Airstrip Gradient Calculation

by Mike Feeney

The history of this simple graph goes back to 1981 when, working for the NZ Civil Aviation Division of the Ministry of Transport, I devised a similar ‘user-friendly’ means for pilots to quickly determine to what extent airstrip slope increased its effective operational length. It was published in articles I wrote for their “Flight Safety” journal and was primarily intended as an aid for the training of pilots undergoing specialized flight instruction for an Agricultural Pilot Rating.

In the early 2000s, I joined Wanganui Aero Work, a large New Zealand operator of fixed-wing agricultural aircraft and Part 135 helicopters. In my role as as Quality Assurance and Safety Manager, I was involved in airstrip standards, including advising growers on improvement methods and, on a few occasions, the siting and works planning for new airstrips. At this time, there were no country-wide standards for farm airstrips; particularly for the increasing number of heavy turbo-prop aircraft which are unable to economically operate from many of the historic strips which suited types such as the Fletcher FU24, DHC-2 Beaver, Cessna 188 Agwagon, etc.

Some pilots may operate their aircraft from sloping rural airstrips. This article may well prove of interest to them. If you are not sure how to work out the gradient of an airstrip, there is an easy method which you can use.

Simply note your altimeter reading at the top and bottom of the airstrip (or you could use your GPS if you are viewing several satellites), then walk out the length and use the formula:

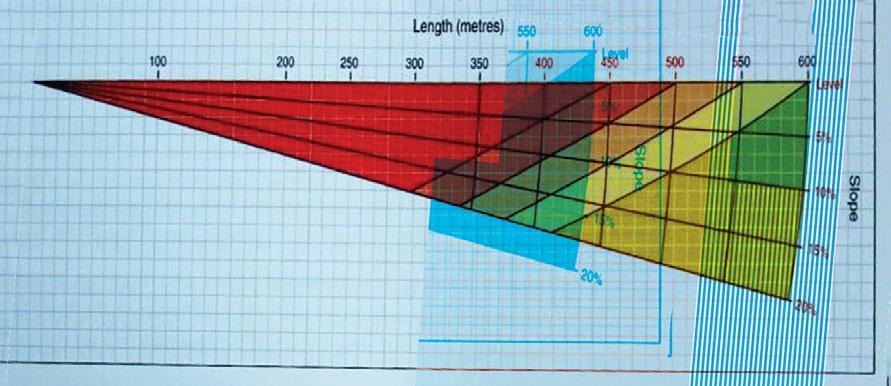
Height difference divided by airstrip length and multiply by 100. Example for a typical airstrip: Length = 1,300 feet. Height difference =90 feet = 90/1,300 = .06923....7% for practical purposes. An examplefor a really steep ag-strip: 150/800 = 18.75 % (5% is about 3 degrees).

When you look at the 20% slope on the graph, you may think it does not appear to be that steep. Let me assure you that when you are approaching such an airstrip, particularly with a tailwind which is quite normal during ag-operations, it will appear to be much fore-shortened and not to be attempted without training by an experienced person. I have operated from airstrips steeper than 20% and, until one gets used to them, they appear rather daunting indeed. In the earlier days with under-powered aircraft, such as the Fletcher FU-24, 225 and 240 BHP models, you needed to touch down well up the strip and keep moving to reach the loading area as it might prove very difficult to taxi up. I do recall having to keep the power well up in the FU-24 to prevent the aircraft from falling back onto its tail, then carefully turning to take off again and make another attempt. But, I was new to the Fletcher then and soon learned to be much more ‘aggressive’ and just fly straight at the airstrip face, get the nose coming up and up and up, whilst pouring on the power as one touched down looking up at the sky. Most exhilarating indeed!

Recalling the periods when I was training new chums into steep strips, I was very wary of those pilots who were overly timid. Some had a strong tendency to ‘stalk’ the airstrip and get too low and too slow, ending up using far too much power just to make the threshold, thus leaving themselves with little reserve with which to execute the transition needed to equal the airstrip slope during the flare. This was particularly pronounced at the high altitude strips in Papua New Guinea. The look on their faces when they went for more power and found that the throttle was already wide open! (This was using non-turbocharged engines when the max power available could be only 60% of that at sea level)

For take-off, one carefully selected an aiming point in the distance, opened to max power and simply fell off the loading area into space. Woe you, if you failed to use the same aiming target each take-off. The effect of gravity is non-linear and is a function of the sine of the airstrip slope. For example: Slope 12 degrees = sine 12 = 0.20791 = about one fifth of the aircraft’s weight will be the vertical component. So, if the aircraft weighs 5,000 lbs., then acceleration will be enhanced by the equivalent of 1,000 lbs of thrust. This equates to another 300 BHP. In the case of a 400 BHP FU-24, this is a large help as this aircraft has a static thrust of about 1,500 lbs. An overloaded FU-24-400 might haul a tonne from a 250-metre steep airstrip, but needs close to 450- 500 metres from a level grassed surface.

Let’s look at an extreme, ridiculous example. Say the strip has a slope of 80 degrees; virtually vertical. The sine of 80 degrees is 0.98481...near enough to unity. So the acceleration force will be the weight of the aircraft plus the propeller thrust. That is 32 feet per second, plus thrust (ignoring drag). Flying airspeed will be attained in a few seconds, but is the take-off distance really almost zero? It all depends on how we define take-off distance. I define it for sloping airstrips as that distance which is required to lift off and reach such an airspeed as will enable the aircraft to sustain flight clear of ground effect and attain at least level flight.

As you rocket off the end of a steep strip, you have an increasing rate of descent until you can execute the energy exchange required to attain level flight. This eats up distance with a heavy aeroplane. With our near-vertical airstrip case, the real take-off distance will be considerable, unless you want to just keep on diving. And there is no such thing as a ‘free lunch’. Even on moderate slopes, you become airborne well below your starting point due to the trade-off. If you need to climb to your target spreading area, you will burn a lot more fuel to make up for the so-called ‘free ride’!

Of course, many airstrips have a variable slope; generally steeper at the top and becoming more level towards the end. Some may even rise somewhat and then fall. So what we are considering is the “mean” or average slope. There are some variables here which I shall not venture into now. However, for practical purposes, just remember that if there is a favorable height difference between the point where you begin rolling and the spot where you lift off, then you benefit by that difference by way of potential energy.

Another complex matter is the effect that the surface has on take-off ground roll. The main predicating factors are tyre pressure, profile and wheel loading. Most New Zealand grasssurfaced airstrips are actually in a ‘plastic’ state and deform under the force exerted by a tyre. During the earlier stages of the roll, a sort of moving ‘chock’ is created in front of the tyre. The effect lessens as wing lift increases until the aircraft is beginning to ‘ride’ over the grass.

The experienced ag-pilot can gain a fairly reasonable idea of airstrip plasticity and expected rolling resistance by simply walking the airstrip and every now and then digging the heel of one’s boot into the surface. You sort of get to know how sluggish the aircraft will be during the early part of the takeoff...it’s a ‘feel’ thing.

When I was measuring take-off performance of ag-aircraft on soft surfaces, I would get down on the ground straight after the aircraft had passed to measure the surface deformation and observe it slowly resuming its former shape. Some loader drivers and farmers must have considered me to be at least slightly eccentric if I had not explained what I was doing. Oh well, perhaps they were right!

The graph in this article is not a “legal” item of performance data. It is a guide only. It has been used by many ag-pilots, none have advised that it is significantly in error. As I said earlier, it is a result of a huge number of directly observed takeoffs by overloaded ag-aircraft and from my own ag and bush flying experience.