Velocity and Acceleration

A scalar will be a quantity that has a magnitude but no direction. Scalars can be negative, depending on the scale. For example, it can be -20 degrees Celsius, which is because of the scale that determines temperature. There is no arrow in a scalar quantity. Distance and speed are scalars; however, velocity and displacement are vectors.

In order to describe the direction of a specific vector, there must be a coordinate system. In one dimension, the coordinate system is a line that starts from the left and ends on the left, usually a number that is along the x-axis. Movement to the right is positive, while movement to the left is negative. If using an up and down motion, movement upward is positive and movement downward is negative. This is done on the y-axis. Sometimes, with falling objects, movement downward is considered positive. In reality, it doesn’t matter which direction is positive as long as you define this clearly. If not defined, use the x-axis and y-axis as is seen in mathematics to define movement in one direction.

VELOCITY AND ACCELERATION

Velocity and acceleration take time into consideration. Time, in physics, represents change or an interval in which change occurs. It cannot be possible to know that time has passed unless something changes during that time. As mentioned, the SI unit for time is the second, with the change being a certain number of units per second.

As mentioned, something should change if time is a factor. There can be the length of a certain event, beginning at noon and ending at 12:30 pm. In such cases, the elapsed time is 30 minutes (note that the use of seconds here would be inappropriate). As time moves forward, this will always be a positive number and is therefore a scalar and not a vector. The delta symbol is used to represent the change in time (or delta-t). For simplicity’s sake, motion is said to start at time zero so that there is no definite need to use the delta-t designation and just “t” is used to represent time.

Velocity is the displacement of something over time. It can be listed in miles per hour or kilometers per hour. In SI units, velocity will be in meters per second. The average velocity is the displacement divided by time. This is a vector because displacement is a vector so it can be a negative number. If the object moved -4 meters relative to the initial

placement over 5 seconds, the total velocity will be -0.8 meters per second. This does not say anything about the actual velocity at any given point in those five seconds; it only lists the average velocity over that time period.

There is such a thing as the instantaneous velocity, which is easy to represent as you look at a car’s speedometer. It is the velocity at a specific instant. The speedometer will show the magnitude of the change in distance over time but will not show the direction. For this reason, speed is a scalar measurement, while velocity is a vector measurement. Instantaneous velocity is the velocity of the object over an infinitesimally small period of time. In calculus, this is the limit of the change in distance as time approaches zero.

While speed and velocity are used in everyday language in the same way, remember that they are different. Instantaneous speed is the magnitude of the instantaneous velocity (or the absolute value of the velocity without a direction). It will always be a positive number. The average speed is the total distance traveled divided by an elapsed period of time. The average speed can exceed the average velocity because it represents the total distance traveled. If you start at one point, go ten miles and return in an hour, the velocity will be zero but the average speed will be 20 miles per hour.

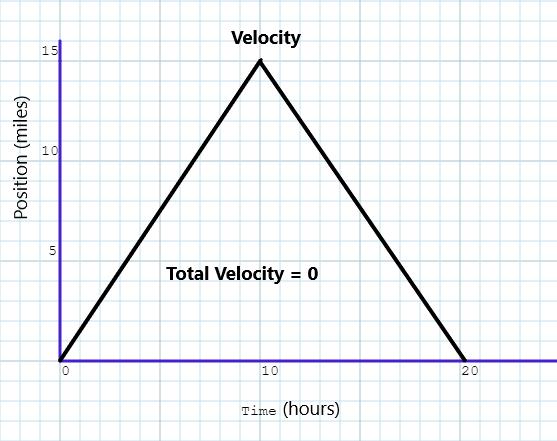
Graphing can be used to describe motion. In such cases, the graph will be the position of the individual or object over time. Graphs can be very simple, assuming that the speed is constant during the time period. It also makes the assumption that the route taken of the person or object is a straight line, which is not always the case. Figure 1 shows the representation of a zero-velocity situation:

Figure 1.

Acceleration is the change in velocity over time. The greater the acceleration, the greater is the change in velocity over time. The average acceleration is the rate at which velocity changes or the delta-v divided by the delta-t. The SI units for acceleration are meters per second squared. This is the velocity change every second. Remember that velocity is a vector; this means it can change in direction as well as magnitude. Acceleration is always in the direction of the change in velocity, it is not always in the direction of motion. A slowing down of acceleration is opposite to the direction of its motion; this is referred to as deceleration.

Negative acceleration is not the same as deceleration. Negative acceleration is acceleration in a negative direction. It might or might not be deceleration because an object can be accelerating quickly but in the opposite direction from where it started. If acceleration has the same sign as the velocity, the individual or object is said to be speeding up. If acceleration has the opposite sign as the velocity, the object can be said to be slowing down. Since velocity is a vector, so is acceleration. Deceleration changes the magnitude of the velocity but does not necessarily affect the direction of the object.

There is also instantaneous acceleration, which is done similarly to instantaneous velocity and speed. It is done by calculating the acceleration over an infinitesimally

small period of time. This can be done using calculus or by using algebra and a very small period of time. If the acceleration and the velocity have the same sign, the object is speeding up (in either direction). If the acceleration and the velocity have different signs, the object is decelerating. The average acceleration is the delta-v divided by the delta-t or the change in velocity over change in time.

In determining the average velocity, one must assume that the acceleration is going to be a constant value. With this in mind, the average velocity will be the starting velocity and the ending velocity, divided by two. If the velocity goes from 30 miles an hour to 60 miles an hour, the average velocity will be 45 miles per hour during that time. There will be a linear relationship between the displacement and the average velocity so that, if velocity 1 is twice the velocity 2, the person will go twice as far in the first instant versus the second instant.

You can also calculate the final velocity of an object by knowing the initial velocity and the rate of acceleration or deceleration (plus the time frame). If an object is traveling at 10 meters per second and decelerates at 1 meter per second squared, you can calculate the final velocity after x number of seconds, although, if it decelerates at 1 meter per second squared, you can determine that, after ten seconds, the final velocity will be zero. Again, this relies on the fact that acceleration is a constant, which may or may not be true but must be assumed if you don’t have the advantage of complex calculus equations to determine the exact change in velocity.

When solving these types of equations, there are several things that need to be taken into account besides the fact that time always starts at zero and that acceleration is held at a constant. It helps to draw a simple sketch so you know what the vectors look like. Remember that velocity, acceleration, and displacement are vectors and you can draw them out to identify the known quantities and what the problem is asking for.

Then find the equation that fits for the problem. If there is one equation, there will be one unknown. If there are two unknowns, there should be two equations. Keep track of the units of measurement and make sure the problem has all the same units of time, velocity, distance, etcetera. Finally, make sure the answer is reasonable and compares with what you know to be true of natural phenomena.