Projectile Motion

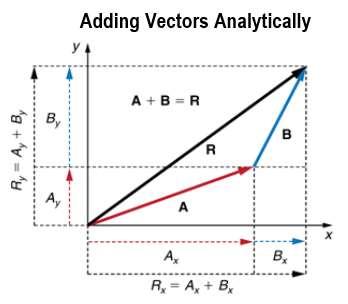
Figure 10.

Once the components of Rx and Ry are determined, the totality of R can be determined along with the angle theta. What you need to know is that the adding and subracting of vectors is done in the same way. You can use the equations you already know to get each angle and each component of the graphed out problem so you can solve for the angle and magnitude of the resultant vector R.

PROJECTILE MOTION

Projectile motion can be termed the movement of an object that is thrown or somehow projected into the air. The object thrown is known as the projectile and its path is referred to as the trajectory. After being thrown, its motion is subject to the laws of gravity. We’ve already covered the motion of falling objects. In our discussion, as in previous ones, air resistance is considered negligible. You need also to remember that you can consider the movements in perpendicular directions (as in the x and y axis) separately. Finally, you need to know that all forces, except gravity are also negligible. Upwards direction will be positive and the force of gravity will be negative. Figure 11 describes a vector at a certain point (x, y) called S, because of a projectile’s trajectory:

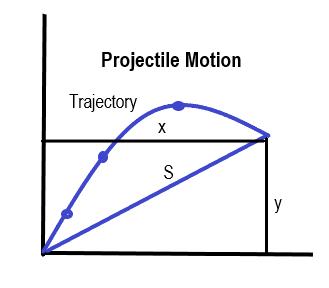
Figure 11.

So, how can the motion of a projectile be determined using physics. The first step involves graphing the projectile’s trajectory on an x and y axis. These are by nature perpendicular. You remember from what we talked about is that the length of x is equal to the displacement vector S multiplied by cosine of angle theta and the length of y is equal to the displacement vector S multiplied by the sine of angle theta.

When it comes to the velocity V, there will be a velocity in the x direction called the Vx and a velocity in the Y direction called Vy. Because these are vectors too, the Vx equals the velocity multiplied by the cosine of theta and the Vy equals the velocity multiplied by the sine of theta.

You will need to treat the motion as two independent one-dimensional movements: one being horizontal and one being vertical. There will be kinematic equations for horizontal and vertical motion, which are listed in Figure 12:

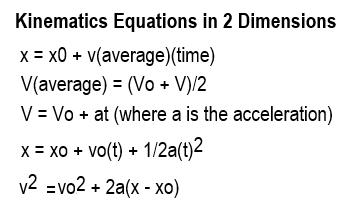
Figure 12.

Once you know the knowns and the equations, you will be able to solve for the unknowns. These types of problem-solving abilities are the same as solving for onedimensional kinematics. The final step is solving for the x and y motions, determining the final vector or the total displacement S and velocity V using what you know about vector addition and subtraction via analytical methods.

The same equations apply to any vector (as seen in the displacement equations in two directions), including the velocity vectors. The same thing applies to the angle theta. What you need to know is that, at any given period of time, there will be a velocity in the x direction and a velocity in the y direction. Over the length of the trajectory, the velocity in the x and y direction can be determined using equations you already know. You need to know, though, that there are other ways to determine velocity based on calculus, which are beyond the scope of this course.

Let’s look at an example: You shoot a shell of fireworks in the air and decide that the fireworks should explode in the air at its peak above the ground. It is shot off at a 75degree angle at a speed of 70 meters per second. At what height should the shell explode and when will this happen?

The height is called the apex or the highest point Y above the ground. You know that the velocity squared is equal to the velocity initial squared minus 2 times the force of gravity times the difference between Y and the initial Y). At the apex (with regard to Y anyway), the velocity will be zero (because the fireworks are turning around). You also know that