Tension

TENSION

Tension is a force along the length of a medium, such as that of a rope or cable. The connector should be considered to be a flexible connector, such as a rope, string, cable, wire, or chain. It can only exert force that is parallel to its length. Tension represents a pull and cannot represent a push because the connector is flexible and has no ability to do any pushing. The actual force starts at each end of the rope or flexible connector and extends toward the middle of the connector. This is an example of Newton’s third law because it shows an equal and opposite force that doesn’t cause any movement unless one is actively pulling on the connector.

When hanging an object from a rope, the net force will be zero if the object isn’t moving. This means that the weight is equal to the tension. This means that the force of tension and the force of the weight of the object are equal and opposite. This is the truth if one neglects the mass of the rope. This means that the tension on a 1-kilogram mass is equal to that mass multiplied by the force of gravity or 9.8 Newtons. If we cut the rope and put in a spring instead, the spring would extend out to a length that equals the downward force (weight) of the object or 9.8 Newtons.

Even if there are pullies and traction systems, the force is still just parallel to the flexible connector attached to the object. This tension is transmitted throughout the length of the connector undiminished except for the friction factors. The pullies will change the direction of the tension but will not change its magnitude as long as there is no friction.

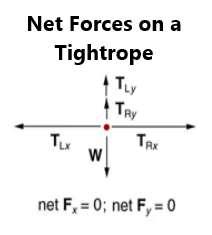
Consider the case of a person standing on a tightrope. The tightrope will dip at an angle on both sides to a degree called theta and there will be forces of tension to the left and right of the person, called tension left and tension right. This is added to the downward force of the weight of the individual. These are the three forces at play with a tightrope situation. The net external force will be zero because the person is stationary on the tightrope.

The coordinate system in this type of situation must be chosen. The goal is to have a convenient horizontal x-axis and a perpendicular y-axis. The x-axis is chosen as the ground, while the y-axis is perpendicular to this. The rope itself cannot be an x-axis

because it bends in the middle where the person is standing and is itself not a straight line. The tension vectors have a horizontal and vertical component (usually just a small vertical component) if the angle of the rope is minor. This leads to five forces in actuality (because the two tension forces have two components each) and these are added to the weight of the person on the tightrope.

Trigonometry will determine the x and y components of the tension on either side. The tension in the x direction or the horizontal direction will equal the total tension on one side multiplied by the cosine of theta, while the vertical component of the tension is the total tension multiplied by the sine of theta. The tension to the left and the tension to the right are equal.

Now, remember that the sum of the vertical tension to the left, vertical tension to the right, and the weight of the person equals zero because the person isn’t moving. Two times the vertical component of the right and left will equal the weight of the person. This means that 2 times the tension times the sine of theta equals the weight of the person on the tightrope. While this sounds complicated, the important thing is to draw the vectors or forces and resolve the vertical and horizontal components. Figure 16 shows the forces added together:

Figure 16.