Tension and Compression

TENSION AND COMPRESSION

Tension and compression can be applied to a rod or wire with a resultant change in length called delta L. This delta L will be produced when a force is applied on top of the rod or wire in order to stretch it or compress it.

As it turns out, the change in length is proportional to its original length and the force applied. It is inversely proportional to the cross-sectional area of the rod or wire. This makes sense because a lesser cross-sectional area and a greater original length will make it easier to have compression or tension affect the length of the rod or wire.

There is also a constant called the Young’s modulus or the elastic modulus, which is dependent on the substance. Things with a large Young’s modulus will have a large tensile stiffness because they deform less for a given tension or compression. The units for this constant are 109 Newtons per meter squared.

You should also know the definitions for stress and strain. Stress is the ratio of force to the surface area of the object, while strain is the ratio of the change in length or delta-L and the total length or L. When you use the equation for tension and compression, you get stress equaling the Young’s modulus multiplied by the strain. These equations are listed in figure 21:

Figure 21.

So far, we have talked about tension and compression acting on a rod or wire. What about sideways stretch? This is referred to as shearing force, in which there is deformation called delta-x. It is perpendicular to delta-L rather than parallel as is the case with tension and compression. There are similar equations, however. Figure 22 shows shear force as well as tension and compression:

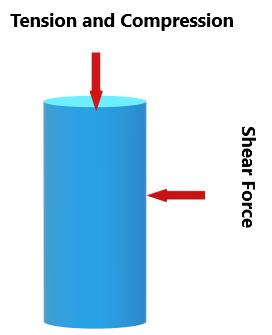
Figure 22.

Shear deformation or delta-x is proportional to the force applied and the length of the object, while it is inversely proportional to the surface area of the object and another constant, referred to as the “shear modulus”, which is dependent on the substance of the object. Longer objects will have a greater shear deformation, while thicker objects will have a lesser shear deformation.