Centripetal Force

Because the two velocities are identical, this will lead to an isosceles triangle (which is one that has two equal sides). Based on the manipulation of knowns and equations, the centripetal acceleration is the same thing as velocity squared divided by the radius. This means that the smaller the radius, the greater is the centripetal acceleration.

You can also demonstrate a relationship between the centripetal acceleration and the angular velocity. The relationship is that the centripetal acceleration is equal to the radius multiplied by the angular velocity squared. This means the centripetal acceleration is directly proportional to the radius and the square of the angular velocity.

CENTRIPETAL FORCE

There can be forces that result in centripetal acceleration. A few examples, include tension on the rope attached to a tether ball and the force of gravity affecting the moon. There are also forces placed on the tube in a spinning centrifuge. What’s true is that any force that causes uniform circular motion is referred as a centripetal force. The direction of this force is in the direction of centripetal acceleration, even though these are not the same thing.

This brings in Newton’s second law of motion, which states that Force equals mass times acceleration. In the case of uniform circular motion, the acceleration being referred to is the centripetal acceleration. When it relates to angular velocity, force equals mass times the radius times the square of the angular velocity. Using these equations, you can do a number of problems. Let’s try one:

How do you calculate the coefficient of friction car tires need on a flat curve? This basically involves calculating the centripetal force on a car that turns a certain radius at a certain linear velocity and then calculating the static friction that will keep the tires from slipping.

First, the centripetal force, which is mass times the velocity squared divided by the radius. Imagine a 900 kg car that negotiates a 500-meter radius at 25 meters per second. Doing the math, you get 900 times 25 squared divided by 500 or 1125 Newtons. Next, you need a certain coefficient of friction to prevent the car from moving out to a greater radius (spinning out of the circle).

Friction is the same thing as the centripetal force because it’s a flat curve. The static friction, if you can remember in the previous chapter is mu times the weight or mu times the mass times the force of gravity. You can calculate mu by taking the centripetal force and dividing by the mass and the force of gravity. This leads to a coefficient of friction of 0.13. You can also manipulate the numbers to get mu equals velocity squared divided by the radius and divided by the force of gravity.

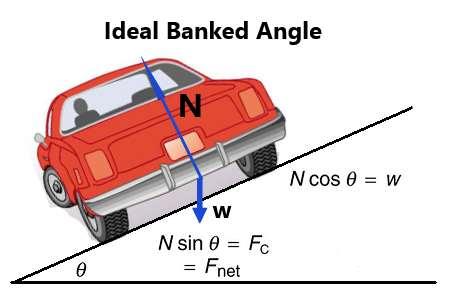
There is the issue of banked curves to think of because banked curves allow the car to drive faster around a curve. There is the concept of an “ideally banked curve”, which is the angle at which a curve can be negotiated without the aid of friction between the tires and the road. In an ideal banking situation, the Normal Force in the horizontal and vertical directions must equal the centripetal force and the weight of the car, respectively. This would be the banking of a “frictionless” surface. Figure 25 shows this situation:

Figure 25.

In the case of the car, the external forces on the car are the weight of the car and the normal force of the road (which is perpendicular to the surface of the banked curve). The two forces must add to give a net external force that is horizontal toward center of the curvature with a magnitude equal to the centripetal force.

This leads back to trigonometry and the study of forces that have horizonal and vertical components. The normal force multiplied by the sine of theta must equal the centripetal