Conservative and Nonconservative Forces

Note that the mass cancels out in the equation. This is consistent with what you already know—that the speed of falling objects is the same thing regardless of the mass. You should also know that, when friction is negligible, the speed of a falling body depends only on its initial speed and height and not on the path the object takes. It can fall directly or take a circuitous path, such as a rollercoaster on its path. The same is true of going uphill—as long as friction is not a factor (which it normally is).

CONSERVATIVE AND NONCONSERVATIVE FORCES

We have so far led up to the idea that force is what creates work. Some forces, such as gravitational force, for which work can be done against or for, depends only on the starting point and ending point of the object and not on the path. This is called a conservative force. Potential energy is also a conservative force as it does not necessarily mean the same thing as gravitational potential energy. Think of winding up a toy or an old-fashioned watch. These will also store potential energy. In both cases, stored energy is recoverable as work. In short, conservative force is one that depends only on the starting and ending point of a motion and not on the path taken.

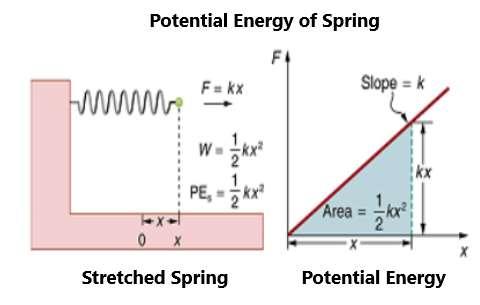
Let’s look at the potential energy stored in a spring. This can, in some situations, obey Hooke’s law, which states that the magnitude of the force on the spring is proportional to the deformation of the spring. In such cases, the amount of deformation is equal to the amount of stretching or compression of the spring in total length. The force equals the spring’s force constant (which depends on the spring) and the change in length. The average force of the spring will be half of its stretched length multiplied by a force constant.

The potential energy of a spring can be defined as one-half the force constant times the distance stretched squared (based on the work-energy theorem). The distance stretched is actually the difference between the length of the unstretched or uncompressed spring and the length it is stretched out. It does not depend on the path taken, just on the stretch or squeeze of the spring. Figure 34 shows the force and potential energy of a stretched spring:

Figure 34.

Remember that, according to the work-energy theorem, the net work by all forces acting on a system is equal to its change in kinetic energy. Remember too that the work net equals one-half mass times the velocity squared (see figure 33). These two values are the same thing (change in kinetic energy and net work). If only conservative forces act on a system the work net equals the work by conservative forces).

What this means is that, if things like gravitational force or spring force does work, this will equal the change in potential energy but will be opposite in direction. Take this to mean that the total kinetic energy and total potential energy added together will equal a constant if only conservative forces are involved. This leads to the equation stating that there is conservation of mechanical energy. The total kinetic energy plus the total kinetic energy equals the system’s mechanical energy. This is seen in figure 35:

Figure 35.

What this means is that the total mechanical energy is constant over the system. It just changes form from kinetic to potential energy and vice versa.

Let’s use an example. You have a toy car that weighs 0.1 kg and is propelled by a spring that rises 0.18 meters from the starting point. The spring is compressed 4 cm (0.04 m) with a force of 250 newtons per meter. If friction is negligible, how fast does the car go initially and how fast does it go at the top of the slope? This is described in figure 36:

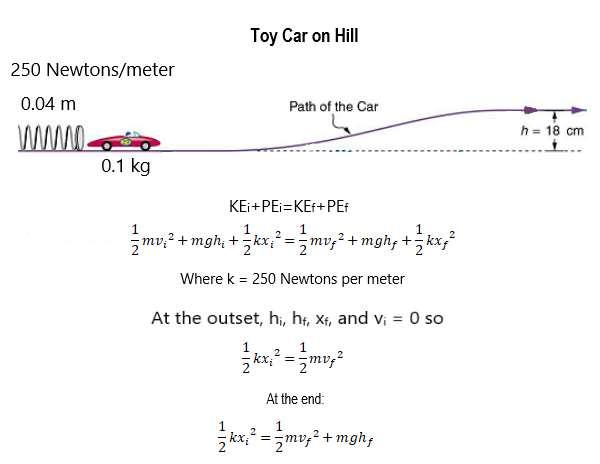
Figure 36.

Using these equations in figure 36, you can solve for the initial and final velocity. In the beginning, the initial height, final height, initial speed, and final compression of the spring is zero, so the velocity is going to be related to the mass of the object, the compression of the spring, and the force constant. Putting in the numbers and solving for the velocity, you get 2 meters per second. This is the speed the car takes as it gets out