Rotational Motion

squared. If the angular velocity increases, the angular acceleration is positive; if the angular velocity decreases, then the angular acceleration is negative.

The important thing to know, for example, with tires on the ground, is the linear acceleration and linear velocity. Remember that the linear velocity is tangent to the circle at the point of interest. This means that linear acceleration, is referred to as tangential acceleration. Centripetal acceleration, which is in the direction of the center of the circle, is perpendicular to the tangential acceleration. They are independent of one another. Tangential acceleration is directly related to the angular acceleration and is related to an increase or decrease in velocity but not necessarily its direction.

If you’ll remember, linear acceleration is proportional to a change in the magnitude of the velocity; with circular motion, linear velocity equals the radius times the angular velocity. What you need to know is that tangential acceleration is equal to the radius times the angular acceleration and this means that angular acceleration is the tangential acceleration divided by the radius.

ROTATIONAL MOTION

Let’s look at the kinematics of rotational motion. This involves finding the relationships between the angular velocity, angular acceleration, and time. Remember that, in linear motion, the velocity is equal to the initial velocity plus the acceleration multiplied by time. If the linear velocity is equal to the angular velocity times the radius and the tangential acceleration is equal to the radius times the angular acceleration. This means that angular velocity equals the initial angular velocity plus the angular acceleration multiplied by the time. The radius cancels out of the equation. Figure 51 describes these equations:

Figure 51.

The kinematics for rotational motion is very similar to translational kinematics we saw in chapter one and chapter 2. The difference is that, instead of x for distance, you use the angle theta, which is the number of radians traversed, and instead of average velocity, you use the average angular velocity. The angular velocity squared becomes the initial velocity squared plus two times the angular acceleration times the angle theta. The values you are looking for are described in this picture of a fishing reel, figure 52:

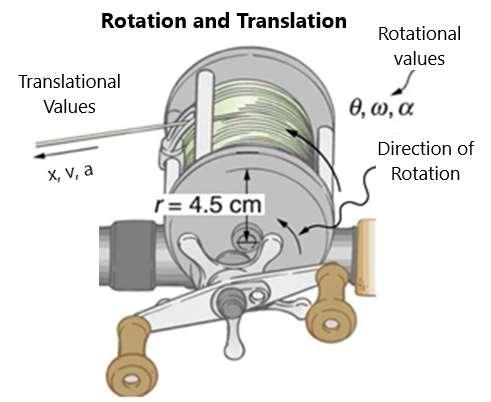
Figure 52.

With the understanding of the kinematics of rotational motion, this leads to the dynamics of angular motion, which includes the forces involved in this type of motion. An example of this is the forces applied to a door in opening it. If the door is opened too close to the hinge, the door will not open easily and will open more slowly. The further out the force applied, the greater is the angular acceleration, which is inversely proportional to the mass. What this means is that the greater the mass of the door or the wheel being spun, the smaller is the angular acceleration.

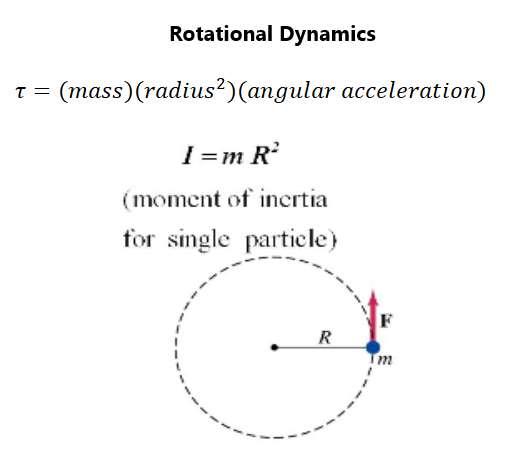
The actual relationship is force equals mass times the radius times the angular acceleration, which is not much different from force equals mass times acceleration, which is something you already know from linear dynamic equations. Remember that torque is the turning effectiveness of a given force. The applied force will be perpendicular to the radius, in which force equals mass times the radius times the angular acceleration. Torque then equals mass times the square of the radius times the angular acceleration.

Figure 53 describes this relationship:

Figure 53.