Collisions of Rotating Objects

the earth is tidal friction. This is small enough that it would take tens of millions of years before there will be a change in the Earth’s spin. This is the only external torque applied to the earth’s spin.

A skater had increased angular velocity when she pulls her arms in because she changes her moment of inertia. The moment of inertia is related to the radius squared and the angular momentum equals the inertia times the angular velocity. Because angular momentum is preserved, the decrease in moment of inertia will greatly increase the velocity. The work done in pulling her arms in will increase the rotational kinetic energy.

COLLISIONS OF ROTATING OBJECTS

When certain objects collide, we have been assuming that there is no rotational spin, while in reality, things like billiard balls and bowling pins will spin. Baseball pitchers throw curve balls by putting a spin on the ball and tennis players can put a “top spin” on a tennis ball.

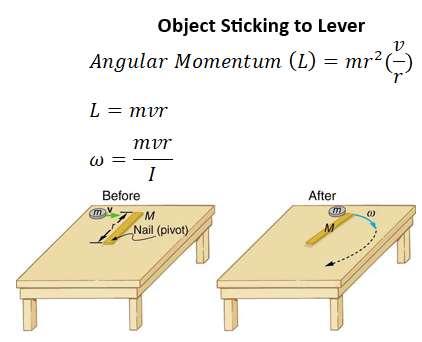
A simple collision involves hitting an object against a motionless stick that is attached as a lever on its far side. If the object sticks to the lever, both objects will spin about the pivot point. Angular momentum will be conserved but not kinetic energy because the two objects result in an inelastic collision. There is no torque observed at the pivot point because its anchored to a frictionless surface. If the object is seen as a point mass, the moment of inertia will be the mass times the radius squared. The angular momentum will be the inertia times the angular velocity so, if you know the value of the radius and the mass of the object striking the lever, you can determine the inertia. Figure 55 shows the equations involved:

Figure 55.

The example in figure 55 assumes that the mass of the lever is negligible but it can be done by adding the mass of the lever and the object that strikes it. The kinetic energy before the collision is the incoming object’s translational kinetic energy. Because this is an inelastic situation, the translational kinetic energy gets completely translated into rotational kinetic energy. The incoming kinetic energy is one-half mass times the square of the velocity. The final kinetic energy will be one-half the inertia times the square of the angular velocity.

In looking at the picture in figure 55, you can imagine that the force applied to the tip of the lever will be all translated into rotational energy and forward force on the nail itself, while force applied to the nail or pivot point will have no rotational energy and the force will be reflected back on the object. Somewhere in between is a point that results in no net force on the nail itself. This is called the percussion point.

The percussion point is the same thing as the “sweet spot” in a tennis racquet or baseball bat. This is when there is no net force on your hand when you hit the ball. Hitting the sweet spot will result in less tennis elbow or force on your batting arm. This is described in figure 56:

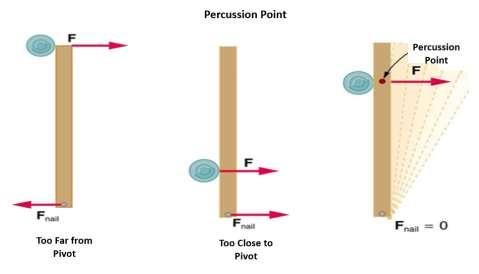
Figure 56.

While rotational kinetic energy is a scalar and not a vector, rotational angular momentum is a vector. It is affected by the torque on the system. The angular momentum is defined by the right-and rule. Both the angular momentum and the angular velocity are vectors. The direction of the angular momentum will be the same as the direction of the angular velocity. Both of these will point along the axis of rotation. If you stick out your right hand and curve your fingers in the direction of rotation, the angle of the angular velocity and momentum will be in the direction of your thumb. This is seen in figure 57:

Figure 57.

Gyroscopes will rotate around a vertical axis and the torque will be horizontal and perpendicular to its angular momentum. If the gyroscope is not spinning, it will acquire angular momentum in the direction of the torque so that it will tip over. Figure 58 shows a top that stays upright as long as it is spinning.

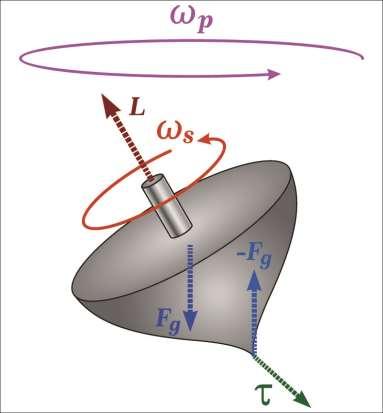
Figure 58.

The Earth is itself a giant gyroscope. Its angular momentum is along its axis, pointing in the direction of the North Star.