Archimedes Principle

For these devices and for blood pressure machines, the units are often millimeters of mercury rather than Pascals.

ARCHIMEDES PRINCIPLE

This topic gets into the idea that some things are buoyant and others are not. Buoyancy involves things being able to float in water as well as things floating in air, such as helium balloons. If the buoyant force is greater than the object’s weight, the object will rise; likewise, if the weight is greater than its buoyancy, the object will sink. The buoyant force is the net upward force on any object within a fluid. This will be the difference between the upward force and the downward force.

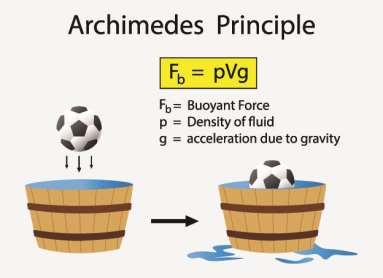
According to Archimedes principle, the buoyant force on an object equals the weight of the fluid it displaces. This is valid, whether the object is partially or completely submerged. Boats will float because of their shape. They will displace more water, experiencing a greater buoyant force. It turns out that you can calculate the buoyant force on an object. Figure 61 shows the buoyant force of an object according to Archimedes principle:

Figure 61.

The density plays a great role in Archimedes’ principle. It is the average density of an object that will determine whether or not it floats. If the average density is less than that of the surrounding fluid, it will float. This is because fluid will contain more mass and more weight in that same volume. The buoyant force will be greater than the weight of the object. Dense objects—denser than the fluid—will sink. Unloaded ships are less dense so they are less submerged. The fraction submerged is the ratio of the volume of the subject divided by the volume of the total object. This is equivalent to the ratio between the volume of the fluid divided by the volume of the object.

What this means is that the volume submerged (which is the same thing as the volume of fluid displaced) is related to the density. From what we know about density, volume, and mass, the average density of the object divided by the density of the fluid will equal the fraction submerged. So, obviously, a packed ship with a greater density will have a greater submersion ratio and will be submerged in water to a greater degree.

This leads to a discussion of what’s known as specific gravity. This is the ratio of the density of an object compared to water. It has no units because it is a ratio. The calculation for specific gravity is that it equals the average density divided by the specific gravity of water. Figure 62 is an example of a hydrometer, which is a tube that has a dense substance in the bottom dropped in a fluid. It sinks to a calibrated level, depending on the density of the fluid:

Figure 62.