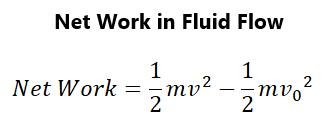
5 minute read
Bernoulli’s Equation
by AudioLearn
As the cross-sectional area of a conduit decreases, the speed must increase in order to have the same flow rate. The ratio of the area and velocity must be the same in order to have the flow rate be the same through a conduit. This is referred to as the equation of continuity, which applies to any incompressible fluid.
BERNOULLI’S EQUATION
Advertisement
So, when fluid flows into a channel that is narrower, its speed increases. This means that its kinetic energy increases. One has to wonder where this kinetic energy comes from as energy is neither created nor destroyed. This goes back to the idea that net work equals one-half mass times velocity squared minus one-half mass times the initial velocity squared. This is shown in figure 65:
Figure 65.
Net work done will increase the fluid’s kinetic energy. Remember, too, that the pressure equals area times force so that the pressure will drop in a rapidly-moving fluid. This explains why shower curtains bulge inward when the shower is on and running. In the same way, cars will experience a force toward a parallel-moving truck passing beside a car. This is because the high velocity of the truck will create negative pressure in the air (which is a fluid) around it.
This leads to Bernoulli’s equation, which is the relationship between pressure and velocity in fluids. This is described in figure 66:
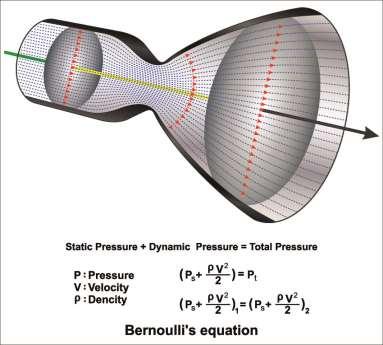
Figure 66.
This basically means that the absolute pressure plus one-half times the density times the pressure times the velocity squared plus the density times the force of gravity times the height equals a constant. Figure 67 shows the Bernoulli’s equation:

Figure 67.
This basically means that there is conservation of energy for an incompressible fluid in the absence of any friction. You need to know that there are other forms of energy that come into play including thermal energy because of fluid viscosity. It applies to static fluids and moving fluids.
In the absence of movement, there are static fluid forces indicating that pressure = the pressure at the surface of the fluid plus density times gravity times height. We already know this because we know that pressure is greater with greater height below the surface. This is the change in potential energy of a fluid.
At a constant height the kinetic energy will be conserved, so that the pressure drops at increasing speed. The difference in pressure is related to one-half times the density times the change in velocity squared. The change in pressure is proportional to the change in velocity squared.
There are many processes that pertain to Bernoulli’s principle, which uses reduced pressure in high-velocity situations in order to move things about. This is known as “entrainment”. It allows for pumps to raise water over small heights. Examples of using entrainment include atomizers that squeeze a jet of air that result in droplets of perfume being entrained. The lift of an airplane wing is an example of Bernoulli’s principle. Wings are tilted to allow air to flow faster over the top. This reduces the pressure on top of the wing, leading to “lift” or a net upward force. Sails of ships will also apply Bernoulli’s principle. Height too is proportional to the square root of the velocity.
Pouring a fluid such as water is not difficult, and yet, pouring fluid like pancake syrup is more difficult. This is because of “fluid friction”, which is its viscosity. So far, we have been dealing with fluid that has no viscosity and therefore has “laminar flow” or nonturbulent flow. Turbulence will happen because of velocity, resulting in characteristic swirls and eddies that mix layers of fluid together.
When fluid becomes turbulent, the layers will mix and there will be velocities in different directions. Consider the movement of smoke rising. It will first rise faster in laminar flow but will rise more slowly and will swirl more easily in turbulent flow because the turbulence will increase the friction between the fluid molecules, restricting its flow. Figure 68 shows laminar flow and turbulent flow:
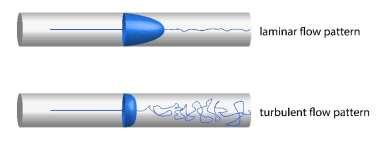
Figure 68.
The lines of flow are referred to as streamlines. These will be smooth and continuous in a forward direction in laminar flow but will break up and be in all directions in turbulent flow. There will be friction between the layers of laminar flow that will restrict its flow. Force is directly proportional to velocity but, at a certain speed, the velocity will be slowed down because of an increase in turbulence. Force is also directly proportional to the coefficient of viscosity, identified by the Greek letter eta (η).
Consider flow between two plates of a certain area. The greater the viscosity coefficient, the greater the force required. Force equals the coefficient of viscosity multiplied by the velocity and the cross-sectional area, divided by the length between two plates. The SI units for the coefficient of viscosity is Newton-seconds-meters squared. The viscosity of a fluid varies from fluid to fluid.
Fluid flow happens because of a difference in pressure. The flow will be from high pressure to low pressure. The greater the difference between two points, the greater the flow rate. It is related to the difference in pressure between two ends of a tube divided by the resistance to flow. Resistance to flow is related to many things that affect flow rate. It is greater in longer tubes and is greater with high viscosity. Turbulence is going to increase resistance, while increased diameter of a tube will decrease resistance to flow.
If viscosity is zero, the fluid is frictionless and resistance to flow will be zero. The speed of a viscous fluid will be greatest at the midstream of the flow because of the drag effects at the boundaries. Poiseuille’s law is that for resistance of a fluid. It results in the following equation for resistance of a fluid in a horizontal tube of uniform radius and length. This is outlined in figure 69:
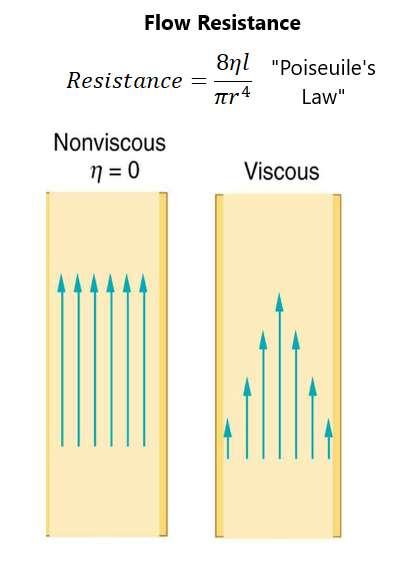
Figure 69.
What this means is that just by doubling the radius, the resistance will go down by a factor of 16. This has a much greater impact on resistance than on any other factor. This law has been specifically applied to blood because it explains why there needs to be a pressure difference put upon by the heart in order to overcome changes in resistance by the changes in radius put upon by things like plaques. Flow will be equal to the difference in pressure times pi times radius to the fourth divided by eight times the coefficient of friction times the length. This looks like what’s seen in figure 70:








