max ebb: current events

— CURRENT EVENTS

example. Can anyone tell me whether the waves are bigger or smaller on an ebb tide?” The sailor in the class knew the answer, of course. “Ebb tides make the water rougher,” he said. “Waves will be higher and steeper on an ebb. A flood tide will do the opposite, and smooth them out.” “Right!” confirmed the instructor. “Why do you think that’s true?” “An ebb tide adds to the wind speed, so there’s more wind over the water.” “Good, but there’s another reason. Ebb tides make the waves think the bay is larger, because the water is moving opposite to the wave direction. So the waves have more fetch.” That’s when I noticed Lee Helm sitting in the back corner over by the buffet table. She put her hand over her face and shook her head. “There’s going to be trouble,” I thought to myself.

The instructor gave a brief introduction to the use of the tide book, and gave some examples of tidal current adding to the wind speed or subtracting

from the wind speed. Lee looked like she was ready to explode. When she finally raised her hand, she started speaking without waiting for the instructor to call on her. “But like, if the ebb tide makes the waves behave as though the fetch were longer, I mean, wouldn’t the waves be smoother and more regular in an ebb tide instead of short and steep?” “The change in apparent fetch is probably not the main cause of rougher water in an ebb tide,” said the instructor. “But if you do the math, you find that a two or three-knot change in wind speed doesn’t have much effect on wave steepness you see at the Gate,” Lee said. “We know that ebb tides really do cause steeper waves,” said the sailor. “But on a sailboat,” Lee argued, “true wind is measured relative to the water. If you’re in 20 knots of wind, that’s like, 20 knots over the water surface. It doesn’t matter if the water is flowing in or out. We both know from experience that 20 knots over the water in an ebb is going to make different waves than 20 knots over the water in a flood, and no one here has even come close to explaining why.” “Uh, do we really have to get into that level of detail?” said the instructor. He also sensed trouble and was desperately trying to back out. “I would kind of like to sort this out,” said one of the students. “I always wondered why ebb tide water was rougher, because, as she just pointed out, the change in wind speed isn’t really all that big.”

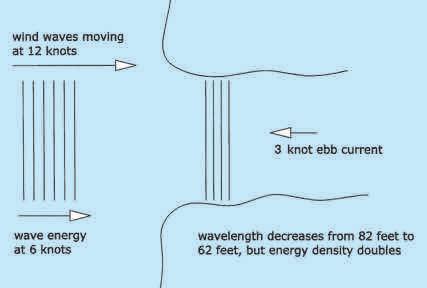
“Maybe it’s the sheer stress or turbulence from the bottom, or some such,” offered another student. “It’s the current gradient,” Lee volunteered without waiting for the floor. “It’s not the direction or speed of the current, but the change in current along the direction that waves are moving that makes the water rough or smooth.” All eyes were on Lee for a more detailed explanation. Having some idea what was coming, it was my turn to cover my face. “When waves move from no current to ebb current, the wave energy is like, concentrated. The waves become steeper. The same as when the waves go from weak ebb to stronger ebb, or from strong flood to weaker flood. Can I have the lights, please?” Not knowing what else to do, I flipped on the house lights while Lee walked over to the big poster easel in front of the room. She tore off the sheet of paper that listed sea kayak safety gear, and started a new diagram. “Here’s the ocean with like, no current, and here’s an inlet with three knots of ebb tide. Let’s say we have wind waves at four-second intervals, so the wavelength is . . .” She hit some buttons on her calculator watch. “. . . 5.121 times T squared, which is 82 feet. The speed of the wave in deep water is 82 divided by 4, or 20.5 feet per second, or 12 knots. And like, you can get the same result using the hull speed formula: 1.34 times the square root of 82 feet is 12 knots. But the energy in those waves only moves at half the speed of the wave form, so the wave energy is moving at 6 knots.” “Wait just a second,” said the sailor

Above, Lee’s diagram, showing how wave energy density doubles when 82-ft long waves moving at 12 knots encounter a 3 knot contrary current gradient. Left, whether you can do the math or not, waves are bumpy.

MAX EBB

in the audience. “How do you get from 12 knots to 6 like that?” “The group velocity in deep water is half the celerity, or half the speed of each wave,” Lee replied. “It’s a basic fact of water waves, and it’s very easy to observe every time you see a powerboat wake headed at your kayak. Each wave form moves twice as fast as the group of waves, so new waves are always forming at the back of the group, the waves in back are always moving to the front of the group, and the waves at the front of the group are always fading out. That’s why it takes longer than you’d first guess for the wave group to reach you. But like, that’s another lecture topic.” “Okay, I’ll take your word that we have wave energy moving at six knots,” he agreed. “At least for now.” “Cool. I’ll email you the proof. Now back to our wave group,” Lee continued. “When the wave group moving at six knots runs into a three-knot increase in ebb current, suddenly the wave energy density is doubled! And like, if the waves were anywhere near steep enough to break, then doubling the wave energy density is almost certain to make them break.” “But ocean swells have a much longer period than four seconds,” noted the instructor. "So the effect on swells is going to be much smaller.” “True, but there is always wave energy at the shorter wavelengths. I mean, when the weather report gives the wave period, that’s the peak in the spectrum. For wind waves there is always a lot of wave action at shorter wavelengths mixed in. And like, for this hypothetical case of a three-knot current gradient, any wave with celerity less than six knots — which is about a two second wave period with a wavelength of 20.5 feet — will be completely stopped when it hits a three-knot opposing current, and the energy density goes to infinity.” “But most waves are bigger than that,” said the instructor. “For sure, but there’s still some energy in that part of the spectrum, even if the amplitude is very low. And like, even the small amount of energy at that frequency will pile up. The energy density can’t really go to infinity - the waves break to dissipate the energy. That’s what tide rip is: A place where wave energy is moving more slowly than a contrary current gradient. Even in zero wind and in what looks like flat water, the wave energy will accumulate until the waves break.” “Is that why we can see whitecaps in Raccoon Strait on a calm day?” asked one of the kayakers. “Yes, the Point Stuart shoal,” said Lee. “Except that instead of the current coming out of an inlet, it changes speed over the shoal because of the change in water

depth. Same result, though. Waves hit opposing current, and some of the wave energy is too slow to make any progress against it.” “What if the tide is flooding, or any situation where the current is going with the waves?” “Waves get flattened out when they encounter a favorable current gradient. Think of it as upwelling that spreads out the wave energy. Likewise, you can think of an adverse current gradient as downwelling that leaves wave energy stranded on the surface.” “This is all very interesting,” conceded the instructor as he glanced at his watch, “but we’re getting behind schedule and we still have some important topics to cover tonight.” I dimmed the lights so the slide show could continue, picked up my bowls of chips and made for the bar. Lee walked out behind me.

“Since when are you a sea kayaker?” I asked as soon as we had closed the door. “And since when do you need to take a beginner class like this one?” “They had to have a yacht club member here to host the meetings,” she explained. “But you’re not a yacht club member.” “Shhh! The manager might hear that. He thinks I am. And like, there’s a free dinner in it. When one of the club members I know from windsurfing who usually hosts these meetings asked me to cover for him tonight, I said sure. I’m still like, a starving graduate student,” she said as she grabbed a big handful of chips from one of the snack bowls I was carrying. “Well, I think you earned your dinner anyway with the wave energy and current gradient lecture,” I said. “There might even be a couple of people in there who understood some of it.”

Lee went back into the dining room and I brought the chips to the bar for the football fans. But the game, if the truth be known, was not nearly as interesting as what had been going on in kayak ground school. I snuck out during a commercial to eavesdrop some more on the lecture. “How can you tell how deep the water will be when the waves break?” asked the instructor. “There’s a rule of thumb,” he answered his own question. “The height is three-quarters of the water depth. So if the waves are 3 feet high, trough to crest, they will break in 4 feet of water.” “Then how is it that waves can also break in an ebb current where the water is deep?” asked one of the students. “Waves break when they get too steep,” said the sailor. "They can break in water of any depth if the ratio of wave height to wave length is greater than, I think something like 1 in 10.”

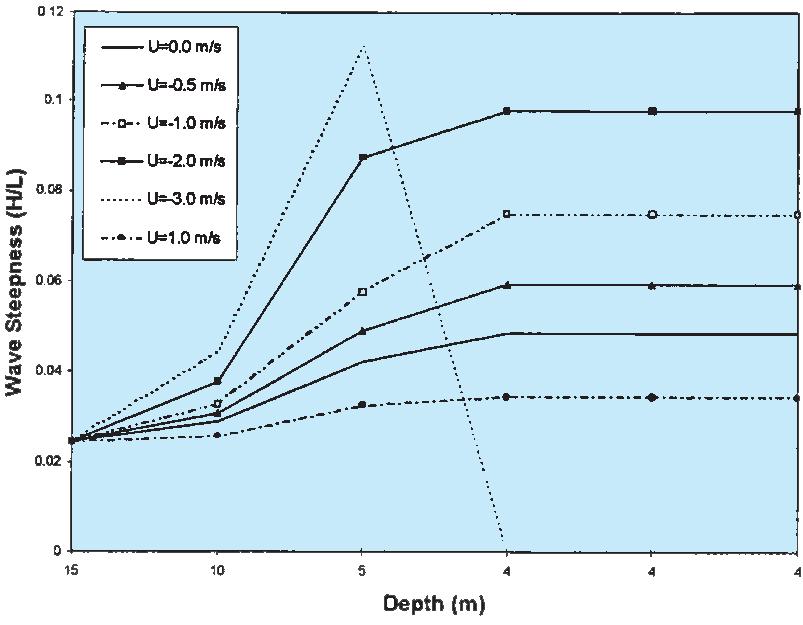
Example problem solved using the Army Corps of Engineers program to compute the interaction of waves, water depth and current gradient. The bottom curve shows wave height versus location in a shoaling inlet for a favorable current gradient, the next curve up is in zero current, and contrary current curves are above. The diagonal dashed line shows where the wave breaking criteria are exceeded.