Lesson 14: Values Integration

Associating values or standards of behavior with mathematical concepts can serve 35 a source of motivation for the students. Values integration will help the students get life lessons through math. If the students find a learning material engaging and meaningful, then they will ask for more (since curiosity will start to kick in). Curiosity s the force behind lifelong learning!

E x p e r ie n c e

The valuing part can be done before closing the lesson. Listed below are the mathematical concepts vis-a-vis the sample questions and/or moral lessons that you might want your learners to reflect on.

You may ask your students to reflect on and write about mathematical concepts in relation to values or standards of behavior related to their lesson.

Math Topic Reflection Questions 1. Whole Numbers Connect the lesson to the concept of 'wholeness'— comprising the full quantity, the start of forming a complete and harmonious whole, and the state of being unbroken and undamaged.

1. What were your experiences in the past that make you feel "whole" or "complete"? 2. Bullying can make a person's heart broken/not whole. Cite a specific event in the past in which you or your classmate has experienced bullying (in any form). How did you respond to the situation? What can you do to stand up against persons who break or damage people's hearts? 2. Order of Operations Relate this lesson to the importance of obeying rules/order for self-management and doing things one step at a time.

1. Why are rules important? 2. What aspect of obeying rules did you find quite challenging in the past? 3. What step-by-step process do you follow in solving your problems?

3. Factors and Multiples

4. Addition and Subtraction of Fractions

5. Geometry (Triangles)

6. Patterns Associate this with the idea of organizing things. You group all items that have a common factor together.

1. What are some benefits of being organized? 2. How do you deal with people who are having a hard time organizing things? Relate this to the idea that most of us tend to be attracted to people who are similar to us.

1. What are the qualities would you like your friends to have? Do you also possess these qualities? 2. Reflect on the saying: "Opposites attract." Do you believe in this saying? 3. Should you listen to the opinion of a person that is not like you? Why or why not?

Fractions that are dissimilar can still be combined. You just have to do some modifications to the denominators to make them similar. Just like in real life, you live in a very diverse world. Even if two people are different (in faith, gender, faith, socioeconomic status, etc.), they can still work harmoniously. A key value that you need to develop is modifying your attitude and genuinely respecting other people. Relate this lesson to the rigidity of triangles.

Other polygons can be easily deformed. If you make a rectangle or a square from metal wires with hinges at the corners, you will find that it does not stay in that orientation. It can be transformed into an ordinary parallelogram. In a triangle, each edge is supported by the other two edges. This characteristic makes a triangle stable. You have to act like triangles, and you have to make sure that you have a strong support group. A person develops a pattern of behavior if he/she repeats an activity over and over again.

1. What are the personal behavior patterns that you wish to break? Why? 2. What are the personal behavior patterns that you wish to form? Why?

7. Data Presentation

Give examples where the use of a bar graph or a pictograph is abused. You should not let your students be easily manipulated by misleading statistics.

What's wrong with this?

1. Both graphs are presenting the same data set.

"MASSIVE INCREASE IN HOUSE PRICES THIS YEAR!"

Average House Price {£)

What can you say about the first graph? Second graph? Which graph presents a more accurate reflection on the increase in house prices?

2. Which graph is misleading? Why?

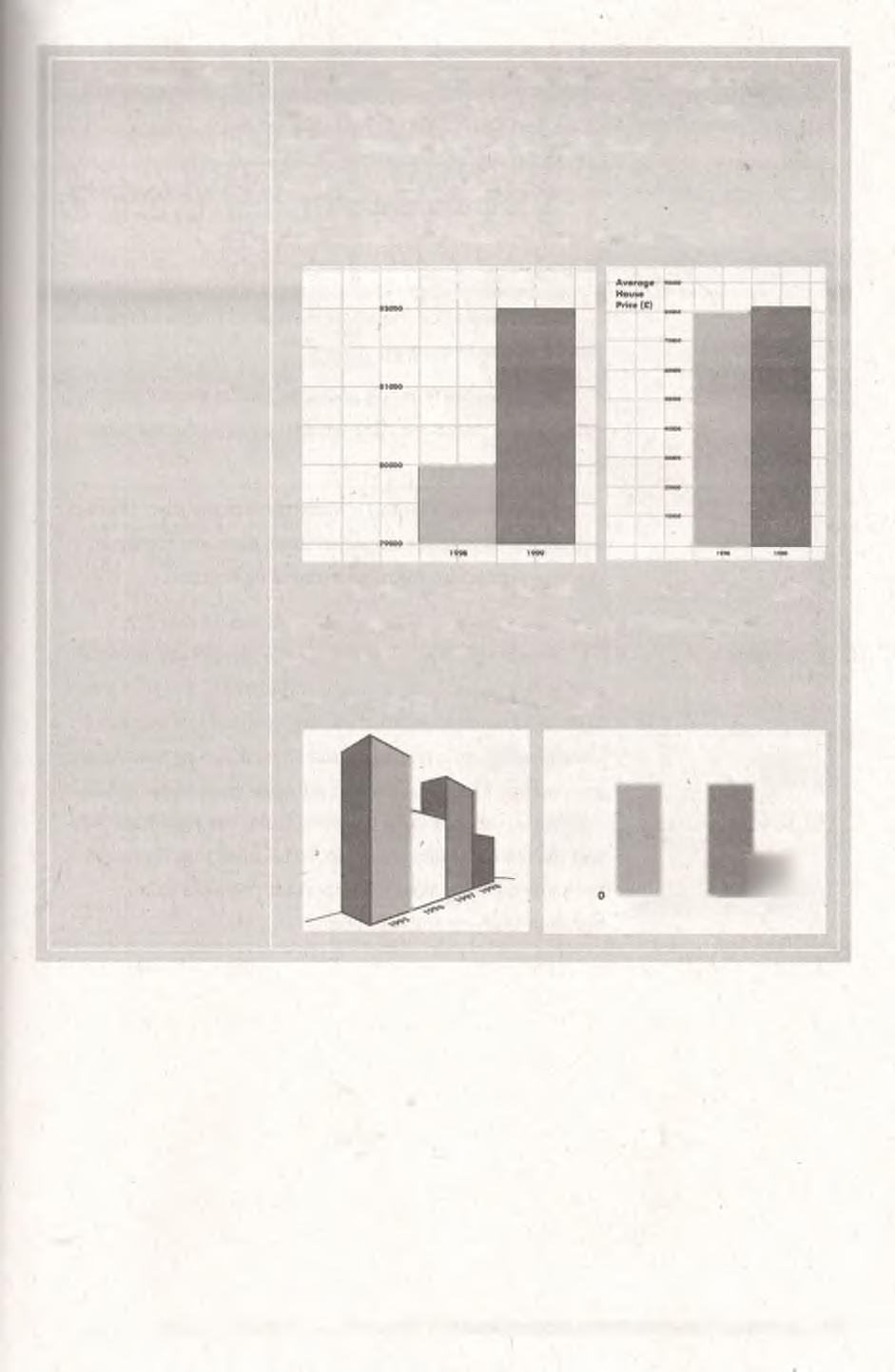
N um ber of singles 2 0 0 , 0 0 0 sold Num ber o f singles sold

100, 000

m

L _ ___ IliiM il -

1995 1996 1997 1998

8. Area

9. Polygons

10. Solving Equations In mathematics, the whole is equal to the sum of its parts (Area Addition Postulate).

Try to deviate from this postulate, and let the students reflect on the statement: "The whole is greater than the sum of its parts."

For example, a laptop is made up of many parts that do nothing by themselves but when these parts are combined, the final product performs an astounding function.

"Alone we can do so little; together we can do so much." Increasing the number of sides of a polygon approximates a circle. In ancient times, a circle is considered as a perfect shape. In life, if you want to improve yourself, you shall undergo many trials. Increasing the number of trials means gaining new insights/ perspectives. These new insights will make you a better person. An equation is like a weighing scale. The right-hand side and the left-hand side are balanced because they represent the same quantity. Why is it important to keep a balance between studying and relaxation?

In our society, it is really vital to educate people in the traditional values of our country. There is a growing demand for teachers to deliberately teach values, through settinjg a good example and discussing/processing moral issues with the learners. It is :nere^ fore crucial to the formation of the students that you deliberately use an eclectic n ix o f methods to convey the important values that the students must uphold.

A ss e s s

D o the following to help you think of creative ways to integrate values in your lesson.

1. Browse the DepEd mathematics curriculum guide. Choose a topic from Grades 4 to 6. Write the topic and grade level below.

How would you inject values into this particular topic? Put it in a situation where the students can relate to. Imagine you are talking to your students. Write your script below. If you plan to use materials, write a note about it.

C h a l le n g e

Reflect on the following questions.

1. Do you foresee problems or difficulties in integrating values into your curriculum ?

2. In what mathematics topics in Grades 4 to 6 do you think this strategy is moist appropriate? Why do you think so?

This activity will test your skill in spontaneously integrating values in a math class setting. This activity will be part of the learning portfolio that you will compile at the end of this module.

Consider this situation. A student consulted with you and raised the following points.

"Hi, Teacher! Our lesson on Solving Equations is not that hard. But why do we study something that we probably will never use in life? If I buy candy in a store, do I need to solve for 'x' before getting the candy that I want?"

How will you tap into your student's affective domain for him/her to understand the relevance of your lesson in his/her life?

Topic: Solving for the Unknown in an Equation

Possible Values Integration Point

i

Summ ary

There is a growing demand for teachers to deliberately teach values and this is possible even in the mathematics classroom. All that teachers need do is to be intentional about it and reflect on ways to inject values in their lessons.

O b je c tiv e

Design collaborative activities that will encourage involvement, interdependen and fair division of labor among the students

Introduction

When transitioning from primary to intermediate grades, children develop a re; strong bond with one friend. Some child psychologists point out that it is easier some kids to relate to just one co-learner rather than socializing with a big gro at the same time. Teachers, however, can provide intermediate graders with ma opportunities for interactions. Within collaborating groups, children learn to 1 things out, conjecture, explore, justify, evaluate, and convince others of their findinj Collaborative tasks provide enriching opportunities for the learners to explore oth students' perspectives that may differ from their own. Thus, these can develop stronger sense of empathy among the students.

Group activities, if facilitated carelessly, could waste classroom time. Because this, it is important for teachers like you to ensure that the group activities are ca re f-; designed and successfully implemented. This lesson aims to help you prepare, mor : : and process collaborative tasks in your classroom that will maximize your student capacity to socialize with each other.

T h i n k " _

Vygotsky's Social Learning Theory

Collaborative learning branches out from the zone of proximal development ZPI theory of Vygotsky. 1

Vygotsky defined the ZPD as follows:

"The zone of proximal development is the distance between the a ^ ja developmental level as determined by independent problem solving and the eve 3 potential development as determined through problem solving under adult gu zzrm or in collaboration with more capable peers."