24 ĐỀ THỰC CHIẾN CHUẨN MINH HỌA KỲ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2023 MÔN TOÁN (ĐỀ SỐ 12-16) by Dạy Kèm Quy Nhơn Official

ĐỀ ÔN TẬP THI TỐT NGHIỆP THPT MÔN TOÁN

ễ

Thanh Tú eBook Collection 24 ĐỀ THỰC CHIẾN CHUẨN MINH HỌA KỲ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2023 BÀI THI MÔN TOÁN - BẢN GIÁO VIÊN (ĐỀ SỐ 12-16)

Ths Nguy

QUA EMAIL

COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO

TAILIEUCHUANTHAMKHAO@GMAIL

BỘ ĐỀ THỰCCHIẾN2023 KỲ THITỐTNGHIỆPTHPTQUỐCGIANĂM2023

ĐỀ SỐ 12 Bàithimôn:TOÁN (Đề gồmcó06trang) Thờigianlàmbài:90phút,khôngkể thờigianphát đề

Họ vàtênthísinh: Số báodanh:

Câu 1: Cho hàm số ()fx có bảng biến thiên như sau:

Hàm số đã cho đạt cực đại tại điểm nào dưới đây?

A. 1 x = . B. 2 x = . C. 0 x = . D. 5 x = .

Lờigiải

ChọnC

Từ bảng biến thiên, hàm số ()fx đạt cực đại tại 0 x = .

Câu 2: Đồ thị của hàm số nào dưới đây có dạng như hình vẽ bên

Lờigiải

=−

ChọnB

A. () ( ) () d fxxfx ′ ′ =  . B. () ( ) () d fxxfx ′ =−  .

C. () ( ) () d fxxfx ′ ′ =−  D. () ( ) () d fxxfx ′ = 

Lờigiải

ChọnD

Gọi ( )Fx là một nguyên hàm của hàm số ( )fx .

Ta có ( ) ( )Fxfx ′ = hay () ( ) () d fxxfx ′ =  .

Câu 5: 2 1 d sin x x  bằng

A. tan xC + B. cot xC−+ C. cot xC + D. tan xC−+ Lờigiải

ChọnB

Áp dụng công thức trong bảng nguyên hàm, ta có: 2 1 dcot sin xxC x =−+  .

Câu 6: Cho hai số phức 122;12 zizi =−=+ . Phần ảo của số phức 21zz bằng

A. 3. B. 2 . C. 2i . D. 3i . Lờigiải

ChọnA

Ta có: 21 . zz ( )( ) 12243 iii=+−=+

Khi đó số phức 21 . zz có phần ảo bằng 3.

Câu 7: Môđun của số phức 23 zi =− bằng:

A. 13 B. 5 C. 13 D. 5

Lờigiải

ChọnC

Số phức ()2 2 232313ziz =−  =+−= .

Câu 8: Từ một nhóm gồm 5 học sinh nam và 8 học sinh nữ, có bao nhiêu cách chọn ra 2 học sinh bất kì?

A. 2 13C . B. 2 13A . C. 22 58CC + . D. 13 .

Lờigiải

ChọnA

Đồ thị hàm số trên có dạng của đồ thị hàm bậc bốn trùng phương

42 yaxbxc =++ , hệ số 0 a < , có 3 cực trị nên 0 ab < .

Câu 3: Nghiệm của phương trình 1 28 x+ = là A. 2 x = . B. 3 x = .

ChọnA

4 x = .

Lờigiải

Ta có 113 2822132 xx xx ++=⇔=⇔+=⇔= .

Câu 4: Mệnh đề nào dưới đây đúng?

1 x = .

Từ một nhóm gồm 5 học sinh nam và 8 học sinh nữ  Tổng cộng có 13 học sinh. Chọn ra 2 học sinh bất kì trong 13 học sinh thì có 2 13C cách chọn.

Câu 9: Cấp số nhân ( ) n u có 122,1uu== thì công bội của cấp số nhân này là

A. 2 . B. 2 . C. 1 2 . D. 1 2 .

Lờigiải

ChọnD

Công bội của cấp số nhân đã cho là: 2 1

1 2 u q u == .

A. 424.yxx =−−

424.yxx =−+

3 2.yxx =−+

3 2.yxx

Câu 10: Cho hàm số ()fx liên tục trên ℝ và có bảng xét dấu của đạo hàm như sau

ChọnA

Áp dụng công thức () 1 log .ln a x xa ′ = v

Câu 16: Trong không gian Oxyz , cho véctơ () 3;2;1

Số điểm cực trị của hàm số đã cho là

A. 3 B. 4 C. 1 D. 2

Lờigiải

ChọnB

Do hàm số liên tục trên ℝ và đạo hàm ()fx ′ đổi dấu khi x lần lượt đi qua 4 điểm 1;0xx=−= ; 1;2xx== nên hàm số đã cho có 4 điểm cực trị.

Câu 11: Cho số phức 21zi=+ , điểm nào dưới đây là điểm biểu diễn số phức z ?

A. () 1;2 G B. () 2;1 T C. () 2;1 K D. () 1;2 H

Lờigiải

ChọnA

Do 2112 zii =+=+ nên 12 zi =− .

Vậy z có điểm biểu diễn là () 1;2 G .

Câu 12: Cho hai số thực ; xy thỏa mãn 45;43 xy== thì 4xy + bằng

A. 5 . B. 2 . C. 10 D. 15

Lờigiải

ChọnD

Ta có 44.45.315 xyxy + === .

Câu 13: Một khối chóp có đáy là hình vuông cạnh a , chiều cao bằng 4a có thể tích là

A. 3 4a . B. 3 4 3 a . C. 3 16 3 a . D. 3 16a .

Lờigiải

ChọnB

Ta có thể tích khối chóp là 23114 ..4 333 VBhaaa ===

Câu 14: Phương trình () 3 log512 x −= có nghiệm là

A. 2 x = . B. 8 5 x = . C. 9 5 x = D. 11 5 x =

Lờigiải

ChọnA

Điều kiện 1 510 5 xx−>⇔>

Ta có () 2 3 log512513 xx−=⇔−= 5102 xx ⇔=⇔= .

Câu 15: Đạo hàm của hàm số 3log yx = là

A. 1 ln3 x . B. ln3 x . C. ln3 x . D. 1 x .

Lờigiải

A. () 7;4;4 . B. () 1;8;2 . C. () 1;8;2 . D. () 7;4;4 .

Gọi () ;; Bxyz , ta có () 4;6;3ABxyz=−−+ . Do ABa = nên

Khi đó () 1;8;2 B .

Câu 17: Cho hàm số ()fx có đồ thị như hình vẽ bên:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. () 1;0 . B. () 0;1 . C. () 1;1 . D. () 2;1 . Lờigiải

ChọnA

Dựa vào hình vẽ ta thấy hàm số đồng biến trên () 1;0 và () 1; +∞ .

Câu 18: Tiệm cận ngang của đồ thị hàm số 2 21 x y x = + là

A. 1 2 x =− B. 1 y = C. 1 2 y =− D. 2 x =

Lờigiải

ChọnC

Ta có 2

Nên tiệm cận ngang của đồ thị hàm số

21 x y x = + là

2 y =−

Câu 19: Trong không gian Oxyz , phương trình mặt cầu có tâm () 2;1;2 I , bán kính bằng 3 là

′ =

ới điều kiện 0;1;0aax>≠> ta được () 3

log ln3

a và điểm ()

A , tọa độ điểm B thỏa mãn

4;6;3

ABa = là

Lờ

igiả

ChọnC

431 628 312 xx yy zz −=−=  −=⇔= +==−

→+∞→+∞

2 1

limlim 1

2 xx x x x x →−∞→−∞ ==− + +

21 limlim

212

xx x x x x

==− + + ;

212

A. ()()() 222 2123xyz +++++= . B. ()()() 222 2123xyz −+−+−= .

C. ()()() 222 2129xyz +++++= D. ()()() 222 2129xyz −+−+−=

Lờigiải

ChọnD

Phương trình mặt cầu có tâm ( )2;1;2 I bán kính bằng 3 là ()()() 222 2129xyz −+−+−=

Câu 20: Một khối lăng trụ có diện tích đáy bằng 3 và thể tích bằng 6 thì chiều cao bằng

A. 6 . B. 4 . C. 2 . D. 3 .

Lờigiải

ChọnC

Ta có thể tích lăng trụ có diện tích đáy B , chiều cao h là: 6 .2 3 V VBhh B =  === .

Câu 21: Trong không gian Oxyz , cho ba điểm ( )4;3;2 A , ( )6;1;7 B , ( )2;8;1 C Đường thẳng qua gốc

O và trọng tâm tam giác ABC có phương trình là

A. 413 xyz == B. 211 xyz == C. 231 xyz == D. 211 xyz ==

Lờigiải

ChọnB

Gọi G là trọng tâm của tam giác ABC , khi đó ta có ( )4;2;2 G .

Có ( )4;2;2 OG =− là VTCP của đường thẳng OG . Chọn ( )2;1;1 u =− là VTCP của đường thẳng OG

Đường thẳng OG đi qua ( )0;0;0 O có VTCP ( )2;1;1 u =− có phương trình chính tắc là:

211 xyz ==

Câu 22: Trong không gian Oxyz , cho ba điểm ( )2;1;3 A , ( )4;0;1 B , ( )10;5;3 C . Véctơ nào dưới đây là

véctơ pháp tuyến của mặt phẳng ( )ABC ?

A. ( )1;2;2 . B. ( )1;2;2 . C. ( )1;2;0 . D. ( )1;8;2 .

Lờigiải

Vậy mặt cầu ( ) S có tâm ( )1;2;2 I bán kính bằng 2

Câu 24: Trong các hàm số sau hàm số nào đồng biến trên ℝ ?

A. 3 32yx=+ . B. 4 31yx=− . C. 41 3 x y x + = . D. tan yx = .

Lờigiải

ChọnA

Ta thấy:

3 32yx=+ ta có 2 90, yxx ′ =≥∀∈ ℝ . Vậy hàm số đồng biến trên ℝ

4 31yx=− ta có 3 01200yxx ′ >⇔>⇔> . Vậy hàm số đồng biến trên ( ) 0; +∞ .

41 3 x y x + = có điều kiện xác định 3 x ≠ nên hàm số không đồng biến trên ℝ .

tan yx = có điều kiện xác định () cos0 2 xxkk π π ≠⇔≠+∈ ℤ nên hàm số không đồng biến trên ℝ

Câu 25: Diện tích xung quanh của hình trụ có đường cao h , bán kính đáy r bằng

A. 2 rhπ B. 2 rhπ C. 2rh D. 2 hπ

Lờigiải

ChọnB

Diện tích xung quanh của hình trụ có đường cao h , bán kính đáy r bằng 2 rhπ

Câu 26: Một hình nón có diện tích xung quanh bằng 2 5 aπ , bán kính đáy bằng a thì độ dài đường sinh bằng

A. 3a B. 5a C. 5a D. 32a

Lờigiải

ChọnA

Ta có ( )2;1;2 AB =− ; ( )12;6;0 AC =− .Khi đó ()() .,.12;24;240nkABACkk  ==≠  với n

là véctơ pháp tuyến của mặt phẳng ( )ABC

Vậy một véctơ pháp tuyến của mặt phẳng ( )ABC là ( )1;2;2 n = .

Câu 23: Trong không gian Oxyz , mặt cầu ( ) 222 :24450 Sxyzxyz++−−−+= có bán kính bằng

A. 14 B. 2 C. 14 D. 4

Lờigiải

ChọnB

Vì mặt cầu ( ) S có phương trình là

222 24450xyzxyz++−−−+= ()()() 222 1224xyz ⇔−+−+−=

ChọnB

Gọi , Rl lần lượt là bán kính đường tròn đáy và độ dài đường sinh của hình nón đã cho.

Theo giả thiết ta có 2 5 Rlaππ = và Ra = nên 2 5 5 a la a π π ==

Câu 27: Đồ thị hàm số 1 1 = + x y x cắt trục tung tại điểm có tọa độ là

A. ( )0;1 B. ( )0;1 C. ( )1;0 D. ( )1;1

Lờigiải

ChọnB

Xét hàm số 1 1 = + x y x , cho 0 = x ta có 10 1 10 == + y

Vậy đồ thị hàm số 1 1 = + x y x cắt trục tung tại điểm có tọa độ là ( )0;1

Câu 28: Với a là số thực dương tùy ý, khi đó ( ) 6 8log a bằng

A. 2 2log a B. 2 18log a C. 2 3log a D. 2 2log + a

Lờigiải

ChọnA

Ta có () 3 6 8 22 2 1 log6.log6.log2log 3 === aaaa

Câu 29: Nếu () 1 0 d2;fxx =  ()() 1 0 2d8fxgxx −=−  thì () 1 0 d gxx  bằng

A. 5 B. 5 C. 6 D. 3 Lờigiải

ChọnB



1 dd85 2 gxxfxx  ⇔=+=  

Câu 30: Trong không gian Oxyz , đường thẳng 11 : 122 xyz d == không đi qua điểm nào dưới đây?

A. () 0;2;1 M B. () 3;4;5 F C. () 1;0;1 N D. () 2;2;3 E Lờigiải

ChọnA

Ta thấy: 01211 122 =≠ nên đường thẳng 11 : 122 xyz d == không đi qua điểm () 0;2;1 M

31451 122 == nên đường thẳng 11 : 122 xyz d == đi qua điểm () 3;4;5 F

11011 122 == nên đường thẳng 11 : 122 xyz d == đi qua điểm () 1;0;1 N

21231 122 == nên đường thẳng 11 : 122 xyz d == đi qua điểm () 2;2;3 E .

Câu 31: Cho hai số phức 122;24 zizi =−=− khi đó môđun của số phức 112zzz + bằng

A. 1 B. 5 5 C. 55 D. 5

Lờigiải

ChọnC

Ta có: 112zzz + 2(2)(24) iii=−+−− 211i =−

Do đó 112 . zzz + 211i =− ()2 2 211=+− 55 = .

Câu 32: Cho hình chóp . SABCD có đáy là hình thoi tâm O , tam giác ABD đều cạnh 2a . Cạnh bên SA

vuông góc với mặt đáy và 32 2 a SA = . Góc giữa đường thẳng SO và mặt phẳng () ABCD bằng

ChọnC

° C.

Lờigiải

Vì ()SAABCD ⊥ nên () () , SOABCDSOA = .

Mặt khác AO là đường cao của tam giác ABD đều cạnh 2.36 2 22 aa aAO  == .

a SA SOASOA AO a ===  =°

Xét SOA∆ vuông tại A có: 32 2 tan360 6 2

Vậy góc giữa đường thẳng SO và mặt phẳng () ABCD bằng 60°

Câu 33: Cho hình chóp tam giác đều . SABC cạnh đáy bằng a và góc giữa mặt phẳng () SBC với mặt phẳng đáy () ABC bằng 60° . Khoảng cách từ A đến mặt phẳng () SBC bằng A. 4 a . B. 8 a . C. 3 4 a . D. 3 8 a . Lờigiải ChọnC

Gọi D là trung điểm của BC , G là trọng tâm tam giác ABC . Khi đó ADBC ⊥ , SDBC ⊥ , ()SGSBC ⊥ .

Vì ()() SBCABCBC ∩= , ADBC ⊥ , SDBC ⊥ nên góc giữa hai mặt phẳng () SBC và

() ABC là góc SDA . Suy ra 60 SDA =° .

Vì ADBC ⊥ , SDBC ⊥ nên ()BCSAD ⊥ . Trong tam giác SAD hạ GESD ⊥ suy ra ()GESBC ⊥ hay () () , dGSBCGE = . Suy ra () (),3 dASBCGE =

Ta có: ()() 1 0 2d8fxgxx −=−  ()() 11 00 d2d8fxxgxx ⇔−=− 

() () 11 00

° D. 90°

A. 45° B. 30

Xét tam giác đều ABC cạnh a có đường cao 3 2 a AD = suy ra 3 6 a GD =

Câu 37: Chọn ngẫu nhiên 2 viên bi từ một hộp gồm 5 viên bi đen và 4 viên bi trắng. Xác suấ

được chọn cùng màu bằng

t để 2 viên bi

Xét tam giác EGD vuông tại E có 60 EDG =° suy ra sin60 GE GD °= hay sin60 3 6

GE a °=

Suy ra 4 a GE = Vì ( ) ( ) ,3 dASBCGE = nên () () 3 , 4 a dASBC = Vậy () () 3 , 4 a dASBC =

ChọnC

Lờigiải

Số phần tử của không gian mẫu là: ( ) 2 9 36 nCΩ==

Gọi A là biến cố: “Chọn được 2 bi cùng màu ”.

12ln d e x Ix x + =  nếu đặt 12ln tx =+ thì I bằng 1 d 2 tt 

11 5 xt xet

Khi đó số phần tử của biến cố A là: ( ) 22 54 16 nACC=+= .

Vậy xác suất của biến cố A là: () ( ) () 164 369 nA PA n === Ω .

Câu 38: Cho hàm số ( )fx có đạo hàm trên ℝ và 21 e x+ là một nguyên hàm của hàm số ( ) e. x fx ′ trên ℝ và ( ) 01 f = . Khi đó ( )1 f bằng

A. 2e1 B. 2 2e2e1 −+ C. 2 ee1 −+ D. 3 ee2 2 −+ Lờigiải



12ln 1 ddd 22 .

e x t Ixttt x + ===

Câu35: Gọi , Mm là giá trị lớn nhất và giá trị nhỏ nhất của hàm số () 21 1 x fx x = + trên đoạn [ ]0;4 , giá trị của 53Mm bằng A. 4 B. 10 C. 8 D. 3 Lờigiải

ChọnB

Hàm số () 21 1 x fx x = + xác định trên [ ]0;4

(

0;4 7 4 5

01 mMinfxf===−

0;4

ChọnB 21 e x+ là một nguyên hàm của hàm số ( ) e. x fx ′ nên

() () 21 e.e xx fx + ′ ′ = 212e x+ = () 21 1 2e 2e e

x x x fx + + ′ ⇔== .

Ta có ()() ()() 1 1 0 0 d10fxxfxff ′ ==− 

()()() 1 0 10d fffxx ′  =+  1 1 11 0 0 12ed12e xx x ++=+=+  2 2e2e1=−+ .

Câu39: Một cuộn túi nilon đựng rác có dạng hình trụ gồm 120 túi nilon giống nhau được cuốn quanh một lõi rỗng hình trụ bán kính đáy của phần lõi là 1,5cm r = , bán kính đáy của cả cuộn nilon là 3cm R = . Biết độ dày mỗi túi nilon là 0,05mm . Chiều dài mỗi túi nilon gần nhất với kết quả nào dưới đây?

A. 34cm B. 33cm C. 36cm D. 35cm Lờigiải

ChọnD

Gọi , xy lần lượt là chiều rộng và chiều dài của mỗi túi nilon đựng rác.

Khi cuộn túi nilon quanh lõi thì ta cuốn theo chiều dài túi nilon, nên chiều rộng túi nilon là chiều cao hình trụ

Thể tích của cuộn túi nilon là: 22 VRhrh ππ=− 22 .3..1,5.6,75xxx πππ =−=

ờigiải ChọnC

Ta có:

xxx xxx −−−+>⇔−<−−+ 

2 11 2432 55

Vậy tập nghiệm của bất phương trình là: ( )6;1

2 56061xxx ⇔+−<⇔−<< .

Mặt khác do cuộn túi nilon được cuốn từ 120 túi nilon nên thể tích của cuộn túi nilon còn được tính bởi công thức: 0,005...1200,6 Vxyxy ==

Suy ra 6,750,6xxyπ = 6,7545 35,343 0,64 y ππ ⇔==≈

Vậy chiều dài mỗi túi nilon gần với 35cm nhất.

2 2 1 1

5 2 1 2d

Câu 34: Xét tích phân () 2 2 1 2 2 1 2d e tt  D. 5 2 1

e tt  B.

tt  C.

ờigiải ChọnD Đặt 12ln tx =+ 2d d x t x  = dd 2 tx x  =

Đổi cận: 2

=  =   =  =  Khi đó () 2 2 55 2 2 111

5310

Ta có: () ( ) ( ) () () 22 21121 3 0 11 xx fx xx +−− ′ ==> ++ [ ]0;4 x ∀∈

)fx  đồng biến trên [ ]0;4 nên [] ()()

MMaxfxf=== , [] ( ) ( )

Mm  −=

Câu 36: Tập nghiệm của bất phương trình

2 243211 55

xxx −−−+ >   là A. ( ) ( ) ;16; −∞−∪+∞ . B. ( ) ( ) ;61; −∞−∪+∞ . C. ( )6;1 D. ( )1;6 .

2 2432

A. 1 4 B. 1 9 C. 4 9 D. 5 9

Câu40: Có bao nhiêu số phức z thoả mãn 131 zizi +−=−− và 3 2 z z + là một số thuần ảo?

A. 1. B. 2 . C. 4 . D. 3 .

Lờigiải

ChọnA

Đặt () , zxyixy=+∈ ℝ . Gọi () ; Mxy là điểm biểu diễn của z .

131 zizi +−=−− ()() ()() 2222 1311 xyxy ⇔++−=−+− () 20 xy ⇔−+=∆ . ()() ()2 2

3.2 33 22 2 xyixyi zxyi zxyi xy −++− −+− == +++ ++ () () 22 2222 65 . 22 xyxy i xyxy +−− =+ ++++

3 2 z z + là một số thuần ảo () 22 2 2

≠−   ⇔+−−  =  ++  22

z xyx xy

2 6 0 2

2 60 z xyx ≠−  ⇔  +−−= 

 M thuộc đường tròn () C có tâm 1 ;0 2 I    , bán kính 5 2 R = và MD ≠ .

() () 5 , 22 dIR ∆=< nên () ∆ cắt () C tại hai điểm phân biệt trong đó có điểm D .

Vậy có một số phức z thỏa yêu cầu bài toán.

Câu 41: Trong không gian Oxyz , cho điểm () 1;1;1 A , mặt phẳng () :30Pxyz++−= và đường thẳng

2 : 121 xyz d == . Xét đường thẳng ∆ qua A , nằm trong () P và cách đường thẳng d một

khoảng cách lớn nhất. Đường thẳng ∆ đi qua điểm nào dưới đây?

A. () 2;1;0 M B. () 1;1;3 N C. () 3;3;3 P D. () 1;2;4 Q

ChọnB

Lờigiải

Gọi () ;; Hxyz là hình chiếu vuông góc của A trên d .

x ytt zt

 ℝ

Ta th

y ∆

Đặt () 4 log44 ttmxtmxmx −=⇔−=⇔=+

Phương trình đã cho trở thành () 1 4240 2 xt xtx +−−+−= 221 1 22 2 xtxt−+ ⇔−=++

() ()() 22111 222211 22 xtxt−+ ⇔+−=++

Xét hàm số () 1 2 2 a gaa =+ có () 1 2ln20, 2 a gaa ′ =+>∀∈ ℝ nên hàm số đồng biến trên ℝ

Do đó ()()() 1221221 gxgtxt ⇔−=+⇔−=+ () 4 2212log21 txmxx ⇔=−−⇔−=−−

() 21 2 log212 x mxxmx ⇔−=−−⇔−= () 21 2* x mx ⇔=+

Xét hàm số () 21 2 x hxx=+ có () 212 12.2ln212ln2 xx hx ′ =−=− .

() () 2 2 1 02ln21logln2 2 x hxx ′ =⇔=⇔= .

Trên đoạn [] 2;2 ta có bảng biến thiên của ()hx :

Phương trình () * có nghiệm [] 2;2 x ∈− {} 1;2;3;4;5;6 m ⇔∈ .

Vậy có 6 giá trị m thỏa mãn yêu cầu bài toán.

2 121 1121110

xyz xyz

Dấu bằng xảy ra ⇔ AH ∆⊥ . Ta có () AH P ∆⊥ 

=   ⇔= 



 ==  ⇔   −+−−−=  () 2 02;0;0 0 

x yH z

∆⊂  P uAH un ∆ ∆  ⊥    ⊥    VTCP của ∆ là (),0;2;2 PuAHn ∆  ==−  .

Câu 43: Cho hình chóp SABC có đáy ABC là tam giác vuông cân đỉnh ,2AABa = . Gọi I là trung điểm của BC , hình chiếu vuông góc của đỉnh S lên mặt phẳng () ABC là điểm H thỏa mãn

2 HAHI =− , góc giữa SC và mặt phẳng () ABC bằng 60° . Thể tích khối chóp . SABC bằng

3 30 9 a . B.

3 5 6 a . C.

Lờigiải

3 15 6 a . D.

3 15 12 a .

ChọnA

.0 d

Hd AHu ∈     =   ()()()

Khi đó (),3ddAH∆≤= .

=   ∆=−∈  

ấ

Suy ra phương trình của () 1;1;3 N

:12, 12

i qua điểm ()

Câu 42: Cho phương trình () 4 1 4log20 2 x xmxm +−−−−= ( m là tham số). Số giá trị nguyên của m để phương trình đã cho có nghiệm thuộc đoạn [] 2;2 là

A. 3 . B. 6 . C. 5 . D. vô số. Lờigiải

ChọnB

Ta có ABC∆ là tam giác vuông cân đỉnh A , I là trung điểm của BC

Hình chiếu vuông góc của đỉnh S lên mặt phẳng () ABC là điểm H thỏa mãn 2 HAHI =− nên

ta có H là trọng tâm của ABC∆ 1 33 a IHIA  == .

Xét IHC∆ vuông tại I : () 2 2 22 10 33 CHIHICaaa  =+=+=  

Ta lại có ()SHABC ⊥ suy ra H là hình chiếu vuông góc của S trên () ABC .

Mà (){} SCABCC ∩=  Góc giữa SC và mặt phẳng () ABC là góc 60 SCH =°

Do đó tan SH SCH HC = 1030 .tan60.3 33 aa SHHC  =°==

Vậy 111 332SABCABC VSSHABACSH ∆  ===

() 3 2 13030 2. 639 aa a =

Câu 44: Cho hàm số ()fx thỏa mãn () 4 4 3 f = và () () 1 1 fxxfx x  ′ =+−

, 0 x ∀> . Khi đó () 4 1 d xfxx  bằng

ờigiải ChọnB

Với mọi 0 x > ta có: ()() fxxfxxx ′ +=+ () ()xfxxx ′ ⇔=+ .

Lấy nguyên hàm hai vế ta được: () 2 2 23 x xfxxxC =++ .

Mà () 4 48 3 fC =  =− ()

2 2 8 23 x xfxxx  =+−

Vậy () 44 2 11

2157 d8d. 2330 x xfxxxxx  =+−=−  

Câu 45: Cho các số thực , bc sao cho phương trình 2 0 zbzc++= có hai nghiệm phức 12 ; zz thỏa mãn

1 332zi−+= và ()() 1222ziz+− là số thuần ảo. Khi đó bc + bằng:

A. 1 B. 12 C. 4

Lờigiải

ChọnC

Trườnghợp1: Nếu các nghiệm của phương trình là các số thực ; xy thì

1 3333 zixi −+=−+ ()2 392 x =−+> mâu thuẫn với giả thiết.

( )

Trườnghợp2: Các nghiệm phức của phương trình không là các số thực, khi đó với

121 zxyizzxyi =+  ==−

Khi đó: ()()() 22 1 3323321zixy −+=⇔−++=

Và:

( )( ) ( ) ( ) 12222.2 zizxyixyi +−=++−−

( ) ( ) ( ) ( ) .2.22.2. xxyyxyxyi =−+++−+−

là một số thuần ảo khi và chỉ khi phần thực bằng 0 tức là:

( ) ( ) ( ) 22 .2.202202 xxyyxyxy −++=⇔+−+= .

Giải hệ gồm ( )1 và ( )2 : ()() 22 22

 −++=   +−+=   22

332 220 xy xyxy

=−  ⇔  +−+= 

4 220 yx xyxy

=−  ⇔  −+=  2 2 x y

4 2880 yx xx

=  ⇔  =−  1222i;22izz  =−=+ .

Vì vậy theo Vi-et ta có: ( ) ( ) ()() 12 12

22i22i4 .22i.22i8 zzb zzc

+=−=−++=    ==−+=   484 bc  +=−+=

Câu 46: Cho hàm số ( ) 3 3 fxxx =−+ và ( ) ( ) 2sin gxfxm =++ ( m là tham số thực). G

Chọn A Đặt [ ] ( ) [ ] [] ( ) [] ( ) 3 1;3 1;3 2sin1;33,1;3maxmin50 txgtttmtgtgt =+∈  =−−∈  += .

 =−−− 

gtmm gtmm ymym gt

 =−−− =−−=−    =

{} [] () 1;3  

 =−=−   −−+−=⇔=−  =−−=−−  

max1818 2185017/ min22

gtmm mmmtm gtmm

[] ( ) [] () () 1;3 1;3

Trường hợp 2: Nếu 18018 mm −<⇔> thì

 =−=−   ++−=⇔=  =−−=+  

min1818 2185033/ max22

gtmm mmmtm gtmm

[] ( ) [] () () 1;3 1;3







A. 1283 30 B. 157 30 C. 157 30 D. 1283 30



 



maxmin50

+= ℝ ℝ

Tổ

ầ

ử

ủ

ằ

B. 1

C. 2 . D. 9 . Lời giả

ọi S là tập các giá trị của tham số m để ( ) ( )

gxgx

ng các ph

n t

a S b

16 .

1;3 1;3

Xét hàm số: [ ] 3233301;3yttmytt ′ =−−  =−≥∀∈ ()() [] ( ) { } [] ()

maxmax2;18 minmin2;18 12,318 min0

Trường hợp 1: Nếu 202mm −−>⇔<− thì

Trường hợp 3: Nếu ()()2180218mmm −−−+≤⇔−≤≤ thì

 =−−−

=  

maxmax2;18 min0

gtmm gt

[] () {} [] () 1;3 1;3

Nhận xét: [] () {} [] 1;3 maxmax2;1850,2;18 gtmmmm =−−−<∀∈−  ∈∅

Vậy {} 17;33 S =− nên tổng các phần tử của S bằng 16.

Câu 47: Trong không gian Oxyz , cho mặt phẳng () :0Pxyz++= và mặt cầu () S có tâm () 0;1;2 I bán

kính 1 R = . Xét điểm M thay đổi trên () P . Khối nón () N có đỉnh là I và đường tròn đáy là

đường tròn đi qua tất cả các tiếp điểm của tiếp tuyến kẻ từ M đến () S . Khi () N có thể tích lớn

nhất, mặt phẳng chứa đường tròn đáy của () N có phương trình là 0 xaybzc+++= . Giá trị của abc ++ bằng

A. 2 . B. 0 . C. 3. D. 2 . Lờigiải

ChọnB

Vì mặt cầu () S có tâm () 0;1;2 I và bán kính 1 R = . Đặt xIM = () (),3xdIP  ≥= .

Gọi A là tiếp điểm của tiếp tuyến kẻ từ M đến () S . Khi đó tiếp điểm A nằm trên đường tròn

() C có tâm H bán kính rHA = .

ChọnB

Phương trình hoành độ giao điểm của ( ) mC và trục Ox là: ( ) 3222320xxmxm−−−+=

Ta có 222 1 AMIMIAx=−=− 2 .1AIAMx AH IMx  == . Khi đó: 22IHIAAH =−

2 11 1 x xx =−= .

Do đó 2 1 3 N VrIH π = () 2 2 11 3 x gx xx π == ) () ()

Dấu bằng đạt tại () 31;0;1xM=⇔− là hình chiếu của I trên mặt phẳng () P

Suy ra () 2 AS AM ∈    =   ()() ()()

tiếp điểm.

 +−+−= 

Vậy 1120 abc++=+−=

22 2 22 2

⇔  +++−=   20 xyz  ++−= là mặt phẳng chứa các

121 112 xyz xyz

Câu48: Cho hàm số () 3222 32 yxxmxm =−−−+ () mC . Biết rằng đồ thị hàm số cắt trục hoành tại ba

điểm phân biệt () ,, ABC ABCxxx << và có hai điểm cực trị , MN . Số các giá trị của tham số m để MNAC = là

=  =  ⇔−−−=⇔⇔   −−= =±+    .

()() 22 22 2

1 1 120 20 11

x x xxxm xxm xm

Suy ra ( ) mC cắt trục Ox tại ba điểm phân biệt ( ) () ( ) 22 11;0,1;0,11;0 AmBCm −+++ và 2 21 ACm =+ .

Ta có, 22 362yxxm ′ =−−+ , ( ) 22 036201yxxm ′ =⇔−−+= , phương trình ( )1 luôn có

nghiệm 12 , xx với mọi giá trị của tham số m Áp dung định lý Vi-et ta có

Gọi hai điểm cực trị là ( ) ( ) 1122 ;,; MxyNxy

Đường thẳng qua hai điểm cực trị , MN là () 2 2 222 1 33 m ymx + =−++ .

Nên ta có () () () () () () 2 2 22 2 2 2 21212112 44 1114 99 MNxxmxxmxxxx  =−++−=+++−

=++−−=+++

() () () ()

2 3 2222 44416 114211 93327 mmmm

Theo giả thiết MNAC = () () () ()() 3 3 222222416416 11211141 327327 mmmmmm ⇔+++=+⇔+++=+

() ()() ()()

3 2222222 4164169 1141141 3273272 mmmmm ⇔+++=+⇔++=⇔+=

2 33 11 22 mm ⇔+=⇔=±− .

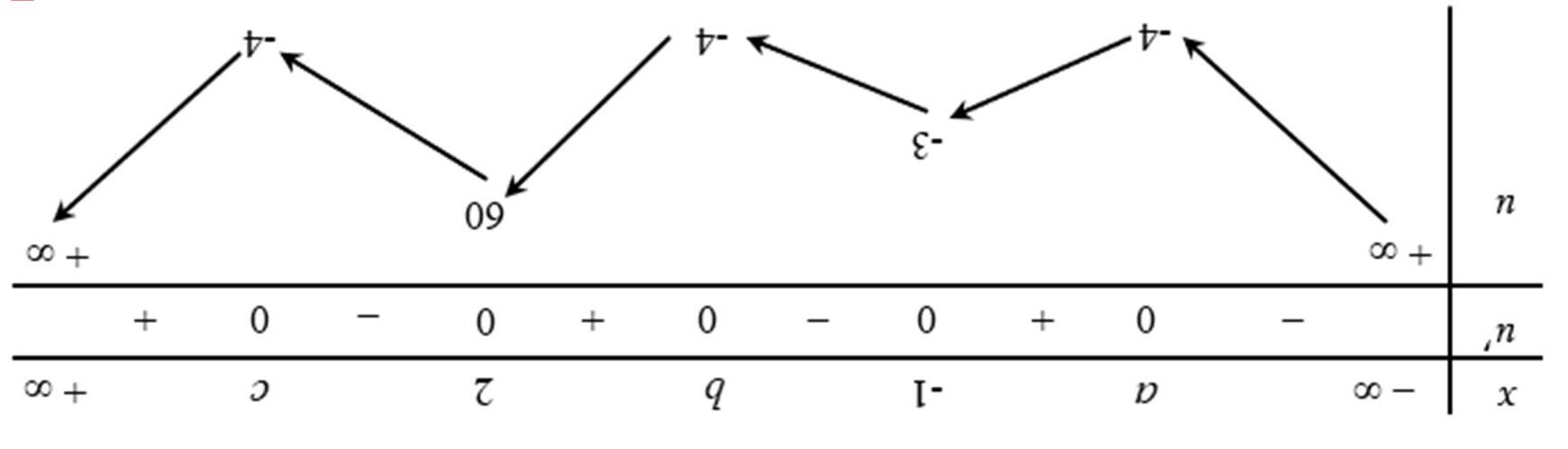
Câu49: Cho hàm số ( ) 42 fxaxbxc =++ có đồ thị như hình vẽ. Biết rằng ( )fx đạt cực trị tại các điểm

1x ; 2x ; 3x thỏa mãn 31 2 xx=+ và ()() ()132 2 0 3 fxfxfx++= . Gọi 1S , 2S , 3S , 4S là diện

tích các hình phẳng trong hình vẽ bên. Tỉ số 12 34

SS SS + + gần nhất với kết quả nào dưới đây?

 

3; 23 max3 27 gxg  +∞  ≤== .

A. 1. B. 2 . C. 0 . D. 3 Lờigiải



 

12 2 12

2 3 xx m xx += 

 −+ =





 



n tích

Khi đó 1234 SSSS +++ a =

ật có các kích thước 1; ()() 23 fxfx a =

Do đó 34SS+= () 12aSS −+ 28217 60 aa=− ()71142 60 a =

SS SS +  + () 28217 71142 = 0,6 ≈ .

12 34

Câu 50: Có tất cả bao nhiêu giá trị nguyên của y sao cho tương ứng với mỗi giá trị y luôn tồn tại không quá

15 số nguyên x thỏa mãn điều kiện ( ) ( ) ( ) 22 202120222 loglog16logxyyyxy ++++≥− ?

A. 2021 B. 4042 C. 2020 D. 4041 Lờigiải

ChọnD

Điều kiện 2 0 0 xy xy

Ta có bất phương trình ( ) ( ) ( ) 22 202120222 loglog16log0 xyyyxy ++++−−≥

Xét ( ) ( ) ( ) ( ) 22 202120222 loglog16log fxxyyyxy =++++−− với xy > , y ∈ ℤ .

Ta có: () () () ( ) () () 2 2 2 ln2ln2021ln2ln2021 11 ' ln2 ln2021..ln2021.ln2 xyy fx xy xyxyxy =−= ++− .

Ta có: ( ) ( )ln2ln2021ln2ln2021xyxy >  −<−

Suy ra ( ) ( ) 22 ln2ln2021ln2ln2021ln20210, xyyyyy −−−<−−<∀∈ ℤ

Do đó ( ) '0,, fxxyy<∀>∈ℤ

Ta có bảng biến thiên của ( )fx là:

Yêu cầu bài toán ( ) 160 fy ⇔+< ( ) ( ) 22 202120222 log16log16log16 yyyy ⇔+++++<

log16 log164 log2022 yy yy ++ ⇔+++< () 2 2021 2022

() ( ) 2 2021 2 2021 2021

4 log162,00 1log2021 yy ⇔++<≈ + 2022

4 1log2021 2 1620212021,992020,99yyy + ⇔++<⇔−≤≤ .

Do y ∈ ℤ nên { }2021;2020;...;2020 y ∈−− .

Vậy có tất cả 4041 giá trị nguyên y thỏa yêu cầu bài toán.

A. 0,65 B. 0,7 C. 0,55 D. 0,6 Lờigiải ChọnD Hàm số () 42 fxaxbxc =++ có đạo hàm như sau: () 3 420fxaxbx ′ =+= 2 0 2 x b x a =   ⇔  =−  0 2 x b x a =   ⇔  =±−   () 0 ab < Do đó hàm số cóba điểm cựctrị 1x ; 2 0 x = ; 31 xx =− vậy 31 2 xx=+ 11 2 xx ⇔−=+ 1 1 x ⇔=− 3 1 x  = Suy ra ()()() 411fxaxxx ′ =+− () 3 4axx=− ()() fxfxdx ′  =  () 42 2 axxc=−+ Do ()() ()132 2 0 3 fxfxfx++= ()() () 2 1100 3 fff ⇔−++= ()() 2 0 3 cacac ⇔−+−+= 3 4 ca⇔= Vậy () 42 3 2 4 fxaxx=−+  Xét () 0 fx = 42 3 20 4 xx ⇔−+= 1 2 3 2 x x  =±   ⇔  =±   Vậy () 1 2 1 0 Sfxdx==  () 1 2 0 fxdx =  1 2 42 0 3 2 4 axxdx  −+    72 30 a = . () 1 2 1 2 Sfxdx==  () 1 1 2 fxdx −=  1 42 1 2 3 2 4 axxdx −−+   14217 60 a = .

ra 12SS+= 72 30 a 14217 60 a += 28217 60 a

Suy

có

SSSS

1234

+++ là diệ

hình chữ nh



 2

xy 

⇔  > 



−>

0 xy

BỘ

ĐỀ THỰCCHIẾN2023 KỲ THITỐTNGHIỆPTHPTQUỐCGIANĂM2023

ĐỀ SỐ 13

Bàithimôn:TOÁN

(Đề gồmcó06trang) Thờigianlàmbài:90phút,khôngkể thờigianphát đề

Họ vàtênthísinh:

Số báodanh:

Câu1: Cho số phức 43 zi =−+ . Số phức iz là

A. 34i + B. 34i C. 34i −+ D. 34i

Lờigiải

ChọnD

Ta có ()4334 iziii =−+=−−

Câu2: Cấp số cộng () nu có 1 2 u =− , công sai 4 d = . Số hạng thứ 4 của cấp số cộng đã cho là.

A. -8. B. 14. C. 10. D. -128.

Lờigiải

ChọnC

Ta có: 41 323.410uud=+=−+=

Câu3: Tích phân 4 1

1 d 2 x x  là

A. 2 B. 1 2 C. 1 4 D. 1

Lờigiải

ChọnD

Ta có: 4 4 1 1

1 d1 2 xx x == 

Câu4: Cho hàm số ()fx có bảng xét dấu của đạo hàm như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. () ;2−∞− . B. () 2;1 . C. () 1;3 . D. ()0;3.

Lờigiải

ChọnB

Nhìn vào bảng xét dấu của đạo hàm, áp dụng định lý mở rộng ta có: hàm số ()fx đồng biến

trên các khoảng ()2;1và () 3;+∞

Câu5: Nghiệm của phương trình 21233xx+− = là

A. 1 x = . B. 3 x =− . C. 1 x =− . D. 3 x = .

Lờigiải

Câu6: Trong không gian Oxyz , véc tơ nào dưới đây là một véc tơ pháp tuyến của mặt phẳng () Oxz ?

A. () 1;1;0 n =− B. () 0;1;0 n = C. () 1;0;1 n = D. () 1;1;1 n =− Lờigiải

ChọnB

Mặt phẳng () Oxz vuông góc với trục Oy nên nhận véc tơ () 0;1;0 nj== làm VTPT.

Câu7: Với a là số thực dương tùy ý, 3 2 a bằng

A. 2 3 a B. 6 a C. 3 2 a D. 5 a Lờigiải

ChọnA

Với a là số thực dương ta có, 2 3 2 3 aa =

Câu8: Trong mặt phẳng tọa độ Oxy , điểm biểu diễn số phức 52 zi =− có tọa độ là

A. () 2;5 . B. () 5;2 . C. () 2;5 . D. () 5;2 . Lờigiải

ChọnB

Điểm biểu diễn số phức 52 zi =− là () 5;2 .

Câu9: Cho hàm số bậc ba ()fx có đồ thị như hình vẽ bên:

ChọnB

Ta có 21233xx+− = 2123 xxx ⇔+=−⇔=− .

Giá trị cực tiểu của hàm số đã cho bằng

A. 2 . B. 3 . C. 1. D. 2 . Lờigiải

ChọnD

Dựa vào đồ thị ta thấy hàm số đạt cực tiểu tại 3 x = và giá trị cực tiểu là 2 y =−

Câu10: Trong không gian Oxyz , đường thẳng nào dưới đây đi qua điểm () 1;2;1 M ?

A. 2 121 : 213 xyz d −−+ == . B. 3 121 : 231 xyz d −+− == .

C. 4 121 : 213 xyz d ++− == . D. 1 121 : 231 xyz d −++ == . Lờigiải

ChọnB

Từ phương trình chính tắc của đường thẳng 3d ta thấy đường thẳng 3d đi qua điểm () 1;2;1 M

Câu11: Tập xác định của hàm số ()()2 log1fxx=+ là

A. ( ) 1; −+∞ B. ( );1−∞− C. { }\1 ℝ D. ( ) 1; +∞

Lờigiải

ChọnC

Điều kiện xác định: ()2 101xx+>⇔≠−

Vậy tập xác định của hàm số là { }\1 D =− ℝ .

Câu12: Thể tích của khối hộp chữ nhật có ba kích thước 5;7;8 là

A. 35 . B. 280 . C. 40 . D. 56 .

Lờigiải

ChọnB

Thể tích của khối hộp chữ nhật là 5.7.8280 =

Câu13: Cho hai số phức 1 23zi=− và 2 15 zi =+ . Môđun của số phức 12 3zz + bằng

A. 185 B. 57 C. 40 D. 56

Lờigiải

ChọnA

Ta có ()2 2 1212 38113811185 zzizz +=−+  +=−+=

Câu14: Họ nguyên hàm của hàm số () 1 1 fx x = là

A. ln1xC −+ B. ( )ln1xC −+ C. 2 1 xC x −+ D. ()2 1 1 C x −+

Lờigiải

ChọnA

Ta có () () 11 ddd1ln1 11 fxxxxxC xx ==−=−+

Câu15: Cho khối chóp có diện tích đáy 3 B = và thể tích 6 V = . Chiều cao h của khối chóp đã cho bằng

A. 18 B. 2 C. 4 D. 6

Lờigiải

ChọnD

Ta có: 133.6 .6 33 V VBhhh B =  ==  =

Câu16: Trong không gian Oxyz , cho hai vectơ ( )1;3;2 u , ( )2;5;1 v . Vectơ uv + có tọa độ là

A. ( )1;8;3 B. ( )3;8;3 C. ( )3;8;3 D. ( )1;8;3

Lờigiải

A. 3 3 yxx =−+ B. 3 33yxx=−− C. 4223yxx=−− D. 4223yxx=−+− Lờigiải

ChọnC Đây là đồ thị của hàm số bậc bốn trùng phương có hệ số 0 a > .

Câu18: Cho hàm số ()fx có đạo hàm liên tục trên đoạn [] 1;2 . Biết ()11 f = , ()24 f = . Khi đó 2 1 '()d fxx  bằng

A. 3. B. 4 C. 4. D. 3 . Lờigiải

ChọnA

2 '()d21413. 1 fxxfxff==−=−=

Câu19: Cho khối nón bán kính đáy 4 r = chiều cao 9 h = . Thể tích của khối nón đã cho bằng

A. 126π B. 36π C. 48π D. 108π Lờigiải

ChọnC

Thể tích của khối nón đã cho là 2211 ..4.948 33 Vrhπππ===

Câu20: Trong không gian Oxyz , cho mặt cầu () 222 :22420 Sxyzxyz+++−+−= . Tâm của () S có

tọa độ là

A. () 1;1;2 B. () 1;1;2 C. () 1;1;2 D. () 2;2;4

Lờigiải

ChọnA

Ta có: ( ) ( )12;35;211;8;3uvuv +=−++−−  +=− .

Câu17: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?

ChọnB

Mặt cầu () S có tâm () 1;1;2 I

Câu21: Họ nguyên hàm của hàm số ()3sin fxx = là

A. 3sin xC−+ B. 3cos xC + C. 3cos2xC + D. 3cos xC−+ . Lờigiải

ChọnD

Ta có 3sind3cosxxxC =−+  .

Câu22: Cho hình trụ có thiết diện qua trục là hình vuông cạnh bằng 4a . Diện tích xung quanh của hình

trụ đã cho bằng

A. 2 16 aπ . B. 2 4 aπ . C. 2 64 aπ . D. 2 8 aπ .



Ta có () ()() 2 1 

Gọi ,, Rhl lần lượt là bán kính đáy, chiều cao, đường sinh của hình trụ

Theo bài ra ta có, hình trụ có thiết diện qua trục là hình vuông ABCD cạnh bằng 4a nên:

4 2 22 ABa Ra === , 4 lhADa ===

Diện tích xung quanh của hình trụ là: 2 22.2.416 xq SRlaaa πππ=== .

Câu23: Trong không gian Oxyz , cho điểm () 0;1;2 M và mặt phẳng () :4320Pxyz+−−= . Đường

thẳng

∆ đi qua M và vuông góc với mặt phẳng () P có phương trình tham s

A. 5! B. 3 5A C. 3 5C D. 35

Lờigiải

ChọnB

Mỗi cách xếp chỗ ngồi cho 3 học sinh vào một dãy ghế hàng ngang gồm 5 ghế, mỗi học sinh ngồi một ghế là một chỉnh hợp chập 3 của 5.

Vậy số cách sắp xếp là: 3 5A .

Câu26: Số đường tiệm cận của đồ thị hàm số 2 2 9 65 x y xx = −+ là

A. 2. B. 4. C. 1. D. 3. Lờigiải

ChọnC

Tập xác định: [] {}3;3\1 D =− . Ta có 2 1 650 5 x xx x =  −+=⇔  =  .

Do 2 2 11

9 limlim 65 xx

x y xx ++→→ ==−∞ −+ , 2 2 11

tiệm cận đứng là 1 x =

x y xx →→ ==+∞ −+ nên đồ thị hàm số có một

9 limlim 65 xx

Do []53;3 x =∉− nên đồ thị hàm số không nhận 5 x = là tiệm cận đứng.

Vì hàm số có tập xác định là [] {}3;3\1 D =− nên đồ thị hàm số không có tiệm cận ngang.

Vậy đồ thị hàm số đã cho chỉ có 1 tiệm cận đứng là 1 x =

Câu27: Cho hình chóp SABC có đáy là tam giác đều cạnh a , SA vuông góc với mặt phẳng đáy và

3 2 a SA = . Gọi M là trung điểm của BC , góc giữa đường thẳng SM và mặt phẳng () ABC bằng

A. 045 B. 030 . C. 060 D. 090

Lờigiải ChọnC

:1 23

Câu24: Hàm số nào sau đây nghịch biến trên ℝ

A. 1 1 x y x + = .

C. ()2 1 yx=−+ .

ChọnD

xt yt zt

B. 2 1 yx=−− .

D. 32335yxxx =−+−+ .

Lờigiải

Hàm số 1 1 x y x + = có tập xác định là {}\1 D = ℝ , nên hàm số không nghịch biến trên ℝ

Hàm số 2 1 yx=−− có [ ) '20,0; yxx=−≤∀∈+∞ , nên hàm số không nghịch biến trên ℝ

Hàm số ()2 1 yx=−+ có [ ) '220,1; yxx=−−≤∀∈−+∞ , nên hàm số không nghịch biến trên ℝ

Hàm số 32335yxxx =−+−+ có 2 '3630, yxxx =−+−≤∀∈ ℝ , nên hàm số nghịch biến trên ℝ

Câu25: Có bao nhiêu cách xếp chỗ ngồi cho 3 học sinh vào một dãy ghế hàng ngang gồm 5 ghế, mỗi học sinh ngồi một ghế

Ta có ABC∆ đều, cạnh a nên

3 2 a AM = ()SAABC ⊥ nên góc giữa đường thẳng SM và mặt phẳng () ABC là góc SMA

3 2 tan360

Trong SMA∆ vuông tại A ta có: 0

a SA SMASMA AM a ===  = .Vậygócgiữa đường thẳng SM và mặt phẳng () ABC là 060

Lờigiải ChọnA

ố

zt =   =−   =−+  . B. 4 1

xt yt zt =   =−+   =−  . C. 4 1 32 x yt zt =   =−   =−+  . D. 4 1 23 xt y zt =   =−   =−  . Lờ

ải

ọ

∆⊥

∆ có

ỉ

=−

là A.

32 x yt

igi

nB Ta có: () P



vec-tơ ch

phương () 4;1;3 u

Mặt khác ∆ đi qua () 0;1;2 M nên =   ∆=−+   =− 

Câu28: Với a là số thực dương tùy ý, ta có

A. 4log4 a a = . B. 4log2 a a = . C. 2log4 a a = . D. 2 log4aa = .

Lờigiải

ChọnA

Với ,0;1bcb>≠ ta luôn có logb c bc = . Do vậy ta có 4log4 a a =

Câu29: Đồ thị hàm số 36 2 x y x + = cắt trục hoành tại điểm có hoành độ bằng

A. 3. B. 3 C. 0. D. 2

Lờigiải

ChọnD

Tập xác định: {}\2 D = ℝ . Cho 36 002 2 x yx x + =⇔=  =− .

Câu30: Cho số phức 26 zi =− , khi đó số phức 13 z i + có phần ảo bằng

A. 6 5 B. 6 5 i C. 8 5 D. 8 5 i

Lờigiải

ChọnA

Ta có ()() 2613 26161286 13191055 ii ii i i ===−− ++

Câu31: Hàm số 2 () 1 x fx x = đồng biến trên khoảng nào dưới đây

A. () 1;2 B. () 2;1 C. () 2; −+∞ D. () 1; −+∞

Lờigiải

ChọnB

Tập xác định {}\1 DR = Đạo hàm () ' 2 1 ()0, 1 fxxD x =>∀∈

Bảng biến thiên

Từ bảng biến thiên suy ra hàm số đồng biến trên khoảng () ;1−∞ và () 1; +∞ .

Câu32: Tập nghiệm của bất phương trình 0,50,5 log(28)log(24) xx +<−+ là

A. () 1; −+∞ B. () 4;1 C. () 1;2 D. ()() ;12; −∞−∪+∞

ChọnC

Lờigiải

Điều kiện 280 42 240 x x x +>   −<<  −+> Khi đó ta có: 28241 xxx +>−+  >−

Kết hợp với điều kiện suy ra 12 x −<< .

Câu33: Một lớp học có 15 học sinh nữ và 25 học sinh nam. Giáo viên chủ nhiệm cầ

sự lớp gồm 3 học sinh. Tính xác suất để ban cán sự lớp có cả nam và nữ.

A. 251 1976 . B. 2625 9880 . C. 1425 1976 . D. 450 988 . Lờigiải

ChọnC

Không gian mẫu có số phần tử: ( ) 3 40 9880 nCΩ==

Gọi biến cố A : “Ban cán sự lớp gồm 3 học sinh có cả nam và nữ”

Trườnghợp1: Ban cán sự có 1 nữ và 2 nam: 12 1525CC

Trườnghợp2: Ban cán sự có 2 nữ và 1 nam: 21 1525CC

( ) 1221 15251525..7125nACCCC  =+= () ( ) () 71251425 98801976 nA PA n  === Ω

Câu34: Chọn ngẫu nhiên một số tự nhiên trong 10 số tự nhiên đầu tiên. Xác suất để chọn được số chia hết cho 3 bằng

A. 3 10 B. 4 9 C. 7 10 D. 2 5 Lờigiải ChọnD

Ta có ( ) 1 10 10 nCΩ==

Gọi biến cố A “chọn được số chia hết cho 3 ”. Trong 10 số tự nhiên đầu tiên, các số chia hết cho 3 gồm: 0;3;6;9 , nên ta có ( ) 4 nA = . Vậy () ( ) () 42 105 nA PA n === Ω

Câu35: Cho hình chóp tứ giác đều .DSABC có độ dài cạnh đáy bằng 4 và độ dài cạnh bên bằng 6 Khoảng cách từ S đến mặt phẳng ( )ABCD bằng

A. 25 . B. 27 . C. 2 . D. 7 . Lờigiải

ChọnB

Gọi = IACBD ∩

Vì giả thiết hình chóp tứ giác đều .DSABC nên ( )SIABCD ⊥ . Hay () () , SABCD dSI =

Xét SIA∆ vuông tại I có: 6 SA = , 11 .4222 22 AIAC=== 22 36827 SISAAI=−=−=

Câu36: Trong không gian Oxyz , cho điểm ( )1;1;3 A . Gọi I là hình chiếu của A trên mặt phẳng ( )Oyz phương trình mặt cầu tâm I qua A là

A. ()() 22 2 131xyz+−+−= B. ()() 22 2 1310xyz++++= 27

C. ()() 22 2 131xyz++++= . D. 20471025131026 −++= .

Lờigiải

ChọnC

Vì I là hình chiếu của điểm A trên mặt phẳng ( )Oyz  ( )0;1;3 I .

chọn một ban cán

Câu37: Biết ()Fx là một nguyên hàm của

xx FCFxF

++ ++

Quãng đường xe đi được trong 10 phút đầu tiên kể từ khi hết đèn đỏ là A. 8.160 m B. 8.610 m C. 10.000 m D. 8.320 m Lờigiải

ChọnA

Phương trình Parabol của chuyển động có dạng () 2 a0yxbxca=++≠

Phương trình vận tốc của chuyển động () 2 a0vtbtca=++≠

Đỉnh của Parabol có tọa độ () ()5;100051001 2 b Iab a  =  +=

Đồ thị hàm số đi qua điểm ()0;00Oc  =

Đồ thị hàm số đi qua điểm ()() 5;100025510002 Iabc  ++=

 ⇔  +==

Với 2 6(40).6400.6960tv =  =−+=

Phương trình đường thẳng có dạng 960 y =



A. 4 B. 2 C. 2 D. 22 Lờigiải ChọnC ( ) , zxyixy=+∈ ℝ .

Ta có: 2221 xyiixyii +−+=+−+

⇔ ( ) 2222 444422121 xxyyxxyy −++++=−++++ ⇔ 22 4 xy+= .

Suy ra 22 2 zxy=+=

Câu39: Một ô tô sau khi chờ hết đèn đỏ đã bắt đầu chuyển động với vận tốc được biểu thị bằng đồ thị là

đường cong Parabol. Biết rằng sau 5 phút thì xe đạt vận tốc cao nhất 1000 m/phút và bắt đầu giảm tốc, đi được 6 phút thì xe bắt đầu chuyển động đều

Câu40: Cửa hàng A có đặt trước sảnh một cái nón lớn với chiều cao 1.35m và sơn cách điệu hoa văn trang trí một phần mặt ngoài của hình nón ứng với cung nhỏ AB như hình vẽ. Biết 01.45,150ABmACB== và giá tiền để trang trí là 2.000.000 đồng mỗi mét vuông. Hỏi số tiền mà cửa hàng A cần dùng để trang trí là bao nhiêu?

A. 4.215.000 đồng. B. 4.510.000 đồng. C. 3.021.000 đồng. D. 3.008.000 đồng. Lờigải

ChọnD

( ) 2022 2 2 ln1 () 1

fx x  ++   = + và (0)1 F = . Giá trị của (1) F bằng A. () 2023 ln122023 2023 +− B. () 2023 ln122023 2023 ++ C. ( )2023 122023 2023 +− . D. ( )2023 122023 2023 ++ . Lờigiải ChọnB Ta có ( ) 2022 2 2 ln1

1 xx Fxdx x  ++ 

+  . Đặt ( ) 2 2 1

 = +

2023 2



 Theo giả

ết ta có

2023 2023 2

 

Ta có: ()1;0;0.1IAIA== . Suy ra bán kính của mặt cầu tâm I qua A là 1 R  

Vậy mặt cầu tâm I qua A có phương trình là ()() 22 2 131xyz++++=

()

 =

ln1

txxdtdx

=++

Vậy ( )

2023 2022 ln1 () 20232023 xx t FxtdtCC  ++ 

==+=+

thi

( ) ()

ln1 ln122023 (0)11()1(1) 20232023

=⇔=  =+  = .

Câu38: Cho số phức z thoả mãn 2221 zizi −+=−+ . Môđun của z bằng

Từ () 1 và () 2 ta có hệ phương trình 10040 2551000400 aba abb +==−

Quãng đường đi được 610 2 06 (40400) +9608.160 sxxdxdxm =−+=

Gọi O , R là bán kính đường tròn ngoại tiếp ABC∆ cũng là bán kính của đường tròn đáy của hình nón. Khi đó diện tích đường tròn đáy của hình nón là: 2 () O SR π = Áp dụng định lý sin ta có: 0 1,45 1,45 2sin150 2sin AB RROAOBABABC ACB ===  ===  ∆ đều 060 AOB  =  diện tích hình quạt AOB là: 20 2 () 0 .6011 . 66 360 quatAOB O R SRS ππ ===

Do đó diện tích mặt được sơn chiếm 1 6 diện tích xung quanh của hình nón.

Vì vậy số tiền cần sơn là: 6622611 .2.10.2.10.1,45.1,351,451,504.2.103.008.000 66 TRlππ ==+≈= đồng.

Câu41: Cho hàm số () 21 11 xm fx x ++ = ++ với m là tham số thực. Gọi S là tập hợp các giá trị nguyên

dương của m để hàm số có giá trị lớn nhất trên đoạn [] 1;8 nhỏ hơn 3. Số phần tử của tập S là

A. 1 B. 3 C. 0 D. 2

Lờigiải

ChọnD

Điều kiện xác định của hàm số là 1 x ≥− . Đặt 1 tx=+ , với [][] 1;80;3xt ∈−  ∈ .

Khi đó hàm số ()fx trở thành () 2 1 tm gt t + = + . Ta có () ()2 2 1 m gt t ′ = +

Trườnghợp1: Nếu () 22mgt =  =  [] () 0;3 max23 gt =< ( tm)

Đặt () () 2 1 2,1 x tt=≥ phương trình trở thành: ( ) ( ) 2 2320,1fttmtm=−+−= .

Với ()2 1101txx =⇔−=⇔= có duy nhất một nghiệm x

Với ()2 22 11log1log txtxt >⇔−=⇔=± có hai nghiệm x .

Vậy phương trình đã cho có bốn nghiệm phân biệt khi và chỉ khi phương trình ( )1 có hai nghiệm

12 , tt thỏa mãn ()

2 12

'0320 12222 12320 1.10 ∆>−+>   <<⇔>⇔>⇔>  

−+−> >

mm ttSmm mm f  

Vậy các số nguyên cần tìm là { }3,4,...,2020 m ∈ . Vậy có 2018 giá trị thỏa mãn.

Câu43: Trong không gian Oxyz , cho hai điểm ( ) ( )1;1;3,0;1;1AB và mặt phẳng

( ) :2230Pxyz+−−= Đường thẳng ∆ song song với mặt phẳng ( )P , cắt cả hai đường thẳng

12 3511 :,: 212121 ddxyzxyz −+−+ ==== và tạo với AB một góc lớn nhất có phương trình là

C. 231 212 xyz ++− == D. 11 122 xyz−+ == Lờigiải

ChọnC

Ta có ( ) ( ) 12 , AdPBdP =∩=∩ .

Mặt phẳng ( )P có véc tơ pháp tuyến là ( )2;2;1 n và ( )1;2;2 AB

Gọi ( ) ( ) 1 2 32;;52;;12;1 MdMtttNdNhhh =∩∆  +−−=∩∆  +−−

Suy ra ( ) 32;21;42 MNhththt  −−+−−++

Do ∆ song song với mặt phẳng ( )P nên ( ).078801MNnht=⇔−−=

Ta lại có ∆ tạo với AB một góc lớn nhất ( ).04902ABABMNht ⊥∆  =⇔++=

Từ ( )1 và ( )2 suy ra 11 2; 4 ht=−=

−< 

>  

20 ⇔⇔<< =< <    Trườnghợp3: [] ()() 0;3

m m m gtg m <  −>   ⇔⇔< +  =< <    Kết hợp các trường hợp

23 max03 2 20 2 6 max33 3 4

3 m m m m gtg

Vậy ∆ đi qua ( )2;3;1 N và có véc tơ chỉ phương ( )42;1;2uMN==− có phương trình 231 212 xyz ++− ==

m < mà m nguyên dương {} 1;2 m  ∈ Vậy tập S có 2 phần tử. Câu42: Có bao nhiêu số nguyên [] 2020;2020 m ∈− để phương trình ()

22 4.2320 x xx mm −+ −+−= có

ốn nghiệm phân biệt?

Lờigiải

Câu44: Cho khối lăng trụ . ABCABC′′′ có đáy là tam giác đều, góc giữa hai mặt phẳng ( ) ABC′′′ và ( ) BCCB′′ bằng 60° , hình chiếu vuông góc của B′ lên mặt phẳng ( ) ABC trùng với trọng tâm tam giác ABC . Khoảng cách giữa hai đường thẳng AA′ và BC′′ bằng 3a . Thể tích khối lăng trụ đã cho bằng

A. 3 83 a . B. 3 83 3 a . C. 3 86 3 a . D. 3 86 a . Lờigiải ChọnA

Trườnghợp2: [] ()() 0;3

trên suy ra

2 2 1

A. 2018 B. 2022 C. 2020 D. 2016

ChọnA



A. 231 122 xyz ++− == B. 113 212 xyz−++ ==

Gọi M là trung điểm BC , O là trọng tâm tam giác ABC , H là hình chiếu vuông góc của O lên BM ′ . Giả sử cạnh đáy bằng x

Ta có ()BOABC ′ ⊥ và

()() () ()() ()

,, ABCBCCBABCBCCBBMO ′′′′′′′′ == .

()() () () () () () ,,,3,33 dAABCdAABCCBdABCCBdOBCCBOHa ′′′′′′′′′′ =====

OHa  = .

Ta gọi các giao điểm của d và () C lần lượt là ()() () 0;2,;2,;2 BBCC ABxxCxx−+−+ với

xxm xxm +=−   =−  .

Ta có diện tích của tam giác MBC là () 1 ,22 2 MBC SBCdMBC ∆ =⋅⋅=

Phương trình d được viết lại là: :220 dyxxy=−+⇔+−= .

Mà ()() 22

312 2 ,,2 2 11 dMBCdMd +− ==== +

Do đó: () 2 2 2.22 416 , 2 MBC S BCBC dMBC ∆ ===⇔=

Ta lại có: ()()()() () 2 222 2 22CBCBCBCB BCxxyyxxxx=−+−=−+−+−−+

()()()() 22222168CBBCCBCB xxxxxxxx =−+−=−=⇔−=

() ()() 2 2 4.824328BCBC xxxxmm ⇔+−=⇔−−−= 2 0 4120 3 m mm m =  ⇔−=⇔  =  (thỏa mãn)

Vậy {} 22 0;3039. S =  +=

Thể tích khối lăng trụ 2 3 3 ..83 24 ABC xx VBOSa ′ ===

x OM x BOOM

Câu46: Trong không gian Oxyz , cho hai điểm ()() 3;1;2,1;3;2AB và đường thẳng 453 : 212 xyz d == .Mặt cầu () S qua hai điểm , AB vàtiếpxúcvới đườngthẳng d có bán kính nhỏ nhất thì hoành độ tâm mặt cầu khi đó bằng A. 3 . B. 1 4 . C. 5 4 . D. 3 2 . Lờigiải

ChọnC

Câu45: Cho hàm số () 322312yxmxmx =++−+ có đồ thị là () C và đường thẳng :2dyx=−+ S

là tập các giá trị m thỏa mãn () d cắt () C tại 3 điểm phân biệt ()0;2,, ABC sao cho diện tích

tam giác MBC bằng 22 , với () 3;1 M . Tính tổng bình phương các phần tử của S ?

A. 4 . B. 3 . C. 9 . D. 25 .

Lờigiải

ChọnC

Phương trình hoành độ giao điểm của () d và đồ thị () C : () 3223122xmxmxx ++−+=−+ () 322310xmxmxx ⇔++−+= () 322320xmxmx ⇔++−= 2 0 2320 x xmxm

=  ⇔  ++−=  (1)

Với 0 x = , ta có giao điểm là ()0;2. A



Gọi mặt cầu () S có tâm I và bán kính là R

Mặt cầu () S qua hai điểm , AB nên I thuộc mặt phẳng () P là mặt phẳng trung trực của AB

Ta có () :220Pxyz−+=

Nhận xét thấy đường thẳng ()dP ⊥ tại () 2;6;1 H , hình chiếu vuông góc của I lên () d là H

Do đó mặt cầu () S tiếp xúc với () d tại H

Mặt cầu () S qua hai điểm , AH nên I thuộc mặt phẳng () Q là mặt phẳng trung trực của AH

m m m mm m

Ta có () :2102270Qxyz−+−−= .



Trong tam giác BOM ′ có 222 111 OHBOOM =+ , trong đó 3 6 .tan60 2     ′ =°=  

Suy ra 222 1412 4 xa axx =+  =

() d cắt () C tại 3 điểm phân biệt khi và chỉ khi phương trình (1) có 2 nghiệm phân biệt khác 0. ≠  −≠   ⇔⇔  >  ′ ∆=−+>    < 

2 3203 (*)3202 1

, BCxx là nghiệm của phương trình (1). Theo định lí Viet, ta có: 2 .32 BC BC

Vì ()() ; IPIQ ∈∈ nên () I ∈∆ với ∆ là giao tuyến của ()() , PQ .

  =+

xt y zt



Hay 2 41 2 4 Rtt=−+ . Suy ra, minR khi 151 ;3; 444 tI  =   

Câu47: Có bao nhiêu số phức z có phần thực và phần ảo đều là các số nguyên thỏa mãn

346 zizizizi ++−=++− và 10 z ≤ ?

A. 12 . B. 2 . C. 10 . D. 5 . Lờigiải

ChọnA

Gọi M là điểm biểu diễn số phức z , ()()() 0;1,0;3,(0;4),0;6 ABCD .

Ta có 346 ziziziziMAMBMCMD ++−=++−⇔+=+

Theo bất đẳng thức tam giác ta có 10 MCMDCD+≥=

Do đó 00 2(5).MAMBMCMDaa +=+=≥

Vi vậy M thuộc hai elip ()() 12 , EE có cùng độ lớn là 0 2a và tâm của hai elip này trùng nhau

tại () 0;1 I là trung điểm của , ABCD . Do đó ()() () () 10 12 20 

Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại 3 điểm phân biệt có hoành độ 1x , 2x , 3x

thỏa mãn 123 9 xxx++= . Khi đó điện tích hình phẳng giới hạn bởi các đường ()yfx = ; ()ygx = ; 1 x = ; 2 x = bằng

A. 3 4 . B. 3 2 . C. 1 4 . D. 1 2 . Lờigiải

ChọnA

Tại các điểm cực trị α , β của ()fx thì ()() 0 ggαβ== , do đó

()()() gxcxxαβ=−− và ()()() 2 343 fxaxxbaxxαβ ′ =++=−−

Trường hợp 1: ()000 0;11011059 Mazaa +  ≤⇔+≤⇔≤≤ trường hợp này có 5 số

phức thỏa mãn.

Trườnghợp2: ()000 0;110110512 Mazaa  ≤⇔−≤⇔≤≤ trường hợp này có 12 số

phức thỏa mãn.

Vậy có tổng 12 số phức thỏa mãn.

Câu48: Cho hai hàm số () 3221fxaxxbx=+++ và () 2 4 gxcxxd =++ có bảng biến thiên như sau

==

Do đó ()() ()22 31 434443 ckak gxkfxcxxdkaxxbkca dkbdb 



 .

Phương trình hoành độ giao điểm 3222134 axxbxaxxb +++=++ ()()3223410axaxbxb ⇔+−+−+−= .

Vậy 2 32 1 

13 374d 34 Sxxxx =−+−+=

Câu49: Cho hàm đa thức ()yfx = Hàm số ()yfx ′ = có đồ thị như hình vẽ sau:



Ta có 1 :3 1 2 

∆= 

 =−

() 2 2 13 1;3;24 22 IttRAItt 

 +−  ==−++−− 

0;1 0;1 Ma MEE Ma  + =∩  

′ =⇔++=++⇔=⇔= 

Suy ra () 3221fxaxxbx=+++ và () 2 34 gxaxxb =++

Theo Vi-et 123 32 9 a xxx a ++== 1 3 a ⇔=− () 2 4 gxxxb  =−++ đạt giá trị lớn nhất tại 0 4 2 2 x == và giá trị lớn nhất bằng ()21413gbb=⇔+=⇔=− 13cd  =−  =−

Có bao nhiêu giá trị của m để []0;6, m ∈ 2m ∈ ℤ để hàm số () () 2 212 gxfxxxm =−−−+ có đúng 9 điểm cực trị?

ĐỀ THỰCCHIẾN2023 KỲ THITỐTNGHIỆPTHPTQUỐCGIANĂM2023

ĐỀ SỐ 14 Bàithimôn:TOÁN (Đề gồmcó06trang) Thờigianlàmbài:90phút,khôngkể thờigianphát đề

Họ vàtênthísinh:………………………………………………

Số báodanh:

Câu1: Đạo hàm của hàm số 5 log yx = là

A. ' ln5 x y = B. ln5 ' y x = C. 'ln5yx = D. 1 ln5 y x =

Lờigiải

Tập xác định: ( ) 0;+∞ . Khi đó đạo hàm: () 5 1 log' ln5 x x =

Câu2: Rút gọn biểu thức 3 32 aa với 0 a < , ta được kết quả là

A. 2a B. 2 a C. a D. 0

Lờigiải

Tập xác định: D = ℝ Với 0 a < ta có: 332 2 aaaaaaa −=−=+=

Câu3: Họ các nguyên hàm của hàm số ( ) 23 x fxe + = là

A. 23 1 2 x eC + + B. 23 1 3 x eC + + C. 23 2 x eC + + D. 23 x eC + +

Lờigiải 2323 1 2 xx edxeC ++=+ 

Câu4: Nếu cấp số nhân ( ) nu có 234,8uu=−= . Giá trị của 1u bằng

A. 16 . B. 2 . C. 2 . C. 16 .

Lờigiải

Ta có 3 2 2 u q u ==− . Do đó 2 1 4 2 2 u u q ===

Câu5: Nghiệm của phương trình ( ) log231 x −= là

A. 3 x = . B. 3 2 x = . C. 2 x = . D. 13 2 x = .

Lờigiải

Ta có: () 1 13 log2312310 2 xxx −=⇔−=⇔=

Câu6: Đườngcongtronghìnhbênlà đồ thị củamộthàmsố trongbốnhàmsố đượcliệtkê ở bốnphương án A,B,C,D dưới đây. Hỏi hàm số đó là hàm số nào?

A. 3 31yxx=−+ . B. 4221 x yx −+ = . C. 3 31yxx=−++ . D. 4221yxx=−++ . Lờigiải

Căn cứ vào hình dáng đồ thị, loại 2 phương án B và D.

Đồ thị có nhánh cuối cùng đi lên, suy ra hệ số a dương.

Câu7: Với a là số thực dương tùy ý, 5 25 log a bằng

A. 52log a B. 5

5 log a C. 5

2 log a D. 55log a

Lờigiải

Ta có 5555 25 loglog25log2logaa a =−=− .

Câu8: Trong không gian Oxyz , cho mặt phẳng () :320Pxz−+= . Vectơ nào sau đây là một vectơ pháp tuyến của () P ?

A. () 3 3;0;1 n =− . B. () 2 3;1;2 n =− . C. () 1 0;3;1 n =− . D. () 4 3;1;0 n =− .

Lờigiải

Từ phương trình mặt phẳng () P suy ra () 3 3;0;1 n =− là một vectơ pháp tuyến của () P .

Câu9: Trong không gian Oxyz , cho mặt cầu ()()() 22 2 :1216Sxyz−+++= . Tâm của mặt cầu () S có tọa độ là

A. () 1;2;1 B. () 1;2;0 C. () 1;2;0 D. () 1;2;1

Lờigiải

Từ phương trình mặt cầu suy ra tâm của mặt cầu () S có tọa độ là () 1;2;0

Câu10: Một khối chóp có đáy là hình vuông cạnh bằng 2 và chiều cao bằng 6. Thể tích khối chóp bằng

A. 6 B. 24 C. 8 D. 12

Lờigiải

Thể tích khối chóp: 11 ..4.68 33 VSh=== .

Câu11: Trong mặt phẳng Oxy , điểm biểu diễn số phức 35 zi =−+ có tọa độ là

A. () 3;5 B. () 3;5 C. () 5;3 D. () 5;3

Lờigiải

Điểm biểu diễn số phức 35 zi =−+ có tọa độ là () 3;5 .

Câu12: Đồ thị hàm số 4223yxx=−− cắt trục tung tại điểm có hoành độ bằng

BỘ

A. 3 . B. 2 . C. 3 ± . D. 0 .

Lờigiải

Đồ thị hàm số cắt trục tung tại điểm có hoành độ bằng 0 .

Câu13: Tích phân 2 1

1 2 dx x  +    bằng

A. ln21. B. ln23 + . C. ln2+1. D. ln22 + .

Lờigiải

+=+=+

1 2dln2ln22 xxx x

A. 1 y = B. 2 y =− C. 4 y =− D. 2 y =

Lờigiải

A. () d fxxxxC =−+  2 126 B. () d fxxxxC =−+  43

C. () d fxxxxC =++  43 D. () d fxxxxC =−+  4343 32 Lờigiải

Ta có () () dd fxxxxxxxC =−=−+ 324343 .

Câu19: Một hình nón có bán kính đáy 3 ra = và độ dài đường sinh 2 la = . Diện tích xung quanh của hình nón đó bằng

A. 2 3 aπ . B. 2 43 aπ . C. 2 83 aπ . D. 2 23 aπ .

Lờigiải

Diện tích xung quanh của hình nón 2 3.223 xq Srlaaa πππ ===

Câu20: Cho hàm số bậc bốn ()fx có bảng biến thiên như sau:

x y x →+∞→+∞

Xét 24 limlim2 1 xx

x y x →−∞→−∞

+ == .

+ == và 24 limlim2 1 xx

Suy ra đồ thị hàm số có tiệm cận ngang là đường thẳng 2 y =

Câu15: Có bao nhiêu cách chọn ra 3 học sinh từ một nhóm gồm 40 học sinh?

A. 340 B. 3 40C C. 403 D. 3 40A

Lờigiải Số cách chọn 3 học sinh từ nhóm có 40 học sinh là: 3 40C

đườ

ng thẳng d là

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. () 4;3 . B. () 4; −+∞ . C. () 1;0 . D. () 0;1

Lờigiải

Dựa vào bảng biến thiên của hàm số, ta có hàm số đồng biến trên () 1;0 .

Câu21: Cho hai số phức 1 2 zi =− và 2 1 zi =+ . Số phức 12 2zz + là

A. 5 i . B. 5 i + . C. 3i . D. 15i −+ .

Lờigiải

A. 2 B. 4 C. 5

Ta có: ()() 12 22215 zziii +=−++=−

Câu22: Cho hàm số bậc ba ()yfx = có bảng biến thiên như sau:

Vậy phần thực của số phức 1 z i + bằng 1

Câu18: Cho hàm số ( ) fxxx =− 3243 . Trong các khẳng định dưới đây, khẳng định nào đúng?

Giá trị cực đại của hàm số đã cho bằng

A. 2 B. 2 C. 1 D. 1 Lờigiải Dựa vào bảng biến thiên ta thấy giá trị cực đại của hàm số đã cho bằng 1

Câu23: Nghiệm của phương trình 35 216 x = là

A. 13 3 x = . B. 1 x = . C. 3 x = . D. 1 3 x =− .

Lờigiải

Ta có: 35354 216223543 xx xx =⇔=⇔−=⇔= .

Vậy phương trình đã cho có nghiệm 3 x = .

Câu24: Thể tích khối lập phương có độ dài cạnh 2a bằng:

Ta có 2 2 1 1  

 .

Câu14: Tiệm cận ngang của đồ thị hàm số 24 1 x y x + = là đường thẳng

A. 2 13 3

yt z =−+   =−   =  B. 12

yt zt =+   =−−   =  C. 2 13 3

z =+   =−−   =  D. 12 3 3 xt yt zt =−+   =−   =  Lờigiải Đường thẳng 13 : 213 xyz d −+ == đi qua điểm ( )1;3;0 M và có một vectơ chỉ phương ( )2;1;3 u =−

3 3

zt =+   =−−   = 

Câu16: Trong không gian Oxyz , cho đường thẳng 13 : 213 xyz d −+ == . Phương trình tham số của

xt yt

nên có phươ

ng trình tham số

xt yt

Câu17: Cho số phức 46 zi =− . Phần thực của số phức 1 z i + bằng

1 Lờigiải Ta có ( )( ) ()() 461 46210 15 11112 ii zii i iiii ====−− +++−

A. 3 2 3 a . B. 3 8 3 a . C. 3 2a . D. 3 8a .

Lờigiải

ể tích khối lập phương có độ dài cạnh 2a là: ()3 3 28 Vaa == .

Câu25: Cho hàm số ()fx có bảng xét dấu đạo hàm như sau:

Hàm số đã cho đạt cực đại tại điểm nào dưới đây

A. 0 x = B. 1 x = C. 3 x = D. 2 x =−

Lờigiải.

Từ bảng xét dấu của đạo hàm ()fx ′ ta thấy được hàm số đạt cực đại tại điểm 1 x = vì dấu của

()fx ′ đổi dấu từ dương sang âm.

Câu26: Cho hình trụ tròn xoay có đường sinh là l , đường cao là h và bán kính đáy là r . Công thức diện tích xung quanh của hình trụ tròn xoay là

A. xq Srh π = B. 2 xq Srh π = C. 2 xq Srh π = D. xq Srl π =

Lờigiải.

Theo công thức tính diện tích xung quanh của hình trụ là 2 xq Srl π = mà lh = nên 2 xq Srh π = .

Câu27: Các số thực , xy thỏa mãn ()() 31235 xyiii +−−+=+ , với i là đơn vị ảo là

A. 1,2xy== B. 4 ,1 3 xy== C. 1,1xy=−= D. 2,2xy=−=

Lờigiải.

Ta có: ()() 31235 xyiii +−−+=+ () 322135 xyyii ⇔−+++=+ 323 215 xy y

1 2 x y

Câu28: Nếu () 1 0 3 fxdx =  thì () 1 0 25fxdx +    bằng

A. 5 B. 6 C. 1 D. 11

Lờigiải

Ta có: ()() 11 1 0 00 25252.3511 fxdxfxdxx+=+=+= 

Câu29: Hàm số nào dưới đây nghịch biến trên ℝ ?

A. 4

Ở câu D: 2 '3250, yxxx =−+−<∀∈ ℝ . Suy ra hàm số ngh

Câu30: Trong không gian Oxyz , cho hai

Suy ra ( )2;2;2 G .

Câu31: Trong không gian Oxyz , cho hai điểm ( )2;1;3 M và ( )4;3;5 N . Mặt phẳng trung trực

a đoạn thẳng MN có phương trình là

A. 490xyz+−−= B. 4150xyz++−= C. 4150xyz+++= D. 490xyz+−+= Lờigiải

Gọi ( )3;2;1 P là trung điểm của MN

Mặt phẳng trung trực của MN đi qua ( )3;2;1 P và nhận ( )2;2;8 MN =− làm vtpt có phương trình là: ( ) ( ) ( ) 2322810 xyz −+−−+= hay 490xyz+−−=

Câu32: Một hộp đựng 9 chiếc thẻ được đánh số từ 1 đến 9. Rút ngẫu nhiên ra hai thẻ rồi nhân hai số ghi trên hai thẻ lại với nhau. Xác suất để kết quả nhận được là một số chẵn bằng

A. 1 2 . B. 13 18 . C. 5 18 . D. 1 6 Lờigiải

Số phần tử của không gian mẫu ( ) 2 9nC Ω=

Gọi A là biến cố hai thẻ có tích hai số ghi trên hai thẻ là một số chẵn ( ) 211 445 nACCC =+

Vậy xác suất cần tìm là () ( ) () 211 445 2 9

13 18 nA CCC PA nC + === Ω

Câu33: Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh 2a , SA vuông góc với mặt phẳng đáy và 2 SAa = . Góc giữa đường thẳng SD và mặt phẳng ( ) SAC bằng

A. 60° . B. 30° . C. 45° . D. 90° . Lờigiải

  ⇔  

 



  ⇔   =  

 −+=



1 yx=−− B. 2 32yxx=−++ C. 3 31 x y x + = D. 32 5 yxxx =−+− Lờigiải Do hàm số nghịch biến trên ℝ nên loại câu A, B và C.

ị

ế

trên ℝ

ch bi

ểm ( )

A và ( )5;4;6 B . Tọa độ trọng tâm của tam giác OAB là: A.

C. ( )2;2;2 . D. ( )2;2;2 . Lờigiải Gọi ( ) ;; GGGGxyz là trọng tâm của tam giác OAB 2 3 2 3 2 3 ABO G ABO G ABO G xxx x yyy y zzz z ++  ==   ++   ==−   ++  ==  

đi

1;2;0

( )4;6;6

B. ( )3;3;3 .

củ

So sánh các giá trị này ta được giá trị nh

10 () 210 xkhix fx xkhix  +≥  =  +<

=−=

Gọi O là giao điểm của AC và BD . Ta có ()

DOAC DOSAC DOSA ⊥   ⊥  ⊥ 

Suy ra góc giữa SD và mặt phẳng () SAC là góc OSD

Mặt khác 2 2 DB DOa == , 22 22SDSAADa =+=

Suy ra 1 sin 2 OD OSD SD == . Vậy góc giữa SD và mặt phẳng () SAC là 30° .

Câu34: Trong không gian Oxyz , cho điểm (1;4;3)A . Gọi I là hình chiếu vuông góc của A trên trục

Ox . Phương trình mặt cầu có tâm I và qua điểm A là

A. 222 (1)25 +++=xyz B. 222 (1)25 −++=xyz

C. 222 (1)5 +++=xyz D. 222 (1)5 −++=xyz

Lờigiải

Hình chiếu vuông góc của điểm (1;4;3)A trên trục Ox là (1;0;0) I

Bán kính của mặt cầu là

222 (11)(40)(30)5 RIA==−+−+−−= .

Vậy phương trình mặt cầu cần tìm là

222 (1)25 −++=xyz .

Câu35: Tập nghiệm của bất phương trình 2 5 11 216

x >   là

A. (;3)(3;) −∞−∪+∞ B. (3;3) C. (;3) −∞ D. (3;) +∞

Lờigiải

Đặt 11 ln;1;1 txdtdxxtxet xe =  == 

===− 

fxx dxfttdttdfttftftdt x

(1)(1)235 ffIII =+−−=+−=− .

Ta có 10101 22 11010

Vậy 1



fxx dx x =−=

'(ln)ln 532 e e

Câu38: Từ một khối gỗ dạng khối lăng trụ đứng .'''ABCABC có 30,40,50 ABcmBCcmCAcm === và chiều cao '100; AAcm = người ta tiện để thu được một khối trụ có cùng chiều cao với khối gỗ ban đầu và đường tròn đáy là đường tròn nội tiếp tam giác ABC . Thể tích của khối trụ gần nhất với giá trị nào dưới đây?

A. 3 62500cm . B. 3 60000cm . C. 3 31416cm . D. 3 6702cm . Lờigiải

xx xxx  >⇔>⇔−<⇔<⇔−<<

Ta có 22 554 22 1111 54933 21622

Vậy tập nghiệm của bất phương trình đã cho là (3;3) .

Câu36: Giá trị nhỏ nhất của hàm số 2 8 yx x =+ trên đoạn 1 ;2 2    bằng

A. 8 . B. 15 2 . C. 65 4 . D. 3 62 . Lờigiải

Xét tam giác ABC có: 222 CABABC =+ nên tam giác ABC vuông tại B .

Gọi r là bán kính đường tròn nội tiếp tam giác ABC ta có:

1 30.40

2 10 1 304050

2() ABC BABC S r cm p BABCCA ∆ ==== ++ ++

Thể tích khối trụ là: 22

3 ..10.1001000031416 Vrhcm πππ ===≈ .



Ta có 3 22

′ =−=

yx  ′ =⇔=∈   165 24 y  =   , ()28 y = , () ()2 333 3 8 4462 4 y =+=

828

. Cho 3 1 04;2 2

ỏ

ất của hàm số đã cho trên 1 ;2 2    bằng 3 62 .

  . Tích phân 1 '(ln)ln e e fxx dx x  bằng A. 14 3 B. 4 3 C. 4 D. 2. Lờigiải

Câu37: Cho hàm số 2 2  = 111 1 1 1 111

'(ln)ln'().(())()() e e

()()()(21)(1)3 33 Iftdtftdtftdttdttdt ==+=+++=+=  .

n lượt tại , MN sao cho 2 ANAM =

M  là trung điểm của đoạn thẳng AN () 1

Gọi Md ∈ có tọa độ () 31;1;22Mttt+−−+ () 2

Từ () 1 và () 2 () 2;2;2MAMAMA Nxxyyzz  () 61;2;41Nttt  +−+

Do ()()()()612241401NPtttt ∈  +++−++=  =− () 5;2;5 N 

Đường thẳng ∆ có 1 vectơ chỉ phương là ()() 6;0;223;0;1 AN =−=−

Gọi H là hình chiếu vuông góc của S lên đáy () SHABCDSHAB  ⊥  ⊥

Xét SAB∆ vuông tại S có SH là đường cao đồng thời là đường trung tuyến SAB  ∆ vuông cân tại S 1 2 SHABa  ==

Gọi N là trung điểm của cạnh CD , {}HNBDO ∩= , {}HCBDI ∩=

=−

xt y zt

Vậy phương trình đường thẳng ∆ là: 13 2 3

Câu40: Cho hình chóp . SABCD có đáy là hình vuông cạnh 2, a hình chiếu vuông góc của S lên đáy là trung điểm cạnh AB , 90 ASB =° . Khoảng cách từ C đến mặt phẳng () SBD bằng

Ta có // OHBC , theo định lý Thales 11 22 IHOHIH ICBCIC ==  =

Lại có (){} () () () () () () () () ; 1 ;2; ;2 dHSBD IH HCSBDIdCSBDdHSBD dCSBDIC ∩=  ==  =

Trong mặt phẳng () ABCD , từ H kẻ HPBD ⊥ tại P () 1

Do ()() 2 SHABCDSHBD ⊥  ⊥

Từ () 1 và () 2 ()() 3 BDSHP  ⊥ . Mặt khác ()() 4 BDSBD ⊂

Từ () 3 và () 4 ()() SHPSBD  ⊥ theo giao tuyến SP

Trong mặt phẳng () SHP , hạ HQSP ⊥ tại Q ()() () ; HQSBDdHSBDHQ  ⊥  =

Xét HPB∆ vuông tại P , có 2 sin.sin45 2 HPa HBPHPHB HB =  =°=

Xét SHP∆ vuông tại H , có đường cao HQ 22 .3 3 HSHPa HQ HSHP  == + () () () () 23 ;2;2 3 a dCSBDdHSBDHQ  ===

Câu41: Có bao nhiêu số phức z thỏa mãn 2(2) zi + là số thuần ảo và ()()2 ziz+− là số thực?

A. 1 B. 0 C. 2 D. 4 Lờigiải Đặt zxyi =+ suy ra ()()()()() 2 22 2 2 222222 zixyiixyixyxyi +=++=++=−+++  

Ta có ()2 2 zi + là số thuần ảo suy ra: ()() () () 2222 2 2 2021 2 2 xy yx xyxy xy yx =+ =−   −+=⇔=+⇔⇔   =−+ =−−  

Câu39: Trong không gian Oxyz , cho điểm () 1;2;3 A , đường thẳng 112 : 312 xyz d −+− == và mặt phẳng () :240Pxyz+++= Đường thẳng ∆ qua A cắt d và () P lần lượt tại , MN sao cho 2 ANAM = có phương trình là A. 13 2 33 xt y zt =−   =−   =+  . B. 13 22 33 xt yt zt =−   =−+   =+  . C. 13 22 3 xt yt zt =−   =−+   =−  . D. 13 2 3 xt y zt =−   =−   =+  . Lờigiải Đường thẳng ∆ qua A cắt d và () P lầ

  =−   =+ 

A. 26 3 a B. 6 3 a C. 3 3 a D. 23 3 a Lờigiải

nh v

minh họa sau:

ẽ

( ) ()()()()



+−=++−−=++−−

()()()() () () 22

()

Gọi O làtâm củamặt đáy .ABCD

Dễ dàng chứng minh được: Góc giữa SD và () SAC là góc OSD . Suy ra 030 OSD = .

Đặt ()0. BCxx=> Ta tính được: 2 2 x OAOD==

Xét SAO∆ vuông tại A: 2 222 4 2 x SOSAAOa=+=+ .

Xét SOD∆ vuông tại O: 2 2 2 2 2121 tan:44 2222 33 ODxxxx OSDaa SO ==+=⇔=+

22 2 1 42 232 xx axa  ⇔=+⇔=   . Diện tích mặt đáy ABCD là: 22 4 ABCD SABa ==

Vậy thể tích khối chóp S.ABCD là: 3 2 118 ...2.4. 333SABCDABCD a VSASaa===

Câu44: Có bao nhiêu cặp số nguyên () ; xy thỏa mãn 12020; 2 xy ≤≤≥ và

() 2 2 log2x xxxyxxyx+−=−− ?

A. 2021. B. 6. C. 2020. D. 11. Lờigiải

Với 12020; 2 xy ≤≤≥ ta có: () 2 2 log2x xxxyxxyx+−=−−

⇔+−=+−−⇔−+=−+−

xx x xx x

() ()

22 1loglog1loglog11 222 log2loglog11loglog11*

2222 22222

⇔−+=−+−⇔+=−+− Xét hàm số: () 2 log fttt =+ với 1 t ≥ . Ta có: () 1 '10,1. ln2 ftt t =+>∀≥

() ()() ()()()

xyxyxxyy xx xyyyy xxx

Suy ra: ()ft là hàm số đồng biến trên nửa khoảng [ ) 1; +∞

Ta có: () () 222 *111 xxx ffyyy xxx  ⇔=−⇔=−⇔=+   .

Để 2 2 x x yx x ∈⇔∈⇔ℤℤ⋮ x ⇔ là ước của 2x

Dễ thấy ước của 2x đều có dạng 2k

Mà {} 2 120201220200log20200;1;2;3;4;5;6;7;8;9;10 k xkk≤≤  ≤≤⇔≤≤  ∈

Vậy {} 012345678910 2;2;2;2;2;2;2;2;2;2;2 x ∈ có 11 số hạng.

=−+++−+−+=−+++−−  

220 2 xy−−= T

2 220 212202 22023 2 2204 3 x yx y yx xy yx x yx xy xy y  =     =−  =    =−   −−=      =−− ⇔⇔   =    =−−      −−=    −−=−    =   Vậy có hai số phức z thỏa mãn yêu cầu bài toán. Câu42: Cho hàm số ()() 1 3 0 4 fxxxfxdx =−  và ( ) 10 f > . Khi đó ( )4 f bằng? A. 64 B. 60 C. 62 D. 63 Lờigiải Ta có: ( ) 3 4 fxxmx =− với 0 m ≥ . Khi () 3 0 0402 2 x fxxmxxm xm =   =⇔−=⇔=   =−  Do ( ) 10 f > 3 11 14.1021 42 mmmm  −>⇔<⇔<⇔< Suy ra: 1121 333 000 2 ()444 m m mfxdxxmxdxxmxdxxmxdx ==−=−+−

() () 21 44 33 22 0 2 1 2 4422 4402 m m xx m xmxdxxmxdxmxmx m  =−++−=++−   ( ) () ( ) () 4 4 4 2 2 2 2 2 1 2202.122 444 m m mmmmm    =+−+−−−      () () 22222

222 1 11482830321210

8 m mmmmmmm m  =   =−+⇔−+=⇔−+=⇔   =   Do 1 4 m < nên 1 8 m = thỏa mãn. Vậ

33 4

()2212 2121222 zizxyiixyixyixyi xxyyxyxyixxyyxyi  =−=−=

Ta có ( )()2 ziz+− là số thực suy ra: ( )

ừ

(1) và (2) suy ra hệ phương trình: ()



11 4824882 44 mmmmmmm =−++−−−=−+

441

y () ()

4464262 22 x fxxf =−

A. 3 8 3 a B. 3 4 3 a C. 3 8. a D. 3 4. a Lờigiải

Câu43: Cho khối chóp SABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng đáy và 2 SAa = . Biếtgócgiữa đường thẳng SD vàmặtphẳng ( ) SAC bằng 030 .Thể tíchkhốichóp đã cho bằng:

Khi đó: 2 2 22 1121 2

k k x k k y x =+=+=+∈ ℤ với ;010kk∈≤≤ ℕ

Mà ;010kk∈≤≤ ℕ nên 22 20212122. kk kkkky−≥  ≥  +≥  ≥

Vậy có 11 cặp số nguyên () ; xy thỏa mãn bài toán.

Câu45: Cho hàm số 432 () fxaxbxcxdxa =++++ có đồ thị hàm số ()yfx ′ = như hình vẽ bên. Hàm số ()()()122 ygxfxfx ==−− đồng biến trên khoảng nào dưới đây?

Câu46: Hai số phức z , w thay đổi nhưng luôn thỏa mãn đẳng thức

() 2 2022.2022 12122 w z izizi + +−−=+− . Giá trị lớn nhất của w là

A. 20212 4 B. 10112 2 C. 20232 4 D. 2019 Lờigiải

ChọnB

Ta có: zizi −=+ nên 2 2 2 21 zizzizi −−=−=+ .

A. 13 ; 22    . B. () ;0−∞ . C. () 0;2 . D. () 3; +∞ .

Lờigiải

ChọnD

Ta có 32 '()432 fxaxbxcxd =+++ , theo đồ thị thì đa thức '()fx có ba nghiệm phân biệt là 1,0,1 nên ()() ()2 3422 '()41144()21 fxaxxxaxaxfxaxaxaax =+−=−  =−+=−

Dựa vào đồ thị hàm số '()yfx = ta có 0 a > nên {}()0,\1fxx>∀∈± ℝ . ()()()()()()()() '()12'2122'2'12212'2 gxfxfxfxfxfxfxfxfx =−−+−−=−−−−−−

−∈−   

Phương trình () 2 2022.2022 12122 w z izizi + +−−=+− () () 2 20221 122 w

z izii + ⇔++=+− () () () 22 2022 22 w

zi zizii + ⇔+−+++= () 1 .

Điều kiện: w0 ≠ suy ra 0 zi+≠ hay 0 zi+> .

Đặt tzi =+ , 0 t > ta có phương trình () 1 ()() () 22 2022 22 w

zi tti + ⇔−++=

Xét ()122;0 13 ; 13 22 2; 22

∈     −∈      , dấu của '()fx không cố định trên 13 ; 22    nên ta không kết

x x x

luận được tính đơn điệu của hàm số ()gx trên 13 ; 22   

Xét () () () () () 121;'120 ;0 '()0 22;'20 xfx x gx xfx

−∈+∞−> 

∈−∞  <  −∈+∞−> 

biến trên () ;0−∞

Khi () () () 123;1 0;2 20;2 x x x

. Do đó, hàm số ()gx nghịch

−∈−   ∈   −∈   , dấu của '()fx không cố định trên () 3;1 và () 0;2 nên ta

không kết luận được tính đơn điệu của hàm số ()gx trên 13 ; 22   

−∈−∞−−< 

∈+∞  > 

Xét () () () () () 12;5'120 3; '()0 2;1'20 xfx x gx xfx

−∈−∞−−< 

Do đó, hàm số ()gx đồng biến trên () 3; +∞

2222

2022

()() ()

w 24 tt tt

 −++=⇔==

22w202210112

= 2 2 zi ⇔+= 10112 w 2 i ⇔=− .

Câu47: Cho hàm số () 32 1; fxaxbxcx=++− () 2 1 gxmxnx=++ có đồ thị như hình vẽ bên

Biết rằng ()20 f ′′ = và hai đồ thị hàm số đã cho cắt nhau tại ba điểm phân biệt có hoành độ 123 ,, xxx thỏa 123 7 xxx++= . Diện tích của hình phẳng gạch sọc trong hình vẽ thuộc khoảng nào dưới đây?

A. 2 0; 5   

B. 21 ; 52   

C. 13 ; 25   

Lờigiải

D. 3 ;1 5   

Ta có () 2 32 fxaxbxc ′ =++ , () 62 fxaxb ′′ =+ . Cho ()201220fab ′′ =⇔+= 6 ba⇔=−





4 2 2

t t

2 2 4 t t

110112 w10112. 2 4 2. t

⇔≤= dấ

bằng xảy ra khi

Do ( )fx bậc 3 và ( )gx bậc hai và quan sát đồ thị đã cho ta thấy tại các điểm cực trị 0x của

hàm số ( )fx thì ( ) 0 0 gx = nên ( ) ( )gxkfx ′ = ( ) 22132 mxnxkaxbxc ⇔++=++

=  

mka nkagxkaxx kc

() () 2 3 12341 1

 =−  =−+   =  .

Ta lại có ()() 1 min2 3 gxg==− 11 112 39 kaka  −=−  = . Khi đó () () 2 1 43 3 gxxx=−+

Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là

()() () () 322 1 1430* 3 fxgxaxbxcxxx=⇔++−−−+=

Theo đề phương trình ( )* có 3 nghiệm 123 ,, xxx thỏa 123 7 xxx++=

Suy ra

Δ 0 0 0 S P >   ⇔>   >  ()2 240 20 0 mm m m  +−>   ⇔+>   >   0 m ⇔> . Do [] 2023;2023 0 m m m ∈     > ∈−  ℤ nên {} 1;2;3;...;2023 m ∈ .

Câu49: Trong không gian Oxyz , cho hai điểm ()() 2;1;3,6;5;5AB . Xét khối nón () N ngoại tiếp mặt cầu đường kính AB có B là tâm đường tròn đáy khối nón. Gọi S là đỉnh của khối nón () N

ba a aa

11 6 1 33 7 3

−++ ==  = 1 3 3 kc  =  = . Khi đó () 32 1 231 3 fxxxx=−+− .

Phương trình ( )* trở thành ()322

Khi thể tích của khối nón () N nhỏ nhất thì mặt phẳng qua đỉnh S và song song với mặt phẳng chứa đường tròn đáy của () N có phương trình 20 xbyczd+++= . Tính Tbcd =++

A. 24 T = B. 12 T = C. 36 T = D. 18 T = Lờigiải ChọnB

xxxxxx

−+−=−+⇔=

11 231432 33

() 513

  =−+−−+−   

11 43231d0,5851 33 Sxxxxxx

A. 2023 . B. 2020 . C. 2023 . D. 2022 . Lờigiải

ChọnA

Hàm số ( )yfx = và hàm số ( )yfx = cùng có tập xác định là ℝ

Lại có, hàm số ( )yfx = là hàm số đa thức bậc 4 trùng phương nên có tối đa 3 điểm cực trị là

1x , 2x , 3x và đồ thị hàm số ( )yfx = cắt trục hoành tại tối đa 4 điểm phân biệt có hoành độ là

4x , 5x , 6x , 7x .

Do đó, hàm số ( )yfx = có nhiều nhất là 7 điểm cực trị là các điểm 1x , 2x , 3x , 4x , 5x , 6x , 7x

Hàm số ( )yfx = có nhiều điểm cực trị nhất ⇔ đồ thị hàm số ( )yfx = phải cắt trục hoành

⇔

Gọi chiều cao khối chóp () 0 SBhh=> và bán kính đường tròn đáy BCR =

Ta có: () 2 1 .1 3 VRh π = và ()4;4;26ABAB =  =

Xét mặt cầu có đường kính AB : ta có bán kính là 3 2 AB r == và tâm () 4;3;4 I

Vì SHI∆ đồng dạng với SBC∆ 22 33 SIIHh SCBCR hR ⇔=⇔= + () () () 2 2 2 222 222 2 3 99 3992 6 h h RhhR hRRhh  ⇔=⇔−−=⇔=  +

Thay () 2 vào () 1 ta có: 22 2 19 ..3. 36 6 hh Vh h hh ππ== với 6 h >

Xét () () () 2 2 22 26 12 3.3. 66 hhh hh V hh ππ ′ == . Ta được bảng biến thiên như sau:

513 2

513 2 x

x  =  

  +  =   .

Vậy diện tích hình phẳng cần tìm là:  ≃

2 232 0

Câu48: Cho hàm số ( ) ( ) 42 2 fxxmxm =−++ với m là tham số thực. Số giá trị nguyên của [ ]2022;2022 m ∈− để hàm số ( )yfx = có số điểm cực trị nhiều nhất là

tại 4 điểm phân biệt (khi đó hàm số ( )yfx = chắc chắn có 3 điểm cực trị)

phương trình ( ) 2 20tmtm−++= phải có 2 nghiệm dương phân biệt

Vậy minV khi 12 SBh== A  là trung điểm của SB () 2;3;1 S 

Vậy mặt phẳng () P đi qua S , vuông góc với AB nên có một VTPT là () 4;4;2 nAB== hay

() 2;2;1 n = nên ta có ()()()() :222310:2290 PxyzPxyz++++−=⇔+++=

Câu50: Có bao nhiêu cặp số nguyên () 3;;0;2023xyy  ∈  thỏa mãn phương trình () 42 11 loglog 24 xxyx

A. 90854 B. 90990 C. 22021 D. 2 20211

Lờigiải



   ?

+++=−

ChọnB Điều kiện: 0 1 4 11 0 24 yx x xx   −>   ≥−    +++>   . Ta có: () 42 11 loglog 24 xxyx  +++=−   () 2 42 11 loglog 24xyx  ⇔++=−    () 22 11 loglog 24xyx  ⇔++=−⇔    2 1111 2442yxxyx  −=++⇔=++    . Vì () 2 11121 4242 m yxxmxmm + ∈  ++∈  +=∈  =+ ℤℤℕ ; khi đó ()2 1 ym=+ Mà ()2 33 0;202312023020232023190989,03ymm  ∈  +≤  ≤≤−≈  Do đó có 90990 giá trị của m , ứng với đó có 90990 cặp () ; xy thỏa mãn yêu cầu bài toán.

Lờigiải

BỘ

ĐỀ THỰCCHIẾN2023 KỲ THITỐTNGHIỆPTHPTQUỐCGIANĂM2023

ĐỀ SỐ 15 Bàithimôn:TOÁN

(Đề gồmcó06trang) Thờigianlàmbài:90phút,khôngkể thờigianphát đề

Họ vàtênthísinh:

Số báodanh:

Câu1: Số phức 22 zi =−− có số phức liên hợp là

A. −+22i B. 22i C. + 22i D. −+ 2 i

Lờigiải

ChọnA

Ta có 2222 zizi =−−  =−+

Câu2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số ()fx , trục hoành và hai đường thẳng

0;1xx== bằng

A. ()  1 0 fxdx B. () π 1 2 0 fxdx C. ()  1 0 fxdx D. () 

Lờigiải

fxdx

ChọnC

Dựa vào đồ thị ta thấy ( ) ( ) ′ ≥∀∈−0,2;3fxx và dấu "" = chỉ xảy ra tại 1 x = nên hàm sốđồng

biến trên khoảng ( )2;3

Câu4: Khối cầu ( ) S có bán kính R có thể tích bằng

Thể tích khối cầu được tính bằng công thức: 3 4 3 VR π =

Câu5: Họ nguyên hàm của hàm số () 1 2 fxx x =+ là

A. 2 1 2 C x −+ B. 2 2 1 xC x −+ C. 2 ln|| xxC ++ D. 2ln||xxC −+

Lờigiải

ChọnD

Diện tích hình phẳng giới hạn bởi đồ thị hàm số ()fx , trục hoành và hai đường thẳng 0;1xx== bằng ()  1 0 fxdx

Câu3: Cho hàm số ()fx xác định và liên tục trên đoạn    3;3 và có đạo hàm ()′ fx trên khoảng () 3;3 Đồ thị của hàm số ()′ = yfx như hình vẽ sau

ChọnC

Ta có 2 11 2d2ddln|| xxxxxxxC xx

Câu6: Cho , ab là các số thực dương. Mệnh đề nào sau đây đúng?

A. ( ) log.loglog abab =+ B. ( ) log.log.log abab =

C. log log log aa bb = . D. logloglog a ba b =− .

Lờigiải

ChọnA

Theo quy tắc tính lôgarit ta có ( ) logloglog abab =+

Câu7: Trong không gian Oxyz , cho véc tơ a thỏa mãn =+−23 aikj . Tọa độ của véc tơ a là

A. ( )2;1;3 B. ( )2;3;1 C. ( )1;2;3 D. ( )1;3;2

Lờigiải

Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên các khoảng () 3;1 và () 1;3

B. Hàm số nghịch biến trên các khoảng () 1;1

C. Hàm số đồng biến trên các khoảng () 2;3

D. Hàm số nghịch biến trên các khoảng () 3;1 và () 1;3 .

ChọnB

Tọa độ của véc tơ a là ( )2;3;1

Câu8: Thể tích khối lập phương có cạnh 2a bằng

A. 3 8a . B. 3 2a . C. 3a . D. 3 6a Lờigiải

ChọnA

Khối lập phương cạnh 2a có thể tích là: ( ) == 3 3 28 Vaa

Câu9: Cho hàm số ( )fx có bảng biến thiên như sau

1 0

2 4 R B. π 3 4 3 R C. π 3 1 3 R D. π 3R Lờigiải

ChọnB

+=+=++   .

Hàm số đã cho đạt cực đại tại điểm nào dưới đây?

A. = 0 x B. = 2 x C. =−1 x D. =−2 x

Lờigiải

ChọnA

Từ bảng biến thiên ta thấy hàm số đạt cực đại tại = 0 x

Câu10: Từ hai chữ số 1 và 9 lập được bao nhiêu số tự nhiên có hai chữ số:

A. 4 . B. 2 . C. 81 . D. 72

Lờigiải

ChọnA

Từ hai chữ số 1 và 9 lập được các số tự nhiên có có hai chữ số là: 99;11;19;91 .

Câu11: Trong không gian Oxyz , cho đường thẳng 213 d: 312 xyz −++ == . Điểm nào sau đây không

thuộc đường thẳng d ?

A. () 2;1;3 N . B. () 5;2;1 P . C. () 1;0;5 Q . D. () 2;1;3 M

Lờigiải ChọnD

ChọnA

Đồ thị của hàm số đi qua điểm () 2;0 và có tiệm cận đứng 1 x = nên hàm số đó là: 2 1 x y x =

Câu14: Cho hình chóp tứ giác . SABCD có tất cả các cạnh bằng nhau. Góc giữa hai đường thẳng , SACD bằng

A. 30° B. 90° . C. 45° D. 60° Lờigiải

ChọnD () () ,,60SACDSAABSAB===° ( vì SAB∆ đều).

Câu15: Giá trị nhỏ nhất của hàm số () 42 2 =−+ fxxx trên đoạn [] 2;2

Thay tọa độ điểm () 2;1;3 N vào phương trình đường thẳng d ta có

221133 312 −−+−+ == suy ra Nd ∈

Thay tọa độ điểm () 5;2;1 P vào phương trình đường thẳng d ta có 522113

suy ra Pd ∈

Thay tọa độ điểm () 1;0;5 Q vào phương trình đường thẳng d ta có 120153 312 −−+−+

suy ra Qd ∈ .

Thay tọa độ điểm () 2;1;3 M vào phương trình đường thẳng d ta có

ra Md ∉

221133 312 −−++ ≠≠ suy

Câu12: Cho cấp số cộng () n u có số hạng đầu 1 2 u = và công sai d3 = . Giá trị của 5u bằng

A. 11 . B. 5 . C. 14 . D. 15

Lờigiải

ChọnC

Ta có 51 4d24.314 uu=+=+= .

Câu13: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. 2

A. -1. B. 8. C. 1. D. -8. Lờigiải

ChọnD

Đạo hàm: () 3 0 4401 1

x fxxxx x

=   ′ =−+=⇔=   =−

Bảng biến thiên:

Từ bảng biến thiên suy ra () 8 minfx =−

Câu16: Nghiệm của phương trình 2 381 = x là

A. 4 = x B. 2 = x C. 4=− x D. 2=− x .

Lờigiải

ChọnB

2 3 3812log8142 =⇔==⇔= x xx

Câu17: Cho hàm số ()fx có bảng biến thiên như sau

312 −−+−+

2 1

D. 2 2 x y x + =

1 x y x = B. 2 1 x y x + = C.

x y x = +



Số nghiệm của phương trình () 320 fx −= là

A. 0 B. 1 C. 2 D. 3 Lờigiải

ChọnD

Ta có ()() 2 320 3 fxfx−=⇔= . Đường thẳng 2 3 y = cắt đồ thị hàm số ()yfx = tại ba điểm

phân biệt, do đó phương trình () 320 fx −= có 3 nghiệm phân biệt.

Câu18: Đạo hàm của hàm số () 3 log23yx=− tại điểm 2 x = bằng

A. 2ln3 B. 1 C. 2 ln3 D. 1 2ln3

Lờigiải

ℝ . Số điểm cực trị của hàm

số đãcholà

A. 0 B. 1 C. 2 D. 3 Lờigiải

ChọnC

Phương trình ()()() 23 110fxxxx ′ =−+= có hai nghiệm bội lẻ là 0,1xx==− và một nghiệm

bội chẵn là 1 x = nên hàm số đã cho có 2 điểm cực trị là 0,1xx==− .

Câu22: Một người gửi tiền vào ngân hàng với lãi suất không thay đổi là 8% / năm. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi được nhập vào vốn ban đầu. Hỏi số tiền ít nhất người đó phải gửi vào ngân hàng để thu về tổng số tiền 500 triệu đồng sau đúng 3 năm kể từ ngày gửi (kết quả làm triệu) là bao nhiêu?

A. 394 B. 396 C. 397 D. 395 Lờigiải

ChọnC

Gọi A (triệu) là số tiền người đó gửi ban đầu. Sau 3 năm kể từ ngày gửi, số tiền thu về là: ()3 31.1,08CArA =+=

ChọnC

Ta có () () () () 23 22 2 23ln323ln3ln3 x yy xx

′ ′′ ==  = .

Câu19: Trong không gian Oxyz , cho ba điểm () 2;1;1 A , () 1;0;4 B , () 0;2;1 C . Mặt phẳng đi qua

A và vuông góc với BC có phương trình là

A. 250xyz−−= B. 2550xyz−−−= C. 2550xyz−−+= D. 2550 xyz−+−=

Lờigiải

ChọnB

Ta có: () 1;2;5 BC =−− . Mặt phẳng đi qua A và vuông góc với BC có phương trình là

()()() 1221510 xyz −−−−+= 2550xyz ⇔−−−=

Câu20: Kí hiệu 0z là nghiệm phức có phần ảo dương của phương trình 2 44100 zz−+= Điểm nào

dưới đây là điểm biểu diễn cho số phức 0iz ?

A. 13 ; 22 M    . B. 13 ; 22 N    . C. 31 ; 22 P    . D. 31 ; 22 Q    .

Lờigiải

ChọnC

 =+  ⇔   =− 

13 22 13 22

zi zi Vì 0z là nghiệm phức có phần ảo dương của phương trình đã cho nên 0 13 22 zi =+ 0 1331 2222 iziii   =+=−+   . Vậy điểmbiểudiễnchosố phức 0iz là 31 ; 22 P   

Giải phương trình 3 3 500 .1,08500396,92 1,08 AA =  =≈

Vậy số tiền ít nhất người đó phải gửi vào ngân hàng để thu về tổng số tiền 500 triệu đồng sau đúng 3 năm kể từ ngày gửi (kết quả làm triệu) là 397 triệu đồng.

Câu23: Trong không gian Oxyz , mặt cầu tâm () 1;2;1 I cắt mặt phẳng () :2210Pxyz−+−= theo

giao tuyến là một đường tròn có bán kính bằng 22 có phương trình là

A. ()()() 222 1219xyz ++++−= . B. ()()() 222 1219xyz −+−++= .

C. ()()() 222 1213xyz ++++−= . D. ()()() 222 1213xyz −+−++= . Lờigiải

ChọnB

Giả sử đường tròn giao tuyến của mặt phẳng () P và mặt cầu () S có tâm H , bán kính HM . () () , IHdIP = ()2 22

2221 1 212 == +−+ .

Ta có: 2 44100 zz−+=

Câu21: Cho hàm số ()yfx = có đạo hàm ()()() 23 11, fxxxxx ′ =−+∀∈

Bán kính của mặt cầu () S là rIM = ()2 2 1223=+=

Vậy phương trình của mặt cầu () S : ()()() 222 1219xyz −+−++=

Câu24: Cho số phức (),, zabiab=+∈ ℝ thỏa mãn ()11 abii +−=−+ . Môđun của z bằng

A. 5 . B. 1. C. 10 . D. 5 .

Lờigiải

ChọnD

Do ()11 abii +−=−+ nên 11 112 aa bb =−=− ⇔  −== . Vậy ()2 222125 zab=+=−+=

Câu25: Cho khối lăng trụ đứng .'''ABCABC có đáy ABC là tam giác vuông tại C , biết 2 ABa = , ACa = , '2 BCa = . Thể tích của khối lăng trụ đã cho bằng

A. 3 3 6 a . B. 3 4 3 a . C. 3 3 2 a . D. 3 4a .

Lờigiải

ChọnC

Ta có: 22 3 BCABACa =−= ( ABC∆ vuông tại C ) và có 22'' BBBCBCa =−=

Thể tích: 3 113 '.'....3 222 ABC a VBBSBBACBCaaa ====

Câu26: Tập nghiệm của bất phương trình () 2 log243 x +< là

A. () ;2−∞− . B. () 2;2 . C. () ;2−∞ . D. () 2; −+∞

Lờigiải

ChọnB () 3 2 log2430242 xx +<⇔<+< 0248 x ⇔<+< 22 x ⇔−<<

Câu27: Cắt một hình trụ bởi một mặt phẳng qua trục thu được thiết diện là một hình vuông có cạnh bằng

3a . Diện tích xung quanh của hình trụ đã cho bằng: A.

Bán kính đáy là: 3 2 a r = . Độ dài đường sinh là: 3 la = .

Diện tích xung quanh của hình trụ là: 2 3 22..39 2 xq a Srlaa πππ=== .

Câu28: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 2 1 2 xx y x +− = + là :

A. 2 B. 1 C. 4 D. 3

Lờigiải

ChọnD

Tập xác định : ( ] [ ) { };10;/2 D =−∞−∪+∞−

Ta có : lim1 x y →−∞ =− , lim1 x y →+∞ = , () 2 lim x y →− =−∞ , () 2 lim x y + →− =+∞ .

Vậy đồ thị hàm số có hai tiệm cận ngang 1;1yy==− và một đường tiệm cận đứng 2 x =− .

Câu29: Cho () =  2 1

1 2 fxdx , () =  4 3

3 4 fxdx . Khi đó ()()

43 12 fxdxfxdx bằng?

A. 3 8 B. 5 4 C. 5 8 D. 1 4 Lờigiải

ChọnB

135 244 fxdxfxdxfxdxfxdx−=+=+=

Câu30: Trong không gian Oxyz , mặt phẳng đi qua điểm ( )1;2;3 A và chứa 1 21 : 121 y xz d −+ == có phương trình là:

A. 5380 xyz−−−= B. 5320 xyz++−=

C. 35780 xyz−−+= D. 357140 xyz++−= Lờigiải

ChọnA

Đường thẳng d có ( ) () 2;1;1 1;2;1. d

I u    =−  

Vì ( )P chứa d và đi qua A nên ta có () ( ),5;3;1 d P nIAu ==−−  .

Khi đó ( )P có ( ) () () 1;2;3 5;3;1 P

   =−−   nên ( ) ( ) ( ) ( ) −−+−−= :513230Pxyz

A n

⇔−−−=5380. xyz

Câu31: Họ các nguyên hàm của hàm số () 21 x fx x = + trên khoảng 1 ; 2   −+∞     là

A. () 1 221 3 xxC −++ . B. () 1 121 3 xxC −++ .

C. 1 21 3 xxC ++ . D. () 1 2121 6 xxC −++ .

2 9 aπ B. 2 27 2 aπ C. 2 9 2 aπ D. 2 13 6 aπ

ải

ờigi

ChọnA



Ta có: ()()()() 4324 1213  .

ChọnB

Ta có 21 x Idx x = +

Khi đó () 2 32 2 1111 .11 222323 ttt ItdttdttCtC

() 1211 211211 233 x xCxxC  +   =+−+=+−+    

Câu32: Bất phương trình ( ) 921.3230 xx mm −+−−> nghiệm đúng với mọi số thực x khi và chỉ khi

A. 3 2 m <− B. 3 2 m ≤− C. 3 2 m >− D. 3 2 m ≥−

Lờigiải

ChọnB

Đặt 3x t = , 0 t > . Phương trình đã cho trở thành : ( ) ( )( ) 2 21.230(*) 123023(0) tmtm ttmtmdot −+−−> ⇔+−−>⇔>+>

Bất phương trình đã cho nghiệm đúng với mọi số thực x khi và chỉ khi bất phương trình (*) nghiệm đúng với mọi 0 t > . Khi đó 3 230 2 mm+≤⇔≤−

Câu33: Hàmsố ( ) 32 fxaxbxcxd =+++ có ( ) 02 f = và ( ) ( ) 3 442,. fxfxxxx −=+∀∈ ℝ Tích

Gọi () , zabiab=+∈ ℝ Theo bài ra ta có () () 22 3234223 zzizabiiab +=+⇔+=++

Vậycóvôsố số phức z thỏamãn điềukiện đã cho.

Câu35: Hàmsố 32 ()3(21)1 fxxxmx =−++−− nghịchbiếntrên khoàng (0;) +∞ khivàchìkhi

A. 3 m ≤− B. 1 m ≤− C. 1 m ≤ D. 3 m ≤ Lờigiải

ChọnB

Tậpxác định: D = ℝ

Đặt ()() 323211yfxxxmx ==−++−− có đạohàm 2 3621yxxm ′ =−++− .

Hàm số nghịch biến trên khoảng () 0; +∞ ()0,0;yx ′ ⇔≤∀∈+∞ () 2 2361,0; mxxx ⇔≤−+∀∈+∞ () 1

Xéthàmsố () 2 361gxxx=−+ trênkhoảng () 0; +∞ có () 66gxx ′ =− ; () 01gxx ′ =⇔= .

Bảngbiếnthiên:

Dựavàobảngbiếnthiên tacó () () 0; min2 gx +∞ =− .

Do đó () 1 ⇔ () () 1; 2minmgx −+∞ ≤ 221 mm ⇔≤−⇔≤− . Vậy 1 m ≤− thoả yêucầubài toán.

Câu36: Trong không gian Oxyz , cho đường thẳng 131 : 111 xyz d −−+ == và mặt phằng

():100. Paxbyz+−−= Biết rằng d nằmtrong () P ,giátrị cùa ab + bằng

A. 2 B. 0 C. 1 D. 5 Lờigiải

ChọnD

Chọn điểm () 1;3;1 Ad −∈ và điểm () 2;2;0 Bd ∈

Mà đườngthẳng d nằmtrongmặtphẳng () P suyra ()()() 1;3;1;2;2;0 ABP −∈

Thaytọa độ củahai điểm ; AB vàophươngtrìnhmặtphẳng () P ,tacó:

31102 221003 aba abb +−== ⇔  +−== Vậy 235. ab+=+=

Lờigiải

∫ . Đặt 2 2121 txtxtdtdx =+⇒=+⇒= .

   ==−=−+=−+     ∫∫



phân () 1 0 Ifxdx

ng A. 148 63 . B. 146 63 . C. 149 63 . D. 145 63 Lời giải ChọnA Ta có: ( ) ( ) () 3 442, 02 fxfxxxx f  −=+∀∈   =   ℝ () 3 4 64463

23 2 a aa

cc c d d  =  −=    −== ⇔⇔  =++  −=  =  =   =  Vậy

11 3

   . Câu34: Có baoo nhiêu số phức z thỏa mãn ( ) 323? zziz +=+ A. 1. B. 0. C. 2. D. Vô số Lờigiải ChọnD

=  bằ

160042 2 422633

bbb fxxx

()

00 42148 2 63363Ifxdxxxdx  ==++=

() () 22 222 22 22 222 0 0 0 42 0 4 23 3 43 a a b aab b aab bab ab bab ≥   ≥   ≥ =+  ⇔⇔⇔≥  =+ =+   =   =+ 

Câu37: Có bao nhiêu số thực dương m để giá trị lớn nhất của hàm số 3 31yxx=−+ trên đoạn

[] 1;2mm++ bằng 53

A. 2 . B. 3 . C. 0 . D. 1.

Lờigiải

Câu39: Cho hình hộp chữ nhật ABCDABCD ′′′′ có ABBCa == và 2 CCa ′ = . Gọi M và N l

ChọnD

Ta có 2 1 330 1 x yx x

=  ′ =−=⇔  =− 

Ta có bảng biến thiên:

Dựatheobảngbiếnthiên thì để giátrị lớnnhấtcủahàmsố 3 31yxx=−+ trên đoạn [] 1;2mm++

bằng 53 thì 110mm+>⇔>

Khi đó [] ()()()() 3 1;2 max2232153 mm fxfmmm ++ =+=+−++=

3269500mmm ⇔++−= 2 m ⇔= .

Vậy có 1 giá trị của m thỏa mãn yêu cầu bài toán.

Câu38: Cho hình nón đỉnh S có chiều cao bằng 5 , cắt hình nón bởi mặt phẳng qua S và dây cung AB

trên đường tròn đáy sao cho 6 AB = , thiết diện thu được có diện tích bằng 15. Diện tích xung quanh của hình nón bằng:

A. 252π . B. 441π . C. 253π . D. 334π .

Lờigiải

ChọnD

Gọi bán kính đường tròn đáy là R , khi đó 222 9 OIRIAR=−=−

Khi đó 222292516SIOIhRR =+=−+=+ .

Lại có 2 11 15.15.6.1615 22

SAB SABSIR=⇔=⇔+= 2 1653RR ⇔+=⇔= .

Khi đó độ dài đường sinh là: 22223534 lRh=+=+= .

Vậy diện tích xung quanh hình nón là: .3.34334 xq SRlπππ ===

′ ′ == 

i có () () ;;5 DJ dDMNPdDMNP DJ

Mặt khác () () () 1 ;;; 3 DI dDMNPdAMNPdAMNP AI ==  



⊥

∩=  ⊥  = 

′′

Vậy () 222 2

a a ANAKa dMNBDAH ANAK a a

′′ ==== +  +  

Cách2. Đặtcáctrục Ox , Oy và Oz vàohìnhnhư sau

ần lượt là trung điểm của cạnh BC và AA′ . Khoảng cách giữa hai đường thẳng BD′′ và MN bằng A. 517 17 a B. 517 68 a C. 317 68 a D. 317 76 a Lờigiải ChọnA Cách1. Gọi P là trung điểm CD , IMPAD =∩ , JINDD′ =∩ , KACMP =∩

== 

Ta có ()()()////;;; MPBDMPBDdBDMNdBDMNPdDMNP ′′′′′′′ 

ạ

 .



Dễ thấy ()() ()() ()() ()() ; trong   

NAKMNP NAKMNPAKAHMNPdAMNPAH AHNKHNKNAK 

⊥∈

Suyra () () 55

;;

33 dMNBDdAMNPAH

==   với 2 AA ANa ′ == ; 332 2 44 a AKAB== .

32 55.5517 4 ;.. 33317 32 4

ự

ó: ()() 11 322 00



413426744231 d2d0,875; 9939850522xfxfxxxxxxxx ′ =−+−=−≈−∈−−

Câu41: Trong không gian Oxyz , cho hai điểm ( )0;1;2 A và ( )3;1;2 B . Gọi ( )P là m

ặ

ấ

ọa độ

A.    1 ;0;0 2 M . B.    1 ;0;0 3 M . C. ( )1;0;0 M . D.  

ChọnA

Gọi phương trình mặt phẳng ( )P là 0 axbyczd+++=

Do mặt phẳng ( )P đi qua điểm ( )0;1;2 A nên 20bcd++= .



() () () 2 2 22 2222 22

323 99 ,

Từ đó suy ra ( ) ( ) , dBP đạt giá trị lớn nhất bằng 9 6 3 2 2

c a =− .

1 b

  .

Câu42: Cho hàm số bậc ba ( )yfx = . Biết rằng hàm số ( ) 2 1 yfx ′ =− có đồ thị đối xứng qua trục Oy , như hình vẽ

Chọ

0;2;4 B′

2;0;4 D′ Tacó

Khi đó

MNBDMB

dMNBD MNBD 



==== 

 Câu40:

Khi

1 0

A.    1 0; 2 B.    1 ;2 2 C.    31 ; 22 D.    1 ;0 2 L

ọ

Do đồ thị hàm số đi qua điểm ()() 0;2,1;1 và điểm () 3;1 nên 2 1 27931 d abcd abcd =   +++=   +++=  Ta có () 2 32 fxaxbxc ′ =++ , do điểm 0 x = là cực trị của hàm số nên ()000fc ′ =  = . Giải hệ 4 phương trình 4 ẩn ở trên ta thu được 4 9 13 9 0 2 a b c d  =    =−   =   =  . Suy ra () 32413 2 99 fxxx=−+ Khi đ

n 2 a = ,tacó () 1;2;0 M , () 0;0;2 N , () 

và ()

() 1;2;2 MN =−− , () 2;2;0 BD′′ =− và () 1;0;4 MB′ =−  (),4;4;6MNBD  ′′ = 

() () 222 ;. 1.40.44.6 1017517 ; 1717 446 ;

′′′ −++

′′

′′ ++

Cho hàm số đa thức ()yfx = có đồ thị như hình vẽ dưới đây

đó ()()

d xfxfxx ′  thuộc khoảng nào dưới đây?

ờigiả

nC D

a vào đồ thị ta thấy () 32 fxaxbxcxd =+++

 .

t phẳng đi qua A và song song với véc-tơ ( )1;1;1 u =− và cách điểm B một khoảng lớn nh

t. T

giao

iểm M của ( )P và trục Ox là

1 ;0;0 3 M Lờigiải

222 222

aa +++ ==== ++ ++  +++ ++  

Do ( ) // Pu nên pháp tuyến của ( )P là () ( ) ;; P nabc = vuông góc với u . Suy ra 0 abc−+= . Khoảng cách từ B đến mặt phẳng ( )P là

abcda a dBP aacc

abc acac

Xét hàm ( ) 2 222fttt=++ , hàm số đạt giá trị nhỏ nhất bằng 3

khi

t =− .

= khi

 

  = 

Ta chọn 2 a = theo phần trên ta suy ra

=−

Do đó phương trình mặt phẳng ( ) :210Pxyz+−+= .

Tọa độ giao điểm của ( )P với trục Ox là điểm ( );0;0Mm thay vào phương trình mặt phẳng ( )P ta có 1 210 2 mm+=⇔=− . Vậy tọa độ điểm 1 ;0;0

M 

Đặt () 2 2 12 x gxf xx  =+  

Đồ thị hàm số ()ygx ′ = cắt trục Ox tại bao nhiêu điểm?

A. 5. B. 4. C. 3. D. 7. Lờigiải

ChọnA

Do hàm số ()yfx = là hàm bậc ba nên hàm số () 2 1 yfx ′ =− phải là hàm bậc bốn. Vì hàm số

này có đồ thị đối xứng qua Oy nên hàm số () 2 1 yfx ′ =− phải là hàm trùng phương.

Đặt () () () 242 10hxfxaxbxca ′ =−=++> . Ta có () 3 42 hxaxbx ′ =+

Do đồ thị ()yx h = có điểm cực trị () 2;1 A và đi qua điểm () 1;1 B nên ta có:

. Suy ra () ()24221623 1 999hxfxxx ′ =−=−+

Ta có () () 2 12 1,0gxfx xx  =−+≠   có () 32222

212211 111gxff xxxxxx

Phương trình hoành độ giao điểm của đồ thị ()ygx ′ = và Ox là: () 2 11 011gxf xx ′′ =⇔−=  

Đặt 1 t x = ta được phương trình ()() () 22 1 1110 tftfxx x ′′ −=  −=∀≠ .

Xét phương trình: ()24242 12162319

1216230 999 fxxxxx xxx ′ −=⇔−+=⇔−−+= .

Ta thấy hàm số () 42 9 21623Fxxx x =−−+ lên tục trên () 0; +∞

Trên () ;0−∞ dễ dàng nhận thấy () 0 Fx = có 2 nghiệm phân biệt ()()453;2,2;1xx∈−−∈−− do

()() () 9 344;2;118 2 FFF−=−=−−=

Từ đó suy ra phương trình: () 2 1 1 fx x ′ −= có 5 nghiệm phân biệt (minh họa đồ thị).

Suy ra phương trình () 0 gx ′ = có 5 nghiệm phân biệt.

Vậy đồ thị hàm số ()ygx ′ = cắt trục Ox tại 5 điểm phân biệt.

Câu43: Có bao nhiêu số nguyên m để tồn tại 2 số phức z thoả mãn 12 zmizmi −+=−+ và 3 || 2 z = A. 5. B. 3. C. 4. D. 6. Lờigiải ChọnA

 −++=−++ 

112 9 4  ⇔ 

()()()() 2222 22

tâm O bán kính 3 2 R =

Có () () 133374190367,1598;;10;;338 1041263324

FFFFF  =−===−=  .

Suy ra () () 134 .0;10;.30 1043 FFFFF  <=<  nên phương trình có 3 nghiệm phân biệt

()()1230;1,1,2;xxx∈=∈+∞ .

()()() ()

2 22

2242301 9 2 4  ⇔ 

mambm ab 

Phương trình () 1 là phương trình đường thẳng, phương trình () 2 là phương trình đường tròn

Để tồn tại số phước z thoả mãn đề bài thì đường thẳng có phương trình () 1 phải cắt đường tròn có phương trình () 2

2 22

Nghĩa là () () ,1 dOR ≤ ()()

m mm ⇔≤ −+− ()() 22 2 121mmm ⇔≤−+−

42562mmm ⇔≤−+ () () 2 2 1220mmm ⇔−+−≤ 1313 m ⇔−−≤≤−+

Vì m ∈ℤ nên {} 2;1;0;1;2 m ∈−−

Câu44: Đường thẳng () 01ymm=<< cắt đường cong 4221yxx=−+ tại hai điểm phân biệt thuộc góc phần tư thứ nhất của hệ tọa độ Oxy và chia thành hai hình phẳng có diện tích 1S , 2S như hình

vẽ. Biết 12SS = . Mệnh đề nào dưới đây đúng?

() () () 2 9 20 3240 16 211641 9 1 11 23 9 a h ab habcb abc h c  =  ′ =  +=     =−⇔++=−⇔=−  ++= =    =  

  .

′′′ =−−=−−

Đặt () , zabiab=+∈ ℝ . Theo giả thiết ta có ()() ()()112 3 2 

ambiabmi abi  

ambabm ab 

 −++=−++

 −+−−=

3 3 2 2242

Câu45: Chotứ diện ABCD có 2 ACBDa == .Gọi , HK lần lượt là hình chiếu vuông góccủa A và

ng thẳng CD . Biết HCCDDK == ; góc giữa AH và BK bằng 60° . Thể tích khối t

Ta có: ()2 23AHBKaaa ==−= (Định lý Pytago).

Dựng hình chữ nhật HKBE , ta có 3 HEBKa == và HEBK ∥

Suy ra ()() ,, AHBKAHHE =

Ta lại có : () HKAH HKAHE HKHE ⊥   ⊥  ⊥  , mà ()HKHKBE ⊂ ()() AHEHKBE  ⊥

Trườnghợp1: 60 AHE =° .Khi đótamgiác AHE đều.Suy rahìnhchiếuvuônggóccủa A

trên () HKBE là trung điểm I của HE suy ra 33 3. 22 AIaa == .

3 1111313 ........3. 3323224ABCDBCD a VAISAIBKCDaaa

(đvtt).

Trường hợp 2: 120 AHE =° .Khi đó 2 11333 ..sin1203.3. 2224 AHE a SAHHEaa=°==

(đvdt) suy ra ()() ()

2 33 2. 23 4 ,, 2 3 AHE

a S dAHEdAHKBEa HE a ==== .

Thể tích khối tứ diện là: () () () () 111 .,..,.. 332ABCDBCD VdAHKBESdAHKBEBKCD ==

3 1313 ...3. 3224 a aaa  ==   (đvtt).

Câu46: Từ 12 học sinh gồm 5 học sinh giỏi, 4 học sinh khá và 3 học sinh trung bình. Giáo viên muốn thành lập 4 nhóm làm 4 bài tập lớn khác nhau, mỗi nhóm 3 học sinh. Xác suất để nhóm nào cũng có học sinh giỏi và học sinh khá bằng

A. 6 385 B. 36 385 C. 3 770 D. 1 6160 Lờigiải ChọnB

Ta có: () 3333 12963 nCCCC Ω=

Gọi A là biến cố từ 12 học sinh lập 4 nhóm khác nhau, mỗi nhóm 3 học sinh và nhóm nào cũng có học sinh giỏi và học sinh khá

A. 2 0; 5 m  ∈  B. 21 ; 52 m  ∈   C. 13 ; 25 m  ∈   D. 3 ;1 5 m  ∈   Lờigiải ChọnA Phương trình hoành độ giao điểm đường cong và đường thẳng () 01ymm=<< : () 22 2 422 22 11 211 11 xmxm xxmxm xmxm −==+ −+=⇔−=⇔⇔  −=−=−  Hoành độ giao điểm thuộc cung phần tư thứ nhất là: 1 1 xm =+ và 2 1 xm =− Ta có () () 1 1 42 42 12 0

 () () () () () 1 1 4242 0 1 1 1 1 4242 42 0 0 1

21d21d021d0

m m

+ + + ⇔−+−=−−+− ⇔−+−+−+−=⇔−+−=   ( ) ( ) 53 53 1 0 2121 0110 5353 m mm xx xmx mmm + ++  ⇔−+−=⇔−++−+=   ( ) ( ) () () ()() () () () 42 2 121 121 10110 5353 1 2 5162 101010; 53

mm mm mmm m mmmm ++ ++ ⇔−+−=⇔−+−+= + ⇔−+−=+≠⇔+=⇔=∈ 

1 21d21d m m m SSxxmxmxxx + =⇔−+−=−+−

21d21d

m m m

xxmxxxmx xxmxxxmxxxmx

9815

A. 3 3 6 a . B. 3 3 3 a . C. 3 3 4 a . D. 3 3 8 a Lờigiải ChọnC

lên đườ

ứ diện ABCD bằng

====  







Ta mô tả ()nA như sau:

Số cách chia 4 học sinh khá cho 4 nhóm có 4! cách.

Số cách chia 5 họcsinhgiỏicho 4 nhómcó 2 5 .4.3! C cách (vì 5 họcsinhgiỏimàchỉ có 4 nhóm nên sẽ có một nhóm có 2 học sinh giỏi. Vì vậy ta chọn 2 học sinh giỏi trong 5 học sinh giỏi và chọn 1 nhóm trong 4 nhóm cho 2 học sinh giỏi vừa chọn. Còn lại 3 học sinh giỏi sắp xếp vào 3 nhóm còn lại).

Bây giờ đã có một nhóm đủ 4 học sinh. Thế thì 3 học sinh trung bình cho vào 3 nhóm còn lại có 3! cách.

Ta có: () 2 5 4!.4.3!3!nAC=×× () () () 36 385 nA PA n  == Ω

Câu47: Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ

Tổng tất cả các giá trị nguyên của tham số m để hàm số ()()()() 2 4 gxffxfxm =−− có 17

điểm cực trị là

()

Bảng biến thiên của hàm số

Vậy số giao điểm của các đường thẳng 2;;2ymymym =−==+ với đồ thị ()ux là 12 điểm phân biệt {} 3260 1581;0;1;...;571652 3260 m mmS m −≤−< ⇔⇔−≤<  ∈−  = −≤+<

Câu48: Có bao nhiêu số nguyên m để tồn tại đúng hai cặp số thực () ; xy thỏa mãn đồng thời các điều kiện: ()() () 71 218.24 +++− +−+++= xyxyxyxy và 21?+++= xyxym

A. 49. B. 48. C. 47. D. Vô số. Lờigiải

ChọnC

Đặt =+ txy , giả thiết đầu tiên trở thành

() () () ()() 718 0 21824218210 8 +−+ =  −++=⇔−++−=⇔  =−

tttt t tttt t

Khi đó ()() 01;82+=+=− xyxy

Tập hợp các điểm () ; xy thỏa mãn () 1 và () 2 lần lượt nằm trên 2 đường thẳng ()() 12:0;:80. +=++=dxydxy

Từ giả thiết () 2 , ta có: () 2121 xyxymxymxy +++=⇔+=−+

⇔+=++−−+ ⇔+−−+−=⇔−+−=+

()()() 22 22 22

21222 22101113 xymxyxyxy xyxymxym

Tập hợp các điểm thỏa mãn (3) là đường tròn tâm () 1;1 I bán kính 1=+Rm

Khi đó yêu cầu bài toán ()() 12 ,,2152149. dIdRdIdmm ⇔<<⇔<+<⇔<<

Vậy có 47 giá trị m thỏa mãn yêu cầu bài toán.

ChọnA Ta

()() ()() () 2 2 2 4 40 4 24 fx x f x fx g xfxm ffxfxm ffxm ′ ′ ′ = −−=

()()

()()() ()()() 2 2 2 2 2 2 2 2 01 24022 4043 41 42424 42 42425 fx fxfx fxfxmfxfxm fxfxmvoly fxfxmfxfxm fxfxm fxfxmfxfxm ′  =  −=⇔=   −−=⇔−=  ⇔ −−=−      −−=−=+ −−=⇔⇔    −−=−−=−      Dễ thấy () 1 có 2 nghiệm đơn (vì có 2 cực trị) và () 2 có 3 nghiệm đơn Vậy tổng số nghiệm đơn của phương trình ()()() 3;4;5 là 12 thì thỏa mãn Đặt ()()()()()

{} {} 2 1;2

;; x uuxfxfxufxfxu xabc ∈−  ′′′ ==−  =−  =⇔  ∈   Các nghiệm trên được sắp thứ tự từ nhỏ đến lớn như sau: 12 abc <−<<<

1652 B. 1653 C. 1654 D. 1651 Lờigiải

có: () ()()() ()() ()

()() ()()() ()()()()()

()

()() ()()

4220

=−

()()

4 ufxfx



Câu49: Cho hàm số () 2 1 xm fx x = + . Gọi S là tập hợp tất cả các giá trị m nguyên của tham số m sao

cho () 0; 2

min7sin0 fx π   

= . Tổng các phần tử của S bằng

A. 10 . B. 3 . C. 15 . D. 6 . Lờigiải

ChọnD

Đặt 7sin tx = . Khi đó: []0;0;7 2 xt π  ∈  ∈   . Yêu cầu bài toán [] () 0;7 min0 ft ⇔=

Ta có: () 2 1 tm ft t = + luôn xác định trên [] 0;7

Với 1 2 m =− thì () 1 ft =  Loại 1 2 m =−

Với 1 2 m ≠− thì ta có: ()() 72 02;7 8 m fmf=−= . Ta xét các trường hợp sau:

Trườnghợp1: ()() 727 0.702.00 82 m ffmm ≤⇔−≤⇔≤≤

Khi đó: [] () 0;7 min0 ft = 7 0 2 m  ≤≤ thỏa yêu cầu bài toán {} 0;1;2;3 m m ∈ →∈ ℤ

Ta có 12 53ABRR=>+= . Gọi ; PQ lần lượt là tâm vị tự trong và ngoài của

( ) ( ) 12 ; SS . Qua P và Q vẽ các tiếp tuyến EF và HK .

Suy ra minmax =EF; MNMNHK = .

===



PAPE R PEPA EF PFPBR PBPF

Ta có 1 2 

Trườnghợp2: ()() 7 72 0.702.0 2 8 0

m m ffm m

 >  >⇔−>⇔  < 

Khi đó: [] () 0;7 min0 ft >  Không có giá trị m thỏa đề bài.

Do đó: {} 0;1;2;3 S = . Vậy tổng các phần tử của S bằng 6 .

Câu50: Trong không gian Oxyz . Cho 2 điểm ()() 1;0;1;1;3;5AB xét đường thẳng d thay đổi cách A

một khoảng bằng 2 ; cách B một khoảng bằng 1. Gọi ; MN là hình chiếu vuông góc của ; AB

lên d tích giá trị lớn nhất và giá trị nhỏ nhất của MN là:

A. 26 B. 85 C. 45 D. 86

Lờigiải

ChọnD

Gọi 1S mặt cầu tâm A bán kính bằng 1 2 R = .

Gọi 2S mặt cầu tâm B bán kính bằng 2 1 R = .

ặ

ầu

t c

Ta có 1 2  == 

108 33 24. 54 33 =  == 

2 25. 2 QAQB R QHQA QBAB QHQK QKQBR =  ===  ==  =

Ta có: 2222 1 1024626QHQARHK =−=−=  = . Do đó .86EFHK =

Lờigiải

BỘ

ĐỀ THỰCCHIẾN2023 KỲ THITỐTNGHIỆPTHPTQUỐCGIANĂM2023

ĐỀ SỐ 16

Bàithimôn:TOÁN

(Đề gồmcó06trang) Thờigianlàmbài:90phút,khôngkể thờigianphát đề

Họ vàtênthísinh:………………………………………………

Số báodanh:

Câu1: Một hình nón có chiều cao và bán kính đáy cùng bằng 2 thì diện tích xung quanh bằng

A. 42π B. 82π C. 8π D. 4π

Lờigiải

ChọnA

Ta có : 22222222.2.2242 xq lRhSRlπππ =+=+=  ===

Câu2: Mệnh đề nào dưới đây sai?

A. sindcosxxxC =+  . B. 2 1 dcot sin xxC x =−+  .

C. 2 1 dtan cos xxC x =+  D. cosdsinxxxC =+ 

Lờigiải

ChọnA

Áp dụng công thức nguyên hàm: sindcosxxxC =−+ 

Câu3: Tập xác định của hàm số ( ) ( ) 3 1 fxx=− là

A. ( ) 1; +∞ B. [ ) 1; +∞ C. ( ) { };\1−∞+∞ D. ( );1 −∞

Lờigiải

ChọnB

Điểm biểu diễn cho số phức 12 zi =−+ trên mặt phẳng tọa độ Oxy là () 1;2 N

Câu7: Cho hàm số ()fx có bảng biến thiên như sau:

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. () ;0−∞ . B. () 2;0 . C. () 2;2 . D. () 0;2 . Lờigiải

ChọnD

Từ bảng biến thiên của hàm số ()fx ta có hàm số nghịch biến trên các khoảng () ;2−∞− và () 0;2

Câu8: Trong không gian Oxyz , mặt cầu () 222 :8106250 Sxyzxyz++−+−+= có bán kính bằng

A. 75 . B. 25 . C. 5 . D. 75 .

Lờigiải

ChọnC

Vì 3 α =− là số nguyên âm nên điều kiện 101xx−≠⇔≠ . Suy ra tập xác định của hàm số ( ) ( ) 3 1 fxx=− là ( ) { };\1 D =−∞+∞

Câu4: Thể tích khối chóp có chiều cao bằng 3a và diện tích đáy bằng 2 2a là

A. 3 a B. 3 3a C. 3 6a D. 3 2a

Lờigiải

ChọnD

Thể tích khối chóp cần tìm là: 23 1 .2.32 3 Vaaa == .

Câu5: Cho cấp số nhân ( ) n u với 1 4

ChọnC

Viết lại ()()()() 222 :45325Sxyz−+++−= . Vậy bán kính của mặt cầu bằng 5

Câu9: Với a là một số thực tùy ý, khi đó () 2 2 log8a+ bằng

A. 36 a + . B. 2 a + . C. 1 2 a + . D. 1 36 a + . Lờigiải

ChọnA

Ta có () () () 32 2 22 log8log23236 a a aa + +  ==+=+  .

Câu10: Đường tiệm cận ngang của đồ thị hàm số () 2 1 fx x = là

A. 0 y = . B. 2 y = . C. 2 y =− . D. 1 x = . Lờigiải

ChọnA

=−   =  . Công bội của cấp số nhân đã cho bằng

3 24 u u

A. 2 B. 22 C. 2 D. 22 Lờigiải

ChọnA

Theo công thức số hạng tổng quát của cấp số nhân, ta có: 33 41.3.242uuqqq =  −=  =− .

Câu6: Trong mặt phẳng Oxy , điểm nào dưới đây là điểm biểu diễn số phức 12 zi =−+ ?

A. ( )1;2 M . B. ( )1;2 N . C. ( )1;2 P . D. ( )1;2 Q .

Ta có: 2 limlim0 1 xx y x →+∞→+∞ == , 2 limlim0 1 xx y x →−∞→−∞ ==

Vậy đường thẳng 0 y = là đường tiệm cận ngang của đồ thị hàm số

Câu11: Cho hàm số ()fx có bảng biến thiên như sau:

ChọnD

Ta có: 22.2.312 Vrhπππ===

xt dyt zt

Số nghiệm của phương trình () 320 fx −+= là

A. 2 . B. 0 . C. 3 . D. 1.

Lờigiải

ChọnC

Ta có: ()() 2 320 3 fxfx −+=⇔= .

Khi đó số giao điểm của đường thẳng

2 3 y = () Ox với đồ thị hàm số ()yfx = chính là số nghiệm phân biệt của phương trình () 320 fx −+= .

Ta có 2 01 3 << . Quan sát vào bảng biến thiên, ta thấy đường thẳng 2 3 y = cắt đồ thị hàm số

()yfx = tại 3 điểm phân biệt nên phương trình () 320 fx −+= có ba nghiệm phân biệt.

Câu12: Cho hàm số ()fx có bảng biến thiên như sau:

Giá trị cực tiểu của hàm số đã cho bằng

A. 2 B. 3 C. 0 D. 4

Lờigiải

ChọnD

Từ bảng biến thiên ta thấy hàm số có giá trị cực tiểu là 4 CTy =− .

Câu13: Nghiệm của phương trình () 2 log110 x −+= là

A. 2 x = B. 3 x = C. 3 2 x = D. 5 2 x =

Lờigiải

ChọnC

Điều kiện: 1 x > . Ta có: ()() 22 13 log110log111 22 xxxx −+=⇔−=−⇔−=⇔= (tm).

Vậy phương trình có nghiệm là 3 2 x =

Câu14: Cho khối trụ có bán kính đáy 2 r = , chiều cao 3 h = . Thể tích khối trụ đã cho bằng

A. 6π B. 16π C. 4π D. 12π

Lờigiải

Câu16: Cho () 3 0

ng 1 :23 5

xt dyt zt

=−   =+   =−  có một vectơ chỉ phương là () 1;3;1 u =−− .

5 d 3 fxx =  ; () 4 0

3 d 5 fxx =  .Tích phân () 4 3 d fxx  bằng

A. 16 15 B. 14 15 C. 17 15 D. 8 15 Lờigiải

ChọnA

Ta có: ()()()() 3444 0303

ChọnD

 .



16 dddd 15 fxxfxxfxxfxx +=

A. 3i . B. 2 . C. 2i . D. 3 . Lờigiải

Ta có ()() 21.12.243 =+−=+ zziii . Vậy phần ảo của số phức 21zz bằng 3 .

Câu18: Từ một nhóm học sinh gồm 6 nam và 4 nữ, có bao nhiêu cách chọn ra hai học sinh gồm 1 nam và 1 nữ

A. 2 10C B. 11 64 + CC C. 2 10A D. 11 64CC

Lờigiải

ChọnD

Theo quy tắc nhân, số cách chọn ra hai học sinh gồm 1 nam (từ 6 học sinh nam) và 1 nữ (từ 4 học sinh nữ) là 11 64CC .

Câu19: Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. 42 2 yxx =−+ B. 42 2 yxx =− C. 32 3 yxx =− D. 32 3 yxx =−+

Lờigiải

ChọnA

Câu15: Trong không gian Oxyz đường thẳng 1 :23 5 =−   =+   =−  . Một vectơ chỉ phương của d là A. () 1;3;1 u =− . B. () 1;3;1 u = . C. () 1;3;1 u =−− . D. () 1;2;5 u = . Lờigiải ChọnC Đường thẳ

=−

Câu17: Cho hai số phức 1 2 =− zi và 2 12=+ zi . Khi đó phần ảo của số phức 21 . zz bằng

Từ hình vẽ ta thấy:

Nhánh bên phải của đồ thị đi xuống nên hệ số 0 a < . Do đó ta loại phương án C và B.

Đồ thị hàm số có 3 điểm cực trị nên ta chọn phương án A là đáp án.

Thật vậy, phương án A có hàm số là hàm bậc bốn trùng phương có 1 a =− , 2 b = nên 0 ab <

Suy ra hàm số có 3 điểm cực trị.

Câu20: Cho hai số phức 1 12 zi =+ , 2 1 zi =− . Số phức 1 2

z z là

A. 13 22 i −+ B. 13 22 i C. 13i −+ D. 31 22 i

Lờigiải

ChọnA

Ta có: ( )( ) ()() 1 2

121 121313 111222 ii zii i ziii ++ +−+ ====−+ −−+

Câu21: Trong không gian Oxyz cho các véctơ ( )1;0;3 a = , ( )2;2;5 b =− . Tọa độ véctơ ab là

A. ( )1;2;8 B. ( )3;2;2 C. ( )3;2;2 D. ( )2;0;15

Lờigiải

ChọnB

Ta có: ( ) ( )12;02;353;2;2 ab−=+−−=−−

Câu22: Trong không gian Oxyz cho mặt phẳng ( ) :230Pxyz−+−= . Véctơ nào dưới đây là một véctơ pháp tuyến của mặt phẳng ( )P ?

A. ( )2;1;1 B. ( )3;1;1 C. ( )2;1;1 D. ( )2;1;1

Lờigiải

ChọnC

Ta thấy một véc tơ pháp tuyến của mặt phẳng ( )P là ( )'2;1;1 n hay ( )2;1;1 n là một véc tơ

pháp tuyến của mặt phẳng ( )P .

x x sincos ππ

≥

Lờigiải ChọnC

Điều kiện 0 x ≠ ( )1

có 3 1 52510 sincoscos

ππππ  =−=<   nên 44 2

02 2 x x <≤  ⇔  ≤−  thoã mãn ( )1 . Vậy trên đoạn [ ]99;100 có 100 số thỏa mãn bài toán.

A. 045

B. 0



⊥

Ta có 0 3 145 3 SAa tan AB a αα ===  =

Câu25: Cho hàm số ()fx xác định trên {}\1 ℝ và có bảng xét dấu ()' fx như sau

Số điểm cực trị của hàm số đã cho là

A. 4. B. 1. C. 2. D. 3. Lờigiải

ChọnC

Hàm số ()fx xác định trên {}\1 ℝ nên hàm số không có cực trị tại 1. x =

Dựa vào bảng xét dấu ()' fx ta thấy hàm số đạt cực trị tại 1, x =− 0. x =

Vậy số điểm cực trị của hàm số đã cho là 2.

Câu26: Tính nguyên hàm 2 xxdx +  bằng cách đặt 2 tx=+ ta thu được nguyên hàm nào dưới đây?

A. () 2 2.ttdt  B. () 2 22. ttdt  C. ()22 22. ttdt  D. 2 2. tdt 

Lờigiải

ChọnC



Câu27: Cho số phức () , zabiab=+∈ ℝ thỏa mãn ()11 abii +−=−+ . Giá trị của ab bằng

A. 0. B. 1. C. 2. D. 2. Lờigiải

ChọnC

Ta có () 11 11.2. 112 aa abiiab bb =−=− +−=−+⇔⇔  =−  −==

Câu28: Gọi 12 , zz là hai nghiệm phức của phương trình 2 220zz−+= , trong đó 1z có phần ảo âm. Số phức 12 2 zz + bằng

A. 3 i + B. 3 i C. 2 D. 2 i + Lờigiải

ChọnA

Ta có 2 1 220 1 zi zz zi =−  −+=⇔  =+ 

Do 1z có phần ảo âm nên 1 1 zi =− và 2 1 zi =+ .

Vậy: () 1221213. zziii +=−++=+

060 L



Câu23: Số nghiệm nguyên thuộc đoạn [ ]99;100 của bất phương trình 4 3 510   là

A. 5 . B. 101. C. 100 . D. 4 .

51055 x

sincossinsinxx xxx ππππ

3444 00

x xx x

≥⇔≥⇔≤⇔−≤⇔≤



C. 0

ờigiải

Câu24: Cho hình chóp . SABC có đáy là tam giác vuông tại B , 3 ABa = . Cạnh bên 3 SAa = vuông góc với đáy. Góc giữa hai mặt phẳng ( )SBC và ( )ABC bằng

ChọnA



Ta có () () SAABCSABC BCSAB ABBC  ⊥  ⊥  ⊥

Mà ()() SBCABCBC ∩= nên ()() () , SBCABCSBA α ==

Đặt 2 222 txtxtdtdx =+  =+⇔= ()22 222. xxdxttdt  +=−

Câu29: Một hình nón và một hình trụ có cùng chiều cao h và bán kính r đồng thời diện tích xung quanh

của chúng bằng nhau. Tỉ số h r bằng

A. 3 3 . B. 3 . C. 1 2 . D. 2 .

Lờigiải

ChọnA

Ta có ππ =⇔=⇔=+⇔=⇔= 22 3 223. 3 xqtruxqnon h SSrhrlhrhrh r

Câu30: Giá trị nhỏ nhất của hàm số () 3 2 x fx x = + trên đoạn 0;4   bằng

A. ( )0 f . B. ( )4 f . C. ( )2 f . D. ( )3 f .

Lờigiải

ChọnA

Ta có: () ()2 5 '0 2 fx x => + , 0;4 x ∀∈   nên hàm số đồng biến trên   0;4

Do đó ( ) ( ) 0;4 min0 x fxf ∈  =

Câu31: Cho 0 a > , 0 b > và 1 ab ≠ thỏa mãn 3ln7ln0 ab+= , khi đó 3 log ab ba bằng

A. 3 . B. 3 . C. 1 3 . D. 1 3 .

Lờigiải

ChọnC

Gọi h là chiều cao mực nước trong ly nước hình trụ

Thể tích phần nước trong ly: 2 1 .4.16 Vhh ππ==

Thể tích viên bi đá hình cầu: 3 2 4 3 VR π = .

Vì khi thả viên bi đá vào ly nước thì mực nước trong cốc tăng lên 9 32 cm nêntacóphươngtrình:

2 3 12 9943 .4.1616 323232 hVVhhRRππππ

 +=+⇔+=+⇔=   ( cm ).

Câu34: Trong không gian Oxyz , mặt phẳng đi qua điểm ( )1;1;1 M và vuông góc với đường thẳng

121 : 221 xyz ∆==+−− có phương trình là

A. +++= 2230 xyz . B. −−=20xyz . C. ++−= 2230 xyz . D. −−−=220xyz . Lờigiải

ChọnC

Domặtphẳngvuônggócvới đườngthẳngnênVTPTmặtphẳngcầntìmcùngphươngvớiVTCP

của đường thẳng ∆ . Suy ra ( )2;2;1 Pn =

Vậy phương trình mặt phẳng cần tìm: ( ) ( ) ( ) 2121102230 xyzxyz −+−++=⇔++−= .

Câu35: Cho khối lăng trụ đứng .'''ABCABC có đáy ABC là tam giác vuông tại ,,'2 AABACaAAa === . Thề tích của khối lăng trụ đã cho bằng

ChọnD

Ta có:

373 3 77 3

11 3ln7ln01ababaab b b +=⇔=⇔=⇔== .

Khi đó 2 7

72 3 99 321 loglog.log.log293 b ab b bb babbbb ===−=− .

Câu32: Số giao điểm của hai đường cong 4 2 yx=− và 2 3 yx = là

A. 3 B. 4 . C. 2 D. 0 Lờigiải

ChọnC

Phương trình hoành độ giao điểm:

ChọnD

Thể tích của khối lăng trụ: ABC VSAA ∆ ′ =

Câu36: Trong không gian ,Oxyz cho bốn điểm ( )1;0;0 M , ( )0;2;0 N , ( )0;0;3 P , ( )1;1;2 Q . Đường thẳng d đi qua Q và vuông góc với mặt phẳng ( )MNP đi qua điểm nào dưới đây?

A. ( )5;4;4 B. ( )6;3;2 C. ( )5;2;4 D. ( )7;2;6 Lờigiải

2 4242

x xxxxx xvn

 + =  +  −=⇔−−=⇔⇔=±  =  

317 317 2 23320 2 317 ()

ChọnA

Vậy số giao điểm của hai đườngcong 4 2 yx=− và 2 3 yx = là2.

Câu33: Thả một viên bi đá hình cầu vào một ly nước hình trụ cóbán kính đáy bằng 4cm , người ta thấy

mực nước trong cốc tăng lên 9 32 cm . Bán kính viên bi đá bằng

A. 3 2 cm . B. 3cm . C. 3 2 cm . D. 2cm .

Mặt phẳng ( )MNP có phương trình: 1 123 xyz++= 63260 xyz ⇔−+−= . Suy ra mặt phẳng ( )MNP nhận vectơ ( )6;3;2 n =− là một vectơ pháp tuyến.

Đường thẳng d đi qua ( )1;1;2 Q và vuông góc với mặt phẳng ( )MNP nên đường thẳng d đi qua ( )1;1;2 Q và nhận vectơ ( )6;3;2 n =− là một vectơ chỉ phương.

xt ytt zt

=+   =−∈   =−+  ℝ

16 13,. 22

Suy ra đường thẳng d có phương trình tham số: ()

ờigiải

A. 3 2 6 a B. 3 2a C. 3 2 3 a D. 3 2 2 a Lờigiả

3 2

aa =

a =

Xét từng phương án

Thay tọa độ điểm ( )5;4;4 vào phương trình đường thẳng d ta có

Suy ra điểm ( )5;4;4 thuộc đường thẳng d hay đường thẳng d đi qua điểm ( )5;4;4 .

Lần lượt thay tọa độ các điểm ( )6;3;2 , ( )5;2;4 , ( )7;2;6 vào phương trình đường thẳng d ta đều được hệ vô nghiệm, tức là đường thẳng d không đi qua các điểm này.

Câu37: Chọn ngẫu nhiên một số gồm 3 chữ số, xác suất để chọn được số gồm toàn chữ số lẻ và các chữ

số tăng dần từ trái qua phải bằng

A. 1 45 B. 1 72 C. 1 90 D. 1 36

Lờigiải

ChọnC

Có 9.10.10900 = số có 3 chữ số. Vậy chọn ngẫu nhiên một số có 3 chữ số có 1 900 900 C = cách.

Chọn 3 chữ số lẻ trong 5 chữ số lẻ có 3 5 10 C = cách và với mỗi cách chọn 3 chữ số lẻ trên ta lập

được duy nhất một số thỏa mãn điều kiện các chữ số tăng dần từ trái qua phải. Vậy có tất cả

10.110 = số có 3 chữ số lẻ và các chữ số tăng dần từ trái qua phải.

Suy ra xác suất cần tìm bằng: 101 90090 = .

Câu38: Giả sử A , B là hai điểm phân biệt trên đồ thị hàm số 3x12 y = sao cho A là trung điểm của đoạn thẳng OB . Khi đó đoạn thẳng AB có độ dài bằng

1ln1 .dln.dln.'dlnln aaa a xxxxa

1 111

 ∫∫∫

A. 2 a B. 2 2 a C. 217 17 a D. 2 3 a Lờigiải ChọnC

Gọi N là trung điểm của AB và// 2 a ANMNAC  = .Mặt khác ACABMNAB ⊥  ⊥

Gọi H là hình chiếu vuông góc của A lên cạnh () 1 SNAHSN  ⊥

Ta có (),2MNANMNSAMNAH ⊥⊥  ⊥ . Từ (1) và (2) suy ra

() ()(), AHSMNdASMNAH ⊥  = Khi đó:

a a SAANa dACSMdACSMNdASMNAH SAAN a a

ChọnD

====== +

,,,17

2 2.

Câu41: Chohàmsố ()yfx = có đạohàm () 2 23fxxx ′ =−−+ với x ∀∈ ℝ .Số giátrị nguyêncủa thamsố m thuộc [] 10;10 để hàmsố () ()22 sin3sin2gxfxxmm =+−++ đồng biến trên 25 ; 36    ππ là

Ta có: () ()22 sin3sin2gxfxxmm =+−++

()() () () () 2 2 2sin.cos3cossin3sincos2sin3sin3sin gxxxxfxxmxxfxxm ′′ ′ =++−=++−

()gx đồng biến trên 25 ; 36    ππ () 25 0,; 36 gxx  ′ ⇔≥∀∈   ππ

516 413 422 t t t −=+  =−  −=−+ 1 t ⇔=−

ChọnD Gọi ( ) 1 31 1;2 x Ax

( ) 2 31 2 ;2 x Bx A

điểm của đoạn thẳng OB 2 1 2 1 3x1 3x1 22 2 2 22 OB A OB A xxx xx yy y  +   ===    ⇒   +  ===     21 1 21 3161 31 2 22 2 22 xx x xx  =     ⇔   ==     11 21 63 2 11 220 42 xx xx  =    ⇔   −=    1 1 21 3 3 2 20() 22 x x xx VN  =     ⇔ =     =   1 2 1 3 2 3 x x    =    ⇔    =     . Suy ra: 1 ;1 3 A         và 2 ;2 3 B         . Vậy 10 3 AB = . Câu39: Với mọi số thực 0 a > thì 1 1ln .d a x xx ex x + ∫ bằng A. a ee . B. ln a ea . C. a ee . D. ln a ea . Lờigiải ChọnB

4 3 . B. 23 3

C. 210 3 . D. 10 3 .

ờigiải

;

là trung

()()

xx 

Ta có: 

exxexxexexea

 =+===    

Câu40: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại A, ABa = , SA vuông góc với mặt phẳng đáy và 2 SAa = . Gọi M là trung điểm của BC . Khoảng cách giữa hai đường thẳng AC và SM bằng

4 2

()() () () () 222  +  

.217

A. 5 B. 6 C. 14 D. 15 Lờigiải

2536

Từ ()()() 1,2,3 suy ra () 1 1 x fx x + = , nên () 2 2 2 1 1 x fx x + =

Phương trình hoành độ giao điểm của 2 đồ thị hàm số () 2yfx = và 1 ymx=+ :

2 22 2 1 1111 1 x mxxmxx x + =+⇔+=+− , do 1 x =± không phải nghiệm.

() ()()

() 2 20xmxxm ⇔+−= () 2

=  ⇔  =+−= 

0 20 x gxmxxm

Để 2 đồ thị cắt nhau tại 2 điểm phân biệt , MN có hoành độ khác 0 thì phương trình () 0 gx =

có 2 nghiệm phân biệt khác 0 () 0 00 g

′ ∆>  ⇔  ≠  

2 10 0 0 m m m  +> ⇔⇔≠  −≠

Gọi 12 , xx là nghiệm phương trình () 0 gx = , khi đó tọa độ , MN :

()() 1122 ;1,;1MxmxNxmx++

Gọi I là trung điểm MN thì I có tung độ:

có ()

+ = ()

363 max 4 ux

() ()012 11 2 22 MN yyymxmx =+=++ 12 20 2 m m

Vậy trung điểm I của MN luôn nằm trên trục hoành với mọi tham số 0 m ≠ .

Vậy có vô số giá trị nguyên của tham số m thỏa yêu cầu bài toán.

Kết hợp với m ∈ ℤ và thuộc [] 10;10 ta được {} 10,9,...,0,7,...,10 m ∈−− . Vậy có 15 số nguyên m thỏa mãn bài toán.

Câu42: Cho hàm số () axb yfx cxd + == + có bảng biến thiên như hình vẽ

Câu43: Có bao nhiêu số nguyên m để tập nghiệm của bất phương trình () 33 log33logxmx +> chứa đúng 2 số nguyên? A. 18 B. 15 C. 17 D. 16 Lờigiải ChọnD

Ta có: () 33 log33logxmx +> 3

0 3 x xmx >  ⇔  +>  3

0 30 x xxm >  ⇔  −−< 

Xét hàm số () 3 3 yfxxxm ==−− trên () 0; +∞

Có () 2 1 330 1 x fxx x =−  ′ =−=⇔  = 

Bảng biến thiên:

Biết ()01 f = , có bao nhiêu giá trị nguyên của tham số m để đường thẳng 1 ymx=+ cắt đồ thị hàm số () 2yfx = tại 2 điểm phân biệt , MN có hoành độ khác 0 sao cho trung điểm của MN nằm trên trục hoành.

A. 7 . B. 8 . C. 13 . D. Vô số.

Lờigiải

ChọnD

Đồ thị hàm số ()yfx = có tiệm cận ngang: ()111 a yac c =−  =−  =−

Đồ thị hàm số ()yfx = có tiệm cận đứng: ()112 d xdc c =  −=  =−

Ta có: () ()0113 b fbd d =  =  =

Dựa vào bảng biến thiên, tập nghiệm của bất phương trình () 33 log33logxmx +> chứa đúng 2 số nguyên chỉ xảy ra khi tập nghiệm của bất phương trình có dạng () 0; a và 23 a <≤ hay () () 20 30 f f <    ≥   202 218 18018 mm m mm −<> ⇔⇔⇔<≤ −≥≤

xxfxxmx  ′ ⇔++−≥∀∈   ππ ()

fxxmx  ′ ⇔+−≤∀∈   ππ Theo giả thiết: () 2 1 230 3 x fxxx x ≥  ′ =−−+≤⇔  ≤−  , ta có: () 2 2 2 25sin3sin1,;

sin3sin0,;

36 xxmx fxxmx xxmx   +−≥∀∈      ′ +−≤∀∈⇔     +−≤−∀∈     ππ ππ ππ 2

sin3sin1,;

  +≥+∀∈     ⇔   +≤−∀∈     ππ ππ .(1) Xét hàm số () 2 sin3sin uxxx =+ trên 25 ; 36    ππ , ta

ππ   

   = ππ

3631563



−≥≥  ⇔⇔ +≤≤ 

() () 2 25 cos2sin3sin3sin0,; 36

2 25 sin3sin0,; 36

3625 sin3sin3,;

2 25

36 25sin3sin3,; 36 xxmx xxmx

;

7 min

, do đó (1)

3 44 73 1 44 mm mm

 

   

=−+=

Vậy có 16 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Câu44: Ông A có một cái cổng hình chữ nhật, lối vào cổng có dạng parabol có kích thước như hình vẽ

Ông A cần trang trí bề mặt (phần gạch chéo) của cổng. Ông A cần bao nhiêu tiền để trang trí,

biết giá thành trang trí là 1.200.000 đồng 2 /1m ?

A. 20 triệu đồng. B. 10 triệu đồng. C. 8 triệu đồng. D. 16 triệu đồng.

Lờigiải

ChọnD

Chọn hệ trục tọa độ như hình vẽ, khi đó () P có phương trình dạng: 2 yaxb =+ .

Khi đó: ()() 5 ;0;0;5 2 P  ∈   nên ta có hệ phương trình:

Khi đó diện tích phần cổng () P là:

Suy ra diện tích phần cần trang trí là: 2 5040

Vậy số tiền cần dùng để trang trí là: 40 1200000.16000000 3 == T (đồng).

Câu45: Xét các số thực không âm x và y thoả mãn () 2 2log16 xyxy+++≥ . Giá trị nhỏ nhất của biểu

thức 22428 Pxyxy =+++ bằng

A. 20 . B. 9 . C. 15 . D. 16 . Lờigiải

ChọnC

Cách1:

Có: ()()() 2 2 2log1621log128 xyxyxyyxy +++≥⇔+++++−≥ 

Nếu 14 xy++< thì () 2 log120 xy++−< do đó ()() 2 21log128 xyyxy +++++−< 

Nếu 14 xy++≥ thì () 2 log120 xy++−≥ do đó ()() 2 21log128 xyyxy +++++−≥  .

Vậy () 2 2114 log6 +++≥⇔++≥ xxyyxy

Bài toán trở thành tìm giá trị nhỏ nhất của P , với điều kiện 14++≥xy .

Ta có 1414 ++≥⇔+≥− xyxy . Xét hai trường hợp:

Nếu 0,4≥≥xy , suy ra 2 4.48.496≥+= P .

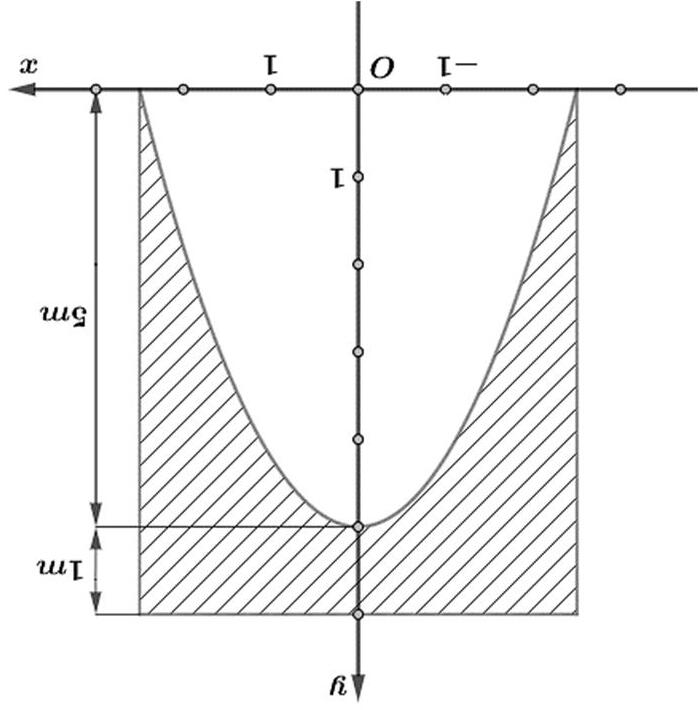
Nếu 0,4≥≤xy , ta có 22142158 +≥−⇔+≥−+ xyxxyy .

Suy ra () 2 2 22 15 248488 =≥++++++ Pyyxxyyyy 2 51515 + ⇔≥≥ y P

Vậy giá trị nhỏ nhất của P bằng 15 khi 3,0==xy .

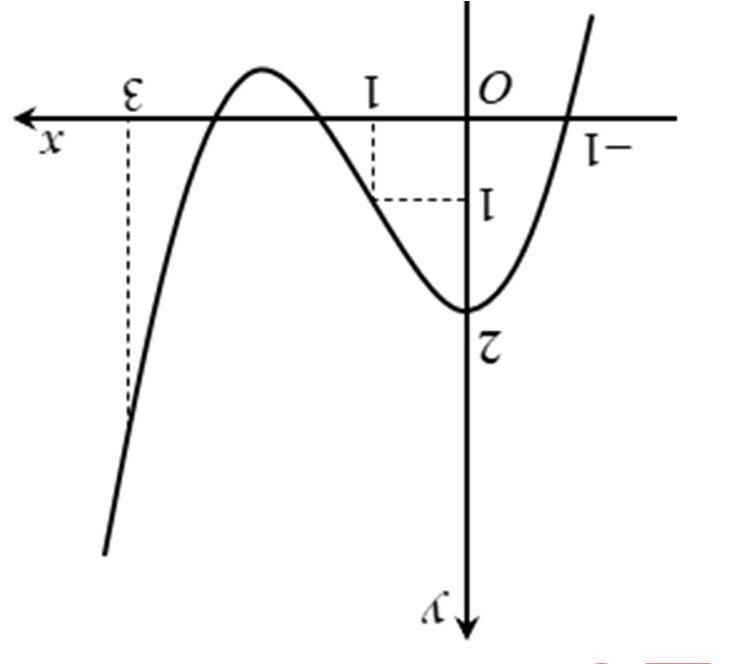
Cách2:

Đặt 2 yY = ()()() 2 2 2log1621log128 xyxyxyyxy +++≥⇔+++++−≥ 

Nếu 14 xy++< thì () 2 log120 xy++−< do đó ()() 2 21log128 xyyxy +++++−< 

Nếu 14 xy++≥ thì () 2 log120 xy++−≥ do đó ()() 2 21log128 xyyxy +++++−≥ 

Vậy 14260xyxY ++≥⇔+−≥

2222428240 PxyxyxYxYP =+++⇔+++−=

Y 1 F

+−≥   có nghiệm không âm, thì đường tròn (*) có tâm (1;2) I bán kính 25 RIF≥= 52515⇔+≥⇔≥ PP . Vậy min 15 = P

Để hệ 22 2 2 40(* 60 ) Y xY xYxP +++  −=

Câu46: Cho hàm số ()fx liên tục trên ℝ và có đồ thị như hình vẽ bên:

Số nghiệm thuộc đoạn [] ;3 ππ của phương trình () 2 1 2cos21 2sin fx x −+= là

A. 24 . B. 12 . C. 16 . D. 18 . Lờigiải

2 5 0. 2 5   =+      = 

b 4 5 5

b  =  ⇔   = 

2 4

=−+

hay ()

Pyx

5 2 2 1 5 2

53  =−+=    Sxdx

450 5

5.6 33 S =−= .

ChọnA Đặt [] 2cos211;3, txx =−+∈−∀ x O I

Ta có: () 2 11222 2sin1cos222cos22cos2111 xxxxt ==== −−−+++

Phương trình trở thành: () () 2 * 1 ft t = + , (với 1 t ≠− ). Kết hợp với [] 1;3 t ∈− ta xét nghiệm của

ương trình () * trên nửa khoảng ( ]1;3

Đồ thị hàm số 2 1 y x = + có tiệm cận ngang 0 y = , tiệm cần đứng 1 x =− và đi qua các điểm đặc

biệt ()() 1 0;2,1;1,3; 2    . Xét sự tương giao trên cùng một hệ trục tọa độ:

Đặt 0 ABx=> suy ra ABBCBBx ′ ===

Trong mặt phẳng () BBCB ′′ hạ BHBC ′ ⊥ . Suy ra ()BHABC ′ ⊥

Ta có: () ()'//,, BBCCCCABBBABBBA ′′′′′′  == ( do BBA ′ nhọn)

Dựa vào đồ thị, trên ( ]1;3 thì đồ thị hàm số 2 1 y x = + cắt đồ thị hàm số ()yfx = tại ba điểm

phân biệt có hoành độ ()0,1,1;3xxxa===∈

Bảng biến thiên của hàm số: 2cos21tx=−+ trên đoạn [] ;3 ππ

Dựavàobảngbiếnthiên:

Với 0 t = , phương trình có 8 nghiệm phân biệt.

Với 1 t = , phương trình có 8 nghiệm phân biệt.

Với () 1;3 ta=∈ , phương trình có 8 nghiệm phân biệt.

Vậy phương trình đã cho có tất cả 24 nghiệm thuộc đoạn [] ;3 ππ

Câu47: Cho khối lăng trụ ABCABC′′′ có đáy là tam giác đều. Mặt bên BBCC ′′ là hình thoi có BBC ′

nhọn và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách và góc giữa hai đường thẳng

′ và AB′ lần lượt bằng 435 ; 7 α với 7 cos 4 α = . Thể tích khối lăng trụ đã cho bằng

A. 123 . B. 125 . C. 36 . D. 96 .

Lờigiải

ChọnB

′′′′ +−+− ′ ′′ ===⇔== ′′′

Xét ABB′ ∆ có: 222222 7 cos 2.cos 2.222 BBABABxABxABx BBA ABxBBA BBABxABx

Xét ABH∆ có 222 22 2cos60 AHABBHABBHxBHxBH ° =+−⋅⋅=+−⋅

Xét AHB′ ∆ có () 22222 2 222 7 4 ABBHAHBHABAHxBHxBH x ′′′′ =+−+⇔−=⋅ =−

Xét BBH ′ ∆ có 2222222 2 BHBBBHxBHHxBBH ′ −⇔ −== ′′ =− () 2 22 2 22 2 7 44 xx BHxBHxBH xBHxBH ⇔=−+=+− +−⋅ 4 x BH ⇔= Suy ra 15 4 x BH ′ = . Khi đó 3 35 16 ABCABCABC x VBHSV ′ =⋅== .

.'.'.

()()

3 1111 135 ..,.sin, 236 316 2 23 BACCBACCAABCABC x VABCCd V A VVBCCABCC′′′′′′ ′′′′′ =⇔ = = ′ = 23 174353135 ..4 6274316 xx x ⇔=⇔=

Vậy 125 ABCABC V = .

Câu48: Trong không gian Oxyz , cho mặt phẳng () :210 −++=Pxyz , và hai điểm () 2;1;0 A , () 33;0;1 B . Điểm M di động trên () P , giá trị nhỏ nhất của biểu thức 7 =−+ TMAMB bằng

A. 378 B. 153 C. 376 D. 373 Lờigiải

ChọnD

Ta thấy , AB nằm cùng phía so với mặt phẳng () P

Gọi , HK lần lượt là hình chiếu vuông góc của , AB lên () P

Mặt phẳng () P có VTPT là () 2;1;1 n =−

Đường thẳng AH đi qua A và nhận n làm VTCP nên 21 : 211 xyz AH −+ ==

Do ()()0;0;16 =∩   = HAHPHAH

Đường thẳng BK đi qua B và nhận n làm VTCP nên 331 : 211 xyz BK −+ ==

Do () ()3;3;3132KBKPKBK =∩   = và 3 HK =

Đặt 0 =>MKx . Khi đó 3 ≤+=+ MHMKHKx

Ta có 2276718 =−+=−+++ TMAMBMHMK ()2 222 63718718615 Txxxxx  ≥−++++=+−++

Xét hàm () 22 718615fxxxx =+−++ trên () 0; +∞ ; () 22

73 18615 xx fx xxx + ′ =− +++

()()() 32 1 02142672270 2 fxxxxxx ′ =⇔−+++=⇔= .

Bảng biến thiên

Gọi OACBD =∩ ; I là trung điểm AE .

Dễ dàng chứng minh được: ()()()() ;;; AKSCDAHSBCSCAKHSCAKE ⊥⊥⊥⊥

()() AKHAKE  ≡  ,,, AKEH cùng thuộc 1 mặt phẳng.

Ta có: ()() ; AKKEAHHE AKSCDAHSBC AKKCAHHC ⊥⊥ ⊥  ⊥ 

0180 AKEAHE  +=  Tứ giác AKEH nội tiếp đường tròn đường kính AE , có tâm I là trung điểm AE .

Ta có: 090 AKCAECAHC=== 2 AC KOEOHO  === .

()OIHKE  ⊥  Khối nón cần tìm có đỉnh là O , đường cao là OI , bán kính đáy

RAI==

2 AE

Ta có: 2222 2222 .2.2 2; 22 SAACaa ACaAEa SAACaa ==== ++ 2 a R  = . 2 2 2 222 2 2222 ACaaa

Thể tích của khối nón cần tìm là: 2 3 2 11 ... 332224 aaa VRh π ππ  ===  

Câu50: Cho ()fx là hàm đa thức và cho hàm đa thức bậc ba ()() 1 gxfx=+ thỏa mãn

()()()() 1312xgxxgx ′′ −+=++ . Số điểm cực trị của hàm số () 2 245yfxx=−+ là

Từ bảng biến thiên, suy ra () () min 0;

1 min373 2 Tfxf +∞

 ===  

Câu49: Cho hình chóp SABCD có đáy là hình vuông cạnh a , 2 SAa = vuông góc với đáy. Gọi ,, HEK lần lượt là hình chiếu vuông góc của A lên ,, SBSCSD . Khối nón có đường tròn đáy là đường tròn ngoại tiếp tam giác HKE và có đỉnh thuộc mặt phẳng () ABCD có thể tích bằng

A. 1. B. 3 . C. 2 . D. 5 . Lờigiải

ChọnB

()()()() 11gxfxgxfx ′′ =+  =+

()()()() 1312xgxxgx ′′ −+=++ hay ()()()() 1413xfxxfx ′′ −+=++

Cho () () ()()() 40 1 34 1 30 f x fxaxx x f

′ =  =   ′  =−−  =− ′ =    .

() () () 2 2 24544.245 yfxxyxfxx ′′ =−+  =−−+

A. 3 24 aπ B. 3 12 aπ C. 3 8 aπ D. 3 6 aπ Lờigiải ChọnA P H M K A B

⊥⊥

  ==−=−=−=     

hOIAOAIAI

() 22 2 22 1 22 11 440 2 024542410 2450 22 24532420 2 1 x xx x x yxxxx fxx x xxxx x =    == = −=    ′ =⇔⇔−+=⇔−+=⇔    ′ −+= +     = −+=−+=   =  Vậy hàm số có 3 cực trị