40 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP THPT MÔN TOÁN - 2022 - MỨC ĐỘ ĐIỂM KHÁ - GIỎI (CHUYÊN ĐỀ 1-8)

Dạng1.Tìmkhoảng đơn điệucủahàmsố g(x)=f[u(x)]khibiết đồ thị hàmsố f’(x)

Cách1:

Bước1: Tính đạo hàm của hàm số ()gx , ()()() . gxuxfux ′′′ =   .

Bước2: Sử dụng đồ thị của ()fx ′ , lập bảng xét dấu của ()gx ′

Bước3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số

Cách2:

Bước1: Tính đạo hàm của hàm số ()gx , ()()() . gxuxfux ′′′ =  

Bước2: Hàm số ()gx đồng biến () 0 gx ′ ⇔≥ ; (Hàm số ()gx nghịch biến () 0 gx ′ ⇔≤ ) (*)

Bước3: Giải bất phương trình () * (dựa vào đồ thị hàm số ()yfx ′ = ) từ đó kết luận khoảng đồng biến, nghịch biến của hàm số Câu1. (Đề ThamKhảo2018) Cho hàm số () = yfx . Hàm số '() = yfx có đồ thị như hình bên. Hàm số (2)=− yfx đồng biến trên khoảng

Hàm số () 52=− yfx đồng biến trên khoảng nào dưới đây? A. () 3;4 B. () 1;3 C. () ;3−∞− D. () 4;5 Lờigiải ChọnD Ta có () 52 ′′ =− yfx ()252 ′ =−−fx 0 ′ = y () 2520 ′ ⇔−−= fx 523 521 521

−=−   ⇔−=−   −= 

x x x

=   ⇔=   = 

()520 ′ −<fx 523 1521 −<−  ⇔ −<−< x x 4 23 >  ⇔  <<  x x ; ()520 ′ −>fx 521 3521 −>  ⇔ −<−<− x x 2 34 <  ⇔  <<  x x Bảng biến thiên

A. () 2; +∞ B. () 2;1 C. () ;2−∞− D. () 1;3 Lờigiải ChọnB Cách1: Ta thấy '()0fx < với (1;4) 1 ∈   <−  x x nên ()fx nghịch biến trên () 1;4 và () ;1−∞− suy ra ()() gxfx =− đồng biến trên (4;1) và () 1; +∞ . Khi đó (2)fx đồng biến biến trên khoảng (2;1) và () 3; +∞ Cách2: Dựa vào đồ thị của

4 3 2

x x x .

Dựa vào bảng biến thiên hàm số () 52=− yfx đồng biến trên khoảng () 4;5 Câu3. (Mã103-2019) Cho hàm số ()fx , bảng xét dấu của ()fx ′ như sau:

Hàm số () 32 yfx =− đồng biến trên khoảng nào dưới đây? A. () 0;2 B. () 2;3 C. () ;3−∞− D. () 3;4 Lờigiải ChọnD Ta có ()() 2.320320yfxfx ′′′ =−−≥⇔−≤ 3233 132112. xx xx −≤−≥ ⇔⇔  −≤−≤≤≤  Vậy chọn A.

Câu4. (Mã102-2019) Cho hàm số ()fx có bảng dấu ()fx ′ như sau:

Hàm số (52)yfx =− nghịch biến trên khoảng nào dưới đây?

A. () 3;5 . B. () 5; +∞ . C. () 2;3 . D. () 0;2 . Lờigiải ChọnD

ịch biến trên khoảng nào dưới đây? A. ()2;1. B. ()2;4. C. ()1;2. D. ()4;. +∞ Lờigiải ChọnA ()2.32 yfx ′′ =−− Hàm số nghịch biến khi ()() 02.320320yfxfx ′′′ ≤⇔−−≤⇔−≥

Dựa vào bảng biến thiên, suy ra hàm số () 2 2 yfxx =+ nghịch biến trên khoảng () 2;1 . Chú ý: Cách xét dấu ()gx ′ : Chọn giá trị () 2 01;1220(0)(0)0 xxxgf′′ =∈−−+  +=  => ( dựa theo bảng xét dấu của hàm ()fx ′ ). Suy ra () ()01;12gxx ′ >∀∈−−+ , sử dụng quy tắc xét dấu đa thức “ lẻ đổi, chẵn không” suy ra dấu của ()gx ′ trên các khoảng còn lại Câu7. (Chuyên Thái Nguyên -2019) Cho hàm số ()yfx = có đạo hàm ()' fx trên ℝ . Hình vẽ bên là đồ thị của hàm số ()yfx = . Hàm số () () 2 gxfxx =− nghịch biến trên khoảng nào trong các khoảng dưới đây?

A. 3 ; 2  −+∞   . B. 3 ; 2  −∞   . C. 1 ; 2  +∞   . D. 1 ; 2  −∞   . Lờigiải

Phươngpháp

Hàm số ()ygx = nghịch biến trên ()()() ;'0; abgxxab ⇔≤∀∈ và bằng 0 tại hữu hạn điểm.

Cáchgiải

Ta có: ()() () 2 '12' gxxfxx =−−

Hàm số ()ygx = nghịch biến trên ()()() ;'0; abgxxab ⇔≤∀∈ và bằng 0 tại hữu hạn điểm.

Ta có ()() '13'20gf−=−>  Loại đáp án A, B và D

Câu8. (ChuyênLêHồngPhongNam Định2019) Cho hàm số ()' yfx = có đồ thị như hình vẽ

Hàm số () 2 2 yfx =− đồng biến trên khoảng nào dưới đây A. () ;0−∞ B. () 0;1 C. () 1;2 D. () 0; +∞ Lờigiải ChọnB Hàm số () 2 2 yfx =− có () 2 '2.'2 yxfx =−−

Ta có bảng xét dấu của ()3:fx ′

Từ bảng xét dấu ta thây hàm số () 3 yfx =− đồng biến trên khoảng ()1;2.

Câu10. (THPT Minh Châu Hưng Yên 2019) Cho hàm số ()yfx = . Hàm số ()' yfx = có đồ thị như hình vẽ. Hàm số 2 ()(2).gxfx=− Mệnhvđề nào sai?

A. Hàm số ()gx nghịch biến trên () ;2−∞− B. Hàm số ()gx đồng biến trên () 2; +∞

C. Hàm số ()gx nghịch biến trên () 1;0 D. Hàm số ()gx nghịch biến trên () 0;2

Lờigiải ChọnA

Ta có 2 2 2 2

x x x gxxfxxx fx x x

0 0 0 '()2.'(2)0211 (2)0 2 22

=  =  =    =−=⇔⇔−=−⇔=±    −=    =± −=  

Từ đồ thị '()fx ta có 22 2 '(2)020 2 x fxx x >  −>⇔−>⇔  <− 

BBT

Từ BBT ta thấy đáp án C sai

Câu11. (THPT Việt ĐứcHàNội2019) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ và đồ thị hàm số ()yfx = như hình bên.

Hỏi hàm số ()() 32 gxfx =− nghịch biến trên khoảng nào trong các khoảng sau?

A. () 1; −+∞ B. () ;1−∞− C. () 1;3 D. () 0;2 Lờigiải ChọnB

Dựa vào bảng xét dấu ()gx ta thấy hàm số () 2 2 yfx=− nghịch biến trên khoảng () 0;2

Câu13. (ChuyênKHTN-2020) Cho hàm số () = yfx có bảng xét dấu đạo hàm như sau.

=−   =⇔=   =  Khi đó ()() '2'32 gxfx =−− Với ()()

Ta có () 2 '02 5

x fxx x

x x gxfxxx x x

5 2 322 1 '0'320322 2 325 1

 =  −=−     =⇔−=⇔−=⇔=    −=   =−    Bảng biến thiên:

Câu12. (ChuyênLêQuý Đôn ĐiệnBiên2019) Cho hàm số ()yfx = có bảng xét dấu đạo hàm như sau: Hàm số () 2 2 yfx=− nghịch biến trên khoảng nào dưới đây? A. () 2;1 B. () 2; +∞ C. () 0;2 D. () 1;0 Lờigiải Xét hàm số () () 2 2 gxfx=−

 ≥  ⇔   ≤≤  

Hàm số () 23=− yfx đồng biến trên khoảng nào sau đây? A. () 2;3 . B. () 1;2 . C. () 0;1 . D. () 1;3 . Lờigiải ChọnA Đặt ()()()() 233.23 ′′ =−  =−− gxfxgxfx Ta có ()()0230 ′′≥⇔−≤ gxfx 233 0231 −≤−  ⇔  ≤−≤  x x 5 3 12 33

x x . Suy ra hàm số ()gx đồng biến trên các khoảng 12 ; 33    và 5 ; 3  +∞   , do đó hàm số đồng biến trên khoảng () 2;3 .

Câu14. (Chuyên Bến Tre -2020) Cho hàm số ()yfx = biết hàm số ()fx có đạo hàm ()fx ′ và hàm số ()yfx ′ = có đồ thị như hình vẽ Đặt ()() 1 gxfx=+ . Kết luận nào sau đây đúng?

A. Hàm số ()gx đồng biến trên khoảng () 3;4 .

B. Hàm số ()gx đồng biến trên khoảng () 0;1

C. Hàm số ()gx nghịch biến trên khoảng () 2; +∞ .

D. Hàm số ()gx nghịch biến trên khoảng () 4;6 Lờigiải

()() 1 gxfx=+

Ta có: ()() 1 gxfx ′′ =+

Hàm số ()gx đồng biến ()() 154 010 11302 xx gxfx xx +>> ′′ ⇔>⇔+>⇔⇔ <+<<< .

Hàm số ()gx nghịch biến ()() 31524 010 110 xx gxfx xx <+<<< ′′ ⇔<⇔+>⇔⇔ +<< .

Vậy hàm số ()gx đồng biến trên khoảng () 0;2 ; () 4; +∞ và nghịch biến trên khoảng () 2;4 ; () ;0−∞ .

Câu15. (Chuyên Phan Bội Châu - Nghệ An - 2020) Cho hàm số () = yfx có bảng xét dấu đạo hàm như sau:

x −∞ 5 2 +∞

y ′ + 0 0 +

Hàm số () () 32=− x gxf đồng biến trên khoảng nào sau đây A. () 3; +∞ . B. () ;5−∞− . C. () 1;2 . D. () 2;7 . Lờigiải ChọnC

Ta có () ()'2ln2.'32 =−− xxgxf . Để ()()32 =− x gxf đồng biến thì () () '2ln2.'320 =−−≥ xxgxf () '320532203 ⇔−≤⇔−≤−≤⇔≤≤ xx fx Vậy hàm số đồng biến trên () 1;2 .

Câu16. (ChuyênVĩnhPhúc-2020) Cho hàm số ()fx có đạo hàm liên tục trên ℝ và có đồ thị của hàm số ()′ = yfx như hình vẽ. Xét hàm số () () 2 2 =−gxfx . Mệnh đề nào dưới đây sai?

Ta có () ()()() 2222.22.2 ′ ′′′ =−−=− gxxfxxfx .

Hàm số nghịch biến khi () 0 gx ′ ≤ () 2 .20xfx ′ ⇔−≤

A. Hàm số ()gx nghịch biến trên () 0;2 B. Hàm số ()gx đồng biến trên () 2; +∞ C. Hàm số ()gx nghịch biến trên () 1;0 . D. Hàm số ()gx nghịch biến trên () ;2−∞− .

+ Với () 2

0 20 x fx ≤    ′ −≥   2

x fx x fx

Từ đồ thị hình của hàm số ()′ = yfx như hình vẽ, ta thấy

+ Với () 2

0 20 x fx ≥    ′ −≤   2

 ≤    ′ −≥   ⇔  ≥    ′ −≤  

0 20 0 20

() ()

2 2

() 02fxx ′ ≤⇔≤ và () 0 fx ′ ≥ 2 x ⇔≥

0 22 x x ≤  ⇔  −≥  2

0 4 x x ≤  ⇔  ≥ 

0 22 x x ≥  ⇔  −≤  2

x x x

0 2 2

≤   ⇔ ≥   ≤−  2 x ⇔≤−

0 4 x x ≥  ⇔  ≤  02 x ⇔≤≤

Như vậy hàm số nghịch biến trên mỗi khoảng () ;2−∞− , () 0;2 ; suy ra hàm số đồng biến trên () 2;0 và () 2; +∞ .

Do ()() 1;02;0−⊂− nên hàm số đồng biến trên () 1;0 . Vậy C sai.

Câu17. (Đại Học Hà Tĩnh - 2020) Cho hàm số ()yfx = . Biết rằng hàm số ()yfx ′ = có đồ thị như hình vẽ bên dưới.

Hàm số () 2 3 yfx =− đồng biến trên khoảng A. () 0;1 B. () 1;0 C. () 2;3 D. () 2;1 Lờigiải ChọnB

Cách1: Đặt () () 2 3 ygxfx ==− .

Ta có: () () 2 2.3 gxxfx ′′ =−−

() () 2 02.30gxxfx ′′ =⇔−−= () 2

0 30 x fx =  ⇔  ′ −=  

Bảng xét dấu của ()gx ′ :

x x x x

2 2 2

=   −=−  ⇔  −=−   −= 

0 36 31 32

x x x x

0 3 2 1

=   =±  ⇔  =±  =± 

() () 2 22gxxfx ′′ =+ , kết hợp với đồ thị hàm số ()yfx ′ = ta đượ

x x x x gx x fx x x x

=  =   =  +=−   ′ =⇔⇔⇔=    ′ += +=     =−   += 

() () 2 2 2 2

0 0 0 22 0 3 20 22 3 25

1 0 0 0 1 + 2 3 0 0 +

x ( ) gx ′ + +∞ −∞ + 3 0 0 2 0

Suy ra hàm số () 2 3 yfx =− đồng biến trên mỗi khoảng: ()()()() 3;2,1;0,1;2,3; −−−+∞ .

Vậy hàm số () 2 3 yfx =− đồng biến trên khoảng () 1;0 .

Cách2:

Dựa vào đồ thị của ()yfx ′ = ta chọn ()()()() 612yfxxxx ′ ==++− Đặt () () 2 3 ygxfx ==−

Ta có: () ()()()() 22222.32941 gxxfxxxxx ′′ =−−=−−−− . () 0 gx ′ =

Từ đồ thị đã cho ta có () 22 0 5 x fx x −<< ′ >⇔  > 

Suy ra () 22 2 22

222403 20 253 3 xxx fx xx x

  −<+<−<<> ′ +>⇔⇔⇔   +>> <−   

Và lập luận tương tự () 2 2 2 2

225 200333 22 x fxxx x  <+< ′ +<⇔⇔<<⇔−<<  +<− 

Bảng biến thiên ( Dấu của ()gx ′ phụ thuộc vào dấu của 2 x và () 2 2 fx ′ + trên từng khoảng)

x x x x

=   =±  ⇔  =±  =± 

0 3 2 1

Bảng xét dấu của ()gx ′ : x ( ) gx ′ + +∞ −∞ + 3 0 0 2 0

1 0 0 0 1 + 2 3 0 0 + Suy ra hàm số () 2 3 yfx =− đồng biến trên mỗi khoảng: ()()()() 3;2,1;0,1;2,3; −−−+∞ Vậy hàm số () 2 3 yfx =− đồng biến trên khoảng () 1;0 Câu18. (Sở Ninh Bình) Cho hàm số bậc bốn ()yfx = có đạo hàm trên ℝ Đồ thị hàm số ()' yfx = như hình vẽ. Hàm số () 2 2 yfx=+ nghịch biến trên khoảng nào dưới đây?

Dựa vào bảng biến thiên hàm số nghịch biền trên () ;3−∞− và () 0;3 chọn đáp án. Câu19. (HậuLộc2-ThanhHóa-2020) Cho hàm số ()yfx = có đồ thị hàm đạo hàm ()yfx ′ = như hình vẽ. Hàm số ()() 20192020 gxfx =− đồng biến trên khoảng nào trong các khoảng sau?

A. () 2;3 . B. () 3;2 . C. () 1;1 . D. () 1;0 . Lờigiải ChọnB Đặt () () 2 2 gxfx=+ , hàm số có đạo hàm trên ℝ

A. () 1;0 B. () ;1−∞− C. () 0;1 D. () 1;+∞ Lờigiải ChọnD Ta có ()()()() 2019202020192020202020192020 gxxfxfx ′ ′′′ =−−=−− ,

260260 026.230 230230 xx gxxfxx fxxfxx −≥−≤  ′ ′ ≥⇔−−≥⇔∪′′ −≥−≤ 

=− đồng biến thì ()() () ()() 2 22

Trường hợp 1. () 2 2 2

 ≤  −≥  ⇔⇔≤ −≤ ′ −≥    −≥ 

x x x xx fxx xx

1 260 3 1 231 3 230 232

Trường hợp 2. () 2 2

 −≤  ≥  ⇔  ′ −≤   ≤−≤  hệ vô nghiệm

x x fxx xx

1 260 3 230 1232

Vậy hàm số () () 2 23 gxfxx =− đồng biến trên khoảng 1 ; 3  −∞  

Câu21. Cho hàm số ()fx liên tục trên R và có đồ thị '()fx như hình vẽ. Tìm số điểm cực trị của hàm số 2 ()yfxx =+ ?

A. 10 . B. 11. C. 12 . D. 13 . Lờigiải ChọnB

Ta có 2 '(21)'() yxfxx =++ ; 2 xxm += có nghiệm khi và chỉ khi 1 4 m ≥− . Dựa vào đồ thị ta thấy đồ thị hàm '()fx cắt trục hoành tại 5 điểm trong đó 1 điểm có hoành độ nhỏ hơn 1 4 và có một tiệm cận. Khi đó ứng với mỗi giao điểm có hoành độ lớn hơn 1 4 và 1 điểm không xác định thì '0 y = có hai nghiệm. Từ đây dễ dàng suy ra hàm 2 ()yfxx =+ có 11 cực trị.

Câu22. (Chuyên ĐH Vinh

suy ra đáp là D.

Dạng 2. Tìm khoảng đơn điệu của hàm số g(x)=f[u(x)]+v(x) khi biết đồ thị, bảng biến thiên củahàmsố f’(x)

Cách1:

Bước1: Tính đạo hàm của hàm số ()gx , ()()()() . gxuxfuxvx ′′′′ =+   .

Bước2: Sử dụng đồ thị của ()fx ′ , lập bảng xét dấu của ()gx ′

Bước3: Dựa vào bảng dấu kết luận khoảng đồng biến, nghịch biến của hàm số

Cách2:

Bước1: Tính đạo hàm của hàm số ()gx , ()()()() gxuxfuxvx ′′′′ =+  

Bước2: Hàm số ()gx đồng biến () 0 gx ′ ⇔≥ ; (Hàm số ()gx nghịch biến () 0 gx ′ ⇔≤ ) (*)

Bước3: Giải bất phương trình () * (dựa vào đồ thị hàm số ()yfx ′ = ) từ đó kết luận khoảng đồng biến, nghịch biến của hàm số

Cách3:(Trắcnghiệm) Bước1: Tính đạo hàm của hàm số ()gx , ()()()() gxuxfuxvx ′′′′ =+  

Bước 3: Hàm số ()gx đồng biến trên K () 0, gxxK ′ ⇔≥∀∈ ; (Hàm số ()gx nghịch biến trên K () 0, gxxK ′ ⇔≤∀∈ ) (*)

Bước3: Lần lượt chọn thay giá trị từ các phương án vào ()gx ′ để loại các phương án sai.

Câu1. (Đề ThamKhảo2019) Cho hàm số ()fx có bảng xét dấu của đạo hàm như sau

x −∞ 1 2 3 4 +∞ ( )fx ′ 0 + 0 + 0 0 +

Hàm số () 3 323 yfxxx =+−+ đồng biến trên khoảng nào dưới đây?

()

ChọnB

B. ()1;0. C. ()0;2. D. ()1;. +∞ Lờigiải

Ta có: () () 2 323yfxx′′ =+−−

Với ()()() 1;021;220xxfx ′ ∈−  +∈  +> , lại có () 2 300;1;0xyx ′ −<  >∀∈−

Vậy hàm số () 3 323 yfxxx =+−+ đồng biến trên khoảng ()1;0.

Chú ý: +) Ta xét ()()()() 2 1;21;23;420;30 xxfxx ′ ∈⊂+∞  +∈  +<−>

Suy ra hàm số nghịch biến trên khoảng () 1;2 nên loại hai phương án A,D. +) Tương tự ta xét ()()()() 2 ;22;020;300;;2xxfxxyx ′′ ∈−∞−  +∈−∞  +<−>  <∀∈−∞−

Hàm số ()gx nghịch biến ()() 20 '0' 4 2 t t gxft t −≤≤  ≤  ≥−   ≥ 

y – 2

1 – 2 O

x

4 Trang 18

Như vậy () 13 2120 12 22 12 4123 2 2

x x x fx x x

 ≤≤  −≤−≤ ′ −≥    ≤−   ≤−  

Vậy hàm số ()() 2 12 gxfxxx =−+− nghịch biến trên các khoảng 13 ; 22    và 3 ; 2  −∞−   .

Mà 313 1;; 222  ⊂   nên hàm số ()() 2 12 gxfxxx =−+− nghịch biến trên khoảng 3 1; 2   

Câu3. (ChuyênLêQuý Đôn ĐiệnBiên2019) Cho hàm số ()fx có bảng xét dấu của đạo hàm như sau

Hàm số () 3 1122019yfxxx =−+−+ nghịch biến trên khoảng nào dưới đây?

A. () 1; +∞ B. () 1;2 C. () ;1−∞ D. () 3;4 Lờigiải Ta có ()()() ()222 1312369369 yfxxftttfttt ′′′′ =−+−=++−=−−−+ , với 1 tx=−

Nghiệm của phương trình 0 y ′ = là hoành độ giao điểm của các đồ thị hàm số () 2 ;369yftytt ′ ==−−+ .

Vẽ đồ thị của các hàm số () 2 ;369yftytt ′ ==−−+ trên cùng một hệ trục tọa độ như hình vẽ sau:

Dựa vào đồ thị trên, ta có BXD của hàm số () () 2 369yfttt ′′ =−−−+ như sau: () 0 1 t <−

Vậy hàm số nghịch biến trên khoảng () 0 ;1 tt ∈ . Do đó hàm số nghịch biến trên khoảng ()() 0 1;21;1xt∈⊂+ .

Câu4. (ChuyênPhanBộiChâuNghệ An2019) Cho hàm số ()fx có bảng xét dấu đạo hàm như sau: Hàm số () 2 211 yfxxx =−++− nghịch biến trên những khoảng nào dưới đây A. () ;2−∞− . B. () ;1 −∞ . C. () 2;0 . D. () 3;2 . Lờigiải. () 2 211 1 x yfx x ′′ =−−+− + . Có 2 10 1 x x −< + , () 2;0 x ∀∈− Bảng xét dấu: ()() 210,2;0 fxx ′  −−<∀∈− () () 2 2110,2;0 1 x fxx x ′  −−+−<∀∈− + .

Câu5. (Sở VĩnhPhúc2019) Cho hàm số bậc bốn ()yfx = có đồ thị của hàm số ()yfx ′ = như hình vẽ bên.

Hàm số 32 3()69 yfxxxx =+−+ đồng biến trên khoảng nào trong các khoảng sau đây? A. () 0;2 . B. () 1;1 . C. () 1; +∞ . D. () 2;0 . Lờigiải

Hàm số 432 (),(0) fxaxbxcxdxea =++++≠ ; 32 ()432 fxaxbxcxd ′ =+++ . Đồ thị hàm số ()yfx ′ = đi qua các điểm (4;0),(2;0),(0;3),(2;1) nên ta có:

5 96 2564880 7 321240 24 3 7 321241 24 3

a abcd abcd b d c abcd d

 =  −+−+=    −+−+= =  ⇔  =−  =−  +++=    =−  Do đó hàm số () 3223251555 3()69;3()433 24812 yfxxxxyfxxxxxx  ′′ =+−+=+−+=+−  11 00 2

=−   ′ =⇔=   =  . Hàm số đồng biến trên các khoảng (11;0) và ( ) 2; +∞ .

x yx x

y x 2 2 2 O

y x 2 2 2 O

Câu6. (Học Mãi 2019) Cho hàm số ( )yfx = có đạo hàm trên ℝ . Đồ thị hàm số ( )yfx ′ = như hình bên. Hỏi đồ thị hàm số ( ) 2 yfxx =− có bao nhiêu điểm cực trị? A. 4 B. 3 C. 2 D. 1 Lờigiải ChọnB Đặt ( ) ( ) 2 gxfxx =− ( ) ( ) 2 gxfx ′′  =− Vẽ đường thẳng 2 y = .  phương trình ( ) 0 gx ′ = có 3 nghiệm bội lẻ  đồ thị hàm số ( ) 2 yfxx =− có 3 điểm cực trị.

2 y =

(THPT Ho

ng Hoa

ám Hưng Yên 2019) Cho hàm số ()yfx = liên tục trên ℝ . Hàm số

()yfx ′ = có đồ thị như hình vẽ. Hàm số ()() 20192018 1 2018 x gxfx=−+ đồng biến trên khoảng nào dưới đây?

A. () 1;0 B. () 2;3 C. () 2;1 D. () 0;1 Lờigiải ChọnA

Ta có ()() 2 2 320182.3 fxxfx ′ ′ −+=−− 

A. () 2 ; 3 B. () 0 ; 1 C. () -1 ; 0 D. () 1 ; 2 Lờigiải Ta có ()()11 gxfx ′′ =−− ()()() 011011gxfxfx ′′′≥⇔−−≥⇔−≥ 110 . 123 xx xx −≤−≤ ⇔⇔−≥≥ Từ đó suy ra hàm số ()() 20192018 1 2018 x gxfx=−+ đồng biến trên khoảng () -1 ; 0 .

Câu8. (Sở NinhBình2019) Cho hàm số ()yfx = có bảng xét dấu của đạo hàm như sau

Hàm số () 22019yfx=−+ nghịch biến trên khoảng nào trong các khoảng dưới đây?

A. () 4;2 . B. () 1;2 . C. () 2;1 . D. () 2;4 . Lờigiải

Xét ()()22019ygxfx ==−+

x x gx x x

=−   =−  ′ =⇔  =  = 

Ta có ()()() () 220192 gxfxfx ′ ′′ =−+=− , () 2 1 0 2 4

Dựa vào bảng xét dấu của ()fx ′ , ta có bảng xét dấu của ()gx ′ : Dựa vào bảng xét dấu, ta thấy hàm số ()ygx = nghịch biến trên khoảng () 1;2

Câu9. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số ()yfx = . Biết đồ thị hàm số ()yfx ′ = có đồ thị như hình vẽ bên. Hàm số () 2 32018yfx=−+ đồng biến trên khoảng nào dưới đây?

 = =   −=− =±  ′ −−=⇔⇔  =± −=−   =±  −= 

x x x x xfx x x x x

() 2 2 2 2

0 0 36 3 2.30 2 31 1 32

Bảng xét dấu của đạo hàm hàm số đã cho

Từ bảng xét dấu suy ra hàm số đồng biến trên () 1;0 x −∞ 3 2 1 0 1 2 3 +∞ ( ) 2 3 fx ′ 0 + 0 0 + 0 + 0 0 + 0 ( ) 2 23xfx ′ 0 + 0 0 + 0 0 + 0 0 +

Câu10. (Chuyên Biên Hòa - Hà Nam - 2020) Cho hàm số đa thức ()fx có đạo hàm trên ℝ . Biết ()00 f = và đồ thị hàm số ()yfx ′ = như hình sau.

Hàm số ()() 2 4 gxfxx =+ đồng biến trên khoảng nào dưới đây?

Lời giải

ChọnB

Xét hàm số ()() 2 4 hxfxx =+ trên ℝ .

Vì ()fx là hàm số đa thức nên ()hx cũng là hàm số đa thức và ()() 0400hf==

Ta có ()()42 hxfxx ′′ =+ . Do đó ()() 1 0 2 hxfxx ′′ =⇔=−

Hàm số () 2 ()2122020 gxfxxx =−−++ đồng biến trên khoảng nào?

A. (0;1) . B. (3;1) . C. (1;3) . D. (2;0) . Lờigiải ChọnA

Ta có đường thẳng yx = cắt đồ thị hàm số ()yfx ′ = tại các điểm 1;1;3xxx=−== như hình vẽ

sau:

Dựa vào sự tương giao của đồ thị hàm số ()yfx ′ = và đường thẳng 1 2 yx =− , ta có

(){} 02;0;4hxx ′ =⇔∈−

Suy ra bảng biến thiên của hàm số ()hx như sau:

Từ đó ta có bảng biến thiên của hàm số ()() gxhx = như sau:

Dựa vào bảng biến thiên trên, ta thấy hàm số ()gx đồng biến trên khoảng () 0;4 .

Câu11. (Chuyên Thái Bình - 2020) Cho hàm số ()fx liên tục trên ℝ có đồ thị hàm số ()yfx ′ = cho như hình vẽ

Dựa vào đồ thị của hai hàm số trên ta có 1 () 13 x fxx x <−  ′ >⇔  <<  và 11 () 3 x fxx x −<< ′ <⇔  > 

+ Trường hợp 1: 101xx−<⇔< , khi đó ta có () 2 ()2122020 gxfxxx =−−++ Ta có () ()212(1) gxfxx ′′ =−−+− .

()() 11102 ()0212(1)011 132 xx gxfxxfxx xx −<−<<<  ′′′ >⇔−−+−>⇔−<−⇔⇔ −><−

Kết hợp điều kiện ta có 01 ()0 2 x gx x <<  ′ >⇔  <−  . + Trường hợp 2: 101xx−>⇔> , khi đó ta có () 2 ()2122020 gxfxxx =−−++ () ()212(1) gxfxx ′′ =−−− ()() 110 ()0212(1)011 11324 xx gxfxxfxx xx −<−< ′′′ >⇔−−−>⇔−>−⇔⇔

Dựa vào đồ thị hàm số ()yfx ′ = suy ra () 03fxx ′ ≤∀< và () 03fxx ′ >∀> () ()ee2 xxgxf′′ =−

Hàm số () ()e22020 x gxf=−− nghịch biến nếu () 0 gx ′ < () ee20 xx f ′ ⇔−< ()e20 x f ′ ⇔−< e23e5ln5 xx x ⇔−<⇔<⇔<

Vậy hàm số đã cho nghịch biến trên 3 1; 2    .

Câu14. (LýNhânTông-BắcNinh-2020) Cho hàm số ()fx có đồ thị hàm số ()fx ′ như hình vẽ.

Hàm số () 2 cos yfxxx =+− đồng biến trên khoảng

A. () 2;1 . B. () 0;1 . C. () 1;2 . D. () 1;0 . Lờigiải

ChọnC

Đặt hàm ()() 2 cos gxfxxx =+−

Ta có: ()()sin.cos21gxxfxx ′′ =−+−

Vì []cos1;1 x ∈− nên từ đồ thị ()fx ′ ta suy ra () []cos1;1fx ′ ∈− .

Do đó () sin.cos1 xfx ′ −≤ , x ∀∈ ℝ .

Ta suy ra ()()sin.cos2112122 gxxfxxxx ′′=+−≥−+−=− () 0,1gxx ′  >∀> . Vậy hàm số đồng biến trên () 1;2 .

Câu15. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số ()fx . Hàm số ()yfx ′ = có đồ thị như hình vẽ

Vì [] 2 215 0,3;5 4 tt t −++ ≥∀∈− . Mà []()0,3;2ftt ′ ≤∀∈−

Nên () [] 2 215 4 3;2 tt ftt −++ ∈− ′ ≤  .

Suy ra 1 32122 2 xx −≤+≤⇔−≤≤ . Vậy chọn phương án D.

Câu17. (Chuyên Thái Bình - Lần 3 - 2020) Cho hàm số ()yfx = liên tục trên ℝ có đồ thị hàm số ()yfx ′ = cho như hình vẽ.

Hàm số () 2 ()2122020 gxfxxx =−−++ đồng biến trên khoảng nào? A. () 0;1 . B. () 1 3; . C. () 1;3 . D. () 0 2; . Lờigiải ChọnA

+Với 1 x > , ta có ()()()2 2112021gxfxx=−−−+ ()()() 2121gxfxx ′′  =−−−

Hàm số đồng biến ()()()() 2121011* fxxfxx ′′ ⇔−−−>⇔−>− .

Đặt 1 tx=− , khi đó ()() 1324 * 10() tx ftt txloai <<<< ′ ⇔>⇔  <−< .

+Với 1, x < ta có ()()()2 2112021gxfxx=−−−+ ()()() 2121 gxfxx ′′  =−−+−

Hàm số đồng biến ()()()() 2121011** fxxfxx ′′ ⇔−−+−>⇔−<−

Đặt 1 tx =− , khi đó ()() 110201 ** 322 txx ftt txx −<<<<<<  ′ ⇔<⇔   ><−<−  .

Vậy hàm số ()gx đồng biến trên các khoảng () ;2−∞− , () 0;1 , () 2;4

Câu18. (Sở PhúThọ -2020) Cho hàm số ()yfx = có đồ thị hàm số ()fx ′ như hình vẽ

Hàm số () ()12020 x gxfe=++ nghịch biến trên khoảng nào dưới đây?

B. 1 ;1 2    . C. 1 0; 2    . D. () 1;1 . Lờigiải ChọnC () () 1 xx gxefe ′′ =+ Do 0, x ex >∀ nên () () 010 x gxfe ′′≤⇔+≤ 13 x e ⇔+≤ ln2 x ⇔≤ , dấu bằng xảy ra tại hữu hạn điểm.

Nên ()gx nghịch biến trên () ;ln2−∞ So với các đáp án thì chỉ có C thỏa mãn.

Câu19. (THPT Anh Sơn - Nghệ An - 2020) Cho hàm số ()yfx = có bảng xét dấu của đạo hàm như sau. Hàm số () 22019yfx=−+ nghịch biến trên khoảng nào trong các khoảng dưới đây? A. () 2;4 B. () 4;2 C. () 2;1 D. () 1;2 Lờigiải ChọnD Ta có ()'2' yfx =− () 2 1 '02'0 2 4

x x yfx x x

=−   =−  =⇔−=⇔  =  = 

Từ bảng xét dấu của ()' fx ta có Từ bảng xét dấu ta có hàm số nghịch biến trên khoảng () ;2−∞− , () 1;2 và () 4; +∞

( ) ( ) 310xxgx−−>

Vậy hàm số ()120192020yfxx =−++ nghịch biến trên các khoảng () ;0−∞ và () 3; +∞

.

Biết () 2, fxx>∀∈ ℝ . Xét hàm số ()() () 32 3232020gxffxxx=−−+− . Khẳng định nào sau

đây đúng?

A. Hàm số ()gx đồng biến trên khoảng () 2;1 .

B. Hàm số ()gx nghịch biến trên khoảng () 0;1 .

C. Hàm số ()gx đồng biến trên khoảng () 3;4

D. Hàm số ()gx nghịch biến trên khoảng () 2;3 .

Lờigiải ChọnD

Ta có: ()()() () 2 '2''3236 gxfxffxxx =−−−+ .

Vì () 2, fxx>∀∈ ℝ nên () 321 fx −<− x ∀∈ ℝ

Từ bảng xét dấu ()' fx suy ra () () '320, ffxx−<∀∈ ℝ

Từ đó ta có bảng xét dấu sau:

Từ bảng xét dấu trên, loại trừ đáp án suy ra hàm số ()gx nghịch biến trên khoảng () 2;3 .

Câu22. Cho hàm số ()fx có bảng biến thiên như sau:

( )hx

30

Hàm số () () () () 32 3. yfxfx =− nghịch biến trên khoảng nào dưới đây?

A. () 1;2 . B. () 3;4 . C. () ; 1 −∞ . D. () 2; 3 .

Lờigiải Chọn D

Ta có () () ()()() 2 3..6.. yfxfxfxfx ′′′ =− ()()() = 3..2 fxfxfx ′  

Hàm số ()()() 11hxfxgx =−−− nghịch biến trên khoảng nào dưới đây? A. 1 ;1 2    B. () 1; +∞ C. () 2; +∞ D. 1 1; 2   

Lờigiải

ChọnD

Ta có: ()()() 11hxfxgx ′′′ =−−−

Dựa vào hình vẽ ta có hàm số ()hx nghịch biến () 0 hx ′ ⇔< ()() 11fxgx ′′ ⇔−<− ⇔ 1 21 2 011

 −<−<−  <−<  ⇔ 1 1 2 12

x x

 −<<  << 

x x

Do đó hàm số ()hx nghịch biến trên các khoảng 1 1; 2    và () 1;2

2.222.2 2121 xxfxxxfxx gx fxxfxx

′ ′′ ′ == −+−+ . () () 2 2 2 2

=  =  −=  

−=−

 ′ −= −=− 

1 2201 0221 20213 23

−=

x x x xx gx x fxx xx x xx Trang 32

Hàm số 3 ()(7)(51)42 kxfxgxhx =+++−+  đồng biến trên khoảng nào dưới đây?

A. 5 ;0 8    B. 5 ; 8  +∞   C. 3 ;1 8    D. 3 ;1 8    Lờigiải ChọnC Ta có: ()(7)5(51)443

(THPTHoàngHoaThám- ĐàNẵng-2021) Cho hàm số ()fx có bảng xét dấu của ()' fx nh

 . Suy ra ( (( () )) ) 2 1 '23 3 t fttt t = == =   =−−+⇔ =−−+⇔ =−−+⇔ =−−+⇔   =− =−=−    Bảng xét dấu:

≤−−   ⇔ −≥   −≤ 

m m m

 ⇔ 



thị hàm số ()yfx ′ = như hình bên. Có bao nhiêu số nguyên dương a để hàm số () 4sincos2 yfxxa =+− nghịch biến trên 0; 2 π    ?

4cos.sin2sin24sincos2 4sincos2 xfxxfxxa gx fxxa

′ −+−   ′  = +−  

Ta có ()() 4cos.sin2sin24cossinsin xfxxxfxx ′′ −=−  Với 0; 2 x π  ∈  thì ()() cos0,sin0;1sinsin0 xxfxx ′ >∈  −< .

Hàm số ()gx nghịch biến trên 0; 2 π    khi () 4sincos20,0; 2 fxxax π +−≥∀∈  () 2 4sin12sin,0; 2 fxxax π ⇔+−≥∀∈ 

Đặt sin tx = được ()() 2 412,0;1 fttat+−≥∀∈ (*). Xét ()()()()() 2 4124441 htftthtfttft ′′′ =+−  =−=−  .

Với () 0;1 t ∈ thì ()() 0 htht ′ <  nghịch biến trên () 0;1

Do đó (*) ()() 2 14112.13ahf ⇔≤=+−= . Vậy có 3 giá trị nguyên dương của a thỏa mãn.

Câu4. (Chuyên Quang Trung-2020) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ và có đồ thị ()yfx ′ = như hình vẽ. Đặt ()() ()2 1 12019 2 gxfxmxm=−−−−+ , với m là tham số thực. Gọi

S là tập hợp các giá trị nguyên dương của m để hàm số ()ygx = đồng biến trên khoảng () 5;6

Tổng tất cả các phần tử trong S bằng

A. 4 B. 11 C. 14 D. 20 Lờigiải

Xét hàm số ()() ()2 1 12019 2 gxfxmxm=−−−−+

()()() 1 gxfxmxm ′′ =−−−−

Xét phương trình ()() 01 gx ′ =

Đặt xmt −= , phương trình () 1 trở thành ()()()() 1012fttftt ′′ −−=⇔=−

Nghiệm của phương trình () 2 là hoành độ giao điểm của hai đồ thị hàm số ()yft ′ = và 1 yt=−

Ta có đồ thị các hàm số ()yft ′ = và 1 yt=− như sau: Căn cứ đồ thị các hàm số ta có phương trình () 2 có nghiệm là: 11 11 33

Gọi S là tập hợp tất cả các giá trị nguyên thuộc khoảng () 6;6 của tham số m để hàm số ()()()223232 gxfxmxmxm =−++−++ nghịch biến trên () 0;1 . Khi đó, tổng giá trị các phần tử của S là A. 12. B. 9. C. 6. D. 15. Lờigiải ChọnB

Xét ()()() '2'3223 gxfxmxm =−−++−+ . Xét phương trình () '0gx = , đặt

txm txm txm

=−=−  =  =+  ==+

Ta có bảng biến thiên của ()ygx = Để hàm số ()ygx = đồng biến trên khoảng () 5;6 cần 15 56 16 2 35

m m m m m

 −≤  ≤≤   ⇔ +≥    ≤   +≤ 

Vì * mm ∈  ℕ nhận các giá trị 1;2;5;614 S  = . Câu5. (Sở Hà Nội - Lần 2 - 2020) Cho hàm số 432 ,0yaxbxcxdxea =++++≠ . Hàm số () ' yfx = có đồ thị như hình vẽ

32 txm =−+ thì phương trình trở thành () 2 2.'04 2 0

t t ftt t

 =−   −−=⇔=     = 

Từ đó, () 123 '0,,531 222 mmm gxxxx ++−+ =⇔=== . Lập bảng xét dấu, đồng thời lưu ý nếu 1xx > thì 1tt < nên () 0 fx > . Và các dấu đan xen nhau do các nghiệm đều làm đổi dấu đạo hàm nên suy ra ()(213'0;; gxxxxx≤⇔∈∪−∞

Vì hàm số nghịch biến trên () 0;1 nên ()() '0,0;1gxx≤∀∈ từ đó suy ra 35 01 22 1 1 2

 ++ ≤<≤   −+  ≤   và giải ra các giá trị nguyên thuộc () 6;6 của m là -3; 3; 4; 5. Từ đó chọn câu B

mm m

Câu6. (Chuyên Quang Trung - Bình Phước - Lần 2 - 2020) Cho hàm số () = yfx có đạo hàm liên tục trên ℝ và có đồ thị ()′ = yfx như hình vẽ bên. Đặt ()() ()2 1 12019 2 =−−−−+gxfxmxm , với m là tham số thực. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số () = ygx đồng biến trên khoảng () 56 ; . Tổng tất cả các phần tử trong S bằng:

A. 4 B. 11 C. 14 D. 20 Lờigiải

Ta có ()()() 1 ′′ =−−−− gxfxmxm

Cho ()()01′′ =⇔−=−− gxfxmxm

Đặt () 1 −=  =− ' xmtftt

Khi đó nghiệm của phương trình là hoành độ giao điểm của đồ thị hàm số ()′ = yft và và đường thẳng 1=−yt

ChọnD

Tacó () ()'2019ln2019.'2019 xx gxfm =− .

Talại có hàm số 2019x y = đồng biến trên [] 0;1

Với [] 0;1 x ∈ thì []20191;2019 x ∈ mà hàm ()yfx = đồng biến trên () 1; +∞ nên hàm () '2019x yf = đồng biến trên [] 0;1

Mà () []20191;'201900;1 xxfx ≥>∀∈ nên hàm () ()2019ln2019.'2019 xxhxf = đồng biến trên [] 0;1

Bảng xét dấu của ()′ gt

t fttt t

Dựa vào đồ thị hàm số ta có được () 1 11 3

 =−  ′ =−⇔=   = 

Từ bảng xét dấu ta thấy hàm số ()gt đồng biến trên khoảng () 11 ; và () 3 +∞ ; Hay 111111 333 −<< −<−<  −<<+ ⇔⇔  >−>>+  txmmxm txmxm

Để hàmsố ()gx đồng biếntrên khoảng () 56 ; thì 156156 3562  −≤<≤+  ≤≤ ⇔ +≤<≤ mmm mm

Vì m là các số nguyên dương nên {} 1256 = ;;; S

Vậy tổngtất cả các phần tử của S là: 125614 +++= .

Câu7. Cho hàm số ()yfx = liên tục có đạo hàm trên ℝ . Biết hàm số ()' fx có đồ thị cho như hình vẽ.

Có bao nhiêu giá trị nguyên của m thuộc [] 2019;2019 để hàm só () ()20192 x gxfmx =−+ đồng biến trên [] 0;1

Hay ()() []00,0;1hxhx≥=∀∈

Do vậy hàmsố ()gx đồng biến trên đoạn [] 0;1 () []'0,0;1gxx ⇔≥∀∈

() []2019ln2019.'2019,0;1 xx mfx ⇔≤∀∈ [] ()() 0;1 min00 x mhxh ∈ ⇔≤==

Vì m nguyên và [] 2019;2019 m ∈−  có 2020 giá trị m thỏa mãn yêu cầu bài toán. Câu8. Cho hàm số ()yfx = có đồ thị ()fx ′ như hình vẽ. Có bao nhiêu giá trị nguyên () 2020;2020 m ∈− để hàm số ()() () 2 23ln12 gxfxxmx =−−+− đồng biến trên 1 ;2 2    ? A. 2020 B. 2019 C. 2021 D. 2018 Lờigiải ChọnB + Ta có ()() 2 2 2232 1 x gxfxm x ′′ =−−− + Hàm số ()gx đồng biến trên 1 ;2 2    khi và chỉ khi ()()() 2 1 0,1;223,;2 12 x gxxmfxx x  ′′≥∀∈−⇔≤−−∀∈  +  () 2 1 ;2 2

x mfx x  ∈ 

min23 1 x

 ′ ⇔≤−− +  () 1

+ Đặt 23tx=− , khi đó () 1 ;22;1 2 xt  ∈⇔∈−   .

Từ đồ thị hàm ()fx ′ suy ra ()() 0,2;1ftt ′ ≥∀∈− và () 0 ft ′ = khi 1 t =−

Tức là () 1 230,;2 2 fxx  ′ −≥∀∈   () 1 ;2 2

′  −= khi 1 x = () 2

min230 x fx  ∈ 

+Xét hàm số () 2 1 x hx x =− + trên khoảng 1 ;2 2    .Ta có () () 2 2 2

1 1 x hx x ′ = + và () 2 0101hxxx ′ =⇔−=⇔=± .

Bảngbiếnthiên củahàm số ()hx trên 1 ;2 2    như sau:

Từ bảng biến thiên suy ra () 1 2 hx ≥− () 1 ;2 2

Từ () 1 , () 2 và () 3 suy ra 1 2 m ≤−

Từ bảng biến thiên suy ra 9 m ≥

Kết hợp với m thuộc đoạn [] 2020;2020 và m nguyên nên {} 9;10;11;...;2020 m ∈ .

Vậy có 2012 số nguyên m thỏa mãn đề bài.

Câu10. Cho hàm số ()fx xác định và liên tục trên R . Hàm số ()yfx ′ = liên tục trên ℝ và có đồ thị như hình vẽ.

 =− khi 1 x = () 3

1 min 2 x hx  ∈ 

Kết hợp với m ∈ ℤ , () 2020;2020 m ∈− thì {} 2019;2018;....;2;1 m ∈−−−−

Vậy có tất cả 2019 giá trị m cần tìm.

Câu9. Cho hàm số ()fx liên tục trên ℝ và có đạo hàm ()()()2226 fxxxxxm ′ =−−+ với mọi x ∈ ℝ .

Có bao nhiêu số nguyên m thuộc đoạn [] 2020;2020 để hàm số ()() 1 gxfx =− nghịch biến trên khoảng () ;1−∞− ? A. 2016 . B. 2014 . C. 2012 . D. 2010 . Lờigiải ChọnC Ta có: ()()()()()() 22 111161 gxfxxxxxm  ′′ =−=−−−−−−−+ ()()() 2 2 1145xxxxm =−+++− Hàmsố ()gx nghịch biến trên khoảng () ;1−∞− () 0,1gxx ′ ⇔≤∀<−

Xét hàm số ()() ()2 1 222020 2 gxfxmmx=−+−+ ,với m là tham số thực. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số () = ygx nghịch biến trên khoảng () 3;4 . Hỏi số phần tử của S bằng baonhiêu? A. 4 . B. 2 . C. 3 . D. Vô số. Lờigiải ChọnB Tacó ()()() ''22 gxfxmmx =−−− Đặt ()()() ' hxfxx =−− . Từ đồ thị hàm số ()' yfx = và đồ thị hàm số yx =− trên hình vẽ suy ra: ()() 31 0' 3 x hxfxx x −≤≤ ≤⇔≤−⇔  ≥ 

khoảng () ;1−∞− ,ta có bảng biến thiên:

Câu12. Cho các hàm số () 3 4 fxxxm =++ và () ()()() 22223 201820192020gxxxx =+++ . Có bao nhiêu giá trị nguyên của thamsố [] 2020;2020 m ∈− để hàm số () ()gfx đồng biến trên () 2; +∞ ?

A. 2005 . B. 2037 . C. 4016 . D. 4041. Lờigiải

ChọnB Tacó () 3 4 fxxxm =++ , () ()()() 23 22212102 121020201820192020... gxxxxaxaxaxa =+++=++++ .

Suy ra () 2 34fxx ′ =+ , () 119 12102 1210...2 gxaxaxax ′ =+++

Và () () ()()() () () () 119 12102 1210...2 gfxfxafxafxafx ′    ′ =+++   

Ta có ()() 3212321 '20 2323 xmmxm gxhxm xmxm −≤−≤−≤≤+  =−≤⇔⇔ −≥≥+

Suy ra hàm số () = ygx nghịch biến trên các khoảng () 23;21 mm−+ và () 23; m ++∞ Do đóhàmsố () = ygx nghịch biến trên khoảng () 3;4 233 3 3 214 2 0 233

m m m m m

 −≤   ≤≤   ⇔⇔ +≥   ≤   +≤  Mặt khác,do m nguyên dương nên {}{} 2;32;3mS ∈  = . Vậy số phần tử của S bằng 2. Từ đó chọn đápánB.

Câu11. Cho hàm số ()fx có đạo hàm trên ℝ là ()()() 13fxxx ′ =−+ . Có bao nhiêu giá trị nguyên của thamsố m thuộc đoạn [] 10;20 để hàmsố () 2 3 yfxxm =+− đồng biến trênkhoảng () 0;2 ? A. 18 B. 17 C. 16 D. 20 Lờigiải ChọnA Ta có () () () 2 2 3233 yfxxmxfxxm ′′′ =+−=++− . Theo đề bài ta có: ()()() 13fxxx ′ =−+ suy ra () 3 0 1 x fx x <−  ′ >⇔ 

()()()() () () ( ) 108 12102 1210...2 fxfxafxafxa ′ =+++ Dễ thấy 121020;;...;;0aaaa > và () 2 340fxx ′ =+> , 2 x ∀> Do đó ()()() () () () 108 12102 1210...20fxafxafxa ′ +++> , 2 x ∀>

Hàm số () ()gfx đồng biến trên () 2; +∞ khi () () 0 gfx ′  ≥  , 2 x ∀>  () 0 fx ≥ , 2 x ∀> ⇔ 3 40xxm++≥ , 3 x ∀> ⇔ 3 4 mxx ≥−− , 2 x ∀>  [ ) () 3 2; max416mxx +∞ ≥−−=−

Vì [] 2020;2020 m ∈− và m ∈ℤ nên có2037 giá trị thỏa mãn m

Câu13. Cho hàm số có đạo hàm ()() () 2 2 121fxxxxmx ′ =+++ với mọi Có bao nhiêu số nguyên âm m để hàmsố ()() 21gxfx=+ đồng biến trên khoảng () 3;5 ? A. 3 B. 2 C. 4 D. 6 Lờigiải ChọnA Tacó: () 22 2'(21)2(21)(22)[(21)2(21)1]gxfxxxxmx ′ =+=++++++ Đặt 21tx=+ Để hàm số đồng biến trên khoảng () 3;5 khi vàchỉ khi ()() 0, 3;5 gxx ′ ≥∀∈ ()() () 2 2 2 1 (21)0, 7;11210,7;112,7;11 t ttmtttmttmt t ⇔++≥∀∈⇔++≥∀∈⇔≥∀∈

( )yfx = x ∈ ℝ ( )gx

Xét hàmsố 2 1 () t ht t = trên [] 7;11 ,có 2 2 1 '() t ht t −+ = BBT:

Vì {3;2;1} mm ∈  ∈−−− ℤ . Câu14. Cho hàmsố ()yfx = có bảng biến thiên như sau

A. ()() ;3,5; −∞+∞ . B. ()() ;1,1; −∞−+∞ . C. () 1;1 . D. () 3;5 . Lờigiải. ChọnB

Có bao nhiêu số nguyên 2019 m < để hàmsố () () 2 2 gxfxxm =−+ đồng biến trên khoảng () 1;+∞ ? A. 2016. B. 2015. C. 2017. D. 2018. Lờigiải ChọnA Ta có () ()() () () 22 2 22212 gxxxmfxxmxfxxm ′ ′′′ =−+−+=−−+ Hàmsố ()ygx = đồngbiếntrên khoảng () 1;+∞ khi và chỉ khi ()() 0,1;gxx ′ ≥∀∈+∞ và

() 0 gx ′ = tại hữu hạn điểm () () () 2 2120,1; xfxxmx ′ ⇔−−+≥∀∈+∞

() () 2 20,1;fxxmx ′ ⇔−+≥∀∈+∞ () () 2 2

Hàm số ()22 yfx ′ =−+ có đồ thị () C như sau: Dựa vào đồ thị () C ta có: ()()()()()() 222,;13;20,;13;fxxfxx ′ ′ −+>∀∈−∞+∞⇔−>∀∈−∞+∞ ∪∪ . Đặt *2xx=− suy ra: ()()() *0,*;11;fxx ′ >∀∈−∞−+∞ ∪ Vậy: Hàmsố ()fx đồngbiếntrên khoảng ()() ;1,1; −∞−+∞

22,1; 20,1; xxmx xxmx

 −+≥∀∈+∞  ⇔  −+≤∀∈+∞  

Xét hàm số 2 2 yxxm =−+ ,ta có bảng biến thiên

Dựa vào bảng biến thiên ta có

TH1: () 2 22,1;123 xxmxmm −+≥∀∈+∞⇔−≥⇔≥ .

TH2: () 2 20,1;xxmx−+≤∀∈+∞ : Không có giá trị m thỏa mãn.

Vậy có 2016 số nguyên 2019 m < thỏa mãn yêu cầu bài toán.

Câu15. Cho hàm số ()yfx = có đạo hàm là hàm số ()fx ′ trên ℝ . Biết rằng hàm số ()22 yfx ′ =−+ có đồ thị như hình vẽ bên dưới.Hàm số ()fx đồngbiếntrên khoảng nào?

Câu16. Cho hàm số ()yfx = có đạo hàm là hàm số ()fx ′ trên ℝ . Biết rằng hàm số ()22 yfx ′ =+− có đồ thị như hình vẽ bên dưới. Hàmsố ()fx nghịch biến trênkhoảng nào?

A. ()() 3;1,1;3 . B. ()() 1;1,3;5 . C. ()() ;2,0;2−∞− . D. ()() 5;3,1;1 . Lờigiải ChọnB Hàm số ()22 yfx ′ =+− có đồ thị () C như sau:

()()()()()() 222,3;11;320,3;11;3fxxfxx ′ ′ +−<−∀∈−−⇔+<∀∈−−∪∪

Đặt *2xx=+ suy ra: ()()() *0,*1;13;5fxx ′ <∀∈− ∪

Vậy: Hàm số ()fx đồng biến trên khoảng ()() 1;1,3;5

Câu17. Cho hàm số ()yfx = có đạo hàm là hàm số ()fx ′ trên ℝ . Biết rằng hàm số ()22 yfx ′ =−+

có đồ thị như hình vẽ bên dưới.Hàm số ()fx nghịch biến trên khoảng nào?

A. () ;2−∞ B. () 1;1 C. 35 ; 22    D. () 2; +∞ Lờigiải.

ChọnB Hàmsố ()22 yfx ′ =−+ có đồ thị () C như sau:

Dựa vào đồ thị () C ta có: ()()()() 222,1;320,1;3fxxfxx ′′−+<∀∈⇔−<∀∈ .

Đặt *2xx=− thì ()() *0,*1;1 ′ <∀∈−fxx

Vậy: Hàm số ()fx nghịch biến trên khoảng () 1;1

Cáchkhác:

Tịnh tiến sang trái hai đơn vị và xuống dưới 2 đơn vị thì từ đồ thị () C sẽ thành đồ thị của hàm ()′ = yfx . Khi đó: ()() 0,1;1fxx ′ <∀∈−

Vậy: Hàm số ()fx nghịch biến trên khoảng () 1;1 . Phân tích: Cho biết đồ thị của hàm số ()fx ′ sau khi đã tịnh tiến và dựa vào đó để xét sự đồng biến của hàm số ()fx Câu18. Cho hàm số ()yfx = có đạo hàm cấp 3 liên tục trên ℝ và thỏa mãn ()()()() 23.14fxfxxxx ′′′ =−+ với mọi x ∈ ℝ và ()()()() 2 2. gxfxfxfx ′′′ =−   . Hàm số () () 2 2 hxgxx

Tacó ()()()()()()()()() 22.2.2.; gxfxfxfxfxfxfxfxfx ′′′′′′′′′′′′′

Khi đó () () () () ()()()() 222223 22222222124 hxxgxxxxxxxxx ′ ′ =−−=−−−−−−+ () 0 1 0 2 12

=   =  ′ =⇔  =  =±   Tacó bảng xét dấu của ()hx ′

x x hx x x

Suy ra hàmsố () () 2 2 hxgxx =− đồng biến trênkhoảng () 1;2 .

Câu19. Cho hàm số ()yfx = xác định trên ℝ . Hàm số () ()'232ygxfx==++ có đồ thị là một parabol với tọa độ đỉnh () 2;1 I và đi qua điểm () 1;2 A . Hỏi hàm số ()yfx = nghịch biến trên khoảng nàodưới đây? A. () 5;9 B. () 1;2 C. () ;9−∞ D. () 1;3 Lờigiải ChọnA Xét hàmsố () ()'232gxfx=++ có đồ thị là một Parabol nên có phương trình dạng: () 2 () ygxaxbxcP ==++

b baab a abcabc g

Vì () P có đỉnh () 2;1 I nên () 2 440 2 421421 21

 = −=+=   ⇔⇔  ++=−++=−  =−  . () P đi qua điểm () 1;2 A nên ()122gabc=⇔++=

Tacó hệ phươngtrình 403 42112 211

+==  ++=−⇔=− ++== nên () 2 31211gxxx=−+ .

aba abcb abcc

Đồ thị của hàm ()ygx = là

Theo đồ thị ta thấy '(23)0'(23)2213 fxfxx +≤⇔++≤⇔≤≤

Đặt 3 23 2 t txx=+⇔= khi đó 3 '()01359 2 t ftt ≤⇔≤≤⇔≤≤

Câu21. Cho hàm số ()yfx = có đạo hàm () 2 '23,. fxxxx=+−∀∈ ℝ Có bao nhiêu giá trị nguyên

của tham số m thuộc đoạn [] 10;20 để hàm số () ()2231gxfxxmm=+−++ đồng biến trên

()0;2?

A. 16. B. 17. C. 18. D. 19. Lờigiải

ChọnC

Tacó ()() 2 3 '230*. 1 t fttt t ≤−  =+−≥⇔  ≥ 

+−≤−∀∈+≤−∀∈ ⇔⇔  +−≥∀∈+≥+∀∈ 

33,0;233,0;2 31,0;231,0;2 xxmxxxmx xxmxxxmx

(**)

Có ()() () 2 '23'3 gxxfxxm =++− Vì ()230,0;2 xx+>∀∈ nên ()gx đồng biến trên ()()() 0;2'0,0;2 gxx ⇔≥∀∈ () () 2 '30,0;2 fxxmx ⇔+−≥∀∈ () () () () 2 2 2 2

Có () 2 3 hxxx =+ luôn đồng biếntrên () 0;2 nên từ (**)  31013 101 mm mm −≥≥ ⇔ +≤≤− Vì [] 10;20 m m  ∈−    ∈   ℤ Có 18 giá trị của thamsố m. Vậy có 18 giá trị của thamsố m cần tìm. Câu22. Cho hàm số ()yfx = có đạohàm liêntục trên ℝ và đồ thị của hàm số ()' yfx = như hình vẽ. Đặt ()() ()2 1 12019 2 gxfxmxm=−−−−+ với m là tham số thực. Gọi S là tập các giá trị nguyên dương của m để hàm số ()ygx = đồng biến trên khoản () 5;6 .Tổng các phần tử của S bằng: A. 4 B. 11. C. 14 D. 20. Lờigiải ChọnC Tacó ()()() ''1 gxfxmxm =−−−−

Ta có ()() 1111 '0 33 xmmxm gxhxm xmxm −≤−≤−≤≤+  =−≥⇔⇔ −≥≥+

Do đóhàmsố ()ygx = đồng biến trên các khoảng () 1;1mm−+ và () 3; m ++∞

 −≤  ≤≤   ⇔⇔ +≥    ≤   +≤ 

m m m m m

Do vậy,hàmsố ()ygx = đồng biến trên khoảng () 5;6 15 56 16 2 35

Do m nguyên dương nên {} 1;2;5;6 m ∈ ,tức {} 1;2;5;6 S =

Tổngcác phần tử của S bằng 14.

Câu23. Cho hàmsố ()yfx = là hàm đa thức có đồ thị hàmsố ()yfx ′ = như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m , ,20202020mZm∈−<< để hàm số () ()222 8 6 3 gxfxmxxx

′ ′ ⇔≤−−+∀∈−⇔≥∀∈− −−+ () () () 2 2 3;0 max 223 fx m xx

()() () () () () 2 22 2 223,3;0,3;0 223 fx fxmxxxmx xx

′ ⇔≥ −−+ .

Ta có ()22 30093 xxfx ′ −<<  <<  ≤− dấu “ = ” khi 2 11xx=⇔=−  ()() 2 2 2 23140234,3;0 xxxxxx −−+=−++  <−−+≤∀∈− 2 11 , 234xx ⇔≥ −−+ dấu “ = ” khi 1 x =− Suy ra () () 2 2 33 2.48 223 fx xx

′ ≤= −−+ , () 3;0 x ∀∈− ,dấu “ = ” khi 1 x =− . () () () 2 2 3;0

′  =− ++ . Vậy 3 8 m ≥− ,mà m ∈ ℤ , 20202020 m −<< nêncó 2020 giá trị của thamsố m thỏamãnbài toán. Câu24. Cho hàm số ()fx .Hàm số ()yfx ′ = có đồ thị như hình sau.

3 max 8 223 fx xx

Cótất cả bao nhiêu giá trị nguyêndương của tham số m đề hàm số 2020 2 ) ( 4 ) ( 2 + + = mx x m x f x g đồng biến trên khoảng).2;1( A. 2 B. 3 C. 0 D. 1 Lờigiải ChọnA Tacó m x m x f x g 2 2 ) 4 ) + = 2(*) ) )0 m x m x f x g ≥ ⇔ ≥ Đặt m x t = thì )2 (*) t t f ≥ ⇔

Vẽ đường thẳng 2 x y = trên cùng hệ trục Oxy với đồ thị ()yfx ′ = như hình vẽ sau

Từ đồ thị ta có    + ≥ ≤ ≤ ⇔    ≥ ≤ ≤ ⇔ ≥ 4 2 4 0 2 2 ) m x m x m t t t t f

Hàmsố ) ( x g đồngbiếntrên khoảng ⇔ )2;1( () 2;1 0 ) ∈ ∀ ≥ x x g    ≤ ≤ ≤ ⇔    ≤ + ≤ < ≤ ⇔ 3 3 2 1 4 2 1 2 m m m m m

Vì m nguyên dương nên {}.3;2∈ m Vậy có hai giá trị nguyên dương của m đề hàmsố ) (x g đồng biến trên khoảng).2;1(

Câu25. Cho hàm số ()fx có đạo hàm ()()()() 114; fxxxxx ′ =+−−∀∈ ℝ .Có bao nhiêu số nguyên

2020 m < để hàmsố () 2 1 x gxfm x  =− +  đồng biến trên () 2; +∞

A. 2018 B. 2019 C. 2020 D. 2021 Lờigiải ChọnB

Ta có: () ()2 32 1 1 x gxfm x x ′′ =−− +  + .

Hàmsố ()gx đồngbiến trên () 2; +∞ ⇔ ()() 0;2;gxx ′ ≥∀∈+∞ () () 2 32 0;2; 1 1 x fmx x x ′ ⇔−−≥∀∈+∞  +  + ⇔ () 2 0;2; 1 x fmx x ′ −≤∀∈+∞ + 

Ta có: () 0 fx ′ ≤ ⇔ ()()()1140xxx+−−≤ ⇔ 1 14 x x ≤−   ≤≤ 

 −≤−∀∈+∞  +   ≤−≤∀∈+∞  +  Hàmsố () 2 1 x hxm x =− + ; () 2; x ∈+∞ có bảng biến thiên:

2 1;2;1 1 2 14;2;2 1

Căn cứ bảng biến thiên suy ra: Điều kiện () 2 khôngcó nghiệm m thỏa mãn. Điều kiện () 1 ⇔ 1 m −≤− ⇔ 1 m ≥ ,kết hợp điều kiện 2020 m < suy ra có 2019 giá trị m thỏa mãn yêu cầu bài toán. Nhậnxét: Có thể mở rộng bài toán đã nêu như sau:

Cho hàm số ()fx có đạo hàm ()()()() 114; fxxxxx ′ =+−−∀∈ ℝ .Có bao nhiêu số nguyên 2020 m < để hàm số () () 2 1 x gxfhm x =+ +  đồng biến trên () 2; +∞

Câu26. Cho hàm số ()yfx = có đạo hàm ()() '1 xfxxe =+ , có bao nhiêu giá trị nguyên của tham số m trong đoạn [] 2019;2019 để hàm số ()() 2 ln2ygxfxmxmx ==−+− nghịch biến trên () 2 1; e A. 2018. B. 2019. C. 2020. D. 2021. Lờigiải ChọnB

Trên () 2 1; e ta có () ()() 1 '.'ln2ln121 gxfxmxmxxm x =−+=+−−

Để hàm số ()ygx = nghịch biến trên () 2 1; e thì ()() () 2 'ln1210,1; gxxxmxe =+−−≤∀∈ () () () 2 2

⇔+−−≤∀∈ + ⇔≤∀∈

ln1210,1; ln1 ,1; 21

xxmxe x mxe x

x mx x x mx x Trang 54

Xét hàmsố () ln1 21 x hx x + = trên () 2 1; e ,ta có () () () 2 2

x x hxxe x =<∀∈ ,từ đây suy ra

1 2ln '0,1; 21

1 m ≥ .Vậy có 2019 giá trị nguyên của m thỏa bài toán.

Câu27. (Liên trường Quỳnh Lưu - Hoàng Mai - Nghệ An - 2021) Cho hàm số ()yfx = có đạo hàm ()() 1 xfxxe ′ =+ . Có bao nhiêu giá trị nguyên của tham số m trong [] 2020;2021 để hàm số ()() 2 ln42gxfxmxmx =−+− nghịchbiếntrong () 2020 ; ee . A. 2018 B. 2020 C. 2021 D. 2019 Lờigiải ChọnB

Tacó () () () ln 11 ln24ln124ln124 x gxfxmxmxemxmxmxm xx ′′ =−+=+−+=+−+

Hàm số nghịch biến trongkhoảng () 2020 ; ee khi và chỉ khi () 2020 ln140,; xmxmxee +−+≤∀∈ () 2020 ln1 2,; 2 x mxee x + ⇔≥∀∈

nghịch biến trên

khoảng

+−− ′ ==∈

1 1ln1 1ln ,; 22

Ta có () () () () () 2020 22

xx xx x gxxee xxx

() () 2020 0,, gxxee ′ <∀∈

BBT x e 2020 e ( )gx ′ ()gx 2 2 e

Quansát bảngbiếnthiên ta có 21 22 22 mmm ee ≥⇔≥  ≥ .Vậy có 2020 giá trị nguyên của thamsố m

Câu28. (ChuyênKHTN-2021) Cho hàm số ()fx có bảngxét dấu của đạo hàm như sau:

Có bao nhiêu giá trị nguyên của tham số m thỏa mãn 1010 m −<< vàhàmsố 2 (2) yfxxm =++ đồng biến trên khoảng (0;1) ? A. 5 B. 4 C. 6 D. 1 Lờigiải

ChọnC Xét 2 ()(2) ygxfxxm ==++

Ta có: 2 ''()2(1)'(2) ygxxfxxm ==+++

Vì 10(0;1)xx+>∀∈ nên để hàm số 2 (2) yfxxm =++ đồng biến trên khoảng (0;1) khi và chỉ khi 2 '(2)0(0;1) fxxmx++>∀∈ ,dohàmsố 2 2 xxm ++ luôn đồng biến trên (0;1) nên Đặt 2 2 txxm =++ .Vì (0;1) x ∈ nên (;3)tmm∈+

m m m m m

2 333 33332

A. 23 B. 21 C. 5 D. 17 Lờigiải ChọnA () ()()() ()()()

gxfxxmxxmxxm fxxmxxmxxm

332333 332363

2 333 2 333

gxxfxxmxxmxxmx fxxmxxmxxmx

=−−++−−+−−+− =−−++−−+−−−+ Tacó () ()()()()()() 2 232323 '91'318133613 gxxfxxmxxxmxxxm =−+−−+−+−−+++−−+ Để hàm số nghịch biến trên () 1;2 ()() ()()() () ()()() ()

≤∀∈−⇔−−++−−+−−−+≥∀∈− ⇔−−+≥−−−++−−+∀∈− Đ ặt 3 3 txxm =−−+ .Với () 1;2 x ∈− ()() 2 '3301;214;4 txxtmm =−−<∀∈−  ∈−+ Xét bất phương trình () 1 ()() 2 '241 fttt ≥−+ Đồ thị hàm số ()' yft = và 2 24 ytt =−+ trên cùng hệ trục tọa độ

'01;2'3234301;2 '323431;2

+≤−  ≤−   ⇔ ≥    =    +≤  Mà 1010 m −<< nên {9;8;7;6;5;0} m =−−−−− Vậy có tất cả 6 giá trị nguyên của tham số m thỏa mãn đề bài. Câu29. (THPT ĐồngQuan-HàNội-2021) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ . Hàm số ()' yfx = có đồ thị như hình vẽ. Số tham số m nguyên thuộc đoạn [] 20;20 để hàm số ()gx Trang 56 () 1;2 biết

Câu30. (THPT ChuVănAn-Thái Nguyên-2021) Cho hai hàm số ()fx và ()gx có một phần đồ thị biểu diễn đạo hàm ()fx ′ và ()gx ′ như hình vẽ Biết rằng hàm số ()()() 2 2021 yhxfxgxax ==−−+ luôn tồn tại một khoảng đồng biến () ; αβ Số giá trị nguyên dương của a thỏa mãn là A. 4 B. 2 C. 3 D. 1 Lờigiải

ChọnC

Ta có: ()()() 2yhxfxgxa ′′′′ ==−− . Hàm số ()yhx = đồng biến khi ()()()() 2 2 00 yfxgxafxgxa ′′′′′ ≥⇔−−≥⇔≥+

Đồ thị hàm số () 2 ygxa ′ =+ là đồ thị hàm số ()ygx ′ = tịnh tiến lên phía trên 2 a đơn vị.

Hàm số ()()() 2 2021 yhxfxgxax ==−−+ luôn tồn tại một khoảng đồng biến () ; αβ khi 2 1133aa<⇔−≤≤

Mà * a + ∈ Z , suy ra: {} 1;2;3 a ∈

Câu31. (THPT PTNKCơ sở 2- TP.HCM-2021) Cho hàm số ()fx xác định và liên tục trên ℝ . Hàm số '()yfx = liên tục và có đồ thị như hình vẽ

Xét hàm số () ()2 1 ()222020 2 gxfxmmx=−+−+ , với m là tham số thực. Gọi S là tập hợp các giá trị nguyên dương của m để hàm số ()ygx = nghịch biến trên khoảng () 3;4 . Số phần tử của S bằng bao nhiêu? A. 4. B. 3. C. 2. D. Vô số Lờigiải ChọnC

Ta có ()()'()'22 gxfxmxm =−+−

'()0'()(2) gxftttxm =⇔=−=− 323 121 323

txm txm txm

=−=−  ⇔=⇔=+  ==+

Từ đồ thị suy ra 23 '()0 2321 xm gx mxm >+  <⇔  −<<+ 

Vậy hàm số ()ygx = nghịch biến trên khoảng () 3;4 khi

ng1.Bàitoáncựctrị hàmsố chứadấutrị tuyệt đối

Bàitoán: Đồ thị hàm số () = yfx có bao nhiêu điểm cực trị (Áp dụng định nghĩa). 2 2 2().() ()() ()

′ ′ ==  = fxfx yfxfxy fx () () ()01 0 ()02 =  ′ =   ′ =  fx y fx

Số nghiệm của () 1 chính là số giao điểm của đồ thị () = yfx và trục hoành 0 = y . Còn số nghiệm của () 2 là số cực trị của hàm số () = yfx , dựa vào đồ thị suy ra () 2 . Vậy tổng số nghiệm bội lẻ của () 1 và () 2 chính là số cực trị cần tìm.

Dạng toán này mình làm tựa theo đề tham khảo 2018, vẫn xuất hiện ở dạng toán hàm hợp, các bạn học chú ý nhé!

Câu1. (ChuyênVinh–Lần2). Đồ thị () C có hình vẽ bên. Tất cả các giá trị của tham số m để hàm số () yfxm =+ có ba điểm cực trị là: A. 1 m ≤− hoặc 3 m ≥ B. 3 m ≤− hoặc 1. m ≥ C. 1 m =− hoặc 3 m = D. 13. m ≤≤ Giải

Cách 1:

Do () yfxm =+ là hàm số bậc ba Khi đó, hàm số () yfxm =+ có ba điểm cực trị ⇔ hàm số () yfxm =+ có D .0CCTyy ≥ (hình minh họa)

()() 1 130 3 m mm m ≤−  ⇔+−+≥⇔→  ≥  Đáp án A

Cách 2:

Ta có () yfxm =+ = () () () () () () () 2 2

. ′ + ′ +  = +

fxmfx fxmy fxm Để tìm cực trị của hàm số () yfxm =+ , ta tìm x thỏa mãn 0 y = hoặc y không xác định. () () () () 1 2 0 ′ =  ⇔  =−   fx fxm

Dựa vào đồ thị, suy ra hàm số có 2 điểm cực trị 12 , xx trái dấu.

Suy ra (1) có hai nghiệm 12 , xx trái dấu.

Vậy để đồ thị hàm số có 3 cực trị thì (2) có một nghiệm khác 12 , xx

Số nghiệm của (2) chính là số giao điểm của đồ thị () C và đường thẳng ym =− .

Do đó để (2) có một nghiệm thì dựa vào đồ thị ta có điều kiện:

→ Đáp án. A. Chú ý:

11 33 mm mm −≥≤−  ⇔  −≤−≥ 

Nếu 0xx = là cực trị của hàm số ()yfx = thì () 0 0 fx = hoặc không tồn tại () 0 ′ fx .

Câu2. (Đề Tham Khảo 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 4323412 yxxxm =−−+ có 7 điểm cực trị?

A. 5 B. 6 C. 4 D. 3 Lờigiải.

Dựa vào BBT thì hàm số () 3 =−yfx có 3 cực trị.

Câu4. (CụmLiênTrườngHảiPhòng2019) Tìm số các giá trị nguyên của tham số m để đồ thị hàm số 4222212yxmxmm =−++− có bảy điểm cực trị A. 1 B. 4 C. 0 D. 2

Lờigiải Đồ thị hàm số 4222212yxmxmm =−++− có bảy điểm cực trị khi và chỉ khi đồ thị hàm số 4222212yxmxmm =−++− cắt trục hoành tại bốn điểm phân biệt 42222120xmxmm−++−= có bốn nghiệm phân biệt khi và chỉ khi



−<<    ⇔>     −−−+  <∨>    

m m mm

  −+−>     >     +−>    43 0 197197 44

()22 2

mmm m mm

2120 20 2120

197 3 4 m −+ ⇔<< Vậy không có giá trị nguyên của tham số m để đồ thị hàm số 4222212yxmxmm =−++− có bảy điểmcựctrị

Câu5. (Sở Vĩnh Phúc 2019) Có bao nhiêu giá trị nguyên của tham số m để hàm số 43223412 yxxxm =−−+ có đúng5 điểmcựctrị? A. 5 B. 7 C. 6 D. 4 Lờigiải Xéthàmsố 4322()3412 fxxxxm =−−+ ; 32 ()121224 fxxxx ′ =−− 123 ()00;1;2 fxxxx ′ =⇔==−= .Suyra,hàmsố ()yfx = có3 điểmcựctrị  Hàmsố 43223412 yxxxm =−−+ có5 điểmcựctrị khi đồ thị hàmsố ()yfx = cắttrụchoành tại2 điểmphânbiệt ⇔ 4322 34120 xxxm−−+= có2nghiệmphânbiệt. Phươngtrình 43224322 341203412 xxxmxxxm −−+=⇔−++= (1). Xéthàmsố 432g()3412 xxxx =−++ ; 32 g()121224 xxxx ′ =−++

đãchocó 3 điểmcựctrị là A. 2 B. 4 C. 3 D. 1 Lờigiải ChọnB

Đặt ( ) 42221fxxmxm =−+− , ( ) 3 44 fxxmx ′ =− , () 2

0 0 x fx xm

+Trườnghợp1: hàm số có một cực trị [ ]2;0 m  ∈− .

=  ′ =⇔  = 

Đồ thị hàm số ( )yfx = có một điểm cực trị là ( )0;21Am .

Do [ ]2;0 m ∈− 210 A ym  =−< nên đồ thị hàm số ( )yfx = cắt trục hoành tại 2 điểm phân biệt

nên hàm số ( )yfx = có 3 cực trị  có 3 giá trị nguyên của m thỏa ycbt.

+Trườnghợp2: hàm số có ba cực trị ( ]0;2 m  ∈

Khi đó đồ thị hàm số có 3 điểm cực trị là ( )0;21Am , ( ) 2 ;21Bmmm−+− , ( ) 2 ;21Cmmm−−+−

Do 10 a => nên hàm số ( ) yfx = có 3 điểm cực trị khi hàm số ( )yfx = có 0 BCyy=≥ 2 210mm ⇔−+−≥ 1 m ⇔= . Nếu 0 BCyy=< (trong bài toán này không xảy ra) thì hàm số có ít nhất 5 điểm cực trị Vậy có 4 giá trị của m thỏa ycbt.

Câu8. (ChuyênBắcNinh2019) Tập hợp các giá trị của m để hàm số 432 34121yxxxm =−−+− có 7 điểm cực trị là: A. (0;6) B. (6;33) C. (1;33) D. (1;6) Lờigiải ChọnD

Xét hàm số 432 ()34121 fxxxxm =−−+− , Có ( ) +∞ = →+∞ x f x lim , ( ) +∞ = →−∞ x f x lim ( ) 322 ()121224122 fxxxxxxx =−−=−− 0 ()01 2

=   =⇔=−   =  . Bảng biến thiên:

x fxx x

Từ bảng biến thiên, ta có hàm số ()yfx = có 7 điểm cực trị ⇔ đồ thị hàm số ()yfx = cắt Ox tại 4 điểm phân biệt 60116mmm ⇔−<<−⇔<< .

Câu9. (THPT Kinh Môn - 2018) Cho hàm số 32 ()(21)(2)2yfxxmxmx ==−−+−+ . Tìm tất cả các giá trị của tham số m để hàm số ()yfx = có 5 điểm cực trị A. 5 2 4 m <≤ B. 5 2 4 m −<< C. 5 2 4 m −<< D. 5 2 4 m << Lờigiải Ta có: () 2 '32212 yxmxm =−−+− Hàm số ()yfx = có 5 điểm cực trị khi chi khi hàm số ()fx có hai cực trị dương. 0 0 0 S P

∆>  ⇔>   > 

Gọi S là tập hợp các giá trị nguyên dương của tham số m để hàm số () 1 yfxm =−+ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng A. 9 B. 12 C. 18 D. 15

Lờigiải Nhận xét: Số giao điểm của ()() : Cyfx = với Ox bằng số giao điểm của ()() :1Cyfx ′ =− với Ox

Vì 0 m > nên ()() :1 Cyfxm ′′ =−+ có được bằng cách tịnh tiến ()() :1Cyfx ′ =− lên trên m đơn vị

 −−−>    ⇔>    >  

()() () 2 21320 221 0 3 2 0 3

mm m m

 −−>   ⇔>   <  

2 450 1 2 2

mm m m

5 2 4 m ⇔<<

Câu10. (Chuyên Đh Vinh - 2018) Cho hàm số ()yfx = có đạo hàm () ()() 32322 fxxxxx ′ =−− với mọi x ∈ ℝ . Hàm số () 12018 fx có nhiều nhất bao nhiêu điểm cực trị? A. 9 . B. 2018 . C. 2022 . D. 11. Lờigiải Ta có ()()()32220fxxxx ′ =−−= có 4 nghiệm và đổi dấu 4 lần nên hàm số ()yfx = có 4 cực trị. Suy ra () 0 fx = có tối đa 5 nghiệm phân biệt. Do đó () 12018 yfx =− có tối đa 9 cực trị

Câu11. (THPTThạchThanh2-ThanhHóa-2018) Hình vẽ bên là đồ thị của hàm số ()yfx =

TH1: 03 m << . Đồ thị hàm số có 7 điểm cực trị. Loại.

TH2: 3 m = . Đồ thị hàm số có 5 điểm cực trị. Nhận.

TH3: 36 m << Đồ thị hàm số có 5 điểm cực trị. Nhận.

TH4: 6 m ≥ . Đồ thị hàm số có 3 điểm cực trị. Loại.

Vậy 36 m ≤< . Do * m ∈ℤ nên {} 3;4;5 m ∈ .

Vậy tổng giá trị tất cả các phần tử của S bằng 12

Để (2) có 4 nghiệm phân biệt thì ()fx cắt trục hoành tạ

−+< <    ⇔⇔<< >   >  

50 10 2 010 0 0 2

m m m mm

Vậy có 9 giá trị nguyên của tham số m để hàm số 4323412 2 m yxxx =+−+ có 7 điểm cực trị.

Câu13. (THPTNguyễnTấtThành-YênBái-2018) Cóbaonhiêugiátrị nguyêncủathamsố m để hàm số 32 3 yxxm =−+ có 5 điểm cực trị? A. 5 B. 3 C. 6 D. 4

Lờigiải Hàm số 32 3 yxxm =−+ có 5 điểm cực trị ⇔ đồ thị hàm số 32 3 yxxm =−+ có hai điểm cực trị và nằm về hai phía của trục hoành ⇔ phương trình () 32301xxm−+= có ba nghiệm phân biệt.

Xét bbt của hàm số 32 3 yxx =−

2 0 360 2 x yxx x

=  ′ =−=   = 

Từ đó ta được () 1 có ba nghiệm phân biệt 4004 mm ⇔−<−<⇔<< . Vậy có 3 giá trị nguyên của m thỏa mãn.

Câu14. (ChuyênNguyễnThị MinhKhai-SócTrăng-2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 53 32560 yxxxm =−++ có 7 điểm cực trị?

A. 42 B. 21 C. 40 D. 20

Lờigiải

2 =− yfxm có 5 điểm cực trị khi và chỉ khi A. () 4;11 ∈ m . B. 11 2; 2  ∈   m . C. 3 = m . D. 11 2; 2  ∈   m . Lờigiải Từ BBT của hàm số () = yfx ta có bảng biến thiên của hàm số () 2 =− yfxm như sau

Đồ thị hàm số () 2 =− yfxm gồm hai phần:

+ Phần đồ thị của hàm số () 2 =− yfxm nằm phía trên trục hoành.

+ Phần đối xứng với đồ thị của hàm số () 2 =− yfxm nằm phía dưới trục hoành qua trục Ox

Do đó, đồ thị hàm số () 2 =− yfxm có 5 điểm cực trị khi và chỉ khi

()() 421120 mm −−< 11 2; 2 m  ⇔∈   .

Câu16. (THPTNguyễnHuệ -TtHuế -2018) Hình vẽ bên là đồ thị của hàm số ()yfx = . Gọi S là tập hợp các giá trị nguyên dương của tham số m để đồ thị hàm số () 2 yfxm =−+ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng A. 15 B. 18 C. 9 D. 12

Lờigiải

Cách 1: dùng đồ thị.

- Nhận thấy: số giao điểm của ()() : Cyfx = với Ox bằng số giao điểm của ()() 1 :2Cyfx=− với Ox

Vì 0 m > nên ()() 2 :2 Cyfxm =−+ có được bằng cách tịnh tiến ()() 1 :2Cyfx=− lên trên m đơn vị

- Đồ thị hàm số () 2 yfxm =−+ có được bằng cách lấy đối xứng qua trục hoành Ox phần đồ thị () 2C nằm phía dưới trục Ox và giữ nguyên phần phía trên trục Ox

- Lại do m ∗ + ∈ ℤ nên {} 3;4;5 m ∈ hay {} 3;4;5 S =

Vậy tổng giá trị tất cả các phần tử của S bằng 12.

Câu17. (Sở HưngYên-2018) Cho hàm số 32()3 fxxxm =−+ với [] 5;5 m ∈− là tham số. Có bao nhiêu giá trị nguyên của m để hàm số ()fx có đúng ba điểm cực trị A. 3 B. 0 C. 8 D. 6 Lờigiải

Xét hàm số 32()3 gxxxm =−+ có 2 0 '()0360 2 x gxxx x =  =⇔−=⇔  = 

Bảng biến thiên

+ Trường hợp 1: 03 m << : đồ thị hàm số có 7 điểm cực trị (loại).

+ Trường hợp 2: 3 m = : đồ thị hàm số có 5 điểm cực trị (thỏa mãn).

+ Trường hợp 3: 36 m << : đồ thị hàm số có 5 điểm cực trị (thỏa mãn).

+ Trường hợp 4: 6 m ≥ : đồ thị hàm số có 3 điểm cực trị (loại).

Vậy 36 m ≤< Do m ∗ + ∈ ℤ nên {} 3;4;5 m ∈ hay {} 3;4;5 S = .

Vậy tổng giá trị tất cả các phần tử của S bằng 12

* Cách 2: đạo hàm hàm số hợp.

- Ta có: () 2 yfxm =−+ () 2 2 fxm=−+ 

- Xét ()20 fx ′ −= () 1

′ −+− ′  = −+  

Từ bảng biến thiên ta thấy để hàm số ()fx có đúng ba điểm cực trị thì đồ thị hàm số ()gx phải có đúng một giao điểm hoặc tiếp xúc với Ox .

Điều kiện này tương đương với 00 404 mm mm ≤≤ ⇔  −+≥≥  . Kết hợp điều kiện [] 5;5 m ∈− ta có {} 5;4;3;2;1;0;4;5 m ∈−−−−− . Vậy có 8 giá trị thoả mãn.

() () () () 2

2.2 2 fxmfx y fxm

+ Do phương trình () 0 fx ′ = có 3 nghiệm phân biệt nên phương trình ()20 fx ′ −= cũng có 3 nghiệm phân biệt.

- Xét ()20fxm−+= () 2 fxm⇔−=− () 2

+ Nếu 63 m −<−<− 36 m ⇔<< thì phương trình () 2 có 2 nghiệm phân biệt khác 3 nghiệm của () 1

+ Nếu 3 m −=− 3 m ⇔= thì () 2 có 3 nghiệm phân biệt (trong đó có 2 nghiệm đơn khác 3 nghiệm của () 1 và 1 nghiệm kép trùng với 1 nghiệm của () 1 )

Tóm lại : với 36 m ≤< thì hai phương trình () 1 và () 2 có tất cả 5 nghiệm bội lẻ phân biệt và y ′ đổi dấu khi x đi qua các nghiệm đó, hay đồ thị hàm số () 2 yfxm =−+ có 5 điểm cực trị.

Câu18. (ChuyênHùngVương-BìnhDương-2018) Cho hàm số ()yfx = có bảng biến thiên như sau. Đồ thị hàm số ()20172018 yfx=−+ có bao nhiêu điểm cực trị? A. 2 B. 3 C. 5 D. 4 Lờigiải Có () 2017 =−yfx bằng cách tịnh tiến sang bên phải 2017 đơn vị ta có bảng biến thiên của hàm số () 2017 yfx=−

Tịnh tiến đồ thị hàm số () 2017 fx lên trên 2018 đơn vị và lấy trị tuyệt đối ta có bảng biến thiên của hàm số ()20172018 yfx=−+

Từ đồ thị hàm số của ()fx ′ suy ra ()fx ′ cùng dấu với

23 0 xx<<

Suy ra: ()fx ′ cùng dấu với ()()() 123 xxxxxx

Từ bảng biến thiên, suy ra hàm số có 3 cực trị.

Câu19. (Chuyên Ngữ -Hà Nội -2018) Hàm số ()fx có đạo hàm ()fx ′ trên ℝ . Hình vẽ bên là đồ thị của hàm số ()fx ′ trên ℝ . Hỏi hàm số () 2018 yfx=+ có bao nhiêu điểm cực trị?

A. 5 B. 3 C. 2 D. 4 Lờigiải

Cách1: Từ đồ thị hàm số của ()fx ′ ta thấy ()fx có hai cực trị dương nên hàm số ()yfx = lấy đối xứng phần đồ thị hàm số bên phải trục tung qua trục tung ta được bốn cực trị, cộng thêm giao điểm của đồ thị hàm số () 2018 yfx=+ với trục tung nữa ta được tổng cộng là 5 cực trị

Do 1 0 xx−> nên ( )( ) () 22 2

′ ′′′ == cùng dấu với ()() 23 2 . x xxxx x .

x yfxxfx x

Vậy hàm số () 2018 yfx=+ có 5 cực trị

Câu20. (Sở-Nam Định-2018) Cho hàm số ()yfx = có bảng biến thiên như hình vẽ

Đồ thị hàm số () 2 yfxm =− có 5 điểm cực trị khi và chỉ khi

A. () 4;11 m ∈ . B. 11 2; 2 m  ∈  . C. 3 m = . D. 11 2; 2 m  ∈   . Lờigiải

Từ bảng biến thiên ta có đồ thị hàm số ()yfx = có hai điểm cực trị Để đồ thị hàm số () 2 yfxm =− có 5 điểm cực trị thì đồ thị ()yfx = cắt đường thẳng 2 ym = tại 523 −= điểm phân biệt 4211 m ⇔<< 11 2 2 m ⇔<<

Câu21. (Sở HưngYên-2021) Gọi X là tập hợp các số nguyên [] 2021;2021 m ∈− sao cho đồ thị hàm số () 32 21 yxmxmxm =−+++ có 5 điểm cực trị. Tổng các phần tử của X là A. 0 B. 4036 C. 1 D. 1 Lờigiải ChọnC +) Xét hàm số ()()32 21 fxxmxmxm =−+++

Ta có ()() 2 3221 fxxmxm ′ =−++ () 2 2 2 13 21330, 24 mmmm  ′ ∆=+−=+++>   với mọi m ∈ ℝ

Suy ra hàm số ()fx luôn có 2 điểm cực trị, với mọi m ∈ ℝ +) ()()32 0210fxxmxmxm =⇔−+++= () 1

′ ∆=+> ⇔  −≠ 

Hàm số đã cho có 5 điểm cực trị ⇔ phương trình ( )1 có 3 nghiệm phân biệt ⇔ phương trình ( )2 có 2 nghiệm phân biệt, khác 1 2 0 130 mm m

m m m

1 0 1 3

 <−   >  ⇔   ≠  

Vì m ∈ ℤ và [ ]2021;2021 m ∈− nên { }2021;2020;...;2;1 m ∈±±± .

Suy ra { }2021;2020;...;2;1 X =±±± .

Vậy tổng các phần tử của tập X bằng 1.

Dạng2.Số điểmcựctrị củahàmhợp

Bàitoán: Cho hàm số ()yfx = (Đề có thể cho bằng hàm, đồ thị, bảng biến thiên của

()() ,' fxfx ). Tìm số điểm cực trị của hàm số ()yfu = trong đó u là một hàm số đối với x

Ta thực hiện phương pháp tương tự xét số điểm cực trị của hàm số ()yfx =

Bước1. Tính đạo hàm ()''.' yufu =

Bước2. Giải phương trình () '0 '0 '0 u y fu =  =⇔  = 

Bước3.Tìm số nghiệm đơn và bội lẻ hoặc các điểm mà ' y không xác định. Kếtluận

Câu1. (Đề Tham Khảo 2020 Lần 1) Cho hàm số bậc bốn ()yfx = có đồ thị như hình bên. Số điểm cực trị của hàm số () () 32 3 gxfxx =+ là A. 5 . B. 3 . C. 7 . D. 11. Lờigiải ChọnC Từ đồ thị ta có bảng biến thiên của hàm số ()yfx = như sau x

Ta có đồ thị của hàm () 32 3 hxxx =+ như sau

Từ đồ thị ta thấy: Đường thẳng ya = cắt đồ thị hàm số ()yhx = tại 1 điểm.

Đường thẳng yb = cắt đồ thị hàm số ()yhx = tại 3 điểm.

Đường thẳng yc = cắt đồ thị hàm số ()yhx = tại 1 điểm.

Như vậy phương trình () 0 gx ′ = có tất cả 7 nghiệm đơn phân biệt.

Vậy hàm số () () 32 3 gxfxx =+ có 7 cực trị.

Câu2. (Mã101-2019) Cho hàm số ()yfx = , bảng biến thiên của hàm số ()' fx như sau:

Số điểm cực trị của hàm số () 2 2 yfxx =− là A. 9. B. 3. C. 7. D. 5. Lờigiải ChọnC Ta có () () 2 21.2 yxfxx ′′ =−−

Phương trình (1) vô nghiệm, các phương trình (2),(3),(4) đều có hai nghiệm phân biệt khác 1 và do ,, bcd đôi một khác nhau nên các nghiệm của phương trình (2),(3),(4) cũng đôi một khác nhau. Do đó () 2 20fxx ′ −= có 6 nghiệm phân biệt. Vậy 0 y ′ = có 7 nghiệm phân biệt, do đó số điểm cực trị của hàm số () 2 2 yfxx =− là 7.

Câu3. (Mã104-2019) Cho hàm số ()fx , bảng biến thiên của hàm số ()fx ′ như sau:

Câu4. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hàm số ()fx có đạo hàm liên tục

hàm số ()yfx ′ = như hình vẽ bên. Hàm số ()2244 yfxxxx =+−− có bao nhiêu điểm cực trị

thuộc khoảng () 5;1 ?

Số điểm cực trị của hàm số () 2 44 yfxx =+ là A. 5. B. 9. C. 7. D. 3. Lờigiải ChọnC

Có () () () () 2 2 448444 fxxxfxx ′ ′ +=++ , () () () 2 2

x fxx fxx

1 2 440 440

 =− ′  +=⇔  ′ +=   .

A. 5 B. 4 C. 6 D. 3 Lờigiải ChọnA Đặt () ()2244 gxfxxxx =+−− ()() () ()() () 2 2 244242441 gxxfxxxxfxx′′′  =++−+=++− .

2 2 2

Từ bảng biến thiên trên ta có () () () () ()

xxa xxa fxx xxa xxa

44;1 441;0 440 440;1 441;

 +=∈−∞−  +=∈−  ′ +=⇔  +=∈   +=∈+∞ 

2 1 2 2 2 2 3 2 4

. (1)

Xét () 2 44 gxxx =+ , () 84gxx ′ =+ , () 1 0 2 gxx ′ =⇔=− ta có bảng biến thiên

Kết hợp bảng biến thiên của ()gx và hệ (1) ta thấy:

Phương trình () 2 1 44;1 xxa+=∈−∞− vô nghiệm.

Phương trình () 2 2 441;0 xxa+=∈− tìm được hai nghiệm phân biệt khác 1 2

Phương trình () 2 2 440;1 xxa+=∈ tìm được thêm hai nghiệm mới phân biệt khác 1 2 .

Phương trình () 2 2 441; xxa+=∈+∞ tìm được thêm hai nghiệm phân biệt khác 1 2 .

Vậy hàm số () 2 44 yfxx =+ có tất cả 7 điểm cực trị.

x xx gx xx xxa

+=   +=−  ′ =⇔  +=  +=∈  

Ta có () ()

240 44(1) 0 40(2) 41;5(3)

. Xét phương trình () 2 41;5xxa+=∈ , ta có BBT của hàm số 2 4 yxx =+ trên () 5;1 như sau:

Suy ra (1) có nghiệm kép 2 x =− , (2) có 2 nghiệm phân biệt 4;0xx=−= , (3) có 2 nghiệm phân biệt 12 ; xxxx == khác 2;0;4 . Do đó phương trình () 0 gx ′ = có 5 nghiệm trong đó có 2 x =− là nghiệm bội ba, các nghiệm 4;0xx=−= ; 12 ; xxxx == là các nghiệm đơn. Vậy ()gx có 5 điểm cực trị

Câu5. (Chuyên Hưng Yên - 2020) Cho hàm số ()yfx = có đạo hàm đến cấp hai trên ℝ và có bảng xét dấu của hàm số ()' yfx = như hình sau: Hỏi hàm số ()() 3 2 123 3 x gxfxxx =−+−+ đạt cực tiểu tại điểm nào trong các điểm sau?

A. 3 x = B. 0 x = C. 3 x =− D. 1 x = Lờigiải

Vây hàm số () () 3 =+ gxfxx đạt cực tiểu tại điểm 0 0 = x .

Câu7. (ChuyênKHTN-2020) Cho hàm số () = yfx liên tục trên ℝ , có đồ thị ()′ fx như hình vẽ

y

y=f'(x)

O 2x

Số điểm cực tiểu của hàm số () () 2 =−+ gxfxx là A. 1 B. 4 C. 3 D. 2 Lờigiải ChọnA

Ta có () () ()() () 2 2 21 ′′ =−+  =−+−+ gxfxxgxxfxx . ()() () () 2 2 2 2

 =  −+=  ′′  =⇔−+−+=⇔⇔−+=   ′ −+=    −+=  

x x gxxfxxxx fxx xx

1 2102 02100 0 2

 =   ⇔=   =  

x x x

1 2 1 0

Do đó ()() () () ()

 −+>   ′ −+>   ′′ >⇔−+−+>⇔  −+<   ′ −+<  

x fxx gxxfxx x fxx 2 2 2

210 0 0210 210 0

2 2 2

  < <           −+> >   <           < −+< ⇔⇔⇔       <<      > >          << <−+<  

1 1 2 2 2 1 0 0 0 1 1 2 1 1 2 2 01 02

x x xx x x x xx x x x x xx Bảng biến thiên x −∞ 0 1 2 1 +∞

()gx

Vậy hàm số có 1 điểm cực tiểu.

Câu8. (Chuyên Lam Sơn - 2020) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ , bảng biến thiên

của hàm số ()' fx như sau:

Câu9. (Sở BắcGiang-2018) Cho hàm số ()yfx = có đúng ba điểm cực trị là 2;1;0

liên tục trên ℝ . Khi đó hàm số () 2 2 yfxx =− có bao nhiêu điểm cực trị?

A. 3 B. 8 C. 10 D. 7 Lờigiải

Số điểm cực trị của hàm số () 2 2 yfxx =+ là A. 4. B. 5. C. 1. D. 7. Lờigiải ChọnB

Ta có () () () () 2 2 1 '22'20 '201 x yxfxx fxx

=−   =++=⇔ +=  

Vì hàm số ()yfx = có đúng ba điểm cực trị là 2;1;0 và có đạo hàm liên tục trên ℝ nên () 0 fx ′ = có ba nghiệm là 2;1;0 (ba nghiệm bội lẻ). Xét hàm số () 2 2 yfxx =− có () () 2 22.2 yxfxx ′′ =−− ; () () 2 022.20yxfxx ′′ =⇔−−= 2 2 2

=   −=−  ⇔  −=−   −= 

x xx xx xx

1 22 21 20

=   ⇔=   = 

x x x

1 0 2

Do 0 y ′ = có một nghiệm bội lẻ ( 1 x = ) và hai nghiệm đơn ( 0 x = ; 2 x = ) nên hàm số () 2 2 yfxx =− chỉ có ba điểm cực trị

Câu10. (Mã102-2019) Cho hàm số ()fx , bảng biến thiên của hàm số ()' fx như sau

2 2 2

Đồ thị hàm số 2 2 yxx =+ có dạng

xxa xxb xxc

Từ BBT ta thấy phương trình () () ()() ()

 +=<−  ⇔+=∈−   +=>  

212 121;13 214

.

Từ đồ thị hàm số 2 2 yxx =+ ta thấy phương trình (2) vô nghiệm; phương trình (3) ; phương trình (4) đều có 2 nghiệm phân biệt. Do đó '0 y = có 5 nghiệm đơn phân biệt. Vậy hàm số () 2 2 yfxx =+ có 5 điểm cực trị

Số điểm cực trị của hàm số () 2 2 yfxx =+ là A. 9 B. 5 C. 7 D. 3 Lờigiải ChọnC

Ta có () () 2 22 2 2

x xxaa yxfxxxxbb xxcc xxdd

220 2,1 '22'202,10 2,01 2,1

+=   +=<−   =++=⇔+=−<<  +=<<   +=> 

Xét hàm số () 2 44 gxxx =− , ta có () 1 840 2 gxxx ′ =−=⇔=

Bảng biến thiên

Từ bảng biến thiên của ()gx ta có: Vì () ;1 a ∈−∞− nên () 1 vô nghiệm. Vì () 1;0 b ∈− nên () 2 có 2 nghiệm phân biệt. Vì () 0;1 c ∈ nên () 3 có 2 nghiệm phân biệt. Vì () 1; d ∈+∞ nên () 4 có 2 nghiệm phân biệt.

Vậy hàm số () 2 44 yfxx =− có 7 điểm cực trị

Cáchkhác: Ta có: () () 2 84.44 yxfxx ′′ =−−

840 084.440 440 x yxfxx fxx −=  ′′ =⇔−−=⇔  ′ −=  

() () () 2 2

+ 1 840 2 xx−=⇔=

 −=<−  −=−<<  ′ −=⇔  −=<<  −=>  

xxaa xxbb fxx xxcc xxdd

4411 44102 440 44013 4414

2 2 2 2 2

+ () ()() ()() ()() ()()

+ Phương trình 22 44440 xxmxxm −=⇔−−= có nghiệm khi 440 m ′ ∆=−≥ hay 1 m ≤

Từ đó, ta có phương trình () 1 ; () 2 ; () 3 luôn có hai nghiệm phân biệt. Phương trình () 4 vô nghiệm.

Do đó, hàm số đã cho có 7 cực trị.

Câu12. (ChuyênAnGiang-2018) Cho hàm số ()yfx = Đồ thị của hàm số ()yfx ′ = như hình bên.

Hàm số () () 2gxfx = có bao nhiêu điểm cực trị?

A. 4 B. 3 C. 5 D. 2

Từ đồ thị ()yfx ′ = ta có () 2 0 0 1 3

x x fx x x

=−   =  ′ =⇔  =  = 

;

() 3 0 21 x fx x >  ′ >⇔ −<< ; () 2 0 13 x fx x <−  ′ <⇔  <<  .

Ta có () () 2 2 gxxfx ′′ = ; () () 2 2 2 2

x x x x gxx fx x x x

Ta có () 2 2 2

=   =  =  =   ′ =⇔⇔⇔=±    ′ = =     =±   = 

0 00 1 01 03 3 0

 −<<  ≠   <<  ′ >⇔⇔   > >    <−  

x x x fx x x x

11 0 01 0 3 3 3

Ta có bảng biến thiên Từ bảng biến thiên ta có hàm số () () 2gxfx = có 5 điểm cực trị

Câu13. (THPT Lê Văn Thịnh Bắc Ninh 2019) Cho hàm số ()yfx = xác định trên ℝ và hàm số ()yfx ′ = có đồ thị như hình vẽ. Tìm số điểm cực trị của hàm số () 2 3 yfx=−

A. 4 B. 2 C. 5 D. 3 Lờigiải ChọnD

Quan sát đồ thị ta có đổi dấu từ âm sang dương qua nên hàm số có một điểm cực trị là 2 x =− ( ) yfx ′ = 2 x =− ( ) yfx =

Ta có ()() 2232.3yfxxfx ′ ′′ =−=−   2 2

0 0 0321 2 31

x x xx x x

 = =   =⇔−=−⇔=±   =± −=   Mà 2 x =± là nghiệp kép, còn các nghiệm còn lại là nghiệm đơn nên hàm số () 2 3 yfx=− có ba cực trị

Câu14. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hàm số ()fx có đạo hàm là ()fx ′ . Đồ thị của hàm số ()yfx ′ = như hình vẽ bên. Tính số điểm cực trị của hàm số () 2 yfx = trên khoảng

() 5;5 .

A. 2 . B. 4 . C. 3 . D. 5 . Lờigiải

Xét hàm số () () () ()22 2 gxfxgxxfx ′′ =  = .

0 0 0 x gx fx =  ′ =⇔  ′ =   2 2

() () 2

=  =   ⇔=⇔   =±   = 

x x x x x

0 0 0 2 2

Ta có bảng xét dấu: Từ đó suy ra hàm số () 2 yfx = có 3 điểm cực trị.

Câu15. (ChuyênVinh-2018) Cho hàm số bậc bốn ()yfx = . Hàm số ()yfx ′ = có đồ thị như hình vẽ bên. Số điểm cực đại của hàm số ( ) 2 22yfxx=++ là

A. 1 B. 2 C. 4 D. 3

Từ bảng xét dấu của ()gx ′ suy ra hàm số có 5 điểm cực trị

Câu17. Cho hàm số ()yfx = xác định và liên tục trên ℝ có đồ thị như hình vẽ. Hàm số () () 2 24gxfxx=−− có bao nhiêu điểm cực tiểu?

A. 1. B. 3 . C. 2 . D. 4 . Lờigiải Chọn B. Ta có: ()() () 2 2124gxxfxx ′′ =−−− .

1 01240 240 x gxxfxx fxx =  ′′ =⇔−−−=⇔  ′ −−=   2 2

()() () () 2 2

=   =+ =     ⇔−−=−⇔=−     −−= =+    =− 

x x x xxx xx x x

1 13 1 24213 240 15 15

(Tất cả đều là nghiệm bội lẻ).

Ta chọn 2 x =− để xét dấu của ()gx ′ : ()()() 22.3.4gf ′′ −=−

Vì hàm số ()yfx = đồng biến trên khoảng () 0; +∞ do đó: ()40 f ′ >

Suy ra: ()20 g ′ −< .

Theo tính chất qua nghiệm bội lẻ ()gx ′ đổi dấu, ta có bảng xét dấy ()gx ′ như sau: x −∞ 15 13 1 13 + 15 + +∞ ( )gx ′ 0 + 00 + 00 +

Từ bảng xét dấu, suy ra hàm số ()ygx = có 3 điểm cực tiểu.

Câu18. (ĐặngThúcHứa-Nghệ An-2018) Biết rằng hàm số ()fx có đồ thị được cho như hình vẽ bên.

Tìm số điểm cực trị của hàm số ()yffx =  



BBT:

Dựa vào BBT suy ra hàm số ()yffx =   có bốn điểm cực trị

Câu19. (Sở Bình Phước - 2018) Cho hàm số ()yfx = liên tục và có đạo hàm trên [] 0;6 Đồ thị của hàm số ()yfx ′ = trên đoạn [] 0;6 được cho bởi hình bên dưới. Hỏi hàm số () 2 yfx =  có tối đa bao nhiêu cực trị.

Do đó, hàm số () 2 yfx =  có tối đa 7 điểm cực trị nên có tối đa 7 cực trị

Câu20. Biết rằng hàm số ()fx có đồ thị được cho như hình vẽ bên. Tìm số điểm cực trị của hàm số ()yffx =   ?

y -4

A. 3 . B. 7 . C. 6 . D. 4 . Lờigiải

Ta có ()() 2 yfxfx ′′ = nên () () 0 0 0 fx y fx  = ′ =⇔  ′ =  

Từ đồ thị ta suy ra () 0 fx = có tối đa 4 nghiệm, () 0 fx ′ = có tối đa 3 nghiệm.

x

A. 5. B. 4. C. 3. D. 6. Lờigiải ChọnB

Ta có: () () ()()() '. yffxfxffx ′ ′′ ==  ; () () () 0 '0 0 fx y ffx  ′ =  =⇔  ′ = 

+ () 0 0 2 x fx x  = ′ =⇔  =  vì hàm số ()fx có hai điểm cực trị 0;2xx==

+ () () () () 0 0 2 fx ffx fx  = ′  =⇔ =  

2 O x

y y=2 a -4

2 2 O b

Quan sát đồ thị ta thấy phương trình () 0 fx = có một nghiệm bội chẵn 0 x = và một nghiệm đơn hoặc bội lẻ 2 xa=> Kẻ đường thẳng 2 y = nhận thấy phương trình () 2 fx = có một nghiệm đơn hoặc bội lẻ xba => Do đó y ′ có các điểm đổi dấu là 0;2,, xxxaxb ==== . Vậy hàm số có 4 điểm cực trị.

điểm cực trị của hàm số ()()()gxffx = là.

A. 3. B. 7. C. 6. D. 5. Lờigiải ChọnC

Ta có ()()()()''.' gxfxffx = . () () () () '0 '0 '0 fx gx ffx

=  =⇔  =   () 0 '0 2 x fx x =  =⇔  =  . () () ()() ()() 0* '0 2** fx ffx fx =  =⇔  =  

Dựa vào đồ thị suy ra:

Nhìn bảng biến thiên ta thấy hàm số ()()()gxffx = có6 cực trị

Câu22. (Sở GDBắcNinh-2019) Cho hàm số ()yfx = có đồ thị như hình vẽ

Biết tất cả các điểm cực trị của hàm số ()yfx = là 2 ; 0 ; 2 ; a ; 6 với 46 a << . Số điểm cực trị của hàm số () 62 3 yfxx =− là A. 8. B. 11. C. 9. D. 7. Lờigiải ChọnB Từ đồ thị ta có -2; 0; 2; a ; 6 là tất cả các nghiệm của ()fx ′ .

Tacó: () () ()() 62562 3663 yfxxxxfxx ′ ′′ =−=−−

=−   = 

Phương trình (*) có hai nghiệm 1 2 x x

=−<<   =<<   =>  () '0gx = có nghiệm

xmn xnn xpp

10 01 2

() 5 62

660 '0 30 xx y fxx  −= =⇔  ′ −=  

62 62 62 62 62

0,1 32 30 32 3 36

xx xx xx xx xxa xx

==±   −=−   −=  ⇔  −=  −=   −= 

==±   =±   ==±  ⇔  =±  =±>   =±> 

Ta có bảng biến thiên của hàm số () 62 3 gxxx =−

xx x xx x xmm xnnm

0,1 1 0,3 2 ,2 ,

4

1 0 2

. Bảngbiếnthiên

=−   =   =  =   =  =  Trang 18

x xm x xn x xp

Dựa vào bảng biến thiên của hàm số () 62 3 gxxx =− , ta suy ra 1± là nghiệm kép của phương trình 6232xx−=− và 0 là nghiệm kép của phương trình 6230xx−= . Do đó 1± và 0 là nghiệm kép của () 62 3 fxx ′ . Do vậy 1± và 0 là nghiệm bội ba của y ′ Các nghiệm khác 1± và 0 của y ′ đều là nghiệm đơn. Vậy hàm số đã cho có 11 cực trị

Câu23. (Toán Học Tuổi Trẻ 2019) Cho hàm số (x) f xác định trên ℝ và có đồ thị ()fx ′ như hình vẽ bên. Đặt ()() gxfxx =− . Hàm số đạt cực đại tại điểm thuộc khoảng nào dưới đây?

A. 3 ;3 2         B. () 2;0 C. () 0;1 D. 1 ;2 2         Lờigiải

x gxfxgxfxx x

 =   ′′′′=−=⇔=⇔=−   = 

Ta có ()()()() 1 1;011 2

Bảng xét dấu của ()gx ′ :

+ 0 2 0 -1 1 + x g'(x)0 -∞ +∞

Từ bảng xét dấu nhận thấy ()gx đạt cực đại tại ()12;0 x =−∈− .

Câu24. (ThptHoàngHoaThámHưngYên2019) Cho hàm số (1)yfx ′ =− có đồ thị như hình vẽ.

Hàm số () 24fxx y π = đạt cực tiểu tại điểm nào? A. 1 x = . B. 0 x = . C. 2 x = . D. 1 x =− . Lờigiải:

nên () 2 fx ′ = 2 0 1

x x x

=−   ⇔=   =  . Do 2 x =− và 1 x = là nghiệm bội chẵn nên ta có bảng biến thiên sau: x −∞ 2 0 1 +∞ y ′ 00 + 0 + y +∞ +∞

Từ bảng biến thiên ta có hàm số đạt cực tiểu tại 0 x = Câu25. (THPTMinhChâuHưngYên2019) Cho hàm số ()yfx = có đạo hàm liên tục trên R và đồ thị hàm số ()yf'x = như hình vẽ bên. Số điểm cực trị của hàm số () yfx20172018x2019 =−−+ là. A. 3 B. 4 C. 1 D. 2 Lờigiải ChọnC

Ta có: ()()() fx20172018x20190fx201720180fx20172018 ′ ′′ −−+=⇔−−=⇔−= 

Dựa vào đồ thị hàm số ()yf'x = suy ra phương trình () fx20172018 ′ −= có 1 nghiệm đơn duy nhất. Suy ra hàm số () yfx20172018x2019 =−−+ có 1 điểm cực trị.

Câu26. (ChuyênTháiBình-2018) Cho hàm số '()yfx = có đồ thị như hình vẽ dưới đây:

ủa hàm số 2()1()e5fxfx y + =+ .

A. 1. B. 2 . C. 4 . D. 3 . Lờigiải

Ta có 2()1()e5fxfx y + =+ ()()2()1() 2.e.5ln5 fxfxyfxfx + ′′′ =+ ()() 2()1() 2e5ln5 fxfx fx + ′ =+

Nhận xét 2()1() 2e5ln50, fxfx x + +>∀ làm cho ()fx xác định nên dấu của y ′ phụ thuộc hoàn toàn vào ()fx ′ .

Vì vậy do ()fx ′ đổi dấu 3 lần nên số điểm cực trị của hàm số 2()1()e5fxfx y + =+ là 3

Câu27. (THPTQuỳnhLưu-Nghệ An-2018) Cho hàm số ()yfx = có bảng biến thiên như sau

Hàm số () 21yfx=+ đạt cực tiểu tại điểm A. 2 x = . B. 0 x = . C. 1 x = . D. 5 x = . Lờigiải

Ta có: () 21yfx=+  () 2 yfx ′′ = .

Suy ra: Điểm cực tiểu của hàm số ()yfx = cũng chính là điểm cực tiểu của hàm số () 21yfx=+ .

Vậy: Hàm số () 21yfx=+ đạt cực tiểu tại điểm 0 x =

=−  ′′′ =⇔+=⇔=−⇔ 

Đặt ()() 2 gxfxx =+ suy ra ()()() 0

1 0202 1 x gxfxfx xx

Trên () 0 1; x thì ()()220fxfx ′′ >−⇔+> .

Trên () 0 ; x +∞ thì ()()220fxfx ′′ <−⇔+< .

Vậy hàm số ()() 2 gxfxx =+ có 1 cực trị

Câu29. Cho hàm số ()fx có đồ thị ()fx ′ như hình vẽ dưới. Hàm số ()() 3 2 252001 3 x gxfxxx =−+−+ có bao nhiêu điểm cực trị?

A. 3 B. 1 C. 2 D. 0 Lờigiải ChọnC Có ()() 2 45gxfxxx ′′ =−+− ()() 2 045 fx gxxx ′ =−  =⇔ + ′

Ta có đồ thị hàm số 2 45yxx=−+ và đồ thị hàm ()yfx ′ = như hình vẽ dưới

Quan sát hình vẽ ta thấy () 0 gx ′ = có 3 nghiệm phân biệt trong đó chỉ có 1 nghiệm bội chẵn

Câu30. Cho hàm số ()yfx = có đạo hàm trên ℝ và không có cực trị, đồ thị của hàm số ()yfx = là

đường cong của như hình vẽ dưới đây.

Xét hàm số () ()() 2 2 1 2.2 2 hxfxxfxx =−+   . Mệnh đề nào sau đây đúng?

A. Đồ thị của hàm số ()yhx = có điểm cực tiểu là () 1;0 M

B. Hàm số ()yhx = không có cực trị

C. Đồ thị hàm số ()yhx = có điểm cực đại là () 1;2 N .

D. Đồ thị hàm số ()yhx = có điểm cực đại là () 1;0 M . Lờigiải

ChọnA

Theo bài ra ta có

( ) ( ) ( ) ( ) ( ) '.22.4 hxfxfxfxxfxx ′′ =−++ ( ) ( ) ( ) ( ) ( ) 222 fxfxxfxx ′ =−−− () () () ()22 fxfxx ′ =−−

Từ đồ thị ta thấy ()yfx = nghịch biến nên () '0fx < suy ra () 20 fx ′ −<

Suy ra ()()020hxfxx ′ =⇔−=

Từ đồ thị dưới ta thấy () 201fxxx−=⇔= .

Ta có bảng biến thiên:

Suy ra đồ thị của hàm số ()yhx = có điểm cực tiểu là () 1;0 M .

Lờigiải

ChọnD

Suy ra () 1 2 2

x gxxx x

1 '12660 1 2

=   =−−=⇔  =−  Đồ thị hàm số lên - xuống – lên. Hàm số ()() 2 '361gxfxxx =−−+ đạt cực tiểu, cực đại lần lượt tại 12 1 1, 2 x x ==− . Suy ra ()()() 32 111 1.243614.3.6.111 222 mgg   ==−−+−−+=−     

hình vẽ. Hàm số () 2 yfxx =− có bao nhiêu điểm cực trị? A. 2 . B. 1. C. 0 . D. 3 . Lờigiải ChọnB Đặt ()() gxfx ′ = () 32 gxaxbxcxd =+++ Đồ thị hàm số ()gx đ

00 20 22 dd abcdb abcdac ==   +++=−⇔=  −+−+=+=−  Do đó: ()()

32 3

x −∞ +∞ 1 +∞ +∞ ( )hx 0 A. 0 m = B. 371 16 m = C. 1 16 m = D. 11 m =−

()()() 2 3 23212yfxxxxx ′′ =−=−−=+−

1 0 2 x y x

=  ′ =⇔  = 

Dấu của y ′

+ 0 0 2 x y' 1 + ∞ ∞

Do đó hàm số có 1 điểm cực trị.

Câu33. (KimLiên-HàNội2019) Cho hàm số ()yfx = có đạo hàm trên ℝ . Biết hàm số ()yfx =′ có đồ thị như hình vẽ

Hàm số () 2 yfxx =− có bao nhiêu cực trị? A. 3 B. 2 C. 0 D. 1 Lờigiải ChọnB

Hàm số ()() gxfxx =+ đạt cực tiểu tại điểm

A. 1 x = B. 2 x =

C. Không có điểm cực tiểu. D. 0 x = . Lờigiải ChọnA

Xét hàm số ()() gxfxx =+ có ()() 1 gxfx′=′+ Dựa vào đồ thị hàm số ()yfx =′ có:

() 0 gx′= () 1 fx ⇔′=− 0 1 2

x x x

=   ⇔=  =   Bảng biến thiên

Từ đó suy ra hàm số ()ygx = đạt cực tiểu tại điểm 1 x =

Câu34. Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ và đồ thị hàm số ()yfx ′ = là parabol như hình bên dưới.

Ta có () 2 yfx ′′ =− . () 020yfx ′′ =⇔−= () 2 fx ′ ⇔= 1

0 1 x xx =  ⇔  =>  .

Dựa vào đồ thị ()yfx ′ = và đường thẳng 2 y = , ta có bảng biến thiên sau Vậy hàm số () 2 yfxx =− có hai điểm cực trị

Câu35. Cho hàm số đa thức ()yfx = có đạo hàm trên ℝ , ()00 f < và đồ thị hình bên dưới là đồ thị của đạo hàm ()fx ′ . Hỏi hàm số ()() 3 gxfxx =+ cóbao nhiêu cực trị?

A. 4. B. 5. C. 3. D. 6. Lờigiải ChọnB

Đặt ()() 3 hxfxx =+ ()() 3 hxfx ′′ =+ ()()()0303hxfxfx ′′′ =⇔+=⇔=−

Theo đồ thị của hàm số ()fx ′ thì phương trình () 3 fx ′ =− có 4 nghiệm {} 1;0;1;2

Ta có bảng biết thiên

0 x h'x() hx()

Khẳng định nào sau đây là đúng?

A. Hàm số 2 () yfxxx =−− đạt cực đại tại 0 x =

B. Hàm số 2 () yfxxx =−− đạt cực tiểu tại 0 x = C. Hàm số 2 () yfxxx =−− không đạt cực trị tại 0 x =

D. Hàm số 2 () yfxxx =−− không có cực trị Lờigiải ChọnA

Xét hàm số () 2 () gxfxxx =−−

Tập xác định: D = ℝ

Ta có ()() 21gxfxx ′′ =−−

1 1 +

Cho ()() 0 021 2 x gxfxx x =  ′′ =⇔=+⇔  =  .

+ 0 0

+ + ∞ + ∞

2 0 f0()

Theo bảng biến thiên ta có phương trình () 0 hx = có hai nghiệm 1 1; x <− và 2 1 x > (do có ()00 f < ) Khi đó ta có

Dựa vào đồ thị ta có: ()() 1130gf′′ =−< , ()() 3370gf′′ =−< nên 0 x = là nghiệm đơn và 2 x = là nghiệm kép. Bảng biến thiên

Từ bảng biến thiên ta có 0 x = là điểm cực đại.

+ 0 ∞ ∞ x2 + ∞ + ∞ x 1 0 0 f0()

Vậy hàm số ()() 3 gxfxx =+ có 5 cực trị.

0 x gx()=hx() Trang 28

1 1 + ∞ ∞

Câu37. (THPT Minh Khai) Cho hàm số Cho hàm số ()yfx = liên tục trên ℝ và hàm số ()() 2 222019gxfxxx =−++ . Biết đồ thị hàm số ()yfx ′ = như hình vẽ.

Số điểm cực trị của hàm số () x yg = là A. 5 B. 3 C. 2 D. 4 Lờigiải

Trang 27

∗ ()()222gxfxx ′′ =−+ , ()()01gxfxx ′′ =⇔=−

Đường thẳng 1 yx=− đi qua các điểm () 1 ;2 , () 1 ; 0 , () 3 ; 2

Từ bảng biến thiên ta suy ra 1 CDx =− .

Câu39. (THPT Hoàng Hoa Thám - Hưng Yên 2019) Cho hàm số ()yfx = có đạo hàm trên ℝ và có đồ thị là đường cong như hình vẽ Đặt () ()3()4 gxffx=+ . Tìm số cực trị của hàm số ()gx

Quan sát vào vị trí tương đối của hai đồ thị trên hình vẽ, ta có BBT của hàm số () x yg ′ = như sau

∗ Đồ thị hàm số () x yg = nhận trục Oy làm trục đối xứng nên từ BBT trên ta suy ra BBT của hàm số () x yg = như sau Vậy hàm số () x yg = có 5 điểm cực trị.

Câu38. Cho hàm số ()fx xác định trên ℝ và có đồ thị ()fx như hình vẽ

Đặt ()() gxfxx =− . Hàm số ()gx đạt cực đại tại điểm nào sau đây? A. 1. x = B. 2. x = C. 0 x = . D. 1. x =− Lờigiải

ChọnD

Ta có ()()() ''10'1 gxfxfx=−=⇔=

Từ đồ thị ta thấy đường thẳng 1 y = cắt đồ thị ()fx tại ba điểm có hoành độ là 1,1xx=−= và 2 x = Bảng biến thiên

A. 2. B. 8. C. 10. D. 6. Lờigiải ChọnB

Ta có: ()()()() ()()()() () () () '0 '3'.','03'.' '0 fx gxfxffxgxfxffx ffx

=  ==⇔⇔  =  

Từ đồ thị hàm số trên ta thấy: + Phương trình () '0fx = có 2 nghiệm phân biệt là 0; xx α == với () 1;3 α∈ . + Phương trình () () () () 0 '0 fx ffx fx α

=  =⇔  =  

+ Phương trình () 0 fx = có 3 nghiệm phân biệt khác 2 nghiệm trên. + Phương trình ()fx α = với () 1;3 α∈ có 3 nghiệm phân biệt khác các nghiệm trên.

Vậy phương trình () '0gx = có 8 nghiệm phân biệt và ()' gx đổi dấu qua các nghiệm.

Do đó hàm số ()gx có 8 điểm cực trị.

Câu40. (HSG 12 - Sở Quảng Nam - 2019) Cho hàm số (x) yf = có đạo hàm trên ℝ , đồ thị hàm số ()yfx = là đường cong ở hình vẽ. Hỏi hàm số () [] () 2 ()41hxfxfx=−+ có bao nhiêu điểm cực trị?

=>  =   ′′′ =−=⇔⇔=−   ′ =   =  Do đó, ta có bảng biến thiên: Suy ra đồ thị hàm số ()ygx = có ba điểm cực không nằm trên trục hoành và bốn giao điểm với Ox Vậy đồ thị hàm số ()() yhxgx == có số cực trị là 347 += Câu41. (THPT Thăng Long - Hà Nội - 2019) Cho hàm số ()yfx = , hàm số ()yfx ′ = có đồ thị như hình bên. Hàm số 25sin1(5sin1) ()23 24 xx gxf  =++   có bao nhiêu điểm cực trị trên khoảng (0;2) π

xaa fx gxfxfxfxx fx x Trang 32

A. 9 B. 7 C. 6 D. 8 Lờigiải ChọnB

=   ⇔   ′ =−    

x xx f

Ta có: () 5sin15 ()5coscos5sin1 22 x gxxfxx ′′ =+−   . () 5sin15 ()05coscos5sin10 22 x gxxfxx ′′ =⇔+−=   cos0 5sin15sin1 22

+) ()10 fx += () * ⇔ ()() 4 5110130 xx+−++= ⇔

x x x x

+≈   +≈   +≈−  +≈− 

11,278 10,606 10,606 11,278

Phươngtrìnhcóbốnnghiệm phânbiệt khác 0 +) ()() () ()() 1 423 211025103120200 tx fxxfxttttt =+ ′ +++=  −++−−=

432 3020402060 tttt ⇔−−++= ⇔

≈   ≈   ≈−  ≈− 

t t t t

1,199 0,731 0,218 1,045

Phươngtrìnhcóbốnnghiệm phânbiệt khác 0 vàkháccácnghiệm củaphươngtrình () * . Vậysố điểmcựctrị của hàm số ()gx là 9 Câu43. (Mã102-2020Lần1) Chohàmsố bậcbốn ()fx cóbảngbiếnthiênnhư sau: Số điểm cựctrị củahàm số ()()gxxfx=−  4 2 1 là A. 7 B. 8 C. 5 D. 9 Lờigiải ChọnC Tacó ()()()()()()() () 4 33 2 2.14112.1121 gxxfxxfxfxxfxfxxfx ′′ ′ =−+−−=−−+−  

x gxfx fxxfx

0 0101 12102

Vậy ()()() ()()()

 =  ′ =  −=   ′ −+−=  Phương trình () 1 có 4 nghiệm phân biệt Phương trình () 2 có ()()()()() 12121 fxxfxfxxfx ′′ −=−−  =−+ Từ bảng biến thiên suy ra hàm ()fx là bậc bốn trùng phương nên ta có () fxxx=−+− 42 361 thay vào ()()() 21 fxxfx ′ =−+ vô nghiệm Vậy hàm ()gx có 5 điểm cực trị

Câu44. (Mã103-2020Lần1) Cho hàm số bậc bốn ()fx có bảng biên thiên như sau:

Số điểm cực trị của hàm số 42 ()[(1)]gxxfx=− là A. 7 B. 5 C. 9 D. 11 Lờigiải

ChọnC

Ta có : 422 ()483()16(1) fxxxfxxx ′ =−+  =−

+TH3: (1)2.'(1)0 fxxfx+++= . Từ bảng biến thiên ta có hàm số thỏa mãn là 42 ()5102 fxxx=−+− () (1)2.'(1)0(1)2(1).'(1)2'(1)0 fxxfxhxfxxfxfx  +++=⇔=++++−+=

Với 1 tx=+ ta có: 4233 ()51022(2020)2(2020)0 htttttttt =−+−+−+−−+= ⇔ 432 4540504020 tttt −++−−=

Lập bảng biến thiên ta suy ra có 4 nghiệm 4 t  nghiệm x

Vậy có 9 cực trị

Bài toán tìm cực trị của hàm số ()()() gxfuxhx =+  

Bước1. Tìm cực trị của hàm số ()()() vxfuxhx =+  

Bước2. Sử dụng phương pháp biến đổi đồ thị hàm số trị tuyệt đối để tìm số cực trị của hàm số ()gx

Ta có 3 ()2.(1).[2(1).(1)] gxxfxfxxfx ′′ =−−+− 3 0 ()0(1)0 2(1).(1)0

 =  ′ =⇔−=   ′ −+−= 

Câu46. (Mã101–2020Lần2) Cho hàm số ()fx có ()00. f = Biết ()yfx ′ = là hàm số bậc bốn và có đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số () 3 () gxfxx =− là

x gxfx fxxfx

(1) (2) (3)

Phương trình (1) có 0 x = (nghiệm bội ba).

Phương trình (2) có cùng số nghiệm với phương trình ()0fx = nên (2) có 4 nghiệm đơn.

Phương trình (3) có cùng số nghiệm với phương trình : 422 2()(1).()02(483)16(1)(1)0 fxxfxxxxxx ′ ++=⇔−+++−= 432 2416321660 xxxx ⇔+−−+= có 4 nghiệm phân biệt. Dễ thấy 9 nghiệm trên phân biệt nên hàm số ()0gx = có tất cả 9 điểm cực trị.

Câu45. (Mã104-2020Lần1) Cho hàm số bậc bốn ()fx có bảng biến thiên như sau

A. 5. B. 4. C. 6. D. 3. Lờigiải ChọnA Xét () 3 () hxfxx =− Có () ()23 '3'1 hxxfx=− () ()() ()() 233 2 1 0310 01 3 hxxfxfxx x ′′′=⇔−=⇔=≠

Đặt 3 322 xtxt =  = phương trình (1) trở thành: () ()() 32

1 02 3 ftt t ′ =≠

Vẽ đồ thị hàm 32

1 3 y x = trên cùng hệ trục tọa độ với hàm ()yfx ′ = .

12 39 yy tt ′ =−⇒= đổi dấu khi qua 0 và đồ thị hàm số có tiệ

m

Dựa vào đồ thị ta có: () 3 3 3 32 3

  =<=<=<  ′ =⇔⇔⇔    => => =>     Bảng biến thiên

000 1 0 0 3 0 tbxbxb ft ta xa txa

Dựa vào bảng biến thiên ta thấy phương trình () 0 hx = có 3 nghiệm phân biệt và hàm số ()hx có 2 điểm cực trị không nằm trên trục hoành, do đó hàm số ()()gxhx = có 5 điểm cực trị.

Câu48. (Mã103-2020Lần2) Cho hàm số ()fx có ()00 f = . Biết ()yfx ′ = là hàm số bậc bốn và có đồ thị như hình vẽ. Số điểm cực trị của hàm số () ()42gxfxx =− là

Dựa vào BBT ta thầy hàm số () 3 () gxfxx =− có 5 điểm cực trị Câu47. (Mã102-2020Lần2) Cho hàm số ()fx có ()00 f = . Biết ()yfx ′ = là hàm số bậc bốn và có đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số () () 3 gxfxx =+ là A. 4. B. 5. C. 3. D. 6. L

A. 4. B. 3. C. 6. D. 5. Lờigiải ChọnD

Trang 37

Xét hàm số () ()42hxfxx =− có () ()34 42 hxxfxx ′′ =− . () () () 4 2

=   ′ =⇔  ′ = 

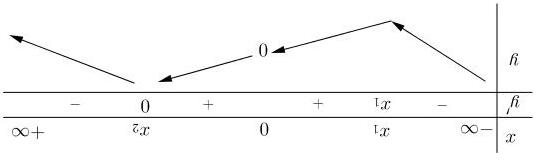
x hx fx x

0 0 1 * 2

Xét phương trình () * : Đặt 4 tx = thì () * thành () 1 2 ft t ′ = với 0 t > .

() ()() ()() 244 2 1 1:210 02 2 xfxfxx x ′′ +=⇔=−≠

Đặt () 42 0 xtxtt =  => phương trình (2) trở thành: () ()() 1 0 3 2 ftt t ′ =−>

Vẽ đồ thị hàm 1 2 y x =− trên cùng hệ trục tọa độ với hàm ()yfx ′ =

Dựa vào đồ thị, phương trình () * có duy nhất một nghiệm 0 a > . Khi đó, ta được 4 xa =± . Bảng biến thiên của hàm số () ()42hxfxx =− Số cực trị của hàm số () ()42gxfxx =− bằng số cực trị của hàm () ()42hxfxx =− và số nghiệm đơn hoặc bội lẻ của phương trình () 0 hx = Dựa vào bảng biến thiên của hàm ()fx thì số cực trị của ()gx là 5.

Câu49. (Mã104-2020 Lần 2) Cho hàm số ()fx có ()00. f = Biết ()yfx ′ = là hàm số bậc bốn và có đồ thị là đường cong trong hình bên. Số điểm cực trị của hàm số ()42 () gxfxx =+ là A.

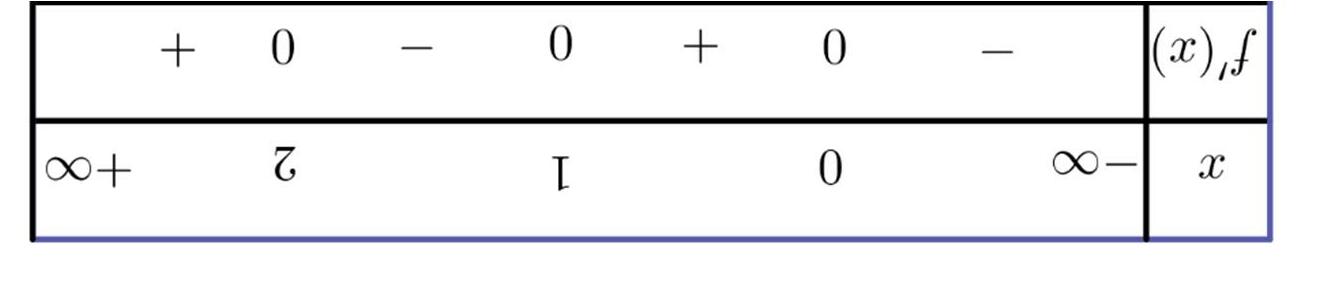
Dựa vào đồ thị ta có: phương trình (3) có nghiệm duy nhất 4 4 4 0 xa taxa xa

Bảng biến thiên:

 = =>  =⇔  =−  

Dựa vào BBT ta thầy hàm số ()42 () gxfxx =+ có 5 điểm cực trị

Câu50. (Chuyên Quang Trung - 2020) Cho hàm số ()yfx = liên tục trên ℝ có đạo hàm ()fx ′ liên tục trên ℝ và có bảng xét dấu như hình vẽ bên

Hỏi hàm số () 2 2 yfxx =− có tất cả bao nhiêu điểm cực trị?

A. 4 B. 7 C. 9 D. 11

Tập xác định của hàm số: D = ℝ . * () () 2 2 yhxfxx ==− () () () 2 2..22. x yhxfxxx x ′′′ ==−− () 2 2 2

 Đồ thị hàm số () 1=−yfx có được bằng cách tịnh tiến đồ thị hàm số

Dựa vào đồ thị, ta được: 2 2 −≥ m hoặc 63 2 −<−≤− m

[] ;12;12 4 612 ∈∈− ≤−  ⇔→  ≤<  ℤ mm m m có 15 giá trị m nguyên thỏa mãn yêu cầu bài toán.

=   =−   =   =  =−  =−   ′ =⇔−=⇔   =+   −=   =−−   −=  =+    =−−  

x x x x x x hxxx x xx x xx x x

1 1 1 2 1 2 020 12 21 12 22 13 13

.

Ta thấy phương trình () 0 hx ′ = có 8 nghiệm đơn () 1 ()hx ′ không tồn tại tại 0 x = mà 0 x = thuộc tập xác định đồng thời qua đó ()hx ′ đổi dấu () 2 Từ () 1 và () 2 suy ra hàm số đã cho có 9 điểm cực trị.

Câu51. (Chuyên Thái Bình - 2020) Cho () = yfx là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [] 12;12 để hàm số ()() 21 =−+ gxfxm có 5 điểm cực trị?

Câu52. (Chuyên Vĩnh Phúc- 2020) Cho hàm số () 32 fxaxbxcxd =+++ (với ,,, abcd ∈ ℝ và 0 a ≠ ) có đồ thị như hình vẽ. Số điểm cực trị của hàm số () () 2 24 gxfxx =−+

A. 13 . B. 14 . C. 15 . D. 12 . Lờigiải ChọnC Đặt ()()()() 21 =−+  = hxfxmgxhx .

 Số điểm cực trị của ()gx = số điểm cực trị của () = yhx + số giao điểm của () = yhx với trục Ox khác với điểm cực trị của () = yhx  Hàm số () = yfx có 3 điểm cực trị. Suy ra hàm số () = yhx cũng có 3 điểm cực trị

 Hàm số ()gx có 5 điểm cực trị khi và chỉ khi ()() 01 2 =⇔−=− m hxfx có 2 nghiệm phân biệt

khác điểm cực trị của ()hx

A. 2. B. 5. C. 4. D. 3. Lờigiải. ChọnD Dựa vào đồ thị hàm số ()yfx = có hai điểm cực trị là 2;0xx=−= . () () 2 24 gxfxx =−+ liên tục trên ℝ ()() () 2 '44'24 gxxfxx =−+−+ () 2 2

x gxxx xx

440 '0240 242

−+=  =⇔−+=  −+=− ()2

=   =  ⇔  =  −=  

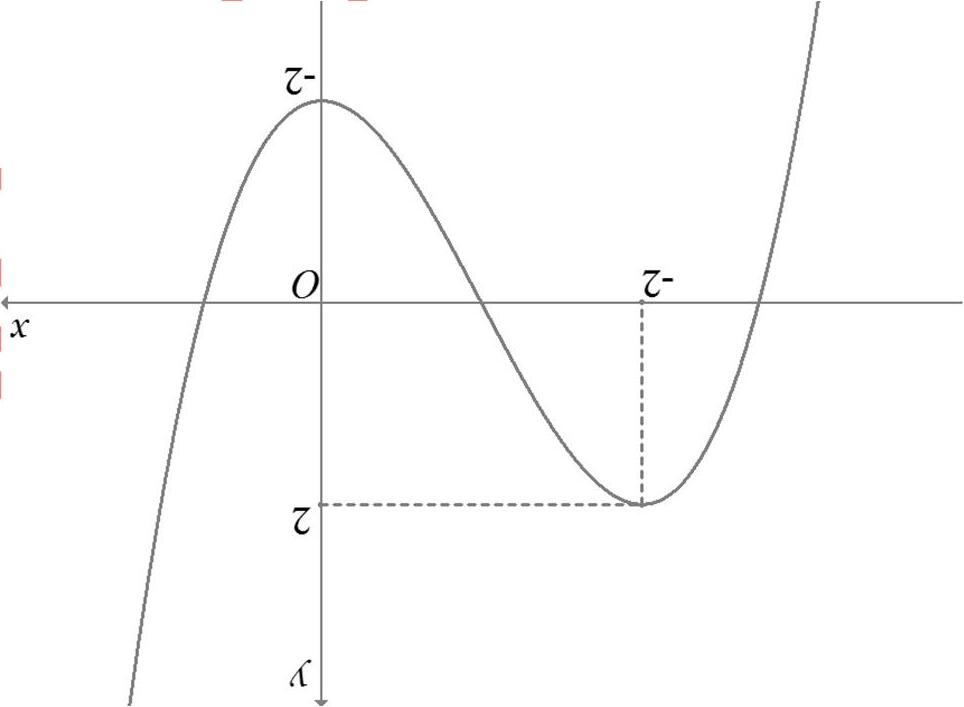
x x x x

1 0 2 10

Như vậy ()gx có 3 nghiệm, trong đó 1 là nghiệm bội 3, 0 và 2 là nghiệm đơn nên ()gx có 3 điểm cực trị.

Câu53. (Sở PhúThọ -2020) Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ

Số điểm cực tiểu của hàm số () () 2 gxfxx =−+ bằng

A. 1 B. 5 C. 2 D. 3 Lờigiải ChọnD

A. 3 B. 7 C. 6 D. 4 Lờigiải ChọnA

Ta có () 2 2 '()1' 2  + =−−−  xx xx gxexfe

Bảng biến thiên Suy ra, hàm số () () 2 gxfxx =−+ có ba đi

m c

c ti

u. Câu54. (Sở Bắc Ninh - 2020) Chohàmsố ()fx liêntụctrên ℝ vàcó đồ thị như hìnhvẽ.Hàmsố 2 2 () 2  + =−  x xx gxfe có bao nhiêu điểm cực trị?

Xét () 2 2

ex xx gxexfe xx fe

10 2 '()01'022'0 2

x xx x

 −−=  +  =⇔−−−=⇔  +   −=     

x x x x

2 2 2

 −−=  +  −=−   ⇔ +  −=   +  −=  

ex xx e xx e xx e

10 1 2 2 2 2 2 1 3 2 2 4 4 2

() () () ()

Ta xét 2 2 ()1;() 2 + =−−=− xx xx uxexvxe

Ta có '()1;'()00 =−=⇔= x uxeuxx '()1;'()1 =−=−− xx uxevxex Bảng biến thiên:

Vậy ()0≥∀∈ℝ uxx

Xét hàm số 2 2 () 2 + =− x xx vxe

Ta có '()10=−−≥∀∈  ℝ x vxexx hàm số đồng biến trên ℝ Bảng biến thiên:

Khi đó các phương trình (2),(3),(4) có nghiệm duy nhất và '()gx đổi dấu qua các nghiệm đó. Vậy hàm số ()gx có 3 điểm cực trị.

Câu55. (Sở Yên Bái - 2020) Cho hàm số () = yfx có đạo hàm trên ℝ Đồ thị hàm số ()′ = yfx như hình bên. Đặt ()() 2 21 =++gxfxx . Khẳng định nào sau đây đúng?

Dựa vào bảng biến thiên, hàm số đạt cực tiểu tại 0 = x .

Câu56. (KimLiên-HàNội-2020) Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số 4323412 yxxxm =−−+ có 5 điểm cực trị? A. 16 B. 28 C. 26 D. 27 Lờigiải ChọnD Xét hàm số () 4323412 fxxxxm =−−+ . Ta có () 32 1212240fxxxx ′ =−−= 0 1 2

=   ⇔=−   = 

x x x

A. Hàm số () = ygx nghịch biến trên khoảng () 1; +∞

B. Hàm số () = ygx đồng biến trên khoảng () 1;0 .

C. Hàm số () = ygx đạt cực tiểu tại 0 = x

D. Hàm số () = ygx đạt cực đại tại 1 = x Lờigiải ChọnC

()()22′′ =+ gxfxx

()() 0 ′′ =⇔=− gxfxx .

Ta vẽ thêm đường thẳng =− yx và đồ thị.

Khi đó phương trình () 0 ′ = gx có các nghiệm 1=− x , 1 = x , 2 = x .

Ta có bảng biến thiên

Bảng biến thiên: Vậy với mọi m hàm số ()fx luôn có ba điểm cực trị. Do đó để hàm số ()yfx = có 5 điểm cực trị khi và chỉ khi phương trình () 0 fx = có đúng hai nghiệm đơn hoặc nghiệm bội lẻ 0 50 320

≤   ⇔ −≥   −< 

m m m

0 532 m m ≤  ⇔  ≤< 

Vì m là số nguyên dương cho nên có 27 số m thỏa đề bài.

Câu57. (Lý NhânTông -BắcNinh- 2020) Cho hàm số ()yfx = có bảng biến thiên như hình vẽ dưới đây:

Hàm số (2)yfx = đạt cực đại tại A. 1 2 x = B. 1 x =− C. 1 x = D. 2 x =−

Đặt 2() txyft =⇒= .

Vậy () () 2 20hxfxx=−= có hai nghiệm phân biệt. (2)

Từ (1) và (2) ta được: hàm số () () 2 2 gxfxx =− có 3 điểm cực trị.

Câu59. (HảiHậu-Nam Định-2020) Cho hàm số ()yfx = đồng biến trên () 4; +∞ có đồ thị như hình

Vậy hàm số (2)yfx = đạt cực đại tại điểm 1 x = và 1 2 x =−

Từ bảng biến thiên ta thấy hàm số ()yft = đạt cực đại tại 1 121 2 222 1

tx x tx x

   =−=− =−   ⇒⇒  ==  = 

vẽ. Số điểm cực trị của hàm số (22)yfx=− bằng

5 3 1 4 O 1

Câu58. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ và ()() 00;44ff=> . Biết hàm ()yfx ′ = có đồ thị như hình vẽ Số điểm cực trị của hàm số () () 2 2 gxfxx =− là

A. 2 B. 1 C. 4 D. 3 Lờigiải ChọnD Xét hàm số () () 2 2 hxfxx =−

Ta có: () () 2 22hxxfx ′′ =− ; () () 2 1 0 hxfx x ′′ =⇔= (vô nghiệm 0 x ∀≤ ). Đặt 2 ,0txxtt =  =∀>

Khi đó: () 1 ft t ′ = (*). Nhận thấy trên khoảng () 0;1 thì () 1 wt t = nghịch biến và ()ft ′ đồng biến, do đó (*) nếu có nghiệm là duy nhất. Mặt khác: ()()()() 0.1221280hhf ′′′ =−−=−< và ()hx ′ liên tục trên [] 0;1 nên ()() 000;1:0xhx ′ ∃∈= . Vậy () 0 hx ′ = có nghiệm duy nhất () 0 0;1 x ∈ và ()hx có một điểm cực tiểu (vẽ bảng biến thiên).

(1)

Xét phương trình: () () 2 020hxfxx =⇔−= (**).

Ta có: ()() 0000hfx ==  = là một nghiệm của (**).

Mặt khác: () ()()() () () () ()000101 .22440;2:0 hxhfxxfxxhx =−−<  ∃∈=

Nên (**) có nghiệm ()10 ;2 xx ∈ .

y 2 Trang 48

x

A. 7 B. 5. C. 4 D. 9 Lờigiải ChọnD () () () () '2'' (22)'22(22)22(22)(22) x gxfxgxxfxxfxfx x =−  =−−=−−=− () ()'0(22)0(22)00 x gxfxfxx x =⇔−=⇔−=≠

Dựa vào đồ thị ta có

x x fx x x

0 2 ()0 3 4

 = =±   −=    = =±  −=    →−=⇔⇔⇔    =± −= =      −=  =±   =  

x x x x x x fx x x x x x x

=   =  =⇔  =  =  1 1 220 2 2 222 (22)0 5 5 223 2 2 224 3 3

Ta có bảng xét dấu ()' gx

Suy ra hàm số (22)yfx=− có 9 điểm cực trị

Câu60. (Hải Hậu - Nam Định - 2020) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị hàm số ()yfx ′ = như hình vẽ dưới đây:

Tìm điểm cực đại của hàm số ()() 20192020. fxfx y =−

A. 2 . B. 3 . C. 0 . D. 1. Lờigiải ChọnA

Từ đồ thị hàm số ()yfx ′ = ta có bảng xét dấu của ()yfx ′ = như sau:

Xét hàm số ()() () ()() () 201920202019ln20192020ln2020 fxfxfxfxyyfx ′′ =−  =−+

Vì ()() 2019ln20192020ln20200 fxfx+>

Nên () ()() () 2019ln20192020ln2020 fxfx yfx ′′ =−+ có bảng xét dấu như sau:

Vậy hàm số ()()20192020fxfx y =− có hai điểm cực đại.

Câu61. (Kìm Thành - Hải Dương - 2020) Cho hàm số ()yfx = là một hàm đa thức có bảng xét dấu ()fx ′ như sau

Xét hàm số () () ()() () 2 22 2

 =   =   ′′ 

x x hxfxxhxxfxxxx xxx

1 1 2 2 2101 15 1 2

Bảngxétdấuhàmsố () () 2 hxfxx =− Hàm số () () 2 hxfxx =− có 2 điểm cực trị dương, vậy hàm số () () () 2 2 gxfxxfxx =−=− có5 điểmcựctrị

Số điểm cực trị của hàm số () () 2 gxfxx =−

A. 5 . B. 3 . C. 1. D. 7 . Lờigiải ChọnA

Ta có () () () 2 2 gxfxxfxx =−=− . Số điểm cực trị của hàm số ()fx bằng hai lần số điểm

cực trị dương của hàm số ()fx cộng thêm 1.

Câu62. (TrầnPhú-QuảngNinh-2020) Cho đồ thị ()yfx = như hìnhvẽ dưới đây: Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số () 2 1 2018 3 yfxm =++ có 5 điểm cực trị. Tổng tất cả các giá trị của các phần tử trong tập S bằng A. 6 B. 5 C. 7 D. 9 Lờigiải ChọnC Đặt ()() () ()() ()

1 20182018 1 3 2018 1 3 2018 3

2 2 2

fxfxm gxfxmgx fxm

 ′ +++  ′ =++  = ++ Phươngtrình () ()() () () 2

fx gx m fx

′ +=   ′ =⇔  +=−  

201801 0 20182 3

Dựavào đồ thị tathấyphươngtrình () 1 luôncó3nghiệmphânbiệt. Vậy để đồ thị hàmsố ()ygx = có5 điểmcựctrị thìphươngtrình () 2 phảicó2nghiệm đơnphân biệt () {}

 −>   ⇔∈⇔∈ −<−≤− 

2 * 2

2 3 3;4 63 3

m mm m

ℕ . Vậytổngcácphầntử là7.

Biếtrằng en > .Số điểmcựctrị củahàmsố () () 2 yffxx ′ =− bằng A. 7 B. 10 C. 14 D. 6 Lờigiải ChọnA

Tacó () () () () ()()()'2'.''2'()2.''2 yfxxffxxfxffxx =−−=−− () () () '20 '0 ''20 fx y ffxx

−=  =⇔  −=   .

+ ()() '20'2 fxfx−=⇔= có3nghiệm.

+ () () () () 2 (1) ''20 2 (2) fxxm ffxx fxxn −=  −=   −=   .

Xétphươngtrình ()()() 1:20 fxxmm−=< , đặt ()()()()2''2gxfxxgxfx =−  =− .

()() 1 2

=<   =⇔=⇔=   =>  .

'0'20 xxm gxfxx xxn

Bảngbiếnthiên:

Từ bảngbiếnthiên  phươngtrình () 1 có2nghiệm.

Xétphươngtrình ()()() 2:2fxxnne −=< , đặt ()()()()2''2hxfxxhxfx =−  =−

()() 1 2

=<   =⇔=⇔=   =>  .

'0'20 xxm hxfxx xxn

Bảngbiếnthiên:

Từ bảngbiếnthiên  phươngtrình(2)có2nghiệm.

Vậyhàmsố () () 2 yffxx ′ =− có7 điểmcựctrị

Câu64. (ChuyênHạ Long-QuảngNinh-2021) Chohàmsố ()yfx = cóbẳngbiếnthiênnhư sau Số điểmcực đạicủahàmsố () () 2 2 2 gxfxx=+ là A. 3 B. 4 C. 2 D. 1 Lờigiải ChọnC Tacó () () () ()() () 2 222 222412 gxfxxfxxxfxx ′  ′ ′ =+=+++  () () ()

 −±+ =>   +=>    +=    =− =−   ′ =⇔+=⇔⇔     += ′ +=    =    +=−   =−  Vì 1 a > nên có thứ tự các nghiệm của () 0 gx ′ = là: 12345 11811118 1 4424 a a xxxxx −−+−++ =<=−<=−<=<= .

a xa xxaa fxx x x gxx xx fxx x xx x

() () 2 2 2 2 2

118 1 2 1 4 20 1 1 0410 4 4 1 21 20 2 22 1

V

() 0 gx

= có 5 nghiệm đơn như trên suy ra ()gx ′ đổi dấu khi x chạy qua các nghiệm đơn.

Với () () 34 11 0;0; 42 xx  ∈−∈   . Xét ()()() 02.000gff ′′ => . Suy ra () 0 gx ′ > trên khoảng 11 ; 42    hay khoảng () 34 ; xx . Ta có bảng xét dấu của ()gx ′ như sau

Ta có hàm ()fx liên tục trên ℝ nên hàm số () () 2 2 2 gxfxx=+ cũng liên tục trên ℝ

Vậy hàm số () () 2 2 2 gxfxx

f a f b f c f

'(0)0 2 (0)1 4 '(1)0 1 (1)0

=  =   =  ↔=− ±=  =   ±= 

−<=

Câu66. (THPTMaiAnhTuấn-ThanhHóa-2021) Cho hàm số ()fx thỏa mãn ()()220,ff

A. 5. B. 7. C. 6. D. 4. Lờigiải ChọnA

Xét hàm số ()() 43211 24 43 hxfxxxxx =+−−+ Ta có ()()()()() 32 2 4414hxfxxxxfxxx ′′′ =+−−+=−−− ()()()() 2 014hxfxxx ′′ =⇔=−−

Vẽ đồ thị hàm số ()() 2 14yxx=−− lên cùng hệ trục tọa độ với đồ thị ()fx ′ thì hai đồ thị này cắt nhau tại 3 điểm 1;2xx==±

Mà ()() 28 220, 3 hf−=−−< (do ()20 f −< ); ()() 23 11, 12 hf=+ ()() 2 220, 3 hf=+> do ()20 f = Bảng biến thiên

Từ bảng biến thiên suy đồ thị hàm số ()hx có 3 điểm cực trị và cắt trục hoành tại 2 điểm phân biệt nên đồ thị hàm số ()() gxhx = có 5 cực trị

Câu67. (THPTHậuLộc4-ThanhHóa-2021) Cho hàm số bậc bốn ()fx có bảng biến thiên như sau:

. Suy ra 42 ()241. =−+fxxx Khi đó 4 424424 4 1 242(2)  =−=−  yxxxx x . Có 43232 '2.4..(2).(32) =−−yxxx Và '0=⇔ y 0 = x (nghiệm bội lẻ); 2 =± x (nghiệm bội lẻ); 2 3 =± x Do đó, hàm số y có 5 cực trị. Trang 54 đồ

trình: ()()() 413210 fxxfx ′ +−−+= () ()()43232 4416163321648320 xxxxxxx ⇔−−−+−−−−−= ()432432 166464123161664640 xxxxxxx ⇔−−−+−−−++= 432432 1664641248481921920 xxxxxxx ⇔−−−+++−−= 432 3216256192120 xxxx ⇔−−−+= 432 84644830 xxxx ⇔−−−+=

Xét hàm số () 432 8464483hxxxxx =−−−+

Ta có: () 32 3248128120hxxxx ′ =−−+= 1 2 3

Bảng biến thiên:

xx xx xx

=   ⇔=   =  với 123 1012 xxx <−<<<<<

Từ bảng biến thiên suy ra phương trình () 0 hx = có 4 nghiệm phân biệt Mà ()2233 h =− 2 x  = không là nghiệm của phương trình () 0 hx =  Phương trình () 0 gx ′ = có 5 nghiệm phân biệt Vậy hàm số () () () 4 3 2 1 x gx fx = +   có 5 điểm cực trị.

Câu68. (THPT ĐồngQuan-HàNội -2021) Cho hàm số ()yfx = liên tục trên các khoảng () ;2−∞ và () 2; +∞ có đồ thị như hình vẽ.

ChọnC

Ta có: () ()4321gxfxx=−+ () ()() 34224 '4.'62.2.'3 gxxfxxxxfx  =−=−

Số điểm cực trị của hàm số () () 212gxfx=−+ là A. 5 . B. 4 . C. 2 . D. 3 . Lờigiải ChọnC () () () () () 221 212''212 21 x gxfxgxfx x =−+  =−+ Ta có () () () () 2121 1 '0'21202122124 2 2124 3 212 2 212 2121 2

 −+=−   =⇔−+=⇔−+=⇔−+=   −+=    =  −=  ⇔−=⇔⇔   −=−   =−   ()' gx không xác định tại 1 2 x = và ()' gx đổi dấu tại 1 2 x = , nhưng tại 1 2 x = thì ()gx không xác định ( vì ()fx kxđ tại x=2). Vậy hàm số có 2 điểm cực trị là 13 , 22 xx==

xVN gxfxxVNx x x x x x x

Câu69. (THPT Đồng Quan - Hà Nội - 2021) Cho hàm đa thức bậc bốn ()yfx = , hàm số ()yfx = có đồ thị như hình vẽ

Số điểm cực tiểu của hàm số () ()4321gxfxx=−+ là

 =  =⇔  =   () () ()

2 4

x gx fx x

0 '0 3 '* 2

Xét () () ()

0 0 3 ' 2 * 00 1 3 1 ' 2

 =−   <   =−    <   =− =−    =∨=∨=∨=    ⇔⇔⇔=−    >>   =      =∨=∨=    = =     =  

xf x xa x xc fx xfxaxcxd x xd xx x xxbxe fx xb x xe

4 4 4 4 4444 4 4 4 444 4 4 4 4 4

Bảng biến thiên: Vậy hàm số ( )gx có 4 điểm cực tiểu. Câu70. (Sở HàTĩnh-2021) Cho hàm số ()yfx = có đạo hàm ()fx ′ có đồ thị như hình vẽ bên.

Số điểm cực đại của hàm số ()() 3 1 9 gxfxx =− là A. 4 . B. 1. C. 2 . D. 3 . Lờigiải ChọnB

 Ta có ()() 2 1 3 gxfxx ′′ =− ()() 2 0 1 3 f gxxx ′ = ′ =⇔ (1).  Vẽ parabol () P : 2 1 3 yx = . Ta thấy () P đi qua các điểm () () 114 1;,0;0,1;,2;,3;3 333    Parabol này cắt đồ thị ()yfx ′ = tại các điểm có hoành độ lần lượt là ()() 1;0,1;2ab∈−∈ và () 2; c ∈+∞ . Suy ra (1) có các nghiệm là: ,, xaxbxc ===  Bảng biến thiên của hàm ()() 3 1 9 gxfxx =− như sau: Từ bảng biến thiên ta thấy hàm số đã cho có một điểm cực đại.

x + + 00 −∞ b c +∞ a 0

Số điểm cực đại của đồ thị hàm số () () () () 24 2 1 43322 2 ygxfxxxx ==−+−−+− là A. 3 B. 7 C. 4 D. 5 Lờigiải ChọnA Ta có: () () () () 24 2 1 43322 2 gxfxxxx =−+−−+− () () ()()()3 2 43.226222 gxfxxxxx ′′ =−+−−−+− () () () () 2 2 2243622xfxxx ′ =−−+−+− () () () () 0 2 2

=  ′ =⇔  ′ −+=−−   (*) () () ()() 2 2 222 433243344432fxxxfxxxxxx ′′ −+=−−⇔−+=−+−=−−++

21 0 4332(*) xn gx fxxx

Đặt: 2 43txx=−+ suy ra phương trình trở thành: '()2ftt=−+

Phương trình trên tương ứng với tương giao giữa đồ thị '()yft = và đường thẳng 2 yt=−+

Dựa vào hình vẽ trên, ta thấy phương trình có 3 nghiệm là 0,1,2ttt=== 22 22 22

==   −+=−+= =     ⇔=⇔−+=⇔−+=⇔=−=+       = −+=−+= =−=+   

xx xxxx t txxxxxx t xxxx xx

1,3 430430 0 143142022;22 2 432410 23;23

Từ đó, ta có bảng biến thiên của hàm ()gx như sau: Dựa vào BBT trên, ta kết luận hàm số ()gx có 3 điểm cực đại

Câu72. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hàm bậc ba ()yfx = có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số () 2 1 yxfx=−  là

A. 9 . B. 7 . C. 6 . D. 5 . Lờigiải ChọnB  Đặt: () 32 fxaxbxcxd =+++ () 2 32 fxaxbxc ′  =++ Ta có: đồ thị giao với trục Oy tại điểm () 0;1 1 d  =

abc abc abc abc

−+=   ++=    +++=−  −+−+=

b a c

 Đồ thị hàm số ()yfx = có hai điểm cực trị là ()() 1;3;1;1 nên 320 320 11 13

=   ⇔=   =−  () 3 31fxxx  =−+ .

0 1 3

()()()() 3 322 1131133136 fxxxxxfxxx ′  −=−−−+=−+  −=− .  ()() 2 1 gxxfx=−    ()()()() 2111gxxfxfxxfx ′′ =−−+−  . () ()() 3232 233493gxxxxxx ′  =−+−+

Suy ra () 32 32

x x x x gxxxx x xx x x

0 2,532 0 1,347 03300,879 2,076 4930 0,694 0,52

=   ≈  =   ≈   ′ =⇔−+=⇔≈−     ≈ −+=   ≈   ≈−  ()gx ′ là phương trình bậc 7 và có 7 nghiệm phân biệt nên hàm số ()gx có 7 điểm cực trị.

Câu73. (Trung Tâm Thanh Tường - 2021) Cho ()() , fxgx là các hàm đa thức bậc 3 có đồ thị như hình vẽ bên. Đặt ()()() hxfxgx =− . Số điểm cực trị của hàm số ()hx là

A. 7 . B. 7 . C. 3 . D. 9 . Lờigiải ChọnA Theo đồ thị của ()() , fxgx thì hai đồ thị cắt nhau tại 3 điểm có hoành độ lần lượt là 2 , 1, 4 nên ()()()() 214hxaxxx =+−− với 0 a > (do hệ số của 3 x của ()fx dương còn hệ số của 3 x của ()gx âm).

 đồ thị của ()yhx = có dạng:

 Đồ thị hàm số ()yhx = được vẽ dựa trên đồ thị hàm số ()yhx = như sau:

+ Bước 1: Giữ nguyên phần đồ thị bên phải trục tung, bỏ phần bên trái rồi lấy đối xứng phần bên phải trục tung qua trục tung. + Từ đồ thì có được qua bước 1, giữ nguyên phần đồ thị trên trục hoành, lấy đối xứng với phần đồ thị dưới trục hoành.

ftt ⇔=− .

Ta vẽ đồ thị hai hàm số ()' yft = và 1 yt=− trên cùng một hệ trục tọa độ

Từ đó suy ra số điểm cực trị của hàm số ()hx là 7. Câu74. Cho ()fx là hàm bậc bốn thỏa mãn ()00 f = . Hàm số ()' fx có đồ thị như hình vẽ

Dựa vào đồ thị ta thấy () 20 '1 2 t ftt t −<< >−⇔  > 

Khi đó: 2 2

2010 21 2 xxx xx xx −<+<−<<  ⇔   <−∨< +>  

Bảng biến thiên:

Vậy hàm số ()() gxhx = có 7 điểm cực trị

Câu75. Cho hàm số ()yfx = là hàm số bậc bốn thỏa mãn ()00. f = Hàm số ()' yfx = có bảng biến thiên như sau:

Hàm số () ()22gxfxx =− có bao nhiêu điểm cực trị?

A. 1 B. 3 C. 5 D. 7 Lờigiải

Đặt () () () 22 00. hxfxxh =−  =

Ta có () () () 2 2

0 '2'20. '1 x hxxfxx fx =  =−=⇔  =  

Dựa vào bảng biến thiên của hàm số ()' tfx = ta có phương trình () '1fx = có duy nhất một nghiệm và nghiệm đó dương. Gọi 0x là nghiệm của phương trình () '1fx = . Suy ra ()22 00 '1. fxxxxx =⇔=⇔=±

Ta có ()()43232'432 yfxaxbxcxdxefxaxbxcxd ==++++  =+++ () lim'0. x fxa →+∞ =+∞  > Khi đó () ()22hxfxx =− là hàm bậc 8 và ()()limlim xx hxhx →+∞→+∞ ==+∞ Lập bảng biến thiên của ()hx ta có Dựa vào bảng biến thiên ta có hàm số ()() gxhx = có 5 điểm cực trị. Câu76. Cho ()fx là hàm số bậc bốn thỏa mãn () 1 0 ln2 f =− . Hàm số ()fx ′ có bảng biến thiên như sau:

Từ đó, phương trình (*) 2 00 xtxt ⇔−=⇔=±− . Bảng biến thiên

Từ bảng biến thiên suy ra hàm số ()() gxhx = có 5 điểm cực trị

Câu77. Cho hàm số ()yfx = có đạo hàm () 3 '42 fxxx =+ và ()01. f = Số điểm cực tiểu của hàm số () ()32 23gxfxx=−− là

A. 0 B. 2 C. 1 D. 3 Lờigiải ChọnB

Ta có: () ()34242 fxxxdxxxC =+=++  và ()011.fC =  = Do đó ta có: () 42 10,. fxxxx =++>∀

Ta có: () 222 '3(22).(23).'(23) gxxfxxfxx =−−−−− .

x gx xxxx

220 '0 4232230

() ()() 3 22

−=   =⇔ −−+−−=  

x x x

1 1 3

=   ⇔=−   =  .

x −∞ 1 1 3 +∞ '()gx 0 + 0 0 + ()gx +∞ +∞

0 0 21(*)

x x hx fx =  ′ =⇔  ′ −=−   . Đặt 2 ,0txt=−≤ . Phương trình (*) trở thành: ()()ftut ′ = , với () 21 t ut =−

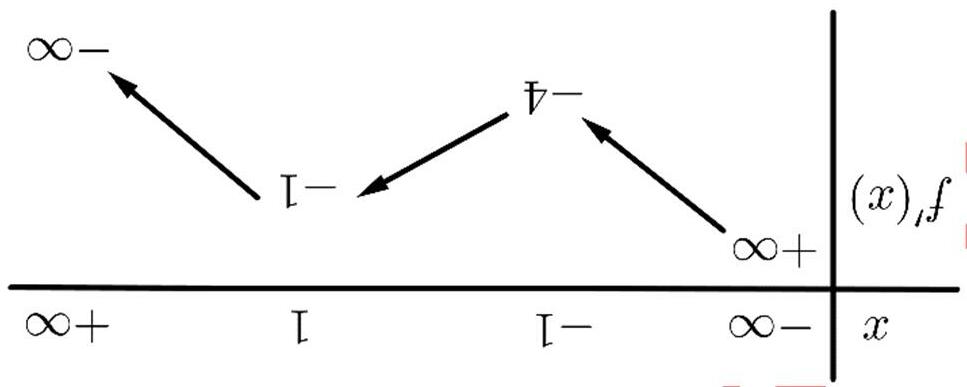
Bảng biến thiên: Từ bảng biến thiên suy ra hàm số ()ygx = có hai cực tiểu.

Câu78. (ChuyênLêHồngPhong-Nam Định-2021) Cho hàm số ()fx có đạo hàm ()fx ′ liên tục trên ℝ và có bảng biến thiên ()fx ′ như sau:

Tìm số điểm cực tiểu của hàm số () () 3 3 gxfxx =−

A. 1. B. 2 . C. 3 . D. 0 . Lờigiải ChọnB

Ta thấy () () 3 3 gxfxx =− là hàm chắn.

Ta chỉ xét 0 x > khí đó hàm số () () 3 3 gxfxx =− () ()23 33gxxfx ′′  =−

Ta có () ( ) ( ) 233 2 1 0330 gxxfxfx x ′′′ =⇔−=⇔=

Đặt 3 3 txxt =  = khi đó ta được: () 3 2 1 ft t ′ =

Xét hàm số ()() 3 2 1 htft t ′ =− Vì ()() 3 5 2 00 3 htftt t ′′′=+>∀> nên ()ht là hàm đồng biến

Bảng biến thiên của ()ht là

Vậy phương trình () 0 ht = chỉ có một nghiệm 0 ta=>

Bảng biến thiên của hàm số ()gx khi 0 x > là

Vậy hàm số ()gx có 2 điểm cực tiểu và 1 điểm cực đại.

Câu79. (Chuyên Hùng Vương - Gia Lai - 2021) Cho ()fx là hàm số bậc ba thỏa mãn ()02 f = và ()10 f ′ = . Hàm số ()fx ′ có bảng biến thiên như sau

Hàm số ( ) ( ) ( ) 3232021gxfxfx=−− có bao nhiêu điểm cực trị?

A. 7 B. 6 C. 9 D. 11

Lờigiải ChọnA

Giả sử () 32 fxaxbxcxd =+++

Ta có () 2 32. fxaxbxc ′ =++ Dựa vào bảng biến thiên, ta suy ra đồ thị hàm số ()fx ′ đối xứng nhau qua trục tung nên là hàm chẵn suy ra 0. b = Khi đó () 2 3. fxaxc ′ =+ Mặt khác cũng từ bảng biến thiên và giả thiết, ta có () () 03 31 303 11 f ca acc f

′ =−  =−=  ⇔⇔  +==− ′ =   

Khi đó ()()23 333. fxxfxxxC ′ =−  =−+ Mà ()022.fC=⇔= Vậy () 3 32.fxxx=−+ Xét hàm số ( ) ( ) ( ) 3232021,hxfxfx=−− ta thấy ()hx là một hàm chẵn nên nhận trục tung là trục đối xứng, vì vậy số điểm cực trị của ()hx chính bằng hai lần số cực trị dương của hàm số ()()() 3232021pxfxfx=−− cộng thêm 1. Xét hàm số ()()() 3232021pxfxfx=−− trên () 0; +∞ ta có ( ) ( ) ( ) ( ) ( ) 2 36. pxfxfxfxfx ′′′ =−

() () () ()

fx x x pxfxxxx xx fx x

0 330 1 003200 322 2 3

2 3 3

′ =  −=  =   ′ =⇔=⇔−+=  =     −+= = =    (do 0 x > ). Bảng biến thiên Từ bảng biến thiên, ta suy ra số điểm cực trị của hàm số ()hx là 2.215. +=

Mặt khác, đồ thị của hàm số ()gx đối xứng qua ,Ox do đó số điểm cực trị của hàm số ()gx

bằng số điểm cực trị của hàm số ()hx cộng với số nghiệm bội lẻ của phương trình () 0. hx =

Dựa vào bảng biến thiên ta có thấy ( ) 0 hx = có hai nghiệm bội đơn.

Vậy hàm số ()gx có tất cả 527 += điểm cực trị

Câu80. (Chuyên ĐHSP-2021) Cho ()fx là hàm số bậc bốn thỏa mãn () 1 0 2021 f = . Hàm số ()fx ′ có bảng biến thiên như sau:

Hàm số () 3 () gxfxx =+ có bao nhiêu điểm cực trị? A. 1. B. 5 . C. 2 . D. 3 . Lờigiải ChọnD

1 3 ft t ′ =

Từ đồ thị hàm ()ft ′ và hàm 32

1 3 y t = , ta suy ra phương trình () 32

1 3 ft t ′ = có đúng một nghiệm () 0 0* tt=>  có đúng một nghiệm 0 0 xx=> . Từ đó ta có bảng biến thiên :

Suy ra ()gx có 3 điểm cực trị

Câu81. (Chuyên Biên Hòa - 2021) Hàm số () 2

()yfx = là

1 khi 0 6 khi 0

x xex fx xxx  +−>  =  +≤   . Số điểm cực trị của hàm số

A. 4 . B. 2 . C. 1. D. 3 . Lờigiải ChọnD Tập xác định D = ℝ

Ta có () () () () () 2 0000 limlim10;limlim60;00 x xxxx fxxefxxxf++ →→→→ =+−==+==  Hàm số liên tục tại 0 x =

Ta có () ()() 00

fxf xe f xx + +

+− ′ === .

+ →→

0 1 0limlim0 0 x xx

Ta có () ( ) ( ) () 2 000

+ ′ ===+=  Hàm số không tồn tại đạo hàm tại 0 x = Với () 01 xxfxxe >  =+− .

fxf xx f x xx →→→

0 6 0limlimlim66 0 xxx

Tính () 1010 xx fxeex ′ =−=⇔=⇔= . Với () 2 06 xfxxx ≤  =+ Tính () 2603fxxx ′ =+=⇔=−

Số điểm cực trị của hàm số ()yfx = là 3 .

Câu82. (Cụm Ninh Bình – 2021) Cho hàm số ()yfx = liên tục, xác định trên ℝ và có đồ thị như hình vẽ. Hàm số () () 2 4 gxfxx =− có bao nhiêu điểm cực trị? A. 9 . B. 5 . C. 11. D. 7 . Lờigiải Ta có () () () () () () 222 2 2 444214 gxfxxgxxxfxxxfxx x  ′ ′′′ =−  =−−=−−   

Hàm số ()gx ′ không xác định tại 0 x = . () () () 2 2 2

Có ()()lim0lim x x fxagx →+∞ →+∞ =−∞  <  =−∞  tồn tại số 1 α > thỏa

Có () 0lim x agx →−∞ <  =+∞  tồn tại số 0 β < thỏa mãn () 0 g β > ( ) 120190gabc=++−> ()020190 g =−< Vậy ()() 1.0gg α < và ()()()() 1.00,0.0gggg β << , mà ()gx liên tục trên ℝ suy ra phương trình () 0 gx = có 3 nghiệm phân biệt. Từ đó đồ thị hàm số ()ygx = có 2 điểm cực trị và cắt trục hoành tại 3 điểm phân biệt. Vậy hàm số ( )ygx = có 5 điểm cực trị. Tức là số điểm cực trị của hàm số ( )2019 ygx=− là 5.

x x x gxxx x fxx xx

2 2 2 044 25 40 41

 = =±   =  ′   =⇔⇔−=−⇔  =±+ ′ −=      −=  . Bảng xét dấu: Vậy hàm số ()gx có 5 điểm cực trị.

Câu84. (Sở Nam Định - 2021) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ và ()30 f −= đồng thời có bảng xét dấu đạo hàm như sau: Hàm số ()()() () 62 432 21613442gxxxfxxx =+−+−−−−− có bao nhiêu điểm cực trị? A. 7 . B. 6 . C. 3 . D. 5 . Lờigiải ChọnD Đặt ()()() () 62 432 21613442hxxxfxxx =+−+−−−−− ()()() ()() 5 32432 '12112134128.'442 hxxxxxxfxxx  =+−+−−−−−−−− ()()() ()()()222432 1212221212.'442 xxxxxxxxfxxx =+++++++−−−− ()() 22432 12(1)222'442 xxxxxfxxx =+++++−−−−  Mà () 2 432442222xxxxx −−−−=−+−≤−   , x ∀∈ ℝ nên dựa vào bảng xét dấu của ()fx ta suy ra () 432 '4420 fxxx−−−−≥ . ()243222'4420, xxfxxxx  +++−−−−>∀∈ ℝ

Do đó dấu của ()' hx cùng dấu với ()()() 2 1212 uxxxx =++ , tức là đổi dấu khi đi qua các điểm 2;1;0xxx=−=−=

Vậy hàm số ()hx có 3 điểm cực trị.

Ta có ()()1330hf−=−−= nên đồ thị hàm số ()yhx = tiếp xúc Ox tại 1 x =− và cắt trục Ox tại 3 điểm phân biệt.

Vậy ()ygx = có 5 điểm cực trị

Câu83. (Sở Quảng Bình - 2021) Cho hàm số ()() 32 1, 0 fxaxbxcxa =+++≠ với các số thực ,, abc thỏa mãn 2019 abc++> và () lim x fx →+∞ =−∞ . Số điểm cực trị của hàm số () 2019 ygx=− với ()() 2020 gxfx=− là A. 3 B. 2 C. 4 D. 5 Lờigiải Ta có: Số điểm cực trị của hàm số () 2019 ygx=− bằng với số điểm cực trị của hàm số ()ygx = Mà ()() 32 20202019gxfxaxbxcx =−=++− Trang 72

()()() 2 42fxfxm ⇔+=− Để ()()gxhx = có 5 điểm cực trị khi và chỉ khi PT () 2 có 2 nghiệm đơn hoặc nghiệm bội lẻ phân biệt Xét hàm số ()()() 2 4 txfxfx =+ Ta có Bảng biến thiên của ()tx : Từ YCBT () txm⇔=− có hai nghiệm đơn hoặc nghiệm bội lẻ pb ()()  −≥>≤−<− −≤<    −<−≤−<−≤ ⇔⇔⇔    ∈    −≤≤∈−≤≤   ℤ ℤ

mtamta m mm m mmm {} 5;4;3;2;1;0;1;2;3. m ⇔∈−−−−−

55 54 4545 55;55

Cách2: Ta có bảng biến thiên của hàm số () = yfx : Xét hàm số ()()() 2 4 hxfxfxm =++

Gọi ,, abc () abc << là ba điểm cực trị của hàm số ()yfx =

Khi đó: ()()()6;2;2fafbfc=−=−=

Xét hàm ()() 2020 hxfx=+ với x ∈ ℝ .

ha mfaf mm

mm

5;4;3;2;1;0;1;2;3

Câu2. (Sở BìnhPh

()yfx = có đồ thị như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số thực m để hàm số ()() 2 2020 gxfxm =++ có 5 điểm cực trị?

c-2020) Cho hàm s

A. 1. B. 2. C. 4. D. 5. Lờigiải

Khi đó: ()()()() 2020.20202020hxfxxfx ′′′′ =++=+ () 2020 02020 2020

=−   ′ =⇔=−   =−  .

xa hxxb xc

Bảng biến thiên của hàm ()hx

Hàm số ()() 2 2020 gxfxm =++ có 5 điểm cực trị

⇔ Phương trình () 2 20200fxm++= có đúng 2 nghiệm không thuộc

{} 2020;2020;2020abc 2 2 2

 =±  =   ⇔=−⇔−<<−     << <<   

2 2 262 26 26

m m mm m m

.

Vậy có 2 giá trị nguyên của m là 2 m = và 2 m =− thì hàm số ()() 2 2020 gxfxm =++ có 5 điểm cực trị.

Câu3. (Chuyên Lào Cai - 2020) Cho hàm số ()fx có đạo hàm ()()()() 43 222423618.fxxxxxmxm ′ =++++++ Có tất cả bao nhiêu giá trị nguyên của m để hàm số ()fx có đúng một điểm cực trị?

m ⇔−<< {} 2; 1; 0;1; 2 m  ∈−−

Trườnghợp2. Phương trình () * có nghiệm kép 2 3 4360 3 m m m =  ⇔∆=−=⇔  =− 

Trườnghợp3. Phương trình () * có hai nghiệm phân biệt 1x , 2x . Trong đó 1 4. x =−

Phương trình có hai nghiệm phân biệt 2 12 3 , 4360 3 m xxm m <−  ⇔∆=−>⇔  > 

Theo định lí Viète ta có 122

426 .4.618 Sxxxm Pxxxm

Tìm tất cả các giá trị của tham số m để đồ thị hàm số ()()() 2 22 hxfxfxm =++

điểm cực trị.

A. 1 m > B. 1 m ≥ C. 2 m ≤ D. 2 m >

Lờigiải ChọnB Số cực trị của hàm số ()()() 2 22 hxfxfxm =++ bằng số cực trị của hàm số ()()() 2 22=++ yxfxfxm cộng với số giao điểm (khác điểm cực trị) của đồ thị hàm số ()()() 2 22=++ yxfxfxm và 0 y =

Xét hàm số ()()() 2 22 gxfxfxm =++ ()()()()()() 2221gxfxfxfxfxfx ′′′′ =+=+ () () () ()

 =  ′ =  ′  =⇔⇔=  ′  =   =< 

x fx gxx fx x αα

1 0 03 1 0

BBT Hàm số ()hx có 3 điểm cực trị 1 20 2 mm ⇔≥⇔≥ Đáp án B là gần kết quả nhất

Câu5. (THPT Hàm Rồng - Thanh Hóa - 2018) Cho hàm số ()fx có đạo hàm ()()()3 2 1315fxxxax ′ =−− . Tập hợ

0 y ′ = ⇔ 2

x x x x axxa

  =±  =   =   =   −+−= 

2 0 3 4 3 540 (1)

Suy ra ()gx có 5 điểm cực trị khi và chỉ khi () 2 và () 3 có hai nghiệm phân

−>   −+>  ⇔  −+≠   −+−≠ 

160 1620 16320 163220

m m m m

<   <  ⇔  ≠   ≠ 

m m m m

16 18 16 18

16 m ⇔< .

m nguyên dương và 16 m < nên có 15 giá trị m cần tìm.

Câu7. Cho hàm số ()yfx = xác định trên ℝ và hàm số '()yfx = có đồ thị như hình bên. Biết rằng '()0fx < với mọi ()() ;3,49;. x ∈−∞−∪+∞ Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ()()5 gxfxmx=−+ có đúng hai điểm cực trị.

  ≠  ∆=−> ≠   −≠   ≠   ≠    ≠    

a aa g g g g g

0 54.40 20 20 00 30 4 0 3

2

⇔

≠   −<<   ≠±   ≠    ≠  

a a a a a

0 55 44 5 4 0 15 13

⇔

−<<  ≠    ≠ 

a a a

55 44 0 15 13

( 0 x = là nghiệm kép ). đặt ( ) 2 54 gxaxxa =−+− Ycbt thỏa mãn khi phương trình 0 y ′ = có 6 nghiệm bội lẻ ⇔ phương trình ( )1 có hai nghiệm phân biệt khác 2;0;1;4± . (Nếu ( ) 00 = g thì 0 y ′ = chỉ có 5 nghiệm bội lẻ). Điều kiện: () () () ()

Câu6. (ChuyênVinh-2018) Cho hàm số ( )yfx = có đạo hàm ()() ( ) 2 2 12 fxxxx ′ =−− với x ∀∈ ℝ Có bao nhiêu giá trị nguyên dương của tham số m để hàm số ( ) 2 8 fxxm −+ có 5 điểm cực trị? A. 15 . B. 17 . C. 16 D. 18 Lờigiải Đặt ( ) ( ) 2 8 gxfxxm =−+ ()() ( ) 2 2 12 fxxxx ′ =−−  ()()( ) ( )( ) 2 222 2881882 gxxxxmxxmxxm ′ =−−+−−+−+− ( ) 0 gx ′ = () ()

A. 7. B. 8. C. 6. D. 5. Lờigiải ChọnB '()'() gxfxm =−

Số điểm cực trị của hàm số ()gx bằng số nghiệm đơn (bội lẻ) của phương trình '(). fxm =

Dựa và đồ thị ta có điều kiện 05 1013 m m <≤   ≤<  .

Vậy có 8 giá trị nguyên dương của m thỏa mãn.

Câu8. (ChuyênVĩnhPhúc2019) Cho hàm số ()yfx = . Hàm số ()yfx ′ = có đồ thị như hình vẽ dưới đây.

y 3 2 0 1

x

7

Tìm m để hàm số 2 ()yfxm =+ có 3 điểm cực trị.

u

5

Do hàm số 2 ()yfxm =+ là hàm chẵn nên hàm số có 3 cực trị khi và chỉ khi hàm số này có đúng 1 điểm cực trị dương. ( ) 22()2 yfxmyxfxm ′′ =+  =+

0 0

′

+==−

+==− Đồ thị hàm số ( )yfx ′ = tiếp xúc trục hoành tại điểm có hoành độ là 1 x = nên các nghiệm của pt 2 1 xm =− (nếu có) không làm ( ) 2 fxm ′ + đổi dấu khi x đi qua, do đó các điểm cực trị của hàm số 2 ()yfxm =+ là các điểm nghiệm của hệ 2 2

∆>  ∆> ⇔  ≠   ≠ 

0 0 50 50 h p

1 2

−>   −>  ⇔⇔<  −+≠ −+≠

, (Với ( ) 2 108hxxxm=−++ và ( ) 2 106pxxxm=−++ ). 170 190 17 170 190

m m m m m

.

Vậy có 16 giá trị nguyên dương m thỏa mãn.

0 3

x xm xm

=   =−   =−  Hệ trên có duy nhất nghiệm dương khi và chỉ khi 0 03 30 m m m −≤ ⇔≤<  −> 

Câu9. (THPTHàmRồng-ThanhHóa-2019) Cho hàm số ()() ( ) 2 2 243fxxxx ′ =−−+ với mọi x ∈ R

. Có bao nhiêu giá trị nguyên dương của m để hàm số ( ) 2 109yfxxm =−++ có 5 điểm cực trị? A. 18 B. 16 C. 17 D. 15 Lờigiải ChọnB

Câu10. (Chuyên Bắc Giang - Lần 4 - 2019) Cho hàm số ( )yfx = có đạo hàm ()()()() ( ) 2 22 21211fxxxxmxm ′ =−−−++− , x ∀∈ℝ . Có bao nhiêu giá trị nguyên của m để hàm số ( ) ( ) gxfx = có 5 điểm cực trị? A. 3. B. 5. C. 2. D. 4. Lờigiải ChọnC

Dựa vào cách vẽ đồ thị hàm số ( ) ( ) gxfx = , số điểm cực trị của đồ thị hàm số ( ) ( ) gxfx = bằng số điểm cực trị dương của đồ thị hàm số ( )yfx = cộng thêm 1. Để hàm số ( ) ( ) gxfx = có 5 điểm cực trị thì đồ thị hàm số ( )yfx = có 2 cực trị dương.

Ta có () 2 01 3

=   ′ =⇔=   =  , 2 x = là nghiệm kép nên khi qua giá trị 2 x = thì ( )fx ′

x fxx x

không bị đổi dấu. Đặt ( ) ( ) 2 109gxfxxm =−++ khi đó ( ) ( ) ( )'.210 gxfux ′ =− với 2 109uxxm=−++ .

x xxm gx xxm xxm

−=   −++−=  ′ =⇔  −++=   −++= 

2100 10920 0 1091 1093

=   −++−=  ⇔  −++=   −++= 

x fxx xmxm

=   ′ =⇔=   −++−= 

1 02. 2110*

Ta có () ()()22

Có 2 x = là nghiệm bội 2, 1 x = là nghiệm đơn.

Vậy ( ) 222110xmxm−++−= có hai nghiệm phân biệt, có một nghiệm dương 1 x ≠ , có một nghiệm 0 x ≤

Trường hợp 1: Có nghiệm 0 x = khi đó ( ) 2222110101 xmxmmm −++−=⇔−=⇔=±

Với 1 m = , có ()()222 0 211040TM 4 x xmxmxx x

=  −++−=⇔−=⇔  = 

() () ()

2 2 2 2

5 10920 10801 10602

Với 1 m =− , có ( ) 222211000 xmxmxx −++−=⇔=⇔= (Loại)

Trường hợp 2: ( ) 222110xmxm−++−= có hai nghiệm phân biệt, có một nghiệm dương 1 x ≠ , có một nghiệm âm

x xxm xxm xxm Trang 10

Vì 0 mm ∈  = ℤ Vậy có hai giá trị nguyên của m thỏa mãn. Câu11. (Sở GD Quảng Nam - 2019) Cho hai hàm đa thức ()yfx = , ()ygx = có đồ thị là hai đường cong ở hình vẽ. Biết rằng đồ thị hàm số ()yfx = có đúng một điểm cực trị là A , đồ thị hàm số ()ygx = có đúng một điểm cực trị là B và 7 4 AB = . Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng () 5;5 để hàm số ()() yfxgxm =−+ có đúng 5 điểm cực trị? A. 1. B. 3 . C. 4 . D. 6 . Lờigiải ChọnB Đặt ()()() hxfxgx =− , ta có: ()()() hxfxgx ′′′ =− ; () 0 0 hxxx ′ =⇔= ; () 1 0 hxxx =⇔= hoặc 2xx = ( 102 xxx << ); ()()() 000 7 4 hxfxgx=−=−

Bảng biến thiên của hàm số ()yhx = là:

Suy ra bảng biến thiên của hàm số ()()() ykxfxgx ==− là:

Do đó, hàm số () ykxm =+ cũng có ba điểm cực trị.

Vì số điểm cực trị hàm số () ykxm =+ bằng tổng số điểm cực trị của hàm số () ykxm =+ và số nghiệm đơn và số nghiệm bội lẻ của phương trình () 0 kxm+= , mà hàm số () ykxm =+ cũng có ba điểm cực trị nên hàm số ()() yfxgxm =−+ có đúng năm điểm cực trị khi phương trình () 0 kxm+= có đúng hai nghiệm đơn (hoặc bội lẻ). Dựa vào bảng biến thiên của hàm số ()ykx = , phương trình () 0 kxm+= có đúng hai nghiệm đơn (hoặc bội lẻ) khi và chỉ khi 7 4 m −≥ 7 4 m ⇔≤− Vì m∈ℤ , 7 4 m ≤− và () 5;5 m ∈− nên {} 4;3;2 m ∈−−− .

Câu12. (Sở GDBạcLiêu- 2019) Cho hàm số ()()() 322122yfxxmxmx ==−−+−+ . Tập hợp tất cả các giá trị của tham số m để hàm số ()yfx = có 5 điểm cực trị là ; a c b    , (với , , abc là các số nguyên, a b là phân số tối giản). Giá trị của biểu thức 222 Mabc =++ là A. 40 M = . B. 11 M = . C. 31 M = . D. 45 M = . Lờigiải ChọnD Hàm số ()()() 322122yfxxmxmx ==−−+−+ có đạo hàm là ()()() 2 32212 yfxxmxm ′=′=−−+− - Để hàm số ()yfx = có 5 điểm cực trị thì hàm số ()yfx = có hai điểm cực trị 12 , xx dương. Tương đương với phương trình () 0 fx′= có 2 nghiệm dương phân biệt.

Để hàm số ()()() 2 ()|23||| gxfxfxmhxm =++=+ có đúng 7 điểm cực trị thì phương trình () hxm =− phải có 4 nghiệm phân biệt, hay 0550 mm <−<⇔−<< Câu14. (THPTThanhChương-Nghệ An- 2018) Có bao nhiêu giá trị nguyên của tham số m để hàm số 32 1 (3)(37)1 3 =−−++− yxmxmx có 5 điểm cực trị? A. 3 B. 5 C. 2 D. 4 Lờigiải

Ta có ()() ()()

 −−++−≥   =  −−−−+−< 

x mxmxkhix y x mxmxkhix ()() ()() 2 2

3 2 3 2

3371,0 3 3371,0 3

2337,0 2337,0 xmxmkhix y xmxmkhix  −−++>  ′  =  −−−−+<  . Dễ thấy tại 0 x = đạo hàm không tồn tại 0 x  = là một điểm cực trị Để hàm số có 5 điểm cực trị thì phương trình ()() 2 23370 −−++=xmxm có 2 nghiệm dương phân biệt

 + >    ∆> <   ⇔>⇔  >   <   >−  

m m P S m m

973 2 973 '0 2 0 0 3 7 3

7973 32 ⇔−<< m . Do m nguyên nên {} 2;1;0∈−− m Câu15. (Đề MinhHọa2021) Cho hàm số ()fx là hàm số bậc bốn thoả mãn ()00 f = . Hàm số ()fx ′ có bảng biến thiên như sau:

() 1 có một nghiệm 0 ta=> .  Bảng biến thiên

 Vậy hàm số ()gx có 3 cực trị

Câu16. (Mã104-2021Lần1) Cho hàm số ()yfx = có đạo hàm ()()() 2 916, fxxxx ′ =−−∀∈ ℝ . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số () ( ) 3 7 gxfxxm =++ có ít nhất 3 điểm cực trị? A. 16 . B. 9 . C. 4 . D. 8 . Lờigiải ChọnD

Ta có: () 9 0 4 x fx x

=  ′ =⇔  =±  () ()() () ( ) 23 3 2 3

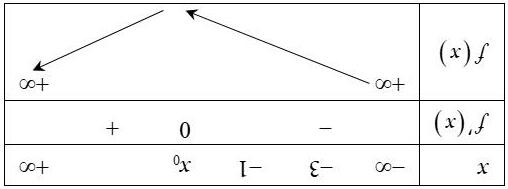
377 .7 7

xxx gxfxxm xx

++ ′′ =++ + +) ()gx ′ không xác định tại 0 x = và ()() () 23 2 3

377 7

xxx xx

++ + đổi dấu khi qua 0 x = nên 0 x = là một điểm cực trị của hàm số +) ( ) 33 333 33

xxmxxm fxxmxxmxxm xxmxxm

++=−+=−−  ′ ++=⇔++=⇔+=−+   ++=+=−+

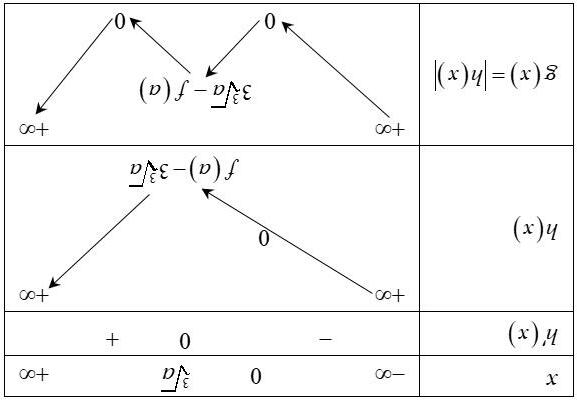
7474 707474 7979

() 1

Ta có bảng biến thiên của hàm số ()ux với () 3 7 uxxx =+ Để hàm số ()gx có ít nhất 3 điểm cực trị thì hệ () 1 phải có ít nhất 2 nghiệm đơn hoặc nghiệm bội lẻ khác 0 . Mà ta lại thấy 944mmm −+>−+>−− Nên suy ra 909mm−+>  <

đi

m

i h

a hàm s

()gx . Mặt khác

Xéthàmsố () 3 6 hxxx =+ ,vì () 2 360, hxxx ′=+>∀∈ ℝ nên ()hx đồngbiếntrên ℝ .Tacó bảngbiếnthiêncủahàmsố ()() 3 6 kxhxxx ==+ như sau: Hàmsố () () 3 6 gxfxxm =++ cóítnhất3 điểmcựctrị khiphươngtrình () 3 60fxxm ′++= cóítnhấthainghiệmkhác0. Điềunàyxảyrakhivàchỉ khi 80 m −> hay 8 m < . Kếthợp điềukiện m nguyêndươngta được {} 1;2;3...;7 m ∈ .Vậycó7giátrị của m thoả mãn.

Câu18. (Mã 101 - 2021 Lần 1) Chohàmsố ()yfx = có đạohàm ()()() 2 79, fxxxx ′ =−−∀∈ ℝ .Có baonhiêugiátrị nguyênd

điểm cực trị. Tổng các phần tử của S là A. 2. B. 4. C. 8. D. 10. Lờigiải ChọnA Xét hàm số () () ()()() () () () ()

2 2 22 22

1 211 11 '01111 1313

yfxm yxfxm xx yxmxm xmxm

=−+ ′′ •=−−+ ==  •=⇔−+=−⇔−=−−   −+=−=−  Để hàm số có 3 điểm cực trị thì {} 103131;0;1;2 mmmm−−≤<−⇔−≤<  ∈− Vậy tổng các phần tử của S là 2 Câu21. (Chuyên Thoại NgọcHầu-AnGiang-2021) Cho hàm số ()yfx = có đồ thị như hình vẽ bên dưới: Tìm tất cả các giá trị của tham số m để đồ thị hàm số ()()() 2 hxfxfxm =++ có đúng 3 cực trị A. 1 4 m ≥ B. 1 m ≤ C. 1 m < D. 1 4 m > Lờigiải ChọnD Xét ()()() 2 gxfxfxm =++ ()()()() '2''0 gxfxfxfx  =+= () () '0 1 2

=   ⇔  =−  

fx fx

Tacó: ( ) '0fx = có hai nghiệm là 0;3xx== và () 1 2 fx =−  có một nghiệm là 0 xa=<

nên hàm số ( )x g có ba cực trị. Do đó để đồ thị hàm số ( ) ( ) ( ) 2 hxfxfxm =++ có đúng 3 cực trị thì phương trình ( ) ( ) 2 0 fxfxm++= vô nghiệm 1 140 4 mm ⇔∆=−<⇔>

Câu22. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hàm số ( )yfx = có đạo hàm ( ) ( )( ) 22121fxxxxmxm ′ =−+++ với mọi x ∈ ℝ . Có bao nhiêu số nguyên 10 m >− để hàm số ( ) ( ) gxfx = có 5 điểm cực trị? A. 6 . B. 7 . C. 9 . D. 8 . Lờigiải ChọnC

Hàm số ( ) ( ) gxfx = là hàm số chẵn nên ( )gx có 5 điểm cực trị khi ( )fx có đúng 2 điểm cực trị dương, hay phương trình ( ) ( )( ) 22 01210fxxxxmxm ′ =⇔−+++= có đúng 2 nghiệm bội lẻ dương.

Cóbaonhiêugiátrị nguyên [] 10,10 m∈− để hàmsố ()() 2021 gxfxmx=++ có đúng1cựctrị?

x fxx xmxm

 =  ′ =⇔=   +++= 

0 01 210*

A. 20 . B. 16 . C. 15 . D. 18 . Lờigiải ChọnD Tacó ()()()()() '''0'1 gxfxmgxgxm =+⇔=⇔=− Số nghiệmcủa () 1 làsố giao điểmcủa2 đồ thị hàmsố ()' yfx = và đường : dym =−

Tacó () () 2

Xétcáctrườnghợp

+Trườnghợp ( )* có 1 nghiệmdươngkhác 1 và 1 nghiệmbằng 0 ,hay 10 1 20 m m m +=  ⇔=−  −>

+ Trường hợp ( )* có hai nghiệm trái dấu, trong đó nghiệm dương khác 1, hay 2 1210 1 3 10 1

mm m m m m

 +++≠ ≠−   ⇔⇔<− +<   <− 

Vậyvới 1 m ≤− thì ( )gx có 5 điểmcựctrị Vì 10 m >− nên { }9;8;...;1 m∈−−− ,có 9 giátrị Câu23. (Sở VĩnhPhúc-2021) Chohàmsố ( )fx .Biết ( ) ' fx làhàmbậc3.Có đồ thị như hìnhvẽ sau

Dựavào đồ thị trên. Để ()gx có đúng1cựctrị thì điềukiệnlà [] { } 10,10 14,5,6,7,8,9,10,10,9,8,7,6,5,4,3,2 3

m mm m

 ∈−  <−⇔∈−−−−−−−−−   >  Số giátrị của m là 16

Câu24. (Sở Lào Cai - 2021) Chohàm số 432 1 () 4 fxxaxbxcx =+++ có đồ thị () C của hàm '()yfx = như hìnhvẽ sau:

  = =   =   với 1x lànghiệmcủaphươngtrình '()1fx =− và 234 ,, xxx làbanghiệmcủaphươngtrình '()2fx = , 1234 02 xxxx <<<<< Bảngxétdấu '()ygx =

nhìnvàobảngtrên,hàmsố ()()'() gxffx = có3cựctrị

●Tìmsố cựctrị củahàmsố ()()'() hxffx = BBTcủahàmsố ()yfx =

1 2 '()0 '()'().''(())0()0 ()2

Tacó: 1 2 3 4

x x fx xx hxfxffxfx xx fx xx xx

=−   =  =   =  ==⇔=⇔   =   =   =  =  

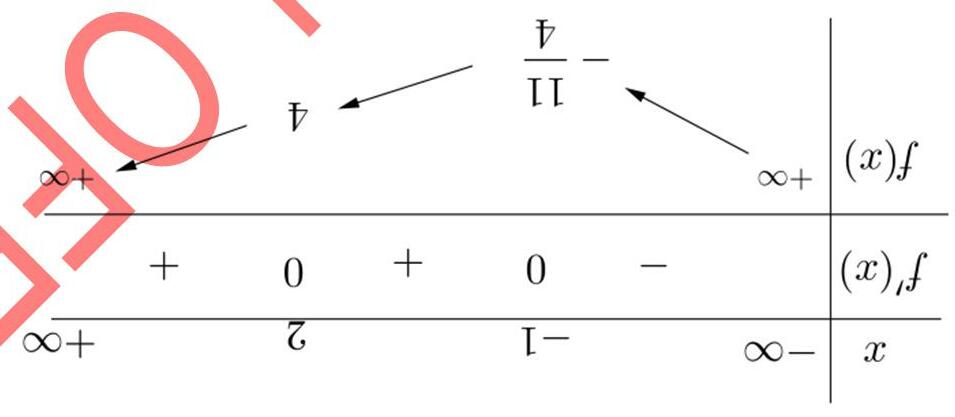
Với 12 , xx lànghiệmcủaphươngtrình ()0,fx = 34 , xx lànghiệmcủaphươngtrình ()2fx = và 312412xxxx<<−<<<

Bảngxétdấu '()yhx = nhìnvàobảngtrên,hàmsố ()()'() hxffx = có5cựctrị

Vậytổngcó8cựctrị.

Câu25. (THPT PTNK Cơ sở 2 - TP.HCM - 2021) Cho hàm số ()yfx = có đạo hàm ()() () 2 2 '2 fxxxx =−− với x ∀∈ ℝ .Gọi S làtậphợptấtcả cácgiátrị nguyêndươngcủathamsố m để hàmsố 2 1 6 2 fxxm  −+   có 5 điểmcựctrị.Tínhtổngcácphầntử của S ?

A. 154 B. 17 C. 213 D. 153

( ) () ( ) () 3222222 2568022340* xmxxmxxmxm  +−+−=⇔−+−+= 

( )1 thì

00 1 60 2 xxm

th

nghi

a ph

() () () 222

2 23401 x gxxmxm

=  ⇔  =+−+=   Để đồ thị hàm số ( )yfx = có hai điểm cực trị nằm khác phía đối với trục Ox thì đồ thị hàm số

( )yfx = phảicắttrụchoành tại3 điểmphân biệt ( )* ⇔ có3 nghiệm phân biệt ( )1 ⇔ có 2nghiệm

Vậy số hàm số ( )yfx = có hai điểm cực trị nằm khác phía đối với trục Ox là 19

ng trình ( )2 hay nói cách khác phương trình ( ) ( )1,2 không có nghiệmchung. Vì vậy, để hàm số 2 1 6 2 fxxm  −+   có 5 điểm cựctrị thì phươngtrình ( ) ( )1,2 cóhai nghiệmphânbiệtkhác 6 hay {}

1 2 2 2

m

∆>  −>   ∆>    ⇔−>⇔<→∈ −+≠     ≠≠ −+≠   

0 90 2 0 1 1 90181,2,...,17 .66.60 2 2 18,19 1 .66.61 2

Xác suất cần tìm là: 19 . 21 P =

+ ∈

m m mm m mm m

ℤ Vậy tổng các giá trị của m là: 12...17153 +++= . Câu26. (THPTPTNKCơ sở 2-TP.HCM-2021) Cho { }020Ann=∈≤≤ ℤ và F là tập hợp các hàm số ( ) ( ) 3222 2568 fxxmxxm =+−+− có mA ∈ . Chọn ngẫu nhiên một hàm số ( )fx từ F . Tính xác suất để đồ thị hàm số ( )yfx = có hai điểm cực trị nằm khác phía đối với trục Ox A. 18 21 B. 19 20 C. 9 10 D. 19 21 Lờigiải ChọnD

Ta có: { } ( ) 0202121. AnnAFdomA =∈≤≤  =  Ω==∈ ℤ Xét hàm số: ( ) ( ) ( ) ( ) 322222 256832256. fxxmxxmfxxmx ′ =+−+−  =+−+

Cách 2: Xét hàm số: ( ) ( ) ( ) ( ) 322222 256832256. fxxmxxmfxxmx ′ =+−+−  =+−+

( ) ( ) ( ) 22 03225601fxxmx ′′ =⇔+−+= .

 +

22810

;y;N;y MMNNMxx c

a đồ th

hàm số là

Hai điểm cực trị nằm về 2 phía của trục hoành, suy ra: ()()()() 2 y.y000 MNMNMNMN axbaxbaxxabxxb <⇔++<⇔+++< () 2432 252 2.0224752206410401880 3 t aabbtttt ⇔++<⇔−+−+> (2).

Sử dụng CASIO - FX 580 giải được (2) đúng với t ∀∈ℝ Vậy số hàm số ()yfx = có hai điểm cực trị nằm khác phía đối với trục Ox là 19 .

Xác suất cần tìm là: 19 21 P =

Câu27. (Chuyên LêKhiết - Quảng Ngãi - 2021) Cho hàm số ()fx có đạo hàm liên tục trên ℝ , đồ thị hàm số '()yfx = có đúng bốn điểm chung với trung hoành như hình vẽ dưới.

+ Vì đồ thị hàm số () 3 ()32021 gxfxxm =−++ thu được bằng cách tịnh tiến

3 ()yfxx =+ theo vector () 2021;0 vm=−− nên để hàm số () 3 ()32021,0 gxfxxmx =−++>

có đúng 5 điểm cực trị thì điều kiện là 20210 20212021,(0;1)2021 20210 am amaam am −−>   −−≤<−∈  =− −−−≤

Vậy có một giá trị của m.

Câu28. (ChuyênLongAn-2021) Cho hàm số ()fx liên tục trên ℝ và có bảng biến thiên dưới đây

Có bao nhiêu giá trị nguyên của m để hàm số ( ) 3 32021yfxxm =−++ có 11 điểm cực trị A. 0 . B. 2 . C. 5 . D. 1 . Lờigiải ChọnD

+ Vì hàm số ( ) 3 32021yfxxm =−++ là hàm số chẵn nên để hàm số có 11 điểm cực trị thì hàm số () 3 ()32021,0 gxfxxmx =−++> có đúng 5 điểm cực trị + Ta có : + Sử dụng phương pháp ghép trục ta có bảng biến thiên của () 3 3,0yfxxx=−> x 0 a 1 b c d e +∞ 3 3 uxx =− 0 -1 -2 -1 1 2 4 ()fu

Có bao nhiêu giá trị nguyên của tham số m để hàm số ()652021 yfxm =−++ có 3 điểm cực đại?

A. 5 B. 6 C. 7 D. 4 Lờigiải ChọnB  Xét hàm số ()652021 yfxm =−++ . Đặt () () () () 2 2

665665 6565 65 65 xx uxxu x x

′ =−=−  == .

Khi đó ()665 5 00 656 x ux x ′ =⇔=  = Với () 7 224 6 xuf =  =  =− ; Bảng biến thiên

Suy ra hàm số () 2021 yfum =++ có ba điểm cực đại

Do { }2023;2022;2021;2020;2019;2018 mm ∈  ∈−−−−−− ℤ .

Vậy có 6 giá trị nguyên của m để hàm số đã cho có 3 cực đại.

Câu29. (Chuyên ĐHSP-2021) Cho hàm số ()yfx = liên tục trên ℝ , có bảng biến thiên như sau:

Đặt ()() 2 hxmfx=−− ( m là tham số). Có bao nhiêu giá trị nguyên của m sao cho hàm số ()yhx = có đúng 5 điểm cực trị?

A. Vô số B. 12 C. 0 D. 10 Lờigiải ChọnD

Xét hàm số ()() 2 gxmfx=−− , ()() 22 20 22 xaxa gxfx xbxb −==+ ′′ =−−=⇔⇔−==+ .

Bảng biến thiên hàm số ()gx : Để hàm số ()yhx = có 5 cực trị khi đồ thị hàm số ()ygx = cắt trục hoành tại 3 điểm phân biệt, tức là: 60556mmm −<<+⇔−<< Vậy: Có 10 giá trị của m thỏa yêu cầu đề bài. Câu30. (ChuyênBiênHòa-2021) Cho hai hàm đa thức ()() , yfxygx == có đồ thị là hai đường cong ở hình vẽ.

Biết rằng đồ thị hàm số ()yfx = có hai điểm cực trị là , FG ; đồ thị hàm số ()ygx = có hai điểm cực trị là , EH và 2,4HGFE== . Số giá trị nguyên của tham số () 10;10 m∈− để hàm số

()() 22 yfxxgxxm =−−−+ có đúng 7 điểm cực trị là

A. 7 B. 8 C. 5 D. 6 Lờigiải ChọnB Đặt () ()() 22 hxfxxgxxm =−−−+ ()() ()() 22 21 hxxfxxgxx ′′′ =−−−− () ()() 2 22 2

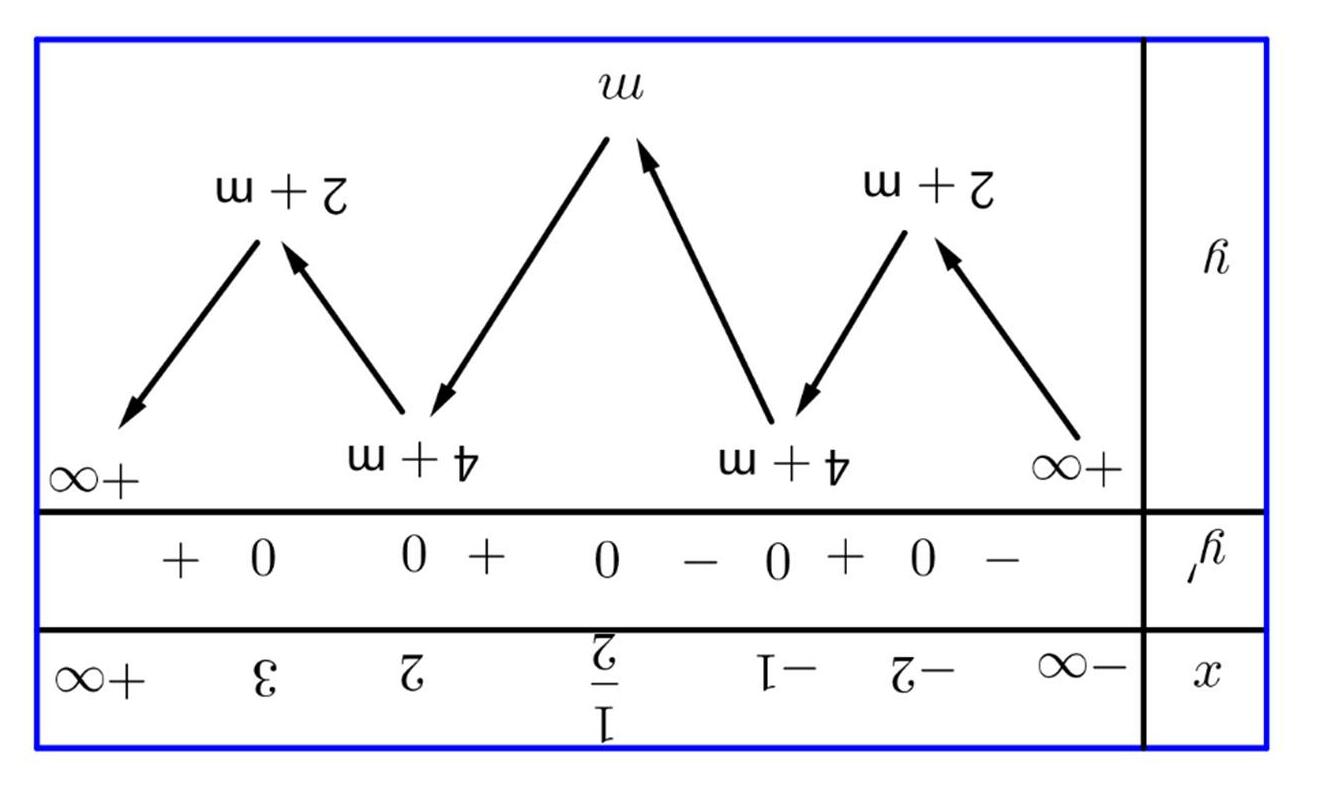
xx xx fxxgxx hxxxxx x xx

2 2;1 0 63;2 210 11 22

 −=  ==−  ′′ −=−  ′ =⇔⇔−=⇔==−   −=    == 

Bảngbiếnthiêncủahàmsố ()yhx =

 ∈−−−−−−−−

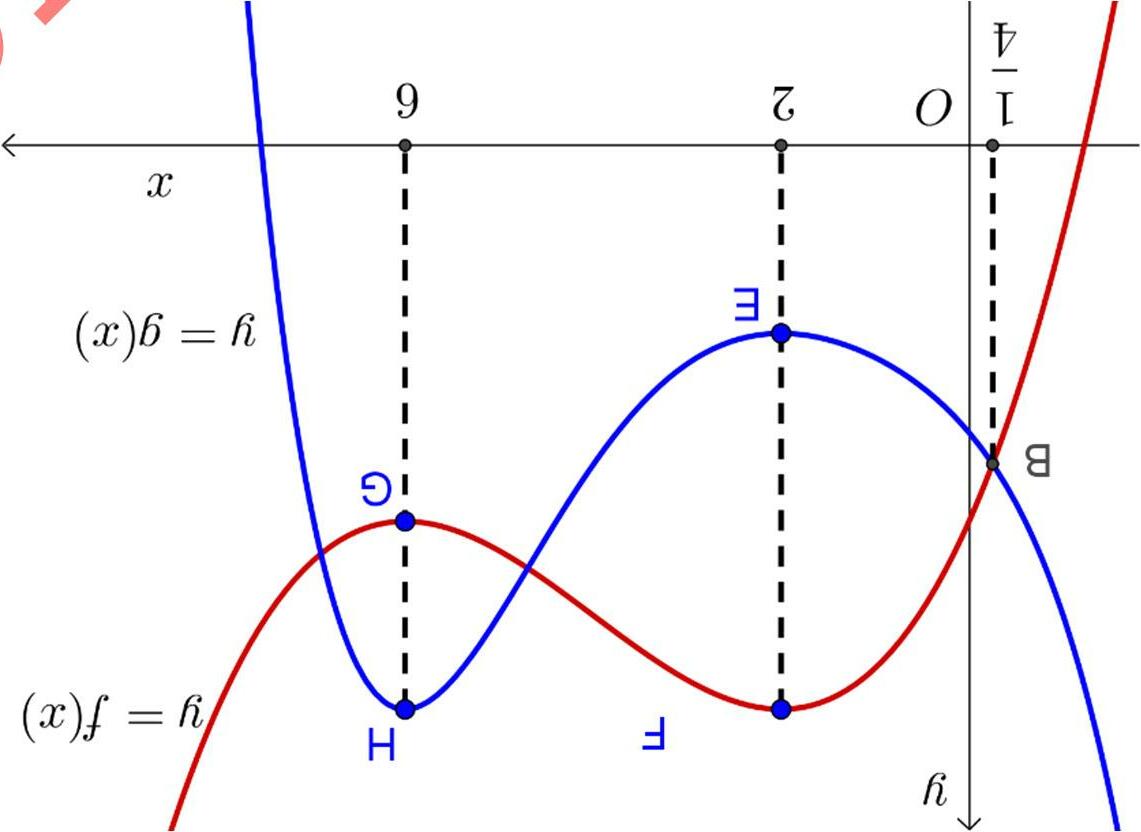
Trường hợp 1: Phương trình có hai nghiệm phân biệt khác 0,,ab

0

'()0 '()0 () 2 () 2 x fxxa gx mxb fx m fx =   ==    =⇔⇔  =  =

m m mm

 <<  <<  ⇔   <−   <−  

Dựa vào bảng biến thiên ta thấy: 15 210 2 2 1 2

Trường hợp 2: Phương trình () 2 m fx = có ba nghiệm, trong đó có đúng một nghiệm trùng 0 x = , xa = hoặc xb = .

m m mm

Dựa vào bảng biến thiên ta thấy: 1 2 2 2 1 2

 =  =  ⇔   =−   =−  

Kết hợp cả hai trường hợp ta có 2027 số nguyên m thuộc đoạn [] 2020;2021

Câu32. (Đại Học Hồng Đức - 2021) Gọi S là tập hợp tất cả các số thực m sao cho đồ thị hàm số () 422 24132yxmxmm =−−−+− có đúng 5 điểm cực trị. Số phần tử [] 2021;2021 mS ∈−∩ có giá trị nguyên là: A. 2020 . B. 2021 . C. 4040 . D. 4041. Lờigiải ChọnA y x O f(x)

|f(x)|

số ()ygx = có đúng một điểm cực trị là A và 7 4 AB = . Có bao nhiêu số nguyên () 2021;2021 m∈− để hàm số ()() yfxgxm =−+ có đúng 5 điểm cực trị? A. 2019 . B. 2021 . C. 2022 . D. 2020 . Lờigiải ChọnA

 Đặt: ()()() hxfxgx =− ; ()()() 1 2 0 xx hxfxgx xx

=  =⇔=⇔  = 

()()() hxfxgx ′′′ =− ; () 0 0 hxxx ′ =⇔= . Từ các đồ thị đã cho, ta có: 102 xxx <<

()()()()() 00000 7 4 hxfxgxgxfxAB =−=−−=−=−   .

Bảng biến thiên của ()hx và ()hx :

x −∞ 1x 0x 2x +∞ ( )hx ′ 0 + + ( )hx +∞ 7 4

7 4 0

Từ bảng biến thiên, ta thấy: hàm số ()yhx = có 3 điểm cực trị

Ox

+∞

+∞ ( )hx +∞ 0

 Đồ thị hàm số () yhxm =+ có cùng số điểm cực trị với đồ thị hàm số ()yhx = . Do đó, hàm số () yhxm =+ cũng có 3 điểm cực trị

 Hàm số () yhxm =+ có số điểm cực trị bằng số điểm cực trị của hàm số () yhxm =+ cộng số giao điểm không trùng với các điểm cực trị của đồ thị hàm số () yhxm =+ với trục Ox Vì vậy, để hàm số () yhxm =+ có đúng 5 điểm cực trị thì đồ thị hàm số () yhxm =+ và trục Ox phải có 2 giao điểm khác các điểm cực trị hay đường thẳng ym =− phải cắt đồ thị hàm số

()yhx = tại 2 điểm phân biệt khác các điểm cực trị

Từ bảng biến thiên của hàm số ()yhx = , điều kiện của m thỏa mãn ycbt là: 77 44 mm −≥⇔≤−

() 2021;2021 m∈− và m ∈ ℤ  {} 2020;2019;...;2 m∈−−−

Vậy số giá trị nguyên của m thỏa mãn là: 2019.

Dạng1.Góccủa đườngthẳngvới đườngthẳng

Để tính góc giữa hai đường thẳng 12 , dd trong không gian ta có thể thực hiện theo hai cách

Cách 1. Tìm góc giữa hai đường thẳng 12 , dd bằng cách chọn một điểm O thích hợp ( O thường nằm trên một trong hai đường thẳng).

ChọnC Vì // AABB ′′ nên ()() ,, AABCBBBCBBC ′′′′′ ==

Từ O dựng các đường thẳng '' 12 , dd lần lượt song song ( có thể tròng nếu O nằm trên một trong hai đường thẳng) với 1d và 2d . Góc giữa hai đường thẳng 12 , dd chính là góc giữa hai đường thẳng 12 , dd

Lưuý1: Để tính góc này ta thường sử dụng định lí côsin trong tam giác 222 cos 2 bca A bc +− = .

Cách 2. Tìm hai vec tơ chỉ phương 12 , uu của hai đường thẳng 12 , dd

Khi đó góc giữa hai đường thẳng 12 , dd xác định bởi () 12 12 12

. cos, uu dd uu =

Lưuý2: Để tính 1212 ,, uuuu ta chọn ba vec tơ ,, abc không đồng phẳng mà có thể tính được độ dài và góc giữa chúng,sau đó biểu thị các vec tơ 12 , uu qua các vec tơ ,, abc rồi thực hiện các tính toán.

Câu1. (Mã101-2021Lần1) Cho hình lăng trụ đứng ABCABC′′′ có tất cả các cạnh bằng. Góc giữa đường thẳng AA′ và BC′ bằng A. 030 B. 090 C. 045 D. 060 Lờigiải

Ta có: 0tan145 BC BBCBBC BB

′′ ′′ ==  = ′

Câu2. (Mã 103 - 2021 - Lần 1) Cho hình lăng trụ đứng ABCABC′′′ có tất cả các cạnh bằng nhau (tham khảo hình bên dưới).

A B

C C' B'

Góc giữa hai đường thẳng AB ′ và CC′ bằng A. 45° B. 30° C. 90° D. 60° Lờigiải ChọnA

A' A B

A'

C C' B'

Ta có: CC // ' BB . Nên () ';'ABCC = () ';'ABBB = ''ABB ( ''ABB là góc nhọn). Mặt khác,

tam giác ''ABB là tam giác vuông cân ( '' ABBB = và '' ABBB ⊥ ) suy ra ''45ABB =° Vậy góc giữa hai đường thẳng AB và ' CC bằng 45°

Câu3. (Mã 102 - 2021 Lần 1) Cho hình lăng trụ đứng ABCABC′′′ có tất cả các cạnh bằng nhau (tham khảo hình bên).

Góc giữa hai đường thẳng ' AB và ' CC bằng A. 30° . B. 90° . C. 60° . D. 45° . Lờigiải ChọnD

Góc giữa hai đường thẳng AA′ và BC ′ bằng A. 090 . B. 0 45 . C. 0 30 . D. 060 . Lờigiải ChọnB

Ta có: //C AAC′′ nên: ()() ,, AABCCCBC ′′′′  = Mặt khác tam giác BCC′ vuông tại C′ có CCBC ′′′ = nên là tam giác vuông cân. Vậy góc giữa hai đường thẳng AA′ và BC ′ bằng 0 45 .

Câu4. (Mã 104 - 2021 Lần 1) Cho hình lăng trụ đứng .'''ABCABC có tất cả các cạnh bằng nhau ( tham khảo hình bên).

Ta có '//'BBCC (do ' BB và ' CC là cạnh bên của hình lăng trụ).

Suy ra () () ','',' ABCCABBB = .

Tứ giác ''ABBA là hình vuông (do .'''ABCABC là lăng trụ đứng có tất cả các cạnh bằng nhau) nên '45ABB =°

Vậy () () ','',''45ABCCABBBABB===° .

Câu5. (Đề Tham Khảo 2018) Cho tứ diện OABC có , , OAOBOC đôi một vuông góc với nhau và OAOBOC == . Gọi M là trung điểm của BC (tham khảo hình vẽ bên dưới). Góc giữa hai đường thẳng OM và AB bằng

A. 045 B. 090 C. 030 D. 060 Lờigiải ChọnD

Đặt OAa = suy ra OBOCa == và 2 ABBCACa === Gọi N là trung điểm AC ta có // MNAB và 2 2 a MN =

Suy ra góc () (),, = OMABOMMN . Xét OMN

Trong tam giác OMN có 2 2 a ONOMMN=== nên OMN là tam giác đều

Suy ra 060 OMN = . Vậy () () 0,,60 ==OMABOMMN

Câu6. (Chuyên Long An - 2021) Cho hình lập phương . ABCDEFGH . Góc giữa cặp véc tơ AF và EG bằng A. 30° . B. 120° . C. 60° . D. 90° . Lờigiải ChọnC

Ta có ()() ,, AFEGAFACCAF ==

CAF∆ là tam giác đều, nên 60 CAF =° .

Câu7. (THPTNguyễnHuệ -PhúYên-2021) Hình chóp SABC có ,, SASBSC đôi một vuông góc với nhau và SASBSC == . Gọi I là trung điểm của AB . Góc giữa SI và BC bằng A. 30° . B. 60° . C. 45° . D. 90° . Lờigiải ChọnB

1 2 cos; . 2

Ta có: () () 2

SASBBC SIBCSABCSBBC SIBC BC SIBCBC BC

+ + === 2 SBBC BC = 2 ..cos135SBBC BC ° = 2 .2.cos135 2 SBSB SB ° = 2.cos1351 22 ° ==−

Suy ra: ();120SIBC =° ();60SIBC  =° .

Câu8. (THPT Nguyễn Đức Cảnh - Thái Bình - 2021) Cho hình lập phương 1111 ABCDABCD có cạnh a . Gọi I là trung điểm .BD Góc giữa hai đường thẳng 1 AD và 1 BI bằng A. 120° B. 30. ° C. 45° D. 60° Lờigiải ChọnB

Ta có 11 // BCAD ()() 1111 ,, ADBIBCBI  = Vì 1111 ABCDABCD là hình lập phương cạnh a nên 11 26 2;; 22 BCaICBIaa ===

Xét 1 BIC∆ có: 222 11 1 11

3 cos 2.2 BIBCIC IBC BIBC +− == 1 30. IBC  =° Do đó ()()11111,,30.ADBIBCBIIBC===°

Câu9. (THPT Lê Quy Đôn Điện Biên 2019) Cho tứ diện ABCD với 0 3 ,60, 2 ACADCABDABCDAD ==== . Gọi ϕ là góc giữa hai đường thẳng AB và CD Chọn khẳng định đúng về góc ϕ

Lờigiải

Ta có () 00 ......60..60 ABCDABADACABADABACABADcosABACcos =−=−=− 0031 ..60..60. 24 ABADcosABADcosABAD =−= () .11 , .44 ABCD cosABCDcos ABCD ϕ ==  =

Câu10. (THPT Hoàng Hoa Thám Hưng Yên 2019) Cho hình hộp chữ nhật ABCDABCD ′′′′ , biết đáy ABCD là hình vuông. Tính góc giữa AC ′ và BD A. 90° B. 30° C. 60° D. 45° Lờigiải Vì ABCD là hình vuông nên BDAC ⊥ Mặt khác () AAABCDBDAA ′′ ⊥  ⊥ Ta có () ' BDAC BDAACBDAC BDAA ⊥  ′′  ⊥  ⊥  ⊥  Do đó góc giữa AC ′ và BD bằng 90° . Câu11. (Chuyên KHTN 2019) Cho tứ diện ABCD có 2 ABCDa == . Gọi M , N lần lượt là trung điểm AD và BC . Biết 3 MNa = , góc giữa hai đường thẳng AB và CD bằng. A. 045 B. 090 C. 060 D. 030 Lờigiải

Gọi P là trung điểm AC , ta có // PMCD và // PNAB , suy ra () (),, ABCDPMPN = . Dễ thấy PMPNa == Xét PMN∆ ta có 22222231 cos 2.2..2 PMPNMNaaa MPN PMPNaa +−+− ===− () 0000 120,18012060MPNABCD  =  =−= .

B

N M

B' C' A'

C D A D'

Câu12. (ChuyênLươngVănChánhPhúYên2019) Cho hình lập phương ABCDABCD ′′′′ ; gọi M là trung điểm của BC′′ . Góc giữa hai đường thẳng AM và BC ′ bằng A. 45° B. 90° C. 30° D. 60° Lờigiải Giả sử cạnh của hình lập phương là 0 a > Gọi N là trung điểm đoạn thẳng BB′ . Khi đó, // MNBC′ nên ()() ,, AMBCAMMN ′ =

Xét tam giác ABM ′′ vuông tại B′ ta có: AM ′ 22ABBM ′′′ =+ 2 2 4 a a =+ 5 2 a =

Xét tam giác AAM ′ vuông tại A′ ta có: 22AMAAAM ′′ =+ 2 2 5 4 a a =+ 3 2 a =

có ABa = và

Trong tam giác AMN ta có:

cos AMN 222 2.. MAMNAN MAMN +− =

+− = 2 2 64 4 62 a a = 1 2 =

aaa aa

222925 444 2..32 22

Suy ra 45 AMN =° Vậy ()() ,, AMBCAMMN ′ = = 45 AMN =° .

Câu13. (Chuyên Hạ Long - 2018) Cho hình chóp . SABC có độ dài các cạnh SASBSCABACa ===== và 2 BCa = . Góc giữa hai đường thẳng AB và SC là? A. 45° . B. 90° . C. 60° . D. 30° . Lờigiải

2 AAa ′ = . Góc giữa hai đường thẳng AB′ và BC′ bằng A. 60° . B. 45° . C. 90° . D. 30° . Lờigiải

Ta có 2 BCa = nên tam giác ABC vuông tại A . Vì SASBSCa === nên hình chiếu vuông góc của S lên () ABC trùng với tâm I của đường tròn ngoại tiếp tam giác ABC Tam giác ABC vuông tại A nên I là trung điểm của BC

Ta có ()cos,ABSC ()cos,ABSC = . .

ABSC ABSC =

. ABSC = ()ABSIIC + . ABSI = 1 2 BABC =− 1 ..cos45 2 BABC =−° 2 2 a =−

()cos,ABSC =

2 2 2 a a 1 2 = () , ABSC  60 =°

Ta có ()() ABBCABBBBCCC ′′′′ =++ ABBCABCCBBBCBBCC ′′′′ =+++

ABBCABCCBBBCBBCC ′′′′ =+++ 22 2 3 002 22 aa a =−+++=

Suy ra ()cos, .

ABBC ABBC ABBC

′′ ′′ = ′′ () 2 3 1 2 ,60 2 3.3

a ABBC aa ′′ ==  =°

Câu15. (Kim Liên - Hà Nội - 2018) Cho tứ diện ABCD có DADBDCACABa ===== , 45 ABC =° . Tính góc giữa hai đường thẳng AB và DC . A. 60° . B. 120° . C. 90° . D. 30° . Lờigiải

Cách2: ()cos,ABSC ()cos,ABSC = . .

ABSC ABSC = Ta có . ABSC ()SBSASC=− .. SBSCSASC=− ..cos90..cos60SBSCSASC =°−° 2 2 a =−

a ABSC a ==

2 2 2 1 cos, 2 Trang 10

Ta có tam giác ABC vuông cân tại A , tam giác BDC vuông cân tại D . Ta có () ... ABCDDBDACDDBCDDACD =−=− () () 2 1 cos,cos, 2 DBCDDBCDDACDDACDa =−=− Mặt khác ta lại có ()() .1 .cos.cos, 2 ABCD ABCDABCDABCDABCD ABCD =⇔==− () () ,120,60ABDCABCD  =°  =° .

Câu16. (ChuyênTrầnPhú-HảiPhòng-2018) Cho hình lập phương ABCDABCD ′′′′ . Gọi M , N lần lượt là trung điểm của AD , . BB′ Cosin của góc hợp bởi MN và ' AC bằng

3 C. 5 3

MNAC MNACMNAC MNAC

′ ′′ === ′ .

2 4 Lờigiải * Xét hình lập phương ABCDABCD ′′′′ cạnh a * Đặt , , , ...0aABbADcAAabcaabbcac ′ ===  ====== * Ta có: 222 11113 2244 2 MNANAMABBNAMabcMNaaaa =−=+−=−+  =++= 222 3 ACABADAAabcACaaaa ′′′ =++=++  =++= 2222 11 22 ACMNaaaa ′ =−+= () () . 2 cos;cos; 3 .

Câu17. (Cụm 5 Trường Chuyên - ĐBSH- 2018) Cho hình chóp SABCD có đáy là hình chữ nhật, 2 ABa = , BCa = . Hình chiếu vuông góc H của đỉnh S trên mặt phẳng đáy là trung điểm của cạnh AB , góc giữa đường thẳng SC và mặt phẳng đáy bằng 060 . Tính cosin góc giữa hai đường thẳng SB và AC A. 2 7 B. 2 35 C. 2 5 D. 2 7 Lờigiải

() () , SCABCD = () , SCCH = 060 SCH =

()cos, SBAC SBAC SBAC = ()() SBACSHHBABBC =++ .... SHABSHBCHBABHBBC =+++

.. HBABHBBC=+ 22 1 2 2 ABa== 5 ACa = , 22 2 CHaaa =+= , .tan6SHCHSCHa == . 22SBSHHB =+ ()2 2 67aaa=+=

()cos, SBAC SBAC SBAC = 2 2 7.5 a aa = 2 35 = .

Câu18. (Chuyên Thái Bình - 2018) Cho hình chóp tứ giác đều SABCD có đáy ABCD là hình vuông, E là điểm đối xứng của D qua trung điểm SA . Gọi M , N lần lượt là trung điểm của AE và BC . Góc giữa hai đường thẳng MN và BD bằng A. 90° . B. 60° . C. 45° . D. 75° . Lờigiải

Gọi I là trung điểm SA thì IMNC là hình bình hành nên // MNIC

Ta có ()BDSAC ⊥ BDIC  ⊥ mà // MNICBDMN  ⊥ nên góc giữa hai đường thẳng MN và BD bằng 90° .

Cách khác: có thể dùng hệ trục tọa độ của lớp 12, tính tích vô hướng .0BDMN = Câu19. (ChuyênTháiBình-2018) Cho hình chóp đều SABCD có tất cả các cạnh đều bằng a . Gọi M , N lần lượt là trung điểm của AD và SD . Số đo của góc giữa hai đường thẳng MN và SC là A. 45° . B. 60° . C. 30° . D. 90° .

Lờigiải

Gọi P là trung điểm của CD

Ta có: // NPSC ()() ,, MNSCMNNP  = .

Xét tam giác MNP ta có: 2 a MN = , 2 a NP = , 2 2 a MP = 22 22 44 aa MNNP  +=+ 2 2 a = 2 MP = MNP  ∆ vuông tại N 90 MNP  =° ()() ,, MNSCMNNP  = 90 =°

Câu20. (Sở Quảng Nam - 2018) Cho hình lăng trụ ABCABC′′′ có đáy ABC là tam giác vuông tại A , ABa = , 3 ACa = . Hình chiếu vuông góc của A′ lên mặt phẳng () ABC là trung điểm H của BC , 3 AHa ′ = . Gọi ϕ là góc giữa hai đường thẳng AB ′ và BC ′ . Tính cosϕ. A. 1 cos 2 ϕ = . B. 6 cos 8 ϕ = . C. 6 cos 4 ϕ = . D. 3 cos 2 ϕ = . Lờigiải Gọi E là trung điểm của AC ; D và K là các điểm thỏa BDHKAB′′ == Ta có ()BKABC ′ ⊥ và // BDAB ′′

2222336.BCBKCKaaa ′′ =+=+= 222 cos 2.. BDBCCD CBD BDBC

′′ +− ′ = ′′ 222 4676 8 2.2.6 aaa aa +− ==

Câu21. (Sở YênBái-2018) Cho tứ diện đều ABCD , M là trung điểm của cạnh BC . Tính giá trị của ()cos,ABDM A. 3 2 B. 3 6 C. 1 2 D. 2 2 Lờigiải Giả sử cạnh của tứ diện đều bằng .a Gọi N là trung điểm của AC Khi đó: () (),, ABDMMNDM =

Ta có: 3 22 ,.MNDMDNaa === 2 222 3 4 26 3 2 22

a MNMN NM MNM aa +− === Vậy () 3 6 cos,. ABDM =

DD cosD . ..D ..

Câu22. (Sở Nam Định - 2018) Cho hình lăng trụ . ABCABC′′′ có đáy ABC là tam giác đều cạnh a , tam giác ABC ′ đều nằm trong mặt phẳng vuông góc với () ABC . M là trung điểm cạnh CC′ . Tính cosin góc α giữa hai đường thẳng AA′ và BM .

A. 222 os 11 c α = B. 33 os 11 c α = C. 11 os 11 c α = D. 22 os 11 c α = Lờigiải

a AABM aa ′ = 33 11 = Câu23. (Sở HàTĩnh-2018) Cho hình lăng trụ tam giác đều . ABCMNP có tất cả các cạnh bằng nhau. Gọi I là trung điểm cạnh AC . Côsin của góc giữa hai đường thẳng NC và BI bằng A. 6 4 . B. 15 5 . C. 6 2 . D. 10 4 . Lờigiải Giả sử các cạnh của lăng trụ bằng a Gọi K là trung điểm của MP // BINK  ()() ,, NCBINCNK  = ABCMNP là lăng trụ tam giác đều ()CPMNP  ⊥

22

5 2 a =

Trong tam giác MND ta có: 222 3 cos 2..6 MNMDND NMD MNMD +− == () 3 cos,cos 6 ABDMNMD==

Câu25. (ĐHQG Hà Nội - 2020) Cho hình chóp SABCD có đáy hình vuông. Cho tam giác SAB vuông tại S và góc SBA bằng 030 . Mặt phẳng () SAB vuông góc mặt phẳng đáy. Gọi , MN là trung điểm , ABBC . Tìm cosin góc tạo bởi hai đường thẳng () , SMDN . A. 2 5 B. 1 5 C. 1 3 D. 2 3

Góc gi

ữ

Ta phải chọn điểm M trên d, mà có thể tính khoảng cách được đến mặt phẳng (P). Còn A là giao điểm của d và mặt phẳng (P).

     

SAB SH ABSHAB

⊥ ∩=⊥ ⊂⊥

ABCD SABABCDABABCD SHS

Trong () SAB , kẻ SHAB ⊥ tại H . Ta có: ()() ()() () () ,

Kẻ tia Az // SH và chọn hệ trục tọa độ Axyz như hình vẽ sau đây.

Trong tam giác SAB vuông tại S , 0 3 .cos.cos30 2 a SBABSBAa===

Trong tam giác SBH vuông tại H , 3 .cos 4 a BHSBSBH== và 3 .sin 4 a SHBHSBA== 3 44 aa AHABBHa=−=−= 3 0;;00;; 444 HSaaa        . 0;;0 2 a M    , () ;0;0Da , ;;0 2 a Na  

a SMDN SMDN SNDN aa ===

Câu1. (Đề Minh Họa 2021) Cho hình hộp chữ nhật . ABCDABCD ′′′′ có 2 ABAD== và 22 AA′ = (tham khảo hình vẽ bên). Góc giữa đường thẳng CA′ và mặt phẳng () ABCD bằng:

ng thẳng d và mặt phẳng (P) là

ặt ph

Trên d chọn điểm B khác A, dựng BH vuông góc với (P) tại H. Suy ra AH là hình chiếu vuông góc của d trên mặt phẳng (P).

Vậy góc giữa d và (P) là góc BAH .

A

C' C

D

D' A' B' B

A. 0 30. B. 045 C. 060 D. 0 90. Lờigiải ChọnB

Vì ()AAABCD ⊥ nên góc giữa đường thẳng CA′ và mặt phẳng () ABCD bằng góc ACA ′

Ta có 22 22. ACABBC=+=

′ ′ ===

Khi đó ta có () 22 tan1. 22 AA ACA AC

Vậy số đo góc 0 45. ACA ′ =

Câu2. (Đề Minh Họa 2020 Lần 1) Cho hình chóp SABCD có đáy là hình vuông cạnh 3a , SA vuông góc với mặt phẳng đáy và 2 SAa = . Góc giữa SC và mặt phẳng () ABCD bằng

Trang 18

A. 045 B. 060 C. 030 D. 090

Lờigiải ChọnC

SC

0 21 tan 30 3.23 SAa SCASCA AC a ===  = Câu3. (Đề ThamKhảo2020Lần2) Cho hình chóp . SABC có SA vuông góc với mặt phẳng (), ABC 2, SAa = tam giác ABC vuông cân tại B và 2 ACa = (minh họa nhứ hình bên). Góc giữa đường thẳng SB và mặtphẳng () ABC bằng A. 30. ° B. 45. ° C. 60. ° D. 90. ° Lờigiải ChọnB Ta có () () SBABCB AB SAABC ∩= 

là hìnhchiếu của SB trên mặt phẳng () ABC () () , SBABCSBA  = Dotam giác ABC vuông cântại ()2 2222222222. 4 BABABaABBCACaABa  ⇔⇔⇔ + = === Xét tam giácvuông SAB vuôngtại ,A có 2 SAABaSAB ==  ∆ vuôngcântại A 45. SBA  =° Câu4. (Mã 101 - 2020 Lần 1) Cho hình chóp . SABC có đáy ABC là tam giác vuông tại B , ABa = , 2 BCa = , SA vuông góc với mặt phẳng đáy và 15 SAa = (tham khảo hình bên).

S

lên m

Trong tam giác ABC vuông tại B có: 222245 ACABBCaaa =+=+= .

Trong tam giác SAC vuông tại A có: 15 tan3 5 SAa SCA AC a === 60 SCA ⇒=°

Vậy () ();60SCABC =° .

Câu5. (Mã 102 - 2020 Lần 1) Cho hình chóp . SABC có đáy là tam giác vuông tại B , 3,3, ABaBCa == SA vuông góc với mặt phẳng đáy và 2 SAa = (tham khảo hình vẽ).

Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 60 B. 045 C. 030 D. 090 Lờigiải ChọnC

C A B Trang 20

23 tan 30. 3 33

SAa SCASCA AC aa ===⇒= +

Ta có: () () ; SCABCSCA = () () 0 2 2

Vậy () () o;30SCABC = .

Câu6. (Mã 103 - 2020 Lần 1) Cho hình chóp SABC và có đáy ABC là tam giác vuông tại ,B ,3; ABaBCa == SA vuông góc với mặt phẳng đáy và 30 SAa = (tham khảo hình bên). Góc giữa đường thẳng SC và mặt đáy bằng

A. 45° B. 90° C. 60° D. 30° Lờigiải ChọnC

Do AC là hình chiếu vuông góc của SC trên mặt phẳng () ABC nên () () , SCABCSCA =

Ta có: 22 10 ACABBCa =+= Khi đó 0 30 tan360 10 SAa SCASCA AC a ===  = .

Câu7. (Mã104-2020Lần1) Cho hình chóp . SABC có đáy ABC là tam giác vuông tại B , ABa = ; 2 BCa = ; SA vuông góc với mặt phẳng đáy và SAa = . Góc giữa đường thẳng SC và đáy bằng A. 090 . B. 045 . C. 060 . D. 030 . Lờigiải ChọnD

Ta có góc giữa đường thẳng AC ′ và mặt phẳng () ABCD bằng góc giữa AC ′ và AC và bằng góc ′ ACA .

Ta có 22 2 ACABBCa =+=

Ta có : Góc SC và đáy là góc SCA Xét tam giác SCA vuông tại A có: 22 3 ACABBCa =+= 0tan30 3 SAa SCASCA AC a ==  = Câu8. (Mã101– 2020Lần 2) Cho hình hộp chữ nhật ABCDABCD ′′′′ có ,6 ABBCaAAa ′ === (tham khảo hình dưới). Góc giữa đường thẳng AC ′ và mặt phẳng () ABCD bằng: A. 60° . B. 90° . C. 30° . D. 45° . Lờigiải ChọnA

Trang 21

Xét tam giác ACA ′ ∆ có 6 tan360 2

′ ′′ ===  =° AAa ACAACA AC a Vậy góc AC ′ và mặt phẳng () ABCD và bằng 60° .

Câu9. (Mã 102 - 2020 Lần 2) Cho hình hộp chữ nhật D.'''' ABCABCD có ABa = , D22 Aa = , '3 AAa = (tham khảo hình bên). Góc giữa đường thẳng ' AC và mặt phẳng () DABC bằng

A. 45° B. 90 ° C. 60° D. 30 ° Lờigiải ChọnD

Ta thấy: hình chiếu của ' AC xuống () DABC là AC do đó () () () ';D';' ACABCACACACA ==

Ta có: 22D3aACABA=+= .

Xét tam giác ' ACA vuông tại C ta có: () '33 tan' 33 AAa ACA ACa === '30ACA °  = .

Câu10. (Mã 103 - 2020 Lần 2) Cho hình hộp chữ nhật ′′′′ ABCDABCD , có ′ == ABAAa ,

2 = ADa (tham khảo hình vẽ). Góc giữa đường thẳng ′ AC và mặt phẳng () ABCD bằng

Câu12. (Mã 103 2018) Cho hình chóp SABC có đáy là tam giác vuông tại C , ACa = , 2 BCa = , SA vuông góc với mặt phẳng đáy và SAa = . Góc giữa đường thẳng SB và mặt phẳng đáy bằng A. 60° B. 90° C. 30° D. 45° Lờigiải ChọnC

A. 30 . B. 45 . C. 90 . D. 60 . Lờigiải ChọnA Vì ABCD là hình chữ nhật, có = ABa , 2 = ADa nên ()2 222 23==+=+= ACBDABADaaa Ta có () () ();; ′′′ == ACABCDACCAACA

Do tam giác ′ AAC vuông tại A nên 1 tan 33

′ ′ === AAa AAC AC a  30 ′ = AAC

Có ()SAABC ⊥ nên AB là hình chiếu của SA trên mặt phẳng () ABC () ( ) (),, SBABCSBABSBA  == Mặt khác có ABC∆ vuông tại C nên 22 3 ABACBCa =+= Khi đó 1 tan 3 SA SBA AB == nên () (),30SBABC =°

Câu13. (Mã 102 - 2019) Cho hình chóp . SABC có SA vuông góc với mặt phẳng () ABC , 2 SAa = , tam giác ABC vuông tại B , ABa = và 3 BCa = (minh họa như hình vẽ bên).

Góc giữa đường thẳng SC và mặt phẳng () ABC bằng A. 30° . B. 60° . C. 45° . D. 90° . Lờigiải ChọnC

Vì SA vuông góc với mặt phẳng () ABC , suy ra góc giữa đường thẳng SC và mặt phẳng () ABC bằng SCA

23 tan 360 3

AAAAa ACA ACA AC ABAD aa Trang 24

′′ ′====  ′=° + +

Trang 23

Mà 22

2 tan1 3 SAa SCA AC aa === +

SBABCSBABSBA

==

Câu14. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hình chóp SABC có SA vuông góc với mặt phẳng () ABC , 2 SAa = , tam giác ABC vuông tại A và 1 ,sin 3 ACaB== (minh họ như hình bên). Góc giữa đường thẳng SB với mặt phẳng () ABC bằng A. 0 90. B. 0 30. C. 0 45. D. 0 60. Lờigiải ChọnC Ta có ()() () , SAABCSBABCSBA ⊥  = 12 sincos 33 BB =  = ; 1 tan2 2 AC BABa AB ==  = Vậy tam giác SAB vuông cân tại A Suy ra () () 0,45SBABCSBA==

Tam giác ABC vuông tại B nên: 22 (2)3ABaaa =−=  SAB∆ vuông cân tại A 45 SBA  =

Vậy () (),45SBABC =

Câu16. (Sở Lào Cai - 2021) Cho hình lập phương . ABCDABCD ′′′′ . Gọi M , N lần lượt là trung điểm AC và BC′′ , α là góc giữa đường thẳng MN và mặt phẳng () ABCD ′′′′ . Tính giá trị α . A. 2 sin 2 α = B. 25 sin 5 α = C. 1 sin 2 α = D. 5 sin 5 α = Lờigiải ChọnB

S

Trang 25

Giả sử cạnh hình lập phương là a . Gọi O′ là tâm của hình vuông ABCD ′′′′ . Suy ra ON ′ là hình chiếu của MN lên () ABCD ′′′′

Do đó góc giữa MN và () ABCD ′′′′ là góc giữa MN và ON ′ .

Tam giác OMN ′ vuông tại O có 1 2 ONa ′ = , OMa ′ = nên 222 2

OMOMa ONM MN ONOMa a

′′ ′ ==== ′′ + +

25 sin 5 4

Câu17. (Sở Tuyên Quang - 2021) Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , đường thẳng SA vuông góc với mặt phẳng đáy và 2 SAa = . Góc giữa đường thẳng SC và mặt phẳng () ABCD là α . Khi đó tan α bằng

A. 22 . B. 2 . C. 2 . D. 2 3 .

Lờigiải ChọnC

Ta có: () () ; SCABCDSCA α == .

Xét tam giác SAC vuông tại A có: tan SA SCA AC = 2 2 a a = 2 = tan2 α ⇒=

Câu18. (ChuyênThoạiNgọcHầu-AnGiang-2021) Cho hình chóp SABCD có đáy là hình vuông ABCD cạnh bằng 3a , SA vuông góc với mặt đáy () ABCD , 5 SBa = . Tính sin của góc giữa cạnh SC và mặt đáy () ABCD

A. 32 4 . B. 234 17 . C. 4 5 . D. 22 3 . Lờigiải ChọnB

Do ()SAABCD ⊥ nên AC là hình chiếu của SC lên mặt phẳng () ABCD . Do đó góc giữa cạnh SC và mặt đáy () ABCD là SCA

Xét tam giác ABC có 22 32ACABBCa =+= Xét tam giác SAB có 22 4 SASBABa =−=

Xét tam giác SAC có 22 34 SCSAACa =+= .

Xét tam giác SAC có 4234 sin 17 34 SAa SCA SC a === .

Trang 27

Vậy sin của góc giữa cạnh SC và mặt đáy () ABCD bằng 234 17

Câu19. (ChuyênLêHồngPhong-TPHCM-2021) Cho hình chóp . SABC có đáy ABC là tam giác đều cạnh a , cạnh SA vuông góc với mặt phẳng đáy và 2 SAa = , gọi M là trung điểm của SC . Tính cosin của góc α là góc giữa đường thẳng BM và () ABC .

A. 7 cos 14 α = B. 27 cos 7 α = C. 21 cos 7 α = D. 5 cos 7 α = Lờigiải ChọnC Trong mặt phẳng () SAC , dựng MHAC ⊥ tại H . Do ()() // SAABCSAACABCSAMH ⊥  ⊥⊂  Khi đó: ()MHABC ⊥ Suy ra: () ( ) () 2 2

3 21 2 coscos,cos,cos 7 32 22

a BH BMABCBMBHMBH BM aa α ======   +    

Câu20. (Chuyên Hoàng VănThụ -HòaBình -2021) Cho hình chóp SABCD có đáy là hình vuông cạnh a , () ,2SAABCSAa ⊥= . Góc giữa đường thẳng SC và mặt phẳng () ABCD bằng A. 60 . B. 90 . C. 45 . D. 30 . Lờigiải ChọnC

S

Ta có 2 ACa = suy ra SAC∆ vuông cân tại A Góc giữa SC và mp () ABCD chính là góc 45 SCA ∧ =°

Câu21. (Sở Yên Bái - 2021) Cho hình chóp SABCD có đáy là hình vuông canh ,a SA vuông góc với mặt phẳng đáy và 6 SAa = . Góc giữa đường thẳng SC và mặt phẳng () ABCD bằng A. 60. o B. 45. o C. 90. o D. 30. o Lờigiải Chọn A.

Ta có AC là hình chiếu của SC lên mặt đáy () ABCD () () () () () 0 ,,tan3,60. SA SCABCDSCACSCASCASCABCD AC  ==  ==  =

Câu22. (THPTLươngThế Vinh-2021) Cho hình chóp . SABCD có đáy là hình thoi tâm O , ABD∆ đều cạnh 2, aSA vuông góc với mặt phẳng đáy và 32 2 a SA = . Góc giữa đường thẳng SO và mặt phẳng () ABCD bằng A. 45° . B. 90° . C. 30° . D. 60° . Lờigiải ChọnD

Ta có: ABCD là hình thoi có tâm là O O  là trung điểm của BD Mà ABD∆ đều nên AOBD ⊥

Lại có ()() () , SAABCDSOABCDSOA ⊥  =

Xét ABO∆ có: () 2 2 22 26 2 22 aa AOABBOa  =−=−=   

Ta có: 32 2 tan360 6 2

a SA SAOSOA AO a ===  =°

Câu23. (THPT Đặng Thúc Hứa - Nghệ An - 2021) Cho khối lăng trụ đứng . ABCABC′′′ có 6 AAa ′ = , đáy ABC là tam giác vuông cân tại B và BABCa == . Góc giữa đường thẳng AC ′ và mặt phẳng đáy bằng A. 45° B. 90° C. 60° D. 30° Lờigiải ChọnC

Ta có: () AAABCAC ′ ⊥  là hình chiếu của AC ′ lên mặt phẳng () ABC Khi đó () () (),, ACABCACACACA ′′′ ==

′ ′′ ===  =° A D C

Câu24. (THPT Chu Văn An - Thái Nguyên - 2021) Cho chóp SABC có đáy là tam giác vuông tại B . 3,3 ABaBCa == . SA vuông góc với đáy và 2 SAa = . Góc giữa SC và đáy là A. 90° . B. 45° C. 60° D. 30° Lờigiải ChọnD 12 ACa = 0

Ta có: 322 tan.360 2 6 SAa SOASOA AO a ===  =° .

Vậy () ();60SOABCD =° .

Câu26. (Trung Tâm Thanh Tường - 2021) Cho hình chóp . SABC có ()SAABC ⊥ , 3 SAa = , tam giác ABC vuông tại B có 2,3ACaBCa == . Góc giữa SB và mặt phẳng () ABC bằng A. 90° B. 45° C. 30° D. 60° Lờigiải ChọnD

S

21 tan 123 30

a SCA a SCA

==  =

Câu25. (THPT Quảng Xương 1-Thanh Hóa - 2021) Cho hình chóp . SABCD có đáy là hình thoi tâm O , ABD∆ đều cạnh 2 a , SA vuông góc với mặt phẳng đáy và 32 2 a SA = . Góc giữa đường thẳng SO và mặt phẳng () ABCD bằng A. 45° B. 30° C. 60° D. 90° Lờigiải ChọnC

Tam giác ABD đều cạnh 2 a , suy ra ()23 6 22 a a AO == . Vì ()SAABCD ⊥ , suy ra OA là hình chiếu của OS lên mặt phẳng () ABCD , suy ra: () () ; SOABCDSOA =

Trang 31

A

a3 2a a3

C B

Ta có () ()2 2 22 23 ABACBCaaa =−=−=

Dễ thấy () () ();; SBABCSBABSBA == . Khi đó 3 tan360 SAa SBASBA ABa ===  =° Vậy () ();60SBABC =° .

Câu27. (THPTTrầnPhú- ĐàNẵng-2021) Cho hình chóp tứ giác SABCD có đáy ABCD là hình vuông tâm I , cạnh a . Biết SA vuông góc với mặt đáy () ABCD và 3 SAa = (tham khảo hình vẽ bên). Khi đó tang của góc giữa đường thẳng SI và mặt phẳng () ABCD là:

Lờigiải ChọnA

Ta có: 12 22 a AIAC==

Mà ()SAABCD ⊥ nên AI là hình chiếu của SI trên mặt phẳng () ABCD  () () ();; SIABCDSIAISIA == (do tam giác SAI vuông tại A ) Vậy () () tan;tan6 SA SIABCDSIA AI === .

Câu28. (ChuyênBiênHòa-2021) Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh a , O là giao điểm của AC và BD 60 ABC =° ; SO vuông góc với () ABCD và 3 SOa = . Góc giữa SB và mặt phẳng () SAC bằng A. () 25;27°° B. () 62;66°° C. () 53;61°° D. () 27;33°° Lờigiải ChọnA Ta có : 60; ABCABC =°∆ cân tại B nên ABC∆ đều cạnh a Suy ra : 3 2 a BO = Do ()OBSAC ⊥ nên góc giữa SB và mặt phẳng () SAC chính là góc BSO Ta có tam giác SOB vuông tại O nên 1 tan26,56 2 BO BSOBSO SO ==  ≈°

SABC ABC B 3 ABa = BCa = SA ( )ABC 2 SAa = SC ( )ABC 45° 30° 60° 90°

A

a a3

Hìnhchiếucủa lênmặt phẳng là . Khi đó .

SC ( )ABC AC () ( ) (),, SCABCSCACSCA == ABC B ()2 22232 ACABBCaaa =+=+=

SAC A 2 tan145 2 SAa SCASCA ACa ===  =°

Xéttamgiác vuôngtại có: . Xéttamgiác vuôngtại có: . Câu30. (Sở QuảngBình-2021) Cho hìnhchóp . SABCD có đáy ABCD là hình vuông cạnh a , biết ()SAABCD ⊥ và 2 SAa = .Gócgiữa đườngthẳng SC vàmặtphẳng () ABCD bằng A. 60 ˚ . B. 45˚ . C. 30˚ . D. 90 ˚ . Lờigiải

Tacó: ()SAABCD ⊥ nên AC làhìnhchiếucủa SC trênmặtphẳng () ABCD . Do đó: () () (),, SCABCDSCACSCA == Xéthìnhvuông ABCD tacó: 2 ACa = Xét SAC △ vuôngtại A , tacó: 2 tan145 2 SAa SCASCA AC a ===  = ˚

Câu31. (Chuyên TuyênQuang-2021) Cho hình chóp . SABCD có đáy là hình thoi tâm O , tam giác ABD đều cạnh bằng 2 a , 32 2 a SA = và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SO vàmặt phẳng () ABCD bằng A. 060 B. 045 C. 030 D. 090 Lờigiải ChọnA

Ta có AO là hình chiếu vuông góc của SO trên mp () ABCD nên góc giữa giữa đường thẳng SO và mặt phẳng () ABCD bằng gócgiữa SO và AO Xét tam giác SAO vuôngtại A có 32 2 a SA = ; 6 2 a AO = 0

32 2 tan360 6 2

a SA SOASOA OA a ===  = Vậy góc giữa giữa đường thẳng SO và mặt phẳng () ABCD bằng 060 . Câu32. (Chuyên Vinh - 2021) Cho hình lăng trụ tam giác đều . ABCABC′′′ có ABa = , 2 AAa ′ = . Góc giữa đường thẳng AC ′ và mặt phẳng () ABBA′′ bằng A. o45 B. o75 C. o60 D. o30 Lờigiải ChọnD

Gọi M là trung điểm AB . Do tam giác ABC đều nên CMAB ⊥ Lại có CMAA ′ ⊥ nên suy ra ()() () (),, CMABBAACABBAACAMMAC ′′′′′′′′ ⊥  ==

Trong tam giác vuông CMA′ , ta có o

3 21 sin30 32

a MC MACMAC AC a ′′ ===  = ′

Vậy góc giữa đường thẳng AC ′ và mặt phẳng () ABBA′′ bằng o30

Câu33. (CụmLiênTrườngHảiPhòng2019) Cho khối chóp SABC có ()SAABC ⊥ , tam giác ABC vuông tại B , 2 ACa = , BCa = , 23SBa = . Tính góc giữa SA và mặt phẳng () SBC A. 45° B. 30° C. 60° D. 90° Lờigiải

Trong () SAB kẻ AHSB ⊥ () HSB ∈

Vì () SABC BCSABBCAH ABBC

 ⊥   ⇒⊥⇒⊥   ⊥  

Mà SBAH ⊥ do cách dựng nên ()AHSBC ⊥ , hay H là hình chiếu của A lên () SBC suy ra góc giữa SA và () SBC là góc ASH hay góc ASB .

Tam giác ABC vuông ở B 22 3 ABACBCa ⇒=−=

Tam giác SAB vuông ở A 1 sin30 2 AB ASBASB SB ⇒==⇒=°

Câu34. (Chuyên Bắc Ninh 2019) Cho hình chóp SABCD có đáy là hình thang vuông tại 1và B ,2 ABBCaADa === . Biết SA vuông góc với đáy () ABCD và SAa = . Gọi , MN lần lượt là trung điểm , SBCD . Tính sin góc giữa đường thẳng MN và mặt phẳng () SAC A. 5 5 B. 55 10 C. 35 10 D. 25 5 Lờigiải ChọnC

Ta gọi , EF lần lượt là trung điểm của SCAB

Ta có // MENF ( do cùng song song với BC . Nên tứ giác MENF là hình thang, và / () () MFISA MFABCD SAABCD   ⊥  ⊥  hay tứ giác MENF là hình thang vuông tại , MF Gọi , KNFACIEKM =∩=∩ thì ()IMNSAC =∩

Ta có: () NCAC NCSAC NCSA ⊥   ⊥  ⊥  hay E là hình chiếu vuông góc của N lên () SAC Từ đó ta có được, góc giữa MN và () SAC là góc giữa MN và CI Suy ra, gọi Q là góc giữa MN và () SAC thì sin CN IN α = 12 D 22 a NCC== ; 2 2 3 INKN INMN MME ==  = 22 210 33 a MFFN =+= Vậy 35 sin 10 CN IN α == .

Câu35. (Mã 102 - 2018) Cho hình chóp . SABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và 2 SAa = . Góc giữa đường thẳng SC và mặt phẳng đáy bằng A. 45° B. 60° C. 30° D. 90° Lờigiải ChọnA

Do ()SAABCD ⊥ nên góc giữa đường thẳng SB và mặt phẳng đáy bằng góc SBA

Ta có cos AB SBA SB = 1 2 = 60 SBA  =° .

Vậy góc giữa đường thẳng SB và và mặt phẳng đáy bằng bằng 60°

Câu37. (Mã 101 - 2019) Cho hình chóp . SABC có SA vuông góc với mặt phẳng () ABC , 2 SAa = , tam giác ABC vuông tại ,B 3 ABa = và BCa = (minh họa như hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng () ABC bằng:

Do ()SAABCD ⊥ nên góc giữa đường thẳng SC và mặt phẳng đáy bằng góc SCA . Ta có 2 SAa = , 2 ACa = tan SA SCA AC  = 1 = 45 SCA  =° Vậy góc giữa đường thẳng SC và và mặt phẳng đáy bằng bằng 45° .

Câu36. (Mã 101 - 2018) Cho hình chóp . SABCD có đáy là hình vuông cạnh a , SA vuông góc với mặt phẳng đáy và 2 SBa = . Góc giữa đường thẳng SB và mặt phẳng đáy bằng A. 45° B. 60° C. 90° D. 30° Lờigiải ChọnB

A. 045 . B. 030 . C. 060 . D. 090 . Lờigiải ChọnA

Ta có SA ⊥ () ABC nên AC là hình chiếu của SC lên mặt phẳng () ABC Do đó () () (),, SCABCSCACSCA ==

Tam giác ABC vuông tại ,B 3 ABa = và BCa = nên 22242 ACABBCaa =+== Do đó tam giác SAC vuông cân tại A nên 045 SCA = Vậy () () 0,45SCABC =

Câu38. (Đề Tham Khảo 2018) Cho hình chóp tứ giác đều SABCD có tất cả các cạnh bằng a . Gọi M là trung điểm của SD (tham khảo hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng () ABCD bằng

A. 2 2 B. 3 3 C. 2 3 D. 1 3 Lờigiải ChọnD

Gọi O là tâm của hình vuông. Ta có ()SOABCD ⊥ và 2 2 2 22 aa SOa=−=

Gọi M là trung điểm của OD ta có // MHSO nên H là hình chiếu của M lên mặt phẳng () ABCD và 12 24 a MHSO== .

Do đó góc giữa đường thẳng BM và mặt phẳng () ABCD là MBH .

A. 30o B. 90o C. 60o D. 45o Lờigiải ChọnD

Ta có () ⊥ SAABC nên đường thẳng AC là hình chiếu vuông góc của đường thẳng SC lên mặt phẳng () ABC .

Do đó, () () (),, α === SCABCSCACSCA (tam giác SAC vuông tại A ).

Tam giác ABC vuông cân tại B nên 22== ACABa

Suy ra tan1 == SA SCA AC nên 45 α = o

Câu40. (Sở Vĩnh Phúc 2019) Cho hình chóp tứ giác đều SABCD có tất cả các cạnh bằng 2a . Gọi M là trung điểm của SD Tính tan của góc giữa đường thẳng BM và mặt phẳng () ABCD

A. 2 2 . B. 3 3 . C. 2 3 . D. 1 3 . Lờigiải

a MH MBH BH a ===

Khi đó ta có 2 1 4 tan 3 32 4

Vậy tang của góc giữa đường thẳng BM và mặt phẳng () ABCD bằng 1 3

Câu39. (Mã 104 - 2019) Cho hình chóp . SABC có SA vuông góc với mặt phẳng () ABC , 2 = SAa , tam giác ABC vuông cân tại B và 2 = ABa (minh họa như hình vẽ bên). Góc giữa đường thẳng SC và mặt phẳng () ABC bằng

Trong tam giác SOD dựng //, MHSOHOD ∈ ta có ()MHABCD ⊥ Vậy góc tạo bởi BM và mặt phẳng () ABCD là MBH

Ta có 2222 1112 42 2222 a MHSOSDODaa ==−=−= 3332 22 442 a BHBDa=== Vậy 1 tan 3 MH MBH BH == .

Câu41. (Chuyên BắcGiang2019) Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a và

()SAABCD ⊥ . Biết 6 3 a SA = . Tính góc giữa SC và () ABCD A. 30° B. 60° C. 75° D. 45° Lờigiải ChọnA

Ta có 2 ACa = Vì AC là hình chiếu của SC lên () ABCD nên góc giữa SC và () ABCD là góc giữa SC và AC Xét SAC∆ vuông tại A, ta có: 6 3 3 tan 3 2

a SCA a == . Suy ra 030 SCA =

Câu42. (ChuyênHùngVươngGiaLai 2019) Cho hình chóp . SABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và 3 SAa = . Gọi α là góc giữa SD và () SAC . Giá trị sinα bằng A. 2 4 B. 2 2 C. 3 2 D. 2 3 Lờigiải

Xét SAD∆ vuông tại A : 22 32 SDaaa =+= .

Xét SOD∆ vuông tại O : có 2 SDa = ,

sinsin 24 aDO ODDSO SD α =  === .

Câu43. (Sở Bắc Giang 2019) Cho hình chóp tam giác . SABC có đáy là tam giác đều cạnh a . Tam giác SAB cân tại S và thuộc mặt phẳng vuông góc với đáy. Biết SC tạo với mặt phẳng đáy một góc 60 ° , gọi M là trung điểm của BC . Gọi α là góc giữa đường thẳng SM và mặt phẳng () ABC . Tính cos α . A. 6 cos 3 α = B. 3 cos 3 α = C. 3 cos 10 α = D. 1 cos 10 α = Lờigiải

Gọi H là trung điểm AB dễ thấy ()SHABC ⊥ . SC tạo với mặt phẳng đáy một góc 60° suy ra 60 SCH =° Có 33 .tan 22 aa HCSHHCSCH =  == Dễ thấy SMH α = , 1101 cos 222 10 aaHM HMACSM SM α ==  =  ==

Câu44. (THCS - THPT Nguyễn Khuyến 2019) Cho hình chóp tứ giác đều SABCD có ABa = , O là trung điểm AC và SOb = . Gọi () ∆ là đường thẳng đi qua C , () ∆ chứa trong mặt phẳng () ABCD và khoảng cách từ O đến () ∆ là 14 6 a . Giá trị lượng giác ()() ()cos, SA ∆ bằng A. 22

2 342 a ba B. 22

2 324 a ab + C. 22324 a ab + D. 22342 a ba Lờigiải

Gọi () ∆′ là đường thẳng đi qua A và song song với () ∆ . Hạ ()() ()''OHH⊥∆∈∆ . Do O là trung điểm của AC và ()() //'∆∆ nên () () () (),', dOdO∆=∆ hay 14 6 a OH = .

Do . SABCD là hình chóp tứ giác đều nên đáy ABCD là hình vuông và ()SOABCD ⊥ .

Do AHOH ⊥ và AHSO ⊥ nên, suy ra AHSH ⊥

Do ABCD là hình vuông cạnh a nên 2 ACa = , suy ra 2 2 a OA = Áp dụng Định lí Pitago vào tam giác vuông AHO ta có 222 OAOHAH =+ , suy ra 22 22 214 263 aaa AHOAOH  =−=−=    .

Áp dụng Định lí Pitago vào tam giác vuông SAO ta có 222 SAOASO =+ , suy ra 2 22 222224 22 aab SAOASOb  + =+=+=    .

Do ()() //'∆∆ nên ()() () ()() () 22

2 cos,cos,cos 324 AHa SASASAH SA ab ′ ∆=∆=== + .

Câu45. (HSG Bắc Ninh 2019) Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, ,3ABaADa == . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Cosin của góc giữa đường thẳng SD và mặt phẳng () SBC bằng A. 13 4 B. 3 4 C. 25 5 D. 1 4 Lờigiải

Gọi , HM lần lượt là trung điểm của , ABSB ; O là tâm của hình chữ nhật ABCD . Ta có // MOSD Dễ thấy () BCSABBCAM ⊥  ⊥ , mà SBAM ⊥ nên ()AMSBC ⊥ .

Xét tam giác AMO , có: 3 2 a AM = ; 22 11 3 22 AOACaaa ==+= ; 2 2 22222 2 11113 3 222222 aa MOSDSHHDSHHAADaa   ==+=++=++=      . AMO  ∆ cân tại O () 2 2 2 2 3 ; 13 16 4 sin 4

a AM a MO dOAM AMO OMOMa  ==== () () 13 cos;sin 4 SDSBCAMO  ==

Câu46. (Sở HàNội2019) Cho hình chóp . SABC có đáy là tam giác vuông tại C , CH vuông góc với AB tại H , I là trung điểm của đoạn HC . Biết SI vuông góc với mặt phẳng đáy, 90 ASB =° . Gọi O là trung điểm của đoạn AB , O′ là tâm mặt cầu ngoại tiếp tứ diện SABI . Góc tạo bởi đường thẳng OO′ và mặt phẳng () ABC bằng A. 60° . B. 30° . C. 90° . D. 45° . Lờigiải

Do 90 ASB =° nên tâm O′ của mặt cầu ngoại tiếp tứ diện SABI nằm trên đường thẳng d đi qua trung điểm O của đoạn thẳng AB và ()dSAB ⊥ . () 1 Trong mặt phẳng () SCH kẻ IKSH ⊥ tại K Theo giả thiết ()SIABC ⊥ suy ra SIAB ⊥ . Từ SIAB ⊥ và ABCH ⊥ suy ra () ABSCHABIK ⊥  ⊥

Từ IKSH ⊥ và ABIK ⊥ ta có ()IKSAB ⊥ . () 2

Từ () 1 và () 2 ta có IKd . Bởi vậy () () () () () ()';;; OOABCdABCIKABC ==

Vì ()() SCHABC ⊥ nên IH là hình chiếu vuông góc của IK trên mặt phẳng () ABC . Bởi vậy () () ();, IKABCIKIHHIKHSI === .

Do tam giác ABC vuông tại C và SAB vuông tại S nên 2 AB COSO== .

Xét hai tam giác vuông CHO và SHO có COSO = , cạnh OH chung nên () c.g.c CHOSHO∆=∆ , bởi vậy CHSH =

Xét tam giác SIH vuông tại I có 22 CHSH IH == , ta có 1 sin30 2 IH HSIHSI SH ==  =° Vậy () ()';30OOABC =°

Câu47. (Sở Bắc Ninh 2019) Cho hình chóp . SABCD có đáy ABCD là hình thoi cạnh a và 60 =° ABC . Hình chiếu vuông góc của điểm S lên mặt phẳng () ABCD trùng với trọng tâm của tam giác ABC , gọi ϕ là góc giữa đường thẳng SB và mặt phẳng () SCD , tính sinϕ biết rằng = SBa A. sin 3 2 ϕ = B. sin 1 4 ϕ = C. sin 1 2 ϕ = D. sin 2 2 ϕ = Lờigiải

Cách 1: ● Gọi O là trọng tâm của tam giác ABC . Dựng đường thẳng d qua O và // dSB , d cắt SD tại K . Khi đó góc giữa SB và () SCD chính là góc giữa OK và () SCD ● Vì () ⊥ SOABCD  ⊥ SOCD

Ta lại có: ∆ABC đều ( ∆ABC cân tại B và 60 =° BAC ).  ⊥  ⊥ ABCOCDCO ()()()  ⊥  ⊥ CDSCOSCDSCO .

Gọi H là hình chiếu của O trên SC , khi đó ta có: () ⊥   ⊥  ⊥ 

OHSC OHSCD OHCD . Do đó góc giữa SB và mặt phẳng () SCD là: ϕ= OKH

Ta có: sinsin ϕ == OH OKH OK .

● Tứ diện SABC là tứ diện đều cạnh a nên ta tính được: 3 3 = a OC , 6 3 = a SO 2 3  = a OH .

Vì 2 // 3  == OKDO OKSB SBDB 22 33  == OKSBa

Vậy: 2 sin 2 ϕ == OH OK Cách 2:

Trước hết ta chứng minh được sin(; )) ( ))(,( = dBSC SCD D SB SB (như hình trên).

Gọi O là trọng tâm tam giác ABC . Khi đó ta có ⊥ COCD

Dựng ⊥ OHSC suy ra () ⊥ OHSCD . Ta tính được 362 , 333 ==  = OCSOOHaaa

(,())(,()) a2a 223 2 22 ====

Vậy 2 2 2 sin(;()) 2 == SBSCD a a

Câu48. (Sở Bình Phước - 2018) Cho hình chóp SABCD có đáy là hình vuông cạnh a , ()SAABCD ⊥ , SAx = . Xác định x để hai mặt phẳng () SBC và () SCD hợp với nhau góc 60° A. 2 xa = B. xa = C. 3 2 a x = D. 2 a x = Lờigiải 22SBSDSAAD ==+ = 22 xa + SDCSBC∆=∆ ; BMSC ⊥ ; DMSC ⊥ ; BMDM = ; MSC ∈ 22SCSAAC =+ = 22 2 xa + ; . SDCD MD SC = = 22 22 2 axa xa + + ()() () () ;;60SBCSDCBMBD==° .

TH1: 60 BMD =°  MDBD = ⇔ 22 22 2 2 axa a xa + = + (vô nghiệm).

TH2: 120 BMD =°  3 BDMD = ⇔ 22 22

3 2 2 axa a xa + = + ⇔ xa = .

Câu49. (Sở Lào Cai - 2018) Cho hình chóp SABC có đáy là tam giác vuông tại B , cạnh bên SA vuông góc với mặt đáy, 2a AB = , 060 BAC = và 2 SAa = . Góc giữa đường thẳng SB và mặt phẳng () SAC bằng A. 045 B. 060 C. 030 D. 090 Lờigiải

Kẻ () BHACHAC ⊥∈ và theo giả thiết BHSA ⊥ nên ()BHSAC ⊥ Do đó, SH là hình chiếu vuông góc của SB lên mặt phẳng () SAC Suy ra, (,())(,)S SBSACSBSHBH ==

Mà ta có: 6 SBa = , 0 sin603HBABa == 1 sin(S) 2 BH  = 0S45BH  =

Câu50. (Chuyên Hạ Long - 2018) Cho hình chóp . SABCD có đáy ABCD là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy, 2 SAa = . Gọi M , N lần lượt là hình chiếu vuông góc của điểm A trên các cạnh SB , SD . Góc giữa mặt phẳng () AMN và đường thẳng SB bằng A. o45 B. o90 C. o120 D. o60 Lờigiải

Ta có ()BCSAB ⊥ BCAM  ⊥ ()AMSBC  ⊥ AMSC  ⊥ . Tương tự ta cũng có ANSC ⊥ ()AMNSC  ⊥ . Gọi ϕ là góc giữa đường thẳng SB và () AMN Chuẩn hóa và chọn hệ trục tọa độ sao cho () 0;0;0 A , () 0;1;0 B , () 1;0;0 D , () 0;0;2 S , () 1;1;0 C , () 1;1;2 SC =− , () 0;1;2 SB =− . Do ()AMNSC ⊥ nên () AMN có vtpt SC sinϕ= 3 23 3 2 = o60 ϕ =

Câu51. (Sở Bắc Giang - 2018) Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, ABa = , 3 BCa = , SAa = và SA vuông góc với đáy ABCD . Tính sin α , với α là góc tạo bởi giữa đường thẳng BD và mặt phẳng () SBC A. 7 sin 8 α = . B. 3 sin 2 α = . C. 2 sin 4 α = . D. 3 sin 5 α = . Lờigiải

Đặt hệ trục tọa độ Oxyz như hình vẽ. Khi đó, ta có () 0;0;0 A , () ;0;0Ba , () 0;3;0Da , () 0;0; Sa

Ta có () () ;3;01;3;0BDaaa=−=− , nên đường thẳng BD có véc-tơ chỉ phương là () 1;3;0 u =−

Ta có () ;0; SBaa =− , () 0;3;0BCa = () 22 ,3;0;3SBBCaa  =  () 2 31;0;1 a = .

Như vậy, mặt phẳng () SBC có véc-tơ pháp tuyến là () 1;0;1 n = .

Trong mặt phẳng () ABC kẻ BHAC ⊥

Mà BHSA ⊥ ()BHSAC  ⊥

Góc giữa đường thẳng SB và mặt phẳng () SAC bằng BSH

Do đó, α là góc tạo bởi giữa đường thẳng BD và mặt phẳng () SBC thì . sin un un α = () () 2 2 2222

−++ = −++++

1.13.00.1 130.101

2 4 =

Câu52. (Chuyên ĐHSPHN- 2018) Cho hình chóp . SABC có đáy là tam giác vuông tại B , cạnh bên SA vuông góc với mặt phẳng đáy, 2 ABa = , 060 BAC = và 2 SAa = . Góc giữa đường thẳng SB và mặt phẳng () SAC bằng A. 0 30. B. 0 45. C. 0 60. D. 0 90. Lờigiải

Xét tam giác ABH vuông tại H , 0.sin60BHAB = 3 2. 2 a = 3 a = 0.cos60AHAB = 1 2. 2 a = a =

Xét tam giác SAH vuông tại S , 22SHSAAH =+ ()2 2 2 aa=+ 3 a = .

Xét tam giác SBH vuông tại H có 3 SHHBa == suy ra tam giác SBH vuông tại H Vậy 045 BSH = .

Câu53. (Chuyên Vĩnh Phúc - 2018) Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a , tâm O . Gọi M và N lần lượt là trung điểm của SA và BC . Biết rằng góc giữa MN và () ABCD bằng 060 , cosin góc giữa MN và mặt phẳng () SBD bằng: A. 41 41 . B. 5 5 . C. 25 5 . D. 241 41 . Lờigiải

B A

A. 3 4 B. 3 4 C. 1 4 D. 3 7 Lờigiải

Gọi E , F lần lượt là trung điểm SO , OB thì EF là hình chiếu của MN trên () SBD . Gọi P là trung điểm OA thì PN là hình chiếu của MN trên () ABCD .

Theo bài ra: 60 MNP ° = . Áp dụng định lý cos trong tam giác CNP ta được: 222 2..cos45NPCPCNCPCN ° =+− 2 22 323225 2... 444228 aaaaa =+−=    . Suy ra: 10 4 a NP = , 30 .tan60 4 a MPNP ° == ; 30 2 2 a SOMP== 22 22SBSOOBa =+= 2 EFa  = .

Ta lại có: MENF là hình bình hành ( vì ME và NF song song và cùng bằng 1 2 OA ). Gọi I là giao điểm của MN và EF , khi đó góc giữa MN và mặt phẳng () SBD là NIF 2425 cos. 25 10 IKa NIF IN a === .

Câu54. (Chuyên Vinh -2018) Cho hình chóp SABCD có đáy ABCD là hình bình hành, 2 ABa = , BCa = , 120 ABC =° . Cạnh bên 3 SDa = và SD vuông góc với mặt phẳng đáy (tham khảo hình vẽ bên). Tính sin của góc tạo bởi SB và mặt phẳng () SAC

Ta có () () () () ; sin; dBSAC SBSAC SB = () ; dDSAC SB =

Xét tam giác ABC ta có 22 2..cos ACBABCBABCBAC =+− 7 a = . 222 24 BABCAC BO + =− 222 473 242 aaaa + =−= 3 BDa  = và 22SBSDBD =+ 2233aa=+ 6 a = .

° = 21 14 = . Gọi K là hình chiếu của D lên AC , và I là hình chiếu của D lên SK . Ta có ACDK ACDI ACSD ⊥   ⊥  ⊥  . Do đó DISK DIAC ⊥   ⊥  () () ; dDSACDI  = .

Mặt khác sin DK C DC = .sin DKDCC  = 21 2. 14 a = 21 7 a =

Xét tam giác SDK ta có 22

SDDK DI SDDK = + 22

Vậy () () () ; sin; dDSAC SBSAC SB = DI SB =

a a aa = +

6 4 6

21 3. 7 21 3 49

6 4 a = .

a a = 1 4 = Trong mặt phẳng () SDK kẻ DISK ⊥ suy ra () () ; dDSACDI = Câu55. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp SABCD có SA vuông góc với mặt phẳng đáy, 3 SAa = , tứ giác ABCD là hình vuông, 2 BDa = (minh họa như hình bên). Góc giữa đường thẳng SB và mặt phẳng () SAD bằng

Từ giả thiết ta có ()SOABCD ⊥ Gọi I là trung điểm OA thì MI là đường trung bình của SOA∆ // MISO  ()MIABCD  ⊥ I  là hình chiếu của M trên mặt phẳng () ABCD IN  là hình chiếu của MN trên mặt phẳng () ABCD . Suy ra () ( ) () ,,60 =  =° MNABCDMNINMNI .

A. 0° . B. 30° . C. 45° . D. 60° . Lờigiải ChọnB Đáy ABCD là hình vuông có đường chéo 2 BDa = nên cạnh ABa = . Ta có: () ABAD ABSAD ABSA ⊥   ⊥  ⊥  SA  là hình chiếu của SB trên mặt phẳng () SAD () ( ) (),, SBSADSBSABSA  ==

Trong tam giác vuông BSA , ta có: 3 tan 3 3 ABa BSA AS a === 30 BSA  =° Vậy, () (),30SBSAD =° .

Câu56. (Chuyên Thái Bình - 2020) Cho hình chóp tứ giác đều . SABCD có đáy là hình vuông tâm O , cạnh a . Gọi , MN lần lượt là trung điểm của SA và BC . Góc giữa đường thẳng MN và mặt phẳng () ABCD bằng 60° . Tính cos của góc giữa đường thẳng MN và mặt phẳng () SBD . A. 41 4 B. 5 5 C. 25 5 D. 241 4 Lờigiải ChọnC

Ta có 1 22 a NCBC== ; 332 44 a ICAC== . Áp dụng định lý cosin trong INC∆ ta có 222 2..cos INCICNCICNNCI =+− 2 2 2 2 32325 2...cos45 42428 aaaaa IN    =+−°=      10 4 a IN  = . Do MIN∆ vuông tại I nên cos IN MNI MN = 10110 : cos60422 INaa MN  === °

Lại có () , ACBDACSOACSBD ⊥⊥  ⊥ . Gọi E là trung điểm OBEN  là đường trung bình của BOC∆ // ENOC  hay // ENAC ()NESBD  ⊥ hay E là hình chiếu của N trên mặt phẳng () SBD

Gọi F là trung điểm của SOMF  là đường trung bình của SAO∆ // MFAO  hay // MFAC

()MFSBD  ⊥ hay F là hình chiếu của M trên mặt phẳng () SBD .

Ta có // MFNE nên bốn điểm ,,, ENFM cùng nằm trên một mặt phẳng.

Trong mặt phẳng () ENFM gọi ()JMNEFJMNSBD =∩  =∩ (do ()EFSBD ⊂ ).

Suy ra () ( ) (),, MNSBDMNEFEJN == (do 90 <° EJN ).

Ta có 112 244 a ENOCAC=== ; 112 244 a MFAOAC=== ENMF  = , mà // ENMF

Câu58. (THPT Nguyễn Viết Xuân - 2020) Chohìnhlăngtrụ đứng . ABCABC′′′ có , 120 ABACaBAC===° .Gọi , MN lầnlượtlàtrung điểmcủa BC′′ và CC′ .Biếtthể tích khốilăngtrụ . ABCABC′′′ bằng 3 3 4 a .Gọi α làgócgiữamặtphẳng () AMN vàmặ

Vậy () 3 coscos, 4 kn kn kn α ===

Câu59. (Chuyên Hạ Long - Quảng Ninh - 2020) Chohìnhchóp SABCD có đáy ABCD làhình vuôngcạnhbằng 2a .Tamgiác SAB cântại S và ()() SABABCD ⊥ .Biếtthể tíchcủakhối chóp . SABCD là 3 4 3 a . Gọi α là góc giữa SC và () ABCD . Tính tan α . A. 5 tan 5 α = . B. 25 tan 5 α = . C. 3 tan 3 α = . D. 7 tan 7 α = . Lờigiải ChọnA

ChọnC

Gọi O là tâm đường tròn ngoại tiếp đáy.

Vì SABC là tứ diện đều cạnh a nên 6 3 ha =

Gọi H là chân đường vuông góc từ N xuống () ABC H  là trung điểm của OC 2 2 223 3323 a MHMCaa   ==−=  

Gọi H là trung điểm AB . Vì SAB∆ cân tại S nên SHAB ⊥ Vì ()() ()() SABABCD SABABCDAB  ⊥   ∩=   nên suy ra ()SHABCD ⊥ . Khi đó ta có: 1 3 SABCDABCD VSHS = 3 SABCD ABCD

Vì N là trung điểm của SC nên 16 26 NHha == Góc giữa đường thẳng MN và mặt phẳng () ABC là NMH

Vậy 632 tan: 632 NH NMHaa MH  ===   

4 3. 3 2

3 2

V SH S  = ()

a a = a = Lại có HC là cạnh huyền trong tam giác vuông BHC nên 22 5 HCBHBCa =+= . Mặtkhác,do ()SHABCD ⊥ , () () HABCD ∈ nên HC làhìnhchiếucủa SC lênmặtphẳng () ABCD . Suy ra () () , SCABCDSCH α == Vậy, trong tam giác vuông SHC , tantan SH SCH HC α == 5 a a = 5 5 = .

Câu60. (ChuyênLêHồngPhong-Nam Định-2020) Cho tứ diện đều SABC cạnh a . Gọi , MN lần lượt là trung điểm của các cạnh , ABSC . Tính tan của góc giữa đường thẳng MN và mặt phẳng () ABC . A. 3 2 . B. 1 2 . C. 2 2 . D. 1. Lờigiải

57

Dạng3Góccủamặtvớimặt

Để tìm góc giữa hai mặt phẳng, đầu tiên tìm giao tuyến của hai mặt phẳng.

Sau đó tìm hai đường thẳng lần lượt thuộc hai mặt phẳng cùng

vuông góc với giao tuyến tại một điểm.

Góc giữa hai mặt phẳng là góc giữa hai đường thẳng vừa tìm.

Nhữngtrườnghợp đặcbiệt đề hayra:

Trườnghợp1: Hai tam giác cân ACD và BCD có chung cạnh đáy CD.

Gọi H trung điểm của CD, thì góc giữa hai mặt phẳng

(ACD) và (BCD) là góc AHB

Trườnghợp2: Hai tam giác ACD và BCD bằng nhau có chung cạnh CD. Dựng AHCDBHCD ⊥  ⊥ .

Vậy góc giữa hai mặt phẳng (ACD) và (BCD) là góc AHB

Trườnghợp3: Khi xác định góc giữa hai mặt phẳng quá khó, ta nên sử dụng công thức sau: () () () , sin ,

dAQ dAa φ=

Với ϕ là góc giữa hai mặt phẳng (P) và mặt phẳng (Q). A là một điểm thuộc mặt phẳng (P) và a là giao tuyến của hai mặt phẳng (P) và (Q).

Trườnghợp4: Có thể tìm góc giữa hai mặt phẳng bằng công thức '.cosSS ϕ =

Trường hợp 5: Tìm hai đường thẳng d và d' lần lượt vuông góc với mặt phẳng (P) và mặt phẳng (Q). Góc giữa hai mặt phẳng là góc giữa d và d'.

ườnghợp6:CÁCHXÁC ĐỊNHGÓCGI

Bước 1: xác dịnh giao tuyến d của mặt bên và mặt đáy.

Bước 2: từ hình chiếu vuông góc của đỉnh, dựng AHd ⊥ .

Bước 3: góc cần tìm là góc SHA .

Với S là đỉnh, A là hình chiếu vuông góc của đỉnh trên mặt đáy.

Vídụ điểnhình: Cho hình chóp S.ABC có SA vuông góc với đáy (ABC).Hãy xác định góc giữa mặt bên (SBC) và mặt đáy (ABC).

Ta có BC là giao tuyến của mp (SBC) và (ABC).

Từ hình chiếu của đỉnh là điểm A, dựng AHBC ⊥ .

Vì () BCSA BCSAHBCSH BCAH ⊥   ⊥  ⊥  ⊥  .

Kết luận góc giữa hai mặt phẳng (SBC) và (ABC) là gócSHA.

Câu1. (ChuyênKHTN-2021) Cho hình lăng trụ tam giác đều ABCABC′′′ có cạnh đáy bằng a và cạnh bên bằng 3 2 a . Góc giữa hai mặt phẳng () ABC ′ và () ABC bằng A. 30° B. 60° C. 45° D. 90° Lờigiải ChọnB

Câu2. (Chuyên Quốc Học Huế - 2021) Cho hình lập phương . ABCDABCD ′′′′ có , OO′ lần lượt là tâm của các hình vuông ABCD và ABCD ′′′′ . Góc giữa hai mặt phẳng () ABD ′ và () ABCD bằng A. AAD ′ . B. AOC ′ . C. AOA ′ . D. OAA ′ . Lờigiải ChọnC

Gọi O là tâm hình vuông ABCD . Khi đó ()SOABCD ⊥  Gọi H là trung điểm cạnh CD . Ta có: OHCD ⊥ và 2 CD HDOHa ===  Do SCD∆ cân tại S nên SHCD ⊥  Vậy góc giữa mặt bên () SCD và mặt phẳng () ABCD là góc SHO 

Trong SHD∆ vuôngtại H ta có 222252 SHSDHDaaa =−=−= . Khi đó 1 cos60 22 OHa SHOSHO SHa ===  =°

Câu4. (ChuyênQuốcHọcHuế -2021) Cho hình lập phương ABCDABCD ′′′′ có , OO′ lần lượt là tâm của hình vuông ABCD và ABCD ′′′′ . Góc giữa hai mặt phẳng ( )ABD ′ và ( )ABCD bằng A. AOA ′ B. OAA ′ C. ADA ′ D. AOC ′ Lờigiải Chọn A.

Ta có ABCD là hình vuông nên AOBD ⊥ , đồng thời BDAA ′ ⊥ ()BDAAO ′  ⊥ BDAO ′  ⊥ Ta có ()() ABDABCDBD AOBD AOBD

′ ∩=   ⊥   ′ ⊥  ()() () ();; ABDABCDAOAOAOA ′′′  ==

Câu3. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a cạnhbênbằng 5a . Góc giữa mặt bên và mặt phẳng đáy bằng A. 60° B. 30° C. 70° D. 45° Lờigiải ChọnA

B' B

A' D' D A

O' O

C' C

()() ABDABCDBD ′ ∩= Có AOBD ⊥ Mà AO là hình chiếu vuông góc của AO ′ trên () ABCD AOBD ′  ⊥ . Vậy góc giữa () ABD ′ và () ABCD là AOA ′

Câu5. (ChuyênLêKhiết-QuảngNgãi-2021) Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại A , cạnh ACa = , các cạnh bên 6 2 a SASBSC=== . Tính góc tạo bởi mặt bên () SAB và mặt phẳng đáy () ABC . A. 6 π B. 4 π C. arctan2 D. arctan2

vuông cạnh a , SA vuông góc với mặt phẳng () ABCD và 3.SAa = Gọi ϕ là góc giữa hai mặt phẳng () SBC và () ABCD Giá trị tanϕ là A. 3. B. 3 3 C. 6 2 D. 3 2 Lờigiải ChọnA

Ta có ()() () () ()() ,,, ,

∩=   ⊂⊥  ==   ⊂⊥  3 tantan3 SAa SBA ABa ϕ ====

SBCABCDBC SBSBCSBBCSBCABCDSBABSBA ABABCDABBC

Câu7. (Sở Cần Thơ - 2021) Cho hình chóp SABCD có đáy ABCD là hình vuông, SA vuông góc với mặt phẳng () ABCD . Góc giữa hai mặt phẳng () SCD và mặt phẳng () ABCD là

A. SDC . B. SCD . C. DSA . D. SDA. Lờigiải ChọnD

Ta có () SCD ∩ () ABCD = CD

Mặt khác () CDSADCDSD ⊥  ⊥ , lại có ADCD ⊥

Vậy góc giữa hai mặt phẳng () SCD và mặt phẳng () ABCD là SDA.

Câu8. (Sở SơnLa-2021) Cho hìnhchóp . SABC có đáytam giác đều cạnh a . Cạnhbên 3 SAa = vuông góc với mặt đáy () ABC . Gọi ϕ là góc giữa hai mặt phẳng () SBC và () ABC . Khi đó sinϕ bằng

A. 3 5 . B. 25 5 . C. 23 5 . D. 5 5 . Lờigiải

S

A. 1713 65 B. 1813 65 C. 613 65 D.

65 Lờigiải Ch

ọi , PQ lần lượt là trung điểm củ

A C B 13

m của AA , khi đó mặt phẳng ( )''ABC song song với mặt phẳng ( )MNQ

góc giữa hai mặt phẳng ( )''ABC và ( )MNP cũng bằng góc giữa hai mặt phẳng ( )MNQ và ( )MNP . Ta có: ( ) ( ) () () ()() ();; ;

MNPMNQMN PEMNPPEMNMNPMNQPEQ QEMNQQEMN

∩=   ⊂⊥  =   ⊂⊥  hoặc ()() () 0;180 MNPMNQPEQ =−

Tam giác ABC đều có cạnh 233 AP  =

Tam giác APQ vuông tại A nên ta có: 22223110 PQAPAQ=+=+=

Tam giác ' AQE vuông tại A nên ta có: 2 222313 ''1 22 QEAEAQ  =+=+=  

Tam giác PEF vuông tại F nên ta có: 2 222 35 2 22 PEFPFE  =+=+=  

EPEQPQ PEQ EPEQ

+− +− ===−

Áp dụng định lý hàm số côsin vào tam giác PQE ta có: 222 2513 10 13 44 cos 2..65 2..513 22

Do đó: ()() () () 0 13 cos;''cos180cos 65 MNPABCPEQPEQ =−=−=

Câu2. (Mã 101 2018) Cho hình lập phương . ABCDABCD ′′′′ có tâm O . Gọi I là tâm của hình vuông ABCD ′′′′ và M là điểm thuộc đoạn thẳng OI sao cho 2 MOMI = (tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng () MCD′′ và () MAB bằng A. 785 85 B. 1713 65 C. 613 65 D. 685 85 Lờigiải ChọnA

Giao tuyến của () MAB và () MCD′′ là đường thẳng KH như hình vẽ

Gọi J là tâm hình vuông ABCD , LN lần lượt là trung điểm của CD′′ và AB

Ta có: () CDLIMCDLMLMKH ′′′′ ⊥  ⊥  ⊥

Tương tự () ABNJMABMNMNKH ⊥  ⊥  ⊥ .

Suy ra góc giữa hai mặt phẳng () MAB và () MCD′′ chính là góc giữa 2 đường thẳng (,) MNML

Gọi cạnh hình lập phương là 1. Ta có 10 6 LM = , 34 6 MN = , 2 NL = .

Ta có: 222 785 cos 2.85 MNMLNL LMN MNML +−− ==

Suy ra cosin của góc giữa hai mặt phẳng () MAB và () MCD′′ là 785 85

Câu3. (ChuyênHùngVương-GiaLai-2020) Cho hình chóp . SABC có SA vuông góc với mặt phẳng () 3 ,2 a ABCSA = , tam giác ABC đều cạnh bằng a (minh họa như hình dưới). Góc tạo bởi giữa mặt phẳng () SBC và () ABC bằng

A. 090 B. 030 C. 045 D. 060

Lờigiải ChọnC

Gọi M là trung điểm BC . ABC ∆ đều cạnh a nên AMBC ⊥ và 3 2 a AM = Ta có ()SAABC ⊥  Hình chiếu của SM trên mặt phẳng () ABC là AM . Suy ra SMBC ⊥ (theo định lí ba đường vuông góc).

Có ()() () () , ,

SBCABCBC AMABCAMBC SMSBCSMBC

∩=   ⊂⊥   ⊂⊥  . Do đó góc giữa mặt phẳng () SBC và () ABC là góc giữa SM và

AM , hay là góc SMA (do () SAABCSAAMSAM ⊥  ⊥  ∆ vuông).

3 2 tan145 3 2

a SA SMASMA AM a ===  = .

Câu5. (THPTNguyễnKhuyến2019) Chohìnhchóp SABCD có đáy ABCD làhìnhthoitâm

Xét tam giác SAM vuông tại A có 0

Vậy góc cần tìm là 045

Câu4. (Sở Bắc Giang -2019) Cho hình chóp SABCD có đáy ABCD là hình chữ nhật, ABa = , 2 ADSAa == , () ⊥ SAABCD . Tính tang của góc giữa hai mặt phẳng () SBD và () ABCD . A. 5 2 B. 5 C. 1 5 D. 2 5 Lờigiải Ta có: () () SBDABCDBD ∩= Hạ AHBD ⊥ tại H Ta có () AHBD BDSAHBDSH BDSA ⊥ 

thẳng SO vuông góc với mặt phẳng () ABCD . Biết ABSBa == , 6 3 a SO = . Tìm số đo của

giữahaimặtphẳng () SAB và (). SAD A. 30° B. 45° C. 60° D. 90° Lờigiải ChọnD Gọi M trung điểm SA .Tacó SAB∆ cântại (1) BBMSA  ⊥ Vì () SOABCDSOBD ⊥  ⊥ , lại có O trung điểm BD SBD  ∆ cântại S nên SDSBa == SAD  ∆ cântại D nên (2) DMSA ⊥ Lại có ()() (3) SABSADSA ∩= Từ ()() ()(1);(2);(3),SABSADBMD  = hoặc ()() (),180 SABSADBMD =°− Xét 323 33 SOBOBBDaa∆  =  = . Xét 6 3 a AOBOAOC∆  == . Xét 23131 3232 aa SOCSCOMSCBD∆  =  === Do đó BMD∆ vuôngt

Đặt 6 ;' 2 =  == x ABxBCxAA

xx AOCOABBOx

2 2..12 2 2 tan 3 1. 1.2 , 2

2 2 22

BOBOBO BKO SAAC OK dASC SAAC

suy ra 060 BKO = . Câu7. (Chuyên Phan Bội Châu Nghệ An 2019) Cho hình hộp chữ nhật .'''' ABCDABCD có mặt ABCD là hình vuông, '6 2 = AB AA . Xác định góc giữa hai mặt phẳng () ' ABD và () ' CBD . A. 030 B. 045 C. 060 D. 090 Lờigiải +Gọi O là giao điểm của hai đường chéo hình vuông ABCD .

''2 = ACx .  '' ∆ AOC đều  0''60 = AOC

Vậy góc giữa hai mặt phẳng ( ) ' ABD và ( ) ' CBD bằng 060 .

Cách khác: Gắn hệ trục tọa độ Oxyz vào hình hộp chữ nhật .'''' ABCDABCD để tìm góc giữa hai mặt phẳng ( ) ' ABD và ( ) ' CBD .

Câu8. (ChuyênLươngVănChánh-PhúYên-2018) Cho hình lăng trụđứng ABCABC′′′ có đáy ABC là tam giác cân, với ABACa == và góc 120 BAC =° ,cạnhbên AAa ′ = .Gọi I làtrung điểmcủa CC′ .Cosincủagóctạobởihai mặtphẳng ( ) ABC và ( ) ABI ′ bằng A. 11 11 . B. 33 11 . C. 10 10 . D. 30 10 . Lờigiải

+ ===== + Trang 16

Tacó 222 2..cos BCABACABACBAC =+− 22 1 2... 2 aaaa =+−−  2 3a = 3 BCa  =

Xéttamgiácvuông BAB ′ có 22ABBBAB ′′ =+ 22 aa=+ 2 a = .

Xéttamgiácvuông IAC có 22IAICAC =+ 2 2 4 a a =+ 5 2 a = .

Xéttamgiácvuông IBC′′ có 22BIBCCI ′′′′ =+ 2 2 3 4 a a =+ 13 2 a = .

Xéttamgiác IBA ′ có 2 222 5 2 4 a BAIAa ′ +=+ 2 13 4 a = 2 BI ′ = IBA ′  ∆ vuôngtại A

 1 . 2 IBA SABAI ′ = 15 .2. 22 a a = 2 10 4 a = .

Lại có 1 ..sin 2 ABC SABACBAC = 13 .. 22 aa = 2 3 4 a = .

Gọigóctạobởi haimặtphẳng () ABC và () ABI ′ là α

Tacó ABC∆ làhìnhchiếuvuônggóccủa ABI ′ ∆ trênmặt phẳng () ABC .

Do đó .cosABCIBASS α ′ = 22310 .cos 44 aa α  = 30 cos 10 α  =

Câu9. (Chuyên Hùng Vương -Phú Thọ -2018) Cho hình chóp SABC có SAa = , ()SAABC ⊥ , tam giác ABC vuông cân đỉnh A và 2 BCa = . Gọi M , N lần lượt là trung điểm của SB , SC Côsincủagóctạobởihai mặt phẳng () MNA và () ABC bằng A. 2 4 . B. 2 6 . C. 3 2 . D. 3 3 . Lờigiải

Gọi I , K lầnlượtlàtrung điểmcủa MN và BC .

 I làtrung điểmcủa SK .

Tacó ()() ////. AMNABCAxMNBC ∩=

ABC∆ cântại A AKBC  ⊥ AKAx  ⊥ .

AMN∆ cântại A AIMN  ⊥ AIAx  ⊥ .

Do đó ()() () , AMNABC () , AIAK = IAK = hoặcbùvớigóc IAK

ABC∆ vuôngtại A có AK là đườngtrungtuyếnnên 2 BC AK = 2 2 a =

a a SAAKa + + === Xét AIK∆ có 222 cos 2. IAAKIK IAK IAAK +− =

2 2 22 6 2 224

 +− 

222 626 424 3 3 2..62 42

aaa aa  == Câu10. (Chuyên Hoàng Văn Thụ - Hòa Bình - 2018) Cho hình chóp SABCD có ABCD là hình thoi cạnh bằng a và góc A bằng 60° , cạnh SC vuông góc với đáy và 6 2 a SC = . Giá trị lượng giác cô-sincủagócgiữahai mặtphẳng () SBD và () SCD bằng A. 6 6 B. 5 5 C. 25 5 D. 30 6 Lờigiải Từ () SCABCDSCBD ⊥  ⊥

Kẻ CKSO ⊥ ,từ () BDSACBDCK ⊥  ⊥ .Như vậy () CKSBDCKSD ⊥  ⊥

Kẻ CHSD ⊥ ,do CKSD ⊥ nênsuyra ()SDCHK ⊥ .

Mặtkhác ()() CHKSBDHK ∩= và ()() CHKSCDCK ∩= nêngócgiữahaimặtphẳng () SBD

và () SCD bằng CHK

là

() SCD .

A. 60° . B. 120° . C. 45° . D. 90° . Lờigiải

hình thoi cạnh a ,

Trongtam giác SCD vuôngtại C ,tacó: 2 22222 1111153 3 5 6 2

a CH CHCDSCaa a =+=+=  =   

Vì ABCD làhìnhthoi cạnhbằng a vàgóc A bằng 60° nên 3 2 a CO =

Tacó 22SBSAAB =+ 2 2 610 22 a aa  =+=    .

. Xéttamgiác CHK vuôngtại K ,tacó 22 22 3 52 10 aaa HKCHCK=−=−= . 36 cos: 6 105 HKaa CHK CH === . Vậy,cô-sincủagócgiữahaimặtphẳng () SBD và () SCD bằng 6 6 .

Vì tamgiác ABD đềunên 3 2.2.3 2 ACAOaa ===

Suyra 22SCSAAC =+ () 2 2 632 3 22 a aa  =+=   

Kẻ BHSC ⊥ ,tacó SCBD SCHD SCBH ⊥   ⊥  ⊥  . Như vậy ()() ()()( ) ,

SBCSCDSC BHSCSBCSCD DHSC

∩=   ⊥    ⊥  .

Xéttamgiác SBC tacó 222 cos 2. HCBCSCSB C BCBCSC +− == 2 2 a HC  = .

Suyra 22 2 2 a HDHBBCHC==−= Tacó 222 cos0 2. HBHDBD BHD HBHD +− == 90 BHD  =° .Vậy ()() (),90SBCSCD =° Câu12. (Chuyên Thái Bình 2018) Cho hình chóp . SABC có đáy ABC là tam giác vuông cân tại B , 2 ACa = , tam giác SAB và tam giác SCB lần lượt vuông tại A , C . Khoảng cách từ S đến mặt phẳng () ABC bằng 2a . Côsincủagócgiữahaimặtphẳng () SAB và () SCB bằng

a CK CKCOSCa aa =+=+=  =    Trang 20

Lờigiải

Chọnhệ trụctọa độ saocho () 0;0;0 B , () 2;0;0 Aa , () 0;2;0Ca , () ;; Sxyz Tacó () :0ABCz = , () 2;; ASxayz =− , () ;2; CSxyaz =− Do .0ASAB = ()220xaa  −= 2 xa  = , () (),2 dSABCa = 2 za  = () 0 z > .0CSCB = ()220yaa  −= 2 ya  = () 2;2;2 Saaa  . Tacó () 0;2;2 ASaa = , () 2;0;2 CSaa = , () 2;2;2 BSaaa = () SBC có1vtpt () 2;0;1 n =− , () SAB có1vtpt () 0;2;1 m =− cosϕ  1 3.3 = 1 3 =

Câu13. (Chuyên Thái Bình 2018) Cho hình lăng trụ đứng ABCABC′′′ có ABACa == , góc 120 BAC =° , AAa ′ = . Gọi M , N lần lượt là trung điểm của BC′′ và CC′ . Số đo góc giữa mặt phẳng () AMN vàmặtphẳng () ABC bằng A. 60° B. 30° C. 3 arcsin 4 D. 3 arccos 4 Lờigiải

Gọi H làtrung điểm BC , 3 BCa = , 2 a AH =

Chọnhệ trụctọa độ () 0;0;0 H , ;0;0 2 a A   , 3 0;;0 2 a B     , 3 0;;0 2 a C     ,

() 0;0; Ma , 3 0;; 22 aa N     .Gọi ϕ làgócgiữamặtphẳng () AMN vàmặtphẳng () ABC

() AMN cómột vtpt , nAMAN =  313 ;; 244  =   

() ABC cómột vtpt HM () 0;0;1 = ,từ đó cos nHM nHM ϕ =

3 4 1.1 = 3 4 =

Câu14. (Chuyên Đh Vinh-2018) Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , cạnh bên 2 SAa = và vuông góc với mặt phẳng đáy. Gọi M là trung điểm cạnh SD . Tang của góc tạo bởihaimặtphẳng () AMC và () SBC bằng

A. 5 5 B. 3 2 C. 25 5 D. 23 3 Lờigiải

và chuẩnhóacho 1 a = saocho () 0;0;0 A , () 0;1;0 B , () 1;0;0 D , () 0;0;2 S

Tacó M làtrung điểm SD 1 ;0;1 2 M     , () 1;1;0 C 1 ;0;1 2 AM  =   , () 1;1;0 AC = , 1 ,1;1; 2 AMAC   =−   () AMC  cómột vtpt () 2;2;1 n =− () 0;1;2 SB =− , () 1;1;2 SC =− , (),0;2;1SBSC  =  () SBC  cómộtvtpt () 0;2;1 k = Gọi α làgócgiữahaimặt phẳng ()

ngthời ()() BCDACDCD ∩= ()()( ) ,90BCDACDBEA

Tacó CFAB DFAB ⊥   ⊥  ()ABCFD  ⊥ ()()( ) (),, ABCABDCFFD⇔= Vậy để ()() ABCABD ⊥ thì (),90 CFFDCFD =°=  trung tuyến FE của tam giác CFD bằng nửacạnhhuyền 1 2 FECD⇔=

Tacó EAB∆ vuôngcântại E 2222 222 AEACCEax EF  === Vậy 22 2 ax x = 22 2 2 ax x ⇔= 2 2 3 a x ⇔= 3 3 xa⇔=

Câu16. (Chuyên Vinh - 2018) Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , mặt bên SAB làtamgiác đềuvànằmtrongmặtphẳngvuônggócvớimặtphẳng () ABCD .Gọi G làtrọng tâm của tam giác SAB và , MN lần lượtlà trung điểm của , SCSD (tham khảohình vẽ bên). Tính côsincủagócgiữahaimặtphẳng () GMN và () ABCD . A. 239 39 B. 3 6 C. 239 13 D. 13 13 Lờigiải

Oxyz như hìnhvẽ.Khi đó 3 0;0; 2 S     ; ;0;0 2 a A   ; ;0;0 2 a B    ; ;;0 2 a Ca   ; ;;0 2 a Da  

suyra 3 0;0; 6 a G     ; 3 ;; 424 aaa M     ; 3 ;; 424 aaa N    

() 222 cos, 2.. BIDIBD BIDI BIDI +− = 1 2 =− (),120BIDI  =° Vậy ()(),60BACDAC  ′′ =°  .

Câu18. (Chuyên Trần Phú - Hải Phòng - 2018) Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và D , 2 ABADa == , CDa = . Gọi I là trung điểm cạnh ,AD biết hai mặt phẳng

() SBI , () SCI cùng vuông góc với đáy và thể tích khối chóp SABCD bằng 3 315 5 a . Tính góc giữa hai mặt phẳng () SBC , () ABCD A. 30° B. 36° C. 45° D. 60° Lờigiải Diện tích hình thang () 1 2 ABCD SADABCD =+ 1 2.3 2 aa = 2 3a = , 5 CBACa == . Độ dài đường cao 3 SABCD ABCD

V SI S =

3.315 315 5 35

3 2

a a a == . Vẽ IHCB ⊥ tại H ()BCSIH  ⊥ BCSH  ⊥ . Ta có ()()( ) , SBCABCD = () , IHSHSHI = . ICBABCDIDCAIB SSSS =−− 22 22 3 3 22 aa aa =−−= 2 .3 IHCBa  = 35 5 a IH  =

S SS S ϕϕ =  == Câu20. (Sở Ninh Bình 2020) Cho hình chóp . SABC có đáy

trị cosin của góc giữa hai mặt phẳng () SAB và () SCB bằng A. 22 3 . B. 1 3 . C. 2 3 . D. 5 3 . Lờigiải ChọnC

+ Gọi , OI lần lượt là trung điểm của , ACSB chúng ta có O là tâm của đường tròn ngoại tiếp tam giác ABC và vì các tam giác , ∆∆SABSCB lần lượt vuông tại A và C nên I là tâm mặt cầu ngoại tiếp tứ diện SABC do đó () ⊥ OIABC + Gọi D là hình chiếu của S lên mặt phẳng () ABC ta có // SDOI và 2 = SDOI suy ra O là trung điểm của BD . Từ đây ta có ABCD là hình vuông cạnh bằng 2 2 2 = a a và = SDa + Gọi , HK lần lượt là hình chiếu của D lên , SCSA ta có () ⊥  ⊥ SDABCDSDBC đồng thời ABCD là hình vuông nên ⊥ BCDC từ hai ý này ta có () ⊥  ⊥ BCSCDBCDH , từ đó suy ra () ⊥ DHSCB Chứng minh tương tự ta có () ⊥ DKSAB + Vì vậy góc giữa hai mặt phẳng () SCB và () SAB bằng góc giữa hai đường thẳng DK và DH + Xét 2 tam giác vuông , ∆∆SADSCD bằng nhau ta có hai đường cao 6 3 == a DKDH + Trong tam giác SAC ta có 2 2 12 33 ===  = HKSHSDa HK ACSCSC , trong tam giác DHK có 222 2 cos 2.3 DHKDKH HDK DHKD +− ==

Câu21. (Sở BắcNinh-2020) Cho hình chóp SABCD có đáy là hình thoi cạnh 0 ,120, aABCSA = vuông góc với mặt phẳng () ABCD Biết góc giữa hai mặt phẳng () SBC và () SCD bằng 0 60, khi đó A. 6 . 4 a SA = B. 6. SAa = C. 6 2 a SA = D. 3 2 a SA = Lờigiải ChọnA

Gọi O là giao điểm của ,.ACBD Gọi H là hình chiếu vuông góc của O trên SC Khi đó () DSCHB ⊥ vì ,. SCBDSCOH ⊥⊥ Vậy góc giữa hai mặt phẳng () SBC và () SCD là góc giữa hai đường thẳng ,.HBHD Vì .SCDSBCHBHD =∆  = △ Đặt ()0. SAxx=>

Cách 1: Gọi O là trung điểm BC

Ta có: 3 .cos30 cos30 3 2. 2

o o BOa BOABABaAC =⇔==== và .sin30 2 o a AOAB== .

Ta có 22 222 0222 2 2 602 2. 3

HBBD HBHDBD cosHBHBBD BD HBHD HB

 = +−  =⇔=−⇔  =  

Ta có ()..1CHOCSAOHCSCOSA ≈∆  = △

Trong tam giác ABC ta có 3, 2 a ACaOBBDa ==  =

TH1 : 22 3 2 a HBBDaOHHBOB ==  =−= . Thay vào (1)ta có 223.xxa =+ (vônghiệm). TH2 : 22 333 336 BDaa HBOHHBOB ==  =−= Thay vào (1) ta có () 22 22236 3 1244 aaa xaxx +=  = Câu22. (Sở BìnhPhước-2020) Cho hình lăng trụ đứng . ABCABC′′′ có đáy là tam giác cân đỉnh A . Biết 3 BCa = và 30o ABC = , cạnh bên AAa ′ = . Gọi M là điểm thỏa mãn 23CMCC′ = . Gọi α là góc tạo bởi hai mặt phẳng () ABC và () ABM ′ , khi đó sin α có giá trị bằng A. 66 22 . B. 481 22 . C. 3 22 . D. 418 22 . Lờigiải ChọnD

Theo đề bài: 331 23 2222 a CMCCCMCCCCCMCCCMCCCM ′′′′′′′′ =⇔=⇔+=⇔=  = .

Gọi α là góc giữa hai mặt phẳng () ABC và () ABM ′ .

Theo công thức diện tích hình chiếu ta có: .coscos

BOa BOABABaAC =⇔==== và .sin30 2 o a AOAB== . Theo đề bài: 331 23 2222 a CMCCCMCCCCCMCCCMCCCM ′′′′′′′′ =⇔=⇔+=⇔=  = . Coi 1 a = . Gắn hệ trục tọa độ Oxyz như hình vẽ với () 0;0;0 O , 1 0;;0 2 A   , 3 ;0;0 2 B     , 3 ;0;0 2 C     , 3 ;0;1 2 B ′   , 33 ;0; 22 M   

đ



ẳ

a SA SIA AI a ===

Xét tam giác SAI vuông tại A ta có 1 2 tan. 33 2

Suy ra 30. SIA =° Vậy ()() (),30.SBCABC =°

Câu24. (KìmThành-HảiDương-2020) Cho hình chóp . SABC có đáy ABC là tam giác vuông cân tại A , 2 ABa = , SA vuông góc với mặt đáy và góc giữa SB và mặt đáy bằng 60° . Gọi α là góc giữa hai mặt phẳng () SBC và () ABC . Giá trị cosα bằng A. 15 5 B. 2 5 C. 1 7 D. 2 7 Lờigiải ChọnC

Ta có ;0; 22 aa AM  =   , 0;; 22 aa AN  =   nên mặt phẳng () AMN

222 1 ,;; 444 aaa nAMAN   ==−−   .

()() ;0;,0;; SBaaSDaa =−=− nên mặt phẳng () SBD có vectơ pháp tuyến là () 222 2 ,;; nSBSDaaa  ==  Khi đó

444 12 444 444 12

aaa nn nn aaa aaa ϕ −−+ === ++++

. 444 1 cos 3 . 161616

2 22 sin1cos 3 ϕϕ  =−=

Câu26. (ChuyênNguyễnTrãi-HảiDương-Lần2-2020) Cho hình lăng trụ đứng .'''ABCABC có đáy ABC là tam giác cân với == ABACa và góc 120 = o BAC và cạnh bên ' = BBa . Gọi I là trung điểm của ' CC . Tính cosin góc giữa hai mặt phẳng () ABC và () ' ABI A. 3 10 . B. 30 10 . C. 30 30 . D. 10 30 . Lờigiải ChọnB

Ta có: 3 sin60 2 a OBAB=°= ; cos60 2 a OAAB=°= • Giả sử 1 a = suy ra 1 ;0;0 2 A           , 3 0;;0 2 B             , 3 0;;0 2 C             , 31 0;;22 I             , 3 0;;1 2 B 

Dạng1.Khoảngcáchtừ điểm đếnmặtphẳng

Bàitoán1:Tínhkhoảngcáchtừ hìnhchiếuvuônggóccủa đỉnh đếnmộtmặtbên

Phương pháp xác định khoảng cách từ hình chiếu của đỉnh đến một mặt phẳng bên.

Bước1: Xác định giao tuyến d

Bước2: Từ hình chiếu vuông góc của đỉnh, DỰNG AHd ⊥ ( Hd ∈ ).

Bước3: Dựng ()AISHISH ⊥∈ .Khoảng cách cần tìm là AI

Với S là đỉnh, A là hình chiếu vuông góc của đỉnh trên mặt đáy.

Vídụ điểnhình: Cho hình chóp S.ABC có SA vuông góc với đáy (ABC). Hãy xác khoảng cách từ điểm A đến mặt bên (SBC).

Ta có BC là giao tuyến của mp (SBC) và (ABC).

Từ hình chiếu của đỉnh là điểm A, dựng AHBC ⊥ tại H. Dựng AISH ⊥ tại I Vì ()()() BCSA BCSAHSBCSAH BCAH ⊥   ⊥  ⊥  ⊥  . Mặt phẳng (SBC) vuông góc với mặt phẳng (SAH) theo giao tuyến SH có AISH ⊥ nên ()() () , AImpSBCdAmpSBCAI ⊥  = Bàitoán2:Tínhkhoảngcáchtừ một đểmbấtkỳ đếnmộtmặtphẳng Thường sử dụng công thức sau: Công thức tính tỉ lệ khoảng cách: () () () () , ,

dMmpP MO AO dAmpP = Ở công thức trên cần tính khoảng cách từ điểm M đến mặt phẳng (P). Câu1. (Mã 101 - 2021 Lần 1) Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại ,B 2 ABa = và SA vuông góc với mặt phẳng đáy. Tính khoảng cách từ C đến mặt phẳng () SAB bằng A. 2a B. 2a C. a D. 22a Lờigiải ChọnB

Vì ()SAABC ⊥ suy ra CBSA ⊥ . Tam giác ABC vuông tại ,B nên CBAB ⊥ (2). Từ (1) và (2), ta suy ra ()CBSAB ⊥ nên khoảng cách từ C đến mặt phẳng () SAB bằng CB. Mà tam giác ABC vuông cân tại ,B suy ra 2 ABBCa == Vậy (;()) 2. CSAB dCBa ==

Câu2. (Mã103-2021-Lần1) Cho hình chóp . SABC có đáy là tam giác vuông cân tại C , ACa = và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng () SAC bằng A. 1 2 a B. 2a C. 2 2 a D. a Lờigiải ChọnD

Ta có: SA vuông góc với mặt đáy suy ra SABC ⊥

Tam giác ABC vuông cân tại C suy ra BCa = và ACBC ⊥

Vậy khoảng cách từ B đến mặt phẳng () SAC bằng BCa = .

Câu3. (Mã102-2021Lần1) Cho hình chóp SABC có đáy là tam giác vuông cân tại C , 3 ACa = và SA vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng () SAC bằng A. 3 2 a . B. 32 2 a . C. 3a . D. 32a . Lờigiải ChọnC

Ta có ABC∆ vuông cân tại C nên () 1 BCAC ⊥ và 3 ACBCa == Mặt khác ()() 2 SAABCSABC ⊥  ⊥ Từ () 1 và () 2 suy ra ()() (),3 BCSACdBSACBCa ⊥  == Vậy khoảng cách từ B đến mặt phẳng () SAC bằng 3a .

Câu4. (Mã 104 -2021 Lần 1) Cho hình chóp SABC có đáy là tam giác vuông cân tại B , 4 ABa = và SA vuông góc với mặt phẳng đáy. Khoảng cách từ C đến mặt phẳng () SAB bằng

A. 4 a B. 42a C. 22a D. 2 a Lờigiải ChọnA

Ta có: () () () () () :

⊥    ⊥⊥  ⊥   ∩=   tại B

gt do Trong mp

BCAB BCSASAABCBCSAB SABABSAA

Suy ra () () , dCSABCB = Xét ABC ∆ vuông cân tại B có: 4 BCABa == Vậy () (),4 dCSABa =

Câu5. (Đề Minh Họa 2021) Cho hình chóp tứ giác đều . SABCD có độ dài cạnh đáy bằng 2 và độ dài cạnh bên bằng 3 (tham khảo hình vẽ bên). Khoảng cách từ S đến mặt phẳng ABCD bằng: A. 7. B. 1 C. 7 D. 11. Lờigiải ChọnA Gọi O là tâm đáy ABCD . Vì . SABCD là hình chóp đều nên SO là đường cao khối chóp. Khi đó ();. dSABCDSO = Ta có 22222 11 2327. 22 AOACABACSOSAAO ==+=  =−=−=

Câu6. (Sở Lào Cai - 2021) Cho tứ diện OABC có OA , OB , OC đôi một vuông góc và 2 OAOBa == , 2 OCa = . Khoảng cách từ điểm O đến mặt phẳng () ABC bằng A. 2 a B. a C. 2 a D. 3 4 a Lờigiải ChọnB

A. 3 a . B. 3a . C. 3 3 a . D. 23 a . Lờigiải ChọnB

đáy bằng

Ta có 2 13 ..sin 24 ABC a SABACBAC == .

Mà () () () () 3 1 .,,23 3 SABC SABCABC ABC

V VSdSABCdSABCa S =  == Khi đó () () () () 1 ,,3 2 dMABCdSABCa == .

Câu9. (THPT Chu Văn An - Thái Nguyên - 2021) Cho lăng trụ đứng ABCABC′′′ có tất cả các cạnh đều bằng a . Gọi M là trung điểm của CC′ (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng () ABC ′ bằng

A. 21 7 a . B. 2 4 a . C. 21 14 a . D. 2 2 a .

SABC ABC ABC ∆ ∆

3. 3 1232 2 22., 2 2 2

S a

a V a a SABACdSABC ==  === Trang 6

Lờigiải ChọnC Gọi , HK lần lượt là hình chiếu của A lên BC và AH ′ .

Suy ra 3 2 a AH =

Câu11. (THPT Trần Phú - ĐàNẵng - 2021) Cho hình lập phương .'''' ABCDABCD cạnh

, I là trung điểm CD (tham khảo hình vẽ). khoảng cách từ I đến mặt phẳng () ''BDDB bằng A. 2 4 a B. 4 a C. 6 4 a D. 3 4 a Lờigiải ChọnC

Do ()''' CIBDDBD ∩= nên ta có () () () () ,'' '1 '2 ,'' dIBDDB ID CD dCBDDB == . Gọi {}MBDAC =∩ . Khi đó 6 22 ACa CM == Vậy () () () () 16 ,'',''. 224 CMa dIBDDBdCBDDB=⋅==

Câu12. (Chuyên Tuyên Quang - 2021) Cho hình lăng trụ đều .'''ABCABC có tất cả các cạnh bằng 2022. Khoảng cách từ điểm A đến mặt phẳng () ''BCCB bằng A. 10113 B. 20223 C. 20222 D. 10112 Lờigiải ChọnA

Gọi H là trung điểm của BC

Ta có () '' ' AHBC AHBBCC AHBB ⊥   ⊥  ⊥  () (),''10113dABCCBAH  ==

B' A B C A' A' C' B' A C B H

H

Câu13. (Cụm Ninh Bình – 2021) Cho hình lăng trụ đứng ABCABC′′′ có đáy ABC là tam giác vuông tại B , ABa = , 2 AAa ′ = . Tính theo a khoảng cách từ điểm A đến mặt phẳng () ABC ′ . A. 23 . 5 a B. 5 . 3 a C. 3 . 3 a D. 25 . 5 a Lờigiải Vẽ ()() () '','. AHABAHABCdAABCAH ⊥  ⊥  =

Ta có: ()()2222

'.2.25 . 5 4 ' AAABaaa AH aa AAAB === + +

Trang 9

Mà SA ; AB ; AD đôi một vuông góc  () () 2 222 1111 ; SAABAD dASBD =++    () () 2 ; 3 a dASBD =

Vậy khoảng cách từ điểm G đến mặt phẳng () SBD là: () () () () 12 ;; 39 a dGSBDdASBD== .

Câu15. (Sở Hòa Bình - 2021) Cho hình hộp chữ nhật .' ABCDABCD′′′ có ,2 ABaADa == ( tham khảo hình vẽ bên dưới).

C' B'

A

A' D' D C B

Khoảng cách từ điểm A đến mặt phẳng () BDDB′′ bằng A. 5 2 a B. 5 a C. 5 5 a D. 25 5 a Lờigiải ChọnD

Câu16. (Sở Nam Định-2021) Cho hình chóp S ABC có đáy là tam giác đều có cạnh bằng 3, mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy (tham khảo hình vẽ dưới đây). Khoảng cách từ đỉnh S đến mặt phẳng ( ABC) bằng A. 3 2 B. 33 2 C. 3 D. 3 2 Lờigiải ChọnB

Gọi H là trung điểm của AB  SH ⊥ AB và SH = 33 2 (do SAB là tam giác đều có cạnh bằng 3)

Ta có (SAB) ⊥ ( ABC) (SAB) ∩ ( ABC) = AB SH ⊥ AB

      SH ⊥ ( ABC)

Khoảng cách từ đỉnh S đến mặt phẳng ( ABC) bằng SH = 33 2 .

Câu17. (Chuyên Vinh - 2021) Cho hình chóp . SABCD có đáy ABCD là hình chữ nhật 3 ABa = , BCa = , các cạnh bên của hình chóp cùng bằng 5 a . Gọi M là trung điểm của SC . Tính khoảng cách từ M đến mặt phẳng () ABCD : A. 2a . B. 2 a . C. 3 a . D. .a Lờigiải ChọnD

S

M O D C

B A

H

Gọi O là giao của hai đường chéo. Dễ thấy cạnh bên của hình chóp bằng nhau nên chân đường cao của hình chóp chính là tâm của đáy.

Ta có 2222 1 32 2 ACABBCaaaAOACa =+=+=  ==

Khi đó ta có 222252 SOSAAOaaa =−=−= . Gọi H là chân đường cao hạ từ M xuống () () ; ACdMABCDMH  =

Câu19. (Mã 103 - 2020 Lần 1) Cho hình lăng trụ đứng ABCABC

cạnh a và 2 AAa ′ = . Gọi M là trung điểm của AA ′ (tham khảo hình vẽ bên). Khoảng cách từ M đến mặt phẳng () ABC ′ bằng

Câu18. (Mã102-2020 Lần1) Cho lăng trụ đứng . ABCABC′′′ có đáy ABC là tam giác đều cạnh a và 2 AAa ′ = . Gọi M là trung điểm của CC′ (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng () ABC ′ bằng A. a 5 5 . B. a25 5 . C. a257 19 . D. a57 19 . Lờigiải ChọnD Gọi , HK lần lượt là hình chiếu của A lên BC và AH ′ .

A. 57 19 a B. 5 5 a C. 25 5 a D. 257 19 a Lờigiải ChọnA

′ ′′ ===  == ′ ′

dMABC MIMA BH dMABCdBABC BIBB dBABC

Gọi IBMAB′ =∩ và K là trung điểm AC . Ta có () () () () () () () () , 11 ,, 222 ,

Xét tam giác BBK ′ có ()22 222 11111257 19 2 3 2

a BH BHBBBK a a =+=+  = ′   

Vậy () () 57 , 219 BHa dMABC ′ ==

Câu20. (Mã 104 - 2020 Lần 1) Cho hình lăng trụ đứng . ABCABC′′′ có tất cả các cạnh bằng a . Gọi M là trung điểm của AA′ (tham khảo hình vẽ).

A. 2 4 a B. 21 7 a C. 2 2 a D. 21 14 a Lờigiải ChọnD

′ ′′ ===  =⋅ ′′

Trong () ABBA′′ , gọi E là giao điểm của BM và AB′ . Khi đó hai tam giác EAM và EBB ′ đồng dạng. Do đó () () () () () () () () , 11 ,22,, dMABC EMMA dMABCdBABC dBABCEBBB

Từ B kẻ BNAC ⊥ thì N là trung điểm của AC và 3 2 a BN = , BBa ′ = Kẻ BIBN ′ ⊥ thì () () 22

21 , 7 BBBNa dBABCBI BBBN

′ ′ === ′ + . Vậy () () () () 121 ,,214 a dMABCdBABC ′′ =⋅= .

Câu21. (Mã 101 - 2020 Lần 1) Cho hình lăng trụ đứng ABCABC′′′ có tất cả các cạnh bằng a . Gọi M là trung điểm của CC′ (tham khảo hình bên). Khoảng cách từ M đến mặt phẳng () ABC ′ bằng

A. 21 14 a . B. 2 2 a . C. 21 7 a . D. 2 4 a .

dMABC CM CC dCABC

′ ′ == ′ ′′ .

() CMABCC ′′ ∩= , suy ra () () () () , 1 2 ,

Ta có 23 11133 .... 333412CABCABCABCABC aa VVCCSa ′′′′′ ∆ ′ ====

Lại có 2 ABa ′ = , CBa = , 2 ACa ′ = 2 7 4 ABC a S ′  = .

Suy ra () () 3 2

a V a dCABC S a ′′ ′ ∆

3 3. 3 21 12 , 7 7 4

′′ === Vậy () () () () 112121 ,,.22714 aa dMABCdCABC ′′′ === .

CABC ABC

Câu22. (Mã 101 2018) Cho hình chóp SABC có đáy là tam giác vuông đỉnh B , ABa = , SA vuông góc với mặt phẳng đáy và 2 SAa = . Khoảng cách từ A đến mặt phẳng () SBC bằng A. 25 5 a B. 5 3 a C. 22 3 a D. 5 5 a Lờigiải ChọnA

S H

Ta có () BCAB BCSAB BCSA ⊥   ⊥  ⊥  .

2a A C B

a

Câu23. (Mã1022018) Cho hình chóp SABC có đáy là tam giác vuông đỉnh B , ABa = , SA vuông góc với mặt phẳng đáy và SAa = . Khoảng cách từ điểm A đến mặt phẳng () SBC bằng A. 6 3 a B. 2 2 a C. 2 a D. a Lờigiải ChọnB S A B

C H Kẻ AHSB ⊥ trong mặt phẳng () SBC Ta có: () BCAB BCSAB BCSA ⊥   ⊥  ⊥  BCAH  ⊥ Vậy () AHBC AHSBC AHSB ⊥   ⊥  ⊥  () () 12 , 22 a dASBCAHSB  ===

Câu24. (Mã103-2019) Cho hình chóp . SABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ D đến mặt phẳng () SAC bằng A. 2 2 a . B. 21 7 a . C. 21 14 a . D. 21 28 a . Lờigiải ChọnB

* Gọi OACBD =∩ và G là trọng tâm tam giác ABD , I là trung điểm của AB ta có ()SIABCD ⊥ và () () () () () () () () ; 2;2.; ; dDSAC DG dDSACdISAC IG dISAC ==  = .

* Gọi K là trung điểm của AO , H là hình chiếu của I lên SK ta có () ; IKACIHSAC ⊥⊥ () () () () ;2.;2. dDSACdISACIH  ==

* Xét tam giác SIK vuông tại I ta có: 32 ; 224 aBOa SIIK=== 222222 111416283 323 27 a IH IHSIIKaaa =+=+=  = () () () () 21 ;2.;2. 7 a dDSACdISACIH  ===

Câu25. (Mã101-2019) Cho hình chóp . SABCD có đáy là hình vuông cạnh ,a mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (minh họa như hình vẽ bên). Khoảng cách từ A đến mặt phẳng () SBD bằng A. 21 14 a . B. 21 7 a C. 2 2 a D. 21 28 a . Lờigiải ChọnB

⊥  ⊥ 

= .

VVa ABCDdBSCDdSCD SS  ==== .

( ;2;2;CDaSCDSDaSCa ∆=== )

Câu27. (Mã 102 - 2019) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy ( minh họa như hình vẽ bên). Khoảng cách từ C đến mặt phẳng () SBD bằng

Gọi H là trung điểm của .AB Khi đó, (). SHABCD ⊥ Gọi O là giao điểm của AC và BD suy ra ACBD ⊥ . Kẻ HKBD ⊥ tại K ( K là trung điểm BO ).

Kẻ HISH ⊥ tại I. Khi đó: () () () () ,2,2. dASBDdHSBDHI ==

Xét tam giác , SHK có: 3 , 2 a SH = 12 24 a HKAO== .

Khi đó: 2222 1112821 314 a HI HISHHKa =+=  = Suy ra: () () 21 ,2. 7 a dASBDHI==

Câu26. (Đề Tham Khảo 2019) Cho hình chóp . SABCD có đáy là hình thoi cạnh a , o60 BAD = , SAa = và SA vuông góc với mặt phẳng đáy. Khoảng cách tứ B đến () SCD bằng? A. 21 3 a . B. 15 3 a . C. 21 7 a . D. 15 7 a . Lờigiải ChọnC

A. 21 14 a B. 2 2 a C. 21 7 a D. 21 28 a Lờigiải ChọnC

H

D B C

S A M Trang 20

Gọi H là trung điểm của ().ABSHABSHABCD  ⊥  ⊥

Từ H kẻ HMBD ⊥ , M là trung điểm của BI và I là tâm của hình vuông.

Ta có: (SHM) BDHM BD BDSH ⊥   ⊥  ⊥ 

Từ H kẻ HKSMHKBD ⊥  ⊥ ( Vì (SHM) BD ⊥ )

()d(H;(SBD))HK.HKSBD  ⊥  = Ta có: 2 . 244 AIACa HM === 3 2 a SH = . 2222

23 .21 42 14 23 42

aa HMHSa HK HMHSaa === +  +   2121 (;())(;())2(;())22.. 147 aa dCSBDdASBDdHSBDHK===== Vậy: (;())dCSBD 21 7 a = Câu28. (Mã 103 2018) Cho hình chóp SABCD có đáy là hình vuông cạnh 3a , SA vuông góc với mặt phẳng đáy và SAa = . Khoảng cách từ A đến mặt phẳng () SBC bằng A. 6 6 a B. 3 3 a C. 5 3 a D. 3 2 a Lờigiải ChọnD Ta có: BCAB BCSA ⊥   ⊥   ()BCSAB ⊥  ()() ()() SABSBC SABSBCSB ⊥    ∩=  

Trong mặt phẳng () SAB : Kẻ AHSB ⊥  () () ; AHdASBC = 222 111 AHSAAB =+ 22 11 3 aa =+ 2 4 3a = .  () () 3 ; 2 a dASBCAH== . Chọn D

Câu29. (ChuyênVĩnhPhúc2019) Cho tứ diện đều ABCD có cạnh bằng a . Tính khoảng cách từ A đến mặt phẳng () BCD A. 6 2 a . B. 6 3 a . C. 3 2 a . D. 2a . Lờigiải: ChọnB Gọi ,, EFG lần lượt là trung điểm của , BDCD và trọng tâm tam giác BCD

Tam giác BCD đều nên suy ra 33 22 BCa CE == 23 33 a CGCE== Tam giác ACG vuông tại G nên ta có 22 2222 26 333 aaa AGACCGaAG =−=−=  =

Vậy () () 6 , 3 a dABCDAG==

Câu30. (ChuyênBắcGiang2019) Cho hình chóp DSABC có () DSAABC ⊥ , đáy DABC là hình chữ nhật. Biết D2aA = , SAa = . Khoảng cách từ A đến () DSC bằng: A. 3a 7 B. 3a2 2 C. 2a 5 D. 2a3 3 Lờigiải ChọnC Gọi H là hình chiếu của A lên DS ta chứng minh được () DAHSC ⊥ 222 1112a D 5 AH AHSAA =+  =

Câu31. (ChuyênLamSơnThanhHóa2019) Cho hình chop . SABC có đáy là tam giác vuông tại A , ABa = , 3 ACa = , SA vuông góc với mặt phẳng đáy và 2 SAa = . Khoảng cách từ điểm A đến mặt phẳng () SBC bằng: A. 57 19 a B. 257 19 a C. 23 19 a D. 238 19 a Lờigiải ChọnB

Vậy () 2 , 3 a dOSCD =   .

A K

H O

Ta có 2222222222 11111111119 3412 AKAHASABACASaaaa =+=++=++= Suy ra 23 19 a AK = hay 257 (,()) 19 a dASBC = . Câu32. (Hùng Vương Bình Phước 2019) Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng a và chiều cao bằng 2 a . Tính khoảng cách d từ tâm O của đáy ABCD đến một mặt bên theo a . A. 25 3 a d = . B. 3 2 a d = . C. 5 2 a d = . D. 2 3 a d = . Lờigiải . SABCD là hình chóp tứ giác đều nên ABCD là hình vuông và ()SOABCD ⊥ . Vẽ OH vuông góc với CD tại H thì H là trung điểm CD , 2 a OH = . Dễ thấy ()()() CDSOHSCDSOH ⊥  ⊥ nên kẻ OK vuông góc với SH tại K thì ()OKSCD ⊥ (), dOSCD    OK =

Câu33. (Chuyên TrầnPhúHải Phòng 2019) Cho khối chóp . SABCD có đáy ABCD là hình vuông cạnh a , ()SAABCD ⊥ và 2 SAa = . Gọi M là trung điểm cạnh SC . Khoảng cách từ điểm M đến mặt phẳng () SBD bằng A. 2 4 a B. 10 10 a C. 2 2 a D. 10 5 a Lờigiải Do M là trung điểm SC nên () () () () () () 11 ;;; 22 dMSBDdCSBDdASBD == Gọi H là hình chiếu của A lên ()() () ; mpSBDdASBDAH  = Lại có ,, ASABAD đôi một vuông góc nên ()2 2222222 11111115 2 2 AHASABADaaa a =++=++= () () 1010 ; 510 AHdMSBDaa  =  =

D

Câu34. (THPT Gang Thép Thái Nguyên 2019) Cho hình chóp SABC có đáy ABC là tam giác vuông tại A , ABa = , 3 ACa = ; SA vuông góc với đáy, 2 SAa = . Khoảng cách từ điểm A đến mặt phẳng () SBC bằng A. 23 7 a B. 3 7 a C. 3 19 a D. 23 19 a Lờigiải

a a OSOHa OK OSOHa a

2. .2 2 3 2 4

=== + + .

S B C Trang 24

Ta có () () SAABC SABC BCABC ⊥    ⊥  ⊂  

K

H

Trong () ABC , kẻ AHBC ⊥ , mà () BCSABCSAHBCSH ⊥  ⊥  ⊥

Trong () SAH , kẻ AKSH ⊥ , mà SHBC ⊥ ()AKSBC  ⊥ hay () () ; dASBCAK =

Vì ABC∆ vuông tại A nên 22 2 BCABACa =+= .

Mặt khác có AH là đường cao nên .3 2 ABACa AH BC ==

Vì SAH∆ vuông tại A nên 22 19 2 a SHSAAH=+= .

Vậy có AK là đường cao .23 19 SAAHa AK SH == .

Nhậnxét. Trong thực hành làm toán trắc nghiệm ta nên áp dụng bài toán sau: Cho tứ diện OABC có ,, OAOBOC đôi một vuông góc với nhau vàHlà hình chiếu của O lên mặt phẳng () ABC . Khi đó 2222 1111 OHOAOBOC =++ .

Câu35. (Chuyên SơnLa2019) Cho hình chóp . SABC có đáy ABC là tam giác đều cạnh a , = SAa và SA vuông góc với mặt phẳng đáy. Khoảng cách từ điểm A đến mặt phẳng () SBC bằng: A. 2 2 a B. 3 7 a C. 21 7 a D. 15 5 a Lờigiải

A C B Trang 26

Mà AHSM ⊥ () 2 . Từ () 1 và () 2 suy ra ()AHSBC ⊥ Do đó () () , dASBCAH = Xét tam giác SAM vuông tại A , có 222 111 AHAMAS =+ 2 2 11 3 2 a a =+   

2 7 3a = 3 7 AHa  = 21 7 a =

Câu36. (Thpt Lê Văn Thịnh Bắc Ninh 2019) Cho hình chóp đều SABCD , cạnh đáy bằng a , góc giữa mặt bên và mặt đáy là 60° . Tính khoảng cách từ điểm B đến mặt phẳng () SCD A. 4 a B. 3 4 a C. 3 2 a D. 2 a Lờigiải ChọnC

* Ta có: () () () () ; 2 ; dBSCDBD dOSCDOD == () () () () ;2.;2 dBSCDdOSCDOH  == . Trong đó H là hình chiếu vuông góc của O lên () SCD

* Gọi I là trung điểm của CD ta có: ()() ()() () () ;;60SICDSCDABCDOISIS SCDABCDC D

  ⊥  ===°   ⊥ 

∩= Xét tam giác SOI vuông tại O ta có: 3 .tan60 2 a SOOI ° == . Xét SOI∆ , ta có 222222 1114416 33 OHOIOSaaa =+=+= () () 33 ; 42 OHdBSCDaa  =  =

D IO OIC

Câu37. (Chuyên Vĩnh Phúc 2019) Cho hình chóp SABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường tròn đường kính 2 ADa = và có cạnh SA vuông góc với mặt phẳng đáy () ABCD với 6 SAa = . Tính khoảng cách từ B đến mặt phẳng () SCD . A. 2 a . B. 3 a . C. 2 2 a . D. 3 2 a . Lờigiải

Từ giả thiết suy ra: 2 AD ABBCCDa ==== , 3 ACa = Gọi EABCD =∩ , suy ra tam giác ADE đều. Khi đó C là trung điểm của ED và ACED ⊥ Dựng AHSC ⊥ thì ()AHSCD ⊥ , suy ra () [] , dASCDAH = Xét tam giác SAC vuông tại A , có AH là đường cao Suy ra: 222 111 2 AHa AHSAAC =+  = Mà () [] () [] 112 ,,222 a dBSCDdASCDAH ===

Câu38. (THPT Minh Châu Hưng Yên 2019) Cho khối chóp . SABCD có đáy ABCD là hình thang vuông tại A và B , ,ABBCa == 2.ADa = Hình chiếu của S lên mặt phẳng đáy trùng với trung điểm H của AD và 6 2 a SH = Tính khoảng cách d từ B đến mặt phẳng () SCD A. 6 8 a d = B. da = C. 6 4 a d = D. 15 5 a d = Lờigiải ChọnC

Tam giác HCD vuông tại H có 2 CDa = và 2 2 a HM =

Ta có () () () ()//,, BHCDdBSCDdHSCDHK  ==

Gọi M là trung điểm của CD , K là hình chiếu của H lên SM

Trang 27

Tam giác SHM vuông tại H có 22

.6 4 HMHSa HK HMHS == + Vậy () () 6 , 4 a dBSCD =

Câu39. (Chuyên Quang Trung Bình Phước 2019) Cho tứ diện OABC có ,, OAOBOC đôi một vuông góc với nhau 3. ===OAOBOC Khoảng cách từ O đến ()mpABC là A. 1 3 B. 1 C. 1 2 D. 1 3 Lờigiải ChọnB

Gọi 'A là chân đường cao kẻ từ A lên ,BC ' C là chân đường cao kẻ từ C lên AB Gọi H là giao của AA’ với CC’ suy ra H là trực tâm của tam giác .ABC Ta dễ dàng chứng minh được (). ⊥ OHABC Do đó: (;()). = dOABCOH Tính OH

Ta có: Tam giác 'OAA vuông tại ,O có OH là đường cao. Suy ra : 222 111 ' =+ OHOAOA (1)

Lại có: Tam giác OBC vuông tại ,B có 'OA là đường cao. Suy ra: 222 111 =+ OAOBOC (2)

Từ (1) và (2) suy ra: 2222 1111 =++ OHOAOBOC Thay 3 ===OAOBOC vào, ta được: 2 1111 11. 333 =++=⇔= OH OH Vậy (;())1. ==dOABCOH

Câu40. (Thpt Cẩm Giàng 2 2019) Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh a ,

60 ABC =° . Cạnh bên SA vuông góc với đáy, 2 SCa = . Khoảng cách từ B đến mặt phẳng () SCD là

A. 15 5 a B. 2 2 a C. 2 5 a D. 530 3 a Lờigiải

Cách1:Sử dụngkiếnthức ở lớp11. ABCD là hình thoi cạnh a , 60 ABC =° ,ABC  ∆ ACD∆ là các tam giác đều cạnh a.

Xét SAC∆ vuông tại A có: 22SASCAC =− 22 4aa=− 3 a = Vì // ABCD nên () // ABSCD . Do đó () () () (),, dBSCDdASCD =

Kẻ AHCD ⊥ () HCD ∈ . Suy ra H là trung điểm của cạnh CD , 3 2 a AH = .

Kẻ AKSH ⊥ () KSH ∈ () 1

Ta có: CDAH CDSA ⊥   ⊥  ()CDSAH  ⊥ CDAK  ⊥ () 2

Từ (1) và (2) suy ra: ()AKSCD ⊥ () () , dASCDAK  = .

Xét SAH∆ vuông ở A : 222 111 AKAHSA =+ 22 41 33aa =+ 2 5 3a = 15 5 a AK  =

Vậy () () 15 , 5 a dBSCD =

Cách2:Tínhkhoảngcáchthôngquatínhthể tích.

ABCD là hình thoi cạnh a , 60 ABC =° ,ABC  ∆ ACD∆ là các tam giác đều cạnh a

Xét SAC∆ vuông tại A có: 22SASCAC =− 22 4aa=− 3 a = Vì // ABDC nên () // ABSDC . Do đó () () () () 3 ,, SACD SCD

V dBSCDdASCD S∆

== 1 . 3 SACDACDVSAS∆ = 2 13 3. 34 a a = 3 4 a = .

Xét SAC∆ và SAD∆ có: ADACa == , SA chung, 90 SACSAD==° Do đó SACSAD∆=∆ SCSD  = SCD  ∆ cân tại S . Gọi H là trung điểm CD SHCD  ⊥

Xét SHC∆ vuông ở H : 22SHSCCH =− 2 2 4 4 a a =− 15 2 a = . 1 2 SCD SSHCD ∆ = 115 22 a a = 2 15 4 a = () () , dASCD

3 2

3. 4 15 4

a a = 15 5 a = Vậy () () 15 , 5 a dBSCD = .

Câu41. (Chuyên Biên Hòa-Hà Nam -2020) Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và ;D 2;ABADa == DCa = . Điểm I là trung điểm đoạn ,AD hai mặt phẳng () SIB và () SIC cùng vuông góc với mặt phẳng () ABCD . Mặt phẳng () SBC tạo với mặt phẳng () ABCD một góc 60° . Tính khoảng cách từ D đến () SBC theo a A. 15 5 a . B. 915 10 a . C. 215 5 a . D. 915 20 a . Lờigiải ChọnA

Theo đề ta có (). SIABCD ⊥

Gọi K là hình chiếu vuông góc của I trên BC .

Suy ra: Góc giữa hai mặt phẳng ()()( ) ,60SBCABCDSKI==°

Gọi E là trung điểm của ,AB .MIKDE =∩

Do BCDE là hình bình hành nên () // DESBC () () () () () (),,, dDSBCdDESBCdMSBC  ==

Gọi H là hình chiếu vuông góc của M trên SK . Suy ra () () , dMSCDMH =

Dễ thấy: 111 222 IMAUKNMK === 15 22 INIMMKKNMKMKMKMK =++=++=

Suy ra: 22 2225 555 a MKINIDDN==+= .

Trong tam giác , MHK ta có: 15 .sin60 5 a MHMK=°=

Câu42. (Chuyên ĐH Vinh - Nghệ An -2020) Cho hình chóp . SABC có đáy là tam giác vuông tại ,, AACaI = là trung điểm SC . Hình chiếu vuông góc của S lên () ABC là trung điểm H của BC . Mặt phẳng () SAB tạo với () ABC một góc 60° . Tính khoảng cách từ I đến mặt phẳng () SAB

A. 3 4 a B. 3 5 a C. 5 4 a D. 2 3 a Lờigiải. ChọnA

Gọi M là trung điểm cạnh AB thì MH là đường trung bình của tam giác ABC nên , 2 //AC a MHMH = MHAB  ⊥ . Mặt khác, do ()SHABC ⊥ nên ()SMHBC ⊥ . Suy ra góc giữa () SAB và () ABC là góc giữa

SM và MH ; lại có SHMH ⊥ nên góc này bằng góc SMH . Từ giả thiết suy ra 60 SMH =° . Gọi K là hình chiếu của H lên SM thì ()HKSAB ⊥ .

tam giác vuông 33 ,.tan60, 224 aaa SMHSHMHMHHK =°==

ọi khoảng cách từ ,, ICH đế

Cách 2: IH là đường trung bình của tam giác SBC nên () //// IHSBIHSAB 

Trang 31

() () () () 3 ,, 4 a ISABHSAB  ==dd

Câu43. (Chuyên Hưng Yên - 2020) Cho hình chóp . SABC có đáy ABC là tam giác cân, BABCa == và 30 BAC =° . Cạnh bên SA vuông góc với mặt phẳng đáy và SAa = . Gọi D là điểm đối xứng với B qua AC . Khoảng cách từ B đến mặt phẳng () SCD bằng A. 221 7 a B. 2 2 a C. 21 14 a D. 21 7 a

Lời giải ChọnD

Tam giác ABC cân tại B có 30 BAC =° và D đối xứng với B qua AC nên tứ giác ABCD là hình thoi có 120 ADCABC==° .

Trong mặt phẳng () ABC , kẻ AH vuông góc với đường thẳng CD tại H . Khi đó CDAH ⊥ và CDSA ⊥ nên ()CDSAH ⊥ . Do đó ()() SCDSAH ⊥

Trong mặt phẳng () SAH , kẻ AKSH ⊥ tại K . Khi đó, ()AKSCD ⊥ và (), AKdASCD =  

Ta có 3 .sin60 2 a AHAD=°= Áp dụng hệ thức lượng trong tam giác vuông SAH , ta có 2222 1117 3 AKAHSAa =+= . Từ đó, 21 7 a AK = Vì () // ABSCD nên ()() 21 ,, 7 a dBSCDdASCDAK === 

Câu44. (ChuyênLamSơn-2020) Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh a . Tam giác ABC là tam giác đều, hình chiếu vuông góc của đỉnh S lên mặt phẳng () ABCD trùng với trọng tâm tam giác ABC . Góc giữa đường thẳng SD và mặt phẳng () ABCD bằng 30° . Tính khoảng cách từ điểm B đến mặt phẳng () SCD theo a . A. 21 7 a B. 3 a C. a D. 221 3 a Lờigiải

Diện tích tam giác ∆SCD : ()()() 2 7 6 ∆ =−−−= SCD a SppSCpSDpCD (đvdt). ( 2 ++ = SCSDCD p là nửa chu vi tam giác ∆SCD ). Vậy khoảng cách từ điểm B đến mặt phẳng () SCD : () () 3 2

a VVa dBSCD SS a

==== BSCDSBCD SCDSCD

3 3. 3.3.21 18 , 7 7 6 ∆∆

Câu45. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Cho hình chóp SABCD có đáy là hình vuông, ,ABa = SA vuông góc với mặt phẳng đáy và 2 SAa = (minh họa như hình vẽ bên dưới ). Gọi M là trung điểm của CD , khoảng cách giữa điểm M và mặt phẳng () SBD bằng A. 2 3 a . B. 2 a . C. 2 a . D. 3 a . Lờigiải ChọnD

Gọi I là giao điểm của AM và BD , O là tâm hình vuông ABCD . Ta có 1 (,()(,()) 2 dMSBDdASBD = Dựng AH vuông góc với SO tại H Ta có

Từ đó ta có: () () 222 2

33 .3 44 , 8 33 44

aa OKSOa dOSBCOH OKSOaa ==== +   +    

.

Câu47. (Chuyên Hùng Vương - Phú Thọ - 2020) Cho hình chóp SABCD có ()SAABCD ⊥ , 6 SAa = , ABCD là nửa lục giác đều nội tiếp đường tròn đường kính 2 ADa = . Khoảng cách từ điểm B đến mặt phẳng () SCD bằng A. 6 2 a . B. 3 2 a . C. 2 2 a . D. 3 4 a . Lờigiải ChọnC

Gọi I là trung điểm AD và H là trung điểm SD suy ra () // HISAHIABCD  ⊥

Do ABCD là nửa lục giác đều và I là trung điểm AD nên // BICD Suy ra () () () (),, dBSCDdISCD = .

Do ABCD là nửa lục giác đểu nên dễ thấy ICD∆ là tam giác đều. Gọi M là trung điểm CD suy ra ()CDHIM ⊥ . Trong () IHM kẻ IKHM ⊥ . Ta có: () () () IKHM IKSCD IKCDCDHIM

Câu48. (Chuyên Lào Cai - 2020) Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh

2a và 0 90. SBASCA== Biết góc giữa đường thẳng SA và mặt đáy bằng 450. Tính khoảng cách từ điểm B đến mặt phẳng (SAC).

A. 15 5 a B. 215 5 a C. 215 3 a D. 251 5 a Lờigiải ChọnB

Gọi I là trung điểm của SA.

Tam giác SAB và SAC là các tam giác vuông tại , BCISIAIBIC  === Gọi G là trọng tâm tam giác đều ()ABCIGABC  ⊥

Trong (SAG) kẻ ()() // SHIGHCGSHABC ∈  ⊥

Dễ thấy khi đó IG là đường trung bình của tam giác 2 SAHSHIG  =

Tam giác ABC đều cạnh = 22323 2. 323 aa aAG  ==

Ta có: () () () 0,,45 SAABCSAAHSAHAIG ===  ∆ vuông cân tại G 2343 2 33 IGAGSHIGaa⇔==  == ()2 3 23 11434 ... 33343SABCABC a aa VSHS  === Ta có: , GAGBGCGAGH === ( IG là đường trung bình của tam giác SAH) GAGBGCGHG  ===  là tâm đường tròn ngoại tiếp tứ giác ABHC.  AH là đường kính đường tròn ngoại tiếp tứ giác ABHC 090 ACH ⇔= (góc nội tiếp chắn nửa đường tròn) Ta có: 22 432 2 3 3 AHAGCHAHACaa

Vậy () () 3 2

a Va dBSAC S a ===

Trang 37

4 3. 3215 3 , 5 215 3

SABC SAC

Câu49. (ChuyênVĩnhPhúc-2020) Cho hình chóp . SABC có đáy ABC là tam giác đều cạnh a , SA vuông góc với mặt phẳng () ABC ; góc giữa đường thẳng SB và mặt phẳng ABC bằng 60° Gọi M là trung điểm cạnh AB . Khoảng cách từ B đến () SMC bằng A. 39 13 a . B. 3 a . C. a . D. 2 a . Lờigiải ChọnA

Ta có () () SBABCSBASAaa ,60tan60.3 ==°⇒=°= Vì M là trung điểm của AB  () () () ()dBSMCdASMC ,, = . Dựng AH vuông góc với SM tại H () () dASMCAH , ⇒= mà 1 22 a AMAB== .

Xét tam giác vuông SAM∆ ta có: 222222

111141339 3313 a AH AHSAAMaaa =+=+=  = .

Câu50. (Sở Phú Thọ - 2020) Cho hình chóp . SABCD có đáy ABCD là hình chữ nhật tâm O , cạnh ,2ABaADa == . Hình chiếu vuông góc của S trên mặt phẳng () ABCD là trung điểm của đoạn OA . Góc giữa SC và mặt phẳng () ABCD bằng 30° . Khoảng cách từ C đến mặt phẳng () SAB bằng A. 922 44 a B. 322 11 a C. 22 11 a D. 322 44 a Lờigiải ChọnB

Gọi H là trung điểm AO , ta có ()SHABCD ⊥ .

Góc giữa SC và () ABCD bằng SCH bằng 30°

Ta có 4 CAHA = , suy ra () () () (),4, dCSABdHSAB = Kẻ , HIABHKSI ⊥⊥ , ta suy ra ()HKSAB ⊥ . () () , dHSABHK = . 12 44 a HIAD== 333 44 a CHAC== Suy ra 3 .tan30 4 a SHCH=°= .

Xét tam giác SHI vuông tại H có HK là đường cao. Suy ra 22222 1111616 92 HKHSHIaa =+=+ 3 222 a HK = () () () () 3322 ,4,4. 11 222 dCSABdHSABaa === .

Câu51. (Sở NinhBình) Cho hình chóp SABC có SAa = , tam giác ABC đều, tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách từ B đến mặt phẳng () SAC bằng A. 42 7 a . B. 42 14 a . C. 42 12 a . D. 42 6 a . Lờigiải ChọnA

Gọi ,, HMN lần lượt là trung điểm của các cạnh ,, ABACAM

Do tam giác SAB vuông cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy ()SHABC  ⊥

Kẻ () 1 HKSN ⊥

Ta có: () ACHN ACSHN ACSH ⊥   ⊥  ⊥  () 2 ACHK  ⊥ .

Từ () 1 và () 2 ()HKSAC  ⊥ () () ; dHSACHK  = .

Ta có () () () ();2; dBSACdHSAC =

 =    =  

ABa a SH

Do tam giác SAB vuông cân tại S và SAa = 2 2 2

Do tam giác ABC đều

 =      =  

a BM a HN

6 2 6 4

Xéttamgiácvuông SHN ,tacó 22

.42 14 SHHN HKa SHHN == + .

Vậy () () () () 42 ;2;2 7 dBSACdHSACHKa === .

Câu52. (Bỉm Sơn - Thanh Hóa - 2020) Chohìnhchóp có đáy làhìnhchữ nhật, .Tamgiác cântại vànằmtrongmặtphẳngvuônggócvới đáy.Góc giữa đườngthẳng vàmặtphẳng bằng .Gọi làtrung điểmcủa ,hãy tínhtheo khoảngcáchtừ đếnmặtphẳng . A. B. C. D. Lờigiải ChọnD

SABCD ABCD ,2 ABaADa == SAB S SC ( )ABCD 45° M SD a M ( ) SAC 21513 89 a d = 1315 89 a d = 21315 89 a d = 1513 89 a d =

dBSAC BA dBSACdHSAC HA dHSAC ==  = ( ) ( ) ( ) ( ) ,,.dMSACdHSAC = ( ) SAC HIAC ⊥ HKSI ⊥ ( ) () () () ACHIgt ACSHIACHK ACSHSHABCD  ⊥   ⊥  ⊥  ⊥⊥   ( ) () ()()

Câu53. (HậuLộc2-ThanhHóa-2020) Cho hình chóp SABCD có đáy ABCD là hình thang vuông tại A và B , 222 ADABBCa === , SA vuông góc với đáy, góc giữa SB và mặt phẳng đáy bằng 0 60 . Gọi H là hình chiếu vuông góc của A lên SB . Khoảng cách từ H đến mặt phẳng () SCD bằng A. 3 a . B. 330 20 a . C. 330 10 a . D. 330 40 a . Lờigiải ChọnD Kẽ () //// HKSCHKSCD  . Khi đó () () () (),, dHSCDdKSCD = Ta có () () 0 .tan.tan;.tan603 SAABSBAaSBABCDaa ==== . 22 2 SBSAABa  =+= Mà 2 2 2 1 . 4 BHAB ABBHSB SBSB =  == . Vì // HKSC nên 13 444 BKaa BKKC BC =  =  = .

// KCAD nên

() () () () ; 33 ;; 88 ; dKSCD KC dKSCDdASCD AD dASCD ==  = .

ọi F là hình chiếu vuông góc của A lên SC .

() ACDC DCSACDCAF SADC ⊥

vuông cạnh a , tâm O . Hình chiếu vuông góc của ′A lên mặt phẳng () ABCD trùng với O

Biết tam giác ′ AAC vuông cân tại ′A . Tính khoảng cách h từ điểm D đến mặt phẳng () ′′ABBA

A. 6 6 = a h . B. 2 6 = a h . C. 2 3 = a h . D. 6 3 = a h . Lờigiải ChọnD

Ta có: 2222 2 =+=+= ACABBCaaa .

Vì tam giác ′ AAC vuông cân tại ′A nên ta có: 2 22 ′ == ACa AO .

Gọi M là trung điểm của AB . Suy ra ⊥ OMAB

Trong mặt phẳng () ′ AOM : kẻ ′ ⊥ OHAM

Ta có: () ′ ⊥ ABAOM (vì ⊥ ABOM và ′ ⊥ ABAO ). Suy ra ⊥ ABOH .

Vì () ′ ⊥  ′′  ⊥  ⊥  OHAM OHABBA OHAB . Do đó: () () ; ′′ = dOABBAOH Do ,, DOB thẳng hàng và 2 = DBOB nên () () () () ;2;2 ′′′′ == dDABBAdOABBAOH

′ === ′ +   +     Lờigiải ChọnC

Từ A kẻ đường thẳng vuông góc với BD tại H , ta có: () ()()() // BDSAH MNSAHAMNSAH MNBD ⊥    ⊥  ⊥   

Mặt khác ()() AMNSAHSE ∩= , suy ra: () () ();; dSAMNdSAE =

d = . D. 5 da = .

Xét tam giác vuông SAH có: 22

..225 5 4 ABADaaa AH BD aa === + . 2 222 20230 4 255 aa SHSAAHa=+=+=

Vì MN là đường trung bình của tam giác SBD nên E là trung điểm của SH , suy ra: 130 25 a AESH== () 2 .2.256 ; 2.3 30 2.5. 5

SAESAHSS ASAHaaa dSAE AEAEAE a ∆∆ ===== .

Câu56. (KìmThành-HảiDương-2020) Cho hình chóp . SABC có đáy ABC là tam giác vuông tại A , biết ()SAABC ⊥ và 2 ABa = , 3 ACa = , 4 SAa = . Khoảng cách từ điểm A đến mặt phẳng () SBC bằng A. 2 11 a d = B. 629 29 a d = C. 1261 61 a d = D. 43 12 a Lờigiải ChọnC

H K

A C B

Ta có () () SAABC SABC BCABC ⊥    ⊥  ⊂   .

Trong () ABC , kẻ AHBC ⊥ , mà () BCSABCSAHBCSH ⊥  ⊥  ⊥

Trong () SAH , kẻ AKSH ⊥ , mà SHBC ⊥ ()AKSBC  ⊥ hay () () ; dASBCAK = .

Vì ABC∆ vuông tại A nên 22 13 BCABACa =+=

Mặt khác có AH là đường cao nên .613 13 ABACa AH BC == .

Vì SAH∆ vuông tại A nên 22 2793 13 a SHSAAH=+= .

Vậy có AK là đường cao .1261 61 SAAHa AK SH ==

Câu57. (Trường VINSCHOOL - 2020) Cho hình chóp SABCD có đáy là hình chữ nhật, cạnh

2 ABADa == . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy () ABCD

Khoảng cách từ điểm A đến mặt phẳng () SBD bằng A. 3 4 a B. 3 2 a C. 2 a D. 2a Lờigiải ChọnA

Trang 45

Suy ra ()HISBD ⊥ () () , dHSBDHI  = .

Ta có 2 222 5 42 aa BDABADa=+=+= , 3 2 a SH =

aa HGBHADBHa HG ADBDBD a =  ===

Lại có BGH∆ đồng dạng với BAD∆ nên . .5 22 10 5 2

Khi đó 22 222 11111 35 210 HISHHG aa =+=+   

Suy ra 3 8 a HI = Lại có () () () () 33 ,2,2.2. 84 aa dASBDdHSBDHI====

Câu58. (ThanhChương1-Nghệ An-2020) Cho hình chóp SABC , có đáy là tam giác vuông tại A , 4 ABa = , 3 ACa = . Biết 23SAa = , 30 SAB = và ()() SABABC ⊥ . Khoảng cách từ A đến mặt phẳng () SBC bằng

A. 37 14 a B. 87 3 a C. 67 7 a D. 37 2 a Lờigiải ChọnC

Gọi SH là đường cao của khối chóp SH  là đường cao của tam giác SAB SAH∆ có 30,90.cos3033 SAHSHAAHSAaSHa ==  ==  = () () () ();4; dASBCdHSBC  = Tính khoảng cách từ H đến mặt phẳng () SBC : Từ H kẻ HKBC ⊥ tại K , kẻ HISK ⊥ tại I () () ; dHSBCHI  = Mà HBKCBA∆∆ ∼ .3 5 BHHKBHCA HKa BCCABC  =  == 2222 1112837 914 a HI HISHHKa  =+=  = () () 67 ;. 7 a dASBC  = Câu59. (Tiên Lãng - Hải Phòng - 2020) Cho hình lăng trụ đứng ABCABC′′′ có ABa = , 2 ACa = , 0120 BAC = . Gọi M là trung điểm cạnh CC′ thì 090 BMA′ = . Tính khoảng cách từ điểm A đến mặt phẳng () BMA′ A. 7 7 a B. 5 3 a C. 5 7 a D. 5 5 a Lờigiải ChọnB

Ta có: 222 2...cos BCABACABACBAC =+− ()2 2 0222..2.cos1207 aaaaa =+−= Đặt 2 CCxCMMCx ′′ =  ==

Vì . ABCABC′′′ là hình lăng trụ đứng nên ta có tam giác BCM vuông tại C và tam giác ACM ′′ vuông tại C′

Ta có: 22222 7 BMBCCMax =+=+ ; ()2 222222 24 AMACCMaxax ′′′′ =+=+=+ ; 22222 4 ABAAABxa ′′ =+=+ .

Vì 090 BMA′ = nên tam giác BMA′ vuông tại M , do đó: 222 ABBMAM ′′ =+ 222222474 xaaxax ⇔+=+++ 2255xaxa⇔=⇔=

Ta có: 1 ..sin 2 ABC SABACBAC = () 1 .., 2 ABdCAB = (),3dCABa  = Lại có: () () () () (),,, dMABAdCABAdCAB ′′ == ( vì () // CCABA ′′ và ()() ABCABA′ ⊥ ).

Suy ra.

Ta có: 2 1 .5 2 ABA SABAAa ′ == ; 2 1 .33 2 MBA SMBMAa ′ == .` () () () () 11 ..,.., 33 AABMABAMBA VSdMABASdABMA ′′ ′ ′′ == () () 5 , 3 a dABMA′  =

Dạng2.Khoảngcáchcủa đườngthẳngvới đườngthẳng

Ta có các trường hợp sau đây:

a) Giả sử a và b là hai đường thẳng chéo nhau và ab ⊥

- Ta dựng mặt phẳng () α chứa a và vuông góc với b tại B .

- Trong () α dựng BAa ⊥ tại A , ta được độ dài đoạn AB là

khoảng cách giữa hai đường thẳng chéo nhau a và b .

b) Giả sử a và b là hai đường thẳng chéo nhau nhưng không vuông góc với nhau.

Cách1:

- Ta dựng mặt phẳng () α chứ a và song song với b .

- Lấy một điểm M tùy ý trên b dựng '() MM α ⊥ tại M

- Từ ' M dựng '// bb cắt a tại A

- Từ A dựng //'ABMM cắt b tại B , độ dài đoạn AB là khoảng cách giữa hai đường thẳng chéo nhau a và b

Cách2:

- Ta dựng mặt phẳng () a α ⊥ tại O , () α cắt b tại I .

- Dựng hình chiếu vuông góc của b là ' b trên () α .

- Trong mặt phẳng () α , vẽ OHb ⊥ , ' Hb ∈

- Từ H dựng đường thẳng song song với a cắt b tại B

- Từ B dựng đường thẳng song song với OH cắt a tại A .

- Độ dài đoạn thẳng AB là khoảng cách giữa hai đường thẳng chéo nhau a và b .

Câu1. (Đề ThamKhảo2018) Cho lập phương ABCDABCD′′′′ có cạnh bằng a ( tham khảo hình vẽ bên ).Khoảng cách giữa hai đường thẳng BD và AC′′ bằng

A. 3 2 a B. 2a C. 3a D. a Lờigiải ChọnD

Ta có khoảng cách giữa hai đường thẳng chéo nhau BD và AC′′ bằng khoảng cách giữa mặt phẳng song song () ABCD và () ABCD ′′′′ thứ tự chứa BD và AC′′ . Do đó khoảng cách giữa hai đường thẳng BD và AC′′ bằng a

Câu2. (ChuyênLamSơn-ThanhHóa-2021) Cho hình chóp . SABCD có đáy ABCD là hình vuông tâm O cạnh a , SO vuông góc với mặt phẳng () ABCD và SOa = . Khoảng cách giữa SC và AB bằng:

.

i

a

a a

B O a

SN a

C D A

ọnB  // ABCD ⇒ ()() () () () () ()d;d;d;2.d; ABSCABSCDASCDOSCD === (*)  Hình chóp OSCD là tam diện vuông tại O : () () 22 2222 2 2 11111115 d; 22 22 OSCDOSOCODaa aa =++=++=   

⇔ () () 5 d; 5 a OSCD = (*) ⇔ ()() () 25 d;2.d; 5 a ABSCOSCD== .

Câu3. (Chuyên ĐHVinh-Nghệ An-2021) Cho hình chóp tứ giác đều . SABCD có cạnh đáy bằng ,a O là tâm của mặt đáy. Khoảng cách giữa hai đường thẳng SO và CD bằng A. 2 a B. a C. 2 2 a D. 2a Lờigiải ChọnA

Vì SABCD là hình chóp tứ giác đều nên ABCD là hình vuông và ()SOABCD ⊥

Gọi M là trung điểm của CD

Khi đó OMSO ⊥ (do ()SOABCD ⊥ và ()OMABCD ⊂ ).

Mà OMCD ⊥ (do OCD∆ là tam giác cân tại O ).

Suy ra (),. 22 ADa dSOCDOM===

Câu4. (THPT TriệuSơn-ThanhHóa-2021) Cho hình chóp . SABCD có đáy là hình vuông cạnh bằng 2a , cạnh bên SA vuông góc với mặt đáy. Khoảng cách giữa hai đường thẳng SA và BD bằng

Gọi O là tâm của hình vuông ABCD , ta có AOBD ⊥ Mặt khác () SAABCDSAAO ⊥  ⊥ .

Vậy AO là đoạn vuông góc chung của hai đường thẳng SA và BD nên () 1 ;2 2 dSABDAOACa === .

Câu5. (ChuyênLongAn-2021) Cho hình chóp . SABCD có ()SAABCD ⊥ , đáy ABCD là hình chữ nhật với 5 ACa = và 2 ADa = . Tính khoảng cách giữa SD và BC .

A. 3 a . B. 3 4 a . C. 3 2 a . D. 2 3 a . Lờigiải ChọnA

A. 2 a B. 2a C. a D. 3 a Lờigiải ChọnA

Câu7. (Đề Minh Họa 2020 Lần 1) Cho hình chóp SABCD có đáy là hình thang, 2 = ABa , === ADDCCBa , SA vuông góc với mặt phẳng đáy và 3 = SAa (minh họa như hình bên). Gọi M là trung điểm của AB . Khoảng cách giữa hai đường thẳng SB và DM bằng A. 3 4 a B. 3 2 a C. 313 13 a D. 613 13 a Lờigiải ChọnA Ta có M là trung điểm của AB . Theo giả thiết suy ra ABCD là nửa lục giác đều nội tiếp đường tròn đường kính AB

Trong tam giác SAN vuông tại A có: 222 111 AHASAN =+ , trong đó 3 ASa = , 1 22 a ANAB==

2 2 22 2 2 2 22 2

Xét tam giác SAC vuông tại A , ta có () () () ()

3.3 .9 4 33 === + +

aa ACSAa AH ACSA aa

3 2  = AHa . Vậy () () () 113 ,,224 === a dDMSBdASBCAH

Câu8. (Mã 101 – 2020 Lần 2) Cho hình chóp . SABC có đáy ABC là tam giác vuông cân tại A . ABa = , SA vuông góc với mặt phẳng đáy và 3 SAa = . Gọi M là trung điểm của BC (tham khảo hình bên). Khoảng cách giữa hai đường thẳng AC và SM bằng A. 2 2 a . B. 39 13 a . C. 2 a . D. 21 7 a . Lờigiải

ChọnB

Cách1(Phươngpháphìnhhọccổ điển): Gọi N là trung điểm của AB , khi đó // MNAC . Gọi H là hình chiếu của A lên SN . Dễ dàng chứng minh được ()AHSMN ⊥ . Suy ra ()() () () (),,, dACSMdACSMNdASMNAH === .

Suy ra 39 13 a AH = . Vậy () 39 , 13 a dACSM = .

Cách2(Phươngpháptọa độ hóa):

Chọn 1 a = , gắn bài toán vào hệ trục tọa độ Axyz , trong đó () 0;0;0 A , () 1;0;0 B , () 0;1;0 C , () 0;0;3 S , 11 ;;0 22 M    .

Ta có: () ,. , ,

SMACAS dSMAC SMAC

  =   với 11 ;;3 22 SM  =−  , () 0;1;0 AC = , () 0;0;3 AS =

Suy ra () 39 , 13 dSMAC = , hay () 39 , 13 a dSMAC =

Câu9. (Mã101 - 2018) Cho hình chóp . SABCD có đáy là ình chữ nhật, ,2, ABaBCa == SA vuông góc với mặt phẳng đáy và .SAa = Khoảng cách giữa hai đường thẳng AC và SB bằng A. 6 2 a B. 2 3 a C. 2 a D. 3 a Lờigiải ChọnB

A

x O C

Từ B kẻ ()////, BxACACSBBx 

Suy ra ()() () () (),,,,, dACSBdACSBBxdASBBx ==

Từ A kẻ ()AKBxKBx ⊥∈ và AHSK ⊥

Do () AKBx BxSAKBxAH SABx ⊥   ⊥  ⊥  ⊥  Nên ()() (),,, AHSBBxdASBBxAH ⊥  =

Ta có BKA∆ đồng dạng với ABC∆ vì hai tam giác vuông có KBABAC = (so le trong Suy ra ..225 5 5 AKABABCBaaa AK CBCACA a =  ===

dMABC VS VS dAABC = 111 224 == 3 1 12 MOBC Va  =

Xét tam giác vuông cân AOB : 12 22 OMABa ==

Xét tam giác vuông BOC : ()2 2 115 2 222 ONBCaaa ==+=

Xét tam giác BAC : ()2 2 115 2 222 MNACaaa ==+= .

Trong tam giác cân OMN , gọi H là trung điểm của OM ta có 22 32 NH 4 NMHMa=−= .

Suy ra 2 13 28 OMN SOMNHa == Vậy () 3 2 ; 3 MOBN OMN

V dBOMNa S ==

Câu11. (THPTViệt ĐứcHàNội2019) Cho lăng trụ đứng ABCABC′′′ có đáy ABC là tam giác vuông tại A với 3 ACa = . Biết BC′ hợp với mặt phẳng () AACC ′′ một góc 30o và hợp với mặt

phẳng đáy góc α sao cho 6 sin 4 α = . Gọi , MN lần lượt là trung điểm cạnh BB′ và AC′′ Khoảng cách giữa MN và AC′ là: A. 6 4 a B. 3 6 a C. 5 4 a D. 3 a Lờigiải ChọnA +) Ta có: () () A ,30 A o CC BCBCA ′ ′ = ′ ′ = +) Mặt khác () () ,ABC BCCBC α ′′ == +) Gọi 22 3 ABxBCax =  =+ () 22 33 .tan 5 ax CCBC α + ′  == .cot303 o ACABx ′  == +) Mặt khác ta có: 222 23'6 ACCCACxaCCaACa ′′′ +=  =  =  = +) Gọi P là trung điểm của BC′′ , ta có: Do mặt phẳng ()() // MNPABC′ nên ()() () () () () () 1 ,,,, 2 dMNACdMNABCdNABCdAABC ′′′′′ == = +) Kẻ ()AHACAHABC ′′′′ ⊥  ⊥ () () 16 , 22 a dAABCAH ′′′  == () , 6 4 dMN a AC′ =  Câu12. (Chuyên Lam Sơn Thanh Hóa 2019) Cho hình chóp

ờigiải ChọnC

Do hình chóp . SABC đều nên SG là đường cao của hình chóp ( G là trọng tâm tam giác đều ABC ). Kẻ MHSA ⊥ tại H thì MH là đoạn vuông góc chung của SA và BC . Vậy khoảng cách giữa hai đường thẳng SA và BC bằng MH

Ta có 23 133 4 343 SABC aa VSGSGa ==  = , 3 3 a AG = , 2 222373 16 93 aa SAAGSGa=+=+= . Ta có .3.4.36 .. 7 2.73 SGAMaaa SAMHSGAMMH SA a =  ===

Câu13. (Mã1022018) Cho hình chóp . SABCD có đáy là hình chữ nhật, ABa = , 2 BCa = , SA vuông góc với mặt phẳng đáy và SAa = . Khoảng cách giữa hai đường thẳng BD , SC bằng A. 421 21 a B. 221 21 a C. 30 12 a D. 30 6 a Lờigiải ChọnB

Gọi O là tâm hình chữ nhật và M là trung điểm SA , ta có: () // SCBMD

Do đó () , dSCBD () () , dSCBMD = () () , dSBMD = () () , dABMDh==

Ta có: ,, AMABAD đôi một vuông góc nên 2222222 1111411 4 hAMABADaaa =++=++ Suy ra: 221 21 a h = . Câu14. (Mã 104 2018) Cho tứ diện OABC có ,, OAOBOC đôi một vuông góc với nhau, OAa = và 2 OBOCa == . Gọi M là trung điểm của BC . Khoảng cách giữa hai đường thẳng OM và AB bằng

A. 6 3 a B. a C. 25 5 a D. 2 2 a Lờigiải ChọnA

Ta có OBC∆ vuông cân tại O , M là trung điểm của BC OMBC  ⊥

Dựng hình chữ nhật OMBN , ta có () () // // OMBN OMABN BNABN     ⊂  

()() () () (),,, dABOMdOMABNdOABN  ==

Gọi H là hình chiếu vuông góc của O trên AN ta có: () BNON BNOAN BNOA ⊥   ⊥  ⊥  OHBN  ⊥ mà OHAN ⊥

()OHABN  ⊥ () () , dOABNOH  = OAN∆ vuông tại O , đường cao OH 222 111

Câu15. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hình chóp SABCD có ()SAABCD ⊥ , đáy ABCD là hình chữ nhật với 5 ACa = và 2 BCa = . Tính khoảng cách giữa SD và BC A. 3 2 a B. 3 a C. 2 3 a D. 3 4 a Lờigiải

Không mất tính tổng quát, giả sử 1 a = . Gọi H là trung điểm của AB . Kẻ ()HMBCMBC ⊥∈ ; ()HNSMNSM ⊥∈

Ta có () ()()() () () () // //,,, BCAD BCSADdBCSDdBCSADdBSAD BCSAD    ==  ⊄   Có () SAABCDSAAB ⊥  ⊥ Ta có ()() () ,

BAAD BASABASADdBSADBA SAADA

⊥   ⊥  ⊥  =   ∩=  . Xét tam giác vuông 2222 ,523 BACBAACBCaaa =−=−= . Vậy () () () ,3,3 dBSADadBCSDa =  =

Câu16. (ChuyênVĩnhPhúcNăm2019) Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh a , ACa = . Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính khoảng cách giữa hai đường thẳng AD và SC , biết góc giữa đường thẳng SD và mặt đáy bằng 60° . A. 906 29 a B. 609 29 a C. 609 19 a D. 600 29 a Lờigiải ChọnB

Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy nên ()SHABCD ⊥ Áp dụng định lý hàm số cos : 222 1117 2..cos12012.1. 4224 DHDAAHDAAH  =+−°=+−−=   7 2 DH  = Theo đề bài: 60 SDH =° .tan60.3721 22 SHDH  =°== Lại có: .sin60.133 224 HMHB=°==

Ngoài ra: () BCSHMBCHN ⊥  ⊥ ()HNSBC  ⊥ ; 222 111116 21 HNSHHM  =+= 609 58 HN  = . Chú ý rằng () // ADSCB nên khoảng cách giữa AD và SC là khoảng cách giữa A vàmặt phẳng () SBC , bằng 2 lần khoảng cách từ H (theo định lý Ta-let), 609 2 29 dHN==

Câu17. (THPTLêQuy Đôn ĐiệnBiên2019) Chohìnhchóp SABC có đáy làtamgiác đều cạnhbẳng 4 ,gócgiữa SC vàmặt phẳng () ABC là 45° .Hình chiếu của S lên mặt phẳng () ABC là điểm H thuộc cạnh AB sao cho 2 HAHB = . Tính khoảng cách giữa hai đường thẳng SA và BC

hình chóp.

Xét tam giác SAM vuông tại A có AH là đường cao, suy ra

Vậy () 21 , 7 dBCSM = .

2 32 ab ba + B. 22 2 ab ba + C. 2 22 32 ab ba + D. 22 32 ab ba + Lờigiải

,

Trên tia đối của tia DC lấy điểm N sao cho 2 3 DNGFDM == . Từ đó ta có DNFG và

BEND là hai hình bình hành và ( ) ( ) // BDGNEF .

Trên đoạn thẳng OD lấy điểm K sao cho 1 3 KDDF ODSD == , từ đó ta có // FKSO mà

( ) SOABCD ⊥ suy ra ()FKABCD ⊥

Hạ KPEN ⊥ và KHPF ⊥ , do ()FKABCD ⊥ nên FKKP ⊥

Do () ENKP ENFKPENKH ENFK ⊥   ⊥  ⊥  ⊥  mà KHPF ⊥ suy ra ( ) KHNEF ⊥

Khi đó: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ,EF,,, dDGdDGNEFdBDGNEFdKNEFKH ==== .

Ta có: 22 . 33233 CDCDa BEGFMD===== Do // FKSO nên 1 3 FKDF SODS == , suy ra 1 33 b FKSO== Hạ EJBD ⊥ . Do 22 //,,EJBDKP.sin45. 326 aa ENBDKPENEJBE Ο ⊥⊥  ==== . Áp dụng hệ thức lượng vào tam giác vuông FKP với đường cao KH ta có: ( ) 22 22 222 22 22

A. 2327 79 a . B. 237 79 a . C. 2237 79 a . D. 5237 316 a . Lờigiải

92 11111 32 2 3 6

ba ab KH KHKFKPab b ba a

+ =+=+=  = +      Vậy () 22 ,EF 32 ab dDG ba = + .

Câu20. (THPTHoàngHoaThámHưngYên2019) Cho hình chóp . SABC có đáy ABC là tam giác đều cạnh 23 a , mặt bên SAB là tam giác cân với 120 ASB =° và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm của SC và N là trung điểm của MC . Tính khoảng cách giữa hai đường thẳng AM , BN .

Cách1: Gọi H là trung điểm AB . Vì ()() SABABC ⊥ nên ()SHABC ⊥ Chọn hệ trục tọa độ Oxyz , với OH ≡ , HBOx ≡ , HCOy ≡ , HSOz ≡ Ta có: 22 3 HCACAHa =−= ; tan AH SHa ASH == Khi đó: () 0;0;0 H , () 0;0; Sa , () 3;0;0 Aa , () 3;0;0 Ba , () 0;3;0Ca , 3 0;; 22 aa M    , 9 0;; 44 aa N    .

Thể tích tứ diện NCPB là: () () 3 111113 ,...SH...PC.a.3a.a3 3342248NCPBCBP a VdNABCSBP ∆ ====

Khoảng cách từ C đến () NBP là: () () 3 2237 , 79 NCPB NBP

== Vậy khoảng cách giữa hai đường thẳng , AMBN là 2237 79 a

V a dCNBP S∆

Cách3: Kẻ KINE ⊥ , INE ∈ . Khi đó: ()()() () () () () () 8 ////,,,, 5 NPAMAMNPBdAMBNdMNPBdCNPBdKNPB  === .

Ta có: ()() () , KINE KINPBdKNPBKI KIBP ⊥   ⊥  =  ⊥  .

Suy ra: ()() 8 ////, 5 NPAMAMNPBdAMBNKI  =

Trong tam giác vuông NKE ta có: () 2222 111126452372237 , 7531679 KIdAMBNaa KIKNKEa =+=  =  = .

Câu21. (ChuyênBắcNinh2019) Cho tứ diện đều ABCD có cạnh bằng 3 cm. Gọi M là trung điểm của CD . Khoảng cách giữa AC và BM là: A. 211 11 cm B. 322 11 cm C. 32 11 cm D. 2 11 cm Lờigiải

Gọi , IG lần lượt là trung điểm của AC và trọng tâm của tam giác ABC .

Ta có 222222 22

111111114 ()() 32 aa AHABACADaa =++=++= 14 a AH  =

trung

MNAC

() || ACBMN

dACBMdACBMNdABMNdNBMNh

() () () ()

ọi K là trung điểm của MN , ta có 22 11911 ... 2216 BMN SBKMNBMMKMN ==−= . Ta có: ..2.2.14 DACB DNMB

V DADCDB VDNDMDB === 1 4 DACBDBMNVV⇔= 921 .. 163 BMN hS ⇔= 921911322 .. 1631611 hh ⇔=⇔= . Câu22. (THCS-THPTNguyễnKhuyến2019) Cho tứ diện ABCD có các cạnh ,, ABACAD vuông góc với nhau đôi một và 23. ADACABa === Gọi ∆ là đường thẳng chứa trong mặt () BCD sao cho khoảng cách từ điểm A đến ∆ là nhỏ nhất và khoảng cách lớn nhất giữa hai đường thẳng ∆ và AD là d Khẳng định nào sau đây là đúng?.

A. 14 . 14 da = B. 34. ada << C. 34 . 147 aa d << D. 4.da > Lờigiải

Gọi H là hình chiếu vuông góc của A lên (). BCD Khi đó ta có H là trực tâm của tam giác BCD Với mọi đường thẳng ∆ nằm trong () BCD thì (;). dAAH ∆≥ Do đó đường thẳng ∆ thỏa mãn phải đi qua điểm H

Kẻ () HKADKAD ⊥∈ khi đó , HK là hai điểm cố định lần lượt nằm trên &. AD ∆

Hiển nhiên, khoảng cách giữa & AD ∆ là độ dài đoạn vuông góc chung của chúng nên (;). dADHK ∆≤ Dấu bằng xảy ra khi . HK ⊥∆

Ta có: 11313 cossin.sin. 14 1414 AH a HAKHAKHKHAHAK AD ==  =  ==

34 . 147 aa d  <<

Câu23. (Mã 102 - 2020 Lần 2) Cho hình chóp SABC có đáy là tam giác ABC vuông cân tại A , ABa = , SA vuông góc với mặt phẳng đáy, 2 SAa = , M là trung điểm của BC . Khoảng cách giữa AC và SM là

A. 2 a B. 2 2 a C. 217 17 a D. 2 3 a Lờigiải ChọnC

Gọi N là trung điểm AB, ta có // ACMN

Gọi N là trung điểm của AB nên // MNAC

Nên ()()() () () ()//;;; ACSMNdACSMdACSMNdASMN  ==

Ta có () // MNACMNSAB  ⊥

Trong mặt phẳng () SAB kẻ AHSN ⊥ tại H nên ()AHSMN ⊥ Nên () () 22

.217 ; 17 ANASa dASMNAH ANAS === +

Câu24. (Mã 103 - 2020 Lần 2) Cho hình chóp . SABC có đáy ABC là tam giác vuông cân tại A , AB=a . SA vuông góc với mặt phẳng đáy và = SAa . Gọi M là trung điểm của BC . Khoảng cách giữa hai đường thẳng AC và SM bằng A. 3 3 a . B. 2 2 a . C. 2 a . D. 5 5 a . Lờigiải ChọnD

Cách1:

a a ASANa AH ASAN a a Cách2: (Tọa độ hóa) Chọn hệ Oxyz sao cho OA ≡ , các tia ,, OxOyOz lần lượt đi qua B , C , S . Chọn 2 a = , ta có ()()()() 0;0;0, 2;0;0, 0;2;0, 0;0;2 ABCS . Suy ra () 1;1;0 M

Ta có () () () 0;2;0 ,4;0;2 1;1;2 AC ACSM SM   =  ⇒=−−   

=−

1;1;0 AM = ()() ,.4.10.12.04ACSMAM  ⇒=−++−=−   .

y () ()() 22 2 ,. 4 25 , 5 5 , 402 ACSMAM a dACSM ACSM

Suy ra: () // ACSMN nên ()() (),, dACSMdACSMN = () () , dASMN = Kẻ AHSN ⊥ tại H . Vì , MNACACABMNAB ⊥  ⊥ , mà MNSA ⊥ () MNSANMNAH  ⊥  ⊥ Ta có: ()() () , AHSN AHSMNAHdASMN AHMN ⊥   ⊥  =  ⊥ 

Xét tam giác vuông SAN vuông tại A ta có: 2 22222 111119 22 4 a AHSAANaa =+=+= 2 3 a AH  = () 2 , 3 a dACSM  =

Câu26. (Chuyên KHTN-2020) Cho hình chóp SABCD có đáy là hình chữ nhật ,2== ABaADa , SA vuông góc với mặt phẳng đáy và = SAa . Gọi M là trung điểm của AD . Tính khoảng cách giữa hai đường thẳng BM và SD

Gọi I là trung điểm của BC .

Vì // BMDI nên () // BMSDI .

Do đó ()() () () (),,, == dBMSDdBMSDIdMSDI

dMSDIdASDI

,,

Suy ra 2 2 2 =  = a AJAKa Mặt khác 222222 1111136 223 =+=+=  = a AH AHAKSAaaa

Do đó () () 16 ,.26 == a dMSDIAH .

Cáchkhác: Gọi =∩ EDIAB thì 22== AEABa . ()() () () () 1 ,,, 2 == dBMSDdBSDIdASDE Vì . SADE là tứ diện vuông tại A nên đặt () () , = hdASDE thì ta có 22222222 111111136 4423 =++=++=  = a h hSAADAEaaaa .

Suy ra () 6 , 26 == ha dBMSD

Câu27. (ChuyênLươngVănTỵ -NinhBình-2020) Cho hình chóp . SABC có đáy ABC là tam giác vuông cân tại ,A mặt bên () SBC là tam giác đều cạnh a và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Khoảng cách giữa hai đường thẳng SA và BC bằng

Gọi H là trung điểm của BC. Khi đó ()SHABCD ⊥ . Do tam giác ABC vuông cân tại A nên AHBC ⊥ và 2 a AH = . Dựng điểm D sao cho ABCD là hình bình hành. Khi đó ()() () () (),,, dSABCsBCSADdHSAD == Kẻ () () 3 3 22 , 4

aa a HISAdHSADHI a ⊥  === .

Câu28. (Chuyên Thái Bình - 2020) Cho hình chóp SABCD có đáy là hình chữ nhật với 2, ABaBCa == , tam giác đều SAB nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa BC và SD là A. 3a . B. 3 2 a . C. 25 5 a . D. 5 5 a . Lờigiải ChọnA

Ta có () () () // // BCAD ADSADBCSAD BCSAD

  ⊂    ⊂ /  , do đó ()() () () (),,, dBCSDdBCSADdBSAD == .

Tam giác SAB đều, gọi H là trung điểm SA thì BHSA ⊥ (1).

Ta có ()() ()()() SABABCD ADSABSABSAD ADAB ⊥    ⊥  ⊥  ⊥   (2).

Từ (1) và (2) suy ra ()BHSAD ⊥ , do đó () () 23 ,3 2 a dBSADBHa === .

Câu29. (Chuyên Bắc Ninh - 2020) Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , SAa = và SA vuông góc với mặt đáy. M là trung điểm SD . Tính khoảng cách giữa SB và CM A. 3 6 a B. 2 3 a C. 3 2 a D. 3 3 a Lờigiải ChọnD

Cách 1

Gọi E là điểm đối xứng với D qua A , N là trung điểm của SE và K là trung điểm của BE

Ta có các tứ giác NMCB và ACBE là các hình bình hành.

Có () // CMSBE nên ()() () () () () (),,,, === dCMSBdCMSBEdCSBEdASBE

ABE∆ vuông cân tại A có ABa = nên AKBE ⊥ và 2 2 a AK = .

Kẻ AHSK ⊥ , HSK ∈ .

Có () BEAK BESAK BESA ⊥   ⊥  ⊥  BEAH  ⊥ Có AHBE AHSK ⊥   ⊥  ()() () , AHSBEdASBEAH  ⊥  =

Chọn hệ trục tọa độ Oxyz sao cho: ()()()() 0;0;0,;0;0,0;;0,0;0; ABaDaSa () ;;0Caa  , 0;; 22 aa M   

Ta có 2 2 a AK = , 22 3 2 a SKSAAK=+= ; SAAK AH SK =

2 . 3 2 3 3 2

a a a a == . Vậy () 3 , 3 a dCMSB = . Cách 2:

Ta có () ;; SCaaa =− , ();0;,a;; 22 aa SBaaMC  =−=−  222 ,;; 222    =−   aaa SBMC . Khoảng cách giữa hai đường thẳng SB và CM là: () ,. , ,

  =  

SBMCSC dSBCM SBMC

333 444

aaa a aaa == ++ Vậy () 3 , 3 a dCMSB = .

222 3 3 444

Câu30. (Chuyên Bến Tre - 2020) Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a , 2 SAa = và vuông góc với () ABCD . Gọi M là trung điểm của SD . Tính khoảng cách d giữa hai đường thẳng SB và CM. A. 3 a d = B. 2 2 a d = C. 2 3 a d = D. 6 a d = Lờigiải ChọnC

K I H S

O M

D C B

a HK HKHMHIHKaHKa a =+⇔=+⇔=⇔=    Vậy ()() () 2 ,2,2 3 a dSBCMdHACMHK === Câu31. (Chuyên Hùng Vương -Gia Lai - 2020) Cho lăng trụ đứng tam giác ABCABC′′′ có đáy là một tam giác vuông cân tại B , 2,ABAAa ′ == M là trung điểm BC (minh họa như hình dưới). Khoảng cách giữa hai đường thẳng AM và BC ′ bằng

A A. 2 a B. 2 3 a C. 7 7 a D. 3 a Lờigiải ChọnB Gọi N là trung điểm BB′ () //// MNBCBCAMN ′′  Khi đó ()() () () (),,, dAMBCdBCAMNdCAMN ′′ == Ta có () BCAMNM ∩= và MBMC = nên () () () (),, dCABMdBABM = . Gọi h là khoảng cách từ B đến mặt phẳng () ABM . Tứ diện BAMN có ,, BABMBN đôi một vuông góc nên: 22222 11111 hBHBABMBN ==++ 2 ABaBC == . 112 222 a BNBBAAa ′′ ==== 1 2 BMBCa == Suy ra 2 2 22222 1111942 4493 hhaa haaaa =++=  =  =

Gọi D là điểm đối xứng của C qua A ta có tứ giác ′′ADAC là hình bình hành do đó // ′′ ADAC , suy ra khoảng cách (,)(,())(,()) ′′′′′ == dACBAdACABDdAABD

Theo giả thiết ′′′ABCABC là lăng trụ đều nên () ′ ⊥ AAABC hay () ′ ⊥ AAABCD suy ra (1) ′ ⊥ AABD

Ta có ∆ABD có = ABAD nên là tam giác cân tại A , gọi I là trung điểm BD ta có (2) ⊥ AIBD

Xét tam giác ∆BCD có , AI lần lượt là trung điểm của , DCDB nên 1 1 2 ==AIBC

Trong mặt phẳng (') AAI dựng ;(3)⊥∈′′ AHAIHAI .

Từ (1) và (2) suy ra (')(4) ⊥  ⊥ BDAAIBDAH .

Từ (3) và (4) suy ra (') ⊥ AHABD do đó khoảng cách (,()) = dASBDAH .

Trong tam giác ' AAI vuông tại A ta có 22

.'2 5 (') == + AIAA AH AIAA

Từ đây chọn đáp án A.

Câu34. (Đại Học Hà Tĩnh - 2020) Cho lăng trụ đứng ABCABC′′′ có đáy là tam giác vuông và ABBCa == , 2 AAa ′ = , M là trung điểm của BC . Tính khoảng cách d của hai đường thẳng AM và BC ′ .

A. 6 6 a d = . B. 2 2 a d = . C. 7 7 a d = . D. 3 3 a d = . Lờigiải ChọnC

Cách1: A

Do ABC∆ vuông và có ABBC = nên ABC∆ vuông cân tại B . Chọn hệ trục tọa độ Oxyz như hình vẽ. Không mất tính tổng quát, ta giả sử 1 a = .

A′

B′ C ′ M

N K H

Ta có: () () () 1 1;0;0,0;;0,0;0;2,0;1;0 2 AMBC  ′   . () () 1 1;;0,0;1;2,1;1;0 2 AMBCAC  ′ =−=−=−   ; 2 ,;2;1 2 AMBC   ′ =−−−    .

B C

Do ABC∆ vuông và có ABBC = nên ABC∆ vuông cân tại B Gọi N là trung điểm của BB′ , ta có: ( ) // BCAMN ′ Khi đó: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ,,,, dAMBCdBCAMNdCAMNdBAMN ′′ === . Kẻ BHAM ⊥ tại H và kẻ BKNH ⊥ tại K

Ta có: ( ) , BHAMBNAMAMNBHBKAM ⊥⊥  ⊥  ⊥ Do BKNH ⊥ , BKAM ⊥ nên ( ) BKAMN ⊥ Suy ra: ( ) ( ) , dBAMNBK = Mặt khác: 22

.5 5 BMBAa BH BMBA == + ; 22

.7 7 BHBNa BK BHBN == + Vậy ()() () 7 ,, 7 a dAMBCdBAMNBK ′ ===

AMBCAC dAMBC AMBC

−+  ′  ′ ===  ′  ++

Khi đó: () 2 20 ,. 2 7 , 7 1 , 21 2

Trong trường hợp tổng quát, ta có: () 7 , 7 a dAMBC ′ =

Câu35. (ĐHQGHà Nội -2020) Cho lăng trụ đứng ///ABCABC có tất cả các cạnh bằng a. Gọi M là trung điểm của AA . Tính khoảng cách giữa hai đường thẳng BM và / BC A. 3 5 a B. 3 10 a C. 3 22 a D. 3 7 a Lờigiải ChọnB

GọiOvàIlầnlượtlàtrung điểmcủaB/C/,BC. Chọnhệ trụctọa độ Oxyz saocho: ////31 (0;0;0);Ox(;0;0);(0;;0);(0;0;1) 22 OAACOyCIOzI ∈  ∈  ∈  / 111331 (0;;0);(0;;1);(0;;1);(;0;1);(;0;) 222222 BCBAM  / 31133 (0;1;1);(;;),(1;;) 22222 BCBMBMBC  ==  =  (0;1;0) BC  = Vậykhoảngcáchgiữahai đườngthẳng BM và BC là: / /

Gọi H là trung điểm cạnh AB , I là trung điểm cạnh AO . Suy ra ()SHABCD ⊥ , ()(),45SACABCDSIH==° .Do đó 12 24 a SHIHBO=== . Gọi N làtrung điểmcạnh CD ,khi đó HNAB ⊥ Chọnhệ trụctọa độ trongkhônggiannhư hìnhvẽ,tacótọa độ các điểm () 0;0;0 H , 22 0;;0;0;0;;;;0;;;;;;0 2422482 aaaaaaa ASDaMCa        . Nên () 22 ;;;;;;;;0 24824 aaaaa AMSCaACaa  ==−=  

BCBMBC dBMBC BMBC

3 ., 3 2 (;) 3310 , 1 44

  ===  ++  nênchọn đápánB Câu36. (Sở PhúThọ -2020) Chohìnhchóp SABCD có đáy ABCD làhìnhvuôngcạnh a .Hìnhchiếu vuông góc của S trên mặt phẳng () ABCD là trung điểm của cạnh AB , góc giữa mặt phẳng () SAC và đáybằng 45° .Gọi M làtrung điểmcủacạnh SD .Khoảngcáchgiữahai đường AM và SC bằng A. a B. 2 4 a C. 5 10 a D. 5 5 a Lờigiải ChọnD

Kẻ

Tacótứ diện làtứ diệnvuông

Vìtứ diện ABCD có ,, ABACAD đôimộtvuônggócvớinhau,nêntachọnhệ trụctọa độ Axyz như hìnhvẽ (với A làgốctọa độ, đườngthằng AC nằmtrêntrục Ax , AD nằmtrên trục Ay và AB nằmtrêntrục Az ). Từ đósuyra: () 0;0;0 A , () 0;0;1 B vì BAz ∈ , () 1;0;0 C vì CAx ∈ , () 0;2;0 D vì DAy ∈ . Vì I làtrung điểmcủa BC nên 11 ;0; 22 I    Từ đó,taquayvề bàitoántínhkhoảngcáchgiữahai đườngthẳngchéonhautronghệ tọa độ khônggian Axyz . Tacó () 111 ;0;,0;2;1,1;;1 222 AIBDAIBD  ==−  =−    và () 0;0;1 AB = . Tacó () () () 2 2 2

1 1.0.01.1 ,. 2 2 , 3 , 1 11 2

AIBDAB dAIBD AIBD

. ABCABC′′′ ABBCa == 2 AAa ′ = M BC AM BC ′

−++   ===    −++   Câu38. (Sở YênBái-2020) Chohìnhlăngtrụ đứng có đáylàtamgiácvuôngcântại B , biết , , làtrung điểm của . Tínhkhoảng cách giữa hai đường thẳng và . A. 7 7 a . B. 25 5 a . C. 6 2 a . D. 15 5 a . Lờigiải ChọnA

Câu39. (Đặng Thúc Hứa - Nghệ An - 2020) Chohìnhchóp tứ giác đều . SABCD có cạnh đáy bằng 2a , cạnh SA tạo với mặt phẳng đáy một góc o30 . Khoảng cách giữa hai đường thẳng SA và CD bằng A. 215 5 a . B. 314 5 a . C. 210 5 a . D. 45 5 a . Lờigiải ChọnC Gọi O làtâmcủamặt đáy, M làtrung điểmcủa AB , H làhìnhchiếucủa O trên SM Tacó () () () oo 2 ,,30tan30 3 a SAABCDSAOASAOSAOSOAO ==  =  == . Tacó () , ABOMABSOABSOMABOH ⊥⊥ 

Câu41. (Liên trường Nghệ An - 2020) Cho tứ diện ABCD

0 90,2, ABCADCACDBCaCDa ===== , góc giữa đường thẳng AB và mặt phẳng () BCD bằng 0 60 . Tính khoảng cách giữa hai đường thẳng AC và BD A. 6 31 a B. 26 31 a C. 23 31 a D. 3 31 a Lờigiải ChọnC

Gọi H là chân đường cao của tứ diện ABCD .

Ta có: BCAB BCHB BCAH ⊥   ⊥  ⊥  () 1

Lại có: CDAD CDHD CDAH ⊥   ⊥  ⊥  () 2

Mà 90 BCD =° Từ đây ta suy ra HBCD là hình chữ nhật. Mặt khác: () (),60ABBCDABH==° . Suy ra: .tan603AHHBa =°= Chọn hệ trục OxyzHDBA ≡ như hình vẽ

Ta có: () 0;0;0 H , () 0;0;3Aa , () 0;;0Ba , () 2;;0Caa , () 2;0;0Da () 2;;3ACaaa =− , () 2;;0BDaa =− , () 0;;3ABaa =− . Vậy () () () () 3 22 2 222

ACBDAB aa dACBC ACBD aaa

,. 23293 , 31 , 3234

  ===  −+−+− 

Câu42. (LýNhânTông-BắcNinh-2020) Cho tứ diện OABC có ,, OAOBOC đôi một vuông góc với nhau và OAOBa == , 2 OCa = . Gọi M là trung điểm của AB . Khoảng cách giữa hai đường thẳng OM và AC bằng A. 2 3 a . B. 25 5 a . C. 2 2 a . D. 2 3 a . Lờigiải ChọnD

Dựng // AEOM , khi đó () // OMCAE . Do đó ()()() ,,(),() dOMACdOMCAEdOCAE ==

Dựng OKAE ⊥ , ta có: () () () AEOK AECOK AEOCCOAC VìB ⊥    ⊥  ⊥⊥  

Mà ()AECAE ⊂ nên ()() CAECOK ⊥ .

Ta có ()() CAECOKCK ∩= . Kẻ OHCK ⊥ , khi đó ()OHCOK ⊥ . Suy ra () ,() dOCAEOH =

Xét tam giác OAB ta có : 22 2 ABOAOBa =+=

Dễ thấy OKAM là hình chữ nhật nên 2 22 ABa OKAM===

Xét tam giác COK ta có : () 22 2222 1111112 3 2 2 2

OHa OHOKOCOH a a =+  =+  =   

.

Câu43. (Nguyễn Huệ - Phú Yên - 2020) Cho hình chóp SABC có đáy là tam giác vuông tại A , ,2, ABaACaSA == vuông góc với mặt phẳng đáy và 2 SAa = . Gọi G là trọng tâm của ABC∆ . Khoảng cách giữa hai đường thẳng SG và BC bằng A. 2 7 a B. 6 3 a C. 26 9 a D. 4 7 a Lờigiải ChọnA

Gọi M là trung điểm của BC . Trong mp () SAM dựng // SMSG ′ . Suy ra 3 3 2 SASAa ′ ==

Do đó ()() () () (),,, dSGBCdSGSBCdGSBC ′′ ==

Vì 3 AMGM = nên () () () () 1 ,, 3 dGSBCdASBC ′′ =

Kẻ AHBC ⊥ ta có ()BCSAH ′ ⊥

Kẻ () () , AKSHAKdASBC ′′ ⊥  =

Ta có 222 1112 5 a AH AHABAC =+  = . Suy ra 222 1116 7 a AK AKSAAH =+  = ′

Do đó () () 12 , 37 a dGSBCAK ′ ==

Câu44. (NguyễnTrãi-TháiBình-2020) Cho hình chóp . SABCD có đáy ABCD là hình bình hành và 11, ===SASBSC góc 30,∠=° SAB góc 60,∠=° SBC góc 45 ∠=° SCA . Tính khoảng cách d giữa hai đường thẳng AB và SD .

A. 222 . B. 22 . C. 22 2 . D. 411 . Lờigiải ChọnB

Trong tam giác ∆SAB ta có 222 2..cos30113=+−°⇔= SBSAABSAABAB

Trong tam giác ∆SBC ta có 11,60 ==∠=°SBSCSBC nên ∆SBC đều suy ra 11 = BC

Trong tam giác ∆SCA ta có 11,45 ==∠=°SCSASCA nên ∆SCA vuông cân tại S suy ra 112 = AC

Xét tam giác ABC có 222 += BCACAB do vậy ∆ABC vuông tại C Gọi I là hình chiếu của S lên mặt phẳng () ABCD vì == SASBSC nên I là tâm của đường tròn ngoại tiếp tam giác ABC , vì ∆ABC vuông tại C nên I là trung điểm của AB và () (1) ⊥  ⊥ SIABCDSICD . Vẽ (2), (3) ⊥⊥ IKCDIHSK

Từ (1) và (2) suy ra () (4) ⊥  ⊥ CDSIKCDIH

Từ (3) và (4) suy ra () ⊥ IHSCD do đó khoảng cách (,()) = dISCDIH

Ta lại có // ABCD suy ra khoảng cách (,)(,())(,()) === dABSDdABSCDdISCDIH .

Trong mặt phẳng đáy vẽ ⊥ CJAB ta suy ra .116 3 === CACB IKCJ AB .

Trong tam giác SAB cân tại S có 2 2 11 42 =−= AB SISA

Trong tam giác SIK vuông tại I ta có 22 22 == + IKSI IH IKSI

Câu45. (TiênDu-BắcNinh-2020) Cho hình lăng trụ tam giác ABCABC′′′ có cạnh bên bằng 2 a , đáy ABC là tam giác vuông tại ,3, BBCaABa == . Biết hình chiếu vuông góc của đỉnh A′ lên mặt đáy là điểm M thoả mãn 3AMAC = . Khoảng cách giữa hai đường thẳng AA′ và BC bằng A. 210 15 a . B. 210 45 a . C. 714 17 a . D. 714 51 a .

Dựng hình bình hành ABCD , vì tam giác ABC là tam giác vuông tại B nên ABCD là hình chữ nhật.

Suy ra () //// BCADBCAAD ′  . Do đó ()() () () (),,, dBCAAdBCAADdCAAD ′′′ == Mà 3AMAC = nên () () () (),3, dCAADdMAAD ′′ = Kẻ ()() MHADAMHAADAH ′′′ ⊥  ⊥= Kẻ ()() () , MKAHMKAADMKdMAAD ′′′ ⊥  ⊥  = Mặt khác ta có 22 22 1214 2 333 ACABBCaAMACAMAAAMaa ′′ =+=  ==  =−= Và 111 // 3333 MHAMa MHCDMHCDAB CDAC  ==  === . Suy ra 22 2222 22 1111111135210 141445 33

a MK MKAMMHMKMKa a a =+⇔=+⇔=⇔= ′     

. Vậy ()() () () () 210210 ,,3,33 4515 aa dBCAAdCAADdMAADMK

Gọi OACBD =∩ , M là trung điểm SC Trong tam giác SAC , dựng đường trung trực của đoạn thẳng SC cắt SO tại I , I là tâm mặt cầu ngoại tiếp hình chóp . SABCD , bán kính 92 8 a RSI== . Vì độ dài cạnh bên lớn hơn độ dài cạnh đáy nên tâm I của mặt cầu ngoại tiếp hình chóp thuộc đoạn SO . Gọi x là độ dài cạnh bên của hình chóp. Ta có SOC∆ đồng dạng với SMI∆

với 2 ABa = , 3 ADa = (tham khảo hình vẽ). Tam giác SAB cân tại S và nằm trong mặ

vuông góc với mặt đáy; góc giữa mặt phẳng () SCD và mặt đáy là 45° . Gọi H là trung điểm cạnh AB . Tính theo a khoảng cách giữa hai đoạn thẳng SD và CH . A. 311 11 a . B. 314 7 a . C. 310 109 a . D. 385 17 a . Lờigiải ChọnB Cách1:

 =      ⇔−+=⇔−+=⇔  SABABCD SABABCD SHABSHSAB

x a xx xaxa aa x a Ta có: ()() ()() () ;

     =   2 9 8 x a  =   không thỏa vì 2 xa < 2 93 x xa a  =⇔=   . Suy ra ()2 222 38 SOaaa ⊥   ∩   ⊥⊂  ()SHABCD  ⊥ Kẻ HKCD ⊥ ( K là trung điểm của CD ) ()CDSHK  ⊥ CDSK  ⊥ ()() () ();; SCDABCDSKHK  = 45 SKH ==° SHK  ∆ vuông cân tại H 3 SHHKa  == . Kẻ d qua D song song với HC cắt AB tại E 10 EDHCa  ==

0;0;3 Sa . Ta có: () 3;;0HCaa =− , () 3;;3 SDaaa =− , () 0;0;3 SHa =− .

() 222;3;9;6 HCSDaaa  =  () .; ; ;

   =   () ()()() 2 222222

SHHCSD dCHSD HCSD

aa aaa = ++ = 314 7 a

6.3 396

Dạng3.Khoảngcáchcủa đườngvớimặt,mặtvớimặt Ở dạngtoánnàychúngta đềuquyvề dạngtoán1

Cho đường thẳng ∆ và mặt phẳng () α song song với nhau. Khi đó khoảng cách từ một điểm bất kì trên ∆ đến mặt phẳng () α được gọi là khoảng cách giữa đường thẳng ∆ và mặt phẳng () α () () () () ,,, ddMM αα ∆=∈∆

α H

Cho hai mặt phẳng () α và () β song song với nhau, khoảng cách từ một điểm bất kì trên mặt phẳng này đến mặt phẳn kia được gọi là khoảng cách giữa hai mặt phẳng () α và () β .

α M M'

M β

N N'

()() () () () () (),,, ddMdNαββα == ()(),, MNαβ∈∈ .

Câu1. (ChuyênNguyễnBỉnhKhiêm-QuảngNam-2020) Cho hình chóp . SABCD có đáy ABCD là hình thang vuông tại A và D , 3,ABa = ADDCa == . Gọi I là trung điểm của AD , biết hai mặt phảng () SBI và () SCI cùng vuông góc với đáy và mặt phẳng () SBC tạo với đáy một góc 060 . Tính theo a khoảng cách từ trung điểm cạnh SD đến mặt phẳng () SBC . A. 17 5 a B. 6 19 a C. 3 15 a D. 15 20 a Lờigiải ChọnB

Kẻ ()()() () 0;S60IKBCKBCSBCABCDKI ⊥∈  == Gọi MADBC =∩ . Ta có 1 32 MDa MD MA =  = Ta có MIK∆ đồng dạng với MBA∆ nên suy ra () 2 2

IKMIa BAMB a a

25 15 3 3 2

===  +   2525 .3 155 a IKa  == Gọi N là trung điểm của SD Ta có () () () () () () 11 ,,, 24 dNSBCdDSBCdISBC == Từ I kẻ IHSK ⊥ suy ra () () () () 0 ,.sin60,1515 520 IHdISBCIKdNSBCaa ===  = Câu2. (THPTLêXoayVĩnhPhúc2019) Cho hình chóp SABCD có đáy là hình thang vuông tại A và D , SD vuông góc với mặt đáy () ABCD , 2,2ADaSDa == . Tính khoảng cách giữa đường thẳng CD và mặt phẳng () SAB A. a 2 B. a2. C. 2a 3 D. a3 2 Lờigiải

Ta có: ABAD ABSD ⊥   ⊥  nên ()ABSAD ⊥

Kẻ DHSA ⊥ tại H . Do ()DHSAD ⊂ nên ABDH ⊥ .

Ta có: () DHSA DHSAB DHAB ⊥   ⊥  ⊥ 

Do // DCAB nên () // DCSAB

Vậy khoảng cách giữa đường thẳng CD và mặt phẳng () SAB là DH .

Xét SAD∆ vuông tại D có: 222 111 DHSDAD =+ () () 22 2 113 4 2 2 a a a =+= 2 3 a DH  = . Khoảng cách giữa đường thẳng CD và mặt phẳng () SAB là 2 3 a

Câu3. Cho hình chóp . SABCD có đáy ABCD là hình vuông cạnh a , SA vuông góc với đáy và 2 SAa = . Gọi M là trung điểm của SD . Tính khoảng cách d giữa đường thẳng SB và mặt phẳng () ACM

A. 3 2 a d = B. da = C. 2 3 a d = D. 3 a d = Lờigiải ChọnC

Gọi O là tâm hình vuông. Ta có: ////() MOSBSBACM  (,())(,())(,()) dSBACMdBACMdDACM  == ( vì O là trung điểm BD )

Gọi I là trung điểm AD //() (,())2(,()) MISAMIABCD dDACMdIACM  ⊥    = 

Trong () ABCD kẻ IKAC ⊥ tại K

Trong () MIK kẻ IHMK ⊥ tại H (1)

Ta có: ,()(2) ACMIACIKACMIKACIH ⊥⊥  ⊥  ⊥ Từ (1) & (2)()(,())IHACMdIACMIH  ⊥  =

Ta có: ()() () () ()//;; MNABCdMNABCdMABC  = Mà () () () () () () () () ; 1113 ;; 2223 ; dMABC AM a dMABCdOABCOH AO dOABC ==  === Câu5. (Chuyên Nguyễn Quang Diêu - Đồng Tháp - 2018) Cho hình lập phương ABCDABCD′′′′ cạnh a . Gọi I , J lần lượt là trung điểm của BC và AD . Tính khoảng cách d giữa hai

Trong tam giác MIK ta có: 22

IM.IK IH= IM+IK Biết 2 2

⋅ =====  == + Vậy: 2 (,()) 3 a dSBACM =

a a SAODBDaa MIaIKIH a a

2 2 4 , 22443 8

Câu4. (THPTLương ĐắcBằng-ThanhHóa-2018) Cho hình chóp . OABC có đườngcao 2 3 a OH = . Gọi M và N lần lượt là trung điểm OA và OB . Khoảng cách giữa đường thẳng MN và () ABC bằng: A. 2 a B. 3 3 a C. 3 a D. 2 2 a Lờigiải

GIÁTRỊLỚNNHẤT-GIÁTRỊNHỎNHẤTCỦAHÀMSỐ Chuyên đề 5

Dạng1: Tìm m để [] () () ; max0. yfxmaa αβ =+=>

Phươngpháp: Cách1:Trước tiên tìm [] () [] ()() ; ; max;min. fxKfxkKk αβ αβ ==>

Kiểm tra {}max, . 222 mKmkmKmkKk mKmk ++++−−− ++≥≥=

TH1:

TH2: 2 Kk a > m  ∈∅ Cách2: Xét trường hợp

TH1: mKa MaxmK mKmk  +=  =+⇔  +≥+  

TH2: mka Maxmk mkmK  +=  =+⇔  +≥+  

+=+=−=−=−−  =⇔∨⇔∨  +>+<>−<−  Vậy 12mSS ∈∪ Dạng3: Tìm m để [] () ; max yfxm αβ =+ không vượt quá giá trị M cho trước. Phươ +≥−  ≤  ⇔−−≤≤−  +≤  Dạng4: Tìm m để [] () ; min yfxm αβ =+ không vượt quá giá trị a cho trước. Phươngpháp: Trước tiên tìm [] () [] ()() ; max;min. fxKfxkKk αβ αβ ==> Để [] ()() ; min 0 . 00 mkamKamakmaK yamKmkKmk mkmKmkmK αβ

+≤+≥−≤−≥−−  ≤⇔∨∨++<⇔∨∨−<<−  +≥+≤≥−≤− 

Dang5: Tìm m để [] () ; max ab yfxm =+ đạt min.

Phươngpháp: Trước tiên tìm [] () [] ()() ; max;min. ab ab fxKfxkKk ==>

Đề hỏi tìm . 2 Kk mm +  =− Đề hỏi tìm min của [] ; max ab y  giá trị này là . 2 Kk

Dạng6: Tìm m để [] () ; min ab yfxm =+ đạt min.

Phươngpháp: Trước tiên tìm [] () [] ()() ; ; max;min. ab ab fxKfxkKk ==>

Đề hỏi tìm ()() 0 mmKmkKmk  ++≤⇔−≤≤− Đề hỏi tìm min của [] ; min ab y  giá trị này là 0.

Dạng7: Cho hàm số () yfxm =+ .Tìm m để [] [] () ; ; max.min0 ab ab yhyh≤> hoặc max Min +=

Phươngpháp: Trước tiên tìm [] () [] ()() ; ; max;min. ab ab fxKfxkKk ==>

TH1: 1 cungdau . Kmkm Kmkm KmhkmmS +≥+ ++ +≤+→∈

TH2: 2 cungdau kmKm Kmkm kmhKmmS +≥+ ++ +≤+→∈

Vậy 12. mSS ∈∪

Dạng8: Cho hàm số () yfxm =+ .

Phươngpháp: Trước tiên tìm [] () [] ()() ; ; max;min. ab ab fxKfxkKk ==>

BT1: Tìm m để [] [] ; minmax ab ab yymKmkαα +=⇔+++=

BT2: Tìm m để [] [] ; min*max* ab ab yymKmkββ =⇔++=

Câu1. (Đề Tham Khảo 2018) Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số 3 3 yxxm =−+ trên đoạn [] 0;2 bằng 3. Số phần tử của S là A. 0 B. 6 C. 1 D. 2 Lờigiải ChọnD Xét hàm số () 3 3 fxxxm =−+ , ta có () 2 33fxx ′ =− . Ta có bảng biến thiên của ()fx :

TH 1 : 202 mm +<⇔<− . Khi đó [] () () 0;2 22 maxfxmm =−−+=− 231 mm −=⇔=− (loại).

TH 2 : 20 20 0 m m m +>  ⇔−<<  <  . Khi đó : 2222 mmm −=−>>+ [] () () 0;2 22 maxfxmm =−−+=− 231 mm −=⇔=− (thỏa mãn).

Trang 2

TH 3 : 0 02 20 m m m >  ⇔<<  −+< .Khi đó: 2222 mmm −=−<<+ [] ( ) 0;2 2 maxfxm =+

231 mm +=⇔= (thỏamãn).

TH 4: 202 mm −+>⇔> .Khi đó [] ( ) 0;2 2 maxfxm =+ 231 mm +=⇔= (loại).

Câu2. (Đề MinhHọa2020Lần1) Gọi S làtậphợptấtcả cácgiátrị thựccủathamsố msaochogiátrị lớn nhất của hàm số ( ) 3 3 fxxxm =−+ trên đoạn [ ]0;3 bằng 16. Tổng tất cả các phần tử của S là: A. 16 B. 16 C. 12 D. 2 Lờigiải ChọnA

TH2: ( ) ( ) 0.10(1)010 ffmmm <⇔+<⇔−<< [] () [] () 0;1 0;1

=−

−≥+

Do đó tổng tất cả các phần tử của S bằng 16 Câu3. (Đề ThamKhảo2020Lần2) Cho hàm số () 1 xm fx x + = + ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho [] ( ) [] ( ) 0;1 0;1 maxmin2 fxfx+= . Số phần tử của S là A. 6 B. 2 C. 1 D. 4 Lờigiải ChọnB

Do hàm số () 1 xm fx x + = + liên tục trên [ ]0;1 .

Khi 1 m = hàm số là hàm hằng nên [] ( ) [] ( ) 0;1 0;1 maxmin1 fxfx==

Khi 1 m ≠ hàm số đơn điệu trên đoạn [ ]0;1 nên

+ Khi ( ) ( )0;1ff cùng dấu thì [] () [] () () () 0;1 0;1

1 maxmin01 2 m fxfxffm + +=+=+

+ Khi ( ) ( )0;1ff trái dấu thì

1 maxmax0;1max; 2 m fxffm  +  ==   . TH1: ()() 1 0.10(1)0 0 m ffmm m ≤−  ≥⇔+≥⇔

[] ( ) 0;1 min0 fx = , [] () () () {} 0;1

2 2 maxmin25 1 2 3 2

m m fxfxm m m

=±  =    +=  ⇔=− +   =   =   (khôngthoả mãn).

Số phầntử của S là 2

Câu4. (THPT Đông Sơn 1 - Thanh Hóa 2019) Tìm m để giá trị lớn nhất của hàm số 3 321yxxm=−+− trên đoạn [ ]0;2 lànhỏ nhất.Giátrị của m thuộckhoảngnào? A. 3 ;1 2    . B. 2 ;2 3    . C. [ ]1;0 . D. ( )0;1 . Lờigiải ChọnD

Xéthàm số ( ) 3 321yfxxxm ==−+− trên đoạn [ ]0;2 .

Tacó () [ ] 2 10;2 '330 1 x fxx x  =−∉ =−=⇔  = 

Tacó ( ) 021fm=− , ( ) 123fm=− và ( ) 221fm=+

Suyra [] ( ) { } { } 0;2 21;23;2123;21 maxfxmaxmmmmaxmmP =−−+=−+=

Trườnghợp1:Xét () 1 23214420 2 mmmm −≥+⇔−−≥⇔≤

Khi đó 232Pm=−≥ , 1 2 m ∀≤ .Suyra min 1 2 2 Pm=⇔=

Trườnghợp2:Xét () 1 23214420 2 mmmm −<+⇔−−<⇔> .

Khi đó 212Pm=+> , 1 2 m ∀> .Suyra minP khôngtồntại.

Vậy 1 2 m = .

Câu5. (Sở VĩnhPhúc2019) Tính tổngtất cả các giá trị của tham số m saocho giá trị lớn nhất củahàm số 2 2 yxxm =−+ trên đoạn [ ]1;2 bằng 5 A. 1 . B. 2 . C. 2 . D. 1. Lờigiải Tacó 2 22 2 x y xxm ′ = −+ , 01yx ′ =  = .

Do đó yêu cầu bài toán tương đương ( ) ( ) ( ) { } max1,2,15 yyy−= { } max3,,15 mmm ⇔+−= .

+ Trường hợp 1 m ≥− , ta có { } max3,,15352 mmmmm +−=⇔+=  = + Trường hợp 1 m <− ta có { } max3,,15154 mmmmm +−=⇔−=  =− . Vậy tổng các giá trị m bằng 2

Câu6. (THPT Nguyễn Huệ 2018) Cho hàm số 2 24yxxa=++− ( a là tham số ). Tìm a để giá trị lớn nhất của hàm số trên đoạn [ ]2;1 đạt giá trị nhỏ nhất A. 1 a = B. 3 a = C. 2 a = D. 5 a = . Lờigiải

Hàm

ã cho xác định và liên tục trên đoạn [ ]2;1

Ta có: () () 2 2 2415yxxaxa =++−=++−∗ Đặt () [ ] [ ] 2 1, 2;10;4txxa =+∈−  ∈ Lúc đó hàm số trở thành: ( ) 5 ftta=+− với [ ]0;4 t ∈ Nên ( ) { } { } 0;40;4 2;1 0;4 maxmaxmax(0);(4)max5;1 tt x t yftffaa     

aaa

Câu8.

lớnnhấtcủahàmsố trên [ ]1;3 .Khi M nhậngiátrị nhỏ nhấtcóthể được,tính 2 ab + . A. 2 B. 4 C. 4 D. 3 Lờigiải

Xéthàmsố ( ) 2 fxxaxb =++ .Theo đề bài, M làgiátrị lớnnhấtcủahàmsố trên [ ]1;3

Mf Mf Mf

≥−   ≥   ≥ 

1 3 1

Suyra ( ) () ()

 ≥−+  ⇔≥++   ≥++  419321 Mababab  ≥−+++++−−−

1 93 1

Mab Mab Mab

1932(1) ababab ≥−+++++−−− 48 M  ≥ 2 M  ≥ Nếu 2 M = thì điềukiệncầnlà 19312 ababab −+=++=−−−= và 1 ab−+ , 93ab++ , 1 ab cùngdấu 19312 19312 ababab ababab −+=++=−−−=  ⇔  −+=++=−−−=−  2 1 a b =−  ⇔  =− 

Ngượclại,khi 2 1 a b =−   =−  tacó,hàmsố ( ) 2 21fxxx=−− trên [ ]1;3

Xéthàmsố ( ) 2 21gxxx=−− xác địnhvàliêntụctrên [ ]1;3 ( ) 22gxx ′ =− ; ( ) [ ]011;3gxx ′ =⇔=∈− M làgiátrị lớnnhấtcủahàmsố ( )fx trên [ ]1;3 () () () { } max1;3;1 Mggg  =− =2 . Vậy 2 1 a b =−   =−  .Tacó: 24ab+=− .

Câu9. Chohàmsố ( ) 322 127yxxmx =++++ .Giátrị lớnnhấtcủahàmsố trên đoạn [ ]3;1 cógiátrị nhỏ nhấtbằng A. 26 B. 18 C. 28 D. 16 Lờigiải

ChọnB

Xét ( ) 322 127uxxmx =++++ trên đoạn [ ]3;1 tacó: 22 3210, uxxmx ′ =+++>∀

Do đó [] ( ) 2 3;1 max126 Auum ==−=− ; [] ( ) 2 3;1 min363 auum ==−=− . Do [] { } 22 3;1 Mmaxmax26,63 ymm==−− và 22 43266372 Mmm≥−+−≥ Vậy 18 M ≥ . Dấubằngxảyrakhi 22 26631822 mmm −=−=⇔=±

Câu10. (Sở QuảngNam-2018) Cóbaonhiêugiátrị thựccủa tham số m để giátrị lớnnhấtcủahàm số 2 24yxxm=++− trên đoạn [ ]2;1 bằng 4 ? A. 1 B. 2 C. 3 D. 4 Lờigiải ( ) 2 24fxxxm=++− có ( ) 22fxx ′ =+ , ( ) 01fxx ′ =⇔=− .Do đó [] { } 2 2;1 max24max1;4;5 xxmmmm ++−=−−− Tathấy 541mmm−<−<− vớimọi m ∈ ℝ ,suyra [] 2;1 max y chỉ cóthể là 5 m hoặc 1 m .

Nếu [] 2;1 max5 ym=− thì 54 51 m mm  −=   −≥−   1 m ⇔= . Nếu [] 2;1 max1 ym=− thì 14 15 m mm  −=   −≥−   5 m ⇔= Vậy { }1;5 m ∈ . Câu11. (Chuyên Nguyễn Thị Minh Khai - Sóc Trăng - 2018) Gọi S là tập hợp tất cả các giá trị của tham số m sao cho giá trị lớn nhất của hàm số 3239 yxxxm =−−+ trên đoạn [] 2;4 bằng 16 . Số phầntử của S là A. 0 B. 2 C. 4 D. 1 Lờigiải Xéthàmsố () 3239 fxxxxm =−−+ trên đoạn [] 2;4 . 2 369fxx ′ =−− ; () 1 0 3 x fx x

=−  ′ =⇔  =  (thỏamãn). ( ) ( ) ( ) ( ) 22;15;327;420 fmfmfmfm −=−+−=+=−+=−+ [] () [] () 2;4 2;4 min27;max5 fxmfxm  =−=+ [] () {} 2;4 maxmax27;5 fxmm  =−+ +)Trườnghợp1:Nếu ( )275*mm−≤+ [] () 2;4

Để [] () 0;2 max20 gx ≤ thì () () 020 220 g g

≤    ≤   2020 620 m m  −≤  ⇔  +≤   014 m ⇔≤≤ .

Mà m ∈ ℤ nên {} 0;1;2;...;14 m ∈

Vậytổngcácphầntử của S là 105 .

Câu13. GọiSlàtậphợptấtcả cácgiátrị thựccủathamsố msaochogiátrị lớnnhấtcủahàmsố 2 sin2sin yxxm =−+ bằng 1.Số phầntử củaSlà A. 0 B. 1 B. 4 D. 3 Lờigiải ChọnA

Đặt [] () 2 sin1;12xttyttm =∈−  =−+ Xéthàmsố () 2 2 ftttm =−+ có () []'22011;1 fttt=−=⇔=∈− Có ()()13,11fmfm −=+=− .Khi đó () [] {} () [] {} 1;1 1;1

11 max5516 21 m fxmm m

=   =+  +=⇔  =−  Đốichiếu điềukiện ()*11 m  = +)Trườnghợp1:Nếu ()275**mm−>+ [] () 2;4

TH1: 311mmm+≥−⇔≥− () () () 2 max31 4 ml fxm ml =−   =+=⇔  =−  

43 max272716 11 m fxmm m

=   =−  −=⇔  =  (Khôngthỏamãn điềukiện () ** ). Vậy { }11 S = S  có 1 phầntử. Câu12. (ChuyênHạ Long2018) Gọi S làtậptấtcả cácgiátrị nguyêncủathamsố m saochogiátrị lớn nhất của hàm số 42119 3020 42 yxxxm =−++− trên đoạn [] 0;2 không vượt quá 20 . Tổng các phầntử của S bằng A. 210 B. 195 C. 105 D. 300 Lờigiải Xéthàmsố () 42 1193020 42 gxxxxm =−++− trên đoạn [] 0;2 Tacó () 3 1930gxxx ′ =−+ ; ()

TH1: 311mmm+<−⇔<− () () () 2 max11 0 ml fxm ml =   =−=⇔  =    Khôngtồntạimthỏamãn

7

Xéthàmsố 44 11 xaxax ya xx ++ ==+ ++ .

Tacó () 43 2

xxx yy x x

4 34 0 3 1 0

=+−=+    =+−=−  

 =− +  ′′ =  =⇔  + =  . Bảng biến thiên

fxmmm fxmmm

maxmax3;13 minmin3;11

Câu14. (ChuyênHưngYên-2020) Cho hàm số 4 1 xaxa y x ++ = + , với a là tham số thực. Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [ ]1;2 . Có bao nhiêu giá trị nguyêncủathamsố a để 2 Mm ≥ ? A. 10 . B. 14 . C. 5 . D. 20 . Lờigiải ChọnB

Tr

Trường hợp 3.

Đặt 42 1 ()144830 4 fxxxxm =−++− là hàm số xác định và liên tục trên [ ]0;2 . Với mọi [ ]0;2 x ∈ ta có 3 '()0284802 fxxxx =⇔−+=⇔= Suy ra [] { } 0;2 max()max(0);(2) fxff = Theo đề [] 0;2

 −≤   +≤−  −≤  ≤⇔⇔   +≤  +≤    −≤+   303030060 016 3014304416 mm m mm −≤−≤≤≤  ⇔⇔⇔≤≤  −≤+≤−≤≤  .

3030 1430 3030 max()30 1430 1430 3014

m mm m fx m m mm

 +<   ⇔−<<−   +>  

a a a

1 0 161 2 16 32 0 3

Do { } 0;1;2;...;16. mmS ∈  ∈= ℤ Vậytổngtấtcả 17giátrị trongtập S là 136 . Câu16. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số ( ) 432 342448 xxxx fxeeeem =−−++ . Gọi A, B lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàmsố đã cho trên [ ]0;ln2 .Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc [ )23;10 thỏamãn 3 AB ≤ .Tổngcácphầntử củatậpSbằng A. 33 B. 0 C. 111 D. 74 Lờigiải ChọnA Đặt [ ] [ ],0;ln21;2 x text =∈  ∈

Xéthàmsố ( ) 432 |342448| htttttm =−−++ trên [ ]1;2 . Đặt ( ) 432 342448 gtttttm =−−++

 =−−     ≥⇔−−≥+⇔≤−     =+  

Ma Mmaaa ma

Nếu 11611635 232312 aaaaa +>+⇔−−>+⇔<− thì 1 11667 2 22 16 2318 3

Kết hợp điều kiện, ta có 1667 318 a −<≤− . Suy ra có 2 giá trị nguyên của a thỏa mãn điều kiện.

Nếu 11611635 232312 aaaaa +≤+⇔−−≤+⇔≥− thì 16 16119 3 22 1 329 2

Ma Mmaaa ma

 =+     ≥⇔+≥−−⇔≥−     =−−  

Kết hợp điều kiện, ta có 191 92 a −≤<− . Suy ra có 2 giá trị nguyên của a thỏa mãn điều kiện. Vậy có 14 giá trị nguyên của a thỏa mãn điều kiện. Câu15. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Gọi S là tập hợp tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số 42 1 144830 4 yxxxm =−++− trên đoạn [ ]0;2 không vượt quá 30 . Tổng giá trị các phần tử của tập hợp S bằng bao nhiêu? A. 120 B. 210 C. 108 D. 136 Lờigiải ChọnD Trang 10

( ) 32 12124848gtttt ′ =−−+ ; ( ) 0 gt ′ = 2[1;2] 2 1

t t t

=−∉   ⇔=   =  ; ( ) 123gm=+ , ( ) 216gm=+ . TH1: 1610 m −≤< 23160mm  +≥+≥ [] ( ) 1;2 max Aht  = 23 m =+ ; [] ( ) 1;2 min Bht = 16 m =+

−≤<

m m mm m

1610 1610

−≤<  ⇔  +≤+ ≥    25 10 2 m  ≤< . Do đó: có 22 giá trị TH2: 2316 m −≤<− 2323, |16|16mmmm  +=++=−− . Dễ thấy 0 B = . Suy ra 2316 160 1619.5 19.523() 2316 230 mm m m VL m mm m  +<−−  −−≤ −≤<−

Tacó ()() () 2523 01;1;1 62 mm ggg=−=−=

- Nếu ( ) () 10 25 10 23 g m g m

 −≥  ≥ ⇔   ≥ ≤−     thì [] ( ) 1;1 min0 fx = ,không thỏamãnbàitoán.

- Nếu ( ) () 10 2325 10 g m g

−<   ⇔−<<  <  

Mà m nguyên nên { }3;2;1;0;1;2;3;4 m ∈−−− .

 ∈+   ∈+   . Xétcáctrường hợp + 0max4;min24103 ayayaaa ≥  =+=  +=  = , nhận. + 4max;min44107 ayayaaaa ≤−  =−=−−  −−−=  =− ,nhận. + {} 0 40min0;max4; 40 a ayyaa a <  ⇔−<<  =∈+−  +>  4106 1010 aa aa +==  −==−  (Loại). Vậy tồn tạihai giátrị a thỏamãn. Câu18. (Chuyên Hùng Vương - Gia Lai - 2020) Cho hàm số ( ) 32 3 fxxxm =−+ . Có bao nhiêu số nguyên m để giátrị nhỏ nhấtcủahàmsố ( )fx trên đoạn [ ]1;3 không lớn hơn 2020? A. 4045 B. 4046 C. 4044 D. 4042 Lờigiải ChọnA Với 32 3 uxxm =−+ có 2 36;00;2uxxuxx ′′ =−=⇔== Do đó [] ( ) ( ) ( ) { } { } [] ()()() {} {} 1;3 1;3

 ==−−=−   ==−−=   * Nếu [] ( ) { } 1;3 404min4202020244,...,2024. mmfxmmm −≥⇔≥  =−≤⇔≤  ∈ * Nếu [] ( ) { } 1;3 0min202020202020;...;0. mfxmmm ≤  =−≤⇔−≤  ∈− * Nếu 0m4 << khi đó [] [] [] ( ) 1;31;3 1;3 min0;max0min0 uufx <>  = (thỏamãn). Vậy { }2020,...,2024 m ∈− có tấtcả 4045 số nguyên thỏamãn. Câu19. (Chuyên Lê Hồng Phong - Nam Định - 2020) Xét hàm số () 24 24 mxx fx x −+ = + , với m là tham số thực. Có bao nhiêu số nguyên m thỏamãn điều kiện [] ( ) 1;1 0min1 fx << ? A. 4 B. 8 C. 2 D. 1 Lờigiải ChọnB Cách1: Xéthàmsố () 24 24 mxx gx x −+ = + liên tụctrên [ ]1;1 và ( ) ( )fxgx = .

minmin1;3;2min2;;44 maxmax1;3;2max2;;4 Trang 12

uuuummmm uuuummmm

Ta có () ()2

x m x gx x

212 4 4 24

+ + + ′ = + .

TH1: 0 m ≥ . Khi đó ( ) [ ]01;1gxx ′ >∀∈− . Do đó hàm số ( )gx đồng biến trên [ ]1;1 Mà ( ) ( ) 0111gg =−  >− . Do đó ( ) 110 g −<< . Vậy [] ( ) 1;1 0min1 fx << hay { }0;1;2;3;4 m ∈ thỏa mãn bài toán. TH2: 0 m < . Xét hàm số () 212 4 x hx x + = + trên [ ]1;1 . Ta có () () [] 2 01;1 44 x hxx xx + ′ =>∀∈− ++ .

Khi đó dễ thấy () 1014 ; 35 hx  ∈  

* Khi ( ) [ ] ( ) [ ]1401;101;1mmhxxgxx ′ =−  +>∀∈−  >∀∈− hay hàm số ( )gx đồng biến trên [ ]1;1 . Khi đó ( ) 110 g −<< nên [] ( ) 1;1 0min1 fx << . Vậy 1 m =− thỏa mãn.

* Khi { }3;2 m ∈−− ( ) [ ] ( ) [ ]401;101;1 mhxxgxx ′  +<∀∈−  <∀∈− hay hàm số ( )gx nghịch biến trên [ ]1;1 . Khi đó ( ) ( ) ( ) 10110ggg −>  −<−< nên [] ( ) 1;1 0min1 fx << . Vậy { }3;2 m ∈−− thỏa mãn.

Do đó { }3;2;1;0;1;2;3;4 m ∈−−− hay có 8 giá trị nguyên của m Cách2

Nhận thấy ( )fx liên tục trên [ ]1;1 nên tồn tại giá trị nhỏ nhất của ( )fx trên đoạn [ ]1;1

Ta có ( ) [ ] () 0,1;1 01 fxx f  ≥∀∈−   =   nên suy ra [] ( ) 1;1 0min1 x fx ∈− ≤≤ Vậy điều kiện [] () [] ( ) [] () 1;1 1;1 1;1

min0 (1) 0min1 min1 (2) x x x

fx fx fx ∈− ∈− ∈−

>   <<⇔  ≠   .  Ta có ( )1 ⇔ Phương trình 240mxx−+= vô nghiệm trên [ ]1;1 ⇔ Phương trình 24 x m x + = vô nghiệm trên [ ] { }1;1\0 Xét hàm số () [] {} 24 ,1;1\0 x gxx x + =∀∈− () [] {} 2 8 0,1;1\0 4 x gxx xx =<∀∈− + Bảng biến thiên

Từ bảng biến thiên suy ra điều kiện phương trình 24 x m x + = vô nghiệm trên

[] {}1;1\0 ⇔ 2325 m −<< . Do m nguyên nên {} 3;2;1;0;1;2;3;4 m ∈−−− .  Để giải () 2 trước hết ta đi tìm điều kiện để [] () 1;1 min1 x fx ∈− = . Do ()01 f = nên [] ()() 1;1 min0 x fxf ∈− = , mà ()01;1 ∈− , suy ra x = 0 là điểm cực trị của hàm số ( )fx Đặt () () / 24 00 24 mxx hxh x −+ =  = + 3 2 m ⇔=− . Do đó với m nguyên thì (2) chắc chắn xảy ra.

Vậy {} 3;2;1;0;1;2;3;4 m ∈−−− thỏa mãn điều kiện ( )2 Kết luận: Có 8 giá trị nguyên của m thỏa mãn yêu cầu. Câu20. (Chuyên Sơn La - 2020) Gọi S là tập hợp những giá trị của tham số m để giá trị lớn nhất của hàm số 3 ()12 fxxxm =−+ trên đoạn [1;3] bằng 12 .Tổng tất cả các phần tử của tập S bằng A. 25. B. 4. C. 15. D. 21. Lờigiải ChọnA

Xét hàm số 3 2 ()12(13)'()31202,2 gxxxmxgxxxx =−+≤≤=−=⇔==− (1)11,(2)16,(3)9 gmgmgm =−=−=−

Suy ra [1;3] max(){16;9} fxmm=−− Giả sử 161228,4mmm −=⇔== thử lại ta thấy 4 m = nhận. Giả sử 91221,3mmm−=⇔==− thử lại ta thấy 21 m = nhận. Vậy 4 m = và 21 m = .

Câu21. (Chuyên Thái Nguyên - 2020) Gọi 0S là tập tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số 42 1 1448 4 yxxxm =−++ trên đoạn [] 2;4 không vượt quá 30 . Số phần tử của S là A. 50 B. 49 C. 66 D. 73 Lờigiải ChọnB Xét hàm số () 42 1 1448 4 fxxxxm =−++ ( ) 3 2848fxxx ′ =−+

() ( ) () ()

6 04 2

xktm fxxtm xtm

=−   ′ =⇔=   =  ( ) ( ) 244;432fmfm =+=+ [] ( ) [] ( ) 2;4 2;4 min32;max4 fxmfxm  =+=+ [] { } 2;4 maxmax44;32 ymm  =++ .

Để giá trị lớn nhất của hàm số 42 1 1448 4 yxxxm =−++ trên đoạn [ ]2;4 không vượt quá 30 thì 4430 7414 6214 622 3230 m m m m m  +≤ −≤≤−  ⇔⇔−≤≤−−≤≤− +≤    .

Câu22. (Đại Học Hà Tĩnh - 2020) Có bao nhiêu giá trị của tham số m để giá trị nhỏ nhất của ham số ( ) 2 e4exx fxm =−+ trên đoạn [ ]0;ln4 bằng 6? A. 3 B. 4 C. 2 D. 1 Lờigiải ChọnC

Đặt e x t = , vì [ ]0;ln4 x ∈ [ ]1;4 t  ∈ Khi đó yêu cầu bài toán trở thành tìm m để giá trị nhỏ nhất của hàm số ( ) 2 4 ftttm =−+ trên đoạn [ ]1;4 bằng 6. Đặt 2 4 stt =− , vì [ ]1;4 t ∈ [ ]4;0 s  ∈− Xét hàm số ( ) gssm =+ với [ ]4;0 s ∈− suy ra hàm số ( )gs đồng biến trên đoạn [ ]4;0

Khi đó giá trị nhỏ nhất của ( ) fssm =+ , [ ]4;0 s ∈− chỉ đạt tại các đầu mút.

 =−=   >−  

fsm mm

TH1: [] ( ) 4;0 min46 4

 =   =− ⇔⇔=   >−  thỏa mãn.

m m m mm

10 2 10 4

TH2: [] ( ) 4;0 min6 4

fsm mm

 ==   <−  

m m m mm

6 6 6 4

 =   =− ⇔⇔=−   >−  thỏa mãn.

Vậy có 2 giá trị của tham số m thỏa mãn yêu cầu bài toán. Câu23. (Đặng Thúc Hứa - Nghệ An - 2020) Gọi S là tập tất cả các giá trị nguyên của tham số m sao cho giá trị lớn nhất của hàm số 3 1 910 3 yxxm=−++ trên đoạn [ ]0;3 không vượt quá 12 . Tổng giá trị các phần tử của S bằng bao nhiêu? A. 7 . B. 0 . C. 3. D. 12 . Lờigiải ChọnA

Xét hàm số () 3 1 910 3 gxxxm=−++ . Dễ thấy hàm số ()gx liên tục trên đoạn [ ]0;3

=  ′ =⇔  =−∉ 

Ta có ( ) 2 9 gxx ′ =− ; () [] 3 0 30;3 x gx x

Theo yêu cầu bài toán, [][] ( ) 0;30;3 maxmax12 ygx=≤ ( ) () 012 312 g g

 ≤  ⇔  ≤   1012 812 m m  +≤  ⇔  −≤   42 m ⇔−≤≤

Mà m∈ℤ nên { }4;3;2;1;0;1;2 m ∈−−−− Vậy tổng các phần tử của S là 7 Câu24. (Đô Lương 4- Nghệ An-2020) Gọi S là tập tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số 42 1 144830 4 yxxxm =−++− trên đoạn [ ]0;2 không vượt quá 30 . Tổng tất cả các giá trị của S là A. 180. B. 136. C. 120 D. 210 . Lờigiải ChọnB

Có [] ( ) ( ) [ ] 0;3 max6060,0;3 fxfxx =⇔≤∀∈ và [ ] 0 0;3 x ∃∈ sao cho ( ) 0 60. fx =

Có ( ) 3 3 6021559602155609 fxxxmxxxmx ≤⇔−+−+≤⇔−+−≤− [ ] 3 33 9602155609224552665,0;3. xxxmxxxmxxx ⇔−≤−+−≤−⇔−+−≤≤−++∀∈ Có [ ] 3 266529,0;3 xxx −++≥∀∈ nên [ ] 3 2665,0;329.mxxxm ≤−++∀∈⇔≤

Tương tự 3 2245523 xx −+−≤− nên [ ] 3 22455,0;323. xxmxm −+−≤∀∈⇔≥−

Vậy 2329 m −≤≤ thì ( ) [ ] 60,0;3.fxx≤∀∈

Để [ ] 0 0;3 x ∃∈ sao cho ( ) 0 60 fx = thì 3 3

22455 2665 xxm xxm −+−=  −++= có nghiệm trên [ ] 0;3.

Hay 29 23 m m ≥   ≤−  Vậy 29 23 m m

Xét 42 1 144830 4 uxxxm =−++− trên đoạn [ ]0;2 . [ ] [] [] 3 60;2 02848020;2 40;2

 =−∉  ′ =⇔−+=⇔=∈   =∉  .

x uxxx x

Khi đó [] ( ) { } { } 0;2 max umax(0),2max30,1414 uummm ==−+=+

Suy ra [] { } 0;2 max-30,14Maxymm =+ .

Trườnghợp1: [] 0;2 14 Maxym=+ 22 1430 1430 1430 301430 mm mm m m   +≥− +≥−  ⇔  +≤ −≤+≤     88704 4416 m m ≥  ⇔ −≤≤ 8 4416 m m ≥  ⇔ −≤≤ 816 m ⇔≤≤ , mà m∈ ℤ { }8;9;10;...;16 m ⇔∈ .

Trườnghợp2: [] 0;2 -30 Maxym = 22 3014 1430 3030 303030 mm mm m m   −≥+ +≤−  ⇔  −≤ −≤−≤     88704 060 m m ≤  ⇔  ≤≤  8 060 m m ≤  ⇔  ≤≤  08 m ⇔≤≤ , mà m∈ℤ { }0;1;2;...;8 m ⇔∈ Vậy tổng các giá trị m thỏa mãn là: 012...16136 ++++= . Câu25. (Liên trường Nghệ An - 2020) Biết giá

i ChọnC

=   =−  thì [] ( ) 0;3 max60. fx = Khi đó tổng các giá trị của m là 29236. −= Câu26. (Lý Nhân Tông - Bắc Ninh - 2020) Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số 3 3 yxxm =−+ trên đoạn [ ]0;2 bằng 3 . Số phần tử của S là A. 2. B. 6. C. 1. D. 0. Lờigiải ChọnA

Xét hàm số 3 ()3 gxxxm =−+ , ta có [ ] [] 2 10;2 '()330 10;2 x gxx x

 =−∉ =−=⇔  =∈   . ( )0 gm = , ( ) 12gm=− , ( ) 22gm=+ .

Vậy giá trị lớn nhất của hàm số ( ) 3 3 fxxxm =−+ bằng max của { } ;2;2Fmmm =−+

TH1: 3 3. 3 m m m

=  =⇔  =− 

Với { }33;1;5mF =  = loại vì max bằng 5. Với { }33;5;1mF =−  = loại vì max bằng 5.

TH2: 5 23. 1 m m m

=  −=⇔  =− 

Với { }55;3;7mF =  = loại vì max bằng 7.

Với { }11;3;1mF =−  = có max bẳng 3. Chọn 1. m =−

TH3: 1 23. 5 m m m

=  +=⇔  =− 

Với { }11;1;3mF =  = có max bằng 3. Chọn 1. m = Với { }55;7;3mF =−  = loại vì max bẳng 7.

Vậy { }1;1 S =−  có 2 giá trị m thoả mãn yêu cầu đề bài.

Câu27. (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số ( ) 432 2 =−++ fxxxxm ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho [] ( ) [] ( ) 1;2 1;2 minmax10 +=fxfx . Số phần tử của S là?

A. 2 . B. 3 . C. 5 . D. 1. Lờigiải ChọnA

16

Đặt ()()43232

x gxxxxmgxxxxx x

=    ′ =−++  =−+=⇔=   = 

0 1 24620 2 1

Bảng biến thiên của hàm ( )gx

Dựa vào bảng biến thiên của ( )gx ta suy ra bảng biến thiên của ()() 432 2 ==−++ fxgxxxxm . Ta có các trường hợp sau:

Trường hợp 1: 0 ≥ m . Bảng biến thiên của ()() 432 2 ==−++ fxgxxxxm

Dựa vào bảng biến thiên ta có [] ( ) [] ( ) 1;2 1;2 minmax104103 +=⇔++=⇔= fxfxmmm (TM)

Trường hợp 2: 11 00 1616 <<+⇔−<< mmm . Bảng biến thiên:

Dựa vào bảng biến thiên ta có [] () [] () 1;2 1;2 minmax1004106 +=⇔++=⇔= fxfxmm (Loại)

Trường hợp 3: 11 0 1616 +=⇔=−mm . Tương tự ta có: [] () [] () 1;2 1;2 minmax1004106 +=⇔++=⇔= fxfxmm (Loại) Trường hợp 4: 11 044 1616 +<<+⇔−<<− mmm . Bảng biến thiên:

Dụa vào bảng biến thiên ta có [] () [] () [] () [] () () 1;2 1;2 1;2 1;2

minmax10 0410 6 010 10 minmax10

fxfx

fxfx

Trường hợp 5: 404 +=⇔=−mm . Ta có: [] () [] () 1;2 1;2 minmax1001010 +=⇔−=⇔=− fxfxmm (Loại)

m m m m

+=  ++=  =   ⇔⇔    +−= =− +=    

Trường hợp 6: 404 +<⇔<−mm . Ta có: [] () [] () 1;2 1;2 minmax104107 fxfxmmm +=⇔−−−=⇔=− (Thỏa mãn)

Vậy { }7;3 m ∈−

(Loại)

Câu28. (Hải Hậu- Nam Định -2020) Có tất cả bao nhiêu giá trị nguyên dương của tham số m để hàm số 2248 () 2 mxx fx x −+ = + có giá trị nhỏ nhất trên đoạn [] 1;1 là a thỏa mãn 01. a <<

A. 3. B. 4. C. 5. D. 2. Lờigiải Chọn D. Đặt [] 2,1;11;3txxt  =+∈−  ∈  ; 2 2. xt=−

Hàm số đã cho trở thành 2 24t4 () mtm gt t = Xét hàm 2 24t4 () mtm ht t = trên đoạn 1;3  

Ta có 2 2 2(2) '() mt ht t + =

Th1: 0 m = thì ()4()41;34 htgtta  =−  =∀∈  =  (loại).

Th2: 0 m ≠ thì hàm số ()ht đồng biến hoặc nghịch biến trên 1;3  

Ta có 243 (1)24;(3) 3 m hmh=−−=

Nếu 2 (1).h(3)0 23 m h m

≤−  ≤⇔  ≥  và hàm số ()ht liên tục trên đoạn 1;3   suy ra đồ thị hàm số ()ht trên đoạn 1;3   cắt trục hoành 0 a  = (loại).

Nếu (1).h(3)0223 hm>⇔−<< . Khi đó, () (1)0;30hh<< 243 3 m a  = . Suy ra 3 4 m m

=   =  là các giá trị nguyên dương để 01 a <<

(Lương Thế Vinh - Hà Nội - 2020) Cho hàm số 4223 yxxm =−+ với m là tham số. Biết

rằng có đúng hai giá trị 12 , mm của m để giá trị nhỏ nhất của hàm số đã cho trên [] 1;2 bằng

2021. Tính giá trị 12mm A. 1 3 B. 4052 3 C. 8 3 D. 4051 3 Lờigiải ChọnD

Khi đó: [] ( ) [] ( ) ( ) 1;4 1;4 max3min331727 fxfxmmm ≤⇔−+≤−−⇔≤− .

+Nếu ( )( ) 3170173mmm −+<⇔−<< thì [] ( ) { } { } [] ( ) 1;4 1;4 maxmax17,3max17,30;min0 fxmmmmfx =+−=+−>=

Khi đó, không thỏa điều kiện [] ( ) [] ( ) 1;4 1;4 max3minfxfx ≤

=  ′ =⇔  =± 

Xét hàm số () 4223 fxxxm =−+ , ta có () ()32 4441fxxxxx ′ =−=− () 0 0 1 x fx x

Bảng biến thiên của hàm số trên [] 1;2 :

Vì [] 1;2 min2021 y =  phương trình () 0 fx = không có nghiệm thuộc [] 1;2

Trường hợp 1 : 1 310 3 mm−>⇔> . Ta có [] 1;2 min31312021 ymm=−=−= 2022 3 m ⇔=

Trường hợp 2 : 8 380 3 mm+<⇔<− . Ta có [] 1;2 min38382021 ymm=+=−−= 2029 3 m ⇔=− . Vậy 12 202220294051 333 mm−=+=

Câu30. (Thanh Chương 1 - Nghệ An - 2020) Cho hàm số () 3231fxxxm=−++ ( m là tham số thực). Gọi S là tập hợp tất cả các giá trị nguyên của m thuộc đoạn [ ]2020;2020 sao cho [] () [] () 1;4 1;4 max3minfxfx ≤ . Số phần tử của S là A. 4003 B. 4002 C. 4004 D. 4001 Lờigiải ChọnB Xét hàm số ()() 32 2 3136 yfxxxmyfxxx ′′ ==−++ 

Do đó: 27 13 m m ≤−   ≥  kết hợp với [ ]2020;2020 m ∈− ta có [ ] [ ]2020;2713;2020 m∈−−∪

Vậy 4002 giá trị nguyên của m cần tìm.

Câu31. (ChuyênLêQuý Đôn- ĐiệnBiên-2021) Cho hàm số () 2 2 xm fx x + = + ( m là tham số). Gọi S là

tập hợp tất cả các giá trị của m sao cho [] ( ) [] ( ) 1;3 1;3 maxmin2 fxfx+= . Số phần tử của S bằng A. 1. B. 0. C. 2 . D. 3 . Lờigiải ChọnC

Ta có () ()2 22 ,2 2 m fxx x ′ =∀≠− + .

Nếu ( ) 11,2mfxx =  =∀≠− , khi đó [] ( ) [] ( ) 1;3 1;3 maxmin1 fxfx== 1232 35 mm++ =+ .

Nếu 1 m ≠ ta có ( )fx là hàm số đơn điệu trên đoạn [ ]1;3 , () () 1232 1,3 35 ffmm ++ ==

+) Nếu ()() 31 1.30 22ffm≤⇔−≤≤− thì [] ( ) [] ( ) ( ) 1;3 1;3 min0,max1 fxfxf == hoặc

m ff m ⇔⇔

mm mm  +=−

thì [] ( ) [] ( ) 1;31;3 minmaxfxfx + ( ) ( )13ff=+

 ==−  ⇔   ==−   Kết hợp điều kiện xét thì không có giá trị m . +) Nếu ()() 1 2 1.30 3 2 

++



=−  

 >−  >⇔   <−   

1232 35 mm++ =+ . Do đó [] () [] () 1;3 1;3 1232 maxmin22 35 mm fxfx ++ +=⇔+= 3 2 1232 2 11 35 4 1 11) 2 1232 2 35 ( lo¹i do m mm m mm m mm  <−  

   =≠ >− 

igiải

Theo bài ra, ta có: ( ) () ()

Mab Mf MfMab MfMabab

 ≥−++ ≥−    ≥⇔≥++  ≥ ≥++=−−− 

1 1 339 1 221222

Suy ra: 4139222139222 Mabababababab ≥−++++++−−−≥−+++++−−− 482 MM ⇔≥⇔≥ . Điều kiện cần để 2 M = là 13912ababab −++=++=−−−= và 1 ab −++ , 39 ab++ , 1 ab cùng dấu 13912 13912 ababab ababab −++=++=−−−= ⇔ −++=++=−−−=− 2 1 a b =−  ⇔  =− 

Ngược lại, với 2 1 a b =−   =−  thì ( ) 2 21fxxx=−− .

Xét hàm số ( ) 2 21gxxx=−− trên đoạn [ ]1;3

Ta có: ( ) 22gxx ′ =− ; ( ) 01gxx ′ =⇔= [ ]1;3∈− Do M là giá trị lớn nhất của hàm số ( )fx trên đoạn [ ]1;3 nên () () () { } max1;3;12Mggg=−= .

Từ đó suy ra với 2 1 a b =−   =−  thỏa mãn yêu cầu bài toán. Vậy 24ab+=−

Câu34. (Trung Tâm Thanh Tường -2021) Cho hàm số ( ) 3 15212 fxxxmxm =−++− . Giá trị nhỏ nhất của [] ( ) 2;3 max Mfx = bằng A. 36 . B. 9 C. 25 D. 27 . Lờigiải ChọnB Đặt [] ( ) 2;3 max afx = Ta có ( ) [ ],2;3fxax≤∀∈− và điều kiện [ ]120,2;3amxx +−≥∀∈−

Xét hàm () 3 3 hxxxm =−+ trên đoạn [] 2;3

Ta có () 2 '33hxx=− BBT của hàm ()hx

≥−   ⇔≥+   ≥− 

am am am

Hệ () 543 *18 36

Trường hợp 1: min18 am=+ nếu 18543436 9 1836218 mmm m mmm +≤−≤ ⇔⇔≤+≤−≤

Trường hợp 2: min36am =− nếu 36543218 9 3618218 mmm m mmm −≤−≤ ⇔⇔=−≤+≥

Trường hợp 3: min543am =− nếu 543369 9 543189 mmm m mmm −≤−≥ ⇔⇔≥−≤+≥

Vậy giá trị nhỏ nhất của [] () 2;3 max Mfx = bằng 27

Ta có bảng biến thiên của hàm số ()ygx = :

A. ( )2 f ; ( )5 f . B. ( )0 f ; ( )5 f . C. ( )2 f ; ( )0 f . D. ( )1 f ; ( )5 f . Lờigiải

Dựa vào đồ thị hàm số ()fx ′ ta có bảng biến thiên.

max24 yf   

=−

Từ bảng biến thiên ta có: trên 3 ;2 2    hàm số ()()24 gxfxx =− đạt giá trị lớn nhất tại 1 x = và () 3;1 2

Câu2. Cho hàm số ()yfx = xác định và liên tục trên ℝ , đồ thị của hàm số ()yfx ′ = như hình vẽ

Giá trị lớn nhất của hàm số ( )yfx = trên đoạn [ ]1;2 là A. () 1 f B. () 1 f C. () 2 f D. () 0 f Lờigiải () 1 01 2

=−   ′ =⇔=   =  .

x fxx x

Từ đồ thị hàm ()yfx ′ = ta có bảng biến thiên

Từ đó suy ra giá trị lớn nhất của hàm số trên [] 1;2 là () 1 f .

Câu3. Cho hàm số ()yfx = có đạo hàm là hàm ()fx ′ Đồ thị của hàm số ()yfx ′ = được cho như hình vẽ. Biết rằng ()()()() 0325ffff +=+ . Giá trị nhỏ nhất, giá trị lớn nhất của ()yfx = trên đoạn [] 0;5 lần lượt là:

fxf ff

Khi đó: ( ) [] ( ) ()() 0;5 min2 32

=     >  , mà ()()()() 0325ffff +=+ ()()()() 0225ffff  +<+ ()() 05ff  < . Vậy giá trị nhỏ nhất, giá trị lớn nhất của ( )yfx = trên đoạn [ ]0;5 lần lượt là: ( )2 f ; ( )5 f .

Câu4. Cho hàm số ()fx có đạo hàm là ()fx ′ Đồ thị của hàm số ()yfx ′ = được cho như hình vẽ bên. Biết rằng ()()()()() 012354 fffff +−=− . Tìm giá trị nhỏ nhất m và giá trị lớn nhất M của ()fx trên đoạn [] 0;5 .

A. ()() 5,3mfMf == B. ()() 5,1mfMf == C. ()() 0,3mfMf == D. ()() 1,3mfMf == Lờigiải ChọnA Từ đồ thị ta có bảng biến thiên của ()fx trên đoạn [] 0;5

() 3 Mf  = và ()()()() 13,43ffff << ()()()()()()()()() 5013430505 ffffffffmf −=−+−<  <  =

Câu5. Cho hàm số ()yfx = có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số

() ()23211 438 33gxfxxxxx =−+−++ trên đoạn [] 1;3 .

A. 15. B. 25 3 C. 19 3 D. 12. Lờigiải ()() ()22 42468gxxfxxxx ′′ =−−+−+ () () 2 2244xfxxx  ′ =−−+− Với [] 1;3 x ∈ thì 40 x −> ; 2 344 xx ≤−≤ nên () 2 40fxx ′ −> .

Suy ra () 2 2440 fxxx ′ −+−> , [] 1;3 x ∀∈ . Bảng biến thiên

Suy ra [] ()() 1;3 max2 gxg = ()4712 f =+=

Câu6. Cho hàm số ()yfx = liên tục trên .ℝ Đồ thị của hàm số ()yfx ′ = như hình bên. Đặt ()()()2 21.gxfxx=−+ Mệnh đề dưới đây đúng.

v

=−   ′′ =⇔=+⇔=

Dựa vào bảng biến thiên suy ra [] ()() 3;3 max1. gxg =

Câu7. Cho hàm số có đạo hàm cấp hai trên . Biết , và bảng xét dấu của như sau: Hàm số đạt giá trị nhỏ nhất tại điểm thuộc khoảng nào sau đây? A. () ;2017−∞− B. () 2017; +∞ C. () 0;2 D. () 2017;0 Lờigiải Dựa vào bảng xét dấu của ( )fx ′′ ta có bảng biến thiên của hàm sồ ( )fx ′

Đặt 2017 tx=+

Ta có ( ) ( ) ( ) 2017201820182017.2018 yfxxfttgt =++=+−= ()() 2018 gtft ′′ =+ .

Dựa vào bảng biến thiên của hàm số ( )fx ′ suy ra phương trình ( ) gt ′ có một nghiệm đơn () ;0 α∈−∞ và một nghiệm kép 2 t = .

Ta có bảng biến thiên ( ) gt Hàm số ()gt đạt giá trị nhỏ nhất tại () 0 ;0 t α =∈−∞ Suy ra hàm số đạt giá trị nhỏ nhất tại 0x mà ()()002017;0;2017xx+∈−∞⇔∈−∞−

( )yfx = ℝ ( ) 03 f ′ = ( ) 22018 f ′ =− ( )fx ′′ ( ) 20172018 yfxx =++ 0x ( ) 20172018 yfxx =++

Câu8. Cho hàm số ()fx có đạo hàm là ()fx ′ Đồ thị của hàm số ()yfx ′ = được cho như hình vẽ dưới đây:

x gxfxxx x   =  Và với ()()();3:10xfxxgx ′′ ∈−∞−<+  < với ( ) ( ) ( ) 3;1:10xfxxgx ′′ ∈−>+  > , với ()()() 1;3:10xfxxgx ′′ ∈<+  < Trang 28

Biết rằng ()()()() 1012ffff −+<+ . Giá trị nhỏ nhất và giá trị lớn nhất của hàm số ()yfx = trên đoạn [ ]1;2 lần lượt là:

A. () 1 f ; () 2 f . B. () 2 f ; () 0 f . C. () 0 f ; () 2 f . D. () 1 f ; () 1 f . Lờigiải

Từ đồ thị của hàm số ( )yfx ′ = ta có bảng biến thiên của hàm số ( )yfx = trên đoạn [ ]1;2 như sau

Hàm số ()yfx = đạt giá trị nhỏ nhất trên đoạn 7 0; 2    tại điểm 0x nào dưới đây?

A. 0 0 x = . B. 0 7 2 x = . C. 0 1 x = . D. 0 3 x = . Lờigiải ChọnD Dựa vào đồ thị hàm số ()' yfx = ta có bảng biến thiên trên đoạn 7 0; 2    như sau:

Nhận thấy  [] ()() 1;2 min1 fxf = .

 Để tìm [] () 1;2 max fx ta so sánh () 1 f và () 2 f .

Theo giả thiết, ()()()()()()()() 10122101 ffffffff −+<+⇔−−>−

Từ bảng biến thiên, ta có ( ) ( ) 010ff−> . Do đó ( ) ( ) ( ) ( )21021 ffff−−>⇔>−

Hay [] ()() 1;2 max2 fxf = .

Câu9. Cho hàm số ()yfx = liên tục trên đoạn 7 0; 2    có đồ thị hàm số ()' yfx = như hình vẽ.

Do đó hàm số đạt giá trị nhỏ nhất tại 0 3 x = .

Câu10. Cho hàm số ()yfx = Đồ thị hàm ()yfx ′ = như hình vẽ

Đặt ()() 3 33 hxfxxx =−+ . Tìm mệnh đề đúng trong các mệnh đề sau: A. () [3;3] max()31 hxf = . B. ( ) [3;3] max()33 hxf=− . C. () [3;3] max()33 hxf = D. () [3;3] max()30 hxf = Lờigiải ChọnB

Ta có: ()() 2 333hxfxx ′′ =−+ ()() () 2 31hxfxx′′ ⇔=−− .

Đồ thị hàmsố 2 1 yx=− làmột parabol có toạ độ đỉnh () 0;1 C , điqua () 3;2 A , () 3;2 B .

Từ đồ thị hai hàm số ()yfx ′ = và 2 1 yx=− tacó bảng biếnthiên củahàmsố ()yhx =

 Trên khoảng () 3;1 đồ thị hàm số ()fx ′ nằm phía dưới () P nên () () 2 33 0 22 fxxxgx  ′′ <+−  <    Trên khoảng () 1;1 đồ thị hàm số ()fx ′ nằm phía trên () P nên () () 2 33 0 22 fxxxgx  ′′ >+−  >   .

 Trên khoảng () 1; +∞ đồ thị hàm số ()fx ′ nằm phía dưới () P nên () () 2 33 0 22 fxxxgx  ′′ <+−  <  

Bảng biến thiên

Với () ()333hf−=− , () ()333hf =

Vậy () [3;3] max()33 hxf=− . Câu11. Cho hàm số ()yfx = có đồ thị ()yfx ′ = ở hình vẽ bên. Xét hàm số ()() 32 133 2018, 342 gxfxxxx =−−++ mệnh đề nào dưới đây đúng? A. [] ()() 3;1 min1 gxg=− B. [] () ()() 3;1

31 min 2 gg gx −+ = C. [] ()() 3;1 min3 gxg=− D. [] ()() 3;1 min1 gxg = Lờigiải ChọnA

Ta có ()() () 223333 2222gxfxxxfxxx ′′′ =−−+=−+−  .

Vẽ parabol () 2 33 : 22Pyxx=+− . Ta thấy () P đi qua các điểm có toạ độ () 3;3 , () 1;2 , () 1;1

Trang 31

Từ bảng biến thiên, ta có [] ()() 3;1 min1 gxg=− .

Câu12. Cho hàm số ()yfx = có đạo hàm liên tục trên R . Hàm số ()' yfx = có đồ thị như hình sau:

Cho bốn mệnh đề sau:

1) Hàm số ()yfx = có hai cực trị 2) Hàm số ( )yfx = đồng biến trên khoảng ( ) 1; +∞ 3) ()()() 124.fff >>

4) Trên đoạn [] 1;4 , giá trị lớn nhất của hàm số ()yfx = là ()1. f Số mệnh đề đúng trong bốn mệnh đề trên là: A. 3. B. 1. C. 4. D. 2. Lờigiải ChọnD Dựa vào đồ thị của hàm số ( ) ' yfx = ta thấy: () 1 '01 4

x fxx x

=−   =⇔=   = 

()()() '0;11;4fxx<⇔∈−∞−∪

()()() '01;14;fxx>⇔∈−∪+∞ Ta có bảng biến thiên của hàm số ( )yfx =

Dựa vào bảng biến thiên đáp án đúng là mệnh đề số 3 và 4

Câu13. Cho hàm số ()yfx = có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số () ()23211 438 33gxfxxxxx =−+−++ trên đoạn []1;3.

A. 25 . 3 B. 15. C. 19 . 3 D. 12. Lờigiải ChọnD

Ta thấy [] 1;1 x ∀∈− ta có ( ) ( ) () 2 20 sin0sin0 fxf x

Dấu “=” xảy ra khi 0 x =

 ≤   −≤=  , do đó ()()() 00gxgf ≤=

Câu15. Cho hàm số ()yfx = liên tục trên ℝ sao cho [] () 1;2 max3 fx = . Xét hàm số ()() 31 gxfxm =−+ .

Tìm tất cả các giá trị của tham số m để [] () 0;1 max10 gx =− A. 13 B. 7 C. 13 D. 1 Lờigiải ChọnC Đặt 31ux=− ()() gxfum  =+ [][] 0;11;2xu ∈  ∈− . Do ()fx liên tục trên ℝ nên [] () [] () () [] () 0;11;21;2 maxmaxmax3 gxfumfumm =+=+=+ . Để [] () 0;1 max1013 gxm=⇔=−

Câu16. Cho hàm số ()yfx = có đạo hàm cấp 2 trên ℝ , hàm số ()yfx ′ = có đồ thị như hình vẽ bên.

Ta có () () () 22 2 4 4.(42x)x6822(4) 2 x gxfxxxxfxx  ′′ ′ =−−+−+=−−+   Xét thấy [] 22 1;3344(4)0xxxfxx ′ ∀∈⇒≤−≤⇒−> Mặt khác 4 0 2 x > [] 1;3 x ∀∈ Suy ra ( ) 02gxx ′ =⇔= ()1(3)(4)519171732 3333 19191934 (3)(3)(4)5 3333 (2)5712.

=+<+=+= =+<+=+= =+= ()()() 132ggg⇒<< Vậy [] () 1;3 max12 gx = tại 2. x =

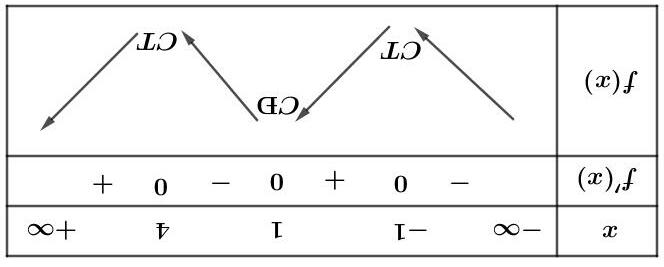
gff gff g

Câu14. Cho hàm số ()yfx = . Hàm số ()yfx ′ = có bảng biến thiên như hình vẽ bên. Giá trị lớn nhất của hàm số ( ) ( ) 2 2sin gxfxx =− trên đoạn [] 1;1 là

A. () 1 f B. () 0 f C. () 2 f D. () 1 f Lờigiải ChọnB Ta có [][] 1;122;2xx ∈−  ∈− Từ bảng biến thiên của ()' yfx = thì bảng biến thiên ()yfx = như sau:

() 02hxx ′ =⇔=

Từ đồ thị ta có bảng biến thiên:

Và ( ) ( ) ( ) ( )0606ffgg −<− ( ) ( ) ( ) ( )0066fgfg ⇔−<− Hay ()() 06hh < Vậy [] ()() 0;6 max6 hxh = ; [] ()() 0;6 min2 hxh = .

Câu19. (ChuyênLàoCai-2020) Cho hàm số ()fx liên tục trên ℝ , có đồ thị như hình vẽ

max1ftm ∈ =++ (với 3 txx =+ và [] 2 0;2 max21 x xxmm ∈  −++=+  ). [] () 0;10 max1415 x fxmmm ∈ ≤++=++=+

Suy ra: [] () 0;2

x gxmx t ∈

=  =+⇔⇔=  = 

1 max51 2 x

Theo giả thiết, ta có: [] () 0;2 max8583 x gxmm ∈ =⇔+=⇔= Câu18. Cho hai hàm số ( )yfx = , ( )ygx = có đạo hàm là ( )fx ′ , ( )gx ′ . Đồ thị hàm số ( )yfx ′ = và ()gx ′ được cho như hình vẽ bên dưới.

Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số 2 8 1 1 x yfm x  =+−  +  có giá trị lớn nhất không vượt quá 2020 ? A. 4029 . B. 4035. C. 4031. D. 4041. Lờigiải ChọnC Đặt 2 8 1 x t x = + . Ta có: () 2 2 2

88 1 x t x −+ ′ = + ; 01tx ′ =⇔=±

Biết rằng ()()()() 0606ffgg −<− . Giá trị lớn nhất, giá trị nhỏ nhất của hàm số ()()() hxfxgx =− trên đoạn [] 0;6 lần lượt là: A. ( )6 h , ( )2 h B. ( )2 h , ( )6 h C. ( )0 h , ( )2 h D. ( )2 h , ( )0 h Lờigiải Ta có ()()() hxfxgx ′′′ =−

t t t

44;4 24;4 24;4

 =−∈−  ⇔=−∈−   =∈−  Ta có: ()40,810,2hmm −≈+−=− ; ( ) 4615hmm=+−=+ ; ()21,610,6hmm −≈+−=+ ; ( ) 2415hmm=−+−=− [] () 4;4 MaxMaxyht = ℝ {} Max5;5 mm =+− Yêu cầu bài toán 52020 52020 m m  +≤  ⇔  −≤   202052020 202052020 m m −≤+≤ ⇔ −≤−≤ 20252015 20152025 m m −≤≤ ⇔ −≤≤ 20152015 m ⇔−≤≤ . Vậy có tất cả 4031 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. Câu20. (Sở HưngYên-2020) Cho hàm số ()yfx = liên tục trên ℝ có đồ thị ()yfx ′ = như hình bên. Đặt ()()()2 21gxfxx=−−

()()00htft ′′ =⇔= [] [] []

Khi đó ()ygx = đạt giá trị nhỏ nhất trên đoạn [] 3;3 tại A. 3 x =− . B. 3 x = . C. 0 x = . D. 1 x = . Lờigiải. ChọnA Ta có ()()()()()() () 2 2121 gxfxxgxfxx ′′ =−−  =−− . Vẽ đồ thị hàm số 1 yx=− trên cùng hệ trục tọa độ với đồ thị hàm số ()yfx ′ =

Dựa vào đồ thị ta thấy + ()()()()()() 1 3 3 1 013;013dd gxxgggxxgg ′′ >  >−<  >  . Do đó ()ygx = đạt giá trị nhỏ

nhất trên đoạn [ ]3;3 tại 3 x = hoặc 3 x =− + Phần hình phẳng giới hạn bởi ();1;3;1yfxyxxx ′ ==−=−= có diện tích lớn hơn phần hình phẳng giới hạn bởi ();1;1;3yfxyxxx ′ ==−== nên () () ()() 13 31 33 dd gxxgxxgg ′′ >  >− 

Vậy ()ygx = đạt giá trị nhỏ nhất trên đoạn [] 3;3 tại 3 x =− .

Câu21. (KimLiên-HàNội-2020) Cho hàm số ()fx . Biết hàm số ()fx ′ có đồ thị như hình dưới đây. Trên [] 4;3 , hàm số ()()()2 21 gxfxx =+− đạt giá trị nhỏ nhất tại điểm

A. 3 x =− B. 4 x =− C. 3 x = D. 1 x =− Lờigiải ChọnD Xét hàm số ()()()2 21 gxfxx =+− trên [] 4;3 Ta có: ( ) ( ) ( ) 221 gxfxx ′′ =−− ()()01 gxfxx ′′ =⇔=− . Trên đồ thị hàm số ()fx ′ ta vẽ thêm đường thẳng 1 yx =−

()03 f ′ = , ()22020 f ′ =− , () lim x fx →−∞

′ =−∞ và bảng xét dấu của ()fx

Hàm số ()20192020 yfxx =++ đạt giá trị nhỏ nhất tại điểm 0x thuộc khoảng nào sau đây?

x fxxx x

Từ đồ thị ta thấy () 4 11 3

=−   ′ =−⇔=−   = 

Bảng biến thiên của hàm số ()gx như sau:

Vậy [] ()() 4;3 min11 gxgx=−⇔=− .

Câu22. (Yên Lạc 2 - Vĩnh Phúc - 2020) Cho hàm số ()yfx = có đạo hàm cấp hai trên ℝ . Biết ()()() 03,220180fff ′′′ ==−= , và bảng xét dấu của ()fx ′′ như sau

Hàm số () 12018 yfx=−− đạt giá trị nhỏ nhất tại 0x thuộc khoảng nào sau đây?

A. () ;2015−∞− . B. () 1;3 . C. () 1009;2 . D. () 2015;1 . Lờigiải. ChọnC

Từ bảng xét dấu của ()fx ′′ và giả thiết ()()() 03,220180fff ′′′ ==−= suy ra bảng biến thiên của hàm số ( )yfx ′ = như sau

A. ( );2019−∞− . B. ( )0;2 . C. ( )2019;0 . D. ( ) 2019; +∞ . Lờigiải ChọnA Theo giả thiết ta có

Ta có ()20192020 yfx ′′ =++ () 020192020yfx ′′  =⇔+=−

Từ bảng biến thiên trên ta có 20192019 0 201922017 xaxa y xx +==− ′ =⇔⇔ +==− , với 0 a < .

Từ đó ta có bảng biến thiên của hàm số ()20192020 yfxx =++

Từ bảng biến thiên có hàm số ( ) 20192020 yfxx =++ đạt giá trị nhỏ nhất tại 0 2019 xa=− . Vì 0 a < nên () 0 ;2019 x ∈−∞− .

Câu24. (Chuyên Thoại Ngọc Hầu - An Giang - 2021) Cho hai hàm số () 32 fxxaxbxc =+++ và () 2 4 gxx x =+ . Trên đoạn [] 1;4 , hai hàm số ()fx và ()gx có cùng giá trị nhỏ nhất và đạt tại cùng một điểm. Biết rằng điểm ( )1;4 A thuộc đồ thị của hàm số ( )fx . Tìm giá trị lớn nhất của hàm số ()fx trên đoạn [] 1;4 A. [] () 1;4 max9 fx = . B. [] () 1;4 max23 fx = . C. [] () 1;4 max11 fx = . D. [] () 1;4 max19 fx = . Lờigiải ChọnC Ta có: ()() 2 3 8 32;1fxxaxbgx x ′′ =++=− Xét () 3 8 0102gxx x ′ =⇔−=⇔= Ta có: ()()() [] () 1;4

17 15;23;4min3 4 ggggx ===  = tại 2 x = .

Trang ′′ như hình sau:

[] 1;1 bằng 11 ? 2 A. 2 . B. 4 . C. 3 . D. 5 . Lờigiải ChọnB

Ta có ()() gxgx −= nên ()gx chẵn hay đồ thị của hàm số ()ygx = đối xứng qua trục tung. [][][] () () [] () () 3 3 1;10;10;1 0;1 max()max()max3max3. gxgxfxxfmfxxfm   ==++=++ 

Xét hàm số () 3 3 yfxx =+ trên [] 0;1 . Đặt [] [] 3 [0;1]0;4 30;4maxmax()3.txxtyft =+  ∈  == Khi đó [] () 1;1

115 max()3(). 22gxfmfm=+=⇔= Vậy có 4 giá trị m thỏa mãn yêu cầu bài toán.

Câu26. (THPT Hậu Lộc 4 - Thanh Hóa - 2021) Cho hàm số ( ) 32()ln1 fxaxbxcxx =+−++ với ,, abc là các số thực dương, biết (1)3,(5)2ff=−= . Xét hàm số ()3(32)2(32) gtftftm =−+−+ , gọi S là tập hợp tất cả các giá trị thực của m sao cho [] 1;1 max()10 gt = . Số phần tử của S là A. 1 B. 2 C. 3 D. 4 Lờigiải

Xét hàm số ()32()ln1 fxaxbxcxx =+−++ xác định trên ℝ

Ta có () () 323 2

1 ln1ln 1 fxaxbxcxxaxbxc xx

−=−−−−++=−−−  ++ 

( ) () 32 ln1 axbxcxxfx =−−+++=− , suy ra ( )fx là hàm số lẻ (5)(5)ff  −=−

Mặt khác ta lại có: () 2 2 3 1 c fxaxb x ′ =+− +

Xét hàm số ()3(32)2(32) htftftm =−+−+ , có '()6'(32)6'(32) hxftft =−−+−

11 '()6'(32)'(32)63(32)(32) 1(32)1(32) htftftattc tt

      =−−−=−−−+−     +−+−    

[] 22 22

( ) ( ) 2222 61(32)1(32)31(32)1(32) ttattc  =+−−+−+−++−+   2222 32321 '()01(32)1(32)0(32)(32) 32231 ttt hxtttt ttt −=−= =⇔+−−+−=⇔−=−⇔⇔  −=−=−

Do (1)3(1)2(1)5(1)15;(1)3(5)2(5)(5)2 hfffhfff =+==−−=+−==

Do đó [] 1;1 max()2Agtm==+ , [] 1;1 min()15Bgtm==−

Ta có [] ( ) { } 1;1 maxmax15,2 gtmm =−+

Trườnghợp1: [] () 1;1

152 max15 mm gtm  −≥+   =−  

152 1510 mm m  −≥+  ⇔  −=   5 m ⇔=

Trườnghợp2: [] () 1;1

215 max2 mm gtm  +>−   =+  

215 210 mm m  +>−  ⇔  +=   8 m ⇔= .

Vậycó 2giá trị của tham số m thỏa mãn yêu cầu bài toán là 5,8mm==

Câu27. (THPT Lê Lợi - Thanh Hóa - 2021) Cho hàm số ( ) 2 242.yfxxx ==−− Gọi S là tổng tất cả các giá trị của tham số m để hàm số ( ) ( ) ( ) 2 2 ygxfxfxm ==−+ đạt giá trị lớn nhất trên đoạn [ ]1;3 bằng 15. Tổng S thuộc khoảng nàosau đây? A. ( ) 25;15. B. ( ) 14;1. D. ( ) 1;8. D. ( ) 8;12. Lờigiải ChọnA Xét hàm số ( ) 2 242yfxxx ==−− có ( ) ( ) ( ) 44;0114fxxfxxf ′′ =−=⇔=  =−

hàm số ( ) ( ) ( ) 2 2 hxfxfxm =−+ có ( ) ( ) ( ) 21hxfxfx ′′ =− 

Khi đó [] () 1;3 max24;Bhxm==+ [] () 1;3 min1.bhxm==−

Mà [] () 1;3 max1515 2 BbBb gx ++− =⇔= 2232530 m ⇔++= 9 14 m m =−  ⇔  =−  Vậy tổngcác giá trị của m là () 23.25;15.−∈−−

Câu28. (THPT Triệu Sơn - Thanh Hóa - 2021) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ. Khi đó hiệu của giá trị lớn nhất và giá trị nhỏ nhất của hàm số () 32 2 ()3log19151 hxfxxxx =−+−++ trên đoạn [] 1;4 bằng:

A. 54 B. 7 C. 33 D. 3 Lờigiải ChọnC

max()(1)4 min()(4)2 gxg gxg

+Xét hàm số () 2 ()log1 gxfx=− Đặt [] 2 log1,1;1txt=−∈− . Ta có: [] []

==    ==   (1)

1;4 1;4

Dựa vào đồ thị ta có bảng biến thiên Giá trị nhỏ nhất của hàm số ()()221gxfxx=−+ trên đoạn 1 ;1 2    bằng ()() 121gf=− .

max()(1)8 min()(4)19

+Xét hàm số 32 ()9151 kxxxx=−++ có [] []

1;4 1;4

kxk kxk

==    ==−   (2) Từ (1) và (2) ta có: [] [] [] [] 1;4 1;4 1;4 1;4

==    −=  ==−  

max()(1)20 min()(4)13max()min()33 hxh hxhx hxh

( )fx ℝ ( ) 0 gx ′ = 1. y =

y -2

2 O 1

x

x x x gxf xx

Câu30. Cho hàm số ()fx , đồ thị hàm số ()yfx ′ = là đường cong trong hình bên. Giá trị nhỏ nhất của hàm số () 2 x gxf  =   trên đoạn [] 5;3 bằng A. () 2 f B. () 1 f C. () 4 f D. () 2 f Lờigiải ChọnA () 2 4 1 2 00 2 22 1 2

 =−  =−  ′′ =⇔=⇔⇔    =    =  

. () 0024 22 xx gxfx ′′ <⇔<⇔<−⇔<−   . Bảng biến thiên

Giá trị nhỏ nhất củahàm số ()gx trên [] 5;3 bằng ()() 42gf−=− .

hàm

1 ;2 2    bằng

A. 1 2 f    B. ()03 f + C. ()16 f + D. ()312 f +

Lờigiải

ChọnC Đặt []210;3txt =−  ∈ , xét hàm số ()() 33htftt=++ trên [] 0;3 .

=   =⇔=   =  . ()()() //031;3hxfxx >⇔>−⇔∈ ()()() //030;1hxfxx <⇔<−⇔∈

Ta có bẳng biến thiên sau

t htt t

Ta có ()()// 3 hxfx=+ , () 0 01 2

Ta có [] ()()() 0;3 min116 hthf==+ .

Câu33. Cho hàm số () , fx đồ thị của hàm số ()yfx = là đường cong như hình vẽ. Giá trị nhỏ nhất của hàm số ()()2143gxfxx =+−− trên đoạn 3 ;1 2    bằng

A. () 0 f B. ()11 f −+ C. ()25 f D. ()13 f

Lờigiải

Ta thấy hàm số đạt giá trị lớn nhất tại [] 4;2 22max()(2)(2)2. txgxgf =  =−  =−=−

Câu35. Cho hàm số ()yfx = có đạo hàm trên ℝ và hàm số '()yfx = có đồ thị như hình vẽ. Trên

[] 2;4 , gọi 0x là điểm mà tại đó hàm số () 2 ()1ln816 2 x gxfxx  =+−++   đạt giá trị lớn nhất.

Khi đó 0x thuộc khoảng nào? A. 1 ;2 2    . B. 5 2; 2    . C. 1 1; 2    . D. 1 1; 2    . Lờigiải ChọnD Ta có 2 12812 '()'1'1. 22816224gxffxxx xxx +  =+−=+− +++ Cho 4 '()0'1. 24 x gxf x  =⇔+=  +  Đặt []10;3 2 x tt =+  ∈ Phương trình trở thành 42 '(). 221 ft tt == ++ Vẽ đồ thị 2 1 y x = + lên cùng một hệ tọa độ ta được:

Từ đồ thị ta thấy hàm số đạt giá trị lớn nhất tại 10.tx =  =

Câu36. Cho hàm số đa thức ()yfx = có đạo hàm trên ℝ . Biết rằng ()00 f = , () 319 3 24 ff  −==−   và đồ thị hàm số ()yfx ′ = có dạng như hình vẽ

Ta có bảng biến thiên như sau:

() 3 03;0; 2 hxx  ′ =⇔∈− 

Từ đó ta có bảng biến thiên của hàm số ()() gxhx = như sau

Vậy giá trị lớn nhất của ()gx trên 3 2; 2    là 29 2 .

Câu37. Cho ()fx là hàm số liên tục trên ℝ , có đạo hàm ()fx ′ như hình vẽ bên dưới. Hàm số () 2 2 x yfxx =+− có giá trị nhỏ nhất trên [] 0;1 là

Hàm số ()() 2 42 gxfxx =+ giá trị lớn nhất của ()gx trên 3 2; 2    là

A. 2 . B. 39 2 . C. 1. D. 29 2 . ChọnD Lờigiải

Xét hàm số ()() 2 42 hxfxx =+ xác định trên ℝ

Hàm số ()fx là hàm đa thức nên ()hx cũng là hàm đa thức và ()() 0402.00hf=+=

Khi đó ()()()() 440' hxfxxhxfxx ′′′ =+  =⇔=−

Dựa vào sự tương giao của đồ thị hàm số ()yfx ′ = và đường thẳng yx =− , ta có

A. () 0 f B. () 1 1 2 f + C. () 1 1 2 f D. 13 28 f    Lờigiải ChọnC

Đặt ()() 2 2 x hxfxx =+− . Ta có ()() 1 hxfxx ′′ =+−

A. ()01. f B. ()34. f C. () 214. f D. ()316. f Lờigiải ChọnC

Ta có ()()() ′′ =−+ 221gxfxx ()()  = ′′ =⇔=+⇔  =±  1 01 3 x gxfxx x .

Dựa vào hình vẽ ta có bảng biến thiên

Suy ra giá trị lớn nhất của hàm số ()()() =−+ 2 21gxfxx trên đoạn [] 3;3 là ()()=− 1214gf

Câu39. (Chuyên Lương Văn Chánh - Phú Yên -2021) Cho hàm số ()yfx = liên tục trên ℝ sao cho

đoạn [] 3;3 bằng

Dựa vào bảng biến thiên và đồ thị hàm số ta có giá trị lớn nhất của hàm số ( ) gx đạt tại 1 2 x =− () 1 1212026 2 gf   −=−+ 

Đặt [] 31 2,;3;1 22 txxt  =∈−  ∈−   Khi đó phương trình ( )* trở thành phương trình sau: ()() () 2 2 11 2210** 22ftttfttt ′′ ++−=⇔=−−+ Ta có đồ thị như sau: ()

x t fttx t x

 =−  =−     ′ =⇔=−  =−    =    =  

3 2 3 1 01 2 1 1 2

Ta có bảng biến thiên như sau:

Maxgtgm Mingtgm

==+ ==−

319 11

Câu41. (Chuyên Bắc Giang - 2021) Cho hàm số () 3 31fxxx=−+ . Có bao nhiêu giá trị nguyên của m để giá trị nhỏ nhất của hàm số () 2sin1 yfxm =++ không vượt quá 10? A. 45. B. 43. C. 30. D. 41. Lờigiải ChọnD Đặt []2sin1,1;3txt =+∈− Xét hàm số ()() [] 3 31,1;3gtftmttmt=+=−++∈− ( ) 2 '3301 gttt=−=⇔=± [] ()() [] ()() 1;3 1;3

+TH1: Nếu 1910(1)mmm +>−>> Để thỏa mãn YCBT thì 11011mm−≤⇔≤  111 m <≤ (1) +TH2: Nếu 0191(19) mmm >+>−<− Để thỏa mãn YCBT thì 191029mm+≥−⇔≥−  2919 m −≤<− (2) +TH3: Nếu 1019191mmm −≤≤+⇔−≤≤ thì min0 y = ( hiển nhiên đúng) (3) Từ (1),(2),(3) suy ra 2911 m −≤≤ Vậy có 41 số nguyên thỏa mãn. Câu42. (Sở Nam Định-2021) Cho hàm số ()yfx = có bảng biến thiên như sau:

Tìm giá trị lớn nhất của hàm số ( ) sinx3cos12cos24cos10yfxxx =−+−+− A. 2 B. 5 C. 9 D. 2 Lờigiải ChọnB Ta có: 2 sinx3cos2sin();cos22cos1 3 xxxx π −=−=−

ạng

Ứng dụ

Giả sử hình hộp chữ nhật có kích thước như hình vẽ. Ta có dung tích của bể cá: = Vabc

Mặt khác theo giả thiết ta có: 226,5 2 ++=   =  abbcac ab

Khi đó 2 2 6,52 2. 6 = b Vb b 3 6,52 3 ⇔= bb V

Xét hàm số: () 3 6,52 3 = bb fb . Có BBT

2 266,5 2  += ⇔  =  bbc ab

 =  ⇔   = 

b c b ab

2 6,52 6 2

1 2 2 2  ′ =−−+−   . a fxaxaax axa

222 2222

12123 2222  −++−− ==    . axaaaxaax xaxa () 2 0 3 ′ =⇔= a fxx Vậy diện tích lớn nhất của tam giác ABC là 2 2a3 318  ==   Sfa Câu 2.(Mã 101 2018) Ông A dự định dùng hết 2 6,5m kính để làm một bể cá có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm). A. 3 2,26 m B. 3 1,61 m C. 3 1,33 m D. 3 1,50 m Lời giải

Vậy bể cá có dung tích lớn nhất là: 3 39 1,50 6  =    fm

Câu 3.(Mã 104 2017) Một vật chuyển động theo quy luật 32 1 6 3 stt =−+ với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?

A. 243 (m/s) B. 27 (m/s) C. 144 (m/s) D. 36 (m/s)

Lời giải

Ta có: 2 12 vstt ′ ==−+ ; 212vt ′ =−+ ; 06vt ′ =⇔=

t v ′ v

0 9 6 0 + 36 3 max 530 1,01 27 Vm  =≈

Nhìn bbt ta thấy vận tốc đạt giá trị lớn nhất khi 6 t = . Giá trị lớn nhất là ()636m/s v = .

Câu 4.(Mã 103 2018) Ông A dự định sử dụng hết 2 5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A. 3 1,01 m B. 3 0,96 m C. 3 1,33 m D. 3 1,51 m Lời giải Chọn A

Câu 5. Một loại thuốc được dùng cho một bệnh nhân và nồng độ thuốc trong máu của bệnh nhân được giám sát bởi bác sĩ. Biết rằng nồng độ thuốc trong máu của bệnh nhân sau khi tiêm vào cơ thể trong t giờ được cho bởi công thức () 2 1 t ct t = + () / mgL . Sau khi tiêm thuốc bao lâu thì nồng độ thuốc trong máu của bệnh nhân cao nhất? A. 4 giờ. B. 1 giờ. C. 3 giờ. D. 2 giờ.

Lời giải

Xét hàm số () 2 1 t ct t = + , (0) t > () () 2 2 2

1 1 t ct t ′ = + () 1 0 1 t ct t =  ′ =⇔  =− 

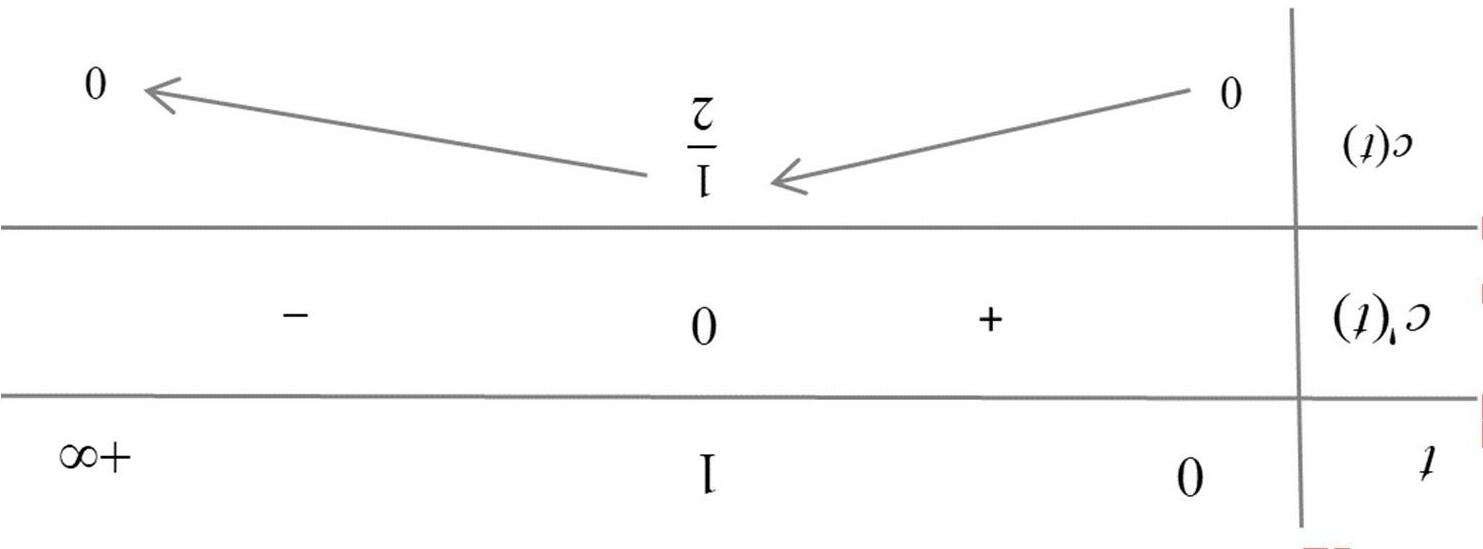
Gọi , xy lần lượt là chiều rộng và chiều cao của bể cá (điều kiện ,0xy > ). Ta có thể tích bể cá 2 2 Vxy = Theo đề bài ta có: 2 22.225 xyxyx++= 2 625 xyx ⇔+= 2 52 6 x y x ⇔= (Điều kiện kiện 2 0520yx>⇔−> 5 0 2 x  << ) 23 2 5252 2 63 xxx Vx x  == 2 56 3 x V ′  = 2 0560Vx ′  =⇔−= 5 6 x ⇔=

Với 1 t = giờ thì nồng độ thuốc trong máu của bênh nhân cao nhất.

Câu 6.(Dề Minh Họa 2017) Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng x (cm), rồi gập tấm nhôm lại như hình vẽ dưới đây để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.

A. 3 x = B. 2 x = C. 4 x = D. 6 x = Lời giải

Chọn B

Ta có : ()hxcm = là đường cao hình hộp

Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: () 122xcm

Vậy diện tích đáy hình hộp () () 2 2 122 Sxcm =− . Ta có: () 00 0;6 12206 xx x xx >> ⇔⇔∈ −><

Thể tích của hình hộp là: ()2 .1 .22 VSxhx =− =

Xét hàm số: ()() 2 .1220;6yxxx =−∀∈

Ta có : ()()()() 2 '1224122122126 yxxxxx =−−−=−− ; ()() '0122.12602 yxxx =⇔−−=⇔= hoặc 6 x = (loại).

Suy ra với 2 x = thì thể tích hộp là lớn nhất và giá trị lớn nhất đó là ()2128 y =

Câu 7.(Chuyên Lê Quý Đôn Điện Biên 2019) Một sợi dây có chiều dài 28m được cắt thành hai đoạn để làm thành một hình vuông và một hình tròn. Tính chiều dài (theo đơn vị mét) của đoạn dây làm thành hình vuông được cắt ra sao cho tổng diện tích của hình vuông và hình tròn là nhỏ nhất? A. 56 4 π + B. 112 4 π + C. 84 4 π + D. 92 4 π + Lời giải

Gọi chiều dài của đoạn dây làm thành hình vuông là x ( m ) ( 028 x << )

=> chiều dài của đoạn dây làm thành hình tròn là 28 x ( m )

+) Diện tích hình vuông là: 2 2 416 xx =  

+) Bán kính hình tròn là: R = 28 2 x π

=> Diện tích hình tròn: 2 2 2 2878456 . 24 xxx R ππ ππ −−+ ==  

+) Tổng diện tích hai hình: 22 2 78456414196 16416 xxx xx π ππππ −++ +=−+  

Xét 2 414196 () 16 fxxx π πππ +  =−+   . Nhận thấy ()fx đạt giá trị nhỏ nhất tại 2 b x a == () 1416112 244 π πππ = ++ Vậy chiều dài của đoạn dây làm thành hình vuông để tổng diện tích của hai hình đạt giá trị nhỏ nhất là 112 4 π + m

Câu 8.(THPTMinhChâuHưngYên2019) Cho một tấm nhôm hình chữ nhật có chiều dài bằng 10cm và chiều rộng bằng 8cm . Người ta cắt bỏ ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng ()xcm , rồi gập tấm nhôm lại (như hình vẽ) để được một cái hộp không nắp. Tìm x để hộp nhận được có thể tích lớn nhất.

A. 8221 3 x = B. 1027 3 x = C. 921 9 x + = D. 921 3 x =

Lời giải Chọn D

Ta có : ()hxcm = là đường cao hình hộp

Vì tấm nhôm được gấp lại tạo thành hình hộp nên cạnh đáy của hình hộp là: () 102 xcm và () 82xcm

Thể tích của hình hộp là: ()() .102.82Sx Vxx h ==

Xét hàm số: ()()() .102.820;4yxxxx =−−∀∈

Ta có : 2 '127280yxx=−+ ; () ()

x x xx x x

Vậy diện tích đáy hình hộp ()()() 2 10282 Sxxcm =−− . Ta có: () 0 0 10200;4 4 820

>  >   −>⇔⇔∈ <   −> 

2 52 6 ⇔= x y x (Điều kiện kiện 2 0520>⇔−>yx 5 0 2  << x ) 23 2 5252 2 63  == xxx Vx x

921 4 3 '0 921 3

xl y xn

 + =>   =⇔  =   Suy ra với 921 3 x = thì thể tích hộp là lớn nhất và giá trị lớn nhất.

Câu 9.(Mã 103 2018) Ông A dự định sử dụng hết 2 5 m kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)? A. 3 1,01 m B. 3 0,96 m C. 3 1,33 m D. 3 1,51 m

Lời giải Chọn A

A'

2 56 3 ′  = x V 2 0560 ′  =⇔−=Vx 5 6 ⇔= x x 3 ma 530 1,01 27  =≈ m V

Câu 10. Một người nông dân có 15.000.000 đồng muốn làm một cái hàng rào hình chữ E dọc theo một con sông (như hình vẽ) để làm một khu đất có hai phần chữ nhật để trồng rau. Đối với mặt hàng rào song song với bờ sông thì chi phí nguyên vật liệu là 60.000 đồng một mét, còn đối với ba mặt hàng rào song song nhau thì chi phí nguyên vật liệu là 50.000 đồng một mét. Tìm diện tích lớn nhất của đất rào thu được

A. 2 3125 m B. 2 50 m C. 2 1250 m D. 2 6250 m

C' B'

y x 2 x C

D A

D' B

Gọi , xy lần lượt là chiều rộng và chiều cao của bể cá (điều kiện ,0 > xy ).

Ta có thể tích bể cá 2 2 = Vxy

Theo đề bài ta có: 2 22.225 ++=xyxyx 2 625⇔+= xyx

Lời giải Chọn D Gọi x là chiều dài 1 mặt hàng rào hình chữ E ( trong ba mặt song song, 0 x > ). Gọi y là chiều dài mặt hàng rào hình chữ E song song với bờ sông ( 0 y > ). Số tiền phải làm là: 5005 .3.50000.6000015.000.000 2 x xyy +=⇔= Diện tích đất: 2 ..25050055 22 x Sxyxxx ===−

Ta có: '2505 Sx =− '0250550. Sxx =⇔−⇔= Bảng biến thiên:

x + + ∞

0 6250

- ∞ 0

Câu 11.(Chuyên Long An-2019) Ông Khoa muốn xây một cái bể chứa nước lớn dạng một khối hộp chữ nhật không nắp có thể tích bằng 3 288 m Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500000 đồng/ 2 m . Nếu ông Khoa biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi ông Khoa trả chi phí thấp nhất để xây dựng bể đó là bao nhiêu (Biết độ dày thành bể và đáy bể không đáng kể)? A. 90 triệu đồng. B. 168 triệu đồng. C. 54 triệu đồng. D. 108 triệu đồng. Lời giải

Chọn D

Theo bài ra ta có để chi phí thuê nhân công là thấp nhất thì ta phải xây dựng bể sao cho tổng diện tích xung quanh và diện tích đáy là nhỏ nhất. Gọi ba kích thước của bể là a , 2a , c ()() () 0,0amcm>>

Ta có diện tích cách mặt cần xây là 22 24226 Saacacaac =++=+ Thể tích bể 2 .2.2288Vaacac===  2 144 c a = . Suy ra 2222 3 2 144864432432432432 26.223.2..216 Saaaaa aaaaaa =+=+=++≥= Vậy 2 min 216m S = , khi đó chi phí thấp nhất là 216.500000108 = triệu đồng.

C D B A

A. 1003. B. 1063. C. 1083. D. 1203. Lời giải Chọn C

Xét hàm số () 2sinsin2 fxxx =+ với () 000;90 x ∈ có () 2cos2cos2 fxxx ′ =+

Ta có: () 2 1 cos 02cos2cos202coscos10 2 cos1

x fxxxxx x

 =  ′ =⇔+=⇔+−=⇔  =− 

Do () 000;90 x ∈ nên ta nhận 0 1 cos60 2 xx=⇔= . Ta có bảng biến thiên: Từ bảng biến thiên ta thấy: () () 000;90

33 max 2 fx ≤ đạt được tại 060 x = () 2 max1083Sm  = khi góc ở đáy CD của hình thang bằng 060 () 060 CD==

Câu 13.(Sở GD Quảng Nam - 2019) Cho nửa đường tròn đường kính 2 AB = và hai điểm C , D thay đổi trên nửa đường tròn đó sao cho ABCD là hình thang. Diện tích lớn nhất của hình thang ABCD bằng

Gọi H là hình chiếu vuông góc của D lên AB , I là trung điểm của đoạn CD và O là trung điểm của AB Đặt DHx = , 01 x << . Ta có 22222221 DCDIOHODDHx ===−=−

Diện tích của hình thang ABCD là () () () 2 11 2 ABCDDH Sfxxx + ===+− Ta có () 22 2

Vậy diện tích lớn nhất của hình thang ABCD bằng 33 4

Câu 14.(THPT Lương Văn Tụy - Ninh Bình 2018) Một người đàn ông muốn chèo thuyền ở vị trí A tới điểm B về phía hạ lưu bờ đối diện, càng nhanh càng tốt, trên một bờ sông thẳng rộng 3km (như hình vẽ). Anh có thể chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B , hay có thể chèo trực tiếp đến B , hoặc anh ta có thể chèo thuyền đến một điểm D giữa C và B và sau đó chạy đến B . Biết anh ấy có thể chèo thuyền 6km/h , chạy 8km/h và quãng đường 8km BC = . Biết tốc độ của dòng nước là không đáng kể so với tốc độ chèo thuyền của người đàn ông. Tính khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến B .

A. 3 2 . B. 9 7 . C. 73 6 . D. 7 1 8 + .

Lời giải

 Cách 1: Anh chèo thuyền của mình trực tiếp qua sông để đến C và sau đó chạy đến B

112 1 xx fx x −+− ′ = () 22 01120fxxx ′ =⇔−+−= (*) Đặt 2 1 tx =− , (điều kiện 0 t ≥ ) khi đó phương trình (*) trở thành 2 1 210 1 2

=−   +−=⇔  =  1 t =− loại. 1 2 t = ta có 22133 1 242 xxx −=⇔=⇔=± Bảng biến thiên

Thời gian chèo thuyền trên quãng đường AC : 3 0,5 6 = (giờ)

t tt t

Thời gian chạy trên quãng đường CB : 8 1 8 = (giờ)

Tổng thời gian di chuyển từ A đến B là 1,5 (giờ).

 Cách 2: chèo trực tiếp trên quãng đường 22 3873 AB =+= mất h 73 126 6 ′ ≈ .

 Cách 3:

Gọi () km x là độ dài quãng đường BD ; ()8km x là độ dài quãng đường CD

Thời gian chèo thuyền trên quãng đường 2 9 ADx=+ là: 2 9 6 x + (giờ)

Thời gian chạy trên quãng đường DB là: 8 8 x (giờ)

Tổng thời gian di chuyển từ A đến B là () 2 98 68 xx fx +− =+

Xét hàm số () 2 98 68 xx fx +− =+ trên khoảng () 0;8

Ta có () 2

1 8 69 x fx x ′ =− + ; () 2 9 0394 7 fxxxx ′ =⇔+=⇔=

Bảng biến thiên

Dựa vào BBT ta thấy thời gian ngắn nhất để di chuyển từ A đến B là h 7 1120 8 ′ +≈

Vậy khoảng thời gian ngắn nhất để người đàn ông đến B là h 7 1120 8 ′ +≈

Dạng 4. Dùng phương pháp hàm số để tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức

Câu 1.(HSG 12 - Sở Quảng Nam - 2019) Cho ba số thực ,, xyz thỏa mãn 0,0,1xyz≥≥≥ , 2 xyz++= .Biết giá trị lớn nhất của biểu thức Pxyz = bằng a b với * , ab ∈ ℕ và a b là phân số tối giản. Giá trị của 2ab + bằng A. 5 B. 43 C. 9 D. 6 Lời giải

Chọn D

Ta có: () 22 23 21 ..z44 224 xyz Pxyzzzzz +−  =≤==−+  

Xét hàm số () () 23 1 44 4 fzzzz =−+ trên [] 1;2

Ta có: () () () 2 2 () 1 483;0 3 4 2

zloai fzzzfz z

 =  ′′ =−+=⇔  = 

Bảng biến thiên: Dựa vào bảng biến thiên, ta có: 1 4 P ≤ .

Vậy max 1 4 P = khi 1 1 2

=    ==   1;426abab  ==  +=

z xy

Câu 2.(Chuyên Bắc Giang Nam 2019) Cho 22 2 xxyy−+= . Giá trị nhỏ nhất của 22 Pxxyy =++ bằng: A. 2 3 B. 1 6 C. 1 2 D. 2 Lời giải Chọn A Xét 2222 22 22 Pxxyyxxyy xxyy ++++ == −+

+nếu 0 y = thì 2 2 x = . Do đó 2 2 Px== suy ra min2 P = +nếu 0 y ≠ ta chia tử mẫu cho 2 y ta được

Đặt () [ ]4,1;2txyt =−+∈ . Ta có: () ( ) ( ) 2 2242 4242810826fttttttt =−+−++=−++ . ( ) 3 4208fttt ′ =−+ () [ ] [] [] 2

t t ftt tt t

21;2 2 0121;2 210 121;2

 =∈  =  ′ =⇔⇔=−+∈   +−=   =−−∈   ( ) ( ) 125;218ff== Suy ra [] ( ) ( ) [] ( ) ( ) 1;2 1;2 min218;max125 mftfMftf ====== Vậy 43 Mm+= . Câu4. (Chuyên LêQuý Đôn- QuảngTrị -2019) Cho x , 0 y > thỏa mãn 3 2 xy+= và biểu thức 41 4 P xy =+ đạt giá trị nhỏ nhất. Tính 22 xy + A. 153 100 B. 5 4 C. 2313 1156 D. 25 16 Lờigiải ChọnA Từ 3 2 xy+= suy ra 3 2 yx =− . Ta có: 3 0, 2 xy << . Xét hàm () 41 3 4 2

Px x x =+   

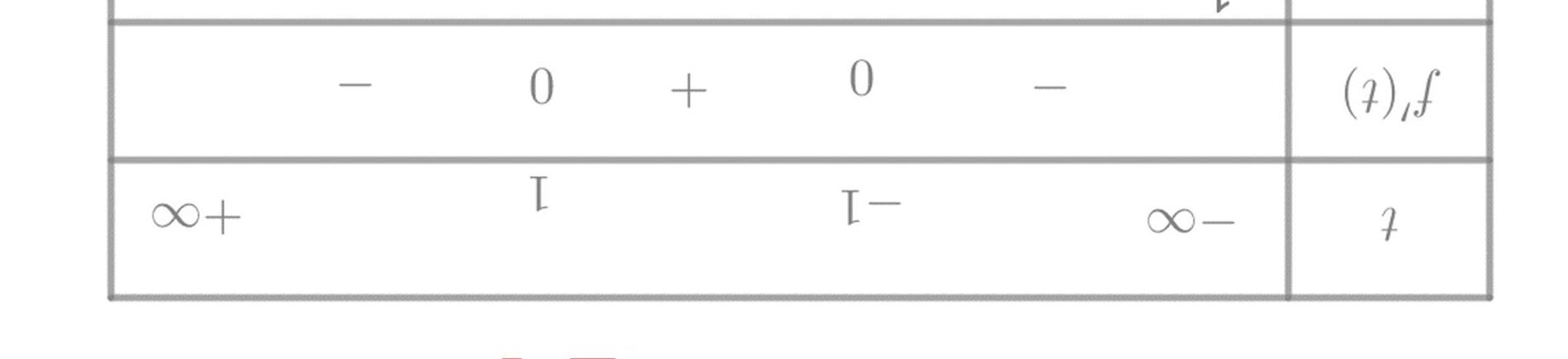
41 64 xx =+ trên khoảng 3 0; 2    , ta có: () ()2 2 44 64 Px x x ′ =−− ( ) 0 Px ′ = ()2 2 44 64 x x ⇔= ( )2 2 64 xx⇔=− 64 46 xx xx

=−  ⇔  =− 

x x

6 5 2

 =  ⇔  =  . Bảng biến thiên của ( )Px trên 3 0; 2    :

   . ()2542 f −=−− ; ()01 f = ; ()10 f = ; ()2542 f =−+ . ()() () () 2;2 2;2

MQftf mQftf

maxmax01 minmin2542

   

 ====    ===−=−−   . Vậy 442 Mm+=−−

Câu6. (Sở LàoCai-2019) Cho hàm số () 432 1 fxxaxbxcx=++++ . Biết rằng đồ thị hàm số ()yfx = có ít nhất một giao điểm với trục hoành. Bất đẳng thức nào sau đây là đúng? A. 222 4 3 abc++> . B. 222 4 3 abc++< . C. 222 4 3 abc++≥ . D. 222 4 3 abc++≤ . Lờigiải ChọnC Phương trình hoành độ giao điểm () 432 101 xaxbxcx++++= Nhận xét 0 x = không phải là nghiệm. Với 0 x ≠ phương trình trở thành

() () 23 1 10 axbxcxx x  ⇔++=−+≠  

()()() 2 2 3222242 1 1 xaxbxcabcxx x +=++≤++++  22 32 2 222 42 2 2

11 111

xx xx abc xx x x

 ++  ⇔++≥= ++ ++ () () () 22 2 2 2 12 2,2'0,2 11 ttt txtfttftt xt t + =+  ≥  =∀≥  =>∀≥ + + Bảng biến thiên Vậy để đồ thị hàm số ()yfx = có ít nhất một giao điểm với trục hoành thì 222 4 3 abc++≥ Câu7. (THPTTrầnNhânTông2018) Cho hai số thực , xy thỏa mãn: () 3 9235350 xyxyxxy +−−+−= Tìm giá trị nhỏ nhất của ()() 33263312 xyxxy Pxy ++++− =+

Ta có ( ) 3 9235350 xyxyxxy +−−+−= ( ) 3 2763535235 xxxyxyxy ⇔+=−−+−

Xét hàm ( ) 3 2 fttt =+ với ( ) 0; t ∈+∞ có ( ) ( ) 2 '3200; fttt=+>∀∈+∞ nên hàm số liên tục và đồng biến trên ( ) 0; +∞ . Khi đó ta có 335 xxy=− 0 x  ≥ và 2 935 xxy=− Với 0 x = thì ( ) 05 l =− với 0 x > thì ( )( ) 33263312 xyxxy Pxy ++++− =+ ( )( ) 3326932 xyxxy xy ++++− =+ ( )( ) 33 6322 xyxyxy xy ++−+− =+ ( ) 33223324 xyxyxy xy ++−++ =+ ()() 3 24xyxy =+−++ Mà 2 955545 424. 3333 x xyxxx xxx + +=+=+≥= Đặt txy =+ thì45 3 t ≥ Xét ( ) 3 24fttt=−+ với45 3 t ≥ . Khi đó ( ) 2 320ftt ′ =−> với45 3 t ∀≥ Do đó () 453629615 39 ftf  + ≥=    Suy ra 3629615 9 P + ≥ . Vậy GTNN của P là 3629615 9 + Câu8. (THPTNguyễnHuệ -NinhBình-2018) Cho ,0xy > và 5 4 xy+= sao cho biểu thức 41 4 P xy =+ đạt giátrị nhỏ nhất.Khi đó A. 22 25 32 xy+= B. 22 17 16 xy+= C. 22 25 16 xy+= D. 22 13 16 xy+= Lờigiải Từ 55 44 xyyx +=  =− ,nên 41 54 P xx =+ .

Xéthàmsố 41 54 P xx =+ với 5 0 4 x << ()2 2 44 54 P x x ′ =−+ ; ()2 2 054 Pxx ′ =⇔=− 10;5 4 55 0; 34

Bảngbiếnthiên Như vậy: min5 P = khi 1 x = ; 1 4 y = . Khi đó 22 17 16 xy+= .

  =∈     ⇔   =∉   

x x

.

Câu9. (Xuân Trường - Nam Định -2018) Cho , xy là hai số thực dương thay đổi thỏa mãn điều kiện ()() 1 111 xyxyyx y ++−≤−− .Tìmgiátrị lớnnhấtcủabiểuthức () 22

2 6 3 xyxy P xy xxyy +− =− + −+ ? A. 57 330 . B. 75 303 . C. 57 330 + . D. 57 30 + . Lờigiải ()() 1 111 xyxyyx y ++−≤−− ()() ( ) 22 1110yxyxyyxyy ⇔++−++−≤ () () () 1110xyyyxyxyy  ⇔+−++++≤  101 xyyxyy ⇔+−≤⇔+≤ 2 2 11111 42 x yyyy ⇔≤−+=−− 

9476 243 B. 76 C. 193 3 D. 148 3 Lờigiải Điềukiện 2;3xy≥≥− . ( ) 1223xyxy ++=−++ ( ) ( ) 2 141223xyxyxy ⇔++=+++−+ .(*) Vì 2231 xyxy −+≤++ nêntừ (*)suyra ()() 2 181xyxy ++≤++ 7 xy ⇔+≤ Vì 2230 xy−+≥ nêntừ (*)suyra ()() 2 141xyxy ++≥++ 10 14 xy xy ++≤  ⇔  ++≥  10 14 xy xy ++=  ⇔  ++≥  1 3 xy xy +=−  ⇔  +≥  .

Do 2 x ≥ nên 2 2 xx ≥ , 2 12 yy +≥ ,suyra () 22 12 xyxy ++≥+ .Từ đótacó () () ()()472247 31.2331.263 xyxyxyxy Mxyxyxyxy +−−−+−−− =+++−+≤+++−++ .

Đặt txy =+ với 1 t =− hoặc 37 t ≤≤ .

Xéthàmsố ()()47 31263 tt fttt =++−+ ,tacó () 2188 1 243 f −= ()()477 3ln321.2ln26 tttftt ′ =+−+− . ()()427 3ln31ln222.ln20 t t ftt ′′ =++−>   , [] 3;7 t ∀∈

Suyra ()ft ′ đồngbiếntrên () 3;7 ,mà ()ft ′ liêntụctrên [] 3;7 và ()()3.70ff′′ < nênphươngtrình () 0 ft ′ = cónghiệmduynhất () 0 3;7 t ∈ .

0 t f'(t)

37

to +

1484 3 f(to) f(t)

Suyra () ()4722 148 31.23 3 xyxy Mxyxy +−−− =+++−+≤ Đẳngthứcxảyrakhi 2 x = , 1 y =

Câu11. (Cụm 5 Trường Chuyên - Đbsh - 2018) Tìm giá trị nhỏ nhất của hàm số 11 sincostancot sincos yxxxx xx =+++++ A. 21. B. 221 + . C. 21 + . D. 221. Lờigiải Tacó 11 sincostancot sincos yxxxx xx =+++++ 1sincos sincos sin.cos xx xx xx ++ =++ Đặt sincos txx =+ 2sin 4 x π  =+  , {} 22 ;\1 22 t  ∈−  , 2 1 sin.cos 2 t xx = .

Suyra 2 1 1 2

t yt t + =+ 2 1 t t =+ .

 =+  ⇔  =−+  ()23220, g =+> ()20, g −< ()212210 g −+=−+<

Xét hàm số () 2 1 gtt t =+ , () ()2 2 1 1 gt t ′ =− () () 2 2 12 1 t t = , () 0 gt ′ = () () 21 21t/m tl t

Đặt 3245 tzzz =−+ , với 250 22 327 zt≤≤  ≤≤

Do đó xét hàm số () 4 53 ft t =+  , với 50 2 27 t ≤≤

- 2

-2+1 2 g(t)

0 t g'(t) 1 +

g - 2+1 () g - 2 ()

+∞ +∞ +∞ g 2 ()

g - 2 () g - 2+1 () g 2 () -∞ y=g(t)

+=−  ++=   ⇔  ++= =−+=−+   Lại có: ()2 4 xyxy +≥ () () 2 2 2 44542 3 zzzz  −≥−+  ≤≤ . Dấu "" = xảy ra khi xy = . Và ()()()() 3 333 33 xyzxyzxyzxyzxyxy ++=++++++++ ()() 33334123 xyzxyzxyxy  ++=−+−+ ()() 2 64345zz=−−+ Ta có: () 333 111 Pxyz xyz  =++++  () 32 32 5 312154 45 zzz zzz  =−++  −+  .

Do đó ( ) min 225 Pf== đạt tại 1 xy== , 2 z = .

Câu 13. (Sở Bắc Ninh - 2018) Gọi M , m lần lượt là giá lớn nhất, giá trị nhỏ nhất của hàm số 20182018sincos yxx =+ trên ℝ . Khi đó: A. 2 M = , 1008 1 2 m = B. 1 M = , 1009 1 2 m = C. 1 M = , 0 m = D. 1 M = , 1008 1 2 m = Lời giải

Ta có: 20182018ysincosxx=+ ( ) ( ) 2210091009sin1sinxx=+− .

Đặt 2 sin tx = , 01 t ≤≤ thì hàm số đã cho trở thành ()1009 1009 1 ytt =+−

Xét hàm số ()()1009 1009 1 fttt =+− trên đoạn [ ]0;1

Ta có: ()()1008 1008 1009.1009.1 fttt ′ =−− ( ) 0 ft ′ = ()1008 1008 1009100910 tt ⇔−−= 1008 1 1 t t  ⇔=   1 1 t t ⇔= 1 2 t ⇔=

Mà ( ) ( ) 101ff== , 1008 11 22 f  =  

Suy ra [] ( ) ( ) ( ) 0;1 max011 ftff=== , [] () 1008 0;1

11 min 22 ftf  ==   Vậy 1 M = , 1008 1 2 m =

Câu 14. (Chuyên Long An - 2018) Cho các số thực x , y thỏa mãn ( ) 233xyxy +=−++ . Tìm giá trị nhỏ nhất của biểu thức ( ) 22 415 Pxyxy =++ . A. min80 P =− . B. min91 P =− . C. min83 P =− . D. min63 P =− . Lời giải

Ta có ( ) 233xyxy +=−++ ()() () 2 483.34 xyxyxyxy ⇔+=++−+≥+ () 4 1 0 xy xy +≥  ⇔  +≤  Mặt khác áp dụng bất đẳng thức Bunhiacopski ta được: ( ) ( ) ( )2332282xyxyxyxy +=−++≤+⇔+≤ . Từ ( )1 và ( )2 ta có [ ]4;8 xy+∈ Ta lại có ( )( ) ( ) 33039xyxyxy ++≥⇔≥−+− . Đặt txy =+ suy ra ( ) ()2 22 2 4154742163 Pxyxyxyxytt ==++=++≥−− Xét hàm số ( ) 2 42163fttt=−− , với [ ]4;8 t ∈ Ta có () [] 21 82104;8 8 fttt ′ =−=⇔=∉ . Do đó [] ( ) ( ) 4;8 min483 ftf==− Do đó 83 P ≥− suy ra min83 P =− khi () 4 7 233 3 xy x xyxy y

+=  =   ⇔  +=−++ =−    .

Câu 15. (THPT Trần Phú - Đà Nẵng - 2018) Cho hai số thực x , y thỏa mãn: ( ) 3 2 272131321 yyxxxy ++−=−++ .Tìmgiátrị lớnnhấtcủabiểuthức 2 Pxy =+ . A. 10 P = B. 4 P = . C. 6 P = . D. 8 P = . Lời giải ( ) 3 2 272131321 yyxxxy ++−=−++ ( ) ( ) ( ) 32 233112113121 yyyyxxxx ⇔−+−+−=−−+−−− . ()() ( ) () 3 3 2112111 yyxx ⇔−+−=−+−

Xét hàm số ( ) 3 2 fttt =+ trên [ ) 0; +∞ Ta có: ( ) 2 61ftt ′ =+ 0 > với 0 t ∀≥ ( ) ft  luôn đồng biến trên [ ) 0; +∞ . Vậy ( ) 111yx⇔−=− 11 yx⇔=+−

2221 Pxyxx  =+=++− với () 1 x ≤ .

Xét hàm số () 221 gxxx =++− trên ( ];1−∞ .

Ta có: () 1 1 1 gx x ′ =− 11 1 x x = () 00gxx ′ =  =

Bảng biến thiên ()gx :

Từ bảng biến thiên của hàm số ()gx suy ra giá trị lớn nhất của P là: ( ] () ;1 max4 gx −∞ =

Câu 16. (Chuyên Trần Phú - Hải Phòng 2018) Cho x , y là các số thực dương thỏa mãn điều kiện: 2 30 23140 xxy xy  −+=  +−≤  . Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 223 322 Pxyxyxx =−−+

A. 8 . B. 0 . C. 12 . D. 4 . Lời giải

Theo giả thiết ta có 2 2 3 30 x xxyy x + −+=  =

Từ bất phương trình 2 549 231400 xx xy x −+ +−≤⇔≤ 9 1 5 x ⇔≤≤ .

Mặt khác ta có 232 222

33 33 xxyxxyx xyxxyxyy =−=−   =+=+ 

Thay vào ta được 38 Pyx =−+ 2 3 38 x x x  + =−+   9 5x x =−

Xét hàm số () 9 5 fxx x =− trên đoạn 9 1; 5    .

Ta có () 2 99 50,1; 5 fxx x  ′ =+≥∀∈   do đó () 9 1; 5

min14 f   

==− và 9 1; 5

9 max4 5 f   

Suy ra tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P bằng 0

 ==  

nh - 2018) Biếtrằng bấtphươngtrình ( ) 22422 11212mxxxxxx +−+≤−++−+ có nghiệm khi và chỉ khi ( ;2 mab ∈−∞+  với , ab ∈Z . Tính giá trị của Tab =+ A. 3 T = . B. 2 T = . C. 0 T = . D. 1 T = . Lời giải Điều kiện: 11 x −≤≤ ( ) 22422 11212mxxxxxx +−+≤−++−+ ( ) 222422 11212mxxxxxx ⇔+−+≤−++−+ Đặt 22 242

Đặt 22 ; axybxy =+= ta được: ()() 2 22 28244150 abbabaabb +≥+⇔−−≥

5 2 a b  ≥ . Suy ra: 22 55 22 xyxy t xyyx + ≥⇔=+≥ .

Ta có: 3322 332249xyxy P yxyx  =+−+  ()() () 3232 4392491218 ttttttft =−−−=−−+= với 5 2 t ≥

Khảo sát hàm số ()ft với 5 2 t ≥ ta được () 23 4 ft ≥− . Vậy chọn C

 ≤≤  =+−   −=−   . Khi đó, bất phương trình trở thành: () 2 2 1 11 1 tt mtttm t ++ +≤++⇔≤ + (vì [ ]1;2 t ∈ nên 10 t +> ). Xét hàm số () 2 1 1 tt ft t ++ = + trên 1;2   . () 2 2 0,1;2 1 tt ftt t +  ′ =>∀∈  + suy ra hàm số đồng biến trên 1;2   . ()() 1;2

12 1 21 t txx xxt

3 min1 2 ftf   == ; () ( ) 1;2 max2122 ftf   ==−+ Bất phương trình đã cho có nghiệm khi và chỉ khi bất phương trình 2 1 1 tt m t ++ ≤ + có nghiệm 1;2 t  ∈  ( ) 1;2 max122mftm   ⇔≤⇔≤−+ 2 a  = , 1 b =− 1 ab  += .

ng thỏa mãn ( ) ( )( ) 22 22 xyxyxyxy ++=++ Giá trị nhỏ nhất của biểu thức 3322 332249xyxy P yxyx  =+−+  A. 25 4 . B. 5 . C. 23 4 . D. 13 . Lời giải Ta có ( ) ( )( ) 22 22 xyxyxyxy ++=++ ( ) 22 xyxy≥+ .

Câu 19. (THPT Kim Liên - Hà Nội - 2018) Cho các số thực dương x , y thỏa mãn 5 2 4 xy+= . Tìmgiá trị nhỏ nhất minP của biểu thức 21 4 P xy =+ A. min 34 5 P = B. min 65 4 P = C. minP không tồn tại. D. min 5 P = Lời giải Từ giả thiết ta có 5 2 4 yx =− . Vì 0 y > nên 55 20 48 xx−>  < . Do đó 5 0 8 x << . Ta có 2 21211015 5588542 4

x P xxxxx x =+=+= −−+   

với5 0 8 x << . () ()() () () () 2 22 2 2 2 2

12016050 85 xx P xx

15851651015120751602405075 8585 xxxxxxxxx P xxxx

−+− ′ = −+ . Có 2

−−+−−+−−−−++− ′ == −+−+ () 2 2 2

x Pxx x

55 0; 68 0120160500 15 0; 28

 =∉    ′ =  −+−=    =∈    

. Bảng biến thiên

Câu 20. (Chuyên Quốc Học Huế - 2021) Cho hàm số 2322(1)21xmmxmm y xm −++++ = có đồ thị ( ) m C ( m là tham số thực). Gọi A là điểm thỏa mãn vừa là điểm cực đại của ( ) m C ứng với một giá trị m vừa là điểm cực tiểu của ( ) m C ứng với giá trị khác của m. Giá trị của a để khoảng cách từ A đến đường thẳng ( ) ( ) :10dxaya−++= đạt giá

10 3 4 7

()fx ′ + 00 + ()fx 5849 490 ()max gx tại 10 3 a =− nên () ()max , dAd tại 10 3 a =−

Câu 21. (Chuyên Hạ Long - Quảng Ninh - 2021) Cho , xy làcácsố thựcdươngthoả mãn điềukiện 2 30 23140 xxy xy  −+=  +−≤  . Tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 223 322 Pxyxyxx =−−+ thuộc khoảng nào sau đây? A. () 2;2 B. () ;1−∞− C. () 1;3 D. () 0; +∞ Lời giải Chọn A Ta có 2 2 3 30 x xxyy x + −+=  = thay vào 23140 xy+−≤ ta có bất phương trình 2 39 231401 5 x xx x + +−≤⇔≤≤ . Thay 2 3 x y x + = vào 223 322 Pxyxyxx =−−+ ta có () 2 22 422 2 32 3 336959 3223322 xxxxx Pxxxxxxxx xxxx  ++++− =−−+=+−−+=   2 2 599 0,1; 5 x Px x + 

Ta có: () ( ) 2221 abcaabcaabcabc +≥++≥+≥+ 1 abc a bc +  ≥ + .

Tương tự ta có: 1 bca b ca + ≥ +

Suy ra: 202112021Aabccc ≥+++=−++

Xét hàm số ( ) [ ]12021;0;1fcccc =−++∈

Ta có () [] 1 10,0;1 22021 fcc c ′ =−+<∀∈ +

Vậy ( )fc là hàm số nghịch biến nên ta có ( ) ( ) 12022. fcf≥=

t nên

phương

TIỆMCẬNĐỒTHỊHÀMSỐ

Dạng Xác địnhtiệmcậncủa đồ thị hàmsố gkhibiếtbảngbiếnthiênhàmsố f(x)

Câu1. (THPT LươngVănCan-2018) Cho đồ thị hàm số () 31 1 x yfx x == . Khi đó đường thẳng nào

sau đây là đường tiệm cận đứng của đồ thị hàm số () 1 2 y fx = ?

A. 1 x = B. 2 x =− C. 1 x =− D. 2 x = Lờigiải () 31 22 1 x fx x =⇔= 31221 xxx  −=−⇔=−

Với () 1 2 y fx = ta có ()() 11 lim;lim xx yy +− →−→− =−∞=+∞

Vậy đồ thị hàm số () 1 2 y fx = có đường tiệm cận đứng 1 x =−

Câu2. Cho hàm số ()yfx = có đồ thị như hình vẽ

Số tiệm cận đứng của đồ thị hàm số () 2019 1 y fx = là

A. 1 B. 2 C. 3 D. 4 Lờigiải ChọnC

Từ đồ thị của hàm số ()yfx = suy ra tập xác định của hàm số ()yfx = là D = ℝ

Vậy đồ thị hàm số () 2019 1 y fx = có 3 đường tiệm cận đứng.

Câu3. (Chuyên Thái Bình - 2020) Cho hàm số ()fx xác định và liên tục trên {}\1 ℝ có bảng biến thiên như sau: Hỏi đồ thị hàm số () 1 y fx = có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang? A. 4 B. 3 C. 2 D. 1 Lờigiải ChọnA

Ta có: () () 11 lim2lim 2 xx fx fx →−∞→−∞ =  = ; () () 11 lim2lim 2 xx fx fx →+∞→+∞ =−  =− .

Suy ra đồ thị hàm số () 1 y fx = có hai đường tiệm cận ngang là 1 2 y = và 1 2 y =− .

Dựa vào bảng biến thiên của hàm số ()yfx = ta thấy: phương trình () 0 fx = có hai nghiệm phân biệt 12 1 xx <−<

Khi đó: ()() 12 0 fxfx== .

Ta có: () () () 1 1 1

lim0 1 lim 0 xx xx

fx fx fxkhixx → →

Do đó chọn A.

 =   =+∞  >→   và () () () 2 2 2

 =   =+∞  >→   .

lim0 1 lim 0 xx xx

fx fx fxkhixx → →

Vậy đồ thị hàm số () 1 y fx = có hai tiệm cận đứng là đường thẳng 1xx = và 2xx =

Câu4. (ChuyênVĩnhPhúc-2020) Cho hàm số ()yfx = thỏa mãn () lim1 x fx →−∞ =− và () lim x fxm →+∞ = . Có bao nhiêu giá trị thực của tham số m để hàm số () 1 2 y fx = + có duy nhất một tiệm cận

ngang. A. 1 B. 0 C. 2 D. Vô số

Ta có () 1 limlim1 2 xx y fx →−∞→−∞ ==  + Đồ thị hàm số có tiệm cận ngang 1 y =

TH 1: Nếu 1 m =− thì () 1 lim1 2 x fx →−∞ = + và () 1 lim1 2 x fx →+∞ = + thì đồ thị hàm số có một tiệm cận.

TH 2: Nếu 1 m ≠− Để đồ thị hàm số có một tiệm cận ngang () 1 lim 2 x fx →+∞ ⇔ + không có giá trị hữu hạn 202mm ⇔+=⇔=− Vậy khi {} 2;1 m ∈−− thì đồ thị hàm số có duy nhất một tiệm cận ngang. Câu5. (KimLiên-HàNội2019) Cho hàm số ()yfx = thỏa mãn 4(tan)cos fxx = . Tìm tất cả các giá trị thực của m để đồ thị hàm số 2019 () () gxfxm = có hai tiệm cận đứng. A. 0 m < . B. 01 m << . C. 0 m > . D. 1 m < . Lờigiải ChọnB () 4 2 2

1 (tan)cos(tan) 1tan fxxfx x =⇔= + 22 1 () (1) ft t  = + Hàm số 22

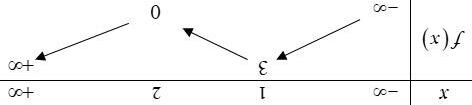
20192019 ()() 1 () (1) gxgxfxmm x

=  = +

Hàm số ()gx có hai tiện cận đứng khi và chỉ khi phương trình 22 1 0 (1) m x −= + có hai nghiệm phân biệt 22 1 (1)101 xm m ⇔+=>⇔<<

Câu6. (THPT Quỳnh Lưu 3 Nghệ An 2019) Cho hàm số ()yfx = xác định, liên tục trên ℝ và có bảng biến thiên như hình bên dưới: Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số () 1 21 y fx = là: A. 4 . B. 3 . C. 1. D. 2 . Lờigiải

Đặt () () 1 21 hx fx =

*) Tiệm cận ngang:

Ta có: () () 1 limlim0 21 xx hx fx →+∞→+∞ == . () () 1 limlim0 21 xx hx fx →−∞→−∞ ==

Suy ra đồ thị hàm số có một đường tiệm cận ngang 0 y = .

*) Tiệm cận đứng: Xét phương trình: () 210 fx −= () 1 2 fx ⇔=

Dựa vào bảng biến thiên ta thấy phương trình () 1 2 fx = có ba nghiệm phân biệt ,, abc thỏa mãn 12 abc <<<< Đồng thời ()()()limlimlim xaxbxc hxhxhx +−+ →→→ ===+∞ nên đồ thị hàm số ()yhx = có ba đường tiệm cận đứng là xa = , xb = và xc = . Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số ()yhx = là 4.

Câu7. (BìnhGiang-HảiDương-2019) Cho hàm số ()yfx = liên tục trên {}\1 ℝ và có bảng biến thiên như sau:

Đồ thị () 1 23 y fx = + có bao nhiêu đường tiệm cận đứng?

A. 2. B. 0. C. 1. D. 3. Lờigiải ChọnA

Đặt () () 1 23 == + ygx fx có tử số là 10, x ≠∀∈ ℝ

Ta có ()() 3 230 2 fxfx+=⇔=− (1).

Trang 4

Từ bảng biến thiên có phương trình (1) có 2 nghiệm phân biệt: 12(;0),(0;1)xx∈−∞∈ .

Do đó đồ thị hàm số () 1 23 y fx = + có 2 đường tiệm cận đứng.

Câu8. (Chuyên Thoại Ngọc Hầu 2018) Cho hàm số ()yfx = liên tục trên {}\1 ℝ và có bảng biến thiên như sau:

Mà số nghiệm thực của phương trình () 1 2 fx = bằng số giao điểm của đồ thị

với đường thẳng 1 2 y =

Dựa vào bảng biến thiên ta thấy đường thẳng 1 2 y = cắt đồ thị hàm số ()yfx = tại 2 điểm phân

biệt. Vậy đồ thị hàm số () 1 21 y fx = có 2 tiệm cận đứng.

Lại có () 1 lim1 21 x fx

=  đồ thị hàm số có một tiệm cận ngang là 1 y = .

Vậy tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số () 1 21 y fx = là 3 .

Đồ thị hàm số () 1 25 y fx = có bao nhiêu đường tiệm cận đứng?

A. 0 B. 4 C. 2 D. 1 Lờigiải

Ta có: ()() () 5 2501 2 fxfx−=⇔= . Phương trình () 1 có 4 nghiệm phân biệt 1234 ,,,1xxxx ≠ và giới hạn của hàm số () 1 25 y fx = tại các điểm 1234 ,,, xxxx đều bằng ±∞ Mặt khác () 1

1 lim0 25 x fx ± → = nên 1 x = không phải tiệm cận đứng.

Vậy đồ thị hàm số () 1 25 y fx = có 4 đường tiệm cận đứng.

Câu9. (ChuyênHưngYên2019) Cho hàm số ()yfx = có bảng biến thiên như hình dưới đây.

Câu10. (THPT Bạch Dằng Quảng Ninh 2019) Cho hàm bậc ba ()yfx = có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số () ()() 22 2

43 2 xxxx y xfxfx +++ =   có bao nhiêu đường tiệm cận đứng?

A. 2 B. 3 C. 4 D. 6 Lờigiải

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số () 1 21 y fx = là A. 0. B. 1. C. 2. D. 3. Lờigiải

Số tiệm cận đứng của đồ thị hàm số () 1 21 y fx = đúng bằng số nghiệm thực của phương trình

()() 1 210 2 fxfx−=⇔= .

() ()() ()()() ()() 22 2

43 131 ..2 2 xxxx xxxx y xfxfx xfxfx +++ +++ ==   

Điều kiện tồn tại căn 2 xx + : 0 1 x x ≥   ≤− 

Xét phương trình ()()() () 2

x xfxfxfx fx

0 200 2

 =  −=⇔=    =  Với 0 x = ta có ()()() ()() ()() ()() 0 0

x xfxfxfx fx

0 00 1

+++ +++ ==+∞     . Suy ra 0 x = là tiệm cận đứng. Với () 0 fx = 3 x  =− (nghiệm bội 2) hoặc xa = (loại vì 10 a −<< ). Ta có: ()()() ()() 3

131 131 limlim ..2 ..2 x x

xxxx xxx xfxfx xfxfx + + → →

 =  −=⇔=    =  () 11,01 0 2 xxx fx x  =<< =⇔  =  . () 22 33

x fxxxx xxx

1 1,12 ,2

131 lim ..2 x

xxxx xfxfx + →−

+++ =−∞   nên 3 x =− làtiệm cận đứng. Với () 2 fx =  () ()

x xbb xcc

1 31 3

xxxx xfxfx + →

 =−  =−<<−   =<−  (nghiệm bội 1). Tacó: ()()() ()() 131 lim0 ..2 xb

+++ =  

=   =⇔=<<   =>  suy ra ()()()() 23 11 fxaxxxxx −=−−− . Khi đó ta có () () ()() ()() ()() 2 2

321 121 .1 xxx xxx gx xfxfx xfxfx −+− ==    . () ()() ()()()()() ()()()() 2 2 123 1 23

x x

xxxx xfxfx + →

+ →− →−

1 1

 +++  =     +++  =     

xxxx xfxfx xxxx xfxfx

()()() ()() ()()() ()()

131 lim0 ..2 131 lim0 ..2

nên 1 x =− không là tiệm cận đứng. ()()() ()() 131 lim ..2 xb

121 1 2 .2.1 xxx x gx axxxxxxxx xaxxxaxxxxx = = 1 0, xxx == không phải tiệm cận đứng của đồ thị hàm số ()ygx = không thỏa mãn điều kiện 0 1 x ≥ . Đồ thị hàm số ()gx có 3 đường tiệm cận đứng là: 232,, xxxxx === .

Câu12. (THPT Quỳnh Lưu- Nghệ An- 2019) Cho hàm số bậc ba () 32 fxaxbxcxd =+++ có đồ thị như hình vẽ sau.

+++ =+∞   (do xb+ → thì () 2 fx + → )nên xb = làtiệmcận đứng. ()()() ()() 131 lim ..2 xc

+++ =+∞   (do xc + → thì () 2 fx → )nên xc = làtiệmcận đứng. Vậy đồ thị hàmsố có4tiệmcận đứng.

xxxx xfxfx + →

Câu11. (Lý Nhân Tông - Bắc Ninh 2019) Cho hàm số () 32 fxaxbxcxd =+++ có đồ thị như hình vẽ

bên.Hỏi đồ thị hàmsố () () ()() 2 2

321xxx gx xfxfx −+− =   cóbaonhiêutiệmcận đứng?

Hỏi đồ thị hàm số () () ()()() 2 2

321 1 xxx gx xfxfx −+− = +− có bao nhiêu tiệm cận đứng?

A. 5 B. 4 C. 6 D. 3 Lờigiải ChọnD

Ta có () ()() ()()() 121 11 xxx gx xfxfx = +− 

lim xx gx → cókếtquả là +∞ hoặc −∞ thì 0xx = làtiệm c

ận đứngcủacủa đồ thị hàmsố ()gx Nhận xét 2:Dựavào đồ thị hàmsố ()fx tacó: () ()()2 1 2 fxaxxx=−−

lim xx gx + → hoặc () 0 Trang 8

Đkxđ: () ()

 ≥  ≠   ≠ 

x fx fx

1 0 1

Dựa vào đồ thị hàm số ()yfx = , ta có: () 1

1 1 x fxxx xx

2 0 x fx xx =  =⇔  =  với 2 x = là nghiệm kép, () 1 0;1 x ∈ () 2 3

=   =⇔=   =  với () 231;2;2xx∈> .

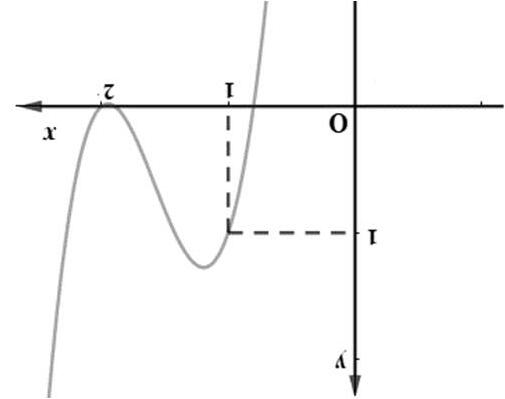
Vì hàm số 3 yxx =+ đồng biến trên ℝ do đó () 3 00;;1xxxx+=∈−∞ có một nghiệm duy nhất.

Vậy đồ thị hàm số () 3 1 3 y fxx = ++ có 1 tiệm cần đứng.

Câu15. (THPTMinhKhai2020) Cho hàmsố () 32 yfxaxbxcxd ==+++ có đồ thị như bêndưới.

x xx fx fxfx x fx xx xxxx trên ℝ và có

1 ; 0 1 1 ==≠ xx gx a axxxxxxx axxxxxxxx . Vậy đồ thị hàm số () = ygx có 4 đường tiệm cận đứng. Câu14. (Chuyên Bắc Giang 2019) Cho hàm số ()yfx = xác định, liên

 =   =<−  =   −=⇔⇔ =   =    =>   =<−≠  ảng

Hỏi đồ thị hàmsố () ()()() 2 2

22 3 xxx y xfxfx =   cóbaonhiêu đườngtiệmcận đứng

A. 4 . B. 6 . C. 3 . D. 5 . Lờigiải ChọnC

t

c

biến thiên như hình bên dưới.

. Khi đó () ()()()() ()()()() () 2 2 123 123 Trang 10

b

=   =−   ′ =   ′ = 

y y y y

01 23 00 20

=   =    +=   +=− 

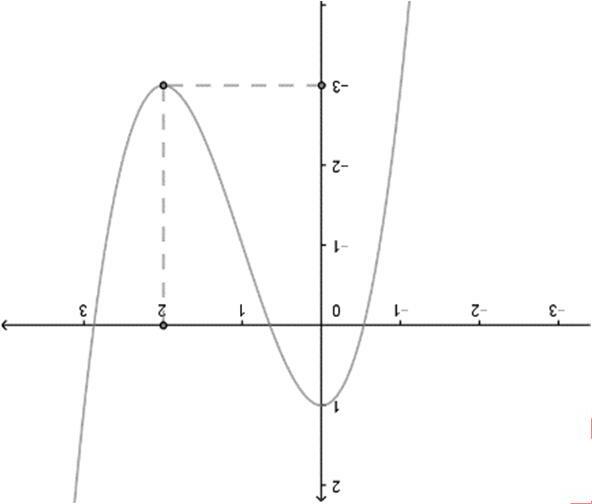
d c ab ab

1 0 1240 844

a b c d

Ta có () 2 32 yxaxbxc ′ =++ Dựa vào đồ thị hàm số, ta thấy hàm số đạt cực trị tại 0 x = , 2 x = . Do đó, ta có hệ () () () ()

=   =−    =   = 

1 3 0 1

vẽ. Hỏi đồ thị hàm số ()() ()() 22 2

xxx y fxfx có tổng cộng bao nhiêu tiệm cận đứng?

42 23 −+ =  +− 

232

22 lim 331 xx

xxx xxxx + → =+∞ −−+ , () () () 2

xxx xxxx + → =+∞ −−+

2 2 232

22 lim 331 xx

Suyra 1xx = và 2xx = cũnglàcác đườngtiệmcận đứngcủa đồ thị hàmsố. Câu16. (YênPhong1-2018) Cho hàm số 32 yaxbxcxd =+++ , () 0 a ≠ có đồ thị như hình dưới đây. Hỏi đồ thị hàm số () () () () 2 2 143 fx gx xxx = +−+ có bao nhiêu đường tiệm cận đứng? A. 2 . B. 1. C. 3 . D. 4 . Lờigiải Điều kiện xác định: () 2

fx x xx

 ≥  ≠−   −+≠ 

0 1 430

x x x x

2 1 1 3

≥   ≠−  ⇔  ≠   ≠ 

2 3 x x ≥  ⇔  ≠ 

Vậy đồ thị hàm số () () () () 2 2 143 fx gx xxx = +−+ có một đườ

A. 5. B. 2. C. 3. D. 4. Lờigiải ChọnD ()() ()() 22 2

42 23 −+ =  +− 

2 2 22 23 +− =  +− 

xxx fxfx

xxx y fxfx ()() ()()

Tacó: ()() 2 230  +−= fxfx () () 1 3

 =  ⇔  =−   fx fx

=<− = ⇔=> = =−

xmm x xnn x x

() ()

2 0 2 2 2

Dựa vào đồ thị ta thấy các nghiệm 0;2xx==± là các nghiệm kép (nghiệm bội 2) và đa thức ()() 2 23fxfx +−  có bậc là 8 nên ()() ()()()() 2 22 22

22 22 +− = +−−− xxx y axxxxmxn Vậy hàm số có các tiệm cận đứng là 0;2;; ==== xxxmxn .

Câu18. (Chuyên Quang Trung - Bình Phước - 2021) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ . Đồ thị ()yfx = như hình vẽ. Số đường tiệm cận đứng của đồ thị hàm số ()() 2 2 2 xx y fxfx +− = là

Lờigiải

ChọnA

Xét hàm số ()() ()() ()() 2 2 12 2 1 xx xx y fxfx fxfx −+ +− ==  

Xét phương trình ()() () () 0 10 1 fx fxfx fx =  −=⇔   =  

Với () 0 fx = () () 1 2 xkep xdon =  ⇔  =−   1 x  = là TCĐ, 2 x =− không là TCĐ.

Vậy đồ thị hàm số có 3 đường tiệm cận khi và chỉ khi phương trình () fxm = có hai nghi

m phân biệt 01 m ⇔<< Vậy 01 m << thì đồ thị hàm số () 2 1 y fxm = có 3 tiệm cận.

x fxxx xx

Với ()() () 1 2

 =  =⇔=∈   =∈−−   0 x = , 1xx = , 2xx = đều là các đường TCĐ

0 10;1 2;1

Vậy đồ thị hàm số có 4 đường TCĐ. Câu19. (ChuyênLêQuý Đôn- ĐiệnBiên-2021) Cho hàm số ()yfx = xác định trên ℝ , có bảng biến thiên như hình vẽ.

Câu20. (THPT Đồng Quan - Hà Nội - 2021) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ và có bảng biến thiên như hình vẽ: Số đường tiệm cận (đứng và ngang) của đồ thị hàm số () () 2

1 144 y fxx = +−− là

A. 5 B. 2 C. 3 D. 4 Lờigiải ChọnD Điều kiện: () () 2 22 40 14 14 xx x fx fx <−∨>  −>   ⇔  +≠ +≠    

Với giá trị nào của m thì đồ thị hàm số () 2 1 y fxm = có tổng số đường tiệm cận ngang và tiệm

cận đứng bằng 3. Chọn đáp án đúng. A. 01 m <≤ . B. 01 m ≤≤ . C. 01 m << . D. 0 m = . Lờigiải ChọnC

Ta có () 2 11 limlim xx y fxmm →±∞→±∞ == vì () lim0 x fx →±∞ = . Do đó:

Nếu 0 m = thì đồ thị hàm số () 2 1 y fxm = không có tiệm cận ngang.

Mặt khác phương trình ()() 2 00fxmfx−=⇔= vô nghiệm nên đồ thị hàm số không có tiệm cận đứng.

Nếu 0 m ≠ thì đồ thị hàm số () 2 1 y fxm = có một tiệm cận ngang là 1 y m = .

+ 0 m < : Phương trình () 2 0 fxm−= vô nghiệm vô nghiệm nên đồ thị hàm số không có tiệm cận đứng.

+ 0 m > : () () () 2 0 fxm fxm fxm  =  −=⇔  =− 

Dựa vào bảng biến thiên ta thấy phương trình () fxm =− vô nghiệm với 0 m ∀>

Xét () () ()

α α β β

12;0 11;1 14121 14; 13;

()() () ()()

xl x fxxxl x xn

=−∈−  +=∈−    +=⇔+=⇔=     +=∈+∞ =−∈+∞   Khi đó: +/ 2 lim x y →− =−∞ , 2 lim x y + → =+∞ , ()() 11 lim,lim xx yy ββ−+ →−→− =+∞=−∞ nên đồ thị hàm số có 3 tiệm cận đứng. +/ lim0 x y →−∞ = , lim0 x y →+∞ = nên đồ thị hàm số có 1 tiệm cận ngang.

Câu21. (Liên Trường Nghệ An – 2021) Cho ()fx là hàm đa thức bậc ba và có đồ thị như hình vẽ bên dưới.

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [] 100;100 để đồ thị hàm số 2 1 () mx y fxm + = có đúng hai đường tiệm cận? A. 100 B. 99 C. 2 D. 196 Lờigiải

TH1: 0 m = 1 () y fx  =

Đồ thị hàm số có một TCN 0 y = và ba tiệm cận đứng nên 0 m = không thoả mãn.

TH2: 0 m <

Đồ thị hàm số không có TCN

Yêu cầu bài toán () fxm⇔= có nghiệm, trong đó có đúng hai nghiệm thoả mãn 2 10 mx +≥

Mà m là số nguyên nên dựa vào đồ thị ta chỉ cần xét } { 2;1 m ∈−−

+ Với 2 12 2 ()2 x my fx =−  = + . Khi đó ()2fx =− có hai nghiệm 120;2xxa==> . Nghiệm 2x không thoả mãn điều kiện 2 120 x −≥ nên 2 m =− không thoả mãn

+ Với 2 1 1 ()1 x my fx =−  = + Khi đó ()1fx =− có hai nghiệm ( ) ( ) 121;0;0;1xbxc=∈−=∈ . Cả

hai nghiệm đều thoả mãn điều kiện 2 10 x −≥ nên 1 m =− thoả mãn.

TH3: 0 m > . Khi đó 2 10,mxxR+≥∀∈

Đồ thị hàm số cómộtTCN 0 y =

Yêucầubàitoán () fxm⇔= có đúngmột nghiệm 2 xRm∈⇔>

Vì m nguyênthuộc đoạn [] [] {} 100;100 3;1001 mZ m ∈     ∈∪−   nêncó 99 giátrị

00xyd =  =<

Câu2. (Đề Tham Khảo 2020 Lần 2) Cho hàm số () 1 ax fx bxc + = + () ,, abc ∈ ℝ có bảng biến thiên như

sau:

Trong các số , ab và c có bao nhiêu số dương? A. 2. B. 3. C. 1. D. 0. Lờigiải ChọnC

Hàm số () 1 ax fx bxc + = + có đường tiệm cận đứng là đường thẳng c x b =− và đường tiệm cận ngang

là đường thẳng a y b =

Từ bảng biến thiên ta có: 2 2 1

 −=  ⇔==−   =   () 1

c c b ab a b

Mặt khác: () ()2 ' acb fx bxc = +

Vì hàm số đã cho đồng biến trên các khoảng () ;2−∞ và () 2; +∞ nên () ()2 '00 acb fxacb bxc =>⇔−> + () 2

Thay () 1 vào () 2 , ta được: 2 2 0001 22 cc ccc −+>⇔−+>⇔<< . Suy ra c là số dương và a, b là số âm. Câu3. (Mã101-2020Lần1) Cho hàm số 32 yaxbxcxd =+++ () ,,, abcd ∈ ℝ có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số a , b , c , d ?

A. 4 B. 1 C. 2 D. 3 Lờigiải Chọn C. Ta có lim x y →+∞ =+∞  0 a <

2x là hoành độ hai điểm cực trị của hàm số suy ra 1x , 2x nghiệm phương trình 2 320yaxbxc ′ =++= nên theo định lý Viet:

+) Tổng hai nghiệm 12 2 0 3 b xx a +=−>  0 b a <  0 b >

+) Tích hai nghiệm 12 0 3 c xx a =>  0 c <

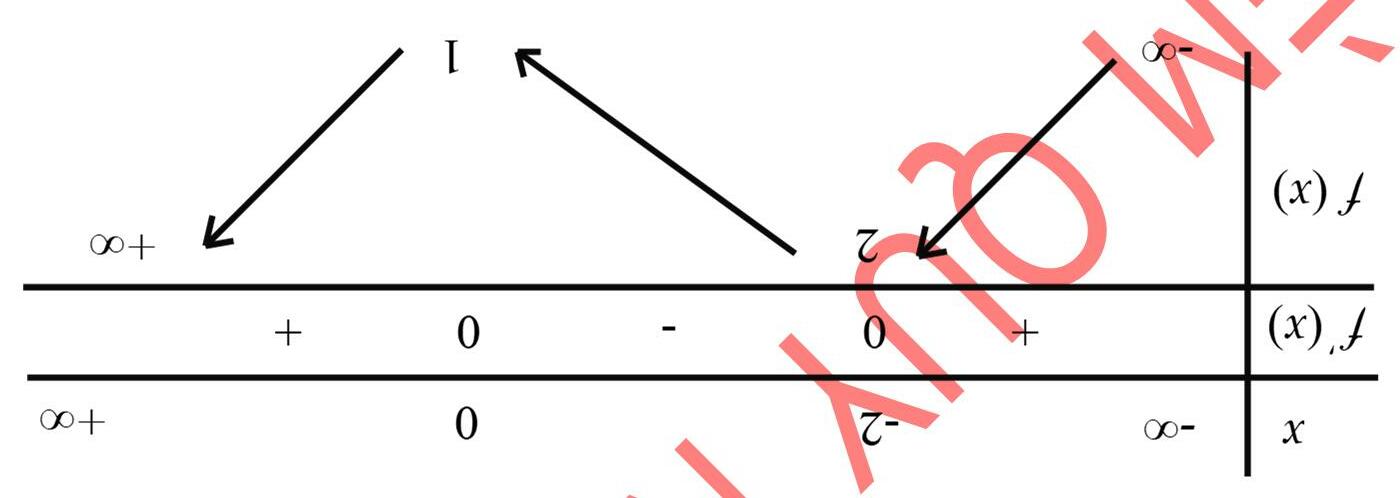
Lại có đồ thị hàm số cắt trục tung tại điểm có tung độ dương nên 0 d > . Vậy có 2 số dương trong các số a , b , c , d .

Câu4. (Mã 102 - 2020 Lần 1) Cho hàm số yaxbxcxd =+++ 32 () ,,, abcd ∈ ℝ có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các hệ số ,,, abcd ?

A. 4 B. 2 C. 1 D. 3 Lờigiải

ChọnC Ta có: 2 32 ′ =++ yaxbxc Dựa vào đồ thị ta thấy 0 < a Hàm số có 2 cực trị âm nên

A. 4 B. 3 C. 1 D. 2 Lờigiải ChọnC

Ta có () lim x fxa →+∞ =−∞  < 0 Đồ thị hàm số có hai điểm cực trị nằm cùng phía của trục tung nên acc >  < 00 Đồ thị hàm số có điểm uốn nằm bên phải trục tung nên abb <  > 00 Đồ thị hàm số cắt trục tung ở dưới trục hoành d  < 0

Câu5. (Mã 103 - 2020 Lần 1) Cho hàm số () 32 ,,, yaxbxcxdabcd =+++∈ ℝ có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số ,,, abcd ? A. 4 B. 2 C. 1 D. 3 Lờigiải ChọnC Ta có 2 32 yaxbxc ′ =++ . Dựa vào đồ thị ta thấy 0 a <

  −> ′ ∆>  <    <⇔−<   <   >   >  

y bac b b S c a P c a Đồ thị cắt trục Oy tại điểm ( ) 0; d nên 0 > d Vậy có đúng 1 số dương trong các số ,,, abcd Câu7. (Mã102-2020Lần2) Cho hàm số ()() 32 ,,, fxaxbxcxdabcd =+++∈ ℝ có bảng biến thiên như sau

2 90 0 0 2 00 0 3 0 0 3

Hàm số có 2 cực trị âm nên

y bac b b S c a P c a

    −> ′ ∆>  <   <⇔−<   <   >  >    Đồ thị cắt trục Oy tại điểm () 0; d nên 0 d > Vậy có đúng một số dương trong các số ,,, abcd

2 90 0 0 2 00 0 3 0 0 3

Câu6. (Mã104-2020Lần1) Cho hàm số () 32 ,,, =+++∈ yaxbxcxdabcd R có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số ,,, abcd ?

Có bao nhiêu số dương trong các số ,,, abcd ? A. 2 . B. 4 . C. 1. D. 3 . Lờigiải ChọnD Từ dáng điệu sự biến thiên hàm số ta có 0. a > Khi 0 x = thì 10 yd==>

Mặt khác () 2 32 fxaxbxc ′ =++ . Từ bảng biến thiên ta có () 2 0 0 x fx x =−  ′ =⇔  =  .

Từ đó suy ra 2 0;230 3 b cba a ==−  => .

Vậy có 3 số dương là ,, abd .

Câu8. (Mã 103 -2020 Lần2) Cho hàm số ()() 32 ,,, fxaxbxcxdabcd =+++∈ ℝ có bảng biến thiên như sau:

Có bao nhiêu số dương trong các số ,,, abcd ? A. 4 B. 2 C. 3 D. 1 Lờigiải ChọnD Ta có: ()() 32 ,,, fxaxbxcxdabcd =+++∈ ℝ ( ) 2 32 fxaxbxc ′  =++ Đồ thị hàm số ()fx có hai điểm cực trị ()() 0;1,4;5AB nên ta có hệ: () () () ()

 = =−   =−     =− +++=−   =− ⇔⇔  = ′ =  =  ++= ′  =   =− 

a f d f abcd b c f c abc f d

1 01 1 8 45 641645 3 4 0 00 0 4880 40 1

. Trong các số ,,, abcd có 1 số dương.

Câu11. Cho hàm số 32 =+++ yaxbxcxd có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

A. 0, 0, 0, 0 <>>< abcd B. 0, 0, 0, 0 <<>< abcd . C. 0, 0, 0, 0 ><<> abcd D. 0, 0, 0, 0 <><< abcd . Lờigiải ChọnA Dựa vào đồ thị suy ra hệ số 0 < a  loại phương án C 2 320 ′ =++=yaxbxc có 2 nghiệm 12 , xx trái dấu (do hai điểm cực trị của đồ thị hàm số nằm hai phía với Oy ) 3.00  <  > acc  loại phương án D. Do ()()0;0. ∩=  < COyDdd

Câu12. (THPT Nguyễn Khuyến 2019) Cho hàm số 42 yaxbxc =++ có đồ thị như hình bên. Mệnh đề nào dưới đây là đúng?

A. 0,0,0abc><> B. 0,0,0abc><< C. 0,0,0abc>>< D. 0,0,0abc<>< Lờigiải

ChọnB

Ta có đồ thị có hình dạng như trên với hàm bậc bốn trùng phương có hai điểm cực tiểu và một điểm cực đại nên 0,0ab>< . Giá trị cực đại nhỏ hơn 0 nên 0 c <

Câu13. (ChuyênTrầnPhúHảiPhòng2019) Cho hàm số + = + axb y cxd có đồ thị như sau.

Mệnh đề nào sau đây đúng?

A. 0; 0 acbd>> B. 0; 0 abcd<< C. 0; 0 bcad>< D. 0; 0 adbd>< Lờigiải Theo đồ thị:

Tiệm cận ngang: 0 => a y c () 1

Tiệm cận đứng: 00 =−>  < dd x cc () 2 000 =  =−<  > bb yx aa () 3

Câu14. (THPTThiệuHóa–ThanhHóa2019) Cho hàm số () 32 0 yaxbxcxda =+++≠ có đồ thị như hình vẽ dưới đây. Chọn khẳng định đúng về dấu của a , b , c , d ?

A. 1,0,1.abc>>< B. 1,0,1.abc><> C. 1,0,1.abc<>< D. 1,0,1.abc>>> Lờigiải

Theo bài ra, đường tiệm cận đứng của đồ thị hàm số là 1 d x c =−

Đường tiệm cận ngang của đồ thị hàm số là: 1 . 1 a y c =

Nhìn đồ thị ta thấy: 0 1 d x c =−> mà 0101dcc <⇒−>⇒>

1 0101 1 a yaa c =>⇒−>⇒>

Đồ thị cắt trục tung tại điểm có tung độ bằng 00 b b d <⇒> .

Câu16. (Sở NinhBình2019) Cho hàm số 42 yaxbxc =++ ( 0 a ≠ ) có đồ thị như hình vẽ dưới đây.

A. 0 a > , 0 b > , 0 d > , 0 c > B. 0 a > , 0 cb >> , 0 d < C. 0,0,0,0.abcd >>>> D. 0 a > , 0 b < , 0 c < , 0 d > lờigiải ChọnD

Dựa vào đồ thị ta có 0 a > , đồ thị cắt Oy tại 1 điểm có tung độ dương nên 0 d > , đồ thị có 2 cực trị trái dấu nên 12.000 c xxc a <  <  < . Vậy đáp án D

Câu15. (ToánHọcTuổiTrẻ 2019) Cho hàm số () () 1 ,0 1 axb yd cxd −+ =< −+ có đồ thị như hình trên. Khẳng định nào dưới đây là đúng?

Mệnh đề nào dưới đây đúng? A. 0 a < , 0 b > , 0 c < B. 0 a < , 0 b < , 0 c > C. 0 a < , 0 b > , 0 c > D. 0 a < , 0 b < , 0 c < Lờigiải Đồ thị cắt trục tung tại điểm () 0; c , từ đồ thị suy ra 0 c < Mặt khác đồ thị hàm số có ba điểm cực trị nên 0 y ′ = có ba nghiệm phân biệt, hay ()32 42220yaxbxxaxb ′ =+=+= có ba nghiệm phân biệt. Suy ra , ab trái dấu. Mà 00ab <  > Câu17. (CụmLiênTrườngHảiPhòng2019) Hàm số 32 yaxbxcxd =+++ có đồ thị như hình vẽ bên dưới:

Đối chiếu lại, ta suy ra 1 c =− , 1 a =− , 2 b = . Vậy ( ) ( ) 2312.2310Tabc=++=−++−=

Câu19. (THPTViệt ĐứcHàNội2019) Cho hàm số 32 yaxbxcxd =+++ có đồ thị như hình bên. Trong các mệnh đề sau mệnh đề nào đúng?

Khẳng định nào là đúng?

A. 0 a < , 0 b < , 0 c < , 0 d < . B. 0 a > , 0 b > , 0 c > , 0 d < . C. 0 a > , 0 b > , 0 c < , 0 d > D. 0 a > , 0 b < , 0 c < , 0 d > Lờigiải

+ Dựa vào hình dạng đồ thị ta khẳng định được 0 a > . + Đồ thị cắt trục Oy tại điểm có tọa độ () 0; d . Dựa vào đồ thị suy ra 0 d >

+ Ta có: 2 32 yaxbxc ′ =++ . Hàm số có hai điểm cực trị 1x , 2x () 12xx < trái dấu nên phương trình 0 y ′ = có hai nghiệm phân biệt 1x , 2x trái dấu. Vì thế 3.0 ac < , nên suy ra 0 c < .

+ Mặt khác từ đồ thị ta thấy 1 2

1 1 x x

 >−     >   nên 12 0 xx+> Mà 12 2 3 b xx a += nên suy ra 2 0 3 b a > 0 b ⇒< Vậy 0 a > , 0 b < , 0 c < , 0 d >

Câu18. (THPT Ba Đình 2019) Cho hàm số axb y xc + = + có đồ thị như hình bên dưới, với a , b , c ∈ ℤ

Tính giá trị của biểu thức 23 Tabc =++ ?

A. 8 T =− . B. 2 T = . C. 6 T = . D. 0 T = . Lờigiải

Từ đồ thị hàm số, ta suy ra  Đồ thị hàm số có tiệm cận đứng là đường thẳng 1 x = , tiệm cận ngang là đường thẳng 1 y =−  Đồ thị hàm số đi qua các điểm () 2;0 A , () 0;2 B

Từ biểu thức hàm số axb y xc + = + (vì đồ thị hàm số là đồ thị hàm nhất biến nên 0 acb−≠ ), ta suy ra  Đồ thị hàm số có tiệm cận đứng là đường thẳng xc =− , tiệm cận ngang là đường thẳng ya =  Đồ thị hàm số đi qua ;0 b A a    , 0; b B c   

A. 0,0,0abbccd<>< B. 0,0,0abbccd<<> C. 0,0,0abbccd>>< D. 0,0,0abbccd>>> Lờigiải ChọnA Từ dáng điệu của đồ thị ta có ngay được: ⊕ lim;lim0 xx yya →+∞→−∞ =+∞=−∞  > . ⊕ Đồ thị hàm số cắt trục tung tại một điểm có tung độ dương nên 0 d > Ta có: 2 '32 yaxbxc =++ Mặt khác dựa vào đồ thị ta thấy phương trình '0 y = có hai nghiệm trái dấu và tổng hai nghiệm

này luôn dương nên 00 20 3

<  <     < −>    (do 0 a > )

ac c b b a

Do đó: 0,,0abbccd<>< .

Câu20. (THPT Lương Thế Vinh Hà Nội 2019) Cho hàm số 32 yaxbxcxd =+++ có đồ thị như hình dưới. Khẳng định nào sau đây đúng ?

A. 0,0,0,0abcd <<<< B. 0,0,0,0abcd <>>> C. 0,0,0,0abcd <><> D. 0,0,0,0abcd <>>< Lờigiải ChọnD

- Dựa vào hình dáng của đồ thị suy ra hệ số 0 a < - Đồ thị cắt trục Oy tại điểm có tung độ âm nên 0 d < . - Ta thấy đồ thị như hình vẽ có hai điểm cực trị, hoành độ các điểm cực trị trái dấu suy ra phương trình 2 320yaxbxc ′ =++= có 2 nghiệm 12 , xx trái dấu kéo theo 3.00 acc <  > .

- Mặt khác 12 00 23 xxb b a + =−>  > .

Câu21. (THPT Chuyên Bắc Ninh 2019) Cho hàm số có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng ? 42 yaxbxc =++

10

A. 0,0,0abc><< B. 0,0,0abc<<< C. 0,0,0abc<>< . D. 0,0,0abc><> Lờigiải ChọnC

- Dựa vào hình dạng đồ thị suy ra 0 a <

- Hàm số có 3 điểm cực trị nên 00abb <  >

- Giao điểm với trục tung nằm dưới trục hoành nên 0 c < .

Câu22. (Chuyên Lê Quý Đôn Quảng Trị 2019) Cho hàm số axb y cxd + = + có đồ thị như trong hình bên dưới. Biết rằng a là số thực dương, hỏi trong các số ,, bcd có tất cả bao nhiêu số dương?

Khẳng định nào là đúng? A. 0 a < , 0 b < , 0 c < , 0 d < . B. 0 a > , 0 b > , 0 c > , 0 d < . C. 0 a > , 0 b > , 0 c < , 0 d > D. 0 a > , 0 b < , 0 c < , 0 d > Lờigiải

ChọnD

+ Dựa vào hình dạng đồ thị ta khẳng định được 0 a > . + Đồ thị cắt trục Oy tại điểm có tọa độ () 0; d . Dựa vào đồ thị suy ra 0 d > .

+ Ta có: 2 32 yaxbxc ′ =++ . Hàm số có hai điểm cực trị 1x , 2x () 12xx < trái dấu nên phương trình 0 y ′ = có hai nghiệm phân biệt 1x , 2x trái dấu. Vì thế 3.0 ac < , nên suy ra 0 c < . + Mặt khác từ đồ thị ta thấy 1 2

A. 1 . B. 2 . C. 0 . D. 3 . Lờigiải ChọnB

Nhìn vào đồ thị ta thấy

• tiệm cận ngang a y c = nằm trên trục hoành nên 0 c > (vì 0 a > )

• tiệm cận đứng d x c = nằm bên trái trục tung nên 0. d c < Suy ra 0 d > (vì 0 c > )

• giao điểm của đồ thị và trục tung nằm bên dưới trục hoành nên 0. b d < Suy ra 0 b < (vì 0 d > )

Vậy 0,0cd>>

Câu23. (Cụm liên trường Hải Phòng 2019) Hàm số 32 yaxbxcxd =+++ có đồ thị như hình vẽ bên dưới:

 >−     >   nên 12 0 xx+> Mà 12 2 3 b xx a += nên suy ra 2 0 3 b a > 0 b ⇒< . Vậy 0 a > , 0 b < , 0 c < , 0 d >

1 1 x x

Câu24. (ChuyênNguyễn Huệ 2019) Cho hàm số axb y cxd + = + có đồ thị như hình vẽ bên. Khẳng định nào

sau đây là khẳng định đúng?

A. 0 0 ad bc <   >  B. 0 0 ad bc <   <  C. 0 0 ad bc >   <  D. 0 0 ad bc >   >  Lờigiải ChọnC

Nhận xét từ đồ thị:

+ Giao với trục hoành tại 0 o b x a =−>  a và b trái dấu (1).

+ Giao với trục tung tại 0 o b yb d =<  và d trái dấu (2).

+ Tiệm cận đứng: 0 d xd c =−<  và c cùng dấu (3).

Từ (1) và (2) suy ra: a và d cùng dấu hay 0 ad >

Từ (2) và (3) suy ra: b và c trái dấu hay 0 bc <

Câu25. Tìm đồ thị hàm số ()yfx = được cho bởi một trong các phương án dưới đây, biết

()()()2 fxaxbx =−− với ab < . A. B. . C. . D. . Lờigiải ChọnA Có ()()()()()()()()() 2 .22223 fxbxaxbxbxbxaxbxbax ′ =−−+−−−=−−−+−=−−+− () 0 2 3

D. 0,0,0,0abcd >><< Lờigiải

ChọnD

Từ đồ thị ta có 00xyd =  =< , từ dạng đồ thị suy ra 0 a > Mặt khác 2 '32 yaxbxc =++ từ đồ thị ta có phương trình '0 y = có hai nghiệm trái dấu suy ra 0 ac < mà 0 a > suy ra 0 c < Hơn nữa phương trình '0 y = có hai nghiệm phân biệt 12 2 1 3 b xx a +=−=− suy ra 320 abb =  > .

Vậy chọn đáp án D. Câu27. (Gia Lai 2019) Hàm số 42 yaxbxc =++ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?

xb fx ab x

=   ′ =⇔ +  =  .

Có 22 33 abbb b ++ <= Ta có bảng biến thiên

A. 0 a > , 0 b > , 0 c < . B. 0 a < , 0 b > , 0 c < . C. 0 a > , 0 b < , 0 c > D. 0 a > , 0 b < , 0 c < Lờigiải ChọnC Dựa vào đồ thị: + lim x y →+∞ =+∞ ⇒ 0 a > + Đồ thị hàm số có ba điểm cực trị ⇒ 0 ab < ⇒ 0 b < . + Giao điểm của đồ thị hàm số và trục tung có tung độ dương ⇒ 0 c > . Vậy 0 a > , 0 b < , 0 c > .

Câu28. (THPT Thăng Long 2019) Cho hàm số 42 yaxbxc =++ có đồ thị như hình vẽ. Tìm kết luận đúng

Từ đó chọn đáp án A

Câu26. Cho đường cong () 32 : Cyaxbxcxd =+++ có đồ thị như hình bên.

A. 0 ab+> . B. 0 bc > . C. 0 ab > . D. 0 ac > . Lờigiải ChọnB

Từ hình vẽ ta thấy: Đồ thị hàm số có bề lõm hướng lên 0 a ⇒> Đồ thị hàm số cắt trục tung tại điểm có tung độ âm 0 c ⇒< . Đồ thị hàm số có 3 điểm cực trị 00abb ⇒<⇒< Vậy chỉ có 0 bc > .

Câu29. (THPT Cẩm Bình Hà Tỉnh 2019) Cho hàm số 42 (0)yaxbxca =++≠ có đồ thị như hình bên. Hãy chọn mệnh đề đúng.

Khẳng định nào sau đây là đúng?

A. 0,0,0,0abcd ><<< .

B. 0,0,0,0abcd>><> .

C. 0,0,0,0abcd <>>< . Trang 14

Trang 13

A. 0,0,0abc<<= . B. 0,0,0abc<>= C. 0,0,0abc><= D. 0,0,0abc><> Lờigiải ChọnC

Dựa vào hình dạng đồ thị hàm số ta nhận thấy : Hệ số 0 a > Đồ thị hàm số đi qua gốc tọa tọa 0 c ⇒= Hàm số có 3 điểm cực trị .00abb ⇒<⇒< Câu30. (ChuyênLongAn2019) Cho hàm số 32 () yfxaxbxcxd ==+++ có đồ thị như hình vẽ ở bên. Mệnh đề nào sau đây đúng?

Dựa vào hình dạng đồ thị hàm số ta nhận thấy : Hệ số 0 a < . Hàm số có 3 điểm cực trị .00abb ⇒<⇒> Đồ thị hàm số đi qua gốc tọa tọa 0 c ⇒= . Vậy 0,0,0abc<>=

Câu32. (THPT Cộng Hiền 2019) Cho hàm số 42 yaxbxc =++ có đồ thị như hình vẽ bên. Hỏi khẳng định nào sau đây đúng?

A. 0,0,0abc><< B. 0,0,0abc>>< C. 0,0,0abc><> D. 0,0,0abc<>< Lờigiải ChọnA Nhìn vào đồ thị ta có: Khi x ∈ ( ) 2; +∞ hàm số đồng biến 0 a  > . Hàm số có 3 điểm cực trị nên 0 a.b < mà 00ab >  < . ()010ycc =−=  < .

Câu33. (SGD Điện Biên - 2019) Cho hàm số 3 ax y xc + = + có đồ thị như hình vẽ bên. Tính giá trị của 2.ac

fda fabcdb fabcc fabcd

. Câu31. (THPT Trần Phú 2019) Cho hàm số bậc bốn trùng phương 42 yaxbxc =++ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng? A. 0,0,0abc<>> . B. 0,0,0abc><> . C. 0,0,0abc<>= D. 0,0,0abc><< Lờigiải

=== =+++==−   =++==  =++== Trang

′ ′

16

A. 23.ac−= B. 23.ac−=− C. 21.ac−=− D. 22.ac−=− Lờigiải ChọnA

Đồ thị hàm số có TCN 111. 1 a ya =−⇔=−⇔=− Mặt khác Đồ thị hàm số có TCĐ 2 x = nên 202. cc +=⇔=− () 212.23.ac  −=−−−=

Dựa vào đồ thị ta thấy các điểm () 3;0 và 3 0; 2    thuộc vào đồ thị hàm số đã cho nên ta được hệ phương trình

Vậy 0 ba<< .

.33 0 3 3.03 20

a c a c

+  =   +  + −= + 

=−  ⇔  =−  () 212.23.ac  −=−−−=

330 36 a c +=  ⇔  −= 1 2 a c

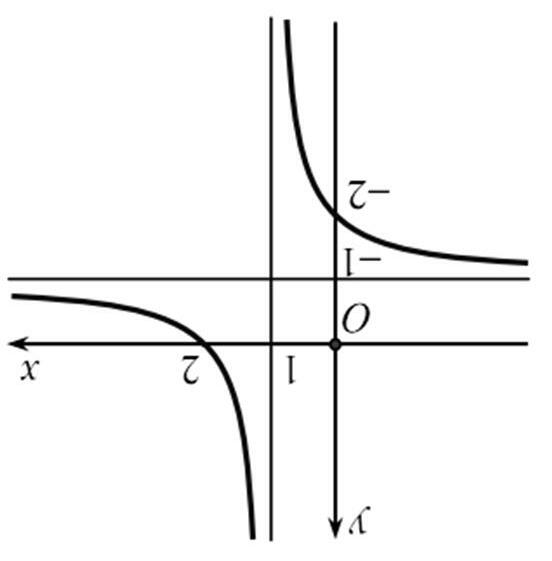
Câu34. Hình vẽ bên là đồ thị hàm số axb y cxd + = +

Mệnh đề nào dưới đây đúng? A. 0 ad > và 0 bd > B. 0 ad > và 0 ab < C. 0 bd < và 0 ab > D. 0 ad < và 0 ab < Lờigiải ChọnB

Đồ thị hàm số giao với trục Ox tại điểm có hoành độ b x a =− , giao với Oy tại điểm có tung độ b y d = .

Câu36. (Chuyên Lương Văn Chánh - Phú Yên - 2020) Đồ thị trong hình bên dưới là của hàm số axb y xc + = + (với ,, abc ∈ ℝ ).

Khi đó tổng abc ++ bằng A. 1 B. 1 C. 2 D. 0 Lờigiải ChọnD Đồ thị hàm số axb y xc + = + có đường tiệm cận ngang ya = , đường tiệm cận đứng xc =− và cắt

Oy tại điểm 0; b c    Từ đồ thị hàm số ta có đường tiệm cận ngang 1 y =− , đường tiệm cận đứng 1 x = và cắt Oy tại điểm ( )0;2 . Từ đó suy ra: 111 111 22 2

  =−=−=−    −=⇔=−⇔=−  =−=  =− 

. Vậy 1120 abc++=−−+=

Dựa vào hình vẽ ta có 00 0 0 0 00

bb ab aa ad bbbd dd

 −><  <   ⇔⇔  >  <  << 

Trong các phương án chỉ có phương án B thỏa mãn.

Câu35. Cho hàm số 1 axb y x = có đồ thị như hình vẽ dưới đây:

Khẳng định nào sau đây đúng?

A. 0 ba<< . B. 0 ab<< . C. ba > và 0 a < . D. 0 ab << . Lờigiải

ChọnA

Ta thấy đồ thị hàm số có tiệm cận ngang 1 y =− suy ra 1 a =−

Do đồ thị hàm số đi qua điểm () 2;0 nên 20202 abbb −=⇔−−=⇔=−

aaa ccc bbcb c

Câu37. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số 2 () ax fx bxc = () ,,,0abcb∈≠ ℝ có bảng biến thiên như sau: Tổng các số ()2 abc ++ thuộc khoảng nào sau đây A. () 1;2 B. () 2;3 C. 4 0; 9    D. 4 ;1 9    Lờigiải ChọnC

Ta có 2 lim x

axa bxcb →∞ = , theo giả thiết suy ra 33 a ab b =⇔=− Hàm số không xác định tại 10 xbcbc =  −=⇔=

n trên t

ng khoảng xác định nên () ()2 2 0 acb fx bxc ′ => với mọi x

1 Suy ra 2 22 2032000 33 acbbbbb −>⇔−−>⇔−<<⇔<−< Lại có 3 abcbbbb ++=−++=− . Suy ra ()2 2 4 0; 9 abcb  ++=∈   Vậy tổng abc ++ thuộc khoảng 4 0; 9   

Câu38. (ChuyênHùngVương-GiaLai-2020) Cho hàm số () axb fx cxd + = + (,,,abcd ∈R và 0 c ≠ ). Biết rằng đồ thị hàm số đã cho đi qua điểm () 1;7 và giao điểm hai tiệm cận là () 2;3 . Giá trị biểu thức 234 7 abcd c +++ bằng A. 7 B. 4 C. 6 D. 5 Lờigiải ChọnC + Ta có đồ thị hàm số () axb fx cxd + = + có đường tiệm cận ngang là a y c = , đường tiệm cận đứng là d x c = .

ố có tiệm cận đứng là đường thẳng 2 x = và tiệm cận ngang là đường thẳng 1 y = nên ta có hệ 2

c c b cbcb a ababa b acbbb acb b abc

    −=  <<  =−=−    =⇔=⇔=⇔−<<  −>−−> −>   −<<     ++= 

2 01 22 1 1 0 2 020 1 0 0 2 0

Dựa vào hệ trên ta có các phát biểu ()() 1,4 là sai, ()() 2,3 đúng. Câu40. (Đô Lương 4 - Nghệ An - 2020) Ta xác định được các số ,, abc để đồ thị hàm số 32 yxaxbxc =+++ đi qua điểm () 1;0 và có điểm cực trị () 2;0 . Tính giá trị biểu thức 222 Tabc =++ . A. 25. B. 1. C. 7. D. 14. Lờigiải ChọnA Ta có 32232 yxaxbxcyxaxb ′ =+++  =++ .

   =   =    ⇒   −=    =−    

a ac c ddc c

Theo bài ra, ta có: 3 3 2 2

. + Điểm () 1;7 thuộc đồ thị hàm số ()fx nên 3 7710 2 abcb bc cdcc −+−+ =⇔=⇔= −+−+ Vậy 2342.(3)3.(10)426 77 abcdcccc cc ++++++ == .

(ChuyênLê HồngPhong -Nam Đị

Theo đề, ta có hệ phương trình () () () ()()() ()()

abca abcb abc

++=−=  ⇔−+=⇔=   −+=−=− 

13 4280 4124

 =+++  =    −=⇔=−+−+−+  ′ −= =−+−+   

abc y yabc y ab

Vậy ()2 2222230425. Tabc=++=++−=

32 32 2

01.1.1 10 2002.2.2 2003.22.2

Câu41. (Lê Lai - Thanh Hóa - 2020) Cho hàm số có đồ thị như hình vẽ. Tính ?

32 yaxbxcxd =+++ Sab =+ 2 S =− 0 S = 1 S = 1 S =−

A. B. C. D. Lờigiải ChọnA Vì đồ thị hàm số cắt trục tung tại điểm 2 y = nên 2 d = . 2 32 yaxbxc ′ =++ Hàm số đạt cực trị tại 0 x = và 2 x = nên

Đồ thị hàm số 1 axb y cx + = + có đường tiệm cận đứng là đường thẳng 1 x c =− và

=− ++= ′ =      Từ đồ thị ta nhận thấy () ()22842844212 yabdabab =−⇔++=−⇔+=−⇔+=− Thay () 1 vào () 2 ta tìm được 1,3ab==− . Vậy 2 S =−

1 1240

abc

Câu42. (Lý Nhân Tông - Bắc Ninh - 2020) Cho hàm số 32 yaxbxcxd =+++ có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?

ngang là đường thẳng a y c =

Nhìn vào bảng biến thiên, ta thấy 1 11 c c −=−  = và 22 a a c =  = (vì 1 c = ).

Ta có ()2 1 abc y cx ′ = + . Vì hàm số đã cho đồng biến trên các khoảng () ;1−∞− và () 1; −+∞ nên () 33 2 00202880 abc yabcbbbb bxc ′ =>⇔−>⇔−>⇔<⇔<⇔−< + Vậy tập các giá trị b là tập nghiệm của bất phương trình 3 80. b −<

Câu44. (TiênDu-BắcNinh-2020) Cho hàm số axb y cxd + = + (với ,,, abcd là số thực) có đồ thị như hình

A. 0,0,0,0abcd <<>< . B. 0,0,0,0abcd <><< . C. 0,0,0,0abcd ><<> . D. 0,0,0,0abcd <>>< . Lờigiải ChọnD Ta có: 2 32 yaxbxc ′ =++ , 62 yaxb ′′ =+ Từ đồ thị ta thấy:  lim x y →+∞ =−∞ . Ta suy ra 0 a <  ( ) 000yd <  < loại C. Đồ thị hàm số có hai điểm cực trị với hoành độ 1x , 2x trái dấu và 12 0 xx+> . Ta suy ra phương trình '0 y = có hai nghiệm trái dấu và 12 0 xx+> .

Ta suy ra 12 0 3 c xx a =< , 0 c  > loại B. Hơn nữa, 12 0 30 0

dưới đây. Tính giá trị biểu thức 23 abd T c −+ =

b xx b a a

 +=−>   >   <  . Lọai A.

Câu43. (Nguyễn Huệ - Phú Yên - 2020) Cho hàm số ()1,, axb yabc cx + =∈ + ℝ có bảng biến thiên như sau:

A. 6 = T . B. 0 = T . C. 8=− T . D. 2 = T . Lờigiải ChọnC Từ đồ thị ta có TCĐ: 111 dd x cc =  =  =− dc  =− TCN: 11 a yac c =−  =−  =− Đồ thị cắt trục hoành tại điểm: 2222 bbb x acc =  =  =  = 2 bc  =

Vậy 2343 8 abdccc T cc −+−−− ===−

Câu45. (ThanhChương 1 - Nghệ An - 2020) Cho hàm số 32 yaxbxcxd =+++ có đồ thị như hình vẽ. Trong các số ,, abc và d có bao nhiêu số dương?

Tập các giá trị b là tập nghiệm của bất phương trình nào dưới đây? A. 3 80. b −≤ B. 2 40. b −+> C. 2 320.bb−+< D. 3 80. b −< Lờigiải ChọnD

A. 1 B. 4 C. 3 D. 2 Lờigiải ChọnD

Từ hình dạng đồ thị hàm số ta có 0 a > Đồ thị hàm số cắt trục tung tại điểm có tung độ âm 0 d  <

Ta có: 2 '32 yaxbxc =++ Hàm số có hai điểm cực trị trái dấu '0 y  = có hai nghiệm trái dấu 0 ca ⇔< Mà 0 a > nên 0 c <

Ta lại có: ''62 yaxb =+ ''0620 3 b yaxbx a =⇔+=⇔=−

Từ đồ thị hàm số ta thấy tâm đối xứng có hoành độ âm. Do đó 0 3 b a −< Mà 0 a > nên 0 b > Vậy trong các số ,, abc và d có 2 số dương là a và b

Câu46. (TiênLãng-HảiPhòng-2020) Cho hàm số () 6 = ax fx bxc () ,, ∈ ℝ abc có bảng biến thiên như

sau:

Trong các số ,, abc có bao nhiêu số âm? A. 0 B. 3 C. 1 D. 2 Lờigiải ChọnD

Từ bảng biến thiên của hàm số, ta thấy đồ thị có hai đường tiệm cận, trong đó tiệm cận đứng là đường thẳng 2 x =− và tiệm cận ngang là đường thẳng 1 y = .

Câu47. (Chuyên Ngoại Ngữ Hà Nội- 2021) Cho hàm số 1 ax y bxc = + với ,, abc ∈ ℝ có

như hình vẽ:

Hỏi trong ba số ,, abc có bao nhiêu số dương? A. 0. B. 3. C. 2. D. 1. Lờigiải ChọnC

Cho 1 000.xyc c =  =<⇔> Đường tiện cận đứng 220 c xcbb b ==  =−  < (do 0 c > ).

Tiệm cận ngang 10 a yaba b ==−⇔=−  > (do 0 b < ).

Khi đó 0 0. 0

b a c

<   >   > 

Câu48. (Chuyên ĐHSP Hà Nội - 2021) Cho hàm số 32 yaxbxcxd =+++ (,,,) abcd ∈ ℝ có đồ thị là đương cong như hình vẽ bên.

c b a b

 =−     =  

Suy ra 2 1

0 0 bc ab <    >  () () 1 0,0,0 2 0,0,0 bca bca ><>  ⇔  <>< 

Lại có hàm số nghịch biến trên mỗi khoảng xác định () ()2 6 0 acb fx bxc −+ ′ =< 6 acb  >

Ta thấy () 1 không thể xảy ra do nếu 0 b > thì 60acb>> ; và () 2 có thể xảy ra do nếu 0,0ca>< thì 60 bac<< Vậy trong các số ,, abc có hai số âm.

Có bao nhiêu số dương trong các số ,,, abcd ? A. 0 B. 1 C. 2 D. 3 Lờigiải ChọnA Dựa vào giáo điểm của đồ thị với trục tung ta có 0 d < , dựa vào dáng của đồ thị suy ra 0 a < 2 32 yaxbxc ′ =++ dựa vào đồ thị ta có phương trình 0 y ′ = có hai nghiệm phân biệt âm suy ra 00 3 2 00 3

c c a b b a

 >  <    −<  <  

Câu49. (THPT Phan Đình Phùng - Quảng Bình - 2021) Cho hàm số () 4 ax fx bxc = + () ,, abc ∈ ℝ có

bảng biến thiên như sau:

A. 0 . B. 1. C. 2 . D. 3 . Lờigiải

Trong các số ,, abc có bao nhiêu số dương?

A. 3. B. 0. C. 2. D. 1. Lờigiải ChọnC

Ta có: () 4 000fc c =−>  <

Tiệm cận đứng của đồ thị hàm số: 00 c xb b =−>  > .

Tiệm cận ngang của đồ thị hàm số: 00 a ya b =>  >

Vậy trong các số ,, abc có 2 số dương.

Câu50. (THPT Đào Duy Từ - Hà Nội - 2021) Cho đồ thị của hàm số () 42 fxaxbxc =++ như hình vẽ bên. Khẳng định nào sau đây là đúng?

y O

x

A. 2 0;0;0;40abcbac ><>−= . B. 2 0;0;0;40abcbac >>>−= . C. 2 0;0;0;40abcbac ><>−> . D. 2 0;0;0;40abcbac ><>−< . Lờigiải

ChọnA

Đồ thị có tiệm cận đứng d x c =− mà 00 d c c −>  >

Đồ thị có tiệm cận ngang a y c = mà 00 a a c >  > .

Đồ thị cắt trục Ox mà tại điểm có hoành độ b a mà 00 b b a −<  > .

Vậy trong các số ,, abc có 3 số dương.

Câu52. (Sở CầnThơ -2021) Cho hàm số ( và ) có đồ thị như sau:

 ++=  ++= 

  = +=     2 2 2 4 ..0040 224 bbacb abcbac aaa   ++=  =  −=   . Câu51. (Sở QuảngBình-2021) Cho hàm số axb y cxd + = + có đồ thị như hình vẽ bên dưới, trong đó 0 d < . Trong Trang 26

0 0 420 2

axbxcaxbxc b axbxx a

Khẳng định nào sau đây đúng? A. B. C. D. Lờigiải ChọnD

Đồ thị hàm số có tiệm cận đứng , tiệm cận ngang .

Đồ thị cắt trục tung tại điểm .

bxc y xa = 0 a ≠ ,, abc ∈ ℝ 0;0;0abc<>< 0,0,0abc<<> 0,0,0abc><< 0,0,0abc>>< bxc y xa = xa = yb = 0; c a   

> 

>   >  ⇔ >   < <   

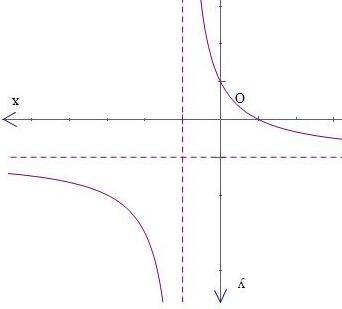
00 00 00

Câu53. (Sở CầnThơ -2021) Cho hàm số 32 yaxbxcxd =+++ () ,,, abcd ∈ ℝ có đồ thị như sau:

Có bao nhiêu số dương trong các số ,,, abcd ? A. 4 . B. 2 . C. 1. D. 3 . Lờigiải ChọnC Đồ thị hàm số cắt trục tung tại điểm có tung độ dương 0 d  > lim00 x ya →+∞ <  < Ta có: 2 32 yaxbxc ′ =++ Đồ thị hàm số có 2 điểm cực trị nằm về bên trái trục tung nên phương trình 0 y ′ = có 2 nghiệm phân biệt 12 0 xx<<

Khi đó theo Viet ta có: 12 12



Câu55. (LiênTrườngNghệ An– 2021) Cho hàm số 42 ()(,,) fxaxbxcabcR =++∈ có đồ thị cho bởi hình vẽ bên. Chọn khẳng định đúng:

A. ba > . B. 0 abc+> C. 0 ac−> D. 0 abc < Lờigiải Ta có lim()0 x fxa →±∞ =+∞  > ; Hàm số có 3 điểm cực trị nên 00abb <  < Đồ thị hàm số cắt trục tung tại điểm nằm phái dưới trục hoành nên 0 c < Vậy 0; 0; 0 abc><< suy ra 0 ac−> .

Câu56. (Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam - 2021) Cho hàm số 32 yaxbxcxd =+++ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng?

b xx a c xx a

 +=−<     =>  

2 0 3 .0 3

Vậy trong các số ,,, abcd chỉ có 0 d > . Câu54. (ChuyênBiênHòa-2021) Cho hàm số 42 yaxbxc =++ có đồ thị như hình vẽ sau:

Trong các khẳng định sau, khẳng định nào đúng? A. 0;0;0abc<<> B. 0;0;0abc><> C. 0;0;0abc<>> D. 0;0;0abc><< Lờigiải

ChọnC

Tập xác định: D = ℝ . Ta có: ()32'4222 yaxbxxaxb =+=+ .

a a b b c c a Trang 28

. Từ đó suy ra 0 b < và 0 c < .

A. 0, 0, 0, 0 abcd <>>> B. 0, 0, 0, 0 abcd <<=> C. 0, 0, 0, 0 abcd <>=> D. 0, 0, 0, 0 abcd ><>> Lờigiải ChọnC

Nhánh cuối đồ thị đi xuống nên 0 a < Điểm uốn lệch bên phải trục Oy nên 00abb <  > Đồ thị có 2 cực trị trong đó một cực trị thuộc Oy nên 0 c = Đồ thị cắt trục tung tại điểm có tung độ dương nên 0 d >

Câu57. (Sở CầnThơ -2021) Cho hàm số () 2 ax fx bxc + = + , () ,,, abcd ∈ ℝ có đồ thị như sau:

Khẳng định nào dưới đây đúng? A. 0 bac <<< . B. 0 bac <<< . C. 0 abc <<< . D. 0 bca <<< . Lờigiải ChọnC Khi 2 012xyc c =  ==  = Tiệm cận đứng 2 112 c xb bb =−=  −=  =− . Tiệm cận ngang 224 2 aa ya b ==  =  =− . Vậy 0 abc <<< Dạng2. Đồ thị hàmsố chứadấugiátrị

ng2

Từ đồ thị ()() = Cyfx : suy ra đồ thị () () ′ = Cyfx :

và () = yfx là hàm chẵn nên đồ thị () C′ nhận Oy làm trục đối xứng.

*Cáchvẽ () ′ C từ () C :

 Giữ nguyên phần đồ thị bên phải Oy của đồ thị ()() = Cyfx :  Bỏ phần đồ thị bên trái Oy của () C , lấy đốixứngphần đồ thị được giữ qua Oy

Vídụ: Từ đồ thị ( ) ( ) ==− Cyfxxx 3 :3 suy ra đồ thị () ′ =− Cyxx 3 :3 Biến đổi () C :

 Bỏ phần đồ thị của () C bên trái Oy, giữ nguyên () C bên phải Oy  Lấy đối xứng phần đồ thị được giữ qua Oy

y O -2

y O -2

2 -1 1

ệt đối(BIẾN ĐỔI ĐỒ THỊ) Dạng1 Từ đồ thị ()() = Cyfx : suy ra đồ thị ()() ′ = Cyfx : Ta có: () ()() ()()  ≥  ==  −<  yfxfxkhifx fxkhifx 0 0 *Cáchvẽ () ′ C từ () C :  Giữ nguyên phần đồ thị phía trên Ox của đồ thị (C): () = yfx  Bỏ phần đồ thị phía dưới Ox của (C), lấy đốixứngphần đồ thị bị bỏ qua Ox. Ví dụ: Từ đồ thị ( ) ( ) 3 :3 Cyfxxx ==− suy ra đồ thị =− yxx 3 3 Biến đổi () C : Bỏ phần đồ thị của () C dưới ,Ox giữ nguyên () C phía trên .Ox Lấy đối xứng phần đồ thị bị bỏ qua Ox .

( ) 3 :3 Cyxx =− ( )′ =− Cyxx 3 :3 Dạ

x

y 2 -1 O 1 Trang 30

y 2 -1 O 1

y O -2

( ) =− Cyxx 3 :3 () ′′ =− Cyxx 3 :3

2 -1 1 x

x

-1 1 x

() ′ =− Cyxx 3 :3

Chú ý với dạng: () = yfx ta lần lượt biến đổi 2 đồ thị () = yfx và () = yfx Ví dụ: Từ đồ thị ( ) ( ) ==− Cyfxxx 3 :3 suy ra đồ thị =− yxx 3 3 . Biến đổi () C để được đồ thị () ′ =− Cyxx 3 :3 . Biến đổi () ′ =− Cyxx 3 :3 ta được đồ thị () ′′ =− Cyxx 3 :3

Dạng3 Từ đồ thị ()()() = Cyuxvx :. suy ra đồ thị ( ) ( ) ( ) ′ = Cyuxvx :. . Ta có: () () ()()()() ()()()() uxvxfxkhi ux yuxvxuxvxfxkhi ux .0 . .0  =≥  ==  −=<  *Cáchvẽ () ′ C từ () C :  Giữ nguyên phần đồ thị trên miền () ≥ ux 0 của đồ thị ()() = Cyfx :  Bỏ phần đồ thị trên miền () < ux 0 của () C , lấy đốixứngphần đồ thị bị bỏ qua Ox Vídụ a) Từ đồ thị ()()==−+Cyfxxx32 :231 suy ra đồ thị () () ′ =−−−Cyxxx 2 :121

Vídụ b) Từ đồ thị ()()== x Cyfx x : 1 suy ra đồ thị () ′ = x Cy x : 1

Đồ thị (C’):  Giữ nguyên (C) với 1 x ≥  Bỏ (C) với < x 1 . Lấy đối xứng phần đồ thị bị bỏ qua Ox.

x khi x x x y x x khi x x

(C)

Nhận xét: Trong quá trình thực hiện phép suy đồ thị nên lấy đối xứng các điểm đặc biệt của (C): giao điểm với Ox, Oy, CĐ, CT…

 ∈+∞   ==  −∈−∞ 

1; 1 1 ;1 1

Đồ thị (C’): Bỏ phần đồ thị của () C với x ,1 < giữ nguyên () C với 1. x > Lấy đối xứng phần đồ thị bị bỏ qua Ox

y 1 O 1

Nhận xét: Đối với hàm phân thức thì nên lấy đối xứng các đường tiệm cận để thực hiện phép suy đồ thị một cách tương đối chính xác.

Câu1. Cho hàm số 3232yxx=−+ có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 3232.yxx=−+ B. 3 2 32yxx=−+ C. () 2 122.yxxx=−−− D. () 2 122.yxxx =−−− Hướngdẫn Ta có: ( )( ) 32232122yxxxxx =−+=−−−

Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Toàn bộ đồ thị ứng với 1 x ≥ được giữ nguyên. Phần đồ thị ứng với 1 x < lấy đối xứng qua trục hoành.  Chọn đápán C.

x Trang 32

A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 Lờigiải ChọnA () ()() ()() 2 2 2

xxx yxx xxx

 −−≥  =−−=  −−−< 

21,2 21 21,2

Đồ thị gồm 2 phần: +) Giữ nguyên phần đồ thị đã cho ứng với 2 x ≥ . +) Lấy đối xứng phần đồ thị đã cho ứng với 2 x < qua trục Ox Hình1 nhận vì đồ thị là hàm () 2 21yxx=−− Hình2 loại vì đồ thị là hàm () ()211yxxx =−−+ Hình3 loại vì đồ thị hàm số ()() 2 21yxx=−− Hình4 loại vì đồ thị hàm ()() 2 21yxx=−−

Câu3. (THPTViệt ĐứcHàNội2019) Cho hàm số ()yfx = có đồ thị hàm số ()yfx = như hình vẽ

Chọn kết luận đúng trong các kết luận sau: A. ( ) 32 44fxxxx=−++− B. ( ) 32 44fxxxx=−−+ C. () 32 44fxxxx=−−+− D. () 32 44.fxxxx=+−− Lờigiải ChọnA Do đồ thị giao với trục Oy tại điểm có tung độ bằng 4 và lim x y →+∞ =−∞

ng trình 32 0 axbxcxd+++= (0) a ≠ có đúng hai nghiệm thực. Hỏi đồ thị hàm số 32 yaxbxcxd =+++ có bao nhiêu điểm cực trị?

A. 4. B. 5. C. 2. D. 3. Lờigiải ChọnD

Ta có: Phương trình 32 0 axbxcxd+++= (0) a ≠ có đúng hai nghiệm thực Nên đồ thị hàm số 32 yaxbxcxd =+++ được minh họa như hình vẽ Gọi m là số điểm cực trị của hàm số ()yfx = và k là nghiệm bội lẻ của phương trình () 0 fx = .  Số điểm cực trị của đồ thị hàm số ()yfx = là mk + Vậy đồ thị hàm số 32 yaxbxcxd =+++ có số điểm cực trị là 21 + Câu5. (ChuVănAn-HàNội-2019) Cho hàm số ()() 2 21yxx=−− có đồ thị như hình vẽ

Ta có () ()() ()() 2 2 2

Một trong bốn hình dưới đây là đồ thị của hàm số () 2 21yxx=−− . Hỏi đó là hình nào?

Hình 1 Hình 2 Hình 3 Hình 4

A. Hình 2. B. Hình 4. C. Hình 3. D. Hình 1. Lờigiải ChọnC

Gọi () C là đồ thị hàm số ()() 2 21yxx=−−

 −−≤−≥  =−−=  −−−−<< 

2111 21 2111 xxkhixhayx yxx xxkhix

Cách vẽ đồ thi như sau: + Giữ nguyên phần đồ () C ứng với ( ][ ) ;11; x ∈−∞−∪+∞ ta được () 1C + Lấy đối xứng phần ( ) C ứng với ( )1;1 x ∈− qua trục hoành ta được ( ) 2C

Khi đó đồ thị hàm số () 2 21yxx=−− gồm () 1C và () 2C .

Câu6. Cho hàm số 3232yxx=−+ có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 3232.yxx=−+ B. 3 2 32yxx=−+ C. () 2 122.yxxx=−−− D. () 2 122.yxxx =−−− Hướngdẫn Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Toàn bộ đồ thị phía “phải” Oy sau đó lấy đối xứng sang trái.  Chọn đápán B.

Câu7. Cho hàm số 1 21 x y x −+ = có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 1 21 x y x −+ = B. 1 21 x y x + = C. 1 21 x y x −+ = D. 1 21 x y x −+ = Hướngdẫn Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Toàn bộ đồ thị phía bên phải Oy được giữ nguyên Sau đó, được lấy đối xứng sang trái. Chọn đápán B.

Câu8. Cho hàm số 3269 yxxx =−+ có đồ thị như Hình 1. Khi đó đồ thị Hình 2 là của hàm số nào dưới đây?

A. 3269=−+− yxxx . B. 3269=−+ yxxx .

C. 3 2 69=−+ yxxx D. 3269=++ yxxx

Lờigiải ChọnC

+/ Loại đáp án A vì: ()32326969 =−+−=−−+ yxxxxxx

+/ Loại đáp án B, vì đồ thị của hàm số 3269 yxxx =−+ giữ lại phần đồ thị phía trên trục hoành

và chỉ lấy đối xứng phần dưới trục hoành của đồ thị Hình 1.

+/ Loại đáp án D vì hệ số của 2 x khác -6.

+/ Đồ thị ở đáp án C là đồ thị của hàm số dạng ()yfx = . Chọn đáp án C

Câu9. (CụmliêntrườngHảiPhòng-2019) Cho hàm số 21 x y x = + có đồ thị như Hình 1. Đồ thị Hình 2 là của hàm số nào trong các đáp án A, B, C, D dưới đây?

A. 3232.yxx=−+ B. 3 2 32yxx=−+

C. () 2 122.yxxx=−−− D. () 2 122.yxxx =−−− Hướngdẫn

Ta có: ()()32232122yxxxxx =−+=−−− Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy

Toàn bộ đồ thị ứng với 13 13 x x

 ≥+  ≤−   được giữ nguyên.

Phần đồ thị ứng với 1313 x −≤≤+ lấy đối xứng qua trục hoành.  Chọn đápán D.

Câu11. Cho hàm số 3232yxx=−+ có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 3232.yxx=−+ B. 3 2 32yxx=−+ C. () 2 122.yxxx=−−− D. () 2 122.yxxx =−−− Hướngdẫn

Ta có: ()()32232122yxxxxx =−+=−−− Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Toàn bộ đồ thị nằm phía trên Ox được giữ nguyên. Phần đồ thị phía dưới Ox được lấy đối xứng qua Ox  Chọn đápán A.

Câu12. Cho hàm số 21 x y x = + có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 21 x y x = + . B. 21 x y x = + C. 21 x y x = + D. 21 x y x = + Lờigiải ChọnA

Câu10. Cho hàm số 3232yxx=−+ có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 21 x y x = + B. 21 x y x = + C. 21 x y x = + D. 21 x y x = + Hướngdẫn Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Toàn bộ đồ thị phía trên Ox giữ nguyên Toàn bộ phần phía dưới Ox được lấy đối xứng lên trên  dạng ( )fx . Chọn đápán C.

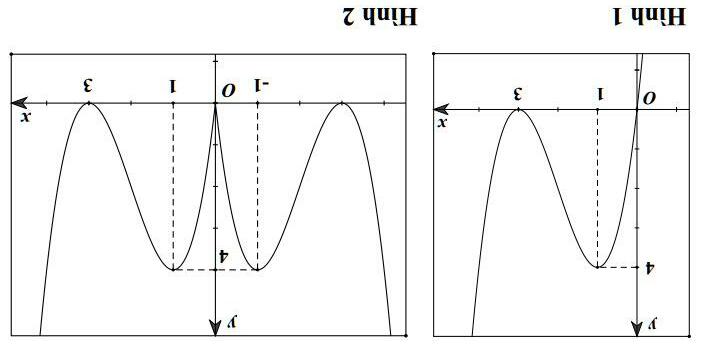
Câu13. Cho hàm số 1 2 x y x −+ = có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 1 . 2 x y x −+ = B. 1 2 x y x + = C. 1 2 x y x −+ = D. 1 2 x y x −+ = Hướngdẫn

Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy

Toàn bộ đồ thị phía bên trái đường thẳng 1 x = được giữ nguyên Toàn bộ đồ thị phía bên phải đường thẳng 1 x = lấy đối xứng qua Ox Chọn đápán C.

Chú ý:

x x xx y xx x x

−+  ≤  −+  ==  −+ −> 

1 ,1 1 2 1 2 ,1 2

Câu14. Cho hàm số 1 2 x y x + = + có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. ()() 2 123.yxxx =−−− B. () 2 123.yxxx=−−−

C. () 2 123yxxx =−−−− D. () 2 123yxxx =−−−

Hướngdẫn Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy Toàn bộ đồ thị nằm bên trái (ứng với 1) x ≤ đường thẳng 1 x = được giữ nguyên Toàn bộ đồ thị nằm bên phải (ứng với 1) x > đường thẳng 1 x = được lấy đối xứng qua Ox  Chọn đápán C.

Câu16. Cho hàm số 1 2 x y x + = −+ có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 1 . 2 x y x + = + B. 1 2 x y x + = + C. 1 . 2 x y x + = + D. 1 . 2 x y x + = + Hướngdẫn

Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy

Toàn bộ đồ thị phía bên phải đường thẳng 2 x =− được giữ nguyên

Toàn bộ đồ thị phía bên trái đường thẳng 2 x =− lấy đối xứng qua Ox Chọn đápán D.

Câu15. Cho hàm số ()() 2 123yxxx =−−− có đồ thị như hình 1. Đồ thị hình 2 là của hàm số nào dưới đây?

A. 1 2 x y x + = + B. 1 2 x y x + = C. 1 2 x y x + = −+ D. 1 2 x y x + = + Hướngdẫn

Từ đồ thị ban đầu (hình 1) sang đồ thị thứ 2 (hình 2) ta thấy

Toàn bộ đồ thị phía bên trái đường thẳng 1 x =− (ứng với 1) x ≤− được giữ nguyên

Toàn bộ đồ thị phía bên phải đường thẳng 1 x =− (ứng với 1) x ≤− được lấy đối xứng qua trục Ox Chọn đápán B.

đó để () 1C và () 2C cắt nhau tại đúng bốn điểm phân biệt thì

là A. [ ) 2; +∞ . B. () ;2−∞ . C. () 2; +∞ . D. ( ];2−∞ . Lờigiải ChọnA

Xét phương trình 321 2 211 xxxx xxm xxxx +++=+−+ −−+ 321 2 211 xxxx xxm xxxx ⇔+++−++= −−+ (1)

xxxx x xxxxxxxx pxxx xxxxxxxx xx xxxx

Hàm số () 321 2khi2 321 211 2 321 211 22khi2 211

1111 0,2;\1;0;1;2 211 1111 20,2 211 TƯƠNGGIAOĐỒTHỊHÀMSỐ Chuyên đề 8 Trang 2

 +++−≥−   −−+ =+++−++=  −−+  +++++<−  −−+ 

.

x x xxx px x x xxx Do

nghiệm phân biệt. Điều này xảy ra khi và chỉ khi đường thẳng ym = cắt đồ thị hàm số ()

ypx =

Câu2. (Mã 103 2019) Chohaihàmsố 112 123 xxxx y xxxx −++ =+++ +++ và 2 yxxm =+−− ( m làtham

Xét () {} 112 2,\3;2;1;0 123 xxxx fxxxxD xxxx −++ =+++−++∈=−−− +++ ℝ

Ta có () () ()

−++  +++−∈−+∞∪=   +++ =  −++  +++++∈−∞−∪=  +++ 

112 2,2; 123 112 22,;2 123

Có () () () () () () ()

1 2

xxxx xDD xxxx fx xxxx xxDD xxxx

 +++∀∈  +++  ′ =   ++++∀∈  +++ 

1 222 2 2 222 2

1111 , 123 1111 2, 123

xD x xxx fx xD x xxx

Dễ thấy () 12 0, fxxDD ′ >∀∈∪ , ta có bảng biến thiên

f'(x) +∞ -∞ x -3 -2 10 +

+ + + + f(x)

-∞

+∞ +∞ +∞ +∞ -∞

2 -∞ -∞ -∞

 +++>∀∈−+∞−  −−+  ′ =   ++++>∀<−  −−+  nên hàm số ()ypx = đồng biến trên mỗi khoảng () ;1−∞− , () 1;0 , () 0;1 , () 1;2 , () 2; +∞ . Mặt khác ta có () lim2 x px →+∞ = và () lim x px →−∞ =−∞ Bảng biến thiên hàm số ()ygx = : phương trình (1) phải có 4

Hai đồ thị cắtnhautại đúng4 điểmphânbiệnkhivàchỉ khi phươngtrình () 1 có đúng4nghiệm phân biệt, từ bảng biến thiên ta có: 22mm −≥⇔≤−

Câu3. (Mã 102 2019) Chohaihàmsố 123 1234 xxxx y xxxx +++ =+++ ++++ và 1 yxxm =+−+ ( m làtham số thực) có đồ thị lần lượt là () 1C và () 2 C . Tập hợp tất cả các giá trị của m để () 1C và () 2 C cắt nhau tại đúng 4 điểm phân biệt là A. ( ];3−∞ B. () ;3−∞ C. [ ) 3; +∞ D. () 3; +∞ Lờigiải ChọnC Điều kiện 1; x ≠− 2; x ≠− 3 x ≠− và 4 x ≠− Ta có phương trình hoành độ giao điểm

++++∈−∞−−  −++ 

. Mặt khác ()() lim;lim3 xx FxFx →+∞→−∞ =+∞= ()()()() ()()()() 2211 0011

lim;lim;lim;lim lim;lim;lim;lim xxxx xxxx

→−→−→−→− →→→→

FxFxFxFx FxFxFxFx +−+− +−+−

=+∞=−∞=−∞=+∞ =−∞=+∞=−∞=+∞ . Bảng biến thiên Để phương trình có 4 nghiệm thì 33mm −≤⇔≥− .

Câu5. Cho hai hàm số 2222 124368 123 xxxxxxx y xxxx −−−+−+ =+++ và 2 yxxm =+−+ (là tham số thực) có đồ thị lần lượt là 1 () C và 2 () C . Tính tổng tất cả các giá trị nguyên thuộc khoảng (15;20) của tham số m để 1 () C và 2 () C cắt nhau tại nhiều hơn hai điểm phân biệt. A. 210 . B. 85 . C. 119 . D. 105 . Lờigiải ChọnB Xét phương trình hoành độ giao điểm 2222 124368 2 123 xxxxxxx xxm xxxx −−−+−+ +++=+−+ 2222

Dựa vào bảng biến thiên ta thấy đường thẳng ym = luôn cắt đồ thị hàm số ()ygx = tại năm điểm phân biệt nên 1 () C và 2 () C luôn cắt nhau tại đúng năm điểm phân biệt với mọi giá trị của m . Kết hợp điều kiện m nguyên thuộc (15;20) nên {} 14;13;...;18;19 m ∈−− . Khi đó tổng tất cả các giá trị m là 151617181985 S =++++= Câu6. Chohaihàmsố 12 11 ++ =++ −+ xxx y xxx và20203 =++ x yem ( m làthamsố thực)có đồ thị lần lượtlà 1 () C và 2 () C . Có bao nhiêu số nguyên m thuộc (2019;2020) để 1 () C và 2 () C cắt nhau tại 3 điểm phân biệt? A. 2692 B. 2691 C. 2690 D. 2693 Lờigiải ChọnA

Xét phương trình hoành độ giao điểm 12 20203 11 ++ ++=++ −+ x xxx em xxx 12 20203 11 ++ ⇔++−−= −+ x xxx em xxx (1).

Đặt 12 ()2020 11 ++ =++−− −+ x xxx gxe xxx .

Ta có ()2 22 111 ()0 (1)1 ′ =−−−−< + x gxe xx x với mọi x thuộc các khoảng sau () ;1−∞− ,

() 1;0 , () 0;1 và () 1; +∞ nên hàm số ()ygx = nghịch biến trên mỗi khoảng đó. Mặt khác ta có lim()2017 →−∞ =− x gx và lim() x gx →+∞ =−∞ Bảng biến thiên hàm số ()ygx =

Câu7. Tìmtậphợptấtcả cácgiátrị củathamsố m để đồ thị haihàms

111 11 342 ym xx =−++ cắt nhau tại 2 điểm phân biệt? A. () ;0−∞ . B. () ;1−∞ . C. ( ];1−∞ . D. ( ];2−∞ . Lờigiải ChọnC

Xét phương trình hoành độ giao điểm: () () 2 111 21111* 342 +−=−++ xxm xx Điều kiện:

Do đó để 1 () C và 2 () C cắt nhau tại đúng ba điểm phân biệt thì phương trình (1) phải có ba nghiệm phân biệt. Điều này xảy ra khi và chỉ khi đường thẳng 3 = ym cắt đồ thị hàm số ()ygx = tại ba điểm phân biệt khi và chỉ khi 2017 32017672,3 3 ≥−⇔≥−≈−mm Do m nguyên thuộc (2019;2020) nên {} 672;671;...;2019 m ∈−− . Vậy có tất cả 2692 giá trị m thỏa mãn.

−≥≥   ≠⇔≠  ≠≠ 

101 44 33 22

xx xx xx Ta có: () * ⇔ () 2 111 21111 342 xxm xx +−−+−=

Xét hàm số () 2 111 ()21111 342 fxxx xx =+−−+− trên [ ) 4 1;\;2 3  +∞  

Nhận thấy, hàm số ()fx liên tục trên các khoảng () 44 1;,;2,2; 33  +∞   

Ta có, () 2 111 ()21111 342 fxxx xx

′  ′ =+−−+−  

() () () 2 2241211331 21342 xxx x xx =−++++ () () 2 22 1081331 0 21 342 xx x xx −+ =++> với [ ) 4 1;\;2 3  ∀∈+∞   x

Suy ra, hàm số ()fx đồng biến trên [ ) 4 1;\;2 3  +∞  

Bảng biến thiên

Từ bảng biến thiên ta suy ra đồ thị hai hàm số () 2 211yxx=+− và 111 11 342 ym xx =−++ cắt nhau tại 2 điểm phân biệt khi ( ];1 m ∈−∞ .

112 123 xxxx y xxxx −++ =+++ +++ và 1 22 x ym =+ ( là tham số thực) có đồ thị lần lượt là 1 () C và 2 () C . Tập hợp tất cả các giá trị của để 1 () C và 2 () C cắt nhau tại đúng năm điểm phân biệt là

A. () 2; +∞ . B. ( ];2−∞ . C. () ;2−∞ . D. () ;4−∞ . Lờigiải ChọnC

Xét phương trình hoành độ giao điểm 1 112 22 123 x xxxx m xxxx −++ +++=+ +++ 1 123 22 1234 x xxxx m xxxx +++ ⇔+++−= ++++ .

Đặt 1 123 ()2 1234 x xxxx gx xxxx +++ =+++− ++++

Ta có () () () 1 222 2 1111 ()2ln20 123 x gx x xxx ′ =++++> +++

với mọi x thuộc các khoảng sau () ;3−∞− , () 3;2 () 2;1 , () 1;0 và () 0; +∞ nên hàm số ()ygx = đồng biến trên mỗi khoảng đó Mặt khác ta có lim()4 x gx →+∞ = và và lim() x gx →−∞ =−∞ . Bảng biến thiên hàm số ()ygx =

với mọi x thuộc các khoảng sau () ;1−∞− , () 1;0 , () 0;1 , () 1;2 , () 2;3 và () 3; +∞ nên hàm số

()ygx = nghịch biến trên mỗi khoảng đó. Mặt khác ta có lim() x gx

= Bảng biến thiên hàm số ()ygx =

=+∞ và và lim()1 x gx

Do đó để và cắt nhau tại đúng năm điểm phân biệt thì phương trình (1) phải có 5 nghiệm phân biệt. Điều này xảy ra khi và chỉ khi đường thẳng 2 ym = cắt đồ thị hàm số ()ygx = tại 5 điểm phân biệt khi và chỉ khi 242 mm<⇔< Câu9. Cho hai hàm số 222 12 1243 xxx y xxxxx =++ −−−+ và 1 yxxm =−++ ( là tham số thực) có đồ thị lần lượt là 1 () C và 2 () C . Số các giá trị m nguyên thuộc khoảng () 20;20 để 1 () C và 2 () C cắt nhau tại năm điểm phân biệt là A. 22 . B. 39 . C. 21. D. 20 . Lờigiải ChọnC Xét phương trình hoành độ giao điểm

Do đó để 1 () C và 2 () C cắt nhau tại đúng năm điểm phân biệt thì phương trình (1) phải có năm nghiệm phân biệt. Điều này xảy ra khi và chỉ khi đường thẳng ym = cắt đồ thị hàm số ()ygx = tại năm điểm phân biệt khi 1 m ≤ , do m nguyên thuộc (20;20) nên {} 19;18;...;0;1 m ∈−− . Vậy có tất cả 21 giá trị m thỏa mãn.

Câu10. Gọi S là tập hợp tất cả các giá trị của tham số m để bất phương trình () ()24322210mxmxxmx −+++−≥ nghiệm đúng với mọi x ∈ ℝ . Số phần tử của tập S là

A. 3 . B. 2 . C. 0 . D. 1. Lờigiải ChọnD Đặt ()() ()2432221 fxmxmxxmx =−+++−

Ta có ()() () () ()243222322 2121 fxmxmxxmxxmxmxxm =−+++−=−+++−  . Giả sử 0 x = không phải là nghiệm của phương trình ()() ()2322210gxmxmxxm=−+++−= thì hàm số ()() ()2432221 fxmxmxxmx =−+++− sẽ đổi dấu khi qua điểm 0 x = , nghĩa là () ()24322210mxmxxmx −+++−≥ không có nghiệm đúng với mọi x ∈ ℝ Do đó, để yêu cầu bài toán được thỏa mãn thì một điều kiện cần là ()() ()2322210gxmxmxxm=−+++−= phải có nghiệm 0 x = , suy ra 2 101mm−=⇔=± Điều kiện đủ: Với () ()43222 1,331 mfxxxxxxx ==−+=−+ khi đó ()110 f =−< không thỏa mãn điều kiện () ()24322210mxmxxmx −+++−≥ nghiệm đúng với mọi x ∈ ℝ . (loại) Với () ()43222 1,10mfxxxxxxx ==−+=−+≥ , x ∈ ℝ Vậy {} 1 S =− .

Câu11. Có bao nhiêu cặp số thực (;) ab để bất phương trình ()()() 2 1220xxaxbx −+++≥ nghiệm đúng với mọi x ∈ ℝ A. 3 B. 2 C. 0 D. 1 Lờigiải

Đặt ( ) ( )( )( ) 2 122fxxxaxbx =−+++

Giả sử 1 x = không phải là nghiệm của phương trình ( ) ( )( ) 2 220gxxaxbx=+++= thì hàm số ( ) ( )( )( ) 2 122fxxxaxbx =−+++ sẽ đổi dấu khi qua điểm 1 x = , nghĩa là

( )( )( ) 2 1220xxaxbx −+++≥ không có nghiệm đúng với mọi x ∈ ℝ

Do đó, để yêu cầu bài toán được thỏa mãn thì một điều kiện cần là ( ) ( )( ) 2 220gxxaxbx=+++= có nghiệm 1 x = suy ra 20 ab++= (1)

Lí luận tương tự có ( ) ( )( ) 2 120hxxaxbx=−++= cũng phải nhận 2 x =− là nghiệm, suy ra

4220 ab−+= (2)

Từ (1) và (2) ta có hệ 201 42201 aba abb ++==− ⇔  −+==− Điềukiện đủ: Với 1 1 a b =−   =−  có ()()()( ) ()() 22 2 122120fxxxxxxx=−+−−+=−−+≤ , x ∈ ℝ

Vậykhôngtồntại cặpsố thực (;) ab nàothỏamãnyêucầubàitoán. Câu12. Trong số các cặp số thực ( ) ; ab để bất phương trình ( )( )( ) 2 10xxaxxb −−++≥ nghiệm đúng với mọi x ∈ ℝ ,tích ab nhỏ nhấtbằng

A. 1 4 . B. 1. C. 1 4 . D. 1. Lờigiải ChọnC

Đặt ( ) ( )( )( ) 2 1 fxxxaxxb =−−++ và ( ) ( )( ) 2 gxxaxxb =−++

Giả sử 1 x = khôngphải lànghiệmcủaphươngtrình ( ) ( )( ) 2 0 gxxaxxb=−++= thìhàm số ( ) ( )( )( ) 2 1 fxxxaxxb =−−++ sẽ đổidấukhiqua điểm 1 x = , nghĩa ( )( )( ) 2 10xxaxxb −−++≥ khôngcónghiệm đúngvớimọi x ∈ ℝ .

=    ≥  ≥   suy ra tích ab nhỏ nhất khi 1 4 ab =

Và với 1 1, 4 ab== , tích 1 4 ab = thì bất phương trình đã cho tương đương với ()() () 2 2 2 11 11010 42 xxxxxx  −−++≥⇔−+≥   thỏa mãn với mọi x ∈ ℝ (nhận)

Trong trường hợp 2: Tích 1 4 4 ab =>

Vậy tích ab nhỏ nhất khi 1 4 ab = .

Câu13. Cho 2 hàm số 753 31yxxxm =+++− và 22 yxxm =−−− ( m là tham số thực) có đồ thị lần lượt là () 1C , () 2C . Tập hợp tất cả các giá trị của m để () 1C cắt () 2C là A. m ∈ ℝ B. () 2; m ∈+∞ C. () ;2 m ∈−∞ D. [ ) 2; m ∈+∞ Lờigiải ChọnA

Xét phương trình hoành độ giao điểm: 753 3122 xxxmxxm +++−=−−− 753 251(1)xxxxxm ⇔++−−+=−+ Xét hàm số 753 ()2 fxxxxxx =++−−+

ườngh

xa =

1 0, a xxbx =   ++≥∀∈  ℝ hoặclàphươngtrình 2 0 xxb++= cóhai nghiệm 1 x = và =  ++=⇔+−=⇔  =−  Vì xa = cũnglànghiệmcủaphươngtrìnhnên 2 a =− . Trang 10

Ta có [ ) () 753 753

2khi 2; () 22khi ;2 xxxx fx xxxxx

 ++>∈+∞  ′ =  +++>∈−∞   .

7530khi 2; () 75320khi ;2 xxxx fx xxxx

 +++∈+∞  =  +++−∈−∞   () () 642 642

x +

+∞ ∞

+ 2 +∞ ∞ f '(x) f(x)

() lim x fx →−∞ =−∞ ; () lim x fx →+∞ =+∞ . Bảng biến thiên: Từ bảng biến thiên ta thấy phương trình () 1 luôn có nghiệm với mọi m ∈ ℝ .Vậy để () 1C cắt () 2C thì m ∈ ℝ

Câu14. Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn [] 2019;2019 để phương trình () () 2 3231512423 xxmxxmxx ++−+−−+=−−+ có nghiệm thực? A. 2019 . B. 4032 . C. 4039 . D. 4033 . Lờigiải ChọnB

Phương trình đã cho ()() () 1134312130 xxxmxx ⇔−−+−+−−+= . (*)

Đặt () 213 txxgx =−−+= , với [] ()() 2 3;11134314xxxxt ∈−  −−+−=+ .

Có () () 11 0,3;1 123 gxx xx ′ =−<∀∈− −+ . Suy ra ()gx nghịch biến trên khoảng () 3;1 [] ()() 3;1 min12 gxg  ==− : [] ()() [] 3;1 max342;4 gxgt =−=  ∈−

Từ (*) 2 40 tmt  ++= Nếu 0040 t =  += (vô lí).

Nếu []2;4\{0} t ∈− , ta có () 2 44 t mtft tt ==−−=

 ∈−  ≥   ∈−−−  ≤−   ∈  ℤ Vậy có () 201941.24032 −+= giá trị nguyên của tham số thực m Câu15. (ChuyênNguyễnBỉnhKhiêm-QuảngNam-2020) Tập hợp tất cả các số thự 643322 3 3 22 2

C.

4

64332261536100 xxmxmxmx xxmxmx fxfmx

D. 9 0

m

c của tham số m để 61536100 232131 21(*)

có đúng hai nghiệm phân biệt +−+−−+= ⇔+++=+++ ⇔+=+

ều

ệ

x ≠    ≥   . Xét trên (){} 0;\10 +∞

phương trình hoành độ giao điể

của ()

và ()

2C

Suy ra phương trình () 0 gx ′ = có một nghiệm duy nhất 17 ;10 2 α  ∈   . Lại có ()9,220 g ′ > nên () 9,22;10 α∈ . Ta có bảng biến thiên của ()gx trên (){} 0;\10 +∞ : Từ đó suy ra phương trình ()mgx = có 3 nghiệm dương phân biệt khi và chỉ khi () 81 25 mg α <<

Dựa vào BBT, phương trình ().() fxmfx ′ = có 2020 nghiệm phân biệt khi và chỉ khi 0 m > hoặc 0 m < . Kết hợp với điều kiện m là số nguyên thuộc [] 2020;2020 nên {} |20202020,0.mnnn ∈∈−≤≤≠ ℤ

Trên khoảng () 9,22;10 thì 2

Xét hàm số

440 218 3 10

<     <     nên ()()() 3736;37gxg α <  ∈ . Vậy những giá trị m nguyên dương thỏa mãn yêu cẩu bài toán là 1; 2; 3; …; 36 hay có 36 giá trị của m cần tìm.

x x x

nghiệm duy nhất 1 ;1 2 t  ∈−  Đặt 3232 3 2 3232 41233434123343 39 39412364 tttmutttmu uttm uttmuttm −−=+=+++ =++   =++=++  ()()()332222

Ta

tìm m để phương trình 3239 mttt =−− có nghiệm duy 1 ;1 2 t 

′ ′ =⇔= ′ ==++++ Ta có () () () () {} 2222 1111 ()0,\1;2;3...;2020 1232020 gx x xxxx ′ =++++<∀∈ …ℝ Bảng biến thiên: Trang 14

cầ

toánxãyrakhivà

Ngh

khi

hai hàm

Với 11 1;; 23 x  ∈−−−  : Khônglànghiệm củaphươngtrình(1). Với 11 1;; 23 x ∉−−−  tacó: () ()()() 432 1222103111 1222 1213112131 xxxx mxmxx xxxxxx −−−++ ⇔=−⇔=−−+++ ++++++

Xéthàmsố () 111 22 12131 fxxx xxx =−−+++ +++ , 11 \1;; 23 x ∀∈−−−  ℝ

Suyra: () () () () 222 2

2123 2 12131 x fx xxx x ′ =−−−−− +++ . Tacó: () () () () () () () () ()

x xxx fx x xxx

123 4khi0; 12131 12311 khi ;0\1;; 23 12131

222 222

 −−−−∈+∞ +++  ′ =    −−−−∞−−−   +++ 

và ()fx ′ khôngxác địnhtại 0 x = .

Bảngbiếnthiên: Dựavàobảngbiếnthiên tathấy để phươngtrình(1)có3nghiệm phânbiệt thì 0 m ≥ .Do đócó 2021giátrị nguyêncủatham số m thỏamãnyêucầubàitoán.

Câu21. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số ()2 2 23 () 3 xxmxm yC x −+−− = và đường thẳng ():2 dyx = ( làtham số thực). Số giátrị nguyêncủa [] 15;15 m ∈− để đườngthẳng () d cắt đồ thị () C tại bốn điểm phânbiệt là A. 15 . B. 30 . C. 16 . D. 17 . Lờigiải ChọnA Xétpthoành độ giao điểmcủahai đồ thị:

m

Vậy số giá trị nguyên của [ ]15;15 m ∈− đồng thời thỏa mãn ( )** và ( )*** là 15.

Câu22. (Thanh Chương 1 - Nghệ An - 2020) Chohaihàmsố 642661yxxx=+++ và ( ) 3 15315 yxmxmx =−+− có đồ thị lần lượt là ( ) 1C và ( ) 2C . Gọi S là tập hợp tất cả các giá trị nguyên của tham số m thuộc đoạn [ ]2019;2019 để ( ) 1C và ( ) 2C cắt nhau tại hai điểm phân biệt. Số phần tử của tập hợp S bằng A. 2006 B. 2005 C. 2007 D. 2008 Lờigiải ChọnA Ta biết ( ) 1C cắt ( ) 2C tại hai điểm phân biệt khi và chỉ khi phương trình ( ) ( ) 6423661153151xxxxmxmx +++=−+− có hai nghiệm phân biệt.

Điều kiện: ()15015*mxmx −≥⇔≥

Nếu 0 x = thì phương trình () 1 vô nghiệm. Suy ra 0 x ≠

Khi đó () () 32 3 1 16615315 xxxmxmx x ⇔+++=−+− () 3 3 11 315315 xxmxmx xx  ⇔+++=−+−   .

Xét hàm số () 3 3 fttt =+ . Tập xác định D = ℝ () 2 330, fttt ′ =+>∀∈ ℝ . Suy ra hàm số () 3 3 fttt =+ đồng biến trên ℝ .

Do đó () () 1 1152 xmx x ⇔+=− .

Nếu 1 00xx x <  +<  Phương trình () 2 vô nghiệm 0 x  >

18

Khi đó 0 1 0

>    +>   nên () 2 2 2 2 11 2215215 xmxmxx xx ⇔++=−⇔=+++

m x x

Đặt () 2 2 1 215,0gxxxx x =+++> . () 3 2 215gxx x ′ =−+ . Phương trình () 0 gx ′ = có một nghiệm 1 2 x = trên khoảng () 0; +∞ Bảng biến thiên

Suy ra () 1 có hai nghiệm phân biệt khi và chỉ khi 55 4 m > ( thỏa 0 m > ). Kết hợp với m nguyên và [] 2019;2019 m ∈− ta có được m nguyên

Dạng2.Tươnggiaohàmhợp,hàm ẩn

Câu1. (Mã104-2021Lần1) Cho hàm số bậc bốn ()yfx = có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình () () 0 ffx = là A. 12. B. 10 . C. 8 . D. 4 . Lờigiải ChọnB Nhìn vào đồ thị ta thấy ()0fx = có 4 nghiệm phân biệt theo thứ tự ,,, abcd

A. 9 B. 7 C. 3 D. 6 Lờigiải ChọnB

fxaa fxbb ffx fxcc fxdd

,;1 ,1;0 0 ,0;1 ,1;

Ta có: () () ()() ()() ()() ()()

=∈−∞−   =∈−  =⇔  =∈   =∈+∞ 

Dựa vào đồ thị ta thấy:

Phương trình () fxa = có 2 nghiệm thực phân biệt.

Phương trình () fxb = có 4 nghiệm thực phân biệt.

Phương trình () fxc = có 4 nghiệm thực phân biệt. Phương trình () fxd = vô nghiệm trên ℝ . Vậy phương trình () () 0 ffx = có 10 nghiệm thực phân biệt.

Câu2. (Mã102-2021Lần1) Cho hàm số bậc ba ()yfx = có đồ thị là đường cong trong hình bên. Số nghiệm thực phân biệt của phương trình () () 1 ffx = là

TH1

fxaa ffxfx fxbb

=<−   =⇔=   =<< 

11 102 123

Dựa vào đồ thị hàm số ()yfx = suy ra () () ()()() ()() ()()()

()() 1 fxaa=<−  phương trình có một nghiệm.

TH2

() 0 fx =  phương trình có ba nghiệm phân biệt.

TH3

()() 12fxbb=<<  phương trình cóbanghiệm phân biệt. Các nghiệm của (1); (2); (3) là đôi một khác nhau. Vậy () () 1 ffx = có 7 nghiệm nghiệm phân biệt.

Câu3. (Mã 103 -2021-Lần 1) Cho hàm số bậc bốn ()yfx = có đồ thị là đường cong trong hình bên dưới:

Số nghiệm thực phânbiệt của phương trình () () 0 ffx = là A. 4 . B. 10 . C. 12 . D. 8 . Lờigiải ChọnB

fxaa fxbb ffx fxcc fxdd

=<−   =−<<  =⇔  =<<   => 

1 10 0 01 1

Ta có: () () ()() ()() ()() ()()

 Phương trình () fxa = với 1 a <− vô nghiệm.

 Phương trình ( ) fxb = với 10 b −<< có 4 nghiệm phân biệt.

 Phương trình () fxc = với 01 c << có 4 nghiệm phân biệt.

 Phương trình ( ) fxd = với 1 d > có 2 nghiệm phân biệt.

Câu4. (Mã101-2021Lần1) Cho hàm số bậc ba ()yfx = có đồ thị là đường cong trong hình bên.

Số nghiệm thuộc đoạn [] ;2 ππ của phương trình () 2sin30 fx += là A. 4 . B. 6 . C. 3 . D. 8 . Lờigiải

ChọnB

Đặt sin tx = . Do [] ;2 x ππ∈− nên [] 1;1 t ∈−

Khi đó ta có phương trình ()() 3 230 2 ftft+=⇔=−

Dựa vào bảng biến thiên ta thấy phương trình () 3 2 ft =− có 2 nghiệm () 1;0 ta=∈− và () 0;1 tb=∈

Trườnghợp1: () 1;0 ta=∈−

Ứng với mỗi giá trị () 1;0 t ∈− thì phương trình có 4 nghiệm 123402.xxxx πππ −<<<<<<<

Trườnghợp2: () 0;1 tb=∈

Ứng với mỗi giá trị () 0;1 t ∈ thì phương trình có 4 nghiệm 56 0. xx π <<<

Hiển nhiên cả 6 nghiệm trong 2 trường hợp trên đều khác nhau.

Số nghiệm thực phân biệt của phương trình (())1ffx = là: A. 9 . B. 3 . C. 6 . D. 7 . Lờigiải ChọnD

Vậy phương trình đã cho có 6 nghiệm thuộc đoạn [] ;2 ππ

Câu6. (Đề ThamKhảo2020Lần2) Cho hàm số ()fx có bảng biến thiên như sau

fx ffxfxaa fxbb

=   =⇔=<−   =< 

Ta có: ()0 (())1() (1) () (1<2)

Ta dựa vào đồ thị:

Phương trình ()0fx = có 3 nghiệm. Phương trình () fxa = có 1 nghiệm. Phương trình () fxb = có 3 nghiệm. Vậy phương trình (())1ffx = có 7 nghiệm phân biệt.

Câu5. (Đề MinhHọa2020Lần1) Cho hàm số ()fx có bảng biến thiên như sau:

Số nghiệm thuộc đoạn 5 0; 2 π    của phương trình ()sin1fx = là

A. 7 B. 4 C. 5 D. 6 Lờigiải ChọnC

Đặt sin tx = , [] 5 0;1;1 2 xt π  ∈  ∈−  

Khi đó phương trình ()sin1fx = trở thành () []1,1;1ftt=∀∈−

Đây là phương trình hoành độ giao điểm của hàm số ()yft = và đường thẳng 1 y = .

Dựa vào bảng biến thiên, ta có () () () 1;0 1 0;1 ta ft tb =∈−  =   =∈   .

Ứng với mỗi giá trị () 1;0 t ∈− thì phương trình sin xt = có 2 nghiệm 12 , xx thỏa mãn 12 2 xx ππ <<< Trườnghợp2: () 0;1 tb=∈

4 3 ()'() k gxfx x ′ =+ .  Với xc > , nhìn hình ta ta thấy ()0fx ′ > 4 3 ()()0 k gxfx x ′′  =+>

()0gx  = có tối đa một nghiệm. Mặt khác ()0 lim() x

=   =  =    +=⇔=−⇔=>⇔ =≠     =>   =≠    ()0fx = có một nghiệm dương xc =  Xét phương trình 3 () k fx x = với 0,0xk≠> Đặt 3 ()() k gxfx x =− .

0 ()0 ()0 ()10()1()0 ()(do0) ()0 ()(do0)

<    =+∞   và ()gx liên tục trên () ;c +∞

gc gx →+∞

 ()0gx = có duy nhất nghiệm trên () ;c +∞ .

 Với 0 xc<< thì 3 ()0 k fx x <<  ()0gx = vô nghiệm.  Với 0 x < , nhìn hình ta ta thấy ()0fx ′ > 4 3 ()()0 k gxfx x ′′  =+>

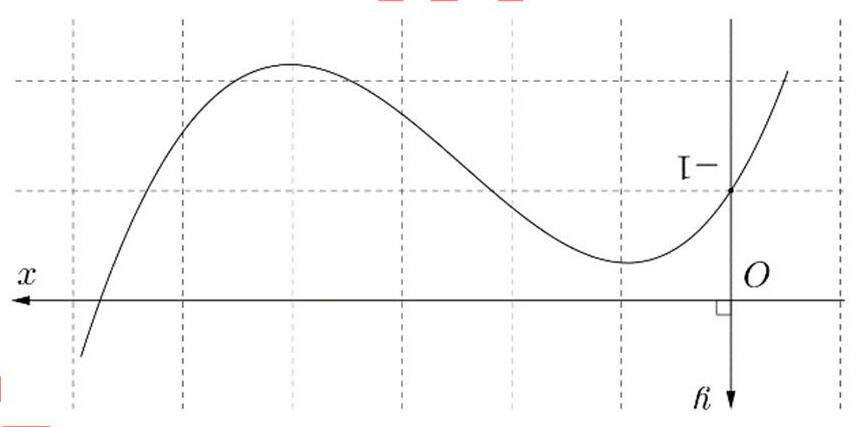
()0gx  = có tối đa một nghiệm.

x fx xfx a fxfxfxfxxfxa fxx x xfxb b fxx x Trang 26

Mặt khác 0 lim()0 lim() x x

>    =−∞   và ()gx liên tục trên () ;0−∞

gx gx → →−∞

 ()0gx = có duy nhất nghiệm trên () ;0−∞

Tóm lại ()0gx = có đúng hai nghiệm trên {}\0 ℝ .

Suy ra hai phương trình 3 () a fx x = , 3 () b fx x = có 4 nghiệm phân biệt khác 0 và khác c .

Vậy phương trình () 3 ()10fxfx += có đúng 6 nghiệm.

Câu8. (Mã102-2020Lần1) Cho hàm số ()fx có đồ thị là đường cong như hình vẽ bên dưới.

Số nghiệm thực phân biệt của phương trình () () 3 10 fxfx += là A. 6 B. 4 C. 5 D. 8 Lờigiải ChọnA

3 333 3

xfxa fxfxfxfxxfxb xfx

 =∈−−  +=⇔=−⇔=∈−−   =  

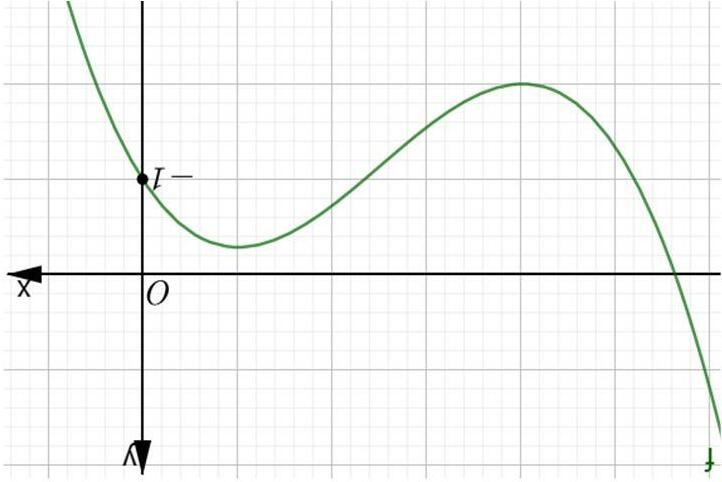
6;51 1013;22 03

Dựa vào đồ thị, ta thấy () () () () ()()() ()()() ()()

nên các phương trình ()() fxgx = và ()() fxhx = có nghiệm duy nhất. + Trên khoảng () 0; +∞ , ta có ()() ()() ()()

 =−∞=−   ==   ==−∞  

lim;lim1 limlim0 limlim

x x xx xx

2 2 2 2 2

xfx xfxa fxfx xfxb xfxc

()0 ()1 ()20 ()2 ()3

 =  =  +=⇔  =  =  

() () () ()

với 0 abc<<<

0 00

→+∞ → →+∞→+∞ →→

nên các phương trình ()() fxgx = và ()() fxhx = có nghiệm duy nhất. Do đó, phương trình () () 3 10 fxfx += có 6 nghiệm phân biệt. Câu9. (Mã 103 - 2020 Lần 1) Cho hàm số bậc bốn ()yfx = có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực phân biệt của phương trình () 2 ()20fxfx += là A. 8 B. 12 C. 6 D. 9 Lờigiải ChọnD

fxfx gxhx gxhx Trang 28

+ ++

Xét phương trình ()() 2 ()10 f m xm x => Gọi , αβ là hoành độ giao điểm của () :() Cyfx = và Ox ; 0 αβ << . 2 (1)()0 fx m x ⇔−= . Đặt 2 ()() gxfx x m =− Đạo hàm 3 2 ()() m gxfx x ′′ =+

Trường hợp 1: 3 2 ;()0;0()0 m xfxgx x α ′′ <<<  <

Ta có () 2 0 li,() m x

m gxg α α →−∞ =− +∞< = . Phương trình () 0 gx = có một nghiệm thuộc () ;α −∞

Trường hợp 2: x αβ <<

()0fx < , 2 0 m x > suy ra ()0(,)gxx αβ <∀∈

Trường hợp 3: 3 2 ;()0;0()0 m xfxgx x β ′′ >>>  >

Ta có () 2 0 li,() m x

m gxg β β →−∞ =− +∞< = . Phương trình () 0 gx = có một nghiệm thuộc (;) β +∞ .

Vậy phương trình () 2 m fx x = có hai nghiệm 0 m ∀>

Ta có: 2 ()00()0xfxxfx=⇔=∨= : có ba nghiệm.

Vậy phương trình () 1 có 9 nghiệm.

Câu10. (Mã104-2020Lần1) Cho hàm số ()yfx = có đồ thị là đường cong trong hình vẽ bên.

Số nghiệm thực của phương trình () () 2 2 fxfx = là:

A. 6. B. 12. C. 8. D. 9. Lờigiải ChọnD

Ta có: () () 2 2 fxfx =

2 2 2 2

() () () ()

xfx xfxa xfxb xfxc

 =  =<    =<   =< 

0 0 0 0

Xét phương trình: () 2 0 xfx = () 0 0 x fx =  ⇔  =  mà () 0 fx = có hai nghiệm () 2.0xfx  = có ba nghiệm.

Xét phương trình: () 2 0 xfxa=<

Do 2 0 x ≥ ; 0 x = không là nghiệm của phương trình () 2 0 a fx x  =<

Xét () () 23 2 aa gxgx xx ′ =  =

Bảng biến thiên:

Số nghiệm của phương trình () () 2e1 x ff+= là A. 4 B. 2 C. 1 D. 3 Lờigiải ChọnB

Đặt e0 x u => , từ đồ thị suy ra: () 3,0fuu≥−∀> Đặt () 2 tfu =+ , 1 t ≥− Ứng với mỗi nghiệm 1 t =− , có một nghiệm 1 u = Ứng với mỗi nghiệm () 1;2 t ∈− , có hai nghiệm () 0;2 u ∈ . Ứng với mỗi nghiệm 2 t > , có một nghiệm 2 u >

Phương trình () 1 ft = có một nghiệm 1 t =− và một nghiệm 2 t > . Vậy phương trình đã cho có hai nghiệm.

Câu12. Cho hàm số () = yfx có đạo hàm cấp 2 trên ℝ và có đồ thị ()fx ′ là đường cong trong hình vẽ bên.

Từ bảng biến thiên với () 0 fx < () 2 a fx x  = có 2 nghiệm.

Tương tự: () 2 xfxb = và () 2 xfxc = () ,0bc < mỗi phương trình cũng có hai nghiệm.

Vậy số nghiệm của phương trình () () 2 2 fxfx = là 9 nghiệm.

Câu11. Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ sau

ChọnC

Hàm số () = yfx có đạo hàm cấp 2 trên ℝ nên hàm số ()fx và ()fx ′ xác định trên ℝ Do đó, tập xác định của hàm số ()gx là . D = ℝ Ta có: ()()()() () () () () () () () ()

x x fx xx gxfxffxgx ffx fx fx fx

1 3 1 01 ; .1,2 0 1011 11 12

Từ đồ thị ta cũng có:  ()() 1 1101 . 2

0

 =   =  ′′ =   =∈ ′′′′′′ =−=⇔⇔   ′′ −=   ′ −=−   ′ −=   ′ −= 

Ta có ()()() ()gxffxfx ′′′ = () () () () 0 0 0 ffx gx fx

 ′ =  ′ =⇔  ′ =   Có () () ()

xxx x fx xxx x

x fxfxx x

=   ′′ −=−⇔=⇔=−   =   ()() () () 1 2

; -1 112. 2 ; + xx fxfx xx

=∈−∞  ′′ −=⇔=⇔  =∈∞  

; 123. ; + xxx fxfx xxx

=∈−∞  ′′ −=⇔=⇔  =∈∞    ()() () () 31 42

Vậy phương trình () 0 gx ′ = có 9 nghiệm.

Câu13. (THPT Cẩm Bình HàTỉnh2019) Cho hàm số ()fx liên tục trên ℝ và có đồ thị như hình vẽ

Đặt ()()()gxffx = . Hỏi phương trình () 0 gx ′ = có mấy nghiệm thực phân biệt?

A. 14 B. 10 C. 8 D. 12 Lờigiải ChọnB

11 22

=−<<− = ′ =⇔ =<< =

,21 0 0 ,12 2

; () () () () () ()

 =   =  ′ =⇔  =   = 

0 0 2

fxx fx ffx fxx fx

1 2

Dựa vào đồ thị ta thấy: () 0 fx = có 3 nghiệm phân biệt là 2,0,2xxx=−== , trong đó có 2 nghiệm trùng với nghiệm của () 0 fx ′ = () 1fxx = có 3 nghiệm phân biệt ()()()3452;1,1;1,2;xxx ∈−−∈−∈+∞ () 2fxx = có 1 nghiệm duy nhất () 6 ;2 x ∈−∞− . () 2 fx = có 1 nghiệm duy nhất () 7 ;2 x ∈−∞− .

Cũng từ đồ thị có thể thấy các nghiệm 1234567 ,,,,,,,2,0,2 xxxxxxx đôi một khác nhau. Vậy () 0 gx ′ = có tổng cộng 10 nghiệm phân biệt. Câu14. Biết rằng đồ thị hàm số ()yfx = được cho như hình vẽ sau

()yfx = liên tục trên R và có đồ thị như hình vẽ bên. Phương trình () ()10 ffx −= có tất cả bao nhiêu nghiệm thực phân biệt?

Tập nghiệm của phương trình () = fxr có số phần tử là

A. 4 B. 3 C. 1 D. 2 Lờigiải

ChọnB

Ta có () 32 432 ′ =+++ fxmxnxpxq () 1

Dựa vào đồ thị ()′ = yfx ta thấy phương trình () 0 ′ = fx có ba nghiệm đơn là 1, 5 4 , 3 .

Do đó ()()()() 1453 ′ =+−− fxmxxx và 0 ≠ m . Hay () 32 413215 ′ =−−+ fxmxmxmxm () 2 .

Từ () 1 và () 2 suy ra 13 3 =− nm , =− pm và 15 = qm .

Khi đó phương trình () = fxr ⇔ 432 0 +++=mxnxpxqx ⇔ 43213150 3  −−+=   mxxxx

⇔ 432 3133450 −−+= xxxx ⇔ ()()2 3530 +−=xxx ⇔ 5 03 3 =∨=−∨= xxx . Vậy tập nghiệm của phương trình () = fxr là 5 ;0;3 3  =−  S .

A. 6 B. 5 C. 7 D. 4 Lờigiải ChọnC

Câu17. (Chuyên Bắc Giang 2019) Cho hàm số () 432 yfxmxnxpxqxr ==++++ , trong đó ,,,, mnpqr ∈ ℝ . Biết rằng hàm số ()' yfx = có đồ như hình vẽ dưới.

xx fxxx xx

=∈−−   =⇔=∈−   =∈ 

2;1 01;0 1;2

Ta có () () () ()

1 2 3

fxx ffxfxx fxx

−=∈−−   −=⇔−=∈−   −=∈ 

12;1 1011;0 11;2

Khi đó: () () ()() ()() ()()

1 2 3

=+∈−   ⇔=+∈   =+∈ 

fxx fxx fxx

()() ()() ()()

11;0 10;1 12;3

1 2 3

+ Ta thấy hai phương trình ()() 1 11;0fxx=+∈− ; ()() 2 10;1fxx=+∈ đều có ba nghiệm phân biệt.

Phương trình ()() 3 12;3fxx=+∈ có một nghiệm.

Vậy phương trình () ()10 ffx −= có 7 nghiệm.

Câu16. (Đề thamkhảo2019) Cho hàm số () 432 =++++ fxmxnxpxqxr ,. Hàm số ()′ = yfx có đồ thị như hình vẽ bên dưới:

Tập nghiệm của phương trình () 16842 fxmnpqr =++++ có tất cả bao nhiêu phần tử. A. 4 B. 3 C. 5 D. 6 Lờigiải ChọnA

Từ đồ thị ta thấy () '0114 fxxxx =⇔=−∨=∨= Ta có bảng biến thiên

Phương trình ()()() 168422 fxmnpqrfxf =++++⇔= Từ bảng biến thiên ta thấy phương trình có 4 nghiệm.

4 3 2 1 4 3 2 1 O -1 -2 -3

y x -4 -3 -2 -1

y=f(x)

5 y=g(x)

Do đó: ( ) ( ) 0 fgx =

xxx x fxxxx xxx xxx

 =−<<−  =−   =⇔=<<   =<<   =<< 

36

32 1 012 23 45

11 22 33 44

() () () ()

.

gxx gx gxx gxx gxx

 =  =−   ⇔=   =   = 

( ) ( ) ()() ()() ()() ()()

1 2 3 4

1 12 3 4 5

Phương trình ( )1 có đúng 1 nghiệm; Phương trình ( )2 có đúng 3 nghiệm; Phương trình ( )3 có đúng 3 nghiệm; Phương trình ( )4 có đúng 3 nghiệm; Phương trình ( )5 có đúng 1 nghiệm. Tất cả các nghiệm trên đều phân biệt nên phương trình ( ) ( ) 0 fgx = có đúng 11 nghiệm.

xxx xxx x

21 01 3

 =−<<−  ⇔=<<   = 

Quan sát đồ thị ta thấy: ( ) 0 gx = ( ) () 55 66

 =  ⇔=   = 

fxx fxx fx

6 7 38

5 6

Do đó ( ) ( ) 0 gfx = ( ) ( ) ()() ()()

Phương trình ( )6 có 5 nghiệm; Phương trình ( )7 có 5 nghiệm; Phương trình ( )8 có 1 nghiệm.

Tất cả các nghiệm này đều phân biệt nên phương trình ( ) ( ) 0 gfx = có đúng 11 nghiệm.

Vậy tổng số nghiệm của hai phương trình ( ) ( ) 0 fgx = và ( ) ( ) 0 gfx = là 22 nghiệm.

Câu20. (THPT Nghĩa Hưng 2019) Cho hàm số ( ) yfx = có đạo hàm liên tục trên R . Hàm số ( ) yfx ′ = có đồ thị như hình vẽ bên dưới:

y 4 2 2

O 1 2 3 1 2 3 4 5 6 7 x

Số nghiệm thuộc đoạn 2;6    của phương trình ( ) ( )0 fxf = là

A. 5 B. 2 C. 3 D. 4 Lờigiải

Từ đồ thị của hàm số ( ) ' fx ta có BBT

Gọi 1S là diện tích hình phẳng giới hạn bởi () ';0;0;2yfxyxx ====

Gọi 2S là diện tích hình phẳng giới hạn bởi () ';0;2;5yfxyxx ==== Gọi 3S là diện tích hình phẳng giới hạn bởi () ';0;5;6yfxyxx ==== ()()() 2 1 0 '02Sfxdxff =−=−  ; ()()() 5 2 2 '52Sfxdxff ==−  ; ()()() 6 3 5 '56Sfxdxff =−=−  Từ đồ thị ta thấy ()()()()()() 21 520250 SSffffff >  −>−  > và ()()()()()()()() 132 02565260 SSSffffffff +<  −+−<−  > Khi đó ta có BBT chính xác ( dạng đồ thị chính xác ) như sau: Vậy phương trình ()() 0 fxf = có 2 nghiệm thuộc đoạn 2;6    Câu21. (ChuyênVĩnhPhúc2019) Cho hàm số ()yfx = có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ dưới. Đặt ()() gxffx =   . Tìm số nghiệm của phương trình () 0 gx ′ = A. 2 B. 8 C. 4 D. 6 Lờigiải

Ta có: ()()() () () 0 0 0 fx gxfxffx ffx

′ =  ′′′ ==⇔    ′ =     () *

Theo đồ thị hàm số suy ra. () 1

0 0 x fx xa =  ′ =⇔  =  , với 1 23 a << . () ()() ()() 1

0,1 0 ,2 fx ffx fxa =  ′ =⇔    =   .

Phương trình () 1 : () 0 fx = có 3 nghiệm phân biệt khác nghiệm phương trình () * Phương trình () 2 : () 1fxa = có 3 nghiệm phân biệt khác nghiệm phương trình () 1 và phương trình () * .

Vậy phương trình ban đầu có 8 nghiệm phân biệt.

Câu22. (THPTHậuLộc2-ThanhHóa-2019) Cho hàm số () 432 yfx=axbxcxdxe =++++ có đồ thị như hình vẽ bên đây, trong đó a,b,c,d,e là các hệ số thực. Số nghiệm của phương trình () () ()()210ffxfxfx++−= là

A. 3. B. 4. C. 2. D. 0. Lờigiải

ChọnB

Từ hình vẽ ta có dạng đồ thị của hàm trùng phương nên () 42 0 bdfxaxcxe ==  =++

Ta có () 3 42 fxaxcx. ′ =+

′ =  +==    =⇔=⇔=  =+  ++== =   () 2 2 fxxx  =+ và () () ()() 2 2 ffxfxfx. =+ Như vậy phương trình () () ()()210 ffxfxfx. ++−= ()()()() 2 2210fxfxfxfx ⇔+++−= với () 0 fx. ≥ Đặt ()() 0 tfxt=≥ ta được phương trình () 0 gt = với () 2 321 gtttt. =−−+ Nhận thấy: Hàm số ()gt liên tục trên đoạn [] 01 ; và ()()010g.g < () 0 gt  = có ít nhất 1 nghiệm thuộc () 01 ; Hàm số ()gt liên tục trên đoạn [] 14 ; và ()() 140g.g <

Từ đồ thị () () () () 42

10 4201 00002 12 11

f aca feefxxx. acec f

Mà () 0 gt = là phương trình bậc hai chỉ có tối hai nghiệm nên () 0 gt = có duy nhất một nghiệm thuộc () 01 ; . Suy ra () () ()()210ffxfxfx++−= có duy nhất một nghiệm ()() 01 fx;. ∈ Suy ra phương trình () fxa = với () 01a; ∈ luôn có 4 nghiệm x phân biệt.

Dựa vào đồ thị ta có () () 10 ffx += () () 1 ffx =−

+ Với () 2 fxa=<− 1 2

2 2 xx xx =<−  ⇔  =>  .

Câu24. (S

 −=− ′′ −=−−+−−−+−=

( ) ( )00fg = ( ) ( )fxgx = ( ) ( ) , fxgx ′′ ( ) ( )fxgx =

nam fgmnapbqc fgmnapbqcpbm qcm fgmnapbqc Tĩnh

- 2019) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ. Tập hợp nghiệm của phương trình () () 10 ffx += có bao nhiêu phần tử?

Hà

fxa fxb fx fxc

Trang 40

=<−   =∈−−  ⇔  =   => 

() ()() () ()

2 2;1 0 2

xx xx xx xx

3 4 5 6

2 2;1 1;0 2

+ Với ()() 2;1 fxb=∈−− () ()

=<−   =∈−−  ⇔  =∈−   => 

 ==−  ⇔=∈   =∈ 

xx xx xx

7 8 9

+ Với () 2 fxc=> vô nghiệm.

2 0;1 2;3

+ Với () 0 fx = () ()

Ta thấy hàm số ()yfx = đơn điệu trên () ;2−∞− , ()() 13 fxabfx =≠= nên 13xx ≠ .

Hàm số ()yfx = đơn điệu trên () 2; +∞ , ()() 69 0 fxbfx =≠= nên 69xx ≠

Vậy phươngtrình đã cho có 9 nghiệm phân biệt.

Câu25. (THPTNguyễn ĐứcCảnh-2019) Cho hàm số ()fx có bảng biến thiên

Phương trình ( ) 2 23fxx−= có bao nhiêu nghiệm?

A. 1. B. 2. C. 3. D. 4. Lờigiải ChọnB

Ta có () 2

22 22 x tx xx ′ = , () 0;2 x ∈ ()() 010;2txx ′ =⇔=∈

Bảngbiếnthiên của ()tx : 01 t  ≤≤ , [] 0;2 x ∀∈

Lúc này, phương trình ( ) 2 23fxx−= trở thành ()() 3 1 ft = với [] 0;1 t ∈

Theobảng biến thiên của hàm số ()ft trên đoạn [] 0;1 thì đường thẳng 3 y = cắt đồ thị hàm số ()yft = tại đúng 1 điểm có hoành độ thuộc khoảng () 0;1 nên phương trình () 2 có đúng 1 nghiệm 0tt = với () 0 0;1 t ∈

Phương trình ()cos10ffx −=  có bao nhiêu nghiệm thuộc đoạn [] 0;2π ?

Khi đó, phương trình () 2 0 12xxt⇔−= () 2 , () 0 0;1 t ∈

Mặt khác, theobảng biến thiên của hàm số ()tx , với mỗi () 0 0;1 t ∈ thì đường thẳng 0yt = cắt đồ thị hàm số ()ytx = tại đúng2 điểm phânbiệt nên phương trình () 2 có đúng 2 nghiệm phânbiệt.

A. 2 B. 5 C. 4 D. 6 Lờigiải ChọnC

Vậy phương trình ( ) 2 23fxx−= có đúng 2 nghiệm.

fxa ffxfxb fxc

Dựa vào đồ thị hàm số ta thấy: () ()() ()() ()()

cos12;1 cos10cos11;0 cos11;2

=+∈−   ⇔=+∈   =+∈ 

−=∈−−   −=⇔−=∈−    −=∈  ()() ()() ()()

fxa fxb fxc

cos11;0 cos10;1 cos12;3

x fxax x

cos11 cos1cos1;02 cos13

• Xét phương trình () () ()() ()

α α α

=<−   =+⇔=∈−   => 

1 2 3

Vì []cos1;1 x ∈− nên phương trình ()() , 13 vô nghiệm và phương trình () 2 có 2 nghiệm thuộc đoạn [] ; π02

x fxbx x

cos14 cos1cos1;05 cos16

• Xét phương trình () () ()() ()

β β β

=<−   =+⇔=∈−   => 

1 2 3

Vì []cos1;1 x ∈− nên phương trình ()() , 46 vô nghiệm và phương trình () 5 có 2 nghiệm thuộc đoạn [] ; π02 .

ng trình ()cos1cos2 fxcxt=+⇔=> (vô nghiệm)

Nhận xét hai nghiệm của phươngtrình () 5 không trùng với nghiệm nào của phương trình () 2 nên phương trình ()cos10ffx −=  có 4 nghiệm phận biệt.

Câu27. (Chuyên Lương Văn Tỵ - Ninh Bình - 2020) Cho hàm số () 32 fxaxbxbxc =+++ có đồ thị như hình vẽ: Số nghiệm nằm trong ;3 2 π π    của phương trình ()cos1cos1fxx+=+ là A. 2 B. 3 C. 5. D. 4. Lờigiải ChọnC

Trang 43

xa fxxxb x

=∈−∞   =⇔=∈   = 

Từ đồ thị ta có () () () ;0 0;1 2

xa fxxxb x

+=∈−∞   +=+⇔+=∈   += 

Do đó () () () cos1;0 cos1cos1cos10;1 cos12

=−=∈−∞−   ⇔=−=∈−   = 

Phương trình (2) có 2 nghiệm nằm trong ;3 2 π π    .

cos1;1() cos11;0(1) cos1(2)

() () 1 2

xatVN xbt x

Dựa vào đường tròn lượng giác, phương trình (1) có 3 nghiệm nằm trong ;3 2 π π    .

Vậy phương trình ban đầucó tất cả 5 nghiệm nằm trong ;3 2 π π   

Câu28. (Chuyên Lê Hồng Phong - Nam Định - 2020) Cho hàm số ()fx liên tục trên ℝ và có bảng biến thiên như sau:

Số nghiệm thuộc khoảng () ;ln2 −∞ củaphương trình () 2019120210 x fe−−= là A. 1. B. 2 . C. 3. D. 4 . Lờigiải ChọnB Đặt 1 xte =− ; () ;ln2 x ∈−∞ () 1;1 t  ∈−

Nhậnxét: ()ln1 xt =−  với mỗi giátrị của () 1;1 t ∈− ta được một giá trị của () ;ln2 x ∈−∞

Phương trình tương đương: () 2021 2019 ft =

Sử dụng bảng biến thiên của ()fx cho ()ft như sau:

vào b

ng biến thiên tathấyphương trình () 2021 2019 ft = có 2 nghiệm () 12,1;1tt ∈− .

Vậy phương trình () 2019120210 xfe−−= có2 nghiệm () ;ln2 x ∈−∞

Câu29. (ChuyênTháiBình-2020) Cho ()yfx = là hàm số đa thức bậc 3 và có đồ thị như hình vẽ bên.

Hỏi phương trình () ()cos10ffx −= có bao nhiêunghiệm thuộc đoạn [] 0;3π ?

ố nghiệm thuộc đoạn 55 ; 44

A. 2 B. 4 C. 5 D. 6 Lờigiải ChọnD

Đặt cos tx = , với [][] 0;31;1xt π ∈  ∈−

Với 1 t = , phương trình cos tx = có hai nghiệm [] 0;3 x π ∈ .

Với 1 t =− , phương trình cos tx = cóhai nghiệm [] 0;3 x π ∈

Với 11 t −<< , phương trình cos tx = có ba nghiệm [] 0;3 x π ∈

Thay cos tx = vào phương trình () ()cos10ffx −= , ta được phương trình:



      

+)Phươ

trình (1)có

nghiệ

1;0 t

Vậy phương trình đã cho có 6 nghiệm.

suy ra ph

ng trình đã cho có 3 nghiệm. +)Phương trình (2)có 1 nghiệm () 1;0 t ∈− , suy ra phương trình đã cho có 3 nghiệm. +)Phương trình (3)có 1 nghiệm 1 t > , suy ra phương trình đã chovô nghiệm.

        −=∈     sin(1;0) 4 xa π  −=∈−  có 2 nghiệm. sin(0;1) 4 xb π  −=∈  có 3 nghiệm. Vậy phương trình có 5 nghiệm. Câu31. (BỉmSơn-ThanhHóa-2020) Cho hàm số có đạo hàm trên và có đồ thị là đường cong tronghìnhvẽ bên dưới. Đặt . Tìm số nghiệm của phươngtrình . A. B. C. D. Lờigiải ChọnA Tacó .

( )yfx = ℝ ( ) ( )gxffx =   ( ) 0 gx ′ = 8 2 4 6 ()() () () ( ) () ()()

′ =  ′ =   ′′ ==⇔⇔=     ′ =      =∈ 

0 0 '.00 0 1;3 () fx fx gxfxffxfx ffx fxm

Phương trình có 2 nghiệm

Phương trình có 3 nghiệm

Phương trình có 3 nghiệm

1;3 fxm=∈

Vậy phương trình có 8 nghiệm.

Câu32. (ĐặngThúcHứa-Nghệ An-2020)

fx

Lờigiải ChọnB

Đặt ()tfx = , 0 t ≥

Tacó: () () () 2 210fftttf++−= (*).

Xét 0 t = : ()() (*)010 ff ⇔−= (không thỏa).

Xét 0 t > : Ta có () 0 ft > và () 2 20fttt++>

Theo đồ thị, hàm ()fu đồng biến trên () 0; +∞ .

Do đó, (*) () () ()() 2 2 2121fftttffttt ⇔++=⇔++= () 2 12 fttt⇔=−− ()()ftgt⇔= (**)(với () 2 12,0gtttt=−−> )

(1)có2 nghiệm trong 0;9 2 π    . (2)có5 nghiệm trong 9 0; 2 π    (3)vônghiệm. Vậy phương trình đã cho có 7 nghiệm trong 0;9 2 π    Câu33. (Hậu Lộc 2 - Thanh Hóa - 2020) Cho hàm số ()() 32 ,,, yfxaxbxcxdabcd ==+++∈ ℝ có đồ thị như hình vẽ bên. Số nghiệm của phương trình () () ()() ( ) () 210fffxfxfxf++−= là A. 2. B. 3. C. 1. D. 0.

Vì hàm ()ft đồng biến và ()gt nghịch biến trên () 0; +∞ nên phươngtrình (**) có nghiệm duy nhất t α = Theo đồ thị hàm ()() , ftgt ta có () 0;1 α∈

Khi đó, ()() 22,0;1 tfxααα =⇔=∈ (***).

Vì đồ thị hàm ()fx cắt đường thẳng 2 y α = tại 3 điểm phân biệt nên phương trình (***)có 3 nghiệm phân biệt.

Câu34. (LýNhânTông-BắcNinh-2020) Cho hàm số () = yfx liên tục trên ℝ và có đồ thị như hình vẽ. Phươngtrình () ()10−= ffx có tất cả bao nhiêu nghiệm thực phân biệt?

A. 6 . B. 5 . C. 7 . D. 4 . Lờigiải

ChọnC

Suy ra () ()10−= ffx () () ()

−=   ⇔−=   −= 

fxa fxb fxc

1 1 1

=∈−−   ⇔=∈−   =∈ 

xa xb xc

2;1 1;0 1;2

Từ đồ thị của hàm số () = yfx suy ra () 0 = fx () () ()

() () ()

fxa fxb fxc

=+   ⇔=+   =+ 

1 1 1

+Do ()() 2;111;0∈−−  +∈− aa  Phương trình () 1 =+fxa có 3 nghiệm phân biệt. +Do ()() 1;010;1∈−  +∈  bb Phương trình () 1 =+fxb có3 nghiệm phân biệt. +Do ()() 1;212;3 ∈  +∈  cc Phương trình () 1 =+fxc có 1 nghiệm. Vậy phương trình () ()10−= ffx có 3317 ++= nghiệm. Câu35. (Nguyễn Trãi - Thái Bình - 2020) Cho hàm số ()yfx = có đồ thị ()' yfx = như hình vẽ. Xét hàm số ()() 3 224365gxfxxxm =+−−− với m là số thực. Để () 0,5;5gxx ≤∀∈− thì điều kiện của m là

A. () 2 545 3 mf≥−− B. () 2 5 3 mf ≤ C. () 2 025 3 mf≤− D. () 2 5 3 mf ≥ Lờigiải ChọnD

Tacó ()() 3 0224365gxfxxxm ≤⇔+−≤+ Đặt ()() 3 224 hxfxxx =+− thì bất phương trình ()()0365gxhxm ≤⇔≤+

()()() () ()22 '2'2.342'32 hxfxxfxx =+−=−−+

Vẽ đồ thị hàm số 2 32yx=−+ trên cùng hệ trục tọa độ với hàm số ()yfx = .

Ta thấy () 2 '32fxx≥−+ 5;5 x ∀∈− nên () '0,5;5hxx ≥∀∈−

Suy ra () ()5,5;5hxhx ≤∀∈− hay () () () 5;5 max52565 hxhf   ==+ Do đó () () 5;5 365,5;5max365hxmxhxm    ≤+∀∈−⇔≤+  () () 2 25653655 3 fmmf⇔+≤+⇔≥ Câu36. (THPT Nguyễn Viết Xuân - 2020) Cho hàm số ()fx có đồ thị như hình vẽ Đặt ()()() 1 gxffx=− . Số nghiệm của phương trình () 0 gx ′ = là A. 6 . B. 10 . C. 9 . D. 8 . Lờigiải ChọnC Ta có ()()()() .1gxfxffx ′′′ =−

′ =  ′′′ =⇔−=⇔  ′ −=   +) () () () () ()

()()()() () () () 0 0.10 10 fx gxfxffx ffx

xaa fxx xaa

1;0 01 1;2

11 22

 =∈−  ′ =⇔=   =∈   +) () () () () ()

−==+∈  ′ −=⇔−=⇔=  −==+∈

fxafxa ffxfxfx fxafxa

110;11 101122 112;33

11 22

()()() ()() ()()()

Từ đồ thị suy ra  phương trình (1) có hai nghiệm phân biệt ()()122;1;2;3bb∈−−∈  phương trình (2) có hai nghiệm phân biệt ()()11222;;;3cbcb ∈−∈  phương trình (3) có hai nghiệm phân biệt ()()11222;;;3dcdc ∈−∈ Vậy phương trình đã cho có 9 nghiệm phân biệt.

Câu37. (TiênDu-BắcNinh-2020) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ bên

Số nghiệm thuộc đoạn 7 0; 2 π    của phương trình ((cos))0ffx = là

A. 7 B. 5 C. 8 D. 6 Lờigiải

ChọnB Đặt (cos) fxt = ta được phương trình ()0ft = Quan sát đồ thị ()yfx = ta suy ra 1 2 3

(2;1) ()0(0;1). tt(1;2)

tt fttt =∈∈−−   =⇔=∈   =∈ 

* Với 1tt = ta có 1 (cos) fxt = . Xét tương giao giữa hai đồ thị ()yfx = và () 1112;1(cos)cos1ytfxtxx =∈−−  =⇔=<− nên phương trình vô nghiệm.

xx ytfxtxx xx

* Với 2tt = ta có 2 (cos) fxt = . Xét tương giao giữa hai đồ thị ()yfx = và () 2 223 4

=<−   =∈  =⇔=∈   =∈ 

cos1 0;1(cos)cos(0;1). cos(1;2)

Chỉ có 3 cos xx = thỏa mãn. Khi đó tồn tại 3 giá trị 7 0; 2 x π  ∈   tương ứng để 3 cos xx = .

* Với 3tt = tương tự ta có 5 6 7

=<−   =∈−   => 

xx xx xx

cos1 cos(1;0). cos1

Chỉ có 6 cos xx = thỏa mãn. Khi đó tồn tại 2 giá trị 7 0; 2 x π  ∈   tương ứng để 6 cos xx = Vậy phương trình đã cho có 5 nghiệm thuộc đoạn 7 0; 2 π   

Câu38. (Lương Thế Vinh - Hà Nội - 2020) Cho hàm số () = yfx có đồ thị nhưu hình vẽ bên. Tìm số nghiệm thuộc đoạn [] 2017;2020ππ của phương trình () 32cos8 = fx

Xét trên đoạn [] 2;2 , đường thẳng 8 3 = y cắt đồ thị hàm số ()ft tại hai điểm () 1 2;1∈−− t và () 2 1;2 ∈ t .

Từ bảng biến thiên của t , ứng với giá tị 1t , ta tìm được 3 nghiệm x thỏa 1 2cos = xt , tươngtự, ta cũng tìm được 3 nghiệm x thỏa 2 2cos = xt

Vậy phương trình () 32cos8 = fx có 6 nghiệm x thuộc đoạn [] 2017;2020ππ

Câu39. (Chuyên Quang Trung - Bình Phước - 2021) Cho hàm số ()yfx = có bảng biến thiên như hình bên.

A. 8 B. 3 C. 4 D. 6 Lờigiải ChọnD Đặt 2cos = tx , ta có bảng biến thiên của t như sau Khi đó ()() 8 32cos8 3 =⇔=fxft . Vẽ thêm đường thẳng 8 3 = y trên đồ thị () = yfx đã cho.

Phương trình sincos 230 2 xx f +  +=   có bao nhiêu nghiệm trên 37 ; 44 ππ   

A. 3 B. 4 C. 5 D. 6 Lờigiải ChọnA

Ta có: sincossin 24 xx x π + =+  Đặt sin 4 xt π +=  , [] 1;1 t ∈−

Phương trình tương đương: () ()() () 1 2

;1 3 2 1;0 ttloai ft tt =∈−∞−  =−⇔  =∈−  

Với 37 ; 44 x ππ  ∈−  , ta có bảng biến thiên của t như sau:

Dựa vào bảng biến thiên, ta thấy phương trình 2tt = có 3 nghiệm 37 ; 44 x ππ  ∈−  .

Câu40. (LiêntrườnghuyệnQuảngXương-ThanhHóa-2021) Cho hàm số ()yfx = có đạo hàm cấp hai trên R và có đồ thị '()yfx = là đường cong trong hình vẽ bên. Đặt ()('()1)gxffx=− . Gọi S là tập nghiệm của phương trình '()0gx = . Số phần tử của tập S là A. 8 B. 6 C. 10 D. 9 Lờigiải ChọnC  Ta có: ()('()1)'()"().'('()1) gxffxgxfxffx =−  =−

Phương trình

fxfx fx gxfxfx ffx fxfx

''()0''()0 '()0 '()0'()11'()0 '('()1)0 '()12'()3

== =   =⇔⇔−=−⇔=   −=  −==

Ta có đồ thị '()yfx = có cực trị tại 0

f f fx

=      =      = 

"(1)0 2 "0 3 ''()0

0

x x xx

=    =   =∈  

1 2 3 (1;2)

''()0fx  = có 3 nghiệm 0

=   =  =   cùng với 1 x = là nghiệm bội chẵn

x xx x

1 2; 3

Tại phương trình '()0fx = ta thấy có 2 nghiệm bội lẻ 1,2xx=−= và nghiệm bội chẵn 1 x =

Tại phương trình '()3fx = ta thấy có 2 nghiệm mà đường thẳng 3 y = cắt đồ thị ()yfx = đó là hai điểm 1 (;1) xx=∈−∞− và 2 (2;) xx=∈+∞

Vậy từ đó ta thấy phương trình '()0gx = tổng cộng có tất cả 10 nghiệm.

Câu41. (Chuyên Thoại Ngọc Hầu -An Giang - 2021) Cho hàm số ()yfx = liên tục trên ℝ có đồ thị như hình vẽ bên dưới.Gọi () 1C và () 2C lần lượt là đồ thị của hai hàm số ()()() 2 yfxfxfx ′′′ =−   và 2021x y = .Số giao điểm của () 1C và () 2C là

A. 1 B. 0 C. 2 D. 4 Lờigiải ChọnB Số giao điểm () 1C và () 2C là nghiệm của phương trình ()()()() 2 .2021* x fxfxfx ′′′ −=   Từ đồ thị ta thấy ()fx cắt trục Ox tại bốn điểm phân biệt có hoành độ lần lượt là 1234 ;;; xxxx nên phương trình () 0 fx = có bốn nghiệm phân biệt 1234 ;;; xxxx ()()()()() 1234 fxaxxxxxxxx  =−−−−

2 2 2 t t t ≥−  ⇔⇔=  =± 

Với 2 t = thì () 32342fxx−+= Sử dụng phương pháp ghép trục ta có BBT:

ễn ĐứcCảnh-TháiBình-2021) Cho hàm số ()yfx = có đồ thị như hình vẽ bên Số nghiệm thực của bất phương trình () ()23232 2348342 fxxfxx−++≤−++

Vậy bất phương trình đã cho có 4 nghiệm thực phân biệt. Câu43. (THPTQuế Võ1-BắcNinh-2021) Cho hàm số ()fx bảng biến thiên như sau:

Số nghiệm thuộc đoạn 9 0; 2 π    của phương trình (2sin1)1fx += là

A. 5. B. 6. C. 7. D. 4. Lờigiải ChọnC

Xét phương trình (2sin1)1fx += (1). Đặt 2sin1tx=+ . '2cos tx = '0cos0. 2 txxk π π =⇔=⇔=+ () k ∈ ℤ

Vì 9 0; 2 x π  ∈   nên 3579 0;;;;; 22222 x πππππ  ∈   . Bảng biến thiên

t ta tb

1 1;3 3;

Phương trình (1) trở thành ()1ft = () ()

 =−  ⇔=∈   =∈+∞  .

Căn cứ bảng biến thiên ta có

+ Với 1 t =− phương trình (1) có 2 nghiệm.

+ Với ta = phương trình (1) có 5 nghiệm.

+Với tb = phương trình (1) vô nghiệm.

Vậy phương trình có 7 nghiệm.

Câu44. (THPTQuảngXương1-ThanhHóa-2021) Biết đồ thị hàm số bậc bốn ()yfx = được cho bởi

hình vẽ bên dưới. Tìm số giao điểm củađồ thị hàm số ()()()() 2 ygxfxfxfx ′′′ ==−   và trục hoành A. 4 . B. 0 . C. 6 . D. 2 . Lờigiải

ChọnB

Ta có phương trình hoành độ giao điểm của hai đồ thị ()ygx = và Ox là: ()()()()()() () () 2 2 .0.00

phân biệt có hoành độ 1234 ,,, xxxx . Giả sử ()()()()()12341234 ,0, fxaxxxxxxxxaxxxx =−−−−≠<<< Ta có: ()()()()()()() 234134 fxaxxxxxxaxxxxxx ′ =−−−+−−− ()()()()()() 124123 axxxxxxaxxxxxx +−−−+−−−

f −+ += là A. 2 B. 3 C. 6 D. 5 Lờigiải ChọnC

′ =+++ Ta có: () () () () () () 2222 1234

1111 0 0 fx fx xxxxxxxx bằng 0 Câu45. (THPT Đào Duy Từ - Hà Nội - 2021) Cho hàm số ()yfx = liên tục trên ℝ và có bảng biến thiên như sau: Trang 60

1111 fx fxxxxxxxxx

′  ′ =⇔−−−−=   vô nghiệm. Vậy số giao điểm của đồ thị hàm số ()ygx = và trục hoành Số nghiệm của phương trình () 42 342 210 xx

()() 42 42 4242 42

xx xxxxxx xx

−+ −+−+−+ −+

ffaa bb

342 342342342 342

 =   +=⇔=−⇔=<−  =>  

22(1) 210212(1)(2) 2(5)(3)

Giải (1): 42

1 2234213410 1 3

2 3424242 2

xx x xxxx x −+  =  =⇔−+=⇔−+=⇔  =  

Suy ra phương trình (1) có 4 nghiệm phân biệt. Phương trình (2) vô nghiệm. Phương trình (3) 42 3424242 2 2 2342log342log0(4) xx bxxbxxb −+ =⇔−+=⇔−+−= Phương trình (4) có hai nghiệm trái dấu nên phương trình (3) có hai nghiệm phân biệt khác với 4 nghiệm của (1) Vậy, phương trình đã cho có 6 nghiệm Câu46. (THPT ĐàoDuyTừ -HàNội-2021) Cho hàm số ()yfx = là hàm số bậc 3 , có đồ thị như sau: Phương trình () () 2 sincos122sinsincossin2 4 fxxxfxxx π  ++=++−   có bao nhiêu nghiệm thực thuộc đoạn 55 ; 44 ππ    ? A. 1. B. 3 . C. 4 . D. 6 . Lờigiải ChọnB yt =

'()yft =

Phương trình đã cho trở thành () 1 2 ft = . Dựa và đồ thị ta thấy phương trình có 3 nghiệm là () () ()

ta tb tc

1;0 1;2 2;3

=∈−   =∈   =∈  .

Dựa vào bảng biến thiên của hàm số 163txx=+−+ ta có Phương trình 163 taxxa =⇔+−+= có 2 nghiệm và phương trình 163 tbxxb =⇔+−+= có 1 nghiệm và Phương trình 163 tcxxc =⇔+−+= có 1nghiệm. Vậy phương trình () 21631 fxx+−+= có 4 nghiệm.

Câu48. (THPTTriệuSơn-ThanhHóa-2021) Cho hai hàm ()yfx = và ()ygx = liên tục trên ℝ và có đồ thị như hình vẽ. Khi đó tổng số nghiệm của phương trình () () 0 fgx = và () () 0 gfx = là

Ta có () ()

gx gx fgxgx gxaa gxbb

 =−   =−  =⇔=   =∈   =∈  

() () () ()() () ()() ()

3(4) 1(5) 01(6) ,1;2(7) ,4;5(8)

. Dựa vào đồ thị hàm số ( )gx suy ra phương trình ( )4 có 1 nghiệm; phương trình ( ) ( ) ( )5;6;7 mỗi phương trình có 3 nghiệm và phương trình ( )8 có 1 nghiệm. suy ra phương trình ( ) ( ) 0 fgx = có 11 nghiệm. Vậy tổng số nghiệm của phương trình ( ) ( ) 0 fgx = và ( ) ( ) 0 gfx = là 21.

Ta có: () 32 33 143 4 fxxxx =−+− , () 2 33 314 2 fxxx ′ =−+ , () 633 2 fxx ′′ =−

Vậy: () * có 2 nghiệm thực.

Câu51. (Sở CầnThơ -2021) Cho hàm số bậc ba có đồ thị như sau:

( )yfx =

 Ta có: (0)0 f = suy ra 0 c = suy ra () sin2021 2021. x x fx e = . () sin2021 00sin20210 2021. x x fxx e =⇔=⇔= 2021 () 2021 k xkxk π π ⇔=⇔=∈ ℤ [] 20212021 1;1643,6643,6xkk ππ ∈−  ≤≤⇔−≤≤ . {-643;...;643} k  ∈ Vậy có 1287 nghiệm. Câu50. (Sở Bạc Liêu - 2021) Cho

()() 2 2212130fxfx+−+−=

xxx x x x

fxfxexfxeefxx efxxefxxxx efxxc hàm số ( ) 32 3 yfxxaxbx ==++− , a , b là các số thực thỏa mãn () 20 24330 ab ab +−>   ++<  . Hỏi phương trình ()()() 2 2.fxfxfx ′′′ =   có bao nhiêu nghiệm?

A. 2 B. 4 C. 3 D. 1 Lờigiải ChọnB Không mất tính tổng quát, chọn 33 4 a =− , 14 b = . Khi đó: Hai số a , b thỏa hệ () 20 24330 ab ab +−>   ++< 

′′ ⇔−=⇔−= ′′ ⇔=⇔= ⇔=+ Trang 64

 +=−  +−+−=⇔  += 

11 12130 13 fx fxfx fx

()() ( ) () 2 2 22 2

() ( ) 2 2 2

 +=− +=−⇔⇔=±  +=  

Số nghiệm của phương trình là A. 3. B. 4. C. 5. D. 2. Lờigiải ChọnB    .

11 111 12 xVN fxx x

() ( ) 2 2 2 2

 += +=⇔⇔=−>⇔=±−  +=>  

10 13111 12 xVN fxxaxa xa

(Các nghiệm không trùng với các nghiệm )  Vậy số nghiệm phương trình là 4.

1 xa=±− 1 x =± ()() 2 2212130fxfx+−+−=

Câu52. (Sở CầnThơ -2021) Cho hàm số () 32 fxxbxcxd =+++ có đồ thị là đường cong trong hình bên dưới.

Số nghiệm của phương trình () () () 41ffxfx+=+ là A. 7 B. 4 C. 3 D. 2

ĐỐITƯỢNGHỌCSINHGIỎI9-10 ĐIỂM

Dạng3.Biệnluậntươnggiaohàmhợp,hàm ẩnchứaTHAMSỐ

Câu1. (Đề ThamKhảo2019) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình () sin fxm = có nghiệm thuộc khoảng () 0;π là

ặt khác: ()() 003gf==− ; () () () 222222ggf−=+=−= ; ()() 242gf=−=− ; ()() 403gf==−

A. () 1;3 B. [ )1;1 C. [ )1;3 D. () 1;1 Lờigiải ChọnB

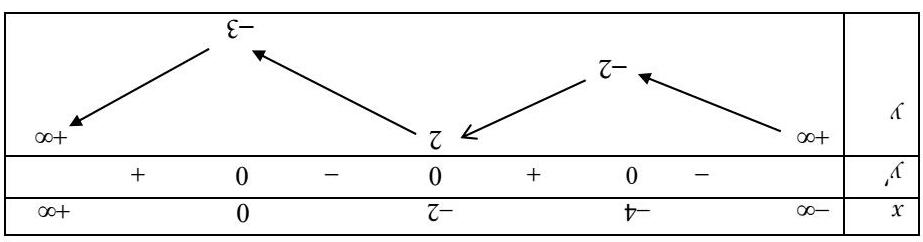
Đặt ()( ]sin0;0;1txxt π =  ∀∈  ∈ Vậy phương trình trở thành () ftm = . Dựa và đồ thị hàm số suy ra [ ) 1;1. m ∈−

Câu2. (Mã102-2020Lần2) Cho hàm số () = yfx có bảng biến thiên như hình vẽ: Có bao nhiêu giá trị nguyên của tham số m để phương trình () 2 64fxxm −= có ít nhất ba nghiệm thực phân biệt thuộc khoảng () 0; +∞ ? A. 25. B. 30. C. 29. D. 24. Lờigiải ChọnB Ta đặt: () () 2 4 gxfxx =− . ()() () 2 244 gxxfxx ′′ =−− ()()()() 222 2244424 xxxxxxx =−−+−+− (dựa vào bảng biến thiên) () () () 3 2 22424 xxxxx =−−+−

Ta có bảng biến thiên: Từ bảng biến thiên ta được: yêu cầu bài toán tương đương 32 6 m −<≤

1812 m ⇔−<≤ . Vậy có tất cả 30 giá trị của tham số m thỏa mãn yêu cầu bài toán. Câu3. (Mã103-2020Lần2) Cho hàm số ()fx có bảng biến thiên như sau

Trang 2

Có bao nhiêu giá trị nguyên của tham số m để phương trình () 2 34fxxm −= có ít nhất ba nghiệm thực phân biệt thuộc khoảng () 0; +∞ ? A. 15 B. 12 C. 14 D. 13 Lờigiải ChọnA Đặt 2 4 uxx =− (1) Ta có BBT sau: Ta thấy:

+ Với 4 u <− , phương trình (1) vô nghiệm.

+ Với 4 u =− , phương trình (1) có một nghiệm 20 x => .

+ Với 40 u −<< , phương trình (1) có hai nghiệm 0 x >

+ Vơi 0 u ≥ , phương trình (1) có một nghiệm 0 x >

Khi đó () () 2 34 3 m fxxmfu −=  = (2), ta thấy:

+ Nếu 39 3 m m =−⇔=− , phương trình (2) có một nghiệm 0 u = nên phương trình đã cho có một nghiệm 0 x >

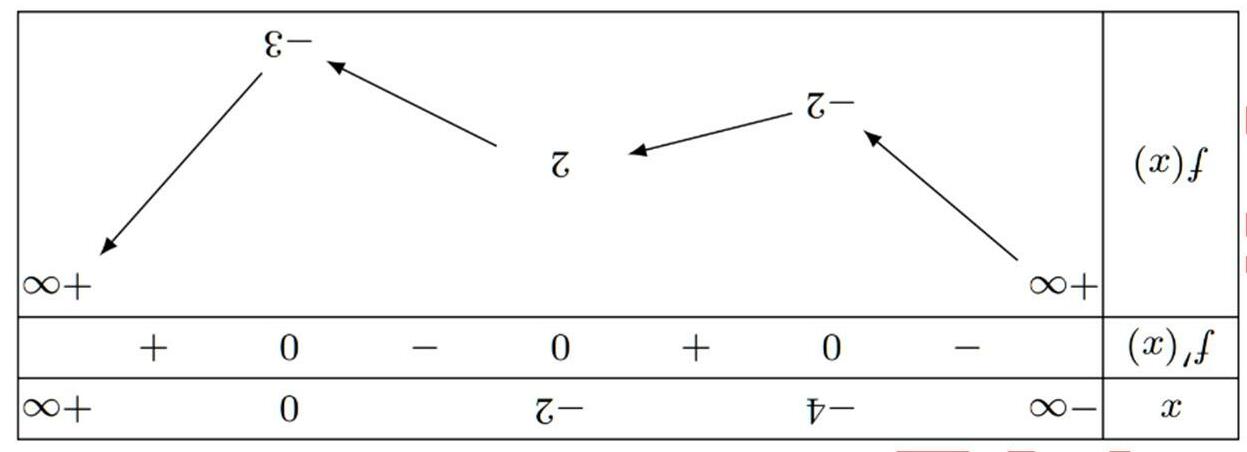
+ Nếu 3296 3 m m −<<−⇔−<<− , phương trình (2) có một nghiệm 0 u > và một nghiệm () 2;0 u ∈− nên phương trình đã cho có ba ngiệm 0 x >

+ Nếu 26 3 m m =−⇔=− , phương trình (2) có một nghiệm 4 u =− , một nghiệm () 2;0 u ∈− và một nghiệm 0 u > nên phương trình đã cho có bốn nghiệm 0 x > . + Nếu 2266 3 m m −<<⇔−<< , phương trình (2) có một nghiệm 4 u <− , hai nghiệm () 4;0 u ∈− và một nghiệm 0 u > nên phương trình đã cho có năm nghiệm 0 x > + Nếu 26 3 m m =⇔= , phương trình (2) có một nghiệm 4 u <− , một nghiệm 2 u =− và một nghiệm 0 u > nên phương trình đã cho có ba nghiệm 0 x > + Nếu 26 3 m m >⇔> , phương trình (2) có một nghiệm 4 u <− và một nghiệm 0 u > nên phương trình đã cho có một nghiệm 0 x > Vậy 96 m −<≤  có 15 giá trị m nguyên thỏa ycbt.

Câu4. (Mã101–2020Lần2) Cho hàm số ()fx có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số m để phương trình () 2 54fxxm −= có ít nhất 3 nghiệm phân biệt thuộc khoảng () 0; +∞ A. 24 B. 21 C. 25 D. 20

Lờigiải Chọn C. Đặt 2 4 txx =− . Ta có 2402txx ′ =−=⇔= Bảng biến thiên

Dựa vào bảng biến thiên ta có 321510 5 m m −<≤⇔−<≤ . Vì m nguyên nên {} 14;13;....;10 m ∈−− . Do đó có 25 giá trị nguyên của m thỏa mãn đề bài.

Câu5. (Mã104-2020Lần2) Cho hàm số ()fx có bảng biến thiên như sau:

Có bao nhiêu giá trị nguyên của tham số m để phương trình () 2 44fxxm −= có ít nhất 3 nghiệm thực phân biệt thuộc khoảng () 0; +∞ ? A. 16 B. 19 C. 20 D. 17 Lờigiải ChọnC

Ta có ()() 22 444 4 m fxxmfxx−=⇔−= Đặt 2 42402txxtxx ′ =−  =−=⇔=

Vì ()0;4xt ∈+∞  ≥− Ta có () 4 m ft = Phương trình đã cho có ít nhất 3 nghiệm phân biệt thuộc khoảng () 0; +∞ 32128 4 m m  −<≤⇔−<≤ mà m nguyên nên {} 11;10;...;0;1;...;8 m ∈−−

Vậy có 20 giá trị nguyên của m thỏa mãn.

Dựa vào sự tương giao của đồ thị hàm số ()yft ′ = và parabol 2 33 22ytt=+− trên đoạn [] 3;1 thì (){} 03;1gtt ′ =⇔∈−− . Suy ra bảng biến thiên của hàm số ()gt trên đoạn [] 3;1 như sau:

3 2 3

−−+>+ ⇔<−−+− Đặt sin2tx=− (với ; 22 x ππ  ∈−  thì () 3;1 t ∈−− , khi đó bất phương trình được viết lại thành: () () () ()2 3 5122 22 22 34 t t mftt  −+ +  <−++− hay () () 32 2365 23 * 3212mftttt <−−++ . Xét hàm số ()() 32 2365 23 3212gtftttt =−−++ trên đoạn [] 3;1 Ta có ()() 2 2233gtfttt ′′ =−−+ . Do đó ()() 2 33 0 22gtfttt ′′ =⇔=+−

fxxmxx x x mfxx Trang 6

2sin5cos2 2sin2sin 34 2sin512sin 2sin2sin 34

Bất phương trình đã cho nghiệm đúng với mọi ; 22 x ππ  ∈−  khi và chỉ khi bất phương trình () * nghiệm đúng với mọi () 3;1 t ∈−− . Điều đó tương đương với ()()12119 12 mgf≤−=−+ dựa vào tính liên tục của hàm số ()gt

Câu7. (Chuyên Lam Sơn - 2020) Cho hàm số ()yfx = , hàm số ()yfx ′ = liên tục trên ℝ và có đồ thị như hình vẽ bên. Bất phương trình () 2 2 fxxxm >−+ (m là tham số thực) nghiệm đúng với mọi () 1;2 x ∈ khi và chỉ khi

A. ()22 mf≤− B. ()11 mf≤+ C. ()11 mf≤− D. () 2 mf ≤ Lờigiải ChọnD

Ta có: ()() () 2 2 1;2 fxxxmx>−+∀∈ ⇔ ()() () () 2 2 1;2* fxxxmx−+>∀∈ . Gọi ()() () 2 2 gxfxxx =−−  ()()() 22gxfxx ′′ =−− Theo đồ thị ta thấy ()() [] () 22 1;2 fxxx ′ <−∀∈  () [] () 0 1;2 gxx ′ <∀∈ . Vậy hàm số ()ygx = liên tục và nghịch biến trên [] 1;2 Do đó () * ⇔ [] ()()() 1;2 min22mgxgf ≤== Câu8. (ChuyênBếnTre-2020) Cho hàm số ()yfx = Đồ thị hàm số ()yfx = như hình vẽ. Cho bất phương trình () 3 33 fxxxm ≥−+ ( m là tham số thực). Điều kiện cần và đủ để bất phương trình () 3 33 fxxxm ≥−+ đúng với mọi 3;3 x ∈−  là A. ()31 ≥ mf . B. ()33≥−mf . C. ()30 ≤ mf . D. ()33 ≤ mf . Lờigiải ChọnD Ta có ()()≥−+⇔−+≥ 3 3 3333 fxxxmfxxxm Đặt ()() 3 33 gxfxxx =−+ . Tính ()() 2 '3'33 gxfxx=−+ Có ()() 2 '0'1 gxfxx=⇔=− Nghiệm của phương trình () '0gx = là hoành độ giao đi

x fxxx x

 =−  =−⇔=   = 

Dựa vào đồ thị hàm số ta có: () 2 3 '10 3

BBT x 3 1 3 ( ) ' gx 0 0 0 ()gx ( ) 3 g ( )3 g Để bất phương trình nghiệm đúng với mọi 3;3 x ∈− thì () () () 3;3 min333mgxgf   ≤==

Câu9. (ChuyênHùngVương-GiaLai-2020) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ bên dưới. Gọi S là tập hợp tất cả giá trị nguyên của tham số m để phương trình ()sin22sin fxmx −+= có nghiệm thuộc khoảng () 0;π . Tổng các phần tử của S bằng

A. 4 . B. 1. C. 3 . D. 2 . Lờigiải ChọnD

Đặt sin tx = , với () 0; x π ∈ ( ]0;1 t  ∈

Ta được phương trình: ()()2222fttmfttm −=−⇔=+− (1)

Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số ()yft = và đường thẳng () 22 ytmr =+− .

Gọi () :21pyx=+ song song với đường thẳng () :2yt∆= và đi qua điểm () 0;1 A Gọi :23qyx=− song song với đường thẳng () :2yt∆= và đi qua điểm () 1;1 B Để phương trình ()sin22sin fxmx −+= có nghiệm thuộc khoảng () 0;π thì phương trình (1) phải có nghiệm ( ]0;1 t ∈ , suy ra đường thẳng r nằm trong miền nằm giữa hai đường thẳng q và p ( có thể trùng lên q và bỏ p ) {}{} 321131;0;1;21;0;1;2 mmmS  −≤−<⇔−≤<  ∈−  =− Do đó tổng các phần tử là: 10122 −+++= Câu10. (ChuyênHùngVương-GiaLai-2020) Cho hàm số () 3 2 fxxx=++ . Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình ()() ()33 3 2 ffxfxmxx ++=−−+ có nghiệm [] 1;2 x ∈− ? A. 1750 B. 1748 C. 1747 D. 1746 Lờigiải ChọnA Xét hàm số 3 ()2fttt=++ , ta có 2 ()310, fttt ′ =+>∀∈ ℝ Do đó hàm số f đồng biến trên ℝ Ta có () 3 3 ()()() ffxfxmfx ++=− 333 3 ()()()()0(1)xfxfxmfxfxxm ⇔−=++⇔+++=

()()()() ()() [1;2] [1;2] minmax012 117480 17481.

hxhxhh mm m

⋅≤⇔−⋅ ⇔−+≤ ⇔−≤≤ Do m nguyên nên tập các giá trị m thỏa mãn là {1748;1747;;0;1} S =−−… . Vậy có tất cả 1750 giá trị nguyên của m thỏa mãn.

Câu11. (ChuyênQuangTrung-2020) Cho hàm số ()fx liên tục trên [] 2;4 và có bảng biến thiên như

hình vẽ bên. Có bao nhiêu giá trị nguyên của m để phương trình 2 22.() xxxmfx +−= có nghiệm thuộc đoạn [] 2;4 ?

A. 6 B. 5 C. 4 D. 3 Lờigiải ChọnC Dựa vào bảng biến thiên ta có [] () 2;4 (4)2 Minfxf== và [] () 2;4 (2)4 Maxfxf==

Hàm số 2 ()22 gxxxx =+− liên tục và đồng biến trên [] 2;4

Suy ra [] () 2;4 (2)2Mingxg== và [] () 2;4 (4)442Maxgxg==+

Ta có 2 2 22() 22.() ()() xxxgx xxxmfxmm fxfx +− +−=⇔=⇔=

Xét hàm số () () () gx hx fx = liên tục trên [] 2;4

Vì ()gx nhỏ nhất và ()fx lớn nhất đồng thời xảy ra tại 2 x = nên

2 1 ()(2) 22 Mingx g Minhxh Maxfxf ====

[] [] () [] () () () 2;4 2;4 2;4

Vì ()gx lớn nhất và ()fx nhỏ nhất đồng thời xảy ra tại 4 x = nên

4 ()(4)222 4 Maxgx g Maxhxh Minfxf ====+

[] [] () [] () () () 2;4 2;4 2;4

Từ đó suy ra phương trình () hxm = có nghiệm khi và chỉ khi 1 222 2 m ≤≤+ Vậy có 4 giá trị nguyên của m để phương trình có nghiệm. Câu12. (Chuyên Sơn La - 2020) Cho hàm số ()fx liên tục trên ℝ và có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình ()()() 2 cos2019cos20200 fxmfxm+−+−= có đúng 6 nghiệm phân biệt thuộc đoạn 0;2π   là

Trang 10

cos0 cos1 cos1() 2 x fxxk xxxVN π π =  =−⇔⇔=+  =>  Vì [] 3 0;2; 22 xx ππ π  ∈  ∈   * Với ()cos2020 fxm =− Đặt [] ()cos1;1txt=∈− Với ( ]1;1 t ∈− thì phương trình cos tx = có hai nghiệm phân biệt thuộc [] 0;2π Với 1 t =− thì phương trình cos tx = có một nghiệm thuộc [] 0;2π Phương trình trở thành () 2020 ftm =− Để phương trình (1) có tất cả 6 nghiệm phân biệt thì phương trình ()cos2020 fxm =− có 4 nghiệm phân biệt, hay phương trình () 2020 ftm =− có hai nghiệm ( ]1;1 t ∈−

Dựa vào đồ thị ta có để phương trình () 2020 ftm =− có hai nghiệm ( ]1;1 t ∈− thì 12020120192021 mm −<−≤⇔≤<

Vì m nguyên nên {} 2019;2020 m ∈

Vậy có 2 giá trị nguyên của m thỏa mãn.

Câu13. (Chuyên VĩnhPhúc -2020) Cho hàm số ()yfx = . Hàm số ()yfx ′ = có đồ thị như hình bên.

Biết () ff e 1 11;2    −=−=      . Tìm tất cả các giá trị của m để bất phương trình

()() fxxm ln <−+ nghiệm đúng với mọi 1 1; x e    ∈−      .

A. 2 m ≥ B. 3 m ≥ C. 2 m > D. 3 m > Lờigiải ChọnB

Ta có ()() ln fxxm <−+ ()() ln mfxx ⇔>−− . Xét hàm số ()()() ln gxfxx =−− trên 1 1; e   

Có ()() 1 gxfx x ′′ =− . Trên 1 1; e    có () 0 fx ′ > và 1 0 x < nên () 1 0,1;gxx e  ′ >∀∈−− 

 hàm số ()gx đồng biến trên 1 1; e   

Vậy nên ()() ln fxxm <−+ nghiệm đúng với mọi 1 1; x e  ∈−−  () 1 ,1;mgxx e ⇔≥∀∈−−  1 mg e ⇔≥− 

Câu14. (Sở Phú Thọ - 2020) Cho hàm số ()yfx = liên tục trên ℝ thỏa mãn ()()15,30ff−=−= và có bảng xét dấu đạo hàm như sau:

Số giá trị nguyên dương của tham số m để phương trình () 2 324 fxxxm −++−= có nghiệm trong khoảng () 3;5 là A. 16 . B. 17 . C. 0 . D. 15 . Lờigiải ChọnD

Đặt ()() 2 324 gxfxxx =−++− với () 3;5 x ∈

Ta có: ()() 2 321 4 x gxfx x ′′ =−−+− + .

Với () 3;5 x ∈ :

Ta có: () 23;1 x −∈−− nên ()20fx ′ −> suy ra () 320 fx ′ −−< .

Ta có: 2 1 4 xx x x <= +

Suy ra ()() () 2 3210,3;5 4 x gxfxx x ′′=−−+−<∀∈ + nên hàm số nghịch biến trên () 3;5 .

Suy ra () ()()() 2 35 m53355295 in4 gxgf==−++−=− ; () ()()() ;

2 35 3 ma3313412 x31 gxgf==−++−=+ Để phương trình () 2 324 fxxxm −++−= có nghiệm thì 2951213 m −≤≤+ mà m nguyên dương nên {} 1,2,...,15 m ∈ tức là có 15 giá trị

Câu15. (Sở PhúThọ -2020) Cho hàm số ()yfx = liên tục trên ℝ và thỏa mãn () 1 11,2 e ff  −=−=   . Hàm số ()fx ′ có đồ thị như hình vẽ. Bất phương trình ()() 2 ln fxxxm <−++ nghiệm đúng với mọi 1 1; e x  ∈−−  khi và chỉ khi

A. 0 m > B. 2 1 3 e m >− C. 2 1 3 e m ≥− D. 0 m ≥ Lờigiải ChọnC

Điều kiện: 00xx −>⇔< Bất phương trình đã cho tương đương với ()() 2 ln fxxxm −−−< (*).

Xét hàm số ()()() 2 ln gxfxxx =−−− trên 1 1; e    .

Ta có ()() 1 2 gxfxx x ′′ =−− . Với 1 1; e x  ∈−−  thì () 1 0;20fxx x ′ >−−> nên () 0 gx ′ > .

Do đó hàm số ()gx đồng biến trên 1 1; e   

Suy ra (*) nghiệm đúng với mọi 1 1; e x  ∈−−  khi và chỉ khi 22 11111 ln3 eeeee mgf ≥−=−−−=−  

Câu16. (Sở HàTĩnh-2020) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ.

Có bao nhiêu giá trị nguyên của tham số m để phương trình () () cos ffxm = có nghiệm thuộc khoảng 3 ; 22 ππ    ? A. 2. B. 4. C. 5. D. 3. Lờigiải. ChọnB Khi 3 ; 22 x ππ  ∈   thì [ )cos1;0 x ∈− .

hàm số ()yfx = ta thấy khi [ )cos1;0 x ∈− thì () [ )cos1;1fx ∈− ; khi đó () () [ )cos1;3ffx ∈− Do đó phương trình () () cos ffxm = có nghiệm thuộc khoảng 3 ; 22 ππ    khi và chỉ khi 13 m −≤< Vậy có 4 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán. .

Vì. nên ta có ()2()2 16.2(4()).416.204 fxfxfxx +−≤+=∀∈ ℝ

225454014mmmmm  −+≥⇔−+≤⇔≤≤

Câu19. (HậuLộc 2 -Thanh Hóa- 2020) Cho hàm số ()yfx = , hàm số ()yfx ′ = liên tục trên ℝ và có đồ thị như hình vẽ bên. Bất phương trình () x mefx +< có nghiệm với mọi () 1;1 x ∈− khi và chỉ khi.

A. ()() 1 min1;1mfef e ≤−−−  B. ()01 mf<− C. ()() 1 min1;1mfef e  <−−−  D. ()01 mf≤−

Lờigiải

ChọnA

Ta có: ()() x xmefxmfxe +<⇔<− Xét hàm số ()() xgxfxe =− với () 1;1 x ∈− ()()()()() ;00 xxx gxfxegxfxefxe ′′′′′ =−=⇔−=⇔=

31 32  −+=− ⇔  −+=  xxm xxm

31 313  −+=− ⇔  −+=−+  xxm xxm Để phương trình đã cho có nghiệm thuộc đoạn [] 1;2 thì 31 331 −≤−≤ −≤−+≤ m m 13 26 −≤≤ ⇔  ≤≤  m m . [] 1;6  ∈− m Do ∈ ℤ m nên có 8 giá trị m để phương trình đã cho có nghiệm. Câu18. (Sở Yên Bái - 2020) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ bên. Số các giá trị nguyên của tham số m để bất phương trình ()2()2() 16.8(5).4((4()).16 fxfxfx mmfx≤−+−− nghiệm đúng với mọi số thực x là A. 3. B. 5. C. 1. D. 4. Lờigiải ChọnD ()2()2()2()2() 16.8(5).4((4()).16516.2(4()).4 fxfxfxfxfx mmfxmmfx ≤−+−−⇔−+≥+−

32 32 Trang 16

Dễ thấy với ()() 0 1;1;01;10xfex ′ ∈−==  = là nghiệm của phương trình () xfxe ′ = hơn nữa là nghiệm duy nhất (Minh họa bằng hình vẽ)

Dựa vào vị trí đồ thị hình vẽ trên ta có bảng biến thiên

Qua bảng biến thiên và chỉ xét trong khoảng () 1;1 ()()() {} ()() 1 min1;1min1;1 mgxmggmfef e <⇔≤−⇔≤−−− 

A. 12103 ; 9  −∞     . B. 1283 ; 9  +∞    . C. 12103 ; 9  +∞     . D. 1283 ; 9  −∞     . Lờigiải ChọnD Xét hàm số ()()() hxfxgx =− .

Vì đồ thị hàm số ()fx tiếp xúc với đồ thị hàm số ()gx tại điểm có hoành độ 3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là 1 và 3 suy ra ()()()()()() 2 313hxfxgxaxxx =−=++− .

Nhận xét từ đồ thị khi x →±∞ thì phần đồ thị ()fx nằm dười ()gx nên 0 a <

Mặt khác ta có ()() 1 027211 27 haa ==−−−=−  =

x e gxfxx x   =+>∀∈  Bảng biến thiên: (*) thỏa mãn khi ()() 2 4;16 min4 mgxfe   ≤=+ . Câu21. (KìmThành-HảiDương-2020) Cho hàm số đa thức bậc bốn ()yfx = và ()ygx = có đồ thị như hình vẽ dưới đây đường đậm hơn là đồ thị hàm số ()yfx = . Biết rằng hai đồ thị tiếp xúc với nhau tại điểm có hoành độ là 3 và cắt nhau tại hai điểm nữa có hoành độ lần lượt là 1 và 3 . Tìm tập hợp tất các giá trị thực của tham số m để bất phương trình ()() fxgxm ≥+ nghiệm đúng với mọi [] 3;3 x ∈−

Xét hàm () ()()() () 2 432 11 313463627 2727 yhxxxxxxxx ==++−=+−−−

Ta có () () ()() 32 2 11 41212363412 2727 yhxxxxxx ′′ ==+−−=+− .

Suy ra 3 03 3

x yx x

x

=−   ′ =  =   =−  . Bảng biến thiên 12+83) 9 12-83 9

3 3 0 0 0 - - + + -3 -3 h(x)

h'(x)

0 0 -∞ -∞

Xét ()()() 2 cos3cos2100fxmfxm+−+−= . Ta có ()2 7 m ∆=− .

Do đó () () cos5(1) cos2(2) fxm fx  =−  =   .

xa fxx x

=<−    =⇔=   = 

Với () cos1 1 cos2cos 2 cos1

Trường hợp này được 3 nghiệm trong ; 3 π π   

() 3 tfxm =+

t . Ta có () () 3 3

ftxm fxtm  =−   =−   ()()33 fttfxx  +=+ (2)

Xét hàm số ()()()()324235120, gufuugufuuuuu ′′ =+  =+=+≥∀ Khi đó (2) ()() gtgxtx ⇔=⇔= () () 3 3 fxmxxfxm ⇔+=⇔−= 5323 xxm⇔+=

Xét hàm số ()()53422560, hxxxhxxxx ′ =+  =+≥∀

Ta có bảng biến thiên của hàm số ()hx :

Để phương trình đã cho có đúng 4 nghiệm phân biệt thuộc đoạn ; 3 π π    thì (1) có đúng 1 nghiệm trong ; 3 π π    và không trùng với nghiệm của các phương trình 1 cos;cos1 2 xx== () 5 ftm ⇔=− với cos tx = có đúng 1 nghiệm trong 1 1; 2     45217 mm  −≤−<⇔≤< .

Do m nguyên nên có 6 giá trị của m thỏa mãn.

Câu24. (Trần Phú - Quảng Ninh - 2020) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình ()sin3sin yfxxm ==+ có nghiệm thuộc khoảng () 0;π . Tổng các phần tử của S bằng

Từ bảng biến thiên suy ra để (1) có nghiệm thuộc đoạn [] 1;2 3348116 mm ⇔≤≤⇔≤≤ Mà {} 1;2;3;...;16 mm ∈  ∈ ℤ suy ra có 16 giá trị của m thỏa mãn bài toán.

Câu23. (Tiên Lãng - Hải Phòng - 2020) Cho hàm số ()fx liên tục trên ℝ và có bảng biến thiên như hình vẽ Số giá trị nguyên của tham số m để phương trình ()()() 2 cos3cos2100fxmfxm+−+−= có

A. 5 . B. 8 . C. 6 . D. 10 . Lờigiải ChọnD

Đặt sin tx = , ()( ]0;0;1xt π ∈⇔∈ Phương trình ()sin3sin fxxm =+ có nghiệm thuộc khoảng () 0;π khi và chỉ khi phương trình () 3 fttm =+ có nghiệm thuộc ( ]0;1 khi và chỉ khi đồ thị hàm số ()yfx = và đường thẳng :3 dyxm =+ có điểm chung với hoành độ ( ]0;1 x ∈ .

1 :34 yx ∆=− là đường thẳng qua điểm () 1;1 và 2 :31 yx ∆=+ là đường thẳng qua điểm () 0;1 Đồ thị hàm số ()yfx = trên ( ]0;1 là phần đường cong nằm giữa hai đường thẳng 1∆ và 2 ∆

Vậy phương trình () 3 fttm =+ có nghiệm thuộc nửa khoảng ( ]0;1 khi và chỉ khi d dao động trong miền giới hạn bởi 1∆ và 2 ∆ (không trùng với 2 ∆ ) khi và chỉ khi {} 414;3;2;1;0 mm −≤<⇔∈−−−− .

Vậy tổng các giá trị của S bằng 10 .

Câu25. (NK HCM-2019) Cho ()fx là một hàm số liên tục trên đoạn []2;9, biết ()()()1293fff−=== và ()fx có bảng biến thiên như sau: Tìm m để phương trình ()() fxfm = có ba nghiệm phân biệt thuộc đoạn []2;9. A. ( ] (){} () 2;9\1;26. m ∈−−∪ B. [] (){} () 2;9\1;26. m ∈−−∪ C. ( ] {} 2;9\6. m ∈− D. [] {} 2;9\2;6. m ∈−− Lờigiải ChọnA

Phương trình ()() fxfm = có ba nghiệm phân biệt thuộc đoạn [] 2;9 khi () 43. fm −<≤

Trên ()2;0, hàm số ()fx đồng biến và ()13 f −= nên () 4321. fmm −<≤⇔−<≤−

Trên ()0;6, hàm số ()fx nghịch biến và ()23 f = nên () 4362. fmm −<≤⇔>≥

Trên ()6;9, hàm số ()fx đồng biến và ()93 f = nên () 4369. fmm −<≤⇔<≤

Vậy điều kiện của m là: ( ][ )( ] ( ] (){} () 2;12;66;92;9\1;26.mm ∈−−∪∪⇔∈−−∪

Câu26. (Chuyên Đại học Vinh 2019) Cho hàm số ()yfx = có đồ thị như hình vẽ. Có bao nhiêu số nguyên m để phương trình () 3 3 fxxm −= có 6 nghiệm phân biệt thuộc đoạn [] 1;2 ? A. 3 . B. 2 . C. 6 . D. 7 .

ChọnB

Đặt () [] 3 3,1;2tgxxxx ==−∈− () 2 1 330 1 x gxx x

=  ′ =−=⇔  =− 

Bảng biến thiên của hàm số ()gx trên [] 1;2

Lờigiải

Suy ra với 2 t =− , có 1 giá trị của x thuộc đoạn [] 1;2 ( ]2;2 t ∈− , có 2 giá trị của x thuộc đoạn [] 1;2 . Phương trình () 3 3 fxxm −= có 6 nghiệm phân biệt thuộc đoạn [] 1;2 khi và chỉ khi phương trình () ftm = có 3 nghiệm phân biệt thuộc ( ]2;2 . (1) Dựa vào đồ thị hàm số ()yfx = và m nguyên ta có hai giá trị của m thỏa mãn điều kiện (1) là: 0, 1. mm==−

Câu27. (Hội8trườngchuyên ĐBSH2019) Cho hàm số ()yfx = có đồ thị như hình vẽ bên dưới.

Số giá trị nguyên dương của m để phương trình () 2 451 fxxm −++= có nghiệm là A. Vô số. B. 4 . C. 0 . D. 3 . Lờigiải ChọnD Đặt 2 45txx=−+ . Ta có ()2 211 tx=−+≥ .

() () 2 4511fxxm −++= trở thành phương trình ()() 12 ftm=− .

Sử dụng các nhận xét ở trên và đồ thị của hàm số ()yfx = ta có () 1 có nghiệm ⇔ () 2 có nghiệm thuộc [ ) 1; +∞ 123mm ⇔−≤⇔≤ Vậy tập hợp các giá trị nguyên dương của m thỏa yêu cầu bài toán là {} 1;2;3

Câu28. Cho hàm số ()yfx = xác định, liên tục trên ℝ và có đồ thị như hình vẽ dưới. Có bao nhiêu giá trị nguyên của m để phương trình ( ) 2 234693 fxxm −−=− có nghiệm

Tìm m để phương trình ()() 2 22210fxfxm−−−= có nghiệm trên () ;1−∞ A. () 1; −+∞ B. [ ) 2; −+∞ C. () 2; −+∞ D. [ ) 1; −+∞ Lờigiải ChọnB

Ta có: ()()()()() 2 2 2221022211 fxfxmfxfxm −−−=⇔−−= .

Đặt ()tfx = , với () ;1 x ∈−∞ thì ()2;2 x ∈−∞ , ki đó () [ ) 20;tfx=∈+∞ . Phương trình () 1 trở thành: () 2 212ttm −−= () 1 có nghiệm trên () ;1−∞ tương ứng khi và chỉ khi () 2 có nghiệm trên [ ) 0; +∞ . Xét () [ ) 2 21,0;gtttt=−−∈+∞ , có ()()22,01gttgtt ′′ =−=⇔= . Bảng biến thiên của ()gt :

A. 13 . B. 12 . C. 8 . D. 10 . Lờigiải ChọnA Điều kiện: 2 2 6900 3 xxx −≥⇔≤≤ Đặt 2 3469 txx =−− ; 2 0 3 x ≤≤

Từ bảng biến thiên suy ra phương trình () 2 có nghiệm [ ) 0; t ∈+∞ khi và chỉ khi 2 m ≥−

Câu30. Cho hàm số () 32 fxaxbxcxd =+++ có đồ thị như hình vẽ

Ta có: () () 2

1231 69 x tx xx ′ = ; 2 0 3 x << ; () 1 0 3 txt ′ =⇔= ( nhận ). () 12 03;1;3. 33 ttt ==−=  

Nên 13 t −≤≤

Mặt khác: () 3 2 m ft = , [] 1;3 t ∈− có nghiệm. Từ đồ thị ta có 3 5175 2 m m −≤≤⇔−≤≤ Do m nguyên nên có 13 giá trị m là 7 , 6 , 5 , 4 , 3 , 2 , 1, 0 , 1, 2 , 3 , 4 , 5 . Câu29. (ChuyênBắcGiang2019) hàm số ()yfx = có bảng biến thiên

Gọi S là tập hợp các giá trị của ()mm∈ℝ sao cho ()()()() 3 12110,. xmfxmfxfxx  −−−+−≥∀∈  ℝ Số phần tử của tập S là A. 0. B. 3. C. 2 D. 1. Lờigiải ChọnC Từ đồ thị ta thấy ()fx =1. Đặt ()()()() 3 211gxmfxmfxfx =−−+− ()()()()() 3 12110,* xmfxmfxfxx  −−−+−≥∀∈  ℝ

bên.

Phương trình (2sin) fxm = có đúng ba nghiệm phân biệt thuộc đoạn [] ; ππ khi và chỉ khi A. {}3;1. m ∈− . B. ()3;1. m ∈− . C. [ ) 3;1. m∈− . D. ( ] 3;1. m∈− Lờigiải ChọnA

Đặt 2sin tx = (*), [][] ;2;2.xt ππ∈−  ∈−

Khi đó phương trình (2sin) fxm = trở thành () ftm = (1). Số nghiệm của PT(1) bằng số giao điểm của đồ thị hàm số ()yft = và đường thẳng ym = Nhận thấy:

Với {} 2;2 t ∈− thì PT(*) có 1 nghiệm [] ; x ππ∈−

Với 0 t = thì PT(*) có 3 nghiệm phân biệt [] ; x ππ∈− .

Với (){} 2;2\0 t ∈− thì PT(*) có 2 nghiệm phân biệt [] ; x ππ∈−

Do đó, dựa vào đồ thị đã cho ta có: +) TH 1: 3 m <− thì phương trình (1) có một nghiệm 2 t <− . Suy ra 3 m <− bị loại

+) TH 2: 3 m =− thì PT(1) có hai nghiệm là 1 t = và 2 t =− . Suy ra 3 m =− là giá trị thỏa mãn.

+) TH 3: 31 m −<< thì phương trình (1) có ba nghiệm phân biệt thuộc khoảng (2;2) . Suy ra 31 m −<< bị loại.

+) TH 4: Xét trường hợp 1 m = thì PT(1) có hai nghiệm là 1 t =− và 2 t = . Suy ra 1 m = là giá trị thỏa mãn.

+) TH 5: 1 m > thì phương trình (1) có một nghiệm 2 t > . Do đó 1 m > bị loại.

Vậy các giá trị m cần tìm là {}3;1. m ∈− Chọn. A.

Câu32. Cho hàm số ()yfx = xác định và liên tục trên ℝ và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của m để phương trình () 2 30 2.339202119 x fxm −−=− +− có nghiệm.

A. 15 B. 14 C. 10 D. 13 Lờigiải ChọnD Ta có: ()2 2 2 943530213020912 xxxxx −=−−  ≤+− + ≤ 2 3021 33393. xx +  ≤−−≤ Đặt [] 2 339;3 30123. x txt =−−  ∈− +− Khi đó, phương trình () () 2 30 2.33920191 21 x fxm +− −−=− () 22019 ftm ⇔=− () () 2019 2 2 m ft ⇔= Phương trình () 1 có nghiệm khi và chỉ khi phương trình () 2 có nghiệm []3;3. t ∈− Dựa vào đồ thị hàm số ()yfx = ta có, phương trình () 2 có nghiệm [] 3;3 t ∈− khi và chỉ khi 2019 51102019220092021 2 m mm −≤≤⇔−≤−≤⇔≤≤

Vì m ∈ ℤ nên {} 2009,2010,...,2021 m ∈ . Vậy có 13 giá trị m nguyên thỏa mãn yêu cầu bài toán.

Câu33. (Thi thử cụm Vũng Tàu - 2019) Cho hàm số ()yfx = xác định, liên tục trên ℝ và có đồ thị như hình vẽ bên. Có bao nhiêu giá trị nguyên của m để phương trình ( ) 2 234693 fxxm −−=− có nghiệm.

A. 9 . B. 17 . C. 6 . D. 5 . Lờigiải ChọnA Điều kiện: 2 2 6900 3 xxx −≥⇔≤≤ Đặt 2 2 3469,0; 3 txxx  =−−∈   . Ta có: 2

61812 4.00; 26933 x tx xx  ′ =−=  =∈  Bảng biến thiên cho 2 3469 txx =−− .Vì [] 2 0;1;3 3 xt  ∈  ∈−  

Chọn B.

Theo hình vẽ ta có ()yfx ′ = là hàm số bậc ba nên 0 a ≠ () 32 432 fxaxbxcxd ′ =+++ () 2 1262 fxaxbxc ′′  =++

Theo giả thiết, ta có: () () ()

′ =  =  =−    ′ =⇔+++=⇔  ==   = ′′ =  

00 0 4 301082760 0 0 00

f d ba fabcd cd c f

() 43 4 fxaxaxe  =−+ () 43 0 40 4 x fxeaxax x =   =⇔−=⇔  =  .

Phương trình trở thành: ()() [] () 3 23,1;3.* 2 m ftmftt=−⇔=∈− Phương trình ( ) 2 234693 fxxm −−=− có nghiệm () 3 2 m ft ⇔= có nghiệm [] 1;3 t ∈− 3 6212342912, 2 m amama ⇔−≤≤−+⇔−≤−≤−+⇔−≤≤−+ với [] () 1;3

1 max2,0; 2 ftaa  =+∈  

Mà {} 9;8;7;..;1 mm ∈  ∈−−−−  ℤ có 9 giá trị m nguyên thỏa ycbt.

Câu34. (SGD Điện Biên - 2019) Cho hàm số () 432 yfxaxbxcxdxe ==++++ với () ,,,, abcde ∈ ℝ . Biết hàm số ()yfx ′ = có đồ thị như hình vẽ, đạt cực trị tại điểm () 0;0 O và cắt trục hoành tại () 3;0 A . Có bao nhiêu giá trị nguyên của m trên [] 5;5 để phương trình () 2 2 fxxme −++= có bốn nghiệm phân biệt.

Khi đó () () 2 21fxxme −++= () ()

 −=+ −++=  ⇔⇔   −++= −=−  

11 20 24 13 xm xxm xxm xm

2 2 2 2

Mà [] {}5;54;5mm ∈∩−  ∈ ℤ

Vậy có 2 giá trị m thỏa đề bài.

+>   ⇔−>⇔>   +≠−  .

PT () 1 có bốn nghiệm phân biệt 10 303 13

m mm mm

Câu35. Cho hàm số () = yfx liên tục và có đạo hàm trên đoạn [] 2;4 và có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số m để hệ phương trình () 2 3

9 40 621860

 −≥    −+−+−=  x fxxxm có ba nghiệm phân biệt? A. 9 B. 11 C. 10 D. 8 Lờigiải ChọnD

= ℤ mm . Vậy có 8 số nguyên m . Câu36. (Hậu Lộc 2-Thanh Hóa 2019) Cho hàm số ()yfx = liên tục trên đoạn [] 05 ; và có bảng biến thiên như hình sau:

nghiệm đúng với mọi [] 05 x;. ∈ A. 2014. B. 2015. C. 2019. D. Vô số Lờigiải ChọnA

Trên [] 05 ; , ta có: () () () 3102 320191022019 xx mfxxfxxm. fx +− +≤−−⇔≤−

Xét hàm số () 3102 gxxx =+− trên đoạn [] 05;. () 31310223 2310223102 xx gx xxx.x ′ =−=

Cho () []0305 gxx;. ′ =⇔=∈

Do ()010 g = , ()35 g = và ()515 g = nên [] ()() 05 35 ; maxgxg. == Mặt khác [] ()() 05 31 ; minfxf== nên () 3102 2019 xx m fx +− ≤− , [] 05x;∀∈ [] () 05

31025 201920192014 1 ;

xx mmin . fx  +− ⇔≤−=−=   

Câu37. (HậuLộc 2-ThanhHóa-2019) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ bên. Số giá trị nguyên của tham số m để phương trình ()()() 2 201820190fcosxmfcosxm+−+−= có đúng 6 nghiệm phân biệt thuộc đoạn [] 02 ; π là

A. 5. B. 3. C. 2. D. 1. Lờigiải ChọnC

Ta có ()()() 2 201820190fcosxmfcosxm+−+−= () () 1 2019 fcosx fcosxm. =−  ⇔  =−  

Dựa vào đồ thị ta có: () () () 01 1 12 cosx fcosx cosxk =  =−⇔  =>  

PT có 2 nghiệm thỏa mãn, PT vô nghiệm. Yêu cầu: phương trình ()() 201920191fcosxmm =−−≠ có thêm 4 nghiệm thuộc [] 02;. π Nhận xét:

[] 11t; ∉− , phương trình cosx=t vô nghiệm.

+ Với mỗi ( ]11t; ∈− , phương trình cosx=t có 2 nghiệm [] 02 x;. π ∈

+ Với 1 t =− , phương trình cosxt = có đúng 1 nghiệm [] 02 x;. π ∈

Như vậy, 12019120182020 mm −<−≤⇔≤≤

Câu38. (THPTGiaLộcHảiDương2019) Cho hàm số () = yfx có bảng biến thiên như sau

() 31ftm=+ có nghiệm thuộc [] 1 2;11 3 m −⇔−≤≤ . Câu40. (THPTLêQuý Đôn ĐàNẵng2019) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ. Tập hợp các giá trị thực của tham số m để phương trình ( ) 2 41 fxxm −−= có nghiệm là

Tìm m để phương trình () 220190 +−=fxm có 4 nghiệm phân biệt. A. () 0;2 ∈m B. () 2;2∈− m C. () 4;2∈− m D. () 2;1∈−m Lờigiải () 220190 +−=fxm () 2019 2 ⇔+= m fx () * . Ta có bảng biến thiên của hàm số ()() 2019 ygxfx==+ như sau: Phương trình () * có 4 nghiệm phân biệt khi 21 2 −<< m 42⇔−<< m Câu39. Cho hàm số ()yfx = liên tục trên R và có đồ thị như hình vẽ dưới đây. Tập hợp tất cả các giá trị thực của tham số m để phương trình () 2 2231fxxm+−=+ có nghiệm thuộc khoảng []0;1. A. [] 0;4 . B. [] 1;0

A. [] 2;0 . B. [] 4;2 . C. [] 4;0 . D. [] 1;1 . Lờigiải Phương trình ( ) 2 41 fxxm −−= có điều kiện 04 x ≤≤ . Ta có bảng biến thiên

Từ bảng biến thiên suy ra, với 04 x ≤≤ thì 2 1411 xx −≤−−≤ . Đặt 2 41txx=−− , 11 t −≤≤ .(Có thể biến đổi ()2 421tx=−−− 11 t  −≤≤ ). Phương trình đã cho trở thành () ftm = (1). Phương trình đã cho có nghiệm ⇔ (1) có nghiệm [] 1;1 t ∈− 40 m ⇔−≤≤ .

Câu41. (Chuyen Phan Bội Châu 2019) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ dưới đây.

Tập hợp tất cả các giá trị thực của tham số m để phương trình 2 (4) fxm −= có nghiệm thuộc nửa khoảng [2;3) là:

A. [-1;3] B. [-1;(2)] f C. (-1;(2)] f D. (-1;3] Lờigiải Đặt 2 ()4 tgxx ==− với [-2;3) x ∈ .

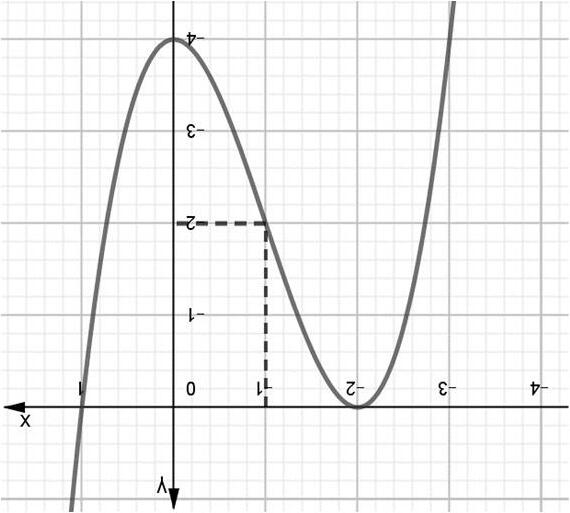
'()00[2;3)gxx=⇔=∈− .

Ta có:

(0)2g = , (2)2g −= , (3)1 g =

Mà hàm số ()gx liên tục trên [-2;3)

Suy ra, (1;2] t ∈

Từ đồ thị, phương trình () ftm = có nghiệm thuộc khoảng (1;2] khi (1;3] m∈−

Câu42. (ChuyênDạiHọcVinh2019) Cho hàm số ()yfx = có đồ thị như hình vẽ

Có bao nhiêu số nguyên m để phương trình 1 1 32 x fxm ++=  có nghiệm thuộc đoạn [] 2;2 ?

A. 11 B. 9 C. 8 D. 10 Lờigiải ChọnC

Đặt 1 2 x t =+ , khi 22 x −≤≤ thì 02 t ≤≤

Phương trình đã cho trở thành () 1 22 3 fttm +−= () 663 fttm⇔+−= .

Xét hàm số ()() 66gtftt=+− trên đoạn [] 0;2

Ta có ()() 6 gtft ′′ =+ . Từ đồ thị hàm số ()yfx = suy ra hàm số ()ft đồng biến trên khoảng

() 0;2 nên ()() 0,0;2ftt ′ >∀∈ ()() 0,0;2gtt ′  >∀∈ và ()010 g =− ; ()212 g = .

Bảng biến thiên của hàm số ()gt trên đoạn [] 0;2

ương trình đã cho có nghiệm thuộc đoạn [] 2;2 khi và chỉ khi phươ

nghiệm thuộc đoạn [] 0;2 hay 10312 m −≤≤ 10 4 3 m ⇔−≤≤

Mặt khác m nguyên nên {} 3;2;1;0;1;2;3;4 m ∈−−− Vậy có 8 giá trị m thoả mãn bài toán.

Câu43. Cho hàm số ()yfx = có đồ thị như hình vẽ. Tìm số giá trị nguyên của m để phương trình () 2 2 fxxm −= có đúng 4 nghiệm thực phân biệt thuộc đoạn 37 ; 22    .

A. 1 B. 2 C. 3 D. 4 Lờigiải ChọnB

Xét phương trình () 2 2 fxxm −= () 1 Đặt 2 2 txx =− , với 37 ; 22 x  ∈− 

Ta có 22tx ′ =− ; '01tx=⇔= . Bảng biến thiên của hàm số 2 2 txx =− trên đoạn 37 ; 22    .

Dựa vào bảng biến thiên suy ra 21 1; 4 t  ∈− 

Xét 1 t =− khi đó phương trình () 1 thành ()14 fmm −=  =

Với 4 m = phương trình () () 2 2 2

21 24* 2 xx fxx xxa  −=− −=⇔  −=  với 23 a << .

Dễ thấy () * có tối đa 3 nghiệm (không thỏa mãn yêu cầu).

Xét 0 21 1; 4 t  ∈−   

Nhận xét với mỗi 0 21 1; 4 t  ∈−    thì có 2 giá trị 37 ; 22 x  ∈−  thỏa mãn 2 0 2 txx =−

Do đó phương trình () 2 2 fxxm −= có 4 nghiệm thực phân biệt thuộc đoạn 37 ; 22    khi phương

trình () ftm = có 2 nghiệm phân biệt 21 1; 4 t  ∈−    . Hay đường thẳng ym = phải cắt đồ thị hàm

số ()yft = tại 2 điểm với 21 1; 4 t  ∈−    .

Mà m ∈ ℤ nên từ đồ thị hàm số ()yfx = ta có 3;5mm== thỏa mãn yêu cầu.

KL: Có 2 giá trị nguyên của m thỏa mãn yêu cầu bài.

Câu44. (Thanh Tường Nghệ An 2019) Cho hàm số () = yfx là hàm đa thức với hệ số thực. Hình vẽ bên dưới là một phần đồ thị của hai hàm số: () = yfx và ()′ = yfx .

Tập các giá trị của tham số m để phương trình () = x fxme có hai nghiệm phân biệt trên [] 0;2 là nửa khoảng [ ) ; ab . Tổng + ab gần nhất với giá trị nào sau đây? A. 0.81. B. 0.54 . C. 0.27 . D. 0.27 . Lờigiải

Nhận xét: Đồ thị hàm ()yfx ′ = cắt trục hoành tại điểm 0x thì 0x là điểm cực trị của hàm ()yfx = . Dựa vào hai đồ thị đề bài cho, thì () 1C là đồ thị hàm ()yfx = và () 2C là đồ thị hàm ()yfx ′ = Xét phương trình hoành độ giao điểm của đồ thị hàm số () = yfx và = x yme ta có: () = x fxme () ⇔= x fx m e .

Đặt () () = x fx gx e ta có: () ()()′ ′ = x fxfx gx e ()()() () 0

 =  ′′ =⇔=⇔=   =∈− 

1 02 1;0

x gxfxfxx xx .

Dựa vào đồ thị của hai hàm số: () = yfx và ()′ = yfx ta được: Yêu cầu bài toán ta suy ra: () 2 2 0 ≤< f m e (dựa vào đồ thị ta nhận thấy ()() 022 =≈−ff ) 0,270⇔−≤< m Suy ra: 0,27,0=−=ab Vậy 0,27+=−ab

Câu45. (VTED 2019) Cho hai hàm số ()yfx = và ()ygx = là các hàm xác định và liên tục trên ℝ và có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là đồ thị của hàm số ()yfx = ). Có bao nhiêu số nguyên m để phương trình () () 121 fgxm −−= có nghiệm thuộc đoạn 5 1; 2   

để phương trình () ftm = có nghiệm thuộc đoạn [] 3;4 [] () [] () [] () 3;4 3;4 3;4 minmaxmin2 ftmftftm ⇔≤≤⇔≤≤ trong đó [] ()() 3;4 min1;0 ft ∈− . Vậy các số nguyên cần tìm là {} 0,1,2 a ∈ Câu46. (THPT Yên Khánh A- Ninh Bình - 2019) Cho hàm số ()yfx = liên tục trên đoạn [] 1;9 và có đồ thị là đường cong trong hình vẽ dưới đây Có bao nhiêu giá trị nguyên của tham số m để bất phương trình () ()() () () () 2 2 16.328.43.6 fx fxfxfxfxmm  −+−≥−  nghiệm đúng với mọi giá trị thuộc [] 1;9 ? A. 32 B. 31 C. 5 D. 6 Lờigiải

ChọnB Dễ thấy () []42,1;9 fxx −≤≤∀∈− (1) nên ()() []4.20,1;9fxfxx −+−≥∀∈−   .

Do đó ()() [] 2 280,1;9fxfxx  −+−≥∀∈−  (2).

fx fx fxfxmm  ⇔−+−≥−    nghiệm đúng với mọi [] 1;9 x ∈− []

Bất phương trình () 17 fxxxm +++−≥ có nghiệm thuộc [] 1;3 khi và chỉ khi A. 7 m ≤ B. 7 m ≥ C. 222 m ≤− D. 222 m ≥− Lờigiải ChọnA

Bất phương trình () 17 fxxxm +++−≥ có nghiệm thuộc [] 1;3 khi và chỉ khi [] () () 1;3 Max17 fx mxx +++ ≤−

Xét hàm số () 17 gxxx =++− trên đoạn [] 1;3 .

Ta có () 1171 212727.1 xx gx xxxx −−+ ′ =−= +−−+ () 0 gx ′ = 710 xx ⇔−−+= 3 x ⇔= . ()1822 g −== , ()3224 g =+=

Suy ra [] () 1;3 Max4 gx = tại 3 x = . (1)

      ⇔=−+−≥−    fx  ≥   và ()() () [] 2 2 28.0,1;9 3

() ()() () 2 2 1;9

12 min16.28.3 23

fx fx x fxfxmm α ∈−       (3). Từ (1) và (2) ta có () 2 11 22

fx fxfxx   −+−≥∀∈−    Suy ra () ()() () [] 2 12 16.28.4,1;9 23

fx fx fxfxx  −+−≥∀∈−   Dấu “=” xảy ra khi và chỉ khi ()() 2178.fxxxaa =⇔=−∨=<< Do đó 4 α = và (3) 2 4314 mmm ⇔≥−⇔−≤≤ . Vì m nguyên nên {} 1;0;1;2;3;4 m ∈− Câu47. (THPT Yên Khánh A-Ninh Bình-2019) Cho hàm số ()yfx = liên tục trên [] 1;3 và có đồ thị như hình vẽ Trang 38

Mặt khác, dựa vào đồ thị của ()fx ta có [] () 1;3 Max3 fx = tại 3 x = .(2)

Từ (1) và (2) suy ra [] () () 1;3 ax1 M77 fxxx++−= + tại 3 x =

Vậy bất phương trình đã cho có nghiệm thuộc [] 1;3 khi và chỉ khi 7 m ≤ .

Câu48. (THPTYênKhánhA-NinhBình-2019) Cho hàm số () = yfx có đạo hàm liên tục trên đoạn [] 3;3 và đồ thị hàm số ()′ = yfx như hình vẽ dưới đây

Biết ()16 = f và ()() ()2 1 2 + =− x gxfx . Mệnh đề nào sau đây là đúng?

A. Phương trình () 0 = gx có đúng hai nghiệm thuộc đoạn [] 3;3

B. Phương trình () 0 = gx không có nghiệm thuộc đoạn [] 3;3

C. Phương trình () 0 = gx có đúng một nghiệm thuộc đoạn [] 3;3

D. Phương trình () 0 = gx có đúng ba nghiệm thuộc đoạn [] 3;3 Lờigiải ChọnC Ta có

Từ bảng biến thiên suy ra phương trình () 0 = gx có đúng một nghiệm thuộc đoạn [] 3;3

Câu49. (Chuyên Sơn La - Lần 2 - 2019) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ

Các giá trị của tham số m để phương trình () () 3 2 2

4 3 25 mm fx fx + =+ + có ba nghiệm phân biệt là A. 37 2 m = B. 33 2 m =± C. 37 2 m =± D. 3 2 m = Lờigiải ChọnA () ()()() () ()()() () ()

3 2322 2 3 222

mm fxmmfxfx fx mmfxfxfx

+ =+⇔+=++ + ⇔+=++++ Xét hàm số ()() 3 2 ,'310, fttttfttt =+∀∈  =+>∀∈ ℝℝ ()()() () () ()

4 34325 25 22252525

fmffxmfx m m m m fx fx

 =+⇔=+ >  >   ⇔⇔  = =±   

225225 0 0 45 45 2 2

22 2 2 2

Với () 2 45 2 m fx =− từ đồ thị ta thấy chỉ có 1 nghiệm. Vậy để phương trình có 3 nghiệm phân biệt thì phương trình () 2 45 2 m fx = phải có hai nghiệm () 2 45374,0 22 m mm ⇔=⇔=> .

Câu50. (THPTNgôQuyền-BaVì-2019) Cho hàm số () 32 fxaxbxcxd =+++ có đồ thị như hình vẽ sau đây. Hỏi có bao nhiêu giá trị nguyên của tham số thực m để phương trình () () ffxm = có 4 nghiệm phân biệt thuộc đoạn [] 1;2 ?

Ta có bảng biến thiên

A. 5 . B. 4 . C. 0 . D. 3 . Lờigiải

ChọnD

Đặt ()()()gxffx = ()()() () . gxffxfx ′′′ = .

Cho ()()() () 0.0gxffxfx ′′′ =⇔= () () () 0 0 fx ffx

′ =  ⇔  ′ =  

+ () 1 0 1 x fx x =  ′ =⇔  =−  ( hoành độ các điểm cực trị ).

+ () () () () 1 0 1 fx ffx fx =  ′ =⇔  =−  

Dựa vào đồ thị, ta có:

+ Khi () 10fxx=⇔= ; () 2;1 xa=∈−− ; () 1;2 xb=∈

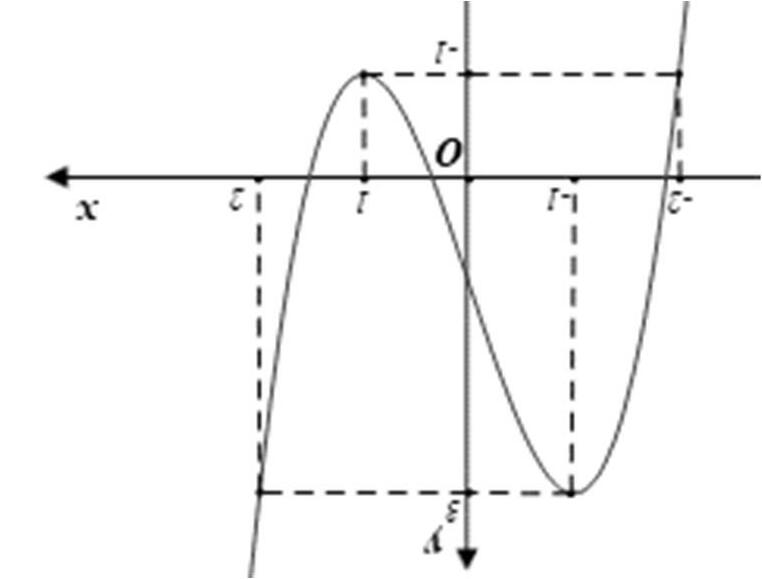
+ Khi () 11fxx=−⇔= ; 2 x =− .

Bảng biến thiên

Phương trình () () ffxm = có 4 nghiệm phân biệt thuộc đoạn [] 1;2 13 m ⇔−<<

Mà m là số nguyên nên {} 0;1;2 m ∈

Vậy có 3 giá trị của m thỏa đề bài.

Câu51. (THPTNguyễn ĐứcCảnh-TháiBình-2019) Cho hàm số () 32 28 gxxxx =+− . Có bao nhiêu số nguyên m để phương trình () () () 327ggxmgx+−=+ có đúng 6 nghiệm thực phân biệt A. 7 . B. 8 . C. 24 . D. 25 . Lờigiải ChọnD Đặt () 322 3283628 tgxtxxxtxx ′ =+  =+−+  =+− .

Từ bảng biến thiên suy ra mỗi giá trị 289 2; 27 t  ∈−  sẽ có tương ứng 3 giá trị x

t gtmt gtmt

1 2 237 21

  ≥− ≥−  ⇔⇔   =−−− =+−−−−  

t t mttt mttttt

1 1 2 2 231211 28441

 ≥−  ⇔−=++⇔   −=+  () 32 322

() () () 327ggxmgx+−=+ () () ()()2

Phương trình đã cho có 6 nghiệm thực phân biệt khi và chỉ khi phương trình () 1 có 3 nghiệm phân biệt 1289 ; 227 t  ∈−   

Xét hàm số () 32 23121ftttt=−−− với 1289 ; 227 t  ∈−    . () 2 6612fttt ′ =−− () 1 0 2 t ft t =−  ′  =⇔  =  .

Ta có bảng biến thiên

Từ bảng biến thiên, phương trình đã cho có 6 nghiệm thực phân biệt ( ]21;4 m ∈− .

Câu52. (Sở GDBạc Liêu-2019) Cho hàm số 32 ()287 =+−+fxxxx . Gọi S là tập hợp tất cả các giá trị nguyên dương của tham số m để phương trình (()3)2()5 −+=−ffxmfx có 6 nghiệm thực phân biệt. Tổng các phần tử của S bằng A. 25 . B. 66 . C. 105 . D. 91. Lờigiải ChọnD Đặt ()3=−tfx . * 32 ()3284(1)=−⇔=+−+ tfxtxxx Đặt 322 11 ()284;()628;()0 4316 327

xy gxxxxgxxxgx xy Bảng biến thiên

=  =−   ′′ =+−+=+−=⇔  =−  = 

Số nghiệm

của phương trình (2) chính là số giao điểm của đồ thị hàm số () = yht và = ym Dựa vào bảng biến thiên ta có + 14 > m thì phương trình (2) vô nghiệm. + 14 = m hoặc 11<− m thì phương trình (2) có 1 nghiệm. + 1114−≤< m thì phương trình (1) có 2 nghiệm phân biệt. Phương trình (()3)2()5 −+=−ffxmfx có 6 nghiệm thực phân biệt khi phương trình (1) có 3 nghiệm phân biệt và phương trình (2) có 2 nghiệm phân biệt. Vậy phương (()3)2()5 −+=−ffxmfx có 6 nghiệm thực phân biệt khi phương trình (2) có hai nghiệm phân biệt 1316 227 −≤< t Dựa vào bảng biến thiên ta được kết quả là 1114−≤< m . Suy ra {} 1;2;...;13 S = Tổng các phần tử của 1...11121391 S =++++=

Câu53. (Quang Trung - Bình Phước - 2019) Cho hàm số ()fx liên tục trên ℝ . Hàm số ()fx ′ có đồ thị như hình vẽ:

Số nghiệm của phương trình (1) chính là số giao điểm của đồ thị hàm số () = ygx và = yt

Dựa vào bảng biến thiên ta có

+ 1<− t hoặc 316 27 > t thì phương trình (1) có 1 nghiệm.

+ 1=− t hoặc 316 27 = t thì phương trình (1) có 2 nghiệm. + 316 1 27 −<< t thì phương trình (1) có 3 nghiệm phân biệt. * Ta có (()3)2()5()21(2) −+=−⇔+=+ ffxmfxftmt Điều kiện để phương trình (2) có nghiệm 1 2 ≥− t

1

2 2 1

y x O

Bất phương trình () 2 2sin2sin fxxm −< đúng với mọi () 0; x π ∈ khi và chỉ khi A. () 1 0 2 mf>− . B. () 1 1 2 mf>− . C. () 1 1 2 mf≥− . D. () 1 0 2 mf≥− . Lờigiải ChọnB Đặt 2sin xt = . Vì () 0; x π ∈ nên () 0;2 t ∈

Bất phương trình trở thành () 2 2 t ftm −< . Đặt ()() 2 2 t gtft=− với () 0;2 t ∈ .

Bất phương trình đúng với mọi () 0;2 t ∈ khi và chỉ khi () () 0;2 max gtm < .

Ta có ()() gtftt ′′ =− .

thị ()yft ′ = và đường thẳng yt = với () 0;2 t ∈ .

Dựa vào đồ thị ta được nghiệm ()10;2 t =∈ .

Cũng dựa vào đồ thị ta thấy khi () 0;1 t ∈ thì () ftt ′ > () 0 gt ′  > , khi () 1;2 t ∈ thì () ftt ′ < () 0 gt ′  < Bảng biến thiên:

Phương trình () 1 có nghiệm ()() 1323348116 hmhmm

Do {} 1;2;3;4;...;16 mZm ∈  ∈ Vậy có 16 giá trị nguyên của tham số m

Câu55. (Chuyên ĐHVinh-Nghệ An-2021) Cho hai hàm số () 2

3 3 x ux x + = + và ()fx , trong đó đồ thị

hàm số ()yfx = như hình vẽ bên. Hỏi có bao nhiêu số nguyên m để phương trình () () fuxm = có đúng 3 nghiệm phân biệt?

Dựa vào bảng biến thiên ta thấy () ()() 0;2 max1 gtg = () 1 1 2 f =− .

Vậy bất phương trình đã cho đúng với mọi () 0; x π ∈ khi và chỉ khi () 1 1 2 mf>− .

Câu54. (Lương Thế Vinh - Hà Nội - 2019) Cho hàm số () 5334 fxxxm =+− . Có bao nhiêu giá trị nguyên của tham số m để phương trình () () 3 3 ffxmxm +=− có nghiệm thuộc [] 1;2 ? A. 15 B. 16 C. 17 D. 18 Lờigiải ChọnB Đặt () () 3 3 tfxmtfxm =+  =+ Ta có hệ () () ()() 3 33

A. 1 B. 4 C. 3 D. 2 Lờigiải ChọnC

Đặt () 2

xx x x x ux x xx

+ +− + == + ++ () '01uxx=⇔=

3 3 x tux x + == + () () ()

3 3 33 3 ' 3 33

2 2 2 22

Dựa vào BBT, ta có ()( ]1;2 ux ∈− Phương trình () () fuxm = trở thành () ftm = , ( ]1;2 t ∈− Dựa vào đồ thị đã cho ta có:

+ Khi 2 m = : phương trình () 0 2 2 t ft t =  =⇔   =  phương trình () () fuxm = có 2 nghiệm phân biệt.

+ Khi 1 m = : phương trình () 1 ft = có 3 nghiệm ()()()1231;0,0;1,1;2ttt ∈−∈∈  phương trình () () fuxm = có 4 nghiệm phân biệt.

+ Khi {} 0;1;2 m ∈−− : phương trình () ftm = có 2 nghiệm ()()120;1,1;2tt∈∈  phương trình () () fuxm = có 3 nghiệm phân biệt.

Câu56. (THPTNguyễn ĐứcCảnh-TháiBình-2021) Biết hàm số () 32 fxaxbxcxd =+++ đạt cực trị tại 1 x = và 2021 x = . Có bao nhiêu số nguyên m để phương trình ( ) ( )fxfm = có ba nghiệm phân biệt? A. 4037 B. 2019 C. 4001 D. 2021 Lờigiải ChọnA Ta có ()()32232 fxaxbxcxdfxaxbxcx ′ =+++  =++ Do hàm số có 2 điểm c

Có bao nhiêu giá trị nguyên của tham số m để phương trình () () 42cos ffxm += có nghiệm 0; 2 x π  ∈  A. 4 B. 5 C. 3 D. 2 Lờigiải ChọnA Đặt cos tx = , với 0; 2 x π  ∈  () 0;1 t  ∈ . Từ đồ thị suy ra ()()()()() ()2;0420;4420;2ftftuft ∈−  +∈  =+∈ . Ta có () fum = với () 0;2 u ∈ Phương trình đã cho có nghiệm 0; 2 x π  ∈  khi và chỉ khi phương trình () fum = có nghiệm () 0;2 u ∈ 22 m ⇔−≤< Do m ∈ ℤ nên {} 2;1;0;1 m ∈−− .

Số nghiệm của phương trình () 3 1 2625 2 fxxm−+=− bằng số giao điểm của đồ thị hàm số () () 3 262gxfxx=−+ và đường thẳng 1 5 2 ym=− .

Kẻ đường thẳng 1 5 2 ym=− trên cùng bảng biến thiên của ()gx Điều kiện để đường thẳng 1 5 2 ym=− cắt đồ thị hàm số () () 3 262gxfxx=−+ tại 6 điểm phân biệt là: 1 052 2 m <−< ⇔ 1014 m << . Vì m∈ ℤ ⇒ {} 11;12;13 m ∈ Vậy có 3 số nguyên m thỏa mãn ycbt.

Câu59. (THPT Thanh Chương 1- Nghệ An - 2021) Cho hàm số 2 ()1 fxxx =++ . Số giá trị nguyên của tham số m để phương trình () 141 ()0 141 xm xfx fxm ++− −= −−+− có hai nghiệm phân biệt là

A. 2 . B. 3 . C. 6 . D. 4 . Lờigiải ChọnD

Tacó: 2 2 ()1'()10, 1 x fxxxfxx x =++  =+>∀∈ + ℝ

Suy ra hàm số 2 ()1 fxxx =++ luôn đồng biến trên ℝ Mặt khác, talại có: 2 2

11 ()1 1() fxxx fx xx −=−++== ++

Nên phương trình tiếp theo tương đương với: () 141 ()0 141 xm xfx fxm ++− −= −−+− () () ()1411410 xfxxmfxm

10 1 62 411 x x mxx xmx

−≥  ≥   ⇔  =−+ +−=−    . Xét hàm 2 ()62,1()2603 ypxxxxpxxx ′ ==−+∀≥  =−=⇔= (nhận). Ta có BBT của hàm ()px như sau: Dựa vào BBT trên để phương trình có hai nghiệm phân biệt thì ( ] ( ](3);(1)7;3mppm ∈⇔∈−− Như vậy, ta kết luận có tất cả 4 giá trị nguyên thỏa mãn yêu cầu đề bài. Câu60. (THPT Nguyễn Huệ - Phú Yên - 2021) Cho hàm số () 32 231yfxxx ==−+ . Tập hợp các giá trị m để phương trình () 2sin1 2 x fffm  +   =     có nghiệm là đoạn [] ; ab . Khi đó giá trị 2 48ab + thuộc khoảng nào sau đây? A. 23 7; 2    . B. () 2;5 . C. 4339 ; 32    . D. 3765 ; 34    . Lờigiải ChọnD Ta có: 2 66 yxx ′ =− . 0 y ′ = 0 1 x x nên [] 2sin1 0;1 2 x ff  +   ∈     . Phương trình () 2sin1 2 x fffm  +   =     có nghiệm () 01 fm ⇔≤≤ 32 32

Câu61. (THPT Hoàng Hoa Thám - Đà Nẵng - 2021) Cho hàm số () 2 52 21 xx fx x ++ = + . Có tất cả

bao

nhiêu giá trị nguyên dương của tham số m để bất phương trình ( ) 22 202131828318284042 fxxmxxm −+−−+≥+ nghiệm đúng với mọi x thuộc đoạn [ ]2;4 A. 673. B. 808 . C. 135 . D. 898 . Lờigiải ChọnA  Đặt ()() 22 318283(3)13244uxxxxx =−+=−+=−−+ do đó ta có với [ ]2;4 x ∀∈ thì [ ]1;2 u ∈ .  Biến đổi BPT ta được ( ) 2021.4042 fumum−≥+ ( ) ( )202121 fumu ⇔   ≥+  .  Ta có () 2 52 21 xx fx x ++ = + nên () 22 52 22 2121 uuuu fu uu +++ −=−= ++ do vậy bất phương trình được biến đổi tiếp ( ) () 2 2021 2021 1 2121 uu u mum uu + ≥+⇔≤ ++ .  Lúc này yêu cầu bài toán tương đương [] 2021 ,1;2 21 u mu u ≤∀∈ + [] 1;2 min() u mgu ∈ ⇔≤ .  Xét hàm số [] 2021 (),1;2 21 u guu u =∈ + ta có () [] 2 2021 ()0,1;2 21 guu u ′ =>∀∈ + dovậy hàm số ( )gu tăng trên đoạn [ ]1;2 . Vì vậy [] () 1;2

=  ⇔  =  . Bảngbiếnthiên: Ta có: 2sin1113 sin; 2222 x x + =+∈−  suy ra [] 2sin1 0;1 2 x f +  ∈   2310 230 mm mm  −+≥  ⇔  −≤   13 22 m ⇔−≤≤ Vậy 2 13 484.8.13 42 ab+=+= Trang 52

u gug u ∈ === + .  Kết hợp với m là các số nguyên dương ta được { }1;2;3;...;673 m ∈ . Vậytìm được 673 số nguyên dương thỏa mãn yêu cầu bài toán.

Câu62. (Chuyên Lương Văn Chánh - Phú Yên - 2021) Cho hàm số ( ) 3 25m fxxx=+− . Có bao nhiêu giá trị nguyên của m thuộc đoạn [ ]6;6 để bất phương trình ( ) ( ) ffxx ≥ đúng với mọi x thuộc khoảng ( )2;6 .

A. 5 B. 11 C. 8 D. 6 Lờigiải ChọnC

Ta có ( ) ( ) ( ) ( ) ( ) ( ) ffxxffxfxfxx ≥⇔+≥+ .

Xét hàm số ( ) ( ) htftt =+ trên tập số thực ℝ Ta có ( ) 2 '330, httt=+>∀∈ ℝ . Suy ra hàm số ( ) ( ) htftt =+ luôn đồngbiếntrên tập ℝ . Suy ra ( ) ( ) ( ) ( ) ( ) 3 5m ffxfxfxxfxxxx +≥+⇔≥⇔+≥ . Để ( ) ( ) 3 5m ffxxxx≥⇔+≥ đúng với mọi x thuộc khoảng ( )2;6 [] ( ) 33 5 2;6 min5225log10 mm xxm ⇔+≥⇔+≥⇔≤

Do m là số nguyên thuộc đoạn [ ]6;6 nên { }6;5;4;3;2;1;0;1 m ∈−−−−−− . Vậycó 8 giátrị nguyêncủa m cần tìm.

là tập hợp tất cả các giá trị nguyên của tham số m để phương trình ()sin3sin fxxm =+ có nghiệm thuộc khoảng () 0;π . Tổngcác phần tử của S bằng

A. -6. B. -5. C. -8. D. -10. Lờigiải ChọnD

A. 0 . B. 1. C. 2019 . D. 2020 . Lờigiải ()()22222 121322 fmfxmxmxmxm −−−++−<−+ ()() 222222 21321311 xmxmfxmxmmfm ⇔−++−−−++−<−−− () *

Ta có: () 2 10,1;2021 mm −<∀∈ . ()() 2 222 213210,1;2021, xmxmxmmmx −++−=−−−+<∀∈∀∈ ℝ . Xét hàm số ()() ,0.gttftt=−< Có ()()10,0gtftt ′′=−>∀< ( do từ đồ thị ta có () 0,0fxx ′ <∀< ) Vậy ()gt là hàm số đồng biến trên () ;0−∞ . () * có dạng ()() 222 2131 gxmxmgm −++−<− 222 2131 xmxmm ⇔−++−<− ()2 2222 2 xmxmmxmm ⇔−+−<⇔−−< ( luôn đúng () 1:2021,.mx ∀∈∀∈ ℝ

Xét phương trình ()sin3sin fxxm =+ () 1 . Đặt sin tx = , ta cóphương trình ( ) 3 fttm =+ ( )2 , phương trình ( )1 có nghiệm ( ) 0; x π ∈ khi và chỉ khi phương trình () 2 cónghiệm ( ]0;1 t ∈ Số nghiệm của () 2 bằng số giao điểm của đồ thị hàm số ()yft = , ( ]0;1 t ∈ và đường thẳng 3 ytm =+ Đường thẳng 3 ytm =+ đi qua điểm () 0;1 A nên có phươngtrình 31.yt=+ Đường thẳng 3 ytm =+ đi qua điểm () 1;1 B nên có phương trình 34.yt=− Từ đó ta cógiá trị m thỏa mãn bài toán là [ )4;1 m ∈− . Các giá trị nguyên của m là tập { }4;3;2;1;0 S =−−−− , vậy tổng các phần tử bằng -10.

Câu64. (Liên Trường Nghệ An – 2021) Cho hàm số bậc ba ()yfx = có đồ thị của hàm số ()yfx ′ = được cho bởi hình vẽ bên. Có bao nhiêu giá trị nguyên của tham số m trong khoảng () 1;2021 để bất phương trình ()()22222 121322 fmfxmxmxmxm −−−++−<−+ có nghiệm?

Vì m nguyên nên { }2;3;...;2020 m∈ . Vậy có 2019 giá trị của m thỏa mãn yêu cầu bài toán. Câu65. (Sở Nam Định - 2021) Cho hàm số ()yfx = liên tục trên ℝ thỏa mãn điều kiện (0)22,()0, ffxx=>∀∈ ℝ và 2 ().()(21).1(), fxfxx xfx ′ =+∀+∈ ℝ . Tất các giá trị m để phương trình 2 22()50 xxmfx+−+= có nghiệm là 157 715;2,, abab     +       ∈  ℚ Tính tổng Sab =+ A. 2. S = B. 3. S = C. 4. S = D. 1. S = Lờigiải ChọnA

Câu 1.(Mã1032019) Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ dưới đây. Số nghiệm thực của phương trình () 3 3 3 2 fxx−= là

Với 4 2 t < phương trình: 3 4 3 txx =− cho ta 1 nghiệm.

Vậy phương trình đã cho có tất cả 8 nghiệm. Chọn C

Câu 2.(Mã 104 2019) Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình () 3 2 3 3 fxx−= là

A. 7 B. 3 C. 8 D. 4

Lời giải Chọn C Đặt 3 3 txx =− ta có phương trình () () 3 * 2 ft = .

Từ đồ thị hàm số ()yft = và đường thẳng 3 2 y = ta suy ra phương trình () * có 4 nghiệm

1234 202 tttt <−<<<<<

Xét hàm 3 3 txx =− . Ta có 2 1 330 1 x tx x

=  ′ =−=⇔  =−  Ta có bảng biến thiên

Với 1 2 t <− phương trình: 3 1 3 txx =− cho ta 1 nghiệm.

Với 2 20 t −<< phương trình: 3 2 3 txx =− cho ta 3 nghiệm.

Với 3 02 t << phương trình: 3 3 3 txx =− cho ta 3 nghiệm.

A. 10 B. 3 C. 9 D. 6

Lời giải

Chọn A Đặt () 3 3 tgxxx ==− (1) Ta có () 2 '3301 gxxx =−=⇔± Bảng biến thiên

ft ft ft

Dựa vào bảng biến thiên ta có với () 2;2 t ∈− cho ta 3 giá trị x thỏa mãn (1) {} 2;2 t ∈− cho ta 2 giá trị x thỏa mãn (1) ()() ;22; t ∈−∞−∪+∞ cho ta 1 giá trị x thỏa mãn (1). Phương trình () 3 2 3 3 fxx−= (2) trở thành () () ()

 =  =⇔   =−  

2 2 3 2 3 3

Dựa vào đồ thị ta có:

+ Phương trình () 2 3 ft = có 3 nghiệm thỏa mãn 12322ttt −<<<<  có 7 nghiệm của phương trình (2).

+ Phương trình () 2 3 ft =− có 3 nghiệm thỏa mãn 456 22 ttt <−<<<  có 3 nghiệm của phương trình (2).

Vậy phương trình đã cho có 10 nghiệm. Câu 3.(Mã 101 2019) Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình () 3 4 3 3 fxx−= là

Dựa vào đồ thị hàm số ()ft ta thấy phương trình (1) có 4 nghiệm phân biệt 1 2, t <− 2 20, t −<< 3 02 t << , 4 2 t >

Mỗi nghiệm t của phương trình () 1 , ta thay vào phương trình 3 3 txx =− để tìm nghiệm x .

Khi đó

+ 1 2 t <−  phương trình 3 3 txx =− có 1 nghiệm.

+ 2 20 t −<<  phương trình 3 3 txx =− có 3 nghiệm.

A. 7 . B. 4 . C. 3 . D. 8 . Lời giải Chọn D Đặt 32333txxtx ′ =−  =− . Ta có bảng biến thiên

+ 3 02 t <<  phương trình 3 3 txx =− có 3 nghiệm.

+ 4 2 t >  phương trình 3 3 txx =− có 1 nghiệm.

Vậy phương trình () 3 4 3 3 fxx−= có 8 nghiệm.

Câu 4.(Mã 102 2019) Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ bên. Số nghiệm thực của phương trình () 3 1 3 2 fxx−=

Khi đó () () 4 1 3 ft =

A. 6 B. 10 C. 12 D. 3

Mỗi phương trình 3 3 , -3 xx α= 3 4 , -3 xx α= 3 5 -3 xx α = , 3 6 -3 xx α= đều có một nghiệm

Từ đó suy ra phương trình () 2 1 3 2 fxx−= có 10 nghiệm.

Câu 5.(Chuyên Lam Sơn - 2020) Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ bên.

fxx fxx fxx

 −=  −=⇔   −=−  

3 3 3

1 31 1 2 3 1 2 32 2

Ta có () () () () ()

xx fxxxx xx

3 11 33 22 3 33

+) () () () () ()

320 1 13302 2 32

αα αα αα

Số nghiệm thực của phương trình () 3 31fxx−= là A. 10 . B. 8 . C. 9 . D. 7 .

 −=−<<  ⇔−=⇔−=<<   −=>   +) () () () () ()

3 44 33 55 3 66

Xét hàm số 3 3, yxxD=−= ℝ

Ta có 2 '33yx=− Bảng biến thiên

α αα αα

32 1 2332 2 32

xxx fxxxx xx

 −=<−  ⇔−=−⇔−=>   −=>  

Dựa vào bảng biến thiên ta có Phương trình: 3 1 3 xx α−= có 3 nghiệm.

Phương trình: 3 2 3 xx α−= có 3 nghiệm.

Lời giải Chọn C Xét phương trình () 3 31fxx−= (1) Đặt 3 3 txx =− , ta có bảng biến thiên của hàm số () 3 3 tgxxx ==− như sau:

Từ bảng biến thiên, ta thấy + Với mỗi 0 2 t > hoặc 0 2 t <− , phương trình 3 0 3 txx =− có một nghiệm; + Với mỗi 0 22 t −<< , phương trình 3 0 3 txx =− có 3 nghiệm.

Khi đó, (1) trở thành () () () 1 1 1 ft ft ft =  =⇔  =−  

tt fttt tt

2;0 10;2 2;

* TH 1: () () () ()

=∈−   =⇔=∈   =∈+∞ 

1 2 3

+ Với () 1 2;0 tt=∈−  Phương trình 3 1 3 txx =− có 3 nghiệm;

+ Với () 2 0;2 tt=∈  Phương trình 3 2 3 txx =− có 3 nghiệm;

+ Với () 3 2; tt=∈+∞  Phương trình 3 3 3 txx =− có 1 nghiệm;

+ Phương trình () 2 có hai nghiệm phân biệt 12 , xx thỏa mãn 1 1 2 2

* TH 2: () () () 4 5

;2 1 2; tt ft tt =∈−∞−  =−⇔  =∈+∞  

+ Với () 4 ;2 tt=∈−∞−  Phương trình 3 4 3 txx =− có 1 nghiệm;

+ Với () 5 2; tt=∈+∞  Phương trình 3 5 3 txx =− có 1 nghiệm. Mặt khác, các nghiệm này đều phân biệt. Vậy phương trình () 3 31fxx−= có 9 nghiệm phân biệt. Câu 6.(Chuyên Thái Nguyên - 2020) Cho hàm số ()yfx = liên tục trên ℝ và có bảng biến thiên như hình vẽ

Từ bảng biến thiên suy ra:

+) Phương trình: ()20191 fx +=− có 3 nghiệm. +) Phương trình: ()20194041 fx += có 1 nghiệm.

Vậy phương trình đã cho có 4 nghiệm.

2 313 3 31112 33

x x xbb x

 =  +=   ⇔  +=<−−   =<−  

Vậy phương trình đã cho có 3 nghiệm. Câu 7.(Nguyễn Huệ - Phú Yên - 2020) Cho hàm số ()yfx = có bảng biến thiên như sau: Số nghiệm của phương trình ()201920202021 fx +−= là A. 4 . B. 6 . C. 2 . D. 3 . Lời giải Chọn A Ta có : ()201920202021 fx +−=⇔ () () () () 20192020202120191 20192020202120194041 fxfx fxfx +−=−+=− ⇔  +−=+= 

Câu 8.(Chuyên Hạ Long - Quảng Ninh - 2021) Cho hàm số bậc ba ()yfx = có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực phân biệt của phương trình ( ) 22 1 41 2021 fxx−−−= là

Nhìn vào đồ thị ()yfx = trên ta có được: 32 (),0 2 0 3 (1)(2)0,"(1)0 fxaxbxcxa a fff  =++≠  =>  === 

Như vậy ta suy ra ()() 2 ()12 3 fxxxx=−− . Mà hàm số đó có cực trị bằng 43 9 tại 0xx = nên suy ra ()00 4333 93fxx −+ =  =

Như vậy: () 3343 (3)4,30,2, 39 fff +− ==−=   

Từ đó, ta phác họa được đồ thị ()yfu = với 2 3 utt=−− như sau:

Dựa vào hình vẽ trên, ta kết luận phương trình 1 () 2021 gx = có tất cả 10 nghiệm phân biệt.

Câu 9.(THPT Đồng Quan - Hà Nội - 2021) Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ

Số nghiệm trên khoảng () ;4 ππ của phương trình () 2cos21fx = là

A. 48 B. 29 C. 31 D. 40. Lời giải

Đặt 2cos2 tx =

Vì ( ) ;4 x ππ∈− nên [ ]0;2 t ∈

Phương trình trở thành: ( ) 1 ft =

Từ đồ thị hàm số ta suy ra phương trình ( ) 1 ft = có các nghiệm thuộc [ ]0;2 là 1 2 t t =   = 

Với

xk x tx xxk

1 cos2 161cos22 21 cos2 23

±   =+ =   =⇔=⇔⇔   −±   ==+    

π π π π

Vì ()

−<+<  −<+< ∈−   −<+<  −<+< 

k k x k k

π πππ π πππ ππ π πππ π πππ

4 6 4 6 ;2 4 3 4 3

Với cos21 2 cos21 2

 <<    <<  ⇔   <<   <<    phương trình có 20 nghiệm thuộc khoảng ( ) ;4 ππ .

xk x t x xk

=  =   =⇔⇔   =− =+  

π π π

723 66 525 66 411 33 213 33

Số nghiệm của phương trình () () 2 ffx = là A. 4 B. 5 C. 9 D. 7 Lờigiải ChọnD

k k k k

Ta có: () () () () () () 2 2 2 ffx ffx ffx

 =  =⇔  =−   Dựa vào bảng biến thiên ta thấy:

() () ()() () ()() () ;4 2 3; fxaa ffx fxbb =∈−∞− =⇔ =∈+∞ () () 2 ffx =− () ()() () ()() ()

fx fxdd fxee

4 1;3 3;

=− ⇔=∈ =∈+∞

.

Vì () 414 ;2 37 4 222

kk x kk

πππ ππ π πππ

−<<−<<   ∈−  ⇔  −<+<<< 

 phương trình có 9 nghiệm thuộckhoảng ( ) ;4 ππ .

Vậy phương trình đã cho có tất cả 29 nghiệm.

Câu10. (Sở TuyênQuang-2021) Cho hàm số ( )yfx = liên tục trên ℝ và có bảng biến thiên như hình vẽ

()() () ;4 fxaa=∈−∞− vô nghiệm. ()() () 3; fxbb=∈+∞ có 2 nghiệm. () 4 fx =− có 1 nghiệm. ()() () 1;3 fxdd=∈ có 2 nghiệm.

()() () 3; fxee=∈+∞ có 2 nghiệm. () () 2 ffx ⇒= có 7 nghiệm.

(TrungTâmThanhTường-2021) Cho hàm đa thức ()yfx = có đồ thị như hình vẽ.

Đặt () () 2 gxfx = . Số nghiệm của phương trình ()().210gxgx −=  là A. 11. B. 10. C. 13. D. 12. Lờigiải ChọnD

Ta có ()() () () () ()

fx gxfx gxgx fx gx fx fx

 =   ==      −=⇔⇔⇔=     = =       =− 

2 2 2 2 2

() () () () () ()

01 00 1 .210 2 1 1 2 2 2 1 3 2

. Từ đồ thị hàm số ()yfx = suy ra +) ()() 2 2 2

1 10;1 1

 =<−  ⇔=∈   =>  . Suy ra phương trình (1) có 4 nghiệm phân biệt.

xa xb xc

1, 20;1, 1,

 =<−≠  ⇔=∈≠   =>≠  

xdda xeeb xffc

2 2 2

+) () () ()() ()

. Suy ra phương trình (2) có 4 nghiệm phân biệt khác 4 nghiệm phân

biệt của phương trình (1). +) () () ()() ()

1,, 30;1,, 1,,

 =<−≠  ⇔=∈≠   =>≠  

xmmda xnneb xppfc

2 2 2

. Suy ra phương trình (3) có 4 nghiệm phân biệt khác 4 nghiệm phân biệt của phương trình (1) và 4 nghiệm phân biệt của phương trình (2). Vậy phương trình ()().210gxgx −=  có tất cả 12 nghiệm.s

Câu12. (THPTTriệuSơn-ThanhHóa-2021) Hàm số ()yfx = liên tục trên ℝ và có bảng biến thiên như hình vẽ

Phương trình () 2 2325fx +−= có bao nhiêu nghiệm?

A. 3 . B. 5 . C. 6 . D. 4 . Lờigiải ChọnA

Gọi () () 2 232gxfx=+− . Ta có: () () 2 '4.'23 gxxfx=+ . () 2 2

x gxxx x

0 '02310 233

=   =⇔+=−⇔=   += 

Ta có bảng biến thiên:

Mà () () () 5 5 5 gx gx gx

=  =⇔  =−   . Từ bảng biến thiên ta thấy phương trình có 3 nghiệm.

Câu13. (Sở TuyênQuang-2021) Cho hàm số () 2 yfxaxbxc ==++ có đồ thị () C (như hình vẽ)

Với () 1 fx =− , ta được 2 nghiệm x .

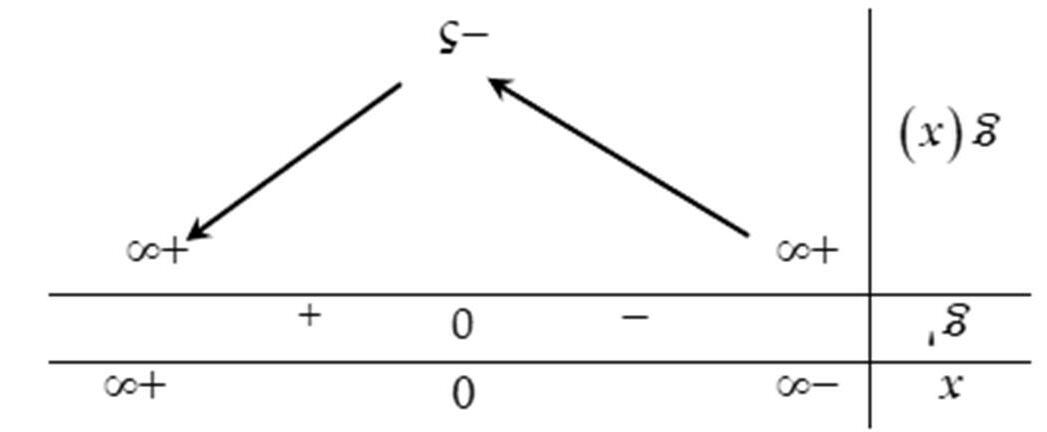
Để phương trình đã cho có 6 nghiệm phân biệt, tức là phương trình () 3 fxm =− có 4 nghiệm phân biệt.

Hay {}133041;2;3 m mmm ∈ −<−<⇔<<→∈ ℤ

Như vậy có 3 giá trị nguyên của m thỏa mãn.

Câu14. (Chuyên Biên Hòa - HàNam - 2020) Cho hàm số 32 () yfxaxbxcxd ==+++ có đồ thị như hình dưới đây

Có bao nhiêu giá trị nguyên của tham số m để phương trình () () () 2 230fxmfxm+−+−= có 6 nghiệm phân biệt? A. 2. B. 3. C. 1. D. 4. Lờigiải ChọnB Xét phương trình () () () 2 230fxmfxm+−+−= Nhận thấy ()() () () 1 1230 3 fx mm fxm  =−  −−+−=  =−  

Từ đồ thị hàm số ()fx , suy ra đồ thị hàm số ()fx như sau:

Có tất cả bao nhiêu giá trị nguyên của tham số () 5;5 m ∈− để phương trình 2 ()(4)()240 fxmfxm−+++= có 6 nghiệm phân biệt A. 2 B. 4 C. 3 D. 5 Lờigiải ChọnC

Để bất phương trình () 2 fxmm +< có nghiệm ta suy ra điều kiện 0 m >

() () 222 fxmmmfxmm +<⇔−<+< () () 3 fxm fxm >−   ⇔  <   .

Dựa vào đồ thị hàm số ()yfx = suy ra phương trình () 1 có 4 nghiệm phân biệt.

Suy ra phương trình đã cho có 6 nghiệm phân biệt () 2 có 2 nghiệm phân biệt khác các nghiệm của phương trình ()1.

Ta có phương trình () 2 là phương trình hoành độ giao điểm của hai đường ()yfx = và 2 ym=+ . Số nghiệm phương trình () 2 là số giao điểm của 2 đồ thị hàm số ()yfx = và 2 ym=+ . Dựa vào hình vẽ đồ thị hàm số ()yfx = ta được phương trình ()2fxm=+ có 2 nghiệm phân biệt khác các nghiệm của phương trình ()2fx = 20 2 24 2 22

m m m m m

+=  =−   ⇔+>⇔   >  +≠   Do m ∈ ℤ và (){} 5;52;3;4mm ∈−  ∈− . Vậy có 3 giá trị nguyên () 5;5 m ∈− thỏa mãn điều kiện bài toán. Câu15. (ChuyênTháiBình-2020) Cho hàm số ()yfx = liên tục trên đoạn [] 1;4 và có đồ thị như hình vẽ.

Có bao nhiêu giá trị nguyên của m thuộc đoạn [] 10;10 để bất phương trình () 2 fxmm +< đúng với mọi x thuộc đoạn [] 1;4 A. 6 B. 5 C. 7 D. 8 Lờigiải

Bất phương trình () 2 fxmm +< đúng với mọi x thuộc đoạn [] 1;4 () () 3 fxm fxm >−   ⇔  <   đúng với mọi x thuộc đoạn [] 1;4 [] () [] () 1;4 1;4

−<  ⇔  >   .

3min max

mfx mfx

Từ đồ thị hàm số ()yfx = ta suy ra [] () [] () 1;4 1;4 min2; max3fxfx=−= [] () [] () 1;4 1;4

2 3min 32 3 3 3 max 3

mfx m m m m mfx m

−<  −<− >    ⇔⇔⇔> > >   >   (thỏa mãn điều kiện 0 m > )

Vậy trên đoạn [] 10;10 có 7 giá trị nguyên của m thỏa mãn điều kiện bài toán.

Câu16. (Sở NinhBình) Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ.

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình () () 2 2sin610fxfmm=++ có nghiệm?

A. 2. B. 3. C. 4. D. 1. Lờigiải. ChọnB

Từ đồ thị suy ra hàm số ()yfx = đồng biến trên nửa khoảng [ ) 0; +∞

Do 2 2sin0;6100 xmm≥++> nên () () 2 2 2sin6102sin610 fxfmmxmm =++⇔=++ .

Mà 02sin2 x ≤≤ nên yêu cầu bài toán tương đương 22 0610268042 mmmmm ≤++≤⇔++≤⇔−≤≤− . Vậy có 3 số nguyên m thỏa mãn

Câu17. (LiêntrườnghuyệnQuảngXương-ThanhHóa-2021) Cho hàm số ()fx liên tục trên ℝ và có đồ thị như hình vẽ

Nhìn vào hình trên ta thấy hàm số ()fx luôn đồng biến trên [] 2;3 nên phương trình

() 2 3sincos1 2(2)4 2cossin4 xx ffm xx   +=++ −+  hay phương trình () () 2 2(2)4ftfm+=++ có

nghiệm khi và chỉ khi phương trình 2 2(2)4tm+=++ có nghiệm t thỏa mãn điều kiện 223 t ≤+≤ 22 2(2)434102525 mmmm⇔≤++≤  +−≤⇔−≤≤+ Mà m ∈ ℤ nên có tất cả 5 giá trị m thỏa mãn.

Câu18. (LiêntrườngNghệ An-2020) Cho hàm số ()fx là hàm số đa thức bậc bốn. Biết ()00 f = và đồ thị hàm số ()yfx ′ = có hình vẽ bên dưới.

Có bao nhiêu giá trị nguyên của tham số m để phương trình () 2 3sincos1 2(2)4 2cossin4 xx ffm xx   +=++ −+  có nghiệm? A. 3 B. 5 C. 4 D. 2 Lờigiải ChọnB  Ta có: 1sin1,1cos1 xx −≤≤−≤≤ nên suy ra 2cossin40,xxx −+>∀∈ℝ Đặt 3sincos1 (2cossin4)3sincos1 2cossin4 xx ttxxxx xx =  −+=−− −+ (21)cos(3)sin(41) txtxt ⇔+−+=−+ . Phương trình trên có nghiệm khi 222 9 (21)(3)(41)1223 11 ttttt +++≥+⇔≤≤  ≤+≤ .

Tập nghiệm của phương trình () 2sin11 fxm −−= (với m là tham số) trên đoạn [] 0;3π có tất cả bao nhiêu phần tử? A. 8 B. 20 C. 12 D. 16 Lờigiải ChọnD Đồ thị đã cho là đồ thị hàm số bậc ba có hai điểm cực trị 0 x = và 2 x = nên có dạng () 32 fxaxbxcxd ′ =+++ . Lần lượt thay thế các dữ kiện từ hình vẽ, ta được 2 3

2 1 0 3 322200 2 2

d a c b abc d abd

=  =    = =−    ⋅⋅+⋅⋅==  = −++=−  

Suy ra ()() 4 323322 4 x fxxxfxxxC ′ =−+  =−++

Mà ()() 4 3 0002 4 x fCfxxx =  =  =−+ .

Câu19. (Sở Hà Nam - 2019) Cho hàm số () 2 43fxxx=−+ . Có bao nhiêu giá trị nguyên của tham số m để phương trình () () () 2 650fxmfxm−−−+= có 6 nghiệm thực phân biệt? A. 1. B. 2 . C. 4 . D. 3 . Lờigiải

Ta có () 1 013 13

x fxx x

=   ′ =⇔=−   =+ 

Suy ra bảng biến thiên

Từ đó ta có bảng biến thiên của () 1 fx

Vì []1sin1,0;3 xx π −≤≤∀∈ nên 02sin13 x ≤−≤

Đặt 2sin1tx=− , [] 0;3 t ∈

Dựa vào bảng biến thiên, suy ra phương trình () 1 ftm −= có tối đa 2 nghiệm th = , tk = . Do đó

ChọnD

Hàm số () 2 43fxxx=−+ có bảng biến thiên

Đặt () ()1* tfx=≥−

Nhận xét:

+ với () * 0 1 tx<−→∈∅

Hàm số ()yfx = có bảng biến thiên

x

x -1 f(x )

-∞ +∞

3 f(x)

0 +∞ 2 -1 +∞

0 3 2 -∞ +∞ +∞ -2 -1 +∞

+ với () * 001;3tt=−>→ 2 nghiệm + với () * 0 3 t =→ 3 nghiệm

+ với () () * 0 1;3 t ∈−→ 4 nghiệm

Phương trình trở thành () 2 650tmtm−−−+= 1 5 t tm =−  ⇔  =− 

Yêu cầu bài toán suy ra {}153485;6;7 m mmm ∈ −<−<⇔<<→∈ ℤ .

±+  =  −=±  ⇔   −=±±+   =  

h x xh xkk x

1 sin 2sin1 2 2sin11 sin 2

.

Trên [] 0;3π , mỗi phương trình có nhiều nhất 4 nghiệm, do đó phương trình đã cho có nhiều nhất 16 nghiệm.

Câu20. Cho hàm số () 32 yfxaxbxcxd ==+++ có đồ thị như hình bên dưới

Có bao nhiêu giá trị nguyên của tham số m để phương trình ()()() 2 5440fxmfxm−+++= có 7 nghiệm phân biệt? A. 1 . B. 2 . C. 3. D. 4 . Lờigiải ChọnC Phương trình tương đương với ()() () () () () () () () () () () () () () () () ()

Có bao nhiêu giá trị nguyên của tham số m để phương trình () 2 3sincos1 44 2cossin4 xx ffmm xx    =++     −+  có nghiệm. A. 4 . B. 5 . C. Vô số. D. 3 . Lờigiải

ChọnD

Ta có 3sincos1 0 2cossin4 xx xx ≥ −+ , x∀ và ()2 2 4420mmm++=+≥ , m∀ . Nhìn vào đồ thị hàm số

fxfxmfx fxfxmfx fx fxfxm fxm

−+−−= ⇔−−−−=  =  ⇔−−−=⇔ =+  

2 5440 4140 41 410. 12

Từ đồ thị hàm số ()yfx = , ta suy ra đồ thị hàm số ()yfx = như sau Dựa vào đồ thị hàm số ()yfx = , suy ra phương trình () 1 luôn có 3 nghiệm phân biệt. Vì vậy, yêu cầu bài toán tương đương với phương trình () 2 có 4 nghiệm phân biệt khác 4 Suy ra 014130,1,2. mmm <+<⇔−<<  =

Vậy có 3 giá trị nguyên của tham số m thỏa bài toán.

Câu21. Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ

()yfx = ta thấy hàm số đã cho đồng biến trên [) 0;+∞ suy ra phương trình đã cho tương đương () 2 3sincos1 441 2cossin4 xx mm xx =++ −+

Đặt () 3sincos1 * 2cossin4 xx P xx = −+ vì 2cossin40 xx−+> , x∀ nên ()()()() *3sin12cos412 PxPxP ⇔−−+=+ Phương trình () 2 có nghiệm ()()() 222 9 4131211 11 PPPPP ⇔+≤−++⇔≤≤⇒≤

Suy ra phương trình () 1 có nghiệm [] 2 4413;1mmm ⇔++≤⇔∈−−⇒ Có ba giá trị nguyên của m thỏa mãn bài toán.

Câu22. (Sở HàNội2019) Cho hàm số bậc bốn ()yfx = có đồ thị như hình vẽ. Số giá trị nguyên của tham số m để phương trình () fxmm += có 4 nghiệm phân biệt là

A. 2. B. Vô số. C. 1. D. 0. Lờigiải

Đặt 0 txm=+≥

Với 0 t =  xm =

Với mỗi giá trị 0 t > sẽ ứng với 2 giá trị x

Ta có phương trình () : ftm = () 0 t ≥ () *

Để phương trình có 4 nghiệm phân biệt thì () * có 2 nghiệm phân biệt dương

Ta có () () () 3232 223230323* xxmmxxmm −+−−=⇔−+=−

Từ đồ thị của hàm số ()yft = trên miền 0 t ≥ 3 4 1

Vậy có 1 giá trị nguyên thỏa mãn

 =    =− 

m m

Câu23. (THPT Thiệu Hóa – Thanh Hóa 2019) Có bao nhiêu số nguyên m để phương trình () () 223230xxmm−+−−= có 4 nghiệm phân biệt.

A. 3 B. 12 C. 7 T = D. 5 Lờigiải ChọnA

Xét hàm số: () 3232yfxxx ==−+ có đồ thị như hình vẽ: Từ đồ thị của hàm số ta có: Phương trình (*) có 4 nghiệm phân biệt 32 232 mm ⇔−<−< Mà () 32 2 33mmmmm ∈  −∈⇔−∈ ℤℤℤ () {} () ()

m m m mm ml m ml

2

3 0 3 31;0;1 1 0 1

 =  = =±    −∈−    = =    =− 

Câu24. (ChuyênLamSơnThanhHóa2019) Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ . Biết (0)0 f = và ()fx ′ được cho như hình vẽ bên. Phương trình () fxm = ( với m là tham số) có nhiều nhất bao nhiêu nghiệm?

Lờigiải ChọnB

BBT của hàm số ()yfx =

BBT của hàm số ()yfx =

BBT của hàm số ()yfx =

Suy ra phương trình () fxm = có nhiều nhất là 6 nghiệm.

Câu25. (THPTHàNam -2019) Cho hàm số () 2 43fxxx=−+ . Có bao nhiêu giá trị nguyên của tham số m để phương trình () () () 2 650fxmfxm−−−+= có 6 nghiệm thực phân biệt? A. 1 B. 2 C. 4 D. 3 Lờigiải ChọnD

Hàm số () 2 43fxxx=−+ có bảng biến thiên

3 f(x)

0 +∞ 2 -1 +∞

Hàm số ()yfx = có bảng biến thiên

x

f(x)

x -1

-∞ +∞

0 3 2 -∞ +∞ +∞ -2 -1 +∞

Đặt () ()1* tfx=≥− Nhận xét:

+ với () * 0 1 tx<−→∈∅ + với () * 001;3tt=−>→ 2 nghiệm + với () * 0 3 t =→ 3 nghiệm + với () () * 0 1;3 t ∈−→ 4 nghiệm Phương trình trở thành () 2 650tmtm−−−+= 1 5 t tm =−  ⇔  =− 

Yêu cầu bài toán suy ra {}153485;6;7 m mmm ∈ −<−<⇔<<→∈ ℤ

Câu26. (Chuyên Vinh - 2021) Cho hàm số ()yfx = liên tục trên ℝ . Đồ thị của hàm số () 1 yfx =− được cho trong hình vẽ bên. Có bao nhiêu giá trị nguyên của m để phương trình 1 1 2 x fm x  +=  +  có đúng 3 nghiệm phân biệt thuộc [] 1;1 ?

A. 3 B. 4 C. 2 D. 1 Lờigiải ChọnA Đặt () () ()2 131 22 2 gxfgxfxx xx x  ′′ =  =  ++  + . Nhậnxét: Dựa vào đồ thị, hàm số () 1 yfx =− đạt cực trị tại các điểm 0;1xx==± nên hàm số ( )yfx = sẽ đạt cực trị tại các điểm 0;1;2xxx=== Giải phương trình ()

x x x x gxx x x x x

 =⇔=−  +   ′ =⇔=⇔=  +   =⇔=−  + 

11 0. 22 1 011. 2 1 21. 2

Bảng biến thiên: Phương trình đã cho tương đương với () () 1 1 gxm gxm

=−   =−−   Để phương trình có đúng 3 nghiệm phân biệt thuộc [ ]1;1 thì Trườnghợp1:

Yêu cầu bài toán ⇔ {} 11320 2;1 21121 mm m mm <−≤−≤< ⇔→∈−− −<−−≤−≤<  Trườnghợp2: Yêu cầu bài toán ⇔ 211 1. 12 m m m −≤−≤ →=  −−=− Vậy có 3 giá trị của m thoả mãn. Câu27. (ChuyênTháiBình-2021) Cho hàm số () 32 yfxaxbxcxd ==+++ có bảng biến thiên như sau: Tìm m để phương trình ()12 fxm −+= có 4 nghiệm thỏa mãn 1234 1 xxxx <<<<

A. 26. m << B. 36. m << C. 24. m << D. 46. m << Lờigiải ChọnD Đặt ()()12 gxfx=−+ Ta có: ()() 1 gxfx ′′ =− () () () 11006 0 11222 xg x gx x xg

=  =  −=−  ′ =⇔⇔   −= =  =  