WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM

Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group ÔN TẬP THI TỐT NGHIỆP THPT MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection 40 CHUYÊN ĐỀ PHÁT TRIỂN ĐỀ MINH HỌA THEO TỪNG CÂU KỲ THI TỐT NGHIỆP
NĂM
TOÁN
BẢN HS-GV (1446
THPT
2023 MÔN
-
TRANG)
vectorstock
com/28062405
KIẾN THỨC CẦN NHỚ:
Số phức zabi có phần thực là ,a phần ảo là b
Số phức liên hợp zabi và cần nhớ 21.i
Số phức zabi có điểm biểu diễn là (;).Mab
Số phức liên hợp zabi có điểm biểu diễn (;).Nab
Hai điểm M và N đối xứng nhau qua trục hoành Ox
;zz ;zzzz ;zzzz
..;zzzz ; zz zz
22 . zzab
CHUYÊNĐỀ21:MODULE–SỐPHỨCLIÊNHỢP–CÁCPHÉPTOÁNSỐPHỨC–ĐIỂM
BIỂUDIỄNSỐPHỨCTRÊNMẶTPHẲNGPHỨC
Hai số phức bằng nhau khi thực bằng thực và ảo bằng ảo.
Mô đun của số phức z là: 22zab
(;)Nab
Phép cộng hai số phức Cho số phức 1 zabi và 2 zcdi Khi
12.... zzabicdiacbdi
Phép trừ hai số phức
Chọn D
7;6 . D. 7;6 .
Lời giải
Ta có điểm biểu diễn số phức 76 zi có tọa độ là 7;6 .
Câu 12: _TK2023 Cho số phức 29 zi , phần thực của số phức 2 z bằng
A. 77 B. 4 C. 36
85 Lời giải 2 2 29297736 zizii .
Vậy phần thực của số phức 2 z bằng 77
Câu 16:_TK2023 Phần ảo của số phức 23 zi là A. 3 B. 2
Lý thuyết.
giải
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT
. zzzz
zz zz
zzzzzz zzzzzz
đó
12 zzabicdiacbdi
12 zzabicdiacbdadbci ..() kzkabikakbi Phép chia hai số phức 11212 2 22222222 2222 .. zzzzzabicdiacbdbcadiacbdbcad i zzzcdcdcdcd z Câu 1:_TK2023 Trên mặt phẳng tọa độ, điểm biểu diễn số phức 76 zi có tọa độ là A. 6;7 . B. 6;7 . C.
Phép nhân hai số phức
D.
C.
D. 3.
2.
Lời
x y b a (;)Mab
zabi zabi
Câu 35:_TK2023 Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức z thỏa mãn 21zi là
một đường tròn. Tâm của đường tròn đó có tọa độ là.
A. 0;2 . B. 2;0 . C. 0;2 . D. 2;0 . Lời giải

Đặt zxyi , với , xy .
Từ giả thiết 2 2 2121zixy
Do đó tập hợp điểm biểu diễn số phức z là đường tròn tâm 0;2I , bán kính 1R
Câu 1: Trên mặt phẳng tọa độ, cho 2;3M là điểm biểu diễn của số phức z Phần
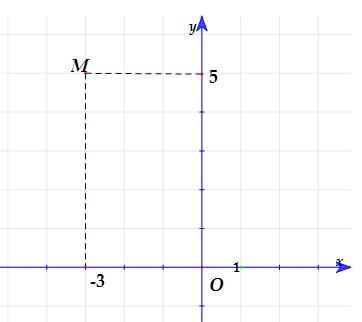
5: Trong hình vẽ bên, điểm M biểu diễn số phức
thực của z bằng A. 2 . B. 3. C. 3 . D. 2 . Câu 2: Cho số phức z thỏa mãn .52 izi Phần ảo của z bằng A. 5 B. 2 C. 5 D. 2 Câu 3: Môđun của số phức 12i
A. 5
B. 3
C. 5 . D. 3 . Câu 4:
Tính z . A. 5z B. 5z C. 2z D. 3z Câu
z Số phức z là: A. 12i . B. 2i . C. 12i . D. 2i . Câu 6: Điểm M trong hình vẽ bên biểu diễn số phức z Tính module của z A. 2z . B. 8z . C. 34z . D. 34z . Câu 7: ĐiểmM trong hình vẽ là biểu diễn hình học của số phức z Tính module của z x y M -1
bằng
.
.
Cho số phức 2 zi .
A. 5z . B. 5z . C. 3z . D. 1z . Câu 8: Cho hai số phức 11 zi và 223 zi . Tính môđun của số phức 12zz . A. 121zz B. 125zz C. 1213zz D. 125zz Câu 9: Gọi 1z , 2z lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên. Tính 12zz x y -4 3 2 O1 M N A. 229 B. 20 C. 25 D. 116 Câu 10: Cho 1224,35 zizi Xác định phần thực của 2 12 . wzz A. 120 B. 32 C. 88 D. 152 Câu 11: Cho hai số phức 143 zi và 212.zi Phần thực của số phức 1 2 z z bằng A. 1. B. 2 5 . C. 2 . D. 11 5 . Câu 12: Cho số phức 22 1 i z i . Môđun của z cùng môđun với số phức nào sau đây? A. 12 wi . B. 2 wi . C. 12 wi . D. 2w . Câu 13: Cho số phức z thỏa mãn 1243 izi , phần thực của số phức iz bằng A. - 2. B. 0. C. - 1. D. 1. Câu 14: Cho số phức 23 zi . Số phức 2 w 2 z zi có phần thực bằng A. 15 B. 15 29 C. 15 D. 15 29
15: Cho số phức 2 (1)(12) zii có phần ảo là A 2i B. 2 C. 2 D. 4
Trong mặt phẳng phức, điểm 3;7M biểu diễn số phức z . Môđun của số phức 2 . wizz bằng: A. 22 B. 8 C. 443 D. 3730
Cho số phức z thoả điều kiện (1)130 izi . Tích của phần thực và phần ảo của số phức z bằng
Câu
Câu 16:
Câu 17:
Câu 21: Cho hai số phức 124,12 zizi Số phức liên hợp của số phức 1
A. 2 B. 2 C. 2i D. 2i Câu 18: Cho số phức z thoả mãn: 2 (32)(2)4izii Tổng phần thực và phần ảo của số phức z bằng A. 3. B. 0. C. 2. D. 1. Câu 19: Cho 2 số phức 1 zmi và 2(2) zmmi (m là tham số thực). Có bao nhiêu giá trị dương của tham số m để 12zz là một số thuần ảo? A. 0 B. 3 C. 2 D. 1 Câu 20: Cho hai số phức 112 zi và 21 zi . Phần thực của số phức 1 2
z
A. 3 2 B. 1 2 C. 3 2 D. 1 2
2
z
A. 67 55 i
B.
i . C. 43i . D. 67 1717 i . Câu 22:
. Tìm phần ảo của số phức . uzw . A. 7 B. 5i C. 5. D. 7i Câu 23:
, zxyixy thỏa mãn 1234 izzi . Tính giá trị của biểu thức 32 Sxy A. 12S B. 11S C. 13S D. 10S Câu 24: Tổng phần thực
số
mãn 12 izizi bằng A. 6 B. 2 C. 2 D. 6 Câu
thoả mãn (1)232 izzi . Tính Pab A. 1P . B. 1 2 P . C. 1 2 P . D. 1P Câu 26: Cho số phức z thỏa mãn 2 3224izii . Mô đun của số phức 1 wzz bằng. A. 2 B. 10 C. 5 D. 4 Câu 27: Modun của số phức 3 zi bằng A. 8. B. 10 . C. 10. D. 22 . Câu 28: Cho số phức 32 zi , khi đó 2z bằng A. 62i . B. 64i . C. 34i . D. 64i . Câu 29: Cho số phức z thỏa mãn 135 zii . Tính môđun của z A. 17z B. 16z C. 17z D. 4z Câu 30: Cho số phức 212 zi . Tính mô đun của số phức 1 z .
z
bằng
z
là
.
67 55
Cho hai số phức 13,2 ziwi
Cho số phức
và phần ảo của
phức z thoả
25: Cho số phức (,)zabiab
Câu 37: Cho hai
A. 1 5 . B. 5 . C. 1 25 . D. 1 5 .
31: Cho số phức z thỏa mãn 2 1343 izi Môđun của z bằng A. 5 4 B. 5 2 C. 2 5 D. 4 5 Câu 32: Cho số phức z thỏa mãn 2343134 izii Môđun của z bằng A. 2 B. 4 C. 22 D. 10 Câu 33: Cho số phức z thỏa mãn 2 3224izii Mô đun của số phức 1 wzz bằng. A. 2 . B. 10 . C. 5 . D. 4 . Câu 34: Cho hai số phức 11 zi và 223 zi . Tính môđun của số phức 12.zz A. 125zz . B. 125zz . C. 121zz . D. 1213zz . Câu 35: Cho hai số phức 12 zi và w3i Môđun của số phức
z bằng A. 52 . B. 26 . C. 26 . D. 50.
i Mô đun của số phức zw A. 40 . B. 8 . C. 22 . D. 210 .
Câu
.w
Câu 36: Cho hai số phức 22 zi
và w2
số phức 42 zi và 1 wi Môđun của số phức . zw bằng A. 22. B. 8. C. 210. D. 40. Câu 38: Cho hai số phức 13 zi và 1 wi Môđun của số phức
A. 25 . B. 22 . C. 20 . D. 8.
mãn 23162izizi . Môđun
bằng A. 13 B. 5 C. 5 D. 13
mãn 24819 izzii Môđun của z bằng A. 13 B. 5 C. 13 D. 5 Câu 41: Cho số phức z thoả mãn 323716. ziizi Môđun của z bằng A. 3. B. 5. C. 5. D. 3. Câu 42: Cho số phức z thỏa mãn 32310 ziizi . Môđun của z bằng A. 3 B. 3 C. 5 D. 5 Câu 43: Cho số phức 23 zi Số phức 3 wz là A. 69 wi B. 69 wi C. 69 wi D. 69 wi Câu 44: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z Khi đó số phức 5 wz là
. zw bằng
Câu 39: Cho số phức z thỏa
của z
Câu 40: Cho số z thỏa
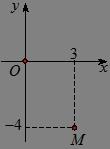



A. 1520 wi . B. 1520 wi . C. 1520 wi . D. 1520 wi . Câu 45: Trong hình vẽ bên, điểm M biểu diễn số phức z . Khi đó số phức 2 wz là A. 42 wi . B. 42 wi . C. 42 wi . D. 42 wi . Câu 46: Điểm M trong hình vẽ bên dưới biểu thị cho số phức Khi đó số phức 4 wz là x y 2 M 3 O A. 812. wi B. 812. wi C. 812. wi D. 812. wi Câu 47: Điểm M trong hình vẽ bên biểu diễn số phức z . Khi đó số phức 234 wzi là A. 96 wi . B. 914 wi . C. 914 wi . D. 914 wi . Câu 48: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Khi đó số phức 5 wz là

A. 1520 wi . B. 1520 wi . C. 1520 wi . D. 1520 wi . Câu 49: Trong hình vẽ bên, điểm M biểu diễn số phức z . Khi đó số phức 2 wz là A. 42 wi . B. 42 wi . C. 42 wi . D. 42 wi . Câu 50: Cho hai số phức 112 zi và 234 zi Số phức 121223zzzz là A. 10i . B. 10i . C. 118i . D. 1110i . Câu 51: Cho số phức 46 zi Tìm số phức . wizz A. 1010 wi . B. 1010 wi . C. 1010 wi . D. 210 wi . Câu 52: Cho số phức 32 zi . Tìm số phức 21 wziz . A. 78 wi . B. 78 wi C. 35 wi . D. 35 wi Câu 53: Cho số phức 1 1 3 zi . Tính số phức 3 wizz . A. 8 3 w . B. 8 3 wi . C. 10 3 wi . D. 10 3 . Câu 54: Cho số phức 25 zi Số phức wizz là: A. 73 wi B. 33 wi C. 37 wi D. 77 wi Câu 55: Cho số phức 32 zi . Tìm số phức 21 wziz A. 35 wi B. 78 wi C. 35 wi D. 78 wi Câu 56: Cho hai số phức 113 zmi và 22 zmi m . Tìm tất cả các giá trị của tham số m để 12zz là số thực. A. 2;3m . B. 2 5 m . C. 3;2m . D. 3;2m . Câu 57: Cho 20171 zi Tìm z A. 1008100822 zi B. 100810082 zi C. 1008100822 zi D. 100810082 zi Câu 58: Nếu 23zi thì z z bằng: A. 56 2 11 i i B. 512 13 i C. 512 13 i D. 34 7 i Câu 59: Cho số phức 35 wi . Tìm số phức z biết 34 wiz . A. 1127 2525 zi . B. 1127 2525 zi . C. 1127 2525 zi . D. 1127 2525 zi . Câu 60: Cho số phức z thỏa mãn: 1234560 zii Tìm số phức 1 wz
diễn số phức z . Phần thực của z bằng
.
Câu 64: Trên mặt phẳng tọa độ, biết 3;1M là điểm biểu diễn số phức z Phần ảo của z bằng
3.
.
Câu 65: Trên mặt phẳng tọa độ, biết 1;3M là điểm biểu diễn số phức z . Phần ảo của z bằng
3
1
3


Câu 66: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Phần thực của z bằng
Câu 67: Trong hình vẽ bên, điểm M biểu diễn số phức z . Phần thực của z bằng
1.
1.
Câu 68: Điểm M trong hình vẽ bên dưới biểu thị cho số phức Phần ảo của z bằng
.
A. 71 2525 wi B. 71 255 wi C. 71 2525 wi D. 71 2525 wi Câu 61: Cho số phức 32 zi Tìm số phức 21 wziz A. 35 wi B. 35 wi C. 78 wi D. 78 wi Câu 62: Trên mặt phẳng tọa độ, biết 3;1M là điểm biểu diễn số phức z Phần thực của z bằng A. 1 B. 3 C. 1 D. 3 Câu 63: Trên mặt phẳng tọa độ, biết 1;3M là điểm biểu
A. 3
B. 1
C. 3
D. 1
.
.
.
B.
C.
D.
A. 1
1.
3.
A.
B.
C.
D.
1
A. 4 B. 4 C.
D. 3
3
A.
B.
C.
D. 2
3.
x y 2 M 3 O A. 3. B. 2. C. 2. D. 3.
Câu 69: Điểm M trong hình vẽ bên biểu diễn số phức z . Phần ảo của z bằng A. 3. B. 3.
5.
Câu 70: Trên mặt phẳng tọa độ, điểm biểu diễn số phức 12 zi là điểm nào dưới đây? A. 1;2Q
1;2P
Câu 71: Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức 12 zi ? A. 1;2Q . B. 2;1M .


Câu 72: Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn của số phức 32 zi ?
.
Câu 73: Điểm M trong hình vẽ bên là điểm biểu diễn số phức
Câu 74: Điểm nào trong hình vẽ bên là điểm biểu diễn của số phức 12 zi ?
Câu 75: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên?
C.
D.
5.
C.
D.
B.
1;2N
1;2M
C.
D.
2;1P .
1;2N .
A.
P
B.
Q
C. 3;2N . D. 2;3M .
3;2
2;3
.
A. 12 zi B. 12 zi C. 2 zi D. 2 zi
A. P B. M C. Q D. N
Câu 76: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Tìm phần thực và phần ảo của số phức z A. Phần thực là 3 và phần ảo là 4
phần

Câu 77: Trong hình vẽ bên, điểm M biểu diễn số phức z Số phức z là:


A. 112 zi B. 212 zi C. 32 zi D. 42 zi
i B. Phần thực là 3 và phần ảo là 4 C. Phần thực là 4 và
ảo là 3i D. Phần thực là 4 và phần ảo là 3
A. 12i B. 2i C. 12i D. 2i


Câu 78: Điểm M trong hình vẽ bên dưới biểu thị cho số phức x y 2 M 3 O A. 32. i B. 23. i C. 23. i D. 32. i Câu 79: Điểm M trong hình vẽ bên biểu diễn số phức z . Chọn kết luận đúng về số phức z . A. 35 zi B. 35 zi C. 35 zi D. 35 zi Câu 80: ĐiểmM trong hình vẽ là biểu diễn hình học của số phức nào dưới đây? x y 2 -1 O A. 2 zi B. 2 zi C. 12 zi D. 12 zi Câu 81: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức liên hợp của số phức 32zi ? A. M . B. N . C. Q . D. P .

Câu 82: Trong hình vẽ bên, điểm M biểu diễn số phức z . Số phức z là: A. 12i . B. 2i . C. 12i . D. 2i . Câu 83: Cho hai số phức 13 zi và 21.zi Phần ảo của số phức 12zz bằng A. 2. B. 2. i C. 2. D. 2. i Câu 84: Cho hai số phức 12 zi và 213 zi Phần thực của số phức 12zz bằng A. 1 B. 3 C. 4 D. 2 Câu 85: Cho hai số phức 132 zi và 22 zi . Số phức 12zz bằng A. 5i . B. 5i . C. 5i . D. 5i . Câu 86: Cho hai số phức 112 zi và 22 zi . Số phức 12zz bằng A. 3i B. 3i C. 3i D. 3i Câu 87: Cho hai số phức 112 zi và 24 zi Số phức 12zz bằng A. 33i B. 33i C. 33i D. 33i Câu 88: Cho hai số phức 113 zi và 23 zi Số phức 12zz bằng A. 24i B. 24i C. 24i D. 24i Câu 89: Cho hai số phức 12 zi và 21 zi . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn của số phức 122 zz có tọa độ là A. 0;5 B. 5;1 C. 1;5 D. 5;0 Câu 90: Cho hai số phức 11 zi và 22 zi Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức 12 2 zz có tọa độ là A. (3;5) B. (5;2) C. (5;3) D. (2;5) Câu
điểm biểu diễn số phức z biết z thỏa mãn phương trình 135 izi A. 1;4M . B. 1;4M . C. 1;4M . D. 1;4M .
91: Tìm tọa độ điểm M là
trình 2 (32)(2)4izii Tìm tọa độ điểm M biểu diễn số phức z. A. 1;1M B. 1;1M C. 1;1M D. 1;1M Câu
2
Điểm
dưới
là
toạ độ? A. 1;2.M B. 2;1.P C. 2;1.N D. 1;2.Q
Câu 92: Cho số phức z thỏa mãn phương
93: Cho số phức
zi
nào
đây
biểu diễn của số phức wiz trên mặt phẳng
Câu 94: Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình 135 izi A. 1;4M B. 1;4M C. 1;4M D. 1;4M Câu 95: Cho số phức z thỏa mãn 1243 zii Phần ảo của số phức z bằng A. 2 5 B. 2 5 C. 11 5 D. 11 5 Câu 96: Cho số phức z thỏa mãn 1243 zii . Phần thực của số phức z bằng A. 2 5 . B. 2 5 . C. 11 5 . D. 11 5 . Câu 97: Cho số phức z thỏa mãn 1243 zii Phần ảo của số phức liên hợp z của z bằng A. 2 5 B. 2 5 C. 11 5 D. 11 5 Câu 98: Cho số phức z thỏa mãn 1243 zii . Phần thực của số phức liên hợp z của z bằng A. 2 5 . B. 2 5 . C. 11 5 . D. 11 5 . Câu 99: Cho số phức z thỏa mãn 3453 zii . Phần ảo của số phức liên hợp z của z bằng A. 27 25 . B. 27 25 . C. 11 25 . D. 11 25 . Câu 100: Cho số phức z thỏa mãn 3453 zii Phần thực của số phức liên hợp z của z bằng A. 27 25 B. 27 25 C. 11 25 D. 11 25 Câu 101: Cho số phức z thỏa mãn 4572 zii . Phần ảo của số phức z bằng A. 38 41 . B. 38 41 . C. 27 41 . D. 27 41 . Câu 102: Cho số phức z thỏa mãn 4572 zii . Phần thực của số phức z bằng A. 38 41 . B. 38 41 . C. 27 41 . D. 27 41 . Câu 103: Cho số phức , zabiab thỏa mãn 1232 izzi Tính Pab A. 1P B. 1 2 P C. 1 2 P D. 1P Câu 104: Cho số phức , zxyixy thỏa mãn 1234 izzi Tính giá trị của biểu thức 32 Sxy . A. 12S B. 11S C. 13S D. 10S Câu 105: Tổng phần thực và phần ảo của số phức z thoả mãn 12 izizi bằng A. 6 B. 2 C. 2 D. 6
Câu 106: Cho số phức (,)zabiab thoả mãn (1)232 izzi Tính Pab A. 1P B. 1 2 P C. 1 2 P D. 1P Câu 107: Tìm số phức z biết 45277 zzi . A. 37 zi B. 37 zi C. 37 zi D. 37 zi Câu 108: Tìm mô đun của số phức z biết 2111122 zizii A. 1 9 B. 2 3 C. 2 9 D. 1 3 Câu 109: Tính mô đun của số phức z thỏa mãn 12140 zizii với i là đơn vị ảo. A. 6 . B. 5 . C. 2 . D. 3 . Câu 110: Tìm số phức z thỏa mãn 2319 zizi . A. 2 zi B. 2 zi C. 2 zi D. 2i Câu 111: Cho số phức 2 zi , số phức 23iz bằng A. 18i B. 74i C. 74i D. 18i Câu 112: Cho số phức 23 zi , số phức 1iz bằng A. 5i B. 15i C. 15i D. 5i Câu 113: Cho hai số phức 11 zi và 212 zi Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức 123zz có tọa độ là: A. 1;4 B. 1;4 C. 4;1 D. 4;1 Câu 114: Cho số phức z thỏa mãn 1243 zii . Tìm số phức liên hợp z của z . A. 211 55 zi B. 211 zi 55 C. 211 z 55 =i D. 211 z 55 =i Câu 115: Cho số phức z thỏa mãn 135 zii . Tính môđun của z A. 17z . B. 16z . C. 17z . D. 4z . Câu 116: Cho số phức 12 zi Tìm tổng phần thực và phần ảo của số phức 2 wzz A. 3 B. 5 C. 1 D. 2 Câu 117: Cho số phức z thỏa mãn 1357. izi Mệnh đề nào sau đây đúng? A. 134 55 zi . B. 134 55 zi . C. 134 55 zi . D. 134 55 zi . Câu 118: Cho số phức z thỏa mãn phương trình 2 (32)(2)4izii . Tìm tọa độ điểm M biểu diễn số phức z A. 1;1M B. 1;1M C. 1;1M D. 1;1M
Câu 119: Số phức liên hợp của số phức 2 zi là A. 2 zi B. 2 zi C. 2 zi D. 2 zi Câu 120: Số phức liên hợp của số phức 35 zi là: A. 35 zi . B. 35 zi . C. 35 zi . D. 35 zi . Câu 121: Số phức liên hợp của số phức 25 zi là A. 25 zi B. 25 zi C. 25 zi D. 25 zi Câu 122: Số phức liên hợp của số phức 25 zi là A. 25 zi . B. 25 zi . C. 25 zi . D. 25 zi . Câu 123: Số phức liên hợp của số phức 35 zi là A. 35 zi . B. 35 zi . C. 35 zi . D. 35 zi . Câu 124: Số phức liên hợp của số phức 32 zi là. A. 32i B. 32i C. 23i D. 32i Câu 125: Số phức liên hợp của số phức 12i là: A. 12i B. 12i C. 2i D. 12i Câu 126: Số phức liên hợp của số phức 2 zi là A. 2 zi B. 2 zi C. 2 zi D. 2 zi Câu 127: Cho số phức 343 zi . Khi đó số phức liên hợp của z là A. 129 zi B. 129 zi C. 129 zi D. 129i Câu 128: Cho hai số phức 11 zi và 223.zi Số phức liên hợp của 12zzz là: A. 32 zi B. 32 zi C. 32 zi D. 32 zi Câu 129: Cho hai số phức 12 zi và 232 zi Số phức liên hợp của 12zzz là A. 1 zi B. 1 zi C. 1 zi D. 1 zi Câu 130: Số phức liên hợp của số phức 1 1 z i là A. 11 22 zi B. 11 22 zi C. 11 22 zi D. 11 22 zi Câu 131: Cho hai số phức 112 zi và 223 zi . Số phức liên hợp của 1232 wzz là A. 112 wi . B. 112 wi . C. 112 wi . D. 113 wi . Câu 132: Cho số phức 31 zii Số phức liên hợp của z là A. 12 zi . B. 12 zi . C. 2 zi . D. 1z . Câu 133: Cho 13 zi là số phức liên hợp của z . Tìm số phức z ? A. 13 zi B. 13 zi C. 13 zi D. 13 zi Câu 134: Cho 20212022 zi là số phức liên hợp của z Tìm số phức z A. 20212022 zi . B. 20212022 zi . C. 20212022 zi . D. 20212022 zi . Câu 135: Số phức đối của 57 zi là? A. 57 zi B. 57 zi C. 57 zi D. 57 zi
z z là số thuần ảo. Tính tổng của các
định sau?
A. Tập hợp điểm biểu diễn của số phức w là đường tròn tâm 33;14I
B. Tập hợp điểm biểu diễn số phức w là đường tròn có tâm 33;14I
C. Tập hợp điểm biểu diễn số phức w là đường tròn có tâm 33;14I .
D. Tập hợp điểm biểu diễn số phức w là đường tròn có bán kính 10R
Câu 146: Cho số phức z thỏamãn 12ziz .Trongmặt phẳng phức,quỹtích điểmbiểu diễn các số phức z
A. là đường thẳng 310 xy
C. là đường thẳng 310 xy
. B. là đường thẳng 310 xy
. D. là đường thẳng 310 xy
Câu 147: Tập hợp các điểm biểu diễn số phức z thỏa mãn
54325 ziz là đường thẳng có phương
A. 86250 xy
xy
860 xy
Câu 136: Cho số phức z có phần thực là số nguyên và z thỏa mãn 273 zziz . Môđun của số phức 21 wzz bằng A. 445w . B. 425w . C. 37w . D. 457w Câu 137: Có bao nhiêu số phức z thỏa mãn 3220ziz A. 4 B. 3 C. 2 D. 6 Câu 138: Có bao nhiêu số phức z thỏa 1234 zizi và 2 zi zi là một số thuần ảo A. 0. B. Vô số. C. 1. D. 2. Câu 139: Có bao nhiêu số phức z thỏa mãn (2)10zi và .25zz A. 2 . B. 3 . C. 1. D. 4 . Câu 140: Cho số phức zabi , ab thỏa mãn 31zz và 2 zzi là số thực. Tính ab A. 2. B. 0. C. 2. D. 4. Câu 141: Cho số phức zabi , ab thỏa mãn 130zizi Tính 23 Sab A. 6S B. 6S C. 5S D. 5S
,
.82
. Tính giá trị của biểu thức Pab A. 10 B.
C.
D.
có đúng một số phức thỏa mãn 6zm và 4
phần tử của tập S . A. 10. B. 0. C. 16. D. 8. Câu 144: Cho số phức zabi ,,0aba thỏa .121310 zzzzzi Tính Sab A. 17S B. 5S C. 7S D. 17S Câu 145: Chosố phức z thỏamãn 3510zi và 213914 wzii .Khẳng địnhnào đúng trong các
Câu 142: Cho số phức
zabiab
thỏa mãn 255zi
và
zz
8
35
7 Câu 143: Gọi S là tập hợp các số thực m sao cho với mỗi mS
khẳng
.
.
trình:
D.
B. 86250
C. 86250 xy
Câu 148: Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức z thỏa mãn điều kiện 22zi là
A. Đường tròn tâm 1;2I , bán kính 2R B. Đường tròn tâm 2;1I , bán kính 2R
C. Đường tròn tâm 2;1I , bán kính 2R . D. Đường tròn tâm 1;2I , bán kính 2R .
Câu 149: Xét các số phức z thỏa mãn 44ziz là số thuần ảo. Trên mặt phẳng tọa độ, tập hợp tất cả
các điểm biểu diễn hình học của z là một đường tròn có bán kính bằng
A. 22 . B. 2 . C. 2 . D. 4 .
Câu 150: Trong mặt phẳng tọa độ Oxy , tập hợp điểm M biểu diễn số phức z thỏa mãn điều kiện 12zi là
A. Đường tròn tâm 1;1I , bán kính 2R . B. Đường tròn tâm 1;1I , bán kính 4R .
C. Đường tròn tâm 1;1I , bán kính 2R . D. Đường tròn tâm 1;1I , bán kính 4R .
Câu 151: Trên mặt phẳng toạ độ Oxy , tập hợp điểm biểu diễn các số phức z thoả mãn điều kiện
(2)2zii là:
A. 22 (2)(1)4 xy .
C. 22 (1)(2)4 xy
B. 22 (1)(2)4 xy .
D. 22 (1)(1)9 xy
Câu 152: Tập hợp các điểm biểu diễn số phức z thỏa mãn 12zi là đường tròn có phương trình
A. 22 114 xy .
C. 22 114 xy .
B. 22 114 xy .
D. 22 114 xy .
Câu 153: Cho Gọi () C là tập hợp điểm biểu diễn số phức z thỏa mãn 448zzzz . Diện tích hình phẳng được giới hạn bởi () C là
A. 24 B. 4 C. 16 D. 8
Câu 154: Chosốphức 12wiz với 12 izzi .Biếtrằngtậphợpcácđiểmbiểudiễnsốphức w là đường thẳng Khoảng cách từ điểm (1;2)A đến bằng
22
Câu 155: Gọi H làhình biểu diễntập hợpcác số phức z trongmặt phẳng tọađộ Oxy sao cho 235 zz , và số phức z có phần thực không âm. Tính diện tích hình H A. 2 B. 5
5 2
5 4
Câu 156: Cho số phức z thỏa mãn điều kiện 123zi . Tập hợp các điểm biểu diễn số phức
1 wzi trong mặt phẳng tọa độ Oxy là hình phẳng H có diện tích bằng
Câu 157: Xét các số phức z thỏa mãn
A.
B.
C.
D. 2 2
0
2
C.
D.
A. 9S B. 9S C. 18S D. 18S
là
3 wz là
1 1 zi zzi
số thực. Tập hợp các điểm biểu diễn của số phức
một parabol có đỉnh
A. 39 ; 22 I B. 39 ; 22 I C. 333 ; 48 I D. 39 ; 22 I
KIẾN THỨC CẦN NHỚ:
Số phức zabi có phần thực là ,a phần ảo là b
Số phức liên hợp zabi và cần nhớ 21.i
Số phức zabi có điểm biểu diễn là (;).Mab
Số phức liên hợp zabi có điểm biểu diễn (;).Nab
Hai điểm M và N đối xứng nhau qua trục hoành Ox
;zz ;zzzz ;zzzz
..;zzzz ; zz zz
22 . zzab
CHUYÊNĐỀ21:MODULE–SỐPHỨCLIÊNHỢP–CÁCPHÉPTOÁNSỐPHỨC–ĐIỂM
BIỂUDIỄNSỐPHỨCTRÊNMẶTPHẲNGPHỨC
Hai số phức bằng nhau khi thực bằng thực và ảo bằng ảo.
Mô đun của số phức z là: 22zab
(;)Nab
Phép cộng hai số phức Cho số phức 1 zabi và 2 zcdi Khi
12.... zzabicdiacbdi
Phép trừ hai số phức
Chọn D
7;6 . D. 7;6 .
Lời giải
Ta có điểm biểu diễn số phức 76 zi có tọa độ là 7;6 .
Câu 12: _TK2023 Cho số phức 29 zi , phần thực của số phức 2 z bằng
A. 77 B. 4 C. 36
85 Lời giải 2 2 29297736 zizii .
Vậy phần thực của số phức 2 z bằng 77
Câu 16:_TK2023 Phần ảo của số phức 23 zi là A. 3 B. 2
Lý thuyết.
giải
TÀI LIỆU ÔN THI TỐT NGHIỆP THPT
. zzzz
zz zz
zzzzzz zzzzzz
đó
12 zzabicdiacbdi
12 zzabicdiacbdadbci ..() kzkabikakbi Phép chia hai số phức 11212 2 22222222 2222 .. zzzzzabicdiacbdbcadiacbdbcad i zzzcdcdcdcd z Câu 1:_TK2023 Trên mặt phẳng tọa độ, điểm biểu diễn số phức 76 zi có tọa độ là A. 6;7 . B. 6;7 . C.
Phép nhân hai số phức
D.
C.
D. 3.
2.
Lời
x y b a (;)Mab
zabi zabi
Câu 35:_TK2023 Trên mặt phẳng tọa độ, biết tập hợp điểm biểu diễn số phức z thỏa mãn 21zi là
một đường tròn. Tâm của đường tròn đó có tọa độ là.
A. 0;2 . B. 2;0 . C. 0;2 . D. 2;0 . Lời giải

Đặt zxyi , với , xy .
Từ giả thiết 2 2 2121zixy
Do đó tập hợp điểm biểu diễn số phức z là đường tròn tâm 0;2I , bán kính 1R
Câu 1: Trên mặt phẳng tọa độ, cho 2;3M là điểm biểu diễn của số phức z Phần thực của z bằng
A. 2 . B. 3. C. 3 . D. 2 .
Lời giải
Ta có 2;3M là điểm biểu diễn của số phức 23.zzi Vậy phần thực của z bằng 2.
Câu 2: Cho số phức z thỏa mãn .52 izi Phần ảo của z bằng
A. 5. B. 2 . C. 5 . D. 2 .
Lời giải Đặt ; zabiab
izi i z i zi zi
A.
5 .
3 .
. Câu
.52 52 25 25
Vậy phần ảo của z bằng -5.
B.
C 5
D. 3
Câu 3: Môđun của số phức 12i bằng
.
. Lời giải
4:
A. 5z B. 5z C. 2z D. 3z Lời giải
diễn số phức z
Số phức z là: A. 12i . B. 2i . C. 12i . D. 2i . Lời giải
Ta có 22 12125 i
Cho số phức 2 zi Tính z
Ta có 2 215z Câu 5: Trong hình vẽ bên, điểm M biểu
.

Điểm 2;1M
độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức 2 zi suy ra 2 zi . Câu 6: Điểm M
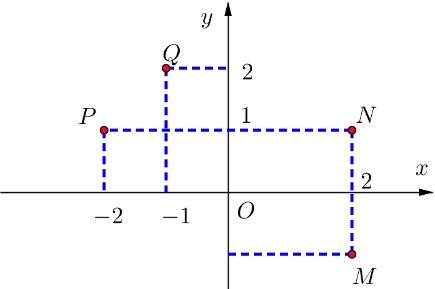
z A. 2z . B. 8z . C. 34z . D. 34z . Lời giải Tọa độ điểm 22 3;5353534Mziz . Câu 7: ĐiểmM trong hình vẽ là biểu diễn hình học của số phức z . Tính module của z . x y M 2 -1 O A. 5z . B. 5z . C. 3z . D. 1z . Lời giải Điểm (2;1)M nên nó biểu diễn cho số phức 22 2215ziz . Câu 8: Cho hai số phức 11 zi và 223 zi . Tính môđun của số phức 12zz . A. 121zz . B. 125zz . C. 1213zz . D. 125zz . Lời giải Ta có 1212123323213zziiizzi Câu 9: Gọi 1z , 2z lần lượt có điểm biểu diễn là M và N trên mặt phẳng phức ở hình bên. Tính 12zz x y -4 3 2 O1 M N
trong hệ tọa
trong hình vẽ bên biểu diễn số phức z Tính module của
A. 229 . B. 20 . C. 25 . D. 116. Lời giải Từ hình bên ta có tọa độ 3;2M biểu diễn số phức 132 zi Tọa độ 1;4N biểu diễn 214 zi . Ta có 1242 zzi 22 124225zz Câu 10: Cho 1224,35 zizi Xác định phần thực của 2 12 . wzz A. 120 B. 32 C. 88 D. 152 Lời giải Ta có 2 22351630 zizi 2 12.2416301524 wzziii . Vậy phần thực của w là 152. Câu 11: Cho hai số phức 143 zi và 212.zi Phần thực của số phức 1 2 z z bằng A. 1. B. 2 5 . C. 2 . D. 11 5 . Lời giải Ta có 1 22 2 43(43)(12)1052. 12(12)(12)12 ziiii i ziii Vậy phần thực của số phức 1 2 z z là 2. Câu 12: Cho số phức 22 1 i z i . Môđun của z cùng môđun với số phức nào sau đây? A. 12 wi . B. 2 wi . C. 12 wi . D. 2w . Lời giải
phần
A.
B. 0. C. - 1. D. 1. Lời giải Ta có: 43 12432 12 i izizi i Suy ra 212 iziii Vậy phần thực của số phức iz bằng 1. Câu 14: Cho số phức 23 zi Số phức 2 w 2 z zi có phần thực bằng A. 15. B. 15 29 . C. 15. D. 15 29 . Lời giải Ta có 325 23156 w 225292929 ziii i zii
Ta có: 22zizz , 22
ww . Câu 13: Cho số phức z thỏa mãn 1243 izi
,
thực của số phức iz bằng
- 2.
Câu 15: Cho số phức 2 (1)(12) zii có phần ảo là
A 2i B 2 C. 2 D. 4
Lời giải
Ta có 2 (1)(12)42 ziii .
Vậy số phức z có phần ảo 2b .
Câu 16: Trong mặt phẳng phức, điểm 3;7M biểu diễn số phức z . Môđun của số phức 2 . wizz
bằng:
A. 22 . B. 8 . C. 443 . D. 3730 .
Lời giải 47393730wiw
Câu 17: Cho số phức z thoả điều kiện (1)130 izi Tích của phần thực và phần ảo của số phức z
2 . B. 2 . C. 2i . D. 2i . Lời giải
Ta có: (1)130 izi
B 0. C. 2. D. 1.
Lời giải
Ta có: 2 (32)(2)4(32)15 iziiizi 15 11 32 i zzizi i
Tổng phần thực và phần
bằng A.
Đặt
zxyi
(1)()130 i130 (1)(3)0 10 30 2 1 ixyii xyixyi xyixy xy xy x y Suy ra .2xy Câu 18: Cho số phức z thoả mãn: 2 (32)(2)4izii Tổng phần thực và phần ảo của số phức z bằng A. 3.
ảo là 0. Câu 19: Cho 2 số phức 1 zmi và 2(2) zmmi (m là tham số thực). Có bao nhiêu giá trị dương của tham số m để 12zz là một số thuần ảo? A. 0 . B. 3. C. 2 . D. 1. Lời giải 2 12 (2)2(22) zzmimmimmmi 12zz là một số thuần ảo 2 2 20 1 m mm m .
Vậy có 1 giá trị dương của tham số m để 12zz là một số thuần ảo. Câu 20: Cho hai số phức 112 zi và 21 zi Phần thực của số phức 1 2 z z bằng A. 3 2 . B. 1 2 . C. 3 2 . D. 1 2 . Lời giải 1 2 12 1 zi zi 2 121 1 ii i 2122 2 iii 1313 222 i i Phần thực của số phức 1 2 z z bằng 1 2 Câu 21: Cho hai số phức 124,12 zizi Số phức liên hợp của số phức 1 2 z z là A. 67 55 i . B. 67 55 i . C. 43i . D. 67 1717 i . Lời giải Ta có 1 2 467 1255 zi i zi Vậy số phức liên hợp là 67 55 i Câu
Tìm
ảo của số phức uzw . A. 7 . B. 5i . C. 5. D. 7i . Lời giải
phần ảo của số phức là 7. Câu 23: Cho số phức , zxyixy thỏa mãn 1234 izzi . Tính giá trị của biểu thức 32 Sxy A. 12S B. 11S C. 13S D. 10S Lời giải Có 2232 123413 247 3 x xy izziS x y . Câu 24: Tổng phần thực và phần ảo của số phức z thoả mãn 12 izizi bằng A. 6 B. 2 C. 2 D. 6 Lời giải Chọn A Giả sử số phức z có dạng: ,, zxyixy Ta có: 12 izizi 12 ixyiixyii 22 xyyii 204 22 xyx yy 6xy Tổng phần thực và phần ảo của số phức z bằng 6 . Câu 25: Cho số phức (,)zabiab thoả mãn (1)232 izzi Tính Pab
22: Cho hai số phức 13,2 ziwi .
phần
.13217 uzwiii
2 3110w
Câu 27: Modun của số phức 3 zi bằng
A. 8. B. 10 . C. 10. D. 22 . Lời giải
Ta có: 22 3110z
Câu 28: Cho số phức 32 zi , khi đó 2z bằng
62i B. 64i
Ta có: 223264 zii .
Câu 29: Cho số phức z thỏa mãn
giải
A. 1P B. 1 2 P C. 1 2 P D. 1P Lời giải (1)232(1)()2()32(3)()32 izziiabiabiiababii 1 332 23 2 aba abb Suy ra: 1Pab Câu 26: Cho số phức z thỏa mãn 2 3224izii . Mô đun của số phức 1 wzz bằng. A. 2 B 10 C. 5 D. 4 Lời giải
2
iziiizizi .
đó:
Ta có:
322432151
Do
1111213 wzzzzziiiii
A.
C.
D.
Lời
34i
64i
135 zii Tính môđun của z A. 17z . B. 16z . C. 17z . D. 4z . Lời giải 35 13514 1 i ziizi i 22 1417z . Câu 30: Cho số phức 212 zi Tính mô đun của số phức 1 z A. 1 5 . B. 5 . C. 1 25 . D. 1 5 . Lời giải Ta có 2 2 1214434 ziiii 1134 342525 i zi Do đó 22 1341 25255z Câu 31: Cho số phức z thỏa mãn 2 1343 izi . Môđun của z bằng
A. 5 4 B. 5 2 C. 2 5 D. 4 5 Lời giải Ta có 2 43 13 i z i 2 435 134 i z i Câu 32: Cho số phức z thỏa mãn 2343134 izii . Môđun của z bằng A. 2 B. 4 C. 22 D. 10 Lời giải 2343134 izii239797 23 i iziz i 9723 49 ii z 3913 3 13 i zzi Vậy 9110z . Câu 33: Cho số phức z thỏa mãn 2 3224izii . Mô đun của số phức 1 wzz bằng. A. 2 B 10 C. 5 D. 4 Lời giải Ta có: 2 322432151 iziiizizi . Do đó: 1111213 wzzzzziiiii 2 3110w
34: Cho hai số phức 11 zi và 223 zi Tính môđun của số phức 12zz A. 125zz B. 125zz C. 121zz D. 1213zz Lời giải 1212332 zziii nên ta có: 22 12323213zzi Câu 35: Cho hai số phức 12 zi và w3i . Môđun của số phức .wz bằng A. 52 B. 26 C. 26 D. 50 Lời giải Ta có 22 .w.w.w12.3152. zzz Câu 36: Cho hai số phức 22 zi và w2i . Mô đun của số phức zw A. 40 B. 8 C. 22 D. 210 Lời giải zw22262210 iii Câu 37: Cho hai số phức 42 zi và 1 wi . Môđun của số phức zw bằng A. 22. B. 8. C. 210. D. 40. Lời giải
Câu
Ta có: .42162. zwiii Suy ra .40210.zw
Câu 38: Cho hai số phức 13 zi và 1 wi . Môđun của số phức . zw bằng
A. 25 B. 22 C. 20 D. 8
Lời giải
Ta có: 11 wiwi
.13142 zwiii
Từ đây ta suy ra: 22 .4225zw
Câu 39: Cho số phức z thỏa mãn 23162izizi . Môđun của z bằng
A. 13 . B. 5. C. 5 . D. 13.
Lời giải Gọi zxyi .
23162izizi
23162ixyiixyii
22316222 xyixiyixyii
232 21622 xyx yxy 30 414 y xy 2 3 x y Suy ra 23 zi . Vậy 13z . Câu 40: Cho số z thỏa mãn 24819 izzii . Môđun của z bằng A. 13 B. 5 C. 13 D. 5 Lời giải Gọi ;,.zabizabiab
Ta có:
iabiabiii ababi aba abb Vậy 3213.ziz Câu 41: Cho số phức z thoả mãn 323716. ziizi Môđun của z bằng A. 3. B. 5. C. 5. D. 3. Lời giải
24819 24819 264819 283 64192 izzii

Đặt ; zabiab . Theo đề ta có 323716 abiiiabii 3332233716 abiiabiaibi 3353716 ababi 37371 3531635132 ababa ababb . Vậy 22 125z . Câu 42: Cho số phức z thỏa mãn 32310 ziizi . Môđun của z bằng A. 3 B. 3 C. 5 D. 5 Lời giải Đặt ,, zxyixy 32310 32310 53310 3 5310 2 1 ziizi xyiiixyii xyxyii xy xy x y 2 zi Vậy 5z Câu 43: Cho số phức 23 zi Số phức 3 wz là A. 69 wi B. 69 wi C. 69 wi D. 69 wi Lời giải Số phức 332369 wzii Câu 44: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Khi đó số phức 5 wz là A. 1520 wi B. 1520 wi C. 1520 wi D. 1520 wi Lời giải Số phức 55341520 wzii Câu 45: Trong hình vẽ bên, điểm M biểu diễn số phức z Khi đó số phức 2 wz là



A. 42 wi B. 42 wi C. 42 wi D. 42 wi Lời giải Điểm 2;1M trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức 2 zi suy ra 22242 wzii Câu 46: Điểm M trong hình vẽ bên dưới biểu thị cho số phức Khi đó số phức 4 wz là x y 2 M 3 O A. 812. wi B. 812. wi C 812. wi D. 812. wi Lời giải Điểm 2;3M biểu thị cho số phức 234423812 ziwzii Câu 47: Điểm M trong hình vẽ bên biểu diễn số phức z Khi đó số phức 234 wzi là A. 96 wi B. 914 wi C. 914 wi D. 914 wi Lời giải Tọa độ điểm 3;53523534914 Mziwiii Câu 48: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z Khi đó số phức 5 wz là
118i .
Ta có 121223zzzz
Câu 51: Cho số
Ta

A. 1520 wi . B. 1520 wi . C. 1520 wi . D. 1520 wi . Lời giải Số phức 55341520 wzii Câu 49: Trong hình vẽ bên, điểm M biểu diễn số phức z Khi đó số phức 2 wz là A. 42 wi B. 42 wi C. 42 wi D. 42 wi Lời giải Điểm 2;1M trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức 2 zi suy ra 22242 wzii .
50: Cho hai số phức 112 zi và 234 zi Số phức
là
10
C.
D.
Lời giải
11811210 iii
Câu
121223zzzz
A.
i . B. 10i .
1110i .
2123341234 iiii
. Tìm số phức wizz A. 1010 wi . B. 1010 wi . C. 1010 wi . D. 210 wi . Lời giải
phức 46
zi
có:
zi . wizz4646iii1010i . Câu 52: Cho số phức 32 zi Tìm số phức 21 wziz A. 78 wi . B. 78 wi . C. 35 wi . D. 35 wi . Lời giải Ta có 3232 zizi Sử dụng MTCT ta có: 22 13213278 wziziiii . Câu 53: Cho số phức 1 1 3 zi . Tính số phức 3 wizz . A. 8 3 w . B. 8 3 wi . C. 10 3 wi . D. 10 3 . Lời giải 1118 1313 3333 wiiiii . Câu 54: Cho số phức 25 zi Số phức wizz là: A. 73 wi B. 33 wi C. 37 wi D. 77 wi Lời giải 33 wizzi .
46 zi46
Câu 55: Cho số phức 32 zi . Tìm số phức 21 wziz A. 35 wi . B. 78 wi . C. 35 wi . D. 78 wi . Lời giải Ta có 2 3213278 wiiii Câu 56: Cho hai số phức 113 zmi và 22 zmi m . Tìm tất cả các giá trị của tham số m để 12 . zz là số thực. A. 2;3m . B. 2 5 m . C. 3;2m . D. 3;2m . Lời giải 12 . zz 132 mimi 2 2263 mimimim 2526mmmi là số thực khi 2 60 mm 3 2 m m Câu 57: Cho 20171 zi Tìm z A. 1008100822 zi B. 100810082 zi C. 1008100822 zi D. 100810082 zi Lời giải Chọn C Ta có 20171 zi 2100811ii 1008 21ii 10082504 21ii1008100822i . Câu 58: Nếu 23zi thì z z bằng: A. 56 2 11 i i B. 512 13 i C. 512 13 i D. 34 7 i Lời giải Vì 2332 zii nên 32 zi , suy ra. 3232 32512 329413 ii zii zi . Câu 59: Cho số phức 35 wi . Tìm số phức z biết 34 wiz . A. 1127 2525 zi B. 1127 2525 zi C. 1127 2525 zi D. 1127 2525 zi Lời giải 3511271127 34 3425252525 i wizzizi i Câu 60: Cho số phức z thỏa mãn: 1234560 zii . Tìm số phức 1 wz . A. 71 2525 wi . B. 71 255 wi . C. 71 2525 wi . D. 71 2525 wi . Lời giải Gọi zabi , với , ab . Ta có: 1234560 zii . 2123456068886100 abiiiababi
Câu 62: Trên mặt phẳng tọa độ, biết
3;1M là điểm biểu diễn số phức z Phần thực của z bằng A. 1. B. 3. C. 1. D. 3.
Chọn B
Điểm 3;1M là điểm biểu diễn số phức z , suy ra 3 zi
Vậy phần thực của z bằng 3
Câu 63: Trên mặt phẳng tọa độ, biết 1;3M là điểm biểu diễn số phức z Phần thực của z bằng
A. 3 B. 1 C. 3 D. 1

Lời giải
Chọn B
Ta có 1;3M là điểm biểu diễn số phức z13 zi .
Vậy phần thực của z bằng 1
Câu 64: Trên mặt phẳng tọa độ, biết 3;1M là điểm biểu diễn số phức z . Phần ảo của z bằng
A. 1. B. 3. C. 1.
Lời giải
Điểm 3;1M là điểm biểu diễn số phức z , suy ra 3 zi
Vậy phần ảo của z bằng 1.
D. 3.
Câu 65: Trên mặt phẳng tọa độ, biết 1;3M là điểm biểu diễn số phức z . Phần ảo của z bằng
A. 3. B. 1. C. 3 . D. 1.
Lời giải
Ta có 1;3M là điểm biểu diễn số phức z13 zi
Vậy phần ảo của z bằng 3.
Câu 66: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z Phần thực của z bằng
32 688032171 251 86100125252525 25 a ab ziwzi ab b . Câu 61: Cho số phức 32 zi Tìm số phức 21 wziz A. 35 wi B. 35 wi C. 78 wi D. 78 wi Lời giải Ta có 3232 zizi . Khi đó 22 13213278 wziziiii .
Lời
giải
C. 3 .
Lời giải
3 .
Điểm M trong hình vẽ bên là điểm biểu diễn của số phức 34 zi Phần thực của z bằng 3.
Câu 67: Trong hình vẽ bên, điểm M biểu diễn số phức z Phần thực của z bằng
A. 1. B. 3.


C. 1. D. 2 .
Lời giải
Điểm 2;1M trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức 2 zi suy ra phần thực của z bằng 2.
Câu 68: Điểm M trong hình vẽ bên dưới biểu thị cho số phức. Phần ảo của z bằng
Điểm 2;3M biểu thị cho số phức 23 zi Phần ảo của z bằng 3
Câu 69: Điểm M trong hình vẽ bên biểu diễn số phức z Phần
A. 4
B.
.
4 .
D.
x y 2 M 3 O A. 3. B. 2. C. 2. D 3. Lời giải
ảo của z bằng A. 3 B. 3 C. 5 D. 5 Lời giải Tọa độ điểm 3;535 Mzi . Phần ảo của z bằng 5 Câu 70: Trên mặt phẳng tọa độ, điểm biểu diễn số phức 12 zi là điểm nào dưới đây? A. 1;2Q . B. 1;2P . C. 1;2N . D. 1;2M .
Chọn B
Điểm biểu diễn số phức 12 zi là điểm
1;2


Câu 71: Trên mặt phẳng tọa độ, điểm nào dưới đây là điểm biểu diễn số phức 12 zi ?
diễn
Câu 72: Trên mặt phẳng tọa độ, điểm nào dưới đây là
Lời giải
P .
B. 2;1M . C. 2;1P . D. 1;2N . Lời giải
A. 1;2Q .
là điểm 1;2N .
Chọn D Điểm biểu
số phức 12 zi
32 zi ? A. 3;2P . B. 2;3Q . C. 3;2N . D. 2;3M . Lời giải Chọn C Ta có: ; zabiNab là điểm biểu diễn của số phức z 32 zi 3;2N
Điểm M trong hình
bên là điểm biểu diễn số phức A. 12 zi B. 12 zi C. 2 zi D. 2 zi Lời giải Chọn D Theo hình vẽ 2;12 Mzi Câu 74: Điểm
A. P B. M C. Q D. N Lời giải
trên
điểm 12Q;
điểm biểu diễn của số phức
Câu 73:
vẽ
nào trong hình vẽ bên là điểm biểu diễn của số phức 12 zi ?
Chọn C Ta có điểm biểu diễn của số phức 12 zi
hệ trục tọa độ Oxy là
Câu 75: Số phức nào dưới đây có điểm biểu diễn trên mặt phẳng tọa độ là điểm M như hình bên?
Lời giải
Chọn C
Điểm 2;1M là điểm biểu diễn số phức 12 zi

Câu 76: Điểm M trong hình vẽ bên là điểm biểu diễn của số phức z . Tìm phần thực và phần ảo của số phức z
A. Phần thực là 3 và phần ảo là 4i
C. Phần thực là 4 và phần ảo là 3i
Chọn B
B. Phần thực là 3 và phần ảo là 4
D. Phần thực là 4 và phần ảo là 3
Lời giải

Nhắc lại:Trên mặt phẳng phức, số phức zxyi được biểu diễn bởi điểm (;)Mxy
Điểm M trong hệ trục Oxy có hoành độ 3x và tung độ 4y
Vậy số phức z có phần thực là 3 và phần ảo là 4
Câu 77: Trong hình vẽ bên, điểm M biểu diễn số phức z Số phức z là:

Điểm 2;1M trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức 2 zi suy ra 2 zi
Câu 78: Điểm M trong hình vẽ bên dưới biểu thị cho số phức
A. 112 zi B. 212
zi
C. 32 zi
D. 42 zi
B. 2i
12i
2i
A. 12i
C.
D.
Lời giải


x y 2 M 3 O A. 32. i B. 23. i C. 23. i D. 32. i Lời giải Điểm 2;3M
số phức 23.zi Câu
đúng về số phức z . A. 35 zi . B. 35 zi . C. 35 zi . D. 35 zi . Lời giải Tọa độ điểm
Mzizi .
x y M 2 -1 O A. 2 zi B. 2 zi C. 12 zi D. 12 zi Lời giải Điểm (2;1)M nên nó biểu diễn cho số phức 2 zi Câu
32zi ? A. M B. N C. Q D. P
biểu thị cho
79: Điểm M trong hình vẽ bên biểu diễn số phức z . Chọn kết luận
3;53535
Câu 80: ĐiểmM trong hình vẽ là biểu diễn hình học của số phức nào dưới đây?
81: Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức liên hợp của số phức
Lời giải
Số phức liên hợp của số phức 32zi là 23 zi Điểm biểu diễn số phức z là 2;3N
Vậy điểm biểu diễn số phức liên hợp của số phức 32zi là N .
Câu 82: Trong hình vẽ bên, điểm M biểu diễn số phức z Số phức z là:
A. 12i B. 2i C. 12i D. 2i

Lời giải
Điểm 2;1M trong hệ tọa độ vuông góc cuả mặt phẳng được gọi là điểm biểu diễn số phức 2 zi suy ra 2 zi Câu 83: Cho hai số phức 13 zi
số phức
12zz bằng A. 2. B. 2. i C. 2. D. 2. i Lời giải Chọn C Ta có: 21 zi . Do đó 12(3)(1)22. zziii Vậy phần ảo của số phức 12zz bằng 2. Câu 84: Cho hai số phức 12 zi và 213 zi Phần thực của số phức 12zz bằng A. 1. B. 3 . C. 4 . D. 2. Lời giải Chọn B Ta có 1234 zzi . Phần thực của số phức 12zz bằng 3. Câu 85: Cho hai số phức 132 zi và 22 zi Số phức 12zz bằng A. 5i B. 5i C. 5i D. 5i Lời giải Chọn C Ta có: 123225 zziii . Câu 86: Cho hai số phức 112 zi và 22 zi Số phức 12zz bằng A. 3i B. 3i C. 3i D. 3i Lời giải Chọn C Tacó: 121223 zziii . Câu 87: Cho hai số phức 112 zi và 24 zi Số phức 12zz bằng
và 21.zi Phần ảo của
Chọn A
Câu 90: Cho hai số phức 11 zi và 22 zi Trên mặt phẳng tọa độ Oxy , điểm biểu diễn số phức 12 2 zz có tọa độ là
A. (3;5) B. (5;2)
Chọn C
Ta có 122(1)2(2)53 zziii
C. (5;3)
Lời giải
D. (2;5)
Do đó điểm biểu diễn số phức 12 2 zz có tọa độ là (5;3)
Câu 91: Tìm tọa độ điểm M là điểm biểu diễn số phức z biết z thỏa mãn phương trình 135 izi .
A. 1;4M B. 1;4
A. 33i B. 33i C. 33i D. 33i Lời giải Chọn C Ta có: 1212433 zziii . Câu 88: Cho hai số phức 113 zi và 23 zi Số phức 12zz bằng A. 24i B. 24i C. 24i D. 24i Lời giải Chọn A Ta có 1213313324 zziiiii Câu 89: Cho hai số phức 12 zi và 21 zi . Trên mặt phẳng tọa độ Oxy , điểm biểu diễn của số phức 122 zz có tọa độ là A. 0;5 B. 5;1 C. 1;5 D. 5;0 Lời giải Chọn B Ta có 12 25 zzi . Nên ta
M C. 1;4M D. 1;4M Lời giải Ta có 135 izi 35 1 i z i 14 zi . Suy ra 14 zi Vậy 1;4M
92: Cho số phức z thỏa mãn phương trình 2 (32)(2)4izii . Tìm tọa độ điểm M biểu diễn số phức z A. 1;1M B. 1;1M C. 1;1M D. 1;1M Lời giải Chọn C Ta có 242 1 32 ii zi i nên 1;1M .
Câu
Câu 93: Cho số phức 2 zi Điểm nào dưới đây là biểu diễn của số phức wiz trên mặt phẳng toạ độ? A. 1;2.M
2;1.N
Lời giải
1;2.Q
Chọn A
Ta có: 212 wiziii .
Vậy điểm biểu diễn số phức wiz là điểm 1;2.M
Câu 94: Tìm tọa độ điểm M là điểm biểu diễn số phức z
C.
D.
B. 2;1.P
biết z thỏa mãn phương trình 135 izi . A. 1;4M B. 1;4M C. 1;4M D. 1;4M Lời giải Ta có 135 izi 35 1 i z i 14 zi Suy ra 14 zi . Vậy 1;4M . Câu 95: Cho số phức z thỏa mãn 1243 zii Phần ảo của số phức z bằng A. 2 5 B. 2 5 C. 11 5 D. 11 5 Lời giải Vì 1243 zii nên 43 12 i z= i 22 4312 12 ii 211 5 i 211 55 =i . Suy ra 211 z 55 =i . Vậy phần ảo của z là 11 5 . Câu 96: Cho số phức z thỏa mãn 1243 zii . Phần thực của số phức z bằng A. 2 5 . B. 2 5 . C. 11 5 . D. 11 5 . Lời giải Vì 1243 zii nên 43 12 i z= i 22 4312 12 ii 211 5 i 211 55 =i . Suy ra 211 z 55 =i . Vậy phần thực của z là 2 5 . Câu 97: Cho số phức z thỏa mãn 1243 zii . Phần ảo của số phức liên hợp z của z bằng A. 2 5 . B. 2 5 . C. 11 5 . D. 11 5 . Lời giải Vì 1243 zii nên 43 12 i z= i 22 4312 12 ii 211 5 i 211 55 =i .
Suy ra 211 z 55 =i Vậy phần ảo của z là 11 5 Câu 98: Cho số phức z thỏa mãn 1243 zii Phần thực của số phức liên hợp z của z bằng A. 2 5 B. 2 5 C. 11 5 D. 11 5 Lời giải Vì 1243 zii nên 43 12 i z= i 22 4312 12 ii 211 5 i 211 55 =i . Suy ra 211 z 55 =i . Vậy phần thực của z là 2 5 Câu 99: Cho số phức z thỏa mãn 3453 zii Phần ảo của số phức liên hợp z của z bằng A. 27 25 B. 27 25 C. 11 25 D. 11 25 Lời giải Vì 3453 zii nên 5327112711 3425252525 i z=izi i Vậy phần ảo của z là 11 25 Câu 100: Cho số phức z thỏa mãn 3453 zii . Phần thực của số phức liên hợp z của z bằng A. 27 25 . B. 27 25 . C. 11 25 . D. 11 25 . Lời giải Vì 3453 zii nên 5327112711 3425252525 i z=izi i Vậy phần ảo của z là 27 25 Câu 101: Cho số phức z thỏa mãn 4572 zii Phần ảo của số phức z bằng A. 38 41 B. 38 41 C. 27 41 D. 27 41 Lời giải Vì 4572 zii nên 7238273827 4541414141 i z=izi i Vậy phần ảo của z là 27 41 . Câu 102: Cho số phức z thỏa mãn 4572 zii . Phần thực của số phức z bằng A. 38 41 . B. 38 41 . C. 27 41 . D. 27 41 . Lời giải
Vì 4572 zii nên 7238273827 4541414141 i z=izi i Vậy phần thực của z là 38 41 27 41 Câu 103: Cho số phức , zabiab thỏa mãn 1232 izzi . Tính Pab A. 1P B. 1 2 P C. 1 2 P D. 1P Lời giải Ta có 12321232 332 1 332 23 2 izziiabiabii ababii aba abb Vậy 1Pab Câu 104: Cho số phức , zxyixy thỏa mãn 1234 izzi Tính giá trị của biểu thức 32 Sxy . A. 12S B. 11S C. 13S D. 10S Lời giải Có 2232 123413 247 3 x xy izziS x y Câu 105: Tổng phần thực và phần ảo của số phức z thoả mãn 12 izizi bằng A. 6 B. 2 C. 2 D. 6 Lời giải Chọn A Giả sử số phức z có dạng: ,, zxyixy Ta có: 12 izizi 12 ixyiixyii 22 xyyii . 204 22 xyx yy 6xy Tổng phần thực và phần ảo của số phức z bằng 6 . Câu 106: Cho số phức (,)zabiab thoả mãn (1)232 izzi Tính Pab A. 1P B. 1 2 P C. 1 2 P D. 1P Lời giải (1)232(1)()2()32(3)()32 izziiabiabiiababii
1 332 23 2 aba abb . Suy ra: 1Pab . Câu 107: Tìm số phức z biết 45277 zzi . A. 37 zi B. 37 zi C. 37 zi D. 37 zi Lời giải Giả sử , zabiabR , khi đó 4()5()2779277 abiabiiabii 9273 37 77 aa zi bb Câu 108: Tìm mô đun của số phức z biết 2111122 zizii A. 1 9 B. 2 3 C. 2 9 D. 1 3 Lời giải Chọn B Giả sử zabizabi Do đó 2111122 zizii 22111122 abiiabiii 2212211122 ababiababii 1 221123323 2211201 3 a abab ab ab abab b Khi đó 222 3 zab Câu 109: Tính mô đun của số phức z thỏa mãn 12140 zizii với i là đơn vị ảo. A. 6 . B. 5 . C. 2 . D. 3 . Lời giải Giả sử: zxyi , , xy . Ta có: 12140 zizii 12140xyiixyiii 23410 xyxi 2340 10 xy x 2 1 y x 125ziz . Câu 110: Tìm số phức z thỏa mãn 2319 zizi A. 2 zi . B. 2 zi . C. 2 zi . D. 2i . Lời giải Giả sử zabi , ab . Ta có:
Vậy 2 zi
Câu 111: Cho số phức 2 zi , số phức 23iz bằng
A. 18i . B. 74i . C. 74i .
18i . Lời giải
Chọn C
Ta có: 2323274 iziii .
Câu 112: Cho số phức 23 zi , số phức 1iz bằng A. 5i B. 15i C. 15i
5i Lời giải Chọn C
Ta có 23 zi23 zi Do đó 11.2315 iziii
Câu 113: Cho hai số phức 11 zi và 212 zi Trên mặt phẳng tọa độ Oxy , điểm biểu diễn
2319 zizi 2319 abiiabii 33319 ababii 31
2 1 a b .
339 ab ab
D.
D.
số phức 123zz có tọa độ là: A. 1;4 B. 1;4 C. 4;1 D. 4;1 Lời giải Chọn D 12 331124 zziii . Suy ra: Tọa độ điểm biểu diễn là: 4;1. Câu 114: Cho số phức z thỏa mãn 1243 zii Tìm số phức liên hợp z của z A. 211 55 zi B. 211 zi 55 C. 211 z 55 =i D. 211 z 55 =i Lời giải Vì 1243 zii nên 43 12 i z= i 22 4312 12 ii 211 5 i 211 55 =i Vậy nên 211 z 55 =i . Câu 115: Cho số phức z thỏa mãn 135 zii Tính môđun của z A. 17z B. 16z C. 17z D. 4z Lời giải 35 13514 1 i ziizi i 22 1417z Câu 116: Cho số phức 12 zi Tìm tổng phần thực và phần ảo của số phức 2 wzz A. 3 B. 5 C. 1 D. 2 Lời giải Chọn B Ta có 1212 zizi
22(12)1232 wzziii Vậy tổng phần thực và phần ảo của số phức w là 5 Câu 117: Cho số phức z thỏa mãn 1357. izi Mệnh đề nào sau đây đúng? A. 134 55 zi B. 134 55 zi C. 134 55 zi D. 134 55 zi Lời giải 57134134 1357. 135555 i izizzizi i Câu 118: Cho số phức z thỏa mãn phương trình 2 (32)(2)4izii Tìm tọa độ điểm M biểu diễn số phức z. A. 1;1M B. 1;1M C. 1;1M D. 1;1M Lời giải Chọn C Ta có 242 1 32 ii zi i nên 1;1M . Câu 119: Số phức liên hợp của số phức 2 zi là A. 2 zi B. 2 zi C 2 zi D. 2 zi Lời giải Chọn C Số phức liên hợp của số phức 2 zi là 2 zi Câu 120: Số phức liên hợp của số phức 35 zi là: A. 35 zi B. 35 zi C. 35 zi D. 35 zi Lời giải Chọn A Câu 121: Số phức liên hợp của số phức 25 zi là A. 25 zi B. 25 zi C. 25 zi D. 25 zi Lời giải Chọn D Số phức liên hợp của số phức 25 zi là 25 zi . Câu 122: Số phức liên hợp của số phức 25 zi là A. 25 zi . B. 25 zi . C. 25 zi . D. 25 zi . Lời giải Chọn A Ta có số phức liên hợp của số phức 25 zi là 25 zi . Câu 123: Số phức liên hợp của số phức 35 zi là A. 35 zi B. 35 zi C. 35 zi D. 35 zi Lời giải Chọn B
có: 35 zi 35 zi . Câu 124: Số phức liên hợp của số phức 32 zi là.
Ta
Chọn A
Số phức liên hợp của số phức zabi là số phức zabi từ đó suy ra chọn đáp ánB.
Câu 125: Số phức liên hợp của số phức 12i là:
12i. B. 12i .
Chọn B
Theo định nghĩa số phức liên hợp của số phức ,, zabiab là số phức ,, zabiab .
Câu 126: Số
A.
B. 32
C.
D.
Lời
32i
i
23i
32i
giải
A.
C.
D.
Lời
2i .
12i .
giải
A. 2
B. 2 zi . C. 2 zi . D. 2 zi . Lời
. Câu 127: Cho số phức 343 zi . Khi đó số phức liên hợp của z là A. 129 zi . B. 129 zi . C. 129 zi . D. 129i . Lời giải Ta có:
. Số phức liên hợp của z là: 129 zi . Câu 128: Cho
số phức 11 zi và 223.zi Số phức liên hợp của 12zzz là: A. 32 zi B. 32 zi C. 32 zi D. 32 zi Lời giải Ta có: 1212332 zzziii . Số phức liên hợp của 12zzz là 32 zi Câu 129: Cho hai số phức 12 zi và 232 zi Số phức liên hợp của 12zzz là A. 1 zi B. 1 zi C. 1 zi D. 1 zi Lời giải Ta có: 122321 zzziii Số phức liên hợp của z là 1 zi . Câu 130: Số phức liên hợp của số phức 1 1 z i là A. 11 22 zi B. 11 22 zi C. 11 22 zi D. 11 22 zi Lời giải Ta có: 11111 1111122 ii zi iii Số phức liên hợp của z là 11 22 zi . Câu 131: Cho hai số phức 112 zi và 223 zi . Số phức liên hợp của 1232 wzz là
phức liên hợp của số phức 2 zi
là
zi
.
giải Số phức liên hợp của z là 2 zi
343129 zii
hai
Câu 132: Cho số phức 31 zii Số phức liên hợp của z
Ta có: 3 1112 ziiiii .
Số phức liên hợp của z là: 12 zi .
Câu 133: Cho 13 zi là số phức liên hợp của z Tìm số phức z ?
A. 13 zi . B. 13 zi .
Số phức z là 13 zi .
13 zi . D. 13 zi .
giải
Câu 134: Cho 20212022 zi là số phức liên hợp của z . Tìm số phức z .
A. 20212022 zi B. 20212022 zi C. 20212022 zi D. 20212022 zi
Số phức z là 20212022 zi .
Câu 135: Số phức đối của 57 zi là? A. 57 zi B 57 zi
Câu 136: Cho số phức z có phần thực là số nguyên và z thỏa
A. 112 wi . B. 112 wi . C. 112 wi . D. 113 wi . Lời giải Ta có:
wzziii Số
z là: 112 wi
A. 12 zi . B. 12 zi . C. 2 zi . D. 1z . Lời giải
12 32312223112
phức liên hợp của
là
C.
Lời
Lời giải
C.
D.
57 zi
57 zi Lời giải Số phức đối của z là z Suy ra 57 zi .
mãn 273 zziz . Môđun của số phức 21 wzz bằng A. 445w . B. 425w . C. 37w . D. 457w Lời giải Đặt , zabiab Khi đó: 273 zziz222273 ababiiabi 223730ababi 3 5 7 4() 3 3 4 b a a b a Do a nên 443421457aziwiw Câu 137: Có bao nhiêu số phức z thỏa mãn 3220ziz . A. 4 B. 3 C. 2 D. 6 Lời giải Chọn A
Vậy phương trình có 4 nghiệm
Câu 138: Có bao nhiêu số phức z thỏa
2 332 2 0 202z020 202 z zizzizzziz ziz Gọi zxyizxyi với , xy thay vào 2 có: 22 2 22 22 2 0 20 2020 22x100 2101 1 30 x xyy yy xyyyixyyx xy y y x 0 0 2 3 1 3 1 xy x y x y x y 0 2 3 3 z zi zi zi
zizi và 2 zi zi là một số thuần ảo A. 0. B. Vô số. C. 1. D. 2. Lời giải Đặt (,)zxyixy Theo bài ra ta có 2222 1234 12345 xyixyi xyxyyx Số phức 2 22 222123 w 11 zixyixyyxyi zixyi xy w là một số ảo khi và chỉ khi 2 22 21012 107 23 57 xyy x xy y yx Vậy 1223 77 zi .Vậy chỉ có 1 số phức z thỏa mãn Câu 139: Có bao nhiêu số phức z thỏa mãn (2)10zi và .25zz . A 2 B. 3 C. 1 D. 4 Lời giải Gọi số phức cần tìm là , zabiab Ta có: 222 .25(1) zzzab Lại có: (2)102(1)10 ziabi
1234
2221 zziabiabiiabiabi
2122 aabbabi
22 22 22 (2)(1)10 (2)(1)10 42510(2) ab ab abab Thay vào ta được: 2542510210 abba Nên 222225(210)25abaa 2 50 540750 34 ab aa ab Vậy Vậy có 2 số phức z thoả mãn là 5z và 34 zi Câu 140: Cho số phức zabi , ab thỏa mãn 31zz và 2 zzi là số thực. Tính ab A. 2. B. 0. C. 2. D. 4. Lời giải Ta có zabi , ab +) 31zz 31 abiabi 222231 abab 2222
abab 480 a 2a . +)
31
2 zzi là số thực 220ab Thay 2a tìm được 2b . Vậy 0ab . Câu 141: Cho số phức zabi , ab thỏa mãn 130zizi Tính 23 Sab A. 6S B. 6S C. 5S D. 5S Lời giải Ta có 130zizi 22 130ababi 22 10 30 a bab 2 1 13* a bb 22 3 * 13 b bb 3 4 3 b b 4 3 b Vậy 1 4 3 a b 236Sab . Câu 142: Cho số phức , zabiab thỏa mãn 255zi và .82zz Tính giá trị của biểu thức Pab . A. 10 . B. 8 . C. 35 . D. 7 . Lời giải
Theo giả thiết ta có 22 22 22 543 2551 2 82822 b a ab ab ab Thay 1 vào 2 ta được 2 9 2943015210169 29 b bb b Vì b nên 91ba . Do đó 8Pab . Câu 143: Gọi S là tập hợp các số thực m sao cho với mỗi mS có đúng một số phức thỏa mãn 6zm và 4 z z là số thuần ảo. Tính tổng của các phần tử của tập S A. 10. B. 0. C. 16. D. 8. Lời giải Cách 1: Gọi zxiy với , xy ta có 2 2222 444 4444 zxiyxiyxiyxxyiy zxiyxyxy là số thuần ảo khi 2 22 4024xxyxy Mà 22 636zmxmy Ta được hệ phương trình 2 2 2 2 2 2 2 2 2 2 2 36 36423642 24423642 42 m x mxm xmy m m yx xy y m Ycbt 2236 420 42 m m 236 22 42 m m hoặc 236 22 42 m m 10m hoặc 2m hoặc 6m Vậy tổng là 102668 Câu 144: Cho số phức zabi ,,0aba thỏa .121310 zzzzzi . Tính Sab . A. 17S . B. 5S . C. 7S . D. 17S . Lời giải Ta có: .121310 zzzzzi 22221221310 ababbii 22221213 210 abab b 2225122513 5 aa b 2 2 2513 251 5 a aVN b 12 5 a b 12 5 a b , vì 0a Vậy 7Sab .






































