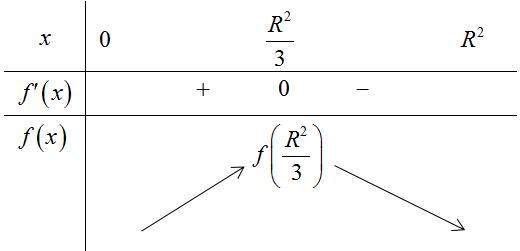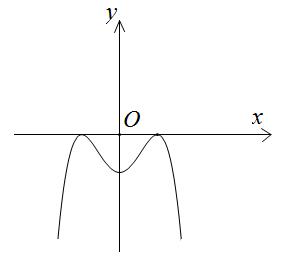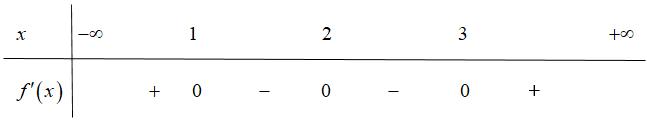70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC (1-10) by Dạy Kèm Quy Nhơn Official

ĐỀ THI THỬ TỐT NGHIỆP THPT MÔN TOÁN

Nguyễn Thanh Tú eBook Collection 70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (1-10) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

Ths

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH TRƯỜNG THPTLÝTHÁI TỔ

ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022–2023

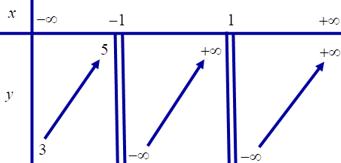
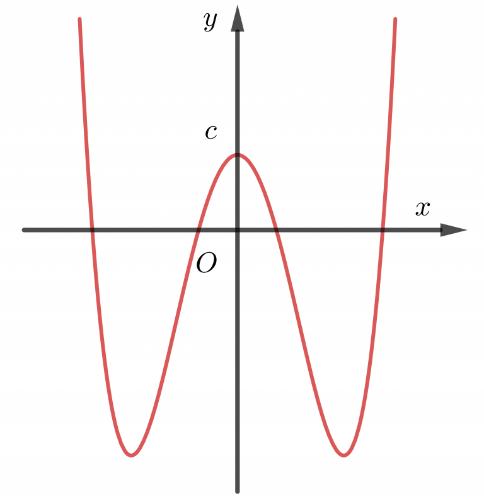
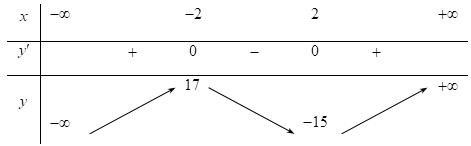
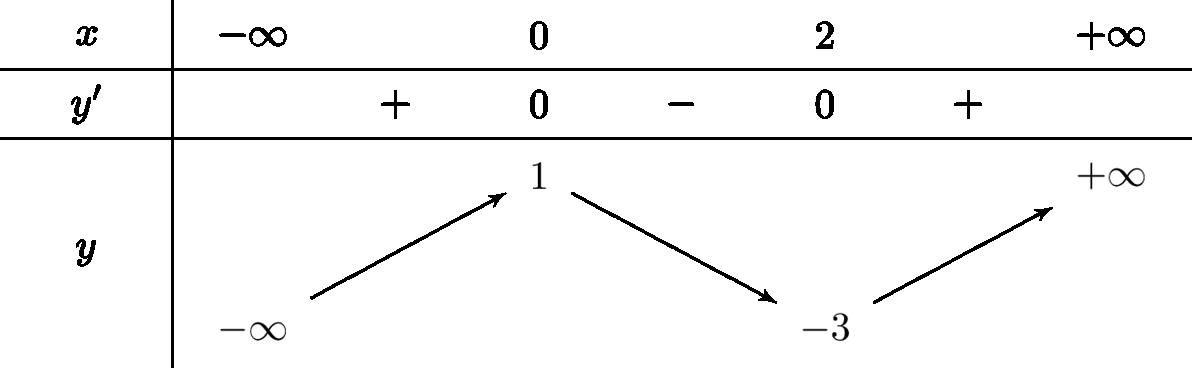
Chohàm số .Xétcác mệnh đề sau: 2 1   x y x

1)Hàm số đã cho đồng biến trên 1;. 

2)Hàm số đã cho nghịch biến trên \1

3)Hàm số đã chokhôngcó điểm cực trị.

4)Hàm số đã cho nghịch biến trêncác khoảng và  ;11;. 

Số các mệnh đề đúng là

A. . B. . C. . D. . 4 2 3 1

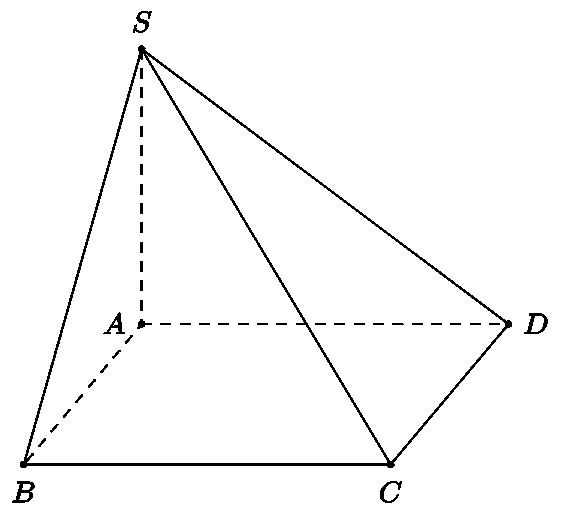
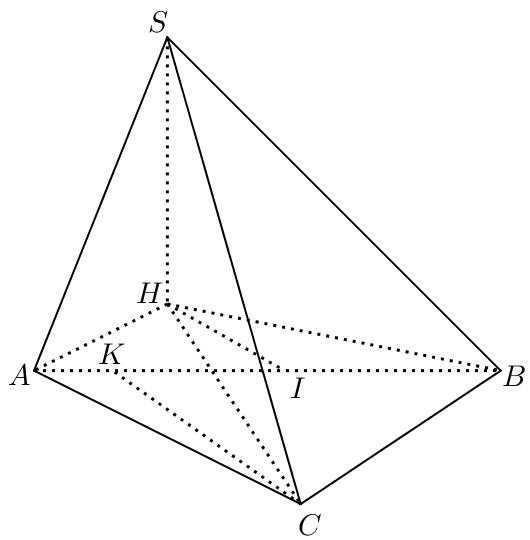
Câu5: Chohìnhchóp tứ giác có đáy làhìnhvuông cạnh , cạnh bên vuônggóc . SABCDABCD 2a SA

với mặt phẳng đáy và .Tính thể tích khối chóp . 32 SAa  . SABCD

42 a 3 122 a 32a 3 32 a

Câu6: Thể tích của khối trụ có chiều cao cmvàbánkính đáy cm bằng

Câu7: Cho biểu thức ,trong đó làphân số

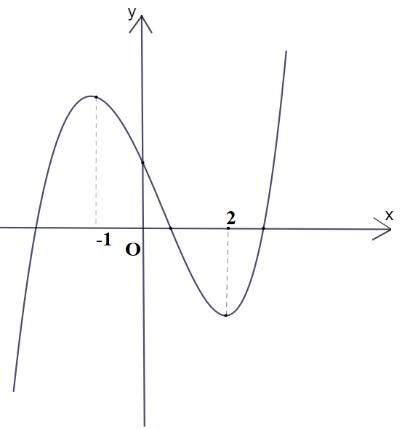
DẠYKÈMQUYNHƠN OFFICIAL

LẦN 1 Câu1: Chohàm số liên tục trên có bảng xét dấu của như sau: yfx   fx  Số điểm cực tiểu của hàm số đã cholà A. B. C. D. 3 1 4 2 Câu2: Nghiệm của phương trình là 223 1 1 5 5 xx x    A. B. Vô nghiệm C. D. 1;2xx 1;2xx 1;2xx Câu3:

đáy và chiều cao là 6B 4h A. B. C. D. 24 12 96 8

Thể tích của khối chópcó diện tích

Câu4:

A. B. C. D. 3



r A. cm B. cm C. cm D. cm 48 3 12 3 7 3 36 3

tối giản. Gọi Khẳng định 354282 m n m n 22Pmn  nàosau đây đúng? A. B. C. D.  425;430P  430;435P  415;420P  420;425P Câu8: Gọi là số nguyên dương bất kì, ,công thức nào dưới đây đúng? n 2n A. B. C. D.  2! 2! n An n  22! ! n n A n   2! 2!2!n An n  22!2! ! n n A n 

Câu9: Gọi lần lượt là độ dài đường sinh, chiều caovàbánkính mặt đáy. Diện tíchxungquanh

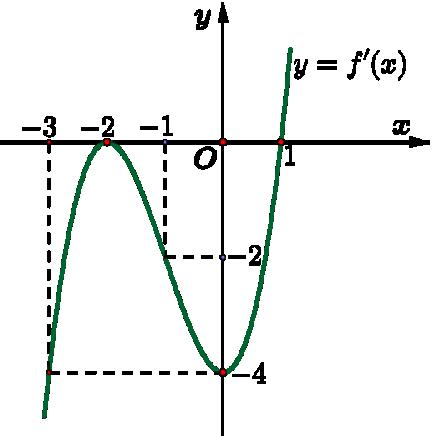
DẠYKÈMQUYNHƠN OFFICIAL

,, lhr của hìnhnónlà: xq S A. B. C. D. 21 3xq Srh  xq Srl  xq Srh  2 xq Srl 

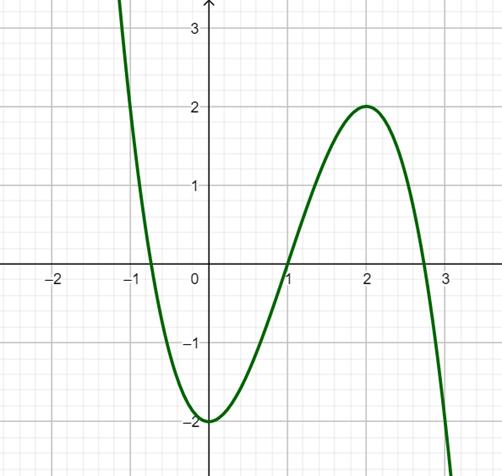
vàhàm số làhàm số bậc bacó đồ thị là yfx   yfx   đường

Hàm số nghịch

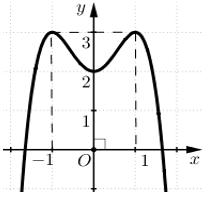
yfx  A. B. C. D.  ;1  2;0  1;  1; Câu11: Tìm tất cả cácgiá trị thực của tham số để hàm số có tập xác định là m  2 ln24yxmx   . A. B.  2;2m ;22;m C. . D. .  ;22;m  2;2m Câu12: Cho cấp số nhân có vàcông bội .Giá trị của bằng  n u12u 3q 2u A. . B. . C. . D. . 2 3 1 9 3 2 6 Câu13: Chohàm số liên tục trên đoạn vàcó đồ thị như hình vẽ bên dưới. Gọi lần yfx   1;2 , Mm lượt làgiá trị lớn nhất vàgiá trị nhỏ nhất của hàm số đã chotrên đoạn .Tacó bằng: 1;22Mm  A. B. C. D. 1 1 4 7 Câu14: Hìnhbát diện đều thuộc loại khối đa diện nàosaudây? A. B. C. D.  4;3  3;3  3;4  3;5

Câu10: Chohàm số có đạo hàmtrên

congtronghình vẽ.

biến trên

DẠYKÈMQUYNHƠN OFFICIAL

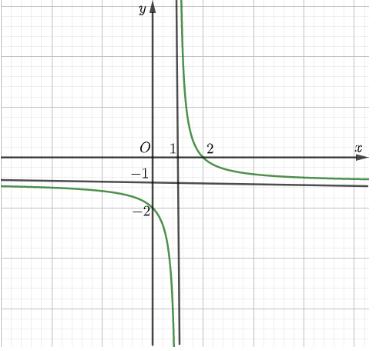
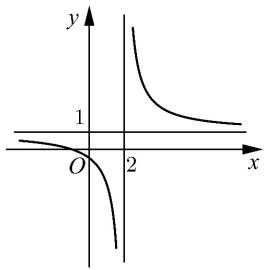
Câu15: Chohàm số có đồ thị như hình vẽ bên dưới. Giá trị của tổng bằng: 1 axb y cx   Sabc  A. B. C. D. 0S 2S 2S 4S Câu16: Tích tất cả các nghiệm của phương trình là 2 33 log2log70 xx A. B. C. D. 7 9 1 2 Câu17: Tổng số đường tiệm cận đứng vàngang của đồ thị hàm số là 2 2 1 2 x y xx   A. B. C. D. 0 2 1 3 Câu18: Lăng trụ tamgiác có

chóp bằng: '''ABCABC V '’’ AABC A. B. C. D. 3 . 4 V .V 2 . 3 V . 3 V Câu19: Với các số

mãn , biểu thức bằng ,0ab 227abab 3logba A. .B. .  33 1 21loglogab  33 1 1loglog 2 ab  C. D. .  33 1 23loglogab  33 1 2loglog 2 ab  Câu20: Đồ thị hàm số nào dưới đây có dạng như đường congtronghình vẽ? A. B. C. D. 3222yxx 3222yxx 4222yxx 4222yxx  Câu21: Gọi lần lượt làgiá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn , Mm 32391yxxx =--.Tínhgiá trị .  1;5 2 TMm  A. . B. . C. . D. 16T= 26T= 20T= 36T=

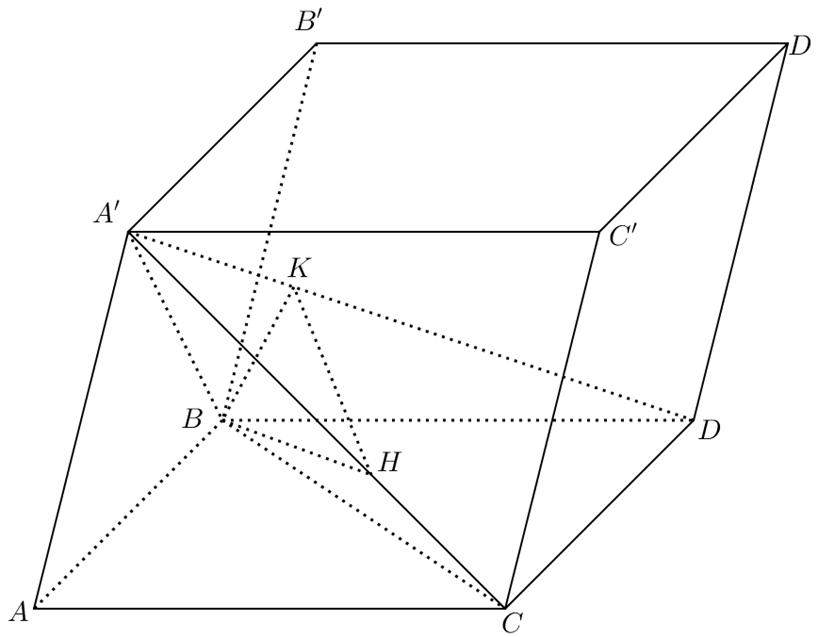
thể tích bằng .Khi đó, thể tích khối

thỏa

Câu22: Tập xác định của hàm số là ()21 yx=-

1;

A. . B. . C. .

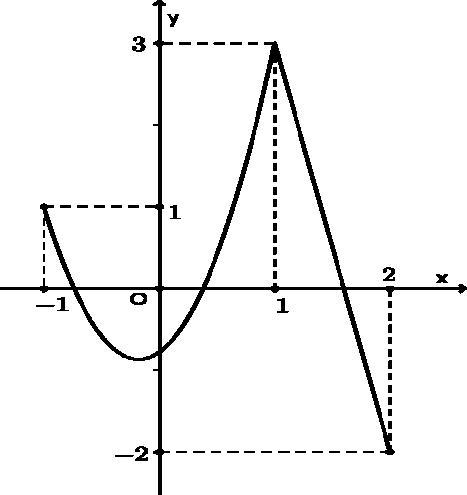
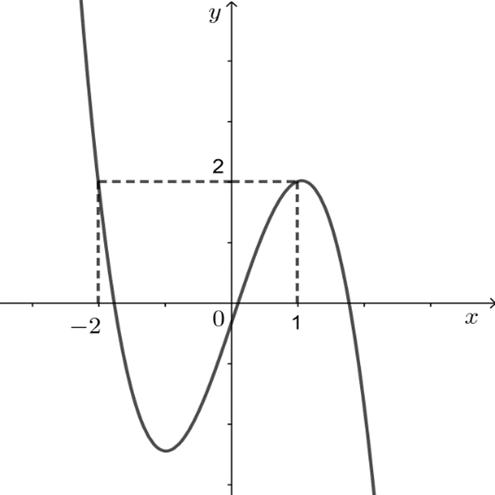
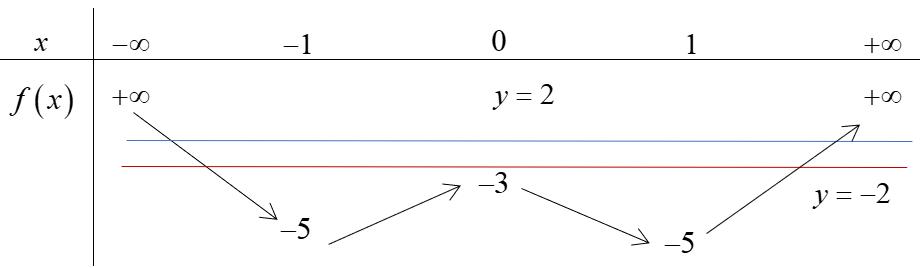
Câu23: Cho đồ thị hàm số liên tục trên vàcó đồ thị như hình vẽ

Số nghiệm của phương trình là  231 fx

A. 4. B. 5. C. 2.

Câu24: Mệnh đề nào dưới đây sai?

A. Hìnhchópcó đáy làhìnhthoicó mặt cầu ngoại tiếp.

B. Hìnhchóp tứ giác đều có mặt cầu ngoại tiếp.

C. Hìnhchópcó đáy làtamgiáccó mặt cầu ngoại tiếp.

D. Hìnhchópcó đáy làhình chữ nhật có mặt cầu ngoại tiếp.

Câu25: Hàm số nào dưới đây khôngcó cực trị?

DẠYKÈMQUYNHƠN OFFICIAL

\1  ;1

D. .  

yfx  

A. B. C. D. 42yx 34yx  33 yxx  22 Vxx 

sai dưới đây. ,0xy,  A. . B. . C. . D. . xyxy   xyxy   xxx   xx  Câu27: Chohàm số xác định trên tập . Số được gọi làgiá trị lớn nhất của hàm số yfx  DM trên nếu yfx  D A. với mọi và tồn tại saocho  fxM  xD  0 xD   0 fxM  B. với mọi .  fxM  xD  C. với mọi  fxM  xD  D. với mọi và tồn tại saocho .  fxM  xD  0 xD   0 fxM  Câu28: Tập nghiệm của bất phương trình là 3 28 x A. . B. . C. . D. . 6;  0;  6;  3;

Chohàm số có bảng biến thiên như sau: fx

Câu26: Cho và .Tìm đẳng thức

Câu29:

Giá trị cực đại của hàm số đã cholà:

Cóbaonhiêugiá trị nguyên của tham số để hàm số

Tổng các giá trị nguyên của tham số để phương trình m có đúng 8 nghiệm thực phân biệt thuộc khoảng

22 2 342410 fxxmfxxm

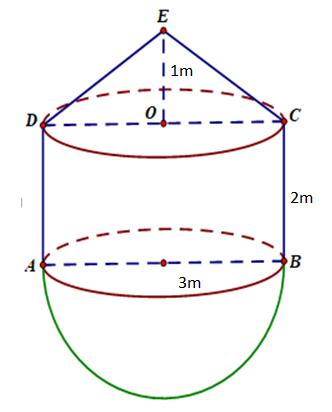
Câu33: Chohình trụ cóhai đáy làhaihìnhtròn và , thiết diện qua trục của hình trụ làhình

vuông. Gọi

DẠYKÈMQUYNHƠN OFFICIAL

A. . B. . C. . D. .

3 2

nhật, vàcác cạnh bên của SABCDABCD 3,4ABAD hìnhchóp

thể

khối cầu ngoại tiếp hìnhchóp đã cho. 60 A. . B. . C. . D. . 2503 3 V  1253 6 V  5003 27 V  503 27 V 

m  3 2 1211fxmxmxx   không có điểm cực đại? A. . B. . C. . D. . 4 6 5 3 Câu32: Chohàm số có bảng biến thiên như sau:  2 yfx 

2 0

Câu30: Chohìnhchóp có đáy làhình chữ

tạo với mặt đáy một góc .Tính

tích

Câu31:



  ? 0; A.

C. D.

7 6 3 13

 O

điểm lần lượt nằm trênhai đường trònvà . Biết và AB  'O O 2 ABa  khoảng cách giữa và bằng .Tính diện tíchxungquanh

hình trụ. AB'OO3 2 a A. . B. . C. . D. . 2 4 a 14 2 a 14 4 a 14 3 a Câu34: Cho khối chóp có đáy làhìnhvuông cạnh cạnh bên vàvuônggóc SABCD ,a  0SAyy với mặt phẳng đáy .Trên cạnh lấy điểm và đặt Tính thể  ABCD ADM (0) AMxxa  tích lớn nhất của khối chóp biết max V .,SABCM222 xya  A. B. C. D. 33 8 a 33 9 a 33 3 a 33 7 a

và làhai

của

Câu35: Chohai mặt phẳng và

songsong với nhauvàcùng cắt khối cầu tâm bánkính

thànhhaihìnhtròncócùngbánkính.Xéthìnhnóncó đỉnh trùng với tâm của một tronghaihình trònnàyvàcóđáylàhìnhtròncònlại.Khidiệntíchxungquanhcủahìnhnónlàlớnnhất,khoảng

cách giữa hai mặt phẳng và bằng: h

; 44

Câu36: Chohàm số liên tục trên đoạn vàcó bảng biến thiên như hình vẽ bên dưới.

Có tất cả baonhiêugiá trị thực của tham số thuộc đoạn để giá trị lớn nhất của hàm

Câu38: Chohàm số , với làtham số. Giả sử đồ thị cắt trục hoành tại

3269 yxxxmC   m  C ba điểm phân biệt cóhoành độ thỏa mãn . Khẳng định nàosau đây đúng? 123 xxx 

A. . B. . 123134xxx 123 134 xxx 

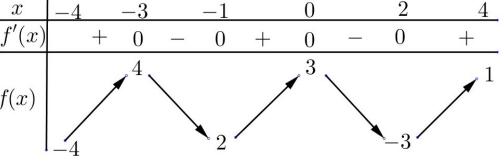
C. D. 123 0134 xxx 

1 23 0134xxx

Câu39: Chocótháp nước như hình dưới đây, tháp được thiết kế gồm thânthápcó dạng hình trụ, phần máiphíatrên dạng hìnhnónvà đáy là nửa hình cầu. Khônggianbêntrongtoàn bộ tháp được minh họa theohình vẽ với đường kính đáy hình trụ, hình cầu và đường kính đáy của hìnhnón đều bằng 3m, chiều caohình trụ là2m, chiều cao của hìnhnónlà1m.

Thể tích của toán bộ khônggianbêntrongtháp nước gần nhất với giá trị nàosau đây?

DẠYKÈMQUYNHƠN OFFICIAL

 P Q

O 43

 P Q A. B. C. D. 46.h 83.h 43.h 8.h





số



 3

 ; 115 A. B. C. D. 9. 8. 10. 11. Câu37: Gọi là tập nghiệm của

trình trên . Tổng các phần S 2 2 2 2log22log32 x x  tử của bằng

; 44

cógiá trị lớn nhất trên đoạn bằng ?

gxfxxfm

322

phương

B. C. D. 42.  82.  6. 62. 



DẠYKÈMQUYNHƠN

OFFICIAL A. B. C. D.  315 2 Vm    3 32 48 a Vm    37 Vm    333 4 Vm   Câu40: Cóbaonhiêu số nguyên dương của tham số m để hàm số đồng biến trên khoảng cos1 10cos x y xm    0; 2     A. B. C. D. 9 12 10 20 Câu41: Cho khối lăng trụ có khoảng cách giữa hai đường . ABCABC 3, ABa4, ACa5, BCa thẳng và bằng Gọi lần lượt làtrung điểm của và (tham khảo ABBC2a, MN AB, AC hình vẽ dưới đây). Thể tích của khối chóp là V ABCNM M N C B A' C' B' A A. B. C. D. 37 Va 38 Va 36 Va 34 Va Câu42: Chohình lập phương có cạnh bằng Gọi làgóc giữa và . .  ABCDABCD a  ACD ABCD Giá trị của bằng: tan A. B. . C. . D. . 2. 3 3 1 2 2 Câu43: Cho đồ thị Gọi làba điểm phân biệt thuộc saocho trực tâm của 2 : 1 Cx y x   ,, ABC  C H tamgiác thuộc đường thẳng . Độ dài đoạn thẳng bằng ABC :310 yx  OH A. . B. C. . D. . 5OH 25.OH 10OH 5OH Câu44: Cóbaonhiêu cặp số nguyên thỏa mãn và ?  ; xy 04000 x  5 5 5252log14 yyxx  A. . B. . C. . D. . 5 2 4 3 Câu45: Cho khối lăng trụ có đáy làtamgiácvuôngcân tại và .Hình ABCABC ABC B 2 ACa  chiếu vuônggóc của trên mặt phẳng làtrung điểm của cạnh và . A  ABC H AB 2AAa   Tính thể tích của khối lăng trụ đã cho. V A. B. C. D. 33Va  36 6 a V 2 22Va  36 2 a V Câu 46: Chohìnhthang ABCD vuông tại A và D có Tính thể tích V của khối tròn 226.CDABAD xoaysinhra bởi hìnhthang ABCD khiquanhxungquanh đường thẳng BC.

Câu47: Có tất cả baonhiêugiá trị nguyên của tham số m để hàm số đồng 432 363  yxmxxm biến trên khoảng ? 0;

B. C. D. 5 6 4 7

DẠYKÈMQUYNHƠN

Câu48: Cho phương trình ( làtham số thực). Có tất cả baonhiêu

2 22 4loglog570   x xx mm giá trị nguyên dương của m để phương trình đã chocó đúng hai nghiệm phân biệt?

A. B. C. Vô số D. 47 49 48

Câu49: Chohìnhchóp có ;Singóc giữa hai . SABC4,32, ABaBCa 

mặt phẳng và bằng Bánkính mặt cầu ngoại tiếp hìnhchóp

A B C D A. B. C. D. 1352 4 V   362V 632 2 V   452 2 V  

OFFICIAL

 A.

 



ABCSACSBC    

45;90

 SAB SBC 2 . 4 A. B. C. D. 183 6 a 183 3 a 53 12 a 35 12 a Câu50: Một hộp có6viênbixanh,4viênbi đỏ và5viênbivàng. Chọn ngẫu nhiên5viênbitrong hộp, tínhxác suất để 5viênbi được chọn có đủ bamàuvà số viênbi đỏ lớn hơn số viênbivàng. A. . B. . C. . D. . 190 1001 310 1001 6 143 12 143 ---------- HẾT ----------

đã cho bằng

1)Hàm số đã cho đồng biến trên 1;. 

2)Hàm số đã cho nghịch biến trên \1

3)Hàm số đã chokhôngcó điểm cực trị.

4)Hàm số đã cho nghịch biến trêncác khoảng và  ;1 1;

DẠYKÈMQUYNHƠN OFFICIAL

Số các mệnh đề đúng là

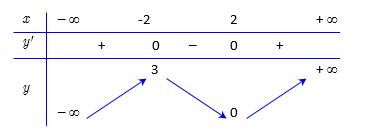
BẢNG ĐÁP ÁN 1.D 2.A 3.D 4.B 5.A 6.D 7.D 8.A 9.B 10.A 11.D 12.D 13.B 14.C 15.C 16.B 17.C 18.C 19.B 20.C 21.D 22.C 23.B 24.A 25.B 26.B 27.D 28.C 29.C 30.C 31.A 32.B 33.C 34.A 35.D 36.C 37.A 38.C 39.A 40.A 41.C 42.A 43.B 44.D 45.D 46.C 47.B 48.A 49.A 50.A Câu1: Chohàm số liên tục trên có bảng xét dấu của như sau: yfx   fx  Số điểm cực tiểu của hàm số đã cholà A. . B. . C. . D. . 3 1 4 2 Lời giải Chọn D Dựa vào bảng xét dấu đạo hàm,tacóhàm số đạt cực tiểu tại .0;4xx Vậy hàm số đã chocóhai điểm cực tiểu. Câu2: Nghiệm của phương trình là 223 1 1 5 5 xx x    A. . B. Vô nghiệm. C. . D. . 1;2xx 1;2xx 1;2xx Lời giải Chọn A Phương trình đã cho tương đương 22312 1 5520 2 xxx x xx x     Vậy phương trìnhcó nghiệm .1;2xx Câu3: Thể tích của khối chópcó diện tích đáy và chiều cao là 6B 4h A. B. C. D. 24 12 96 8 Lời giải Chọn D 11 648 33  kch VBh Câu4: Chohàm số .Xétcác mệnh đề sau:

2 1   x y x

A. B. C. D. 4 2 3 1

Lời giải

Chọn B

Tacó: nênhàm số đã chokhôngcó điểm cực trị, nghịch 2 23 0;1 11    x y y x x x

biến trêncác khoảng và  ;1 1;

Câu5: Chohìnhchóp tứ giác có đáy làhìnhvuông cạnh , cạnh bên vuônggóc . SABCDABCD 2a SA

với mặt phẳng đáy và .Tính thể tích khối chóp . 32 SAa  SABCD A. B. C. D. 3 42 a 3 122 a 32a 3 32 a Lời

DẠYKÈMQUYNHƠN OFFICIAL

giải Chọn A Diện tíchhìnhvuông là ABCD2224 Saa  Suyra thể tích khối chóp là . SABCD 23 11 32442 33 VSASaaa   Câu6: Thể tích của khối trụ có chiều cao cmvàbánkính đáy cm bằng V 4h 3r A. cm B. cm C. cm D. cm 48 3 12 3 7 3 36 3 Lời giải Chọn D Thể tích khối trụ là cm. 223436VRh  3 Câu7: Cho biểu thức ,trong đó làphân số tối giản. Gọi Khẳng định 354282 m n m n 22Pmn  nàosau đây đúng? A. B. C. D.  425;430P  430;435P  415;420P  420;425P Lời giải Chọn D Tacó 3 8441414 3 3 333 3 3 53 2 5 5 555515 42842242242422222     Từ đó suyra ,14m15n Vậy .22 1415421420;425P Câu8: Gọi là số nguyên dương bất kì, ,công thức nào dưới đây đúng? n 2n

Câu9: Gọi lần lượt là độ dài đường sinh, chiều caovàbánkính mặt đáy. Diện tíchxungquanh ,, lhr

DẠYKÈMQUYNHƠN

Hìnhnóncóbánkính đáy , đường sinhnên diện tíchxungquanh . r l xq

Câu10: Chohàm số có đạo hàmtrên vàhàm số làhàm số bậc bacó đồ

A. B. C. D.  2! 2! n An n  22! ! n n A n   2! 2!2!n An n  22!2! ! n n A n  Lời giải Chọn A

.  2! 2! n An n 

của

xq S A. . B. . C. . D. . 21 3xq Srh  xq Srl  xq Srh  2 xq Srl  Lời giải Chọn

OFFICIAL

Công thức đúng là

hìnhnónlà:



là 

  yfx   đường congtronghình vẽ. Hàm số nghịch biến trên yfx  A. B. C. D.  ;1  2;0  1;  1; Lời giải Chọn A Dựa vào đồ thị, ta thấy .Do đó hàm số nghịch biến trên khoảng . 0,1fxx   ;1 Câu11: Tìm tất cả cácgiá trị thực của tham số để hàm số có tập xác định là m  2 ln24yxmx   . A. B.  2;2m ;22;m C. . D. .  ;22;m  2;2m Lời giải Chọn D Hàm số có tập xác định là .  2 ln24yxmx   2240, xmxx 

Srl

thị

yfx

Câu14: Hìnhbát diện đều thuộc loại khối đa diện nàosaudây?

DẠYKÈMQUYNHƠN

Câu15: Chohàm số có đồ thị như hình vẽ bên dưới. Giá trị của tổng bằng: 1

OFFICIAL Khi đó hay .  2 2 10 4022 40 a m m m         2;2m Câu12: Cho cấp số nhân có vàcông bội .Giá trị của bằng  n u12u 3q 2u A. . B. . C. . D. . 2 3 1 9 3 2 6 Lời giải Chọn D Số hạng thứ hai . 21.2.36uuq Câu13: Chohàm số liên tục trên đoạn vàcó đồ thị như hình vẽ bên dưới. Gọi lần yfx   1;2 , Mm lượt làgiá trị lớn nhất vàgiá trị nhỏ nhất của hàm số đã chotrên đoạn .Tacó bằng: 1;22Mm  A. B. C. D. 1 1 4 7 Lời giải Chọn B Tacó 3 21 2 M Mm m   

A. B. C. D.  4;3  3;3  3;4  3;5 Lời giải Chọn C

axb

Sabc

y cx  



DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D. 0S 2S 2S 4S Lời giải Chọn C Tacó: Tiệm cận ngang: 1a y c  Tiệm cận đứng: 1 1x c  Từ đây suyra: . 1 1 a c    Lại có đồ thị cắt trục hoành tại nên hay 2x20 ab 22.ba Vậy 1212Sabc Câu16: Tích tất cả các nghiệm của phương trình là 2 33 log2log70 xx A. B. C. D. 7 9 1 2 Lời giải Chọn B Điều kiện: 0.x Khi đó: 122 31 1 2 2 33 112 22 32 2 log1223log2log70 .39. log1223 x x xx xx x x                Câu17: Tổng số đường tiệm cận đứng vàngang của đồ thị hàm số là 2 2 1 2 x y xx   A. B. C. D. 0 2 1 3 Lời giải Chọn C Tập xác định  1;00;1D Hàm số khôngcó tiệm cận ngang  là tiệm cận đứng 0 lim x y 0x Câu18: Lăng trụ tamgiác có thể tích bằng .Khi đó, thể tích khối chóp bằng: '''ABCABC V '’’ AABC

A. . 3222yxx

B. . 3222yxx

C. . 4222yxx

D. 4222yxx 

DẠYKÈMQUYNHƠN

OFFICIAL A. B. C. D. 3 . 4 V .V 2 . 3 V . 3 V Lời giải Chọn C ' ' ’’(/(’’))’’ 1 . 3 3 AABC AABCABC VVdS   Câu19: Với các số thỏa mãn , biểu thức bằng ,0ab 227abab 3logba A. .B. .  33 1 21loglogab  33 1 1loglog 2 ab  C. D. .  33 1 23loglogab  33 1 2loglog 2 ab  Lời giải Chọn B Tacó:      22 2 2 2 2 3 3 3 33 3 33 loglog log log 7 29 9 9 2.2loglog 1 1loglog 2 ab ab ab aabb abab abab ab ab ab ab            Câu20:

như đường congtronghình vẽ?

Đồ thị hàm số nào dưới đây có dạng

Lời

Chọn C Đồ thị hàmtrùng phương có . lim0 x ya  

giải

C Vì số mũ nguyênâmnênhàm số xác định khivà chỉ khi .101 xx

Vậy tập xác định là .{} 1D\ =

Câu23: Cho đồ thị hàm số liên tục trên vàcó đồ thị như hình vẽ 

Số nghiệm của phương trình là  231 fx

A. 4. B. 5. C. 2. D. 6. Lời giải Chọn B

2312 231 2311 fx fx

Tacó . 

Dựa vào đồ thị, phương trình có nghiệm phân biệt, phương trình có

nghiệm phân biệt. Các nghiệm khácnhaunên phương trình đã chocó nghiệm. 5

Câu24: Mệnh đề nào dưới đây sai?

A. Hìnhchópcó đáy làhìnhthoicó mặt cầu ngoại tiếp.

DẠYKÈMQUYNHƠN OFFICIAL

B. Hìnhchóp tứ giác đều có mặt cầu ngoại tiếp.

C. Hìnhchópcó đáy làtamgiáccó mặt cầu ngoại tiếp.

Câu21: Gọi lần lượt làgiá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn , Mm 32391yxxx =--.Tínhgiá trị .  1;5 2 TMm  A. . B. . C. . D. 16T= 26T= 20T= 36T= Lời giải Chọn D Hàm số liên tục vàxác định trên . 32391yxxx =---  1;5 Đạo hàm , 2 369yxx     11;5 0 31;5 x y x     Tacó .  112,328,54

  

 

=A. . B. . C. . D. .   1; \1 

 Lời

yy y

Vậy .4,28,236MmMm

Câu22: Tập xác định của hàm số là ()21 yx

Chọn

yfx 



  

fx fx fx              



2

2 1fx3

D. Hìnhchópcó đáy làhình chữ nhật có mặt cầu ngoại tiếp. Lời giải

Chọn A

Hìnhthoikhông nội tiếp được đường tròn,do đó hìnhchópcó đáy làhìnhthoikhôngcó mặt

cầu ngoại tiếp.

Bản wordpháthành từ websiteTailieuchuan.vn

Câu25: Hàm số nào dưới đây khôngcó cực trị?

Chọn B

Hàm số xác định với mọi 34yx  x

Tacó 30,.yx 

Vậy hàm số nàykhôngcó cực trị.

Câu26: Cho và .Tìm đẳng thức sai dưới đây. ,0xy

DẠYKÈMQUYNHƠN OFFICIAL

A. . B. . C. . D. . 42yx 34yx  33 yxx  22 Vxx  Lời giải

,  A. . B. . C. . D. . xyxy   xyxy   xxx   xx  Lời giải Chọn B Câu27: Chohàm số xác định trên tập . Số được gọi làgiá trị lớn nhất của hàm số yfx  DM trên nếu yfx  D A. với mọi và tồn tại saocho  fxM  xD  0 xD   0 fxM  B. với mọi .  fxM  xD  C. với mọi  fxM  xD  D. với mọi và tồn tại saocho  fxM  xD  0 xD   0 fxM  Lời giải Chọn D Câu28: Tập nghiệm của bất phương trình là 3 28 x A. . B. . C. .

6;  0;  6;  3; Lời giải Chọn C 3

2822336 x x xx  Vậy

D. .

tập nghiệm của bất phương trình đã cholà . 6;T Câu29: Chohàm số có bảng biến thiên như sau: fx Giá trị cực đại của hàm số đã cholà:

Gọi .Khi đó, là trục của hìnhchóp . OACBD  SO . SABCD

Gọi làtrung điểm của của . Kẻ đường trung trực của cạnh cắt tại .Khi đó, M SD SDSOII làtâm khối cầu ngoại tiếp hìnhchóp . SABCD

DẠYKÈMQUYNHƠN OFFICIAL

A. . B. . C. . D. . 2 0 3 2 Lời giải Chọn C

cạnh bên của . SABCDABCD 3,4ABAD hìnhchóp tạo với mặt đáy một góc .Tính thể tích khối cầu ngoại tiếp hìnhchóp đã cho. 60 A. . B. . C. . D. . 2503 3 V  1253 6 V  5003 27 V  503 27 V  Lời giải Chọn C 60o I M O D B A C S

Câu30: Chohìnhchóp có đáy làhình chữ nhật, vàcác

 2

2S SMSIMISMSDSD SI SOSDOD SOO   Tacó: .Xéttamgiác

,tacó: 22 115 34 222 ODBD SOD O , . 53 tan60D 2 SOO    5 cos60 OD SD   Suyra . Vậy 2 553 5323 2 SI 3 4535003 3327 V       Câu31: Cóbaonhiêugiá trị nguyên của tham số để hàm số m  3 2 1211fxmxmxx   không có điểm cực đại? A. . B. . C. . D. . 4 6 5 3 Lời giải Chọn A

Tacó: suyra . SMISOD

vuông tại

Mà . 0,1,2mm

Vậy có4giá trị nguyên của tham số thỏa yêu cầu đề bài. m

Câu32: Chohàm số có bảng biến thiên như sau:

kép

Tổng các giá trị nguyên của tham số

phương trình m

DẠYKÈMQUYNHƠN OFFICIAL

Với ,tacó: là một parabol với hệ số suyrahàm số chỉ có1 1m 2 31fxxx  30a điểm cực tiểu thỏa yêu cầu đề bài. Với ,tacó:.1m  3 2 1211fxmxmxx   Suyra .Khi đó, hàm số khôngcó điểm cực đại hàm số  2 '312211 fxmxmx    khôngcó cực trị phương trình vô nghiệm hoặc có nghiệm

 



  2 213110

 2 4720 mm  1 2 4 m 

'0fx







2 yfx

có đúng 8 nghiệm thực phân biệt thuộc khoảng  22 2 342410 fxxmfxxm   ? 0; A. B. C. D. 7 6 3 13 Lời giải Chọn B Xéthàm số .  24 gxfxx  Có .Cho .  2 '24'4 gxxfxx    2 2 '0 '401 x gxfxx      Tacó:  2 2 2 2 42 4 '404222 040 4 xxx fxxxx=x xxx= x              Bảng biến thiên x 022222 4 ' gx 0000

để

22 2 342410 fxxmfxxm

Dựa vào bảng biến thiênta thấy phương trình có tối đa là5 nghiệm phân biệt

Do đó, để phương trình có đúng 8 nghiệm phân

22 2 342410 fxxmfxxm

. Thế vào phương trình(2)ta được .Khi , phương

DẠYKÈMQUYNHƠN

gx22 2 33



    2 32102 gxmgxm   Tacó: .   2 2 2

m mmmm m    

OFFICIAL

Lại có: .

24.3.1081640,4

 gxhm 



  biệt thì

 

     2gx 7m 7m trình(2)cóhai nghiệm thỏa yêu cầu.   2 1 gx gx     TH2. .   32 22 gx gx        2 2 24 3 2 6 24 2 2 6 mm mm           182412 122412 mm mm      Với ,tacó: (vôlí). 4m 18612 122212 m  Với ,tacó: , . 4m 182212 85 12612 m m       7,6mm  Vậy

bàilà .

 7766  Câu33:

, thiết diện qua trục của hình trụ làhình  O 'O vuông. Gọi và làhai điểm lần lượt nằm trênhai đường trònvà . Biết và AB  'O O 2 ABa  khoảng cách giữa và bằng .Tính diện tíchxungquanh của hình trụ. AB'OO3 2 a A. . B. . C. . D. . 2 4 a 14 2 a 14 4 a 14 3 a Lời giải Chọn C

TH1.

2 22 gx gx

có tổng cácgiá trị nguyên của tham số thỏa yêu cầu đề

Chohình trụ cóhai đáy làhaihìnhtròn và

Thiết diện qua trục làhìnhvuôngnên . '2  AAR

Tacó: . 2222222 14 ''4434 4 aAAABABRRaaR  

Câu34: Cho khối chóp có đáy làhìnhvuông cạnh cạnh bên vàvuônggóc . SABCD ,a 0.SAyy

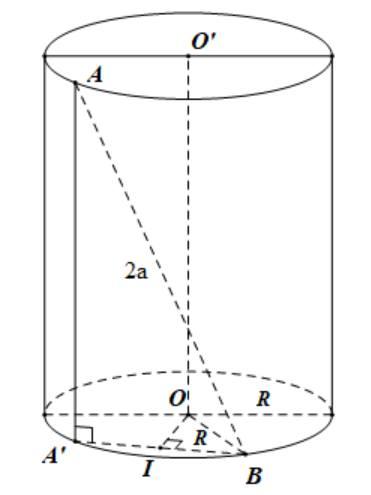
DẠYKÈMQUYNHƠN OFFICIAL

Dựng

đáy. '//'AAOO' AO  I ' ABR Suyra:khoảng cách giữa và là . AB'OO 3 2 Oa I Và:

2 222 223'243

IBOBOIR

  

(), gọi làtrung điểm , làbánkính

4 a

ABIBRa

 với



(0).AMxxa  tích

 A. B. C. D. 33 8 a 33 9 a 33 3 a 33 7 a Lời giải Chọn A Theo đề bài,tacó và . 0xa 22 yax  Khi đó  22111 3326SABCM ABCM xaa VSSA yaaxxa      Taxéthàm số với 22fxxaax  0xa

mặt phẳng đáy .Trên cạnh lấy điểm và đặt Tính thể

ABCD ADM

lớn nhất của khối chóp biết max

,SABCM222 xya

DẠYKÈMQUYNHƠN

OFFICIAL  22 22 2 fxaxa x ax    0 2 afxx  Tacó bảng biến thiên của fx Vậy suyra (đvtt).  2 0; 33 max 24 a faa xf    3 (0;a) 3 max 8SABCM a V Câu35: Chohai mặt phẳng và songsong với nhauvàcùng cắt khối cầu tâm bánkính  P Q O 43 thànhhaihìnhtròncócùngbánkính.Xéthìnhnóncó đỉnh trùng với tâm của một tronghaihình trònnàyvàcóđáylàhìnhtròncònlại.Khidiệntíchxungquanhcủahìnhnónlàlớnnhất,khoảng cách giữa hai mặt phẳng và bằng: h  P Q A. B. C. D. 46h 83h 43h 8.h Lời giải Chọn D B O' O A ; .   ,   dPQOOh ABR vuông tại nên OAB O 2 222 . 4   h OAABOBR vuông tại nên  OAO O 2 2 2222 23 44   h hOAOOOAhRR Diện tíchxungquanh của hìnhnón: . 2 2 2 23 .... 44            h h SOAOARR Đặt 2 ,0 4  h xx

DẠYKÈMQUYNHƠN

Câu36: Chohàm số liên tục trên đoạn vàcó bảng biến thiên như hình vẽ bên dưới.

Có tất cả baonhiêugiá trị thực của tham số thuộc đoạn để giá trị lớn nhất của hàm m

cógiá trị lớn nhất trên đoạn bằng ?

Giả sử giá trị lớn nhất của hàm trên đoạn bằng

gx 1;132(m) f

OFFICIAL Xét với .  22 422..3.23    fxRxRxRRxx20;  xR .  2 22 26 2 3     Rx fx RxRx .  2 2 0260 3   R fxRxx Diện tíchxungquanh của hìnhnón đạt giá trị lớn nhất khi đạt giá trị lớn nhất trên fx .Khi đó . 20; R  222 2 2 2433423 8 343333 RhR RR x h h  

fx  ; 44

số

gxfxxfm  3322  ; 115 A. B. C. D. 9. 8. 10. 11. Lời giải Chọn C TH1:



 ; 44

Theo giả thiết tacó . Thử lại tacó không thoả

Với Dựa vàoBBT của hàm số tacó5giá trị thoả mãn.

1fm

TH2: Giả sử giá trị lớn nhất của hàm trên đoạn bằng

Theo giả thiết tacó . Thử lại tacó không thoả

Với . Dựa vàoBBT của hàm số tacó5giá trị thoả mãn.

Vậy có10giá trị m thoả mãn đề bài.

Câu37: Gọi là tập nghiệm của phương trình trên . Tổng các

Câu38: Chohàm số , với làtham số. Giả sử đồ thị cắt trục hoành

ba điểm phân biệt cóhoành độ thỏa mãn . Khẳng định nàosau đây đúng? 123 xxx 

A. B. 123134xxx 123 134 xxx 

C. . D. . 123 0134 xxx  1 23 0134xxx

DẠYKÈMQUYNHƠN OFFICIAL

(m)4

f f f   

fm

32(m)5(m)1



fx m



f

gx 1;132(m)

(m)1

f f f   4fm

32(m)5(m)4



fx m

1fm

S 2 2 2 2log22log32 x x  tử

S A. B. C. D. 42 

 6 62  Lời giải Chọn A Điều kiện xác định của phương trìnhlà (*) 2 2201 33 0 x x x x        Với điều kiện (*) phương trình 2 2 2 2log22log32 x x   2 2 2 2 log22log32 x x     22 2 log2232 xx      2 2234 xx          2 2 223228401 223228802 xx xx xx xx             Phương trình(1)cócác nghiệm  22;22x Nx L   Phương trình(2)có nghiệm 2 xN  Vậy tập nghiệm của phương trình đã cholà . Tổng các nghiệm bằng . 

S 42 

phần

của bằng

22;2

tại  32

yxxxmC   m  C

(1).Xéthàm số với

3269 fxxxx  x Tacó . 2 1 '31290 3 x fxxx x   Tacó  32 0 0690 3 x fxxxx x   

Lời giải Chọn

Phương trìnhhoành độ giao điểm của đồ thị (C) với trục hoành

32 32 69069 xxxmmxxx 

4694

BBT của hàm số fx

Đồ thị (C) cắt trục hoành tại 3 điểm phân biệt cóhoành độ thoả mãn 123 xxx 

Phương trình(1)có3 nghiệm  123 xxx 

Đường thẳng cắt đồ thị hàm số tại 3 điểm cóhoành độ

ym  fx 123 xxx 

Dựa vàoBBTtasuyra . 123 0134 xxx 

Bản wordpháthành từ websiteTailieuchuan.vn

Thể tích của toán bộ khônggianbêntrongtháp nước gần nhất với giá trị nàosau đây?

DẠYKÈMQUYNHƠN OFFICIAL

x   

và 

4 x fx xxx



A. B. C. D.  315 2 Vm   32 48 a V  37 Vm    333 4 Vm   Lời giải Chọn A Tacó: Vnón , Vtrụ 2 133 324 OE        2 399 2 242 AD      

Vậy thể tích của toán bộ khônggianbêntrongtháp nước bằng:

Câu40: Cóbaonhiêu số nguyên dương của tham số m để hàm số đồng biến trên khoảng

DẠYKÈMQUYNHƠN OFFICIAL

Thể tích phần còn lại 3 427 3..9 8 224 cau V V    

3993015 42442  

cos1

   0; 2      A. B. C. D. 9 12 10 20 Lời giải Chọn A Đặt cos,0;0;1 2 txx t      Ta thấy hàm số nghịchbiến trên khoảng nên để hàm số đồng cos tx  0; 2     cos1 10cos x y xm    biến trên khoảng khivà chỉ khihàm số nghịch biến trên khoảng 0; 2     1 10 t y tm     0;1 Tacó .  2 10 0,0;110 10 fm t t m tm     Lại có 100 0 100 10101 10 m m m tm t mm        Khi đó tacó: . 10 00101;...;9 10 m m m m m m           Câu41: Cho khối lăng trụ có khoảng cách giữa hai đường . ABCABC 3, ABa4, ACa5, BCa thẳng và bằng Gọi lần lượt làtrung điểm của và (tham khảo ABBC2. a, MN AB, AC hình vẽ dưới đây). Thể tích của khối chóp là V . ABCNM M N C B A' C' B' A A. B. C. D. 37 Va 38 Va 36 Va 34 Va Lời giải

10cos x y xm

DẠYKÈMQUYNHƠN

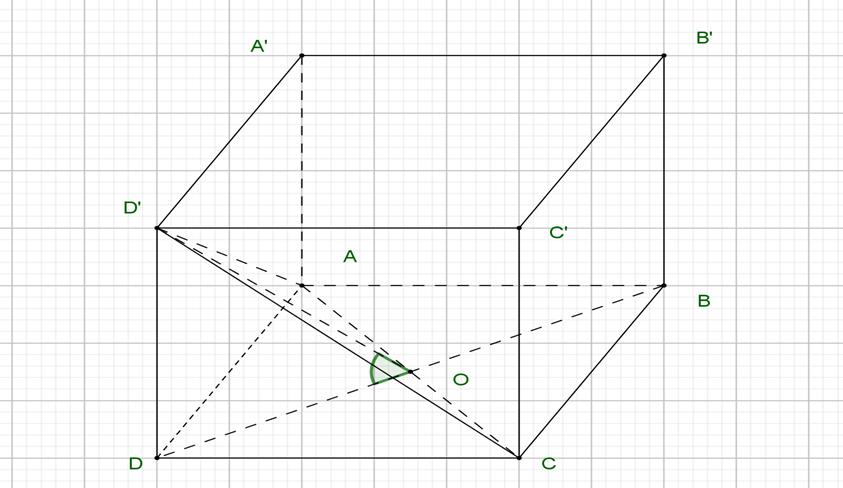
OFFICIAL Chọn C M N C B A' C' B' A Gọi V là thể tích khối lăng trụ. Vì BMCN làhìnhthangcóhai đáy BC, MN và nêntacó 2 BCMN    1 111 ;.;. 2 222 BMN BCNSdBMNMNdNBCBCS      Suyra . 33311 . 22232ABCNMABMNABCN ABCNNABCVVVVV VV    Tacó đáy làtamgiác vuông tại A nên: . ABC 26ABC Sa   Vì    // ; ;2 BCABCdABBCdBCABCdBABCah        Với h là chiều cao của khối lăng trụ. Suyra 23 31 .2.612 6 2 ABC ABCNM VhSaaaVVa   Câu42: Chohình lập phương có cạnh bằng . Gọi làgóc giữa và . .  ABCDABCD a  ACD ABCD Giá trị của bằng: tan A. B. C. D. 2 3 3 1 2 2 Lời giải Chọn A Gọi làtrung điểm của .Tamgiác cân tại .Do đó góc giữa O AC ' DAC' DDOAC   ACD và là ABCD  ' 'tan 2 2 2 DDa DOD DOa  Câu43: Cho đồ thị . Gọi làba điểm phân biệt thuộc saocho trực tâm của 2 : 1 Cx y x   ,, ABC  C H tamgiác thuộc đường thẳng . Độ dài đoạn thẳng bằng ABC :310 yx  OH

5 21 5 5 5252log145log115521 y y yxx xx y   () 1

Đặt . ()5 log115t xtx+=Þ+=

Phương trình trở thành: () 1 ()21555215 t y t y ++=++() 2

Xéthàm số trên . ()55ufuu=+ 

nênhàm số đồng biến trên . ()55ln50, u fu u

¢=+>"Î ()fu 

Do đó ()()() 22121 ftfyty Û=+Û=+

() 21 5 log121155251 y y xyx x+ Þ+=+Û+=Û=-

Vì 25 1400114001 0400005251400025 log2085525 y y x y££Þ£-£Û££Û££ »

Do ,có3giá trị của ynên cũng có3giá trị của {} 0,1,2yy  ÎÞÎ x

Vậy có3 cặp số nguyên .() ; xy

Câu45: Cho khối lăng trụ có đáy làtamgiácvuôngcân tại và .Hình . ABCABC ABC B 2 ACa  chiếu vuônggóc của trên mặt phẳng làtrung điểm của cạnh và . A

ABC H AB 2AAa  

Tính thể tích của khối lăng trụ đã cho.

DẠYKÈMQUYNHƠN

OFFICIAL A. . B. C. . D. . 5OH 25.OH 10OH 5OH Lời giải Chọn B Do . ;310HHxx   Mà làba điểm phân biệt thuộc nên trực tâm của tamgiác cũng thuộc ,, ABC  C H ABC  C dó đó  2 1 1 2 310 2 131012440 x x x x x xxx x xx                 Vậy  2;42;425.HOH OH   Câu44: Cóbaonhiêu cặp số nguyên thỏa mãn và ?  ; xy 04000 x  5 5 5252log14 yyxx  A. B. C. D. 5 2 4 3 Lời giải Chọn D Tacó: .   

 

V A. B. C. D. 33Va  36 6 a V 2 22Va  36 2 a V Lời giải Chọn D

DẠYKÈMQUYNHƠN

OFFICIAL Dotamgiác vuôngcân tại và nên ABC B2 ACa  2 2 2 aABBCaAH Xéttamgiác tacó: AAH  226 2 aAHAAAH     Vậy: 36 . 2 ABCABCABC aVSAH     Câu46: Chohìnhthang ABCD vuông tại A và D có Tính thể tích V của khối tròn 226CDABAD xoaysinhra bởi hìnhthang ABCD khiquanhxungquanh đường thẳng BC. A B C D A. B. C. D. 1352 . 4 V   362V 632 . 2 V   452 . 2 V   Lời giải Chọn C

DẠYKÈMQUYNHƠN OFFICIAL

Thể tích khối trònxoaysinhrasaukhiquayhìnhthang xungquanh cạnh được ABCD BC tính như sau: với là thể tích khối nóncó đỉnh là có đáy làhìnhtròntâm  122 VVV  1V C , là khối nón đỉnh có đáy làhìnhtròntâmtâm B2V H I Tamgiác vuôngcân tại nên BCD B 232BCBDAB Nên 2 2 1 11 ..32.32182 33 VBCBD       Dễ dàng chứng minh được làhìnhvuôngnên BAHE 32 232 2 AEHBAB HI  Nên 2 2 2 11323292 33224 VIAIH          Vậy  12 632 2 2 VVV    Câu47: Có tất cả baonhiêugiá trị nguyên của tham số m để hàm số đồng 432 363  yxmxxm biến trên khoảng ? 0; A. B. C. D. 5 6 4 7 Lời giải Chọn B Đặt 432 363  fxxmxxm Do .  432 limlim3630     x x fxxmxxm Nên đồng biến trên  yfx  0;   0 00 ,0; ,0; 0 0                    fx f x x fx fx

Để phương trìnhcó đúng hai nghiệm phân biệt: TH1: . 7 log0011 m mm

TH2: .

DẠYKÈMQUYNHƠN

4 7 2log27493;4;;48 

OFFICIAL   32 3 30 ,0; 4,0; 123120 4               m m x x xmxx mx x .  0; 3 3 438 min48             x m m m m xm x Vậy .38  m Câu48:

tất cả baonhiêu   2 22 4loglog570   x xx mm giá trị

dương của m để phương trình đã chocó đúng hai nghiệm phân biệt? A. B. C. Vô số D. 47 49 48 Lời giải Chọn A Xét phương trình   2 22 4loglog570   x xx m Điều kiện: . 70log 70         x xxm m x Phương trình tương đương 2 5 22 4 7 2 4loglog50 2 70 log            x x xx x m xm

Cho phương trình ( làtham số thực). Có

nguyên

5 4 5 2

m mm Vậy có tất cả giá trị thỏa mãn. 47m Câu49: Chohìnhchóp có ;Singóc giữa hai SABC4,32, ABaBCa   45;90ABCSACSBC     mặt phẳng và bằng Bánkính mặt cầu ngoại tiếp hìnhchóp đã cho bằng  SAB SBC 2 . 4 A. . B. . C. . D. . 183 6 a 183 3 a 53 12 a 35 12 a Lời giải Chọn A

Do nên nằm trên mặt cầu đường kính , , SAACSBBC   ,,, SABC SC

Tacó . 222 02 2..sin451010ACABBCABBC aACa  

Gọi làhình chiếu vuônggóc của lên . H S ABC

Tacó và nên . CASA CASH  CAHA 

Tương tự: .CBHB 

Khi đó nội tiếp đường tròn đường kính nên . ABCH HC 025 sin45 AC HC a

Tacó: 222HBHCBCa  

Gọi làhình chiếu vuônggóc của và của lên .Khi đó và vuôngcân , KI CHAB CKB

6 15nC  Gọi là biến cố “5viênbi được chọn có đủ bamàuvà số viênbi đỏ lớn hơn số viênbivàng” A

* Số cách lấy được bixanh, bi đỏ vàbivànglà:221 221 645 .. CCC

* Số cách lấy được bixanh, bi đỏ vàbivànglà:131 131 645CCC

DẠYKÈMQUYNHƠN OFFICIAL

Khi đó . 221131 645645570nACCCCCC

HIB nên và . 32 3 2 Ca K a 2 HB HIa  Do đó     , 1 3 , dHSABHI CKdCSAB  Tacó .       2,2 23 sin ,. , 4 4 42 2 dCSAB a a dCSABCB dHSAB CB      Khi đó .   2 2 2 2222 2 111413 3 , Sa H SH HIaaadHSAB    Vậy ,suyrabánkính mặt cầu . 2 22 2183 20 33 a a SCSHHC a  183 6 a R Câu50: Một hộp có6viênbixanh,4viênbi đỏ và5viênbivàng. Chọn ngẫu nhiên5viênbitrong hộp, tínhxác suất để 5viênbi được chọn có đủ bamàuvà số viênbi đỏ lớn hơn số viênbivàng. A. B. C. D. 190 1001 310 1001 6 143 12 143 Lời giải Chọn A Tacó số phần tử của khônggian mẫu 





DẠYKÈMQUYNHƠN

OFFICIAL Vậy .  5 15 570190 1001 nA PA nC  

TRƯỜNG THPTCHUYÊNTHÁIBÌNH

ĐỀ THI THỬ TỐT NGHIỆP THPT– NĂM HỌC 2022–2023

LẦN 1

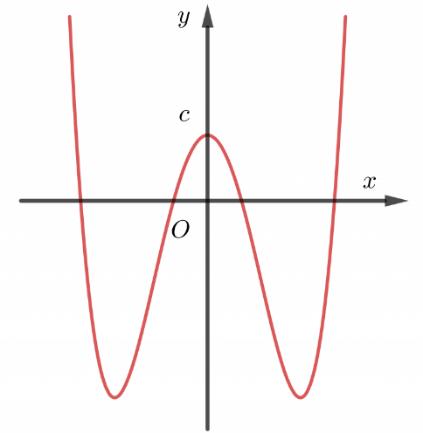
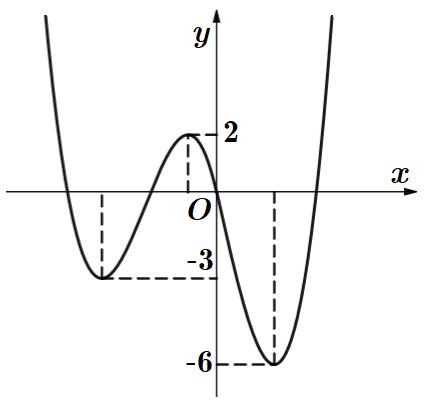
Câu1: Chohàm số có đồ thị là đường congtronghìnhbên. Dấu của các hệ số

thực là ,, abc

42 fxaxbxd 

0,0,0abc 0,0,0abc 0,0,0abc 0,0,0.abc

Câu2: Chohìnhchóp có đáy làtamgiác đều và vuônggóc với đáy, . Khoảng . SABCABC

DẠYKÈMQUYNHƠN OFFICIAL

. B. .

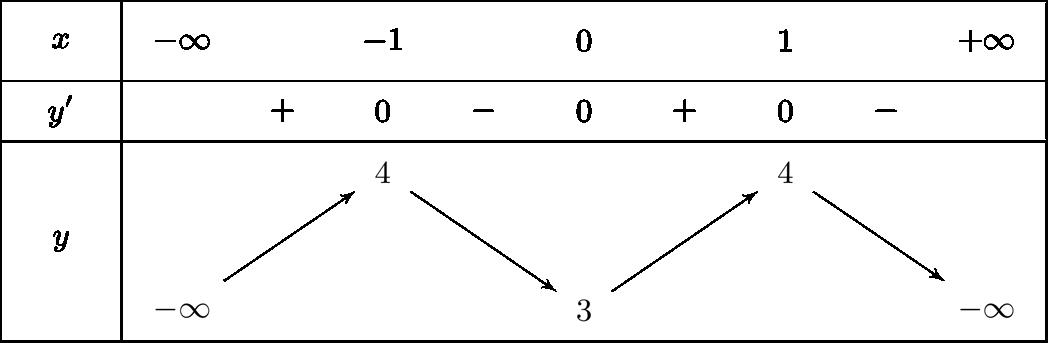
 cách từ đến mặt phẳng bằng C

SAB A. B. C. D. 2 2 a a 3 2 a . 2 a Câu3: Chọn

hai số chẵn bằng A. . B. . C. . D. 11 15 1 5 4 5 4 15 Câu4: Cho cấp số cộng có sống hạng đầu vàcôngsai .Giá trị bằng  n u 13u 4d 5u A. . B. 768. C. . D. 19. 23 13 Câu5: Chohàm số có đồ thị là đường congtronghìnhbên.Hàm số 32() 0fxaxbxcxda  nghịch biến trong khoảng nào dưới đây? yfx  A. B. C. D.  0;2  2;2  2;  2;0 Câu6: Giá trị nhỏ nhất của hàm số trên đoạn bằng 321 34 3 fxxxx   4;0 A. B. C. D. 8 3 5 4 17 3

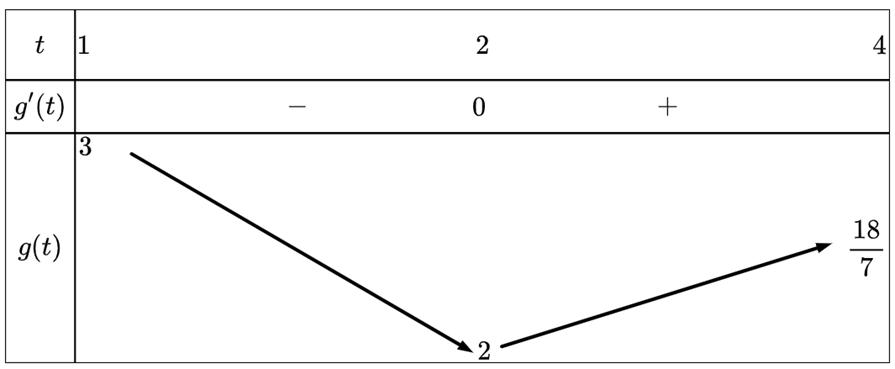
ABa

()

ngẫu nhiênhai số trong15 số nguyên dương đầu tiên.Xác suất chọn được

Câu7: Chohàm số có bảng biến thiên như sau:

số đã cho đạt cực tiểu tại

Tìm tất cả cácgiá trị thực của tham số để hàm số

Chohìnhchóp tứ giác đều có cạnh bên gấp đôi cạnh đáy. Tỉ lệ giữa diện tíchxungquanhvà

DẠYKÈMQUYNHƠN OFFICIAL

yfx  Hàm

A. B. C. D. 5x 1x 3x 1x Câu8:

có

m 33 fxxmx  A. . B. . C. . D. . 2m 0m 0m 0m Câu9:

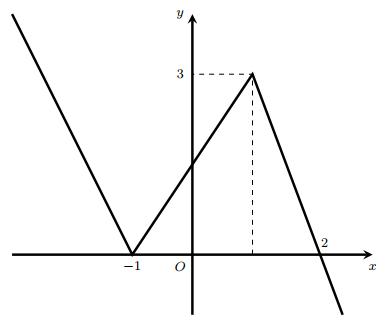
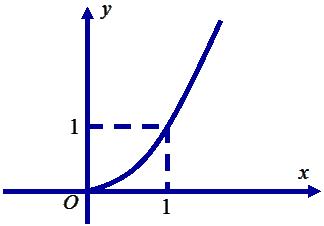
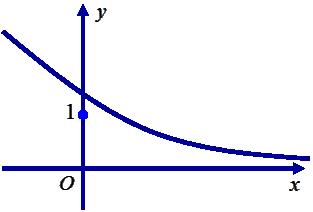
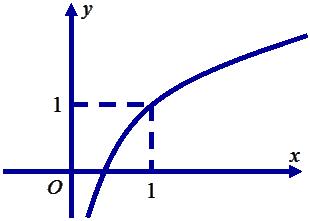
diện tích đáy của hìnhchóp đã cho bằng A. B. C. D. 15 3 3 43 Câu10: Chohàm số có đạo hàmliên tục trên và dấu của đạo hàmcho bởi bảng sau: yfx   Hàm số có mấy điểm cực trị? A. B. C. D. 0 3 2 1 Câu11: Gọi , làtọa độ cácgiao điểmcủa đồ thị hàmsố vớitrục  ; AAAxy ; BBBxy 243 2 xx y x   hoành.Tính . ABPxx  A. . B. . C. . D. . 4P 3P 1P 2P Câu12: Chokhốichópcó đáylàhìnhvuôngcạnh vàchiềucaobằng .Thể tíchkhốichóp đãcho a 2a bằng A. . B. . C. . D. . 34 3 a 32 3 a 32a 34a Câu13: Chohàmsố có đồ thị như hìnhvẽ bên. yfx  Giátrị lớnnhấtcủahàmsố trên đoạn là 21gxfx   1;2 A. . B. . C. . D. . 3 5 6 2

cực trị.

của đồ thị hàm

Câu17: Cho khối hộp chữ nhật cóhaikích thước là2;3và độ dài đường chéo bằng 5. Thể tích khối hôp đã cho bằng

Câu18: Trong mặt phẳng cho18 điểm phân biệt trong đó khôngcóba điềm nào thẳng hàng. Số tamgiác cócác đỉnh thuộc 18 điểm đã cholà

DẠYKÈMQUYNHƠN

60ABC

Câu19: Cho khối chóp có đáy làhìnhthoi cạnh , , cạnh bên vuông .

SA góc với đáy, mặt bên tạo với đáy một góc . Thể tích khối chóp bằng  SCD 60 . SABCD

Câu20: Cho cấp số nhân có và .Giá trị của bằng

Câu21: Đường congtronghìnhbênlà đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án , , , dưới đây. Hỏi hàm số đó làhàm số nào? ABCD

Câu14: Chokhốilăngtrụ đứng có , đáy làtamgiácvuôngcântại và . ABCABCBBa   ABC B .Tínhthể tích củakhốilăngtrụ đãcho. ABa  V A. B. C. D. 3 2 a V 3 3 a V 3Va  3 6 a V Câu15: Chohìnhlậpphương cócạnhbằng ,gọi làgócgiữa đườngthẳng và ABCDABCD  a AB  mặtphẳng .Tính .  BBDD  sin A. B. C. D. 3 4 1 2 3 2 3 5 Câu16: Chohàm số xác

,có

biến

như sau: yfx   1;1 Số đường

cận

cận đứng và đường tiệm cận ngang)

yfx  là A. . B. . C. . D. . 3 4 2 1

OFFICIAL

định trên

bảng

thiên

tiệm

(đường tiệm

số

A. B. C. D.

23 43 123 63

A. B. C. D. 6 3 18A 18! 3 3 18C

C. . D. . 3 23 a 3

a 33a 32a

SABCDABCD 2a 



 n u13

26u

3u A. . B.

u



. 15 18 12 9

DẠYKÈMQUYNHƠN

OFFICIAL A. . B. . C. . D. . 331yxx 4221yxx 331yxx 4221yxx   Câu22: Chohàm số với vàcó bảng biến thiên như sau: 3ax yxb    , ab Giá trị của là ab  A. B. C. D. 1 3 1 3 Câu23: Giá trị cực đại của hàm số là 3121yxx   A. . B. . C. . D. . 2 2 17 15 Câu24: Với và làhai số nguyên dương tuỳ ý thoả mãn , mệnh đề nào dưới đây đúng? kn kn  A. B. C. D.  ! ! k n Cn nk  ! ! k n Cn k   ! !! k n Cn knk   !! ! k n knk C n 

A. . B. . C. . D. . 12 10 11 7

có vuônggóc với mặt phẳng và .Tamgiác có . SABCSA ABCSAa  ABC .Tính số đo góc giữa đường thẳng và mặt phẳng 3ABa  SB  ABC A. . B. . C. . D. . o60 o90 o30 o45

Câu25: Hình đa diện hìnhbêncóbaonhiêu mặt?

Câu26: Chohìnhchóp

Câu27: Chohìnhchóp có đáy làtamgiác đều cạnh . Cạnh bên vàvuônggóc . SABCABC a 3SAa 

với đáy. Gọi làgóc giữa hai mặt phẳng và .Khi đó bằng   SBC ABCsin A. . B. . C. . D. . 25 5 5 5 3 5 23 5

Câu28: Chohàm số có đồ thị là đường congtronghìnhbên.Giá trị của biểu

32 fxxbxcxd 

thức bằng  20Tff  A. B. C. D. 10 6 4 8

Câu29: Trongcáchàm số sau,hàm số nào đồng biến trên từng khoảng xác định?

Câu30: Chohàm số bậc bốn có bảng

DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D. 4222yxx   21 1 x y x   332yxx   2 1 x y x  

biến thiên như sau: yfx  Phương trình có mấy nghiệm? 2fx A. . B. . C. . D. . 6 2 4 5 Câu31: Chohàm số có đồ thị . Viết phương trình tiếp tuyến với tại điểm 3234fxxx    C  C thuộc cóhoành độ bằng . A C 1 A. . B. . C. . D. . 53yx  35yx 35yx  53yx Câu32: Đường tiệm cận ngang của đồ thị hàm số 12 2 x y x  A. B. C. D. 2x 2y 2x 1y Câu33: Chohìnhchóp có đáy làhìnhvuông cạnh , vuônggóc với đáy, Khoảng SACBD aSA SAa  cách giữa hai đường thẳng và là SBCD A. . B. . C. . D. . 2a 3a a 2a Câu34: Chohàm số . Mệnh đề nào dưới đây đúng? 332yxx

A. Hàm số đồng biến trên .

B. Hàm số nghịch biến trên .  1;1

C. Hàm số nghịch biến trên .

D. Hàm số nghịch biến trên

Câu35: Trongcáchàm số sau,hàm số nàocó điểm cực trị? 3

Câu36: Một khối chópcó chiều cao bằng và diện tích đáy bằng Nếu giữ nguyên chiều cao và h B h diện tích đáy tăng lên lần thìta được một khối chóp mới có thể tíchlà 3

Câu37: Tìm tất cả cácgiá trị thực của tham số để hàm số

Câu38: Đồ thị hàm số có tất cả baonhiêu đường tiệm cận đứng và

Câu39: Chohàm số có bảng xét dấu đạo hàm như sau: yfx

số đã cho đồng biến trên khoảng nào dưới đây?

3;4

DẠYKÈMQUYNHƠN OFFICIAL

2;4 Câu40: Cóbaonhiêugiátrị thựccủathamsố để tíchgiá trị lớn nhất vàgiá trị nhỏ nhất của hàmsố m trên đoạn bằng ?



 1;

.  1;1  ;1

A. . B. . C. . D. . 4223yxx  3231yxxx   4223yxx  1 2 x y x   

A. . B. . C. . D. . 1 6 VBh  1 2 VBh  VBh  1 3 VBh 

đồng biến trên . m 321yxxmx  A. B. C. D. 4 3 m 1 3 m 4 3 m 1 3 m

đường tiệm cận ngang? 4 1 x y x   A. . B. . C. . D. . 2 3 0 1

 Hàm



0;11 A. . B. . C. . D. . 2 3 0 1 Câu41: Chohàm số với làtham số. Gọi là tập hợp tất cả cácgiá trị nguyên của 23mxm y xm  m S để hàm số đồng biến trên khoảng .Tìm số phần tử của m  2; S A. . B. . C. . D. . 4 1 3 5 Câu42: Chohình hộp có và . ABCDABCD   060BADBACDAC   2,3,7ABADAC   Thể tích của khối hộp bằng V ABCDABCD  A. . B. . C. . D. . 212 242 142 122 Câu43: Cho phương trình Tìm tất cả cácgiá trị của tham số để phương trình  323101xxm m cóba nghiệm thỏa mãn  1 123 ,, xxx 123 1 xxx  A. . B. . C. . D. . 1m 31 m  31 m  13 m  Câu44: Chohàm số với làtham số. Cóbaonhiêugiá trị nguyên của 32 3 fxxxm    4;4m để hàm số có đúng 3 điểm cực trị? m yfx 

. B. . C. .

1;3

;1

4232 2 fxxmxxm 

Câu45: Tìm tất cả cácgiá trị của tham số để đồ thị hàm số có đúng một

cực đại.

Câu46: Chohàm số , với có đồ thị tiếp xúc trục hoành tại điểm cóhoành

32 fxaxbxcxd  0a

độ bằng và cắt đường thẳng tại hai điểm phân biệt cóhoành độ lần lượt là và , 1 21ym  04 với làtham số. Số nghiệm của phương trình là.

. B. . C. . D. . 2 0 3 1

Câu47: Hỏi có tất cả baonhiêugiá trị nguyên của tham số để hàm số  20;20m

4 23 22 341262121 fxxmxmmxmx

nghịch biến trên khoảng ?

Chohìnhchóptamgiác đều có cạnh đáy bằng . Gọi lần lượt làtrung điểm SABC 3a , MN

DẠYKÈMQUYNHƠN OFFICIAL

A. 6. B. 8. C. 5. D. 4.



 

C. . D. .

m m    1m 0m 01 m 

4 2 12022ymxmx

điểm

. B. .

1 0

m 

3fxf 

    0;1 A. . B.

C. . D. . 2

của

Biết mặt phẳng vuônggóc với mặt phẳng .Tính thể tích của khối , SBSC  AMN  SBC chóp . . ABCNM A. B. C. D. 3 315 16 a 3 315 48 a 3 315 32 a 315 32 a Câu49: Chohàm số .Hàm số có bảng biến thiên như sau: ()yfx  ()yfx   Điều kiện cần và đủ của tham số để bất phương trình nghiệm đúng với mọi m 21 ()2 fxxm  là [1;2]x A. . B. . C. . D. . (2)2mf  (2)2mf  1 (1)2mf  1 (1)2mf  Câu50: Cho khối đa diện (minh họa như hình vẽ bên)trong đó là khối hộp chữ nhật ABCDABCD  với , , là khối chópcócác cạnh bên bằng nhauvà . 2 ABADa AAa   . SABCD 3SAa  Thể tích khối tứ diện bằng SABD 



20 19

Câu48:

DẠYKÈMQUYNHƠN

OFFICIAL A. B. C. D. 32 2 a 32a 32 3 a 32 6 a ---------- HẾT ----------

DẠYKÈMQUYNHƠN

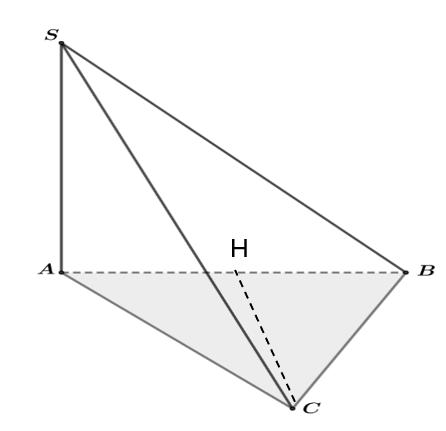
Chohìnhchóp có đáy làtamgiác đều và vuônggóc với đáy, . Khoảng .

BẢNG ĐÁP ÁN 1234567891 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 2 0 2 1 2 2 2 3 2 4 2 5 CCBDDCCBACABBDBACDACCDCCB 2 6 2 7 2 8 2 9 3 0 3 1 3 2 3 3 3 4 3 5 3 6 3 7 3 8 3 9 4 0 4 1 4 2 4 3 4 4 4 5 4 6 4 7 4 8 4 9 5 0 CAABCBBCCCCBCADCABABDBCDC HƯỚNG DẪN GIẢI Câu1: Chohàm số có đồ thị là đường congtronghìnhbên. Dấu của các hệ số 42 fxaxbxd  thực là ,, abc A. . B. . C. . D. 0,0,0abc 0,0,0abc 0,0,0abc 0,0,0.abc Lời giải Chọn C Tacó đồ thị cóhình dạng như trên với hàm bậc bốn trùng phương cóhai điểm cực tiểu và một điểm cực đại nên .Giá trị cực đại

0,0ab

 Câu2:

SABCABC

 cách từ đến mặt phẳng bằng C

SAB A. . B. . C. . D. 2 2 a a 3 2 a . 2 a Lời giải Chọn C Trong vẽ ()ABCCHAB 

OFFICIAL

lớn hơn nên .

00 c

SA ABa

()

Câu3: Chọn ngẫu nhiênhai số trong15 số nguyên dương đầu tiên.Xác suất chọn được hai số chẵn bằng

Gọi Alà biến cố: “Chọn được hai số chẵn trong15 số nguyên dương đầu tiên” 2 7AC 

DẠYKÈMQUYNHƠN OFFICIAL

Tacó  SAABCSACH CHSAB CHAB       Nên .  (;) 3 2 CSAB adCH

A. B. C. D. 11 15 1 5 4 5 4 15 Lời giải Chọn B Khônggian



mẫu 2 15C

. 2 7 2 15 1 5 A AC P C   Câu4:

số cộng có sống hạng đầu vàcôngsai .Giá trị bằng  n u 13u 4d 5u A. B.

C. D. 19.

Lời giải Chọn D Tacó . 1 51 1434.419 n uunduud   Câu5: Chohàm số có đồ thị là

số 32() 0fxaxbxcxda  nghịch

đây? yfx  A. . B. . C. . D. .  0;2  2;2  2;  2;0 Lời giải Chọn D Xéthàm số: yfx  '' yfx  Đề hàm số nghịch biến yfx   '0'00220 yfx x x  

Cho cấp

768.

23 13

đường congtronghìnhbên.Hàm

biến trong khoảng nào dưới

DẠYKÈMQUYNHƠN OFFICIAL

Câu6: Giá trị nhỏ nhất của hàm số trên đoạn bằng 321 34 3 fxxxx   4;0 A. B. C. D. 8 3 5 4 17 3 Lời giải Chọn C Xéthàm số trên đoạn 321 34 3 fxxxx   4;0 Tacó 223fxxx  Giải    14;0 0 34;0 x fx x     Tacó .  8 35;4;04 3 f f f    Suyra . 4;0 min40 fxf  Câu7: Chohàm số có bảng biến thiên như sau: yfx  Hàm số đã cho đạt cực tiểu tại A. B. C. D. 5x 1x 3x 1x Lời giải Chọn C Hàm số đã cho đạt cực tiểu tại .3x Câu8: Tìm tất cả cácgiá trị thực của tham số để hàm số có cực trị. m 33 fxxmx  A. . B. . C. . D. . 2m 0m 0m 0m Lời giải Chọn B Tacó . 2 33 fxxm  Để hàm số có cực trị thì phương trình cóhai nghiệm phân biệt 33 fxxmx  0fx   0300 mm  Câu9: Chohìnhchóp tứ giác đều có cạnh bên gấp đôi cạnh đáy. Tỉ lệ giữa diện tíchxungquanhvà diện tích đáy của hìnhchóp đã cho bằng A. . B. . C. . D. . 15 3 3 43 Lời giải Chọn A

Gọi làhìnhchóp đều có cạnh đáy . SABCD 2.ABaSAa 

Diện tíchxungquanh của hìnhchóplà 2 2 2 1 1 44415 24SBC aSSaa a  

Diện tích đáy của hìnhchóplà .2 2 Sa 

Vậy . 1 2 15 S S 

Câu10: Chohàm số có đạo hàmliên tục trên và dấu của đạo hàmcho bởi bảng sau:

Hàm số có mấy điểm cực trị?

A. B. C. D. 0 3 2 1 Lời giải Chọn C

Từ BBTta thấy

DẠYKÈMQUYNHƠN OFFICIAL



yfx  

đổi dấu quacácgiá trị nênhàm số đã chocó2 điểm cực trị. fx  2;1xx Câu11: Gọi , làtọa độ cácgiao điểmcủa đồ thị hàmsố vớitrục  ; AAAxy ; BBBxy 243 2 xx y x   hoành.Tính . ABPxx  A. . B. . C. . D. . 4P 3P 1P 2P Lời giải Chọn A Phươngtrìnhhoành độ giao điểmcủa đồ thị hàmsố vớitrụchoànhlà 243 2 xx y x   2 143 0 23 x xx x x    Vậy 4ABPxx  Câu12: Chokhốichópcó đáylàhìnhvuôngcạnh vàchiềucaobằng .Thể tíchkhốichóp đãcho a 2a bằng A. B. C. D. 34 3 a 32 3 a 32a 34a Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL

Thể tíchkhốichóplà .2312 ..2 33 Vaaa   Câu13: Chohàmsố có đồ thị như hìnhvẽ bên. yfx  Giátrị lớnnhấtcủahàmsố trên đoạn là 21gxfx   1;2 A. B. C. D. 3 5 6 2 Lời giải Chọn B Giátrị lớnnhấtcủahàmsố trên đoạn là 21gxfx   1;2 .  1;2 1;2 max2max12.315 gxfx   Câu14: Chokhốilăngtrụ đứng có , đáy làtamgiácvuôngcântại và ABCABCBBa   ABC B .Tínhthể tích củakhốilăngtrụ đãcho. ABa  V A. . B. . C. . D. . 3 2 a V 3 3 a V 3Va  3 6 a V Lời giải Chọn D Thể tích củakhốilăngtrụ đãcholà . V 3 211 .. 326 a Vaa   Câu15: Chohìnhlậpphương cócạnhbằng ,gọi làgócgiữa đườngthẳng và . ABCDABCD  a AB  mặtphẳng .Tính .  BBDD  sin A. . B. . C. . D. . 3 4 1 2 3 2 3 5 Lời giải Chọn B

DẠYKÈMQUYNHƠN

Câu17: Cho khối hộp chữ nhật cóhaikích thước là2;3và độ dài đường chéo bằng

OFFICIAL Gọi làtrung điểm của M BD Tacó nên . AMBBDD     , ABBBDDABM   Xéttamgiác vuông tại ,tacó . ABM  M 1 sin 2 AM AB     Câu16: Chohàm số xác định trên ,có bảng biến thiên như sau: yfx   1;1 Số đường tiệm cận (đường tiệm cận đứng và đường tiệm cận ngang) của đồ thị hàm số yfx  là A. . B. . C. . D. . 3 4 2 1 Lời giải Chọn A Tacó ; nên đường tiệm cận đứng là ; . 1 lim x y  1 lim x y  1x 1x Lại có nên

. lim3 x y   3y Vậy đồ thị hàm

đường tiệm cận nganglà

số có3 đường tiệm cận.

đã cho

A. . B. . C. . D. . 23 43 123 63 Lời giải Chọn C

5. Thể tích khối hôp

bằng

Câu18: Trong mặt phẳng cho18 điểm phân biệt trong đó khôngcóba điềm nào thẳng hàng. Số tamgiác

Mỗi tamgiáclà một tổ hợp chập 3 của 18 phần tử.

Số cáctamgiáccócác đỉnh thuộc 18 điểm đã cholà

DẠYKÈMQUYNHƠN OFFICIAL

Xéthình hộp chữ nhật có ; . ABCDABCD  2AB 3AD Gọi (với ). AAx   0x Xéttamgiác có . ABC 22222313ACABBC Xéttamgiác có . ACA 2222251323ACAAACxx    Thể tích khối hộp

cholà . 2323123VABADAA   

cócác

A. B. C. D. 6 3 18A 18! 3 3 18C Lời giải

đã

đỉnh thuộc 18 điểm đã cholà

Chọn

. 3 18C Câu19: Cho khối chóp có đáy làhìnhthoi cạnh , , cạnh bên vuông . SABCDABCD 2a  60ABC  SA góc với đáy, mặt bên tạo với đáy một góc . Thể tích khối chóp bằng  SCD 60 . SABCD A. B. C. D. 3 23 a 3 33 a 33a 32a Lời giải Chọn A M D C B A S Tamgiác cân(do bởi làhìnhthoi)có nênnó đều. ABCABAC  ABCD  60ABC  Gọi làtrung điểm cạnh suyra ; M CDAMCD 

DẠYKÈMQUYNHƠN

OFFICIAL Tacó suyra nên , với CDAM CDSA    CDSM     , ,60SCDABCDSMAMSMA    tacó . 3 23 2 AMaa  tan603SAAM a    Thể tích khối chóp là . . SABCD 2 31113 232223 3334SABCD ABCD ABC VSASSASaaa     Câu20: Cho cấp số nhân có và .Giá trị của bằng  n u13u 26u 3u A. . B. . C. . D. . 15 18 12 9 Lời giải Chọn C Tacó . 22 2 3 1 6 12 3 u u u  Câu21: Đường congtronghìnhbênlà đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án , , , dưới đây. Hỏi hàm số đó làhàm số nào? ABCD A. . B. . C. . D. . 331yxx 4221yxx 331yxx 4221yxx   Lời giải Chọn C -Hàm số bậc , hệ số .30 a Câu22: Chohàm số với vàcó bảng biến thiên như sau: 3ax yxb    , ab Giá trị của là ab 

Chọn D

Tiệm cận đứng .22xbb

Tiệm cận ngang 1ya

Suyra .3ab

TacóBBT:

Từ bảng biến thiêntacó .17CDy

Câu24: Với và làhai số nguyên dương tuỳ

Câu25: Hình đa diện hìnhbêncóbaonhiêu mặt?

DẠYKÈMQUYNHƠN OFFICIAL

A. . B. . C. . D. . 1 3 1 3 Lời giải

Câu23:

cực đại của hàm số là 3121yxx   A. B. C. D. 2 2 17 15 Lời giải Chọn C Tacó 2 312yx   2 0 2 x y x  

Giá trị



mãn ,

đề

kn kn  A. . B. . C. . D. .  ! ! k n Cn nk  ! ! k n Cn k   ! !! k n Cn knk   !! ! k n knk C n  Lời giải

thoả

mệnh

nào dưới đây đúng?

Chọn C Lí thuyết.

A. B. C. D. 12 10 11 7 Lời giải

Chọn B

Lý thuyết.

Câu26: Chohìnhchóp có vuônggóc với mặt phẳng và .Tamgiác có SABCSA ABCSAa  ABC .Tính số đo góc giữa đường thẳng và mặt phẳng . 3ABa  SB  ABC A. B. C. D. o60 o90 o30 o45

giải

Tacó:góc giữa đường thẳng và mặt phẳng chínhlàgóc giữa hai đường thẳng SB  ABC SB và , đó chínhlàgóc . AB  SBA

Xéttamgiác

DẠYKÈMQUYNHƠN OFFICIAL

a a3 A B C S

Lời

Chọn C

vuông tại có . SAB A   o 1 tan 30 33 SAa SBA SBA ABa  Vậy góc giữa đường thẳng và mặt phẳng bằng . SB  ABC o30

Chohìnhchóp có đáy làtamgiác đều cạnh Cạnh bên vàvuônggóc SABCABC a 3SAa  với đáy. Gọi làgóc giữa hai mặt phẳng và .Khi đó bằng   SBC ABCsin A. B. C. D. 25 5 5 5 3 5 23 5

Câu27:

DẠYKÈMQUYNHƠN

OFFICIAL Lời giải Chọn A φ a a3 H A B C S Gọi làtrung điểm của .Khi đó, chínhlàgóc . H BC   SHA Xéttamgiác vuông tại có . SAH A   2 2 325 sin 335 2 SA a SHA SH aa      Vậy 25sin 5 Bản wordpháthành từ websiteTailieuchuan.vn Câu28: Chohàm số có đồ thị là đường congtronghìnhbên.Giá trị của biểu 32 fxxbxcxd  thức bằng  20Tff  A. . B. . C. . D. . 10 6 4 8 Lời giải Chọn A   32 2 32 fxxbxcxdfxxbxc   Kết hợp đồ thị, tacó: 32 23 1 3 3 6 2 2 26 3 b b fxxxxd c c              Vậy  2010Tff   Câu29: Trongcáchàm số sau,hàm số nào đồng biến trên từng khoảng xác định?

xác định của nó. Câu30: Chohàm số bậc bốn có bảng biến thiên như sau:

Phương trình có mấy nghiệm?

2fx

Bảng biến thiên:

Dựa vào bảng biến thiên,tacó: phương trình cóhai nghiệm, phương trình cóhai nghiệm  1  2 (vàcác nghiệm nàyphân biệt) nên phương trình có4 nghiệm. 2fx

Câu31: Chohàm số có đồ thị

DẠYKÈMQUYNHƠN

A. . B. . C. . D. . 4222yxx   21 1 x y x   332yxx   2 1 x y x   Lời giải Chọn B Tacó nênhàm số đồng biến

từng khoảng 2 213 0,1 11 x y y x x x      21 1 x y x  

OFFICIAL

trên

yfx 



 A.

Lời giải Chọn C    21 2 22 fx fx fx   

B. C.

6 2 4 5

Viết phương trình tiếp tuyến với tại điểm 3234fxxx    C  C thuộc cóhoành độ bằng . A C 1 A. . B. . C. . D. . 53yx  35yx 35yx  53yx Lời giải Chọn B Gọi là điểm thuộc đồ thị cóhoành độ bằng M  C 1 1;2M Tacó nên hệ số góc tiếp tuyến của tại là . 2 36 fxxx    C 1;2M 13f 

Vậy phương trình tiếp tuyến của tại là

Câu32: Đường tiệm cận ngang của đồ thị hàm

Tập xác định của hàm số là

Tacó .Suyra là đường tiệm cận ngang của đồ thị hàm số 12 limlim2

Câu33: Chohìnhchóp có đáy làhìnhvuông cạnh , vuônggóc với đáy, Khoảng SACBD aSA SAa 

cách giữa hai đường thẳng và là SBCD

C. Hàm số nghịch biến trên .

D. Hàm số nghịch biến trên

Câu35: Trongcáchàm số sau,hàm số nàocó điểm cực trị?

DẠYKÈMQUYNHƠN OFFICIAL

C

 



1;2

 31235yx yx

số 12 2 x y x 

. C. . D. .

 2y 2

 1

 Lời

A. . B.

giải Chọn B

.

D

 

2 x x x y x

  2y 12 2 x y x 

A. B. C. D. 2a 3a a 2a Lời giải Chọn C a a a C A D B S Tacó làhìnhvuông cạnh nên và mà ,suyra . ABCD aADa  // CDAB// ABSAB // CDSAB Do đó   ,,, dSBCDdCDSABdDSAB   Lại có do làhìnhvuôngvà do ,suyra ADAB  ABCD ADSA  SAABCD  ADSAB  hay . Vậy .   , dDSABADa   , dSBCDa 

Chohàm số . Mệnh đề nào dưới đây đúng? 332yxx

Hàm số đồng biến trên .

Hàm số nghịch biến trên .  1;1  1;

Câu34:



 ;1 Lời giải

1;1

Tacó . 2 2

yxyx x   



Chọn C

33033011

Vậy hàm số nghịch biến trên khoảng

1;1

DẠYKÈMQUYNHƠN

A. . B. . C. . D. . 4223yxx  3231yxxx   4223yxx  1 2 x y x    Lời giải Chọn C Xéthàm số ,có nênhàm số có1 điểm cực trị. 4223yxx  3 4400yxxyx    Xéthàm số ,có nênhàm số có2 3231yxxx   2 110 3 0 3 23yx x yx      điểm cực trị. Xéthàm số ,có nênhàm số có3 điểm cực trị. 4223yxx  3 0 4401 1 x yxxyx x          Xéthàm số ,có nênhàm số khôngcó cực trị. 1 2 x y x    2 1 0,2 2 y x x     Cáchkhác: Hàm số có3 điểm cực trị nênhàm số có3 điểm cực trị là 42 yaxbxc  0ab  . 4223yxx  Câu36: Một khối chópcó chiều cao bằng và diện tích đáy bằng . Nếu giữ nguyên chiều cao và h B h diện tích đáy tăng lên lần thìta được một khối chóp mới có thể tíchlà 3 A. B. C. D. 1 6 VBh  1 2 VBh  VBh  1 3 VBh  Lời giải Chọn C Thể tích của khối chóp mới là: . 1 3 3 VBhBh  Câu37: Tìm tất cả cácgiá trị thực của tham số để hàm số đồng biến trên . m 321yxxmx  A. . B. . C. . D. . 4 3 m 1 3 m 4 3 m 1 3 m Lời giải Chọn B Tập xác định . D Tacó . 2 32 yxxm  Khi đó hàm số đồng biến trên khivà chỉ khi  0, yx 2 320, xxmx  2 32, mxxx  (1). 2 32, mxxx  Xéthàm số hay .  2 2 111 3233, 33gxxxx x       1 3maxgx 

OFFICIAL

Câu38: Đồ thị hàm số có tất cả baonhiêu đường tiệm cận đứng

là đường tiệm cận đứng. 1

đồ thị hàm số đã cho chỉ có một đường tiệm cận: 1x

Bản wordpháthành từ websiteTailieuchuan.vn

Câu39: Chohàm số có bảng xét dấu đạo hàm như sau:

yfx 

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

Lời giải Chọn A

Từ bảng xét dấu suyrahàm số đồng biến trên . 1;3

Câu40: Cóbaonhiêugiátrị thựccủathamsố để tíchgiá trị lớn nhất vàgiá trị nhỏ nhất của hàmsố m trên đoạn bằng ?

4232 2 fxxmxxm  0;11

A. . B. . C.

DẠYKÈMQUYNHƠN OFFICIAL

. 1 3 m

Từ (1)suyra

tiệm

ngang? 4 1 x y x   A. . B. . C. . D. . 2 3 0 1 Lời giải Chọn C Tập xác định .Do đó đồ thị hàm số khôngcó đường tiệm cận ngang. 1;4D Xét 11 4 limlim 1 x x x y x        Vì và mặt khác khi . 1 lim450 x x   1 lim10 x x   10x 1x  Suyra đường

x

và đường

cận

thẳng

Vậy



 1;3 

 ;1 

B. C. D.

3;4

2;4



. D. . 2 3 0 1 Lời giải Chọn D Tacó với   3 22 22 44341130fxxxmxxxxmx       0;1x  Suyra . 0;1 0;1 max0;min1 fxffxf   Theoyêu cầu bàitoántacó   2 32 0.11 11 10 ff mmm mmm   .  2 1101mm m  Câu41: Chohàm số với làtham số. Gọi là tập hợp tất cả cácgiá trị nguyên của 23mxm y xm  m S để hàm số đồng biến trên khoảng .Tìm số phần tử của m  2; S

DẠYKÈMQUYNHƠN

OFFICIAL A. . B. . C. . D. . 4 1 3 5 Lời giải Chọn C Tacó .  2 2 23mm y xm   Để thoả mãntacó . 2213 30 12 2 2 m mm m m m         Vậy  0;1;2S Câu42: Chohình hộp có và . ABCDABCD   060BADBACDAC   2,3,7ABADAC   Thể tích của khối hộp bằng V ABCDABCD  A. . B. . C. . D. . 212 242 142 122 Lời giải Chọn A Gọi và . :2HACAH    :2KADAK    Khi đó là tứ diện đều có cạnh bằng 2nên thể tích . . ABHK  1 22 3 V Tacó . 1 1 4472 21212 ABCD ABCD VAHAK VV VACAD       Do . 36212ABCDABCDAABCDABCDV VV      Câu43: Cho phương trình Tìm tất cả cácgiá trị của tham số để phương trình  323101.xxm m cóba nghiệm thỏa mãn  1 123 ,, xxx 123 1 xxx  A. . B. . C. . D. . 1m 31 m  31 m  13 m  Lời giải Chọn B Xéthàm số 32 2 0 31360 2 x yxxyxxy x       Bảng biến thiên:

DẠYKÈMQUYNHƠN

Để phương trình có3 nghiệm phân biệt thì .  323101xxm 31 m  Từ kết hợp định lívi–et: 1 123 23 10 1 10,10 x xxx xx       123 1231223311231110 10 1310 1 xxx xxxxxxxxxxxx m m     Kết hợp điều kiện ta được: 31 m  Câu44: Chohàm số với làtham số. Cóbaonhiêugiá trị nguyên của 32 3 fxxxm    4;4m để hàm số có đúng 3 điểm cực trị? m yfx  A. 6. B. 8. C. 5. D. 4. Lời giải Chọn A Xéthàm số: .    32 2 0 3360 2 x gxxxgxxxgx x       Bảng biênthiên: Số điểm cực trị của hàm số bằng số điểm cực trị cộng với số nghiệm bội lẻ nên để hàm số fx có đúng 3 điểm cực trị thì: fx 40mm Do .  44;0;1;2;3;4 ;4 m m m        Câu45: Tìm tất cả cácgiá trị của tham số để đồ thị hàm số có đúng một m 4 2 12022ymxmx   điểm cực đại.

OFFICIAL

Lời giải

Chọn B

TH1: .Khi đó hám số suy biến thànhhàm bậc haicó dạng là một parabol 0m 22022yx

có bề lõmquay xuống nên đồ thị hàm số có1 điểm cực trị vàlà điểm cực đại. Suyra (thỏa 0m mãn)

TH2: .Khi đó hàm số đã cholàhàm bậc bốn trùng phương. 0m

Tacó nhận xétsau về hàm bậc bốn trùng phương: .420yaxbxca 

Hàm số cóba điểm cực trị khivà chỉ khi . 0ab

Hàm số có một điểm cực trị khivà chỉ khi ..0ab

Do đó tacóhai khả năng cho TH2:

 KN1: Đồ thị hàm số có một điểm cực trị và đó là điểm cực đại thì



: Đồ thị hàm số cóba điểm cực trị trong đó cóhai điểm cực tiểu và1 điểm cực đại thì

Vậy kết hợp các trường hợp trênta được thỏa mãnyêu cầu bàitoán. 1m

Câu46: Chohàm số , với có đồ thị tiếp xúc trục hoành tại điểm cóhoành 32 fxaxbxcxd  0a

độ bằng và cắt đường thẳng tại hai điểm phân biệt cóhoành độ lần lượt là và , 1 21ym  04

với làtham số. Số nghiệm

DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D. 1 0 m m    1m 0m 01 m 

. 0000 0 .00101 aam m m abbm m                      

0000 01 .00101 aam m m abbm m                      

KN2



của

trình là. m  3fxf  A. B. C. D. 2 0 3 1 Lời giải Chọn D Do đồ thị tiếp xúc trục hoành tại điểm cóhoành độ bằng nên đồ thị 32 fxaxbxcxd  1 còn cắt trục hoành

01x Khi đó   2 32 01 fxaxbxcxdaxxx  Do đồ thị cắt đường thẳng tại hai điểm phân biệt cóhoành 32 fxaxbxcxd  21ym  độ lần lượt là và nêntacó: 04 .     0 0 00 0 021.21 9 .9.4 9.421 2 421 fmaxm axaxx axmfm                  Suyra .  2 32 9 1 2fxaxbxcxdaxx    Vậy . 2 32 9 311202132023103 2fxfaxx axxx x      

phương

tại một điểm khác nữa, ta giả sử điểm đó cóhoành độ .

DẠYKÈMQUYNHƠN

Câu47: Hỏi có tất cả baonhiêugiá trị nguyên của tham số để hàm số  20;20m nghịch biến trên khoảng ? 4 23 22 341262121 fxxmxmmxmx     0;1 A. . B. . C. . D. . 2 20 19 21 Lời giải Chọn B Tacó: .    3 22 2 '0,0;1121212122120,0;1fxx x mxmmxmx   2 2 12110,0;1xxmxxmxx    22 120,0;1xxmxmx  Vì nênyêu cầu bàitoán .(*) 0;110x x    2220,0;1 gx xmxmx   Xét .  4 gx mm TH1:

0 gx 

a

gxx 

(không thỏa mãn).  1 0 0 gx m m   TH3: .  4 1 00 0 gx m mm m    Khi đó có2 nghiệm phân biệt (giả sử ). 0gx 12 , xx 12xx  Tacó bảng xét dấu của như sau: gx Theoyêu cầu bàitoántacó   00 10 g g      2 0 0 11 21201 2 m m m m mm m              Do nênta nhận Vậy có tất cả 20giá trị thỏa mãn.  20;20 m m        20;19;;1m Câu48: Chohìnhchóptamgiác đều có cạnh đáy bằng . Gọi lần lượt làtrung điểm . SABC 3a , MN của . Biết mặt phẳng vuônggóc với mặt phẳng .Tính thể tích của khối , SBSC  AMN  SBC chóp . ABCNM A. B. C. D. 3 315 16 a 3 315 48 a 3 315 32 a 315 32 a Lời giải Chọn C

OFFICIAL

,do (không thỏa mãn).

TH2:

OFFICIAL G H I M N A S B C Gọi làtrung điểm (do cân tại ). H BCBCSH  SBC S Gọi là trọng tâm và . G ABC ISHMN  Do làchóp đều . . SABC SGABC Tacó: là đường trungbình của tại MN // SBCMNBCMNSH  I Vậy: .     , AMNSBC AMNSBCMNSHAMNSHAI SHMNSHSBC         Lại có làtrung điểm (do ) là đường trung tuyến . I SHIMN  AI SAH Suyra cân tại SAH 33 22 ABa ASAAH Xét vuông tại : . SGA G 2 2 223235 . 2322 aaaSGSAAG     Mặt khác: . 2 313313315 . ... 4443432 SAMN MNABCSABC SABC VSMSN AB VV SG a VSBSC     Câu49: Chohàm số .Hàm số có bảng biến thiên như sau: ()yfx  ()yfx   Điều kiện cần và đủ của tham số để bất phương trình nghiệm đúng với mọi m 21 ()2 fxxm  là [1;2]x

DẠYKÈMQUYNHƠN

OFFICIAL A. . B. . C. . D. . (2)2mf  (2)2mf  1 (1)2mf  1 (1)2mf  Lời giải Chọn D Đặt  21 ()2gxfxxgxfxx    ' 00 gxfxxfxx    Dưa vào đồ thị 2hàm số và đồ thị hàm số ta được Do đó ' yfx  yx  0,1;2gxx hàm số nghịch biến trên . gx 1;2 1 1;2max11 2gxgf  Yêu cầu bàitoán . 1;2 1 max1 2mgxf   Câu50: Cho khối đa diện (minh họa như hình

là khối

nhật . ABCDABCD  với

. 2 ABADa AAa   . SABCD 3SAa  Thể tích khối

SABD  A. B. C. D. 32 2 a 32a 32 3 a 32 6 a Lời giải Chọn C

vẽ bên)trong đó

hộp chữ

, , là khối chópcócác cạnh bên bằng nhauvà

tứ diện bằng

DẠYKÈMQUYNHƠN

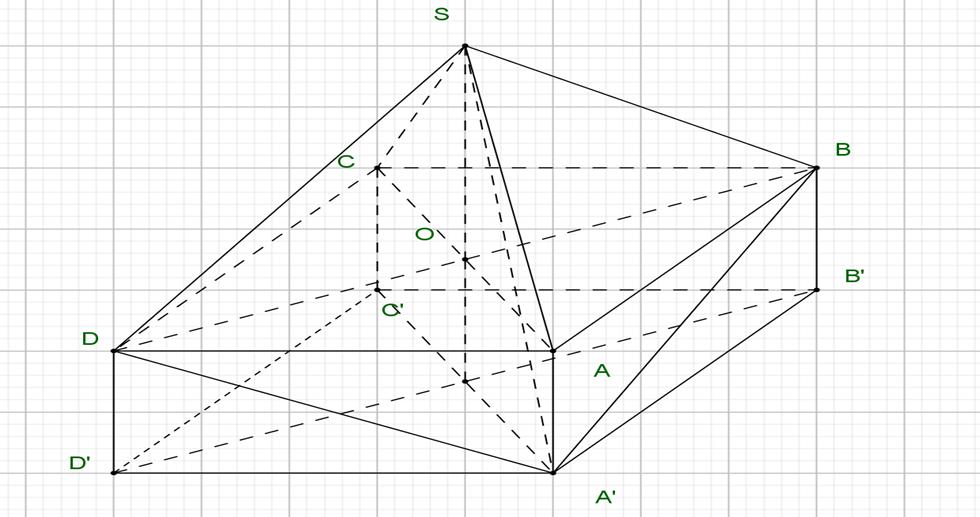
OFFICIAL Giả sử . OACBD  Do .Tacó SASBSCSD SOABCD OAOBOCOD    ' ASBDSABD VV   Do   ' '//' ' ,, ' ASBDASBD AABB dASBDdASBDVV BBSBD         Tacó .AOSO AOSBD AOBD   Tamgiác vuông tại . SOB 2222 32 OSOSBOBaaa    1 ,1 3SABDASBD VVAOk  Với là diện tíchtamgiác . . k 2 11 222,2 22 SBDkSOBDaaa    23AOa  Thay(2),(3)vào(1)ta được 3 2 ' 12 22 33ASBDSABD a VVaa     HẾT 

SỞ GIÁO DỤC VÀ ĐÀO TẠO HẢI DƯƠNG

ĐỀ THI THỬ TỐT NGHIỆP THPT

TRƯỜNG: THPTKINHMÔN

LẦN 1 NĂM HỌC 2021–2022

Câu1: BCH đoàn trường THPTKinhMôn muốn phát động phongtrào kế hoạch nhỏ cho học sinh trồng 4hàngcây, mỗi hàng5cây phủ xanhsân vận động của trường. Vì đất xấu nênBCH Đoàn trường quyết định đào các hố sâuhình hộp chữ nhật vàmua đất phùsa đổ đầy vào đó. Biết mỗi hố sâu 2m, miệng hố làhìnhvuôngkích thước cạnh là1m. Số tiền BCH Đoàn phải chichomua đất là baonhiêu nếu giá đất là nghìn đồng 175 31m

Câu2: Chohàm số có bảng biến thiên như dưới đây. yfx 

Hỏi

DẠYKÈMQUYNHƠN OFFICIAL

D. triệu.

A. triệu.

triệu.

12 14 10 7

đồ thị hàm số cóbaonhiêu tiệm cận A. . B. . C. . D. . 3 2 4 1 Câu3: Cóbaonhiêucách xếp 4 bạn namvà2 bạn nữ thành một hangngang. A. . B. . C. . D. . 48 120 8 720 Câu4: Khối chópcó chiều cao bằng 1và diện tích đáy là có thể tíchlà. 2 a A. . B. . C. . D. . 3 a 2 3 a 2 a 3 3 a Câu5: Cho cấp số cộng với .Tìm số hạng đầu vàcôngsai .  n u 32 n un 1u d A. B. 12;2ud 15;3ud C. D. 13;5ud 15;2ud Câu6: Khoảng nghịch biến của hàm số là 321 3 3 yxxx  A. B.  3;  ;13;  C. . D. .  ;1  1;3 Câu7: Chohàm số liên tục trên có bảng biến thiên như hình vẽ  yfx  ;11; 

tích của mặt cầu cóbánkính được tínhtheocông thức nào dưới đây?

qua trục, ta được thiết diện là một hìnhvuôngcóchuvilà8.

DẠYKÈMQUYNHƠN OFFICIAL

Khi đó số điểm cực tiểu của hàm số bằng: A. . B. . C. . D. . 2 1 0 3 Câu8: Chohìnhchóp có đáy làhìnhthoi cạnh ,góc , cạnh vuông SABCDABCD a  0120BAD SA góc với đáy và .Tínhgóc giữa hai mặt phẳng và 2  Sa A   SBC ABCD A. B. C. D. 060 030 045 090 Câu9: Với các số thực bất kì, mệnh đề nàosau đây đúng? , ab A. B. C. D. 5 5 5 a ab b   5 5 5 a ab b  5 5 5 a ab b  5 5 5 aa b b  Câu10: Họ nguyênhàm của

là: sin fxxx  A. B. 2 cos 2 xxC 2 cos 2 xxC  C. D. 1cosxC 1cosxC  Câu11:

S r A. B. C. D. 21 3 Sr   24 Sr   2Sr   24 3 Sr   Câu12: Chohàm số

nàosau

là đúng? 3 yx  Fx A. B.  2016FF  201FF C. D.  208FF  204FF Câu13: Cắt hình trụ bởi một mặt

Diện tíchxungquanh của hình trụ đã cho bằng A. B. C. D. 4.  2 3  2.  8 Câu14: Đạo hàm của hàm số là 2 2xx y   A. B. 2 212ln2. xx yx   2 2ln2. xx y    C. D. 21 2ln2. x y    2 212xx yx   Câu15: Chohàm số . Đồ thị của hàm số làhìnhnàotrong bốn hình dưới đây: ln yfxxx  yfx  

hàm số

Diện

có một nguyênhàmlà . Khẳng định

đây

phẳng

DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D. Câu16: Mệnh đề nào dưới đây sai? A. B. 2 1dtan cos xxC x   1dlnxxC x  C. D. sindcos. xxxC  3 3d. ln3 x xxC  Câu17: Chohàm số có đồ thị như hình dưới đây. Tìm tất cả cácgiá trị thực của tham số 42 2 yxx  để phương trình có bốn nghiệm phân biệt. m 4220xxm x y 1 1 -O 1 A. B. C. D.  01. m 1.m  01. m 0.m Câu18: Số nghiệm của phương trình là  2 3 3 log1log212 x x   A. B. C. D. 3 2 0 1 Câu19: Đường cong của hình dưới đây là đồ thị của hàm số với làcác số thực. Mệnh    axb ycxd,,, abcd đề nào dưới đây đúng?

Câu20: Đồ thị hàm số nàotrongcáchàm số dưới đây

Câu21: Các mặt của khối tám mặt đều làcác

DẠYKÈMQUYNHƠN OFFICIAL

A. B.  y0,2 x  y0,x2 C. D. 

 y0,1

y0,x1

A. B. 1 y x  2 1 . 1y x   C. D. 4 1 . 1y x   2 1 . 1y xx  

A. Bátgiác

B. Tamgiác đều. C.

D. Ngũ giác đều.

khối nóncó chiều cao vàbánkính đáy . Thể tích khối nón đã cho bằng: 6h 3r A. . B. . C. . D. . 54 6 18 36 Câu23: Cho là số thực dương tùyý,khi đó bằng a 5 2log 22 a    A. . B. . C. . D. . 2 3 25loga 2 3 25loga 2 2 5log3 a 2 3 5log2 a Câu24: Chohàm số . Mệnh đề nàosau đây đúng? 3 1 32 fx x  A. . B. . 2 1 d 332 fxx C x    2 1 d 632 fxx C x    C. D. 2 1 d 332 fxx C x    2 1 d 632 fxx C x    Câu25: Chohàm số có đồ thị như hình vẽ. Chọn đáp án đúng? 32 yfxaxbxcxd  A. , , , . B. , , , . 0a0b0c0d 0a0b0c0d C. , , , . D. , , , . 0a0b0c0d 0a0b0c0d Câu26: Thể tích của khối lập phương có cạnh bằng 2 bằng

có tiệm cận đứng?

đều.

Tứ giác đều.

Câu22: Cho

DẠYKÈMQUYNHƠN

OFFICIAL A. B. C. D. 2 8 3 8 4 Câu27: Cho tứ diện cóba đường thẳng , , vuônggóc với nhau từng đôi một, , . SABC SASBSC 3SA , . Diện tích mặt cầu ngoại tiếp bằng 4SB 5SC . SABC A. B. C. D. 50 75 100 25 Câu28: Cho khối chóp có thể tích , , làhai điểm lần lượt nằm trênhai cạnh , . SABC VMN SBSC saocho .Tính thể tích khối đa diện theo 2 3 SMCN SBCS  AMNCBV A. B. C. D. 7 9 V 4 9 V 2 9 V 5 9 V Câu29: Cho khối chóp lục giác đều có cạnh đáy bằng , cạnh bên bằng , thể tích khối chóp đó: 1 2 A. . B. . C. . D. . 32 2 2 2 33 2 3 2 Câu30: Giá trị lớn nhất của hàm số trên đoạn làbaonhiêu? 3 ()32 fxxx [1;2] A. B. C. D. 2 0 4 2 Câu31: Cho là một nguyênhàm của hàm số , biết .Giá trị của : Fx 1 21fx x   01F  2F A. . B. . C. . D. . 1 1ln3 2  1 1ln5 2  1ln3  1 1ln3 2  Câu32: Lăng trụ có thể tích bằng . lần lượt làtrung điểm các cạnh . Thể ABCABC   27,MN , AABB tích khối chóp bằng: MNAC A. . B. . C. . D. 9 2 27 2 9 3 Câu33: Tập nghiệm của bất phương trình là 115.62.3 x x   A. B. C. D.  2 ;log5  2 log5;0 2 log5;0 1 ; 10    Câu34: Chohàm số cógiá trị cực đại vàgiá trị cực tiểu . Mệnh đề nào dưới 4223yxx CDy CTy đây đúng? A. B. 315CDCTyy 23CTCDyy C. D. 25 CDCTyy 12CDCTyy Câu35: Viết phương trình tiếp tuyến của đồ thị tại điểm cóhoành độ bằng 42 :23Cyxx 2 A. B. 22yx 2443yx C. D. 24yx 2443yx  Câu36: Số nghiệm thực của phương trình . 243 91 xx 

Câu42: Cho khối lăng trụ tamgiác có đáy làtamgiácvuông tại thoả mãn . '''ABCABC A , đồng thời cùng tạo với đáy một góc . Gọi lần

 ' , ' , ' AAABAC

làtrung điểm của các cạnh .Tính thể tích khối tứ diện '' , '' ,

Câu43: Một côngtychuyên

DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D. 1 0 2 3 Câu37: Chohìnhchóp có đáy làhình chữ nhật, tamgiác đều cạnh và nằm . SABCDABCD SAB a trong mặt phẳng vuônggóc với đáy. Biết góc giữa và bằng ,tính thể tích khối SC SAD30 chóp . . SABC A. . B. . C. . D. . 36 6 a 3 4 a 36 12 a 3 2 a Câu38: Cho phương trình:  3 3 3 sin2cos222cos12cos232cos2 xx xm xm xm    Tổngtấtcảcácgiátrịnguyêncủathamsố đểphươngtrìnhtrêncóđúng nghiệm m 1 2 0; 3 x      A. . B. . C. . D. . 8 12 10 9 Câu39: Chocác số thực dương thỏa mãn .Tìmgiá trị lớn , xy  22 2 1 log 221xy xxyy xy      nhất của biểu thức . 23 1 Pxy xy    A. B. C. D. 8 1 2 1 2 Câu40: Tập hợp tất cả cácgiá trị thực của tham số để phương trình cóhai m 1 4220 xx mm  nghiệm phân biệt thuộc là  0;2 A. . B. . 18 ;12; 7     2;2 C. D.  ;12;  18 2; 7    Câu41: Chohàm số . Số điểm cực trị của hàm số đã cholà 235

C. D.

yxx

1 2 3

lượt

ABACBC MNAH A. B.

D. 33 2 a 3 2 a 3 4 a 32 3 a

ABaACa

0 60,,MNH

sản xuất chậu trồng câycó dạng hình trụ khôngcó nắp, chậu có thể tích Biết giá vật liệu làm mặt xungquanh chậu là đồng, để làm đáy chậu 30,5m 21m 100.000 21m là đồng. Số tiền ít nhất để mua vật liệu làm một chậu gần nhất với số nào dưới đây? 200000 A. đồng. B. đồng C. đồng D. đồng 349.000 725000498000369000

DẠYKÈMQUYNHƠN

4034. 2027. 4032. 2022. Câu48: Chohàm số với đạo hàm .Có tất cả baonhiêugiá trị

Câu44: Tìm tất cả cácgiá trị của để đồ thị hàm số có đúng hai đường tiệm cận m 2 11 3 x y xmxm   đứng A. B.  0; 1 0; 2    C. D. 1 0; 2     ;120;  Câu45: Chọn ngẫu nhiênba số trong tập hợp Biết xác suất để ba số tìm được ,, abc  1;2;3;;20S thỏa mãn chia hết cho là với làcác số nguyên dương, phân số tối 222 abc  3, m n , mn m n giản. bằng Smn  A. B. C. D. 58. 127. 85. 239. Câu46: Hàm số nghịch biến trên khoảng khi: 4mx y xm     ;0 A. B. C. D. 20 m  2m 2m 0m Câu47: Chohàm số đa thức bậc bốn có đồ thị như hình vẽ dưới đây:  yfx Gọi là tập hợp tất cả cácgiá trị nguyên của tham số để hàm số S  2022;2022m có điểm cực trị. Số phần tử của tập



2 2

 fxxxxmx nguyên của tham số để hàm số có đúng điểm cực trị? m  yfx 1 A. B. C. D. 5. 3. 4. 6. Câu49: Tất cả cácgiá trị của tham số để phương trình có nghiệm duy nhá́t là: m loglog(1) mxx A. hoặc .B. . C. và ,D. . 0m 4m 10 m  0m 4m 0m Câu50: Chohìnhchóp đều có đáy làhìnhvuông cạnh bằng , cạnh bên SABCDABCD a 2 SAa  .Khoảng cách giữa 2 đường thẳng và bằng SDAB

OFFICIAL

là  22  yfxm9 S

C. D.

 yfx

125

DẠYKÈMQUYNHƠN

OFFICIAL A. . B. . C. . D. . 7 30 a 30 2 7 a 30 7 a 14 15 a ---------- HẾT ----------

HƯỚNG DẪN GIẢI CHI TIẾT

A. triệu. B. triệu. C. triệu. D. triệu. 12 14 10 7

Lời giải

Chọn D

Số hố câylà .4520 

Mỗi hố có thể tíchlà .32.1.12m

Số tiền để chi đổ đất là đồng20.2.1750007.000.000

Câu2: Chohàm số có bảng biến thiên như dưới đây.

Hỏi đồ thị hàm số cóbaonhiêu tiệm cận

A. . B. . C. . D. . 3 2 4 1 Lời giải

A Tacó là một tiệm cận đứng.

lim 2

một tiệm cận đứng.

một tiệm cận ngang

Vậy đồ thị hàm số có3 đường tiệm cận.

Câu3: Cóbaonhiêucách xếp 4 bạn namvà2 bạn nữ thành một hangngang.

. B. . C. . D. . 48 120 8 720

DẠYKÈMQUYNHƠN OFFICIAL

giải

1.D 2.A 3.D 4.B 5.B 6.D 7.B 8.B 9.C 10.B 11.B12.D13.A14.A15.B16.B17.C18.D19.A20.A 21.B22.C23.D24.B25.D26.C27.A28.A29.D30.C 31.B32.A33.A34.C35.B36.C37.A38.C39.D40.D 41.C42.C43.A44.C45.B46.A47.A48.D49.A50.D

BẢNG ĐÁP ÁN



yfx 

(2)

  là

0 lim0 x yx   là

lim00 x yy  

Chọn

Lời

Chọn D

Hàm số nghịch biến khivà chỉ khi . 2 023013yxx x

Vậy hàm số đã cho nghịch biến trên khoảng . 1;3

Câu7: Chohàm số liên tục trên có bảng biến thiên như hình vẽ

Khi đó số điểm cực tiểu của hàm số bằng:

A. B. C. D. 2 1 0 3

Lời giải Chọn B

Dựa vào bảng biến thiênta thấy hàm số đã chokhôngxác định tại và đổi dấu từ 1x fx

“âm”sang “dương” khiqua nênnó chỉ có điểm cực tiểu. 3x 1 Câu8: Chohìnhchóp có đáy làhìnhthoi cạnh ,góc

DẠYKÈMQUYNHƠN OFFICIAL

Cóbaonhiêucách xếp 4 bạn namvà2 bạn nữ thành một hangnganglà 6!720  Câu4: Khối chópcó chiều cao bằng 1và diện tích đáy là có thể tíchlà. 2 a A. B. C. D. 3 a 2 3 a 2 a 3 3 a Lời giải Chọn B Thể tích của khối chóplà . 2 21 .1. 33 a Va Câu5: Cho cấp số cộng với .Tìm số hạng đầu vàcôngsai .  n u 32 n un 1u d A. . B. . C. . D. . 12;2ud 15;3ud 13;5ud 15;2ud Lời giải Chọn B Tacó và . 13.125u  1323123 nn duunn      Vậy 15;3ud Câu6: Khoảng nghịch biến của hàm số là 321 3 3 yxxx  A. . B. .  3;  ;13;  C. D.  ;1  1;3 Lời giải Chọn D Tacó . 223yxx  







 ;11; 

 yfx

vuông . SABCDABCD a  0120BAD SA

2  Sa A   SBC ABCD A. . B. . C. . D. . 060 030 045 090

, cạnh

góc với đáy và .Tínhgóc giữa hai mặt phẳng và

DẠYKÈMQUYNHƠN OFFICIAL

Diện tích của mặt cầu cóbánkính được tínhtheocông thức

Lời giải Chọn B φ H C A D B S Từ giả thiết suyratamgiác đều. Do đó, gọi làtrung điểm của thì ABC H BC  . SHA Xéttamgiác vuông tại có SAH A 0 33 3 , tan 30. 222 3  a a SA SAAHAB AH  Vậy góc giữa hai mặt phẳng và bằng  SBC ABCD 0 30. Câu9: Với các số thực bất kì, mệnh đề nàosau đây đúng? , ab A. B. C. D. 5 5 5 a ab b   5 5 5 a ab b  5 5 5 a ab b  5 5 5 aa b b  Lời giải Chọn C Câu10: Họ nguyênhàm của hàm số là: sin fxxx  A. B. C. D. 2 cos 2 xxC 2 cos 2 xxC  1cosxC 1cosxC  Lời giải Chọn B Tacó:  2 dsindcos 2 xfxxxxx xC   

nào dưới đây? S r A. B. C. D. 21 3 Sr  24 Sr  2Sr  24 3 Sr  Lời giải Chọn B Câu12: Chohàm số có một nguyênhàmlà . Khẳng định nàosau đây là đúng? 3 yx  Fx A. B. C. D.  2016FF 201FF  208FF 204FF Lời giải Chọn D

Câu11:

DẠYKÈMQUYNHƠN OFFICIAL

Câu13: Cắt hình trụ bởi một mặt phẳng qua trục, ta được thiết diện là một hìnhvuôngcóchuvilà8.

  4 3 4 4 4 20 20 4 44 x FxxdxC FF CC 

 



Diện tíchxungquanh

A. B. C. D. 4 2 . 3  2 8.  Lời giải Chọn A h l r Thiết diện thu được làhìnhvuông ,nên . ABCD 8 22 4 lr Diện tíchxungquanh của hình trụ là: . 22.1.24 xq Srl Câu14: Đạo hàm của hàm số là 2 2xx y   A. B. 2 212ln2. xx yx   2 2ln2. xx y    C. D. 21 2ln2. x y    2 212xx yx   Lời giải Chọn A Tacó .   2 2 2 2 2 2212ln2ln2 xx xx xx y xx x            Câu15: Chohàm số Đồ thị của hàm số làhìnhnàotrong bốn hình dưới đây: ln yfxxx  yfx  





của hình trụ đã cho bằng

C. D. Lời giải Chọn B

Tacó . lnln1yfxxxx  

Đồ thị hàm số có tập xác định nên nằm phíabên phải trục hoành.Do đó loại phương yfx  

án C.

Đồ thị hàm số đi qua điểm nên loại phương án A. yfx    1;1

Đồ thị hàm số cắt trục hoành tại điểm nên loại phương án D. yfx   1 ;0 e 

Câu16: Mệnh đề nào dưới đây sai?

A. B. 2 1dtan. cos xxC x 

1dln. xxC x 

C. D. sindcosxxxC  33d ln3 x xxC

Câu17: Chohàm số

đồ thị như hình dưới đây. Tìm tất cả cácgiá trị thực của tham số 42 2 yxx

DẠYKÈMQUYNHƠN OFFICIAL

A. B.

 



 Lời

Chọn

x 



giải

B Vì . 1dlnxxC

để

m 

x y 1 1 -O 1 A.

C. D.



0

Lời

Chọn

có



phương trình có bốn nghiệm phân biệt.

4220xxm

 01 m 1m

01 m

giải

42 42202 xxmxxm

Số nghiệm của phương trìnhlà số giao

4 nghiệm phân

dưới đây là đồ thị của hàm số với làcác số thực. Mệnh    axb ycxd,,, abcd

đề nào dưới đây đúng?

Chọn A

x  y0,x2.  y0,x1.  y0,1.

B. C. D.

Lời giải

Dựa vào đồ thị ta nhận thấy tiệm cận đứng bằng 2vààm số nghịch biến vậy chọn A

Câu20: Đồ thị hàm số nàotrongcáchàm số dưới đây có tiệm cận đứng?

Lời giải

DẠYKÈMQUYNHƠN OFFICIAL

Chọn A

đồ thị hàm số và đường thẳng 42 2 yxx  ym 

. 01 m Câu18:

nghiệm

là  2 3 3 log1log212 x x   A. B. C. D. 3 2 0 1 Lời giải Chọn D Điều

  2 2 2 log1log212 x x    2 2 2 2 2 log1log21log4 x x    2 2 2 log121log4 xx       22 214 xx   2 2 2 2 210212 212230 xxVN xx xx xx            . 3 2 1 x x     Thử lại tacó một nghiệm thỏa mãn. 3 2 x Câu19: Đường cong của hình

điểm của

Để phương trìnhcó đúng

biệt

Số

của phương trình

kiện: 1 ,1 2 xx

 y0,2.

A. B. C. D. 1 y x  2 1 1y x   4 1 1y x   2 1 1y xx  

. 2 1 . 1y xx  

Câu21: Các mặt của khối tám mặt đều làcác

A. Bátgiác đều. B. Tamgiác đều. C. Tứ giác đều. D. Ngũ giác đều.

Các mặt của khối tám mặt đều

Cho khối nóncó chiều cao

DẠYKÈMQUYNHƠN OFFICIAL

+)Xéthàm số TXĐ . 1 .y x   0;D Tiệm cận đứng của đồ thị là 0 1 lim xx   0x +)Hàm số có TXĐ . Vậy đồ thị hàm số khôngcó tiệm cận đứng 4 1 . 1y x   D +)Hàm số có TXĐ . Vậy đồ thị hàm số khôngcó tiệm cận đứng. 2 1 . 1y x   D +)Hàm số có TXĐ . Vậy đồ thị hàm số khôngcó tiệm cận đứng

D

Lời giải Chọn B

làcáctamgiác

Câu22:

vàbánkính đáy . Thể tích khối nón đã cho bằng: 6h 3r A. . B. . C. . D. . 54 6 18 36 Lời giải Chọn C Thể tích khối nón đã cho bằng . 2211 3618 33 Vrh    Câu23: Cho là số thực dương tùyý,khi đó bằng a 5 2log 22 a    A. B. C. D. 2 3 25loga 2 3 25loga 2 2 5log3 a 2 3 5log2 a Lời giải Chọn D 5 5 2 22 2 3 logloglog225log2 22 a a a      Câu24: Chohàm số . Mệnh đề nàosau đây đúng? 3 1 32 fx x  A. B. 2 1 d 332 fxx C x    2 1 d 632 fxx C x    C. D. 2 1 d 332 fxx C x    2 1 d 632 fxx C x    Lời giải Chọn B .  3 3 2 11 1 dd32d32 33 2 632 fxx xxx C x x       Câu25: Chohàm số có đồ thị như hình vẽ. Chọn đáp án đúng? 32 yfxaxbxcxd 

đều.

DẠYKÈMQUYNHƠN

OFFICIAL A. , , , . B. , , , . 0a0b0c0d 0a0b0c0d C. , , , . D. , , , 0a0b0c0d 0a0b0c0d Lời giải Chọn D Tacó và : 32 yfxaxbxcxd  2 32 fxaxbxc   00fd  ,do đó lim x fx   0a  Tổng hai điểm cực trị của hàm số 12 2 00 3 b xx b a   Tíchhai điểm cực trị của hàm số 1200 3 c xx c a  Vậy, , , , . 0a0b0c0d Câu26: Thể tích của khối lập phương có cạnh bằng 2 bằng A. B. C. D. 2 8 3 8 4 Lời giải Chọn B Thể tích của khối lập phương : . 3 28V Câu27: Cho tứ diện cóba đường thẳng , , vuônggóc với nhau từng đôi một, , SABC SASBSC 3SA , . Diện tích mặt cầu ngoại tiếp bằng 4SB 5SC SABC A. B. C. D. 50 75 100 25 Lời giải Chọn A

DẠYKÈMQUYNHƠN

OFFICIAL 5 4 3 S C B A Bánkính mặt cầu ngoại tiếp bằng SABC 22252 22 SASBSC R    Diện tích mặt cầu ngoại tiếp bằng SABC 2 450SR Câu28: Cho khối chóp có thể tích , , làhai điểm lần lượt nằm trênhai cạnh , . SABC VMN SBSC saocho .Tính thể tích khối đa diện theo 2 3 SMCN SBCS  AMNCBV A. B. C. D. 7 9 V 4 9 V 2 9 V 5 9 V Lời giải Chọn A N M A C B S Tacó: 21 33 7 9 AMNCB SAMN SMSN VVVV V SBSC VV V     Câu29: Cho khối chóp lục giác đều có cạnh đáy bằng , cạnh bên bằng , thể tích khối chóp đó: 1 2 A. . B. . C. . D. . 32 2 2 2 33 2 3 2 Lời giải Chọn D

DẠYKÈMQUYNHƠN

OFFICIAL O F E D C B A S Chóp lục giác đều có đáy làhình lục giác đều. Lục giác đều được ghép . SABCDEF ABCDEF từ 6tamgiác đều chung đỉnh tâm làtâm lục giác đều, vuônggóc đáy. O SO  2 2 2 333 6111333 42 .. 3322 211 day day S VSh h              Câu30: Giá trị lớn nhất của hàm số trên đoạn làbaonhiêu? 3 ()32 fxxx [1;2] A. B. C. D. 2 0 4 2 Lời giải Chọn C  3 2 ()3233 fxxxfxx   011fxxx  Xét : , ,  1;2x 14f10f24f Vậy . 1;2 4Maxfx Câu31: Cho là một nguyênhàm của hàm số , biết .Giá trị của : Fx 1 21fx x   01F  2F A. . B. . C. . D. . 1 1ln3 2  1 1ln5 2  1ln3  1 1ln3 2  Lời giải Chọn B Tacó  11 dln21 212 Fx xxC x     .  1 01ln2.0111 2 F CC   1 1 2ln2.211ln51 2 2 F  

DẠYKÈMQUYNHƠN

OFFICIAL Câu32: Lăng trụ có thể tích bằng lần lượt làtrung điểm các cạnh Thể ABCABC 27,MN , AABB tích khối chóp bằng: MNAC A. . B. . C. . D. 9 2 27 2 9 3 Lời giải Chọn A N M A B C A' B' C' .     1 3,1279 ,662 ABC MNAC CABN MNAC ABCABCABCABCABC SdNABC VV V VV SdBABC       Câu33: Tập nghiệm của bất phương trình là 115.62.3 x x   A. B. C. D.  2 ;log5  2 log5;0 2 log5;0 1 ; 10    Lời giải Chọn A Tacó 1 11 1 2 2 2 6222 5.62.3321log11log5log5 555 x x x x x x x          Vậy tập nghiệm của bất phương trình .  2 ;log5S Câu34: Chohàm số cógiá trị cực đại vàgiá trị cực tiểu . Mệnh đề nào dưới 4223yxx CDy CTy đây đúng? A. B. C. D. 315CDCTyy 23CTCDyy 25 CDCTyy 12CDCTyy Lời giải Chọn C Tập xác định D Tacó , 3 44 yxx  1 00 1 x yx x      Bảng biến thiên

DẠYKÈMQUYNHƠN

Chohìnhchóp có đáy làhình chữ nhật, tamgiác đều cạnh và

Từ bảng biến thiênsuyra , . 3CTy 4CDy Vậy 25 CDCTyy Câu35: Viết phương trình tiếp tuyến của đồ thị tại điểm cóhoành độ bằng 42 :23Cyxx 2 A. B. C. D. 22yx 2443yx 24yx 2443yx  Lời giải Chọn B Gọi là tọa độ tiếp điểm  2;MMy Tacó 42 22235My Tacó suyra 3 44 yxx  3 2424224ky  Vậy phương trình tiếp tuyến của đồ thị là .  24252443yx x   Câu36: Số nghiệm thực của phương trình . 243 91 xx  A. . B. . C. . D. . 1 0 2 3 Lời giải Chọn C Tacó: . 2432 1 91430 3 xx x xx x    Câu37:

nằm SABCDABCD SAB a trong mặt phẳng vuônggóc với đáy. Biết góc giữa và bằng ,tính thể tích khối SC SAD30 chóp .SABC A. . B. . C. . D. . 36 6 a 3 4 a 36 12 a 3 2 a Lời giải Chọn A M O N D K H B A C S I

OFFICIAL

DẠYKÈMQUYNHƠN

. ,,, HKMN ,,, ABSAADSDOACBD 

đó, tacó

đó .

OKSC   ,, SCSADOKSAD 

.Do , lại có ADAB ADSABADSA ADSH   // MNSAADMN  OMAD  (vì ). Từ đây suyra . Kẻ suyra // OMCD  ADOMNOMNSAD    OIMN  .OISAD  Từ đây tacó .    ,O,30OKSADKKIOKI    Xéttamgiác có màtamgiác đều cạnh suy OMN 111 2,,22 MNSAONSBOMAB    SAB a ratamgiác đều cạnh .Do đó tacó: . OMN 2 a 33 . 224 Oaa I Xéttamgiác vuông tại ,tacó . OKI I 3 sin30 sin302 OI OIa OK OK   Suyra .Xéttamgiác vuông tại có: 2O3SCKa  SHC H 2222222 SCSHHCSCSHHBBC  .  22 2 2 3 3 2 22 aa a BCBCa      Từ đó tacó: . 3 1136 2 3326SABCDABCD aaVSSHaa    Câu38: Cho phương trình .  3 3 3 sin2cos222cos12cos232cos2 xx xm xm xm    Tổngtấtcảcácgiátrịnguyêncủathamsố đểphươngtrìnhtrêncóđúng nghiệm . m 1 2 0; 3 x      A. . B. . C. . D. . 8 12 10 9 Lời giải Chọn C Tacó:  3 3 3 sin2cos222cos12cos232cos2 xx xm xm xm    .(2)   3 3 3 3 2sinsin22cos22cos22cos2 xxxm xm xm     Xéthàm số , với .Tacó: suyrahàm số luôn đồng 32 fttt  0t 2 '610, fttt  ft biến. Mà  3 3 23 sin0 2sin2cos2sin2cos2 sin2cos2 x fxfxm xxm xxm     

OFFICIAL Gọi lần lượt làtrung điểm của và

Khi

,do

Tacó:

DẠYKÈMQUYNHƠN

OFFICIAL (vì ) . 23 1cos2cos2 xxm  2 sin0,0; 3 xx      32 2coscos1xxm  Đặt ,vì .Xéthàm số với cos vx  2 1 0;cos;1 3 2 x vx       32 21gvvv  .Có .Cho . 1 ;1 2 v   2 '62 gvvv   2 0 '06201 3 v gv vv v      Bảng biến thiên v1 2 1 3 01 ' gv00 gv11 28 27 4 Dựa vào bảng biến thiênsuyra phương trìnhcó đúng 1 nghiệm trên khi 2 0; 3     1 28 4 27 m m     Do . Vậy tổng tất cả giá trị nguyên của tham số thỏa yêu cầu đề  4,3,2,1mm  m bàilà: .432110  Câu39: Chocác số thực dương thỏa mãn .Tìmgiá trị lớn , xy  22 2 1 log 221xy xxyy xy      nhất của biểu thức . 23 1 Pxy xy    A. . B. . C. . D. . 8 1 2 1 2 Lời giải Chọn D Phương trình   22 22 2 1 2log2 1 2 xy xyxy xy     Đặt , với thì 221uxy2 vxy  ,0uv 22logu vu v  (*) 2 22log2loguuvv  Xét với . Dễ thấy . 22log fttt  0t  '210,0 ln2ft t t  Suyra đồng biến trên nên . ft  0;  22 * 111uvxy  Gọi tâm ,bánkính .  ; Mxy:MC  1;1I 1R

DẠYKÈMQUYNHƠN

OFFICIAL Mặt khác .  23 :230 1 PxyMPxPyP xy       Để tồn tại điểm chung giữa và  C  2 2 35 ; 1 23 P dIR PP    2 6 7201202 7 PP P   Suyra .  22 1111 max2 2 20 x Pxy y y               Câu40: Tập hợp tất cả cácgiá trị thực của tham số để phương trình cóhai m 1 4220 xx mm  nghiệm phân biệt thuộc là  0;2 A. B. C. D. 18 ;12; 7    2;2  ;12;  18 2; 7    Lời giải Chọn D Đặt .Do . 2xt  0;21;4x t  Khi đó phương trìnhthành 2220tmtm .   2 2 2 2120 ,1;4 21 t tmt m gtt t    Tacó: ,cho .  2 2 '224 21 tt gt t     1 '0 2 tloai gt tnhan    Tacó và bảng biến thiên của : 18 22,13,4 7ggg gt Yêu cầu bàitoán . 18 2; 7 m    Câu41: Chohàm số . Số điểm cực trị của hàm số đã cholà 235yxx A. . B. . C. . D. . 1 2 3 0 Lời giải Chọn C Đặt .Tacó 235gxxx  3 '0230 2 gx x x 

Mặt khác .  329 0 2gxx  

Tacó bảng biến thiên của như sau: gx

Dựa vào bảng biến thiên,tacó có3 điểm cực trị.  ygx

Câu42: Cho khối lăng trụ tamgiác có đáy làtamgiácvuông tại thoả mãn . '''ABCABC A , đồng thời cùng tạo với đáy một góc . Gọi lần ,3ABaACa  ' , ' , ' AAABAC 0 60,,MNH

lượt làtrung điểm của các cạnh .Tính thể tích khối tứ diện '' , '' , ABACBC MNAH

. B. . C. .

2 a

giải Chọn C

Gọi làhình chiếu của lênmp ,khi đó cáctamgiác là O 'A ABC ' , ' , ' AOAAOBAOC

DẠYKÈMQUYNHƠN OFFICIAL

2 a

4 a

2 3 a Lời

 cáctamgiácvuông tại và bằng nhau.Khi đó hay O OAOBOC  OH ' AHABC  Tacó . 0 2 '.tan603BCaHBaAHHBa   Do đó . 3 'ABC 111 '33 3322 A ABC aVSAHaaa    Gọi làgiao điểm của và , làgiao điểm của và , làgiao điểm của K ' ACNAI ' ABMAL và .Tacó và . KI' AH ''1 2 KAIA KIBC KCIB  '1 2 LA LH 

DẠYKÈMQUYNHƠN

OFFICIAL    ' A'MN 1 1 , 2';22 3 3 MNAHHAMN AMN AMN AAMNA VVSdHAMNSdAAMNVV     Mặt khác, (vì khối hai khối tứ diện cócùng chiều cao nhưng ) ' ' 1 4 AAMNAABCVV  ' 1 4AMN ABCSS  Do đó 33 'ABC' 111 2 42224MNAH A AABC aa V VV   Câu43: Một côngtychuyên sản xuất chậu trồng câycó dạng hình trụ khôngcó nắp, chậu có thể tích . Biết giá vật liệu làm mặt xungquanh chậu là đồng, để làm đáy chậu 30,5m 21m 100000 21m là đồng. Số tiền ít nhất để mua vật liệu làm một chậu gần nhất với số nào dưới đây? 200000 A. đồng B. đồng C. đồng D. đồng 349000 725000498000369000 Lời giải Chọn A Gọi , lần lượt làbánkínhvà chiều cao của chậu hình trụ. xmhm Vì thể tích chậu bằng nên . 30,5m 2 2 00,5 ,5 xhh x    Diện tíchxungquanh của chậu là nên số tiền mua vật liệu để làm mặt xungquanh  22xhm là (đồng). 2 0,5100.0002.100.0002..100.000 xh x x x      Diện tích đáy của chậu là nên số tiền mua vật liệu để làm đáy chậu là 22 xm (đồng). 2 2200000200000x x    Số tiền mua vật liệu làm một cái chậu là 2 2 2 3 100.000 50.00050.000 50.00050.000 200000 2000003 200000 T x x x x xx xx        hay . 32 350000.200000.348734,2055T    Câu44: Tìm tất cả cácgiá trị của để đồ thị hàm số có đúng hai đường tiệm cận m 2 11 3 x y xmxm   đứng A. B.  0; 1 0; 2    C. . D. . 1 0; 2     ;120;  Lời giải Chọn C TH1: Phương trình có nghiệm .Khi đó hàm số 230xmxm 1x 1 2 m  hàm số chỉ có một tiệm cận đứng là do đó  2 1111 1313 22 2 x x y xxxx        3 2 x 1 2 m không thoả mãn.

Tachiathành tập: Số chia hết cho, số chia dư , số chia dư 3 33132

Số chia hết cho 3: 3;6;9;12;15;18

Số chia dư 31: 1;4;7;10;13;16;19

Số chia dư 32: 2;5;8;11;14;17;20 Nếu

0mod30mod3,1mod31mod3,2mod31mod3

Nên để tacócácTHsau: 

DẠYKÈMQUYNHƠN OFFICIAL

TH2: Phương trình khôngcó nghiệm 230xmxm 1x 1 2 m  Khi đó hàm số cóhai đường tiệm cận đứng khivà chỉ khi phương trình 2 11 3 x y xmxm   có2 nghiệm phân biệt lớn hơn 230xmxm 12 , xx 1  12 12 0 2 110 xx xx        2 12 4300 2 2 1310 2 m mm m m m mm m                    1 0 2 m  Kết hợp TH1vàTH2tacógiá trị cần tìmlà . m 1 0 2 m  Câu45: Chọn ngẫu nhiênba số trong tập hợp Biết xác suất để ba số tìm được ,, abc  1;2;3;;20S thỏa mãn chia hết cho là với làcác số nguyên dương, phân số tối 222 abc  3, m n , mn m n giản. bằng Smn  A. B. C. D. 58 127 85 239 Lời giải Chọn B Số cách

số từ tập hợp là: . 3 S3 201140C

lấy ngẫu nhiên

 2 2 2

a a a a a a      

2220mod3abc TH1: Lấy số từ cùng một trong tập trên: 3 3 333 67790CCC TH2: Lấy số từ tập các số chia dư và một số từ tập các số chia dư : 2 31 3221 77147CC TH3: Lấy số từ tập các số chia dư và một số từ tập các số chia dư : 2 32 3121 77147CC Vậy xác suất cần tínhlà: 321471479032 127. 95114095 mm mn nn     Câu46: Hàm số nghịch biến trên khoảng khi: 4mx y xm     ;0 A. B. C. D. 20 m  2m 2m 0m Lời giải Chọn A

DẠYKÈMQUYNHƠN

OFFICIAL Tacó: khi:  2 2 44 00 mx m y y x xmxm      2422 0 20 00 m m m m m         Câu47: Chohàm số đa thức bậc bốn có đồ thị như hình vẽ dưới đây:  yfx Gọi là tập hợp tất cả cácgiá trị nguyên của tham số để hàm số S  2022;2022m có điểm cực trị. Số phần tử của tập

 22  yfxm

S A. B. C. D.

Lời giải Chọn A Đặt . 22  gxfxm Tacó

 0 2;0 1 0 fx gxfxfxgxfx      Từ đồ thị hàm số ta thấy có nghiệm đơn nên có điểm cực trị. yfx  17 gx7 Xét .     22 22 0 0 2fxm gxfxmfxmfxm    Do có điểm cực trị nên để có điểm cực trị thì phương gx7 22   yfxmgx9 trình phải có nghiệm bội lẻ hay phải có nghiệm bội lẻ . 0gx 2  22 6 6    m m . Vậy có giá trị .  2022;...;6;6;...;2022 S 4034m Câu48: Chohàm số với đạo hàm .Có tất cả baonhiêugiá trị  yfx 2 2 125  fxxxxmx nguyên của tham số để hàm số có đúng điểm cực trị? m  yfx 1 A. B. C. D. 5. 3. 4. 6. Lời giải Chọn D Tacó: . 2 2 2 0 012501 250 x fxxxxmx x xmx     

là

4034 2027 4032 2022

DẠYKÈMQUYNHƠN OFFICIAL

Hàm số có đúng điểm cực trị chỉ có đúng một nghiệm bội lẻ.  yfx 1 0 fx TH1: vô nghiệm hoặc có nghiệm kép 2250xmx 25055m m   2;1;0;1;2m  TH2: có nghiệm là . 2250xmx 12603  m m Với , . 3m2 2 0 016501 5 (béich½n) (béich½n) (béilÎ) x fxxxxx x x       Suyra thỏa mãnyêu cầu. 3m Vậy .  2;1;0;1;2;3m Câu49: Tất cả cácgiá trị của tham số để phương trình có nghiệm duy nhá́t là: m loglog(1) mxx A. hoặc .B. . C. và ,D. . 0m 4m 10 m  0m 4m 0m Lời giải Chọn A .loglog(1),1 mxx Điều kiện của phương trình 0 10 mx x    2 1,0,01,0,0 loglog(1) 2. 210 1 xmxxmx mxx xmx mxx              Đặt (2). .  221hxxmx   24 hmm + Với 2 0 040. 4 h m mm m    Với không thỏa mãn điều kiện. 0m Với phương trìnhcó nghiệm thỏa mãnyêu cầu bàitoán. 4m 1x + Với 2 0 040. 4 h m mm m     Do nênđểphươngtrìnhcónghiệmduynhấtđiềukiệnlà có2nghiệm 0,0mx 0hx 12 , xx thỏa mãn . 121100xxh m  Kết luận: Để phương trìnhcó nghiệm duy nhất khi hoặc 0m 4m Câu50: Chohìnhchóp đều có đáy làhìnhvuông cạnh bằng , cạnh bên . SABCDABCD a 2 SAa  .Khoảng cáchgiữa 2 đường thẳng và bằng SDAB A. . B. . C. . D. . 7 30 a 30 2 7 a 30 7 a 14 15 a Lời giải Chọn D

DẠYKÈMQUYNHƠN

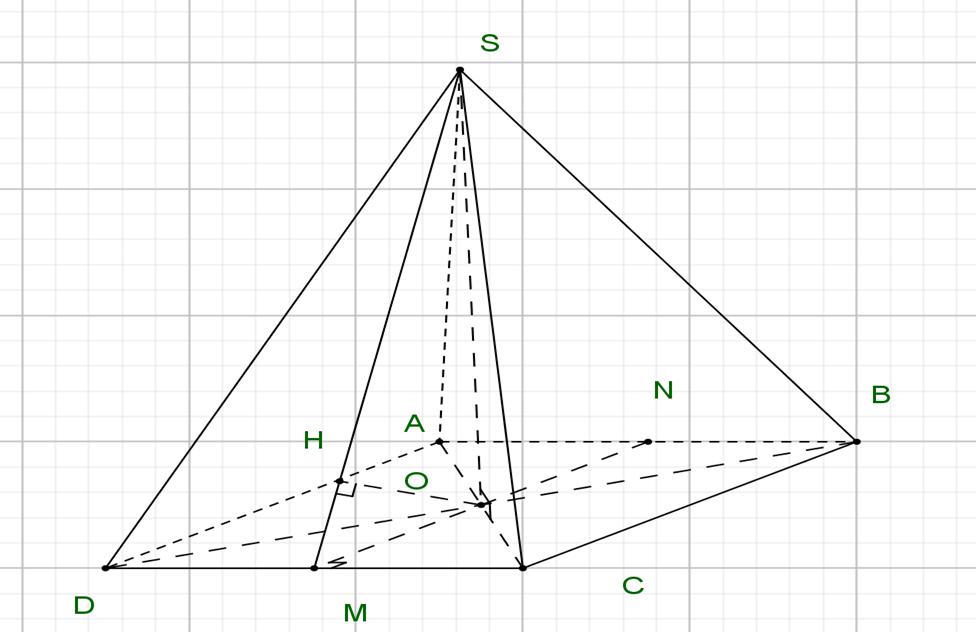
OFFICIAL Tacó2 đường thẳng và chéonhau. SDAB Gọi lần lượt làtrung điểm của ,, MNO ,, ABCDAC Do .    // // ,,2, ABCD ABSADdABSDdMSADdOSAD CDSAD          Trong kẻ  SOM , MHSMHSM   Tacó .    , , OHSM OHSCDdOSCDOH OHCDDoCDSOMOHSOM          Tamgiác vuông tại SOM O 22222 2 1111130 77 24 aaOHOSOM a  210 14 ,2 30 15 Oa H dABSDOHa    ---------- HẾT ---------

SỞ

DẠYKÈMQUYNHƠN OFFICIAL

Câu1:

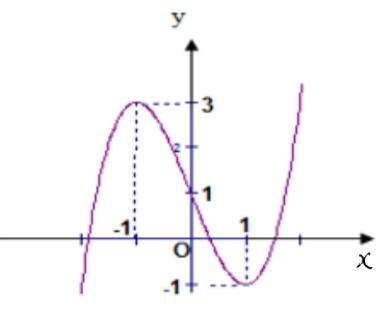
LIÊN

THỬ TỐT NGHIỆP THPT NĂM HỌC 2022–2023

GIÁO DỤC VÀ ĐÀO TẠO BẮC GIANG TRƯỜNG THPTNGÔ SĨ

THI

Trongcáchàm số sau,hàm số nàocó đồ thị như hìnhbên? A. . B. . C. . D. . 1 21 x y x    1 21 x y x   21 x y x   1 21 x y x   Câu2: Chohàm số liên tục trên vàcó đồ thị như hình vẽ dưới đây. Khẳng định nàosau yfx   đây đúng? A. B. C. D. 1;1 max3 fx 1; maxfx   1;1 max1 fx 1; max3 fx   Câu3: Giá trị của tham số để hàm số đạt cực đại tại là m 3221 1 3 yxmxmmx   1x A. B. C. D. 1m 0m 2m 3m Câu4: Tập nghiệm của bất phương trình là  log21 x A. . B. . C. . D. .  ;8  2;  2;8  8; Câu5: Số nghiệm thực của phương trình là 3 3 1 3 3log1log53 x x A. B. C. D. 1 2 3 0 Câu6: Cho .Tính 4 0 ()10fxdx 2 0 (2). Ifxdx  A. . B. . C. . D. 6I 4I 36I 5I Câu7: Cho khối trụ cóbánkính đáy và chiều cao . Thể tích của khối trụ đã cho bằng 3r 5h A. . B. . C. . D. . 30 15 5 45

DẠYKÈMQUYNHƠN OFFICIAL

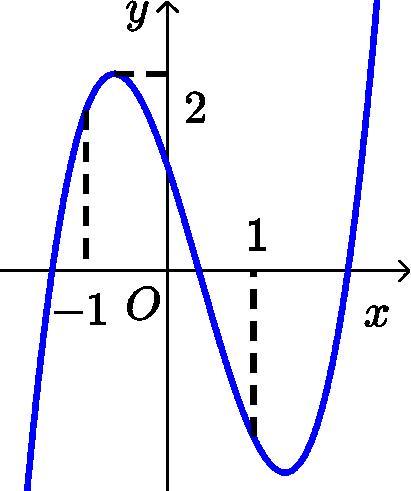
Câu8: Chohàm số có đồ thị như hình vẽ bên  yfx Hàm số đã cho đồng biến trên khoảng nào dưới đây A. B. C. D.  3;  1;3  2;  ;2 Câu9: Chohìnhnóncóbánkính đáy và độ dài đường sinh . Diện tíchxungquanh của hình 2r 5l nón đã cho bằng A. . B. . C. . D. . 200 3  20 10 3  10 Câu10: Hàm số có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng 32  yaxbxcxd A. B. 0,0,0,0 abcd 0,0,0,0 abcd C. . D. . 0,0,0,0 abcd 0,0,0,0  abcd Câu11: Giá trị nhỏ nhất của hàm số trên đoạn bằng 22 2ex fxx   1;2 A. . B. . C. . D. . 22e 22e 42e 2 e Câu12: Hàm số nào dưới đây đồng biến trên ? ;  A. . B. . C. . D. . 1 2 x y x  33 yxx  1 3 x y x    33 yxx  Câu13: Chohìnhchóp . Gọi , , , lần lượt làtrung điểm của các cạnh , , , . SABCDIJKH SASBSC .Tính thể tích khối chóp biết thể tích của khối chóp là SD SABCD SIJKH2.

DẠYKÈMQUYNHƠN

OFFICIAL H K J I A D B C S A. B. C. D. 8 16 4 2 Câu14: Cắt hìnhnón bởi một mặt phẳng đi qua trục ta được thiết diện là một tamgiácvuôngcâncó cạnh huyền bằng .Tính thể tích của khối nón đó. 6a V A. . B. . C. . D. . 36 3 a V   36 4 a V   36 6 a V   36 2 a V   Câu15: Số hạng thứ của cấp số cộng có số hạng đầu bằng vàcôngsai là 11 3 2d A. . B. . C. . D. . 19 17 23 21 Câu16: Tìmgiá trị lớn nhất của hàm số trên đoạn 328169fxxxx    1;3 A. . B. . C. . D. . 1;3 max6 x fx   1;3 13 max 27 x fx   1;3 max5 x fx   1;3 max0 x fx   Câu17: Cho khối chópcó diện tích đáy 3B và chiều cao 2h . Thể tích khối chóp đã cho bằng A. B. C. D. 3 12 6 2 Câu18: Chohàm số có đồ thị như hìnhbên.Tìm tất cả cácgiá trị thực của tham số để 42 2 yxx  m phương trình có bốn nghiệm thực phân biệt. 42 2 xxm  x y 1 -1 0 1 A. . B. . C. . D. . 0m 01 m  01 m  1m Câu19: Chosô thực dương. Rút gọn biểu thức ta được biểu thức nàosau đây? a 1 4 . Paa  A. B. C. D. 1 2a 1 4a 9 4a 3 4a Câu20: Chohàm số có bảng biến thiên như sau:

DẠYKÈMQUYNHƠN

tiết kiệm vào một ngânhàng với lãi suất năm. Biết rằng nếu khôngrút tiền 6,1%/ ra khỏi ngânhàngthì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tínhlãicho năm tiếp theo. Hỏi sauít nhất baonhiêu năm người đó thu được (cả số tiền gửi ban đầu vàlãi) gấp đôi số

OFFICIAL Hàm số đã cho đạt cực tiểu tại A. . B. . C. . D. . 3x 1x 2x 2x Câu21: Phương trình có tập nghiệm là 2sin30 x A. . B. . 2, 3 kk        2 2,2, 33 kkk             C. . D. . 5 2,2, 66 kkk             2, 6 kk        Câu22: Cho làcáchàm số xác định vàliên tục trên . Mệnh đề nàosau đây sai?  , fxgx  A. B.  fxdxfxc    ddd fxgxxfxxgxx        C. với mọi . D. .  dd kfxxkfxx   k  ddd fxgxxfxxgxx          Câu23: Cho , biểu thức cógiá trị bằng baonhiêu? 0,1aa 3loga Da  A. B. C. D. 1 3 3 3 1 3 Câu24: Cho , với làcácphân số tối giản. Tổng bằng 1 2 2 0 (1)x xedxabe   ;,, abab   ab A. . B. . C. . D. . 3 1 2 1 5 Câu25: Tập nghiệm của phương trình là 2 log12 x A. B. C. D. 4x 3x 3x 5x Câu26: Biết ,.Khi đó tínhtheo và bằng 6 log2a 6 log5b 3 log5I ab A. . B. . C. . D. . 1 b I a   1 b I a  1 b I a  b I a  Câu27: Số giao điểm của đường cong và đường cong là 321yxx 21yx A. . B. . C. . D. . 1 2 3 0 Câu28: Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số có phương trình lần lượt 1 2 x y x   là A. . B. . C. . D. . 2;1xy 1 2; 2xy 1;2xy 2;1xy Câu29: Một người gửi

tiền gửi ban đầu, giả định trong khoảng thời giannàylãi suất khôngthay đổi và người đó không

tiền ra?

Câu30: Giá trị cực đại của hàm số

Câu32: Chohìnhchóp có vuônggóc với mặt phẳng , .Tamgiác . SABCSA  ABC2 SAa  ABC vuôngcân tại và (minh họa như hình vẽ) BABa

Góc giữa đường thẳng và mặt phẳng bằng SC  ABC

A. B. C. D. 90 60 30 45

Câu33: Khối đa diện đều loại là khối  3;5

A. Tứ diện đều. B. Lập phương C. Hai mươi mặt đều D. Tám mặt đều

Câu34: Chohàm số liên tục trên . Gọi Slà diện tíchhình phẳng giới hạn bởi các đường fx  (như hình vẽ). Mệnh đề nào dưới đây đúng?

Câu35: Chọn ngẫu nhiênhai số khácnhau từ số nguyên dương đầu tiên.Xác suất để chọn được hai

DẠYKÈMQUYNHƠN OFFICIAL

A. năm. B. năm. C. năm. D. năm. 11 12 13 10

là

yxx A. B. C. D. 3 4 1 0 3 4

23 1yx  A. . B. . C. . D. . \1   1;  ;1  ;11; 

rút

421

Câu31: Tìm tập xác định của hàm số



,0,1,2yfxyxx   A.

 1 2 1 1 dd Sfxxfxx   1 2 1 1 dd Sfxxfxx    C. D.  1 2 1 1 dd Sfxxfxx   1 2 1 1 dd Sfxxfxx   

21 số có tổng là một số chẵn bằng A. B. C. D. 221 441 1 2 10 21 11 21

DẠYKÈMQUYNHƠN OFFICIAL

Chohìnhchóp có đáy làhìnhvuông cạnh ,hai mặt phẳng và . SABCDABCD a  SAB SAD cùngvuônggóc với mặt phẳng ;góc giữa đường thẳng và mặt phẳng  ABCD SC  ABCD bằng .Tínhtheo thể tích khối chóp . 60 a SABCD A. . B. . C. . D. . 36 3 a 33a 332a 36 9 a Câu37: Đạo hàm của hàm số là 12x ye  A. B. C. D. 12 2 x e y   122x ye   122x ye   12x ye   Câu38: Chohình lập phương cạnh (tham khảo hình vẽ bên). Khoảng cách giữa hai . ABCDABCD  a đường thẳng và bằng ABBC C' D' B' A' C B D A A. B. C. D. 3 3 a 2 2 a 3a 2a Câu39: Số giá trị nguyên của thuộc để đồ thị hàm số có đúng ba m 10;10   2 2 1.3 12 xxx y xmxm    đường tiệm cận là A. . B. C. . D. . 20 18 17 19 Câu40: Cho làhàm số đa thức bậc bốn vàhàm số có đồ thị là đường cong như hình fx yfx   dưới đây.

Câu36:

số cóbaonhiêu điểm cực trị thuộc khoảng ?

Xét khối tứ diện có cạnh ,các cạnh còn lại có cạnh bằng .Tìm

tứ diện lớn nhất là ABCD

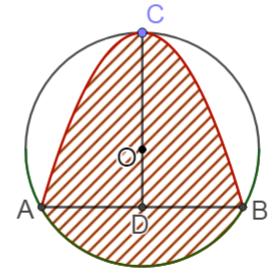
Một hoa văn hìnhtròntâm , ngoại tiếp tamgiác đều có cạnh

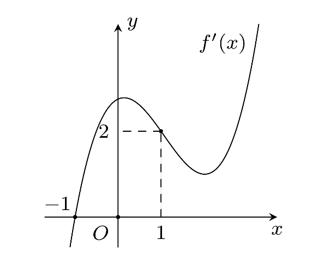
DẠYKÈMQUYNHƠN OFFICIAL

Hàm

cos2

  0;2 A. B. C. D. 0 2 3 1 Câu41:

để thể

khối

A. . B. . C. . D. . 23 62 32 26

điểm: là một phần của parabol. ,, ABC Diện tích phần gạch chéo bằng A. . B. . C. . D. . 237,54cm 29,83cm 227,71cm 236,75cm Câu43: Gọi là tập tất cả các số nguyên để hàm số nghịch biến S m 32 2 1 56 3 yxmxmxm   trên . Tổng các phần tử của bằng  S A. B. C. D. 20 10 18 15 Câu44: Chohình giới hạn bởi đồ thị hàm số ,cungtròncó phương trình () H 33 9 yx  24 yx  (với và trục hoành (phần tô đậm tronghình vẽ) 02) x 

sin1 4 x gxfx 

tích ABCDADx 

Câu42:

Đường cong O ABC 43 ABcm  quaba

Biếtthểtíchcủakhốitrònxoaytạothànhkhiquay quanhtrụchoànhlà , () H 3 ac V bd       trong đó và làcácphân số tối giản. Tính . * ,,, abcd, ac bd Pabcd 

A. B. C. D. 40P 46P 16P 14P

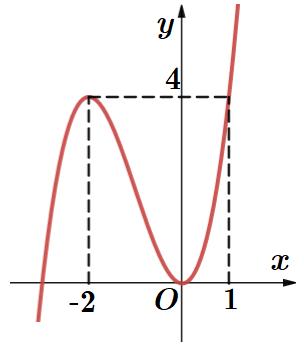
Câu45: Chohàm số thỏa mãn .Tìmgiá trị lớn  ygx 32 2673231  gxgxgxxx

nhất của biểu thức 2  Pgxx

A. B. C. D. 0 1 4 6

Câu46: Chohàm số liên tục trên vàcó đồ thị như hình vẽ dưới đây.

Tập hợp tất cả cácgiá trị thực của

DẠYKÈMQUYNHƠN OFFICIAL

 yfx 

tham số để phương trình có nghiệm m  22231 fxxm thuộc khoảng là  0;1 A. B. C. D. 1 ;1 3     0;1  0;4  1;0 Câu47: Cho bất phương trình .Cóbaonhiêu số nguyên dương 432 42 32 2 ln 20 3 xxx xxm xxm    m để bất phương trình nghiệm đúng với . 0;3x  A. . B. . C. . D. . 3 2 4 0 Câu48: Chohàm số liên tục trên có đồ thị như hình vẽ fx 

DẠYKÈMQUYNHƠN OFFICIAL

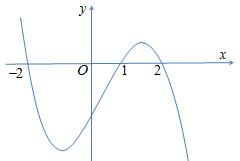
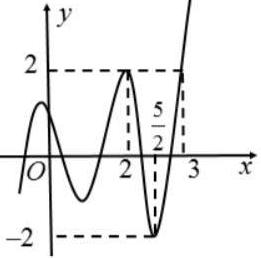
Cóbaonhiêugiá trị nguyên dương nhỏ hơn của tham số để phương trình 10 m có nghiệm phân biệt?  2222 xx mm f f  2 A. B. C. D. 6 7 9 4 Câu49: Chohàm số Đồ thị hàm số như hình vẽ bên dưới và . ()yfx  ()yfx   220ff Hàm số đồng biến trên khoảng nàotrongcác khoảng sau? 2 gxfx  A. B. . C. . D. .  4;3  2;4  0;2  3;1 Câu50: Biết và .Tính 1 0 ()5xfxdx    11f 1 0 (). Ifxdx  A. B. C. D. 4I 4I 6I 6I ---------- HẾT ----------

Câu1: Trongcáchàm số sau,hàm số nàocó đồ thị như hìnhbên?

Đồ thị hàm số tronghình vẽ có đường tiệm cận nganglànên loại các phương án D.

Đồ thị hàmsô cắt trục hoành tại điểm có tọa độ nên loại phương ánAvà C.  0;1

Câu2: Chohàm số liên tục trên vàcó đồ thị như hình vẽ dưới đây. Khẳng định nàosau

đây đúng?

DẠYKÈMQUYNHƠN OFFICIAL

BẢNG ĐÁP ÁN 1234567891 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 2 0 2 1 2 2 2 3 2 4 2 5 BADCBDDADCDBBBBDDBDCBCDBC 2 6 2 7 2 8 2 9 3 0 3 1 3 2 3 3 3 4 3 5 3 6 3 7 3 8 3 9 4 0 4 1 4 2 4 3 4 4 4 5 4 6 4 7 4 8 4 9 5 0 BBDBBADCACACADCBAADCCBCBD HƯỚNG

DẪN GIẢI CHI TIẾT

A. B. C. D. 1 21 x y x    1 21 x y x   21 x y x   1 21 x y x   Lời

giải Chọn

yfx  

A. . B. . C. . D. . 1;1 max3 fx 1; maxfx   1;1 max1 fx 1; max3 fx   Lời giải Chọn A

DẠYKÈMQUYNHƠN

OFFICIAL +) nên phương ánA đúng. 1;1 max3 fx +Không tồn tại giá trị lớn nhất của hàm số trên . yfx  1; Câu3: Giá trị của tham số để hàm số đạt cực đại tại là m 3221 1 3 yxmxmmx   1x A. B. C. D. 1m 0m 2m 3m Lời giải Chọn D Đặt: .  3221 1 3 fxxmxmmx   Tacó: .   2 2 21;22 fxxmxmmfxxm      Để hàm số đạt cực đại tại yfx  1x    2 0 1030 3 10220 1 mL f mm m f m m                    Vậy, thìhàm số hàm số đạt cực đại tại 3m yfx  1x Câu4: Tập nghiệm của bất phương trình là  log21 x A. B. C. D.  ;8  2;  2;8  8; Lời giải Chọn C Bất phương trình .  202 log212108 x x x x x             Vậy tập nghiệm của bất phương trình là  log21 x  2;8T Câu5: Số nghiệm thực của phương trình là 3 3 1 3 3log1log53 x x A. B. C. D. 1 2 3 0 Lời giải Chọn B Điều kiện: 10 5* 50 x x x     Với điều kiện (*) phương trình   3 3 1 3 3 3 3log1log53log1log51 x x x x    . 2 3 log15115362037 xx xx xx x    Vậy số nghiệm thực của phương trình đã cholà2. Câu6: Cho .Tính 4 0 ()10 fxdx 2 0 (2). Ifxdx A. . B. . C. . D. 6I 4I 36I 5I Lời giải

Chọn D

Đặt 22 txdtdx

Đổi cận: 02 04 x t

Câu7: Cho khối trụ cóbánkính đáy và chiều cao . Thể tích của khối trụ đã cho bằng 3r 5

Thể tích của khối trụ: 22 ...3.545 Vrh

Câu8: Chohàm số có đồ thị như hình vẽ bên

Hàm số đã cho đồng biến trên khoảng nào dưới đây

DẠYKÈMQUYNHƠN OFFICIAL

*  2 4 0 0 11 (2) .105 22      Ifxdxftdt

h A. B. C. D.



 45 Lời giải Chọn

 5



yfx

A. B. C. D.  3;  1;3  2;  ;2 Lời giải Chọn

Đặt

txdtdx Đổi cận: 02 04 x t *  2 4 0 0 11 (2) 105 22      Ifxdxftdt Câu9: Chohìnhnóncóbánkính đáy và độ dài đường sinh . Diện tíchxungquanh của hình 2r 5l nón đã cho bằng A. . B. . C. . D. . 200 3  20 10 3  10 Lời giải



22

Chọn D

Thể tích của khối trụ: 22 ...3.545 Vrh

Diện tíchxungquanh: 2510 Srl Câu10: Hàm số có đồ

yaxbxcxd

* Hệ số 0a

* Đồ thị cắt trục tung tại điểm  0;0 Add 0 d

*Hàm số cóhai điểm cực trị trái dấu 00 acc

* Đồ thị hàm số cóhai điểm cực trị ,trong đó hay  ;,; A BAayBby  ba ba

Hàm số cótâm đối xứng   0;IIy

 babbb a a

000 32 

0,0,0,0 abcd

Câu11: Giá trị nhỏ nhất của hàm số trên đoạn bằng

DẠYKÈMQUYNHƠN OFFICIAL

B. .

abcd 0,0,0,0 abcd C. D. 0,0,0,0 abcd 0,0,0,0  abcd Lời giải Chọn

thị như hình vẽ bên. Mệnh đề nào dưới đây đúng 32 

0,0,0,0

32 yaxbxc

Vậy

22 2ex fxx   1;2 A. B. C. D. 22e 22e 42e 2 e Lời giải Chọn D Tacó .  22222 2e22e2e2 x xx fxxx xx       11;2 0 21;2 x fx x     Khi đó ; ; . 21ef 422ef21ef

DẠYKÈMQUYNHƠN

OFFICIAL Vậy 2 1;2 min1e fxf Câu12: Hàm số nào dưới đây đồng biến trên ? ;  A. . B. . C. . D. . 1 2 x y x  33 yxx  1 3 x y x    33 yxx  Lời giải Chọn B Xéthàm số ,tacó . 33 yxx  2 330, yxx  Vậy hàm số đồng biến trên . 33 yxx   ;  Câu13: Chohìnhchóp . Gọi , , , lần lượt làtrung điểm của các cạnh , , , SABCDIJKH SASBSC .Tính thể tích khối chóp biết thể tích của khối chóp là SD . SABCD . SIJKH2 H K J I A D B C S A. B. C. D. 8 16 4 2 Lời giải Chọn B Tacó và nên và 1 .. 8 SIJK SABC VSISJSK VSASBSC   1 .. 8 SIHK SADC VSISHSK VSASDSC   1 8 SIJKSABCVV  1 8 SIHKSADCVV  Do đó suyra .   1 1 8 8 SIJKHSIJKSIHK SABCSADC SABCDVVVVVV   88216SABCDSIJKHVV   Câu14: Cắt hìnhnón bởi một mặt phẳng đi qua trục ta được thiết diện là một tamgiácvuôngcâncó cạnh huyền bằng .Tính thể tích của khối nón đó. 6a V A. . B. . C. . D. . 36 3 a V   36 4 a V   36 6 a V   36 2 a V   Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL

Gọi thiết diện qua trục của hìnhnónlàtamgiác . OMN Theo đề tacó,tamgiác vuôngcân tại có .Do đó, OMN O 6 MNa 6 6 , . 2222   MNa MNa r hOI Vậy khối nóncó 2 3 2 1166.6 ... 33224       aaaVrh   Câu15: Số hạng thứ của cấp số cộng có số hạng đầu bằng vàcôngsai là 11 3 2d A. . B. . C. . D. . 19 17 23 21 Lời giải Chọn B Tacó  11110310.217.  uud Câu16: Tìmgiá trị lớn nhất của hàm số trên đoạn 328169fxxxx    1;3 A. B. C. D. 1;3 max6 x fx   1;3 13 max 27 x fx   1;3 max5 x fx   1;3 max0 x fx   Lời giải Chọn D Tacó:     2 4 1;3 3161603 41;3 x fxxxfx x         Và:   1;3 4115 10,,36max0 327 x ff f fx         Câu17: Cho khối chópcó diện tích đáy 3B và chiều cao 2h . Thể tích khối chóp đã cho bằng A. B. C. D. 3. 12. 6. 2. Lời giải Chọn D

Thể tích khối chóp: 1 2 3

Tacó: 1113 4424 Paaaaa 

Câu20: Chohàm số có bảng biến thiên như sau: Hàm số đã cho đạt cực tiểu tại

DẠYKÈMQUYNHƠN OFFICIAL

VBh

tất

cácgiá trị thực của tham số để 42 2 yxx  m phương trình có bốn nghiệm thực phân biệt. 42 2 xxm  x y 1 -1 0 1 A. . B. . C. . D. . 0m 01 m  01 m  1m Lời giải Chọn B Dựa vàohình ảnh đồ thị hàm số thì phương trình có bốn nghiệm thực phân biệt 42

 khi: .

m 

Chosô

biểu thức ta được biểu thức nàosau đây? a 1 4 Paa  A. . B. . C. . D. . 1 2a 1 4a 9 4a 3 4a Lời giải

Câu18: Chohàm số có đồ thị như hìnhbên.Tìm

cả

2 xxm

Câu19:

thực dương. Rút gọn

Chọn D

A. . B. . C. . D. .

 1x 2x 2x Lời giải Chọn C Dựa vào bảng biến thiên,hàm số đạt cực tiểu tại 2x Câu21: Phương trình có tập nghiệm là 2sin30 x A. . B. . 2, 3 kk        2 2,2, 33 kkk             C. D. 5 2,2, 66 kkk             2, 6 kk       

DẠYKÈMQUYNHƠN

OFFICIAL Lời giải Chọn B . 3 2sin30sinsinsin 23 x x x   2 23() 2 3 xk k xk              Câu22: Cho làcáchàm số xác định vàliên tục trên . Mệnh đề nàosau đây sai?  , fxgx  A. .B. .  fxdxfxc    ddd fxgxxfxxgxx        C. với mọi . D. .  dd kfxxkfxx   k  ddd fxgxxfxxgxx          Lời giải Chọn C với mọi  dd kfxxkfxx   0k Câu23: Cho , biểu thức cógiá trị bằng baonhiêu? 0,1aa 3loga Da  A. B. C. D. 1 3 3 3 1 3 Lời giải Chọn D 3 11 loglog33 a a Daa   Câu24: Cho , với làcácphân số tối giản. Tổng bằng 1 2 2 0 (1)x xedxabe   ;,, abab   ab A. . B. . C. . D. . 3 1 2 1 5 Lời giải Chọn B Đặt ; chọn 1dd uxux  2 dd, x vex  21 2 x ve  . 1 1 1 2 2 2 0 0 0 11 (1)(1)d 22 x x x xedxxeex    1 2 2 2 0 1111131 2424444 x e e e          31 ; 44 ab  Vậy 1 2 ab Câu25: Tập nghiệm của phương trình là 2 log12 x A. . B. . C. . D. . 4x 3x 3x 5x Lời giải Chọn C Tacó: .  2 2 log12123 x xx 

DẠYKÈMQUYNHƠN OFFICIAL

Câu29: Một người gửi tiết kiệm vào một ngânhàng với lãi suất năm. Biết rằng nếu khôngrút tiền 6,1%/ ra khỏi ngânhàngthì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn để tínhlãicho năm tiếp theo. Hỏi sauít nhất baonhiêu năm người đó thu được (cả số tiền gửi ban đầu vàlãi) gấp đôi số tiền gửi ban đầu, giả định trong khoảng thời giannàylãi suất khôngthay đổi và người đó không rút tiền ra?

Câu26: Biết ,.Khi đó tínhtheo và bằng 6 log2a 6 log5b 3 log5I ab A. . B. . C. . D. . 1 b I a   1 b I a  1 b I a  b I a  Lời giải Chọn B Tacó: . 6 6 3 666 llog5log5 og5 . log3log6log21 b I a   Câu27: Số giao điểm của đường cong và đường cong là 321yxx 21yx A. B. C. D. 1 2 3 0 Lời giải Chọn B Phương trìnhhoành độ giao điểm của đường cong và đường cong là 321yxx 21yx 32232 0 1120 2 x xxxxx x    Vậy số giao điểm của hai đồ thị bằng 2. Câu28: Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số có phương trình lần lượt 1 2 x y x   là A. . B. . C. . D. . 2;1xy 1 2; 2xy 1;2xy 2;1xy Lời giải Chọn D Tacó: . 1 1 limlim1;limlim1 2 2 x x x x x x y y x x           Và . 22 22 1 1 limlim;limlim 2 2 x x x x x x y y x x            Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số có phương trình lần lượt

x   là .2;1xy

A. năm. B. năm. C. năm. D. năm. 11 12 13 10 Lời giải Chọn B Gọi số tiền ban đầu người đó gửi là (đông), A 0A Số tiền lãivà gốc

năm là . n  16,1%n Ta Tacó .  16,1% 16,1%216,1%2log211,7 n n a a n      Vậy sauít nhất năm người đó thu được (cả số tiền gửi ban đầu vàlãi) gấp đôi số tiền gửi 12 ban đầu

1 2 x y

Câu30: Giá trị cực đại của hàm số là 421yxx A. B. C. D. 3 4 1 0 3 4 Lời giải Chọn B Tacó . 3 42 yxx   Giải 0 02 2 x y x     Bảng biến thiên: Từ BBT,giá trị cực đại của hàm số là. 421yxx1 Câu31: Tìm tập xác định của hàm số 23 1yx  A. B. C. D. \1   1;  ;1  ;11;  Lời giải Chọn A Hàm số xác định khivà chỉ khi . 2101x x  Do đó tập xác định của hàm số là: .\1D  Câu32: Chohìnhchóp có vuônggóc với mặt phẳng , .Tamgiác . SABCSA  ABC2 SAa  ABC vuôngcân tại và (minh họa như hình vẽ) BABa  Góc giữa đường thẳng và mặt phẳng bằng SC  ABC A. B. C. D. 90 60 30 45 Lời giải Chọn D

Tacó

Do vậy .  ,45SCABC 

Câu33: Khối đa diện đều loại là khối  3;5

A. Tứ diện đều. B. Lập phương. C. Hai mươi mặt đều. D. Tám mặt đều. Lời giải

Chọn C

Khối đa diện loại là khối hai mười mặt đều.

Câu34: Chohàm số liên tục trên . Gọi Slà diện tíchhình phẳng giới hạn bởi các đường

(như hình vẽ). Mệnh đề nào dưới đây đúng?

DẠYKÈMQUYNHƠN OFFICIAL

thấy với ,   , SCABCSCA   tan SA SCA AC 

Nhận

, nên . 2SAa  22ACABa   tan145 SCASCA

 3;5

fx 

,0,1,2yfxyxx   A. B.  1 2 1 1 dd Sfxxfxx   1 2 1 1 dd Sfxxfxx    C. D.  1 2 1 1 dd Sfxxfxx   1 2 1 1 dd Sfxxfxx    Lời giải Chọn A Dựa vào đồ thị, tacó .  1 2 1 1 dd Sfxxfxx  Câu35: Chọn ngẫu nhiênhai số khácnhau từ số nguyên dương đầu tiên.Xác suất để chọn được hai 21 số có tổng là một số chẵn bằng A. B. C. D. 221 441 1 2 10 21 11 21 Lời giải Chọn C Tacó . 2 21nC  Gọi là biến cố: “Chọn được hai số có tổng là một số chẵn”. A Khi đó nênxác suất cần tìmlà: . 22 1011nACC    22 1011 2 21 10 21 nACC PA nC    

Câu36: Chohìnhchóp có đáy làhìnhvuông cạnh ,hai mặt phẳng và . SABCDABCD a  SAB

cùngvuônggóc với mặt phẳng ;góc giữa đường thẳng và mặt phẳng  ABCD SC 

bằng .Tínhtheo thể tích khối chóp . 60 a SABCD

DẠYKÈMQUYNHƠN OFFICIAL

SAD

ABCD

A. . B. . C. . D. . 36 3 a 33a 332a 36 9 a Lời giải Chọn A Tacó

    SABABCD

SABSADSA        làhình chiếu vuônggóc của lên . AC SC ABCD Do đó:      , ,60SCABCDSCACSCA    Tamgiácvuông vuông tại có . SAC A  .tan6SAACSCAa   Vậy thể tích khối chóp: . 3 211 6 3 6 3 3 SABCDABCD aVSSAaa    Câu37: Đạo hàm của hàm số là 12x ye  A. B. C. D. 12 2 x e y   122x ye   122x ye   12x ye   Lời giải Chọn C Tacó 1212 2x x ee   Câu38: Chohình lập phương cạnh (tham khảo hình vẽ bên). Khoảng cách giữa hai ABCDABCD  a đường thẳng và bằng ABBC

SADABCDSAABCD

DẠYKÈMQUYNHƠN

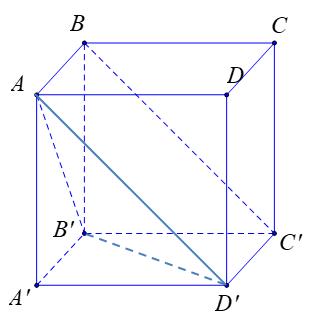
OFFICIAL C' D' B' A' C B D A A. B. C. D. 3 3 a 2 2 a 3a 2a Lời giải Chọn A Tacó       // ,, , , BCADABD dBCABdBCABDdCABDdAABDd            Hìnhchóp cóba cạnh đôi một vuônggócnên . AABD  ,, AAABAD  . 22222 11113 dAAABADa   Vậy . 3 3 da  Câu39: Số giá trị nguyên của thuộc để đồ thị hàm số có đúng ba m 10;10   2 2 1.3 12 xxx y xmxm    đường tiệm cận là A. . B. C. . D. . 20 18 17 19 Lời giải Chọn D Tacó     2 2 2 1313 1212 xxxxxx y xmxmxxm      

DẠYKÈMQUYNHƠN

OFFICIAL Điều kiện 0 3 1 2 x x x xm         Với điều kiện trênthì     2 2 2 2 13133 12122 xxxxxxxx y xmxmxxmxm         Tacó là tiệm cận ngang của đồ thị hàm số. 2 l3 im11 2 x xx y xm    là tiệm cận ngang của đồ thị hàm số. 2 l3 im11 2 x xx y xm    Để đồ thị hàm số có3 tiệm cận thì cần cóthêm1 tiệm cận đứng 202 231 m m m m       Do nêncó giá trị nguyên.  ,10;10mm  19 Câu40: Cho làhàm số đa thức bậc bốn vàhàm số có đồ thị là đường cong như hình fx yfx   dưới đây. Hàm số cóbaonhiêu điểm cực trị thuộc khoảng ? cos2sin1 4 x gxfx    0;2 A. B. C. D. 0 2 3 1 Lời giải Chọn C Ta có    sin2 '()cos'sin1cos'sin1cossincos'sin1sin 2 x gxxfx xfxxxxfxx       cos0 '()0'(sin1)sin x gxfxx      +) 3 cos0; 22 xxx   +) '(sin1)sin fxx  Đặt với sin1tx   2;0t trở thành . '(sin1)sin fxx  '()1ftt

Vẽ đường thẳng cắt đồ thị hàm số tại hai điểm 1yt '()yft  .1 2 3 12;0;12;0;2;0t t ta   

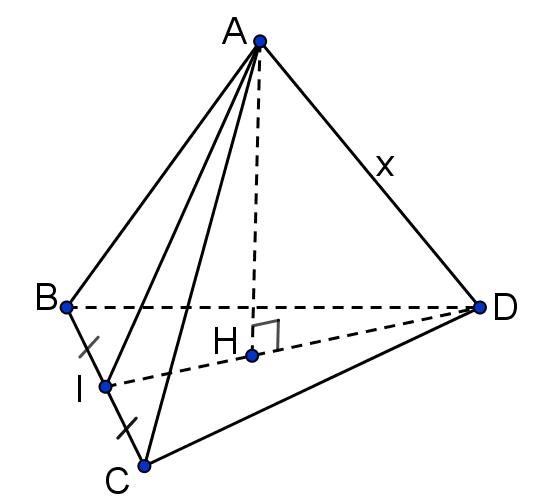
Với  11sin11sin00;2tx xx

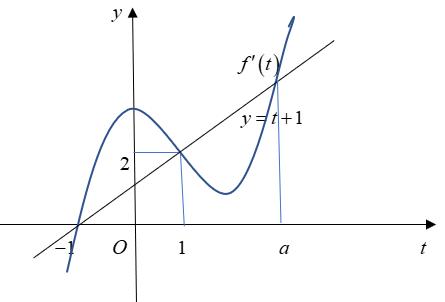
Vậy cóba nghiệm đơn phân biệt nênhàm số có3 điểm cực trị. '()0gx

Câu41: Xét khối tứ diện có cạnh ,các cạnh còn lại có cạnh bằng .Tìm để thể tích ABCDADx  43x khối tứ diện lớn nhất là ABCD

A. B. C. D. 23 62 32 26 Lời giải Chọn B

Gọi làtrung điểm của . Từ giả thiết suyratamgiác

DẠYKÈMQUYNHƠN OFFICIAL

vàtamgiác làcáctam I BC ABC DBC giác đều có cạnh bằng .Do đó . 43 BCAI BCAIDAIDBCD BCDI   Trong mặt phẳng gọi làhình chiếu của lên cạnh ,tacó . AIDH AID AHBCD   2 11133 4343243 33342ABCD BCD BCD VSAHSAI       Dấu xảy rakhi . Vậy khi thì thể tích tứ ""  262AHAIHIxAI 62x diện lớn nhất. ABCD

Câu42: Một hoa văn hìnhtròntâm , ngoại tiếp tamgiác đều có cạnh . Đường cong

DẠYKÈMQUYNHƠN OFFICIAL

43 ABcm  quaba điểm:

,, ABC Diện tích phần gạch chéo bằng A. B. C. D. 237,54cm 29,83cm 227,71cm 236,75cm Lời giải Câu43:ChọnA. Do tam giác là tam giác đều có cạnh nên ABC 43cm và .   3 2 436 4 2 3 CD cmOCCDcm   2 ODcm  Gắn trục toạ độ như hình vẽ, tacó Oxy 23;2,23;2,0;4A B C Phương trình đường Parapol đi qua3 điểm có đỉnh có dạng . ,, ABCC 24 yaxP  Thay toạ độ điểm vào suyra  23;2B  P 1 2 a 21 :4 2 Pyx  Phương trình đường tròntâm bánkính là Phương trình một phần O 4OA 2216xy cung nhỏ có dạng AB 216 yx  Vậy diện tích phần gạch chéo bằng  23 2 2 2 23 1 41637,54 2 x x cm                Câu44: Gọi là tập tất cả các số nguyên để hàm số nghịch biến S m 32 2 1 56 3 yxmxmxm   trên . Tổng các phần tử của bằng  S A. B. C. D. 20 10 18 15 Lời giải Chọn A Tacó: . Để hàm số đã cho nghịch biến trên khivà chỉ khi: 2 '256 yxmxm  

O ABC

là một phần của parabol.

Câu45: Chohình giới hạn bởi đồ thị hàm số

và trục hoành (phần tô đậm tronghình vẽ) 02) x 

Biếtthểtíchcủakhốitrònxoaytạothànhkhiquay quanhtrụchoànhlà , () H 3 ac

DẠYKÈMQUYNHƠN OFFICIAL

2 2 '2560,

m   Vì .  

mm m    

56061yxmxmxmm

6;5;4;;120

 24 yx 

,cungtròncó phương trình () H

9 yx

(với

V bd       trong đó và

tối giản. Tính . * ,,, abcd, ac bd Pabcd  A. B. C. D. 40P 46P 16P 14P Lời giải Chọn D Phương trìnhhoành độ giao điểm: 236262 2 31 4 427108033 927 xxxxxx xx   Ta thấy thể tích của khối trònxoay tạo thànhkhiquay quanh trục hoành bằng () H 12VVV  Trong đó: +) .Tacó: 3 1 3 0;3,, 9 Vx yxOx              . 3 3 3 7 3 6 1 0 0 0 31 3dd. 9272777 x V xxxx              +) .Tacó:  2 2 3;2,4,Vx yxOx     2 2 2 3 2 2 2 2 3 3 3 8 16 4d4d4843333 33 3 x V xx xxx                  Khi đó tacó: . 12 16320316 33 3773 VVV                Suyra: . 20 7 14 16 3 a b Pabcd c d       

làcácphân số

DẠYKÈMQUYNHƠN

OFFICIAL Câu46: Chohàm số thỏa mãn .Tìmgiá trị lớn  ygx 32 2673231  gxgxgxxx nhất của biểu thức 2  Pgxx A. B. C. D. 0 1 4 6 Lời giải Chọn C 32 2673231  gxgxgxxx 32 2662232211    gxgxgxgx xxx   3 21121111     gxgx xxx Xéthàm số 32  fttt Tacó đồng biến trên 2 610ftttft  ;   111 11212    gx xgxxPxx Tacó 2 2 212121141144     Pxxxx x Đẳng thức xảy rakhi .1100 x x Câu47: Chohàm số liên tục trên vàcó đồ thị như hình vẽ dưới đây.  yfx  Tập hợp tất cả cácgiá trị thực của tham số để phương trình có nghiệm m  22231 fxxm thuộc khoảng là  0;1 A. B. C. D. 1 ;1 3     0;1  0;4  1;0 Lời giải Chọn C Đặt  2 222132;1 txxx t   2 0;1 2;1 2 0;1 2;1 max22max4 min22min0              x t x t fxx ft fxx ft Để có nghiệm thuộc khoảng  22231 fxxm 0;104  m

DẠYKÈMQUYNHƠN

OFFICIAL Câu48: Cho bất phương trình .Cóbaonhiêu số nguyên dương 432 42 32 2 ln 20 3 xxx xxm xxm    m để bất phương trình nghiệm đúng với . 0;3x  A. . B. . C. . D. . 3 2 4 0 Lời giải Chọn B Do nên điều kiện xác định của phương trìnhlà 43220xxxx  3230xxm Ta có 432 42 32 2 ln 20 3 xxx xxm xxm      432432 3232 ln2 2ln33 xxxxxxxxmxxm   * Xéthàm số trên khoảng tacó hàm số ln fttt   0;   1 10,0;ft t t  đồng biến trên khoảng ln fttt   0; Do đó 43232 42 * 2342 xxxxxmxxm  ** Để bất phương trình nghiệm đúng với thì bất phương trình nghiệm đúng với  *  0;3x   ** . 0;3x  Xét hàm số trên đoạn ta có 4242gxxx  0;3 .   3 2 48420,0;3gxxxxx x  Khi đó  0;3 0;3 max3119;min02 gxg gxg   Vậy bất phương trình nghiệm đúng với  **  0;3 0;3min02x mgxg  Do là số nguyên dương nên . m 1;2mm Câu49: Chohàm số liên tục trên có đồ thị như hình vẽ fx  Cóbaonhiêugiá trị nguyên dương nhỏ hơn của tham số để phương trình 10 m có nghiệm phân biệt?  2222 xx mm f f  2

DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D. 6 7 9 4 Lời giải Chọn C Đặt .Tacó phương trình 22xxt  22mmftf Do nên . 222 xx 2t Ứng với mỗi giá trị của thì phương trình vô nghiệm. 2t 22xxt Ứng với mỗi giá trị của thì phương trình có đúng một nghiệm. 2t 22xxt Ứng với mỗi giá trị của thì phương trình cóhai nghiệm phân biệt. 2t 22xxt Phương trình cóhai nghiệm phân biệt khi phương trình  2222 xx mm f f  có đúng một nghiệm .  22mmftf 2t Từ đồ thị hàm số tacó phương trình có đúng một nghiệm yfx   22mmftf 2t khi .     2 2 55 222 2210122 22 222 232102223 mm m m mm mm mm mm f f                Xét phương trình . 25221 2.21011 22 2 m m m m m m     Xét bất phương trình . 2 2 2 35235log2 223.210 23535 2log2 m mm m m m                        Do là số nguyên dương nhỏ hơn nên có giá trị của . m 10 1;2;3;4;5;6;7;8;9m 9 m Câu50: Chohàm số . Đồ thị hàm số như hình vẽ bên dưới và . ()yfx  ()yfx   220ff Hàm số đồng biến trên khoảng nàotrongcác khoảng sau? 2 gxfx  A. . B. . C. . D. .  4;3  2;4  0;2  3;1

DẠYKÈMQUYNHƠN OFFICIAL

220ff

Lời giải Chọn B Dựa vào đồ thị hàm số như hình vẽ bên dưới và . ()yfx  

 Tacó bảng biến thiên của hàm số ()yfx   2 '2.' gxfxgxfxfx    21 '02.'00. 2 x gxfxfxfx x      Câu51: Biết và .Tính 1 0 ()5xfxdx    11f 1 0 (). Ifxdx  A. B. C. D. 4I 4I 6I 6I Lời giải Chọn B . Đặt 1 0 ()5Ixfxdx      . ux dudx dvfxdxvfx                   0 1 1 1 1 0 0 0 .()().56.Ixfxfxdxfxdxxfx      ---------- HẾT ----------

SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC NINH TRƯỜNG LƯƠNG TÀI SỐ 2-LẦN 2

ĐỀ THI THỬ TỐT NGHIỆP THPT

NĂM HỌC 2022–2023

Câu1: Hình lập phương có tất cả baonhiêu mặt?

8 12 4

Câu2: Với là số thực dương, viết biểu thức dưới dạng lũy thừa của .

Câu3: Chohình trụ cóbánkính đáy r và độ dài đường sinh l.Công thức tính diện tíchxungquanh của

trụ đã cholà

Câu4: Một khối chópcó diện tích đáy

chiều cao

Câu5: Công thức tính thể tích của một khối lăng trụ có diện tích đáy và chiều cao là B h

Câu6: Công thức tính thể tích của một khối nóncóbánkính đáy vàchièucao là r

Bánkính của khối cầu có đường kính bằng là

DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D.

x 232Txx  x A. . B. . C. . D. . 1 2Tx  4 3Tx  8 3Tx  7 2Tx 

hình

A. B. 2 xq 22 Srlr  xq Srl  C. . D. . xq 2 Srl  xq 4 Srl 

. Thể tích của khối chóp đã cholà 6B 4h A. B. C. D. 12V 24V 8V 48V

A. B. C. D. VBh  1 3 VBh  2 VBh  3 VBh 

A. B. C. D. 24 3 Vrh  2 Vrh  21 3 Vrh  22 Vrh  Câu7:

A. B. C. D. 12 Ra  2 Ra  3 Ra  6 Ra  Câu8: Cho cấp số cộng có số hạng và .Tìmcôngsai của cấp số cộng đã cho  n u 13u 26u d A. B. C. D. 3d 1 2 d 2d 3d Câu9: Chohàm số liên tục trên đoạn vàcó đồ thị như hình vẽ. Trên đoạn hàm yfx   3;1  3;1 số đạt giá trị lớn nhất tại điểm nào dưới đây? A. B. C. D. 0x 2x 1x 3x Câu10: Trongcáchàm số được cho bởi các phương án A, B, C, D dưới đây, hàm số nào đồng biến trên tập xác định của nó. A. . B. . C. . D. . 0,5log yx  21log yx  0,2log yx  2log yx  Câu11: Nghiệm của phương trình là 2 log13 x

Câu18: Chohàm số có bảng biến thiên như hình vẽ.

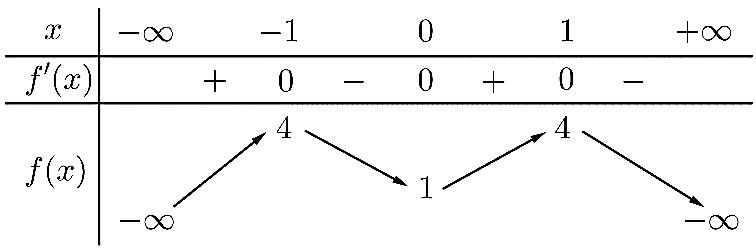
số đã cho nghịch biến trên khoảng nào dưới đây?

DẠYKÈMQUYNHƠN

OFFICIAL A. B. C. D. 10x 9x 7x 8x Câu12: Chohàm số có bảng biến thiên như hình vẽ. yfx  Giá trị cực tiểu của hàm số đã cho bằng A. . B. . C. . D. . 2 3 1 5 Câu13: Chohàm số liên tục trên vàcó bảng xét dấu như hình vẽ. yfx   fx  Điểm cực đại của hàm số đã cholà A. B. C. D. 4x 1x 1x 2x Câu14: Đường congtronghình vẽ là đồ thị của hàm số nào dưới đây? A. B. 42 241.yxx   332.yxx  C. D. 3231yxx 42 241yxx Câu15: Đường tiệm cận ngang của đồ thị hàm số là 32 1 x y x  A. B. C. D. 3x 3y 2y 1x Câu16: Một hìnhnóncóbánkính đáy , chiều cao . Độ dài đường sinh của hìnhnónlà 5r 4h A. B. C. D. 32.l 3.l 41.l 9.l Câu17: Tập xác định của hàm số là 31yx  A. . B. . C. . D. .  3;  \1  1;



 Hàm

A. B. C. D.  1;0  1;1  ;1  0;1 Câu19: Tập nghiệm của bất phương trình là 2 327 x A. B. C. D. ;1 1; 5; 1; Câu20: Với x, y làcác số thực dương và . Khẳng định nàosau đây là sai? 01 a  A. B. loglog n a a xnx   logloglog a a a xyxy 

yfx

D.  logloglog a a a xyxy 

a a a

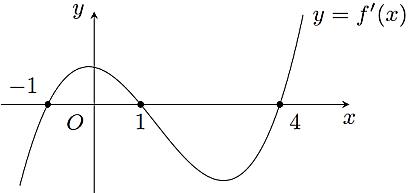
Câu24: Đồ thị hàm số cắt trục hoành tại tất cả baonhiêu điểm? 3 231yxx 

Câu25: Chohàm số xác định trên vàcó .Hàm số đã chocó

các chữ số 1,2,3,4,5có thể tạo được tất cả baonhiêu

cạnh bằng .Tính thể tích của khối trụ đã cho. 23a

Câu30: Chohìnhchóp S.ABC có cạnh bên SA vuônggóc với mặt đáy (ABC

thiết diện là một hình

DẠYKÈMQUYNHƠN OFFICIAL

y    

logloglog

x xy

trên đoạn 

fxxx  1;3 A. B. C. D. 7 8 3 5 Câu22:

có .Tính khoảng cách giữa hai đường thẳng '''' ABCDABCD 6 ACa  và . AC''BD A. . B. . C. . D. . 2a 3a 2a 3a Câu23: Chohàm số liên tục trên vàcó đồ thị của hàm số như hình vẽ. Hàm số yfx   ' fx đồng biến trên khoảng nào dưới đây? yfx  A. B. C. D.  1;4  4;  1;4  ;1

Câu21: Tìmgiá trị lớn nhất của hàm số

3233

Chohình lập phương



A. B. C.

1 0 2 3

tất cả yfx   2 '12 fxxxx  baonhiêu điểm cực trị? A. 2. B. 1. C. 3. D. 0. Câu26: Từ một nhóm học sinh gồm 6namvà8 nữ, chọn ngẫu nhiên3 học sinh.Tínhxác suất chọn được 3 học sinh nữ. A. B. C. D. 14 19 5 91 2 13 11 13 Câu27: Cho cấp số nhân có số hạng đầu là ,công bội .Tìm số

?  n v 18v 2q 3v A. B. C. D. 364v 312v 314v 332v Câu28:

số tự nhiêncó3 chữ số đôi một khác nhau. A. 243. B. 125. C. 10. D. 60. Câu29:

vuôngcó

A. B. C. D. 323 Va  393 Va  363 Va  333 Va 

hạng

Từ

Cho khối trụ (T), cắt khối trụ (T) bằng mặt phẳng qua trục của nóta được

.Khi 2 SAa  4 SBa  thìgóc giữa SB và mặt phẳng

ABC

bằng. A. B. C. D. 45.  90.  60.  30. 

cả

23 22 1 4 2 xx x    

)và

(

)

Câu31: Phương trình có tất

baonhiêu nghiệm?

DẠYKÈMQUYNHƠN

Chohàm số có đồ thị như hình vẽ. Tập nghiệm của phương trình yfx 

số phần tử là

B. C. D. 7 10

Có tất cả baonhiêugiá trị nguyên dương của tham số m saochohàm số xác

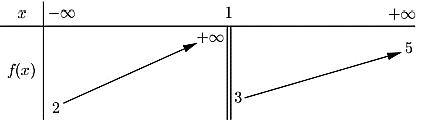
OFFICIAL A. B. C. D. 1. 2. 0. 3. Câu32: Chokhốihộpchữnhật có .Thểtíchcủakhốihộp '''' ABCDABCD'3,4,5 AAaABaACa  đã cholà. A. B. C. D. 3 36.Va  3 12.Va  3 60.Va  3 20.Va  Câu33: Chotamgiác ABC vuông tại A,xoaytamgiác ABC quanh cạnh AB ta được hìnhnón(N).Tính diện tíchxungquanh của nón(N) biết rằng  6,30.ABaABC    A. . B. . C. . D. . 224 xq Sa  248 xq Sa  2366 xq S a 2723 xq S a Câu34: Đạo hàm của hàm số là 22412x y   A. . B. . 224 '12.ln12 x y   223'22412x yx   C. D. 224'212x y   224 '212ln12 x y   Câu35: Chohàm số có bảng biến thiên như hình vẽ. yfx  Tổng số tiệm cận ngangvà tiệm cận đứng của đồ thị hàm số đã cholà A. . B. . C. . D. . 3 2 1 4 Câu36:

 

 có

9 6



 định

 A. B.

C. D. 1. 3. 2.

thì bằng 24 faxb x x     min11 fxf  maxfx  A. B. C. D. 11 20 5 12 3 4 1 4

'230ffx

Câu37:

lnx yemx

trên khoảng ? 0;

Vô số.

Câu38: Chohàm số , với a, b làtham số. Nếu

Câu39: Chohìnhchóptamgiác có đáy làtamgiác đều cạnh cạnh bên vuônggóc SABCABC 2, a SA

với đáy. Góc giữa và mặt phẳng đáy bằng . Gọi và lần lượt làtrung điểm SB  ABC60MN

của và Tính thể tích khối đa diện SB.SC ?ABCMN

Câu40: Có tất cả baonhiêugiá trị nguyên của tham số m thuộc đoạn saocho đồ thị hàm số

có đúng



trị là–1

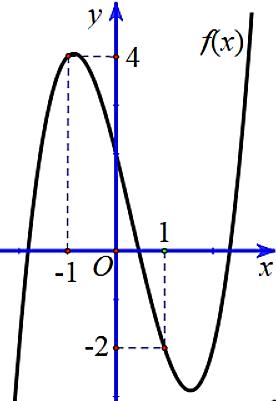
và2thìhàm số có tất cả baonhiêu điểm cực trị?

21yfx

A. 4. B. 5. C. 3. D. 2.

Câu44: Cho khối nón cóbánkính đáy và chiều cao lớn hơn bánkính đáy. Mặt phẳng

đi qua đỉnh nónvà tạo với đáy nón một góc cắt khối nón theo thiết diện là một tamgiác

Câu45: Chohàm số (m làtham số). Có tất

DẠYKÈMQUYNHƠN OFFICIAL

A. . B. . C. . D. . 33 2 a 33a 31 2 a 39 2 a

25;25

2 đường tiệm cận đứng. 2 1 2310 x y xmxm   A. B. C. D. 42. 43. 44. 45. Câu41: Khi đặt thì phương trình trở thành phương trìnhnào dưới 5log tx  2 6 5 5 log25log80 xx đây? A. B. C. D. 28120tt 2120tt 212120tt 23120tt Câu42: Tập nghiệm của bất phương trình có tất cả baonhiêu số  2 9244.3243.8log20 x x x   nguyên? A. 252. B. 250. C. 249. D. 254. Câu43: Chohàm số có đạo hàmtrên . Nếu hàm số đã chocó đúng hai điểm cực





yfx 



 P

ra 

  N

283a  N A. B. C. D. 364a 396a 332a 3192a

cả baonhiêugiá trị nguyên của m để hàm số đã 212    x y xm cho nghịch biến trên khoảng ? 2; A. Vô số. B. 9. C. 7. D. 8. Câu46: Chohàm số có đồ thị như hình vẽ. 32  fxaxbxcxd Tínhgiá trị của biểu thức      5 33  Tfabcdffabcd A. . B. . C. . D. . 2T 4T 8T 6T

có diện tích bằng Thể tích của khối nón bằng

Câu47: Chohìnhchóp S.ABC có cạnh bênSAvuônggóc với đáy, . Gọi M, N lần lượt làhình 26 SAa 

chiếu của A trêncác cạnh SB và SC. Biết góc giữa hai mặt phẳng (AMN)và(ABC) bằng , 60

tính diện tích mặt cầu ngoại tiếp đa diện ABCMN? A.

Câu48: Chohình trụ (T)cóbánkính đáy và chiều cao gấp đôi bánkính đáy. Gọi O và lần 6r 'O

lượt làtâm của hai đáy trụ. Trên đường tròntâm O lấy điểm A,trên đường tròntâm lấy điểm 'O

B saocho thể tích của tứ diện lớn nhất. Tính AB? ' OOAB

A. B. 6. C. 5. D. 30 43

Câu49: Chohàm số bậc ba có đồ thị là đường cong đậm tronghình vẽ và đồ thị hàm số yfx 

có đồ thị là đường cong mảnh như hình vẽ. Đồ thị hàm

có trục đối xứng là đường

DẠYKÈMQUYNHƠN OFFICIAL

B. C. D. 236

 272 Sa  224 Sa  28 Sa 

với



 số

thẳng .Tìmgiá trị lớn nhất của hàm số trên ygx  1 2 x gx đoạn  2;2 A. B. 2;2 max1692. gx 2;2 max198. gx C. D. 2;2 max52. gx 2;2 max2. gx Câu50: Chohàm số .Trên khoảng có tất cả bao  2022202220232ln1 x xfxee xx     25;25 nhiêugiá trị nguyên của tham số m saocho phương trình có  22ln0 xm femfxxx   đúng 3 nghiệm phân biệt? A. B. C. D. 24. 25. 48. 26. ---------- HẾT --------

2 gxfaxbxc  ,, abc

Câu3: Chohình trụ cóbánkính đáy r và độ dài đường sinh l.Công thức tính diện tíchxungquanh của hình trụ đã cholà

A. B. 2 xq 22 Srlr  xq Srl 

Câu6: Công thức tính thể tích của một khối nóncóbánkính đáy vàchièucao là r h

DẠYKÈMQUYNHƠN OFFICIAL

BẢNG ĐÁP ÁNVÀ LỜI GIẢI 1.D 2.C 3.C 4.C 5.A 6.C 7.C 8.A 9.B 10.D 11.B 12.B 13.C 14.A 15.B 16.C 17.D 18.A 19.B 20.B 21.A 22.D 23.B 24.D 25.A 26.C 27.D 28.D 29.C 30.D 31.B 32.A 33.A 34.D 35.A 36.A 37.D 38.D 39.A 40.A 41.A 42.A 43.C 44.C 45.D 46.C 47.D 48.B 49.B 50.A Câu1: Hình lập phương có tất cả baonhiêu mặt? A. B. C. D. 8 12 4 6 Lời giải Chọn D Hình lập phương có tất cả mặt. 6 Câu2: Với là số thực dương, viết biểu thức dưới dạng lũy thừa của . x 232Txx  x A. . B. . C. . D. . 1 2Tx  4 3Tx  8 3Tx  7 2Tx  Lời giải Chọn C

28 232233 .. Txxxxx 

 C. D. xq 2 Srl  xq 4 Srl  Lời giải Chọn C Công thức tính diện tíchxungquanh của hình trụ là . xq 2 Srl 

đáy , chiều cao . Thể tích của khối chóp đã cholà 6B 4h A. B. C. D. 12V 24V 8V 48V Lời giải Chọn C Thể tích của khối chóp đã cholà . 11 .6.48 33 VBh

Câu4: Một khối chópcó diện tích

B h A. B. C. D. VBh  1 3 VBh  2 VBh  3 VBh  Lời giải Chọn

. VBh 

Câu5: Công thức tính thể tích của một khối lăng trụ có diện tích đáy và chiều cao là

A Thể tích khối lăng trụ là

A. B. C. D. 24 3 Vrh  2 Vrh  21 3 Vrh  22 Vrh  Lời giải

DẠYKÈMQUYNHƠN

Chọn C Thể tích khối nónlà . 21 3 Vrh  Câu7: Bánkính của khối cầu có đường kính bằng là R 6a A. B. C. D. 12 Ra  2 Ra  3 Ra  6 Ra  Lời giải Chọn C Bánkính khối cầu là , 6 3 2 a Ra  Câu8: Cho cấp số cộng có số hạng và .Tìmcôngsai của cấp số cộng đã cho  n u 13u 26u d A. B. C. D. 3d 1 2 d 2d 3d Lời giải Chọn A Côngsailà . 21633duu Câu9: Chohàm số liên tục trên đoạn vàcó đồ thị như hình vẽ. Trên đoạn hàm yfx   3;1  3;1 số đạt giá trị lớn nhất tại điểm nào dưới đây? A. . B. . C. . D. . 0x 2x 1x 3x Lời giải Chọn B Từ đồ thị hàm số, trên đoạn ,hàm số đạt giá trị lớn nhất bằng tại  3;1 22x Câu10: Trongcáchàm số được cho bởi các phương án A, B, C, D dưới đây, hàm số nào đồng biến trên tập xác định của nó. A. . B. . C. . D. . 0,5log yx  21log yx  0,2log yx  2log yx  Lời giải Chọn D Xéthàm số : 2log yx  + Tập xác định: . 0; +Tacó hàm số đồng biến trên khoảng 1 0 ln2y x  2log yx   0; Câu11: Nghiệm của phương trình là 2 log13 x A. . B. . C. . D. . 10x 9x 7x 8x Lời giải Chọn B

OFFICIAL

DẠYKÈMQUYNHƠN OFFICIAL

Câu12:

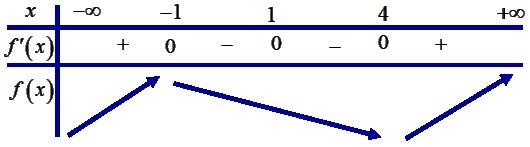
Tacó .  3 2 log13129 x x x 

yfx 

A. . B. . C. . D. . 2 3 1 5 Lời giải Chọn B

dấu như hình vẽ. yfx   fx  Điểm cực đại của hàm

đã cholà A. B. C. D. 4.x 1.x 1.x 2.x Lời giải Chọn C Điểm cực đại của hàm số đã cholà .1x Câu14: Đường congtronghình vẽ là đồ thị của hàm số nào dưới đây? A. B. 42 241yxx   332yxx  C. D. 3231yxx 42 241yxx Lời giải Chọn A Đồ thị tronghình vẽ làhình dạng của hàm bậc bốn .Do đó loại phương ánB 42 yaxbxc  vàC

Chohàm số có bảng biến thiên như hình vẽ.

Giá trị cực tiểu của hàm số đã cho bằng

Giá trị cực tiểu của hàm số đã cho bằng .3 Câu13: Chohàm số liên tục trên vàcó bảng xét

số

DẠYKÈMQUYNHƠN

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

OFFICIAL Lại có .Do đó loại phương ánD lim x y   Câu15: Đường tiệm cận ngang của đồ thị hàm số là 32 1 x y x  A. B. C. D. 3.x 3y 2.y 1.x Lời giải Chọn B Tacó ; . l32 imlim3 1 x x x y x    l32 imlim3 1 x x x y x     Đường tiệm cận ngang của đồ thị hàm số là . 32 1 x y x  3y Câu16: Một hìnhnóncóbánkính đáy , chiều cao . Độ dài đường sinh của hìnhnónlà 5r 4h A. B. C. D. 32.l 3.l 41.l 9.l Lời giải Chọn C Độ dài đường sinh của hìnhnónlà . 22224541lhr Câu17: Tập xác định của hàm số là 31yx  A. B. C. D.  3;  \1  1; Lời giải Chọn D

bảng biến thiên như hình vẽ. yfx 

A. B. C. D.  1;0  1;1  ;1  0;1 Lời giải Chọn A

Tập nghiệm

trình là 2 327 x A. . B. . C. . D. . ;1 1; 5; 1; Lời giải Chọn B 2 23 32733231 x x xx    Câu20:

x, y làcác

và . Khẳng định nàosau đây là sai? 01 a  A. . B. . loglog n a a xnx   logloglog a a a xyxy  C. . D. .  logloglog a a a xyxy  logloglog a a a x xy y     Lời giải Chọn B

Câu18: Chohàm số có

Câu19:

của bất phương

Với

số thực dương

Chọn B Dựa vào đồ thị hàm số ,ta thấy hàm số đồng biến trêncác khoảng và nên

Phương trìnhhoành độ giao điểm: do

hoành tại ba điểm phân biệt.

Câu25: Chohàm số xác định trên vàcó

DẠYKÈMQUYNHƠN

baonhiêu điểm cực trị?

OFFICIAL Câu21: Tìmgiá trị lớn nhất của hàm số trên đoạn . 3233fxxx  1;3 A. . B. . C. . D. . 7 8 3 5 Lời giải Chọn A Tacó (loại) (nhận).   2 2 3603600fxxxfx xxx    hay2 x Khi đó ; và ,do vậy 15f27f33f 1;3 max27 x fxf   Câu22: Chohình lập phương có .Tính khoảng cách giữa hai đường thẳng . '''' ABCDABCD 6 ACa  và . AC''BD A. . B. . C. . D. . 2a 3a 2a 3a Lời giải Chọn D Nhận thấy .    , , dACBDdABCDABCDAA     Tacó nên do vậy . 6 ACa  3 2 AC AAAB a   ,3 dACBDa   Câu23: Chohàm số liên tục trên vàcó đồ thị của hàm số như hình vẽ. Hàm số yfx   ' fx đồng biến trên khoảng nào dưới đây? yfx  A. B. C. D.  1;4  4;  1;4  ;1



  1;1 4; chọn

 A.

Lời

Chọn D

Lời giải

đáp ánB. Câu24: Đồ thị hàm số cắt trục hoành tại tất cả baonhiêu điểm? 3 231yxx

. B. . C. .

. 1 0 2 3

giải

đồ

hàm số cắt trục 3 1 231013 2 x xx x      

đó

thị

cả yfx   2 '12 fxxxx 

.Hàm số đã chocó tất

Tacó: 22 318232vvq

Câu28: Từ các chữ số 1,2,3,4,5có thể tạo được tất cả baonhiêu số tự nhiêncó3 chữ số đôi một khác nhau.

A. 243. B. 125. C. 10. D. 60.

Lời giải

Chọn D

Số các chọn số có3 chữ số đôi một khácnhau: . 3 560A

Câu29: Cho khối trụ (T), cắt khối trụ (T) bằng mặt phẳng qua trục của nóta được thiết diện là một hình

vuôngcó cạnh bằng .Tính thể tích của khối trụ đã cho. 23a

Chọn C

DẠYKÈMQUYNHƠN OFFICIAL

A. 2. B. 1. C. 3. D. 0. Lời giải Chọn A Tacó:  2 '120 fxxxx   0 1 2 x x x      Bảng xét dấu x 012 ' fx + - - + 000 Hàm số có2 cực trị. Câu26: Từ một nhóm học sinh gồm 6namvà8 nữ, chọn ngẫu nhiên3 học sinh.Tínhxác suất chọn được 3 học sinh nữ. A. . B. . C. . D. . 14 19 5 91 2 13 11 13 Lời giải Chọn C -Khônggian mẫu: 3 14C - Gọi Alà biến cố: “Chọn được 3 học sinh nữ” 3 8A nC  3 8 3 14 2 13 A C P C  Câu27: Cho cấp số nhân có số hạng đầu là ,công

?  n v 18v 2q 3v A. . B. . C. . D. . 364v 312v 314v 332v Lời giải

bội .Tìm số hạng

Chọn D

A. B. C. D. 323 Va  393 Va  363 Va  333 Va  Lời giải

DẠYKÈMQUYNHƠN

Vì làhìnhvuôngcó cạnh bằng . ABCD 23 23 3 2 a aR a Suyra: Sđáy . 2 2 233 Raa    Thể tích khối trụ bằng: 2 332363 Vaaa     Câu30: Chohìnhchóp S.ABC có cạnh bên SA vuônggóc với mặt đáy (ABC)và .Khi 2 SAa  4 SBa  thìgóc giữa SB và mặt phẳng (ABC) bằng A. B. C. D. 45 90 60 30 Lời giải Chọn D Vì .    , SAABCSBABCSBA   Tacó vuông tại A suyra . SAB   0 21 sin 30 42 SAa SBA SBA SBa  Câu31: Phương trình có tất cả baonhiêu nghiệm? 23 22 1 4 2 xx x     A. B. C. D. 1 2 0 3 Lời giải Chọn B Tacó: 23 2 3222 2432232 1 1 422 24340 2 2 xx x xxx x xxxxx x          Câu32: Chokhốihộpchữnhật có .Thểtíchcủakhốihộp '''' ABCDABCD'3,4,5 AAaABaACa  đã cholà. A. B. C. D. 336 Va  312 Va  360 Va  320 Va  Lời giải Chọn A Vì . 22 4,5 3 ABaACaADACABa   Khi đó thể tích khối hộp bằng: . 3..3.4.336 VAAABADaaaa    

OFFICIAL

DẠYKÈMQUYNHƠN

OFFICIAL Câu33: Chotamgiác ABC vuông tại A,xoaytamgiác ABC quanh cạnh AB ta được hìnhnón(N).Tính diện tíchxungquanh của nón(N) biết rằng  6,30ABaABC    A. B. C. D. 224 xq Sa  248 xq Sa  2366 xq S a 2723 xq S a Lời giải Chọn A Tacó . 2 2 0 22 tan3023 62343 ACAB aBCABACaaa    Vậy . 2..23.4324 sq SACBCaaa       Câu34: Đạo hàm của hàm số là 22412x y   A. B. 224 '12ln12 x y   223'22412x yx   C. D. 224'212x y   224 '212ln12 x y   Lời giải Chọn D Tacó . 224 224 21412ln12212ln12 x x yx      Câu35: Chohàm số có bảng biến thiên như hình vẽ. yfx  Tổng số

cận ngangvà

cận

của đồ thị hàm số đã cholà A. . B. . C. . D. . 3 2 1 4 Lời giải Chọn A Tacó làcác đường tiệm cận ngang.   lim5;lim25;2 x x fxfxyy     là tiệm cận đứng. 1 lim 1 x fxx   Câu36: Chohàm số có đồ thị như hình vẽ. Tập nghiệm của phương trình yfx    '230ffx có số phần tử là

tiệm

đứng

DẠYKÈMQUYNHƠN

Từ sự tương giaotrênhình vẽ, phương trình có7 nghiệm.   '230ffx

Câu37: Có tất cả baonhiêugiá trị nguyên dương của tham số m saochohàm số xác lnx yemx 

định trên khoảng ? 0;

A. B. Vô số. C. D. 1 3 2 Lời giải Chọn D

Hàm số xác định trên khoảng lnx yemx   0; 0,0; x emxx  ,(*).Tacó: ,0; x e mfxx x   2 1x ex fx x   x01 fx  0

Từ BBTtrên,(*). Vậy cóhaigiá trị nguyên dương của thõaYCBTlà me m 1,2mm

OFFICIAL A. B. C. D. 7 10 9 6 Lời giải Chọn A Từ đồ thị hàm số tacó yfx           1231 1 3 00'230230 2 1 2312 fx fx x fxxffx fx fx x fx fx                     



fx e

DẠYKÈMQUYNHƠN

Câu39: Chohìnhchóptamgiác có đáy làtamgiác đều cạnh cạnh bên

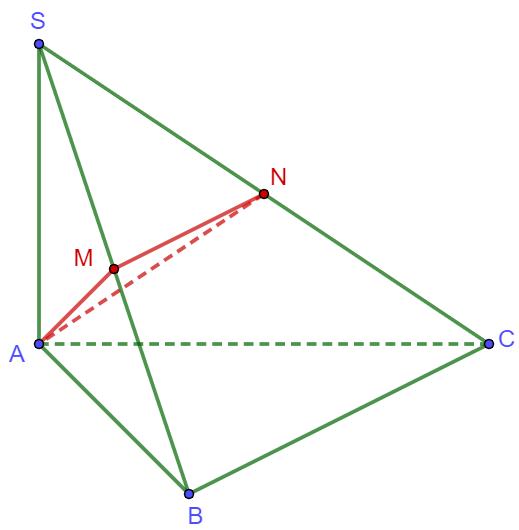
OFFICIAL Câu38: Chohàm số , với a, b làtham số. Nếu thì bằng 24 faxb x x     min11 fxf  maxfx  A. B. C. D. 11 20 5 12 3 4 1 4 Lời giải Chọn D Từ đề bàita phải có . Mặc khác 0a  115,1f ab   2 22 24 4 faxbxa x x     Phương trình luôncóhai nghiệm phân biệt. 2 22 240,(40)axbxaba   Vì nên ,(2)  min1 fxf    2 12.140320abaab  Từ (1)và(2)suyra Do đó . 2,3ab   2 2 2 2 23268 4, 4 x xx fx fx x x       x 14 fx  00 fx1 4 00 1 Vậy 1 max 4fx 

SABCABC

a SA với đáy. Góc giữa và mặt phẳng đáy bằng Gọi và lần lượt làtrung điểm SB  ABC60MN của và Tính thể tích khối

diện SBSC ?ABCMN A. . B. . C. . D. . 33 2 a 33a 31 2 a 39 2 a Lời giải Chọn A Do

vuônggóc

đa

DẠYKÈMQUYNHƠN

OFFICIAL    3 1 , 60tan6023 2 3SABC ABC SAABCSBABCSBASAAB aVSASa     Mà: .3 11 33 . 44 42 SAMN SAMNSABCABCMNSABC SABC VSMSN VVVVa VSBSC     Câu40:

thuộc đoạn saocho đồ thị hàm số  25;25 có đúng 2 đường tiệm cận đứng 2 1 2310 x y xmxm   A. B. C. D. 42. 43. 44. 45. Lời giải Chọn A Để đồ thị hàm số có đúng đường tiệm cận đứng thì phương trình: có 2 223100xmxm hai nghiệm thỏa mãn: phân biệt vàhai nghiệm khác 12 , xx 1 Nên: 2 2 0 3100 5 12310011 11 m mm m mm m m                   Do Có giá trị nguyên thỏa mãn.  ,25;25mm   42 m Câu41: Khi đặt thì phương trình trở thành phương trìnhnào dưới 5log tx  2 6 5 5 log25log80 xx đây? A. . B. . C. . D. . 28120tt 2120tt 212120tt 23120tt Lời giải Chọn A Tacó:   2 2 6 2 5 55 5 5 5 log25log80log25log12log580log8log120 xx x x xx     Đặt thì phương trình trở thành: 5log tx  28120tt Câu42: Tập nghiệm của bất phương trình có tất cả baonhiêu số  2 924432438log20 x x x   nguyên? A. 252. B. 250. C. 249. D. 254. Lời giải Chọn A Điều kiện .   2 2 20 2 2 2254 8log20log282256 x x x x x x x                      Trường hợp 1: (thoả mãn). 2 log282256254 x x x  Trường hợp 2: . 2 8log202254 x x  Tacó .  2 32435 9244.3243.8log209244.3243030 1 x x x x x x x x x        

Có tất cả baonhiêugiá trị nguyên của tham số m

20 x x

Kết hợp điều kiện suyra nghiệm của bất phương trìnhlà . 2254 x 

Vậy bất phương trìnhcó tập nghiệm là .  2;05;254S

Do đó tập nghiệm của bất phương trìnhcó252 số nguyên.

Câu43: Chohàm số có đạo hàmtrên . Nếu hàm số đã chocó đúng hai điểm cực trị là–1

và2thìhàm số có tất cả baonhiêu điểm cực trị?

Cho khối nón cóbánkính đáy và chiều cao lớn hơn bánkính đáy.

DẠYKÈMQUYNHƠN OFFICIAL

  

5254





yfx 

 21yfx A. 4. B. 5. C. 3. D. 2. Lời giải Chọn C Tacó . 2 2 121yfxyxfx   Do đó   2 2 2 2 2 000 02101121 1121 x x x yxfx x xvnx x x x                      Vậy hàm số có tất cả 3 điểm cực trị.  21yfx Câu44:

Mặt phẳng  N 4 ra   P đi qua đỉnh nónvà tạo với đáy nón một góc cắt khối nón theo thiết diện là một tamgiác 60  N có diện tích bằng Thể tích của khối nón bằng 283a  N A. B. C. D. 364a 396a 332a 3192a Lời giải Chọn C 600 I O A S B Gọi thiết diện làtamgiác và làtrung điểm của đoạn SABI AB Tacó và nên . OIAB SIAB   60SIO 

DẠYKÈMQUYNHƠN

OFFICIAL Gọi tacó  4 SOhha  3 tan603 SOh OI   2 22 23 22216 9 h ABAIOBOIa  và . 23 sin603 SOh SI  Do đó 1 2SAB SSIAB  2 2 2 1233 83..216 239 h h a a  2 2 23 12.16 9 haha . 2 4223 14416 9 haha         22 4224 22 36 6 1 161440 3 1223 hanhanha haha hahaloai           Vậy  2 2 3 11 4632 33N Vrhaaa       Câu45: Chohàm số (m làtham số). Có tất cả baonhiêugiá trị nguyên của m để hàm số đã 212    x y xm cho nghịch biến trên khoảng ? 2; A. Vô số. B. 9. C. 7. D. 8. Lời giải Chọn D Tacó với . 2 212212 '     x m y y xmxm  xm Để hàm số nghịch biến trên  2;  2120 '02; ,2;    m yx x xm . 21206 '02; 26 22           m m yx m m m Câu46: Chohàm số có đồ thị như hình vẽ. 32  fxaxbxcxd Tínhgiá trị của biểu thức .      5 33  Tfabcdffabcd A. B. C. D. 2T 4T 8T 6T Lời giải Chọn C Từ đồ thị ta thấy được và  1 4fabcd 1 2fabcd

Câu47: Chohìnhchóp S.ABC có cạnh bênSAvuônggóc với đáy, . Gọi M, N lần lượt làhình 26 SAa

chiếu của A trêncác cạnh SB và SC. Biết góc giữa hai mặt phẳng (AMN)và(ABC) bằng , 60 tính diện tích mặt cầu ngoại tiếp đa diện ABCMN?

DẠYKÈMQUYNHƠN OFFICIAL

   15133    Tff fff    452331134   f ff fff



A. B. C. D. 236 Sa  272 Sa  224 Sa  28 Sa  Lời giải Chọn D Gọi

. là điểm

xứng với qua . O ABCD AO Tacó    , BDAB DBSABDBAMDoAMSAB DBSA     Tacó   1 AMSB AMSDBAMSD AMDB   Tacó     2, DCAC DCSACDCANDoANSAC DCSA       2 ANSC ANSCDANSD ANDC   Từ  1,2SDAMN Do    0 ,,60. SAABCD AMNABCSASD SDAMN         Tamgiác vuông tại SAD  0 26 tan 22. tan60 SA aAASDAD a AD    .    3 AMSDB AMMD DMSDB          4 ANSCD ANND DNSCD      

làtâm đường tròn ngoại tiếp tâmgiác

đối

Do đó tacó làtâm mặt cầu ngoại tiếp đa diện

Diện tích mặt cầu ngoại tiếp hình đa diện là 2 2 2 14428.SR aa

Câu48: Chohình trụ (T)cóbánkính đáy và chiều cao gấp đôi bánkính đáy. Gọi O và lần 6r 'O

lượt làtâm của hai đáy trụ. Trên đường tròntâm O lấy điểm A,trên đường tròntâm lấy điểm 'O

B saocho thể tích của tứ diện lớn nhất. Tính AB? ' OOAB

A. . B. 6. C. 5. D. . 30 43

Lời giải

Chọn B

Gọi làhình chiếu vuônggóc của xuống mặt đáy . A A  O

Tacó làhình chữ nhật. '' OOAA

Tacó ' 111 ''6266 222OOAOOAA SSOOAA     

Gọi làhình chiếu vuônggóc của điểm lên đường thẳng H B OA 

tacó

'' ' BHOA BHOOA BHOO   

Thể tích của khối tứ diện là . ' OOAB ' 1 .2226 3OOA VBHSBHOB

DẠYKÈMQUYNHƠN OFFICIAL

 0

ANDAMDACDABDO  2.

2 AD ABCMNR a

  





  Khi đó tamgiác vuông tại . '' OAB 'O 22 '223' 24126 ABr ABAAAB   Câu49: Chohàm số bậc ba có đồ thị là đường cong đậm tronghình vẽ và đồ thị hàm số yfx  với có đồ thị là đường cong mảnh như hình vẽ. Đồ thị hàm  2 gxfaxbxc  ,, abc số có trục đối xứng là đường thẳng .Tìmgiá trị lớn nhất của hàm số trên ygx  1 2 x gx đoạn  2;2

DẠYKÈMQUYNHƠN

OFFICIAL A. B. 2;2 max1692. gx 2;2 max198. gx C. D. 2;2 max52. gx 2;2 max2. gx Lời giải Chọn B Hàm số 32 fxmxnxpxq  2 32 fxmxnxp  Hàm số cóhai điểm cực trị ; nên fx 0x2x   00 20 f f       Suyra, 0 0 12403 p p mnnm            Do đó, 32 3 fxmxmxq   Từ đồ thị tacó fx   10 02 f f      20 2 mq q   1 2 m q    Vậy 3232fxxx   Tacó 00g32320fccc   1 13 c c   Do nên chọn . c 1c Đồ thị hàm số nhận đường thẳng làm trục đối xứng nên gx 1 2 x 100gg Từ 10g10fab  3 2 13120abab   11 113 ab ab   Do nên chọn , ab 0 abab  Suyra . 2 21axbxcaxax  Có 22212g fa  3 2 2132122 a a   210 213 a a    . 1 2 1 a a     Từ đồ thị hàm số và suyra: và . fxgx lim x fx   lim x gx   Vậy chọn .1a

DẠYKÈMQUYNHƠN

OFFICIAL Khi đó,  2 21gxfaxbxcfxx  Xéthàm số trên đoạn gx  2;2 Đặt . 21uxx 210uxx  1 2;2 2 x  ;; 13 24 u    23u27u 3 ;7 4 u    Vậy .  3 2;2 ;7 4 7198MaxgxMaxfuf      Câu50: Chohàm số .Trên khoảng có tất cả bao  2022202220232ln1 x xfxee xx     25;25 nhiêugiá trị nguyên của tham số m saocho phương trình có  22ln0 xm femfxxx   đúng 3 nghiệm phân biệt? A. B. C. D. 24. 25. 48. 26. Lời giải Chọn A Có nêhàm số có 2 21 0xxxxxx   2022202220232ln1 x xfxee xx    tập xác định là .  Có  2 2 1 ln1ln 1 fxxx xx        1 2 2 ln1ln1 xx xx  Vậy, Hàm số làhàm số lẻ.  fxfx fx Đạo hàm của hàm số là: fx  20222 2022 2022 2 ln1 202220222023 1 x x xx fxe e x       0x  Do đó, hàm số đồng biến trên . fx  Dohàm số làhàm số lẻ và đồng biến trên nênPT đã cho tương đương với PT: fx fx   22 ln xm femfxxx   22 ln xm femfxxx  (1)  22 ln xm exmxx  Đặt 22ln ttxxe  PT(1) trở thành: xm t exmet  Hàm số đồng biến trên nênPT(1) ĐKXĐ: t gtet   2ln xmx 0x  2ln mxxhx  Có ; 2 1hx x  2x x   02hxx  Lập bảng biến thiên của hàm số hx

DẠYKÈMQUYNHƠN OFFICIAL

Từ bảng biến thiênhàm số suyraPT đã chocó3 nghiệm khi hx 2ln220,614m  Do nênsuyra  25;25m  24;23;...;1m Vậy có24 số nguyên thỏa mãnyêu cầu bàitoán. m ---------- HẾT ----------

SỞ

SAABCD sai?

B. C.

. ACSBD . CDSAD . BCSAB . BDSAC

Câu6: Hàm số đồng biến trong khoảng nào dưới đây? 2

A. B. và .  ;11;   ;1 1;

C. D. \1  ;1

Câu7: Một hộp chứa quả cầu màu đỏ khácnhauvà quả cầu màuxanhkhácnhau.Cóbaonhiêu 7 6 cách chọn ra quả cầu khácnhau phải

Câu8: Gọi là tập nghiệm của phương trình Tổng các phần tử

DẠYKÈMQUYNHƠN OFFICIAL

GIÁO DỤC VÀ ĐÀO TẠO VĨNH PHÚC ĐỀ THI THỬ TỐT NGHIỆP THPT– NĂM HỌC 2022–2023– LẦN 1

Hàm số nào dưới đây có đồ thị như đường congtronghình dưới đây? A. B. C. D. 3221. yxx 3231. yxx 4231. yxx 4221. yxx Câu2: Cho là số thực dương. Rút gọn biểu thức về dạng trong đó làphân a 3  Aaaaa m na m n số tối giản và .Tínhgiá trị của biểu thức * ,mn 22 . Tmn A. B. C. D. 2425. 593. 1369. 539. Câu3: Tìm tập xác định của hàm số D  2 3 log43 yxx A. B.  ;13;.D  22;13;22.  D C. D.  ;2222;.  D 1;3.D Câu4: Tính thể tích khối trụ có đường kính đáy bằng , chiều cao bằng 6 3 A. B. C. D. 9.  54.  27.  108.  Câu5: Chohìnhchóp có đáy làhìnhvuôngvà . Mệnh đề nàosau đây . SABCDABCD 

Câu1:

 x y x



3 2 A. B. C. D. 105 76 165 231

có đủ màu?

S 3 2 8 1 2 log2log420   x xx của là S A. B. C. D. 2 5 1 5

Câu9: Giá trị lớn nhất của hàm số trên đoạn

Câu10: Chohìnhchóp có đáy làhìnhvuông cạnh , vuônggóc với đáy. tạo với mặt SABCD aSA SC phẳng một góc Tính thế tích khối chóp

Khối lập phương là khối đa diện loại?

DẠYKÈMQUYNHƠN OFFICIAL

32 1   x

x 

A. B. C. D. 8 14 8 3 14 3

là

2;4

 SAB

SABCD A. B. C. D. 32 3 a 32a 32 3 a 36 3 a

A. B. C. D.

 3;3

3;4 Câu12: Chohình trụ cóbánkính đáy và chiều cao . Diện tíchxungquanh của hình trụ đã cho 3r 4h bằng A. . B. . C. . D. . 42 24 12 36 Câu13: Đường tiệm cận đứng của đồ thị hàm số là 44 1 x y x   A. B. C. D. 4x 1y 4y 1x Câu14: Phương trìnhnàosau đây vô nghiệm? A. B. C. D. 4sin50 x 4sin30 x 4sin10 x 4sin30 x Câu15: Biết ,tính.log2 a b 23logbab A. B. C. D. 23 log2 bab 23 log6 bab 23 log4 bab 23 log7 bab Câu16: Nghiệm của phương trình là 21 327 x  A. B. C. D. 5x 1x 4x 2x Câu17: Mặt cầu có diện tích bằng , thể tích khối cầu bằng  S 20  S A. . B. . C. . D. . 205 3  20 3  45 3  205  Câu18: Tập xác định của hàm số 3 log2y x  A. . B. . C. . D. .  0;  0;  ;2 Câu19: Tính thể tích của khối lập phương , biết V '''' ABCDABCD'6ACa  A. B. C. D. 33 3 a V 3 26Va  3 22Va  3 32Va  Câu20: Cho khối nóncó thiết diện qua trục là một tamgiác đều cạnh Thể tích của khối nón bằng a A. B. C. D. 33 24 a 33 24 a 33 5 a 33 5 a Câu21: Cho và làhai số thực dương thỏa mãn . Mệnh đề nào dưới đây đúng? ab 2 31 3 loglog2 ab A. . B. . C. . D. . 29 ab  29ab 2 ba  2 ab  Câu22: Trongcác mệnh đề sau, mệnh đề nào sai? A. Hai đường thẳng chéonhauthìkhôngcó điểm chung.

30

Câu11:

 4;3  3;5



B. Hai đường thẳng khôngcó điểm chungthìchéonhau.

C. Hai đường thẳng chéonhaukhivà chỉ khichúngkhông đồng phẳng.

D. Hai đường thẳng phân biệt không cắt nhau,khôngsongsong với nhauthìchéonhau.

Câu23: Với là số thực dương tùyý. bằng a 323 5 aa

Câu24: Hàm số có bảng biến thiên như sau:

Số nghiệm thực của phương trình là  290 fx

Câu25: Tính thể tích của khối chópcó diện tích đáy bằng , chiều cao

Câu26: Chohàm số có bảng biến thiên như hình vẽ.

Hàm số cóbaonhiêu điểm cực trị?

A. Cóba điểm. B. Có bốn điểm. C. Cóhai điểm. D. Có một điểm.

Câu27: Gọi lần lượt làgiá trị lớn nhất vàgiá trị nhỏ nhất của hàm số trên đoạn , Mm 21 1 x y x    2;0

Giá trị của biểu thức bằng 5Mm  A. B.

4. 4. 0.

Câu28: Chohìnhnóncóbánkính đường tròn đáy là, chiều cao và độ dài đường sinh. Gọi r h l,xq SV lần lượt là diện tíchxungquanhvà thể tích của khối nón.Trongcácphát biểu sau,phát biểu nào đúng?

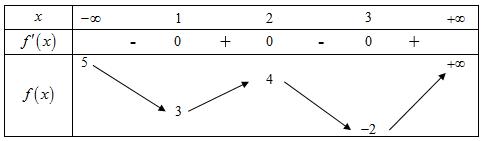
Câu29: Tìm tổng số đường tiệm cận đứng

Câu30: Xétcác số nguyên dương chiacho dư Tổng số

nguyên dương đầu tiên đó bằng

DẠYKÈMQUYNHƠN OFFICIAL

A. . B. . C. . D. . 13 15a 10 3a 15 13a 11 9a

yfx 

A. . B.

C. . D. .

0 1

3 2

A. B. C. D. 18.V 36.V 12.V 16.V

bằng 4. V 9

fx

yfx



A. B. C. D. 2. xq Srl  21 . 3 Vrl  2 .Vrh  . xq Srl 

và tiệm

ngang của đồ thị hàm số 2 32 1 xx y x   A. B. C. D. 1 3 4 2

3150 A. B. C. D. 3900 3725 7500 3800

cận

số

DẠYKÈMQUYNHƠN

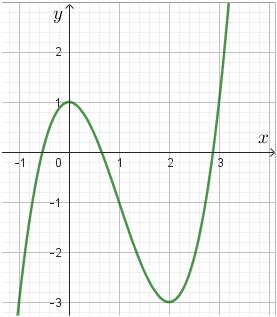
Câu31: Chohìnhchóp đều . Mặt phẳng chứa và đi qua trọng tâm của tamgiác SABCD PAB G cắt lần lượt tại . Tỉ lệ cógiá trị là SAC, SCSD , MN SABMN SABCD V T V  A. B. C. D. 1 4 1 2 3 4 3 8 Câu32: cho với là một số thực. Khẳng định nàosau đây đúng? 2 2 l25 im 2 x axbx L x      L A. B. C. D. 4ab 2211ab 23 ab 22 ab Câu33: Chocác số thực thỏa mãn và .Giá trị của biểu thức , ab 1ab 11 2024 loglog b a ab  bằng 11 loglog ab ab P ba  A. B. C. D. 2018 2024 2022 2020 Câu34: Chohàm số có đồ thị như hình vẽ bên dưới yfx  Số nghiệm phân biệt của phương trình là  420ffx   A. B. C. D. 5 6 3 4 Câu35: Chohai số thực dương thỏa .Tính , ab 91525 logloglogabab   . a b A. B. C. D. 1 2  15 2  15 2   15 2   Câu36: Cho2 số thực dương thỏa mãn: .Tính . 91525 logloglog() abab  a b A. B. C. D. 1 2 15 2 15 2  15 2  Câu37: Chohàm số với làtham số thực. Giả sử làgiá trị dương của tham số để hàm 2 8 xm y x  m 0m m số cógiá trị nhỏ nhất trên đoạn bằng .Giá trị thuộc khoảng nàosau đây [0;3]m 0m A. B. C. D. (20;25) (6;9) (5;6) (2;5)

OFFICIAL

Câu38: Tìmgiá trị của tham số để hàm số liên tục trên m

Câu39: Cắt hìnhnón đỉnh cho trước bởi mặt phẳng qua trục của nó,ta được một tamgiácvuông

câncó cạnh huyền bằng . Biết là một dâycung của đường tròn đáy hìnhnónsaocho 22aBC

mặt phẳng

là tập hợp tất cả cácgiá trị để phương trình có nghiệm phân S m lnln mxxmxm  2

yfx  m có tất cả nghiệm thực phân biệt.

10ffxm 9 A. B. C. D. 3 1 0 2

Câu42: Cóbaonhiêu cặp số nguyên dương thoả mãn điều kiện

và ?2023x

Câu43: Gọi là tập hợp tất cả cácgiá trị nguyên của tham số thực

DẠYKÈMQUYNHƠN OFFICIAL

232 ,2

xx x yx

      A. B. C. D. 3m 3m 6m 5m

2 3,2

xmx



tạo với mặt phẳng đáy nón một góc .Tính diện tíchtamgiác.  SBC 060 SBC A. B. C. D. 2 22 . 9 a 2 42 . 3 a 2 42 . 9 a 2 22 . 3 a Câu40:

biệt. Tập là S A. B. C. D. 1 ;11;. e      1;;. ee 1 ;. e    1;.  Câu41: Chohàm số bậc ba có đồ thị như hình vẽ. Cóbaonhiêu số nguyên để phương trình



Gọi



3 3

yyxx 

 ; xy

392log12

B. C. D. 2 4040 3780 3776

trị lớn nhất của hàm S m số trên đoạn không vượt quá . Tổng giá trị các phần tử 421 144830 4 yxxxm    0;2 30 của tập hợp bằng baonhiêu? S A. . B. . C. . D. . 210 108 136 120 Câu44: Cho phương trình ,( làtham số). Tìm số giá  3 2 32 2 log3421823 m xxxx m  m trị nguyên của tham số để phương trình đã chocó nghiệm duy nhất thuộc ? m 2;4 A. . B. . C. . D. . 3 4 5 2 Câu45: Chohình tứ diện có đáy làtamgiácvuông tại , , . Cạnh OABCOBC OOBa  3OCa  OA vuônggóc với mặt phẳng , , gọi làtrung điểm của .Tính khoảng cách  OBC 3OAa  M BC giữa hai đường thẳng và . h ABOM A. B. C. D. 3 15 ha  5 5 ha  3 2 ha  15 5 ha  Câu46: Tìm tất cả cácgiá trị thực của tham số để phương trình có đúng một nghiệm. m 21 x mx  A. B. C. D. 0 ln2 m m    0m 0 ln2 m m    ln2m Câu47: Chohàm số liên tục trên . Biết đồ thị hàm số như hinh vể sau: ()yfx   ()yfx  

saochogiá

số nghịch biến trên khoảng nàosau đây? 2 ()(13)32023 gxfxxx 

Câu48: Cóbaonhiêu số nguyên saocho ứng với mỗi cókhôngquá242 số nguyêny thỏa mãn x x

2 4 3 log2log()? xyxy 

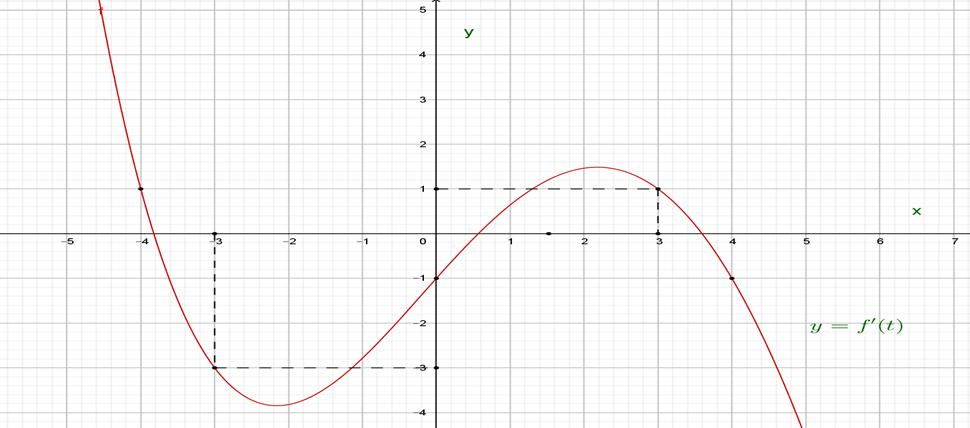
A. B. C. D. 21 40 20 39

Câu49: Chohìnhchóp có đáy làhìnhbìnhhànhtâm . Gọi là điểm thuộc sao . SABCDABCD OI SO cho .Mặtphẳng thay

Câu50: Tại trungtâmthành phố Vĩnh Yên người ta tạo điểm nhấn bằng cáchtrangtríhìnhnóncókích thước như sau: đường sinh ,bánkính đáy Biết rằng tamgiác là thiết

10 Rm SAB diện qua trục của hìnhnónvà làtrung điểm của .Trangtrí một hệ thống đèn điện chạy từ C SB đến trên mặt nón.Tìmgiá trị ngắn nhất của chiều dàidây đèn điện tử.

DẠYKÈMQUYNHƠN OFFICIAL

 A.

2    3 1; 2    (4;1) 11 ;4 2      

Hàm

. B.



, , lầnlượttại 1 3  SISO   BI SASCSD M , , . Gọi , lần lượt làgiá trị lớn nhất,

tỉ số .Tính ? NPmn SBMPN SABCD V V m n A. . B. . C. . D. . 7 5 8 5 9 5 2

đổiđiqua và cắtcáccạnh

giá trị nhỏ nhất của



A. B.

D. 103m 105m 30

20m ---------- HẾT -----------

20 lm

DẠYKÈMQUYNHƠN OFFICIAL

HƯỚNG DẪN GIẢI CHI TIẾT

BẢNG ĐÁP ÁN 1.D 2.B 3.A 4.C 5.A 6.B 7.D 8.D 9.A 10.A 11.A 12.B 13.D 14.A 15.A 16.D 17.A 18.D 19.C 20.B 21.A 22.B 23.A 24.B 25.B 26.C 27.B 28.D 29.D 30.B 31.D 32.A 33.D 34.A 35.C 36.D 37.D 38.D 39.D 40.A 41.B 42.C 43.C 44.B 45.D 46.A 47.A 48.D 49.C 50.B

Câu1: Hàm số nào dưới đây có đồ thị như đường congtronghình dưới đây? A. B. C. D. 3221. yxx 3231. yxx 4231. yxx 4221. yxx Lời giải Chọn D Hình đã cholà đồ thị của hàm số 4221 yxx Câu2: Cho là số thực dương. Rút gọn biểu thức về dạng trong đó làphân a 3  Aaaaa m na m n số tối giản và .Tínhgiá trị của biểu thức * ,mn 22 . Tmn A. B. C. D. 2425. 593. 1369. 539. Lời giải Chọn B 1523 1 3 315 3 3 3 3 88 2 2 44 22 ...... 23,8238593       Aaaaaaaaaaaaaaaaaaaa mnT Câu3: Tìm tập xác định của hàm số D  2 3 log43. yxx A. B.  ;13; D  22;13;22.  D C. D.  ;2222;.  D  1;3D Lời giải Chọn A Hàm số xác định khi  2 3 log43 yxx 2 1 430. 3    x xx x

Vậy tập xác định của hàm số đã cho  ;13;.

Câu4: Tính thể tích khối trụ có đường kính đáy bằng , chiều cao bằng . 6 3

A. B. C. D. 9 54 27 108 Lời giải Chọn C

Hình trụ có đường kính đáy bằng nênnócóbánkính 6 3r

Do đó khối trụ đã chocó thể tích bằng 223327rh  

Câu5: Chohìnhchóp có đáy làhìnhvuôngvà . Mệnh đề nàosau đây . SABCDABCD  SAABCD sai?

A. B. C. D.  ACSBD  CDSAD  BCSAB  BDSAC Lời giải Chọn A S C

A D

Hìnhchóp có đáy làhìnhvuôngnên mà nên B SABCD  CDAD  CDSA  CDSAD đúng.

Hìnhchóp có đáy làhìnhvuôngnên mà nên C . SABCD  BCAB  BCSA  BCSAB đúng.

Hìnhchóp có đáy làhìnhvuôngnên mà nên D . SABCD  ACBD  BDSA  BDSAC

Kết luận sai Thật vậy, giả sử .Khi đó màcó

DẠYKÈMQUYNHƠN OFFICIAL

Câu6: Hàm số đồng biến trong khoảng nào dưới đây?

đúng.

 ACSBD  ACSBD  ACSB  ACSA nên suyra

với  ACSABACBC AC .SBD

trùng (vôlý). Vậy khôngvuônggóc

2 1   x y x

Suyrahàm số đồng biến trên khoảng

Câu7: Một hộp chứa quả cầu màu đỏ khácnhauvà quả cầu màuxanhkhácnhau.Cóbaonhiêu 7 6 cách chọn ra quả cầu khácnhau phải có đủ màu? 3 2

Chọn D

Gọi là biến cố “chọn ra quả cầu khácnhau phải có đủ màu” A 3 2

Biến cố đối của là :“chọn ra quả cầu cùngmàu” AA3

TH1: Chọn ra quả cầu cùngmàu đỏ có 3 3 735C

TH1: Chọn ra quả cầu cùngmàuxanhcó

DẠYKÈMQUYNHƠN OFFICIAL

A. B. và  ;11;  ;1 1; C. D. \1  ;1 Lời giải Chọn B TXĐ: \1D Tacó 2 23 0 11         x y xD xx

và .  ;1 1;

A. B. C. D.

231 Lời giải

105 76 165

3 3 620C Suyra 352055nA Vậy số cách chọn ra quả cầu khácnhau phải có đủ màu: 3 23 1355231 nAC Câu8: Gọi là tập nghiệm của phương trình Tổng các phần tử S 3 2 8 1 2 log2log420   x xx của là S A. B. C. D. 2 5 1 5 Lời giải Chọn D ĐK 2 2 20 22 22 420 222 22                x x x x xx x x   3 2 2 8 1 2 2 2 log2log420log2log420    x xx x xx .  2 2 2 2 2 0 log2log42242505    x x xxxxxxx x Đối chiếu với điều kiện tacó tập nghiệm của phương trìnhlà  0;5S Vậy tổng các phần tử của là S5 Câu9: Giá trị lớn nhất của hàm số trên đoạn là 32 1   x y x  2;4 A. B. C. D. 8 14 8 3 14 3 Lời giải Chọn A

DẠYKÈMQUYNHƠN

OFFICIAL Tacó .Suyrahàm số nghịch biến trên .  2 325 02;4 11       x y x x x  2;4 Vậy giá trị lớn nhất của hàm số trên đoạn là 32 1   x y x  2;43.22 28 21  y Câu10: Chohìnhchóp có đáy làhìnhvuông cạnh , vuônggóc với đáy. tạo với mặt . SABCD aSA SC phẳng một góc Tính thế tích khối chóp  SAB 30 . SABCD A. B. C. D. 32 3 a 32a 32 3 a 36 3 a Lời giải Chọn A Tacógóc giữa và mặt phẳng làgóc Suyra SC  SAB  BSC  30 BSC Xéttamgiác vuông tại tacó: Suyra SBC B  tan BC BSC SB  3 ttan30 an     BCa SB a BSC 2 22 2 32    SASBABaaa Vậy thể tíchhìnhchóp là: SABCD 3 2 112 ....2 333    ABCD aVSSAaa Câu11: Khối lập phương là khối đa diện loại? A. . B. . C. . D. .  4;3  3;5  3;3  3;4 Lời giải Chọn A Câu12: Chohình trụ cóbánkính đáy và chiều cao . Diện tíchxungquanh của hình trụ đã cho 3r 4h bằng A. B. C. D. 42 24 12 36 Lời giải Chọn B Diện tíchxungquanh của hình trụ đã cho bằng 23424 2 xq Srh   Câu13: Đường tiệm cận đứng của đồ thị hàm số là 44 1 x y x   A. . B. . C. . D. . 4x 1y 4y 1x

DẠYKÈMQUYNHƠN OFFICIAL

Lời giải Chọn D Tập xác định .\1D Tacó và nên đồ thị hàm số có đường tiệm cận 11 44 limlim 1 x x x y x        11 44 limlim 1 x x x y x      đứng là .1x Câu14: Phương trìnhnàosau đây vô nghiệm? A. . B. . C. . D. . 4sin50 x 4sin30 x 4sin10 x 4sin30 x Lời giải Chọn A Phương trình nên phương trìnhnàyvô nghiệm. 5 4sin50sin1 4 x x  Câu15: Biết ,tính.log2 a b 23logbab A. . B. . C. . D. . 23 log2 bab 23 log6 bab 23 log4 bab 23 log7 bab Lời giải Chọn A Tacó .  2323 23 23.2llogloglog23log og 2 logloglog2 a a a a b a a a abab b ab b b b         Câu16: Nghiệm của phương trình là 21 327 x  A. . B. . C. . D. . 5x 1x 4x 2x Lời giải Chọn D 213 3273 213 2 x x x    Câu17: Mặt cầu có diện tích bằng , thể tích khối cầu bằng  S 20  S A. . B. . C. . D. . 205 3  20 3  45 3  205  Lời giải Chọn A 2 420 5 SR R   3 4205 33 VR   Câu18: Tập xác định của hàm số .3 log2y x  A. B. C. D.  0;  0;  ;2 Lời giải Chọn D Tacó: 202 xx

Câu22: Trongcác mệnh đề sau, mệnh đề nào sai?

A. Hai đường thẳng chéonhauthìkhôngcó điểm chung.

B. Hai đường thẳng khôngcó điểm chungthìchéonhau.

C. Hai đường thẳng chéonhaukhivà chỉ khichúngkhông đồng phẳng.

D. Hai đường thẳng phân biệt không cắt nhau,khôngsongsong với nhauthìchéonhau.

Lời giải

Chọn B

DẠYKÈMQUYNHƠN OFFICIAL

Hai đường thẳng khôngcó điểm chungthìchéonhau Mệnh đề saivìhai đường thẳng khôngcó

điểm chungthìchúngcó thể songsong.

Câu19:

, biết V . '''' ABCDABCD'6ACa  A. . B. . C. . D. . 33 3 a V 3 26Va  3 22Va  3 32Va  Lời giải Chọn C Tacó: là đường chéohình lập phương ' AC 33 '3 ' 2 3 22 ACAB AC ABa VABa    Câu20: Cho

tamgiác đều cạnh . Thể tích của khối nón bằng a A. . B. . C. . D. . 33 24 a 33 24 a 33 5 a 33 5 a Lời giải 60° B S A Chọn B Khối nóncó và suyra thể tích 2 2 a rar 3 2 ha  2 3 2 1133 332224 aaaVrh      Câu21: Cho và làhai số thực dương thỏa mãn . Mệnh đề nào dưới đây đúng? ab 2 31 3 loglog2 ab A. B. C. D. 29 ab  29ab 2 ba  2 ab  Lời giải Chọn A Tacó . 2 2 2 2 22 31 33 3 3 loglog2loglog2log239 aa ab ab ab bb  

Tính thể tích của khối lập phương

khối nóncó thiết diện qua trục là một



DẠYKÈMQUYNHƠN OFFICIAL

Câu23: Với là số thực dương tùyý. bằng a 323 5 . aa A. B. C. D. 13 15a 10 3a 15 13a 11 9a Lời giải Chọn A Tacó . 31313 333232 5 5515 .. aaaaaa 

sau: yfx  Số nghiệm thực của

trình là  290 fx A. B. C. D. 3 2 0 1 Lời giải Chọn B Tacó Phương trìnhcó nghiệm phân biệt.  9 290 2 fx fx  2 Câu25:

4. V

A. B. C. D. 18.V 36.V 12.V 16.V Lời giải Chọn C Tacó . 11 .9.412 33 VBh Câu26: Chohàm

fx Hàm

yfx  A. Cóba điểm. B.

C. Cóhai điểm. D. Có một điểm. Lời giải 9 2y

Câu24: Hàm số có bảng biến thiên như

phương

Tính thể tích của khối chópcó diện tích đáy bằng , chiều cao bằng

số có bảng biến thiên như hình vẽ.

số cóbaonhiêu điểm cực trị?

Có bốn điểm.

tròn

DẠYKÈMQUYNHƠN

OFFICIAL Chọn C Dựa vào bảng biến thiênta thấy hàm số có2 điểm cực trị là và . fx 1x 1x Câu27: Gọi lần lượt làgiá trị lớn nhất vàgiá trị nhỏ nhất của hàm số trên đoạn . , Mm 21 1 x y x    2;0 Giá trị của biểu thức bằng 5Mm  A. B. C. D. 4 4 0 2 Lời giải Chọn B Vìhàm số đơn điệu trên đoạn nên chỉ đạt GTLN,GTNN tại hai điểm 21 1 x y x    2;0 2;0 Tacó Suyra . Vậy . 21;01ff   1;1Mm 54 Mm Câu28:

h l,xq SV lần lượt là diện tíchxungquanhvà

đúng? A. B. C. D. 2. xq Srl  21 . 3 Vrl  2 .Vrh  . xq Srl  Lời giải Chọn D Câu29: Tìm tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 2 32 1 xx y x   A. B. C. D. 1 3 4 2 Lời giải Tập xác định: 3;\1D Tacó: nên đồ thị hàm số có tiệm

2 l32 im0 1 x xx x   0y        2 12 1 1 1 12 12 1 431 32 34limlim lim 111321132 l437 im 8132 l327 im 18 43 l32 imlim 1132 x x x x x x x xx xx xx x xxxxxxxx x xxx xx x x xx x xxx                             Nên đồ thị hàm số có1 tiệm cận đứng 1x Vậy đồ thị hàm số có2 đường tiệm cận. Câu30: Xétcác số nguyên dương chiacho dư . Tổng số số nguyên dương đầu tiên đó bằng 3150 A. B. C. D. 3900 3725 7500 3800 Lời giải

Chohìnhnóncóbánkính đường

đáy là, chiều cao và độ dài đường sinh. Gọi r

thể tích của khối nón.Trongcácphát biểu sau,phát biểu nào

cận ngang

Gọi dãy số nguyên dương chiacho dư ,có là: 3111,3ud

Tổng số số nguyên dương đầu tiên đó bằng: 50

Câu31: Chohìnhchóp đều . Mặt phẳng chứa và đi qua trọng tâm của tamgiác SABCD

lần lượt tại .

DẠYKÈMQUYNHƠN OFFICIAL

 32 n un 



50 .50249.502.149.3.50 3725 22 2 uu ud S       

150 1

PAB G cắt

lệ cógiá

SCSD , MN SABMN SABCD V T V  A. B. C. D. 1 4 1 2 3 4 3 8 Lời giải

cắt tại

thể tíchtacó: 1;1;2;2 SASBSCSDabc d SASBSMSN  Suyra: . Chọn đáp án D 11223 4....4.1.1.2.28 SABMN SABCD Vabcd T V abc      Câu32: cho với là một số thực. Khẳng định nàosau đây đúng? 2 2 l25 im 2 x axbx L x      L A. B. . C. . D. . 4ab 2211ab 23 ab 22 ab Lời giải Đặt .Vì có nghiệm kép nên để là số thực thì: 25fxaxbx  2 20x 2x L .   202101 2103 0 f ab a a b f              Vậy .4ab



Tỉ

trị là SAC,

Tacó: Trongtamgiác ,kéodàiAG cắt tại Mvà làtrung điểm SAC SCM SC Trongtamgiác ,kéodài

và làtrung điểm SBDBGSDNN SD Áp dụng công thức tỉ số

DẠYKÈMQUYNHƠN OFFICIAL

Câu33: Chocác số thực thỏa mãn và .Giá trị của biểu thức , ab 1ab 11 2024 loglog b a ab  bằng 11 loglog ab ab P ba  A. B. C. D. 2018 2024 2022 2020 Lời giải Chọn D Tacó: 2 11 1 2024log2506log2506log10loglog log log506505 log506505 b b b b a b b b a a a ab a a a      Tacó . 11 loglog1log1logloglog b a b a ab ab P ababab ba    +) Với .Suyra: log506505 ba (loại). 1 11 log 2505 506505506505506505a b P      +) Với .Suyra: log506505 ba 1 111 log 506505 2505 506505 506505506505506505 a b P        (thỏa mãn). Vậy 11 25052020 loglog ab ab P ba   Câu34: Chohàm số có đồ thị như hình vẽ bên dưới yfx  Số nghiệm phân biệt của phương trình là  420ffx   A. B. C. D. 5 6 3 4 Lời giải Chọn A Từ đồ thị của hàm số tacó: yfx 

có3 nghiệm phân biệt khác2.

có2 nghiệm trong đó có nghiệm

Chohai số thực dương thỏa

DẠYKÈMQUYNHƠN

OFFICIAL       4202 420 4223 fxfx ffx fxfx                +) Với

2fx +)

kép . 3fx 2x Số nghiệm

là5.  420ffx   Câu35:

.Tính

ab 91525 logloglogabab   . a b A. B. C. D. 1 2  15 2  15 2   15 2   Lời giải Chọn C Đặt   91525 9 logloglog 1591525* 25 t t ttt t a ababtb ab        Chia cả hai vế của (*)cho ta được: 25t 2 315 529333 1 10 25555315 0 52 t t t t t t                       Tacó . 9315 1552 t t t a b      Câu36: Cho2 số thực dương thỏa mãn: .Tính . 91525 logloglog() abab  a b A. . B. . C. . D. . 1 2 15 2 15 2  15 2  Lời giải Chọn D Đặt 91525 logloglog()t abab  Suyra . 9,15,25 t t tabab  Tacó phương trình: 2 315() 5233 91525 10 55315 5(tm) 2 t t t ttt t l             Vậy 315 . 52 t a b    

Với

phân biệt của phương trình

DẠYKÈMQUYNHƠN OFFICIAL

Câu37: Chohàm số với làtham số thực. Giả sử làgiá trị dương của tham số để hàm 2 8 xm y x  m 0m m số cógiá trị nhỏ nhất trên đoạn bằng .Giá trị thuộc khoảng nàosau đây [0;3]m 0m A. . B. . C. . D. . (20;25) (6;9) (5;6) (2;5) Lời giải Chọn D Tacó: 2 ' 2 8 0,8 (8) m y x x     Do đó .Theo giả thiết 2 [0;3] min(0)8m yy 2 2 [0;3] min332426 8 m y mm  Vậy 026(2;5)m Câu38: Tìmgiá trị của tham số để hàm số liên tục trên m 232 ,2 2 3,2 xx x yx xmx       A. B. C. D. 3m 3m 6m 5m Lời giải Chọn D Tập xác định .  Hàm số đã choliên tục trêncác khoảng và . (;2) (2;)  Do đó hàm số liên tục trên khinóliên tục tại  2x Vậy  2 2 2 2 2 32 limlim(2)limlim(3)3.2 2 x x x x xx fxfxf xmm x           . 2 lim(1)65 x xmm    Câu39: Cắt hìnhnón đỉnh cho trước bởi mặt phẳng qua trục của nó,ta được một tamgiácvuông  NS câncó cạnh huyền bằng Biết là một dâycung của đường tròn đáy hìnhnónsaocho 22aBC mặt phẳng tạo với mặt phẳng đáy nón một góc .Tính diện tíchtamgiác.  SBC 060 SBC A. B. C. D. 2 22 . 9 a 2 42 . 3 a 2 42 . 9 a 2 22 . 3 a Lời giải Chọn D

DẠYKÈMQUYNHƠN

OFFICIAL Gọi thiết diện làtamgiácvuông ,khi đó nênhìnhnóncóbánkính và SAB 22ABa  2ra  chiều cao . 2SOa  Gọi làhình chiếu của trên . H OBC Khi đó nên . BCSOH     ,60SHOSBCABC    Suyra ,do đó . 6 .cot60 3 aOHSO    2223 22 3 aBCBHOBOH   Lại có nên . 26 sin603 SOa SH  2 122 23SBC aSBCSH    Câu40: Gọi là tập hợp tất cả cácgiá trị để phương trình có nghiệm phân S m lnln mxxmxm  2 biệt. Tập là S A. B. 1 ;11; e      1;; ee C. D. 1 ;. e    1;.  Lời giải Chọn A Điều kiện 0;0xm Phương trình lnln mxxmxm  1ln1lnxm xm   Xét ,tacó ; 1ln ,0xfx x x    2 lnxfx x   01fxx  Bảng biến thiên 1ln ,0xfx x x    Dựa vào bảng biến thiêntasuyra hay 1ln 01 m m    11ln0 1ln1 mm e mm m          Câu41: Chohàm số bậc ba có đồ thị như hình vẽ. Cóbaonhiêu số nguyên để phương trình yfx  m có tất cả nghiệm thực phân biệt.   10ffxm 9 A. B. C. D. 3 1 0 2

DẠYKÈMQUYNHƠN

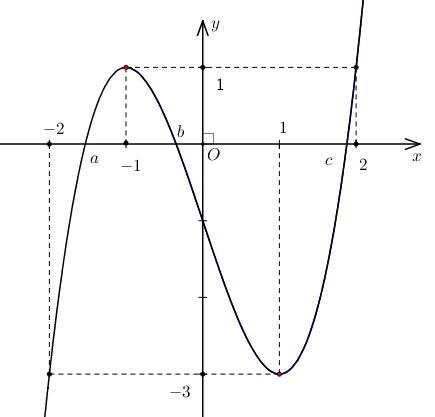
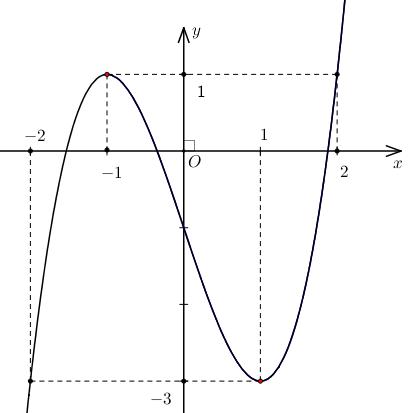
OFFICIAL Lời giải Chọn B Tacó hay         1,2;1 10* 1,1;0 1,1;2 fxmaa ffxm fxmbb fxmcc                1,1 1,2 1,3 fxma fxmb fxmc      Để phương trình có9 nghiệm phân biệt thì mỗi phương trình đều có3 nghiệm  *  1,2,3 phân biệt, khi đó 31122 31122 31122 ma ma mb mb mc mc              Do nêntasuyra  2;1,1;0,1;2a bc    14 2311 41 m m m m      Vì nên m0m Câu42: Cóbaonhiêu cặp số nguyên dương thoả mãn điều kiện  ; xy 3 3 392log12 yyxx  và ?2023x A. . B. . C. . D. . 2 4040 3780 3776 Lời giải Chọn C

3 1log121112726y x x x  Mà và nguyên dương nên . 2023x x  26;27;...;2023x

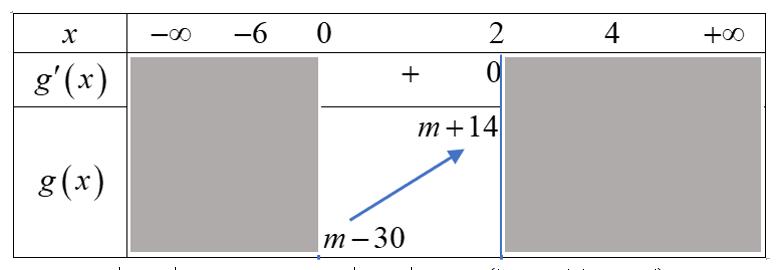
Do đó có1998 cặp số nguyên dương thoả mãn.  ; xy

+) Với . 3 2log12.211243242y x x x 

Mà và nguyên dương nên . 2023x x  242;243;;2023x

Do đó có1782 cặp số nguyên dương thoả mãn.  ; xy

DẠYKÈMQUYNHƠN

Vậy có tất cả 3780 cặp số nguyên dương thoả mãnyêu cầu bàitoán.  ; xy

Câu43: Gọi là tập hợp tất cả cácgiá trị nguyên của tham số thực saochogiá trị lớn nhất của hàm

m số trên đoạn không vượt quá . Tổng giá trị các phần tử

OFFICIAL Tacó 3 3 392log12 yyxx    2 3 33213log13 yyx x    3 log1 2 3 33233log13 x yy x      3 log11 2 3 323log11,1 x yy x    Xéthàm số có nênhàm số đồng 3t yftt 3ln310, tft t  3t yftt  biến. Từ .     3 31 1 log11log21 2 fy x yx f      Mà ,suyra . 2023x 3 3 3 11 log11log20241log202422 2 y yx  Do nguyên dương nên hoặc y 1y 2y +) Với

421 144830 4 yxxxm    0;2 30 của tập hợp bằng baonhiêu? S A. . B. . C. . D. . 210 108 136 120 Lời giải Chọn C Đặt 421 144830 4 gxxm x x   32848xxgx    6 02 4 x gxx x        Bảng biến thiên Tacó . ygx    0;20;2 ax maxmma14,30 xg myx m     Trường hợp 1: Nếu thì 14308mmm    0;2 m14 axym 1430m  301430 m  4416 m  Do đó 816 m 

DẠYKÈMQUYNHƠN

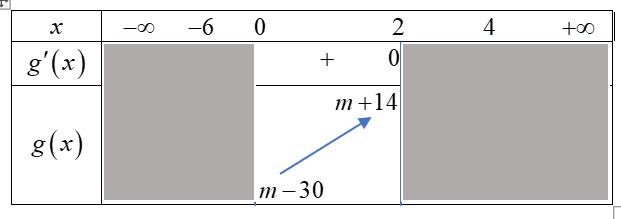
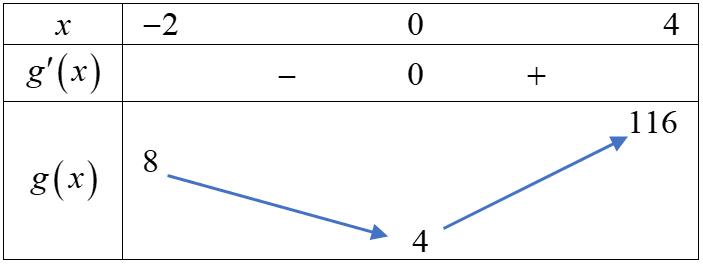
OFFICIAL Trường hợp 2: Nếu thì 14308mmm    0;2 m30 axym  3030m  303030 m 060 m  Do đó 08 m  Vậy .Suyra tổng giá trị các phần tử của tập hợp bằng  0;1;2;3;;16S S136 Câu44: Cho phương trình ,( làtham số). Tìm số giá  3 2 32 2 log3421823 m xxxx m  m trị nguyên của tham số để phương trình đã chocó nghiệm duy nhất thuộc ? m 2;4 A. . B. . C. . D. . 3 4 5 2 Lời giải Chọn B Điều kiện 32340xx Tacó  3 2 32 2 log3421823 m xxxx m     3232 2 2 3log34343log22,1 mm xxxx   Xéthàm số với có nênhàm số 23log yfttt  0t 1 l10,0 n2ft t t  đồng biến trên khoảng . 23log yfttt   0; Từ .  32 324 2 1 234 3 m m fxxf xx  Đặt với có . 3234gxxx 2;4x   2 0 360 2 x gxxxgx x     Bảng biến thiên Từ bảng biến thiênsuyra phương trình đã chocó nghiệm duy nhất thuộc 2;4 24 82116 m m    2 2 3log116 m m    Màtham số nguyênnên . m  2;4;5;6m Vậy có4giá trị nguyên của tham số để phương trình đã chocó nghiệm duy nhất thuộc m 2;4

Câu45: Chohình tứ diện có đáy làtamgiácvuông tại , , .

DẠYKÈMQUYNHƠN OFFICIAL

với mặt phẳng ,

Cạnh OABCOBC OOBa 

OCa

OA vuônggóc

làtrung điểm của .Tính khoảng cách  OBC 3OAa  M BC giữa

h ABOM A. B. C. D. 3 15 ha  5 5 ha  3 2 ha  15 5 ha  Lời giải Chọn D H K D M O A B C

saocho và là đường trungbình

tamgiác . D

BCD Khi đó tacó .     // ,,, OMABDdABOMdOMABDdOABD    Kẻ Lại có (do )suyra . OHBD  BDOA    OAOBC BDOBC      BDAOH  Suyra theogiao tuyến  AOHABD  AH Trong , kẻ suyra . AHOOKAH     , OKABDOKdOABD  Trong :AHO 222222222 111111111 33 OKOHOAODOBOAaaa  Suyra hay . 15 5 Oa K 15 ,5 adABOM Câu46: Tìm tất cả cácgiá trị thực của tham số để phương trình có đúng một nghiệm. m 21 x mx  A. . B. . C. . D. . 0 ln2 m m    0m 0 ln2 m m    ln2m Lời giải Chọn A Tacó: (*). Đặt 21 x mx 21 x mx  2x fxmx  Nhận xét là nghiệm của phương trình . 0x  * Tacó: .  '2ln2 xfx m  Trường hợp 1: khi đó , .Tacó bảng biến thiên của như sau: 0m  '0fxx  fx



gọi

hai đường thẳng và .

Dựng

của

// BDOMOM

DẠYKÈMQUYNHƠN OFFICIAL

Vậy thỏa yêu cầu bàitoán. 0m Trường hợp 2: .Khi đó .Tacó bảng biến thiên của 0m  2 '0logln2 o mfxx fx Yêu cầu bàitoán . Lại có nên . 1 ofx  01f 2 0log0ln2 ln2 o m x m   Tóm lại từ hai trường hợp, ta thấy phương trìnhcó đúng 1 nghiệm .  0 ln2 m m    Câu47: Chohàm số liên tục trên . Biết đồ thị hàm số như hinh vể sau: ()yfx   ()yfx   Hàm số nghịch biến trên khoảng nàosau đây? 2 ()(13)32023 gxfxxx   A. . B. C. . D. . 3 ;2 2    3 1; 2    (4;1) 11 ;4 2       Lời giải Chọn A  2 ()(13)320233(13)61 gxfxxx gxfxx      .  2 0(13)131 3 gxfxx    Đặt ta được phương trình . 31tx 2 ()1 3 ftt   Đặt 2 (),1 3 yftyt   

vào đồ thị để hàm số nghịch biến khi

Câu48: Cóbaonhiêu số nguyên saocho ứng với mỗi cókhôngquá242 số nguyêny thỏa mãn x

Để (1)khôngcóquá242 nghiệm nguyên cókhôngquá242 nghiệm nguyên dương . (2)y

Đặt .Tacó: làhàm số đồng biến

DẠYKÈMQUYNHƠN OFFICIAL

lg4 o() fttt 

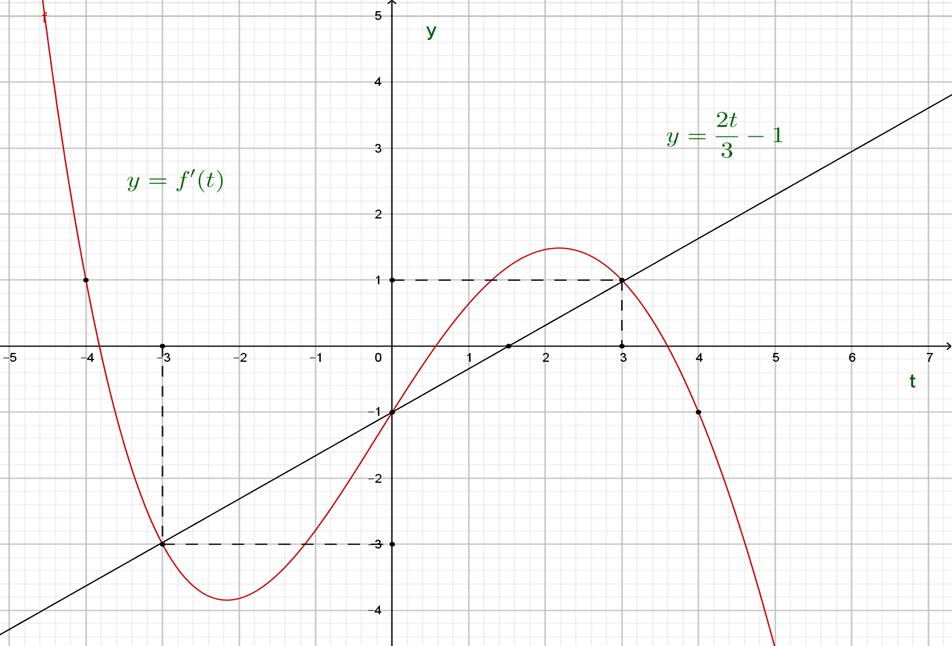
41 313033 . 1332 3 x x x x      

x  2 4 3 log2log()? xyxy  A. B. C. D. 21. 40. 20. 39. Lời giải Chọn D Điều kiện: . 2 20 0 xy xy    Tacó: (1).  2 4 3 log2log() xyxy  3 2log()24xy xy   3 lg4 o 2 2() xyxy Điều kiện: (do . 1xy,,0) xyxy  Đặt .Ta được (1)txyt 3 3 log o4 g 4 l 2 2 2 2 xtxtxxtt 

Dựa

3 log41 3 ()log101 4 ftt t   ()ft trên cókhôngquá242 nghiệm nguyên hay [1;) (2)  1242ft  3 3 log4 log4 2 2 22422422242242019,51996 xx xx x   



Câu49: Chohìnhchóp có đáy làhìnhbìnhhànhtâm . Gọi là điểm thuộc sao . SABCDABCD OI SO cho .Mặtphẳng thayđổiđiqua và cắtcáccạnh , , lầnlượttại 1 3  SISO   BI SASCSD M , , . Gọi , lần lượt làgiá trị lớn nhất, giá trị nhỏ nhất của tỉ số .Tính ? NPmn SBMPN SABCD V V m n

Lại có: Có số nguyên thỏa mãnbàitoán. x

39 x

DẠYKÈMQUYNHƠN

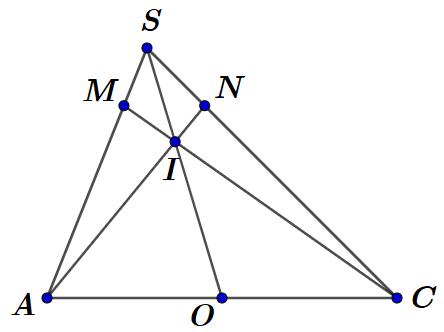
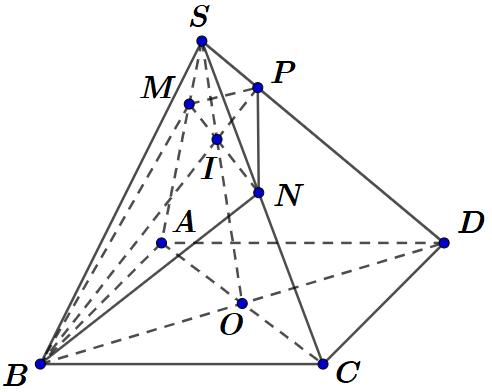
OFFICIAL A. B. C. D. 7 5 8 5 9 5 2 Lời giải Chọn C Áp dụng định lýMenelaustacó . 221 11 5 114   PSIOBDPS PSSD PDISBOPD PDSP Đặt , , , với  SA x SM 1 SB ySB SC z SN 5 SD t SP 66 xzytzx Khi ,Áp dụng định lýMenelaustacó .  NC 11 1 44   MSIOCAMSISCOMS MAISCOMAIOCAMA ,khi đó tacó với 1515  SA x SM  3 456    SBMPN SABCD Vxyzt V xyztxx 15  x Tacó mà . 2 639  xxx 15  x   133 569 155625    xx xx và . 3 25  m 1 15 n 9 5  m n Câu50: Tại trungtâmthành

cáchtrangtríhìnhnóncókích thước như

Biết

tamgiác là thiết 20 lm 10 Rm SAB diện qua trục của hìnhnónvà làtrung điểm của .Trangtrí một hệ thống đèn điện chạy từ C SB đến trên mặt nón.Tìmgiá trị ngắn nhất của chiều dàidây đèn điện tử. AC A. B. C. D. 103m 105m 30m 20m Lời giải

phố Vĩnh Yên người ta tạo điểm nhấn bằng

sau: đường sinh ,bánkính đáy .

rằng

DẠYKÈMQUYNHƠN

OFFICIAL Chọn B Trải hìnhnónra mặt phẳng ta được một hình quạt. Do thiết là thiết diện qua trục nên SAB .  '1' 2  ASBBSAASA Tacóchuvi đường tròn đáy của hìnhnónlà . 20  '20 AA Chuvi đường tròntâm bánkính là . S SA40   '2036018090 40      ASA ASB Hệ thống đèn ngắn nhất đi từ đến là đoạn AC 22222010105ACSASC m ---------- HẾT ----------

DẠYKÈMQUYNHƠN OFFICIAL

ĐẠI HỌC KHOA HỌC TỰ NHIÊN

THPTCHUYÊNKHTN THI THỬ TÔT NGHIỆP THPT- NĂM HỌC 2022–2023– LẦN 1 Câu1: Hàmnàosau đây là một nguyênhàm của hàm số ? 1 2  x y A. . B. . C. . D. . ln2x 2lnx 1 ln 2 x 2 1 2x Câu2: Chohàm số có đạo hàmlà . Số điểm cực trị của hàm số đã cholà fx 2312   fxxxx A. B. C. D. 0 1 2 3 Câu3: Tập nghiệm của bất phương trình 1 2 log210 x A. B. C. D.  ;1  1; 1 ;1 2    1 ; 2    Câu4: Mô-đun của số phức bằng  3412 zii  A. . B. . C. . D. . 25 255 5 55 Câu5: Chohàm số .Tính . 31fxx  1 0 d Ifxfxx   A. B. C. D. 1I 3I 3 2 I 1 2 I Câu6: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 2 2 43 x y xx   A. B. C. D. 0 1 2 3 Câu7: Trongkhônggian với hệ tọa độ ,chohai véc-tơ , .Tíchvô Oxyz  1;2;3u   2;1;2v  hướng của hai véc-tơ và bằng u  v  A. B. C. D. 6 6 10 10 Câu8: Tập xác định của hàm số là  2log4 yxx  A. B. C. D.  0;4  0;2  2;2  2;0 Câu9: Số nghiệm thực của phương trình là 2 224332 x x  A. . B. . C. . D. . 0 1 2 3 Câu10: Khẳng định nàosau đây đúng? A. . B. . 1 23d36 xx x xC  1 12.3d3.6 xx x xC    C. . D. . 13623d ln6 x xxxC  1 13.62.3d 1 x xx x C x     Câu11: Trongkhônggian với hệ trục tọa độ ,cho mặt cầu .Tìm tất cả Oxyz 222 ():23 Sxyzx cácgiá trị thực dương của tham số để mặt phẳng tiếp xúc với mặt cầu m 220xyzm () S A. B. C. D. 7m 5m 6m 19m

TRƯỜNG

Câu12: Cho số phức có phần ảo âm thoả mãn .Tính z (2)2zz 3 zi 

B. C. D. 17 17 5 5

Câu13: Chohìnhchóp tứ giác đều cógóc giữa cạnh bên với đáy một góc .Tínhcosin của SABCD 45 góc giữa mặt bênvà đáy của hìnhchóp đã cho.

Câu14: Cho tập M gồm các số tự nhiêncóba chữ số đôi một khácnhau lấy từ tập Chọn  0;1;2;3;4;5 ngẫu

DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D. 1 3 1 2 1 2 1 3

nhiên một số từ tập M.Tínhxác xuất để số được chọn có chữ số hàng trăm nhỏ hơn chữ số hàng chục. A. . B. . C. . D. . 3 5 2 5 1 3 2 3 Câu15: Biết .Tính .  4 2 d8fxx   2 1 2d Ifxx  A. . B. . C. . D. . 2I 4I 6I 8I Câu16: Cho thỏa mãn .Tính . 0a 1 log2 a log1000a A. . B. . C. . D. . 13 4 4 3 4 3 2 Câu17: Chohìnhchóp có đáy làhìnhvuông cạnh và vuônggóc với đáy. Tính SABCD ,2 aSAa SA theo khoảng cách từ đến mặt phẳng a A  SBD A. B. C. D. 4 9 a 9 4 a 2 3 a 3 2 a Câu18: Số giao điểm của đồ thị hàm số với đường thẳng là: 32ln yxxx  2yx A. . B. . C. . D. . 0 1 2 3 Câu19: Phần ảo của số phức là: 13 1   i z i A. . B. . C. . D. . 4 4i 2i 2 Câu20: Từ các chữ số lập được baonhiêu số chẵn gồm ba chữ số đôi một khácnhau? 0,1,2,3,4,5,6 A. B. C. D. 80 120 68 105 Câu21: Hàm số nào dưới đây khôngcó cực trị? A. . B. . C. . D. . 31yxx 421yxx 31yxx 421yxx Câu22: Thể tích khối chópcó diện tích đáy và chiều cao là 2 a 2a A.. B. . C. . D. . 3 a 32 3 a 32a 31 3 a Câu23: Chohàm số .Tìmcácgiá trị thực của tham số để hàm số có đúng 1 cực 4 2 (21)1yxmx   m trị? A. . B. . C. . D. . 1 2 m 1 2 m 1 2 m 1 2 m

Câu24: Cho cấp số nhân có

() n u

Câu25: Chohàm số có đạo hàmlà .Hàm số đã cho đồng biến trên ()fx '

khoảng nào dưới đây?

Câu26: Trongkhônggian với hệ toạ độ cho mặt cầu

mặt cầu đã chocó toạ độ là:

Oxyz

Câu27: Cho khối chóptamgiác đều S.ABC có cạnh đáy AB=2a, cạnh bên . Thể tích khối chóp 2SAa 

đã cho bằng:

Câu28: Hình chiếu vuônggóc của điểm M(1,-2,3)lên mặt phẳng (Oyz) có toạ độ là:

A. . B. . C. . D. .(1,2,3)(0,2,3)(0,2,3)(1,0,0)

Câu29: Trongkhônggian với hệ tọa độ cho đường thẳng và mặt phẳng Oxyz

DẠYKÈMQUYNHƠN OFFICIAL

 2q 10u A. . B. . C. . D. . 2048 256 512 1024

vàcông bội .Tính



()(1)(2)(3) fxxxx

A. . B. . C. . D. . (2;3)

(1;3) (3;) 

(1;2)

.Tâm

222

Sxyzxy

của

():2430

A. . B. . C. . D. . (1,2,0) (1,2,0)(2,4,0)(2,4,0)

A. . B. . C. . D.

32 3

32 6 a 32 2 a

 .Tìm

B. (-3,1,-3). C. (-1,3,-3). D. (3,1,3). Câu30: Cho số thực a>0,a1.Giá trị của biểu thức bằng:  loga aa A. 6. B. 3. C. D. 3 2 3 4 Câu31: Trongkhônggian với hệ tọa độ cho đường thẳng Viết phương trình Oxyz 11 : 234 dxyz   mặt phẳng qua vàvuônggóc với đường thẳng .  1;0;2M d A. B. 10xy 234100 xyz   C. D. 234100 xyz   23460 xyz Câu32: Chohàm số có đạo hàmlà với làtham số thực. Tìm tất cả các fx  1 fxxxm   m giá trị của để hàm số đồng biến trên . m  ;  A. . B. . C. . D. . 1m 1m 1m 1m Câu33: Tập nghiệm của bất phương trình là 233 x x      A. . B. . C. . D. .  ;1  1;  0; 0;1 Câu34: Trongkhônggian với hệ tọa độ choba điểm , , . Phương Oxyz  1;0;0A  0;1;0B  0;0;1C trình mặt phẳng là  ABC A. B. C. D. 0xyz 1xyz 0xyz 1xyz

: 213 dxyz

tọa độ giao điểm của d và (P). ():280 Pxyz

(1,3,-3).

DẠYKÈMQUYNHƠN OFFICIAL

Câu35: Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức thỏa mãn là z 1 zzi  đường thẳng có phương trình? A. B. C. D. yx  yx  1yx 1yx Câu36: Tìm tất cả cácgiá trị thực của tham số để đường thẳng cắt đồ thị hàm số m ym  224yxx  tại đúng điểm phân biệt. 4 A. B. C. D. 4m 4m 4m 24 m  Câu37: Cho khối nóncó đường kính đáy bằng và chiều cao bằng . Thể tích của khối nón đã cho 4a 2a bằng A. . B. . C. . D. . 38 3 a 332 3 a 38a 332a

Khẳng định nàosau đây đúng? A. . B. .  lndln1 xxxx  lndln1xxxxC  C. . D. .  lndln1xxxxC     lndln1 xxxx  Câu39:

Tìm tất cả cácgiá trị của để tổng giá trị lớn nhất và 1 xm y x   m m giá trị nhỏ nhất

đã chotrên bằng 0;26. A. B. C. D. 4.m 4.m 1.m 1.m Câu40: Số các số nguyên dương thỏa mãn là: x  4202312024.2 x x xx  A. B. C. D. 7. 9. 8. 10. Câu41: Diện tíchhình phẳng giới hạn bởi các đồ thị hàm số và là 2  yx 22 yx A. B. C. D. 0. 8 3 4 3 2 3 Câu42: Cho khối lăng trụ đứng có đáy làtamgiáccân tại và , cạnh bên . ABCABC A  120oBAC ,góc giữa và mặt phẳng bằng . Thể tích khối lăng trụ đã cho bằng AAa   AB  ABC60 A. B. C. D. 313 12 a 33 36 a 33 4 a 33 6 a Câu43: Tìm tất cả cácgiá trị thực của tham số mgiá trị lớn nhất của hàm số là 32 3 yxxm   2;3 trị nhỏ nhất? A. . B. . C. . D. . m8  m8  10m 10m Câu44: Trongkhônggian với hệ tọa độ cho mặt cầu và mạt Oxyz 222 S:22210 xyzxyz   phẳng . Lấy điểm di động trên và điểm di động trên saocho P:250 xyz A  SB  S cùng phương .Tìmgiá trị lớn nhất của độ dài đoạn . BA   2;1;1a  AB A. B. C. 2+ D. 236  436  36 2 36 4 2  Câu45: Cho số phức thỏa mãn .Tìmgiá trị lớn nhất của . z 2 zzzzz  23 zi  A. . B. . C. . D. . 27102  52  752  2052 

Câu38:

Chohàm số với là số thực.

của hàm số

ảo. Tính tổng tất cả các phần tử của .

Câu48: Chohìnhnóncó đỉnh cóbánkính đáy bằng vàgóc ở đỉnh bằng . Thiết diện tạo bởi

DẠYKÈMQUYNHƠN OFFICIAL

Câu46: Chohàm số xác định vàcó đạo hàm cấp haitrên thỏa mãn , fx  0; 00f và .Tính .  0 lim1 x fx x    22 '''12' fxfxxxfx     2f A. . B. . C. . D. . 1ln3  2ln3  2ln3 1ln3 Câu47: Gọi là tập hợp tất cả giá trị thực của tham số saochocó đúng một số phức thỏa mãn M m z và là số thuần

3zm 4zz M A. B. C. D. 2 4

S a

 một mặt

S A. B. C. D. 22 3 a 21 3 a 24 3 a 22 3 a Câu49: Chohàm số xác định vàcó đạo hàmtrên thỏa mãn và fx  0; 4 1f e  với mọi .Tính .  1 21xxfxxfxxe   0x  2 1 x efxdx A. B. C. D. 4ln4. 52ln2. 2 4ln4.  52ln2. 2  Câu50: Biết x,ylàcác số thực thỏa mãn với mọi số thực .Tìmgiá trị lớn nhất 2 232log10xyxa a  0a của biểu thức 34 Pxy  A. B. C. D. 10 13 25 8

120

phẳng đi qua đỉnh vàhìnhnónlà một tamgiáccó diện tích lớn nhất bằng:

DẠYKÈMQUYNHƠN

OFFICIAL BẢNG ĐÁP ÁN 1234567891 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 2 0 2 1 2 2 2 3 2 4 2 5 CCCDCCBACCACDBBACBDCCBBCA 2 6 2 7 2 8 2 9 3 0 3 1 3 2 3 3 3 4 3 5 3 6 3 7 3 8 3 9 4 0 4 1 4 2 4 3 4 4 4 5 4 6 4 7 4 8 4 9 5 0 BBBDCCCDDABACBDAACBBBCADA HƯỚNG DẪN GIẢI CHI TIẾT Câu1: Hàmnàosau đây là một nguyênhàm của hàm số ? 1 2  x y A. . B. . C. . D. . ln2x 2lnx 1 ln 2 x 2 1 2x Lời giải Chọn C là một nguyênhàm của hàm số 11111 lnln 2222  xxxCx xx dd 1 2  x y Câu2: Chohàm số có đạo hàmlà . Số điểm cực trị của hàm số đã cholà fx 2312   fxxxx A. . B. . C. . D. . 0 1 2 3 Lời giải Chọn C 23 0 01201 2 x fxxxx x x        Trongcác nghiệm của phương trình thì làcác nghiệm bội lẻ nênchúnglà 0 fx 0,2xx cực trị của hàm số .Còn là nghiệm bội chẵn nênnókhông phải là cực trị của hàm số fx 1x fx Vậy hàm

đã

2 Câu3: Tập nghiệm của bất phương trình 1 2 log210 x A. B. C. D.  ;1  1; 1 ;1 2    1 ; 2    Lời giải Chọn C Bất phương trình . 1 2 1 log21002111 2 x x x  Vậy tập nghiệm 1 ;1 2 S  

số

chocó cực trị.

DẠYKÈMQUYNHƠN

Câu4: Mô-đun của số phức bằng  3412 zii  A. . B. . C. . D. . 25 255 5 55 Lời giải Chọn D .  3412112 ziii   55z  Câu5: Chohàm số .Tính . 31fxx  1 0 d Ifxfxx   A. . B. . C. . D. . 1I 3I 3 2 I 1 2 I Lời giải Chọn C .  21 1 1 0 0 0 3.113.013 dd 2222 fxIfxfxxfxfx          Câu6: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 2 2 43 x y xx   A. B. C. D. 0 1 2 3 Lời giải Chọn C Hàm số xác định khivà chỉ khi 2 2 20 2 1 1 430 3 x x x x x xx x                 Tập xác định ;2\1D Tacó , 2 2 lim0 43 x x xx   12 2 lim 43 x x xx   Suyra TCĐ: vàTCN: . 1x 0y Câu7: Trongkhônggian với hệ tọa độ ,chohai véc-tơ , .Tíchvô Oxyz  1;2;3u   2;1;2v  hướng của hai véc-tơ và bằng u  v  A. . B. . C. . D. . 6 6 10 10 Lời giải Chọn B Tacó  .1.221326uv   Câu8: Tập xác định của hàm số là  2log4 yxx  A. B. C. D.  0;4  0;2  2;2  2;0 Lời giải Chọn A

số xác định khivà chỉ khi 2 4004 xx x 

Số nghiệm thực của phương trình là 2 224.33.2 x x  A. B. C. D. 0 1 2 3

OFFICIAL

Hàm

Câu9:

DẠYKÈMQUYNHƠN

OFFICIAL Lời giải Chọn C Tacó  2 2 2 22 2 22212222 2 2 2 4332233232221log312log30 x x x xx x xx x    2 1 10 1 x x x   Vậy phương trình đã chocóhai nghiệm. Câu10: Khẳng định nàosau đây đúng? A. B. 1 2.3d3.6 xx x xC  1 123d36 xx x xC    C. D. 13.62.3d ln6 x xxxC  1 13623d 1 x xx x C x     Lời giải Chọn C Tacó 1 3.62.3d32.3d36d ln6 x xx xx x x xxC      Câu11: Trongkhônggian với hệ trục tọa độ ,cho mặt cầu .Tìm tất cả Oxyz 222 ():23 Sxyzx cácgiá trị thực dương của tham số để mặt phẳng tiếp xúc với mặt cầu m 220xyzm () S A. B. C. D. 7m 5m 6m 19m Lời giải Chọn A Tacó .(1;0;0 ): 2 I S R      Để tiếp xúc với thì . () P () S  5() 1 ; 2 7 3 mml dIPR m      Câu12: Cho số phức có phần ảo âm thoả mãn .Tính z (2)2zz 3 zi  A. . B. . C. . D. . 17 17 5 5 Lời giải Chọn C Tacó: 2220zz . Vậy nghiệm phức có phần ảo âm của phương trìnhlà 2220zz 1 1 zi zi   1 zi  313125ziiii  Câu13: Chohìnhchóp tứ giác đều cógóc giữa cạnh bên với đáy một góc .Tínhcosin của SABCD 45 góc giữa mặt bênvà đáy của hìnhchóp đã cho. A. B. C. D. 1 3 1 2 1 2 1 3 Lời giải

tập M.Tínhxác xuất để số được chọn có chữ số hàng trăm nhỏ hơn chữ số

Lời giải Chọn B

- Số tự nhiêncóba chữ số đôi một khácnhau lấy từ tập : abc 

0;1;2;3;4;5

- Gọi Alà biến cố: “số được chọn có chữ số hàng trăm nhỏ hơn chữ số hàng chục”

+Vì chữ số hàng trăm nhỏ hơn chữ số hàng chục và . Đồng thời cứ 1 bộ 2 chữ số thìcó1 0a chữ số đứng trước bé hơn chữ số đứng sau.Suyra số cách chọn , 2 4abC 

+Cách chọn :4c

Số cách chọn 2 4 :.424 A abcnC

DẠYKÈMQUYNHƠN OFFICIAL

Chọn D Gọi cạnh đáy bằng 2aBDa  -Góc giữa cạnh bên với đáy một góc làvuôngcân 45SBD 2 22 BDa SO  - Gọi làtrung điểm góc giữa mặt bênvà đáy là M CDCDOM  SMO  22 1 cos 3 OMOM SMO SMOMSO    Câu14: Cho tập M gồm các số tự nhiêncóba chữ số đôi một khácnhau lấy từ tập Chọn  0;1;2;3;4;5 ngẫu nhiên một số từ

A. . B. . C. . D. . 3 5 2 5 1 3 2 3

hàng chục.



2 4Ω5.60 A 

242 605AP 

.Tính .  4 2 d8fxx   2 1 2d Ifxx  A. B. C. D. 2I 4I 6I 8I Lời giải Chọn B Tacó  2 1 2d Ifxx  Đặt suyra 22 txdtdx  02 14 xt xt   



Câu15: Biết

Câu16: Cho thỏa mãn .Tính . 0a

log1000log1000log3log32224 a a a 

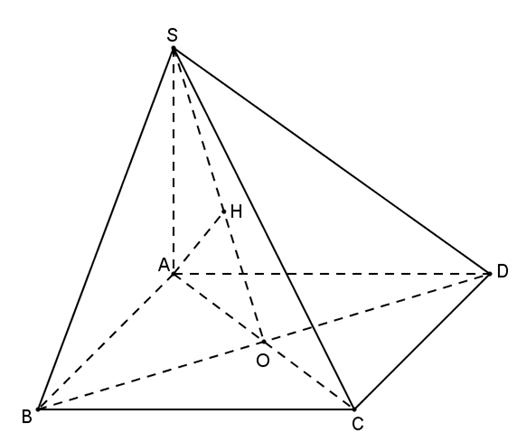
Tacó .

Câu17: Chohìnhchóp có đáy làhìnhvuông cạnh và vuônggóc với đáy. Tính . SABCD ,2 aSAa SA theo khoảng cách từ đến mặt phẳng . a A

DẠYKÈMQUYNHƠN

 2 4 4 1 2 2 11 2ddt=dx=4 22 Ifxxftfx    



log2 a log1000a A. . B. . C. . D. . 13 4 4 3 4 3 2 Lời giải Chọn

OFFICIAL



 11113

 SBD A. . B. . C. . D. .

4 a 2 3 a 3 2 a Lời giải Chọn C

 BDSACBDAH  Lại

nên .

 AHBD    , AHSBDdASBDAH   Trongtamgiác có . ABC 2222 2 2 2 aACABBCaaaAO  Trongtamgiác có . SAO  22 222 2 1111192 2243 2 Aa H AHAOSAaaa      Vậy  2 , 3 adASBDAH Câu18: Số giao điểm của đồ thị hàm số với đường thẳng là: 32ln yxxx  2yx A. . B. . C. . D. . 0 1 2 3 Lời giải

4 9 a 9

Gọi làgiao điểm của và .

ACBD Gọi làhình chiếu của lên . H SO Tacó và nên . BDAC  BDSA 

có và

AHSO

Chọn B

Phương trìnhhoành độ giao điểm của đồ thị hàm số với đường thẳng 32ln yxxx  2yx

là . 322 ln xxxx

Điều kiện 0x

Khi đó phương trình trở thành . 3l0 n2xxx

Xéthàm số , với 3ln2fxxxx  0x

Tacó .Do đó hàm số đồng biến trên 21 310,0fxx x x  3ln2fxxxx 

Khi đó phương trình có nhiều nhất là1 nghiệm. 3l0 n2xxx Nhận thấy là nghiệm của phương trình.

lập được baonhiêu số chẵn gồm ba chữ số đôi một khácnhau?

Chọn C

Số cần tìmcó dạng:  0abca

TH1: , chọn số. 0c 2 5 :20 abA

Suyra lập được số thỏa mãn. 20

TH2: cách chọn 2;4;6:3c

Chọn cách. :4a

Chọn cách. :4b

Suyracó số. 4.4.348 

Vậy có số. 204868 

Câu21: Hàm số nào dưới đây khôngcó cực trị?

DẠYKÈMQUYNHƠN OFFICIAL

Chọn C

khoảng



thị hàm số với đường thẳng có1giao điểm. 32ln yxxx  2yx Câu19: Phần ảo của số phức là: 13 1   i z i A. . B. . C. . D. . 4 4i 2i 2 Lời giải Chọn D Tacó .  22 1131 3 24 12 1112      iiii z i i Vậy phần ảo của số phức là: . 13 1   i z i 2 Câu20: Từ các chữ số

0,1,2,3,4,5,6 A. B. C. D. 80 120 68 105 Lời

 0;

1x Vậy đồ

giải

A. B. C. D. 3

yxx

1yxx 31yxx 421yxx

Lời giải

x xxfxxxx

Do đó hàm số đồng biến trên khoảng . (2;3)

Câu26: Trongkhônggian với hệ toạ độ cho mặt cầu .Tâm của Oxyz 222 ():2430 Sxyzxy

DẠYKÈMQUYNHƠN OFFICIAL

Xéthàm số có .Do đó hàm số khôngcó cực 31yxx'2310, yxx 31yxx trị Câu22: Thể tích khối chópcó diện tích đáy và chiều cao là 2 a 2a A.. B. . C. . D. . 3 a 32 3 a 32a 31 3 a Lời giải Chọn B Thể tích khối chóplà: . 2 312 2 33 Vaaa   Câu23: Chohàm số .Tìmcácgiá trị thực của tham số để hàm số có đúng 1 cực 4 2 (21)1yxmx   m trị? A. . B. . C. . D. . 1 2 m 1 2 m 1 2 m 1 2 m Lời giải Chọn B Hàm số có đúng 1 cực trị . 4 2 (21)1yxmx   1 .0210 2 abmm  Câu24: Cho cấp số nhân có vàcông bội .Tính () n u22u 2q 10u A. . B. . C. . D. . 2048 256 512 1024 Lời giải Chọn C Tacó: . 88 10222512uuq Câu25: Chohàm số có đạo hàmlà .Hàm số đã cho đồng biến trên ()fx ' 2 ()(1)(2)(3) fxxxx  khoảng nào dưới đây? A. . B. . C. . D. . (2;3) (1;2) (1;3) (3;)  Lời giải Chọn A ' 2 (2;3)(2)(3)0()(1)(2)(3)0





 mặt cầu đã chocó toạ độ là: A. . B. . C. . D. . (1,2,0) (1,2,0)(2,4,0)(2,4,0) Lời giải Chọn B Tacótâm của mặt cầu có toạ độ là . 222 ():2430 Sxyzxy (1,2,0)

đáy AB=2a, cạnh

Thể tích khối chóp 2SAa  đã cho bằng:

Câu27: Cho khối chóptamgiác đều S.ABC có cạnh

bên .

Gọi H là trọng tâm của tamgiác ABC và M làtrung điểm của BC

Vậy thể tích của khối chóp đã cholà:

1,2,3M

Oyz

Câu28: Hình chiếu vuônggóc của điểm lên mặt phẳng có toạ độ là:

A. . B. . C. . D. .(1,2,3)(0,2,3)(0,2,3)(1,0,0)

Lời giải

Chọn B

Hình chiếu vuônggóc của điểm M(1,-2,3)lên mặt phẳng (Oyz) có toạ độ là:(0,2,3)

Câu29: Trongkhônggian với hệ tọa độ cho đường thẳng và mặt phẳng Oxyz 12 : 213 dxyz 

.Tìm tọa độ giao điểm của d và (P) ():280 Pxyz

A. (1,3,-3). B. (-3,1,-3). C. (-1,3,-3). D. (3,1,3). Lời giải

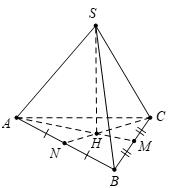
Chọn D

Gọi M(a,b,c) vì M thuộc (d) nênsuyra: 21 2 3

Vì M thuộc (P) nên: 21(2)2.3801 ttt t 

at bt ct

DẠYKÈMQUYNHƠN OFFICIAL

Vậy tọa độ giao điểm của d và (P) là (3,1,3).

A. . B. . C. . D. . 32a 32 3 a 32 6 a 32 2 a Lời giải Chọn B

Tacó 223

33 aAMaAHAM  Mặt khác 2 22 2 (236 2)33 aSHSAAHa a      

. 3 2 11362 3(2)3433 ABC aaVSSHa   



    

DẠYKÈMQUYNHƠN OFFICIAL

Trongkhônggian với hệ tọa độ cho đường thẳng .

Câu30: Cho số thực a>0,a1.Giá trị của biểu thức bằng:  loga aa A. 6. B. 3. C. D. 3 2 3 4 Lời giải Chọn C 1 2 3 4133logloglog142 2 a a a aaa a    Câu31:

trình

11 : 234 dxyz   mặt phẳng qua vàvuônggóc

đường thẳng  1;0;2M d A. . B.

10xy 234100 xyz   C. .D.

234100 xyz  23460 xyz Lời giải Chọn C Đường thẳng có vectơ

phương . d  2;3;4du  Theo đề bài,tacó

phẳng qua điểm

vectơ pháp tuyến  P  1;0;2M  2;3;4dnu  Khi đó: . :2130420234100 Pxyz xyz    Câu32: Chohàm số có đạo hàmlà với làtham số thực. Tìm tất cả các fx  1 fxxxm   m giá trị của để hàm số đồng biến trên . m  ;  A. . B. . C. . D. . 1m 1m 1m 1m Lời giải Chọn C Hàm số đồng biến trên khi  ;    0,10, fxxxxmx     210, xmxmx  2 10 140 a mm       2210mm  . 2 10101m mm   Câu33: Tập nghiệm của bất phương trình là 233 x x      A. . B. . C. . D. .  ;1  1;  0; 0;1 Lời giải

Viết phương

Oxyz

với

chỉ

mặt

vàcó

DẠYKÈMQUYNHƠN

OFFICIAL Chọn D Tacó: . 2 0 00 33 01 121 x xx xx x xxxx                          Do vậy, tập nghiệm của bất phương trìnhlà: . 0;1S Câu34: Trongkhônggian với hệ tọa độ choba điểm , , . Phương Oxyz  1;0;0A  0;1;0B  0;0;1C trình mặt phẳng là  ABC A. . B. . C. . D. . 0xyz 1xyz 0xyz 1xyz Lời giải Chọn D Phương trình mặt phẳng có dạng: .  ABC 11 111 xyz xyz  Câu35: Trong mặt phẳng tọa độ, tập hợp các điểm biểu diễn các số phức thỏa mãn là z 1 zzi  đường thẳng có phương trình? A. . B. . C. . D. . yx  yx  1yx 1yx Lời giải Chọn A Giả sử được biểu diễn bởi điểm .  , zxiyxy  ; Mxy Khi đó   2 222 1 1 10 zzixyxyxyyx   Câu36: Tìm tất cả cácgiá trị thực của tham số để đường thẳng cắt đồ thị hàm số m ym  224yxx  tại đúng điểm phân biệt. 4 A. . B. . C. . D. . 4m 4m 4m 24 m  Lời giải Chọn B Xét phương trìnhhoành độ giao điểm của đường thẳng và đồ thị hàm số : ym  224yxx  22 4244 xxmxxm   Tacó đồ thị hàm số như sau 42 4 yxx 

DẠYKÈMQUYNHƠN OFFICIAL

Từ đồ thị suyra để đường thẳng cắt đồ thị hàm số tại đúng điểm phân ym  224yxx  4 biệt .4m  Câu37: Cho khối nóncó đường kính đáy bằng và chiều cao bằng Thể tích của khối nón đã cho 4a 2a bằng A. B. C. D. 38 3 a 332 3 a 38a 332a Lời giải Chọn A Thể tích của khối nón đã cholà . 2 2 11 ..2.2 33 Vrhaa    38 3 a Câu38: Khẳng định nàosau đây đúng? A. B.  lndln1 xxxx  lndln1xxxxC  C. . D. .  lndln1xxxxC     lndln1 xxxx  Lời giải Chọn C Đặt l1 n uxdudx x dvdx vx         .  lnd.lndlnln1 xxxxxxxxCxxC       Câu39: Chohàm số với là số thực. Tìm tất cả cácgiá trị của để tổng giá trị lớn nhất và 1 xm y x   m m giá trị nhỏ nhất của hàm số đã chotrên bằng 0;26 A. B. C. D. 4m 4m 1m 1m Lời giải Chọn B Tổng giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn bằng khi: 0;26

DẠYKÈMQUYNHƠN

OFFICIAL  2 026 64. 3 m yy m m  Câu40: Số các số nguyên dương thỏa mãn là: x  4202312024.2 x x xx  A. B. C. D. 7 9 8 10 Lời giải Chọn D Tacó:     420231202424202422023220230 2122023220230 22023210 x xx x x x x x x x xx x x x          Do nguyên dương nên x 21210 x x x x  Do đó bpt.  220231;2;;10 x x  Vậy có số nguyên dương thỏa mãn. 10 x Câu41: Diện tíchhình phẳng giới hạn bởi các đồ thị hàm số và là 2  yx 22 yx A. . B. . C. . D. 0. 8 3 4 3 2 3 Lời giải Chọn A Xét phươn trình . 22 2 xx1 x Vậy diện tíchhình phẳng đã cho bằng  1 1 22 2 1 1 82d22d 3     xxxxx Câu42: Cho khối lăng trụ đứng có đáy làtamgiáccân tại và , cạnh bên ABCABC A  120oBAC ,góc giữa và mặt phẳng bằng . Thể tích khối lăng trụ đã cho bằng AAa   AB  ABC60 A. . B. . C. . D. . 313 12 a 33 36 a 33 4 a 33 6 a Lời giải Chọn A .  AAABC   , 60     oAAABCABA

DẠYKÈMQUYNHƠN

OFFICIAL Xéttamgiácvuông có: . ABA   cot 3 aABAAABA    Vậy 3 1 3sin120 2 12 o ABCABC ABC aVAASAAABAC        Câu43: Tìm tất cả cácgiá trị thực của tham số mgiá trị lớn nhất của hàm số là 32 3 yxxm   2;3 trị nhỏ nhất? A. . B. . C. . D. . m8  m8  10m 10m Lời giải Chọn C Xéthàm số liên tục trên đoạn . 32 3 yfxxxm    2;3 +);. 2 36xfxx    00;22;3fxxx  +), ,. 220fm  24fm   30 ffm  Khi đó  2;3 maxmax;20fxmmM   Tacó: .220202010 2020 Mm MmmmmM Mm m         Dấu xảy ra. ""   2010 10 200 mm m mm          Câu44: Trongkhônggian với hệ tọa độ cho mặt cầu và mạt Oxyz 222 S:22210 xyzxyz   phẳng Lấy điểm di động trên và điểm di động trên saocho P:250 xyz A  SB  S cùng phương .Tìmgiá trị lớn nhất của độ dài đoạn . BA  2;1;1a  AB A. B. C. 2+ D. . 236  436  36 2  36 4 2  Lời giải Chọn B +) cótâm ,bánkínhR=2.  S  1;1;1I +) cóVTPT , đường thẳng cóVTVP .  P  1;1;2n  AB  2;1;1a  +)Tacó ,suyragóc giữa và bằng 300  1 sin; 2 ABP AB P +) Gọi làhình chiếu của . trên .Tacó .Do đó khivà chỉ H PA P 2 ABAH  ABmax khi AHmax  36dI;PR2 2 AHmax 

DẠYKÈMQUYNHƠN

+) Vậy 436ABmax Câu45: Cho số phức thỏa mãn .Tìmgiá trị lớn nhất của z 2 zzzzz  23 zi  A. . B. . C. . D. . 27102  52  752  2052  Lời giải Chọn B Đặt biểu diễn .  ,; zxyixyMxy   z Do  2 2 22 2 2 22 112 zzzzzzzzzzxyxy xy     Từ đó suyra: Tập hợp điểm biểu diễn là4 phần của 4 đường tròn như hình vẽ: M z Mà với biểu diễn số phức 2323 TziziMA    2;3A  23i Tacó . 1 23 4 17;5;13;5AIAIAIAI    Do đó 252MaxTAIR Câu46: Chohàm số xác định vàcó đạo hàm cấp haitrên thỏa mãn , fx  0; 00f và .Tính .  0 lim1 x fx x    22 '''12' fxfxxxfx     2f A. . B. . C. . D. . 1ln3  2ln3  2ln3 1ln3 Lời giải Chọn B

OFFICIAL

DẠYKÈMQUYNHƠN

OFFICIAL Do .   0 0 0 lim1lim1'01 0 x x fx fxf f x x     Tacó: ,(1)     2 2 2 '''12'' ''1fxfxxxfxfxxfx           Đặt ,nên(1) trở thành ''''1gxfxxgxfx     2 2 ' ' 1.gx gxgx gx  Lấy nguyênhàmhai vế, ta được    1 1'1 xCgx fxx gx xC xC  Cho .Do đó 1 0'0 1 xf C C    2 1 '1 ln1 12 x fxx fx xC x   Mặt khác .Suyra . Vậy 1 000f C   2 ln1 2fx x x  22ln3f Câu47: Gọi là tập hợp tất cả giá trị thực của tham số saochocó đúng một số phức thỏa mãn M m z và là số thuần ảo. Tính tổng tất cả các phần tử của . 3zm 4zz M A. B. C. D. 2 4 8 10 Lời giải Chọn C Đặt khi đó .Khi đó tập các số phức là đường tròn  zxyi 3 3  zmxmyi z cótâm và .  1C 1;0Im13R Tacó . Để là số thuần ảo khivà chỉ khi 2 22 4444   zzzzxyxyi 4zz .Khi đó tập hợp các số phức là đường tròn cótâm và . 2240xyx z  2C 22;0I 22R Tacó độ dài đường nối tâmlà . 122 IIm Để có một số phức thỏa mãn . z 1212 1212 7 253 213 1                 m IIRRm m IIRRm m m Câu48: Chohìnhnóncó đỉnh cóbánkính đáy bằng vàgóc ở đỉnh bằng . Thiết diện tạo bởi S a 120 một mặt phẳng đi qua đỉnh vàhìnhnónlà một tamgiáccó diện tích lớn nhất bằng: S A. B. C. D. 22 3 a 21 3 a 24 3 a 22 3 a Lời giải Chọn A

DẠYKÈMQUYNHƠN

OFFICIAL Tacó   2 2 222 223 22cos 22cos120322cos      a AB a ABSASBSASBASBSA ASB Tacó diện tích thiết diện là . 2 222'1112 sin 2223  Sl lSAa Đẳng thức xảy rakhi hay . sin1   ''90 ASB Câu49: Chohàm số xác định vàcó đạo hàmtrên thỏa mãn và fx  0; 4 1f e  với mọi .Tính .  1 21xxfxxfxxe   0x  2 1 x efxdx A. B. C. D. 4ln4 52ln2 2 4ln4  52ln2 2  Lời giải Chọn D Tacó  1 21xxfxxfxxe    1 21 x x xefxexfxx     21 x xefxx         21 x xefxdxxdx          2 x xefxxxC  Vì nên .Suyra . 4 1f e  122Cef   2 1 x efxx x  Khi đó  2 2 2 2 1 1 1 2 1 2ln 2 x x efxdxxdxxx x                52ln2. 2  Câu50: Biết x,ylàcác số thực thỏa mãn với mọi số thực .Tìmgiá trị lớn nhất 2 232log10xyxa a  0a của biểu thức 34 Pxy  A. B. C. D. 10 13 25 8 Lời giải Chọn A  2 232log 2 2 2 1 0 0 232logloglog2log23xyxa a xyxaaaxaxy      Đặt ta được bất phương trình log ta  2 20223 txtxy Để bất phương trình đúng với mọi số thực 0a Điều kiện là . 2 2 2 2 '023014 xxyxy   2222 2 3431434125.410.PxyxyP xy P       

DẠYKÈMQUYNHƠN OFFICIAL

Đẳng thức xảy rakhi . 1 0 x y   

DẠYKÈMQUYNHƠN

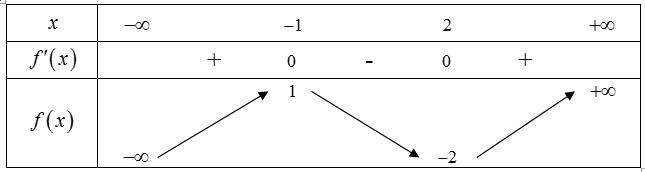
ĐỀ THI THỬ TỐT NGHIỆP THPT– NĂM HỌC 2022–2023- LẦN 2 Câu1: Cho cấp số cộng có ,côngsai Khi đó bằng  n u23u 2.d 4u A. . B. . C. . D. . 5 1 9 7 Câu2: Hàm số nào dưới đây khôngcó điểm cực trị? A. B. C. D. 33 yxx  42yx 34yx  22 yxx  Câu3: Thể tích của khối cầu bánkính bằng R A. . B. . C. . D. . 34 3 R 33 4 R 32R 24R Câu4: Chohình lập phương Góc giữa hai đường thẳng và bằng . '''' .ABCDABCD AC' AD A. B. C. D. 60 30 45 90 Câu5: Chohìnhchóptamgiác đều có độ dài cạnh đáy bằng độ dài cạnh bên bằng SABC ,a 23 3 a Tínhgóc giữa cạnh bênvà mặt đáy của hìnhchóp. A. B. C. D. 60 30 45 90 Câu6: Một hình trụ cóbánkính đáy chiều cao Diện tíchtoàn phần của hình trụ là 5,rcm  7.hcm  A. B. C. D. 2120cm 295cm 260cm 2175cm Câu7: Cho khối chópcó thể tích bằng và diện tích đáy bằng Tính chiều cao của khối 332cm 2 16. cm chóp. A. . B. . C. . D. . 2cm 4cm 3cm 6cm Câu8: Chohàm số thỏa mãn Hàm số đạt yfx   2 123,.fxxxxx    yfx  cực đại tại: A. . B. . C. . D. . 2x 1x 3x 1x Câu9: Chohàm số liên tục trên vàcó bảng biến thiên như sau: fx  Hàm số

A. B. C. D.  2;1  0;1  ;1  ;0 Câu10: Tính đạo hàm của hàm số 223xx y A. B. 22 322 ln3 xx x y   22 3ln3 xx y   C. . D. . 223 ln3 xx y   22 322ln3 xx y x  

OFFICIAL THPTCHUYÊNTHÁIBÌNH

đã cho nghịch biến trên khoảng nào dưới đây?

DẠYKÈMQUYNHƠN

OFFICIAL Câu11: Tíchcác nghiệm của phương trình là 2 2511 3 3 xx  A. B. C. D. 2 0 2 5 2 Câu12: Giá trị lớn nhất của hàm số là 216 yx  A. . B. . C. . D. . 16 4 0 1 Câu13: Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số tương ứng có phương 23 1 x y x   trìnhlà A. và . B. và . C. và . D. và . 2x 1y 1x 3y 1x 2y 1x 2y Câu14: Hàm số nào dưới đây

thiên như hình vẽ sau? A. . B. . C. . D. . 21 2 x y x  4 2 x y x   1 2 x y x  3 2 x y x  Câu15: Số giao điểm của đồ thị hàm số và đường thẳng là 3221yxxx   12 yx  A. . B. . C. . D. . 3 1 0 2 Câu16: Tính thể tích

8và độ

10. A. B. C. D. 256 288 96 384 Câu17: Tập xác định của hàm số là  21yx   A. . B. . C. . D. . 1 ; 2 D     1 \ 2     1 ; 2 D  

hình vẽ: yfx  + x y' y 1 1 + + 0 ∞ ∞ 2 4 ∞ 3 1

số là yfx  A. . B. . C. . D. . 3 2 0 1

có bảng biến

của khối nóncó chiều cao bằng

dài đường sinh bằng

Câu18: Chohàm số có bảng biến thiên như

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm

Câu19: Cho , , làcác số thực dương và Mệnh đề

Câu20: Đường congtronghìnhbên dưới là đồ thị

Câu21: Xéttấtc

Chohìnhchóp có đáy làhình chữ nhật. Các mặt bênvà vuônggóc với . SABCD  SAB

đáy. Góc giữa mặt phẳng và bằng Khoảng cách giữa hai đường

ABCD60,  3BCa  thẳng và bằng ABSC

Câu24: Chohàm số bậc ba có đồ thị hàm số như hình vẽ bên. ()yfx  '()fx

số đồng biến trên khoảng nào dưới đây?

Câu25: Chohìnhnóncó chiều caovàbánkính đáy đều bằng . Mặt phẳng đi qua đỉnh của hình a () P

DẠYKÈMQUYNHƠN OFFICIAL

cắt đường tròn đáy theo một dâycungcó độ dài bằng . Khoảng cách từ tâm của đáy tới a

phẳng bằng () P

abc 1a A.

1 loglog

b b      loglog.log a aa bcbc  C.

bbc c      logloglog a a a bcbc 

nàosau đây sai?

a a

. logloglog a a a

nào

đây? A. B. C. D. 3log yx  3x y 1 3 x y    3 yx 

của hàm số

dưới

ảcácsốthựcdương và thỏamãn Mệnhđề nàodưới đây đúng? ab  2 327loglogaab  A. B. C. D. 2 ab  ab  3 ab  2ab 

Gieo ngẫu nhiên một consúc sắc cân đối và đồng chất 3 lần. Tínhxác suất để tích số chấm xuất hiện trong3 lần gieolà một số lẻ. A. . B. . C. . D. . 7 8 5 8 3 8 1 8 Câu23:



A. B. C. D. 3 2 a 613 13 a 3 2 a 65 5 a

x y  3 4 8 7  Hàm

A. . B. . C. . D. .  1;3  0;7  ;1  3;

nónvà

Câu22:

SAD

SCD

1 ()() gxfx x 

mặt

Số giá trị nguyên của tham số để hàm số

DẠYKÈMQUYNHƠN

Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200m3 . Đáy bể làhình chữ nhật có chiều dài gấp đôi chiều rộng. Chiphí để xây bể là300nghìn đồng/m2 (chiphí được tínhtheo diện tíchxây dựng, bao gồm diện tích đáy và diện tíchxung quanh,khôngtính chiều dày của đáy vàthành bể). Hãyxác định chiphí thấp nhất để xây bể (làm tròn đến triệu đồng).

A. 75 triệu đồng. B. 36 triệu đồng. C. 46 triệu đồng. D. 51 triệu đồng.

Câu34: Chohình hộp đứng có đáy làhìnhvuông, cạnh bên và đường chéo

OFFICIAL A. . B. . C. . D. . 2 2 a 3 3 a 7 7 a 21 7 a Câu26: Cho khối lăng trụ có thể tích bằng Mặt phẳng cắt các cạnh . '''ABCABC 2022.  P ' ,AA' ,BB lần lượt tại saocho .Tính thể tích khối đa 'CC ,, MNP ' ,MAMA  2',NBNB  3 PCPC  diện ABCMNP A. . B. . C. . D. . 1348 7751 6 13480 9 10784 9 Câu27: Số cácgiá trị nguyên của tham số để phương trình cóhai nghiệm m  2 2 log1log8 x mx thực phân biệt là: A. Vô số. B. C. D. 4 5 3 Câu28: Cho khối chóp có vuônggóc với đáy, tamgiác cân tại , SABCSA ABC  ,120ABAC  Thể tích của khối chóp đã cho bằng ,2 ABaSAa  A. B. C. D. 32a 33 6 a 33a 33 3 a Câu29:



    là: A. B. C. D. 3 1 2 0 Câu30:

, với làcác số thực . Biết ,hàm số có 42 yaxbxc  ,, abc 0a lim x y   3 điểm cực trị và phương trình vô nghiệm. Hỏi trong số cóbaonhiêu số dương? 0y 3,,abc A. B. C. D. 2 1 3 0 Câu31: Chohìnhchóp có Diện tích mặt SABC 2,SASBSC  90,ASB   60,BSC   120.CSA  cầu ngoại tiếp hìnhchóp bằng: A. . B. . C. . D. . 4 16 3  16 8 Câu32: Cho lăng trụ đều có cạnh đáy bằng chiều cao bằng Thể tích khối cầu

'''ABCABC 1, 2. tiếp lăng

đã

A. . B. . C. . D. . 323 27  16 3  16 9  323 9  Câu33:

nghịch biến trên m

321 251

ymxmxmx

Chohàm số

ngoại .

trụ

cho bằng:

'ABCDABCD  '3 AAa  Tính

'5. ACa  . ' .ABCDABCD  A. . B. . C. . D. . 34a 324a 38a 3 a

thể tích khối hộp

Câu35: Chohìnhchóp có đáy làhìnhthangvuông tại Biết vuônggóc với SABCDABCD

đáy, góc giữa và đáy bằng Tính thể tích khối chóp 2;4; ABBCaADa

Câu36: Chohìnhchóp có đáy làhìnhvuông cạnh bằng 2; tamgiác . SABCDABCD 2;SA SAC vuông tại và nằm trong mặt phẳng vuônggóc với đáy. Tính thể tích khối chóp S

 1;2S

Câu38: Chohàm số liên tục vàcó bảng biến thiêntrên đoạn như hình dưới. ()fx

Giá trị lớn

2;4

Câu41: Cóbaonhiêu số nguyên saocho tồn tại số thực thỏa mãn và a b 3 ab e

;01;

D. 4.

Câu42: Số cácgiá trị nguyên của tham số để bất phương trình có m 2 2 2 22242 22240 xxxxmxxm   

khôngquá nghiệm nguyênlà: 6

A. 7. B. 4. C. 10. D. 9.

Câu43:

DẠYKÈMQUYNHƠN OFFICIAL

ABSA

 SCD 60.  .. SABCD A. . B. . C. . D. . 386 3 a 346 3 a 386 15 a 346a



SABCD A. B. C. D. 26 3 86 3 26 42 3

Tìm

nghiệm của bất phương trình S  2 1 1 5 5 log1log33. x x A. B.  2;S  ;12;S C.





Câu37:

tập

1;2S



hàm số trên bằng ()yfx   2;4 A. . B. . C. . D. 3 4 19 17 Câu39: Tìm hệ số của số hạng chứa trongkhai triển biểu thức 18 x 12 4 2 2 x x    A. . B. . C. . D. . 25344 126720 0 25344 Câu40: Tập nghiệm của bất phương trình là: 256.550 xx A. . B. . C. . D. .  ;01;  



nhất của

0;1  0;1



229?ab

Vô số. B. 5. C. 6.

Từ các chữ số có thể lập được baonhiêu số tự nhiên gồm chữ số đôi một khác 1;2;3;4;5;6;7 7 nhausaochocó đúng chữ số lẻ đứng cạnh nhau? 3 A. 288. B. 2880. C. 1728. D. 2736. Câu44: Biết phương trình có một nghiệm dạng (trong 212 202220221221 x x xx  xab  đó làcác số nguyên).Tính . , ab 3ab  A. B. C. D. 3 10 7 9

Câu45: Chohàm số bậc bốn có đồ thị như hình vẽ

Số nghiệm của phương trình là:  2()3()0 fxfxfx

Câu46: Cho lăng trụ đều có cạnh đáy bằng góc giữa đường thẳng và mặt phẳng . ABCABC ,a AB bằng .Tính thể tích khối lăng trụ  BCCB30 '''ABCABC

Câu47: Một người thợ có một khối đá hình trụ. Kẻ hai đường kính lần lượt trênhai đáy saocho , MNPQ

Người thợ đó cắt khối đá theocác mặt cắt đi qua3trong4 điểm để thu .MNPQ  ,,, MNPQ

được khối đá cóhình tứ diện Biết rằng và thể tích khối tứ diện MNPQ 80 MNcm  MNPQ

bằng Tìm thể tích của lượng đá bị cắt bỏ (làmtròn kết quả đến 1 chữ số thập phân). 3 64. dm

A. B. C. D. 386,8dm 3237,6dm 3338,6dm 3109,6dm

Câu48: Chohình lăng trụ tứ

DẠYKÈMQUYNHƠN OFFICIAL



yfx 

   A. . B. . C. . D. .

6 9

8 7

C. . D. . 3 4 a 36

a 36 4 a 33 4 a

giác có đáy làhìnhthoi cạnh Biết 'ABCDABCD  ,a  120BAD  góc giữa hai mặt phẳng và bằng với  '''90,ABACAC   ' AAD ''ABBAtan2.  Tính thể tích khối lăng trụ . ' .ABCDABCD  A. . B. . C. . D. . 32a 3 a 32 3 a 3 3 a Câu49: Chohàm số có đồ thị như hình vẽ. Cóbaonhiêugiá trị nguyên ()yfx  ()fx  để hàm số nghịch biến trên ?  2022;2022m  2 23ln12gxfx xmx   1 ;2 2    x y 4 -2-1 01 A. . B. . C. . D. . 2020 2021 2018 2019 Câu50: Chohàm số bậc năm có đồ thị là đường congtronghình vẽ sau. yfx  ()fx 

DẠYKÈMQUYNHƠN

OFFICIAL Số điểm cực trị của hàm số là: 3243 3 322022 4 yfxxxx   A. B. C. D. 8 7 6 10 ---------- HẾT ----------

DẠYKÈMQUYNHƠN

OFFICIAL BẢNG ĐÁP ÁN 1234567891 0 1 1 1 2 1 3 1 4 1 5 1 6 1 7 1 8 1 9 2 0 2 1 2 2 2 3 2 4 2 5 DCAAAADDBDBBCDBCDABBADABD 2 6 2 7 2 8 2 9 3 0 3 1 3 2 3 3 3 4 3 5 3 6 3 7 3 8 3 9 4 0 4 1 4 2 4 3 4 4 4 5 4 6 4 7 4 8 4 9 5 0 BDBCACADBDAACACBBCDCCBADB HƯỚNG DẪN GIẢI Câu1: Cho cấp số cộng có ,côngsai Khi đó bằng  n u23u 2.d 4u A. . B. . C. . D. . 5 1 9 7 Lời giải Chọn D Tacó: 12321uud41313.27uud Câu2: Hàm số nào dưới đây khôngcó điểm cực trị? A. B. C. D. 33 yxx  42yx 34yx  22 yxx  Lời giải Chọn C .Suyrahàm số khôngcó cực trị. 3430yxy   Câu3: Thể tích của khối cầu bánkính bằng R A. . B. . C. . D. . 34 3 R 33 4 R 32R 24R Lời giải Chọn A Lý thuyết. Câu4: Chohình lập phương Góc giữa hai đường thẳng và bằng . '''' .ABCDABCD AC' AD A. B. C. D. 60 30 45 90 Lời giải Chọn A

DẠYKÈMQUYNHƠN

OFFICIAL A B D C C' B' A' D' Tacó .   ,, ACADACBCACB      đều suyra . ACB   60ACB   Câu5: Chohìnhchóptamgiác đều có độ dài cạnh đáy bằng độ dài cạnh bên bằng SABC ,a 23 3 a Tínhgóc giữa cạnh bênvà mặt đáy của hìnhchóp. A. B. C. D. 60 30 45 90 Lời giải Chọn A I A B C S G Gọi là trọng tâm . . G ABC 323 ; 233 a aAIAGAI   Xét tacó: SAG .   3 31 cos 60 22 3 3 a AG SAG SAG SAa  Câu6: Một hình trụ cóbánkính đáy chiều cao Diện tíchtoàn phần của hình trụ là 5,rcm  7.hcm  A. . B. . C. . D. . 2120cm 295cm 260cm 2175cm

số đã cho nghịch biến trên khoảng nào dưới đây?

Từ BBT,hàm số đã cho nghịch biến trên khoảng

Suyrahàm số đã cho nghịch biến trên khoảng

DẠYKÈMQUYNHƠN OFFICIAL

Lời giải Chọn A Diện tíchtoàn phần của hình trụ là: 2 2 22225725120tp Srlr cm   Câu7: Cho khối chópcó thể tích bằng và diện tích đáy bằng Tính chiều cao của khối 332cm 216cm chóp. A. B. C. D. 2cm 4cm 3cm 6cm Lời giải Chọn D Tacó; . 133.32 . 6. 3 16 VVShh cm S  Câu8: Chohàm số thỏa mãn Hàm số đạt yfx   2 123,.fxxxxx    yfx  cực đại tại: A. . B. . C. . D. . 2x 1x 3x 1x Lời giải Chọn D ,trong đó là nghiệm kép.  2 1 12302 3 x fxxxxfxx x          2x Vậy hàm số đạt cực đại tại yfx  1x Câu9: Chohàm

liên

fx  Hàm

A. B. C. D.  2;1  0;1  ;1  ;0 Lời giải Chọn B

số

tục trên vàcó bảng biến thiên như sau:

.

1;2



hàm số 223xx y A. B. 22 322 ln3 xx x y   22 3ln3 xx y  

0;1 Câu10: Tính đạo hàm của

DẠYKÈMQUYNHƠN OFFICIAL

C. . D. . 223 ln3 xx y   22 322ln3 xx y x   Lời giải Chọn D Tacó .  2 2 2 2 322.3.ln3 xx xx y yx   Câu11: Tíchcác nghiệm của phương trình là 2 2511 3 3 xx  A. B. C. D. 2 0 2 5 2 Lời giải Chọn B Tacó . 2 2 25125112 1 333250 3 xx xx xx    TheoViet,tacótíchcác nghiệm bằng .0 Câu12: Giá trị lớn nhất của hàm số là 216 yx  A. . B. . C. . D. . 16 4 0 1 Lời giải Chọn B Tacó , dấu “=”khi . 2 164yx   0x Vậy  4;4 max4 y Câu13: Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số tương ứng có phương 23 1 x y x   trìnhlà A. và . B. và . C. và . D. và . 2x 1y 1x 3y 1x 2y 1x 2y Lời giải Chọn C Tacó nên là tiệm cận ngang của đồ thị hàm số; nên là lim2 x y   2y  1 lim x y   1x tiệm cận đứng của đồ thị hàm số. Câu14: Hàm số nào dưới đây có bảng biến thiên như hình vẽ sau? A. . B. . C. . D. . 21 2 x y x  4 2 x y x   1 2 x y x  3 2 x y x  Lời giải Chọn D Hàm số đồng biến trên và .  ;2 2;

Câu15: Số giao điểm của đồ thị hàm số và đường thẳng là 3221yxxx   12 yx 

A. B. C. D. 3 1 0 2

Lời giải

Chọn B

Xét phương trình

32 32 2 211223201201xxxxxxx xxx x  

Vậyhaiđồthịhàmsốcómộtgiaođiểm.

Câu16: Tính thể tích của khối nóncó chiều cao bằng 8và độ dài đường sinh bằng 10.

A. B. C. D. 256 288 96 384

Lời

DẠYKÈMQUYNHƠN OFFICIAL





giải Chọn C Gọi chiều cao, độ dài đường sinh,bánkính đáy của khối nón lần lượt là ,,.hlr Bánkính đáy của khối nónlà . 22221086rlh    Thể tích của khối nónlà . 2211 6896 33 Vrh    Câu17: Tập xác định của hàm số là  21yx   A. . B. . C. . D. . 1 ; 2 D     1 \ 2     1 ; 2 D   Lời giải Chọn D Điều kiện 1 210 2 xx Tập xác định của hàm số là: .  21yx   1 ; 2 D   Câu18: Chohàm số có bảng biến thiên như hình vẽ: yfx  + x y' y 1 1 + + 0 ∞ ∞ 2 4 ∞ 3 1 Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là yfx  A. B. C. D. 3 2 0 1 Lời giải Chọn A Tacó ; . lim2 x y  lim1 x y  

Do đó đường tiệm cận ngang của đồ thị hàm số là ; . 2y 1y

Lại có nên đường tiệm cận đứng của đồ thị hàm số là

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là3.

Câu19: Cho , , làcác số thực dương và Mệnh đề nàosau đây sai? abc 1.a

A. B. 1 loglog a a b b 

logloglog a aa bcbc 

C. . D. . logloglog a a a bbc c

Chọn B

Áp dụng công thức về logritta thấy:

• . 1 1 logloglog a a a b b b

• .  logloglog a aa bcbc 

• . logloglog a a a bbc

• .  logloglog a a a bcbc 

Nênmệnh đề Bsai.

Câu20: Đường congtronghìnhbên

 logloglog a a a bcbc 

Lời giải

DẠYKÈMQUYNHƠN OFFICIAL

1 lim x y  1x

  



  



 

 

   

là đồ thị của hàm số nào dưới đây? A. B. C. D. 3log yx  3x y 1 3 x y    3 yx  Lời giải Chọn B Dựa vào đồ thị ta thấy, đây là đồ thị hàm số mũ dạngvới x ya  1a Câu21: Xéttấtcảcácsốthựcdương và thỏamãn Mệnhđề nàodưới đây đúng? ab  2 327loglogaab  A. . B. . C. . D. . 2 ab  ab  3 ab  2ab  Lời giải Chọn A .  2 327loglogaab  3 2 2727loglogaab  32 aab 2 ab

dưới

Câu22: Gieo ngẫu nhiên một consúc sắc cân đối và đồng chất 3 lần. Tínhxác suất để tích số chấm xuất hiện trong3 lần gieolà một số lẻ.

Chọn D

Số kết quả của việc gieo ngẫu nhiên một consúc sắc cân đối và đồng chất 3 lần là 3 6216 

216n 

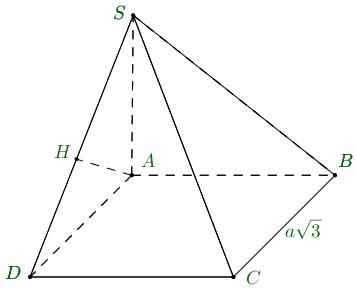
Gọi là biến cố: “tích số chấm xuất hiện trong3 lần gieolà một số lẻ”. A

xảy rakhi kết quả của cả ba lần gieo đều là số lẻ . A 3 327nA 

Vậy, .   1 8 nA PA n  

Câu23: Chohìnhchóp có đáy làhình chữ nhật. Các mặt bênvà vuônggóc với . SABCD  SAB SAD

đáy. Góc giữa mặt phẳng và bằng

DẠYKÈMQUYNHƠN OFFICIAL

A. B. C. D. 7 8 5 8 3 8 1 8

giải

Lời

Khoảng cách giữa hai đường  SCD ABCD60,  3.BCa  thẳng và bằng ABSC A. B. C. D. 3 2 a 613 13 a 3 2 a 65 5 a Lời giải Chọn A và vuônggóc với đáy nên .  SAB SAD SAABCD  Tacó: , , ,  SCDABCDCD   CDSAD   SADABCDAD   .Suyra,góc giữa và là . Vậy .  SADSCDSD   SCD ABCD  SDA  60SDA  .   // ABSCD SCSCD        ,,, dABSCdABSCDdASCD   Gọi làhình chiếu của trên . H ASD Tacó: do ; AHSDAHCD   CDSAD  AHSCD   3 , sin 2 adASCDAHADADS  

Vậy 3 ,2 adABSC

Câu24: Chohàm số bậc ba có đồ thị hàm số như hình vẽ bên. ()yfx  '()fx x

Hàm số đồng biến trên khoảng nào dưới đây? 1 ()() gxfx x 

A. . B. . C. . D. .  1;3  0;7  ;1  3; Lời giải

Chọn B

Tacó: . 2 1 ()() gxfx x 

Từ đồ thị hàm số tacó .Suyra . '()fx '()0,0;7fxx ()0,0;7gxx

Vậy hàm số đồng biến trên khoảng . 1 ()() gxfx x   0;7

Câu25: Chohìnhnóncó chiều caovàbánkính đáy đều bằng . Mặt phẳng đi qua đỉnh của hình a () P nónvà cắt đường tròn đáy theo một dâycungcó độ dài bằng . Khoảng cách từ tâm của đáy tới a mặt phẳng bằng () P

Giả sử hìnhnón đã chocó đỉnh là ,tâm của đáy là và cắt đường tròn đáy theodâycung S O() P

DẠYKÈMQUYNHƠN OFFICIAL

Gọi làtrung điểm của đoạn và làhình chiếu của trên .

ABK OSH

y  3 4 8 7 

A. B. C. D. 2 2 a 3 3 a 7 7 a 21 7 a Lời giải Chọn D

DẠYKÈMQUYNHƠN

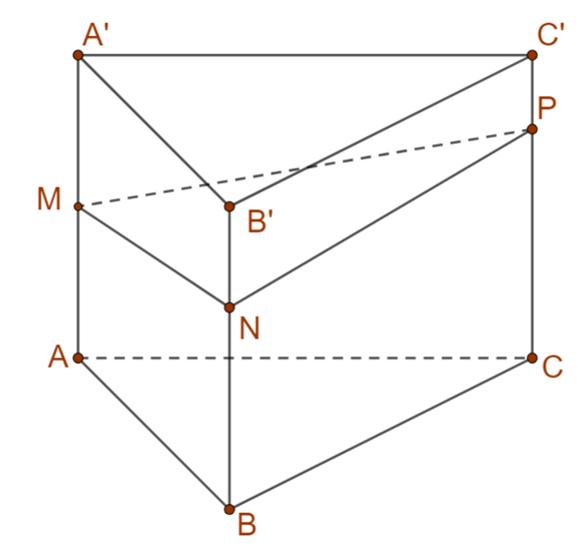
OFFICIAL Ta có: , mà , ABSOOH  ABSOH ABOK OKSH  OKSAB   , dOPOK  Xéttamgiácvuông có (dotamgiác đều có cạnh bằng ), . SOH 3 2 Oa H OAB aSOa  Suyra: . 22 .21 7 OSOHa OK OSOH    Vậy  21 ,7 adOP Câu26: Cho khối lăng trụ có thể tích bằng Mặt phẳng cắt các cạnh . '''ABCABC 2022.  P ' ,AA' ,BB lần lượt tại saocho .Tính thể tích khối đa 'CC ,, MNP ' ,MAMA  2',NBNB  3 PCPC  diện .. ABCMNP A. B. C. D. 1348 7751 6 13480 9 10784 9 Lời giải Chọn B Tacó suyra . 123 ';;2'3'4 MANBPC AABBCC   ''' 23''' 336 ABCMNP ABCABC MANBPC VAABBCC V    Vậy 237751 .2022 366ABCMNPV  Câu27: Số cácgiá trị nguyên của tham số để phương trình cóhai nghiệm m  2 2 log1log8 x mx thực phân biệt là: A. Vô số. B. . C. . D. . 4 5 3 Lời giải Chọn D  2 2 log1log8 x mx 2 10 80 18 x mx xmx        2 1 18 x xmx     2 1 29 x xx m x      

DẠYKÈMQUYNHƠN OFFICIAL

Xéthàm số trên,tacó 229xx y x    1; ; 2 2 '9 x y x  '03yx Bảng biến thiên Để thỏa mãnyêu cầu thì nêncácgiá trị nguyên của tham số là . 48 m  m5,6,7 Câu28: Cho khối chóp có vuônggóc với đáy, tamgiác cân tại , SABCSA ABC  ,120ABAC  . Thể tích của khối chóp đã cho bằng ,2 ABaSAa  A. B. C. D. 32a 33 6 a 33a 33 3 a Lời giải Chọn B Tacó .  2 1 3..sin 2 4 ABC aSABACBAC   Thể tích của khối chóp đã cholà: . 3 13 .. 36 ABC aVSAS   Câu29: Số giá trị nguyên của tham số để hàm số nghịch biến trên m 321 251 3 ymxmxmx     là: A. . B. . C. . D. . 3 1 2 0 Lời giải Chọn C Tacó .Hàm số nghịch biến trên 2 ,'45Dymxmxm    '0, yx  TH1: suyra thỏa mãn. 0:'50,my x 0m

Chohàm số , với làcác số thực Biết

điểm cực trị và phương trình vô nghiệm. Hỏi trong số cóbaonhiêu số dương? 0y 3,,abc

Do nên . lim x y

0a Ta lại cóhàm số có điểm cực trị nên . 3 00abb

Vìnhánh cuối của đồ thị đi lênmà phương trình

DẠYKÈMQUYNHƠN OFFICIAL

TH2: : . 0m 2 005 0 '0 3350 mm m mm         Vậy . 5 01;0 3 m m m    Câu30:

số có 42

 ,, abc 0a lim x y   3

A. B. C. D. 2 1

0 Lời giải Chọn

,hàm

yaxbxc





vô nghiệm nên đồ thị nằm hoàntoàntrên 0y .0Oxc Câu31: Chohìnhchóp có Diện tích mặt . SABC 2,SASBSC  90,ASB   60,BSC   120CSA  cầu ngoại tiếp hìnhchóp bằng: A. B. C. D. 4 16 3  16 8 Lời giải Chọn C Tacó , suyratamgiác đều 2SBSC  60BSC  BSC 2BC  Lại có , suyratamgiác vuôngcân tại . 2SASC  90ASB  ASB S22AB  Mặt khác, , ,áp dụng định lícosinchotamgiác ,ta được: 2SASC  120ASB  ASC

Trong

Xéttamgiácvuông

tại có . ASH H

Tacó .2SISMSMSC SHCSMI SI SCSH SH 

Diện tích mặt cầu ngoại tiếp chóplà. . 2 416SR

Câu32: Cho lăng trụ đều có cạnh đáy bằng chiều cao bằng Thể tích khối cầu ngoại . '''ABCABC 1, 2. tiếp lăng trụ đã cho bằng:

Gọi lần lượt là trọng tâmtamgiác , làtrung điểm của .Khi đó là , II , ABCABCO

tâm mặt cầu ngoại tiếp hình lăng trụ.

Tacó , . 23 33 AIAM 1OI

DẠYKÈMQUYNHƠN

Bánkính mặt cầu ngoại tiếp hình lăng trụ

OFFICIAL .  222 2 2..3.223ACSASCSASCcosASC AC  

có suyratamgiác vuông tại . ABC 2 222 222212BCAB AC   ABC B

Xéttamgiác

điểm

cạnh suyra làtâm đường tròn ngoại tiếp tamgiác . H ACH ABC



Gọi làtrung

của

Mà . SASBSC 

SHABC

cắt đường thẳng tại suyralàtâm  SAC SC SHI

mặt phẳng kẻ đường trung trực canh

mặt cầu ngoại tiếp hìnhchóp.

vuông

2 222

2 SHSAAH      

23 21

 



C. . D. . 323 27  16 3  16 9  323 9  Lời giải

Chọn

II O

 2 222 12 1 33 ROAOIAI    

Thể tích khối cầu ngoại tiếp lăng trụ

Câu33: Người ta cần xây một bể chứa nước sản xuất dạng khối hộp chữ nhật không nắp có thể tích bằng 200m3 . Đáy bể làhình chữ nhật có chiều dài gấp đôi chiều rộng. Chiphí để xây bể là300nghìn đồng/m2 (chiphí được tínhtheo diện tíchxây dựng, bao gồm diện tích đáy và diện tíchxung quanh,khôngtính chiều dày của đáy vàthành bể). Hãyxác định chiphí thấp nhất để xây bể (làm tròn đến triệu đồng).

A. 75 triệu đồng. B. 36 triệu đồng. C. 46 triệu đồng. D. 51 triệu đồng. Lời

Chọn D

Gọi độ dài chiều rộng, chiều

DẠYKÈMQUYNHƠN OFFICIAL

3 3 44232323 . 33327 93 VR      

giải

caohình hộp lần lượt là: Chiều dài của hình hộp là: . , xhm 2x Thể tích khối hộp chữ nhật là: . .2. Vxxh  2 2 100 2002xhh x  Chiphíxây bể thấp nhất khi nhỏ nhất xqdaýSSS  Tacó . 2222 Sxhxhxx  262xhx 2600 2x x  2 23600300300 2 23180000 Sx x x xx  nhỏ nhất bằng khi S 169,3864852 23300 2150 xx x  Tổng chiphí thấp nhất màanh Tiến phải trả là: đ. 300000.169,386485251000000  Câu34: Chohình hộp đứng có đáy làhìnhvuông, cạnh bên và đường chéo 'ABCDABCD  '3 AAa  Tính thể tích khối hộp '5. ACa  . ' .ABCDABCD  A. . B. . C. . D. . 34a 324a 38a 3 a Lời giải Chọn B Xéthình lập phương tacó: . ABCDABCD  222222 ACAAACAAABAD   2222222 2''92''25''8 AAABaABaABa    

DẠYKÈMQUYNHƠN

OFFICIAL 23 '''' '3824 ABCDABCD ABCD V AASaaa    Câu35: Chohìnhchóp có đáy làhìnhthangvuông tại Biết vuônggóc với . SABCDABCD ,. ABSA đáy, góc giữa và đáy bằng Tính thể tích khối chóp 2;4; ABBCaADa   SCD 60.  .. SABCD A. . B. . C. . D. . 386 3 a 346 3 a 386 15 a 346a Lời giải Chọn D Tamgiác vuông tại ACD  , CDCACDCSADCSACDCSC     0 , 60SCDABCDSCA  22 0 22.tan6026ACABBCaSAAC a   3 11(42)2 26 46 332SABCD ABCD aaa VSAS a a     Câu36: Chohìnhchóp có đáy làhìnhvuông cạnh bằng 2; tamgiác . SABCDABCD 2;SA SAC vuông tại và nằm trong mặt phẳng vuônggóc với đáy. Tính thể tích khối chóp S SABCD A. B. C. D. 26 3 86 3 26 42 3 Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL

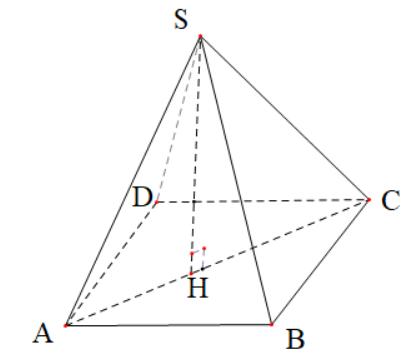
Tacó:

 Tamgiác vuông tại SAC 22 22 (22)(2)6SSCACSA    22 .266 22 6 SASC SH SASC     Diện tíchhìnhvuông :ABCD4ABCDS

tích

..4. 3323SABCD ABCDVSHS   

trình S  2 1 1 5 5 log1log33 x x A. . B. .  2;S  ;12;S C. D.  1;2S  1;2S Lời giải Chọn A ĐK:

BPT tương đương  2 1 1 5 5 2 2 log1log33 133 1 320 2 x x xx x xx x      Kết hợp điều kiện ta được .2x

hình

()fx  2;4

()SHABCD

Thể

khối chóp. :SABCD 11626

Câu37: Tìm tập nghiệm của bất phương

3301 xx

Câu38: Chohàm số liên tục vàcó bảng biến thiêntrên đoạn như

dưới.

DẠYKÈMQUYNHƠN OFFICIAL

Giá trị lớn nhất của hàm số trên bằng ()yfx   2;4 A. . B. . C. . D. 3 4 19 17 Lời giải Chọn C Giá trị lớn nhất của hàm số trên bằng: xảy rakhi . ()yfx  2;4192 x Câu39: Tìm hệ số của số hạng chứa trongkhai triển biểu thức 18 x 12 4 2 2 x x    A. . B. . C. . D. . 25344 126720 0 25344 Lời giải Chọn A Số hạng tổng quáttrongkhai triển là: 412 486 112 212 2 ()()(2)k k kkkk k TCx Cx x    Tacó số hạng chứa nên 18 x486185 kk Vậy hệ số của số hạng chứa trongkhai triển biểu thức là: . 18 x 12 4 2 2 x x    55 12(2)25344C Câu40: Tập nghiệm của bất phương trình là: 256550 xx A. B. C. D.  ;01;   0;1  0;1 ;01;  Lời giải Chọn C . 2 256.550 56.550 15501 xx xx x x     Câu41: Cóbaonhiêu số nguyên saocho tồn tại số thực thỏa mãn và a b 3 ab e 229?ab A. Vô số. B. 5. C. 6. D. 4.

DẠYKÈMQUYNHƠN

OFFICIAL Lời giải Chọn B Tacó:   222 2 3 3 2 3 93.log.log9 1log ab ebaeaaea e       2 2 3 3 3 3 1log1log a e e     Do nên: . a 2;1;0;1;2a Câu42: Số cácgiá trị nguyên của tham số để bất phương trình có m 2 2 2 22242 22240 xxxxmxxm    khôngquá nghiệm nguyênlà: 6 A. 7. B. 4. C. 10. D. 9. Lời giải Chọn B Đặt: 2 2 2 4 2222 2 xxma xxab xxmb        Tacó:   2 224 22 22 2224022220 2222220 22220 abab abab ab b a b           TH1: 2 2 2 2 24242 22222 axxmxxm bxxmxxm                      Để phương trìnhcókhôngquá nghiệm nguyênthì: 6 12230 m m  TH2: 2 2 2 2 24242 22222 axxmxxm bxxmxxm                      Để phương trìnhcókhôngquá nghiệm nguyênthì: 6

42112436 m m m 

Do nêncó: giá trị thỏa mãn. m4m

Câu43: Từ các chữ số có thể lập được baonhiêu số tự nhiên gồm chữ số đôi một khác 1;2;3;4;5;6;7 7

nhausaochocó đúng chữ số lẻ đứng cạnh nhau. 3

A. B.

D. 288. 2880. 1728. 2736.

Chọn C

Giả sử số cần tìmcó dạng: . abcdefg

Lời giải

TH1: Ba chữ số lẻ ở hai vị trí đầu: thìcó cách. , abcefg 3 42A

Do chỉ có đúng ba chữ số lẻ đứng cạnh nhaunên vị trícòn lại có: cách. 4 33!

 3 4 233!864 A

Có: số thỏa mãn.

TH2: Ba chữ số lẻ ở các vị trí giữa thìcó: cách. 3 43.A

Do chỉ có đúng ba chữ số lẻ đứng cạnh nhaunên vị trícòn lại có: cách. 4 2 32!.A

Có: số thỏa mãn.  32 43 32!864 AA

1728 Câu44:

Vậy có số thỏa mãnyêu

DẠYKÈMQUYNHƠN OFFICIAL

Biết phương trình có một nghiệm dạng (trong 212 202220221221 x x xx  xab  đó làcác số nguyên).Tính . , ab 3ab  A. B. C. D. 3 10 7 9 Lời giải Chọn D Tacó  212 2 21 2 2 21 202220221221 202221222212022 202212112022 x x x x x x xx xxxx x x       Xéthàm số , . 220221 t ft t 0;t Tacó nênhàm số đồng biến trên  2022ln2022210,0; t ft tt    yft  khoảng 0; Khi đó .  2 0 2121 12 210 x fxfxxx x xx       Suyra và . 1a 2b Vậy 33129ab Câu45: Chohàm số bậc bốn có đồ thị như hình vẽ yfx 

cầu bàitoán.

DẠYKÈMQUYNHƠN

OFFICIAL Số nghiệm của phương trình là:  2()3()0 fxfxfx    A. B. C. D. 8 7 6 9 Lời giải Chọn C Trường hợp 1: . 00hay1fxxx   Trường hợp 2: . 0101fxx x  Khi đó:         11 22 33 44 1 310 2()3()02.3()0201 1 xaa xaa fxfxfxfxfxfxfx xaa xaa            f(x)= 3 2 a4 a3 a2 a1 So với điều kiện, ta nhận: và . 1xa  3xa  Trường hợp 3: . 0101fx xx       55 66 1 3 2()3()023()02 1 xaa fxfxfx fxfxfxfx xaa         f(x)= 3 2 a6 a5

DẠYKÈMQUYNHƠN

hai đường kính lần lượt trênhai đáy saocho , MNPQ

thợ đó cắt khối đá theocác mặt cắt đi qua3trong4 điểm để thu

khối đá cóhình tứ diện Biết rằng và thể tích khối tứ diện .MNPQ 80 MNcm 

thể tích của lượng đá bị cắt bỏ (làmtròn kết quả đến 1 chữ số thập phân).

OFFICIAL So với điều kiện, ta nhận: 6xa  Nhận thấy các nghiệm trênphân biệt nên phương trình có nghiệm.  2()3()0 fxfxfx   6 Câu46: Cho lăng trụ đều có cạnh đáy bằng góc giữa đường thẳng và mặt phẳng ABCABC ,a AB bằng .Tính thể tích khối lăng trụ  BCCB30 . ''' .ABCABC A. B. C. D. 3 4 a 36 12 a 36 4 a 33 4 a Lời giải Chọn C M C' B' A' C B A Gọi làtrung điểm suyra . M BCAMBC  Khi đó nên do đó AMBC AMBB    AMBCCB     , , ABBCCBABMBABM     Theo đề bài,tacó , nên .  30ABM    3 2 Aa M 333 : tan30232 AMa a BM    Tacó . 22 223 2 22 aaBBBABM a       Thể tích khối lăng trụ là . ABCABC 2336 2 44 ABCABC ABC aaVBBSa      Câu47: Một người thợ có một khối đá hình trụ. Kẻ

Người

MNPQ 

MNPQ được

MNPQ bằng Tìm

364dm A. . B. . C. . D. . 386,8dm 3237,6dm 3338,6dm 3109,6dm Lời giải Chọn B

,,,

DẠYKÈMQUYNHƠN OFFICIAL

Tacó Do đó thể tích khối tứ diện MNPQlà:  PQ ' ' MN PQOMNPQOO   . MNPQMNO' 1 VSPQ 3  1 6OOMNPQ   Trong đó 2 3 1 d(MN,PQ)OOh80h16410h60cm. 6   Vậy thể tích của lượng đá bị cắt bỏ bằng: . 2 2 3 MNPQ 3 VVVRh64406064237,6dm 10 t     Câu48: Chohình lăng trụ tứ giác có đáy làhìnhthoi cạnh Biết . 'ABCDABCD  ,a  120.BAD  góc giữa hai mặt phẳng và bằng với  '''90,ABACAC   ' AAD ''ABBAtan2.  Tính thể tích khối lăng trụ . ' .ABCDABCD  A. . B. . C. . D. 32a 3 a 32 3 a 3 3 a Lời giải Chọn A Gọi lần lượt làtrung điểm của . , MN '' , BCBC .  '''90'''1 ABACACABACANBC   Theobàira đều .  120,BAD ABCABC     2BCAN

DẠYKÈMQUYNHƠN

OFFICIAL Từ  1,2'''' BCAAMNAAMNBCCB   Kẻ . Gọi làhình chiếu vuônggóc của lên .  APBBCCPMN     Q 'A'BB    , , .AADAABBBBCCAABBAQP         . 23 tan2. 3 22 AP a a AP AQ ABa QP       32 ABaBBa    làhình chữ nhật . BBCC  3 ''' 122 2 323AABCCB a a V aa   3 3 3 2 2 662 6 6 ABBCBABC BABC a a VV VV a       Câu49: Chohàm số có đồ thị như hình vẽ. Cóbaonhiêugiá trị nguyên ()yfx  ()fx  để hàm số nghịch biến trên ?  2022;2022m  2 23ln12gxfx xmx   1 ;2 2    x y 4 -2-1 01 A. . B. . C. . D. . 2020 2021 2018 2019 Lời giải Chọn D Tacó 2 2 2232 1 xgxfx m x     Để hàm số nghịch biến trên  2 23ln12gxfx xmx   1 ;2 2     2 1 1 0,;223,;2 2 12 x gxx mfx x x           Xéthàm số . Đặt 2 1 23,;2 12 xhxfx x x      231;1txt Khi đó taxéthàm số  2 2 3 26 2 613 13 2 t t gtft ft tt t           Tacó .  2 2 2 21214 613 ttgtft tt   

DẠYKÈMQUYNHƠN

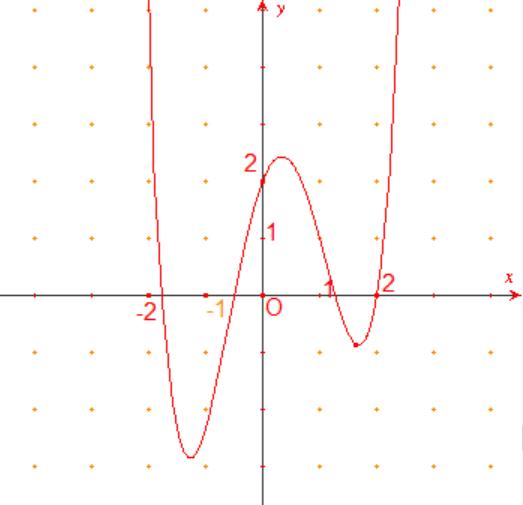
OFFICIAL Từ đồ thị ta thấy được đồng biến trên nên nên ft   1;1  0,1;1ftt .Nên đồng biến trên .  2 2 2 21214 0,1;1 613 ttgtft t tt     gt  1;1 Nên    2 2 1 26 23,;2 ,1;1 12 613 x t mfx x mft t x tt            . 18 ,1;11 5 mgtt mg  Câu50: Chohàm số bậc năm có đồ thị là đường congtronghình vẽ sau. yfx  ()fx  Số điểm cực trị của hàm số là: 3243 3 322022 4 yfxxxx   A. . B. . C. . D. 8 7 6 10 Lời giải Chọn B Tacó   2 32322 3236336363 yxxfxxxxxxfxxx          Xéthàm số  32 3 hxfxx   Tacó      2 32 2 32 32 32 360 321 3630 301 312 xx xxaa hxxxfxx xxbb xxcc                Xéthàm số . 32 3 gxxx  Tacó 2 0 360 2 x gxxx x    

DẠYKÈMQUYNHƠN

OFFICIAL Từ bảng biến thiênta thấy được:          2 11 32 22 32 3 3 32 131 111 0 2 360 0 321 02 301 2 312 x x xx xaa xxaa xaa xxbb xaa xxcc xbab xcbc                           Khi đó tacó được bảng biến thiên của :  32 3 hxfxx   Khi đó phương trình có nghiệm phân biệt khác và   32 32303 fxxxfxxx   5 0 nên phương trình có nghiệm phân biệt. 2  2 32363 yxxfxxx       7 Vậy hàm số có điểm cực trị. 3243 3 322022 4 yfxxxx   7 ---------- HẾT -----------