70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC (21-27) by Dạy Kèm Quy Nhơn Official

Ths

ĐỀ THI THỬ TỐT NGHIỆP THPT MÔN TOÁN

Nguyễn Thanh Tú eBook Collection 70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (ĐỀ SỐ 21-27)

VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL

COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

WORD

TAILIEUCHUANTHAMKHAO@GMAIL

TRƯỜ

NG HOÀI ĐỨC A – HÀ NỘI

THI THỬ TỐT NGHIỆP THPT NĂM HỌC - 2022-2023

ĐỀ 01

Câu 1: Cho hàm số 42 2 yxx =− . Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng () ;2−∞− . B. Hàm số đồng biến trên khoảng () 1;1 .

C. Hàm số nghịch biến trên khoảng () ;2−∞− . D. Hàm số nghịch biến trên khoảng () 1;1 .

Câu 2: Cho hàm số ()yfx = có bảng biến thiên như sau.

Hàm số ()yfx = nghịch biến trên khoảng nào sau đây?

A. () 2;0 . B. () ;2−∞− . C. () 0;2 . D. () 0; +∞ .

Câu 3: Cho hàm số 3213 21 32 yxxx =−++ . Giả sử hàm số đạt cực đại tại điểm xa = và đạt cực tiểu tại xb = thì giá trị biểu thức 25ab là

A. 1. B. 12 . C. 1. D. 8 .

Câu 4: Cho hàm số 322 2 yxmxmx =−+++ . Giá trị của m để hàm số đạt cực tiểu tại 1 x =− là A.

Câu 5: Cho hàm số bậc bốn ()yfx = . Hàm số ()yfx ′ = có đồ thị như hình vẽ

Câu 6: Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số () 31 3 x fx x = trên đoạn [] 0;2

. Giá trị của 3Mm + bằng

A. 0 . B. 4 . C. 2 . D. 1.

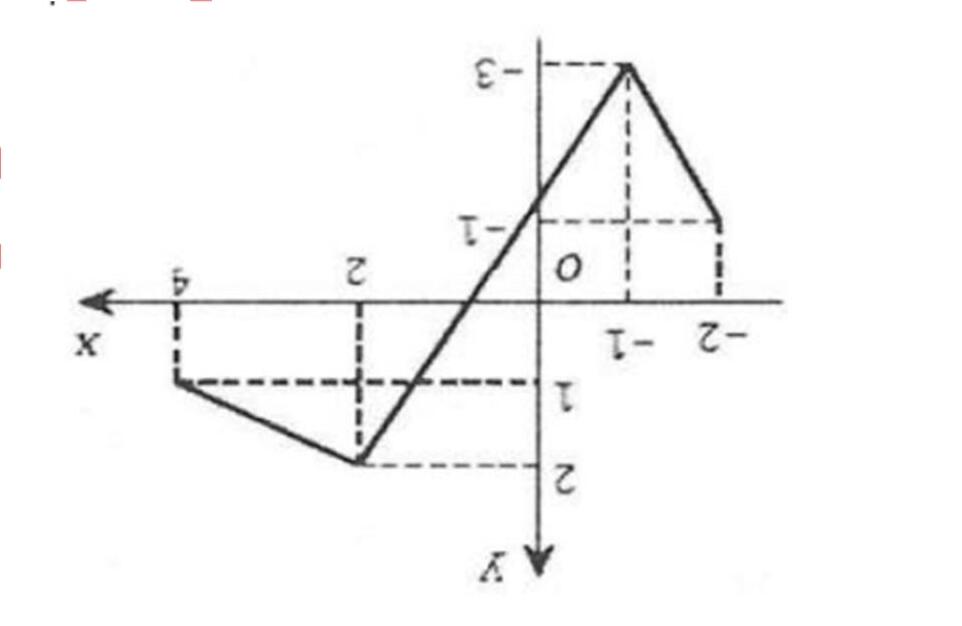
Câu 7: Cho hàm số ()yfx = có đồ thị trên đoạn [] 2;4 như hình vẽ. Tìm giá trị lớn nhất M của hàm số ()yfx = trên đoạn [] 2;4 .

A. 2 . B. 3 . C. 1. D. () 0 f .

Câu 8: Có bao nhiêu số thực m để hàm số 4323412 yxxxm =−−+ có giá trị lớn nhất trên đoạn [] 3;2 bằng 150 ?

A. 2 . B. 0 . C. 6 . D. 4 .

Câu 9: Cho hàm số ()yfx = xác định trên {}\1 ℝ liên tục trên mỗi khoảng xác định và có bảng biến thiên sau.

Số điểm cực trị của hàm số ()() 3211 23 32 gxfxxxx =++−− là

2 .

3 .

0 .

Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

A. 3 . B. 4 . C. 5 . D. 2 .

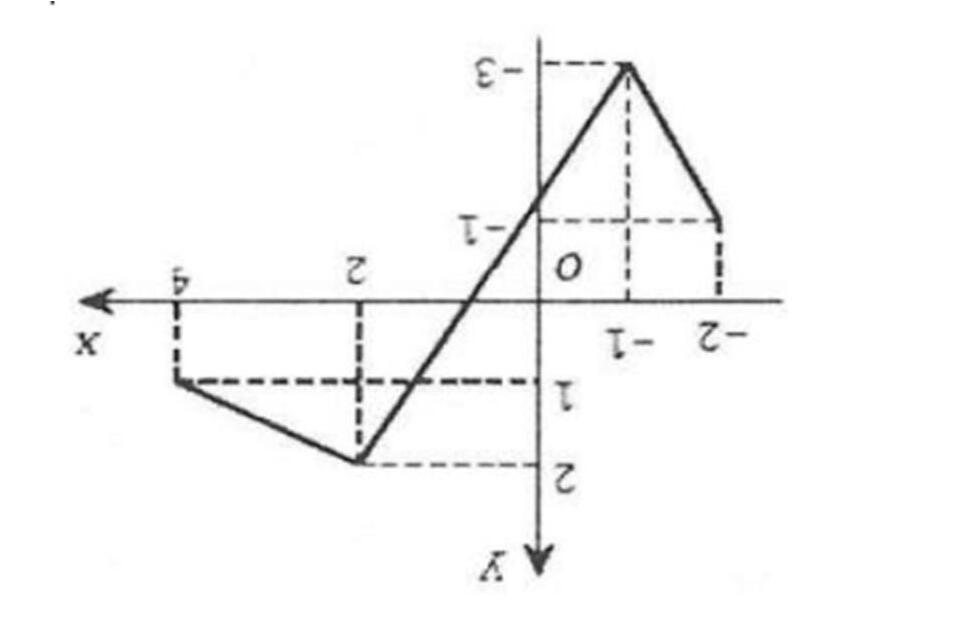
Câu 10: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?

A. 3 32yxx=−+ . B. 3 32yxx=−++ . C. 3232yxx=+ . D. 3232yxx=−−+ .

Câu 11: Có bao nhiêu giá trị nguyên của tham số m để hàm số 432 48xxm yx=− có đúng 7 điểm cực trị?

A. 127 . B. 124 . C. 5 . D. 2 .

B. 3 m

C. 1 3 m m =−   =  . D. 1 3 m m =   =−  .

m =− .

= .

A. 1

Câu 12: Tìm số giao điểm của đồ thị hàm số

2 1 23 x x y x −+ = với đường thẳng 36yx=− .

A. 3 . B. 0 . C. 1. D. 2 .

Câu 13: Cho hàm số 32 3 m yxx=++ có đồ thị () C . Biết đồ thị () C cắt trục hoành tại 3 điểm phân biệt

,, ABC sao cho B là trung điểm của AC . Phát biểu nào sau đây đúng?

A. () 0; m ∈+∞ . B. () ;4 m ∈−∞− . C. () 4;0 m ∈− . D. () 4;2 m ∈−− .

Câu 14: Cho hàm số bậc bốn ()yfx = có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị thực của tham số m để phương trình ()2022612fxmm+=+ có đúng 4 nghiệm thực phân biệt. Tính tổng tất cả các phần tử của S .

212 xx y ++

Câu 20: Cho hàm số 2 22 3 4

xx y −+  =   . Trong các khẳng định sau khẳng định nào đúng?

A. Hàm số đồng biến trên ℝ B. Hàm số nghịch biến trên ℝ

C. Hàm số đồng biến trên khoảng ( );1−∞ D. Hàm số đồng biến trên khoảng ( ) 1; +∞

Câu 15: Tìm m để giá trị lớn nhất của hàm số 3 321yxxm=−+− trên đoạn [] 0;2 là nhỏ nhất. Giá trị của m thuộc khoảng nào?

A. 3 ;1 2    . B. 2 ;2 3    . C. [] 1;0 .

aabb T abab = vớ

Câu 18: Tìm tập xác định D c

oạn

1 ;e e    là A. 2 e1 T =− . B. 2 2 1 e e T =− . C. 2 1 2 e T =+ . D. 2 1 3 e T =+ .

A. 16 P = B. 80 3 P = C. 40 3 P = D. 27 P =

Câu 23: Với a làsố thựcdươngtùyý, ( ) ln8ln(5) aa bằng

A. ( ) () ln5 ln3 a a B. ( ) ln2a C. 8 ln 5    D. ( ) () ln5 ln3

Câu 24: Số nghiệmcủaphươngtrình 761 x x =+ là

A. 0 . B. 1. C. 2 . D. 3 .

Câu 25: Phươngtrình 93.320 xx−+= cóhainghiệm ( ) 1212 , xxxx < . Tính 1223xx + ?

A. 1. B. 2 2log3 . C. 3 3log2 . D. 3 4log2 .

Câu 26: BácBình cần sửalại căn nhàvớichi phí 1 tỷ đồng. Đặt kế hoạch sau 5 năm phải có đủ số tiền trên thì mỗi năm bác Bình cần gửi vào ngân hàng một khoản tiền tiết kiệm như nhau gần nhất bằng giá trị nào sau đây, biết lãi suất của ngân hàng là 7%/năm và lãi hàng năm được nhập vào vốn.

A. 162 triệu đồng. B. 162,5 triệu đồng. C. 162,2 triệu đồng. D. 162,3 triệu đồng.

Câu 27: Số nghiệm của phương trình 3 3 22 4 loglog 3 xx+= .

A. 1. B. 2 . C. 3 . D. 0 .

Câu 28: Biết 9 4 x = là một nghiệm của bất phương trình ( ) ( )( ) 22 log2log23* aa xxxx −−>−++ . Khi đó tập nghiệm của bất phương trình ( )* là

A. 5 1; 2 T  =−  . B. 5 ; 2 T =+∞  . C. ( );1 T =−∞− . D. 5 2; 2 T  =   .

Câu 29: Tìm tập nghiệm S của bất phương trình ( ) 2 42 21.ln0 x x −< .

1 2

97 24 .

D. () 0;1 .

i , ab là hai số thực dương. A. 46Tab = . B. 66Tab = . C. 44Tab = . D. 64Tab = . Câu 17: Tìm tập xác định D của hàm số () log100 2 2 yxx=−− . A. () 1;2 D =− . B. ()\1;2 D =− ℝ . C. {}\1;2 D =− ℝ . D. D = ℝ .

ủ

ố

2 3 1 log2 y

= .

Câu 16: Rút gọn biểu thức () () 2 2231 3 152    . C. ( ] 11 ;0;\;1 22 D  =−∞∪+∞−    . D. () 1 ;0; 2 D  =−∞∪+∞  .

a hàm s

()

A. ( ] 1 ;0; 2 D =−∞∪+∞   . B. () 11 ;0;\;1 22 D =−∞∪+∞−

= .

2 22 xx y + ′ = . B. 2 21 2ln2 xx y ++ ′ = .

Câu 19: Tính đạo hàm của hàm số

C. () 2 21 41.2ln2 xx yx ++ ′ =+ . D. () 2 21 21.2ln2 xx yx ++ ′ =+ .

Câu 21: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 2ln yxx =− trên đ

Câu 22: Cho log4 a x = và log5 b x = . Tính giá trị của biểu thức 3loglogaba b Pxx =+

A. ( ) 1;2 S = . B. { }1;2 S = .

C. ( ) ( ) 2;11;2 S =−−∪ . D. [ ]1;2 S = .

Câu 30: Cho , xy là số thực dương thỏa mãn ( ) 2 lnlnlnxyxy +≥+ . Tìm giá trị nhỏ nhất minP của biểu thức Pxy =+ .

A. min 6 P = B. min 223 P =+ . C. min 322 P =+ . D. min 172 P =+ .

A. 1 4 .

Câu 38: Cho hình lăng trụ đứng tam giác . ABCABC′′′ có đáy là tam giác đều c

phẳng ( ) ABC ′ tạo với đáy một góc 060 . Thể tích khối lăng trụ đã cho là

A. 2 23 4 a . B. 3 3 8 a . C. 3 33 8 a . D. 3 33 4 a .

Câu 31: Có bao nhiêu giá trị nguyên của tham số m để bất phương trình 2 21232e

xmxxm ++−

nghiệm đúng với mọi x∈ℝ ?

A. 8 . B. 5 . C. 6 . D. 7 .

Câu 32: Cho phương trình 2 2 3 2 2 log4 1 xxm xxm x −+ =++− + . Có bao nhiêu giá trị nguyên của tham số

[ ]2022;2022 m∈− để phương trình có hai nghiệm trái dấu?

A. 2022 . B. 2021. C. 2016 . D. 2019 .

Câu 33: Cho hình đa diện. Trong các khẳng định sau, có bao nhiêu khẳng định SAI?

i) Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.

ii) Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.

iii) Mỗi mặt có ít nhất ba cạnh.

iv) Mỗi cạnh là cạnh chung của ít nhất ba mặt.

A. 1. B. 2 . C. 3 . D. 4 .

Câu 34: Cho hình chóp SABC đáy ABC là tam giác đều cạnh a , ( )SAABC ⊥ . Biết mặt phẳng ( ) SBC tạo với đáy một góc 60° . Thể tích khối chóp SABC là

A. 3 3 24 a . B. 3 3 8 a . C. 3 3 6 a . D. 3 3 18 a .

Câu 35: Cho hình chóp . SABCD đáy là hình chữ nhật, 2 ABa = , 3 ADa = . Cạnh bên SA vuông góc với đáy. Gọi M là trung điểm của cạnh CD . Biết SM tạo với mặt phẳng đáy một góc 60° . Tính thể tích V của khối chóp . SABCD .

A. 3 2 Va = . B. 3 43Va = . C. 3 12 Va = .

D. 3 4 Va = .

Câu 36: Cho hình chóp SABC , đáy là tam giác ABC vuông tại B , có 3; ABaBCa == . Tam giác SAC cân tại S và thuộc mặt phẳng vuông góc với đáy, ( ) mpSBC tạo với đáy một góc 060 . Thể tích khối chóp SABC là

A. 3 3 2 a . B. 3 4 a . C. 3 3 3 a . D. 3 2a .

Câu 37: Cho hình chóp SABCD có đáy ABCD là hình chữ nhật. Mặt phẳng ( )α đi qua các điểm ; AB và trung điểm M của SC . Mặt phẳng ( )α chia hình chóp đã cho thành hai phần có thể tích lần

Câu 39: Cho lăng trụ đứng . ABCABC′′′ có đáy ABC vuông cân tại A và ABACa == . Biết diện tích tam giác ABC ′ bằng 2 3 2 a . Thể tích của khổi lăng trụ đã cho bằng

A. 3 2 Va = . B. 3 Va = . C. 3 3 Va = . D. 3 2 a V = .

Câu 40: Cho khối lăng trụ đứng ABCDABCD ′′′′ có đáy là hình chữ nhật ABCD có ABa = ; 3 ADa = . Mặt phẳng ( )ABD ′ tạo với đáy một góc 60° . Thể tích của khối lăng trụ đã cho là:

A. 3 33 2 a . B. 3 3 2 a . C. 3 3 a . D. 3 3 2 a .

Câu 41: Chokhốilăngtrụ . ABCDABCD ′′′′ có đáylàhìnhthoi ABCD tâm O có 2,ACa = 23BDa = . Hình chiếu vuông góc của B′ xuống mặt đáy trùng với trung điểm H của . OB Đường thẳng BC ′ tạo với mặt đáy một góc 45° . Thể tíchcủa khối lăng trụ đã cholà

A. 3 27 a B. 3 23 a C. 3 321 a D. 3 21 a

Câu 42: Cho hình chóp . SABC . Gọi M là trung điểm của AC và G là trọng tâm của tam giác SAC Biết khoảng cách từ điểm M đến mặt phẳng ( ) SBC bằng 6 6 a . Khoảng cách từ điểm G đến mặt phẳng ( ) SBC bằng

A. 6 18 a . B. 6 9 a . C. 6 3 a . D. 6 6 a .

Câu 43: Cho lăng trụ . ABCABC′′′ có thể tích là V . Gọi M , N , P lần lượt là các điểm nằm trên các cạnh AA′ , BB′ , CC′ sao cho 1 3 AM AA = ′ , BN x BB = ′ , CP y CC = ′ . Biết thể tích khối đa diện . ABCMNP bằng 2 3 V . Giá trị lớnnhất của xy bằng

A. 17 21 B. 25 36 C. 5 24 D. 9 16

Câu 44: Thể tích của khối nón có chiều cao h và bán kính r là

A. 2 1 3 rhπ B. 2 rhπ C. 2 4 3 rhπ D. 2 2 rhπ

Câu 45: Hình nón có góc ở đỉnhbằng 60° và chiều cao bằng 3 Độ dài đường sinh của hình nón bằng

A. 2 . B. 22 . C. 23 . D. 3.

Câu 46: Gọi ,, lhr lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức nào sau đây đúng?

 ≤  

lượt 12 ; VV với 12VV < . Tỷ số 1 2 V V bằng

C. 3 8

D. 5 8

3 5 .

Biết

ặ

ạnh bằng a .

A. rh = . B. hl = . C. 222 rhl =+ . D. 222 lhr =+ .

Câu 47: Thể tích của miếng Piza dạng nửa hình trụ có đường kính đáy là 18cm và chiều cao 3cm là

A. 3243cm . B. 381cm π . C. 3 243 cm 2 π . D. 3972cm π .

Câu 48: Thể tích của khối cầu có đường kính 2a bằng

A. 3 4 aπ . B. 3 32 aπ . C. 3 4 3 aπ . D. 3 32 3 aπ .

Câu 49: Cho mặt cầu () ; SOR và điểm A thỏa 2 OAR = . Qua A kẻ một tiếp tuyến tiếp xúc với S tại

B .

HƯỚ

Câu 1: Cho hàm số 42 2 yxx =− . Mệnh đề nào dưới đây đúng?

A. Hàm số đồng biến trên khoảng () ;2−∞− . B. Hàm số đồng biến trên khoảng () 1;1 .

C. Hàm số nghịch biến trên khoảng () ;2−∞− . D. Hàm số nghịchbiếntrên khoảng () 1;1 .

Lời giải

Ta có 3 44 yxx ′ =− . 0 0 1 x y x

=  ′ =⇔  =± 

Bảng biến thiên

Khi đó độ dài đoạn AB bằng

A. 2 R . B. R . C. 2 R . D. 3 R .

Câu 50: Người ta xếp hai quả cầu có cùng bán kính R vào một chiếc hộp hình trụ sao cho các quả cầu tiếp xúc với hai đáy, đồng thời hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ (tham khảohình vẽ).

Suy ra hàm số nghịch biến trên () ;2−∞−

Câu 2: Cho hàm số ()yfx = cóbảng biến thiên như sau.

20 cm .

Biết thể tíchkhối trụ là 3 120 cm , thể tích củakhối cầubằng A. 3 10 cm .

. ---------- HẾT ----------

Hàm số ()yfx = nghịch biến trên khoảng nào sau đây?

A. () 2;0 . B. () ;2−∞− . C. () 0;2 . D. () 0; +∞ .

Lời giải

Dựa vào bảng biến thiên, suy ra hàm số nghịch biến trên () 2;0 và () 2: +∞ .

C. 3

D. 3

1.C 2.A 3.D 4.C 5.C 6.B 7.B 8.A 9.A 10.D 11.D 12.D 13.C 14.D 15.D 16.D 17.C 18.B 19.C 20.C 21.A 22.B 23.C 24.C 25.C 26.B 27.A 28.D 29.C 30.B 31.C 32.D 33.A 34.B 35.D 36.B 37.B 38.C 39.D 40.A 41.D 42.B 43.B 44.A 45.A 46.B 47.C 48.C 49.D 50.C

3 15 cm .

30 cm

ẢNG ĐÁP ÁN

NG DẪ

Ả

CHI

ẾT

N GI

Câu 3: Cho hàm số 3213 21 32 yxxx =−++ . Giả sử hàm số đạt cực đạitại điểm xa = và đạt cựctiểu tại

xb = thì giá trị biểuthức 25ab là

A. 1. B. 12 . C. 1. D. 8 . Lời giải

Vẽ đồ thị hàm số 2 2 yxx=−−+

Đạo hàm 2 32yxx ′ =−+ ; 1 0 2 x y x

=  ′ =⇔  = 

Vì đây là hàm số bậc ba với hệ số 1 0 3 a => nên hàm số đạt cực đại tại 1 x = và đạt cực tiểu tại

2 x = , do đó 2521528 ab−=⋅−⋅=− .

Câu 4: Cho hàm số 322 2 yxmxmx =−+++ . Giá trị của m để hàm số đạt cực tiểu tại 1 x =− là

A. 1 m =− . B. 3 m = . C. 1 3 m m

Lời giải Đạo hàm 22 32,62 yxmxmyxm ′′′ =−++=−+ .

=   =−  .

=−   =  . D. 1 3 m m

Vì hàm số đã cho là hàm số bậc ba nên để hàm số đạt cực tiểu tại 1 x =− khi và chỉ khi () () ()() ()

Suy ra () 0 gx ′ = có 3 nghiệm và đổi dấu qua các nghiệm đó.

Vậy ()gx có ba điểm cực trị

Câu 6: Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số () 31 3 x fx x = trên đoạn [] 0;2

. Giá trị của 3Mm + bằng

⇔⇔  ′′ +> −> −⋅−+>      1;31

 ′ −=  −−+−+=  −−= 

⇔⇔   >−=

=−==−

A. 0 . B. 4 . C. 2 . D. 1. Lời giải

Tập xác định ()() ;33; D =−∞∪+∞ .

Ta có () ()2 8 0,. 3 fxxD x ′ =<∀∈ Suy ra hàm số () 31 3 x fx x = nghịch biến trên từng khoảng

của tập xác định.

Do đó hàm số () 31 3 x fx x = nghịch biến trên đoạn [] 0;2 .

Vậy [] ()() 0;2

1 max0 3 fxf== và [] ()() 0;2 min25 fxf==− . Vậy 1 33.54 3 Mm+=−=− .

Câu 7: Cho hàm số ()yfx = có đồ thị trên đoạn [] 2;4 như hình vẽ. Tìm giá trị lớn nhất M của hàm

số ()yfx = trên đoạn [] 2;4 .

Số điểm cực trị của hàm số ()() 3211 23 32 gxfxxxx =++−− là

A. 1. B. 2 . C. 3 . D. 0 . Lời giải Đạo hàm ()() 2 2 gxfxxx ′′ =++− . ()() 2 02gxfxxx ′′ =⇔=−−+



2 2 2 10 31210 230 260 10 6120 y mm mm m y m

33 mmm mm

Câu 5: Cho hàm số bậc bốn ()yfx = . Hàm số ()yfx ′ = có đồ thị như hình vẽ

. B. 3 . C. 1. D. () 0 f .

Lời giải

Dựa vào cách vẽ đồ thị hàm số ()yfx = ta suy ra [] () 2;4 max33Mfx==−= .

Câu 8: Có baonhiêu số thực m để hàm số 4323412 yxxxm =−−+ có giá trị lớn nh

bằng 150 ?

A. 2 . B. 0 . C. 6 . D. 4 .

Lời giải

Đặt () 4323412 fxxxxm =−−+ . Ta có () 32

fxxxxx

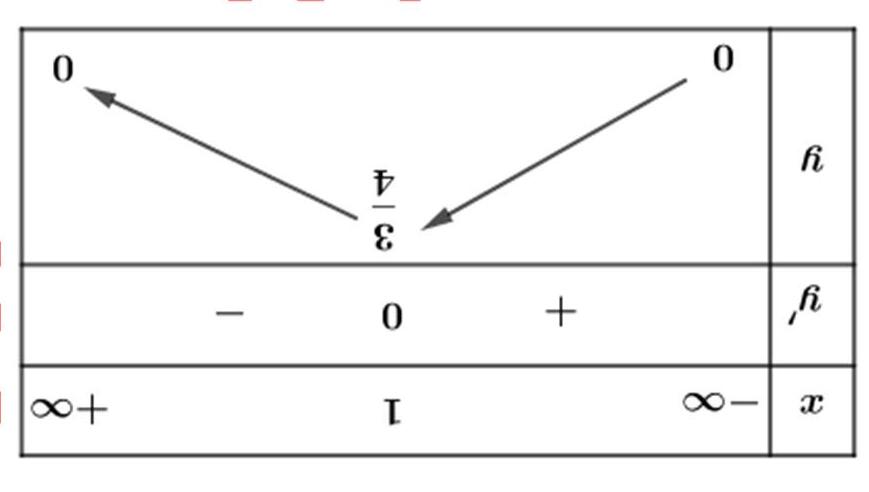
() lim5 x fx →+∞ = nên đồ thị hàm số có một tiệm cận ngang là đường thẳng 5 y = .

() 1 lim x fx → =−∞ và () 1 lim x fx + → =+∞ nên đồ thị hàm số có một tiệm cận đứng là đường thẳng 1 x = .

Vậy hàm số có 3 đường tiệm cận.

Câu 10: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ?

=−−=⇔=−

'12122401

()3243 fm −=+ , ()15 fm −=−+ , () 0 fm = , ()232 fm =−+ .

Khi đó [] ()()()()() {}

A. 3 32yxx=−+ . B. 3 32yxx=−++ . C. 3232yxx=+ . D. 3232yxx=−−+ . Lời giải

Trên hình vẽ là đồ thị của một hàm số bậc ba có hệ số 0 a < , có hai điểm cực trị 2;0xx=−= .

[] ()()()()() {} () ()

Trong các phương án, chỉ có hàm số 3232yxx=−−+ thoả mãn.

maxmax3;1;0;2 3243 232 minmin3;1;0;2 m mTM m m mL mmm m mmmL mmTM mm m m

ymm =+−=          ≤− 

93()

243150 393()

{}  +=   =−     += +=− =−       +≥−≥− −≤≤  ⇔⇔⇔    −=  −==      −=−=−  −≥+     −≤ ≥+   93

Câu 11: Có bao nhiêu giá trị nguyên của tham số m để hàm số 432 48xxm yx=− có đúng 7 điểm cực trị? A. 127 . B. 124 . C. 5 . D. 2 . Lời giải

Xét hàm số () 432 48xxm fxx=− .

Tập xác định D = ℝ . () ()32216434 '412 fxxxxxxx =−= ; ()

Bảng biến thiên của ()yfx = :

Lời giải

Vì () lim3 x fx →−∞ = nên đồ thị hàm số có một tiệm cận ngang là đường thẳng 3 y = .

4 x

x =−   =⇔=   = 

Ta thấy hàm số ()yfx = luôn có 3 điểm cực trị với mọi giá trị của m . Do đó hàm số ()yfx =

có đúng 7 điểm cực trị khi và chỉ khi phương trình () 0 fx = có 4 nghiệm đơn (hoặc bội lẻ), tức là 3030 mmm −−<<−⇔−<< .

Vì m nguyên nên {} 2;1 m ∈−− .

A. 2

ất trên đoạn [] 3;2

2 x

x =  

  = 

Afxffff Afm afm afxffff  ==−− =−=+       ==−+ ==−−     Vậy []

3;2 maxmax243;32150

243150

2433215032

3;2 3;2 3215032150182() 32150118() 32243 393 150243

118182

Do đó có hai giá trị của m thỏa mãn yêu cầu bài toán.

Câu 9: Cho hàm số ()yfx = xác định trên {}\1 ℝ liên tục trên mỗi khoảng xác định và có bảng biến thiên sau.

Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

A. 3 . B. 4 . C. 5 . D. 2 .

'00

fxx

Câu 13: Cho hàm số 32 3 m yxx=++ có đồ thị () C . Biết đồ thị () C cắt trục hoành tại 3 điểm phân biệt ,, ABC sao cho B là trung điểm của AC . Phát biểu nào sau đây đúng?

A. () 0; m ∈+∞ . B. () ;4 m ∈−∞− . C. () 4;0 m ∈− . D. () 4;2 m ∈−− .

Lời giải

Giả sử 123 ,, xxx lầnlượtlàhoành độ củacác điểm ,, ABC . Khi đó 123 ,, xxx lànghiệmcủaphương

trình 32 0 3xm x ++= .

B là trung điểm của AC khi và chỉ khi 13 2132 2 2 xx xxxx + =⇔+= .

Theo định lý Viet ta lại có 2 13 3 xxx+=− + , do đó 2 1 x =− .

Vì 2 1 x =− là nghiệm của phương trình 32 0 3xm x ++= nên 1302 mm −++=⇔=− .

Với 2 m =− , hàm số trở thành 32 2 3 yxx=+− .

Phương trình 32 20 3 xx+= có 3 nghiệm phân biệt 21,31,13xx=−=−± thỏa mãn

132 2 xxx += nên 2 m =− là giá trị cần tìm.

Câu 14: Cho hàm số bậc bốn ()yfx = có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị thực của tham

số m để phương trình ()2022612fxmm+=+ có đúng 4 nghiệm thực phân biệt. Tính tổng tất

cả các phần tử của S .

A. 1 2 . B. 1 2 .

97 24 .

Lời giải

Đặt 2022 txm =+ ( )∗ , khi đó với mỗi 0 t > ta được hai giá trị x thỏa ( )∗ và với 0 t = tồn tại duy nhất một giá trị x thỏa ( )∗ .

Phương trình ( ) 2022612fxmm+=+ có đúng 4 nghiệm thực phân biệt khi và chỉ khi phương trình ( ) 64ftm=+ có hai nghiệm dương phân biệt.

m m m m

. Suy ra 1513 ; 86 S  =−−

 =−   +=  ⇔⇔    +=− =−     



≥−++=−++≥−++=

3 x x x x + =

2 2

   



 ≠ −+=



Câu 12: Tìm số giao điểm của đồ thị hàm số

1 23 x x y x −+ = với đường thẳng 36yx=− . A. 3 . B. 0 . C. 1. D. 2 .

ời giải

ương trình hoành độ giao điểm:

()()

3 3 2 1 2316 730 1 2 x x xxxx x x x =

⇔⇔−+=⇔



= 

. Vậy số giao điểm của đồ thị hàm số 2 1 23 x x y x −+ = với đường thẳng 36yx=− bằng 2 .

97 24 .

15 3 612 8 4 13 6121 6

. Vậy 151397 8624  −+−=−

=−+− trên đoạn [ ]0;2 là nhỏ nhất. Giá trị của m thuộc khoảng nào? A. 3 ;1 2    . B. 2 ;2 3    . C. [ ]1;0 . D. ( )0;1 . Lời giải Đặt ( ) ( ) 3 2 32133fxxxmfxx ′ =−+−  =− . Xét () [ ] [] 2 10;2 0330 10;2 x fxx x  =−∉ ′ =⇔−=⇔  =∈   . Ta có : ( ) () () [] () [] () 0;2 0;2 021 max21, 123 min23. 221 fm fxm fm fxm fm =−  =+    =−   =−   =+  Gọi [] 3 0;2 max321Mxxm =−+− , khi đó { }max23,21Mmm =−+ . Ta có: ( ) ( ) 22321322132214 Mmmmmmm

. Suy ra 2min2MM ≥  = . Dấu “ = ” xảy ra ()() () 2 1 3221 3221 1 2 3221 13 2 32210 4430 22 mm m mm mm m mm m mm   −=+  =   −=+    −=−+ ⇔⇔⇔⇔=   −+>    −<< −−>    . Vậy ( )0;1 m ∈ .

Câu 15: Tìm m để giá trị lớn nhất của hàm số 3 321yxxm

Câu 16: Rút gọn biểu thức ( ) ()

2 2231

aabb T abab = với , ab là hai số thực dương.

Câu 20: Cho hàmsố

3 152

A. 46Tab = . B. 66Tab = . C. 44Tab = . D. 64Tab = .

Lời giải

Ta có ( ) () 2 2231 246125 64 3 335281 152

aabb aabbab T ab ababab abab ==== .

Câu 17: Tìm tập xác định D củahàm số ( ) log100 2 2 yxx=−− .

A. ( )1;2 D =− . B. ( )\1;2 D =− ℝ . C. { }\1;2 D =− ℝ . D. D = ℝ .

Lời giải

Ta có ( ) ( ) 22log1002 22yxxxx =−−=−− .

Hàm số xác định khi 2 1 20 2 x xx x ≠−  −−≠⇔  ≠  . Vậy { }\1;2

2 22 3 4

xx y −+  =   . Trong các khẳng định sau khẳng định nào đúng?

A. Hàmsố đồng biến trên ℝ B. Hàm số nghịch biến trên ℝ

C. Hàmsố đồng biến trên khoảng () ;1−∞ D. Hàmsố đồng biến trên khoảng () 1; +∞ Lời giải

Tập xác định D = ℝ .

xx yx −+  ′ =−

'01

t và giá tr

ℝ .

=−





   . C. ( ] 11 ;0;\;1 22 D =−∞∪+∞−    . D. () 1 ;0; 2 D =−∞∪+∞  . Lời giải Hàm số xác định khi () 2 2 3 20 log20 xx xx  −>   −≠   2 1 0 2 1 0 1 2 2 21 1 xx xx x xx x  <∨>    <∨>  ⇔⇔≠−   −≠  ≠    . Vậy () 11 ;0;\;1 22 D =−∞∪+∞−   . Câu 19: Tính đạo hàm của hàm số 2 212 xx y ++ = . A. 2 22 xx y + ′ = . B. 2 21 2ln2 xx y ++ ′ = . C. () 2 21 41.2ln2 xx yx ++ ′ =+ . D. () 2 21 21.2ln2 xx yx ++ ′ =+ . Lời giải Ta có

′ ′ =++=+ .

Câu 18: Tìm tập xác định D củahàm số () 2 3

log2 y xx = . A. ( ] 1 ;0; 2 D =−∞∪+∞ 

. B. () 11 ;0;\;1 22 D

=−∞∪+∞−

() () 2 2 22121 21.2ln241.2ln2 xxxx yxxx ++++

 

yx  =⇔=

ả

ế

thiên:

đóhàmsố 2 22

Ta có () 2 22 33 22..ln 44 xx y −+  =   đồngbiến trên () ;1−∞

ng bi

3 4

ấ

ị

ỏ

ất của hàmsố 2 2ln yxx =− trên đoạn 1 ;e e    là A. 2 e1 T =− . B. 2 2 1 e e T =− . C. 2 1 2 e T =+ . D. 2 1 3 e T =+ . Lời giải Hàmsố xác địnhtrên 1 ;e e    Ta có 2 1 1;e e 2 20220 1 1;e e x yxyx x x   =−∉     ′′ =−  =⇔−=⇔   =∈     . () 2 22 11111 2ln2lne2 eeeee y  =−=+=+  .

Câu 21: Tổng giá trị lớn nh

2 112ln11 y =−=

()()

ee2lnee2

Vậy 2 1 ;e e maxe2 y    =− . Dấubằng xảyra khi vàchỉ khi e x = .

()()

y =−=−

min1 y   

= . Dấu bằng xảy ra khi và chỉ khi 1 x = .

1 ;e e

22 e21e1 T  =−+=−

Câu 22: Cho log4 a x = và log5 b x = . Tínhgiá trị của biểu thức 3loglogaba b Pxx =+

A. 16 P = B. 80 3 P = C. 40 3 P = D. 27 P =

Lời giải

+Với 1310 x tx =⇔=⇔= .

+Với 3 232log20 x tx =⇔=⇔=> .

Vậy 1233 232.03.log23log2 xx+=+= .

Câu 26: Bác Bình cần sửa lại căn nhà với chi phí 1 tỷ đồng. Đặt kế hoạch sau 5 năm phải có đủ số tiền trên thì mỗi năm bác Bình cần gửi vào ngân hàng một khoản tiền tiết kiệm như nhau gần nhất bằnggiá trị nàosau đây, biếtlãi suất của ngân hàng là 7%/năm và lãi hàng năm đượcnhập vào vốn.

Ta có 31 3loglog log log aba x b x

Pxx a ab b

=+=+

A. 162 triệu đồng. B. 162,5 triệu đồng. C. 162,2 triệu đồng. D. 162,3 triệu đồng. Lời giải

Nếu đầu mỗi năm gửi vào ngânhàng số tiền m , lãi suất không đổi %r /năm vàlãi saumỗi năm được nhập vào vốn thì sau n năm số tiền thu được n T được tính theo công thức

P abab ⇔=+=+= +− +− .

313180 1111 loglogloglog3 4545 xxxx

Câu 23: Với a làsố thựcdươngtùyý, ( ) ln8ln(5) aa bằng

A. ( ) () ln5 ln3 a a B. ( ) ln2a C. 8 ln 5    D. ( ) () ln5 ln3

Lời giải

Tacó () 88 ln8ln(5)lnln55 a aa a

Câu 24: Số nghiệmcủaphươngtrình 761 x x =+ là

A. 0 . B. 1. C. 2. D. 3 .

Lời giải

Phươngtrình 7617610 xx xx =+⇔−−= .

Đặt ( ) 761 x fxx=−− .

Tacó ( ) 7.ln76 x fx ′ =− , ( ) 2 7.ln70 x fxxR ′′ =>∀∈ nênphươngtrình ( ) 0 fx = cókhôngquáhainghiệm.

Lạicó ( ) ( ) 010ff== . Vậyphươngtrình 761 x x =+ cóhainghiệm.

Câu 25: Phươngtrình 93.320 xx−+= cóhainghiệm ( ) 1212 , xxxx < . Tính 1223xx + ?

A. 1. B. 2 2log3 . C. 3 3log2 . D. 3 4log2 .

Lời giải

Đặt ( )30 x tt=> ,khi đótacóphương trình

2 1 320 2 t tt t =  −+=⇔

()() 111 =+−+  n n m Trr r . Ápdụngcôngthứctrên với 5 5;1000000000;7%0,07nTr ==== tacó:

()() 5 100000000010,07110,07 0,07 m  =+−+  ( ) 5 700000001,0711,07 m ⇔=−

() 5 70000000 162,5 1,071,071 m ⇔=≈ triệu đồng.

Câu 27: Số nghiệmcủaphươngtrình 3 3 22

. B. 2.

loglog

t 3 3 22 loglog txxt =  = , ta đượcphươngtrình 3 14 1 33 ttt+=⇔= .

Với ( ) 2 1log12t.mtxx =  =⇔= .

Vậyphươngtrìnhcó 1 nghiệm.

Câu 28: Biết 9 4 x = làmộtnghiệmcủabấtphươngtrình ( ) ( )



 

−==

 = 

Lời giải

+= 1 3 3 22 4

⇔+= 3 22 14 loglog 33

⇔+= . Đặ

xx+= . A. 1

3 .

0 .

Điềukiện 0 x > . Phươngtrình 3 3 22

loglog

Khi đó

A. 5 1; 2 T  =−  . B. 5 ; 2 T =+∞  . C. ( );1 T =−∞− . D. 5 2; 2 T  =   .

( ) 22 log2log23* aa xxxx −−>−++ .

tậpnghiệm củabấtphươngtrình ( )* là

Câu 30: Cho , xy là số thực dương thỏa mãn ( )

c Pxy =+ . A. min 6 P

B. min 223 P =+ . C. min 322 P =+ . D. min 172 P =+ . Lời giải

Tacó ( ) ( ) 222lnlnln1 xyxyxyxyyxx +≥+⇔≥+⇔−≥ .

Vì 2 0 101 0 x xx y  >  −>⇔>  >  .

Với điềukiện 1 x > khi đ

ngtrình ( )* là 5 2; 2 T  =   . Cách2: Vì 9 4 x = là một nghiệm của bất phương trình nên ta có

Lời giải Cách1: Trườnghợp1: 1 a >

2 22 22 230 log2log23 223 aa xx xxxx xxxx −++> −−>−++⇔  −−>−++   2 13 13 5 1 3 2 2350 5 2 x x x x xx x −<<  −<<  <−  ⇔⇔⇔<<  −−>   >   . Trườnghợp2: 01 a <<

2 22 22 20 log2log23 223 aa xx xxxx xxxx  −−>  −−>−++⇔  −−<−++   2 1 1 5 2 2 2 2 5 1 2350 2 x x x x x x xx  <−   <−     >   > ⇔⇔⇔<<   −<< −−<    . Mà 95 2; 42 x  =∈   . Vậytậ

Với 01 a << ta có ()() 2 22 22 2 2350 223 log2log23 1 20 2 aa xx xxxx xxxx x xx x  −−<  −−<−++   −−>−++⇔⇔ <−  −−>   >  5 1 2 5 2 1 2 2 x x x x  −<<  ⇔⇔<<  <−   >  . Vậytậpnghiệmcủabấtphươngtrình ( )* là 5 2; 2 T  =   . Câu 29: Tìmtậpnghiệm S củabấtphươngtrình ( ) 2 42 21.ln0 x x −< . A. ( ) 1;2 S = . B. { }1;2 S = . C. ( ) ( ) 2;11;2 S =−−∪ . D. [ ]1;2 S = . Lời giải Điềukiện: 0 x ≠ . () 2 2 2 42 22 42 2 4 2 2 22 21040 1 1 ln01 21 21.ln0 12 2 40 210 2 1 ln0 11 x x x x x x x xx x x x x x x x x x  −<<    −<−< <−       > >>  −<<−      −<⇔⇔⇔⇔    <<   <− −>  −>          >  <   <     −<< . Kếthợpvới điềukiện 0 x ≠ . Khi đótậpnghiệmcủabấtphươ

2;11;2 S =−−∪ .

()()

pnghiệmcủ

ấtphươ

()() 22 1339 log2log23loglog01 1616aaaa xxxxa −−>−++⇔>⇔<< .

ngtrìnhlà ( ) ( )

+≥+

trị nhỏ nhất minP của biểu th

lnlnlnxyxy

. Tìm giá

ứ

ó ( ) 2 1 yxx −≥ 2 1 x y x ⇔≥ . Tacó () 22 1111 21213223 1111 xx Pxyxxxx xxxx −+ =+≥+=+=++=−++≥+ . Khi đó min 223 P =+ . Dấubằngxảyra ()2 1 1 2 211 1 1 2 x x x  =+   ⇔−=⇔  =−   . Vậy min 223 P =+ Câu 31: Cóbaonhiêugiátrị nguyêncủathamsố m để bấtphươngtrình 2 21232e e2 xmxxm ++− ≤   nghiệm đúngvớimọi x∈ℝ ? A. 8 . B. 5 . C. 6 . D. 7 . Lời giải Tacó: 2 21232e e2 xmxxm ++− ≤   2 212322 ee xmxxm ++−+⇔≤  2 2123 xmxxm⇔++≥−+ ( ) 2 21130xmxm ⇔+++−≥ , ( )* Bấtphươngtrình đãchonghiệm đúngvớimọi x∈ℝ ⇔ Bấtphươngtrình ( )* nghiệm đúngvới mọi x ∈ℝ 0 0 a ′ ∆≤ ⇔  >  ()() 2 1130 10 mm  +−−≤  ⇔  >   2 5050mmm ⇔+≤⇔−≤≤ .

Mà m∈ℤ nên { }5;4;3;2;1;0 m ∈−−−−− .

Câu 32: Cho phương trình 2 2 3 2 2 log4 1 xxm xxm x −+ =++− + . Có bao nhiêu giá trị nguyên của tham số

[ ]2022;2022 m∈− để phươngtrìnhcóhainghiệmtráidấu?

A. 2022 . B. 2021. C. 2016 . D. 2019 .

Lời giải

Điềukiện: 2 2 2 2 020 1 xxm xxm x −+ >⇔−+> + .

Tacó: 2 2 3 2 2 log4 1 xxm xxm x −+ =++− +

( ) ( ) ( ) ( ) 2222 33 log2log13321 xxmxxxxm ⇔−+−+=+−−++

( ) ( ) ( ) ( ) 2222 3 3 log22log1133 xxmxxmxx ⇔−++−+=++++

( ) ( ) ( ) ( ) 2222 3 3 log22log3333 xxmxxmxx ⇔−++−+=+++ , ( )*

Xéthàmsố: ( ) 3log fttt =+ với 0 t > .

Tacó: () 1 10,0 ln3 ftt t ′ =+>∀> .

 Hàmsố ( )ft đồngbiếntrênkhoảng ( ) 0; +∞ .

Khi đó: ( ) ( ) ( ) 22 *233 fxxmfx ⇔−+=+

22 233 xxmx ⇔−+=+

2 30xxm ⇔++−= , ( )**

Phươngtrình đãchocó2nghiệmtráidấu ⇔ phươngtrình ( )** có2nghiệmtráidấu

⇔ ( ) 1.30 m −< ⇔ 3 m > .

Mà m∈ℤ , [ ]2022;2022 m∈− nên { }4;5;6;...;2022 m∈  Có 2019 số nguyên m thỏamãnyêu cầubàitoán.

Câu 33: Chohình đadiện. Trongcáckhẳng địnhsau,cóbaonhiêukhẳng định SAI?

i)Mỗi đỉnhlà đỉnhchungcủaítnhấtbacạnh.

ii)Mỗi đỉnhlà đỉnhchungcủaítnhấtbamặt.

iii)Mỗimặtcóítnhấtbacạnh.

iv)Mỗicạnhlàcạnhchungcủaítnhấtbamặt.

A. 1. B. 2 . C. 3 . D. 4 . Lời giải

Chọn A

“i)Mỗi đỉnhlà đỉnhchungcủaítnhấtbacạnh.” Đúng.

“ii)Mỗi đỉnhlà đỉnhchungcủaítnhấtbamặt.” Đúng

“iii)Mỗimặtcóítnhấtbacạnh. ”Đúng.

“iv)Mỗicạnhlàcạnhchungcủaítnhấtbamặt.”Sai(Mỗicạnhlàcạnhchungcủa đúnghaimặt)

Vậycó1mệnh đề SAI.

Câu 34: Chohìnhchóp . SABC đáy ABC làtamgiác đềucạnh a , ()SAABC ⊥ . Biếtmặtphẳng () SBC

tạovới đáymộtgóc 60° . Thể tíchkhốichóp . SABC là

A. 3 3 24 a . B. 3 3 8 a . C. 3 3 6 a . D. 3 3 18 a . Lời giải Chọn B

Gọi M làtrung điểmcủa BC ,dễ thấygócgiữamặtphẳng () SBC tạovới đáylà 60 SMA =° ; Talạitính được 3 2 a AM = ;suyra 33 .tan.3 22 aa SAAMSMA=== ; Thể tíchkhốichóp . SABC là

2 3 33 . 3 24 338 ABC aa SAS a V ∆ === .

A. 3 2 Va = . B. 3 43Va = . C. 3 12 Va = . D. 3 4 Va = . Lời giải Chọn D

Ta thấy góc giữa SM tạo với mặt phẳng đáy là 60 SMA =° ;

Trong hình chữ nhật ABCD ta dễ tính được 2 AMa = ; suy ra .tan2.3SAAMSMAa ==

Vậy thể tích khối chóp . SABCD là 2 3 23.23 4 33 ABCD SAS aa Va === ▭ .

Câu 36: Cho hình chóp SABC , đáy là tam giác ABC vuông tại B , có 3; ABaBCa == . Tam giác

SAC cân tại S và thuộc mặt phẳng vuông góc với đáy, ()mpSBC tạo với đáy một góc 060 . Thể

tích khối chóp SABC là

A. 3 3 2 a . B. 3 4 a . C. 3 3 3 a . D. 3 2a .

Lời giải

Theo giả thiết, trong tam giác SAC kẻ đường cao ()SHACSHABC ⊥  ⊥ .

Khi đó 1 . 3 SABCABCVSHS ∆ = .

Vậy 231133 33224

SABCABC aaa VSHS ∆ === .

Câu 37: Cho hình chóp . SABCD có đáy ABCD là hình chữ nhật. Mặt phẳng () α đi qua các điểm ; AB và trung điểm M của SC . Mặt phẳng () α chia hình chóp đã cho thành hai phần có thể tích lần lượt 12 ; VV với 12VV < . Tỷ số 1 2

V V bằng

A. 1 4 . B. 3 5 . C. 3 8 . D. 5 8 . Lời giải Qua M kẻ đường thẳng song song với CD cắt SD tại K , khi đó mặt phẳng () α cắt khối chóp theo thiết diện ABMK .

Ta có SABCSADCVV = ; 1 SABMSAMKVVV =+ ;

Ta có

2 13 3. 22 ABC a Saa== .

BCa

HKABSKHHK ⊥  =°== .

Trong tam giác ABC kẻ 60; 22

Xét tam giác SKH , ta có 0 3 tan60.3. 22 aa SHHK=== .

()

2 2 SABCSABMSACDSAMKSABCSABMSAMK VVVVVVVV =−+−=−+ .

..11111

SAMK SAMKSACDSABC

V SASMSK VVV VSASCSD ===  == .

SACD

..22444

..11

SABM SABMSABC SABC

V SASMSB VV VSASCSB ==  = .

..22

1 113 244 SABMSAMKSABCSABCSABC VVVVVV =+=+= .

() 2 115 22 244 SABCSABMSAMKSABCSABCSABC VVVVVVV  =−+=−+=   . Khi

ó 1 2 3 3 4 5 5 4 SABC SABC V V V V

Câu 38: Cho hình lăng trụ đứng tam giác . ABCABC′′′ có đáy là tam giác đều cạnh bằng a . Biết mặt

phẳng () ABC ′ tạo với đáy một góc 060 . Thể tích khối lăng trụ đã cho là

A. 2 23 4 a . B. 3 3 8 a . C. 3 33 8 a . D. 3 33 4 a .

Lời giải

Do đáy ABC đều nên các cạnh ABAC ′′ = . Kẻ 060 AKBCAKA ′′ ⊥  = và 3 2 a AK = ; 2 3 4 ABC a S∆ = .

Xét AAK ′ : 0 33 tan60.3. 22 aa AAAK ′ === .

Khi đó 23 .''' 3333 .. 248 ABCABCABC aaa VAAS∆ ′ === .

Câu 39: Cho lăng trụ đứng ABCABC′′′ có đáy ABC vuông cân tại A và ABACa == . Biết diện tích

tam giác ABC ′ bằng 2 3 2 a . Thể tích của khổi lăng trụ đã cho bằng

A. 3 2 Va = . B. 3 Va = . C. 3 3 Va = . D. 3 2

Ta có: (..) AABAACcgcABAC ∆=∆′′′′  = ABC ′

2222

Vậy 23 .. 22 ABCABCABC aa VAASa ′′′

ủa khối lăng trụ đã cho là: A. 3 33 2 a . B. 3 3 2 a . C. 3 3 a . D. 3 3 2 a . Lời giải

Trong () ABCD gọi M là hình chiếu vuông góc của A lên cạnh BD

′ ⊥  ′′  ⊥  ⊥

Do đó ()() () () ;;60ABDABCDAMAMAMA ′′′===°

ABADaaa AM ABAD aa === + +

..33 2 3

Ta có () 222 2

Xét tam giác AAM ′ vuông tại A : 33

tantan60.tan60.3 22 AAaa AMAAAAM AM

′ ′′ =°=  =°==

a V = . Lời giải Gọi M là trung điểm của canh BC 2

2 a BCaAM==

A′ AMBC ′  ⊥

∆ ′′′ =  =  = Tam giác AAM ′ ∆ vuông tại A nên 22 22 62 22 aa AAAMAMa  ′′ =−=−=   

 ∆ cân tại

Do đó 2 1316 ..2

AAC aa SAMBCAMaAM ′

∆ ′ === . Câu 40: Cho khối lăng trụ đứng ABCDABCD ′′′′ có đáy là hình chữ nhật ABCD có ABa = ; 3 ADa = . Mặt phẳng () ABD ′ tạo với đáy một góc 60° . Thể tích c

Ta có () BDAA BDAAMBDAM BDAM ⊥ 

Vậy 3 333 ...3 22

ABCDABCDABCD VAASaaaa ′′′′ ∆ ′ === .

Câu 41: Cho khối lăng trụ ABCDABCD ′′′′ có đáy là hình thoi ABCD tâm O có 2,ACa = 23BDa = . Hình chiếu vuông góc của B′ xuống mặt đáy trùng với trung điểm H của . OB Đường thẳng

BC ′ tạo với mặt đáy một góc 45° . Thể tích của khối lăng trụ đã cho là

A. 3 27 a . B. 3 23 a . C. 3 321 a . D. 3 21 a .

Lời giải

Ta có () MGSBCS ∩= . Suy ra

dMSBC SM aa dGSBCdMSBC SG dGSBC ==  ===

() () () () () () () () , 32266 ,,. 23369 ,

Câu 43: Cho lăng trụ ABCABC′′′ có thể tích là V . Gọi M , N , P lần lượt là các điểm nằm trên các cạnh AA′ , BB′ , CC′ sao cho

Ta có 3 42 BDa HO == và 2 AC OCa == .

Xét tam giác OHC vuông tại O có: 2 222 37 22 aa HCOHOCa  =+=+=

Ta có () () () ,,45BCABCDBCHCBCH ′′′===° .

Xét BCH ′ ∆ vuông tại H và 45 BCH ′ =° . Suy ra BCH ′ ∆ vuông cân tại H

Do đó 7 2 a BHHC ′ ==

Vậy 3 71 ...2.2321 22 ABCDABCDABCD a VBHSaaa ′′′′ ′ ===

Câu 42: Cho hình chóp . SABC . Gọi M là trung điểm của AC và G là trọng tâm của tam giác SAC

Biết khoảng cách từ điểm M đến mặt phẳng () SBC bằng

mặt phẳng () SBC bằng

6 a . Khoảng cách từ điểm G đến

A. 6 18 a B. 6 9 a C. 6 3 a D. 6 6 a

Lời giải

1 3 AM AA = ′ , BN x BB = ′ , CP y CC = ′ . Biết thể tích khối đa diện . ABCMNP bằng 2 3 V . Giá trị lớn nhất của xy bằng

A. 17 21 B. 25 36 C. 5 24 D. 9 16 Lời giải

Áp dụng công thức tính nhanh, ta có

15 2 33 xyxy  ++=  += Áp dụng bất đẳng thức Cauchy, ta có

Vậy giá trị lớn nhất của xy bằng 25 36 .

AMBNCPV xy V AABBCC V V ′′′

ABCMNP ABCABC

′′′++++ ====

2 33 333

  +  ≤==

() 2 2 5 25 3 4436 xy xy

  

Câu 44: Thể tích của khối nón có chiều cao h và bán kính r là

A. 2 1 3 rhπ B. 2 rhπ C. 2 4 3 rhπ D. 2 2 rhπ

Lời giải

Thể tích của khối nón có chiều cao h và bán kính r là

2 1 3 Vrh π = .

Câu 45: Hình nón có góc ở đỉnh bằng 60° và chiều cao bằng 3 . Độ dài đường sinh của hình nón bằng

A. 2 B. 22 C. 23 D. 3.

Lời giải

Ta có góc ở đỉnh của hình nón bằng 60° nên 30 HOA =° .

Trong tam giác HAO vuông tại H có 2 cos30 OH OA == ° .

Vậy độ dài đường sinh của hình nón bằng 2 .

Câu 46: Gọi ,, lhr lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức nào sau đây đúng?

A. rh = . B. hl = . C. 222 rhl =+ . D. 222 lhr =+ .

Lời giải

Trong hình trụ ta có hl = .

Phương án B đúng, phương án A, C, D là sai.

Câu 47: Thể tích của miếng Piza dạng nửa hình trụ có đường kính đáy là 18cm và chiều cao 3cm là

Ta có thể tích miếng Piza là () 2 3 118243 .3.cm 222 V π π

Câu 48: Thể tích của khối cầu có đường kính 2a bằng

A. 3 4 aπ . B. 3 32 aπ . C. 3 4 3 aπ .

Lời giải

Thể tích của khối cầu là 3344 33 VRa ππ== .

Câu 49: Cho mặt cầu () ; SOR và điểm A thỏa 2 OAR = . Qua A kẻ một tiếp tuyến tiếp xúc với S tại B .

Khi đó độ dài đoạn AB bằng

A. 2 R . B. R . C. 2 R . D. 3 R .

Lời giải

Áp dụng định lý Pi-ta-go với tam giác OAB vuông tại B , ta được:

()2 22222233.ABOAOBRRRABR =−=−=  =

Biết thể tích khối trụ là 3 120 cm , thể tích của khối cầu bằng

A. 3 10 cm . B. 3 15 cm . C. 3 20 cm . D. 3 30 cm .

Lời giải

Gọi , hr lần lượt là chiều cao và bán kính đáy của hình trụ.

Vì hai quả cầu tiếp xúc với đáy nên 2 hR = .

Vì hai quả cầu tiếp xúc với nhau và mỗi quả cầu đều tiếp xúc với đường sinh của hình trụ nên

2 rR = .

2 π

3972cm

Lời giải

A. 3243cm . B. 381cm π . C.

243 cm

. D.

π .



 

D. 3 32 3 aπ .

Theo đề bài, thể tích khối trụ là 3 120 cm nên ta có: ()2 33 15 2.21208120 RRRRππ π =  =  = Vậy thể tích của khối cầu bằng () 3 4415 .20 33 3 cm VRππ π === . ---------- HẾT ----------

TRƯỜ

NG HOÀI ĐỨC A – HÀ NỘI

THI THỬ TỐT NGHIỆP THPT NĂM HỌC - 2022-2023

ĐỀ 02

Câu 1: Hàm số nào trong bốn hàm số liệt kê ở dưới nghịch biến trên từng khoảng xác định của nó?

A. 21 e 2

x y +  =   . B. 1 3

x y  =   . C. 3 e

x y  =   . D. 2017x y = .

Câu 2: Hàm số 32397yxxx=−−+ đồng biến trên khoảng nào sau đây?

A. () 1; +∞ B. () 5;2 C. () ;1−∞ D. () 1;3

Câu 3: Cho hàm số ()yfx = liên tục trên ℝ và có bảng biến thiên như sau:

A. 3. B. 1 C. 2 D. 4

Câu 9: Hai đường tiệm cận của đồ thị hàm số 21 1 x y x + = tạo với hai trục tọa độ một hình chữ nhật có diện tích là

A. 2 B. 1 C. 3. D. 4

Câu 10: Hàm số nào dưới đây có đồ thị như trong hình vẽ bên?

Khẳng định nào sau đây đúng?

A. Hàm số đạt cực tiểu tại điểm 3 x = B. Hàm số có giá trị nhỏ nhất trên ℝ bằng 1.

C. Hàm số có giá trị cực đại bằng 1. D. Hàm số chỉ có một điểm cực trị.

Câu 4: Hàm số 42 3 yxx=−+ có mấy điểm cực trị?

A. 1. B. 2 . C. 3. D. 0.

Câu 5: Hàm số () 2 2 log2 yxx =− nghịch biến trên khoảng nào sau đây?

A. () ;1−∞ B. () ;0−∞ C. () 1;1 D. () 0; +∞

Câu 6: Gọi , mM lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số () 1 1 2 fxxx=−+ trên đoạn 0;3   . Tổng 2 SMm =− bằng

A. 2 = x y . B. 1 3  =   x y . C. 1 3 log = yx . D. 3log = yx .

Câu 11: Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?

Câu 7: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số ()

cos fxxx =+ trên đoạn 0;

A. 3232=−++yxx . B. 3232=−+yxx . C. 3 32=−+yxx . D. 4222=−+−yxx .

Câu 12: Viết phương trình tiếp tuyến của đồ thị () 3 :2ln =+ Cyxxx tại điểm () 1;2 M .

A. 79=−+yx B. 34=−yx C. 75=−yx D. 31=−yx

m cận ngang?

Câu 13: Cho hàm số 21 1 = + x y x có đồ thị () C và đường thẳng :23 =−dyx Đường thẳng d cắt () C tại hai điểm A và B . Tọa độ trung điểm của đoạn AB là A. 3 ;6

C. 2

D. 4

A. 0 = S

=− S

= S

4 π    là A. () () 0; 0; 4 4 1 max;min1 2 fxfx π π       ==− . B. () () 0; 0; 4 4 max;min 46fxfx π π ππ       == . C. () () 0; 0; 4 4 1 max;min1 42 fxfx π π π       =+= D. () () 0; 0; 4 4 11 max;min 422fxfx π π π       =+= Câu 8: Cho hàm số ()yfx = có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và tiệ

2    M

42    M C. 3 ;0 2    M D. 3 ;0 4    M

B. 33 ;

Câu 14: Cho hàm số ()()32322fxxmxmx =−+++ (với m là tham số thực, 0 m > ). Hàm số ()yfx = có bao nhiêu điểm cực trị?

A. 1 B. 3 C. 5 D. 4

Câu 15: Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ và có đồ thị hàm số ()yfx ′ = như hình vẽ sau.

Câu 22: Tìm tất cả các giá trị thực củ

Gọi ()() 3211 2019 32 gxfxxxx =−++− . Biết ()()()() 1102gggg −+>+ . Với [] 1;2 x ∈− thì ()gx đạt giá trị nhỏ nhất bằng

A. () 2 g . B. () 1 g . C. () 1 g . D. () 0 g .

7 35 3

Câu 16: Rút gọn biểu thức

Câu 23: Cho hàm số () 2 1 ln1 fx

mn là các số nguyên dương nguyên tố cùng nhau. Tính 2 Smn

Câu 24: Số nghiệm của phương trình 2 275 21 xx−+ = là

A. 2 B. 1 C. 3 D. 0

Câu 25: Phương trình 93.320 xx−+= có hai nghiệm ( ) 1212 , xxxx < . Giá trị 1223xx + bằng

A. 2 4log3. B. 2. C. 0 . D. 3 3log2 .

Câu 26: Tập nghiệm S của phương trình ( ) 2 2 log32 xx+= là

A. { }1;4 S =− . B. { }1;4 S =− . C. { }1 S = . D. { }4 S = .

Câu 27: Giải phương trình 2 22 log3log20 xx−+= . Ta có tổng các nghiệm là

7 42

aa A aa = với 0 a > . Khẳng định nào sau đây đúng?

A. 2 7 Aa = B. 2 7 Aa = C. 7 2 Aa = D. 7 2 Aa =

Câu 17: Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của x ?

A. () 1 3 21yx=− . B. () 1 2 3 21yx=+ . C. () 3 12 yx =− . D. ()3 12 yx =+ .

Câu 18: Chosố thựcdương , ab với 1 a ≠ .Tìmmệnh đề dúngtrongcácmệnh đề dưới đây.

A. () 2 1 loglog 2 a a abb = . B. () 2 11 loglog 22 a a abb =+ .

C. () 2 1 loglog 4 a a abb = D. () 2 log22loga a abb =+

Câu 19: Hãychobiếtgiátrị của () 2 g ′ nếu () () 2 ln1gxx=+

A. 2 5 . B. 0,8 . C. 2 3 . D. 0,65.

Câu 20: Đạohàmcủahàmsố () 2 cos2 x fx = lànàosố nàosau đây?

A. () 2 cos sin2.2ln2 x x . B. () 2 cos sin2.2ln2 x x . C. () 2 cossin2.2 x x . D. () 2 cos1sin2.2 x x .

Câu 21: Chohaisố a và b với 01 ab <<< .Khẳng địnhnàodưới đâylàkhẳng định đúng?

A. log1log abba << B. 1loglog baab<<

C. 1loglog abba<< D. log1log baab <<

A. 6 . B. 3 . C. 5 2 . D. 9 2 .

Câu 28: Tập nghiệm của bất phương trình ( )( ) 121 32480 xxx++ +−≤

A. 1 ; 4 

Câu 29: Tập nghiệm của bất phương trình 3.910.330 xx−+≤ có dạng [ ] ; Sab = trong đó , ab là các số nguyên. Giá trị biểu thức 52ba bằng

A. 43 3 . B. 8 3 . C. 7 . D. 3 .

Câu 30: Tập nghiệm của bất phương trình ( ) ( ) 2 12 2 loglog11 x −≤− là:

A. ( ) ;55; S  =−∞−∪+∞  . B.  =   S 1;5 . C. =−  S 5;5 D. ) ( =−∪  S 5;11;5 .

Câu 31: Bất phương trình ( ) 22 ln(23)ln1 xxax+>++ nghiệm đúng với mọi số thực x khi

A. 2222 a −<< B. 022 a << C. 02 a << D. 22 a −<<

Câu 32: Tìm số nghiệm nguyên của bất phương trình 22 21510010502 22251500 xxxx xx −++−−+−+<

A. 6. B. 5. C. 4. D. 3.

Câu 33: Hình bát diện đều có bao nhiêu cạnh?

A. 16 . B. 8 . C. 24 . D. 12.

a tham số m để hàm số 1 1 5 mx xm y + +  =   đồng biến trên khoảng 1 ; 2  +∞   ? A.

B. 1

2 m  ∈   C. 1 ;1 2 m  ∈   D. 1 ;1 2 m  ∈−   

( )1;1 m∈−

x 

 

Biết rằng ()()()() 23...20192020 m ffff n ′′′′ ++++= với ,

=−

=− . A. 2 B. 4 C. 2 D. 4

−+∞   

B.  −∞−   

4 C. (  −∞ 

D. )  +∞ 4; .

1 ;

Câu 34: Cho hình chóp SABC có SA , SB , SC đôi một vuông góc. Biết SASBSCa === . Tính thể

tích của khối chóp . SABC

A. 3 6 a . B. 3 3 4 a . C. 3 2 a . D. 3 3 a .

Câu 35: Cho hình chóp . SABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy, SAa = . Thể tích của khối chóp . SABC bằng:

Câu 42: Cho hình chóp . SABCD có thể tích bằng 3 4a , đáy ABCD là hình bình hành. Gọi M là trung điểm cạnh SD . Biết diện tích tam giác SAB bằng 2 a . Tính khoảng cách từ M tới mặt phẳng ( )SAB .

A. 12a . B. 6a . C. 3a . D. 4a .

Câu 43: Cho tứ diện ABCD có 2,7,3===== ABBDADaACaBCa . Biết khoảng cách giữa hai đường thẳng , ABCD bằng a . Tính thể tích của khối tứ diện ABCD

A. 3 26 3 a B. 3 22 3 a C. 3 26a D. 3 22a

Câu 44: Công thức tính diện tích xung quanh của hình nón tròn xoay có bán kính đáy r và độ dài đường sinh l là:

A. = xq Srl B. 2π = xq Srl C. π = xq Srl D. 2 = xq Srl

Câu 45: Hình nón có góc ở đỉnh bằng o60 và chiều cao bằng 3 Độ dài đường sinh của hình nón bằng

A. 3 3 4 a . B. 3 3 6 a . C. 3 4 a . D.

12 a .

Câu 36: Cho hình chóp . SABC có 3,2,3. SASBSCaABACaBCa ====== Thể tích của khối SABC bằng

A. 3 5 2 a B. 3 35 2 a C. 3 35 6 a D.

Câu 37: Cho hình chóp . SABCD có đáy là hình bình hành ABCD . Gọi , MN lần lượt là trung điểm của , SASB và P là điểm bất kì thuộc cạnh CD . Biết rằng thể tích của khối chóp . SABCD là V Tính thể tích khối tứ diện AMNP theo V .

A. 8 V . B. . 12 V C. . 6 V D. . 4 V

Câu 38: Cho hình lập phương ABCDABCD ′′′′ có diện tích mặt chéo ACCA′′ là 2 22 a . Thể tích khối lập phương . ABCDABCD ′′′′ là:.

A. 3 a . B. 3 2a . C. 3 2 a . D. 3 22 a .

Câu 39: Cho khối lăng trụ đều . ABCABC′′′ có ABa = , 2 AAa ′ = . Góc giữa đường thẳng AB ′ và mặt phẳng () BCCB′′ bằng

A. 60° B. 30° C. 45° D. 90°

Câu 40: Cho khối lăng trụ đứng ABCABC′′′ có độ dài cạnh bên bằng 2a , đáy là tam giác ABC vuông cân tại C ; CACBa == . Gọi M là trung điểm của cạnh AA′ . Khoảng cách giữa hai đường thẳng AB và MC ′ bằng

A. 3 3 a . B. 3 a . C. 3 2 a . D. 2 3 a .

Câu 41: Cho khối lăng trụ có đáy là tam giác đều cạnh bằng a và thể tích bằng 3 3a . Chiều cao của khối lăng trụ đã cho bằng

A. 123a B. 63a C. 43a D. 23a

A. 2 l = . B. 22 l = . C. 23 l = . D. 3 l = .

Câu 46: Gọi ;; lhr lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ Đẳng thức nào sau đây đúng?

A. lh = B. hr = C. 222 lrh =+ D. 222 rlh =+

Câu 47: Thể tích của miếng Piza dạng nửa hình trụ có đường kính đáy 18 cm và chiều cao 3 cm là

A. 243 2 π B. 81π C. 243π D. 972π

Câu 48: Cho hình chóp . SABC có ( ) ⊥ SAABC , 3,2==ABAC và 60 =° BAC . Gọi , MN lần lượt là hình chiếu của A lên , SBSC . Tính bán kính R mặt cầu ngoại tiếp hình chóp . ABCNM

A. 2 = R . B. 21 3 = R . C. 4 3 = R . D. 1 = R .

Câu 49: Chomặtcầu ( ) ; SIR vàmặtphẳng ( )P cách I mộtkhoảngbằng 2 R .Khi đóthiếtdiệncủa ( )P và ( ) S là một đường tròn có bán kính bằng

A. R B. 3 2 R C. 3 R D. 2 R

Câu 50: Cho tứ diện ABCD có tam giác BCD vuông tại C , AB vuông góc với mặt phẳng ( )BCD , 5,3== ABaBCa và 4 = CDa . Tính bán kính R của mặt cầu ngoại tiếptứ diện ABCD

A. 52 3 = a R B. 53 3 = a R C. 52 2 = a R D. 53 2 = a R ---------- HẾT ----------

3 5 4

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Hàm số nàotrongbốn hàm số liệt kê ở dưới nghịch biến trên từng khoảng xác định của nó?

Câu 5: Hàm số ( ) 2 2 log2 yxx =− nghịch biến trên khoảng nào sau đây?

A. ( );1−∞ B. ( );0−∞ C. ( )1;1 D. ( ) 0; +∞ Lời giải

Hàm số xác định khi 2 0 20 2 x xx x <  −>⇔  >  . Tập xác định của hàm số là ( ) ( ) ;02; D =−∞∪+∞

Khi đó () 2 22 002201. 2ln2 x yxx xx ′ <⇔<⇔−<⇔<

Kết hợp với tập xác định ta được 00yx ′ <⇔<

x y +  =  

A. 21 e 2

B. 1 3

x y  =   C. 3 e

x y  =   D. 2017x y =

Lời giải

Hàm số x ya = nghịch biến trên ℝ khi 01. a <<

Vậy hàm số 1 3

x y  =   nghịch biến trên ℝ

Câu 2: Hàm số 32397yxxx=−−+ đồng biến trên khoảng nào sau đây?

A. () 1; +∞ B. () 5;2 C. () ;1−∞ D. () 1;3

Lời giải

Ta có 2 369yxx ′ =−−

2 1 03690 3 x yxx x <−  ′ >⇔−−>⇔  > 

Do đóhàm số đồng biến trên () ;1−∞− nên hàm số đồng biến trên ()5;2.

Câu 3: Cho hàm số ()yfx = liên tụctrên ℝ và cóbảng biến thiên như sau:

Vậy hàm số đã cho nghịch biến trên khoảng ( ) ;0.−∞

Câu 6: Gọi , mM lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số () 1 1 2 fxxx=−+ trên đoạn 0;3   . Tổng 2 SMm =− bằng

A. 0 = S . B. 3 2 =− S . C. 2=− S . D. 4 = S . Lời giải

Ta có () 1 1 2 fxxx=−+ () 1111 2 2121 x fx xx +− ′  =−= ++ .

( ) 0110fxxx ′ =⇔+=⇔= .

Ta có ()() 1 01;3 2 ff=−=− và hàm số ( )fx liên tục trên đoạn 0;3  

Vậy 11 ;12210 22 MmSMm  =−=−  =−=−+= 

Câu 7: Giátrị lớn nhất và giá trị nhỏ nhất của hàm số ( ) 2 cos fxxx =+ trên đoạ

Khẳng định nàosau đây đúng?

A. Hàm số đạt cực tiểu tại điểm 3 x =

B. Hàm số có giá trị nhỏ nhất trên ℝ bằng 1.

C. Hàm số có giá trị cực đại bằng 1. D. Hàm số chỉ có một điểm cực trị

Lời giải

Hàm số ()yfx = liên tục trên ℝ và hàm số đạt cựctiểu tại 3 x = . Phương án A đúng.

Hàm số không có giá trị nhỏ nhất trên ℝ nên phương án B sai.

Hàm số có giá trị cực đại bằng 2 nên phương án C sai.

Hàm số có hai điểm cực trị 1 x = và 3 x = nên phương án D sai.

Câu 4: Hàm số 42 3 yxx=−+ có mấy điểm cực trị?

A. 1 B. 2 C. 3. D. 0.

Lời giải

Ta có () 1.10 ab =−<  Hàm số có 3 điểm cựctrị.

BẢNG ĐÁP ÁN 1.B 2.B 3.A 4.C 5.B 6.A 7.C 8.A 9.A 10.D 11.B 12.C 13.B 14.C 15.A.C 16.B 17.B 18.B 19.B 20.A 21.A 22.D 23.C 24.A 25.D 26.A 27.A 28.A 29.C 30.A 31.D 32.C 33.D 34.A 35.D 36.D 37.A 38.D 39.B 40.A 41.C 42.C 43.B 44.C 45.A 46.A 47.A 48.B 49.B 50.C



n 0; 4 π    là A. () () 0; 0; 4 4 1 max;min1 2 fxfx π π       ==− B. () () 0; 0; 4 4 max;min 46fxfx π π ππ       ==

() () 0; 0; 4 4 1 max;min1 42 fxfx π π π       =+= . D. () () 0; 0; 4 4 11 max;min 422fxfx π π π       =+= . Lời giải Ta có ( ) 2 cos fxxx =+ ( ) 12cos.sin1sin2 fxxxx ′  =−=− Cho () 01sin20 4 fxxxk π π ′ =⇔−=⇔=+ . Do 0; 44 xx ππ ∈  =   () 1

ππ ==+   và hàm

ố

liên tục trên đoạn 0; 4 π   

01; 442 ff

( )fx

() () 0; 0; 4 4 1 max;min1 42 fxfx π π π       =+= Câu 8: Cho hàm

ố

)

= có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

Suy ra

(

yfx

A. 3. B. 1 C. 2 D. 4

Lời giải Ta có:

()() lim5;lim3 xx fxfx →+∞→−∞ ==  đồ thị hàm số có hai đường tiệm cận ngang là 3 y = và 5 y = .

()() 11 lim;lim xx fxfx −+ →→ =−∞=+∞  đồ thị hàm số có đường tiệm cận đứng là 1 x =

Vậy đồ thị hàm số có 3 đường tiệm cận.

Câu 9: Hai đường tiệm cận của đồ thị hàm số 21 1 x y x + = tạo với hai trục tọa độ một hình chữ nhật có diện tích là

A. 2 . B. 1. C. 3. D. 4 .

Lời giải

Ta có: lim2;lim2 xx yy →+∞→−∞ ==  đồ thị hàm số có đường tiệm cận ngang là 2 y = .

11 lim;lim xx yy −+ →→ =−∞=+∞  đồ thị hàm số có đường tiệm cận đứng là 1 x =

Hai đường tiệm cận tạo với hai trục tọa độ một hình chữ nhật có kích thước lần lượt là 1 và 2

Vậy diện tích hình chữ nhật là 2 S =

Câu 10: Hàm số nào dưới đây có đồ thị như trong hình vẽ bên?

A. 2 = x y .

B. 1 3  =   x y .

C. 1 3 log = yx . D. 3log = yx .

Lời giải

Từ đồ thị hàm số ta có tập xác định của hàm số là () 0; +∞ suy ra đây là đồ thị của hàm số

logarit log = a yx . Loại đáp án A và

Hàm số đồng biến trên () 0; +∞ nên 1 > a  chọn đáp án

Câu 11: Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số dưới đây?

A. 3232=−++yxx .

B. 3232=−+yxx .

C. 3 32=−+yxx .

Lời giải

D. 4222=−+−yxx .

Trong các đáp án cho thì ta thấy đồ thị trên là đồ thị của hàm số bậc ba có hệ số 0 > a nên:

Loại đáp án A vì hệ số 0 < a

Loại đáp án D vì là hàm số bậc bốn.

Vì đồ thị đi qua điểm () 2;2 nên chỉ có đáp án B thỏa mãn.

Vậy đáp án đúng làB.

Câu 12: Viết phương trình tiếp tuyến của đồ thị () 3 :2ln =+ Cyxxx tại điểm () 1;2 M

A. 79=−+yx . B. 34=−yx . C. 75=−yx . D. 31=−yx . Lời giải

Tập xác định: () 0; =+∞ D .

Ta có 2 6ln1yxx ′ =++ ; () 2 16.1ln117 y ′ =++=

Phương trình tiếp tuyến của đồ thị () 3 :2ln =+ Cyxxx tại điểm () 1;2 M là: ()() 112yyx ′ =−+ () 712⇔=−+ yx 75⇔=− yx

Vậy phương trình tiếp tuyến của đồ thị là 75yx=−

Câu 13: Cho hàm số 21 1 = + x y x có đồ thị () C và đường thẳng :23 =−dyx Đường thẳng d cắt () C tại hai điểm A và B . Tọa độ trung điểm của đoạn AB là

xthoaûmaõny

=  =

21 1 4 2

 =−

1 ;4 2 

3 ;6 2    M B.

42    M C. 3 ;0 2    M D. 3 ;0 4    M Lời giải

33 ;

() () 

 ⇔  =−



xthoaûmaõny

Tập xác định: {}\1 D =− ℝ . Xét phương trình hoành độ giao điểm của d và () C 21 23 1 =− + x x x ()() 21123 ⇔−=+− xxx 2 2123 ⇔−=−− xxx   B

2320⇔−−= xx



Đường thẳng d cắt đồ thị () C tại hai điểm () 2;1 A và

33 ; 42    M

Vậy tọa độ trung điểm của đoạn AB là: 33 ; 42    M

Câu 14: Cho hàm số ()()32322fxxmxmx =−+++ (với m là tham số thực, 0 m > ). Hàm số ()yfx =

có bao nhiêu điểm cực trị?

A. 1 B. 3 C. 5 D. 4

Lời giải

Nhận xét: hàm số ()yfx = là hàm số chẵn nên đồ thị hàm số đối xứng qua Oy. Vì vậy, ta đi

tìm số cực trị dương. Khi đó, số điểm cực trị cần tìm bằng số cực trị dương cộng 1.

Ta có ()() 2 3232 fxxmxm ′ =−++ ; ()() 2 032320fxxmxm ′ =⇔−++= (*).

()2 2 3690mmm ′ ∆=+−=+> với mọi m () 0 fx ′  = luôn có hai nghiệm phân biệt 12 , xx (Giả sử 12xx < ).

m xx m xx   

+=>

 => 

với mọi 0 m >

Bảng biến thiên

Từ bảng biến thiên trên, ta thấy hàm số ()yfx = có 5 điểm cực trị.

Câu 15: Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ và có đồ thị hàm số ()yfx ′ = như hình vẽ sau.

Gọi ()() 3211 2019 32 gxfxxxx =−++− . Biết ()()()() 1102gggg −+>+ . Với [] 1;2 x ∈− thì ()gx đạt giá trị nhỏ nhất bằng

A. () 2 g . B. () 1 g . C. () 1 g . D. () 0 g . Lời giải

Ta có ()()() ()2211gxfxxxfxxx ′′′ =−++=−−−

()() () 2 010gxfxxx ′′ =⇔−−−= () 2 1 fxxx ′ ⇔=−−

Bảng biến thiên

x fxxxx x

=−   ′ =−−⇔=   = 

Dựa vào hình vẽ trên, ta thấy () 2 1 10 2

Tọa độ trung điểm M của đoạn thẳng AB là () 1 2 2 2 2 14 2 2  +− +    =    =  ⇔  +  = +−   =   AB M M AB M M xx x x yy y y 3 4 3 2  =   ⇔   =−   M M x y 

Theo định lý Vi–et ta có () 12 12

23 0 3 2 .0 3 



Suy ra với 0 m > hàm số ()yfx = luôn có hai điểm cực trị dương 12 , xx .

Theo giả thiết: ()()()()()()()()()() 11021201012 gggggggggg −+>+⇔−−>−>  −>

Vậy [] ()() 1;2 min2 gxg =

▪ Chú ý: Cách khác khi không dùng giả thiết ()()()() 1102gggg −+>+ ở đề bài

A. () 1 3 21yx=− . B. () 1 2 3 21yx=+ . C. () 3 12 yx =− . D. ( )3 12 yx =+ .

Câu 18: Chosố thựcdương , ab với 1 a ≠ .Tìmmệnh đề dúngtrongcácmệnh đề dưới đây.

C. () 2 1 loglog 4 a a abb = D. ( ) 2 log22loga a abb =+

Lời giải

Với 0;0ab>> và 1 a ≠ , ta có: () () () 2 1111 logloglogloglog 2222aaaa a abababb ==+=+

Câu 19: Hãychobiếtgiátrị của ( )2 g ′ nếu ( ) ( ) 2 ln1gxx=+ .

A. 2 5 B. 0,8 C. 2 3 D. 0,65

Lời giải

Gọi 1S làdiệntíchhìnhphẳnggiớihạnbởi đồ thị hàmsố ()yfx ′ = , 2 1 yxx=−− , 1,0xx=−=

Hàmsố đãchoxác định vớimọi x ∈ ℝ

Tacó () 2 2 1 x gx x ′ = + nên () 4 20,8 5 g ′ == .

Ta có () ()

2 1 1 1d Sfxxxx ′ =−−−  () () 0 2 1 1d fxxxx  ′ =−−−  () 0 1 d gxx ′ =  () 0 1 gx = ()() 01gg =−−

Gọi 2S là diện tích hình phẳng giới hạn đồ thị hàm số ()yfx ′ = , 2 1 yxx=−− , 0,2xx==

Ta có () ()

2 2 2 0 1d Sfxxxx ′ =−−−  () () 2 2 0 1d fxxxx  ′ =−−−−  ()

2 0 d gxx ′ =− () 2 0 gx=− ()() 20gg=−+ .

Ta có 21SS > ()()()() 2001gggg  −+>−− ()() 21gg ⇔−>−− ()() 21gg ⇔<−

Vậy [] ()() 1;2 min2 gxg = .

aa A aa = với 0 a > . Khẳng định nào sau đây đúng?

354 333

Câu 20: Đạohàmcủahàmsố () 2 cos2 x fx = lànàosố nàosau đây?

A. () 2 cos sin2.2ln2 x x B. () 2 cos sin2.2ln2 x x C. () 2 cossin2.2 x x D. () 2 cos1sin2.2 x x

Lời giải

Tacó () () ()() 2 2 2 cos2cos cos 2.ln2.cos2.ln2.2cos.sinsin2.2.ln2 xx x fxxxxx ′ ′ ==−=− .

Câu 21: Chohaisố a và b với 01 ab <<< .Khẳng địnhnàodưới đâylàkhẳng định đúng?

A. log1log abba << . B. 1loglog baab<< .

C. 1loglog abba<< D. log1log baab <<

Lời giải

Tacó:vì 01 ab <<< nên log1log abba << làkhẳng định đúng.

Câu 22: Tìmtấtcả cácgiátrị thựccủathamsố m để hàmsố 1 1 5 ảng 1 ; 2  +∞   ? A. ( )1;1 m∈− B. 1 ;1 2 m  ∈   C. 1 ;1 2 m  ∈   D. 1 ;1 2 m  ∈−    Lời giải Tacó ()

mxmx xmxmmxm y xm xm

mx xm y + +  =   đồngbiếntrênkho 11 2 2 11111.ln..ln5 555

A. 2 7 Aa = B. 2 7 Aa = C. 7 2 Aa = D. 7 2 Aa = Lờ

giải Với 0 a > , ta có 757 2

Câu 16: Rút gọn biểu thức 7 226 7

7 35 3 7 42 4

. . aaaaa Aa aa aaa ====

77 .. . .

Câu

17: Trong các hàm số sau đây, hàm số nào xác định với mọi giá trị thực của x ?

Lời giả

Tacó 2 210xx+>∀∈ℝ nênhàmsố () 1 2 3 21yx=+ xác địnhvớimọigiátrị thựccủa x .

A. () 2 1 loglog 2 a a abb = . B. () 2 11 loglog 22 a a abb =+ .

++ ++ ′ +−  ′ ==  +  +

. Biết rằng ()()()() 23...20192020 m ffff n ′′′′ ++++= với

số nguyên d

ng nguyên tố cùng nhau. Tính2Smn =− .

4 . C. 2 . D. 4 . Lời giải

Tập xác định: ( ) ( ) ;11; D =−∞−∪∞

Ta có: () () () ()() () () 2 2 12211 ln1 1111 1 fxfx xxxxxxxx xx  ′ =−  ===−  −+−+ 

Khi đó: ( ) ( ) ( ) (

Vì 12xx < nên 1230,log2xx== .

Khi đó: 1233 232.03.log23log2 xx+=+=

Câu 26: Tập nghiệm S của phương trình ( ) 2 2 log32 xx+= là

A. { }1;4 S =− B. { }1;4 S =− C. { }1 S = D. { }4

Điều kiện: 0 3 x x > 

Ta có: 22 3x2 x += ⇔ 2 34=0xx+− ⇔ ( ) () 1 4 xTM xTM =

Vậy tập nghiệm của phương trình là { }1;4 S =− .

Câu 27: Giải phương trình 2 22 log3log20 xx−+= . Ta có tổng các nghiệm là

A. 6 B. 3 C. 5 2 D. 9 2 Lời giải Điều kiện: 0 x >

Ta có: 2 22 log3log20 xx−+= ⇔ 2 2

Tập nghiệm của phương trình là { }2;4 S =

log1 log2 x x

22 24 xTM xTM  ==  ==   .

=   =  ⇔ ( ) () 1 2

Tổng tất cả các nghiệm của phương trình là: 246 +=

Câu 28: Tập nghiệm của bất phương trình ( )( ) 121 32480 xxx++ +−≤

A. 1 ; 4  −+∞    . B.

−∞ ;4 D. )  +∞ 4; Lời giải Do 320 x x+>∀ nên ( )( ) 121121121 3248048048 xxxxxxx ++++++ +−≤⇔−≤⇔≤

2263 1 22226341 4 xx xxxx ++ ⇔≤⇔+≤+⇔≥−⇔≥− .

Vậy tập nghiệm của bất phương trình đã cho là 1 ; 4  −+∞    .

Câu 29: Tập nghiệm của bất phương trình 3.910.330 xx−+≤ có dạng [ ] ; Sab = trong đó , ab là các số nguyên. Giá trị biểu thức 52ba bằng

A. 43 3 . B. 8 3 . C. 7 . D. 3 .

Lời giải

Ta có: 1 3.910.3303311 3 xxx x −+≤⇔≤≤⇔−≤≤

Suy ra [ ]1;1 S =−  1;1ab=−=

Vậy 52527 ba−=+=

Câu 30: Tập nghiệm của bất phương trình ( ) ( ) 2 12 2 loglog11 x −≤− là:

ố đồ

1 ;

 

  () () 1 2 2 2 2

522 mx xm m m xx xmxm + + 

 + + Điều kiện: 2 11 10 1 1 1 1 2 2 2 m m m m m −<<  −>  ⇔⇔−≤< ≥− −≤    . Vậy 1 ;1 2 m  ∈−    . Câu 23: Cho



 

, mn

Hàm s

ng biến trên khoảng

2  +∞

khi và chỉ khi 1 0,; 2 yx  ′ >∀∈+∞

11111 ..ln50,;0,;

⇔>∀∈+∞⇔>∀∈+∞ 

hàmsố () 2 1 ln1 fx x

=−

là các

ươ

)23...20192020 ffff ′′′′ ++++ 111111 ... 1.22.32.33.42019.20202020.2021 =−+−++− 11 1.22020.2021 =− 1010.20211 2020.2021 = Vậy1010.20211;2020.2021 mn=−= , suy ra 22 mn−=− . Câu 24: Số nghiệm của phương trình 2 275 21 xx−+ = là A. 2 . B. 1. C. 3 . D. 0 . Lời giải Ta có: 2 275 21 xx−+ = ⇔ 2 2750 xx−+= ⇔ 1 5 2 x x =    =  Vậy tập nghiệm của phương trình là: 5 1; 2 S  =   .

Phương trình 93.320

có hai nghiệ

1212

xxxx

Giá trị 1223xx + bằng A. 2 4log3. B. 2 . C. 0 . D. 3 3log2 . Lời giải Ta có: 93.320 xx−+= ⇔ ( )2 33.320 xx−+= ⇔ 31 32 x x  =  =  ⇔ 3 0 log2 x x =   = 

Câu 25:

xx−+=

m ( )

< .

S = Lời giải



 <−







=− 

 −∞−   



1 ; 4 C. (

Hình bát diện đều có 12 cạnh.

3 6 a . B. 3 3 4 a . C. 3 2 a . D. 3 3 a . Lời giải

Câu 31: Bất phương trình ( ) 22 ln(23)ln1 xxax+>++ nghiệm đúng với mọi số thực x khi

A. 2222 a −<< . B. 022 a << . C. 02 a << . D. 22 a −<< . Lời giải

Thể tích của khối chóp . SABC là 3 111 .... 366 SBC VSSASASBSCa ∆ ===

222 22

23120 ln(23)ln1 1010 xxaxxax xxax I xaxxax

 ++>++> 

Ta có () ()

Để bất phương trình ( ) 22 ln(23)ln1 xxax+>++ đúng với mọi số thực x thì ( ) I phải đúng với mọi số thực x

Điều này tương đương với ()2 2 2 2 2

8 4.20 422 4 40 a a aa a a

  < −−<  ⇔⇔<⇔−<< <  −<    .

Vậy 22 a −<< thỏa mãn yêu cầu bài toán.

Câu 32: Tìm số nghiệm nguyên của bất phương trình 22 21510010502 22251500 xxxx xx −++−−+−+<

A. 6. B. 5. C. 4. D. 3. Lời giải

Đặt 2 2

215100 1050 xxa xxb  −+=   +−=   . Khi đó bất phương trình trở thành 22()0 ab ab −+−< .

22 abab⇔+<+ (I).

Xét hàm số ()2 ftt =+ trên ( ) ; −∞+∞ . Ta có ( ) ( ) 2ln210, ; ′ =+>∀∈−∞+∞ t ftt

Suy ra, hàm số ()ft đồng biến trên ( ) ; −∞+∞ .

Từ (I) ta lại có 22 ()()2151001050 fafbabxxxx <⇔<⇔−+<+− ( ) 2 25150010;15xxx ⇔−+<⇔∈ .

Vì x ∈ ℤ nên { }11;12;13;14 x ∈

Vậy bất phương trình có 4 nghiệm nguyên.

Câu 33: Hình bát diện đều có bao nhiêu cạnh?

A. 16 B. 8 C. 24 D. 12

Lời giải

3 3 4 a B. 3 3 6 a C. 3 4 a D. 3 3 12 a Lời giải

3 111133 .....sin60.... 3326212 ABC a VSSAABACSAaaa ∆ ==°==

A. ( ) ;55; S  =−∞−∪+∞  . B.  =   S 1;5 C. =−  S 5;5 D. ) ( =−∪  S 5;11;5 Lời giải Ta có: () () () () 2 2 222 122 2 2 2 2 1 1 10 10 25 loglog11log1011 25 14 log12 5 5 x x x x xx xxx xx x x x x  <−   >   −>   −>  <−≤−    −≤−⇔−>⇔−>⇔⇔  >≥  −≥ −≥     ≤−   ≥   . Vậy tập

ệm của bất phương

S 



nghi

trình đ

cho là ( ) ;55;

=−∞−∪+∞

2 2 +>++−+> +>++⇔⇔

Câu 34: Cho hình chóp SABC có SA , SB , SC đôi một vuông góc. Biết SASBSCa === . Tính thể tích của khối chóp . SABC A.

Câu 35: Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy, SAa = . Thể tích của khối chóp SABC bằng:

Thể tích của khối chóp . SABC là:

Câu 36: Cho hình chóp . SABC có 3,2,3. SASBSCaABACaBCa ====== Thể tích của khối

SABC bằng

A. 3 5 2 a . B. 3 35 . 2 a C. 3 35 . 6 a D. 3 5 . 4 a

Lời giải

Gọi H là hình chiếu vuông góc của S lên mặt phẳng () ABC

Do SASBSC == nên H là tâm đường tròn ngoại tiếp tam giác ABC∆

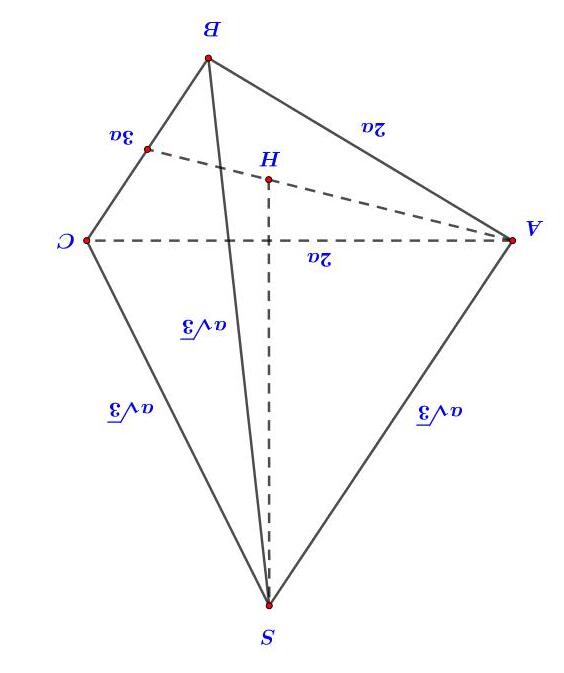
Áp dụng công thức Hê – rông tính diện tích ABC∆ ta được:

()()() 2 37 4 ABC a Sppapbpc ∆ =−−−= . (với p là nửa chu vi).

Sử dụng công thức 4 abc S R = ta tính được bán kính đường tròn ngoại tiếp tam giác ABC∆ là

47 7 a RAH==

Xét HAS∆ có 22 5 7 SHSAAHa =−=

Khi đó ta có 23 113755 33474SABCABC aa VSSHa ∆ ===

Câu 37: Cho hình chóp . SABCD có đáy là hình bình hành ABCD . Gọi , MN lần lượt là trung điểm của , SASB và P là điểm bất kì thuộc cạnh CD . Biết rằng thể tích của khối chóp . SABCD là V .

Tính thể tích khối tứ diện AMNP theo V .

A. 8 V . B. . 12 V C. . 6 V D. . 4 V Lời giải

//;//// PAMNCAMNCSABCDABABSABCDSABCDAMNddd ⊂  ==

Ta có ()()() () () () () () (),,,

Do đó () () () (),,

11111 33448 AMNPAMNSABSABC PAMNCSAB VSdSdVV ∆∆ ====

Câu 38: Cho hình lập phương ABCDABCD ′′′′ có diện tích mặt chéo ACCA′′ là 2 22 a . Thể tích khối lập phương ABCDABCD ′′′′ là:.

A. 3 a B. 3 2a C. 3 2 a D. 3 22 a Lời giải

Đặt cạnh của hình lập phương là x .

Theo bài ra ta có ACCA′′ là hình chữ nhật với ;2AAxACx ′ ==

Diện tích mặt chéo ACCA′′ là 2 22 a nên 2 .2222 xxaxa =⇔= .

Do đó thể tích khối lập phương . ABCDABCD ′′′′ là: 3322Vxa ==

Câu 39: Cho khối lăng trụ đều . ABCABC′′′ có ABa = , 2 AAa ′ = . Góc giữa đường thẳng AB ′ và mặt phẳng () BCCB′′ bằng

A. 60° . B. 30° . C. 45° . D. 90° . Lời giải

Gọi M là trung điểm của cạnh BC′′ , suy ra ()AMBCCB ′′′ ⊥ , MB là hình chiếu vuông góc của AB ′ trên mặt phẳng () BCCB′′ ; Khi đó: () () (),, ′′′′′ == ABBCCBABMBABM .

Xét tam giác ' ABM vuông tại M ta có: 3 3; 2 a ABaAM ′′ ==

Gọi K là trung điểm của cạnh AB ()ABEKC  ⊥ ,

Dựng () , CHEKHEK ⊥∈ ()CHEAB  ⊥ . Khi đó () () , dCABECH =

Xét tam giác ECK vuông tại C có 2 ; 222 ABaCC CKCEa ′ ==== 222 2

a a CKCEa CH CKCEa a

=== + +

2 .3 2 3 2

Vậy khoảng cách giữa hai đường thẳng AB và MC′ là 3 3 a .

Câu 41: Cho khối lăng trụ có đáy là tam giác đều cạnh bằng a và thể tích bằng 3 3a . Chiều cao của khối lăng trụ đã cho bằng

A. 123a B. 63a C. 43a D. 23a Lời giải

3 1 2 sin30 2 3

a AM ABMABM AB a

′ ′′ ===  =° ′ . Vậy góc giữa đường thẳng AB ′ và mặt phẳng () BCCB′′ là 30° .

Câu 40: Cho khối lăng trụ đứng . ABCABC′′′ có độ dài cạnh bên bằng2a , đáy là tam giác ABC vuông cân tại C ; CACBa == . Gọi M là trung điểm của cạnh AA′ . Khoảng cách giữa hai đường thẳng AB và MC ′ bằng

A. 3 3 a B. 3 a C. 3 2 a D. 2 3 a Lời giải

Diện tích đáy của khối lăng trụ là tam giác đều có cạnh bằng a là 2 3 4 a

Gọi E là trung điểm của cạnh CC ′ () //, AEMCECC ′′  ∈ ()() () () () () (),,,, dABMCdMCEABdCEABdCEAB ′′′ === .

a a a = .

Chiều cao của lăng trụ là: 3 2 3 43 3 4

A. 12a . B. 6a . C. 3a . D. 4a . Lời giải

S H D

K M C B

Ta có: 1 2 = SABDSABCDVV (do 1 2 = ABDABCDSS ) 33 1 42 2  == SABD Vaa

Mà: () () 1 ,. 3 SABDSAB VdDSABS∆ = () () 3 2 3.2 ,6 a dDSABa a  ==

Lại có: () () () () , 1 2 ,

dMSAB dDSAB = ( Do M là trung điểm SD ) () () 1 ,.63 2 dMSABaa  ==

Vậy khoảng cách từ M tới mặt phẳng () SAB là 3a .

Câu 43: Cho tứ diện ABCD có 2,7,3===== ABBDADaACaBCa . Biết khoảng cách giữa hai

đường thẳng , ABCD bằng a . Tính thể tích của khối tứ diện ABCD .

A. 3 26 3 a B. 3 22 3 a C. 3 26a D. 3 22a

Lời giải

Do 2,7,3===== ABBDADaACaBCa nên ∆ABD đều và ∆ABC vuông tại B

Dựng hình chữ nhật ABCE () ABECABDEC ()() (),,  == dABCDdABCEDa .

Gọi , MN lần lượt là trung điểm của , ABCE và H là hình chiếu của D lên MN .

Ta có: ⊥   ⊥  ABDM ABMN ()  ⊥  ⊥ ABDMNABDH .

Mà ⊥ DMMN ()  ⊥ DHABCD .

Tam giác DMN có 23 3 2 == a DMa , 3 == MNBCa

 ∆DMN cân tại M và () () , == MIdMDECa MI cũng là đường trung tuyến của tam giác

∆DMN

∆DMI vuông tại I 22 2  =−= DIDMMIa

Mà 2 = DNDI 22  = DNa .

Tam giác DMN có: ..2

∆ == DMN DHMNMIDNS

Ta có o o 3 cos302 cos30 h l l =  == .

Câu 46: Gọi ;; lhr lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình trụ. Đẳng thức nào sau đây đúng?

A. lh = . B. hr = . C. 222 lrh =+ . D. 222 rlh =+ .

Lời giải

Hình trụ có ;; lhr lần lượt là độ dài đường sinh, chiều cao và bán kính đáy. Khi đó, lh = . Chọn A

Câu 47: Thể tích của miếng Piza dạng nửa hình trụ có đường kính đáy 18 cm và chiều cao

3 cm là

A. 243 2 π B. 81π C. 243π D. 972π

Ta có 189dr =  = .

Lời giải

Thể tích của miếng Piza là 2 11243 .81.3 222 Vrhπππ===

Câu 48: Cho hình chóp . SABC có () ⊥ SAABC , 3,2==ABAC và 60 =° BAC . Gọi , MN lần lượt là

hình chiếu của A lên , SBSC . Tính bán kính R mặt cầu ngoại tiếp hình chóp . ABCNM

A. 2 = R . B. 21 3 = R . C. 4 3 = R . D. 1 = R .

Lời giải

..2226

 === MIDNaaa DH MN a .

3 3

Vậy: 3 1126122 ...2.3 33323

∆ === DABCABC aa VDHSaa .

Câu 44: Công thức tính diện tích xung quanh của hình nón tròn xoay có bán kính đáy r và độ dài đường sinh l là:

A. = xq Srl B. 2π = xq Srl C. π = xq Srl D. 2 = xq Srl

Lời giải

Công thức tính diện tích xung quanh của hình nón là: π = xq Srl .

Câu 45: Hình nón có góc ở đỉnh bằng o60 và chiều cao bằng 3 Độ dài đường sinh của hình nón bằng

A. 2 l = . B. 22 l = . C. 23 l = . D. 3 l = .

M N E A B D C H I Lời giải

Câu 50: Cho tứ diện ABCD có tam giác BCD vuông tại C , AB vuông góc với mặt phẳng

, 5,3== ABaBCa và 4 = CDa . Tính bán kính R của mặt cầu ngoại tiếp t

A. 52 3 = a R B. 53 3 = a R C. 52 2 = a R D.

Cách 1 áp dụng công thức tính nhanh () 2 2 4 =+cd h RR

Trong đó bán kính của đường tròn ngoại tiếp tam giác BCD bằng ()() 22 22 34 5

2222 + + ==== d aa BDBCCDa R .

Chiều cao của tứ diện 5 == hABa

Vậy () 2 2 5 552 242  =+=   c

a aa R .

Gọi I là tâm đường tròn ngoại tiếp tam giác  == ABCIAIBIC .

Gọi , EF lần lượt là trung điểm của , ABAC

Ta có

Cách 2

()() () ()()

⊥    ⊥⊥  ⊥⊥⊂   IEAB IESABhayIEMAB IESAdoSAABCIEABC .

Mặt khác tam giác MAB vuông tại M nên E là tâm đường tròn ngoại tiếp tam giác MAB .

Do vậy IE là trục của đường tròn ngoại tiếp tam giác  == MABIMIAIB () * .

Tương tự có IF là trục của đường tròn ngoại tiếp tam giác () **  == NACINIAIC

Từ () * và () ** ====  IAIBICINIMI là tâm của mặt cầu ngoại tiếp hình chóp . ABCNM .

Bán kính mặt cầu .. 4 ∆

ABBCAC RIA S Có 1133 ....2.3.sin60 222 ∆ === ABC SABABsinA

== ABC

Lại có 22222...cos322.3.2.cos607 =+−=+−°=BCABACABACA

Do tam giác BCD vuông tại C nên gọi O là tâm đường tròn ngoại tiếp tam giác BCD  O là trung điểm BC .

Dựng trục d của đường tròn ngoại tiếp tam giác BCD

== R

Do vậy 3.2.721 3 33 4. 2

Câu 49: Cho mặt cầu () ; SIR và mặt phẳng () P cách I một khoảng bằng 2 R . Khi đó thiết diện của () P

và () S là một đường tròn có bán kính bằng

A. R . B. 3 2 R . C. 3 R . D. 2 R .

Lời giải

Gọi r là bán kính của đường tròn giao tuyến.

Ta có () () 2 2

Dựng mặt phẳng () P là mặt phẳng trung trực của cạnh AB cắt AB tại H

Giả sử () ∩= dPI .

Ta có () 1 ∈  == IdIBICID

Lại có ()() 2 ∈  = IPIAIB

Từ () 1 và () 2 ta có === IAIBICID  I chính là tâm mặt cầu ngoại tiếp tứ diện và bán kính ()() 22 22 5552 222  =+=+= 

22 3

22   =−=−=    RR rRdIPR .

() BCD

ứ diện ABCD .

Lời giả

= a R

 aaa

---------- HẾT ----------

RHBOB .

TRƯỜNG THPT TRIỆU QUANG PHỤC HƯNG YÊN

THI THỬ TỐT NGHIỆP THPT NĂM HỌC -2022-2023

Câu 1: Hàm sô nào dưới đây nghịch biến trên tập xác định của nó?

A. 2 3 log yx = B. 5 2 log yx = C. ln yx = D. log yx =

Câu 2: Số các tổ hợp chập 3 của 12 phần tử là

A. 1728 B. 220 C. 36 D. 1320

Câu 3: Cho hình lăng trụ đứng ABCABC′′′ có đáy ABC là tam giác vuông tại B , 2,3ACAB== và

1 AA′ = (tham khảo hình bên).

Góc giữa hai mặt phẳng () ABC′ và () ABC bằng

A. 0 45. B. 0 90. C. 0 30. D. 0 60.

Câu 4: Cho hình chóp đều SABCD . Khẳng định nào sau đây là sai?

A. Các mặt bên tạo với đáy các góc bằng nhau.

B. Tất cả các cạnh đều bằng nhau.

C. Hình chiếu vuông góc của S lên mặt phẳng ABCD là tâm của đáy.

D. Các mặt bên là tam giác cân.

Câu 5: Gọi ,, lhr lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy. Diện tích xung quanh

xq S của hình nón là

A. xq Srl π = B. 2 xq Srl π = C. xq Srh π = D. 2 1 3 xq Srh π =

Câu 6: Một hình lập phương có diện tích mỗi mặt bằng 2 4 cm . Tính thể tích của khối lập phương đó

A. 3 6 cm B. 3 2 cm C. 3 64 cm D. 3 8 cm

Câu 7: Cho khối chóp SABC có chiều bằng 3 , đáy ABC có diện tích bằng 10 . Thể tích khối chóp SABC bằng

A. 15. B. 30. C. 2 . D. 10.

Câu 8: Tập xác định của hàm số () 3 2 yxx =− là

A. ()() ;01; −∞∪+∞ . B. {}\0 ℝ . C. {}\0;1 ℝ . D. () 0;1 .

Câu 9: Một cấp số cộng có 2 5 u = và 3 9 u = . Khẳng định nào sau là khẳng định đúng?

A. 4 12 u = . B. 4 4 u = . C. 4 13 u = . D. 4 36 u = .

Câu 10: Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh ,() ABaSAABCD =⊥ và SAa = . Thể tích khối chóp SABCD bằng

A. 3 6 a . B. 3 2 a C. 3 a D. 3 3 a .

Câu 11: Cho ,0xy > và , αβ∈ ℝ . Tìm đẳng thức sai dưới đây.

A. xxxαβαβ + = B. ()xyxy α αα+=+

C. ()xyxy α αα = D. ()xx β ααβ =

Câu 12: Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số ()() log62 =−+

A. 9. B. 7. C. 8. D. Vô số.

Câu 13: Tập xác định của hàm số () 3 log4yx=− là

A. () 4;+∞ . B. () ;4−∞ . C. () ; −∞+∞ . D. () 5;+∞ .

Câu 14: Phương trình đường tiệm cận ngang của đồ thị hàm số 1 21 x y x = + là

A. 1 2 x = . B. 1 2 x =− . C. 1 2 y = . D. 1 2 y =− .

Câu 15: Số mặt phẳng đối xứng của hình lập phương là:

A. 8. B. 7. C. 6. D. 9.

Câu 16: Cho đồ thị hàm số và như hình vẽ. Khẳng định nào sau đây đúng?

x ya = logb yx =

A. 1,01.ab><< B. 1,1.ab>> C. 01,1. ab <<> D. 01,01. ab <<<<

Câu 17: Hàm số 32 23122022yxxx =+−+ nghịch biến trên khoảng nào sau đây?

A. () ;0−∞ B. () 2;1 . C. () 1; +∞ . D. () ;2−∞− .

Câu 18: Cho cấp số nhân () n u với 1 1 u = và 2 2 u = . Công bội của cấp số nhân đã cho là:

A. 1 2 q =− . B. 1 2 q = . C. 2 q =− . D. 2 q = .

Câu 19: Tập nghiệm của bất phương trình 5 log(1)2 x +> là

A. () 9; +∞ . B. () 24; +∞ . C. () 31; +∞ . D. () 25;; +∞ .

Câu 20: Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 32 1 231 3 yxxx =−++ trên đoạn [] 0;4 . Tính tổng SMn =+

A. 7 3 . B. 1. C. 10 3 . D. 4 .

Câu 21: Cho hình trụ có chiều cao 1 h = và bán kính 2 r = . Diện tích xung quanh của hình trụ đã cho bằng

A. 2π B. 6π C. 4π D. 3π

Câu 22: Tìm m để hàm số () 3211yxmxmx =+−−+ đạt cực tiểu tại 1 x =

 yxx

A. m ∈∅ B. 1 m = C. 0 m = D. 1 m =−

Câu 23: Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [] 40;60 . Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng

A. 2 5 . B. 3 7 . C. 3 5 . D. 4 7 .

Câu 24: Biết rằng phương trình () 2 3 log20212022 xx−= có 2 nghiệm 12 , xx . Tính tổng 12xx + .

A. 2022 12 3 xx+=− B. 3 12 2022 xx+=−

C. 12 2021 xx+= . D. 12 2021 xx+=− .

Câu 25: Cho hàm số ()yfx = có đồ thị là đường cong như hình vẽ bên dưới.

A. () 1;0 . B. () ;1−∞− . C. ()0;. +∞ D. () 2;1.

Câu 29: Chọn khẳng địnhk sai?

A. Mỗi cạnh của khối đa diện là cạnh chung của đúng 2 mặt của khối đa diện.

B. Mỗi mặt của khối đa diện có ít nhất ba cạnh.

C. Mỗi đỉnh của khối đa diện luôn là đỉnh chung của ít nhất 3 mặt.

D. Hai mặt của khối đa diện luôn có ít nhất một điểm chung.

Câu 30: Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 2a , cạnh bên bằng 3a . Tính thể tích V của khối chóp đã cho?

A. 3 47 3 a V = B. 3 4 3 a V = C. 3 47 9 a V = D. 3 47 Va =

Câu 31: Cho khối lăng trụ có diện tích đáy là 2 3a và chiều cao là 2a . Thể tích khối lăng trụ đã cho bằng:

A. 3 a B. 3 3a C. 3 2a D. 3 6a

Câu 32: Cho hàm số ()yfx = có đồ thị là đường cong như hình vẽ

Số nghiệm của phương trình () 2 fx =− bằng

A. 2 B. 3. C. 0. D. 1

Câu 26: Cho hình hộp chữ nhật .'''' ABCDABCD có ;2 ABaBCa == và '3 AAa = (tham khảo hình bên).

Khoảng cách giữa hai đường thẳng BD và ''AC bằng?

A. a . B. 2a. C. 2a. D. 3a .

Câu 27: Nghiệm của phương trình 21233xx = là:

A. 1 3 x = . B. 0 x = . C. 1 x = . D. 1 x =−

Câu 28: Cho hàm số ()yfx = có bảng biến thiên như hình vẽ

Giá trị lớn nhất của hàm số trên [] 2;2 bằng:

A. 0. B. 2 C. 1 D. 3

Câu 33: Với a là số thực dương tùy ý, 4log a bằng

A. 2log a B. 8log a C. 4log a D. 2log a

Câu 34: Cho hàm số 42 ax,(,,)ybxcabc =++∈ ℝ có đồ thị là đường cong như hình vẽ dưới đây.

Mệnh đề nào sau đây đúng?

A. 0,0,0abc>>< B. 0,0,0abc><> C. 0,0,0abc><< D. 0,0,0abc<>>

Câu 35: Đường cong trong hình vẽ bên dưới là của đồ thị hàm số nào sau đây?

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. 22x 1 y x = + B. 4222.yxx=++ C. 21 . 2 x y x −+ = + D. 3 21.yxx=−+

Câu 36: Ông A có 200 triệu đồng gửi tiết kiệm tại ngân hàng với kì hạn 1 tháng so với lãi suất 0,6% trên 1 tháng được trả cuối kì. Sau mỗi kì hạn ông đến tất toán cả gốc lẫn lãi, rút ra 4 triệu đồng để tiêu dùng, số tiền còn lại ông gửi vào ngân hàng theo phương thức trên (phương thức giao dịch và lãi suất không thay đổi trong suốt quá trình gửi). Sau đúng 1 năm (đúng 12 kì hạn) kể từ ngày gửi, ông A tất toán và rút ra toàn bộ số tiền nói trên ở ngân hàng, số tiền đó là bao nhiêu? (làm tròn đến nghìn đông).

A. 165269 (nghìn đông). B. 168269 (nghìn đông).

C. 169234 (nghìn đông). D. 165288 (nghìn đông).

Câu 37: Cho hàm số ()yfx = có bảng biến thiên như hình vẽ:

Số đường tiệm cận của đồ thị hàm số ()yfx = là

A. 2. B. 4. C. 1. D. 3.

Câu 38: Cho hàm số ()yfx = có đồ thị là đường cong như hình vẽ:

Câu 39: Hình bát diện đều có bao nhiêu đỉnh

A. 6. B. 10. C. 8. D. 12

Câu 40: Cho hàm số () = yfx liên tục trên ℝ và ()()()′ =+− 2 21 fxxxx . Hàm số đã cho nghịch biến

trên khoảng nào dưới đây

A. () 1;1 B. () −∞;1 C. () 0;2 D. () 2;3

Câu 41: Cho đường cong () ()()32 :31313. m Cyxmxmx =−−−++ Gọi S là tập các giá trị của tham số m để đồ thị hàm số có hai điểm cực trị , AB sao cho ,, OAB thẳng hàng. Tổng các phần tử của S bằng

A. 3. B. 0. C. 2. D. 1.

Câu 42: Cho tháp nước như hình dưới đây, tháp được thiết kế gồm thân tháp có dạng hình trụ, phần mái phía trên dạng hình nón và đáy là nửa hình cầu. Không gian bên trong toàn bộ tháp được minh họa theo hình vẽ với đường kính đáy hình trụ, hình cầu và đường kính đáy của hình nón đều bằng 3m , chiều cao hình trụ là 2m , chiều cao của hình nón là 1m .

Thể tích của toàn bộ không gian bên trong tháp nước gần nhất với giá trị nào sau đây?

A. () 3 7 Vm π = . B. () 3 8 Vm π = . C. () 3 15 2 Vm π = . D. () 3 33 4 Vm π = .

Câu 43: Cho hàm số ()yfx = liên tục và xác định trên R có đồ thị đạo hàm ()fx được cho như hình vẽ. Hàm số () 2 1 yfx=− đồng biến trên khoảng nào sau đây?

Khẳng định nào sau đây đúng?

A. Đồ thị hàm số có điểm cực đại là ()3;1. B. Đồ thị hàm số có điểm cực đại là ()1;1.

C. Đồ thị hàm số có điểm cực tiểu là ()1;1. D. Đồ thị hàm số có điểm cực đại là ()1;3.

A. () 1; +∞ B. () ;1−∞− C. () 0;1 D. () 1;2

Câu 44: Một cốc thủy tinh hình nón có chiều cao 20cm. Người ta đổ vào cốc thủy tinh một lượng nước sao cho chiều cao của lượng nước trong cốc bằng 3 4 chiều cao cốc thủy tinh, sau đó người ta bịt kín miệng cốc rồi lật úp cốc xuống như hình vẽ thì chiều cao của nước trong cốc bằng bao nhiêu( làm tròn đến chữ số thập phân thứ 2).

Câu 49: Cho khối lăng trụ đứng .''' ABCABC có đáy ABC là tam giác vuông cân tại A , ABC . Góc giữa đường thẳng ' BC và mặt phẳng ( )''ACCA bằng 030 . Thể tích của khối lăng trụ đã cho bằng?

A. 3 a . B. 3 3a . C. 3 122a . D. 3 42a .

Câu 50: Cho hàm số 2 2 21 2 xmx y xx −+ = −+ . Có tất cả bao nhiêu giá trị nguyên của tham số [ ]10;10 m ∈−

giá trị lớn nhất của hàm số lớn hơn hoặc bằng 4

A. 20 . B. 14 . C. 10. D. 18 . ---------- HẾT ----------

A. 3,34cm B. 2,21cm C. 5,09cm D. 4,27cm

Câu 45: Cho hàm số 2 2 22 x y xmxm = . Biết với (,, mabaa bb =∈ ℕ tối giản) thì đồ thị hàm số có đúng

2 đường tiệm cận. Tính ab +

A. 6 ab+= B. 7 ab+= C. 5 ab+= D. 8 ab+=

Câu 46: Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ.

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình

() 3 33210 fxxm−+−+= có 8 nghiệm phân biệt

A. 6. B. 7. C. 8. D. 5.

Câu 47: Xét tất cả các số thực , xy cho sao cho 2 2 54log 4025 xa y a ≤ với mọi số thực dương a . Giá trị lớn nhất của biểu thức 22 3 Pxyxy =++− bằng

A. 60. B. 20. C. 125 2 . D. 80.

Câu 48: Cho ()fx là hàm số bậc bốn và hàm số ()yfx ′ = có đồ thị là đường cong như hình dưới đây.

Hỏi hàm số ()() cos2 sin1 4 x gxfx=−+ có bao nhiêu điểm cực trị thuộc khoảng () 0;2π ?

A. 4 B. 3. C. 5 D. 2

để

HƯỚNG DẪN GIẢI CHI TIẾT.

Câu 1: Hàm sô nào dưới đây nghịch biến trên tập xác định của nó?

A. 2 3 log yx = B. 5 2 log yx = C. ln yx = D. log yx =

Lời giải

Vì hàm số lôgarit log a yx = nghịch biến trên tập xác định của nó khi cơ số a thỏa mãn

01 a <<

Câu 2: Số các tổ hợp chập 3 của 12 phần tử là

A. 1728 . B. 220 . C. 36 . D. 1320 .

Lời giải

Ta có: 3 12 220 C =

Câu 3: Cho hình lăng trụ đứng . ABCABC′′′ có đáy ABC là tam giác vuông tại B , 2,3ACAB== và

1 AA′ = (tham khảo hình bên).

Mặt khác ABBC ABBC ABBB ⊥  ′  ⊥ ′ ⊥

Do đó ()()( ) 0,45ABCABCCBC ′′ ==

(vì 1 CCAA ′′ == và 22 1 BCACAB=−= nên tam giác BCC ′ vuông cân tại C).

Câu 4: Cho hình chóp đều . SABCD . Khẳng định nào sau đây là sai?

A. Các mặt bên tạo với đáy các góc bằng nhau.

B. Tất cả các cạnh đều bằng nhau.

C. Hình chiếu vuông góc của S lên mặt phẳng ABCD là tâm của đáy.

D. Các mặt bên là tam giác cân.

Lời giải

Khẳng định B sai vì hình chóp đều có đáy là đa giác đều, các cạnh bên bằng nhau, chứ cạnh bên chưa chắc đã bằng cạnh đáy.

Câu 5: Gọi ,, lhr lần lượt là độ dài đường sinh, chiều cao và bán kính mặt đáy. Diện tích xung quanh

xq S của hình nón là

A. xq Srl π = B. 2 xq Srl π = C. xq Srh π = D. 2 1 3 xq Srh π = Lời giải Chọn A

Câu 6: Một hình lập phương có diện tích mỗi mặt bằng 2 4 cm . Tính thể tích của khối lập phương đó A. 3 6 cm . B. 3 2 cm . C. 3 64 cm . D. 3 8 cm .

Lời giải

Ta có: Diện tích của một mặt bằng 2 4 cm  mỗi cạnh của hình lập phương bằng 2 cm  thể tích của khối lập phương đó bằng 3328 cm =  phương án D đúng. Chọn D

Câu 7: Cho khối chóp SABC có chiều bằng 3 , đáy ABC có diện tích bằng 10 . Thể tích khối chóp SABC bằng

A. 15 . B. 30 . C. 2 . D. 10.

Góc giữa hai mặt phẳng () ABC′ và () ABC bằng

A. 0 45. B. 0 90. C. 0 30. D. 0 60.

Lời giải

Ta có ()() ABCABCAB ′ ∩=

Ta có: 11 ..3.1010 33 ABC VhS∆ ===

Câu 8: Tập xác định của hàm số ( ) 3 2 yxx =− là

A. ( ) ( ) ;01; −∞∪+∞ . B. { }\0 ℝ . C. { }\0;1 ℝ . D. ( )0;1 . Lời giải

Ta có: {} 2 0 0\0;1 1 x xx x

≠  −≠⇔   ≠  ℝ .

Câu 9: Một cấp số cộng có 2 5 u = và 3 9 u = . Khẳng định nào sau là khẳng định đúng?

A. 4 12 u = . B. 4 4 u = . C. 4 13 u = . D. 4 36 u = .

Lời giải

Gọi 1; ud lần lượt là số hạng đầu và công sai của cấp số cộng. Ta có:

BẢNG ĐÁP ÁN 1.A 2.B 3.A 4.B 5.A 6.D 7.D 8.C 9.C 10.D 11.B 12.B 13.A 14.C 15.D 16.A 17.B 18.D 19.B 20.C 21.C 22.D 23.B 24.C 25.A 26.D 27.C 28.A 29.D 30.A 31.D 32.C 33.D 34.B 35.A 36.A 37.A 38.D 39.A 40.D 41.B 42.C 43.C 44.A 45.B 46.D 47.A 48.B 49.D 50.B



55 1 929 4 uud u uud d =+= =   ⇔⇔  =+= =    Suy ra 41 313uud=+=

21 1 31

Câu 10: Cho hình chóp tứ giác SABCD có đáy là hình vuông cạnh ,() ABaSAABCD =⊥ và SAa = .

Thể tích khối chóp SABCD bằng

A. 3 6 a . B. 3 2 a C. 3 a D. 3 3 a .

Lời giải 3 2 11 .. 333SABCDABCD a VSSAaa ===

Câu 11: Cho ,0xy > và , αβ∈ ℝ . Tìm đẳng thức sai dưới đây.

A. . xxxαβαβ + = B. ( )xyxy α αα+=+

C. ( ) xyxy α αα = D. ( ) xx β ααβ =

Lời giải

Theo tính chất của lũy thừa thì ( )xyxy α αα+=+ sai

Câu 12: Có bao nhiêu giá trị nguyên thuộc tập xác định của hàm số ( )( )log62 =−+

yxx

A. 9 . B. 7 . C. 8 . D. Vô số.

Lời giải

Hàm số xác định ⇔ ( )( ) 620 −+> xx 26⇔−<< x

Do đó, tập xác định ( )2;6=− D

Các giá trị nguyên thuộc D là 1;0;1;2;3;4;5 . Vậy có 7 giá trị nguyên thỏa mãn yêu cầu.

Câu 13: Tập xác định của hàm số ( ) 3 log4yx=− là

A. ( ) 4;+∞ B. ( );4−∞ C. ( ) ; −∞+∞ D. ( ) 5; +∞

Lời giải

Điều kiện xác định của hàm số đã cho là

404xx−>⇔>

Vậy tập xác định của hàm số là ( ) 4; D =+∞ .

Câu 14: Phương trình đường tiệm cận ngang của đồ thị hàm số 1 21 x y x = + là

A. 1 2 x = B. 1 2 x =− C. 1 2 y = D. 1 2 y =−

Lời giải

Hàm số 1 21 x y x = + là hàm số nhất biến axb y cxd + = + nên đồ thị hàm số có đường tiệm cận ngang

là đường thẳng 1 2 a y c == .

Câu 15: Số mặt phẳng đối xứng của hình lập phương là:

A. 8 B. 7 C. 6 D. 9

Lời giải

Hình lập phương . ABCDABCD ′′′′ có 9 mặt đối xứng: 3 mặt phẳng trung trực của ba cạnh

,, ABADAA′ và 6 mặt phẳng mà mỗi mặt phẳng đi qua hai cạnh đối diện.

Câu 16: Cho đồ thị hàm số và như hình vẽ. Khẳng định nào sau đây đúng?

x ya = logb yx =

A. 1,01.ab><< B. 1,1.ab>> C. 01,1. ab <<> D. 01,01. ab <<<<

Lời giải

Từ đồ thị hàm số suy ra hàm số x ya = đồng biến trên ℝ nên 1 a > ; hàm số logb yx = nghịch biến trên () 0; +∞ nên 01 b << .

Câu 17: Hàm số 32 23122022yxxx =+−+ nghịch biến trên khoảng nào sau đây?

A. () ;0−∞ B. () 2;1 . C. () 1; +∞ . D. () ;2−∞− .

Lời giải +) 2 6612yxx ′ =+− ; 1 0 2 x y x =  ′ =⇔  =− 

+) Ta có: ()0,2;1yx ′ <∀∈− . Chọn đáp án B.

Câu 18: Cho cấp số nhân () n u với 1 1 u = và 2 2 u = . Công bội của cấp số nhân đã cho là:

A. 1 2 q =− . B. 1 2 q = C. 2 q =− D. 2 q =

Lời giải

Ta có, công bội: 2 1

2 u q u == . Chọn đáp án D.

Câu 19: Tập nghiệm của bất phương trình 5 log(1)2 x +> là

A. () 9; +∞ . B. () 24; +∞ . C. () 31; +∞ . D. () 25;; +∞ .

Lời giải

Điều kiện: 101xx+>⇔>− .

Khi đó: 5 log(1)212524 xxx +>⇔+>⇔>

Kết hợp điều kiện ta có, tập nghiệm của bất phương trình là: () 24; T =+∞ .

Câu 20: Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 32 1 231 3 yxxx =−++ trên

đoạn [] 0;4 . Tính tổng SMn =+



Dễ thấy hàm số liên tục trên ℝ

Ta có: 2 43yxx ′ =−+

1 0 3 x y x =  ′ =⇔  =  ( ) 01 y = . () 7 1 3 y = . ( ) 31 y = () 7 4 3 y = Vậy [] ()() [] ()() 0;4 0;4

Lời giải

Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [] 40;60 có 21 số nên số phần tử

của không gian mẫu là: () 21 n Ω= .

Gọi A là biến cố “ số được chọn có chữ số hàng đơn vị lớn hơn chữ số hàng chục”.

Khi đó {} 45;46;47;48;49;56;57;58;59 A = , nên () 9 nA =

Vậy xác suất của biến cố A là () () () 93 217 nA PA n === Ω .

Câu 24: Biết rằng phương trình () 2 3 log20212022 xx−= có 2 nghiệm 12 , xx . Tính tổng 12xx +

A. 2022 12 3 xx+=− . B. 3 12 2022 xx+=− .

C. 12 2021 xx+= D. 12 2021 xx+=−

Lời giải.

Phương trình: ()22202222022 3 log2021202220213202130 xxxxxx −=⇔−=⇔−−= luôn có 2 nghiệm phân biệt 12 , xx nên theo định lí Viét ta có: 12 2021 xx+= .

Câu 25: Cho hàm số ()yfx = có đồ thị là đường cong như hình vẽ bên dưới.

 ====    =+=+=  ====   

Myyy SMm myyy

7 max14 710 3 1 33 min031

Câu 21: Cho hình trụ có chiều cao 1 h = và bán kính 2 r = . Diện tích xung quanh của hình trụ đã cho bằng

A. 2π B. 6π C. 4π D. 3π

Lời giải

Ta có: 22.2.14 xq Srlπππ=== .

Câu 22: Tìm m để hàm số ( ) 3211yxmxmx =+−−+ đạt cực tiểu tại 1 x =

A. m ∈∅ B. 1 m = C. 0 m = D. 1 m =−

Lời giải

Tập xác định: D = ℝ

Ta có ( ) 2 '321 yxmxm =+−− .

Hàm số đạt cực tiểu tại 1 x = nên ( ) ( ) '103210101 ymmmm =  +−−=⇔+=⇔=− .

Ta có ( )''621yxm=+− . Suy ra ( ) ( ) ''16.12.1120 y =+−−=>

Vậy khi 1 m =− hàm số đã cho đạt cực tiểu tại 1 x = .

Câu 23: Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [ ]40;60 . Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng

ờ

Số nghiệm của phương trình () 2 fx =− bằng

A. 2 B. 3. C. 0. D. 1

Lời giải

Số nghiệm của phương trình () 2 fx =− bằng số giao điểm của đồ thị hàm số ()yfx = và đường thẳng 2 y =−

Do đó phương trình () 2 fx =− có 2 nghiệm.

Câu 26: Cho hình hộp chữ nhật .'''' ABCDABCD có ;2 ABaBCa == và '3 AAa = (tham khảo hình bên).

Khoảng cách giữa hai đường thẳng BD và ''AC bằng?

A. a B. 2a C. 2a D. 3a Lời giải

Ta có () () () ;'' );('''' '3 BDAC ABCDABCD ddAAa === .

D. 4

A. 7 3 B. 1

10 3

A. 2 5 . B. 3 7 . C.

5 . D. 4 7 .

i giả

Câu 27: Nghiệm của phương trình 21233xx = là:

A. 1 3 x = . B. 0 x = .

Lời giải Ta có 212 332121. xx xxx =⇔−=−⇔=

Câu 28: Cho hàm số ()yfx = có bảng biến thiên như hình vẽ

Gọi Vì hình chóp đều

OACBD =∩

. SABCD ( )SOABCD  ⊥

Ta có: 22 2 22 ACa OAa === 2222927SOSAAOaaa =−=−=

Do đó () 3 2 1147 ...2.7 333 ABCD a VSSOaa ===

Câu 31: Cho khối lăng trụ có diện tích đáy là 2 3a và chiều cao là 2a . Thể tích khối lăng trụ đã cho bằng:

A. 3 a . B. 3 3a . C. 3 2a . D. 3 6a .

Lời giải

Thể tích khối lăng trụ đã cho là: 23.3.26 VShaaa === .

Câu 32: Cho hàm số ()yfx = có đồ thị là đường cong như hình vẽ.

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. () 1;0 . B. () ;1−∞− . C. ()0;. +∞ D. () 2;1.

Lời giải + Ta có ()0,1;0yx ′ >∀∈−  hàm số đồng biến trên ()1;0.

Câu 29: Chọn khẳng địnhk sai?

A. Mỗi cạnh của khối đa diện là cạnh chung của đúng 2 mặt của khối đa diện.

B. Mỗi mặt của khối đa diện có ít nhất ba cạnh.

C. Mỗi đỉnh của khối đa diện luôn là đỉnh chung của ít nhất 3 mặt.

D. Hai mặt của khối đa diện luôn có ít nhất một điểm chung.

Lời giải

Hai mặt của khối đa diện có thể không có điểm chung.

Câu 30: Cho hình chóp tứ giác đều . SABCD có cạnh đáy bằng 2a , cạnh bên bằng 3a . Tính thể tích V của khối chóp đã cho?

3 47 3 a V = B. 3 4 3 a V = C. 3 47 9 a V = D. 3 47 Va =

Lời giải

Giá trị lớn nhất của hàm số trên [] 2;2 bằng:

A. 0 . B. 2 . C. 1. D. 3.

Lời giải

Dựa vào đồ thị hàm số, ta được [] max 2;2 1 y =

Câu 33: Với a là số thực dương tùy ý, 4log a bằng

A. 2log a . B. 8log a . C. 4log a . D. 2log a . Lời giải

Ta có: 4log2logaa =

Câu 34: Cho hàm số 42 ax,(,,)ybxcabc =++∈ ℝ có đồ thị là đường cong như hình vẽ dưới đây.

Mệnh đề nào sau đây đúng?

A. 0,0,0abc>>< B. 0,0,0abc><> C. 0,0,0abc><< D. 0,0,0abc<>>

C. 1 x = . D. 1 x =−

B C D

Lời giải

Do đồ thị hàm số cắt trục Oy tại điểm có tọa độ () 0;c nằm phía trên trục Ox nên 0 c > .

Vì lim

x y →+∞ =+∞ và lim x y →−∞ =+∞ nên 0 a >

Hàm số có ba điểm cực trị nên 00abb <  <

Câu 35: Đường cong trong hình vẽ bên dưới là của đồ thị hàm số nào sau đây?

Số đường tiệm cận của đồ thị hàm số ()yfx = là

A. 2. B. 4. C. 1. D. 3. Lời giải

Chọn A

Dựa vào bảng biến thiên ta có:

()()lim; lim1 xx fxfx →+∞→−∞ =+∞= nên đồ thị hàm số có 1 đường tiệm cận ngang là 1. y = () 0 lim x fx → =−∞ nên đồ thị hàm số có 1 đường tiệm cận đứng là 0. x =

Vậy đồ thị hàm số có 2 đường tiệm cận.

Câu 38: Cho hàm số ()yfx = có đồ thị là đường cong như hình vẽ:

A. 22x . 1 y x = + B. 4222.yxx=++ C. 21 2 x y x −+ = + D. 3 21.yxx=−+

Lời giải

Đây là độ thị của hàm nhất biến nên loại đáp án B và D.

Từ đồ thị suy ra: Tiệm cận đứng 1 x =− và tiệm cận ngang 2 y =− Loại đáp án C.

A. 165269 (nghìn đông). B. 168269 (nghìn đông).

C. 169234 (nghìn đông). D. 165288 (nghìn đông). Lời giải

ng công thức tính số ti

Khẳng định nào sau đây đúng?

A. Đồ thị hàm số có điểm cực đại là ()3;1. B. Đồ thị hàm số có điểm cực đại là ()1;1.

C. Đồ thị hàm số có điểm cực tiểu là ()1;1. D. Đồ thị hàm số có điểm cực đại là ()1;3.

Lời giải

Chọn D Dựa vào đồ thị hàm số ta có điểm cực đại của đồ thị hàm số là ()1;3.

Câu 39: Hình bát diện đều có bao nhiêu đỉnh

A. 6. B. 10. C. 8. D. 12

Lời giải

Ta có hình bát diện đều có 6 đỉnh.

Câu 40: Cho hàm số () = yfx liên tục trên ℝ và

()()()′ =+− 2 21 fxxxx . Hàm số đã cho nghịch biến trên khoảng nào dưới đây

A. () 1;1 . B. () −∞;1 . C. () 0;2 . D. () 2;3

Lời giải

ụ

ền còn lại sau n tháng 11 100 1 100 100 n n n r r SAX r     +−           =+−       Với 200 A = triệu đồng, 0,6% r = và 4 X = triệu đồng ta được 12 12 12 1,0061 200.1,0064.165259 0,006 S =−= . Câu 37: Cho hàm số ()yfx = có bảng biến thiên như hình vẽ:

Áp d

02102

Bảng xét dấu của ( ) ′ fx x −∞ 2 0 1 +∞ ( ) ' fx

Do đó hàm số nghịch biến trên ( )2;3

Câu 41: Cho đường cong ( ) ( ) ( ) 32 :31313. m Cyxmxmx =−−−++ Gọi S là tập các giá trị của tham số m để đồ thị hàm số có hai điểm cực trị , AB sao cho ,, OAB thẳng hàng. Tổng các phần tử của S bằng

A. 3. B. 0. C. 2. D. 1.

Lời giải

Chọn B

Thể tích của toàn bộ không gian bên trong tháp nước gần nhất với giá trị nào sau đây?

A. () 3 7 Vm π = B. () 3 8 Vm π = C. () 3 15 2 Vm π = D. () 3 33 4 Vm π = Lời giải Chọn C

( ) ( ) ( ) ( )

32 2 31313. '36131 yxmxmx yxmxm

=−−−++ ⇒=−−−+

Chia tháp nước thành 3 phần theo thứ tự từ trên xuống phần 1 là hình nón, phần 2 là hình trụ và phần 3 là nửa hình cầu.

223 111 11133 ....1. 33324 VhrEOODm

∆>⇔−−−−>⇔−+>⇔−++>

⇔−+>∀∈ ℝ

Để đồ thị hàm số có hai điểm cực trị , AB thì '0 y = có hai nghiệm phân biệt ( ) ( ) ( ) ( )

03614.3.33036367209441630 921630 y mmmmmm mm

2 22 2

Gọi ( ) d là phương trình đường thẳng đi qua hai điểm cực trị , AB

Ta có: ()

()() 2 2 9131.33 22 :333 33933.19.1 mmm bbc dycxdmx aa

( ) ( ) 22:224 dymmxm =−+−+−

Để ,, OAB thẳng hàng thì điểm O thuộc ( ) d . Từ đó ta có ( ) 222 224042oo ymmxmmm =−+−+−⇔=−⇒=± . Từ đó tập { }2;2 S =− . Tổng các phần tử S là 0.

223 222 39 ..2. 22 VhrDAODm

333 33 22239 ... 33324 VrODm

Thể tích tháp nước là 123 39915 4242 VVVV ππππ =++=++=

Xét ()()()  = 

  = 

1 x

x .

′ =⇔+−=⇔=−

fxxxxx

0 + 0 + 0

          =−+−=−−−+−             

()

() 2

π πππ    ====      () 2

π πππ    ====      () 3

π πππ    ====     

()() 221'2.'1yfxyxfx

Đặt 1 SOx = , thì chiều cao cột nước mới trong cốc là hx và

Bảng biến thiên:

Dựa vào bảng biến thiên: hàm số đồng biến trên khoảng () ()0;10;2 ⊂

Câu 44: Một cốc thủy tinh hình nón có chiều cao 20cm . Người ta đổ vào cốc thủy tinh một lượng nước

sao cho chiều cao của lượng nước trong cốc bằng 3 4 chiều cao cốc thủy tinh, sau đó người ta bịt kín miệng cốc rồi lật úp cốc xuống như hình vẽ thì chiều cao của nước trong cốc bằng bao nhiêu( làm tròn đến chữ số thập phân thứ 2).

11 OAR′ = Rx Rh

Gọi V là thể tích khối nón có chiều cao , bán kính đáy . Ta có 2 1 3 VRh π =

′ = xR R h ′  = h R x R′

Gọi 1V là thể tích khối nón có chiều cao , bán kính đáy . Ta có 23 2 1 2 1 ' 33 Rx VRx h π π ==

Vì 1 n VVV −= nên 232 3 2 2 1937 33644 RxRh Rhxh h ππ π −=  =

A. 3,34cm B. 2,21cm C. 5,09cm D. 4,27cm Lời giải

Gọi lần lượt là bán kính và chiều cao của cốc thủy tinh Ta có 20 hcm =

Gọi lần lượt là chiều cao và bán kính đáy của khối nước lúc ban đầu.

,R h 1 , h 1R

Ta có 11 11 1

 ==    ==    

33 44 3 4

hhhh hR RR hR

Thể tích khối nước: 2 2 11 19 364 n Rh VRh π ==

Khi quay ngược cốc, nước trong cốc được biểu diễn như hình vẽ.

Chiều cao cột nước mới trong cốc là 3 37 13,34 4 hxhcm

−=−=

Câu 45: Cho hàm số 2 2 22 x y xmxm = . Biết với (,, mabaa bb =∈ ℕ tối giản) thì đồ thị hàm số có đúng

2 đường tiệm cận. Tính ab +

A. 6 ab+= B. 7 ab+=

C. 5 ab+= D. 8 ab+= Lời giải

Ta có: 2 2 lim00 22 x

x y xmxm →±∞ =  = là đường tiệm cận ngang của đồ thị hàm số

Đồ thị hàm số có đúng 2 đường tiệm cận khi và chỉ khi đồ thị hàm số có đúng 1 đường tiệm cận đứng () 2 2201xmxm ⇔−−−= có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng 2. ()

∆> ⇔⇔⇔⇔=   ++>     =    =   −−−=   

Vậy 2,57.abab ==  +=

Câu 46: Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ.

A. () 1; +∞ . B. () ;1−∞− . C. () 0;1 . D. () 1;2 . Lời giải

 =−

() 22 2 22 1110222 '10 123 33 xxx fx xx xx   −<−<<<−<< −>⇔⇔⇔   −>> <−>    ∪

=−

200 xx=⇔=



  

2 0 4480

0 4480

5 20 5 22.220 mm vn m mm m f mm  ∆= ++=     

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình

() 3 33210 fxxm−+−+= có 8 nghiệm phân biệt

A. 6. B. 7. C. 8. D. 5.

Lời giải

Xét hàm số ()()()2 21fxaxx=+− . Vì ()02221faa =⇔=⇔= .

()()()2 3 2 213 fxxxxx  =−=−+ +

Phương trình: () () () 3 3 1 33210321 3 m fxxmfxx−+−+=⇔−+= .

Sử dụng phương pháp ghép trục :

Phương trình () 1 có 8 nghiệm phân biệt 1 0217 3 m m <<⇔<< . Vậy có 5 giá trị nguyên m thoả mãn.

Câu 47: Xét tất cả các số thực , xy cho sao cho 2 2 54log 4025 xa y a ≤ với mọi số thực dương a . Giá trị lớn nhất của biểu thức 22 3 Pxyxy =++− bằng

A. 60 . B. 20 . C. 125 2 . D. 80. Lời giải Ta có:

Đặt 5 log ta = khi đó bất phương trình () 1 trở thành () 222 42802248020 xttytxtyx ⇔−≤−⇔−+−≥∀∈ ℝ () 2222 20 42802040 0 a xyxy =>  ′ ⇔⇔∆=−−≤⇔+≤  ′ ∆≤

Khi đó: ()() 22 2222 3403401360Pxyxyxyxy =++−≤+−≤+++=

max 60 P ⇔=

Câu 48: Cho ()fx là hàm số bậc bốn và hàm số ()yfx ′ = có đồ thị là đường cong như hình dưới đây.

Hỏi hàm số ()() cos2 sin1 4 x gxfx=−+ có bao nhiêu điểm cực trị thuộc khoảng () 0;2π ?

A. 4 B. 3. C. 5 D. 2 Lời giải

Ta có: ()()()()() cos.sin1sin.coscossin1sin11gxxfxxxxfxx ′′′ =−−=−−−−

()()()() ()()() cos0 0 cossin1sin11 sin1sin1101 x gxxfxx fxx =  ′′ =⇔−−−−⇔  ′ −−−−= 

Đăt sin1tx=− . Khi đó () 1 trở thành: ()() 12 ftt ′ =+

Số nghiệm của pt () 2 là số giao điểm của đồ thị hàm số ()ft ′ và đường thẳng 1 yt=+

=−−=−  =⇔−= =>−=>

tx tx taaxaa

1sin11 1sin11 1sin11

Từ đồ thi hàm số ta có: ()()

2 2 5

a ≤ () ()() 2 2 2 2 5 5 240 4log4log 40 55 2 55 25loglog5 42loglog8021 y xaxa y aa xaay ⇔≤⇔≤ ⇔−≤−

4log 4025 xa y

49: Cho kh

i l

ng tr

ng .''' ABCABC có đáy ABC là tam giác vuông cân tại A , ABC . Góc giữa đường thẳng ' BC và mặt phẳng () ''ACCA bằng 0 30. Thể tích của khối lăng trụ đã cho bằng?

A. 3 a . B. 3 3a . C. 3 122a . D. 3 42a . Lời giải

'';'''' ' ',''',''30 ⊥   ⊥∩=  ⊥   ===

ABAC ABACCABCACCAC ABAA BCACCABCCAACB 60 BAC  =°

∆

Xét ' ABC

vuông tại A ta

===  =−=−=

()

ACABACBaa CCCAACaaa SABACaaa VSCCaaa

 ===  ===

'.cot'2.tan3023 ''23222. 11 ...2.22 22 .'2.2242

ABC ABCABCABC

∆ ∆

để

2 2

84 250 M x axy xmx xx xmxxx xmxxx xxxmx xmx R xmx m m m m m x −+ −+  −+−+  −+−+⇔  −+−+   −+−− ⇔∀∈  ∀ −++≥    −−≤ −≤≤   ⇔⇔−≤≤ ∈ ≤≤  +−≤   ≤⇔≤ ≤  ≤ −≤ ≤ ℝ Ta thấy [ ]2;4 m∈− thì 4 Maxy ≤ nên ( ] [ ) ;24; m∈−∞−∪+∞ thì 4 Maxy ≥ . Kết hợp với điều kiện [ ] {} 10;10 8;7;6;5;4;3;2;4;5;6;7;8;9;10 m m m  ∈−   ∈−−−−−−−  ∈   ℤ -------HẾT------

sin0

xaaVN π  =  ⇔=⇔=⇔=∈   =+>  ℤ Do () 0;2 xxππ ∈  = Và pt: () cos0 2 xxll π π =⇔=+∈ℤ Do () 2 0;2 3 2 x x x π π π  =  ∈    =   Suy ra

0 gx ′ =

ệm phân biệt: 2 3 2 x x x π π π  =    =   =    Nên hàm

ố

có 3 điểm cực trị thuộc khoả

0;2π

() ()() ()

sin2sin0 sin11

xVNxxkk

()

có 3 nghi

()() cos2 sin1

x gxfx=−+

ng ()

Câu

ố

ụ đứ

Ta có: ()(){} () () () 0

có: ()

0 2 2 22 2 23 .'''

Câu 50: Cho hàm số 2 2 21 2 xmx y xx −+ = −+ . Có tất cả bao nhiêu giá trị nguyên của tham số [ ]10;10 m ∈−

giá trị lớn nhất của hàm số lớn hơn hoặc bằng 4 . A. 20 . B. 14 . C. 10. D. 18 . Lời giả

Ta có:

() () () () () () ()

22 22 22 2 2 2 2 21 2 212 212 221 34270 5

4290 2210 26 24 4 44 4 4. 4.