70-100 ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM 2023 - MÔN TOÁN - CÁC TRƯỜNG - SAU MINH HỌA (28-48) by Dạy Kèm Quy Nhơn Official

WORD VERSION | 2023 EDITION

ĐỀ THI THỬ TỐT NGHIỆP THPT MÔN TOÁN

ễ

ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM HỌC 2022-2023 - MÔN TOÁN - CÁC TRƯỜNG TRÊN CẢ NƯỚC - CÓ LỜI GIẢI (CẬP NHẬT SAU MINH HỌA) (ĐỀ 28-48)

Ths Nguy

n Thanh Tú eBook Collection 70-100

ORDER

TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

NOW / CHUYỂN GIAO QUA EMAIL

TRƯỜNGTHPTBẢOTHẮNG–LÀOCAI

ĐỀ THITHỬ TỐTNGHIỆPTHPT–LẦN1–NĂMHỌC2022-2023

Câu1. Cho hàm số ()fx có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. () ;1−∞ B. () 1;1 C. () ;1−∞− D. () 1; −+∞

Câu2. Cho hàm số 42 yaxbxc =++ có đồ thị như hình vẽ . Số điểm cực trị của đồ thị hàm số là:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. () 1; −+∞ . B. () 1;1 . C. () 1; +∞ D. () 0;1 .

Câu8. Nghiệm của phương trình 2 327 x+ = là

A. 3 x = . B. 2 x = . C. 1 x = . D. 1 x =− .

Câu9. Hình nào sau đây không phải là hình đa diện?

A. 4 B. 1 C. 2 D. 3

Câu3. Cho điểm () 1;2;3 A , () 3;4;5 B . Tọa độ I trung điểm của đoạn AB là

A. () 1;1;4 B. () 1;2;1 C. () 2;0;1 D. () 1;1;0

Câu4. Tập nghiệm S của phương trình () 3 log231 x +=

A. {} 3 S = . B. {} 1 S = . C. {} 1 S =− . D. {} 0 S = .

Câu5. Trong không gian Oxyz , cho mặt cầu ()()()() 222 :1234Sxyz−+−++= . Tọa

độ tâm I và bán kính R của mặt cầu đã cho là

A. () 1;2;3;2IR−= B. () 1;2;3;4IR−=

C. ()1;2;3;2IR−−= D. ()1;2;3;4IR−−=

Câu6. Cho khối lập phương có cạnh bằng 2a . Thể tích khối lập phương đó bằng

A. 3 8a . B. 2 4a . C. 3 8 3 a . D. 3 4a .

Câu7. Cho hàm số bậc bốn ()yfx = có đồ thị trong hình vẽ bên:

A. Hình 1. B. Hình 4. C. Hình 2. D. Hình 3. Câu10. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu ()()()() 222 :22334Sxyz−+++−= . Tìm tọa độ tâm I và bán kính R của mặt cầu () S .

A. ()2;2,3;34IR−= . B. ()2;2;3;26IR−−= .

C. ()4;4;6;34IR−−= D. ()2;2;3;26IR−−=

Câu11. Có bao nhiêu số tự nhiên có hai chữ số khác nhau mà các chữ số được lấy từ tập hợp {} 1;2;3;4;5 X = ?

Câu12. Cho a là số thực dương tùy ý. Giá trị của biểu thức 1 3 Paa = bằng

6 a B.

3 a C. 2 5 a D. 5 6 a

Câu13. Trong không gian Oxyz , cho mặt cầu () S có tâm () 0;2;3 I và có thể tích 36 V π = . Phương trình của () S là

A. ()() 22 2 239xyz+−++= . B. ()() 22 2 239xyz+++−= .

C. ()() 22 2 233xyz+++−= . D. ()() 22 2 233xyz+−+−= .

Câu14. Cho () 1 0 2 fxdx =  và () 1 0 5 gxdx =  khi đó ()() 1 0 2 fxgxdx    bằng

A. 12. B. 1. C. 8 . D. 3 .

A. 25 B. 2 5A C. 5 2. D. 2 5C

A. 1

Câu15. Trong các hàm số sau hàm số nào nghịch biến trên tập số thực?

A. 10 1 x y x + = . B. 322104yxxx =−+−+ .

C. 2 56yxx=−+ . D. 5 yx=+ .

Câu16. Đường tiệm cận ngang của đồ thị hàm số 2 2x6 y x = là

A. 30 x−= . B. 30 y −= . C. 20 x −= . D. 20 y −= .

Câu17. Trong không gian Oxyz , cho hai điểm () 2;5;1 M và () 0;7;1 N . Tọa độ trung điểm I của đoạn thẳng MN là

A. () 1;1;1 I B. () 3;4;2 I C. () 2;2;2 I D. () 6;8;4 I

Câu18. Nếu tăng bán kính đáy của một hình nón lên 4 lần và giảm chiều cao của hình nón đó đi 8 lần thì thể tích khối nón tăng hay giảm bao nhiêu lần?

A. giảm 2 lần . B. tăng 16 lần . C. tăng 2 lần . D. giảm 16 lần .

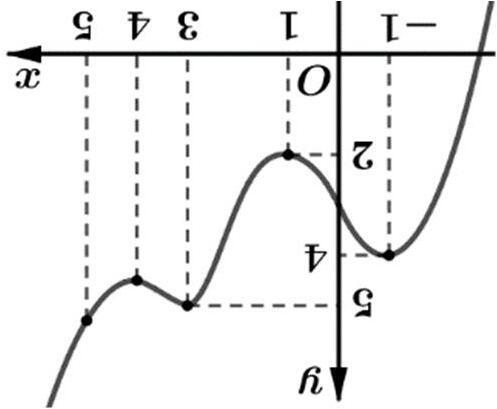
Câu19. Cho hàm số ()yfx = có đồ thị như hình vẽ sau

Tìm số nghiệm thực phân biệt của phương trình ( ) 1 fx = .

A. 1 B. 3 C. 0 D. 2

Câu20. Hàm số x y π = có đạo hàm là

A. xπ B. ln xπ π C. 1 xπ D. ln x ππ

Câu21. Cho a là số thực dương khác 1. Tính 3 log a Ia = .

A. 2 3 I = B. 6 I = C. 3 2 I = D. 1 6 I =

Câu22. Cho cấp số cộng () n u có 1 2 u =− và công sai 3 d = . Tìm số hạng 10u

A. 10 28 u = B. 9 10 2.3 u =− C. 10 25 u = D. 10 29 u =−

Câu23. Diện tích hình phẳng phần gạch chéo trong hình vẽ bên được tính theo công thức nào sau đây?

A. () 2 32 1 256d Sxxxx =+−−  B. () 2 32 1 210d Sxxxx =+−− 

C. () 2 32 1 210d Sxxxx =−−+  D. () 2 32 1 256d Sxxxx =−−++ 

Câu24. Hàm số () 32 54710 FxxxxC =+−++ là nguyên hàm của hàm số nào ?

A. () 432547 432 xxx fx =+− . B. () 2 547fxxx=+− .

C. () 2 1587fxxx=+− . D. () 432547 10 432 xxx fxx =+−+ .

Câu25. Cho hàm số ()yfx = liên tục trên ℝ và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là sai?

A. Hàm số có giá trị lớn nhất bằng 1

B. Hàm số có hai điểm cực tiểu, một điểm cực đại.

C. Hàm số có giá trị nhỏ nhất bằng 3 .

D. Hàm số đồng biến trên () 1;3

Câu26. Mặt cầu có bán kính bằng 2a có diện tích là

A. 2 12 aπ . B. 2 16 aπ . C. 2 8 aπ . D. 2 4 aπ .

Câu27. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số 2 yx = , yx = và các đường thẳng 0 x = , 1 x = bằng

A. 0 2 1 d xxx  . B. 1 2 0 d xxx +  . C. 0 2 1 d xxx +  . D. 1 2 0 d xxx  .

Câu28. Trong không gian Oxyz , cho () 3;1;2 a =− và () 0;4;5 b . Giá trị của . ab bằng:

A. 10. B. 3. C. 6. D. 14

Câu29. Với α là số thực bất kì, mệnh đề nào sau đây sai?

A. 2 1010. α α = B. ( ) 1010. α α = C. ( ) 2 2 1010. αα = D. ( )2 10100. αα =

Câu30. Cho hàm số ( )yfx = có đạo ( ) ( ) ( ) ( ) 23 112 fxxxx ′ =+−− . Số điểm cực trị của hàm số ( )fx là:

A. 1. B. 2. C. 4. D. 3.

Câu31. Cho hình trụ ( ) T có thiết diện cắt bởi mặt phẳng chứa đường cao là hình vuông có diện tích bằng 2 4a . Thể tích khối trụ ( ) T bằng:

A. 3 2 aπ B. 3 8 aπ C. 3 3 aπ D. 3 aπ

Câu32. Gọi ( )α là góc giữa hai vectơ ( )2;1;2 u =− ; ( )3;4;0 v =− . Tính cosα

A. 2 15 .

B. 2 15 . C. 2 15 . D. 2 15 .

Câu33. Hàm số 4286yxx=−++ đồng biến trên khoảng nào dưới đây?

A. ( )2;0 và ( ) 2; +∞ B. ( );2−∞− và ( )0;2 .

C. ( );2−∞− và ( ) 2; +∞ D. ( )2;2

Câu34. Số nghiệm nguyên của bất phương trình ( ) 2 2 2 log223log70 xx−+< là

A. 4 . B. 3. C. vô số. D. 5

Câu35. Hàm số nào sau đây đồng biến trên khoảng ( ) ; −∞+∞ ?

A. ( ) 32 x y =− . B. 32 4

x y  + =  

x y  + =

Câu36. Kí kiệu ( ) H là hình phẳng giới hạn bởi đồ thị hàm số ( )21 x yxe =− , trục tung và trục hoành.

Tính thể tích V của khối tròn xoay khi quay hình ( ) H xung quanh trục Ox

A. ( ) 2 5 Ve π =− . B. 42 Ve =− . C. 2 5 Ve=− . D. ( ) 42 Ve π =− .

Câu37. Một túi chứa 6 bi xanh, 4 bi đỏ. Lấy ngẫu nhiên 2 bi. Tính xác suất để lấy được cả hai bi đều màu đỏ?

A. 4 15 . B. 8 15 . C. 2 15 . D. 7 45 .

Câu38. Tập nghiệm của bất phương trình

Câu39. Cho hàm số ( )fx thỏa mãn hai điều kiện ()() 2 2 3214. fxxxxfx ++−≤   ; x ∀∈ ℝ và () 3 1 d12fxx =  . Giá trị () 2 0 d fxx  bằng

A. 6 B. 8 C. 7 D. 5

A. 22 m −<< . B. 22 m −≤≤ . C. 21 m −<≤ . D. 2 m > .

 

A. 11 ;2;1 3

   B.

Câu43: Có bao nhiêu cặp số nguyên dương ( ) ; xy thoả mãn 12020 x ≤≤ và 1 2 22log(2) yy yxx +=++ ?

A. 2020 B. 2021 C. 11 D. 10 .

Câu44. Cho hình chóp . SABC có đáy là tam giác đều cạnh a , tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích của khối chóp . SABC , biết khoảng cách từ A đến mặt phẳng ( ) SBC bằng 3 3 a

A. 3 5 120 a B. 3 5 40 a C. 3 5 72 a D. 3 5 24 a

Câu45. Cho hình chóp SABC có ( ) SAABC ⊥ và ABC∆ vuông tại C . Gọi O là tâm đường tròn ngoại tiếp SBC∆ , H là hình chiếu vuông góc của O lên mặt phẳng ( ) ABC . Khẳng định nào sau đây là đúng?

2 2 43 1 2 2

x x  >   là

A. ( );1−∞ . B. ( ) 1;2 . C. ( ) ( ) ;12; −∞∪+∞ . D. ( ) 2; +∞ .

A. H là trọng tâm ABC∆ B. H là trung điểm cạnh AC C. H là tâm đường tròn nội tiếp ABC∆ D. H là trung điểm cạnh AB

Câu46. Hàm số nào ( ) = yfx có đồ thị như hình bên dưới.



C. 2 e  =   x y D. 32 3   

Câu40. Tìm tất cả các giá trị của tham số m để hàm số 2 2 mx y mx = nghịch biến trên khoảng 1 ; 2  +∞

   C. 211 ;;1 33    D. ( )2;11;1

Câu41. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có ( ) 1;2;1, A ( ) ( )2;1;3,4;7;5BC Tọa độ chân đường phân giác trong góc B của tam giác ABC là

2111 ;; 333

() 2 2 1 22dt=−  Itt B. () 2 2 1 2dt=−  Itt C. () 2 2 1 22dt=+  Itt D. () 2 2 1 2dt =−  Itt

Câu42. Cho tích phân 3 0 d 11 = ++  x Ix x nếu đặt 1 =+tx thì I là A.

Đồ thị hàm số ()()151=+gxfx có bao nhiêu điểm cực trị?

A. 7 B. 6 C. 5 D. 4

Câu47: Cho hình hộp chữ nhật ′′′′ ABCDABCD , có ,2ABaADa == , góc giữa AC ′ và mặt phẳng () ABCD bằng 30° . Gọi H là hình chiếu vuông góc của A trên AB ′ và K là hình chiều vuông góc của A trên AD ′ . Tính góc giữa hai mặt phẳng () AHK và ABBA′′

A. 45° . B. 30° . C. 60° . D. 90° .

Câu48: Cho hàm số ()fx thỏa mãn ()() 2 .ln2 xfxxfxx ′ += , () 1; x ∀∈+∞ và () 2 ee f = . Giá trị của tích phân () 2 d e e

x Ix fx =  bằng

A. 5 3 I = B. 2 I = C. 1 2 I = D. 3 2 I =

Câu49: Cho hình chóp SABCD có đáy là ABCD là hình vuông, tam giác SAD cân tại S và nằm trong mặt phẳng vuông góc với đáy ABCD . Biết SDa = , gọi K là trung điểm của AB , góc giữa đường thẳng SK với mặt phẳng đáy bằng 60° . Thể tích V của khối chóp . SABCD bằng

3 442 147 a V = B. 3 242 49 a V = C.

3 442 49 a V = D.

3 242 147 a V =

Câu50: Cho ,, abc là các số thực khác 0 thỏa mãn 6924 abc == . Giá trị của biểu thức aa T bc =+ bằng

Câu1. Cho hàm số ()fx có bảng biến thiên như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. () ;1−∞

() 1;1 C. () ;1−∞−

() 1; −+∞

Từ bảng biến thiên của đồ thị hàm số ta thấy ()()() 0;11; ′ >⇔∈−∞−∪+∞fxx

Vậy hàm số đồng biến () ;1−∞− và () 1;+∞ .

Câu2. Cho hàm số 42 yaxbxc =++ có đồ thị như hình vẽ . Số điểm cực trị của đồ thị hàm số là:

A. 4 . B. 1. C. 2 . D. 3 . Lờigiải

Từ đồ thị hàm số ta thấy hàm số có 3 cực trị

Câu3. Cho điểm () 1;2;3 A , () 3;4;5 B . Tọa độ I trung điểm của đoạn AB là

A. () 1;1;4 B. () 1;2;1 C. () 2;0;1 D. () 1;1;0

Lờigiải

Ta có

+−  ===−

  +−+

AB I AB I AB I

xx x yy y zz z

 ===   ++  ===  

13 1 22 24 1 22 35 4 22

A. 11 12 B. 1 3 C. 3 D. 2 ---------HẾT--------BẢNG ĐÁPÁN 1.C 2.D 3.A 4.D 5.A 6.A 7.C 8.C 9.D 10.A 11.B 12.D 13.B 14.C 15.B 16.D 17.A 18.C 19.A 20.D 21.B 22.C 23.D 24.C 25.A 26.B 27.D 28.C 29.C 30.B 31.A 32.D 33.B 34.A 35.D 36.A 37.C 38.B 39.D 40.C 41.C 42.A 43.C 44.B 45.D 46.C 47.A 48.A 49.A 50.A

ờigiải

Vậy tọa độ trung điểm là () 1;1;4 I

Câu4. Tập nghiệm S của phương trình () 3 log231 x += .

A. {} 3 S = B. {} 1 S = C. {} 1 S =− D. {} 0 S =

Lờigiải () 1 3 log231233200 xxxx +=⇔+=⇔=⇔=

Câu5. Trong không gian Oxyz , cho mặt cầu ()()()() 222 :1234Sxyz−+−++= . Tọa

độ tâm I và bán kính R của mặt cầu đã cho là

A. () 1;2;3;2IR−= B. () 1;2;3;4IR−=

C. ()1;2;3;2IR−−= . D. ()1;2;3;4IR−−= .

Lờigiải

Mặt cầu ()()()() 222 :1234Sxyz−+−++= có tâm () 1;2;3 I và bán kính 2 R =

Câu6. Cho khối lập phương có cạnh bằng 2a . Thể tích khối lập phương đó bằng

A. 3 8a . B. 2 4a . C. 3 8 3 a . D. 3 4a .

Lờigiải Thể tích của khối lập phương có cạnh bằng 2a là ()3 3 28 Vaa ==

Câu7. Cho hàm số bậc bốn ()yfx = có đồ thị trong hình vẽ bên:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. () 1; −+∞ . B. () 1;1 . C. () 1; +∞ D. () 0;1 .

Lờigiải

Từ đồ thị hàm số ta suy ra hàm số đồng biến trên khoảng () 1;0 và () 1; +∞ .

Câu8. Nghiệm của phương trình 2 327 x+ = là

A. 3 x = . B. 2 x = . C. 1 x = . D. 1 x =− .

Lờigiải

Phương trình 2 327 x+ = 23 33231 x xx + ⇔=⇔+=⇔=

Vậy phương trình có nghiệm 1 x = .

Câu9. Hình nào sau đây không phải là hình đa diện?

A. Hình 1. B. Hình 4. C. Hình 2. D. Hình 3. Lờigiải

Hình 3 tồn tại cạnh là cạnh chung của 3 đa giác. Do đó hình 3 không là hình đa diện.

Câu10. Trong không gian với hệ tọa độ Oxyz , cho mặt cầu ()()()() 222 :22334Sxyz−+++−= . Tìm tọa độ tâm I và bán kính R của mặt cầu () S .

A. ()2;2,3;34IR−= B. ()2;2;3;26IR−−=

C. ()4;4;6;34IR−−= D. ()2;2;3;26IR−−=

Lờigiải.

Mặt cầu () S có tâm () 2;2;3 I , bán kính 34 R =

Câu11. Có bao nhiêu số tự nhiên có hai chữ số khác nhau mà các chữ số được lấy từ tập hợp {} 1;2;3;4;5 X = ?

A. 25 B. 2 5A C. 5 2. D. 2 5C Lờigiải.

Mỗi số tự nhiên có hai chữ số khác nhau mà các chữ số được tạo thành từ tập hợp X là một chỉnh hợp chập 2 của 5 phần tử

Vậy số các số tự nhiên được tạo thành thỏa mãn yêu cầu bài toán là 2 5A

Câu12. Cho a là số thực dương tùy ý. Giá trị của biểu thức 1 3 Paa = bằng

A. 1 6 a B. 2 3 a C. 2 5 a D. 5 6 a Lờigiải.

Ta có 5 6 1111 1 3332 2 Paaaaaa + ====

Câu13. Trong không gian Oxyz , cho mặt cầu () S có tâm () 0;2;3 I và có thể tích 36 V π = . Phương trình của () S là

A. ()() 22 2 239xyz+−++= B. ()() 22 2 239xyz+++−=

C. ()() 22 2 233xyz+++−= D. ()() 22 2 233xyz+−+−=

Lờigiải

Gọi R là bán kình mặt cầu ( ) S , khi đó 33 4

3636273 3 VRRR πππ =⇔=⇔=⇔=

Mặt cầu ( ) S có tâm ( )0;2;3 I và bán kính 3 R = nên phương trình của ( ) S là

()() 22 2 239xyz+++−=

Câu14. Cho () 1 0 2 fxdx =  và () 1 0 5 gxdx =  khi đó ()() 1 0 2 fxgxdx    bằng

A. 12. B. 1. C. 8 . D. 3 .

Lờigiải

()()()() 111 000 2dd2d22.58fxgxxfxxgxx−=−=−=−

Câu15. Trong các hàm số sau hàm số nào nghịch biến trên tập số thực?

A. 10 1 x y x + = B. 322104yxxx =−+−+

C. 2 56yxx=−+

D. 5 yx=+

Lờigiải

+ Hàm số 322104yxxx =−+−+ có tập xác định là D = ℝ

Ta có 322210434100, ′ =−+−+  =−+−<∀∈ ℝ yxxxyxxx nên hàm số

322104yxxx =−+−+ nghịch biến trên tập số thực.

+ Hàm số 10 1 x y x + = có tập xác định là { }\1 D = ℝ nên phương án A sai.

+ Hàm số 2 56yxx=−+ có tập xác định là D = ℝ

Ta có 2 5 56250 2 ′ =−+  =−<⇔<yxxyxx nên hàm số 2 56yxx=−+ nghịch biến trên

Gọi () ;; III Ixyz là trung đi

 ==

−+

Sau khi tăng bán kính lên 4 lần và giảm chiều cao đi 8 lần, thể tích của khối nón mới là ()2 2 1 11 .4.2.2. 383 h VrrhV ππ ===

Vậy thể tích khối nón tăng 2 lần.

Câu19. Cho hàm số ()yfx = có đồ thị như hình vẽ sau

5 ; 2 

 nên phương án C sai.

+ Hàm số 5 yx=+ đồng biến trên ℝ nên phương án D sai.

Câu16. Đường tiệm cận ngang của đồ thị hàm số 2 2x6 y x = là

A. 30 x−= . B. 30 y −= . C. 20 x −= . D. 20 y −= .

Tập xác định của hàm số là { }2 \ D = ℝ

Ta có: 6 2 26 limlimlim2 2 2 1 xxx

x x y x x →+∞→+∞→+∞ === ,

Lờigiải

6 2 26 limlimlim2 2 2 1 xxx

x x y x x →−∞→−∞→−∞ === .

Vậy đường tiệm cận ngang của đồ thị hàm số là 2 y = hay 20 y −=

Câu17. Trong không gian Oxyz , cho hai điểm ( )2;5;1 M và ( )0;7;1 N . Tọa độ trung điểm I của đoạn thẳng MN là

Tìm số nghiệm thực phân biệt của phương trình () 1 fx = .

A. 1 B. 3 C. 0 D. 2

Lờigiải

 

 .

−∞ 

Lờigiải

A. ( )1;1;1 I .

( )3;4;2 I .

( )2;2;2 I .

( )6;8;4 I .

ủ

ạn

ẳ

ểm c

ng MN .

 

Khi đó 

20 1 2 57 1 2 11 1 2   + 

I I  

x y z 

() 1;1;1 I

Vậy trung điểm của đoạn thẳng MN có tọa độ là () 1;1;1 I .

Câu18. Nếu tăng bán kính đáy của một hình nón lên 4 lần và giảm chiều cao của hình nón đó đi 8 lần thì thể tích khối nón tăng hay giảm bao nhiêu lần?

A. giảm 2 lần . B. tăng 16 lần C. tăng 2 lần . D. giảm 16 lần . Lờigiải

Gọi bán kính và chiều cao của khối nón lần lượt là r và h thì thể tích khối nón là 2 1 3 Vrh π = .

Số nghiệm của phương trình ( ) 1 fx = chính là số giao điểm của đồ thị hàm số ( )yfx = và

đường thẳng 1 y = . Từ đồ thị ta thấy phương trình () 1 fx = có 1 nghiệm duy nhất.

Câu20. Hàm số x y π = có đạo hàm là

A. xπ . B. ln xπ π . C. 1 xπ . D. ln x ππ .

Lờigiải

Ta có () ln. xx y πππ ′ ′ ==

Câu21. Cho a là số thực dương khác 1. Tính 3 log a Ia =

A. 2 3 I = B. 6 I = C. 3 2 I = D. 1 6 I =

Ta có 1 2

Lờigiải

33 loglog3.2.log6 a a a Iaaa ==== .

Câu22. Cho cấp số cộng () n u có 1 2 u =− và công sai 3 d = . Tìm số hạng 10u

A. 10 28 u = B. 9 10 2.3 u =− C. 10 25 u = D. 10 29 u =−

Lờigiải

Theo công thức ta có: ()()1101110129.325 n uunduud =+−  =+−=−+=

Vậy 10 25 u =

Câu23. Diện tích hình phẳng phần gạch chéo trong hình vẽ bên được tính theo công thức nào sau đây?

()()

2 23 1 22832d xxxxx =−++−−+  (Vì [] 23 22832,1;2 xxxxx −++≥−+∀∈− ).

() 2 32 1 256d xxxx=−−++ 

Vậy diện tích hình phẳng phần gạch chéo trong hình vẽ là () 2 32 1 256d Sxxxx =−−++ 

Câu24. Hàm số () 32 54710 FxxxxC =+−++ là nguyên hàm của hàm số nào ?

A. () 432547 432 xxx fx =+− B. () 2 547fxxx=+−

C. () 2 1587fxxx=+− D. () 432547 10 432 xxx fxx =+−+

Lờigiải

()()()() 2 d1587 FxfxxfxFxxx ′ =  ==+− 

Vậy hàm số () 32 54710 FxxxxC =+−++ là nguyên hàm của () 2 1587fxxx=+−

Câu25. Cho hàm số ()yfx = liên tục trên ℝ và có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là sai?

A. Hàm số có giá trị lớn nhất bằng 1.

B. Hàm số có hai điểm cực tiểu, một điểm cực đại.

C. Hàm số có giá trị nhỏ nhất bằng 3

D. Hàm số đồng biến trên () 1;3 .

Lờigiải

Dựa vào bảng biến thiên hàm số không có giá trị lớn nhất suy ra khẳng định hàm số có giá trị lớn nhất bằng 1 là khẳng định sai.

A. ()

256d Sxxxx

Lờigi

Câu26. Mặt cầu có bán kính bằng 2a có diện tích là

A. 2 12 aπ . B. 2 16 aπ . C. 2 8 aπ . D. 2 4 aπ .

Lờigiải

Diện tích mặt cầu là ()2 2 4.216 Saa ππ==

Ta có: ()()

Câu27. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số 2 yx = , yx = và các đường thẳng 0 x =

, 1 x = bằng

=+−− 

2 32 1 210d Sxxxx =+−−  .

Sxxxx =−−+ 

1 256d Sxxxx =−−++  .

()

C. ()

210d

()

ả

1 32228d Sxxxxx =−+−−++ 

ng trình hoành độ giao đi

Câu28. Trong không gian Oxyz , cho () 3;1;2 a =− và () 0;4;5 b . Giá trị của . ab bằng:

A. 10. B. 3. C. 6. D. 14 Lờigiải

Ta có .3.01.(4)2.56.ab =−+−+=

Câu29. Với α là số thực bất kì, mệnh đề nào sau đây sai?

A. 2 1010. α α = B. () 1010.

α = C. ()

Ta có ()2 10100. αα =

Gọi thiết diện cắt hình trụ () T bởi mặt phẳng chứa đường cao là hình vuông ABCD .

Ta có ABCD là hình vuông diện tích bằng 2 4a '2 OBRa OOha ==    == 

Vậy thể tích của khối trụ () 223 .22 T VRhaaa πππ ===

1010. αα = D. ()

10100. αα = Lờigiải

Câu30. Cho hàm số ()yfx = có đạo ()()()() 23 112 fxxxx ′ =+−− . Số điểm cực trị của hàm số ()fx là:

A. 1. B. 2. C. 4. D. 3.

Lờigiải

Ta có ()()()() 23 1120fxxxx ′ =+−−=

=−

Câu32. Gọi () α là góc giữa hai vectơ () 2;1;2 u =− ; () 3;4;0 v =− . Tính cosα

A. 2 15 B. 2 15 C. 2 15 D. 2 15

Lờigiải

Ta có ()() () () 22 2222

.2.31.42.02 212.34015 uv cos uv α −++− ===− ++−−++

Câu33. Hàm số 4286yxx=−++ đồng biến trên khoảng nào dưới đây?

⇔= =

x x x

1 2

Ta có bảng xét dấu sau:

Vậy hàm số có hai cực trị

Câu31. Cho hình trụ () T có thiết diện cắt bởi mặt phẳng chứa đường cao là hình vuông có diện tích

bằng 2 4a . Thể tích khối trụ () T bằng:

A. 3 2 aπ B. 3 8 aπ C. 3 3 aπ D. 3 aπ

Lờigiải

A. () 2;0 và () 2; +∞ B. () ;2−∞− và () 0;2

C. () ;2−∞− và () 2; +∞ D. () 2;2

Tập xác định: D = ℝ

Lờigiải

=  =

′′ =−+=⇔−+=⇔=  =



=−  =

A. 0 2 1 d xxx  B. 1 2 0 d xxx +  C. 0 2 1 d xxx +  D. 1 2 0 d xxx  Lờigiải Phươ

ểm 2 0 1 x xx x =  =⇔  =  1 2 0 d Sxxx  =−  .

2 2

 

33 06 416;04160222 222 

xy yxxyxxxy xy

Bảng biến thiên

Vậy hàm số 4286yxx=−++ đồng biến trên khoảng ( );2−∞− và ( )0;2

Câu34. Số nghiệm nguyên của bất phương trình ( ) 2 2 2 log223log70 xx−+< là

A. 4 . B. 3. C. vô số. D. 5 Lờigiải

Điều kiện: 0 x > ( ) ( ) 2 2 222 2 2 2 2222 11 4 2

d21d 1 1 dd 2

log223log704log223log70

−+<⇔−+< ⇔+−+<⇔−+< ⇔<<⇔<<

xxxx xxxx xx

4(1log)23log704log15log110 11 1log22 4

So với điều kiện ta có 11 4 22 x <<

Vì x ∈  ℤ { }3,4,5,6 x ∈ .

Vậy số nghiệm nguyên của bất phương trình đã cho là 4.

Câu35. Hàm số nào sau đây đồng biến trên khoảng ( ) ; −∞+∞ ?

A. ( ) 32 x y =− . B. 32 4

x y  + =    . C. 2 e  =   x y . D. 32 3

x y  + =    Lờigiải.

244 e Ve ππ   =−−−=−

Ta có

• 0321 <−< nên hàm số ( ) 32 x y =− nghịch biến trên ℝ (loại).

• Ta có 32 01 4 + << nên hàm số 32 4

x y  + =    nghịch biến trên ℝ (loại).

• Ta có 2 01 e << nên hàm số 2 x y e  =   nghịch biến trên ℝ (loại).

• Ta có 32 1 3 + > nên hàm số 32 3

x y  + =    đồng biến trên ℝ (nhận).

Câu36. Kí kiệu ( ) H là hình phẳng giới hạn bởi đồ thị hàm số ( )21 x yxe =− , trục tung và trục hoành.

Tính thể tích V của khối tròn xoay khi quay hình ( ) H xung quanh trục Ox

A. ( ) 2 5 Ve π =− B. 42 Ve =− C. 2 5 Ve=− D. ( ) 42 Ve π =−

Lờigiải.

Phương trình hoành độ giao điểm : ( ) 2101 x xex −=⇔=

Tính thể tích V của khối tròn xoay khi quay hình ( ) H xung quanh trục Ox là () 1 2 2 0 41d x Vxex π =−

Câu37. Một túi chứa 6 bi xanh, 4 bi đỏ. Lấy ngẫu nhiên 2 bi. Tính xác suất để lấy được cả hai bi đều màu đỏ? A. 4 15 . B. 8 15 . C. 2 15 . D. 7 45 . Lờigiải

Ta có số phần tử của không gian mẫu là ( ) 2 10 45 nCΩ==

Gọi A là biến cố “Hai bi được lấy đều màu đỏ”.

Số phần tử của biến cố A là ( ) 2 4 6 nAC==

Xác xuất để lấy được cả hai bi đều màu đỏ là () ( ) () 62 4515 nA PA n === Ω

2 2 43

2 320xx ⇔−+−> ( )1;2 x ⇔∈

2 2 43 1 2 2

x x  > 

. L

24322xx −+−⇔> 2 243 xx⇔−+>−



x x uxx ux ve vex =−   =−    = =     () () () 1 2 2 1 1 2 2 0 0 0 1 1 41d41d 22 x x x xe Vxexxex ππ    =−−=−−−     Xét () 1 2 0 1d x Ixex =−  Đặt 1 1 2 2 1 1 dd 1 1 dd 2 x x ux ux ve vex =  =−     = =    () 11 1 22222 0 00 1113 1d 222424444 xxx eeeee Ixx =−−=−=−+=−  Vậy () 2 2 13 45

Đặt () ( ) 2 2 2    

 là

Câu38. Tập nghiệm của bất phương trình

2;+∞

A. ( );1−∞ . B. ( ) 1;2 . C. ( ) ( ) ;12; −∞∪+∞ .

( )

ờigiải

Bất phương trình 2

x x  >  

Vậy tập nghiệm của bất phương trình

2 2 43 1 2 2

x x  >   là ( )1;2

Câu39. Cho hàm số ( )fx thỏa mãn hai điều kiện ()() 2 2 3214. fxxxxfx ++−≤   ; x ∀∈ ℝ và ()

1 d12fxx =  . Giá trị () 2 0 d fxx  bằng

A. 6 B. 8 C. 7 D. 5 Lờigiải

Ta có ( ) ( ) 223214. fxxxxfx ++−≤ ( ) ( ) ( ) ( ) 1310fxxfxx ⇔−+−−≤   .

Nếu 1 x ≥ thì ( ) 131xfxx +≤≤−

()()() 333 111 1dd31d xxfxxxx  +≤≤− () 3 1 6d10 fxx ⇔≤≤  ( )*

Nếu 1 x ≤ thì ( ) 311 xfxx−≤≤+

()()() 111 111 31dd1d xxfxxxx  −≤≤+ () 1 1 2d2 fxx ⇔−≤≤  ( )**

Vậy hàm số nghịch biến trên khoảng 1 ; 2  +∞   khi 21 m −<≤ .

Câu41. Trong không gian với hệ tọa độ Oxyz , cho tam giác ABC có () 1;2;1, A ()() 2;1;3,4;7;5BC

Tọa độ chân đường phân giác trong góc B của tam giác ABC là

A. 11 ;2;1 3 

Gọi chân đường phân giác trong góc B của tam giác ABC là () ;; Dxyz

Từ ( )* và ( )** ta có ()

3 1 8d12 fxx ⇔≤≤  mà () 3 1 d12fxx =  () 311 11 xkhix fx xkhix −≥   =  +≤  Vậy

()()() 212 001 ddd5fxxfxxfxx =+=

Câu40. Tìm tất cả các giá trị của tham số m để hàm số 2 2 mx y mx = nghịch biến trên kho

A. 22 m −<< B. 22 m −≤≤ C. 21 m −<≤ D. 2 m >



2  +∞  

Tậ

 

Để hàm số 2 2 mx

nghị

ến trên khoảng 1 ; 2  +∞   thì () 2 2 41 0,; 2 2  ′ =<∀∈+∞  m yx mx

40 22 21 1 1 22 m m m m m  −< −<<  ⇔⇔⇔−<≤  ≤ ≤    .

ảng

;

ờigiải

p xác định \ 2 m D  =

ℝ Ta có ()

2 4 2 ′ = m y mx

ch bi

  B. 2111 ;; 333    C. 211 ;;1 33    D. () 2;11;1 Lờigiải

có 261 2 2 104 DABA DCDA DCBC ===  =− () () () 2 3 421 11 722 3 521 1 x xx yyy zz z  =−  −−=−−     −=−−  =   −=−−−  =   

ậy 211

33 D   . Câu42. Cho tích phân 3 0 d 11 = ++  x Ix x nếu đặt 1=+tx thì I là A. () 2 2 1 22dt=−  Itt B. () 2 2 1 2dt=−  Itt C. () 2 2 1 22dt=+  Itt D. () 2 2 1 2dt =−  Itt Lờigiải đặt 2 112dd=+  =+⇔= txtxttx 01 =  = xt ; 32 =  = xt . () 22 2 2 11 1 2d=22d 1 =− +  t Ittttt t

. Ta

;;1

Câu43: Có bao nhiêu cặp số nguyên dương () ; xy thoả mãn 12020 x ≤≤ và 1 2 22log(2) yy yxx +=++ ?

A. 2020 B. 2021 C. 11 D. 10 .

Lờigiải

Ta có: ()() 1 1 2 2 22log22222log2 +=++⇔++=+++ yyyyyy yxxyxx

()() () 11 22 2.2log222log2*. ⇔+=+++ yyyy xx

Đặt 2 ()2log fttt =+ với 0 t > .

Ta có 1 ()20,0 ln2 ftt t ′ =+>∀> suy ra hàm số ()yft = đồng biến trên (0;) +∞

Từ () * ta có 111 (2)(2)222. yyyyy ffxxx =+⇔=+⇔=

Vì 12020 x ≤≤ nên 1 222 122020log11log20201log20201 y yy ≤≤⇔≤−≤⇔≤≤+

Theo bài y nguyên dương suy ra {} 1;2;3;4;5;6;7;8;9;10;11 y ∈ .

Vậy có 11 cặp số nguyên dương () ; xy thỏa yêu cầu bài toán.

Câu44. Cho hình chóp . SABC có đáy là tam giác đều cạnh a , tam giác SAB cân tại S và nằm trong

mặt phẳng vuông góc với đáy. Tính thể tích của khối chóp SABC , biết khoảng cách từ A đến

mặt phẳng () SBC bằng

3 3 a

- Gọi H là trung điểm của AB SHAB  ⊥

( ) ( ) ()() () ()

SABABC SABABCABSHABC SABSHAB

⊥   ∩=  ⊥   ⊃⊥  .

- Gọi I là trung điểm của BC AIBC  ⊥ và 3 2 a AI =

- Kẻ HKBC ⊥ tại K 3 24 BCa HK  ==

() () () () () 1 13 ,, 2 26

 =   ==   ∈ 

HBAB a dHSBCdASBC BSBC

- Gọi H ′ là hình chiếu của H trên SK , ta có: ()() () 3 , 6 HHSK a HHSBCHHdHSBC HHBC

′ ⊥  ′′  ⊥  ==  ′ ⊥ 

′  === ′

2222



33 .15 46 10 33 46

SABCABC aaa VSHS∆ === .

3310440

A. H là trọng tâm ABC∆ .

C. H là tâm đường tròn nội tiếp ABC∆

B. H là trung điểm cạnh AC .

D. H là trung điểm cạnh AB

Lờigiải

A. 3

a B. 3 5 40 a C. 3 5 72 a D. 3 5 24 a

5 120

Lờigiả

a a a B K I H' H S C A

HKHHa SH HKHH aa  

23 111535

S B

()() 1 0 15 =⇔=−hxfx

Dựa vào đồ thị hàm số ()fx suy ra phương trình () 1 15 =− fx có một nghiệm đơn thuộc () 1;0

suy ra đồ thị hàm số ()hx cắt trục hoành tại 1 điểm thuộc () 1;0

O H

⊥   ⊥  ⊥  ⊥ 

BCAC BCSACBCSC BCSA

()

SBC  ∆ vuông tại C .

Mà O là tâm đường tròn ngoại tiếp SBC∆ O  là trung điểm SB .

H là hình chiếu của O lên mặt phẳng () ABC nên suy ra // OHSA , do đó OH là đường trung

bình của tam giác SAB∆ H  là trung điểm AB .

Câu46. Hàm số nào () = yfx có đồ thị như hình bên dưới.

Đồ thị hàm số ()()151=+gxfx có bao nhiêu điểm cực trị?

A. 7 . B. 6 . C. 5 . D. 4 .

Lờigiải

Đặt ()() = gxhx

Nhậnxét: Số cực trị hàm ()gx bằng số cực trị hàm số ()hx cộng với số giao điểm cắt của đồ thị hàm số ()hx với trục hoành.

Ta có ()() 15 ′′ = hxfx ; ()() 2 1 00 1 2

=−   =−  ′′ =⇔=⇔  =  = 

x x hxfx x x

Các nghiệm 1;2=±=±xx đều là các nghiệm đơn suy ra ()hx có bốn cực trị

Vậy ()() = gxhx có năm cực trị.

Câu47: Cho hình hộp chữ nhật . ′′′′ ABCDABCD , có ,2ABaADa == , góc giữa AC ′ và mặt phẳng () ABCD bằng 30° . Gọi H là hình chiếu vuông góc của A trên AB ′ và K là hình chiều vuông góc của A trên AD ′ . Tính góc giữa hai mặt phẳng () AHK và ABBA′′ A. 45° B. 30° C. 60° D. 90° Lờigiải

- Dễ thấy ()BCABBA′′ ⊥ . (*)

- Ta có () () () () AHABgt AHABCAHAC AHBCBCABBA

. (1) () () () () AKADgt AKADCAKAC AKCDCDADDA

(1) và (2) suy ra ()ACAHK ′ ⊥ (**)

′

  ′′  ⊥  ⊥  ′′ ⊥⊥  

′ ⊥   ′′  ⊥  ⊥  ′′ ⊥⊥   . (2)

⊥

ừ

- Từ (*) và (**) suy ra ( ) ( ) ( ) ( ) ,, ABBAAHKBCACBCA ′′′′ == . (3)

- Lại có () ( ) (),, ACABCDACACACA ′′′ == ( vì ( )AAABCD ′ ⊥ ) nên 30 ACA ′ =°

Xét AAC ′ ∆ vuông tại A có 22 3 ACABADa =+= và 30 ACA ′ =°

nên 3 2 cos30 3 2

ACa ACa ′ === ° .

Xét BCA′ ∆ vuông tại B nên có 21 cos45 2 2 BCa BCABCA ACa ′′ ===  =° ′ . (4)

Từ (3) và (4) suy ra ( ) ( ) ( ) ,45ABBAAHK ′′ =° .

Câu48: Cho hàm số ( )fx thỏa mãn ( ) ( ) 2 .ln2 xfxxfxx ′ += , ( ) 1; x ∀∈+∞ và ( ) 2 ee f = . Giá trị của tích phân ()

Gọi I làtrung điểmcủa AD

Tacó SIAD ⊥ (do SAD∆ cântại S )và ()() SADABCD ⊥ nên ()SIABCD ⊥

2 d e e

x Ix fx =  bằng

A. 5 3 I = . B. 2 I = . C. 1 2 I = . D. 3 2 I = . Lờigiải

Với ( ) 1; x ∀∈+∞ , ta có ( ) ( ) 2 .ln2 xfxxfxx ′ += ()() 1 ln.2 fxxfxx x ′ ⇔+= () ().ln2 fxxx ′ ⇔=

Từ ()SIABCD ⊥ nên () () () ,,60 SKABCDSKIKSKI===°

Xéttamgiác SIK vuôngtại I nên tan60.3 SI SIIK IK °=  = . (1)

Gọi độ dàicạnhhìnhvuông ABCD là x .Khi đótacó 2 BDx = .

Xéttamgiác ABD có IK là đườngtrungbìnhnên 2 2 IKx = . (2)

Từ (1),(2)tacó 6 2 SIx = . (*)

Mặtkháctamgiác SDI vuôngtại I nêntacó 2 2 4 x SIa=− . (**)

Từ (*),(**)suyra 2 2222 372 244 7 x xaaxxa =−⇔=⇔= .(Vì ,0ax > )

( ) 2 .ln fxxxC  =+ ( ) 2e.lnee fC  =+ 22 ee C ⇔=+ 0 C ⇔= . ( ) 2 .ln fxxx  = () ln xx fxx  = ()

2 e e

d x Ix fx =  2 e e

ln d x x x =  () () 2 2 e 2 e e e

ln lndln 2 x xx ==  ( ) ()

2lne lne 22 =− 2 213 222 =−=

Câu49: Chohìnhchóp . SABCD có đáylà ABCD làhìnhvuông,tamgiác SAD cântại S vànằmtrong mặtphẳngvuônggócvới đáy ABCD .Biết SDa = ,gọi K làtrung điểmcủa AB ,gócgiữa đường thẳng SK vớimặtphẳng đáybằng 60° .Thể tích V củakhốichóp SABCD bằng

Suyra 626 2 77 SIaa ==

Vậythể tích . SABCD là 2 3 2 1162442 .... 33147 77 ABCD a VSISaa  ===  

Câu50: Cho ,, abc làcácsố thựckhác 0 thỏamãn 6924 abc == .Giátrị củabiểuthức aa T bc =+ bằng

A. 11 12 B. 1 3 C. 3 D. 2

Lờigiải Đặt 6924 abc t === , () 0,1tt>≠ .

2 2

A. 3 442 147 a V = . B. 3 242 49 a V = . C. 3 442 49 a V = . D. 3 242 147 a V = . Lờigiải

6 9 24 1 log log6 1 log log9 1 log log24 t t at bt ct  ==     ==    ==   () 111 log9log24 log6 tt t aa Ta bcbc   =+=+=+   () () 3 11 log6log6.log216.log63 tt tt T ⇔=== Vậy 3 T =

SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HÓA TRƯỜNG THPT YÊN ĐỊNH

ĐỀ THI THỬ TỐT NGHIỆP THPT – NĂM 2022 - 2023

Câu 1. Đồ thị hàm số nào trong các hàm số sau đây có tiệm cận đứng ?

A. 2 1 2 y xx = −+ B. 2 1 1 y x = + C. 4 3 1 y x = + D. 2 y x =

Câu 2. Tích tất cả các nghiệm của phương trình 2 254 24 xx++ = bằng

A. 2 B. 2 C. 1 D. 1

Câu 3. Tập nghiệm của phương trình ()() log1log230 xx−−+= là

A. {} 4 B. ∅ C. {} 2 D. 2 4; 3   

Câu 4. Cho hàm số 3231yxxx=−++ có đồ thị () C và đường thẳng () :1. dyx =− Biết () d cắt () C tại ba điểm phân biệt có hoành độ là 123,,.xxx Tính 123 Txxx =++ ?

A. 3 B. 1 C. 4 D. 2

Câu 5. Tập xác định của hàm số () 2 3 1 yx=− là

A. [ ) 1; +∞ B. () 1; +∞ C. () 0; +∞ D. {}\1 ℝ

Câu 6. Một hình nón có chiều cao bằng 4 bán kính đáy bằng 3 có diện tích toàn phần bằng

A. 9π B. 15π C. 24π D. 12π

Câu 7. Cho hàm số ()fx liên tục trên mỗi khoảng () ;1−∞ và () 1; +∞ và có bảng biến thiên như sau

Câu 10. Thể tích V của khối cầu có bán kính 3 r = bằng

A. 36 . B. 36π . C. 9π . D. 9 .

Câu 11. Biết () 3Fxx = là một nguyên hàm của hàm số ()fx trên R . Giá trị của () () 2 1 2dfxx +  bằng

A. 7 B. 9 C. 15 4 D. 23 4

Câu 12. Cho các hàm số x ya = và xyb = với , ab là những số thực dương khác 1, có đồ thị như hình vẽ Đường thẳng 3 y = cắt trục tung, đồ thị hàm số x ya = và x yb = lần lượt tại ,, HMN . Biết rằng 23HMMN = , khẳng định nào sau đây đủng?

Tập nghiệm của bất phương trình () 20 fx −> là

A. ℝ . B. ( ];1−∞ . C. () ;1−∞ . D. () 1; +∞ .

Câu 8. Cho hàm số ()yfx = có đạo hàm liên tục trên () 0;π thoả mãn ()().cot2.sin fxfxxxx ′ =+ . Biết 2 24 f ππ =   . Tính 6 f π    .

A. 2 36 π B. 2 80 π C. 2 54 π D. 2 72 π

Câu 9. Có bao nhiêu giá trị nguyên của tham số m không vượt quá 10 để hàm số 3 3 x y xm = + đồng biến trên khoảng () 2; −+∞ ?

A. 11 B. 10 C. 12 D. 9

A. 53ab = B. 23ab = C. 35ab = D. 35ab =

Câu 13. Cho khối lăng trụ tam giác ABCABC′′′ có thể tích V . Gọi ,, MNP lần lượt là trung điểm của các cạnh AB′′ ; BC ; CC′ . Mặt phẳng () MNP chia khối lăng trụ đã cho thành 2 phần, phần chứa điểm B có thể tích là 1V . Tỉ số 1V V bằng

Câu 14. Cho hình lăng trụ tam giác đều . ABCABC′′′ có cạnh đáy bằng 2a . Khoảng cách từ B đến mặt phẳng () ACCA′′ bằng

A. 2a . B. 3a . C. 2a . D. 22a .

Câu 15. Nếu () 32d23 fxxxxC =++  thì hàm số ()fx bằng

A. () 43 1 2 fxxxCx =++ . B. () 2 66 fxxxC =++ .

C. () 43 1 2 fxxx =+ D. () 2 66 fxxx =+

Câu 16. Cho () 5 2 d10fxx =  . Khi đó () 2 5 24dfxx   bằng

A. 42 B. 34 C. 32 D. 46

Câu 17. Cho một cấp số cộng có 2 4 u = , 4 2 u = . Hỏi 1u bằng bao nhiêu?

A. 1 5 u = . B. 1 1 u =− . C. 1 6 u = . D. 1 1 u = .

Câu 18. Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới đây?

25 144 B. 37 144

61 144

49 144

A. 4223yxx=−+

C. 4223yxx=−+−

B. 4223yxx=−−

D. 4233yxx=+−

Câu 19. Một hình trụ có bán kính đáy bằng a , chu vi thiết diện qua trục bằng 10a . Thể tích của khối trụ đã cho bằng

A. 3 aπ . B. 3 3 aπ . C. 3 4 aπ . D. 3 5 aπ .

Câu 20. Trong các mệnh đề sau, mệnh đề nào sai?

A. () dln01 xx axaaCa =+<≠  B. cosdsinxxxC =+ 

C. 1 d,1 1 x xxC α α α α

+ =+∀≠− +  . D. ()() d fxxfxC ′ =+  .

Câu 21. Cho hàm số ()yfx = liên tục trên [] 1;3 và có bảng biến thiên như sau

A. 3 . B. 0 . C. 1 . D. 2 .

Câu 24. Số cách sắp xếp 5 người ngồi vào 6 chiếc ghế xếp hàng ngang là:

A. 5 6A B. 6! C. 5 6C D. 5!

Câu 25. Cho hàm số ( )yfx = có đạo hàm ()() ( ) 2 2 19fxxxxmx ′ =−++ với mọi x ∈ ℝ . Có bao nhiêu số nguyên dương m để hàm số ( ) ( ) 3 gxfx =− đồng biến trên khoảng ( ) 3; +∞ ?

A. 6 B. 5 C. 7 D. 8

Câu 26. Cho hàm số ( ) 2 sin1fxxx=++ biết ( )Fx là một nguyên hàm của hàm số ( )fx và ( ) 01 F = . Khí đó ( )Fx bằng?

A. ( ) 3 cos2Fxxxx=−++ . B. () 3 cos2 3 x Fxxx=−++ .

C. () 3 cos 3 x Fxxx =++ . D. () 3 cos2 3 x Fxx=++ .

Câu 27. Tiệm cận đứng của đồ thị hàm số 21 2 x y x = −+ là đường thẳng

Có bao nhiêu giá trị nguyên của m để phương trình () 2 1 45 m fx xx += −+ có nghiệm trên khoảng () 1;2 ?

A. 0 B. 10 C. 5 D. 4

Câu 22. Cho hình nón () N có chiều cao bằng 2a . Cắt () N bởi một mặt phẳng qua đỉnh và cách tâm của đáy

một khoảng bằng a ta được thiết diện có diện tích bằng 2 411 3 a . Thể tích khối nón đã cho bằng

A. 3 45 3 aπ . B. 3 10 3 aπ . C. 3 10 aπ . D.

3 45 9 aπ .

Câu 23. Cho hàm số ()yfx = có đồ thị là đường cong trong hình vẽ dưới đây. Giá trị lớn nhất của hàm số đã cho trên đoạn [] 1;1 bằng bao nhiêu ?

A. 2 x = B. 1 2 x = C. 2 y =− D. 2 x =−

Câu 28. Cho hình chóp tứ giác có đáy là hình vuông cạnh bằng 2 , chiều cao bằng 3. Thể tích của khối chóp đã cho bằng

A. 4 . B. 12 . C. 6 . D. 18 .

Câu 29. Trên khoảng ( );2−∞− , họ nguyên hàm của hàm số () 1 2 fx x = + là

A. 1 2 C x + + B. ln2xC ++ C. ()2 1 2 C x −+ + D. 1 ln2 2 xC ++

Câu 30. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 32 1 93 3 fxxmxx =++− đồng biến trên ℝ ?

A. 5 .B. 4 . C. 7 . D. 6 .

Câu 31. Cho hàm số ( )fx có bảng xét dấu của đạo hàm như sau

x ( )fx ( )fx ′ 1 2 3 0 + 4 3 1

1 2 1 2 3 1 2 1 x y O

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. () 2; +∞ .B. () ;2−∞− C. () 2; −+∞ D. () 2;1 .

Câu 32. Có bao nhiêu số nguyên dương m để phương trình () () 2 e1ln12ee1 xxx mmx−⋅++=+ có hai nghiệm phân biệt không lớn hơn 5 .

A. 29 .B. 27 . C. 28 . D. 26 .

Câu 33. Ông Nam cần xây dựng một bể nước mưa có thể tích () 3 8 Vm = dạng hình hộp chữ nhật với chiều dài gấp 4 3 lần chiều rộng, đáy và nắp đổ bê tông , cốt thép; xung quanh xây bằng gạch và xi măng. Biết rằng chi phí trung bình là 980.000đ 2 /m và ở nắp để hở một khoảng hình vuông có diện tích bằng 2 9 diện tích nắp bể. Tính chi phí thấp nhất mà ông Nam phải chi trả (làm tròn đến hàng nghìn đồng).

A. 22.770.000 đ. B. 27.657.000 đ. C. 20.965.000 đ. D. 23.235.000 đ.

Câu 34. Xét 1 22022 0 2(2)d Ixxx =+  , nếu đặt 2 2 ux=+ thì I bằng

Câu 35. Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh 2a , SA vuông góc với đáy và 6 SAa = . Góc giữa hai mặt phẳng () SBD và () ABCD bằng

A. 90° B. 45° C. 60° D. 30°

Câu 36. Cho hình chóp SABC có đáy ABC là tam giác đều, hình chiếu vuông góc của đỉnh () ABCD S trên mặt đáy là trung điểm H của cạnh AB . Biết 3 2 a SH = và mặt phẳng () SAC vuông góc với mặt phẳng () SBC . Thể tích của khối chóp SABC bằng

A. 3 4 a B. 3 3 8 a C. 3 16 a D. 3 2 a

Câu 37. Với k và n là hai số nguyên dương tùy ý thỏa mãn kn ≤ . Mệnh đề nào dưới đây đúng?

A. () !! ! k n

knk C n = B. () ! !! k n n A knk = C. ! ! k n n C k = D. () ! ! k n n A nk =

Câu 38. Cho hai số dương ,,1aba ≠ , thỏa mãn 2 2 loglog2 a a bb+= . Tính log a b

A. 8 5 . B. 4 5 . C. 2 . D. 4 .

Câu 49. Số nghiệm nguyên của bất phương trình 2 3 52 1 5 5

x x+  <   là

A. 4 . B. 2 . C. 1. D. 3 .

Câu 50. Cho 35log5; log7, ab== khi đó 45 log175 bằng

A. 2 ab a + + . B. () 2 aab a + + . C. ()22 2 b a + + . D. () 2 2 ab a +

Câu 41. Thể tích của khối tứ diện đều cạnh a là

A. 3 2 12 a . B. 3 2 4 a . C. 3 3 12 a . D. 3 3 4 a .

Câu 42. Đồ thị hàm số nào sau đây có hai điểm cực đại và 1 điểm cực tiểu?

A. 4223yxx=−− . B. 3 4 yxx =− . C. 2 2 yxx =− . D. 4223yxx=−+− .

Câu 43: Cho hàm số ()yfx = có bảng biến thiên như sau:

Điểm cực đại của hàm số đã cho là

A. 4 x = B. 3 x =− C. 2 x =− D. 3 x =

Câu 44: Tìm tất cả các giá trị nguyên của m trên () 2021;2021 thỏa mãn ( )( ) 2 2414323 mm mmm−++−+−≥

A. 2020. B. 2021. C. 1. D. 0

Câu 45. Cho ;; abc là ba số thực dương khác 1 Đồ thị hàm số ;; xxx yaybyc === được cho ở hình vẽ dưới đây. Mệnh nào nào sau đây đúng?

A. abc << B. cab << C. bca << D. acb << Câu 46. Cho , ab là các số thực thay đổi thỏa mãn () 22 20 log6841 ab ab ++ −−= và , cd là các số thực dương thay đổi thỏa mãn () 2 2 2 log7223 c ccdd d ++−=+− . Giá trị nhỏ nhất của biểu thức ()() 22 1 acbd −++− là

A. 421 B. 1255 5 C. 291 D. 855 5

Câu 47. Cho hàm số () 1cos fxx =− , x ∀∈ ℝ . Khẳng định nào dưới đây đúng?

A. () dcos fxxxxC =−+  B. () dcos fxxxxC =++ 

A. 3 2022 2 2duu  B. 1 2022 0 d uu  C. 3 2022 2 d uu  D. 3 2022 2 1 d 2 uu 

+ .

C. () dsin fxxxxC =−+  . D. () dsin fxxxxC =++  .

Câu 48. Gọi l , h , R lần lượt là độ dài đường sinh, chiều cao và bán kính của hình trụ () T . Diện tích toàn

phần tpS của hình trụ được xác định theo công thức

A. 2 tp SRlR ππ=+

C. 2 2 tp SRlR ππ=+

Câu 49. Hàm số () 4 2x fx + = có đạo hàm là

B. 2 22 tp SRlR ππ=+

D. 2 tp SRhR ππ=+

A. () 4 4.2 ln2 x fx + ′ = . B. () 4 4.2.ln2 x fx + ′ = . C. () 4 2 ln2 x fx + ′ = . D. () 4 2.ln2 x fx + ′ = .

Câu 50. Cho hàm số () 432 fxaxbxcxdxa =++++ có đồ thị hàm số ()yfx ′ = như hình vẽ bên

12345678910111213141516171819202122232425

DDBABCDDBBBDDBDBABBADBAAA

26272829303132333435363738394041424344454647484950

AAABCACBCCADBBDADCBDCCBDB

Câu 1. Đồ thị hàm số nào trong

x + → =+∞ nên đồ thị có tiệm cận đứng 0 x =

Câu 2. Tích tất cả các nghiệm của phương trình 2 254 24 xx++ = bằng

A. 2 . B. 2 . C. 1 . D. 1.

Lời giải

Hàm số ()()() 122 ygxfxfx ==−− đồng biến trên khoảng nào dưới đây?

A. () 0;2 . B. () 3; +∞ . C. 13 ; 22 

. D. () ;0−∞ .

Chọn D

Có () 22 254254222 242225422520* xxxx xxxx ++++=⇔=⇔++=⇔++=

( )* có 25160∆=−> và 12.1 c xx a ==

Câu 3. Tập nghiệm của phương trình ( ) ( ) log1log230 xx−−+= là

A. { }4 . B. ∅ . C. { }2 . D. 2 4; 3 

Lời giải

Chọn B

Có ( ) ( ) ( ) ( )log1log230log1log23 xxxx −−+=⇔−=+

1234 101 xxx x xx −=+=−

Vậy S =∅

Câu 4. Cho hàm số 3231yxxx=−++ có đồ thị ( )C và đường thẳng ( ) :1. dyx =− Biết ( ) d cắt ( )C tại ba điểm phân biệt có hoành độ là 123,,.xxx Tính 123 Txxx =++ ?

A. 3 B. 1 C. 4 D. 2

Lời giải

Chọn A

Có phương trình hoành độ giao điểm 3232 311320210. xxxxxxxxxx −++=−⇔−+=⇔=∨=∨= Suy ra 0123. T =++=

Câu 5. Tập xác định của hàm số () 2 3 1 yx=− là

 

BẢNG ĐÁP ÁN

HƯỚNG DẪN GIẢI CHI TIẾT

số sau đây có tiệm cận đứng ?

2 1 2 y xx = −+ . B. 2 1 1 y x = + . C. 4 3 1 y x = + . D. 2 y x = . Lời giải Chọn D Các hàm số 2 1 2 y xx = −+ , 2 1 1 y x = + , 4 3 1 y x = + có TXĐ là DR = nên đồ thị không có tiệm cận đứng. Hàm số

x = có ( ) 0; D =+∞ và 0 2 lim x

các hàm

2 y

 

⇔⇔⇔∈∅  −>>

A. [ ) 1; +∞

Chọn B

B. () 1; +∞ C. () 0; +∞ D. {}\1 ℝ

Lời giải

Ta có: ( ) ( ).cot2.sin fxfxxxx ′ =+ ()() cos .2.sin sin x fxfxxx x ′ ⇔=+

′

Điều kiện xác định: 101xx−>⇔>

Tập xác định () 1; D =+∞ .

Câu 6. Một hình nón có chiều cao bằng 4 bán kính đáy bằng 3 có diện tích toàn phần bằng

A. 9π B. 15π C. 24π D. 12π

Lời giải

Chọn C

Theo giả thiết ta có 22 4,35hrlhr ==  =+= . 22.3.5.324 tp Srlrπππππ =+=+=

Câu 7. Cho hàm số ()fx liên tục trên mỗi khoảng () ;1−∞ và () 1; +∞ và có bảng biến thiên như sau

Tập nghiệm của bất phương trình () 20 fx −> là

A. ℝ B. ( ];1−∞ C. () ;1−∞ D. () 1; +∞

Lời giải

Chọn D

Ta có : ()()202fxfx−>⇔> Từ bảng biến thiên suy ra () 21fxx>⇔>

Tập nghiệm bất phương trình là ( ) 1; +∞

Câu 8. Cho hàm số ()yfx = có đạo hàm liên tục trên () 0;π thoả mãn ()().cot2.sin fxfxxxx ′ =+ . Biết

′ ⇔= () 2 sin fx x x ⇔=  





2 24 f ππ =   22 0 44 CC ππ  =+  = . Hay ( ) () 22 .sin sin fx xfxxx x =  = 22 .sin 636672 f ππππ

A. 11 B. 10 C. 12 D. 9

Ta có ()2 333 3 3 xm y xm xm −+ ′ == 

3 3

x y xm

1 330 2 2

3 3 m m m m m >−  +>   ⇔⇔≥ −≤− ≥   

Vì m nguyên nên { }1;2;3;....;10 m ∈ . Vây có 10 giá trị nguyên của tham số m thỏa mãn.

A. 36 B. 36π C. 9π D. 9

Lời giải Chọn B

Ta có 3344 .336 33 Vrπππ===

Câu 11. Biết ( ) 3Fxx = là một nguyên hàm của hàm số ( )fx trên R . Giá trị của () () 2 1 2dfxx +  bằng

A. 7 B. 9 C. 15 4 D. 23 4

Lời giải Chọn B

Ta có () () ()

222 2 2 3 1 1 111 2d2dd29 fxxxfxxxx +=+=+=

2 24 f ππ =   . Tính 6 f π    A. 2 36 π . B. 2 80 π . C. 2 54 π . D. 2 72 π . Lời giải Chọn D

( ) ( ) 2 .sin-.cos 2 sin fxxfxx x x

 



Do đó () () 2 d2d sinsin fxfxxxxxC xx  

′  =  =+



để

= + đồ

ế

Câu 9. Có bao nhiêu giá trị nguyên của tham số m không vượt quá 10

hàm số

ng bi

n trên

khoảng ( ) 2; −+∞ ?

Lờ

i giải Chọn B

′

+  + .

Hàm số 3 3 x y xm = + đồng biến trên khoảng ( ) 2; −+∞ khi

Do m không vượt quá 10 nên 2 10 3 m ≤≤

Câu 10. Thể tích V của khối cầu có bán kính 3 r = bằng

Câu 12. Cho các hàm số x ya = và xyb = với , ab là những số thực dương khác 1, có đồ thị như hình vẽ

Đường thẳng 3 y = cắt trục tung, đồ thị hàm số x ya = và x yb = lần lượt tại ,, HMN . Biết rằng

23HMMN = , khẳng định nào sau đây đủng?

Ta có: 1...HBMEHBGNPCFEVVVV′′=−−

Lại có:

′′′ = ′′ 1

A. 53ab = B. 23ab = C. 35ab = D. 35ab = Lời giải

Chọn D

Ta có () 0;3 H , () log3;3 a M , () log3;3 b N () log3;0 a HM  = , () log3log3;0 ba MN =−

Theo giả thiết, 23HMMN = 23HMMN⇔= () 2log33log3log3 aba⇔=−

5log33log3 ab⇔= 33

53 loglogab ⇔= 33 5log3logba⇔= 53 33 loglogba⇔= 53ba⇔= .

Câu 13. Cho khối lăng trụ tam giác ABCABC′′′ có thể tích V . Gọi ,, MNP lần lượt là trung điểm của các

cạnh AB′′ ; BC ; CC′ . Mặt phẳng () MNP chia khối lăng trụ đã cho thành 2 phần, phần chứa điểm B

có thể tích là 1V . Tỉ số 1V V bằng

HBMEV HBBMBE VBBBABC

′′′ === ′′′′′

• 113133 332228

• 111111 3326272

HBGNV HBBGBN VBBBABC === ′

PCFEV PCCECF VCCCBCA

′′′ === ′′′′′

• 111111 ...... 3322448

Vậy 1 31149 87248144 V V =−−= .

Câu 14. Cho hình lăng trụ tam giác đều ABCABC′′′ có cạnh đáy bằng 2a . Khoảng cách từ B đến mặt phẳng () ACCA′′ bằng

A. 2a B. 3a C. 2a D. 22a

Lời giải Chọn B

Gọi M là trung điểm của AC

Ta có BMAC BMAA ⊥   ′ ⊥  ()BMACCA′′  ⊥ .

Khi đó () () ; 3 BAACA dBMa ′′ ==

Câu 15. Nếu () 32d23 fxxxxC =++  thì hàm số ()fx bằng

A. () 43 1 2 fxxxCx =++

C. () 43 1 2 fxxx =+

B. () 2 66 fxxxC =++

D. () 2 66 fxxx =+

Lời giải Chọn D () ()322 2366 fxxxCxx ′ =++=+

Câu 16. Cho () 5 2 d10fxx =  . Khi đó () 2 5 24dfxx   bằng

A. 42

B. 34

C. 32

Lời giải Chọn B

D. 46

A. 25 144 B. 37 144 C. 61 144 D. 49 144 Lời giải Chọn D

Ta có: • PCEPCNCECN ∆=∆′′  = • PCNHBNHBCP∆=∆  =

• Xét ABC′′′ ∆ , theo định lý menelauyt có: ..1AMBECF MBECFA 

FA ′

• Xét BGN∆ đồng dạng BME ′ ∆ 1 3 BGBN BMBE  == ′′ 1 6 BG BA  = .

()() 555 222 42d4d2d fxxfxxx −=− 

40634=−= .

Câu 17. Cho một cấp số cộng có 2 4 u = , 4 2 u = . Hỏi 1u bằng bao nhiêu?

A. 1 5 u = . B. 1 1 u =− .

C. 1 6 u = . D. 1 1 u = .

Lời giải

Chọn A

4 5 32 1 uud u uud d =+= =   ⇔

=+= =−  

Câu 18. Hàm số nào dưới đây có đồ thị như đường cong trong hình dưới đây?

A. 4223yxx=−+

C. 4223yxx=−+−

Chọn B

B. 4223yxx=−−

D. 4233yxx=+−

Lời giải

Dựa vào đồ thị ta thấy đường cong là hàm bậc 4 trùng phương với hệ số 0 a > , 3 d =− và hàm số có ba cực trị suy ra 00abb<⇔< .

Câu 19. Một hình trụ có bán kính đáy bằng a , chu vi thiết diện qua trục bằng 10a . Thể tích của khối trụ đã cho bằng

A. 3 aπ . B. 3 3 aπ . C. 3 4 aπ . D. 3 5 aπ .

Lời giải

Chọn B

Chu vi thiết diện qua trục là ()()

2222103 Phrhaaha =+=+=⇔=

Thể tích khối trụ là 223 ..33 Vrhaaa πππ === .

Câu 20. Trong các mệnh đề sau, mệnh đề nào sai?

A. () dln01 xx axaaCa =+<≠  . B. cosdsinxxxC =+  .

C. 1 d,1 1 x xxC α α α α

+ =+∀≠− +  . D. ()() d fxxfxC ′ =+  .

Lời giải

Chọn A

Theo công thức () d01 ln x x a axCa a =+<≠  .

x ( )

A. 0 B. 10 C. 5 D. 4

Lời giải

Chọn D

Do ( ) 2 4501;2xxx−+>∀∈ , ta có:

Phương trình () () ()() 2 2 1451 45 m fxmxxfxgx xx +=⇔=−++= −+

Xét ( ) ( )( ) ( ) ( ) ( ) 2 14524101;2gxfxxxxfxx ′′=+−++−+<∀∈

′  +<  ∀∈  <+<  +>

Vì () ( ) () 10 1;2213 10 240

  −<

( )

Yêu cầu bài toán ( ) ( ) 2138gmgm ⇔<<⇔<<

( )2 g

Câu 22. Cho hình nón ( )N có chiều cao bằng 2a . Cắt ( )N bởi một mặt phẳng qua đỉnh và cách tâm của đáy một khoảng bằng a ta được thiết diện có diện tích bằng 2 411 3 a . Thể tích khối nón đã cho bằng

A. 3 45 3 aπ B. 3 10 3 aπ C. 3 10 aπ D. 3 45 9 aπ Lời giải

Chọn B S O A B

H I

Gỉa sử tam giác SAB là thiết diện đi qua đỉnh của hình nón ( )N



Ta có 21 1 41 

( )fx ′ 1 2 3 0 + 4 3 1

Câu 21. Cho hàm số ()yfx = liên tục trên [] 1;3 và có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của m để phương trình () 2 1 45 m fx xx += −+ có nghiệm trên khoảng ( )1;2 ?

fx xx fx x 

Bảng xét dấu: x

′ ( )gx ( )1 g

Do { }4;5;6;7 mm ∈  ∈ ℤ .

Gọi I là trung điểm của AB và kẻ OHSI ⊥ ( ) ( ) ( ) , OHSABdOSABHOa  ⊥  ==

Xét tam giác vuông SOI có : 222222 111111 4 OHSOOIaaOI =+⇔=+ 2 3 a OI  = .

Lại có: 2 222 44 4 3 3 aa SISOIOa=+=+= .

Xét tam giác SAB có :

gxx fxx xxxmxx ′ ⇔−−≤∀∈+∞  ⇔−−−+−+≤∀∈+∞ 

′ ≥∀∈+∞

0,3;. 30,3;. 323390,3;.

ABC

a S a AB a SI === 33 23 ABa BI  == .

2 411 2. 2 233 3 4 3 3

Xét tam giác OIB có: 22 22 433 5 39 aa OBOIIBa =+=+=

Vậy thể tích của khối nón là : 3 22 1110 ..5.2 333 a VrSOaa π ππ ===

Câu 23. Cho hàm số ( )yfx = có đồ thị là đường cong trong hình vẽ dưới đây. Giá trị lớn nhất của hàm số đã

cho trên đoạn [ ]1;1 bằng bao nhiêu ?

A. 3 B. 0 C. 1 D. 2

Lời giải

Chọn A

Theo đồ thị ta thấy: ( ) 13 fx −≤≤ với [ ]1;1 x ∈− nên [] ( ) 1;1 3 Maxfx = .

Câu 24. Số cách sắp xếp 5 người ngồi vào 6 chiếc ghế xếp hàng ngang là:

A. 5 6A . B. 6! . C. 5 6C . D. 5!.

Lời giải

Số cách sắp xếp 5 người vào 6 ghế hàng ngang là 5 6A

Câu 25. Cho hàm số ( )yfx = có đạo hàm ()() ( ) 2 2 19fxxxxmx ′ =−++ với mọi x ∈ ℝ . Có bao nhiêu số

nguyên dương m để hàm số ( ) ( ) 3 gxfx =− đồng biến trên khoảng ( ) 3; +∞ ?

A. 6 B. 5 C. 7 D. 8

Lời giải

Chọn A

Ta có ()()()()() 22 332339. fxxxxmx ′ −=−−−+−+

Khi đó ( ) ( ) 3.gxfx ′′ =−−

( ) 3; x ∀∈+∞ thì ()()2 30,20 xx −≤−≥ suy ra ()()() 2 3390,3:. xmxx −+−+≥∀∈+∞ () () () () 2 2 3:

−+−+ ⇔≤∀∈+∞⇔≤

3939 ,3; 33 xx mxmMin xx +∞

Ta có () () () 2 39 99 323.6 333 x xx xxx −+ =−+≥−=

Suy ra 6. m ≤

Vì m nguyên dương suy ra { }1;2;3;4;5;6 m ∈ .

Câu 26. Cho hàm số ( ) 2 sin1fxxx=++ biết ( )Fx là một nguyên hàm của hàm số ( )fx và ( ) 01 F = . Khí đó ( )Fx bằng?

A. ( ) 3 cos2Fxxxx=−++ B. () 3 cos2 3 x Fxxx=−++

C. () 3 cos 3 x Fxxx =++

Chọn A

D. () 3 cos2 3 x Fxx=++

Lời giải

Ta có () () 3 2 sin1cos 3 x FxxxdxxxC =++=−++  .

Mà () 30 01cos0012 3 FCC =⇔−++=⇔= . Vậy ( ) 3 cos2Fxxxx=−++ .

Câu 27. Tiệm cận đứng của đồ thị hàm số 21 2 x y x = −+ là đường thẳng

A. 2 x = B. 1 2 x = C. 2 y =− D. 2 x =−

Lời giải

Chọn A

Ta có 2

21 lim 2 x

x x → =∞ −+ nên đồ thị hàm số có tiệm cận đứng là 2 x =

Câu 28. Cho hình chóp tứ giác có đáy là hình vuông cạnh bằng 2 , chiều cao bằng 3. Thể tích của khối chóp đã cho bằng

A. 4 B. 12 C. 6 D. 18

Lời giải

Chọn A

Ta có diện tích đáy 2.24 B == nên thể tích khối chóp là 11 .4.34 33 VBh===

Câu 29. Trên khoảng ( );2−∞− , họ nguyên hàm của hàm số () 1 2 fx x = + là

1 2 1 2 3 1 2 1 x y O



Hàm số ( )gx đồng biến trên khoảng ( ) 3; +∞ khi và chỉ khi ( ) ( ) ()() ()()()()() 22

A. 1 2 C x + + B. ln2xC ++ C. ()2 1 2 C x −+ + D. 1 ln2 2 xC ++

Lời giải

Chọn B

Ta có () 1 ln2 2 fxdxdxxC x ==++ +

Câu 30. Có bao nhiêu giá trị nguyên của tham số m để hàm số () 32 1 93 3 fxxmxx =++− đồng biến trên ℝ ?

A. 5 .B. 4 C. 7 D. 6 .

Lời giải

Chọn C

TXĐ: D = ℝ

Ta có () 2 29fxxmx ′ =++

Hàm số đồng biến trên ℝ () 0, fxx ′ ⇔≥∀∈ℝ 2 290, xmxx ⇔++≥∀∈ ℝ 2 9033mm ′ ⇔∆=−≤⇔−≤≤ .

Vì m ∈ ℤ nên {} 3;2;1;0;1;2;3 m∈−−−

Câu 31. Cho hàm số ()fx có bảng xét dấu của đạo hàm như sau

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. () 2; +∞ .B. () ;2−∞− C. () 2; −+∞ D. () 2;1 .

Lời giải

Chọn A

Từ bảng biến thiên suy ra hàm số nghịch biến trên khoảng () 2; +∞ .

Câu 32. Có bao nhiêu số nguyên dương m để phương trình () () 2 e1ln12ee1 xxx mmx−⋅++=+ có hai nghiệm

phân biệt không lớn hơn 5

A. 29 .B. 27 . C. 28 . D. 26 .

Lời giải

Chọn C

Vì 0 x ≠ nên () ln1e1 x mmx +=− ⇔ () ln11ex mmx ++= () 2

Đặt () ln1tmx=+  1ex mx +=

Ta có 1e ee 1e xt x

mx mxmt mt  +=  +=+  +=  () ** .

Xét hàm số đặc trưng: () e u fumu =+ trên ℝ

Ta có () e0 u fum ′ =+> , u ∀∈ ℝ và m + ∈ ℤ

Suy ra ()**e10 x xtmx ⇔=⇔−−=

Xét hàm số ( ) e1 x gxmx=−− , có ( ) e x gxm ′ =− , suy ra ( ) 0ln gxxm ′ =⇔= .

* Nếu 1 m = loại.

* Nếu 1 m > , ta có Để thỏa mãn bài toán thì () 5 e1 50 5 gm≥⇔≤

Kết hợp điều kiện, suy ra {} 2;3;;29 m∈… .

Vậy có 28 giá trị nguyên dương m thỏa mãn.

A. 22.770.000 đ. B. 27.657.000 đ. C. 20.965.000 đ. D. 23.235.000 đ. Lời giải

Chọn B

Gọi chiều rộng của bể là () 3xm . Ta có chiều dài bể là 4 ()xm và chiều cao của bể là () 2 2 3 m x Khi đó tổng diện tích bề mặt xây là: () () 22 2 2 22 2228642864327 34.2.2.3.4.3.42.. 3933333 xx Txxxxxx m xxx =++−=+≥= .

Chi phí C (tính theo đồng) xây dựng là: 327 .980000.98000027657000 3 CT=≥≈ (đồng).

 −=

Ta có () () 2 e1ln12ee1 xxx mmx−⋅++=+ () 1 () () ()2 e1lnx1e10 xx mm ⇔−+−−= () () () e1ln1e10 xx mmx  ⇔−+−−=  () () e10 ln1e10

x x mmx

⇔  +−−=   () e1 ln1e1

x x mmx  = ⇔  +=−  () () 0 / ln1e1 x

xtm mmx

=  ⇔  +=−

Câu 34. Xét 1 22022

2(2)d Ixxx =+  , nếu đặt 2 2 ux=+ thì I bằng

()



 Phương trình () 1 có hai nghiệm phân biệt không lớn hơn 5 ⇔ Phương trình

ln1e1 x mmx +=− có một nghiệm duy nhất khác 0 và nhỏ hơn hoặc bằng 5 .

A. 3 2022 2 2duu  B. 1 2022 0 d uu  C. 3 2022 2 d uu  D. 3 2022 2 1 d 2 uu  Lời giải

Chọn C

Ta có: +) d2duxx = ; +) 02;13xuxu =  ==  =

3 2022 2 d Iuu  =  .

Câu 35. Cho hình chóp . SABCD có đáy ABCD là hình vuông cạnh 2a , SA vuông góc với đáy và 6 SAa =

. Góc giữa hai mặt phẳng () SBD và () ABCD bằng

A. 90° . B. 45° . C. 60° . D. 30° .

Lời giải

Chọn C

Gọi O là giao điểm của AC và BD

Từ đề bài, ta có: +) ,() BDACBDSABDSACBDSO ⊥⊥  ⊥  ⊥

 Ta có , SOBDAOBD ⊥⊥

 ()() () ();; SBDABCDSOAOSOA ==

+) 222tan360 SA ACaAOaSOASOA AO =  =  ==  =°

Câu 36. Cho hình chóp . SABC có đáy ABC là tam giác đều, hình chiếu vuông góc của đỉnh () ABCD S trên mặt đáy là trung điểm H của cạnh AB . Biết 3 2 a SH = và mặt phẳng () SAC vuông góc với mặt phẳng () SBC . Thể tích của khối chóp SABC bằng

A. 3 4 a B. 3 3 8 a C. 3 16 a D. 3 2 a

Chọn A

x H A C B S K

Giả sử ABC là tam giác đều cạnh x .

Kẻ HK vuông góc với SC tại K . Ta có , SCHKSCAB ⊥⊥ (vì ()ABSHC ⊥ ) () , SCAKBAKBK  ⊥  cùng vuông góc với SC  Góc giữa AK và BK là góc giữa () SAC và () SBC 90 22 ABx AKBHK  =°  == . Mặt khác, ta có: () 22 222 3 3 24 xa x CHSCCHSH + =  =+= 222 111 HKCHSH  =+ 222222

33 . .3 22 332 44

xa CHSHax HK CHSHxaxa  === ++ +

Suy ra, tacó phương trình: 222 22

3 32 2 2 xax xxaxa xa =⇔=+⇔= +

 Diện tích tam giác ABC là: () 2 2 33 2. 42 ABC a Sa ∆ ==

 Thể tích của khối chóp SABC là: 23133 3224 aaa V ==

Câu 37. Với k và n là hai số nguyên dương tùy ý thỏamãn kn ≤ . Mệnh đề nào dưới đây đúng?

A. () !! ! k n

knk C n = . B. () ! !! k n n A knk = . C. ! ! k n n C k = . D. () ! ! k n n A nk = .

Lời giải

Chọn D

Mệnh đề đúng là () ! ! k n n A nk =

Câu 38. Cho hai số dương ,,1aba ≠ , thỏa mãn 2 2 loglog2 a a bb+= . Tính log a b

A. 8 5 . B. 4 5 . C. 2 . D. 4 .

Lời giải

Chọn B

Lời giải S

D B C

Ta có 2 2 154 loglog2log2log2log2log225 aaaaa a bbbbbb +=⇔+=⇔=⇔=

52 1 5 5 x x

x xxx ++

<⇔< 

Do x ∈ ℤ nên {} 0;1 x ∈

2 ab a + + B. ()

Chọn D

Lời giải

Ta có: 2 3333335 45 2 33333

log175log5.72log5log72log5log5log7 log175 log45log3.52log3log52.1log5 ++ ==== ++ () 2 2. . 22 ab aab aa + + == ++

Câu 41. Thể tích của khối tứ diện đều cạnh a là

B. 3 2 4

a .

3 3 12 a .

Chọn A

Gọi tứ diện đều cạnh a là . SABC với O là tâm của đáy ABC ()SOABC  ⊥ .

Ta có

2 113 ..sin...sin60 224 ABC a SABACAaa ∆ ==°= và 3 2sin2sin603 BCaa OA A === °

Tam giác SOA có 22 6 3 a SOSAOA=−=

Vậy 23 11362 ... 334312SABCABC aaa VSSO ∆ ===

Câu 42. Đồ thị hàm số nào sau đây có hai điểm cực đại và 1 điểm cựctiểu?

A. 4223yxx=−− . B. 3 4 yxx =− . C. 2 2 yxx =− . D. 4223yxx=−+− . Lời giải

Chọn D

Ta có 4223yxx=−+− 3 44 yxx ′  =−+ .

3 0 0440 1 x yxx x

=  ′ =  −+=⇔  =± 

2 124yx ′′ =−+

Có ()040 y ′′ => 0 x  = là điểm cực tiểu.

Có ()180 y ′′ ±=−< 1 x  =± là hai điểm cực đại.

Câu 43: Cho hàm số ()yfx = có bảng biến thiên như sau:

Điểm cực đại của hàm số đã cho là

A. 4 x = B. 3 x =− C. 2 x =− D. 3 x = Lời giải

Chọn C Điểm cực đại của hàm số đã cho là 2 x =−

Câu 44: Tìm tất cả các giá trị nguyên của m trên () 2021;2021 thỏamãn ( )( ) 2 2414323 mm mmm−++−+−≥

A. 2020. B. 2021. C. 1. D. 0 Lời giải Chọn B

Ta có: ( )( ) 2 2414323 mm mmm−++−+−≥ () ( ) () ()

mmm mmm mm

−++− ⇔≥ ++ ⇔−++−≥++ ⇔−++−≥++

2 2 2 2

mm mm mm

241.3 3 432 241432 131232

Xét hàm số () 2 3 fxxx =++ với 0 x >

2 3

+  <   là A.

D. 3

Lờ

giải Ch

2 2





Câu 39. Số nghiệm nguyên của bất phương trình 1 2 3 x ⇔−<<

4 .

2 .

ọn B Ta có:

52352 1 555 5

22 3523520 xxxx ⇔<+⇔−−<

Số nghiệm nguyên của bất phương trình là 2. Câu 40. Cho 35log5; log7, ab== khi đó 45 log175 bằng

aab a + +

()22

b a + +

() 2 2 ab a + +

D. 3 3 4

A. 3 2 12 a .

Lời giải

Ta có: () 2 22

3 10,0 33 xxx fxx xx ++ ′ =+=>∀> ++

Nên hàm số ()fx đồng biến trên khoảng () 0; +∞

Mà () () 1212210 mmm fmfmm −≥⇔−≥⇔+−≤

Xét hàm số () 21 m fmm=+− :

Ta có: () 2ln210, m fmm ′ =+>∀ nên hàm () 21 m fmm=+− đồng biến

Mặt khác: ()()00fmfm ≤  ≤

Vậy {} 2020;2019;...;0 m∈−−  có 2021 giá trị nguyên m thỏa mãn.

Câu 45. Cho ;; abc là ba số thựcdương khác 1. Đồ thị hàm số ;; xxx yaybyc === được cho

ở hình vẽ dưới đây. Mệnh nào nào sau đây đúng?

A. abc << B. cab << C. bca << D. acb << Lời giải

Chọn D

Do hàm số x ya = nghịch biến trên 1 a  < ℝ

Do hàm số xyb = và x yc = đồng biến trên ,1bc  > ℝ .

Ta có: ()0;:11 x xx bb xbcbc cc  ∀∈+∞>⇔>  >  >  

Vậy acb <<

Câu 46. Cho , ab làcácsố thựcthay đổithỏamãn () 22 20 log6841 ab ab ++ −−= và , cd làcácsố thựcdươngthay

đổi thỏa mãn () 2 2 2 log7223 c ccdd d ++−=+− . Giá trị nhỏ nhất của biểu thức

()() 22 1 acbd −++− là

A. 421 B. 1255 5 C. 291 D. 855 5

Lời giải

Chọn C

Ta có: ()()()() 22 22 22 20 log684120684341* ab abababab ++ −−=⇔++=−−⇔−++=

 ++−=+−  ++−=+−⇔



+−≥>

() () 2 2 2 2 121 log722log27 ** 1;0 1;0 cd cccddd dc dc

≥>

Đặt ()() ;;1; MabNcd . Theo () * ta thấy M thuộc đường tròn tâm () 3;4 I , bán kính

Suy ra min1 291 MNNIR=−=− .

Vậy giá trị nhỏ nhất của biểu thức ()() 22 1291acbd −++−=− .

Câu 47. Cho hàm số () 1cos fxx =− , x ∀∈ ℝ . Khẳng định nào dưới đây đúng?

A. () dcos fxxxxC =−+  . B. () dcos fxxxxC =++  .

C. () dsin fxxxxC =−+  . D. () dsin fxxxxC =++  .

Lời giải

Chọn C

Ta có: () 1cosdsinxxxxC−=−+  .

Câu 48. Gọi l , h , R lần lượt là độ dài đường sinh, chiều cao và bán kính của hình trụ () T . Diện tích toàn phần tpS của hình trụ được xác định theo công thức

A. 2 tp SRlR ππ=+ B. 2 22 tp SRlR ππ=+

C. 2 2 tp SRlR ππ=+ D. 2 tp SRhR ππ=+

Lời giải

Chọn B

Diện tích toàn phần tpS của hình trụ được xác định theo công thức 2 22 tp SRlR ππ=+

Câu 49. Hàm số () 4 2x fx + = có đạo hàm là

A. () 4 4.2 ln2 x fx + ′ = B. () 4 4.2.ln2 x fx + ′ = C. () 4 2 ln2 x fx + ′ = D. () 4 2.ln2 x fx + ′ = Lời giải

Chọn D

Ta có: ()()44 22.ln2 xxfxfx++ ′ =  = .



Lại có: () () 2 2 2 2 2 2 2 

log7223 log7223 230;,0  ⇔ ⇔  

c ccdd c ccdd d d dddc ≥>   



−=−  ++−=++−

1 R =

Từ () ** ta thấy N thuộc nữa đường thẳng 11 21 22xyyx =−⇔=+ ứng với 0,1xy≥≥

Khi đó ()() 22 1 MNacbd =−++− .

Hàm số ()()() 122 ygxfxfx ==−− đồng biến trên khoảng nào dưới đây?

A. () 0;2 . B. () 3; +∞ . C. 13 ; 22    . D. () ;0−∞ .

Lời giải Chọn B

Từ đồ thị hàm số ()fx ′ ta thấy: () 0 0 1 x fx x =  ′ =⇔  =± 

Nên ()()() 4.11fxaxxx ′ =−+ , hay () () 2 41fxaxx ′ =− .

Suy ra: () () ()() 2 22 422 .2..1.1.1 fxaxaxaaxaxx =−+=−=−+

Xét ()()() 122 gxfxfx =−− có: ()()()()() 2122122 gxfxfxfxfx ′′′ =−−−−−− Suy ra:

′ =−−−−−−−−−−−−

()()()()()()()()() 222222 2.4121211.3.2.22.42.21 gxaxxaxxaxxaxx

()()()()()() 32 3 2 22 32.121364.213 axxxxaxxxx =−−−−−−−

()()()()() 3 2 32.1312322 axxxxxxx =−−−−−−

()()() 3 22 32.134113 axxxxx =−−−+

Vì () () 2 41fxaxx ′ =− nên dựa vào đồ thị hàm số ()fx ′ suy ra 0 a >

Nhận xét: ()()()()() 3 2 1321.2.4.41130ga ′ −=−++<

Nên ta có bảng xét dấu:

Dựa vào bảng xét dấu ta có ()gx đồng biến trên khoảng () 3; +∞ .

Câu 50. Cho hàm số () 432 fxaxbxcxdxa =++++ có đồ thị hàm số ()yfx ′ = như hình vẽ bên

 

 

 

  ==∈  

 

==∈  

() () () 0 1173 0;1 8 01 1173 2;3 8 3 x xa gxx xb x = 

′ =⇔=

 = 

SỞ GIÁO DỤC VÀ ĐÀO TẠO THÁI BÌNH

TRƯỜNG THPT CHUYÊN THÁI BÌNH

ĐỀ THI THỬ TỐT NGHIỆP THPT –LẦN 3 – NĂM HỌC 2022 – 2023

Câu 1. Trong không gian Oxyz , cho 23 aijk =−+− . Tọa độ của vectơ a là:

A. ( )2;1;3 B. ( )3;2;1 C. ( )2;3;1 D. ( )1;2;3

Câu 2. Cho hàm số ( )yfx = có bảng biến thiên như hình vẽ

Khẳng định nào sau đây đúng?

A. Giá trị cực đại của hàm số là 3 CDy = B. Giá trị cực đại của hàm số là 4 CDy =

C. Giá trị cực tiểu của hàm số là 3 CTy =− D. Giá trị cực tiểu của hàm số là 1 CTy =

Câu 3. Hàm số nào dưới đây có đồ thị như đường cong trong hình bên dưới?

Câu 10. Trong các hàm số sau, hàm số nào đồng biến trên ℝ ?

. B. () 1 x fx e  =

A. 3 2 yxx =− B. 24 2 yxx =− C. 32 yxx =−+ D. 42 2 yxx =−

Câu 4. Tìm tập xác định D của hàm số ( ) 25 2 yxx=−−

A. D = ℝ B. ( ) 0; D =+∞

C. ( ) ( ) ;12; D =−∞−∪+∞ . D. { }\1;2 D =− ℝ .

Câu 5. Tìm họ nguyên hàm của hàm số ( ) sin3 fxx =

A. cos3xC−+ B. 1 cos3 3 xC−+ C. cos3xC + D. 1 cos3 3 xC +

Câu 6. Cho cấp số nhân ( ) n u có số hạng đầu 1 3 u = và công bội 2 q = . Số hạng thứ năm của cấp số nhân ( ) n u là

A. 5 96 u = B. 5 32 u = C. 5 48 u = D. 5 24 u =

Câu 7. Cho khối hộp chữ nhật ABCDABCD ′′′′ có AAa ′ = , 3 ABa = , 5 ACa = . Thể tích khối hộp bằng

A. 3 12a B. 3 4a C. 3 15a D. 3 5a

Câu 8. Số tổ hợp chập 3 của 12 phần tử là

A. 1728 B. 220 C. 1320 D. 36

Câu 9. Cho hình chóp SABC có đáy ABC là tam giác cân ABACa == , 120 BAC =° các cạnh bên bằng nhau và cùng tạo với mặt phẳng đáy các góc 30° . Thể tích khối chóp SABC là

A. 3 3 12 a B. 3 4 a C. 3 3 4 a D. 3 12 a

 . C. () 1 3

x fx

A. 3 3 yxx =−− B. 1 2 x y x = C. 1 3 x y x + = + D. 3 3 yxx =+

Câu 12. Cho hàm số ()yfx = liên tục trên đoạn [ ]1;5 và có đồ thị trên đoạn [ ]1;5 như hình vẽ bên.

Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( )fx trên đoạn [ ]1;5 bằng

A. 4. B. -1. C. 1. D. 2.

Câu 13. Trong không gian Oxyz , một vectơ chỉ phương của đường thẳng 12 112 xyz −+ == là

A. ( )1;1;2 u =− B. ( )1;1;2 u = C. ( )1;2;0 u =− D. ( )1;2;1 u =−

Câu 14. Trong không gian Oxyz , cho điểm ( )1;2;3 M . Tọa độ điểm A là hình chiếu vuông góc của M trên mặt phẳng ( )Oyz là:

A. ( )1;2;3 A B. ( )1;2;0 A C. ( )1;0;3 A D. ( )0;2;3 A

Câu 15. Hàm số axb y cxd + = + với 0 a > có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?

A. 0,0,0bcd<<< B. 0,0,0bcd<>< C. 0,0,0bcd>>< D. 0,0,0bcd><<

Câu 16. Tính đạo hàm của hàm số ( ) 2 log21yx=+

A. () 1 21.ln2 y x ′ = + B. () 2 21.ln2 y x ′ = + C. 2 21 y x ′ = + D. 1 21 y x ′ = +

Câu 17. Cho hàm số ( )yfx = có bảng biến thiên như hình vẽ. Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là







 

A. () x e fx π  =  fx = .

. D. ( )

Câu 11. Hàm số nào dưới đây đồng biến trên khoảng ( ) ; −∞+∞ ?

A. 0. B. 2. C. 1. D. 3.

Câu 18. Với mọi , ab dương thỏa mãn 3 2 2 loglog5. ab+= Khẳng định nào dưới đây đúng?

A. 32 32 ab = B. 22 32 ab =− C. 23 32 ab = D. 2 32 ab =−

Câu 19. Hàm số ( )log01 a yxa=<≠ có đồ thị là hình bên. Giá trị của cơ số a bằng

A. 1 y = B. 1 x = C. 2 x = D. 2 y =

Câu 28. Giá trị nhỏ nhất của hàm số 3 35yxx=−+ trên đoạn [] 2;4 là

A. [] 2; 4 min3 y = B. [] 2;4 min7 y = C. [] 2; 4 min5 y = D. [] 2; 4 min0 y =

Câu 29. Cho hàm số ()yfx = có bảng biến thiên như sau

A. 4 2 B. 4 C. 2 D. 2

Câu 20. Tìm tập nghiệm S của bất phương trình 4 5 5 1 x >

A. ( ) 5; S =+∞ . B. ( ) 3; S =+∞ . C. ( );5 S =−∞ . D. ( );3 S =−∞ .

Câu 21. Tìm tập nghiệm S của bất phương trình ( ) 2 22 loglogxxx =− .

A. { }2 S = . B. { }0 S = . C. { }0;2 S = . D. { }1;2 S = .

Câu 22. Một chiếc hộp chứa 9 quả cầu gồm 4 quả màu xanh, 3 quả màu đỏ và 2 quả màu vàng (các quả cầu đôi một khác nhau). Lấy ngẫu nhiên 3 quả cầu từ hộp đó. Xác suất để trong 3 quả cầu lấy được có ít nhất 1 quả màu đỏ bằng

A. 1 3 . B. 19 28 . C. 16 21 .

D. 17 42 .

Câu 23. Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B và 2 ABa = . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối chóp SABC

A. 3 3 4 a V = B. 3 3 3 a V = C. 3 3 12 a V =

D. 3 23 3 a V =

Câu 24. Cho khối nón có bán kính đáy bằng 3cm , góc ở đỉnh hình nón là 60° . Thể tích khối nón bằng

A. 3 93 (cm) π . B. 3 33 (cm) π . C. 3 6 (cm). D. 3 3 (cm) π .

Câu 25. Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh 4a . Diện tích xung quanh của hình trụ là

A. 2 8 Sa π = B. 2 24 Sa π = C. 2 16 Sa π = D. 2 4 Sa π =

Câu 26. Tìm nguyên hàm ( )Fx của hàm số () 2 21 2 fxx x =+− biết ( ) 13 F =

A. ( ) ( ) 2 2ln21Fxxxx=+−−+ B. ( ) 2 2ln21Fxxxx=++−+

C. ( ) 2 ln21Fxxxx=+−−+ D. ( ) 2 2ln21Fxxxx=+−−+

Câu 27. Đường tiệm cận đứng của đồ thị hàm số 1 2 x y x = là

Hàm số ()yfx = nghịch biến trên khoảng nào dưới đây?

A. () ;1−∞− . B. () 0;1 . C. () 1;0 . D. () 1;1 .

Câu 30. Cho ()

d3Ifxx==  . Khi đó () 2 0 43d Jfxx =−   bằng:

A. 2 B. 6 C. 8 D. 4

Câu 31. Nếu ()

2 d9fxx =  và () 2 1 d2fxx =  thì () 1 2 d fxx  bằng

A. 7 B. 3 C. 11 D. 7

1 3d 21 Ixx x

=+ +

Câu 33. Trong không gian với hệ trục tọa độ Oxyz , cho () 1;1; 3 H . Phương trình mặt phẳng () P đi qua H cắt các trục tọa độ Ox, Oy, Oz lần lượt tại ,, ABC (khác O ) sao cho H là trực tâm tam giác ABC là

A. 370xyz+++= . B. 3110xyz+−+= . C. 3110xyz+−−= . D. 370xyz++−= .

Câu 34. Trong không gian với hệ trục tọa độ Oxyz , mặt phẳng (P) đi qua () 1;1;3 A và chứa trục hoành có phương trình là

A. 340 yz+−= . B. 30 yz−= . C. 0 xy−= . D. 30xy−= .

Câu 35. Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ dưới đây. Có bao nhiêu giá trị nguyên của tham số m để phương trình () 3 3log1fxm=− có nghiệm duy nhất trên 3

1 ;3 3     ?

A. 2 . B. 4 . C. 3 . D. 1.

2 0



Câu 32. Tính 1 0  

A. 2ln3 + B. 4ln3 + C. 2ln3 + D. 1ln3 +

Câu 36. Cho hàm số ()fx có đạo hàm và liên tục trên đoạn [] () 1;3, 34 f = và () 1 0 21d6fxx ′ +=  Tính giá trị của () 1 f .

A. ()18 f =− . B. ()12 f =− . C. ()116 f = . D. ()110 f = .

Câu 37. Cho hình chóp . SABCD có đáy là hình vuông cạnh a , đường thẳng SA vuông góc với mặt phẳng () ,2ABCDSAa = . Khoảng cách giữa hai đường thẳng SB và AD bằng

A. 6 3 a . B. 2 3 a . C. 3 2 a . D. a .

Câu 38. Trong không gian với hệ trục tọa độ Oxyz , cho () 1;2;3 A ; () 4;2;3 B ; () 4;5;3 C . Diện tích mặt cầu nhận đường tròn ngoại tiếp tam giác ABC làm đường tròn lớn là

A. 9π B. 36π C. 18π D. 72π

Câu 39. Cho hàm số ()yfx = xác định trên R và có đạo hàm ()() 2 (1)1fxxxx=−+ ′ . Hàm số đã cho nghịch biến khoảng nào dưới đây?

A. () 1;0 . B. () ;1−∞− . C. () 0;1 . D. () 1; +∞ .

Câu 40. Trong không gian với hệ tọa độ Oxyz, mặt cầu () S có tâm () 1;2;1 I và có tiếp diện là mặt phẳng () :2250Pxyz+++= , có phương trình là

A. ()()() 222 1214xyz −++++= B. ()()() 222 1211xyz ++−+−=

C. ()()() 222 1214xyz ++−+−= D. ()()() 222 1211xyz −++++=

Câu 41. Cho ()fx là hàm số liên tục trên tập số thực không âm và thỏa mãn () 2 3120.fxxxx ++=+∀≥ Tính () 5 1 d fxx 

. B. 527 3 . C. 61 6 . D. 464

Câu 42. Cho hình lăng trụ đứng ABCABC′′′ có đáy ABC vuông tại ,A 3 ABa = , ACAAa ′ == Giá trị sin của góc giữa đường thẳng AC′ và mặt phẳng () BCCB′′ bằng

A. 10 4 . B. 6 3 . C. 3 3 . D. 6 4 .

Câu 43. Cho hàm số () 2 21fxxx=−+ . Gọi S là tập hợp tất cả các giá trị thực của tham số m để giá trị lớn nhất của hàm số ()()() 2 2 gxfxfxm =−+ trên đoạn [] 1;3 bằng 8 . Tính tổng các phần tử của S

A. 7

B. 2

C. 0

Câu 44. Cho hàm số ()yfx = liên tục trên ℝ . Đồ thị hàm số () 3 ' yfx = được cho trong hình bên. Hàm số ()() 4 1 8 gxfxxx =−− có tối đa bao nhiêu điểm cực đại?

A. 2 B. 3

C. 4 . D. 5 .

D. 5

Câu 45. Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi M là điểm đối x

B và N là trung điểm của SC . Mặt phẳng () MND chia khối chóp SABCD thành hai khối đa diện, trong đó khối đa diện chứa đỉnh S có thể tích 1V , khối đa diện còn lại có thể tích 2V (tham khảo hình vẽ bên).

Tính tỉ số 1 2

A. 1 2

V V

12 7 V V = B. 1 2

5 3 V V = C. 1 2

7 5 V V = D. 1 2

1 5 V V =

Câu 46. Cho hàm số ()() () 2 3ln3 fxaxaxx =−−+ với a là tham số thực. Biết rằng nếu

()() 1;3 max2 fxf   = thì () 1;3 min fxm   = . Khẳng định nào sau đây đúng?

A. () 6;7 m ∈ B. () 7;8 m ∈ C. () 8;9 m ∈ D. () 9;10 m ∈

Câu 47. Cho hàm số ()fx có đạo hàm trên đoạn [] 1;e và thỏa mãn ()10 f = ;

()() []1,1; fxxfxxe ′ −=∀∈  . Tích phân () 1 d e fxx  bằng

Câu 48. Có bao nhiêu số nguyên dương x sao cho tồn tại số thực y lớn hơn 1 thỏa mãn () 2 23 21loglog yx xyxyy x −+ +−−= ?

A. 3. B. 1. C. vô số D. 2.

Câu 49. Trong không gian với hệ tọa độ Oxyz, cho mặt cầu () S có tâm thuộc mặt phẳng ():270 Pxyz++−= và đi qua hai điểm ()() 1;2;1,2;5;3AB . Bán kính nhỏ nhất của mặt cầu () S bằng:

A. 470 3 B. 546 3 C. 763 3 D. 345 3

Câu 50. Trong khoảng () 10;20 có bao nhiêu giá trị nguyên của tham số m để phương trình 2 39 4log(1)log9(1) m xxx+=+ có đúng 2 nghiệm phân biệt.

A. 23. B. 20. C. 8. D. 15. HẾT

của C

ứng

qua

A. 2 1 4 e B. 2 1 2 e + C. 2 1 4 e + D. 2 1 2 e

BẢNG ĐÁP ÁN

12345678910111213141516171819202122232425

DADDBCABDDDCADCBDACBACDAC

26272829303132333435363738394041424344454647484950

DCBCBAACBDAACADCDABCACDBA

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1. Trong không gian Oxyz , cho 23 aijk =−+− . Tọa độ của vectơ a là:

A. ( )2;1;3 B. ( )3;2;1 C. ( )2;3;1 D. ( )1;2;3

Lời giải

Chọn D

Ta có ( )231;2;3aijka =−+−  =−− .

Câu 2. Cho hàm số ( )yfx = có bảng biến thiên như hình vẽ

Khẳng định nào sau đây đúng?

A. Giá trị cực đại của hàm số là 3 CDy = . B. Giá trị cực đại của hàm số là 4 CDy = .

C. Giá trị cực tiểu của hàm số là 3 CTy =− . D. Giá trị cực tiểu của hàm số là 1 CTy = .

Lời giải

Chọn A

Từ bảng biến thiên, giá trị cực đại của hàm số là 3 CDy = .

Câu 3. Hàm số nào dưới đây có đồ thị như đường cong trong hình bên dưới?

Chọn D

Điều kiện 2 1 20 2 x xx x

Tập xác định { }\1;2 D =− ℝ .

Câu 5. Tìm họ nguyên hàm của hàm số ( ) sin3 fxx =

A. cos3xC−+ B. 1 cos3 3 xC−+ C. cos3xC + D. 1 cos3 3 xC +

Lời giải

Chọn B

Ta có 1 sin3cos3 3 xdxxC =−+ 

Câu 6. Cho cấp số nhân ( ) n u có số hạng đầu 1 3 u = và công bội 2 q = . Số hạng thứ năm của cấp số nhân ( ) n u là

A. 5 96 u = . B. 5 32 u = . C. 5 48 u = . D. 5 24 u = .

Lời giải

Chọn C

Áp dụng 1 1 n n uuq = ta được 44 51.3.248uuq=== .

Câu 7. Cho khối hộp chữ nhật . ABCDABCD ′′′′ có AAa ′ = , 3 ABa = , 5 ACa = . Thể tích khối hộp bằng

A. 3 12a . B. 3 4a . C. 3 15a . D. 3 5a .

Lời giải

Chọn A

Nhận thấy ()() 22 22 534 BCACABaaa =−=−= .

Do đó, thể tích hình hộp chữ nhật ABCDABCD ′′′′ là 3 ..3.4.12 VABBCAAaaaa ′ ===

Câu 8. Số tổ hợp chập 3 của 12 phần tử là

A. 1728 B. 220 C. 1320 D. 36

Lời giải

A. 3 2 yxx =− B. 24 2 yxx =− C. 32 yxx =−+ D. 42 2 yxx =−

Lời giải

Chọn D Đồ thị hàm số trên là đồ thị hàm bậc bốn trùng phương dạng ( ) 42 0 yaxbxcxa =++> . 42 2 yxx  =− .

Câu 4. Tìm tập xác định D của hàm số ( ) 5 2 2 yxx=−−

A. D = ℝ

B. ( ) 0; D =+∞

C. ( ) ( ) ;12; D =−∞−∪+∞ . D. { }\1;2 D =− ℝ .

Chọn B

Số tổ hợp chập 3 của 12 phần tử là 3 12 220 C = .

Câu 9. Cho hình chóp . SABC có đáy ABC là tam giác cân ABACa == , 120 BAC =° các cạnh bên bằng nhau và cùng tạo với mặt phẳng đáy các góc 30° . Thể tích khối chóp SABC là

A. 3 3 12 a B. 3 4 a C. 3 3 4 a D. 3 12 a

Lời giải

Chọn D

Gọi O là hình chiếu của S lên mặt phẳng ( )ABC .

Lời giải

≠−  −−≠⇔ 

≠  .

Nhận thấy: () ( ) , SAABCSAO = , () ( ) , SBABCSBO = và () ( ) , SCABCSCO = nên suy ra

OAOBOC == hay O là tâm đường tròn ngoại tiếp tam giác ABC .

Tam giác ABC cân tại A có 120 BAC =° , nên 30 ABCACB==° .

Khi đó: 2 sin AB OA ACB = hay 2.sin30 2sin ABa OAa ACB === °

Ta có: 3 .tan.tan30 3 a SOOASAOa==°=

Thể tích khối chóp . SABC là

Chọn C

Từ đồ thị ta thấy: [] ( ) [] ( ) 1;5 1;5 max3;min2 fxfx==− nên [] ( ) [] ( ) 1;5 1;5 maxmin321 fxfx

Câu 13. Trong không gian Oxyz , một vectơ chỉ phương của đường thẳng 12 112 xyz −+ == là

Câu 14. Trong không gian Oxyz , cho điểm ( )1;2;3

trên mặt phẳng ( )Oyz là:

chi

u vuông góc của M

A. ( )1;2;3 A . B. ( )1;2;0 A . C. ( )1;0;3 A . D. ( )0;2;3 A

Lời giải

Chọn D

Câu 15. Hàm số axb y cxd + = + với 0 a > có đồ thị như hình vẽ bên. Mệnh đề nào sau đây là đúng?

3 1131 ......sin120 333212

SABCABC aa VSOSaa ==°=   .

Câu 10. Trong các hàm số sau, hàm số nào đồng biến trên ℝ ?

A. () x e fx π  =  

B. () 1 x fx e  =  

C. ()

Lời giải

Chọn D

Hàm số mũ x ya = đồng biến trên ℝ khi

1 3

x fx  =   D. ( ) 3x fx =

1 a > do đó chọn đáp án D.

Câu 11. Hàm số nào dưới đây đồng biến trên khoảng ( ) ; −∞+∞ ?

A. 3 3 yxx =−− B. 1 2 x y x = C. 1 3 x y x + = + D. 3 3 yxx =+

Lời giải

Chọn D

Xét đáp án D ta có: 2 '330 yxx=+>∀∈ ℝ nên hàm số đồng biến trên ℝ

Câu 12. Cho hàm số ()yfx = liên tục trên đoạn [ ]1;5 và có đồ thị trên đoạn [ ]1;5 như hình vẽ bên.

Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( )fx trên đoạn [ ]1;5 bằng

A. 0,0,0bcd<<< B. 0,0,0bcd<>< C. 0,0,0bcd>>< D. 0,0,0bcd><< Lời giải

Chọn C

Tiệm cận ngang của đồ thị hàm số là 200 a yc c ==>  > (do 0 a > )

Tiệm cận đứng của đồ thị hàm số là 100 d yd c =−=>  < (do 0 c > )

Giao điểm của đồ thị hàm số với trục tung có tung độ âm nên 00 b b d <  > (do 0 d < ).

Câu 16. Tính đạo hàm của hàm số ( ) 2 log21yx=+

A. () 1 21.ln2 y x ′ = + B. () 2 21.ln2 y x ′ = + C. 2 21 y x ′ = + D. 1 21 y x ′ = + Lời giải

Chọn B

Câu 17. Cho hàm số ( )yfx = có bảng biến thiên như hình vẽ. Tổng số tiệm cận ngang và tiệm cận đứng

của đồ thị hàm số đã cho là

O C B A S

Lời giải

A. 4. B. -1. C. 1. D. 2.

+=−= .

( )1;1;2 u =− . B. ( )1;1;2 u = . C. ( )1;2;0 u =− . D. ( )1;2;1 u =− Lời giải

ọ

n A

điểm A

hình

M .

ọa độ

là

ế

A. 0. B. 2. C. 1. D. 3. Lời giải

Chọn D

Từ bảng biến thiên của hàm số ( )yfx = ta có:

() ( ) 2 lim x fx + →− =−∞  Đồ thị hàm số đã cho nhận đường thẳng 2 x =− là tiệm cận đứng.

( ) 0 lim x fx → =+∞  Đồ thị hàm số đã cho nhận đường thẳng 0 x = là tiệm cận đứng.

( ) lim0 x fx →+∞ =  Đồ thị hàm số đã cho nhận đường thẳng 0 y = là tiệm cận ngang.

Câu 18. Với mọi , ab dương thỏa mãn 3 2 2 loglog5. ab+= Khẳng định nào dưới đây đúng?

A. 32 32 ab = B. 22 32 ab =− C. 23 32 ab = D. 2 32 ab =−

Lời giải

Chọn A

3 2 2 loglog5 ab+= ( ) 32 2 log5 ab ⇔= 32 32 ab ⇔= .

Câu 19. Hàm số ( )log01 a yxa=<≠ có đồ thị là hình bên. Giá trị của cơ số a bằng

Vậy tập nghiệm của bất phương trình là () 3; +∞

Câu 21. Tìm tập nghiệm S của bất phương trình () 2 22 loglogxxx

A. {} 2 S = . B. {} 0 S = . C. {} 0;2 S = . D. {} 1;2 S = .

A. 1 3 B. 19 28 C. 16 21 D. 17 42 Lời giải

Chọn C

Gọi A là biến cố trong ba quả cầu lấy được có ít nhất một quả màu đỏ. Suy ra A là biến cố trong ba quả cầu lấy được không có quả cầu nào màu đỏ.

Không gian mẫu:

3 9 84 C Ω== .

Số cách lấy ra ba quả cầu mà không có quả cầu nào màu đỏ là

() () () 20516 1 842121 PAPAPA ==  =−=

3 6 20 C = . Ta có:

Câu 23. Cho hình chóp . SABC có đáy ABC là tam giác vuông cân tại B và 2 ABa = . Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích V của khối chóp SABC

A. 4 2 B. 4

Chọn C

Lời giải

Ta thấy đồ thị hàm số đi qua điểm có tọa độ ( ) 4 4;4log444 a a ⇔=⇔=

Mà 01 a <≠ nên 2 a =

Câu 20. Tìm tập nghiệm S của bất phương trình 4 5 5 1 x >

A. ( ) 5; S =+∞ . B. ( ) 3; S =+∞ . C. ( );5 S =−∞ . D. ( );3 S =−∞ .

Lời giải

Chọn B

441 5 1 55413 5 xx xx⇔>⇔−− > >⇔>

Diện tích ABC∆ là 2 1 2.22 2 aaa =

D. 2

=− .

Ð xx xL xxxxxxxx xN Kx −> =  =−⇔=−⇔−=⇔  =  >     ⇔>

ời giải Chọn A () () () 2 222 22 0 0 loglog : 20 2 0 1 x

A. 3 3 4 a V = B. 3 3 3 a V = C. 3 3 12 a V = D. 3 23 3 a V = Lời giải

Chọn D

Chiều cao SH của hình chóp SABC là 3 2.3. 2 aa

Vậy, thể tích V của khối chóp SABC là

3 2 123 .2.3. 33 a Vaa==

Câu 24. Cho khối nón có bán kính đáy bằng 3cm , góc ở đỉnh hình nón là 60° . Thể tích khối nón bằng

A. 3 93 (cm) π B. 3 33 (cm) π C. 3 6 (cm). D. 3 3 (cm) π

Lời giải

Chọn A

3 33 tan30 h == °

2 1 .3.3393 3 V ππ==

Câu 25. Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh 4a . Diện tích xung quanh của hình trụ là A. 2 8 Sa π = . B. 2 24 Sa π = .

Lời giải

a ra Saaa ππ

== ==

2.2.416

Câu 26. Tìm nguyên hàm ()Fx của hàm số () 2 21 2 fxx x =+− biết ()13 F = .

A. ()() 2 2ln21Fxxxx=+−−+ B. () 2 2ln21Fxxxx=++−+

C. () 2 ln21Fxxxx=+−−+ . D. () 2 2ln21Fxxxx=+−−+ .

Lời giải

Chọn D ()() 2 2 d21d2ln2 2 FxfxxxxxxxC x  ==+−=+−−+   

Mà ()13 F = nên 1 C =  () 2 2ln21Fxxxx=+−−+

Câu 27. Đường tiệm cận đứng của đồ thị hàm số 1 2 x y x = là

A. 1 y = B. 1 x = C. 2 x = D. 2 y =

Lời giải

xx yy xx ++−− →→→→ ==+∞==−∞ nên đường tiệm cận đứng của đồ thị hàm số là

Chọn C 2222

11 limlim;limlim 22xxxx

2. x = .

Câu 28. Giá trị nhỏ nhất của hàm số 3 35yxx=−+ trên đoạn [ ]2;4 là

A. [] 2; 4 min3 y = . B. [] 2;4 min7 y = . C. [] 2; 4 min5 y = . D. [] 2; 4 min0 y = .

Lời giải

Chọn B

Hàm số liên tục trên đoạn [ ]2;4 .

Ta có 3 35yxx=−+ [ ] 2 330,2;4yxx ′  =−>∀∈ . Vậy [] ( ) 2;4 min27 yy==

Câu 29. Cho hàm số ( )yfx = có bảng biến thiên như sau

Hàm số ( )yfx = nghịch biến trên khoảng nào dưới đây?

A. ( );1−∞− . B. ( )0;1 . C. ( )1;0 . D. ( )1;1 .

Lời giải

Chọn C

Từ bảng biến thiên ta thấy : ( ) ( ) ( ) 01;01;fxx ′ <∀∈−∪+∞ .

Vậy hàm số ( )yfx = nghịch biến trên khoảng ( )1;0

Câu 30. Cho ()

d3Ifxx==  . Khi đó () 2 0 43d Jfxx =−   bằng:

A. 2 B. 6 C. 8 D. 4

Lời giải

Chọn B

()() 222 000 43d4d3d1266.Jfxxfxxx =−=−=−=

Câu 31. Nếu ()

d9fxx =  và ()

d2fxx =  thì ()

d fxx  bằng

A. 7 . B. 3 . C. 11. D. 7 .

Lời giải

Chọn A

C. 2 16 Sa π = . D. 2 4 Sa π = .

n C 2 4 2 2

ọ

2 0

  

2 2

2 1

1 2

1 3d 21 Ixx x  =+

 +

Chọn A

Ta có 1 1 0 0 

2ln3=+ .

Câu 33. Trong không gian với hệ trục tọa độ Oxyz , cho () 1;1; 3 H . Phương trình mặt phẳng () P đi

qua H cắt các trục tọa độ Ox, Oy, Oz lần lượt tại ,, ABC (khác O ) sao cho H là trực tâm tam giác ABC là

A. 370xyz+++= B. 3110xyz+−+= C. 3110xyz+−−= D. 370xyz++−=

Lời giải

Chọn C

Tứ diện OABC có ,, OAOBOC đôi một vuông góc nên H là trực tâm tam giác ABC ()OHABC⇔⊥ () ABC  đi qua điểm H và có véc tơ pháp tuyến là () 1; 1; 3 OH

 phương trình mặt phẳng () P là 3110xyz+−−= .

Câu 34. Trong không gian với hệ trục tọa độ Oxyz , mặt phẳng (P) đi qua () 1;1;3 A và chứa trục hoành

có phương trình là

A. 340 yz+−= . B. 30 yz−= . C. 0 xy−= . D. 30xy−= .

Lời giải

Chọn B

Mặt phẳng (P) đi qua () 1;1;3 A và chứa trục hoành  () P có dạng 0 bycz+=

Mà () P đi qua điểm () 1;1;3 A nên 303 bcbc +=  =−

Chọn 13cb =  =−  phương trình mặt phẳng () P là 30 yz−=

Câu 35. Cho hàm số ()yfx = liên tục trên ℝ và có đồ thị như hình vẽ dưới đây. Có bao nhiêu giá trị

nguyên của tham số m để phương trình () 3 3log1fxm=− có nghiệm duy nhất trên 3

1 ;3 3     ?

C. 3 D. 1 Lờ

giải

3     .

Do đó yêu cầu bài toán tương đương với phương trình ( ) 1 fum=− có nghiệm duy nhất trên [ )1;3 . Từ đồ thị hàm số suy ra 112 2 41556 m mm m mm ∈ −==  →=



ℤ .

A. ( ) 18 f =− B. ( ) 12 f =− C. ( ) 116 f = D. ( ) 110 f = Lời giải Chọn A

Xét () 1 0 21d Ifxx ′ =+  , đặt 212 2 dt txdtdxdx =+  =  = .

Với 01;13xtxt =  ==  = .

Do đó () ( ) ( ) ()() 3 1 

31 1328 22 ff dt IftffI ′ ==  =−=−

A. 6 3 a B. 2 3 a C. 3 2 a D. a Lời giải

Chọn A

Ta có ()()()()() 21222 22111

d9dd9d92d7 fxxfxxfxxfxxfxx =⇔+=⇔=−⇔= .

Câu 32. Tính 1 0  

A. 2ln3 + B. 4ln3 + C. 2ln3 + D. 1ln3 + Lời giải

111 3dln212ln32 2122 Ixxxxx x  =+=++=+  + 

A. 2

B. 4

Chọn D

Đặt [ ) 3 3 1 ;31;3 3lo, 3 g uxu x     ∈∈−  =  . Do hàm số 33log ux = là hàm số đồng biến trên

( ) 0; +∞ nên với [ )1;3 u ∈− phương trình có nghiệm duy nhất trên

3 1 ;3

<−<<<

Câu 36. Cho hàm số ( )fx có đạo hàm và liên tục trên đoạn [ ] ( ) 1;3, 34 f = và () 1 0 21d6fxx ′ +=  Tính giá trị của ( )1 f

Câu 37. Cho hình chóp . SABCD có đáy là hình vuông cạnh a , đường thẳng SA vuông góc với mặt phẳng ( ) ,2ABCDSAa = . Khoảng cách giữa hai đường thẳng SB và AD bằng

Ta có ()() () () (),,, dSBADdADSBCdASBC == .

Do ()BCSAB ⊥ , kẻ AHSBAHBC ⊥  ⊥ . Do đó ()() () , AHSBCdASBCAH ⊥  =

Ta có 22

.26 3 3 SAABaa AH SAAB === + .

Câu 38. Trong không gian với hệ trục tọa độ Oxyz , cho () 1;2;3 A ; () 4;2;3 B ; () 4;5;3 C . Diện tích mặt

cầu nhận đường tròn ngoại tiếp tam giác ABC làm đường tròn lớn là

A. 9π . B. 36π . C. 18π . D. 72π .

Lời giải

Chọn C

Mặt cầu nhận đường tròn ngoại tiếp tam giác ABC làm đường tròn lớn nên tâm mặt cầu là tâm

đường tròn ngoại tiếp tam giác ABC .

Ta có () 3;0;0 AB , () 0;3;0 BC .

Vì .0ABBC = nên tam giác ABC vuông tại B .

Suy ra bán kính mặt cầu là 132 22 RAC==

Vậy diện tích mặt cầu là 2 2 32 44.18 2 SRπππ  ===    .

Câu 39. Cho hàm số ()yfx = xác định trên R và có đạo hàm ()() 2 (1)1fxxxx=−+ ′ . Hàm số đã cho nghịch biến khoảng nào dưới đây?

A. () 1;0 B. () ;1−∞− C. () 0;1 D. () 1; +∞

Lời giải

Chọn A

Lập bảng xét dấu ()fx ′

Dựa vào bảng xét dấu, hàm số ()yfx = nghịch biến trên khoảng () 1;0

Câu 40. Trong không gian với hệ tọa độ Oxyz, mặt cầu () S có tâm () 1;2;1 I và có tiếp diện là mặt phẳng () :2250Pxyz+++= , có phương trình là

A. ()()() 222 1214xyz −++++= . B. ()()() 222 1211xyz ++−+−= .

C. ()()() 222 1214xyz ++−+−= . D. ()()() 222 1211xyz −++++= .

Lời giải

Chọn D

Mặt cầu () S có tâm () 1;2;1 I và có tiếp diện là mặt phẳng () P suy ra () () 222

225 d,1 212 III xyz RIP +++ === ++

Phương trình mặt cầu ()()()() 222 :1211Sxyz−++++=

Câu 41. Cho ()fx là hàm số liên tục trên tập số thực không âm và thỏa mãn () 2 3120.fxxxx ++=+∀≥ Tính () 5 1 d fxx 

()()()()

Ifxxxxxxx =+++=++=

Đặt () 2 31d23d txxtxx =++  =+ , Đổi cận: 01xt =  = 15xt =  =

61 3123d()() 6 fxxxxftdtfxdx =+++==

A. 37 6 B. 527 3 C. 61 6 D. 464 3 Lời giải Chọn C

có:

1 1 2 0 0 61



3123d223d

Suy ra ()() 1 55 2 

A. 10 4 . B. 6 3 . C. 3 3 . D. 6 4 . Lời giải Chọn D

Câu 42. Cho hình lăng trụ đứng . ABCABC′′′ có đáy ABC vuông tại ,A 3 ABa = , ACAAa ′ == Giá trị sin của góc giữa đường thẳng AC′ và mặt phẳng () BCCB′′ bằng

Kẻ ()AHBCAHBCCB′′ ⊥  ⊥ , từ đó () () ; ACACH BCCB′′ ′′ =

Xét ABC∆ vuông tại A : 222 1113 2 AHa AHABAC =+⇔= .

Xét AAC′′ ∆ vuông tại C′ : 22 2 ACAAACa ′′′ =+= .

Xét AHC′ ∆ vuông tại C′ : 6 sin 4 AH ACH AC ′ == ′ .

A. 7 B. 2 C. 0 D. 5 Lời giải

Chọn A

Khi [] () []1;30;4xfx ∈−  ∈ . Đặt () [] 0;4 fxt=∈ .

A. 2 . B. 3 . C. 4 . D. 5 . Lời giải

Chọn B

Đặt ()() 4 1 8 hxfxxx =−−

Ta có: ()() () () '0 3 3 11 ''1'1 22 hx hxfxxfxx = =−−→=+

Đặt 3 xt = . Khi đó phương trình trở thành ()

ftttx

'100

Khi đó, yêu cầu bài toán () 2 2 htttm⇔=−+ có giá trị lớn nhất trên đoạn [] 0;4 bằng 8 () [] [] ()()00

Bảng biến thiên của hàm số ()yhx = :

8,0;4 0;4:8 htt tft  ≤∀∈  ⇔ ∃∈=∗ 

Với mọi [] 0;4 t ∈ , ta có: 2228828ttmttm −+≤⇔−≤−+≤ [] () [] ()2222 0;4 0;4 2828max28min2870 ttmttttmttm ⇔−+−≤≤−++⇔−+−≤≤−++⇔−≤≤

Đồng thời từ () ∗ suy ra 0 7 m m =   =−  . Vậy tổng các phần tử của S là 7

Câu 44. Cho hàm số ()yfx = liên tục trên ℝ Đồ thị hàm số () 3 ' yfx = được cho trong hình bên.

Hàm số ()() 4 1 8 gxfxxx =−− có tối đa bao nhiêu điểm cực đại?

Khi đó, hàm số ()() gxhx = có số điểm cực đại nhiều nhất () 0 hx ⇔= có 4 nghiệm.

Vậy hàm số ()() gxhx = có tối đa 3 điểm cực đại.

Câu 45. Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi M là điểm đối xứng của C qua





    = =  

3 3 3 22 1

2 2 2 tx

t x  =−=−



=+⇔=⇔=

()()

2 2 23 3ln33 3 x fxaxaxxfxaa xx + ′ =−−+  =−− +

fxf   = nên ()20 f ′ = () 7 307 10 aaa  −−=⇔=− () 2 23 710 3 x fx xx + ′  =−+ +

x fx x

() 2 0 15 7

=   ′ =⇔  =  .

( ) ( ) ( ) 1710ln4;21410ln10;32110ln18 fff=−+=−+=−+

Vậy ( ) ( )

= và ( ) ( )

Câu 47. Cho hàm số ( )fx có đạ

) ( ) [ ] 1,1; fxxfxxe ′ −=∀∈

()()()() () () 2 111 1 fxxfxfxxfxxfxfx

′  ⇔=  =+   do [ ] 1; xe ∈ , mà ( ) 10 f = ( ) ln fxxx  = .

 () () 111 ln fxfxxC xxx

e eee fxxxxxxxxxeee  + ==−=−−=

11 dlndlnd 222444   

Câu 48. Có bao nhiêu số nguyên dương x sao cho tồn tại số thực y lớn hơn 1 thỏa mãn

() 2 23 21loglog yx xyxyy x −+ +−−= A. 3. B. 1. C. vô số D. 2. Lời giải Chọn D Điều kiện: 23023 11 11

−+>−<

() 2 23 21loglog yx xyxyy x −+ +−−=

() 2 23 21log2loglog2log yx xyxyyyy x −+ ⇔+−−−=−

() 2 2 23 23loglog yx xyxyy xy −+ ⇔+−−=

() () loglogloglog0 ba abyabyab ⇔−=⇔−+= , với () 2 ,0 23 axy ab byx  = >  =−+ 

Nếu ab > thì () loglog0 a aby b −+> , ab < thì () loglog0 a aby b −+< .

Tính tỉ số 1 2 V V A. 1 2 12 7 V V = B. 1 2 5 3 V V = C. 1 2 7 5 V V = D. 1 2 1 5 V V = Lời giải Chọn C Ta có: 1 3 BK KMNSB BS =∩  = Đặt 2 SABCDSBCDSABC V VVVV =  == ..1 2 CDMN CDMN CDBS VCDCMCNV V VCDCBCS ==  = .2..1 1

BMKI BMKICDMNBMKI BCSA V BMBKBIVVVVV VVVVV VBCBSBA ==  =  =−=−=

= Vậy 1 2 7 5 V V = Câu

()() 1;3

 

1;3

 

đị

ây đúng? A. () 6;7 m ∈ . B. () 7;8 m ∈ . C. () 8;9 m ∈ . D. () 9;10 m ∈ . Lời giải Chọn A

57 .. 6122121212



46. Cho hàm số ()() () 2 3ln3 fxaxaxx =−−+ với a là tham số thực. Biết rằng nếu

max2 fxf

= thì ()

min fxm

= . Khẳng

nh nào sau đ

Vì ()() 1;3 max2

() ()()

1;3



1;3

  ==≈

ỏa mãn ( ) 10 f = ;

 

Tích phân

1 d e fxx  bằng A. 2 1 4 e B. 2 1 2 e + C. 2 1 4 e + D. 2 1 2 e Lời giải Chọn C

max2 fxf 

min16,86mfxf

o hàm trên đoạn [ ]

e và th

(

()

xxx



′′′ −=⇔−=  +=

() 2222 111 1

yxxy yy xx   >⇔> ≥≥

Nên () loglog0 ab a aby b −=⇔ = + 2 23xyyx ⇔=−+ 2 23 1 y x y + ⇔= +

Xét hàm số () 2 23 1 y fy y + = + với 1 y > . Ta có () () 2 2 2

Nên ()fy nghịch biến trên () 1; +∞ .

Bảng biến thiên:

Câu 50. Trong khoảng () 10;20 có bao nhiêu giá trị nguyên của tham số

2 39 4log(1)log9(1) m xxx+=+ có đúng 2 nghiệm phân biệt. A. 23. B. 20. C. 8. D. 15.

−−+ ′ =<∀> +

262 0,1 1 yy fyy y

Chọn A

Lời giải

Với điều kiện: 1 x >− thì phương trình ban đầu () 33 4log(1)1log1 xxmx ⇔+=++

() 3 1 log1 4 x xm ⇔+=

Để phương trình có đúng 2 nghiệm phân biệt thì đồ thị hai hàm số

điểm.

Để tồn tại số thực y lớn hơn 1 thì {} 5 01;2

2 xx<<  ∈

Câu 49. Trongkhônggianvớihệ tọa độ Oxyz,chomặtcầu () S cótâmthuộcmặtphẳng ():270 Pxyz++−= và đi qua hai điểm ( ) ( )1;2;1,2;5;3AB . Bán kính nhỏ nhất của mặt cầu

Gọi I là tâm mặt cầu () S ()IQ  ∈ là mặt phẳng trung trực của ()

=+    =   có 2 giao

yx y xm

() 3 log1 1 4

Từ đồ thị, điều kiện có 2 giao điểm khi 14 4 m m >−⇔>− và () 10;20 m ∈− , m ∈ ℤ {} 3;2;....;19 m  =−−

ằng: A. 470 3

B. 546 3

C. 763 3

D. 345 3 . Lờ

giải Chọ

() S b

AB VTPTAB        =  có dạng: 32160xyz++−= Vậy Id ∈ là giao tuyến của 2 mặt phẳng: 32160 270 xyz xyz ++−=   ++−=  + cho () 2 00;2;11 11 y xCd z =−  =  →−∈  =  và cho () 3 11;3;12 12 y xDd z =−  =  →−∈  =  . + Đường thẳng () () 0;2;11 : 1;1;1 quaC d VTCPCD    =−   có dạng: ()2;2;11 11 xt ytIttt zt =   =−−→−−+   =+  + Bán kính () () () 2 22 2 1382546 14103 393 RIAtttt   ==−++++=++≥      khi 13 3 t =− Vậy min 54613 33 Rkhit==−

37 ;;2 :22 1;3;2 quaM

m để phương trình

HẾT

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH PHÚ THỌ

ĐỀ THI THỬ TNTHPT - NĂM HỌC: 2022-2023 – LẦN 1 – ĐỀ GỐC 2

Câu 1: Từ một nhóm học sinh gồm 5 nam và 9 nữ, có bao nhiêu cách chọ ra hai học sinh?

A. 2 14A B. 14 2. C. 2 14C D. 2 14.

Câu 2: Tập xác định của hàm số () 2023 2 1 yx=− là

A. () 0;+∞ . B. ℝ . C. ()() ;11; −∞−∪+∞ . D. {}\1;1 ℝ .

Câu 3: Cho hàm số ()yfx = có đồ thị như hình vẽ

Số nghiệm của phương trình 2()50 fx −= bằng

A. 0 B. 2 C. 4 D. 3

Câu 4: Phương trình đường tiệm cận ngang của đồ thị hàm số 23 1 x y x −+ = + là

A. 3 2 x = . B. 2 y =− . C. 1 x =− . D. 3 y = .

Câu 5: Nghiệm của phương trình 4 5125 x = là

A. 4 x = . B. 5 x = . C. 7 x = . D. 6 x = .

Câu 6: Đạo hàm của hàm số 2023 log yx = là

A. 1 2023ln y x ′ = B. 1 ln2023 y x ′ = C. 1 y x ′ = D. ln2023 y x ′ =

Câu 7: Cho hàm số () ecos2 x fxx =+ . Khẳng định nào dưới đây là đúng?

A. () sin2 de 2 x x fxxC =++  . B. () sin2 de 2 x x fxxC =−+  .

C. () desin2 x fxxxC =−+  . D. () desin2 x fxxxC =++  .

Câu 8: Cho cấp số nhân () n u có số hạng đầu 1 3 u = và công bội 2 q = . Giá trị của 4u bằng

A. 5 . B. 24 . C. 30 . D. 27 .

Câu 9: Hàm số nào dưới đây có bảng biến thiên như hình vẽ?

A. 3232yxx=+− B. 23 1 x y x + = + C. 4231yxx=−+−

Câu 10: Nếu () 5 0 d7fxx =  và () 5 2 d3fxx =  thì () 2 0 d fxx  bằng

A. 10 B. 4 C. 4 D. 3

Câu 11: Biết phương trình 2 55 log3log10 xx−+= có hai nghiệm 12 , xx . Giá trị 12 . xx bằng

A. 25 . B. 3 . C. 1. D. 125 .

Câu 12: Cho 0,, a ℝ >αβ∈ . Khẳng định nào dưới đây đúng?

A. ()aa β αα+β = B. aaaαβα+β += C. aaaαβα+β = D. a a a

α β−α β =

Câu 13: Cho hàm số 42 yaxbxc =++ có đồ thị như hình vẽ.

Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

A. () 0;2 . B. () 1;3 . C. () 2;0 . D. () 1;3 .

Câu 14: Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. () 0;+∞ . B. () 2;0 . C. () 1;1 . D. () ;0−∞ .

Câu 15: Cho hàm số bậc ba ()yfx = có bảng biến thiên sau:

Giá trị cực đại của hàm số đã cho là

A. 0 . B. 1. C. 1. D. 3 .

Câu 16: Cho () 2 1 d sin xFxC x =+ ∫ . Khẳng định nào dưới đây đúng?

D. 21 1 x y x + = +

A. () 4 sin2 cos x Fx x ′ = B. () cot Fxx ′ =− C. () 2 1 sin Fx x ′ =− D. () 2 1 sin Fx x ′ =

Câu 17: Trong không gian Oxyz , nếu vectơ 23 OMijk =−+ thì tọa độ của điểm M là

A. () 2;3;1 . B. () 2;1;3 . C. () 2;1;3 . D. () 3;2;1 .

Câu 18: Tập nghiệm của bất phương trình () 2 log13 x −< là

A. [) 1;9 . B. () 1;9 . C. () 1;+∞ . D. () ;9−∞ .

Câu 19: Cho khối nón có bán kính đáy 2 r = , thể tích 6 V =π . Chiều cao của khối nón đã cho bằng

A. 3. B. 6 . C. 6. D. 9.

Câu 20: Cho khối chóp có diện tích đáy bằng 6, chiều cao bằng 5. Thể tích của khối chóp đã cho bằng

A. 30 . B. 10 . C. 15 . D. 5 .

Câu 21: Trong không gian Oxyz , mặt phẳng () P đi qua điểm (1;0;1) M và nhận (2;1;3)n làm vectơ pháp tuyến có phương trình là

A. 50 xz++= . B. 50 xz+−= .

C. 2350 xyz−+−= . D. 2350 xyz−++= .

Câu 22: Giá trị lớn nhất của hàm số 42 ()101 fxxx=−+ trên đoạn [3;2] bằng

A. 8. B. 1 C. 1 D. 2

Câu 23: Trong không gian Oxyz , cho mặt cầu 222 ():426110 Sxyzxyz+++−+−= . Tâm của mặt cầu () S có tọa độ là

A. () 1;2;3 . B. () 4;2;6 . C. () 4;2;6 . D. () 2;1;3 .

Câu 24: Cho hàm số () 2 4 xm fx x = + . Gọi 0m là giá trị lớn nhất của tham số m để hàm số đã cho có giá

trị nhỏ nhất trèn đoạn [] 0;6 bằng 4 . Khẳng định nào sau đây đúng?

A. 0 (5;7) m ∈ . B. 0 (1;3) m ∈ . C. 0 (7;9) m ∈ . D. 0 (3;5) m ∈ .

Câu 25: Cho khối lăng trụ đứng . ABCABC′′′ có đáy là tam giác vuông cân tại B , 1 ABAA′ == (tham khảo hình vẽ).

A. 6 B. 9 C.

Câu 27: Cho bất phương trình

Câu 28: Có bao nhiêu giá trị nguyên không âm c

()()()322 1 223 3 ymxmxmxm =−−−+−+ nghịch biến trên ( ) ; −∞+∞

A. 3 . B. 4 . C. 1. D. 2 .

Câu 29: Nếu () 4 0 d5fxx =  và () 4 0 d6gxx =  thì ()() 4 0 23 d fxgxx +   bằng

A. 11 B. 21 C. 27 D. 28

Câu 30: Trong kho đèn trang trí có 7 bóng đèn loại I và 8 bóng đèn loại II, các bóng đèn trong kho khác nhau về màu sắc và hình dáng. Lấy ra 7 bóng đèn bất kì. Xác suất để 7 bóng đèn lấy ra có đủ hai loại và số bóng đèn loại I nhiều hơn số bóng đèn loại II bằng

A. 868 2145 B. 868 2143 C. 521 2145 D. 521 2149

Câu 31: Cho mặt cầu có diện tích bằng 20π . Bán kính của mặt cầu đã cho bằng

A. 5 . B. 25 . C. 5 . D. 10

Câu 32: Cho hình trụ có bán kính đáy 4 r = , đường sinh 6 l = . Diện tích toàn phần của hình trụ đã cho bằng

A. 80π . B. 96π . C. 56π . D. 64π

Câu 33: Cho hàm số ( ) ( ) 42172023fxxmx=−−−+ và ( ) 32520222023gxxxx =−+−+ . Có bao nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) ( ) hxgfx = đồng biến trên khoảng ( ) 2;+∞

A. 16 B. 13 .C. 15 .D. 14

Câu 34: Số nghiệm nguyên của bất phương trình ( ) 222 ln161615 xxxxx +−≤+−

A. 2 . B. 0 . C. 3 . D. 1.

Câu 35: Cho hàm số ( )yfx = thoả mãn () 5 0 4 f =− và ( ) ( ) 42 fxxfx ′ = với mọi x ℝ ∈ . Giá trị của ( )2 f bằng

A. 1 4 .B. 3 4 .C. 5 36 .D. 1

Thể tích của khối lăng trụ đã cho bằng

A. 1 2 B. 1 6 C. 1 3 D. 1 4

Câu 26: Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx là một nguyên hàm của hàm số ()fx trên ℝ thỏa mãn ()() 317FF−= . Khi đó ()

2dfxx

bằng

Câu 36: Cho hàm số ( ) 32 5 log34yxx =−+ có bao nhiêu điểm cực trị?

A. 2 .B. 1.C. 3 .D. 0

Câu 37: Cho hình chóp tứ giác đều SABCD có tất cả các cạnh đều bằng a (tham khảo hình vẽ).

C' B' A' C B

∫

D. 14

21 11

55 xx  −>    có tập nghiệm ( ) ; Sab = . Giá trị của biểu thức 25ab + bằ

C. 0 D. 3

215

5 B. 2

để hàm số

ủa tham số m

Góc giữa đường thẳng SC và mặt phẳng () SBD bằng

A. 90° B. 30° C. 60° D. 45°

Câu 38: Trong không gian Oxyz , mặt cầu () S có tâm thuộc trục Oy và đi qua hai điểm () 2;1;1 A , ( )0;1;3 B có bán kính bằng

A. 3. B. 23. C. 9 . D. 3 .

Câu 39: Cho hình chóp SABC , có đáy là tam giác đều cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy, 3 SBa = . Gọi M là trung điểm của canh AB (tham khảo hình vẽ).

Thể tích của khối hộp chữ nhật đã cho bằng

A. 3 4a . B. 3 26a . C. 3 26 3 a . D. 3 4 3 a .

Khoảng cách từ điểm M đến mặt phẳng () SBC bằng

A. 66 33 a . B. 66 22 a . C. 66 11 a . D. 66 44 a .

Câu 40: Cho hàm số ()yfx = có đồ thị như hình dưới đây:

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình ()4420fxxm++−−+= có nghiệm trong khoảng () 4;4 ?

A. 3 . B. 4 . C. 5 . D. 2 .

Câu 41: Cho khối hộp chữ nhật . ABCDABCD ′′′′ có ,2, ABaADa == diện tích tam giác CBD ′ bằng 2 6a (tham khảo hình vẽ)

Câu 42: Cho hàm số ()fx liên tục trên ℝ Biết ()()1,00fxf>= và thỏa mãn () () 2 121.fxxxfx ′ +=+ Khi đó () 22 0

d fxx ′ ∫ bằng

A. 3 B. 8 C. 1 D. 6

Câu 43: Cho hàm số ()yfx = có đạo hàm trên ℝ thỏa mãn ()11 f = và () () 342 4321 fxxfxxx −=++ với mọi . x ℝ ∈ Khi đó () 4 1

.d xfxx ′ ∫ bằng

A. 15 I = B. 1 I =− C. 14 I = D. 6 I =

Câu 44: Có bao nhiêu số nguyên () 2023;2023 a ∈− để phương trình () 3

11 log871 x xa x +=+ +− có 2 nghiệm phân biệt?

A. 2028 B. 2016 C. 2027 D. 2015

Câu 45: Trong không gian Oxyz , cho hai điểm () 1;2;2 A , () 3;2;6 B . Xét hai điểm M , N thay đổi thuộc mặt phẳng ( )Oxy sao cho 16 MN = . Giá trị nhỏ nhất của AMBN + bằng.

A. 413. B. 45. C. 53. D. 215.

Câu 46: Cho hàm số ()yfx = có đạo hàm liên tục trên ℝ . Biết ()70 f −< và đồ thị ()fx ′ như hình vẽ

Hàm số () ()4262 627412 gxfxxxx =−+−−+ có tối đa bao nhiêu điểm cực trị?

A. 5 . B. 9 . C. 7 . D. 3 .

Câu 47: Cho khối chóp SABCD có đáy là hình vuông cạnh ,a tam giác SAB vuông cân tại ,S tam giác

SCD có 13 4 a SCSD== . Thể tích khối chóp đã cho bằng

A. 3 37 16 a B. 3 13 24 a C. 3 315 64 a D. 15 32 a 3

Câu 48: Cho hình trụ có bán kính đáy bằng 2a . Cắt hình trụ bởi một mặt phẳng song song với trục, cách trục một khoảng bằng a ta được thiết diện là một hình chữ nhật có diện tích bằng 2 83a . Thể tích khối trụ đã cho bằng

A. 3 4 aπ . B. 3 16 aπ . C. 3 32 aπ . D. 3 27 aπ .

Câu 49: Cho lăng trụ đứng ABCABC′′′ có đáy ABC là tam giác vuông tại B , 3 ABBCa ′ == , 60 ACB =° . Lấy hai điểm , MN lần lượt trên hai cạnh AB′ và AC ′ sao cho 2,MBAM ′ = 3 ACAN ′′ = . Thể tích khối đa diện BMNCC ′ bằng

A. 3 26 27 a . B. 3 4 9 a . C. 3 46 27 a . D. 3 83 27 a .

Câu 50: Cho hình nón có thiết diện qua đỉnh là tam giác SAB vuông tại S , ( , AB thuộc đường tròn đáy).

Biết tam giác SAB có bán kính đường tròn nội tiếp bằng 2510 , đường cao SO tạo với mặt phẳng ( )SAB một góc 30° . Diện tích xung quanh của hình nón đã cho bằng

A. 510π . B. 415π . C. 52π . D. 25π . H

1.C2.C3.D4.B5.C6.B7.A8.B9.D10.C 11.C12.C13.A14.A15.C16.D17.C18.B19.D20.B

21.C22.B23.D24.D25.A26.D27.B28.A29.D30.A

31.A32.A33.C34.B35.C36.B37.D38.D39.B40.B

41.A42.B43.A44.B45.A46.C47.D48.B49.C50.A

HƯỚNG DẪN GIẢI

Câu 1: Từ một nhóm học sinh gồm 5 nam và 9 nữ, có bao nhiêu cách chọ ra hai học sinh?

A. 2 14A B. 14 2. C. 2 14C D. 2 14.

Lời giải

Chọn C

Câu 2: Tập xác định của hàm số () 2023 2 1 yx=− là

A. () 0;+∞ . B. ℝ . C. ()() ;11; −∞−∪+∞ . D. {}\1;1 ℝ .

Lời giải

Chọn C

Câu 3: Cho hàm số ()yfx = có đồ thị như hình vẽ

Số nghiệm của phương trình 2()50 fx −= bằng

A. 0 B. 2 C. 4 D. 3

Lời giải

Chọn D

5 2()50() 2 fxfx−=⇔= . Do đó phương trình có ba nghiệm phân biệt.

Câu 4: Phương trình đường tiệm cận ngang của đồ thị hàm số 23 1 x y x −+ = + là

A. 3 2 x = B. 2 y =− C. 1 x =− D. 3 y =

Lời giải

Chọn B.

Câu 5: Nghiệm của phương trình 4 5125 x = là

A. 4 x = B. 5 x = C. 7 x = D. 6 x =

BẢNG ĐÁP ÁN

ẾT

Chọn C

Ta có 443 512555437 xx xx =⇔=⇔−=⇔=

Câu 6: Đạo hàm của hàm số 2023 log yx = là

A. 1 2023ln y x ′ = B. 1 ln2023 y x ′ = C. 1 y x ′ = D. ln2023 y x ′ =

Lời giải

Chọn B

Ta có 2023 1 log ln2023 yxy x ′ =⇒= .

Câu 7: Cho hàm số () ecos2 x fxx =+ . Khẳng định nào dưới đây là đúng?

A. () sin2 de 2 x x fxxC =++  B. () sin2 de 2 x x fxxC =−+ 

C. () desin2 x fxxxC =−+  . D. () desin2 x fxxxC =++  .

Lời giải

Chọn A. () () sin2 decos2de 2 xx x fxxxxC =+=++

Câu 8: Cho cấp số nhân () n u có số hạng đầu 1 3 u = và công bội 2 q = . Giá trị của 4u bằng

A. 5 . B. 24 . C. 30 . D. 27 .

Lời giải

Chọn B.

Ta có 33 41.3.224uuq=== .

Câu 9: Hàm số nào dưới đây có bảng biến thiên như hình vẽ?

A. 3232yxx=+− . B. 23 1 x y x + = + . C. 4231yxx=−+− . D. 21 1 x y x + = + .

Lời giải

Chọn D

Từ bảng biến thiên ta thấy đồ thị hàm số có tiệm cận đứng 1 x =− nên loại A,. C.

Hàm số đồng biến trên các khoảng () ;1−∞− và () 1; −+∞ nên chọn. D.

Câu 10: Nếu ()

5 0 d7fxx =  và () 5 2 d3fxx =  thì () 2 0 d fxx  bằng

A. 10 B. 4 C. 4 D. 3

Lời giải

Chọn C ()()()()()() 525255 002002 dddddd734 fxxfxxfxxfxxfxxfxx =+  =−=−=

Câu 11: Biết phương trình 2 55 log3log10 xx−+= có hai nghiệm 12 , xx . Giá trị 12xx bằng

A. 25 . B. 3 . C. 1. D. 125 .

Lời giải

Chọn C

:0 log3log10 ÐKx xx > −+=

2 55

Đặt 5log tx = ta được phương trình () 2 31050tt−+=∆=> .

Áp dụng Định lí Viet ta được 3 125152512123loglog3log.3.5125ttxxxxxx +=⇔+=⇔=⇔== .

Câu 12: Cho 0,, a ℝ >αβ∈ . Khẳng định nào dưới đây đúng?

A. ()aa β αα+β = . B. aaaαβα+β += . C. . aaaαβα+β = . D. a a a

Lời giải

α β−α β = .

Chọn C.

Câu 13: Cho hàm số 42 yaxbxc =++ có đồ thị như hình vẽ.

Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

A. () 0;2 . B. () 1;3 . C. () 2;0 . D. () 1;3 .

Lời giải

Chọn A

Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là () 0;2 .

Câu 14: Cho hàm số bậc ba ()yfx = có đồ thị như hình vẽ

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. () 0;+∞ . B. () 2;0 . C. () 1;1 . D. () ;0−∞ .

Lời giải

∫∫



Lời giải

Chọn D.

Chọn A

Hàm số đã cho nghịch biến trên khoảng () 0;+∞

Câu 15: Cho hàm số bậc ba ()yfx = có bảng biến thiên sau:

Giá trị cực đại của hàm số đã cho là

A. 0 B. 1 C. 1 D. 3

Lời giải

Chọn C

Giá trị cực đại của hàm số đã cho là 1 y =

Câu 16: Cho () 2 1 d sin xFxC x =+ ∫ . Khẳng định nào dưới đây đúng?

A. () 4 sin2 cos x Fx x ′ = B. () cot Fxx ′ =− C. () 2 1 sin Fx x ′ =− D. () 2 1 sin Fx x ′ =

Lời giải

Chọn D

Có ()() 2 2 11 d sinsin xFxCFx xx ′ =+⇒=

Câu 17: Trong không gian Oxyz , nếu vectơ 23 OMijk =−+ thì tọa độ của điểm M là

A. () 2;3;1 . B. () 2;1;3 . C. () 2;1;3 . D. () 3;2;1 .

Lời giải

Chọn C () 232;1;3OMijkM=−+⇒−

Câu 18: Tập nghiệm của bất phương trình () 2 log13 x −< là

A. [) 1;9 B. () 1;9 C. () 1;+∞ D. () ;9−∞

Lời giải

Chọn B.

Ta có () 2 3

10 1 log13 9 12 x x x x x

  −> >   −<⇔⇔ 

 < −<    

Vậy tập nghiệm của bất phương trình là () 1;9

Câu 19: Cho khối nón có bán kính đáy 2 r = , thể tích 6 V =π . Chiều cao của khối nón đã cho bằng

A. 3. B. 6. C. 6. D. 9.

Lời giải

VV VShh Sr π =⇒==== π π .

Ta có ( )2 2 1333.6 .9 3. .2 d d

Câu 20: Cho khối chóp có diện tích đáy bằng 6, chiều cao bằng 5. Thể tích của khối chóp đã cho bằng

A. 30 . B. 10. C. 15. D. 5 .

Lời giải

Chọn B

Thể tích của khối chóp đã cho 11..6.510 33 d VSh=== .

Câu 21: Trong không gian Oxyz , mặt phẳng () P đi qua điểm (1;0;1) M và nhận (2;1;3)n làm vectơ

pháp tuyến có phương trình là

A. 50 xz++= . B. 50 xz+−= .

C. 2350 xyz−+−= . D. 2350 xyz−++= .

Lời giải

Chọn C

Phương trình mặt phẳng () P : ( ) ( ) ( ) 21103102350 xyzxyz −−−+−=⇔−+−=

Câu 22: Giá trị lớn nhất của hàm số 42 ()101 fxxx=−+ trên đoạn [3;2]bằng

A. 8. B. 1. C. 1. D. 2 . Lời giải

Chọn B ( ) 42101fxxx=−+ . Hàm số liên tục trên [ ]3;2

x fxxxx x

 =∈−   ′ =−=⇔=∈−    =−∈−

53;2

( ) 01 f = ; ( ) ( ) 5524ff=−=− ; ( ) 223 f =− . Suy ra GTLN của hàm số 1

Câu 23: Trong không gian Oxyz , cho mặt cầu 222 ():426110 Sxyzxyz+++−+−= . Tâm của mặt cầu () S có tọa độ là A. ( )1;2;3 B. ( )4;2;6 C. ( )4;2;6 D. ( )2;1;3 Lời giải

Chọn D 222 ():426110 Sxyzxyz+++−+−= có tâm ( )2;1;3

Câu 24: Cho hàm số () 2 4 xm fx x = + . Gọi 0m là giá trị lớn nhất của tham số m để hàm số đã cho có giá trị nhỏ nhất trèn đoạn [ ]0;6 bằng 4 . Khẳng định nào sau đây đúng?

A. 0 (5;7) m ∈ . B. 0 (1;3) m ∈ . C. 0 (7;9) m ∈ . D. 0 (3;5) m ∈ .

Lời giải

∫

()

[]

420053;2

[ ]

03;2



Chọn D () () () 22 2 4 0, 4 4 xmm fxfxm x x −+ ′ =⇒=>∀ + + . Hàm số đồng biến trên [] 0;6 .

Suy ra: [] ()() 2 2 0;6 min04164 4 m fxfmm==−=−⇔=⇔=± suy ra 4 m = .

Câu 25: Cho khối lăng trụ đứng . ABCABC′′′ có đáy là tam giác vuông cân tại B , 1 ABAA′ == (tham khảo hình vẽ).

 >  +

  −−>⇔⇒>⇔<−⇔<⇔−<<



hàm số

()()()322 1 223 3 ymxmxmxm =−−−+−+ nghịch biến trên ( ) ; −∞+∞

Với 2 m = : 4 yx=−+ luôn NB trên ( ) ; −∞+∞ . Do đó 2 m = thỏa mãn.

Với 2 m ≠ : Hàm số nghịch biến trên ( ) ; −∞+∞ ( ) ( ) 2 0,22230, yxmxmxmx ℝ ℝ ′ ⇔≤∀∈⇔−−−+−≤∀∈

 −<   <    ⇔⇔⇔<   −−−+≤

Thể tích của khối lăng trụ đã cho bằng

A. 1 2 B. 1 6 C. 1 3 D. 1 4 Lời giải Chọn A

2 11 .. 22 ABC ABCABC VAASAAAB ′′′ ′′ === .

Câu 26: Cho hàm số ()fx liên tục trên ℝ . Gọi ()Fx là một nguyên hàm của hàm số ()fx trên ℝ thỏa mãn ()() 317FF−= . Khi đó () 3 1

2dfxx ∫ bằng

A. 6 B. 9 C. 5 D. 14

Lời giải Chọn D.

Ta có: ()() ()() 3 1

3 2d223114 1 fxxFxFF ==−=  ∫ .

()()() ()() 2

20 2 2 2230 2230 m m m mmm mmm

−−−−≤    .

Vậy 2 m ≤ thỏa mãn yêu cầu bài toán, mà m nguyên không âm. Do đó { }0;1;2 m ∈⇒ có 3 giá trị của m thỏa mãn bài toán.

Câu 29: Nếu () 4 0 d5fxx =  và () 4

d6gxx =  thì

()() 4 0 23 d fxgxx + 

A. 11. B. 21. C. 27 . D. 28 . Lời giải

Chọn D.

0 00 fxgxxfxxgxx +=+=+=  ∫∫∫

23 d2 d3 d2.53.628

()()()()

A. 868 2145 . B. 868 2143 . C. 521 2145 . D. 521 2149

Lời giải

Chọn A.

Lấy 7 bóng đèn từ 15 bóng đèn thì có số cách là 7 15 6435 C =

( ) 6435 n ⇒ω= .

Gọi biến cố A: “Số bóng đèn loại I nhiều hơn số bóng đèn loại II”.

Lấy 4 bóng đèn loại I và 3 bóng đèn loại II có số cách là 43 78 C.C1960 = .

Lấy 5 bóng đèn loại I và 2 bóng đèn loại II có số cách là 52 78 C.C588 =

Lấy 6 bóng đèn loại I và 1 bóng đèn loại II có số cách là 61 78 C.C56 =

( ) 1960588562604 nA ⇒=++=



bằng A. 5

B. 2

Lờ

giải Chọn B ĐK: 0 x ≠ . Đặt 1 1 5 x t    =      , 0 t > . Bpt trở thành: C' B'

C B A



Câu 27: Cho bất phương trình 21 11 215 55 xx  −>     

có tập nghiệm () ; Sab = . Giá trị của biểu thức 25ab +  

0 .

3 .

()

1 2 5 111 215051010 3KTM 5 x t x tt x t xx

<−  .

Vậy tập nghiệm là ( )1;0 S =− . Do đó 252 ab+=−

Câu 28: Có bao nhiêu giá trị nguyên không âm của tham số m để

A. 3 B. 4 C. 1 D. 2 Lời giải Chọn A

 bằng

4 44

n64352145 A

() ( ) ( ) n 2604868

Câu 31: Cho mặt cầu có diện tích bằng 20π . Bán kính của mặt cầu đã cho bằng

A. 5 B. 25 C. 5 D. 10

Lời giải

16 ln16lnln16ln16 16 x xxxxxx xx

() ( ) 22 ln16ln161616 xxxxxx −++≤++−

Chọn A.

Ta có 222 420455 mc Srrrr =π⇔π=π⇔=⇔= .

Câu 32: Cho hình trụ có bán kính đáy 4 r = , đường sinh 6 l = . Diện tích toàn phần của hình trụ đã cho

bằng

A. 80π B. 96π C. 56π D. 64π

Lời giải

Chọn A.

Ta có ( ) ( ) 2244680 tp Srrl=π+=π+=π .

Câu 33: Cho hàm số ( ) ( ) 42172023fxxmx=−−−+ và ( ) 32520222023gxxxx =−+−+ . Có bao

nhiêu giá trị nguyên của tham số m để hàm số ( ) ( ) ( ) hxgfx = đồng biến trên khoảng ( ) 2; +∞

A. 16 B. 13.C. 15.D. 14

Lời giải

Chọn C.

Ta có ( ) ( ) ( ) ( ) . hxfxgfx ′′′ = ( ) ( ) ( ) ( ) 322 4173102022 xmfxfx =+−−+ .

Để hàm số ( ) ( ) ( ) hxgfx = đồng biến trên khoảng ( ) 2;+∞ cần:

( ) ( ) 02;hxx ′ ≥∀∈+∞ ⇒ ( ) 32 4170 xm+−≥ vì ( ) ( ) ( ) 2 31020220,2 fxfxx −+>∀>

Suy ra 23417mx≤+ .(*)

Xét hàm số ( ) 3 417kxx=+ ta có ( ) 2 '120,2 kxxx=>∀> . Suy ra hàm số ( ) 3 417kxx=+ đồng biến trên khoảng ( ) 2; +∞ .

(*) () ( ) 2 2; min4977mkxm +∞

Vậy có 15 giá trị của m

Câu 34: Số nghiệm nguyên của bất phương trình ( ) 222 ln161615 xxxxx +−≤+− .

A. 2 B. 0 C. 3 D. 1

Lời giải

Chọn B

Điều kiện ( ) 2221601600 xxxxxxx +−>⇔+−>⇔>

() ( ) 22 ln1616ln1616 xxxxxx ⇔+≤+++++ (*)

Xét hàm số ( ) ln fttt =+ trên ( ) 0; +∞

Ta có: () 1 10 ft t ′ =+> trên ( ) 0; +∞ . Suy ra hàm số ( ) ln fttt =+ đồng biến trên ( ) 0; +∞

Từ (*) suy ra 22222 111 1616161516225 14 1414 xxxxxxxxx ≤++⇔+≥⇔+≥⇔≤⇔−≤≤

So với điều kiện ta được 1 0 14 x <≤

Mà x ℤ ∈ nênsuyra không có giátrị nguyên nào của x thoả mãn yêu cầubài toán.

Câu 35: Cho hàm số ( )yfx = thoả mãn () 5 0 4 f =− và ( ) ( ) 42 fxxfx ′ = với mọi x ℝ ∈ . Giá trị của ( )2 f bằng

A. 1 4 .B. 3 4 .C. 5 36 .D. 1.

Lời giải

Chọn C

Ta có: ( ) ( ) 42 fxxfx ′ = ( ) ( ) 4 2 fx x fx

′ ⇒=

Lấy nguyên hàm 2 vế: ( ) ( ) ( ) 5 4 2 1 dd 5 fx x xxxC fxfx∫∫

Theo giả thiết () 5 0 4 f =− suy ra () () 5 455 2 5436Cfxf x =⇒=⇒= +

Câu 36: Cho hàm số ( ) 32 5 log34yxx =−+ cóbao nhiêu điểm cựctrị?

A. 2 .B. 1.C. 3 .D. 0

Lời giải

Chọn B

A ⇒===

⇒≤=⇒−≤≤

Ta có: ( ) () ( ) 2 2 2 +−==−++  

Bất phương trình tương đương

′ =⇒−=+

n xác

x xxxx

nh: ()() 2 32 12 340210

Ta có: () 2 32 36 34ln5 xx y xx ′ = −+

Cho 0 0 2 x y x  =  ′ =⇒  = 

Bảng biến thiên:

Từ bảng biến thiên tathấy hàm số đã cho có1 điểm cực trị.

Câu 37: Cho hình chóp tứ giác đều . SABCD có tất cả các cạnh đều bằng a (tham khảo hình vẽ).

Tam giác OSC vuông tại O có

OC SCa

Góc giữa đường thẳng SC và mặt phẳng () SBD bằng

A. 90° . B. 30° . C. 60° . D. 45° .

Lời giải

Chọn D

Ta có hình vẽ:

Gọi OACBD =∩ ()SOABCD⇒⊥ (do SABCD là hình chóp đều).

Ta thấy ()

 ⊥   ⇒⊥   ⊥   tại O () () ; SCSBDCSO ⇒==ϕ

OCBD OCSBD OCSO

⇒ϕ=°

Câu 38: Trong không gian Oxyz , mặt cầu () S có tâm thuộc trục Oy và đi qua hai điểm () 2;1;1 A , ( )0;1;3 B có bán kính bằng

A. 3. B. 23. C. 9 D. 3 Lời giải

Chọn D.

Gọi I là tâm của mặt cầu () S , bán kính R

() 0;;0IOyIb ∈⇒ . Mặt cầu () S đi qua hai điểm () 2;1;1 A , () 0;1;3 B AIBIR⇔==

22AIBI⇒= ()() 22 41119 bb ⇔+−+=++ 440 b ⇔+= ()10;1;0bI ⇔=−⇒− 3 RIB ⇒==

Khoảngcách từ điểm M đến mặt phẳng () SBC bằng

Lời giải

Chọn B

Ta có hình vẽ sau

Do () ABSBCB ∩= , mà M là trung điểm của cạnh AB nên ta có:

() () () () 1 ;; 2 ddMSBCdASBC ==

ề

ệ



 > 

u ki

đị

−<<

−+>⇔−+>⇔

 

     =    2

⇒ϕ==

2 2 a



sin

OC SC

A. 66 33 a . B. 66 22 a . C. 66 11 a . D. 66 44 a .

Gọi N là trung điểm của cạnh BC . Kẻ AHSN ⊥ tại H (1).

Ta có: () BCAN BCSAN BCSA

 ⊥   ⇒⊥   ⊥   BCAH⇒⊥ . (2)

Từ (1) và (2), ta có: ()AHSBC ⊥ () () ; AHdASBC⇒=

Bảng biến thiên

= 

Trong tam giác vuông ASN có 22

2222 11111

a AN SASBABa

  =−=  

3 2 2

6 AHANSAa =+= 66 11 a AH ⇒=

nên ta có:

Như vậy () () () () 1 ;; 2 ddMSBCdASBC == 166 222 a AH ==

Câu 40: Cho hàm số ()yfx = có đồ thị như hình dưới đây:

Dựa vào bảng biến thiên, để phương trình đã cho có nghiệm thì

Có tất cả bao nhiêu giá trị nguyên của tham số m để phương trình ()4420fxxm++−−+= có nghiệm trong khoảng () 4;4 ?

A. 3 . B. 4 . C. 5 . D. 2 .

Lời giải

Chọn B

Xét phương trình () () 4420 * fxxm++−−+= trong khoảng () 4;4 () ()

442 *442 441 xxm fxxm xxm

 ++−−=  ⇔++−−=−⇔  ++−−=−  

442 441 xxm xxm

 ++−=+  ⇔  ++−=−   Xét hàm số () 44 gxxx =++− trong khoảng () 4;4 .

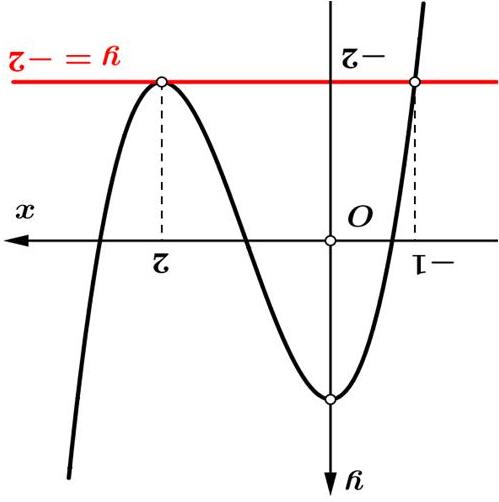
Ta có () () 11 ;00 2424 gxgxx xx ′′=−=⇔= +−

22242222

22142215 mm mm

Mà m ℤ ∈ nên {}{} 1;24;5 m ∈∪

Vậy có 4 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Câu 41: Cho khối hộp chữ nhật . ABCDABCD ′′′′ có ,2, ABaADa == diện tích tam giác CBD ′ bằng

2 6a (tham khảo hình vẽ)

Thể tích của khối hộpchữ nhật đã cho bằng

A. 3 4a . B. 3 26a . C. 3 26 3 a . D. 3 4 3 a . Lời giải

Chọn A

Trong mp(), ABCD kẻ CHBD ⊥ thì () BDCHCBDHC ⊥⇒⊥′′ .

Khi đó

CBD∆ vuông tại C có 22 5 BDBCCDa =+= và

2 126 . 2 5 CBD CBD S a SHCBDHC BD ′ ′ ′′ =⇔== .

Tam giác HCC′ vuông tại C có 22 2.CCHCHCa ′′ =−=

Vậy thể tích khối hôph chữ nhật đã cholà 3 .4 ABCD VSCCa ′ ==

.2 5 BCCDa CH BCCD == +

  

  

<+≤−<≤  ⇔  <−≤+<≤ 