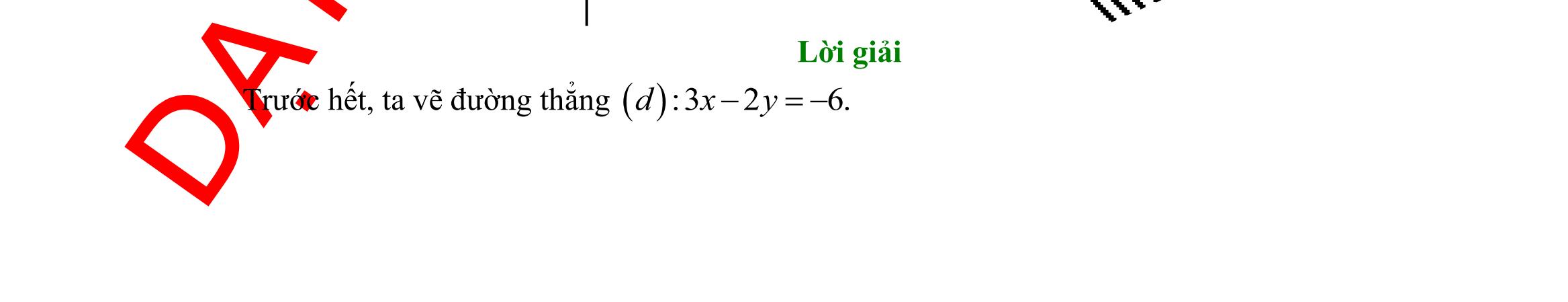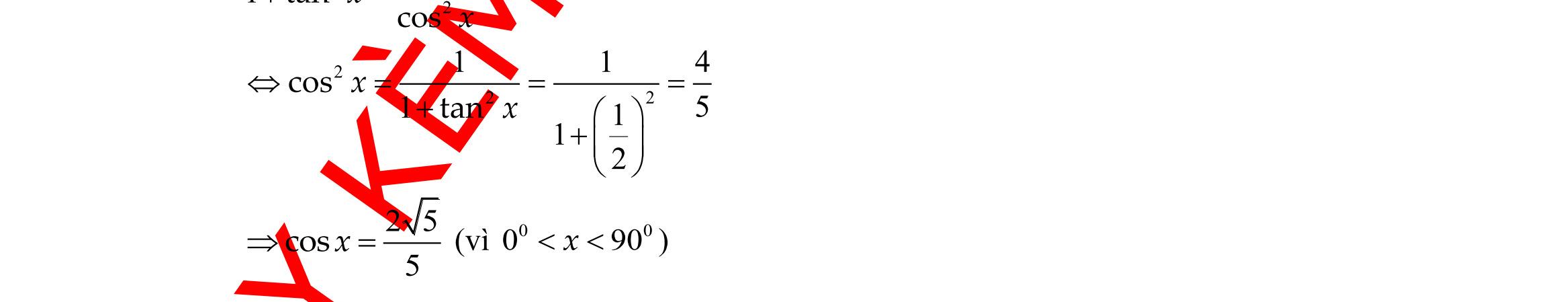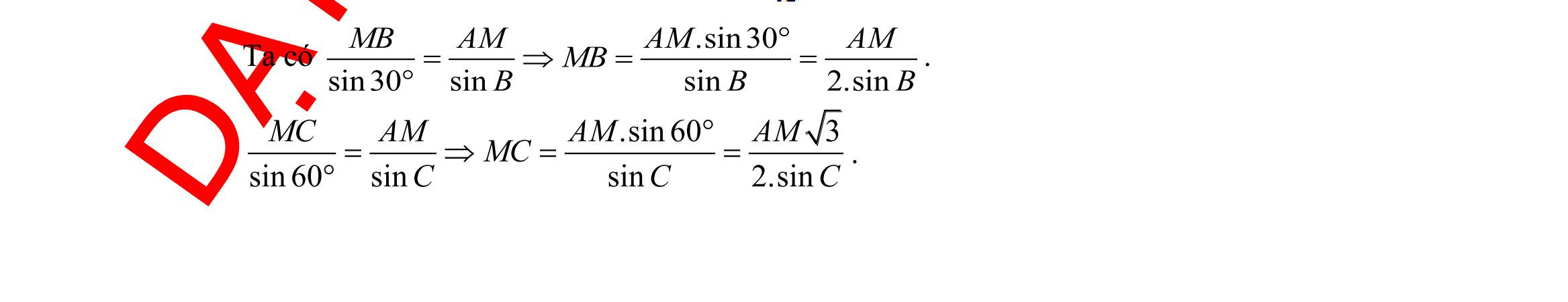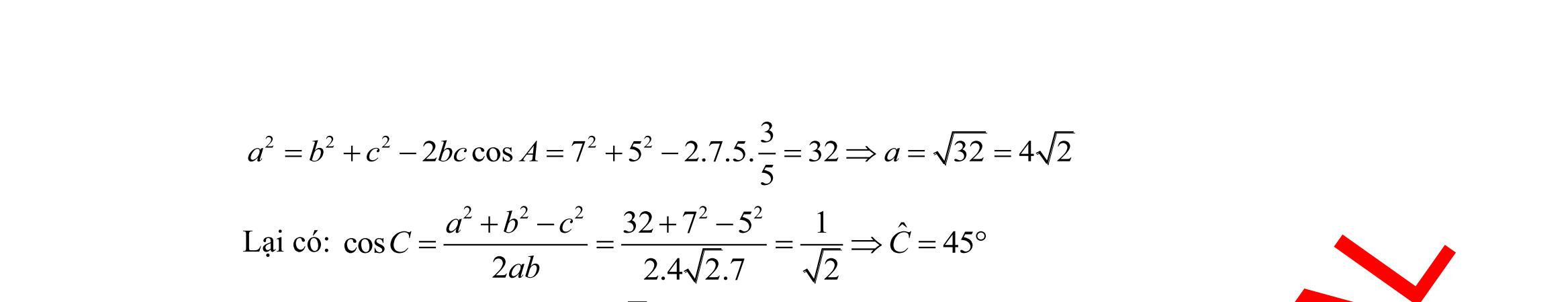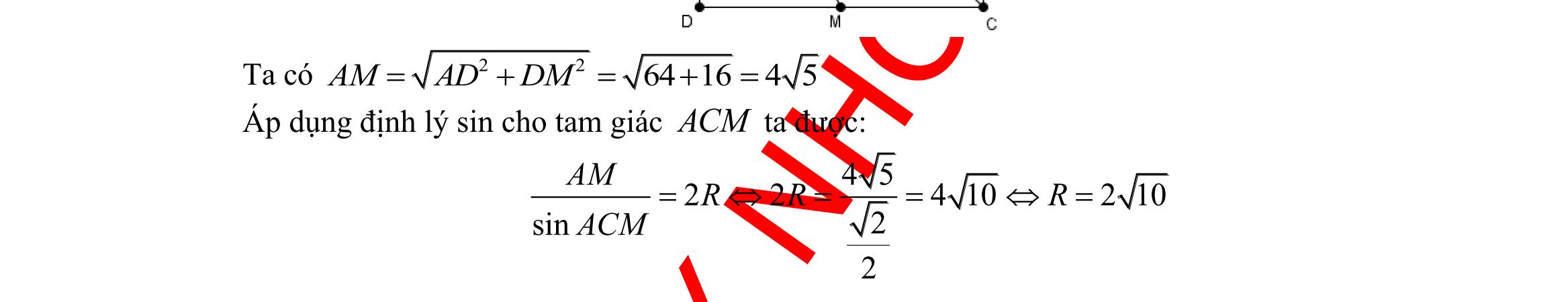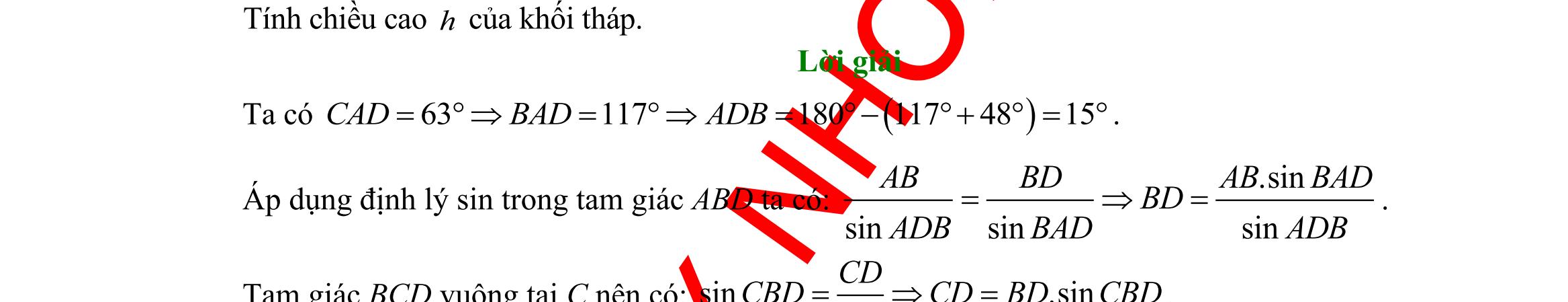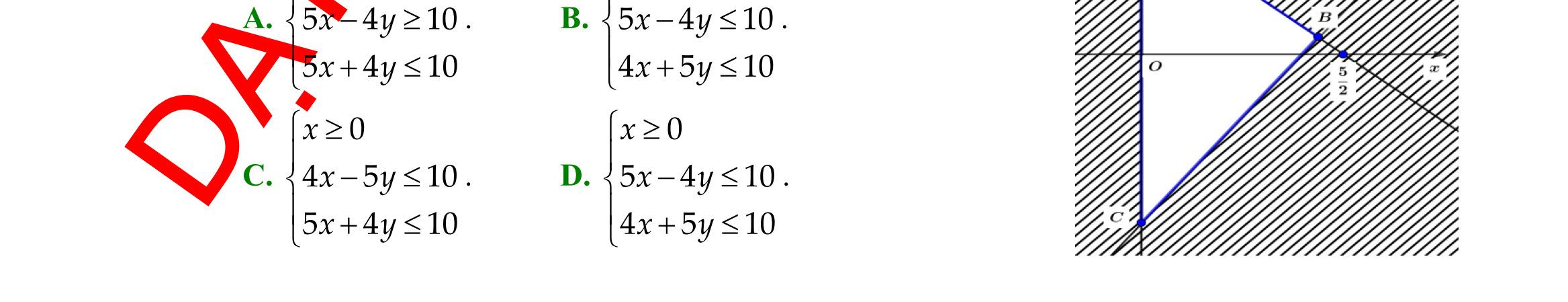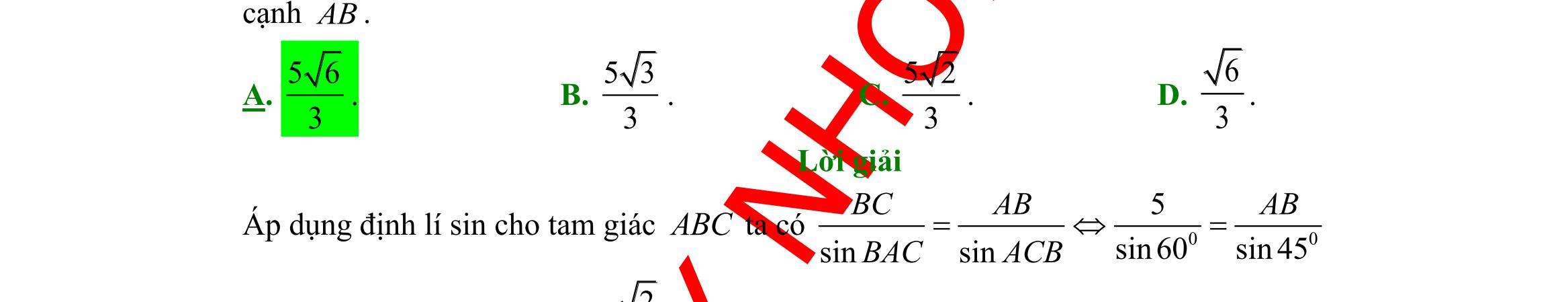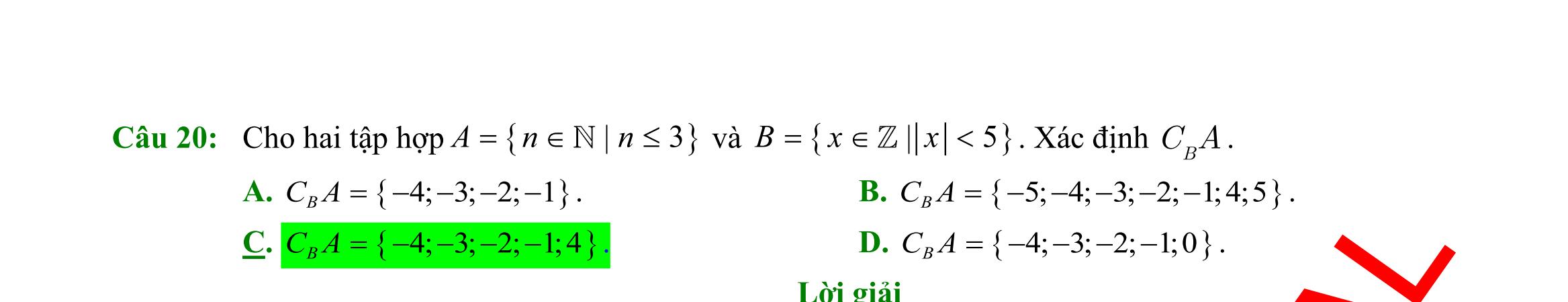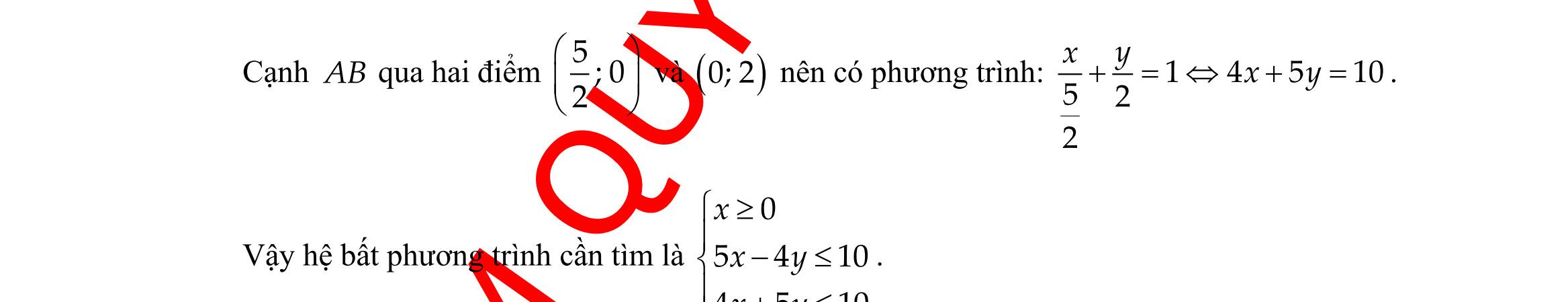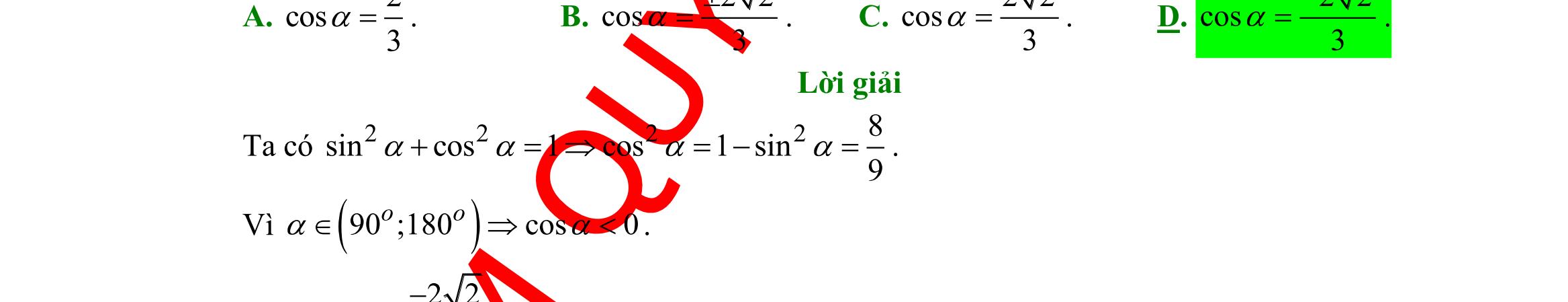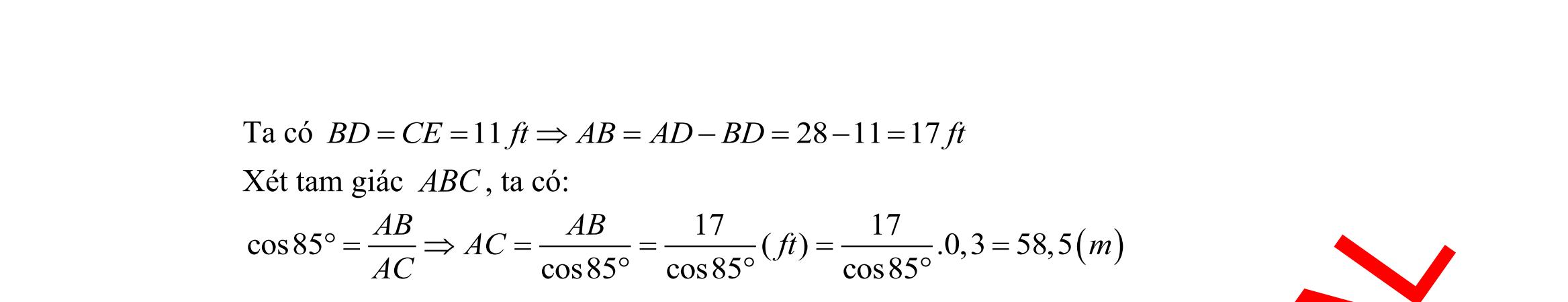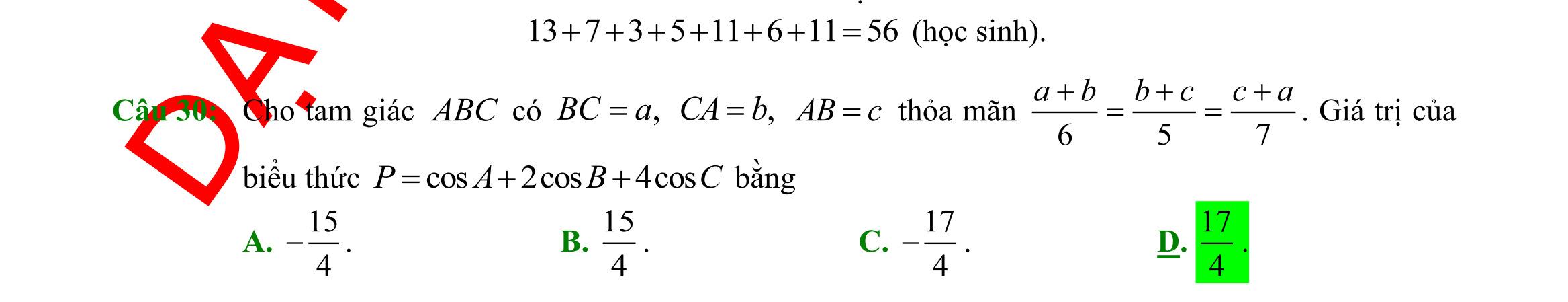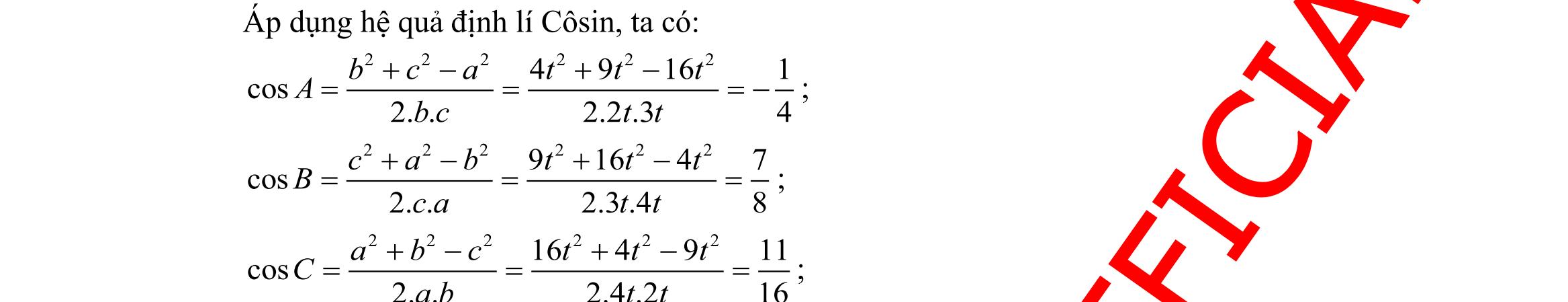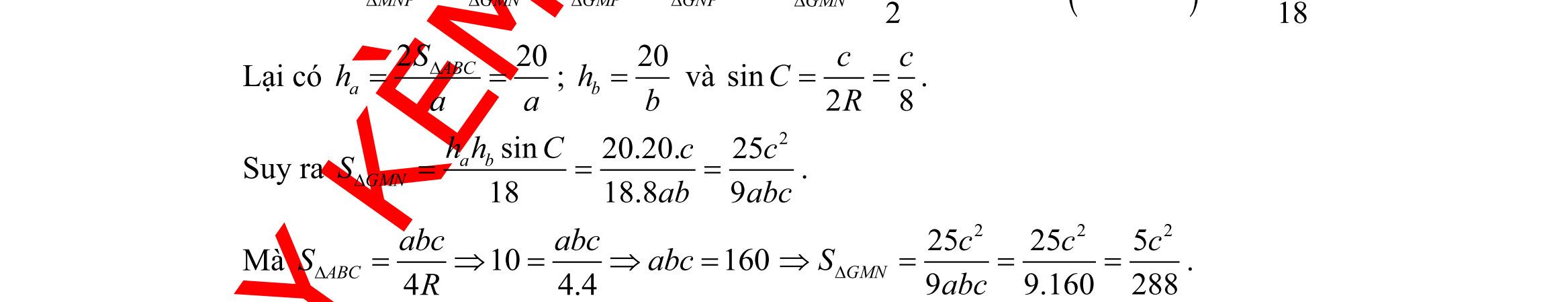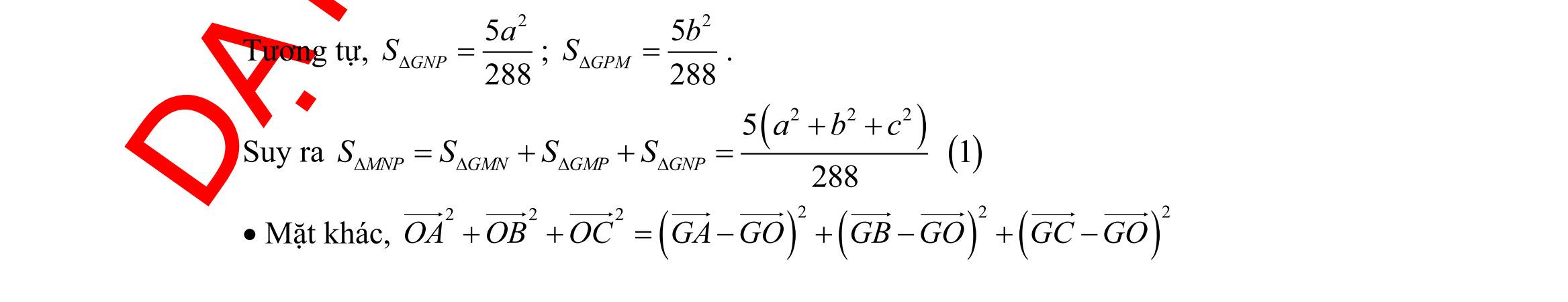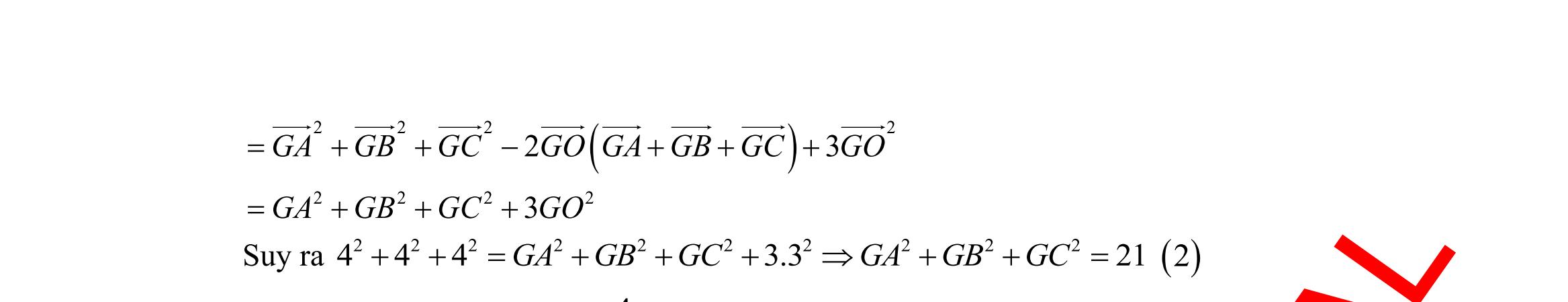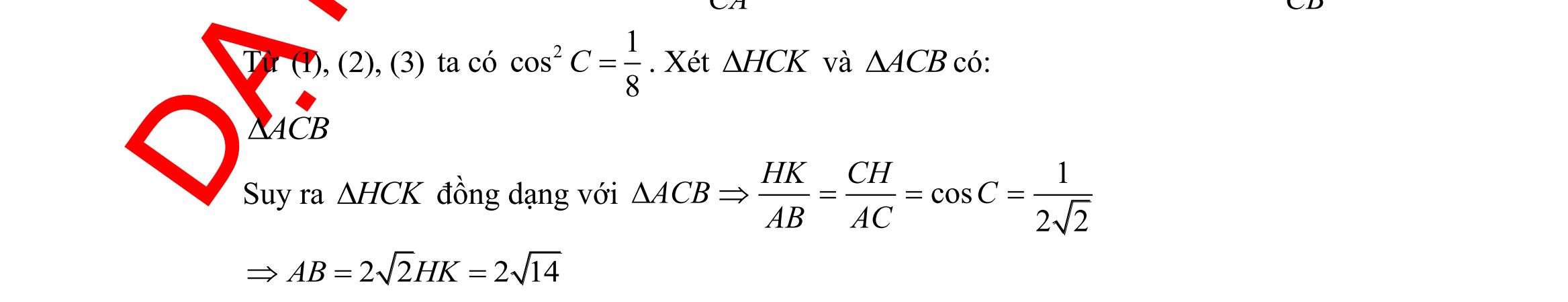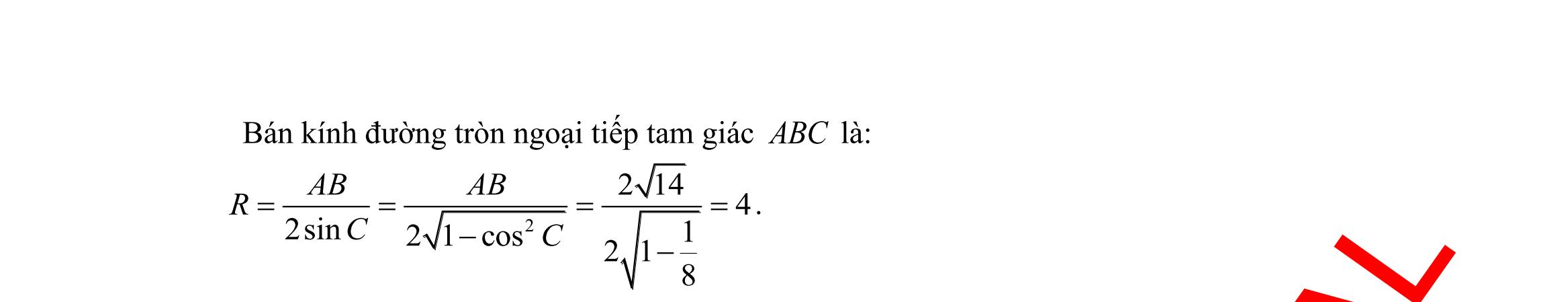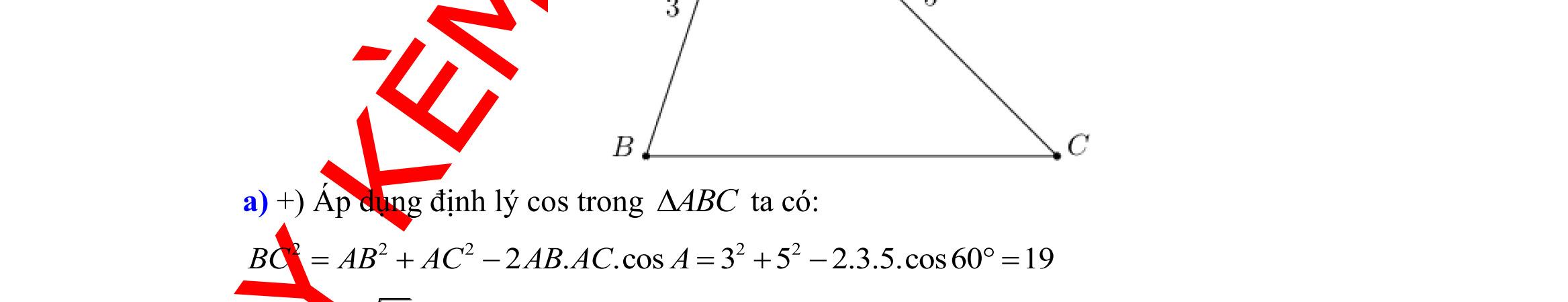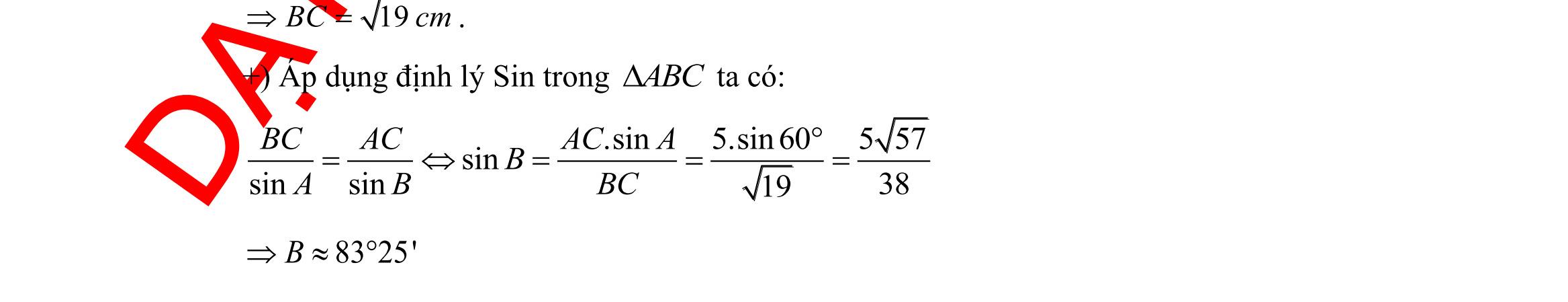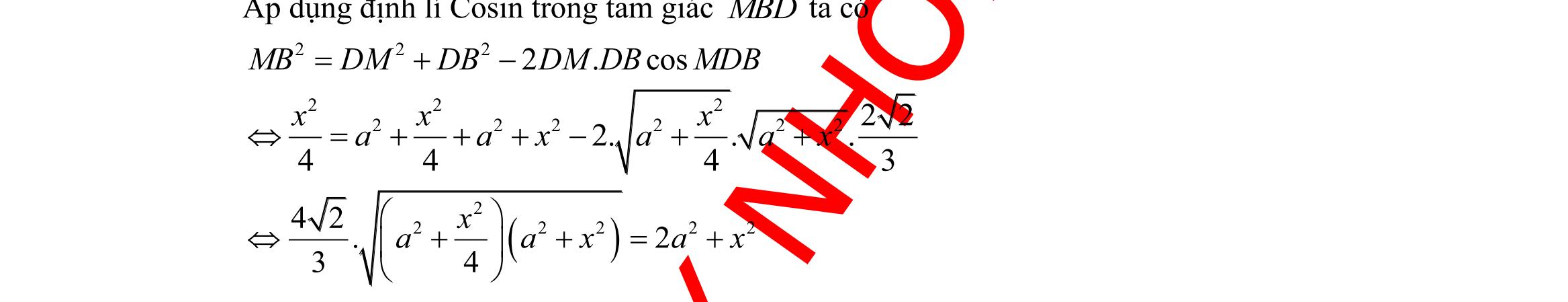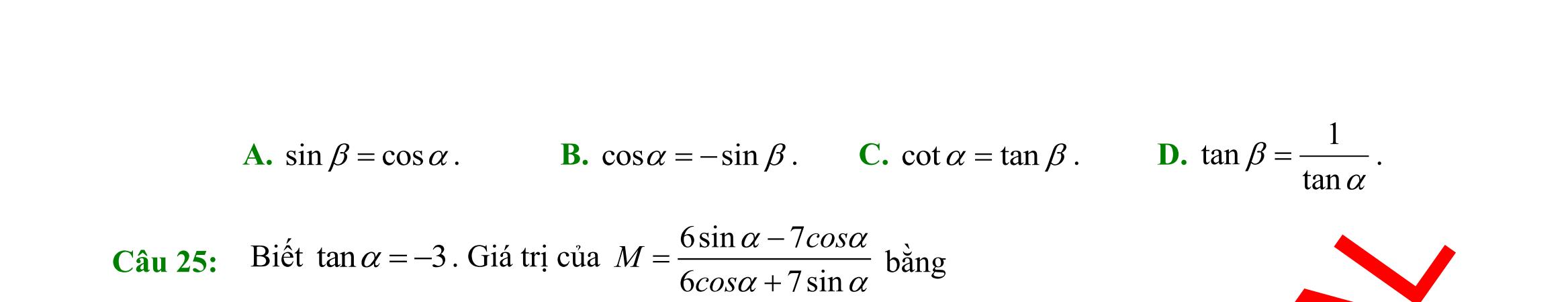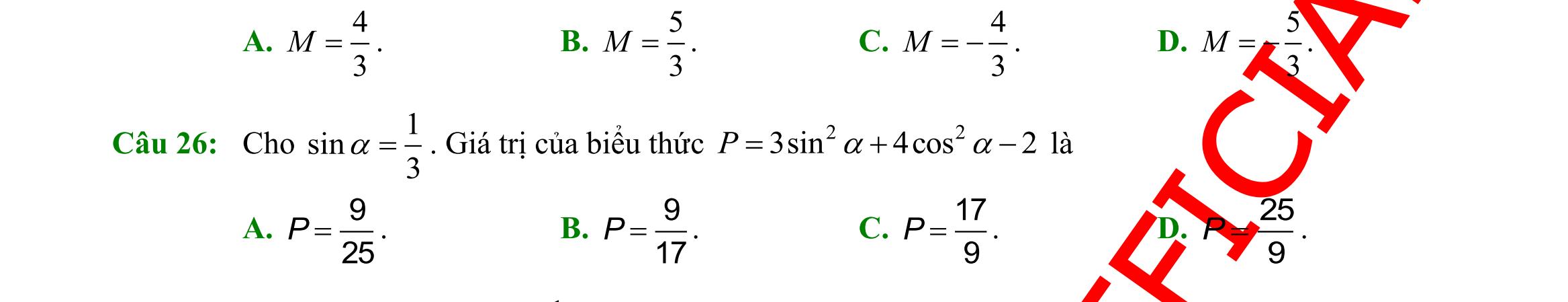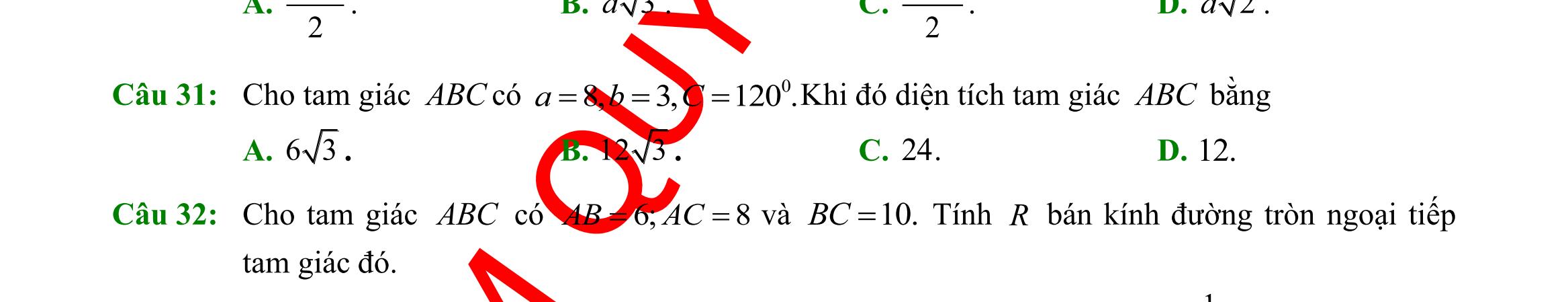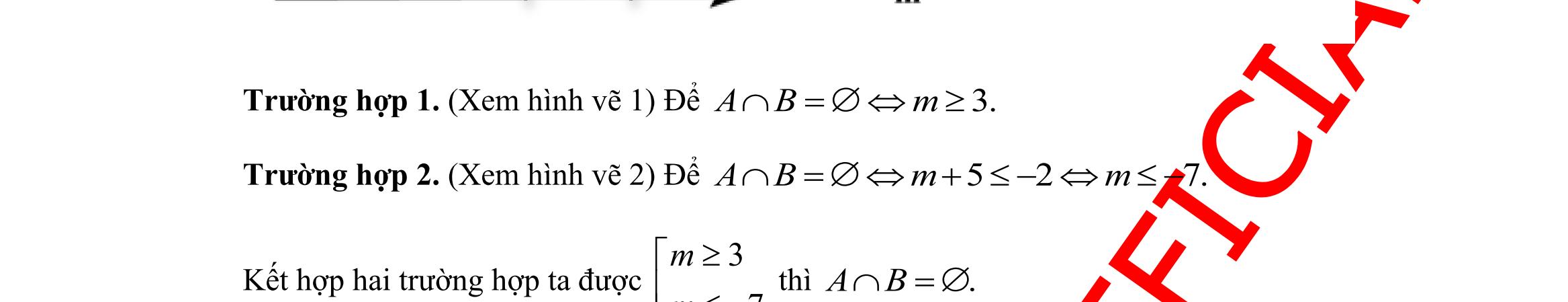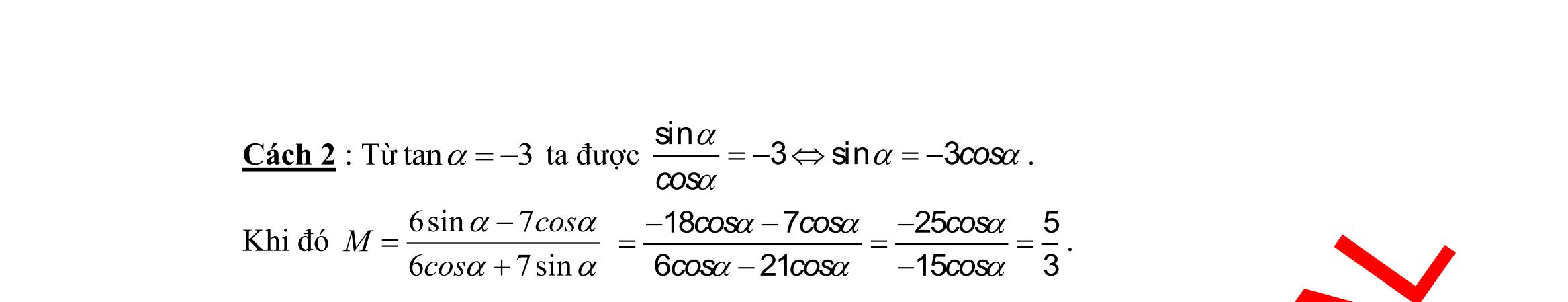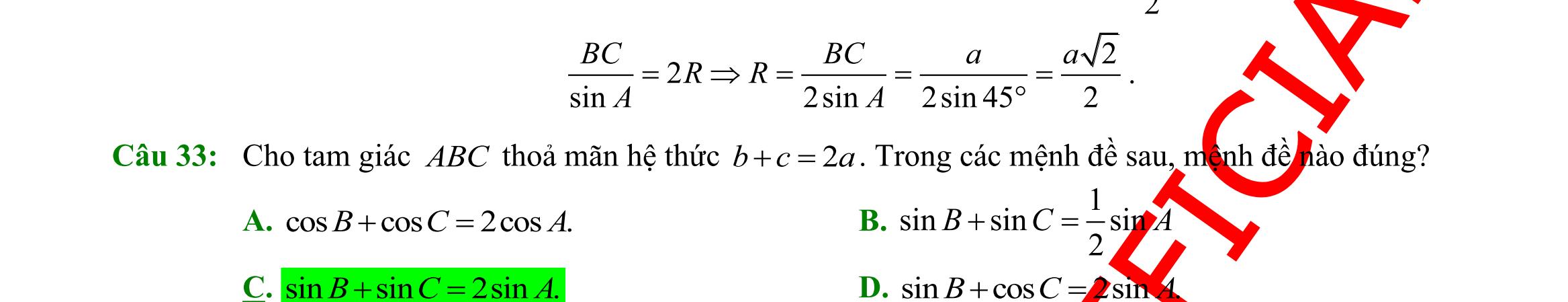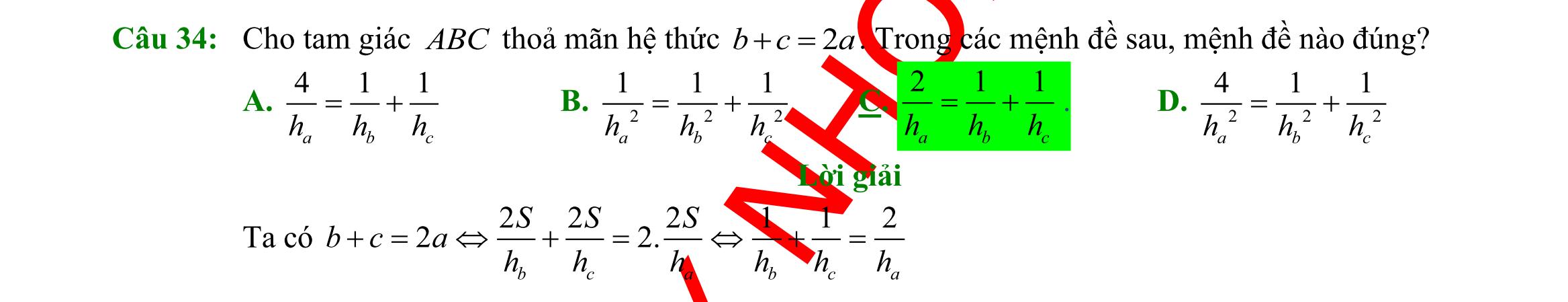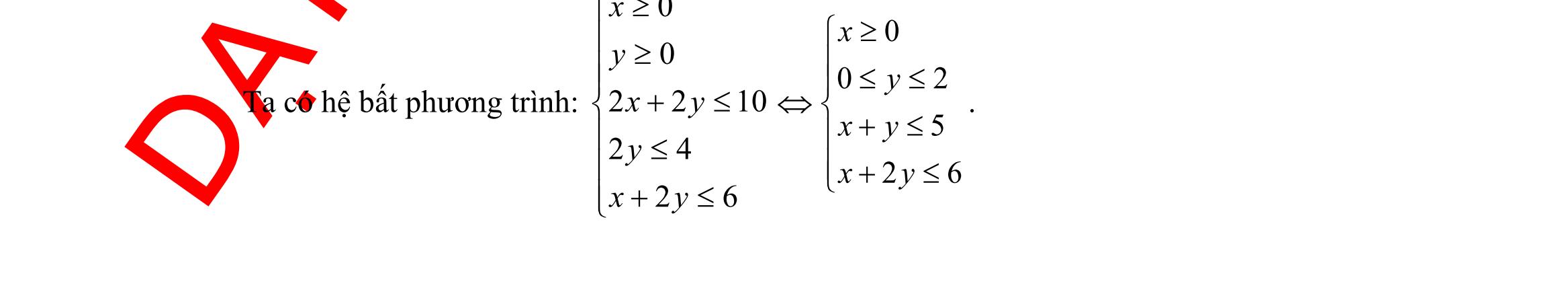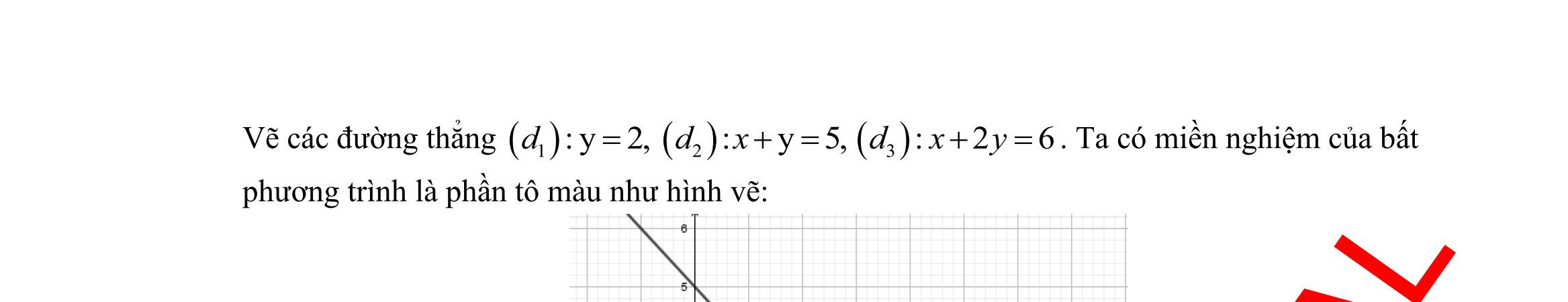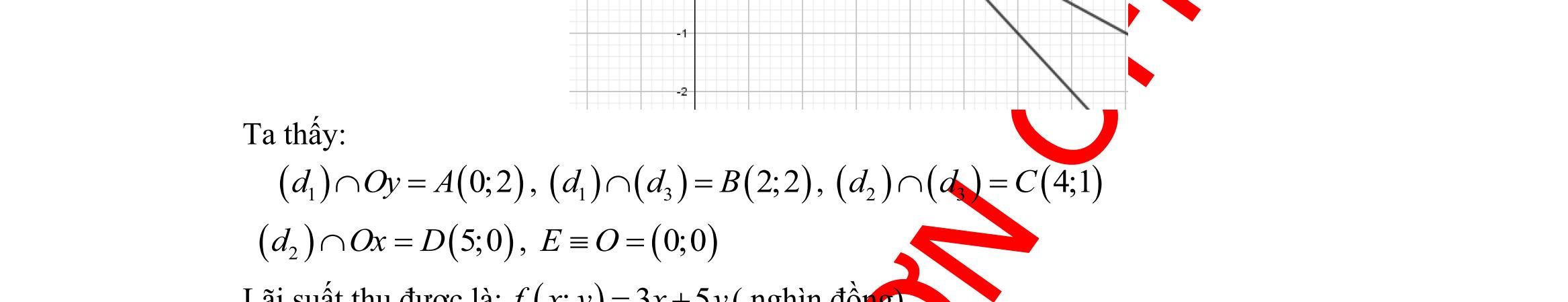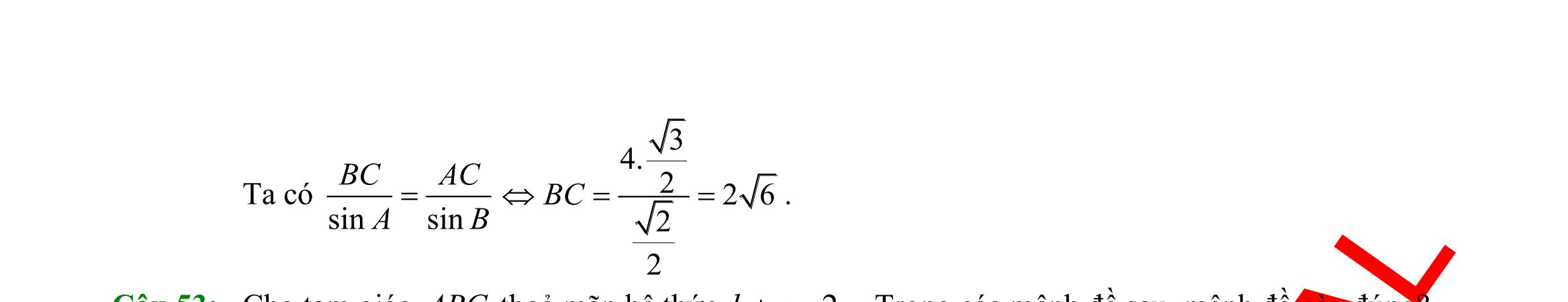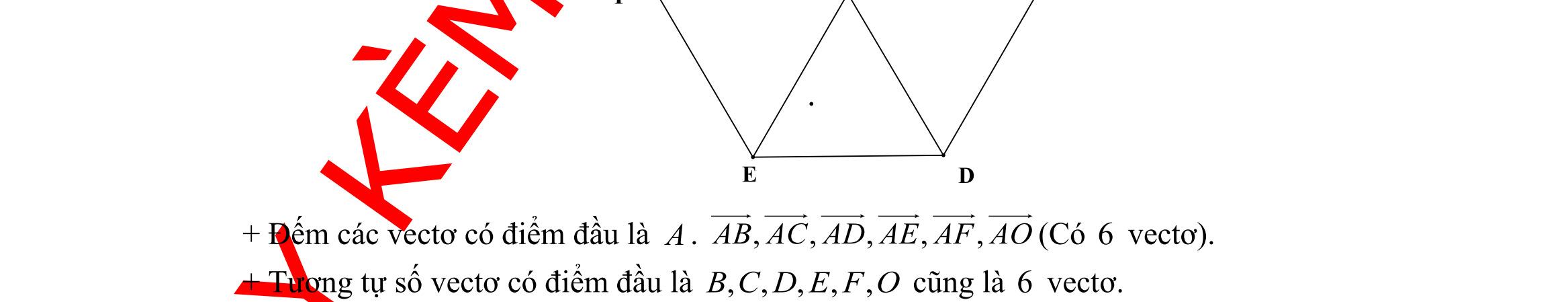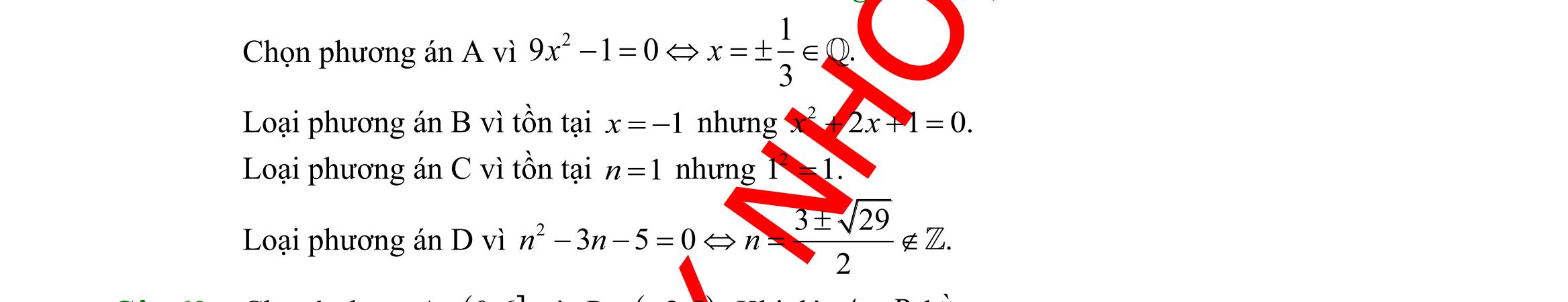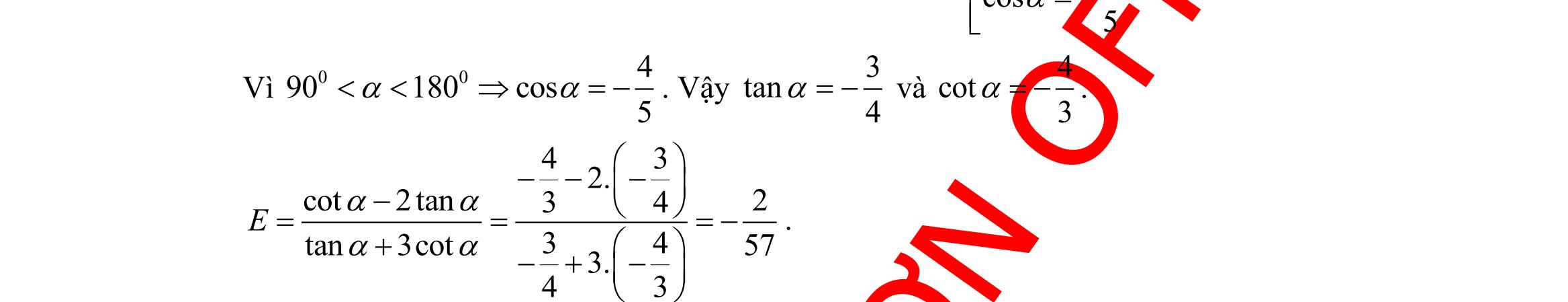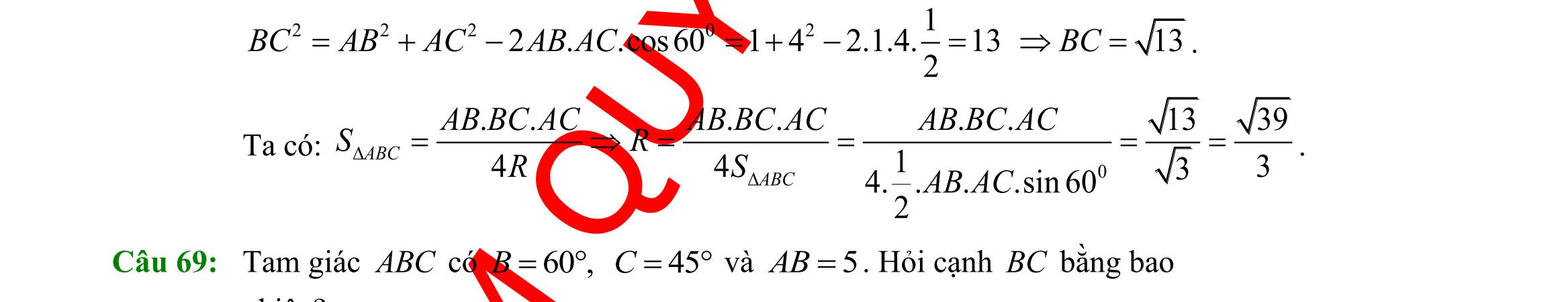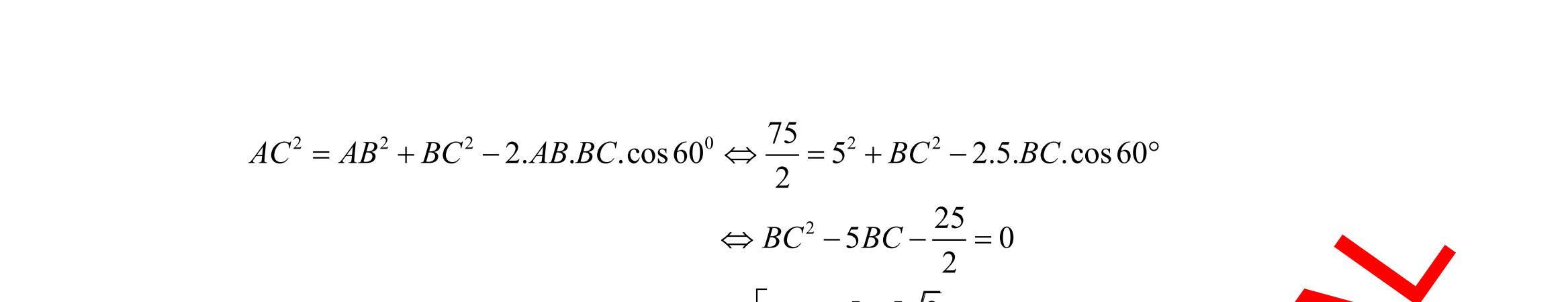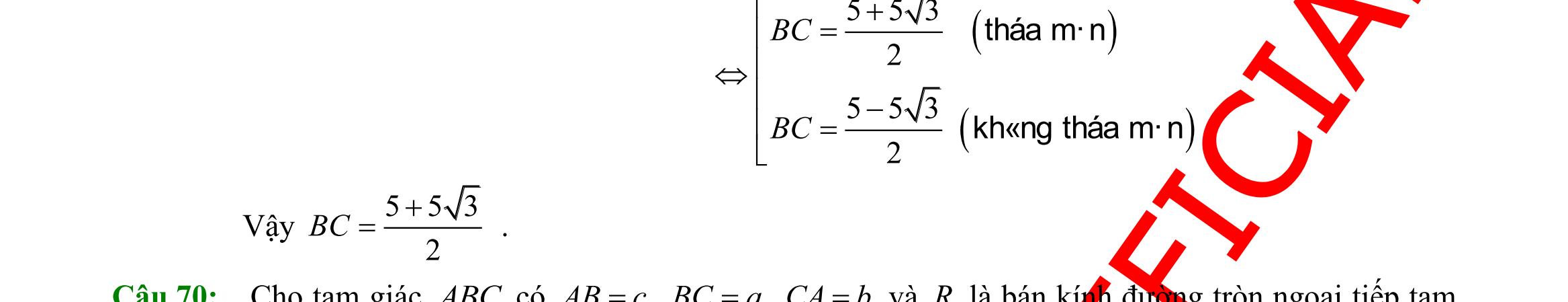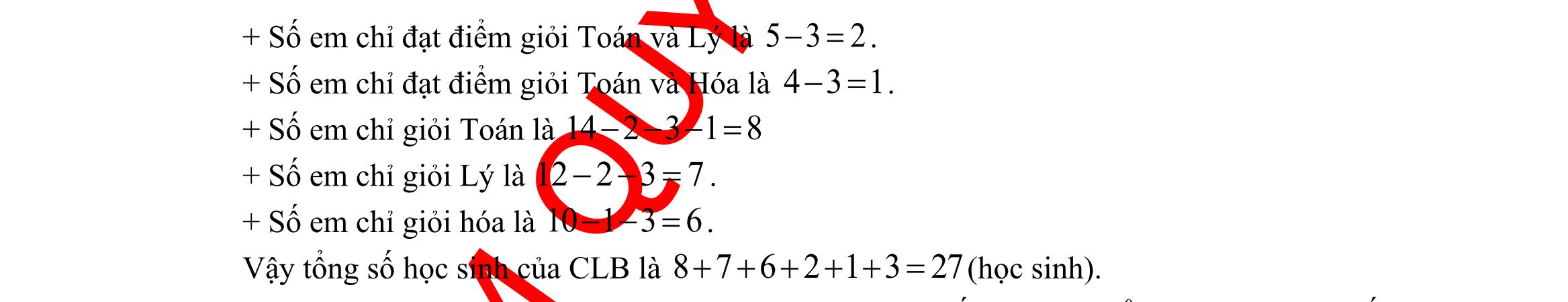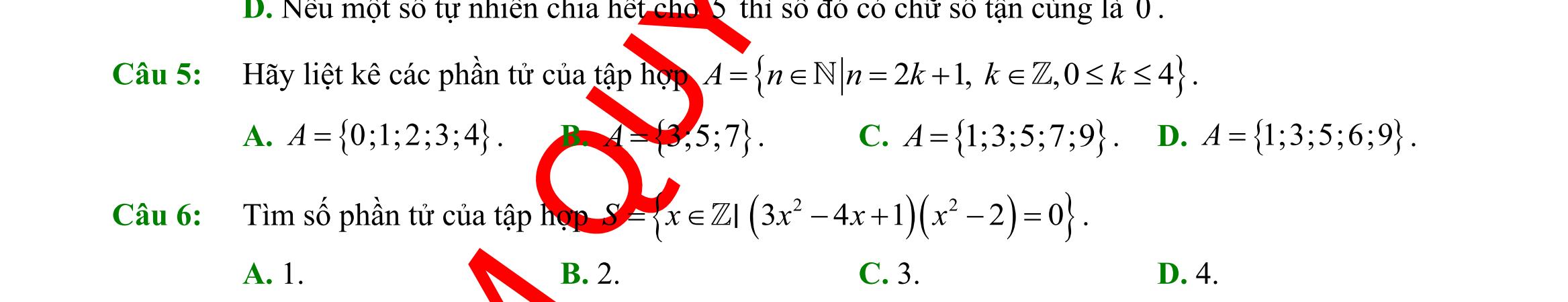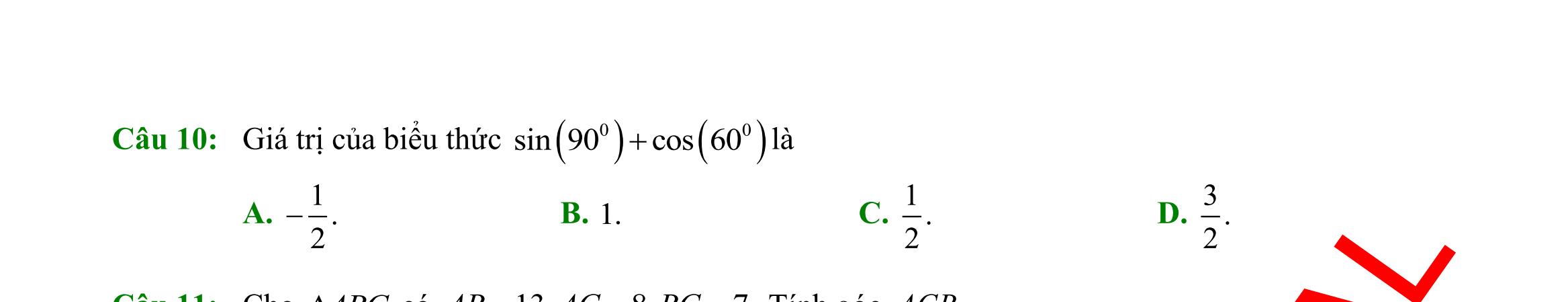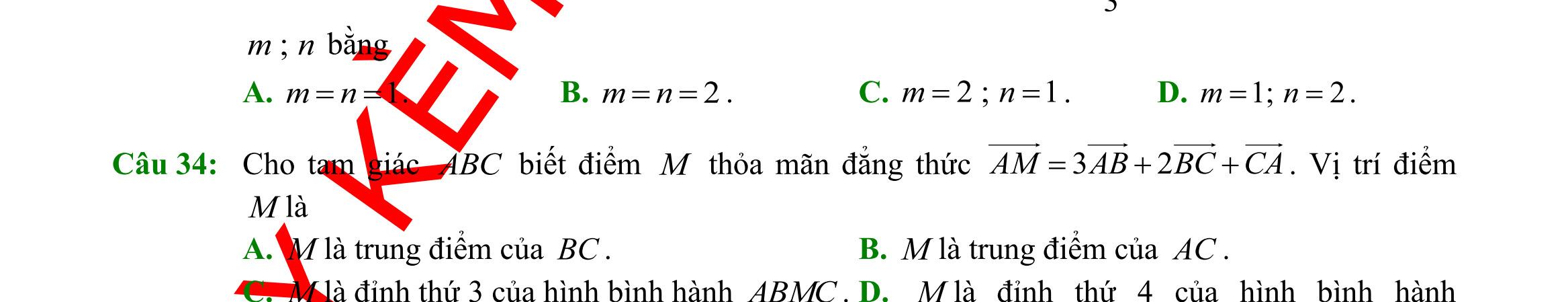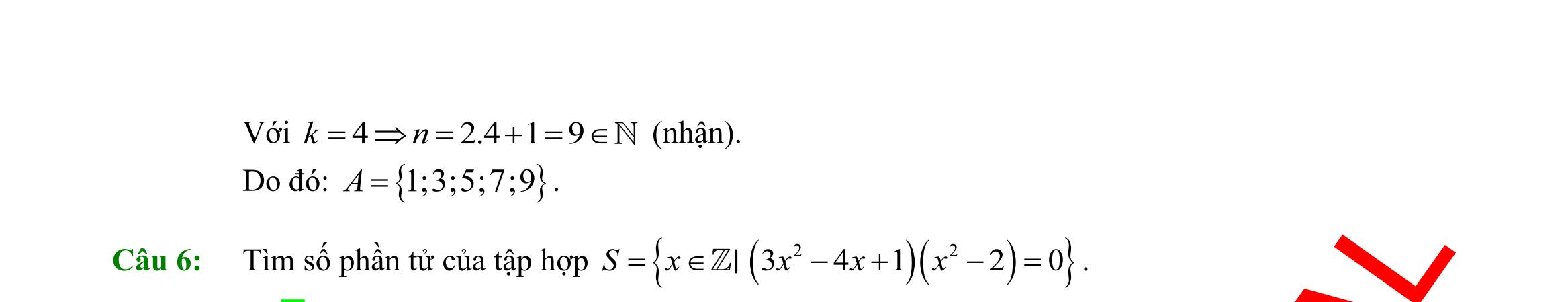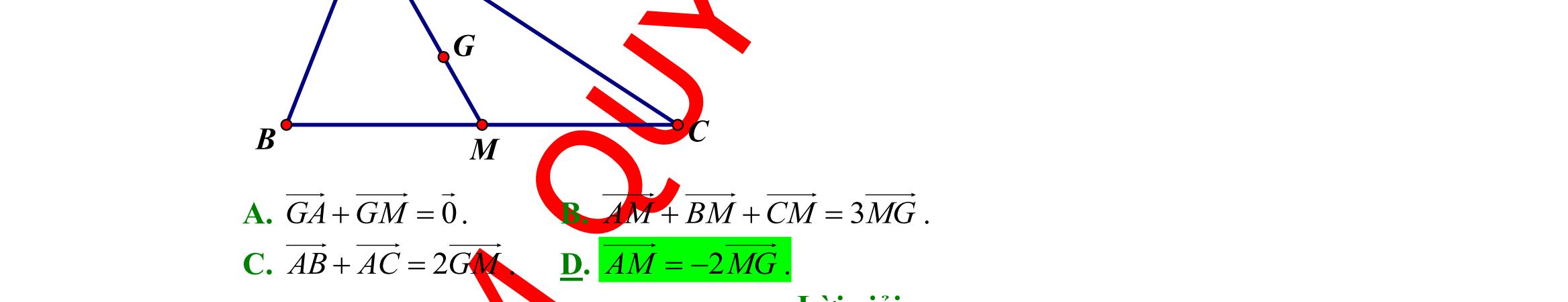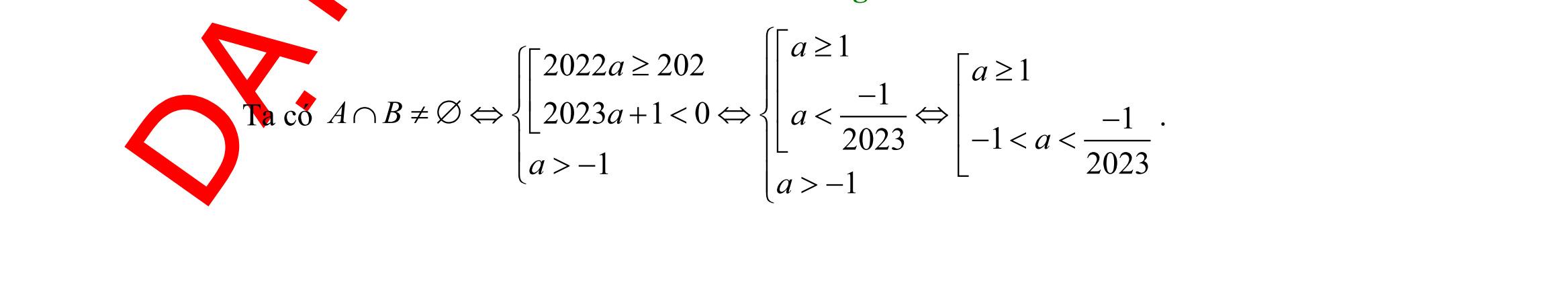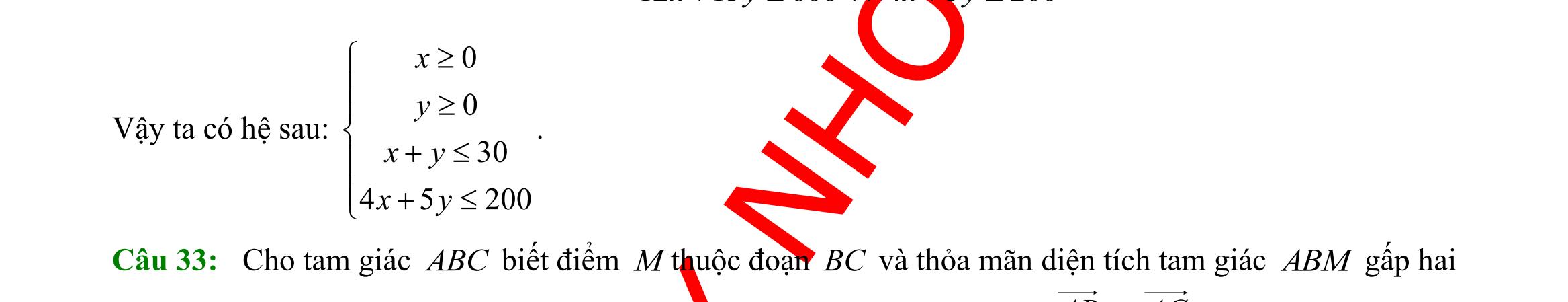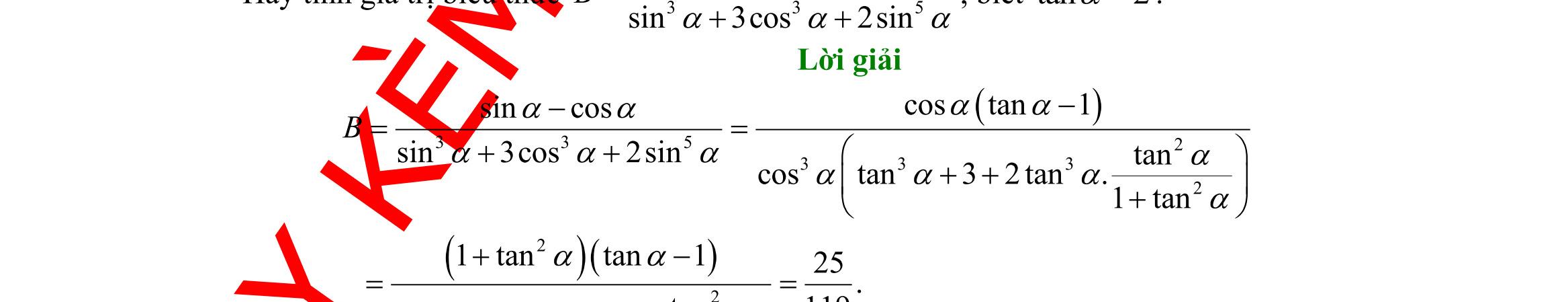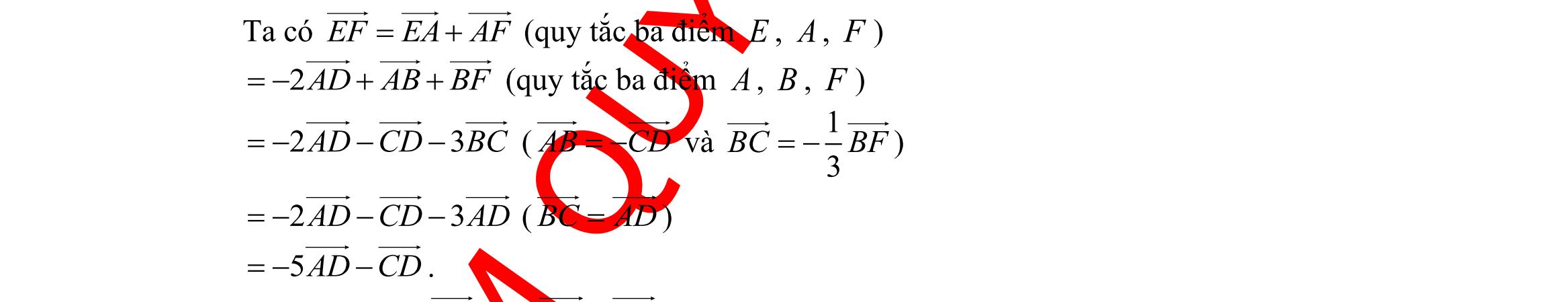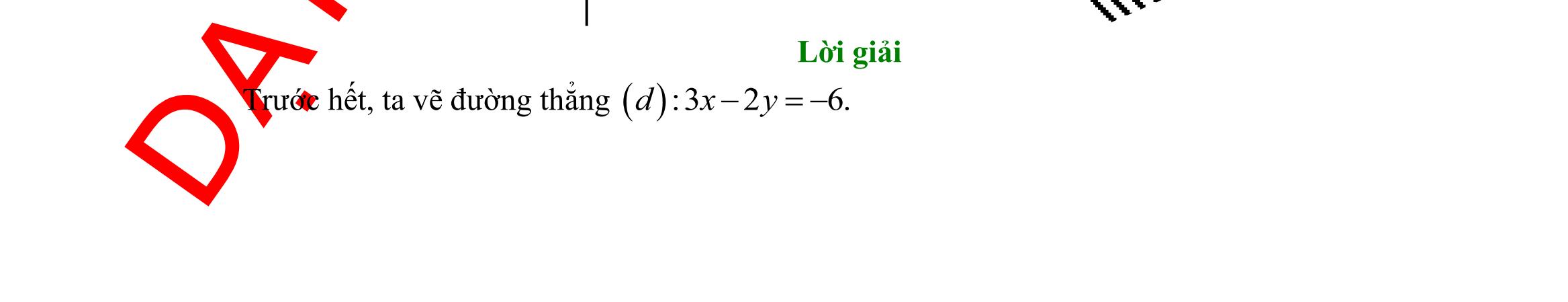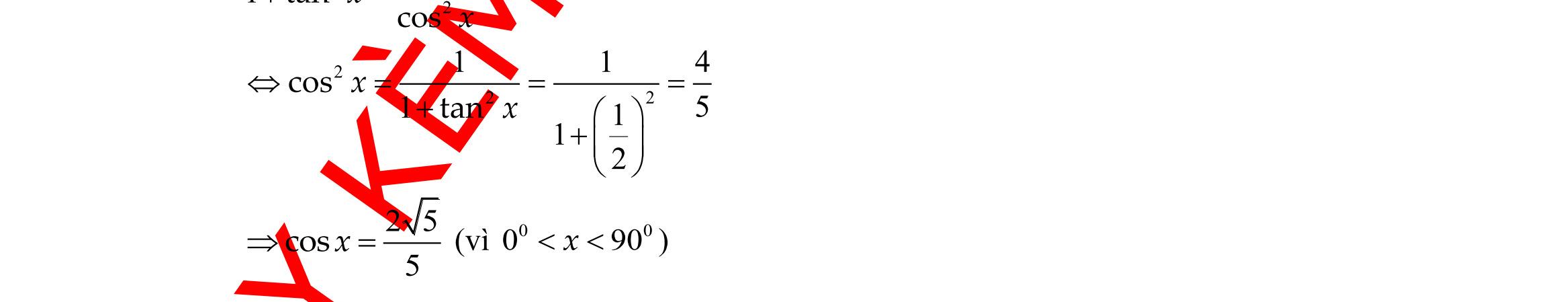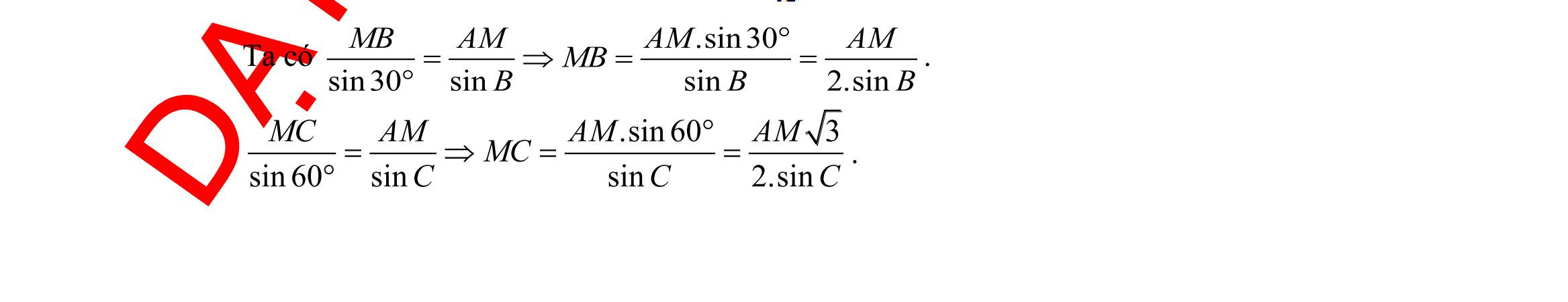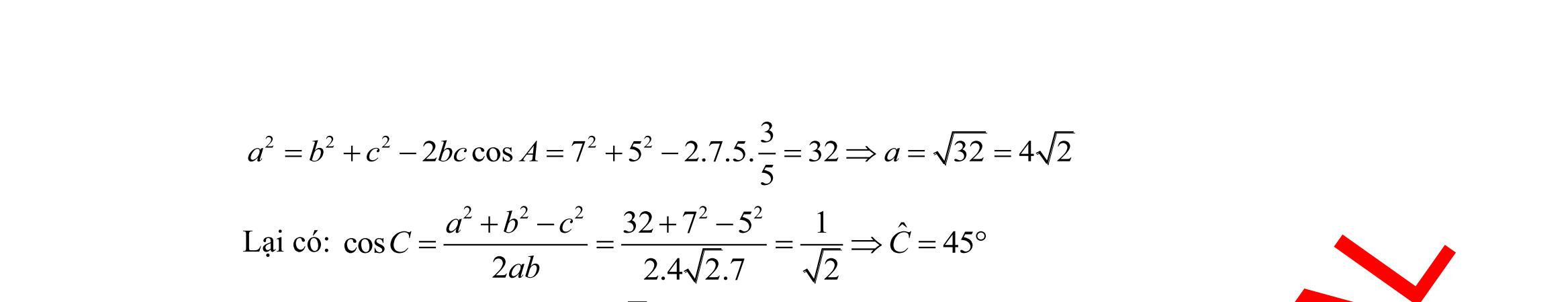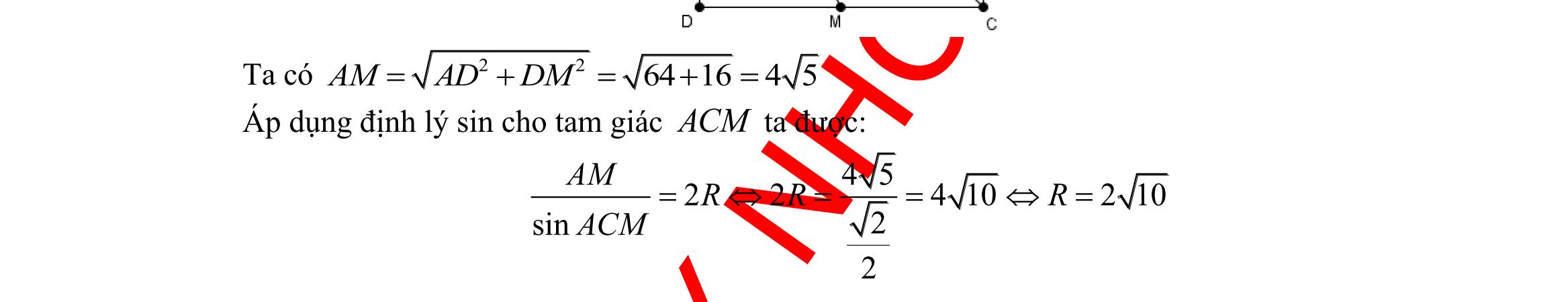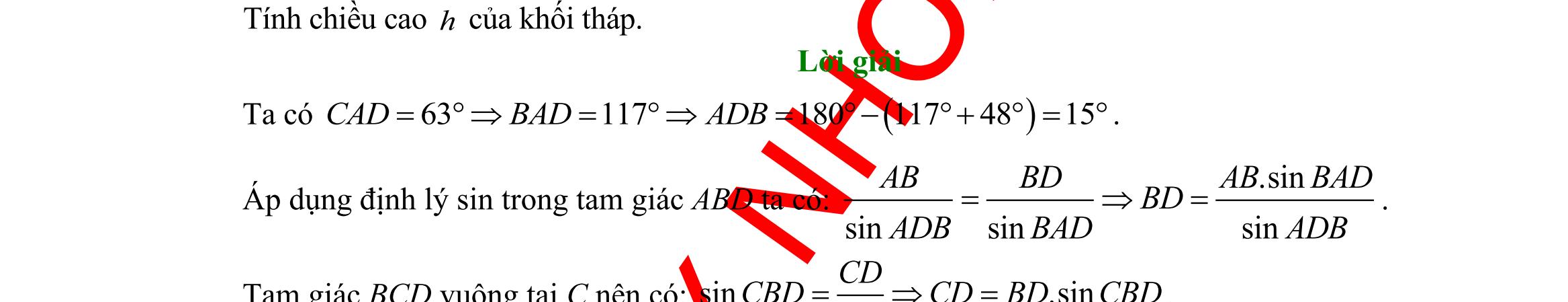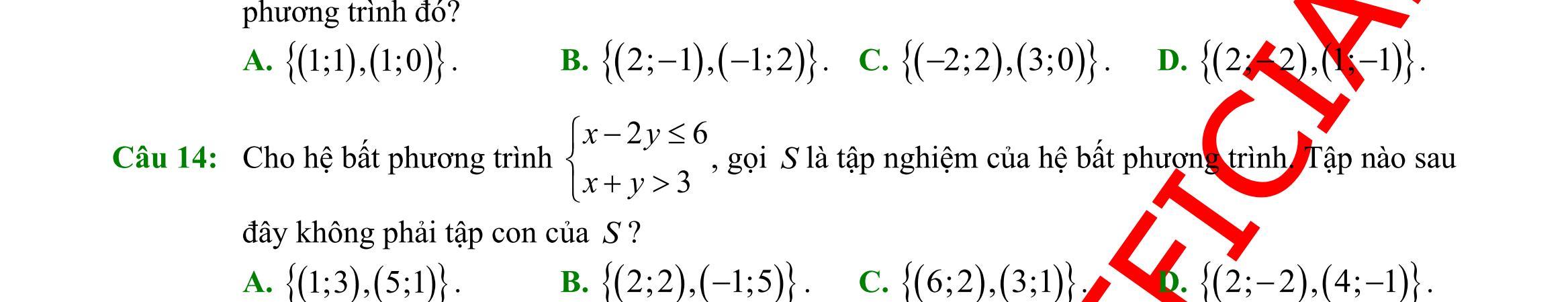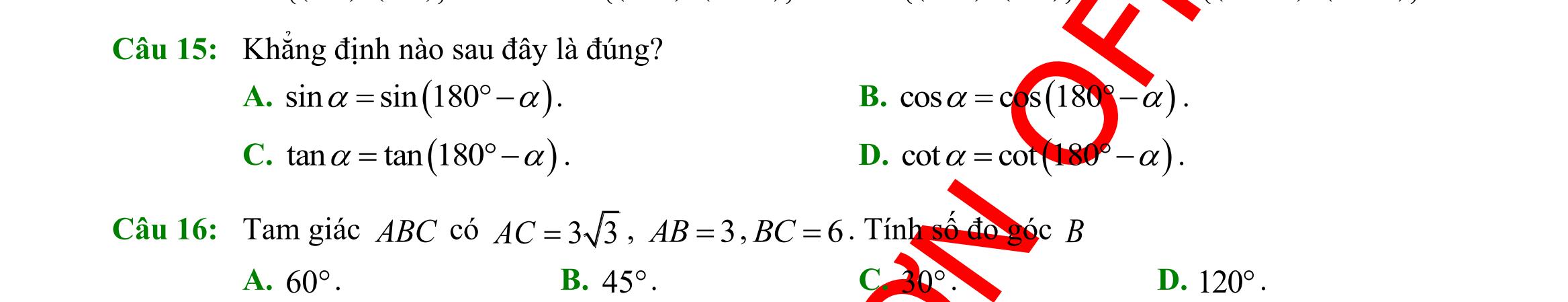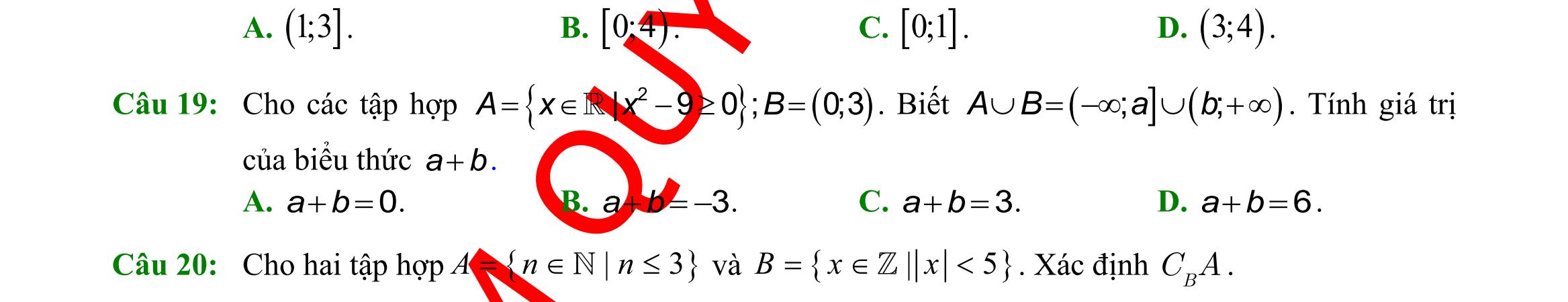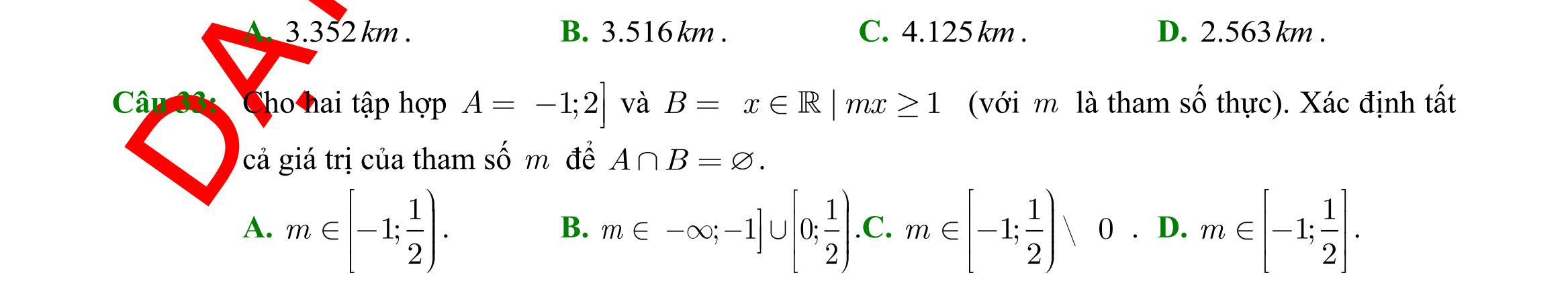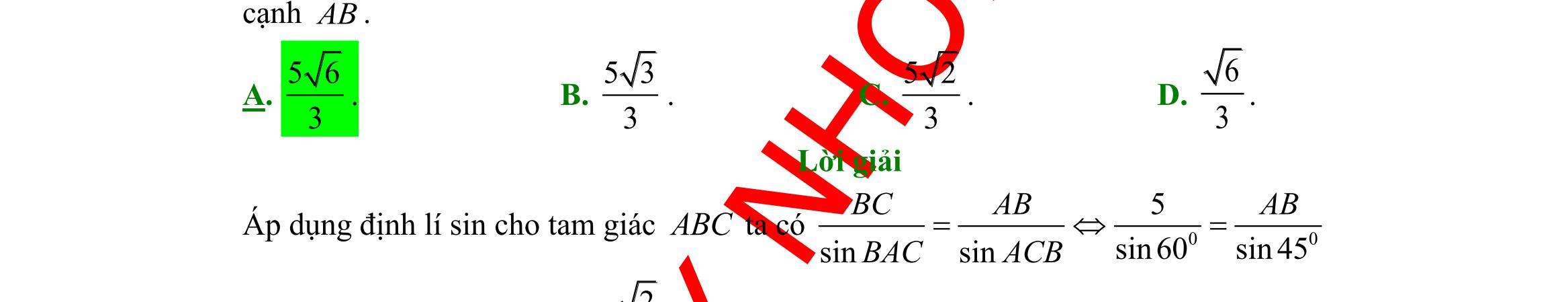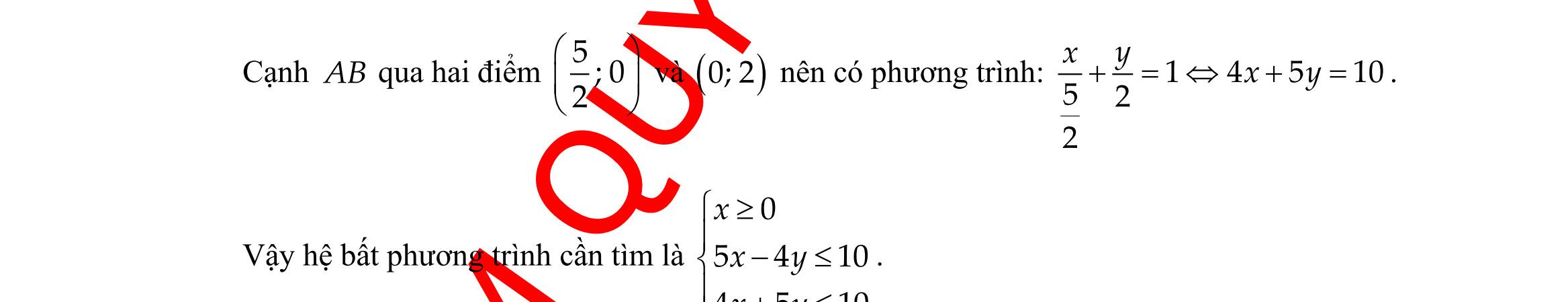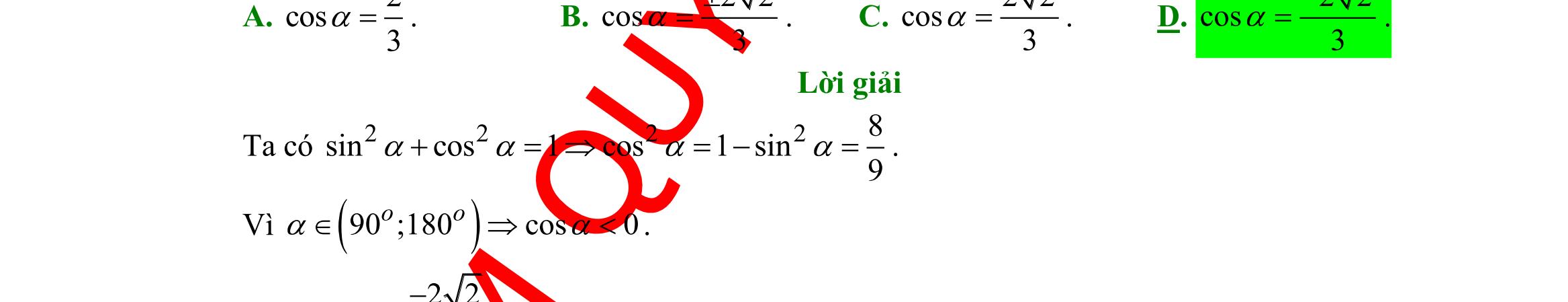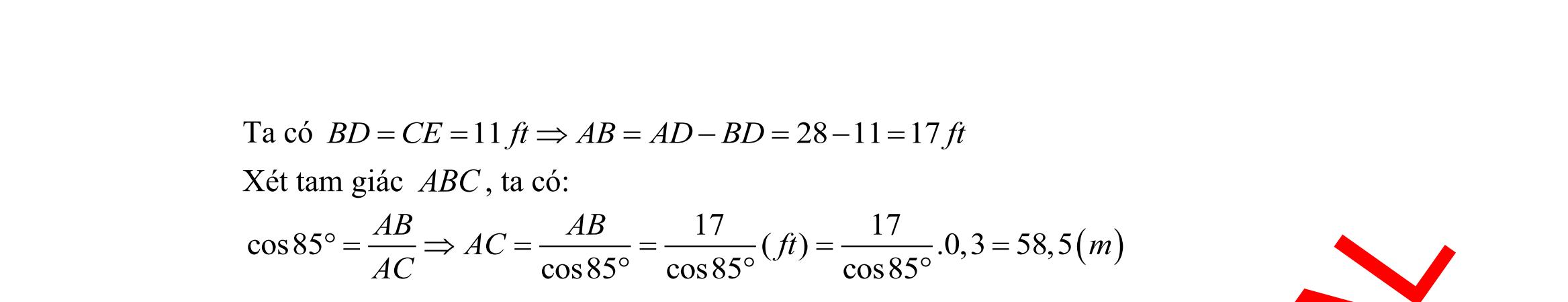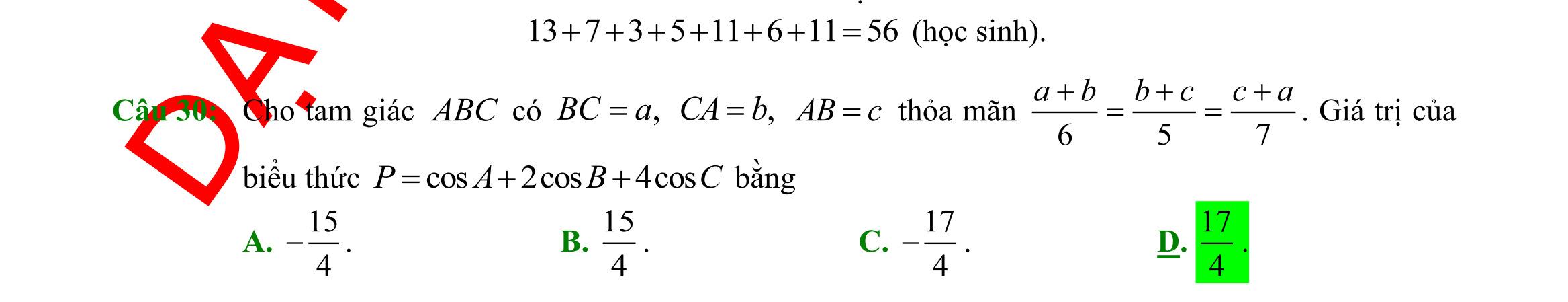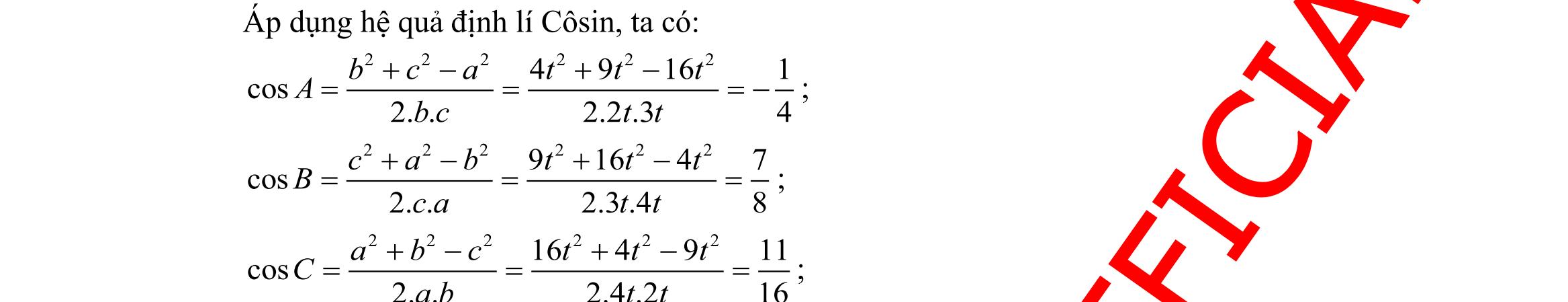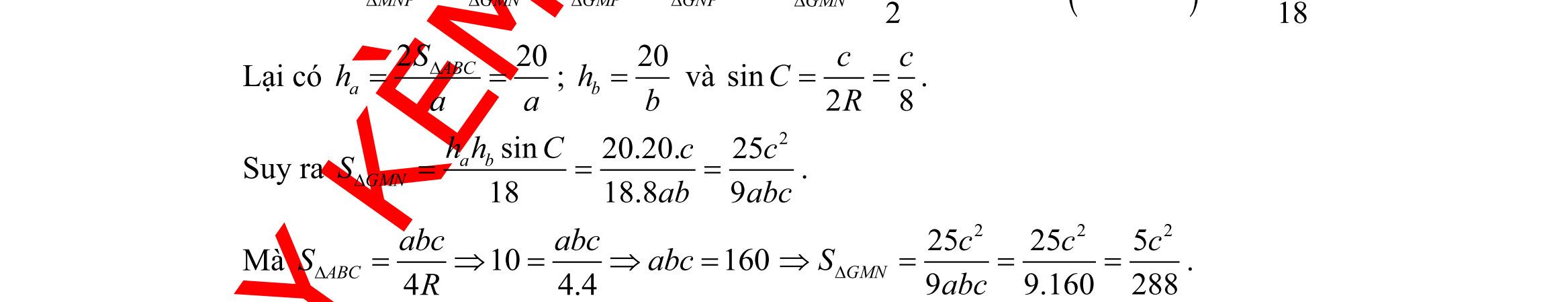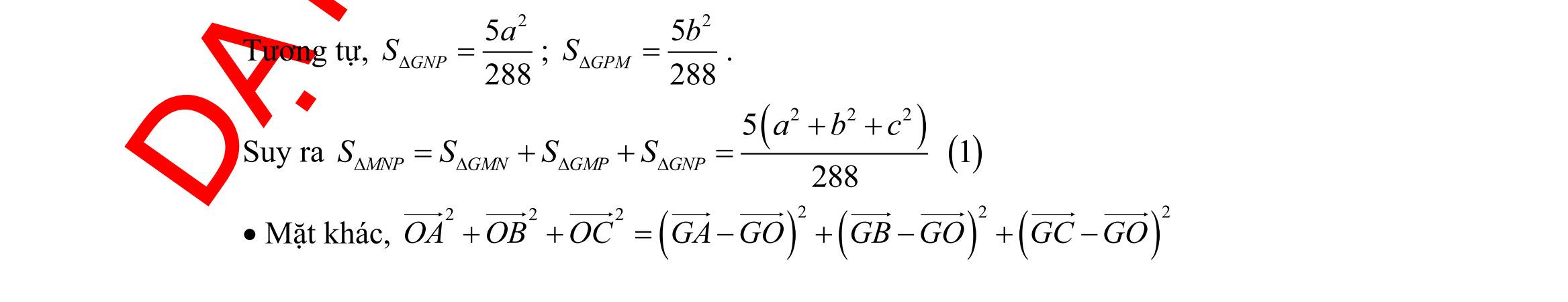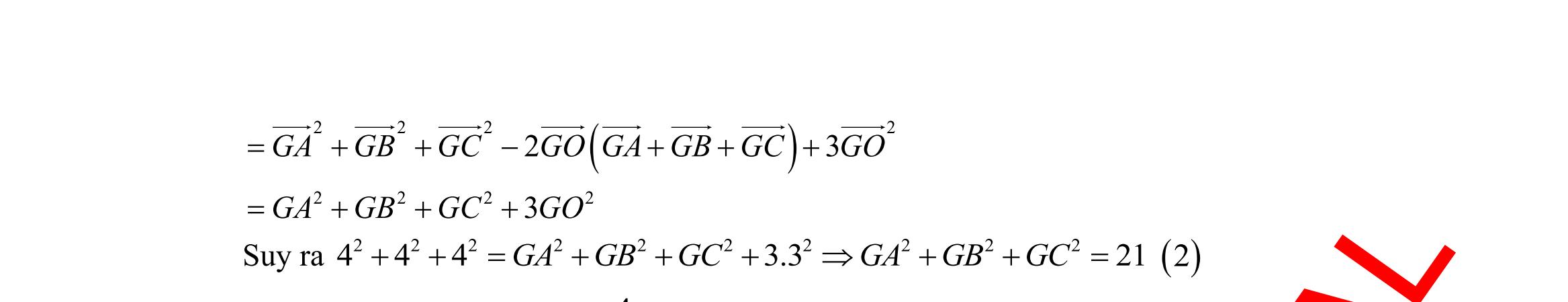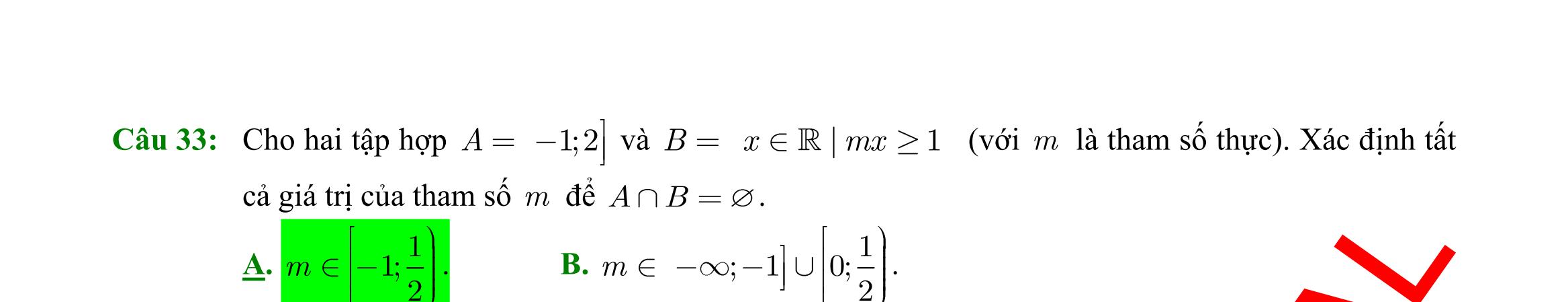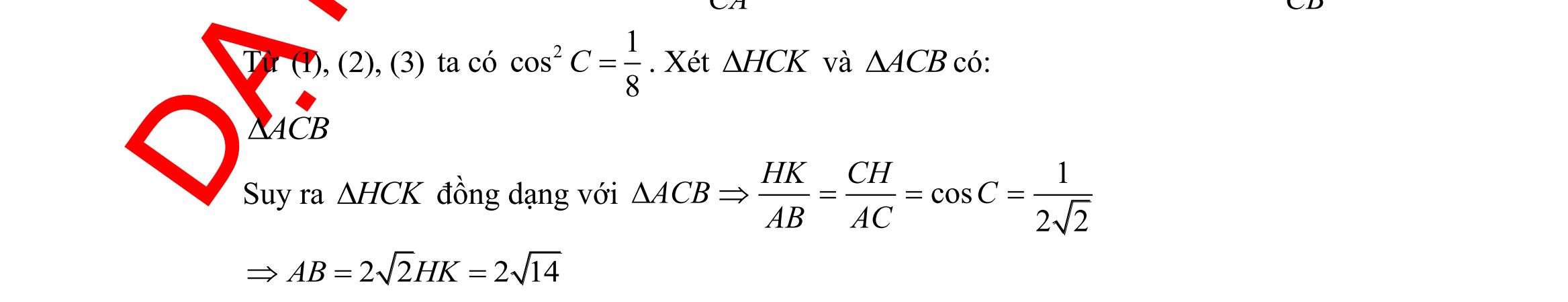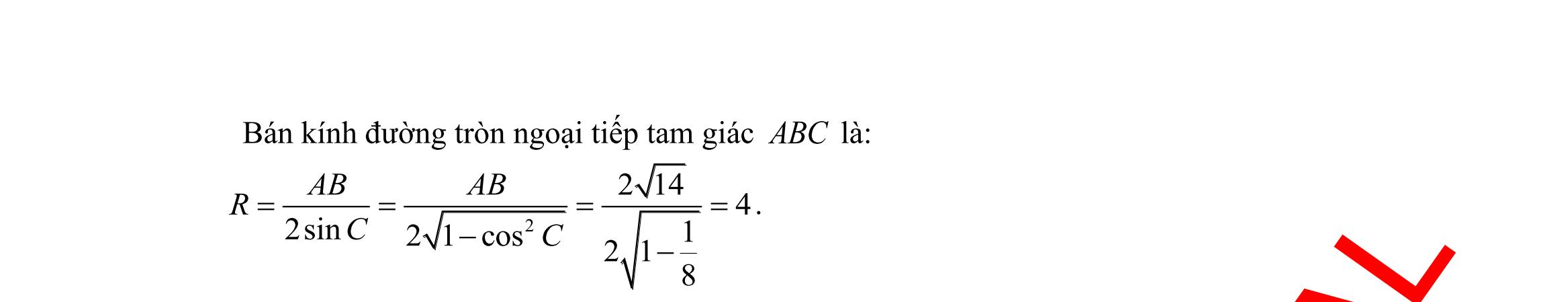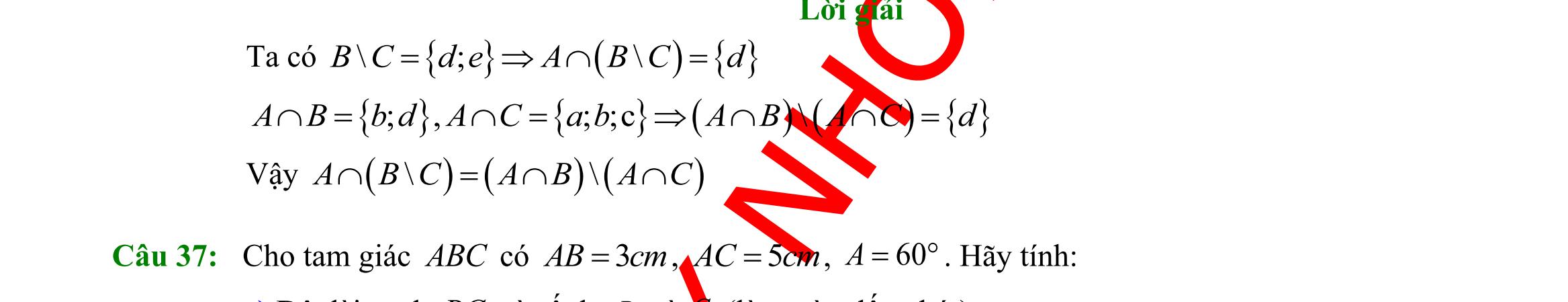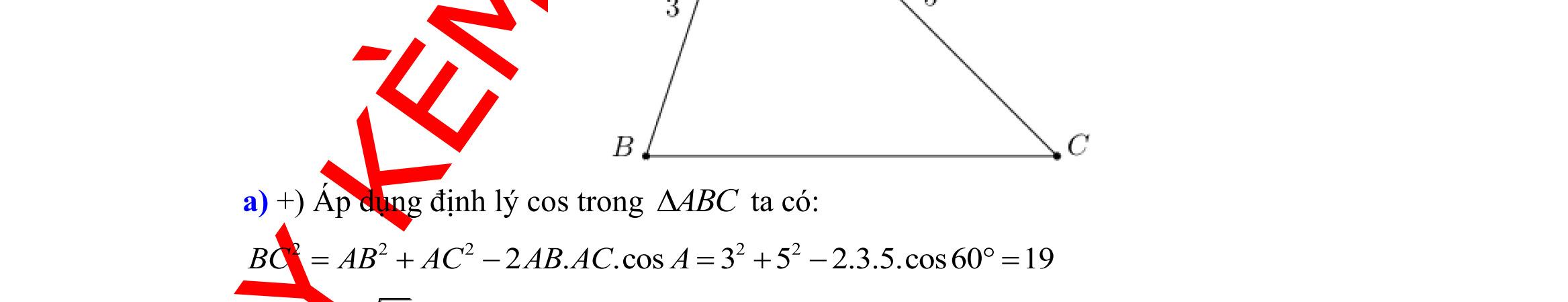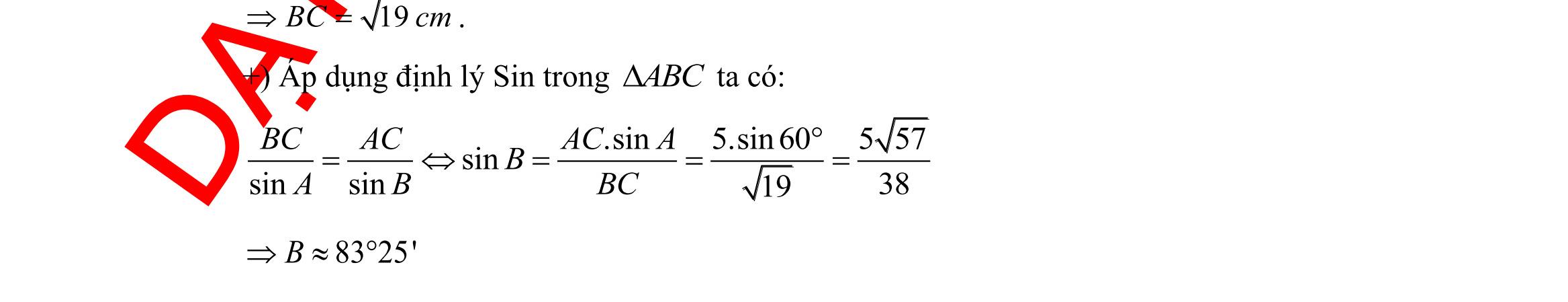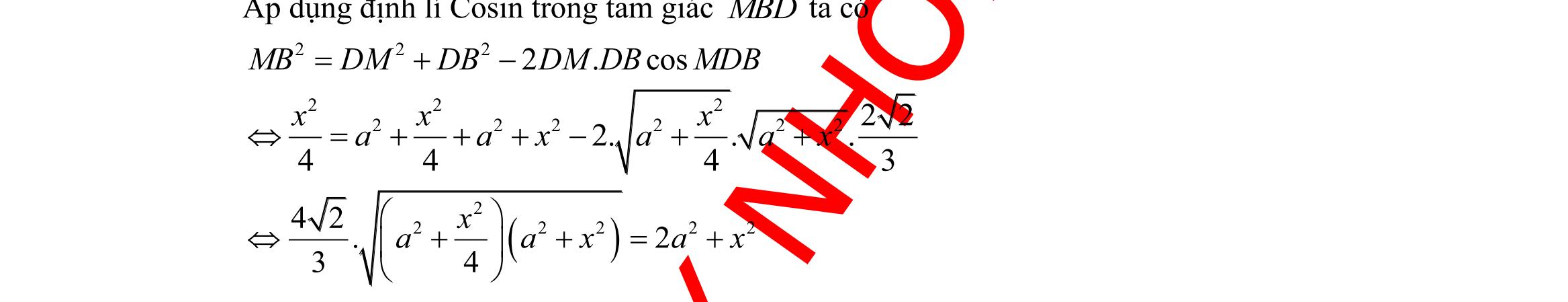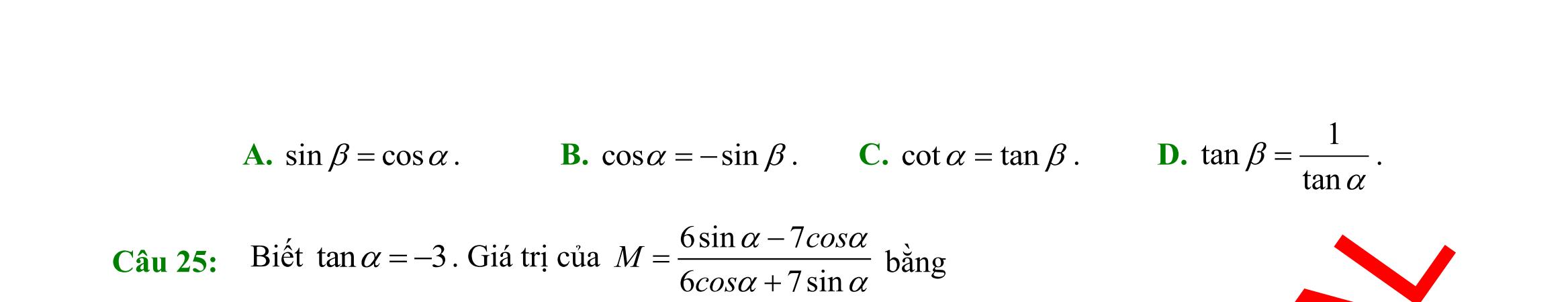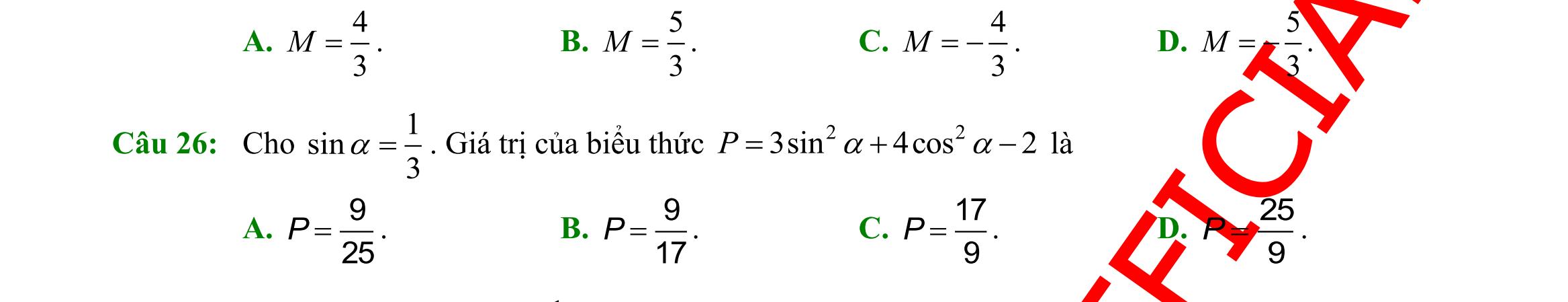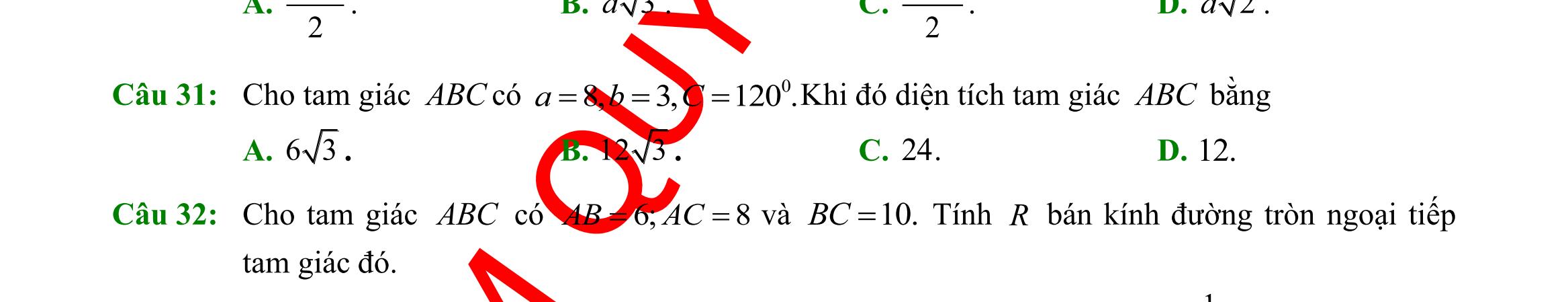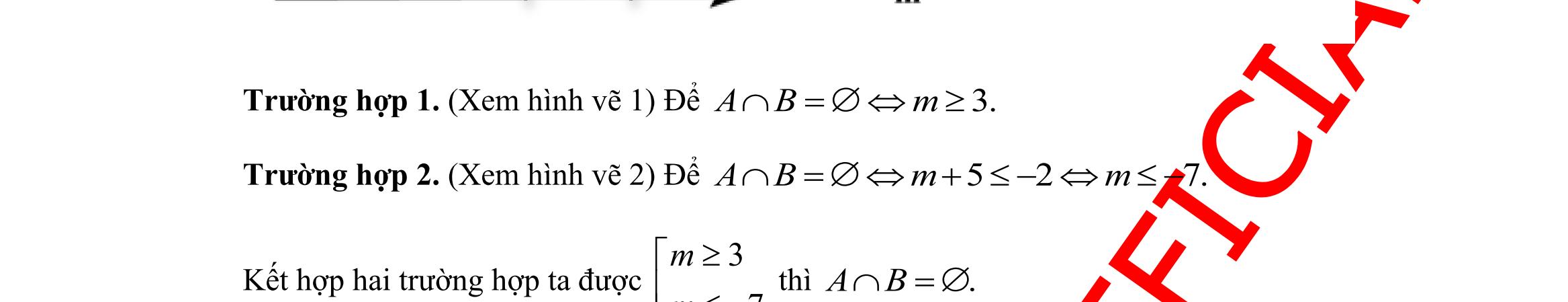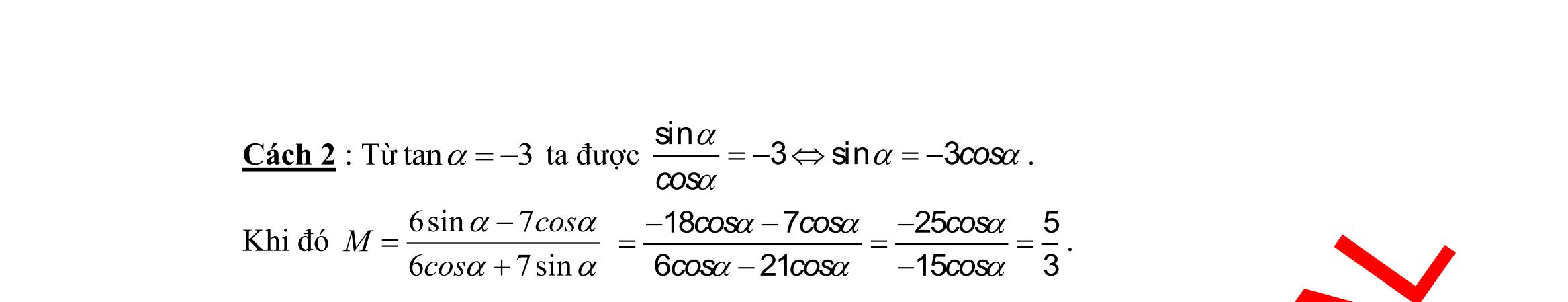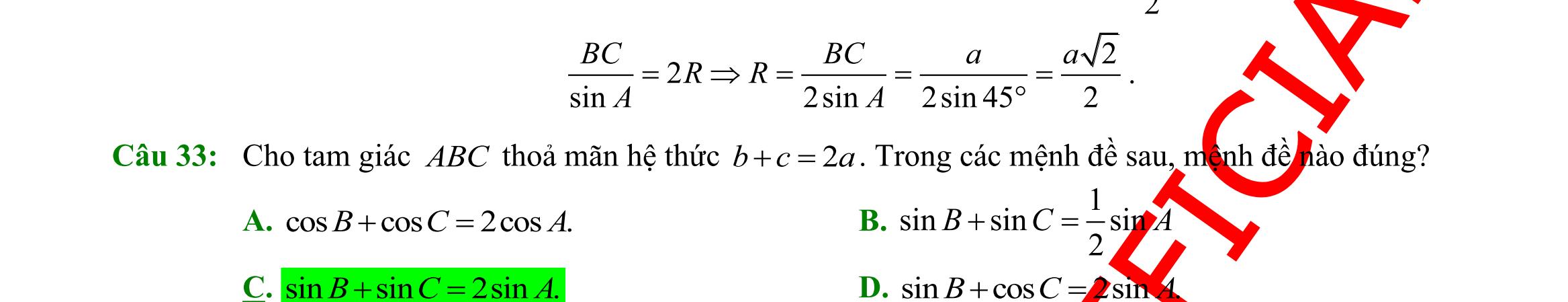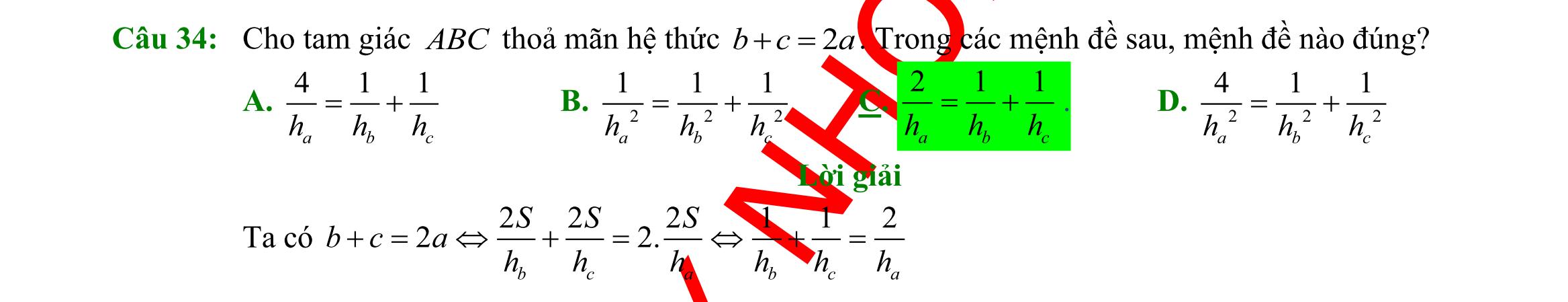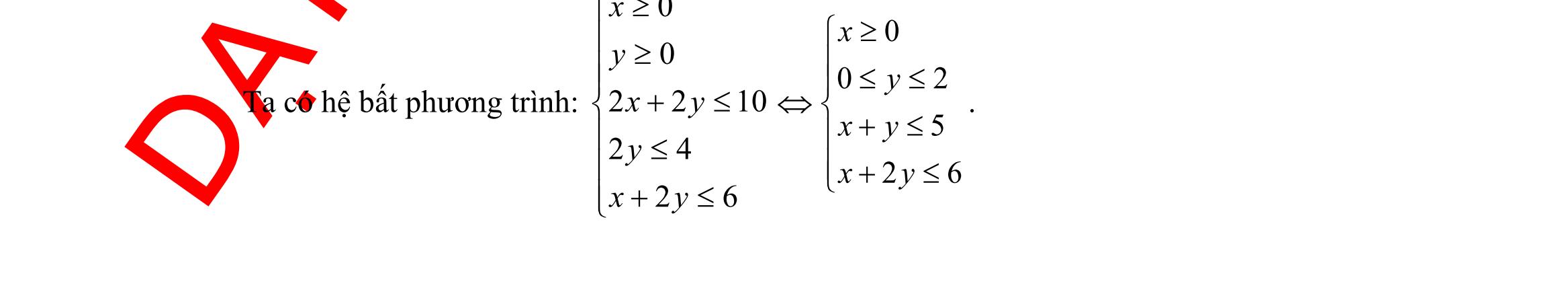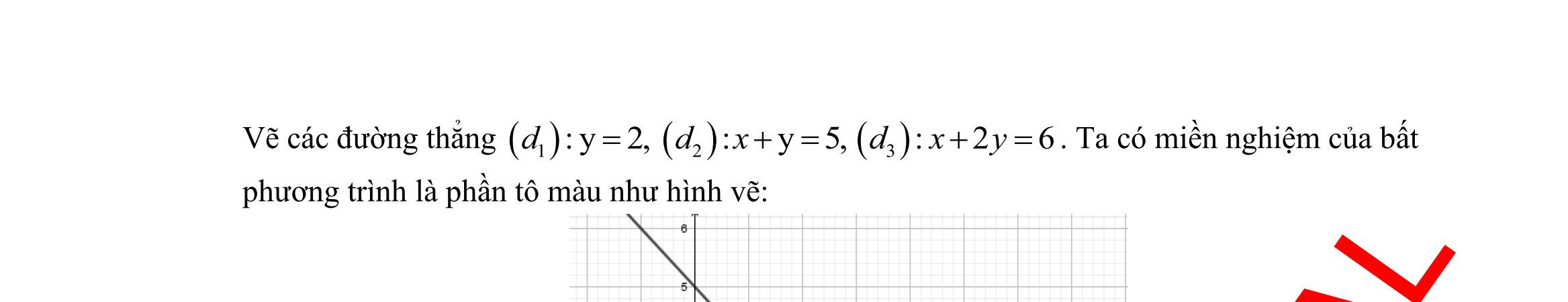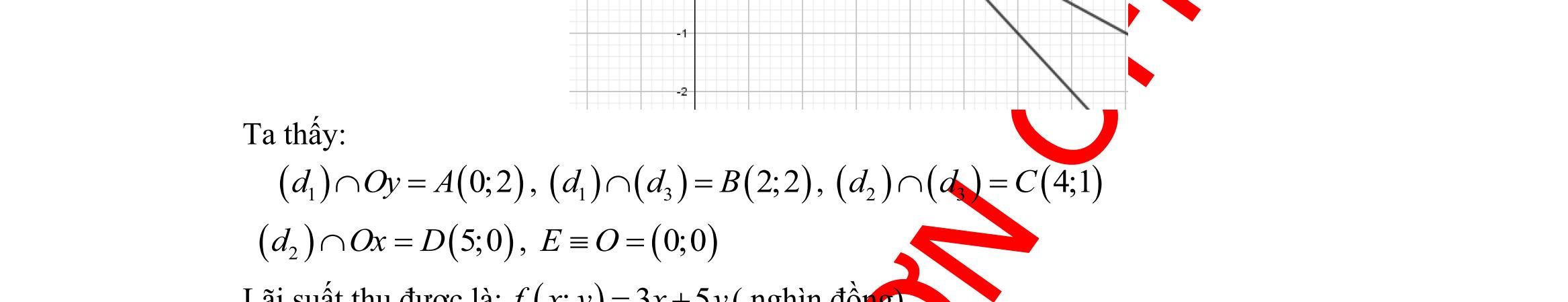DẠYKÈMQUYNHƠN OFFICIALĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection BỘ 5 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN TOÁN 10 CÁNH DIỀU CÓ LỜI GIẢI CHI TIẾT (35 CÂU TRẮC NGHIỆM + TỰ LUẬN) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
Câu
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 ĐỀ SỐ: 01 I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Mệnh đề phủ định của mệnh đề P: “ 2 :20xxx − ” là A. 2 :20xxx − B. 2 :20xxx − C. 2 :20xxx − D. 2 :20xxx − Câu 2: Dùng ký hiệu để viết tập hợp sau :12Axx =− A. ( 1;2A =− B. ( )1;2A =− C. 1;2A =− D. )1;2A =− Câu 3: Kết quả của ( ) 1;30;5− là A. ( )1;0 . B. ( 1;5 . C. ( 0;3 . D. )0;3 . Câu 4: Với giá trị thực nào của x thì mệnh đề chứa biến: “ 2 84 xx − ” trở thành mệnh đề đúng? A. 3x = B. 0x = C. 1x =− D. 6x = Câu 5: Hãy liệt kê các phần tử của tập ( )( ) 222 530.xx Xxx =−+ += A. 2;1.X =− B. 1.X = C. 3 2;1;. 2 X =− D. 3 1;. 2 X =
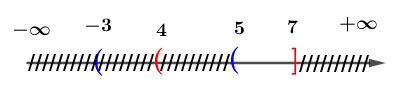
6: Tập 2;3X = có bao nhiêu tập hợp con? A. 3. B. 4. C. 5. D. 2. Câu 7: Cho hai tập hợp }{1;2;3;4A = , }{2;4;6;8B = . Tập hợp AB là A. {2;4}. B. {1;2;3;4;6;8}. C. {6;8}. D. {1;3}. Câu 8: Cho hai tập hợp ,A B thỏa \B1;2{}A = , {3;4}AB= . Khi đó số phần tử của tập hợp A là A. 4. B. 2. C. 3. D. 0. Câu 9: Câu nào trong các câu sau không phải là mệnh đề? A. 52. B. 2 là một số hữu tỷ. C. 225. += D. có phải là một số nguyên không? Câu 10: Hãy liệt kê các phần tử của tập hợp 2 |20Xxxx=++= . A. 0X = . B. 2X = . C. X = . D. X = . Câu 11: Cho n là số tự nhiên, mệnh đề nào sau đây đúng? A. ( ),1nnn + là số chính phương. B. ( ),1nnn + là số lẻ. C. ( )( ),12 nnnn ++ là số lẻ. D. ( )( ),12 nnnn ++ là số chia hết cho 6. Câu 12: Cho )3;2A =− . Tập hợpCA là : A. ( ) ;3.−− B. ( ) 3;. + C. ) 2;. + D. ( ) ) ;32;.−−+ Câu 13: Cho :20,:50AxRxBxRx =+=− . Khi đó \ AB là: A. 2;5 . B. 2;6 .
Câu
Câu
trình bậc nhất hai ẩn ; xy . Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho
B. Hệ bất phương trình bậc nhất hai ẩn là hệ chỉ gồm hai bất phương trình bậc nhất hai ẩn ; xy
Mỗi nghiệm chung của hai bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.
C. Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều phương trình bậc nhất hai ẩn ; xy. Mỗi nghiệm chung của tất cả các phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 2 C. ( )5;+ . D. ( )2;+ . Câu 14: Cho 0;1;2;3;4;2;3;4;5;6AB== . Tập hợp ( ) ( )\\ ABBA bằng: A. 0;1;5;6 B. 1;2 C. 2;3;4 D. 5;6 Câu 15: Trong các mệnh đề sau, mệnh đề nào đúng? A. ,x ( )2 11xx−− B. ,3xx 3x C. 2 ,1nn + chia hết cho 4 D. 2 ,1nn + không chia hết cho 3 Câu 16: Cho các tập hợp khác rỗng 3 1; 2 Amm+ =− và ( ) );33;B =−−+ . Tập hợp các giá trị thực của m để AB là A. ( ) );23;5−− . B. ( )2;3 . C. ( ) ( );23;5−− . D. ( ) ;23;5−− . Câu 17: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 2530 xyz−+ . B. 2 3240 xx+− . C. 2 253 xy+ . D. 235 xy+ . Câu 18: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 230 xy+− ? A. ( )1;3Q B. 3 1; 2 M C. ( )1;1N D. 3 1; 2 P
19: Cặp số nào sau đây không là nghiệm của bất phương trình 25(1)0 xy−− ? A. ( )0;1 B. ( )1;1 C. ( )2;3 D. ( )4;2
20: Đâu là hệ bất phương trình bậc nhất hai ẩn A. 2 22 20 xxy xy −+ − B. ( ) 25 230 xy x −− − C. 2 21 231 xyy xy +− − D. 0 253 234 xy xyxy xy − −+− += Câu 21: Cặp số ( )1;2 là một nghiệm của hệ bất phương trình nào sau đây: A. 30 7 xy xy + − B. 30 33 xy xy − +− C. 70 960 xy xy + − D. 70 230 xy xy − + Câu 22: Chọn khẳng định đúng trong các khẳng định sau đây: A. Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 D. Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc hai có ẩn là x . Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho Câu 23: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình sau: 2310 5320 xy xy ++ −− ? A. ( )1;0 . B. ( )2;1 . C. ( )0;0 . D. ( )3;1 . Câu 24: Miền nghiệm của bất phương trình 326 xy−− là: A. . B. C. D. Câu 25: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 0 5410 5410 y xy xy − + . B. 0 5410 4510 x xy xy − + . C. 0 4510 5410 x xy xy − + . D. 0 5410 4510 x xy xy − + . Câu 26: Một hộ nông dân định trồng đậu và cà trên diện tích 800m2. Nếu trồng đậu thì cần 20 công và thu 3.000.000 đồng trên 100m2 nếu trồng cà thì cần 30 công và thu 4.000.000 đồng trên 100 m2 Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180. Hãy chọn phương án đúng nhất trong các phương án sau: A. Trồng 600m2 đậu, 200m2 cà. B. Trồng 500 m2đậu, 300 m2cà. O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x
C.
Câu
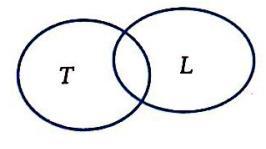
Câu
Câu
A.
Ch
A.
Câu
Câu
Cho tan3
Cho tam
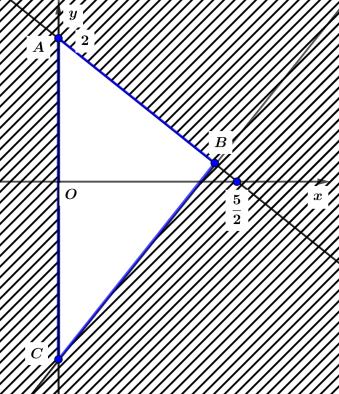
A.
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 4
Trồng 400m2 đậu, 200m2 cà. D. Trồng 200m2 đậu, 600m2 cà.
27: Trong các đẳng thức sau, đẳng thức nào sai? A. oo sin0cos00 += . B. oo sin90cos901 += . C. oo sin180cos1801 +=− D. oo sin60cos6031 2 + +=
28: Giá trị của oo cos60sin30 + bằng
1. B. 3 2 . C. 3 . D. 3 3 .
29:
ọn khẳng định đúng.
sin120sin60 = B. sin120sin30 = C. sin60cos60 = . D. sin60cos120 = .
30:
x = . Giá trị của biểu thức sin2cos 3sincos xx P xx = bằng A. 1 2 . B. 1 8 . C. 1 7 . D. 8.
31:
giác ABC có ,, ABcACbBCa === , R là bán kính đường tròn ngoại tiếp ABC Chọn khẳng định đúng.
sinsinsin abc R ABC === B. 2 sinsinsin abc R ABC === C. .sin2 aAR = . D. .sin aAR = . Câu 32: Cho tam giác ABC . Mệnh đề nào dưới đây sai? A. 222 2cos abcbcA =+− B. 222 cos 2 acb B ac +− = C. 222 cos 2 bca A bc +− = . D. 222 2cos abcbcA =++ . Câu 33: Cho tam giác ABC có 00 3,30,120ABAB=== . Chọn khẳng định đúng. A. 33AC = B. 3AC = C. 23AC = D. 43AC = Câu 34: Tam giác ABC có ba cạnh ;; abc thoả mãn điều kiện ( )( ) 3 abcabcab −+−−=− Khi đó số đo của C là A. 120 B. 30 C. 45 D. 60 Câu 35: Cho tam giác ABC cân tại A biết 120A = và ABACa == . Lấy điểm M trên cạnh BC sao cho 2 5 BMBC = . Tính độ dài AM . A. 6 4 AMa = . B. 7 5 AMa = . C. 3 3 AMa = . D. 11 5 AMa = . II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Cho hai tập 1;2;3A = và 0;1;3;5B = a) Tìm \ BA.
b) Tìm tất cả các tập hợp X thỏa mãn ( )XAB .
Câu 37: Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:

Một đơn vị sản phẩm I lãi ba nghìn đồng, một đơn vị sản phẩm loại II lãi năm nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất.
38: Cho tam giác ABC với ,, abc mmm lần lượt là độ dài đường trung tuyến xuất phát từ đỉnh
ABC
ABC và thỏa mãn
Chứng minh tam giác ABC đều.
OFFICIAL
Sưu
và biên soạn
DẠYKÈMQUYNHƠN
tầm
Page 5
Câu
,,
sinsinsin abc
mmm == .
---------- HẾT ----------
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 6 HƯỚNG DẪN GIẢI CHI TIẾT I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Mệnh đề phủ định của mệnh đề P: “ 2 :20xxx − ” là A. 2 :20xxx − . B. 2 :20xxx − . C. 2 :20xxx − . D. 2 :20xxx − . Lời giải Mệnh đề phủ định của mệnh đề P: “ 2 :20xxx − ” là 2 :20xxx − . Câu 2: Dùng ký hiệu để viết tập hợp sau :12Axx =− . A. ( 1;2A =− . B. ( )1;2A =− . C. 1;2A =− . D. )1;2A =− . Lời giải Ta có ( :121;2Axx=−=− Câu 3: Kết quả của ( ) 1;30;5− là A. ( )1;0 . B. ( 1;5 . C. ( 0;3 . D. )0;3 . Lời giải Ta có ( ) )1;30;50;3 −= Câu 4: Với giá trị thực nào của x thì mệnh đề chứa biến: “ 2 84 xx − ” trở thành mệnh đề đúng? A. 3x = . B. 0x = . C. 1x =− . D. 6x = . Lời giải Với 6x = ta có 2824 (mệnh đề đúng). Câu 5: Hãy liệt kê các phần tử của tập ( )( ) 222 530.xx Xxx =−+ += A. 2;1.X =− B. 1.X = C. 3 2;1;. 2 X =− D. 3 1;. 2 X = Lời giải ( )( )2 2 225301 3 2 x xx x xx =− −+== = + . Do x nên 1x = . Câu 6: Tập 2;3X = có bao nhiêu tập hợp con? A. 3 B. 4 C. 5 D. 2 Lời giải Tập X có các tập con là ,2,3,2;3. Câu 7: Cho hai tập hợp }{1;2;3;4A = , }{2;4;6;8B = . Tập hợp AB là A. {2;4}. B. {1;2;3;4;6;8}. C. {6;8}. D. {1;3}. Lời giải Ta có 2;4AB= . Câu 8: Cho hai tập hợp ,A B thỏa \B1;2{}A = , {3;4}AB= . Khi đó số phần tử của tập hợp A là A. 4 B. 2 C. 3 D. 0
Chọn D
Đáp án A: Cho ( ) 216
Lời giải
không
chính phương nên loại.
Đáp án B: Cho ( ) 216nnn=+= không phải là số lẻ nên loại.
Đáp án C: ( )( )12nnn++ là tích 3 số tự nhiên liên tiếp nên luôn có một số chia hết cho 2 nên ( )( )12nnn++ luôn là một số chẵn.
Đáp án D: ( )( ),12nnnn ++ là tích của 3 số tự nhiên liên tiếp, trong đó luôn có một số chia hết cho 2 và một số chia hết cho 3 nên nó chia
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 Lời giải ( ) ( ) \1;2;3;4AABAB == . Khi đó số phần tử của A là 4 Câu 9: Câu nào trong các câu sau không phải là mệnh đề? A. 52. B. 2 là một số hữu tỷ. C. 225. += D. có phải là một số nguyên không? Lời giải có phải là một số nguyên không? (là câu hỏi nên không phải là mệnh đề). Câu 10: Hãy liệt kê các phần tử của tập hợp 2 |20Xxxx=++= A. 0X = B. 2X = C. X = . D. X = Lời giải Giải phương trình: 2 20xx++= ( )VN nên X là tập rỗng. Từ đó: X = . Câu 11: Cho n là số tự nhiên, mệnh đề nào sau đây đúng? A. ( ),1nnn + là số chính phương. B. ( ),1nnn + là số lẻ. C. ( )( ),12 nnnn ++ là số lẻ. D. ( )( ),12 nnnn ++ là số chia hết cho 6.
nnn=+=
phải là số
hết cho 2.36 = Câu 12: Cho )3;2A =− . Tập hợpCA là : A. ( ) ;3.−− B. ( ) 3;. + C. ) 2;. + D. ( ) ) ;32;.−−+ Lời giải Chọn D ( ) );\3;2CA =−+− ( ) ) ;32;.=−−+ Câu 13: Cho :20,:50AxRxBxRx =+=− . Khi đó \ AB là: A. 2;5 . B. 2;6 . C. ( )5;+ . D. ( )2;+ . Lời giải Ta có :20=+AxRx )2; =−+ A , :50=−BxRx ( ;5=− B . Vậy ( ) \5;.=+ AB Câu 14: Cho 0;1;2;3;4;2;3;4;5;6AB== . Tập hợp ( ) ( )\\ ABBA bằng: A. 0;1;5;6 B. 1;2 C. 2;3;4 D. 5;6 Lời giải.
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8 Ta có ( ) ( ) \0;1 \\0;1;5;6 \5;6 AB ABBA BA = = = Câu 15: Trong các mệnh đề sau, mệnh đề nào đúng? A. ,x ( )2 11xx−− B. ,3xx 3x C. 2 ,1nn + chia hết cho 4 D. 2 ,1nn + không chia hết cho 3 Lời giải A sai vì với 1x = thì ( )2 11xx−=− . B sai vì khi 43x =− nhưng 43x = C sai vì Nếu ( )2 nkk= thì 22141nk+=+ số này không chia hết cho 4 Nếu ( )21 nkk=+ thì 221442nkk+=++ số này cũng không chia hết cho 4 D đúng vì Nếu ( )3 nkk= thì 22191nk+=+ số này không chia hết cho 3. Nếu ( )*31 nkk= thì 221962nkk+=+ số này không chia hết cho 3. Câu 16: Cho các tập hợp khác rỗng 3 1; 2 Amm + =− và ( ) );33;B =−−+ . Tập hợp các giá trị thực của m để AB là A. ( ) );23;5−− B. ( )2;3 C. ( ) ( );23;5−− D. ( ) ;23;5−− Lời giải Để AB thì điều kiện là 3 1 2 13 3 3 2 m m m m + − −− + 5 2 3 m m m − Vậy ( ) ( );23;5m−− . Câu 17: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 2530 xyz−+ . B. 2 3240 xx+− . C. 2 253 xy+ . D. 235 xy+ . Lời giải Theo định nghĩa bất phương trình bậc nhất hai ẩn. Câu 18: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 230 xy+− ? A. ( )1;3Q . B. 3 1; 2 M . C. ( )1;1N . D. 3 1; 2 P . Lời giải
mãn
Câu 20: Đâu
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9 Tập hợp các điểm biểu diễn nghiệm của bất phương trình 230 xy+− là nửa mặt phẳng bờ là đường thẳng 230 xy+−= và không chứa gốc tọa độ. Từ đó ta có điểm 3 1; 2 M thuộc miền nghiệm của bất phương trình 230 xy+− + Cách 2: Thử nghiệm Câu 19: Cặp số nào sau đây không là nghiệm của bất phương trình 25(1)0 xy−− ? A. ( )0;1 B. ( )1;1 C. ( )2;3 D. ( )4;2 Lời giải Thay các cặp số vào bất phương trình ta thấy đáp án B. ( )1;1 không thỏa
nên không phải là nghiệm.
là hệ bất phương trình bậc nhất hai ẩn A. 2 22 20 xxy xy −+ − . B. ( ) 25 230 xy x −− − . C. 2 21 231 xyy xy +− − D. 0 253 234 xy xyxy xy − −+− += Lời giải Loại đáp án A, C vì bpt thứ nhất là bậc 2. Loại D vì 234 xy+= là 1 phương trình. Đáp án B thỏa yêu cầu bpt bậc nhất 2 ẩn. Câu 21: Cặp số ( )1;2 là một nghiệm của hệ bất phương trình nào sau đây: A. 30 7 xy xy + − . B. 30 33 xy xy − +− . C. 70 960 xy xy + − . D. 70 230 xy xy − + . Lời giải Thế 1;2xy== vào hệ 30 33 xy xy − +− ta được 13.20 3.123 − +− (luôn đúng). Nên cặp số ( )1;2 là một nghiệm của hệ bất phương trình 30 33 xy xy − +− . Câu 22: Chọn khẳng định đúng trong các khẳng định sau đây: A. Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn ; xy . Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.
B. Hệ bất phương trình bậc nhất hai ẩn là hệ chỉ gồm hai bất phương trình bậc nhất hai ẩn ; xy .
Mỗi nghiệm chung của hai bất phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.
C. Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều phương trình bậc nhất hai ẩn ; xy. Mỗi nghiệm chung của tất cả các phương trình đó được gọi là một nghiệm của hệ bất phương trình đã cho.
D. Hệ bất phương trình bậc nhất hai ẩn là hệ gồm hai hay nhiều bất phương trình bậc hai có ẩn là x . Mỗi nghiệm chung của tất cả các bất phương trình đó được gọi là một nghiệm của hệ bất phương
Lời
OFFICIAL
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 10
trình đã cho.
giải Theo khái niệm hệ bất phương trình bậc nhất hai ẩn ta chọn câu A. Câu 23: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình sau: 2310 5320 xy xy ++ −− ? A. ( )1;0 B. ( )2;1 C. ( )0;0 D. ( )3;1 Lời giải Ta thay điểm ( )2;1 vào hệ, ta thấy không thỏa mãn. Câu 24: Miền nghiệm của bất phương trình 326 xy−− là: A. . B. C. D. Lời giải O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

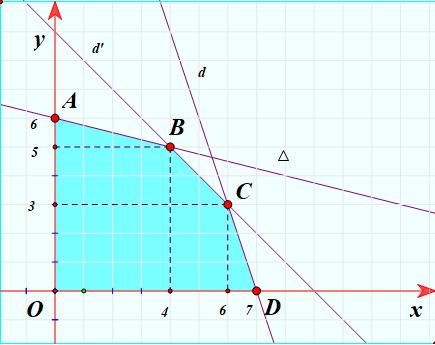
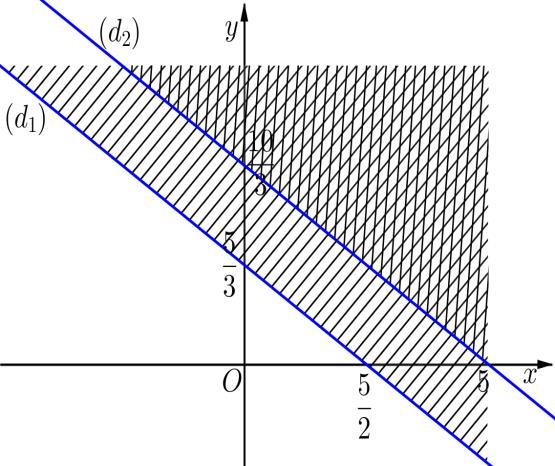
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 11 Trước hết, ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0. Câu 25: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 0 5410 5410 y xy xy − + B. 0 5410 4510 x xy xy − + C. 0 4510 5410 x xy xy − + D. 0 5410 4510 x xy xy − + Lời giải Cạnh AC có phương trình 0x = và cạnh AC nằm trong miền nghiệm nên 0x là một bất phương trình của hệ. Cạnh AB qua hai điểm 5 ;0 2 và ( )0;2 nên có phương trình: 14510 5 2 2 xy xy +=+= . Vậy hệ bất phương trình cần tìm là 0 5410 4510 x xy xy − + . Câu 26: Một hộ nông dân định trồng đậu và cà trên diện tích 800m2. Nếu trồng đậu thì cần 20 công và thu 3.000.000 đồng trên 100m2 nếu trồng cà thì cần 30 công và thu 4.000.000 đồng trên 100 m2 Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180. Hãy chọn phương án đúng nhất trong các phương án sau: A. Trồng 600m2 đậu, 200m2 cà. B. Trồng 500 m2đậu, 300 m2cà. C. Trồng 400m2 đậu, 200m2 cà. D. Trồng 200m2 đậu, 600m2 cà. Lời giải Gọi x là số m2 đất trồng đậu, y là số m2 đất trồng cà. Điều kiện 0x , 0y Số tiền thu được là 34 Txy =+ triệu đồng. Theo bài ra ta có 8 2030180 0 0 xy xy x y + + 8 2318 0 0 xy xy x y + + Đồ thị: O x y 2 3

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 Dựa đồ thị ta có tọa độ các đỉnh ( )0;6A , ( )6;2B , ( )8;0C , ( )0;0O Thay vào 34 Txy =+ ta được max 26T = triệu khi trồng 600m2 đậu và 200 m2 cà. Câu 27: Trong các đẳng thức sau, đẳng thức nào sai? A. oo sin0cos00 += . B. oo sin90cos901 += . C. oo sin180cos1801 +=− .D. oo sin60cos6031 2 + += . Lời giải Ta có : oo sin0cos01 += . Câu 28: Giá trị của oo cos60sin30 + bằng A. 1 B. 3 2 C. 3 D. 3 3 Lời giải Chọn A Cách 1: Ta có oo 11 cos60sin301 22 +=+= Cách 2: Bấm máy Câu 29: Chọn khẳng định đúng. A. sin120sin60 = . B. sin120sin30 = . C. sin60cos60 = . D. sin60cos120 = . Lời giải Chọn A Cách 1: Ta có: ( ) 1 sin120sin180120sin60 2 =−== . Cách 2: Bấm máy 1 sin120sin60 2 == Câu 30: Cho tan3 x = . Giá trị của biểu thức sin2cos 3sincos xx P xx = bằng A. 1 2 . B. 1 8 . C. 1 7 . D. 8. Lời giải Chia cả tử và mẫu của biểu thức P cho cos x ta được sin2cos coscostan2 3sincos 3tan1 coscos xx Pxxx xx x xx ==
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 13 Thay tan3 x = vào biểu thức P ta được 1 8 P = . Câu 31: Cho tam giác ABC có ,, ABcACbBCa === , R là bán kính đường tròn ngoại tiếp ABC Chọn khẳng định đúng. A. sinsinsin abc R ABC === . B. 2 sinsinsin abc R ABC === . C. .sin2 aAR = . D. .sin aAR = . Lời giải Chọn B Câu 32: Cho tam giác ABC . Mệnh đề nào dưới đây sai? A. 222 2cos abcbcA =+− B. 222 cos 2 acb B ac +− = C. 222 cos 2 bca A bc +− = . D. 222 2cos abcbcA =++ . Lời giải Chọn D Câu 33: Cho tam giác ABC có 00 3,30,120ABAB=== . Chọn khẳng định đúng. A. 33AC = . B. 3AC = . C. 23AC = . D. 43AC = . Lời giải Chọn A Ta có: 00 18030CAB=−−= Áp dụng định lí sin ta có: 0 0 sinsin120 .3.33 sinsinsinsin30 ABACB ACAB CBC ==== Câu 34: Tam giác ABC có ba cạnh ;; abc thoả mãn điều kiện ( )( ) 3 abcabcab −+−−=− Khi đó số đo của C là A. 120 . B. 30 . C. 45 . D. 60 . Lời giải Ta có: ( )( ) ( )2 222233 abcabcababcababcab −+−−=−−−=−+−=− Theo hệ quả của định lí hàm cosin: 222 1 cos120 222 abcab CC abab +−− ===−= . Câu 35: Cho tam giác ABC cân tại A biết 120A = và ABACa == . Lấy điểm M trên cạnh BC sao cho 2 5 BMBC = . Tính độ dài AM . A. 6 4 AMa = B. 7 5 AMa = C. 3 3 AMa = D. 11 5 AMa = Lời giải


DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 14 Tam giác ABC cân tại A biết 120A = và ABACa == nên theo định lý côsin ta có: 222 2..cos BCABACABACA =+− 220 2...cos120aaaa=+− 22 1 2... 2 aaaa =+−− 23a= 3BCa= . Lại có: 2 5 BMBC = 23 5 a BM = Do tam giác ABC cân tại A và 120A = 30BC == Áp dụng định lý hàm số côsin với tam giác ABM ta có: 222 2..cos AMBABMBABMB =+− 2 20 2323 2...cos30 55 aa aa =+− 2 2 12233 2... 2552 aa aa=+− 22 2 126 255 aa a =+− 27 25 a = . 7 5 AMa= II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Cho hai tập 1;2;3A = và 0;1;3;5B = . a) Tìm \ BA. b) Tìm tất cả các tập hợp X thỏa mãn ( )XAB Lời giải a) \0;5BA = . b) 1;3AB= nên các tập X thỏa mãn ( )XAB là ; 1 ; 3 ; 1;3 Câu 37: Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:
Một đơn vị sản phẩm I lãi ba nghìn đồng, một đơn vị sản phẩm loại II lãi năm nghìn đồng. Hãy
lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất.
Lời giải
Gọi số sản phẩm loại I cần sản xuất là x ; số sản phẩm loại II cần sản xuất là y ( ,0xy ).
Số máy nhóm A cần sử dụng là: 22 + xy
Số máy nhóm B cần sử dụng là: 2y .
Số máy nhóm C cần sử dụng là: 24 + xy .
Lãi suất thu được là: ( ) ;35 fxyxy =+ (nghìn đồng).
OFFICIAL
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 15
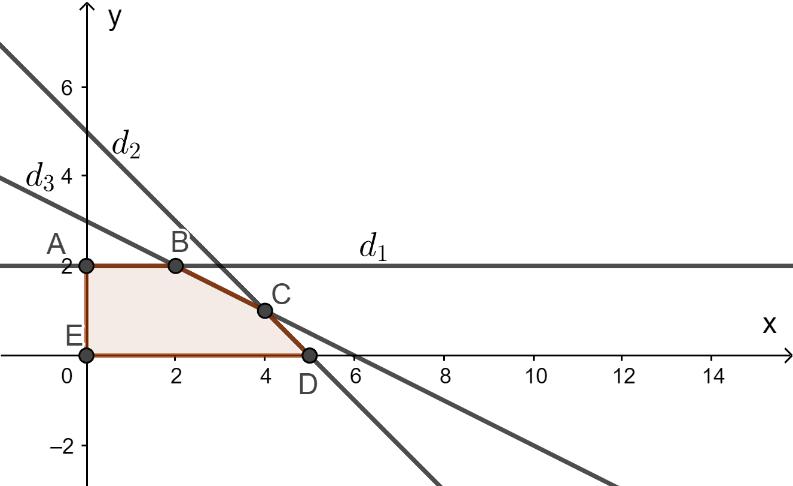
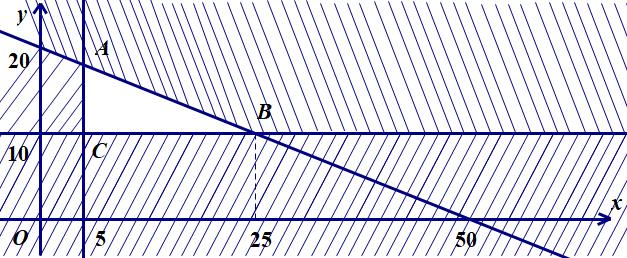
Ta có hệ bất phương trình: 0 0 2210 24 2412 x y xy y xy + + 0 02 5 26 x y xy xy + + . Bài toán trở thành: Tìm , xy thỏa mãn hệ bất phương trình 0 02 5 26 x y xy xy + + sao cho ( ) ;35 fxyxy =+ lớn nhất. Vẽ các đường thẳng ( ) ( ) ( )123 :2,:5,:26 dydxydxy =+=+= . Ta có miền nghiệm của bất phương trình là phần tô màu như hình vẽ: Khi đó ta có: ( ) ( )1 0;2= dOyA , ( ) ( ) ( )13 2;2= ddB , ( ) ( ) ( )23 4;1= ddC ( ) ( )2 5;0= dOxD , ( )0;0=EO . Do đó ( ); fxy đạt giá trị lớn nhất tại ( )4;1C . Vậy phương án sản xuất 4 sản phẩm loại I và 1 sản phẩm loại II sẽ cho lãi cao nhất. Câu 38: Cho tam giác ABC với ,, abc mmm lần lượt là độ dài đường trung tuyến xuất phát từ đỉnh ,, ABC và thỏa mãn sinsinsin abc ABC mmm == . Chứng minh tam giác ABC đều. Lời giải
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 16 Theo định lí sin ta có: ( ) sin sin 21. sinsinsinsin sin Aa abc RBb ABCAa Cc = === = Ta có: sinsinsin abc ABC mmm == ( ) sin sin 2. sin sin a b a c Am Bm Am Cm = = Từ (1) và (2) a b a c am bm am cm = = 2222 2222 .. ba ca ambm amcm = = 222222 22 222222 22 2222 44 2222 44 abacbbca abcbca ac +−+− = +−+− = ( )( )( ) ( )( )( ) 222 222 0 0 abababc acacabc −+++= −+++= ab ac = = abc== . Vậy tam giác ABC đều.
Câu
H
A.
có bao
Câu 2: Mệnh đề nào sau đây
A.
(1)
(2) Ch
ng?
cùng c
(3) 1n là số chính phương
Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào đúng, mệnh đề nào sai?
A. Mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai
B. Mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai
C. Mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai.
D. Mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.
Câu 4: Lập mệnh đề phủ định của mệnh đề:
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 ĐỀ SỐ: 02 I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm)
1: Cho các phát biểu sau đây (I): “17 là số nguyên tố”. (II): “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”. (III): “Các em C14 hãy cố gắng học tập thật tốt nhé !”. (IV): “Mọi hình chữ nhật đều nội tiếp được đường tròn”.
ỏi
nhiêu phát biểu là một mệnh đề?
2 B. 3 C. 1 D. 4
đú
3. B. 2 16. C. 356. D. 366. Câu 3: Với mọi n là số tự nhiên, cho ba mệnh đề sau:
8n + là số chính phương
ữ số tận
ủa n là 4
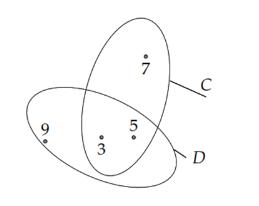
“ Số 6 chia hết cho 2 và 3”. A. Số 6 chia hết cho 2 hoặc 3. B. Số 6 không chia hết cho 2 và 3. C. Số 6 không chia hết cho 2 hoặc 3. D. Số 6 không chia hết cho 2 và chia hết cho 3. Câu 5: Mệnh đề nào sau đây đúng? A. 2 ,1xx − là bội số của 3. B. 2 ,3.xx = C. ,21 x x + là số nguyên tố D. ,22. x xx + Câu 6: Cho các tập hợp 1;2;3;4,2;4;5;8.AB== Tìm tập hợp A B A. 1;2;3;4;5;8.A B = B. 1;2;3;5;8.A B = C. 1;2;3;4;5;6;8.AB= D. 1;3;4;5;8.A B = Câu 7: Cho hai tập hợp 2;4;6;9,1;2;3;4AB== . Tập \ AB bằng tập hợp nào sau đây? A. 2;4 B. 1;3 C. 6;9 D. 6;9;1;3 Câu 8: Cho ba tập hợp
Câu 12: Khẳng định nào sau đây đúng?
A. Hai véc tơ bằng nhau khi chỉ khi độ dài của chúng bằng nhau.
B. Hai véc tơ bằng nhau khi chỉ khi hai véc tơ cùng phương.
C. Hai véc tơ bằng nhau khi chỉ khi hai véc tơ cùng phương và cùng độ dài
D. Hai véc tơ bằng nhau khi chỉ khi hai véc tơ cùng hướng và cùng độ dài.
Câu 13: Khẳng định nào sau đây sai?
A. Hai véc tơ cùng phương với một véc tơ khác véc tơ 0 thì hai véc tơ đó cùng phương.
B. Hai véc tơ cùng hướng với một véc tơ khác véc tơ 0 thì hai véc tơ đó cùng hướng.
C. Hai véc tơ ngược hướng với một véc tơ khác véc tơ 0 thì hai véc tơ đó ngược hướng.
D. Hai véc tơ cùng bằng một véc tơ thứ ba thì hai véc tơ đó bằng nhau.
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 2 :E “Tập hợp các tứ giác”. :F “Tập hợp các hình thang”. :G “Tập hợp các hình thoi”. Trong các mệnh đề sau, mệnh đề nào là sai? A. .F E B. .E G C. .G F D. .G E Câu 9: Cho hai tập hợp 4;7M =− và ( ) ( );23;N =−−+ . Hãy xác định tập hợp MN . A. ) ( )4;23;7MN=− . B. ( ( );23;MN=−+ . C. ( ) ( );23;MN=−−+ D. ) ( 4;23;7MN=−− Câu 10: Lớp 110B có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn của lớp 110B là: A. 9. B. 10. C. 18. D. 28. Câu 11: Cho tập hợp ( ) ( ) 2 ;256Axyxyy =−=+ và , xy . Số phần tử của tập hợp A là A. 7. B. 5. C. 4. D. 6.
Câu 14: Gọi G là trọng tâm tam giác vuông ABC có cạnh huyền 12BC = . Véc tơ GBGC + có độ dài bằng bao nhiêu? A. 2 B. 4 C. 8 D. 23 Câu 15: Có 6 điểm bất kỳ ,,,,, ABCDEF . Tổng véc tơ ABCDEF ++ bằng? A. AFCEDB ++ B. AECBDF ++ C. ADCFEB ++ D. AEBCDF ++ Câu 16: Cho bốn điểm bất kì ,,, ABCO . Đẳng thức nào sau đây đúng? A. OAOBBA =− B. ABOBOA =+ C. ABACBC =+ D. OACACO =− Câu 17: Cho lục giác đều ABCDEF tâm O . Véc tơ vAFBCDE =++ bằng véc tơ nào dưới đây?
A. DA . B. CF . C. BE . D. 0 .
Câu 18: Cho hình vuông ABCD cạnh a , tâm O . Tính theo a độ dài của véc tơ uABODBC =+− .
OFFICIAL
A. 2 2 a B. 32 2 a C. 2a D. a
Câu 19: Cho 2 ab =− , khẳng định nào sau đây là đúng?
A. a và b có giá trùng nhau.
C. a , b ngược hướng và 2 ab =
B. a và b cùng hướng.
D. a , b ngược hướng và 2 ab =−
Câu 20: Cho tam giác ABC có 2AB = cm, 1AC = cm, Oˆ 60A = . Khi đó độ dài cạnh BC là:
A. 1 cm.
Câu 21: Cho tam giác ABC có
5 cm.
. Đường trung tuyến AM ( M là trung điểm c
a BC ) c
7 cm
AB
tam giác
D. 5 cm
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 3
B. 2 cm. C. 3 cm. D.
8cm
= , 10cmBC = , 6cmCA =
ủ
ủa
đó có độ dài bằng A.
B. 6 cm C. 4 cm
Câu 22: Tam giác ABC có 5a = cm, 3b = cm, 5c = cm. Tính số đo góc A . A. O45 B. O30 C. O90 D. o72.54 Câu 23: Nếu ( )00 cossin2090 += thì bằng A. 030 B. 060 C. 045 D. 022,5 Câu 24: Tính sin, biết 5 cos 3 =− và 00 90180 A. 1 3 B. 1 3 . C. 2 3 . D. 2 3 . Câu 25: Tam giác ABC vuông tại A có 6AB = cm, 10BC = cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng A. 1 cm. B. 2 cm. C. 2cm. D. 3cm. Câu 26: Cho a , b , c là những hằng số thực, a và b không đồng thời bằng 0 Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn x và y ? A. 2 0axbxc++ . B. 22 axbyc + . C. axbyc + . D. axbyc += . A D B C O A CB D E F O
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 4 Câu 27: Điểm nào sau đây không thuộc miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− ? A. ( )1;1M . B. ( )0;0O . C. ( )4;2P . D. ( )1;1N . Câu 28: Miền nghiệm không bị gạch chéo được cho bởi hình bên (không kể bờ là đường thẳng d ), là miền nghiệm của bất phương trình nào sau đây? A. 260 xy+− . B. 260 xy+− . C. 260xy+− . D. 260xy+− . Câu 29: Cặp số ( )00 ; xy nào là nghiệm của bất phương trình 334 xy− . A. ( ) ( )00;2;2xy =− . B. ( ) ( )00;5;1xy = . C. ( ) ( )00;4;0xy =− . D. ( ) ( )00;2;1xy = . Câu 30: Miền nghiệm của hệ bất phương trình 2360 0 2310 xy x xy +− −− chứa điểm nào sau đây? A. ( ) 1;2.A B. ( )0;2B . C. ( )1;3C . D. 1 0;. 3 D Câu 31: Miền nghiệm của hệ bất phương trình 10 2 23 xy y xy +− −+ là phần không tô đậm của hình vẽ nào trong các hình vẽ sau? O y x1 2 1 -3 O y x1 2 1 -3 A. B. O y x1 2 1 -3 O y x1 2 1 -3 C. D.

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 5 Câu 32: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A , đi thẳng theo hai hướng tạo với nhau một góc60. Tàu thứ nhất chạy với tốc độ 25 km/h, tàu thứ hai chạy với tốc độ 40 km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km? A. 56,8 km B. 70 km C. 35 km D. 113,6 km Câu 33: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Ta đo được khoảng cách 40mAB = , 045CAB = và 070CBA = Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây? A. 53m B. 30m C. 41,5m D. 41m Câu 34: Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết 04m, 20m, 45AHHBBAC === Chiều cao của cây gần nhất với giá trị nào sau đây? A. 17,5m. B. 17m. C. 16,5m. D. 16m. Câu 35: Giả sử CDh = là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm , AB trên mặt đất sao cho ba điểm , AB và C thẳng hàng. Ta đo được 24 mAB = , 0063, 48CADCBD== Chiều cao h củatháp gầnvớigiátrị nào sauđây? A. 18m B. 18,5m C. 60m D. 61,5m II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Xác định các tập A B ; A B ; \ AB biết 35Ax x=− ; 4Bx x= Câu 37: Cho ABC có đường trung tuyến AM. Gọi I là trung điểm của AM. Chứng minh các đẳng thức
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 6 vectơ sau: a) ABCIAICB +=+ b) 20 IAIBIC++= Câu 38: Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm B trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất. ---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm)
Câu 1: Cho các phát biểu sau đây
(I): “17 là số nguyên tố”.
(II): “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”.
(III): “Các em C14 hãy cố gắng học tập thật tốt nhé !”. (IV): “Mọi hình chữ nhật đều nội tiếp được đường tròn”. Hỏi có bao nhiêu phát biểu là một mệnh đề?
2
Câu (I) là mệnh đề.
Câu (II) là mệnh đề.
3
Câu (III) không phải là mệnh
Câu (VI) là mệnh
Câu 2: Mệnh đề nào sau đây
3.
có 366
Câu 3: V
(1) 8n
ng?
OFFICIAL
giải
là số chính phương
(2) Chữ số tận cùng của n là 4 (3) 1n là số chính phương Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào đúng, mệnh đề nào sai?
A. Mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai
B. Mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai C. Mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai D. Mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.
Lời giải
Ta có số chính phương có các chữ số tận cùng là0,1,4,5,6,9 Nhận thấy giữa mệnh đề (1) và (2) có mâu thuẫn. Bởi vì, giả sử 2 mệnh đề này đồng thời là đúng thì 8n + có chữ số tận cùng là 2 nên không thể là số chính phương. Vậy trong hai mệnh đề này phải có một mệnh đề là đúng và một mệnh đề là sai. Tương tự, nhận thấy giữa mệnh đề (2) và (3) cũng có mâu thuẫn. Bởi vì, giả sử mệnh đề này đồng thời là đúng thì 1n có chữ số tận cùng là 3 nên không thể là số chính phương. Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 7
A.
B.
C. 1 D. 4 Lời giải
đề.
đề.
đú
A.
B. 2 16. C. 356. D. 366. Lời
Ta
=
ới mọi n là số tự nhiên, cho ba mệnh đề sau:
+
Câu 4: Lập mệnh đề phủ định của mệnh đề: “ Số 6 chia hết cho 2 và 3”. A. Số 6 chia hết cho 2 hoặc 3. B. Số 6 không chia hết cho 2 và 3. C. Số 6 không chia hết cho 2 hoặc 3. D. Số 6 không chia hết cho 2 và chia hết cho 3. Lời giải Phủ định của mệnh đề “ Số 6 chia hết cho 2 và 3” là mệnh đề: “Số 6 không chia hết cho 2 hoặc 3” Câu 5: Mệnh đề nào sau đây đúng?
A. 2 ,1xx
− là bội số của 3. B. 2 ,3.xx = C. ,21 x x + là số nguyên tố. D. ,22. x xx +
Lời giải
Đáp án B sai vì 2 33xx== là số vô tỉ. Đáp án C sai với 3 3219x =+= là hợp số. Đáp án D sai với 0 021022.x ==+=
Câu 6: Cho các tập hợp
1;2;3;4,2;4;5;8.AB== Tìm tập hợp A B

A.
Lời giải
Ta
OFFICIAL
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 8
1;2;3;4;5;8.A B = B. 1;2;3;5;8.A B = C. 1;2;3;4;5;6;8.AB= D. 1;3;4;5;8.A B =
có 1;2;3;4;5;8.A B = Câu 7: Cho hai tập hợp 2;4;6;9,1;2;3;4AB== . Tập \ AB bằng tập hợp nào sau đây? A. 2;4 . B. 1;3 . C. 6;9 . D. 6;9;1;3 . Lời giải Ta có: \|;xB6;9ABxxA== . Câu 8: Cho ba tập hợp :E “Tập hợp các tứ giác”. :F “Tập hợp các hình thang”. :G “Tập hợp các hình thoi” Trong các mệnh đề sau, mệnh đề nào là sai? A. .F E B. .E G C. .G F D. .G E Lời giải Ta có mối liên hệ giữa 3 tập hợp trên là: .GFE Câu 9: Cho hai tập hợp 4;7M =− và ( ) ( );23;N =−−+ . Hãy xác định tập hợp MN . A. ) ( )4;23;7MN=− . B. ( ( );23;MN=−+ . C. ( ) ( );23;MN=−−+ D. ) ( 4;23;7MN=−− Lời giải ) ( 4;23;7MN=−− Câu 10: Lớp 110B có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6học sinh giỏi Hóa, 3 học sinh giỏi cả Toán và Lý, 4 học sinh giỏi cả Toán và Hóa, 2 học sinh giỏi cả Lý và Hóa, 1 học sinh giỏi cả 3 môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn của lớp 110B là: A. 9. B. 10. C. 18. D. 28. Lời giải.
A.
B. Hai véc tơ bằng nhau khi chỉ khi hai véc tơ cùng phương.
C. Hai véc tơ bằng nhau khi chỉ khi hai véc tơ cùng phương và cùng độ dài
D. Hai véc tơ bằng nhau khi chỉ khi hai véc tơ cùng hướng và cùng độ dài.
Lời giải
Hai vec tơ bằng nhau khi hai vec tơ có cùng phương cùng chiều và cùng độ dài.
Hai véc tơ cùng phương cùng chiều gọi chung là cùng hướng.
Câu 13: Khẳng định nào sau đây sai?
A. Hai véc tơ cùng phương với một véc tơ khác véc tơ 0 thì hai véc tơ đó cùng phương.
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9 Ta dùng biểu đồ Ven để giải: GiỏiLý+Hóa GiỏiToán+Hóa GiỏiToán+Lý 1 1 1 Hóa Lý Toán 1 3 2 1 Nhìn vào biểu đồ, số học sinh giỏi ít nhất 1 trong 3 môn là: 121311110 ++++++= Câu 11: Cho tập hợp ( ) ( ) 2 ;256Axyxyy =−=+ và , xy . Số phần tử của tập hợp A là A. 7. B. 5. C. 4. D. 6 Lời giải Ta có ( )2 256xyy−=+ ( ) 22316xy −+= ( )( ) 3316xyxy ++−+= Vì 33xyxy++−+ và 30xy++ nên 30xy−+ Do đó ( )( ) 3316xyxy++−+= khi các trường hợp sau xảy ra: TH1: 17 316 2 3115 3 2 x xy xy y ++== −+= += loại do , xy . TH2: 38 32 xy xy ++= −+= 5 33 x y = += 5 33 x y = += 5 0 6 x y y = = =− . TH3: 34 34 xy xy ++= −+= 4 30 x y = += 4 3 x y = =− Do đó ( ) ( ) ( ) ( ) ( ) ( ) 5;0;5;6;5;0;5;6;4;3;4;3A =−−−−−−− Vậy tập hợp A có 6 phần tử. Câu 12: Khẳng định nào sau đây đúng?
Hai véc tơ bằng nhau khi chỉ khi độ dài của chúng bằng nhau.
Câu
B. Hai véc tơ cùng hướng với một véc tơ khác véc tơ 0 thì hai véc tơ đó cùng hướng.
C. Hai véc tơ ngược hướng với một véc tơ khác véc tơ 0 thì hai véc tơ đó ngược hướng.
D. Hai véc-tơ cùng bằng một véc-tơ thứ ba thì hai véc-tơ đó bằng nhau.
Lời giải
Hai véc tơ ngược hướng với một véc tơ khác véc tơ 0 thì hai véc tơ đó
OFFICIAL
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 10
cùng hướng
14: Gọi G là trọng tâm tam giác vuông ABC có cạnh huyền 12BC = . Véc-tơ GBGC + có độ dài bằng bao nhiêu? A. 2. B. 4. C. 8. D. 23 Lời giải Tam giác vuông ABC có cạnh huyền 12BC = nên tam giác vuông tại A G là trọng tâm tam giác ta có 0 GAGBGCGBGCGAGBGCGAGA ++=+=−+=−= Gọi M là trung điểm BC ta có 1 6 2 AMBC== ( trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền) Mà 2 4 3 GAAM== Vậy 4GBGCGAGA +=−== . Câu 15: Có 6 điểm bất kỳ ,,,,, ABCDEF . Tổng véc tơ ABCDEF ++ bằng? A. AFCEDB ++ B. AECBDF ++ . C. ADCFEB ++ . D. AEBCDF ++ Lời giải Ta có ( ) ( ) ABCDEFADDBCFFDEF ADCFEFFDDB ADCFEDDB ADCFEB ++=++++ =++++ =+++ =++ Câu 16: Cho bốn điểm bất kì ,,, ABCO . Đẳng thức nào sau đây đúng? A. OAOBBA =− B. ABOBOA =+ C. ABACBC =+ D. OACACO =− Lời giải Theo quy tắc ba điểm ta có OACACO =− Câu 17: Cho lục giác đều ABCDEF tâm O . Véc tơ vAFBCDE =++ bằng véc tơ nào dưới đây? A. DA . B. CF . C. BE . D. 0 . Lời giải Ta có vAFBCDEAFFEDEAEBABE =++=++=+= . A CB D E F O
Câu 18: Cho hình vuông
A. 2 2 a . B. 32
Lời gi
2a . D. a
i
Ta có uABODBCABBOADAOADDO
Suy ra 2 2 uDOa
Câu 19: Cho 2 ab =− , khẳng định nào sau đây là đúng?
A. a và b có giá trùng nhau.
C. a , b ngược hướng và 2 ab =
Do 2 ab =− nên , ab ngược hướ
Câu
Cho
A.
B. a và b cùng hướng.
OFFICIAL
D. a , b ngược hướng và 2 ab =−
Lời giải
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 11
ABCD cạnh a , tâm O . Tính theo a độ dài của véc tơ uABODBC =+−
2 a . C.
.
ả
=+−=+−=−= .
==
ng và 2 ab =
20:
tam giác ABC có 2AB = cm, 1AC = cm, Oˆ 60A = . Khi đó độ dài cạnh BC là:
1 cm. B. 2 cm. C. 3 cm. D. 5 cm. Lời giải Áp dụng định lý cô sin, ta có 222O 1 2...cos60412.2.1.3 2 BCABACABAC=+−=+−= . Suy ra 3BC = cm. Câu 21: Cho tam giác ABC có 8cmAB = , 10cmBC = , 6cmCA = . Đường trung tuyến AM ( M là trung điểm của BC ) của tam giác đó có độ dài bằng A. 7 cm. B. 6 cm. C. 4 cm. D. 5 cm. Lời giải ( ) 222 28610 5 4 AM +− == cm Câu 22: Tam giác ABC có 5a = cm, 3b = cm, 5c = cm. Tính số đo góc A A. O45 . B. O30 . C. O90 . D. o72.54 . Lời giải 2222223553 cos 22.3.510 bca A bc +−+− === Suy ra o72.54A = Câu 23: Nếu ( )00 cossin2090 += thì bằng A. 030 . B. 060 C. 045 D. 022,5 . A D B C O
Câu
Cách
Cách
Phương
Phương
Phương
Phương
Lời
Cách 1:
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 Lời giải
1: Theo đề bài, 0000 cossin2sin2129036045180 kk +===+=+ .
2: Thử đáp án:
án A: 00 cos30sin3013 2 + += (Loại)
án B: 00 cos60sin6013 2 + += (Loại)
án A: 00 cos45sin452 += (đúng)
án A: 00 cos22,5sin22,51,31 + (Loại)
24: Tính sin, biết 5 cos 3 =− và 00 90180 . A. 1 3 B. 1 3 C. 2 3 D. 2 3
giải
Ta có: 22 sin1cos154 99 =−=−= 2 sin 3 = Do 00 90180 nên sin0 . Vậy 2 sin 3 = . Câu 25: Tam giác ABC vuông tại A có 6AB = cm, 10BC = cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng A. 1 cm. B. 2 cm. C. 2cm. D. 3cm. Lời giải Tam giác ABC vuông tại A có diện tích 11 ..6.824 22 SABAC=== . Bán kính đường tròn nội tiếp là ( ) 24 2 1 6810 2 S r p === ++ cm. Câu 26: Cho a , b , c là những hằng số thực, a và b không đồng thời bằng 0 Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn x và y ? A. 2 0axbxc++ . B. 22 axbyc + . C. axbyc + . D. axbyc += . Lời giải Áp dụng lý thuyết bất phương trình bậc nhất hai ẩn Câu 27: Điểm nào sau đây không thuộc miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− ? A. ( )1;1M . B. ( )0;0O . C. ( )4;2P . D. ( )1;1N . Lời giải Thay toạ độ điểm ( )4;2P vào bất phương trình ta được ( ) ( )42222214 −++−−
26−− sai.
Vậy điểm P không thuộc miền nghiệm của bất phương trình.
Câu 28: Miền nghiệm không bị gạch chéo được cho bởi hình bên (không kể bờ là đường thẳng d ), là miền nghiệm của bất phương trình nào sau đây?
A. 260 xy+− B. 260 xy+− C. 260xy+− D. 260xy+−
Lời giải
Thế điểm ( )0;0O và ( )0;3A vào 4 đáp án
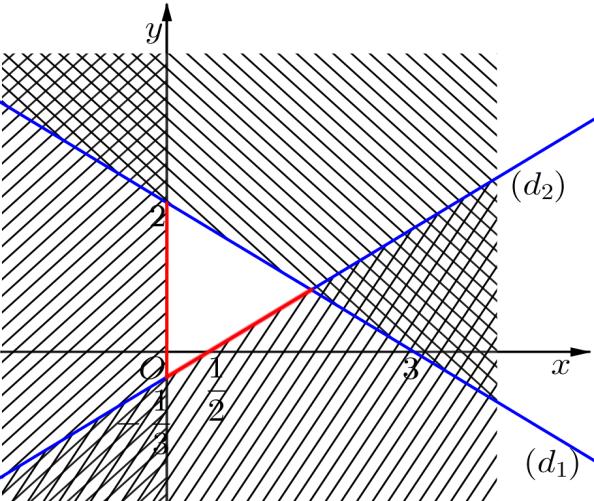

OFFICIAL
Câu
A. ( ) (
;2;2
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 13
ta chọn được đáp án 260 xy+− .
29: Cặp số ( )00 ; xy nào là nghiệm của bất phương trình 334 xy−
)00
xy =− B. ( ) ( )00;5;1xy = C. ( ) ( )00;4;0xy =− D. ( ) ( )00;2;1xy = Lời giải Thế các cặp số ( )00 ; xy vào bất phương trình: ( ) ( )00;2;2xy =− ( ) 334323.24 xy −−− ( ) ( )00;5;1xy = 3343.53.14 xy −− ( ) ( )00;4;0xy =− ( ) 3343.43.04 xy −−− ( ) ( )00;2;1xy = 3343.23.14 xy −− Câu 30: Miền nghiệm của hệ bất phương trình 2360 0 2310 xy x xy +− −− chứa điểm nào sau đây? A. ( ) 1;2.A B. ( )0;2B . C. ( )1;3C . D. 1 0;. 3 D Lời giải Trước hết, ta vẽ ba đường thẳng:
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 14 ( )1 :2360dxy+−= ( )2 :0dx = ( )3 :2310dxy−−= Ta thấy ( )1;1 là nghiệm của các ba bất phương trình. Điều này có nghĩa là điểm ( )1;1 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ Câu 31: Miền nghiệm của hệ bất phương trình 10 2 23 xy y xy +− −+ là phần không tô đậm của hình vẽ nào trong các hình vẽ sau? O y x1 2 1 -3 O y x1 2 1 -3 A. B. O y x1 2 1 -3 O y x1 2 1 -3 C. D. Lời giải Chọn điểm ( )0;4M thử vào các bất phương trình của hệ thấy thỏa mãn. Câu 32: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A , đi thẳng theo hai hướng tạo với nhau một góc60. Tàu thứ nhất chạy với tốc độ 25 km/h, tàu thứ hai chạy với tốc độ 40 km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km? A. 56,8 km B. 70 km C. 35 km D. 113,6 km Lời giải Gọi AB là quãng đường tàu thứ nhất đi được, ta có 25.250AB == km. Gọi AC là quãng đường tàu thứ hai đi được, ta có 40.280AC == km. Gọi BC là khoảng cách giữa hai tàu, ta có 22 2...cos70BCABACABACA =+−= km


DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 15 Vậy sau 2 giờ hai tàu cách nhau 70 km Câu 33: Để đo khoảng cách từ một điểm A trên bờ sông đến gốc cây C trên cù lao giữa sông, người ta chọn một điểm B cùng ở trên bờ với A sao cho từ A và B có thể nhìn thấy điểm C . Ta đo được khoảng cách 40mAB = , 045CAB = và 070CBA = . Vậy sau khi đo đạc và tính toán được khoảng cách AC gần nhất với giá trị nào sau đây? A. 53m. B. 30m. C. 41,5m. D. 41m. Lời giải Áp dụng định lí sin vào tam giác ,ABC ta có sinsin ACAB BC = Vì ( )sinsin C =+ nên ( ) 0 0 .sin40.sin70 41,47 sinsin115m. AB AC == + Câu 34: Từ vị trí A người ta quan sát một cây cao (hình vẽ). Biết 04m, 20m, 45AHHBBAC === Chiều cao của cây gần nhất với giá trị nào sau đây? A. 17,5m. B. 17m. C. 16,5m. D. 16m. Lời giải Trong tam giác AHB, ta có 041 tan1119' 205 AH ABHABH BH === . Suy ra 00 907841'ABCABH=−= . Suy ra ( ) 00 1805619'ACBBACABC=−+= . Áp dụng định lý sin trong tam giác ABC , ta được .sin 17m. sinsinsin ABCBABBAC CB ACBBACACB == Câu 35: Giả sử CDh = là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm , AB trên mặt đất sao cho ba điểm , AB và C thẳng hàng. Ta đo được 24 mAB = , 0063, 48CADCBD== .

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 16 Chiều cao h củatháp gầnvớigiátrị nào sauđây? A. 18m B. 18,5m C. 60m D. 61,5m Lời giải Áp dụng định lí sin vào tam giác ,ABD ta có . sinsin ADAB D = Ta có D =+ nên 000 634815.D =−=−= Do đó ( ) 0 0 .sin24.sin48 68,91 sinsin15m. AB AD == Trong tam giác vuông ,ACD có .sin61,4m.hCDAD == II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Ta có 3;5A =− 444xx− Do đó ( )4;4B =− ( 4;5A B =− . )3;4A B =− \4;5AB = Câu 37: a. ( ) 0ABCIAICBABAICICB +=+−+−= 00CIIBCBCBCB +−=−= b. 2022IM0 IAIBICIA++=+= đpcm vì I là trung điểm của AM Câu 38: Gọi 0, 0xy (tấn) là sản lượng cần sản xuất của sản phẩm A và sản phẩm .B Ta có: 6 xy + là thời gian hoạt động của máy I 23xy + là thời gian hoạt động của máy II 32xy + là thời gian hoạt động của máy .III Số tiền lãi của nhà máy: 43 Txy =+ (triệu đồng). Bài toán trở thành: Tìm 0, 0xy thỏa mãn 636 2323 3227 xy xy xy + + + để 43 Txy =+ đạt giá trị lớn nhất.
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 17 Vẽ hình biểu diễn miền nghiệm của hệ ta được 43 Txy =+ đạt giá trị lớn nhất tại ( )7;3 . Nên sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B thì nhà máy được số tiền lãi lớn nhất. ---------- HẾT ---------
ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023
MÔN: TOÁN 10 ĐỀ SỐ: 03
I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm)
Câu 1: Trong các câu sau, câu nào là mệnh đề?
A. 10 là số chính phương B. abc +=
C. 2 0xx−= D. 21 n + chia hết cho 3
Câu 2: Các phương án sau, đâu là một mệnh đề đúng?
A. 61 . 32 = B. 21. C. 235. += D. 35.
Câu 3: Cho các mệnh đề sau đây:
(I): Nếu tam giác ABC đều thì .ABAC =
(II): Nếu ab + là các số chẵn thì , ab là số chẵn.
(III): Nếu tam giác ABC có tổng hai góc bằng 090 thì tam giác ABC cân.
Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
A. 0
Câu 4: Mệnh đề
A.
Câu 5: Trong các mệnh đề sau, mệnh đề nào sai?
A. Nếu cả hai số chia hết cho 3 thì tổng hai số đó chia hết cho 3
B. Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau.
C. Nếu một số có tận cùng bằng 0thì nó chia hết cho 5.
D. Nếu một số chia hết cho 5 thì nó có tận cùng bằng 0.
OFFICIAL
Câu 6: Cho mệnh đề 2 P:":10" xxx ++ . Mệnh đề phủ định của mệnh đề Pvà tính đúng, sai của nó là:
A. 2 P:":10"
biên soạn
DẠYKÈMQUYNHƠN
Sưu tầm và
Page 1
B. 3 C. 2. D. 1
phủ định của mệnh đề: 2 "," xxx là
2 , xxx . B. 2 , xxx . C. 2 , xxx . D. 2 , xxx .
xxx ++= và P là mệnh đề sai. B. 2 P:":10" xxx ++= và P là mệnh đề đúng. C. 2 P:":10" xxx ++ và P là mệnh đề đúng. D. 2 P:":10" xxx ++= và P là mệnh đề sai. Câu 7: Viết tập hợp ( )( ) 22 /22530Bxxxx =−−+= bằng cách liệt kê các phần tử của tập hợp. A. 3 1; 2 B = . B. 3 2 B = . C. 1B = . D. 3 1;;2;2 2 B =− . Câu 8: Cho tập hợp 23|,5 =+ Axxx . Tập hợp A là: A. 1;2;3;4;5A = B. 1;3;5;7;9;11=A C. 3;4;5;6;7;8=A . D. 3;5;7;9;11;13=A . Câu 9: Hãy liệt kê các phần tử của tập hợp 2 |7520=−−=Xxxx A. 0X = B. 1X = C. 1 1; 2 X = D. 2 1; 7 =− X Câu 10: Cho hai tập hợp 50,6Annn = và 6;12;18;24;30;36;42;48B = . Mệnh đề nào sau đây đúng? A. BA. B. AB . C. = AB . D. =AB . Câu 11: Tập hợp nào sau đây có đúng hai tập hợp con?
A. ;x
Câu 12: Cho
B.
x C.
;;xy D. ;
1;1;5;0;1;3;5.AB=−= Khẳng định nào sau đây đúng?
A. 1.=AB B. 1;3.=AB
C. 1;5.=AB D. 1;3;5.=AB
Câu 13: Cho hai tập hợp 0;2,0;1;2;3;4.AB== Số tập hợp X thỏa mãn AXB = là
A. 2 B. 3 C. 4 D. 5
Câu 14: Cho
17: Cho
A.
Câu 18: Cho
OFFICIAL
A. (2;3] B. (2;4] C. (3;6] D. (4;6]
Câu 19: Cho tập (
4;7A = và (
3;5B
A. ( 3;4 B. (
Câu 20: Cho
A.
Câu
T
AB
4;5 C. (
3;7 D. ( 5;7
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 2
xy
1;3;5;7A = ; 1;2;3;4;5;6B = . Tập hợp \ BA có số phần tử là A. 1. B. 4. C. 2. D. 3. Câu 15: Cho hai tập hợp 1;2;4;6,1;2;3;4;5;6;7;8AB== khi đó tập B CA là A. 3;5;7;8 . B. 4;6 C. 2;6;7;8 D. 1;2;4;6 Câu 16: Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh? A. 54. B. 40. C. 26. D. 68. Câu
tập hợp ( ( ;3; 1;5AB=−= . Khi đó, tập AB là
(1;3] B. (3;5 ] C. (;5] − D. (;1) −
tập hợp ( ) 2;6; [3;4]AB=−=− . Khi đó, tập AB là
=− .
ập
\ là
tập ( 5;8A =− và ( 2;4B =− . Tập A CB là
( ) ( )5;24;8A CB =−− B. ( ) ( 5;24;8A CB =−− C. ( ( )5;24;8A CB =−− . D. ( ( 5;24;8A CB =−− .
21: Cặp số nào sau đây không phải là nghiệm của bất phương trình 2310 xy+− A. 0;0xy== . B. 1;1xy==− . C. 0;2xy==− . D. 1;1xy=−= . Câu 22: Cho hình vẽ bên dưới, miền nghiệm được biểu diễn bởi phần không bị tô màu (không có đường thẳng) là miền nghiệm của bất phương trình nào sau đây? x y 2 2 O A. 2xy . B. 2xy . C. 2xy . D. 2xy . Câu 23: Miền không bị gạch ( không tính đường thẳng) được cho bởi hình sau, là miền nghiệm của bất phương trình nào?
hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
A. 5 lít nước cam và 4 lít nước táo. B. 6 lít nước cam và 5 lít nước táo.
C. 4 lít nước cam và 5 lít nước táo. D. 4 lít nước cam và 6 lít nước táo.
Câu 26: Cho 2 sin 5 x = và 00 90180 x . Tính giá trị cosx.

A. 21 5 B. 21 C. 21 5 D. 1 5
Câu 27: Cho ABC có 06,8,60bcA=== . Tính độ dài cạnh a .
A. 213. B. 312. C. 237. D. 20.
Câu 28: Cho tam giác ABC thoả mãn:
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 A. 260 xy+− . B. 260 xy+− . C. 260xy+− . D. 260xy+− . Câu 24: Miền nghiệm của hệ bất phương trình: 3260 2100 10 xy xy y −+ +− − là miền chứa điểm nào trong các điểm sau? A. ( ) 1;3.M B. ( ) 4;3.N C. ( )1;5P D. ( )2;3Q Câu 25: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g
222 3 bcabc +−= . Khi đó: A. 0 30.A = B. 0 45.A = C. 0 60.A = D. 075A = . Câu 29: Cho hai tập hợp ( ( 1;5;2;7AB== . Tập hợp \ AB là: A. ( 1;2 B. ( )2;5 C. ( 1;7 D. ( )1;2 Câu 30: Cho ABC có 5AB = ;A40= ;B60= . Độ dài BC gần nhất với kết quả nào? A. 3,7 B. 3,3 C. 3,5 D. 3,1 Câu 31: Cho tam giác ABC , biết độ dài của cạnh BC là 10a = và bán kính đường tròn ngoại tiếp tam giác là 10R = . Tính số đo góc A A. 030A = . B. 045A = . C. 060A = . D. 090A = . Câu 32: Cho tam giác ABC , biết độ dài của ba cạnh của tam giác là 10a = , 8b = , 9c = . Số đo góc A gần nhất với kết quả nào sau đây. A. 072 B. 068 C. 086 D. 034 Câu 33: Cho tam giác ABC , biết bán kính đường tròn ngoại tiếp tam giác là 10R = , diện tích tam giác ABC bằng 50 và 030A = . Tính khoảng cách từ đỉnh A đến cạnh BC A. 15. B. 20. C. 10. D. 19 2 .
mình. Bi
t r
ng chi phí cho m
block 1 phút quảng cáo trên đài phát thanh là 10 triệu đồng và chi phí cho một block 10 giây quảng cáo trên đài truyền hình là 25 triệu đồng. Đài phát thanh chỉ nhận các chương trình quảng cáo với ít nhất 5 block, đài truyền hình chỉ nhận các chương trình quảng cáo với số block ít nhất là 10. Theo thống kê của công ty, sau 1 block quảng cáo trên đài phát thanh thì số sản phẩm bán ra tăng 2%, sau 1 block quảng cáo trên đài truyền hình thì số sản phẩm bán ra tăng 4%. Để đạt hiệu quả tối đa thì công ty đó cần quảng cáo bao nhiêu block trên đài phát thanh và đài truyền hình?
38: Cho tam giác ABC
AMAB
. Biết
đoạn AB lấy điểm M sao cho
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 4 Câu 34: Cho tam giác ABC có ;; BCaCAbABc === . Khẳng định nào sau đây là đúng? A. sin SbcA = . B. 2 sin R b B = . C. ( )( )( )Sppapbpc =+++ D. 222 2cos abcbcA =+− Câu 35: Cho tam giác ABC có 3;4;33 ABCACBCS=== . Tính độ dài cạnh AB . A. 13 B. 37 C. 13 D. 37 II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Cho tập ( )( ) 2 |22310Axxxx =−++= ; 2 |(21)20Bxxmxm =+++= với m Tìm m để AB có đúng 3 phần tử và tổng bình phương của chúng bằng 9. Câu 37: Một công ty dự kiến chi 500 triệu đồng cho một đợt quảng cáo sản phẩm của
ế
ằ
ột
Câu
có 8AC = và có góc 120A = . Trên
2 3
=
diện tích tam giác BMC bằng 43BMCS = . Tính độ dài cạnh AB Câu 39: Cho tập hợp ( )2;1A =− và B là tập xác định khác tập rỗng của hàm số 2022 23 3 yxm mx =++− . Có bao nhiêu số nguyên m không lớn hơn 20 để AB là một khoảng? ---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm)
Câu 1: Trong các câu sau, câu nào là mệnh đề?
A. 10 là số chính phương B. abc +=
C. 2 0xx−=
D. 21 n + chia hết cho 3
Lời giải
Các đáp án B, C, D không phải là mệnh đề mà là mệnh đề chứa biến. Chọn A
Câu 2: Các phương án sau, đâu là một mệnh đề đúng?
A. 61 32 = B. 21. C. 235. += D. 35.
Lời giải
Câu 3: Cho các mệnh đề sau đây:
(I): Nếu tam giác ABC đều thì .ABAC =
(II): Nếu ab + là các số chẵn thì , ab là số chẵn.
(III): Nếu tam giác ABC có tổng hai góc bằng 090 thì tam giác ABC cân. Trong các mệnh đề trên, có bao nhiêu mệnh đề đúng?
OFFICIAL
A. 0. B. 3. C. 2. D. 1. Lời giải
Mệnh đề (I) là mệnh đề đúng.
Mệnh đề (II) mệnh đề sai vì còn trường hợp , ab là số lẻ.
Mệnh đề (III) mệnh đề sai vì tam giác ABC vuông chứ không phải là cân.
Vậy chỉ có 1 mệnh đề đúng.
Câu 4: Mệnh đề phủ định của mệnh đề: 2 "," xxx là
A. 2 , xxx . B. 2 , xxx . C. 2 , xxx . D. 2 , xxx .
Lời giải Mệnh đề: 2 "," xxx có mệnh đề phủ định là: 2 "," xxx
Câu 5: Trong các mệnh đề
và biên soạn
DẠYKÈMQUYNHƠN
Sưu tầm
Page 5
sau, mệnh đề nào sai? A. Nếu cả hai số chia hết cho 3 thì tổng hai số đó chia hết cho 3. B. Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau. C. Nếu một số có tận cùng bằng 0thì nó chia hết cho 5 D. Nếu một số chia hết cho 5 thì nó có tận cùng bằng 0. Lời giải D là đáp án cần chọn, vì một số chia hết cho 5 có thể có tận cùng là 5 Câu 6: Cho mệnh đề 2 P:":10" xxx ++ . Mệnh đề phủ định của mệnh đề Pvà tính đúng, sai của nó là: A. 2 P:":10" xxx ++= và P là mệnh đề sai. B. 2 P:":10" xxx ++= và P là mệnh đề đúng. C. 2 P:":10" xxx ++ và P là mệnh đề đúng. D. 2 P:":10" xxx ++= và P là mệnh đề sai. Lời giải Phủ định của mệnh đề 2 P:":10" xxx ++ là 2 P:":10" xxx ++=
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 6 Có: 2 2 13 10, 24 xxxx ++=++ nên mệnh đề 2 P:":10" xxx ++= sai vì phương trình 2 10xx++= vô nghiệm nên không tồn tại x để phương trình 2 10xx++= . Câu 7: Viết tập hợp ( )( ) 22 /22530Bxxxx =−−+= bằng cách liệt kê các phần tử của tập hợp. A. 3 1; 2 B = B. 3 2 B = C. 1B = D. 3 1;;2;2 2 B =− Lời giải Xét ( )( )2222530xxx−−+= 2 2 2 20 1 2530 3 2 x x x xx x = −= = −+= = .Vậy 3 1; 2 B = . Câu 8: Cho tập hợp 23|,5 =+ Axxx . Tập hợp A là: A. 1;2;3;4;5A = B. 1;3;5;7;9;11=A C. 3;4;5;6;7;8=A . D. 3;5;7;9;11;13=A . Lời giải Xét x và 5x nên 0;1;2;3;4;5.x Do đó 3;5;7;9;11;13=A Câu 9: Hãy liệt kê các phần tử của tập hợp 2 |7520=−−=Xxxx A. 0X = . B. 1X = . C. 1 1; 2 X = . D. 2 1; 7 =− X . Lời giải Xét phương trình: 2 1 7520 2 7 = −−= =− x xx x Do x nên 1X = Câu 10: Cho hai tập hợp 50,6Annn = và 6;12;18;24;30;36;42;48B = . Mệnh đề nào sau đây đúng? A. BA B. AB C. = AB D. =AB Lời giải Ta có 0;6;12;18;24;30;36;42;48A = BA . Câu 11: Tập hợp nào sau đây có đúng hai tập hợp con? A. ;x B. x C. ;;xy D. ; xy Lời giải x có hai tập con là x và Câu 12: Cho 1;1;5;0;1;3;5.AB=−= Khẳng định nào sau đây đúng? A. 1.=AB B. 1;3.=AB
Lời giải
Lời

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 C. 1;5.=AB D. 1;3;5.=AB Lời giải 1;5;1;3;5.==AB Suy ra 1;5.=AB Câu 13: Cho hai tập hợp 0;2,0;1;2;3;4.AB== Số tập hợp X thỏa mãn AXB = là A. 2 B. 3 C. 4 D. 5 Lời giải Vì AXB = nên X bắt buộc phải chứa các phần tử {1;3;4} và XB Vậy X có 4 tập hợp đó là 0;1;2;3;4,{1;2;3;4},{1;3;4},0;1;3;4 . Câu 14: Cho 1;3;5;7A = ; 1;2;3;4;5;6B = . Tập hợp \ BA có số phần tử là A. 1 B. 4 C. 2 D. 3
Ta có: \2;4;6BA = Suy ra tập hợp \ BA có 3 phần tử. Câu 15: Cho hai tập hợp 1;2;4;6,1;2;3;4;5;6;7;8AB== khi đó tập B CA là A. 3;5;7;8 . B. 4;6 C. 2;6;7;8 D. 1;2;4;6
giải Ta có: 3;5;7;8B CA = . Câu 16: Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh? A. 54. B. 40. C. 26. D. 68. Lời giải Gọi T, L lần lượt là tập hợp các học sinh giỏi Toán và các học sinh giỏi Lý. Ta có: T : là số học sinh giỏi Toán L : là số học sinh giỏi Lý TL : là số học sinh giỏi cả hai môn Toán và Lý Khi đó số học sinh của lớp là: 6TL+ Mà 25231434TLTLTL =+−=+−= . Vậy số học sinh của lớp là 34640 += . Câu 17: Cho tập hợp ( ( ;3; 1;5AB=−= . Khi đó, tập AB là A. (1;3]. B. (3;5 ] . C. (;5] − . D. (;1) − . Lời giải


DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8 Ta có ( ;5AB=− . Câu 18: Cho tập hợp ( ) 2;6; [3;4]AB=−=− . Khi đó, tập AB là A. (2;3]. B. (2;4]. C. (3;6]. D. (4;6]. Lời giải Ta có ( 2;4AB=− . Câu 19: Cho tập ( 4;7A = và ( 3;5B =− . Tập AB \ là A. ( 3;4 . B. ( 4;5 . C. ( 3;7 . D. ( 5;7 . Lời giải Ta có: AB =\ ( ( ( 4;73;55;7 −=\ Câu 20: Cho tập ( 5;8A =− và ( 2;4B =− . Tập A CB là A. ( ) ( )5;24;8A CB =−− . B. ( ) ( 5;24;8A CB =−− . C. ( ( )5;24;8A CB =−− . D. ( ( 5;24;8A CB =−− . Lời giải ( ( ( ( \5;8\2;45;24;8A CBAB==−−=−− . Câu 21: Cặp số nào sau đây không phải là nghiệm của bất phương trình 2310 xy+− A. 0;0xy== B. 1;1xy==− C. 0;2xy==− D. 1;1xy=−= Lời giải Thử các cặp số , xy vào bất phương trình. Ta có đáp án D Câu 22: Cho hình vẽ bên dưới, miền nghiệm được biểu diễn bởi phần không bị tô màu (không có đường thẳng) là miền nghiệm của bất phương trình nào sau đây? x y 2 2 O A. 2xy B. 2xy C. 2xy D. 2xy
Lời giải
Ta thấy đường thẳng đi qua hai điểm ( )0;2A và ( )2;0B nên đường thẳng có phương
trình :20 xy +−=

Lấy điểm ( )0;0O , không thuộc miền nghiệm của bất phương trình và ta có 002 + nên
hình trên biểu diễn miền nghiệm của bất phương trình 2xy+
Câu 23: Miền không bị gạch ( không tính đường thẳng) được cho bởi hình sau, là miền nghiệm của bất phương trình nào?
A. 260 xy+− .
Từ đồ thị
biên
B. 260 xy+− . C. 260xy+− . D. 260xy+− .
OFFICIAL
Lời giải
DẠYKÈMQUYNHƠN
Sưu tầm và
soạn Page 9
ta thấy: Đường thẳng d đi qua 2 điểm (3;0);(0;6)AB suy ra phương trình là 260 xy+−= Điểm ( )0;0O thuộc miền nghiệm của bất phương trình. Nên đáp án là B Câu 24: Miền nghiệm của hệ bất phương trình: 3260 2100 10 xy xy y −+ +− − là miền chứa điểm nào trong các điểm sau? A. ( ) 1;3.M B. ( ) 4;3.N C. ( )1;5P . D. ( )2;3Q . Lời giải Phương án A: thay 1x = , 3y =− vào từng hệ bất phương trình đã cho, ta được: 150 110 40 − − (không thoả mãn). Phương án B: thay 4x = , 3y = vào từng hệ bất phương trình đã cho, ta được: 120 10 20 (thoả mãn). Phương án C: thay 1x =− , 5y = vào từng hệ bất phương trình đã cho, ta được: 70 70 40 − − (không thoả mãn). Phương án D: thay 2x =− , 3y =− vào từng hệ bất phương trình đã cho, ta được:
được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; Để pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
A. 5 lít nước cam và 4 lít nước táo.
điểm
nhận
mặt phẳng tọa
Oxy
các đường
là phần mặt phẳng (ngũ giác OABCD ) tô màu trên hình vẽ
đó miền nghiệm của hệ bất phương trình
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 10 60 170 40 − − (không thoả mãn). Câu 25: Trong một cuộc thi pha chế, mỗi đội chơi
B. 6 lít nước cam và 5 lít nước táo. C. 4 lít nước cam và 5 lít nước táo. D. 4 lít nước cam và 6 lít nước táo. Lời giải Giả sử , xy là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế. Suy ra 3010xy là số gam đường cần dùng; xy là số lít nước cần dùng; 4 xy là số gam hương liệu cần dùng. Theo giả thiết ta có 00 00 3010210321.* 99 424424 xx yy xyxy xyxy xyxy Số
thưởng
được sẽ là 6080 Pxy . Trong
độ
, vẽ
thẳng: :3210,':90,:4240 dxydxyxy Khi
(*)
Xét các đỉnh của miền khép kín tạo ra bởi hệ (*) là 0;0,0;6,4;5,6;3,7;0 OABCD Ta thấy P đạt giá trị lớn nhất tại 4,5xy . Vậy để đạt được số điểm thưởng cao nhất cần pha chế 4 lít nước cam và 5 lít nước táo. Câu 26: Cho 2 sin 5 x = và 00 90180 x . Tính giá trị cosx. A. 21 5 B. 21 C. 21 5 D. 1 5

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 11 Lời giải 22222242121 sincos1cos1sincos1coscos 25255 xxxxxxx +==−=−== Vì 00 90180 x nên cos0 x . Vậy 21 cos 5 x =− . Câu 27: Cho ABC có 06,8,60bcA=== . Tính độ dài cạnh a A. 213. B. 312. C. 237. D. 20. Lời giải 22202cos36642.6.8.cos6052213abcbcAa =+−=+−== . Câu 28: Cho tam giác ABC thoả mãn: 222 3 bcabc +−= . Khi đó: A. 0 30.A = B. 0 45.A = C. 0 60.A = D. 075A = . Lời giải 222 033 cos30. 222 bcabc AA bcbc +− ==== Câu 29: Cho hai tập hợp ( ( 1;5;2;7AB== . Tập hợp \ AB là: A. ( 1;2 B. ( )2;5 C. ( 1;7 D. ( )1;2 Lời giải ( \\ va 1;2ABxxAxBx = . Câu 30: Cho ABC có 5AB = ;A40= ;B60= . Độ dài BC gần nhất với kết quả nào? A. 3,7. B. 3,3. C. 3,5. D. 3,1. Lời giải C180AB180406080 =−−=−−= Áp dụng định lý sin: 5 sinsinsinsin80.sinsin403,3 BCABAB BCA ACC === . Câu 31: Cho tam giác ABC , biết độ dài của cạnh BC là 10a = và bán kính đường tròn ngoại tiếp tam giác là 10R = . Tính số đo góc A A. 030A = . B. 045A = . C. 060A = . D. 090A = . Lời giải Áp dụng định lý sin ta có: sin101 2202 Aa R === 030A = Câu 32: Cho tam giác ABC , biết độ dài của ba cạnh của tam giác là 10a = , 8b = , 9c = . Số đo góc A gần nhất với kết quả nào sau đây. A. 072 . B. 068 . C. 086 . D. 034 . Lời giải Áp dụng định lý côsin ta có 222 89105 cos 2.8.916 A +− == 072A Câu 33: Cho tam giác ABC , biết bán kính đường tròn ngoại tiếp tam giác là 10R = , diện tích tam giác ABC bằng 50 và 030A = . Tính khoảng cách từ đỉnh A đến cạnh BC .
Gọi
Câu
Suy
A.
Lời

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 A. 15. B. 20. C. 10. D. 19 2 . Lời giải
d là khoảng cách từ đỉnh A đến cạnh BC . Áp dụng định lý sin ta có: 0 2sin2.10.sin3010aRA=== Mặt khác 1 2ABC Sad =
ra 22.50 10 10 ABCdS a === Vậy khoảng cách từ đỉnh A đến cạnh BC là 10d =
34: Cho tam giác ABC có ;; BCaCAbABc === . Khẳng định nào sau đây là đúng?
sin SbcA = B. 2 sin R b B = C. ( )( )( )Sppapbpc =+++ . D. 222 2cos abcbcA =+− .
giải Áp dụng định lí côsin ta có đáp án D đúng Câu 35: Cho tam giác ABC có 3;4;33 ABCACBCS=== . Tính độ dài cạnh AB . A. 13 B. 37 C. 13 D. 37 Lời giải Ta có: 1 ..sin 2ABC SACBCC = 1 .3.4sin 2 C= 33= sin3 2 C = 60C = . Áp dụng định lý côsin trong tam giác ABC ta có: 222 2...cos ABBCACBCACC =+− 22 342.3.4.cos60=+− 22 1 342.3.4.13 2 =+−= . Do đó 13AB = . II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Cho tập ( )( ) 2 |22310Axxxx =−++= ; 2 |(21)20Bxxmxm =+++= với m . Tìm m để AB có đúng 3 phần tử và tổng bình phương của chúng bằng 9. Lời giải ( )( ) 2 |223101;2.Axxxx =−++==− Ta có: 2 (21)201xmxmx +++==− hoặc 2 xm =− . Khi đó AB có đúng 3 phần tử 221 211(*) 2 m m m m −− −− Suy ra 1;2;2 ABm =−− .
Một công ty dự kiế
500 triệu đồng cho một đợt quảng cáo sản phẩm của mình. Biết rằng chi phí cho một block 1 phút quảng cáo trên đài phát thanh là 10 triệu đồng và chi phí cho một block 10 giây quảng cáo trên đài truyền hình là 25 triệu đồng. Đài phát thanh chỉ nhận các chương trình quảng cáo với ít nhất 5 block, đài truyền hình chỉ nhận các chương trình quảng cáo với số block ít nhất là 10. Theo thống kê của công ty, sau 1 block quảng cáo trên đài phát thanh thì số sản phẩm bán ra tăng 2%, sau 1 block quảng cáo trên đài truyền hình thì số sản phẩm bán ra tăng 4%. Để đạt hiệu quả tối đa thì công ty đó cần quảng cáo bao nhiêu block trên đài phát thanh và đài truyền hình?
Lời giải
Gọi , xy tương ứng là số block công ty đó thuê quảng cáo trên đài đài phát thanh và đài truyền hình. Chi phí công ty cần bỏ ra là 1025xy + (triệu đồng).
Mức chi phí cho quảng cáo không quá 500 triệu nên 1025500 xy+ hay 25100 xy+ . Do các điều kiện đài phát thanh và đài truyền hình đưa ra nên 5;10;, xyxy .
Số phần trăm tăng trưởng sản phẩm bán ra nhờ quảng cáo là ( ) ;0,020,04 Fxyxy =+ .
xy +
Ta tìm , xy sao cho ( ) ;0,020,04 Fxyxy =+ đạt giá trị lớn nhất với các điều kiện ( )5* 25 10
100 x y
Biểu diễn miền nghiệm của hệ (*) như hình sau:
Miền nghiệm
Ta
5;10.
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 13 Theo giả thiết: ( ) ( ) 22 22 1 21291. 1 m mm m = −+−+== =− Đối chiếu (*) ta được: 1.m = Vậy 1m = là giá trị cần tìm. Câu 37:
n chi
.
của hệ (*) là miền tam giác ABC với ( ) 5;18;A ( )25;10B và ( )
C
có ( ) 5;180,82F = ; ( ) 25;100,9F = ; ( ) 5;100,5F = . Vậy để đạt hiệu quả tối đa thì công ty đó cần quảng cáo 25 block trên đài phát thanh và 10 block trên đài truyền hình. Câu 38: Cho tam giác ABC có 8AC = và có góc 120A = . Trên đoạn AB lấy điểm M sao cho 2 3 AMAB = . Biết diện tích tam giác BMC bằng 43BMCS = . Tính độ dài cạnh AB Lời giải A B C M
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 14 Ta có 21 33 AMABBMAB == từ đó 1 43123 3 BMCABCABC SSS === . Áp dụng công thức diện tích ta có: 1113 ..sin..sin120.8..123 2222ABC SACABBACACABAB ==== Giải được 6AB = Vậy độ dài cạnh 6AB = . Câu 39: Cho tập hợp ( )2;1A =− và B là tập xác định khác tập rỗng của hàm số 2022 23 3 yxm mx =++− . Có bao nhiêu số nguyên m không lớn hơn 20 để AB là một khoảng? Lời giải Điều kiện xác định: 23023 303 xmxm mxxm ++−− −−− Ta có: ) 23;32330 Bmmmmm =−−−−−− (*). AB là một khoảng AB Ta có 00 32101 1232 mm ABm mm mm = −− −−− Khi đó ( ) ( ( ) ( 0;\0;11;1;20ABmmm ++ Vậy có 19 giá trị của m thỏa mãn yêu cầu bài toán.

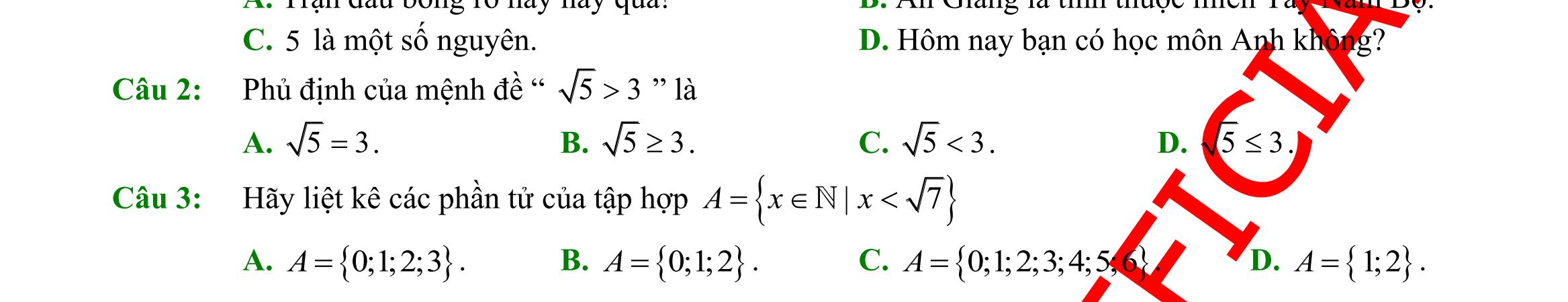















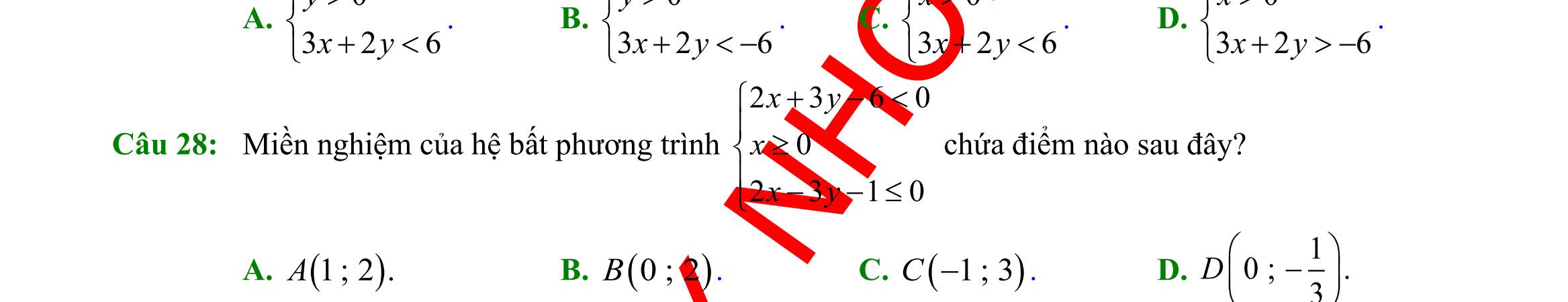

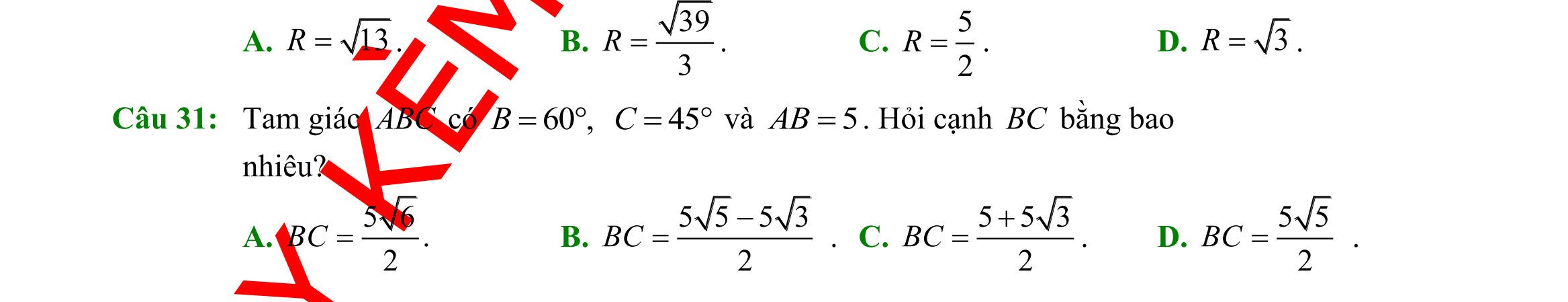






















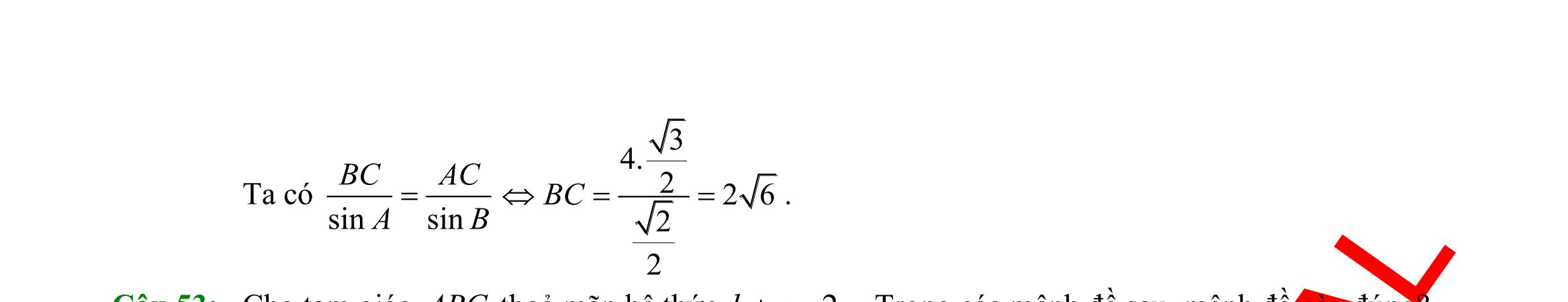








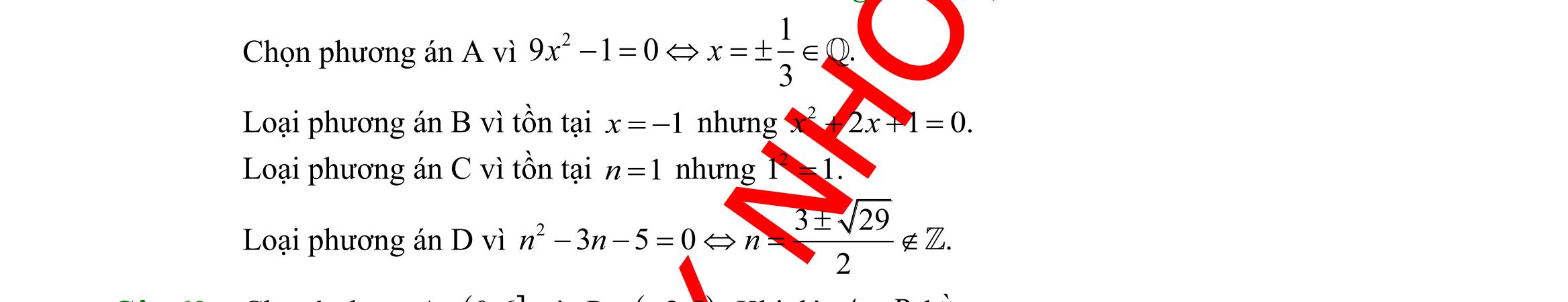



















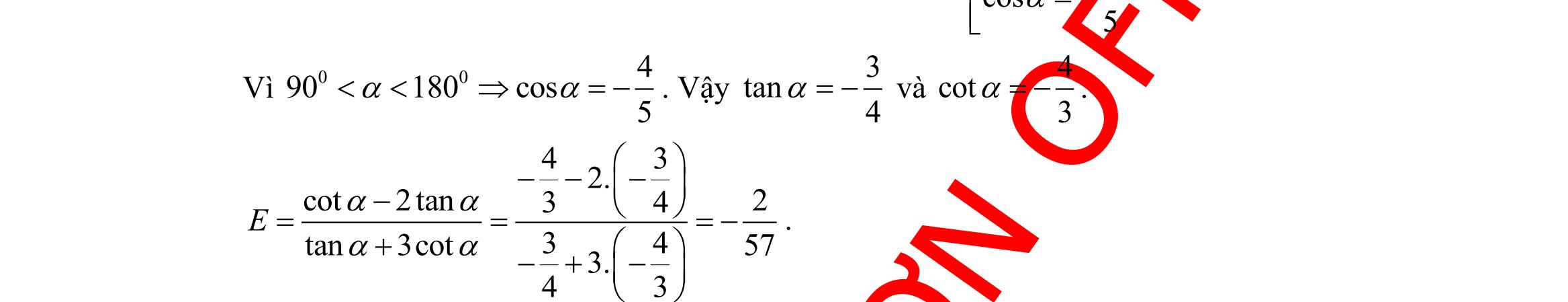

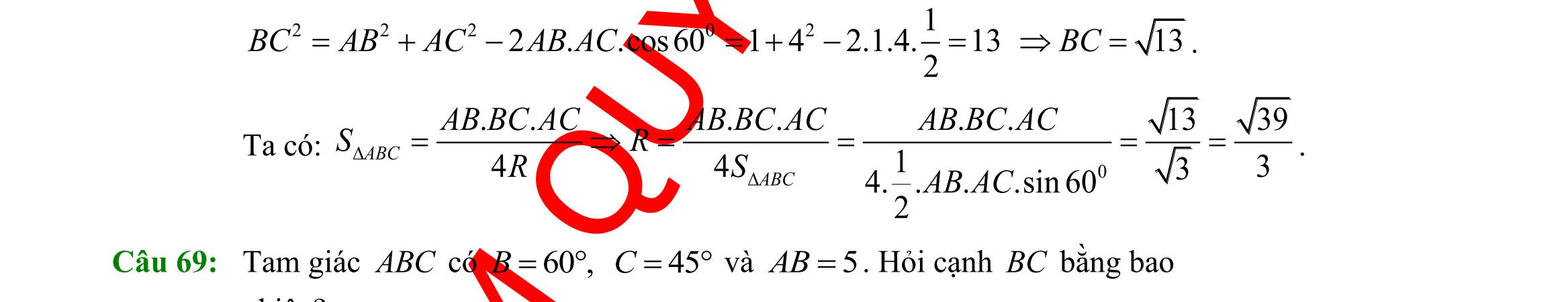


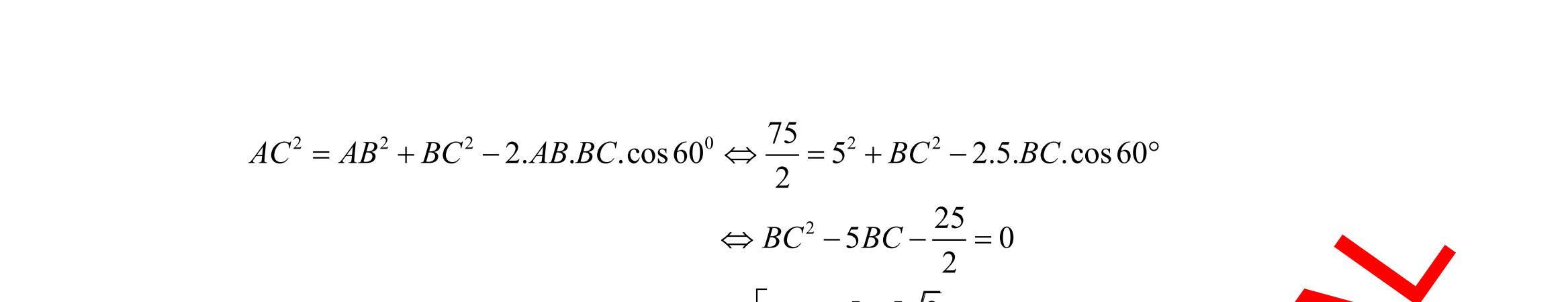
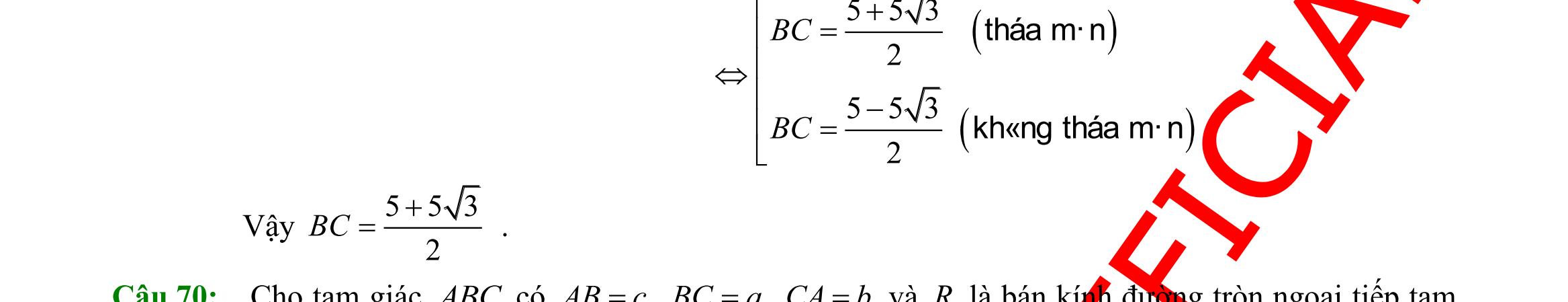









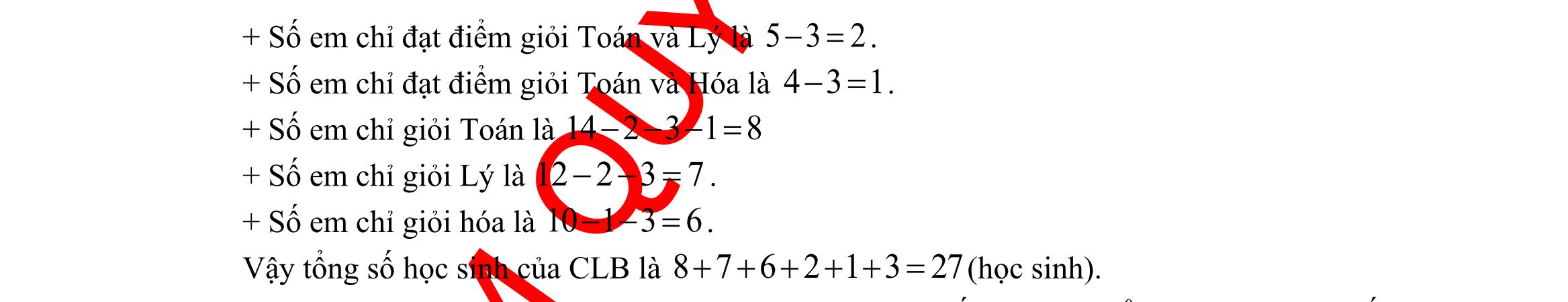




















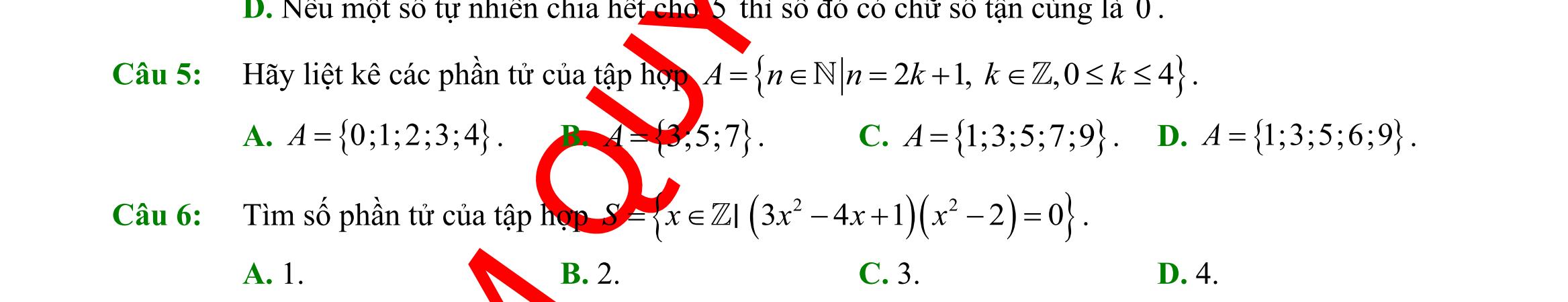


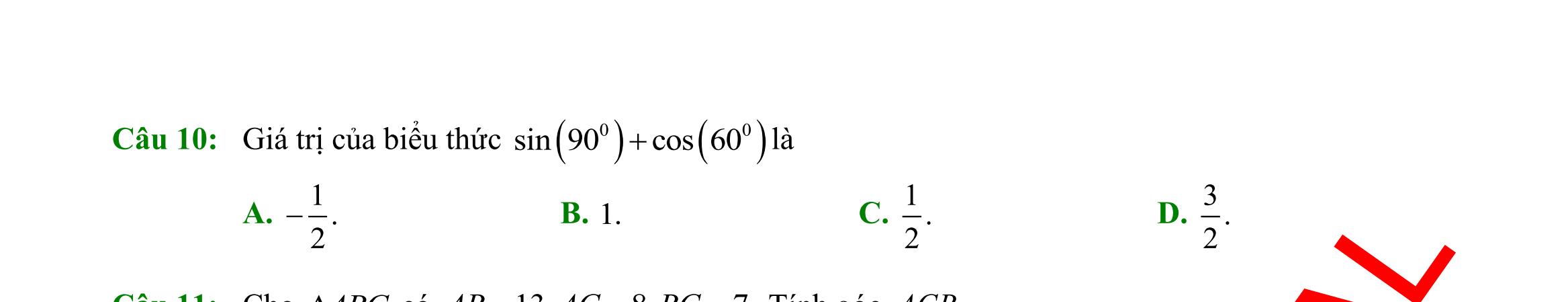











































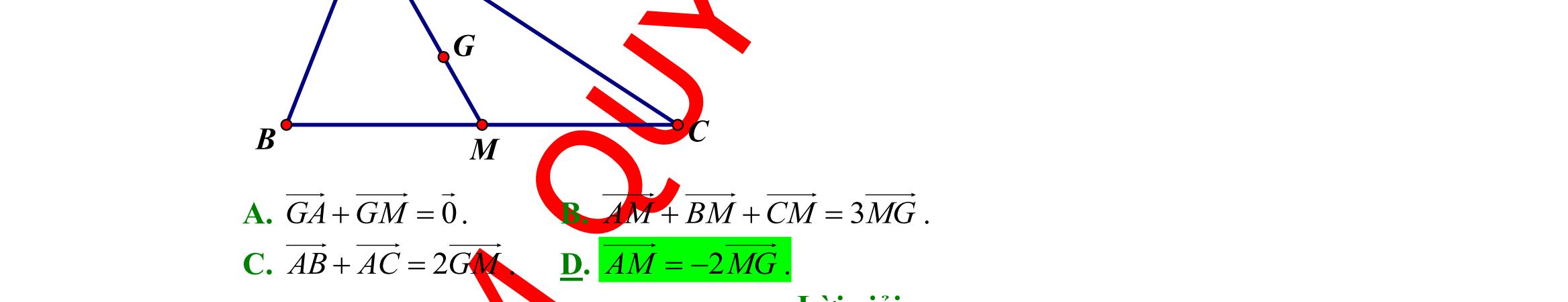






















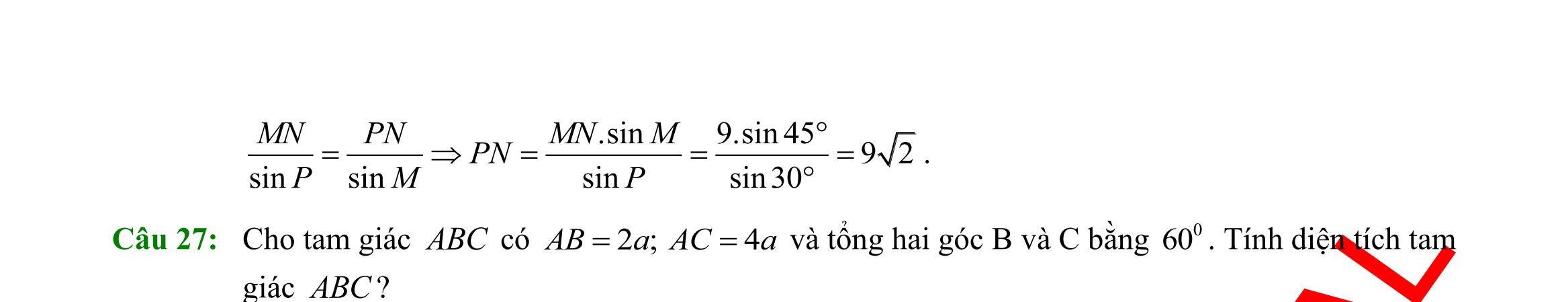






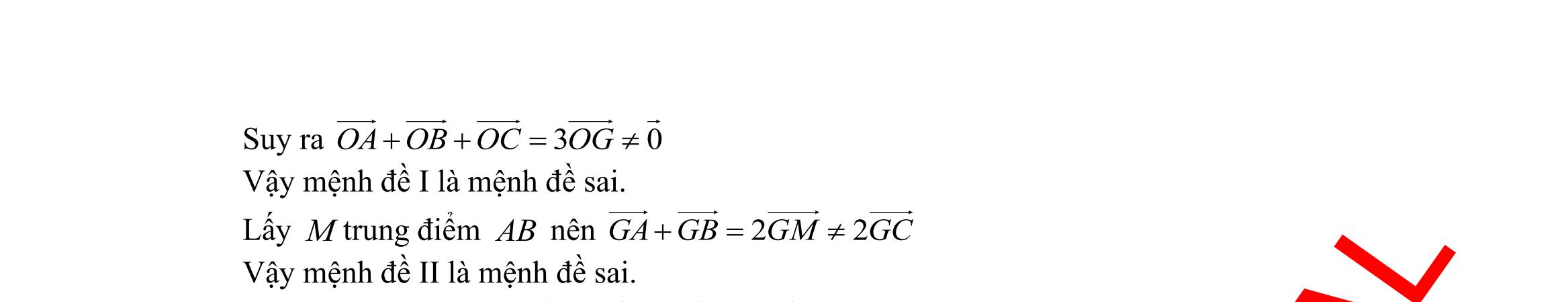





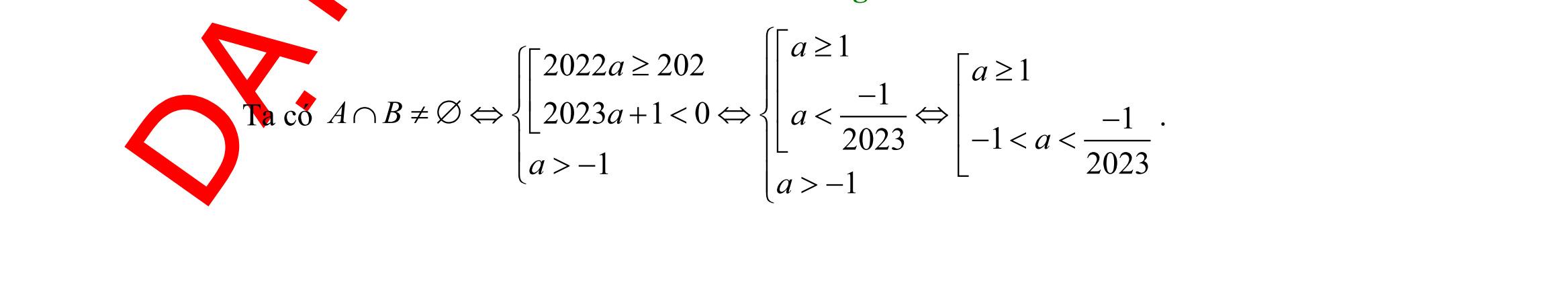



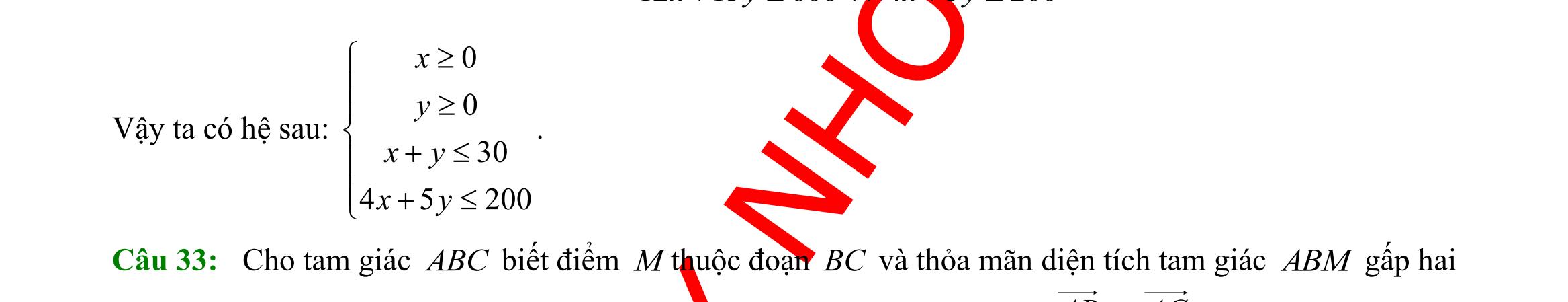















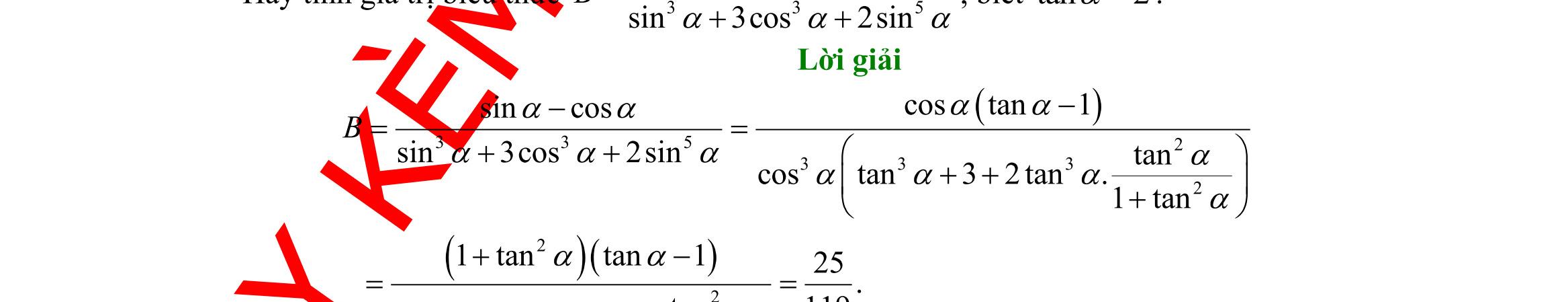





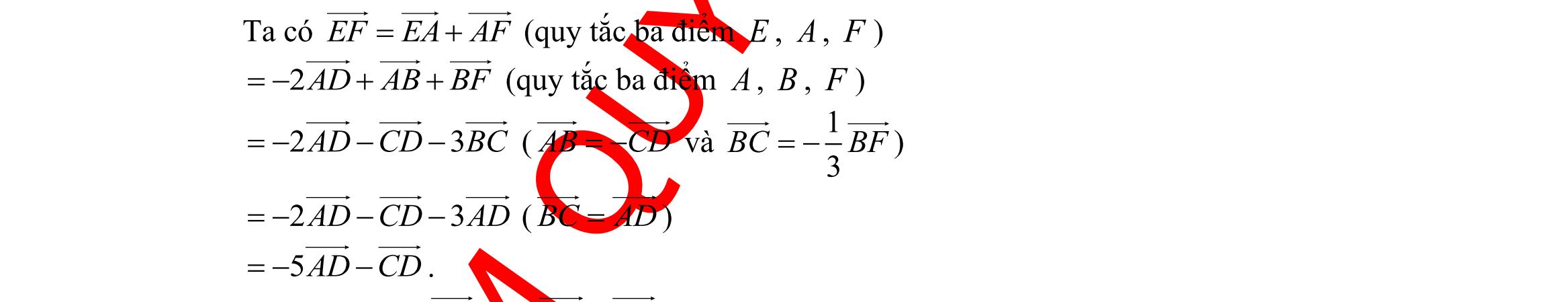











DẠYKÈMQUYNHƠN OFFICIALĐỀ ÔN TẬP KIỂM TRA GIỮA HỌC KỲ MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection BỘ 5 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN TOÁN 10 CHÂN TRỜI SÁNG TẠO CÓ LỜI GIẢI CHI TIẾT (35 CÂU TRẮC NGHIỆM + TỰ LUẬN) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 ĐỀ SỐ: 01 I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Mệnh đề phủ định của mệnh đề “ , xxx=− ” là mệnh đề nào sau đây? A. , xxx=− . B. , xxx− . C. , xxx− . D. , xxx− . Câu 2: Mệnh đề ( ) 2 :",28920220"Pxxxx−+ . Phủ định của mệnh đề P là A. 2, 28920220xxx −+ B. 2, 28920220xxx −+ C. 2, 28920220xxx −+ . D. 2, 28920220xxx −+ . Câu 3: Trong các mệnh đề sau, mệnh đề nào sai? A. ,2 nn laø soá chaün . B. 2 ,0xx . C. 2 , nnn = . D. 2 ,0nn − . Câu 4: Hãy liệt kê các phần tử của tập hợp A gồm các số tự nhiên chia hết cho 7 và nhỏ hơn 50. A. 7;14;21;28;35;42;49A = . B. 7;14;21;28;35;42A = . C. 0;7;14;21;28;35;42;49A = D. 0;14;21;28;35;42;49A = Câu 5: Cho tập hợp 1;2;3;4;5A = . Hãy chỉ ra tính chất đặc trưng của các phần tử của tập hợp A . A. |06.Axx= B. |06.Axx= C. |5.Axx= D. |5.Axx= Câu 6: Cho hai tập hợp ) ( )5;3,1;AB=−=+ . Khi đó AB là tập nào sau đây? A. ( )1;3 B. ( 1;3 C. )5; −+ D. 5;1 Câu 7: Cho hai tập hợp C và D có biểu đồ Ven như hình vẽ. Hãy xác định tập hợp CD A. 3;5;7;9CD= B. 7CD= C. 3;5CD= D. 3;5;7CD= Câu 8: Lớp 10A tham gia thi học sinh giỏi cấp trường, có 25 học sinh tham gia thi môn Toán, 20 học sinh tham gia thi môn Văn và 15 học sinh tham gia thi cả hai môn Toán và Văn. Hỏi lớp 10A có bao nhiêu học sinh tham gia thi ít nhất một trong hai môn trên? A. 35. B. 40. C. 45. D. 30. Câu 9: Cho hai tập hợp 3;2A =− và |1Bxx=− . Tìm AB . A. )3;1AB=−− B. ( 1;2AB=− C. 3;2AB=− D. ( );1AB=−− Câu 10: Cho tập hợp |13Axx=− . Tìm CA . A. (;1)CA =−− . B. ( ( );13;CA =−−+ . C. (;1)[3;)CA =−−+ . D. [3;)CA =+ .
Câu
Câu
Câu
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 2
11: Điểm ( )0;0O thuộc miền nghiệm của bất phương trình nào sau đây? A. 320xy++ . B. 20xy++ . C. 2520 xy+− . D. 220 xy++ .
12: Cặp số nào sau đây không là nghiệm của bất phương trình ( ) 5210 xy−− ? A. ( )0;1 B. ( )1;3 C. ( )–1;1 D. ( )–1;0
13: Miền nghiệm của bất phương trình ( ) ( ) 323413 xyxy +++−+ là phần mặt phẳng chứa điểm A. ( )3;0 B. ( )3;1 C. ( )2;1 D. ( )0;0 Câu 14: Miền nghiệm của bất phương trình ( ) 529227 xxy +−−+ không chứa điểm nào trong các điểm sau? A. ( )0;0 B. ( )2;1 C. ( )2;1 D. ( )2;3 Câu 15: Miền nghiệm của bất phương trình 326 xy−− là A. B. C. D. Câu 16: Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 360 240 xy xy +− ++ B. 360 240 xy xy +− ++ C. 360 240 xy xy +− ++ D. 360 240 xy xy +− ++ Câu 17: Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình 20 2320 xy xy +− −+ là A. ( )0;0 . B. ( )1;1 . C. ( )1;1 . D. ( )1;1 . Câu 18: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2510 250 10 xy xy xy −− ++ ++ ? A. ( )0;0 B. ( )1;0 C. ( )0;2 D. ( )0;2 O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x
Câu 21: Khẳng định
Câu 22: Khẳng định
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 Câu 19: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy + . B. 0 326 y xy +− . C. 0 326 x xy + . D. 0 326 x xy +− . Câu 20: Cho hệ 235(1) 3 25(2) xy xy + + . Gọi 1S là tập nghiệm của bất phương trình (1), 2S là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì A. 12SS B. 21SS C. 2 SS = D. 1 SS
nào sau đây là đúng? A. 22 sin1 cos −= B. 22 sin1 cos −=− C. 22 sin0 cos −= . D. 22 sin1 cos += .
nào sau đây là đúng? A. ( )0sin180 cos −=. B. ( )0sin180 cos −=−. C. ( )0 sin180sin−= D. ( )0 sin180sin−=−. Câu 23: Khẳng định nào sau đây là Sai? A. ( )0sin90 cos −= B. 2 2 1 1cot sin += C. 2 2 1 1tan sco += D. cot sin cos = Câu 24: Cho góc thỏa mãn 4 sin 5 = . Tính giá trị biểu thức 5cos1P =− A. 4 B. 3 C. 3. D. 4 Câu 25: Cho tam giác ABC có 5AB = ; 7BC = ; 8AC = . Số đo góc A bằng A. 90 . B. 60 . C. 30 . D. 45 . Câu 26: Tam giác ABC có 8a = , 3c = , ˆ 60B = . Độ dài cạnh b bằng bao nhiêu A. 7 B. 97 C. 61 D. 49 Câu 27: Cho tam giác ABC thỏa mãn 222 2.0BCACABBCAC +−−= . Khi đó, góc C có số đo là A. ˆ 150C = . B. ˆ 60C = . C. ˆ 45C = . D. ˆ 30C = . Câu 28: Cho hình thoi ABCD cạnh bằng 1 cm và có 60BAD = . Tính độ dài cạnh AC . A. 3.AC = B. 2.AC = C. 23.AC = D. 2.AC = O 2 3 y x
Câu 29: Cho tam giác ABC
A. 5
Câu 30: Tam giác ABC có
A. 56 . 2 AC
B.
bán kính
Tính
tròn ngoại tiếp tam giác ABC
B.
Câu 31: Tìm chu vi tam giác ABC , biết rằng 6AB = và 2sin3sin4sin ABC ==
A. 106 . B. 26
Câu 32: Cho tam giác ABC có 9,18
C. 13
60A
dài cạnh AC
D. 56
AC
D. 526
Bán kính R c
đường tròn ngoại ti
OFFICIAL
3 II. PHẦN TỰ LUẬN (3,0 điểm)
Câu 36: Lớp 10A chọn ra một số h
c sinh tham gia làm bài khảo sát học sinh giỏi môn Toán. Đề thi có 3 câu. Sau khi chấm bài giáo viên tổng kết được như sau: Có 5 học sinh làm được câu 1, có 6 học sinh làm được câu 2, có 4 học sinh làm được câu 3. Có 3 học sinh làm được câu 1 và câu 2, có 2 học sinh làm được câu 1 và câu 3, có 1 học sinh làm được câu 2 và câu 3 và chỉ có 1 học sinh làm được cả 3 câu. Hỏi có t
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 4
có 30, 10ABC== Tính
đường
.
10. C. 10 3 . D. 103 .
ˆˆ 60, 45BC== và 5AB = .
độ
.
=
53.AC = C. 56 . 3 AC =
. 4
=
.
.
.
.
ABAC== và
= .
ủa
ếp tam giác ABC là: A. 3. B. 93 . C. 9. D. 6 . Câu 33: Cho tam giác ABC biết độ dài ba cạnh , , BCCAAB lần lượt là , , abc thỏa mãn hệ thức ( ) ( )2222 bbacca −=− với bc . Khi đó, góc BAC bằng A. 45 B. 60 C. 120 D. 90 Câu 34: Cho tam giác ABC , biết rằng 00 60,45,4ABb=== . Tính cạnh a và c . A. 4,9a và 5,5c B. 5,5a và 4,9c C. 5,5a và 6,3c D. 6,3a và 5,5c Câu 35: Cho hình chữ nhật ABCD biết 1AD = . Giả sử E là trung điểm AB và thỏa mãn 1 sin 3 BDE = . Tính độ dài cạnh AB . A. 22 B. 5 C. 2 D.
ọ
ất cả bao nhiêu học sinh tham gia làm bài khảo sát Câu 37: Tìm giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ với điều kiện 04 0 10 2100 y x xy xy −− +− là Câu 38: Cho tam giác ABC thỏa mãn sinsinsin coscos BC A BC + = + . Chứng minh tam giác ABC vuông. ---------- HẾT ----------
C.
Các số tự
0;14;21;28;35;42;49
Lời giải

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 5 HƯỚNG DẪN GIẢI CHI TIẾT I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Mệnh đề phủ định của mệnh đề “ , xxx=− ” là mệnh đề nào sau đây? A. , xxx=− B. , xxx− C. , xxx− D. , xxx− Lời giải Mệnh đề phủ định của mệnh đề “ , xxx=− ” là mệnh đề “ , xxx− ”. Câu 2: Mệnh đề ( ) 2 :",28920220"Pxxxx−+ . Phủ định của mệnh đề P là A. 2, 28920220xxx −+ B. 2, 28920220xxx −+ C. 2, 28920220xxx −+ D. 2, 28920220xxx −+ Lời giải Chọn D ( ) 2 :",28920220"Pxxxx−+ ( ) 2:", 28920220"Pxxxx −+ Câu 3: Trong các mệnh đề sau, mệnh đề nào sai? A. ,2 nn laø soá chaün . B. 2 ,0xx . C. 2 , nnn = . D. 2 ,0nn − . Lời giải Với 0n = , khi đó 2 00n −= (sai). Nên mệnh đề: 2 ,0nn − là mệnh đề sai. Câu 4: Hãy liệt kê các phần tử của tập hợp A gồm các số tự nhiên chia hết cho 7 và nhỏ hơn 50. A. 7;14;21;28;35;42;49A = . B. 7;14;21;28;35;42A = .
0;7;14;21;28;35;42;49A = D.
A =
nhiên chia hết cho 7 và nhỏ hơn 50 là: 0;7;14;21;28;35;42;49 Câu 5: Cho tập hợp 1;2;3;4;5A = . Hãy chỉ ra tính chất đặc trưng của các phần tử của tập hợp A A. |06.Axx= B. |06.Axx= C. |5.Axx= D. |5.Axx= Lời giải Câu 6: Cho hai tập hợp ) ( )5;3,1;AB=−=+ . Khi đó AB là tập nào sau đây? A. ( )1;3 B. ( 1;3 C. )5; −+ D. 5;1 Lời giải Ta có thể biểu diễn hai tập hợp A và B, tập AB là phần chung không bị gạch ở cả A và B nên ( )1;3x Câu 7: Cho hai tập hợp C và D có biểu đồ Ven như hình vẽ. Hãy xác định tập hợp CD .
gia thi môn Toán, 20
thi
môn Toán và Văn. Hỏi l
p 10A có bao nhiêu
gia
A. 35. B.


trong hai môn trên?
C. 45. D. 30.
Lời giải Kí hiệu A và B lần lượt là tập hợp các
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 6 A. 3;5;7;9CD= B. 7CD= C. 3;5CD= D. 3;5;7CD= Lời giải Tập hợp CD gồm những phần tử vừa thuộc tập C vừa thuộc tập D Nên 3;5CD= Câu 8: Lớp 10A tham gia thi học sinh giỏi cấp trường, có 25 học sinh tham
học sinh tham gia thi môn Văn và 15 học sinh tham gia
cả hai
ớ
học sinh tham
thi ít nhất một
40.
học sinh của lớp 10A tham gia thi môn Toán và Văn. Theo giả thiết, ( ) ( ) ( ) 25,20,15nAnBnAB=== Ta thấy, tổng ( ) ( )nAnB + cho ta số học sinh thi Toán hoặc Văn, đồng thời số bạn thi hai môn được tính hai lần. Do đó, số bạn thi ít nhất một trong hai môn là ( ) ( ) ( ) ( ) 25201530nABnAnBnAB=+−=+−= . Câu 9: Cho hai tập hợp 3;2A =− và |1Bxx=− . Tìm AB A. )3;1AB=−− . B. ( 1;2AB=− . C. 3;2AB=− . D. ( );1AB=−− . Lời giải Ta có 3;2A =− ( );1B =−− Do đó )3;1AB=−− Câu 10: Cho tập hợp |13Axx=− . Tìm CA A. (;1)CA =−− . B. ( ( );13;CA =−−+ .
Chọn
Chọn B
Chọn C
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 C. (;1)[3;)CA =−−+ D. [3;)CA =+ Lời giải Ta có : [1;3)A =− Do đó : (;1)[3;)CA =−−+ Câu 11: Điểm ( )0;0O thuộc miền nghiệm của bất phương trình nào sau đây? A. 320xy++ B. 20xy++ C. 2520 xy+− D. 220 xy++ Lời giải
D Thay toạ độ điểm ( )0;0O vào từng đáp án. Nhận thấy chỉ có mỗi đáp án D là thoả ( )20 Câu 12: Cặp số nào sau đây không là nghiệm của bất phương trình ( ) 5210 xy−− ? A. ( )0;1 B. ( )1;3 C. ( )–1;1 D. ( )–1;0 Lời giải
Ta thế từng cặp ( ); xy từ đáp án vào, nhận thấy đáp án B không thoả vì ( ) 5.123110 −−= . Câu 13: Miền nghiệm của bất phương trình ( ) ( ) 323413 xyxy +++−+ là phần mặt phẳng chứa điểm A. ( )3;0 B. ( )3;1 C. ( )2;1 D. ( )0;0 Lời giải
Ta có ( ) ( ) 323413310 xyxyxy +++−+−+− . Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa bất phương trình trên. Câu 14: Miền nghiệm của bất phương trình ( ) 529227 xxy +−−+ không chứa điểm nào trong các điểm sau? A. ( )0;0 B. ( )2;1 C. ( )2;1 D. ( )2;3 Lời giải Chọn D Ta có ( ) 5292273260 xxyxy +−−++− . Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa bất phương trình trên. Câu 15: Miền nghiệm của bất phương trình 326 xy−− là A. B. O x y 2 3 O 2 3 y x
Lời giải
OFFICIAL
Trước hết,
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 8 C. D.
ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0. Câu 16: Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 360 240 xy xy +− ++ . B. 360 240 xy xy +− ++ . C. 360 240 xy xy +− ++ . D. 360 240 xy xy +− ++ . Lời giải Thay điểm ( )0;0O vào từng đáp án. Đáp án , AB sai vì 03.060 +− . Đáp án D sai vì 2.0040 ++ . Nên ta chọn đáp án C . Câu 17: Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình 20 2320 xy xy +− −+ là A. ( )0;0 . B. ( )1;1 . C. ( )1;1 . D. ( )1;1 . Lời giải Ta thay cặp số ( )1;1 vào hệ ta thấy không thỏa mãn. Câu 18: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2510 250 10 xy xy xy −− ++ ++ ? A. ( )0;0 B. ( )1;0 C. ( )0;2 D. ( )0;2 Lời giải Nhận xét: chỉ có điểm ( )0;2 thỏa mãn hệ. Câu 19: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? O x y 2 3 O x 2 3 y O x y 2 3
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9 A. 0 326 y xy + B. 0 326 y xy +− C. 0 326 x xy + D. 0 326 x xy +− Lời giải Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng ( )1 :0dy = và đường thẳng ( )2 :326.dxy+= Miền nghiệm gồm phần y nhận giá trị dương. Lại có ( )0;0 thỏa mãn bất phương trình 326. xy+ Câu 20: Cho hệ 235(1) 3 25(2) xy xy + + . Gọi 1S là tập nghiệm của bất phương trình (1), 2S là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì A. 12SS . B. 21SS . C. 2 SS = . D. 1 SS . Lời giải Trước hết, ta vẽ hai đường thẳng: ( )1 :235dxy+= ( )2 3 :5 2 dxy+= Ta thấy ( )0;0 là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 21: Khẳng định nào sau đây là đúng? A. 22 sin1 cos −= B. 22 sin1 cos −=− O 2 3 y x
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 10 C. 22 sin0 cos −= . D. 22 sin1 cos += . Lời giải. Câu 22: Khẳng định nào sau đây là đúng? A. ( )0sin180 cos −= . B. ( )0sin180 cos −=− . C. ( )0 sin180sin−= D. ( )0 sin180sin−=− Lời giải. Câu 23: Khẳng định nào sau đây là Sai? A. ( )0sin90 cos −= . B. 2 2 1 1cot sin += . C. 2 2 1 1tan sco += . D. cot sin cos = . Lời giải 2 2 1 1tan sco += sai vì tại 090 = không tồn tại tan. Câu 24: Cho góc thỏa mãn 4 sin 5 = . Tính giá trị biểu thức 5cos1P =− A. 4 . B. 3 . C. 3. . D. 4 Lời giải Ta có: 2 22 cos1sin149 525 =−=−= 3 cos 5 =− (vì 00 90180 ) Vậy 3 5.cos15.14 5 P =−=−−=− Câu 25: Cho tam giác ABC có 5AB = ; 7BC = ; 8AC = . Số đo góc A bằng A. 90 . B. 60 . C. 30 . D. 45 . Lời giải Ta có 5AB = ; 7BC = ; 8AC = Từ đó suy ra 2222228571 60 2.2.8.52 ACABBC cosAA ABAC +−+− ==== . Câu 26: Tam giác ABC có 8a = , 3c = , ˆ 60B = . Độ dài cạnh b bằng bao nhiêu A. 7 B. 97 C. 61 D. 49 Lời giải 8 3 60° A B C Áp dụng định lý cosin cho tam giác ABC
Ta có 222 2cos bacacB
Câu 27: Cho tam giác ABC thỏa mãn
A.
150C =
2.0
Lời giải
. Khi đó, góc C có số đo là
D.
30C =
BCACAB BCAC +− =
ABCD
hình
định lí hàm cosin, ta
Câu 29: Cho tam giác ABC
A. 5
Ta có
Vậy bán kính đường tròn
2
2
Theo đề ra ta có: 222 2.0BCACABBCAC +−−= 222 2. BCACABBCAC+−= 222 2 .
Câu 28: Cho hình thoi ABCD cạnh bằng 1 cm và có 60BAD = Tính độ dài cạnh AC
OFFICIAL
4
5C
kính đường tròn ngoại tiếp tam giác ABC
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 11
=+− 22 832.8.3.cos60497 b =+−== .
222
BCACABBCAC +−−=
ˆ
B. ˆ 60C = C. ˆ 45C =
ˆ
2cos20 C −=
cos
C =
ˆ
= .
A. 3.AC = B. 2.AC = C. 23.AC = D. 2.AC = Lời giải Do
là
thoi, có 60120BADABC== . Theo
có 222 2...cos ACABBCABBCABC =+− 22 112.1.1.cos1203 =+−= 3AC = .
có 30, 10ABC== Tính bán
B. 10 C. 10 3 D. 103 Lời giải
10 210 sin2sin2.sin30 BCBC RR AA ==== .
ngoại tiếp tam giác ABC là 10R = . Câu 30: Tam giác ABC có ˆˆ 60, 45BC== và 5AB = Tính độ dài cạnh AC A. 56 2 AC = B. 53.AC = C. 56 3 AC = D. 56 4 AC = Lời giải Theo định lí sin ta có: 00 556 sinsinsin452 sin60 ABACAC AC CB === Câu 31: Tìm chu vi tam giác ABC , biết rằng 6AB = và 2sin3sin4sin ABC == . A. 106 B. 26 C. 13 D. 526 Lời giải Từ giả thiết 2sin3sin4sin ABC == sin2sin 4 sinsin 3 AC BC = = Theo định lý sin trong tam giác ABC ta có sinsinsin ABBCAC CAB == 6 sin2sin4sin 3 BCAC CC C ==
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 6.2sin 12 sin 64sin8 sin3 C BC C ACC C == == 128626ABACBC ++=++= . Câu 32: Cho tam giác ABC có 9,18ABAC== và 60A = . Bán kính R của đường tròn ngoại tiếp tam giác ABC là: A. 3. B. 93 . C. 9. D. 6 . Lời giải Ta có: 222222...cos9182.9.18.cos6024393BCABACABACABC =+−=+−== 11813 ...sin.9.18.sin60 222ABC SABACA=== ....9.18.93 9. 44 4.813 2 ABACBCABACBC SR RS ==== Câu 33: Cho tam giác ABC biết độ dài ba cạnh , , BCCAAB lần lượt là , , abc thỏa mãn hệ thức ( ) ( )2222 bbacca −=− với bc . Khi đó, góc BAC bằng A. 45 B. 60 C. 120 D. 90 Lời giải Ta có ( ) ( ) ( )22223232332 0bbaccabbaccabcabc −=−−=−−−−= ( )( ) 222222 0 bcbbccabcabc −++−=+−=− Mặt khác : 222 1 cos120 222 bcabc BACBAC bcbc +−− ===−= . Câu 34: Cho tam giác ABC , biết rằng 00 60,45,4ABb=== . Tính cạnh a và c A. 4,9a và 5,5c B. 5,5a và 4,9c C. 5,5a và 6,3c D. 6,3a và 5,5c Lời giải Ta có sinsinsin abc ABC == . Suy ra sin4sin60 sinsin454,9 bA a B == và sin4sin75 sinsin455,5 bC c B == . Câu 35: Cho hình chữ nhật ABCD biết 1AD = . Giả sử E là trung điểm AB và thỏa mãn 1 sin 3 BDE = . Tính độ dài cạnh AB . A. 22 B. 5 C. 2 D. 3 Lời giải
Đề
có
Có 5 học sinh làm được câu 1, có 6
ọc sinh làm được câu
có
h
sinh làm được câu 3. Có 3 học sinh làm được câu 1 và câu 2, có 2 học sinh làm được câu 1 và câu 3, có 1 học sinh làm được câu 2 và câu 3 và chỉ có 1 học sinh làm được cả 3 câu. Hỏi có tất cả bao nhiêu học sinh tham gia làm bài khảo sát
Lời giải
Số học sinh chỉ làm được câu 1 và câu 2 là: 312 −= học sinh.
Số học sinh chỉ làm được câu 1 và câu 3 là: 211 −= học sinh.
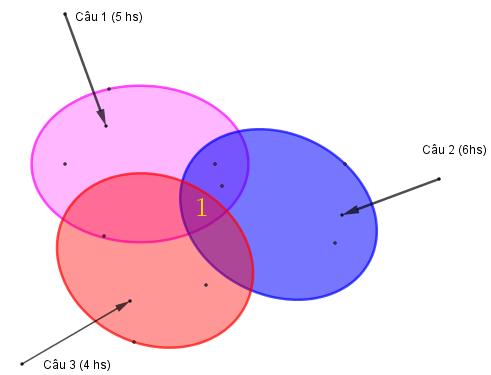
Số học sinh chỉ làm được câu 2 và câu 3 là: 110 −= học sinh.
Số học sinh chỉ làm được câu 1 là: ( ) 51121 −++= học sinh.
Số học sinh chỉ làm được câu 2 là: ( ) 61203 −++= học sinh.
Số học sinh chỉ làm được câu 3 là: ( ) 41102 −++= học sinh.
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 13 xx 1 E D C AB Đặt ( )0AEEBxx== . Ta có: ( )22 11 sin 1214 AD DBE BD xx === ++ Theo định lí sin trong tam giác BDE ta có: 2 2 1 sinsin11 3 14 EBEDxx BDEEBD x + == + 2231.14 xxx=++ ( ) ( ) 22242 91.144410 xxxxx =++−+= 2 12 22 xx == Vậy 22ABx== II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Lớp 10A chọn ra một số học sinh tham gia làm bài khảo sát học sinh giỏi môn Toán.
thi
3 câu. Sau khi chấm bài giáo viên tổng kết được như sau:
h
2,
4
ọc
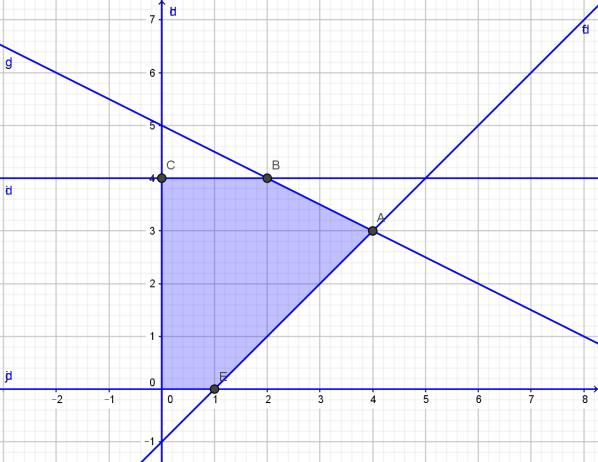
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 14 Tổng số học sinh tham gia làm khảo sát là: 53210 ++= học sinh. Câu 37: Tìm giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ với điều kiện 04 0 10 2100 y x xy xy −− +− là Lời giải Vẽ đường thẳng 1 :10dxy−−= , đường thẳng 1d qua hai điểm ( )0;1 và ( )1;0 . Vẽ đường thẳng 2 :2100dxy+−= , đường thẳng 2d qua hai điểm ( )0;5 và ( )2;4 Vẽ đường thẳng 3 :4dy = Miền nghiệm là ngũ giác ABCOE với ( ) ( ) ( ) ( )4;3,2;4,0;4,1;0ABCE Ta có: ( ) 4;310F = , ( ) 2;410F = , ( ) 0;48F = , ( ) 1;01F = , ( ) 0;00F = . Vậy giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ bằng 10 Câu 38: Cho tam giác ABC thỏa mãn sinsinsin coscos BC A BC + = + . Chứng minh tam giác ABC vuông. Lời giải Ta có: ( )sinsin sinsincoscossinsin coscos BC AABCBC BC + =+=+ + 222222 22222 aacbabcbc RacabRR +−+− +=+ ( ) ( )222222 222 bacbcabc abc RabcR +−++− + = ( ) ( ) ( )222222 2 bacbcabcbcbc +−++−=+ 22322322220abbcbacbccbcbc +−++−−−= 232322 0abbaccbcbc −+−−−= ( ) ( ) ( )223322 0abacbcbcbc +−+−+= ( ) ( )( ) ( )222 0abcbcbbccbcbc +−+−+−+= ( )( )222 0bcabc +−−= 222 0abc −−= 222 abcABC=+ vuông tại A (đpcm).
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 ĐỀ SỐ: 02 I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Trong các khẳng định sau có bao nhiêu khẳng định là mệnh đề? (I): “247 += ”. (II): “310 x −= ”. (III): “Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau”. (IV): “3 là số lẻ”. A. 1 . B. 3. C. 2 . D. 4 . Câu 2: Cho mệnh đề A : “ 2 :10xx + ”. Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A ? A. :A “ 2 :10xx + ”. B. :A “ 2 :10xx + ”. C. :A “ 2 :10xx + ”. D. :A “ 2 :10xx + ” . Câu 3: Cho tập hợp 34Axx=− . Khẳng định nào sau đây đúng? A. 2;1;0;1;2;3;4.A =−− . B. ( 3;4A =− . C. 2;1;0;1;2;3A =−− . D. 3;2;1;0;1;2;3;4A =−−− Câu 4: Cho hai tập hợp ( ( 1;5;2;7AB== . Tập hợp \ AB là: A. ( 1;2 . B. ( )2;5 . C. ( 1;7 . D. ( )1;2 . Câu 5: Cho tập hợp ;;1;2;3Aab = . Số tập con gồm 2 phần tử của tập A là A. 20. B. 10. C. 12. D. 15. Câu 6: Cho các tập hợp 1 5; 2 A =− , ( )3;B =−+ . Khi đó tập hợp AB bằng: A. 1 |3 2 xx − . B. 1 |3 2 xx − . C. 1 |5 2 xx − D. 1 |3 2 xx − Câu 7: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 22 230 xy+ B. 2 20 xy− C. 2 230 xy+ D. 230 xy+ Câu 8: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 530xy+− ? A. (1;2)M . B. ( )1;7N . C. ( )0;2P . D. ( )8;1Q . Câu 9: Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 360 240 xy xy B. 360 240 xy xy C. 360 240 xy xy D. 360 240 xy xy Câu 10: Cặp số nào sau đây là nghiệm của hệ bất phương trình 28 33 − + xy xy ? A. ( )0;1 . B. ( )0;4 . C. ( )1;1 . D. ( )1;1 .

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 2 Câu 11: Tìm hệ bất phương trình bậc nhất hai ẩn trong các hệ sau: A. 250 34100 xy xy +−= −−= B. 40 3260 xy xy −− +− C. 2 330 450 xx xy −− +− D. 2 70 350 xy xy +− −− Câu 12: Cho hệ bất phương trình bậc nhất hai ẩn 50 23200 xy xy +− −− có tập nghiệm S . Khẳng định nào sau đây đúng? A. ( )1;5 S . B. ( )1;2 S . C. ( )2;4 S− . D. ( )5;2 S− . Câu 13: Giá trị của biểu thức 4cos602sin303tan45A =+− bằng A. 1 2 B. 0 C. 1 4 D. 2 Câu 14: Cho 21sin cos =− . Khẳng định nào sau đây đúng? A. 90180 . B. 090 . C. 0180 . D. 0180 . Câu 15: Trên nửa đường tròn đơn vị có hai điểm , MM đối xứng nhau qua trục tung; gọi các góc xOM = , xOM = (như hình vẽ) Hỏi mối liên hệ giữa hai góc và là gì? A. Phụ nhau. B. Bù nhau. C. Bằng nhau. D. Hơn kém nhau 90 . Câu 16: Khăn quàng đội viên có hình tam giác cân với kích thước như trong hình vẽ. Góc lớn nhất của tam giác cân gần nhất với số đo nào? A. 90 B. 120 C. 135 D. 150 Câu 17: Cho tam giác ABC có 14cmAB = , 10cmAC = và 16cmBC = . Tính góc C của tam giác ABC A. 30 B. 45 C. 60 D. 120 Câu 18: Cho tam giác ABC có 3a = , 5b = và 7c = . Tính sin2sinsin SABC =−+ . A. 0 B. 1 C. 2 D. 1
C.
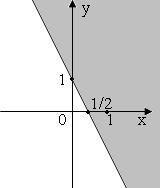
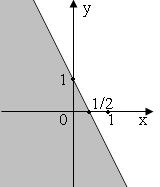
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 Câu 19: Cho tam giác ABC có 5a = , 60A = . Tính bán kính đường tròn ngoại tiếp tam giác ABC A. 103 3 . B. 5 3 . C. 53 . D. 53 3 . Câu 20: Tính diện tích tam giác ABC biết 2b = , 5c = , 30A = A. 10. B. 5. C. 5 2 . D. 53 . Câu 21: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. 2 ,280xx −= . B. 2 525 . C. 7395 D. ( )2 2 ,43xxx −+ Câu 22: Lập mệnh đề phủ định của mệnh đề 2 ":20220" xxx ++ A. 2 :20220xxx ++ . B. 2 :20220xxx ++ . C. 2 :20220xxx ++ . D. 2 :20220xxx ++ Câu 23: Cho hai tập 335 Axxx =++ , 5241Bxxx =−− . Tất cả các số tự nhiên thuộc cả hai tập A và B là: A. 2;3;4;5;6 . B. 1;2;3;4;5;6 . C. 2;3;4;5 . D. Không có. Câu 24: Trong các tập sau, tập nào là tập rỗng? A. |2xx . B. 2 |3210−−= xxx . C. 2 |410−+=xxx D. 2 |430−+=xxx Câu 25: Cho các tập hợp 2 |30Axxx=−= , 0;1;2;3B = . Tập \ BAbằng A. 1;2 . B. 5;6 . C. 0 . D. 0;1 . Câu 26: Biểu diễn hình học của tập nghiệm (phần mặt phẳng không bị tô đậm, tính cả biên) của bất phương trình 21 xy+ là A. . B. .
D. Câu 27: Phần không tô đậm trong hình vẽ biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 4 3 2 -3 O y x A. 23 xy− . B. 23xy− . C. 23xy− . D. 23 xy− . Câu 28: Điểm ( )x;yM là điểm có tung nhỏ nhất thuộc miền nghiệm của hệ bất phương trình 22 2 54 xy xy xy + − +− , khi đó ?Fyx=−= A. 8. B. 2. C. 2. D. 8. Câu 29: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 260 350 10 xy xy x +− −+ + ? A. ( )0;7M B. ( )1;1N C. ( )2;3P . D. ( )1;2Q Câu 30: Biết 2 sin 5 = ( )90180 . Hỏi giá trị tanlà bao nhiêu? A. 221 21 . B. 221 21 . C. 2. D. 2. Câu 31: Cho là góc tù và sin5 13 = Giá trị của biểu thức 3sin2cos + là A. 9 13 . B. 3. C. 9 13 . D. 3. Câu 32: Cho tam giác ABC có 4AB = , 7BC = , 9AC = . Tính sin A A. sin3 3 A = B. sin5 3 A =− C. sin5 3 A = D. sin5 3 A = Câu 33: Cho tam giác ABC có 2,4 ABaACa == và 120BAC = . Tính chiều cao AH của tam giác ABC . A. 23 7 AHa = B. 221 7 AHa = C. 23 7 AHa = D. 221AHa = Câu 34: Cho tam giác ABC cân tại A có cạnh 30b = và o120A = . Bán kính đường ngoại tiếp của tam giác ABC là A. 303R = . B. 153R = . C. 30R = . D. 302R = . Câu 35: Cho tam giác ABC vuông tại A có 4AB = và o60B = . Bán kính đường tròn nội tiếp của tam giác ABC là
chuyền này sản xuất ra sản
loại II. Mỗi sản phẩm loại I, loại II bán ra thu về lợi nhuận lần lượt là 35000 đồng và 50000 đồng. Để sản xuất được sản phẩm loại I thì An phải làm việc trong 1 giờ, Bình phải làm việc trong 30 phút. Để sản xuất được sản phẩm loại II thì An phải làm việc trong 30 phút, Bình phải làm việc trong 45 phút. Một người không thể làm đồng thời hai loại sản phẩm. Biết rằng trong một ngày An không thể làm việc quá 12 giờ, Bình không thể làm việc quá 10 giờ. Tìm lợi nhuận lớn nhất trong một ngày của dây chuyền sản xuất.
Câu 39: Cho hình chữ nhật ABCD có M là trung điểm của AD; N là trung điểm của đoạn BM ; I là trung điểm của đoạn NC . Biết 1AB = và 1 cos 4097 BIM =− . Tìm độ dài cạnh ?BC
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 5 A. 232r =− . B. 232r =+ . C. 23r = . D. 33r = . II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Cho tập 11 | 22 Ax x = và |12Bxx= . Tìm ( ) ( )\ ABAB . Câu 37: Tìm giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ , biết , xy thỏa mãn các điều kiện 04 0 10 2100 y x xy xy −− +− . Câu 38: Trong một dây chuyển sản xuất có hai công nhân là An và Bình. Dây
phẩm loại I và
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT
I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm)
Câu 1: Trong các khẳng định sau có bao nhiêu khẳng định là mệnh đề?
(I): “247 +=
(II): “310
(III): “Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau”. (IV): “3 là số lẻ”.
A. 1 .
Các khẳng định (I), (III), (IV) là mệnh đề.
C. 2 . D. 4 .
Lời giải
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 6
”.
x −= ”.
B. 3.
Câu 2: Cho mệnh đề A : “ 2 :10xx + ”. Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A ? A. :A “ 2 :10xx + ”. B. :A “ 2 :10xx + ”. C. :A “ 2 :10xx + ”. D. :A “ 2 :10xx + ” . Lời giải Mệnh đề phủ định A : “ 2 :10xx + ”. Câu 3: Cho tập hợp 34Axx=− . Khẳng định nào sau đây đúng? A. 2;1;0;1;2;3;4.A =−− B. ( 3;4A =− C. 2;1;0;1;2;3A =−− D. 3;2;1;0;1;2;3;4A =−−− Lời giải Ta có tập hợp 2;1;0;1;2;3;4A =−− Câu 4: Cho hai tập hợp ( ( 1;5;2;7AB== Tập hợp \ AB là: A. ( 1;2 B. ( )2;5 C. ( 1;7 D. ( )1;2 Lời giải Ta có ( \1;2AB = . Câu 5: Cho tập hợp ;;1;2;3Aab = . Số tập con gồm 2 phần tử của tập A là A. 20 B. 10. C. 12 D. 15 Lời giải Các tập con gồm 2 phần tử của tập hợp A là: ;,;1,;2,;3,;1,;2,;3,1;2,1;3,2;3 abaaabbb . Vậy có 10 tập con gồm 2 phần tử của tập A Câu 6: Cho các tập hợp 1 5; 2 A =− , ( )3;B =−+ . Khi đó tập hợp AB bằng: A. 1 |3 2 xx − . B. 1 |3 2 xx − . C. 1 |5 2 xx − D. 1 |3 2 xx − Lời giải
Lời
bất phương trình bậc nhất hai ẩn vì có chứa
xy
Câu 8: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 530xy+−
A. (1;2)M
thấy
giải
phương trình 530xy+− .
Câu 9: Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình nào sau đây?
A. 360 240 xy xy
B. 360 240 xy xy C. 360 240 xy xy D. 360 240 xy xy
Lời giải Thay cặp số ( )0;0O vào các hệ bất phương trình ta được đáp án 360 240 xy xy .
Câu 10: Cặp số nào sau đây là nghiệm của hệ bất phương
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 Ta có 1 3; 2 AB =− 1 |3 2 xx =− . Câu 7: Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? A. 22 230 xy+ . B. 2 20 xy− . C. 2 230 xy+ . D. 230 xy+ .
giải Bất phương trình 230 xy+ là bất phương trình bậc nhất hai ẩn. Các bất phương trình còn lại không phải
22 ,
?
B. ( )1;7N C. ( )0;2P D. ( )8;1Q Lời
Ta
cặp số ( )8;1 thỏa mãn bất phương trình 530xy+− nên điểm ( )8;1Q thuộc miền nghiệm của bất
trình 28 33 − + xy xy ? A. ( )0;1 . B. ( )0;4 . C. ( )1;1 . D. ( )1;1 . Lời giải Lần lượt thay các bộ số ở các phương án vào hệ bất phương trình ta được một nghiệm của hệ bất phương trình trên là ( )1;1 . Câu 11: Tìm hệ bất phương trình bậc nhất hai ẩn trong các hệ sau: A. 250 34100 xy xy +−= −−= . B. 40 3260 xy xy −− +− . C. 2 330 450 xx xy −− +− D. 2 70 350 xy xy +− −− Lời giải Hệ bất phương trình bậc nhất hai ẩn là 40 3260 xy xy −− +− Câu 12: Cho hệ bất phương trình bậc nhất hai ẩn 50 23200 xy xy +− −− có tập nghiệm S . Khẳng định nào sau đây đúng? A. ( )1;5 S . B. ( )1;2 S . C. ( )2;4 S− . D. ( )5;2 S− . Lời giải

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8 Vì 15510 +−= và 2.13.520330 −−=− nên ( )1;5 là nghiệm của hệ bất phương trình bậc nhất hai ẩn 50 23200 xy xy +− −− Vì 12520 +−=− và 2.13.220240 −−=− nên ( )1;2 không là nghiệm của hệ bất phương trình bậc nhất hai ẩn 50 23200 xy xy +− −− . Vì 24570 −−=− và ( ) 2.23.42060 −−−=− nên ( )2;4 không là nghiệm của hệ bất phương trình bậc nhất hai ẩn 50 23200 xy xy +− −− . Vì 52520 −−=− và ( ) 2.53.22040 −−−=− nên ( )5;2 là nghiệm của hệ bất phương trình bậc nhất hai ẩn 50 23200 xy xy +− −− Câu 13: Giá trị của biểu thức 4cos602sin303tan45A =+− bằng A. 1 2 . B. 0 . C. 1 4 . D. 2. Lời giải Ta có 11 4cos602sin303tan454.2.3.10 22 A =+−=+−= Câu 14: Cho 21sin cos =− . Khẳng định nào sau đây đúng? A. 90180 . B. 090 . C. 0180 . D. 0180 . Lời giải Ta có 22 1sin0 coscoscoscos =−== 090 . Câu 15: Trên nửa đường tròn đơn vị có hai điểm , MM đối xứng nhau qua trục tung; gọi các góc xOM = , xOM = (như hình vẽ) Hỏi mối liên hệ giữa hai góc và là gì? A. Phụ nhau B. Bù nhau C. Bằng nhau D. Hơn kém nhau 90 Lời giải Ta có , MM đối xứng nhau qua trục tung và , AA đối xứng nhau qua trục tung nên AMAMAMAMAOMAOM === s®s® Ta có 180AOMMOAAOMMOAAOA +=+== Vậy hai góc ; là hai góc bù nhau.


DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9 Câu 16: Khăn quàng đội viên có hình tam giác cân với kích thước như trong hình vẽ. Góc lớn nhất của tam giác cân gần nhất với số đo nào? A. 90 B. 120 C. 135 D. 150 Lời giải Đặt các đỉnh của hình tam giác như hình vẽ dễ thấy 12 tan59,7119,4 7 BH HCBHCBACB CH == . Vậy chọn 120ACB . Câu 17: Cho tam giác ABC có 14cmAB = , 10cmAC = và 16cmBC = . Tính góc C của tam giác ABC . A. 30 . B. 45 . C. 60 . D. 120 . Lời giải Ta có: 2222221016141 cos 2..2.10.162 ACBCAB C ACBC +−+− === 60C = . Câu 18: Cho tam giác ABC có 3a = , 5b = và 7c = . Tính sin2sinsin SABC =−+ A. 0 B. 1 C. 2 D. 1 Lời giải Ta có: 232.57 sin2sinsin20 22222 abcabc SABC RRRRR −+−+ =−+=−+=== . Câu 19: Cho tam giác ABC có 5a = , 60A = . Tính bán kính đường tròn ngoại tiếp tam giác ABC A. 103 3 . B. 5 3 . C. 53 . D. 53 3 . Lời giải Theo định lý sin: 553 2sin2.sin603 a R A === Câu 20: Tính diện tích tam giác ABC biết 2b = , 5c = , 30A = A. 10 B. 5 C. 5 2 D. 53 Lời giải Diện tích tam giác ABC là 115 sin.2.5.sin30 222 SbcA===
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 10 Câu 21: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. 2 ,280xx −= B. 2 525 C. 7395 . D. ( )2 2 ,43xxx −+ . Lời giải + Với 2x = thì 2 280 x −= nên A là đúng. + Ta có mệnh đề 5 và mệnh đề 2 25 là mệnh đề đúng nên mệnh đề “ 2 525 ” là mệnh đề đúng. Vậy B đúng. + Ta có mệnh đề "73" là mệnh đề sai và mệnh đề "95" là mệnh đề đúng nên mệnh đề “7395 ” là mệnh đề đúng. Vậy C đúng. + Với 1x =− thì ( )2 425x −= ; 2 34x += nên mệnh đề “ ( )2 2 ,43xxx −+ ” là mệnh đề sai. Câu 22: Lập mệnh đề phủ định của mệnh đề 2 ":20220" xxx ++ A. 2 :20220xxx ++ B. 2 :20220xxx ++ C. 2 :20220xxx ++ D. 2 :20220xxx ++ Lời giải Mệnh đề phủ định của mệnh đề 2 ":20220" xxx ++ là mệnh đề 2 :20220xxx ++ . Câu 23: Cho hai tập 335 Axxx =++ , 5741Bxxx =−− . Tất cả các số tự nhiên thuộc cả hai tập A và B là: A. 2;3;4;5;6 . B. 1;2;3;4;5;6 . C. 2;3;4;5 . D. Không có. Lời giải 335 =++ Axxx ( ) 1;.=+ A 5741=−− Bxxx ( ) ;6.=− B ( )1;6=AB 16.= ABxx 16= ABxx 2;3;4;5.= AB Câu 24: Trong các tập sau, tập nào là tập rỗng? A. |2xx B. 2 |3210−−= xxx C. 2 |410−+=xxx . D. 2 |430−+=xxx . Lời giải |20;1== AxxA 2 |32101 =−−== BxxxB . 2 |410 =−+== CxxxC . 2 |4301;3=−+== DxxxD Câu 25: Cho các tập hợp 2 |30Axxx=−= , 0;1;2;3B = . Tập \ BA bằng A. 1;2 . B. 5;6 . C. 0 . D. 0;1 . Lời giải
Biểu diễn hình học của tập nghiệm (phần mặt phẳng không bị tô đậm, tính cả biên) của bất phương trình
Đường thẳng :21dxy+= đi qua hai điểm ( )0;1 và 1 ;0 2 nên ta loại phương án C, D. Xét điểm ( )0;0O có 2.001 + . Do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ là đường thẳng d , không chứa gốc O (tính cả biên) nên la loại phương án B và chọn phương án A.



Câu 27: Phần không tô đậm trong hình vẽ biểu diễn tập nghiệm của bất phương trình nào trong các bất phương trình sau?

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 11 Ta có 2 3 30 0 x xx x = −= = nên 2 |300;3Axxx=−== . Theo định nghĩa \ xB xBA xA nên \1;2BA = . Câu 26:
21 xy+ là A. . B. . C. D. Lời giải
3 2 -3 O y x A. 23 xy− . B. 23xy− . C. 23xy− . D. 23 xy− . Lời giải Nhận xét: Miền nghiệm là phần chứa điểm ( )0;0O nên loại phương án 23xy− và 23 xy− . Đường thẳng d cắt trục Ox tại 3 ;0 2 A , cắt trục Oy tại ( )0;3B nên chọn đáp án 23 xy− .
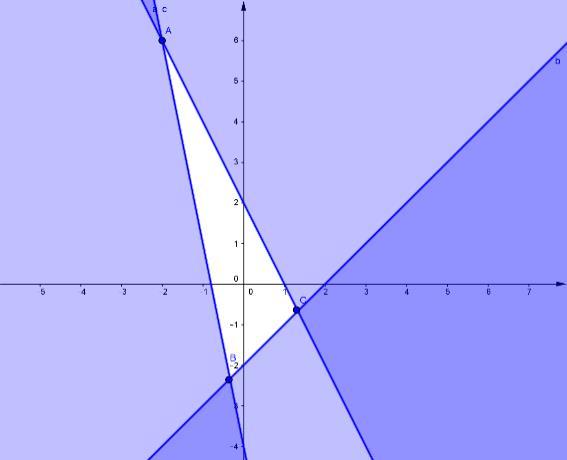
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 12 Câu 28: Điểm ( ); Mxy là điểm có tung nhỏ nhất thuộc miền nghiệm của hệ bất phương trình 22 2 54 xy xy xy + − +− , khi đó ?Fyx=−= A. 8 B. 2 C. 2 D. 8 Lời giải Miền nghiệm của hệ bất phương trình 22 2 54 xy xy xy + − +− trên hệ trục tọa độ Oxy là phần không bị xóa kể cả biên như hình vẽ Dựa vào hình vẽ ta có điểm có tung độ nhỏ nhất thuộc miền nghiệm của hệ bất phương trình là điểm 17 ; 33 B . Khi đó 71 2 33Fyx=−=−=− . Câu 29: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 260 350 10 xy xy x +− −+ + ? A. ( )0;7M . B. ( )1;1N . C. ( )2;3P . D. ( )1;2Q . Lời giải Thay tọa độ của điểm ( )0;7M vào hệ 260 350 10 xy xy x +− −+ + ta được 10 160 10 − không đúng. Thay tọa độ của điểm ( )1;1N vào hệ 260 350 10 xy xy x +− −+ + ta được 30 30 20 − đúng. Thay tọa độ của điểm ( )2;3P vào hệ 260 350 10 xy xy x +− −+ + ta được 10 20 30 − không đúng.
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 13 Thay tọa độ của điểm ( )1;2Q vào hệ 260 350 10 xy xy x +− −+ + ta được 60 20 00 − − không đúng. Vậy điểm thuộc miền nghiệm của hệ bất phương trình là ( )1;1N Câu 30: Biết 2 sin 5 = ( )90180 . Hỏi giá trị tanlà bao nhiêu? A. 221 21 . B. 221 21 . C. 2. D. 2. Lời giải Vì 90180 cos0 2cos1sin =−− 4 1 25 =−− 21 5 =− . Vậy sin tan cos = 221 21 =− . Câu 31: Cho là góc tù và sin5 13 = Giá trị của biểu thức 3sin2cos + là A. 9 13 . B. 3. C. 9 13 . D. 3. Lời giải Ta có 2 14412 cos1sincoscos 16913 =−== . Vì là góc tù nên cos0 , suy ra 12 cos 13 =− Vậy 3sin2cos325129 131313 +=+−=− . Câu 32: Cho tam giác ABC có 4AB = , 7BC = , 9AC = . Tính sin A A. sin3 3 A = . B. sin5 3 A =− . C. sin5 3 A = . D. sin5 3 A = . Lời giải Áp dụng định lí Côsin ABC , ta có: 222 2..cos. BCABACABACA =+− Suy ra: 222 cos 2.. ABACBC A ABAC +− = 222 4972 2.4.93 +− == . Ta có: 2 2222 sincos1sin1cos125 39 AAAA +==−=−= sin5 3 A = (vì sin0 A ). Vậy sin5 3 A = . Câu 33: Cho tam giác ABC có 2,4 ABaACa == và 120BAC = . Tính chiều cao AH của tam giác ABC . A. 23 7 AHa = . B. 221 7 AHa = . C. 23 7 AHa = . D. 221AHa = . Lời giải
Diện tích của tam giác ABC
dụng định lí Côsin ABC
.
Suy ra:
có:
Câu 34: Cho tam giác ABC cân tại A có cạnh 30b = và o120A = . Bán kính đường ngoại tiếp của tam giác ABC là
A. 303R = . B. 153R = . C. 30R = . D. 302R = .
Lời giải
Áp dụng định lí cosin cho tam giác ABC , ta có:
OFFICIAL
2cos30302.30.30.cos1202700
Suy ra 303a =
Áp dụng định lí sin cho tam giác ABC , ta có: 303 30 2sin2sin120 a R A ===
Vậy bán kính đường tròn ngoại tiếp tam giác ABC là 30
Câu 35: Cho tam giác ABC vuông tại
A. 232r
có
232
60B
. Bán kính đường tròn nội tiếp của tam giác ABC là
23r = . D. 33r = .
Lời giải
DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 14
là: 211 ..sin.2.4.sin12023. 22 SABACBACaaa === Áp
Ta
222 2..cos BCABACABACA =+− ( ) ( ) 22 22242.2.4.cos1202827. BCaaaaaBCa =+−==
2 12.2.23221 .. 27 27 Saa SAHBCAH BC a ==== . Vậy 221 7 AHa =
22222o
abcbcA=+−=+−=
R =
A
4AB = và o
=
=− . B.
r =+ . C.
Xét tam giác ABC vuông tại A , ta có: o .tan4.tan6043ACABB=== ; 22 8BCABAC=+= . Ta có diện tích tam giác ABC là Spr = , với r là bán kính đường tròn nội tiếp tam giác ABC và 2 ABBCAC p ++ = . Suy ra ..4.43 232 2 4843 ABACABAC r pABBCAC ====− ++ ++ Vậy bán kính đường tròn nội tiếp tam giác ABC là 232r =− . II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Cho tập 11 | 22 Ax x = và |12Bxx= Tìm ( ) ( )\ ABAB Lời giải Với 2x , ta có: 11 2204 22 xx x − , suy ra ( ) 0;4\2A = .
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 15 Ta có: 12 12 21 x x x −− , suy ra 2;11;2B =−− . ( )2;10;4AB=−− , )1;2AB= Suy ra: ( ) ( ) ( )\2;10;1ABAB=−− )2;4 . Câu 37: Tìm giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ , biết , xy thỏa mãn các điều kiện 04 0 10 2100 y x xy xy −− +− Lời giải Vẽ đường thẳng 1 :10dxy−−= , đường thẳng 1d qua hai điểm ( )0;1 và ( )1;0 Vẽ đường thẳng 2 :2100dxy+−= , đường thẳng 2d qua hai điểm ( )0;5 và ( )2;4 Vẽ đường thẳng 3 :4dy = . Miền nghiệm là ngũ giác ABCOE với ( ) ( ) ( ) ( )4;3,2;4,0;4,1;0ABCE Ta có: ( ) 4;310F = , ( ) 2;410F = , ( ) 0;48F = , ( ) 1;01F = , ( ) 0;00F = Vậy giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ bằng 10 Câu 38: Trong một dây chuyển sản xuất có hai công nhân là An và Bình. Dây chuyền này sản xuất ra sản phẩm loại I và loại II. Mỗi sản phẩm loại I, loại II bán ra thu về lợi nhuận lần lượt là 35000 đồng và 50000 đồng. Để sản xuất được sản phẩm loại I thì An phải làm việc trong 1 giờ, Bình phải làm việc trong 30 phút. Để sản xuất được sản phẩm loại II thì An phải làm việc trong 30 phút, Bình phải làm việc trong 45 phút. Một người không thể làm đồng thời hai loại sản phẩm. Biết rằng trong một ngày An không thể làm việc quá 12 giờ, Bình không thể làm việc quá 10 giờ. Tìm lợi nhuận lớn nhất trong một ngày của dây chuyền sản xuất. Lời giải Gọi x , y lần lượt là số sản phẩm loại I và loại II được sản xuất ( ), xy .
Lợi nhuận trong một ngày của dây chuyển sản xuất là 3500050000 Txy =+ (đồng)
Dựa vào miền nghiệm, ta thấy T chỉ đạt giá trị lớn nhất tại các điểm ,,, OABC .
Mà A có tọa độ không nguyên nên loại.
Tại ( )0;0O 0T = đồng.
Tại ( )8;8B 35000.850000.8680000T =+= đồng.


Tại ( )12;0C 35000.1250000420000T =+= đồng. Vậy lợi nhuận lớn nhất trong ngày là 680000 đồng.
39: Cho hình ch
điể
nh
t
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 16 Ta có hệ bất phương trình sau: ( ) 0,512 0,50,7510 0 0 xy xy x y + + Miền nghiệm của hệ bất phương trình ( ) được biểu diễn là
Câu
ữ
ậ
ABCD có M là trung điểm của AD ; N là trung điểm của đoạn BM ; I là trung
m của đoạn NC . Biết 1AB = và 1 cos 4097 BIM =− . Tìm độ dài cạnh ?BC Lời giải Đặt ( )20BCxx= . Ta có: 222 1BMCMx==+ . ( ) ( ) ( )222222 2 2 22411 91 444 CBCMMBxxx CNx +−++−+ + === . ( ) 22 2 222 2 2 24191 2 44 251 4416 xx BNBCCNx x BI ++ +−+−+ ===
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 17 ( ) 22 2 222 2 2 21191 2 44 9 4416 xx MNMCCNx x MI ++ +−++−+ === . Ta có: 222 cos 2.. IBIMMB BIM IBIM +− = 22 2 22 2519 1 16161 2.25194097 1616 xx x xx ++ +−− =− ++ ( ) 2 222 22 531 4097352519 25194097 x xxx xx =−=++ ++ ( ) ( )( ) ( ) 2 2 2 22242 350 350 409735251902564004811440 x x xxxxx − − −−++=−+= ( )( )( )( ) 2 350 256434354540 x xxxx − −+−+= 2 350 3 4 3 4 4 5 4 5 x x x x x − = = = = 3 4 x = Do đó: 3 2 BC =
Câu
Phát biểu nào dưới
Câu
Phủ
A. Nếu phương trình
axbxc
mệnh
hai nghiệm trái dấu thì .0
B. Nếu phương trình
0axbxc
thì phương trình 2 0axbxc++= có hai nghiệm trái dấu.
C. Phương trình 2 0axbxc++= có hai nghiệm trái dấu khi và chỉ khi .0ac .
D. .0ac là điều cần và đủ để phương trình 2 0axbxc++= có hai nghiệm trái dấu.
Câu 5: Cho tập hợp |2110Ann=+ . Hãy viết tập hợp A bằng cách liệt kê các phần tử của tập hợp.
A. 0;1;2;3;4;5A = B. 0;1;2;3;4;5;6;7;8;9
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 1 ĐỀ ÔN TẬP KIỂM TRA GIỮA HKI NĂM HỌC 2022 2023 MÔN: TOÁN 10 ĐỀ SỐ: 03 I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm)
1:
đây không là một mệnh đề? A. 0axb+= luôn có nghiệm. B. 3 . C. Bạn học giỏi toán! D. 1012
2:
định của mệnh đề 4 là A. 4 . B. 4 C. 4 D. 4 Câu 3: Mệnh đề nào dưới đây sai? A. 2 ,161xx = B. 2 ,320xxx −+= C. 2 ,40xx −= D. 2 ,61130xxx −+= Câu 4: Cho mệnh đề P : “ Phương trình 2 0axbxc++= có hai nghiệm trái dấu”, mệnh đề Q : “ Phương trình 2 0axbxc++= có .0ac ”. Mệnh đề đảo của
đề PQ là
2 0
++= có
ac .
2
++= có .0ac
A = C. 1;2;3;4A = . D. 0;1;2;3;4A = . Câu 6: Tập hợp 2;1;0;1;2A =−− được viết dưới dạng chỉ ra tính chất đặc trưng cho các phần tử của nó là A. |2Axx= B. |2Axx= C. |2Axx= D. |2Axx= Câu 7: Cho tập ( )( ) 2232150Axxxx =−+−= và 22Bxx=− . Khẳng định nào dưới đây là sai? A. 1 AB . B. \2;15AB = . C. \1;0BA =− . D. 1;2AB= . Câu 8: Cho các khẳng định sau: (I) ( )1;1xx=− (II) (III) 1 (IV) Số khẳng định sai là: A. 1. B. 2. C. 3 D. 4.
Câu
sau
A.
Câu 10: Cho hai tập
A.
Câu 11: Biểu diễn
A.
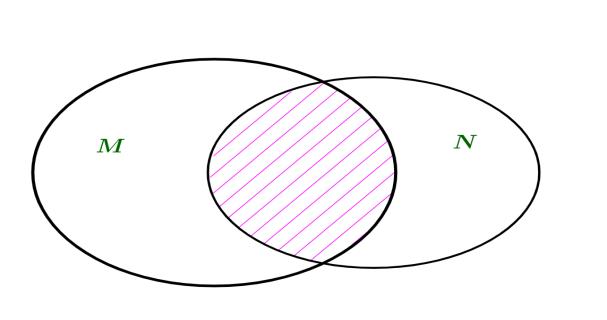
B. C.
Câu 12: Cho hai tập
sau đây đúng?
OFFICIAL
Khẳng định nào sau đây là đúng?

DẠYKÈMQUYNHƠN
Sưu tầm và biên soạn Page 2
9: Cho M , N là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ dưới đây là tập hợp nào
đây?
MN B. \ MN C. M CN D. MN
hợp , MN và MN . Mệnh đề nào
\ MN B. \ MNN = C. \ N NMCM = D. \ MNM =
của tập hợp |13Axx= trên trục số là
.
D.
hợp |12,|3101AxNxBxx =−=+ .
A. 2;3;4;...B CA = B. 3;2;1;2;3;4;...B CA =−−− C. 0;1;2;3;4;...B CA = . D. 2;1;2;3;4;...B CA =−− . Câu 13: Cho các tập hợp: M = xx là bội số của 2 N = xx là bội số của 6 P = xx là ước số của 2 .Q = xx là ước số của 6 . Mệnh đề nào sau đây đúng? A. MN B. QP C. MNN = D. PQQ = Câu 14: Miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− là nửa mặt phẳng không chứa điểm A. ( )0;0 . B. ( )1;1 . C. ( )4;2 . D. ( )1;1 . Câu 15: Bất phương trình nào sau đây là bất phương trình bật nhất hai ẩn? A. 32xy+ . B. 2 3xy+ . C. ( )( ) 325 xyxy−+ D. 3 20y −
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 3 Câu 16: Miền nghiệm của bất phương trình 326 xy−− là A. B. C. D. Câu 17: Phần không bị gạch kể cả bờ trong hình vẽ là miền nghiệm của bất phương trình nào sau đây? f(x)=x-1 Bóng1 -3 -2 -1 1 2 3 4 -3 -2 -1 1 2 3 x y O A. 1+xy . B. xy1 − . C. 1+xy . D. 1xy− . Câu 18: Cho góc x , 00 090 x thỏa mãn 2=cot x . Tìm cos x A. 25 5 =cosx . B. 25 5 =−cos x . C. 1 5 =cos x . D. 5 5 =cos x . Câu 19: Biết 1 cos 2 = với 00 0180 thì A. 030 = B. 045 = C. 060 = D. 0120 = Câu 20: Cho 0 2311'38'' = , khi đó kết quả của sin gần bằng với giá trị nào sau đây nhất A. 0,3907 B. 0,3936 C. 0,3938 D. 0,933 O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x
Câu 21: Cho tam giác ABC có có 8a = , 3c = , 60B = . Độ dài cạnh b bằng bao nhiêu?
A. 49 B. 97 C. 61 D. 7
Câu 22: Cho ABC có BCa = , 120BAC = . Bán kính đường tròn ngoại tiếp ABC là
A. 3 2 a R = B. 2 a R = C. 3 3 a R = D. Ra =
Câu 23: Cho tam giác ABC có 06,4,120ABACA=== . Độ dài cạnh BC bằng.
A. 19 B. 219 C. 319 D. 27
Câu 24: Cho tam giác ABC vuông tại A , ACb = , ABc = . Lấy điểm M trên cạnh BC sao cho góc 30BAM = Tính tỉ số MB MC
A. 3 3 b c . B. 3
3
D. bc bc
Câu 25: Minh và Quân đứng ở hai địa điểm A , B và cách địa điểm C lần lượt là 3km và 4km. Biết rằng các địa điểm ,, ABC tạo thành tam giác vuông tại C . Khi đó Minh và Quân cách nhau một khoảng bằng
OFFICIAL
A. 5km B. 3km C. 7km D. 1km
.
Câu 26: Ba địa điểm ,, ABC tạo thành một tam giác vuông tại A , 3kmAB = và 60oABC = . Bạn Luân đứng ở địa điểm D thẳng hàng với hai địa điểm , BC ( D nằm giữa B và C ) và cách B một khoảng bằng 2 3 khoảng cách giữa hai địa điểm , BC . Khi đó bạn Luân đứng cách địa điểm C một khoảng bằng
A. 4km . B. 2km. C. 3km. D. 5km.
Câu 27: Cho tam giác ABC có b = 7; c = 5, 3 cos 5 =A . Đường cao a h của tam giác ABC là
A. 72 . 2 B. 8. C. 83. D. 803.
Câu 28: Cho hình vuông ABCD có cạnh bằng 8, M là trung điểm của CD. Tính bán kính đường tròn ngoại tiếp tam giác ACM
A. 210 B. 25 C. 310 D. 410
biên soạn
DẠYKÈMQUYNHƠN
Sưu tầm và
Page 4
c b . C.
3 c b .
+
Câu 29: Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là
030 và 055 . Biết khoảng cách giữa hai vị trí A, B là 40m. Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
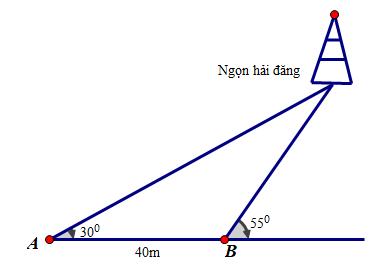
A. 10,3m . B. 67,1m . C. 38,7m. D. 60,8m .
Câu 30: Cho lục giác đều ABCDEF tâm O . Số các véctơ khác véctơ không cùng phương với véctơ
OA (không tính véctơ OA ) là
OFFICIAL
A. 5. B. 6. C. 9. D. 10.
Câu 31: Chọn mệnh đề đúng trong các mệnh đề sau
A. Hai vectơ cùng phương thì cùng hướng.
B. Hai vectơ cùng hướng thì bằng nhau
C. Hai vectơ bằng nhau thì cùng phương
D. Hai vectơ cùng phương thì ngược chiều.
Câu 32: Cho lục giác đều ABCDEF tâm O . Ba vectơ bằng vectơ BA là:
A. ,, OFEDOC . B. ,, CAOFDE . C. ,, OFDECO . D. ,, OFDEOC .
Câu 33: Cho các điểm phân biệt ,, ABC . Đẳng thức nào sau đây đúng?
A. ABBCCA =+ . B. ABBCAC =+ . C. ABCACB =+ . D. ABACCB =+ .
Câu 34: Cho hình bình hành ABCD. Tìm các vec tơ đối của BC mà có điểm đầu, điểm cuối là các đỉnh của hình bình hành ABCD
A. CB và DA B. AD C. CD D. DC và AB
Câu 35: Cho hình bình hành ABCD, giao điểm
Sưu tầm và biên soạn
DẠYKÈMQUYNHƠN
Page 5
của hai đường chéo là O . Tìm mệnh đề sai trong các mệnh đề sau: A. COOBBA −= . B. ABBCDB −= . C. DADBODOC −=− . D. 0DADBDC++= . II. PHẦN TỰ LUẬN (3,0 điểm) Câu 36: Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là bao nhiêu?
Câu 37: Một người thợ mộc làm những chiếc bàn và những chiếc ghế. Mỗi một chiếc bàn khi bán lãi 150 nghìn đồng. Mỗi một chiếc ghế khi bán lãi 50 nghìn đồng. Người thợ mộc có thể làm 40 giờ/tuần và tốn 6 giờ để làm một cái bàn, 3 giờ để làm một cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế ít nhất là gấp 3 số bàn. Một chiếc bàn chiếm chỗ bằng 4 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần. Tìm phương án cho người thợ mộc để trong tuần số lãi thu được là lớn nhất.
Câu 38: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được 24 ABm = , 63CAD = , 48CBD = .
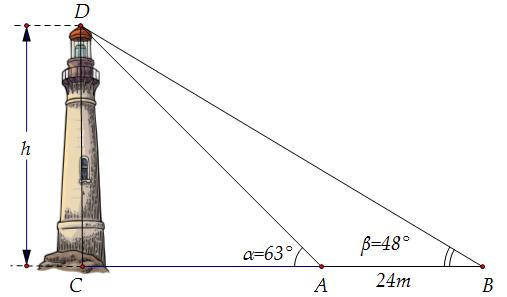
OFFICIAL
Tính chiều cao h của khối tháp.
Câu 39: Cho hình vuông ABCD cạnh a . Trên các cạnh BC , AB lần lượt xác định điểm E , K sao cho 3 CEEB, AKKB. Đường thẳng d đi qua A vuông góc với DE cắt BC tại F , KF cắt DE tại J . Tính EJEF .
và biên soạn
DẠYKÈMQUYNHƠN
Sưu tầm
Page 6
---------- HẾT ----------
Khẳng
DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 7 HƯỚNG DẪN GIẢI CHI TIẾT I. PHẦN TRẮC NGHIỆM (35 câu 7,0 điểm) Câu 1: Phát biểu nào dưới đây không là một mệnh đề? A. 0axb+= luôn có nghiệm. B. 3 C. Bạn học giỏi toán!. D. 1012 Lời giải +) 0axb+= luôn có nghiệm là một mệnh đề đúng. +) 3 : là một mệnh đề đúng +) 1012 : là một mệnh đề sai +) Bạn học giỏi toán!: là một câu cảm thán nên không phải là mệnh đề. Câu 2: Phủ định của mệnh đề 4 là A. 4 . B. 4 . C. 4 . D. 4 . Lời giải Mệnh đề 4 đọc là: pi lớn hơn bốn Vậy phủ định mệnh đề này đọc là: pi không lớn hơn bốn Nên ta có 4 Câu 3: Mệnh đề nào dưới đây sai? A. 2 ,161xx = . B. 2 ,320xxx −+= . C. 2 ,40xx −= . D. 2 ,61130xxx −+= . Lời giải Khẳng định A đúng vì 2 1 161 4 xx== Khẳng định B đúng vì 2 3201;2xxxx −+===
định C đúng vì 2 402,2xxx −==−= trong đó 2 Khẳng định D sai vì với 2 13 61130, 32 xxxx −+=== Câu 4: Cho mệnh đề P : “ Phương trình 2 0axbxc++= có hai nghiệm trái dấu”, mệnh đề Q : “ Phương trình 2 0axbxc++= có .0ac ”. Mệnh đề đảo của mệnh đề PQ là A. Nếu phương trình 2 0axbxc++= có hai nghiệm trái dấu thì .0ac . B. Nếu phương trình 2 0axbxc++= có .0ac thì phương trình 2 0axbxc++= có hai nghiệm trái dấu. C. Phương trình 2 0axbxc++= có hai nghiệm trái dấu khi và chỉ khi .0ac . D. .0ac là điều cần và đủ để phương trình 2 0axbxc++= có hai nghiệm trái dấu. Lời giải Mệnh đề đúng là B. Câu 5: Cho tập hợp |2110Ann=+ . Hãy viết tập hợp A bằng cách liệt kê các phần tử của tập hợp. A. 0;1;2;3;4;5A = . B. 0;1;2;3;4;5;6;7;8;9A = . C. 1;2;3;4A = D. 0;1;2;3;4A = Lời giải

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 8 Ta có |21100;1;2;3;4Ann=+= . Câu 6: Tập hợp 2;1;0;1;2A =−− được viết dưới dạng chỉ ra tính chất đặc trưng cho các phần tử của nó là A. |2Axx= B. |2Axx= C. |2Axx= D. |2Axx= Lời giải Ta có 2;1;0;1;2|2Axx =−−= Câu 7: Cho tập ( )( ) 2232150Axxxx =−+−= và 22Bxx=− . Khẳng định nào dưới đây là sai? A. 1 AB B. \2;15AB = C. \1;0BA =− D. 1;2AB= Lời giải Ta có: 1;2;15;15 1;0;1 A B =− =− Nên: 1,\2;15,\1;0ABABBA ===− . Chọn D Câu 8: Cho các khẳng định sau: (I) ( )1;1xx=− (II) (III) 1 (IV) Số khẳng định sai là: A. 1. B. 2. C. 3 D. 4. Lời giải Các khẳng định (I), (IV) đúng. Các khẳng định (II), (III) sai. Câu 9: Cho M , N là hai tập hợp bất kì. Phần gạch sọc trong hình vẽ dưới đây là tập hợp nào sau đây? A. MN B. \ MN C. M CN D. MN Lời giải Theo biểu đồ Ven thì phần gạch sọc trong hình vẽ là tập hợp MN .
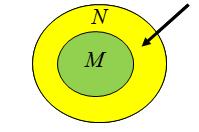

DẠYKÈMQUYNHƠN OFFICIAL Sưu tầm và biên soạn Page 9 Câu 10: Cho hai tập hợp , MN và MN . Mệnh đề nào sau đây đúng? A. \ MN . B. \ MNN = . C. \ N NMCM = . D. \ MNM = . Lời giải Theo giả thiết ta có MN . Ta có sơ đồ Ven, ta có \ N NMCM = Câu 11: Biểu diễn của tập hợp |13Axx= trên trục số là A. . B. . C. . D. . Lời giải Ta có )|131;3Axx== được biểu diễn trên trục số như sau Câu 12: Cho hai tập hợp |12,|3101AxNxBxx =−=+ . Khẳng định nào sau đây là đúng? A. 2;3;4;...B CA = B. 3;2;1;2;3;4;...B CA =−−− C. 0;1;2;3;4;...B CA = .D. 2;1;2;3;4;...B CA =−− . Lời giải Ta có: 0;1A = |31012;1;0;1;2;3;...Bxx=+=−− Dễ thấy AB Ta có 2;1;2;3;4;...B CA =−− Câu 13: Cho các tập hợp: M = xx là bội số của 2 . N = xx là bội số của 6 . P = xx là ước số của 2 Q = xx là ước số của 6 Mệnh đề nào sau đây đúng? A. MN . B. QP . C. MNN = . D. PQQ = . Lời giải