BÀI GIẢNG TOÁN 10 BỘ SÁCH KẾT NỐI TRI THỨC - BÀI TẬP TỰ LUẬN, TRẮC NGHIỆM THEO DẠNG (CHƯƠNG 1-3) by Dạy Kèm Quy Nhơn Official

BÀI GIẢNG TOÁN 10 BỘ SÁCH KẾT NỐI TRI THỨC Ths Nguyễn Thanh Tú eBook Collection BÀI GIẢNG TOÁN 10 BỘ SÁCH KẾT NỐI TRI THỨC VỚI CUỘC SỐNG TÓM TẮT LÝ THUYẾT BÀI TẬP TỰ LUẬN, TRẮC NGHIỆM THEO DẠNG (1935 TRANG) (CHƯƠNG 1 3) WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/30416001

DẠYKÈMQUYNHƠN OFFICIALTÀI LIỆU TOÁN 10 .............. BÀI GIẢNG TOÁN 10 BỘ SÁCH KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 1. TÓM TẮT LÝ THUYẾT 2. BÀI TẬP TỰ LUẬN THEO DẠNG 3. BÀI TẬP TRẮC NGHIỆM THEO DẠNG Học sinh: …………………………… Giáo viên giảng dạy: …………………….. Điện thoại: ………………………

DẠYKÈMQUYNHƠN OFFICIAL

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1 BÀI1:MỆNHĐỀ 1. MỆNH ĐỀ, MỆNH ĐỀ CHỨABIẾN a. Mệnh đề: Mệnh đề là những khẳng định có tính đúng hoặc sai. Người ta gọi là một mệnh đề lôgic (gọi tắt là mệnh đề). Những câu không xác định được tính đúng sai không phải là mệnh đề. Chú ý : Người ta thường sử dụng các chữ cái ,, PQR ,…để biểu thị các mệnh đề. Câu Không phải mệnh đề Mệnh đề đúng Mệnh đề sai 13 là số nguyên tố ? ? ? Tổng độ dài hai cạnh bất kì của một tam giác nhỏ hơn độ dài cạnh còn lại ? ? ? Bạn đã làm bài tập chưa? ? ? ? Thời tiết hôm nay thật đẹp! ? ? ? b. Mệnh đề chứa biến Xét câu “ n chia hết cho 2” (với n là số tự nhiên). Ta chưa khẳng định được tính đúng sai của câu này, do đó nó chưa phải là một mệnh đề Tuy nhiên, nếu thay n bằng số tự nhiên cụ thể thì câu này cho ta một mệnh đề. Chẳng hạn: • Với 5n = ta được mệnh đề “5 chia hết cho 2”. Đây là mệnh đề sai. • Với 10n = ta được mệnh đề “10 chia hết cho 2”. Đây là mệnh đề đúng. Ta nói rằng câu “ n chia hết cho 2” là một mệnh đề chứa biến. 2. MỆNH ĐỀ PHỦ ĐỊNH Để phủ định một mệnh đề P, người ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề P. Ta kí hiệu mệnh đề phủ định của mệnh đề P là P CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I = Mỗi mệnh đề phải hoặc đúng hoặc sai. Một mệnh đề không thể vừa đúng vừa sai Luyện tập 1. Hãy điền dấu ‘’x’’ vào ô thích hợp trong bẳng sau : Mệnh đề P và mệnh đề P là hai phát biểu trái ngược nhau. Nếu P đúng thì P sai, còn nếu P sai thì P đúng.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 P: “2022 chia hết cho 5” ; Q: “Bất phương trình 210 x + có nghiệm”. Vận dụng. Cho mệnh đề Q: “Châu Á là châu lục có diện tích lớn nhất trên thế giới”. Phát biểu mệnh đề phủ định Q và xác định tính đúng sai của hai mệnh đề Q và Q . 3. MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO a. Mệnh đề kéo theo Mệnh đề PQ  chỉ sai khi P đúng và Q sai. Các định lí toán học là những mệnh đề đúng và thường có dạng PQ  . Khi đó ta nói: b. Mệnh đề đảo Nhận xét. Mệnh đề đảo của một mệnh đề đúng không nhất thiết là mệnh đề đúng. a) Hãy phát biểu định lí PQ  Nêu giả thiết, kết luận của định lí và phát biểu định lí này dưới dạng điều kiện cần, điều kiện đủ. b) Hãy phát biểu mệnh đề đảo của mệnh đề PQ  xác định tính đúng sai của mệnh đề đảo này. 4. MỆNH ĐỀ TƯƠNG ĐƯƠNG Nhận xét. Nếu cả hai mệnh đề PQ  và QP  đều đúng thì mệnh đề tương đương PQ  đúng. Khi đó ta nói “ P tương đương với Q ” hoặc “ P là điều kiện cần và đủ để có Q ” hoặc “ P khi và chỉ khi Q ”. Luyện tập 2. Phát biểu mệnh đề phủ định của mỗi mệnh đề sau và xác định tính đúng sai của mệnh đề phủ định đó. Mệnh đề ‘’Nếu P thì Q ’’ được gọi là một mệnh đề kéo theo và kí hiệu PQ  P là giả thiết của định lí, Q là kết luận của định lí, hoặc “ P là điều kiện đủ để có Q ” hoặc “Q là điều kiện cần để có P ”. Mệnh đề QP  được gọi là mệnh đề đảo của mệnh đề PQ  Luyện tập 3 Cho các mệnh đề : “ và chia hết cho ” ; : “ chia hết cho ” Mệnh đề “ P nếu và chỉ nếu Q ” được gọi là một mệnh đề tương đương và kí hiệu là PQ  Luyện tập 4. Phát biểu điều kiện cần và đủ để số tự nhiên chia hết cho

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3 5. MỆNH ĐỀ CÓ CHỨAKÍ HIỆU ∀,∃ Kí hiệu  đọc là ''với mọi'' . Kí hiệu  đọc là ''có một'' (tồn tại một) hay''có ít nhất một''(tồn tại ít nhất một). Cho mệnh đề ", ()"xXPx  Mệnh đề phủ định của mệnh đề ", ()"xXPx là mệnh đề ", ()".xXPx  Mệnh đề phủ định của mệnh đề ", ()"xXPx là mệnh đề ", ()".xXPx Ví dụ: Câu ''Bình phương của mọi số thực đều lớn hơn hoặc bằng 0'' là một mệnh đề. Có thể viết mệnh đề này như sau 2 :0xx  hay 2 0,.xx Kí hiệu  đọc là ''với mọi'' . Ví dụ: Câu ''Có một số nguyên nhỏ hơn 0'' là một mệnh đề. Có thể viết mệnh đề này như sau :0.nn  Kí hiệu  đọc là ''có một'' (tồn tại một) hay''có ít nhất một''(tồn tại ít nhất một).  Mệnh đề phủ định của mệnh đề ", ()"xXPx là ", ()".xXPx Ví dụ: Cho mệnh đề 2 “,70” xxx −+ . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải Phủ định của mệnh đề 2 “,70” xxx −+ là mệnh đề 2 “,70” xxx −+  Mệnh đề phủ định của mệnh đề ", ()"xXPx là ", ()".xXPx Ví dụ: Cho mệnh đề 2 “,60” xxx −−= . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải Phủ định của mệnh đề 2 “,60” xxx −−= là mệnh đề 2 “,60” xxx −− . 1.1. Trong các câu sau, câu nào là mệnh đề? a) Trung Quốc là nước đông dân nhất thế giới; b) Bạn học trường nào? c) Không được làm việc riêng trong trường học; d) Tôi sẽ sút bóng trúng xà ngang. 1.2. Xét tính đúng sai của các mệnh đề sau: HỆ THỐNG BÀI TẬP.II = BÀI TẬP SÁCH GIÁO KHOA.1 =

a) 10 3   ;

b) Phương trình370 x += có nghiệm; c) Có ít nhất một số cộng với chính nó bằng 0; d) 2022 là hợp số.

1.3. Cho hai câu sau:

P: “Tam giác ABC là tam giác vuông”;

Q: “Tam giác ABC có một góc bằng tổng hai góc còn lại”. Hãy phát biểu mệnh đề tương đương PQ  xét tính đúng sai của mệnh

OFFICIAL

ệnh đề 22 :""Pab  và :"0"Qab 

a) Hãy phát biểu mệnh đề PQ  .

b) Hãy phát biểu mệnh đề đảo của mệnh đề ở câu a.

c) Xác định tính đúng sai của mỗi mệnh đề ở câu a và câu b.

1.6. Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó.

Q: “ n  , n chia hết cho n+1”.

1.7. Dùng kí hiệu ,  để viết các mệnh đề sau:

P: “Mọi số tự nhiên đều có bình phương lớn hơn hoặc bằng chính nó”;

một số thực

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4

đề này. 1.4. Phát biểu mệnh đề đảo của mỗi mệnh đề sau và xác định tính đúng sai chúng.

“Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”; Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”. 1.5. Với hai số thực a và b, xét các m

Q: “ Có

cộng với chính nó bằng 0”.  DẠNG 1: XÁC ĐỊNH MỀNH ĐỀ VÀ MỆNH ĐỀ CHỨA BIẾN PHƯƠNG PHÁP Để xác định mệnh đề và mệnh đề chứa biến ta cần biết:  Mệnh đề là một câu khẳng định đúng hoặc sai. Một mệnh đề không thể vừa đúng hoặc vừa sai  Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập X nào đó mà với mỗi giá trị chứa biến thuộc X ta được một mệnh đề Bài 1. Các câu sau đây, có bao nhiêu câu là mệnh đề? (1) Ở đây đẹp quá! BÀI TẬP TỰ LUẬN.2 =

(2) Phương trình 2 310xx−+= vô nghiệm

(3) 16 không là số nguyên tố

(4) Hai phương trình 2 430xx−+= và 2 310xx−++= có nghiệm chung.

(5) Số  có lớn hơn 3 hay không?

(6) Italia vô địch Worldcup 2006

(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.

(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.

Bài 2. Cho ba mệnh đề sau, với n là số t

(1) 8n + là số chính phương

(2) Chữ s

n cùng c

(3) 1n là số chính phương

nhiên

OFFICIAL

ng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào, đúng mệnh đề nào sai?

Biết r

Bài 3. Tại Tiger Cup 98 có bốn đội lọt vào vòng bán kết: Việt Nam, Singapor, Thái Lan và Inđônêxia. Trước khi thi đấu vòng bán kết, ba bạn Dung, Quang, Trung dự đoán như sau:

Dung: Singapor nhì, còn Thái Lan ba.

Quang: Việt Nam nhì, còn Thái Lan tư.

Trung: Singapor nhất và Inđônêxia nhì.

Kết quả, mỗi bạn dự đoán đúng một đội và sai một đội. Hỏi mỗi đội đã đạt giải

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5

ự

ố

ậ

ủa n là 4

ằ

mấy? Bài 4: Trong các phát biểu sau, phát biểu nào không phải là mệnh đề, giải thích? 1/ Hải Phòng là một thành phố của Việt Nam. 2/ Bạn có đi xem phim không? 3/ 10 21 chia hết cho 11 4/ 2763 là hợp số. 5/ 2 320xx−+= Bài 5: Trong các phát biểu sau, phát biểu nào là mệnh đề, xét tính đúng, sai của mệnh đề đó. (I): “17 là số nguyên tố” (II): “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền” (III): “Các em C14 hãy cố gắng học tập thật tốt nhé !” (IV): “Mọi hình thoi đều nội tiếp được đường tròn” Bài 6: Cho các câu sau đây: (I): “Phan xi păng là ngọn núi cao nhất Việt Nam”. (II): “ 2 9,86  ”.

Bài 9. Tìm tất cả các giá trị thực của x để mệnh đề :“211”Px − là mệnh đề đúng?

Bài 10. Tìm tất cả các giá trị thực của x để mệnh đề :“210”Px − là mệnh đề sai?

Bài 11. Tìm tất cả các giá trị thực của x để mệnh đề 2 :“540”Pxx++= là mệnh đề sai?

Bài 12. Xét câu: ( ):Pn “n là số thự nhiên nhỏ hơn 50 và n chia hết cho 12”. Với giá trị nào của n sau đây thì ( )Pn là mệnh đề đúng. Khi đó số các giá trị của n bằng bao nhiêu?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6 (III): “Mệt quá!”. (IV): “Chị ơi, mấy giờ rồi?”. Hỏi có bao nhiêu câu là mệnh đề? Bài 7: Trong các câu sau, có bao nhiêu câu là mệnh đề đúng (I): Hãy cố gắng học thật tốt! (II): Số 20chia hết cho 6 (III): Số 5 là số nguyên tố (IV): Với mọi k  , 2k là số chẵn. Bài 8: Trong các câu dưới đây, câu nào là mệnh đề, câu nào là mệnh đề chứa biến: a) 250 − . b) 4 + x = 3. c) Hãy trả lời câu hỏi này!. d) Paris là thủ đô nước Ý.

 DẠNG 2: XÉT TÍNH ĐÚNG SAI CỦA MỘT MỆNH ĐỀ PHƯƠNG PHÁP Để xét tính đúng, sai của một mệnh đề ta cần nhớ nội dung sau:  Một câu khẳng định đúng là mệnh đề đúng  Một câu khẳng định sai là mệnh đề sai.  Không có mệnh đề vừa đúng vừa sai. Bài 1. Xét tính đúng, sai của mệnh đề sau: M: “π là một số hữu tỉ”. N: “Tổng của độ dài hai cạnh một tam giác lớn hơn độ dài cạnh thứ ba” Bài 2. Xét tính đúng, sai của mệnh đề sau: A: “Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn” . B: “Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn” C: “Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”. D: “Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”.

hay sai:

a) P : “Phương trình 2 10xx++= có nghiệm”.

b) Q : “Năm 2020 là năm nhuận”.

c) R : “327 chia hết cho 3”.

Bài 6. Cho tam giác ABC với đường trung tuyến AM . Xét hai mệnh đề

P : “Tam giác ABC vuông tại A ”;

Q : “Trung tuyến AM bằng nửa cạnh BC ”

a) Phát biểu mệnh đề PQ  và cho biết mệnh đề này đúng hay sai.

b) Phát biểu mệnh đề PQ  và cho biết mệnh đề này đúng hay sai.

Bài 7. Lập mệnh đề phủ định của mệnh đề: “ n  , 2 1nn++ là số nguyên tố”.

Mệnh đề phủ định đó đúng hay sai?

Bài 8. Xét tinh đúng sai của mệnh đề 2 ",66" xxx .

Bài 9. Xét tinh đúng sai của mệnh đề “Với mọ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7 Bài 3. Xét tính đúng, sai của mệnh đề sau: P: “ 2 24. −− ”. Q: “ 2 416. ”. Bài 4. Xét tính đúng, sai của mệnh đề sau: M: “Số nguyên tố lớn hơn 2 là số lẻ”. N: “Số tự nhiên có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5” . P: “Bình phương tất cả các số nguyên đều chia hết cho 2” . Bài 5. Nêu mệnh đề phủ định của mỗi mệnh đề sau và xác định xem mệnh đề phủ định đó đúng

i giá trị n thuộc tập hợp số nguyên, 2 1n + không chia hết cho 3”. Bài 10. Xét tinh đúng sai của mệnh đề “Tồn tại n thuộc tập hợp số nguyên, 2 1n + chia hết cho 4”. Bài 11. Xét tinh đúng sai của mệnh đề “Nếu n  và 2 5n thì 5n ”. Bài 12. Xét tính đúng sai của mệnh đề: “ 32 ,341nnnn +−+ chia hết cho 6”. Bài 13. Xác định tính đúng, sai của mệnh đề A : " 2 ,0xx  " và tìm mệnh đề phủ định của nó. Bài 14. Viết mệnh đề phủ định của mệnh đề 2 :,4410 Axxx −+− và xét tính đúng, sai của mệnh đề đó. Bài 15. Xét mệnh đề chứa biến: ( ) 32 :"320"Pxxxx−+= . Có bao nhiêu giá trị của biến x để mệnh đề trên là mệnh đề đúng ?  DẠNG 3: PHỦ ĐỊNH MỘT MỆNH ĐỀ PHƯƠNG PHÁP

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8  Để phủ định một mệnh đề ta thêm hoặc bớt từ “không” hoặc “không phải” trước vị ngữ của mệnh đề đó.  Ta có thể dùng từ thay thế hoặc đặt lại câu có cùng ý nghĩa.  Mệnh đề phủ định của mệnh đề ' )' ,( xXPx   là , ().'' xXPx    Mệnh đề phủ định của mệnh đề ' )' ,( xXPx   là , ().'' xXPx    Để phủ định mệnh đề kéo theo PQ  ta hiểu PQ  là “ ,()xXPx ta có ( )Qx ” nên mệnh đề phủ định là “ ,()xXPx ta có ( )Qx ” . Phủ định mệnh đề " P " là mệnh đề " không phải P ", kí hiệu P .  Tính chất X thành không X và ngược lại.  Quan hệ = thành quan hệ  và ngược lại.  Quan hệ  thành quan hệ  và ngược lại.  Quan hệ  thành quan hệ  và ngược lại.  ( ), xXPx thành ( ), xXPx  ( ), xXPx thành ( ), xXPx .  ( ),,, xXyYPxy thành ( ),,, xXyYPxy  ( ),,, xXyYPxy thành ( ),,, xXyYPxy Nếu P đúng thì P sai, nếu P sai thì P đúng. Bài 1. Nêu mệnh đề phủ định của các mệnh đề sau. :P " Trong tam giác tổng ba góc bằng 1800" :Q " 6 không phải là số nguyên tố" Bài 2. Lập mệnh đề phủ định của mỗi mệnh đề sau . a) Mọi hình vuông đều là hình thoi. b) Có một tam giác cân không phải là tam giác đều. Bài 3. Lập mệnh đề phủ định của mỗi mệnh đề sau . a) 2 :0xx  b) 2 : nnn . Bài 4. Lập mệnh đề phủ định của mỗi mệnh đề sau a) 2 :250xxx ++= b) 2 :32xxx + .

Bài

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9 Bài 5. Lập mệnh đề phủ định của mỗi mệnh đề sau . :P “Phương trình 2 10x += có nghiệm” :Q “ ,21nNn + là số lẻ” Bài 6. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ ( )*2,1nnn − là bội số của 3”.

7. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ 2 :650xxx −+= ”. Bài 8. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ ,:3xyyx =+ ”. Bài 9. Phát biểu mệnh đề phủ định của mệnh đề “ n chia hết cho 2 và cho 3 thì nó chia hết cho 6”. Bài 10. Phát biểu mệnh đề phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Bài 11. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó a) : nn chia hết cho n b) 2 :2xQx = c) :1xxx + d) 2 :31xRxx =+ Bài 12. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mệnh đề: ( )( ),12 nnnn ++ là số không chia hết cho 6 Bài 13. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định a) ,,1aRbRab + . b) ( )2 22,,2 aRbRabaabb +=++ . c) 2 ,, aRbRab  d) ,, abc  mà 0abc++ thì 222 2 abc abbcca++ −++ .

kéo theo P ⟹ Q: Mệnh đề kéo theo P ⟹ Q chỉ sai khi P đúng và Q sai.

b. Xét tính đúng, sai của mệnh đề kéo theo:

P ⟹ Q chỉ sai khi P đúng và Q sai.

Phương pháp xét tính đúng sai của mệnh đề P ⟹ Q

Quan sát xem P, Q đúng hay sai

Khi đó P ⟹ Q rơi vào mẫu nào trong 4 mẫu sau

1. Đ⟹S→Sai 2. Đ⟹Đ 3. ��⟹Đ 4. ��⟹�� →Đúng Đặc biệ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10 Bài 14. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định P : “ ( )( )( ) :1231nAnnnn =++++ không là số chính phương".  DẠNG 4: MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO, MỆNH ĐỀ TƯƠNG ĐƯƠNG PHƯƠNG PHÁP 1. Mệnh đề kéo theo a. ĐN: Cho hai mệnh đề P và Q. Mệnh đề dạng: “Nếu P thì Q” được gọi là mệnh đề kéo theo Ký hiệu là: P ⟹ Q. Cách xét tính đúng sai của mệnh đề

t: Có hai trường hợp mà chỉ cần nhìn vào một trong hai mệnh đề P hoặc Q ta sẽ biết (P ⟹ Q) luôn đúng: TH1: P sai. TH2: Q đúng. Chú ý: P⟹QchínhlàP∩Q. 2. Mệnh đề tương đương a. Mệnh đề đảo: Mệnh đề Q⟹P được gọi là mệnh đề đảo của mệnh đề P⟹Q b. Mệnh đề tương đương - Điều kiện cần và đủ: Nếu cả hai mệnh đề "P⟹ Q" và "Q⟹P" đều đúng ta nói P và Q là hai mệnh đề tương đương và kí hiệu "P⟺Q" Lúc đó ta nói: P là điều kiện cần và đủ để có Q hay Q là điều kiện cần và đủ để có P. Hoặc P nếu và chỉ nếu Q Hay P khi và chỉ khi Q Hay Điều kiện cần và đủ để có P là Q. Cách xét tính đúng, sai của mệnh đề tương đương : Mệnh đề P ⇔ Q chỉ đúng khi cả hai mệnh đề kéo theo P ⟹ Q và Q ⟹ P đều đúng. Nói cách khác mệnh đề P ⇔ Q đúng nếu cả hai mệnh đề P và Q cùng đúng hoặc cùng sai. Bài 1. Lập mệnh đề PQ  và xét tính đúng sau của nó, với :"4"P   và 2 :"10"Q   . Bài 2. Phát biểu mệnh đề đảo của mệnh đề “Nếu 0A90 = thì ABC là tam giác vuông” và xét tính đúng sai của nó.

Cho mệnh

. L

p mệnh đề PQ

và xét tính đúng sai của nó.

Bài 4. Giả sử ABC là một tam giác đã cho. Lập mệnh đề PQ  và mệnh đề đảo của nó, rồi xét tính đúng sai của chúng với P: "Góc A bằng 90 ", Q: 222 "" BCABAC =+

Bài 5. Cho ABC . Xét mệnh đề P : “ ABC

OFFICIAL

Bài

ABCDlà t

Tổng số đo hai góc đối nhau bằng 180o .

Hãy phát biểu mệnh đề PQ  dưới dạng điều kiện cần và đủ.

Bài 10. Trên một hòn đảo, tôi đã gặp ba người A, B và C, một người là hiệp sĩ, một người khác là kẻ bất lương và người kia là gián điệp. Người hiệp sĩ luôn nói sự thật, kẻ bất lương luôn luôn nói dối và gián điệp có thể nói dối hoặc nói sự thật.

A nói: "Tôi là hiệp sĩ."

B nói, "Tôi là kẻ bất lương."

C nói: "Tôi là gián điệp."

Hỏi ai là gián điệp?

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Bài 3.

đề :"23",Q:"46"P −−

ậ



là tam giác cân” và mệnh đề Q : “ ABC có hai đường trung tuyến bằng nhau”. Lập mệnh đề PQ  và xét tính đúng sai của nó. Bài 6. Phát biểu mệnh đề đảo của định lý: “Trong một tam giác cân, các đường cao ứng với các cạnh bên bằng nhau”. Mệnh đề đảo đó đúng hay sai? Tại sao? Bài 7. Cho mệnh đề chứa biến ( ):53Pnn + chia hết cho 3, với nN  , ( ): Qnn chia hết cho 3, với nN  Phát biểu mệnh đề “ ( ) ( ), nNPnQn ” và từ đó phát biểu mệnh đề đảo. Xét tính đúng sai của mệnh đề đảo.

8. Cho hai mệnh đề P và Q: P:

ứ giác nội tiếp. Q:

Bài 11. Ba anh em An, Bình, Vinh ngồi làm bài xung quanh một cái bàn được trải khăn mới. Khi phát hiện

có vết mực, bà hỏi thì các cháu lần lượt trả lời:

An: “Em Vinh không làm đổ mực, đấy là do em Bình.”

Bình: “Em Vinh làm đổ mực, anh An không làm đổ mực”.

Vinh: “Theo cháu, Bình không làm đổ mực, còn cháu hôm nay không chuẩn bị bài”.

Biết rằng trong 3 em thì có 2 em nói đúng, 1 em nói sai. Hỏi ai làm đổ mực?

Bài 12. Ếch hay cóc?

Trong một đầm lầy ma thuật, có hai loài lưỡng cư biết nói: cóc luôn luôn nói đúng và ếch luôn luôn nói sai.

Bốn loài lưỡng cư, Brian, Chris, LeRoy và Mike sống cùng nhau trong đầm lầy này và chúng đưa ra những tuyên bố sau:

OFFICIAL

Brian: "Mike và tôi là những loài khác nhau."

Chris: "LeRoy là một con ếch."

LeRoy: "Chris là một con ếch."

Mike: "Trong bốn người chúng tôi, ít nhất hai người là cóc."

Có bao nhiêu loài lưỡng cư là ếch?

Câu 1: Câu nào sau đây không là mệnh đề?

A. Tam giác đều là tam giác có ba cạnh bằng nhau.

B. 31 

Câu

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 12

. C. 451 −= . D. Bạn học giỏi quá!

2: Câu nào trong các câu sau không phải là mệnh đề? A.  có phải là một số vô tỷ không?. B. 225 += . C. 2 là một số hữu tỷ D. 4 2 2 = Câu 3: Trong các câu sau, câu nào là mệnh đề? A. 12là số tự nhiên lẻ B. An học lớp mấy? C. Các bạn có chăm học không? D. Các bạn hãy làm bài đi! Câu 4: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Cố lên, sắp tới nơi rồi! b) Số 15 là số nguyên tố. c) Tổng các góc của một tam giác là 180.  d) x là số nguyên dương. A. 3. B. 2. C. 4. D. 1. Câu 5: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng? BÀI TẬP TRẮC NGHIỆM.2 =

bao nhiêu

A. 4.

Câu 8: Cho ba m

(1)

(2)

đề sau,

huy

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 13 A. “ Nếu I là trung điểm của AB thì IA = IB”. B. “ Nếu ABCD là hình bình hành thì ACABAD =+ ’’. C. “ Nếu x > 2 thì 2x  ” . D. “ Nếu , mn là 2 số nguyên dương và cùng chia hết cho 3 thì 22 mn + cũng chia hết cho 3”. Câu 6: Trong các mệnh đề dưới đây, các mệnh đề nào sai. M: “ 2 ,410rr = ”. N: “ 2 ,1nn + chia hết cho 8”. X: “ *,123 nn ++++ không chia hết cho 11”. Q: “ 2 ,1nnn + + là một số chẵn”. E: “ 32 2 263 ,21 xxx x x −+−  + ”. A. N, X, Q B. M, X, Q C. N, Q, E D. M, Q, E Câu 7: Cho các mệnh đề sau: (1) 2a và 3a 6a (2) 39aa  (3) 24aa  (4) 3a và 6a thì 18a (5) 00aba+ và 0b  . (6) 00aba== hoặc 0b = . (7) Hai tam giác bằng nhau khi và chỉ khi hai tam giác đó đồng dạng. (8) Một tam giác là tam giác vuông khi và chỉ khi đường trung tuyến ứng với cạnh

ền bằng một nửa cạnh huyền. Có

mệnh đề sai trong các mệnh đề trên?

B. 6. C.

ệnh

vớ

n là số tự nhiên:

8n + là số chính phương

Chữ số tận cùng của n là 4 (3) 1n là số chính phương Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào đúng, mệnh đề nào sai? A. Mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai B. Mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai C. Mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai D. Mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai. Câu 9: Mệnh đề nào là sau đây sai? A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.

B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông.

C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại

D. Một tam giác là đều khi và chỉ khi nó là tam giác cân và có một góc bằng 60. 

Câu 10: Mệnh đề nào dưới đây đúng?

A. Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

B. Nếu tứ giác ABCD một cặp cạnh đối song song thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCD có một cặp cạnh đối bằng nhau thì tứ giác ABCD là hình bình hành.

D. Nếu tứ giác ABCD có hai đường chéo vuông góc với nhau thì tứ giác ABCD là hình bình hành.

Câu 11: Mệnh đề nào sau đây sai?

A. 2 là số nguyên tố. B. 1 là số nguyên tố.

C. 5 là số nguyên

Câu 12: Trong các

đề sau,

đề nào là mệnh

sai?

A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.

OFFICIAL

B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông.

C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.

D. Một tam giác là đều khi và chỉ khi chúng có hai đường trung tuyến bằng nhau và có một góc bằng 60. 

Câu 13: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có chữ số tận cùng là 5thì số nguyên n chia hết cho 5.

B. Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau.

D. Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD có hai đường chéo vuông góc với nhau.

Câu 14: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có tổng các chữ số bằng 9 thì số tự nhiên n chia hết cho 3.

B. Nếu xy  thì 22 xy 

C. Nếu xy = thì ... txty =

D. Nế

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 14

tố. D. 6 không phải là số nguyên tố.

mệnh

đề

u xy  thì 33 .xy  Câu 15: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. "ABC là tam giác đều  Tam giác ABC cân". B. "ABC là tam giác đều  Tam giác ABC cân và có một góc 60".  C. "ABC là tam giác đều  ABC là tam giác có ba cạnh bằng nhau". D. "ABC là tam giác đều  Tam giác ABC có hai góc bằng 60".  Câu 16: Mệnh đề nào sau đây đúng? A. ( ):1nnn + là số chính phương. B. ( ):1nnn + là số lẻ. C. ( )( ):12nnnn ++ là số lẻ D. ( )( ):12nnnn ++ chia hết cho 6 Câu 17: Trong các mệnh đề sau, mệnh đề nào sai? A. 2 , xxx B. ,66xxx  C. 2 ,1nn + không chia hết cho 3. D. 2 ,7aa = .

Câu 18: Trong các

Câu 19: Trong các mệnh đề sau

nào

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 15

mệnh đề sau, mệnh đề nào đúng? A. 2 ,50xx += . B. 42 ,540xxx ++= . C. 3 , nnn− chia hết cho 3 D. 52 , xxx

mệnh đề

sai?

2399100 444....44 +++++ chia hết cho 5. B. 2 :1nn + không chia hết cho 4 .

:21 nnN − chia hết cho 7

3333 123....100 ++++ không chia hết cho 5050 Câu 20: Có bao nhiêu số nguyên n để mệnh đề “ 32 271 nnn+++ chia hết cho 21 n ” là đúng? A. 3. B. 2. C. 4. D. 5. Câu 21: Cho các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu tứ giác ABCD là hình thang cân thì 2 góc đối bù nhau. B. Nếu ab = thì acbc = C. Nếu ab  thì 22ab  D. Nếu số nguyên chia hết cho 10 thì chia hết cho 5 và 2. Câu 22: Dùng kí hiệu ,  để phát biểu mệnh đề "Có một số hữu tỉ mà nghịch đảo của nó lớn hơn chính nó". A. 1 : nn n  B. 1 : nn n  C. 1 : nn n  D. 1 : nn n  Câu 23: Cho mệnh đề 2 1 “:” 4 Axx x =+− . Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó. A. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. B. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. C. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. D. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề sai. Câu 24: Phủ định của mệnh đề: “Hình thoi có hai đường chéo vuông góc với nhau” là: A. “Hai đường chéo của hình thoi vuông góc với nhau”. B. “Hình thoi có hai đường chéo không vuông góc với nhau”. C. “Hình thoi có hai đường chéo bằng nhau”. D. “Hình thoi là hình bình hành có hai đường chéo vuông góc với nhau”. Câu 25: Phủ định của mệnh đề: “ 2 :1nn + không chia hết cho 3” là: A. “ 2 :1nn + chia hết cho 3”. B. “ 2 :1nn + không chia hết cho 3”. C. “ 2 :1nn + chia hết cho 3”. D. “  2 :1nn+ không chia hết cho 3”. Câu 26: Phủ định của mệnh đề: “ 2 :10xx + ” là: A. “ 2 :10xx + ” B. “ 2 :10xx + ”C. “ 2 :10xx + ”D. “ 2 :10xx += ”

di chuy

A. M

Câu 33: Cho n là s

nhiên,

A. :P ” (

Câu 34: Cho mệnh

ệnh

đây đúng

“Nếu 2ab+ thì một trong hai số a và b nhỏ hơn 1”. Phát biểu mệnh đề trên

bằng cách sử dụng khái niệm “điều kiện đủ”.

A. 2ab+ là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 16 Câu 27: Phủ định của mệnh đề P: “ 2 :320xxx −+= ” là: A. P : “ 2 :320xxx −+ ” B. P : “ 2 :320xxx −+= ” C. P : “ 2 :320xxx −+ ” D. P : “ 2 :320xxx −+ ” Câu 28: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều

ển”.

ọi động vật đều không di chuyển. B. Mọi động vật đều đứng yên. C. Có ít nhất một động vật không di chuyển. D. Có ít nhất một động vật di chuyển. Câu 29: Phủ định của mệnh đề 2 ",531" xxx −= là A. 2" ,53"xxx− B. 2 ",531" xxx −= C. 2 "x,5x31" x − D. 2 ",531" xxx − Câu 30: Cho mệnh đề ( ):Px 2 ",10" xxx ++ . Mệnh đề phủ định của mệnh đề ( )Px là: A. 2 ",10" xxx ++ B. 2 ",10" xxx ++ C. 2 ",10" xxx ++ D. "  2 ,10"xxx++ Câu 31: Cho mệnh đề 2 “:”A xxx=  . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A? A. 2 “:” xxx B. 2 “:” xxx C. 2 “:” xxx D. 2 “:” xxx Câu 32: Cho mệnh đề 2 “:”A xxx=  . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A? A. 2 “:” xxx B. 2 “:” xxx C. 2 “:” xxx D. 2 “:” xxx

ố

ự

đề phủ định của mệnh đề nào sau

),1nnn + không là số chính phương”.

:Q ” ( ),1nnn + là số chẵn”

:R ” ( )( ),12nnnn ++ là số chẵn”.

:M ” ( )( ),12nnnn ++ không chia hết cho 6”

đề:

điều kiện đủ để một trong hai số a và b nhỏ hơn 1. B. Một trong hai số a và b nhỏ hơn 1 là điều kiện đủ để 2ab+ C. Từ 2ab+ suy ra một trong hai số a và b nhỏ hơn 1 D. Tất cả các câu trên đều đúng. Câu 35: Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên? A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong. D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.

Câu 36: Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”.

Phát biểu mệnh đề trên bằng cách sử dụng khái niệm “điều kiện cần”.

A. Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai đường chéo bằng nhau.

B. Điều kiện cần để tứ giác có hai đường chéo bằng nhau là tứ giác đó là hình thang cân.

C. Tứ giác là hình thang cân kéo theo tứ giác đó có hai đường chéo bằng nhau.

D. Cả a, b đều đúng.

Câu 37: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai?

A. Tam giác cân có hai cạnh bằng nhau.

B. x chia hết cho 6 thì x chia hết cho 2 và 3.

C. ABCD là hình bình hành thì AB song song với CD.

D. ABCD là hình chữ nhật thì 90.ABC===

Câu 38: Mệnh đề nào dưới đây sai?

A. Tứ giác ABCD là hình chữ nhật khi và chỉ khi ABCD có ba góc vuông.

B. Tứ giác ABCD là hình bình hành khi và chỉ khi ABCD có hai cạnh đối song song và bằng nhau.

C. Tứ giác ABCD là hình thoi khi và chỉ khi ABCD có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường.

OFFICIAL

D. Tứ giác ABCD là hình vuông khi và chỉ khi ABCD có bốn góc vuông.

Câu 39: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có chữ số tận cùng là 5 thì số nguyên n chia hết cho 5.

B. Nếu tứ giác ABCDcó hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCDlà hình chữ nhật thì tứ giác ABCDcó hai đường chéo bằng nhau.

D. Nếu tứ giác ABCDlà hình thoi thì tứ giác ABCDcó hai đường chéo vuông góc với nhau.

Câu 40: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu tổng hai số 2ab+ thì có ít nhất có một số lớn hơn 1.

B. Trong một tam giác cân hai đường cao bằng nhau.

C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.

D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3.

Câu 41: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?

A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c

B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau.

C. Nếu a chia hết cho 3 thì a chia hết cho 9

D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5.

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 17

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1 BÀI1:MỆNHĐỀ 1. MỆNH ĐỀ, MỆNH ĐỀ CHỨABIẾN a. Mệnh đề: Mệnh đề là những khẳng định có tính đúng hoặc sai. Người ta gọi là một mệnh đề lôgic (gọi tắt là mệnh đề). Những câu không xác định được tính đúng sai không phải là mệnh đề Chú ý : Người ta thường sử dụng các chữ cái ,, PQR ,…để biểu thị các mệnh đề. Câu Không phải mệnh đề Mệnh đề đúng Mệnh đề sai 13 là số nguyên tố. ? ? ? Tổng độ dài hai cạnh bất kì của một tam giác nhỏ hơn độ dài cạnh còn lại ? ? ? Bạn đã làm bài tập chưa? ? ? ? Thời tiết hôm nay thật đẹp! ? ? ? Giải Câu Không phải mệnh đề Mệnh đề đúng Mệnh đề sai 13 là số nguyên tố. x Tổng độ dài hai cạnh bất kì của một tam giác nhỏ hơn độ dài cạnh còn lại x Bạn đã làm bài tập chưa? x Thời tiết hôm nay thật đẹp! x b. Mệnh đề chứa biến Xét câu “ n chia hết cho 2” (với n là số tự nhiên). Ta chưa khẳng định được tính đúng sai của câu này, do đó nó chưa phải là một mệnh đề Tuy nhiên, nếu thay n bằng số tự nhiên cụ thể thì câu này cho ta một mệnh đề. Chẳng hạn: • Với 5n = ta được mệnh đề “5 chia hết cho 2”. Đây là mệnh đề sai. CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I = Mỗi mệnh đề phải hoặc đúng hoặc sai. Một mệnh đề không thể vừa đúng vừa sai Luyện tập 1. Hãy điền dấu ‘’x’’ vào ô thích hợp trong bẳng sau :

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 • Với 10n = ta được mệnh đề “10 chia hết cho 2”. Đây là mệnh đề đúng. Ta nói rằng câu “ n chia hết cho 2” là một mệnh đề chứa biến. 2. MỆNH ĐỀ PHỦ ĐỊNH Để phủ định một mệnh đề P, người ta thường thêm (hoặc bớt) từ “không” hoặc “không phải” vào trước vị ngữ của mệnh đề P. Ta kí hiệu mệnh đề phủ định của mệnh đề P là P . P: “2022 chia hết cho 5” ; Q: “Bất phương trình 210 x + có nghiệm”. Giải Mệnh đề phủ định của P là P : “2022 không chia hết cho 5”. Mệnh đề P là một mệnh đề sai vì 2022:4505 = dư 2. Mệnh đề phủ định của Q là Q : “ Bất phương trình 210 x + vô nghiệm ”. Mệnh đề Q là một mệnh đề sai vì với 1:2.1130x =+= nên 1x = là một nghiệm của bất phương trình 210 x + Vận dụng. Cho mệnh đề Q: “Châu Á là châu lục có diện tích lớn nhất trên thế giới”. Phát biểu mệnh đề phủ định Q và xác định tính đúng sai của hai mệnh đề Q và Q Giải : Mệnh đề phủ định Q : “Châu Á không phải là châu lục có diện tích lớn nhất trên thế giới’’ Mệnh đề Q đúng còn mệnh đề Q là mệnh đề sai. 3. MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO a. Mệnh đề kéo theo Mệnh đề PQ  chỉ sai khi P đúng và Q sai. Các định lí toán học là những mệnh đề đúng và thường có dạng PQ  . Khi đó ta nói: b. Mệnh đề đảo Nhận xét. Mệnh đề đảo của một mệnh đề đúng không nhất thiết là mệnh đề đúng. Mệnh đề P và mệnh đề P là hai phát biểu trái ngược nhau. Nếu P đúng thì P sai, còn nếu P sai thì P đúng. Luyện tập 2. Phát biểu mệnh đề phủ định của mỗi mệnh đề sau và xác định tính đúng sai của mệnh đề phủ định đó. Mệnh đề ‘’Nếu P thì Q ’’ được gọi là một mệnh đề kéo theo và kí hiệu PQ  P là giả thiết của định lí, Q là kết luận của định lí, hoặc “ P là điều kiện đủ để có Q ” hoặc “Q là điều kiện cần để có P ”. Mệnh đề QP  được gọi là mệnh đề đảo của mệnh đề PQ  Luyện tập 3. Cho các mệnh đề : “ và chia hết cho ” ; : “ chia hết cho ”

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3 a) Hãy phát biểu định lí PQ  . Nêu giả thiết, kết luận của định lí và phát biểu định lí này dưới dạng điều kiện cần, điều kiện đủ. b) Hãy phát biểu mệnh đề đảo của mệnh đề PQ  xác định tính đúng sai của mệnh đề đảo này. Giải a) Phát biểu định lí PQ  là Nếu a và b chia hết cho c thì ab + chia hết cho c . Trong đó giả thiết là a và b chia hết cho c , kết luận là ab + chia hết cho c . Phát biểu định lý dưới dạng điều kiện cần : ab + chia hết cho c là điều kiện cần để a và b chia hết cho c . Phát biểu định lý dưới dạng điều kiện đủ : a và b chia hết cho c là điều kiện đủ để ab + chia hết cho c b) Mệnh đề đảo của mệnh đề PQ  là ‘’nếu ab + chia hết cho c thì a và b chia hết cho c ’’. Mệnh đề đảo của mệnh đề PQ  là mệnh đề sai vì 2;7;3abc=== khi đó ab + chia hết cho c nhưng c và b chia hết cho c . 4. MỆNH ĐỀ TƯƠNG ĐƯƠNG Nhận xét. Nếu cả hai mệnh đề PQ  và QP  đều đúng thì mệnh đề tương đương PQ  đúng. Khi đó ta nói “ P tương đương với Q ” hoặc “ P là điều kiện cần và đủ để có Q ” hoặc “ P khi và chỉ khi Q ”. Giải Số tự nhiên n chia hết cho 2khi và chỉ khi số đó có chữ số tận cùng là số chẵn. 5. MỆNH ĐỀ CÓ CHỨAKÍ HIỆU ∀,∃ Kí hiệu  đọc là ''với mọi'' . Kí hiệu  đọc là ''có một'' (tồn tại một) hay''có ít nhất một''(tồn tại ít nhất một). Cho mệnh đề ", ()"xXPx  Mệnh đề phủ định của mệnh đề ", ()"xXPx là mệnh đề ", ()".xXPx  Mệnh đề phủ định của mệnh đề ", ()"xXPx là mệnh đề ", ()".xXPx Ví dụ: Câu ''Bình phương của mọi số thực đều lớn hơn hoặc bằng 0'' là một mệnh đề. Có thể viết mệnh đề này như sau 2 :0xx  hay 2 0,.xx Kí hiệu  đọc là ''với mọi'' . Ví dụ: Câu ''Có một số nguyên nhỏ hơn 0'' là một mệnh đề Có thể viết mệnh đề này như sau :0.nn  Kí hiệu  đọc là ''có một'' (tồn tại một) hay''có ít nhất một''(tồn tại ít nhất một).  Mệnh đề phủ định của mệnh đề ", ()"xXPx là ", ()".xXPx Ví dụ: Cho mệnh đề 2 “,70” xxx −+ . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải Mệnh đề “ P nếu và chỉ nếu Q ” được gọi là một mệnh đề tương đương và kí hiệu là PQ  . Luyện tập 4. Phát biểu điều kiện cần và đủ để số tự nhiên chia hết cho .

Trong các

câu

Bạn học trường nào?

đông dân nhất thế giới;

Không được làm việc riêng trong trường học;

Tôi sẽ sút bóng trúng xà ngang.

Lời giải

Câu a) “Trung Quốc là nước đông dân nhất thế giới.” là mệnh đề là:

Câu b) là câu nghi vấn; Câu c) là câu cầu khiến; Câu d) là câu khẳng định chưa xác định được tính đúng sai)

1.2. Xét tính đúng sai của các mệnh đề

10 3

Phương trình370 x += có nghiệm;

Có ít nhất một

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4 Phủ định của mệnh đề 2 “,70” xxx −+ là mệnh đề 2 “,70” xxx −+ .  Mệnh đề phủ định của mệnh đề ", ()"xXPx là ", ()".xXPx Ví dụ: Cho mệnh đề 2 “,60” xxx −−= . Tìm mệnh đề phủ định của mệnh đề trên? Lời giải Phủ định của mệnh đề 2 “,60” xxx −−= là mệnh đề 2 “,60” xxx −− 1.1.

câu sau,

nào là mệnh đề? a) Trung Quốc là nước

sau: a)

  ; b)

số cộng với chính nó bằng 0; d) 2022 là hợp số. Lời giải Xét tính đúng sai của các mệnh đề sau: a) 10 3   Mệnh đề đúng do 3,14  và 10 3,33 3  nên 10 3   b) Phương trình370 x += có nghiệm. HỆ THỐNG BÀI TẬP.II = BÀI TẬP SÁCH GIÁO KHOA.1 =

Vì phương trình370 x += có nghiệm hữu tỉ 7 3 x = nên mệnh đề là đúng.

c) Có ít nhất một số cộng với chính nó bằng 0;Do tồn tại số thực 0 để 0 + 0 = 0 nên mệnh đề đúng.

d) 2022 là hợp số.

Ta có: 2022 1011.2= nên 2022 là hợp số hay mệnh đề đã cho là đúng.

1.3. Cho hai câu sau:

P: “Tam giác ABC là tam giác vuông”;

Q: “Tam giác ABC có một góc bằng tổng hai góc còn lại”.

Hãy phát biểu mệnh đề tương đương PQ  xét tính đúng sai của mệnh đề này. Lời giải

Mệnh đề tương đương PQ  : “Tam giác ABC là tam giác vuông khi và chỉ khi tam giác ABC có một góc bằng tổng hai góc còn lại”.

OFFICIAL

Mệnh đề PQ  đúng. Thật vậy: + PQ  đúng: Hiển nhiên.

+ Mệnh đề QP  : “Tam giác ABC có một góc bằng tổng hai góc còn lại thì tam giác ABC là tam giác vuông”. Không giảm tổng quát ta giả sử tam giác ABC có: 0 00180 18090 ABC BCBCBC ABC  ++= +++=+= =+

Nên tam giác ABC vuông tại A. Do đó mệnh đề QP  đúng.

1.4. Phát biểu

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5

mệnh đề đảo của mỗi mệnh đề sau và xác định tính đúng sai chúng. P: “Nếu số tự nhiên n có chữ số tận cùng là 5 thì n chia hết cho 5”; Q: “Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau”. Lời giải Mệnh đề đảo của P: “Nếu số tự nhiên n chia hết cho 5 thì n có chữ số tận cùng là 5”. Mệnh đề sai vì số nguyên n cũng có thể có chữ số tận cùng là 0 Mệnh đề đảo của Q: “Nếu tứ giác ABCD có hai đường chéo bằng nhau thì tứ giác ABCD là hình chữ nhật”. Mệnh đề sai (không thỏa mãn dấu hiệu nhận biết hình chữ nhật).

a) Hãy

b) Hãy phát

c) Xác

Mệnh đề QP

sai

1.6. Xác định tính đúng sai của mệnh đề sau và tìm mệnh đề phủ định của nó.

Q: “ n  , n chia hết cho n+1”.

Lời giải

Mệnh đề Q đúng do tồn tại 0n = để 0 chia hết cho 01 + .

Mệnh đề phủ định: Q : “ n  , n không chia hết cho 1n + ”.

1.7. Dùng kí hiệu ,  để viết các mệnh đề sau:

P: “Mọi số tự nhiên đều có bình phương lớn hơn hoặc bằng chính nó”;

Q: “ Có một số thực cộng với chính nó bằng 0”.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6 (Tứ giác có hai đường chéo bằng nhau là hình thangcân) 1.5. Với hai số thực a và b, xét các mệnh đề 22 :""Pab  và :"0"Qab  .

phát biểu mệnh đề PQ  .

biểu mệnh đề đảo của mệnh đề ở câu a.

định tính đúng sai của mỗi mệnh đề ở câu a và câu b. Lời giải a) Mệnh đề PQ  : “Nếu 22ab  thì 0 ab ”. b) Mệnh đề đảo QP  : “Nếu 0 ab thì 22ab  ”. c) Mệnh đề



vì ví dụ có 22(3)4 − nhưng 304−

 đúng.

Lời giải Lời giải 2 :"," Pnnn  :",0"Qxxx+=

1. Các câu sau đây, có bao nhiêu câu là mệnh đề?

(1) Ở đây đẹp quá!

(2) Phương trình 2 310xx−+= vô nghiệm

(3) 16 không là số nguyên tố

(4) Hai phương trình 2 430xx−+= và 2 310xx−++= có nghiệm chung.

(5) Số  có lớn hơn 3 hay không?

(6) Italia vô địch Worldcup 2006

(7) Hai tam giác bằng nhau khi và chỉ khi chúng có diện tích bằng nhau.

(8) Một tứ giác là hình thoi khi và chỉ khi nó có hai đường chéo vuông góc với nhau.

Lời giải

Câu (1) và (5) không là mệnh đề(vì là câu cảm thán, câu hỏi)

Các câu (3), (4), (6), (8) là những mệnh đề đúng

Câu (2) và (7) là những mệnh đề sai.

Bài 2. Cho ba mệnh đề sau, với n là số tự nhiên

(1) 8n + là số chính phương

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7  DẠNG 1: XÁC ĐỊNH MỀNH ĐỀ VÀ MỆNH ĐỀ CHỨA BIẾN PHƯƠNG PHÁP Để xác định mệnh đề và mệnh đề chứa biến ta cần biết:  Mệnh đề là một câu khẳng định đúng hoặc sai. Một mệnh đề không thể vừa đúng hoặc vừa sai  Mệnh đề chứa biến là một câu khẳng định chứa biến nhận giá trị trong một tập X nào đó mà với mỗi giá trị chứa biến thuộc X ta được một mệnh đề Bài

(2) Chữ số tận cùng của n là 4 (3) 1n là số chính phương Biết rằng có hai mệnh đề đúng và một mệnh đề sai. Hãy xác định mệnh đề nào, đúng mệnh đề nào sai? Lời giải Ta có số chính phương có các chữ số tận cùng là 0,1,4,5,6,9. Vì vậy Nhận thấy giữa mệnh đề (1) và (2) có mâu thuẫn. Bởi vì, giả sử 2 mệnh đề này đồng thời là đúng thì 8n + có chữ số tận cùng là 2 nên không thể là số chính phương. Vậy trong hai mệnh đề này phải có một mệnh đề là đúng và một mệnh đề là sai. BÀI TẬP TỰ LUẬN.2 =

Bài

Tương tự, nhận thấy giữa mệnh đề (2) và (3) cũng có mâu thuẫn. Bởi vì, giả sử mệnh đề này

đồng thời là đúng thì 1n có chữ số tận cùng là 3 nên không thể là số chính phương.

Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.

vòng bán k

t qu

i b

Câu

Dung: Singapor nhì, còn Thái Lan ba.

Singapor, Thái Lan và Inđônêxia.

Dung, Quang, Trung dự đoán như sau:

Quang: Việt Nam nhì, còn Thái Lan tư.

Trung: Singapor nhất và Inđônêxia nhì.

n d

đoán đúng m

i và sai m

độ

OFFICIAL

thuẫ

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8

3. Tại Tiger Cup 98 có bốn đội lọt vào vòng bán kết: Việt Nam,

Trước khi thi đấu

ết, ba bạn

ế

ả,

ỗ

ạ

ự

ột độ

ột

i. Hỏi mỗi đội đã đạt giải mấy? Lời giải + Nếu Singapor nhì thì Singapor nhất là sai do đó Inđônêxia nhì là đúng(mâu

n) + Như vậy Thái lan thứ ba là đúng suy ra Việt Nam nhì Singapor nhất và Inđônêxia thứ tư Bài 4: Trong các phát biểu sau, phát biểu nào không phải là mệnh đề, giải thích? 1/ Hải Phòng là một thành phố của Việt Nam. 2/ Bạn có đi xem phim không? 3/ 10 21 chia hết cho 11 4/ 2763 là hợp số. 5/ 2 320xx−+= Lời giải Các phát biểu không phải mệnh đề là 2 và 5 Câu 2 là câu hỏi. Câu 5 là mệnh đề chứa biến. Bài 5: Trong các phát biểu sau, phát biểu nào là mệnh đề, xét tính đúng, sai của mệnh đề đó. (I): “17 là số nguyên tố” (II): “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền” (III): “Các em C14 hãy cố gắng học tập thật tốt nhé !” (IV): “Mọi hình thoi đều nội tiếp được đường tròn” Lời giải

(I) là mệnh đề đúng. Câu (II) là mệnh đề đúng.

(III) không phải là mệnh đề.

(VI) là mệnh đề sai. Bài 6: Cho các câu sau đây:

(I):

(II):

(III):

(IV):

có

(I), (II) là m

(III),

Bài 7: Trong các câu sau, có bao nhiêu câu là m

(I): Hãy

(II): S

(III): S

(IV): V

chia

OFFICIAL

Có hai mệnh đề đúng là (III) và (IV)

i gi

Bài 8: Trong các câu dưới đây, câu nào là mệnh đề, câu nào là mệnh đề chứa biến:

a) 250 − .

b) 4 + x = 3.

c) Hãy trả lời câu hỏi này!.

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9

“Phan xi păng là ngọn núi cao nhất Việt Nam”.

“ 2 9,86  ”.

“Mệt quá!”.

“Chị ơi, mấy giờ rồi?”.

ỏi

bao nhiêu câu là mệnh đề?

ời giải

ệnh đề,

(IV) không là mệnh đề.

ệnh đề đúng

cố gắng học thật tốt!

ố 20

hết cho 6.

ố 5 là số nguyên tố.

ới mọi k  , 2k là số chẵn.

ờ

ả

d) Paris là thủ đô nước Ý. Lời giải a) Mệnh đề đúng. b) Mệnh đề chứa biến. c) Không phải là mệnh đề, câu mệnh lệnh. d) Mệnh đề sai. Bài 9. Tìm tất cả các giá trị thực của x để mệnh đề :“211”Px − là mệnh đề đúng? Lời giải Ta có 2111 211 2110 xx x xx − −−−  . Bài 10. Tìm tất cả các giá trị thực của x để mệnh đề :“210”Px − là mệnh đề sai? Lời giải Mệnh đề :“210”Px − sai khi và chỉ khi 210 x − đúng 1 2 x  Bài 11. Tìm tất cả các giá trị thực của x để mệnh đề 2 :“540”Pxx++= là mệnh đề sai?

Bài 1. Xét tính đúng, sai củ

N: “Tổng của độ dài hai cạnh một tam giác lớn hơn độ dài cạnh thứ ba

Lời giải

Mệnh đề M là một mệnh đề sai vì π là số vô tỉ

Mệnh đề N đúng.

Bài 2. Xét tính đúng, sai của mệnh đề sau:

A: “Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đề

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10 Lời giải Mệnh đề 2 :“540”Pxx++= là mệnh đề sai khi thay giá trị x vào biểu thức 2 54xx++ ta được kết quả khác 0, ta thấy 1;4xx−− thỏa mãn. Bài 12. Xét câu: ( ):Pn “n là số thự nhiên nhỏ hơn 50 và n chia hết cho 12”. Với giá trị nào của n sau đây thì ( )Pn là mệnh đề đúng. Khi đó số các giá trị của n bằng bao nhiêu? Lời giải Các số thỏa mãn yêu cầu bài toán là 0;12;24;36;48.  DẠNG 2: XÉT TÍNH ĐÚNG SAI CỦA MỘT MỆNH ĐỀ PHƯƠNG PHÁP Để xét tính đúng, sai của một mệnh đề ta cần nhớ nội dung sau:  Một câu khẳng định đúng là mệnh đề đúng.  Một câu khẳng định sai là mệnh đề sai.  Không có mệnh đề vừa đúng vừa sai.

a mệnh đề sau: M: “π là một số hữu tỉ”

”

u là số chẵn” . B: “Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn” C: “Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”. D: “Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ”. Lời giải A là mệnh đề sai. Ví dụ: 134 += là số chẵn nhưng 1,3 là số lẻ. B là mệnh đề sai. Ví dụ: 2.36 = là số chẵn nhưng 3 là số lẻ. C là mệnh đề sai. Ví dụ: 134 += là số chẵn nhưng 1,3 là số lẻ. D là mệnh đề đúng. Bài 3. Xét tính đúng, sai của mệnh đề sau: P: “ 2 24. −− ”. Q: “ 2 416. ”.

Nêu mệnh đề

mệnh đề

và xác định xem mệnh đề phủ định đó đúng hay sai:

a) P : “Phương trình 2 10xx++= có nghiệm”.

b) Q : “Năm 2020 là năm nhuận”.

c) R : “327 chia hết cho 3”.

Lời giải

a) P : “Phương trình 2 10xx++= vô nghiệm”. P là mệnh đề đúng.

b) Q : “Năm 2020 không phải là năm nhuận”. Q là mệnh đề sai.

c) R : “327 không chia hết cho 3”. R là mệnh đề sai.

Bài 6. Cho tam giác ABC với đường trung tuyến AM . Xét hai mệnh đề

P : “Tam giác ABC vuông tại A ”;

Q : “Trung tuyến AM bằng nửa cạnh BC ”

a) Phát biểu mệnh đề PQ  và cho biế

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Lời giải Ta có: Suy ra P sai. 2 416 . Suy ra Q đúng. Bài 4. Xét tính đúng, sai của mệnh đề sau: M: “Số nguyên tố lớn hơn 2 là số lẻ”. N: “Số tự nhiên có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5” . P: “Bình phương tất cả các số nguyên đều chia hết cho 2” . Lời giải M là mệnh đề đúng. Vì mọi số lớn hơn 2 mà chẵn thì đêuu chia hết cho 2, nên không thể là số nguyên tố. N là mệnh đề đúng. P là mệnh đề sai. Ví dụ: 2 39 = nhưng 9 không chia hết cho 2. Bài 5.

phủ đị

của mỗi

t mệnh đề này đúng hay sai. b) Phát biểu mệnh đề PQ  và cho biết mệnh đề này đúng hay sai. Lời giải a) “Nếu tam giác ABC đã cho vuông tại A thì trung tuyến AM bằng nửa cạnh BC ”. Mệnh đề này đúng. b) “Tam giác ABC đã cho vuông tại A nếu và chỉ nếu trung tuyến AM bằng nửa cạnh BC ”. Mệnh đề này đúng. Bài 7. Lập mệnh đề phủ định của mệnh đề: “ n  , 2 1nn++ là số nguyên tố”. Mệnh đề phủ định đó đúng hay sai? 2 4222.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 12 Lời giải Mệnh đề phủ định là: “ n  , 2 1nn++ không phải là số nguyên tố”. Mệnh đề phủ định đúng. Ví dụ với 4n = thì 2 121nn++= chia hết cho 3 nên là hợp số Bài 8. Xét tinh đúng sai của mệnh đề 2 ",66" xxx Lời giải Ta có 2 2 2 33 66 22 xx xx xx       Vậy mệnh đề đúng. Bài 9. Xét tinh đúng sai của mệnh đề “Với mọi giá trị n thuộc tập hợp số nguyên, 2 1n + không chia hết cho 3”. Lời giải Với ( ) 22 3191nkknk =+=+ không chia hết cho 3. Với ( ) 22 311961 nkknkk =++=++ không chia hết cho 3. Với ( ) 22 3219124 nkknkk =++=++ không chia hết cho 3. Do đó mệnh đề trên đúng. Bài 10. Xét tinh đúng sai của mệnh đề “Tồn tại n thuộc tập hợp số nguyên, 2 1n + chia hết cho 4”. Lời giải Với ( ) 22 2141nkknk =+=+ không chia hết cho 4. Với ( ) 22 211442nkknkk =++=++ không chia hết cho 4. Vậy mệnh đề trên sai. Bài 11. Xét tinh đúng sai của mệnh đề “Nếu n  và 2 5n thì 5n ”. Lời giải Giả sử n  và 2 5n mà ta có n không chia hết cho 5. Vì n không chia hết cho 5 nên n có thể biểu diễn theo một trong các dạng sau: 51nk= hoặc 52nk= Với 51nk= ta có 2225101nkk=+ không chia hết cho 5. Với 52nk= ta có 2225204nkk=+ không chia hết cho 5. Vậy mệnh đề trên đúng. Bài 12. Xét tính đúng sai của mệnh đề: “ 32 ,341nnnn +−+ chia hết cho 6”. Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 13 n  , ta có: ( ) ( )( )32234132611261 nnnnnnnnnnn +−+=++−+=++−+ . Vì ( )( )12nnn++ là tích 3 số tự nhiên liên tiếp nên ( )( )12nnn++ chia hết cho 6 Lại có 6n chia hết cho 6; 1 không chia hết cho 6. Do đó ( )( ) 1261nnnn++−+ không chia hết cho 6. Vậy mệnh đề đã cho là sai. Bài 13. Xác định tính đúng, sai của mệnh đề A : " 2 ,0xx  " và tìm mệnh đề phủ định của nó. Lời giải Mệnh đề A đúng và (Textranslationfailed) là mệnh đề sai. Bài 14. Viết mệnh đề phủ định của mệnh đề 2 :,4410 Axxx −+− và xét tính đúng, sai của mệnh đề đó. Lời giải Ta có 2 :",4410" Axxx−+− là mệnh đề sai vì ( ) 22 1 4410210 2 xxxx −+−−− Khi đó mệnh đề phủ định 2 :",4410" Axxx−+− là mệnh đề đúng. Bài 15. Xét mệnh đề chứa biến: ( ) 32 :"320"Pxxxx−+= Có bao nhiêu giá trị của biến x để mệnh đề trên là mệnh đề đúng ? Lời giải Ta có 323200,1,2xxxxxx −+==== . Vậy có ba giá trị của x .  DẠNG 3: PHỦ ĐỊNH MỘT MỆNH ĐỀ PHƯƠNG PHÁP  Để phủ định một mệnh đề ta thêm hoặc bớt từ “không” hoặc “không phải” trước vị ngữ của mệnh đề đó.  Ta có thể dùng từ thay thế hoặc đặt lại câu có cùng ý nghĩa.  Mệnh đề phủ định của mệnh đề ' )' ,( xXPx   là , ().'' xXPx    Mệnh đề phủ định của mệnh đề ' )' ,( xXPx   là , ().'' xXPx    Để phủ định mệnh đề kéo theo PQ  ta hiểu PQ  là “ ,()xXPx ta có ( )Qx ” nên mệnh đề phủ định là “ ,()xXPx ta có ( )Qx ” . Phủ định mệnh đề " P " là mệnh đề " không phải P ", kí hiệu P .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 14  Tính chất X thành không X và ngược lại.  Quan hệ = thành quan hệ  và ngược lại.  Quan hệ  thành quan hệ  và ngược lại.  Quan hệ  thành quan hệ  và ngược lại.  ( ), xXPx thành ( ), xXPx  ( ), xXPx thành ( ), xXPx .  ( ),,, xXyYPxy thành ( ),,, xXyYPxy  ( ),,, xXyYPxy thành ( ),,, xXyYPxy . Nếu P đúng thì P sai, nếu P sai thì P đúng Bài 1. Nêu mệnh đề phủ định của các mệnh đề sau. :P " Trong tam giác tổng ba góc bằng 1800" :Q " 6 không phải là số nguyên tố" Lời giải Ta có các mệnh đề phủ định là: :P "Trong tam giác tổng ba góc không bằng 1800 " :Q " 6 là số nguyên tố" Bài 2. Lập mệnh đề phủ định của mỗi mệnh đề sau . a) Mọi hình vuông đều là hình thoi. b) Có một tam giác cân không phải là tam giác đều. Lời giải Ta có các mệnh đề phủ định là: a) Có ít nhất một hình vuông không phải là hình thoi. b) Mọi tam giác cân đều là tam giác đều. Bài 3. Lập mệnh đề phủ định của mỗi mệnh đề sau . a) 2 :0xx  b) 2 : nnn . Lời giải Ta có các mệnh đề phủ định là: a) 2 :0xx  b) 2 : nnn Bài 4. Lập mệnh đề phủ định của mỗi mệnh đề sau a) 2 :250xxx ++= b) 2 :32xxx + Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 15 Ta có các mệnh đề phủ định là: a) 2 :250xxx ++ b) 2 :32xxx =+ Bài 5. Lập mệnh đề phủ định của mỗi mệnh đề sau . :P “Phương trình 2 10x += có nghiệm” :Q “ ,21nNn + là số lẻ” Lời giải Ta có các mệnh đề phủ định là: :P “Phương trình 2 10x += vô nghiệm” :Q “ ,21nNn + là số chẵn” Bài 6. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ ( )*2,1nnn − là bội số của 3”. Lời giải Mệnh đề “ ( )*2,1nnn − là bội số của 3” là mệnh đề đúng vì ( ) ( ) ( ) 2* 1113, nnnnnn −=−+ . Phủ định của mệnh đề “ ( )*2,1nnn − là bội số của 3” là mệnh đề “ ( )*2,1nnn − không phải là bội số của 3”. Bài 7. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ 2 :650xxx −+= ”. Lời giải Mệnh đề “ 2 :650xxx −+= ” là mệnh đề đúng vì 2 1 650 5. x xx x = −+=  = Phủ định của mệnh đề “ 2 :650xxx −+= ” là mệnh đề “ 2 :650xxx −+ ”. Bài 8. Xét tính đúng sai và nêu mệnh đề phủ định của mệnh đề “ ,:3xyyx =+ ”. Lời giải Mệnh đề “ ,:3xyyx =+ ” đúng vì ,3xyx =+ . Phủ định của mệnh đề “ ,:3xyyx =+ ” là mệnh đề “ ,:3xyyx + ”. Bài 9. Phát biểu mệnh đề phủ định của mệnh đề “ n chia hết cho 2 và cho 3 thì nó chia hết cho 6”. Lời giải Phủ định của mệnh đề “ n chia hết cho 2 và cho 3 thì nó chia hết cho 6” là mệnh đề “Có n chia hết cho 2 và cho 3 mà không chia hết cho 6” . Bài 10. Phát biểu mệnh đề phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Lời giải

Phủ định của mệnh đề “Hai tam giác bằng nhau thì diện tích của chúng bằng nhau” là mệnh đề “Có

ai tam giác bằng nhau mà diện tích của chúng khác nhau” .

Bài 11. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó

a) : nn chia hết cho n

2 :2xQx =

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 16

c) :1xxx + d) 2 :31xRxx =+ Lời giải a) : nNn không chia hết cho n . Mệnh đề phủ định đúng. b) 2 :2.xQx  Mệnh đề phủ định đúng. c) :1.xRxx + Mệnh đề phủ định sai. d) 2 :31.xRxx + Mệnh đề phủ định sai. Bài 12. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của mệnh đề: ( )( ),12 nnnn ++ là số không chia hết cho 6 . Lời giải ( )( ),12 nnnn ++ là số chia hết cho 6. Mệnh đề này đúng vì ( )( ),12nnnn ++ là tích của 3 số tự nhiên liên tiếp, trong đó, luôn có một số chia hết cho 2 và một số chia hết cho 3 nên nó chia hết cho 2.36 = Bài 13. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định a) ,,1aRbRab + . b) ( )2 22,,2 aRbRabaabb +=++ . c) 2 ,, aRbRab  d) ,, abc  mà 0abc++ thì 222 2 abc abbcca++ −++ . Lời giải a) Phủ định của mệnh đề là ,,1aRbRab + Mệnh đề phủ định này sai vì với 1;1ab== thì 21ab+= . b) Phủ định của mệnh đề là ( )2 22,,2 aRbRabaabb +++ Mệnh đề phủ định này sai. c) Phủ định của mệnh đề là 2 ,, aRbRab  Mệnh đề phủ định này đúng.

đề dạng: “Nếu P thì Q” được gọi là mệnh đề kéo theo.

Ký hiệu là: P ⟹ Q.

Cách xét tính đúng sai của mệnh đề kéo theo P ⟹ Q: Mệnh đề kéo theo P ⟹ Q chỉ sai khi P đúng và Q sai.

b. Xét tính đúng, sai của mệnh đề kéo theo: P ⟹ Q chỉ sai khi P đúng và Q sai Phương pháp xét tính đúng sai của mệnh đề

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 17 d) Phủ định của mệnh đề là ,, abc  mà 0abc++= thì 222 2 abc abbcca++ −=++ Mệnh đề phủ định này đúng vì 0abc++= ( )2 222 02220abcabcabacbc ++=+++++= 222 2 abc abbcca++ −=++ Bài 14. Phát biểu mệnh đề phủ định của mệnh đề sau. Cho biết tính đúng sai của mệnh đề phủ định P : “ ( )( )( ) :1231nAnnnn =++++ không là số chính phương". Lời giải P : “ ( )( )( ) :1231nAnnnn =++++ là số chính phương". P đúng vì ( )( )( ) ( )( ) ( ) 2222 :1231332131 nAnnnnnnnnnn =++++=++++=++  DẠNG 4: MỆNH ĐỀ KÉO THEO, MỆNH ĐỀ ĐẢO, MỆNH ĐỀ TƯƠNG ĐƯƠNG PHƯƠNG PHÁP 1. Mệnh đề kéo theo a. ĐN: Cho hai mệnh đề P và Q. Mệnh

P ⟹ Q Quan sát xem P, Q đúng hay sai Khi đó P ⟹ Q rơi vào mẫu nào trong 4 mẫu sau 1. Đ⟹S→Sai 2. Đ⟹Đ 3. ��⟹Đ 4. ��⟹�� →Đúng Đặc biệt: Có hai trường hợp mà chỉ cần nhìn vào một trong hai mệnh đề P hoặc Q ta sẽ biết (P ⟹ Q) luôn đúng: TH1: P sai TH2: Q đúng. Chú ý: P⟹QchínhlàP∩Q. 2. Mệnh đề tương đương a. Mệnh đề đảo: Mệnh đề Q⟹P được gọi là mệnh đề đảo của mệnh đề P⟹Q b. Mệnh đề tương đương Điều kiện cần và đủ: Nếu cả hai mệnh đề "P⟹ Q" và "Q⟹P" đều đúng ta nói P và Q là hai mệnh đề tương đương và kí hiệu "P⟺Q".

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 18 Lúc đó ta nói: P là điều kiện cần và đủ để có Q hay Q là điều kiện cần và đủ để có P. Hoặc P nếu và chỉ nếu Q Hay P khi và chỉ khi Q Hay Điều kiện cần và đủ để có P là Q. Cách xét tính đúng, sai của mệnh đề tương đương : Mệnh đề P ⇔ Q chỉ đúng khi cả hai mệnh đề kéo theo P ⟹ Q và Q ⟹ P đều đúng. Nói cách khác mệnh đề P ⇔ Q đúng nếu cả hai mệnh đề P và Q cùng đúng hoặc cùng sai. Bài 1. Lập mệnh đề PQ  và xét tính đúng sau của nó, với :"4"P   và 2 :"10"Q   Lời giải Ta có mệnh đề PQ  là: “Nếu 4  thì 2 10  ”. Vì P sai (và Q sai) nên mệnh đề PQ  là mệnh đề đúng. Bài 2. Phát biểu mệnh đề đảo của mệnh đề “Nếu 0A90 = thì ABC là tam giác vuông” và xét tính đúng sai của nó. Lời giải Ta có mệnh đề PQ  : “Nếu 090A = thì ABC là tam giác vuông” Mệnh đề đảo của mệnh đề trên là QP  : “ Nếu ABC là tam giác vuông thì 90A = ”. Mệnh đề QP  là mệnh đề sai, ví dụ trường hợp ABC vuông tại B Bài 3. Cho mệnh đề :"23",Q:"46"P −− . Lập mệnh đề PQ  và xét tính đúng sai của nó. Lời giải (): PQ  “Nếu 23  thì 46−− ”. Mệnh đề sai. Bài 4. Giả sử ABC là một tam giác đã cho. Lập mệnh đề PQ  và mệnh đề đảo của nó, rồi xét tính đúng sai của chúng với P: "Góc A bằng 90 ", Q: 222 "" BCABAC =+ . Lời giải Với tam giác ABC đã cho, ta có () PQ  : “Nếu góc A bằng 90o thì 222 BCABAC =+ ” là mệnh đề đúng. (): QP  “Nếu 222 BCABAC =+ thì ˆ 90oA = ” là mệnh đề đúng. Bài 5. Cho ABC . Xét mệnh đề P : “ ABC là tam giác cân” và mệnh đề Q : “ ABC có hai đường trung tuyến bằng nhau”. Lập mệnh đề PQ  và xét tính đúng sai của nó. Lời giải Ta có mệnh đề PQ  là: “ ABC là tam giác cân khi và chỉ khi tam giác đó có hai đường trung tuyến bằng nhau”. Vì PQ  và QP  đều là hai mệnh đề đúng nên mệnh đề PQ  đúng.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 19 Bài 6. Phát biểu mệnh đề đảo của định lý: “Trong một tam giác cân, các đường cao ứng với các cạnh bên bằng nhau”. Mệnh đề đảo đó đúng hay sai? Tại sao? Lời giải Mệnh đề đảo: “Trong tam giác, các đường cao ứng với các cạnh bên bằng nhau thì tam giác đó là tam giác cân”. Mệnh đề đảo trên đúng. (Hs tự chứng minh) Bài 7. Cho mệnh đề chứa biến ( ):53Pnn + chia hết cho 3, với nN  , ( ): Qnn chia hết cho 3, với nN  Phát biểu mệnh đề “ ( ) ( ), nNPnQn ” và từ đó phát biểu mệnh đề đảo. Xét tính đúng sai của mệnh đề đảo. Lời giải Mệnh đề: “ ,53nn + chia hết cho 3 thì n chia hết cho 3” Mệnh đề đảo: “ , nn chia hết cho 3 thì 53 n + chia hết cho 3”. Mệnh đề đảo trên đúng. Vì: n chia hết cho 3 suy ra 3, nkk= . Khi đó : 535.3.3153, nkkk +=+=+ 153 331533,. k kk +  Vậy 53 n + chia hết cho 3. Bài 8. Cho hai mệnh đề P và Q: P: ABCDlà tứ giác nội tiếp. Q: Tổng số đo hai góc đối nhau bằng 180o . Hãy phát biểu mệnh đề PQ  dưới dạng điều kiện cần và đủ. Lời giải Điều kiện cần : “ ABCDlà tứ giác nội tiếp là điều kiện cần để tổng số đo hai góc đối nhau bằng 180o ”. Điều kiện đủ: “Trong tứ giác ABCD, tổng số đo hai góc đối nhau bằng 180o là điều kiện đủ đề ABCDlà tứ giác nội tiếp.”

lương

người

A nói: "Tôi

Nếu A nói thật

A là hiệp sĩ.

B hoặc C là kẻ bất lương.

Nếu B là kẻ bất lương ⟹

t quả nhanh nhất, ta sẽ xét hiệp sĩ và gián điệp.

OFFICIAL

Bài 11. Ba anh em An, Bình, Vinh ngồi làm bài xung quanh một cái bàn được trải khăn mới. Khi phát hiện có vết mực, bà hỏi thì các cháu lần lượt trả lời:

An: “Em Vinh không làm đổ mực, đấy là do em Bình.”

Bình: “Em Vinh làm đổ mực, anh An không làm đổ mực”.

Vinh: “Theo cháu, Bình không làm đổ mực, còn cháu hôm nay không chuẩn bị bài”.

Biết rằng trong 3 em thì có 2 em nói đúng, 1 em nói sai. Hỏi ai làm đổ mực?

Lời giải

Nếu An nói đúng thì Bình là người làm đổ, suy ra Bình nói sai, theo đề bài ta có Vinh nói đúng. Nếu

Vinh nói đúng thì Bình không làm đổ mực. Suy ra mâu thuẫn.

Nếu Bình nói đúng, Vinh làm

Vinh làm

ch hay cóc?

nói

Vinh nói đúng. Suy ra thỏa mãn.

Trong m

y ma thuật, có hai loài lưỡng cư biết nói: cóc luôn luôn nói đúng và ếch luôn luôn nói sai.

loài lưỡng cư, Brian, Chris, LeRoy và Mike sống cùng nhau trong đầm lầy này và chúng đưa ra nh

ng tuyên

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 20 Bài 10. Trên một hòn đảo, tôi đã gặp ba người A, B và C, một người là hiệp sĩ, một người khác là kẻ bất

và

kia là gián điệp. Người hiệp sĩ luôn nói sự thật, kẻ bất lương luôn luôn nói dối và gián điệp có thể nói dối hoặc nói sự thật.

là hiệp sĩ." B nói, "Tôi là kẻ bất lương." C nói: "Tôi là gián điệp." Hỏi ai là gián điệp? Lời giải Do tính đúng sai nên để xác định kế

⟹

B nói dối ⟹ Mâu thuẫn Nếu C là kẻ bất lương ⟹ C nói dối ⟹ Thỏa mãn Vậy A là hiệp sĩ, C là kẻ bất lương và B là gián điệp cần tìm.

đổ mực thì An

sai. Dẫn đến

Vậy

đổ mực. Bài 12. Ế

ột đầm lầ

ốn

ữ

bố

Brian: "Mike và tôi là những loài khác nhau."

Chris: "LeRoy là một con ếch."

LeRoy: "Chris là một con ếch."

Mike: "Trong bốn người chúng tôi, ít nhất hai người là cóc."

Có bao nhiêu loài lưỡng cư là ếch?

Cách 1: Trình bày lời văn:

Giả sử Brian là cóc (nói thật)

⟹ Mike là ếch (nói dối)

Lời giải

⟹ Chỉ có 1 con là ếch trong 4 con. Mà Mike đã là ếch

⟹ LeRoy và Chris là đều cóc (nói thật)

Nhưng Chris nói LeRoy là ếch ⟹ mâu thuẫn

Vậy Brian nói dối (là Ếch)

⟹ Brian và Mike cùng là loài ếch (nói dối)

⟹ Chỉ

LeRoy

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 21

có 1 con cóc và 3 con còn lại là ếch (*) • Nếu Chris là Cóc (nói thật) ⟹ LeRoy là ếch (nói dối) ⟹ Thỏa mãn (*) • Nếu LeRoy là Cóc (nói thật) ⟹ Chris là ếch (nói dối) ⟹ Thỏa mãn (*) Vậy có 3 loài lưỡng cư là ếch Cách 2: Dùng bảng Kí hiệu: Cóc : x Ếch: o Brian Chris

Mike x o o o Mâu thuẫn o x o o Thỏa mãn o o x o Thỏa mãn Vậy có 3 loài lưỡng cư là ếch. Câu 1: Câu nào sau đây không là mệnh đề? A. Tam giác đều là tam giác có ba cạnh bằng nhau. B. 31  C. 451 −= D. Bạn học giỏi quá! Lời giải BÀI TẬP TRẮC NGHIỆM.2 =

Câu

là câu

i là mệnh đề

Câu 4: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) Cố lên, sắp tới nơi rồi!

b) Số 15 là số nguyên tố

c) Tổng các góc của một tam giác là 180.  d) x là số nguyên dương.

A. 3. B. 2. C. 4. D. 1.

Chọn B

Câu a) không là mệnh đề

Câu d) là mệnh đề chứa biến Các câu b) c) là các mệnh đề

i giải

Câu 5: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng?

A. “ Nếu I là trung điểm của AB thì IA = IB”.

B. “

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 22 Chọn D Vì “Bạn học giỏi quá!” là câu cảm thán không có khẳng định đúng hoặc sai. Câu 2: Câu nào trong các câu sau không phải là mệnh đề? A.  có phải là một số vô tỷ không?. B. 225 += C. 2 là một số hữu tỷ. D. 4 2 2 = . Lời giải Chọn A

3: Trong các câu sau, câu nào là mệnh đề? A. 12là số tự nhiên lẻ. B. An học lớp mấy? C. Các bạn có chăm học không? D. Các bạn hãy làm bài đi! Lời giải Chọn A

cảm thán không phả

ờ

Nếu ABCD là hình bình hành thì ACABAD =+ ’’. C. “ Nếu x > 2 thì 2x  ” . D. “ Nếu , mn là 2 số nguyên dương và cùng chia hết cho 3 thì 22 mn + cũng chia hết cho 3”. Lời giải Chọn D Đáp án A sai vì IA = IB thì IAB có thể là tam giác cân tại I. Đáp án B sai vì ACABAD =+ thì ,,, ABCD có thể thẳng hàng. Đáp án C sai vì 2x  thì 2x − hoặc 2x  Đáp án D đúng:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 23 Nhận xét: 2 m ( 2 n ) là các số chính phương nên chia cho 3 có thể dư 0 hoặc 1 ( chứng minh bằng cách xét 3,31,32mkmkmk ==+=+ ) Do đó: Nếu 22 , mn cùng chia 3 dư 1 thì 22 mn + chia 3 dư 2 ( trái giả thiết) Nếu 1 trong 2 số 22 , mn có 1 số chia hết cho 3 và số còn lại chia hết cho 3 dư 1 thì 22 mn + chia 3 dư 1 ( trái giả thiết) Suy ra 22 , mn cùng chia hết cho 3. Mà 3 là số nguyên tố nên m, n cùng chia hết cho 3 Câu 6: Trong các mệnh đề dưới đây, các mệnh đề nào sai. M: “ 2 ,410rr = ”. N: “ 2 ,1nn + chia hết cho 8”. X: “ *,123 nn ++++ không chia hết cho 11”. Q: “ 2 ,1nnn + + là một số chẵn”. E: “ 32 2 263 ,21 xxx x x −+−  + ”. A. N, X, Q B. M, X, Q C. N, Q, E D. M, Q, E Lời giải Chọn A Mệnh đề M đúng, vì với 2 ,410 1 2 r r= = Mệnh đề N sai. Ta chứng tỏ mệnh đề phủ định “ 2, 1nn + không chia hết cho 8” là đúng. + Nếu n chẵn thì 2 1n + là một số lẻ nên không chia hết cho 8 + Nếu n lẻ, ( )21 nkk=+ thì ( )2214424.12nkkkk +=++=++ chia 8 dư 2 vì ( )1kk + là số chẵn Mệnh đề X sai. Ta chứng tỏ mệnh đề phủ định “ *,123 nn ++++ chia hết cho 11”. Thật vậy, nếu *11n = thì 12+31166 +++= chia hết cho 11. Mệnh đề Q sai. Ta chứng minh mệnh đề phủ định “ 2 ,1nnn + + là một số lẻ” là đúng. + Nếu n chẵn 2 1nn++ là một số lẻ, + Nếu n lẻ, 21nk=+ thì 221463nnkk++=++ là số lẻ Mệnh đề E đúng vì ( )( )322 22 263213 ,3 2121 xxxxx xx xx −+−+− ==− ++ Câu 7: Cho các mệnh đề sau: (1) 2a và 3a 6a .

(2) 39aa  .

(3) 24aa 

(4) 3a và 6a thì 18a .

(5) 00aba+ và 0b 

(6) 00aba== hoặc 0b =

(7) Hai tam giác bằng nhau khi và chỉ khi hai tam giác đó đồng dạng.

(8) Một tam giác là tam giác vuông khi và chỉ khi đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.

Có bao nhiêu mệnh đề sai trong các mệnh đề trên?

A. 4. B. 6. C. 5. D. 7. Lời giải Chọn C

OFFICIAL

(1) đúng.

(2) sai, ví dụ 63 nhưng 69  .

(3) sai, vì 22 nhưng 24

(4) sai, vì 63 và 66 nhưng 618.

(5) sai, ví dụ a = 5, b = 7 có tổng a + b < 0 nhưng a > 0. (6) đúng.

(7) sai, 2 tam giác đồng dạng có thể không bằng nhau.

(8) đúng.

Câu 8: Cho ba mệnh đề sau, với n là số tự nhiên:

(1) 8n + là số chính phương

(2) Chữ số tận cùng của n là 4 (3) 1n là số chính phương

Biết rằng có hai mệnh đề đúng và một mệnh đề

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 24

sai. Hãy xác định mệnh đề nào đúng, mệnh đề nào sai? A. Mệnh đề (2) và (3) là đúng, còn mệnh đề (1) là sai B. Mệnh đề (1) và (2) là đúng, còn mệnh đề (3) là sai C. Mệnh đề (1) là đúng, còn mệnh đề (2) và (3) là sai D. Mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai. Lời giải Chọn D Ta có số chính phương có các chữ số tận cùng là0,1,4,5,6,9. Vì vậy

đúng thì

này

có

chính

Vậy trong hai m

n thấy giữa mệnh đề (2) và (3) cũng có mâu thuẫn. Bởi vì, giả sử mệnh đề này đồng thời là đúng thì 1n có chữ số tận cùng là 3 nên không thể là số chính phương.

Tương tự,

Vậy trong ba mệnh đề trên thì mệnh đề (1) và (3) là đúng, còn mệnh đề (2) là sai.

Câu 9: Mệnh đề nào là sau đây sai?

A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau.

B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông

C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại.

D. Một tam giác là đều khi và chỉ khi nó là tam giác cân và có một góc bằng 60. 

Lời giải

Chọn A

Vì hai tam giác đồng dạng thì luôn có các góc bằng nhau nên A sai

OFFICIAL

Các mệnh đề B, C, D đúng.

Câu 10: Mệnh đề nào dưới đây đúng?

A. Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

B. Nếu tứ giác ABCD một cặp cạnh đối song song thì tứ giác ABCD là hình bình hành. C. Nếu tứ giác ABCD có một cặp cạnh đối bằng nhau thì tứ giác ABCD là hình bình hành. D. Nếu tứ giác ABCD có hai đường chéo vuông góc với nhau thì tứ giác ABCD là hình bình hành.

Chọn A

Theo định lý đã học suy ra Chọn A Các mệnh đề B, C, D sai.

Câu 11: Mệnh đề nào sau đây sai?

A. 2 là số nguyên tố B. 1 là s

C. 5 là số nguyên t

nguyên t

D. 6 không ph

i là s

ả

nguyên t

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 25

ận thấy giữa mệnh đề (1) và (2) có mâu thuẫn. Bởi vì, giả sử 2

ệnh đề này đồng thời là

chữ số tận cùng là 2 nên không thể là số

phương.

ệnh đề

phải có một mệnh đề là đúng và một mệnh đề là sai.

nhậ

ời gi

ố

ả

ố

ố Lời giải Chọn B Số nguyên tố là số tự nhiên lớn hơn 1, chỉ chia hết cho 1 và chính nó. Vậy B sai. Câu 12: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. Hai tam giác bằng nhau khi và chỉ khi chúng đồng dạng và có một góc bằng nhau. B. Một tứ giác là hình chữ nhật khi và chỉ khi chúng có 3 góc vuông. C. Một tam giác là vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại. D. Một tam giác là đều khi và chỉ khi chúng có hai đường trung tuyến bằng nhau và có một góc bằng 60.  Lời giải Đáp án A sai vì hai tam giác đồng dạng thì các góc tương ứng bằng nhau. Hai tam giác đồng dạng bằng nhau khi chúng có cặp cạnh tương ứng bằng nhau.

Câu 13: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có chữ số tận cùng là 5thì số nguyên n chia hết cho 5.

B. Nếu tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCD là hình chữ nhật thì tứ giác ABCD có hai đường chéo bằng nhau.

D. Nếu tứ giác ABCD là hình thoi thì tứ giác ABCD có hai đường chéo vuông góc với nhau.

Lời giải

Xét mệnh đề đảo của đáp án A: “Nếu số nguyên n chia hết cho 5 thì số nguyên n có chữ số tận cùng là 5”. Mệnh đề này sai vì số nguyên n

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 26

cũng có thể có chữ số tận cùng là 0 Xét mệnh đề đảo của đáp án B: “Nếu tứ giác ABCD là hình bình hành thì tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm mỗi đường”. Mệnh đề này đúng. Câu 14: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu số nguyên n có tổng các chữ số bằng 9 thì số tự nhiên n chia hết cho 3. B. Nếu xy  thì 22 xy  C. Nếu xy = thì ... txty = D. Nếu xy  thì 33 .xy  Lời giải Xét mệnh đề đảo của đáp án A: “Nếu số tự nhiên n chia hết cho 3 thì số nguyên n có tổng các chữ số bằng 9”. Mệnh đề này sai vì tổng các chữ số của n phải chia hết cho 9 thì n mới chia hết cho 9. Xét mệnh đề đảo của đáp án B: “Nếu 22 xy  thì xy  ” sai vì 22 xy xyxy xy    − . Xét mệnh đề đảo của đáp án C: “Nếu .. txty = thì xy = ” sai với 0,.txy= Câu 15: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. "ABC là tam giác đều  Tam giác ABC cân". B. "ABC là tam giác đều  Tam giác ABC cân và có một góc 60".  C. "ABC là tam giác đều  ABC là tam giác có ba cạnh bằng nhau". D. "ABC là tam giác đều  Tam giác ABC có hai góc bằng 60".  Lời giải Mệnh đề kéo théo "ABC là tam giác đều  Tam giác ABC cân" là mệnh đề đúng, nhưng mệnh đề đảo "Tam giác ABC cân ABC là tam giác đều" là mệnh đề sai. Do đó, 2 mệnh đề "ABC là tam giác đều" và "Tam giác ABC cân" không phải là 2 mệnh đề tương đương. Câu 16: Mệnh đề nào sau đây đúng? A. ( ):1nnn + là số chính phương. B. ( ):1nnn + là số lẻ. C. ( )( ):12nnnn ++ là số lẻ. D. ( )( ):12nnnn ++ chia hết cho 6. Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 27 Ta có ( )( )12nnn++ là tích của 3 số tự nhiên liên tiếp nên ( )( )12nnn++ chia hết cho 3 và chia hết cho 2. Vậy ( )( )12nnn++ chia hết cho 6. Câu 17: Trong các mệnh đề sau, mệnh đề nào sai? A. 2 , xxx . B. ,66xxx  . C. 2 ,1nn + không chia hết cho 3. D. 2 ,7aa = . Lời giải Chọn D Câu 18: Trong các mệnh đề sau, mệnh đề nào đúng? A. 2 ,50xx += . B. 42 ,540xxx ++= . C. 3 , nnn− chia hết cho 3. D. 52 , xxx . Lời giải Chọn C Với * n thì ( )( )3 11nnnnn−=−+ là tích 3 số tự nhiên liên tiếp nên 3 nn chia hết cho 3. Với 0n = thì 3 0nn−= chia hết cho 3. Vậy 3 , nnn− chia hết cho 3. Câu 19: Trong các mệnh đề sau mệnh đề nào sai? A. 2399100 444....44 +++++ chia hết cho 5. B. 2 :1nn + không chia hết cho 4 C. :21 nnN − chia hết cho 7. D. 3333 123....100 ++++ không chia hết cho 5050 Lời giải Chọn D Phương án A đúng vì ( )2399100399399 444....444.54.5...4.5544...4 +++++=+++=+++ chia hết cho 5. Phương án B đúng vì +) TH1 : 2, nkk= Ta có : 22141nk+=+ không chia hết cho 4. +) TH1 : 21, nkk=+ Ta có : 221442nkk+=++ không chia hết cho 4. Vậy 2 :1nn + không chia hết cho 4 là mệnh đề đúng. Phương án C đúng vì với 3n = thì 217 n −= chia hết cho 7. Phương án D sai vì: ( ) ( ) ( )3333332333 123....1001100299...5060 ++++=++++++ chia hết cho 101 Lại có ( ) ( ) ( ) 333333233333 123....100199298...406050100 ++++=++++++++ chia hết cho 50. Vậy 3333 123....100 ++++ chia hết cho 5050.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 28 Câu 20: Có bao nhiêu số nguyên n để mệnh đề “ 32 271 nnn+++ chia hết cho 21 n ” là đúng? A. 3. B. 2. C. 4. D. 5. Lời giải Chọn C Ta có : ( )( )322 2714215 nnnnnn +++=++−+ 32 271 nnn+++ chia hết cho 21 n  5 chia hết cho 21 n 2111 2110 2153 2152 nn nn nn nn −==  −=−= −==  −=−=− Vậy có 4 giá trị nguyên của n . Câu 21: Cho các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu tứ giác ABCD là hình thang cân thì 2 góc đối bù nhau. B. Nếu ab = thì .. acbc = . C. Nếu ab  thì 22ab  . D. Nếu số nguyên chia hết cho 10 thì chia hết cho 5 và 2. Lời giải Chọn D "Nếu số nguyên chia hết cho 10 thì chia hết cho 5 và 2" có mệnh đề đảo là "Nếu số nguyên chia hết cho 5 và 2 thì chia hết cho 10" là một mệnh đề đúng. Câu 22: Dùng kí hiệu ,  để phát biểu mệnh đề "Có một số hữu tỉ mà nghịch đảo của nó lớn hơn chính nó". A. 1 : nn n  B. 1 : nn n  C. 1 : nn n  D. 1 : nn n  Lời giải Chọn D Câu 23: Cho mệnh đề 2 1 “:” 4 Axx x =+− . Lập mệnh đề phủ định của mệnh đề A và xét tính đúng sai của nó. A. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. B. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. C. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề đúng. D. 2 1 “:” 4 Axxx=+− . Đây là mệnh đề sai. Lời giải Chọn D 2 1 “:” 4 Axx x =+− vậy 2 1 “:” 4 Axx x =+− . Ta có 2 2 11 0, 42 xxxx  +−+   là mệnh đề đúng. Vậy mệnh đề A là mệnh đề sai.

Câu 24: Phủ định của mệnh đề: “Hình thoi có hai đường chéo vuông góc với nhau” là:

A. “Hai đường chéo của hình thoi vuông góc với nhau”.

B. “Hình thoi có hai đường chéo không vuông góc với nhau”.

C. “Hình thoi có hai đường chéo bằng nhau”.

D. “Hình thoi là hình bình hành có hai đường chéo vuông góc với nhau”.

Câu

góc” là

vuông góc”.

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 29

Lời giải

ọn B

ủ định của “vuông

“không

25: Phủ định của mệnh đề: “ 2

nn + không chia hết cho 3” là: A. “ 2 :1nn + chia hết cho 3”. B. “ 2 :1nn + không chia hết cho 3”. C. “ 2 :1nn + chia hết cho 3”. D. “  2 :1nn+ không chia hết cho 3”. Lời giải Chọn C Phủ định của  là  Phủ định của “không chia hết” là “chia hết” Câu 26: Phủ định của mệnh đề: “ 2 :10xx + ” là: A. “ 2 :10xx + ” B. “ 2 :10xx + ”C. “ 2 :10xx + ”D. “ 2 :10xx += ” Lời giải Chọn B Phủ định của  là  Phủ định của > là  Câu 27: Phủ định của mệnh đề P: “ 2 :320xxx −+= ” là: A. P : “ 2 :320xxx −+ ” B. P : “ 2 :320xxx −+= ” C. P : “ 2 :320xxx −+ ” D. P : “ 2 :320xxx −+ ” Lời giải Chọn D Phủ định của là  Phủ định của = là  Câu 28: Mệnh đề nào sau đây là phủ định của mệnh đề: “Mọi động vật đều di chuyển”. A. Mọi động vật đều không di chuyển. B. Mọi động vật đều đứng yên. C. Có ít nhất một động vật không di chuyển. D. Có ít nhất một động vật di chuyển. Lời giải Chọn C Phủ định của mệnh đề “Mọi động vật đều di chuyển” là mệnh đề “Có ít nhất một động vật không di chuyển”. Câu 29: Phủ định của mệnh đề 2 ",531" xxx −= là A. 2" ,53"xxx− B. 2 ",531" xxx −= C. 2 "x,5x31" x − D. 2 ",531" xxx − Lời giải Chọn C Phủ định của mệnh đề 2 ",531" xxx −= là mệnh đề 2 "x,5x31" x −

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 30 Câu 30: Cho mệnh đề ( ):Px 2 ",10" xxx ++ . Mệnh đề phủ định của mệnh đề ( )Px là: A. 2 ",10" xxx ++ B. 2 ",10" xxx ++ C. 2 ",10" xxx ++ D. "  2 ,10"xxx++ Lời giải Chọn C Phủ định của mệnh đề 2 ",10" xxx ++ là mệnh đề 2 ",10" xxx ++ Câu 31: Cho mệnh đề 2 “:”A xxx=  . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A? A. 2 “:” xxx B. 2 “:” xxx C. 2 “:” xxx D. 2 “:” xxx Lời giải Chọn B Trong mệnh đề phủ định,  đổi thành ,  đổi thành  Phủ định của  là . Câu 32: Cho mệnh đề 2 “:”A xxx=  . Trong các mệnh đề sau, mệnh đề nào là phủ định của mệnh đề A? A. 2 “:” xxx . B. 2 “:” xxx . C. 2 “:” xxx . D. 2 “:” xxx . Lời giải Chọn B Phủ định của  là  Phủ định của  là . Câu 33: Cho n là số tự nhiên, mệnh đề phủ định của mệnh đề nào sau đây đúng? A. :P ” ( ),1nnn + không là số chính phương”. B. :Q ” ( ),1nnn + là số chẵn” C. :R ” ( )( ),12nnnn ++ là số chẵn”. D. :M ” ( )( ),12nnnn ++ không chia hết cho 6” Lời giải Chọn D :P ” ( ),1nnn + là số chính phương” +) với ( ) 112nnn=+= không phải số chính phương A sai. :Q ” ( ),1nnn + là số lẻ”. +) với ( ) 112nnn=+= là số chẵn B sai. :R ” ( )( ),12nnnn ++ là số lẻ” TH1: n chẵn ( )( )12nnn ++ chẵn TH2: n lẻ ( )1n + chẵn ( )( )12nnn ++ chẵn

ab+

đủ để một trong hai số a và b nhỏ hơn 1. B. Một trong hai số a và b nhỏ hơn 1 là điều kiện đủ để 2ab+

C. Từ 2ab+ suy ra một trong hai số a và b nhỏ hơn 1

D. Tất cả các câu trên đều đúng.

Chọn A

Lời giải

Câu 35: Cho mệnh đề: “Nếu 2 góc ở vị trí so le trong thì hai góc đó bằng nhau”. Trong các mệnh đề sau đây, đâu là mệnh đề đảo của mệnh đề trên?

A. Nếu 2 góc bằng nhau thì hai góc đó ở vị trí so le trong

B. Nếu 2 góc không ở vị trí so le trong thì hai góc đó không bằng nhau

C. Nếu 2 góc không bằng nhau thì hai góc đó không ở vị trí so le trong.

D. Nếu 2 góc ở vị trí so le trong thì hai góc đó không bằng nhau.

ời giải

ọn A

Câu 36: Cho mệnh đề: “Nếu một tứ giác là hình thang cân thì tứ giác đó có hai đường chéo bằng nhau”.

Phát biểu mệnh đề

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 31 Vậy ( )( )12nnn++ chẵn n  C sai. :M ” ( )( ),12nnnn ++ chia hết cho 6”. +) ( ) ( ) 2* 6 3** P P P       ( )* Ở trên ta đã chứng minh P luôn chẵn 2P ( )** 3P TH1: 3n 3P TH2: n chia 3 dư 1 ( ) 23n + 3P TH3: n chia 3 dư 2 ( ) 13n + 3P Vậy 3P n  6P . Câu 34: Cho mệnh đề: “Nếu 2ab+ thì một trong hai số a và b nhỏ hơn 1”. Phát biểu mệnh đề trên bằng cách sử dụng khái niệm “điều kiện đủ”.

là điều kiện

trên bằng cách sử dụng khái niệm “điều kiện cần”. A. Điều kiện cần để tứ giác là hình thang cân là tứ giác đó có hai đường chéo bằng nhau. B. Điều kiện cần để tứ giác có hai đường chéo bằng nhau là tứ giác đó là hình thang cân. C. Tứ giác là hình thang cân kéo theo tứ giác đó có hai đường chéo bằng nhau. D. Cả a, b đều đúng. Lời giải Chọn A Câu 37: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo là sai? A. Tam giác cân có hai cạnh bằng nhau. B. x chia hết cho 6 thì x chia hết cho 2 và 3.

C. ABCD

ABCD

hình

Câu 38: Mệnh đề nào dưới đây sai

A. Tứ giác ABCD là hình chữ nhật khi và chỉ khi ABCD có ba góc vuông.

B. Tứ giác ABCD là hình bình hành khi và chỉ khi ABCD có hai cạnh đối song song và bằng nhau.

C. Tứ giác ABCD là hình thoi khi và chỉ khi ABCD có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường.

D. Tứ giác ABCD là hình vuông khi và chỉ khi ABCD có bốn góc vuông.

Lời giải

Chọn D

Mệnh đề ở đáp án D không phải là một mệnh đề tương đương vì hình chữ nhật vẫn có bốn góc vuông nhưng không phải là hình vuông.

OFFICIAL

Câu 39: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu số nguyên n có chữ số tận cùng là 5 thì số nguyên n chia hết cho 5.

B. Nếu tứ giác ABCDcó hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác ABCD là hình bình hành.

C. Nếu tứ giác ABCDlà hình chữ nhật thì tứ giác ABCDcó hai đường chéo bằng nhau.

D. Nếu tứ giác ABCDlà hình thoi thì tứ giác ABCDcó hai đường chéo vuông góc với nhau.

Lời giải Chọn B

Đáp án A sai vì số nguyên n chi hết cho 5 thì số nguyên n có chữ số tận cùng là 5 và 0 ; Đáp án C sai vì hai đường chéo bằng nhau không suy ra được tứ giác là hình chữ nhật ; Đáp án D sai vì hai đường chéo vuông góc với nhau không suy ra được tứ giác là hình thoi.

Câu 40: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng?

A. Nếu tổng hai số 2ab+ thì có ít nhất có một số lớn hơn 1.

B. Trong một tam giác cân hai đường cao bằng nhau.

C. Nếu tứ giác là hình vuông thì hai đường chéo vuông góc với nhau.

D. Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3. Lờ

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 32

là

bình hành thì AB song song với CD. D.

là

chữ nhật thì 90.ABC=== Lời giải Chọn C

i giải Chọn B Tam giác có hai đường cao bằng nhau là tam giác cân là mệnh đề đúng. Câu 41: Trong các mệnh đề sau đây, mệnh đề nào có mệnh đề đảo là đúng? A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c B. Nếu hai tam giác bằng nhau thì diện tích bằng nhau. C. Nếu a chia hết cho 3 thì a chia hết cho 9 D. Nếu một số tận cùng bằng 0 thì số đó chia hết cho 5. Lời giải Chọn C Nếu a chia hết cho 9 thì a chia hết cho 3 là mệnh đề đúng.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 33

BÀI1:MỆNHĐỀ

Câu 1: Trong các câu dưới đây, câu nào không phải là mệnh đề?

A. 16 là số chính phương. B. Bạn bao nhiêu tuổi?

C. Năm 2021 là năm nhuận. D. Tổng các góc của một tứ giác bằng 0360 .

Câu 2: Câu nào sau đây không là mệnh đề?

A. 213 x + .

B. Mặt trời mọc ở hướng Tây.

C. Một tuần có bảy ngày.

D. Hình bình hành có một góc vuông là hình chữ nhật.

Câu 3: Phát biểu nào sau đây không phải là mệnh đề?

A. Bạn là học sinh khối 10 phải không?

B. Tổng ba góc của một tam giác bằng 180 .

C. 2 là số nguyên tố nhỏ nhất.

D. Năm 2022 là năm nhuận.

Câu 4: Trong các câu dưới đây, câu nào là mệnh đề?

A. Bạn có khỏe không?

C. Lớp bạn có bao nhiêu học sinh nữ?

B. Hôm nay trời nóng quá!

D. 111 không phải là số nguyên tố.

Câu 5: Trong các câu sau, câu nào không là một mệnh đề chứa biến?

A. 246 += B.

450

C. 520 xy−= D. 21

chia hết cho 3.

Câu 6: Trong các câu sau đây câu nào không phải là mệnh

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 18

xx−−=

x +

đề? A. Một năm có 365 ngày. B. Học lớp 10 thật vui. C. Pleiku là thành phố của Gia Lai. D. 236 += . Câu 7: Mệnh đề chứa biến 2 :''440"Pxx++= trở thành một mệnh đề đúng với. A. 2x =− . B. 1x =− . C. 1.x = D. 0x = . Câu 8: Trong các câu dưới đây có bao nhiêu câu là mệnh đề? (I) Số 2018 là số chẵn. (II) Hôm nay bạn có vui không? (III) Quảng Phú là một thị trấn của huyện CưMgar. (IV) Tiết 5 rồi, đói bụng quá! A. 4 B. 1 C. 2 D. 3 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

Câu 9: Cho các câu sau đây:

(I): “ Phan xi păng là ngọn núi cao nhất Việt Nam”.

(II): “ 2 9,86  ”.

(III): “ Mệt quá!”.

(IV): “ Chị ơi, mấy giờ rồi?”

Hỏi có bao nhiêu câu là mệnh đề?

A. 4 B. 3 C. 2 D. 1

Câu 10: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) Trời rét quá!

b) Việt Nam nằm ở khu vực Đông Nam Á.

c) 10244. −+=

d) Năm 2020là năm nhuận.

A. 1. B. 2. C. 3. D. 4.

Câu 11: Trong các phát biểu sau, phát biểu nào là mệnh đề?

A. 3 là số nguyên tố lẻ nhỏ nhất.

B. Đề thi hôm nay khó quá!

OFFICIAL

C. Một tam giác cân thì mỗi góc đều bằng 060 phải không?

D. Các em hãy cố gắng học tập!

Câu 12: Trong các phát biểu sau, phát biểu nào là mệnh đề?

A. 3 là số nguyên tố lẻ nhỏ nhất.

B. Đề thi hôm nay khó quá!

C. Một tam giác cân thì mỗi góc đều bằng 060 phải không?

D. Các em hãy cố gắng học tập!

Câu 13: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) 613 x + .

b) Phương trình 2 310xx+−= có nghiệm. c) ,51xx 

d) Năm 2018 là năm nhuận. e) Hôm nay thời tiết đẹp quá!

A. 4. B. 1. C. 2. D. 3.

Câu 14: Trong các câu sau, câu nào là mệnh đề?

A. Không được làm việc riêng trong giờ học. B. Đi ngủ đi. C. Trung Quốc là nước đông dân nhất thế giới. D. Bạn học trường nào?

Câu 15: Trong các câu sau, có bao nhiêu câu là mệnh đề?

a) Hãy đi nhanh lên!

b) Hà Nội là thủ đô của Pháp. c) 57415 ++=

3x  .

A. 4. B. 1. C. 2.

Câu 16: Trong các câu sau câu nào là mệnh đề?

A. Hãy đi nhanh lên!.

B. Hà nội là thủ đô của Việt Nam.

C. Nam ăn cơm chưa?.

D. Buồn ngủ quá!

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 19

Câu 17: Trong các câu sau câu nào là mệnh đề chứa biến?

A. 9 là số nguyên tố.

B. 18 là số chẵn.

C. ( )2 3, xxx+ .

D. Hình chữ nhật có hai đường chéo bằng nhau.

Câu 18: Cho mệnh đề chứa biến ( ) 2 :"511"Pxx với x là số nguyên tố. Tìm mệnh đề đúng trong các mệnh đề sau:

A. ( )3P . B. ( )2P . C. ( )7P . D. ( )5P .

Câu 19: Cho S là mệnh đề “ Nếu tổng các chữ số của một số n chia hết cho 6thì n chia hết cho 6”. Một giá trị của n để khẳng định S sai là:

A. 33. B. 40. C. 42. D. 30.

Câu 20: Trong các phát biểu sau, phát biểu nào là mệnh đề đúng?

A. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.

B. Hình thang có hai cạnh bên bằng nhau là hình thang cân.

C. Bạn có chăm học không?

D.  là một số hữu tỉ.

Câu 21: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

OFFICIAL

A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

Câu 22: Trong các câu sau, câu nào một là mệnh đề đúng?

A. Hà nội là thủ đô của Việt Nam.

C. 7là một số tự nhiên chẵn.

Câu 23: Trong các mệnh đề sau, mệnh đề nào sai?

A. Hà nội là thủ đô của Việt Nam.

C. 5là một số tự nhiên lẻ.

B. 2là một số tự nhiên lẻ.

C.  là một số hữu tỷ.

B. 4là một số tự nhiên chẵn.

C.  là một số hữu tỷ.

Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x ?

A. 52xx  .

B. 52xx  .

C. 2252xx  . D. 52xx++ .

Câu 25: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai?

A. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

B. Tam giác cân có một góc bằng 060 là tam giác đều.

C. Hình bình hành có hai đường chéo bằng nhau là hình vuông.

D. Tam giác có hai đường cao bằng nhau là tam giác cân.

Câu 26: Cho định lý “Nếu hai tam giác bằng nhau thì diện tích bằng nha”. Mệnh đề nào sau đây đúng?

A. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.

B. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.

D. Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

Câu

Mệnh

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 20

27:

đề nào

đây là mệnh đề sai ? A. 2 :0xx  . B. 2 : nnn= . C. :2 nnn . D. 2 : xxx . Câu 28: Trong các mệnh đề sau, mệnh đề nào sai?

A. N

B. N

huy

C. V

hướ

D. Điể

ABC

OFFICIAL

) xBA  . D. ( ) xBA  .

Câu 32: Trong các mệnh đề sau, tìm mệnh đề sai?

A. Nếu a chia hết cho 9thì a chia hết cho 3 B. Nếu một tam giác có một góc bằng 60thì tam giác đó là tam giác đều.

C. Nếu 0ab thì 22ab  . D. Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân.

Câu 33: Cho mệnh đề chứa biến

các giá trị của x để ( )Px là một mệnh đề đúng.

Câu 34: Trong các

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 21

ếu m , n là các số vô tỉ thì mn cũng là số vô tỉ

ếu

là một tam giác vuông thì đường trung tuyến ứng với cạnh huyền bằng nửa cạnh

ền.

ới ba véctơ a , b , c đều khác véctơ 0 , nếu a , b cùng ngược hướng với c thì a , b cùng

ng.

là trọng tâm tam giác ABC khi và chỉ khi 0GAGBGC++= Câu 29: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu hai số a , b cùng chia hết cho c thì ab + chia hết cho c B. Nếu một số nguyên chia hết cho 6 thì nó chia hết cho2 và 3. C. Nếu hai số x , y thỏa mãn 0xy+ thì có ít nhất một trong hai số x , y dương. D. Phương trình bậc hai ( )2 00axbxca++= có a , c trái dấu thì có hai nghiệm phân biệt. Câu 30: Cho hai đa thức ( )Px và ( )Qx . Xét các tập hợp ( ) 0AxPx== , ( ) 0BxQx== và ( ) ( ) 22 0CxPxQx =+=   . Trong các mệnh đề sau, mệnh đề nào đúng? A. CAB = B. CAB = C. \ CAB = D. \.CBA = Câu 31: Cho phần tử x thuộc tập B và tâp B là tập con của A . Trong các khẳng định sau khẳng định nào đúng? A. ( ) xBA  . B. ( ) xBA  . C. (

( ) 32 :"320"Pxxxx−+= . Tìm

A. 0,1,2xxx=== B. 2,3xx=−=− C. 1,2xx=−=− D. 4,2,3xxx==−=

mệnh đề sau, mệnh đề nào là mệnh đề sai? A. :33 n nn + B. 1267  C. 64107  D. ( )2 2:2 xxx − Câu 35: Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì tam giác cân có 2 cạnh bằng nhau” và Q: “Nếu 17 là số chẵn thì 25 là số chính phương”. Hãy chọn khẳng định đúng trong các khẳng định sau A. P đúng, Q sai. B. P đúng, Q đúng. C. P sai, Q đúng. D. P sai, Q sai. Câu 36: Trong các mệnh đề dưới đây, mệnh đề nào là mệnh đề đúng? A. 2 :10xx += . B. 2 :0xx  . C. 2 :210xx − . D. 2 :20xx −= . Câu 37: Mệnh đề nào sau đây là mệnh đề đúng? A. “ :22 x xx + ”. B. “ :21 x x + là số nguyên tố”. C. “ *2:1xx − là bội số của 3”. D. “ 2 :3xx = ”. Câu 38: Cho P Q là mệnh đề đúng. Khẳng định nào sau đây là sai? A. PQ  sai. B. PQ  đúng. C. QP  sai. D. PQ  sai.

Mệnh đề phủ định của mệnh

A. 2018không là một số lẻ.

2018là một số lẻ.

2018 là một số chẵn” là:

2018không là một số chẵn.

Câu 42: Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề: “Mọi động vật đều di chuyển”?

A. Có ít nhất một động vật di chuyển. B. Có ít nhất một động vật không di chuyển. C. Mọi động

Cho m

Cho mệnh đề "Có một học sinh trong lớp 11A không chấp hành luật giao thông " Mệnh đề phủ định của mệnh đề này là :

A. Không có học sinh nào trong lớp 11A chấp hành luật giao thông.

B. Mọi học sinh trong lớp 11A đều chấp hành luật giao thông.

C. Có một học sinh trong lớp 11A chấp hành luật giao thông. D. Mọi học sinh trong

hành luật giao thông.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 22 Câu 39: Số mệnh đề đúng trong các mệnh đề sau: ( ) 1 : Ixx x  . ( ) :20 nIIn . ( ) 2 :90IIIxx−= ( ) 2 :510IVnn+ chia hết cho 5 A. 1 B. 4 C. 2 D. 3 Câu 40: Lập mệnh đề phủ định của mệnh đề 2 ":20180" xxx ++ . A. 2 :20180xxx ++ B. 2 :20180xxx ++ C. 2 :20180xxx ++ D. 2 :20180xxx ++ Câu 41:

đề: “

vật đều không di chuyển. D. Mọi động vật đều đứng yên. Câu 43: Cho mệnh đề 2 :",12" Pxxx + . Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề P ? A. 2 :",12" Pxxx + . B. 2 :",12" Pxxx + . C. 2 :",12" Pxxx + . D. 2 :",12" Pxxx + . Câu 44:

ệnh đề 2 ",30" xxx −+ . Hỏi mệnh đề nào là phủ định của mệnh đề trên A. 2 ",30" xxx −+ . B. 2 ",30" xxx −+ . C. 2 ",30" xxx −+ . D. "  2 ,30"xxx−+ . Câu 45:

lớp 11A không chấp

Câu 46: Cho mệnh đề 2 :":70" Axxx−+ . Mệnh đề phủ định của A là: A. 2 :70xxx −+ B. 2 :70xxx −+ C. 2 :70xxx −+ . D. 2 :70xxx −+ . Câu 47: Cho mệnh đề: 2 ",20" xxx −+ . Mệnh đề phủ định là: A. 2 ",20" xRxx −+ B. 2 ",20" xxx −+ C. 2 ",20" xxx −+ D. 2 ",20" xxx −+ Câu 48: Cho mệnh đề: 2 ",20" xxx −+ . Mệnh đề phủ định sẽ là: A. 2 ",20" xxx −+ . B. 2 ",20" xxx −+ . C. 2 ",20" xxx −+ D. 2 ",20" xxx −+ Câu 49: Lập mệnh đề phủ định của mệnh đề : “ ,21 n nn + “ A. ,21 n nn + . B. ,21 n nn + . C. ,21 n nn + . D. ,21 n nn + . Câu 50: Cho mệnh đề 2 ",320" xxx ++ . Mệnh đề phủ định của mệnh đề trên là

Câu 51: Cho mệnh đề:”Có một học sinh trong lớp 10A không thích học môn Toán ”. Mệnh đề phủ định của mệnh đề này là:

A. ”Mọi học sinh trong lớp 10A đều thích học môn Văn ”.

B. ”Mọi học sinh trong lớp 10A đều không thích học môn Toán ”.

C. ”Có một học sinh trong lớp 10A thích học môn Toán ”.

D. ”Mọi học sinh trong lớp 10A đều thích học môn Toán ”.

Câu 52: Cho tứ giác ABCD. Xét hai mệnh đề

P: “ Tứ giác ABCDlà hình thoi”

Q: “ Tứ giác ABCDcó hai đường chéo vuông góc”.

Phát biểu mệnh đề PQ 

A. Tứ giác ABCDcó hai đường chéo vuông góc thì nó là hình thoi.

B. Tứ giác ABCDlà hình thoi thì nó có hai đường chéo vuông góc.

C. Tứ giác ABCDlà hình thoi khi và chỉ khi nó có hai đường chéo vuông góc.

D. Tứ giác ABCDlà hình thoi nếu nó có hai đường chéo vuông góc.

Câu 53: Trong các định lý sau, định lý nào không có định lý đảo?

A. Nếu tứ giác ABCDlà hình chữ nhật thì nó là hình bình hành có một góc vuông.

B. Nếu tứ giác ABCDlà hình vuông thì nó là hình thoi có hai đường chéo bằng nhau.

C. Nếu tứ giác ABCDlà hình bình hành thì nó là hình thang có hai cạnh bên bằng nhau.

D. Nếu tứ giác ABCDlà hình vuông thì nó là hình chữ nhật có hai cạnh kề bằng nhau.

Câu 54: Cho mệnh đề '''' PQ  . Phát biểu nào sau đây đúng?

A. P là điều kiện đủ để có Q. B. P là điều kiện cần và đủ để có Q.

C. Nếu P thì Q. D. P là điều kiện cần để có Q.

Câu 55: Cho định lí “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây đúng?

A. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.

B. Hai tam giác có diện tích bằng nhau là điều kiện đủ đê chúng bằng nhau.

C. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

D. Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

Câu 56: Mệnh đề nào sau đây có mệnh đề đảo là mệnh đề đúng?

A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c .

B. Nếu ab  thì 22ab  .

C. Nếu số nguyên chia hết cho 14thì chia hết cho cả 7và 2

D. Hai tam giác bằng nhau có diện tích bằng nhau.

Câu 57: Trong các mệnh đề

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 23 A. 2 ,320xxx ++ B. 2 ,320xxx ++ C. 2 ,320xxx ++ D. 2 ,320xxx ++

sau, mệnh đề nào có mệnh đề đảo đúng. A. Nếu xy = thì txty = . B. Nếu xy  thì 33 xy  . C. Nếu số nguyên n có tổng các chữ số bằng 9thì số nguyên n chia hết cho 3. D. Nếu xy  thì 22 xy  Câu 58: Câu “Tồn tại ít nhất một số thực có bình phương không dương” là một mệnh đề. Có thể viết lại mệnh đề đó như sau. A. 2 :0xx  . B. 2 :0xx  . C. 2 :0xx = . D. 2 :0xx  . Câu 59: Mệnh đề ( ) 2 :",70"Pxxxx−+= . Phủ định của mệnh đề P là

biểu

lý “Với mọi số tự nhiên chia hết cho 5thì

chia hết cho

A. Với mọi số tự nhiên

, n chia hết cho 5là điều kiện cần để

1n và 2 1n + đều không chia hết cho 5

B. Với mọi số tự nhiên n , điều kiện cần để n chia hết cho 5là 2 1n và 2 1n + đều không chia hết cho 5.

C. Với mọi số tự nhiên n , điều kiện cần để 2 1n và 2 1n + đều không chia hết cho 5là n chia hết cho 5

D. Với mọi số tự nhiên n , n chia hết cho 5là điều kiện cần và đủ để 2 1n và 2 1n + đều không chia hết cho 5.

Câu 62: Phát biểu định lý đảo của định lý “ Nếu một tam giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

A. Một tam giác là tam giác cân là điều kiện cần và đủ để có tam giác đó có hai góc bằng nhau

B. Một tam giác có hai góc bằng nhau khi và chỉ khi là tam giác đó là tam giác cân.

C. Một tam giác có hai góc bằng nhau là điều kiện đủ để có tam giác đó là tam giác cân.

D. Một tam giác là tam giác cân điều kiện đủ là tam giác đó có hai góc bằng nhau.

Câu 63: Tìm mệnh đề phủ định của mệnh đề: “Tất cả người dân Việt Nam đều được tiêm Vacxin ngừa Côvit.”

A. “Tất cả người dân Việt Nam đều không được tiêm Vacxin ngừa Côvit.”.

B. “Có người dân Việt Nam được tiêm Vacxin ngừa Côvit.”.

C. “Có một người dân Việt Nam không được tiêm Vacxin ngừa Côvit.”.

D. “Có ít nhất một người dân Việt Nam không được tiêm Vacxin ngừa Côvit.”

Câu 64: Cho mệnh

đề phủ định của mệnh đề Pvà tính đúng, sai của

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 24 A. 2 ,70xxx −+ B. 2 ,70xxx −+ C. 2 ,70xxx −+ D. 2 ,70xxx −+ Câu 60: Phủ định của mệnh đề 2 ":2520" xQxx −+= là A. 2 ":2520" xQxx −+ . B. 2 ":2520" xQxx −+ . C. 2 ":2520" xQxx −+ . D. 2 ":2520" xQxx −+= . Câu 61: Sử dụng thuật ngữ “điều kiện cần” để phát

định

2 1n và 2 1n + đều không

5”

đề 2 P:":10" xxx ++ . Mệnh

nó là: A. 2 P:":10" xxx ++= và P là mệnh đề sai. B. 2 P:":10" xxx ++= và P là mệnh đề đúng. C. 2 P:":10" xxx ++ và P là mệnh đề đúng. D. 2 P:":10" xxx ++= và P là mệnh đề sai.

Câu

Trong các câu dưới

A. 16 là s

Năm

chính phương.

BÀI1:MỆNHĐỀ

Câu 2: Câu nào sau đây không là mệnh đề?

A. 213 x +

B. Mặt trời mọc ở hướng Tây.

C. Một tuần có bảy ngày.

D. Hình bình hành có một góc vuông là hình chữ nhật.

Lời giải

Chọn A

213 x − không phải là mệnh đề.

Mặt trời mọc ở hướng Tây là mệnh đề sai.

Một tuần có bảy ngày là mệnh đề đúng.

Hình bình hành có một góc vuông là hình chữ nhật là mệnh đề đúng.

Câu 3: Phát biểu nào sau đây

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 1

đây, câu nào không phải là mệnh đề?

ố

B. Bạn bao nhiêu tuổi? C.

2021 là năm nhuận. D. Tổng các góc của một tứ giác bằng 0360 Lời giải Chọn B

không phải là mệnh đề? A. Bạn là học sinh khối 10 phải không? B. Tổng ba góc của một tam giác bằng 180 C. 2 là số nguyên tố nhỏ nhất. D. Năm 2022 là năm nhuận. Lời giải Chọn A “Bạn là học sinh khối 10 phải không?” là câu nghi vấn, không phải là một mệnh đề Câu 4: Trong các câu dưới đây, câu nào là mệnh đề? A. Bạn có khỏe không? B. Hôm nay trời nóng quá! C. Lớp bạn có bao nhiêu học sinh nữ? D. 111 không phải là số nguyên tố. Lời giải Chọn D Chọn D vì đây là câu khẳng định. Các câu A, C là các câu hỏi, câu B là câu cảm thán. Nên không phải là mệnh đề. CHƯƠNG I MỆNH ĐỀ - TẬP HỢP HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

Câu 5: Trong các câu sau, câu nào không là m

A. 246 += B. 2

C. 520 xy

Chọn A

Câu A là một mệnh đề

D. 21

t mệnh đề chứa bi

chia hết cho 3.

Lời giải

Câu B, C, D là mệnh đề chứa biến.

Câu 6: Trong các câu sau đây câu nào không phải là mệnh đề?

A. Một năm có 365 ngày. B. Học

OFFICIAL

đề: (I) và (III).

Câu 9: Cho các câu sau đây:

(I): “ Phan xi păng là ngọn núi cao nhất Việt Nam”.

(II): “ 2 9,86  ”.

(III): “ Mệt quá!”.

(IV): “ Chị ơi, mấy giờ rồi?”

Hỏi có bao nhiêu câu là mệnh đề?

A. 4 B. 3 C. 2 D. 1

Lời giải

Chọn C

Câu (I) là mệnh đề đúng.

Câu (II) là mệnh đề sai.

Câu (III) là câu cảm thán nên không phải là mệnh đề.

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 2

ộ

ế

450 xx−−=

−=

x +

lớp 10 thật vui. C. Pleiku là thành phố của Gia Lai. D. 236 += Lời giải Chọn B B. Vì đây là một câu cảm thán, không phải là một khẳng định có tính đúng hoặc sai nên B không phải là mệnh đề. Câu 7: Mệnh đề chứa biến 2 :''440"Pxx++= trở thành một mệnh đề đúng với. A. 2x =− . B. 1x =− . C. 1.x = D. 0x = . Lời giải Chọn A Ta có ( ) 22440202xxxx ++=+==− Vậy 2x =− . Câu 8: Trong các câu dưới đây có bao nhiêu câu là mệnh đề? (I) Số 2018 là số chẵn. (II) Hôm nay bạn có vui không? (III) Quảng Phú là một thị trấn của huyện CưMgar. (IV) Tiết 5 rồi, đói bụng quá! A. 4 B. 1 C. 2 D. 3 Lời giải Chọn C Ta có câu là mệnh

Câu (IV) là câu hỏi nên không

là mệnh đề.

Câu 10: Trong các câu sau, có bao nhiêu câu là m

a) Trời rét quá!

Việt Nam nằm ở khu vực Đông Nam Á.

10244.

Năm 2020là năm nhuận.

A. 1. B. 2

Chọn C

Câu b), câu c) và câu d) là mệnh đề

Câu a) là câu cả

Câu

Trong các phát

A. 3 là số nguyên tố l

Đề thi hôm nay khó quá!

C. 3

C. Một tam giác cân thì mỗi góc đều bằng 060 phải không?

D. Các em hãy cố gắng học tập!

Chọn A

Lời giải

Mệnh đề là những phát biểu có tính chất hoặc đúng hoặc sai, do đó phát biểu:”3 là số nguyên tố lẻ nhỏ nhất” là một mệnh đề đúng.

Câu 12: Trong các phát biểu sau, phát biểu nào là mệnh đề?

A. 3 là số nguyên tố lẻ nhỏ nhất.

B. Đề thi hôm nay khó quá!

C. Một tam giác cân thì mỗi góc đều bằng 060 phải không?

D. Các em hãy cố gắ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 3

phải

ệnh đề?

−+= d)

4. Lời giải

m thán nên không phải là mệnh đề

11:

biểu sau, phát biểu nào là mệnh đề?

ẻ nhỏ nhất. B.

ng học tập! Lời giải Chọn A Mệnh đề là những phát biểu có tính chất hoặc đúng hoặc sai, do đó phát biểu:”3 là số nguyên tố lẻ nhỏ nhất” là một mệnh đề đúng. Câu 13: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) 613 x + . b) Phương trình 2 310xx+−= có nghiệm. c) ,51xx  d) Năm 2018 là năm nhuận. e) Hôm nay thời tiết đẹp quá! A. 4. B. 1. C. 2. D. 3. Lời giải Chọn C

Câu 15: Trong các câu sau,

a) Hãy đi nhanh lên!

b) Hà Nội là thủ đô của Pháp

c) 57415 ++= d) 3x

A. 4. B. 1

Chọn C

Câu a) không phải là mệnh đề. Câu d) là mệnh đề chứa biến.

Câu 16: Trong các câu sau câu nào là mệnh đề?

A. Hãy đi nhanh lên!

B. Hà nội là thủ đô của Việt Nam. C. Nam ăn cơm chưa?. D. Buồn ngủ quá!

Chọn B

đề?

D. 3.

Lời giải

Đáp án B đúng vì nó là câu khẳng định có tính đúng sai.

Câu 17: Trong các câu sau câu nào là mệnh đề chứa biến?

A. 9 là số nguyên tố.

B. 18 là số chẵn.

C. ( )2 3, xxx+ .

D. Hình chữ nhật có hai đường chéo bằng nhau.

Lời giải

Chọn C

Đáp án A là mệnh đề sai. Đáp án

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 4 Trong các câu trên có các câu là mệnh đề: Phương trình 2 310xx+−= có nghiệm. Năm 2018 là năm nhuận. Có hai câu là mệnh đề chứa biến: 613 x + ; ,51xx  Và một câu là câu cảm thán. Câu 14: Trong các câu sau, câu nào là mệnh đề? A. Không được làm việc riêng trong giờ học. B. Đi ngủ đi. C. Trung Quốc là nước đông dân nhất thế giới. D. Bạn học trường nào? Lời giải Chọn C

có bao nhiêu câu là mệnh



. C. 2.

ời giải

B là mệnh đề đúng. Đáp án D là mệnh đề đúng. Đáp án C ta có với 0x = ta được mệnh đề đúng là 03. Ta có với 1x = ta được mệnh đề sai là 23. Nên tính đúng sai còn phụ thuộc giá trị của biến. Nó là mệnh đề chứa biến.

Câu 20: Trong các phát biểu sau, phát bi

nào là mệnh đề đúng?

A. Tổng của hai cạnh một tam giác lớn hơn cạnh thứ ba.

B. Hình thang có hai cạnh bên bằng nhau là hình thang cân.

C. Bạn có chăm học không?

D.  là một số hữu tỉ.

Chọn A

i giải

Câu 21: Trong các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Tổng của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

B. Tích của hai số tự nhiên là một số chẵn khi và chỉ khi cả hai số đều là số chẵn.

C. Tổng của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

D. Tích của hai số tự nhiên là một số lẻ khi và chỉ khi cả hai số đều là số lẻ.

Lời giải

Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 5 Câu 18: Cho mệnh đề chứa biến ( ) 2 :"511"Pxx với x là số nguyên tố. Tìm mệnh đề đúng trong các mệnh đề sau: A. ( )3P B. ( )2P C. ( )7P D. ( )5P Lời giải Chọn A ( ) 3:"5911"P  là mệnh đề đúng. Câu 19: Cho S là mệnh đề “ Nếu tổng các chữ số của một số n chia hết cho 6thì n chia hết cho 6”. Một giá trị của n để khẳng định S sai là: A. 33 B. 40 C. 42 D. 30 Lời giải Chọn A Ta có: 33n = có tổng các chữ số bằng 6thì chia hết cho 6nhưng số 33n = không chia hết cho 6 .

ểu

ờ

Câu 22: Trong các câu sau, câu nào một là mệnh đề đúng? A. Hà nội là thủ đô của Việt Nam. B. 2là một số tự nhiên lẻ. C. 7là một số tự nhiên chẵn. C.  là một số hữu tỷ. Lời giải Chọn A Ta thấy: Hà nội là thủ đô của Việt Nam là một mệnh đề đúng. 2là một số tự nhiên lẻ là một mệnh đề sai. 7là một số tự nhiên chẵn là một mệnh đề sai.  là một số hữu tỷ là một mệnh đề sai. Câu 23: Trong các mệnh đề sau, mệnh đề nào sai?

A. Hà nội là thủ đô của Việt

C. 5là một số tự nhiên lẻ.

Chọn C

Ta thấy:

là một số tự nhiên chẵn.

là một số hữu tỷ.

Hà nội là thủ đô của Việt Nam là một mệnh đề đúng.

4là một số tự nhiên chẵn là một mệnh đề đúng.

Trong các mệnh

nào

mệnh đề sai

OFFICIAL

A. Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

B. Tam giác cân có một góc bằng 060 là tam giác đều.

C. Hình bình hành có hai đường chéo bằng nhau là hình vuông.

D. Tam giác có hai đường cao bằng nhau là tam giác cân.

Lời giải

Chọn C

Câu 26: Cho định lý “Nếu hai tam giác bằng nhau thì diện tích bằng nha”. Mệnh đề nào sau đây đúng?

A. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau.

B. Hai tam giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

C. Hai tam giác có diện tích bằng nhau là điều kiện đủ để chúng bằng nhau.

D. Hai tam giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

Chọn D

Vì các định lí toán học là

Khi đó,

mệnh

Lời giải

và thường có dạng P

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 6

Nam. B. 4

C. 

Lời giải

5là một số tự nhiên lẻ là một mệnh đề đúng.  là một số hữu tỷ là một mệnh đề sai. Câu 24: Trong các khẳng định sau, khẳng định nào đúng với mọi giá trị của x ? A. 52xx  . B. 52xx  . C. 2252xx  . D. 52xx++ . Lời giải Chọn D 5252xx++ điều này đúng với mọi x . Câu 25:

đề sau,

ệnh đề

là

những

đề đúng



ta nói: P là điều kiện đủ để có Q , Q là điều kiện cần để có P . Câu 27: Mệnh đề nào sau đây là mệnh đề sai ? A. 2 :0xx  . B. 2 : nnn= . C. :2 nnn . D. 2 : xxx . Lời giải Chọn A Ta có 2 0x  , x  Đáp án A sai. Câu 28: Trong các mệnh đề sau, mệnh đề nào sai? A. Nếu m , n là các số vô tỉ thì . mn cũng là số vô tỉ B. Nếu ABC là một tam giác vuông thì đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền. C. Với ba véctơ a , b , c đều khác véctơ 0 , nếu a , b cùng ngược hướng với c thì a , b cùng hướng. D. Điểm G là trọng tâm tam giác ABC khi và chỉ khi 0GAGBGC++=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 7 Lời giải Chọn A Cho 2m = , 32n = là các số vô tỉ. Khi đó .6mn = là số hữu tỉ. Câu 29: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng? A. Nếu hai số a , b cùng chia hết cho c thì ab + chia hết cho c . B. Nếu một số nguyên chia hết cho 6 thì nó chia hết cho2 và 3 C. Nếu hai số x , y thỏa mãn 0xy+ thì có ít nhất một trong hai số x , y dương. D. Phương trình bậc hai ( )2 00axbxca++= có a , c trái dấu thì có hai nghiệm phân biệt. Lời giải Chọn B + Ta có 51 + chia hết cho3, tuy nhiên 5và 1không chia hết cho 3. Loại A + Nếu một số nguyên chia hết cho2 và 3thì nó chia hết cho 6. Chọn B + Ta có 10  , 20− , tuy nhiên ( ) 1210 +−=− . Loại C + Phương trình 2 0xx−= có hai nghiệm phân biệt, tuy nhiên a , c không trái dấu. Loại. D. Câu 30: Cho hai đa thức ( )Px và ( )Qx . Xét các tập hợp ( ) 0AxPx== , ( ) 0BxQx== và ( ) ( ) 22 0CxPxQx =+=   . Trong các mệnh đề sau, mệnh đề nào đúng? A. CAB = . B. CAB = . C. \ CAB = . D. \.CBA = . Lời giải Chọn A Vì ( ) ( ) 22 0PxQx +=  ( ) ( ) 0 0 Px Qx =    =  ( ) ( )xPxQx . Câu 31: Cho phần tử x thuộc tập B và tâp B là tập con của A . Trong các khẳng định sau khẳng định nào đúng? A. ( ) xBA  B. ( ) xBA  C. ( ) xBA  D. ( ) xBA  Lời giải Chọn B Câu 32: Trong các mệnh đề sau, tìm mệnh đề sai? A. Nếu a chia hết cho 9thì a chia hết cho 3. B. Nếu một tam giác có một góc bằng 60thì tam giác đó là tam giác đều. C. Nếu 0ab thì 22ab  D. Nếu một tam giác có hai cạnh bằng nhau thì tam giác đó là tam giác cân. Lời giải Chọn B Tam giác có một góc bằng 60thì có thể là tam giác vuông hoặc tam giác thường. Câu 33: Cho mệnh đề chứa biến ( ) 32 :"320"Pxxxx−+= . Tìm các giá trị của x để ( )Px là một mệnh đề đúng.

A. P đúng, Q sai.

Chọn

tam giác cân có 2 c

Hãy chọ

khẳng định đúng trong các khẳng định

nh bằng nhau” và Q: “Nế

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 8 A. 0,1,2xxx=== B. 2,3xx=−=− C. 1,2xx=−=− D. 4,2,3xxx==−= Lời giải Chọn A Những giá trị x làm cho ()Px là mệnh đề đúng là nghiệm của phương trình 32320xxx−+= . Do đó 0,1,2xxx=== là các giá trị cần tìm. Câu 34: Trong các mệnh đề sau, mệnh đề nào là mệnh đề sai? A. :33 n nn + . B. 1267  . C. 64107  D. ( )2 2:2 xxx − Lời giải Chọn D Với 1n = thì 33;34 n n =+= nên đáp án A là đúng. Ta có mệnh đề :"12"P  và mệnh đề :"67"Q  là mệnh đề sai nên mệnh đề PQ  hay mệnh đề 1267  là mệnh đề đúng. Đáp án B đúng. Ta có mệnh đề :"64"P  là mệnh đề sai và mệnh đề :"107"Q  là mệnh đề đúng nên mệnh đề PQ  hay mệnh đề 64107  là mệnh đề đúng. Đáp án C đúng. Với 1x =− thì ( )2 29x −= ; 2 1x = nên mệnh đề ( )2 2:2 xxx − là mệnh đề sai. Câu 35: Xét mệnh đề kéo theo P: “Nếu 18 chia hết cho 3 thì

ạ

là số chẵn thì 25 là số chính phương”.

B. P đúng, Q đúng. C. P sai, Q đúng. D. P sai, Q sai. Lời giải

B Mệnh đề PQ  sai khi P đúng, Q sai. Từ đó ta có hai mệnh đề trên đều đúng. Câu 36: Trong các mệnh đề dưới đây, mệnh đề nào là mệnh đề đúng? A. 2 :10xx += B. 2 :0xx  C. 2 :210xx − D. 2 :20xx −= Lời giải Chọn C  Ta có: 22011xx+ với x  . Vậy loạiA.  Ta có: 2 0x  với x  . Vậy loại B.  22 122 210 222 xxx −− , mà 0xx= . Vậy C đúng.  ( )2 202loaixx−== vì x . Vây loạiD. Câu 37: Mệnh đề nào sau đây là mệnh đề đúng? A. “ :22 x xx + ” B. “ :21 x x + là số nguyên tố”. C. “ *2:1xx − là bội số của 3”. D. “ 2 :3xx = ”. Lời giải Chọn A Giả sử chọn , ta được: 1 23  (đúng). Nhưng chọn 3x = , ta được: 85  (sai). 1x =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 9 Vậy :22 x xx + Câu 38: Cho P Q là mệnh đề đúng. Khẳng định nào sau đây là sai? A. PQ  sai. B. PQ  đúng. C. QP  sai. D. PQ  sai. Lời giải Chọn D P Q đúng suy ra PQ  đúng. Vậy mệnh đề sai là D Câu 39: Số mệnh đề đúng trong các mệnh đề sau: ( ) 1 : Ixx x  ( ) :20 nIIn ( ) 2 :90IIIxx−= . ( ) 2 :510IVnn+ chia hết cho 5. A. 1. B. 4. C. 2. D. 3. Lời giải Chọn B Ta có ( ) 1 : Ixx x  là mệnh đề đúng vì 2x =− thỏa mãn. Ta có ( ) :20 nIIn là mệnh đề đúng vì theo tính chất lũy thừa. Ta có ( ) 2 :90IIIxx−= là mệnh đề đúng vì 3x = . Ta có ( )22 51052 nn+=+ là số chia hết cho 5 mệnh đề ( )IV là mệnh đề đúng. Câu 40: Lập mệnh đề phủ định của mệnh đề 2 ":20180" xxx ++ . A. 2 :20180xxx ++ . B. 2 :20180xxx ++ . C. 2 :20180xxx ++ D. 2 :20180xxx ++ Lời giải Chọn D Mệnh đề phủ định của mệnh đề 2 ":20180" xxx ++ là mệnh đề 2 :20180xxx ++ Câu 41: Mệnh đề phủ định của mệnh đề: “2018 là một số chẵn” là: A. 2018không là một số lẻ. B. 2018không là một số chẵn. C. 2018là một số lẻ. D. 2018không là một số chẵn. Lời giải Chọn D Theo mệnh đề phủ định. Câu 42: Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề: “Mọi động vật đều di chuyển”? A. Có ít nhất một động vật di chuyển. B. Có ít nhất một động vật không di chuyển. C. Mọi động vật đều không di chuyển. D. Mọi động vật đều đứng yên. Lời giải Chọn B

A. Không có học sinh nào trong lớp 11A chấp hành luật giao thông.

B. Mọi học sinh trong lớp 11A đều chấp hành luật giao thông.

C. Có một học sinh trong lớp 11A chấp hành luật giao thông.

D. Mọi học sinh trong lớp 11A không chấp hành luật giao thông.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 10 Phủ định của “mọi” là “có ít nhất” Phủ định của “đều di chuyển” là “không di chuyển”. Do đó mệnh đề phủ định của mệnh đề: “Mọi động vật đều di chuyển” là “Có ít nhất một động vật không di chuyển” Câu 43: Cho mệnh đề 2 :",12" Pxxx + . Mệnh đề nào sau đây là mệnh đề phủ định của mệnh đề P ? A. 2 :",12" Pxxx + . B. 2 :",12" Pxxx + . C. 2 :",12" Pxxx + D. 2 :",12" Pxxx + Lời giải Chọn C Câu 44: Cho mệnh đề 2 ",30" xxx −+ . Hỏi mệnh đề nào là phủ định của mệnh đề trên A. 2 ",30" xxx −+ . B. 2 ",30" xxx −+ . C. 2 ",30" xxx −+ . D. "  2 ,30"xxx−+ . Lời giải Chọn C Câu 45: Cho mệnh đề "Có một học sinh trong lớp 11A không chấp hành luật giao thông " Mệnh đề phủ định của mệnh đề này là :

Lời giải Chọn B Câu 46: Cho mệnh đề 2 :":70" Axxx−+ . Mệnh đề phủ định của A là: A. 2 :70xxx −+ . B. 2 :70xxx −+ . C. 2 :70xxx −+ D. 2 :70xxx −+ Lời giải Chọn A Câu 47: Cho mệnh đề: 2 ",20" xxx −+ . Mệnh đề phủ định là: A. 2 ",20" xRxx −+ B. 2 ",20" xxx −+ C. 2 ",20" xxx −+ D. 2 ",20" xxx −+ Lời giải Chọn D Câu 48: Cho mệnh đề: 2 ",20" xxx −+ . Mệnh đề phủ định sẽ là: A. 2 ",20" xxx −+ . B. 2 ",20" xxx −+ . C. 2 ",20" xxx −+ D. 2 ",20" xxx −+ Lời giải

A. ”Mọi học sinh trong lớp 10A đều thích học môn Văn ”.

B. ”Mọi học sinh trong lớp 10A đều không thích học môn Toán ”.

C. ”Có một học sinh trong lớp 10A thích học môn Toán ”

D. ”Mọi học sinh trong lớp 10A đều thích học môn Toán ”.

Lời giải Chọn D

Câu 52: Cho tứ giác ABCD. Xét hai mệnh đề

P: “ Tứ giác ABCDlà hình thoi”

Q: “ Tứ giác ABCDcó hai đường chéo vuông góc”.

Phát biểu mệnh đề PQ 

A. Tứ giác ABCDcó hai đường chéo vuông góc thì nó là hình thoi.

B. Tứ giác ABCDlà hình thoi thì nó có hai đường chéo vuông góc.

C. Tứ giác ABCDlà hình thoi khi và chỉ khi nó có hai đường chéo vuông góc.

D. Tứ giác ABCDlà hình thoi nếu nó có hai đường chéo vuông góc.

Lời giải

Chọn C

Câu 53: Trong các định lý sau, định lý nào không có định lý đảo?

A. Nếu tứ giác ABCDlà hình chữ nhật thì nó là hình bình

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 11 Chọn A Ta có phủ định của mệnh đề ban đầu chính là: 2 ",20" xxx −+ Câu 49: Lập mệnh đề phủ định của mệnh đề : “ ,21 n nn + “ A. ,21 n nn + . B. ,21 n nn + . C. ,21 n nn + . D. ,21 n nn + . Lời giải Chọn A Mệnh đề: “ ( ), xDPx ” có mệnh đề phủ định là: “ ( ), xDPx ” . Nên mệnh đề : “ ,21 n nn + “ có mệnh đề phủ định là: “ ,21 n nn + ”. Câu 50: Cho mệnh đề 2 ",320" xxx ++ . Mệnh đề phủ định của mệnh đề trên là A. 2 ,320xxx ++ B. 2 ,320xxx ++ C. 2 ,320xxx ++ D. 2 ,320xxx ++ Lời giải Chọn B Phủ định của mệnh đề ( ) "," xpx là mệnh đề ( ) "," xpx Câu 51: Cho mệnh đề:”Có một học sinh trong lớp 10A không thích học môn Toán ”. Mệnh đề phủ định của mệnh đề này là:

hành có một góc vuông. B. Nếu tứ giác ABCDlà hình vuông thì nó là hình thoi có hai đường chéo bằng nhau. C. Nếu tứ giác ABCDlà hình bình hành thì nó là hình thang có hai cạnh bên bằng nhau. D. Nếu tứ giác ABCDlà hình vuông thì nó là hình chữ nhật có hai cạnh kề bằng nhau. Lời giải Chọn C

Câu

Nếu tứ giác

Cho m

Phát

Câu 55: Cho định lí “Nếu hai tam giác bằng nhau thì diện tích của chúng bằng nhau”. Mệnh đề nào sau đây

C. Hai tam

D. Hai tam

Chọn D

Câu 56: Mệnh đề nào sau đây có mệnh đề đảo là mệnh đề đúng?

A. Nếu a và b cùng chia hết cho c thì ab + chia hết cho c .

B. Nếu ab  thì 22ab  .

C. Nếu số nguyên chia hết cho 14thì chia hết cho cả 7và 2

D. Hai tam giác bằng nhau có diện tích bằng nhau.

Lời giải

Chọn C

Ta kiểm tra các phương án:

A. Mệnh đề đảo là: “Nếu ab + chia hết cho c thì a và b cùng chia hết cho c ”. Là mệnh đề sai. Thật vậy, với 3,5,2abc=== ta có ab + chia hết cho c nhưng a không chia hết cho c .

B. Mệnh đề đảo là: “Nếu 22ab  thì ab  ”. Là mệnh đề sai. Thật vậy, với 6,5ab=−= ta có 22ab  nhưng ab 

C. Mệnh đề đảo là: “Nếu số nguyên chia hết cho cả 7và 2thì chia hết cho 14”. Là mệnh đề đúng.

Do 7 và 2 là hai nguyên tố cùng nhau nên một số nguyên nào đó chia hết cho 7 và 2 thì nó cũng chia hết cho 7.2, tức chia hết cho 14.

D. Mệnh đề đảo là: “Hai tam giác có diện tích bằng nhau thì bằng nhau ”. Là mệnh đề sai. Thật vậy,

vuông

3,2DEDF

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 12

ABCDlà hình thang có hai cạnh bên bằng nhau thì nó không là hình bình hành. Nó có thể là hình thang cân.

54:

ệnh đề '''' PQ  .

biểu nào sau đây đúng? A. P là điều kiện đủ để có Q. B. P là điều kiện cần và đủ để có Q. C. Nếu P thì Q. D. P là điều kiện cần để có Q. Lời giải Chọn C

đúng? A. Hai tam giác bằng nhau là điều kiện cần và đủ để chúng có diện tích bằng nhau. B. Hai tam giác có diện tích bằng nhau là điều kiện đủ đê chúng bằng nhau.

giác bằng nhau là điều kiện cần để diện tích chúng bằng nhau.

giác bằng nhau là điều kiện đủ để diện tích chúng bằng nhau.

ời giải

xét tam giác đều ABC có cạnh 4 23 và tam giác DEF

ở D ,

Dễ thấy hai tam giác đã cho có diện tích bằng nhau nhưng rõ ràng chúng không bằng nhau. Câu 57: Trong các mệnh đề sau, mệnh đề nào có mệnh đề đảo đúng. A. Nếu xy = thì txty = B. Nếu xy  thì 33 xy  C. Nếu số nguyên n có tổng các chữ số bằng 9thì số nguyên n chia hết cho 3. D. Nếu xy  thì 22 xy  Lời giải Chọn B * A sai khi 0t = .

2 1n và 2 1n + đều không chia hết cho 5.

B. Với mọi số tự nhiên n , điều kiện cần để n chia hết cho 5là 2 1n và 2 1n + đều không chia hết cho 5

C. Với mọi số tự nhiên n , điều kiện cần để

1n và

+ đều không chia hết cho 5là n chia hết cho

D. Với mọi số tự nhiên

họn

, n chia hết cho

là điều kiện

không chia

Lời

giác có hai góc bằng nhau thì tam giác đó là tam giác cân.

A. Một tam giác là tam giác cân là điều kiện cần và đủ để có tam giác đó có hai góc bằng nhau

B. Một tam giác có hai góc bằng nhau khi và chỉ khi là tam giác đó là tam giác cân.

C. Một tam giác có hai góc bằng nhau là điều kiện đủ để có tam giác đó là tam giác cân

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 13 * B đúng vì ( )( )3322 0 xyxyxxyyxy −++ * C sai ví dụ như 114n = . * D sai khi 2;1xy=−= Câu 58: Câu “Tồn tại ít nhất một số thực có bình phương không dương” là một mệnh đề. Có thể viết lại mệnh đề đó như sau. A. 2 :0xx  B. 2 :0xx  C. 2 :0xx = D. 2 :0xx  Lời giải Chọn A Ta có mệnh đề 2 :0xx  Câu 59: Mệnh đề ( ) 2 :",70"Pxxxx−+= . Phủ định của mệnh đề P là A. 2 ,70xxx −+ B. 2 ,70xxx −+ C. 2 ,70xxx −+ . D. 2 ,70xxx −+ . Lời giải Chọn D Phủ định của mệnh đề ( ) 2 :",70"Pxxxx−+= là 2 :,70Pxxx−+ . Câu 60: Phủ định của mệnh đề 2 ":2520" xQxx −+= là A. 2 ":2520" xQxx −+ B. 2 ":2520" xQxx −+ C. 2 ":2520" xQxx −+ D. 2 ":2520" xQxx −+= Lời giải Chọn C Câu 61: Sử dụng thuật ngữ “điều kiện cần” để phát biểu định lý “Với mọi số tự nhiên chia hết cho 5thì 2 1n và 2 1n + đều không chia hết cho 5” A. Với mọi số tự nhiên n , n chia hết cho 5là điều kiện cần để

cần và đủ để 2 1n và 2 1n + đều

hết cho 5

giải C

B Với mọi số tự nhiên n , điều kiện cần để n chia hết cho 5là 2 1n và 2 1n + đều không chia hết cho 5. Câu 62: Phát biểu định lý đảo của định lý “ Nếu một tam

D. Một tam giác là tam giác cân điều kiện đủ là tam giác đó có hai góc bằng nhau.

Lời giải Chọn D

Một tam giác là tam giác cân điều kiện đủ là tam giác đó có hai góc bằng nhau.

Câu 63: Tìm mệnh đề phủ định của mệnh đề: “Tất cả người dân Việt Nam đều được tiêm Vacxin ngừa Côvit.”

A. “Tất cả người dân Việt Nam đều không được tiêm Vacxin ngừa Côvit.”.

B. “Có người dân Việt Nam được tiêm Vacxin ngừa Côvit.”.

C. “Có một người dân Việt Nam không được tiêm Vacxin ngừa Côvit.”.

nhất một người dân Việt Nam

được tiêm Vacxin ngừa

Câu

OFFICIAL

P:":10"

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I ĐẠI SỐ 10 CHƯƠNG I MỆNH ĐỀ - TẬP HỢP Sưu tầm và biên soạn Page 14

“

ó ít

không

Côvit.” Lời giải Chọn D

mệnh đề phủ định của mệnh đề “",()" xXPx là ",()" xXPx .

64: Cho mệnh đề 2 P:":10" xxx ++ . Mệnh đề phủ định của mệnh đề Pvà tính đúng, sai của nó là:

2 P:":10" xxx ++= và P là mệnh đề sai.

xxx ++= và P là mệnh đề đúng. C. 2 P:":10" xxx ++ và P là mệnh đề đúng. D. 2 P:":10" xxx ++= và P là mệnh đề sai. Lời giải Chọn A Mệnh đề phủ định của Plà 2 P:":10" xxx ++= . Xét phương trình 2 10xx++= vô nghiệm nên P là mệnh đề sai.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 25 BÀI 2: TẬPHỢP. CÁC PHÉPTOÁNTRÊNTẬPHỢP 1. KHÁI NIỆM CƠ BẢN VỀ TẬP HỢP a. Tập hợp Tập hợp (còn gọi là tập) là một khái niệm cơ bản của toán học, không định nghĩa. Giả sử đã cho tập hợp .A • Để chỉ a là một phần tử của tập hợp ,A ta viết aA  (đọc là a thuộc A ). • Để chỉ a không phải là một phần tử của tập hợp ,A ta viết aA  (đọc là P không thuộc A ). Chú ý. Số phần tử của tập hợp S được kí hiệu là ( )nS Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu là  Chẳng hạn: Tập các nghiệm của phương trình 2 10x += là tập rỗng. Gọi X là tập nghiệm của phương trình: 2 241430xx−+= Các mệnh đề sau đúng hay sai? a) 13 X ; b) 11 X ; c) ( ) 2nX = . Có thể mô tả một tập hợp bằng một trong hai cách sau Cách 1. Liệt kê các phần tử của tập hợp; Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I = aS  ; phần tử a thuộc tập hợp S aS  ; phần tử a không thuộc tập hợp S Luyện tập 1.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 26 b. Tập hợp con Nhận xét  Từ định nghĩa trên, T là tập con của S nếu mệnh đề sau đúng: , xxTxS  .  Quy ước tập rỗng là tập con của mọi tập hợp. Minh họa T là một tập con của S như Hình 1.3 c. Hai tập hợp bằng nhau Giả sử C là tập hợp các hình bình hành có hai đường chéo vuông góc; D là tập hợp các hình hình vuông. Các mệnh đề sau đây đúng hay sai? a) CD  ; b) CD  ; c) CD = . Nếu mọi phần tử của tập hợp T đều là phần tử của tập hợp S thì ta nói T là một tập hợp con (tập con) của S và ta viết là TS  (đọc là T chứa trong S hoặc T là tập con của S . Người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi đường kín, gọi là biểu đồ Ven (H.1.2) Hai tập hợp S và T được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của T cũng là phần tử của tập hợp S và ngược lại. Kí hiệu ST = . Luyện tập 2.  Thay cho TS  , ta còn viết ST  (đọc là S chứa T ).  Kí hiệu TS  để chỉ T không là tập con của S .

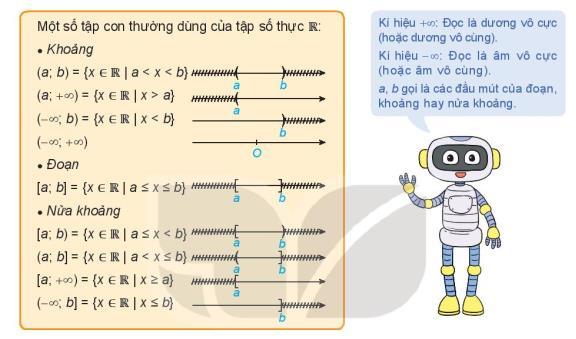
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 27 2. CÁC TẬP HỢP SỐ a. Mối quan hệ giữa các tập hợp số Tập hợp các số tự nhiên  0;1;2;3,4;...= Tập hợp các số nguyên gồm các số tự nhiên và các số nguyên âm:  ...;3;2;1;0;1;2;3...=−−− . Tập hợp các số hữu tỉ gồm các số viết được dưới dạng phân số a b , với ,, 0abb Số hữu tỉ còn được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn. Tập hợp các số thực gồm các số hữu tỉ và các số vô tỉ. Số vô tỉ là các số thập phân vô hạn không tuần hoàn. Cho tập hợp  4;0;1;2C =− . Các mệnh đề sau đúng hay sai? a) C là tập con của ; b) C là tập con của ; c) C là tập con của b. Các tập con thường dùng của Mối quan hệ giữa các tập hợp số:  . Luyện tập 3.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 28 Hãy ghép mỗi dòng ở cột bên trái với một dòng thích hợp ở cột bên phải. 3. CÁC PHÉP TOÁN TRÊN TẬP HỢP a. Giao của hai tập hợp Tập hợp gồm các phần tử thuộc cả hai tập hợp S và T gọi là giao của hai tập hợp S và T , ký hiệu là ST   | STxxSxT = Cho các tập hợp  1;5C = ,  2;3D =− . Hãy xác định tập hợp CD  b. Hợp của hai tập hợp: Tập hợp gồm các phần tử thuộc tập hợp S hoặc T tập hợp gọi là hợp của hai tập hợp S và T , ký hiệu ST   | STxxSxT = . c. Hiệu của hai tập hợp: Luyện tập 4. Luyện tập 5.

Hiệu

u T là tập con của

Phần

Tìm phần bù của các t

p hợ

OFFICIAL

có

thi

và 11 bạn tham gia thi đấ

và cầu lông, trong đó có 16 bạn tham gia thi đấu bóng

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 29

của hai tập hợp S và T là tập hợp gồm các phần tử thuộc tập hợp S mà không thuộc tập hợp T , ký hiệu \ ST .  \| STxxSxT = Nế

tập hợp S , thì \ ST còn được gọi là

bù của T trong S . Ký hiệu là s CT

ậ

p sau trong a) ( );2−− . b)  )5; −+ . Lớp 10A

24tham gia

đấu bóng đá

đá

ầu lông. Giả sử các trận bóng đá và các trận cầu lông không tổ chức đồng thời. Hỏi có bao nhiêu bạn lớp 10A tham gia thi đấu cả bóng đá và cả cầu lông? Gợi ý : Gọi x là số bạn tham gia thi đấu cả bóng đá và cả cầu lông. Luyện tập 7. Vận dụng

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 30 1.8. Gọi X là tập hợp các quốc gia tiếp giáp với Việt Nam. Hãy liệt kê các phần tử của tập hợp X và biểu diễn tâp X bằng biểu đồ Ven. 1.9. Ký hiệu E là tập hợp các quốc gia tại khu vực Đông Nam Á. a) Nêu ít nhất hai phần tử thuộc tập hợp E b) Nêu ít nhất hai phần tử không thuộc tập hợp E c) Liệt kê các phần tử thuộc tập hợp E . Tập hợp E có bao nhiêu phần tử? 1.10. Hãy viết tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử cuả tập hơp :  0;4;8;12;16A = 1.11. Trong các tập hợp sau, tập nào là tập hợp rỗng?  2 |60Axx=−= ;  2 |60Bxx=−= 1.12. Cho  ; Xab = . Các cách viết sau đúng hay sai? Giải thích kết luận đưa ra. a) aX  . b)   aX  . C) X . 1.13. Cho  2;5A = ,  5; Bx = ,  2; Cy = .Tìm x và y để ABC == 1.14. Cho   ( )( ) 22 |4;|53230AxxBxxxxx ==−+−= . a) Liệt kê các phần tử của hai tập hợp A và B b) Hãy xác định các tập hợp , ABAB  và \ AB 1.15. Xác định các tập hợp sau và biểu diễn chúng trên trục số a) (   )4;10;3− . b) (  ( 0;23;1 − . c) ( ) ( 2;1;1−− . d) ( \;3 − 1.16. Để phục vụ cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau: a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó? b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh? c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp? HỆ THỐNG BÀI TẬP.II = BÀI TẬP SÁCH GIÁO KHOA.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 31  DẠNG 1: XÁC ĐỊNH MỘT TẬP HỢP PHƯƠNG PHÁP Để xác định một tập hợp, ta có 2 cách sau:  Liệt kê các phần tử của tập hợp.  Chỉ ra tính chất đặc trưng của tập hợp. Bài 1. Viết lại tập hợp ( )( ) Axxxxx =−+−+= 22 253430 bằng cách liệt kê các phần tử của nó Bài 2. Viết lại tập hợp ( )( ) Axxxxx =−+−+= 22 253430 bằng cách liệt kê các phần tử của nó Bài 3. Viết lại tập hợp  Axx= 5 bằng cách liệt kê các phần tử của nó Bài 4. Viết mỗi tập hợp  A = 0; 1; 2; 3; 4 bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó Bài 5. Viết mỗi tập hợp  A = 9; 36; 81; 144 bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó Bài 6. Liệt kê tất cả các phần tử của tập hợp A gồm các số tự nhiên chia hết cho 3 và nhỏ hơn 25 Bài 7. Liệt kê các phần tử của tập hợp  2 2530=−+=Xxxx . Bài 8. Viết tập hợp ( )( ) 22 9320 =−−+= Bxxxx dưới dạng liệt kê các phần tử. Bài 9. Viết tập hợp ( )( ) 22 5560 =−−+= Axxxx dưới dạng liệt kê các phần tử. Bài 10. Tính tổng tất cả các phần tử của tập hợp 3 2  =  Ax x . Bài 11. Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Tính học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A? Bài 12. Cho ( )2;A =+ , ( );Bm=+ . Tìm điều kiện cần và đủ của m để B là tập con của A ? Bài 13. Xác định số phần tử của tập hợp  |4,2017Xnnn= . Bài 14. Cho hai tập hợp  1;3A = và  ;1Bmm=+ . Tìm tất cả giá trị của tham số m để BA  Câu 15. Số phần tử của tập hợp  2 43220 =−++−= Axxxx Câu 16. Tính tổng các phần tử của tập hợp 43 2 + = +  Axx x BÀI TẬP TỰ LUẬN.2 =

u biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu, 30 em biết chơi cầu lông, 15 em biết chơi cả hai. Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? Bao nhiêu em chỉ biết đánh cầu lông? Sĩ số lớp là bao nhiêu?

Bài 6. Viết lại tập hợp {21| AxxZ và 24} x dưới dạng liệt kê

Bài 7. Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu , 30 em biết chơi cầu lông , 15 em biết chơi

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 32 Câu 17. Liệt kê các phần tử của tập hợp  2238230 =+−++= Axxxxx DẠNG 2: CÁC PHÉP TOÁN VỀ GIAO, HỢP, HIỆU CỦA HAI TẬP HỢP PHƯƠNG PHÁP Giao của hai tập hợp: ABxxAvaxB Hợp của hai tập hợp: ABxxAhoacxB Hiệu cuả hai tập hợp: \ ABxxAvaxB . Phần bù: Cho BA thì \A CBAB . Bài 1. Cho hai tập hợp 1;2;3;7,2;4;6;7;8AB . Xác định các tập hợp AB , AB, \ AB , \.BA Bài 2. Cho tập {0;1;2;3;4;5}X = và tập {0;2;4}A = . Xác định phần bù của A trong X . Bài 3. Gọi n B là tập hợp các bội số của n trong . Xác định tập hợp 24BB ? Bài 4. Cho A là tập hợp tất cả các nghiệm của phương trình 2 43 0xx ; B là tập hợp các số có giá trị tuyệt đối nhỏ hơn 4 Xác định tập hợp \ AB ? Bài 5. Mỗi học sinh của lớp 10A1 đề

cả hai . Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? bao nhiêu em chỉ biết đánh cầu lông? Sĩ số lớp là bao nhiêu? Bài 8. Cho các tập hợp: |3|15|24 AxRxBxRxCxRx a) Hãy viết lại các tập hợp , , ABC dưới kí hiệu khoảng, nửa khoảng, đoạn. b) Tìm ,,\ ABABAB . c) Tìm \ BCAC Bài 9. Cho các tập hợp 3 1; 2 Amm +  =−  và ( )  );33;B =−−+ Tìm tất cả các số thực m để AB= Bài 10. Cho hai tập hợp ( 2;5E = và  23;22Fmm=−+ . Tìm tất cả các giá trị của tham số m để A hợp B là một đoạn có độ dài bằng 5. Bài 11. Cho khoảng 6 ; 2 A m  =−  và khoảng ( )1;Bm=−+ . Tìm tất cả các số thực m để \ ABA =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 33 Bài 12. Cho các tập hợp ( )2;A =+ và )2 7;Bm  =−+  với 0m  . Tìm tất cả các số thực m để \ AB là một khoảng có độ dài bằng 16 . Câu 1: Cho tập hợp  2 10Axxx=++= . Các phần tử của tập A là: A. 0=A B.  0=A C. =A D.  =A Câu 2: Hãy liệt kê các phần tử của tập hợp  saocho 8MxNx = lµíccña . A.  1;4;16;64M = B.  0;1;4;16;64M = C.  1;2;4;8M = D.  0;1;2;4;8M = Câu 3: Cho tập hợp ( )( ) 22–120Axxx =+= . Các phần tử của tập A là: A.  –1;1=A B. –2;–1; }{2 1;=A C. {1}=A D. {1}=A Câu 4: Cho 2 40Axx . Tập hợp A viết lại dạng liệt kê là A. . B.  . C.  )2; −+ . D.  )2;+ . Câu 5: Tập hợp nào là tập hợp rỗng, trong các tập hợp sau? A.  2 |6–710xxx += . B.  |1xx . C.  2 |420xxx−+= D.  2 |430xxx−+= Câu 6: Cho tập hợp ( )( ) 22930=−−= Bxxxx . Tập hợp B được viết dưới dạng liệt kê là A.  3;9;1;2=B B.  3;9;0=−B C.  9;9;0=−B D.  3;3;0=−B Câu 7: Cho tập hợp  3 90=−=Hxxx . Tập hợp H là tập con của tập hợp nào dưới đây ? A.  3;0;1;2=−A . B.  3;1;2;3=−B . C.  0;1;2=C . D.  3;0;2;3=−D . Câu 8: Tập hợp ( )( ) 23240=+−+= Axxxxx có bao nhiêu phần tử? A. 1. B. 3. C. 5. D. 2. Câu 9: Trong các tập hợp sau, tập hợp nào là tập rỗng? A.  2 560+−=xxx B.  2 3520−+= xxx . C.  2 10+−=xxx . D.  2 510+−=xxx . Câu 10: Cho tập hợp  2 1 =+Pnn và 33− n . Viết tập hợp P dưới dạng liệt liệt kê các phần tử. A.  3;2;1;0;1;2;3=−−−P . B.  2;1;0;1;2=−−P . BÀI TẬP TRẮC NGHIỆM.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 34 C.  1;2;5=P . D.  0;1;4=P . Câu 11: Cho tập hợp { Axx = là ước chung của 36và120}. Hãy liệt kê các phần tử của tập hợp A A.   1;2;3;4;6;12.A = B.   1;2;4;6;8;12.A = C.   2;4;6;8;10;12.A = D.   2;3;4;6;12.A = . Câu 12: Số phần tử của tập hợp  2 1,2Akk k=+  là: A. 1. B. 2. C. 3. D. 5. Câu 13: Trong các tập hợp sau, tập hợp nào rỗng? A.  2 40.Axx=−= B.  2 230.Bxxx=++= C.  2 50.Cxx=−= D.  2 120.Dxxx=+−= Câu 14: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A.   1.Axx= B.  2 6710.Bxxx=−+= C.  2 420.Cxxx=−+= D.  2 430.Dxxx=−+= Câu 15: Cho hai tập hợp  0;2A = và   0;1;2;3;4.B = Có bao nhiêu tập hợp X thỏa mãn A XB . A. 2 B. 4 C. 6 D. 8 Câu 16: Tổng tất cả các phần tử của tập hợp  216=+Axx bằng A. 3. B. 9. C. 0. D. 3. Câu 17: Cho tập ( ) ;, =Mxyxy và 22 0.+xy Hỏi tập hợp M có bao nhiêu phần tử? A. 1. B. 2. C. 0. D. Vô số. Câu 18: Cho tập ( ) ( ) 2 43.0 =−+−= Mxxxxm . Có bao nhiêu giá trị nguyên của tham số m để tổng tất cả các phần tử của tập M bằng 4? A. 0. B. 1. C. 2. D. 3. Câu 19: Gọi A là tập hợp các số nguyên  7;7−m sao cho phương trình 2 0−+=xmxm có ít nhất một nghiệm dương. Số phần tử của tập hợp A là A. 9. B. 11. C. 10. D. 12. Câu 20: Cho tập hợp ( ) ( ) 2 ;256 =−=+ Axyxyy và , xy . Số phần tử của tập hợp A là A. 7. B. 5. C. 4. D. 6 Câu 21: Tập hợp nào sau đây chỉ gồm các số vô tỷ? A. *\ . B. \ . C. \ . D.  \0 . Câu 22: Cho tập hợp A . Trong các mệnh đề sau, tìm mệnh đề sai?. A. AA. B. AAA. C. D. A . Câu 23: Cho hai tập hợp ;;;;,;;;; AabcdmBcdmkl . Tìm AB . A. ; ABab B. ;;;;;; ABabcdmkl C. ; ABcd . D. ;; ABcdm .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 35 Câu 24: Cho , , ABC là ba tập hợp được minh họa như hình vẽ bên. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây? A. \ ABC B. \ ABC C. \\ ACAB D. ABC Câu25: Cho hai tập hợp , MN thỏa mãn MN . Mệnhđềnàosauđâyđúng? A. .MNN B. \. MNN C. .MNM D. \. MNM Câu 26: Số phần tử của tập hợp  2 23/,3Akkk =+ là: A. 7 B. 6 C. 5 D. 4 Câu 27: Tập hợp nào sau đây có đúng hai tập hợp con? A.  ;x  B.  x C.  ;;xy  D.  ; xy Câu 28: Cho tập X có biểu diễn trên trục số như hình sau: Khẳng định nào sau đây đúng. A. X là khoảng, ( )5;X =−+ . B. X là khoảng, ( );5X =−− . C. X là nửa khoảng, ( ;5X =−− . D. X là nửa khoảng,  )5;X =−+ . Câu 29: Tập hợp  ) ( 3;10;4− bằng tập hợp nào sau đây? A. ( )0;1 . B.  0;1 . C.  3;4 . D.  3;0 . Câu 30: Cho hai tập hợp  |20;3Axxx = và  2 |50Bxxx=−= Xác định tập hợp AB  A.  0;3;6;9;12;15;18 B.  0;3;5;6;9;12;15;18 C.  3;6;9;12;15;18 . D.  3;5;6;9;12;15;18 Câu 31: Cho hai tập hợp  4;1Am=− , ( 3; Bm =− khác rỗng. Tính tổng tất cả các giá trị nguyên của m để ABB = A. 13. B. 14. C. 12. D. 11. Câu 32: Chonửakhoảng  )5;3A =− vàđoạn  12;52 Bmm =−− .Tìmtấtcảcácsốthực m để AB= A. 15 m − . B. 1 5 m m −   . C. 1 5 m m −   . D. 1 5 m m −   . Câu 33: Cho nửa khoảng ( ; Am =−− và khoảng ( )25;23Bm=− . Gọi S là tập hợp các số thực m để ABA = . Hỏi S là tập con của tập hợp nào sau đây? A. ( );23−− . B. ( ;0− . C. ( )23; −+ . D.  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 36 Câu 34: Cho hai tập hợp ( )1;8Am=− và ( )2;B =+ . Tìm tất cả các giá trị của số thực m để A khác tập rỗng và . A. B. C. D. \ AB = 3m  3m = 39 m  39 m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1 BÀI 2: TẬPHỢP. CÁC PHÉPTOÁNTRÊNTẬPHỢP 1. KHÁI NIỆM CƠ BẢN VỀ TẬP HỢP a. Tập hợp Tập hợp (còn gọi là tập) là một khái niệm cơ bản của toán học, không định nghĩa. Giả sử đã cho tập hợp .A • Để chỉ a là một phần tử của tập hợp ,A ta viết aA  (đọc là a thuộc A ). • Để chỉ a không phải là một phần tử của tập hợp ,A ta viết aA  (đọc là P không thuộc A ). Chú ý. Số phần tử của tập hợp S được kí hiệu là ( )nS Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu là  Chẳng hạn: Tập các nghiệm của phương trình 2 10x += là tập rỗng. Gọi X là tập nghiệm của phương trình: 2 241430xx−+= Các mệnh đề sau đúng hay sai? a) 13 X ; b) 11 X ; c) ( ) 2nX = . Có thể mô tả một tập hợp bằng một trong hai cách sau Cách 1. Liệt kê các phần tử của tập hợp; Cách 2. Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP LÝ THUYẾT.I = aS  ; phần tử a thuộc tập hợp S aS  ; phần tử a không thuộc tập hợp S Luyện tập 1.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 Giải Ta có phương trình: 2 241430xx−+= có hai nghiệm phân biệt là 12 11, 13xx== Suy ra  11;13X = nên mệnh đề a) 13 X là đúng; b) 11 X là sai; c) ( ) 2nX = là đúng b. Tập hợp con Nhận xét  Từ định nghĩa trên, T là tập con của S nếu mệnh đề sau đúng: , xxTxS  .  Quy ước tập rỗng là tập con của mọi tập hợp. Minh họa T là một tập con của S như Hình 1.3 c. Hai tập hợp bằng nhau Nếu mọi phần tử của tập hợp T đều là phần tử của tập hợp S thì ta nói T là một tập hợp con (tập con) của S và ta viết là TS  (đọc là T chứa trong S hoặc T là tập con của S . Người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi đường kín, gọi là biểu đồ Ven (H.1.2) Hai tập hợp S và T được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của T cũng là phần tử của tập hợp S và ngược lại. Kí hiệu ST = .  Thay cho TS  , ta còn viết ST  (đọc là S chứa T ).  Kí hiệu TS  để chỉ T không là tập con của S .

p h

các hình bình hành có hai

ng chéo vuông góc; D là t

Các m

nh đề sau đây đúng hay sai?

p các hình hình vuông.

a) CD

;

c) CD = . Gi

Ta có hình bình hành có hai đường chéo vuông góc là hình thoi. Lại có mọi hình vuông đều là hình thoi. Suy ra CD

nên mệnh

OFFICIAL

p h

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3

ả sử C là tậ

ợp

đườ

ậ

ợ

ệ



 ;

ả



đề a) CD  là sai; b) CD  là đúng; c) CD = là sai, do có hình thoi hai cạnh kề có độ dài không bằng nhau thì không phải là hình vuông.

CÁC TẬP HỢP SỐ a. Mối quan hệ giữa các tập hợp số Tập hợp các số tự nhiên  0;1;2;3,4;...= . Tập hợp các số nguyên gồm các số tự nhiên và các số nguyên âm:  ...;3;2;1;0;1;2;3...=−−− . Tập hợp các số hữu tỉ gồm các số viết được dưới dạng phân số a b , với ,, 0abb . Số hữu tỉ còn được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn. Tập hợp các số thực gồm các số hữu tỉ và các số vô tỉ. Số vô tỉ là các số thập phân vô hạn không tuần hoàn. Cho tập hợp  4;0;1;2C =− . Các mệnh đề sau đúng hay sai? a) C là tập con của ; b) C là tập con của ; c) C là tập con của . Mối quan hệ giữa các tập hợp số:  Luyện tập 2. Luyện tập 3.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4 Giải Đáp án a), c) đúng Đáp án b) sai vì 4 − b. Các tập con thường dùng của Hãy ghép mỗi dòng ở cột bên trái với một dòng thích hợp ở cột bên phải. Giải 1 d, 2 a, 3 b, 4 c 3. CÁC PHÉP TOÁN TRÊN TẬP HỢP a. Giao của hai tập hợp Tập hợp gồm các phần tử thuộc cả hai tập hợp S và T gọi là giao của hai tập hợp S và T , ký hiệu là ST  .  | STxxSxT = Luyện tập 4.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5 Cho các tập hợp  1;5C = ,  2;3D =− . Hãy xác định tập hợp CD  . Giải: Ta có :  1;3CD= b. Hợp của hai tập hợp: Tập hợp gồm các phần tử thuộc tập hợp S hoặc T tập hợp gọi là hợp của hai tập hợp S và T , ký hiệu ST  .  | STxxSxT = Hãy biểu diễn tập AB  bằng biểu đồ Ven, với , AB cho trong HĐ1. HD : Hs trình bày biểu đồ Ven. c. Hiệu của hai tập hợp: Hiệu của hai tập hợp S và T là tập hợp gồm các phần tử thuộc tập hợp S mà không thuộc tập hợp T , ký hiệu \ ST  \| STxxSxT = . Luyện tập 5. Luyện tập 6.

p 10Acó 24tham gia thi đấu bóng đá và cầu lông, trong đó

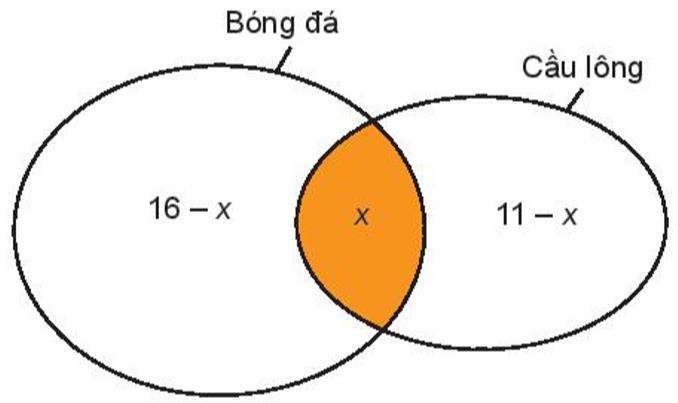
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6 Nếu T là tập con của tập hợp S , thì \ ST còn được gọi là Phần bù của T trong S . Ký hiệu là s CT Tìm phần bù của các tập hợp sau trong a) ( );2−− . b)  )5; −+ Giải: a) ( )  )\;22;−−=−+ . b)  ) ( )\5;;5 −+=−− .

ớ

có 16 bạn tham gia thi đấu bóng đá và 11 bạn tham gia thi đấu cầu lông. Giả sử các trận bóng đá và các trận cầu lông không tổ chức đồng thời. Hỏi có bao nhiêu bạn lớp 10A tham gia thi đấu cả bóng đá và cả cầu lông? Gợi ý : Gọi x là số bạn tham gia thi đấu cả bóng đá và cả cầu lông. Trả lời : 2416111611243 xxx =+−=+−= Ta có ( ) ( ) ( ) ( )nABnAnBnAB =+− Luyện tập 7. Vận dụng

1.8. G

p h

n tâp

t Nam. Hãy li

t kê các phần t

Ven.

Lời giải X ={Trung Quốc, Lào, Campuchia}

1.9. Ký hiệu E là tập hợp các quốc gia tại khu vực Đông Nam Á.

a) Nêu ít nhất hai phần tử thuộc tập hợp E .

b) Nêu ít nhất hai phần tử không thuộc tập hợp E .

c) Liệt kê các phần tử thuộc tập hợp E . Tập hợp E có bao nhiêu phần tử?

Lời giải

a) Hai quốc gia thuộc khu vực Đông Nam Á : Lào, Thái Lan.

b) Hai quốc gia không thuộc khu vực Đông Nam Á : Trung Quốc, Ấn Độ.

c) E = {Việt Nam, Lào, Campuchia, Thái lan,

a t

p h

p X

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7

ọi X là

ậ

ợ

các

ốc gia tiế

giáp

ới Việ

ệ

ử

ủ

ậ

ợ

và

ểu

ễ

ằng

ểu đồ

Indonesia, Singapore, Đông Timor, Philipin, Myanma, Brunei và Myanma} Số phần tử tập hợp E là : ( ) 11nE = . 1.10. Hãy viết tập hợp sau bằng cách nêu tính chất đặc trưng cho các phần tử cuả tập hơp :  0;4;8;12;16A = Lời giải Tập hợp  4|,04Annn = 1.11. Trong các tập hợp sau, tập nào là tập hợp rỗng?  2 |60Axx=−= ;  2 |60Bxx=−= Lời giải Ta có : 2 6 60 6 x x x  = −=  =−  , hai giá trị này không thuộc tập Vậy B = . 1.12. Cho  ; Xab = . Các cách viết sau đúng hay sai? Giải thích kết luận đưa ra. HỆ THỐNG BÀI TẬP.II = BÀI TẬP SÁCH GIÁO KHOA.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8 a) aX  . b)   aX  . C) X Lời giải a) Sai. Vì a là ký hiệu phần tử, viết đúng phải là : aX  b) Đúng. c) Sai. Vì  là 1 tập hợp. không phải là phần tử của X . Viết đúng phải là : X 1.13. Cho  2;5A = ,  5; Bx = ,  2; Cy = .Tìm x và y để ABC == . Lời giải Các tập hợp bằng nhau nếu các phần tử của tập này cũng là phần tử của tập kia. Vậy để cho ABC == thì 2,5xy== . 1.14. Cho   ( )( ) 22 |4;|53230AxxBxxxxx ==−+−= . a) Liệt kê các phần tử của hai tập hợp A và B b) Hãy xác định các tập hợp , ABAB  và \ AB Lời giải a) Ta có :  ....;4;3;2;1;0;1;2;3A =−−−−  2 0 530 5 3 x xx x = −=  = .  2 1 230 3 x xx x = +−=  =− . Khi đó :  3;0;1B =− . b) Ta có : BA  nên ABB = ; ABA = ;  \.....;4;2;1;2;3AB =−−− 1.15. Xác định các tập hợp sau và biểu diễn chúng trên trục số a) (   )4;10;3− . b) (  ( 0;23;1 − . c) ( ) ( 2;1;1−− . d) ( \;3 − Lời giải a) (   )  4;10;30;1 −= . b) (  (  ( 0;23;13;2 −=− . c) ( ) (  ( )2;1;12;1 −−=− .

Để phục v

cho một hội nghị quốc tế, ban tổ chức huy động 35 người phiên dịch tiếng Anh, 30 người phiên dịch tiếng Pháp, trong đó có 16 người phiên dịch được cả hai thứ tiếng Anh và Pháp. Hãy trả lời các câu hỏi sau:

a) Ban tổ chức đã huy động bao nhiêu người phiên dịch cho hội nghị đó?

b) Có bao nhiêu người chỉ phiên dịch được tiếng Anh?

c) Có bao nhiêu người chỉ phiên dịch được tiếng Pháp?

Lời giải Sơ đồ ven minh họa

a) Số người phiên dịch mà ban tổ chức huy động là : 35301649 +−= người.

b) Số người chỉ phiên dịch được tiếng

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9 d) (  ( )\;33;−=+ . 1.16.

ụ

anh là : 351619 −= người. c) Số người chỉ phiên dịch được ttiếng Pháp là : 301614 −= người.  DẠNG 1: XÁC ĐỊNH MỘT TẬP HỢP PHƯƠNG PHÁP Để xác định một tập hợp, ta có 2 cách sau:  Liệt kê các phần tử của tập hợp.  Chỉ ra tính chất đặc trưng của tập hợp. Bài 1. Viết lại tập hợp ( )( ) Axxxxx =−+−+= 22 253430 bằng cách liệt kê các phần tử của nó. Lời giải Ta có ( )( ) x xx x xxxx xx x x  =  −+= −+−+==  −+=  =  = 2 22 2 1 25343025303 4302 1 3 . BÀI TẬP TỰ LUẬN.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10 Vì x  nên 3 1;;3 2 A Bài 2. Viết lại tập hợp ( )( ) Axxxxx =−+−+= 22 253430 bằng cách liệt kê các phần tử của nó. Lời giải Ta có ( )( ) x xx x xxxx xx x x  =  −+= −+−+==  −+=  =  = 2 22 2 1 25343025303 4302 1 3 . Vì x  nên 1;3A Bài 3. Viết lại tập hợp  Axx= 5 bằng cách liệt kê các phần tử của nó. Lời giải Ta có x  5và x  nên 0;1;2;3;4x Vậy 0;1;2;3;4A Bài 4. Viết mỗi tập hợp  A = 0; 1; 2; 3; 4 bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó. Lời giải Ta nhận thấy các phần tử của tập hợp A là các số tự nhiên và nhỏ hơn 5. Do đó  Axx= 5 Bài 5. Viết mỗi tập hợp  A = 9; 36; 81; 144 bằng cách chỉ rõ tính chất đặc trưng cho các phần tử của nó. Lời giải Ta có 293 , 2366 , 2819 , 214412 và các số 3,6,9,12 đều là bội của 3. Do đó ta viết lại tập hợp A bằng cách chỉ ra tính chất đặc trưng là 2 * 3,4Akkk . Bài 6. Liệt kê tất cả các phần tử của tập hợp A gồm các số tự nhiên chia hết cho 3 và nhỏ hơn 25. Lời giải Ta có  0;3;6;9;12;15;18;21;23=A Bài 7. Liệt kê các phần tử của tập hợp  2 2530=−+=Xxxx Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Ta có 2 2530 xx−+= 1 3 2 x x =   = 3 1; 2  =   X . Bài 8. Viết tập hợp ( )( ) 22 9320 =−−+= Bxxxx dưới dạng liệt kê các phần tử. Lời giải Ta có ( )( )22 9320 xxx −−+= 2 2 90 320 x xx  −=   −+= 3 3 1 2 =−  =  =  = x x x x Vậy  3;1;2=B . Bài 9. Viết tập hợp ( )( ) 22 5560 =−−+= Axxxx dưới dạng liệt kê các phần tử. Lời giải Ta có ( )( )22 5560 xxx −−+= 2 2 50 560 x xx  −=   −+= 5 3 2  = =   = x x x . Vậy  2;3=A . Bài 10. Tính tổng tất cả các phần tử của tập hợp 3 2  =  Ax x Lời giải Ta có ( ) 213 2113 32 2352 231 xx xx x xxx xx −==  −−=−= −==  −=−=− Vì x nên loại 1=−x Suy ra  1;3;5=A Vậy tổng tất cả các phần tử của tập hợp A là 1359 ++= Bài 11. Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi hóa, 6 học sinh giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học sinh giỏi cả ba môn Toán, Lý, Hóa. Tính học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A? Lời giải Theo giả thiết đề bài cho, ta có biểu đồ Ven:

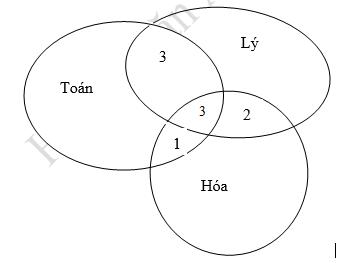
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 12 Dựa vào biểu đồ Ven, ta có Số học sinh giỏi chỉ một môn Toán: 103313 −−−= Số học sinh giỏi chỉ một môn Lý: 103322 −−−= . Số học sinh giỏi chỉ một môn Hóa: 113215 −−−= . Vậy số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là: 325332119 ++++++= Bài 12. Cho ( )2;A =+ , ( );Bm=+ . Tìm điều kiện cần và đủ của m để B là tập con của A ? Lời giải Ta có: BA  khi và chỉ khi xBxA 2m  Bài 13. Xác định số phần tử của tập hợp  |4,2017Xnnn= . Lời giải Tập hợp X gồm các phần tử là những số tự nhiên nhỏ hơn 2017 và chia hết cho 4 Từ 0 đến 2015 có 2016 số tự nhiên, ta thấy cứ 4 số tự nhiên liên tiếp sẽ có duy nhất một số chia hết cho 4. Suy ra có 504 số tự nhiên chia hết cho 4 từ 0 đến 2015. Hiển nhiên 20164. Vậy có tất cả 505 số tự nhiên nhỏ hơn 2017 và chia hết cho 4. Bài 14. Cho hai tập hợp  1;3A = và  ;1Bmm=+ . Tìm tất cả giá trị của tham số m để BA  Lời giải Ta có: 11 132 mm BA mm  +  . Vậy 12 m  Câu 15. Số phần tử của tập hợp  2 43220 =−++−= Axxxx Lời giải B= m;+∞( ) + ∞ - ∞ 2

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 13 Ta có 2 430−+xx và 220 −x nên 2 2 1 430 432201 3 220 1 = −+=  −++−== = −=  = x xx xxxx x x x . Vậy tập A có đúng 1 phần tử. Câu 16. Tính tổng các phần tử của tập hợp 43 2 + = +  Axx x Lời giải Ta có 25 254355 452 21222 21 x xx x xxxx x +=  ++=− =−+  ++++=  +=− 3 7 1 3 =  =−  =−  =− x x x x Suy ra  3;7;1;3=−−−A Vậy tổng các phần tử của tập hợp A là ( ) ( ) ( ) 37138 +−+−+−=− . Câu 17. Liệt kê các phần tử của tập hợp  2238230 =+−++= Axxxxx Lời giải Đặt 2 30=+txx . Phương trình 2238230 +−++= xxxx trở thành 2 2 2802 4 = +−==  =− t ttt t . + 2=t 22 1 32340 4 = +=+−=  =− x xxxx x . Vậy  1;4=−A DẠNG 2: CÁC PHÉP TOÁN VỀ GIAO, HỢP, HIỆU CỦA HAI TẬP HỢP PHƯƠNG PHÁP Giao của hai tập hợp: ABxxAvaxB Hợp của hai tập hợp: ABxxAhoacxB Hiệu cuả hai tập hợp: \ ABxxAvaxB . Phần bù: Cho BA thì \A CBAB . Bài 1. Cho hai tập hợp 1;2;3;7,2;4;6;7;8AB . Xác định các tập hợp AB , AB, \ AB , \.BA Lời giải Ta có 2;7,1;2;3;4;6;7;8,\1;3,\4;6;8ABABABBA

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 14 Bài 2. Cho tập {0;1;2;3;4;5}X = và tập {0;2;4}A = . Xác định phần bù của A trong X Lời giải Vì AX nên \{1;3;5)X CAXA Bài 3. Gọi n B là tập hợp các bội số của n trong . Xác định tập hợp 24BB ? Lời giải Ta có các tập hợp 2 4 2,2;4;6;8;10;... 4,4;8;12;16;... Bxxkk Bxxkk Do đó 244 BBB . Bài 4. Cho A là tập hợp tất cả các nghiệm của phương trình 2 43 0xx ; B là tập hợp các số có giá trị tuyệt đối nhỏ hơn 4 Xác định tập hợp \ AB ? Lời giải Ta có 2 1 76 01;3 3 x xxA x 3;2;1;0;1;2;3B . Do đó \ AB . Bài 5. Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu, 30 em biết chơi cầu lông, 15 em biết chơi cả hai. Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? Bao nhiêu em chỉ biết đánh cầu lông? Sĩ số lớp là bao nhiêu? Lời giải Dựa vào biểu đồ Ven ta suy ra số học sinh chỉ biết đá cầu là 251510 −= . Số học sinh chỉ biết đánh cầu lông là 301515 −= Do đó ta có sĩ số học sinh của lớp 10A1 là 10151540 ++= . Bài 6. Viết lại tập hợp {21| AxxZ và 24} x dưới dạng liệt kê. Lời giải Ta có 242,1,0,1,2,3,4 xZ x x . Suy ra 3;1;1;3;5;7;9C . Bài 7. Mỗi học sinh của lớp 10A1 đều biết chơi đá cầu hoặc cầu lông, biết rằng có 25 em biết chơi đá cầu , 30 em biết chơi cầu lông , 15 em biết chơi cả hai . Hỏi lớp 10A1 có bao nhiêu em chỉ biết đá cầu? bao nhiêu em chỉ biết đánh cầu lông? Sĩ số lớp là bao nhiêu?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 15 Lời giải Dựa vào biểu đồ ven ta suy ra số học sinh chỉ biết đá cầu là 251510 Số học sinh chỉ biết đánh cầu lông là 301515 Do đó ta có sĩ số học sinh của lớp 10A1 là 10151540 Trong số 220 học sinh khối 10 có 163 bạn biết chơi bóng chuyền, 175 bạn biết chơi bóng bàn còn 24 bạn không biết chơi môn bóng nào cả. Tìm số học sinh biết chơi cả 2 môn bóng. Bài 8. Cho các tập hợp: |3|15|24 AxRxBxRxCxRx a) Hãy viết lại các tập hợp , , ABC dưới kí hiệu khoảng, nửa khoảng, đoạn. b) Tìm ,,\ ABABAB c) Tìm \ BCAC . Lời giải a) Ta có: ;3 1;5 2;4ABC . b) Suy ra ;5AB Suy ra 1;3AB Suy ra \;1AB 2;3AC và 2;5BC Suy ra ta có \3;5BCAC Bài 9. Cho các tập hợp 3 1; 2 Amm +  =−  và ( )  );33;B =−−+ . Tìm tất cả các số thực m để AB= . Lời giải Đặt  )3;3XCBX==− AB= XA 13 34 3 2 m mm −−    +   25 30 0 15

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 16 Bài 10. Cho hai tập hợp ( 2;5E = và  23;22Fmm=−+ . Tìm tất cả các giá trị của tham số m để A hợp B là một đoạn có độ dài bằng 5. Lời giải Nhận xét: Kí hiệu X là độ dài của khoảng/nửa khoảng/đoạn X , khi đó 3E = ; 5F = . * TH1: 35 232522 22 EFFEFmmm =−+ . * TH2: 5EFFEFF = . Vậy không có giá trị nào của m thỏa mãn TH2. Bài 11. Cho khoảng 6 ; 2 A m  =−  và khoảng ( )1;Bm=−+ . Tìm tất cả các số thực m để \ ABA = Lời giải 2 6341\10 2224 ABAABmmmm mmm ==−−++−   ( )* Bài 12. Cho các tập hợp ( )2;A =+ và )2 7;Bm  =−+  với 0m  . Tìm tất cả các số thực m để \ AB là một khoảng có độ dài bằng 16 . Lời giải Điều kiện để \ AB  là 22729 3 00 mm m mm −   . Khi đó ( )2 \2;7ABm=− Độ dài khoảng \ AB bằng 16 2 72165mm −−== (do 3m  ). Câu 1: Cho tập hợp  2 10Axxx=++= . Các phần tử của tập A là: A. 0=A B.  0=A C. =A D.  =A Lời giải Chọn C Ta có:  2 10Axxx=++= Vì phương trình 2 10xx++= vô nghiệm nên =A . Câu 2: Hãy liệt kê các phần tử của tập hợp  saocho 8MxNx = lµíccña A.  1;4;16;64M = . B.  0;1;4;16;64M = . C.  1;2;4;8M = . D.  0;1;2;4;8M = . Lời giải Chọn A A. Đúng, căn bậc hai của các số trong tập M đều là ước của 8. B. HS hiểu nhầm số 0 là ước của mọi số tự nhiên. C. HS hiểu nhầm x là ước của 8. BÀI TẬP TRẮC NGHIỆM.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 17 D. HS hiểu nhầm x là ước của 8 và 0 là ước của mọi số tự nhiên. Câu 3: Cho tập hợp ( )( ) 22–120Axxx =+= . Các phần tử của tập A là: A.  –1;1=A B. –2;–1; }{2 1;=A C. {1}=A D. {1}=A Lời giải Chọn A ( )( ) 22–120Axxx =+= Ta có ( )( )22–120 +=xx ( ) 2 2 –10 20vn  =   +=  x x 1 1 =   =− x x   1;1.=− A Câu 4: Cho 2 40Axx . Tập hợp A viết lại dạng liệt kê là A. . B.  . C.  )2; −+ . D.  )2;+ . Lời giải Chọn A Ta có: 22404 xxx ( Vì 2 0, xx ). Câu 5: Tập hợp nào là tập hợp rỗng, trong các tập hợp sau? A.  2 |6–710xxx += B.  |1xx C.  2 |420xxx−+= . D.  2 |430xxx−+= . Lời giải Chọn C Ta có 2 22 420 22 x xx x  =+ −+=  =−  . Vì x nên x . Câu A sai là phương trình có 2 nghiệm hữu tỉ Câu B sai là bất phương trình có 1 nghiệm nguyên 0x = Câu D sai là phương trình có 2 nghiệm là 1x và 3x Câu 6: Cho tập hợp ( )( ) 22930=−−= Bxxxx . Tập hợp B được viết dưới dạng liệt kê là A.  3;9;1;2=B . B.  3;9;0=−B . C.  9;9;0=−B . D.  3;3;0=−B . Lời giải Chọn D Ta có 2 2 90 30 x xx  −=  −= 3 3 3 0 x x x x =−  =  =  = . Vậy  3;3;0=−B . Câu 7: Cho tập hợp  3 90=−=Hxxx . Tập hợp H là tập con của tập hợp nào dưới đây ?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 18 A.  3;0;1;2=−A . B.  3;1;2;3=−B . C.  0;1;2=C . D.  3;0;2;3=−D . Lời giải Chọn D Ta có ( )32 0 9090 3 = −=−=  = x xxxx x . Suy ra  0;3=H (vì x ). Câu 8: Tập hợp ( )( ) 23240=+−+= Axxxxx có bao nhiêu phần tử? A. 1. B. 3. C. 5. D. 2. Lời giải Chọn B Ta có ( )( ) ( )( )( )2322401240 +−+=−++= xxxxxxxx 01 102 200 ==  −==−  +==  xx xx xx (do 2 40, xx+ ). Vì x nên loại 2=−x . Suy ra  0;1=A . Vậy tập hợp A có 2 phần tử. Câu 9: Trong các tập hợp sau, tập hợp nào là tập rỗng? A.  2 560+−=xxx . B.  2 3520−+= xxx . C.  2 10+−=xxx . D.  2 510+−=xxx . Lời giải Chọn C Ta có 2 10+−=xx 15 2 − = x nên  2 10 +−==xxx . Câu 10: Cho tập hợp  2 1 =+Pnn và 33− n . Viết tập hợp P dưới dạng liệt liệt kê các phần tử A.  3;2;1;0;1;2;3=−−−P B.  2;1;0;1;2=−−P C.  1;2;5=P . D.  0;1;4=P . Lời giải Chọn C Ta có 2 1 33 0 1 2 =−  −=−  =   = =  n n n n n n n . Suy ra  1;2;5=P

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 19 Câu 11: Cho tập hợp { Axx = là ước chung của 36và120}. Hãy liệt kê các phần tử của tập hợp A A.   1;2;3;4;6;12.A = B.   1;2;4;6;8;12.A = C.   2;4;6;8;10;12.A = D.   2;3;4;6;12.A = . Lời giải Chọn A Ta có 22 3 362.3 1202.3.5  =  =  . Do đó  1;2;3;4;6;12A = . Câu 12: Số phần tử của tập hợp  2 1,2Akk k=+  là: A. 1. B. 2. C. 3. D. 5. Lời giải Chọn D Vì k  và 2k  nên  2;1;0;1;2k  do đó ( )  2 11;2;5.k + Vậy A có 3 phần tử Câu 13: Trong các tập hợp sau, tập hợp nào rỗng? A.  2 40.Axx=−= B.  2 230.Bxxx=++= C.  2 50.Cxx=−= D.  2 120.Dxxx=+−= Lời giải Chọn B Xét các đáp án:  Đáp án A. Ta có  2 2 402 2 x xA x = −==  =− .  Đáp án B. Ta có 2 230xx++= (phương trình vô nghiệm) B =  Đáp án C. Ta có  2 5055;5xxC −===− .  Đáp án D. Ta có  2 3 1204;3 4 x xxD x = +−==−  =− . Câu 14: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng? A.   1.Axx= B.  2 6710.Bxxx=−+= C.  2 420.Cxxx=−+= D.  2 430.Dxxx=−+= Lời giải Chọn C Xét các đáp án:  Đáp án A. Ta có  1110xxA −=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 20  Đáp án B. Ta có  2 1 67101 1 6 x xxB x =  −+==  =  Đáp án C. Ta có 2 42022 xxxC −+===  Đáp án D. Ta có  2 3 4301;3 1 x xxD x = −+==  = . Câu 15: Cho hai tập hợp  0;2A = và   0;1;2;3;4.B = Có bao nhiêu tập hợp X thỏa mãn A XB . A. 2 B. 4 C. 6 D. 8 Lời giải Chọn C Ta có A XB nên ; XAXB == ,  0;1;2X = ,  0;2;3X = ,  0;2;4X = ,  0;1;2;3X = ,  0;1;2;4X = ,  0;2;3;4X = Vậy có 8 tập X thỏa đề bài. Câu 16: Tổng tất cả các phần tử của tập hợp  216=+Axx bằng A. 3 B. 9 C. 0 D. 3 Lời giải Chọn D Ta có 75 2156216725 22 +−+−− xxxx . Vì x  nên  3;2;1;0;1;2−−−x . Suy ra  3;2;1;0;1;2=−−−A . Vậy tổng tất cả các phần tử của tập hợp A là ( ) ( ) ( ) 3210123 −+−+−+++=− . Câu 17: Cho tập ( ) ;, =Mxyxy và 22 0.+xy Hỏi tập hợp M có bao nhiêu phần tử? A. 1. B. 2. C. 0. D. Vô số. Lời giải Chọn A Ta có 2 22 2 0, 0. 0,   +   xx xy yx Mà 22 0+xy nên chỉ xảy ra khi 22 00.+===xyxy Do đó ta suy ra ( ) 0;0=M nên tập hợp M có 1 phần tử Câu 18: Cho tập ( ) ( ) 2 43.0 =−+−= Mxxxxm . Có bao nhiêu giá trị nguyên của tham số m để tổng tất cả các phần tử của tập M bằng 4? A. 0. B. 1 C. 2 D. 3 Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 21 Ta có ( ) ( ) 2 2 1 430 43.03 0 x xx xxxmx xm xm = −+=  −+−==  −=  = . Nếu 1 3 m m =  = thì  1;3=M . Khi đó tổng các phần tử bằng 4 (thỏa mãn). Nếu 1 3 m m    thì  1;3;= Mm . Khi đó 1340 ++== mm . Vậy có 3 giá trị của tham số m để tổng tất cả các phần tử của tập M bằng 4. Câu 19: Gọi A là tập hợp các số nguyên  7;7−m sao cho phương trình 2 0−+=xmxm có ít nhất một nghiệm dương. Số phần tử của tập hợp A là A. 9 B. 11. C. 10. D. 12 Lời giải Chọn B TH1: Phương trình 2 0−+=xmxm có hai nghiệm trái dấu 00 acm Mặt khác do  7;7−m và m nên  7;6;5;4;3;2;1 −−−−−−−m . TH2: Phương trình 2 0−+=xmxm có nghiệm kép dương 0 0 =    S 4= m TH3: Phương trình 2 0−+=xmxm có hai nghiệm dương phân biệt 120 xx 0 0 0       S P 2 40 0 0 =−  =   = mm Sm Pm ( ) 40 04 0 −  =   = mm Smm Pm . Từ các trường hợp trên suy ra  7;6;5;4;3;2;1;4;5;6;7=−−−−−−−A . Vậy số phần tử của tập hợp A là 11. Câu 20: Cho tập hợp ( ) ( ) 2 ;256 =−=+ Axyxyy và , xy . Số phần tử của tập hợp A là A. 7. B. 5. C. 4. D. 6 Lời giải Chọn D Ta có ( )2 256−=+xyy ( ) 22316−+= xy ( )( ) 3316++−+= xyxy Vì 33++−+xyxy và 30++xy nên 30−+xy Do đó ( )( ) 3316++−+=xyxy khi các trường hợp sau xảy ra:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 22 TH1: 17 316 2 3115 3 2  ++==    −+= +=  x xy xy y loại do , xy . TH2: 38 32 ++=   −+=  xy xy 5 33 =    +=  x y 5 33 =   += x y 5 0 6 =   =  =− x y y . TH3: 34 34 ++=   −+=  xy xy 4 30 =    +=  x y 4 3 =   =− x y . Do đó ( ) ( ) ( ) ( ) ( ) ( ) 5;0;5;6;5;0;5;6;4;3;4;3 =−−−−−−−A Vậy tập hợp A có 6 phần tử. Câu 21: Tập hợp nào sau đây chỉ gồm các số vô tỷ? A. *\ . B. \ . C. \ . D.  \0 . Lời giải Chọn B Tập hợp chỉ gồm các số vô tỷ là \ Câu 22: Cho tập hợp A . Trong các mệnh đề sau, tìm mệnh đề sai?. A. AA. B. AAA. C. D. A . Lời giải Chọn A Ta có A Câu 23: Cho hai tập hợp ;;;;,;;;; AabcdmBcdmkl . Tìm AB . A. ; ABab B. ;;;;;; ABabcdmkl C. ; ABcd . D. ;; ABcdm . Lời giải Chọn D Tập hợp A và tập hợp B có chung các phần tử ,, cdm. Do đó ;; ABcdm . Câu 24: Cho , , ABC là ba tập hợp được minh họa như hình vẽ bên. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây? A. \ ABC . B. \ ABC . C. \\ ACAB D. ABC Lời giải

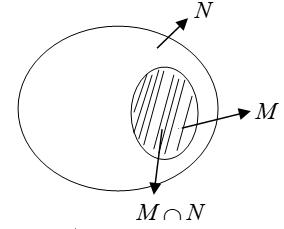
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 23 Chọn B Sử dụng phép toán giao hai tập hợp để tìm AB  , từ đó suy ra đáp án B. Câu25: Cho hai tập hợp , MN thỏa mãn MN Mệnhđềnàosauđâyđúng? A. .MNN B. \. MNN C. .MNM D. \. MNM Lời giải Chọn C Dựa vào biểu đồ Ven Câu 26: Số phần tử của tập hợp  2 23/,3Akkk =+ là: A. 7. B. 6. C. 5. D. 4. Lời giải Chọn D  3;2;1;0;1;2;3k =−−−  3;5;11;21A = . Câu 27: Tập hợp nào sau đây có đúng hai tập hợp con? A.  ;x  . B.  x . C.  ;;xy  . D.  ; xy . Lời giải Chọn B C1: Công thức số tập con của tập hợp có n phần tử là 2n nên suy ra tập  x có 1 phần tử nên có 1 22 = tập con. C2: Liệt kê số tập con ra thì  x có hai tập con là  x và   Câu 28: Cho tập X có biểu diễn trên trục số như hình sau: Khẳng định nào sau đây đúng. A. X là khoảng, ( )5;X =−+ . B. X là khoảng, ( );5X =−− . C. X là nửa khoảng, ( ;5X =−− D. X là nửa khoảng,  )5;X =−+ Lời giải Chọn B Câu 29: Tập hợp  ) ( 3;10;4− bằng tập hợp nào sau đây? A. ( )0;1 B.  0;1 C.  3;4 D.  3;0 Lời giải Chọn C Ta có:  ) (   3;10;43;4 −=− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 24 Câu 30: Cho hai tập hợp  |20;3Axxx = và  2 |50Bxxx=−= Xác định tập hợp AB  A.  0;3;6;9;12;15;18 . B.  0;3;5;6;9;12;15;18 . C.  3;6;9;12;15;18 D.  3;5;6;9;12;15;18 Lời giải Chọn B Ta có tập hợp  |20;3Axxx =  0;3;6;9;12;15;18A = Giải phương trình 2 0 50 5 x xx x = −=  = . Do x  nên  0;5B = .  0;3;5;6;9;12;15;18AB = Câu 31: Cho hai tập hợp  4;1Am=− , ( 3; Bm =− khác rỗng. Tính tổng tất cả các giá trị nguyên của m để ABB = A. 13. B. 14. C. 12. D. 11. Lời giải Chọn B 34115ABBABmmm =−− . m   2;3;4;5m  tổng các giá trị nguyên của m là 234514 +++= . Câu 32: Chonửakhoảng  )5;3A =− vàđoạn  12;52 Bmm =−− .Tìmtấtcảcácsốthực m để AB= A. 15 m − . B. 1 5 m m −   . C. 1 5 m m −   . D. 1 5 m m −   . Lời giải Chọn C 1231 5255 mm AB mm =−− −−  Vậy giá trị m cần tìm là 1 5 m m −   Câu 33: Cho nửa khoảng ( ; Am =−− và khoảng ( )25;23Bm=− . Gọi S là tập hợp các số thực m để ABA = . Hỏi S là tập con của tập hợp nào sau đây? A. ( );23−− . B. ( ;0− . C. ( )23; −+ . D.  . Lời giải Chọn B 252314 23 2323 mm ABABAm mm − =−  −−  Suy ra (  ( ;23;0S =−−− Câu 34: Cho hai tập hợp ( )1;8Am=− và ( )2;B =+ . Tìm tất cả các giá trị của số thực m để A khác tập rỗng và . A. . B. . C. . D. . Lời giải \ AB = 3m  3m = 39 m  39 m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 25 Chọn C Điều kiện: Để khi và chỉ khi , tức là Đối chiếu điều kiện, ta được . 189mm− \ AB = AB  213 mm − 39 m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1 BÀI2:TẬPHỢP.CÁCPHÉPTOÁNTRÊNTẬPHỢP DẠNG 1. PHẦN TỬ CỦA TẬP HỢP, CÁC XÁC ĐỊNH TẬP HỢP Câu 1: Ký hiệu nào sau đây dùng để viết đúng mệnh đề: “3 là một số tự nhiên”? A. 3  B. 3 C. 3  D. 3  Câu 2: Ký hiệu nào sau đây để chỉ 5 không phải là một số hữu tỉ? A. 5  B. 5  C. 5  D. 5  Câu 3: Cho tập hợp  1|,5Axxx=+ . Tập hợp A là: A.  1;2;3;4;5A = B.  0;1;2;3;4;5;6A = C.  0;1;2;3;4;5A = D.  1;2;3;4;5;6A = Câu 4: Hãy liệt kê các phần tử của tập hợp  2 |2310Xxxx=−+= A.  0X = B.  1X = C. 1 1; 2 X  =   D. 3 1; 2 X  =   Câu 5: Liệt kê các phần tử của phần tử tập hợp  2 |2530Xxxx=−+= A.  0X = B.  1X = C. 3 2 X  =   D. 3 1; 2 X  =   Câu 6: Trong các tập sau, tập nào là tập rỗng? A.  |1xx B.  2 |6710xxx −+= C.  2 :420xxx−+= D.  2 :430xxx−== Câu 7: Cho tập hợp ( ) ;|;,1Mxyxyxy =+= . Hỏi tập M có bao nhiêu phần tử? A. 0 B. 1 C. 2 D. 3 Câu 8: Cho tập hợp  2 1\,5Axxx =+ . Hãy liệt kê các phần tử của tập hợp A A.  0;1;2;3;4;5A = B.  1;2;5;10;17;26A = C.  2;5;10;17;26A = D.  0;1;4;9;16;25A = Câu 9: Hãy liệt kê các phần tử của tập hợp:  42 \680Xxxx=−+= . A.  2;4X = B.  2;2X =− CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 C.  2;2X = D.  2;2;2;2X =−− Câu 10: Cho tập hợp ( ) 22 ;\,,0Mxyxyxy=+ . Khi đó tập hợp M có bao nhiêu phần tử? A. 0 B. 1 C. 2 D. Vô số Câu 11: Số phần tử của tập hợp: ( ) 2 22 \21Axxxxx =+=−+ là: A. 0 B. 3 C. 1 D. 2 Câu 12: Số tập con của tập hợp: ( ) 2 22 \3220Axxxxx =+−−= là: A. 16 B. 8 C. 12 D. 10 Câu 13: Số phần tử của tập hợp: ( ) 2 22 \24441Axxxxx =+−=−+ là: A. 0 B. 2 C. 4 D. 3 Câu 14: Hãy liệt kê các phần tử của tập hợp  2 10Xxxx=++= : A. 0=X B.  0=X C. X = D.  X = Câu 15: Số phần tử của tập hợp  2 1/,2=+Akkk là: A. 1. B. 2. C. 3. D. 5. Câu 16: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng: A.  xx1  . B.  2 x6710 xx −+= . C.  2 xx420 x −+= . D.  2 x430 xx −+= . Câu 17: Cho tập hợp ( )( ) 22–120Axxx =+= . Các phần tử của tập A là: A.  –1;1=A B. –2;–1; }{2 1;=A C. {1}=A D. {1}=A Câu 18: Trong các tập hợp sau, tập hợp nào là tập rỗng? A.  2 40Axx=−= B.  2 230Bxxx=++= C.  2 50Cxx=−= D.  2 120.Dxxx=+−= Câu 19: Trong các tập hợp sau, tập hợp nào khác rỗng? A.  2 10Axxx=++= B.  2 20Bxx=−= C. ( )( ) 32–310Cxxx=+= . D. ( ) 2 30Dxxx=+= . DẠNG 2. TẬP HỢP CON, TẬP HỢP BẰNG NHAU Câu 20: Cho hai tập hợp A và .B Hình nào sau đây minh họa A là tập con của B? A. B. C. D. Câu 21: Cho ba tập hợp E, F, G thỏa mãn: , EFFG  và GK  . Khẳng định nào sau đây đúng? A. GF  B. KG  C. EFG == D. EK  Câu 22: Cho tập hợp  0;3;4;6A = . Số tập hợp con gồm hai phần tử của A là:

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3 A. 12 B. 8 C. 10 D. 6 Câu 23: Cho tập hợp  ;; Xabc = . Số tập con của X là A. 4 B. 6 C. 8 D. 12 Câu 24: Trong các tập hợp sau đây, tập hợp nào có đúng một tập hợp con? A.  B.  x C.   D.  , x Câu 25: Cho tập hợp  1;2A = và  1;2;3;4;5B = . Có tất cả bao nhiêu tập X thỏa mãn: AXB  ? A. 5 B. 6 C. 7 D. 8 Câu 26: Chotậphợp  1;2;5;7A = và  1;2;3B = .Cótấtcảbaonhiêutập X thỏamãn: XA  và XB  ? A. 2 B. 4 C. 6 D. 8 Câu 27: Cho tập hợp      1;3,3;,;;3 ABxCxy === . Để ABC == thì tất cả các cặp ( ); xy là: A. ( )1;1 B. ( )1;1 và ( )1;3 C. ( )1;3 D. ( )3;1 và ( )3;3 Câu 28: Cho tập hợp    1;2;3;4,0;2;4AB== ,  0;1;2;3;4;5C = . Quan hệ nào sau đây là đúng? A. BAC  B. BAC = C. AC BC    D. ABC =

29: Cho tập hợp A có 4 phần tử. Hỏi tập A có bao nhiêu tập con khác rỗng? A. 16 B. 15 C. 12 D. 7

30: Số các tập hợp con gồm hai phần tử của tập hợp  ;;;;; Babcdef = là: A. 15 B. 16 C. 22 D. 25

31: Số các tập hợp con có 3 phần tử có chứa a, b của tập hợp  ;;;;;; Cabcdefg = là: A. 5 B. 6 C. 7 D. 8 Câu 32: Trong các tập hợp sau đây, tập hợp nào có đúng hai tập hợp con? A.  ; xy B.  x C.  ;x D.  ;;xy Câu 33: Cho tập hợp  1,2,3,4,,= Axy . Xét các mệnh đề sau đây: ( )I : “3 A”. ( )II : “ 3,4  A”. ( )III : “ ,3, abA  ”. Trong các mệnh đề sau, mệnh đề nào đúng A. I đúng. B. , III đúng. C. , IIIII đúng. D. , IIII đúng. Câu 34: Cho  0;2;4;6=A . Tập A có bao nhiêu tập con có 2 phần tử? A. 4. B. 6. C. 7. D. 8. Câu 35: Cho tập hợp  1;2;3;4=X . Câu nào sau đây đúng? A. Số tập con của X là 16.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4 B. Số tập con của X gồm có 2 phần tử là 8 C. Số tập con của X chứa số 1 là 6. D. Số tập con của X gồm có 3 phần tử là 2 Câu 36: Số các tập con 2 phần tử của  ,,,,, = Babcdef là: A. 15 B. 16 C. 22 D. 25 Câu 37: Số các tập con 3 phần tử có chứa ,  của  ,,,,,,,,, =C là: A. 8 B. 10 C. 12 D. 14 Câu 38: Trong các tập sau đây, tập hợp nào có đúng hai tập hợp con? A.  ; xy . B.  x . C.  ; x . D.  ;; xy . Câu 39: Cho tập hợp  ,,, Aabcd = . Tập A có mấy tập con? A. 16. B. 15. C. 12. D. 10. Câu 40: Khẳng định nào sau đây sai?Các tập AB = với , AB là các tập hợp sau? A. ( )( ) 1;3, 0} –1 {= 3ABxxx ==− . B.  1;3;5;7;9,21, ,04{} ABnnkkk ===+ . C.  2{1;2, 0} 23ABxxx  =−=−= . D.  2, 10ABxxx ==++= . Câu 41: Cho tập hợp    1;5,1;3;5XY== . Tập XY  là tập hợp nào sau đây? A.  1 B.  1;3 C. {1;3;5} D.  1;5 Câu 42: Cho tập    2;4;6;9,1;2;3;4XY== . Tập nào sau đây bằng tập \ XY ? A.  1;2;3;5 B.  1;3;6;9 C.  6;9 D.  1 Câu 43: Cho tập hợp    ;,;; XabYabc == XY  là tập hợp nào sau đây? A.  ;;; abcd B.  ; ab C.  c D. {;;} abc Câu 44: Cho hai tập hợp A và B khác rỗng thỏa mãn: AB  . Trong các mệnh đề sau mệnh đề nào sai? A. \ AB = B. ABA = C. \ BAB = D. ABB = Câu 45: Cho ba tập hợp: ( )  ( )  ( ) ( ) |0,|0,|0 FxfxGxgxHxfxgx =====+= . Mệnh đề nào sau đây là đúng? A. HFG = B. HFG = C. \ HFG = D. \ HGF = Câu 46: Cho tập hợp 2 2 |1 1 Axx x =  +  ; B là tập hợp tất cả các giá trị nguyên của b để phương trình 2 240xbx−+= vô nghiệm. Số phần tử chung của hai tập hợp trên là: A. 1 B. 2 C. 3 D. Vô số Câu 47: Cho hai tập hợp    1;2;3;4,1;2XY== X CY là tập hợp sau đây?

nhiêu học

54: Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5 A.  1;2 B.  1;2;3;4 C.  3;4 D.  Câu 48: Cho A, B, C là ba tập hợp được minh họa bằng biểu đồ ven như hình vẽ. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây? A. ( ) \ ABC  B. ( ) \ ABC  C. ( ) ( )\\ ACAB  D. ( ) ABC  Câu 49: Cho hai tập hợp  0;2A = và  0;1;2;3;4B = . Số tập hợp X thỏa mãn AXB = là: A. 2 B. 3 C. 4 D. 5 Câu 50: Cho hai tập hợp  0;1A = và  0;1;2;3;4B = . Số tập hợp X thỏa mãn B XCA  là: A. 3 B. 5 C. 6 D. 8 Câu 51: Cho tập hợp  1;2;3;4;5A = . Tìm số tập hợp X sao cho  \1;3;5AX = và  \6;7XA = A. 1 B. 2 C. 3 D. 4 Câu 52: Ký hiệu X là số phần tử của tập hợp X. Mệnh đề nào sai trong các mệnh đề sau? A. ABABABAB =+=+ B. ABABABAB +=− C. ABABABAB +=+ D. ABABAB =+= Câu 53: Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao

sinh? A. 54 B. 40 C. 26 D. 68 Câu

Toán, Lý, Hóa? A. 3 B. 4 C. 5 D. 6 Câu 55: Cho tập hợp    1;2;3;4,0;2;4;6AB== . Mệnh đề nào sau đây là đúng? A.  2;4AB= B.  0;1;2;3;4;5;6AB= C. AB  D.  \0;6AB = Câu 56: Ký hiệu H là tập hợp các học sinh của lớp 10A. T là tập hợp các học sinh nam, G là tập hợp các học sinh nữ của lớp 10A. Khẳng định nào sau đây sai? A. TGH = B. TG= C. \ HTG = D. \ GT = Câu 57: Cho A, B, C là ba tập hợp. Mệnh đề nào sau đây là sai? A. ABACBC  B. \\ ABCACB  C. ABACBC  D. , ABBCAC  Câu 58: Cho tập hợp  ;; Aabc = và  ;;;; Babcde = . Có tất cả bao nhiêu tập hợp X thỏa mãn AXB  ? A. 5 B. 6 C. 4 D. 8 Câu 59: Cho hai tập hợp    1;2;3;4;5;1;3;5;7;9AB== . Tập nào sau đây bằng tập AB  ?

Câu

Cho

  6;9. D. .

Câu 67: Cho     0;1;2;3;4,2;3;4;5;6.AB== Tập hợp ( ) ( )\\ ABBA  bằng?

A.   0;1;5;6. B.   1;2. C.   2;3;4. D.

Câu 68: Cho

Câu

Cho

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6 A.  1;3;5 B.  1;2;3;4;5 C.  2;4;6;8 D.  1;2;3;4;5;7;9 Câu 60: Cho tập hợp    2;4;6;9,1;2;3;4AB== . Tập nào sau đây bằng tập \ AB ? A.  1;2;3;5 B.  1;2;3;4;6;9 C.  6;9 D.  Câu 61: Cho các tập hợp    2 :760,:4AxxxBxx =−+== . Khi đó: A. ABA = B. ABAB = C. \ ABA  D. \ BA = Câu 62: Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn và 6 học sinh không chơi môn nào. Số học sinh chỉ chơi 1 môn thể thao là? A. 48 B. 20 C. 34 D. 28 Câu 63: Trong các khẳng định sau khẳng định nào đúng: A. \ = . B. * = . C. * = . D. ** = . Câu 64: Chọn kết quả sai trong các kết quả sau: A. .= ABAAB B. .ABAAB = C. \. ==ABAAB D. \.BABAB== Câu 65: Cho  7;2;8;4;9;12X = ;  1;3;7;4Y = . Tập nào sau đây bằng tập  XY ? A.  1;2;3;4;8;9;7;12 B.  2;8;9;12 C.  4;7 D.  1;3

66:

hai tập hợp  2,4,6,9A = và  1,2,3,4B = .Tập hợp \ AB bằng tập nào sau đây? A.  1,2,3,5=A B.   1;3;6;9. C.

  5;6.

    0;1;2;3;4,2;3;4;5;6.AB== Tập hợp \ AB bằng: A.   0. B.   0;1. C.   1;2. D.   1;5.

69:

    0;1;2;3;4,2;3;4;5;6.AB== Tập hợp \ BA bằng: A.   5. B.   0;1. C.   2;3;4. D.   5;6. Câu 70: Cho     1;5;1;3;5.==AB Chọn kết quả đúng trong các kết quả sau A.   1.=AB B.   1;3.=AB C.   1;5.=AB D.   1;3;5.=AB Câu 71: Cho ( )( )   22*2 22320;330AxxxxxBnn =−−−== . Khi đó tập hợp  AB bằng: A.   2;4. B.   2. C.   4;5. D.   3. DẠNG 3. BIỂU DIỄN TẬP HỢP SỐ Câu 72: Cho tập hợp  \31Axx=− . Tập A là tập nào sau đây? A.  3;1 B.  3;1 C.  )3;1 D. ( )3;1 Câu 73: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp ( 1;4 ?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7 A. B. C. D. Câu 74: Cho tập hợp  \,13Xxxx= thì X được biểu diễn là hình nào sau đây? A. B. C. D. Câu 75: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp  49Axx= : A.   4;9.=A B. (  4;9.=A C.  ) 4;9.=A D. ( ) 4;9.=A DẠNG 4. CÁC PHÉP TOÁN TRÊN TẬP HỢP SỐ Câu 76: Cho tập hợp ( ;1A =−− và tập ( )2;B =−+ . Khi đó AB  là: A. ( )2; −+ B. ( 2;1 C. D.  Câu 77: Cho hai tập hợp  ) ( )5;3,1;AB=−=+ . Khi đó AB  là tập nào sau đây? A. ( )1;3 B. ( 1;3 C.  )5; −+ D.  5;1 Câu 78: Cho ( )  2;1,3;5AB=−=− . Khi đó AB  là tập hợp nào sau đây? A.  2;1 B. ( )2;1 C. ( 2;5 D.  2;5 Câu 79: Cho hai tập hợp (  ( 1;5;2;7AB== . Tập hợp \ AB là: A. ( 1;2 B. ( )2;5 C. ( 1;7 D. ( )1;2 Câu 80: Cho tập hợp ( )2;A =+ . Khi đó R CA là: A.  )2;+ B. ( )2;+ C. ( ;2− D. ( ;2−− Câu 81: Cho các số thực a, b, c, d và abcd  . Khẳng định nào sau đây là đúng? A. ( ) ( ) ( );;; acbdbc = B. ( ) ( ) ( ;;; acbdbc = C. ( )  )  );;; acbdbc = D. ( )  ) ( );;; acbdbc =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8 Câu 82: Cho ba tập hợp      )2;2,1;5,0;1ABC =−== . Khi đó tập ( )\ ABC  là: A.  0;1 B.  )0;1 C. ( )2;1 D.  2;5 Câu 83: Cho tập hợp )3;8CA  =−  , ( ) ( ) 5;23;11.CB =− Tập ( )CAB  là: A. ( )3;3 . B.  . C. ( )5;11 . D. ( ) ( ) 3;23;8.− Câu 84: Cho   ( ) ( ) 1;4;2;6;1;2.ABC === Tìm :ABC  A.   0;4. B.  ) 5;. + C. ( ) ;1.− D.  Câu 85: Cho hai tập  342 Axxx =++ ,  5341Bxxx =−− Tất cả các số tự nhiên thuộc cả hai tập A và B là: A. 0 và 1. B. 1. C. 0 D. Không có. Câu 86: Cho  4;7A =− , ( ) ( );23;B =−−+ . Khi đó AB  : A.  ) (  4;23;7.−− B.  ) ( ) 4;23;7.−− C. (  ( ) ;23;.−+ D. ( )  ) ;23;.−−+ Câu 87: Cho ( ;2A =−− ,  )3;B =+ , ( ) 0;4.C = Khi đó tập ( ) ABC  là: A.   3;4. B. (  ( ) ;23;.−−+ C.  ) 3;4. D. ( )  ) ;23;.−−+ Câu 88: Cho  :20AxRx=+ ,  :50BxRx=− . Khi đó  AB là: A.  2;5 . B.  2;6 . C.  5;2 . D. ( )2; −+ . Câu 89: Cho    :20,:50AxRxBxRx =+=− . Khi đó \ AB là: A.  2;5 . B.  2;6 . C. ( )5;+ . D. ( )2;+ . Câu 90: Cho hai tập hợp  ) ( 2;7,1;9AB=−= . Tìm AB  . A. ( )1;7 B.  2;9 C.  )2;1 D. ( 7;9 Câu 91: Cho hai tập hợp  |51Axx=− ;  |33Bxx=− . Tìm AB  A.  5;3 B. ( )3;1 C. ( 1;3 D.  )5;3 Câu 92: Cho (  ( )1;5,2;7AB=−= . Tìm \ AB . A. ( 1;2 B. ( 2;5 C. ( )1;7 D. ( )1;2 Câu 93: Cho 3 tập hợp ( ;0A =− , ( )1;B =+ ,  )0;1C = . Khi đó ( ) ABC  bằng: A.  0 B. C.  0;1 D.  Câu 94: Cho hai tập hợp  4;7M =− và ( ) ( );23;N =−−+ . Khi đó MN  bằng: A.  ) ( 4;23;7−− B.  ) ( )4;23;7− C. (  ( );23; −+ D. ( )  );23; −−+ Câu 95: Cho hai tập hợp   ( )2;3,1;AB=−=+ . Khi đó ( )CAB  bằng: A. ( )1;3 B. (   );13; −+ C.  )3;+ D. ( );2−−

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9 Câu 96: Chọn kết quả sai trong các kết quả sau: A. ABAAB = B. ABABA = C. \ ABAAB== D. \ ABAAB= Câu 97: Cho tập hợp )3;8 =− CA , ( ) ( ) 5;23;11.=−CB Tập ( )CAB  là: A. ( )5;11 . B. ( ) ( ) 3;23;8.− C. ( )3;3 . D.  . Câu 98: Cho 3 tập hợp: ( ;1A =− ;  2;2B =− và ( )0;5C = . Tính ( ) ( ) ?ABAC= A.  2;1 B. ( )2;5 C. ( 0;1 D.  1;2 DẠNG 5. CÁC BÀI TOÁN TÌM ĐIỀU KIỆN CỦA THAM SỐ Câu 99: Cho tập hợp    ;2,1;2AmmB=+− . Tìm điều kiện của m để AB  . A. 1m − hoặc 0m  B. 10 m − C. 12 m  D. 1m  hoặc 2m  Câu 100: Cho tập hợp ( )0;A =+ và  2 \430Bxmxxm =−+−= . Tìm m để B có đúng hai tập con và BA  . A. 03 4 m m   = B. 4m = C. 0m  D. 3m = Câu 101: Cho hai tập hợp   ( )2;3,;6ABmm =−=+ . Điều kiện để AB  là: A. 32 m −− B. 32 m −− C. 3m − D. 2m − Câu 102: Cho hai tập hợp ( 0;3X = và ( );4Ya = . Tìm tất cả các giá trị của 4a  để XY . A. 3 4 a a    B. 3a  C. 0a  D. 3a  Câu 103: Cho hai tập hợp   (   )\12;;2; AxxBmm ==−−+ . Tìm tất cả các giá trị của m để AB  . A. 4 2 m m   − B. 4 2 1 m m m   −  = C. 4 2 1 m m m   −  = D. 24 m − Câu 104: Cho số thực 0a .Điều kiện cần và đủ để ( ) 4 ;9; −+  a a là: A. 2 0. 3 − a B. 2 0. 3 − a C. 3 0. 4 − a D. 3 0. 4 − a Câu 105: Cho tập hợp    ;2,1;2AmmB=+=− với m là tham số. Điều kiện để AB  là: A. 12 m  B. 10 m − C. 1m − hoặc 0m  D. 1m − hoặc 2m  Câu 106: Cho tập hợp    );2,1;3AmmB=+= . Điều kiện để AB= là: A. 1m − hoặc 3m  B. 1m − hoặc 3m  C. 1m − hoặc 3m  D. 1m − hoặc 3m  Câu 107: Cho hai tập hợp    3;12;4A =−− , ( )1;2Bmm=−+ . Tìm m để AB

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10 A. 5m  và 0m  B. 5m  C. 13 m  D. 0m  Câu 108: Cho 3 tập hợp ( ) ( )3;11;2A =−− , ( );Bm=+ , ( );2 Cm − . Tìm m để ABC . A. 1 2 2 m  B. 0m  C. 1m − D. 2m  Câu 109: Cho hai tập  0;5A = ; ( 2;31Baa=+ , 1a − . Với giá trị nào của a thì AB A. 15 32 a − B. 5 2 1 3 a a     −  C. 5 2 1 3 a a     −  D. 15 32 a − Câu 110: Cho 2 tập khác rỗng (  ( ) 1;4;2;22, AmBmm =−=−+ . Tìm m để AB A. 15 m − B. 15 m  C. 25 m − D. 3m − Câu 111: Cho số thực 0a .Điều kiện cần và đủ để ( ) 4 ;9; −+  a a là: A. 3 0. 4 − a B. 2 0. 3 − a C. 2 0. 3 − a D. 3 0. 4 − a Câu 112: Cho hai tập  0;5A = ; ( 2;31Baa=+ , 1a − . Với giá trị nào của a thì AB A. 5 2 1 3 a a     −  B. 15 32 a − C. 5 2 1 3 a a     −  D. 15 32 a − Câu 113: Cho  AxR\xm25 =− ;  BxR\x2020 = . Có bao nhiêu giá trị nguyên m thỏa AB= A. 3987. B. 3988. C. 3989. D. 2020. Câu 114: Cho 2 tập hợp  2;5Amm=−+ và  0;4B = . Tìm tất cả các giá trị thực của tham số m để BA  . A. 1m − . B. 12 m − . C. 12 m − . D. 2m  . Câu 115: Cho hai tập hợp (;1)Amm=+ và  1;3B =− . Tìm tất cả các giá trị của m để AB= A. 2 3 m m −   . B. 23 m − . C. 2 1 m m   − . D. 2 3 m m −   . Câu 116: Tìm m để AD  , biết (3;7)A =− và (;32) Dmm =− A. 3m =− B. 3m − C. 1m  D. 2m − Câu 117: Cho 2 tập hợp khác rỗng ( 1;4Am=− , ( )2;22Bm=−+ , với m . Tìm m để AB  . A. 15 m  B. 1m  C. 15 m − D. 21 m −− Câu 118: Cho ( )  )2 3;,;12; 4 m AmB +  =−=−−+   . Tìm m để AB= A. 14 2 3 m  B. 26 m  C. 26 m  D. 14 2 3 m 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Câu 119: Cho số thực 0x  . Tìm x để ( ) 9 ;16; x x  −+   A. 3 0 4 x  . B. 3 0 4 x  . C. 3 0 4 x  . D. 3 0 4 x  . Câu 120: Cho hai tập hợpkhác rỗng ( 1;4Am=− và ( ) 2;22,.Bmm=−+ Có bao nhiêu giá trị nguyên dương của m để AB ? A. 5. B. 6. C. 4. D. 3. Câu 121: Cho ( ) ( );,0;AmB=−=+ . Điều kiện cần và đủ để AB= là: A. 0m  . B. 0m  . C. 0m  . D. 0m  . Câu 122: Cho hai tập hợp khác rỗng ( 1;4Am=− và ( )2;22Bm=−+ , m . Tìm tất cả các giá trị của m để AB A. 25 m − B. 3m − C. 3m − D. 35 m −

Câu

Đáp

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 1 BÀI2:TẬPHỢP.CÁCPHÉPTOÁNTRÊNTẬPHỢP DẠNG 1. PHẦN TỬ CỦA TẬP HỢP, CÁC XÁC ĐỊNH TẬP HỢP

1: Ký hiệu nào sau đây dùng để viết đúng mệnh đề: “3 là một số tự nhiên”? A. 3  B. 3 C. 3  D. 3  Lời giải

án A sai vì kí hiệu “  ” chỉ dùng cho hai tập hợp mà ở đây “3” là một số Hai đáp án C và D đều sai vì ta không muốn so sánh một số với tập hợp. Đáp án B. Câu 2: Ký hiệu nào sau đây để chỉ 5 không phải là một số hữu tỉ? A. 5  B. 5  C. 5  D. 5  Lời giải Vì 5 chỉ là một phần tử còn là một tập hợp nên các đáp án A, B, D đều sai. Đáp án C. Câu 3: Cho tập hợp  1|,5Axxx=+ . Tập hợp A là: A.  1;2;3;4;5A = B.  0;1;2;3;4;5;6A = C.  0;1;2;3;4;5A = D.  1;2;3;4;5;6A = Lời giải Vì ,5xx nên    0;1;2;3;4;511;2;3;4;5;6xx += Đáp án D. Câu 4: Hãy liệt kê các phần tử của tập hợp  2 |2310Xxxx=−+= A.  0X = B.  1X = C. 1 1; 2 X  =   D. 3 1; 2 X  =   Lời giải Vì phương trình 2 2310 xx−+= có nghiệm 1 1 2 x x =   =  nhưng vì x  nên 1 2  . CHƯƠNG I MỆNH ĐỀ VÀ TẬP HỢP HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 2 Vậy  1X = . Đáp án B. Câu 5: Liệt kê các phần tử của phần tử tập hợp  2 |2530Xxxx=−+= . A.  0X = B.  1X = C. 3 2 X  =   D. 3 1; 2 X  =   Lời giải Vì phương trình 2 2530 xx−+= có nghiệm 1 3 2 x x =   =  nên 3 1; 2 X  =   Đáp án D. Câu 6: Trong các tập sau, tập nào là tập rỗng? A.  |1xx B.  2 |6710xxx −+= C.  2 :420xxx−+= D.  2 :430xxx−== Lời giải Xét các đáp án: Đáp án A: ,1110xxxx −= . Đáp án B: Giải phương trình: 2 1 6710 1 6 x xx x = −+=  =  . Vì 1xx= . Đáp án C: 2 42022xxx−+== . Vì x  Đây là tập rỗng. Đáp án C. Câu 7: Cho tập hợp ( ) ;|;,1Mxyxyxy =+= . Hỏi tập M có bao nhiêu phần tử? A. 0 B. 1 C. 2 D. 3 Lời giải Vì ; xy  nên x, y thuộc vào tập  0;1;2;... Vậy cặp ( ); xy là ( ) ( )1;0,0;1 thỏa mãn 1xy+= Có 2 cặp hay M có 2 phần tử. Đáp án C. Câu 8: Cho tập hợp  2 1\,5Axxx =+ . Hãy liệt kê các phần tử của tập hợp .A A.  0;1;2;3;4;5A = B.  1;2;5;10;17;26A = C.  2;5;10;17;26A = D.  0;1;4;9;16;25A = Lời giải Đáp án B.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 3 Ta có  2 1\,5Axxx =+ Vì ,5xx nên  0;1;2;3;4;5x  2 11;2;5;10;17;26x + . Câu 9: Hãy liệt kê các phần tử của tập hợp:  42 \680Xxxx=−+= A.  2;4X = B.  2;2X =− C.  2;2X = D.  2;2;2;2X =−− Lời giải Đáp án D. Giải phương trình 42680xx−+= 2 2 2 2 42 x x xx  = =    == . Câu 10: Cho tập hợp ( ) 22 ;\,,0Mxyxyxy=+ . Khi đó tập hợp M có bao nhiêu phần tử? A. 0 B. 1 C. 2 D. Vô số Lời giải Đáp án B. Vì 2 2 0 0 x y      nên 22 00xyxy+== Khi đó tập hợp M có 1 phần tử duy nhất là ( ) 0;0 . Câu 11: Số phần tử của tập hợp: ( ) 2 22 \21Axxxxx =+=−+ là: A. 0 B. 3 C. 1 D. 2 Lời giải Đáp án D. Giải phương trình ( )2 22 21xxxx+=−+ trên ( ) ( )2 2210xxx +−−= ( )( )22110xxxxxx +−+++−= ( )( )221210xxx ++−= 12 12 x x  =−−   =−+  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 4 Câu 12: Số tập con của tập hợp: ( ) 2 22 \3220Axxxxx =+−−= là: A. 16 B. 8 C. 12 D. 10 Lời giải Đáp án A. Giải phương trình ( ) ( )2 22 320 xxxx+−+= Đặt 2 xxt += ta có phương trình 2 0 320 2 3 t tt t = −=  =  Với 0t = ta có 2 0 0 1 x xx x = +=  =− Với 2 3 t = ta có: 2 2 3 xx+= 2 333 3320 3 xxx − +−== Vậy A có 4 phần tử suy ra số tập con của A là 4 216 = Câu 13: Số phần tử của tập hợp: ( ) 2 22 \24441Axxxxx =+−=−+ là: A. 0 B. 2 C. 4 D. 3 Lời giải Đáp án C. Giải phương trình ( )2 22 24441 xxxx +−=−+ ( ) ( )2 22 2421 xxx +−=− 2 2 2421 2421 xxx xxx  +−=−   +−=−+ 2 2 1 3 230 2 12350 5 2 x x xx xxx x =−   = −−=    +−==   =− 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 5 Vậy A có 4 phần tử Câu 14: Hãy liệt kê các phần tử của tập hợp  2 10Xxxx=++= : A. 0=X B.  0=X C. X = D.  X = Lời giải Chọn C Phương trình 2 10xx++= vô nghiệm nên X = . Câu 15: Số phần tử của tập hợp  2 1/,2=+Akkk là: A. 1. B. 2. C. 3. D. 5. Lời giải Chọn C  2 1,2=+Akkk . Ta có ,2kk 22− k   1;2;5.= A Câu 16: Trong các tập hợp sau, tập hợp nào là tập hợp rỗng: A.  xx1  . B.  2 x6710 xx −+= . C.  2 xx420 x −+= . D.  2 x430 xx −+= . Lời giải Chọn C     xx10.== AA  2 x6710 =−+=Bxx . Ta có 2 6710 −+=xx 1 1 6 =   = x x   1.= B  2 xx420 =−+=Cx . Ta có 2 420−+=xx 22 22  =−   =+  x x = C  2 x430 =−+=Dxx . Ta có 2 430−+=xx 1 3 =   = x x   1;3.= D Câu 17: Cho tập hợp ( )( ) 22–120Axxx =+= . Các phần tử của tập A là: A.  –1;1=A B. –2;–1; }{2 1;=A C. {1}=A D. {1}=A Lời giải Chọn A ( )( ) 22–120Axxx =+= . Ta có ( )( )22–120 +=xx ( ) 2 2 –10 20vn  =   +=  x x 1 1 =   =− x x   1;1.=− A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 6 Câu 18: Trong các tập hợp sau, tập hợp nào là tập rỗng? A.  2 40Axx=−= . B.  2 230Bxxx=++= . C.  2 50Cxx=−= . D.  2 120.Dxxx=+−= Lời giải Chọn B    2 402=−== AxxA  2 2 .30 =++==Bxxx B    2 5;5 50=−= =−CxxC    2 1203;4.=+−==− DxxxD Câu 19: Trong các tập hợp sau, tập hợp nào khác rỗng? A.  2 10Axxx=++= B.  2 20Bxx=−= C. ( )( ) 32–310Cxxx=+= . D. ( ) 2 30Dxxx=+= . Lời giải Chọn B  2 10=++=Axxx . Ta có ( )2 10vn++=xx = A  2 20=−=Bxx . Ta có 2 20−=x 2 = x  =B ( )( ) 32–310=+=Cxxx . Ta có ( )( )32–310 +=xx 3 3 = x = C ( ) 2 30=+=Dxxx . Ta có ( )2 30+=xx 0= x   0.= D DẠNG 2. TẬP HỢP CON, TẬP HỢP BẰNG NHAU Câu 20: Cho hai tập hợp A và .B Hình nào sau đây minh họa A là tập con của B? A. B. C. D. Lời giải Hình C là biểu đồ ven, minh họa cho AB  vì mọi phần tử của A đều là của B. Đáp án C. Câu 21: Cho ba tập hợp E, F, G thỏa mãn: , EFFG  và GK  . Khẳng định nào sau đây đúng? A. GF  B. KG  C. EFG == D. EK  Lời giải Dùng biểu đồ minh họa ta thấy EK  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 7 Đáp án D. Câu 22: Cho tập hợp  0;3;4;6A = . Số tập hợp con gồm hai phần tử của A là: A. 12 B. 8 C. 10 D. 6 Lời giải Mỗi tập con gồm hai phần tử của A là:            0;3;,0;4,0;6,3;4,3;6,4;6 . Đáp án D. Câu 23: Cho tập hợp  ;; Xabc = . Số tập con của X là A. 4 B. 6 C. 8 D. 12 Lời giải Số tập con không có phần tử nào là 1 (tập  ) Số tập con có 1 phần tử là 3:      ,, abc . Số tập con có 2 phần tử là 3:      ;,;,; abacbc .  Số tập con có 3 phần tử là 1:  ;; abc . Vậy có 13318 +++= tập con. Đáp án C. Nhận xét: Người ta chứng minh được là số tập con (kể cả tập rỗng) của tập hợp n phần tử là 2n . Áp dụng vào Ví dụ 4 có 3 28 = tập con. Câu 24: Trong các tập hợp sau đây, tập hợp nào có đúng một tập hợp con? A.  B.  x C.   D.  , x Lời giải Vì tập  có tập hợp con là chính nó. Đáp án B có 2 tập con là  và  x . Đáp án C có 2 tập con là  và   . Đáp án D có 4 tập con. Đáp án A. Câu 25: Cho tập hợp  1;2A = và  1;2;3;4;5B = . Có tất cả bao nhiêu tập X thỏa mãn: AXB  ? A. 5 B. 6 C. 7 D. 8 Lời giải

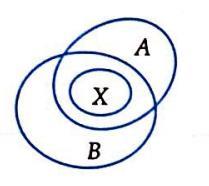
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 8 X là tập hợp phải luôn có mặt 1 và 2. Vì vậy ta đi tìm số tập con của tập  3;4;5 , sau đó cho hai phần tử 1 và 2 vào các tập con nói trên ta được tập X Vì số tập con của tập  3;4;5 là 3 28 = nên có 8 tập X. Đáp án D. Câu 26: Chotậphợp  1;2;5;7A = và  1;2;3B = .Cótấtcảbaonhiêutập X thỏamãn: XA  và XB  ? A. 2 B. 4 C. 6 D. 8 Lời giải Cách 1: Vì XA XB    nên ( )XAB  . Mà  1;2AB= Có 2 24 = tập X Cách 2: X là một trong các tập sau:      ;1;2;1;2 Đáp án B. Câu 27: Cho tập hợp      1;3,3;,;;3 ABxCxy === . Để ABC == thì tất cả các cặp ( ); xy là: A. ( )1;1 B. ( )1;1 và ( )1;3 C. ( )1;3 D. ( )3;1 và ( )3;3 Lời giải Ta có: 1 1 3 x ABC y y =  == =  = Cặp ( ); xy là ( ) ( )1;1;1;3 Đáp án B. Câu 28: Cho tập hợp    1;2;3;4,0;2;4AB== ,  0;1;2;3;4;5C = . Quan hệ nào sau đây là đúng? A. BAC  B. BAC = C. AC BC    D. ABC = Lời giải Đáp án C. Ta thấy mọi phần tử của A đều thuộc C và mọi phần tử của B đều thuộc C nên Chọn C Câu 29: Cho tập hợp A có 4 phần tử. Hỏi tập A có bao nhiêu tập con khác rỗng? A. 16 B. 15 C. 12 D. 7 Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 9 Đáp án B. Vì số tập con của tập 4 phần tử là 4 216= Số tập con khác rỗng là 16115 −= Câu 30: Số các tập hợp con gồm hai phần tử của tập hợp  ;;;;; Babcdef = là: A. 15 B. 16 C. 22 D. 25 Lời giải Đáp án A. Cách 1: Số tập con có 2 phần tử trong đó có phần tử a là 5 tập          ;,;,;,;,, abacadaeaf Số tập con có 2 phần tử mà luôn có phần tử b nhưng không có phần tử a là 4 tập:  ; bc ,  ; bd ,  ; be ,  ; bf . Tương tự ta có tất cả 5432115 ++++= tập. Câu 31: Số các tập hợp con có 3 phần tử có chứa a, b của tập hợp  ;;;;;; Cabcdefg = là: A. 5 B. 6 C. 7 D. 8 Lời giải Đáp án A. Tập con có 3 phần tử trong đó a, b luôn có mặt. Vậy phần tử thứ 3 sẽ thuộc một trong các phần tử c, d, e, f, g (5 phần tử) nên có 5 tập con. Câu 32: Trong các tập hợp sau đây, tập hợp nào có đúng hai tập hợp con? A.  ; xy B.  x C.  ;x D.  ;;xy Lời giải Đáp án B. Vì tập hợp  x có hai tập con là  và chính nó. Câu 33: Cho tập hợp  1,2,3,4,,= Axy . Xét các mệnh đề sau đây: ( )I : “3 A”. ( )II : “ 3,4  A”. ( )III : “ ,3, abA  ”. Trong các mệnh đề sau, mệnh đề nào đúng A. I đúng. B. , III đúng. C. , IIIII đúng. D. , IIII đúng. Lời giải Chọn A 3 là một phần tử của tập hợp A .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 10  3,4 là một tập con của tập hợp A . Ký hiệu:  3,4 A .  ,3, ab là một tập con của tập hợp A . Ký hiệu:  ,3, abA  . Câu 34: Cho  0;2;4;6=A . Tập A có bao nhiêu tập con có 2 phần tử? A. 4. B. 6. C. 7. D. 8. Lời giải Chọn B Có thể sử dụng máy tính bỏ túi để tính số tập con có 2 phần tử của tập hợp A gồm 4 phần tử là: 2 4 6C = Các tập con có 2 phần tử của tập hợp A là: 0;2 ,  0;4; ,  0;6 ,  2;4; ,  2;6 ,   4;6. Câu 35: Cho tập hợp  1;2;3;4=X . Câu nào sau đây đúng? A. Số tập con của X là 16. B. Số tập con của X gồm có 2 phần tử là 8 C. Số tập con của X chứa số 1 là 6 D. Số tập con của X gồm có 3 phần tử là 2. Lời giải Chọn A Số tập con của tập hợp X là: 4 216 = Số tập con có 2 phần tử của tập hợp X là: 2 4 6C = Số tập con của tập hợp X chứa số 1 là: 8  1 ,    1;2,1;3 ,  1;4 ,  1;2;3 ,  1;2;4 ,  1;3;4 ,   1;2;3;4. Số tập con có 3 phần tử của tập hợp X là: 3 4 4C = Câu 36: Số các tập con 2 phần tử của  ,,,,, = Babcdef là: A. 15. B. 16. C. 22. D. 25. Lời giải Chọn A Số các tập con 2 phần tử của  ,,,,, = Babcdef là 2 6 15C = (sử dụng máy tính bỏ túi). Câu 37: Số các tập con 3 phần tử có chứa ,  của  ,,,,,,,,, =C là: A. 8 B. 10 C. 12 D. 14 Lời giải Chọn A Các tập con 3 phần tử có chứa ,  của  ,,,,,,,,, =C là:  ,,  ,  ,,  ,  ,,  ,  ,,  ,  ,,  ,  ,,  ,  ,,  ,   ,,.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 11 Câu 38: Trong các tập sau đây, tập hợp nào có đúng hai tập hợp con? A.  ; xy . B.  x . C.  ; x . D.  ;; xy . Lời giải Chọn B  ; xy có 2 24 = tập con.  x có 1 22 = tập con là  x và  .  ; x có 2 24 = tập con.  ;; xy có 3 28 = tập con. Câu 39: Cho tập hợp  ,,, Aabcd = . Tập A có mấy tập con? A. 16 B. 15 C. 12 D. 10 Lời giải Chọn A Số tập con của tập A là: 4 216 = . Câu 40: Khẳng định nào sau đây sai?Các tập AB = với , AB là các tập hợp sau? A. ( )( ) 1;3, 0} –1 {= 3ABxxx ==− . B.  1;3;5;7;9,21, ,04{} ABnnkkk ===+ . C.  2{1;2, 0} 23ABxxx  =−=−= D.  2, 10ABxxx ==++= Lời giải Chọn C * {3} 1;=A , ( )( ) –130 ==− Bxxx  1;3= B =AB. 1;3;5; *} 9{ 7;=A ,  21, ,04==+ Bnnkkk  1;3;5;7;9= B =AB . ;2}*{1 =−A ,  2 230=−=Bxxx  1;3=− B AB * =A ,  2 10=++=Bxxx = B =AB . Dạng 3. Các phép toán trên tập hợp Câu 41: Cho tập hợp    1;5,1;3;5XY== . Tập XY  là tập hợp nào sau đây? A.  1 B.  1;3 C. {1;3;5} D.  1;5 Lời giải Vì XY  là tập hợp gồm các phần tử vừa thuộc X và vừa thuộc Y nên Chọn D Đáp án D.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 12 Câu 42: Cho tập    2;4;6;9,1;2;3;4XY== . Tập nào sau đây bằng tập \ XY ? A.  1;2;3;5 B.  1;3;6;9 C.  6;9 D.  1 Lời giải Vì \ XY là tập hợp các phần tử thuộc X mà không thuộc Y nên Chọn C Đáp án C. Câu 43: Cho tập hợp    ;,;; XabYabc == XY  là tập hợp nào sau đây? A.  ;;; abcd B.  ; ab C.  c D. {;;} abc Lời giải Vì XY  là tập hợp gồm các phần tử thuộc X hoặc thuộc Y nên Chọn D Đáp án D. Câu 44: Cho hai tập hợp A và B khác rỗng thỏa mãn: AB  . Trong các mệnh đề sau mệnh đề nào sai? A. \ AB = B. ABA = C. \ BAB = D. ABB = Lời giải Vì \ BA gồm các phần tử thuộc B và không thuộc A nên Chọn C Đáp án C. Câu 45: Cho ba tập hợp: ( )  ( )  ( ) ( ) |0,|0,|0 FxfxGxgxHxfxgx =====+= Mệnh đề nào sau đây là đúng? A. HFG = B. HFG = C. \ HFG = D. \ HGF = Lời giải Vì ( ) ( ) ( ) ( ) 0 0 0 fx fxgx gx =  +=  =  mà ( ) ( ) |0 vµ FGxfxgx == Đáp án A. Câu 46: Cho tập hợp 2 2 |1 1 Axx x =  +  ; B là tập hợp tất cả các giá trị nguyên của b để phương trình 2 240xbx−+= vô nghiệm. Số phần tử chung của hai tập hợp trên là: A. 1 B. 2 C. 3 D. Vô số Lời giải Ta có: ( ) 222 2 21 121210101 1 x xxxxxx x +−+−= + Phương trình 2 240xbx−+= có 2 '4 b =− Phương trình vô nghiệm 2240422bbb −− Có 1b = là phần tử chung duy nhất của hai tập hợp. Đáp án A.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 13 Câu 47: Cho hai tập hợp    1;2;3;4,1;2XY== . X CY là tập hợp sau đây? A.  1;2 B.  1;2;3;4 C.  3;4 D.  Lời giải Vì YX  nên  \3;4X CYXY== Đáp án C. Câu 48: Cho A, B, C là ba tập hợp được minh họa bằng biểu đồ ven như hình vẽ. Phần gạch sọc trong hình vẽ là tập hợp nào sau đây? A. ( ) \ ABC  B. ( ) \ ABC  C. ( ) ( )\\ ACAB  D. ( ) ABC  Lời giải Vì với mỗi phần tử x thuộc phần gạch sọc thì ta thấy: ( ) \ xA xBxABC xC      Đáp án B. Câu 49: Cho hai tập hợp  0;2A = và  0;1;2;3;4B = . Số tập hợp X thỏa mãn AXB = là: A. 2 B. 3 C. 4 D. 5 Lời giải Vì AXB = nên bắt buộc X phải chứa các phần tử  1;3;4 và XB  Vậy X có 3 tập hợp đó là:        1;3;4,0;1;3;4,1;2;3;4,0;1;2;3;4 Đáp án C Câu 50: Cho hai tập hợp  0;1A = và  0;1;2;3;4B = . Số tập hợp X thỏa mãn B XCA  là: A. 3 B. 5 C. 6 D. 8 Lời giải Ta có  \2;3;4B CABA== có 3 phần tử nên số tập con X có 3 28 = (tập). Đáp án D.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 14 Câu 51: Cho tập hợp  1;2;3;4;5A = . Tìm số tập hợp X sao cho  \1;3;5AX = và  \6;7XA = . A. 1 B. 2 C. 3 D. 4 Lời giải Vì  \1;3;5AX = nên X phải chứa hai phần tử 2; 4 và X không chứa các phần tử 1; 3; 5. Mặt khác  \6;7XA = vậy X phải chứa 6; 7 và các phần tử khác nếu có phải thuộc A. Vậy  2;4;6;7X = . Đáp án A. Câu 52: Ký hiệu X là số phần tử của tập hợp X. Mệnh đề nào sai trong các mệnh đề sau? A. ABABABAB =+=+ B. ABABABAB +=− C. ABABABAB +=+ D. ABABAB =+= Lời giải Kiểm tra các đáp án bằng cách vẽ biểu đồ Ven cho hai trường hợp AB= và AB Đáp án C. Câu 53: Một lớp học có 25 học sinh giỏi môn Toán, 23 học sinh giỏi môn Lý, 14 học sinh giỏi cả môn Toán và Lý và có 6 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh? A. 54 B. 40 C. 26 D. 68 Lời giải Gọi T, L lần lượt là tập hợp các học sinh giỏi Toán và các học sinh giỏi Lý. Ta có: T : là số học sinh giỏi Toán L : là số học sinh giỏi Lý TL  : là số học sinh giỏi cả hai môn Toán và Lý Khi đó số học sinh của lớp là: 6TL+ . Mà 25231434TLTLTL =+−=+−= . Vậy số học sinh của lớp là 34640 += Đáp án B Câu 54: Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 15 Hóa, 9 em học giỏi cả môn Toán và môn Hóa. Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn Toán, Lý, Hóa? A. 3 B. 4 C. 5 D. 6 Lời giải Gọi T, L, H lần lượt là tập hợp các học sinh giỏi môn Toán, Lý, Hóa. Khi đó tương tự Ví dụ 13 ta có công thức: TLHTLHTLLHHTTLH =++−−−+ 452523201189 TLH=++−−−+ 5TLH = Vậy có 5 học sinh giỏi cả 3 môn. Đáp án C. Câu 55: Cho tập hợp    1;2;3;4,0;2;4;6AB== . Mệnh đề nào sau đây là đúng? A.  2;4AB= B.  0;1;2;3;4;5;6AB= C. AB  D.  \0;6AB = Lời giải Đáp án A. Ta thấy  2;4AB= Câu 56: Ký hiệu H là tập hợp các học sinh của lớp 10A. T là tập hợp các học sinh nam, G là tập hợp các học sinh nữ của lớp 10A. Khẳng định nào sau đây sai? A. TGH = B. TG= C. \ HTG = D. \ GT = Lời giải Đáp án D. Vì \ GTG = . Câu 57: Cho A, B, C là ba tập hợp. Mệnh đề nào sau đây là sai? A. ABACBC  B. \\ ABCACB  C. ABACBC  D. , ABBCAC  Lời giải Đáp án B.

1;3;5

Đáp án

bằng t

1;2;3;4;5;7;9

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 16 Ta có thể dùng biểu đồ Ven ta thấy \\ ABCACB  Câu 58: Cho tập hợp  ;; Aabc = và  ;;;; Babcde = . Có tất cả bao nhiêu tập hợp X thỏa mãn AXB  ? A. 5 B. 6 C. 4 D. 8 Lời giải Đáp án C. Vì AX  nên X phải chứa 3 phần tử  ;; abc của A. Mặt khác XB  nên X chỉ có thể lấy các phần tử a, b, c, d, e Vậy X là một trong các tập hợp sau:    ;;,;;; abcabcd ,  ;;; abce ,  ;;;; abcde Câu 59: Cho hai tập hợp    1;2;3;4;5;1;3;5;7;9AB== . Tập nào sau đây

ập

 ?

 

B.  1;2;3;4;5 C.  2;4;6;8

 

Lời giải

A. Vì AB  gồm các phần tử vừa thuộc A vừa thuộc B. Câu 60: Cho tập hợp    2;4;6;9,1;2;3;4AB== . Tập nào sau đây bằng tập \ AB ? A.  1;2;3;5 B.  1;2;3;4;6;9 C.  6;9 D.  Lời giải Đáp án C. Vì  \| vµ ABxxAxB = Câu 61: Cho các tập hợp    2 :760,:4AxxxBxx =−+== . Khi đó: A. ABA = B. ABAB = C. \ ABA  D. \ BA = Lời giải Đáp án C. Ta có    1;6,\4ABxx ==     0;1;2;3\6\ BABABA == . Câu 62: Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn và 6 học sinh không chơi môn nào. Số học sinh chỉ chơi 1 môn thể thao là? A. 48 B. 20 C. 34 D. 28 Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 17 Đáp án B. Gọi A là tập hợp các học sinh chơi bóng đá B là tập hợp các học sinh chơi bóng bàn C là tập hợp các học sinh không chơi môn nào Khi đó số học sinh chỉ chơi bóng đá là 225232.1420ABAB+−=+−= Câu 63: Trong các khẳng định sau khẳng định nào đúng: A. \ = . B. * = . C. * = . D. ** = . Lời giải Chọn D D đúng do *** = . Câu 64: Chọn kết quả sai trong các kết quả sau: A. .= ABAAB B. .ABAAB = C. \. ==ABAAB D. \.BABAB== Lời giải Chọn B B sai do ABAAB = Câu 65: Cho  7;2;8;4;9;12X = ;  1;3;7;4Y = . Tập nào sau đây bằng tập  XY ? A.  1;2;3;4;8;9;7;12 B.  2;8;9;12 C.  4;7 D.  1;3 Lời giải Chọn C    7;2;8;4;9;12,1;3;7;4==XY   7;4.= XY Câu 66: Cho hai tập hợp  2,4,6,9A = và  1,2,3,4B = .Tập hợp \ AB bằng tập nào sau đây? A.  1,2,3,5=A . B.   1;3;6;9. C.   6;9. D. . Lời giải Chọn C    2,4,6,9,1,2,3,4==AB   \6,9.= AB Câu 67: Cho     0;1;2;3;4,2;3;4;5;6.AB== Tập hợp ( ) ( )\\ ABBA  bằng? A.   0;1;5;6. B.   1;2. C.   2;3;4. D.   5;6. Lời giải Chọn A     0;1;2;3;4,2;3;4;5;6.==AB

Câu 68: Cho

Câu 69: Cho

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 18    \0;1,\5;6 ==ABBA ( ) ( )  \\0;1;5;6= ABBA

    0;1;2;3;4,2;3;4;5;6.AB== Tập hợp \ AB bằng: A.   0. B.   0;1. C.   1;2. D.   1;5. Lời giải Chọn B    0;1;2;3;4,2;3;4;5;6==

 \0;1= AB

    0;1;2;3;4,2;3;4;5;6.AB== Tập hợp \ BA bằng: A.   5. B.   0;1. C.   2;3;4. D.   5;6. Lời giải

ọn D    0;1;2;3;4,2;3;4;5;6==AB   \5;6.= BA Câu 70: Cho     1;5;1;3;5.==AB Chọn kết quả đúng trong các kết quả sau A.   1.=AB B.   1;3.=AB C.   1;5.=AB D.   1;3;5.=AB Lời giải Chọn C     1;5;1;3;5.==AB Suy ra   1;5.=AB Câu 71: Cho ( )( )   22*2 22320;330AxxxxxBnn =−−−== . Khi đó tập hợp  AB bằng: A.   2;4. B.   2. C.   4;5. D.   3. Lời giải Chọn B ( )( ) 22 22320 =−−−= Axxxxx  0;2= A  *2330=Bnn  1;2;3;4;5= B   2.AB = DẠNG 3. BIỂU DIỄN TẬP HỢP SỐ Câu 72: Cho tập hợp  \31Axx=− . Tập A là tập nào sau đây? A.  3;1 B.  3;1 C.  )3;1 D. ( )3;1 Lời giải Theo định nghĩa tập hợp con của tập số thực ở phần trên ta chọn ( )3;1 . Đáp án D.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 19 Câu 73: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp ( 1;4 ? A. B. C. D. Lời giải Vì ( 1;4 gồm các số thực x mà 14 x  nên Chọn A Đáp án A. Câu 74: Cho tập hợp  \,13Xxxx= thì X được biểu diễn là hình nào sau đây? A. B. C. D. Lời giải Giải bất phương trình:     1 1 133;11;3 1 3 33 x x xx x x x   −− −  −  Đáp án D. Câu 75: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp  49Axx= : A.   4;9.=A B. (  4;9.=A C.  ) 4;9.=A D. ( ) 4;9.=A Lời giải Chọn A  49=Axx   4;9.= A DẠNG 4. CÁC PHÉP TOÁN TRÊN TẬP HỢP SỐ Câu 76: Cho tập hợp ( ;1A =−− và tập ( )2;B =−+ . Khi đó AB  là: A. ( )2; −+ B. ( 2;1 C. D. 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 20 Vì  \ hoac ABxxAxB = nên chọn đáp án C. Đáp án C. Câu 77: Cho hai tập hợp  ) ( )5;3,1;AB=−=+ . Khi đó AB  là tập nào sau đây? A. ( )1;3 B. ( 1;3 C.  )5; −+ D.  5;1 Lời giải Ta có thể biểu diễn hai tập hợp A và B, tập AB  là phần không bị gạch ở cả A và B nên ( )1;3x Đáp án A. Câu 78: Cho ( )  2;1,3;5AB=−=− . Khi đó AB  là tập hợp nào sau đây? A.  2;1 B. ( )2;1 C. ( 2;5 D.  2;5 Lời giải Vì với xA xAB xB     hay 21 21 35 x x x − − − Đáp án B. Câu 79: Cho hai tập hợp (  ( 1;5;2;7AB== . Tập hợp \ AB là: A. ( 1;2 B. ( )2;5 C. ( 1;7 D. ( )1;2 Lời giải   ( \\ va 1;2ABxxAxBx = Đáp án A. Câu 80: Cho tập hợp ( )2;A =+ . Khi đó R CA là: A.  )2;+ B. ( )2;+ C. ( ;2− D. ( ;2−− Lời giải Ta có: ( \;2R CAA==− . Đáp án C. Câu 81: Cho các số thực a, b, c, d và abcd  . Khẳng định nào sau đây là đúng? A. ( ) ( ) ( );;; acbdbc = B. ( ) ( ) ( ;;; acbdbc = C. ( )  )  );;; acbdbc = D. ( )  ) ( );;; acbdbc =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 21 Lời giải Đáp án A. Câu 82: Cho ba tập hợp      )2;2,1;5,0;1ABC =−== . Khi đó tập ( )\ ABC  là: A.  0;1 B.  )0;1 C. ( )2;1 D.  2;5 Lời giải Ta có:  ) ( )  )\2;1\0;1 ABABC =−= . Đáp án B. Câu 83: Cho tập hợp )3;8CA  =−  , ( ) ( ) 5;23;11.CB =− Tập ( )CAB  là: A. ( )3;3 . B.  . C. ( )5;11 . D. ( ) ( ) 3;23;8.− Lời giải Chọn C )3;8 =− CA , ( ) ( ) ( )5;23;115;11=−=−CB ( ) );38;  =−−+ A , (  ) ;511;.  =−−+ B (  );511;  =−−+ AB ( ) ( ) 5;11.=− CAB Câu 84: Cho   ( ) ( ) 1;4;2;6;1;2.ABC === Tìm :ABC  A.   0;4. B.  ) 5;. + C. ( ) ;1.− D. . Lời giải Chọn D   ( ) ( )1;4;2;6;1;2=== ABC ( 2;4= AB = ABC . Câu 85: Cho hai tập  342 Axxx =++ ,  5341Bxxx =−− Tất cả các số tự nhiên thuộc cả hai tập A và B là: A. 0 và 1. B. 1. C. 0 D. Không có. Lời giải Chọn A  342=++ Axxx ( ) 1;.=−+ A  5341 =−− Bxxx ( ) ;2.=− B ( )1;2=−AB   12.=− ABxx

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 22  12=− ABxx   0;1.= AB Câu 86: Cho  4;7A =− , ( ) ( );23;B =−−+ . Khi đó AB  : A.  ) (  4;23;7.−− B.  ) ( ) 4;23;7.−− C. (  ( ) ;23;.−+ D. ( )  ) ;23;.−−+ Lời giải Chọn A  4;7=−A , ( ) ( );23; =−−+B , suy ra  ) ( 4;23;7=−−AB Câu 87: Cho ( ;2A =−− ,  )3;B =+ , ( ) 0;4.C = Khi đó tập ( ) ABC  là: A.   3;4. B. (  ( ) ;23;.−−+ C.  ) 3;4. D. ( )  ) ;23;.−−+ Lời giải Chọn C ( ;2=−−A ,  )3; =+B , ( ) 0;4.=C Suy ra (   );23; =−−+AB ; ( )  ) 3;4.=ABC Câu 88: Cho  :20AxRx=+ ,  :50BxRx=− . Khi đó  AB là: A.  2;5 . B.  2;6 . C.  5;2 . D. ( )2; −+ . Lời giải Chọn A Ta có  :20=+AxRx  )2; =−+ A ,  :50=−BxRx ( ;5=− B Vậy   2;5.=− AB Câu 89: Cho    :20,:50AxRxBxRx =+=− . Khi đó \ AB là: A.  2;5 . B.  2;6 . C. ( )5;+ . D. ( )2;+ . Lời giải Chọn C Ta có  :20=+AxRx  )2; =−+ A ,  :50=−BxRx ( ;5=− B Vậy ( ) \5;.=+ AB Câu 90: Cho hai tập hợp  ) ( 2;7,1;9AB=−= . Tìm AB  A. ( )1;7 B.  2;9 C.  )2;1 D. ( 7;9 Lời giải Đáp án B.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 23  ) (   2;71;92;9 −=− Câu 91: Cho hai tập hợp  |51Axx=− ;  |33Bxx=− . Tìm AB  . A.  5;3 B. ( )3;1 C. ( 1;3 D.  )5;3 Lời giải Đáp án B.  ) (  ( )5;1,3;33;1ABAB =−=−=− Câu 92: Cho (  ( )1;5,2;7AB=−= . Tìm \ AB A. ( 1;2 B. ( 2;5 C. ( )1;7 D. ( )1;2 Lời giải Đáp án A. Vì \ AB gồm các phần tử thuộc A mà không thuộc B nên ( \1;2AB =− . Câu 93: Cho 3 tập hợp ( ;0A =− , ( )1;B =+ ,  )0;1C = . Khi đó ( ) ABC  bằng: A.  0 B. C.  0;1 D.  Lời giải Đáp án A. (  ( );01;AB=−+ ( )  0ABC = Câu 94: Cho hai tập hợp  4;7M =− và ( ) ( );23;N =−−+ . Khi đó MN  bằng: A.  ) ( 4;23;7−− B.  ) ( )4;23;7− C. (  ( );23; −+ D. ( )  );23; −−+ Lời giải Đáp án A.  ) ( 4;23;7MN=− Câu 95: Cho hai tập hợp   ( )2;3,1;AB=−=+ . Khi đó ( )CAB  bằng:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 24 A. ( )1;3 B. (   );13; −+ C.  )3;+ D. ( );2−− Lời giải Đáp án D. Ta có:  )2;AB=−+ ( ) ( )\ CABAB = ( ) ( );2CAB =−− Câu 96: Chọn kết quả sai trong các kết quả sau: A. ABAAB = B. ABABA = C. \ ABAAB== D. \ ABAAB= Lời giải Đáp án D. Câu 97: Cho tập hợp )3;8 =− CA , ( ) ( ) 5;23;11.=−CB Tập ( )CAB  là: A. ( )5;11 . B. ( ) ( ) 3;23;8.− C. ( )3;3 . D.  . Lời giải Chọn A )3;8 =− CA , ( ) ( ) ( )5;23;115;11=−=−CB ( ) );38;  =−−+ A , (  ) ;511;.  =−−+ B (  );511;  =−−+ AB ( ) ( ) 5;11.=− CAB Câu 98: Cho 3 tập hợp: ( ;1A =− ;  2;2B =− và ( )0;5C = Tính ( ) ( ) ?ABAC= A.  2;1 . B. ( )2;5 . C. ( 0;1 . D.  1;2 . Lời giải Chọn A  2;1AB=− . ( 0;1AC= ( ) ( )  2;1ABAC=− . DẠNG 5. CÁC BÀI TOÁN TÌM ĐIỀU KIỆN CỦA THAM SỐ Câu 99: Cho tập hợp    ;2,1;2AmmB=+− . Tìm điều kiện của m để AB  . A. 1m − hoặc 0m  B. 10 m − C. 12 m  D. 1m  hoặc 2m  Lời giải Để AB  thì 122 mm −+ 11 10 220 mm m mm −− − + 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 25 Đáp án B. Câu 100: Cho tập hợp ( )0;A =+ và  2 \430Bxmxxm =−+−= . Tìm m để B có đúng hai tập con và BA  A. 03 4 m m   = B. 4m = C. 0m  D. 3m = Lời giải Để B có đúng hai tập con thì B phải có duy nhất một phần tử, và BA  nên B có một phần tử thuộc A. Tóm lại ta tìm m để phương trình 2 430mxxm−+−= (1) có nghiệm duy nhất lớn hơn 0. + Với 0m = ta có phương trình: 3 430 4 xx −−== (không thỏa mãn). + Với 0m  : Phương trình (1) có nghiệm duy nhất lớn hơn 0 điều kiện cần là: ( ) 2 1 '430340 4 m mmmm m =−−=−++==−  = +) Với 1m =− ta có phương trình 2 440xx −−−= Phương trình có nghiệm 2x =− (không thỏa mãn). +) Với 4m = , ta có phương trình 2 4410 xx−+= Phương trình có nghiệm duy nhất 1 04 2 xm== thỏa mãn. Đáp Án B. Câu 101: Cho hai tập hợp   ( )2;3,;6ABmm =−=+ . Điều kiện để AB  là: A. 32 m −− B. 32 m −− C. 3m − D. 2m − Lời giải Điều kiện để AB  là 236mm−+ 2 63 m m −   + 2 3 m m −   − 32 m −− Câu 102: Cho hai tập hợp ( 0;3X = và ( );4Ya = . Tìm tất cả các giá trị của 4a  để XY . A. 3 4 a a    B. 3a  C. 0a  D. 3a  Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 26 Ta tìm a để 3 34 4 a XYaXY a  =   là 3a  Đáp án B. Câu 103: Cho hai tập hợp   (   )\12;;2; AxxBmm ==−−+ . Tìm tất cả các giá trị của m để AB  A. 4 2 m m   − B. 4 2 1 m m m   −  = C. 4 2 1 m m m   −  = D. 24 m − Lời giải Giải bất phương trình:    122;11;2 xx −−    2;11;2A =−− Để AB  thì: 224 22 112 1 mm mm mm m   − −−   −−=   Đáp án B. Câu 104: Cho số thực 0a .Điều kiện cần và đủ để ( ) 4 ;9; −+  a a là: A. 2 0. 3 − a B. 2 0. 3 − a C. 3 0. 4 − a D. 3 0. 4 − a Lời giải Chọn A ( ) ( ) 44 ;9;09 aaa aa  −+   4 90 a a − 49² 0a a  49²0 0 a a −    2 0 3 − a

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 27 Câu 105: Cho tập hợp    ;2,1;2AmmB=+=− với m là tham số. Điều kiện để AB  là: A. 12 m  B. 10 m − C. 1m − hoặc 0m  D. 1m − hoặc 2m  Lời giải : Đáp án B. 122ABmm −+ 11 10 220 mm m mm −− − +  Câu 106: Cho tập hợp    );2,1;3AmmB=+= . Điều kiện để AB= là: A. 1m − hoặc 3m  B. 1m − hoặc 3m  C. 1m − hoặc 3m  D. 1m − hoặc 3m  Lời giải Đáp án C. 33 211 mm AB mm = +−  Câu 107: Cho hai tập hợp    3;12;4A =−− , ( )1;2Bmm=−+ . Tìm m để AB . A. 5m  và 0m  B. 5m  C. 13 m  D. 0m  Lời giải Đáp án A. Ta đi tìm m để AB= 235 145 011 22 mm mm mm m   +−−  −   −−=  + 55 0 m AB m −   hay 5 0 m m     

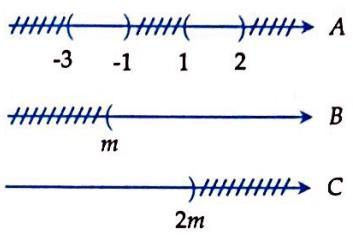
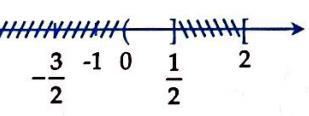
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 28 Câu 108: Cho 3 tập hợp ( ) ( )3;11;2A =−− , ( );Bm=+ , ( );2 Cm − . Tìm m để ABC A. 1 2 2 m  B. 0m  C. 1m − D. 2m  Lời giải Đáp án A. Ta đi tìm m để ABC= TH1: Nếu 20 mmm thì BC= ABC = TH2: Nếu 20 mmm ABC = 3 23 2 22 11 1 221 m m mm m m m   −    −−   Vì 0m  nên 1 0 2 2 m m      )1 ;2; 2 ABCm  =−+    1 2 2 ABCm  Câu 109: Cho hai tập  0;5A = ; ( 2;31Baa=+ , 1a − . Với giá trị nào của a thì AB

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 29 A. 15 32 a − . B. 5 2 1 3 a a     −  . C. 5 2 1 3 a a     −  . D. 15 32 a − . Lời giải Chọn D Ta tìm 5 255 2 A2 3101 1 13113 a a a B a a aa a       = +    −   −−−  − 15 32 ABa − Chọn A Câu 110: Cho 2 tập khác rỗng (  ( ) 1;4;2;22, AmBmm =−=−+ . Tìm m để AB A. 15 m − . B. 15 m  . C. 25 m − . D. 3m − . Lời giải Chọn C Đáp án A đúng vì: Với 2 tập khác rỗng A, B ta có điều kiện 145 25 2222 mm m mm − − +−− . Để 1223ABmmm −+− . So với kết quả của điều kiện thì 25 m − . Câu 111: Cho số thực 0a .Điều kiện cần và đủ để ( ) 4 ;9; −+  a a là: A. 3 0. 4 − a B. 2 0. 3 − a C. 2 0. 3 − a D. 3 0. 4 − a Lời giải Chọn B ( ) ( ) 44 ;9;09 aaa aa  −+   4 90 a a − 49² 0a a  49²0 0 a a −    2 0 3 − a . Câu 112: Cho hai tập  0;5A = ; ( 2;31Baa=+ , 1a − . Với giá trị nào của a thì AB A. 5 2 1 3 a a     −  . B. 15 32 a − . C. 5 2 1 3 a a     −  . D. 15 32 a − . Lời giải Chọn A Trước hết tìm a để AB=. Với 1231aaa−+ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 30 Ta có 5 52 2 3101 3 a a AB a a  =  +  −  . Từ đó, kết hợp điều kiện ta có AB 5 2 1 3 a a     −  . Câu 113: Cho  AxR\xm25 =− ;  BxR\x2020 = . Có bao nhiêu giá trị nguyên m thỏa AB= A. 3987. B. 3988. C. 3989. D. 2020. Lời giải Chọn C Ta có:    AxR\xm25Am25;m25 =−=−+   (   )BxR\x2020B;20202020; ==−−+ Để AB= thì ( )2020m25m2520201 −−+ Khi đó ( ) m252020m1995 11995m1995 m252020m1995 −−− −  + . Vậy có 3989 giá trị nguyên m thỏa mãn. Câu 114: Cho 2 tập hợp  2;5Amm=−+ và  0;4B = . Tìm tất cả các giá trị thực của tham số m để BA  . A. 1m − . B. 12 m − . C. 12 m − . D. 2m  . Lời giải Chọn B Ta có 527mm+−+= . Để BA  20 12 54 m m m − −  + Câu 115: Cho hai tập hợp (;1)Amm=+ và  1;3B =− . Tìm tất cả các giá trị của m để AB=. A. 2 3 m m −   B. 23 m − C. 2 1 m m   − D. 2 3 m m −   Lời giải Chọn A 112 33 mm AB mm =+−−   .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 31 Vậy chọn đáp ánA. Câu 116: Tìm m để AD  , biết (3;7)A =− và (;32) Dmm =− . A. 3m =− B. 3m − C. 1m  D. 2m − Lời giải Chọn B Ta có: 333 3 732242 mmm ADm mmm −−− − −−−  . Câu 117: Cho 2 tập hợp khác rỗng ( 1;4Am=− , ( )2;22Bm=−+ , với m . Tìm m để AB  . A. 15 m  . B. 1m  . C. 15 m − . D. 21 m −− . Lời giải Chọn A Với 2 tập hợp khác rỗng ( 1;4Am=− , ( )2;22Bm=−+ ta có điều kiện 14 222 m m −  +− 5 2 m m    − 25 m − . AB 12 224 m m −−  + 1 224 m m −  + 1 1 m m −   1m  Kết hợp với điều kiện 25 m −15 m  . Câu 118: Cho ( )  )2 3;,;12; 4 m AmB +  =−=−−+   . Tìm m để AB= A. 14 2 3 m  . B. 26 m  . C. 26 m  . D. 14 2 3 m  . Lời giải Chọn A 214 3 43 14 3122 3 26 2 4 m mm ABmmm mm + −  =−−  +    . Câu 119: Cho số thực 0x  . Tìm x để ( ) 9 ;16; x x  −+   A. 3 0 4 x  . B. 3 0 4 x  . C. 3 0 4 x  . D. 3 0 4 x  . Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ I CHƯƠNG I MỆNH ĐỀ TẬP HỢP Sưu tầm và biên soạn Page 32 Để ( ) 9 ;16; x x  −+   thì giá trị của số thực x phải thỏa bất phương trình 9 16x x  Ta có 29 16169 xx x  (do 0x  ) 2 1690 x − 33 44 x − So điều kiện 0x  , suy ra 3 0 4 x  . Câu 120: Cho hai tập hợpkhác rỗng ( 1;4Am=− và ( ) 2;22,.Bmm=−+ Có bao nhiêu giá trị nguyên dương của m để AB ? A. 5 B. 6 C. 4 D. 3. Lời giải Chọn C Ta có , AB là hai tập khác rỗng nên 145 25 2222 mm m mm − − +−− (*). Ta có 1223ABmmm −+− Đối chiếu với điều kiện (*), ta được 25 m − . Do m +  nên  1;2;3;4m . Vậy có 4 giá trị nguyên dương của m thỏa mãn yêu cầu. Câu 121: Cho ( ) ( );,0;AmB=−=+ . Điều kiện cần và đủ để AB= là: A. 0m  . B. 0m  . C. 0m  . D. 0m  . Lời giải Chọn C AB= 0m  . Câu 122: Cho hai tập hợp khác rỗng ( 1;4Am=− và ( )2;22Bm=−+ , m . Tìm tất cả các giá trị của m để AB . A. 25 m − B. 3m − C. 3m − D. 35 m − Lời giải Chọn A Điều kiện để hai tập ( 1;4Am=− và ( )2;22Bm=−+ khác tập rỗng là 14 222 m m −  +− 5 2 m m    − 25 m − ( )* Khi đó AB 122mm −+ 3m −

phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

Trong mặt phẳng tọa độ ,Oxy tập hợp các điểm có tọa độ là nghiệm của bất phương trình ( )1 được gọi là miền nghiệm của nó. Từ đó ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) của bất phương trình axbyc + như sau (tương tự cho bất phương trình axbyc + )

Bước 1. Trên mặt phẳng tọa độ ,Oxy vẽ đường thẳng  : .axbyc +=

Bước 2. Lấy một điểm ( )000 ; Mxy không thuộ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 51 BÀI 3. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Bất phương trình bậc nhất hai ẩn , xy có dạng tổng quát là ( )1axbyc + ( );; axbycaxbycaxbyc +++ trong đó ,, abc là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số. II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Cũng như bất phương trình bậc nhất một ẩn, các bất

c  (ta thường lấy gốc tọa độ O ) Bước 3. Tính 00axby + và so sánh 00axby + với c Bước 4. Kết luận Nếu 00 axbyc + thì nửa mặt phẳng bờ  chứa 0M là miền nghiệm của 00 axbyc + Nếu 00 axbyc + thì nửa mặt phẳng bờ  không chứa 0M là miền nghiệm của 00 axbyc + Chú ý: Miền nghiệm của bất phương trình 00 axbyc + bỏ đi đường thẳng axbyc += là miền nghiệm của bất phương trình 00 .axbyc + 2.1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? a) 236 xy+ ; b) 2 20 xy+ ; c) 2 21 xy− . 2.2. Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng toạ độ: a) 32300 xy+ ; b) 7200 xy+ . CHƯƠNG II BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LÝ THUYẾT.I = BÀI TẬP SÁCH GIÁO KHOA.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 52 2.3. Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau: Phí cố định (nghìn đồng/ngày) Phí tính theo quãng đường di chuyển (nghìn đồng/kilômét) Từ thứ Hai đến thứ Sáu 900 8 Thứ Bảy và Chủ nhật 1500 10 a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng. b) Biểu diển miền nghiệm của bất phương trình ở câu a trên mặt phẳng toạ độ.

Tương tự

phương

phương trình

i tìm

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 53 BÀI 4. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

hệ bất

trình một ẩn

ệ bất

bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn , xy mà ta

ả

các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho. Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn. II. BIỂU DIỄN TẬP NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn ta làm nư sau: Trong cùng hệ toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó. Phần không bị gạch là miền nghiệm cần tìm. III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính. 2.4. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn? a) 0 0; x y    b) 2 0 1; xy yx  + − c) 0 0; xyz y ++   d) 2 2 23 431. xy xy −+  + 2.5. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ: a) 1 0 0; yx x y −−     b) 0 0 24; x y xy     + c) 0 5 0. x xy xy   +  − 2.6. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn; giá tiền 1 kg thịt bò là 250 nghìn đồng; 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn. a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó. b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y. c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất. HỆ THỐNG BÀI TẬP.II = BÀI TẬP SÁCH GIÁO KHOA.1 = BÀI TẬP TỰ LUẬN.2 =

DẠNG 1: CÁC BÀI TOÁN LIÊN BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Câu

D

NG 3: CÁC BÀI TOÁN TH

Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm S là đa giác.

Bước 2: Tính giá trị của F tương ứng với ; xy là tọa độ của các đỉnh của đa giác.

Bước 3: Kết luận:

Giá trị lớn nhất của F là số lớn

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 54

1: Biểu diễn hình học tập nghiệm của bất phương trình 23 xy+ .

2: Biểu diễn hình học tập nghiệm của bất phương trình 320 xy −++

ểu diễn hình học tập nghiệm của bất phương trình 32(25)2(1) xyx +++− . Câu 4: Biểu diễn hình học tập nghiệm của bất phương trình ( ) ( ) 13132 xy +−− DẠNG 2: CÁC BÀI TOÁN HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Biểu diễn hình học tập nghiệm của hệ bất phương trình 36 4 0 0 xy xy x y +  +     Câu 2: Tìm miền nghiệm của hệ bất phương trình 30 23 2 xy xy yx −  +−  + Câu 3: Tìm trị lớn nhất của biểu thức ( ) ;2 Fxyxy =+ , với điều kiện        +    1002 10 0 40 xy xy x y .

Ạ

ỰC TIỄN Bài toán: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức , Txyaxby với ; xy nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn cho trướ

nhất trong các giá trị tìm được. Giá trị nhỏ nhất của F là số nhỏ nhất trong các giá trị tìm được. Câu 1: Một hộ nông dân định trồng đậu và cà trên diện tích 800m2. Nếu trồng đậu thì cần 20 công và thu 3.000.000 đồng trên 100m2 nếu trồng cà thì cần 30 công và thu 4.000.000 đồng trên 100 m2 Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180 Câu 2: Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng?

ệc quá 220 giờ. Tính số tiền lãi lớn nhất trong một tháng của xưởng. Câu 4: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200đơn vị lipit. Mỗi kilogam thịt lợn chứa 600đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 55 Câu 3: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm vi

lượng protein và lipit trong thức ăn? Câu 5: Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ha . Trên diện tích mỗi ha , nếu trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180.

Câu 1: Bất phương trình ( ) 3–2–10 xyx + tương đương với bất phương trình nào sau đây?

A. –2–20xy  . B. 5–2–20 xy

. C. 5–2–10 xy

Câu 2: Cho bất phươngtrình ( ) ( ) 314253 xyx

A. Điể

4;2C thu

D. Điểm ( )5;3D thu

c mi

n nghi

nghi

a b

. D. 4–2–20 xy

. Khẳng định nào dưới đâylà khẳng định đúng?

cho.

phương trình đã cho.

Câu 3: Cho bất phương trình ( ) ( )322521 xyx +++− . Khẳng định nào dưới đây là khẳng định sai?

A. Điểm ( )3;4A thuộc miền nghiệm của bất phương trình đã cho.

B. Điểm ( )2;5B thuộc miền nghiệm của bất phương trình đã cho.

OFFICIAL

C. Điểm ( )1;6C thuộc miền nghiệm của bất phương trình đã cho.

D. Điểm ( )0;0O thuộc miền nghiệm của bất phương trình đã cho.

Câu 4: Cặp số ( )1;–1 là nghiệm của bất phương trình nào sau đây?

A. –30xy+

B. ––0 xy  C. 310xy++ D. ––3–10 xy 

Câu 5: Cặp số nào sau đây là nghiệm của bất phương trình ( ) –2–3 +xyy ?

A. ( )4;–4 B. ( )2;1 C. ( )–1;–2 D. ( )4;4

Câu 6: Cặp số nào sau đây không là nghiệm của bất phương trình ( ) 5210 −−xy ?

A. ( )0;1 B. ( )1;3 C. ( )–1;1 D. ( )–1;0

Câu 7: Miền nghiệm của bất phương trình 326 xy−− là

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 56



−+−−

m ( )0;0O thuộc miền nghiệm của bất phương trình đã cho.

Điểm ( )2;2B thuộc miền nghiệm của bất phương trình đã

Điểm ( )

ộ

ề

ệm

ủ

ất

ộ

ền

ệm củ

ất

A. B. C. D. BÀI TẬP TRẮC NGHIỆM.2 = O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 57 Câu 8: Miền nghiệm của bất phương trình 326 xy+ là A. B. C. D. Câu 9: Miền nghiệm của bất phương trình 326 xy−− là A. B. C. D. O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 58 Câu 10: Miền nghiệm của bất phương trình 326 xy+− là A. B. C. D. Câu 11: Miền nghiệm của hệ bất phương trình           + 6 82 3 93 y yx xy xy là phần mặt phẳng chứa điểm nào sau đây? A. ( )0;0 B. ( )1;2 C. ( )2;1 D. ( )8;4 Câu 12: Miền nghiệm của hệ bất phương trình 10 23 3 2(1)4 2 0 xy y x x  +−   −+     là phần mặt phẳng chứa điểm A. ( )2;1 . B. ( )0;0 . C. ( )1;1 . D. ( )3;4 . Câu 13: Trong các cặp số sau, tìm cặp số không là nghiệm của hệ bất phương trình    + + 0232 02 xy xy A. ( )0;0 . B. ( )1;1 . C. ( )1;1 . D. ( )1;1 . Câu 14: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4 . B. ( )2;4 . C. ( )0;0 . D. ( )3;4 . O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

Hỏi khẳng định nào dưới đây là khẳng định đúng?

A. Điểm ( )2;1A thuộc miền nghiệm của hệ bất phương trình đã cho.

B. Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình đã cho.

C. Điểm ( )1;1C thuộc miền nghiệm của hệ bất phương trình đã cho.

D. Điểm ( )3;4D thuộc miền nghiệm của hệ bất phương trình đã cho.

16: Cho h

bất phương trình

Hỏi khẳng định nào dưới đây là khẳng định đúng?

A. Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình đã cho.

B. Điểm ( )1;0B thuộc miền nghiệm của hệ bất phương trình đã cho.

C. Điểm ( )0;2C thuộc miền nghiệm của hệ bất phương trình đã cho.

D. Điểm ( )0;2D thuộc miền nghiệm của hệ bất phương trình đã cho.

Câu 17: Điểm ( )0;0O

A. 360 240 +−

nào sau đây?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 59 Câu 15: Cho hệ bất phương trình           + + 0 4 21)32( 10 23 x y x xy

Câu

ệ

: 2510 250 10 xy xy xy −−  ++  ++

thuộc miền nghiệm của hệ bất phương trình

 ++ xy xy . B. 360 240 +−  ++ xy xy . C. 360 240 +−  ++ xy xy . D. 360 240 +−  ++ xy xy . Câu 18: Cho hệ bất phương trình ( ) ( ) 3 211 2 4322 xy xy  −   − có tập nghiệm S . Mệnh đề nào sau đây là đúng? A. 1 ;1 4 S−−   B. ( ) ;|432Sxyxy=−= . C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= . Câu 19: Cho hệ 235(1) 3 25(2) xy xy +   +  . Gọi 1S là tập nghiệm của bất phương trình (1), 2S là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 60 Câu 20: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + . B. 0 326 y xy   +− . C. 0 326 x xy   + . D. 0 326 x xy   +− . Câu 21: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 5410 5410 y xy xy   −  + B. 0 4510 5410 x xy xy   −  + C. 0 5410 4510 x xy xy   −  + D. 0 5410 4510 x xy xy   −  + Câu 22: Cho hệ bất phương trình 2 3515 0 0 xy xy x y −  +     . Mệnh đề nào sau đây là sai? A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệ bất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với ( )0;3A , 259 ; 88 B    , ( )2;0C và ( )0;0O B. Đường thẳng : xym+= có giao điểm với tứ giác ABCO kể cả khi 17 1 4 m − O C B 5 2 2A x O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 61 C. Giátrị lớnnhất củabiểuthức xy + ,với x và y thỏamãnhệbất phươngtrình đãcho là 17 4 D. Giátrị nhỏnhất củabiểuthức xy + ,với x và y thõamãn hệbất phươngtrìnhđãcholà0. Câu 23: Giá trị nhỏ nhất của biết thức trên miền xác định bởi hệ 22 24 5 yx yx xy −  −  + là. A. min 1F = khi 2,3xy== B. min 2F = khi 0, 2xy== C. min 3F = khi 1,4xy== . D. min 0F = khi 0, 0xy== . Câu 24: Biểu thức Fyx =− đạt giá trị nhỏ nhất với điều kiện         +  + 0 5 22 22 x xy xy xy tại điểm ; Sxy có toạ độ là A. ( )4;1 . B. ( )3;1 . C. ( )2;1 . D. ( )1;1 . Câu 25: Giá trị nhỏ nhất của biểu thức ( ) ;2 Fxyxy =− , với điều kiện         +   20 20 0 50 xy xy x y là A. 12. B. 10. C. 8. D. 6. Câu 26: Biểu thức Lyx =− , với x và y thỏa mãn hệ bất phương trình 2360 0 2310 xy x xy +−    −− , đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b . Hãy chọn kết quả đúng trong các kết quả sau: A. 25 8 a = và 2b =− B. 2a = và 11 12 b =− C. 3a = và 0b = D. 3a = và 9 8 b = Câu 27: Cho các giá trị , xy thỏa mãn điều kiện 20 210 320 xy xy xy −+  −−  −− . Tìm giá trị lớn nhất của biểu thức 32 Txy =+ A. 19 B. 25. C. 14 D. Không tồn tại. Câu 28: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. ● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu; ● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất? A. 5 lít nước cam và 4 lít nước táo. B. 6 lít nước cam và 5 lít nước táo. C. 4 lít nước cam và 5 lít nước táo. D. 4 lít nước cam và 6 lít nước táo.

Câu 29: M

● Mỗi kg

Xưởng

OFFICIAL

i 30 nghìn.

cao Sao vàng và đựng "Quy sâm đại bổ hoàn". Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau.

• Cách thứ nhất cắt được 3 hộp B1, một hộp cao Sao vàng và 6 hộp Quy sâm.

• Cách thứ hai cắt được 2 hộp B1, 3 hộp cao Sao vàng và 1 hộp Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B1 tối thiểu là 900 hộp, số hộp cao sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?

A. Cắt theo cách một 20x − tấm, cắt theo cách hai 300 tấm.

B. Cắt theo cách một 150 tấm, cắt theo cách hai 100 tấm. C. Cắt theo cách một 50 tấm, cắt theo cách hai 300 tấm. D. Cắt theo cách một 100 tấm, cắt theo cách hai 200 tấm. Câu 32: Một nhà máy sản xuất, sử

máy

c ch

t t

n ph

t s

n phẩm A và sản phẩm B trong một chu trình s

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 62

ột xưởng sản xuất hai loại sản phẩm

sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn;

sản phẩm loại II cần 4 kg nguyên liệu và

giờ, đem lại mức lờ

có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất? A. 30kg loại I và 40 kg loại II. B. 20kg loại I và 40 kg loại II. C. 30kg loại I và 20 kg loại II. D. 25kg loại I và 45 kg loại II. Câu 30: Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B . Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A . Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng. A. 600 đơn vị Vitamin A , 400 đơn vị Vitamin .B B. 600 đơn vị Vitamin A , 300 đơn vị Vitamin B C. 500 đơn vị Vitamin A , 500 đơn vị Vitamin .B D. 100 đơn vị Vitamin A , 300 đơn vị Vitamin .B Câu 31: Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1

đựng

dụng ba

ại

đặ

ủng để

ả

xuấ

ả

ản xuất. Để sản xuất

ộ

ấn sả

ẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất. A. Sản xuất 9 tấn sản phẩm A và không sản xuất sản phẩm B B. Sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm .B C. Sản xuất 10 3 tấn sản phẩm A và 49 9 tấn sản phẩm B D. Sản xuất 6 tấn sản phẩm B và không sản xuất sản phẩm A

phương trình bậc nhất hai ẩn thường có vô số nghiệm và để mô tả tập nghiệm của chúng, ta sử dụng phương pháp biểu diễn hình học.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 1 BÀI 3. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Bất phương trình bậc nhất hai ẩn , xy có dạng tổng quát là ( )1axbyc + ( );; axbycaxbycaxbyc +++ trong đó ,, abc là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số. II. BIỂU DIỄN TẬP NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Cũng như bất phương trình bậc nhất một ẩn, các bất

cho bất phương trình axbyc + ) Bước 1. Trên mặt phẳng tọa độ ,Oxy vẽ đường thẳng  : axbyc += Bước 2. Lấy một điểm ( )000 ; Mxy không thuộc  (ta thường lấy gốc tọa độ O ) Bước 3. Tính 00axby + và so sánh 00axby + với .c Bước 4. Kết luận Nếu 00 axbyc + thì nửa mặt phẳng bờ  chứa 0M là miền nghiệm của 00 .axbyc + Nếu 00 axbyc + thì nửa mặt phẳng bờ  không chứa 0M là miền nghiệm của 00 .axbyc + Chú ý: Miền nghiệm của bất phương trình 00 axbyc + bỏ đi đường thẳng axbyc += là miền nghiệm của bất phương trình 00 .axbyc + CHƯƠNG II BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN LÝ THUYẾT.I =

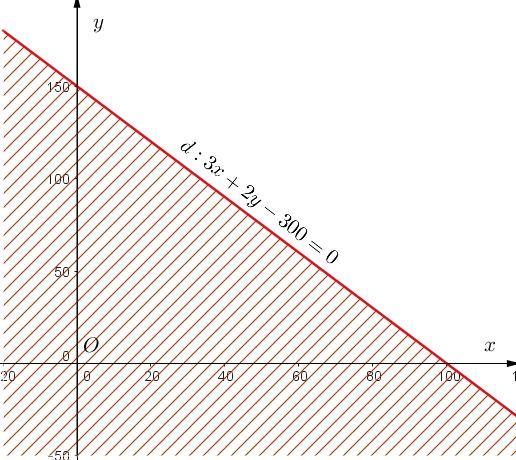
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 2 2.1. Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn? a) 236 xy+ ; b) 2 20 xy+ ;c) 2 21 xy− . Lời giải Bất phương trình bậc nhất hai ẩn là 236 xy+ và 2 2040. xyxy ++ Bất phương trình 2 21 xy− không phải là bất phương trình bậc nhất hai ẩn vì chứa 2 x . 2.2. Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng toạ độ: a) 32300 xy+ ; b) 7200 xy+ . Lời giải Biểu diễn miền nghiệm của bất phương trình 32300 xy+ Bước 1: Vẽ đường thẳng :323000dxy+−= . Bước 2: Ta lấy gốc toạ độ ( )0;0O và tính 3.02.0300 + (vô lí). Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng bờ d không chứa gốc toạ độ và kể đường thẳng d .  Biểu diễn miền nghiệm của bất phương trình 7200 xy+ Bước 1: Vẽ đường thẳng7200 xy+= . Bước 2: Ta lấy điểm ( )0 1;1M và tính 7.120.10 + (vô lí). Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng bờ d không chứa điểm ,M không kể đường thẳng d BÀI TẬP SÁCH GIÁO KHOA.1 =

i x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần (điều kiện 0,0xy )

Số tiền ông An phả

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 3 2.3. Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau: Phí cố định (nghìn đồng/ngày) Phí tính theo quãng đường di chuyển (nghìn đồng/kilômét) Từ thứ Hai đến thứ Sáu 900 8 Thứ Bảy và Chủ nhật 1500 10 a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền ông An phải trả không quá 14 triệu đồng. b) Biểu diển miền nghiệm của bất phương trình ở câu a trên mặt phẳng toạ độ. Gọ

i trả từ thứ 2đến thứ 6là 5.900845008 xx+=+ (nghìn đồng) Số tiền ông An phải trả hai ngày cuối tuần là 2.150010300010 yy+=+ (nghìn đồng) Vì đề bài yêu cầu tổng số tiền ông An phải trả không quá 14 triệu đồng nên ta có ( ) ( ) 4500830001014000453250 xyxy ++++ (nghìn đồng) Miền nghiệm của bất phương trình bậc nhất hai ẩn này được xác định như sau: Bước 1: Vẽ đường thẳng :4532500dxy+−= . Bước 2: Ta lấy gốc toạ độ ( )0;0O và tính 02003250 += . Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa gốc toạ độ, kể đường thẳng d

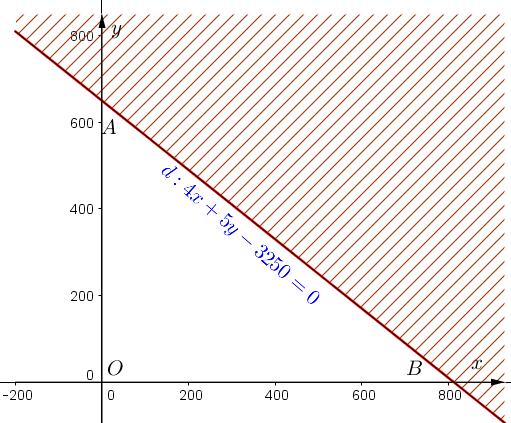
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 4

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 5 BÀI 4. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN I. HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Tương tự hệ bất phương trình một ẩn Hệ bất phương trình bậc nhất hai ẩn gồm một số bất phương trình bậc nhất hai ẩn , xy mà ta phải tìm các nghiệm chung của chúng. Mỗi nghiệm chung đó được gọi là một nghiệm của hệ bất phương trình đã cho. Cũng như bất phương trình bậc nhất hai ẩn, ta có thể biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn. II. BIỂU DIỄN TẬP NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Để biểu diễn miền nghiệm của hệ bất phương trình bậc nhất 2 ẩn ta làm nư sau: Trong cùng hệ toạ độ, biểu diễn miền nghiệm của mỗi bất phương trình trong hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó. Phần không bị gạch là miền nghiệm cần tìm. III. ÁP DỤNG VÀO BÀI TOÁN THỰC TIỄN Giải một số bài toán kinh tế thường dẫn đến việc xét những hệ bất phương trình bậc nhất hai ẩn và giải chúng. Loại bài toán này được nghiên cứu trong một ngành toán học có tên gọi là Quy hoạch tuyến tính. 2.4. Hệ bất phương trình nào sau đây là hệ bất phương trình bậc nhất hai ẩn? a) 0 0; x y    b) 2 0 1; xy yx  + − c) 0 0; xyz y ++   d) 2 2 23 431. xy xy −+  + Lời giải a) 0 0; x y    d) 2 2 23 431. xy xy −+  + 2.5. Biểu diễn miền nghiệm của mỗi hệ bất phương trình sau trên mặt phẳng tọa độ: a) 1 0 0; yx x y −−     b) 0 0 24; x y xy     + c) 0 5 0. x xy xy   +  − Lời giải a) 1 0 0; yx x y −−     HỆ THỐNG BÀI TẬP.II = BÀI TẬP SÁCH GIÁO KHOA.1 =

Bước 1: Vẽ đường thẳng

không thỏa mãn bất phương trình

Do đó miền nghiệm của của bất phương trình

là nửa mặt phẳng bờ 1d không chứa gốc tọa độ O không kể đường thẳng

Bước 2: Vẽ đường thẳng ( )2 :0dx

Vì 10

nên tọa độ điểm ( )1;0 thỏa bất phương trình

Do đó miền nghiệm của bất phương trình

Bước 3: Vẽ đường thẳng ( )3 :0dy =

là nửa mặt phẳng bờ Oy chứa điểm ( )1;0 không kể bờ Oy .

Vì 10− nên tọa độ điểm ( )0,1 thỏa bất phương trình 0y 

Do đó miền nghiệm của bất phương trình 0y  là nửa mặt phẳng bờ Ox chứa điểm ( )0;1 không kể bờ Ox .

Vậy miền nghiệm của hệ là miền không bị gạch.

b) 0

Bước 1: Vẽ đường thẳng ( )1 :0dx =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 6

( )1 :1dxy−+=− Vì 0001 −+=− nên tọa độ điểm ( )0;0O

1xy −+−



0x 



0 24; x y xy     +

2.6. M

Vì 10  nên tọa độ điểm ( )1;0 thỏa bất phương trình 0x 

Do đó miền nghiệm của bất phương trình 0x  là nửa mặt phẳng bờ Oy và đường thẳng 0x = chứa điểm ( )1;0 .

Bước 2: Vẽ đường thẳng ( )2 :0dy =

Vì 10  nên tọa độ điểm ( )0,1 thỏa bất phương trình 0y 

Do đó miền nghiệm của bất phương trình 0y  là nửa mặt phẳng bờ Ox và đường thẳng 0y = chứa điểm ( )0;1 .

Bước 3: Vẽ đường thẳng ( )3 :24dxy+=

Vì 2.0004 += nên tọa độ điểm ( )0;0O thỏa mãn bất phương trình 24 xy+

Do đó miền nghiệm của của bất phương trình24 xy+ là nửa mặt phẳng bờ 3d và đường thẳng 24 xy+= chứa gốc tọa độ O .

Vậy miền nghiệm của hệ là miền không bị gạch.

gia

cần

vị protein và 400 đơn vị lipit trong th

i kilôgam th

t bò ch

800 đơn vị protein và 200 đơn vị lipit. Mỗi kilôgam th

OFFICIAL

mỗi ngày. M

n chứa 600 đơn vị protein và 400 đơn vị lipit. Bi

t l

t rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt l

n; giá tiền 1 kg thịt bò là 250 nghìn đồng; 1 kg thịt lợn là 160 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm của hệ đó.

b) Gọi F (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn F theo x và y.

c) Tìm số kilôgam thịt mỗi loại mà gia đình cần mua để chi phí là ít nhất.

Lời giải

a) Gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giả sử gia đình này mua x kilôgam thịt bò và y kilôgam thịt lợn thì x và y cần thỏa mãn điều kiện: 01,6 x  và 01,1 y  .

Gia đình này cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 7

ột

đình

ít nhất 900 đơn

ức ăn

ỗ

ị

ứa

ị

ợ

ế

ợ

ăn mỗi ngày nên điều kiện tương ứng là 800600900 xy+ và 200400400 xy+ Hay 869 xy+ và 22xy+ Từ các bất phương trình biểu thị các điều kiện của bài toán, ta có hệ bất phương trình sau: 01,6 01,1 869 22 x y xy xy     +  + Biểu diễn miền nghiệm của hệ bất phương trình: ( ) ( ) ( ) ( ) 1 2 3 4 :1,6 :1,1 :869 :22 dx dy dxy dxy = = += +=

Miền nghiệm của hệ trên là miền tứ giác ABCD

(kể cả biên).

b) 250160 Fxy =+ (nghìn đồng)

c) ( ); Fxy đạt giá trị lớn nhất hoặc nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.

( ) ( ) ( )23 0,3;1,1AddA  , ta có ( ) 0,3;1,1250.0,3160.0,191F =+= (nghìn đồng)

( ) ( ) ( )12 1,6;1,1BddB  , ta có ( ) 1,6;1,1250.1,6160.1,1576F =+= (nghìn đồng)

( ) ( ) ( )14 1,6;0,2CddC  , ta có ( ) 1,6;0,2250.1,6160.0,2432F =+= (nghìn đồng)

( ) ( ) ( )34 0,6;0,7DddD  , ta có ( ) 0,6;0,7250.0,6160.0,7262F =+= (nghìn đồng)

Vậy gia đình đó cần mua 0,3kg thịt bò và 1,1kg thịt

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 8

lợn để chi phí là ít nhất. DẠNG 1: CÁC BÀI TOÁN LIÊN BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Biểu diễn hình học tập nghiệm của bất phương trình 23 xy+ Lời giải Vẽ đường thẳng :23. xy += Lấy gốc tọa độ ( ) 0;0,O ta thấy O và có 2.003 + nên nửa mặt phẳng bờ  chứa gốc tọa độ O là miền nghiệm của bất phương trình đã cho (miền không bị tô đậm trong hình). Câu 2: Biểu diễn hình học tập nghiệm của bất phương trình 320 xy −++ Lời giải BÀI TẬP TỰ LUẬN.2 =

Trướ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 9

c hết, ta vẽ đường thẳng ( ):320.dxy−++=

thấy ( )0;0 không là nghiệm của bất phương trình.

ậy miền nghiệm là nửa mặt phẳng bờ ( )d không chứa điểm ( ) 0;0. Câu 3: Biểu diễn hình học tập nghiệm của bất phương trình 32(25)2(1) xyx +++− Lời giải Đầu tiên, thu gọn bất phương trình đề bài đã cho về thành 34110. xy++ Ta vẽ đường thẳng ( ):34110.dxy++= Ta thấy ( )0;0 không là nghiệm của bất phương trình. Vậy miền nghiệm là nửa mặt phẳng (không kể bờ ( )d ) không chứa điểm ( ) 0;0. Câu 4: Biểu diễn hình học tập nghiệm của bất phương trình ( ) ( ) 13132 xy +−− Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 10 Trước hết, ta vẽ đường thẳng ( ) ( ) ( ) :13132.dxy +−−= Ta thấy ( )0;0 không là nghiệm của bất phương trình đã cho. Vậy miền nghiệm là nửa mặt phẳng bờ ( )d không chứa điểm ( ) 0;0. DẠNG 2: CÁC BÀI TOÁN LIÊN HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Biểu diễn hình học tập nghiệm của hệ bất phương trình 36 4 0 0 xy xy x y +  +     Lời giải Vẽ các đường thẳng ( ) ( ) 1 2 2 2 :36 :4 :0 :0 dxy dxy dxOy dyOx += += = = Vì điểm ( )0 1;1M có tọa độ thỏa mãn tất cả các bất phương trình trong hệ trên nên ta tô đậm các nửa mặt phẳng bờ ( )1 ,d ( )2 ,d ( )3 ,d ( )4d không chứa điểm 0M Miền không bị tô đậm (hình tứ giác OCIA kể cả bốn cạnh ,,, AIICCOOA) trong hình vẽ là miền nghiệm của hệ đã cho. Câu 2: Tìm miền nghiệm của hệ bất phương trình 30 23 2 xy xy yx −  +−  + . Lời giải Trước hết, ta vẽ ba đường thẳng: ( )1 :30dxy−= ( )2 :23dxy+=− ( )3 :2dxy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 11 Ta thấy ( )1;0 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )1;0 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 3: Tìm trị lớn nhất của biểu thức ( ) ;2 Fxyxy =+ , với điều kiện        +    1002 10 0 40 xy xy x y Lời giải Vẽ đường thẳng 1 :10dxy−−= , đường thẳng 1d qua hai điểm ( )0;1 và ( )1;0 Vẽ đường thẳng 2 :2100dxy+−= , đường thẳng 2d qua hai điểm ( )0;5 và ( )2;4 . Vẽ đường thẳng 3 :4dy = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 12 Miền nghiệm là ngũ giác ABCOE với ( ) ( ) ( ) ( )4;3,2;4,0;4,1;0ABCE Ta có: ( ) 4;310F = , ( ) 2;410F = , ( ) 0;48F = , ( ) 1;01F = , ( ) 0;00F = . Vậy giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ bằng 10 DẠNG 3: CÁC BÀI TOÁN THỰC TIỄN Bài toán: Tìm giá trị lớn nhất, nhỏ nhất của biểu thức , Txyaxby với ; xy nghiệm đúng một hệ bất phương trình bậc nhất hai ẩn cho trước. Bước 1: Xác định miền nghiệm của hệ bất phương trình đã cho. Kết quả thường được miền nghiệm S là đa giác. Bước 2: Tính giá trị của F tương ứng với ; xy là tọa độ của các đỉnh của đa giác. Bước 3: Kết luận: Giá trị lớn nhất của F là số lớn nhất trong các giá trị tìm được. Giá trị nhỏ nhất của F là số nhỏ nhất trong các giá trị tìm được. Câu 1: Một hộ nông dân định trồng đậu và cà trên diện tích 800m2. Nếu trồng đậu thì cần 20 công và thu 3.000.000 đồng trên 100m2 nếu trồng cà thì cần 30 công và thu 4.000.000 đồng trên 100 m2 Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công không quá 180 Lời giải Gọi x là số 00x m2 đất trồng đậu, y là số 00y m2 đất trồng cà. Điều kiện 0x  , 0y  Số tiền thu được là 34 Txy =+ triệu đồng. Theo bài ra ta có 8 2030180 0 0 xy xy x y +  +      8 2318 0 0 xy xy x y +  +     Đồ thị: Dựa đồ thị ta có tọa độ các đỉnh ( )0;6A , ( )6;2B , ( )8;0C , ( )0;0O Câu 2: Bạn An kinh doanh hai mặt hàng handmade là vòng tay và vòng đeo cổ. Mỗi vòng tay làm trong 4 giờ, bán được 40 ngàn đồng. Mỗi vòng đeo cổ làm trong 6 giờ, bán được 80 ngàn đồng. Mỗi tuần bạn An bán được không quá 15 vòng tay và 4 vòng đeo cổ. Tính số giờ tối thiểu trong tuần An cần dùng để bán được ít nhất 400 ngàn đồng? Lời giải

ờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 13 Gọi , xy  là số vòng tay và vòng đeo cổ trong tuần An làm được. Theo giả thiết ta có 4080400 015 04 xy x y +     Bài toán trở thành tìm nghiệm ( ), xy để 46 Lxy =+ nhỏ nhất. Miền nghiệm của hệ bất phương trình (1) là tam giác ABC với ( ) ( ) ( )0;50,10;0,2;4ABC kể cả miền trong tam giác đó. Tình giá trị của biểu thức 46 Lxy =+ tại tất cả các đỉnh của tam giác ABC ta thấy L nhỏ nhất khi 2,4xy== Vậy số giờ tối thiểu trong tuần An cần dung là 4.26.432L =+= Câu 3: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II . Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 gi

180 giờ và Bình không thể làm việc quá 220 giờ. Tính số tiền lãi lớn nhất trong một tháng của xưởng. Lời giải Gọi x , y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x , y nguyên dương. Ta có hệ bất phương trình sau: 32180 6220 0 0 xy xy x y +  +     Miền nghiệm của hệ trên là Tiền lãi trong một tháng của xưởng là 0,50,4 Txy =+ (triệu đồng). Ta thấy T đạt giá trị lớn nhất chỉ có thể tại các điểm A , B , C . Vì C có tọa độ không nguyên nên loại. Tại ( )60;0A thì 30T = triệu đồng. x y B 90 OA C

Câu 4: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200đơn vị lipit. Mỗi kilogam thịt lợn chứa 600đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 14 Tại ( )40;30B thì 32T = triệu đồng. Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng.

x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn? Lời giải Theo bài ra ta có số tiền gia đình cần trả là 160.110.xy + với x , y thỏa mãn: 01,6 01,1 x y    Số đơn vị protein gia đình có là 0,8.0,6.0,9 xy+ 869 xy + ( )1d . Số đơn vị lipit gia đình có là0,2.0,4.0,422 xyxy ++ ( )2d Bài toán trở thành: Tìm , xy thỏa mãn hệ bất phương trình 01,6 01,1 869 22 x y xy xy     +  + sao cho 160.110. Txy =+ nhỏ nhất. Vẽ hệ trục tọa độ ta tìm được tọa độ các điểm ( )1,6;1,1A ; ( )1,6;0,2B ; ( )0,6;0,7C ; ( )0,3;1,1D . Nhận xét: ( ) 377TA = nghìn, ( ) 278TB = nghìn, ( ) 173TC = nghìn, ( ) 169TD = nghìn. Vậy tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì 0,6x = và 0,7y = . Câu 5: Một hộ nông dân định trồng dứa và củ đậu trên diện tích 8ha . Trên diện tích mỗi ha , nếu trồng dứa thì cần 20 công và thu 3 triệu đồng, nếu trồng củ đậu thì cần 30 công và thu 4 triệu đồng. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu ha để thu được nhiều tiền nhất, biết rằng tổng số công không quá 180. Lời giải O x y A BC D 1 2 1 2 1,6x = 1,1y = 22xy+= 869 xy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 15 Gọi , xy lần lượt là số ha trồng dứa và củ đậu. Có 08;08 xy  ; 8xy+ ; 20301802318 xyxy ++ Số tiền thu được là ( ) ,34 Txyxy =+ Ta có hệ 08 08 8 2318 x y xy xy     +  + Miền nghiệm của hệ là miền tứ giác OABC với ( ) ( ) ( )0;6,6;2,0;8ABC . Khi đó ( ), Txy đạt cực đại tại một trong các đỉnh của OABC. Có ( ) ( ) ( ) ( ) 0,00;0;624;6;226;8;024 TTTT==== . Vậy cần trồng 6 ha dứa và 2 ha củ đậu. Câu 1: Bất phương trình ( ) 3–2–10 xyx + tương đương với bất phương trình nào sau đây? A. –2–20xy  . B. 5–2–20 xy  . C. 5–2–10 xy  . D. 4–2–20 xy  . Lời giải Chọn B ( ) 3–2–10322205220 xyxxyxxy+−+−−− . Câu 2: Cho bất phương trình ( ) ( ) 314253 xyx −+−− . Khẳng định nào dưới đây là khẳng định đúng? A. Điểm ( )0;0O thuộc miền nghiệm của bất phương trình đã cho. B. Điểm ( )2;2B thuộc miền nghiệm của bất phương trình đã cho. BÀI TẬP TRẮC NGHIỆM.3 =

Cho b

phương trình

. Khẳng định nào dưới đây là khẳng định sai?

A. Điểm ( )3;4A thuộc miền nghiệm của bất phương trình đã cho.

B. Điểm ( )2;5B thuộc miền nghiệm của bất phương trình đã cho.

C. Điểm ( )1;6C thuộc miền nghiệm của bất phương trình đã cho.

D. Điểm ( )0;0O thuộc miền nghiệm của bất phương trình đã cho.

Lời giải

Chọn D

Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy ( ) ( )00;0;0xy =

không là nghiệm của bất phương trình đã cho.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 16 C. Điểm ( )4;2C thuộc miền nghiệm của bất phương trình đã cho. D. Điểm ( )5;3D thuộc miền nghiệm của bất phương trình đã cho. Lời giải Chọn A Lần lượt thay toạ độ điểm ở mỗi phương án vào bất phương trình đã cho, ta thấy ( ) ( )00;0;0xy = là nghiệm của bất phương trình đã cho. Câu 3:

ất

( ) ( )322521 xyx +++−

Câu 4: Cặp số ( )1;–1 là nghiệm của bất phương trình nào sau đây? A. –30xy+ . B. ––0 xy  . C. 310xy++ . D. ––3–10 xy  . Lời giải Chọn C ( ) ,31fxyxy=++ . Thay ( ) 1,113110f −=−+=− . Câu 5: Cặp số nào sau đây là nghiệm của bất phương trình ( ) –2–3 +xyy ? A. ( )4;–4 B. ( )2;1 C. ( )–1;–2 D. ( )4;4 Lời giải Chọn D ( ) ( )–2–32323* xyyxyyx +−++ Thay các đáp án vào bpt( )* để kiểm tra Câu 6: Cặp số nào sau đây không là nghiệm của bất phương trình ( ) 5210 −−xy ? A. ( )0;1 . B. ( )1;3 . C. ( )–1;1 . D. ( )–1;0 . Lời giải Chọn B Ta có ( ) 5210 −−xy 5220 xy −+ ; ta thay từng đáp án vào bất phương trình, cặp ( )1;3 không thỏa mãn bất phương trình vì 5.12.320 −+ là sai. Vậy Chọn B Câu 7: Miền nghiệm của bất phương trình 326 xy−− là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 17 A. B. C. D. Lời giải Chọn C Trước hết, ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0. Câu 8: Miền nghiệm của bất phương trình 326 xy+ là O x y 2 3 O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 18 A. B. C. D. Lời giải Chọn A Trước hết, ta vẽ đường thẳng ( ):326.dxy+= Ta thấy ( )0;0 không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng (không kể bờ ( )d ) không chứa điểm ( ) 0;0. Câu 9: Miền nghiệm của bất phương trình 326 xy−− là O 2 3 y x O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 19 A. B. C. D. Lời giải Chọn B Trước hết, ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng (không kể bờ ( )d ) không chứa điểm ( ) 0;0. Câu 10: Miền nghiệm của bất phương trình 326 xy+− là O x y 2 3 O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 20 A. B. C. D. Lời giải Chọn D Trước hết, ta vẽ đường thẳng ( ):326.dxy+=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng (không kể bờ ( )d ) chứa điểm ( ) 0;0. Câu 11: Miền nghiệm của hệ bất phương trình           + 6 82 3 93 y yx xy xy là phần mặt phẳng chứa điểm nào sau đây? A. ( )0;0 . B. ( )1;2 . C. ( )2;1 . D. ( )8;4 . Lời giải O x 2 3 y O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 21 Chọn D Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa hệ bất phương trình trên. Câu 12: Miền nghiệm của hệ bất phương trình 10 23 3 2(1)4 2 0 xy y x x  +−   −+     là phần mặt phẳng chứa điểm A. ( )2;1 . B. ( )0;0 . C. ( )1;1 . D. ( )3;4 . Lời giải Chọn A Nhận xét: chỉ có điểm ( )2;1 thỏa mãn hệ Câu 13: Trong các cặp số sau, tìm cặp số không là nghiệm của hệ bất phương trình    + + 0232 02 xy xy A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )1;1 Lời giải Chọn C Ta dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào không thỏa hệ bất phương trình trên với mọi x Câu 14: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4 . B. ( )2;4 . C. ( )0;0 . D. ( )3;4 . Lời giải Chọn C Nhận xét: chỉ có điểm ( )0;0 không thỏa mãn hệ Câu 15: Cho hệ bất phương trình           + + 0 4 21)32( 10 23 x y x xy Hỏi khẳng định nào dưới đây là khẳng định đúng? A. Điểm ( )2;1A thuộc miền nghiệm của hệ bất phương trình đã cho. B. Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình đã cho.

C. Điểm

)1;1

thuộc miền nghiệm

hệ bất phương trình đã cho.

D. Điểm ( )3;4D thuộc miền nghiệm của hệ bất phương trình đã cho.

Lời giải

Chọn A

Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã

Hỏi khẳng định nào dưới đây là khẳng định đúng?

A. Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình đã cho.

B. Điểm ( )1;0B thuộc miền nghiệm của hệ bất phương trình đã cho.

C. Điểm ( )0;2C thuộc miền nghiệm của hệ bất phương trình đã cho.

D. Điểm ( )0;2D thuộc miền nghiệm của hệ bất phương trình đã cho.

Lời giải

Chọn C

Lần lượt thay toạ độ điểm ở mỗi phương án vào hệ bất phương trình đã cho, ta thấy ( ) ( )00;0;2xy =− là nghiệm của hệ bất phương trình đã cho.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 22

(

của

cho, ta thấy ( ) ( )00;2;1xy = là nghiệm của hệ bất phương trình đã cho. Câu 16: Cho hệ bất phương trình      ++ ++  10 250 2510 xy xy xy .

Câu 17: Điểm ( )0;0O thuộc miền nghiệm của hệ bất phương trình nào sau đây? A. 360 240 +−  ++ xy xy B. 360 240 +−  ++ xy xy C. 360 240 +−  ++ xy xy D. 360 240 +−  ++ xy xy Lời giải Chọn C Thay 0;0xy== vào từng đáp án ta được: 36060 24040 xy xy +−−   ++ (loại A. ); 36060 24040 xy xy +−−   ++ ( LoạiB. ) 36060 24040 xy xy +−−   ++ (thỏa mãn). Vậy Chọn C Câu 18: Cho hệ bất phương trình ( ) ( ) 3 211 2 4322 xy xy  −   − có tập nghiệm S . Mệnh đề nào sau đây là đúng? A. 1 ;1 4 S−−   .

c ti

p ta th

y ( )0;0 là nghi

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 23 B. ( ) ;|432Sxyxy=−= C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= . Lời giải Chọn B Trước hết, ta vẽ hai đường thẳng: ( )1 3 :21 2 dxy−= ( )2 :432dxy−= Thử

ự

ế

ấ

ệm của bất phương trình (2) nhưng không phải là nghiệm của bất phương trình (1). Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của hệ bất phương trình chính là các điểm thuộc đường thẳng ( ):432.dxy−= Câu 19: Cho hệ 235(1) 3 25(2) xy xy +   +  . Gọi 1S là tập nghiệm của bất phương trình (1), 2S là tập nghiệm của bất phương trình (2) và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  . Lời giải Chọn A Trước hết, ta vẽ hai đường thẳng: ( )1 :235dxy+= ( )2 3 :5 2 dxy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 24 Ta thấy ( )0;0 là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ Câu 20: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + . B. 0 326 y xy   +− . C. 0 326 x xy   + . D. 0 326 x xy   +− . Lời giải Chọn A Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng ( )1 :0dy = và đường thẳng ( )2 :326.dxy+= Miền nghiệm gồm phần y nhận giá trị dương. Lại có ( )0;0 thỏa mãn bất phương trình 326. xy+ Câu 21: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 25 A. 0 5410 5410 y xy xy   −  + B. 0 4510 5410 x xy xy   −  + C. 0 5410 4510 x xy xy   −  + D. 0 5410 4510 x xy xy   −  + Lời giải Chọn C Dựa vào hình vẽ, ta thấy đồ thị gồm các đường thẳng: ( )1 :0dx = ( )2 :4510dxy+= ( )3 :5410dxy−= Miền nghiệm gần phần mặt phẳng nhận giá trị x dương (kể cả bờ ( )1d ). Lại có ( )0;0 là nghiệm của cả hai bất phương trình 4510 xy+ và 5410. xy− Câu 22: Cho hệ bất phương trình 2 3515 0 0 xy xy x y −  +     . Mệnh đề nào sau đây là sai? A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệ bất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với ( )0;3A , 259 ; 88 B    , ( )2;0C và ( )0;0O B. Đường thẳng : xym+= có giao điểm với tứ giác ABCO kể cả khi 17 1 4 m − O C B 5 2 2A x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 26 C. Giátrị lớnnhất củabiểuthức xy + ,với x và y thỏamãnhệbất phươngtrình đãcho là 17 4 D. Giátrị nhỏnhất củabiểuthức xy + ,với x và y thõamãn hệbất phươngtrìnhđãcholà0. Lời giải Chọn B Trước hết, ta vẽ bốn đường thẳng: ( )1 :2dxy−= ( )2 :3515dxy+= ( )3 :0dx = ( )4 :0dy = Fyx =− Miền nghiệm là phần không bị gạch, kể cả biên. Câu 23: Giá trị nhỏ nhất của biết thức trên miền xác định bởi hệ 22 24 5 yx yx xy −  −  + là. A. min 1F = khi 2,3xy== B. min 2F = khi 0, 2xy== C. min 3F = khi 1,4xy== D. min 0F = khi 0, 0xy== Lời giải Chọn A Biểu diễn miền nghiệm của hệ bất phương trình 22 24 5 yx yx xy −  −  + trên hệ trục tọa độ như dưới đây:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 27 Nhận thấy biết thức Fyx =− chỉ đạt giá trị nhỏ nhất tại các điểm , AB hoặc C . Ta có: ( ) ( ) ( ) 413;2;321FAFBFC=−===−= . Vậy min 1F = khi 2,3xy== Câu 24: Biểu thức Fyx =− đạt giá trị nhỏ nhất với điều kiện         +  + 0 5 22 22 x xy xy xy tại điểm ; Sxy có toạ độ là A. ( )4;1 . B. ( )3;1 . C. ( )2;1 . D. ( )1;1 . Lời giải Chọn A Cách 1: Thử máy tínhTa dùng máy tính lần lượt kiểm tra các đáp án để xem đáp án nào thỏa hệ bất phương trình trên loại được đáp án D. Ta lần lượt tính hiệu Fyx =− và min3 F =− tại 4,x = 1y = Cách 2: Tự luận: Tọa độ 78 ; 33 A   , 22 ; 33 B    , ( )4;1C . Giá trị F lần lượt tại toạ độ các điểm ,, BCA là 41 ,3; 33 . Suy ra min3 F tại 4;1.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 28 Câu 25: Giá trị nhỏ nhất của biểu thức ( ) ;2 Fxyxy =− , với điều kiện         +   20 20 0 50 xy xy x y là A. 12. B. 10. C. 8. D. 6. Lời giải Chọn B Vẽ các đường thẳng 1 :5dy = ; 2 :20dxy+−= ; 3 :20dxy−−= ; :0; :0OxyOyx== Các đường thẳng trên đôi một cắt nhau tại ( )0;5A Vì điểm ( )0 2;1M có toạ độ thoả mãn tất cả các bất pt trong hệ nên ta tô đậm các nửa mặt phẳng bờ 123,,,, dddOxOy không chứa điểm 0M . Miền không bị tô đậm là đa giác ABCD kể cả các cạnh (hình bên) là miền nghiệm của hệ pt đã cho. Kí hiệu ( ) ();2AAAA FAFxyxy ==− , ta có ()10,()4,()2;()3 FAFBFCFD=−=−==− , 10432 −−− Giá trị lớn nhất cần tìm là 10. Câu 26: Biểu thức Lyx =− , với x và y thỏa mãn hệ bất phương trình 2360 0 2310 xy x xy +−    −− , đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b Hãy chọn kết quả đúng trong các kết quả sau: A. 25 8 a = và 2b =− B. 2a = và 11 12 b =− C. 3a = và 0b = D. 3a = và 9 8 b = Lời giải Chọn B Trước hết, ta vẽ ba đường thẳng: 6 4 2 2 4 6 15 10 5 5 10 15 d3 d2 d1 h x( )=x 2 g x( )=2 x f x( )=5 B A D C O

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 29 ( )1 :2360dxy+−= ( )2 :0dx = ( )3 :2310dxy−−= Ta thấy ( )0;0 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả ba miền nghiệm của cả ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ (kể cả biên). Miền nghiệm là hình tam giác ABC (kể cả biên), với ( ) 0;2,A 75 ;, 46 B    1 0;. 3 C    Vậy ta có 202,a =−= 5711 6412 b =−=− Câu 27: Cho các giá trị , xy thỏa mãn điều kiện 20 210 320 xy xy xy −+  −−  −− . Tìm giá trị lớn nhất của biểu thức 32 Txy =+ . A. 19. B. 25. C. 14. D. Không tồn tại. Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 30 Chọn B Miền nghiệm của hệ đã cho là miền trong tam giác ABC (Kể cả đường biên) trong đó ( )1;1A , ( )2;4B , ( )3;5C . Giá trị lớn nhất của 32 Txy =+ đạt được tại các đỉnh của tam giác ABC Do ( ) 1;13.12.15A TT==+= , ( ) 2;43.22.414B TT==+= và ( ) 3;53.32.525C TT==+= nên giá trị lớn nhất của 32 Txy =+ là 25 đạt được khi 3x = và 5y = . Câu 28: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. ● Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu; ● Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất? A. 5 lít nước cam và 4 lít nước táo. B. 6 lít nước cam và 5 lít nước táo. C. 4 lít nước cam và 5 lít nước táo. D. 4 lít nước cam và 6 lít nước táo. Lời giải Chọn C Giả sử , xy lần lượt là số lít nước cam và số lít nước táo mà mỗi đội cần pha chế Suy ra 3010xy + là số gam đường cần dùng; xy + là số lít nước cần dùng; 4 xy + là số gam hương liệu cần dùng. Theo giả thiết ta có 00 00 3010210321. 99 424424 xx yy xyxy xyxy xyxy    ++  ++  ++  ( )* Số điểm thưởng nhận được sẽ là 6080. Pxy =+ Ta đi tìm giá trị nhỏ nhất của biểu thức P với , xy thỏa mãn ( )* Câu 29: Một xưởng sản xuất hai loại sản phẩm ● Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn; ● Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 nghìn. Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất? A. 30kg loại I và 40 kg loại II. B. 20kg loại I và 40 kg loại II.

phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A . Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng.

A. 600 đơn vị Vitamin A , 400 đơn vị Vitamin .B

B. 600 đơn vị Vitamin A , 300 đơn vị Vitamin .B

C. 500 đơn vị Vitamin A , 500 đơn vị Vitamin B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 31 C. 30kg loại I và 20 kg loại II. D. 25kg loại I và 45 kg loại II. Lời giải Chọn B Gọi ( )0, 0kgxy lần lượt là số sản phẩm loại I và loại II cần sản xuất. Khi đó, tổng số nguyên liệu sử dụng: 24200. xy+ Tổng số giờ làm việc: 30151200. xy+ Lợi nhuận tạo thành: 4030 Lxy =+ (nghìn). Thực chất của bài toán này là phải tìm 0,x  0y  thoả mãn hệ 24200 30151200 xy xy +  + sao cho 4030 Lxy =+ đạt giá trị lớn nhất. Câu 30: Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B . Do tác động

D. 100 đơn vị Vitamin A , 300 đơn vị Vitamin .B Lời giải Chọn D Gọi 0, 0xy lần lượt là số đơn vị vitamin A và B để một người cần dùng trong một ngày. Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị vitamin cả A lẫn B nên ta có: 4001000. xy + Hàng ngày, tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B nên ta có: 600, 500.xy Mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A nên ta có: 0,53. xyx  Số tiền cần dùng mỗi ngày là: ( ) ,97,5. Txyxy =+ Bài toán trở thành: Tìm 0, 0xy thỏa mãn hệ 0600,0500 4001000 0,53 xy xy xyx   +   để ( ) ,97,5 Txyxy =+ đạt giá trị nhỏ nhất.

Câu 31: Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1, đựng cao Sao vàng và đựng "Quy sâm đại bổ hoàn". Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau.

• Cách

• Cách th

hai c

theo

và

vàng và 1 h

p Quy sâm.

p Quy sâm. Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B1 tối thiểu là 900 hộp, số hộp cao sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho

OFFICIAL

t chu trình sản xuất. Để sản xuất một t

n sản phẩm A lãi 4 triệu đồng người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng người ta sử dụng máy I trong 6 giờ, máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy hai hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 32

thứ nhất cắt được 3 hộp B1, một hộp cao Sao vàng

6 hộ

ứ

ắt đượ

2 hộp B1, 3 hộp cao Sao

ộ

tổng số tấm bìa phải dùng là ít nhất?

Cắt theo cách một 20x − tấm, cắt theo cách hai 300 tấm. B. Cắt

cách một 150 tấm, cắt theo cách hai 100 tấm. C. Cắt theo cách một 50 tấm, cắt theo cách hai 300 tấm. D. Cắt theo cách một 100 tấm, cắt theo cách hai 200 tấm. Lời giải Chọn A Gọi 0, 0xy lần lượt là số tấm bìa cắt theo cách thứ nhất, thứ hai. Bài toán đưa đến tìm 0, 0xy thoả mãn hệ 32900 31000 6900 xy xy xy +  +  += sao cho Lxy =+ nhỏ nhất. Câu 32: Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm B trong mộ

ấ

để tiền lãi được nhiều nhất. A. Sản xuất 9 tấn sản phẩm A và không sản xuất sản phẩm .B B. Sản xuất 7 tấn sản phẩm A và 3 tấn sản phẩm B C. Sản xuất 10 3 tấn sản phẩm A và 49 9 tấn sản phẩm .B D. Sản xuất 6 tấn sản phẩm B và không sản xuất sản phẩm .A Lời giải Chọn B Gọi 0, 0xy (tấn) là sản lượng cần sản xuất của sản phẩm A và sản phẩm .B Ta có: 6 xy + là thời gian hoạt động của máy I 23xy + là thời gian hoạt động của máy .II 32xy + là thời gian hoạt động của máy III Số tiền lãi của nhà máy: 43 Txy =+ (triệu đồng).

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 33 Bài toán trở thành: Tìm 0, 0xy thỏa mãn 636 2323 3227 xy xy xy +  +  + để 43 Txy =+ đạt giá trị lớn nhất.

Câu 1: Điểm nào sau đây thuộc mi

A. ( )1;1A

Câu 2: Điểm (1;3)A là

A. 3240

Câu 3: Điể

m thu

n nghi

m c

a b

phương trình 3450 +−xy ?

phương trình:

Câu

Trong các

( )

OFFICIAL

240

A. Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm của bất phương trình axbyc + không được gọi là miền nghiệm của

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 1

ề

ệ

ủ

ất

B. ( )2;0B C. ( )1;2C D.

4;1D

điể

ộc

ền nghiệm của bất

−+− xy B. 30+xy C. 30 −xy D.

−+xy

m (0;3)A là điểm thuộc miền nghiệm của bất phương trình: A. 3240 xy −+− B. 30 xy− C. 240 xy−− D. 30xy+ Câu 4: Điểm nào sau đây không thuộc miền nghiệm của bất phương trình 450−+xy ? A. ( )5;0M B. ( )1;0N C. ( )1;3P D. ( )2;1Q

mệnh đề sau, mệnh đề nào đúng?

nó B. Biểu diễn tập nghiệm của bất phương trình 2310 xy−+ trên hệ trục Oxy là đường thẳng 2310 xy−+= . C. Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm của bất phương trình axbyc + được gọi là miền nghiệm của nó. D. Nghiệm của bất phương trình axbyc + là tập rỗng. Câu 6: Miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− là nửa mặt phẳng không chứa điểm nào trong các điểm sau? A. ( )0;0 . B. ( )1;1 . C. ( )4;2 . D. ( )1;1 . Câu 7: Miền nghiệm của bất phương trình ( ) ( ) 314253 xyx −+−− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )0;0 B. ( )4;2 C. ( )2;2 D. ( )5;3 Câu 8: Miền nghiệm của bất phương trình ( ) ( )322521 xyx +++− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )3;4 . B. ( )2;5 . C. ( )1;6 . D. ( )0;0 . CHƯƠNG II BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

Câu 13: Trong các

( )0;0

Câu 14: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn?

A. 2530 xyz−+

Câu

2 3240 xx+−

253 xy+

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 2 Câu 9: Miền nghiệm của bất phương trình ( ) ( ) 415329 xyx −+−− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )2;5 Câu 10: Miền nghiệm của bất phương trình ( ) ( ) 323413 xyxy +++−+ là phần mặt phẳng chứa điểm nào trong các điểm sau? A. ( )3;0 . B. ( )3;1 . C. ( )1;1 . D. ( )0;0 . Câu 11: Miền nghiệm của bất phương trình ( ) 529227 xxy +−−+ là phần mặt phẳng không chứa điểm nào trong các điểm sau? A. ( )2;1 B. ( )2;3 C. ( )2;1 D. ( )0;0 Câu 12: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 21 xy+ ?

( )2;1 B. ( )3;7 C. ( )0;1 D. ( )0;0

cặp số sau đây, cặp nào không là nghiệm của bất phương trình 450xy−+ ?

( )5;0 . B. ( )2;1 . C. ( )1;3 . D.

C. 2

D. 235 xy+

15: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 230 xy+− ? A. ( )1;3Q . B. 3 1; 2 M    . C. ( )1;1N . D. 3 1; 2 P    . Câu 16: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau? A. 23 xy− . B. 3xy− . C. 23 xy− . D. 23 xy+ .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 3 Câu 17: Hình vẽ nào sau đây biểu diễn miền nghiệm là của bất phương trình nào sau đây? A. 21xy . B. 21xy . C. 2xy . D. 2xy . Câu 18: Miền nghiệm của bất phương trình 23xy+ là phần tô đậm trong hình vẽ của hình nào, trong các hình vẽ dưới đây? A. B. C. D. Câu 19: Miền nghiệm của bất phương trình 320 xy −++ không chứa điểm nào sau đây? A. ( )1;2A B. ( )2;1B C. 1 1; 2 C    D. ( )3;1D Câu 20: Miền nghiệm của bất phương trình 32(25)2(1) xyx +++− không chứa điểm nào sau đây? A. ( )1;2A . B. 12 ; 1111 B    . C. ( )0;3C . D. ( )4;0D . Câu 21: Miền nghiệm của bất phương trình 21 xy+ không chứa điểm nào sau đây? A. ( ) 1;1.A B. ( )2;2B C. ( )3;3C D. ( )1;1D Câu 22: Miền nghiệm của bất phương trình ( ) ( ) 13132 xy +−− chứa điểm nào sau đây? A. ( )1;1A B. ( )1;1B C. ( )1;1C D. ( )3;3D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 4 Câu 23: Miền nghiệm của bất phương trình ( ) 22124xyx −+−+ chứa điểm nào sau đây? A. ( ) 1;1.A B. ( ) 1;5.B C. ( ) 4;3.C D. ( ) 0;4.D Câu 24: Miền nghiệm của bất phương trình 22220 xy−+− chứa điểm nào sau đây? A. ( ) 1;1.A B. ( )1;0B C. ( )2;2C D. ( ) 2;2.D Câu 25: Cho bất phương trình245 xy+ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng ? A. ( )1;1 S B. ( )1;10 S C. ( )1;1 S− D. ( )1;5 S Câu 26: Cho bất phương trình 250xy−+ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )2;2 S . B. ( )1;3 S . C. ( )2;2 S− . D. ( )2;4 S− . Câu 27: Miền nghiệm của bất phương trình 326 xy−− là A. B. C. D. O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 5 Câu 28: Miền nghiệm của bất phương trình 326 xy+ là A. B. C. D. Câu 29: Miền nghiệm của bất phương trình 326 xy+− là A. B. C. D. O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 6 Câu 30: Cho bất phương trình 2320 xy −++ có tập nghiệm là S Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S . B. 2 ;0 2 S     . C. ( )1;2 S− . D. ( )1;0 S . Câu 31: Cặp số ( )(;) 2;3xy = là nghiệm của bất phương trình nào sau đây? A. 43xy  . B. –370xy + . C. 2–3–10 xy  . D. –0xy  . Câu 32: Cặp số ( )00 ; xy nào là nghiệm của bất phương trình 334 xy− . A. ( ) ( )00;2;2xy =− . B. ( ) ( )00;5;1xy = . C. ( ) ( )00;4;0xy =− . D. ( ) ( )00;2;1xy = . Câu 33: Cặp số ( ); xy nào sau đây là một nghiệm của hệ bất phương trình 20 ? 310 −  +− xy xy A. ( ) ( );2;1 =−−xy . B. ( ) ( );4;0 =xy . C. ( ) ( );1;2 =xy . D. ( ) ( );3;4 =−−xy . Câu 34: Trong mặt phẳng Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 31 22 xy xy −  + ? A. ( ) 1;0.P B. ( ) 1;1.N C. ( ) 1;1.M D. ( ) 0;1.Q Câu 35: Trong mặt phẳng với hệ trục tọa độ Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 210 3210 +−  ++ xy xy ? A. ( )1;1 B. ( )0;1 C. ( )1;0 D. ( )1;3 Câu 36: Miền nghiệm của hệ bất phương trình 39 3 xy xy +  − là phần mặt phẳng chứa điểm A. ( )1;2 B. ( )0;0 C. ( )2;1 D. ( )8;4 Câu 37: Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình 20 2320 xy xy +−  −+ là A. ( )0;0 . B. ( )1;1 . C. ( )1;1 . D. ( )1;1 . Câu 38: Miền nghiệm của hệ bất phương trình 10 23 3 2(1)4 2 0 xy y x x  +−   −+     là phần mặt phẳng chứa điểm nào trong các điểm sau? A. ( )2;1 B. ( )0;0 C. ( )1;1 D. ( )3;4

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 7 Câu 39: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4 . B. ( )2;4 . C. ( )0;0 . D. ( )3;4 . Câu 40: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2510 250 10 xy xy xy −−  ++  ++ ? A. ( )0;0 . B. ( )1;0 . C. ( )0;2 . D. ( )0;2 . Câu 41: Miền nghiệm của hệ bất phương trình 0 330 50 xy xy xy −  −+  +− là phần mặt phẳng chứa điểm A. ( )5;3 . B. ( )0;0 . C. ( )1;1 . D. ( )2;2 . Câu 42: Miền nghiệm của hệ bất phương trình 39 3 28 6 xy xy yx y +  −  −   là phần mặt phẳng chứa điểm A. ( )0;0 . B. ( )1;2 . C. ( )2;1 . D. ( )8;4 . Câu 43: Cho hệ bất phương trình 0 250 xy xy +  + có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S B. ( )1;1 S−− C. 1 1; 2 S −  D. 12 ; 25 S −  Câu 44: Miền nghiệm của hệ bất phương trình 36 3 28 4 xy xy yx y +  −  −   là phần mặt phẳng chứa điểm: A. ( )2;1 B. ( )6;4 C. ( )0;0 D. ( )1;2

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 8 Câu 45: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 0 5410 5410 y xy xy   −  + B. 0 5410 4510 x xy xy   −  + C. 0 4510 5410 x xy xy   −  + D. 0 5410 4510 x xy xy   −  + Câu 46: Cho hệ bất phương trình 0 310 x xy    ++  có tập nghiệm là S Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S− . B. ( )1;3 S− . C. ( )1;5 S− . D. ( )4;3 S− . Câu 47: Cho hệ bất phương trình 0 310 x xy    ++  có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )1;2 S− B. ( )2;0 S C. ( )1;3 S− D. ( )3;0 S

48: Cho hệ bất phương trình 3 1 10 2 xy xy −   −+  có tập nghiệm S . Khẳng định nào sau đây là khẳng định đúng ? A. ( )1;2 S− B. ( )2;1 S C. ( )5;6 S− D. S = Câu 49: Cho hệ bất phương trình 3 21 2 432 xy xy  −   − có tập nghiệm S . Khẳng định nào sau đây là khẳng định đúng ? A. 1 ;1 4 S−−   . B. ( ) ;|432Sxyxy=−= . C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= . D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 9 Câu 50: Cho hệ 235(1) 3 25(2) xy xy +   +  . Gọi 1S là tập nghiệm của bất phương trình, 2S là tập nghiệm của bất phương trình và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  . Câu 51: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + B. 0 326 y xy   +− C. 0 326 x xy   + D. 0 326 x xy   +− Câu 52: Miền nghiệm của hệ bất phương trình 20 32 3 xy xy yx −  +−  − chứa điểm nào sau đây? A. ( )1;0A . B. ( )2;3B . C. ( )0;1C . D. ( ) 1;0.D Câu 53: Miền nghiệm của hệ bất phương trình 2360 0 2310 xy x xy +−    −− chứa điểm nào sau đây? A. ( ) 1;2.A B. ( )0;2B C. ( )1;3C D. 1 0;. 3 D    Câu 54: Miền nghiệm của hệ bất phương trình 210 350 x x − −+  chứa điểm nào sau đây? A. Không có B. 5 ;2. 3 B    C. ( ) 3;1.C D. 1 ;10 2 D    Câu 55: Miền nghiệm của hệ bất phương trình 30 2310 y xy −  −+ chứa điểm nào sau đây? A. ( )3;4A . B. ( )4;3B . C. ( )7;4C . D. ( ) 4;4.D O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 10 Câu 56: Miền nghiệm của hệ bất phương trình 20 32 xy xy −  +− không chứa điểm nào sau đây? A. ( ) 1;0.A B. ( ) 1;0.B C. ( )3;4C . D. ( ) 0;3.D Câu 57: Miền nghiệm của hệ bất phương trình 3260 3 2(1)4 2 0 xy y x x −−   −+    không chứa điểm nào sau đây? A. ( )2;2A . B. ( ) 3;0.B C. ( ) 1;1.C D. ( ) 2;3.D Câu 58: Miền nghiệm của hệ bất phương trình 0 33 5 xy xy xy −  −−  + không chứa điểm nào sau đây? A. ( ) 3;2.A B. ( ) 6;3.B C. ( ) 6;4.C D. ( ) 5;4.D Câu 59: Miền nghiệm của hệ bất phương trình 30 23 2 xy xy yx −  +−  + không chứa điểm nào sau đây? A. ( ) 0;1.A B. ( ) 1;1.B C. ( ) 3;0.C D. ( ) 3;1.D

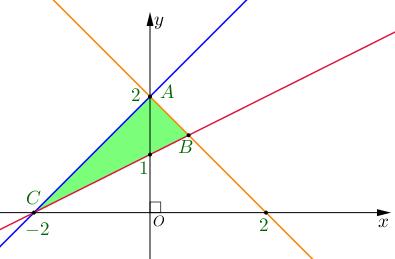
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 11 Câu 60: Miền tam giác ABC kể cả ba cạnh ,, ABBCCA trong hình là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 20 20 220 xy xy xy +−  −+  −+ . B. 20 20 220 xy xy xy +−  −+  −+ . C. 20 20 220 xy xy xy +−  −+  −+ . D. 20 20 220 xy xy xy +−  −+  −+ . Câu 61: Giá trị nhỏ nhất của biểu thức Fyx =− trên miền xác định bởi hệ 22 24 5 yx yx xy −  −  + là A. min1 F = khi 2x = , 3y = B. min2 F = khi 0x = , 2y = C. min3 F = khi 1x = , 4y = . D. min0 F = khi 0x = , 0y = . Câu 62: Giá trị nhỏ nhất của biết thức Fyx =− trên miền xác định bởi hệ 22 2 54 xy xy xy +  −  +− là A. min 3F =− khi 1,2xy==− B. min0 F = khi 0,0xy== C. min 2F =− khi 42 , 33xy==− . D. min 8F = khi 2,6xy=−= . Câu 63: Cho hệ bất phương trình 2 3515 0 0 xy xy x y −  +     . Khẳng định nào sau đây là khẳng định sai? A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệbất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với ( )0;3A , 259 ; 88 B    , ( )2;0C và ( )0;0O . B. Đường thẳng : xym+= có giao điểm với tứ giác ABCO kể cả khi 17 1 4 m − C. Giátrị lớnnhất củabiểuthức xy + ,với x và y thỏamãnhệbất phươngtrình đãcho là 17 4 . D. Giátrị nhỏnhất củabiểuthức xy + ,với x và y thõamãn hệbất phươngtrìnhđãcholà0.

ng tối đa 24g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, m

lít nước táo nhận được 80 điểm thưởng. Đội A pha ch

và dành được điểm thưở

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 12 Câu 64: Giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ với điều kiện 04 0 10 2100 y x xy xy     −−  +− là A. 6. B. 8. C. 10. D. 12. Câu 65: Giá trị nhỏ nhất của biết thức ( ) ;2 Fxyxy =− với điều kiện 05 0 20 20 y x xy xy     +−  −− là A. 10. B. 12. C. 8. D. 6. Câu 66: Biểu thức Fyx = đạt giá trị nhỏ nhất với điều kiện 22 22 5 0 xy xy xy x −+−  −  +   tại điểm ( ); Sxy có toạ độ là A. ( )4;1 . B. ( )3;1 . C. ( )2;1 . D. ( )1;1 . Câu 67: Biểu thức Lyx =− , với x và y thõa mãn hệ bất phương trình 2360 0 2310 xy x xy +−    −− , đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b . Hãy chọn kết quả đúng trong các kết quả sau: A. 25 8 a = và 2b =− B. 2a = và 11 12 b =− C. 3a = và 0b = D. 3a = và 9 8 b = Câu 68: Trong một cuộc thi pha chế, hai đội A, B được sử dụ

ỗi

ế được

lít nước cam và b lít nước táo

ng cao nhất. Hiệu số ab là A. 1. B. 3. C. 1. D. 6. Câu 69: Một hộ nông dân định trồng đậu và cà trên diện tích 2800 m . Nếu trồng đậu trên diện tích 2100 m thì cần 20công làm và thu được 3000000 đồng. Nếu trồng cà thì trên diện tích 2100 m cần 30 công làm và thu được 4000000 đồng. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công làm không quá 180 công. Hãy chọn phương án đúng nhất trong các phương án sau: A. Trồng 2600 m đậu; 2200 m cà. B. Trồng 2500 m đậu; 2300 m cà. C. Trồng 2400 m đậu; 2200 m cà. D. Trồng 2200 m đậu; 2600 m cà.

đa 24 gam hương liệu, 9 lít nước và 210 gam đường để pha chế nước ngọt loại I và nước ngọt loại II. Để pha chế 1 lít nước ngọt loại I cần 10 gam đường, 1 lít nước và 4 gam hương liệu. Để pha chế 1 lít nước ngọt loại II cần 30 gam đường, 1 lít nước và 1 gam hương liệu. Mỗi lít nước ngọt loại I được 80 điểm thưởng, mỗi lít nước ngọt loại II được 60 điểm thưởng. Hỏi số điểm thưởng cao nhất có thể của mỗi đội trong cuộc thi là bao

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 13 Câu 70: Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa (1 sản phẩm mới của công ty) cần thuê xe để chở trên 140 người và trên 9 tấn hàng. Nơi thuê chỉ có hai loại xe A và

. Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng. A. 4 xe A và 5 xe B . B. 5 xe A và 6 xe B . C. 5 xe A và 4 xe B . D. 6 xe A và 4 xe B Câu 71: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi , xy lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính 22 xy + A. 22 1,3xy+= B. 22 2,6xy+= C. 22 1,09xy+= D. 22 0,58xy+= Câu 72: Có hai cái giỏ đựng trứng gồm giỏ A và giỏ B, các quả trứng trong mỗi đều có hai loại là trứng lành và trứng hỏng. Tổng số trứng trong hai giỏ là 20 quả và số trứng trong giỏ A nhiều hơn số trứng trong giỏ B. Lấy ngẫu nhiên mỗi giỏ 1 quả trứng, biết xác suất để lấy được hai quả trứng lành là 55 84 Tìm số trứng lành trong giỏ A. A. 6. B. 14. C. 11. D. 10. Câu 73: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối

nhiêu? A. 540. B. 600 . C. 640 . D. 720. Câu 74: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là. A. 32 triệu đồng. B. 35 triệu đồng. C. 14 triệu đồng. D. 30 triệu đồng.

Câu 75: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200đơn vị lipit. Mỗi kilogam thịt lợn chứa 600đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn?

A. 0,3x = và 1,1y = B. 0,3x = và 0,7y = C. 0,6x = và 0,7y = D. 1,6x = và 0,2y =

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 14

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 1 DẠNG 1. TÌM NGHIỆM BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 1: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 3450 +−xy ? A. ( )1;1A B. ( )2;0B C. ( )1;2C D. ( )4;1D Lời giải Chọn A Thay tọa độ điểm ( )1;1A vào bất phương trình đã cho ta được: ( ) 3.14.150 +−− đúng. Do đó điểm ( )1;1A thuộc miền nghiệm của bất phương trình đã cho. Câu 2: Điểm (1;3)A là điểm thuộc miền nghiệm của bất phương trình: A. 3240 −+− xy B. 30+xy C. 30 −xy D. 240 −+xy Lời giải Chọn A Vì ( ) 3.12.340 −−+− là mệnh đề đúng nên ( )1;3A là điểm thuộc miền nghiệm của bất phương trình 3240 −+− xy . Câu 3: Điểm (0;3)A là điểm thuộc miền nghiệm của bất phương trình: A. 3240 xy −+− B. 30 xy− C. 240 xy−− D. 30xy+ Lời giải Chọn A Thay điểm (0;3)A vào từng đáp án, ta thấy A. 3.(0)2.(3)420 −+−=  nhận B. 3.(0)(3)30 −=− loại C. 2.(0)(3)470 −−=− loại D. (0)3.(3)90 += loại. Câu 4: Điểm nào sau đây không thuộc miền nghiệm của bất phương trình 450−+xy ? A. ( )5;0M . B. ( )1;0N . C. ( )1;3P . D. ( )2;1Q . Lời giải Chọn D CHƯƠNG II BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 2 Thay tọa độ điểm Q vào bất phương trình ta được 245010 −−+− . Do đó điểm Q không thuộc miền nghiệm của bất phương trình đã cho. Câu 5: Trong các mệnh đề sau, mệnh đề nào đúng? A. Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm của bất phương trình axbyc + không được gọi là miền nghiệm của nó B. Biểu diễn tập nghiệm của bất phương trình 2310 xy−+ trên hệ trục Oxy là đường thẳng 2310 xy−+= C. Trong mặt phẳng tọa độ Oxy , tập hợp các điểm có tọa độ là nghiệm của bất phương trình axbyc + được gọi là miền nghiệm của nó D. Nghiệm của bất phương trình axbyc + là tập rỗng Lời giải Chọn C Câu 6: Miền nghiệm của bất phương trình ( ) ( )22221 xyx −++−− là nửa mặt phẳng không chứa điểm nào trong các điểm sau? A. ( )0;0 . B. ( )1;1 . C. ( )4;2 . D. ( )1;1 . Lời giải Chọn C Ta có: ( ) ( )22221 xyx −++−− 22422 xyx−++−− 24xy + Dễ thấy tại điểm ( )4;2 ta có: 42.284 += . Câu 7: Miền nghiệm của bất phương trình ( ) ( ) 314253 xyx −+−− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )0;0 . B. ( )4;2 . C. ( )2;2 . D. ( )5;3 . Lời giải Chọn A Ta có: ( ) ( ) 314253 xyx −+−− 334853 xyx −+−− 2480 xy −+ 240xy −+ Dễ thấy tại điểm ( )0;0 ta có: 02.0440 −+= Câu 8: Miền nghiệm của bất phương trình ( ) ( )322521 xyx +++− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )3;4 B. ( )2;5 C. ( )1;6 D. ( )0;0 Lời giải Chọn D Ta có: ( ) ( )322521 xyx +++− 341022 xyx+++− 3480 xy ++ . Dễ thấy tại điểm ( )0;0 ta có: 3.04.080 ++ Câu 9: Miền nghiệm của bất phương trình ( ) ( ) 415329 xyx −+−− là nửa mặt phẳng chứa điểm nào trong các điểm sau? A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )2;5

xét: chỉ có cặp số ( )2;3 không thỏa bất phương trình.

Câu 12: Trong các cặp số sau đây, cặp nào không là nghiệm của bất phương trình 21 xy+ ?

A. ( )2;1 B. ( )3;7

C. ( )0;1 D. ( )0;0

Lời giải ChọnC.

Nhận xét: chỉ có cặp số ( )0;1 không thỏa bất phương trình.

Câu 13: Trong các cặp số sau đây, cặ

A. ( )5;0

Ta thay

nào

nghi

phương trình

xy−+

( )0;0

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 3 Lời giải Chọn D Ta có: ( ) ( ) 415329 xyx −+−− 4451529 xyx −+−− 25100 xy +− . Dễ thấy tại điểm ( )2;5 ta có: 2.25.5100 +− . Câu 10: Miền nghiệm của bất phương trình ( ) ( ) 323413 xyxy +++−+ là phần mặt phẳng chứa điểm nào trong các điểm sau? A. ( )3;0 . B. ( )3;1 . C. ( )1;1 . D. ( )0;0 . Lời giải ChọnC. Nhận xét: chỉ có cặp số ( )1;1 thỏa bất phương trình. Câu 11: Miền nghiệm của bất phương trình ( ) 529227 xxy +−−+ là phần mặt phẳng không chứa điểm nào trong các điểm sau?

( )2;1 . B. ( )2;3 . C. ( )2;1 . D. ( )0;0 . Lời giải ChọnC.

ận

không là

ệm của bất

450

B. ( )2;1 C. ( )1;3 D.

Lời giải ChọnB.

cặp số ( )2;1 vào bất phương trình 450xy−+ được 2450−−+ đo dó cặp số ( )2;1 không là nghiệm của bất phương trình 450xy−+ . Câu 14: Trong các bất phương trình sau, bất phương trình nào là bất phương trình bậc nhất hai ẩn? A. 2530 xyz−+ B. 2 3240 xx+− C. 2 253 xy+ D. 235 xy+ Lời giải Chọn D Theo định nghĩa bất phương trình bậc nhất hai ẩn. Câu 15: Điểm nào sau đây thuộc miền nghiệm của bất phương trình 230 xy+− ? A. ( )1;3Q B. 3 1; 2 M    C. ( )1;1N D. 3 1; 2 P    Lời giải

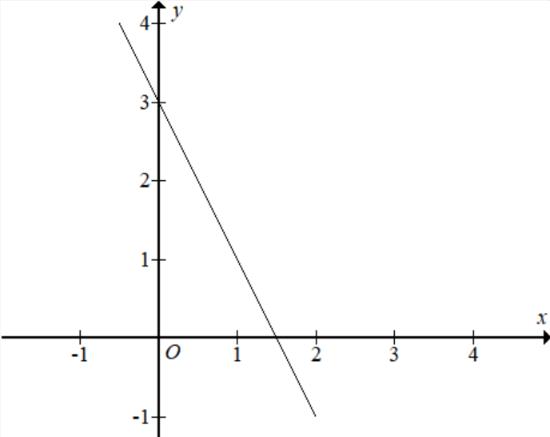
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 4 Chọn B Tập hợp các điểm biểu diễn nghiệm của bất phương trình 230 xy+− là nửa mặt phẳng bờ là đường thẳng 230 xy+−= và không chứa gốc tọa độ Từ đó ta có điểm 3 1; 2 M    thuộc miền nghiệm của bất phương trình 230 xy+− . Câu 16: Miền nghiệm của bất phương trình nào sau đây được biểu diễn bởi nửa mặt phẳng không bị gạch trong hình vẽ sau? A. 23 xy− . B. 3xy− . C. 23 xy− . D. 23 xy+ . Lời giải Chọn A Đường thẳng 23 xy−= đi qua điểm ( ) 3 0;3,;0 2    . Loại B Thay tọa độ điểm ( )0;0O vào vế trái của các bất phương trình ở đáp án A, C, D. Ta thấy đáp án A thỏa mãn. Câu 17: Hình vẽ nào sau đây biểu diễn miền nghiệm là của bất phương trình nào sau đây?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 5 A. 21xy B. 21xy C. 2xy D. 2xy Lời giải Chọn D Câu 18: Miền nghiệm của bất phương trình 23xy+ là phần tô đậm trong hình vẽ của hình nào, trong các hình vẽ dưới đây? A. B. C. D. Lời giải Trong mặt phẳng tọa độ vẽ đường thẳng :23dxy+= , ta thấy d chia thành 2 nửa mặt phẳng thì ta chọn nửa bên trái do 23xy+ . Câu 19: Miền nghiệm của bất phương trình 320 xy −++ không chứa điểm nào sau đây? A. ( )1;2A . B. ( )2;1B . C. 1 1; 2 C    . D. ( )3;1D . Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 6 Trước hết, ta vẽ đường thẳng ( ):320.dxy−++= Ta thấy ( )0;0 không là nghiệm của bất phương trình. Vậy miền nghiệm là nửa mặt phẳng bờ ( )d không chứa điểm ( ) 0;0. Câu 20: Miền nghiệm của bất phương trình 32(25)2(1) xyx +++− không chứa điểm nào sau đây? A. ( )1;2A B. 12 ; 1111 B    C. ( )0;3C D. ( )4;0D Lời giải Chọn B Đầu tiên, thu gọn bất phương trình đề bài đã cho về thành 34110. xy++ Ta vẽ đường thẳng ( ):34110.dxy++= Ta thấy ( )0;0 không là nghiệm của bất phương trình. Vậy miền nghiệm là nửa mặt phẳng không chứa điểm ( ) 0;0. Câu 21: Miền nghiệm của bất phương trình 21 xy+ không chứa điểm nào sau đây? A. ( ) 1;1.A B. ( )2;2B . C. ( )3;3C . D. ( )1;1D . Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 7 Trước hết, ta vẽ đường thẳng ( ):21.dxy+= Ta thấy ( )0;0 không là nghiệm của bất phương trình đã cho. Vậy miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm ( ) 0;0. Câu 22: Miền nghiệm của bất phương trình ( ) ( ) 13132 xy +−− chứa điểm nào sau đây? A. ( )1;1A . B. ( )1;1B . C. ( )1;1C . D. ( )3;3D . Lời giải Chọn A Trước hết, ta vẽ đường thẳng ( ) ( ) ( ) :13132.dxy +−−= Ta thấy ( )0;0 không là nghiệm của bất phương trình đã cho. Vậy miền nghiệm là nửa mặt phẳng bờ ( )d không chứa điểm ( ) 0;0. Câu 23: Miền nghiệm của bất phương trình ( ) 22124xyx −+−+ chứa điểm nào sau đây? A. ( ) 1;1.A B. ( ) 1;5.B C. ( ) 4;3.C D. ( ) 0;4.D Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 8 Đầu tiên ta thu gọn bất phương trình đã cho về thành 280.xy −+− Vẽ đường thẳng ( ):280.dxy−+−= Ta thấy ( )0;0 không là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng không chứa điểm ( ) 0;0. Câu 24: Miền nghiệm của bất phương trình 22220 xy−+− chứa điểm nào sau đây? A. ( ) 1;1.A B. ( )1;0B C. ( )2;2C D. ( ) 2;2.D Lời giải Chọn A Trước hết, ta vẽ đường thẳng ( ):22220.dxy−+−= Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0. Câu 25: Cho bất phương trình245 xy+ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng ? A. ( )1;1 S . B. ( )1;10 S . C. ( )1;1 S− . D. ( )1;5 S . Lời giải ChọnC. Ta thấy ( )1;1 thỏa mãn hệ phương trình do đó ( )1;1 là một cặp nghiệm của hệ phương trình. Câu 26: Cho bất phương trình 250xy−+ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 9 A. ( )2;2 S B. ( )1;3 S C. ( )2;2 S− D. ( )2;4 S− Lời giải Chọn A Ta thấy ( )2;2 S vì 22.250 −+ . Câu 27: Miền nghiệm của bất phương trình 326 xy−− là A. B. C. D. Lời giải Chọn C Trước hết, ta vẽ đường thẳng ( ):326.dxy−=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ ( )d chứa điểm ( ) 0;0. Câu 28: Miền nghiệm của bất phương trình 326 xy+ là O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x O x y 2 3

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 10 A. B. C. D. Lời giải Chọn A Trước hết, ta vẽ đường thẳng ( ):326.dxy+= Ta thấy ( )0;0 không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng không chứa điểm ( ) 0;0. Câu 29: Miền nghiệm của bất phương trình 326 xy+− là O 2 3 y x O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 11 A. B. C. D. Lời giải Chọn D Trước hết, ta vẽ đường thẳng ( ):326.dxy+=− Ta thấy ( )0;0 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng chứa điểm ( ) 0;0. Câu 30: Cho bất phương trình 2320 xy −++ có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S . B. 2 ;0 2 S     . C. ( )1;2 S− . D. ( )1;0 S . Lời giải ChọnB. O x 2 3 y O x 2 3 y O x y 2 3 O x y 2 3 O 2 3 y x

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 12 Ta thấy 2 ;0 2 S     vì 2 2.3.020 2 −++= . Câu 31: Cặp số ( )(;) 2;3xy = là nghiệm của bất phương trình nào sau đây? A. 43xy  B. –370xy + C. 2–3–10 xy  D. –0xy  Lời giải Chọn D Ta có 2310 −=− nên Chọn D Câu 32: Cặp số ( )00 ; xy nào là nghiệm của bất phương trình 334 xy− . A. ( ) ( )00;2;2xy =− B. ( ) ( )00;5;1xy = C. ( ) ( )00;4;0xy =− D. ( ) ( )00;2;1xy = Lời giải Chọn B Thế các cặp số ( )00 ; xy vào bất phương trình: ( ) ( )00;2;2xy =− ( ) 334323.24 xy −−− ( ) ( )00;5;1xy = 3343.53.14 xy −− ( ) ( )00;4;0xy =− ( ) 3343.43.04 xy −−− ( ) ( )00;2;1xy = 3343.23.14 xy −− DẠNG 2. TÌM MIỀN NGHIỆM CỦA HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN Câu 33: Cặp số ( ); xy nào sau đây là một nghiệm của hệ bất phương trình 20 ? 310 −  +− xy xy A. ( ) ( );2;1 =−−xy B. ( ) ( );4;0 =xy C. ( ) ( );1;2 =xy D. ( ) ( );3;4 =−−xy Lời giải Chọn C Thay các cặp số ( ); xy trong các phương án vào hệ bất phương trình trên, ta thấy ( ) ( );1;2 =xy thỏa mãn hệ bất phương trình. Câu 34: Trong mặt phẳng Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 31 22 xy xy −  + ? A. ( ) 1;0.P B. ( ) 1;1.N C. ( ) 1;1.M D. ( ) 0;1.Q Lời giải Chọn C Ta thấy tọa độ điểm M thỏa mãn hệ bất phương trình nên thuộc miền nghiệm của hệ bất phương trình

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 13 Câu 35: Trong mặt phẳng với hệ trục tọa độ Oxy , điểm nào dưới đây thuộc miền nghiệm của hệ 210 3210 +−  ++ xy xy ? A. ( )1;1 B. ( )0;1 C. ( )1;0 D. ( )1;3 Lời giải Chọn A Với 1 1 =−  = x y hệ phương trình 21000 321000 +−  ++  xy xy Câu 36: Miền nghiệm của hệ bất phương trình 39 3 xy xy +  − là phần mặt phẳng chứa điểm A. ( )1;2 B. ( )0;0 C. ( )2;1 D. ( )8;4 Lời giải Chọn D Ta có: ( ) ( ) 3.8491 8432 +   −  cả và đều đúng. Câu 37: Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình 20 2320 xy xy +−  −+ là A. ( )0;0 B. ( )1;1 C. ( )1;1 D. ( )1;1 Lời giải ChọnC. Ta thay cặp số ( )1;1 vào hệ ta thấy không thỏa mãn. Câu 38: Câu nào sau đây đúng?. Miền nghiệm của hệ bất phương trình 10 23 3 2(1)4 2 0 xy y x x  +−   −+     là phần mặt phẳng chứa điểm A. ( )2;1 . B. ( )0;0 . C. ( )1;1 . D. ( )3;4 . Lời giải Chọn A Nhận xét: chỉ có điểm ( )2;1 thỏa mãn hệ Câu 39: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 2310 540 xy xy +−  −+ ? A. ( )1;4 . B. ( )2;4 . C. ( )0;0 . D. ( )3;4 . Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 14 ChọnC. Nhận xét: chỉ có điểm ( )0;0 không thỏa mãn hệ. Câu 40: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình 2510 250 10 xy xy xy −−  ++  ++ ? A. ( )0;0 . B. ( )1;0 . C. ( )0;2 . D. ( )0;2 . Lời giải ChọnC. Nhận xét: chỉ có điểm ( )0;2 thỏa mãn hệ Câu 41: Miền nghiệm của hệ bất phương trình 0 330 50 xy xy xy −  −+  +− là phần mặt phẳng chứa điểm A. ( )5;3 . B. ( )0;0 . C. ( )1;1 . D. ( )2;2 . Lời giải Chọn A Nhận xét: chỉ có điểm ( )5;3 thỏa mãn hệ Câu 42: Miền nghiệm của hệ bất phương trình 39 3 28 6 xy xy yx y +  −  −   là phần mặt phẳng chứa điểm A. ( )0;0 B. ( )1;2 C. ( )2;1 D. ( )8;4 Lời giải ChọnD. Nhận xét: chỉ có cặp số ( )8;4 thỏa bất phương trình 39 xy+ . Câu 43: Cho hệ bất phương trình 0 250 xy xy +  + có tập nghiệm là S . Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S . B. ( )1;1 S−− . C. 1 1; 2 S −  . D. 12 ; 25 S −  . Lời giải Chọn C Thế đáp án, chỉ có 1 1; 2xy==− thỏa mãn hệ bất phương trình  chọn C Câu 44: Miền nghiệm của hệ bất phương trình 36 3 28 4 xy xy yx y +  −  −   là phần mặt phẳng chứa điểm:

có toạ độ thoả mãn t

t c

6;4xy

phương trình đã cho là miề

các bất phương trình trong hệ

vào từng bất phương

mặt phẳng chứa t

t c

các điểm

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 15 A. ( )2;1 B. ( )6;4 C. ( )0;0 D. ( )1;2 Lời giải Chọn A

ận xét: Miền nghiệm của hệ

ất

ấ

ả

ấ

ả

ế

trình trong hệ, ta lần lượt có các mệnh đề đúng: 226;61;82;44  . Vậy ta chọn đáp án B Đáp án A có toạ độ không thoả bất phương trình thứ 3. Đáp án C, D có toạ độ không thoả bất phương trình thứ 1 và 3. Câu 45: Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 0 5410 5410 y xy xy   −  + . B. 0 5410 4510 x xy xy   −  + . C. 0 4510 5410 x xy xy   −  + . D. 0 5410 4510 x xy xy   −  + . Lời giải Chọn D Cạnh AC có phương trình 0x = và cạnh AC nằm trong miền nghiệm nên 0x  là một bất phương trình của hệ Cạnh AB qua hai điểm 5 ;0 2    và ( )0;2 nên có phương trình: 14510 52 2 xy xy +=+= Vậy hệ bất phương trình cần tìm là 0 5410 4510 x xy xy   −  + Câu 46: Cho hệ bất phương trình 0 310 x xy    ++  có tập nghiệm là S Khẳng định nào sau đây là khẳng định đúng? A. ( )1;1 S− . B. ( )1;3 S− . C. ( )1;5 S− . D. ( )4;3 S− . Lời giải ChọnC.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 16 Ta thấy ( )1;5 S− vì 10− . Câu 47: Cho hệ bất phương trình 0 310 x xy    ++  có tập nghiệm là S Khẳng định nào sau đây là khẳng định đúng? A. ( )1;2 S− B. ( )2;0 S C. ( )1;3 S− D. ( )3;0 S Lời giải ChọnD. Ta thấy ( )3;0 S vì 30 33.010    ++  . Câu 48: Cho hệ bất phương trình 3 1 10 2 xy xy −   −+  có tập nghiệm S . Khẳng định nào sau đây là khẳng định đúng ? A. ( )1;2 S− B. ( )2;1 S C. ( )5;6 S− D. S = Lời giải Chọn D Vì không có điểm nào thỏa hệ bất phương trình. Câu 49: Cho hệ bất phương trình 3 21 2 432 xy xy  −   − có tập nghiệm S . Khẳng định nào sau đây là khẳng định đúng ? A. 1 ;1 4 S−−   B. ( ) ;|432Sxyxy=−= C. Biểu diễn hình học của S là nửa mặt phẳng chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= D. Biểu diễn hình học của S là nửa mặt phẳng không chứa gốc tọa độ và kể cả bờ d , với d là là đường thẳng 432 xy−= . Lời giải Chọn B

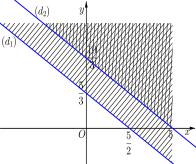
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 17 Trước hết, ta vẽ hai đường thẳng: ( )1 3 :21 2 dxy−= ( )2 :432dxy−= Thử trực tiếp ta thấy ( )0;0 là nghiệm của phương trình nhưng không phải là nghiệm của phương trình. Sau khi gạch bỏ các miền không thích hợp, tập hợp nghiệm của bất phương trình chính là các điểm thuộc đường thẳng ( ):432.dxy−= Câu 50: Cho hệ 235(1) 3 25(2) xy xy +   +  . Gọi 1S là tập nghiệm của bất phương trình, 2S là tập nghiệm của bất phương trình và S là tập nghiệm của hệ thì A. 12SS  . B. 21SS  . C. 2 SS = . D. 1 SS  . Lời giải Chọn B Trước hết, ta vẽ hai đường thẳng: ( )1 :235dxy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 18 ( )2 3 :5 2 dxy+= Ta thấy ( )0;0 là nghiệm của cả hai bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả hai miền nghiệm của hai bất phương trình. Say khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 51: Phần không gạch chéo ở hình sau đây là biểu diễn miền nghiệm của hệ bất phương trình nào trong bốn hệ A, B, C, D? A. 0 326 y xy   + . B. 0 326 y xy   +− . C. 0 326 x xy   + . D. 0 326 x xy   +− . Lời giải Chọn A Dựa vào hình vẽ ta thấy đồ thị gồm hai đường thẳng ( )1 :0dy = và đường thẳng ( )2 :326.dxy+= Miền nghiệm gồm phần y nhận giá trị dương. Lại có ( )0;0 thỏa mãn bất phương trình 326. xy+ Câu 52: Miền nghiệm của hệ bất phương trình 20 32 3 xy xy yx −  +−  − chứa điểm nào sau đây? A. ( )1;0A . B. ( )2;3B . C. ( )0;1C . D. ( ) 1;0.D Lời giải Chọn D Trước hết, ta vẽ ba đường thẳng: ( )1 :20dxy−= ( )2 :32dxy+=− ( )3 :3dyx−= O 2 3 y x

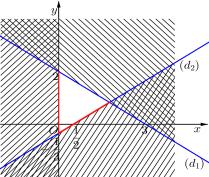
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 19 Ta thấy ( )0;1 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )0;1 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 53: Miền nghiệm của hệ bất phương trình 2360 0 2310 xy x xy +−    −− chứa điểm nào sau đây? A. ( ) 1;2.A B. ( )0;2B . C. ( )1;3C . D. 1 0;. 3 D    Lời giải Chọn D Trước hết, ta vẽ ba đường thẳng: ( )1 :2360dxy+−= ( )2 :0dx = ( )3 :2310dxy−−= Ta thấy ( )1;1 là nghiệm của các ba bất phương trình. Điều này có nghĩa là điểm ( )1;1 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ Câu 54: Miền nghiệm của hệ bất phương trình 210 350 x x − −+  chứa điểm nào sau đây? A. Không có B. 5 ;2. 3 B    C. ( ) 3;1.C D. 1 ;10 2 D    Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 20 Trước hết, ta vẽ hai đường thẳng: ( )1 :210dx −= ( )2 :350dx−+= Ta thấy ( )1;0 là không nghiệm của cả hai bất phương trình. Điều đó có nghĩa điểm ( )1;0 không thuộc cả hai miền nghiệm của hai bất phương trình. Vậy không có điểm nằm trên mặt phẳng tọa độ thỏa mãn hệ bất phương trình. Câu 55: Miền nghiệm của hệ bất phương trình 30 2310 y xy −  −+ chứa điểm nào sau đây? A. ( )3;4A B. ( )4;3B C. ( )7;4C D. ( ) 4;4.D Lời giải Chọn C Trước hết, ta vẽ hai đường thẳng: ( )1 :30dy−= ( )2 :2310dxy−+= Ta thấy ( )6;4 là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm ( )6;4 thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 21 Câu 56: Miền nghiệm của hệ bất phương trình 20 32 xy xy −  +− không chứa điểm nào sau đây? A. ( ) 1;0.A B. ( ) 1;0.B C. ( )3;4C D. ( ) 0;3.D Lời giải Chọn B Trước hết, ta vẽ hai đường thẳng: ( )1 :20dxy−= ( )2 :32dxy+=− Ta thấy ( )0;1 là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm ( )0;1 thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ phần không thích hợp, phần không bị gạch là miền nghiệm của hệ Câu 57: Miền nghiệm của hệ bất phương trình 3260 3 2(1)4 2 0 xy y x x −−   −+    không chứa điểm nào sau đây? A. ( )2;2A B. ( ) 3;0.B C. ( ) 1;1.C D. ( ) 2;3.D Lời giải Chọn C Trước hết, ta vẽ ba đường thẳng: ( )1 :3260dxy−−= ( )2 :43120dxy+−= ( )3 :0dx =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 22 Ta thấy ( )2;1 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )2;1 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 58: Miền nghiệm của hệ bất phương trình 0 33 5 xy xy xy −  −−  + không chứa điểm nào sau đây? A. ( ) 3;2.A B. ( ) 6;3.B C. ( ) 6;4.C D. ( ) 5;4.D Lời giải Chọn A Trước hết, ta vẽ ba đường thẳng: ( )1 :0dxy−= ( )2 :33dxy−=− ( )3 :5dxy+= Ta thấy ( )5;3 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )5;3 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền không thích hợp, miền không bị gạch là miền nghiệm của hệ Câu 59: Miền nghiệm của hệ bất phương trình 30 23 2 xy xy yx −  +−  + không chứa điểm nào sau đây? A. ( ) 0;1.A B. ( ) 1;1.B C. ( ) 3;0.C D. ( ) 3;1.D Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 23 Chọn C Trước hết, ta vẽ ba đường thẳng: ( )1 :30dxy−= ( )2 :23dxy+=− ( )3 :2dxy+= Ta thấy ( )1;0 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm ( )1;0 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Câu 60: Miền tam giác ABC kể cả ba cạnh ,, ABBCCA trong hình là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây? A. 20 20 220 xy xy xy +−  −+  −+ B. 20 20 220 xy xy xy +−  −+  −+ C. 20 20 220 xy xy xy +−  −+  −+ D. 20 20 220 xy xy xy +−  −+  −+ Lời giải FB Người gắn ID: Trần Lộc Chọn A Cạnh AB nằm trên đường thẳng 1 :20dxy+−= Cạnh AC nằm trên đường thẳng 2 :20dxy−+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 24 Cạnh BC nằm trên đường thẳng 3 :220dxy−+= Đường thẳng 1 :20dxy+−= chia mặt phẳng Oxy thành hai nửa mặt phẳng bờ 1d , thay tọa độ ( )0;0O vào vế trái 1d ta có 20− . Vậy nửa mặt phẳng chứa điểm O là miền nghiệm của bất phương trình 20xy+− . Tương tự nửa mặt phẳng chứa điểm O là miền nghiệm của bất phương trình 20xy−+ Nửa mặt phẳng không chứa điểm O là miền nghiệm của bất phương trình 220xy−+ . Từ (1),(2),(3) suy ra miền tam giác ABC kể cả ba cạnh ,, ABBCCA là miền nghiệm của hệ bất phương trình 20 20 220 xy xy xy +−  −+  −+ DẠNG 3. TÌM GIÁ TRỊ NHỎ NHẤT- GIÁ TRỊ LỚN NHẤT Câu 61: Giá trị nhỏ nhất của biểu thức Fyx =− trên miền xác định bởi hệ 22 24 5 yx yx xy −  −  + là A. min1 F = khi 2x = , 3y = . B. min2 F = khi 0x = , 2y = . C. min3 F = khi 1x = , 4y = D. min0 F = khi 0x = , 0y = Lời giải Chọn A Miền nghiệm của hệ 22 24 5 yx yx xy −  −  + là miền trong của tam giác ABC kể cả biên Ta thấy Fyx =− đạt giá trị nhỏ nhất chỉ có thể tại các điểm A , B , C .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 25 Tại ( )0;2A thì 2F = Tại ( )1;4B thì 3F = Tại ( )2;3A thì 1F = . Vậy min1 F = khi 2x = , 3y = Câu 62: Giá trị nhỏ nhất của biết thức Fyx =− trên miền xác định bởi hệ 22 2 54 xy xy xy +  −  +− là A. min 3F =− khi 1,2xy==− . B. min0 F = khi 0,0xy== . C. min 2F =− khi 42 , 33xy==− . D. min 8F = khi 2,6xy=−= . Lời giải Chọn C Biểu diễn miền nghiệm của hệ bất phương trình 22 2 54 xy xy xy +  −  +− trên hệ trục tọa độ như dưới đây: Giá trị nhỏ nhất của biết thức Fyx =− chỉ đạt được tại các điểm ( ) 4217 2;6,;,; 3333 ACB   . Ta có: ( ) ( ) ( ) 8;2;2FAFBFC==−=− . Vậy min 2F =− khi 42 , 33xy==− . Câu 63: Cho hệ bất phương trình 2 3515 0 0 xy xy x y −  +     . Khẳng định nào sau đây là khẳng định sai? A. Trên mặt phẳng tọa độ Oxy , biểu diễn miền nghiệm của hệbất phương trình đã cho là miền tứ giác ABCO kể cả các cạnh với ( )0;3A , 259 ; 88 B    , ( )2;0C và ( )0;0O B. Đường thẳng : xym+= có giao điểm với tứ giác ABCO kể cả khi 17 1 4 m −

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 26 C. Giátrị lớnnhất củabiểuthức xy + ,với x và y thỏamãnhệbất phươngtrình đãcho là 17 4 D. Giátrị nhỏnhất củabiểuthức xy + ,với x và y thõamãn hệbất phươngtrìnhđãcholà0. Lời giải Chọn B Trước hết, ta vẽ bốn đường thẳng: ( )1 :2dxy−= ( )2 :3515dxy+= ( )3 :0dx = ( )4 :0dy = Miền nghiệm là phần không bị gạch, kể cả biên. Câu 64: Giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ với điều kiện 04 0 10 2100 y x xy xy     −−  +− là A. 6 B. 8 C. 10 D. 12 Lời giải Chọn C Vẽ đường thẳng 1 :10dxy−−= , đường thẳng 1d qua hai điểm ( )0;1 và ( )1;0 Vẽ đường thẳng 2 :2100dxy+−= , đường thẳng 2d qua hai điểm ( )0;5 và ( )2;4 . Vẽ đường thẳng 3 :4dy =

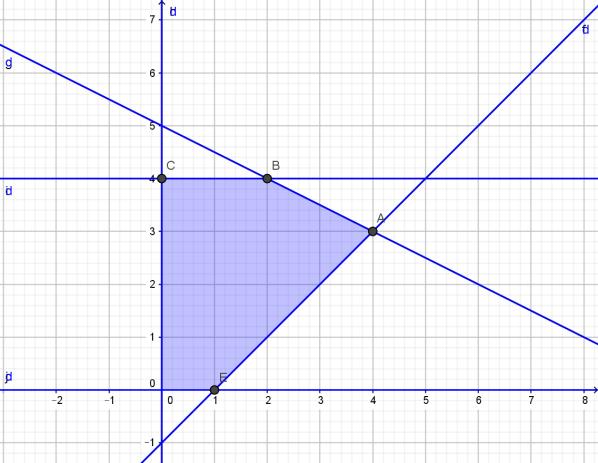
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 27 Miền nghiệm là ngũ giác ABCOE với ( ) ( ) ( ) ( )4;3,2;4,0;4,1;0ABCE Ta có: ( ) 4;310F = , ( ) 2;410F = , ( ) 0;48F = , ( ) 1;01F = , ( ) 0;00F = . Vậy giá trị lớn nhất của biết thức ( ) ;2 Fxyxy =+ bằng 10. Câu 65: Giá trị nhỏ nhất của biết thức ( ) ;2 Fxyxy =− với điều kiện 05 0 20 20 y x xy xy     +−  −− là A. 10. B. 12. C. 8. D. 6. Lời giải Chọn A Biểu diễn miền ngiệm của hệ bất phương trình 05 0 20 20 y x xy xy     +−  −− trên hệ trục tọa độ như dưới đây:. Nhận thấy biết thức Fyx =− chỉ đạt giá trị nhỏ nhất tại các điểm ,, ABC hoặc D . Ta có: ( ) ( ) 7253;2510FAFB=−=−=−=− . ( ) ( ) 224,2202FCFD=−=−=−= . Vậy min 10F =− khi 0,5xy== .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 28 Câu 66: Biểu thức Fyx = đạt giá trị nhỏ nhất với điều kiện 22 22 5 0 xy xy xy x −+−  −  +   tại điểm ( ); Sxy có toạ độ là A. ( )4;1 . B. ( )3;1 . C. ( )2;1 . D. ( )1;1 . Lời giải Chọn A Biểu diễn miền ngiệm của hệ bất phương trình 22 22 5 0 xy xy xy x −+−  −  +   trên hệ trục tọa độ như dưới đây: Nhận thấy biết thức Fyx =− chỉ đạt giá trị nhỏ nhất tại các điểm , AB hoặc C . Chỉ ( )4;1C có tọa độ nguyên nên thỏa mãn. Vậy min 3F =− khi 4,1xy== Câu 67: Biểu thức Lyx =− , với x và y thõa mãn hệ bất phương trình 2360 0 2310 xy x xy +−    −− , đạt giá trị lớn nhất là a và đạt giá trị nhỏ nhất là b . Hãy chọn kết quả đúng trong các kết quả sau: A. 25 8 a = và 2b =− B. 2a = và 11 12 b =− C. 3a = và 0b = D. 3a = và 9 8 b = Lời giải Chọn B

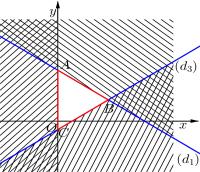
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 29 Trước hết, ta vẽ ba đường thẳng: ( )1 :2360dxy+−= ( )2 :0dx = ( )3 :2310dxy−−= Ta thấy ( )0;0 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa gốc tọa độ thuộc cả ba miền nghiệm của cả ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Miền nghiệm là hình tam giác ABC , với ( ) 0;2,A 75 ;, 46 B    1 0;. 3 C    Vậy ta có 202,a =−= 5711 6412 b =−=− DẠNG 4. ÁP DỤNG BÀI TOÁN THỰC TIỄN Câu 68: Trong một cuộc thi pha chế, hai đội A, B được sử dụng tối đa 24g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu; pha chế 1 lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Đội A pha chế được a lít nước cam và b lít nước táo và dành được điểm thưởng cao nhất. Hiệu số ab là A. 1 B. 3 C. 1 D. 6 Lời giải Chọn C Gọi , xy lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế ( )0;0xy Để pha chế x lít nước cam cần 30x g đường, x lít nước và x g hương liệu. Để pha chế y lít nước táo cần 10y g đường, y lít nước và 4y g hương liệu. Theo bài ra ta có hệ bất phương trình:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 30 ( ) 3010210 9 * 424 0;0 xy xy xy xy +  +  +   . Số điểm đạt được khi pha x lít nước cam và y lít nước táo là ( ) ,y6080 Mxxy =+ . Bài toán trở thành tìm , xy để ( ), Mxy đạt giá trị lớn nhất. Ta biểu diễn miền nghiệm của hệ ( )* trên mặt phẳng tọa độ như sau: Miền nghiệm là ngũ giác ABCDE Tọa độ các điểm: ( )4;5A , ( )6;3B , ( )7;0C , ( )0;0D , ( )0;6E ( ), Mxy sẽ đạt giá trị lớn nhất, giá trị nhỏ nhất tại các đỉnh của miền nghiệm nên thay tọa độ các điểm vào biểu thức ( ), Mxy ta được: ( ) 4;5640M = ; ( ) 6;3600M = , ( ) 7;0420M = , ( ) 0;00M = , ( ) 0;6480M = . Vậy giá trị lớn nhất của ( ); Mxy bằng 640 khi 4;5xy== 4;51abab ==−=− Câu 69: Một hộ nông dân định trồng đậu và cà trên diện tích 2800 m . Nếu trồng đậu trên diện tích 2100 m thì cần 20công làm và thu được 3000000 đồng. Nếu trồng cà thì trên diện tích 2100 m cần 30 công làm và thu được 4000000 đồng. Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được nhiều tiền nhất khi tổng số công làm không quá 180 công. Hãy chọn phương án đúng nhất trong các phương án sau: A. Trồng 2600 m đậu; 2200 m cà. B. Trồng 2500 m đậu; 2300 m cà. C. Trồng 2400 m đậu; 2200 m cà. D. Trồng 2200 m đậu; 2600 m cà. Lời giải Chọn A Giả sử diện tích trồng đậu là x ;suy ra diện tích trồng cà là 8 x Ta có thu nhập thu được là ( ) ( ) ( )348.100001000032Sxxxx  =+−=−+  đồng. Tổng số công là ( ) 2030810240 xxx +−=−+ Theo giả thiết có 102401806 xx −+ x+y=9 x y E D≡O C B A 30x+10y=210 x+4y=24

Câu

Mà

t công

trong m

cáo và bán khuy

n mãi hàng hóa (1 sản phẩm mới c

a công ty) cần thuê xe để chở trên 140 người và trên 9 tấn

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 31

hàm số ( )Sx là hàm nghịch biến trên nên ( )Sx đạt giá trị lớn nhất khi 6x =

đó trồng 2600 m đậu, 2200 m cà.

70:

ộ

ty TNHH

ột đợt quảng

ế

ủ

hàng. Nơi thuê chỉ có hai loại xe A và B . Trong đó xe loại A có 10 chiếc, xe loại B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu, loại B giá 3 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhất. Biết rằng xe A chỉ chở tối đa 20 người và 0,6 tấn hàng. Xe B chở tối đa 10 người và 1,5 tấn hàng. A. 4 xe A và 5 xe B . B. 5 xe A và 6 xe B . C. 5 xe A và 4 xe B . D. 6 xe A và 4 xe B . Lời giải Chọn D Gọi x là số xe loại A ( )010;xx  , y là số xe loại B ( )09;y y  . Khi đó tổng chi phí thuê xe là 43 Txy =+ Xe A chở tối đa 20 người, xe B chở tối đa 10 người nên tổng số người 2 xe chở tối đa được là 2010xy + Xe A chở được 0,6 tấn hàng, xe B chở được 1,5 tấn hàng nên tổng lượng hàng 2 xe chở được là 0,61,5xy + . Theo giả thiết, ta có 010 09 2010140 0,61,59 x y xy xy     +  + ( )* Biểu diễn miền nghiệm của hệ bất phương trình ( )* là tứ giác ABCD kể cả miền trong của tứ giác. Biểu thức 43 Txy =+ đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.

gia đình cần

900 đơn

400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 32 Tại các đỉnh ( ) ( ) ( )5 10;2;10;9;;9;5;4 2 ABCD    , ta thấy T đạt giá trị nhỏ nhất tại 5 4 x y =  = Khi đó min 32T = Câu 71: Một

ít nhất

vị protein và

đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi , xy lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính 22 xy + A. 22 1,3xy+= . B. 22 2,6xy+= . C. 22 1,09xy+= . D. 22 0,58xy+= . Lời giải Chọn A Điều kiện: 01,6 x  ; 01,1 y  Khi đó số protein có được là 800600xy + và số lipit có được là 200400xy + Vì gia đình đó cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là: 800600900à200400400 xyvxy ++ 869à22 xyvxy ++ 01,6 01,1 869 22 x y xy xy     +  + Miền nghiệm của hệ trên là miền nghiệm của tứ giác ABCD Chi phí để mua x kg thịt bò và y kg thịt lợn là 160110 Txy =+ Biết T đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD Tại A: 160.0,6110.0,7173T =+= Tại B: 160.1,6110.0,2278T =+= Tại C: 160.1,6110.1,1377T =+= Tại D: 160.0,3110.1,1169T =+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 33 Vậy T đạt GTNN khi 0,3;1,1xy== 22220,31,11,3xy +=+= Câu 72: Có hai cái giỏ đựng trứng gồm giỏ A và giỏ B, các quả trứng trong mỗi đều có hai loại là trứng lành và trứng hỏng. Tổng số trứng trong hai giỏ là 20 quả và số trứng trong giỏ A nhiều hơn số trứng trong giỏ B. Lấy ngẫu nhiên mỗi giỏ 1 quả trứng, biết xác suất để lấy được hai quả trứng lành là 55 84 . Tìm số trứng lành trong giỏ A. A. 6. B. 14. C. 11. D. 10. Lời giải Chọn C Gọi a là số trứng lành, b là số trứng hỏng trong giỏ A. Gọi x là số trứng lành, y là số trứng hỏng trong giỏ B. Lấy ngẫu nhiên mỗi giỏ 1 quả trứng, xác suất để lấy được hai quả trứng lành: 55 84 ax abxy = ++ Do đó: ( ) ( )( ) ( )( ) ( )2 .55 1484 11 620 5 .55 100 2 ax abxyab a abxyxy x abxyabxyax    +++= = +++=+=  = +++  ++=   Suy ra: Giỏ A có 11 quả trứng lành. Câu 73: Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 gam hương liệu, 9 lít nước và 210 gam đường để pha chế nước ngọt loại I và nước ngọt loại II. Để pha chế 1 lít nước ngọt loại I cần 10 gam đường, 1 lít nước và 4 gam hương liệu. Để pha chế 1 lít nước ngọt loại II cần 30 gam đường, 1 lít nước và 1 gam hương liệu. Mỗi lít nước ngọt loại I được 80 điểm thưởng, mỗi lít nước ngọt loại II được 60 điểm thưởng. Hỏi số điểm thưởng cao nhất có thể của mỗi đội trong cuộc thi là bao nhiêu? A. 540. B. 600 . C. 640 . D. 720. Lời giải Chọn C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 34 Gọi số lít nước ngọt loại I là x và số lít nước ngọt loại II là y. Khi đó ta có hệ điều kiện về vật liệu ban đầu mà mỗi đội được cung cấp: 10302103210 424424 99 ,0,0 xyxy xyxy xyxy xyxy ++ ++   ++    Điểm thưởng đạt được: 8060 Pxy =+ Bài toán đưa về tìm giá trị lớn nhất của biểu thức P trong miền D được cho bởi hệ điều kiện Biến đổi biểu thức 806080600PxyxyP =++−= đây là họ đường thẳng Δ trong hệ tọa độ Oxy Miền D được xác định trong hình vẽ bên dưới: Giá trị lớn nhất của P ứng với đường thẳng Δ đi qua điểm (5;4)A , suy ra: max 80.560.40640PPP+−=→== . Câu 74: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II . Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là. A. 32 triệu đồng. B. 35 triệu đồng. C. 14 triệu đồng. D. 30 triệu đồng. Lời giải Chọn A Gọi x , y lần lượt là số sản phẩm loại I và loại II được sản xuất ra. Điều kiện x , y nguyên dương. x y O 5 6 9 4 3 6 7 9 Δ(P) A

Câu 75: Một gia đình cần ít nhất 900 đơn

protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kiogam thịt bò chứa 800 đơn vị protein và 200đơn vị lipit. Mỗi kilogam thịt lợn chứa 600đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, một kg thịt lợn là 110 nghìn đồng. Gọi x , y lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua. Tìm x , y để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn? A. 0,3x = và 1,1y = B. 0,3x = và 0,7

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 35 Ta có hệ bất phương trình sau: 32180 6220 0 0 xy xy x y +  +     Miền nghiệm của hệ trên là Tiền lãi trong một tháng của xưởng là 0,50,4 Txy =+ Ta thấy T đạt giá trị lớn nhất chỉ có thể tại các điểm A , B , C . Vì C có tọa độ không nguyên nên loại. Tại ( )60;0A thì 30T = triệu đồng. Tại ( )40;30B thì 32T = triệu đồng. Vậy tiền lãi lớn nhất trong một tháng của xưởng là 32 triệu đồng.

vị

y = C. 0,6x = và 0,7y = D. 1,6x = và 0,2y = Lời giải Chọn A Theo bài ra ta có số tiền gia đình cần trả là 160.110.xy + với x , y thỏa mãn: 01,6 01,1 x y    Số đơn vị protein gia đình có là 0,8.0,6.0,9 xy+ 869 xy + ( )1d . Số đơn vị lipit gia đình có là0,2.0,4.0,422 xyxy ++ ( )2d . Bài toán trở thành: Tìm , xy thỏa mãn hệ bất phương trình 01,6 01,1 869 22 x y xy xy     +  + sao cho 160.110. Txy =+ nhỏ nhất. x y B 90 OA C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ II TOÁN 10 BẤT PHƯƠNG TRÌNH HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT 2 ẨN Sưu tầm và biên soạn Page 36 Vẽ hệ trục tọa độ ta tìm được tọa độ các điểm ( )1,6;1,1A ; ( )1,6;0,2B ; ( )0,6;0,7C ; ( )0,3;1,1D . Nhận xét: ( ) 377TA = nghìn, ( ) 278TB = nghìn, ( ) 173TC = nghìn, ( ) 169TD = nghìn. Vậy tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn thì 0,6x = và 0,7y = O x y A BC D 1 2 1 2 1,6x = 1,1y = 22xy+= 869 xy+=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 1 BÀI 5. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180 . I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC (CUNG). 1. Định nghĩa. Trong mặt phẳng tọa độ Oxy .Với góc ( )oo 0180 , ta xác định được duy nhất điểm M trên trên đường nửa đường tròn đơn vị tâm O , sao cho xOM = , biết ( ); Mxy Khi đó: ooosin;cos;tan(90);cot (0,180)yx yx xy  ==== Các số sin,cos,tan,cot được gọi là giá trị lượng giác của góc  Chú ý: Với oo 0180   ta có 0sin1;1cos1  − Từ định nghĩa trên, ta có: CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC LÝ THUYẾT.I = x y OP M(x;y)Q Hình 2.1 tan(90);cotsincos cossin    == 0  180   ( )1 tan0;90;180 cot   =( và );

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 2 2. Dấu của giá trị lượng giác. Góc 0ooo 90180 sin + + cos + tan + cot + II. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU oo oo sin(180)sin ; cos(180)cos tan(180)tan ; cot(180)cot III. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU (BỔ SUNG) o o o o sin(90)cos cos(90)sin tan(90)cot cot(90)tan IV. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC ĐẶC BIỆT Góc 00 300 450 600 900 sin 0 1 2 2 2 3 2 1 cos 1 3 2 2 2 1 2 0 tan 0 3 3 1 3  cot  3 1 3 3 0 V. CÁC HỆ THỨC LƯỢNG GIÁC CƠ BẢN (BỔ SUNG KẾT QUẢ CỦA BÀI TẬP 3.3/TR37) 22 2 2 2 2 sin tan(90); cos cos cot(0;180) sin tan.cot1(0;90;180) sincos1 1 1tan(90) cos 1 1cot(0;180) sin             = = = += += += o oo ooo o oo BÀI TẬP SÁCH GIÁO KHOA. =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 4 DẠNG 1: TÍNH CÁC GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC · Sử dụng định nghĩa giá trị lượng giác của một góc · Sử dụng tính chất và bảng giá trị lượng giác đặc biệt Sử dụng các hệ thức lượng giác cơ bản Câu 1. Tính giá trị các biểu thức sau: a) 222oo o sin90cos90cos180Aabc =++ b) 22 o 2 oo 3sin902cos603tan45B =−+− c) 20222ooooo sin452sin503cos452sin404tan55.tan35C =−+−+ Câu 2. Tính giá trị các biểu thức sau: a) oooo 2222 sin3sin15sin75sin87A =+++ b) ooooo cos0cos20cos40...cos160cos180B =+++++ c) ooooo tan5tan10tan15...tan80tan85C = Câu 1: Giá trị của oo cos60sin30 + bằng bao nhiêu? A. 3 2 B. 3 C. 3 3 D. 1. Câu 2: Giá trị của oo tan30cot30 + bằng bao nhiêu? A. 4 3 B. 13 3 + C. 2 3 D. 2 Câu 3: Trong các đẳng thức sau đây, đẳng thức nào sai? A. oo sin0cos01 += B. oo sin90cos901 += C. oo sin180cos1801 +=− D. oo sin60cos601 += Câu 4: Trong các khẳng định sau, khẳng định nào sai? A. oo cos60sin30 = . B. oo cos60sin120 = . C. oo cos30sin120 = . D. oo sin60cos120 =− . Câu 5: Đẳng thức nào sau đây sai? HỆ THỐNG BÀI TẬP.II == PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 = BÀI TẬP TRẮC NGHIỆM.3 =

Câu

Trong

Câu

Trong

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 5

oo sin45sin452 += B. oo sin30cos601 += C. oo sin60cos1500 += . D. oo sin120cos300 += .

6: Giá trị oo cos45sin45 + bằng bao nhiêu?

1 B. 2 C. 3 D. 0

các đẳng thức sau, đẳng thức nào đúng?

( )o sin180cos−=− B. ( )o sin180sin−=− C. ( )o sin180sin−=. D. ( )o sin180cos−=.

các đẳng thức sau, đẳng thức nào sai?

oo sin0cos00 += B. oo sin90cos901 += C. oo sin180cos1801 +=− . D. oo 31sin60cos60 2 + += . Câu 9: Cho  là góc tù. Điều khẳng định nào sau đây là đúng? A. sin0   . B. cos0   . C. tan0   . D. cot0   . Câu 10: Giá trị của oooo sin36cos6sin126cos84E = là A. 1 2 . B. 3 2 . C. 1. D. 1. Câu 11: Giá trị của biểu thức oo 2222oo sin51sin55sin39sin35A =+++ là A. 3. B. 4. C. 1. D. 2. Câu 12: Giá trị của biểu thức ooooo tan1tan2tan3...tan88tan89A = là A. 0. B. 2. C. 3. D. 1. Câu 13: Tổng ooooo 222222o sin2sin4sin6...sin84sin86sin88 ++++++ bằng A. 21 B. 23 C. 22 D. 24 Câu 14: Giá trị của ooooo tan5.tan10.tan15...tan80.tan85A = là A. 2. B. 1. C. 0. D. 1. Câu 15: Giá trị của 2222 cos73cos87cos3cos17B  =+++ là A. 2 . B. 2. C. 2. D. 1. .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 6 DẠNG 2: TÍNH GIÁ TRỊ CỦA MỘT BIỂU THỨC LƯỢNG GIÁC , KHI BIẾT TRƯỚC MỘT GIÁ TRỊ LƯỢNG GIÁC. Dựa vào các hệ thức lượng giác cơ bản Dựa vào dấu của giá trị lượng giác Sử dụng các hằng đẳng thức đáng nhớ Câu 1. Cho 1 sin 3  = với 00 90180   . Tính cos và tan Câu 2. Cho 2 cos 3  =− và sin0   . Tính sin và cot Câu 3. Cho tan22  =− tính giá trị lượng giác còn lại. Câu 4. Cho 3 cos 4  = với 00 090   . Tính tan3cot tancot A   + = + Câu 5. Cho tan2  = . Tính 33 sincos sin3cos2sin B   = ++ Câu 6. Biết sincosxxm += a) Tìm 44 sincosxx b) Chứng minh rằng 2m  . Câu 1: Cho 1 cos 2 x = . Tính biểu thức 22 3sin4cos Pxx =+ A. 13 4 . B. 7 4 . C. 11 4 . D. 15 4 . Câu 2: Biết 1 cos 3  = . Giá trị đúng của biểu thức 22 sin3cosP =+ là: A. 1 3 B. 10 9 C. 11 9 D. 4 3 Câu 3: Cho biết 1 tan 2  = . Tính cot PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 = BÀI TẬP TRẮC NGHIỆM.3 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 7 A. cot2  = . B. cot2  = . C. 1 cot 4  = . D. 1 cot 2  = . Câu 4: Cho biết 2 cos 3  =− và 0 2    . Tính tan? A. 5 4 B. 5 2 C. 5 2 D. 5 2 Câu 5: Cho  là góc tù và sin5 13  = Giá trị của biểu thức 3sin2cos + là A. 3 B. 9 13 C. 3 D. 9 13 Câu 6: Cho biết sincos a+= . Giá trị của sin.cos bằng bao nhiêu? A. 2sin.cos a = B. sin.cos2a = C. 2sin.cos1 2 a  = D. 2 1sin.cos 2 a  = Câu 7: Cho biết 2 cos 3  =− . Tính giá trị của biểu thức cot3tan 2cottan E   + = + ? A. 19 13 B. 19 13 C. 25 13 D. 25 13 Câu 8: Cho biếtcot5  = . Tính giá trị của 2 2cos5sincos1E  =++ ? A. 10 26 B. 100 26 C. 50 26 D. 101 26 . Câu 9: Cho 1 cot 3  = . Giá trị của biểu thức 3sin4cos 2sin5cos A   + = là: A. 15 13 . B. 13. C. 15 13 . D. 13. Câu 10: Cho biết 2 cos 3  =− . Giá trị của biểu thức cot3tan 2cottan E   = bằng bao nhiêu? A. 25 3 . B. 11 13 . C. 11 3 . D. 25 13 . Câu 11: Biết sincos2 aa+= . Hỏi giá trị của 44 sincosaa + bằng bao nhiêu? A. 3 2 . B. 1 2 . C. 1. D. 0. Câu 12: Cho tancot m+= . Tìm m để 22 tancot7 += . A. 9m = . B. 3m = . C. 3m =− . D. 3m = . Câu 13: Cho biết 3cossin1 −= , oo 090   Giá trị của tan bằng A. 4 tan 3  = B. 3 tan 4  = C. 4 tan 5  = D. 5 tan 4  = Câu 14: Cho biết 2cos2sin2 += , 00 090.   Tính giá trị của cot.  A. 5 cot 4  = B. 3 cot 4  = C. 2 cot 4  = D. 2 cot 2  =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 8 Câu 15: Cho biết 1 cossin. 3 += Giá trị của 22 tancotP =+ bằng bao nhiêu? A. 5 4 P = . B. 7 4 P = . C. 9 4 P = . D. 11 4 P = . Câu 16: Cho biết 1 sincos. 5 −= Giá trị của 44 sincosP =+ bằng bao nhiêu? A. 15 5 P = B. 17 5 P = C. 19 5 P = D. 21 5 P = DẠNG 3: CHỨNG MINH CÁC ĐẲNG THỨC, RÚT GỌN CÁC BIỂU THỨC LƯỢNG GIÁC · Sử dụng các hệ thức lượng giác cơ bản · Sử dụng tính chất của giá trị lượng giác Sử dụng các hằng đẳng thức đáng nhớ . Câu 1. Chứng minh các đẳng thức sau (giả sử các biểu thức sau đều có nghĩa) a) 4422 sincos12sin.cos xxxx +=− b) 1cottan1 1cottan1 xx xx ++ = c) 32 3 cossin tantantan1 cos xx xxx x + =+++ Câu 2. Cho tam giác ABC . Chứng minh ( ) 33 sincoscos 22 .tan2 sincossin 22 BB AC B ACAC B + +−= ++    Câu 3. Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa) a) o o222 sin(90)cos(180)sin(1tan)tan Axxxxx =−+−++− b) 111 .2 sin1cos1cos B xxx =+− +− Câu 4. Chứng minh biểu thức sau không phụ thuộc vào x . 424424 sin6cos3coscos6sin3sin Pxxxxxx =+++++ PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 9 Câu 1: Trong các hệ thức sau hệ thức nào đúng? A. 22 sincos1 += . B. 22 sincos1 2   += . C. 22 sincos1 += . D. 22 sin2cos21 += . Câu 2: Trong các hệ thức sau hệ thức nào đúng? A. 22 sincos1 += . B. 22 sincos1 2   += . C. 22 sincos1 += . D. 22 sincos1 += . Câu 3: Trong các hệ thức sau hệ thức nào đúng? A. sin2cos21 += B. 22 sincos1 += C. 22 sincos1 += D. 22 sincos1 += Câu 4: Rút gọn biểu thức sau ( ) ( ) 22 tancottancot Axxxx =+−− A. 4A = B. 1A = C. 2A = D. 3A = Câu 5: Đơn giản biểu thức ( ) 222 1sincot1cot Gxxx =−+− . A. 2sin x B. 2 cos x C. 1 cos x D. cos x Câu 6: Khẳng định nào sau đây là sai? A. 22 sincos1 += . B. ( )2 2 1 1cotsin0 sin   += . C. ( )tan.cot1sin.cos0  =− . D. ( )2 2 1 1tancos0 cos   += . Câu 7: Rút gọn biểu thức 21sin 2sin.cos x P xx = ta được A. 1 tan 2 Px = B. 1 cot 2 Px = C. 2cot Px = D. 2tan Px = Câu 8: Đẳng thức nào sau đây là sai? A. ( ) ( ) 22 cossincossin2, xxxxx ++−= . B. 2222 tansintansin,90 xxxxx  −= C. 4422 sincos12sincos, xxxxx +=− . D. 6622 sincos13sincos, xxxxx −=− Câu 9: Đẳng thức nào sau đây là sai? A. ( )1cossin sin1cos0,180 xx xx xx  = + B. ( )1 tancot0,90,180 sincos xxx xx  += C. ( )22 22 1 tancot20,90,180 sincos xxx xx  +=− D. 22 sin2cos22 xx+= Câu 10: Biểu thức 2222 tansintansinxxxx −+ có giá trị bằng A. 1. B. 0. C. 2. D. 1. Câu 11: Biểu thức ( )2 cottanaa + bằng A. 22 11 sincos . B. 22 cottan2 aa + . C. 22 11 sincos + . D. 22 cottan2 aa + . BÀI TẬP TRẮC NGHIỆM.3 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 10 Câu 12: Đơn giản biểu thức sin cot 1cos x Ex x =+ + ta được A. sin x . B. 1 cos x . C. 1 sin x . D. cos x . Câu 13: Rút gọn biểu thức sau 22 2 cotcossin.cos cotcot Axxxx xx =+ A. 1A = B. 2A = C. 3A = D. 4A = Câu 14: Biểu thức ( ) ( ) ( )4466 3sincos2sincos fxxxxx =+−+ có giá trị bằng: A. 1 B. 2 C. 3 D. 0 Câu 15: Biểu thức: ( ) 4222 coscossinsin fxxxxx =++ có giá trị bằng A. 1. B. 2. C. 2. D. 1. Câu 16: Trong các mệnh đề sau, mệnh đề nào sai? A. ( )2 sincos12sincos xxxx = . B. 4422 sincos12sincosxxxx += . C. ( )2 sincos12sincos xxxx +=+ . D. 6622 sincos1sincosxxxx += .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 1 BÀI 5. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180 . I. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC (CUNG). 1. Định nghĩa. Trong mặt phẳng tọa độ Oxy .Với góc ( )oo 0180 , ta xác định được duy nhất điểm M trên trên đường nửa đường tròn đơn vị tâm O , sao cho xOM = , biết ( ); Mxy . Khi đó: ooosin;cos;tan(90);cot (0,180)yx yx xy  ==== Các số sin,cos,tan,cot được gọi là giá trị lượng giác của góc  . Chú ý: Với oo 0180   ta có 0sin1;1cos1  − Từ định nghĩa trên, ta có: 2. Dấu của giá trị lượng giác. Góc 0ooo 90180 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC LÝ THUYẾT.I = x y OP M(x;y)Q Hình 2.1 tan(90);cotsincos cossin    == 0  180   ( )1 tan0;90;180 cot   =( và );

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 2 sin + + cos + tan + cot + II. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC BÙ NHAU oo oo sin(180)sin ; cos(180)cos tan(180)tan ; cot(180)cot III. MỐI QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC CỦA HAI GÓC PHỤ NHAU (BỔ SUNG) o o o o sin(90)cos cos(90)sin tan(90)cot cot(90)tan IV. GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC GÓC ĐẶC BIỆT Góc 00 300 450 600 900 sin 0 1 2 2 2 3 2 1 cos 1 3 2 2 2 1 2 0 tan 0 3 3 1 3  cot  3 1 3 3 0 V. CÁC HỆ THỨC LƯỢNG GIÁC CƠ BẢN (BỔ SUNG KẾT QUẢ CỦA BÀI TẬP 3.3/TR37) 22 2 2 2 2 sin tan(90); cos cos cot(0;180) sin tan.cot1(0;90;180) sincos1 1 1tan(90) cos 1 1cot(0;180) sin             = = = += += += o oo ooo o oo

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 3 3.1. Không dùng bảng số hay máy tính cầm tay, tính giá trị của các biểu thức sau: a) ( )( )2sin30cos1353tan150cos180cot60 +−− ; b) 22222 sin90cos120cos0tan60cot135 ++−+ ; c) 2 cos60.sin30cos30 +. Chú ý: ( ) ( ) ( ) ( ) 22222222 sinsin;coscosx;tantan;cotcot  ==== . Lời giải a) ( )( )2sin30cos1353tan150cos180cot60 +−− ( ) ( )( )( )2sin30cos180453tan18030cos180cot60 =+−−−− ( )( )2sin30cos453tan301cot60 =−+−− 1211 2.3.1 22 33  =−+−−    ( )( )222331 23 −++ =− . b) 22222 sin90cos120cos0tan60cot135 ++−+ ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( )( ) ( ) ( ) ( ) 22222 2 22 2 22 sin90cos120cos 0tan60cot135 1cos1806013cot18045 1 1cos 6013cot45. 4 =++−+ =+−+−+− =++−+= c) ( ) 22 11 cos60.sin30cos30.cos301 22 +=+= . 3.2. Đơn giản biểu thức sau: a) sin100sin80cos16cos164 +++. b) ( ) ( ) ( )2sin180.cotcos180.tan.cot180 −+−− với 090   Lời giải. a) sin100sin80cos16cos164 +++ ( ) ( )sin18080sin80cos16cos18016 sin80sin80cos16cos162sin80. =−+++− =++−= b) ( ) ( ) ( )2sin180.cotcos180.tan.cot180 −+−− BÀI TẬP SÁCH GIÁO KHOA. =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 4 cos 2sin.cotcos.tan.cot2sin.cos3cos. sin    =+=+= 3.3. Chứng minh các hệ thức sau: a) 22 sincos1 += ; b) ( )2 2 1 1tan 90; cos   += c) ( )2 2 1 1cot sin0180;  += Lời giải. a) Xét nửa đường tròn tâm O bán kính 1. Ta có sin DO = , cos=OC  . Xét tam giác vuông OBC ta có 22221sincos1ODOC  +=+= b) ( )2 2 1 1tan 90 cos   += Xét 222 2 222 sinsincos1 1tan1 = coscoscos VTVP    + =+=+== c) ( )2 2 1 1cot 0180 sin   += Xét 222 2 222 cossincos1 1cot1 sinsinsin VTVP    + =+=+=== . 3.4. Cho góc ( )0180  thỏa mãn tan3  = . Tính giá trị của biểu thức 2sin3cos 3sin2cos P   = + Lời giải. Ta có tan3cos0 = nên chia cả tử và mẫu của biểu thức P cho cos ta được 2sin3cos2tan33 3sin2cos3tan211 P   === ++

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 5 DẠNG 1: TÍNH CÁC GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC · Sử dụng định nghĩa giá trị lượng giác của một góc · Sử dụng tính chất và bảng giá trị lượng giác đặc biệt Sử dụng các hệ thức lượng giác cơ bản Câu 1. Tính giá trị các biểu thức sau: a) 222oo o sin90cos90cos180Aabc =++ b) 22 o 2 oo 3sin902cos603tan45B =−+− c) 20222ooooo sin452sin503cos452sin404tan55.tan35C =−+−+ Lời giải a) 222oo o sin90cos90cos180Aabc =++ ( ) 22222 .1.0.1 abcac =++−=− b) 22 o 2 oo 3sin902cos603tan45B =−+− ( ) 22 2 12 31231 22  =−+−=    c) 20222ooooo sin452sin503cos452sin404tan55.tan35C =−+−+ ( ) 22 2020 221332sin50cos404244 2222 C  =+−++=+−+=    . Câu 2. Tính giá trị các biểu thức sau: a) oooo 2222 sin3sin15sin75sin87A =+++ b) ooooo cos0cos20cos40...cos160cos180B =+++++ c) ooooo tan5tan10tan15...tan80tan85C = Lời giải: a) ( ) ( )oooo 2222 sin3sin87sin15sin75A =+++ ( ) ( )222oo 2 oo sin3cos3sin15cos15112 =+++=+= b) ( ) ( ) ( )oooooo cos0cos180cos20cos160...cos80cos100B =++++++ ( ) ( ) ( )oooooo cos0cos0cos20cos20...cos80cos800 =−+−++−= HỆ THỐNG BÀI TẬP.II == PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 6 c) ( )( ) ( )oooooo tan5tan85tan15tan75...tan45tan45C = ( )( ) ( )oooooo tan5cot5tan15cot5...tan45cot51 == Câu 1: Giá trị của oo cos60sin30 + bằng bao nhiêu? A. 3 2 B. 3 C. 3 3 D. 1. Lời giải Chọn D Ta có oo 11 cos60sin301 22 +=+= Câu 2: Giá trị của oo tan30cot30 + bằng bao nhiêu? A. 4 3 B. 13 3 + C. 2 3 D. 2 Lời giải Chọn A oo 343 tan30cot303 33 +=+= Câu 3: Trong các đẳng thức sau đây, đẳng thức nào sai? A. oo sin0cos01 += B. oo sin90cos901 += C. oo sin180cos1801 +=− D. oo sin60cos601 += Lời giải Chọn D Giá trị lượng giác của góc đặc biệt. Câu 4: Trong các khẳng định sau, khẳng định nào sai? A. oo cos60sin30 = . B. oo cos60sin120 = . C. oo cos30sin120 = . D. oo sin60cos120 =− . Lời giải Chọn B Giá trị lượng giác của góc đặc biệt. Câu 5: Đẳng thức nào sau đây sai? A. oo sin45sin452 += . B. oo sin30cos601 += . C. oo sin60cos1500 += . D. oo sin120cos300 += . Lời giải Chọn D BÀI TẬP TRẮC NGHIỆM.3 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 7 Giá trị lượng giác của góc đặc biệt. Câu 6: Giá trị oo cos45sin45 + bằng bao nhiêu? A. 1 B. 2 C. 3 D. 0 Lời giải Chọn B Ta có oo cos45sin452 += Câu 7: Trong các đẳng thức sau, đẳng thức nào đúng? A. ( )o sin180cos−=− . B. ( )o sin180sin−=−. C. ( )o sin180sin−=. D. ( )o sin180cos−=. Lời giải Chọn C Câu 8: Trong các đẳng thức sau, đẳng thức nào sai? A. oo sin0cos00 += . B. oo sin90cos901 += . C. oo sin180cos1801 +=− . D. oo 31sin60cos60 2 + += . Lời giải Chọn A Ta có oo sin0cos01 += Câu 9: Cho  là góc tù. Điều khẳng định nào sau đây là đúng? A. sin0   . B. cos0   . C. tan0   . D. cot0   . Lời giải Chọn C Góc tù có điểm biểu diễn thuộc góc phần tư thứ II, có giá trị sin0   , còn cos , tan và cot đều nhỏ hơn 0 . Câu 10: Giá trị của oooo sin36cos6sin126cos84E = là A. 1 2 B. 3 2 C. 1 D. 1 Lời giải Chọn A ( ) ( ) ooooooooooo 1 sin36cos6sin9036cos906sin36cos6cos36sin6sin30 2 E =+−=−== Câu 11: Giá trị của biểu thức oo 2222oo sin51sin55sin39sin35A =+++ là

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 8 A. 3 B. 4 C. 1 D. 2 Lời giải Chọn D ( ) ( ) ( ) ( )2222222 oooo 2 oooo sin51sin39sin55sin35sin51cos51sin55cos55 2A =+++=+++= . Câu 12: Giá trị của biểu thức ooooo tan1tan2tan3...tan88tan89A = là A. 0 B. 2 C. 3 D. 1 Lời giải Chọn D ( ) ( ) ( ) ooooooo tan1.tan89.tan2.tan88...tan44.tan46.tan451A == . Câu 13: Tổng ooooo 222222o sin2sin4sin6...sin84sin86sin88 ++++++ bằng A. 21. B. 23. C. 22 . D. 24 . Lời giải Chọn C 222222 oooooo Ssin2sin4sin6...sin84sin86sin88 =++++++ ( ) ( ) ( )22222 ooooo o2 sin2sin88sin4sin86...sin44sin46 =++++++ ( ) ( ) ( )2222 ooooo 2 o 2 sin2cos2sin4cos4...sin44cos4422 =++++++= . Câu 14: Giá trị của ooooo tan5.tan10.tan15...tan80.tan85A = là A. 2 . B. 1. C. 0 . D. 1. Lời giải Chọn B ( ) ( ) ( ) tan5.tan85.tan10.tan80...tan40tan50.tan451A  == . Câu 15: Giá trị của 2222 cos73cos87cos3cos17B  =+++ là A. 2 . B. 2 . C. 2. D. 1. Lời giải Chọn B ( ) ( ) ( ) ( )ooooooo 22222222o cos73cos17cos87cos3cos73sin73cos87sin872B =+++=+++= . DẠNG 2: TÍNH GIÁ TRỊ CỦA MỘT BIỂU THỨC LƯỢNG GIÁC , KHI BIẾT TRƯỚC MỘT GIÁ TRỊ LƯỢNG GIÁC. Dựa vào các hệ thức lượng giác cơ bản · Dựa vào dấu của giá trị lượng giác · Sử dụng các hằng đẳng thức đáng nhớ PHƯƠNG PHÁP.1 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 9 Câu 1. Cho 1 sin 3  = với 00 90180   . Tính cos và tan Câu 2. Cho 2 cos 3  =− và sin0   . Tính sin và cot Câu 3. Cho tan22  =− tính giá trị lượng giác còn lại. Lời giải: Câu 1. Vì 00 90180   nên cos0   mặt khác 22 sincos1 += suy ra 2 cos1sin1122 93 =−−=−−=− Do đó 1 sin1 3tan cos2222 3    ===− Câu 2. Vì 22 sincos1 += và sin0   , nên 2 sin1cos145 93 =−=−= và 2 cos2 3cot sin55 3    ===− Câu 3. Vì tan220cos0  =− mặt khác 2 2 1 tan1 cos   += Nên 2 111 cos tan1813  =−=−=− ++ Ta có sin122tansintan.cos22. cos33     ===−−=   1 cos1 3cot sin2222 3    ===− Câu 4. Cho 3 cos 4  = với 00 090   . Tính tan3cot tancot A   + = + . Câu 5. Cho tan2  = . Tính 33 sincos sin3cos2sin B   = ++ Lời giải: BÀI TẬP TỰ LUẬN.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 10 Câu 4. Ta có 2 2 2 2 2 11 tan32 tan3 tancos12cos 11tantan1 tancos A        ++ + ====+ + + Suy ra 917 12. 168 A =+= Câu 5. ( ) ( ) ( ) 22 33 33 32 333 sincos tantan1tan1 coscos sin3cos2sin tan32tantan1 coscoscos B       +−+ == +++ ++ Suy ra ( ) ( ) ( ) ( )22121321 2232221382 B +−+ == ++++ . Câu 6. Biết sincosxxm += a) Tìm 44 sincosxx . b) Chứng minh rằng 2m  . Lời giải: a) Ta có ( )2 22 sincossin2sincoscos12sincos xxxxxxxx +=++=+ (*) Mặt khác sincosxxm += nên 2 12sincosm =+ hay 2 1sincos 2 m  = Đặt 44 sincos Axx =− . Ta có ( )( ) ( )( )2222 sincossincossincossincos Axxxxxxxx =+−=+− ( ) ( ) ( )( )222sincossincos12sincos12sincos Axxxxxxxx =+−=+− 2224 2 1132 11 224 Ammmm −−+− =+−=   Vậy 2432 2 Amm +− = b) Ta có 22 2sincossincos1 xxxx+= Kết hợp với (*) suy ra ( )2 sincos2sincos2 xxxx ++ Câu 1: Cho 1 cos 2 x = . Tính biểu thức 22 3sin4cos Pxx =+ A. 13 4 . B. 7 4 . C. 11 4 . D. 15 4 . Lời giải Chọn A Ta có ( ) 2 22222 3sin4cos3sincoscos3113 24 Pxxxxx  =+=++=+=   . Câu 2: Biết 1 cos 3  = . Giá trị đúng của biểu thức 22 sin3cosP =+ là: BÀI TẬP TRẮC NGHIỆM.3 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 11 A. 1 3 . B. 10 9 . C. 11 9 . D. 4 3 . Lời giải Chọn C ( ) 222222 111 cossin3ossincos2cos12cos 39 Pc  ==+=++=+= Câu 3: Cho biết 1 tan 2  = . Tính cot. A. cot2  = B. cot2  = C. 1 cot 4  = D. 1 cot 2  = Lời giải Chọn A 1 tan.cot1cot2 tan   === . Câu 4: Cho biết 2 cos 3  =− và 0 2    Tính tan? A. 5 4 B. 5 2 C. 5 2 D. 5 2 Lời giải Chọn D Do 0tan0 2    . Ta có: 2 2 1 1tan cos   += 2 5 tan 4  = 5 tan 2  =− Câu 5: Cho  là góc tù và sin5 13  = Giá trị của biểu thức 3sin2cos + là A. 3 B. 9 13 C. 3 D. 9 13 Lời giải Chọn B Ta có 22 14412 cos1sincos 16913  =−== Do  là góc tù nên cos0   , từ đó 12 cos 13  =− Như vậy 3sin2cos325129 131313   +=+−=−   . Câu 6: Cho biết sincos a+= . Giá trị của sin.cos bằng bao nhiêu? A. 2sin.cos a = . B. sin.cos2a = . C. 2sin.cos1 2 a  = . D. 2 1sin.cos 2 a  = . Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 12 ( ) 2 22 1sincos12sincossincos 2 a a  =+=+= Câu 7: Cho biết 2 cos 3  =− . Tính giá trị của biểu thức cot3tan 2cottan E   + = + ? A. 19 13 B. 19 13 C. 25 13 D. 25 13 Lời giải Chọn B ( ) ( ) 2 22 2 22 2 2 3 3tan122 cot3tan13tan32cos19 cos 1 2cottan2tan1cos13 11tan1 cos E       +− ++− ====== +++ ++ + . Câu 8: Cho biếtcot5  = . Tính giá trị của 2 2cos5sincos1E  =++ ? A. 10 26 . B. 100 26 . C. 50 26 . D. 101 26 . Lời giải Chọn D ( )222 22 sin2cot5cot3cot5cot111101 sin1cot26 E    =++=++=  + . Câu 9: Cho 1 cot 3  = . Giá trị của biểu thức 3sin4cos 2sin5cos A   + = là: A. 15 13 . B. 13. C. 15 13 . D. 13. Lời giải Chọn D 3sin4sin.cot34cot 13 2sin5sin.cot25cot A   ++ === Câu 10: Cho biết 2 cos 3  =− . Giá trị của biểu thức cot3tan 2cottan E   = bằng bao nhiêu? A. 25 3 B. 11 13 C. 11 3 D. 25 13 . Lời giải Chọn C ( ) ( ) 2 22 2 22 2 2 3 43tan14 cot3tan13tan4cos311 cos 1 2cottan2tan3cos13 31tan3 cos E       −+ ======− −+ . Câu 11: Biết sincos2 aa+= . Hỏi giá trị của 44 sincosaa + bằng bao nhiêu? A. 3 2 . B. 1 2 . C. 1. D. 0. Lời giải Chọn B Ta có: sincos2 aa+= ( )22sincosaa=+ 1 sin.cos 2 aa = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 13 ( ) 2 442222 sincossincos2sincos1211 22 aaaaaa  +=+−=−=   . Câu 12: Cho tancot m+= . Tìm m để 22 tancot7 += A. 9m = B. 3m = C. 3m =− D. 3m = Lời giải Chọn D ( ) 222 7tancottancot2  =+=+− 2 9m = 3m = Câu 13: Cho biết 3cossin1 −= , oo 090   Giá trị của tan bằng A. 4 tan 3  = B. 3 tan 4  = C. 4 tan 5  = D. 5 tan 4  = Lời giải Chọn A Ta có ( ) 22 3cossin13cossin19cossin1  −==+→=+ ( ) 2222 9cossin2sin191sinsin2sin1  =++−=++ 2 sin1 10sin2sin80. sin4 5    =− +−=  =  • sin1  =− : không thỏa mãn vì oo 090   • 43sin4 sincostan. 55cos3    ==⎯⎯→== Câu 14: Cho biết 2cos2sin2 += , 00 090.   Tính giá trị của cot.  A. 5 cot 4  = B. 3 cot 4  = C. 2 cot 4  = D. 2 cot 2  = Lời giải Chọn C Ta có ( ) 222cos2sin22sin22cos2sin22cos  +==−→=− ( ) 2222 2 2sin48cos4cos21cos48cos4cos cos1 6cos8cos20. 1 cos 3     =−+−=−+ = −+=  =  • cos1  = : không thỏa mãn vì oo 090   • 122cos2 cossincot. 33sin4    ==⎯⎯→== Câu 15: Cho biết 1 cossin. 3 += Giá trị của 22 tancotP =+ bằng bao nhiêu? A. 5 4 P = . B. 7 4 P = . C. 9 4 P = . D. 11 4 P = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 14 Lời giải Chọn B Ta có ( )2 11 cossincossin 39  +=→+= 14 12sincossincos. 99  +==− Ta có ( ) 2 222 sincos tancottancot2tancot2 cossin P     =+=+−=+−   2 2222 sincos197 222. sincossincos44    +  =−=−=−−=    Câu 16: Cho biết 1 sincos. 5 −= Giá trị của 44 sincosP =+ bằng bao nhiêu? A. 15 5 P = B. 17 5 P = C. 19 5 P = D. 21 5 P = Lời giải Chọn B Ta có ( )2 sincossincos11 55  −=→−= 12 12sincossincos. 55  −== ( )2 442222 sincossincos2sincosP =+=+− ( )2 17 12sin. 5 cos  =−=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 15 DẠNG 3: CHỨNG MINH CÁC ĐẲNG THỨC, RÚT GỌN CÁC BIỂU THỨC LƯỢNG GIÁC Sử dụng các hệ thức lượng giác cơ bản Sử dụng tính chất của giá trị lượng giác · Sử dụng các hằng đẳng thức đáng nhớ Câu 1. Chứng minh các đẳng thức sau (giả sử các biểu thức sau đều có nghĩa) a) 4422 sincos12sin.cos xxxx +=− b) 1cottan1 1cottan1 xx xx ++ = c) 32 3 cossin tantantan1 cos xx xxx x + =+++ Lời giải a) 44442222 sincossincos2sincos2sincos xxxxxxxx +=++− ( )2 2222 22 sincos2sincos 12sincos xxxx xx =+− =− b) 1tan1 1 1cottan1 tantan 1tan1 1cottan1 1 tantan x xx xx x xx xx + + ++ === c) 323 cossin1sin coscoscos xxx xxx + =+ ( )22 tan1tantan1 xxx =+++ 32 tantantan1 xxx =+++ Câu 2. Cho tam giác ABC . Chứng minh ( ) 33 sincoscos 22 .tan2 sincossin 22 BB AC B ACAC B + +−= ++    Lời giải: Vì 0180ABC++= nên ( )33 0 00 sincos22cos180 .tan cossin180180sin 22 BB B VTB BBB =+−    PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 16 33 22 sincos 22cos.tansincos12 sincossin22 22 BB BBB BVP BB B =+−=++== Suy ra điều phải chứng minh. Câu 3. Đơn giản các biểu thức sau(giả sử các biểu thức sau đều có nghĩa) a) o o222 sin(90)cos(180)sin(1tan)tan Axxxxx =−+−++− b) 111 .2 sin1cos1cos B xxx =+− +− Lời giải: a) 22 2 1 coscossin.tan0 cos Axxxx x =−+−= b) ( )( ) 11cos1cos .2 sin1cos1cos Bxx xxx −++ =− −+ 22 2 2 1212 .2.2 sin1cossinsin 1 212cot sin xxxx x x =−=−  =−=   Câu 4. Chứng minh biểu thức sau không phụ thuộc vào x . 424424 sin6cos3coscos6sin3sin Pxxxxxx =+++++ Lời giải ( ) ( ) 22 224224 1cos6cos3cos1sin6sin3sin Pxxxxxx =−+++−++ ( ) ( ) 42422222 22 4cos4cos14sin4sin12cos12sin1 2cos12sin13 xxxxxx xx =+++++=+++ =+++= Vậy P không phụ thuộc vào x . Câu 1: Trong các hệ thức sau hệ thức nào đúng? A. 22 sincos1 += . B. 22 sincos1 2   += . C. 22 sincos1 += . D. 22 sin2cos21 += . Lời giải Chọn D Công thức lượng giác cơ bản. Câu 2: Trong các hệ thức sau hệ thức nào đúng? BÀI TẬP TRẮC NGHIỆM.3 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 17 A. 22 sincos1 += . B. 22 sincos1 2   += . C. 22 sincos1 += . D. 22 sincos1 += . Lời giải Chọn D Công thức lượng giác cơ bản. Câu 3: Trong các hệ thức sau hệ thức nào đúng? A. sin2cos21 += B. 22 sincos1 += C. 22 sincos1 += D. 22 sincos1 += Lời giải Chọn D Công thức lượng giác cơ bản. Câu 4: Rút gọn biểu thức sau ( ) ( ) 22 tancottancot Axxxx =+−− A. 4A = B. 1A = C. 2A = D. 3A = Lời giải Chọn A ( ) ( )2222 tan2tan.cotcottan2tan.cotcot4 Axxxxxxxx =++−−+= Câu 5: Đơn giản biểu thức ( ) 222 1sincot1cot Gxxx =−+− A. 2sin x B. 2 cos x C. 1 cos x D. cos x Lời giải Chọn A ( ) 222222 1sin1cot1sin.cot11cossin Gxxxxxx  =−−+=−+=−=  Câu 6: Khẳng định nào sau đây là sai? A. 22 sincos1 += B. ( )2 2 1 1cotsin0 sin   += C. ( )tan.cot1sin.cos0  =− D. ( )2 2 1 1tancos0 cos   += Lời giải Chọn C sincos tan.cot.1 cossin xx xx  == Câu 7: Rút gọn biểu thức 21sin 2sin.cos x P xx = ta được A. 1 tan 2 Px = . B. 1 cot 2 Px = . C. 2cot Px = . D. 2tan Px = . Lời giải Chọn B 22 1sincoscos1 cot 2sin.cos2sin.cos2sin2 xxx Px xxxxx ==== . Câu 8: Đẳng thức nào sau đây là sai? A. ( ) ( ) 22 cossincossin2, xxxxx ++−= . B. 2222 tansintansin,90 xxxxx  −=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 18 C. 4422 sincos12sincos, xxxxx +=− . D. 6622 sincos13sincos, xxxxx −=− Lời giải Chọn D ( )( )662222 sincossincos1sincos xxxxxx −=−− Câu 9: Đẳng thức nào sau đây là sai? A. ( )1cossin sin1cos0,180 xx xx xx  = + . B. ( )1 tancot0,90,180 sincos xxx xx  += C. ( )22 22 1 tancot20,90,180 sincos xxx xx  +=− D. 22 sin2cos22 xx+= Lời giải Chọn D 22 sin2cos21 xx+= Câu 10: Biểu thức 2222 tansintansinxxxx −+ có giá trị bằng A. 1 B. 0 C. 2 D. 1 Lời giải Chọn B ( ) ( ) 2 222222222 2 sin tansintansintansin1sincossin0 cos x xxxxxxxxx x −+=−+=−+= Câu 11: Biểu thức ( )2 cottanaa + bằng A. 22 11 sincos . B. 22 cottan2 aa + . C. 22 11 sincos + . D. 22 cottan2 aa + . Lời giải Chọn C ( ) ( ) ( )2 2222 22 11 cottancot2cot.tantancot1tan1 sincos aaaaaaaa aa +=++=+++=+ Câu 12: Đơn giản biểu thức sin cot 1cos x Ex x =+ + ta được A. sin x . B. 1 cos x . C. 1 sin x . D. cos x . Lời giải Chọn C ( ) ( ) sincossincos1cossin.sin cot 1cossin1cossin1cos xxxxxxx Ex xxxxx ++ =+=+= +++ ( ) ( ) ( ) ( ) ( )( ) ( ) 2 cos1cos1coscos1cos1cos1cos1 sin1cossin1cossin xxx xxxx xxxxx ++− +++− === ++ Câu 13: Rút gọn biểu thức sau 22 2 cotcossin.cos cotcot Axxxx xx =+ A. 1A = B. 2A = C. 3A = D. 4A =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 19 Lời giải Chọn A 222 22 22 cotcossin.coscossin.cos11sinsin1 cotcotcotcot xxxxxxx Axx xxxx =+=−+=−+= Câu 14: Biểu thức ( ) ( ) ( )4466 3sincos2sincos fxxxxx =+−+ có giá trị bằng: A. 1 B. 2 C. 3 D. 0 Lời giải Chọn A 4422 sincos12sincos xxxx +=− . 6622 sincos13sincos xxxx +=− ( ) ( ) ( )2222 312sincos213sincos1 fxxxxx =−−−= Câu 15: Biểu thức: ( ) 4222 coscossinsin fxxxxx =++ có giá trị bằng A. 1. B. 2. C. 2. D. 1. Lời giải Chọn A ( ) ( ) 222222 coscossinsincossin1 fxxxxxxx =++=+= . Câu 16: Trong các mệnh đề sau, mệnh đề nào sai? A. ( )2 sincos12sincos xxxx = B. 4422 sincos12sincosxxxx += C. ( )2 sincos12sincos xxxx +=+ . D. 6622 sincos1sincosxxxx += . Lời giải Chọn D ( ) ( ) ( ) ( )333 6622222222 sincossincossincos3sincos.sin.cos xxxxxxxxxx +=+=+−+ 2213sin.cosxx=− .

TH

LƯỢNG TRONG TAM GIÁC

BÀI 5. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC

TỪ 0 ĐẾN 180

OFFICIAL

DẠNG 1. DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC. GIÁ TRỊ LƯỢNG GIÁC

Câu 1: Cho góc ( ) 90;180. Khẳng định nào sau đây đúng?

A. sin và cot cùng dấu. B. Tích sin.cot mang dấu âm.

C. Tích sin.cos mang dấu dương.

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 1

D. sin và tan cùng dấu. Câu 2: Cho  là góc tù. Mệnh đề nào đúng trong các mệnh đề sau? A. tan0.  B. cot0.   C. sin0.   D. cos0.   Câu 3: Cho 0º90º   . Khẳng định nào sau đây đúng? A. ( ) cot90ºtan−=− B. ( ) cos90ºsin−= C. ( ) sin90ºcos−=−. D. ( ) tan90ºcot−=−. Câu 4: Đẳng thức nào sau đây đúng? A. ( )o tan180tanaa+=− B. ( )o cos180cosaa+=− C. ( )o sin180sinaa+= D. ( )o cot180cotaa+=− Câu 5: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) sin180sin  −=− B. ( ) cos180cos  −= C. ( ) tan180tan  −= D. ( ) cot180cot  −=− Câu 6: Cho  và  là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. sinsin = . B. coscos =− . C. tantan =− . D. cotcot = . Câu 7: Cho góc  tù. Điều khẳng định nào sau đây là đúng? A. sin0   B. cos0   C. tan0   D. cot0   CHƯƠNG III HỆ

ỨC

HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 2 Câu 8: Hai góc nhọn  và  phụ nhau, hệ thức nào sau đây là sai? A. sincos = B. tancot = C. 1 cot cot   = D. cossin =− Câu 9: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. 3sin150 2  =− B. 3 cos150 2  = C. 1 tan150 3  =− D. cot1503  = Câu 10: Bất đẳng thức nào dưới đây là đúng? A. sin90sin100   . B. cos95cos100   . C. tan85tan125   . D. cos145cos125   . Câu 11: Giá trị của tan45cot135  + bằng bao nhiêu? A. 2 B. 0 C. 3 D. 1 Câu 12: Giá trị của cos30sin60  + bằng bao nhiêu? A. 3 3 . B. 3 2 . C. 3 . D. 1. Câu 13: Giá trị của cos60sin30  + bằng bao nhiêu? A. 3 2 . B. 3 . C. 3 3 . D. 1 Câu 14: Giá trị của tan30cot30  + bằng bao nhiêu? A. 4 3 . B. 13 3 + . C. 2 3 . D. 2. Câu 15: Trong các đẳng thức sau đây, đẳng thức nào sai? A. sin0cos01  += B. sin90cos901  += C. sin180cos1801  +=− . D. sin60cos601  += . Câu 16: Tính giá trị của biểu thức sin30cos60sin60cos30P =+. A. 1P = B. 0P = C. 3P = D. 3P =− Câu 17: Trong các khẳng định sau, khẳng định nào sai? A. cos60sin30  = . B. cos60sin120  = . C. cos30sin120  = . D. sin60cos120  =− . Câu 18: Đẳng thức nào sau đây sai? A. sin45sin452  += B. sin30cos601  += C. sin60cos1500  += . D. sin120cos300  += . Câu 19: Cho hai góc nhọn  và  ( )  . Khẳng định nào sau đây là sai? A. coscos  . B. sinsin  . C. tantan0 + . D. cotcot  . Câu 20: Cho ABC vuông tại A , góc B bằng 30  . Khẳng định nào sau đây là sai?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 3 A. 1 cos 3 B = B. 3sin 2 C = C. 1 cos 2 C = D. 1 sin 2 B = Câu 21: Tìm khẳng định sai trong các khẳng định sau: A. cos75cos50   . B. sin80sin50   . C. tan45tan60   . D. cos30sin60  = . DẠNG 2. CHO BIẾT MỘT GIÁ TRỊ LƯỢNG GIÁC, TÍNH CÁC GIÁ TRỊ LƯỢNG GIÁC CÒN LẠI Câu 22: Biết 2 cos 3  = ( )090   . Khi đó tan bằng A. 5 2 . B. 5 2 . C. 2 5 . D. 2 5 . Câu 23: Cho góc  thỏa mãn 4 sin 5  = và 90180  . Giá trị của cos bằng A. 2 5 B. 3 5 C. 2 5 D. 3 5 Câu 24: Cho 1 sin 3 x = và 90180 oo x  thì A. 2 cos 3  = . B. 2 cos 3  =− . C. 22 cos 3  = . D. 22 cos 3  =− . Câu 25: Cho 00 90180   và thỏa mãn sin3 5  = . Giá trị của cos bằng. A. 4 5 B. 4 5 C. 2 5 D. 1 5 Câu 26: Cho ( )62 sin;90180 4  + = . Giá trị của tan bằng A. 23 . B. 23−+ . C. 23 + . D. 23 . Câu 27: Cho góc  thỏa mãn 12 sin 13  = và 90180   . Tính cos A. 1 cos= 13  . B. 5 cos 13  =− . C. 1 cos 13  =− . D. 5 cos 13  = . Câu 28: Cho 1 sin 3  = , với 90180  . Tính cos . A. 2 cos 3  = . B. 2 cos 3  =− . C. 22 cos 3  = . D. 22 cos 3  =− . Câu 29: Cho biết 2 cos 3  =− . Tính tan?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 4 A. 5 4 B. 5 2 C. 5 2 D. 5 2 Câu 30: Cho biết 1 tan 2  = . Tính cot A. cot2  = . B. cot2  = . C. 1 cot 4  = . D. 1 cot 2  = . Câu 31: cos bằng bao nhiêu nếu 1 cot 2  =− ? A. 5 5  . B. 5 2 . C. 5 5 . D. 1 3 . Câu 32: Nếu tan3  = thì cos bằng bao nhiêu? A. 10 10 . B. 1 3 C. 10 10  . D. 10 10 . Câu 33: Cho  là góc tù và sin5 13  = Giá trị của biểu thức 3sin2cos + là A. 9 13 B. 3 C. 9 13 D. 3 Câu 34: Biết cot a=− , 0a  . Tính cos A. 2 cos 1 a a  = + . B. 2 1 cos 1 a  = + . C. 2 1 cos 1 a  =− + . D. 2 cos 1 a a  =− + . Câu 35: Cho 1 cos 2 x = . Tính biểu thức 22 3sin4cos Pxx =+ A. 13 4 B. 7 4 C. 11 4 D. 15 4 Câu 36: Cho  là góc tù và 4 sin 5  = . Giá trị của biểu thức 2sincosA =− bằng A. 7 5 . B. 7 5 . C. 1. D. 11 5 . Câu 37: Cho 4 sin, 5  = với 90180  . Tính giá trị của 3 sincos cos M   + = A. 25 27 M = B. 175 27 M = . C. 35 27 M = . D. 25 27 M =− . Câu 38: Cho biết 2 cos 3  =− . Tính giá trị của biểu thức cot3tan 2cottan E   + = + ? A. 19 13 B. 19 13 C. 25 13 D. 25 13

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 5 Câu 39: Cho biếtcot5  = . Tính giá trị của 2 2cos5sincos1E  =++ ? A. 10 26 B. 100 26 C. 50 26 D. 101 26 . Câu 40: Cho 1 3 cot = . Giá trị của biểu thức 3sin4cos 2sin5cos A   + = là: A. 15 13 . B. 13. C. 15 13 . D. 13. Câu 41: Cho biết 2 cos 3  =− . Giá trị của biểu thức cot3tan 2cottan E   = bằng bao nhiêu? A. 25 3 B. 11 13 C. 11 3 D. 25 13 . Câu 42: Biết 1 cos 3  = . Giá trị đúng của biểu thức 22 sin3cosP =+ là: A. 11 9 . B. 4 3 . C. 1 3 . D. 10 9 . Câu 43: Cho tan2  =− . Tính giá trị biểu thức 2sin3cos 3sin2cos P   + = . A. 1 8 P = . B. 7 4 P =− . C. 1 8 P =− . D. 7 4 P = . Câu 44: Cho biết 2 cos 3  =− . Giá trị của cot3tan 2cottan   + = + P bằng bao nhiêu? A. 25 13 =−P B. 19 13 =−P C. 19 13 =P D. 25 13 =P Câu 45: Cho biết 2 cos 3  =− . Tính giá trị của biểu thức cot3tan 2cottan P   + = + ? A. 19 13 P =− . B. 19 13 P = . C. 25 13 P = . D. 25 13 P =− . Câu 46: Cho biết 1 cossin 3 += . Tính giá trị của biểu thức 22 tancotP =+? A. 5 4 P = B. 7 4 P = C. 9 4 P = D. 11 4 P = Câu 47: Cho tan2  = . Tính giá trị của biểu thức 3sin2cos 2sincos A   = + là A. 2 5 B. 4 5 C. 3 2 D. 3 2 Câu 48: Cho tan2 x = . Giá trị của biểu thức 2sin3cos 3sincos xx P xx + = ?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 6 A. 3 5 P = B. 7 5 P = . C. 8 3 P = . D. 5 7 P = . Câu 49: Cho 1 cos 2 x = . Tính biểu thức 22 3sin4cos Pxx =+ . A. 13 4 B. 7 4 C. 11 4 D. 15 4 Câu 50: Rút gọn biểu thức 2 2cos1 sincos Aa aa = + A. sincosaa + B. sincosaa C. cossinaa D. tancosaa + Câu 51: Giá trị của biểu thức 66 sincos Axx =+ bằng .cos4 abx + . Giá trị của 2 ab + là A. 9 8 . B. 11 8 . C. 13 8 . D. 15 8 . DẠNG 3. CHỨNG MINH, RÚT GỌN BIỂU THỨC LƯỢNG GIÁC Câu 52: Đẳng thức nào sau đây là sai? A. ( ) ( ) 22 cossincossin2, xxxxx ++−= B. 2222 tansintansin,90 xxxxx  −= C. 4422 sincos12sincos, xxxxx +=− D. 6622 sincos13sincos, xxxxx −=− Câu 53: Đẳng thức nào sau đây là sai? A. ( )1cossin sin1cos0,180 xx xx xx  = + B. ( )1 tancot0,90,180 sincos xxx xx  += C. ( )22 22 1 tancot20,90,180 sincos xxx xx  +=− D. 22 sin2cos22 xx+= . Câu 54: Trong các hệ thức sau hệ thức nào đúng? A. 22 sincos1 += B. 22 sincos1 2  += C. 22 sincos1 += . D. 22 sin2cos21 += . Câu 55: Trong các hệ thức sau hệ thức nào đúng? A. 22 sincos1 += B. 22 sincos1 2  += C. 22 sincos1 += D. 22 sincos1 += Câu 56: Rút gọn biểu thức sau 22 2 cotcossin.cos cotcot Axxxx xx =+ A. 4A = . B. 2A = . C. 1A = . D. 3A = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 7 Câu 57: Biểu thức ( )2 cottanaa + bằng A. 22 11 sincos . B. 22 cottan2 aa + . C. 22 11 sincos + . D. 22 cottan2 aa + . Câu 58: Rút gọn biểu thức sau ( ) ( ) 22 tancottancot Axxxx =+−− A. 4A = . B. 1A = . C. 2A = . D. 3A = Câu 59: Đơn giản biểu thức ( ) 222 1sincot1cot Gxxx =−+− A. 2sin x . B. 2 cos x . C. 1 cos x . D. cos x . Câu 60: Đơn giản biểu thức sin cot 1cos x Ex x =+ + ta được A. sin x B. 1 cos x C. 1 sin x D. cos x Câu 61: Khẳng định nào sau đây là sai? A. 22 sincos1 += . B. ( )2 2 1 1cotsin0 sin   += . C. ( )tan.cot1sin.cos0  =− . D. ( )2 2 1 1tancos0 cos   += . Câu 62: Rút gọn biểu thức 21 2sin.cos sinx P xx = ta được A. 1 tan 2 Px = . B. 1 cot 2 Px = . C. 2cot Px = . D. 2tan Px = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 8 DẠNG 4. TÍNH GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC Câu 63: Biểu thức cos20cos40cos60...cos160cos180A =+++++ có giá trị bằng A. 1. B. 1. C. 2. D. 2. Câu 64: Cho tancot3. −= Tính giá trị của biểu thức sau: 22 tancotA =+ . A. 12A = . B. 11A = . C. 13A = . D. 5A = . Câu 65: Giá trị của biểu thức tan1tan2tan3...tan88tan89A  = là A. 0 B. 2 C. 3 D. 1 Câu 66: Tổng 222222 sin2sin4sin6...sin84sin86sin88  ++++++ bằng A. 21. B. 23. C. 22. D. 24. Câu 67: Biết sincos2 aa+= . Hỏi giá trị của 44 sincosaa + bằng bao nhiêu? A. 3 2 . B. 1 2 . C. 1. D. 0 . Câu 68: Biểu thức ( ) ( ) ( )4466 3sincos2sincos fxxxxx =+−+ có giá trị bằng: A. 1. B. 2. C. 3. D. 0 . Câu 69: Biểu thức: ( ) 4222 coscossinsin fxxxxx =++ có giá trị bằng A. 1. B. 2. C. 2. D. 1. Câu 70: Biểu thức 2222 tansintansinxxxx −+ có giá trị bằng A. 1. B. 0. C. 2. D. 1. Câu 71: Giá trị của tan5.tan10.tan15...tan80.tan85A  = là A. 2. B. 1. C. 0 . D. 1. Câu 72: Giá trị của 2222 cos73cos87cos3cos17B  =+++ là A. 2 . B. 2. C. 2. D. 1. Câu 73: Cho tancot m+= . Tìm m để 22 tancot7 += . A. 9m = . B. 3m = . C. 3m =− . D. 3m = . Câu 74: Giá trị của sin36cos6sin126cos84E  = là A. 1 2 B. 3 2 C. 1 D. 1 Câu 75: Giá trị của biểu thức 2222 sin51sin55sin39sin35A  =+++ là A. 3 B. 4 C. 1 D. 2 Câu 76: Cho sincosxxm += . Tính theo m giá trị của sin.cos Mxx =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 9 A. 2 1m B. 2 1 2 m C. 2 1 2 m + D. 2 1m + Câu 77: Rút gọn biểu thức 22 4 222 tansintansincossin Pxxxxxx =−++ ta được A. 1P =− B. 0P = C. 2P = D. 1P = Câu 78: Thu gọn biểu thức ( ) ( )22 sin2sin.sin.cossin Axaxxaax =+−+− A. 2 cos Aa = . B. cos2 Aa = . C. 2sin Aa = . D. sin2 Aa = . Câu 79: Tính giá trị của biểu thức cos5cos10cos15...cos170cos175cos180P =++++++ A. 2P = . B. 1P = . C. 0P = . D. 1P =− .

LƯỢNG TRONG TAM GIÁC

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 1 BÀI 5. GIÁ TRỊ LƯỢNG GIÁC CỦA MỘT GÓC TỪ 0 ĐẾN 180 . DẠNG 1. DẤU CỦA CÁC GIÁ TRỊ LƯỢNG GIÁC. GIÁ TRỊ LƯỢNG GIÁC Câu 1: Cho góc ( ) 90;180. Khẳng định nào sau đây đúng? A. sin và cot cùng dấu. B. Tích sin.cot mang dấu âm. C. Tích sin.cos mang dấu dương. D. sin và tan cùng dấu. Lời giải Chọn B Với ( )90;180  , ta có sin0,cos0  suy ra: tan0,cot0  Vậy sin.cot0  Câu 2: Cho  là góc tù. Mệnh đề nào đúng trong các mệnh đề sau? A. tan0.  B. cot0.   C. sin0.   D. cos0.   Lời giải Chọn C tan0.  Câu 3: Cho 0º90º   . Khẳng định nào sau đây đúng? A. ( ) cot90ºtan−=−. B. ( ) cos90ºsin−=. C. ( ) sin90ºcos−=−. D. ( ) tan90ºcot−=−. Lời giải Chọn B Vì  và ( )90º  là hai cung phụ nhau nên theo tính chất giá trị lượng giác của hai cung phụ nhau ta có đáp án B đúng. Câu 4: Đẳng thức nào sau đây đúng? A. ( )o tan180tanaa+=− B. ( )o cos180cosaa+=− CHƯƠNG III HỆ THỨC

HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 2 C. ( )o sin180sinaa+= .D. ( )o cot180cotaa+=− . Lời giải Chọn B Lý thuyết “cung hơn kém 180  ” Câu 5: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. ( ) sin180sin  −=− . B. ( ) cos180cos  −= C. ( ) tan180tan  −= . D. ( ) cot180cot  −=− Lời giải Chọn D Mối liên hệ hai cung bù nhau. Câu 6: Cho  và  là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai? A. sinsin = B. coscos =− C. tantan =− D. cotcot = . Lời giải Chọn D Mối liên hệ hai cung bù nhau. Câu 7: Cho góc  tù. Điều khẳng định nào sau đây là đúng? A. sin0   . B. cos0   . C. tan0   . D. cot0   . Lời giải Chọn D Câu 8: Hai góc nhọn  và  phụ nhau, hệ thức nào sau đây là sai? A. sincos = . B. tancot = . C. 1 cot cot   = . D. cossin =− . Lời giải Chọn D ( ) coscos90sin   =−= . Câu 9: Trong các đẳng thức sau đây, đẳng thức nào đúng? A. 3sin150 2  =− B. 3 cos150 2  = C. 1 tan150 3  =− D. cot1503  = Lời giải Chọn C Giá trị lượng giác của góc đặc biệt. Câu 10: Bất đẳng thức nào dưới đây là đúng? A. sin90sin100   . B. cos95cos100   . C. tan85tan125   . D. cos145cos125   . Lời giải Chọn B Câu 11: Giá trị của tan45cot135  + bằng bao nhiêu? A. 2 B. 0 C. 3 D. 1 Lời giải Chọn B tan45cot135110  +=−= Câu 12: Giá trị của cos30sin60  + bằng bao nhiêu? A. 3 3 . B. 3 2 . C. 3 . D. 1.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 3 Lời giải Chọn C 33 cos30sin603 22  +=+= . Câu 13: Giá trị của cos60sin30  + bằng bao nhiêu? A. 3 2 . B. 3 . C. 3 3 . D. 1 Lời giải Chọn D Ta có 11 cos60sin301 22  +=+= . Câu 14: Giá trị của tan30cot30  + bằng bao nhiêu? A. 4 3 . B. 13 3 + . C. 2 3 . D. 2. Lời giải Chọn A 343 tan30cot303 33  +=+= . Câu 15: Trong các đẳng thức sau đây, đẳng thức nào sai? A. sin0cos01  += B. sin90cos901  += C. sin180cos1801  +=− D. sin60cos601  += Lời giải Chọn D Giá trị lượng giác của góc đặc biệt. Câu 16: Tính giá trị của biểu thức sin30cos60sin60cos30P =+ A. 1P = . B. 0P = . C. 3P = . D. 3P =− . Lời giải Chọn A Ta có: 1133 sin30cos60sin60cos30..1 2222 P =+=+= Câu 17: Trong các khẳng định sau, khẳng định nào sai? A. cos60sin30  = . B. cos60sin120  = . C. cos30sin120  = . D. sin60cos120  =− . Lời giải Chọn B Giá trị lượng giác của góc đặc biệt. Câu 18: Đẳng thức nào sau đây sai? A. sin45sin452  += . B. sin30cos601  += . C. sin60cos1500  += D. sin120cos300  += Lời giải Chọn D Giá trị lượng giác của góc đặc biệt. Câu 19: Cho hai góc nhọn  và  ( )  . Khẳng định nào sau đây là sai?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 4 A. coscos  B. sinsin  C. tantan0 + D. cotcot  Lời giải Chọn B Biểu diễn lên đường tròn. Câu 20: Cho ABC vuông tại A , góc B bằng 30  . Khẳng định nào sau đây là sai? A. 1 cos 3 B = . B. 3sin 2 C = . C. 1 cos 2 C = . D. 1 sin 2 B = Lời giải Chọn A 3 coscos30 2 B  == Câu 21: Tìm khẳng định sai trong các khẳng định sau: A. cos75cos50   B. sin80sin50   C. tan45tan60   D. cos30sin60  = Lời giải Chọn A Lý thuyết. DẠNG 2. CHO BIẾT MỘT GIÁ TRỊ LƯỢNG GIÁC, TÍNH CÁC GIÁ TRỊ LƯỢNG GIÁC CÒN LẠI Câu 22: Biết 2 cos 3  = ( )090   . Khi đó tan bằng A. 5 2 B. 5 2 C. 2 5 D. 2 5 Lời giải Chọn A Ta có: 2 2 1 1tan cos   =+ 2 5 tan 4  = Vì 0 2    nên tan0   , do đó 5 tan 2  = Câu 23: Cho góc  thỏa mãn 4 sin 5  = và 90180  . Giá trị của cos bằng A. 2 5 . B. 3 5 . C. 2 5 . D. 3 5 . Lời giải Ta có 22 cos1sin1169 2525 =−=−= , mặt khác 2   nên cos0  . Suy ta 3 cos 5  =− . Câu 24: Cho 1 sin 3 x = và 90180 oo x  thì A. 2 cos 3  = B. 2 cos 3  =− C. 22 cos 3  = D. 22 cos 3  =− Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 5 Chọn D Ta có 2 122 cos1sin1. 93 =−=−= Mặt khác 00 90180   nên 22 cos0cos. 3 =− Câu 25: Cho 00 90180   và thỏa mãn sin3 5  = . Giá trị của cos bằng. A. 4 . 5 B. 4 . 5 C. 2 . 5 D. 1 . 5 Lời giải Chọn A Ta có 2 2222 sincos1cos1sin1cos3164 5255   +==−=−==   . Vì 00 90180   nên cos0  , suy ra 4 cos. 5  =− Câu 26: Cho ( )62 sin;90180 4  + = . Giá trị của tan bằng A. 23 B. 23−+ C. 23 + D. 23 Lời giải Chọn A Ta có: 2 22 sincos1cos16262 44  +− +==−−=−    , Vậy 62 sin 4 tan23 cos 62 4    + ===−− . Câu 27: Cho góc  thỏa mãn 12 sin 13  = và 90180   . Tính cos A. 1 cos= 13  B. 5 cos 13  =− C. 1 cos 13  =− D. 5 cos 13  = Lời giải Chọn B Vì 90180   cos0   .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 6 Ta có 2 22 cos1sin11225 13169   =−=−=   5 cos 13 5 cos 13    =    =−  Vì cos0  nên 5 cos 13  =− . Câu 28: Cho 1 sin 3  = , với 90180  . Tính cos A. 2 cos 3  = . B. 2 cos 3  =− . C. 22 cos 3  = . D. 22 cos 3  =− . Lời giải Chọn D Ta có 22 cos1sin =− 2 18 1 39  =−=   Mặt khác 90180  nên 22 cos 3  =− . Câu 29: Cho biết 2 cos 3  =− . Tính tan? A. 5 4 . B. 5 2 . C. 5 2 . D. 5 2 . Lời giải Chọn D Do cos0tan0  Ta có: 2 2 1 1tan cos   += 2 5 tan 4  = 5 tan 2  =− Câu 30: Cho biết 1 tan 2  = . Tính cot. A. cot2  = . B. cot2  = . C. 1 cot 4  = . D. 1 cot 2  = . Lời giải Chọn A 1 tan.cot1cot2 tan x x  === Câu 31: cos bằng bao nhiêu nếu 1 cot 2  =− ? A. 5 5  . B. 5 2 . C. 5 5 . D. 1 3 . Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 7 Ta có 1 cottan2 2 =−=− . ( ) 22 222 1111 1tancos cos1tan5 12   +==== + +− . Suy ra 5 cos 5  = Câu 32: Nếu tan3  = thì cos bằng bao nhiêu? A. 10 10 . B. 1 3 . C. 10 10  . D. 10 10 . Lời giải Chọn C Ta có 22 222 1111 1tancos cos1tan1310   +==== ++ . Suy ra 10 cos 10  = Câu 33: Cho  là góc tù và sin5 13  = Giá trị của biểu thức 3sin2cos + là A. 9 13 B. 3 C. 9 13 D. 3 Lời giải Chọn C Ta có 2 14412 cos1sincos 16913   =−== Do  là góc tù nên cos0  , từ đó 12 cos 13  =− Như vậy 3sin2cos325129 131313   +=+−=−   . Câu 34: Biết cot a=− , 0a  . Tính cos A. 2 cos 1 a a  = + B. 2 1 cos 1 a  = + C. 2 1 cos 1 a  =− + D. 2 cos 1 a a  =− + . Lời giải Chọn D Do cot a=− , 0a  nên 00 90180   suy ra cos0  Mặt khác, 1 tan cot   = 1 tan a  =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 8 Mà ta lại có 2 2 1 1tan cos   += 2 2 1 cos 1tan   = + 2 2 2cos 1 a a  = + . Khi đó 2 cos 1 a a  =− + và do 0a  nên 2 cos 1 a a  =− + Câu 35: Cho 1 cos 2 x = . Tính biểu thức 22 3sin4cos Pxx =+ A. 13 4 . B. 7 4 . C. 11 4 . D. 15 4 . Lời giải Chọn A Ta có ( ) 2 22222 3sin4cos3sincoscos3113 24 Pxxxxx  =+=++=+=   Câu 36: Cho  là góc tù và 4 sin 5  = . Giá trị của biểu thức 2sincosA =− bằng A. 7 5 . B. 7 5 . C. 1. D. 11 5 . Lời giải Chọn D Ta có: 2 22 sincos1sin1449 5525   ==−=−=   . Do  là góc tù nên 3 cos0cos 5 = 2.43112sincos 555 A  =−=−= Câu 37: Cho 4 sin, 5  = với 90180  . Tính giá trị của 3 sincos cos M   + = A. 25 27 M = B. 175 27 M = C. 35 27 M = D. 25 27 M =− Chọn D Ta có 2 22 cos1sin149 525   =−=−=   Mà 3 90180cos0cos 5  = Từ đó 3 sincos25 cos27 M   +− == . Câu 38: Cho biết 2 cos 3  =− . Tính giá trị của biểu thức cot3tan 2cottan E   + = + ?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 9 A. 19 13 . B. 19 13 . C. 25 13 . D. 25 13 Lời giải Chọn B ( ) ( ) 2 22 2 22 2 2 3tan1232 cot3tan13tan32cos19 cos 1 2cottan2tan1cos13 11tan1 cos E       +− ++− ====== +++ ++ + Câu 39: Cho biếtcot5  = . Tính giá trị của 2 2cos5sincos1E  =++ ? A. 10 26 B. 100 26 C. 50 26 D. 101 26 . Lời giải Chọn D ( )222 22 sin2cot5cot3cot5cot111101 sin1cot26 E    =++=++=  + . Câu 40: Cho 1 3 cot = . Giá trị của biểu thức 3sin4cos 2sin5cos A   + = là: A. 15 13 . B. 13. C. 15 13 . D. 13. Lời giải Chọn D 3sin4sin.cot34cot 13 2sin5sin.cot25cot A   ++ === . Câu 41: Cho biết 2 cos 3  =− . Giá trị của biểu thức cot3tan 2cottan E   = bằng bao nhiêu? A. 25 3 B. 11 13 C. 11 3 D. 25 13 . Lời giải Chọn C ( ) ( ) 2 22 2 22 2 2 43tan143 cot3tan13tan4cos311 cos 1 2cottan2tan3cos13 31tan3 cos E       −+ ======− −+ . Câu 42: Biết 1 cos 3  = . Giá trị đúng của biểu thức 22 sin3cosP =+ là: A. 11 9 . B. 4 3 . C. 1 3 . D. 10 9 . Lời giải Chọn A ( ) 222222 111 cossin3ossincos2cos12cos 39 Pc  ==+=++=+= Câu 43: Cho tan2  =− . Tính giá trị biểu thức 2sin3cos 3sin2cos P   + = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 10 A. 1 8 P = . B. 7 4 P =− . C. 1 8 P =− . D. 7 4 P = . Lời giải Chọn A Ta có: 2sin3cos 3sin2cos P   + = sincos23 coscos sincos32 coscos     + = 2tan3 3tan2   + = ( ) ( ) 223 1 3228 −+ == Câu 44: Cho biết 2 cos 3  =− . Giá trị của cot3tan 2cottan   + = + P bằng bao nhiêu? A. 25 13 =−P . B. 19 13 =−P . C. 19 13 =P . D. 25 13 =P . Lời giải Chọn C Áp dụng công thức 2 2 1 tan1 cos   += ta được: 22 2 15 tan1tan 24 3  +==    . Nhân tử và mẫu của biểu thức P cho tan, biết rằng tan.cot1  = , ta được 2 2 513 tan.cot3tan19 4 5 2tan.cottan13 2.1 4   + + === + + P . Câu 45: Cho biết 2 cos 3  =− . Tính giá trị của biểu thức cot3tan 2cottan P   + = + ? A. 19 13 P =− B. 19 13 P = C. 25 13 P = D. 25 13 P =− Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 11 Ta có: cot3tan 2cottan P   + = + 22 22 cossin3cos3sinsincos cossin2cossin2 sincos      + + == + + ( )22 22 cos31cos 2cos1cos   +− = +− 19 13 = . Câu 46: Cho biết 1 cossin 3 += . Tính giá trị của biểu thức 22 tancotP =+? A. 5 4 P = . B. 7 4 P = . C. 9 4 P = . D. 11 4 P = . Lời giải Chọn B Ta có: 1 sincos 3 += 1 sincos914 29  ==− ( )2 tancot2P  =+− 2sincos 2 cossin    =+−   2 2 117 22 sin.cos4 4 9   =−=−=      . Câu 47: Cho tan2  = . Tính giá trị của biểu thức 3sin2cos 2sincos A   = + là A. 2 5 B. 4 5 C. 3 2 D. 3 2 Lời giải Ta có: sin tan22sin2cos cos    === 3sin2cos3.2cos2cos4cos4 2sincos2.2coscos5cos5 A   ==== ++ Câu 48: Cho tan2 x = . Giá trị của biểu thức 2sin3cos 3sincos xx P xx + = ? A. 3 5 P = B. 7 5 P = C. 8 3 P = D. 5 7 P = Lời giải Chọn B Chia cả tử và mẫu cho cosx ta được: 2sin3cos2tan32.237 3sincos3tan13.215 xxx P xxx +++ ==== Câu 49: Cho 1 cos 2 x = . Tính biểu thức 22 3sin4cos Pxx =+ A. 13 4 . B. 7 4 . C. 11 4 . D. 15 4 . Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 12 Ta có: ( ) 2 22222 113 3sin4cos3sincoscos3.1. 24 Pxxxxx  =+=++=+=   Câu 50: Rút gọn biểu thức 2 2cos1 sincos Aa aa = + A. sincosaa + . B. sincosaa. C. cossinaa. D. tancosaa + . Lời giải Chọn C Ta có: ( )222 222 2cossincos 2cos1cossincossin sincossincossincos aaa aaa aa aaaaaa −+ ===− +++ Câu 51: Giá trị của biểu thức 66 sincos Axx =+ bằng .cos4 abx + . Giá trị của 2 ab + là A. 9 8 . B. 11 8 . C. 13 8 . D. 15 8 . Lời giải Chọn B Ta có: ( )( )66224224 sincossincossinsin.coscos Axxxxxxxx =+=+−+ ( )2 22222 sincos3sin.cos1sin21.331cos4 442 x xxxxx =+−=−=− ( ) 353 11cos4cos4 888 xx=−−=+ . Vậy 5311 22. 888 ab+=+= DẠNG 3. CHỨNG MINH, RÚT GỌN BIỂU THỨC LƯỢNG GIÁC Câu 52: Đẳng thức nào sau đây là sai? A. ( ) ( ) 22 cossincossin2, xxxxx ++−= . B. 2222 tansintansin,90 xxxxx  −= C. 4422 sincos12sincos, xxxxx +=− . D. 6622 sincos13sincos, xxxxx −=− Lời giải Chọn D ( )( )662222 sincossincos1sincos xxxxxx −=−− Câu 53: Đẳng thức nào sau đây là sai? A. ( )1cossin sin1cos0,180 xx xx xx  = + B. ( )1 tancot0,90,180 sincos xxx xx  += C. ( )22 22 1 tancot20,90,180 sincos xxx xx  +=− D. 22 sin2cos22 xx+= . Lời giải Chọn D

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 13 22 sin2cos21 xx+= . Câu 54: Trong các hệ thức sau hệ thức nào đúng? A. 22 sincos1 += . B. 22 sincos1 2  += . C. 22 sincos1 += . D. 22 sin2cos21 += . Lời giải Chọn D Công thức lượng giác cơ bản. Câu 55: Trong các hệ thức sau hệ thức nào đúng? A. 22 sincos1 += B. 22 sincos1 2  += C. 22 sincos1 += D. 22 sincos1 += Lời giải Chọn D Công thức lượng giác cơ bản. Câu 56: Rút gọn biểu thức sau 22 2 cotcossin.cos cotcot Axxxx xx =+ A. 4A = B. 2A = C. 1A = D. 3A = Lời giải Chọn C 2 2 22 2 22 2 cos cos cotcossin.cossin.cos sin cotcotcoscos sinsin x x xxxxxxAx xxxx xx =+=+ ( )22 222 2 cos1sin sin1sinsin1 cos xx xxx x =+=−+= . Câu 57: Biểu thức ( )2 cottanaa + bằng A. 22 11 sincos B. 22 cottan2 aa + C. 22 11 sincos + D. 22 cottan2 aa + Lời giải Chọn C ( ) ( ) ( )2 2222 22 11 cottancot2cot.tantancot1tan1 sincos aaaaaaaa aa +=++=+++=+ . Câu 58: Rút gọn biểu thức sau ( ) ( ) 22 tancottancot Axxxx =+−− A. 4A = B. 1A = C. 2A = D. 3A = Lời giải Chọn A ( ) ( )2222 tan2tan.cotcottan2tan.cotcot4 Axxxxxxxx =++−−+= . Câu 59: Đơn giản biểu thức ( ) 222 1sincot1cot Gxxx =−+− . A. 2sin x . B. 2 cos x . C. 1 cos x . D. cos x . Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 14 ( ) 222222 1sin1cot1sin.cot11cossin Gxxxxxx  =−−+=−+=−=  Câu 60: Đơn giản biểu thức sin cot 1cos x Ex x =+ + ta được A. sin x B. 1 cos x C. 1 sin x D. cos x Lời giải Chọn C ( ) ( ) sincossincos1cossin.sin cot 1cossin1cossin1cos xxxxxxx Ex xxxxx ++ =+=+= +++ ( ) ( ) ( ) ( ) ( )( ) ( ) 2 cos1cos1coscos1cos1cos1cos1 sin1cossin1cossin xxx xxxx xxxxx ++− +++− === ++ . Câu 61: Khẳng định nào sau đây là sai? A. 22 sincos1 += B. ( )2 2 1 1cotsin0 sin   += C. ( )tan.cot1sin.cos0  =− D. ( )2 2 1 1tancos0 cos   += Lời giải Chọn C sincos tan.cot.1 cossin xx xx  == . Câu 62: Rút gọn biểu thức 21 2sin.cos sinx P xx = ta được A. 1 tan 2 Px = . B. 1 cot 2 Px = . C. 2cot Px = . D. 2tan Px = . Lời giải Chọn B 22 1coscos1 cot 2sin.cos2sin.cos2sin2 sinxxx Px xxxxx ==== . DẠNG 4. TÍNH GIÁ TRỊ BIỂU THỨC LƯỢNG GIÁC Câu 63: Biểu thức cos20cos40cos60...cos160cos180A =+++++ có giá trị bằng A. 1. B. 1. C. 2. D. 2. Lời giải Chọn B Ta có ( ) ( )coscos1800180  =−− nên suy ra ( ) coscos1800 +−= . Do đó: ( ) ( ) ( )cos20cos160cos40cos140cos60cos120A =+++++ ( ) cos80cos100cos180 +++ cos1801 ==− Câu 64: Cho tancot3. −= Tính giá trị của biểu thức sau: 22 tancotA =+ . A. 12A = B. 11A = C. 13A = D. 5A = Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 15 ( )2 22 tancot3tancot9tancot2tan.cot9  −=−=+−= 2222 tancot29tancot11  +−=+= . Câu 65: Giá trị của biểu thức tan1tan2tan3...tan88tan89A  = là A. 0. B. 2. C. 3. D. 1. Lời giải Chọn D ( ) ( ) ( ) tan1.tan89.tan2.tan88...tan44.tan46.tan451A  == . Câu 66: Tổng 222222 sin2sin4sin6...sin84sin86sin88  ++++++ bằng A. 21. B. 23. C. 22. D. 24. Lời giải Chọn C 222222 sin2sin4sin6...sin84sin86sin88S  =++++++ ( ) ( ) ( )222222 sin2sin88sin4sin86...sin44sin46  =++++++ ( ) ( ) ( )222222 sin2cos2sin4cos4...sin44cos4422  =++++++= Câu 67: Biết sincos2 aa+= . Hỏi giá trị của 44 sincosaa + bằng bao nhiêu? A. 3 2 . B. 1 2 . C. 1. D. 0 . Lời giải Chọn B Ta có: sincos2 aa+= ( )22sincosaa=+ 1 sin.cos 2 aa = . ( ) 2 442222 11 sincossincos2sincos12 22 aaaaaa  +=+−=−=   . Câu 68: Biểu thức ( ) ( ) ( )4466 3sincos2sincos fxxxxx =+−+ có giá trị bằng: A. 1. B. 2. C. 3. D. 0 . Lời giải Chọn A 4422 sincos12sincos xxxx +=− . 6622 sincos13sincos xxxx +=− . ( ) ( ) ( )2222 312sincos213sincos1 fxxxxx =−−−= . Câu 69: Biểu thức: ( ) 4222 coscossinsin fxxxxx =++ có giá trị bằng A. 1. B. 2. C. 2. D. 1. Lời giải Chọn A ( ) ( ) 222222 coscossinsincossin1 fxxxxxxx =++=+= . Câu 70: Biểu thức 2222 tansintansinxxxx −+ có giá trị bằng A. 1 B. 0 C. 2 D. 1 Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 16 ( ) ( ) 2 222222222 2 sin tansintansintansin1sincossin0 cos x xxxxxxxxx x −+=−+=−+= . Câu 71: Giá trị của tan5.tan10.tan15...tan80.tan85A  = là A. 2. B. 1. C. 0 . D. 1. Lời giải Chọn B ( ) ( ) ( ) tan5.tan85.tan10.tan80...tan40tan50.tan451A  == Câu 72: Giá trị của 2222 cos73cos87cos3cos17B  =+++ là A. 2 B. 2 C. 2 D. 1 Lời giải Chọn B ( ) ( ) ( ) ( )22222222 cos73cos17cos87cos3cos73sin73cos87sin872B  =+++=+++= Câu 73: Cho tancot m+= . Tìm m để 22 tancot7 += A. 9m = . B. 3m = . C. 3m =− . D. 3m = . Lời giải Chọn D ( ) 222 7tancottancot2  =+=+− 2 9m = 3m = . Câu 74: Giá trị của sin36cos6sin126cos84E  = là A. 1 2 B. 3 2 C. 1 D. 1 Lời giải Chọn A ( ) ( ) 1 sin36cos6sin9036cos906sin36cos6cos36sin6sin30 2 E  =+−=−== Câu 75: Giá trị của biểu thức 2222 sin51sin55sin39sin35A  =+++ là A. 3 B. 4 C. 1 D. 2 Lời giải Chọn D ( ) ( ) ( ) ( )22222222 sin51sin39sin55sin35sin51cos51sin55cos55 2A  =+++=+++= Câu 76: Cho sincosxxm += . Tính theo m giá trị của sin.cos Mxx = A. 2 1m . B. 2 1 2 m . C. 2 1 2 m + . D. 2 1m + . Lời giải Chọn B ( ) ( )2 2222sincossincossincos2sin.cos xxmxxmxxxxm +=+=++= 2 2 1 12sin.cossin.cos 2 m xxmxx +== . Vậy 2 1 2 m M = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 17 Câu 77: Rút gọn biểu thức 22 4 222 tansintansincossin Pxxxxxx =−++ ta được A. 1P =− . B. 0P = . C. 2P = . D. 1P = . Lời giải Chọn B Điều kiện xác định: ( )os0 2 cxxkk   + . Ta có ( ) 4222222 sincossinsincossinsin xxxxxxx +=+= . Nên 22 4 222 tansintansincossin Pxxxxxx =−++ . 2222 tansintansinxxxx=−+ ( ) ( ) 2 22222 2 sin tansin1sincossin0 cos x xxxxx x =−+=−+= . Câu 78: Thu gọn biểu thức ( ) ( )22 sin2sin.sin.cossin Axaxxaax =+−+− A. 2 cos Aa = . B. cos2 Aa = . C. 2sin Aa = . D. sin2 Aa = . Lời giải Chọn C Ta có ( ) ( )22 sin2sin.sin.cossin Axaxxaax =+−+− ( ) ( ) ( ) ( )22 sinsin.sinsinsin xaxxaxaax =+−++−+−   ( ) ( ) ( ) ( )2 sinsin.sinsinsin xaxxaxaax =+−++−+−  ( ) ( ) 22 1cos2cos2cos21cos2 sinsin.sinsin 222 xaxa xaxxaa =+−+=−== Câu 79: Tính giá trị của biểu thức cos5cos10cos15...cos170cos175cos180P =++++++ A. 2P = . B. 1P = . C. 0P = . D. 1P =− . Lời giải Chọn D Áp dụng công thức biến đối ( )coscos180 =−− , ta có: cos5cos10cos15...cos170cos175cos180P =++++++ ( ) ( ) ( ) cos5cos175cos10cos170...cos85cos95cos90cos180P =++++++++ ( ) ( ) ( ) cos5cos5cos10cos10...cos85cos85cos90cos180P =−+−+++++ ( ) 00...0011P =+++++−=− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 88 BÀI 6. HỆ THỨC LƯỢNG TRONG TAM GIÁC Cho tam giác , , , ,ABCBCaCAbABc === S là diện tích tam giác. Giả sử ,, abc hhh lần lượt là độ dài các đường cao đi qua ba đỉnh ,,;ABC ,, abc mmm lần lượt là các đường trung tuyến đi qua ba đỉnh ,,. RABC và r lần lượt là bán kính đường tròn ngoại tiếp và nột tiếp của tam giác ABC . Ta có kết quả sau đây: 1. Định lí côsin 222 2.cos, abcbcA =+− 222 2.cos, bcacaB =+− 222 2.cos. cababC =+− *Hệ quả của định lí côsin 222222222 cos,cos,cos 222 bcaacbbac ABC bcacab +−+−+− === . 2. Định lí sin trong tam giác: 2. sinsinsinC abc R AB === 3. Giải tam giác và ứng dụng thực tế. Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác. 4. Công thức diện tích: a) 111 . 222abc Sahbhch === b) 111 sinsinsin 222 SbcAcaBabC === c) 4 abc S R = CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC LÝ THUYẾT.I = Luyện tập 1. Cho tam giác có và . Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác. Luyện tập 2. Cho tam giác có và . Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác. Luyện tập 3. Giải tam giác , biết và

phút

động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8km/h. Sau 2 giờ kể từ khi động cơ bị hỏng,tàuneođậuđượcvào một hònđảo.

a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu.

b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu.

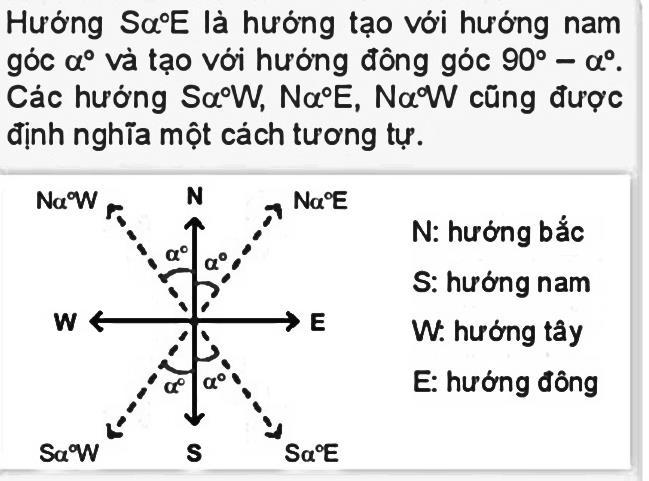
3.9. Trên nóc một tòa nhà có một cột ăng ten

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 89 d) Spr = với ( )1 2 pabc =++ e) Công thức Hê Rông ( )( )( )Sppapbpc =−−− 5. Công thức trung tuyến (bổ sung) 222222222 222 2()2()2() , , 444abc bcaacbabc mmm +−+−+− === 3.5. Cho tam giác ABC có 6,5,8.abc=== Tính cos,,. ASr 3.6. Cho tam giác ABC có 10,45,70.aAB=== Tính ,,.Rbc 3.7. Giải tam giác ABC và tính diện tích của tam giác đó, biết 15,130,6.ABc=== 3.8. Một tàu đánh cá xuất phát từ cảng ,A đi theo hướng 70 SE  với vậ

tốc 70 km/h. Đi được 90

thì

cao 5m. Từ một vị trí quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng ten, với các góc tương ứng là 50và 40 so với phương nằm ngang (H.3.18). a) Tính các góc của tam giác .ABC b) Tính chiều cao của tòa nhà. 3.10. Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một cách xác định bề rộng của hòn đảo (theo chiều ta ngắm được). Đảo Yến nhìn từ bãi biển Vũng Chùa, Quảng Bình Luyện tập 4. Tính diện tích tam giác có BÀI TẬP SÁCH GIÁO KHOA. =

I TAM GIÁC

ng h

núi,

Áp dụng các công thức sách giáo khoa như: định lí

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 90 3.11. Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đườ

ầm xuyên

nối thẳng từ A tới D . Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ? DẠNG 1: GIẢ

{Tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.} +

cosin, hệ quả của định lí cosin, định lí sin, các công thức liên quan đến diện tích để vận dụng vào làm bài. Câu 1. Cho tam giác có 0 4,6,120.ABACA=== Tính độ dài cạnh BC Câu 2. Cho tam giác ABC có 7;8;5abc=== . Tính ,,,. a AShR Câu 3. Cho tam giác ABC có độ dài ba cạnh là 2AB = , 5BC = , 6CA = . Tính độ dài đường trung tuyến MA, với M là trung điểm của BC . Câu 4. Tam giác ABC vuông tại A có 6cmAC = , 10cmBC = . Tính bán kính đường tròn nội tiếp tam giác ABC . Câu 5. Cho tam giác ABC có 7b = , 5c = , 3 cos 5 A = . Tính độ dài đường cao a h của tam giác ABC . Câu 1: Cho ABC có BCa = , 120BAC = . Bán kính đường tròn ngoại tiếp ABC là A. 3 2 a R = B. 2 a R = C. 3 3 a R = D. Ra = ABC HỆ THỐNG BÀI TẬP.II == PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 = BÀI TẬP TRẮC NGHIỆM.3 =

Câu 7: Tam giác ABC

A. 17

Câu 8: Tam giác ABC có 4AB = , 10AC = và đường trung tuy

A. 26 B. 5 C.

6AM = . Tính độ dài cạnh BC .

D. 222

Câu 9: Tam giác ABC có 75,45AB== , 2AC = . Tính cạnh AB .

A. 2 2 . B. 6 . C. 6 2

Câu 10: Tam giác ABC

Câu 11: Tam giác ABC

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 91 Câu 2: Tam giác ABC có 8a = , 3c = , 60B = . Độ dài cạnh b bằng bao nhiêu? A. 49 B. 97 C. 7 D. 61 Câu 3: Cho ABC có 4a = , 5c = , 150B = . Tính diện tích tam giác ABC . A. 10S = . B. 103S = . C. 5S = . D. 53S = . Câu 4: Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 4 . B. 40. C. 32,5. D. 65,8. Câu 5: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 60. Biết ( )200mCA = , ( )180mCB = . Khoảng cách AB bằng bao nhiêu? A. ( )228m B. ( )2091m C. ( )112m D. ( )168m Câu 6: Tam giác ABC có góc A nhọn, 5AB = , 8AC = , diện tích bằng 12. Tính độ dài cạnh BC A. 23 B. 4 C. 5 D. 32

có 4AB = , 6AC = và trung tuyến 3BM = . Tính độ dài cạnh BC .

. B. 25 . C. 4. D. 8.

ến

. D. 6 3 .

có 60B = , 45C = , 3AB = . Tính cạnh AC .

36 2 B. 32 2 C. 6 D. 26 3

có các góc 75,45AB== Tính tỉ số AB AC

6 3 . B. 6 . C. 6 2 . D. 1,2. Câu 12: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết ABc = và os() 1 c 3 AB+= . A. 2 2 c B. 32 8 c C. 92 8 c D. 3 2 c Câu 13: Tam giác ABC có các góc 105A = , 45B = . Tính tỉ số AB AC A. 2 2 . B. 2 . C. 2 2 . D. 6 3 . Câu 14: Tam giác ABC có 4AB = , 5AC = , 6BC = . Tínhcos() BC + . A. 1 8 B. 1 4 C. –0,125 D. 0,75 Câu 15: Tam giác có ba cạnh lần lượt là 2,3,4. Góc bé nhất của tam giác có sin bằng bao nhiêu? A. 15 8 B. 7 8 C. 1 2 D. 14 8

Câu

Tam giác

Câu 17: Hình vuông ABCD có

Tìm

dài

n th

ng DF

trung

A. 13

Câu 18: Tam giác

Câu

dài AM bằng bao nhiêu?

trên cạnh BC sao cho 3 BC BM = .

A. 17 3 a . B. 5 3 a . C. 22 3 a . D. 2 3 a

Câu 20: Tam giác ABC có ( ) 1 cosAB 8 +=− , 4AC = , 5BC = . Tính cạnh AB

A. 46 . B. 11. C. 52 . D. 6.

Câu 21: Tam giác ABC có

A. 215

Câu 22: Tam giác ABC có

A. 6.

Câu 23: Tam giác ABC có

Câu

Cho tam

Tính

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 92

16:

có ba cạnh lần lượt là 3, 8, 9. Góc lớn nhất của tam giác có cosin bằng bao nhiêu?

1 6 . B. 1 6 . C. 17 4 . D. 4 25 .

cạnh bằng a . Gọi E là trung điểm cạnh

là

điểm

ạnh AE .

độ

đoạ

ẳ

. B. 5 4 a . C. 3 2 a . D. 3 4 a .

ABC có 12BC = , 9CA = , 6AB = . Trên cạnh BC lấy điểm M sao cho 4BM = . Tính độ dài đoạn thẳng AM A. 25. B. 32 . C. 20 . D. 19 .

19: Tam giác ABC vuông tại A có ABACa == . Điểm M nằm

Độ

7AB = , 5AC = và ( ) 1 cos 5 BC+=− . Tính BC

. B. 422 . C. 415 . D. 222

5BC = , 3AC = và cot2 C = . Tính cạnh AB

B. 2 . C. 9 5 .

210 .

3AB = , 4AC = và tan22 A =−

cạnh BC

32 . B. 43. C. 33. D. 7.

24:

giác ABC có cạnh BCa = , cạnh CAb = . Tam giác ABC có diện tích lớn nhất khi góc C bằng: A. o60 B. o90 C. o150 D. o120 Câu 25: Cho tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm , EF sao cho các góc MPE , EPF , FPQ bằng nhau. Đặt , , , MPqPQmPExPFy ==== . Trong các hệ thức sau, hệ thức nào đúng? A. MEEFFQ == . B. 222 MEqxxq =+− . C. 222 MFqyyq =+− . D. 222 2 MQqmqm =+− . Câu 26: Tính góc C của tam giác ABC biết ab  và ( ) ( )2222 aacbbc −=− . A. 150C = B. 120C = C. 60C = D. 30C = Câu 27: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết 12AB = và 1 cot()3 AB+= . A. 210 B. 910 5 C. 510 D. 32

Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin, các công thức liên quan

ng vào làm bài.

Câu 1. Cho tam giác ABC thỏa sin

Câu 2. Chứng minh trong tam giác

Cho tam giác ABC

Cho tam giác

Tam giác ABC là tam giác gì?

tam giác

là tam giác

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 93 Câu 28: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết 10AB = và 1 tan()3 AB+= A. 510 9 B. 10 3 C. 10 5 D. 510 Câu 29: Tam giác ABC có 4AB = , 6AC = , 1 cos 8 B = , 3 cos 4 C = .Tính cạnh BC . A. 7. B. 5. C. 33. D. 2. Câu 30: Cho tam giác cân ABC có 0120A = và ABACa == . Lấy điểm M trên cạnh BC sao cho 2 5 BC BM = . Tính độ dài AM A. 3 3 a . B. 11 5 a . C. 7 5 a . D. 6 4 a . DẠNG 2: HỆ THỨC LIÊN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC, NHẬN DẠNG TAM GIÁC

đến diện tích để vận dụ

2cos sin

C B =

ABC ta có: 2.sin.sin a hRBC = Câu 3.

. Chứng minh ( )..sinsinsin SRrABC =++ . Câu 4.

ABC thỏa 333 2 2.cos bca a bca abC  +− = +−  = . Chứng minh

ABC

đều. Câu 5. Chứng minh trong tam giác ABC ta có: sin.cossin.cossin BCCBA += Câu 1: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: A. 222 2 24a bca m + =+ . B. 222 2 24a acb m + =− . C. 222 2 22 4a cba m +− = D. 222 2 24a abc m + =− Câu 2: Trong tam giác ABC , câu nào sau đây đúng? A. 222 2.cos abcbcA =++ . B. 222 2.cos abcbcA =+− . C. 222 .cos abcbcA =++ . D. 222 .cos abcbcA =+− . Câu 3: Nếu tam giác ABC có 222 abc + thì: A. A là góc tù. B. A là góc vuông. C. A là góc nhọn. D. A là góc nhỏ nhất. PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 = BÀI TẬP TRẮC NGHIỆM.3 =

Câu 8: Cho tam giác ABC

Câu 9: Trong tam giác ABC , hệ thức nào sau đây sai?

Câu 10: Cho tam giác ABC

abc

. Trong các mệnh đề sau, mệnh đề nào đúng?

A. coscos2cosBCA += . B. sinsin2sinBCA += .

C. 1 sinsinsin 2 BCA += . D. sincos2sinBCA += .

Câu 11: Tam giác ABC có 120A = thì câu nào sau đây đúng?

A. 222 3 abcbc =+− . B. 222 abcbc =++ . C. 222 3 abcbc =++ . D. 222 abcbc =+− .

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 94 Câu 4: Tam giác ABC có ba cạnh thoả mãn điều kiện ( )( ) 3 abcabcab +++−= . Khi đó số đo của C là A. 120 B. 30 C. 45 D. 60 Câu 5: Cho tam giác ABC . Khẳng định nào sau đây là đúng? A. ( )222222 2 3abc mmmabc ++=++ . B. ( )222222 4 3abc mmmabc ++=++ . C. ( )222222 1 3abc mmmabc ++=++ . D. ( )222222 3 4abc mmmabc ++=++ . Câu 6: Cho tam giác ABC thỏa mãn .cos caB = . Khẳng định nào sau đây là đúng? A. Tam giác ABC là tam giác cân. B. Tam giác ABC là tam giác nhọn. C. Tam giác ABC là tam giác vuông. D. Tam giác ABC là tam giác tù Câu 7: Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây? I. ( )( )( )2 Sppapbpc =−−− II. ( )( )( )( )216Sabcabcabcabc =+++−−+−++ . A. Chỉ I. B. Chỉ II. C. Cả I và II. D. Không có.

, các đường cao ,, abc hhh thỏa mãn hệ thức 32abc hhh =+ . Tìm hệ thức giữa , , abc .

321 abc =− . B. 32abc =+ . C. 32abc =− . D. 321

=+ .

.sin sin bA a B = B. sin.sincA C a = C. 2.sin aRA = D. .tan bRB =

thỏ

mãn hệ thức 2 bca +=

12: Trong tam giác ABC , điều kiện để hai trung tuyến vẽ từ A và B vuông góc với nhau là: A. 222225 abc += . B. 222335 abc += . C. 222223 abc += . D. 222 5 abc += . Câu 13: Trong tam giác ABC , nếu có 2 . abc = thì : A. 2 111 abc hhh =− B. 2 . abc hhh = C. 2 111 abc hhh =+ D. 2 122 abc hhh =+ Câu 14: Trong tam giác ABC , nếu có 2 abc hhh =+ thì : A. 211 sinsinsinABC =+ B. 2sinsinsinABC =+ C. sin2sin2sinABC =+ . D. 211 sinsinsinABC =− . Câu 15: Trong tam giác ABC , câu nào sâu đây đúng? A. 2a bc m + = . B. 2a bc m +  . C. 2a bc m +  . D. a mbc =+ .

Câu

Cho

ABC có

abc

góc

là góc

góc vuông.

Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin, các công thức liên quan đến diện tích để vận dụng vào làm bài.

Câu 1: Hai chiế

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 95 Câu 16: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện ( )( ) 3 abcabcab +++−= . Tính số đo của góc C . A. 45 . B. 60 . C. 120 . D. 30 .

17:

tam giác ABC , xét các bất đẳng thức sau: I. abc − . II. abc + . III. abc mmmabc ++++ Hỏi khẳng định nào sau đây đúng? A. Chỉ I, II. B. Chỉ II, III. C. Chỉ I, III. D. Cả I, II, III. Câu 18: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện 222 3 bcabc +−= . Tính số đo của góc A . A. 45 . B. 60 . C. 120 . D. 30 . Câu 19: Tam giác ABC .cos.cos aBbA = . Tam giác ABC là tam giác gì? A. Tam giác vuông. B. Tam giác đều. C. Tám giác vuông cânD. Tam giác cân. Câu 20: Cho tam giác ABC vuông tại A , ACb = , ABc = . Lấy điểm M trên cạnh BC sao cho góc 30BAM =  Tính tỉ số MB MC . A. 3 3 b c B. 3 3 c b C. 3c b D. bc bc + Câu 21: Mệnh đề nào sau đây sai? A. Nếu 222 abc + thì A là góc tù. B. Nếu tam giác

một

tù thì 222 abc + C.

ếu 222

+ thì A

nhọn. D.

ếu 222

=+ thì A là

DẠNG 3: ỨNG DỤNG THỰC TẾ

c tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 060 . Tàu thứ nhất chạy với tốc độ 30/kmh , tàu thứ hai chạy với tốc độ 40/kmh. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km ? Câu 2: Từ một đỉnh tháp chiều cao 80 CDm = , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 7212' và 0 3426' so với phương nằm ngang. Ba điểm ,, ABD thẳng hàng. Tính khoảng cách AB (chính xác đến hàng đơn vị)? PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 =

Câu 3: Cho tam giác ABC có 13,8,7abc=== . Tính góc A, suy ra S, ha, R, r, ma.

Câu 4: Cho tam giác ABC có ABAC4,5 và A 3 cos 5 . Tính cạnh BC, và độ dài đường cao kẻ từ A.

Câu 5: Cho tam giác ABC có , ABAC104 và A 060 . a) Tính chu vi của tam giác b) Tính tanC

Câu 6: Giải tam giác ABC biết AB00 60,40 và c 14 .

Câu 7: Giải tam giác ABC , biết: bAC00 4,5;30;75

Câu 8: Cho tam giác ABC

Cho tam giác

từ A và bán kính đường tròn n

OFFICIAL

tam giác.

Câu 10: Cho tam giác ABC thỏa mãn 2 sinsin.sinABC . Ch

ng minh rằng a) 2 abc b) 1 cos 2 A

Câu 11: Tam giác ABC có ,, BCaCAbABc và trung tuyến AMABc chứng minh rằng: 222 222 )2() )sin2(sinsin) aabc bABC

Câu 12: Cho tam giác ABC . Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là 222 5 bca

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 96

cân tại A biết 03;30aBC=== . Tính R, r, cạnh c, b, suy ra S Câu 9:

ABC nội tiếp đường tròn bán kính bằng 3, biết 00 30,45AB . Tính độ dài trung tuyến kẻ

ộ

tiếp

ứ

. Câu 13: Chứng minh rằng trong mọi tam giác ABC ta có; a) .cos.cos abCcB b) sinsincossincos ABCCB Câu 14: Chứng minh rằng trong mọi tam giác ABC ta có: 2sinsin a hRBC Câu 15: Tìm tính chất đặc biệt của tam giác ABC biết:2cos.cos.cos aAbCcB =+ Câu 16: Nhận dạng tam giác ABC biết: 333 2 2cos(1) (2) abC abc a abc Câu 17: Nhận dạng tam giác ABC biết: .sinsinsin abc aAbBcChhh Câu 18: Cho tam giác ABC . Chứng minh tam giác ABC cân nếu .sin a hcA BÀI TẬP TỰ LUẬN TỔNG HỢP. =

tam giác

H

LƯỢNG TRONG

lượt

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 1 BÀI 6.

Ệ THỨC

TAM GIÁC Cho

, , , ,ABCBCaCAbABc === S là diện tích tam giác. Giả sử ,, abc hhh lần

là độ dài các đường cao đi qua ba đỉnh ,,;ABC ,, abc mmm lần lượt là các đường trung tuyến đi qua ba đỉnh ,,. RABC và r lần lượt là bán kính đường tròn ngoại tiếp và nột tiếp của tam giác ABC . Ta có kết quả sau đây: 1. Định lí côsin 222 2.cos, abcbcA =+− 222 2.cos, bcacaB =+− 222 2.cos. cababC =+− *Hệ quả của định lí côsin 222222222 cos,cos,cos 222 bcaacbbac ABC bcacab +−+−+− === . Áp dụng định lý cosin : 22222 2 2..cos45582.5.8.89402 2 oBCABACABAC=+−=+−=− 89402BC =− . Áp dụng định lý cosin : ( ) ( ) 22222 0 8940258 cos0,0202919' 2 289402.5 acb BB ac +−−+− ==− 0000 18045919'26,83''4350'33,17''C −− 2. Định lí sin trong tam giác: 2. sinsinsinC abc R AB === Giải Áp dụng Định lí sin cho tam giác ABC ta có: CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC LÝ THUYẾT.I = Luyện tập 1. Cho tam giác có và . Tính độ dài các cạnh và độ lớn các góc còn lại của tam giác. Luyện tập 2 Cho tam giác có và . Tính số đo các góc, bán kính đường tròn ngoại tiếp và độ dài cạnh còn lại của tam giác.

Áp dụng Đị

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 2 0 0 .sin5.sin80 sin0,62 2R8 sinsin 8 2sin2.sin804,06 cB bcC b BC b R B  ==  ==   ===  3. Giải tam giác và ứng dụng thực tế. Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác. Giải

nh lí côsin cho tam giác ABC , ta có: 2222202.cos32452.32.45.cos872898,27abcbcA=+−=+−= Suy ra 53,84a . Áp dụng Định lí sin cho tam giác ABC , ta có: 0 53,8432 sin87sinB = Suy ra 0 032.sin87 sin0,59369' 53,84 BB = Ta có 0 180()180(369'87)5651'. ooooCAB=−+=−+= Chú ý. Áp dụng các Định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính ( gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau: • Biết hai cạnh và góc xen giữa; • Biết ba cạnh; • Biết một cạnh và hai góc kề. 4. Công thức diện tích: a) 111 . 222abc Sahbhch === b) 111 sinsinsin 222 SbcAcaBabC === c) 4 abc S R = Luyện tập 3. Giải tam giác , biết và

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 3 d) Spr = với ( )1 2 pabc =++ e) Công thức Hê Rông ( )( )( )Sppapbpc =−−− Giải Ta có 180()180(3045)105. oooooACB=−+=−+= Áp dụng Định lí sin cho tam giác ABC ta có: 0 000 22.sin45 22. sin45sin30sin30 c c === Ta có: 011 sinA.2.22.sin10513. 22 Sbc===+ 5. Công thức trung tuyến (bổ sung) 222222222 222 2()2()2() , , 444abc bcaacbabc mmm +−+−+− === 3.5. Cho tam giác ABC có 6,5,8.abc=== Tính cos,,. ASr Lời giải Ta có 22222258653 cos 22.5.880 bca A bc +−+− === Nửa chu vi là 65819 222 abc P ++++ === . Áp dụng công thức Heron ta có: ()()()658191919193399 22224Sppapbpc  =−−−=−−−=   Do 3399 .. 38 S Sprr p === 3.6. Cho tam giác ABC có 10,45,70.aAB=== Tính ,,.Rbc Lời giải Áp dụng định lý sin ta có 10 252. sin2sin2.sin45 aa RR AA ====  Ta có sin10.sin70 13,289sinsinsinsin45 abaB b ABA  ===  Vì sin10.sin65 1801806512,82 sinsin45 aC ABCCABc A  ++==−−===  Luyện tập 4. Tính diện tích tam giác có BÀI TẬP SÁCH GIÁO KHOA. =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 4 3.7. Giải tam giác ABC và tính diện tích của tam giác đó, biết 15,130,6.ABc=== Lời giải Ta có 18018035ABCCAB ++==−−= Áp dụng định lý sin ta có: sin6sin15 sinsin352,71 sin6sin130sinsinsin sinsin358,01 cA a abcC ABCcB b C  ==  ==   ==  Diện tích của tam giác là: 11 ..sin.2,71.6.sin1306,228 22 SacB== 3.8. Một tàu đánh cá xuất phát từ cảng ,A đi theo hướng 70 SE  với vận tốc 70 km/h. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc 8km/h. Sau 2 giờ kể từ khi động cơ bị hỏng,tàuneođậuđượcvào một hònđảo. a) Tính khoảng cách từ cảng A tới đảo nơi tàu neo đậu. b) Xác định hướng từ cảng A tới đảo nơi tàu neo đậu. Lời giải a) Theo giả thiết ta có: 105,16, ABkmBCkm == Góc 7018070110BASABC==−= Khoảng cách từ A tới đảo tàu neo đậu bằng đoạn .AC Áp dụng định lý côsin ta có:

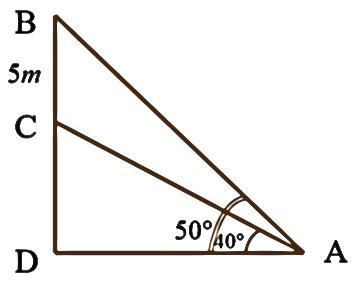
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 5 22 2..cos ACABBCABBCB =+− 22 105162.105.16.cos110115,5km=+−= b) Ta có 222 cos0,994617706176342 2. ABACBC BACASAC ABAC +−  ==−= Vậy hướng từ cảng A tới đảo nơi tàu neo đậu là 6342 SE  . 3.9. Trên nóc một tòa nhà có một cột ăng ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng ten, với các góc tương ứng là 50và 40 so với phương nằm ngang (H.3.18). a) Tính các góc của tam giác .ABC b) Tính chiều cao của tòa nhà. Lời giải a) Ta có 504010BAC =−= , 9040180130ABCBADACBABCBAC=−==−−= b) Áp dụng định lý sin trong tam giác ABC ta có .sin5.sin40 18,51.sinsinsinsin10 BCACBCB AC ABA  ===  Xét tam giác ACD vuông tại D có .sin4011,9CDAC= Vậy chiều cao của tòa nhà là: 11,9718,9. m+= 3.10. Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một cách xác định bề rộng của hòn đảo (theo chiều ta ngắm được). Đảo Yến nhìn từ bãi biển Vũng Chùa, Quảng Bình Lời giải

Gọi , BC là hai vị trí ngoài cùng mà ta quan sát khi nhìn từ bãi biển

OFFICIAL

Từ một điểm A trên bãi biển dùng giác kế ta xác định được góc BAC = .

Lấy điểm , ED trên bãi biển sao cho ,, EAD thẳng hàng và có độ dài đoạn ; EAxADy == mét.

Ta xác định được EAB =. Từ đó suy ra được CAD

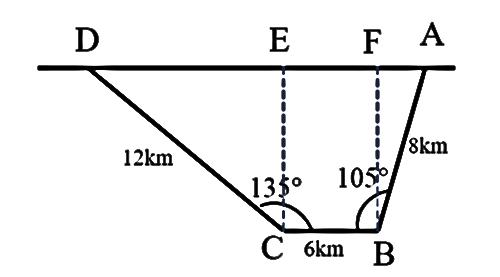
Ta dùng giác kế ta xác định được các góc ;

Từ đó áp dụng định lí sin cho hai tam giác ABE và ADC ta xác định được AB và AC .

Sau đó ta sử dụng đị

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 6

= .

AEBADC .

nh lý cosin trong ABC tính được bề rộng BC của hòn đảo. 3.11. Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong Hình 3.19. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ A tới D . Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ? Lời giải Dựng , CEBF vuông góc với AD. Xét tam giác CDE vuông tại E có 45DC== .sin4562. DECDkm==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 7 Xét tam giác ABF vuông tại F có 15B = ( ) .sin152622. AFABkm==− Mặt khác 6 EFBCkm == 6422616,56. ADDEEFFAkm =++=++ Vậy độ dài đường mới sẽ giảm 9,44km so với đường cũ. DẠNG 1: GIẢI TAM GIÁC {Tìm một số yếu tố của tam giác khi cho biết các yếu tố khác.} + Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin, các công thức liên quan đến diện tích để vận dụng vào làm bài. Câu 1. Cho tam giác có 0 4,6,120.ABACA=== Tính độ dài cạnh BC Lời giải 222220 2..cosA642.6.4.cos120BCABACABAC=+−=+− 22 1 642.6.4.7676219. 2 BC =+−=== Câu 2. Cho tam giác ABC có 7;8;5abc=== . Tính ,,,. a AShR Lời giải + 2222228571 cos 22.8.52 bca A bc +−+− === 60A = . + 11 ..sin.8.5.sin60103 22 SbcA=== . + Ta có: 122.103203 277 aa SahhS a ==== . + Ta có: ....7.8.573 443 4.103 abcabc SR RS ==== Câu 3. Cho tam giác ABC có độ dài ba cạnh là 2AB = , 5BC = , 6CA = . Tính độ dài đường trung tuyến MA, với M là trung điểm của BC Lời giải Áp dụng công thức tình độ dài trung tuyến ta có: ABC HỆ THỐNG BÀI TẬP.II == PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 8 222 24 ABACBC MA + =− 222 26555 242 + =−= . Câu 4. Tam giác ABC vuông tại A có 6cmAC = , 10cmBC = . Tính bán kính đường tròn nội tiếp tam giác ABC . Lời giải Do tam giác ABC vuông tại A có 6cmAC = , 10cmBC = nên 22ABBCAC =− 22 1068=−= . Diện tích tam giác ABC là 1 . 2ABC SABAC  = 24= Bán kính đường tròn nội tiếp tam giác ABC là 2 ABCS r ABBCCA  = ++ 2.24 6810 = ++ 2= . Câu 5. Cho tam giác ABC có 7b = , 5c = , 3 cos 5 A = . Tính độ dài đường cao a h của tam giác ABC . Lời giải Theo định lí hàm cos ta có 222 2cos abcbcA =+− 3 49252.7.5. 5 =+− 32= 42a = . Ta lại có: 3 cos 5 A = 4 sin 5 A = . Diện tích tam giác ABC là 1 sin 2ABC SbcA  = 14 .7.5. 25 = 14= . Vì 1 2 ABCa Sah  = nên 2 ABC a S h a  = 28 42 = 72 2 = Vậy 72 2a h = Câu 1: Cho ABC có BCa = , 120BAC = . Bán kính đường tròn ngoại tiếp ABC là A. 3 2 a R = . B. 2 a R = . C. 3 3 a R = . D. Ra = . Lời giải Chọn D a c bha BH C A BÀI TẬP TRẮC NGHIỆM.3 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 9 Theo định lý sin trong tam giác ta có 2 sin BC R BAC = 13 2sin1203 aa R ==  Câu 2: Tam giác ABC có 8a = , 3c = , 60B = . Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 . C. 7. D. 61 . Lời giải Chọn C 222 2cos bacacB =+− 22 832.8.3cos60 =+− 49= 7b = . Câu 3: Cho ABC có 4a = , 5c = , 150B = . Tính diện tích tam giác ABC . A. 10S = B. 103S = C. 5S = D. 53S = Lời giải Chọn C Diện tích tam giác ABC là 1 sin 2 SacB = 1 .4.5sin150 2 = 5= Câu 4: Một tam giác có ba cạnh là 52, 56, 60. Bán kính đường tròn ngoại tiếp tam giác đó là A. 65 4 . B. 40. C. 32,5. D. 65,8. Lời giải Chọn C Ta có: 525660 2p ++ = 84= Áp dụng hệ thức Hê rông ta có: ( )( )( )84845284568460S =−−− 1344= . Mặt khác 4 abc S R = 4 abc R S = 52.56.60 4.1344 = 32,5= . Câu 5: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 60. Biết ( )200mCA = , ( )180mCB = . Khoảng cách AB bằng bao nhiêu? A. ( )228m B. ( )2091m C. ( )112m D. ( )168m Lời giải Chọn B

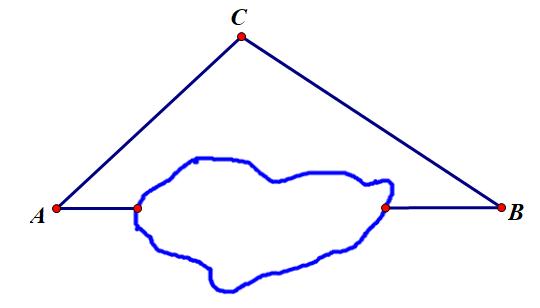
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 10 222 2..cos6036400ABCACBCACB=+−= ( )2091mAB = Câu 6: Tam giác ABC có góc A nhọn, 5AB = , 8AC = , diện tích bằng 12. Tính độ dài cạnh .BC A. 23. B. 4. C. 5. D. 32 . Lời giải Chọn C Ta có: 122.123 ...sinsin365212 2.5.85 S SABACAAA ABAC ===== 222222...cos582.5.8.cos365212255 BCABACABACABC  =+−=+− . Câu 7: Tam giác ABC có 4AB = , 6AC = và trung tuyến 3BM = . Tính độ dài cạnh BC A. 17 B. 25 C. 4 D. 8 Lời giải Chọn B Ta có: 222 2 24 ABBCAC BM + =− 2 222 2 4 AC BCBMAB  =+−   2 22 6 2342025 4 BC =+−==   Câu 8: Tam giác ABC có 4AB = , 10AC = và đường trung tuyến 6AM = . Tính độ dài cạnh BC . A. 26 . B. 5. C. 22 . D. 222 . Lời giải Chọn D 4 6 3 M B A C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 11 Ta có: 222 2 24 ACABBC AM + =− 2222 222 104 446 22 ACAB BCAM ++ =−=−=   88222 BC == . Câu 9: Tam giác ABC có 75,45AB== , 2AC = . Tính cạnh AB . A. 2 2 B. 6 C. 6 2 D. 6 3 Lời giải Chọn B Ta có: .sin.sin2.sin(1807545)6 sinsinsinsinsin45 bcbCACC ABc BCBB ====== . Câu 10: Tam giác ABC có 60B = , 45C = , 3AB = . Tính cạnh AC . A. 36 2 . B. 32 2 . C. 6 . D. 26 3 . Lời giải Chọn A Ta có: .sin.sin3.sin603.6 sinsinsinsinsin452 bccBABB ACb BCCC ====== . Câu 11: Tam giác ABC có các góc 75,45AB== Tính tỉ số AB AC A. 6 3 B. 6 C. 6 2 D. 1,2 Lời giải Chọn C Ta có: sinsin(1807545)6 sinsinsinsin452 bcABcC BCACbB −− =====  . Câu 12: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết ABc = và os() 1 c 3 AB+= 4 10 6 M A B C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 12 A. 2 2 c B. 32 8 c C. 92 8 c D. 3 2 c Lời giải Chọn B Ta có 1 coscos()3 CAB=−+=− . Do đó 2 122 sin1 33 C  =−−=   . 32 2 sin2sin8 ABABc RR CC === Câu 13: Tam giác ABC có các góc 105A = , 45B = . Tính tỉ số AB AC . A. 2 2 . B. 2 . C. 2 2 . D. 6 3 . Lời giải. Chọn A Ta có: sinsin(18010545)2 sinsinsinsin452 bcABcC BCACbB −− =====  . Câu 14: Tam giác ABC có 4AB = , 5AC = , 6BC = . Tínhcos() BC + A. 1 8 B. 1 4 C. –0,125 D. 0,75 Lời giải Chọn C Ta có 4==cAB , 5==bAC , 6==aBC Tính 8 1 2 cos 222 = + = bc bca A Để ý 0,125 8 1 cos()cos+===BCA Câu 15: Tam giác có ba cạnh lần lượt là 2,3,4. Góc bé nhất của tam giác có sin bằng bao nhiêu? A. 15 8 B. 7 8 C. 1 2 D. 14 8 Lời giải Chọn A Góc bé nhất ứng với cạnh có số đo bé nhất.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 13 Giả sử 2,3,4===abc . Ta có 222 7 cos 2..8 bca A bc +− == Do đó 8 15 8 7sin1 2 =     =A Câu 16: Tam giác có ba cạnh lần lượt là 3, 8, 9. Góc lớn nhất của tam giác có cosin bằng bao nhiêu? A. 1 6 . B. 1 6 . C. 17 4 . D. 4 25 Lời giải Chọn B Góc lớn nhất tương ứng với cạnh lớn nhất: 222 3891 cos 2.3.86  +− ==− . Câu 17: Hình vuông ABCD có cạnh bằng a . Gọi E là trung điểm cạnh BC , F là trung điểm cạnh AE . Tìm độ dài đoạn thẳng DF . A. 13 4 a . B. 5 4 a . C. 3 2 a . D. 3 4 a Lời giải Chọn A Ta có: 2 2 5 22 AEDEaaa  ==+=   Dùng công thức độ dài trung tuyến: 2 2 22222 2 5 4513 2421616 a a DADEAEaa DF + + =−=−= 13 4 a DF = Câu 18: Tam giác ABC có 12BC = , 9CA = , 6AB = . Trên cạnh BC lấy điểm M sao cho 4BM = . Tính độ dài đoạn thẳng AM A. 25. B. 32 . C. 20 . D. 19 . Lời giải F E DC A B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 14 Chọn D 222222612911 cos 2.2.6.1216 ABBCAC B ABBC +−+− === 2222 11 2..cosB642.6.4.19 16 AMABBMABBM=+−=+−= . Câu 19: Tam giác ABC vuông tại A có ABACa == . Điểm M nằm trên cạnh BC sao cho 3 BC BM = . Độ dài AM bằng bao nhiêu? A 17 3 a . B. 5 3 a . C. 22 3 a . D. 2 3 a . Lời giải Chọn B 2222 2BCABACaaa =+=+= 22BCABa == 2 3 a BM = 2 2202 2225 2..cos452.. 3323 AMABBMABBMaaaaa  =+−=+−=    . Câu 20: Tam giác ABC có ( ) 1 cosAB 8 +=− , 4AC = , 5BC = . Tính cạnh AB A. 46 . B. 11. C. 52 . D. 6. Lời giải Chọn A Vì trong tam giác ABC ta có AB + bù với góc C nên ( ) 11 coscos 88 ABC +=−= 2222 1 2..cos452.4.5.6 8 ABACBCABBCC=+−=+−= . Câu 21: Tam giác ABC có 7AB = , 5AC = và ( ) 1 cos 5 BC+=− . Tính BC A. 215 . B. 422 . C. 415 . D. 222 . Lời giải B A C M

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 15 Chọn A Vì trong tam giác ABC ta có BC + bù với góc A nên ( ) 1 cosBC 5 +=− 1 cos 5 A = 2222 1 2..cosA752.7.5.215 5 BCABACABAC=+−=+−= Câu 22: Tam giác ABC có 5BC = , 3AC = và cot2 C = . Tính cạnh AB A. 6. B. 2 . C. 9 5 . D. 210 . Lời giải Chọn B Từ giả thiết cot2 C = , ta suy ra C là góc nhọn 2 22 11142 cot2tancoscos 21tan515 1 2 CCCC C ====== + +−   2222 2 2..cos352.3.5.2 5 ABACBCABBCC=+−=+−= Câu 23: Tam giác ABC có 3AB = , 4AC = và tan22 A =− . Tính cạnh BC A. 32 . B. 43. C. 33. D. 7. Lời giải Chọn C Từ giả thiết tan22 A =− , ta suy ra A là góc tù 2 2 2 1111 tan22coscos 1tan93 1(22) AAA A =−====− + + 2222 1 2..cosA342.3.4.33 3 BCABACABAC  =+−=+−−=   Câu 24: Cho tam giác ABC có cạnh BCa = , cạnh CAb = . Tam giác ABC có diện tích lớn nhất khi góc C bằng: A. o60 B. o90 C. o150 D. o120 Lờigiải Chọn B Diện tích của tam giác ABC là: 1 ..sin 2 SabC = S lớn nhất khi sinC lớn nhất, hay sin190oCC== .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 16 Câu 25: Cho tam giác MPQ vuông tại P . Trên cạnh MQ lấy hai điểm , EF sao cho các góc MPE , EPF , FPQ bằng nhau. Đặt , , , MPqPQmPExPFy ==== . Trong các hệ thức sau, hệ thức nào đúng? A. MEEFFQ == . B. 222 MEqxxq =+− . C. 222 MFqyyq =+− . D. 222 2 MQqmqm =+− . Lờigiải Chọn C Từ giả thiết, suy ra 30 3 oMPEEPFFPQMPQ ==== Tam giác MPF có 60oMPFMPEEPF=+= ; 222 2...cos MFMPPFMPPFMPF =+− 2222 1 2... 2 qyyqqyyq =+−=+− Câu 26: Tính góc C của tam giác ABC biết ab  và ( ) ( )2222 aacbbc −=− . A. 150C = B. 120C = C. 60C = D. 30C = Lời giải Chọn C Ta có: ( ) ( )2222 aacbbc −=− ( )332 0abcab −−−= ( )( ) ( )222 0abaabbcab −++−−= 222 0aabbc ++−= 222 cos 2 abc C ab +− = 1 2 =− . Do đó: 120C = Câu 27: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết 12AB = và 1 cot()3 AB+= . A. 210 . B. 910 5 . C. 510 . D. 32 . Lời giải Chọn A Ta có: 1 cot()3 AB+= nên 1 cot 3 C =− , suy ra3cossinCC =− . q m x y M P Q E F

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 17 Mà 22 sincos1 CC+= sin3310 1010 C == . 2210 sin2sin ABAB RR CC === . Câu 28: Tính bán kính đường tròn ngoại tiếp tam giác ABC biết 10AB = và 1 tan()3 AB+= . A. 510 9 B. 10 3 C. 10 5 D. 510 Lời giải Chọn D Ta có: 1 tan()3 AB+= nên 1 tan 3 C =− Do đó 3sincosCC =− , mà 22 sincos1 CC+= sin110 1010 C == . 2510 sin2sin ABAB RR CC === . Câu 29: Tam giác ABC có 4AB = , 6AC = , 1 cos 8 B = , 3 cos 4 C = .Tính cạnh BC . A. 7. B. 5. C. 33. D. 2. Lời giải Chọn B 8 63 1cossin 2 ==BB , 4 7 1cossin 2 ==CC 16 9coscos()sinsincoscos =+== ABCBCBC Do đó 5.cos.2.22 =+= BCABACABACA . Câu 30: Cho tam giác cân ABC có 0120A = và ABACa == . Lấy điểm M trên cạnh BC sao cho 2 5 BC BM = . Tính độ dài AM A. 3 3 a . B. 11 5 a . C. 7 5 a . D. 6 4 a . Lời giải Chọn C

giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 18 22022 1 2cos1202..3 2 BCABACABACaaaaa  =+−=+−−=   23 5 a BM = 2 2202 232337 2..cos302.. 5525 AMABBMABBMaaaaa  =+−=+−=    . DẠNG 2: HỆ THỨC LIÊN HỆ GIỮA CÁC YẾU TỐ TRONG TAM GIÁC, NHẬN DẠNG TAM GIÁC Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin, các công thức liên quan đến diện tích để vận dụng vào làm bài. Câu 1. Cho tam giác ABC thỏa sin 2cos sin A C B = Tam giác ABC là tam giác gì? Lời

Ta có: sin 2cos sin A C B = 2cosa C b = 222 2.cos2. 2 abCababc ab +− == 2222 aabcbc =+−= Tam giác ABC cân tại A. Câu 2. Chứng minh trong tam giác ABC ta có: 2.sin.sin a hRBC = Lời giải Áp dụng định lí sin trong tam giác ta có: 22.sin sin b RRBb B == Do đó: 2.sin.sin a hRBC = .sin a hbC= ( đúng) Câu 3. Cho tam giác ABC . Chứng minh ( )..sinsinsin SRrABC =++ . Lời giải Ta có : .... 2222 abcabc VPRrrrpS RRR ++  =++===   ( đpcm). Câu 4. Cho tam giác ABC thỏa 333 2 2.cos bca a bca abC  +− = +−  = . Chứng minh tam giác ABC là tam giác đều. Lời giải 30 a a A B C M PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 19 Ta có: 333333223 2 222 2.2.cos 2 bcabcaabaca a bca abCababc ab  +−=+− +− =  +−  +−= =  ( )( )222 222 0bcbbcca abc a a  +−+−=   +−=  22 2.cosA01 cos 60 2 bcbc A A bcbc bc −+=  = =   ==   = Vì tam giác ABC cân có 1 góc bằng 60  nên tam giác ABC là tam giác đều. Câu 5. Chứng minh trong tam giác ABC ta có: sin.cossin.cossin BCCBA += Lời giải 222222 2222 babccacb VT RabRac +−+− =+ 2222222 2 sin 4442 abcacbaa A aRaRaRR +−+− =+=== Câu 1: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: A. 222 2 24a bca m + =+ B. 222 2 24a acb m + =− C. 222 2 22 4a cba m +− = . D. 222 2 24a abc m + =− . Lời giải Chọn C Theo công thức đường trung tuyến ta có 222222 2 22 244a bcabca m ++− =−= Câu 2: Trong tam giác ABC , câu nào sau đây đúng? A. 222 2.cos abcbcA =++ B. 222 2.cos abcbcA =+− C. 222 .cos abcbcA =++ . D. 222 .cos abcbcA =+− . Lời giải Chọn B Áp dụng định lí hàm số cos tại đỉnh A ta có: 222 2.cos abcbcA =+− Câu 3: Nếu tam giác ABC có 222 abc + thì: A. A là góc tù. B. A là góc vuông. C. A là góc nhọn. D. A là góc nhỏ nhất. Lời giải Chọn C Ta có 222 2cos abcbcA =+− 222 cos 2 bca A bc +− = do 222 abc + nên cos0 A  Câu 4: Tam giác ABC có ba cạnh thoả mãn điều kiện ( )( ) 3 abcabcab +++−= . Khi đó số đo của C là A. 120 B. 30 C. 45 D. 60 Lời giải Chọn D BÀI TẬP TRẮC NGHIỆM.3 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 20 Ta có: ( )( ) ( )2 222233 abcabcababcababcab +++−=+−=+−= Theo hệ quả của định lí hàm cosin: 222 1 cos60 222 abcab CC abab +− ==== . Câu 5: Cho tam giác ABC . Khẳng định nào sau đây là đúng? A. ( )222222 2 3abc mmmabc ++=++ . B. ( )222222 4 3abc mmmabc ++=++ . C. ( )222222 1 3abc mmmabc ++=++ . D. ( )222222 3 4abc mmmabc ++=++ . Lời giải Sử dụng công thức trung tuyến, ta có: ( ) 222222222 222222 2222223 4444abc bcacababc mmmabc +−+−+− ++=++=++ Câu 6: Cho tam giác ABC thỏa mãn .cos caB = . Khẳng định nào sau đây là đúng? A. Tam giác ABC là tam giác cân. B. Tam giác ABC là tam giác nhọn. C. Tam giác ABC là tam giác vuông. D. Tam giác ABC là tam giác tù Lời giải Ta có: .cos caB = 222222 . 22 acbacb cac acc +−+− == 222 cba+= Theo định lí pi ta go tam giác ABC vuông tại A . Câu 7: Diện tích S của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây? I. ( )( )( )2 Sppapbpc =−−− II. ( )( )( )( )216Sabcabcabcabc =+++−−+−++ . A. Chỉ I. B. Chỉ II. C. Cả I và II. D. Không có. Lời giải Chọn C Ta có: I. đúng vì là công thức Hê rông tính diện tích tam giác. Khi đó: 2 ... 2222 abcabcabcabc S +++−−+−++ = ( )( )( )( )216Sabcabcabcabc =+++−−+−++ . Do đó II. đúng Câu 8: Cho tam giác ABC , các đường cao ,, abc hhh thỏa mãn hệ thức 32abc hhh =+ . Tìm hệ thức giữa , , abc A. 321 abc =− B. 32abc =+ C. 32abc =− D. 321 abc =+ Lời giải Chọn D Kí hiệu ABCSS = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 21 Ta có: 32abc hhh =+ 3.22.22 SSS abc =+ 321 abc =+ Câu 9: Trong tam giác ABC , hệ thức nào sau đây sai? A. .sin sin bA a B = B. sin.sincA C a = C. 2.sin aRA = D. .tan bRB = Lời giải Chọn D Theo định lí hàm số sin ta có: 2 sinsinBsinC abc R A === Suy ra: + .sin sinsinBsin abbA a AB == . + sin.sin sinsinC accA C Aa == . + 22.sin sin a RaRA A == + 2sintan sinB22cosB bbb RRBRB=== . Câu 10: Cho tam giác ABC thỏa mãn hệ thức 2 bca += . Trong các mệnh đề sau, mệnh đề nào đúng? A. coscos2cosBCA += B. sinsin2sinBCA += C. 1 sinsinsin 2 BCA += . D. sincos2sinBCA += . Lời giải Chọn B Ta có 2sin 22sin sinsinsin 2sin aRA abc RbRB ABC cRC =  ====   = . Mà 22sin2sin4sinsinsin2sin bcaRBRCRABCA +=+=+= Câu 11: Tam giác ABC có 120A = thì câu nào sau đây đúng? A. 222 3 abcbc =+− B. 222 abcbc =++ C. 222 3 abcbc =++ . D. 222 abcbc =+− . Lời giải Chọn B Áp dụng định lí hàm số cos tại đỉnh A ta có: 222 2.cos abcbcA =+− . 222 2.os120abcbcc =+− 222 abcbc=++ Câu 12: Trong tam giác ABC , điều kiện để hai trung tuyến vẽ từ A và B vuông góc với nhau là: A. 222225 abc += B. 222335 abc += C. 222223 abc += D. 222 5 abc += Lời giải Chọn D Vì hai trung tuyến vẽ từ A và B vuông góc với nhau nên ABG vuông tại G với G là trọng tâm tam giác ABC . Khi đó: 222 cGAGB =+ 222222 2 4 92424 bcaacb c  ++ =−+− 

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 22 22 22 4 944 ab cc  =++  2225cab=+ Câu 13: Trong tam giác ABC , nếu có 2 abc = thì : A. 2 111 abc hhh =− B. 2 . abc hhh = C. 2 111 abc hhh =+ D. 2 122 abc hhh =+ Lời giải Chọn B Ta có: 2 . abc = 2 222 abc SSS hhh  =  2 111 . abc hhh = 2 . abc hhh= Câu 14: Trong tam giác ABC , nếu có 2 abc hhh =+ thì : A. 211 sinsinsinABC =+ B. 2sinsinsinABC =+ C. sin2sin2sinABC =+ . D. 211 sinsinsinABC =− . Lời giải Chọn A Ta có : 2 abc hhh =+ 222 2. SSS abc =+ 211 abc =+ 211 2.sin2.sin2.sin RARBRC =+ 211 sinsinsinABC =+ . Câu 15: Trong tam giác ABC , câu nào sâu đây đúng? A. 2a bc m + = . B. 2a bc m +  . C. 2a bc m +  . D. a mbc =+ . Lời giải Chọn C Ta có: 222 2 24a bca m + =− ( ) ( ) 22 2 4 bcbca ++−− = Vì ( )2 2bcabca −− ( )2 2 4a bc m +  2a bc m +  . Câu 16: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện ( )( ) 3 abcabcab +++−= . Tính số đo của góc C . A. 45 . B. 60 . C. 120 . D. 30 . Lời giải Chọn B Ta có: ( )( ) 3 abcabcab +++−=  ( )2 2 3 abcab +−=  222 abcab +−= . Mà 222 1 cos 22 abc C ab +− ==  60C = . Câu 17: Cho tam giác ABC , xét các bất đẳng thức sau: I. abc − II. abc + .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 23 III. abc mmmabc ++++ . Hỏi khẳng định nào sau đây đúng? A. Chỉ I, II B. Chỉ II, III C. Chỉ I, III D. Cả I, II, III Lời giải Chọn D Ta có I. và II. đúng vì đây là bất đẳng thức tam giác Ta có: 222 2 24a bca m + =− ( ) ( ) 22 2 4 bcbca ++−− = . Vì ( )2 2bcabca −− ( )2 2 4a bc m +  2a bc m +  Tương tự ta có: 2b ac m +  ; 2c ac m +  Do đó: abc mmmabc ++++ . Vậy III. Đúng. Câu 18: Tam giác ABC có các cạnh a , b , c thỏa mãn điều kiện 222 3 bcabc +−= . Tính số đo của góc A . A. 45 . B. 60 . C. 120 . D. 30 . Lời giải Chọn D Ta có: 222 3 bcabc +−=  2cos3 bcAbc =  3 cos30 2 AA== Mà 222 1 cos 22 abc C ab +− ==  60C = . Câu 19: Tam giác ABC .cos.cos aBbA = . Tam giác ABC là tam giác gì? A. Tam giác vuông. B. Tam giác đều. C. Tám giác vuông cânD. Tam giác cân. Lời giải Chọn D Ta có: .cos.cos aBbA =  222222 22 abacbbca acbc +−+− =  22 abab == . Vậy tam giác ABC cân. Câu 20: Cho tam giác ABC vuông tại A , ACb = , ABc = . Lấy điểm M trên cạnh BC sao cho góc 30BAM =  Tính tỉ số MB MC . A. 3 3 b c B. 3 3 c b C. 3c b D. bc bc + Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 24 . Ta có .sin30 sin30sinsin2.sin MBAMAMAM MB BBB  ===  .sin603 sin60sinsin2.sin MCAMAMAM MC CCC  ===  Do đó sin3 3sin33 MBCcc MCb Bb === Câu 21: Mệnh đề nào sau đây sai? A. Nếu 222 abc + thì A là góc tù. B. Nếu tam giác ABC có một góc tù thì 222 abc + . C. Nếu 222 abc + thì A là góc nhọn. D. Nếu 222 abc =+ thì A là góc vuông. Lời giải Chọn B Ta có : 222 cos 2 bca A bc +− = . Do đó : * 222 abc + thì cos0 A  do đó A là góc tù nên A. đúng * 222 abc + thì cos0 A  do đó A là góc nhọn nên C. đúng. * 222 abc =+ thì cos0 A = do đó A là góc vuông nên D. đúng. * Nếu tam giác ABC có góc B tù thì 222 bac + ; nếu góc C tù thì 222 cab + do đó B. sai. DẠNG 3: ỨNG DỤNG THỰC TẾ Áp dụng các công thức sách giáo khoa như: định lí cosin, hệ quả của định lí cosin, định lí sin, các công thức liên quan đến diện tích để vận dụng vào làm bài. Câu 1: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 060 . Tàu thứ nhất chạy với tốc độ 30/kmh , tàu thứ hai chạy với tốc độ 40/kmh. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km ? 60 ° 30 ° B A C M PHƯƠNG PHÁP.1 = BÀI TẬP TỰ LUẬN.2 =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 25 Lời giải Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: 1 30.260. Skm == Sau 2h quãng đường tàu thứ hai chạy được là: 2 40.280. Skm == Vậy: sau 2h hai tàu cách nhau là: 220 12122..cos602013.SSSSS =+−= Câu 2: Từ một đỉnh tháp chiều cao 80 CDm = , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 7212' và 0 3426' so với phương nằm ngang. Ba điểm ,, ABD thẳng hàng. Tính khoảng cách AB (chính xác đến hàng đơn vị)? Lời giải Ta có: Trong tam giác vuông CDA: 0 00 80 tan7212'25,7. tan7212'tan7212' CDCD AD AD === Trong tam giác vuông CDB : 0 00 80 tan3426'116,7. tan3426'tan3426' CDCD BD BD === Suy ra: khoảng cách 116,725,791. ABm =−= Câu 3: Cho tam giác ABC có 13,8,7abc=== . Tính góc A, suy ra S, ha, R, r, ma. Lời giải 222 2220 1 2coscos120 22 bca abcbcAAA bc +− =+−==−= 113sin56.143 222 12283 . 213 7.8.13133 443 4.143 22.143 .3 7813 aa SbcA SahhS a abcabc SR RS S Sprr abc === === ==== ==== ++++ 222 2 57 242aa bca mm + =−= Câu 4: Cho tam giác ABC có ABAC4,5 và A 3 cos 5 . Tính cạnh BC, và độ dài đường cao kẻ từ A Lời giải Áp dụng định lí côsin ta có BÀI TẬP TỰ LUẬN TỔNG HỢP. =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 26 22222 3 2..cos452.4.5.17 5 BCABACABACA Suy ra 17BC Vì AA22 sincos1 nên AA 2 94 sin1cos1 255 Theo công thức tính diện tích ta có ABC SABACA114 ..sin.4.5.8 225 (1) Mặt khác 11 ..17. 22 ABCaa Sahh (2) Từ (1) và (2) suy ra 11617 .17.8 217 aa hh Vậy độ dài đường cao kẻ từ A là 1617 17a h Câu 5: Cho tam giác ABC có , ABAC104 và A 060 . a) Tính chu vi của tam giác b) Tính tanC Lời giải a) Theo định lí côsin ta có ..cos , BC BC 222010421046076 872 Suy ra chu vi tam giác là ,,p 21048722272 b) (Hình 2.23a) Kẻ đường cao BH ta có cosAHAB HC 0 605 541 . .sinBHAB 0 6053 . Vậy tantanCBCHHB HC 53 Câu 6: Giải tam giác ABC biết AB00 60,40 và c 14 Lời giải Ta có CAB00000 180180604080 10 4 A B C H Hình 2.23a

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 27 Theo định lí sin ta có cA aa C 0 0 sin14.sin60 sin12,3 sin80 cB bb C 0 0 sin14.sin40 sin9,1 sin80 Câu 7: Giải tam giác ABC , biết: bAC00 4,5;30;75 Lời giải Ta có 00000 180180307575 BACC suy ra tam giác ABC cận tại A 4,5cb == Theo định lí sin ta có bA aa B 0 0 sin4,5.sin30 sin2,33 sin75 Câu 8: Cho tam giác ABC cân tại A biết 03;30aBC=== . Tính R, r, cạnh c, b, suy ra S Lời giải Áp dụng định lí sin: 3 21 sin2sin 23 2 aa RR AA ==== 0 2sin301bcR === 13 .sin 24 SbcA== 3 (23)2 S r p ==− . Câu 9: Cho tam giác ABC nội tiếp đường tròn bán kính bằng 3, biết 00 30,45AB . Tính độ dài trung tuyến kẻ từ A và bán kính đường tròn nội tiếp tam giác. Lời giải Ta có CAB00000 1801803045105 Theo định lí sin ta có aRA 0 2sin2.3.sin303 , bRB 0 2 2sin2.3.sin456.32 2 cRC 0 2sin2.3.sin1055,796

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 28 Theo công thức đường trung tuyến ta có a bca m 2222 2 22185,7969 4423,547 Theo công thức tính diện tích tam giác ta có 0 1sin sin 22 32.5,796sin30 0,943 3325,796 ABC SprbcArbcA p Câu 10: Cho tam giác ABC thỏa mãn 2 sinsin.sinABC . Chứng minh rằng a) 2 abc b) 1 cos 2 A Lời giải a) Áp dụng định lí sin ta có sin,sin,sin222 ABCabc RRR Suy ra 2 22 sinsin.sin. 222 abc ABCabc RRR đpcm b) Áp dụng định lí côsin và câu a) ta có 22222 21 cos 2222 Abcabcbcbcbc bcbcbc đpcm Câu 11: Tam giác ABC có ,, BCaCAbABc và trung tuyến AMABc chứng minh rằng: 222 222 )2() )sin2(sinsin) aabc bABC Lời giải a) Áp dụng công thức đường trung tuyến Ta có 22 2222222 22222() aa bcAMcabc (*) b) Theo định lí sin ta có 2 sinsinsin abc R ABC 222 222 222 4sin 4sin 4sin aRA bRB cRC Thay vào (*) ta có đpcm

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 29 Câu 12: Cho tam giác ABC . Chứng minh rằng điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là 222 5 bca . Lời giải Gọi G là trọng tâm của tam giác ABC . Khi đó hai trung tuyến kẻ từ B và C vuông góc với nhau khi và chỉ khi tam giác GBC vuông tại G 22 2222 22 33bc GBGCBCmma (*) Mặt khác theo công thức đường trung tuyến ta có 222222 222()2() , 44bc acbabc mm Suy ra bc mma 222(*)4 9 222222 2422 944 acbabc a 222249 abca 222 5 bca Câu 13: Chứng minh rằng trong mọi tam giác ABC ta có; a) .cos.cos abCcB b) sinsincossincos ABCCB Lời giải a) Áp dụng định lí côsin ta có: 222222 222222 .. 22 2 VPbcabccab abca abccab aVT a b) sinsincossincos ABCCB .cos.cos 222 abcCB RRR abCcB .cos.cos Câu 14: Chứng minh rằng trong mọi tam giác ABC ta có: 2sinsin a hRBC Lời giải 2 2sinsin2sin 2a Sb hRBCRC aR 1 sin 2 SabC (đúng) Câu 15: Tìm tính chất đặc biệt của tam giác ABC biết:2cos.cos.cos aAbCcB =+ Lời giải Yêu cầu bài toán tương đương với:

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 30 0 2(2sin)cos(2sin)cos2sincos 2sin.cossin()sin 1 cos(sin0)60 2 RAARBCRCB AABCA AdoAA =+ =+= == Câu 16: Nhận dạng tam giác ABC biết: 333 2 2cos(1) (2) abC abc a abc Lời giải Áp dụng định lí cosin ở (1) và thế vào (2) 222 (1) abc abc a 222 0 (2) 1 cos60 2 abcbc AA KL: Tam giác ABC đều. Câu 17: Nhận dạng tam giác ABC biết: .sinsinsin abc aAbBcChhh Lời giải Áp dụng công thức diện tích ta có 11 sin 22 a SbcAah suy ra .sinsinsin abc aAbBcChhh 222222 abcSSSSSS bccaababc 222 222 0 abcabbcca abbcca abc Vậy tam giác ABC đều. Câu 18: Cho tam giác ABC . Chứng minh tam giác ABC cân nếu .sin a hcA Lời giải Sử dụng công thức 11 sin* 22 a SahbcA thay .sin a hcA vào (*) được: aa bhahab suy ra tam giác ABC cân tại C

BÀI 6. HỆ THỨC LƯỢNG TRONG TAM GIÁC

DẠNG 1. ĐỊNH LÝ COSIN, ÁP DỤNG ĐỊNH LÝ COSIN ĐỂ GIẢI TOÁN

Câu 1: Cho tam giác ABC , mệnh đề nào sau đây đúng?

A. 222 2cos abcbcA =++ .

B. 222 2cos abcbcA =+− .

C. 222 2cos abcbcC =+− . D. 222 2cos abcbcB =+− .

Câu 2: Cho tam giác ABC , có độ dài ba cạnh là ,, BCaACbABc === . Gọi a m là độ dài đường trung tuyến kẻ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây sai?

A. 222 2 24a bca m + =− .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 1

B. 222 2cos abcbcA =++ . C. 4 abc S R = . D. 2 sinsinsin abc R ABC === . Câu 3: Cho tam giác ABC có 8,10ab== , góc C bằng 060 . Độ dài cạnh c là? A. 321=c B. 72=c C. 211=c D. 221=c Câu 4: Cho ABC có 06,8,60bcA=== . Độ dài cạnh a là: A. 213. B. 312. C. 237. D. 20. Câu 5: Cho ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . Câu 6: Cho ABC có 9AB = ; 8BC = ; 0B60 = . Tính độ dài AC . A. 73 B. 217 C. 8 D. 113 Câu 7: Cho tam giác ABC có 2,1ABAC== và 0 60.A = Tính độ dài cạnh .BC A. 2.BC = B. 1.BC = C. 3.BC = D. 2.BC = Câu 8: Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61. CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

Câu

Cho

Câu

Cho

Góc

Câu 15: Cho tam giác ABC

30.

Câu 16: Cho các

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 2 Câu 9: Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ? A. 13 B. 3. C. 10 D. 1 Câu 10: Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7=b ; 5=c ; 4 cos 5 A = . Tính độ dài của a . A. 32 . B. 72 2 . C. 23 8 . D. 6.

11: Cho 30xOy =.Gọi , AB là 2 điểm di động lần lượt trên , OxOy sao cho 2AB = . Độ dài lớn nhất của OB bằng bao nhiêu? A. 4. B. 3. C. 6. D. 2. Câu 12: Cho ;;cab là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2 aabac + . B. 222 2 acbac ++ . C. 222 2 bcabc ++ . D. 2abbcb + .

13:

tam giác ABC có 4AB = cm, 7BC = cm, 9AC = cm. Tính cos A

2 cos 3 A =− . B. 1 cos 2 A = . C. 1 cos 3 A = . D. 2 cos 3 A = .

14:

tam giác ABC có 222 0abc+− . Khi đó:

Góc 090C  B. Góc 090C  C.

090C = D. Không thể kết luận được gì về góc C

thoả mãn: 222 3 bcabc +−= . Khi đó:

A = B. 0 45.A = C. 0 60.A = D. 075A = .

điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu? A. 090 . B. 0 60. C. 0 45. D. 0 30. Câu 17: Cho tam giác ABC , biết 24,13,15.abc=== Tính góc A? A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'. Câu 18: Cho tam giác ABC , biết 13,14,15.abc=== Tính góc B? A. 0 5949'. B. 0 537'. C. 0 5929'. D. 0 6222'. Câu 19: Cho tam giác ABC biết độ dài ba cạnh , , BCCAAB lần lượt là ,, abc và thỏa mãn hệ thức ( ) ( )2222 bbacca −=− với bc  Khi đó, góc BAC bằng A. 45 B. 60 C. 90 D. 120 Câu 20: Tam giác ABC có ,, ABcBCaCAb === . Các cạnh ,, abc liên hệ với nhau bởi đẳng thức ( ) ( )2222 bbacac −=− . Khi đó góc BAC bằng bao nhiêu độ.

Câu 21: Cho tam giác ABC vuông cân

trong tam giác ABC sao cho ::1:2:3MAMBMC

A. 135

khi

góc

bao nhiêu?

Câu 22: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau:

A. 222 2 . 24a bca m + =+ B. 222 2 . 24a acb m + =− C. 222 2 24a abc m + =− D. 222 2 22 4a cba m +−

Câu 23: Tam giác ABC có 9AB = cm, 15BC = cm, 12AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là A. 10cm

B. 9cm

C. 7,5cm

Câu 24: Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyế

Câu

Tam giác

D. 120

D. 8cm

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 3

30 . B. 60 . C. 90 . D. 45 .

tại A và M là điểm nằm

đó

AMB

ằng



90

150



n 13BM = . Tính độ dài AC

11 B. 4 C. 9 2 D. 10

25: Cho ABC vuông ở ,A biết 30,C = 3.AB = Tính độ dài trung tuyến ?AM

3 B. 4 C. 5 2 D. 7 2

26:

ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3BM = . Độ dài đoạn AM bằng bao nhiêu? A. 9. B. 9. C. 3. D. 1 108. 2 Câu 27: Gọi 222 abc Smmm =++ là tổng bình phương độ dài ba trung tuyến của tam giác ABC . Trong các mệnh đề sau mệnh đề nào đúng? A. 222 3() 4 Sabc =++ . B. 222Sabc =++ . C. 222 3() 2 Sabc =++ .D. 222 3()Sabc =++ . Câu 28: Cho ABC có 2AB = ; 3AC = ; 0A60 = . Tính độ dài đường phân giác trong góc A của tam giác ABC . A. 12 5 B. 62 5 C. 63 5 D. 6 5 DẠNG 2. ĐỊNH LÝ SIN, ÁP DỤNG ĐỊNH LÝ SIN ĐỂ GIẢI TOÁN Câu 29: Cho tam giác ABC . Tìm công thức sai: A. 2. sin a R A = B. sin. 2 Aa R = C. sin2. bBR = D. sin sin. cA C a =

Câu 33: Cho ABC có 5AB = ;A40= ;B60= . Độ

BC g

. D. 6 .

n nhất v

i k

t qu

nào?

A. 3,7. B. 3,3. C. 3,5. D. 3,1.

Câu 34: Cho tam giác ABC thoả mãn hệ thức 2

A. coscos2cos.

sinsinsin

Câu 35: Tam giác ABC có 16,8

A. 29,9.

Câu 36: Tam giác ABC có

A. 68. B.

14,1.

các mệnh đề sau, mệnh đề nào đúng?

sincos2sin.

ng bao nhiêu?

17,5. D. 19,9.

Tính

DẠNG 3. DIỆN TÍCH TAM GIÁC, BÁN KÍNH ĐƯỜNG TRÒN

Câu

D. 200.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 4 Câu 30: Cho ABC với các cạnh ,, ABcACbBCa === . Gọi ,, RrS lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và diện tích của tam giác ABC . Trong các phát biểu sau, phát biểu nào sai? A. 4 abc S R = B. sin a R A = C. 1 sin 2 SabC = D. 222 2cos abcabC +−= Câu 31: Cho tam giác ABC có góc 60BAC = và cạnh 3BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC A. 4R = B. 1R = C. 2R = D. 3R = Câu 32: Trong mặt phẳng, cho tam giác ABC có 4cmAC = , góc 60A = , 45B = . Độ dài cạnh BC là A. 26 . B. 223 + . C. 232

dài

ầ

ớ

ế

ả

bca += . Trong

BCA += B. sinsin2sin. BCA +=

2 BCA += . D.

BCA +=

a = ; 0 5613'B = ; 071C = . Cạnh c bằ

0 6812'A = , 0 3444'B = , 117.AB =

AC ?

168. C. 118.

37: Chọn công thức đúng trong các đáp án sau: A. 1 sin. 2 SbcA = B. 1 sin. 2 SacA = C. 1 sin. 2 SbcB = D. 1 sin. 2 SbcB = Câu 38: Cho hình thoi ABCD có cạnh bằng a . Góc 30BAD = . Diện tích hình thoi ABCD là A. 2 4 a . B. 2 2 a . C. 2 3 2 a . D. 2 a . Câu 39: Tính diện tích tam giác ABC biết 3,5,6ABBCCA=== . A. 56 B. 48 C. 6 D. 8 Câu 40: Cho ABC có 6,8,10.===abc Diện tích S của tam giác trên là: A. 48. B. 24. C. 12. D. 30.

Câu 41: Cho ABC có 0 4,5,150.===acB Diện tích của tam giác là:

A. 53. B. 5. C. 10. D. 103.

Câu 42: Một tam giác có ba cạnh là 13,14,15. Diện tích tam giác bằng bao nhiêu?

A. 84. B. 84. C. 42. D. 168.

Câu 43: Cho các điểm (1;2),(2;3),(0;4). ABC Diện tích ABC bằng bao nhiêu?

A. 13 2 B. 13. C. 26. D. 13 4

Câu 44: Cho tam giác ABC có (1;1),(3;3),(6;0). ABC Diện tích ABC là

A. 12. B. 6. C. 62. D. 9.

Câu 45: Cho tam giác ABC có 4,6,8abc=== . Khi đó diện tích của tam giác là:

A. 915. B. 315. C. 105. D. 2 15. 3

Câu 46: Cho tam giác ABC . Biết 2AB = ; 3BC = và 60

OFFICIAL

tích tam

Câu

Tam giác

tam giác

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 5

ABC = . Tính chu vi và diện

giác ABC .

57 + và 3 2 B. 57 + và 33 2 C. 57 và 33 2 D. 519 + và 3 2

47:

ABC có các trung tuyến 15 a m = , 12bm = , 9 c m = .Diện tích S của

ABC bằng

72. B. 144. C. 54. D. 108. Câu 48: Cho tam giác ABC có 3 7;5;cos 5 bcA === . Độ dài đường cao a h của tam giác ABC là. A. 72 2 B. 8 C. 83 D. 803 Câu 49: Cho tam giác ABC có 2;4 ABaACa == và 120BAC = . Tính diện tích tam giác ABC ? A. 28 Sa = . B. 2 23Sa = . C. 2 3Sa = . D. 24 Sa = . Câu 50: Cho tam giác ABC đều cạnh a . Bán kính đường tròn ngoại tiếp tam giác ABC bằng A. 3 2 a . B. 3 3 a . C. 3 4 a . D. 2 2 a . Câu 51: Cho tam giác ABC có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác ABC bằng A. 12. B. 3. C. 6 . D. 24.

Câu

Cho

Câu

Cho tam giác ABC

giác

Câu 54: Cho tam giác ABC

A. 1 B. 8 9 C. 4 5 D. 3 4

bằng

Câu 55: Cho ABC có 84,13,14,15.Sabc ==== Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là:

A. 8,125. B. 130. C. 8. D. 8,5.

Câu 56: Cho ABC có 103S = , nửa chu vi 10=p . Độ dài bán kính đường tròn nội tiếp r của tam giác trên là:

A. 3. B. 2. C. 2. D. 3.

Câu 57: Một tam giác có ba cạnh là 26,28,30. Bán kính đường tròn nội tiếp là:

A. 16. B. 8. C. 4. D. 42.

Câu 58: Một tam giác có ba cạnh là 52,56,60.Bán kính đường tròn ngoại tiếp là:

A. 65 . 8 B. 40. C. 32,5. D. 65 . 4

Câu 59: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn ngoại tiếp là?

A. 6. B. 8. C. 13 2 . D. 11 2 .

Câu 60: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu?

A. 2. B. 22. C. 23. D. 3. Câu 61: Tam giác với ba cạnh là 6;8;10 có bán kính đường tròn ngoại tiếp bằng bao nhiêu?

A. 5. B. 42.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 6

52:

tam giác ABC đều cạnh 2a . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. 2 3 a . B. 4 3 a . C. 8 3 a . D. 6 3 a .

53:

có 6BC = , 2AC = và 31AB =+ . Bán kính đường tròn ngoại tiếp tam

ABC bằng:

5 . B. 3 . C. 2 . D. 2.

có 3AB = , 4AC = , 5BC = . Bán kính đường tròn nội tiếp tam giác

C. 52. D. 6. Câu 62: Cho hình chữ nhật ABCD có cạnh 4,6ABBC== , M là trung điểm của , BCN là điểm trên cạnh CD sao cho 3 NDNC = . Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng A. 35 B. 35 2 C. 52 D. 52 2 Câu 63: Cho tam giác đều ABC ;gọi D là điểm thỏa mãn 2 DCBD = . Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác ADC Tính tỉ số R r

khoảng cách AB?

A. 71. m B. 91. m C. 79. m D. 40. m

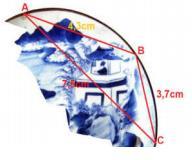
Câu 67: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và Bdưới một góc 0 5616'. Biết 200 CAm = , 180 CBm = . Khoảng cách AB bằng bao nhiêu?

A. 180. m B. 224. m C. 112. m D. 168. m

Câu 68: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ ( 4,3AB = cm;

BC =

;

CA = cm). Bán kính của chiếc đĩa này bằng.

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 7 A. 5 2 B. 577 9 + C. 755 9 + D. 757 9 + DẠNG 4. ỨNG DỤNG THỰC TẾ Câu 64: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 7824' o . Biết 250,120 CAmCBm == . Khoảng cách AB bằng bao nhiêu? A. 266. m B. 255. m C. 166. m D. 298. m Câu 65: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 060 . Tàu thứ nhất chạy với tốc độ 30/kmh , tàu thứ hai chạy với tốc độ 40/kmh. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km ? A. 13. B. 2013. C. 1013. D. 15. Câu 66: Từ một đỉnh tháp chiều cao 80 CDm = , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 7212' và 0 3426'. Ba điểm ,, ABD thẳng hàng. Tính

3,7

7,5

A. 5,73 cm B. 6,01cm C. 5,85cm D. 4,57cm Câu 69: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, 063CAD = ; 048CBD = . Chiều cao h của khối tháp gần với giá trị nào sau đây? A. 61,4 m. B. 18,5 m. C. 60 m. D. 18 m. BÀI TẬP TỔNG HỢP Câu 70: Cho tam giác ABC có 8,10==BCCA , và 60 =ACB . Độ dài cạnh AB bằng A. 321. B. 72 . C. 211. D. 221.

Câu 71: Cho tam giác ABC có ;; BCaCAbABc === biết 8,10ab== , gócC bằng60. Độ dài cạnh c là?

A. 321=c . B. 72=c . C. 211c = . D. 221c = .

Câu 72: Cho tam giác ABC có 7b = ; 5c = và 3 cos 5 A = . Tính a

A. 42 B. 2 C. 2 D. 3

Câu 73: Trong ABC có ,, === ABcACbBCa . Đẳng thức nào sau đây đúng?

A. 222 2cos abcbcA =++ . B. 222 2cos abcbcA =+− .

C. 222 cos abcbcA =++ D. 222 cos abcbcA =+−

Câu 74: Cho tam giác ABC có 4,6ABAC== và 120.A = Độ dài cạnh BC là

A. 19. B. 27. C. 319. D. 219.

OFFICIAL

Câu 75: Tam giác ABC có 120A = thì câu nào sau đây đúng?

A. 222 3 abcbc =+− B. 222 abcbc =++

C. 222 3 abcbc =++ . D. 222 abcbc =+− .

Câu 76: Cho ABC có 0 60,8,5.Bac=== Độ dài cạnh b bằng:

A. 7. B. 129. C. 49. D. 129 .

Câu 77: Cho tam giác ABC có = BCa ; = ACb ; = ABc , có 222 2=++ abcbc . Số đo của góc A là:

A. 150

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 8

B. 120 C. 45 D. 135 Câu 78: Cho ABC có A60, 3, 4 ABcmACcm=== . Tính cạnh BC . A. 10BC = B. 13BC = C. 12BC = D. 11BC = Câu 79: Cho tam giác ABC có 06,8,60ABcmACcmABC === . Tính độ dài cạnh BC A. 337 + . B. 10. C. 337 . D. 9. Câu 80: Xét tam giác ABC có 3AB = cm , 5AC = cm , 1 cos 2 BAC = . Độ dài cạnh BC bằng: A. 19 B. 7 C. 4 D. 34 Câu 81: Tam giác ABC có 5AB = cm, 5BC = cm, 3AC = cm. Giá trị cos A là A. 2 3 B. 1 2 C. 3 10 D. 3 10 Câu 82: . Tam giác ABC có 3,8ABBC== . Gọi M là trung điểm của BC . Biết 513 cos 26 AMB = và 3AM  . Tính độ dài cạnh AC . A. 13AC = B. 7AC = C. 13AC = D. 7AC =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 9 Câu 83: Cho tam giác ABC có 4AB = , 7AC = và 9BC = . Gọi M là điểm trên cạnh BC sao cho 2 MCMB = . Gọi H là trung điểm của đoạn thẳng BC . Đường trung trực của đoạn thẳng BC cắt AM tại I . Tính độ dài đoạn thẳng AI . A. 33 2 B. 27 2 C. 3 D. 32 3 Câu 84: Cho tam giác ABC có ,, BCaCAbABc === , trọng tâm G và diện tích S . Đặt BGC = , mệnh đề nào sau đây đúng? A. 222 5 cot 4 bca S  +− = .B. 222 5 cot 12 bca S  ++ = . C. 222 5 cot 12 bca S  = D. 222 5 cot 12 bca S  +− = Câu 85: Cho hình vuông ABCD có cạnh bằng 6, E là trung điểm của CD. Tính bán kính đường tròn ngoại tiếp tam giác ACE . A. 310 2 B. 35 2 C. 310 D. 35 Câu 86: Tam giác ABC có ˆ 6812A   = , ˆ 3444B   = , 117.AB = Tính AC ? A. 68. B. 168. C. 118. D. 200. Câu 87: Tam giác ABC có độ dài cạnh 3cm=AB ; 6cm=AC và 60 =A . Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng A. 3=R . B. 33=R . C. 3=R . D. 6=R . Câu 88: Cho ABC có 45,75AB== . Tính tỉ số AB BC A. 6 2 B. 13 2 + C. 632 6 + D. 6 3 Câu 89: Cho tam giác ABC có 60, 75BC== và 10AC = Khi đó, độ dài cạnh BC bằng A. 106 3 . B. 56 . C. 56 3 . D. 10. Câu 90: Cho tam giác ABC có 5AC = thoả mãn sinBtanBsinsinAC= . Gọi G là trọng tâm tam giác ABC . Tính giá trị biểu thức 22SGAGC =+ Câu 91: Cho tam giác ABC có 5AB = , 6AC = , 7BC = . Tính diện tích tam giác ABC . A. 123 . B. 96 . C. 66 . D. 36 . Câu 92: Cho tam giác ABC có 5,12,13.abc=== Bán kính đường tròn ngoại tiếp R của tam giác bằng A. 13. B. 6,5. C. 26. D. 7,5.

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 10

93: Cho ABCDlà hình thoi, 0 120,2BADAB== . Diện tích tam giác ABC bằng A. 3 B. 23 C. 3 2 D. 4

94: Cho tam giác ABC có các cạnh 6AB = , 8AC = , 10BC = . Bán kính đường tròn nội tiếp tam giác ABC là A. 12r = B. 3r = C. 5r = D. 2.r =

95: Cho tam giác ABC có 6;9;60ABcmACcmBAC===. Diện tích tam giác ABC là A. 2273 2 Scm = . B. 227 2 Scm = . C. 2273 4 Scm = . D. 227 4 Scm = .

96: Tính diện tích hình bình hành ABCDbiết 0;3;60ABaBCaABC === A. 2 a . B. 23 2 a . C. 2 2 a . D. 2 3 2 a . Câu 97: Tam giác ABC có 4, 30, 75ACBACACB=== . Tính diện tích tam giác .ABC A. 8ABCS = B. 43ABCS = C. 4ABCS = D. 83ABCS = Câu 98: Cho hình bình hành ABCDcó 3,7,60ABBCBAC=== . Diện tích hình bình hành ABCDlà A. 213 B. 213 2 C. 123 D. 63 Câu 99: Hai chiếc tàu thuỷ P và Q trên biển cách nhau 100m và thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển. Từ P và Q người ta nhìn chiều cao AB của tháp dưới các góc 015BPA = và 055BQA = . Tính chiều cao của tháp Câu 100: Trên nóc một tòa nhà có một cột ăng ten cao 4m . Từ vị trí qua sát A cao 9m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng-ten dưới góc 050 và 035 so với phương ngang. Chiều cao của tòa nhà gần nhất với số nào dưới đây? A. 14 m B. 21,1 m C. 17,8 m D. 18,7 m Câu 101: Giả sử CDh = là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm , AB trên mặt đất sao cho ba điểm ,, ABC thẳng hàng. Ta đo được 30 ABm = , 63CAD = ; 48CBD = . Chiều cao h của khối tháp gần với giá trị nào sau đây? A. 64,6. m B. 30. m C. 61,4. m D. 76,8. m

ỨC

NG

TAM

DẠNG 1.

NH LÝ COSIN, ÁP DỤNG ĐỊNH LÝ COSIN ĐỂ GIẢI TOÁN

Câu 1: Cho tam giác

Câu 2: Cho tam giác

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 1 BÀI 6. HỆ TH

LƯỢ

TRONG

GIÁC

ĐỊ

ABC , mệnh đề nào sau đây đúng? A. 222 2cos abcbcA =++ . B. 222 2cos abcbcA =+− . C. 222 2cos abcbcC =+− . D. 222 2cos abcbcB =+− . Lời giải Chọn B Theo đị

lý cosin trong tam giác ABC , ta có 222 2cos abcbcA =+− .

ABC , có độ dài ba cạnh là ,, BCaACbABc === . Gọi a m là độ dài đường trung tuyến kẻ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác và S là diện tích tam giác đó. Mệnh đề nào sau đây sai? A. 222 2 24a bca m + =− . B. 222 2cos abcbcA =++ . C. 4 abc S R = . D. 2 sinsinsin abc R ABC === . Lời giải Chọn B Theo định lý hàm số cosin trong tam giác ta có 222 2cos abcbcA =+− Câu 3: Cho tam giác ABC có 8,10ab== , góc C bằng 060 . Độ dài cạnh c là? A. 321=c . B. 72=c . C. 211=c . D. 221=c . Lời giải Chọn D Ta có: 2222202..cos8102.8.10.cos6084221cababCc =+−=+−== Câu 4: Cho ABC có 06,8,60bcA=== . Độ dài cạnh a là: A. 213. B. 312. C. 237. D. 20. Lời giải Chọn A Ta có: 22202cos36642.6.8.cos6052213abcbcAa =+−=+−== . Câu 5: Cho ABC có 0 60,8,5.===Bac Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 . CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC HỆ THỐNG BÀI TẬP TRẮC NGHIỆM.III ==

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 2 Lời giải Chọn A Ta có: 2222202cos852.8.5.cos60497 bacacBb =+−=+−== Câu 6: Cho ABC có 9AB = ; 8BC = ; 0B60 = . Tính độ dài AC A. 73 . B. 217 . C. 8. D. 113 . Lời giải Chọn A Theo định lý cosin có: 222 2..cos73ACBABCBABCABC =+−= 73AC = Vậy 73AC = . Câu 7: Cho tam giác ABC có 2,1ABAC== và 0 60.A = Tính độ dài cạnh BC A. 2.BC = B. 1.BC = C. 3.BC = D. 2.BC = Lời giải Chọn C Theo định lý cosin ta có: 220 2..cos60BCABACABAC =+− 22 1 212.2.1. 2 =+− 3.= Câu 8: Tam giác ABC có 0 8,3,60.acB=== Độ dài cạnh b bằng bao nhiêu? A. 49. B. 97 C. 7. D. 61. Lời giải Chọn C Ta có: 2222202cos832.8.3.cos60497 bacacBb =+−=+−== . Câu 9: Tam giác ABC có 0 150,3,2. === CBCAC Tính cạnh AB ? A. 13 . B. 3. C. 10. D. 1. Lời giải Chọn A Theo định lí cosin trong ABC ta có: 222 2..cos=+− ABCACBCACBC 13= 13= AB . Chọn A Câu 10: Cho ;;cab là độ dài 3 cạnh của tam giác ABC . Biết 7=b ; 5=c ; 4 cos 5 A = . Tính độ dài của a A. 32 . B. 72 2 . C. 23 8 . D. 6. Lời giải Chọn A Áp dụng định lí cosin cho tam giác ABC ta có: 22222 4 2.cos752.7.5.18 5 abcbcA=+−=+−= . Suy ra: 1832a == .

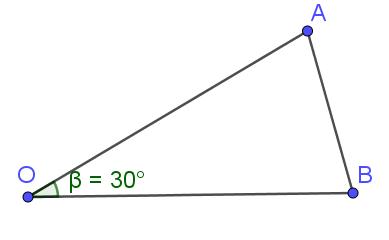
DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 3 Câu 11: Cho 30xOy =.Gọi , AB là 2 điểm di động lần lượt trên , OxOy sao cho 2AB = . Độ dài lớn nhất của OB bằng bao nhiêu? A. 4. B. 3. C. 6. D. 2. Lời giải Chọn A Áp dụng định lí cosin: 22222 3 2..cos3042.. 2 ABOAOBOAOBOAOBOAOB =+−=+− 223..40OAOBOAOB −+−= . Coi phương trình là một phương trình bậc hai ẩn OA. Để tồn tại giá trị lớn nhất của OB thì 222 (*)0(3)4(OB4)0164 OBOBOB −− . Vậy max4 OB = Câu 12: Cho ;;cab là độ dài 3cạnh của một tam giác. Mệnh đề nào sau đây không đúng? A. 2 aabac + . B. 222 2 acbac ++ . C. 222 2 bcabc ++ . D. 2abbcb + . Lời giải Chọn C Do 222 2.cos2 bcabcAbc +−=  222 2 bcabc ++ nên mệnh đề C sai. Áp dụng bất đẳng thức tam giác ta có 2 abcaabac ++ ;đáp án A đúng. Tương tự 2acbabbcb ++ ;mệnh đề D đúng. Ta có: 222 2.cos2 acbacBac +−= 222 2 acbac++ ;mệnh đề B đúng. Câu 13: Cho tam giác ABC có 4AB = cm, 7BC = cm, 9AC = cm. Tính cos A A. 2 cos 3 A =− B. 1 cos 2 A = C. 1 cos 3 A = D. 2 cos 3 A = Lời giải Chọn D Ta có 222 cos 2.. ABACBC A ABAC +− = 222 4972 2.4.93 +− == . Câu 14: Cho tam giác ABC có 222 0abc+− . Khi đó: A. Góc 090C  B. Góc 090C  C. Góc 090C = D. Không thể kết luận được gì về góc .C Lời giải Chọn B Ta có: 222 cos 2 abc C ab +− = Mà: 222 0abc+− suy ra: 0cos090 CC . Câu 15: Cho tam giác ABC thoả mãn: 222 3 bcabc +−= . Khi đó: A. 0 30.A = B. 0 45.A = C. 0 60.A = D. 075A = .

Ta có: 222 033 cos30. 222 bcabc AA bcbc +−

Câu 16: Cho các điểm (1;1),(2;4),(10;2). ABC Góc BAC bằng bao nhiêu?

A. 090 . B. 0 60. C. 0 45. D. 0 30.

Chọn A

Ta có: (1;3)AB = , (9;3)AC =−

ABAC BACBAC ABAC ===

Suy ra: 0. cos090. .

Câu 17: Cho tam giác ABC , biết 24,13,15.abc===

Tính góc A?

A. 0 3334'. B. 0 11749'. C. 0 2837'. D. 0 5824'.

i gi

OFFICIAL

DẠYKÈMQUYNHƠN

CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 4

ời giải

ọn

====

ời

ải

ờ

ải Chọn B Ta có: 222222 01315247 cos11749'. 22.13.1515 bca AA bc +−+− ===− Câu 18: Cho tam giác ABC , biết 13,14,15.abc=== Tính góc B? A. 0 5949'. B. 0 537'. C. 0 5929'. D. 0 6222'. Lời giải Chọn C Ta có: 222222 013151433 cos5929'. 22.13.1565 acb BB ac +−+− === Câu 19: Cho tam giác ABC biết độ dài ba cạnh , , BCCAAB lần lượt là ,, abc và thỏa mãn hệ thức ( ) ( )2222 bbacca −=− với bc  . Khi đó, góc BAC bằng A. 45 B. 60 C. 90 D. 120 Lời giải Chọn D Ta có ( ) ( ) ( )22223232332 0bbaccabbaccabcabc −=−−=−−−−= ( )( ) 222222 0 bcbbccabcabc −++−=+−=− . Mặt khác 222 1 cos120 222 bcabc BACBAC bcbc +−− ===−= Câu 20: Tam giác ABC có ,, ABcBCaCAb === . Các cạnh ,, abc liên hệ với nhau bởi đẳng thức ( ) ( )2222 bbacac −=− . Khi đó góc BAC bằng bao nhiêu độ A. 30 B. 60 C. 90 D. 45 Lời giải Chọn B Theo bài ra, ta có: ( ) ( ) 22223223332200bbacacbabaccbcabac −=−−=−=+−−= ( )( ) ( ) ( )( ) 222222222 000 bcbbccabcbcbbccabbcca +−+−+=+−+−=−+−=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 5 222 222 11 cos60 222 bca bcabcBACBAC bc +− +−==== . Câu 21: Cho tam giác ABC vuông cân tại A và M là điểm nằm trong tam giác ABC sao cho ::1:2:3MAMBMC = khi đó góc AMB bằng bao nhiêu? A. 135 B. 90 C. 150 D. 120 Lời giải MBx = 2 MAx= ; 3 MCx = với 02 xBC = Ta có 222 1431 cos 2.1.24 BAMxxx xx +−+ == 22214915 cos 44 MACxxx xx +−− == . 22223115 1 44 xx xx  +− +=   4224 9611102516 xxxx +++−+= . 42 342020 xx −+= 2 2 5221() 175 522 17 xl x  + =   =  . 222 cos 2. AMBMAB AMB AMBM +− = 22 41 2.2. xx xx +− = 2 2 51 4 x x = 251022082 1: 1717  =−   2 2 = . Vậy 135AMB = Câu 22: Cho tam giác ABC , chọn công thức đúng trong các đáp án sau: A. 222 2 24a bca m + =+ B. 222 2 24a acb m + =− C. 222 2 . 24a abc m + =− D. 222 2 22 . 4a cba m +− = Lời giải Chọn D Ta có: 222222 2 22 . 244a bcabca m ++− =−= Câu 23: Tam giác ABC có 9AB = cm, 15BC = cm, 12AC = cm. Khi đó đường trung tuyến AM của tam giác có độ dài là A. 10cm. B. 9cm. C. 7,5cm. D. 8cm. Lời giải Chọn C Ta có 222 2 24 ABACBC AM + =− 222 91215225 244 + =−= 15 2 AM = . Câu 24: Cho tam giác ABC có 3,5ABBC== và độ dài đường trung tuyến 13BM = . Tính độ dài AC .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 6 A. 11. B. 4. C. 9 2 . D. 10 . Lời giải Chọn B Theo công thức tính độ dài đường trung tuyến;ta có: ( ) 222222 2 2 35 134 2424 BABCACAC BMAC ++ =−=−= . Câu 25: Cho ABC vuông ở ,A biết 30,C = 3.AB = Tính độ dài trung tuyến ?AM A. 3 B. 4 C. 5 2 D. 7 2 Lời giải Chọn A AM là trung tuyến ứng với cạnh huyền nên 1 2 AMBCBMMC === . Xét BAC có 903060B =−= Xét tam giác ABM có BMAM = và 60B = suy ra ABM là tam giác đều. 3AMAB == Câu 26: Tam giác ABC có 6,42,2.abc=== M là điểm trên cạnh BC sao cho 3BM = . Độ dài đoạn AM bằng bao nhiêu? A. 9. B. 9. C. 3. D. 1 108. 2 Lời giải Chọn C Ta có: Trong tam giác ABC có 66aBC== mà 3BM = suy ra M là trung điểm .BC Suy ra: 222 22 93 24a bca AMmAM + ==−== Câu 27: Gọi 222 abc Smmm =++ là tổng bình phương độ dài ba trung tuyến của tam giác ABC . Trong các mệnh đề sau mệnh đề nào đúng? A. 222 3() 4 Sabc =++ B. 222Sabc =++ C. 222 3() 2 Sabc =++ D. 222 3()Sabc =++ Lời giải Chọn A 13 5 3 M CB A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 7 Ta có: 222222222 222222 24242443().abc bcaacbabc Smmmabc +++ =++=−+−+−=++ Câu 28: Cho ABC có 2AB = ; 3AC = ; 0A60 = . Tính độ dài đường phân giác trong góc A của tam giác ABC A. 12 5 B. 62 5 C. 63 5 D. 6 5 Lời giải Chọn C Gọi M là chân đường phân giác góc A. Ta có 222 2..cos77.BCABACABACABC =+−== Lại có 2 3 BMAB CMAC == Suy ra 27 5 BM = Áp dụng định lý cosin trong tam giác ABM ta được: 222 22222 108 2..cos2... 2..25 ABBCAC AMABBMABBMABCABBMABBM ABBC +− =+−=+−= 63 . 5 AM = CÁ CH 2 Gọi M là chân đường phân giác trong của góc A . Vì đoạn thẳng AM chia tam giác ABC thành hai phần nên ta có: 111 ..sin..sin..sin 222ABCABMACM SSSABACBACABAMBAMACAMMAC =+=+ ( ) ..sin60 .sin30 ABAC AM ABAC  = + 63 5 AM = Vậy 63 5 AM = DẠNG 2. ĐỊNH LÝ SIN, ÁP DỤNG ĐỊNH LÝ SIN ĐỂ GIẢI TOÁN Câu 29: Cho tam giác ABC . Tìm công thức sai: A. 2. sin a R A = B. sin. 2 Aa R = C. sin2. bBR = D. sin sin. cA C a =

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 8 Lời giải Chọn C Ta có: 2. sinsinsin abc R ABC === Câu 30: Cho ABC với các cạnh ,, ABcACbBCa === . Gọi ,, RrS lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và diện tích của tam giác ABC . Trong các phát biểu sau, phát biểu nào sai? A. 4 abc S R = . B. sin a R A = . C. 1 sin 2 SabC = . D. 222 2cos abcabC +−= . Lời giải Chọn B Theo định lí Sin trong tam giác, ta có 2 sin a R A = Câu 31: Cho tam giác ABC có góc 60BAC = và cạnh 3BC = . Tính bán kính của đường tròn ngoại tiếp tam giác ABC A. 4R = . B. 1R = . C. 2R = . D. 3R = . Lời giải Chọn B Ta có: 3 21 sin2sin 2.3 2 BCBC RR AA ==== Câu 32: Trong mặt phẳng, cho tam giác ABC có 4cmAC = , góc 60A = , 45B = . Độ dài cạnh BC là A. 26 . B. 223 + . C. 232. D. 6 . Lời giải Chọn A Ta có sinsin BCAC AB = 4.3 2 26 2 2 BC == . Câu 33: Cho ABC có 5AB = ;A40= ;B60= . Độ dài BC gần nhất với kết quả nào? A. 3,7 B. 3,3 C. 3,5 D. 3,1 Lời giải Chọn B C180AB180406080 =−−=−−= Áp dụng định lý sin: 5 sinsinsinsin80.sinsin403,3 BCABAB BCA ACC ===  Câu 34: Cho tam giác ABC thoả mãn hệ thức 2 bca += . Trong các mệnh đề sau, mệnh đề nào đúng? A. coscos2cos. BCA += B. sinsin2sin. BCA += C. 1 sinsinsin 2 BCA += D. sincos2sin. BCA += Lời giải

L

Câu

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 9 Chọn B Ta có: 2 2sinsin2sin. sinsinsinsinsinsin2sinsinsin bc abcbcbcbc RBCA ABCABCABC + ++ ======+= + Câu 35: Tam giác ABC có 16,8a = ; 0 5613'B = ; 071C = . Cạnh c bằng bao nhiêu? A. 29,9. B. 14,1. C. 17,5. D. 19,9.

ời giải Chọn D Ta có: Trong tam giác ABC : 00000 180180715613'5247'ABCA ++==−−= . Mặt khác 0 0 .sin16,8.sin71 sinsinsinsinsinsin19,9. sin5247' abcacaC c ABCACA =====

36: Tam giác ABC có 0 6812'A = , 0 3444'B = , 117.AB = Tính AC ? A. 68. B. 168. C. 118. D. 200. Lời giải Chọn A Ta có: Trong tam giác ABC : 00000 1801806812'3444'774'ABCC ++==−−= . Mặt khác 0 0 .sin117.sin3444' 68. sinsinsinsinsinsin sin774' abcACABABB AC ABCBCC ===== DẠNG 3. DIỆN TÍCH TAM GIÁC, BÁN KÍNH ĐƯỜNG TRÒN Câu 37: Chọn công thức đúng trong các đáp án sau: A. 1 sin. 2 SbcA = B. 1 sin. 2 SacA = C. 1 sin. 2 SbcB = D. 1 sin. 2 SbcB = Lời giải Chọn A Ta có: 111 sinsinsin 222 SbcAacBabC === Câu 38: Cho hình thoi ABCD có cạnh bằng a . Góc 30BAD = . Diện tích hình thoi ABCD là A. 2 4 a . B. 2 2 a . C. 2 3 2 a . D. 2 a . Lời giải Chọn B Ta có ..sinABCD SABADBAD = 21 ..sin30 2 aaa== Câu 39: Tính diện tích tam giác ABC biết 3,5,6ABBCCA=== A. 56 B. 48 C. 6 D. 8 Lời giải Chọn A Ta có: 356 7 22 ABACBC p ++++ === Vậy diện tích tam giác ABC là: ( )( )( ) ( )( )( ) 773767556SppABpACpBC =−−−=−−−= .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 10 Câu 40: Cho ABC có 6,8,10.===abc Diện tích S của tam giác trên là: A. 48. B. 24. C. 12. D. 30. Lời giải Chọn B Ta có: Nửa chu vi ABC : 2 abc p ++ = . Áp dụng công thức Hê rông: ()()()12(126)(128)(1210)24Sppapbpc =−−−=−−−= . Câu 41: Cho ABC có 0 4,5,150.===acB Diện tích của tam giác là: A. 53. B. 5. C. 10. D. 103. Lời giải Chọn B

có: 011 ..sin.4.5.sin1505. 22ABC SacB  === Câu 42: Một tam giác có ba cạnh là 13,14,15. Diện tích tam giác bằng bao nhiêu? A. 84. B. 84. C. 42. D. 168. Lời giải Chọn A Ta có: 131415 21 22 abc p ++++ === Suy ra: ()()()21(2113)(2114)(2115)84Sppapbpc =−−−=−−−= . Câu 43: Cho các điểm (1;2),(2;3),(0;4). ABC Diện tích ABC bằng bao nhiêu? A. 13 . 2 B. 13. C. 26. D. 13 . 4 Lời giải Chọn A Ta có: (3;5)34ABAB=−= , (1;6)37ACAC=−= , (2;1)5BCBC== Mặt khác 37345 22 ABACBC p ++++ == Suy ra: 13 ()()(). 2SppABpACpBC =−−−= Câu 44: Cho tam giác ABC có (1;1),(3;3),(6;0). ABC Diện tích ABC là A. 12. B. 6. C. 62. D. 9. Lời giải Chọn B Ta có: (2;2)22ABAB=−= , (5;1)26ACAC== , (3;3)32BCBC== . Mặt khác .0 ABBCABBC =⊥ Suy ra: 1 .6. 2ABC SABBC  == Câu 45: Cho tam giác ABC có 4,6,8abc=== . Khi đó diện tích của tam giác là: A. 915. B. 315. C. 105. D. 2 15. 3 Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 11 Ta có: 468 9. 22 abc p ++++ === Suy ra: ()()()315.Sppapbpc =−−−= Câu 46: Cho tam giác ABC . Biết 2AB = ; 3BC = và 60ABC = . Tính chu vi và diện tích tam giác ABC . A. 57 + và 3 2 B. 57 + và 33 2 C. 57 và 33 2 . D. 519 + và 3 2 . Lời giải Chọn B Ta có: 222 2...cos492.2.3.cos601367ACABBCABBCABC=+−=+−=−= . Suy ra 7AC = Chu vi tam giác ABC là 237ABACBC++=++ . Diện tích tam giác ABC là 1133 ..sin.2.3.sin60 222ABC SABBCABC  === . Câu 47: Tam giác ABC có các trung tuyến 15 a m = , 12bm = , 9 c m = .Diện tích S của tam giác ABC bằng A. 72. B. 144. C. 54. D. 108. Lời giải 1 Chọn A Theo bài toán ta có 222 22 222 222 22222 222 222 22 15 24 1022900 1222576413 24 22324 273 9 24 a b c bca m bcaa acb macbb abc abcc m  + =−= =+−=  + =−=+−==   +−= = + =−=  Ta có 521373 2 abc p ++ ==++ , áp dụng công thức He rong ta có ()()()72ABC Sppapbpc=−−−= . Cách 2: Đặt ,, BCaCAbABc === , Theo định lý trung tuyến có: J K I BC A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 12 ( ) ( ) ( ) 2222 2222 2222 42 42 42 a b c mabc mbac mcba  +=+  +=+  +=+  222 222 222 22900 22576 22324 abc abc abc −++=  −+=   +−= 2 2 2 100 208 291 a b c  =  =   = 2 2 2 10010 208413 292 273 aa bb c c = =   ==   = = Có ( )( )( )ABC Sppapbpc =−−− , ( )1 2 pabc =++ Suy ra 72ABCS = Câu 48: Cho tam giác ABC có 3 7;5;cos 5 bcA === . Độ dài đường cao a h của tam giác ABC là. A. 72 2 B. 8 C. 83 D. 803 Lời giải Chọn A 2222 3 2cos752.7.5.3242 5 abcbcA =+−=+−== 2 22 sin1cos1316 525 AA  =−=−=   . Suy ra 4 sin 5 4 sin 5 A A  =   =−  vì 00180 A  nên 4 sin 5 A= 114 sin.7.5.14 225 SbcA=== mà 1172 .14.42. 222 aaa Sahhh === Câu 49: Cho tam giác ABC có 2;4 ABaACa == và 120BAC = . Tính diện tích tam giác ABC ? A. 28 Sa = . B. 2 23Sa = . C. 2 3Sa = . D. 24 Sa = . Lời giải Chọn B Diện tích của tam giác ABC là 211 ..sin.2.4.sin12023 22ABC SABACBACaaa === . Câu 50: Cho tam giác ABC đều cạnh a . Bán kính đường tròn ngoại tiếp tam giác ABC bằng A. 3 2 a . B. 3 3 a . C. 3 4 a . D. 2 2 a . Lời giải Chọn B Gọi G là trọng tâm ABC . Bán kính đường tròn ngoại tiếp 233 323 RAGaa === Câu 51: Cho tam giác ABC có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác ABC bằng A. 12 B. 3 C. 6 D. 24 Lời giải Chọn C Theo đề bài tam giác ABC có chu vi bằng 12 nên nửa chu vi là 12 2p = ; bán kính đường tròn nội tiếp bằng 1, tức là ta có: 1r = . Diện tích tam giác ABC là: .6.16Spr=== .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 13 Câu 52: Cho tam giác ABC đều cạnh 2a . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC . A. 2 3 a B. 4 3 a C. 8 3 a D. 6 3 a Lời giải Chọn A Gọi H, K lần lượt là trung điểm cạnh ,;ABBC I là giao điểm của AH và CK . Lúc đó, I là tâm đường tròn ngoại tiếp tam giác ABC Ta có: 23 3 2 a AHa == . Do đó: 222 3. 33 3 RAIAHaa ==== Câu 53: Cho tam giác ABC có 6BC = , 2AC = và 31AB =+ . Bán kính đường tròn ngoại tiếp tam giác ABC bằng: A. 5 . B. 3 . C. 2 . D. 2. Lời giải Chọn C Áp dụng định lý cosin ta có 222 1 cos 22 bca A bc +− == suy ra 60A = Áp dụng định lý sin ta có 2 2sin a R A == Câu 54: Cho tam giác ABC có 3AB = , 4AC = , 5BC = . Bán kính đường tròn nội tiếp tam giác bằng A. 1. B. 8 9 . C. 4 5 . D. 3 4 . Lời giải Chọn A Vì 222 ABACBC += nên tam giác ABC vuông tại A Do đó bán kính đường tròn nội tiếp ( ) 1 23.41 1345 2 SABAC r p ABACBC ==== ++ ++ Câu 55: Cho ABC có 84,13,14,15.Sabc ==== Độ dài bán kính đường tròn ngoại tiếp R của tam giác trên là: A. 8,125. B. 130. C. 8. D. 8,5. I K H A B C

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 14 Lời giải Chọn A Ta có: ....13.14.1565 444.848ABC abcabc SR RS ==== . Câu 56: Cho ABC có 103S = , nửa chu vi 10=p . Độ dài bán kính đường tròn nội tiếp r của tam giác trên là: A. 3. B. 2. C. 2. D. 3. Lời giải Chọn D Ta có: 103 3. 10 S Sprr p ==== Câu 57: Một tam giác có ba cạnh là 26,28,30. Bán kính đường tròn nội tiếp là: A. 16. B. 8. C. 4. D. 42. Lời giải Chọn B Ta có: 262830 42. 22 abc p ++++ === ()()()42(4226)(4228)(4230) 8. 42SprrSppapbpc pp ===== Câu 58: Một tam giác có ba cạnh là 52,56,60.Bán kính đường tròn ngoại tiếp là: A. 65 8 B. 40. C. 32,5. D. 65 4 Lời giải Chọn C Ta có: 525660 84. 22 abc p ++++ === Suy ra: ()()()84(8452)(8456)(8460)1344Sppapbpc =−−−=−−−= . Mà 52.56.6065 444.13442 abcabc SR RS ==== Câu 59: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn ngoại tiếp là? A. 6. B. 8. C. 13 2 . D. 11 2 . Lời giải Chọn C Ta có: 222 13 51213. 2 R +== . Câu 60: Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu? A. 2. B. 22. C. 23. D. 3. Lời giải Chọn A Ta có: 51213 15 2p ++ == . Mà 222 1 51213.5.1230. 2 S +=== Mặt khác .2. S Sprr p === Câu 61: Tam giác với ba cạnh là 6;8;10 có bán kính đường tròn ngoại tiếp bằng bao nhiêu?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 15 A. 5. B. 42. C. 52. D. 6. Lời giải Chọn A Ta có: 222 10 68105. 2 R +=== Câu 62: Cho hình chữ nhật ABCD có cạnh 4,6ABBC== , M là trung điểm của , BCN là điểm trên cạnh CD sao cho 3 NDNC = . Khi đó bán kính của đường tròn ngoại tiếp tam giác AMN bằng A. 35 B. 35 2 C. 52 D. 52 2 Lời giải Chọn D Ta có 3,110MCNCMN=== 3,45BMABAM=== 6,345ADNDAN=== 10545 22 AMANMN p ++++ == ( )( )( ) 15 2AMN SppAMpANpMN =−−−= Bán kính của đường tròn ngoại tiếp của tam giác AMN là: ..52 42 AMN AMANMN R S == Câu 63: Cho tam giác đều ABC ;gọi D là điểm thỏa mãn 2 DCBD = . Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác ADC Tính tỉ số R r . A. 5 2 B. 577 9 + C. 755 9 + D. 757 9 + Lời giải Chọn D Ta có 22 DCBDDCDB ==− . Do đó 2 DCDB = .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 16 Gọi S là diện tích của tam giác ACDvà E là trung điểm của BC Đặt ABa = . Suy ra 22 2 2 22 2233 3346 327 266 ABC SSaa ADAEEDaaa  ===     =+=+=     . Hơn nữa ( ) ( ) 34 2 3 57 57.2775726 6.36108..27 436 ADDCAC Srar araar S ADDCBCaRR S RR  +++== ++ ==  ==  Hay ( ) ( ) ( )44757757.12757 121081089 ar aRR Rrr +++ === . DẠNG 4. ỨNG DỤNG THỰC TẾ Câu 64: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và B dưới một góc 7824' o . Biết 250,120 CAmCBm == . Khoảng cách AB bằng bao nhiêu? A. 266. m B. 255. m C. 166. m D. 298. m Lời giải Chọn B Ta có: 222222..cos2501202.250.120.cos7824'64835255. o ABCACBCBCACAB =+−=+− Câu 65: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 060 . Tàu thứ nhất chạy với tốc độ 30/kmh , tàu thứ hai chạy với tốc độ 40/kmh. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km ? A. 13. B. 2013. C. 1013. D. 15. Lời giải Chọn B Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: 1 30.260. Skm == Sau 2h quãng đường tàu thứ hai chạy được là: 2 40.280. Skm == Vậy: sau 2h hai tàu cách nhau là: 220 12122..cos602013.SSSSS =+−= Câu 66: Từ một đỉnh tháp chiều cao 80 CDm = , người ta nhìn hai điểm A và B trên mặt đất dưới các góc nhìn là 0 7212' và 0 3426'. Ba điểm ,, ABD thẳng hàng. Tính khoảng cách AB? A. 71. m B. 91. m C. 79. m D. 40. m Lời giải Chọn B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 17 Ta có: Trong tam giác vuông CDA: 0 00 80 tan7212'25,7. tan7212'tan7212' CDCD AD AD === Trong tam giác vuông CDB : 0 00 80 tan3426'116,7. tan3426'tan3426' CDCD BD BD === Suy ra: khoảng cách 116,725,791. ABm =−= Câu 67: Khoảng cách từ A đến B không thể đo trực tiếp được vì phải qua một đầm lầy. Người ta xác định được một điểm C mà từ đó có thể nhìn được A và Bdưới một góc 0 5616'. Biết 200 CAm = , 180 CBm = . Khoảng cách AB bằng bao nhiêu? A. 180. m B. 224. m C. 112. m D. 168. m Lời giải Chọn A Ta có: 2222202..cos2001802.200.180.cos5616'32416180. ABCACBCBCACAB =+−=+− Câu 68: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ ( 4,3AB = cm; 3,7BC = cm; 7,5CA = cm). Bán kính của chiếc đĩa này bằng. A. 5,73 cm. B. 6,01cm. C. 5,85cm. D. 4,57cm. Lời giải Chọn A Bán kính R của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác ABC . Nửa chu vi của tam giác ABC là: 4,33,77,531 224 ABBCCA p ++++ === cm. Diện tích tam giác ABC là: ( )( )( ) 5,2SppABpBCpCA =−−− cm2 . Mà 5,73 44 ABBCCAABBCCA SR RS == cm. Câu 69: Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm A, B trên mặt đất sao cho ba điểm A, B, C thẳng hàng. Ta đo được AB = 24m, 063CAD = ; 048CBD = . Chiều cao h của khối tháp gần với giá trị nào sau đây? A. 61,4 m. B. 18,5 m. C. 60 m. D. 18 m. Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 18 Ta có ( ) 000000 631171801174815CADBADADB===−+= Áp dụng định lý sin trong tam giác ABD ta có: .sin sinsinsin ABBDABBAD BD ADBBADADB == Tam giác BCD vuông tại C nên có: sin.sin CD CBDCDBDCBD BD == Vậy 00 0 .sin.sin24.sin117.sin48 sinsin1561,4 ABBADCBD CDm ADB === BÀI TẬP TỔNG HỢP Câu 70: Cho tam giác ABC có 8,10==BCCA , và 60 =ACB . Độ dài cạnh AB bằng A. 321 B. 72 C. 211 D. 221 Lời giải Chọn D Ta có: 222222..cos8102.8.10.cos6084 =+−=+−=ABBCCABCCAC 221= AB . Câu 71: Cho tam giác ABC có ;; BCaCAbABc === biết 8,10ab== , gócC bằng60. Độ dài cạnh c là? A. 321=c B. 72=c C. 211c = D. 221c = Lời giải Chọn D Ta có: 222222..cos8102.8.10.cos6084221cababCc =+−=+−== . Câu 72: Cho tam giác ABC có 7b = ; 5c = và 3 cos 5 A = . Tính a A. 42 . B. 2. C. 2 . D. 3. Lời giải Chọn A Áp dụng định lí hàm số Cosin vào tam giác ABC có 222 3 2..Cos25492.5.7.32 5 BCABACABACA 42BC Câu 73: Trong ABC có ,, === ABcACbBCa Đẳng thức nào sau đây đúng?

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 19 A. 222 2cos abcbcA =++ . B. 222 2cos abcbcA =+− . C. 222 cos abcbcA =++ . D. 222 cos abcbcA =+− . Lời giải Chọn B Theo định lí hàm số cos, trong ABC ta luôn có: 222 2cos=+− abcbcA Câu 74: Cho tam giác ABC có 4,6ABAC== và 120.A = Độ dài cạnh BC là A. 19. B. 27. C. 319. D. 219. Lời giải Chọn D Xét ABC có 222 2..cos BCABACABACA =+− Hay 22222..cos462.4.6.cos120219.BCABACABACA=+−=+−= Câu 75: Tam giác ABC có 120A = thì câu nào sau đây đúng? A. 222 3 abcbc =+− B. 222 abcbc =++ C. 222 3 abcbc =++ D. 222 abcbc =+− Lời giải Chọn B Áp dụng định lí hàm số cos tại đỉnh A ta có: 222 2.cos abcbcA =+− . 222 2.os120abcbcc =+− 222 abcbc=++ . Câu 76: Cho ABC có 0 60,8,5.Bac=== Độ dài cạnh b bằng: A. 7. B. 129. C. 49. D. 129 Lời giải Chọn A Ta có: 2222202cos852.8.5.cos60497 bacacBb =+−=+−== Câu 77: Cho tam giác ABC có = BCa ; = ACb ; = ABc , có 222 2=++ abcbc . Số đo của góc A là: A. 150 . B. 120 . C. 45 . D. 135 . Lời giải Chọn D Ta có: 222 22 cos 222 +−−− === bcabc A bcbc 135 = A . Câu 78: Cho ABC có A60, 3, 4 ABcmACcm=== . Tính cạnh BC . A. 10BC = B. 13BC = C. 12BC = D. 11BC = Lời giải Chọn B Áp dụng định lí cosin ta có: 2220 343.4.cos60BC =+− 13BC = . Câu 79: Cho tam giác ABC có 06,8,60ABcmACcmABC === . Tính độ dài cạnh BC .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 20 A. 337 + B. 10 C. 337 D. 9 Lời giải Chọn A Ta có 222222 2 1 2..cos862.6.. 2 337 6280. 337() ACABBCABBCABCBCBC BC BCBC BCl =+−=+−  =+ −−=  =−  Câu 80: Xét tam giác ABC có 3AB = cm , 5AC = cm , 1 cos 2 BAC = . Độ dài cạnh BC bằng: A. 19 B. 7 C. 4 D. 34 Lời giải Chọn A Theo định lí Cosin trong tam giác, ta có: 222 2...cos BCABACABACBAC =+− 22 1 352.3.5.9251519 2 =+−=+−= Vậy 19BC = Câu 81: Tam giác ABC có 5AB = cm, 5BC = cm, 3AC = cm. Giá trị cos A là A. 2 3 . B. 1 2 . C. 3 10 . D. 3 10 . Lời giải Chọn C Áp dụng định lí hàm số cosin ta có: 2222225353 cos 2..2.5.310 ABACBC A ABAC +−+− === . Câu 82: . Tam giác ABC có 3,8ABBC== . Gọi M là trung điểm của BC . Biết 513 cos 26 AMB = và 3AM  . Tính độ dài cạnh AC . A. 13AC = . B. 7AC = . C. 13AC = . D. 7AC = . Lời giải Chọn D Ta có: M là trung điểm của BC 4. 2 BC BM == Trong tam giác ABM ta có: 222 cos 2. AMBMAB AMB AMBM +− = 222 2..cos0.AMAMBMAMBBMAB −+−=

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 21 A B MC 2 2013133() 70 13713133() AM AMAM AM  −+==  =  thoaû maõn loaïi 13.AM = Ta có: AMB và AMC là hai góc kề bù. 513 coscos 26 AMCAMB =−=− Trong tam giác AMC ta có: 222 2..cos ACAMCMAMCMAMC =+− 513 13162.13.4.497. 26 AC  =+−−==    Câu 83: Cho tam giác ABC có 4AB = , 7AC = và 9BC = . Gọi M là điểm trên cạnh BC sao cho 2 MCMB = . Gọi H là trung điểm của đoạn thẳng BC . Đường trung trực của đoạn thẳng BC cắt AM tại I . Tính độ dài đoạn thẳng AI . A. 33 2 . B. 27 2 . C. 3. D. 32 3 . Lời giải Chọn A 9BC = 3BM = và 6MC = . 2222224972 cos 2.2.4.93 ABBCAC ABC ABBC +−+− === 2 coscos 3 ABMABC == 222 2..cos AMABBMABBMABM =+− 22 2 432.4.3.9 3 =+−= 3AM = . 2222223341 cos 2.2.3.39 AMBMAB AMB AMBM +−+− === 1 coscos 9 HMIAMB == .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 22 93 3 22 MHBHBM=−=−= 3127 : 292cos MH MI HMI === . Vậy 2733 3 22 AIAMMI=+=+= . Câu 84: Cho tam giác ABC có ,, BCaCAbABc === , trọng tâm G và diện tích S . Đặt BGC = , mệnh đề nào sau đây đúng? A. 222 5 cot 4 bca S  +− = B. 222 5 cot 12 bca S  ++ = C. 222 5 cot 12 bca S  = .D. 222 5 cot 12 bca S  +− = . Lời giải Chọn D Gọi GBCR là bán kính đường tròn ngoại tiếp tam giác GBC Ta có 222 222222 cos 2. cot. sin.. 2 GBC GBCGBC GBGCBC GBGCGBGCBCGBGCBC R BCGBGCBC GBGCBC RR    +− +−+− ==== 222 4 GBC GBGCa S +− = ( ) ( ) 222222 2422 944 4 3 cabbac a S  +−+−  +−   = 222 5 12 bca S +− = . Câu 85: Cho hình vuông ABCD có cạnh bằng 6, E là trung điểm của CD. Tính bán kính đường tròn ngoại tiếp tam giác ACE A. 310 2 B. 35 2 C. 310 D. 35 Lời giải Chọn A

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 23 Ta có 22 36935=+=+=AEADDE Áp dụng định lý sin cho tam giác ACE ta được: 35310 2 sin22 2. 2 === AE RRR ACE Câu 86: Tam giác ABC có ˆ 6812A   = , ˆ 3444B   = , 117.AB = Tính AC ? A. 68 B. 168 C. 118 D. 200 Lời giải Chọn A Ta có trong tam giác ABC : 1801806812'3444'774'ABCC ++==−−= . Mặt khác .sin117.sin3444' 68. sinsinsinsinsinsinsin774' abcACABABB AC ABCBCC  =====  Câu 87: Tam giác ABC có độ dài cạnh 3cm=AB ; 6cm=AC và 60 =A . Bán kính R của đường tròn ngoại tiếp tam giác ABC bằng A. 3=R . B. 33=R . C. 3=R . D. 6=R . Lời giải Chọn C Xét tam giác ABC ta có: 222 2..cos=+− BCABACABACA 222362.3.6.cos6027=+−= BC 222+=BCABAC Do đó tam giác ABC vuông tại B . Vậy bán kính R của đường tròn ngoại tiếp tam giác ABC : ( )6 3cm 22 === AC R . Câu 88: Cho ABC có 45,75AB== . Tính tỉ số AB BC A. 6 2 . B. 13 2 + . C. 632 6 + . D. 6 3 . Lời giải 6 DE C A B

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 24 Chọn A Áp dụng định lí hàm số sin trong tam giác ABC , ta có ( )sin1804575 sinsin606 sinsinsinsin45sin452 ABBCABC CABCA −−  =====  Câu 89: Cho tam giác ABC có 60, 75BC== và 10AC = . Khi đó, độ dài cạnh BC bằng A. 106 3 . B. 56 . C. 56 3 . D. 10. Lời giải Chọn A Ta có 180607545A =−−= Áp dụng định lí Sin cho tam giác ABC , ta có: .sin10.sin45106 sinsinsinsin603 BCACACA BC ABB  ====  Câu 90: Cho tam giác ABC có 5AC = thoả mãn sinBtanBsinsinAC= . Gọi G là trọng tâm tam giác ABC . Tính giá trị biểu thức 22SGAGC =+ Lời giải sinBtanBsinsin = AC 2 sinBcosBsinsin= AC 2222 2 4222 +− = bacbac RacRR 22222 =+−bacb 222 3+=acb Mà 5==bAC suy ra 22 75+=ac Do đó: 22222222 22222275175 25 3242434346  +++  =+=−+−=+=+=    bcaabcac SGAGCb Câu 91: Cho tam giác ABC có 5AB = , 6AC = , 7BC = . Tính diện tích tam giác ABC A. 123 B. 96 C. 66 . D. 36 Lời giải Chọn C Nửa chu vi của tam giác ABC : 9 2 ABACBC p ++ == Áp dụng công thức Herong, diện tích của tam giác ABC là ( )( )( ) ( )( )( ) 995969766SppABpACpBC =−−−=−−−= . Câu 92: Cho tam giác ABC có 5,12,13.abc=== Bán kính đường tròn ngoại tiếp R của tam giác bằng A. 13. B. 6,5. C. 26. D. 7,5. Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 25 Chọn B Có 51213 15. 22 abc p ++++ === Do đó ( )( )( ) ( )( )( ) 15.1551512151330.ABC Sppapbpc  =−−−=−−−= Mà 5.12.13 6,5. 444.30ABC abcabc SR RS ==== Câu 93: Cho ABCDlà hình thoi, 0 120,2BADAB== . Diện tích tam giác ABC bằng A. 3 . B. 23 . C. 3 2 . D. 4. Lời giải Chọn A Giả thiết suy ra tam giác ABC đều 01 .2.2.sin603 2ABCS == Câu 94: Cho tam giác ABC có các cạnh 6AB = , 8AC = , 10BC = . Bán kính đường tròn nội tiếp tam giác ABC là A. 12r = B. 3r = . C. 5r = . D. 2.r = Lời giải Chọn D Ta có 222 BCABAC =+ ABC vuông tại A Khi đó 11 ..6.824 22ABC SABAC  === . Gọi r là bán kính đường tròn nội tiếp, p là nửa chu vi tam giác ABC , ta có 24 .2 12 S Sprr p ==== . Câu 95: Cho tam giác ABC có 6;9;60ABcmACcmBAC===. Diện tích tam giác ABC là A. 2273 2 Scm = B. 227 2 Scm = C. 2273 4 Scm = D. 227 4 Scm = Lời giải Chọn C 2113273 ...sin.6.9. 2224 SACABBACcm === . Câu 96: Tính diện tích hình bình hành ABCDbiết 0;3;60ABaBCaABC === . A. 2 a . B. 23 2 a . C. 2 2 a . D. 2 3 2 a . Lời giải

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 26 Chọn B Ta có 2 D ..sin.3sin603 2 o ABC SABBCBaaa === Câu 97: Tam giác ABC có 4, 30, 75ACBACACB=== . Tính diện tích tam giác .ABC A. 8ABCS = B. 43ABCS = C. 4ABCS = D. 83ABCS = Lời giải Chọn C Ta có ( )0180 75 ABCBACACBACB =−+== . Suy ra tam giác ABC cân tại A nên 4ABAC== Diện tích tam giác ABC là 1 .sin4. 2ABC SABACBAC  == Câu 98: Cho hình bình hành ABCDcó 3,7,60ABBCBAC=== . Diện tích hình bình hành ABCDlà A. 213 B. 213 2 C. 123 D. 63 Lời giải Chọn C Ta có 222 cos 2.. ABACBC BAC ABAC +− = 2 2 1949 22.3. 8 3400 5() AC AC AC ACAC ACL +− = = −−=  =− Vậy 8AC = . Suy ra 1 22...sin3.8.sin60123 2ABCDABC SSABACA==== Câu 99: Hai chiếc tàu thuỷ P và Q trên biển cách nhau 100m và thẳng hàng với chân A của tháp hải đăng AB ở trên bờ biển. Từ P và Q người ta nhìn chiều cao AB của tháp dưới các góc 015BPA = và 055BQA = . Tính chiều cao của tháp

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 27 Lời giải Ta có 000 551540PBQ =−= . Áp dụng định lí sin cho tam giác PBQ ta có 0 000100100.sin15 sin15sin40sin40 BQ BQ == Chiều cao của tháp là 000 0 100 sin55.sin55.sin15.33 sin40 ABBQm == Câu 100: Trên nóc một tòa nhà có một cột ăng ten cao 4m . Từ vị trí qua sát A cao 9m so với mặt đất, có thể nhìn thấy đỉnh B và chân C của cột ăng ten dưới góc 050 và 035 so với phương ngang. Chiều cao của tòa nhà gần nhất với số nào dưới đây? A. 14 m B. 21,1 m C. 17,8 m D. 18,7 m Lời giải Chọn D Hạ AHBC ⊥ , HBC  . Từ giả thiết ta có: 00 50;35BAHCAH== nên 015BAC = Tam giác AHB vuông tại H có 00 9040BBAH=−= .

DẠYKÈMQUYNHƠN OFFICIAL CHUYÊN ĐỀ III TOÁN 10 CHƯƠNG III HỆ THỨC LƯỢNG TRONG TAM GIÁC Sưu tầm và biên soạn Page 28 Áp dụng định lí sin trong tam giác ABC có: 00 sin40sin15 ACBC = 0 0 4sin40 sin15 AC = Xét tam giác AHC vuông tại H có 00 0 4sin40sin35 sin5,7 sin15 CHACCAHm == . Vậy chiều cao của tòa nhà xấp xỉ: ( )45,7918,7 m++= . Câu 101: Giả sử CDh = là chiều cao của tháp trong đó C là chân tháp. Chọn hai điểm , AB trên mặt đất sao cho ba điểm ,, ABC thẳng hàng. Ta đo được 30 ABm = , 63CAD = ; 48CBD = . Chiều cao h của khối tháp gần với giá trị nào sau đây? A. 64,6. m B. 30. m C. 61,4. m D. 76,8. m Lời giải Chọn D Ta có ( ) 000000 631171801174815CADBADADB===−+= Áp dụng định lý sin trong tam giác ABD ta có: .sin sinsinsin ABBDABBAD BD ADBBADADB == Tam giác BCD vuông tại C nên có: sin.sin CD CBDCDBDCBD BD == Vậy 00 0 .sin.sin30.sin117.sin48 sinsin1576,8. ABBADCBD CDm ADB ===