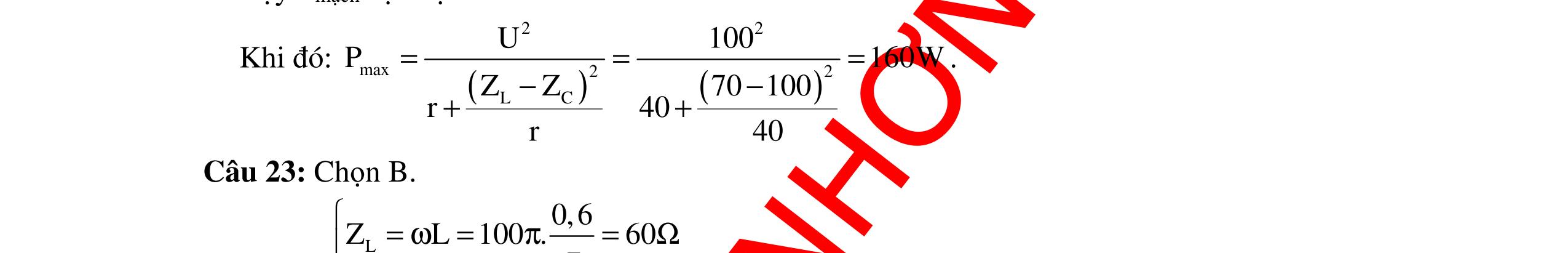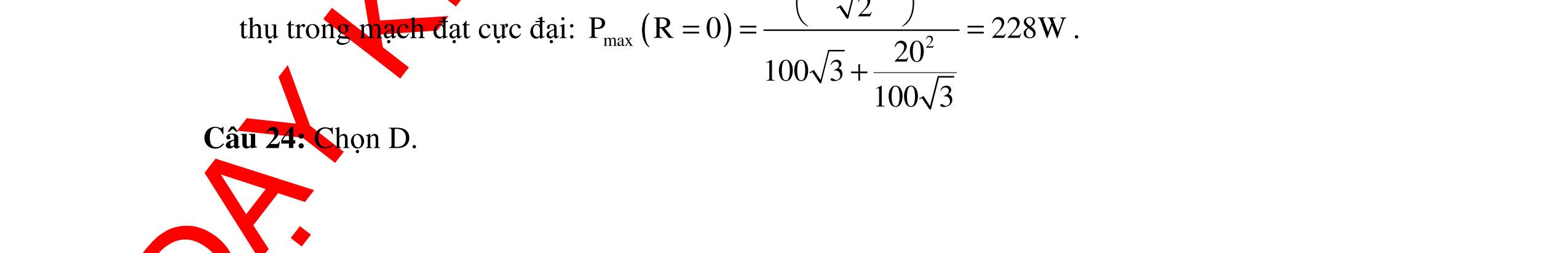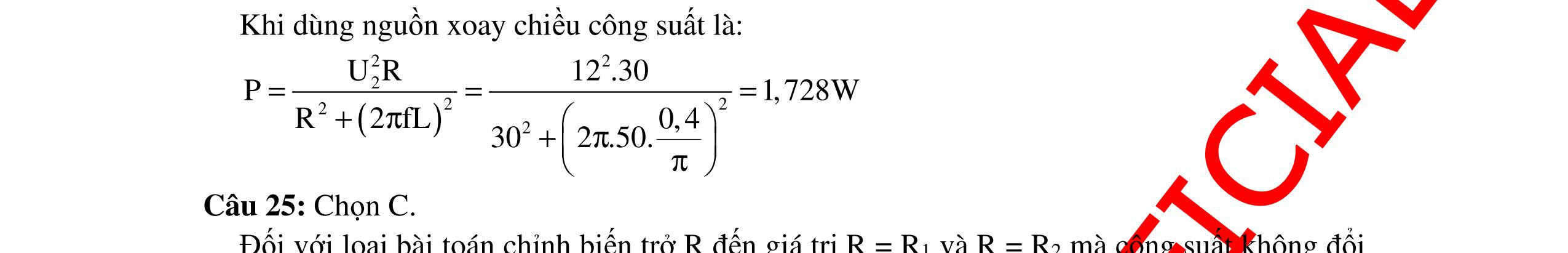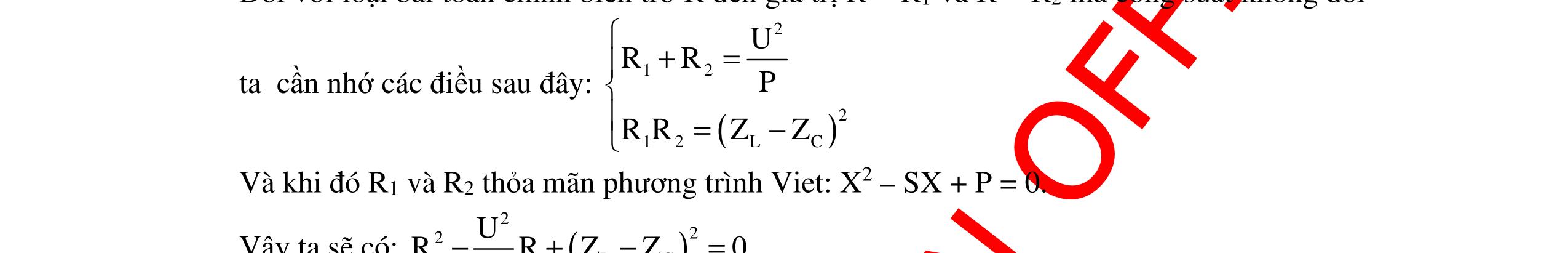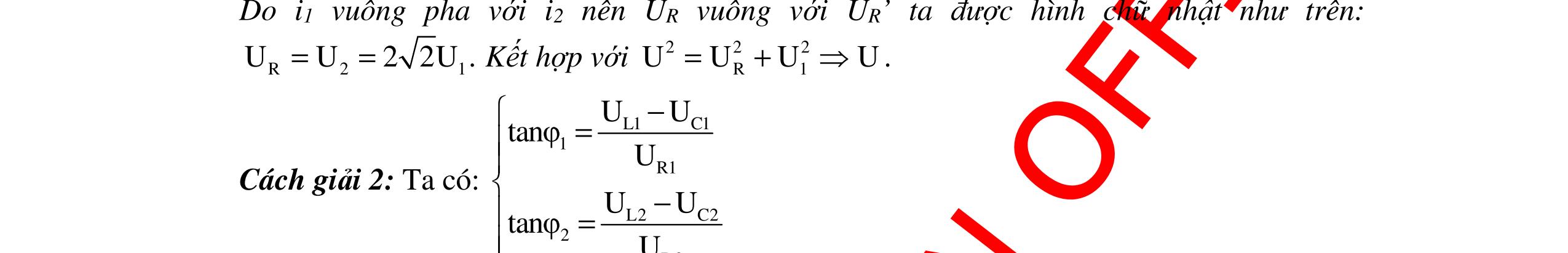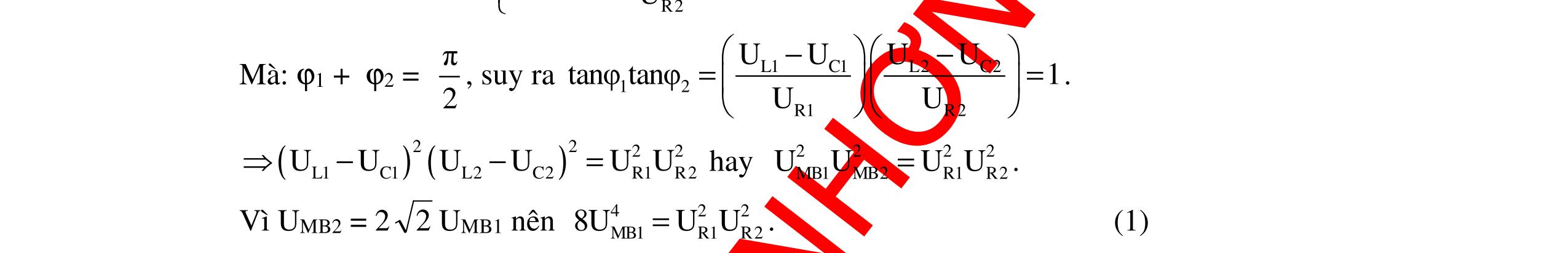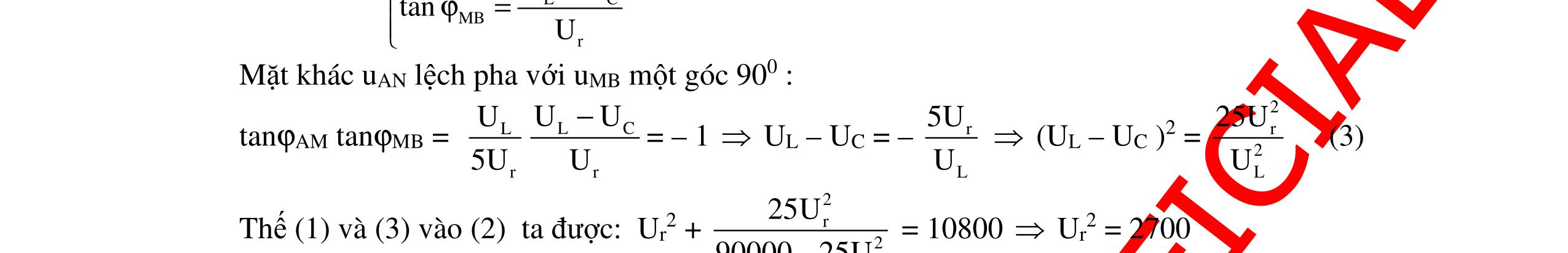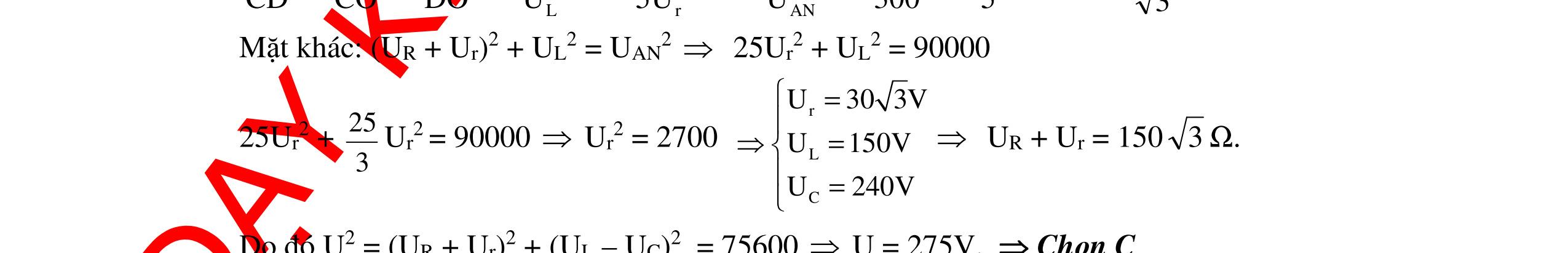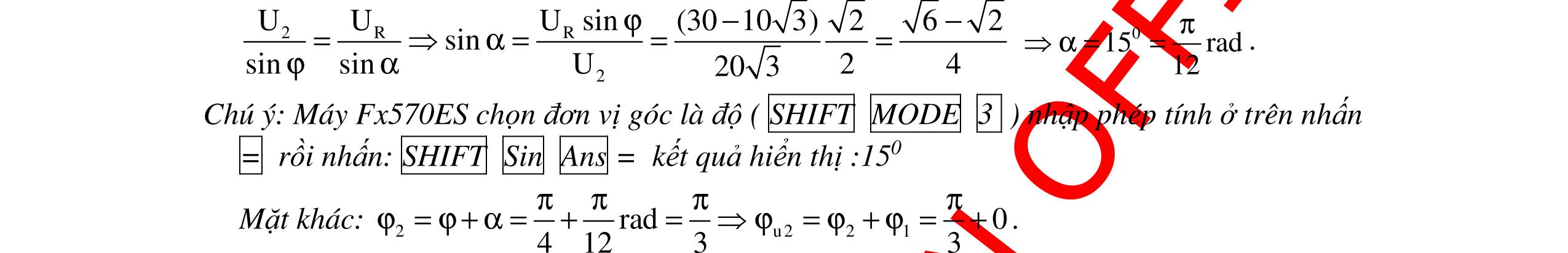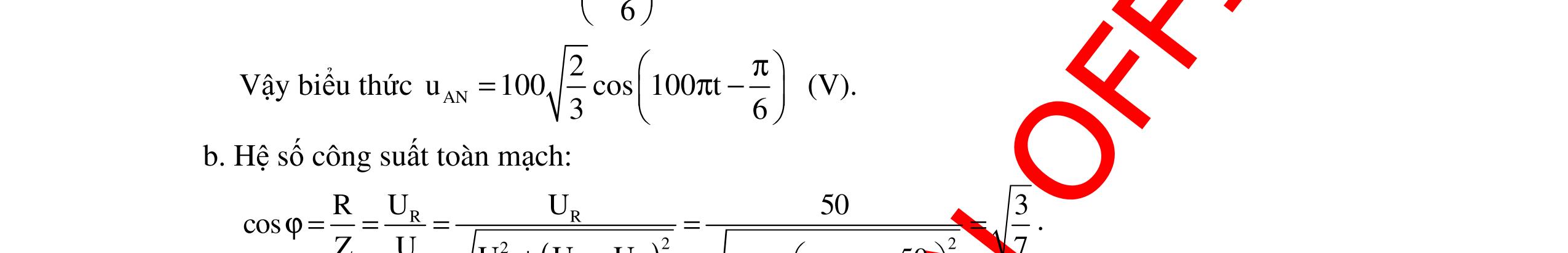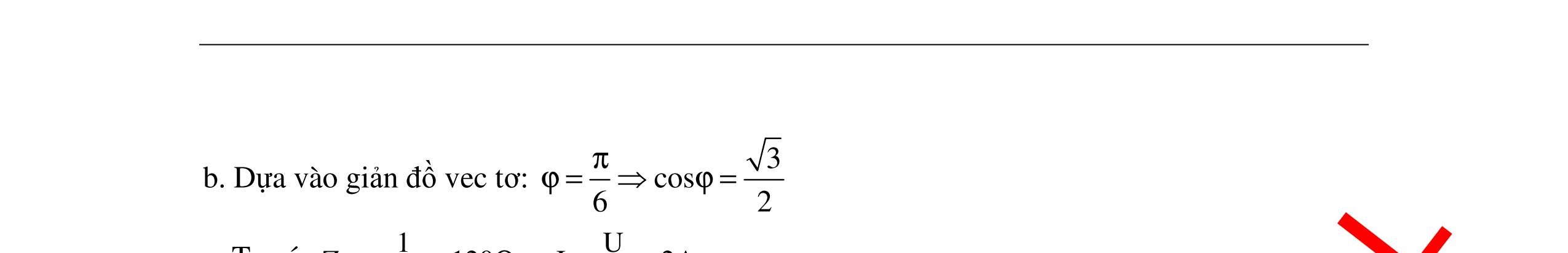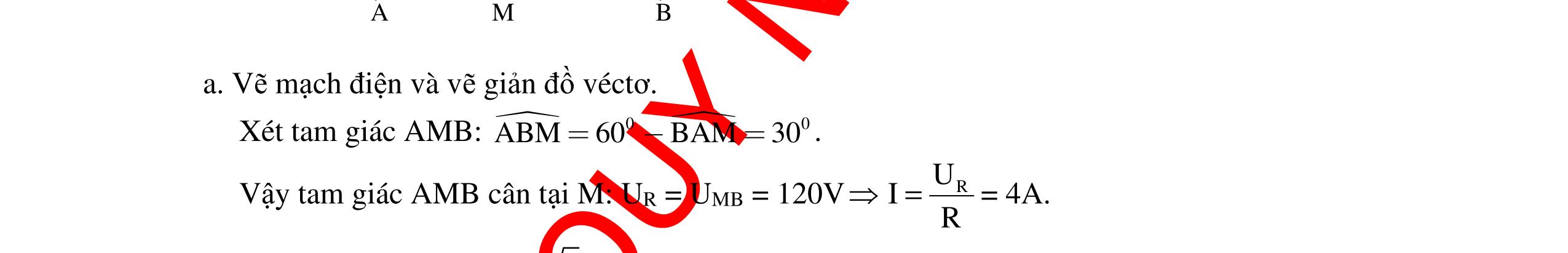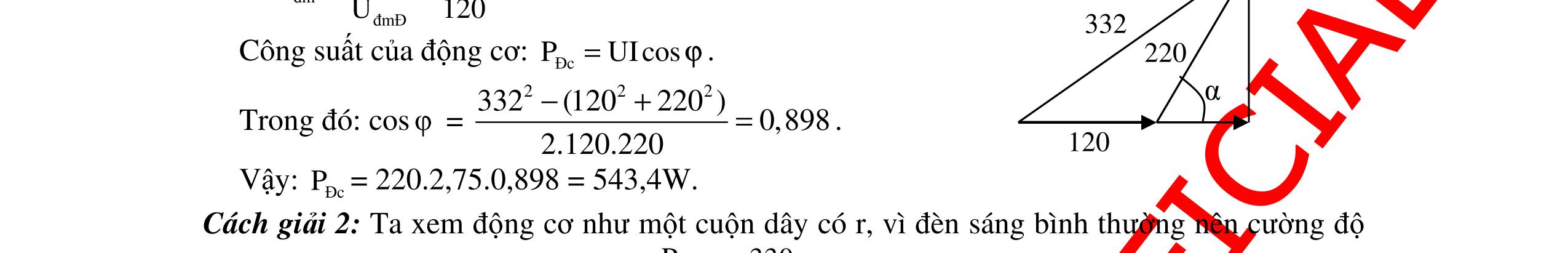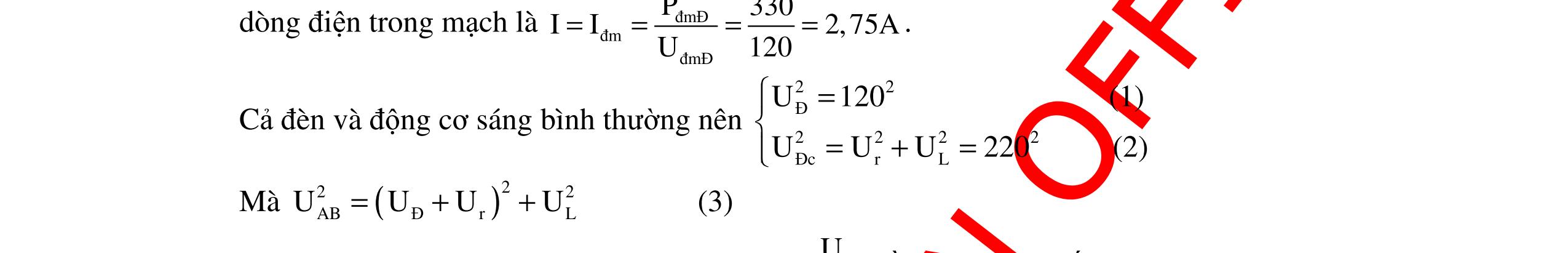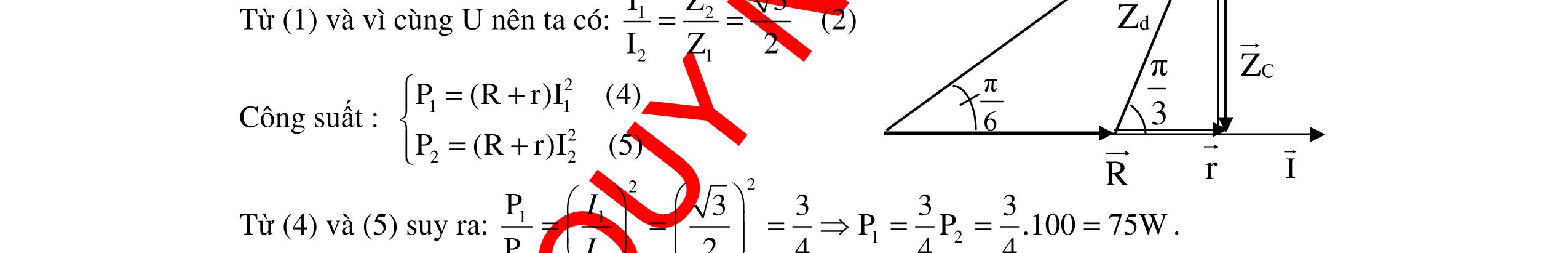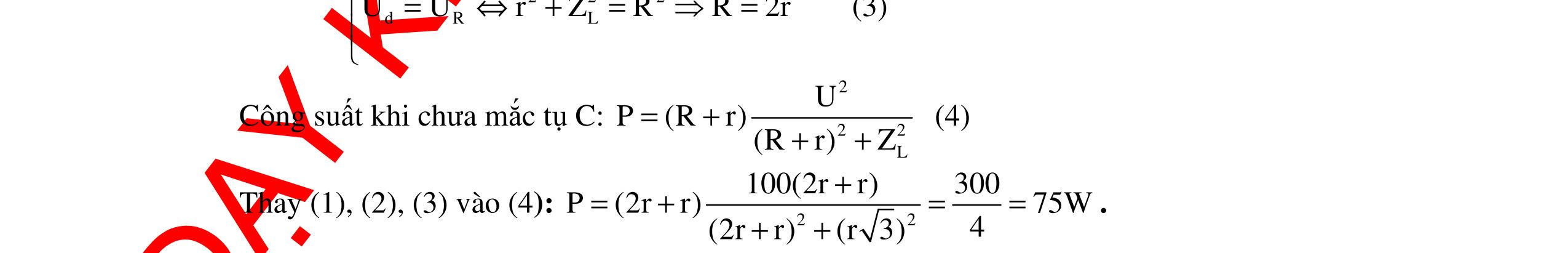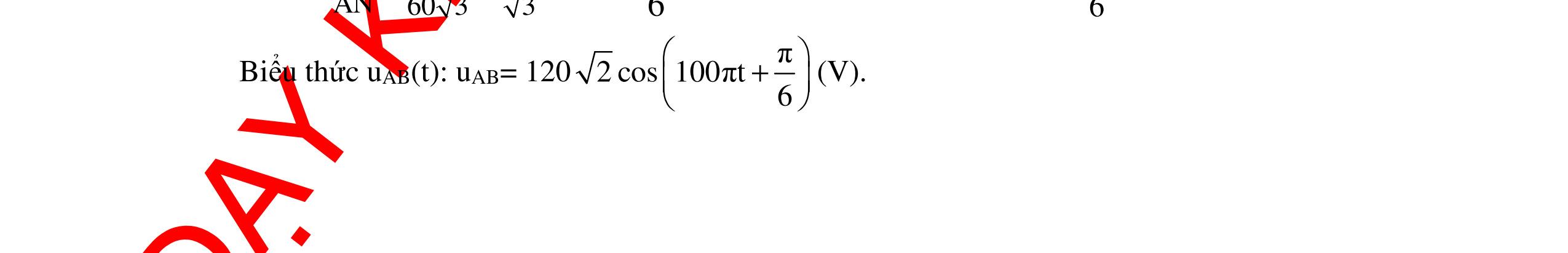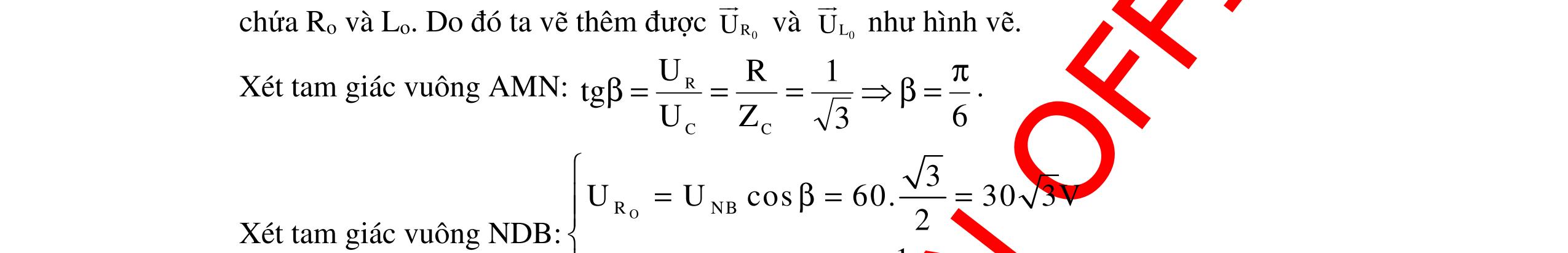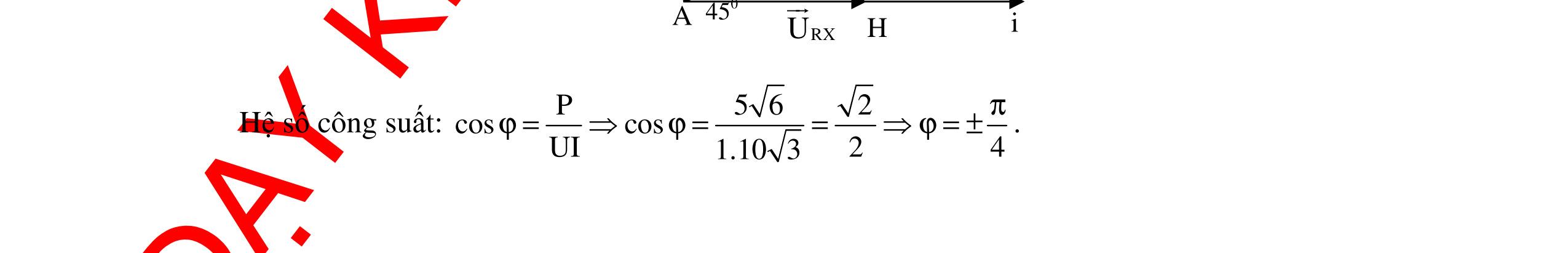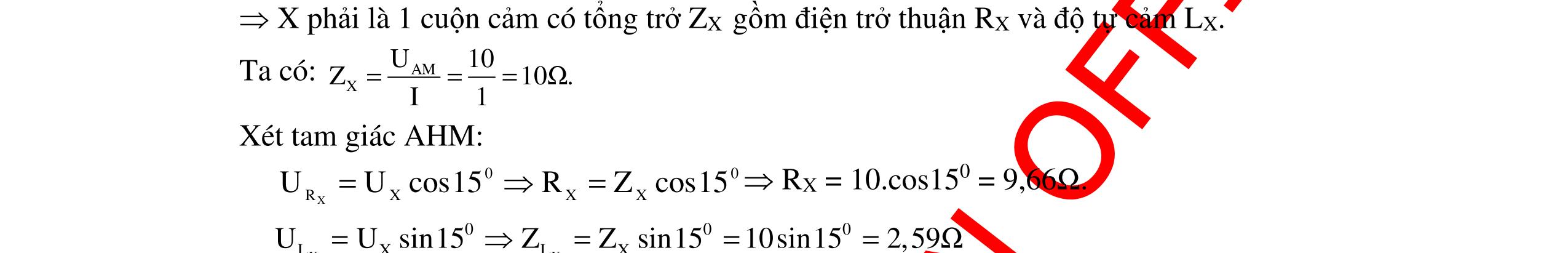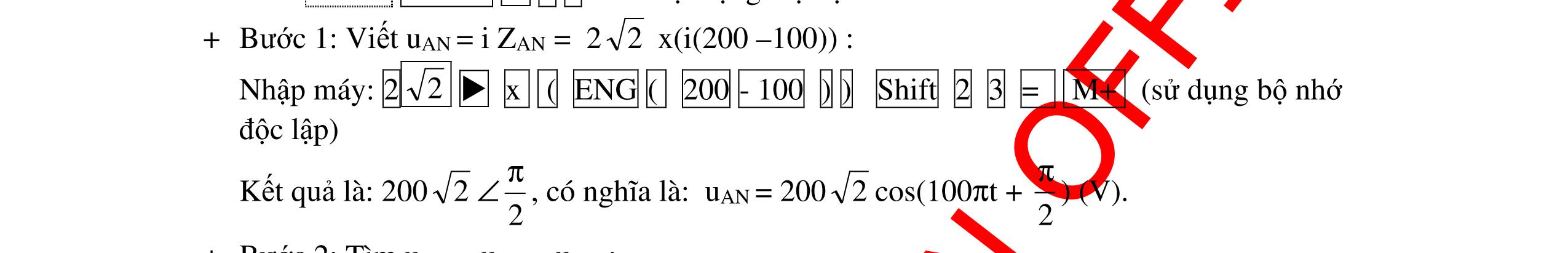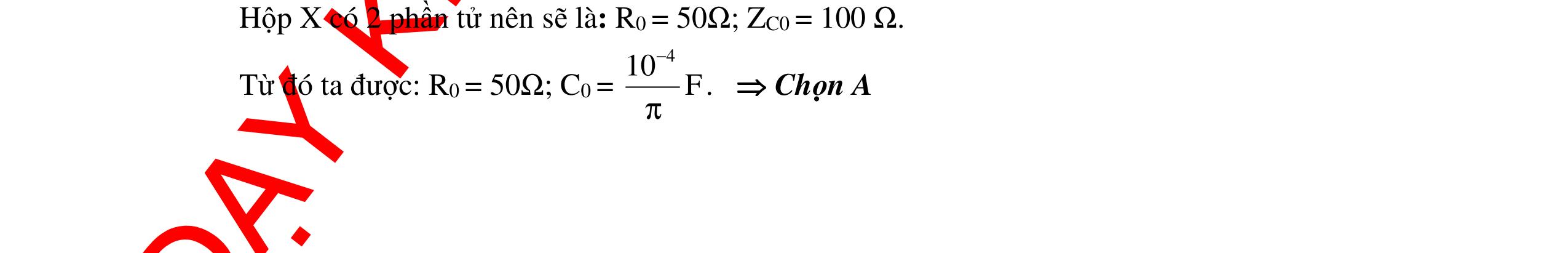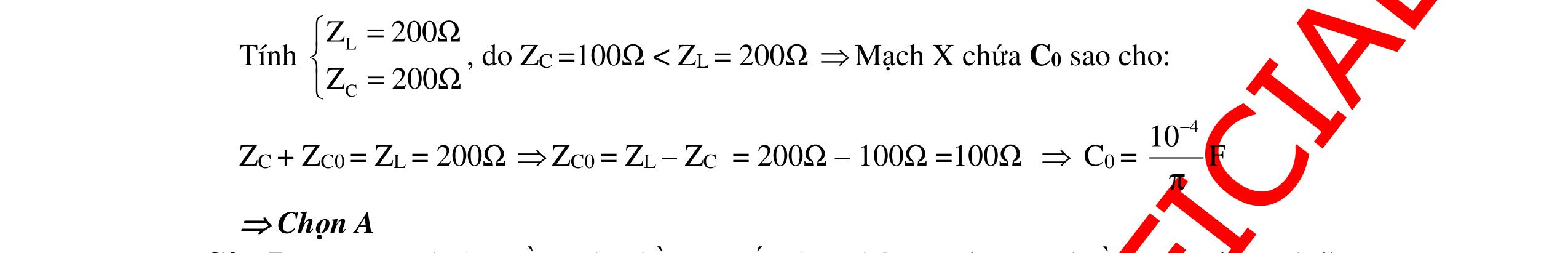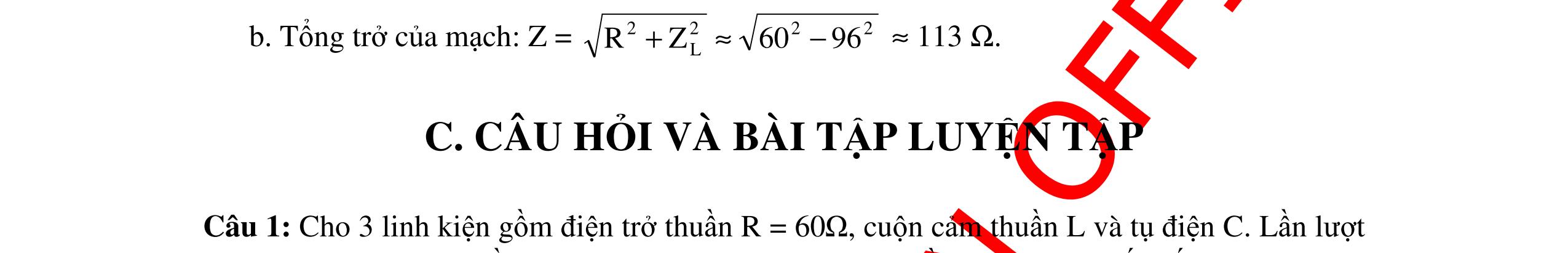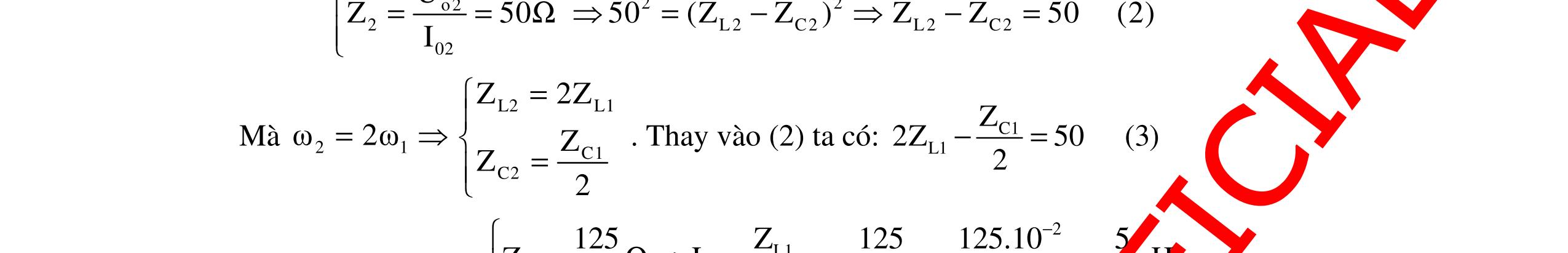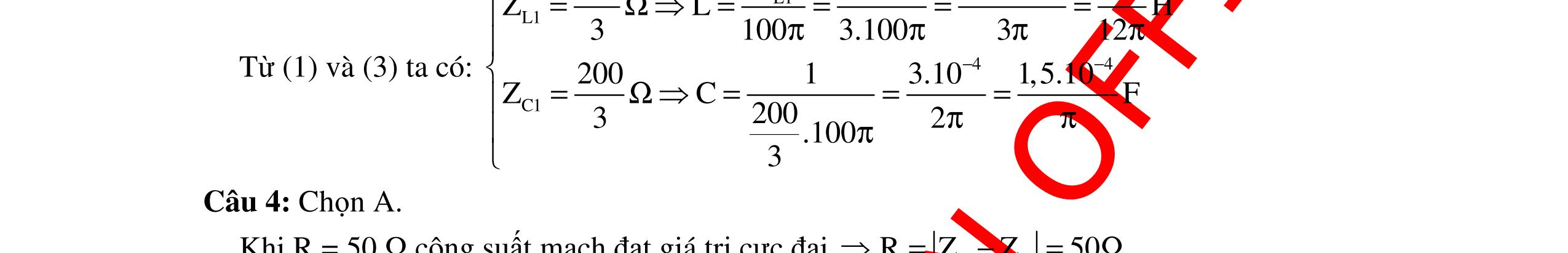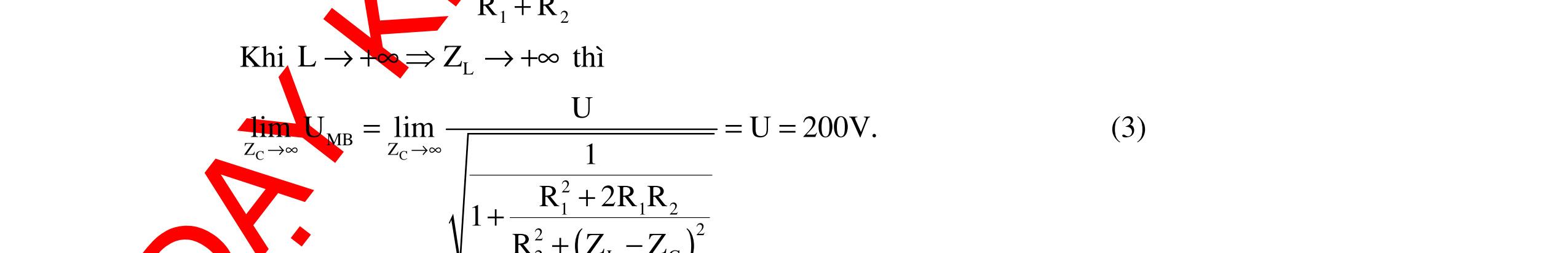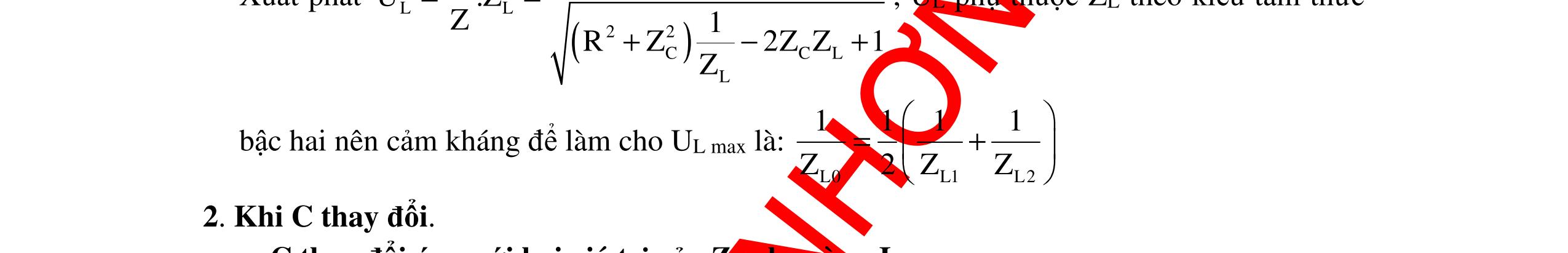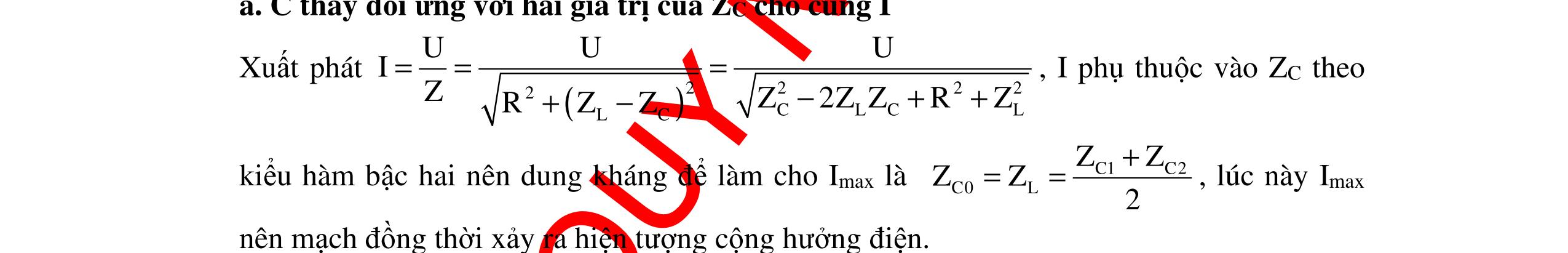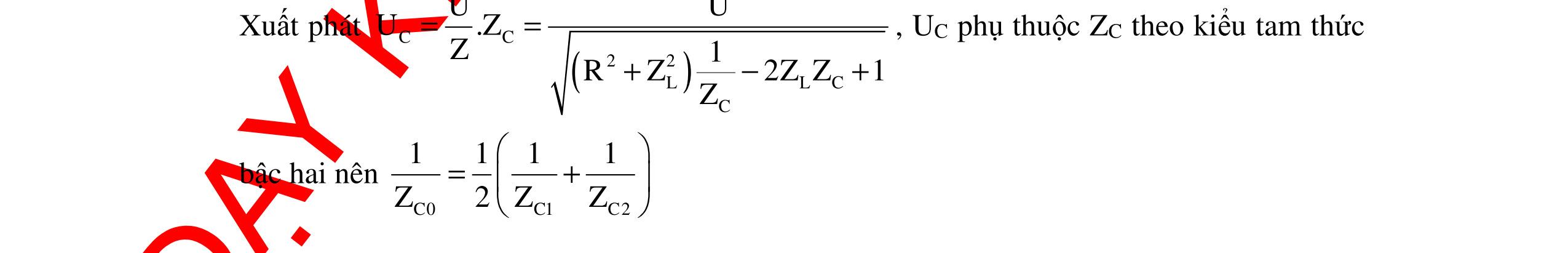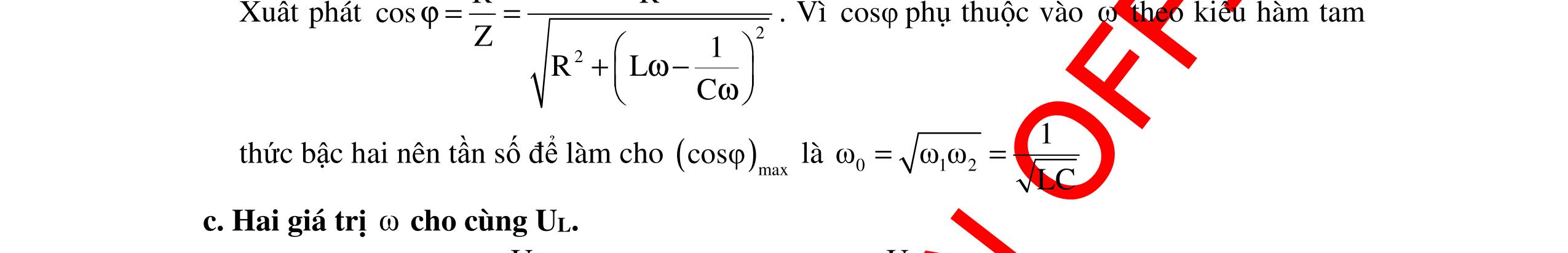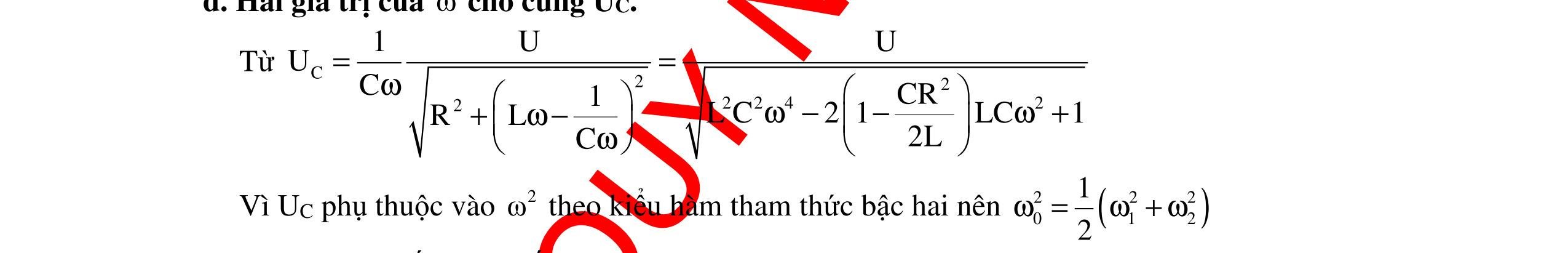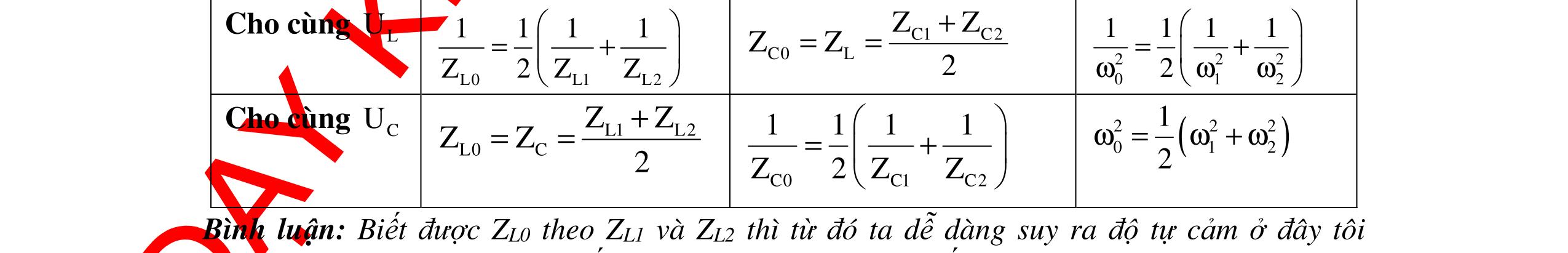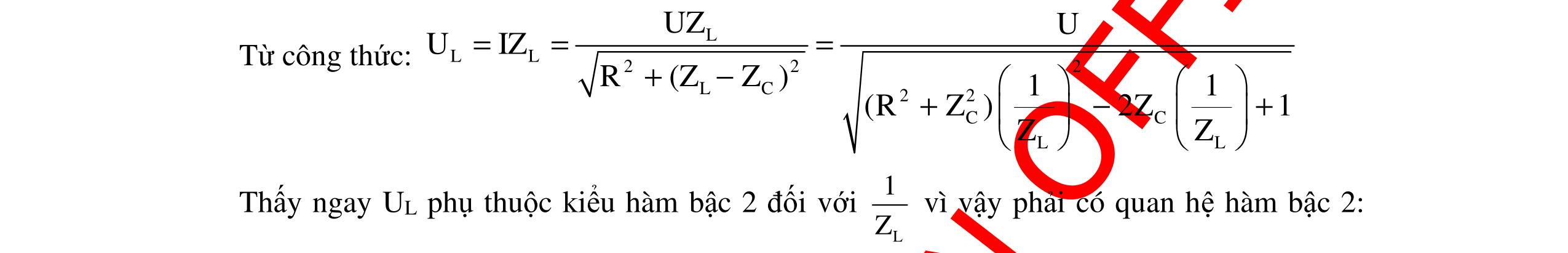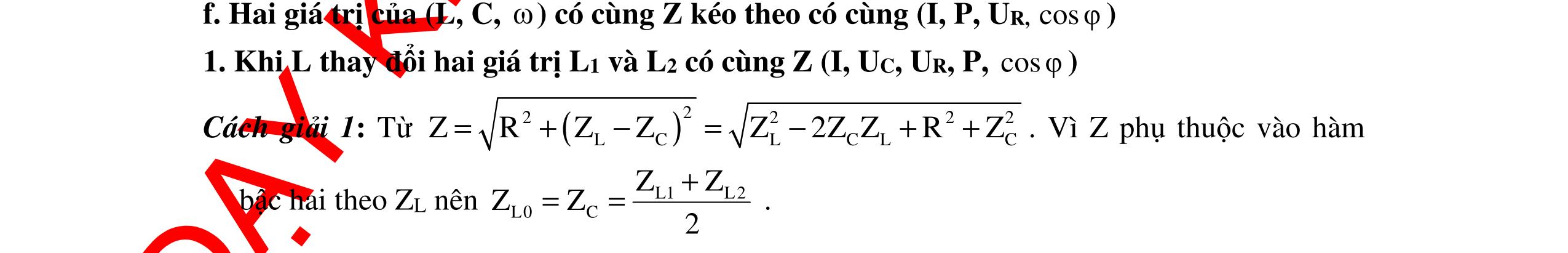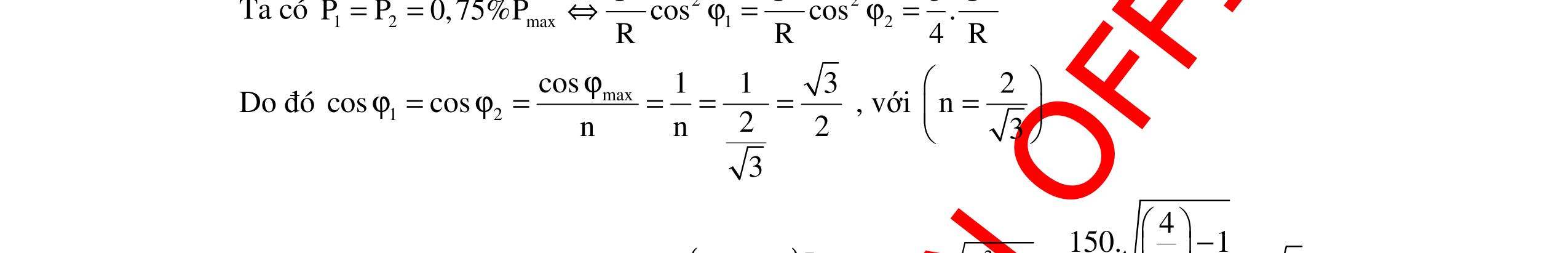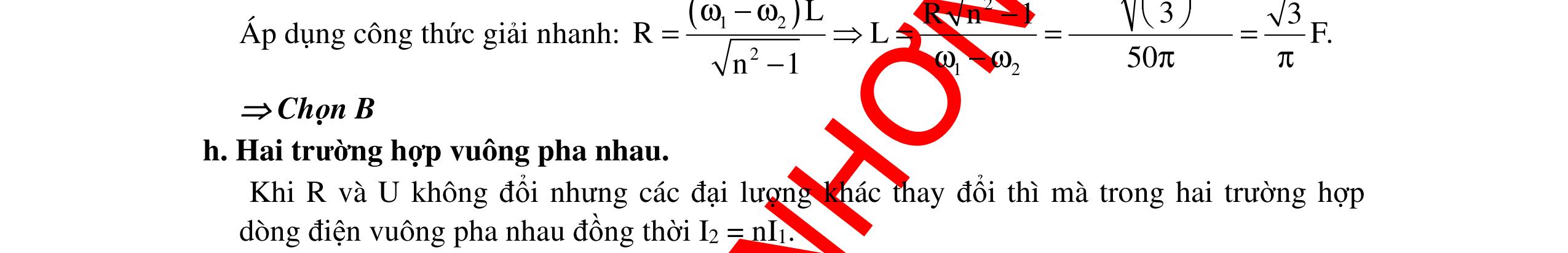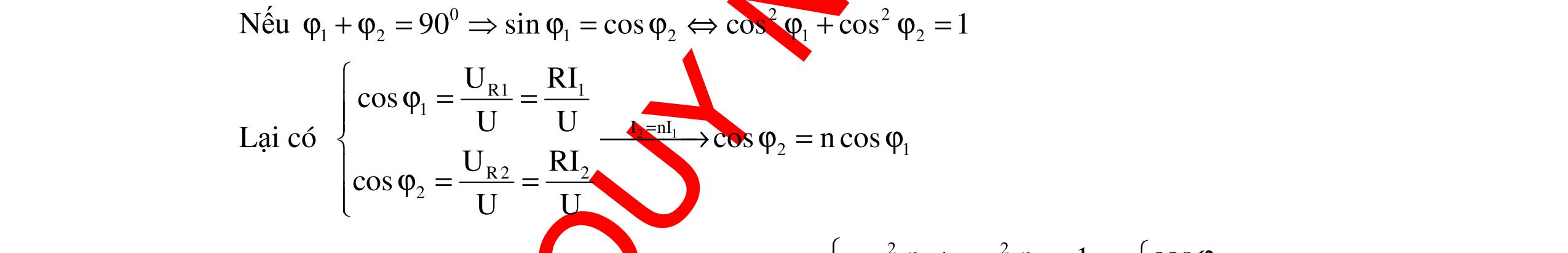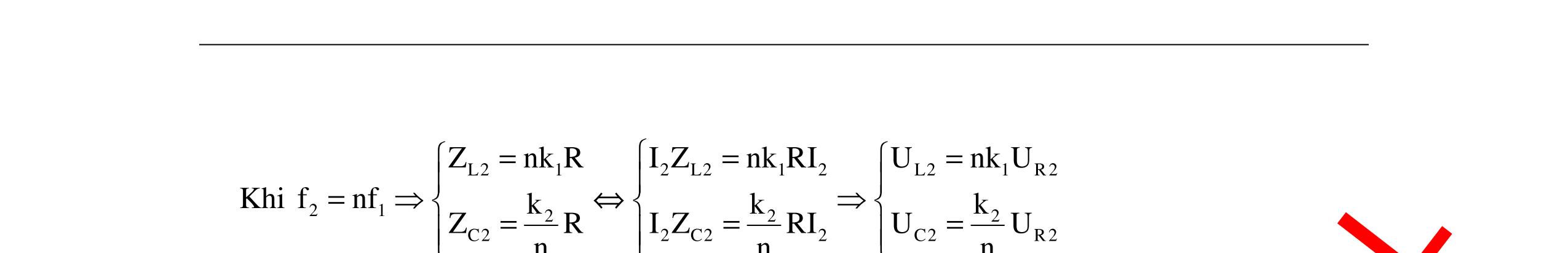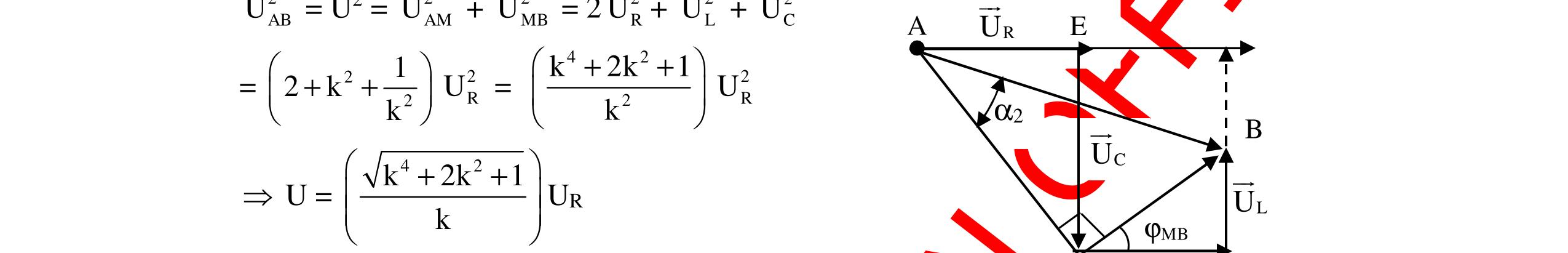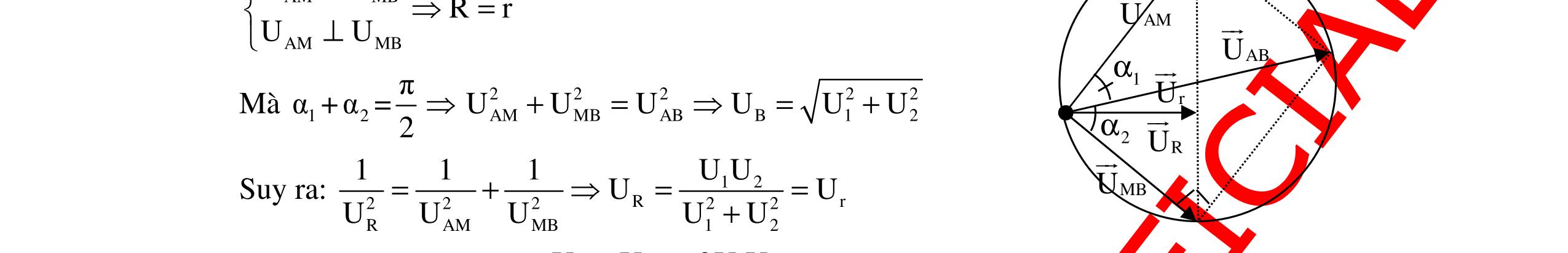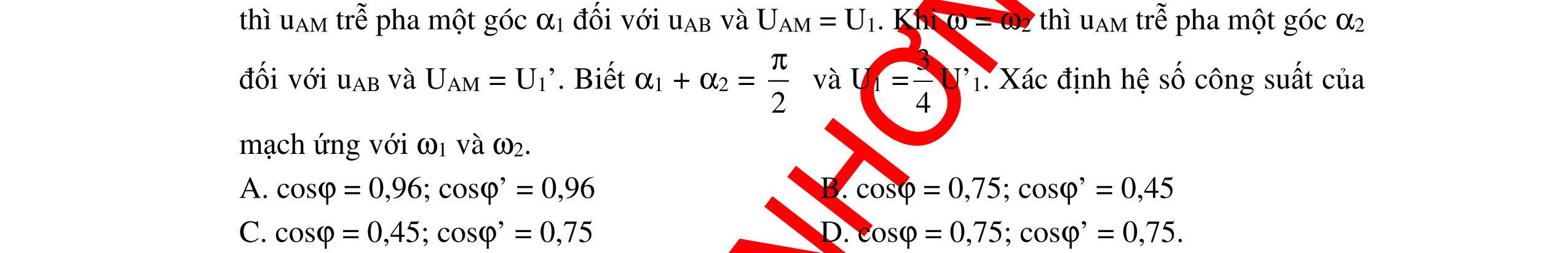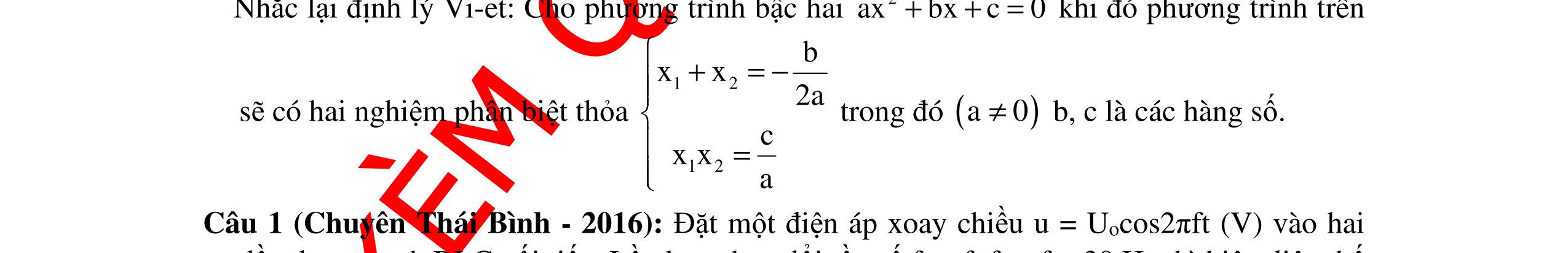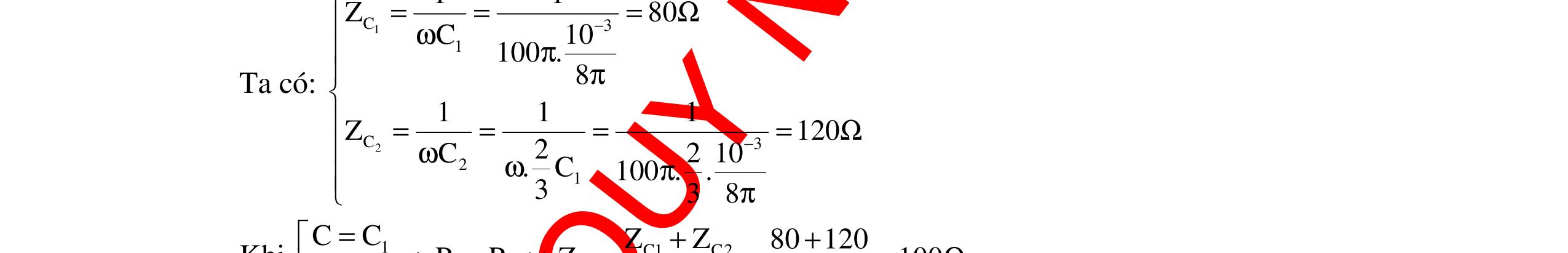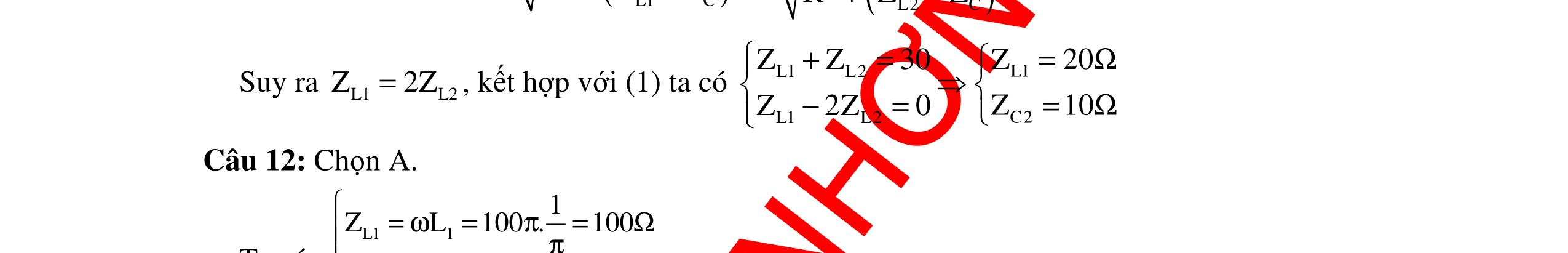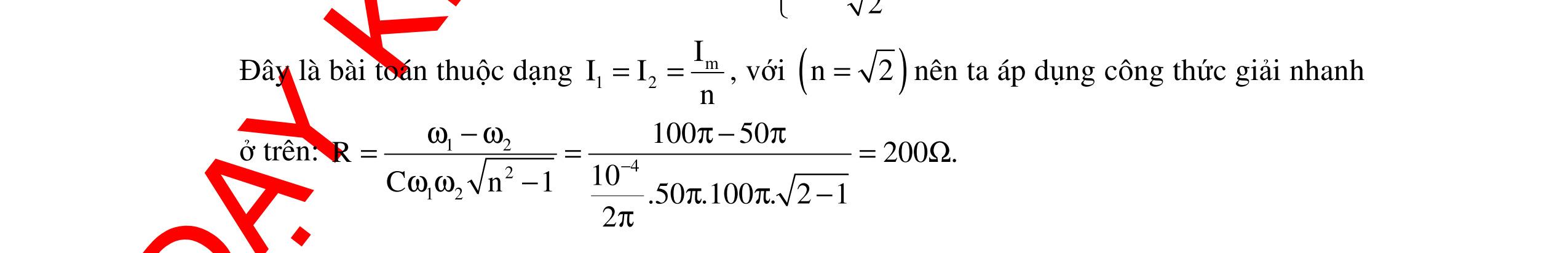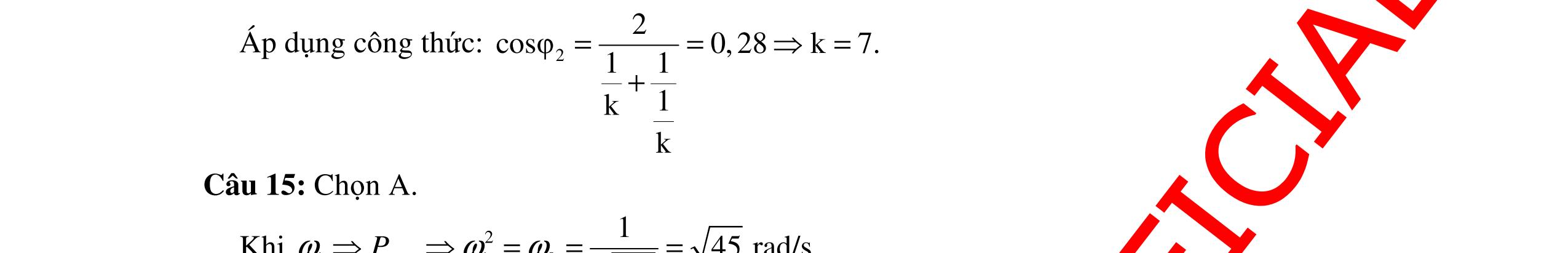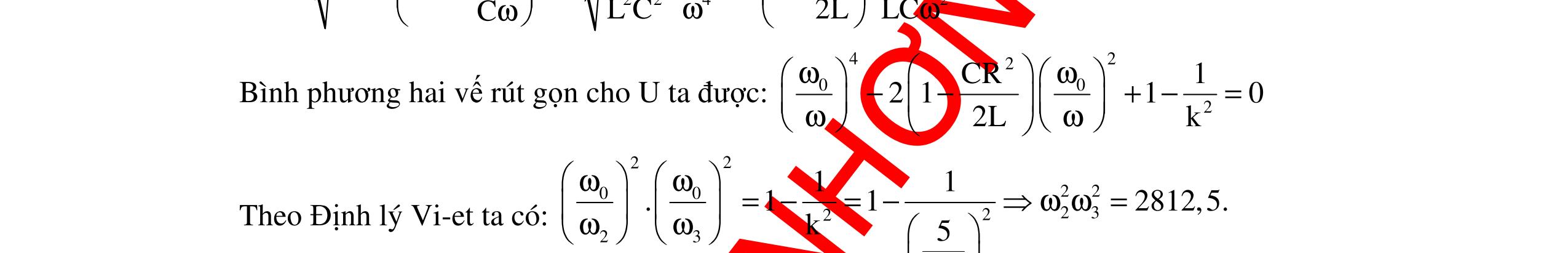CHUYÊN ĐỀ ĐIỆN XOAY CHIỀU VẬT LÝ 12 - GV NGUYỄN XUÂN TRỊ - CHỦ ĐỀ 01-13 by Dạy Kèm Quy Nhơn Official

CHUYÊN ĐỀ ĐIỆN XOAY CHIỀU VẬT LÝ 12 Ths Nguyễn Thanh Tú eBook Collection CHUYÊN ĐỀ ĐIỆN XOAY CHIỀU VẬT LÝ 12 - GV NGUYỄN XUÂN TRỊ - CHỦ ĐỀ 01-13 (KIẾN THỨC CƠ BẢN - CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI) WORD VERSION | 2022 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/10212086

DẠYKÈMQUYNHƠNOFFICIAL 3 Chương II: M MM MẠCH CHCH ðI ðIðI ðIỆN XOAY CHIỀU UU U CHỦ ĐỀ 1: ĐẠI CƯƠNG VỀ DÒNG ĐIỆN XOAY CHIỀU A. TÓM TẮT KIẾN THỨC CƠ BẢN I. Suất điện động xoay chiều: Cho khung dây dẫn phẳng có N vòng, diện tích S quay đều với vận tốc ω, xung quanh trục vuông góc với với các đường sức từ của một từ trường đều có cảm ứng từ B . Theo định luật cảm ứng điện từ, trong khung dây xuất hiện một suất điện động biến đổi theo định luật dạng cosin với thời gian gọi tắt là suất điện động xoay chiều: 00 eEcos(t) =ω+ϕ 1. Từ thông gởi qua khung dây: Từ thông gửi qua khung dây dẫn gồm N vòng dây có diện tích S quay trong từ trường đều B Giả sử tại t = 0 thì: =  Φ=ω+ϕ=Φ+ϕ 0 (n,B)fNBScos(t)cos(wt) (Wb) Từ thông gởi qua khung dây cực đại 0 NBSΦ= ; ω là tần số góc bằng tốc độ quay của khung (rad/s) Đơn vị: Φ : Vêbe(Wb); N: vòng; B: Tesla (T); S: 2 m . 2. Suất điện động xoay chiều tức thời: (t) d eNBSsin(t)NBScos(t) dt 2 Φ ′π =−=−Φ=ωω+ϕ=ωω+ϕ− e =E0cos(ωt + ϕ0). Đặt E0= NBωS : Suất điện động cực đại; 0 2 π ϕ=ϕ− Đơn vị :e, E0 (V) • Chu kì và tần số liên hệ bởi: 2 2f2n T π ω==π=π với n là số vòng quay trong 1s. • Suất điện động do các máy phát điện xoay chiều tạo ra cũng có biểu thức tương tự như trên. II. Điện áp xoay chiều -Dòng điện xoay chiều. 1. Biểu thức điện áp tức thời: Nếu nối hai đầu khung dây với mạch ngoài thành mạch kín thì biểu thức điện áp tức thời mạch ngoài là: u = e – ir. Xem khung dây có 2 r0 ≈ thì 00 ueEcos(t) ==ω+ϕ . Tổng quát : 0u uUcos(t) =ω+ϕ . 2. Khái niệm về dòng điện xoay chiều. Là dòng điện có cường độ biến thiên tuần hoàn với thời gian theo quy luật của hàm số sin hay cosin, với dạng tổng quát: i = I0cos(ωt + ϕi) * i: giá trị của cường độ dòng điện tại thời điểm t, được gọi là giá trị tức thời của i (cường độ tức thời). * I0 > 0: giá trị cực đại của i (cường độ cực đại). α n Bω

dòng

Các giá

* Lý do

chia cho

các giá tr

dòng

chi

u dụng của dòng điện xoay chiều.

- Khi sử dụng dòng điện xoay chiều, ta không cần quan tâm đến các giá trị tức thời của i và u vì chúng biến thiên rất nhanh, ta cần quan tâm tới tác dụng của nó trong một thời gian dài.

- Tác dụng nhiệt của dòng điện tỉ lệ với bình phương cường độ

DẠYKÈMQUYNHƠNOFFICIAL 4 * ω > 0: tần số góc. * f: tần số của i. T: chu kì của i. * (ωt + ϕ): pha của i. * ϕi: pha ban đầu. 3. Độ lệch pha giữa điện áp u và cường độ dòng điện i. Đại lượng : ϕ=ϕ−ϕ ui gọi là độ lệch pha của u so với i. Nếu ϕ > 0 thì u sớm pha (nhanh pha) so với i. Nếu ϕ < 0 thì u trễ pha (chậm pha) so với i. Nếu ϕ = 0 thì u đồng pha (cùng pha) so với i. 4. Giá trị hiệu dụng: Dòng điện xoay chiều cũng có tác dụng toả nhiệt như dòng điện một chiều. Xét về mặt toả nhiệt trong một thời gian dài thì dòng điện xoay chiều 0i iIcos(t) =ω+ϕ tương đương với dòng điện một chiều có cường độ không đổi có cường độ bằng 0I 2 "Cường độ hiệu dụng của dòng điện xoay chiều bằng cường độ của một dòng điện không đổi,nếu cho hai dòng điện đó lần lượt đi qua cùng một điện trở trong những khoảng thời gian bằng nhau đủ dài thì nhiệt lượng toả ra bằng nhau. Nó có giá trị bằng cường độ

điện cực đại

2 ".

trị hiệu dụng của

điện xoay

ều: 0I I 2 = , 0U U 2 = , 0E E 2 = .

sử dụng

ị hiệ

dòng điện nên không phụ thuộc vào chiều dòng điện. - Ampe kế đo cường độ dòng điện xoay chiều và vôn kế đo điện áp xoay chiều dựa vào tác dụng nhiệt của dòng điện nên gọi là ampe kế nhiệt và vôn kế nhiệt, số chỉ của chúng là cường độ hiệu dụng và điện áp hiệu dụng của dòng điện xoay chiều. 5. Nhiệt lượng toả ra trên điện trở R trong thời gian t nếu có dòng điện xoay chiều i(t) = I0cos(ω ωt + ϕi) chạy qua là: Q = RI2t. 6. Công suất toả nhiệt trên R khi có dòng điệnxoay chiều chạy qua: P = R I2 . B. DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI Dạng 1: Xác định suất điện động cảm ứng Phương pháp: Thông thường bài tập thuộc dạng này yêu cầu ta tính từ thông, suất điện động cảm ứng xuất hiện trong khung dây quay trong từ trường. Ta sử dụng các công thức sau để giải: - Tần số góc: ω=π 02n , Với n0 là số vòng quay trong mỗi giây bằng tần số dòng điện xoay chiều. - Biểu thức từ thông: φ=φω+ϕ 0cos(t) , Với φ0 = NBS. - Biểu thức suất điện động: =ω+ϕ 0 eEsin(t)

DẠYKÈMQUYNHƠNOFFICIAL 5 Với E0 = NBS ω; ϕ= (B,n) lúc t = 0. - Vẽ đồ thị: Đồ thị là đường hình sin: có chu kì : π = ω 2 T , có biên độ: 0E BÀI TẬP VẬN DỤNG Câu 1 (Quốc gia – 2017) Một máy phát điện xoay chiều ba pha đang hoạt động ổn định. Suất điện động trong ba cuộn dây của phần ứng có giá trị el, e2 và e3 Ở thời điểm mà e1 = 30 V thì│e2 - e3│= 30 V. Giá trị cực đại của e1 là: A. 51,9 V. B. 45,1 V. C. 40,2 V. D. 34,6 V. Hướng dẫn: Gia sử e1 = Ecosωt. Khi đó e2 = Ecos(ωt + 2 3 π ) = Ecosωt cos 2 3 π - Esinωt sin 2 3 π e2 = Ecos(ωt + 2 3 π ) =1 2 Ecosωt3 2 Esinωt e3 = Ecos(ωt2 3 π ) =1 2 Ecosωt + 3 2 Esinωt  │ e2 - e3│ = E 3 sinωt = 3 Esinωt = 3 22E30 = 30  E2 – 900 = 300  E2 = 1200  E = 34.6 (V)    Chọn D Câu 2 (ĐH 2008): Một khung dây dẫn hình chữ nhật có 100 vòng, diện tích mỗi vòng 600 cm2 , quay đều quanh trục đối xứng của khung với vận tốc góc 120 vòng/phút trong một từ trường đều có cảm ứng từ bằng 0,2T. Trục quay vuông góc với các đường cảm ứng từ Chọn gốc thời gian lúc vectơ pháp tuyến của mặt phẳng khung dây ngược hướng với vectơ cảm ứng từ. Biểu thức suất điện động cảm ứng trong khung là A. e48sin(40t)(V). 2 π =ππ− B. e4,8sin(4t)(V). =ππ+π C. e48sin(4t)(V). =ππ+π D. e4,8sin(40t)(V). 2 π =ππ− Hướng dẫn: Ta có: ( ) ( ) ( ) BScosteN'NBSsint4,8sin4tV.Φ=ω+π  −Φ=ωω+π=π+π  Chọn D Câu 3 (Bến Tre – 2015): Từ thông qua mỗi vòng dây dẫn của một máy phát điện xoay chiều một pha có biểu thức 2 2.105 cos100t(Wb) 3 π  ϕ=π+π  . Với stato có 4 cuộn dây nối tiếp, mỗi cuộn có 25 vòng, biểu thức của suất điện động xuất hiện trong máy phát là A. 5 e2sin100t(V). 3 π =−π+  B. e200sin100t)(V). 3 π  =π−  C. 5 e200sin100t(V). 3 π  =−π−  D. 5 e2sin100t(V). 3 π =π+  Hướng dẫn:

DẠYKÈMQUYNHƠNOFFICIAL 6 Ta có: ( ) ( )0 eNBSsintNsint =ωω+ϕ=ωΦω+ϕ () 2 2.1055 e100.4.25.sin100t2sin100tV. 33 ππ   =ππ+=π+π     Chọn D Câu 4: Một khung dây dẫn phẳng có diện tích S = 50 cm2, có N = 100 vòng dây, quay đều với tốc độ 50 vòng/giây quanh một trục vuông góc với các đường sức của một từ trường đều có cảm ứng từ B = 0,1 T. Chọn gốc thời gian t = 0 là lúc vectơ pháp tuyến n của diện tích S của khung dây cùng chiều với vectơ cảm ứng từ B và chiều dương là chiều quay của khung dây. a. Viết biểu thức xác định từ thông Φ qua khung dây. b. Viết biểu thức xác định suất điện động e xuất hiện trong khung dây. c. Vẽ đồ thị biểu diễn sự biến đổi của e theo thời gian. Hướng dẫn: a. Khung dây dẫn quay đều với tốc độ góc: ω = 50.2π = 100π rad/s. Tại thời điểm ban đầu t = 0, vectơ pháp tuyến n của diện tích S của khung dây có chiều trùng với chiều của vectơ cảm ứng từ B của từ trường. Đến thời điểm t, pháp tuyến n của khung dây đã quay được một góc bằng ωt . Lúc này từ thông qua khung dây là: NBScos(t)ϕ=ω Như vậy, từ thông qua khung dây biến thiên điều hoà theo thời gian với tần số góc ω và với giá trị cực đại (biên độ) là Ф0 = NBS. Thay N = 100, B = 0,1 T, S = 50 cm2 = 50. 10-4 m2 và ω = 100π rad/s ta được biểu thức của từ thông qua khung dây là : 0,05cos(100πt)ϕ= (Wb) b. Từ thông qua khung dây biến thiên điều hoà theo thời gian, theo định luật cảm ứng điện từ của Faraday thì trong khung dây xuất hiện một suất điện động cảm ứng. Suất điện động cảm ứng xuất hiện trong khung dây được xác định theo định luật Lentz: (t) d e'NBSsin(t)NBScost dt 2 ϕ π  =−=−ϕ=ωω=ωω−  Như vậy, suất điện động cảm ứng xuất hiện trong khung dây biến đổi điều hoà theo thời gian với tần số góc ω và với giá trị cực đại (biên độ) là E0 = ωNBS. Thay N = 100, B = 0,1 T, S = 50 cm2 = 50. 10-4 m2 và ω = 100π rad/s ta được biểu thức xác định suất điện động xuất hiện trong khung dây là: e5cos100t 2 π  =ππ−  (V) hay e15,7cos314t 2    π ≈− (V) c. t (s) e (V) 0 + 15,715,7 0,005 0,015 0,0250,01 0,02 0,03

DẠYKÈMQUYNHƠNOFFICIAL 7 Suất điện động xuất hiện trong khung dây biến đổi điều hoà theo thời gian với chu khì T và tần số f lần lượt là: 22 T0,02 100 ππ === ωπ s; 11 f50 T0,02 === Hz Đồ thị biểu diễn sự biến đổi của suất điện động e theo thời gian t là đường hình sin có chu kì tuần hoàn T = 0,02 s. Bảng giá trị của suất điện động e tại một số thời điểm đặc biệt như: 0 s, T 0,005 4 = s, T 0,01 2 = s, 3T 0,015 4 = s, T0,02 = s, 5T 0,025 4 = s và 3T 0,03 2 = s : t (s) 0 0,005 0,01 0,015 0,02 0,025 0,03 e (V) 0 15,7 0 -15,7 0 15,7 0 Đồ thị biểu diễn sự phụ thuộc của e theo t như hình trên hình vẽ. Câu 5: Dòng điện xoay chiều chạy qua một đoạn mạch có cường độ biến đổi điều hoà theo thời gian được mô tả bằng đồ thị ở hình dưới đây. a. Xác định biên độ, chu kì và tần số của dòng điện. b. Đồ thị cắt trục tung (trục Oi) tại điểm có toạ độ bao nhiêu ? Hướng dẫn: a. Biên độ chính là giá trị cực đại I0 của cường độ dòng điện. Dựa vào đồ thị ta có biên độ của dòng điện này là: I0 = 4 A. Tại thời điểm 2,5.10-2 s, dòng điện có cường độ tức thời bằng 4A. Thời điểm kế tiếp mà dòng điện có cường độ tức thời bằng 4 A là 2,25.10-2 s. Do đó chu kì của dòng điện này là: T = 2,25.10-2 – 0,25.10-2 = 2.10-2 s, tần số của dòng điện này là: 2 11 f50 T2.10 === Hz. b. Biểu thức cường độ dòng điện xoay chiều: 0i iIcos(t) =ω+ϕ Tần số góc của dòng điện này là : ω 2f2.50100 =π=π=π rad/s. Tại thời điểm t = 0,25.10-2 s, dòng điện có cường độ tức thời i = I0 = 4 A, nên suy ra 0i0 Icos(100.0)I π+ϕ= hay i cos1 4 π  +ϕ=  Suy ra : π ϕ=− i 4 rad . Do đó biểu thức cường độ của dòng điện này là : 0 iIcos100πt(A)4cos100t(A) 44 ππ  =−=π−   t(10-2 s) i (A) 0 +4 4 0,250,75 1,25 1,752,252,75 3,25

c độ góc ω .

+ Có 2 điểm M ,N chuyển động tròn đều có hình chiếu lên Ou là u, nhưng N có hình chiếu lên Ou có u đang tăng (vận tốc là dương),còn M có hình chiếu lên Ou có u đang giảm (vận tốc là âm).

+ Ta xác định xem vào thời điểm ta xét điện áp u có giá trị u và đang biến đổi thế nào (ví

DẠYKÈMQUYNHƠNOFFICIAL 8 Tại thời điểm t = 0 thì dòng điện có cường độ tức thời là : 0 0 Iπ 4 iIcos100.0(A)22 4 22  =π−===   A 2,83≈ A. Vậy đồ thị cắt trục tung tại điểm có toạ độ (0 s, 22 A). Dạng 2: Giải toán điện xoay chiều bằng cách sử dụng mối liên hệ giữa chuyển động tròn đều và dao động điều hòa. 1. Ta dùng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều để tính. Theo lượng giác: 0 u=Ucos(ωt+ φ) được biểu diễn bằngvòngtròntâm Obán kínhU0,quayvớitố

dụ chiều âm)  ta chọn M rồi tính góc MOA φ= ; còn nếu theo chiều dương ta chọn N và tính NOA φ=− theo lượng giác. 2. Dòng điện xoay chiều i = I0cos(2π ππ πft + ϕ ϕi) * Mỗi giây đổi chiều 2f lần * Nếu cho dòng điện qua bộ phận làm rung dây trong hiện tượng sóng dừng thì dây rung với tần số 2f. BÀI TẬP VẬN DỤNG Câu 1: Biểu thức cường độ dòng điện xoay chiều chạy qua một đoạn mạch là 0 iIcos(100t)(A) =π , với 0 I0 > và t tính bằng giây (s). Tính từ lúc 0 s, xác định thời điểm đầu tiên mà dòng điện có cường độ tức thời bằng cường độ hiệu dụng? Hướng dẫn: Biểu thức cường độ dòng điện 0 iIcos(100t)(A) =π có dạng dao động điều hoà. Do đó, tính từ lúc 0 s, tìm thời điểm đầu tiên để dòng điện có cường độ tức thời bằng i, u t i (t) u (t) 0 -U0 O u U0 u M N ϕ O i + α I0A 2 P Q(C) D

DẠYKÈMQUYNHƠNOFFICIAL 9 cường độ hiệu dụng 0I iI 2 == cũng giống như tính thời gian t tính từ lúc 0 s. Vì pha ban đầu của dao động bằng 0, nghĩa là lúc 0 s thì I đang có giá trị i = I0, nên thời điểm cần tìm chính bằng thời gian ngắn nhất để I biến thiên từ điểm mà i = I0 đến vị trí có 0I iI 2 == . Ta sử dụng tính chất hình chiếu của một chất điểm chuyển động tròn đều lên một đường thẳng nằm trong mặt phẳng quỹ đạo là một dao động điều hoà với cùng chu kì để giải bài toán này. Thời gian ngắn nhất để i = I0 đến vị trí có 0I iI 2 == (từ P đến D) chính bằng thời gian vật chuyển động tròn đều với cùng chu kì đi từ P đến Q theo cung tròn PQ. Tam giác ODQ vuông tại D và có OQ = A, A OD 2 = nên ta có: OD2 cos OQ2 α== . Suy ra: π α= 4 rad. Thời gian chất điểm chuyển động tròn đều đi từ P đến Q theo cung tròn PQ là : 14t 4ω π α === ωω . Trong biểu thức của dòng điện, thì tần số góc ω = 100π rad/s nên ta suy ra tính từ lúc 0 s thì thời điểm đầu tiên mà dòng điện có cường độ tức thời bằng cường độ hiệu dụng là: π 1 t 44.100π 400 π === ω s. Câu 2: Biểu thức cường độ dòng điện xoay chiều chạy qua một đoạn mạch là 0 πiIcos(100πt)(A) 6 =− , với 0I 0> và t tính bằng giây (s). Tính từ lúc 0 s, xác định thời điểm đầu tiên mà dòng điện có cường độ tức thời bằng cường độ hiệu dụng ? Hướng dẫn: Cách giải 1: Ta sử dụng tính chất hình chiếu của một chất điểm chuyển động tròn đều lên một đường thẳng nằm trong mặt phẳng quỹ đạo là một dao động điều hoà với cùng chu kì để giải bài toán này. Thời gian ngắn nhất để 0 I3 i 2 = đến i = I0 ( cung MoQ) rồi từ i = I0 đến vị trí có 0I iI 2 == (từ P đến D) bằng thời gian vật chuyển động tròn đều với cùng chu kì đi từ Mo đến P rồi từ P đến Q theo cung tròn 0 MPQ . Ta có góc quay ππ 5π α 6412 =+= . Mo O i + α I00 2 I P Q(C) D

DẠYKÈMQUYNHƠNOFFICIAL 10 Tần số góc của dòng điện ω = 100π rad/s. Suy ra chu kỳ T = 0,02 s. Thời gian quay: TT1 ts 128240 =+= hay 5π 5π 1 ts 12ω 12.100π 240 === . Cách giải 2: Dùng sơ đồ thời gian: Thời gian ngắn nhất để 0 I3 i 2 = đến i = I0 là: 1 T t 12 = . Thời gian ngắn nhất để i = I0 đến 0I iI 2 == là: 2 T t 8 = Vậy 12 TT1 ttts 128240 =+=+= . Câu 3: Đặtvàohai đầumột đoạnmạchRLCmột điệnápxoaychiềucóphươngtrình: u2002cos(100πt)= (V). Tính thời gian từ thời điểm u = 0 đến khi u1102(V) = . Hướng dẫn: Cách giải 1: Chọn lại gốc thời gian: t = 0 lúc u = 0 và đang tăng, ta có phương trình mới: πu2002cos(100πt) 2 =− (V) và u/  0 . Khi u =110 2 V lần đầu ta có: 1 cos100πt 2 = và πsin(100πt)0 2 −< . Giải hệ phương trình ta được 1 ts 600 = . Cách giải 2: Dùng giản đồ véctơ Thời gian từ thời điểm u = 0 đến khi u = 1102 ( V) lần đầu tiên: π α 16 ts ω 100π 600 ∆=== hay: α 30π 1 ts ω 180.100π 600 ∆=== Câu 4: Cho dòng điện xoay chiều ( )i4cos20t (A)=π . Ở thời điểm t1: dòng điện có cường độ i = i1 = -2A và đang giảm, hỏi ở thời điểm t2 = t1 + 0,025s thì i = i2 = ? Hướng dẫn: Cách giải 1: Tính ∆ϕ = ω ∆t = 20π.0,025 = 2 π (rad)  i2 vuông pha i1 22222 1222 ii4 2i16 i23(A) +=  +=  =± . Vì i1 đang giảm nên chọn i2 = - 2 3(A). iI0O I0/2 0 I3 2 0I 2 - I0 T/8 T/12 M uu N α = π/6 1102 0

DẠYKÈMQUYNHƠNOFFICIAL 11 Cách giải 2: Bấm máy tính Fx 570ES với chú ý: 4SHIFTMODE : đơn vị góc là Rad. Bấm nhập máy tính: 2 4 cosshift cos23 42  −π +=−    2 i23(A) =− . Chú ý: Xác định cường độ dòng điện tức thời: Ở thời điểm t1 cho i = i1, hỏi ở thời điểm t2 = t1 + ∆t thì i = i2 = ? (Hoặc Ở thời điểm t1 cho u = u1, hỏi ở thời điểm t2 = t1 + ∆t thì u = u2 = ?) Phương pháp giải nhanh: Về cơ bản giống cách giải nhanh của dao động điều hòa. * Tính độ lệch pha giữa i1 và i2 : ∆ϕ= ω∆ t hoặc: Tính độ lệch pha giữa u1 và u2 : ∆ϕ= ω∆ t * Xét độ lệch pha: + Nếu (đặc biệt) i2 và i1 cùng pha  i2 = i1 i2 và i1 ngược pha  i2 = - i1 i2 và i1 vuông pha  222 120 iiI += + Nếu ∆ϕbất kỳ: dùng máy tính : 1 20 0 i iI cosshift cos I   =±+∆ϕ     * Quy ước dấu trước shift: dấu (+) nếu i1 dấu ( – ) nếu i1 ↑ Nếu đề không nói đang tăng hay đang giảm, ta lấy dấu (+) Câu 5: Tại thời điểm t, điện áp điện áp u2002cos100t(V) 2 π  =π−  có giá trị 1002 (V) và đang giảm. Sau thời điểm đó 1 300 s , điện áp này có giá trị là bao nhiêu? Hướng dẫn: Cách giải 1: ∆ϕ = ω∆t = 100π. 1 300 = 3 π rad. Vậy độ lệch pha giữa u1 và u2 là 3 π . Vẽ vòng tròn lượng giác sẽ thấy: Với u1 =1002 V thì u2 = -1002 V Cách giải 2: Bấm máy tính Fx 570ES với chú ý: 4SHIFTMODE : đơn vị góc là Rad: Bấm nhập máy tính: 1002 2002 cosshift cos141(V)1002(V) 32002   π +≈−≈−      Câu 6: Điện áp ở hai đầu một đoạn mạch là u = 160cos100πt (V) (t tính bằng giây). Tại thời điểm t1, điện áp ở hai đầu đoạn mạch có giá trị là 80V và đang giảm. Đến thời điểm t2 = t1 + 0,015s, điện áp ở hai đầu đoạn mạch có giá trị bằng A. 403V B. 803 V C. 40V D. 80V π/3 10021002

DẠYKÈMQUYNHƠNOFFICIAL 12 Hướng dẫn: Cách giải 1: Ta có: cos100πt1 = 1 0 u U = 1 2 = cos(± π 3 ); u đang giảm nên 100πt1 = π 3  t1 = 1 300 s Tại thời điểm t2 = t1+ 0,015 s = 5,5 300 s  u2 = 160cos100πt2 = 160cos 5,5 3 π = 3 160 2 =803 (V).    Chọn B Cách giải 2: Ta có: t2 = t1 + 0,015s = t1+ 3T 4 . Với 3T 4 ứng góc quay 3π 2 . Nhìn hình vẽ thời gian quay 3T 4 (ứng góc quay 3π 2 ). M2 chiếu xuống trục u => u = 803 V. T0,02s0,015s23T 1004 π ==  = π 2 3 u160cos160.803V. 62 π ===  Chọn B Cách giải 3: ∆ϕ = ω∆t = 100π.0,015 = 1,5π (rad). Độ lệch pha giữa u1 và u2 là 3π 2 Bấm máy tính Fx 570ES với chú ý: 4SHIFTMODE : đơn vị góc là Rad. Bấm nhập máy tính: 803 160shiftcos803V. 1602 π  +=  Chọn B Dạng 3: Điện lượng qua tiết diện dây dẫn Điện lượng qua tiết diện S trong thời gian t là q với: q = it. Điện lượng qua tiết diện S trong thời gian từ t1 đến t2 là Δq: Δq = iΔt  2 1 t t qidt =  Chú ý: Bấm máy tính phải để ở chế độ rad. BÀI TẬP VẬN DỤNG u(V) 2t 3 2 π160 M2 O + π/3 80 803 16 0 M1 3π/2 t1

DẠYKÈMQUYNHƠNOFFICIAL 13 Câu 1: Cho đoạn mạch RLC mắc nối tiếp. Dòng điện xoay chiều hình sin chạy qua một đoạn mạch có biểu thức có biểu thức 0 πiIcos100πt 6 =+  A. Tính từ thời điểm dòng điện qua mạch triệt tiêu, sau khoảng 1 4 chu kì thì điện lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch là A. 0 B. 0I C 100π C. 0I C 25π D. 0I C 50π Hướng dẫn: Gọi t1 là thời điểm dòng điện qua mạch triệt tiêu, ta có: 0111 πππ 1 0Icos100πt100πtts. 662300 =+  +=  =  Thời điểm t2 sau t1: 21 T12π 1 tts. 43004.100π 120 =+=+= Điện lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch từ thời điểm t1 đến t2 là: 2 1 1 1 t 300 120 0 0 t11 300300 I ππqidtIcos100πtdtsin100πt 6100π 6  ∆==+=+   0I 1 π 1 πsin100π.sin100π. 100π 12063006  =+−+  00 II πsin π sinC. 100π 1100π  =−=−   Chọn B Câu 2: Cho dòng điện xoay chiều πi πcos100πt 2  =−  (A) chạy qua bình điện phân chứa dung dịch H2SO4 với các điện cực bằng bạch kim. Tính điện lượng qua bình theo một chiều trong thời gian 16 phút 5 giây? Hướng dẫn: Cách giải 1: Chu kì của dòng điện T = π ω 2 = π π 2 100 = 50 1 s = 0,02s. Khi t = 0 thì i = 0. Khi t = 4 1 T thì i = πcos(100π 4 02,0 –π 2 ) = π = I0 Trong khoảng thời gian T 4 điện lượng chuyển qua mạch ∆q = Q0 = ω 0I = π 0I 100 C = 10-2C. Điện lượng chuyển qua bình theo một chiều trong một chu kỳ là: q1 = 2∆q = 2.10-2C Số chu kỳ trong t = 16 phút 5s = 965s là N = t T = 02,0 965 = 48250. Điện lượng qua bình theo một chiều trong thời gian 16 phút 5 giây là: Q = Nq1 = 965 C.

DẠYKÈMQUYNHƠNOFFICIAL 14 Cách giải 2: Áp dụng công thức tt t 00 0 qidtcos100tdtcos100td100t 210022 ππππ  ∆==ππ−=π−π−  π  Điện lượng chuyển qua một tiết diện thẳng của đoạn mạch trong thời gian t = T 4 là: ∆q = 0.005 2 0 11 sin100t10C. 1002100 π  −π−==   Điện lượng chuyển qua bình theo một chiều trong một chu kỳ là: q1 = 2∆q = 2.10-2C Số chu kỳ trong t = 16 phút 5s = 965s là N = t T = 02,0 965 = 48250. Điện lượng qua bình theo một chiều trong thời gian 16 phút 5 giây là: Q = Nq1 = 965 C. C. CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Một khung dây dẫn quay đều quanh trục quay xx’ với vận tốc 150 vòng/phút trong một từ trường có cảm ứng từ B vuôn góc với trục quay của khung. Từ thông cực đại gởi qua khung là 10 Wb π . Suất điện động hiệu dụng trong khung có giá trị A. 25V B. 252 V C. 50V D. 502 V Câu 2: Từ thông qua một vòng dây dẫn là 22.10 cos100tWb 4 π Φ=π+π  . Biểu thức suất điện động cảm ứng xuất hiện trong cuộn dây là: A. e2sin100t(V) 4 π  =−π+  B. e2sin100t (V)=π C. e2sin100t (V)=−π D. e2sin100t(V) 4 π  =π+  Câu 3: Tại thời điểm t, điện áp πu2002cos(100πt) 2 =− (trong đó u tính bằng V, t tính bằng s) có giá trị 1002V và đang giảm. Sau thời điểm đó 1 s 300 , điện áp này có giá trị là A. 100V. B. 1003V. C. 1002V. D. 200 V. Câu 4: Vào cùng một thời điểm nào đó, hai dòng điện xoay chiều 101 iIcos(t) =ω+ϕ và i2 = Iocos(ωt + ϕ2) đều cùng có giá trị tức thời là 0,5Io, nhưng một dòng điện đang giảm, còn một dòng điện đang tăng. Hai dòng điện này lệch pha nhau một góc bằng. A. 5π 6 B. 2π 3 C. π 6 D. 4π 3

DẠYKÈMQUYNHƠNOFFICIAL 15 Câu 5: Dòng điện xoay chiều hình sin chạy qua một đoạn mạch có biểu thức có biểu thức cường độ là 0 πiIcos ωt 2  =−  , với I0 > 0. Tính từ lúc t0 (s)= , điện lượng chuyển qua tiết diện thẳng của dây dẫn của đoạn mạch đó trong thời gian bằng nửa chu kì của dòng điện là A.0 B. 02I ω C. 0π 2I ω D. 0πI ω 2 Câu 6: Dòng điện xoay chiều có biểu thức i = 2sin100πt (A) chạy qua một dây dẫn. Điện lượng chạy qua một tiết diện dây trong khoảng thời gian từ 0 đến 0,15s là : A. 0 B. 4 100π C C. 3 100π C D. 6 100π C Câu 7: Dòng điện xoay chiều có biểu thức i2cos100πt (A)= chạy qua dây dẫn. Điện lượng chạy qua một tiết điện dây trong khoảng thời gian từ 0 đến 0,15s là : A. 0 B. 4 100π C C. 3 100π C D. 6 100π C HƯỚNG DẪN GIẢI Câu 1: Chọn A. Khung quay với vận tốc 150 vòng/phút = 2,5 vòng/giây suy ra f = 2,5 Hz. Tần số góc: 2f2.2,55π rad/s.ω=π=π= Biểu thức suất điện động cảm ứng do máy phát tạo ra: ( )eNBScost =ωω+ϕ Suất điện động cực đại: 00 10 ENBS.550V. =ω=φω=π= π Suất điện động hiệu dụng trong khung: 0E 50 E252V. 22 === Câu 2: Chọn D. Ta có: ' 2 ' (t) 2.10 ecos100t2sin100tV. 44 ππ =−Φ=−π+=π+  π  Câu 3: Chọn C. Dùng mối liên quan giữa dao động điều hòa và chuyển động tròn đều, khi t = 0 , u ứng với chuyển động tròn đều ở C. Vào thời điểm t , u = 1002V và đang giảm nên ứng với chuyển động tròn đều tại M với MOB Δφ= . Ta có : u1002 Δφ U 2002 == Suy ra 0 0 Δφ 0,021 t60s ω 360300 === . Vì vậy thêm 1 s 300 u ứng với chuyển động tròn đều ở B với MOB= 600 C’ M ϕ 0,5I0 I0 cos O B C M’

DẠYKÈMQUYNHƠNOFFICIAL 16 Suy ra lúc đó u = 1002V. Câu 4: Chọn B. Dùng mối liên quan giữa dao động điều hòa và chuyển động tròn đều: Đối với dòng i1 khi có giá trị tức thời 0,5I0 và đăng tăng ứng với chuyển động tròn đều ở M’, còn đối với dòng i2 khi có giá trị tức thời 0,5I0 và đăng giảm ứng với chuyển động tròn đều ở. Bằng công thức lượng giác, ta có : π φ MOBM'OB 3 ===  2πMOM' 3 =  suy ra 2 cường độ dòng điện tức thời i1 và i2 lệch pha nhau 2π 3 Câu 5: Chọn B. Ta có : π0,5T ω =  dqi dt =  π ω 0 0 πqidtIcos(ωt) 2 ==−   π ω 0 0 0 πIsin(ωt) 2I2q ωω == . Câu 6: Chọn B. Ta có: dqi dt =  0,15 0 qidt2sin100πt==  0,15 0 2cos100πt4 q 100π 100π =−= C. Câu 7: Chọn A. Ta có: dqi dt =  0,15 0 qidt2cos100πt==  0,15 0 2sin100πt q0 100π == . CHỦ ĐỀ 2 VIẾT BIỂU THỨC CỦA u HOẶC i A. TÓM TẮT LÝ THUYẾT CƠ BẢN B C’ M Δϕ U0 cos O B C

DẠYKÈMQUYNHƠNOFFICIAL 17 I. Đoạn mạch chỉ có một phần tử R, L hoặc C 1. Đoạn xoay chiều chỉ có trở thuần Sơ đồ mạch điện: Tính chất của điện trở R: có tác dụng cản trở, làm giảm cường độ của dòng điện đi qua nó. + Mắc nối tiếp: 12 RRR... =++ ( 12 RR,R,... > ) tăng điện trở + Mắc song song: 12 111 ... RRR =++ ( 12 RR,R,... < ) giảm điện trở Biểu thức điện áp và dòng điện trong mạch: u(t) = U0cos(ωt + ϕ)  uU i==2cos(ωt+) RR ϕ Đặt : 0 0 U Ι = R thì 0 iIcos(ωt φ)I2cos(ωt φ)=+=+  i , u cùng pha. Định luật Ôm : U I R = Giản đồ véctơ: 2. Đoạn mạch chỉ có tụ điện C: uC trễ pha so với i góc π 2 . Định luật Ôm: I = C C U Z ; với ZC = 1 ω C là dung kháng của tụ điện. + Mắc nối tiếp: 12 111 ... CCC =++ ( 12 CC,C,... < ) giảm điện dung + Mắc song song: 12 CCC... =++ ( 12 CC,C,... > ) tăng điện dung Đặt điện áp uU2cosωt= vào hai đầu một tụ điện thì cường độ dòng điện qua nó có giá trị hiệu dụng là I. Tại thời điểm t, điện áp ở hai đầu tụ điện là u và cường độ dòng điện qua nó là i. Hệ thức liên hệ giữa các đại lượng là: 2222 2222 00CC iuiu 11 IU2I2U +=⇔+=  22 22 ui 2 UI += . Cường độ dòng điện tức thời qua tụ: πiI2cos ωtA 2  =+  . Ý nghĩa của dung kháng - ZC là đại lượng biểu hiện sự cản trở dòng điện xoay chiều của tụ điện. - Dòng điện xoay chiều có tần số cao (cao tần) chuyển qua tụ điện dễ dàng hơn dòng điện xoay chiều tần số thấp. C BA ARB O RU I x O I x CU

DẠYKÈMQUYNHƠNOFFICIAL 18 - ZC cũng có tác dụng làm cho i sớm pha π 2 so với u. Giản đồ véctơ của mạch: 3. Mạch điện xoay chiều chỉ có cuộn cảm Sơ đồ mạch điện. Tính chất của cuộn cảm. Mỗi cuộn dây có hai phần tử: điện trở r và độ tự cảm L . Riêng cuộn cảm thuần chỉ có L. Trường hợp nếu rút lỏi thép ra khỏi cuộn cảm thì độ sáng đèn tăng lên  Cuộn cảm có tác dụng cản trở dòng điện xoay chiều. Tác dụng cản trở này phụ thuộc vào độ tự cảm cuộn dây. Biểu thức điện áp ở hai đầu mạch điện và dòng điện trong mạch: Giả sử i = I0cosωt  u = LωI0cos(ωt+ π 2 ) = U0cos(ωt + π 2 ) Nếu u = U0cosωt  i = I0cos(ωt –π 2 ) i = I0cos(ωt + ϕi)  u = U0cos(ωt + π 2 + ϕi)  u sớm pha hơn i một góc: π 2 Ta có: 222222 222222 00LL iuiuiu 112 IU2I2UIU +=⇔+=  += Biểu thức định luật ôm cho đoạn mạch: I = L U ω . Cảm kháng : ZL = ωL Đơn vị: Ôm ( Ω ) Ý nghĩa của cảm kháng - ZL là đại lượng biểu hiện sự cản trở dòng điện xoay chiều của cuộn cảm. - Cuộn cảm có L lớn sẽ cản trở nhiều đối với dòng điện xoay chiều, nhất là dòng điện xoay chiều cao tần. - ZL cũng có tác dụng làm cho i trễ pha π 2 so với u. Giản đồ véctơ cho đoạn mạch: Chú ý: a. 1 0,318= π ; 2 0,636= π ; 1 0,159 2 = π b. Công thức tính điện dung của tụ phẳng: C = 9 S 9.10.4πd ε . ε : Hằng số điện môi. S: Phần diện tích giữa hai bản tụ (m2). d: Khoảng cách giữa hai bản tụ(m). L A B x I LU O

DẠYKÈMQUYNHƠNOFFICIAL 19 - Điện môi bị đánh thủng là hiện tượng khi điện trường tăng vượt qua một giá trị giới hạn náo đó sẽ làm cho điện môi mất tính cách điện. - Điện áp giới hạn là điện áp lớn nhất mà điện môi không bị đánh thủng. II. Đoạn mạch RLC không phân nhánh Đặt điện áp uuU2cos(ωt φ )=+ vào hai đầu mạch. Độ lệch pha ϕ giữa u và i xác định theo biểu thức: tanϕ = LCZZ R = 1 L C R ω− ω Với ui φφφ =− Cường độ hiệu dụng xác định theo định luật Ôm: I = U Z . Với Z = 22 LCR (Z Z)+− là tổng trở của đoạn mạch. Cường độ dòng điện tức thời qua mạch: iuiI2cos(ωt φ )I2cos(ωt φφ)=+=+− . Cộng hưởng điện trong đoạn mạch RLC: Khi ZL = ZC hay ω = 1 LC thì: + Imax = U R , Pmax = 2U R , u cùng pha với i (ϕ = 0). + Khi ZL > ZC thì u nhanh pha hơn i (đoạn mạch có tính cảm kháng). + Khi ZL < ZC thì u trể pha hơn i (đoạn mạch có tính dung kháng). + R tiêu thụ năng lượng dưới dạng toả nhiệt, ZL và ZC không tiêu thụ năng lượng điện. III. Đoạn mạch có RLrC không phân nhánh Đặt điện áp uuU2cos(ωt φ )=+ vào hai đầu mạch. Độ lệch pha ϕ giữa uAB và i xác định theo biểu thức: tanϕ = LCZZ Rr + = 1 L C Rr ω− ω + . Với ui φφφ =− Cường độ hiệu dụng xác định theo định luật Ôm: I = U Z Với Z = ()2 2 LCRr (Z Z)++− là tổng trở của đoạn mạch. Cường độ dòng điện tức thời qua mạch: iuiI2cos(ωt φ )I2cos(ωt φφ)=+=+− Cách nhận biết cuộn dây có điện trở thuần r: C A B R L NM C A B R L,r NM

DẠYKÈMQUYNHƠNOFFICIAL 20 + Xét toàn mạch, nếu: Z ≠ ()2 2 LCRr (Z Z)++− ; U ≠ 22 RLC U(UU) +− hoặc P ≠ I2R hoặc cosϕ ≠ R Z  thì cuộn dây có điện trở thuần r ≠ 0. + Xét cuộn dây, nếu: Ud ≠ UL hoặc Zd ≠ ZL hoặc Pd ≠ 0 hoặc cosϕd ≠ 0 hoặc ϕd ≠ π 2  thì cuộn dây có điện trở thuần r ≠ 0. IV. Phương pháp truyền thống 1. Mạch điện chỉ chứa một phần tử (hoặc R, hoặc L, hoặc C) Mạch điện chỉ có điện trở thuần: u và i cùng pha: ϕ= ϕu - ϕ i = 0 hay ϕu = ϕ i Ta có: iiI2cos(ωt + φ )= thì RiuU2cos(ωt + φ )= ; với RU I R = . Câu 1: Điện áp giữa hai đầu một đoạn mạch điện xoay chiều chỉ có điện trở thuần R = 100Ω có biểu thức πu2002cos100πt (V)4  =+  . Biểu thức của cường độ dòng điện trong mạch là : A. i = π22cos100πt(A) 4    B. i = π22cos100πt(A) 4  +   C. i = π22cos100πt(A) 2  +   D. i = π2cos100πt(A) 2    Hướng dẫn: Tính I0 hoặc U200 I2A R100 === ; i cùng pha với u hai đầu R, nên ta có: ϕi = ϕu = π 4 . Suy ra: i = π22cos100πt(A) 4  +      Chọn B Mạch điện chỉ có tụ điện: uC trễ pha so với i góc π 2  ϕ= ϕu – ϕ i = –π 2 hay ϕu = ϕ i –π 2 ; ϕ i = ϕu + π 2 Nếu đề cho iI2cosωt= thì viết: πuU2cos ωt 2  =−  và Định luật Ôm: C C U I Z = với C 1 Z ωC = . Nếu đề cho uU2cosωt= thì viết: πiI2cos ωt 2 =+  . Câu 2: Điện áp giữa hai đầu một đoạn mạch điện xoay chiều chỉ có tụ có điện dung C = 410 F π có biểu thức u2002cos100πt(V)= . Biểu thức của cường độ dòng điện trong mạch là:

DẠYKÈMQUYNHƠNOFFICIAL 21 A. i = 5π 22cos100t(A) 6  π+   B. i = π22cos100πt(A) 2  +   C. i = π22cos100πt(A) 2    D. i = π 2cos100t(A) 6  π−   Hướng dẫn: Tính C 4 11 Z 10ωC 100π. π == =100Ω. Tính Io hoặc U200 I2A R100 === ; i sớm pha góc 2 π so với u hai đầu tụ điện. Suy ra: i = π22cos100πt(A) 2  +   .   Chọn B Mạch điện chỉ có cuộn cảm thuần: uL sớm pha hơn i góc π 2  ϕ= ϕu – ϕ i = –π 2 hay ϕu = ϕ i + π 2 ; ϕ i = ϕu –π 2 Nếu đề cho iI2cosωt= thì viết: πuU2cos ωt 2 =+  V và định luật Ôm: L L U I Z = với LZ ωL= . Nếu đề cho uU2cosωt= thì viết: πiI2cos ωtA 2  =−  Câu 3: Hiệu điện thế giữa hai đầu một đoạn mạch điện xoay chiều chỉ có cuộn cảm có độ tự cảm L = 1 H π có biểu thức πu2002cos100πt(V) 3 =+  . Biểu thức cường độ dòng điện trong mạch là : A. i = 5π 22cos100t(A) 6  π+   B. i =22cos100t(A) 6 π  π−   C. i = π 22cos100t(A) 6  π+   D. i = π 2cos100t(A) 6  π−   Hướng dẫn: Tính LZ ωL= = 100π. 1 π =100Ω. Tính I0 hoặc L U200 I2A Z100 === ; i trễ phagóc π 2 so với u hai đầu cuộn cảm thuần, nên ta có: πππ 326 −=− . Suy ra: i =22cos100t(A) 6 π  π−   Chọn B

DẠYKÈMQUYNHƠNOFFICIAL 22 2. Mạch RLC không phân nhánh Phương pháp giải: Tìm Z, I ( hoặc I0 )và ϕ Tính tổng trở Z: Tính LZ ωL= .; C 11 Z ωC2πfC == và 22 LC ZR(ZZ) =+− Định luật Ôm: U và I liên hệ với nhau bởi U I Z = ; Io = o U Z Tính độ lệch pha giữa u hai đầu mạch và i: LCZZ tanφ R = Viết biểu thức u hoặc i + Nếu cho trước: iI2cosωt= thì biểu thức của u là uU2cos(ωt + φ)= . Hay i = Iocosωt thì u = Uocos(ωt + ϕ). + Nếu cho trước: uU2cosωt= thì biểu thức của i là: iI2cos(ωt φ)=− Hay u = Uocosωt thì i = Iocos(ωt – ϕ) . Khi: (ϕu ≠ 0; ϕi ≠ 0 ) ta có : ϕ = ϕu – ϕi  ϕu = ϕi + ϕ; ϕi = ϕu – ϕ + Nếu cho trước iiI2cos(ωt φ )=+ thì biểu thức của u là: iuU2cos(ωt + φ + φ)= . Hay i = Iocos(ωt + ϕi) thì u = Uocos(ωt + ϕi + ϕ). + Nếu cho trước uuU2cos(ωt φ )=+ thì biểu thức của i là: uiI2cos(ωt + φφ)=− . Hay u = Uocos(ωt + ϕu) thì i = Iocos(ωt +ϕu – ϕ). Chú ý: Với mạch điện không phân nhánh có cuộn dây không cảm thuần (R ,L,r, C) thì: 22 LC Z(Rr)(ZZ) =++− và LCZZ tan φ Rr = + . BÀI TẬP VẬN DỤNG Câu 1: Mạch điện xoay chiều gồm một điện trở thuần R = 50Ω, một cuộn thuần cảm có hệ số tự cảm 1 LH π = và một tụ điện có điện dung -42.10 CF π = mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng ( )i5cos100πtA= .Viết biểu thức điện áp tức thời giữa hai đầu mạch điện. Hướng dẫn: Cảm kháng: L 1 Z ωL100π.100Ω π === . Dungkháng: C -4 11 Z50 2.10ωC 100π. π ===Ω . Tổng trở: () ()2 222 LC ZRZZ5010050502 =+−=+−=Ω Định luật Ôm: Uo= IoZ = 5.50 2 = 250 2 V.

DẠYKÈMQUYNHƠNOFFICIAL 23 Tính độ lệch pha giữa u hai đầu mạch và i: LC ZZ10050 tanφ 1 R50 === π φ 4  = Biểu thức điện áp tức thời giữa hai đầu mạch điện: πu2502cos100πt 4 =+  (V). Câu 2: Một mạch điện xoay chiều RLC không phân nhánh có R = 100 Ω ; -410 CF π = ; L = 2 π H. Cường độ dòng điện qua mạch có dạng: i = 2cos100 π t (A). Viết biểu thức tức thời điện áp của hai đầu mạch và hai đầu mỗi phần tử mạch điện. Hướng dẫn: Cảm kháng: L 2 ZL.100200 =ω=π=Ω π . Dung kháng: C 4 11 Z .C10 100. == ω π π = 100 Ω Tổng trở: Z = 2222 LC R(ZZ)100(200100)1002 +−=+−=Ω Hiệu điện thế cực đại : U0 = I0.Z = 2.1002 V =200 2 V. Độ lệch pha: LCZZ 200100 π tanφ 1 φ R1004 ===  = Pha ban đầu của hiệu điện thế: ui π0 4 ϕ=ϕ+ϕ=+= 4 π Biểu thức hiệu điện thế: u = 0u πUcos(t)2002cos100t 4  ω+ϕ=π+  (V). Hiệu điện thế hai đầu R: uR = U0Rcos Ru (t) ω+ϕ . Với : U0R = I0.R = 2.100 = 200 V. Trong đoạn mạch chỉ chứa R: uR cùng pha i: uR = U0Rcos Ru (t) ω+ϕ = 200cos100πt V. Hiệu điện thế hai đầu L: uL = U0Lcos Lu (t) ω+ϕ . Với : U0L = I0.ZL = 2.200 = 400 V. Trong đoạn mạch chỉ chứa L: uL nhanh pha hơn cường độ dòng điện 2 π : L ui 0 222 πππ ϕ=ϕ+=+= rad  uL = U0Lcos Ru (t) ω+ϕ = 400cos π100t 2  π+   V. Hiệu điện thế hai đầu C :uC = U0Ccos Cu (t) ω+ϕ với : U0C = I0ZC = 2.100 = 200V. Trong đoạn mạch chỉ chứa C : uC chậm pha hơn cường độ dòng điện 2 π : L ui 0 222 πππ ϕ=ϕ−=−=− rad.  uC = U0Ccos Cu (t) ω+ϕ = 200cos π100t 2  π−   V.

DẠYKÈMQUYNHƠNOFFICIAL 24 Câu 3: Mạch điện xoay chiều gồm một điện trở thuần R = 40Ω, một cuộn thuần cảm có hệ số tự cảm 0,8 LH π = và một tụ điện có điện dung 42.10 CF π = mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng i3cos100πt (A)= a. Tính cảm kháng của cuộn cảm, dung kháng của tụ điện và tổng trở toàn mạch. b. Viết biểu thức điện áp tức thời giữa hai đầu điện trở, giữa hai đầu cuộn cảm, giữa hai đầu tụ điện, giữa hai đầu mạch điện. Hướng dẫn: a. Cảm kháng: L Z0,8 ωL100π.80 π ===Ω . Dung kháng: C 4 11 Z50 2.10ωC 100π π ===Ω Tổng trở: () ()2 222 LC ZRZZ40805050 =+−=+−=Ω . b. • Vì uR cùng pha với i nên : R0R uUcos100πt= với UoR = IoR = 3.40 = 120V. Vậy u120cos100πt= (V). • Vì uL nhanh pha hơn i góc π 2 nên: L0L πuUcos100πtV 2 =+  Với UoL = IoZL = 3.80 = 240V. Vậy L πu240cos100πt 2 =+  (V). • Vì uC chậm pha hơn i góc π 2 nên: C0C πuUcos100πtV 2  =−  . Với UoC = IoZC = 3.50 = 150V. Vậy C πu150cos100πt 2  =−  V. Áp dụng công thức: LC ZZ80503 tan φ R404 === φ 37 ≈ o 37π φ 0,2π rad. 180  =≈ Biểu thức hiệu điện thế tức thời giữa hai đầu mạch điện: ( )o uUcos100πt φ=+ , với Uo= IoZ = 3.50 = 150V. Vậy ( )u150cos100πt0,2π=+ (V). Câu 4: Một đoạn mạch điện xoay chiều gồm một điện trở thuần R = 80Ω, một cuộn dây thuần cảm có độ tự cảm L = 64mH và một tụ điện có điện dung C400μF= mắc nối tiếp. a. Tính tổng trở của đoạn mạch. Biết tần số của dòng điện f = 50Hz. b. Đoạn mạch được đặt vào điện áp xoay chiều có biểu thức u282cos314t = (V). Lập biểu thức cường độ tức thời của dòng điện trong đoạn mạch.

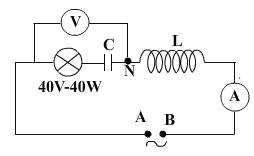
DẠYKÈMQUYNHƠNOFFICIAL 25 Hướng dẫn: a. Tần số góc: ω 2πf2π.50100π=== rad/s. Cảm kháng: 3 LZ ωL100π.64.1020 ==≈Ω . Dung kháng: C 6 11 Z80 ωC100π.40.10 ==≈Ω Tổng trở: () ()2 222 LC ZRZZ802080100 =+−=+−=Ω b. Cường độ dòng điện cực đại: 0 0 U282 I2,82 Z100 === A. Độ lệch pha của hiệu điện thế so với cường độ dòng điện: LC ZZ20803 tan φ R804 ===− φ 37 ≈− o iu 37π φφφφ 37 180  =−=−== o rad. Vậy 37πi2,82cos314t 180 =+  (A). Câu 5: Cho mạch điện xoay chiều như hình vẽ. Biết 1 LH 10π = , 310 CF 4π = và đèn ghi (40V - 40W). Đặt vào 2 điểm A và N một hiệu điện thế AN u1202cos100πt (V)= . Các dụng cụ đo không làm ảnh hưởng đến mạch điện. a. Tìm số chỉ của các dụng cụ đo. b. Viết biểu thức cường độ dòng điện và điện áp toàn mạch. Hướng dẫn: a. Cảm kháng: L 1 Z ωL100π.10 10π ===Ω Dung kháng: C 3 11 Z40 10ωC 100π 4π ===Ω . Điện trở của bóng đèn: đ 22 đm đm U40 R40 P40 ===Ω . Tổng trở đoạn mạch AN: đ 2222 ANC ZRZ4040402 =+=+=Ω . Số chỉ của vôn kế: 0 AN AN U1202 U120 22 === V. Số chỉ của ampe kế: AN A AN U1203 II2,12 Z 4022 ====≈ A.

DẠYKÈMQUYNHƠNOFFICIAL 26 b. Biểu thức cường độ dòng điện có dạng: ( )oiiIcos100πt φ=+ (A). Ta có: đ C AN Z40 tan φ 1 R40 ==−=− AN π φ 4  =− rad.  AN iuANAN π φφφφ 4 =−=−= rad; o 3 II2.23 2 === A. Vậy πi3cos100πt 4 =+  (A). Hiệu điện thế giữa hai điểm A, B có dạng: ( )ABou uUcos100πt φ=+ (V). Tổng trở của đoạn mạch AB: () ()đ 2 222 ABLC ZRZZ40104050 =+−=+−=Ω ooAB UIZ3.50150 === V. Ta có: đ LC AB ZZ10403 tan φ R404 ===− AB 37π φ 180  =− rad. uiAB π 37ππ φφφ 418020  =+=−= rad. Vậy AB πu150cos100πt 20 =+  (V). Câu 6: Sơ đồ mạch điện có dạng như hình vẽ, điện trở R = 40Ω, cuộn thuần cảm 3 LH 10π = , tụ điện 310 CF 7π = . Điện áp AF u120cos100πt (V)= . Hãy lập biểu thức của: a. Cường độ dòng điện qua mạch. b. Điện áp hai đầu mạch AB. Hướng dẫn: a. Cảm kháng: L 3 Z ωL100π.30 10π ===Ω . Dung kháng: C 3 11 Z70 10ωC 100π. 7π ===Ω. Tổng trở của đoạn AF: 2222 AFL ZRZ403050 =+=+=Ω oAF o AF U120 I2,4 Z50  === A. Góc lệch pha AFφ : L AFAF Z3037π tanφ 0,75 φ R40180 ===  ≈ rad. Ta có: AF iuAFAFAF 37π φφφ 0 φφ 180 =−=−=−=− rad. Vậy 37πi2,4cos100πt 180  =−  (A). C A B R L F

DẠYKÈMQUYNHƠNOFFICIAL 27 b. Tổng trở của toàn mạch: () 22 Z403070402 =+−=Ω oo UIZ2,4.402962 === V. Ta có: LC AB AB ZZ3070 π tan φ 1 φ R404 ===−  =− rad. uABi π 37π 41π φφφ 418090  =+=−−=− rad. Vậy 41πu962cos100πt 90  =−  (V). Câu 7: Cho mạch điện xoay chiều như hình vẽ, R = 100Ω, L là độ tự cảm của cuộn dây thuần cảm, 410 CF 3π = , RA ≈ 0. Điện áp AF u502cos100πt (V)= Khi K đóng hay khi K mở, số chỉ của ampe kế không đổi. a. Tính độ tự cảm L của cuộn dây và số chỉ không đổi của ampe kế b. Lập biểu thức của cường độ dòng điện tức thời trong mạch khi K đóng và khi K mở. Hướng dẫn: a. Theo đề bài, điện áp và số chỉ ampe kế không đổi khi K đóng hay khi K mở nên tổng trở Z khi K mở và khi K đóng bằng nhau ( )2 222 đ LCC ZZRZZRZ =⇔+−=+ m ( )2 2 LCC ZZZ −= LCCLC LCCL ZZZZ2Z ZZZZ0 −=  =   −=−  = Ta có: C 4 11 Z173 10ωC 100π. 3π ===Ω LC Z2Z2.173346 ===Ω L Z346 L1,1 ω 100π  ==≈ H. Số chỉ ampe kế bằng cường độ dòng điện hiệu dụng khi K đóng: A đ 2222 đ C U50 II0,25 Z RZ100173 ==== ++ U A . b. Biểu thức cường độ dòng điện: - Khi K đóng: Độ lệch pha: C đ Z173 tan φ 3 R100 ===− đ π φ 3  = rad. Pha ban đầu của dòng điện: đ iu đđ π φφφφ 3 =−=−= . Vậy đ πi0,252cos100πt 3 =+  (A). - Khi K mở: Độ lệch pha: LC m ZZ346173 tan φ 3 R100 === m π φ 3  = . (Loại)

DẠYKÈMQUYNHƠNOFFICIAL 28 Pha ban đầu của dòng điện: m iumm π φφφφ 3 =−=−=− Vậy: m πi0,252cos100πt 3  =−  (A). Câu 8: Cho mạch điện như hình vẽ: UAN = 150V, UMB =200V. Độ lệch pha UAM và UMB là π 2 Dòng điện tức thời trong mạch là: i = I0 cos 100πt (A), cuộn dây thuần cảm. Hãy viết biểu thức UAB. A. uAB = 139 2 cos(100πt + 0,53) V. B. uAB = 139 2 cos(100πt + 0,5) V. C. uAB = 139 3 cos(100πt + 0,5) V. D. uAB = 139 3 cos(100πt + 0,53) V. Hướng dẫn: Ta có: 22 ANCR ANCR UUUUUU150V =+  =+= (1) 22 MBLR MBLR UUUUUU200V =+  =+= (2) Vì UAN và UMB lệch pha nhau π 2 nên LC 12 RR UU tanφ tanφ 11 UU =−⇔= hay U2 R = UL.UC (3) Từ (1), (2) và (3) ta có UL = 160V, UC = 90V, R U120V = () 22 ABRLC UUUU139V =+−= ; LC R UU7 tanφφ 0,53rad U12 ==  = . Vậy uAB = 139 2 cos(100πt + 0,53) V.   Chọn A Câu 9: Cho mạch điện không phân nhánh gồm R = 100 3 Ω, cuộn dây thuần cảm L và tụ điện 410 CF 2π = Đặt vào 2 đầu đoạn mạch điện một hiệu điện thế xoay chiều u = 100 2 cos100πt (V). Biết hiệu điện thế ULC = 50V, dòng điện nhanh pha hơn hiệu điện thế. Hãy tính L và viết biểu thức cường độ dòng điện i trong mạch. Hướng dẫn: Ta có ω = 100π rad/s, U = 100V, C 4 11 Z200 C10 100π 2π ===Ω ω . Hiệu điện thế 2 đầu điện trở thuần là: 2 RLC UUU503V =−= . Cường độ dòng điện RU I0,5A R == và LC LC U Z100 I ==Ω R CL N M AB

DẠYKÈMQUYNHƠNOFFICIAL 29 Vì dòng điện nhanh pha hơn hiệu điện thế,mà trên giản đồ Frexnen,dòng điện được biêủ diễn trên trục hoành vậy hiệu điện thế được biểu diễn dưới trục hoành nghĩa là ZL < ZC. Do đó: ZC – ZL =100Ω  ZL = ZC – 100 = 100Ω. Suy ra LZ L0,318H ω == . Độ lệch pha giữa u và i : LC ZZ1 π tanφφR6 3 ==−  =− . Vậy πi0,52cos100πt(A) 6  =+  V. Phương pháp dùng số phức để tìm biểu thức i hoặc u với máy tính Casio FX-570ES; FX-570ES PLUS; VINACAL-570ES PLUS. 1. Tìm hiểu các đại lượng xoay chiều dạng phức Đại lượng điện Công thức Dạng số phức trong máy tính FX-570ES Cảm kháng ZL ZL ZLi (Chú ý trước i có dấu cộng là ZL) Dung kháng ZC ZC – ZCi (Chú ý trước i có dấu trừ là ZC) Tổng trở L ZLω= ; C 1 Z ωC = () 22 LCZRZZ =+− LC ZR(ZZ)i =+− = a + bi (với a = R; b = ZL – ZC ) Nếu ZL > ZC: Đoạnmạch có tính cảm kháng Nếu ZL< ZC: Đoạnmạch có tính dung kháng Cường độ dòng điện i = I0cos(ωt + ϕi ) iiφ 00iiII φ==∠ Điện áp u = U0cos(ωt + ϕu ) uiφ 00uuUU φ==∠ Định luật Ôm U I Z = u iuiZ Z =  = u Z i  = Chú ý: LC ZR(ZZ) =+− i (tổng trở phức Z có gạch trên đầu: R là phần thực, (ZL – ZC ) là phần ảo). Cần phân biệt chữ i sau giá trị b = (ZL – ZC ) là phần ảo, khác với chữ i là cường độ dòng điện. 2. Chọn cài đặt máy tính: CASIO fx – 570ES; 570ES Plus. Chọn chế độ Nút lệnh Ý nghĩa- Kết quả Chỉ định dạng nhập / xuất toán Bấm: SHIFT MODE 1 Màn hình xuất hiện Math. Thực hiện phép tính số phức Bấm: MODE 2 Màn hình xuất hiện chữ CMPLX Dạng toạ độ cực: r∠θ Bấm: SHIFT MODE 3 2 Hiển thị số phức dạng: A ∠ϕ Hiển thị dạng đề các: a + ib. Bấm: SHIFT MODE 3 1 Hiển thị số phức dạng: a+bi Chọn đơn vị đo góc là độ (D) Bấm: SHIFT MODE 3 Màn hình hiển thị chữ D

DẠYKÈMQUYNHƠNOFFICIAL 30 Chọn đơn vị đo góc là Rad (R) Bấm: SHIFT MODE 4 Màn hình hiển thị chữ R Nhập ký hiệu góc ∠ Bấm SHIFT (-) Màn hình hiển thị ∠ Nhập ký hiệu phần ảo i Bấm ENG Màn hình hiển thị i 3. Lưu ý chế độ hiển thị kết quả trên màn hình Sau khi nhập, ấn dấu = có thể hiển thị kết quả dưới dạng số vô tỉ, muốn kết quả dưới dạng thập phân ta ấn SHIFT = (hoặc nhấn phím SD ) để chuyển đổi kết quả Hiển thị BÀI TẬP VẬN DỤNG Câu 1: Mạch điện xoay chiều gồm một điện trở thuần R = 50Ω, một cuộn thuần cảm có hệ số tự cảm 1 LH π = và một tụ điện có điện dung 42.10 CF π = mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng ( )i5cos100πtA= .Viết biểu thức điện áp tức thời giữa hai đầu mạch điện. Hướng dẫn: Ta có: L 1 Z ωL100π.100 π ===Ω ; C 4 11 Z50 2.10ωC 100π. π ===Ω Và ZL – ZC = 50 Ω . Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX. Bấm SHIFT MODE 3 2 : dạng hiển thị toạ độ cực:( r∠θ ) Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D Ta có: 0iLC uiZIX[R(ZZ)i] ==∠ϕ+− 50X(5050i)=∠+ (X là phép nhân hai số phức) Nhập máy: 5 SHIFT (-) 0 X ( 50 + 50 ENG i ) = Hiển thị: 353.55339∠45 = 250 2 ∠45. Vậy biểu thức tức thời điện áp của hai đầu mạch: u = 250 2 cos(100πt + π 4 ) (V). Câu 2: Một mạch điện xoay chiều RLC không phân nhánh có R = 100 Ω ; C = 410 F π ; L = 2 π H. Cường độ dòng điện qua mạch có dạng: i = 2 2 cos100 π t(A). Viết biểu thức điện áp tức thời của hai đầu mạch? Hướng dẫn: Ta có: L 2 Z ωL100π.200 π ===Ω ; C 4 11 Z 10ωC 100π π === 100 Ω Và ZL – ZC = 100 Ω .

DẠYKÈMQUYNHƠNOFFICIAL 31 Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX. Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r∠θ ) Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D Ta có: 0iLC uiZIX(R(ZZ)i ==∠ϕ+− 220X(100100i) =∠+ ⊳ (X là phép nhân hai số phức) Nhập máy: 2 2 SHIFT (-) 0 X ( 100 + 100 ENG i ) = Hiển thị: 400∠45. Vậy biểu thức tức thời điện áp của hai đầu mạch: u = 400cos( 100πt + π 4 ) (V). Câu 3: Khi đặt hiệu điện thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm L = 1 4π H thì cường độ dòng điện 1 chiều là 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp u150cos120πt (V)= thì biểu thức cường độ dòng điện trong mạch là: A. πi52cos(120πt)(A) 4 =− B. πi5cos(120πt)(A) 4 =+ C. πi52cos(120 πt)(A) 4 =+ D. πi5cos(120πt)(A) 4 =− Hướng dẫn: Khi đặt hiệu điện thế không đổi (hiệu điện thế 1 chiều) thì đoạn mạch chỉ còn có R: R = U I = 30Ω Ta có: L 1 ZL12030 4 =ω=π=Ω π ; i = u15020 3030iZ ∠ = + a. Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX. Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r∠θ ) Chọn đơn vị góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D Nhập máy: 150 2 : ( 30 + 30 ENG i ) = Hiển thị: 5∠- 45 Vậy biểu thức cường độ dòng điện qua mạch là: πi5cos(120πt)(A) 4 =− .   Chọn D b. Với máy FX570ES: Bấm MODE 2 màn hình xuất hiện: CMPLX. Chọn đơn vị góc là độ (R), bấm: SHIFT MODE 4 màn hình hiển thị R Nhập máy: 150 2 : ( 30 + 30 ENG i ) = Hiển thị dạng phức: 3.535533..-3.535533…i. Bấm SHIFT 2 3 : Hiển thị: 5∠π 4 . Biểu thức cường độ dòng điện qua mạch là: πi5cos(120πt)(A) 4 =−   Chọn D

DẠYKÈMQUYNHƠNOFFICIAL 32 VI. Bài toán cộng điện áp xoay chiều dùng máy tính FX-570ES 1. Phương pháp 1: Phương pháp giản đồ véctơ: Dùng phương pháp tổng hợp dao động điều hoà. Ta có: u1 = U01 1 cos(t) ω+ϕ và u2 = U02 2 cos(t) ω+ϕ Thì điện áp tổng trong đoạn mạch nối tiếp: u = u1 + u2 = 011022 Ucos(t)Ucos(t) ω+ϕ+ω+ϕ Điện áp tổng có dạng: u = U0 cos(t) ω+ϕ Với: U0 2 = U2 01+ U02 2 + 2U02U01cos 12(φφ ), 12 12 0102 0102 UsinUsin tan UcosUcos ϕ=ϕ+ϕ ϕ+ϕ Câu 1: Cho mạch xoay chiều gồm: Đoạn AM chứa: R, C mắc nối tiếp với đoạn MB chứa cuộn cảm L, r. Tìm uAB = ? Biết: + uAM = 100 π2cos100πt 3    (V) 0AM 1 U1002V 3  =   π ϕ=−  + uMB = 100 π2cos100πt 6  +   (V) 0MB 2 U1002V 6  =   π ϕ=  Hướng dẫn: Cách giải 1: Dùng công thức tổng hợp dao động: uAB = uAM + uMB + U0AB = () () 22 ππ 100210022.1002.1002.cos200V 36  ++−−=   . + 1002sin1002sin 36 tan 121002cos1002cos 36 ππ  −+  πϕ=  ϕ=− ππ  −+   . Vậy uAB = 200 πcos100πt 12    (V). Cách giải 2: Dùng máy tính FX-570ES: uAB = uAM + uMB để xác định U0AB và ϕ a. Chọn chế độ của máy tính: CASIO fx – 570ES ; 570ES Plus Các thao tác lệnh: Thực hiện phép tính về số phức Bấm: MODE 2 Màn hình xuất hiện chữ CMPLX Dạngtoạ độ cực: r∠θ (A∠ϕ) Bấm: SHIFT MODE 3 2 Hiển thị số phức dạng r ∠θ Tính dạng toạ độ đề các: a + ib. Bấm: SHIFT MODE 3 1 Hiển thị số phức dạng a+bi Chọn đơn vị góc là độ (D) Bấm: SHIFT MODE 3 Màn hình hiển thị chữ D Hoặc chọn đơn vị góc là Rad (R) Bấm: SHIFT MODE 4 Màn hình hiển thị chữ R Hình uAM BA R L,r uMB M C

DẠYKÈMQUYNHƠNOFFICIAL 33 Nhập ký hiệu góc ∠ Bấm: SHIFT (-) Màn hình hiển thị ký hiệu ∠ Chuyển từ a + bi sang A∠ ϕ Bấm: SHIFT 2 3 = Màn hình hiển thị dạng A∠ ϕ Chuyển từ A∠ ϕ sang a + bi Bấm: SHIFT 2 4 = Màn hình hiển thị dạng a + bi b. Xác định U0 và ϕ ϕϕ ϕ bằng cách bấm máy tính: + Với máy FX570ES: Bấm MODE 2 màn hình xuất hiện: CMPLX. Nhập U01 bấm SHIFT (-) nhập φ1; bấm +, Nhập U02, bấm SHIFT (-) nhập φ2 nhấn = kết quả. Nếu hiển thị số phức dạng: a + bi thì bấm SHIFT 2 3 = hiển thị kết quả: A∠ϕ + Với máy FX570MS: Bấm MODE 2 màn hình xuất hiện chữ: CMPLX. Nhập U01, bấm SHIFT (-) nhập φ1, bấm + , Nhập U02, bấm SHIFT (-) nhập φ2 nhấn =. Sau đó bấm SHIFT + = hiển thị kết quả là: A SHIFT = hiển thị kết quả là: φ + Lưu ý chế độ hiển thị kết quả trên màn hình: Sau khi nhập, ấn dấu = hiển thị kết quả dưới dạng số vô tỉ, muốn kết quả dưới dạng thập phân ta ấn SHIFT = (hoặc dùng phím SD ) để chuyển đổi kết quả Hiển thị Câu 2: Cho mạch xoay chiều gồm: Đoạn AM chứa: R, C mắc nối tiếp với đoạn MB chứa cuộn cảm L, r. Tìm uAB = ? Biết: + uAM = 100 π2cos100πt 3    (V) 0AM 1 U1002V 3  =   π ϕ=−  + uMB = 100 π2cos100πt 6  +   (V) 0MB 2 U1002V 6  =   π ϕ=  Cách giải 2a: Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX Chọn đơn vị đo góc là D (độ): SHIFT MODE 3 Nhập máy:100 2 SHIFT (-) ∠ (-60) + 100 2 SHIFT (-) ∠ 30 = Hiển thị kết quả: 200∠-15. Vậy uAB = 200 ( )0 cos ωt15 (V) hay uAB = 200 πcos100πt 12    (V) Cách giải 2b: Chọn đơn vị đo góc là R (Radian): SHIFT MODE 4 Nhập máy:100 2 SHIFT (-).∠ (-π/3) + 100 2 SHIFT (-) ∠(π/6 = Hiển thị kết quả: 200∠ π 12 . Vậy uAB = 200 πcos100πt 12    (V) Chú ý: Nếu cho u1 = U01cos(ωt + ϕ ϕ1) và u = u1 + u2 = U0cos(ω ωω ωt + ϕ) . uAM AB R L,r uMB M C

DẠYKÈMQUYNHƠNOFFICIAL 34 Tìm dao động thành phần u2: u2 = u - u1 .với: u2 = U02cos(ωt + ϕ2). Xác định U02 và ϕ2 * Với máy FX570ES : Bấm chọn MODE 2 Nhập U0, bấm SHIFT (-) nhập φ; bấm - (trừ), Nhập U01, bấm SHIFT (-) nhập φ1 nhấn = kết quả (Nếu hiển thị số phức thì bấm SHIFT 2 3 = kết quả trên màn hình là: U02 ∠ ϕ2 * Với máy FX570MS : Bấm chọn MODE 2 Nhập U0, bấm SHIFT (-) nhập φ bấm - (trừ), Nhập U01, bấm SHIFT (-) nhập φ1 nhấn = bấm SHIFT (+) =, ta được U02 ; bấm SHIFT (=) ; ta được φ2 Câu 3: Nếu đặt vào hai đầu một mạch điện chứa một điện trở thuần và một cuộn cảm thuần mắc nối tiếp một điện áp xoay chiều có biểu thức πu1002cos ωt 4  =+  (V), thì khi đó điện áp hai đầu điện trở thuần có biểu thức R u100cosωt= (V). Biểu thức điện áp giữa hai đầu cuộn cảm thuần sẽ là A. L πu100cos ωt 2  =+  (V). B. L πu1002cos ωt 4  =+  (V). C. L πu100cos ωt 4  =+  (V). D. L πu1002cos ωt 2  =+  (V). Hướng dẫn: Cách giải 1: Với máy FX-570ES: Bấm MODE 2 màn hình xuất hiện: CMPLX Chọn đơn vị đo góc là D (độ): SHIFT MODE 3 Nhập máy:100 2 SHIFT (-).∠ (45) - 100 SHIFT (-). ∠ 0 = Hiển thị kết quả: 100∠90. Vậy L πu100cos ωt 2  =+  (V)    Chọn A Cách giải 2: Với máy FX-570ES: Bấm MODE 2 màn hình xuất hiện: CMPLX Chọn đơn vị đo góc là R (Radian): SHIFT MODE 4 Nhập máy:100 2 SHIFT (-).∠ (π/4) - 100 SHIFT (-). ∠ 0 = Hiển thị kết quả: 100∠ π 2 . Vậy L πu100cos ωt 2  =+  (V)   Chọn A Câu 4: Đoạn mạch AB có điện trở thuần, cuộn dây thuần cảm và tụ điện mắc nối tiếp. M là một điểm trên trên đoạn AB với điện áp uAM = 10cos100πt (V) và AB u10cos100tV) 2 3( π =π−    . Tìm biểu thức điện áp uAB? A. AB u202cos(100t)(V) =π B. AB u102cos100t(V) 3 π =π+    C. AB u20cos100tV) 3 (π =π+    D. AB u20cos100tV) 3 (π =π−    u1 AB X Y u2 M

DẠYKÈMQUYNHƠNOFFICIAL 35 Hướng dẫn: Cách giải 1: Với máy FX570ES: Bấm MODE 2 màn hình xuất hiện: CMPLX Chọn đơn vị đo góc là độ (D): SHIFT MODE 3 Nhập máy:10 SHIFT (-).∠ 0 + 10 3 SHIFT (-). ∠ -90 = Hiển thị kết quả : 20∠-60. Vậy AB u20cos100tV) 3 (π =π−      Chọn D Cách giải 2: Với máy FX570ES: Bấm MODE 2 màn hình xuất hiện: CMPLX Chọn đơn vị đo góc là Radian (R): SHIFT MODE 4 Nhập máy:10 SHIFT (-).∠ 0 + 10 3 SHIFT (-). ∠ (-π/2 = Hiển thị kết quả: 20∠ 3 π . Vậy AB u20cos100tV) 3 (π =π−       Chọn D C. CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Cho 3 linh kiện gồm điện trở thuần R = 60Ω, cuộn cảm thuần L và tụ điện C. Lần lượt đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch nối tiếp RL hoặc RC thì biểu thức cường độ dòng điện trong nạch lần lượt là 1 i2cos100t(A) 12 π  =π−  và 2 7 i2cos100t(A) 12 π  =π−  . Nếu đặt điện áp trên vào hai đầu đoạn mạch RLC nối tiếp thì dòng điện trong mạch có biểu thức: A. i22cos100t(A) 3 π =π+  B. i2cos100t(A) 3 π =π+  C. i22cos100t(A) 4 π =π+  D. i2cos100t(A) 4 π =π+  Câu 2: Cho đoạn mạch điện AB gồm R, L, C mắc nối tiếp với R là biến trở. Giữa AB có một điện áp 0 uUcos(ωt φ)=+ luôn ổn định. Cho R thay đổi, khi R = 42,25 Ω hoặc khi R = 29,16 Ω thì công suất tiêu thụ của đoạn mạch như nhau; khi R = R0 thì công suất tiêu thụ của đoạn mạch đạt giá trị lớn nhất, và cường độ dòng điện qua mạch πi2cos(100πt) 12 =+ (A). Điện áp u có thể có biểu thức A. 7πu140,42cos(100πt)(V) 12 =+ B. 5πu70,22cos(100πt)(V) 12 =− C. πu140,42cos(100πt)(V) 3 =− D. πu70,22cos(100πt)(V) 3 =+ Câu 3: Cho đoạn mạch điện xoay chiều AB không phân nhánh gồm một cuộn cảm thuần, một tụ điện có điện dung C thay đổi được, một điện trở hoạt động 100Ω. Giữa AB có một điện áp xoay chiều luôn ổn định πu=110cos(120πt) 3 (V). Cho C thay đổi, khi C = 125 μF 3π thì điện áp giữa hai đầu cuộn cảm có giá trị lớn nhất. Biểu thức của điện áp giữa hai đầu cuộn cảm là:

DẠYKÈMQUYNHƠNOFFICIAL 36 A. L πu=1102cos(120πt+ 6) (V). B. L πu= 220cos(120πt + )6 (V). C. L πu= 220cos(120πt + )2 (V). D. L πu= 1102cos(120πt + )2 (V). Câu 4: Đặt điện áp xoay chiều 0 πu=Ucos(120πt) 3 + vào hai đầu một cuộn cảm thuần có độ tự cảm 1 L=H. 6π Tại thời điểm điện áp giữa hai đầu cuộn cảm là 402V thì cường độ dòng điện qua cuộn cảm là 1A . Biểu thức của cường độ dòng điện qua cuộn cảm là A. πi= 32cos(120πt)A 6 B. πi= 3cos(120πt)A 6 C. πi= 22cos(120πt)A 6 + D. πi= 2cos(120πt)A 6 + Câu 5: khi đặt dòng điện áp xoay chiều vào hai đầu mạch gồm điện trở thuân R mắc nối tiếp một tụ điện C thì biểu thức dòng điện có dang: i1 = I0 cos(ωt + π 6 )(A). Mắc nối tiếp thêm vào mạch điiện cuộn dây thuần cảm L rồi mắc vào điện áp nói trên thì biểu thức dòng điện có dạng i2 = I0 cos(ωt –π 3 )(A). Biểu thức hai đầu đoạn mạch có dạng: A. u = U0 cos(ωt + π 12 )(V) B. u = U0 cos(ωt + π 4 )(V) C. u = U0 cos(ωt –π 12 )(V) D. u = U0 cos(ωt –π 4 )(V) Câu 6: Một đoạn mạch gồm cuộn cảm có độ tự cảm L và điện trở thuần r mắc nối tiếp với tụ điện có điện dung C thay đổi được. Đặt vào hai đầu mạch một hiệu điện thế xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Khi điều chỉnh để điện dung của tụ điện có giá trị C = C1 thì điện áp hiệu dụng giữa hai đầu tụ điện và hai đầu cuộn cảm có cùng giá trị và bằng U, cường độ dòng điện trong mạch khi đó có biểu thức 1 πi26cos100πt(A) 4  =+  . Khi điều chỉnh để điện dung của tụ điện có giá trị C = C2 thì điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại. Cường độ dòng điện tức thời trong mạch khi đó có biểu thức là A. 2 5πi23cos100πt(A) 12  =+  B. 2 5πi22cos100πt(A) 12  =+  C. 2 πi22cos100πt(A) 3  =+  D. 2 πi23cos100πt(A) 3  =+  Câu 7: Đặt điện áp xoay chiều có giá trị hiệu dụng 60 V vào hai đầu đoạn mạch R, L, C mắc nối tiếp thì cường độ dòng điện qua đoạn mạch là i1 = 0 Icos(100t) 4 π π+ (A). Nếu ngắt bỏ tụ điện C thì cường độ dòng điện qua đoạn mạch là 20 iIcos(100t) 12 π =π− (A). Điện áp hai đầu đoạn mạch là:

DẠYKÈMQUYNHƠNOFFICIAL 37 A. u602cos(100t) 12 π =π− (V). B. u602cos(100t) 6 π =π− (V). C. u602cos(100t) 12 π =π+ (V). D. u602cos(100t) 6 π =π+ (V). Câu 8: Cho ba linh kiện: điện trở thuần R60=Ω , cuộn cảm thuần L và tụ điện C. Lần lượt đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch nối tiếp RL hoặc RC thì biểu thức cường độ dòng điện trong mạch lần lượt là 1 i2cos(100t)(A) 12 π =π− và 2 7 i2cos(100t)(A) 12 π =π+ . Nếu đặt điện áp trên vào hai đầu đoạn mạch RLC nối tiếp thì dòng điện trong mạch có biểu thức: A. πi22cos(100πt)(A) 3 =+ B. πi2cos(100πt)(A) 3 =+ C. πi22cos(100πt)(A) 4 =+ D. πi2cos(100πt)(A) 4 =+ Câu 9: Đặt điện áp 0 uUcost 2 π  =ω−  vào hai đầu đoạn mạch chứa một điện trở thuần và một tụ điện mắc nối tiếp. Khi đó, dòng điện trong mạch có biểu thức 0 iIcost 4 π  =ω−  Mắc nối tiếp vào mạch tụ thứ hai có cùng điện dung với tụ đã cho. Khi đó, biểu thức dòng điện qua mạch là: A. ( )0 i0,63Icost0,147(A) =ω−π B. ( )0 i0,63Icost0,352(A) =ω−π C. ( )0 i1,26Icost0,147(A) =ω−π D. ( )0 i1,26Icost0,352(A) =ω−π Câu 10: Mạch điện xoay chiều chỉ có tụ điện với điện dung C. Đặt vào hai đầu tụ điện một điện áp xoay chiều có biểu thức 0 uUcos(t) =ω+ϕ V. Cường độ dòng điện tức thời của mạch có biểu thức là A. i = U0ωCsin(ωt + ϕ + π 2 ) A B. i = U0ωCcos(ωt + ϕ –π 2 ) A C. i = U0ωCcos(ωt + ϕ + π 2 ) A D. i = 0U Cω cos(ωt + ϕ + π 2 ) A Câu 11: Đặt vào giữa hai đầu một đoạn mạch điện chỉ có tụ điện có điện dung C = 410 π F một điện áp xoay chiều có biểu thức u = 200cos(100πt –π 6) V. Dòng điện xoay chiều chạy qua đoạn mạch có biểu thức A. i = 2cos(100πt + π 3) A B. i = 2cos(100πt + π 2) A C. i = 2cos(100πt + π 3) A D. i = 2cos(100πt –π 6) A

DẠYKÈMQUYNHƠNOFFICIAL 38 Câu 12: Cho đoạn mạch xoay chiều có R = 40 Ω , L = 1 π H, C = 410 0,6π F, mắc nối tiếp điện áp 2 đầu mạch u1002cos100t =π (V). Cường độ dòng điện qua mạch là: A. πi2,5cos(100πt)(A) 4 =+ B. πi2,5cos(100πt)(A) 4 =− C. πi2cos(100πt)(A) 4 =− D. πi2cos(100πt)(A) 4 =+ Câu 13: Một đoạn mạch điện gồm điện trở R = 50Ω mắc nối tiếp với cuộn thuần cảm L = 1 2π (H). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u1002cos(100t) 4 π =π− (V). Biểu thức của cường độ dòng điện qua đoạn mạch A. i = 2cos(100πt – π 2 )(A). B. i = 2 2 cos(100πt – π 4 ) (A). C. i = 2 2 cos100πt (A). D. i = 2cos100πt (A). Câu 14: Nếu đặt vào hai đầu một mạch điện chứa một điện trở thuần và một tụ điện mắc nối tiếp một điện áp xoay chiều có biểu thức πu1002cos ωt 4  =+  (V), khi đó điện áp hai đầu điện trở thuần có biểu thức R u100cosωt= (V). Biểu thức điện áp giữa hai đầu tụ điện sẽ là A. C πu100cos ωt 2  =−  (V). B. C πu1002cos ωt 4  =+  (V). C. C πu100cos ωt 4  =+  (V). D. C πu1002cos ωt 2  =+  (V). HƯỚNG DẪN GIẢI: Câu 1: Chọn C. Cách giải 1: Theo đề ( )12 0102RLRC LC φ = φ 1 IIZZ ZZ    =⇒=⇒   =  Mặt khác ( ) () ()1 12 2 1 u1 u u2 φφ = φ 2 φφ π φ 3 24φφ = φ i ii i   + ⇒==    Từ ()() ()L 1L Zπ2,3 φ 3Z603 Ω 3R ⇒=⇒=⇒= ( )001RL UIZ1202V⇒== . Khi RLCnt ⇒ cộng hưởng: i = 0U R cos(100πt + uφ ) = 2 2 cos(100πt + π 4 )(A).

DẠYKÈMQUYNHƠNOFFICIAL 39 Cách giải 2: Ta thấy cường độ hiệu dụng trong đoạn mạch RL và RC bằng nhau suy ra ZL = ZC độ lệch pha φ1 giữa u và i1 và φ2 giữa u và i2 đối nhau: tanφ1= – tanφ2 Giả sử điện áp đặt vào các đoạn mạch có dạng: u = U 2 cos(100πt + φ) (V). Khi đó φ1 = φ – (– π 12 ) = φ + π 12 , φ2 = φ –7π 12 . tanφ1 = tan(φ + π 12 ) = – tanφ2 = – tan( φ –7π 12 ) tan(φ + π 12 ) + tan( φ –7π 12 ) = 0  sin(φ + π 12 + φ –7π 12 ) = 0. Suy ra φ = π 4 ⇒ tanφ1 = tan(φ + π 12 ) = tan( π 4 + π 12 ) = tan π 3 = ZL/R ⇒ ZL = R 3 và U = I1 22 L1 RZ2RI120 +== (V). Mạch RLC có ZL = ZC ⇒ có sự cộng hưởng I = U R = 120 60 = 2 (A) và i cùng pha với u: u = U 2 cos(100πt + π 4 ) . Vậy i = 2 2 cos(100πt + π 4 ) (A). Câu 2: Chọn B. Ta có: R0 = 12 RR42,25.29,16 = = 35,1 Ω khi đó thì 0LC RZZ =− . Khi đó tính được 000 L 0 UIR22.35,170,22Ω ZZ 5π tanφ = R12   ===     =    Suy ra: 5πu70,22cos(100πt)(V) 12 =− . Câu 3: Chọn B. Khi thay đổi c để ULmax thì LCZZ = ,tù đó sua ra U0L = I0R = 220V. Mà khi đó thì u,i cùng pha, từ đó suy ra uL ππ φ 32 =+ = π 6 Suy ra: L πu= 220cos(120πt + )6 (V). Câu 4: Chọn B. Áp dụng công thức độc lập: 1 I i U u 2 0 2 2 0 2 +=  2 0 2 2 L 2 iI Z u +=  I0 = 3A φi = 326 π = ππ . Suy ra: πi= 3cos(120πt)A 6 Câu 5: Chọn C. Giả sử u = U0 cos(ωt + ϕ). Gọi ϕ1; ϕ2 góc lệch pha giữa u và i1; i2. Ta có: tanϕ1 = CZ R = tan(ϕ –π 6 ); tanϕ2 = LCZZ R = tan(ϕ + π 3 ).

DẠYKÈMQUYNHƠNOFFICIAL 40 Mặt khác cường độ dòng điện cực đại trong hai trường hợp như nhau, nên Z1 = Z2  ZC 2 = (ZL – ZC)2  ZL = 2ZC . Vì vậy: tanϕ2 = LCZZ R = CZ R = tan(ϕ + π 3 )  tan(ϕ –π 6 ) = – tan(ϕ + π 3 )  tan(ϕ –π 6 ) + tan(ϕ + π 3 ) = 0  sin(ϕ –π 6 + ϕ + π 3 ) = 0  ϕ –π 6 + ϕ + π 3 = 0  ϕ = –π 12 . Suy ra: u = U0 cos(ωt –π 12 )(V). Câu 6: Chọn B. Khi C = C1 , UD = UC = U  Zd = ZC1 = Z1 Zd = Z1  22 LC1 r(ZZ) +− = 22 LrZ +  ZL – ZC1 = ± ZL  ZL = C1Z 2 (1) Zd = ZC1  r2 + ZL 2 = ZC1 2  r2 = 2 C13Z 4  r = 2 C13Z 2 (2) tanϕ1 = C1 C1 LC1 C1 Z ZZZ21 r 33 Z 2 ==−  ϕ1 = π 6 Khi C = C2 UC = UCmax khi ZC2 = 222 LC1 C1 LC1 ZrZ 2Z ZZ 2 + == Khi đóZ2 = 22222 1 LC2C1C1C1C1 3Zc r(ZZ)Z(2Z)3Z3Z 42 +−=+−== tanϕ2 = C1 C1 LC2 C1 Z ZZ2Z 2 3 r 3 Z 2 ==−  ϕ2 = π 3 U=I1Z1 =I2Z2  I2 =I1 11 2 ZI23 2 Z33 === (A) Cường độ dòng điện qua mạch: i2 = I2 22 πππ 5πiI2cos(100πt)22cos(100πt)46312 =+−+=+ (A). Câu 7: Chọn C. Cách giải 1: Gọi biểu thức của u = Uocos(100πt+ φ) Ta thấy : I1 = I2 suy ra Z1 = Z2 hay C LCLL Z ZZZZ 2 −= == . Lúc đầu: LC L 1 ZZZ tan RRϕ==− ⇒ i1 = Io cos(100πt+ φ + φ1) ⇒ φ + φ1 = 4 π .

DẠYKÈMQUYNHƠNOFFICIAL 41 Lúc sau: L 2 Z tan φ R = ⇒ i2 = Io cos(100πt+ φ – φ2 ) ⇒ φ – φ2 = –12 π . Mà 12φφ = ⇒ φ = 12 π . Vậy u602cos(100t) 12 π =π+ (V).   Chọn C Cách giải 2: Ta thấy I1 = I2 ⇒ (ZL – ZC)2 = ZL 2 ⇒ ZC = 2ZL LC L 1 ZZZ tan RRϕ==− (*)tanϕ1 = R Z L (**) ⇒ ϕ1 + ϕ2 = 0. ϕ1 = ϕu –4 π ; ϕ2 = ϕu + 12 π ⇒ 2ϕu 4 π + 12 π = 0 ⇒ ϕu = 12 π Do đó u602cos(100t) 12 π =π+ (V). Câu 8: Chọn A. Pha ban đầu của i: CL 23 ϕ−ϕ π ϕ==  01 0 I I cos = ϕ =22 . Suy ra: πi22cos(100πt)(A) 3 =+ . Chú ý: Ta có thể mở rộng bài toán này như sau: Mắc mạch RL vào hiệu điện thế u thì dòng điện là i1 = I0 cos(ωt + ϕL). Mắc mạch RC vào hiệu điện thế u thì dòng điện là i2 = I0 cos(ωt + ϕC). Mắc mạch RLC vào hiệu điện thế u thì dòng điện là i = ' 0I cos(ωt + ϕ). Ta luôn có mối quan hệ: (vẽ giản đồ hoặc sử dụng công thức tanϕta dễ dàng chứng minh được): CL LC ' 0 0 2 ZZRtan I I cos ϕ=ϕ−ϕ   ==ϕ   = ϕ  . Vậy bài toán này trong mạch RLC ta có thể tính và viết được biểu thức của: R, L, C, u, i, P ... Câu 9: Chọn A.Ta có: 00C uUcostiIcostRZ 24 ππ  =ω−  =ω−  =  . Mắc thêm tụ nữa thì 020020 C2C 2I0,63III Z2Z5 φ 0,417π tan φ 2  == =  = = Vậy: ( )0 i0,63Icost0,147(A) =ω−π Câu 10: Chọn B. Với đoạn mạch chỉ có tụ C thì 0 00 C iu U U2 IUC 1Z C 22  ===ω   ω  ππϕ=ϕ+=ϕ+  i = U0ωCcost 2 π  ω+ϕ−   A.

DẠYKÈMQUYNHƠNOFFICIAL 42 Câu 11: Chọn A. Dung kháng của mạch là ZC = 4 11 C10 100. π = ω π = 100 Ω. Với đoạn mạch chỉ có tụ C thì 0 0 C iu U 200 I2A Z100 2623  ===   ππππϕ=ϕ+=−+=   i = 2cos(100πt + π 3) A . Câu 12: Chọn B. Ta có: L 1 ZL.100π 100 =ω==Ω π ; C 4 11 Z 10.C 100. 0,6π == ω π = 60 Ω Và ZL – ZC = 40 Ω . Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX. Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r∠θ ) Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D Ta có : 0u LC U φiu ZR(ZZ)i ∠ == +− 10020 4040 ∠ = + . i Nhập 100 2 SHIFT (-) 0 : ( 40 + 40 ENG i ) = Hiển thị: 2,5∠-45 Biểu thức tức thời cường độ dòng điện qua mạch là: i = 2,5cos(100πt – π 4 ) (A). Câu 13: Chọn A. Ta có : L 0,5 ZL10050 =ω=π=Ω π và ZL – ZC = 50 Ω – 0 = 50 Ω Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX. Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r∠θ ) Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D Ta có : 0u L U φiu ZRZ ∠ == + i 100245 5050 ∠− = + i Nhập 100 2 SHIFT (-) - 45 : ( 50 + 50 ENG i ) = Hiển thị: 2∠- 90 Biểu thức tức thời cường độ dòng điện qua mạch là: i = 2cos( 100πt – π 2 ) (A). Câu 14: Chọn A. Cách giải 1: Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX Chọn đơn vị đo góc là độ (D): SHIFT MODE 3 Nhập máy:100 2 SHIFT (-).∠ (-45) - 100 SHIFT (-). ∠ 0 = Hiển thị kết quả : 100∠-90. Vậy C πu100cos ωt 2  =−  (V) Cách giải 2: Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX Chọn đơn vị đo góc là Radian(R): SHIFT MODE 4 Nhập máy:100 2 SHIFT (-).∠ (-π/4) - 100 SHIFT (-). ∠ 0 = Hiển thị kết quả: 100∠ π 2 . Vậy C πu100cos ωt 2  =−  (V).

DẠYKÈMQUYNHƠNOFFICIAL 43 CHỦ ĐỀ 3 GIÁ TRỊ TỨC THỜI CỦA ĐIỆN ÁP VÀ DÒNG ĐIỆN A. TÓM TẮT LÝ THUYẾT CƠ BẢN + Cường độ dòng điện trong mạch: 0i iIcos(t) =ω+ϕ + Hiệu điện thế hai đầu điện trở : () () R R ui R0Ru0Ri uUcostUcost ϕ=ϕ   =ω+ϕ=ω+ϕ  + Hiệu điện thế hai đầu cuộn cảm thuần: () () L L ui L0Lu0Li0Li 2 uUcostUcostUsint 2 π ϕ=ϕ+   π  =ω+ϕ=ω+ϕ+=−ω+ϕ   + Hiệu điện thế hai đầu tụ điện : () () C C ui C0Cu0Ci0Ci 2 uUcostUcostUsint 2 π ϕ=ϕ−   π  =ω+ϕ=ω+ϕ−=ω+ϕ   Biểu diễn cả bốn hàm RLCi; u; u; u trên cùng một đường tròn lượng giác như sau: + Cường độ dòng điện trong mạch: 0i iIcos(t) =ω+ϕ là hàm cosin  cùng chiều trục cosin có chiều (+) từ trái sang phải với biên độ là max0iI = + Hiệu điện thế hai đầu điện trở: ( )R0RiuUcos ωt φ=+ là hàm cosin  cùng chiều trục cosin có chiều (+) từ trái sang phải với biên độ là R max0RuU = + Hiệu điện thế hai đầu cuộn cảm thuần: ( )L0Li uUsint=−ω+ϕ làhàmtrừ sin  ngượcchiều trụcsinnêncóchiều(+)hướngtừ trênxuốngvớibiên độ Lmax0LuU = . Pha L ui π φφ 2 =+ + Hiệu điện thế hai đầu tụ : ( )C0Ci uUsint=ω+ϕ là hàm sin  cùng chiều trục sin nên có chiều (+) hướng từ dưới lên với biên độ Cmax0CuU = . Pha C ui π φφ 2 =− Trong các đề thi ĐH và CĐ thường cho dạng trắc nghiệm xác định các giá trị tức thời của điện áp hoặc dòng điện trong mạch điện xoay chiều. Dạng này có nhiều cách giải. Sau đây là 3 cách thông thường. Xét ví dụ điển hình sau: O Lu Cu Ru i

DẠYKÈMQUYNHƠNOFFICIAL 44 Câu 1: Đặt điện áp xoay chiều có u = 100 2 cosωt (V) vào hai đầu đoạn mạch gồm điện trở R nối tiếp với tụ điện C có ZC = R. Tại thời điểm điện áp tức thời trên điện trở là 50V và đang tăng thì điện áp tức thời trên tụ là: A. – 50V. B. – 50 3V. C. 50V. D. 50 3V. Hướng dẫn: Cách giải 1: Dùng phương pháp đại số: R = ZC  UR = UC. Ta có: U2 = UR 2 + Uc 2 = 2UR 2  UR = 50 2 V = UC. Mặt khác: CZ tanφ = R = 1  π = 4ϕ− . Suy ra pha của i là ( π ωt+ 4 ). Xét đoạn chứa R: uR = U0Rcos( π ωt+ 4 ) = 50  cos( π ωt+ 4 ) = 2 1 . Vì uR đang tăng nên u'R > 0 suy ra sin( π ωt+ 4 ) < 0  sin( π ωt+ 4 ) = – 2 3 (1) và uC = U0Ccos( π ωt+ 4 –π 2 ) = U0Csin( π ωt+ 4 ) (2) Thế U0C = 100V và thế (1) vào (2) ta có uC = – 50 3V.    Chọn B Cách giải 2: Dùng phương trình lượng giác Do ZC = R  uR = 100cos( π ωt+ 4 ) V; uC = 100cos ( t 4 π ω− ) V Theo đề: uR =50V  100cos( π ωt+ 4 ) = 50  cos( π ωt+ 4 ) = 1 2  ( π ωt+ 4 ) = 3 π + k2π. (do đang tăng)  ωt = 3 π 4 π + k2π = 7 12 π + k2π. Ta có: uC = 100cos( t 4 π ω− ) = 100cos( 7 12 π 4 π + k2π ) = 100cos( 5 6 π + k2π) = 3 100503V 2 −=− . Cách giải 3: Dùng giản đồ vectơ uR =100cos( π ωt+ 4 ) (V) uC = 100cos( t 4 π ω− ) (V) Các vectơ tại thời điểm t: điện áp tức thời trên điện trở là 50V. Véctơ 0RU hợp với trục ngang u một góc 3 π . Do 0CU chậm pha 2 π so với véctơ 0RU nên nó hợp với trục ngang u một góc: 5 236 πππ −−=− π/3π/6 0RU 0CU 0U 50503 u(V)

DẠYKÈMQUYNHƠNOFFICIAL 45 Dễ thấy: uC = 100cos( 5 6 π ) = – 50 3V. Do ZC = R nên 0U chậm pha 4 π so với véc tơ 0RU , nên nó hợp với trục ngang u một góc: 7 3412 πππ −−=− . Suy ra uC = 100 2 cos( 7 12 π ) =5050336,6V −=− .  Chọn B Cách giải 4: Sử dụng vòng tròn lượng giác Từ ZC = R  U0C = U0R = 0U 1002 100V 22 == 2222 RRCC RC 2222 0R0C0C0C 2222 C0CR uuuu uu11 UUUU uUu10050503V ⊥  +=⇔+=  =±−=±−=± Dựa vào hình vẽ dễ dàng có được C u503V =−  Chọn B Cách giải 5: Áp dụng hệ thức độc lập (công thức vuông pha): Từ ZC = R  U0C = U0R = 100V mà Ru 50 i RR == còn 0 0 U I R = Áp dụng hệ thức độc lập trong đoạn chứa tụ C: 2 R 22 2 CC 2222C 0C0 0 u uu i R 11u503V UI100 U R    +=⇔+=  =±    vì đang tăng nên chọn C u503V =− .  Chọn B Nhận xét: Với cách giải bằng vòng tròn lượng giác, thời gian tìm ra đáp án ngắn hơn nhiều với việc chỉ cần nhớ nhanh các giá trị đặc biệt của hàm cos và sin thôi. Cách giải theo phương trình lượng giác cũng không khó gì nhưng phải viết nhiều phương trình nên hơi mất thời gian. Cách giải bằng vòng tròn lượng giác được áp dụng rất nhiều trong các chương có phương trình dao động điều hòa vì thế tôi khuyên các bạn nên có gắn học để nắm rõ phương pháp này. Từ ví dụ trên ta thấy dùng vòng tròn lượng giác hoặc dùng các công thức vuông pha sẽ giải nhanh hơn. I. Dùng giản đồ vectơ hay phương pháp đường tròn lượng giác: + Ta xét: ( )0 uUcost=ω+ϕ được biểu diễn bằng OM quay quanh vòng tròn tâm O bán kính U0, quay ngược chiều kim đồng hồ với tốc độ góc ω. + Có 2 điểm M, N chuyển động tròn đều có hình chiếu lên Ou là u, thì: - N có hình chiếu lên Ou lúc u đang tăng (thì chọn góc âm phía dưới), α-U0 OuU0 u N α M O Lu Cu Ru100 i 50 503Cu =− Ru ↑ Ru ↓100

DẠYKÈMQUYNHƠNOFFICIAL 46 - M có hình chiếu lên Ou lúc u đang giảm (thì chọn góc dương phía trên)  vào thời điểm t ta xét điện áp u có giá trị u và đang biến đổi : - Nếu u theo chiều âm (đang giảm)  ta chọn M rồi tính góc 0α UOM= - Nếu u theo chiều dương (đang tăng) ta chọn N và tính góc 0α UON=− . Câu 1: (Tìm khoảng thời gian ngắn nhất để điện áp biến thiên từ giá trị u1 đến u2) Đặt vào hai đầu đoạn mạch RLC một điện áp xoay chiều có phương trình: u2202cos100t (V)=π . Tính thời gian từ thời điểm u = 0 đến khi u = 1102 (V). Hướng dẫn: Cách giải 1: Chọn lại gốc thời gian: t = 0 lúc u = 0 và đang tăng, ta có phương trình mới: u2202cos100t (V)2 π  =π−  và u’ > 0. Khi u =110 2 V lần đầu ta có: 1 cos100t 2 π= và sin100t0 2 π π−<  . Giải hệ hương trình ta được t = 1 600 (s). Cách giải 2: Dùng phương pháp giản đồ véctơ (Hình vẽ vòng tròn lượng giác) Thời gian từ thời điểm u = 0 đến khi u = 1102 (V) lần đầu tiên: π α 16Δts ω 100π 600 === .Hay: α 301 Δts ω 180.100π 600 === π . Câu 2: (Tìm khoảng thời gian ngắn nhất để dòng điện biến thiên từ giá trị i1 đến i2) Cường độ dòng điện xoay chiều qua mạch là 0 πiIcos100πt(A) 6  =−  , với 0I 0> và t tính bằng giây. Tính từ lúc 0s, xác định thời điểm đầu tiên mà dòng điện có cường độ tức thời bằng cường độ hiệu dụng ? Hướng dẫn: Cách giải 1: Ta sử dụng tính chất hình chiếu của một chất điểm chuyển động tròn đều lên một đường thẳng nằm trong mặt phẳng quỹ đạo là một dao động điều hoà với cùng chu kì để giải bài toán này. Thời gian ngắn nhất để 0 I3 i 2 = đến i = I0 ( cung MoQ) rồi từ i = I0 đến vị trí có 0I iI 2 == (từ P đến D) bằng thời gian vật chuyển động tròn đều với cùng chu kì đi từ Mo đến P rồi từ P đến Q theo cung tròn 0 MPQ Ta có góc quay ππ 5π α 6412 =+= . Tần số góc của dòng điện ω = 100π rad/s. Suy ra chu kỳ T = 0,02 s. Thời gian quay: TT1 ts 128240 =+= hay 5π 5π 1 ts 12ω 12.100π 240 === . M uu N π/6 1102 O Mo O i + α I00 2 I P Q(C) D

DẠYKÈMQUYNHƠNOFFICIAL 47 Cách giải 2: Dùng sơ đồ thời gian: Thời gian ngắn nhất để 0 I3 i 2 = đến i = I0 là : 1 T t 12 = Thời gian ngắn nhất để i = I0 đến 0I iI 2 == là: 2 T t 8 = . Vậy 12 TT1 ttts 128240 =+=+= Câu 3: (Xác định cường độ dòng điện tức thời) Đặt vào hai đầu tụ có điện dung 310 CF 5 = π một điện áp có dạng u1502cos100t(V) =π . Tính cường độ dòng điện khi điện áp bằng 75 2 (V). Hướng dẫn: Cách giải 1: Ta có: C 3 0 0 C 11 Z50 C10 100. 5 U 1502 I32A Z50  ===Ω ω π π  ===   Phương trình cường độ dòng điện tức thời: i32sin100t(A) =−π Khi u = 75 2  2 13 costsint1cost 22 ω=  ω=±−ω=±  336 i32.A. 22  =±=±    Cách giải 2: Từ công thức 2222 2222 0 22C0 2 00 C uiUu 1uiZUi UIZ +=⇔+=  = 136.756A. 502 =±=± Câu 4: Cho dòng điện xoay chiều ( ) i4cos20t(A) =π . Ở thời điểm t1 dòng điện có cường độ i = i1 = -2A và đang giảm, hỏi ở thời điểm t2 = t1 + 0,025s thì i = i2 = ? Hướng dẫn: Cách giải 1: Tính ∆ϕ = ω ∆t = 20π.0,025 = 2 π (rad)  i2 vuông pha i1 22222 1222 ii4 2i16 i23(A) +=  +=  =± Vì i1 đang giảm nên chọn i2 = - 2 3(A). iI0O I0/2 0 I3 2 0I 2 - I0 T/8 T/12

DẠYKÈMQUYNHƠNOFFICIAL 48 Cách giải 2: Bấm máy tính Fx 570ES với chú ý: 4SHIFTMODE : đơn vị góc là Rad. Bấm nhập máy tính: 2 4 cosshift cos23 42  −π +=−    2 i23(A) =− . Chú ý: Xác định cường độ dòng điện tức thời: Ở thời điểm t1 cho i = i1, hỏi ở thời điểm t2 = t1 + ∆t thì i = i2 = ? (Hoặc Ở thời điểm t1 cho u = u1, hỏi ở thời điểm t2 = t1 + ∆t thì u = u2 = ?) Phương pháp giải nhanh: Về cơ bản giống cách giải nhanh của dao động điều hòa. * Tính độ lệch pha giữa i1 và i2 : ∆ϕ= ω∆ t hoặc: Tính độ lệch pha giữa u1 và u2 : ∆ϕ= ω∆ t * Xét độ lệch pha: + Nếu (đặc biệt) i2 và i1 cùng pha  i2 = i1 i2 và i1 ngược pha  i2 = - i1 i2 và i1 vuông pha  222 120 iiI += . + Nếu ∆ϕbất kỳ: dùng máy tính : 1 20 0 i iI cosshift cos I   =±+∆ϕ     * Quy ước dấu trước shift: dấu (+) nếu i1 dấu ( – ) nếu i1 ↑ Nếu đề không nói đang tăng hay đang giảm, ta lấy dấu (+) Câu 5 (ĐH 2010): Tại thời điểmt nào đó,một điện ápxoaychiều u2002cos100t(V) 2 π  =π−  đang có giátrị 1002 (V) và đang giảm.Sau thời điểm đó 1 s 300 , điện áp này có giá trị là bao nhiêu? Hướng dẫn: Cách giải 1: ∆ϕ = ω∆t = 100π. 1 300 = 3 π rad. Vậy độ lệch pha giữa u1 và u2 là 3 π . Vẽ vòng tròn lượng giác sẽ thấy: Với u1 =1002 V thì u2 = -1002 V Cách giải 2: Bấm máy tính Fx 570ES với chú ý: 4SHIFTMODE : đơn vị góc là Rad: Bấm nhập máy tính: 1002 2002 cosshift cos141(V)1002(V) 32002   π +≈−≈−      . Câu 6 (CĐ 2013): Điện áp ở hai đầu một đoạn mạch là u = 160cos100πt (V) (t tính bằng giây). Tại thời điểm t1, điện áp ở hai đầu đoạn mạch có giá trị là 80V và đang giảm. Đến thời điểm t2 = t1 + 0,015s, điện áp ở hai đầu đoạn mạch có giá trị bằng A. 403V B. 803 V C. 40V D. 80V π/3 10021002

DẠYKÈMQUYNHƠNOFFICIAL 49 Hướng dẫn: Cách giải 1: Ta có: cos100πt1 = 1 0 u U = 1 2 = cos(± π 3 ). u đang giảm nên 100πt1 = π 3  t1 = 1 300 s. Tại thời điểm t2 = t1+ 0,015 s = 5,5 300 s  u2 = 160cos100πt2 = 160cos 5,5 3 π = 3 160 2 =803 (V).    Chọn B Cách giải 2: Ta có: t2 = t1 + 0,015s = t1+ 3T 4 . Với 3T 4 ứng góc quay 3π 2 . Nhìn hình vẽ thời gian quay 3T 4 (ứng góc quay 3π 2 ). M2 chiếu xuống trục u  u = 803 V. T0,02s0,015s23T 1004 π ==  = π 2 3 u160cos160.803V. 62 π === Chọn B Cách giải 3: ∆ϕ = ω∆t = 100π.0,015 = 1,5π (rad). Độ lệch pha giữa u1 và u2 là 3π 2 Bấm máy tính Fx 570ES với chú ý: 4SHIFTMODE : đơn vị góc là Rad. Bấm nhập máy tính: 803 160shiftcos803V. 1602 π  +=     Chọn B Câu 7: Tại thời điểm t, điện áp u = 200 2 cos(100 π πt 2 ) (trong đó u tính bằng V, t tính bằng s) có giá trị 100 2 V và đang tăng. Sau thời điểm đó 1 s 600 , điện áp này có giá trị A. 1006 V B. 1006 V C. 1002 V D. 100V. Hướng dẫn: Chu kỳ: 221 T(s) 10050 ππ === ωπ u(V) 2t 3 2 π160 M2 O + π/3 80 803 16 0 M1 3π/2 t1

DẠYKÈMQUYNHƠNOFFICIAL 50 Theo bài ra: 0 0 1 t1T 600 t 1 T1212 50 Uu10021 u U22 2002   ∆ ==  ∆=     ==  =  Tại thời điểm t: 0U u 2 =↑ sau đó T Δt 12 = : 0 U3 2002.3 u1006V 22 =↑== Chọn A Câu 8 (Sư phạm Hà Nội lần 1 năm 2013): Cường độ dòng điện tức thời chạy qua một đoạn mạch xoay chiều là ( )i2cos100πt A,= t đo bằng giây. Tại thời điểm 1t , dòng điện đang giảm và có cường độ bằng 1A. Đến thời điểm 1 tt0,005s =+ cường độ dòng điện bằng. A. 3A. B. 2A . C. 3A. D. 2A . Hướng dẫn: Tại thời điểm 1t ta có 1 π φ 3 = . Tại thời điểm 2t ta có π i2cos100π.0,0053A 3  =+=−   .    Chọn A Câu 9: Điện áp giữa hai bản tụ điện có biểu thức 0 πuUcos100πt 3  =−  (V). Xác định các thời điểm mà cường độ dòng điện qua tụ bằng 0 ? Hướng dẫn: Giá trị của cường độ dòng điện trong mạch xem như là tọa độ của hình chiếu của một vật chuyển động tròn đều lên trục 0i. Cường độ dòng điện có giá trị i = 0 khi vật chuyển động tròn đi qua điểm M1 và M2. Góc quay được: 1k 100tk2t 330050 44k 100tk2t 330050 π π=+π=+    π π=+π=+  Câu 10: Điện áp giữa hai bản tụ có biểu thức: 0 πuUcos100πt 3  =−  (V). Xác định các thời điểm mà cường độ dòng điện qua tụ điện có giá trị bằng giá trị cường độ dòng điện hiệu dụng và đang giảm. M2 M (t = M0) 1 -U0C O U0C i I0-I0 O Lu Cu u 0U 0 2 U u =↑ 0 2 U u =↓ 0 3 2 U u =↑

DẠYKÈMQUYNHƠNOFFICIAL 51 Hướng dẫn: Giá trị của cường độ dòng điện trong mạch xem như là tọa độ của hình chiếu của một vật chuyển động tròn đều lên trục 0i. Cường độ dòng điện của tụ có giá trị bằng giá trị cường độ dòng điện hiệu dụng và đang giảm tương ứng vật chuyển động tròn đều ở điểm M. 0 i 1 π cos αα I4 2 ==  = Các thời điểm mà cường độ dòng điện qua tụ điện có giátrị bằngcường độ dòng điệnhiệudụngvà đanggiảm: 1k 100tk2t(s) 34120050 ππ π=−+π  =+ với k0;1;2... = Câu 11: Điện áp giữa hai bản tụ có biểu thức: 0 πuUcos100πt 3  =−  (V) (t tính bằng s). Xác định thời điểm mà điện áp giữa hai bản tụ có giá trị bằng 1 2 giá trị điện áp cực đại và đang giảm lần thứ 2017. Hướng dẫn: Giá trị của điện áp giữa hai bản tụ có giá trị bằng 1 2 giá trị điện áp cực đại và đang giảm tương ứng vật chuyển động tròn đều ở vị trí M. 0 u 1 cos U23 π α==  α= Thời điểm điện áp giứa hai bản tụ có giá trị bằng 1 2 giá trị điện áp cực đại và đang giảm lần thứ 2017 khi bán kính OM quay được 2016 vòng và quay thêm một góc 2 3 π . Ta có: 2120986049 100t2016.2ts. 33150 ππ π=π+=  = Câu 12: Điện áp giữa hai bản tụ có biểu thức: 0 πuUcos100πt 3  =−  (V), (t tính bằng s). Xác định khoảng thời gian ngắn nhất từ lúc cường độ dòng điện trong mạch có giá trị bằng cường độ dòng điện hiệu dụng đến lúc điện áp giữa hai bản tụ có giá trị bằng giá trị điện áp hiệu dụng. Hướng dẫn: Khoảng thời gian ngắn nhất từ lúc cường độ dòng điện trong mạch có giá trị bằng cường độ dòng điện hiệu dụng đến lúc điện áp giữa hai bản tụ có giá trị bằng giá trị điện áp hiệu dụng khi vật chuyển động tròn đều đi từ M1 đến M2 với thời gian nhỏ nhất. π/3 M t = 0 α 0 I/2 -U0C O -uc U0 C i I0I0 α t = 0 U0/2 M -U0C O -uc U0C iI0-I0

DẠYKÈMQUYNHƠNOFFICIAL 52 00 iu 1 cos IU4 2 π α===  α= . Bán kính quay được góc 2 π : minmin 1 100tts 2200 π π=  = . Câu 13: Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u2202cos π100πt 6  =   (V). Thời gian ngắn nhất từ thời điểm ban đầu đến khi điện áp tức thời có giá trị 110 2 V và đang tăng là: A. 1 120 s. B. 200 1 s. C. 11 300 s. D. 11 600 s. Hướng dẫn: Theo bài ra ta có vòng tròn lượng giác sau: tại t = 0: 0 U3 u 2 =↑ tại t = tmin : 0U u 2 =↑ Thời gian ngắn nhất: 00 min U3U uu 22 T3TT11T11 t 1241212600(s). =↑→=↑    ∆=++==   Chọn D Câu 14: Trong một đoạn mạch xoay chiều có RLC mắc nối tiếp, tần số dòng điện là 50Hz. Tại một thời điểm điện áp hai đầu cuộn cảm thuần có độ lớn bằng một nửa biện độ của nó và đang giảm dần. Sau khoảng thời gian ngắn nhất là bao nhiêu thì điện áp giữa hai bản tụ điện có độ lớn cực đại? A. 1 ts 150 ∆= B. 1 ts 300 ∆= C. 1 ts 600 ∆= D. 1 ts 100 ∆= Hướng dẫn: Theo bài ra ta có vòng tròn lượng giác sau. 0L 0C LC0C CC0C minmin U uuUU3uuU 2 2 tt TTT1 1243150(s).  =↓→= =−↑→=    ∆=∆ =+==   Chọn A M2 0 U/2 M1 0 I/2 π/4 -U0C O -uc U0C i I0-I0 O 0U u 0 3 2 U u =↑ 0 2 U u =↑ O u Cu Ru i 0CC Uu = 0 0 2 3 2 L C L C U U u u  =↓    =−↑ 

DẠYKÈMQUYNHƠNOFFICIAL 53 Câu 15: Điện áp giữa hai bản tụ có biểu thức: 0 πuUcos100πt 3  =−  (V), (t tính bằng s). Trong một chu kì khoảng thời gian cường độ dòng điện qua tụ điện có giá trị độ lớn lớn hơn 1 2 giá trị cường độ dòng điện cực đại là bao nhiêu? Hướng dẫn: Trong một chu kì khoảng thời gian cường độ dòng điện qua tụ điện có độ lớn lớn hơn 1 2 giá trị cường độ dòng điện cực đại khi vật chuyển động tròn đều đi từ M1 đến M2 và 1 M' đến 2 M': 0 i 1 cos I23 π α==  α= Trong chu kì bán kính quay được góc: 44 100tts 3300 π π=  = . Câu 16: Điện áp giữa hai bản tụ có biểu thức: 0 πuUcos100πt 3  =−  (V). Trong khoảng thời gian 2013 300(s) tính từ thời điểm t = 0, cường độ dòng điện qua tụ điện có giá trị bằng giá trị cường độ dòng điện hiệu dụng bao nhiêu lần? Hướng dẫn: Thời điểm cường độ dòng điện có giá trị bằng cường độ dòng điện hiệu dụng khi vật chuyển động tròn đều ở vị trí M1 và M2 0 i 1 cos I4 2 π α==  α= Bán kính OM quay được góc trong thời gian 2013 (s)300 là: 2013 t100671335.2 300 ω=π=π=π+π . Vậy trong thời gian 2013 300(s) bán kính OM quay được 335 vòng và quay thêm được góc π. Mỗi vòng bán kính qua vị trí cường độ dòng điện có giá trị bằng giá trị hiệu dụng là 2 lần. Từ hình vẽ ta thấy được cường độ dòng điện có giá trị bằng giá trị hiệu dụng trong khoảng thời gian 2013 (s) 300 là 671 lần. Câu 17: Đặt điện áp: ( )0 uU2cos100πt V= vào hai đầu một mạch điện xoay chiều gồm cuộn dây thuần cảm độ tự cảm L = 0,5π H mắc nối tiếp với tụ điện có điện dung 410 CF = π . Tại thời điểm t, cường độ dòng điện và điện áp qua mạch là i = 2A; u = 200V. Giá trị của U là: A. ≈158V. B. ≈210V. C. ≈224V. D. ≈180V. M1 M’2 M’1M2 α -U0C O -uc U0C i I0-I0 N M2 t = 0 M1 α α -U0C O -uc,q U0C i I0-I0

DẠYKÈMQUYNHƠNOFFICIAL 54 Hướng dẫn: Ta có: L C 4 ZL100.0,550 11 Z100 C10 100. =ω=ππ=Ω   ===Ω ω π π Tổng trở của đoạn mạch: ()2 LC ZZZ50. =−=Ω Ta thấy ZC > ZL nên uLC = uL + uC cùng pha với uC. Từ hình vẽ ta thấy: u200 sin U2U2 iiZ2.50100 cos I2U2U2U2  α==    α====  Thay vào công thức: sin2α + cos2α = 1 22 200100 1U5010158V. U2U2   +=  =≈    Chọn A Câu 18: Cho mạch điện xoay chiều gồm điện trở thuần R, cuộn dây thuần cảm L và tụ điện C = 310 π F mắc nối tiếp. Biểu thức điện áp giữa hai bản tụ điện là 3u502cos100t 4 π  =π−  (V). Cường độ dòng điện trong mạch khi t = 0,01(s) là A. +5A. B. - 5A. C. -5 2 A. D. +5 2 A. Hướng dẫn: Muốn tìm cường độ dòng điện tại một thời điểm cụ thể nào đó thì việc làm bắt buộc là phải viết được phương trình của cường độ dòng điện sau đó chỉ cần thay t vào phương trình là có ngay đáp án. Dung kháng của tụ điện: C 3 11 Z10. 10ωC100π. π ===Ω Biểu thức cường độ dòng điện trong mạch (nhanh pha hơn điện áp hai đầu tụ một góc 2 π ): C 0C u C U 5023 icostcos100t(A) Z21042 πππ  =ω+ϕ+=π−+   Hay i52cos100t(A) 4 π  =π−  Khit=0,01(s)thìcường độ dòng điệntrongmạch: 2 i52cos100.0,01(A)52cos52.5A. 442 ππ  =π−=π−=−=−    Chọn B α α I0 uLC t i 2O 20 U0

DẠYKÈMQUYNHƠNOFFICIAL 55 2. Dòng điện xoay chiều i = I0cos(2π ππ πft + ϕ ϕϕi). Số lần dòng điện đổi chiều sau khoảng thời gian t. * Mỗigiây đổichiều2flần. * Số lần đổichiềusaukhoảngthờigiant:2tflần. * Nếuphaban đầu ϕi = π 2 ± thìtrongmộtchukỳ dòng điện đổichiều(2f–1)lần. * Nếuphaban đầu ϕi π 2 ≠± thìtrongmộtchukỳ dòng điện đổichiều2flần. Câu 1: Cho dòng điện xoay chiều có cường độ π i10cos120tA 2 =π+  chạy qua một đoạn mạch điện.Số lầnmạch điện đổichiềutrong1slà A.100lần B.60lần C.119lần D.120lần Hướng dẫn: Vì ϕi = π 2 + vàf=60Hz  Số lầnmạch điện đổichiềutrong1slà: ( ) ( ) N2f12.601119 =−=−= lần. Chọn C Câu 2: Cho dòng điện xoay chiều có cường độ π i4cos100tA 3 =π+  chạy qua một đoạn mạch điện.Số lầnmạch điện đổichiềutrong1slà A.99lần B.400lần C.100lần D.50lần Hướng dẫn: Vì ϕi = ππ 32 +≠± vàf=50Hz  Số lầnmạch điện đổichiềutrong1slà: N2f2.50100 === lần.  Chọn C Câu 3: Cho dòng điện xoay chiều có cường độ π i2cos100tA 2 =π+  chạy qua một đoạn mạch điện.Số lầndòng điệncó độ lớn1Atrong1slà A.200lần B.400lần C.100lần D.50lần Hướng dẫn: Ta sẽ đi tìm số lần dòng điện có có độ lớn 1A trong 1s. Số chu kỳ có trong 1s là 1 =N T  Số lần dòng điện có độ lớn trong 1s. Độ lớncủadòng điệnxoaychiều: i1i1A. =  =± Khi i0 t0 v0 = =   > 0 Lần1Lần4 Lần3 Lần2 t=0 -2 2-1 1

- Thờigian đènsáng:

U4 tarccos U =

* Trong khoảng thời gian t = nT:

- Thờigian đènsáng: ss tnt =∆

- Thờigian đènt

tnttt =∆=−

DẠYKÈMQUYNHƠNOFFICIAL 56 Từ sơ đồ nhậnthấy,trongmộtchukỳ dòng điệncó độ lớn1Alà4lần. Số chukỳ trong1s: 11 N50 T0,02 === chukỳ Số lầndòng điệncó độ lớn1Atrong1slà: N4.50200 == lần.  Chọn A 3. Công thức tính thời gian đèn huỳnh quang sáng trong một chu kỳ Khi đặt điệnápu=U0cos(ωt+ ϕu)vàohai đầubóng đèn,biết đènchỉ sánglênkhi u ≥ U1.Gọi Δt làkhoảngthờigian đènsángtrongmộtchukỳ 4Δφt ω ∆= với 10φ MOU∆= ; 1 0 U cos φ U ∆= , (0< ∆ϕ < π 2 ) - Thờigian đèntắttrongmộtchukì: tsΔtTt =−∆ * Trong khoảng thời gian

= nT:

ω .

ắt: tts

. Câu 1: Một đèn nêon mắc với mạch điện xoay chiều có điện áp hiệu dụng 220V và tần số 50Hz.Biết đènsángkhi điệnápgiữa2cựckhôngnhỏ hơn155V. a.Trongmộtgiây,baonhiêulần đènsáng?Baonhiêulần đèntắt? b.Tínhtỉ số giữathờigian đènsángvàthờigian đèntắttrongmộtchukỳ củadòng điện? c.Tínhthờigian đènsángtrong1phút? Hướng dẫn: a.Tacó: u2202sin100πt (V)= Trong một chu kỳ có 2 khoảng thời gian thỏa mãn điều kiện đèn sáng u155 ≥ . Do đó trong một chu kỳ, đèn chớpsáng2lần,2lần đèntắt. Số chukỳ trongmộtgiây:n=f=50chukỳ. Trong một giây đèn chớp sáng 100 lần, đèn chớp tắt 100lần. U uO M'2 M2 M'1 M1 -U U0 0 1-U1 Sáng Sáng Tắt Tắt Sáng Tối U 1 U 0 C’ M’ M U0 2 ϕ U0 2 U0 cos U0 O B E’ E C

DẠYKÈMQUYNHƠNOFFICIAL 57 b.Tìmkhoảngthờigian đènsángtrongnửachukỳ đầu 220 2sin(100πt)155 ≥  1 sin(100πt) 2 ≥  π 5π 100πt 66 ≤≤  15 sts 600600 ≤≤ Thờigian đènsángtrongnửachukỳ: 511 ts 600600150 ∆=−=  Thờigian đènsángtrongmộtchukỳ: t 11 2.s 15075 == saùng Thờigian đèntắttrongchukỳ: 111 tTts 5075150 =−=−=taétsaùng Tỉ số thờigian đènsángvàthờigian đèntắttrongmộtchukỳ: 1 t 75 2 t1 150 == saùng taét . c.Thờigian đènsángtrong1phút: 1 60f.60.50.40s. 75 tt = == saùng trong1 phuùtsaùng trong1chu kyø Chú ý: Có thể giải bài toán trên bằng phương pháp nêu trên: 155u ≥  1552202 2 = = U0 2 . Vậy thời gian đèn sáng tương ứng chuyển động tròn đều quay góc EOM và góc E'OM' . Biễu diễn bằng hình ta thấy tổng thời gian đèn sáng ứng với thời gian tsáng = 4t với t là thời gian bán kính quét góc BOM φ= ; với 0 0 U 12cosφ U2 ==  π φ 3 = Áp dụng: t π4. 413 ss 100π 30075 === saùng  1 tt 75 2 tTt1 150 = == saùngsaùng taéttaét . Câu 2: Đặt điện áp xoay chiều có trị hiệu dụng U = 120V tần số f = 60 Hz vào hai đầu một bóng đèn huỳnh quang. Biết đèn chỉ sáng lên khi điện áp đặt vào đèn không nhỏ hơn 60 2 V.Tỉ số thờigian đènsángvà đèntắttrong30phútlà A.3lần. B. 1 3 lần. C.2lần D. 1 2 lần. Hướng dẫn: Giả sử biểuthức điệnáp:u=120 2 cos(ωt+ ϕ)(V) Đènsángkhi |u| = |120 2 cos(ωt+ ϕ)| ≥ 60 2  |cos(ωt+ ϕ)| ≥ 0,5 Trongmộtchukỳ Tkhoảngthờigian để:|cos(ωt+ ϕ)| ≥ 0,5là 3 2 T  2 t t = saùng taét

DẠYKÈMQUYNHƠNOFFICIAL 58 Khif=60HzthìT= 60 1 s.Trongkhoảngt=30phút=1800s=108000T. Do đótỉ số thờigian đènsángvà đèntắttrong30phútlà2lần.    Chọn C Câu 3 (Sư phạm Hà Nội lần 1 năm 2013): Một đèn ống được mắc vào mạng điện xoay chiều 220V50Hz, điện áp mồi của đèn là 1102V . Biết trong một chu kỳ của dòng điện, đènsángvàtắthailần.Khoảngthờigianmộtlần đèntắtlà. A. 1 s. 150 B. 1 s. 50 C. 2 s. 150 D. 1 s. 300 Hướng dẫn: Đènsángkhigiátrị điệnáptứcthờilớnhơn hoặcbằng 1102V Tacó 0U u1102. 2 == Trongmộtchukỳ, đèntắt2lầnnênthờigian 1lần đèntắtlà: 00 UU 00 22 TTT1 ttts. 12126300 →→   =+=+==  Chọn D Câu 4: Mắc một bóng đèn vào nguồn điện xoay chiều có điện áp tức thời là u2202cos100t (V)=π thì đènchỉ phátsángkhi điệnáp đặtvào đèncó độ lớnkhôngnhỏ hơn110 6V.Khoảngthờigian đènsángtrong 1 2 chukỳ là A. 1 s 300 B. 2 s 300 C. 1 s 150 D. 1 s 200 Hướng dẫn: Tacó: 0 u10063 U2 2202 == 0 3 uU 2  = Theobàira: đènchỉ phátsángkhi điệnáp đặt vào đèncó độ lớnkhôngnhỏ hơn110 6V vìthế trong 1 2 chukỳ đènsánghếtthờigian: 00 00 U3U3 UU 22 ttt TTT1 s. 12126300  ↑→→↓    =+ =+==  Chọn A O Tắt 0U0 2 U Tắt 0 2 U 0U O Tắt u 0U 0 3 2 U ↑ Tắt 0 3 2 U −↓ 0U 0 3 2 U ↓ 0 3 2 U −↑

DẠYKÈMQUYNHƠNOFFICIAL 59 II. Các công thức vuông pha, cùng pha: 1. Đoạn xoay chiều chỉ có trở thuần + Biểuthức điệnápvàdòng điệntrongmạch:u(t)=U0cos(ωt+ ϕ)  () ()()R0R R 0 U uU2 icostcostIcost RRR ==ω+ϕ=ω+ϕ=ω+ϕ  i,ucùngpha: () 22 R2 22 0R0 ui 2cost UI+=ω+ϕ 2. Đọan mạch chỉ có tụ điện : + Biểuthức điệnáp ở hai đầumạch điệnvà cường độ dòng điệntrongmạch: Giả sử : u=U0cosωt  i=I0cos(ωt+ 2 π ) Nếu:i=I0cosωt  u=U0cos(ωt 2 π ) Nếu:i=I0cos(ωt+ ϕi )  u=U0cos(ωt 2 π + ϕi)  utrễ phahơnimộtgóc: 2 π Tacó: 222222 222222 0C0C uiuiui 112 UI2U2IUI +=⇔+=⇔+= với: U0C =I0ZC 2 22 20 C u iI Z  += ; với: () 22 2 22 21 CC0C 22 12 uu1 ZCuiIZ Cii =  ω+=  = ω− 3. Mạch điện xoay chiều chỉ có cuộn cảm: + Biểuthứcdòng điệntrongmạch:i=I0cosωt(A) + Biểuthức điệnáp ở hai đầumạch điện:uL =U0cos(ωt+ 2 π ) NếuuL =U0cosωt  i=I0cos(ωt 2 π ) Nếu i=I0cos(ωt+ ϕi)  uL =U0cos(ωt+ 2 π + ϕi)  usớmphahơnimộtgóc: 2 π Tacó: 222222 222222 0L0L uiuiui 112 UI2U2IUI +=⇔+=⇔+= với: U0L =I0ZL 2 22 20 L u iI Z  +=  2 2 2 1 2 1 2 2 L ii uu Z = L A B C AB R

DẠYKÈMQUYNHƠNOFFICIAL 60 4. Mạch điện xoay chiều chứa L và C: uLC vuông pha với i 2 2 LC 22 0LC0 u i 1 UI +=  2 2 2 1 2 1 2 2 LC ii uu Z = 5. Đoạn mạch có R và L : uR vuông pha với uL 22 LR 22 0L0R uu 1 UU += ; 22 LR 2222 00 uu 1 UsinUcos += ϕϕ 6. Đoạn mạch có R và C: uR vuông pha với uC 2 2 C R 22 0C0R u u 1 UU += ; 2 2 C R 2222 00 u u 1 UsinUcos += ϕϕ 7. Đoạn mạch có RLC : uR vuông pha với uLC 2 2 LC R 22 0LC0R u u 1 UU += ; 2 2 LC 22 0LC0 u i 1 UI += 2 2 LC R 2222 00 u u 1 UsinUcos += ϕϕ  222 00R0LCUUU =+ với U0LC =U0R tanϕ  2 LC22 2R0R u uU tan += ϕ 8. Từ điều kiện cộng hưởng 2 0LC1ω= : Xétvới ω thay đổi a. 22 00 LC1 LLL CCtan RRR ωω ω− ω−ω− ω ωω ϕ=== 2 0 L const. Rtan ω ω− ω == ϕ b. ZL = ω ωωL và C 1 Z C = ω 2 2 LL 2 C0C0 ZZ LC ZZ ωω  =ω=  = ωω  đoạnmạchcótínhcảmkhángZL > ZC  ωL > ω0  đoạnmạchcótínhdungkhángZL < ZC  ωC < ω0  khicộnghưởngZL = ZC  ω = ω0 c. I1 =I2 <Imax  ω1ω2 = 2 0ω . Nhânthêmhaivế LC  ω1ω2LC= 2 0ω LC=1  ZL1 = ω1Lvà C2 2 1 Z C = ω  ZL1 =ZC2 vàZL2 =ZC1 d. cosϕ ϕϕ1 = cosϕ ϕϕ ϕ2  ω ωω ω1ω ωω ω2LC = 1 thêm điều kiện L = CR2 () 2 1 1 222 L1C1 12 21 R1 coscos RZZ 1 ϕ=  ϕ= +−ωω +− ωω  0LCU 0U 0RU ϕ LU RLU O CU ϕ ϕR RU RCU

DẠYKÈMQUYNHƠNOFFICIAL 61 9. Khi L thay đổi; điện áp hai đầu cuộn cảm thuần L  URC ⊥ URLC  từ giản đồ véctơ: UL max ⇔ tanϕRCtanϕRLC = – 1 ⇔ C 2 C 2 L Z ZR Z + =  22 LLC ZZZZ =+  22 LmaxC U URZ R =+ hay 22 RC Lmax C UU U U + =  2222 LmaxRC UUUU =++  22 LmaxCLmaxUUUU =+  2 C 2 LmaxLmax UU 1 UU +=  2 C 2 LL ZZ 1 ZZ += 10. Khi C thay đổi; điện áp hai đầu tụ C  URL ⊥URLC  UC max ⇔ tanϕRLtanϕRLC = – 1  L 2 L 2 C Z ZR Z + =  22 CCL ZZZZ =+  22 CmaxL U URZ R =+ hay 22 RL Cmax L UU U U + =  2222 CmaxRL UUUU =++  22 CmaxLCmaxUUUU =+  2 L 2 CmaxCmax UU 1 UU +=  2 L 2 CC ZZ 1 ZZ += 11. Khi URL ⊥ ⊥⊥ URC ⇔ ZLZC = R2  2 RC 2 RL RLRC R UU UU U + =  tanϕRLtanϕRC = – 1 12. Điện áp cực đại ở hai đầu tụ điện C khi ω ωω ω thay đổi Với 2 C 2 L 2R C 2L ω= (1)  ω2 = 2 Cω = 2 0ω – 2 2 2L R (2)  cách viết kiểu (2) mới dễ nhớ hơn (1). với ZL = ωCL và C C 1 Z C = ω  2 2 LC C 2 C0 Z LC Z ω =ω= ω Từ Cmax 22 2UL U R4LCRC = (3) Từ (2) và (3) suy dạng công thức mới: Cmax 2 L C U U Z 1 Z =     22 L 22 CmaxC ZU 1 UZ +=  22 L 22 CC ZZ 1 ZZ +=  2 L 22 C ZZZ =+  2tanϕRLtanϕRLC = – 1  24 C 24 Cmax0 U 1 U ω += ω

DẠYKÈMQUYNHƠNOFFICIAL 62 13. Điện áp ở đầu cuộn dây thuần cảm L cực đại khi ω ωω ω thay đổi Từ L 22 2 2LCRC ω= (1)  22 22 L0 11RC 2 =− ωω (2)  cách viết kiểu (2) mới dễ nhớ hơn (1). với ZL = ωLL và C L 1 Z C = ω  2 C0 22 LLL Z 1 ZLC ω == ωω Từ Lmax 22 2UL U R4LCRC = (3)  dạng công thức mới Lmax 2 C L U U Z 1 Z =     22 C 22 LmaxL ZU 1 UZ +=  22 C 22 LL ZZ 1 ZZ +=  222 LC ZZZ =+  2tanϕRCtanϕRLC = – 1  24 0 24 LmaxL U 1 U ω += ω 14. Máy phát điện xoay chiều một pha Từ thông ( )0 cost Φ=Φω+ϕ Suất điện động cảm ứng: ()()00 d esintEsint dt Φ =−=ωΦω+ϕ=ω+ϕ  1 E e 2 0 2 0 =        +        Φ Φ . BÀI TẬP VẬN DỤNG: Câu 1: Đặt điện áp uU2cosωt= (V) vào hai đầu một tụ điện thì cường độ dòng điện qua nó có giá trị hiệu dụng là I. Tại thời điểm t, điện áp ở hai đầu tụ điện là u và cường độ dòng điện qua nó là i. Hệ thức liên hệ giữa các đại lượng là A. 22 22 ui1 UI4 += B. 22 22 ui 1 UI += C. 22 22 ui 2 UI += D. 22 22 ui1 UI2 += Hướng dẫn: Do mạch chỉ có tụ C nên u và i luôn vuông pha nhau. Theo bài ra: phương trình của u có dạng: 0 uUcosωt= (1) Suy ra phương trình của i có dạng: 00 iIcostIsint 2 π  =ω+=−ω   (2) Từ (1) và (2) suy ra 22 2222 2222 00 iuiuiu 112 IU2I2UIU  +=⇔+=  +=  Vì thế C đúng và dễ dàng thấy được các đáp án còn lại đều sai. Trong các đáp án sai thì đáp án B sẽ khiến nhiều bạn nhầm lẫn nhất.  Chọn C

DẠYKÈMQUYNHƠNOFFICIAL 63 Câu 2: Đặt điện áp xoay chiều u = U0cosωt (V) vào hai đầu đoạn mạch chỉ có điện trở thuần. Gọi U là điện áp hiệu dụng giữa hai đầu đoạn mạch; i, I0 và I lần lượt là giá trị tức thời, giá trị cực đại và giá trị hiệu dụng của cường độ dòng điện trong đoạn mạch. Hệ thức nào sau đây sai? A. ui 0 UI −= B. 00 UI 0 UI −= C. 22 22 00 ui 1 UI += D. 00 UI 2 UI += Hướng dẫn: Do mạch chỉ có điện trở thuần R nên u và i luôn cùng pha nhau. Theo bài ra: phương trình của u có dạng: 0 uUcosωt= (1) Suy ra phương trình của i có dạng: 0 iIcost =ω (2) Từ (1) và (2) suy ra 00 uiuiui 000 UIUI U2I2 −=⇔−=  −= Vì thế đáp án A đúng. Từ đáp án D ta có : 00 UIUI112 2 UI U2I2222 +=+=+== Vì thế D đúng. Từ đáp án B ta có : 00 UIUI11 0 UI U2I222 −=−=−= Vì thế B đúng. Từ (1) và (2) suy ra 22 2 22 00 ui 2cost1 UI +=ω≠ Vì thế C sai.   Chọn A Câu 3: Đặt điện áp 0 uUcost =ω (V) vào 2 đầu cuộn cảm thuần có 1 LH 3 = π . Ở thời điểm t1 các giá trị tức thời của u và i lần lượt là 100V và - 2,5 3A. Ở thời điểm t2 có giá trị là 100 3V và - 2,5A. Tìm giá trị của ω? Hướng dẫn: Do mạch chỉ có L nên u và i luôn vuông pha nhau. Phương trình của i có dạng: 00 iIcostIsint 2 π  =ω−=ω   (1) và phương trình của u có dạng: 0 uUcost =ω (2) Từ (1) và (2) suy ra 22 00 ui 1 UI  +=  Ta có hệ 2 2 00 0 22 0 00 2,53100 1 IU I5A 2,51003U200V 1 IU  +=  =   =  +=    

DẠYKÈMQUYNHƠNOFFICIAL 64 Mà 000 0 L0 UUU 200 I120π rad/s. ZLIL1 5. 3 ==  ω=== ω π Cau 4: Đặt điện áp xoay chiều 0 uUcos100t =π (V) vào hai đầu cuộn dây thuần cảm 5 LH = π Khi hiệu điện thế có giá trị u = 50V thì cường độ dòng điện là 3 iA 10 = . Hiệu điện thế cực đại hai đầu cuộn dây là A. 100 3V B. 100 2 V C. 100V D. 100 2 V Hướng dẫn: Cảm kháng: L 5 ZL100.50. =ω=π=Ω π Áp dụng : 2 0 2 2 L L Ii Z u +=        2 222222 0L0 3 UuZiU50500.100V. 10  ⇔=+⇔=+=       Chọn C Câu 5: Mạch R nối tiếp với C. Đặt vào 2 đầu mạch một điện áp xoay chiều có tần số f = 50Hz. Khi điện áp tức thời 2 đầu R là 20 7 V thì cường độ dòng điện tức thời là 7 A và điện áp tức thời 2 đầu tụ là 45V. Đến khi điện áp 2 đầu R là 40 3 V thì điện áp tức thời 2 đầu tụ C là 30V. Tìm giá trị của C? A. 33.10 F 8π B. 32.10 F 3π C. 410 F π D. 310 F 8π Hướng dẫn: Các bài toán liên quan tới sự vuông góc thì việc đầu tiên các bạn nên nghĩ tới là hệ thức độc lập theo thời gian. Điều này chúng ta đã gặp rất nhiều trong chương dao động cơ vì thế bài toán này được giải quyết nhanh như sau: Do mạch chỉ có R nối tiếp với C nên Ru và Cu luôn vuông pha nhau. Nếu gọi phương trình của i có dạng: 0 iIcost =ω (1) + Phương trình của Ru có dạng: R0R uUcosωt= (2) + Phương trình của Cu có dạng: C0C0C uUcostUsint 2 π  =ω−=ω   (3) Từ (2) và (3) suy ra 22 RC 0R0C uu 1 UU  +=  Ta nhận thấy hiệu điện thế hai đầu R và C vuông pha nhau, nên:

DẠYKÈMQUYNHƠNOFFICIAL 65 2 2 00C 0 RC 2 2 0C 00C 20745 1 IRIZ IR80 UU 40330IZ60 1 IRIZ  +=  =⊥   =  +=   Ta lại có trong đoạn mạch chỉ có R thì i và u cùng pha nên: 3 R 0C 0R00 ui20772.10I4Z15CF. UI80I3 =  =  =  =  = π    Chọn B Câu 6: Một mạch điện AB gồm tụ C nối tiếp với cuộn cảm thuần L. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có tần số 2 LC ω= . Điểm giữa C và L là M. Khi uMB = 40V thì uAB có giá trị A. 160V B. -30V C. -120V D. 200V Hướng dẫn: Ta có: 2 2 C 22 2 2 0C0 C L 2222 L0C0L 22 0L0 u i 1 UI u u uUU i 1 UI  +=    = +=   , với U0C = ZCI0 và U0L = ZLI0 L LLC C Z uuu Z  =  =− (uL ngược pha với uC). Vậy uAB = uL + uC = –3uC = –120V.   Chọn C Câu 7: Một mạch điện xoay chiều AB gồm một điện trở thuần R, một cuộn cảm thuần có độ tự cảm L, một tụ điện có điện dung C thay đổi được mắc nối tiếp theo đúng thứ tự. Điểm M nằm giữa cuộn cảm và tụ điện. Đặt vào hai đầu mạch điện một điện áp xoay chiều uU2cost =ω (V) . Biết rằng R, L, U, ω có giá trị không đổi. Điều chỉnh điện dung của tụ điện sao cho UMB max, khi đó điện áp hiệu dụng giữa hai đầu điện trở R là 150V, trong điều kiện này, khi điện áp tức thời giữa hai đầu đoạn mạch AB là 1506 V thì điện áp tức thời giữa hai đầu đoạn mạch AM là 506 V. Điện áp hiệu dụng giữa hai đầu đoạn mạch AB là: A. 100 3 V B. 150 2 V C. 150V D. 300V Hướng dẫn giải: Khi UC max thì UAM vuông pha với UAB Ta có: 2222 ABAMABAM 2222 0AB0AMABAM 22AB ABR 222222 RAMABAMABR uuuu 12 UUUU U300V. 1111UU UUUUUU  +=⇔+=    = =+⇔=    Chọn D

DẠYKÈMQUYNHƠNOFFICIAL 66 CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Trong mạch điện xoay chiều RLC mắc nối tiếp thì A. Điện áp tức thời ở hai đầu đoạn mạch bằng tổng các điện áp tức thời trên các phần tử. B. Điệnáphiệudụng ở hai đầu đoạnmạchbằngtổngcác điệnáphiệudụngtrêncácphầntử C. Điện áp cực đại ở hai đầu đoạn mạch bằng tổng các điện áp cực đại trên các phần tử. D. Dòng điện tức thời trong mạch bằng tổng các dòng điện tức thời qua các phần tử Câu 2: Xét hai điện áp xoay chiều u1 = U 2 cos(ωt π 4 ) (V) và u2 = U 2 cos(ωt + φ ) (V) (biết φ π 4 ≠− và 22 33 ππ −≤ϕ≤ ). Ở thời điểm t cả hai điện áp tức thời cùng có giá trị U2 2 . Giá trị của φ bằng A. π 2 B. 2π 3 C. 5π 12 D. π 4 Câu 3: Mạch điện xoay chiều không phân nhánh gồm điện trở thuần R, cuộn cảm thuần có cảm kháng LZ và tụ điện có dung kháng CLZ2Z = . Vào một thời điểm khi hiệu điện thế trên điện trở và trên tụ điện có giá trị tức thời tương ứng là 40V và 30V thì hiệu điện thế giữa hai đầu mạch điện là: A. 50V B. 85V C. 25V D. 55V Câu 4: Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết dung kháng của tụ điện bằng 2 lần cảm kháng của cuộn cảm. Tại thời điểm t, điện áp tức thời giữa hai đầu điện trở và điện áp tức thời giữa hai đầu mạch có giá trị tương ứng là 40 V và 60 V. Khi đó điện áp tức thời giữa hai đầu tụ điện là A. 20V. B. 40V. C. -20V. D. -40V. Câu 5: Đặt điện áp u2402cos100t(V) =π vào hai đầu đoạn mạch RLC mắc nối tiếp. Biết R60, =Ω cuộn dây thuần cảm có độ tự cảm 1,2 LH = π và tụ điện có điện dung 310 CF. 6 = π Khi điện áp tức thời giữa hai đầu cuộn cảm bằng 240V thì độ lớn của điện áp tức thời giữa hai đầu điện trở và giữa hai bản tụ điện lần lượt bằng A. 1203V và 120V B. 120V và 1203V C. 1202V và 1203V D. 240V và 0V Câu 6: Đặt vào hai đầu đoạn mạch RLC nốitiếp một điện ápxoay chiều có giá trị hiệu dụng và tần số không đổi. Tại thời điểm t1 các giá trị tức thời uL1 = 205 3 V, uC1 = 205 V, uR1 = 20V. Tại thời điểm t2 các giá trị tức thời uL2 = 20V; uC2 = - 60V, uR2 = 0. Tính biên độ điện áp đặt vào hai đầu đoạn mạch. A. 60V B. 50V C. 40v D. 403 V

DẠYKÈMQUYNHƠNOFFICIAL 67 Câu 7: Đoạn mạch xoay chiều AB mắc nối tiếp thứ tự gồm cuộn dây thuần cảm có độ tự cảm L, đoạn mạch X và tụ điện có điện dung C. Gọi P là điểm nối giữa cuộn dây và X, Q là điểm X và tụ. Nối A, B với nguồn xoay chiều có tần số f. Biết 224π fLC1 = , AQ u802cost(V) 3 π =ω+  và PB u1602cost(V) =ω Điện áp hiệu dụng hai đầu đoạn mạch AB bằng A. 60 11 V B. 40 14 V C. 40 7 V D. 20 14 V Câu 8: Đặt điện áp u = U0cosωt vào hai đầu đoạn mạch RLC nối tiếp có L thuần cảm thì đoạn mạch xẩy ra cộng hưởng. Gọi i là cường độ dòng điện tức thời trong đoạn mạch, P là công suất tiêu thụ của mạch; uLvà uR lần lượt là điện áp tức thời giữa hai đầu cuộn cảm và giữa hai đầu điện trở. Quan hệ nào sau đây không đúng? A. u cùng pha với i. B. u trễ pha so với uL góc π 2 C. P = 2 u R . D. u = uR Câu 9: Đặt điện áp xoay chiều ổn định vào hai đầu đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Biết điện áp hai đầu đoạn mach AM và điện áp hai đầu đoạn mạch MB lệch pha nhau góc π 3 rad. Tại thời điểm t1 giá trị tức thời của hai điện áp uAM và uMB đều bằng 100V. Lúc đó, điện áp tức thời hai đầu mạch AB có giá trị bằng A. 100 2 V B. 200 V C. 100 V D 100 3 V Câu 10: Vào cùng một thời điểm nào đó, hai dòng điện xoay chiều có cường độ dòng điện là i1 = I0cos( ω t + 1ϕ ) (A) và i2 = I0cos( ω t + 2ϕ ) (A) có cùng giá trị tức thời là 0,5I0; nhưng một dòng điện có cường độ đang tăng còn một dòng điện có cường độ đang giảm. Hai dòng điện này lệch pha nhau A. 3 2π rad. B. 2 π rad. C. π rad. D. 3 π rad. Câu 11: Đặt điện áp xoay chiều u = 200 2 cos100πt (V) vào 2 đầu mạch gồm điện trở thuần R = 100Ω nối tiếp với cuộn cảm thuần 2 LH = π và tụ 410 LF = π . Khi điện áp tức thời hai đầu cuộn cảm bằng 200V và đang giảm thì cường độ dòng điện tức thời bằng A. 3A. B. 2 A. C. 1A. D. 2A. Câu 12: Đặt điện áp xoay chiều u = 220 2 cos100πt (V) vào 2 đầu đoạn mạch gồm điện trở R = 50Ω, cuộn cảm thuần ZL = 100Ω và tụ điện ZC = 50Ω mắc nối tiếp. Trong một chu kì khoảng thời gian điện áp 2 đầu mạch thực hiện thực hiện công âm là? A. 12,5 ms B. 17,5 ms C. 15 ms D. 5 ms Câu 13: Đoạn mạch xoay chiều AB gồm các đoạn mạch: đoạn mạch AM chứa điện trở thuần R, đoạn mạch MN chứa tụ điện C và đoạn mạch NB chứa cuộn dây thuần cảm mắc nối tiếp nhau. Đặt vào hai đầu A, B điện áp xoay chiều 0 uUcost (V)=ω thì điện áp hiệu dụng

DẠYKÈMQUYNHƠNOFFICIAL 68 trên các đoạn mạch AM, MN, NB lần lượt là 302V , 902V và 602V . Lúc điện áp giữa hai đầu AN là 30V thì điện áp giữa hai đầu mạch là: A. 81,96 B. 42,43V C. 90V D. 60V Câu 14: Đặt vào hai đầu đoạn mạch RLC nối tiếp một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Tại thời điểm t1 các giá trị tức thời uL1 = – 10 3V, uC1 = 30 3V, uR1 = 20 3V. Tại thời điểm t2 các giá trị tức thời uC2 = – 60 3V, uR2 = 0. Biên độ điện áp đặt vào 2 đầu mạch là: A. 50V. B. 403V. C. U0 = 60 V D. 80 V. Câu 15: Cho một mạch điện xoay chiều AB gồm điện trở thuần R = 100Ω, cuộn dây thuần cảm L, tụ điện có điện dung C. Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều u = 220 2 cos100πt (V), biết ZL = 2ZC. Ở thời điểm t hiệu điện thế hai đầu điện trở R là 60V, hai đầu tụ điện là 40V. Hỏi hiệu điện thế hai đầu đoạn mạch AB khi đó là: A. 220 2 V B. 20 V C. 72,11 V D. 100 V Câu 16: Cho mạch điện RLC, tụ điện có điện dung C thay đổi. Điều chỉnh điện dung sao cho điện áp hiệu dụng của tụ đạt giá trị cực đại. Khi đó điện áp hiệu dụng hai đầu điện trở bằng 75 V. Khi điện áp tức thời hai đầu mạch là 756V thì điện áp tức thời của đoạn mạch RL là 256V Điện áp hiệu dụng của đoạn mạch là A. 756V B. 753V C. 150 V D. 1502V Câu 17: Đặt vào hai đầu đoạn mạch RLC nối tiếp một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Tại thời điểm t1 các giá trị tức thời uL(t1) = -30 3V, uR(t1) = 40V. Tại thời điểm t2 các giá trị tức thời uL(t2) = 60V, uC(t2) = -120V, uR(t2) = 0V. Điện áp cực đại giữa hai đầu đoạn mạch là: A. 50V B. 100 V C. 60 V D. 50 3V Câu 18: Đoạn mạch xoay chiều chứa 3 linh kiện R, L, C. Đoạn AM chứa cuộn dây thuần cảm L, MN chứa R và NB chứa C. Biết R = 50 Ω , ZL = 50 3 Ω ; ZC = 3 503 Ω . Khi uAN = 80 3V thì uMB = 60V. Giá trị cực đại của uAB là: A. 150V B. 50 7V C. 100V D. 100 3V Câu 19: Đặt điện áp u100cost =ω (V) vào hai đầu đoạn mạch AB mắc nối tiếp gồm điện trở thuần, một cuộn cảm thuần và một tụ điện có điện dung thay đổi được. Thay đổi điện dung của tụ điện cho tới khi UC max = 100V. Khi đó, vào thời điểm điện áp tức thời giữa hai đầu đoạn mạch AB có giá trị bằng 100V thì điện áp tức thời giữa hai đầu cuộn cảm thuần có giá trị. A. -50V B. 50 2 V C. 50V D. -50 2 V M NLA RB C

DẠYKÈMQUYNHƠNOFFICIAL 69 Câu 20: Cho đoạn mạch điện xoay chiều AB gồm tụ điện C mắc nối tiếp với cuộn cảm thuần L theo thứ tự trên. Điểm M nối giữa tụ điện và cuộn cảm. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị hiệu dụng U không đổi, tần số góc 2 LC ω= . Khi điện áp giữa A và M là 30V thì điện áp giữa hai đầu đoạn mạch bằng A. 90V B. – 120V C. 0 D. – 90V Câu 21: Đặt vào hai đầu một tụ điện điện áp xoay chiều có biểu thức u = U0cosωt (V). Điện áp và cường độ dòng điện qua tụ điện tại thời điểm t1, t2 tương ứng lần lượt là: u1= 60V; i1 = 3A; u2 = 602 V; i2 = 2 A. Biên độ của điện áp giữa hai bản tụ và cường độ dòng điện qua bản tụ lần lượt là : A. Uo = 120 2 V, Io = 3A B. Uo = 120 2 V, Io =2A C. Uo = 120V, Io = 3A D. Uo = 120V, Io =2A. Câu 22: Đặt giữa hai đầu đoạn mạch RLC nối tiếp điện áp xoay chiều có giá trị hiệu dụng không đổi và tần số f = 50Hz. Tại thời điểm t, điện áp tức thời giữa hai đầu cuộn cảm đạt giá trị cực đại và bằng 120V. Biết rằng ZL = 2ZC = 2R. Tính điện áp tức thời giữa hai đầu đoạn mạch tại thời điểm 1 t 300 + s. A. 82V B. 60V C. 60 2 V D. 67V Câu 23: Đoạn mạch xoay chiều AB gồm các đoạn mạch: đoạn mạch AM chứa điện trở thuần R, đoạn mạch MN chứa tụ điện C và đoạn mạch NB chứa cuộn dây thuần cảm mắc nối tiếp nhau. Đặt vào hai đầu A,B điện áp xoay chiều 0 uUcost =ω (V) thì điện áp hiệu dụng trên các đoạn mạch AM, MN, NB lần lượt là 302V , 902V và 602V . Lúc điện áp giữa hai đầu AN là 30V thì điện áp giữa hai đầu mạch là A. 81,96 B. 42,43V C. 90V D. 60V Câu 24: Đặt một điện áp xoay chiều ổn định vào hai đầu đoạn mạch nối tiếp gồm điện trở thuần R; cuộn dây thuần cảm và tụ điện. Tại thời điểm t1 các giá trị tức thời của điện áp hai đầu cuộn dây; hai đầu tụ điện và hai đầu điện trở R lần lượt là uL = – 20 3V; uC = 60 3V, uR = 30V. Tại thời điểm t2 các giá trị tức thời là u’L = 40V; u’C = – 120V, u’R = 0. Điện áp cực đại giữa hai đầu đoạn mạch là A. 100V B. 120V C. 80 3V D. 60V Câu 25: Tại một thời điểm t nào đó, hai dòng điện xoay chiều có phương trình ( )101 iIcost(A) =ω+ϕ , ( )202 iIcost(A) =ω+ϕ có cùng giá trị tức thời bằng 0,5I0 nhưng một dòng đang tăng và một dòng đang giảm. Xác định khoảng thời gian ngắn nhất t∆ tính từ thời điểm t để 12ii =− ? A. t 3 ∆=π ω B. t 2 ∆=π ω C. t 4 ∆=π ω D. t ∆=π ω Câu 26: Đặt một điện áp xoay chiều u vào hai đầu của một đoạn mạch gồm điện trở R mắc nối tiếp với một tụ điện có điện dung C. Điện áp tứ thời hai đầu điện trở R có biểu

DẠYKÈMQUYNHƠNOFFICIAL 70 thức R u502cos(2ft)(V) =π+ϕ . Vào một thời điểm t nào đó điện áp tức thời giữa hai đầu đoạn mạch và hai đầu điện trở có giá trị u502V = và R u252V =− . Xác định điện áp hiệu dụng giữa hai bản tụ điện. A. 603V. B. 100 V. C. 50V. D. 503V Câu 27: Một mạch điện AB gồm tụ C nối tiếp với cuộn cảm thuần L. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có tần số 2 ω LC = Điểm giữa C và L là M. Khi uAM = 40V thì uAB có giá trị A. 160V B. -30V C. -120V D. 200V Câu 28 (ĐH 2013): Đặt điện áp u2202cos100πt= (V) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở 20Ω, cuộn cảm thuần có độ tự cảm 0,8 π H và tụ điện có điện dung 310 6π F. Khi điện áp tức thời giữa hai đầu điện trở bằng 1103 V thì điện áp tức thời giữa hai đầu cuộn cảm có độ lớn là A. 330V. B. 440V. C. 4403 V. D. 3303 V. Câu 29: Điện áp xoay chiều giữa hai đầu đoạn mạch có biểu thức u = Uocos100πt (V). t tính bằng giây. Vào thời điểm nào sau đây điện áp tức thời u đang giảm và có giá trị bằng điện áp hiệu dụng U A. 7 ts 400 = . B. 3 ts 400 = C. 9 ts 400 = . D. 1 ts 400 = . Câu 30: Một đoạn mạch xoay chiều gồm 3 phần tử mắc nối tiếp: điện trở thuần R, cuộn dây có (L; r) và tụ điện có điện dung C. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều, khi đó điện áp tức thời ở hai đầu cuộn dây và hai đầu tụ điện lần lượt là: ud = 80 6 cos(ωt + π 6 ) V, uC = 40 2 cos(ωt –2π 3 ) V, điện áp hiệu dụng ở hai đầu điện trở là UR = 60 3 V. Hệ số công suất của đoạn mạch trên là A. 0,862. B. 0,908. C. 0,753. D. 0,664. Câu 31: Đặt điện áp xoay chiều có u = 100 2 cosωt (V) vào hai đầu mạch gồm điện trở R nối tiếp với tụ C có ZC = R. Tại thời điểm điện áp tức thời trên điện trở là 50V và đang tăng thì điện áp tức thời trên tụ là: A. – 50V. B. – 50 3V. C. 50V. D. 50 3V.

DẠYKÈMQUYNHƠNOFFICIAL 71 HƯỚNG DẪN GIẢI: Câu 1: Chọn A. A. Điện áp tức thời ở hai đầu đoạn mạch bằng tổng các điện áp tức thời trên các phần tử đúng vì RLCuuuu =++ B. Điện áp hiệu dụng ở hai đầu đoạn mạch bằng tổng các điện áp hiệu dụng trên các phần tử sai vì () 22 RLC UUUU =+− C. Điện áp cực đại ở hai đầu đoạn mạch bằng tổng các điện áp cực đại trên các phần tử sai vì () 22 00R0L0C UUUU =+− D. Dòng điện tức thời trong mạch bằng tổng các dòng điện tức thời qua các phần tử sai vì dòng điện tức thời trong mạch không bằng tổng các dòng điện tức thời qua các phần tử. Câu 2: Chọn C. Hai điện áp cùng tần số góc và cùng biên độ ( )01020 UUUU2 === vì thế ta biểu diễn hai điện áp trên trong một vòng tròn lượng giác. Theo bài ra ta có: 1 2 21 54 2 12 3 π ϕ=− π  ϕ=ϕ= πϕ−ϕ=  Câu 3: Chọn D. Theo bài ra ta có: C CLCLL u 30 Z2Zu2uu15V 22 =  =−  =−=−=− (vì LCu; u ngược pha nhau nên LC uu0 ≤ ) Ta luôn có: RLC uuuu40153055V. =++=−+= Câu 4: Chọn B. Theo bài ra ta có: C CLCLL u Z2Zu2uu 2 =  =−  =− (vì LCu; u ngược pha nhau nên LC uu0 ≤ ) Ta luôn có: CC RLCRCR uu uuuuuuu 22 =++=−+=+ ( ) ( )CR u2uu2604040V. =−=−= Câu 5: Chọn B. Theo bài ra: Điện trở thuần: R60=Ω Cảm kháng: L Z120=Ω O Lu Cu u 2U0 2 U 0 1 2 U u = 0 2 2 U u = 2 3 π

bài toán

Câu

không có gì khó

Bài toán này mang tính tổng quát h

a các ph

a các giá tr

bài toán có đủ cả ba phần tử R, L, C. Cách giải bài toán này là phải viết phương trình của từng u giữa hai đầu các phần tử bằng cách vận dụng tính chất nhanh pha, chậm pha 2

DẠYKÈMQUYNHƠNOFFICIAL 72 Dung kháng: C Z60=Ω Tổng trở: Z602=Ω 0 0 U 2402 I4A. Z 602  === 0R 0L 0C U240V U480V U240V =   =  = Từ đây ta có vòng tròn lượng giác biểu diễn ba đại lượng trên. Khi điện áp tức thời giữa hai đầu cuộn cảm bằng 0 L U u240V 2 == chính là hai điểm trên hình vẽ, vì chỉ xét về độ lớn nên ta chỉ cần xét một điểm, ở đây ta xét điểm phía bên phải. Nhận xét: để tìm các giá trị tức thời thì cách giải này là trực quan, dễ hiểu và ít tốn thời gian nhất. Những điều này chúng ta đã học qua trong chương dao động cơ nên để làm được các

dạng này

cả.

ọn B.

vì

ữ

ần tử, sau đó liên hệ giữ

ị của cos và sin và cuối cùng là tìm được kết quả. Tuy hơi dài một chút nhưng giải cũng không mất nhiều thời gian lắm. Giả sử dòng điện qua mạch có biểu thức: i = I0cosωt (A). Khi đó: uR = U0Rcosωt (V); uL = U0Lcos(ωt + π 2 ) (V) và uC = U0Ccos(ωtπ 2 ) (V) Khi t = t1: uR1 = U0Rcosωt1 = 20 (V) (1) uL1 = U0Lcos(ωt1 + π 2 ) =3 205  U0Lsinωt1 = 3 205 (V) (2) uC1 = U0Ccos(ωt1π 2 ) = 20 5  U0C sinωt1 = 20 5 (V) (3) Khi t = t2: uR2 = U0Rcosωt2 = 0 (V)  cosωt2 = 0  sinωt2 = ± 1 (4) uL2 = U0Lcos(ωt2 + π 2 ) = 20 (V)  U0Lsinωt2 = 20 (V) (5) uC2 = U0Ccos(ωt2π 2 ) = - 60 (V)  U0C sinωt2 = - 60 (V) (6) Từ (4) , (5), (6) ta có U0L = 20 (V) (1) ; U0C = 60 (V) (2) Thay U0C = 60 (V) vào (3)  sinωt1 = 3 5 O Lu Cu Ru2401203 120Cu =− 240 480 240Lu = 0 0 0 2 2 3 2 L C R L C R U U U u u u  =↓   =−↑   =↑ 

DẠYKÈMQUYNHƠNOFFICIAL 73  cosωt1 = ± 3 2 Thay vào (1) ta được U0R = 1 20 cost ω = 30 (V) (3) Từ (1); (2) và (3) ta có: U0 = 22 0R0L0C U(UU) +− = 50 (V). Câu 7: Chọn C. Theo bài ra ta có hình vẽ mô tả mạch điện như sau: Ta có: () () AQXL PBXC uuu802costV 3 uuu1602cost V  π =+=ω+    =+=ω Theo bài ra: 22 LCLC 4fLC1ZZuu0 π=  =  += (vì Lu ngược pha với Cu ) Ta lại có: ABLXCX uuuuu =++=  () casio AQPBXABABAQPB fx500ES 1 uu2u2uuuu 2 +==  =+→ ( )AB u4014cost0,333(V) =ω+ Điện áp hiệu dụng hai đầu đoạn mạch AB: 0AB AB U 4014 U407V. 22 === Câu 8: Chọn C. Khi đoạn mạch xảy ra cộng hưởng thì u cùng pha với i (A đúng), u trễ pha so với uL góc π 2 (B đúng), u cùng pha với uR nên u = uR (D đúng), P là công suất tiêu thụ của mạch P = 22Uu RR ≠ nên (C sai) Câu 9: Chọn B. Ta luôn có giá trị điện áp tức thời uAB = uAM + uMB Tại t = t1 thì uAM = uMB = 100V  uAB = uAM + uMB = 200 (V). Câu 10: Chọn A. Hai dòng điện cùng tần số góc và cùng biên độ ( )01020 III == vì thế ta biểu diễn hai điện áp trên trong một vòng tròn lượng giác như hình vẽ. Theo bài ra ta có: 0 1 21 0 2 I i 22 I 3 i 2  =↑ π  ϕ−ϕ=  =↓  XA P Q B L C O Lu Cu i0I0 2 I 0 1 2 I i =↑ 0 2 2 I i =↓ 2 3 π

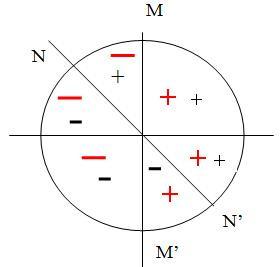
DẠYKÈMQUYNHƠNOFFICIAL 74 Câu 11: Chọn A. Theo bài ra: Điện trở thuần: R100=Ω Cảm kháng: L Z200=Ω Dung kháng: C Z100=Ω Tổng trở: Z1002=Ω 0 0 U 2002 I2A Z 1002  === 0L U400V = Từ đây ta có vòng tròn lượng giác biểu diễn hai đại lượng trên. Khi điện áp tức thời giữa hai đầu cuộn cảm bằng 0 L U u200V 2 == và đang giảm chính là điểm trên hình vẽ. Từ hình vẽ dễ dàng ta dễ dàng có 0 I3 i3A. 2 == Câu 12: Chọn D. Chu kì của dòng điện T = 0,02 (s) = 20 (ms) Dễ dàng tính được tổng trở: Z = 50 2 Ω Độ lệch pha giữa u và i: tanϕ = LCZZ R = 1  ϕ = 4 π Biểu thức cường độ dòng điện qua mạch i = 4,4cos(100πt4 π ) (A). Biểu thức tính công suất tức thời: p = ui = 965 2 cos100πt cos(100πt4 π ). Điện áp sinh công âm cung cấp điện năng cho mạch khi p < 0. Hay biểu thức Y = cos100πt cos(100πt4 π ) < 0. Xét dấu của biểu thức Y = cosα.cos(α4 π ) trong một chu kì 2π: cosα > 0 khi2 π < α < 2 π . Vùng phía phải đường thẳng MM’: cos(α4 π ) > 0 khi2 π < α4 π < 2 π hay khi - 4 π < α < 3 4 π : Vùng phía trên đường thẳng NN’. Theo hình vẽ dấu cộng và dấu trừ lớn hơn ứng với dấu của cosα và nhở hơn là dấu của cos(α4 π ). O Lu Cu i23 400 200Lu = 0 0 2 3 2 L L U I i u  =↓    =↑ 

DẠYKÈMQUYNHƠNOFFICIAL 75 Ta thấy vùng Y < 0 khi cosα và cos(α4 π ) trái dấu từ N đến M và từ N’ đến M’. Như vậy trong một chu kì Y < 0 trong t = 2 T 8 = T 4 . Do đó Trong một chu kì, khoảng thời gian điện áp hai đầu đoạn mạch sinh công âm cung cấp điện năng cho mạch bằng: 4 20 = 5 ms. Câu 13: Chọn A. Cách giải 1: Độ lệch pha giữa u và i: LC R UU tan1 U4 π ϕ==−  ϕ=−  u trễ pha hơn uR một góc 4 π Ta có điện áp hiệu dụng hai đầu mạch: () 22 RLC UUUU60V =+−=  điện áp cực đại hai đầu mạch: U0 = 602V Điện áp cực đại hai đầu R: U0R = 60V. Khi uR = 30V = 1 2 U0R  Δφ = 3 π  Δφ’ = Δφ – ϕ = 34 ππ = 12 π . Ta có u = U0cosΔφ’= 602 cos 12 π = 81,96 V. Cách giải 2: Nhận thấy UR vuông pha với UL: 22 RL L 0R0L uu 1u603V. UU  +=  =±  Tương tự, uR vuông pha với UC: 22 RC C 0R0C uu 1u903V. UU  +=  =±  Vậy um = uR + uL + uc = 30 + 60 3– 90 3= – 21,96V (do uL và uC ngược pha nhau) hoặc um = 30 – 60 3+ 90 3 = 81,96V. Câu 14: Chọn D. Theo bài toán, ta có uC và uR vuông pha nên: 2 22 C2R2 22220C 0C0R0C0R 2 222 C1 R1 22220R 0C0R0C0R uu60.30 11U603V. UUUU uu30.320.3 11U40V. UUUU  +=⇔+=  =    +=⇔+=  =  Vì uL và uR vuông pha nên: 2222 L1R1 22220L 0L0R0C0R uu10.320.3 11U203V. UUUU +=⇔+=  = Biên độ điện áp đặt vào 2 đầu mạch là: () 222 00R0L0C0 UUUUU80V. =−  = uR uU 0R U Δφ φ Δφ’

DẠYKÈMQUYNHƠNOFFICIAL 76 Câu 15: Chọn B. Ta có điện áp hai đầu đoạn mạch ở thời điểm t là: uAB = uR + uC + uL = 20(V) (vì uCvà uL ngược pha nhau). Câu 16: Chọn C. Cách giải 1: Khi C thay đổi để UCmax ta có giản đồ như hình bên: Nhận thấy uRL vuông pha với u  2 2 RL RL u u 2 UU   +=    22 RL 375033750 2 UU += (1) Hệ thức lượng trong tam giác vuông ta có: 222222 RRLRL 111111 UUU75UU +=  += (2) Từ hệ (1) và (2) ta có: URL = 50 3 (V) và U = 150(V). Cách giải 2: Ta có ( ) ( ) ( ) ( ) 2222 22222222 RRL RLR 1111256256256256 UUU75UUU75 =+=  +== (1) Mặt khác: ( ) ( ) 22 22 RL 2222 RLRL uu756256 22 UUUU ==  += (2) Lấy (2) – (1), ta được: 2 300004 U150V. U3 =  = Cách giải 3: Khi thay đổi C để UCmax thì ta có: () () 222222 RL RRL 2222 RL 22 22 RL RL 111111 UUU75UU uu 2756256 UU2 UU =+=+     == +=   222 RL 22 RL 111 75UU U150V. 191 UU1875  =+   =  +=  Câu 17: Chọn B. Ta có: uR = U0R cosωt uL = U0L cos(ωt + 2 π ) = - U0L sinωt uC = U0C cos(ωt2 π ) = U0C sinωt RU RLU U CU

DẠYKÈMQUYNHƠNOFFICIAL 77 Tại thời điểm t2: uR(t2) = U0R cosωt2 = 0V  cosωt2 = 0 => sinωt2 = ±1 uL(t2) = - U0L sinωt2 = 60V  U0L = 60V uC(t2) = U0C sinωt2 = -120V  U0C = 120V Tại thời điêmt t1: uR(t1) = U0R cosωt1 = 40V. uL(t1) = - 60 sinωt1 = -30 3V  sinωt1 = 2 3  cosωt1 = ± 2 1  do đó U0R = 80 V  U0 2 = U0R 2 + (U0L – U0C)2 = 802 + 602  U0 = 100 V. Câu 18: Chọn B. Ta có: ZLZC = R2  uAN vuông pha với uMB (Vì LC ANMB ZZ tan.tan.1 RR ϕϕ==− ) Quan hệ các đại lượng vuông pha: 22 ANMB 0AN0MB u u 1 IZIZ  +=   I0 = 3 A. Tổng trở: Z = () 22 LC 5021 RZZ 3 +−=  U0 = I0Z = 50 7V. Chú ý: Gặp dạng cho điện áp tức thời thì thường xét hai đại lượng vuông pha! Câu 19: Chọn A. Ta có U = 50 2 V; U0C = 100 2 V. Bạn cần nắm vững điều chỉnh C để UCmax ta có: ABR,Luu ⊥ 222 2222 R,LC R,L 22 2 RL0C0L C L L UUUU1002.502.50 U1002 UU;U502U2.50U50 U100  +=  =−=   ⇔  == + = ==  V Gọi biểu thức C0CL0L uUcos(t)thìuUcos(t) =ω+α=ω+α+π Do đó khi C Lu1002cos(t)100 thìu502cos(t)50(V)=ω+α==ω+α+π=− . Câu 20: Chọn D. Ta có: LL2 LC CC UZ LC4U4U4.30120V. UZ ==ω=  === Do UAM = UC = 30V nên UL = – 120V. Vậy U = 30 – 120 = – 90V. Câu 21: Chọn D. Ta có: u = U0cosωt (V)  u2 = U 2 0cos2ωt(1) i = 0 C U cost Z2 π  ω+   = 0 C U Z sinωt  (iZC)2 = U 2 0sin2ωt(2) Cộng (1) và (2) vế theo vế ta có: (iZC)2 + u2 =U 2 0 (3) Thay giá trị cho vào (3) ta được: ( ) ( ) ( ) 222 2 CC 3Z602Z602 +=+ (4) Từ (3) và (4) ta giải ra kết quả: ZC = 60 Ω và U0 = 120V . Vậy I0 = 0 C U 120 Z60 = = 2A.

DẠYKÈMQUYNHƠNOFFICIAL 78 Câu 22: Chọn A. Tổng trở: () 22 LCLoLoo ZRZZR2ZZ2UU2U602V =+−=  =  =  = Độ lệch pha: L LC uiuu ZZ tan1. R44 ππ ϕ==  ϕ−ϕ=  ϕ−ϕ= Mặt khác: 0 o 1T ttttuUcos1581,96V. 30063 π →+  →+  ∆θ=  == Câu 23: Chọn A. Do UR vuông pha với UL nên: 22 RL 0R0L uu1 UU  +=   uL =3 60± V. Vì uR vuông pha với UC nên: 22 RC 0R0C uu1 UU  +=   uC =3 90± V. Vậy um = uR + uL + uc = 30 + 603– 903= – 21,96V(do uL và uC ngược pha nhau) hoặc um = 30 – 603+ 903= 81,96V. Câu 24: Chọn A. Cách giải 1: Vì uL và uR vuông pha, tại thời điểm t2 ta có: ''22 RL 0R0L uu1 UU  +=   '2 L 0L u1 U  =   uL’ = 40V = U0L Vì uC và uR vuông pha, tại thời điểm t2 ta có: 22'' RC 0R0C uu1 UU  +=   '2 C 0C u 1 U  =   uC’ = – 120V = – U0C  U0C = 120V. Theo hình vẽ trục uL, từ thời điểm t1 đến thời điểm t2 là: ∆t = T 6 + T 4 Theo hình vẽ trục uR, ứng tới khoảng thời gian ∆t thì suy ra thời điểm t1: uR = 0RU 2 = 30V  U0R = 60V. Điện áp cực đại giữa hai đầu đoạn mạch: U0 2 = 602 + (40 – 120)2  U0 = 100V. uL-40-20 3 040 (t1)(t2 T/6) T/4 uR-U0R 0RU 2 U0R 0 (t1)(t2) T/6 T/4

DẠYKÈMQUYNHƠNOFFICIAL 79 Cách giải 2: Quan hệ các đại lượng vuông pha ta có: 22 RL 0R0L uu1 UU  +=  và 22 RC 0R0C uu1 UU  +=  Ở thời điểm t2 có u’R = 0  |u’L| = U0L = 40V và |u’C| = U0C = 120V. Thời điểm t1 có: 0L0R LR U3U |u||u| 22 =  = = 30V  U0R = 60V. Vậy () 22 00R0L0C UUUU =+− = () 22604060 +− = 100V. Câu 25: Chọn B. Dùng giản đồ véctơ Tạithời điểmban đầudòng điệntứcthờitạovớitrục nằmngang 1 góc:MOPQOP3 π == và gócIOM6 π = sauthờigianngắnmỗivéctơ quaythêmmộtgócnhư nhau (hình vẽ). Góc QONMOH = Mà 2 QONNOM3π += và 2 HOMNOMHON2HOI 3 π +=== Suy raHOI3 π = . Vậy quay bé nhất để 12ii =− là:HOM. 632 πππ =+= HOM = 30 + 60 = 900 Thời gian là:t2∆=π ω . Câu 26: Chọn D. Ta có: u = uR + uC  uC = u – uR = ( ) 502252752V −−= Do uR và uC vuông pha nên: ( ) ( ) () ( ) 222 2 2 C R 2222 2 0C0R0C 0C u752252752u1 111 UUUU4 502 +=  +=⇔+= ( ) ( ) 22 220CC 0C0C 752752131502150 1UU503V U4U433 ⇔+=⇔=  =  == . Câu 27: Chọn C. Do 2 ω LC = LC 4 ωLZ4Z ωC  =  = Mà L LCLC C Z uuu4u Z =−  =−  uAB = uL + uC = – 3uC = – 3.40 = –120V. M N P Q H KO I

DẠYKÈMQUYNHƠNOFFICIAL 80 Câu 28: Chọn B. Cách giải 1: Ta có: Z202=Ω , I0 = 11A, Và 0R0 0L0L UIR11.20220V UIZ11.80880V ===  === Vì UR và UL vuông pha nên khi: uR = 1103 V 0R R 2203U3 u1103 22  === V Thì 0L L U880 u440V 22 === Cách giải 2: () ( ) () () 0R 0L 22 RL RL L R0R0L 11U220V Z202IA 2U880V uu uu 1u440V u1103UU  = =→=→  =  ⊥  →+=→=  =   Vòng trong ứng với uR, vòng ngoài ứng với uL. Câu 29: Chọn D. Khi t = 0 : u = U0 Ở thời điểm t : 0U uU 2 == và đang giảm π 1 α 100πtts. 4400  ==  = Câu 30: Chọn B. Ta có: dC π 2π 5π φφ =+= 636  uC chậm so với i một góc π 2 vậy ud nhanh pha so với i một góc π 2 Vì tanφd = tan π 3 = L r U U nên Lr U=3U mà 2222 drLr U=U+U=4U rLU=403 (V) và U=120(V) RrU+U cosφ ==0,908 U  Câu 31: Chọn B.Từ ZC = R  U0C = U0R = 100V mà R u50 i== RR còn 0R 0 U I= R Áp dụng hệ thức độc lập trong đoạn chỉ có tụ C: R2 22 2 CC 222 0C00R2 u uu() iR +=1=1 UI100U() R  + 2 CC u=7500u=± 503V ; vì đang tăng nên chọn C u=503V . 220 110√3 300600- 880 -440 UL UR U0 RQ0/2 R π/3 0R U3 2 0LU 2 O 0 2 U U0 α •• u

DẠYKÈMQUYNHƠNOFFICIAL 81 CHỦ ĐỀ 4: QUAN HỆ GIỮA CÁC ĐIỆN ÁP HIỆU DỤNG A. TÓM TẮT KIẾN THỨC CƠ BẢN Phương pháp giải: Dùng các công thức Công thức tính U: Biết UL, UC, UR : 222 RLC UU(UU) =+−  22 RLC UU(UU) =+− Biết u = U0cos(ωt + ϕu) hay : uuU2cos(ωt φ )=+ với 0U U 2 = Công thức tính I: Biết i = I0cos(ωt + ϕi) hay iiI2cos(ωt φ )=+ với : 0I I 2 = Biết U và Z hoặc UR và R hoặc UL và L hoặc UC và C: RLC LC UUUU I ZRZZ ==== BÀI TẬP VẬN DỤNG Câu 1: Điện áp đặt vào hai đầu một đoạn mạch R, L, C không phân nhánh. Điện áp hai đầu R là 80V, hai đầu L là 120V, hai bản tụ C là 60V. Điện áp hiệu dụng hai đầu đoạn mạch là: A. 260V B. 140V C. 100V D. 20V Hướng dẫn: Điện áp ở hai đầu đoạn mạch: 2222 RLC UU(UU)80(12060)100 =+−=+−= (V).  Chọn C Câu 2: Điện áp xoay chiều đặt vào hai đầu một đoạn mạch R, L, C không phân nhánh. Điện áp hiệu dụng hai đầu mạch là 100V, hai đầu cuộn cảm thuần L là 120V, hai bản tụ C là 60V. Điện áp hiệu dụng hai đầu R là: A. 260V B. 140V C. 80V D. 20V Hướng dẫn: Cách giải 1: Ta có: 222222 RLCRLC UU(UU)UU(UU)100(12060)80V =+−  =−−=−−=    Chọn C Cách giải 2: Sử dụng SOLVE của Máy tính Fx 570ES ( COMP: MODE 1 ) SHIFT MODE 1 : Math Chú ý: Nhập biến X là phím: ALPHA ) : màn hình xuất hiện X Nhập dấu = là phím : ALPHA CALC : màn hình xuất hiện = Chức năng SOLVE là phím: SHIFT CALC và sau đó nhấn phím = hiển thị kết quả X = Với máy FX570ES: Bấm: MODE 1 Dùng công thức : 222 RLC UU(UU) =+− với biến X là UR

DẠYKÈMQUYNHƠNOFFICIAL 82 Bấm: 100 x2 ALPHA CALC =ALPHA ) X x2 + ( 120 - 60 ) x2 Màn hình xuất hiện: 1002 = X2 +(120 - 60)2 Tiếp tục bấm:SHIFT CALC SOLVE = . Màn hình hiển thị: X = UR = 80V.  Chọn C Câu 3: Điện áp đặt vào hai đầu một đoạn mạch R, L, C không phân nhánh. Điện áp hiệu dụng hai đầu mạch là 200V, hai đầu L là 240V, hai bản tụ C là 120V. Điện áp hiệu dụng hai đầu R là: A. 200V B. 120V C. 160V D. 80V Hướng dẫn: Điện áp ở hai đầu R: Ta có: 222 RLC UU(UU) =+−  2222 RLC UU(UU)200(240120)160V =−−=−−= .   Chọn C Câu 4: Cho mạch như hình vẽ, điện trở R, cuộn dây thuần cảm L và tụ C mắc nối tiếp. Các vôn kế có điện trở rất lớn, V1 chỉ UR = 15V, V2 chỉ UL = 9V, V chỉ U = 13V. Hãy tìm số chỉ V3, biết rằng mạch có tính dung kháng? A. 12 V B. 21 V C. 15 V D. 51 V Hướng dẫn: Áp dụng công thức tổng quát của mạch nối tiếp R, L, C ta có: 222 RLC UU(UU) =+− Hay: 222222 RLCLCLC UU(UU)1315(UU)UU12. −=−  −=−  −=± Vì mạch có tính dung kháng nên CLU> U Hay trong biểu thức trên ta lấy nghiệm CCLU12U= U1291221(V)=−  +=+= . UC chính là số chỉ vôn kế V3    Chọn B Câu 5: Cho một đoạn mạch RLC không phân nhánh, cuộn dây thuần cảm, độ tự cảm của cuộn dây có thể thay đổi được. Khi thay đổi giá trị của L thì thấy ở thời điểm điện áp hiệu dụng giữa hai đầu điện trở cực đại thì điện áp này gấp 4 điện áp hiệu dụng giữa hai đầu cuộn dây. Khi điện áp hiệu dụng giữa hai đầu cuộn dây cực đại thì điện áp này so với điện áp hiệu dụng giữa hai đầu điện trở khi đó gấp: A. 4,25 lần. B. 2,5 lần. C. 4 lần. D. 4 2 lần. Hướng dẫn: Khi URmax (mạch có cộng hưởng), ta có: UL = UC và URmax = U = 4UL  R = 4ZC (1) Khi ULmax ta có: ULmax = 22 RC C UU U + (2) Từ (1) suy ra UR = 4UC (3) Từ (2) và (3) suy ra ULmax = 4,25 UR.  Chọn A Câu 6: Cho đoạn mạch như hình vẽ, cuộn dây L thuần cảm, AB πu200cos10πt 2 =+  (V) CR V1 V2 V3 V L

DẠYKÈMQUYNHƠNOFFICIAL 83 và 0 πiIcos10πt 4 =+  (A). Tìm số chỉ các vôn kế V1 và V2. A. 100V và 200V B. 100V C. 200V và 100V D. 200V Hướng dẫn: Độ lệch pha của uAB so với i: ui πππ φφφ 244 =−=−= rad. Suy ra LLL LR RR ZUU π tanφ tanUU RU4U ==⇔=  = Ta có: 22 22222 RLRR RL U1200 UUU2UUUU100(V) 22 2  =+=  ==  ==  AB AB .  Chọn B Câu 7: Đặt một điện áp xoay chiều vào hai đầu đọan mạch L,R,C mắc nối tiếp theo thứ tự đó. Điện áp hai đầu các đọan mạch chứa L, R và R, C lần lượt có biểu thức LR πu150cos100πt(V) 3 =+  ; RC πu506cos100πt(V) 12  =−  . Cho R = 25Ω. Cường độ dòng điện trong mạch có giá trị hiệu dụng bằng: A. 3,0 A B. 3 2 A C. 2 A D. 3,3 A Hướng dẫn: Vẽ giản đồ véc tơ như hình vẽ ta có: ∠ MON = ππ 5π 31212  −−=   MN = UL + UC OM = URL = 75 2 (V) ON = URC = 50 3 (V) Áp dụng ĐỊNH LUẬT cosin cho tam giác OMN: MN = UL + UC = 22 LRRCLRRC 5πUU2UUcos 12 +− ≈ 118 (V) UR 2 = ULR 2 – UL 2 = URC 2 – UC 2  UL 2 – UC 2 = ULR 2 – URC 2 = 3750 (UL + UC )(UL – UC ) = 3750  UL + UC = 3750 118 = 32 (V) Ta có hệ phương trình: UL – UC =118 (V); UL + UC = 32 (V) Suy ra UL = 75 (V)  UR = 222 LRL UU75 −= = 75 (V). Do đó I = RU R = 3 (A).  Chọn A Câu 8: Đặt một điện áp xoay chiều vào hai đầu mạch điện nối tiếp gồm R, cuộn cảm thuần L và tụ C có điện dung C thay đổi khi C = C1 thì điện áp hiệu dụng trên các phần tử lần lượt O UR N UCR ULR M

DẠYKÈMQUYNHƠNOFFICIAL 84 là UR = 40V, UL = 40V, UC = 70V. Khi C = C2 thì điện áp hiệu dụng hai đầu tụ là 50 2 V, địện áp hiệu dụng hai đầu điện trở R bằng: A. 25 2 V B. 25 3 V C. 25V D. 50V Hướng dẫn: Khi C = C1 , UR = UL  ZL = R Điện áp đặt vào hai đầu mạch 22 RLC UU(UU)50 =+−= V Khi C = C2  U’R = U’L thì 2 22 RLC UU'(U'U)50 =+−= V  U’R = 25 2 V.    Chọn A Câu 9: Cho mạch điện AB có hiệu điện thế không đổi gồm có biến trở R, cuộn dây thuần cảm L và tụ điện C mắc nối tiếp. Gọi U1, U2 , U3 lần lượt là hiệu điện thế hiệu dụng trên R, L và C. Biết khi U1 = 100V, U2 = 200V, U3 = 100 V. Điều chỉnh R để U1 = 80V, lúc ấy U2 có giá trị A. 233,2V. B. 100V. C. 50 V. D. 50V. Hướng dẫn: Cách giải 1: Ta có 2222 123123 UU(UU)U'(U'U') =+−=+− = 100 2 V. Suy ra : (U’2 – U’3)2 = U2 – U’1 2 = 13600 U2 – U3 = I(Z2 – Z3) =100V (1) U’2 – U’3 = I’(Z2 – Z3) = 13600 V (2) Từ (1) và (2) suy ra: I' I = 100 13600  2 2 U' U = 2 2 I'Z IZ = I' I = 100 13600  U’2 = 100 13600 U2 = 233,2 V. Chọn A Cách giải 2: Điện áp 2 đầu mạch: 22 123 UU(UU)1002V =+−= . Nhận thấy U2 = 2U1 nên ta luôn có: UL = 2UC (chú ý R đang thay đổi). Ta luôn có: 22 RLC UU(UU)1002V =+−= . Khi UR = 80V thì 2 2 L RL U UUU1002V 2  =+−=   . Suy ra: 2 2 L LL2 U 80U1002VUU233,2V 2  +−=  ==  .   Chọn A Câu 10: Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần R mắc nối tiếp với tụ điện C có điện dung thay đổi được, đoạn mạch MB là cuộn dây thuần cảm có độ tự cảm L. Thay đổi C để UAM max thì thấy các điện áp hiệu dụng giữa hai đầu điện trở và cuộn dây lần lượt là UR = 100 2 V, UL = 100V. Khi đó điện áp hiệu dụng giữa hai đầu tụ điện là: A. UC = 100 3 V B. UC = 100 2 V C. UC = 200 V D. UC = 100V Hướng dẫn: 2 2

DẠYKÈMQUYNHƠNOFFICIAL 85 Ta có: 22 C AM 22222 LCLCLLC 2222 CC URZ 11 U R(ZZ)R(ZZ)Z2ZZ 1 RZRZ + === +−+−− + ++ . Để UAM = UAM max thì biểu thức y = 2 LLC 22 C Z2ZZ RZ + = ymin  đạo hàm y’ = 0  ( )( ) ( )( )222 22 CLLLCCCLC RZ2ZZ2ZZ2Z0ZZZR0. +−−−−=⇔−−= Hay UC 2 – ULUC – UR 2 = 0 ⇔ UC 2 – 100UC – 20000 = 0 ⇔ UC = 200V (loại nghiệm âm).  Chọn C C. CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Một đoạn mạch xoay chiều mắc nối tiếp gồm điện trở thuần R, tụ điện C và cuộn dây thuần cảm có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ổn định , khi điều chỉnh độ tự cảm của cuộn cảm đến giá trị L0 thì điện áp hiệu dụng hai đầu các phần tử R, L, C có giá trị lần lượt là 30 V, 20 V và 60 V. Khi điều chỉnh độ tự cảm đến giá trị 2L0 thì điện áp hiệu dụng hai đầu điện trở bằng bao nhiêu? A. 50V B. 50 V 3 C. 150 V 13 D. 100 V 11 Câu 2: Một cuộn dây không thuần cảm nối tiếp với tụ điện C trong mạch xoay chiều có điện áp u = U0cosωt (V) thì dòng điện trong mạch sớm pha hơn điện áp u là φ1 và điện áp hiệu dụng hai đầu cuộn dây là 30V. Nếu thay C1 = 3C thì dòng điện chậm pha hơn u góc φ2 = 900 – φ1 và điện áp hiệu dụng hai đầu cuộn dây là 90V. Giá trị của U0 là A. 5 60 V. B. 60 V. C. 30 2 V. D. 5 63 V. Bài 3: Cho đoạn mạch như hình vẽ, cuộn dây L thuần cảm, AB u200cos100t 2 π =π+  (V) và 0 iIcos100t 4 π =π+  (A). Tìm số chỉ các vôn kế V1 và V2. A. 200V B. 100V C. 200V và 100V D. 100V và 200V Câu 4: Đặt một điện áp xoay chiều vào hai đầu đọan mạch L, R, C mắc nối tiếp theo thứ tự đó. Điện áp hai đầu các đọan mạch chứa L, R và R, C lần lượt có biểu thức RL u150cos100tV 3 π =π+  ; RC u506cos100tV 12 π  =π−  . Cho R= 25Ω. Cường độ dòng điện trong mạch có giá trị hiệu dụng bằng: A 3,0A B. 3 2 A C. 2 A D. 3,3A Câu 5: Đặt một điện áp xoay chiều vào hai đầu mạch điện nối tiếp gồm R, cuộn cảm thuần L và tụ C có điện dung C thay đổi khi C = C1 thì điện áp hiệu dụng trên các phần tử lần lượt là UR = 40V, UL = 40V, UC = 70V. Khi C = C2 thì điện áp hiệu dụng hai đầu tụ là 50 2 V, địện áp hiệu dụng hai đầu điện trở R bằng: A. 25 2 V B. 25 3 V C. 25V D. 50V

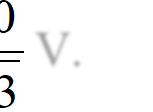
DẠYKÈMQUYNHƠNOFFICIAL 86 Câu 6: Cho mạch điện AB có hiệu điện thế không đổi gồm có biến trở R, cuộn dây thuần cảm L và tụ điện C mắc nối tiếp. Gọi U1, U2 , U3 lần lượt là hiệu điện thế hiệu dụng trên R, L và C. Biết khi U1 = 100V, U2 = 200V, U3 = 100 V. Điều chỉnh R để U1 = 80V, lúc ấy U2 có giá trị A. 233,2V. B. 100V. C. 50 V. D. 50V. HƯỚNG DẪN GIẢI Câu 1: Chọn C. Khi L1 = L0 điện áp hiệu dụng đặt vào hai đầu mạch: U = () 22 R1L1C1UUU = 50 V. Do UR1 = 30V; UL1 = 20 V; UC1 = 60V  ZC = 2R; ZL1 = 2R 3 Khi điều chỉnh L2 = 2L0  ZL2 = 2ZL1 = 4R 3 . Khi đó tổng trở của mạch: Z () 22 L2CRZZ 2 2 4R13 R2RR 33  −−=   = = Điện áp hiệu dụng hai đầu điện trở bằng UR2 = U Z R = 13 150 V. Câu 2: Chọn B. Ta có: d1 d2 2112 d2 d1 U30V U 3I3IZ3Z U90V U =  =  =  = = () () 2 2 2222 C1 LC1LLLC1 Z RZZ9RZ2RZZZ 3   +−=+−  +=  (1) Mặt khác: 211212tantan1 22 ππ ϕ=−ϕ  ϕ+ϕ=  ϕϕ=− (vì ϕ1 < 0) C1 L LC1LC2LC1 Z ZZZZZZZ 3 .1.1 RRRR ⇔=−⇔=− () C12222 LC1L LLC1C1 Z ZZZR3R3Z4ZZZ0 3  ⇔−−=−⇔+−+=   ()222 C1L Z5RZ⇔=+ (2) Từ (1) và (2) ta được: 2 C1LC1C1L 55 ZZZZZ 22 =  = Mà: ()222L LLC1L C1 5Z2R 2RZZZZ 2Z5R = +==   = (3) 2 2

DẠYKÈMQUYNHƠNOFFICIAL 87 Từ đó suy ra: Z1 2 = R2 +(ZL – ZC1)2 = 10R2  Z1 = R 10 và Zd1 = 22 LRZ + = R 5 . Suy ra: d11 d1d1 d11d1 U ZU UU2U. ZZZ =  == Do đó U0 = U 2 = 2Ud1 = 60V. Câu 3: Chọn B. Độ lệch pha của uAB so với i: ui rad 244 πππ ϕ=ϕ−ϕ=−= LL LR R ZU tantan1UU RU4 π  ϕ====  = Ta có: 22 22222 AB ABRLRR LR U1200 UUU2UUUU100V. 22 2  =+=  ==  ==  Câu 4: Chọn A. Vẽ giản đồ véc tơ như hình vẽ ta có: 5 MON 31212  πππ  =−−=    MN = UL + UC OM = URL = 75 2 V ON = URC = 50 3 V Áp dụng định lí cosin cho tam giác OMN: MN = UL + UC = 22 RLRCRLRC 5 UU2UUcos 12 π +− ≈ 118V UR 2 = ULR 2 – UL 2 = URC 2 – UC 2  UL 2 – UC 2 = ULR 2 – URC 2 = 3750 (UL + UC)(UL – UC) = 3750  UL + UC = 3750 118 = 32V Ta có hệ phương trình: UL – UC =118 V UL + UC = 32 V Suy ra UL = 75V  UR = 222 RLL UU75 −= = 75V. Do đó I = RU R = 3A. Câu 5: Chọn A. Khi C = C1 thì UR = UL  ZL = R Điện áp đặt vào hai đầu mạch: U = () 22 RLC1UUU +− = 50 V Khi C = C2 thì U’R = U’L Điện áp hai đầu mạch: U = () '22 RLC2UU'U +− = 50 V  U’R = 25 2 V. Câu 6: Chọn A. Cách giải 1: Ta có: U = () 22 123 UUU +− = () 22 123 U'U'U' +− = 100 2 V O UR N UCR ULR M

DẠYKÈMQUYNHƠNOFFICIAL 88 Suy ra: (U’2 – U’3)2 = U2 – U’1 2 = 13600 U2 – U3 = I(Z2 – Z3) =100V (1) U’2 – U’3 = I’(Z2 – Z3) = 13600 V (2) Từ (1) và (2) suy ra: I' I = 100 13600  2 2 U' U = 2 2 I'Z IZ = I' I = 100 13600  U’2 = 100 13600 U2 = 233,2V. Cách giải 1: Điện áp 2 đầu mạch: U = () 22 123 UUU +− = 100 2 V Nhận thấy 21 U2U = nên ta luôn có: LCU2U = (chú ý R đang thay đổi) Ta luôn có: () 22 RLC UUUU1002V =+−= . Khi UR = 80V thì 2 2 L RL U UUU1002V 2  =+−=   2 2 L L L2 U 80U1002VUU233,2V. 2  +−=  == 

DẠYKÈMQUYNHƠNOFFICIAL 89 CHỦ ĐỀ 5 ĐOẠN MẠCH XOAY CHIỀU RLC MẮC NỐI TIẾP A. TÓM TẮT KIẾN THỨC CƠ BẢN 1. Đoạn mạch xoay chiều chứa R, L Điện áp và tổng trở của mạch: 22 RLRL 22 RLL UUU ZRZ  =+  =+  Định luật Ohm cho đoạn mạch: 22 RL RLRL0 22 RL LL 22 0R0L 0RL0R0L 0 22 RL LL UU UUUI I ZUZRZ2 UU UUU I 2I ZUZ RZ  + =====  +  + ===== +  Điện áp nhanh pha hơn dòng điện góc φ, xác định từ biểu thức LL R R 22 RRL L UZ tan UR URR cos ULZ RZ  ϕ==    ϕ=== + Giản đồ véc tơ: Khi đó: ϕu = ϕi + ϕ Chú ý: Để viết biểu thức của u, uL, uR trong mạch RL thì ta cần phải xác định được pha của i, rồi tính toán các pha theo quy tắc      = =+ ui ui R L ϕϕ π ϕϕ 2 Câu 1: Tính độ lệch pha của u và i, tổng trở trong đoạn mạch điện xoay chiều RL biết tần số dòng điện là 50 Hz và a. R = 50 Ω, L = 3 2π H. b. R = 100 2 Ω, L = 2 π H Hướng dẫn: Áp dụng các công thức L 22 RLL L Z.L2fL ZRZ Z tan R  =ω=π  =+   ϕ=

DẠYKÈMQUYNHƠNOFFICIAL 90 a. Ta có: ZL = 50 3 Ω  2222 RLL L ZRZ50(503)100 Z503 tan3 R50  =+=+=Ω   ϕ=== ⇔ Z100 3 =Ω  π ϕ=  b. Ta có: Z = 100 2 Ω  2222 RLL L ZRZ(1002)(1002)200 Z1002 tan1 R 1002  =+=+=Ω  ϕ===  ⇔ Z200 4 =Ω   π ϕ=  Câu 2: Cho mạch điện xoay chiều gồm hai phần tử R, L mắc nối tiếp với R = 50 3 Ω, L = 1 2π H. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểu thức u120cos100t 4 π =π+  V. a. Tính tổng trở của mạch. b. Viết biểu thức cường độ dòng điện chạy qua đoạn mạch. c. Viết biểu thức điện áp hai đầu cuộn cảm thuần, hai đầu điện trở. Hướng dẫn: a. Từ giả thiết ta tính được Z = 50 Ω  2222 RLL ZRZ(503)50100 =+=+=Ω . b. Ta có I0 = 0U 120 Z100 = = 1,2 A. Độ lệch pha của điện áp và dòng điện là φ thỏa mãn: tanφ = ZL R = 50 50 3 = 1 3  ϕ = π 6 rad. Mà điện áp hai đầu mạch nhanh pha hơn dòng điện nên: φu = φi + φ  φi = φu – φ = π 4 –π 6 = π 12 Vậy biểu thức cường độ dòng điện qua mạch là i = 1,2cos(100πt + π 12) A. c. Viết biểu thức uL và uR. Ta có 0L0L 0R0 UIZ60V UIR603V ==   ==  Do uL nhanh pha hơn i góc π 2 nên: Luϕ = φi + π 2 = π 12 + π 2 = 7π 12  uL = 60cos(100πt + 7π 12). Do uR cùng pha với i nên Ruϕ = φi = π 12  uR = 60 3cos(100πt + π 12) V.

DẠYKÈMQUYNHƠNOFFICIAL 91 Câu 3: Cho một đoạn mạch điện xoay chiều chỉ có cuộn cảm thuần L và điện trở R. Nếu đặt vào hai đầu đoạn mạch điện áp i22cos100t 6 π  =π−  ; u = 100cos(100πt + 4 π )V thì cường độ dòng điện trong mạch là i = 2cos100πt (A). Tính giá trị của R và L. Hướng dẫn: Từ giả thiết ta có 0RL 0 U100V I2A 4  =  =  πϕ=  0RL22 RL L 0 L U Z502RZ I Zπ tan1 4R  ==Ω=+    ==   L R50 1 Z50LH. 2 =Ω   =Ω  = π Câu 4: Cho một đoạn mạch điện xoay chiều gồm điện trở R = 50 Ω và cuộn cảm thuần có hệ số tự cảm L = 3 2π H. Cường độ dòng điện chạy qua đoạn mạch có biểu thức i22cos100t 6 π  =π−  A. Viết biểu thức điện áp hai đầu mạch, hai đầu điện trở, hai đầu cuộn cảm. Hướng dẫn: Cảm kháng của mạch ZL = ω.L = 50 3 Ω  ZRL = 100Ω Viết biểu thức của u: Điện áp cực đại hai đầu đoạn mạch U0L = I0ZL = 200 2 V. Độ lệch pha của u và i: tanφ = 3  φ = π 3 = φu – ϕi ⇔ ϕu = ϕi + π 3 = π 6 Từ đó ta được u = 200 2cos(100πt + π 6) V. Viết biểu thức của uR: Điện áp cực đại hai đầu điện trở U0R = I0ZL = 100 2 V. uR và i cùng pha nên: Ruϕ = φi = –π 6  uR = 100 2cos(100πt –π 6) V. Viết biểu thức của uL: Điện áp cực đại hai đầu cuộn cảm thuần U0L = I0ZL= 100 6 V. u nhanh pha hơn i góc π 6 nên: Luϕ = φi + π 6 = 0  uL = 100 6cos(100πt) V. 2. Đoạn mạchxoay chiều chứa R, C Điện áp và tổng trở của mạch: 22 RCRC 22 RCC UUU ZRZ  =+  =+ 

DẠYKÈMQUYNHƠNOFFICIAL 92 Định luật Ôm cho đoạn mạch: 22 RCRC RC0 22 RC CC 22 0R0C 0RC0R0C 0 22 RC CC UU UUI U I ZUZRZ2 UU UUU I 2I ZUZ RZ  + =====  +  + ===== +  Điện áp chậm pha hơn dòng điện góc φ, xác định từ biểu thức: CC R UZ tan URϕ=−=− ; ϕ = ϕu – ϕi Giản đồ véctơ: Chú ý: Để viết biểu thức của u, uC, uR trong mạch RC thì ta cần phải xác định được pha của i, rồi tính toán các pha theo quy tắc      = = ui ui R C ϕϕ π ϕϕ 2 Câu 1: Cho mạch điện xoay chiều gồm hai phần tử R, C mắc nối tiếp với R 100 Ω, C = 410 π F. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểu thức u200cos100t 3 π =π+  V. a. Tính tổng trở của mạch. b. Viết biểu thức cường độ dòng điện chạy qua đoạn mạch. c. Viết biểu thức điện áp hai đầu tụ điện, hai đầu điện trở thuần. Hướng dẫn: a. Ta có ZL = 100 Ω tổng trở của mạch là ZRC = 22 CRZ + 100 2 Ω. b. Ta có 0 0 U I Z = = 2 A. Độ lệch pha của điện áp và dòng điện là φ thỏa mãn tanφ = –ZC R = –1  ϕ = –4 π Mà φu – φi = φ  φi = φu – φ = 7π 12 rad. Vậy biểu thức cường độ dòng điện qua mạch là i = 2cos(100πt + 7π 12) A. c. Viết biểu thức uC và uR. Ta có U0C = I0ZC = 100 2 V và uC chậm pha hơn i góc π 2 nên Cuϕ = φi –π 2 = π 12

DẠYKÈMQUYNHƠNOFFICIAL 93  uC = 100 2cos(100πt + π 12) V. Ta có U0R = I0R = 100 2 V và uR cùng pha với i nên Ruϕ = φi = 7π 12  uR = 100 2cos(100πt + 7π 12) V. Câu 2: Cho một đoạn mạch điện xoay chiều chỉ có tụ điện C và điện trở R. Nếu đặt vào hai đầu đoạn mạch một điện áp u1002cos100t =π (V) thì cường độ dòng điện trong mạch là i2cos100t 4 π =π+  iA. Tính giá trị của R và C. Hướng dẫn: Từ giả thiết ta có 0RC 0 U100V I2A 4  =  =  πϕ=−  0RC22 RC C 0 C U Z502RZ I Z tan1 4R  ==Ω=+   −π  =−=  ⇔ 3 C R50 10 Z50CF. 52 =Ω   =Ω  =  Câu 3: Đoạn mạch điện xoay chiều nối tiếp gồm điện trở R = 50 Ω và tụ điện C = 200 π 3 µF. Viết biểu thức điện áp tức thời giữa hai bản của tụ điện và ở hai đầu đoạn mạch. Cho biết biểu thức cường độ dòng điện i2sin100t 3 π =π+  A. Hướng dẫn: Ta có ω = 100π rad  ZC = 1 ωC = 50 3 Ω. Tổng trở của mạch RC: 22 RCC ZRZ =+ = 100 Ω. Từ giả thiết ta có I0 = 2 A  00RC 0R0 0C0C UIZ1002V UIR502V UIZ506V  ==   ==  ==  Viết biểu thức điện áp giữa hai đầu tụ C: Do uC chậm pha hơn i góc π 2 nên Cuϕ – φi = –π 2  Cuϕ = φi –π 2 = –π 6 rad. Biểu thức hai đầu C là uC = 50 6cos(100πt –π 6) V.

DẠYKÈMQUYNHƠNOFFICIAL 94 Viết biểu thức điện áp giữa hai đầu đoạn mạch RC: Độ lệch pha của u và i là tanφ = –ZC R = – 3  ϕ = –π 3 rad. Mà ϕ = RCuϕ – ϕi ⇔ RCuϕ = ϕ + ϕi = 0  uRC = 100 2cos100πt V. 3. Đoạn mạch xoay chiều chứa L, C Điện áp và tổng trở của mạch: CLC CLC UUU ZZZ  =−  =−   LC LCC0 L LCLCLC 0L0C 0LC0L0C 0 LCLCLC UU UUI U I ZZZZZ2 UU UUU II2 ZZZZZ  =====    =====  * Giản đồ véctơ: -Khi UL > UC hay ZL > ZC thì uLC nhanh pha hơn i góc π 2. (Hình a). Khi đó ta nói mạch có tính cảm kháng. -Khi UL < UC hay ZL < ZC thì uLC chậm pha hơn i góc π 2. (Hình b). Khi đó ta nói mạch có tính dung kháng. Câu 1: Một đoạn mạch gồm một tụ điện C có dung kháng 100 Ω và một cảm thuần có cảm kháng200 Ω mắcnốitiếpnhau. Điệnáphai đầucuộncảmcóbiểuthức L u100cos100t 6 π =π+  V. Viết biểu thức điện áp ở hai đầu tụ điện. Hướng dẫn: Ta có I0 = 0L0C LC UU 100 Z200Z ==  U0C = ZC 2 = 50 V. Mặt khác C L ui ui 2 2 π ϕ=ϕ−   πϕ=ϕ+   LCC uuu 5 66 ππ ϕ−ϕ=π  ϕ=−π=− rad. Vậy biểu thức hai đầu điện áp qua tụ C là uC = 50cos(100πt –5π 6 ) V. Câu 2: Đoạn mạch gồm cuộn dây thuần cảm có độ tự cảm L 2 = π H mắc nối tiếp với tụ điện 4 1 10 CF = π rồi mắc vào một điện áp xoay chiều tần số 50 Hz. Khi thay tụ C1 bằng một tụ Hình a Hình b

DẠYKÈMQUYNHƠNOFFICIAL 95 C2 khác thì thấy cường độ dòng điện qua mạch không thay đổi. Điện dung của tụ C2 có giá trị bằng: A. 4 2 10 CF 2 = π B. 4 2 2.10 CF = π C. 4 2 10 CF 3 = π D. 4 2 3.10 CF = π Hướng dẫn: Ta có I = 0LC0LC LCLC UU ZZZ = Do I không đổi nên 12 LCLC ZZZZ −=− ⇔ 12 12 LCLC LCCL ZZZZ ZZZZ −=−  −=−  ⇔ 12 21 CC CLC ZZ Z2ZZ =  =−  Từ giả thiết ta tính được 1 L C Z200 Z100 =Ω   =Ω   2CZ = 300Ω  C2 = 410 3π F. 4. Mạch điện xoay chiều RLC mắc nối tiếp Điện áp và tổng trở của mạch: () () () 2 22 2 RLC00R0L0C 22 LC UUUUUUUU ZRZZ  =+−  =+−   =+− Định luật Ohm cho mạch: () () () () 22 RLC RLC0 22 LCLC 22 00R0L0C 0R0L0C 0 22 LCLC UUU UIUUU I ZRZZ 2RZZ UUU UUUU I I2 ZRZZ RZZ  +− ====== +−   +− ======  +− Độ lệch pha của điện áp và cường độ dòng điện trong mạch là φ, được cho bởi LCLC R UUZZ tan URϕ== ; ϕ = ϕu – ϕi - Khi UL > UC hay ZL > ZC thì u nhanh pha hơn i góc φ. (Hình 1). Khi đó ta nói mạch có tính cảm kháng. - Khi UL < UC hay ZL < ZC thì u chậm pha hơn i góc φ. (Hình 2). Khi đó ta nói mạch có tính dung kháng. Giản đồ véc tơ: O ϕ O ϕ

DẠYKÈMQUYNHƠNOFFICIAL 96 Câu 1: Cho mạch điện RLC có R = 10 3 Ω, L = 3 10π H, C = 310 2π F. Đặt vào hai đầu mạch điện áp xoay chiều có giá trị hiệu dụng 120 V, tần số 50 Hz. a. Tính tổng trở của mạch. b. Tính cường độ hiệu dụng của dòng điện qua mạch. c. Điện áp hiệu dụng trên từng phần tử R, L, C. Hướng dẫn: a. Tính tổng trở của mạch. Ta có ZL = ωL = 30Ω; ZC = 20 Ω. Tổng trở của mạch () 22 LCZRZZ =+− = 20 Ω. b. Cường độ hiệu dụng qua mạch I = U R = 6 A. c. Điện áp hiệu dụng trên từng phần tử là R LL CC UIR603 UIZ180 UIZ120  ==Ω ==Ω  ==Ω Câu 2: Cho đoạn mạch RLC gồm R = 80 Ω, L = 318 mH, C = 79,5 µF. Điện áp giữa hai đầu đoạn mạch có biểu thức u1202cos100t =π V. a. Viết biểu thức cường độ dòng điện chạy trong mạch và tính điện áp hiệu dụng giữa hai đầu mỗi dụng cụ b. Tính điện áp hiệu dụng giữa hai đầu R, hai đầu L và hai đầu C. c. Viết biểu thức điện áp hai đầu R, hai đầu L, hai đầu C. Hướng dẫn: a. Ta có ω = 100πn rad  ZL = ωL ≈ 100 Ω và ZC = 1 ωC ≈ 40 Ω. Tổng trở của mạch là () 22 LCZRZZ =+− = 100 Ω. Cường độ dòng điện của mạch : I = U Z = 1 A  I0 = 2 A. Gọi ϕ là độ lệch pha của u và i, ta có LCZZ tan Rϕ= = 3 4  ϕ ≈ 0.64 rad. Mà φ = φu – φi  φi = φu – φ = – 0,64 rad. Vậy biểu thức cường độ dòng điện trong mạch là i = 2cos(100πt – 0,64) A. b. Theo a ta có I = 1 A, điện áp hiệu dụng giữa hai đầu mỗi phần tử là R LL CC UIR80 UIZ180 UIZ40 ==Ω  ==Ω  ==Ω c. Viết biểu thức hai đầu mỗi phần tử R, L và C. Biểu thức điện áp giữa hai đầu R: UR = 80 V  U0R = 80 2 V. Do uR cùng pha với i nên Ruϕ = φ1 = 0,64 rad  uR = 80 2cos(100πt – 0,64) V.

DẠYKÈMQUYNHƠNOFFICIAL 97 Biểu thức điện áp giữa hai đầu L: UL = 100 V  U0L = 100 2 V Do uL nhanh pha hơn i góc π 2 nên Luϕ – φi = π 2  Luϕ = π 2 + φi = π 2 – 0.64 rad Biểu thức điện áp hai đầu L là uL = 100 2cos(100πt + π 2 – 0,64  V. Biểu thức điện áp giữa hai đầu C: UC = 40 V  U0C = 40 2 V. Do uC chậm pha hơn i góc π 2 nên Cuϕ – φi = –π 2  Cuϕ = φi –π 2 = –π 2 – 0.64 rad. Biểu thức điện áp hai đầu tụ C là uC = 40 2cos(100πt –π 2 – 0,64  V. Câu 3: Cho đoạn mạch RLC gồm R = 10Ω, L = 1 10π H, C = 310 2π F. Điện áp hai đầu cuộn cảm có biểu thức u202cos100t 2 π =π+  V. a. Viết biểu thức cường độ dòng điện chạy trong mạch. b. Viết biểu thức điện áp hai đầu đoạn mạch u, hai đầu điện trở uR, hai đầu tụ điện uC, uRL, uRC Hướng dẫn: a. Từ giả thiết ta có () 22 L LC C R10 Z10ZRZZ102 Z20 =Ω  =Ω  =+−=Ω  =Ω Từ đó ta được I0 = 0L L U Z = 2 2 A. Do uL nhanh pha hơn i góc π 2 nên Luϕ – φi = π 2  φi = Luϕ –π 2 = 0  i = 2 2cos100πt A. b. Viết biểu thức u, uR, uC, uRL, uRC Viết biểu thứ của u: Ta có U0 = I0Z = 2 2.10 2 = 40 V. Độ lệch pha của u và i: LCZZ tan Rϕ= = – 1  ϕ = –π 4 = φu – φi ⇔ φu = φi –π 4 . Từ đó ta có biểu thức của điện áp hai đầu mạch u = 40cos(100πt –π 4) V. Viết biểu thức của uR: Ta có U0R = I0R = 2 2.10 = 20 2 V. Độ lệch pha của uR và i: φu = φi = 0  uR = 20 2cos(100πt –π 4) V. Viết biểu thức của uC: Ta có U0C = I0ZC = 2 2.20 = 40 2 V. Độ lệch pha của uC và i: Cuϕ – φi = –π 2  uC = 40 2cos(100πt –π 2) V. Viết biểu thức của uRL: Ta có U0RL = I0ZRL = 2 2. 22 LRZ + = 40 V.

DẠYKÈMQUYNHƠNOFFICIAL 98 Độ lệch pha của uRL và i: LZ tan Rϕ= = 1  ϕRL = π 4 = RLuϕ – ϕi ⇔ RLuϕ = π 4 Từ đó ta có: uRL = 40cos(100πt + π 4) V. Viết biểu thức của uRC: Ta có U0RC = I0ZRC = 2 2. 22 CRZ + = 20 10 V. Độ lệch pha của uRC và i: CZ tan Rϕ=− = – 2  ϕRC ≈ –63π 180 = RCuϕ – ϕi ⇔ RCuϕ = –63π 180 + ϕi = –63π 180. Từ đó ta có: uRC = 20 10cos(100πt –63π 180 ) V. Câu 4: Cho đoạn mạch RLC gồm R = 40Ω, L = 3 10π H, C = 310 7π F. Điện áp hai đầu đoạn mạch RL có biểu thức RL u120cos100t =π V. a. Viết biểu thức cường độ dòng điện chạy trong mạch. b. Viết biểu thức điện áp hai đầu đoạn mạch. Hướng dẫn: a. Từ giả thiết ta có () 22 LC L 22 CRLL R40 ZRZZ102 Z30 Z70ZRZ50 =Ω  =+−=Ω =Ω   =Ω=+=Ω Từ đó ta được I0 = 0RL RL U Z = 2,4 A. Mặt khác LZ 3 tan R4ϕ==  ϕRL = 37π 180 = RLuϕ – ϕi = –37π 180  i = 2,4cos(100πt –37π 180 ) A. b. Độ lệch pha của u và i: LCZZ 3070 tan1 R40 ϕ===−  φ = –π 4 = φu – φi ⇔ φu = ϕi –π 4 = –41π 90 Đồng thời U0 = I0Z = 96 2 V  u = 96 2cos(100πt –41π 90 ) V. 5. Cuộn dây không thuần cảm có điện trở hoạt động a. Xét cuộn dây không cảm thuần (L, r): Khi mắc cuộn dây có điện trở r và độ tự cảm L vào mạch điện xoay chiều, ta xem cuộn dây như đoạn mạch r nối tiếp với L có giản đồ vectơ như hình vẽ dưới: + Tổng trở cuộn dây: 2222 cdL ZrZr(L) =+=+ω Trong đó: ZL = ω L. + Điện áp hai đầu cuộn dây nhanh pha hơn cường độ dòng điện một góc dφ được tính theo công thức: 0L L d 0r U Z tan φ Ur ==

DẠYKÈMQUYNHƠNOFFICIAL 99 + Biên độ, giá trị hiệu dụng của cường độ dòng điện và điện áp theo các công thức: 0d0d 0 22 d L UU I Z rZ == + và dd 22 d L UU I Z rZ == + . + Công suất tiêu thụ của cuộn dây: P = UdIcos φ d = Ir2 hay Pr = 2 2 Ur Z . + Hệ số công suất của cuộn dây: cos φ d = 22 d L rr Z Zr = + . + Cách nhận biết cuộn dây có điện trở thuần r: - Xét toàn mạch, nếu: Z ≠ 22 LC R(ZZ) +− ; U ≠ 22 RLC U(UU) +− hoặc P ≠ I2R hoặc cosϕ ≠ R Z  thì cuộn dây có điện trở thuần r ≠ 0. - Xét cuộn dây, nếu: Ud ≠ UL hoặc Zd ≠ ZL hoặc Pd ≠ 0 hoặc cosϕd ≠ 0 hoặc ϕd ≠ 2 π  thì cuộn dây có điện trở thuần r ≠ 0. b. Mạch RLrC không phân nhánh: - Điện trở thuần tương đương là: R + r. - Tổng trở của cả đoạn mạch RLrC nối tiếp là: 22 LC Z(Rr)(ZZ) =++− - Độ lệch pha giữa điện áp hai đầu đoạn mạch RLrC với cường độ dòng điện là: LCZZ tan Rrϕ= + + Sự liên hệ giữa các điện áp hiệu dụng: 222 RrLC U(UU)(UU) =++− ; rR cosφ Z + = + Công suất tiêu thụ toàn mạch: 2PUIcosφ I(rR)==+ + Công suất tiêu thụ trên R: 2 R PRI = Câu 1: Cho mạch điện như hình vẽ, trong đó: 410 C π = F, L = 1 2π H, r = 10Ω, R = 40Ω. Biểu thức dòng điện trong mạch i = 2 2 cos100πt (A). a. Tính tổng trở của mạch? b. Độ lệch pha ϕ và công suất của toàn mạch? Hướng dẫn: a. Cảm kháng: L 1 ZLω 100π 50 2π ===Ω . Dung kháng: C 4 11 Z 10ωC 100π. π == = 100 Ω . Tổng trở: Z = 2222 LC (rR)(ZZ)(1040)(50100)502 ++−=++−=Ω . C A B R L, r C A B R L,r NM

DẠYKÈMQUYNHƠNOFFICIAL 100 b. Công suất tiêu thụ của mạch điện. Ta có: LCZZ 50100 π tan φ 1 φ rad rR10404 ===−  =− ++ . Công suất tiêu thụ của mạch điện: P = UIcosϕ hoặc P = I2(r + R) = 22.(10 + 40) = 200W. Câu 2: Cho mạch như hình vẽ. Cuộn dây có r = 100Ω, 1 LH = π ; tụ điện có điện dung 410 CF 2 = π . Điện áp xoay chiều hai đầu đoạn mạch AB u1002cos100t (V)=π .Tính độ lệch pha giữa điện áp uAB và uAM? Tính UC? Hướng dẫn: Ta có: L C 4 1 ZL100.100 11 Z200 C10 100. 2  =ω=π=Ω π  ===Ω ω π π Độ lệch pha: LC AB AB L AMAM ZZ 100200 tan1 r1004 Z100 tan1 r1004 −π ϕ===−  ϕ=−   π ϕ===  ϕ=  Độ lệch pha giữa điện áp uAB và uAM : AB/AMABAM 442 πππ ϕ=ϕ−ϕ=−−=− Khi đó: UC = IZC C 2222 LC UZ 100.100 r(ZZ)100(100200) == +−+− = 50 2Ω . Câu 3: Một cuộn dây có hệ số tự cảm L được mắc nối tiếp với một tụ có điện dung C rồi mắc vào 2 điểm A, B của mạch điện xoay chiều có tần số f. Đo điện áp giữa hai đầu đoạn mạch AB, giữa hai đầu cuộn dây và giữa hai cực của tụ điện bằng vôn kế có điện trở rất lớn, ta lần lượt được: UAB = 37,5 V, UL = 50V, UC = 17,5 V. Đo cường độ dòng điện bằng một ampekế có điện trở không đáng kể, ta thấy I = 0,1 A. Khitần số f thay đổi đến giátrị fm = 330Hz thì cường độ dòng điện trong mạch đạt giá trị cực đại. Tính độ tự cảm L, điện dung C, và tần số f của điện áp trên. Hướng dẫn: Giả sử cuộn dây thuần cảm không có điện trở r thì: UAB = UL – UC = 50 – 17,5 = 32,5V. Không phù hợp với đề bài, nên cuộn dây phải có điện trở r. Ta có tổng trở cuộn dây: d d U 50 Z500 I0,1 ===Ω Dung kháng của tụ điện: C C U 17,5 Z175 I0,1 ===Ω . L,r M C V BA

DẠYKÈMQUYNHƠNOFFICIAL 101 Tổng trở: AB AB U 37,5 Z375. I0,1 ===Ω Khi f = fm, trong mạch có cộng hưởng (Imax) nên: 2 m ω = 1 LC () 22 2 m m 111 LC 2f(2..330)  === ωπ π (1) Mặt khác: ZAB 2 = r2 + (ZL – ZC)2 = r2 + ZL 2 – 2ZLZC + ZC 2  ZAB 2 = Zd 2 + ZC 2 – 2ZLZC  2ZLZC = Zd 2 + ZC 2 – ZAB 2 = 5002 + 1752 - 3752 = 14.104  2L ω 1 Cω = 444LL 214.107.10L7.10C CC =  =  = (2) Thế (2) vào (1) ta được: 7.104C2 = 2 1 (2.π.330)  C = 1,82.10-6 F; L = 7.104C = 7.104.1,82.10-6 = 0,128H Mà: ZC = 1 Cω = 6 c 111 f500 C.2.fC.2..Z1,82.10.2.3,14.175  === ππ Hz. Câu 4 (ĐH 2008): Cho đoạn mạch điện xoay chiều gồm cuộn dây mắc nối tiếp với tụ điện. Độ lệch pha của hiệu điện thế giữa hai đầu cuộn dây so với cường độ dòng điện trong mạch là 3 π . Hiệu điện thế hiệu dụng giữa hai đầu tụ điện bằng 3 lần hiệu điện thế hiệu dụng giữa hai đầu cuộn dây. Độ lệch pha của hiệu điện thế giữa hai đầu cuộn dây so với hiệu điện thế giữa hai đầu đoạn mạch trên là A. 0. B. 2 π . C. 3 π . D. 2 3 π . Hướng dẫn: Ta có: () L cd 22222 CLrCL Z π tanφ ==tg=3 r3 U=3.U+UZ=3Z+r      L LC cd C Z=3r ZZ π 2π tanφ ==3 φ = φφ = Z=23rr33           Chọn D

DẠYKÈMQUYNHƠNOFFICIAL 102 CHỦ ĐỀ 6 HIỆN TƯỢNG CỘNG HƯỞNG ĐIỆN A. TÓM TẮT KIẾN THỨC CƠ BẢN 1. Cộng hưởng điện: Điềukiện: ZL =ZC ( LC UU) =  21 ωLLCω 1 Cω =⇔= hay 1 LC ω= . Các biểu hiện cơ bản của hiện tượng cộng hưởng điện: + Tổng trở cực tiểu: min ZZR == + Điện áp hai đầu điện trở cực đại bằng điện áp cả mạch: Rmax UU = + Cường độ dòng điện trong mạch cực đại: Imax = R min UUU ZRR == + Điện áp và cường độ dòng điện cùng pha (tức φ = 0) + Hệ số công suất cực đại: cosφ = 1. + Công suất tiêu thụ cực đại: 2 2 max U PPRIUI R ==== . 2. Ứng dụng: tìm L, C, f khi có cộng hưởng điện + Số chỉ ampe kế cực đại, hay cường độ dòng điện hiệu dụng đạt giá trị lớn nhất. + Cường độ dòng điện và điện áp cùng pha, điện áp hiệu dụng: LCR UUUU =  = + Hệ số công suất cực đại, công suất cực đại.... Chú ý: Nếu đề bài yêu cầu mắc thêm tụ 2C với 1C để mạch xảy ra cộng hưởng, tìm cách mắc và tính 2C ta làm như sau: + Khi mạch xảy ra cộng hưởng thì tđ CLZZ = + So sánh giá trị tđCZ và 1CZ  Cách ghép 2C với 1C : - Nếu tđ CC1ZZ > (Hay tđ 1 CC) <  2C ghép nối tiếp 1C 2tđ 1 2 CCC2 C 1 ZZZC Z  =−  = ω - Nếu tđ 1CCZZ < (Hay tđ 1 CC) >  2C ghép song song 1C 1tđ 2 1tđ 2 CC C2 CCC ZZ 1 ZC ZZZ  =  = −ω BÀI TẬP VẬN DỤNG

DẠYKÈMQUYNHƠNOFFICIAL 103 Câu 1: Cho mạch điện như hình vẽ. uAB = 200 2 cos100πt (V). R =100 Ω ; 1 L π = H; C là tụ điện biến đổi; VR →∞ . Tìm C để vôn kế V có số chỉ lớn nhất. Tính Vmax? A. 100 2 V, 1072,4µF. B. 200 2 ; 410 F π . C. 100 2 V; 410 π µF. D. 200 2 ; 410 π µF. Hướng dẫn: Số chỉ của Vôn Kế (V) là giá trị điện áp hiệu dụng giữa hai đầu đoạn mạch chứa R và L. Ta có: UV = 22 RLL 22 LC U IZRZ. R(ZZ) =+ +− Do R, L không đổi và U xác định  UV = UVmax  cộng hưởng điện, nên ZL = ZC  C = 2 1 Lω = 2 1 1 (100) π π = 410 π F.    Chọn B Câu 2: Cho mạch điện xoay chiều như hình vẽ. Biết R = 50Ω, 1 L π = H. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u2202cos100πt= (V). Biết tụ điện C có thể thay đổi được. a. Xác định C để điện áp đồng pha với cường độ dòng điện. b. Viết biểu thức dòng điện qua mạch. Hướng dẫn: a. Để u và i đồng pha: φ 0= thì trong mạch xảy ra hiện tượng cộng hưởng điện. Suy ra: ZL = ZC 1 ωL ωC  = () 4 2 2 1110 C 1ω L π100π π  === F. b. Do trong mạch xảy ra cộng hưởng điện nên Zmin = R oo o min UU2202 I4,42 ZR50  ==== (A) Pha ban đầu của dòng điện: iu φφφ 000=−=−= Vậy i4,42cos100πt= (A). V C A B R L C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 104 Câu 3 (ĐH 2009): Đặt điện áp xoay chiều có giá trị hiệu dụng 120V, tần số 50 Hz vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần 30 Ω, cuộn cảm thuần có độ tự cảm 0,4 π H và tụ điện có điện dung thay đổi được. Điều chỉnh điện dung của tụ điện thì UL max bằng A. 150 V. B. 160 V. C. 100 V. D. 250 V. Hướng dẫn giải: Ta có: L LL LmaxmaxL min ZL0,4 ω 2π.5040 π ZZ40 UIZU.U.120.160V ZR30  ===Ω    =====     Chọn B Câu 4: Cho mạch điện xoay chiều như hình vẽ Biết R = 200Ω, 2 L π = H, 410 C π = F. Đặt vào hai đầu mạch điện một điện áp xoay chiều u100cos100πt= (V). a. Tính số chỉ của ampe kế. b. Khi R, L, C không đổi để số chỉ của ampe kế lớn nhất, thì tần số dòng điện phải bằng bao nhiêu? Tính số chỉ ampe kế lúc đó. (Biết rằng dây nối và dụng cụ đo không làm ảnh hưởng đến mạch điện). Hướng dẫn: a. Cảm kháng: L 2 Z ωL100π.200 π ===Ω Dung kháng: C 4 11 Z100 10ωC 100π π ===Ω . Tổng trở của mạch: () ()2 222 LC ZRZZ2002001001005 =+−=+−=Ω. Ta có : o o U1001 I Z 10055 === (A). Số chỉ của ampe kế : o A I1 II0,32 25.2 ==== (A). b. Ta có: () 22 LC U I RZZ = +− . Để số chỉ của ampe kế cực đại IAmax thì Zmin : LC ZZ0 −= LCZZ = 1 2πfL 2πfC  = 4 11 f35,35 2π LC 2210 π . ππ  === Hz. Số chỉ ampe kế cực đại: IA max = max min UU100 I0,35 ZR 2.200 ==== (A). CL M A B R A

DẠYKÈMQUYNHƠNOFFICIAL 105 Câu 5: Đặt điện áp uU2cosωt= (V) vào hai đầu đoạn mạch AB gồm hai đoạn mạch AN và NB mắc nối tiếp. Đoạn AN gồm biến trở R mắc nối tiếp với cuộn cảm thuần có L, đoạn NB chỉ có tụ điện với điện dung C. Đặt 1 1 ω 2LC = . Để điện áp hiệu dụng giữa hai đầu đoạn mạch AN không phụ thuộc R thì tần số góc ω bằng A. 1ω . 22 B. 1ω 2. C. 1ω . 2 D. 2ω1. Hướng dẫn: Cách giải 1: Ta có: 22 22 L AN 22 LC RZ U.U R(ZZ) + = +−  222 222 LCLCC AN 2222 LCLC R(ZZ)2ZZZ U.U.U R(ZZ)R(ZZ) +−− =− +−+−  2 222 LCC AN 22 LC 2ZZZ UU.U R(ZZ) =− +− Để UAN không phụ thuộc R thì: 2ZL = ZC hay 1 11 2Lωωω 2 Cω 2LC =  == .   Chọn B Cách giải 2: Điện áp hiệu dụng hai đầu mạch AN là: () 22 ANAN L 222 LCCLC 22 L UU UIZRZ RZZZ2ZZ 1 RZ ==+= +− + + Để UAN không phụ thuộc vào R thì 2 CLC Z2ZZ0 −= , suy ra 2 1 1 ω (1) 2LC 1 ω (2) 2LC  =    =  Từ (1) và (2) ta được 21ωω 2=   Chọn B Câu 6: Cho mạch điện xoay chiều AB gồm R, L, C mắc nối tiếp. Biết 2 RC16L = Đoạn mạch đang cộng hưởng. Biết điện áp hiệu dụng của toàn đoạn mạch AB là 120V. Tính điện áp hiệu dụng RLCU,U,U ? Hướng dẫn: Giả thiết cho: 2 RC16L = ⇔ 2 RC16L ω=ω ⇔ 2 L C 1 R.16Z Z = (1) và đoạn mạch cộng hưởng nên : LCZZ = (2) . Từ (1) và (2) ta được: 222 LCR16Z16Z ==  RLC U4U4U == Do U2 = 120V  RLC U120V;UU30V === .

DẠYKÈMQUYNHƠNOFFICIAL 106 Câu 7: Đặt điện áp xoay chiều có giá trị hiệu dụng 200V và tần số không đổi vào hai đầu A và B của đoạn mạch mắc nối tiếp theo thứ tự gồm biến trở R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi. Gọi N là điểm nối giữa cuộn cảm thuần và tụ điện. Các giá trị R, L, C hữu hạn và khác không. Với C = C1 thì điện áp hiệu dụng giữa hai đầu biến trở R có giá trị không đổi và khác không khi thay đổi giá trị R của biến trở. Với C = 1C 2 thì điện áp hiệu dụng giữa A và N bằng A. 200 V. B. 1002 V. C. 100 V. D. 2002 V. Hướng dẫn: Cách giải 1: Khi C = C1 thì hiêu điện thế hiệu dụng hai đầu biến trở là 1 1 R 222 LCLC 2 UU UIRR R(ZZ)(ZZ) 1 R === +−− + . Để UR không phụ thuộc vào R thì 1LC ZZ0 −= (hiện tượng cộng hưởng), suy ra 1LCZZ = . Khi 1C C 2 = , thì 1 CCL Z2Z2Z == thì 22 22 ANL 22L LC U UIRZRZ R(ZZ) =+=+ +− 22 L 22 LC URZ U200V. R(Z2Z) + === +−    Chọn A Cách giải 2: Với C = C1 thì điện áp hiệu dụng giữa hai đầu biến trở R có giá trị không đổi và khác không khi thay đổi giá trị R của biến trở  mạch cộng hưởng  ZL = ZC, C = C1 2  ZC1 = 2ZC Điện áp hai đầu A và N: 22 22 ANL 22L LC U UIRZRZU200V R(ZZ) =+=+== +− . Chọn A C. CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Cho mạch điện không phân nhánh gồm R = 40Ω, cuộn dây có r = 20Ω và L = 0,0636H, tụ điện có điện dung thay đổi. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có f = 50Hz và U = 120V. Điều chỉnh C để điện áp hiệu dụng hai đầu cuộn dây đạt giá trị cực đại, giá trị đó bằng: A. 40V B. 80V C. 46,57V D. 40 2 V Câu 2: Một mạch điện xoay chiều RLC không phân nhánh có R = 100 Ω , L = 2 π H, tụ điện có điện dung C thay đổi được. Đặt vào hai đầu đoạn mạch một C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 107 điện áp xoay chiều AB π u2002cos(100t) 4 =π+ (V). Giá trị của C và công suất tiêu thụ của mạch khi điện áp giữa hai đầu R cùng pha với điện áp hai đầu đoạn mạch nhận cặp giá trị nào sau đây: A. C = 410 2π F, P = 400W B. C = 410 π F, P = 300W C. C = 310 π F, P = 400W C. C = 410 2π F, P = 200W Câu 3: Mạch điện R, L, C nối tiếp, điện áp hai đầu mạch u = 220 2 cos ω t (V) và ω có thể thay đổi được. Tính điện áp hiệu dụng 2 đầu R khi biểu thức dòng điện có dạng 0 iIcost =ω : A. 220 2 V B. 220V C. 110V D. 120 2 V. Câu 4: Cho đoạn mạch như hình vẽ. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều AB u632cosωt (V)= , A R0 = , VR =∞ . Cuộn dây thuần cảm có cảm kháng L Z200=Ω , thay đổi C cho đến khi Vôn kế V chỉ cực đại 105V. Số chỉ của Ampe kế là : A. 0,25A B. 0,3A C. 0,42A D. 0,35A Câu 5: Một mạch điện không phân nhánh gồm điện trở R =100Ω,cuộn thuần cảm có L thay đổi được và tụ có điện dung C. Mắc mạch vào nguồn có u1002cos(100t)V 6 π =π+ . Thay đổi L để điện áp hai đầu điện trở có giá trị hiệu dụng UR = 100V. Biểu thức nào sau đây đúng cho cường độ dòng điện qua mạch: A. i2cos100t) 6 π =π+ (A) B. icos(100t) 6 π =π+ (A) C. i2cos(100t) 4 π =π+ (A) D. i2cos100t =π (A) Câu 6: Với mạch điện xoay chiều RLC mắc nối tiếp, khi tần số dòng điện bằng f thì ZL = 6Ω vàZc =9Ω. Thay đổitầnsố dòng điện đếngiátrị fo để mạchxảy racộnghưởng điện,khi đó: A. f < fo B. f = fo C. f > fo D. không tồn tại HƯỚNG DẪN GIẢI Câu 1: Chọn D. Ta có: L Z2πfL2π.50.0,063620 ===Ω . Điện áp hiệu dụng hai đầu cuộn dây: Ud = IZd . Vì Zd không phụ thuộc vào sự thay đổi của CnênUd đạtgiátrị cực đạikhi max II = .Suy ratrongmạchphải cócộnghưởng điện.Lúc đó: V CL MA B R A

DẠYKÈMQUYNHƠNOFFICIAL 108 max 2222 dL U120 I2A Rr4020 ZrZ2020202  === ++  =+=+=Ω dmaxd UIZ2.20240256,57 ==== (V). Câu 2: Chọn A. Ta thấy khi uR cùng pha với uAB nghĩa là uAB cùng pha với cường độ dòng điện i. Xảy ra cộng hưởng điện: ZL = ZC  L 1 C Z = ω . Với ZL = L ω = 200 Ω  C= 410 2π F. Suy ra công suất P = Pmax = 22 U200 400W R100 == . Câu 3: Chọn B. Dựa vào dạng của phương trình cường độ dòng điện ta thấy lúc này u và i cùng pha. Nên trong mạch xảy ra cộng hưởng điện. Khi đó uR = u = 220 2 cos ω t (V)  UR = 2202 2 =220V. Câu 4: Chọn C. Khi mạch có cộng hưởng thì AB2222 LCAM maxL U63 ZZURZ105R200R150. RR =  =+⇔=+  =Ω Khi đó: I = RAB UU63 RR150 == = 0,42A . Câu 5: Chọn A. Theo đề ta có U = 100V, UR = 100V. Vậy UR = U, do đó trong mạch xảy ra cộng hưởng điện. Lúc này i cùng pha với u và U100 I1A R100 === Do i cùng pha với u suy ra: I0 = I2 = 2A . Vậy π i2cos(100t) 6 =π+ (A). Câu 6: Chọn C. Do lúc đầu: ZL = 6Ω và Zc = 9Ω, suy ra ZL < ZC  phải tăng f  tăng ZL cho nên để mạch xảy ra cộng hưởng điện thì: f > fo .

DẠYKÈMQUYNHƠNOFFICIAL 109 CHỦ ĐỀ 7 : ĐỘ LỆCH PHA A. TÓM TẮT KIẾN THỨC CƠ BẢN 1. Phương pháp chung: + LCZZ tanφ R = hay LC R UU tanφ U = . Thường dùng công thức này vì có dấu của ϕ. + R cos Zϕ= hay RU cos φ U = ; cosϕ = P UI . Lưu ý công thức này không cho biết dấu của ϕ + sinϕ LCZZ Z = hay LCUU sin φ U = . + Kết hợp với các công thức định luật ôm : RLCMN LCMN UUUUU I RZZZZ ===== + Lưu ý: Xét đoạn mạch nào thì áp dụng công thức cho đoạn mạch đó. + Độ lệch pha của hai đoạn mạch ở trên cùng một mạch điện: 12 ϕ−ϕ=±∆ϕ , khi đó: - Nếu 0∆ϕ= (hai điện áp đồng pha) thì 1212 tantanϕ=ϕ  ϕ=ϕ . Lúc này ta có thể cộng các biên độ điện áp thành phần: 1212 UUUZZZ =+  =+ . - Nếu 2 ∆ϕ=±π (hai điện áp vuông pha), ta dùng công thức: 12 tantan1 ϕϕ=− - Nếu ∆ϕ bất kì ta dùng công thức: 12 12 tantan tan 1tantan ∆ϕ=ϕ−ϕ +ϕϕ hoặc dùng giản đồ véctơ. + Thay giá trị tương ứng của hai đoạn mạch đã biết vào 1tan ϕ và 2tan ϕ (Với : LCZZ tan Rϕ= ). a. Xác định các đại lượng khi biết hai đoạn mạch có điện áp cùng pha, vuông pha. Câu 1: Cho mạch điện xoay chiều như hình. R1 = 4Ω, 2 1 10 CF 8 = π , R2 = 100Ω, 1 LH = π , f = 50Hz. Tìm điện dung C2, biết rằng điện áp uAE và uEB cùng pha. Hướng dẫn: Ta có EB EBui AEuAE i φφφ φφφ   =−  =− Vì uAE và uEB đồng pha nên AEEBuuφφ = AEEBφφ = AEEBtanφ tanφ = 12 CLC 12 ZZZ RR ⇔−= 21 2 CLC 1 R ZZZ R  =+ 2C 100 Z1008300 4  =+=Ω 2 4 2 C 1110 C 2πfZ2π.50.3003π  === (F). E R1 B m A L,R2C1 C2

DẠYKÈMQUYNHƠNOFFICIAL 110 Câu 2: Cho mạch điện như hình vẽ. UAN = 150V, UMB = 200V, uAN và uMB vuông pha với nhau, cường độ dòng điện tức thời trong mạch có biểu thức 0 iIcos100πt= (A). Biết cuộn dây là thuần cảm. Hãy viết biểu thức uAB. Hướng dẫn: Ta có: 22 ANRC UUU150 =+= V (1) 22 MBRL UUU200 =+= V (2) Vì uAN và uMB vuông pha nhau nên: MBANMBAN ππ φφφφ 22 −=  =+ (Với MBφ 0> , ANφ 0< ) MBANAN π tanφ tan φ cot φ2   =+=−   MBMBAN AN 1 tanφ tanφ tanφ 1 tanφ ⇔=−  =− LC2 RLC RR UU.1UUU UU  =  = (3) Từ (1), (2) và (3), ta suy ra : UL = 160V , UC = 90V, UR = 120V. Ta có : () ()2 222 ABRLC UUUU12016090139 =+−=+−≈ V LC R UU160907 tanφφ 0,53 U12012 ===  = rad. Vậy ( )AB u1392cos100πt0,53=+ (V). Câu 3: Cho vào đoạn mạch hình bên một dòng điện xoay chiều có cường độ 0 iIcos100πt= (A). Khi đó uMB và uAN vuông pha nhau, và biểu thức MB πu1002cos100πt 3 =+  (V). Hãy viết biểu thức uAN và tìm hệ số công suất của đoạn mạch MN? Hướng dẫn: Do pha ban đầu của i bằng 0 nên MB MBui ππ φφφ 0 33 =−=−= rad. Dựa vào giản đồ vectơ, ta có các giá trị hiệu dụng của UL, UR, UC là: UR = UMB cosϕMB = π 100cos50 3 = V LRMB πUUtanφ 50tan503 3 === V Vì uMB và uAN vuông pha nhau nên: MBANAN ππ φφφ26 −=  =− R A B NM C L R CL,r = 0 A B NM

DẠYKÈMQUYNHƠNOFFICIAL 111 Ta có: MBANtanφ tanφ 1=− LC RR UU .1 UU ⇔=− 22 R C L U5050 U U 5033  === V. Ta có: R AN 0 AN AN U501002 UU100 πcosφ 33 cos 6 ===  =    V. Vậy biểu thức AN 2 πu100cos100πt 36  =−  V. Hệ số công suất toàn mạch: () RR 2 22 RLC2 RUU503 cos φ ZU UUU7 5050350 3 ===== +−  +−  Câu 4: Đoạn mạch xoay chiều với điện áp hai đầu đoạn mạch ổn định , có RLC ( L thuần cảm ) mắc nối tiếp. Biết : điện áp hiệu dụng hai đầu đoạn mạch lệch pha là ϕ = π 6 so với cường độ dòng điện hiệu qua mạch . Ở thời điểm t , điện áp tức thời ở hai đầu đoạn mạch chứa LC là uLC = 100 3 V và điện áp tức thời hai đầu điện trở R là uR = 100 V .Biểu thức điện áp cực đại hai đầu điện trở R là : A. 200 V B. 173,2 V C. 321,5 V D. 316,2 V Hướng dẫn: Đoạn mạch chứa LC và R  uLC vuông pha với uR Áp dụng công thức: 1 U u U u 2 R0 R 2 LC0 LC =        +         2 LC22 R0R u uU tanφ  +=  Suy ra: U0R = 316,2V.   Chọn D Câu 5: Đoạn mạch xoay chiều với điện áp hai đầu đoạn mạch AB ổn định, có R, L, C (L thuần cảm) mắc nối tiếp. Biết thời điểm t1, điện áp tức thời ở hai đầu đoạn mạch chứa LC là uLC = 50 3 V và điện áp tức thời hai đầu điện trở R là uR = 50 3 V; ở thời điểm t2 điện áp tức thời ở hai đầu đoạn mạch chứa LC là uLC = 150V và điện áp tức thời hai đầu điện trở R là uR = 50V. Độ lệch pha giữa điện áp tức thời hai đầu đoạn mạch so với cường độ dòng điện tức thời ở thời điểm t1 là : A. π 3 B. π 6 C. π 4 D. π 5 Hướng dẫn: Áp dụng: 1 U u U u 2 R0 R 2 LC0 LC =        +         U0LC = 100 3 V và U0R = 100 V. Khi đó: LC LC0LC1R 111 R0R1 u uU sintu1 .tantanttantt uUcosttan6 3 ω π ==ϕω  ω==  ω= ωϕ    Chọn B ) α

DẠYKÈMQUYNHƠNOFFICIAL 112 Câu 6: Đặt vào hai đầu đoạn mạch RLC nối tiếp một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Tại thời điểm t1 các giá trị tức thời uL(t1) = – 30 3 V, uR(t1) = 40V. Tại thời điểm t2 các giá trị tức thời uL(t2) = 60V, uC(t2) = – 120V, uR(t2) = 0V. Điện áp cực đại giữa hai đầu đoạn mạch là: A. 50V B. 100 V C. 60 V D. 50 3 V Hướng dẫn: Đây là bài tập dạng pha vuông góc hay còn gọi là vế phải bằng 1: 1 U u U uu 2 R0 R 2 LC0 LC =        +        + `Khi đó: 2222 L1R1 0L0R0L0R uu30340 11 UUUU   +=  +=     (1) 2222 L2C2R2 0LC0R0LC0R uu u600 11 UUUU  + +=  +=  (2) Từ (2)  uL + uC = U0LC = 60 V. Và vì uR2 = 0  uL2 = U0L = 60 V và uC = – U0C = 120 V. Thay vào U0L = 60 V vào (1)  U0R = 80 V. Suy ra U0 = 100V.    Chọn B b. Xác định các đại lượng khi biết hai đoạn mạch có điện áp lệch pha góc ϕ. Câu 1: Một mạch điện không phân nhánh gồm điện trở thuần R = 75 Ω , cuộn cảm có độ tự cảm L = 5 4π H và tụ điện có điện dung C. Dòng điện xoay chiều qua mạch: i = 2 cos 100 π t (A). Độ lệch pha giữa điện áp và cường độ dòng điện là π 4 . Tính C và viết biểu thức điện áp giữa hai đầu đoạn mạch trên. Hướng dẫn: Ta có: ZL= ωL= 100π 5 4π =125Ω Độ lệch pha giữa u và i: tanϕ = LCZZ R ⇔ tan π 4 = LCZZ R ⇔ 1 = 125 75 CZ . Suy ra: C75125Z =−  CC CC 75125ZZ50 75Z125Z200 =−  =Ω  =−  =Ω  3 C 4 C C 1110 CF Z100.505 1110 ZF Z100.200  === ωππ  === ωππ a. Trường hợp C = 310 F 5π , thì () ()2 222 LC ZRZZ7512550752 =+−=+−=Ω . Ta có: U0 = I0Z = 2.75 2 =150 2 V; ϕ = π 4 nên: u = 150 2 cos(100πt+ π 4 )(V).

DẠYKÈMQUYNHƠNOFFICIAL 113 b. Trường hợp C = 410 F π , thì () ()2 222 LC ZRZZ75125200752 =+−=+−=Ω. Ta có: U0 = I0Z = 2.75 2 = 150 2 V; ϕ = π 4 nên: u = 150 2 cos(100πt π 4 )(V). Câu 2: Cho đoạn mạch như hình vẽ: f = 50 Hz; L= 1 2π H thì MBU trễ pha 900 so với ABU và MNU trễ pha 1350 so với ABU . Tính điện trở R? A. R = 50 Ω B. R1002=Ω C. R = 100 Ω D. R802=Ω Hướng dẫn: Ta có: ZL= Lω = 1 2π .100π = 50 Ω . Do MBU trễ pha 900 so với ABU nên ta có: MBMBAB AB 1 tan φ tan φ tan φ 1 tan φ =−⇔=− . Hay : ()C2 CLC LC LC Z 1R RZZZ ZZ RZZ R =−=−  =− (1) Mặt khác MNU trễ pha 1350 so với ABU nên: 00000 MNABABMNφφ 135 φφ 1359013545−=−  =+=−+= (Do đoạn MN chỉ chứa C nên 0 MNφ 90=− ). Vậy : LC ABLC ZZ tan φ 1ZZR R ==  −= (2) Thay (2) vào (1) ta có: L LCCC Z100 ZZZZ50 22 −=  ===Ω . Thay vào (2): LC RZZ1005050 =−=−=Ω    Chọn C Câu 3: Đoạn mạch xoay chiều R, L, C nối tiếp như hình vẽ, biết R = 100W; UR = 50V; UL = 50V;UC = 100V; f = 50Hz. a. Tính L, C? b. Tính ZAB? UAB? c. Tính uANuMBϕ−ϕ ? Dựa vào giản đồ tìm UAB. Hướng dẫn: a. Ta có: R L L L 4 C C C U 50 I0,5A R100 UZ501001 Z100LH I0,5100 U 1001110 Z200CF I0,5Z100.2002   ===    ===Ω  === ωππ  ===Ω  === ωππ  C A B R L NM NM R A B L C

DẠYKÈMQUYNHƠNOFFICIAL 114 b. () 22 LCZRZZ =+− =1002 Ω ;UAB = I.Z = 50 2 V. c. Giản đồ vectơ: 1ϕ góc lệch pha của uAN so với I tan L 11 Z 1 R4 π ϕ==  ϕ= uMB trễ pha so với i 1 góc 2 π (vì ZC > ZL). Vậy uAN sớm pha hơn uMB một góc: 1 3 2424 ππππ ϕ+=+= . Dựa vào giản đồ ta có:NB = 2MN và 1 4 π ϕ= nên tam giác ANB là tam giác vuông cân tại A vì vậy AB = AN. Câu 4 (ĐH 2009): Đặt điện áp u = U0cosωt (V) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, tụ điện và cuộn cảm thuần có độ tự cảm L thay đổi được. Biết dung kháng của tụ điện bằng R3 Điều chỉnh L để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại, khi đó A. Điện áp giữa hai đầu điện trở lệch pha 6 π so với điện áp giữa hai đầu đoạn mạch. B. Điện áp giữa hai đầu tụ điện lệch pha 6 π so với điện áp giữa hai đầu đoạn mạch. C. Trong mạch có cộng hưởng điện. D. Điện áp giữa hai đầu cuộn cảm lệch pha 6 π so với điện áp giữa hai đầu đoạn mạch. Hướng dẫn: Vẽ giản đồ vectơ, chỉnh L để ULmax dùng định lý hàm sin ta có: () () () L Lmax RCRCLRCL UUU U sinU;UsinU;UsinU;U =  = góc tạo bởi ( )RC πU;U 2 = Đặt ( )RRCα U;U= với tan CZ π α 3 α R3 ==  =  điện áp giữa hai đầu tụ điện lệch pha 2 π so với điện áp giữa hai đầu đoạn mạch và điện áp giữa hai đầu cuộn cảm lệch pha 3 π so với điện áp giữa hai đầu đoạn mạch. Điện áp giữa hai đầu điện trở lệch pha 6 π so với điện áp giữa hai đầu đoạn mạch.  Chọn A A N B M

DẠYKÈMQUYNHƠNOFFICIAL 115 Câu 5: Đặt một điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch AB gồm cuộn cảm thuần có độ tự cảm L, điện trở thuần R và tụ điện có điện dung C mắc nối tiếp theo thứ tự trên. Gọi UL, UR và UC_lần lượt là các điện áp hiệu dụng giữa hai đầu mỗi phần tử. Biết điện áp giữa hai đầu đoạn mạch AB lệch pha 2 π so với điện áp giữa hai đầu đoạn mạch NB (đoạn mạch NB gồm R và C). Hệ thức nào dưới đây là đúng? A. 2222 RCL UUUU =++ . B. 2222 CRL UUUU =++ C. 2222 LRC UUUU =++ D. 2222 RCL UUUU =++ Hướng dẫn: Cách giải 1: Ta có: 2222222 LRC PQOPOQUUUU =+  =++ Cách giải 2: Ta có: ABNB LCC22 LCRC RR tantan1 UUU .1UUUU (1) UU ϕϕ=−  =−  =+ Mà: () 222 RLC UUUU =+− 222 RLLCC UU2UUU =+−+ ( )22222 RLCRC UUU2UU =++−+ (2) Từ (1) và (2) suy ra: 22222222 LRCLRC UUUUUUUU =−−  =++   Chọn C C. CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Cho đoạn mạch xoay chiều u = U0cosωt (V) ổn định, có R, L, C (L thuần cảm) mắc nối tiếp với R thay đổi. Khi R = 20 Ω thì công suất trên điện trở R cực đại và đồng thời khi đó điều chỉnh tụ C thì điện áp hiệu dụng hai đầu tụ C sẽ giảm. Dung kháng của tụ sẽ là: A. 20 Ω B . 30 Ω C . 40 Ω D . 10 Ω Câu 2: Đoạn mạch xoay chiều với điện áp hai đầu đoạn mạch AB ổn định, có R, LC ( L thuần cảm )mắc nối tiếp. Biết thời điểm t1, điện áp tức thời ở hai đầu đoạn mạch chứa LC là uLC = 7,5 7 V và điện áp tức thời hai đầu điện trở R là uR = 30V; ở thời điểm t2 điện áp tức thời ở hai đầu đoạn mạch chứa LC là uLC = 15V và điện áp tức thời hai đầu điện trở R là uR = 20 3 V. Điện áp hiệu dụng hai đầu đoạn mạch AB là: A. 45 V B. 50 V C. 25 2 V D. 60 V Câu 3: Đoạn mạch xoay chiều AB chứa 3 linh kiện R, L, C. Đoạn AM chứa L, MN chứa R và NB chứa C. R50=Ω , L Z503 = Ω, C 503 Z 3 = Ω. Khi giá trị điện áp tức thời Q O H P R CL M N B A

DẠYKÈMQUYNHƠNOFFICIAL 116 AN u803 = V thì MB u60V = . Giá trị tức thời ABu có giá trị cực đại là: A. 150V. B. 100V. C. 507 V. D. 1003 V. Câu 4: Đoạn mạch xoay chiều với điện áp hai đầu đoạn mạch ổn định, có R, L, C (L thuần cảm) mắc nối tiếp. Biết thời điểm t, điện áp tức thời ở hai đầu đoạn mạch chứa LC là uLC = 100 3 V và điện áp tức thời hai đầu điện trở R là uR = 100 V; độ lệch pha giữa điện áp hiệu dụng ở hai đầu đoạn mạch và cường độ dòng điện hiệu là π 3 . Pha của điện áp tức thời hai đầu điện trở R ở thời điểm t là: A. π 6 B. π 4 C. π 3 D. π 5 Câu 5: Cho mạch xoay chiều như hình vẽ: C31,8 μF= , f = 50 Hz. Biết AEU lệch pha EBU một góc 1350 và i cùng pha với ABU . Tính giá trị của R? A. R = 50 Ω B. R502=Ω C. R = 100 Ω D. R = 200 Ω Câu 6: Đoạn mạch xoay chiều AB chứa 3 linh kiện R, L, C. Đoạn AM chứa L, MN chứa R và NB chứa C. R50=Ω , L Z503 = Ω, C 503 Z 3 = Ω. Khi giá trị điện áp tức thời AN u803 = V thì MB u60V = . Giá trị tức thời ABu có giá trị cực đại là: A. 150V. B. 100V. C. 507 V. D. 1003 V. Câu 7: Đặt vào hai đầu đoạn mạch RLC nối tiếp một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Tại thời điểm t1 các giá trị tức thời uL(t1) = – 10 3 V, uC(t1) = 30 3 V, uR(t1) = 15V. Tại thời điểm t2 các giá trị tức thời uL(t2) = 20V, uC(t2) = – 60V, uR(t2) = 0V. Tính biên độ điện áp đặt vào 2 đầu mạch? A. 60 V. B. 50V. C. 40 V. D. 403 V. Câu 8: Đoạn mạch AB gồm một cuộn dây có độ tự cảm L = 1 2π H, một tụ điện có điện dung C = 410 F π và một điện trở thuần R = 50Ω mắc như hình vẽ Điện trở của cuộn dây nhỏ không đáng kể Điện áp giữa 2 đầu đoạn mạch AB có tần số 50Hz và có giá trị hiệu dụng là U = 100V. Tính độ lệch pha của điện áp giữa 2 điểm A và N đối với điện áp giữa 2 điểm M và B. A. 3π 4 B. π 4 C. π 2 D. 3π 4 C A B R L NM R CL M N B A E C A B R, L

DẠYKÈMQUYNHƠNOFFICIAL 117 HƯỚNG DẪN GIẢI Câu 1: Chọn C. Khi R thay đổi, công suất trên điện trở R cực đại khi LCRZZ =− (1) Đồng thời lúc này điều chỉnh tụ C thì điện áp hai hiệu dụng đầu tụ C giảm. Chứng tỏ khi LCC maxRZZ20U =−=Ω  Áp dụng khi 22 L C maxC L RZ UZ Z +  = (2) và đương nhiên ZC > ZL Từ (1) suy ra ZL = ZC – R (3). Thay (3) vào (2) ta được ZC = 2R = 40 Ω. Câu 2: Chọn C. Áp dụng công thức 1 U u U u 2 0R R 2 0LC LC =        +         U0 2 = U0LC 2 + U0R 2  U  điện áp hệu dụng hai đầu đoạn AB là U = 25 2 V. Câu 3: Chọn C. Ta có: tanϕANtanϕMB = LC 503 Z Z503 3 ..1 RR5050    ==−    . Hai đoạn mạch AN và MB có pha vuông góc 2222 ANANMBMB 0AN0MB0RL0RC uuuu11 UUIZIZ  +=  +=  (1) Với 22 ANC 22 MBC ZRZ100 100 ZRZ 3  =+=Ω  =+=  (2) Suy ra: 3AI 0 =  22 AB max0AB0ABLC uUIZ3.R(ZZ)507V ===+−= Câu 4: Chọn B. Điện áp tức thời: uLC = U0LC cos(ωt + π 2 ) = U0LC sinωt uR = U0R cosωt Và uLC vuông pha với uR  LC LC0LC R R0R u uU sintu .tan.tanttant1t uUcosttan4 ω π ==ϕω  ω==  ω= ωϕ . Câu 5: Chọn C. Theo giả thiết u và i cùng pha nên trong mạch xảy ra hiện tượng cộng hưởng ta có: LC 6 11 ZZ100 ωC100π.31,8.10 ====Ω .

DẠYKÈMQUYNHƠNOFFICIAL 118 Mặt khác đoạn EB chứa tụ C nên EB π φ 2 =− Suy ra: 0 AEEBφφ 135−= hay : 0000 AEEBφφ 1359013545=+=−+= . Vậy L0 AEL Z tanφ tan451RZ100 R ===  ==Ω Câu 6: Chọn C. Ta có: tanϕANtanϕMB = 1 50 3) 503 ( . 50 503 R Z . R Z LC == Hai đoạn mạch AN và MB có pha vuông góc 2222 ANANMBMB 0AN0MB0RL0RC uuuu11 UUIZIZ  +=  +=  (1) Với 22 ANC 22 MBC ZRZ100 100 ZRZ 3  =+=Ω  =+=  (2) Từ (1) và (2) ta được: I3A 0 = suy ra uUIZ3RZ)507V 2 LC 2 ABMAX0AB0AB===+= . Câu 7: Chọn B. Đâylàbàitậpdạngphavuônggóchaycòngọilàvế phảibằng1: 1 U u U uu 2 R0 R 2 LC0 LC =        +        + . Khi đó: 2222 L1C1R1 0LC0R0LC0R uu u20315 11 UUUU   + +=  +=     (1) 2222 L2C2R2 0LC0R0LC0R uu u400 11 UUUU  + +=  +=  (2) Từ (2)  U0LC = 40V. Thay vào (1)  U0R = 30 V  U0 2 = U0LC 2 +U0R 2  U0 = 50V. Câu 8: Chọn A. Độ lệch pha của ANu đối với i : AN AN L u u 1 2π Z.50. ωL π2πtanφ 1 φ RR504 ====  = . Độ lệch pha của MBu đối với i: AN MB 4 LC u u 11 2π.50. 110 2π ωL2π.50.ZZ ωπ C πtanφ φ RR02 ====−∞  =− Vậy: ANMBuu ππ 3π φφφ 424  ∆=−=−−=   .

DẠYKÈMQUYNHƠNOFFICIAL 119 CHỦ ĐỀ 8 : BÀI TOÁN NGƯỢC XÁC ĐỊNH CÁC GIÁ TRỊ CỦA MẠCH RLC Tính tổng trở Z, điện trở R - cảm kháng ZL – dung kháng ZC – độ tự cảm L và điện dung C A. TÓM TẮT LÝ THUYẾT CƠ BẢN Giả thiết đề cho Sử dụng công thức Chú ý Cường độ hiệu dụng và điện áp hiệu dung. Áp dụng định luật ôm: C RLAM LCAM U UUU U I RZZZZ ===== Cho n dự kiện tìm được (n – 1) ẩn số Độ lệch pha φ LCZZ tan Rϕ= hoặc R cos Zϕ= kết hợp với định luật ôm Thường tính R Z cos = ϕ Công suất P hoặc nhiệt lượng Q 2 PRIUIcos==ϕ hoặc 2 QRIt = với định luật ôm ThườngdùngtínhI: P I R = Ápdụng địnhluậtômtínhZ + Nhớ các công thức về định luật Ôm, công thức tính tổng trở.... Biết U và I: U Z I = Biết ZL, ZC và R: () 22 LCZRZZ =+− : LZ ωL= , C 1 Z ωC = với L có đơn vị (H) và C có đơn vị (F) . Biết R và ϕ hoặc cosϕ : R Z cos = ϕ . Nếu cuộn cảm có điện trở hoạt động r thì mạch RLrC sẽ có điện trở thuần tương đương là R + r; khi đó () 22 LCZ(rR)ZZ =++− + Công thức tính điện trở R: Nếu biết L, C và ϕ: tính theo: LCZZ tan Rϕ= . Nếu cuộn cảm có điện trở r: LCZZ tan Rrϕ= + Biết Z và ϕ hoặc cosϕ : R = Zcosϕ. Nếu cuộn cảm có điện trở r: Rr cos Z + ϕ= Biết P và I: 2PRI = ; Nếu cuộn cảm có điện trở r. Công suất toàn mạch : P = (r + R)I2

DẠYKÈMQUYNHƠNOFFICIAL 120 + Công thức tính cảm kháng ZL và dung kháng Zc: LZ ωL2πfL== ; C 11 Z ωC2πfC == . - Biết Z và R, tính được hiệu: 22() LC ZZZR −=±− sau đó tính được ZL nếu biết Zc và ngược lại, từ đó tính L và C - Chú ý thêm : LC L ZZ C = ; cộng hưởng điện : ZL= ZC hay : 2 ω LC1 = hay 1 ω LC = . - Khi bài toán cho các điện áp hiệu dụng thành phần và hai đầu mạch, cho công suất tiêu thụ nhưng chưa cho dòng điện thì hãy lập phương trình với điện áp hiệu dụng. - Khi tìm ra UR sẽ tìm R P I U = sau đó tìm RLC LC UUU R; Z; Z. III === - Công suất thiêu thụ : 22 2 222R LC UU PUIcosφ IRRRIU ZR(ZZ) ===== +− . - Hệ số công suất R kcosφ Z == = RPU UIU = . - Nhiệt lượng toả ra trên mạch (chính là trên R): Q = RI2t ( t có đơn vị: s, Q có đơn vị: J). - Cũng cần phải nghĩ đến giản đồ véctơ vẽ mạch điện đó để bảo đảm hệ phương trình không bị sai. BÀI TẬP VẬN DỤNG Câu 1: Tính tổng trở của các mạch điện sau: a. Cho mạch RLC không phân nhánh: UC = 4V; UR = 16V; UL = 20V; I = 2A. b. Cho Mạch RL nối tiếp có R = 20Ω; u lệch pha 60o so với i. c. Cho Mạch RC nối tiếp có R = 10Ω; u lệch pha 30o so với i. d. Cho Mạch RLC nối tiếp có R = 60Ω; hệ số công suất 0,6. Hướng dẫn: a. Đề cho I và các UC; UR, UL nên ta dùng các công thức : R = RU I = 16 2 = 8 Ω; ZL = LU I = 20 2 = 10Ω; ZC = CU I = 4 2 = 2Ω. Suy ra: () 2222 LC ZR(ZZ)810282 =+−=+−=Ω . b. Đề cho: R = 20 Ω; ϕ = π 3 nên ta có: tan ϕ = LZ R  ZL = Rtan ϕ = 20 3 Ω c. Đề cho: R = 10 Ω; ϕ = π 6 nên ta có: tan ϕ = CZ R  ZC = – Rtan ϕ = 10 3 3 Ω d. Đề cho: R = 60 Ω; cos ϕ= 0,6 mà cosϕ = R Z  Z = R cosφ = 60 0,6 = 100 Ω.

DẠYKÈMQUYNHƠNOFFICIAL 121 Câu 2: Cho mạch điện xoay chiều như hình vẽ. UAB = const; f = 50Hz, điện trở các khóa K và ampe kế không đáng kể 410 C π = F. Khi khóa K chuyển từ vị trí 1 sang 2 thì số chỉ của ampe kế không thay đổi. Tính độ tự cảm L của cuộn dây? A. 210 H π B. 110 H π C. 1 H π D. 10 H π Hướng dẫn: Ta có: C 4 11 Z100Ω 10ωC 100π. π ω 100π rad/s  ===    =  Khi khóa K ở vị trí 1 mạch là hai phần tử R và C nên ta có: ABAB 22 AB C UU I ZRZ == + (1) Khi khóa K ở vị trí 2 thì mạch bao gồm hai phần tử là R và L nên ta có: ABAB 22 AB L UU I' Z'RZ == + (2) Theo đề I = I’ nên (1) = (2) : 2222 2222CL CL 11 RZRZ RZRZ =  +=+ ++ L LC Z1001 ZZ100LH ω 100ππ  ==Ω  ===    Chọn C Câu 3: Một mạch điện xoay chiều ABDEF gồm các linh kiện sau đây mắc nối tiếp (xem hình vẽ). Một cuộn dây cảm thuần có hệ số tự cảm L. Hai điện trở giống nhau, mỗi cái có giá trị R. Một tụ điện có điện dung C. Đặt giữa hai đầu A, F của mạch điện một điện áp xoay chiều có giá trị hiệu dung UAF = 50V và có tần số f = 50Hz. Điện áp giữa hai đầu các đoạn mạch AD và BE đo được là UAD = 40V và UBE = 30V. Cường độ dòng điện hiệu dụng trong mạch là I = 1A. a. Tính các giá trị R, L và C. b. Tính hệ số công suất của mạch điện. c. Tính độ lệch pha giữa các hiệu điện thế UAD và UDF A B C A 1 2 K R L C A F R ED RL B

DẠYKÈMQUYNHƠNOFFICIAL 122 Hướng dẫn: a. Tổng trở Z = 22 AF LC U50 (2R)(ZZ)50 I1 +−===Ω 22 LC 4R(ZZ)2500⇔+−= (1) Lại có ZAD = 22 AD L U40 RZ40 I1 +===Ω 22 L RZ1600⇔+= (2) ZBE = 22 BE C U30 RZ30 I1 +===Ω 22 C RZ900⇔+= (3) Từ (2) và (3) ta có: 4R2 + 2 22 LC Z2Z5000 += (4) Từ (1) suy ra: 4R2 + 22 LCLC ZZ2ZZ2500 +−= (5) Lấy (4) trừ (5) ta có: 222 LCLCLC ZZ2ZZ(ZZ)2500 ++=−= LC ZZ50 +=Ω ( loại nghiệm LC ZZ500) +=−Ω< (6) Lấy (2) trừ (3) ta có: 700= 22 LCLCLCZZ(Z+ Z)(ZZ)−=− (7) Thay (6) vào (7) suy ra: 700 = 50 LC (ZZ) LC 700 ZZ14 50 ⇔−== (8) Từ (6) và (8) suy ra L C Z32 Z18 =Ω  =Ω L 6 C Z32 L0,102H ω 2π.50 11 C177.10F Z ω 100π.18  ===     ===   Thay vào (2) : R = 2 L1600Z = 24 Ω . b. Hệ số công suất cos 2R2.24 φ 0,96 Z50 === . c. uAD sớm pha hơn i là φ 1 với tan φ 1 = L Z4 R3 = ; uDF sớm pha hơn i là φ 2 với tan φ 2 = C Z3 R4 =− Ta có tan φ 1tan φ 2 = – 1 nghĩa là uAD sớm pha hơn uDF là π 2 . Câu 4: Đặt vào điện áp 0 uUcost =ω V, trong đó U0 không đổi nhưng ω thay đổi được vào 2 đầu đoạn mạch gồm điện trở R = 60 Ω , cuộn cảm thuần L và tụ điện C mắc nối tiếp. Khi ω=ω thì cường độ dòng điện hiệu dụng trong mạch cực đại và bằng Im. Khi ω=ω hoặc ω=ω thì cường độ dòng điện hiệu dụng trong mạch như nhau và bằng m I 2 . Biết 21 120 rad/s.ω−ω=π Giá trị của độ tự cảm L bằng: A. 43 H 4π B. 3 H 2π C. 1 H 2π D. 2 H π

DẠYKÈMQUYNHƠNOFFICIAL 123 Hướng dẫn giải: Ta có: 2 120 12 1 LC ωω=ω⇔= ωω  ZC1 = ZL2 (ta lại có ZL2 > ZL1). Mặt khác: m m 122 LC U I R I UUU I Z22R R(ZZ)  =   ====  +− (vì Im là lúc mạch cộng hưởng). Khi đó: 4R2 = R2 + (ZL2 – ZC2)2  3R2 = (ZL2 – ZL1)2 = L2 (ω1 – ω2)2  R 3 = L (ω2 – ω1) = 60 3 (Ω) Suy ra: 21 6036033 LH 1202 === ω−ωππ .   Chọn B CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Chomạch điệnnhư hình vẽ: u1202cos100πt= (V); cuộn dây có r = 15Ω; 2 LH 25π = , C là tụ điện biến đổi. Điện trở vôn kế lớn vô cùng. Điều chỉnh C để số chỉ vôn kế lớn nhất. Tìm C và số chỉ vôn kế lúc này? A. 2 V 10 CF, U136V 8π == B. 2 V 10 CF, U163V 4π == C. 2 V 10 CF, U136V 3π == D. 2 V 10 CF, U186V 5π == Câu 2: Mạch điện xoay chiều gồm một cuộn dây có điện trở r = 30Ω, độ tự cảm L0,4 π = H mắc nối tiếp với tụ điện có điện dung C. Điện áp tức thời giữa hai đầu đoạn mạch là: u120cos100πt= (V). Với giá trị nào của C thì công suất tiêu thụ của mạch có giá trị cực đại và giá trị công suất cực đại bằng bao nhiêu? A. 410 C 2π = F và max P120 = W. B. 4C10 π = F và max P1202 = W. C. 310 C 4π = F và max P240 = W. D. 310 C π = F và max P2402 = W. Câu 3: Cho mạch điện không phân nhánh. R = 100Ω, cuộn dây có độ tự cảm L = 0,318 H, f = 50Hz, tụ điện có điện dung thay đổi. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng U1002 = V. Điều chỉnh C để mạch có cộng hưởng điện. Giá trị C và cường độ dòng điện khi đó là: A. C = 31,8µF và I2 = A. B. C = 31,8µF và I22 = A. C. C = 3,18µF và I32 = A. D. C = 63,6µF và I = 2A. V r, L C A B

DẠYKÈMQUYNHƠNOFFICIAL 124 Câu 4: Cho mạch điện gồm R, L, C nối tiếp. R thay đổi, 1 L π = H, 310 C 4π = F. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u752cos100πt= (V). Công suất trên toàn mạch là P = 45W. Điện trở R có giá trị bằng bao nhiêu? A. R = 45Ω B. R = 60Ω C. R = 80Ω D. câu A hoặc C Câu 5: Cho đoạn mạch gồm điện trở thuần R = 100Ω và tụ điện có điện dung C mắc nối tiếp. Biết biểu thức hiệu điện thế giữa 2 đầu đoạn mạch u = 100cos100πt V và cường độ hiệu dụng trong mạch I = 0,5 A. Tính tổng trở của đoạn mạch và điện dung của tụ điện? A. Z = 100 2 Ω; C = 410 F π B. Z = 200 2 Ω; C = 410 F π C. Z = 50 2 Ω; C = 410 F π D. Z = 100 2 Ω; C = 310 F π Câu 6: Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi, tần số 50Hz vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L thay đổi được và tụ điện có điện dung. Điều chỉnh độ tự cảm L đến giá trị 1 H 5π hoặc 4 H 5π thì cường độ dòng điệntrongmạchcógiátrị hiệudụngnhư nhauvàlệchphanhaulà 2π 3 .Giátrị củaRbằng A. 30 Ω . B. 30 3 Ω . C. 10 3 Ω . D. 40 Ω . Câu 7: Mạch điện xoay chiều nối tiếp AMB có tần số 50Hz. AM chứa L và R = 50 3 Ω. MB chứa tụ điện C = 410 F π . Điện áp uAM lệch pha π 3 so với uAB. Giá trị của L là A. 3 π H. B. 1 π H. C. 1 2π H. D. 2 π H. HƯỚNG DẪN GIẢI: Câu 1: Chọn A. Do vôn kế mắc vào hai đầu cuộn dây nên số chỉ vôn kế là: 22 Vddd 22 LC UU UUIZZ.r(ωL) Z r(ZZ) ====+ +− . Do Zd không phụ thuộc C nên nó không đổi. Vậy biểu thức trên tử số không đổi. Số chỉ Vôn kế lớn nhất khi mẫu số bé nhất: 22 LCmin(r(ZZ)) +− Điều này xảy ra khi cộng hưởng điện: LC ZZ8==Ω .

DẠYKÈMQUYNHƠNOFFICIAL 125 Suy ra: 210 CF 8π = . Lúc đó Z = r. Số chỉ vôn kế : 22 Vd U UU.r(ωL) r ==+ 2212015.15(8)=+ 120 .17136V 15 == Câu 2: Chọn C. Công suất: () 2 2 22 LC Ur PIr rZZ == +− Ta có Pmax ⇔ CL 1 ZZ ωL ωC =⇔= () 3 2 2 1110 C 0,4ω L4π100π . π  === F và 22 max U120 P240 r2.30 === W. Câu 3: Chọn A. Cảm kháng: L Z2πfL2π.50.0,318100 ===Ω Mạch có cộng hưởng khi ZC = ZL = 100Ω. 4 C 1110 C 2πfZ2π.50.100 π  === F 31,8= µF. Khi đó: max U1002 I===2 R100 A. Câu 4: Chọn D. Ta có: L 1 Z ωL100π.100 π ===Ω ; C 3 11 Z40 10ωC 100π. 4π ===Ω Công suất tiêu thụ: () () 22 22 2 22LC LC URU PIRRRZZ0 RZZP ==⇔−+−= +− () 2 2275R80 RR100400 45R45 =Ω ⇔−+−=⇔  =Ω Câu 5: Chọn A. Theo định luật Ôm Z = U I = 100 2 Ω. Từ công thức Z = 2222 CC RZ100Z +=+ . Suy ra ZC = 2222 ZR2.100100100 −=−=Ω  C= C 1 ωZ = 410 F π . Câu 6: Chọn C. Ta có: ZL1 = 20Ω và ZL2 = 80Ω Từ I1 = I2  Z1 = Z2  (ZL1 – ZC)2 = (ZL2 – ZC)2  ZC = L1L2ZZ 2 + = 50Ω.

DẠYKÈMQUYNHƠNOFFICIAL 126 Khi đó: tanϕ1 = L1CZZ R = 30 R ; tanϕ2 = L2CZZ R = 30 R  ϕ2 = – ϕ1 Vậy: ϕ2 – ϕ1 = 2ϕ2 = 2π 3  ϕ2 = π 3  R = 30 π tan 3 = 3 30 = 10 3 Ω. Câu 7: Chọn C. Ta có: C 4 11 Z100Ω 10ωC 100π. π R503  ===     =Ω Khi đó: L RL LC RL RL RL RL Z tan R ZZ tantan tan= R1tantantan()3 3  ϕ=  ϕ−ϕ ϕ  ϕ−ϕ== +ϕϕ π ϕ−ϕ=  LLC LLC ZZZ RR 3 ZZZ 1. RR ⇔= + Suy ra: ( )2 C2 2LL LLC RZ 3503.10033.50Z100Z RZ(ZZ) =⇔=+− +− 22 LLL 1 Z100Z3.5050.1000Z50LH. 2 ⇔−+−=⇔=Ω⇔= π

DẠYKÈMQUYNHƠNOFFICIAL 127 CHỦ ĐỀ 9 HAI ĐOẠN MẠCH XOAY CHIỀU MẮC NỐI TIẾP A. TÓM TẮT KIẾN THỨC CƠ BẢN 1. Hai đoạn mạch điện xoay chiều cùng pha Hai đoạn mạch AM gồm R1L1C1 nối tiếp và đoạn mạch MB gồm R2L2C2 nối tiếp mắc nối tiếp với nhau, nếu có: UAB = UAM + UMB  uAB; uAM và uMB cùng pha ABAMMB uuu tantantan ϕ=ϕ=ϕ . 2. Hai đoạn mạch R1L1C1 và R2L2C2 xoay chiều có các điện áp u1 và u2 lệch pha nhau ∆ ∆∆ ∆ϕ ϕϕ Với 11 22 LC 1 1 LC 2 2 ZZ tan R ZZ tan R  ϕ=    ϕ=  (giả sử ϕ1 > ϕ2) Khi đó: ϕ1 – ϕ2 = ∆ϕ  12 12 tantan tan 1tantan ϕ−ϕ =∆ϕ +ϕϕ 3.Trường hợp đặc biệt Nếu hai đoạn mạch trên cùng một mạch điện mà có 2 ∆ϕ=π (vuông pha nhau, lệch nhau góc 900) thì: tanϕ1tanϕ2 = 1. 4. Các ví dụ Ví dụ 1: Mạch điện ở hình 1 có uAB và uAM lệch pha nhau ∆ϕ. Hai đoạn mạch AB và AM có cùng i và uAB chậm pha hơn uAM  ϕAM – ϕAB = ∆ϕ  AMAB AMAB tantan tan 1tantan ϕ−ϕ =∆ϕ +ϕϕ Nếu uAB vuông pha với uAM thì: LLC AMAB ZZZ tan φ tan φ 1 1 RR =−  =− Ví dụ 2: Mạch điện ở hình2: Khi C =C1 vàC =C2 (giả sử C1 >C2)thìi1 vài2 lệch phanhau ∆ϕ. Hai đoạn mạch RLC1 và RLC2 có cùng uAB Gọi ϕ1 và ϕ2 là độ lệch pha của uAB so với i1 và i2 thì có ϕ1 > ϕ2  ϕ1 – ϕ2 = ∆ϕ Nếu I1 = I2 thì ϕ1 = – ϕ2 = 2 ∆ϕ Nếu I1 ≠ I2 thì tính 12 12 tantan tan 1tantan ϕ−ϕ =∆ϕ +ϕϕ B. BÀI TẬP VẬN DỤNG Hình1 R L C M A B Hình2 R L C M A B

DẠYKÈMQUYNHƠNOFFICIAL 128 Câu 1: Đặt vào hai đầu đoạn mạch hình vẽ một hiệu điện thế uAB = Uocos100t (V). Biết C1 = 40μF, C2 = 200μF, L = 1,5H. Khi chuyển khoá K từ (1) sang (2) thì thấy dòng điện qua ampe kế trong hai trường hợp này có lệch pha nhau 90o Điện trở R của cuộn dây là: A. R = 150Ω B. R = 100Ω C. R = 50Ω D. R = 200Ω Hướng dẫn: Khi K ở vị trí (1), đoạn mạch AM chứa các phần tử RLC1 Khi K ở vị trí (2), đoạn mạch MB chứa các phần tử RLC2 Ta có: 1 2 L C 6 1 C 6 2 ZL100.1,5150 11 Z125 C100.40.10 11 Z50 C100.200.10   =ω==Ω  ===Ω ω  ===Ω ω Hai dòng điện iAM và iMB vuông pha nhau nên: 12 LCLC AMMB ZZZZ tan φ tan φ 11 RR =−⇔=− ()()()() 12 12 22 422 4 LCLCLCLC ZZZZRRZZZZ ⇔−−=⇔=−− ()() 422 R1501251505050. =−−=Ω    Chọn C Câu 2 (ĐH 2010): Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM có điện trở thuần 50 Ω nối tiếp với cuộn cảm thuần có độ tự cảm 1 LH π = đoạn mạch MB chỉ có tụ điện với điện dung C thay đổi được. Đặt điện áp 0 uUcos100t =π (V) vào hai đầu đoạn mạch AB. Điều chỉnh C của tụ điện đến giá trị C1 sao cho điện áp hai đầu đoạn mạch AB lệch pha 2 π so với điện áp hai đầu đoạn AM. Giá trị của C1 bằng A. 58.10 π F B. 510 π F C. 54.10 π F. D. 52.10 π F Hướng dẫn: Ta có: L 1 ZL100.100 R50  =ω=π=Ω π  =Ω A C2 B (1) (2) C1 KL,R A R L C M A B

DẠYKÈMQUYNHƠNOFFICIAL 129 Độ lệch pha giữa hiệu điện thế hai đầu đoạn mạch AN và i là: L AM Z tan φ R = (1) Độ lệch pha giữa u và i là 1LCZZ tan φ R = (2). Khi điện áp hai đầu đoạn mạch AB lệch pha 2 π so với điện áp hai đầu đoạn AM, thì: LLC1 AMAM ZZZ tantan11 2RR π ϕ+ϕ=  ϕϕ=−  =− 1 2 5 CL1 L R8.10 ZZ125CF. Z  =+=Ω  = π   Chọn A Câu 3 (ĐH 2011): Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần R1 mắc nối tiếp với tụ điện có điện dung C, đoạn mạch MB gồm điện trở thuần R2 mắc nối tiếp với cuộn cảm thuần có độ tự cảm L. Đặt điện áp xoay chiều có tần số và giá trị hiệu dụng không đổi vào hai đầu đoạn mạch AB. Khi đó đoạn mạch AB tiêu thụ công suất bằng 120 W và có hệ số công suất bằng 1. Nếu nối tắt hai đầu tụ điện thì điện áp hai đầu đoạn mạch AM và MB có cùng giá trị hiệu dụng nhưng lệch pha nhau 3 π , công suất tiêu thụ trên đoạn mạch AB trong trường hợp này bằng A. 75 W. B. 90 W. C. 160 W. D. 180 W. Hướng dẫn: Ban đầu, mạch xảy ra cộng hưởng: () 2 2 1 12 12 U P120U120RR RR ==  =+ + (1) Lúc sau, khi nối tắt C, mạch còn R1R2L: AMMB AMMB UU 3 =  ∆ϕ=ϕ−ϕ=π  Từ giản đồ vectơ ta có: L12 L 12 ZRR 1 tanZ 6RR 33 π+ ϕ=  ϕ==  = + Suy ra: ()() 2 2 21212 2 U PRRIRR Z =+=+ () ( ) () 12 12 2 2 12 12 120RR RR90W. RR RR 3 + =+= +  ++    Chọn B Câu 4 (ĐH 2011): ĐoạnmạchABgồmhai đoạnmạchAMvàMBmắcnốitiếp. ĐoạnAM gồm điện trở thuần R1 = 40 Ω mắc nối tiếp với tụ điện có điện dung 310 CF 4 = π , đoạn mạch MB gồm điện trở thuần R2 mắc với cuộn thuần cảm. Đặt vào A, B điện áp xoay chiềucógiátrị hiệudụngvàtầnsố không đổithì điệnáptứcthời ở hai đầu đoạnmạchAM ϕ π/3

DẠYKÈMQUYNHƠNOFFICIAL 130 và MB lần lượt là: AM 7 u502cos100t(V) 12 π  =π−  và MB u150cos100t (V)=π . Hệ số côngsuấtcủa đoạnmạchABlà A.0,84. B.0,71. C.0,86. D.0,95. Hướng dẫn: Cách giải 1: Tacó: C 3 C AM AM 1 11 Z40 10C 100. 4 Z 40 tan1 R404  ===Ω ω π π  π ϕ=−=−=−  ϕ=−  Từ hìnhvẽ có: L MBMBL2 2 Z tan3ZR3 3R π ϕ=  ϕ==  = Xét đoạnmạchAM: AM AM U50 I0,6252A Z 402 === Xét đoạnmạchMB: MB222 MB2L2 L R60U Z120RZ2R I Z603 =Ω  ===+=   =Ω  Hệ số côngsuấtcủamạchABlà: () () 12 2 22 2 12LC RR 4060 cos 0,84. RR(ZZ)4060(60340) + + ϕ== ++−++− ≃ Chọn A Cách giải 2: Dùng máyFx570ES. Tổngtrở phứccủa đoạnmạchAB: ABAMMBMB ABAMAM AMAM uuuu ZZ1Z iuu  + ===+  Cài đặtmáy:Bấm MODE 2 xuấthiện:CMPLX.bấm: SHIFT MODE 4 Chọn đơnvị là Rad(R) Nhậpmáy: 150 1X(4040) 7 π502 12   +−=  ∠−  i Hiểnthị có2trườnghợp: A φ ab ∠  + i . Tamuốnhiểnthị ϕ,nếumáyhiện:a+bithìbấm:SHIFT23= Kếtquả:118,6851133 ∠ 0,5687670898. Bấmtiếp:cos(0,5687670898)=0,842565653.    Chọn A Câu 5: Đặt điệnáp u2202cos100t (V)=π vàohai đầu đoạnmạchABgồmhai đoạnmạch AMvàMBmắcnốitiếp đoạnAMgồm điệntrở thuầnRmắcnốitiếpvớicuộncảmthuần L, đoạnmạchMBchỉ cótụ điệnC.Biết điệnápgiữahai đầumạchAMvà điệnápgiữahai 7π/12 π/4 π/3

DẠYKÈMQUYNHƠNOFFICIAL 131 đầu đoạnmạchMBcógiátrị hiệudụngbằngnhaunhưnglệchphanhau 2 3 π Điệnáphiệu dụnggiữahai đầu đoạnmạchAMbằng. A.220V B. 220 3 V C.110V D. 2202 V Hướng dẫn: Từ giải đồ vectơ,tacó: () AMMBAMMB 22 tantan 33 ππ ϕ−ϕ=⇔ϕ−ϕ= AMMB AMMB tantan2 tan3 1tantan3 ϕ−ϕ π ⇔==− +ϕϕ AM MB AM MB tan 1 tan 3 1 tan tan ϕ ϕ ⇔=− +ϕ ϕ L AM AM Z011 3tan 0tanR 3 ⇔=−⇔ϕ== +ϕ R LL UR ZU 33 ⇔=⇔= (1) Mặtkhác: 2 222222 R RLCRLRRCR U 42 UUUUUUUU 33 3 ==+=+=  = (2) Talạicó: ()2 22222 RLCRLLCC UUUUUU2UUU =+−=+−+ 2222 CLCCCLC UU2UUU2U2UU ⇔=−+=− (3) Thay(1)và(2)vào(3) ta được: 222 RR RR UU 44 U2.U2.2U 33 33 =−= R RLC U3 U1103V 2 2.1103 UU220V 3  ==     ===     Chọn A Nhận xét: Khi làm bài trắc nghiệm để tính nhanh được bài này thì ta có thể nhẩm để lấy điểm quan trọng nhất của bài giải là: Mạch MB chứa tụ điện mà CU trễ pha 2 π so với I . Mà AMRLUU ≡ lệch pha 2 3 π so với MBCUU ≡  độ lệch pha giữa φAM và φi là 6 π . Khi đó: L R LL ZU R tanZU 6R 33 π =  =  = . Câu 6: Mộtmạch điệnxoaychiềuABDEFgồmcáclinhkiệnsau đâymắcnốitiếp(xemhìnhvẽ): - Mộtcuộndâycảmthuầncóhệ số tự cảmL. C A F R ED RL B

DẠYKÈMQUYNHƠNOFFICIAL 132 - Hai điệntrở giốngnhau,mỗicáicógiátrị R. - Mộttụ điệncó điệndungC. Đặtgiữahai đầuA,Fcủamạch điệnmột điệnápxoaychiềucógiátrị hiệudụngUAF = 50Vvàcótầnsố f=50Hz. Điệnápgiữahai đầucác đoạnmạchADvàBE đo đượclàUAD =40VvàUBE =30V.Cường độ dòng điệnhiệudụngtrongmạchlàI=1A. a.Tínhcácgiátrị R,LvàC. b.Tínhhệ số côngsuấtcủamạch điện. c.Tính độ lệchphagiữacáchiệu điệnthế UAD vàUDF. Hướng dẫn: a.Tổngtrở Z= 22 AF LC U50 (2R)(ZZ)50 I1 +−===Ω 22 LC 4R(ZZ)2500⇔+−= (1) LạicóZAD = 22 AD L U40 RZ40 I1 +===Ω 22 L RZ1600⇔+= (2) ZBE = 22 BE C U30 RZ30 I1 +===Ω 22 C RZ900⇔+= (3) Từ (2)và(3)tacó:4R2 + 22 LC 2Z2Z5000 += (4) Từ (1)tacó: 4R2 + 22 LCLC ZZ2ZZ2500 +−= (5) Lấy(4)trừ (5): 222 LCLCLC ZZ2ZZ(ZZ)2500 ++=+= LC ZZ50 +=Ω (loạinghiệm LC ZZ500) +=−Ω< (6) Lấy(2)trừ (3)ta được:700= 22 LCLCLC ZZ(Z+Z)(ZZ) −=− (7) Thay(6)vào(7)ta được:700=50 LC (ZZ) LC 700 ZZ14 50 ⇔−== (8) Từ (6)và(8)suyra L C Z32 Z18 =Ω  =Ω L 6 C Z32 L0,102H 2.50 11 C177.10F Z100.18  === ωπ    === ωπ  Thayvào(2)ta đươc:R= 2 L1600Z =24 Ω b.Hệ số côngsuất: 2R2.24 cos φ 0,96 Z50 === c. Do uAD sớm pha hơn i là 1φ với tan 1φ = LZ 4 R3 = ; uDF sớm pha hơn i là 2φ với tan 2φ = CZ 3 R4 =− . Tacótan 1φ tan 2φ =–1nghĩalàuAD sớmphahơnuDF là π 2 .

DẠYKÈMQUYNHƠNOFFICIAL 133 Câu 7 (THPT Chuyên ĐHSP Hà Nội lần 7 – 2015): Giả sử cómộtnguồn điệnxoaychiều cóhiệu điệnthế hiệudụng ổn định,còntầnsố thay đổi trongphạm vi rộng.Mạchxoay chiềukhôngphânnhánhR1L1C1 xảyracộnghưởngvớitầnsố góc ω1.Mạchxoaychiều không phân nhánh R2L2C2 xảy ra cộng hưởng với tần số góc ω2. Nếu mắc nối tiếp hai mạch điện đóvớinhaurồimắcvàonguồnthì để xảyracộnghưởng,tầnsố góccủadòng điệnlà: A. ω = 12 2 22 2 11 LL LL + ω+ω B. ω = 12 2 22 2 11 CC LL + ω+ω C. ω = 12 1122 LL LL + ω+ω D. ω = 12 1122 CC LL + ω+ω Hướng dẫn: Nếughépnốitiếp: b12 111 CCC =+ Nếughépnốitiếp: Lb = L1 + L2 KhimạchgồmR1C1L1 cótầnsố góccộnghưởnglà: 11 2 1111 11 ω C(1) L ωLC =  = KhimạchgồmR2C2L2 cótầnsố góccộnglà: 22 2 2222 11 C(2) LLC ω=  = ω KhimạchgồmR1C1L1 mắcnốitiếpR2C2L2 thìtầnsố góccộnghưởnglà: bb 1 ω LC = 12 b 12 bb12 b12 12 12 CC C MàCC11 LCCC LLL CC(LL)  = +  ω==  =++ + 22 2211 222222 112211222211 12 22221212 11221122 11LL LLLLLL 1111LL .(LL).(LL)LLLL ω+ω + ωωωωω+ω === +++ ωωωω Chọn A Câu 8: Cho mạch điện RLC (cuộn dây không thuần cảm), L = 1 π H, C = 50 π µF, R = 2r. R mắc vào hai điểm A, M; cuộn dâymắcvàohai điểmM,N;tụ Cmắcvàohai điểmN,B; Mắcvàomạchhiệu điệnthế AB0 uUcos100t 12 π =π+  (V). BiếtUAN =200V,hiệu điệnthế tứcthờigiữahai điểmMN lệch pha so với hiệu điện thế tức thời giữa hai điểm AB là 2 π . L ; R C • A • B • N • M

DẠYKÈMQUYNHƠNOFFICIAL 134 a. Xác định các giá trị U0, R, r A. 200V; Ω; 100Ω B. 400V; Ω; Ω C. 100V; Ω; 100Ω D. 200V; Ω; Ω b. Viết biểu thức dòng điện trong mạch? A.i22cos100t 3 π =π+  AB.i2cos100t 3 π  =π−  A C.icos100t 3 π =π+  AD.i2cos100t 3 π =π+  A Hướng dẫn: a. Ta có: L C 6 1 ZL100.100 11 Z200 C50.10 100.  =ω=π=Ω π  ===Ω ω π π Và LC AB L MN ZZ 100 tan R3r Z100 tan Rr  ϕ==−    ϕ==   uMN sớm pha hơn uAB góc 2 π  tanϕABtanϕMN = – 1  2 100 r 1003 1 3r200 R2r 3  =Ω  =    ==Ω  Mặt khác: AB MNAN UZ 1 UZ == (Vì Z = ZAN = 200Ω)  UAB = UMN = 200V. Do đó U0 = 200V.    Chọn D b. Ta có: LC AB AB ZZ1001 tan R3r6 3 π ϕ==−=−  ϕ=− : uAB chậm pha hơn i góc 6 π Mà: I = ABU Z = 1 A. Biểu thức dòng điện: i =cos(100πt + 12 π + 6 π ) =cos(100πt + 3 π )A.  Chọn D 2 3 200 3 200 3 100 2 3 200 2 3 200 3 100 2 22

DẠYKÈMQUYNHƠNOFFICIAL 135 C. CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Cho mạch điện xoay chiều RLC mắc nối có R = 100Ω; 410 CF. 2 = π Khi đặt vào AB một điện áp xoay chiều có tần số f=50HzthìuAB vàuAM vuôngphavớinhau.Giátrị Llà: A. 1 H 2π B. 3 H π C. 3 H π D. 1 H π Câu 2: Mạch điện xoay chiều AB gồm điện trở thuần R = 80Ω nối tiếp với hộp X. Trong hộp X chỉ chứa một phần tử là điện trở thuần R’ hoặc cuộn thuần cảm L, hoặc tụ C. Biết u1002cos120tV 4 π =π+  . Dòng điện qua R có cường độ hiệu dụng 1 A và trễ pha hơn uAB.Phầntử tronghộpXcógiátrị: A. R’=20Ω B. C = 310 F 6π C. L= 1 2π H D. L= 6 10π H Câu 3: Cho mạch điện xoay chiều AB chứa R, L, C nối tiếp, đoạn AM có điện trở thuần và cuộndâythuần cảm 2R =ZL, đoạnMB cótụ C điệndungcóthể thay đổi được. Đặthai đầu mạch vào hiệu điện thế xoay chiều u = U0cosωt (V), có U0 và ω không đổi. Thay đổi C = C0 công suất mạch đạt giá trị cực đại, khi đó mắc thêm tụ C1 vào mạch MB công suất toạn mạch giảm một nửa, tiếp tục mắc thêm tụ C2 vào mạch MB để công suất của mạch tăng gấp đôi.Giátrị C2 là: A. 0C 2 hoặc3C0 B. 0C 2 hoặc2C0 C. 0C 3 hoặc2C0 D. 0C 2 hoặc3C0 Câu 4: Đoạn mạch xoay chiều AB chứa 3 linh kiện R, L, C. Đoạn mạch AM chứa L, MN chứa R, NB chứa C, R =50Ω, ZL= 50 Ω, ZC = 50 3 Ω. Khi uAN = 80V thì uMB =60V. Giátrị uAB cực đại(U0)là. A.100V B.100V C.150V D. 507 V Câu 5: Mạch điện AB gồm đoạn AM và đoạn MB. Điện áp ở hai đầu mạch ổn định u2202cos100t =π (V). Điện áp ở hai đầu đoạn AM sớm pha hơn cường độ dòng điện một góc 300 Đoạn MB chỉ có một tụ điện có điện dung C thay đổi được. Chỉnh C để ( )AMMB max UU + .Khi đó điệnáphiệudụng ở hai đầutụ điệnlà A. 440V B. 2203V C. 220V D. Câu 6: Mạch điện xoay chiều nối tiếp AMB có tần số 50Hz. AM chứa L và R = 50 3 Ω. MB chứatụ điệnC = 410 π F. Điện ápuAM lệchpha 3 π sovớiuAB.Giátrị củaLlà: A. 3 π H. B. 1 π H. C. 1 2π H. D. 2 π H. 33 3 2202 V R L C M A B

DẠYKÈMQUYNHƠNOFFICIAL 136 HƯỚNG DẪN GIẢI Câu 1: ChọnA. Tacó: C 4 11 Z200 10C 50.2. 2 R100  ===Ω ω π π =Ω  Khihai đoạnmạchuAB vàuAM vuôngphavớinhau,thì: LC AMMB ZZ tan φ tan φ 1 1 RR  =−  =−  22 L L C Z R100501 Z50LH. Z2002.502  ===Ω  === ωππ Câu 2: ChọnC. VìItrễ phahơnuAB nên hộpXchứaphầntử L. Khi đó: L L 222 L R80 Z U601 Z100Z60LH. I1202 ZRZ =Ω   ==Ω  =Ω  === ωππ =+  Câu 3: ChọnC. KhiC =C0 thìcôngsuấtcực đại,ta có: 0 CL ZZ2R == Khimắcthêm tụ C1 (coimạchcótụ C01)thìcôngsuấtcủamạchgiảm mộtnửa: () 0 01 0 01 C 2 2 max010 C LC 0 C 01 L C Z C2CP ZRPZZ2R 22 2C3Z CZ2R Z3R 3 2  === =  −=     == ==   Từ đótaxác định đượcC1 =C0 hoặcC1 =2C0. Để côngsuất củamạchtănggấp đôi(cực đại) cần mắcthêm tụ C2 (coimạchcóC012). Tacó 0120 CCZZ = ,taxác định được 010 0 01 C2C 2C C 3 =   =  Câu 4: ChọnD. Tacó: L AN AN L MB MB Z503 tan3 R503 50 Z1 3tan R506 3  π ϕ===  ϕ=    π ϕ=−=−=−  ϕ=−  VậyuAN vuôngphavới uMB nêntacó

DẠYKÈMQUYNHƠNOFFICIAL 137 2222 AN MBAN MB 0AN0MB0AN0MB uuuu11 UUIZIZ  +=⇔+=   VớiZAN =100Ω,ZMB = 100 3 Ω Suyra: 22 20 0 1803603 1I3A. I100100  +=  =   Vậy:U0 = I0Z=50V. Câu 5: ChọnC. Tacó:UR =Ucos|ϕ| UAM = R 0 U cos30 = 2 3 Ucos|ϕ| UC =URtan300 +Usin|ϕ| =Ucos|ϕ| +Usin|ϕ| Đặty=UAM +UC = Ucos|ϕ| + Ucos|ϕ| +Usin|ϕ| = U(cos|ϕ| +sin|ϕ|) Suyra:y’=U( 3 sin|ϕ| +cos|ϕ|) ymax  y’=0  sin|ϕ| =cos|ϕ|  tan|ϕ| =  |ϕ| =300 VậyUC =220V. Câu 6: ChọnC. Tacó φAM/i + φi/AB = 3 π . Lấytanhaivế ta được: LCL AM/ii/AB AM/ii/ABLCL 2 ZZZ tantan RR 33 1tantanZ(ZZ) 1 R + ϕ+ϕ =⇔= −ϕϕ ( )22 CLCL ZR3RZZZ ⇔=−+ Thaysố vàgiảiphươngtrìnhta đượcZL =50Ω  L= 1 2π H. CHỦ ĐỀ 10 7 3 1 3 2 3 1 3 3 3 1

DẠYKÈMQUYNHƠNOFFICIAL 138 CÔNG SUẤT. HỆ SỐ CÔNG SUẤT A. TÓM TẮT LÝ THUYẾT CƠ BẢN I. Công suất mạch điện xoay chiều không phân nhánh RLC. 1. Công suất tiêu thụ trong mạch RLC không phân nhánh. + Côngsuấttứcthời:P =UIcosϕ +UIcos(2ωt+ ϕ) + Côngsuấttrungbình: P =UIcosϕ =RI2 . + Côngsuấttiêuthụ củamạch điệnxoay chiều: + Hệ số côngsuất: R cos Zϕ= (cosϕ cógiátrị từ 0 đến1) + Biến đổi ở cácdạngkhác: 2 2 R R 2 2 2 R U PRIUI R UR PZIcos Z U cos U  ===   =ϕ=   ϕ=  2. Ý nghĩa của hệ số công suất cosϕ ϕ + Trườnghợpcosϕ =1  ϕ =0:mạchchỉ cóR,hoặc mạchRLC cócộnghưởng điện (ZL =ZC)thì:P =Pmax = UI= 2U R . + Trường hợp cosϕ = 0 tức là ϕ = ± 2 π : Mạch chỉ có L, hoặc C, hoặc có cả L và C mà khôngcóR thì:P =Pmin =0. + Côngsuấthaophítrên đườngdâytảilà: Php =rI2 = 2 22 rP Ucos ϕ Với r(Ω) điệntrở của đườngdâytải điện. + Từ (8)  Nếu cosϕ nhỏ thì Php lớn, do đó người ta phải tìm cách nâng cao cosϕ. Quy địnhcosϕ ≥ 0,85. + Với cùng một điện áp U và dụng cụ dùng điện tiêu thụ một công suất P, tăng cosϕ để giảm cường độ hiệudụngItừ đógiảm đượchao phívìtỏanhiệttrêndây. + Để nâng cao hệ số công suất cosϕ của mạch bằng cách thường mắc thêm tụ điện thích hợp vào mạch điện sao cho cảm kháng và dung kháng của mạch xấp xỉ bằng nhau để cosϕ ≈ 1. BÀI TẬP VẬN DỤNG PUIcos=ϕ

DẠYKÈMQUYNHƠNOFFICIAL 139 Câu 1: Cho mạch điện AB, trong đó 44.10 CF = π , 1 LH 2 = π , r = 25Ω mắc nối tiếp. Biểu thức điệnápgiữahai đầu mạch uAB =50 2 cos100πtV.Tínhcôngsuấtcủatoànmạch? A.50 2 W. B.25W. C.100W. D.50W. Hướng dẫn: Dễ dàngtính được: () () C 4 L 2222 LC 11 Z25 C4.10 100. 1 U50 ZL100.50I2A 2 Z 252 ZrZZ255025252 ===Ω ω π π   =ω=π=Ω  === π  =+−=+−=Ω   Côngsuấttiêuthụ củamạch điện: P = I2r=2.25 =50W.   Chọn D Câu 2: Đặt một hiệu điện thế xoay chiều vào hai đầu đoạn mạch là: AB u1202cos100tV 4 π  =π−  và cường độ dòng điện qua mạch i32cos100tA 12 π =π+  .Tínhcôngsuấttiêuthụ của đoạnmạch? A.P =180W B.P =120W C.P =100W D.P =50W Hướng dẫn: Tacó: 0 0 I32 I3A 22 U1202 U120V 22  ===    ===  Mặtkhác: pha(u)pha(i)100t100t4123 πππ  −=ϕ  ϕ=π−−π+=−   . Vậy 1 coscos 32 π  ϕ=−=   Suyracôngsuấttiêuthụ của đoạnmạchlà: 1 PUIcos120.3.180W 2 =ϕ== Chọn A Câu 3: Cho mạch điện xoay chiều như hình vẽ: R nối tiếp với cuộn dây có r, L. R = 50 Ω ; điện áp hiệu dụng 2 đầu R là UR =100V;r=20 Ω .Côngsuấttiêuthụ của đoạnmạchlà A.P =180W B.P =240W C.P =280W D.P =50W A BR r, L

DẠYKÈMQUYNHƠNOFFICIAL 140 ROR1 RM R2 P Pmax P<Pmax Hướng dẫn: Tacó: R U100 I2A R50 === . Khi đó: ( ) ( ) 22 PRrI50202280W =+=+= .  Chọn C Câu 4: Cho mạch R, L, C mắc nối tiếp, cuộn dây thuần cảm. Đặt vào hai đầu đoạn mạch một hiệu điện thế u100cos100t (V)=π . Biết cường độ dòng điện trong mạch có giá trị hiệu dụng là 2 A, và lệch pha so với điện áp hai đầu mạch một góc 36,80. Tính công suất tiêu thụ củamạch ? A.P =80W B.P =200W C.P =240W D.P =50W Hướng dẫn: Côngsuấttoànmạch: ( )0 PUIcos502.2.cos36,880W =ϕ== .  Chọn C 3. R thay đổi để P = Pmax Khi L,C, ω không đổi thì mối liên hệ giữa ZL và ZC không thay đổi nên sự thay đổi của R khônggâyrahiệntượng cộnghưởng. Tìm côngsuấttiêuthụ cực đạicủa đọanmạch: Tacó: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + DoU=constnên để P = Pmax thì ()2 LC min ZZ R R  +    Ápdụngbất đẳngthứcCô-sicho2số dươngR và ()2 LCZZ R ta được: () () 22 LCLC LC ZZZZ R2R.2ZZ RR +≥=− Vậy ()2 LC min ZZ R R  +    là LC2ZZ lúc đódấu“=”củabất đẳngthứcxảyranêntacó: LCRZZ =− C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 141 Khi đó: 22 max LC max LC UUZR2 P 2R2ZZUU I Z 1UR2 II ZZ2R2 costan1 Z2   =  ==  ==    == ϕ==  ϕ=  Câu 1: Chomạch điệnnhư hìnhvẽ:BiếtL= 1 π H, C= 42.10 π F, uAB = 200cos100πt V. R phải có giá trị bằng bao nhiêu để côngsuấttoả nhiệttrênRlàlớnnhất?Tínhcôngsuất đó. A.50 Ω;200W B.100 Ω;200W C.50 Ω;100W D.100 Ω;100W Hướng dẫn: Tacó: L C 4 U1002V 1 ZL100.100 11 Z50 2.10C 100.    =  =ω=π=Ω π  ===Ω ω π π CôngsuấtnhiệttrênR: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + . DoU=constnên để P=Pmax thì ()2 LC min ZZ R R  +    . Ápdụngbất đẳngthứcCô-sicho2số dươngRvà ()2 LCZZ R ta được: () () 22 LCLC LC ZZZZ R2R.2ZZ RR +≥=− Vậy ()2 LC min ZZ R R  +    là LC2ZZ lúc đódấu“=”củabất đẳngthứcxảyranêntacó: LC RZZ50=−=Ω . Khi đó: 22 max U1002 P200W 2R2.50   ===      Chọn A C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 142 Câu 2: Cho mạch R, L, C. R có thể thay đổi được, U = URL = 100 2 V, UC = 200V. Xác định công suất tiêu thụ trong mạch. Biết tụ điện có điện dung 410 C 2 = π F và tần số dòng điệnf=50Hz. A.100W B.100 2 W C.200W D.200 2 W Hướng dẫn: Tacó: C C U 200 I1A Z200 === Côngsuấttiêuthụ trongmạch: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + DoU=constnên để P=Pmax thì ()2 LC min ZZ R R  +    Ápdụngbất đẳngthứcCô-sicho2số dươngRvà ()2 LCZZ R ta được: () () 22 LCLC LC ZZZZ R2R.2ZZ RR +≥=− Vậy ()2 LC min ZZ R R  +    là LC2ZZ lúc đódấu“=”củabất đẳngthứcxảyranêntacó: LCRZZ =− Suyra: max ZR2 2 PUIcos1002.1.100WR2 2cos Z2 =   =ϕ== ϕ==      Chọn A Câu 3: Cho đoạn mạch xoay chiều RLC mắc nối tiếp có cuộn dây thuần cảm kháng có độ tự cảm L, tụ điện có điện dung C, R là một điện trở thuần thay đổi được. Đặt một điện áp xoaychiều ổn định ở hai đầu đoạnmạchABcóbiểuthức AB u120cos100t =π (V).KhiR= 100Ω thì thấy mạch tiêu thụ công suất cực đại. Xác định cường độ dòng điện trong mạch lúcnày? A.2A. B. 2 A. C.2 2 A. D. 2 2 A Hướng dẫn:

DẠYKÈMQUYNHƠNOFFICIAL 143 Côngsuấtcủamạch: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + . KhiP=Pmax thì ()2 LC LC min ZZ RRZZ R  +⇔=−   Suyra: () 22 LC UUU200 I A Z R21002RZZ ===== +− .    Chọn B Câu 4: Cho đoạn mạch xoay chiều RLC mắc nối tiếp: cuộn dây thuần cảm kháng có độ tự cảm L, tụ điện có điện dung C, R là một điện trở thuần thay đổi được. Đặt hai đầu mạch một điện áp xoay chiều ổn định. Điều chỉnh điện trở đến giátrị R =60Ω thì mạch tiêu thụ côngsuấtcực đại.Xác địnhtổngtrở củamạchlúcnày? A.30 2 Ω. B.120Ω. C.60Ω. D.60 2 Ω. Hướng dẫn: Côngsuấttiêuthụ củamạch: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + Để P=Pmax thì ()2 LC LC min ZZ RRZZ R  +⇔=−   . Suyra: () 22 LC ZRZZR2602. =+−==Ω   Chọn D Câu 5: Cho mạch điện gồm cuộn dây có điện trở r = 20Ω và độ tự cảm L = 2 π H, tụ điện có điệndungC= 410 π Fvà điệntrở thuầnRthay đổi đượcmắcnốitiếpvớinhau. Đặtvàohai đầu mạch điện một hiệu điện thế xoay chiều u240cos100t =π (V). Khi R = Ro thì công suấttiêuthụ trêntoànmạch đạtgiátrị cực đại.Khi đócôngsuấttiêuthụ trên điệnthở Rlà: A.P=115,2W B.P=224W C.P=230,4W D.P=144W Hướng dẫn: Tacó: L C 4 2 ZL100.200 11 Z100 C10 100.  =ω=π=Ω π  ===Ω ω π π Côngsuấtcủamạch: () ()() () () 2 2 2 222 LCLC URU PIRr RrZZZZ Rr Rr =+== ++−− ++ +

DẠYKÈMQUYNHƠNOFFICIAL 144 DoU=constnên để P=Pmax thì ()2 LC LC min ZZ RrRrZZ Rr  ++⇔+=− +   Khi đó: ( )2 2 max LC U1202 P144W 2ZZ2200100 ===    Chọn D 4. R thay đổi để có công suất P (P < Pmax): Có hai giá trị R1, R2 đều cho công suất P < Pmax a. Tìm R để mạch có công suất P < Pmax: Côngsuấttiêuthụ củamạch: () () 22 22 2 22LC LC URU PIRRRZZ0 RZZP ==⇔−+−= +− VậyRlànghiệmcủaphươngtrìnhbậchai,dễ dànggiảiphươngtrình để đượckếtquả có2 nghiệm:R1 vàR2 Theo ĐịnhlýViettacó: () 2 12 2 12LC U RR P RRZZ  +=   =− Câu 1: Cho đoạn mạch xoay chiều như hình vẽ. Biết cuộn dây thuần cảm 1 LH = π và tụ 310 CF 4 = π . Đặt vào hai đầu đoạnmạchmộthiệu điệnthế AB u752cos100t V=π .CôngsuấttrêntoànmạchlàP=45W. Tínhgiátrị R? A. R45=Ω B. R60=Ω C. R80=Ω D.CâuAhoặcC Hướng dẫn: Tacó: L C 3 1 ZL100.100 11 Z40 C10 100. 4  =ω=π=Ω π  ===Ω ω π π Côngsuấttoànmạch: 22 P PIRI R =  = (1) Mặtkhác: () ()2 22222 ABABLCABLC UIZIRZZUIRZZ==+−  =+− (2) Thay(1)vào(2)tacó: () () 2 2 2222 AB ABLC LC UP URZZRRZZ0 RP  =+−⇔−+−=  () 2 2 21 2 2 75R45 RR100400R125R36000 45R80 =Ω  −+−=  −+=   =Ω VậyR1 =45Ω hoặcR2 =80Ω.   Chọn D A BR L C

DẠYKÈMQUYNHƠNOFFICIAL 145 Câu 2: Cho mạch điện RLC như hình vẽ. Biết 1 LH = π , 310 CF 6 = π , AB u200cos100t =π (V). R phải có giá trị bằngbaonhiêu để côngsuấttoả nhiệttrênRlà240W? Hướng dẫn giải: Côngsuấttiêuthụ củamạch: () () 2 22 22 22LC LC UR PIRPRURPZZ0 RZZ ==⇔−+−= +− ()21 2 2 R30 240R1002R240.16000 160 R 3 =Ω  ⇔−+=   =Ω  Câu 3: Cho mạch điện RLC nối tiếp biết 2 LH = π , 6125.10 CF = π , R biến thiên. Điện áp hai đầumạch AB u1502cos100t =π (V). a. KhiP=90W.TínhR. b.TìmR để côngsuấttiêuthụ cógiátrị cực đại,tínhgiátrị cực đại đó. Hướng dẫn: a. Tacó: L C 6 2 ZL100.200 11 Z80 C125.10 100.  =ω=π=Ω π  ===Ω ω π π Côngsuấttiêuthụ củamạch: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + (1) () 22 1 2 2 150120R16090R250 20080RR90 R R =Ω  =  +=   =Ω + VậyvớiR=160 Ω hoặc90Ω côngsuấttiêuthụ trênmạchbằng90W. b.Từ (1)tanhậnthấyPmax khi ()2 LCRZZ =− hay LC RZZ20080120 =−=−=Ω . Suyra: 22 max U150 P93,75W. 2R2.120 === Câu 4: Cho đoạn mạchxoay chiều R, C mắcnốitiếp. Rlàmột biến trở, tụ điện có điện dung 410 CF = π . Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ổn định U. Thay đổi R ta C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 146 thấyvớihaigiátrị củaRlàR=R1 vàR=R2 thìcôngsuấtcủamạch điện bằngnhau.Tính tích 12RR ? A. 0 12 RR10 = B. 1 12 RR10 = C. 2 12 RR10 = D. 4 12 RR10 = Hướng dẫn: Tacó: C 4 11 Z100 10C 100. ===Ω ω π π KhiR=R1 thìcôngsuấttiêuthụ củamạch: 22 2 1111 222 1C UU PIRRR ZRZ === + (1) KhiR=R2 thìcôngsuấttiêuthụ củamạch: 22 2 2222 222 2C UU PIRRR ZRZ === + (2) Từ (1)và(2)suyra: 22 24 22221212C 1C2C UU RRRRZ10 RZRZ =  == ++ .   Chọn D b. Biết hai giá trị của điện trở là R1 và R2 mạch có cùng công suất P, tìm công suất P. b1. Biết hai giá trị của điện trở là R1 và R2 mạch có cùng công suất P Côngsuấttiêuthụ củamạch: () () 22 22 2 22LC LC URU PIRRRZZ0 RZZP ==⇔−+−= +− với R1 và R2 là hai nghiệm của phương trình trên. Theo định lí Viét đối với phương trình bậchai,tacó: 2 12 U RR P += và ()2 12LC RRZZ =− . b2. Với 2 giá trị của điện trở là R1 và R2 mạch có cùng công suất P. Tính R0 để mạch có công suất cực đại Pmax theo R1 và R2. Côngsuấttiêuthụ củamạch: () () 2 2 2 0 0 222 0LCLC 0 0 UR U PIR RZZZZ R R === +−− + . KhiP=Pmax thì ()2 LC 00LC 0 min ZZ RRZZ R  +⇔=−   (1) Vớigiátrị của điệntrở làR0 mạchcócôngsuấtcực đạiPmax,theo(1)thì 0LC RZZ =− . Với2giátrị của điệntrở làR1 vàR2 mạchcócùngcôngsuấtP,thì ()2 12LC RRZZ =− . Suyra: 012RRR = .Khi đó: max 120 2P RR.R P += C A B R L NM

DẠYKÈMQUYNHƠNOFFICIAL 147 Câu 1: Đặt vào hai đầu một điện trở thuần một hiệu điện thế xoay chiều có giátrị cực đại U0 công suất tiêu thụ trên RlàP. Khi đặt vào hai đầu điện trở đó một hiệu điện thế không đổi cógiátrị U0 thìcôngsuấttiêuthụ trênRlà A.P B.2P C. 2 P D.4P Hướng dẫn: Khi đặthiệu điệnthế xoaychiềuthì: 22 2 0 0 UU PIR R2R === (1) Khi đặthiệu điệnthế không đổithì: 2 2 0U P'IR R == (2) Từ (1)và(2)suyra: P' 2P'2P P =  = .    Chọn B Câu 2: Đặt điện áp ( )uU2cost=ω+ϕ (V) vào hai đầu mạch gồm một cuộn dây nối tiếp vớitụ Cthay đổi được.KhiC=C1 thì độ lệchphagiữadòng điệnvà điệnáphai đầumạch là600 vàkhi đó mạch tiêu thụ một công suất 50W. Điều chỉnh C để công suất tiêu thụ của mạchcực đạilà A.100W. B.200W. C.50W. D.250W. Hướng dẫn: KhiC=C1 thì 3 π ϕ= nên LC LC ZZ tantan3ZZ3R R3 π ϕ===  −= . Côngsuấttiêuthụ củamạch: () 2222 2 222 LC URURUU P4P200W RZZR3R4RR ===⇔== +−+ KhiP=Pmax thì 2 LCmax U ZZP200W R =  == .    Chọn B Câu 3: Cho đoạnmạchRLCmắcnốitiếp,cuộn dâycảmthuần, điệntrở Rthay đổi được. Đặt hai đầu đoạnmạchmột điệnápxoaychiềucó điệnáphiệudụnglà200V.KhiR=R1 vàR=R2 thìmạchcócùngcôngsuất.Biết 12 RR100+=Ω .KhiR=R1 côngsuấtcủamạchlà: A.400W. B.220W. C.440W D.880W. Hướng dẫn: Cách giải 1: Tacó: C 4 11 Z100 10C 100. ===Ω ω π π . KhiR=R1 thìcôngsuấttiêuthụ củamạch: () 22 2 1111 22 2 1LC UU PIRRR ZRZZ === +− (1) KhiR=R2 thìcôngsuấttiêuthụ củamạch: () 22 2 2222 22 2 2LC UU PIRRR ZRZZ === +− (2) Từ (1)và(2)suyra: () () () 122 222212LC 1LC2LC RR RRZZ RZZRZZ =  =− +−+− .

DẠYKÈMQUYNHƠNOFFICIAL 148 Suyra: 222 1 1 2 11212 URU200 P400W. RRRRR100 ==== ++   Chọn A Cách giải 2: Côngsuấttiêuthụ củamạch: () () 22 22 2 22LC LC URU PIRRRZZ0 RZZP ==⇔−+−= +− với R1 và R2 là hai nghiệm của phương trình trên. Theo định lí Viét đối với phương trình bậchai,tacó: 2 12 U RR P += (1) ()2 12LC RRZZ =− Sử dụngphươngtrình(1): 222 12 12 UU200 RRP400W. PRR100 +=  === +    Chọn A Câu 4: Cho đoạnmạchRLCmắcnốitiếp:cuộndâythuầncảmkhángcó độ tự cảmL,tụ điện có điệndungC,Rthay đổi được. Đặtmột điệnápxoaychiều ổn định ở hai đầu đoạnmạch có giátrị hiệu dụng U, tần số f. Điều chỉnh R thì thấy có hai giátrị 40Ω và 90Ω mạch tiêu thụ cùngmộtcôngsuất.Xác địnhR0 để mạchtiêuthụ côngsuấtcực đại? A.60Ω. B.65Ω. C.130Ω. D.98,5Ω. Hướng dẫn: Côngsuấttiêuthụ củamạch: () () 2 2 2 0 0 222 0LCLC 0 0 UR U PIR RZZZZ R R === +−− + KhiP=Pmax thì ()2 LC 00LC 0 min ZZ RRZZ R  +⇔=−   (*) Vớigiátrị của điệntrở làR0 mạchcócôngsuấtcực đạiPmax,theo(*)thì 0LC RZZ =− Với2giátrị của điệntrở làR1 vàR2 mạchcócùngcôngsuấtP,thì ()2 12LC RRZZ =− Suyra: 012 RRR40.9060 ===Ω .  Chọn A Câu 5: Mạch điệnxoay chiềugồm điệntrở thuầnRvàcuộndâythuầncảmkhángL.KhiR= R0 mạch có công suất trong mạch đạt giá trị cực đại Pmax. Nếu chỉ tăng giá trị điện trở lên R’=2R0 thìcôngsuấtcủamạchlà:(các đạilượngkhác(U,f,L)không đổi) A.2Pmax. B. max P 2 . C.0,4Pmax. D.0,8Pmax Hướng dẫn: KhiPmax thì 0L 2 max 0 RRZ U P 2R ==   =  .

DẠYKÈMQUYNHƠNOFFICIAL 149 KhiR’=2R0 thìZ= 5 R0  0 U I 5.R =  P=R’I2 = 2 0 2U 5R . Lậptỉ số: max P4 0,8 P5 ==  P=0,8Pmax.    Chọn D 5. Công suất tiêu thụ cực đại khi mạch RLC có cộng hưởng. Nếu giữ không đổi điện áp hiệu dụng U giữa hai đầu đoạnmạchvàthay đổitầnsố góc ω (hoặcthay đổif,L, C) sao cho 1 ωL= ωC (hay ZL = ZC) thì có hiện tượng cộng hưởng điện. Điều kiện xảy ra hiện tượng cộng hưởngtrongmạchRLCnối tiếp: LCZZ 11 L CLC =   ω=  ω= ω Lúcmạchcócộnghưởngthì:Tổngtrở: min RRmax ZZR UUU ==  == Cường độ dòng điện: max U II R == Côngsuấtcủamạchkhicócộnghưởng đạtgiátrị cực đại: 2 max U PP R == Mạchcócộnghưởngthì điệnápcùngphavớicường độ dòng điện,nghĩalà: ui 0 cos1 ϕ=  ϕ=ϕ  ϕ= Điệnápgiữahai điểmM,BchứaLvàC đạtcựctiểu:ULC min =0. Lưu ý: L và C mắc liên tiếp nhau. a. Bài toán tính công suất khi mạch có cộng hưởng Câu 1: Trong đoạnmạchxoaychiềugồm điệntrở R,tụ điệncó điệndungCbiên đổi đượcvà cuộn dây chỉ có độ tự cảm L mắc nối tiếp với nhau. Điện áp tức thời trong mạch là u = U0cos100πt (V). Ban đầu độ lệch pha giữa u và i là 600 thì công suất tiêu thụ của mạch là 50W.Thay đổitụ C để uAB cùngphavớiithìmạchtiêuthụ côngsuất: A. 200W B. 50W C. 100W D. 120W Hướng dẫn: Cách giải 1: Tacó: 060 P50W ϕ= = .Khiuvàicùngphathì 2 max U P R = Mặtkhác: LC0 LC ZZ tantan603ZZ3R R ϕ===  −= C A B R L NM

DẠYKÈMQUYNHƠNOFFICIAL 150 ()2 222 LC ZRZZR3R2R =+−=+= Suyra: 222 2max URUU PP4P200W Z4RR ===>=== .    Chọn A Cách giải 2: Ban đầu,tacó: ()LC0 LC ZZ tantan603ZZ3R R ϕ==±=  −=± ()2 222 LC ZRZZR3R2R =+−=+= (1) Và 2 22 2 U PIRRU200R Z ==  = (2) Khiuvàicùngphatacó: 2 max U P R = (3) Từ (2)và(3)tacó: max 200R P200W R == .    Chọn A Câu 2: Cho đoạn mạch RLC mắc nối tiếp: R = 200 Ω, cuộn dây thuần cảm kháng có độ tự cảm L, tụ điện có điện dung C thay đổi được. Đặt một điện áp xoay chiều ổn định ở hai đầu đoạn mạch AB có biểu thức AB u200cos100t =π (V). Điều chỉnh C để mạch tiêu thụ côngsuấtcực đại.Tínhcôngsuấttrongmạchlúcnày? A. 100W B. 50W C. 200W D. 150W Hướng dẫn: Côngsuấtcủamạchkhicócộnghưởng đạtgiátrị cực đại: 2 2 max 200 U 2 PP100W R200    ==== .    Chọn A Lưu ý: Bài toán áp dụng khi mạch có cộng hưởng thì điện áp cùng pha với cường độ dòng điện, nghĩa là: ui 0 cos1 ϕ=  ϕ=ϕ  ϕ= rất dễ nhầm với 22 max LC ZR2 UUUU IP Z2R2ZZ R2 R2 costan1 Z2  =   ==  ==   ϕ==  ϕ=  Công suất của mạch khi có cộng hưởng đạt giá trị cực đại: 2 max U PP R == rất dễ nhầm với 22 max LC UU P 2R2ZZ == .

DẠYKÈMQUYNHƠNOFFICIAL 151 Câu 3: Cho đoạn mạch RLC mắc nối tiếp: cuộn dây thuần cảm kháng có độ tự cảm L thay đổi được, tụ điện có điện dung C, R = 50 Ω. Đặt hai đầu mạch một điện áp xoay chiều ổn định u = 50 2 cos100πt (V). Điều chỉnh L để điệnápgiữahai điểmMvàBnhỏ nhất. Tínhcôngsuấttiêuthụ củamạchlúcnày? A.50W B.100W C.200W D.150W Hướng dẫn: Dễ thấyUMB min=ULC min=0. ĐiềukiệnxảyrahiệntượngcộnghưởngtrongmạchRLCnốitiếp: LCZZ 11 L CLC =   ω=  ω= ω Mạchcócộnghưởngthì điệnápcùngphavớicường độ dòng điện,nghĩalà: ui 0 cos1 ϕ=  ϕ=ϕ  ϕ= Côngsuấtcủamạchkhicócộnghưởng đạtgiátrị cực đại: () 22 max 50U PP50W R50 ==== .  Chọn A b. Bài toán xác định hệ số công suất khi mạch có cộng hưởng Câu 1: Đoạnmạch điệnxoaychiềukhôngphânnhánhgồmcuộndâycó độ tự cảmL, điệntrở thuầnRvàtụ điệncó điệndungC.Khidòng điệncótầnsố góc 1 LC chạyqua đoạnmạch thìhệ số côngsuấtcủa đoạnmạchnày A.phụ thuộc điệntrở thuầncủa đoạnmạch. B.bằng0. C.phụ thuộctổngtrở của đoạnmạch. D.bằng1. Hướng dẫn: Dễ thấyPmax khimạchcócộnghưởng,khi đó điệnápcùngphavớicường độ dòng điện, nghĩalà: ui 0 cos1 ϕ=  ϕ=ϕ  ϕ= Chọn D Câu 2: Cho mạch điện RLC nối tiếp, trong đócuộn L thuần cảm, R là biến trở Điện áp hiệu dụng U = 200V, f = 50Hz, biết ZL = 2ZC, điều chỉnh R để công suất của hệ đạt giá trị lớn nhấtthìdòng điệntrongmạchcógiátrị làI= 2 A.Giátrị củaC,Llà: A. 1 mF 10π và 2 H π B. 3 mF 10π và 4 H π C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 152 C A B R2 L M R1 C. 1 F 10π và 2 mH π D. 1 mF 10π và 4 H π Hướng dẫn: Tacó: () 22 22 LC UU PUI Z RZZ === +− VậyPmax khivàchỉ khi: LCRZZ =− hay CRZ = (vì LCZ2Z = ) Khi đó,tổngtrở củamạch: () 22 LC U ZRZZ1002 I ==+−=Ω C C L LC 11 Z100CmF Z10 Z2 Z2Z200LH  =Ω  == ωπ    ==Ω  == ωπ   Chọn A Câu 3: Một đoạn mạch AB gồm hai đoạn mạch AM và BM mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần R1 mắc nối tiếp với tụ điện có điện dung C, đoạn mạch MB gồm điện trở thuần R2 mắc nối tiếp với cuộn cảm thuần có độ tự cảm L. Đặt điện áp xoay chiều 0 uUcost =ω (U0 và ω không đổi) vào hai đầu đoạn mạch AB thì công suất tiêu thụ của đoạn mạch AB là 85 W. Khi đó 2 1 LC ω= và độ lệch pha giữa uAM và uMB là 900. Nếu đặt điệnáptrênvàohai đầu đoạnmạchMBthì đoạnmạchnàytiêuthụ côngsuấtbằng A.85W B.135W. C.110W. D.170W. Hướng dẫn: Khi 2 1 LC ω= trongmạchcócộnghưởng:ZL =ZC vàcôngsuấttiêuthụ của đoạnmạch đượctínhtheocôngthức: 2 12 U P RR = + Tacó: C 1 1 L 212 1 21 Z tan R Z tantantan1 R 2  ϕ=    ϕ=  ϕϕ=−  π ϕ−ϕ=   CL LC12 21 Z Z .1ZZRR RR  =−  == Khi đặt điện áp trên vào đoạn mạch MB thì công suất tiêu thụ trên đoạn mạch: 222 2 22 222 222 2L21212 URURU PIRP85W RZRRRRR ====== +++ .

DẠYKÈMQUYNHƠNOFFICIAL 153    Chọn A Câu 4: Cho một mạch điện gồm biến trở Rx mắc nối tiếp với tụ điện có C63,8F =µ và một cuộndâycó điệntrở thuầnr=70Ω, độ tự cảm 1 LH = π Đặtvàohai đầumột điệnápU=200V có tần số f = 50Hz. Giá trị của Rx để công suất của mạch cực đại và giá trị cực đại đó lần lượt là A. 0; 378,4WΩ B. 20; 378,4WΩ C. 10; 78,4WΩ D. 30; 100WΩ Hướng dẫn: Tacó: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + . Với xx L C RRrR7070 ZL100 1 Z50 C   =+=+≥Ω =ω=Ω   ==Ω ω Khi đó () 22 2 22 LC URU PIR 3500RZZ R R === +− + P =Pmax khi mẫu số y =R + 3500 R có giátrị nhỏ nhất với R ≥ 70Ω Xét sụ phụ thuộccủay vào R: Lấy đạo hàm y’theo R tacó 2 3500 y'1R =− 2 3500 y'010R50 R =⇔−=  =Ω Khi R <50 Ω thì nếu R tăng y giảm.(vì y’<0) Khi R >50 Ω thì nếu R tăng thì y tăng. Do đó khi R ≥ 70Ω thìmấu số y có giátrị nhỏ nhất khi R =70Ω. Công suất củamạch có giátrị lớn nhất khi Rx =R– r=0: () 2 max 22 LC Ur 378,4W rZZ == +− P Chọn A 6. Với hai giá trị của cuộn cảm L1 và L2 mạch có cùng công suất. Tìm L để Pmax. Với hai giátrị củacuộn cảm L1 vàL2 mạch có cùng công suất P1 =P2  Z1 =Z2  |ZL1 ZC|= |ZL2 ZC|  L1L2 C12 C ZZ 22 ZLL 2ZC + =  +== ω Với Lmạch có công suất cực đại (mạch xảy racộng hưởng)ZL =ZC suy ra:

DẠYKÈMQUYNHƠNOFFICIAL 154 L1L212 L ZZLL ZL 22 ++ =  = Câu 1: Cho mạch điện RLC mắc nối tiếp theo thứ tự R, L, C trong đó cuộn dây thuần cảm có độ tự cảm L thay đổi được, điện trở thuần R = 50Ω. Đặt vào hai đầu đoạn mạch hiệu điện thế xoay chiều có tần số f = 50Hz. Thay đổi L người ta thấy khi L = L1 và khi 21 3 LLL 2 == thì công suất tiêu thụ trên đoạn mạch như nhau nhưng cường độ dòng điện tứcthời vuông phanhau. Giátrị L1 và điện dung C lần lượt là: A. 1 1 LH = π và 45,36.10 CF. 2 = π B. 1 2 LH = π và 45,36.10 CF. 2 = π C. 1 1 LH = π và 45,36.10 CF. = π D. 1 2 LH = π và 45,36.10 CF. = π Hướng dẫn: Khi công suất tiêu thụ trên đoạn mạch như nhau: P1 =P2  I1 = I2  Z1 =Z2  (ZL1 – ZC)2 =(ZL2 – ZC)2 . Do ZL1 ≠ ZL2 nên ZL1 –ZC =ZC – ZL2 =ZC L1 3 Z 2  L1 23 Z 2  +    =2ZC Tacó: L1C L1 1 1C L2C L1 2 ZZ 23Z tan R4R 3 ZZLZ tan223Z RR4R   ϕ==       −+ ϕ===    Cường độ dòng điện tứcthời vuông phanhau nên ϕ1 + ϕ2 = 2 π  tanϕ1tanϕ2 =– 1  2 L1Z =16R2  ZL1 =4R=200Ω  L1 1 Z2002 LH. 100 === ωππ Dung kháng củatụ: ()CL1 2323 ZZ.200523 44  ++ ===+Ω    () 415,36.10 CF. 100.523  == π+π  Chọn D 7. Với hai giá trị của tụ điện C1 và C2 mạch có cùng công suất. Tìm C để Pmax Với hai giátrị củatụ điện C1 vàC2 mạch có cùng công suất P1 =P2  Z1 =Z2  |ZL1 ZC|= |ZL2 ZC|  C1C2 L L 12 ZZ 11 Z2Z2L 2CC + =  +==ω Với điện dung củatụ điện C mạch có công suất cực đại (mạch xảy racộng hưởng)ZL =ZC suy ra:

DẠYKÈMQUYNHƠNOFFICIAL 155 C1C2 12 C 1212 ZZ 2CC211 ZC 2CCCCC + =  =+  = + Câu 1: Đặt điện áp xoay chiều u = 200 2 cos 100πt (V) vào hai đầu đoạn mạch R, L, C mắc nối tiếp. Điện dung C củatụ điện thay đổi được. Khi C =C1= 410 2π FvàC = C2 = 410 π Fthì mạch có cùng công suất P =400W. a.Tính R vàL. b.Tính hệ số công suất củamạch ứng với C1 ,C2. Hướng dẫn: + Khi C =C1= 410 2π F tacó: 1C 4 1 11 Z200. C10 100. 2 ===Ω ω π π Tổng trở: () ()1 2 222 1LCL ZRZZRZ200. =+−=+− Công suất: () 2 2 11 22 L UR PIR. RZ200 == +− (1) + Khi C =C2 = 410 π Ftacó: 2C 4 2 11 Z00. C10 100. ===Ω ω π π Tổng trở: () ()2 2 222 2LCL ZRZZRZ100. =+−=+− Công suất: () 2 2 22 22 L UR PIR. RZ100 == +− (2) Từ (1)và (2)tacó P1 =P2: () () 22 L 2222L LL Z URUR15Z150LH. RZ200RZ10010 ⇔=⇔=Ω  == +−+−ωπ Tìm R: () () 2 2 1 2 22 2 L UR200.R P400R50. RZ200R150200 =⇔=  =Ω +−+− b.Hệ số công suất khi C =C1 = 410 2π : () () 1 2222 1 L RR502 cos . Z RZ200501502002 ϕ==== +−+− Hệ số công suất khi C = C2 = 410 π : () () 2 2222 2 L RR502 cos . Z RZ100501501002 ϕ==== +−+−

DẠYKÈMQUYNHƠNOFFICIAL 156 Câu 2: Cho mạch điện RLC mắc nối tiếp theo thứ tự R, L, C trong đó cuộn dây thuần cảm có tụ điện C thay đổi được. Thay đổi C người ta thấy khi 4 1 2.10 CCF == π và khi 4 2 2.10 CCF 3 == π thì cường độ dòng điện trên đoạn mạch trong hai trường hợp là như nhau. Để công suất tiêu thụ củamạch đạt cực đại thì C có giátrị: A. 43.10 F 2π B. 410 F 2π C. 410 F π D. 42.10 F π Hướng dẫn: Cách giải 1: Tacó: () ()1 2 12 2222 LCLC UU II RZZRZZ =⇔= +−+− ( ) ( )12 22 LCLC ZZZZ ⇔−=− Vì 12 CCZZ ≠ nên () 12 12 CC LCLCL ZZ ZZZZZ 2 + −=−−  = (1) Khi P =Pmax thì mạch xảy rahiện tượng cộng hưởng điện LCZZ = (2) Từ (1)và (2)ta được: 12 CC C 12 ZZ1111 Z 2C2CC +  =  =+  () 44 4 12 44 12 2.102.10 2CC2.10 3 C2F CC2.102.10 3  + + ππ ===  π  ππ  Chọn D Cách giải 2: Ta có: () 22222 LCCLCL UU I Z2ZZRZRZZ == +−−++ Nhậnthấy,Iphụ thuộckiểuhàmbậchaitheoZC,vìvậyphảicómốiquanhệ hàmbậchai: ()CT12 1 xxx 2 =+ tứclà 12 CC C 12 ZZ1111 Z 2C2CC +  =  =+  () 44 4 12 44 12 2.102.10 2CC 2.103 C2F 2.102.10CC . 3  + + ππ ===  π  ππ  .    Chọn D Câu 3: ChomachR,L,Cmắcnốitiếp,vớiCcóthể thay đổi,Lkhôngthay đổi. Đặtvàohai đầu đoạn mạch điện áp u1002cos100t =π (V). R = 100 3 Ω. khi C tăng thêm 2 lần thì công suất tiêu thụ không đổi, nhưng cường độ dòng điện có pha thay đổi 1 góc 3 π . Công suâttiêuthụ củamạch: A. 252W B.25W C.40W D. 253W

DẠYKÈMQUYNHƠNOFFICIAL 157 Hướng dẫn: Vớihaigiátrị củatụ điệnC1 vàC2 mạchcócùngcôngsuất: ()1212 1212LCLCLCC 1 PPZZZZZZZZZ 2 =⇔=⇔−=−  =+ Mà: 122 CCLC 3 Z2ZZZ 2 =  = Đề cho 21 3 π ϕ−ϕ= vàhaigóclệchphabằngnhauvà đốinhaunên: 1 12 2 6 tantan 6 π  ϕ=−    −ϕ=ϕ π ϕ=   Talạicó: 1 LLL LC 21 ZZZ2ZZ333 33 R3R3R3 =−⇔=−⇔= () 2 12 L 22 LC CL CC Z3R1003.3300 ZRZZ20022 ZZ.300200 U10033 I0,5A Z200Z2Z400  ===Ω  =+−=Ω  ===Ω    === ==Ω  Côngsuấttiêuthụ: () () () 222 222 2 2 LC URUR100.1003 P253W ZRZZ1003300400 ==== +− +− Chọn D Các đồ thị công suất của dòng điện xoay chiều L, C, ω ωω = const, R thay đổi. R, C, ω ωω = const, L thay đổi. 22 max LC UU P 2R2ZZ == Khi LCRZZ =− Dạng đồ thị như sau: 2 max U P R = Khi LC 2 1 ZZL C =  = ω Dạng đồ thị như sau: ROR1 R0 R2 P Pmax P<Pmax LO L0 P Pmax

DẠYKÈMQUYNHƠNOFFICIAL 158 R, L, ω ωω ω = const, C thay đổi. R, L, C = const, f thay đổi. 2 max U P R = Khi LC 2 1 ZZL C =  = ω Dạng đồ thị như sau: 2 max U P R = Khi LC 1 ZZf 2LC =  = π Dạng đồ thị như sau: Câu 4: Đặt điệnáp ft2cos2uU=π (Ukhông đổi,tầnsố fthay đổi được)vàohai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Khi tần số là f1 thì cảm kháng và dung kháng của đoạn mạch có giá trị lần lượtlà6 Ω và8 Ω .Khitầnsố làf2 thìhệ số côngsuấtcủa đoạnmạchbằng1.Hệ thứcliên hệ giữaf1 vàf2 là A. .f 3 4 f21 = B. .f 2 3f 21 = C. .f 3 2f 21 = D. .f 4 f321 = Hướng dẫn: Vớitầnsố f1: () 1 1 1 1 L1 L2 1 C C 1 Z2fL6 Z 3 2fLC1 Z8 Z4 2fC =π=Ω    =π===Ωπ  (1) Vớitầnsố f2 mạchxảyracộnghưởng,tacó: ()2 2 L2 2 C Z 2fLC1 Z =π= (2) fO f0 P Pmax O C0 P Pmax

DẠYKÈMQUYNHƠNOFFICIAL 159 Chiatừngvế của(2)cho(1)ta được: 2 21 1 f 22 ff f 33 =  = .    Chọn C Câu 5: ChomachR,L,Cmắcnốitiếp,vớiCcóthể thay đổi,Lkhôngthay đổi. Đặtvàohai đầu đoạn mạch điện áp u1002cos100t =π (V).R = 100 3 Ω.khiC tăngthêm2lần thi công suất tiêu thụ không đổi, nhưng cường độ dòng điện có pha thay đổi 1 góc 3 π . Công suâttiêuthụ củamạch: A. 252W B.25W C.40W D. 253W Hướng dẫn: Vớihaigiátrị củatụ điệnC1 vàC2 mạchcócùngcôngsuất: ()1212 1212LCLCLCC 1 PPZZZZZZZZZ 2 =⇔=⇔−=−  =+ Mà: 122 CCLC 3 Z2ZZZ 2 =  = . Đề cho 21 3 π ϕ−ϕ= vàhaigóclệchphabằngnhauvà đốinhaunên: 1 12 2 6 tantan 6 π  ϕ=−    −ϕ=ϕ π ϕ=   Talạicó: 1 LLL LC 21 ZZZ2ZZ333 33 R3R3R3 =−⇔=−⇔= () 2 12 L 22 LC CL CC Z3R1003.3300 ZRZZ20022 ZZ.300200 U10033 I0,5A Z200Z2Z400  ===Ω  =+−=Ω  ===Ω    === ==Ω  Côngsuấttiêuthụ: () () () 222 222 2 2 LC URUR100.1003 P253W ZRZZ1003300400 ==== +− +−    Chọn D Câu 6: Cho mạch điện xoay chiều RLC mắc nối tiếp, R là biến trở. Đặt vào hai đầu đoạn mạchmột điệnápxoaychiều uU2cost =ω (V).Khithay đổigiátrị củabiếntrở Rtathấy cóhaigiátrị R=R1 =25Ω hoặcR=R2 =75Ω thìmạchtiêuthụ cùngmộtcôngsuấtP. Hệ số côngsuấtcủamạch ứngvớihaigiátrị củabiếntrở R1 vàR2 lầnlượtlà: A. 12 cos0,50;cos0,87 ϕ=ϕ= B. 12 cos0,50;cos0,80 ϕ=ϕ= C. 12 cos0,87;cos0,50 ϕ=ϕ= D. 12 cos0,80;cos0,50 ϕ=ϕ= Hướng dẫn:

DẠYKÈMQUYNHƠNOFFICIAL 160 VìvớiR=R1 =25Ω hoặcR=R2 =75Ω thìmạchcócùngcôngsuấtthìchúnglànghiệm củaphươngtrình: () () 22 22 2 22LC LC URU PIRRRZZ0 RZZP ==⇔−+−= +− Theo địnhlíViet: ()2 12LC RRZZ =− Tacó: () 11 1 2222 1LC112 RR 25 cos 0,50 RRR2525.75RZZ ϕ==== +−++ . Tươngtự: () 22 2 2222 2LC212 RR753 cos 0,87 2RRR7525.75RZZ ϕ==== +−++ ≃ . Chọn A Câu 7: Đặt điệnápxoaychiềucógiátrị hiệudụngU=100Vvào2 đầudoạnmạchAB. Đoạn mạch AB gồm 2 đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm có điện trở thuầnR vàcuộncảmthuầnL; đoạnmạchMBcó điệntrở thuầnR vàtụ điệnC.Biết điện áp hiệu dụng ở 2 đầu đoạn AM và MB lần lượt là 60V và 80V. Tìm hệ số công suất của đoạnmạchAB? A.1,00 B.0,96 C.0,71 D.0,50 Hướng dẫn: Dễ thấy: 222 ABAMMBAMMB UUUUU =+  ⊥ ,suyraUL +UC =UAB (1) Tacó: 22 LAMR 22 CMBR UUU UUU  =−  =−  (2) Từ (1)và(2)tacó: 22222222 ABAMRMBRAMRABMBR UUUUUUUUUU =−+−⇔−=−− 2222222 AMRABABMBRMBR UUU2UUUUU ⇔−=−−+− 222222 ABMBRMBMBRR UUUUUU64U48V ⇔−=⇔−=  = Hệ số côngsuất: R AB 2U2.48 cos0,96 U100 ϕ=== . Chọn B II. Mạch không phân nhánh RLrC (Cuộn dây không thuần cảm có r). 1. Công suất tiêu thụ trong mạch RrLC không phân nhánh (cuộn dây có L, r) Côngsuấttiêuthụ củacả đọanmạchxoaychiều: C A B R L,r NM

DẠYKÈMQUYNHƠNOFFICIAL 161 () ( ) ()() 2 2 22 LC URr PUIcosIRr RrZZ + =ϕ=+= ++− . Hệ số côngsuấtcủacả đọanmạch: ( ) ( ) ()() 22 LC RrRr cos Z RrZZ ++ ϕ== ++− . Côngsuấttiêuthụ trên điệntrở R: ()() 2 2 R 22 LC UR PIR RrZZ == ++− ,với ()() 22 LCZRrZZ =++− Côngsuấttiêuthụ củacuộndây: ()() 2 2 r 22 LC Ur PIr RrZZ == ++− . Hệ số côngsuấtcủa đọanmạchchứacuộndây: d 22 d L rr cos ZrZϕ== + . (HaymạchcóRLCcuộndâycó điệntrở trongr(R,L,r,C) Côngsuấttiêuthụ củacả đọanmạchxoaychiều: () ( ) ()() () 2 2 2 222 LCLC URrU PIRr RrZZZZ Rr Rr + =+== ++−− ++ + TìmR để côngsuấttoànmạchcực đạiPmax: ()2 LC max LCLC min ZZ PRrRrZZRZZr Rr  ⇔++⇔+=−⇔=−−  +   Khi đó: () 22 max LC UU P 2Rr2ZZ == +− TìmR để côngsuấttrênRcực đạiPR max: () 222 LCRrZZ =+− Câu 1: Một đoạnmạch điệnxoaychiềugồmmộtcuộndâycó điệntrở thuầnr=20Ω và độ tự cảmL= 0,8 π H,tụ điện 410 CF 2 = π và điệntrở thuầnRthay đổi đượcmắcnốitiếp. Điệnáp hai đầu đoạn mạch ổn định. Để mạch tiêu thụ công suất cực đại thì R phải có giá trị nào sau đây? A.100 Ω. B.120 Ω. C.60 Ω. D.80 Ω. Hướng dẫn: Tacó: L C 4 0,8 ZL100.80 11 Z200 C10 100. 2  =ω=π=Ω π  ===Ω ω π π Côngsuấttiêuthụ củacả đọanmạchxoaychiều:

DẠYKÈMQUYNHƠNOFFICIAL 162 () ( ) ()() () 2 2 2 222 LCLC URrU PIRr RrZZZZ Rr Rr + =+== ++−− ++ + Để côngsuấttoànmạchcực đại ()2 LC max min ZZ PRr Rr  ⇔++ +   . LCLC RrZZRZZr8020020100 ⇔+=−⇔=−−=−−=Ω .  Chọn A Câu 2: Một đoạnmạch điệnxoaychiềugồmmộtcuộndâycó điệntrở thuầnr=30Ω và độ tự cảmL= 0,8 π H,tụ điện 310 CF 4 = π và điệntrở thuầnRthay đổi đượcmắcnốitiếp. Điệnáp hai đầu đoạnmạch ổn định. Để côngsuấttiêuthụ trênRcực đạithìRphảicógiátrị nào sau đây? A.100 Ω. B.120 Ω. C.50 Ω. D.80 Ω. Hướng dẫn: Tacó: L C 3 0,8 ZL100.80 11 Z40 C10 100. 4  =ω=π=Ω π  ===Ω ω π π Côngsuấttiêuthụ củacả đọanmạchxoaychiều: ()() () 2 2 2 R 22 22 LC LC URU PIR RrZZrZZ R2r R === ++− +− ++    Để côngsuấttrênRcực đạiPR max: () () () 2 22 2 LCLC2 22 LC min rZZrZZ RRRrZZ RR +−+− +⇔=⇔=+−   Hay () 22 R30804050 =+−=Ω .  Chọn C 2. Công suất tiêu thụ cực đại của cả đoạn mạch R thay đổi: (L, r, C, ω ω không đổi) R thay đổi để Pmax: Khi L, C, ω không đổi thì mối liên hệ giữa ZL và ZC không thay đổi nên sự thay đổi củaRkhônggâyrahiệntượngcộnghưởng Côngsuấttiêuthụ củacả đọanmạchxoaychiều: C A B R L ,r

DẠYKÈMQUYNHƠNOFFICIAL 163 () ( ) ()() () 2 2 2 222 LCLC URrU PIRr RrZZZZ Rr Rr + =+== ++−− ++ + TìmR để côngsuấttoànmạchcực đạiPmax: ()2 LC max LCLC min ZZ PRrRrZZRZZr Rr  ⇔++⇔+=−⇔=−−  +   Khi đó: () 22 max LC UU P 2Rr2ZZ == +− 3. Công suất tiêu thụ cực đại trên R: Côngsuấttiêuthụ củacả đọanmạchxoaychiều: ()() () 2 2 2 R 22 22 LC LC URU PIR RrZZrZZ R2r R === ++− +− ++    Để côngsuấttrênRcực đạiPR max: () () () 2 22 2 LCLC2 22 LC min rZZrZZ RRRrZZ RR +−+− +⇔=⇔=+−   Khi đó: () 2 Rmax 22 LC U P 2r2rZZ = ++− Lưu ý: Có khi kí hiệu r thay bằng R0 Câu 1: Mộtbiến trở R mắcnốitiếpvới cuộndâycó điện trở thuần 0 R15=Ω và độ tự cảm L = 1 5π H như hình vẽ. Biết điện áp hai đầu đoạn mạch là AB u402cos100t =π (V).Côngsuấttoả nhiệttrênbiếntrở cóthể đạtgiátrị cực đạilàbao nhiêu khi ta dịch chuyển con chạy của biến trở? Tính giá trị của biến trở lúc đó và công suấtcực đại đó? Hướng dẫn: Tacó: L 0 1 ZL100.50 5 U 402 U40V 22  =ω=π=Ω π   ===  Côngsuấttoả nhiệttrênR: () 22 2 R 222 2 0L0L 0 URU PIR RZRRZ R2R R === +++ ++ A L,R0R B

DẠYKÈMQUYNHƠNOFFICIAL 164 Để Pmax thì 22 0L222 0L min RZ RRRZ R  + +⇔=+  (vì2R0 làmộtsố không đổi). Khi đó: () () 2222 0L 22 max 0 RRZ154025 U40 P20W 2RR22515  =+=+=Ω  === ++ . Câu 2: Cho đoạn mạch điện gồm diện trở R = 40 Ω mắc nối tiếp với cuộn dây có điện trở hoạt độngbằng10 Ω vàtụ điệncó điệndungC. Đặtvào2 đầu đoạnmạchmột điệnápu= 110 2 cosωt(V),thì điệnápgiữa2bảntụ điệnlệch pha90o sovớiu.Tínhcôngsuấttiêu thụ củatoànmạch.Tínhcôngsuấttiêuthụ củacuộndây? Hướng dẫn: Khi điệnápgiữa2bảntụ điệnlệchpha90o sovớiunêntrongmạchxảyracộnghưởng. Do đó: max U110 I2,2A Rr4010 === ++ . Côngsuấttoànmạch: 22 max U110 P242W Rr4010 === ++ . Côngsuấttiêuthụ củacuộndây: 22 d PIr2,2.1048,4W === Câu 3: Cho mạch điện xoay chiều gồm các phần tử điện R, L, C mắc nối tiếp. Điện áp giữa hai đầu mạch là AB u1002cos100t =π (V), điện trở R thay đổi; cuộn dây có Ro = 30Ω, 1,4 LH = π ; C31,8F =µ Điều chỉnh R để công suất tiêu thụ của điện trở R đạt giá trị lớn nhấtthìRvàPR cógiátrị là: A.R=30Ω ;PR =125W. B.R=50Ω ;PR =250W. C.R=30Ω ;PR =250W. D.R=50Ω ;PR =62,5W. Hướng dẫn: Tacó: L C 6 1,4 ZL100.140 11 Z100 C100.31,8.10  =ω=π=Ω π   ===Ω ωπ Côngsuấttiêuthụ củacả đọanmạchxoaychiều: ()() () 2 2 2 R 22 22 0LC 0LC 0 URU PIR RRZZRZZ R2R R === ++− +− ++    Để côngsuấttrênRcực đạiPR max:

DẠYKÈMQUYNHƠNOFFICIAL 165 () () () 2 22 2 0LC0LC2 22 0LC min RZZRZZ RRRRZZ RR +−+− +⇔=⇔=+−   Khi đó: () () () () 2222 0LC 22 Rmax 0 RRZZ3014010050 U100 P62,5W 2RR25030  =+−=+−=Ω   === ++     Chọn D Câu 4: Đặt một điện áp u = 80cosωt (V) vào hai đầu đoạn mạch nối tiếp gồm điện trở R, tụ điệnCvàcuộndâykhôngthuầncảmthìthấycôngsuấttiêuthụ củamạchlà40W, điệnáp hiệudụngUR =ULr =25V;UC =60V. Điệntrở thuầnrcủacuộndâybằngbaonhiêu? A.15Ω B.25Ω C.20Ω D.40Ω Hướng dẫn: Tacó: 2222 rLLr UUU25 +== (1) Mặckhác: ()() 2 222 0 RrLC U UUUUU 2  =++−=   ()() 2 22 rL 80 25UU603200 2  ⇔++−==   22 rrLL 62550UUU120U36003200 ⇔+++−+= rL 12U5U165⇔−= (2) Giảihệ phươngtrình(1)và(2)ta được: * L r U3,43V U24,76V =  = nghiệmnàyloạivìlúcnàyU>40 2 . * L r U20V U15V =  = Khi đó: Rr r UU25151P40I1A cos801 U80Ucos. 2 222 PUIcosU15r15 I1 ++ === === ϕ     =ϕ  ===Ω   Chọn A Câu 5: Một đoạnmạch điệnxoaychiềugồmmột điệntrở thuầnR,mộtcuộndâycó điệntrở r và độ tự cảmL,mộttụ điệncó điệndungCmắcnốitiếp.Cácgiátrị củar,L,Ckhông đổi, giá trị của điện trở thuần R thay đổi được. Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều u2002cos100t =π (V). Khi 1 RR50==Ω hoặc 2 RR95==Ω thì công suất ϕ

DẠYKÈMQUYNHƠNOFFICIAL 166 tiêu thụ của đoạn mạch AB có cùng một giá trị bằng 8000 W 41 . Khi 0RR = thì công suất của đoạnmạchAB đạtgiátrị lớnnhất.Giátrị của 0R là A. 70Ω B. 80Ω C. 90Ω D. 60Ω Hướng dẫn: Tacó: ()()() 22 tđ1tđ212 2 tđ1tđ2LC LC U200 RRRR2r205r30 8000P 41 R.RZZ50309530ZZ100  +=++===  =Ω     =−=++  −=Ω Côngsuấttiêuthụ củacả đọanmạchxoaychiều: () ( ) ()() () 2 2 2 222 LCLC URrU PIRr RrZZZZ Rr Rr + =+== ++−− ++ + . TìmR để côngsuấttoànmạchcực đạiPmax: ()2 LC max min ZZ PRr Rr  ⇔++ +   LCLC RrZZRZZr1003070 ⇔+=−⇔=−−=−=Ω    Chọn A Câu 6: Mộtmạch điênxoaychiềugồmbiếntrở R,cuộndâycó độ tự cảmLvà điệntrở thuần r,tụ điệncó điệndungCmắcnốitiếp(với LC ZZr −> ).KhiR=R1 hoặcR=R2 thìcông suất tỏa nhiệt trên biến trở R có cùng một giá trị. Khi R = R0 thì công suất tỏa nhiệt trên toànmạchlớnnhất.Liênhệ nàosau đây đúng? A. 2 120RRR = B. ( )( ) 2 120 RrRrR ++= C. ()()()2 120 RrRrRr ++=+ D. () 22 120 RRrRr −=+ Hướng dẫn: Côngsuấttỏanhiệttrênbiếntrở R: ()() 2 2 22 LC UR PIR RrZZ == ++− Theogiả thuyết: ()() ()()12 1 2 RR 2222 1LC2LC RR PP RrZZRrZZ =⇔= ++−++− ()()()() 22 122121LC21 RRRRrRRZZRR ⇔−−−=−− DoR1 ≠ R2 nên: () 22 12LC RRrZZ −=− (1) Côngsuấttỏanhiệttrêntoànmạch: () ( ) ()() () 2 2 2 222 LCLC URrU PIRr RrZZZZ Rr Rr + =+== ++−− ++ +

DẠYKÈMQUYNHƠNOFFICIAL 167 Để côngsuấttrênRcực đạiPmax: ()2 LC min ZZ Rr Rr  ++  +   () ()() 2 LC22 LC ZZ RrRrZZ Rr ⇔+=⇔+=− + ()() 22 LC0 ZZRr −=+ (2) Từ (1)và(2)tacó: () 22 120 RRrRr −=+ .  Chọn D Câu 7: Mạch điện xoay chiều gồm biến trở R, cuộn dây và tụ điện mắc nối tiếp. Biết cuộn dâycó điệntrở thuầnr=30Ω, độ tự cảm 0,6 LH = π ,tụ điệncó điệndung 310 CF 2 = π . Đặt vào hai đầu đoạn mạch một điện áp xoay chiều 220V – 50Hz. Để công suất tiêu thụ trên biếntrở đạtcực đạithìgiátrị củabiếntrở phảibằng A.0 Ω B.10 Ω C.40 Ω . D.50 Ω Hướng dẫn: Tacó: L C 3 0,6 ZL100.60 11 Z20 C10 100. 2  =ω=π=Ω π  ===Ω ω π π Côngsuấttiêuthụ củacả đoạnmạchxoaychiều: ()() () 2 2 2 R 22 22 LC LC URU PIR RrZZrZZ R2r R === ++− +− ++    Để côngsuấttrênRcực đạiPR max: () () () 2 22 2 LCLC2 22 LC min rZZrZZ RRRrZZ RR +−+− +⇔=⇔=+−   Khi đó: () () 2222 LC RrZZ30602050 =+−=+−=Ω   Chọn D Câu 8: Đặt điệnápu=400cos100πt(utínhbằngV,ttínhbằngs)vàohai đầu đoạnmạchAB gồm điện trở thuần 50 Ω mắc nối tiếp với đoạn mạch X. Cường độ dòng điện hiệu dụng qua đoạn mạch là 2 A. Biết ở thời điểm t, điện áp tức thời giữa hai đầu AB có giá trị 400 V; ở thời điểm 1 t 400 + (s), cường độ dòng điện tức thời qua đoạn mạch bằng không và đanggiảm.Côngsuấttiêuthụ điệncủa đoạnmạchXlà A.400W. B.200W. C.160W. D.100W. Hướng dẫn: Cách giải 1: Ở thời điểmt:u=400V  φu =2kπ.

DẠYKÈMQUYNHƠNOFFICIAL 168 Ở thời điểm 1 t 400 + :i=0, đanggiảm  φ’ i = 2 π +2kπ  tạithời điểmt: φi = 24 ππ +2kπ. Góclệchphagiữauvài: ∆φ = φu – φi = 4 π  Côngsuất:P=UIcos∆φ =400W. Côngsuấttiêuthụ điệncủa đoạnmạchXlà: PX =P–PR =UIcosϕ –I2R=200 2 .2 2 2 –22.50=200W.   Chọn B Cách giải 2: Giả sử i=2 2 cos(100πt-ϕ). Ở thời điểmt: u=400V  cos100πt=1vàkhi đósin100πt=0. Ở thời điểm 1 t 400 + :cos(100πt– ϕ + 4 π ).=0và đanggiảm  cos100πtcos( 4 π – ϕ)–sin100πt.sin( 4 π – ϕ)=0  cos( 4 π – ϕ)=0.  ϕ = 42 ππ = 4 π  uchậmphahơnigóc 4 π .Suyracosϕ =cos 4 π Côngsuấttiêuthụ của đoạnmạchXlà: PX =P–PR =UIcosϕ –I2R=200 2 .2 2 2 –22.50 =200W.   Chọn B Câu 9: Cho đoạn mạch xoay chiều AB gồm hai đoạn AMvàMBmắcnốitiếp.Biết đoạnAMgồm điệntrở thuầnRmắcnốitiếpvới tụ điện có điện dungCthay đổi được; đoạn mạch MB chỉ có cuộn dây. Đặt vào hai đầu A, B một điện áp xoay chiều có biểu thức u1002cos100t =π (V) rồi điều chỉnh tụ điện có điện dung 323.10 CF 15 = π thì mạch xảy ra cộng hưởng điện. Biết khi đó các điện áp tức thời uAM và uMB vuông pha nhau, công suất tiêu thụ trên đoạn AM bằng 1 4 côngsuấttiêuthụ trêntoànmạch.Côngsuấttiêuthụ trêntoànmạchkhi đóbằng A.100W. B.50W. C.200W. D. 753 W. Hướng dẫn: C A B R L, r M

DẠYKÈMQUYNHƠNOFFICIAL 169 Khimạchxảyracộnghưởng điệnthì: C 3 LC LC 11 Z153 C 23.10 100. UU 15 ZZ153 ===Ωω π  =π  ==Ω  VìuAM vàuMB vuôngphanhaunêncuộndâyphảicó điệntrở trong. C L AMMB ZZ tantan1.1 Rrϕϕ=−  =− ( )2 22 CLL2 ZZRrZZRr1531875⇔=  ==== (1) Talạicó:IAM =Itoàn mạch. MàPAM =0,25Ptoàn mạch  R=0,25(R+r)  4R=(R+r) (2) Từ (1)và(2)ta được:R=25Ω  r=75Ω Lúcnàycôngsuấttoànmạch: 22 U100 P100W Rr2575 === ++    Chọn A Câu 10: Cho mạch RLC,có C thay đổi được điện áp hai đầu đoạn mach uU2cos100t =π (V).Khi 4 1 10 CCF 2 == π hoặc 4 2 10 CCF == π thìmạchtiêuthụ cùngcôngsuấtnhưngcác dòng điệni1 vài2 lệchphanhau 3 π .Xác địnhRnếubiết 1,5 LH = π Hướng dẫn: Mạchtiêuthụ cùngcôngsuất: 12max1212 PPPIIZZ =<⇔=⇔= 2 1212 1111 LL2L CCCC ⇔ω−=ω−  ω=+ ωω . Khicôngsuấttrongmạchcực đạivớiC=C0;vìLvà ω làkhông đổi: 22 12 0 0 001212 2CC1111 LC1L2C CCCCCC ω=  ω=  =+  = + Tầnsố góccủamạch 44 012 12 44 111 100π rad/s LC2CCL1010 CC1,52.. 2 . 1010 2 ω==== + ππ π ππ

DẠYKÈMQUYNHƠNOFFICIAL 170 Tacó: 1 2 L C 4 1 C 4 2 1,5 ZL100.150 11 Z200 C10 100. 2 11 Z100 C10 100.     =ω=π=Ω π  ===Ω ω π π   ===Ω ω π π Talạicó: 1 2 LC 1 LC 2 21 ZZ 50 tan0 RR ZZ 50 tan0 RR 3  ϕ==<   ϕ==>  π ϕ−ϕ=  Khi đó: () 21 21 12 5050 tantan RR tan tan3R503 5050 1tantan3 1. RR   ϕ−ϕπ  ϕ−ϕ=⇔==  =Ω +ϕϕ +−  Câu 11: Mạch điệnxoaychiềuRLCghépnốitiếp, đặtvàohai đầumạchmột điệnápu=U0cosωt (V). ĐiềuchỉnhC=C1 thìcôngsuấtcủamạch đạtgiátrị cực đạiPmax =400W. Điềuchỉnh C=C2 thìhệ số côngsuấtcủamạchlà 2 3 .Côngsuấtcủamạchkhi đólà A.200W B.200 3 W C.300W D.150 3 W Hướng dẫn: Cách giải 1: Khi C = C1 thì công suất của mạch đạt cực đại vậy trong mạch xảy ra hiện tượng cộng hưởng: 2 2 11 U PIRcos400W R ==ϕ= Khithay đổiC=C2 thìhệ số côngsuấtcủamạchlà 2 3 cos 2ϕ= . (1) Từ giản đồ Fre-nentathu đượcnhư sau: LC LC ZZ 3 tantanZZR 6R3 π ϕ==  −= (2)

DẠYKÈMQUYNHƠNOFFICIAL 171 Lấy(1)thayvào(2)ta được: 22 2 2 2 U3U33 P...400300W 32R44 RR 3 ====  +   . VậyP2 cầntìmlà300W.   Chọn C Công thức giải nhanh cho dạng này: 2 22 Rmax U PPcos.cos R =ϕ=ϕ Cách giải 2: Khi C = C1  công suất cực đại 2 max U P R =  tương đương công suất cực đại trên điện trở R(cộnghưởng)  2 Rmax U P R = KhiC=C2 thìcôngsuấtP=UIcosϕ =I2Rvới U I Z = Côngsuấtcầntìm: 2222 22 22 URURU3 P.cos.cos400.300W ZRZR4 ==ϕ=ϕ== . Lí do là khi C thay đổi thì I thay đổi, với đề cho thì chỉ có L, R, U, ωlà không đổi.  Chọn C Cách giải 3: KhiC=C1: Pmax =UI1 (1) KhiC=C2 : P= UI2 cosϕ (2) Từ (1)và(2)ta được: 22 max max11 IcosIcosP PP PII ϕϕ =  = (3) Với: 1 1 2 1 2 2 UU I ZR I cos UU I Icos ZR  ==    =ϕ ==ϕ  (4) Từ (3)và(4)ta được: 2 max 3 PPcos.400300W 4 =ϕ== .   Chọn C Cách giải 4: Tacó: 2 2 2 max R32R cosZ Z2 3 UU333 PIRR.P.400.300W. ZR444  ϕ==  =    ======     Chọn C Câu 12: Đoạn mạch gồm một cuộn dây có điện trở R và độ tự cảm L nối tiếp với một tụ điện biến đổi có điện dungC thay đổi được. Điện áp xoay chiều ở hai đầu mạch là

DẠYKÈMQUYNHƠNOFFICIAL 172 u=U 2 cos(ωt+ 6 π )(V).Khi C=C1 thìcôngsuấtmạchlàPvàcường độ đòng điệnqua mạch laø: i = I 2 cos(ωt + 3 π ) (A). Khi C = C2 thì công suất mạch cực đại là P0. Tính côngsuấtcực đạiP0 theoP. A. 0 4 PP 3 = B. 0 2 PP 3 = C. 0 P4P = D. 0 P2P = Hướng dẫn: Cách giải 1: TheobàiratacógóclệchphagiữauvàikhiC=C1: 636 πππ ϕ=−=− . Tacó: 2 2 1 1 1 33U PUIcosUI 22Z3U P RR2R4R cosZ Zcos3  =ϕ==    = ϕ=  == ϕ  (1) KhiC=C2 thìcôngsuấtmạchcực đại:(mạchRLCcócộnghưởng điện(ZL =ZC))thì: 2 0max U PP R == (2) Từ (1)và(2): 0 4 PP 3 =  Chọn A Cách giải 2: KhiC=C2 thìcôngsuấtmạchcực đại P0:cosϕ =1=> ϕ =0:mạchRLCcócộnghưởng điện(ZL =ZC))thì: 2 0max U PP R == (1) KhiC=C1 thìcôngsuấtmạchlàPvà 636 πππ ϕ=−=− : ()2 LC2 LCLC ZZ 31 tantanZZRZZR 6R33 π  ϕ=−=  −=−  −=  (2) Thế (2)vàocôngthức: () 2 22 LC UR P RZZ = +− Tacó: () 222 22 22 LC URUR3U P. 1 4RRZZ RR 3 === +− + (3) Từ (1)và(3)suyra: 0 4 PP 3 =   Chọn A Công thức giải nhanh cho dạng này: 2 22 Rmax U PPcos.cos R =ϕ=ϕ

DẠYKÈMQUYNHƠNOFFICIAL 173 Câu 13: Mạch điệnxoaychiềumắcnốitiếpgồmbiếntrở R,cuộndâythuầncảmLvàtụ điện C. Đặtvàohai đầu đoạnmạch điệnápxoaychiềucógiátrị hiệudụngU=100Vvàtầnsố f không đổi. Điều chỉnh để R = R1 = 50Ω thì công suất tiêu thụ của mạch là P1 = 60W và góclệchphacủa điệnápvàdòng điệnlà ϕ1. Điềuchỉnh để R=R2 =25Ω thìcôngsuấttiêu thụ củamạchlàP2 vàgóclệchphacủa điệnápvàdòng điệnlà ϕ2 vớicos2ϕ1 +cos2ϕ2 = 4 3 ,Tỉ số 2 1 P P bằng: A.1 B.2 C.3 D.4 Hướng dẫn: Cách giải 1: Tacó: 2 22 111 2 2 22 12 U P.coscos0,3 R cos0,45 3 coscos 4  =ϕ  ϕ=    ϕ= ϕ+ϕ=   Suyra: 2 2 2 22 1 PU P.cos1803 RP=ϕ=  =    Chọn C Cách giải 2: Tacó: 2 111111111 22 1 1111 2 222222222 222 122 PUIcosIRIRUcosI2cos (1) P3 PUIcos2Ucoscos (2) 2U10 PUIcosIRIRUcosI4cos (3) 3339 coscoscos 441020 =ϕ=  =ϕ  =ϕ =ϕ=ϕ  ϕ== =ϕ=  =ϕ  =ϕ ϕ+ϕ=  ϕ=−= (4)          Từ (1),(2),(3)và(4)suyra: 2 222222 2 111111 9 PIcos4coscoscos20 ..223 PIcos2coscoscos3 10 ϕϕϕϕ ===== ϕϕϕϕ Chọn C Câu 14: Đặt điện áp xoay chiều u = 120 6 cosωt (V) vào hai đầu đoạn mạch AB gồm hai đoạnmạchAMvàMBmắcnốitiếp. ĐoạnAMlàcuộndâycó điệntrở thuầnrvàcó độ tự cảmL, đoạnMBgồm điệntrở thuầnRmắcnốitiếpvớitụ C. Điệnáphiệudụngtrên đoạn MBgấp đôi điện áphiệu dụngtrên Rvàcường độ dòng điệnhiệu dụngtrongmạchlà0,5 A. Điện áp trên đoạn MB lệch pha so với điện áp hai đầu mạch là 2 π . Công suất tiêu thụ điệntrongmạchlà: A.150W B.90W C.20W D.100W

DẠYKÈMQUYNHƠNOFFICIAL 174 Hướng dẫn: Tacó: 222 MBRCC U2URZ4RZR3 =⇔+=  = Mặckhác: LC MBMBAB LC ABLC ZZ tan3 R36 ZZ 1Rr tanZZ Rr 33 ππ ϕ==−  ϕ=−  ϕ=   + ϕ==  −=  + Khi đó: ()() () () 2 22222 AB LC 2 4U ZRrZZRr2403 3I =++−=+== Rr360 +=Ω Côngsuấttiêuthụ điệntrongmạchlà:P=(R+r)I2 =90W.  Chọn B Câu 15: Đặtmột điệnápxoaychiềucógiátrị hiệudụngUvàtầnsố fkhông đổivàohai đầu đoạnmạchgồmbiếntrở Rmắcnốitiếpvớitụ điệncó điệndungC.Gọi điệnáphiệudụng giữahai đàu biến trở,giữahai đầu tụ điện vàhệ số công suất của đoạn mạch khi biến trở cógiátrị R1 lầnlượtlà 11 RC1U,U,cos ϕ .Khibiếntrở cógiátrị R2 thìcácgiátrị tương ứng nói trên lần lượtlà 22 RC2U,U,cos ϕ ,biết rằng sự liên hệ: 1 2 R R U9 U16 = và 2 1 C C U9 U16 = .Giátrị của 1cos ϕ là: A.1 B. 1 2 C.0,49 D. 3 2 Hướng dẫn: Tacó: 1 21 2 2 21 1 R RR R C CC C U 916 UU (1)U169 U 99 UU (2)U1616  =  =    =  =  Khi đó: 112211 22 22222 RCRCRC 169 UUUUUUU 916 =+=+=+  M C A B RL, r

DẠYKÈMQUYNHƠNOFFICIAL 175 111111 2 22 222 RRCCCR 16916 UUUUUU 9169  ⇔−=−  =   Suyra: 11 1 1 2 22 2222 RCRR 16916 UUU1UUU 99  +=+=+  =     1R 1 22 U9 cos0,49 U916⇒ϕ== + ≃ .  Chọn C TÓM TẮT CÁC CÔNG THỨC VỀ CÔNG SUẤT Dạng toán Kết quả Bổ sung Bàitoánthuận:chocác đạilượngtìmP PUIcos=ϕ ; P=RI2 R cos Zϕ= ChoPtìmLhoặctìmC 2 2 LC RU ZZR P −=− TìmR để Pmax R=|ZL ZC|; 2 max U P 2R = ChoPtìmR () 2 22 LC U RRZZ0 P −+−= Biết hai giá trị của điện trở là R1 và R2 mạchcócùngcôngsuấtP 2 12 U RR P += 2 12 U P RR = + Với 2 giá trị của điện trở là R1 và R2 mạch có cùng công suất P. Với giá trị của điện trở là R0 thì mạch có công suất cực đạiPmax. 012 RRR = 2 max U P 2R = Mạch có RLC cuộn dây có điện trở trong r (R, L, r, C).Tìm R để công suất toànmạchcực đạiPmax R+r=|ZL ZC| 2 max U P 2(Rr) = + Mạch có RLC cuộndâycó điệntrở r(R, L, r, C) . TìmR để côngsuấttrênRcực đạiPRmax R2 =r2 +(ZL ZC)2 Thay đổi f (hay ω) hoặc L hoặc C để Pmax Khimạchcócộnghưởng: ZL =ZC; 1 L C ω= ω 2 max U PP R == Vớihaigiátrị tầnsố ω = ω1 hoặc ω = ω2 thìcôngsuấtPcócùngmộtgiátrị. Với ω = ω0 thìPmax 012 ω=ωω hay 12fff = 2 max U P R =

DẠYKÈMQUYNHƠNOFFICIAL 176 Với hai giá trị của cuộn cảm L1 và L2 mạchcócùngcôngsuất. Với Lmạchcócôngsuấtcực đại. L1L2 C ZZ Z 2 + = L1L2 L ZZ Z 2 + = ; 12LL L 2 + = 2 max U P R = Vớihaigiátrị củatụ điệnC1 vàC2 mạch cócùngcôngsuất. Với điện dung của tụ điện C mạch có côngsuấtcực đại. C1C2 L ZZ Z 2 + = C1C2 C ZZ Z 2 + = ; 12 12 2C.C C CC = + 2 max U P R = III. Hệ số công suất mạch điện xoay chiều không phân nhánh. 1. Xác định hệ số công suất trong mạch điện xoay chiều bằng máy tính CASIO fx–570ES; 570ES Plus a. Hệ số công suất của đoạn mạch: ĐoạnmạchRLC: R cos Zϕ= hay RU cos Uϕ= ĐoạnmạchRrLC: Rr cos Z + ϕ= hay RrUU cos U + ϕ= Đọanmạchchứacuộndây: d 22 d L rr cos ZrZϕ== + Tổngtrở: () 22 LCZRZZ =+− Tổngtrở phức: ( )LC ZRZZi =+− Dùngcôngthứcnày: u Z i = Tínhcosϕ :Saukhibấmmáytínhtacó: ZZ=∠ϕ ;sau đóbấmcosϕ =Kếtquả. Nếutínhcosϕd thì: d d u Z i = .Saukhibấmmáytacó: d ddZZ=∠ϕ sau đóbấmcosϕd = Kếtquả. b. Chọn cài đặt máy tính: CASIO fx–570ES ; 570ES Plus

DẠYKÈMQUYNHƠNOFFICIAL 177 Chọnchế độ Nútlệnh Ýnghĩa-Kếtquả Chỉ địnhdạngnhập/xuấttoán Bấm:SHIFT MODE 1 MànhìnhxuấthiệnMath. Thựchiện phéptínhvề số phức Bấm:MODE 2 MànhìnhxuấthiệnCMPLX Hiểnthị dạngtoạđộ cực:r∠θ Bấm:SHIFTMODE 32 Hiểnthị số phứcdạng:A ∠ϕ Hiểnthị dạng đề các:a+bi. Bấm:SHIFTMODE 31 Hiểnthị số phứcdạng: a+bi Chọn đơnvị đogóclà độ (D) Bấm:SHIFT MODE 3 Mànhìnhhiểnthị chữ D Chọn đơnvị đogóclàRad(R) Bấm:SHIFT MODE 4 Mànhìnhhiểnthị chữ R Nhậpkýhiệugóc ∠ Bấm SHIFT (-) Mànhìnhhiểnthị ∠ Với máy FX - 570ES : Kết quả hiển thị: Câu 1: ĐoạnmạchABgồmhai đoạnmạchAMvàMBmắcnối tiếp. Đoạn AM gồm điện trở thuần R = 100Ω mắc nối tiếp với cuộn cảm thuần 1 LH = π . Đoạn MB là tụ điện có điện dung C. Biểu thức điện áp trên các đoạn mạch AM và MB lần lượt là: AM u1002cos100t (V)4 π =π+  và MB u200cos100t (V)2 π  =π−  . Hệ số công suất của đoạnmạchABlà: A. 2 2 B. 3 2 C. 1 2 D. 3 4 Hướng dẫn: Cách giải 1: M C A B RL Nếu đang thực hiện phép tính số phức: Bấm SHIFT 2 màn hình xuất hiện như hình bên Nếu bấm tiếp phím 1 = hiển thị: arg (θ hay ϕ) Nếu bấm tiếp phím 2 = hiển thị: Conjg (a – bi ) Nếu bấm tiếp phím 3 = hiển thị: dạng tọa độ cực (r∠θ) Nếu bấm tiếp phím 4 = hiển thị: dạng đề các (a + bi)

DẠYKÈMQUYNHƠNOFFICIAL 178 Tacó: L AM AM AM MB C 1 ZL100.100 Z1002 U1002 IA Z2 1002 U1002.2 Z200 I 2  =ω=π=Ω π =Ω   ===   ===Ω  Suyra: () () 2222 LC ZRZZ1001002001002 =+−=+−=Ω Và R1002 cos Z2 1002 ϕ=== .    Chọn A Cách giải 2: Tacó: ZAM =(100+100i). Tổngtrở phứccủa đoạnmạchAB: ABAMMBMB AB AMAM AMAM uuuu ZZ1Z iuu  + ===+  Dùng máy Fx570ES. Cài đặt máy: Bấm MODE 2 xuất hiện: CMPLX. Bấm: SHIFT MODE 4xuấthiện:(R) Nhậpmáy: () 200 2 1X100100i 1002 4 π  ∠−  ++ π  ∠  .Bấmdấu=.Hiểnthị:có2trườnghợp: A abi ∠ϕ  + (Ta không quan tâm đến dạng hiển thị này: Ví dụ máy hiển thị: 141,4213562∠ π 4 (Dạng A∠ϕ)) Tamuốnlấygiátrị ϕ thỉ bấmtiếp:SHIFT 2 1 =Hiểnthị: π 4 (Đâylàgiátrị của ϕ) Bấmtiếp:cos =cos(Ans → Kếtquả hiểnthị : 2 2 . Đâylàgiátrị củacosϕ cầntính 2 cos φ 2 = .   Chọn A Câu 2: ĐoạnmạchABgồmhai đoạnmạchAMvàMBmắcnốitiếp. ĐoạnAMgồm điệntrở thuần R1 = 40 Ω mắc nối tiếp với tụ điện có điện dung C = π4 10 3 F, đoạn mạch MB gồm điệntrở thuầnR2 mắcvớicuộnthuầncảm. ĐặtvàoA,B điệnápxoaychiềucógiátrị hiệu dụngvàtầnsố không đổithì điệnáptứcthời ở hai đầu đoạnmạchAMvàMBlầnlượtlà: )V)(12 7 t100cos(2u50 AM π =π và MB u150cos100t (V)=π . Hệ số công suất của đoạn mạchABlà A.0,84. B.0,71. C.0,86. D.0,95. Hướng dẫn:

DẠYKÈMQUYNHƠNOFFICIAL 179 Cách giải 1: Tacó: C 3 C AM AM 1 11 Z40 10C 100. 4 Z 40 tan1 R404  ===Ω ω π π  −π ϕ===−  ϕ=−  Từ hìnhvẽ: L MBMBL2 2 Z tan3ZR3 3R π ϕ=  ϕ==  = . Xét đoạnmạchAM: AM AM U5052 IA Z8 402 === Xét đoạnmạchMB: MB222 MB2L2 L R60U Z120RZ2R I Z603 =Ω  ===+=   =Ω  Hệ số côngsuấtcủamạchABlà: ()() 12 22 12LC RR cos0,84 RRZZ + ϕ=≈ ++− .    Chọn A Cách giải 2: Dùng máy Fx570ES. Tổngtrở phứccủa đoạnmạchAB: ABAMMBMB AB AMAM AMAM uuuu ZZ1Z iuu  + ===+  Cài đặtmáy:BấmMODE 2xuấthiện:CMPLX.Bấm:SHIFT MODE 4Chọn đơnvị là Rad(R) Nhậpmáy: ()150 1X4040i 7502 12   +−= π  ∠−  Hiểnthị có2trườnghợp: A abi ∠ϕ  + (Ta không quan tâm đến dạng hiển thị này. Nếu máy hiện dạng a+bi thì có thể bấm: SHIFT 2 3 = Kết quả: 118,6851133 ∠0,5687670898 ( A∠ϕ) ) Ta muốn hiển thị ϕ thì bấm: SHIFT 2 1 Hiển thị: arg( , Bấm = Hiển thị: 0,5687670898 (Đâylàgiátrị của ϕ) Muốntínhcosϕ:Bấmtiếp:cos =cos(Ans Hiểnthị :0,842565653=0,84làgiátrị củacosϕ.  Chọn A Câu 3: Mạch điệngồmmộtcuộndâycó điệntrở Rmắcnốitiếpvớimộttụ C.Mạch được đặt dưới điện áp u luôn ổn định. Biết giá trị hiệu dụng CcdU3U = , độ lệch pha của điện áp hai đầu cuộn dây so với cường độ dòng điện qua mạch là 3 π . Tính hệ số công suất của mạch? Hướng dẫn: I UAM UMB 7π/12 π/4 π/3

DẠYKÈMQUYNHƠNOFFICIAL 180 Giả sử cd U1 = (đơnvị)  C U3 = và cdU nhanhphahơndòng điệngóc 3 π : cd U1 3 =∠π Và CU chậmphamộtgóc 2 π sovớidòng điện: C U3 2 =∠−π Tacó: cdCuuu =+ . Dùng máy Fx570ES: BấmMODE 2xuấthiện:CMPLX.Bấm:SHIFT MODE 4Chọn đơn vị làRad(R) Nhập máy: [][][][] SHIFT23 131 323 = πππ∠+∠−←→∠−  . Ta muốn hiển thị ϕ thì bấm: SHIFT 2 1Hiểnthị:arg(,Bấm= Hiểnthị: 3 π (Đâylàgiátrị của ϕ) cd u/i UU cos0,5 3 =    π ϕ=−  ϕ=  Muốntínhcosϕ:Bấmtiếp:cos =cos(Anshiểnthị:0,5=0,5làgiátrị củacosϕ Câu 4: Một đoạnmạchxoaychiềugồm3phầntử mắcnốitiếp: điệntrở thuầnR,cuộndâycó độ tự cảm L và điện trở thuần r, tụ điện có điện dung C. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều,khi đó điện áp tứcthời ở hai đầu cuộn dây vàhai đầu tụ điện lần lượt có biểu thức: d u806cost (V)6 π =ω+  và C 2 u402cost (V) 3 π  =ω−  , điện áp hiệu dụng ở hai đầu điệntrở làUR = 603 V.Hệ số côngsuấtcủa đoạnmạchtrênlà A.0,862. B.0,908. C.0,753. D.0,664. Hướng dẫn: Cách giải 1: Từ giản đồ vectơ tatínhtoán được: r L U403V cos0,908 U120V =   ϕ= =    Chọn B Cách giải 2: Dùng máy Fx570ES Tacó: R 2 u603.2cost606cost(V) 326 πππ  =ω−+=ω−   0 iIcost(A) 6 π   =ω−  Mặckhác: RdC 0u 2 uuuu606806402U 663 πππ  =++=∠−+∠+∠−=∠ϕ   . Với uiu 6 π ϕ=ϕ−ϕ=ϕ+ Dùng máy Fx570ES : Bấm MODE 2xuấthiện:CMPLX.Bấm:SHIFT MODE 4Chọn đơnvị làRad(R)

DẠYKÈMQUYNHƠNOFFICIAL 181 Nhậpmáy: 2 606806402 663 πππ  ∠−+∠+∠−   Bấm= Hiểnthị :.....(khôngquantâm) Bấm:SHIFT21 Hiểnthị :arg(Bấm= Hiểnthị :–0,09090929816(Đâylàgiátrị của ϕu) Bấm- ( 6 π )Bấm= Hiểnthị 0,4326894774(Đâylàgiátrị của ϕ). Muốntínhcosϕ:Bấmtiếp:cos =cos(Ans Hiểnthị:0,907841299 =0,908.    Chọn B Cách giải 3: Vì đề khôngchoI0 nêntachobằng1 đơnvị: 0i iI1Zu 6i=∠ϕ=∠−π  = với ZZ=∠ϕ . Nhập: 2 606806402 663 πππ  ∠−+∠+∠−   Bấm: 1 6 ∠−π Bấm= Hiểnthị:…..(khôngquantâm) Bấm:SHIFT 2 1 Hiểnthị:arg(Bấm= Hiểnthị:0,4326894774(Đâylàgiátrị của ϕ). Muốntínhcosϕ:Bấmtiếp:cos =cos(Ans Hiểnthị:0,907841299 =0,908làgiátrị củacosϕ. Chọn B Câu 5: Chomạch điệnxoaychiềuRLCmắcnốitiếp,cuộndâythuầncảm.BiếtL=CR2 . Đặt vàohai đầu đoạnmạch điệnápxoaychiều ổn định,mạchcócùnghệ số côngsuấtvớihaigiátrị củatầnsố góc 50(rad)s/1 ω=π và 200(rad)s/2 ω=π .Hệ số côngsuấtcủa đoạnmạchbằng A. 2 13 . B. 2 1 . C. 2 1 . D. 12 3 Hướng dẫn: Ápdụngcôngthức: 2 2 RR cos Z 1 RL C ϕ== +ω− ω  Docosφ1 =cosφ2 tacó: 22 12 12 11 LL CC  ω−=ω−  ωω  mà ω1 ≠ ω2 nên 12 1212 111 LLLC CC  ω−=−ω−  = ωωωω  (1) TheobàiraL=CR2 (2) Từ (1)và(2)tacó: 12 2 1 2 1 12 1 RR L 100 RR2 cos 11 Z C113 R100RRL C  == ωωπ   ϕ===  == +ω− ωωπ  ω  . Chọn A

DẠYKÈMQUYNHƠNOFFICIAL 182 Câu 6: Đặt vào hai đầu đoạn mạch RL nối tiếp một điện áp xoay chiều uU2cost =ω (V). Trong đó u tính bằng (V), thời gian t(s). Tần số f thay đổi được. Ban đầu tần số bằng f1 công suất đoạn mạch là P 1 , tăng tần số lên gấp đôi thì công suất đoạn mạch giảm xuống với 21 3 PP 4 = .Khităngtầnsố lêngấp3tầnsố ban đầuthìcôngsuất đoạnmạchlà: A. 1 1 P 8 B. 1 9 P 17 C. 1 3 P 17 D. 1 5 P 8 Hướng dẫn: Cách giải 1: Tacó: 2 1 222 12L 222 21L RZPZ 4 PZRZ3 + === + Theo đề: 211 2 22 21LLL1 8U f2fZ2ZR8ZP 9R =  =  =  = (1) và: 31 31LL f3fZ3Z =  = 31 2222 3 2222 LL22 URURUR8U P 8 RZR9Z17R RR 9  ==== ++ + (2) (Lấy(2)chia(1)ta được: 3 31 1 P 99 PP P1717 =  = .    Chọn B Cách giải 2: Côngsuất đoạnmạch: 1 2 21 3 2 1 22 L 2222 1L 2 222222 LL2L 2 3 22 L UR P RZ PRZ URUR4 PP RZRZPRZ3 UR P RZ  = +  + =  =  == +++    = +  211 3 2 2222 LLL1 222 3 221 L22 8U R3Z4Z8ZP 9R URUR8U9 PP 9 RZ17R17 RR 8  =−=  =    ==== + +   Chọn B Cách giải 3: Dùng chuẩn hóa số liệu. Khif=f1 thìchọn 1L Z1=Ω . Khif=f2 =2f1 thì 2L Z2=Ω . Khif=f3 =3f1 thì 3L Z3=Ω Tacó: 2 1 22 222 12L 2222 21L RZ PZR24 R8 PZRZR13 + + ====  =Ω ++

DẠYKÈMQUYNHƠNOFFICIAL 183 1 3 22 22 3L 1 2222231 13L RZP Z R199 PP PZRZR31717 + +  ====  = ++ .   Chọn B Chú ý: Loại bài tập này nên lập tỉ số, không nên biến đổi dài dòng ! Câu 7: Cho đoạn mạch AB gồm hai đoạn mạch AM nối tiếp với MB.Biết đoạn AM gồm R nối tiếp với C vàMB cócuộn cảm có độ tự cảm L và điện trở r. Đặt vào AB một điện áp xoaychiềuu=U 2 cosωt(v).Biết R=r= L C , điệnáphiệudụnggiữahai đầuMBlớn gấpn= 3 điệnáphai đầuAM.Hệ số côngsuấtcủa đoạnmạchcógiátrị là A.0,887 B.0,755 C.0,866 D.0,975 Hướng dẫn: Vẽ giản đồ véctơ như hìnhvẽ. Từ giả thuyết: 22 LLC LC C L Rr C ZLRrZZ L Z1ZZC C  ==     =ω==   = = ω  Mặckhác: ( ) ()() 222222 AMRCC 222222222 MBrLLL UUUIRZ UUUIrZIRZ =+=+ =+=+=+ XéttamgiácOPQ,tacó: LCPQUU =+ ()() 2222 LCLC PQUUIZZ =+=+ ( ) ( )2222222 LLCCLC IZ2ZZZIZZ2R =++=++ (1) Và ( )22222222222 AMMBRLCLC OPOQUU2UUUIZZ2R +=+=++=++ (2) Từ (1)và(2)tathấy: PQ2 =OP2 +OQ2  TamgiácOPQvuôngtạiO. Từ UMB =nUAM = 3 U AM ,tacó: AM MB U 1 tanPOEPOE U6 3 OQEQOE36  π ==⇒=     ππ  =⇒=     Tứ giácOPEQlàhìnhchữ nhật Do đógóclệchphagiữauvàitrongmạch: ϕ =900 –600 =300 Vìvậycosϕ =cos300 = 866 2 3 = .   Chọn C Câu 8: Chomạch điệnABgồmhai đoạnmạchAMnốitiếpvớiMB,trong đóAMgồm điện trở R nối tiếp với tụ điện có điện dung C, MB có cuộn cảm có độ tự cảm L. Đặt vào hai Q ϕ FO P E

DẠYKÈMQUYNHƠNOFFICIAL 184 đầu đoạn mạch một điện áp xoay chiều uU2cost =ω (V). Biết uAM vuông pha với uMB vớimọitầnsố ω.Khimạchcócộnghưởng điệnvớitầnsố ω0 thì AMMBUU = .Khi ω = ω1 thìuAM trễ phamộtgóc α1 đốivớiuAB vàUAM =U1.Khi ω = ω2 thìuAM trễ phamộtgóc α2 đối với uAB và ' AM1 UU = . Biết 12 2 π α+α= và ' 11 3 UU 4 = . Xác định hệ số công suất của mạch ứngvớitầnsố ω1 vàtầnsố ω2 A.cosϕ =0,75;cosϕ’=0,75. B.cosϕ =0,45;cosϕ’=0,75. C.cosϕ =0,75;cosϕ’=0,45. D.cosϕ =0,96;cosϕ’=0,96. Hướng dẫn: Tacó: C AM L MB Z tan R Z tan r  ϕ=    ϕ=  VìuAM vuôngphavớiuMB vớimọitầnsố ω nên: C L AMMB LC ZZ tantan1.1RrZZ Rr ϕϕ=−⇔=−⇔= Khi ω = ω0 mạchcócộnghưởngvàUAM =UMB  r=R=>R2 =ZLZC Vẽ giãn đồ vectơ như hìnhvẽ TaluôncóUR =Ur UAM =UAB cosα =Ucosα (α làgóctrễ phacủauAM sovớiuAB) U1 =Ucosα1 (1) U’1 =Ucosα2 = Usinα1 (2) (do 12 2 π α+α= ) Từ (1)và(2)suyra: ' 1 1MBAM11 1 U 44 tanUUtanU U33ϕ==  =ϕ= . HaitamgiácvuôngEAMvàFBM đồngdạng(vìcó AMMAEMBF==ϕ cùngphụ với ϕMB). Từ đósuyra: LR C RAM1 LRMB 1 CR 4 UU U UUU3 3 4 UUU43 U 3UU 4  =  ====    =  22222222 ABAMMBRLCRR 62525 UUUU2UUUUUU 14412 ==+=++=  = M R A B C L,r A ϕMB E Ur = UR F α1 B M

DẠYKÈMQUYNHƠNOFFICIAL 185 ZC - ZL ZL R O Z Vậycosϕ = R2U U = 25 24 =0,96. Tươngtự tacókếtquả đốivớitrườnghợp ω2 U1 =Ucosα1 =Usinα2 (1) ' 1U =Ucosα2 (2) Từ (1)và(2)suyra: 1 2 ' 1 ' MBAM21 U3 tan U4 3 UUtanU 4 ϕ==  =ϕ= Hai tam giác vuông EAM và FBM đồng dạng (vì có AMMAEMBF==ϕ cùngphụ với ϕMB) Từ đósuyra: ' LR C RAM1 ' LRMB 1 CR 3 UU U UUU4 4 4 UUU34 U UU 3 3  =  ====    =  22'2'22222 ABAMMBRLCRR 62525 UUUU2UUUUUU 14412 ==+=++=  = Vậycosϕ’= R2U U = 25 24 =0,96.    Chọn D Câu 9: Cho đoạnmạchRLCmắcnốitiếp(cuộndâythuầncảm)vớiCR2 <2L. Đặtvàohai đầu đoạn mạch điện áp 0 uUcost =ω (V) với ω thay đổi được. Điều chỉnh ω để UC max, khi đó điện áp hiệu dụng trên điện trở gấp 5 lần điện áp hiệu dụng trên cuộn dây.Hệ số công suất của đoạnmạchkhi đó: A. 5 31 . B. 2 29 . C. 5 29 . D. 3 19 Hướng dẫn: Với ω thay đổi để UC max Tacó: ω2 = 2LC-R2C2 2L2C2  ZL = L CR2 2  ZL 2 =ZLZCR2 2 ⇔ ZL R. ZC -ZL R = 1 2 Ở hìnhvẽ bên:   tana1 = ZL R tana2 = ZC -ZL R  tan α1tanα2 = 1 2 Cũngtừ hìnhvẽ,tacó: Z2 =(ZC –ZL)2 +R2 ⇔ Z2 =(ZC –ZL)2 +2ZL(ZC –ZL) ϕMB Ur = UR F A E α2 B M

DẠYKÈMQUYNHƠNOFFICIAL 186 Biến đổihệ thứctrêntacó:ZC 2 =Z2 +ZL 2    Chọn B Bài 10: Đoạn mạch AB gồm ba đoạn mạch mắc nối tiếp: Đoạn mạch AM chứa điện trở R, đoạnmạchMNcuộndây,và đoạnmạchNBchứatụ điệncó điệndungC. Đặtvàohai đầu đoạn mạch AB điện áp xoay chiều u1202cos2ft =π (V). Thay đổi f thì thấy: Khi f = f1 thìhệ số côngsuấtcủa đoạnmạchANlà0,6vàhệ số côngsuấtcủatoànmạchlà0,8.Khi f=f2 =100Hzthìhệ số côngsuấttoànmạchlà1.Giátrị củaf1 là A.90Hz. B.60Hz. C.80Hz. D.70Hz. Hướng dẫn: Khif=f1: () () 2 2 2 2 1 1tan cos L AN ANL 1 1tan cos LC AB ABLC 22 2 L11 1 C22 2AB Z 44 cos0,6tanZRr 3Rr3 ZZ 33 cos0,8tanZZRr 4Rr4 Zf LC Zf 1 , cos1 LC =+ϕ ϕ =+ϕ ϕ  ϕ=→ϕ==  =+ +   ϕ=→ϕ=±=  −=±+ +   ω =ω==  ω   ω=−ϕ=  Với: () () L LCC 12 C Z 37164 ZZRrZRrff151,2Hz. 412Z7 7 −=+  =+  =  == Với: () () L LCC 12 C Z 325164 ZZRrZRrff80Hz. 412Z255 −=−+  =+  =  == Chọn C CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Cho đoạn mạch xoay chiều không phân nhánh. Điện trở R = 50 Ω , cuộn dây thuần cảm 1 LH = π và tụ 310 CF 22 = π Điện áp hai đầu mạch: u2602cos100t =π (V). Công suấttoànmạch: A.P =180W B.P =200W C.P =100W D.P =50W Câu 2: Điện áp hai đầu đoạn mạch R, L, C mắc nối tiếp là AB u2002cos100tV 3 π  =π−  , cường độ dòng điện qua đoạn mạch là i2cos100t A=π . Công suất tiêu thụ của đoạn mạchbằng A.200W. B.100W. C.400W. D.141W.

DẠYKÈMQUYNHƠNOFFICIAL 187 Câu 3: Cho đoạnmạchxoaychiềugồmbiếntrở R,cuộnthuầncảmL= 1 π Hvàtụ điệnC= 310 4π F mắc nối tiếp. Đặt vào hai đầu đoạn mạch điện áp xoay chiều u = 120 2 cos100πt V. Điện trở củabiếntrở phảicógiátrị baonhiêu để côngsuấtcủamạch đạtgiátrị cực đại? A.R =120Ω. B.R =60Ω. C.R =100Ω. D.R =80Ω Câu 4: Cho đoạnmạchxoaychiềugồmbiếntrở R,cuộnthuầncảmL= 1 π Hvàtụ điệnC= 310 4π F mắc nối tiếp. Đặt vào hai đầu đoạn mạch điện áp xoay chiều u = 120 2 cos100πt V. Điều chỉnh giá trị của biến trở để công suất của mạch đạt giá trị cực đại. Giá trị cực đại của công suấtlàbaonhiêu? A.Pmax =60W. B.Pmax =120W. C.Pmax =180W. D.Pmax =1200W. Câu 5: Cho đoạn mạch xoay chiều gồm biến trở R, cuộn thuần cảm L và tụ điện C mắc nối tiếp. Đặt vào hai đầu đoạn mạch điện áp xoay chiều u = 220 2 cos100πt (V). Điều chỉnh biến trở đến giá trị R = 220Ω thì công suất của mạch đạt giá trị cực đại. Giá trị cực đại của côngsuấtlàbaonhiêu? A.Pmax =55W. B.Pmax =110W. C.Pmax =220W. D.Pmax =110 2 W. Câu 6: Cho đoạn mạch xoay chiều RLC mắc nối tiếp: cuộn dây thuần cảm kháng có độ tự cảm 1 LH = π , tụ điện có điện dung 410 CF 2 = π , R là một điện trở thuần thay đổi được. Đặt một hiệu điện thế xoay chiều ổn định ở hai đầu đoạn mạch AB có biểu thức: uAB = 200cos100πt(V).Xác địnhR để mạchtiêuthụ côngsuất80W. A.50Ω,200Ω. B.100Ω,400Ω. C.50Ω,200Ω. D.50Ω,200Ω Câu 7: Mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm, R là biến trở. Điều chỉnh R = R0 thì công suất trên mạch đạt giá trị cực đại. Tăng R thêm 10Ω thì công suất tiêu thụ trên mạchlàP0,sau đógiảmbớt5Ω thìcôngsuấttiêuthụ trênmạchcũnglàP0.Giátrị củaR0 là A.7,5Ω B.15Ω C.10Ω D.50Ω Câu 8: Cho đoạn mạch RLC mắc nối tiếp: cuộn dây thuần cảm kháng có độ tự cảm L, tụ điện có điện dung C, R thay đổi được. Đặt một điện áp xoay chiều ổn định ở hai đầu đoạn mạch có U = 100V, f = 50Hz. Điều chỉnh R thì thấy có hai giá trị 30Ω và 20Ω mạch tiêu thụ cùngmộtcôngsuấtP.Xác địnhP lúcnày? A.4W. B.100W. C.400W D.200W. Câu 9: Cho đoạn mạch RLC mắc nối tiếp: cuộn dây thuần cảm kháng có độ tự cảm L, tụ điện có điện dung C, R thay đổi được. Đặt một điện áp xoay chiều ổn định ở hai đầu đoạn mạch có giá trị hiệu dụng U, tần số f. Điều chỉnh R thì thấy có hai giá trị 60Ω và 30Ω mạch tiêu thụ cùngmộtcôngsuấtP =40W.Xác địnhUlúc này? A.60V. B.40V. C.30V. D.100V. Câu 10: Cho đoạn mạch RLC nối tiếp,R thay đổi được, hiệu điện thế hai đầu đoạn mạch u = 60 2 cos100πt (V). Khi R1 = 9Ω hoặc R2 = 16Ω thì công suất trong mạch như nhau. Hỏivớigiátrị nàocủaR thìcôngsuấtmạchcực đại,giátrị cực đại đó?

DẠYKÈMQUYNHƠNOFFICIAL 188 A.12Ω;150W B.12;100W C.10Ω;150W D.10Ω;100W Câu 11: Có ba phần tử R, cuộn thuần cảm có ZL = R và tụ điện ZC = R. Khi mắc nối tiếp chúng vào nguồn xoay chiều có điện áp hiệu dụng và tần số dòng điện không đổi thì công suất của mạch là 200W. Nếu giữ nguyên L và C, thay R bằng điện trở Ro = 2R thì công suấtcủamạchlàbaonhiêu? A.P =200W B.P =400W C.P =100W D.P =50W Câu 12: Cho đoạn mạch RLC mắc nối tiếp: R không đổi, cuộn dây thuần cảm kháng có độ tự cảm L, tụ điện có điện dung C thay đổi được. Đặt một điện áp xoay chiều ổn định ở hai đầu đoạn mạch AB có biểu thức: uAB = U0cosωt (V). Điều chỉnh C để mạch tiêu thụ công suấtcực đại.Xác địnhhệ số côngsuấtcủamạchlúcnày? A.1. B. 4 π . C.0. D. 2 2 Câu 13: Cho mạch điện xoay chiều không phân nhánh. R = 100Ω, 410 CF = π , cuộn dây thuần cảm có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp u200cos100t =π (V). Độ tự cảm L bằng bao nhiêu thì công suất tiêu thụ trong mạch là 100W. A. 1 H π B. 1 H 2π C. 2 H π D. 4 H π Câu 14: Nếu đặt điện áp u1 = U 2 cosωt (V) vào hai đầu đoạn mạch gồm tụ điện và điện trở thuần nối tiếp thì công suất tiêu thụ của mạch là P = P1 và hệ số công suất là 0,5. Nếu đặt điện áp u2 = Ucos 3 ωt (V) vào hai đầu đoạn mạch trên thì công suất tiêu thụ của mạch là P = P2 .Hệ thứcliênhệ giữaP1 vàP2 là: A. P1 = P2 B. 2 1 P P 2 = C. P1 = 2P2 D. P1 = 2 P2 Câu 15: Đặt điện áp xoay chiều u = U0cosωt (V) vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. ĐiệndungCcủatụ điệnthay đổi được.Vớihaigiátrị của điệndungC1 =3µFvàC2 =4µF mạchcócùng côngsuất. Tìm C để mạchcóPmax. A.C =7µF. B.1µF. C.5µF. D.3,43µF. Câu 16: Đặt điện ápxoaychiều cógiá trị hiệu dụngkhông đổi,tần số 50 Hzvào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung C đến giá trị 410 4π F hoặc 410 2π F thì côngsuấttiêuthụ trên đoạnmạch đều cógiátrị bằngnhau.Giátrị của Lbằng: A. 1 3π H B. 1 2π H C. 3 π H D. 2 π H Câu 17: Cho đoạnmạchxoaychiềugồmbiếntrở R,cuộndâykhôngthuầncảmcó điệntrở r=ZL mắc nối tiếp. Điều chỉnh R để công suất tiêu thụ trên cuộn dây là lớn nhất. Hệ số công suất củamạchkhi đólà:

DẠYKÈMQUYNHƠNOFFICIAL 189 A. 3 2 B.0,75 C.0,5 D. 1 2 Câu 18: Cho đoạn mạch gồm hai phần tử R và C. Biết R = 50Ω và ZC = 50 3 Ω, biểu thức cường độ dòng điện trong mạch là i2cos100t 3 π =π+  (A). Nếu muốn điện áp hai đầu đoạn mạch cùng pha với cường độ dòng điện trong mạch thì phải lắp nối tiếp vào mạch mộtcuộndâycó độ tự cảm bằngbaonhiêu?Tính côngsuấtcủamạchkhi đó? A.L= 2 2π H;P =160W. B.L= 3 π H;P =173,2W C.L= 3 2π H;P =200W D.L= 3 2π H;P =100W Câu 19: Đặt điện áp u = U0cos 100t 12 π  π−   (V) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở, cuộn cảm và tụ điện có cường độ dòng điện qua mạch là 0 iIcos100t 2 π =π+  ( A).Hệ số côngsuấtcủa đoạnmạchbằng: A.1,00 B.0,87 C.0,71 D.0,50 Câu 20: Một mạch điệnxoay chiều gồm AM nồitiếp MB. Biết AM gồm điện trở thuần R1, tụ điện C1, cuộn dây thuần cảm L1 mắc nối tiếp. Đoạn MB có hộp X, biết trong hộp X cũng có các phần tử là điện trở thuần, cuộn cảm, tụ điện mắc nối tiếp nhau. Đặt điện áp xoay chiều vào hai đầu mạch AB có tần số 50Hz và giá trị hiệu dụng là 200V thì thấy dòng điện trong mạch có giá trị hiệu dụng 2A. Biết R1 = 20Ω và nếu ở thời điểm t (s), uAB = 200 2 V thì ở thời điểm 1 t 600 + (s) dòng điện AB i0 = và đang giảm. Công suất của đoạn mạch MB là: A.266,4W B.120W C.320W D.400W Câu 21: Mạch điện xoay chiều gồm một cuộn dây mắc nối tiếp với tụ điện. Cuộn dây có điện trở r = 30Ω, độ tự cảm 0,4 LH = π , tụ điện có điện dung C. Biểu thức điện áp tức thời giữa hai đầu đoạn mạch là u120cos100t =π (V). Với giá trị nào của C thì công suất tiêu thụ củamạch cógiátrị cực đạivàgiátrị côngsuất cực đạibằngbaonhiêu? A. 410 CF 2 = π và max P120W = . B. 410 CF = π và max P1202W = . C. 310 CF 4 = π và max P240W = . D. 310 CF = π và max P2402W =

DẠYKÈMQUYNHƠNOFFICIAL 190 Câu 22: Cho mạch điện gồm cuộn dây có điện trở r = 40Ω và độ tự cảm 0,7 LH = π , tụ điện có điện dung 410 CF = π và điện trở thuần R thay đổi được mắc nối tiếp với nhau. Đặt vào hai đầu mạch điện một hiệu điện thế xoay chiều u1002cos100t =π (V). Thay đổi R thì côngsuấttiêuthụ trêntoànmạch đạtgiátrị cực đại.Khi đó: A.Pmax =166,7W. B.Pmax =320W. C.Pmax =160W. D.Pmax =333W. Câu 23: Một đoạn mạch nối tiếp gồm cuộn dây có điện trở thuần r = 100 3 Ω và độ tự cảm 0,6 LH = π , tụ điện có điện dung 310 CF 4 = π , điện trở R có giá trị thay đổi được. Điện áp đặt vào hai đầu đoạn mạch u = 200 2 cos100πt (V). Thay đổi giá trị của R để công suất tiêuthụ trongmạch đạtcực đại.Xác địnhgiátrị cực đạicủacôngsuấttrongmạch. A.200W B.228W C.100W D.50W Câu 24: Xét cuộn dây có độ tự cảm 0,4 LH = π . Nếu đặt vào hai đầu cuộn dây điện áp không đổiU1 =12Vthìcường độ dòng điệnquacuộndâylà I1 =0,4A.Nếu đặt vàohai đầucuộn dây này điện áp xoay chiều có giá trị hiệu dụng U2 = 12 V, tần số f = 50 Hz thì công suất tiêuthụ ở cuộndâylà: A.1,2W. B.1,6W. C.4,8W. D.1,728W. Câu 25: Cho một đoạn mạch gồm cuộn cảm thuần và biến trở mắc nối tiếp với điện áp hiệu dụng ở 2 đầu đoạnmạchlàU=24Vkhông đổi.Khibiếntrở cógiátrị R1 =18Ω hoặcR2 =128Ω thì công suất tiêu thụ của đoạn mạch đều là P. Cảm khẳng ZL của cuộn dây và công suất cực đại của đoạnmạchkhithay đổibiếntrở tương ứnglà: A.ZL =24Ω vàPmax =12W B.ZL =24Ω vàPmax =24W C.ZL =48Ω vàPmax =6W D.ZL =48Ω vàPmax =12W Câu 26: Đặt điện áp xoay chiều u = 200√2cos100πt (V) vào hai đầu đoạn mạch gồm điện trở thuần, cuộn dây không thuần cảm và tụ điện (có điện dung thay đổi được) mắc nối tiếp. Điều chỉnh điện dung của tụ điện bằng 42.10 CF 3 = π thì mạch xảy ra cộng hưởng điện. Biết khi đó điệnáphiệudụng ở hai đầucuộn dâybằng điệnáphiệudụng ở hai đầumạchvàgấp đôi điệnáphiệudụnghai đầu điệntrở R.Côngsuấtnhiệttrêncuộndâykhi đóbằng A.50W. B.100W. C.200W. D.250W. Câu 27: Mạch điện RCL nối tiếp có C thay đổi được. Điện áp hai đầu đoạn mạch u1502cos100t =π (V). Khi 6 1 62,5.10 CCF == π thì mạch tiêu thụ công suất cực đại Pmax = 93,75W. Khi 3 2 10 CCF 9 == π thì điện áp hai đầu đoạn mạch RC và cuộn dây vuông phavớinhau, điệnáphiệudụnghai đầucuộndây khi đólà:

DẠYKÈMQUYNHƠNOFFICIAL 191 A. 90V B. 120V. C.75V D.75 2 V Câu 28: Cho đoạn mạch RLrC gồm một biến trở R, một cuộn dây có độ tự cảm L điện trở thuần r, một tụ điện có điện dung C nối tiếp. Điện áp ở hai đầu đoạn mạch có giá trị hiệu dụng và tần số f không đổi. Biết f = 50Hz, 0,4 LH = π ; r =10Ω; 310 CF 8 = π . Khi thay đổi R tới giá trị 15 Ω thì công suất của mạch là P. Phải tăng giá trị của R thêm bao nhiêu để công suấttiêuthụ củamạchvẫnlàP. A.43 Ω B.54 Ω. C.39Ω D.64Ω Câu 29: Mạch điện xoay chiều mắc nối tiếp RLC, cuộn dây thuần cảm. Điện trở R và tần số dòng điện f có thể thay đổi. Ban đầu ta thay đổi R đến giá trị R = R0 để công suất tiêu thụ trênmạch cực đại làP1.Cố địnhchoR = R0 vàthay đổif đến giátrị f=f0 để côngsuấtmạchcực đạiP2.SosánhP1 vàP2 A.P1 =P2 B.P2 =2P1 C.P2 = 2P1 D.P2 =2 2P1. Câu 30: Đặt điện áp xoay chiều u = 120 2 cos(100πt + 3 π ) vào hai đầu đoạn mạch gồm một cuộn dây thuần cảm L, một điện trở R và một tụ điện 410 CF = π mắc nối tiếp. Biết điện áp hiệu dụng trên cuộn dây L và trên tụ điện C bằng nhau và bằng một nửa trên điện trở R. Côngsuấttiêuthụ trên đoạnmạch đóbằng: A.144W B.72W C.240W D.100W Câu 31: Cho mạch điện gồm R, L, C nối tiếp với R biến trở, cuộn cảm thuần. Mắc mạch này vào mạng điện xoay chiều ( )0 uUcost=ω+ϕ (V), khi R = R0 thì công suất tiêu thụ của mạch là cực đại và bằng Pmax. Khi công suất tiêu thụ của mạch là P = Pmax n thì giá trị điện trở R là: A. ( )2 0Rnn1R =±− . B. ( )2 0Rnn1R =+− . C. ( )2 0Rnn1R =−− . D. ( ) 2 0Rn1R =− Câu 32: Đoạn mạch AB nối tiếp gồm chỉ các phần tử như điện trở thuần, cuộn cảm và tụ điện. Đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần R = 50 Ω mắc nối tiếp với tụ điện có điện dung kháng 50 Ω . Biểu thức điện áp trên đoạn mạch AM và MB lần lượt là: AM u80cos100t (V)=π và MB u100cos100t (V)2 π =π+  .Hệ số côngsuấtcủa đoạnmạchAB là: A.0,99 B.0,84. C.0,86. D.0,95. Câu 33: Đoạn mạch gồm 2 đoạn mạch AM và MB mắc nối tiếp. Đoạn AM gồm điện trở thuần 1R nốitiếpvới cuộncảm thuầnL, đoạnmạch MB gồm điệntrở thuần 2 R50=Ω nối C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 192 tiếp tụ điện 42.10 CF = π . Biết điện áp tức thời AM 17 u2002cos100t (V)12 π =π+  và MB u80cos100t (V)=π .Tínhhệ số côngsuấtcủa đoạnmạch AB. A.0,91 B.0,74. C.0,72. D.0,90. Câu 34: Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắcnốitiếp. Đoạnmạch AM chỉ cóbiến trở R, đoạnmạch MB gồm điện trở thuần r mắc nối tiếp với cuộn cảm thuần có độ tự cảm L. Đặt vào AB một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Điều chỉnh R đến giá trị 80 Ω thì công suất tiêu thụ trên biến trở đạt cực đại và tổng trở của đoạn mạch AB chia hết cho 40. Khi đó hệ số công suất của đoạn mạch MB và của đoạnmạchAB tương ứnglà A. 8 3 và 8 5 . B. 118 33 và 160 113 . C. 17 1 và 2 2 . D. 8 1 và 4 3 Câu 35: Đặt một điện áp xoay chiều u = U0cosωt (V) vào hai đầu một đoạn mạch AB gồm điện trở R, cuộn dây cảm thuần L và tụ điện có điện dung C mắc nối tiếp. Tụ C có điện dung thay đổi được. Thay đổi C, khi 1CCZZ = thì cường độ dòng điện trễ pha 4 π so với điện áp hai đầu đoạn mạch, khi 21 CCC ZZ6,25Z == thì UC max. Tính hệ số công suất của mạch. A.0,6 B.0,8 C.0,7 D.0,9 Câu 36: Đặt điện ápu = Uocosωt(V)(Uovà ω không đổi)vàohai đầu đoạn mạchmắcnốitiếp gồm có biến trở R, tụ điện có dung kháng 80 3 Ω, cuộn cảm có điện trở thuần 30 Ω và cảm kháng 50 3 Ω. Khi điều chỉnh trị số của biến trở R để công suất tiêu thụ trên biến trở cực đạithìhệ số côngsuấtcủa đoạnmạchbằng A. 2 1 . B. 1 2 . C. 7 2 . D. 7 3 . Câu 37: Cho mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Tần số của hiệu điện thế thay đổi được. Khi tần số là f1 và 4f1 công suất trong mạch như nhau và bằng 80% công suất cực đạimàmạchcóthể đạt được.Khif=3f1 thìhệ số côngsuấtlà: A.0,894 B.0,853 C.0,964 D.0,47 Bài 38: Mạch điện xoay chiều R, L, C nối tiếp gồm điện trở R, cuộn cảm (L, r) và tụ C. Khi hiệu điện thế 2 đầu đoạn mạch là u652cost =ω (V) thì các điện áp hiệu dụng trên điện trở và cuộn dây đều bằng 13V. Còn điện áp trên tụ là65V,côngsuấttiêu thụ trêntoànmạchlà25W.Hệ số côngsuấtcủa mạchlà A. 3 13 B. 5 13 C. 10 13 D. 12 13 • B R L,r A M C A B RL,r

DẠYKÈMQUYNHƠNOFFICIAL 193 HƯỚNG DẪN GIẢI Câu 1: ChọnB. Tacó: () () C 3 AB L AB 2222 ABLC 11 Z220 C10 100. 22 1U 260 ZL100.100I2A Z130 ZRZZ50100220130 ===Ω ω π π   =ω=π=Ω  === π  =+−=+−=Ω   Vậy côngsuấttoànmạch: 22 PIR2.50200W === Câu 2: ChọnB. Tacó: 0 0 I2 I1A 22 U2002 U200V 22  ===    ===  Mặtkhác: pha(u)pha(i)100t100t43 ππ −=ϕ  ϕ=π−−π=− . Vậy 1 coscos 32 π  ϕ=−=   Suyracôngsuấttiêuthụ của đoạnmạchlà: 1 PUIcos200.1.100W 2 =ϕ== . Câu 3: ChọnA. Tacó: L C 3 1 ZL100.100 11 Z40 C10 100. 4  =ω=π=Ω π  ===Ω ω π π Côngsuấttiêuthụ trongmạch: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + DoU=constnên để P = Pmax thì ()2 LC min ZZ R R  +    . Ápdụngbất đẳngthứcCô-sicho2số dươngR và ()2 LCZZ R ta được:

DẠYKÈMQUYNHƠNOFFICIAL 194 () () 22 LCLC LC ZZZZ R2R.2ZZ RR +≥=− Vậy ()2 LC min ZZ R R  +    là LC2ZZ lúc đódấu“=”củabất đẳngthứcxảyranêntacó: LC RZZ1004060 =−=−=Ω . Câu 4: ChọnA.Tacó: L C 3 1 ZL100.100 11 Z40 C10 100. 4  =ω=π=Ω π  ===Ω ω π π Côngsuấtcủamạch: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + DoU=constnên để P = Pmax thì ()2 LC LC min ZZ RRZZ R  +⇔=−   . Khi đó: 22 max LC U120 P60W 2ZZ210040 === Câu 5: ChọnB. Côngsuấtcủamạch: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + DoU=constnên để P = Pmax thì ()2 LC LC min ZZ RRZZ R  +⇔=−   . Khi đó: 22 max U220 P110W 2R2.50 === Câu 6: ChọnC. Tacó: L C 4 1 ZL100.100 11 Z200 C10 100. 2  =ω=π=Ω π  ===Ω ω π π

DẠYKÈMQUYNHƠNOFFICIAL 195 Côngsuấttiêuthụ củamạch: () () 22 22 2 22LC LC URU PIRRRZZ0 RZZP ==⇔−+−= +− ( ) () 2 22 1002 RR1002000 80  −+−= 21 2 R50 R250R100000 R200 =Ω  −+=   =Ω VậyR1 =50Ω hoặcR2 =200Ω Câu 7: ChọnC. Côngsuấttiêuthụ củamạch: () () 2 2 2 0 0 222 0LCLC 0 0 UR U PIR RZZZZ R R === +−− + KhiR=R0 max0LC PRZZ ⇔=− KhiR1 =R0 +10hayR2 =R0 –5thìmạchcócùngcôngsuất: ()()() 2 2 12LC00000 RRZZR10R5R5R500R10 =−  +−=  −=  =Ω . Câu 8: ChọnC. Từ côngthức: 2 12 U RR P +=  22 12 U100 P200W RR3020 === ++ . Câu 9: ChọnA. Từ côngthức: 2 12 U RR P +=  2 12 P40 U3600U60V RR6030 ===  = ++ Câu 10: ChọnA. Côngsuấttiêuthụ củamạch: () () 2 2 2 0 0 222 0LCLC 0 0 UR U PIR RZZZZ R R === +−− + . KhiP =Pmax thì ()2 LC 00LC 0 min ZZ RRZZ R  +⇔=−   (1) Vớigiátrị của điệntrở là R0 mạchcócôngsuấtcực đạiPmax,theo(1)thì 0LC RZZ =− Với2giátrị của điệntrở làR1 vàR2 mạchcócùng côngsuấtP,thì ()2 12LC RRZZ =− . Suyra: 012 RRR9.1612 ===Ω .Khi đó: 22 max 0 U60 P150W 2R2.12 === . Câu 11: ChọnC. VìZL =ZC nên ở haitrườnghợp đềuxảyrahiệntượngcộnghưởng điện,côngsuất đều đạt cực đại.

DẠYKÈMQUYNHƠNOFFICIAL 196 Tacó: 1 2 1 1 2 2 2 2 ZR U P200W P200R P100W 22Z2R U P 2R =   ==    === =    =    Câu 12: ChọnA. Dễ thấyPmax khimạchcócộnghưởng,khi đó điệnápcùngphavớicường độ dòng điện, nghĩalà: ui 0 cos1 ϕ=  ϕ=ϕ  ϕ= Câu 13: ChọnC. Tacó: C 4 11 Z100 10C 100. P100 I1A R100  ===Ω ω π π   ===  Mặckhác: 2 2 2 UR200100 PIRRZU1002 ZP100 2 ==  ===Ω Suyra: () 22 L Z100Z1001002 =+−=Ω L L L Z0 Z 2002 Z200LH 100 =    =Ω  === ωππ (loaïi) Câu 14: ChọnA. ĐoạnmạchR ntC: Khi đặtvàohai đầu đoạnmạch điệnápu1 =U 2 cosωt: 11 1 R cos0,5Z2R Zϕ==  = . Tổngtrở đoạnmạchtrongtrườnghợpdùngu1 : ()1 1 1 1 2 22222 1CC C C 1 ZRZ2RRZ Z1 Z11R33C CC =+⇔=+   == ==ω  ωω  (1) Côngsuấttiêuthụ của đoạnmạch: 22 2 2 1 11 2 1 UUU PIRRR Z2R4R  ====   (2) Khi đặtvàohai đầu đoạn mạch điệnápu2 =Ucos 3 ωt: 2C 2 11 Z C 3C == ω ω (3) Sosánh (1)và(3) tacó: 2C ZR = Tổngtrở đoạnmạchtrongtrườnghợpdùngu2: