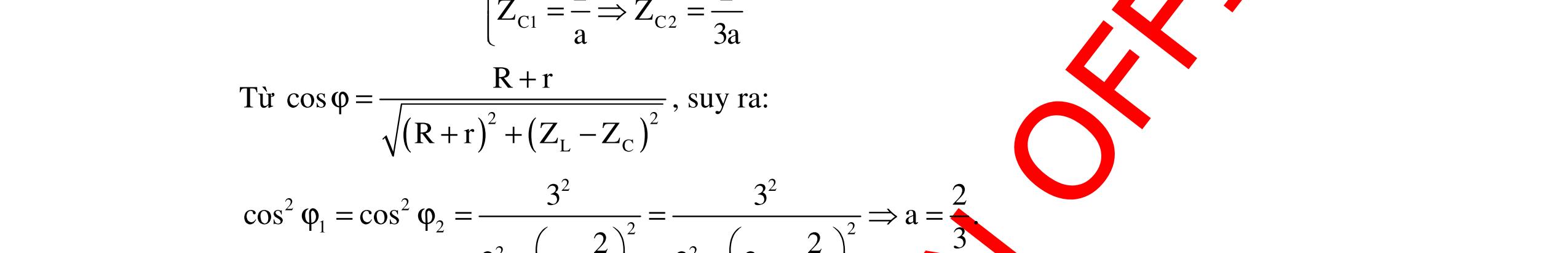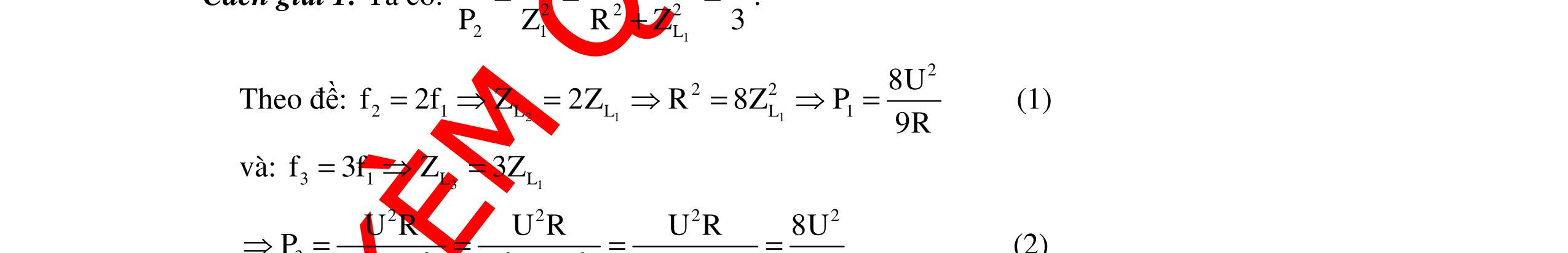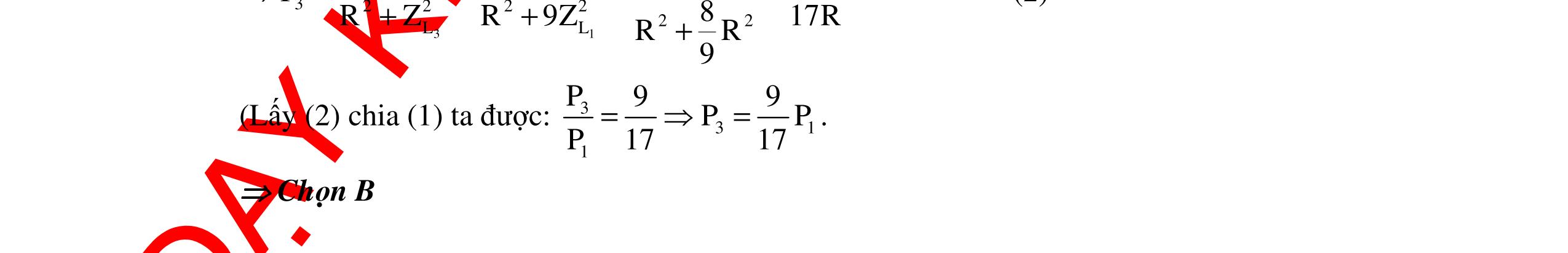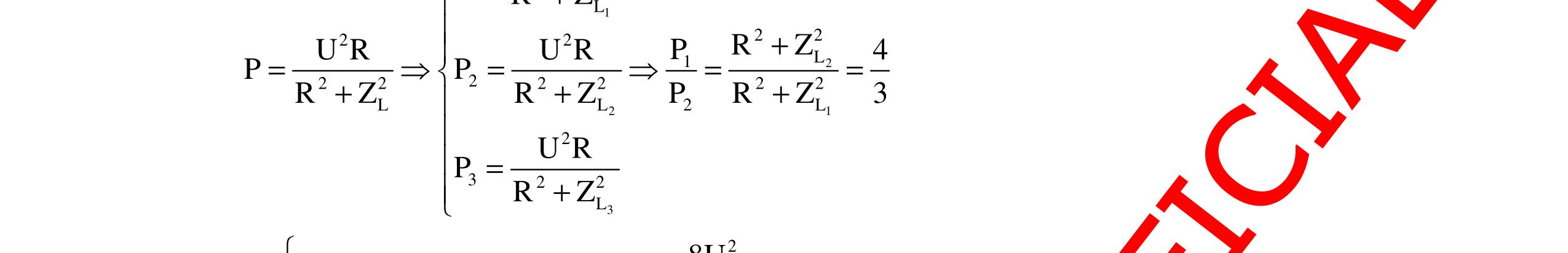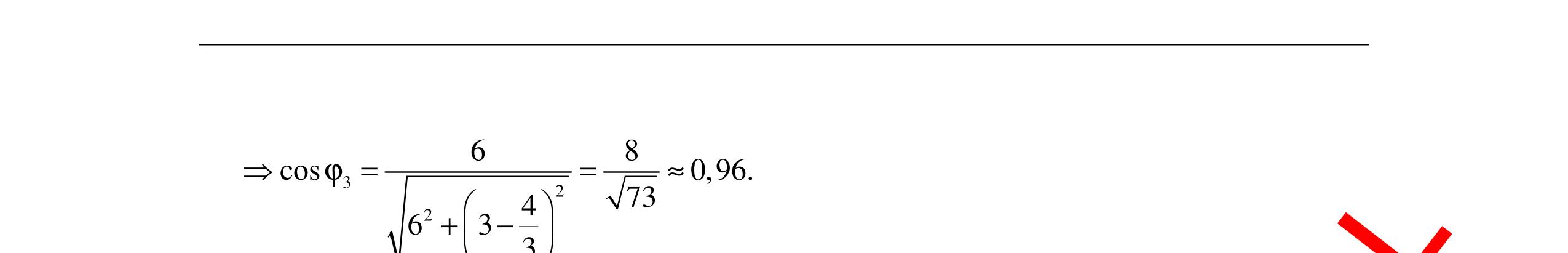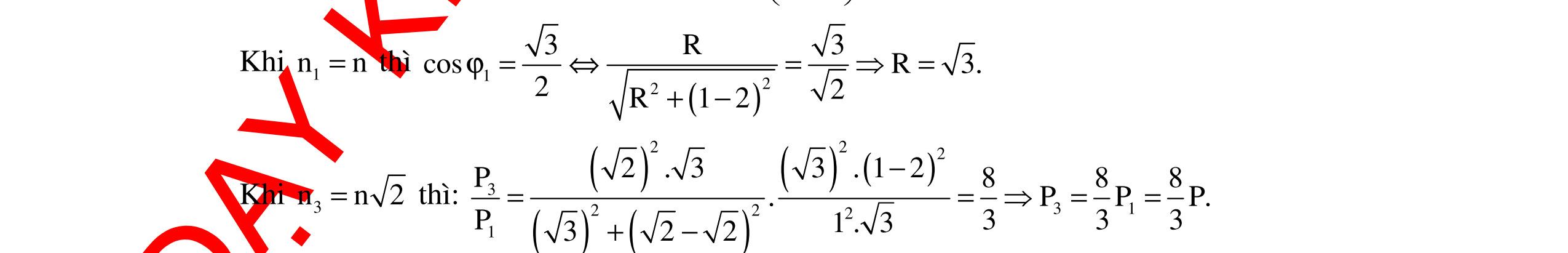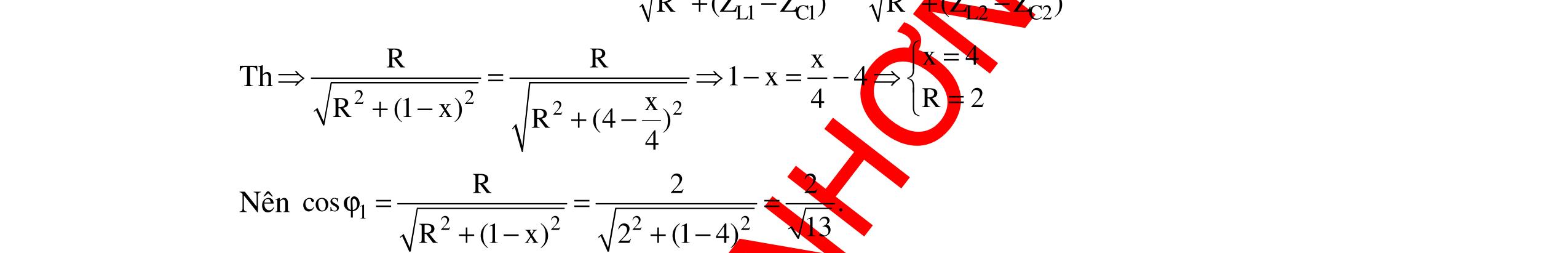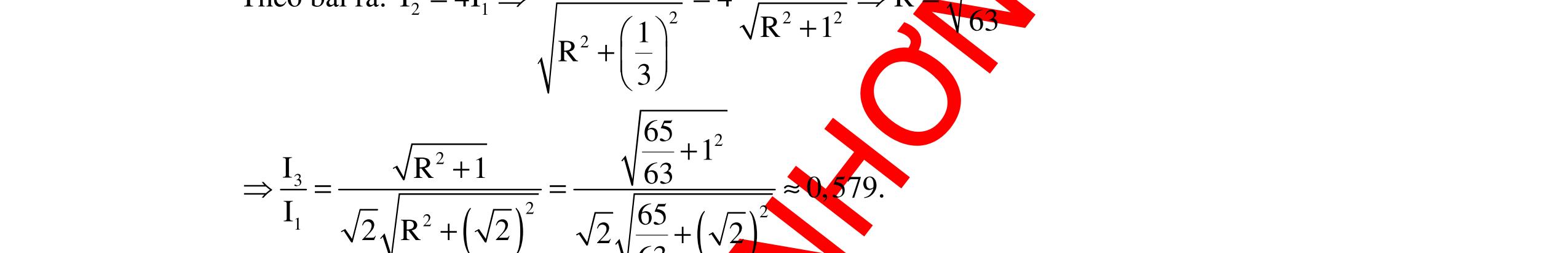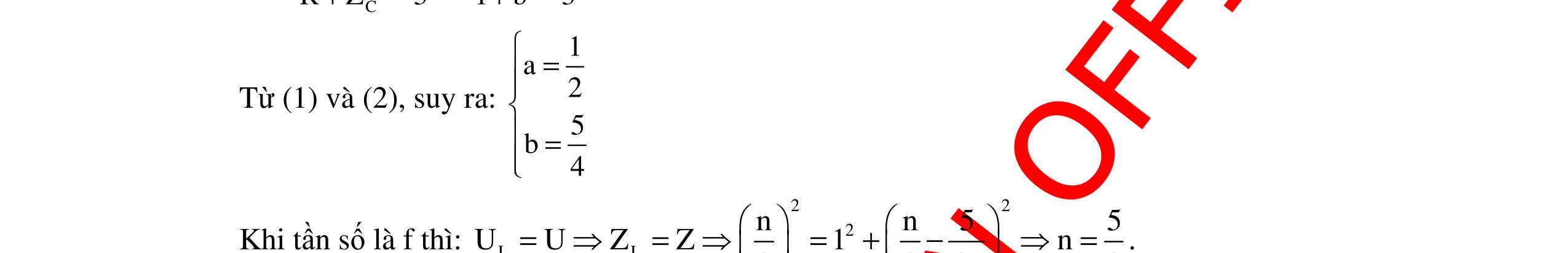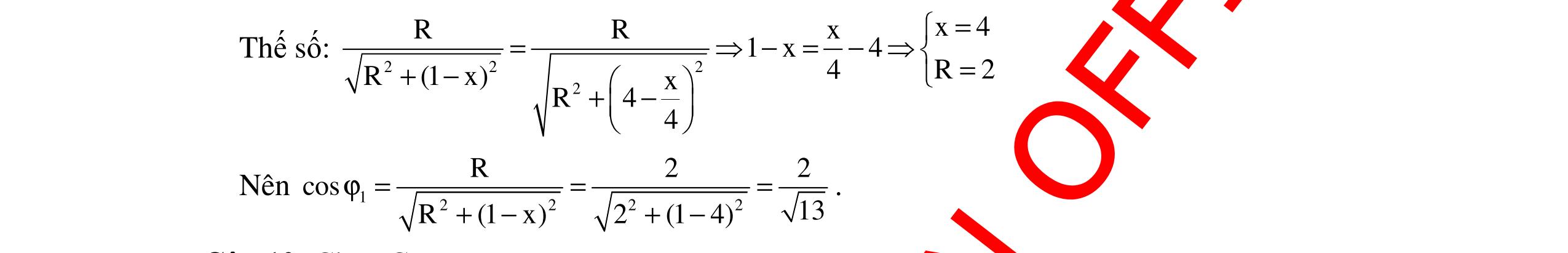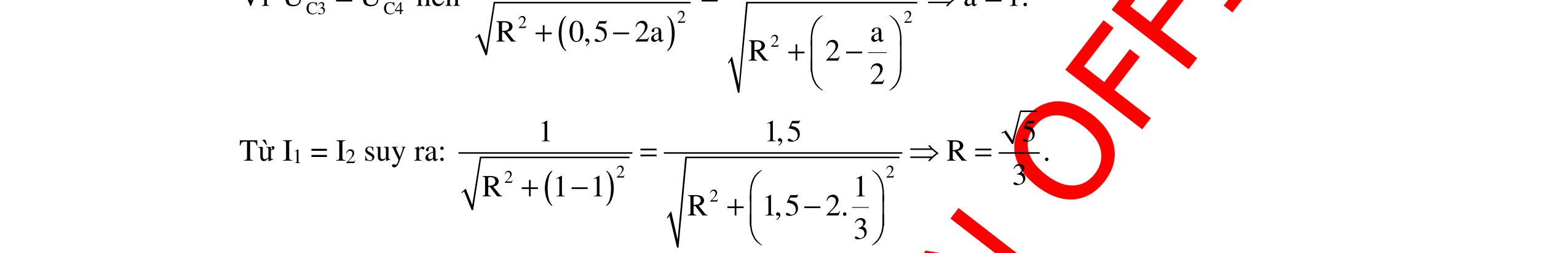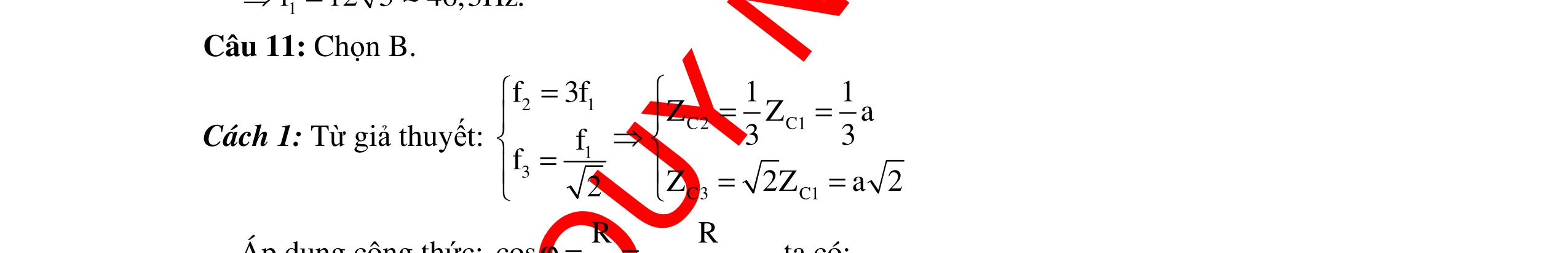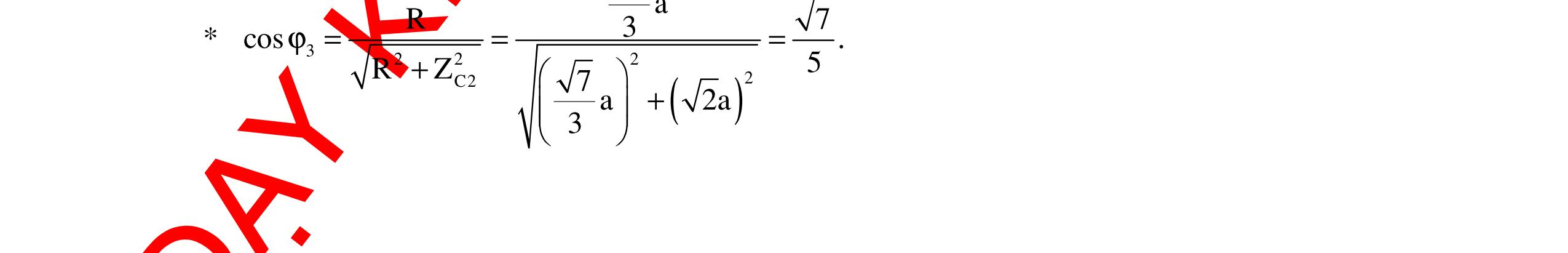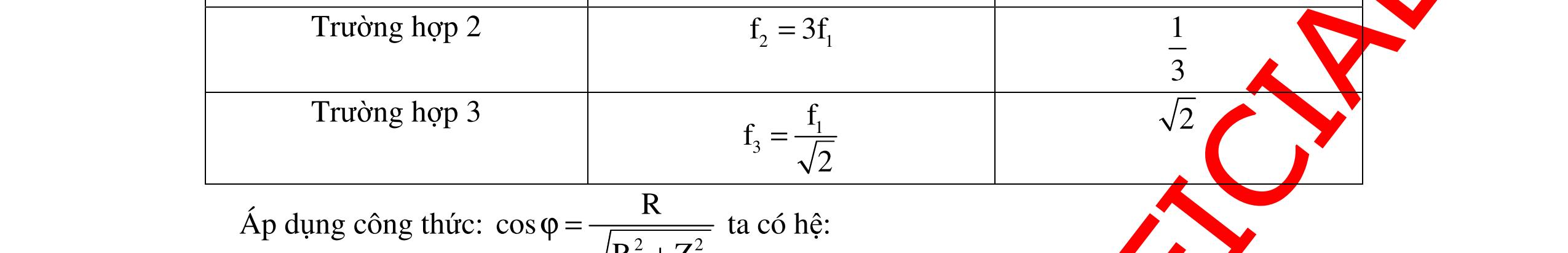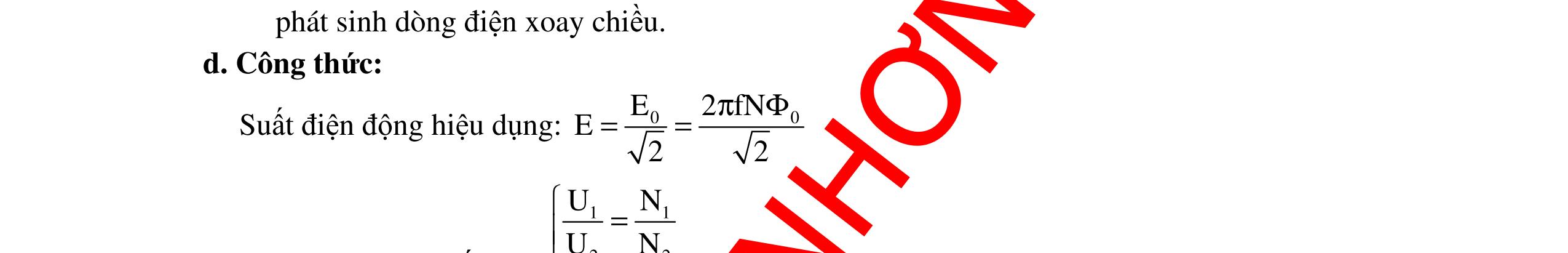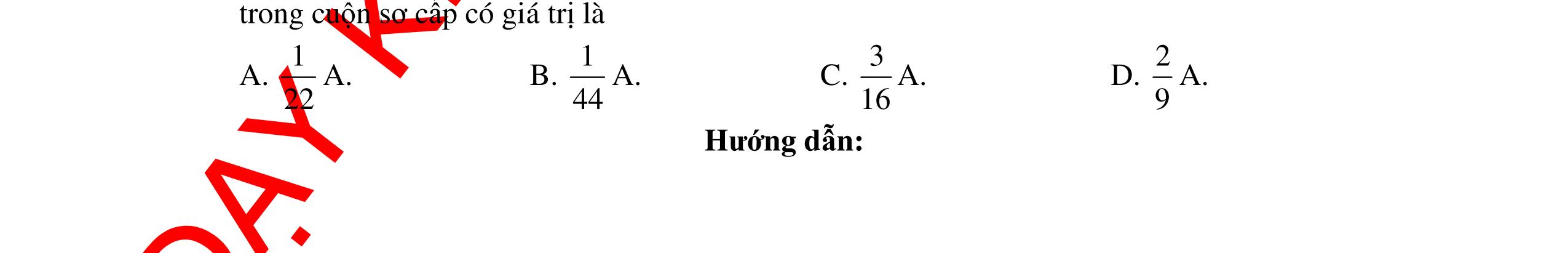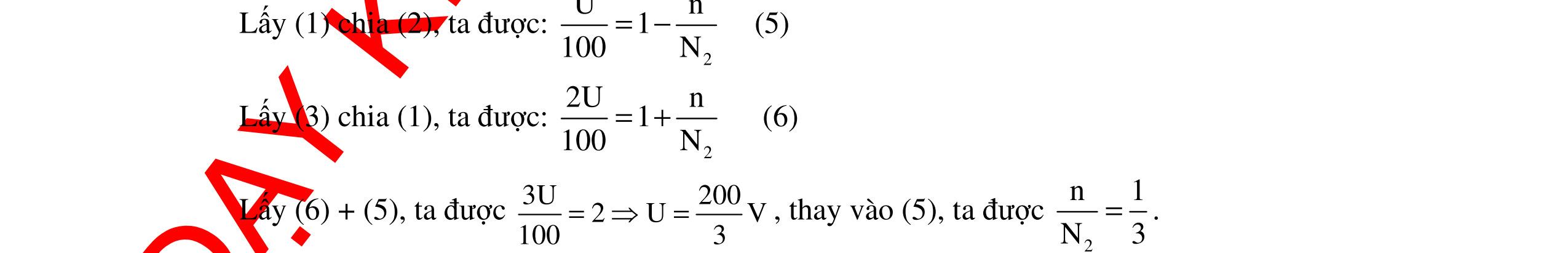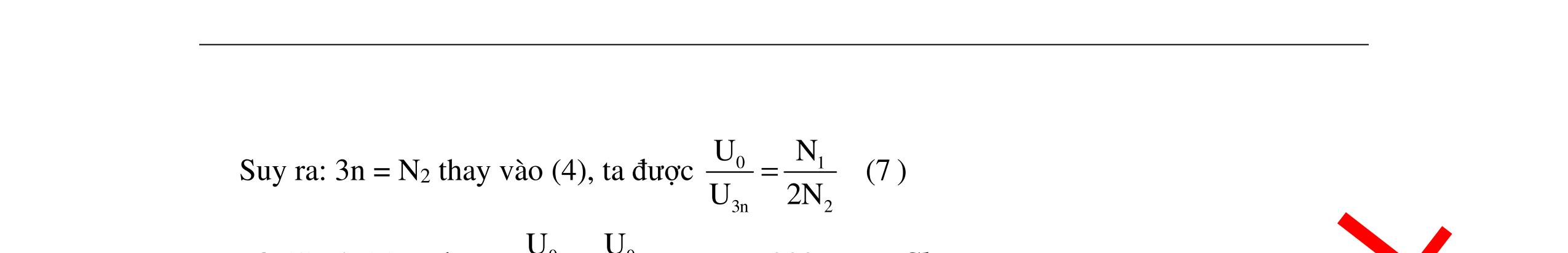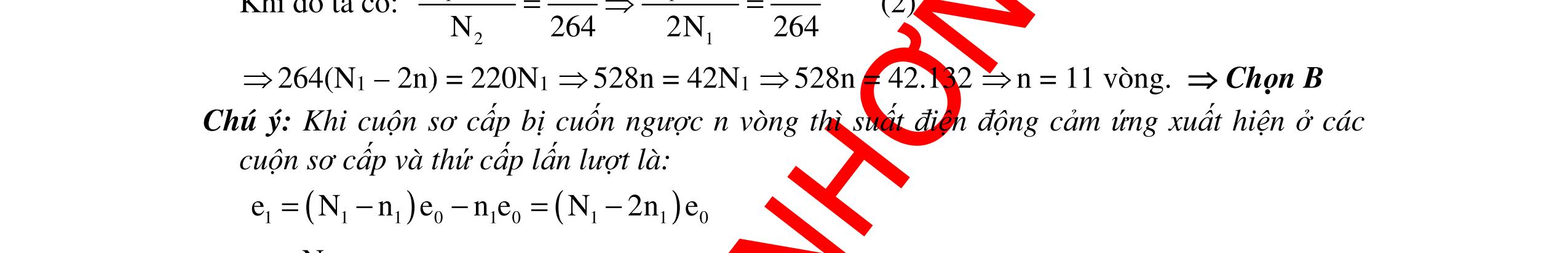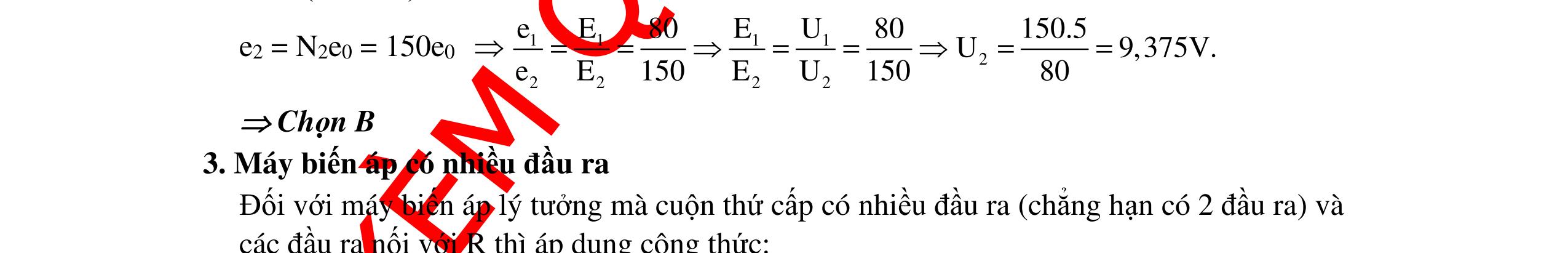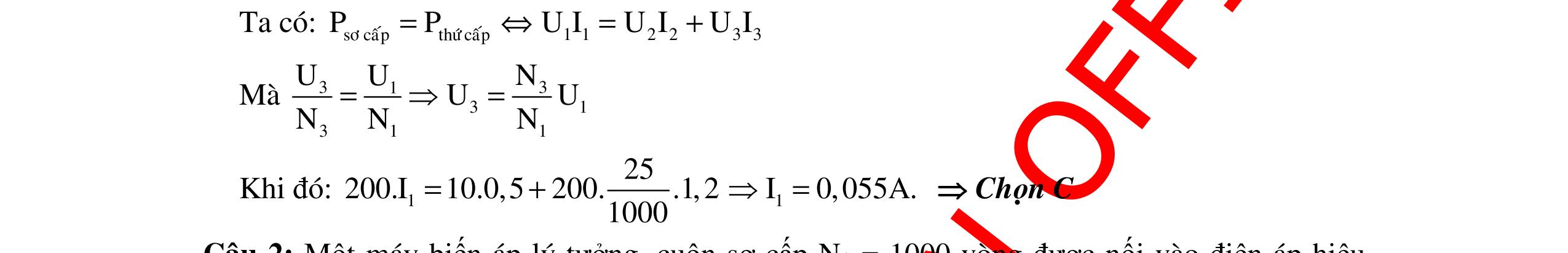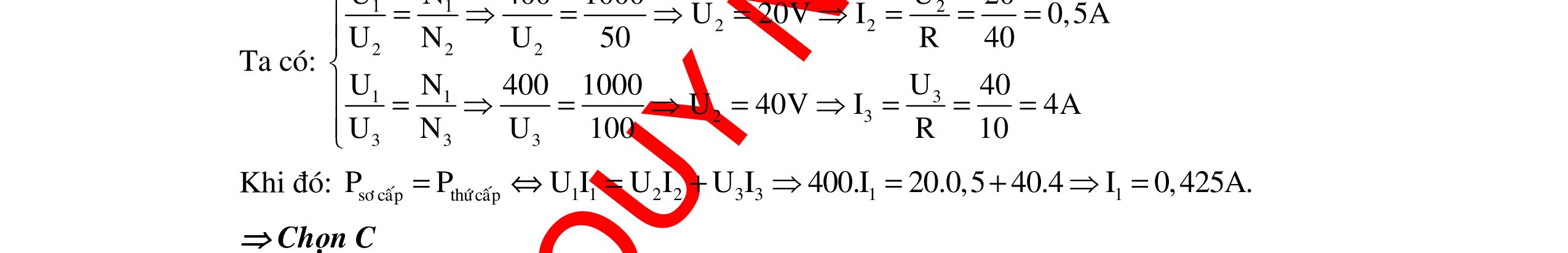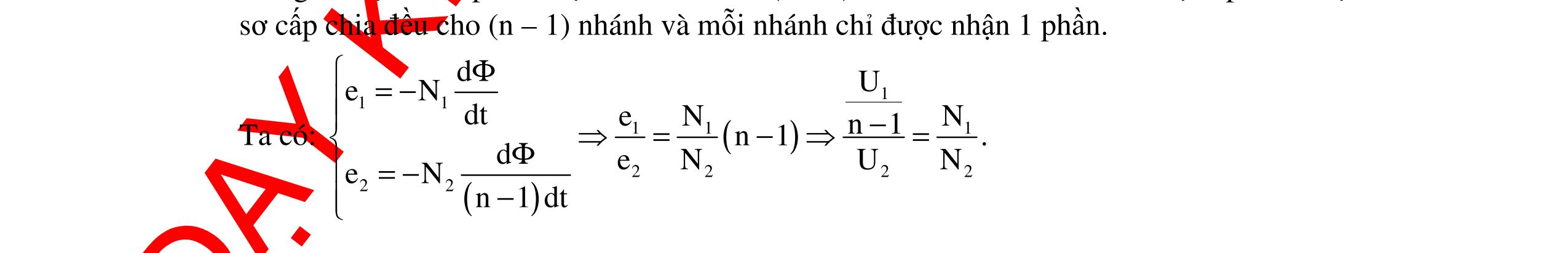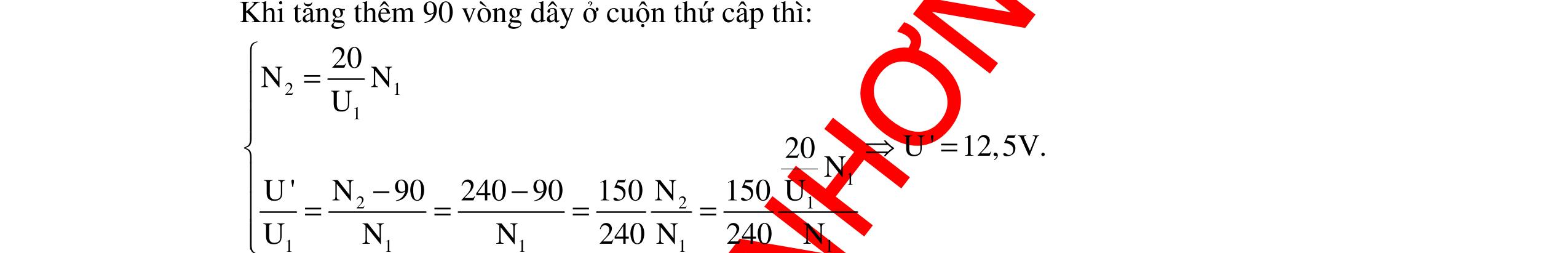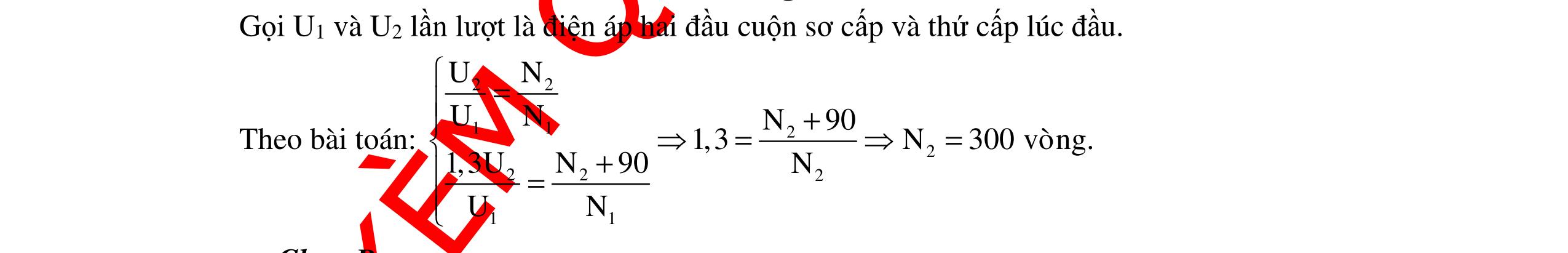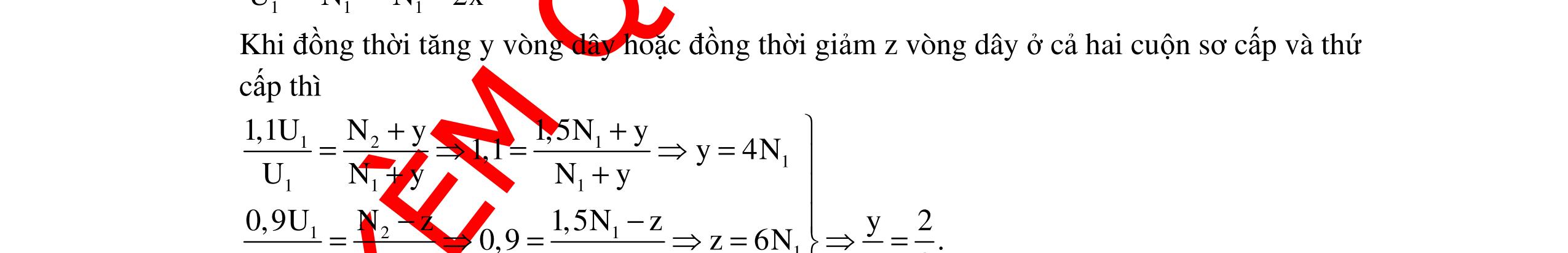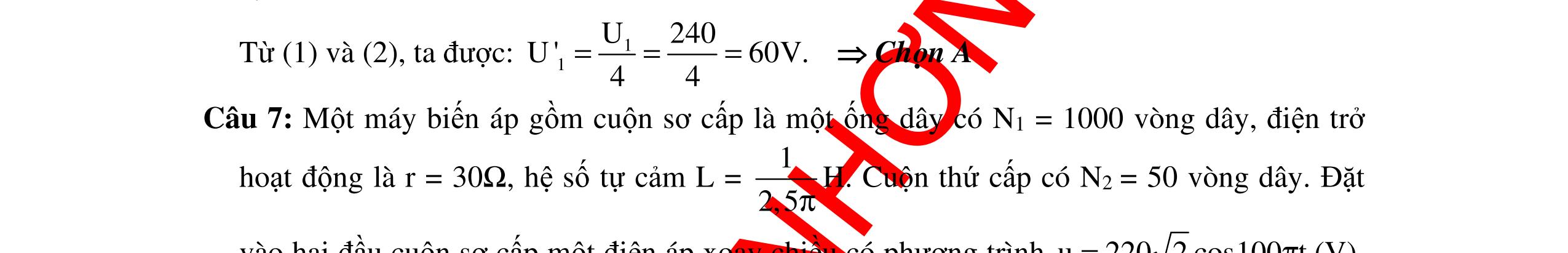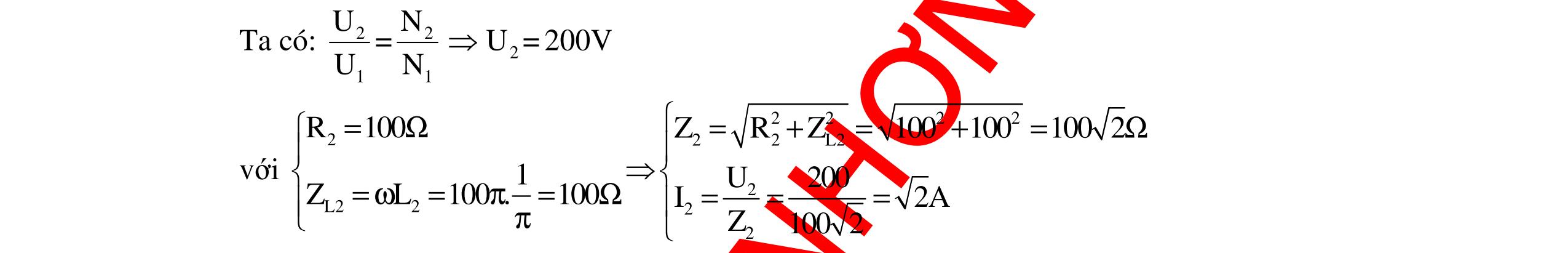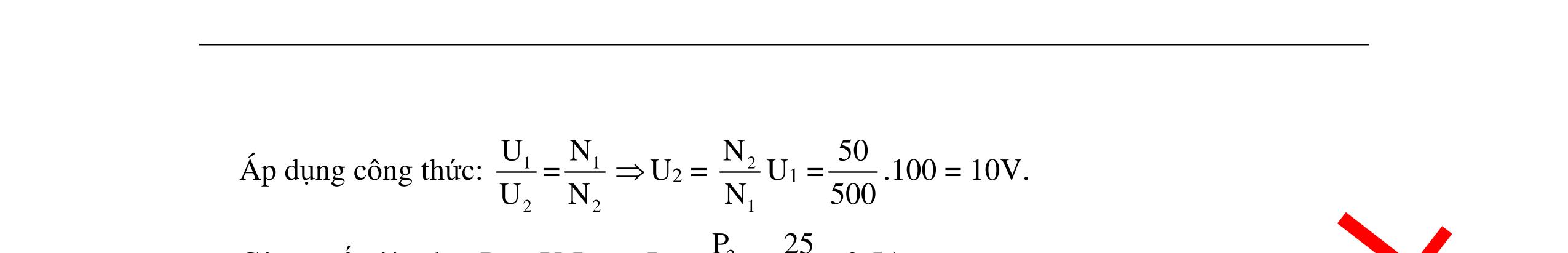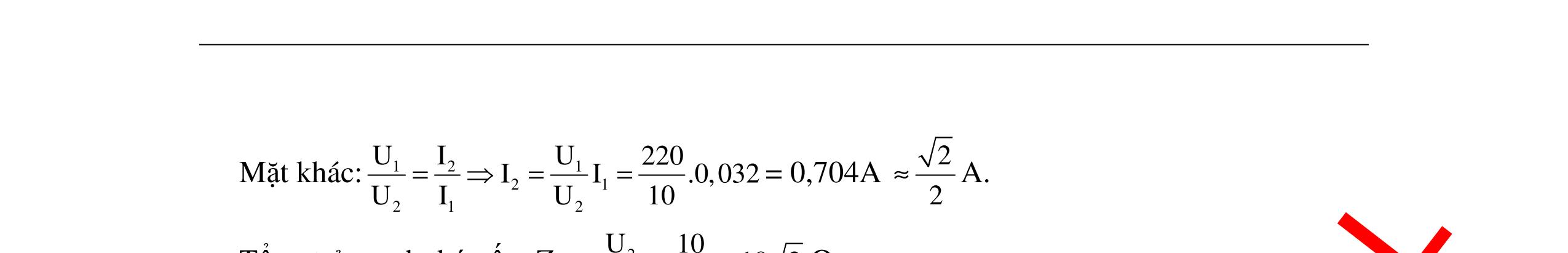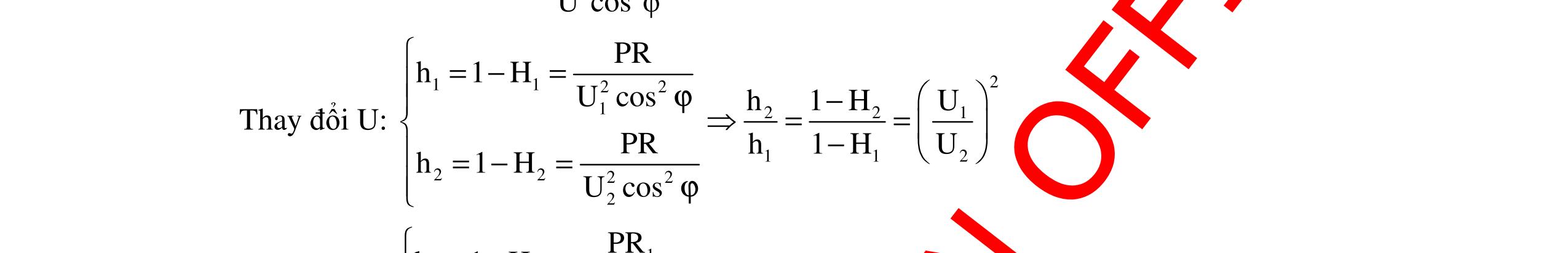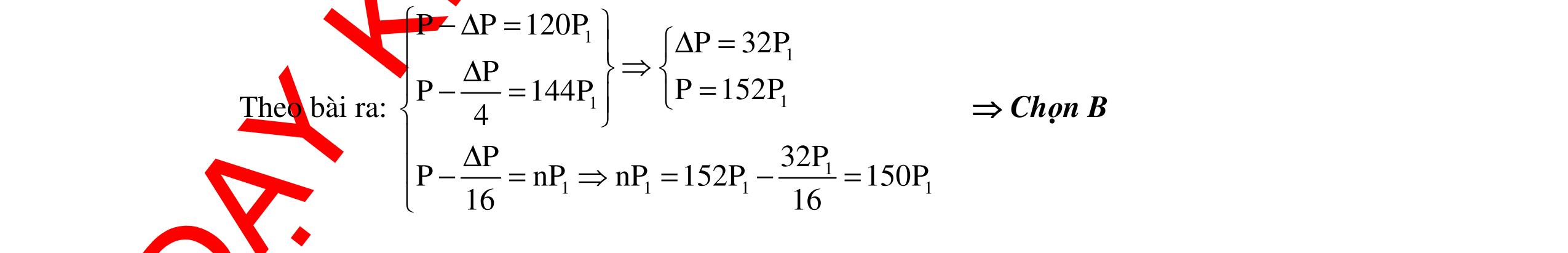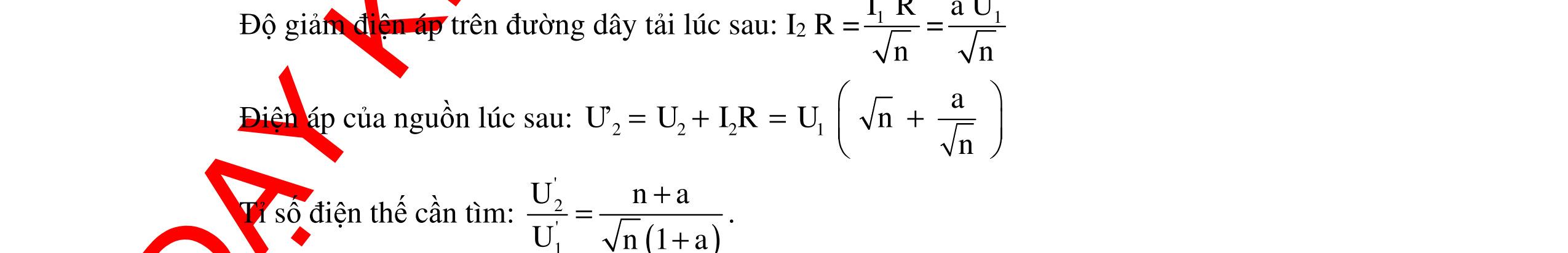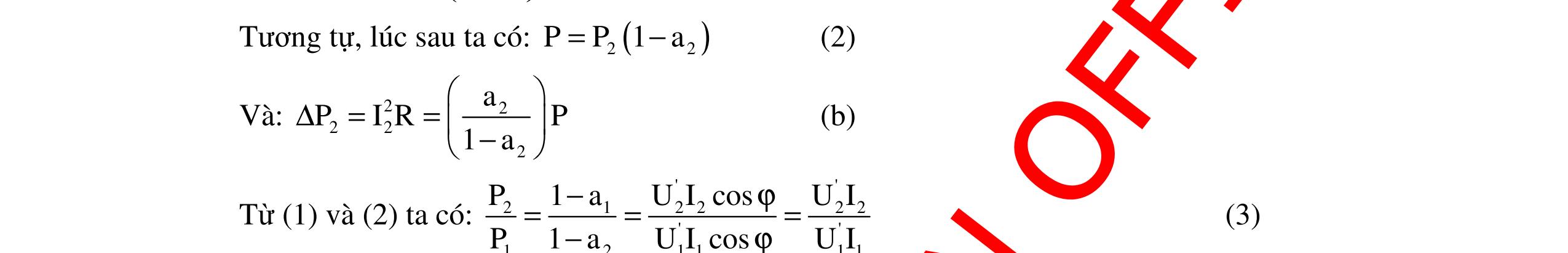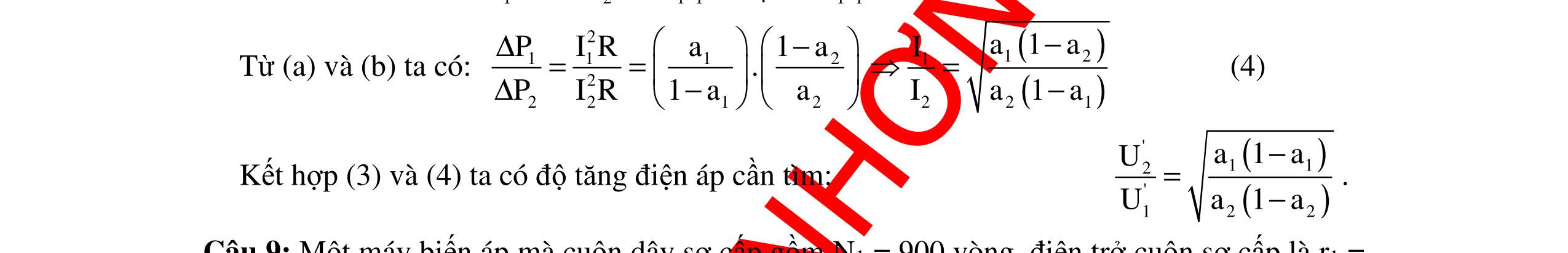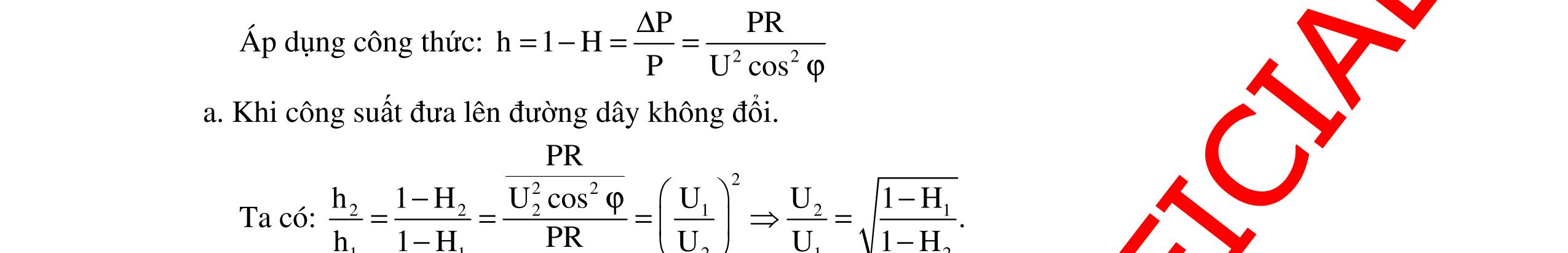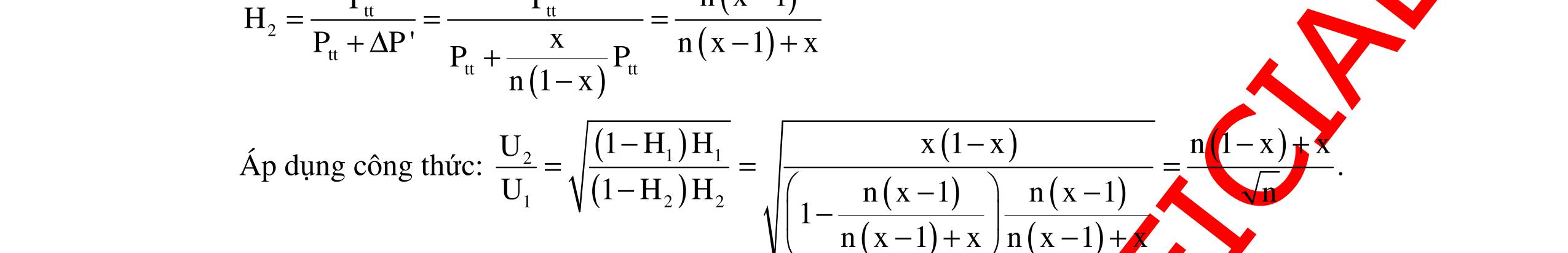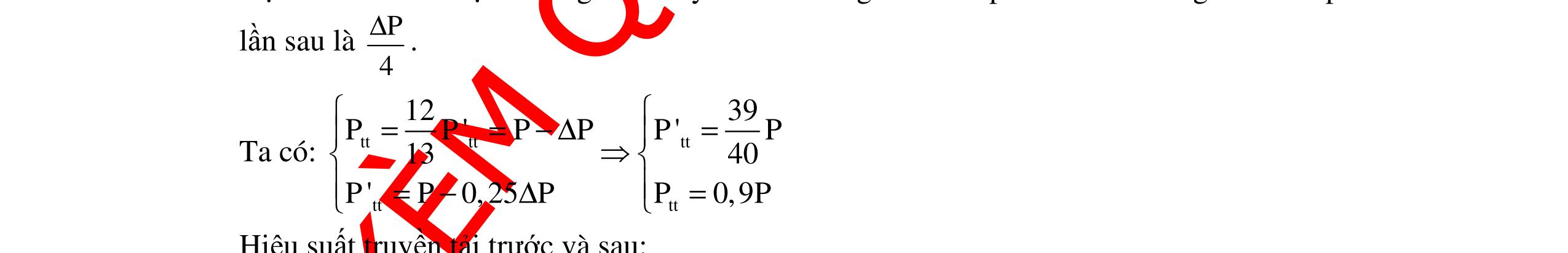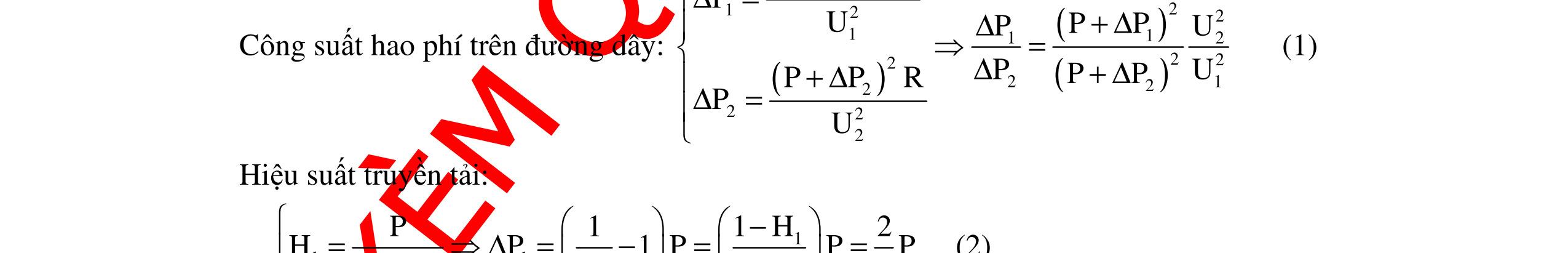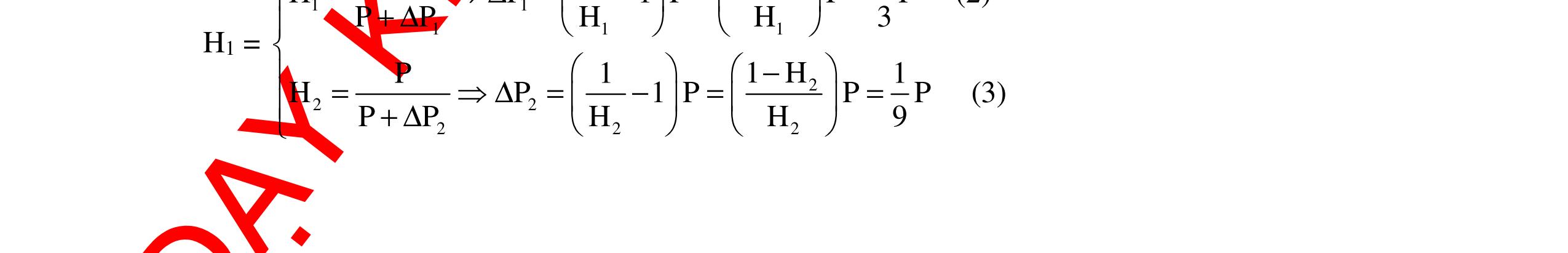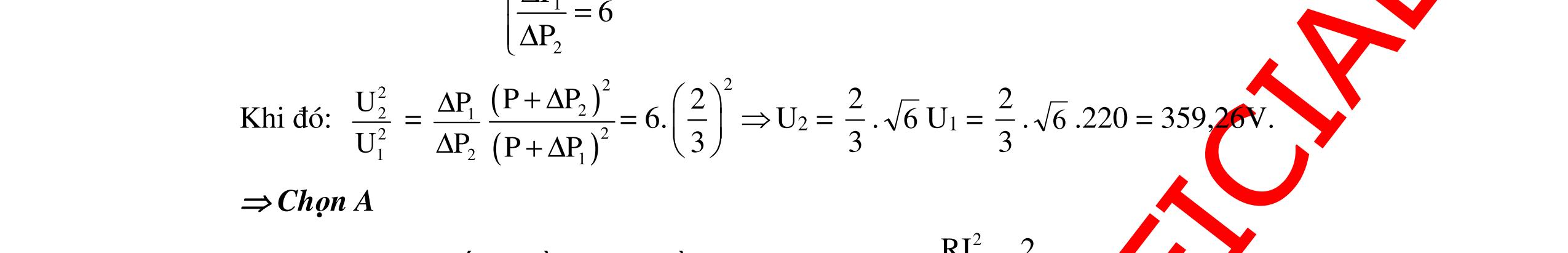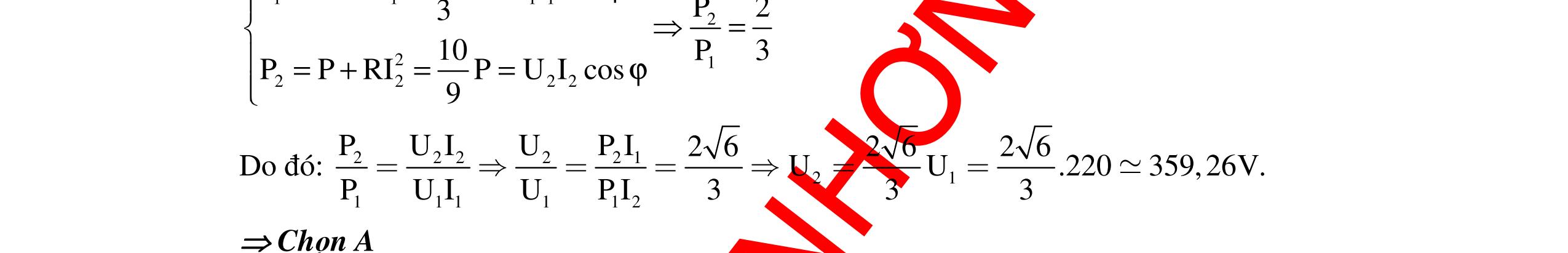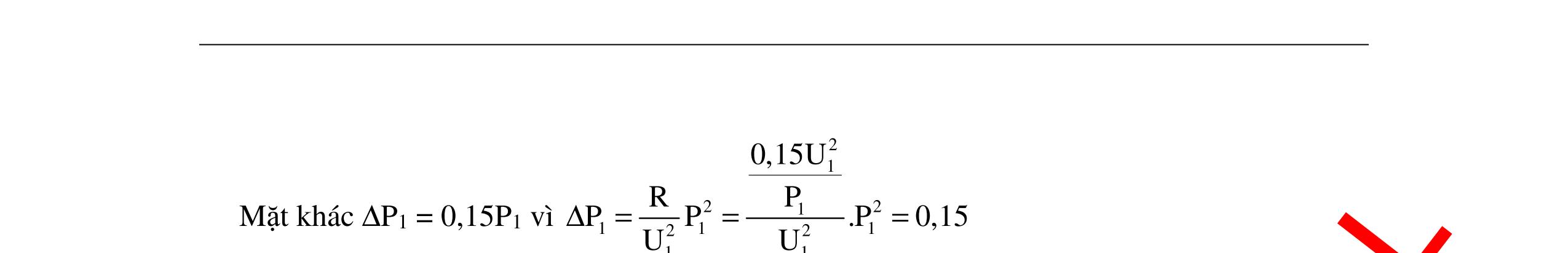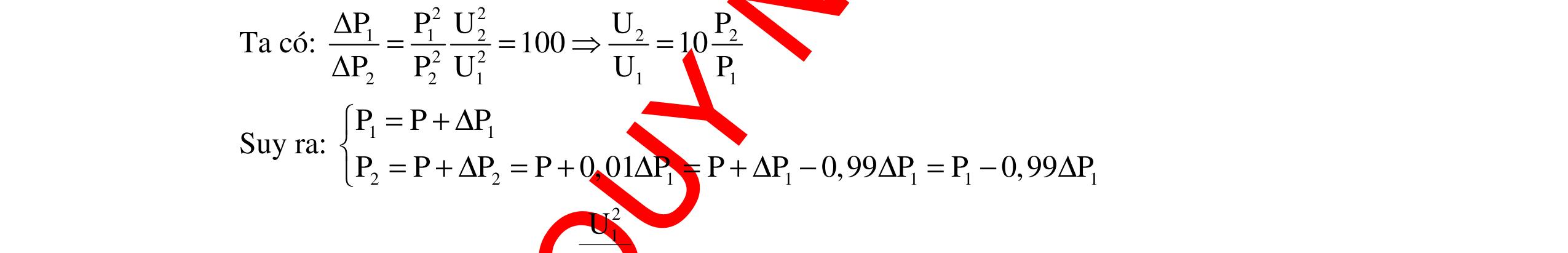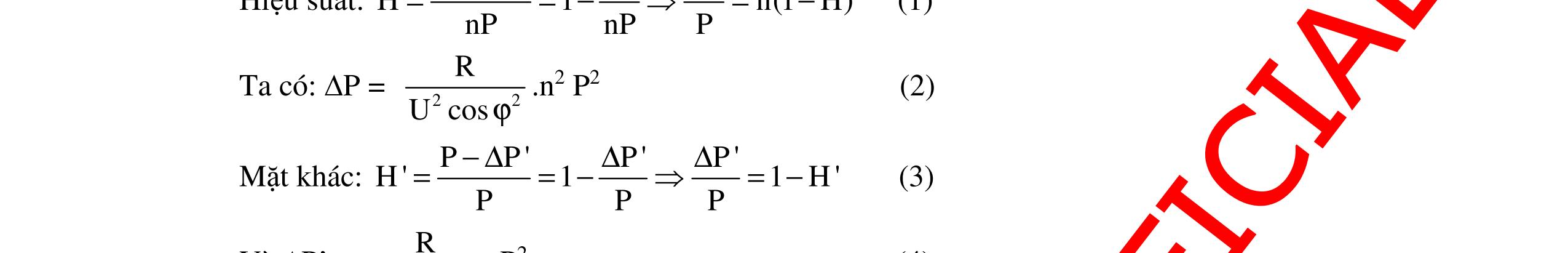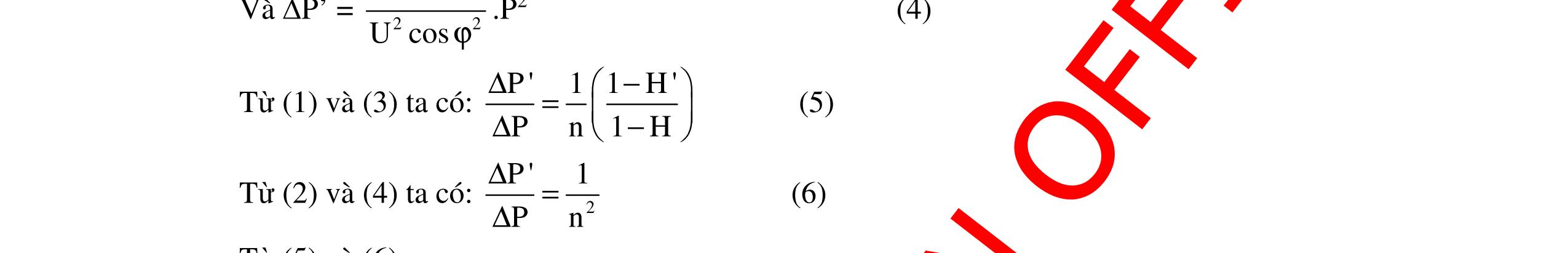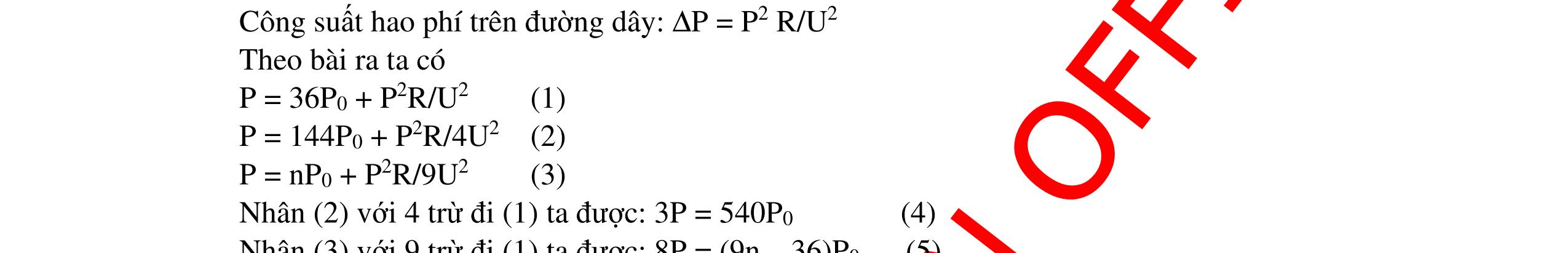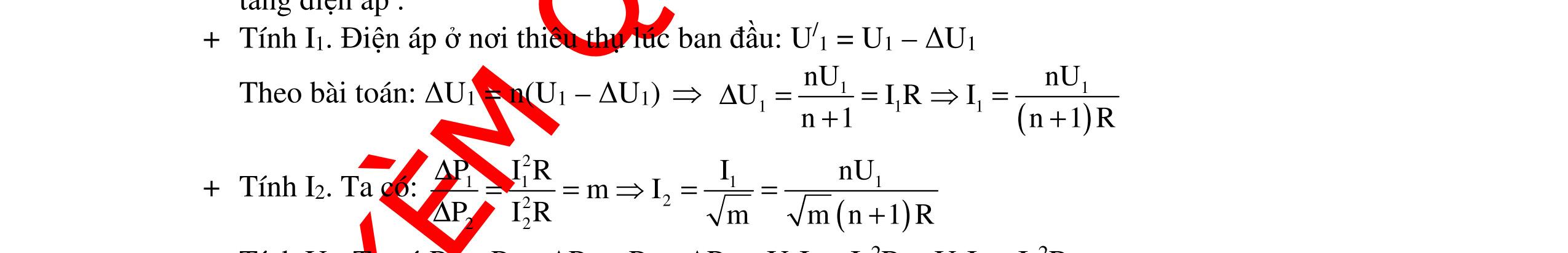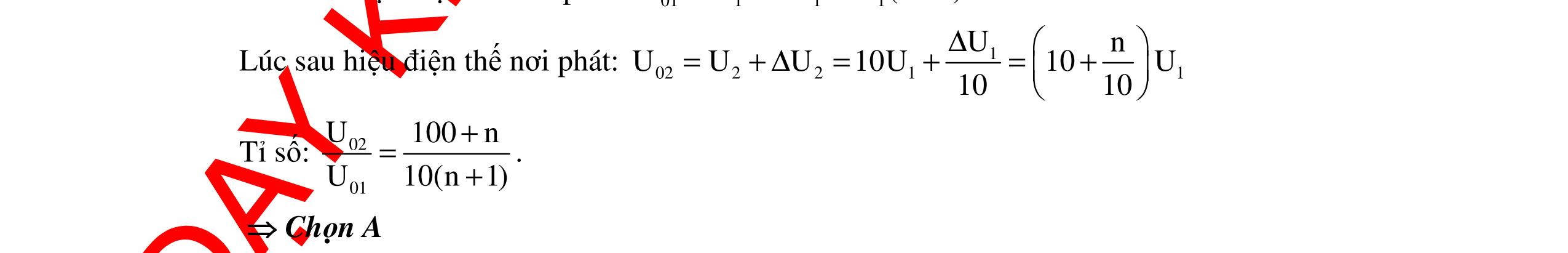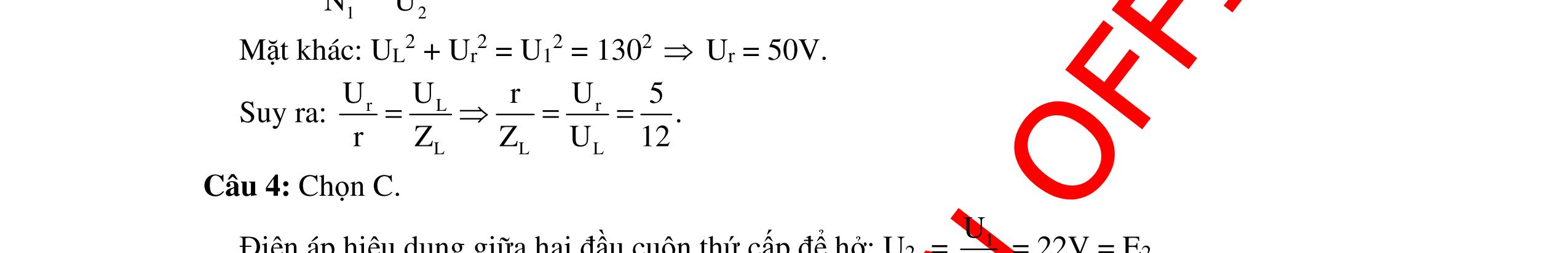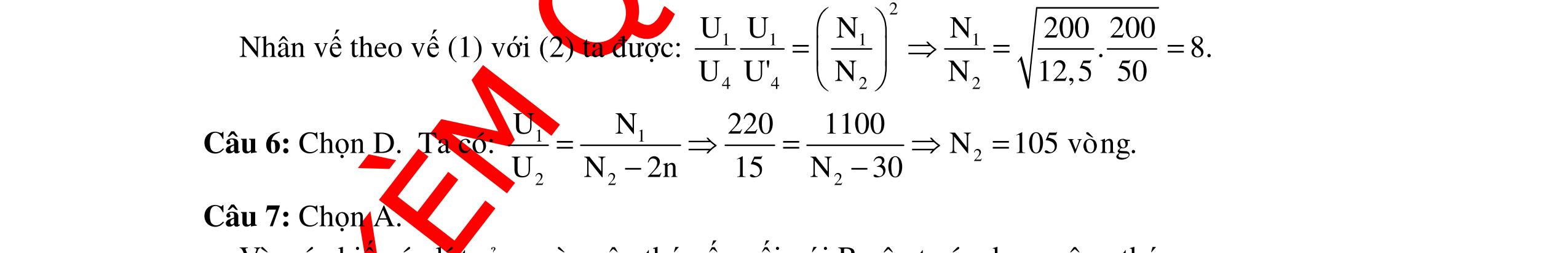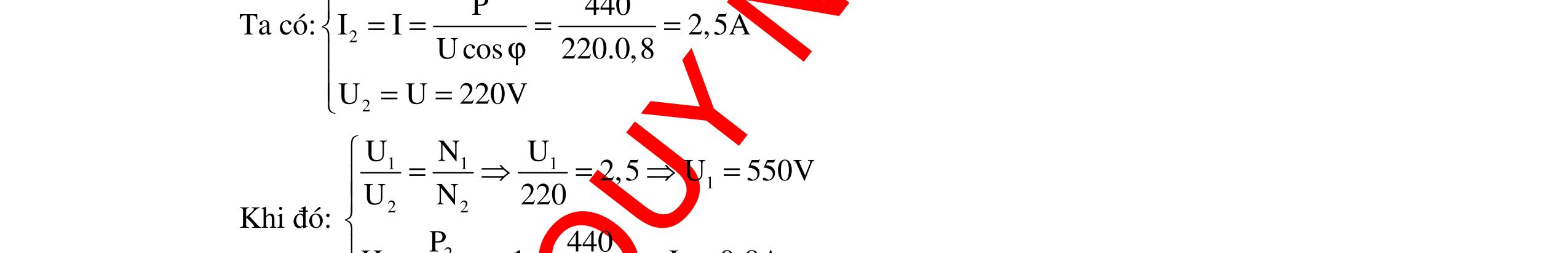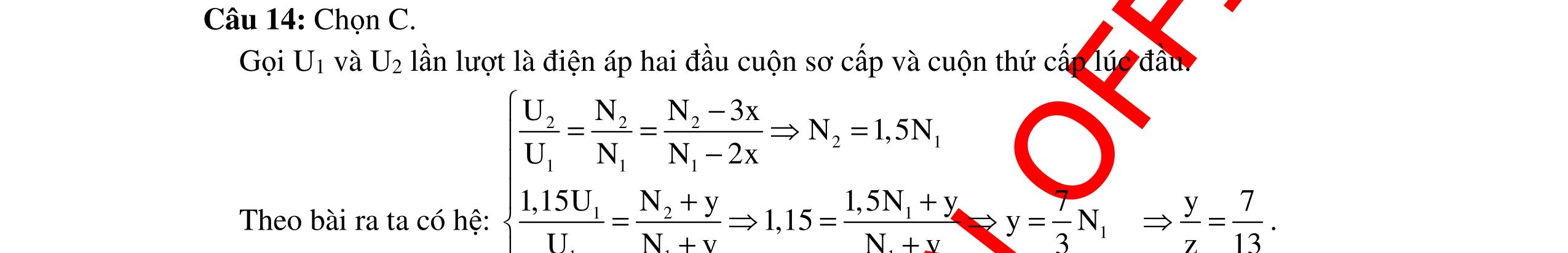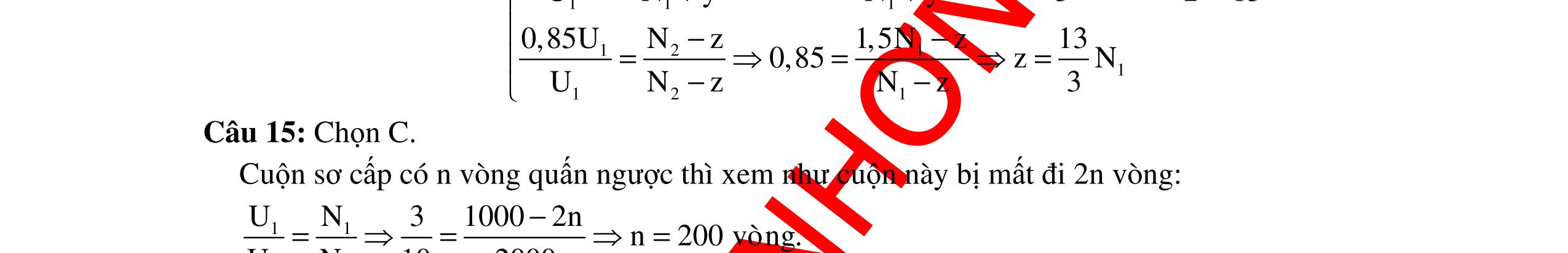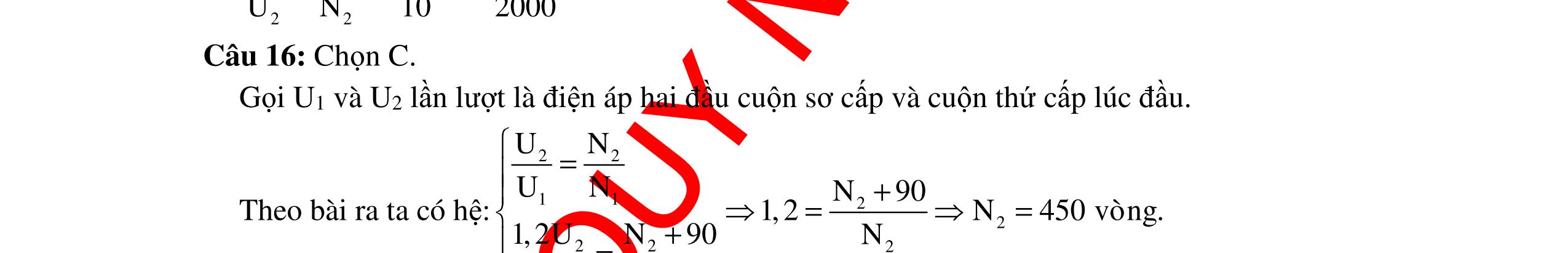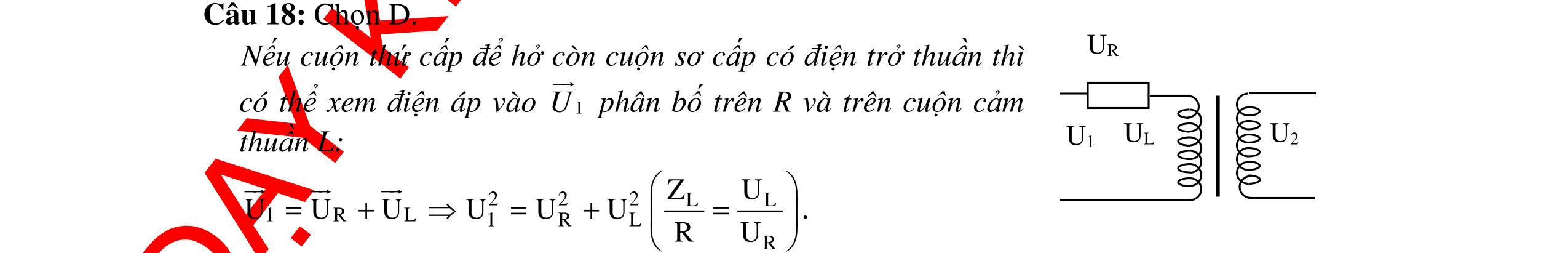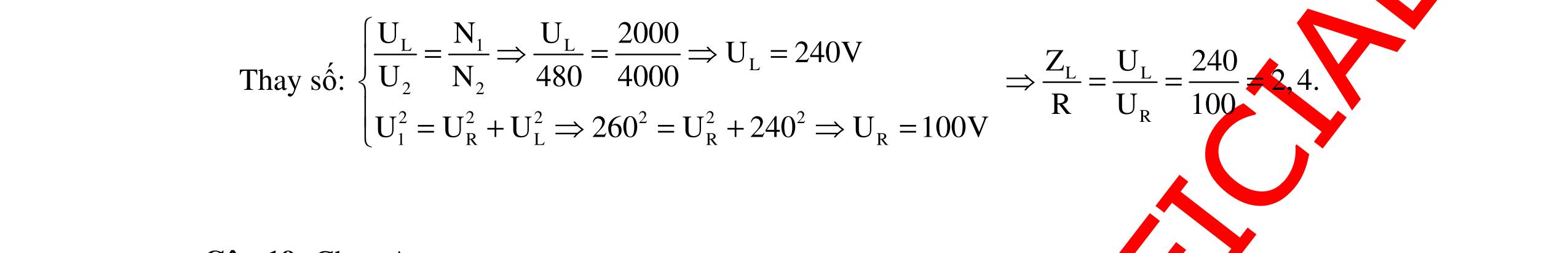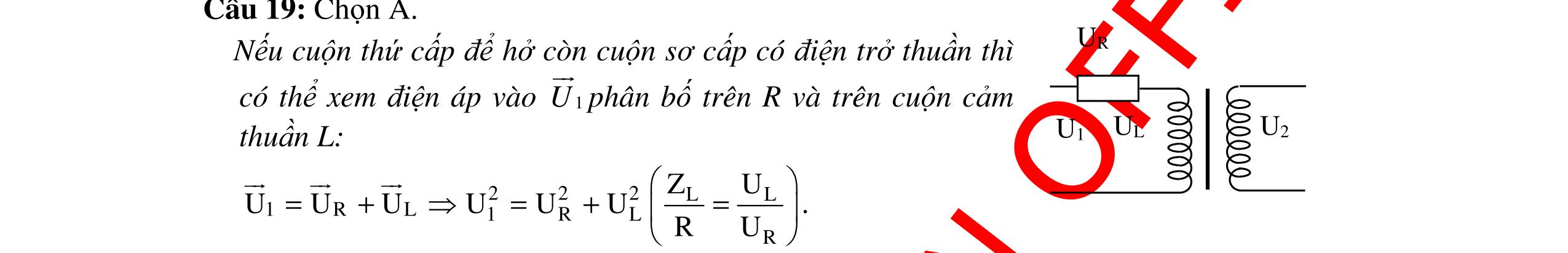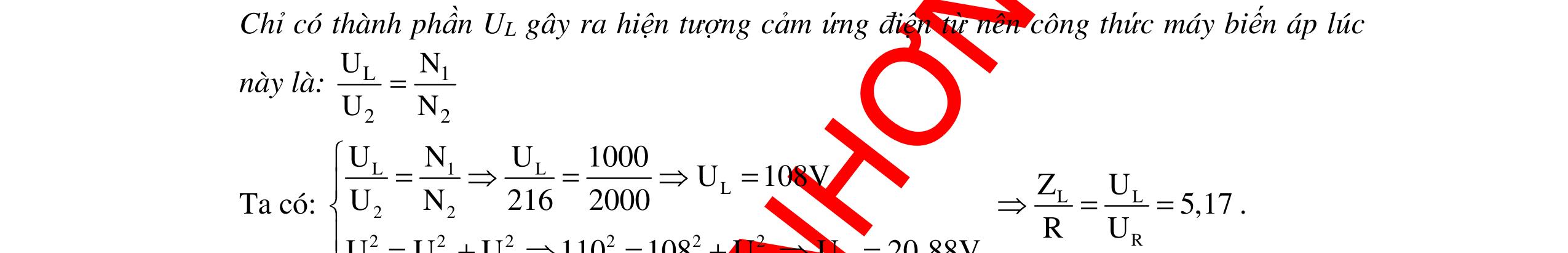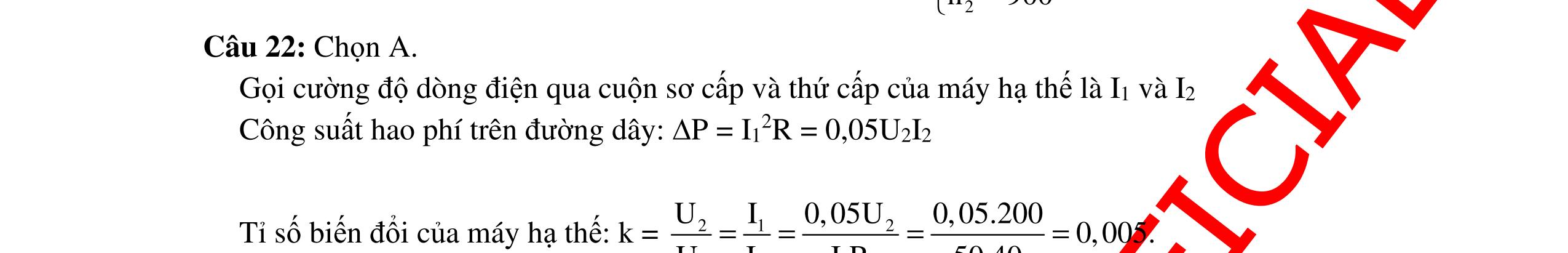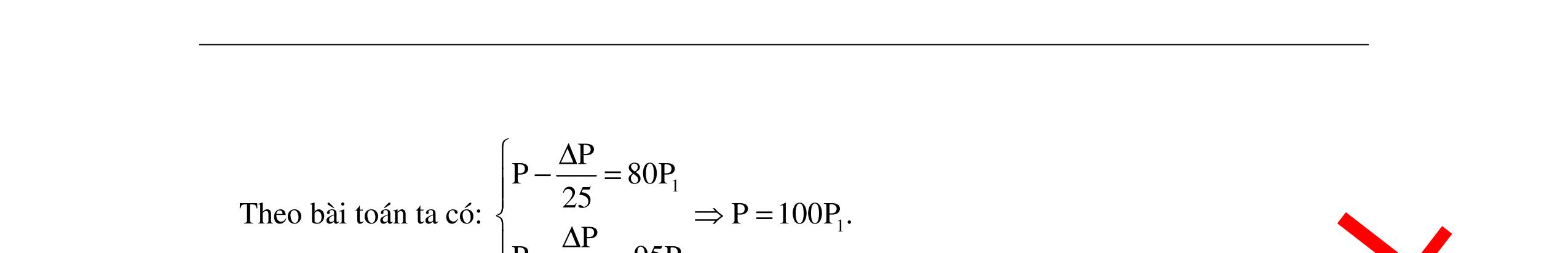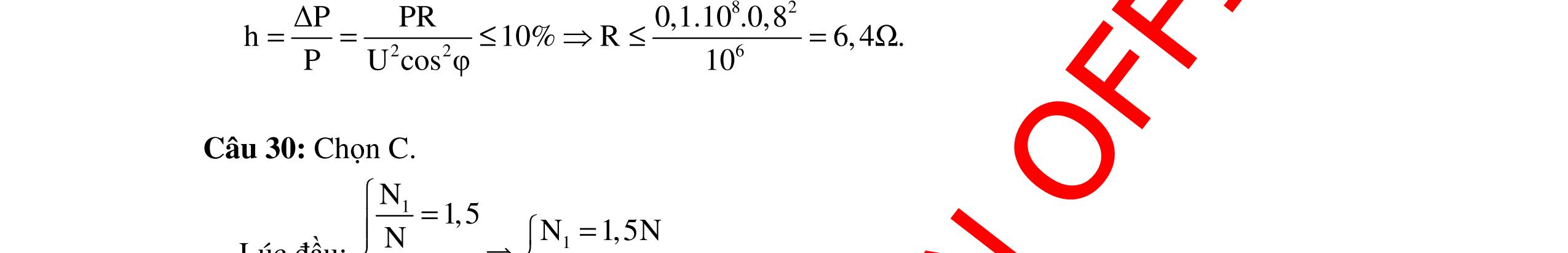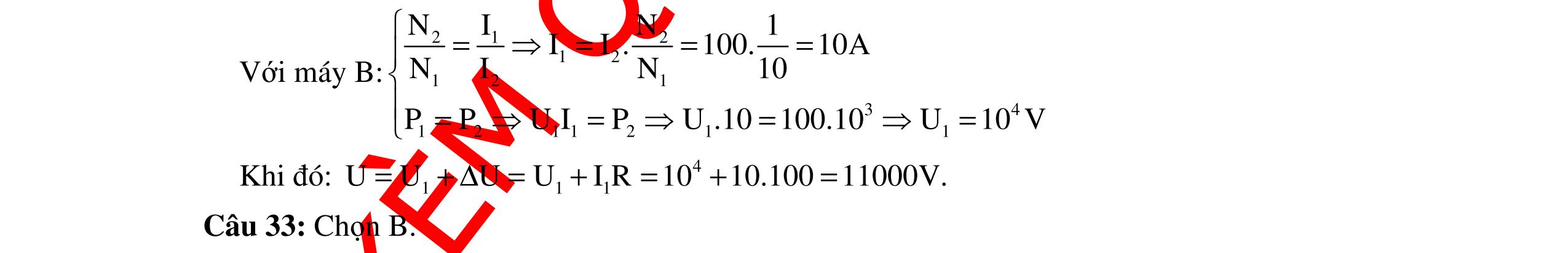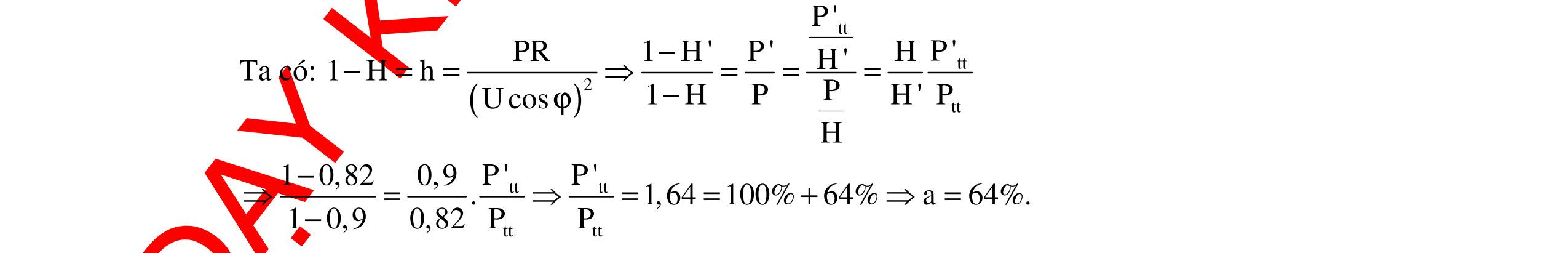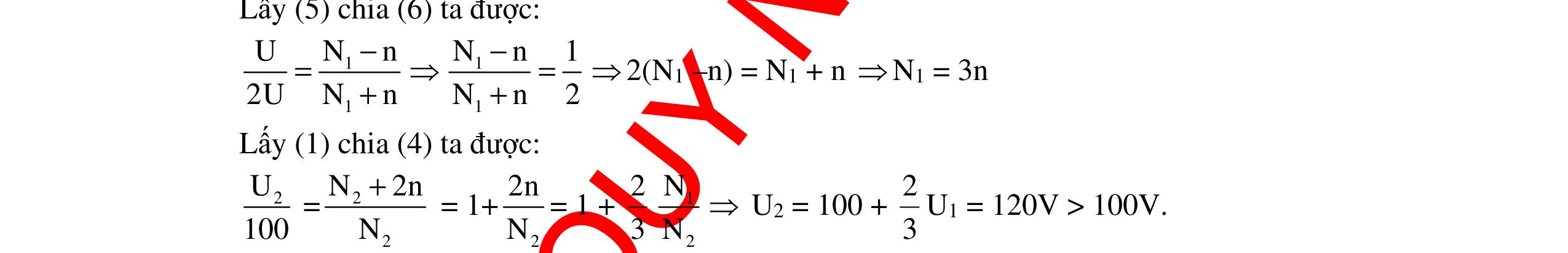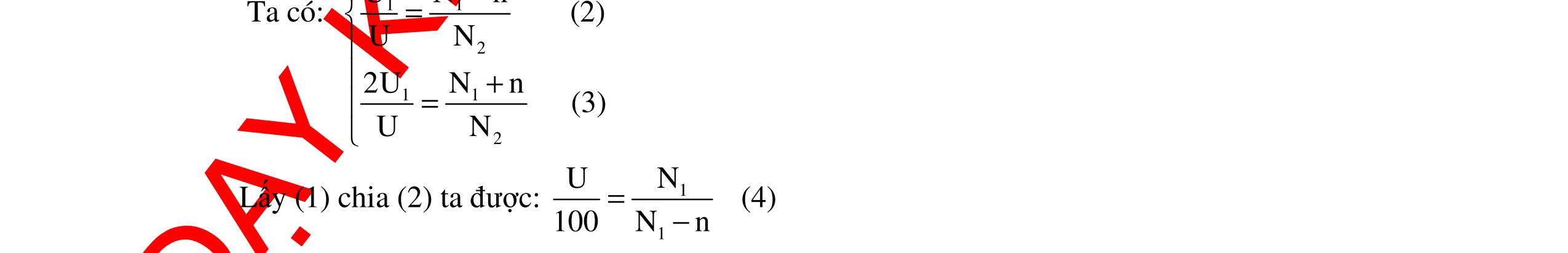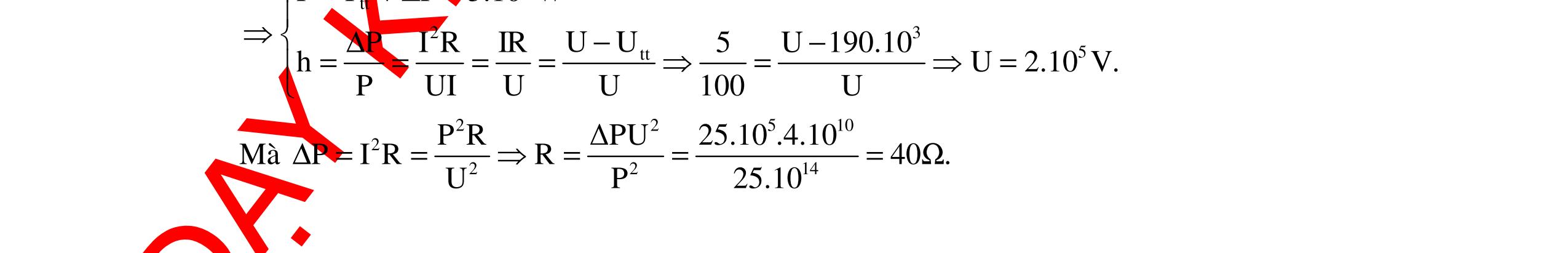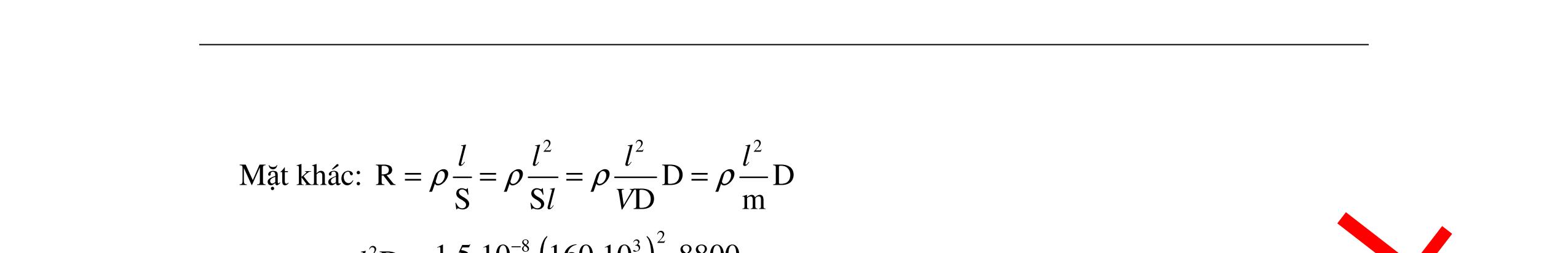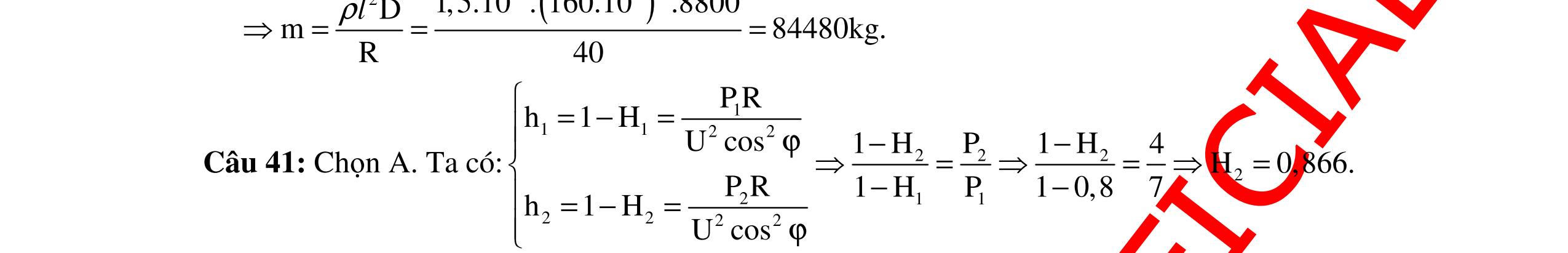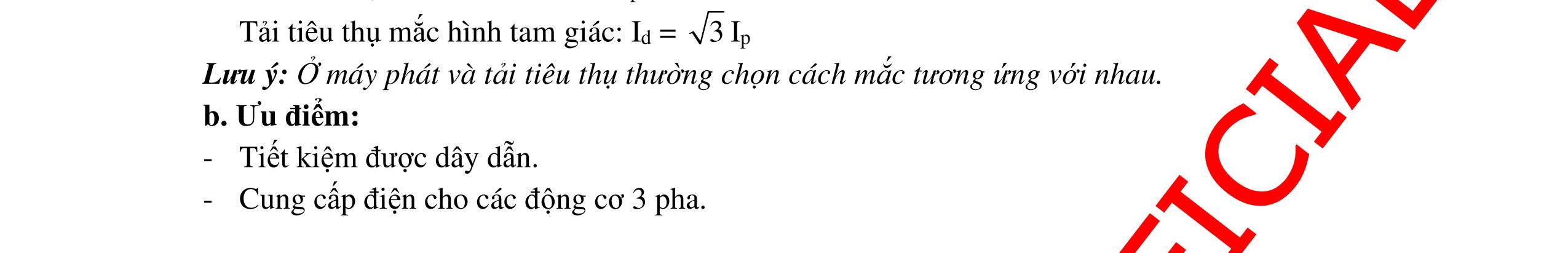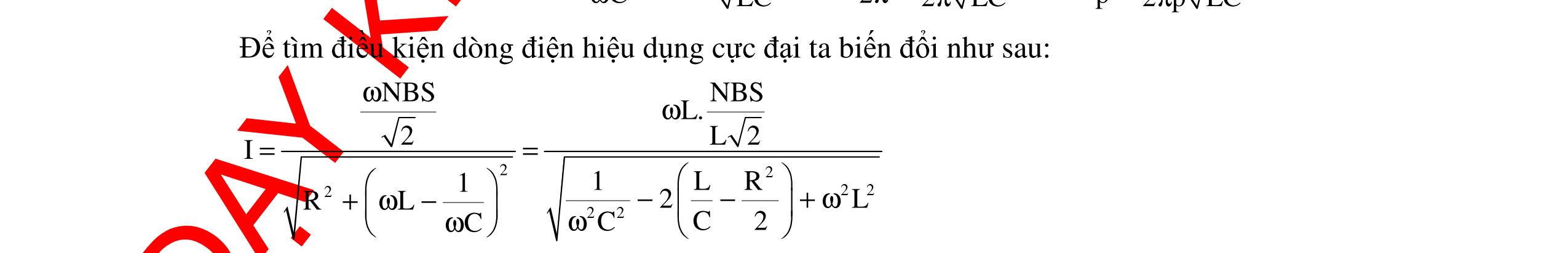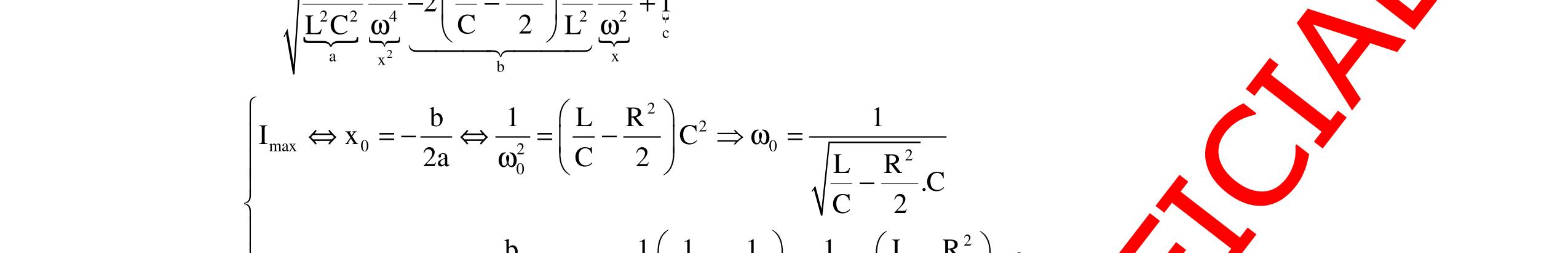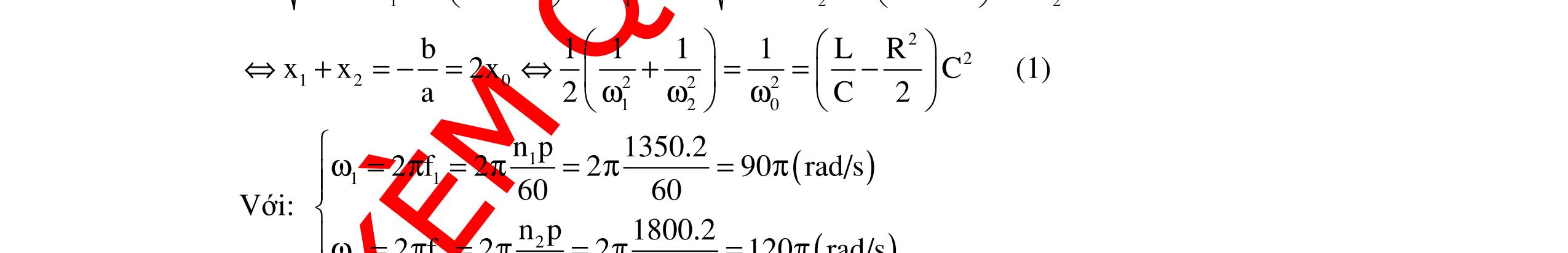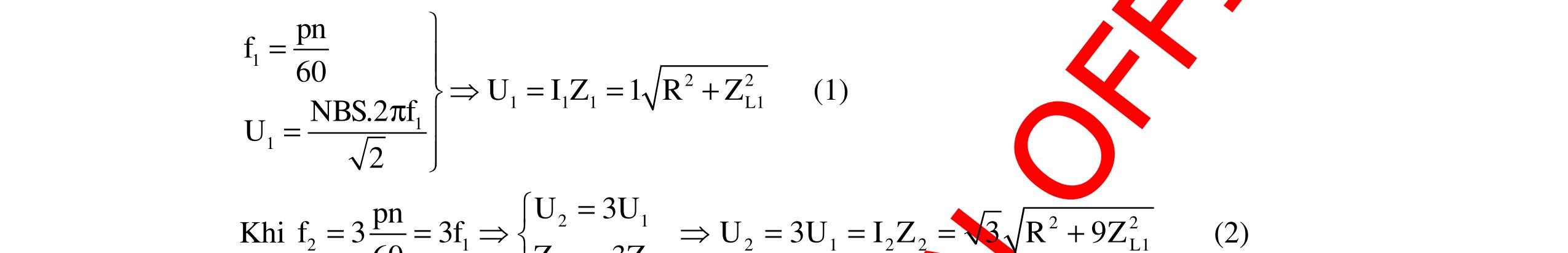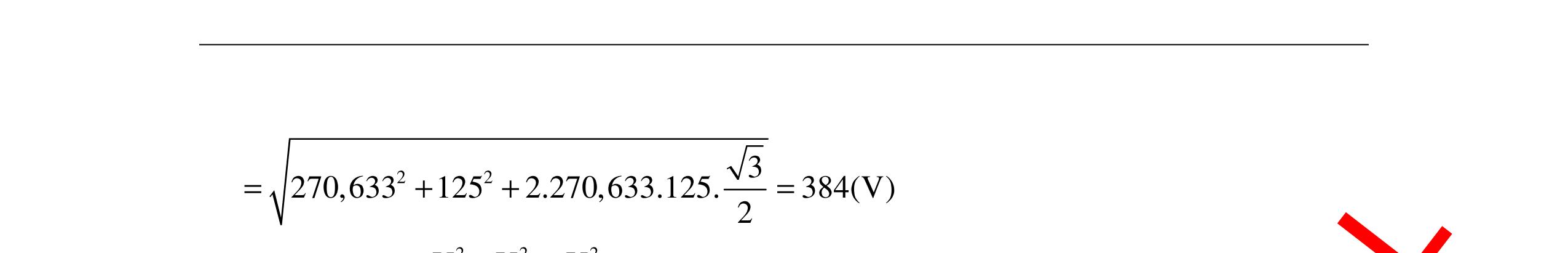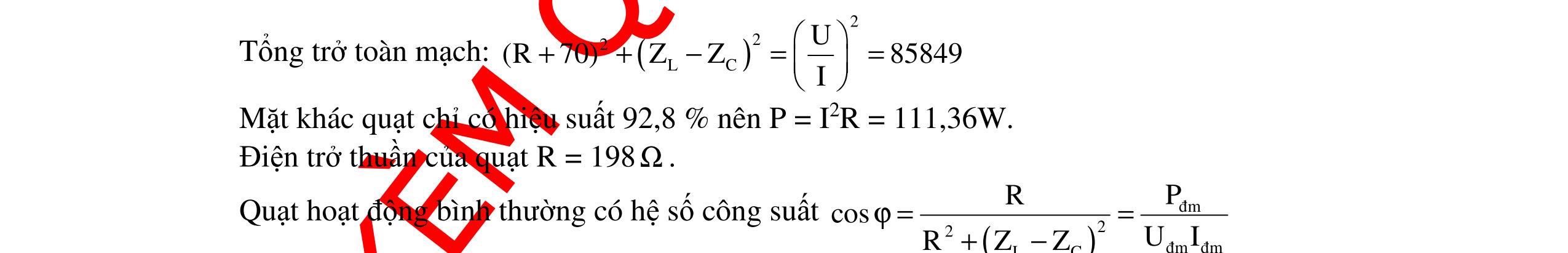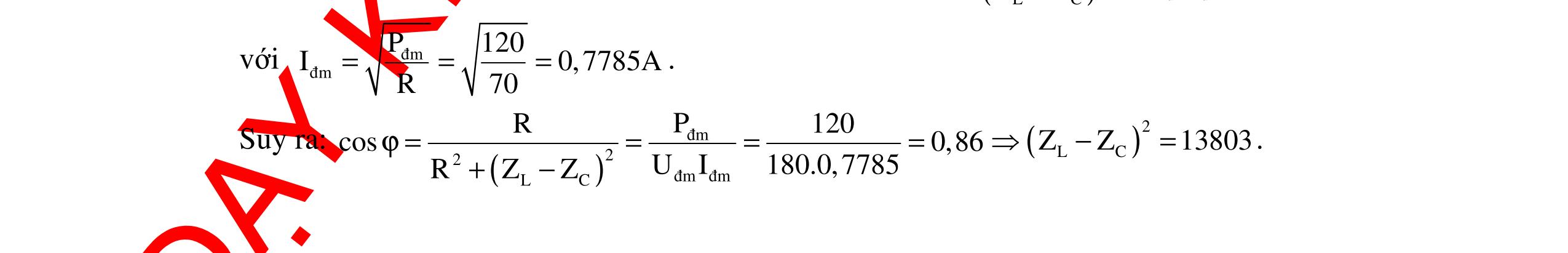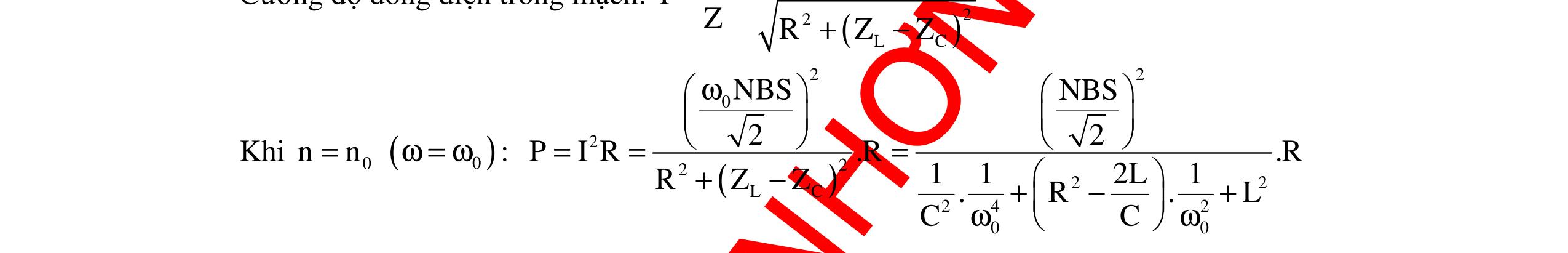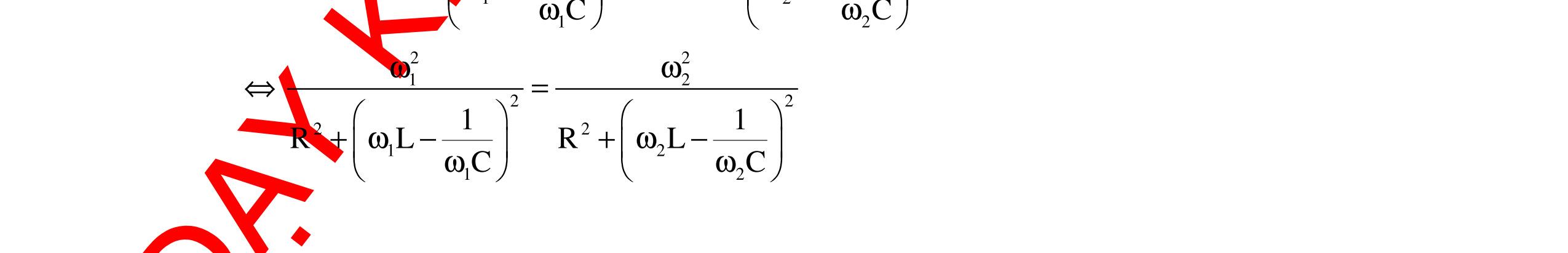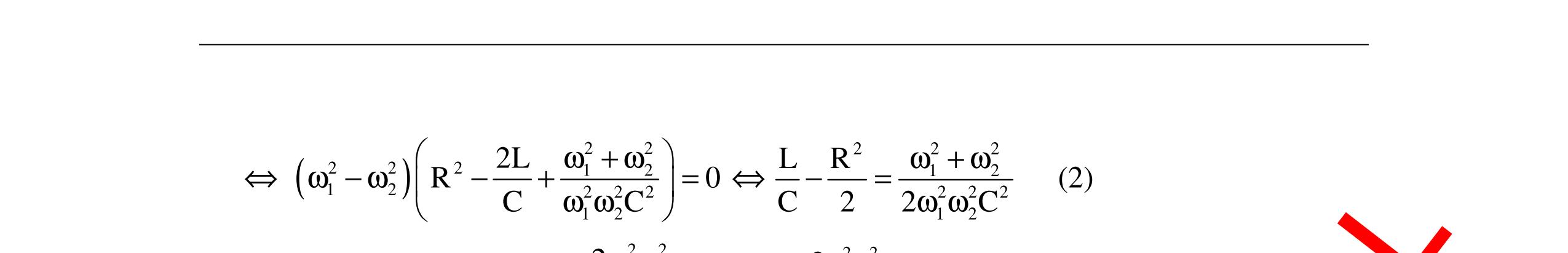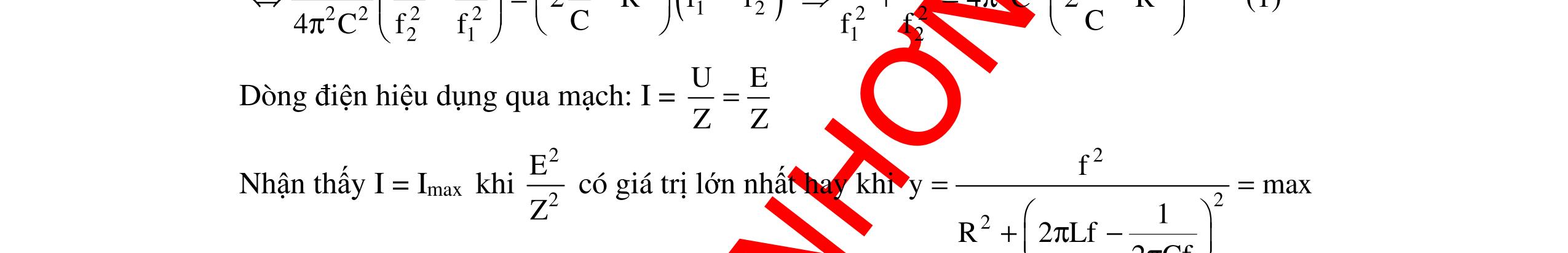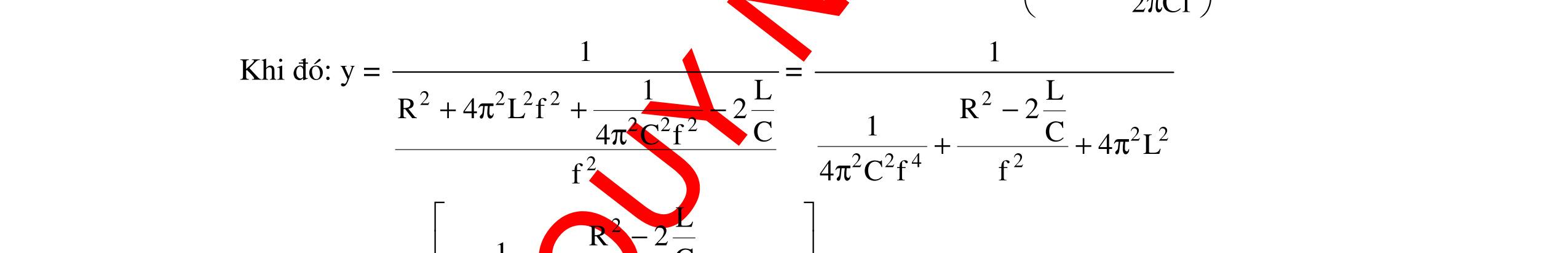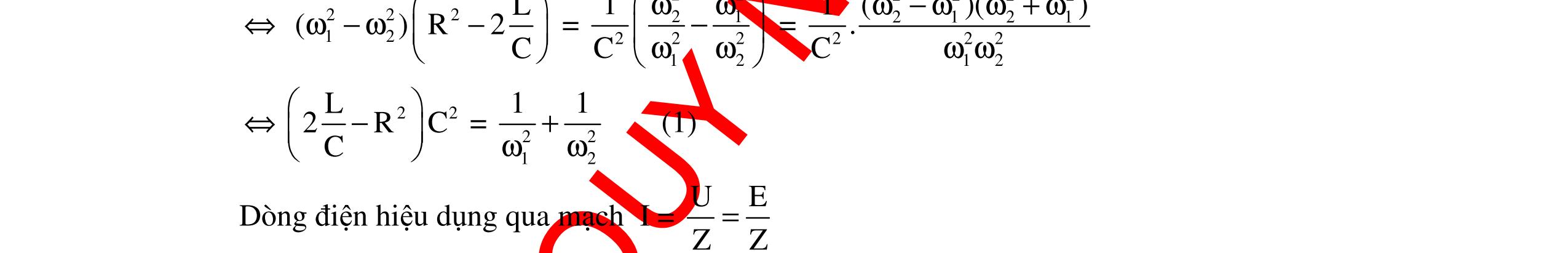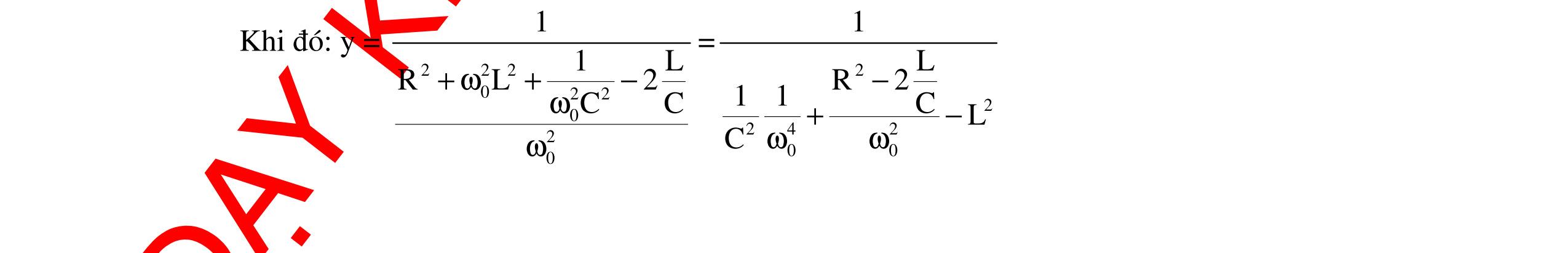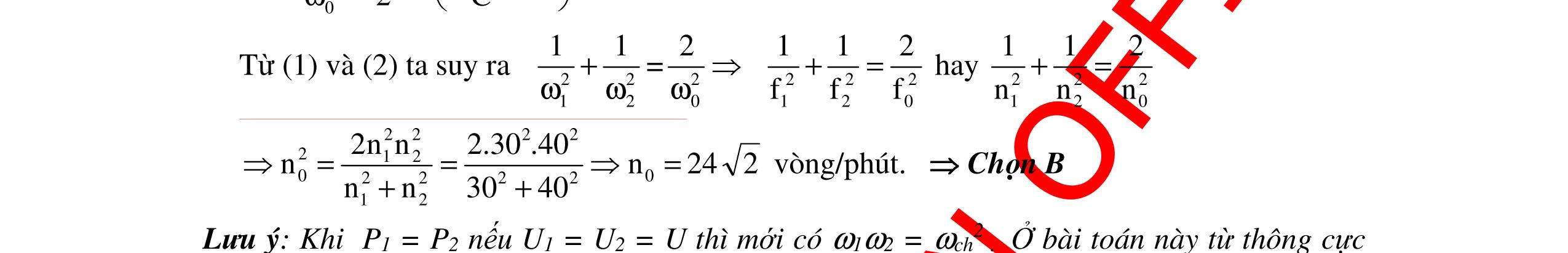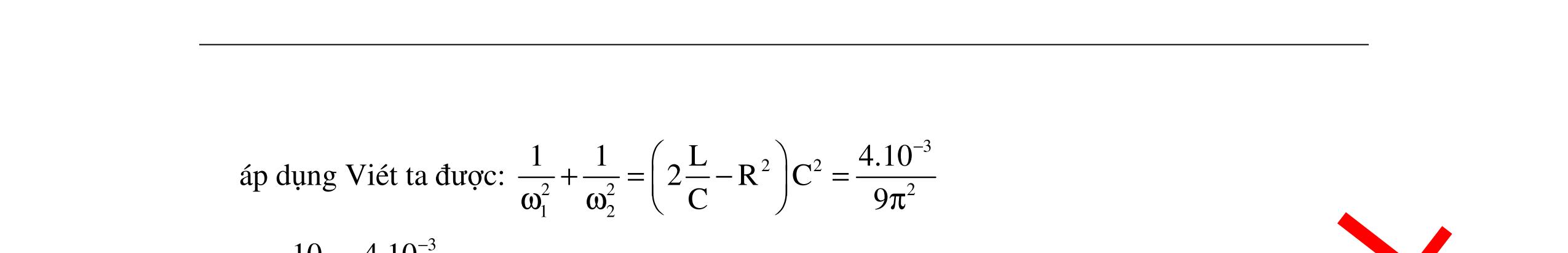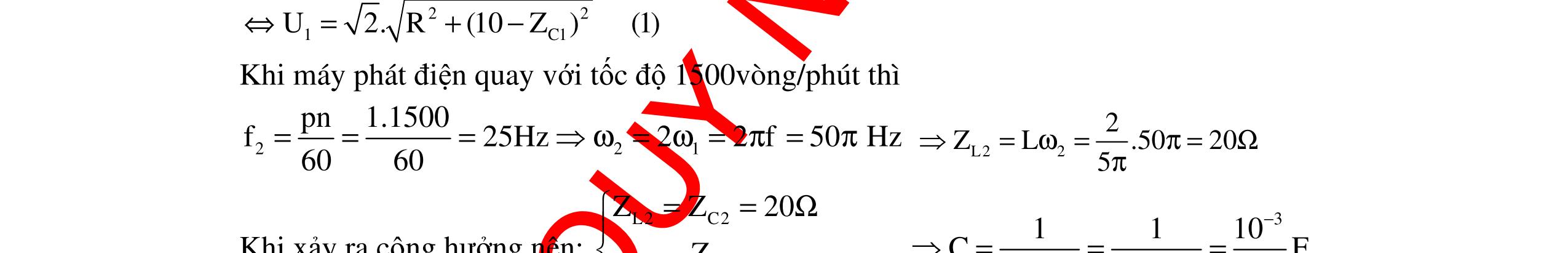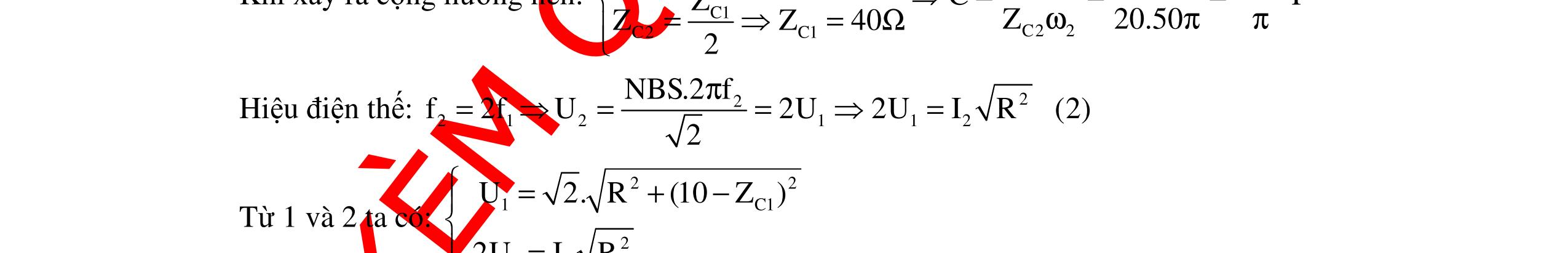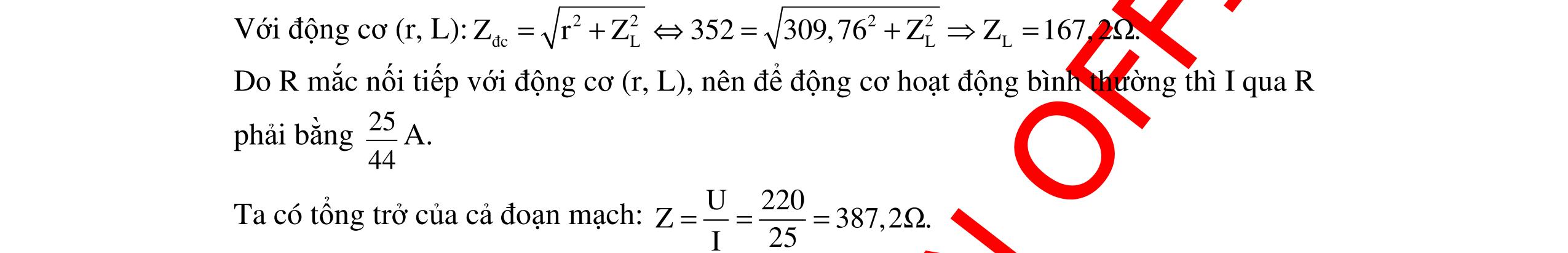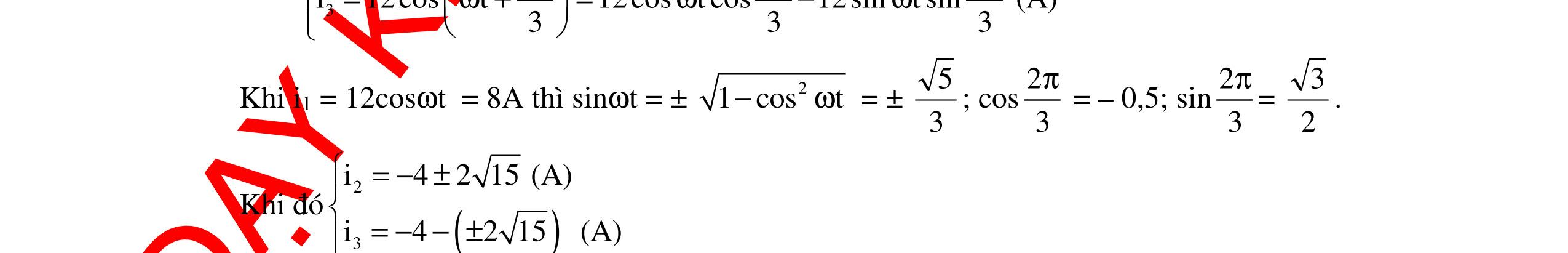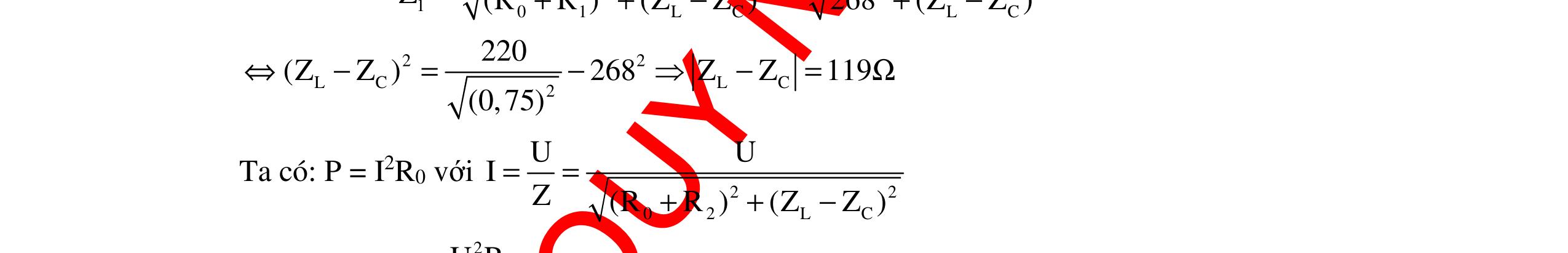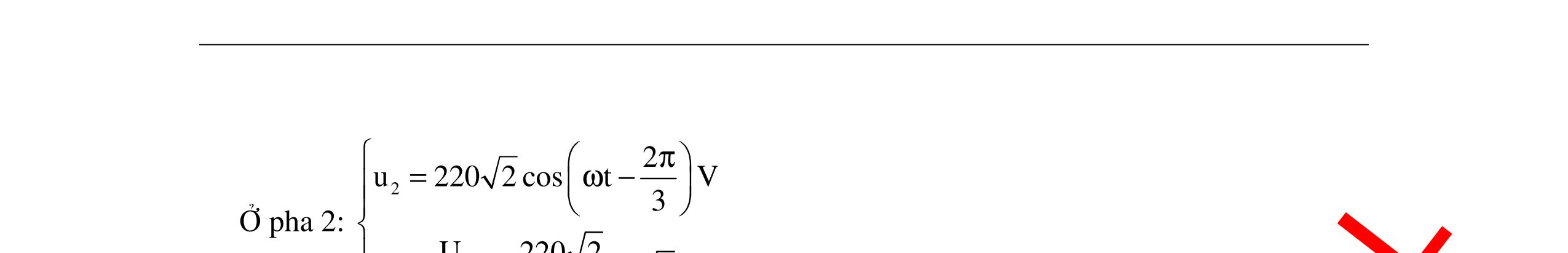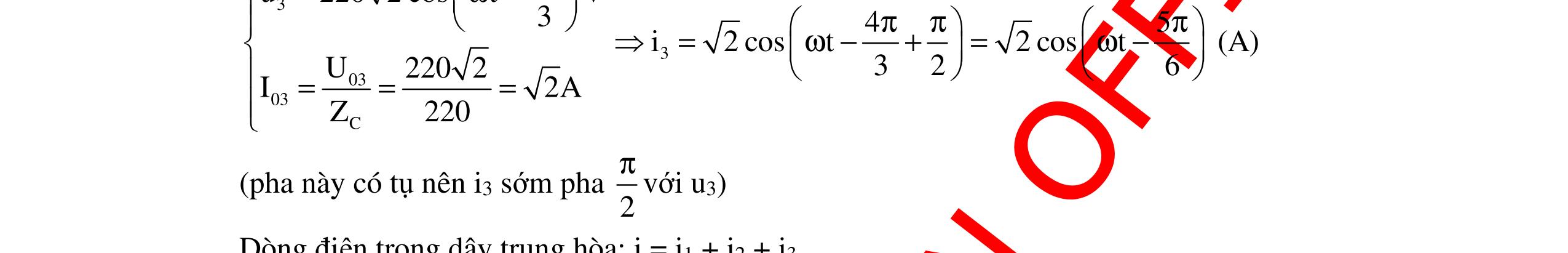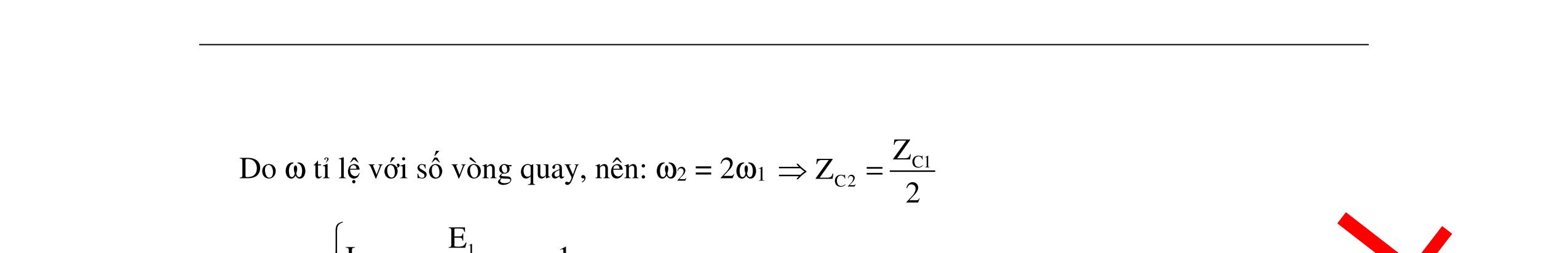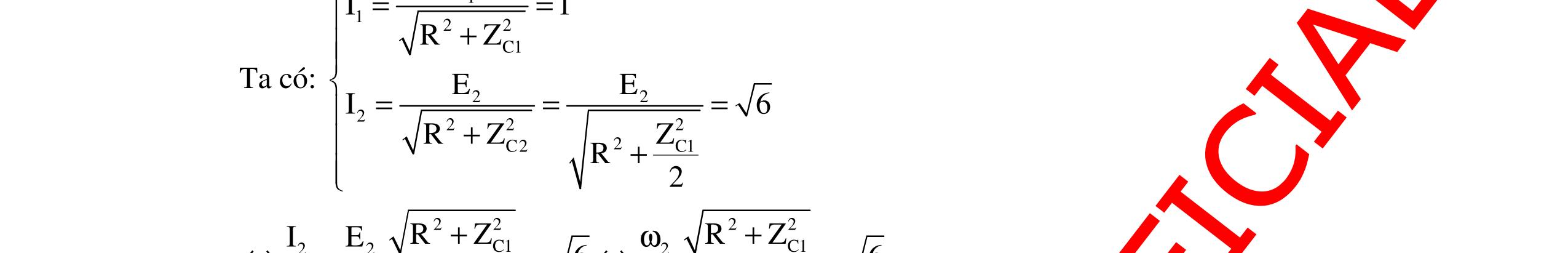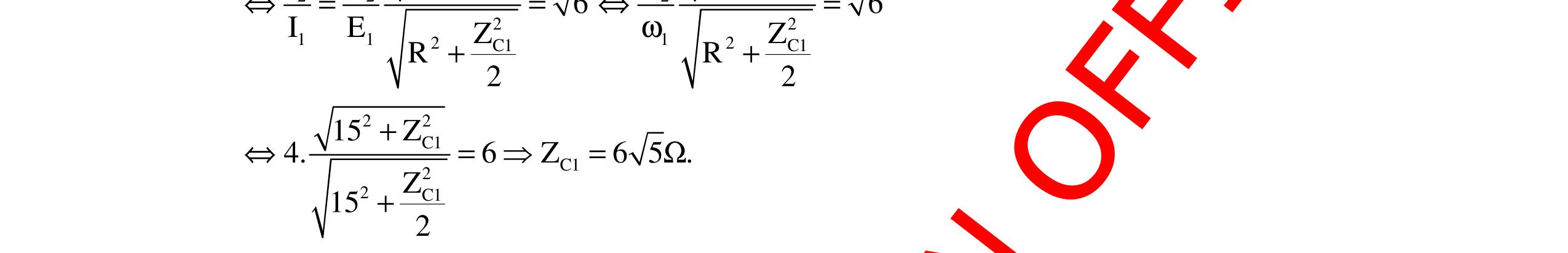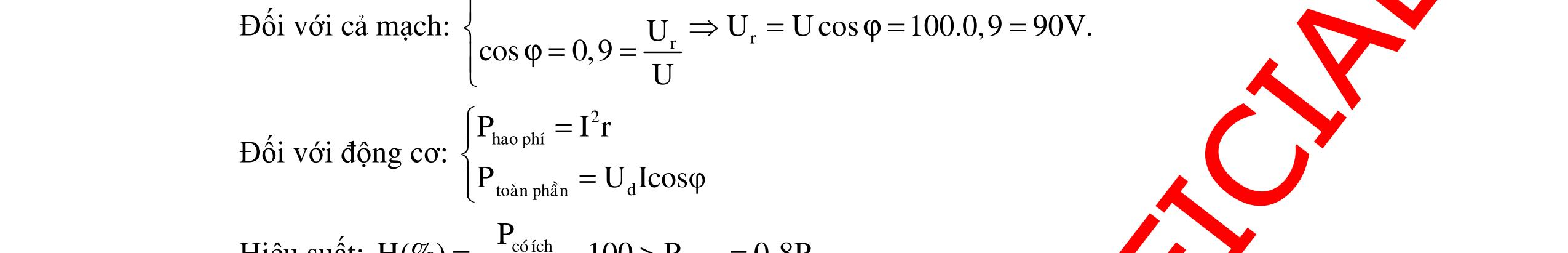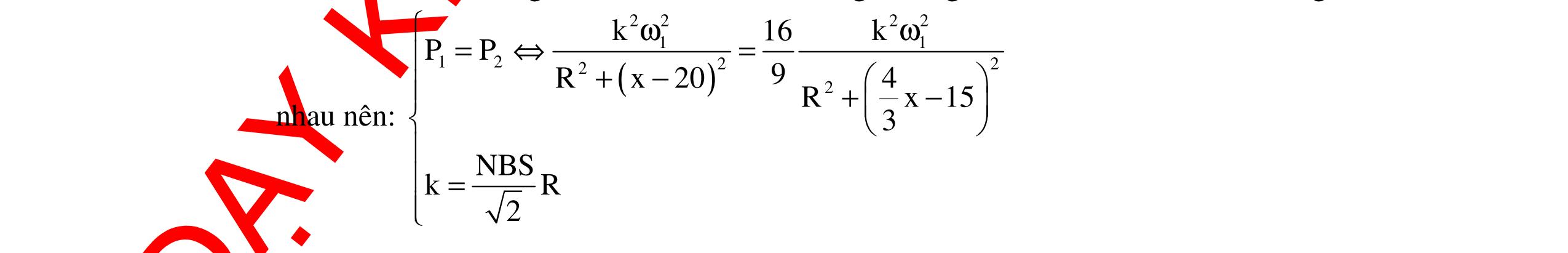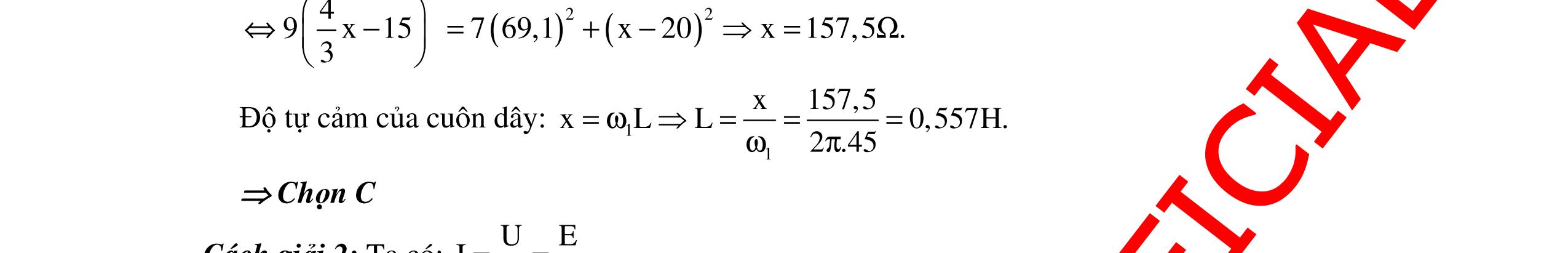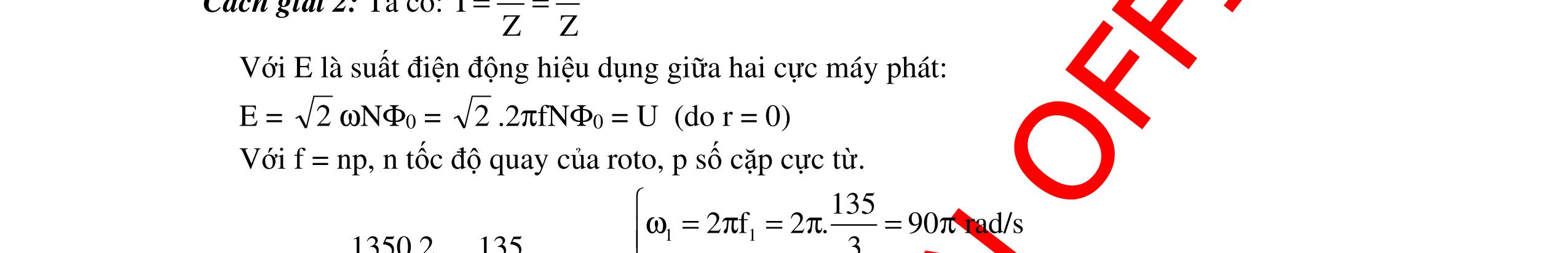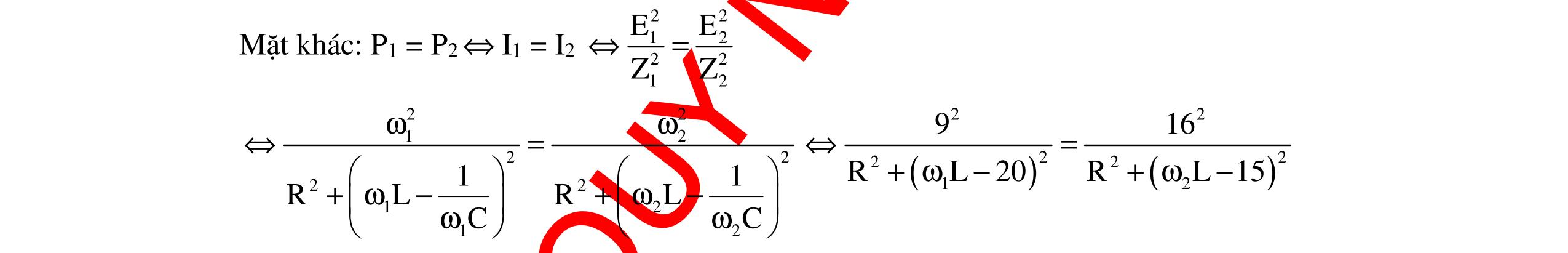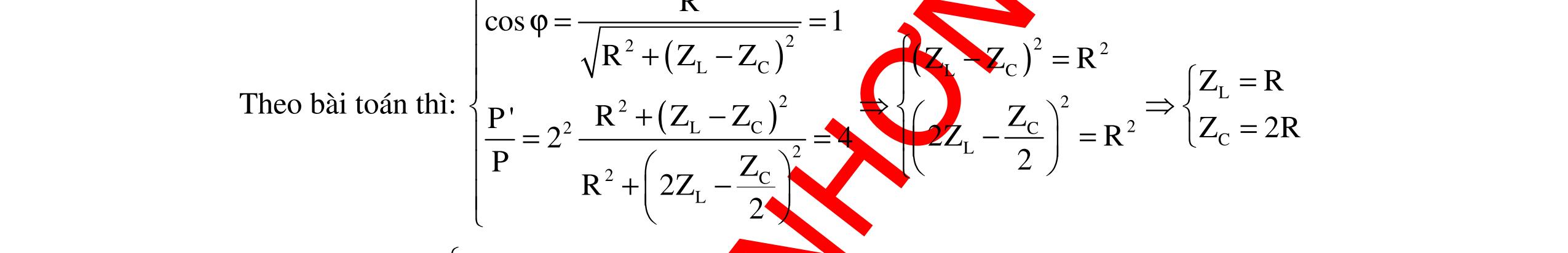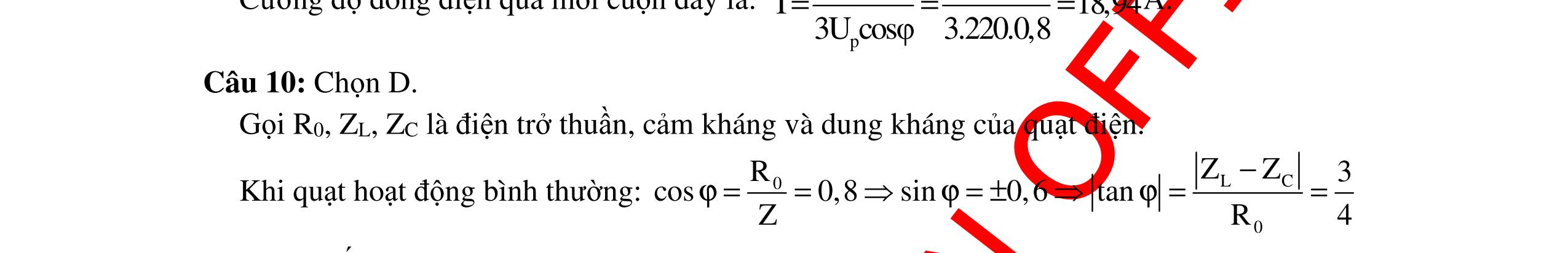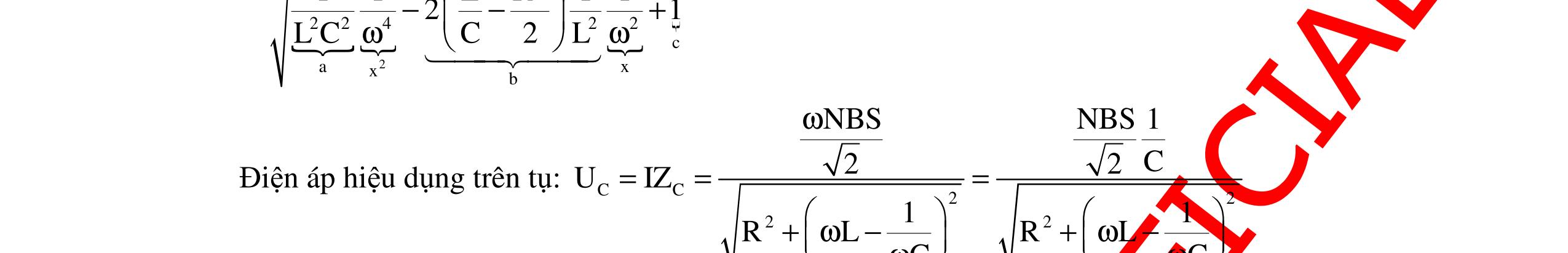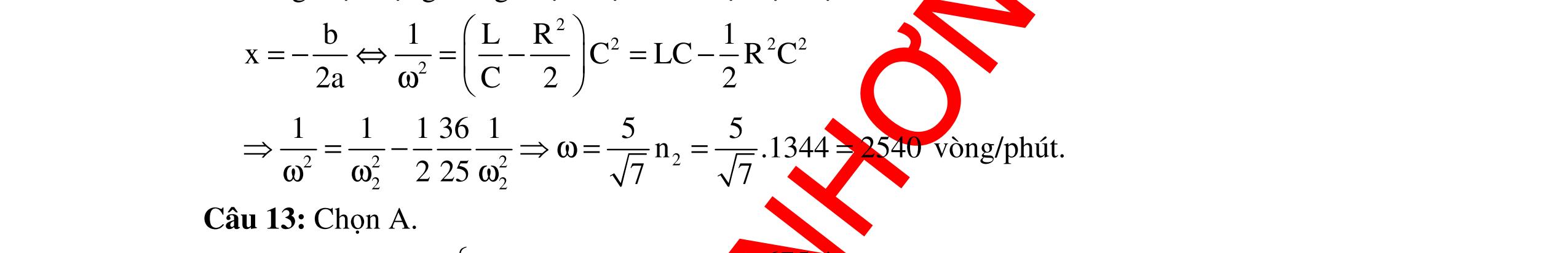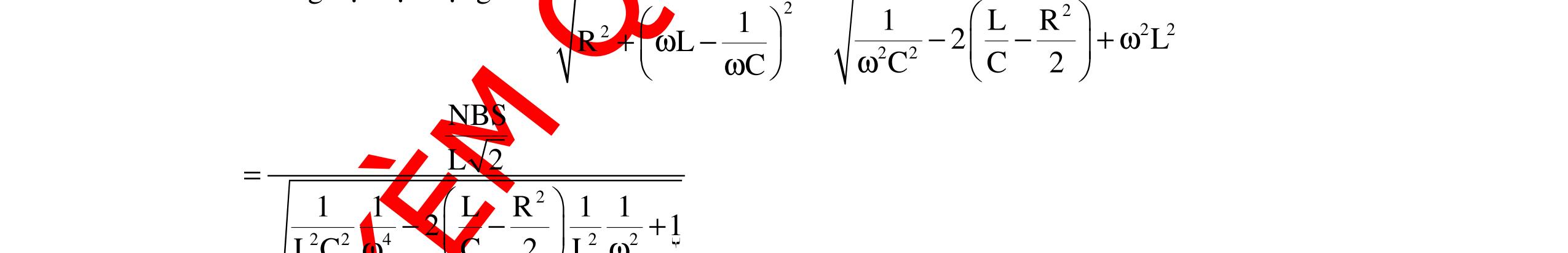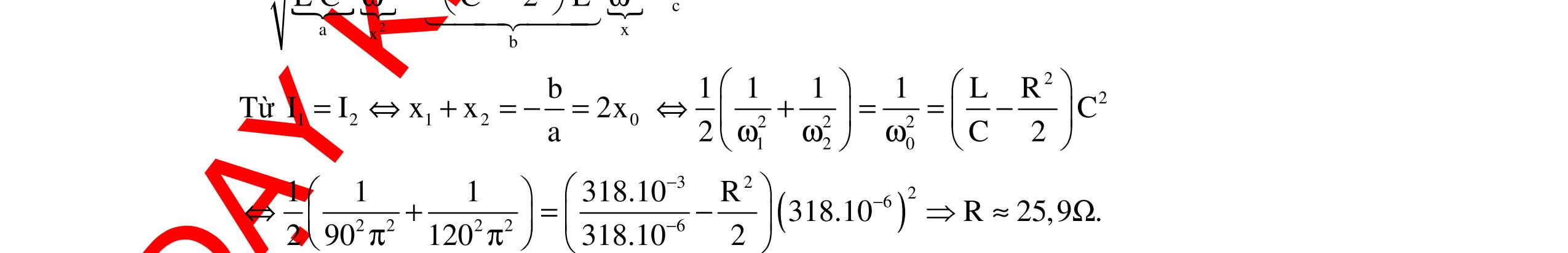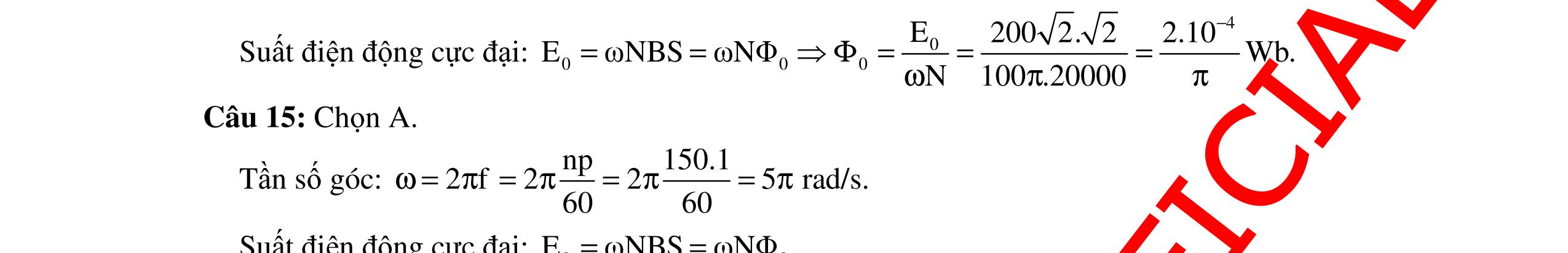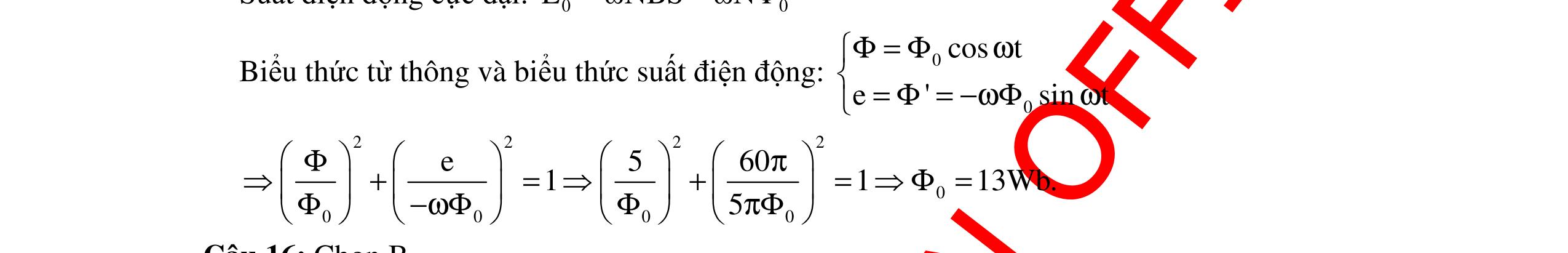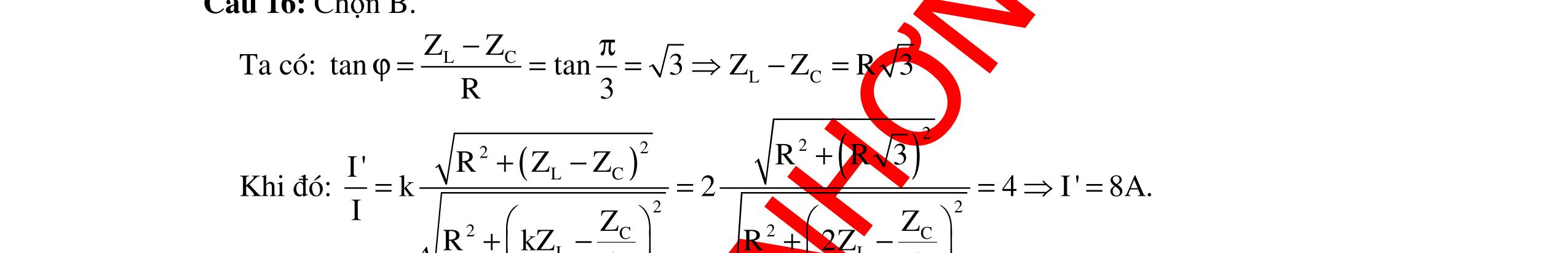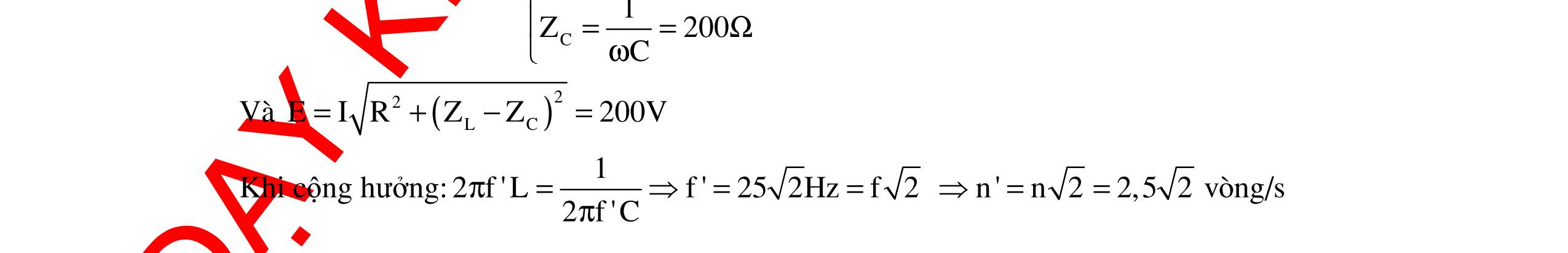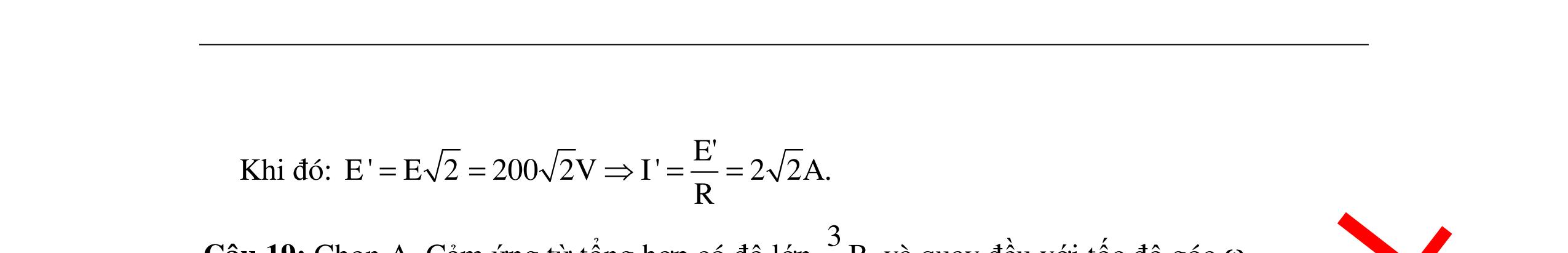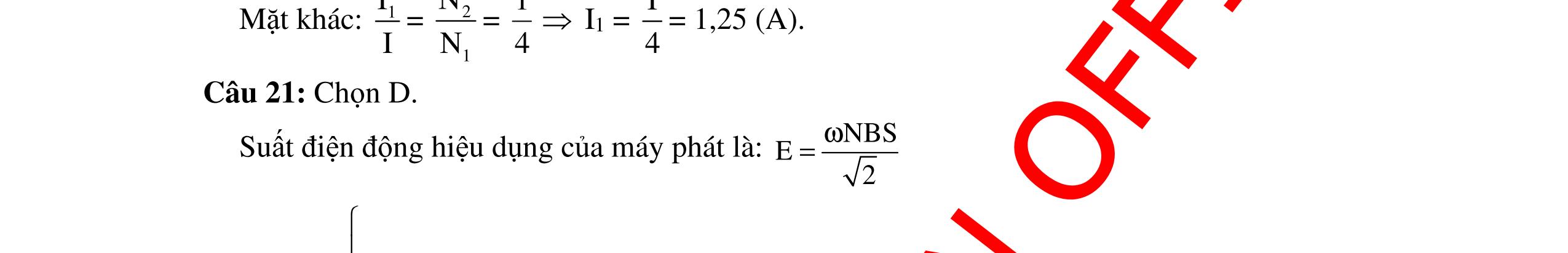CHUYÊN ĐỀ ĐIỆN XOAY CHIỀU VẬT LÝ 12 - GV NGUYỄN XUÂN TRỊ - CHỦ ĐỀ 14-18 by Dạy Kèm Quy Nhơn Official

CHUYÊN ĐỀ ĐIỆN XOAY CHIỀU VẬT LÝ 12 Ths Nguyễn Thanh Tú eBook Collection CHUYÊN ĐỀ ĐIỆN XOAY CHIỀU VẬT LÝ 12 - GV NGUYỄN XUÂN TRỊ - CHỦ ĐỀ 14-18 (KIẾN THỨC CƠ BẢN - CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI) WORD VERSION | 2022 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/10212086

DẠYKÈMQUYNHƠNOFFICIAL 297 CHỦ ĐỀ 14: CỰC TRỊ ĐIỆN XOAY CHIỀU LIÊN QUAN ĐẾN ĐIỆN ÁP A. TÓM TẮT LÝ THUYẾT CƠ BẢN MỘT SỐ KIẾN THỨC TOÁN HỌC CẦN VẬN DỤNG KHI GẶP CÁC DẠNG BÀI TÌM CỰC TRỊ 1. Phương pháp 1: Dùng bất đẳng thức Cô-si Áp dụng bất đẳng thức Cô-si cho 2 số dương a, b: ab ab 2 + ≥ đẳng thức xảy ra khi a = b () () min max abab ab ab 2  += + =  Lưu ý: Áp dụng: + Tích không đổi khi tổng nhỏ nhất. + Tổng không đổi khi tích lớn nhất. 2. Phương pháp 2: + Định lí hàm số sin trong tam giác: abc sinAsinBsinC == + Định lí hàm số cosin trong tam giác: 222 abc2bccosA =+− max max (cos)10 (sin)1 2 α=⇔α=   π α=⇔α=  3. Phương pháp 3: Dựa vào hàm số bậc 2: 2 yf(x)axbxc(a0) ==++≠ + Nếu a > 0 thì đỉnh Parabol a x 2b =− có 2 min 4acb y 4a4a ∆− =−= + Nếu a < 0 thì đỉnh Parabol a x 2b =− có 2 max 4acb y 4a4a ∆− =−= + Đồ thị: A CB b a c a > 0 O x y ymin a < 0 O x y ymax

DẠYKÈMQUYNHƠNOFFICIAL 298 4. Phương pháp 4: Dùng đạo hàm Nội dung: + Hàm số y = f(x) có cực trị khi f ’(x) = 0 + Giải phương trình f ’(x) = 0 + Lập bảng biến thiên tìm cực trị + Vẽ đồ thị nếu bài toán yêu cầu khảo sát sự biến thiên. Ngoài các phương pháp trên còn có một số phương pháp khác để khảo sát max, min của một đại lượng vật lí. Tùy theo biểu thức của đại lượng vật lí có dạng hàm nào mà áp dụng bài toán để giải. Có những hàm số không có cực trị, chỉ có tính đồng biến hay nghịch biến ta tìm được max, min trong miền nào đó. Trong đoạn [a,b]: f(b)max khi x = b f(a)min khi x = a I. Sự thay đổi L trong mạch RLC mắc nối tiếp với cuộn dây thuần cảm. Xét mạch điện xoay chiều có hiệu hiệu thế hai đầu ổn định: 0u uUcos(t) =ω+ϕ . L là một cuộn dây thuần cảm có giá trị thay đổi, R và C không đổi. 1. Khảo sát sự biến thiên của công suất theo cảm kháng ZL Ta có công suất toàn mạch là: 2 22 LC UR P R(ZZ) = +− , với R, C là các hằng số, nên công suất của mạch là một hàm số theo biến số ZL Đạo hàm của P theo biến số ZL ta có: ( )2 CL L 222L LC 2RUZZ P'(Z)P'(Z)0 R(ZZ) =  =  +−  khi LCZZ = Bảng biến thiên LZ -∞ 0 LCZZ = +∞ ( )LP'Z - 0 + ( )LPZ = 2 max U P R 2 22 C U PR RZ = + U Đồ thị của công suất theo ZL : A B CR L y xbaO f(a) f(b) ZLZL = ZCO P Pmax

DẠYKÈMQUYNHƠNOFFICIAL 299 Nhận xét đồ thị: + Có hai giá trị của cảm kháng cho cùng một giá trị công suất + Công suất của mạch cực đại khi 12 LL LC ZZ ZZ 2 + == , với 12LLZ;Z là hai giá trị của cảm kháng cho cùng một giá trị công suất. Kết luận: Từ việc khảo sát sự biến thiên sự thay đổi công suất vào giá trị của ZL sẽ cho phép định tính được sự tăng hay giảm của P theo ZL. Từ đó ta có thể tiên đoán được sự thay đổi của công suất theo giá trị của ZL trong một số bài toán. 2. Có hai giá trị L1 ≠ ≠≠ ≠ L2 cho cùng giá trị công suất Vì có hai giá trị của cảm kháng cho cùng giá trị công suất nên: 1 2 22 12 2222 LCLC URUR PP R(ZZ)R(ZZ) =⇔= +−+− Khai triển biểu thức trên ta thu được: 12 12 12 22LCLC LCLC LCLC ZZZZ (ZZ)(ZZ) ZZ(ZZ) −=− −=−⇔  −=−−  (loaïi) (nhaän) Suy ra : 12 LL C12 2 ZZ 2 ZLL 2C + =⇔+= ω 3. Giá trị ZL để hiệu điện thế ULmax Phương pháp 1: Dùng phương pháp đại số - Lấy cực trị là tọa độ đỉnh. Ta có: LL LL 22222 LCLLCC UZUZ UIZ R(ZZ)RZ2ZZZ === +−+−+ Chia cả tử và mẫu cho LZ và rút gọn ta được: () L 22 CC 2 LL UU U RZ2Z111y ZZ == +−+ Để LmaxminZy ⇔ . Đặt L 1 x Z = , ta có hàm 2 yaxbx1 =++ với 22 C C aRZ b2Z  =+  =−  (*) Vì a > 0 nên 2 min 4acb y 4a4a ∆− =−= khi b x 2a =− (**) Thay a, b ở (*) vào (**) ta được: 2222 CCC 22L LCCC 1ZRZRZ ZL ZRZZZ ++ =  =  = +ω và 2222 C min 22Lmax C C L URZ 4acbRU yU4a4aRZR Z 1 Z ∆−+ =−==  == +

DẠYKÈMQUYNHƠNOFFICIAL 300 Phương pháp 2: Dùng phương pháp đạo hàm, khảo sát LU theo LZ . Ta có: () () L LL 22 22 LC CC 2 LL UZUU UIZ RZZ11y RZ2Z1 ZZ ==== +− +−+ Nhận thấy LmaxminUy ⇔ và Lmax min U U y = với () 22 CC 2 LL 11 yRZ2Z1 ZZ =+−+ Khảo sát hàm số y: Ta có: () 22 CC L 1 y'2RZ2Z Z =+− . () 22 C CC 22 LLC 11Z y'02RZ2Z0ZZRZ =  +−=  = + Lập bảng biến thiên ta sẽ thu được cực trị và dạng của đồ thị:  ymin khi 22 CC 22L LCC 1ZRZ Z ZRZZ + =  = + Khi đó: 22 C Lmax C L URZ U U R Z 1 Z + == Phương pháp 3: Dùnggiản đồ vectơ rồidựavàophép tính hình học để khảo sát Ta có: ABAMMNNB uuuu =++ Hay dạng vectơ: ABAMMNNB UUUU =++ Theo cách vẽ các vectơ nối tiếp nhau, theo giản đồ này ta có: AB R L C ABUU AMU MNAKU NBU ==  =  ==  = U 0 0 ZL UL O U ULmax UL(V) β K A M α α N B ϕ

DẠYKÈMQUYNHƠNOFFICIAL 301 Áp dụng định lí hàm số sin trong ∆ABK ta có: L L U ABAKUsin UU sinsinsinsinsin =⇔=β  = αβαβα Trong ∆KBN vuông tại N ta có: R 22 RC C U KNR sin KBU RZ α=== + Nên 22 C L sinURZ UU.sin sinR β+ ==β α Lúc này ta thấy LU chỉ phụ thuộc vào sin β . Vậy nên khi sin1 β= thì: 22 C LLmax C L URZU UU RZ 1 Z + === và khisin1. 2 β=π  β=  α=ϕ 22 LCC L C C RZZRZ tantanZ. ZRZ −+  α=ϕ  =  = Chú ý: Khi LLmaxUU = , theo phương pháp giản đồ vectơ nêu trên, điện áp giữa các phần tử có mối liên hệ: 2222 LRC UUUU =++ Tóm lại: +Khi 22 C L C RZ Z Z + = thì 22 C Lmax RZ UU R + = +Khi ULmax thì hiệu điện thế tức thời ở hai đầu mạch luôn nhanh pha hơn uRC một góc 900 4. Có hai giá trị L1 ≠ ≠≠ L2 cho cùng giá trị UL, giá trị L để ULmax tính theo L1 và L2. Khi có hai giá trị của L cho cùng một giá trị hiệu điện thế: 1 2 1212 1 2 LL LLL1L2 2222 LCLC ZZ UUZIZI R(ZZ)R(ZZ) =⇔=⇔= +−+− Bình phương và khai triển biểu thức trên ta thu được: 1 2 11 22 2 2 L L 222222 CLLCCLLC ZZ RZZ2ZZRZZ2ZZ = ++−++− Theo kết quả phần trên khi hiệu điện thế giữa hai đầu cuộn dây cực đại thì 22 CRZ=+LCZZ với giá trị ZL là giá trị làm cho ULmax . Thay vào biểu thức trên: 1 2 1122 22 LL 22 LCLLCLCLLC ZZ ZZZ2ZZZZZ2ZZ = +−+− 121212 22 LLLLLLL (ZZ)Z2ZZ(ZZ) ⇔−=− Vì L1 ≠ L2 nên đơn giản biểu thức trên ta thu được: 12 12 LL 12 L LL12 2ZZ2LL ZL ZZLL =⇔= ++ với giá L là giá trị cho ULmax

DẠYKÈMQUYNHƠNOFFICIAL 302 Chú ý: - Khi L = L1 hoặc L = L2 mà công suất P (hoặc cường độ hiệu dụng I) không đổi thì ta có ZC = 2 12 LL ZZ + - Khi UL cực đại thì ta có ( )2222 max LRC UUUU =++ - Khi UL cực đại thì điện áp hai đầu đoạn mạch RC vuông pha với điện áp u của hai đầu mạch. - Khi L = L1 hoặc L = L2 mà UL không đổi, đồng thời khi L = L0 mà UL đạt cực đại thì ta có hệ thức liên hệ giữa các đại lượng là 012 211 LLL =+ (*). Chứng minh (*): 1212 12 LLLL UUIZIZ =⇔= ⇔ 1 2 1 2 2222 ()() = +−+− LL LCLC ZZ RZZRZZ ⇔ 2222222 ()()() 122112 LLLLCLLC RZZZZZZZZ = ⇔ 1212 2 ()() −+ LLLL RZZZZ 1221221 1 ()()()()  =−−−−+−  LLCLLCLLCLLC ZZZZZZZZZZZZ ⇔ 1212121212 2 ()()()2() −+=−−+LLLLCLLLLCLL RZZZZZZZZZZZZ ⇔ 121212 1212 2 ()2() ()() −−+ = −+ CLLLLCLL LLLL ZZZZZZZZ R ZZZZ 1212 12 2() ()  −+  = + CLLCLL LL ZZZZZZ ZZ ⇔ 12 12 2 2 ()  =−  +  LL CC LL ZZ RZZ ZZ 12 12 22 2 ⇔+= + LL CC LL ZZ RZZ ZZ Từ đó ta được 12 12 22 2+ = + CLL CLL RZZZ ZZZ Khi L = L0 mà UL đạt cực đại thì 0 22 + = C L RZ Z ZC ⇔ 12 0 12 2 = + LL L LL ZZ Z ZZ  12 012 1 2 + = LL LLL ZZ ZZZ ⇔ 012 211 LLL ZZZ =+ ⇔ 012 211 LLL =+ 5. Giá trị ZL để hiệu điện thế URLmax Khi R và L mắc nối tiếp nhau thì: 22 22L RLL 2222 LCLC 22 L URZUU UIRZ R(ZZ)R(ZZ)y RZ + =+=== +−+− + Đặt 22 LC 22 L R(ZZ) yRZ +− = + , ta có 22 LC RLmaxmin 22 L min UyR(ZZ) RZ  +− ⇔=  +  .

DẠYKÈMQUYNHƠNOFFICIAL 303 Đạo hàm của y theo biến số ZL ta thu được: () 2222 'LCLLLC L 222 L 2(ZZ)(RZ)2ZR(ZZ) y(Z) RZ −+−+− = + () 222 ' CLCLC L 222 L ZZZZZR y(Z) RZ  = + Cho y’(ZL) = 0 ta có: 222 CLCLC ZZZZZR0 −−= . Nghiệm của phương trình bậc hai này là: 1 2 22 CC L L 22 CC L Z4RZ ZZ0 2 Z4RZ Z0 2  ++ ==>   −+ =<  . Lậpbảngbiếnthiêntacó: ZL 0 22 CC L Z4RZ Z 2 ++ = +∞ y’(ZL) - 0 + y(ZL) 2 22 CC4RZZ 2R  +−    Từ bảngbiếnthiênta đượcymin ⇔ 22 CC L ZZ4R Z 2 ++ = Thaygiátrị củaZL ta được: ymin = 2 2222 CCC 4R 4R2Z2ZZ4R +++ = () 2 2 22 CC 4R Z4RZ +− Suy ra: URL max = min U y = 22 CCC L 2URU Z4RZZ 1 Z = +− BÀI TẬP VẬN DỤNG Câu 1: Cho mạch điện như hình vẽ Điện áp giữa hai đầu AB có biểu thức u200cos100t =π (V) . Cuộn dây thuần cảm có L thay đổi được, điện trở R = 100Ω, tụ điện có điện dung 410 CF = π . Xác định L sao cho điện áp hiệu dụng giữa hai điểm M và B đạt giá trị cực đại, tính hệ số công suất của mạch điện khi đó. Hướng dẫn: MC A BR L V

DẠYKÈMQUYNHƠNOFFICIAL 304 Dung kháng: C 4 11 Z100. C10 100. ===Ω ω π π Cách giải 1: Phương pháp đạo hàm Ta có: () () AB ABAB MBLL 22 22 LC CC 2 LL UUU UIZZ RZZ11y RZ2Z1 ZZ ==== +− +−+ Nhận thấy LmaxminUy ⇔ và Lmax min U U y = với () () 22222 CCCC 2 LL 11 yRZ2Z1RZx2Zx1 ZZ =+−+=+−+ (với L 1 x Z = ) Khảo sát hàm số y: Ta có: ( )22 CCy'2RZx2Z =+− () 22 C CC 22 C Z y'02RZx2Z0x RZ =  +−=  = + Bảng biến thiên: x 0 C 22 C Z RZ + +∞ y’-0 + y miny  ymin khi C 22 C Z x RZ = + hay 22 22 CC 22L LCC ZRZ 1100100 Z200 ZRZZ100 + + =  ===Ω + L Z2002 L 100  === ωππ H . Hệ số () () 2222 LC RR1002 cos Z2 RZZ100200100 ϕ==== +−+− . Cách giải 2: Phương pháp dùng tam thức bậc hai Ta có: () () AB ABAB MBLL 22 22 LC CC 2 LL UUU UIZZ RZZ11y RZ2Z1 ZZ ==== +− +−+ Đặt ()222 CC 2 LL 11 yRZ2Z1axbx1 ZZ =+−+=−+ (với L 22 C C 1 x Z aRZ b2Z  =   =+  =−   )

DẠYKÈMQUYNHƠNOFFICIAL 305 I CU U LU RU 1U φ α O P Q 1φ UMB max khi ymin: Vì 22 C aRZ0 =+> nên tam thức bậc hai đạt cực tiểu khib x 2a =− hay () 22 22 CCC 2222L L CCC 2ZZRZ1 100100 Z200 ZRZZ100 2RZ −+ + =−=  ===Ω ++ LZ 2002 L 100  === ωππ H. Hệ số côngsuất: () () 2222 LC RR1002 cos Z 2RZZ100200100 ϕ==== +−+− . Cách giải 3: Phươngphápdùnggiản đồ Fre-nen. Đặt RLC 1RC UUUU UUU  =++  =+  Tacó: CC 1 R UZ 100 tan1 UR100 ϕ==== 1 4 π  ϕ= . Vì 1122244 πππππ α+ϕ=  α=−ϕ=−= Xéttam giácOPQvà đặt 1β=ϕ+ϕ Theo địnhlýhàm số sin,tacó: L L U UU Usin sinsinsin =  αβα=β VìUvà R 22 1 C U R sin U RZ α== + không đổinênULmax khisinβ cực đạihay sinβ =1 2 π  β= . Vì 11 244 β=ϕ+ϕπππ  ϕ=β−ϕ=−= . Hệ số côngsuất: 2 coscos 42 π ϕ== . Mặtkhác: LC LC ZZ tan1ZZR200 R ϕ==  =+=Ω LZ 2002 L 100  === ωππ H. Dungkháng: C 4 11 Z100. C10 100. ===Ω ω π π Câu 2 (THPT Chuyên ĐHSP Hà Nội lần 7 – 2015): Mạch điện AB gồm R, L, C nối tiếp, uAB =U 2 cosωt(V).Chỉ cóLthay đổi được.KhiL thay đổitừ L=L1 = 2C 1 ω đến L=L2 = C CR1 2 222 ω ω+ thì:

DẠYKÈMQUYNHƠNOFFICIAL 306 A.Cường độ dòng điệnluôntăng. B.Tổngtrở củamạchluôngiảm. C.Hiệu điệnthế hiệudụnggiữahai đầucuộn cảm luôntăng. D.Hiệu điệnthế hiệudụnggiữahaibảntụ luôntăng. Hướng dẫn: KhiLthay đổitừ L=L1 = 2C 1 ω  L1CZZ = :Cộnghưởng KhiLthay đổitừ L=L2 = C CR1 2 222 ω ω+  22 C L2 C RZ Z Z + = .   Chọn C Câu 3: Mạch điện xoay chiều gồm 3 phần tử R, L, C trong đó L thuần cảm thay đổi được có hiệu điện hiệu thế dụng hai đầu mạch không đổi. Khi chỉnh L đến giá trị L = L1 và L = L2 thì mạch có cùng hiệu điện thế hiệu dụng hai đầu cuộn cảm như nhau. Vậy khi chỉnh L = L3 ta đượcmạch cóhiệu điệnthế hai đầucuộn cảm cực đại.Mốiquanhệ giữaL1,L2,L3 là: A.L3 = L1L2 B. 1 L3 2 = 1 L2 2 + 1 L3 2 C. 2 L3 = 1 L2 + 1 L1 D. 2 L3 2 = 1 L2 2 + 1 L3 2 Hướng dẫn: KhichỉnhL đếnL=L3 thìUL cực đạisuyraZL3 = R2 +ZC 2 ZC KhichỉnhL đến2giátrị L=L1 hoặcL=L2 thìUL như nhaukhông đổivậytacó: UL1 =UL2 ⇔ I1.ZL1 = I2.ZL2 ⇔ ZL1 Z1 = ZL2 Z1 ,bìnhphươngquy đồngta được:  ZL1 2    R2 +(ZL2 ZC )2    =ZL2 2    R2 +(ZL1 ZC )2    Biến đổibiểuthứcta được: R2 +ZC 2 ZC = 2.ZL1ZL2 ZL1 + ZL2  ZL3 = 2.ZL1ZL2 ZL1 + ZL2  2 ZL3 = 1 ZL1 + 1 ZL2  2 L3 = 1 L1 + 1 L2 . Chú ý: Khảo sát và tính toán tương tự với C ta có C3 = 1 2 (C1 + C2) Câu 4: Cho mạch điện RLC mắc nối tiếp theo thứ tự R, L, C trong đó cuộn dây thuần cảm có độ tự cảm Lthay đổi được.Thay đổiL ngườitathấykhi 1 5 LLH == π vàkhi 2 1 LLH 2 == π thì cường độ dòng điện trên đoạn mạch trong hai trường hợp là như nhau. Để công suất tiêuthụ củamạch đạtcực đạithìLcógiátrị: A. 11 H π B. 11 H 4π C. 11 H 2π D. 11 H 3π Hướng dẫn: Cách giải 1: Tacó: () ()1 2 12 2222 LCLC UU II RZZRZZ =⇔= +−+− ( ) ( )12 22 LCLC ZZZZ ⇔−=−

DẠYKÈMQUYNHƠNOFFICIAL 307 Vì 12 LLZZ ≠ nên () 12 12 LL LCLCC ZZ ZZZZZ 2 + −=−−  = (1) KhiP =Pmax thìmạchxảyrahiệntượngcộnghưởng điện LCZZ = (2) Từ (1)và (2)ta được: 12 LL 12 L 51 ZZ LL 112 ZLH 2224 ++ + ππ =  === π   Chọn B Cách giải 2: Ngoại trừ R biến thiên, còn với các trường hợp L và C hay ω mà cho cùng I, P, ... thì điều tương tự nhau, vì vậy, mặc dù bài toán cho hai giá trị của L cho cùng I nhưng tìm L để Pmax thìtachỉ cầngiảimộttronghaitrườnghợpsau: + Cóhaigiátrị củaL chocùng I,tìm L để Pmax. + Cóhaigiátrị củaL chocùngP,tìm L để Pmax Tasẽ giảibàitoánnàytrongtrườnghợpthứ nhất. Tacó: () 22222 LCLLCC UU I RZZZ2ZZRZ == +−−++ Nhận thấy, I phụ thuộc kiểu hàm bậc hai theo ZL, vì vậy phải có mối quan hệ hàm bậc hai: ()CT12 1 xxx 2 =+ tứclà 12 LL 12 L 51 ZZ LL 112 ZLH 2224 ++ + ππ =  === π .    Chọn B Chú ý: 1. Mạch RLC có C biến đổi cho hai giá trị C1 và C2 a. Có hai giá trị C1 và C2 cho độ lệch pha giữa dòng điện và hiệu điện thế trong hai trường hợp là như nhau. Từ 1 2 2222 1212LCLC coscosZZR(ZZ)R(ZZ) ϕ=ϕ  =  +−=+− 12 LCLC ZZ(ZZ) −=−− b. Ngoài ra, khi gặp bài toán C biến thiên C1, C2 làm cho hoặc I1 = I2 hoặc P1 = P2 thì cảm kháng cũng được tính trong trường hợp 12φφ = tức là: 12 CC L ZZ Z 2 + = . c. Khi 1CC = và 2CC = (giả sử 2CC > ) thì 1i và 2i lệch pha nhau Δφ . Gọi 1φ và 2φ là độ lệch pha của ABu so với 1i và 2i thì ta có 1212 φφφφφ >  −=∆ + Nếu 12II = thì 12 Δφ φφ 2 =−= + Nếu 12II ≠ thì tính 12 12 12 tan φ tan φtan(φφ )tan Δφ1tan φ tan φ −== + d. Nếu C biến thiên, có hai giá trị C1, C2 làm cho hoặc I1 = I2 hoặc P1 = P2 hoặc 12φφ = . Tìm C để có cộng hưởng điện.

DẠYKÈMQUYNHƠNOFFICIAL 308 Ta có: 12 12 CCC 1212 111112CC Z(ZZ)C 2C2CCCC  =+  =+  = + e. Nếu C biến thiên, có hai giá trị C1, C2 làm cho hiệu điện thế trên tụ bằng nhau trong hai trường hợp. Tìm C để hiệu điện thế trên tụ đạt giá trị cực đại thì: 12 12 12 CCC 11111CC C(CC)C Z2ZZ22  + =+  =+  =   2. Mạch RLC với L biến đổi, có hai giá trị L1 và L2 a. Nếu L biến thiên, có hai giá trị L1, L2 cho hoặc I1 = I2 hoặc P1 = P2 hay cho cùng độ lớn của sự lệch pha của u và i thì dung kháng CZ tính được bao giờ cũng bằng trung bình cộng của cảm kháng LZ theo biểu thứ : 12 LL C ZZ Z 2 + = b. Nếu L biến thiên, có hai giá trị L1, L2 cho hoặc I1 = I2 hoặc P1 = P2 hay cho cùng độ lớn của sự lệch pha của u và i. Tìm L để có cộng hưởng điện maxuiuimaxmax (II,,0,(cos)1,PP,...) =ϕ=ϕ∆ϕ=ϕ=ϕ=ϕ== thì bao giờ ta cũng thu được: 12LL L 2 + = . c. Nếu cuộn dây thuần cảm với L biến thiên, có hai giá trị L1, L2 cho cùng một hiệu điện thế trên cuộn dây. Để hiệu điện thế trên cuộn dây đạt cực đại thì L có giá trị là: 12 1111 L2LL  =+  hay 12 12 2LL L LL = + Câu 5: Cho mạch điện RLC mắc nối tiếp theo thứ tự R, L, C trong đó cuộn dây thuần cảm có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch hiệu điện thế xoay chiều có tần số f. Thay đổi L người ta thấy khi 1 3 LLH == π và khi 2 1 LLH 2 == π thì hiệu điện thế trên cuộn dâythuầncảm lànhư nhau. Để hiệu điệnthế trên cuộndây đạtcực đạithì Lcógiátrị: A. 7 H 6π B. 6 H 7π C. 6 H 5π D. 5 H 6π Hướng dẫn: Cách giải 1: KhiLbiếnthiên, để hiệu điệnthế trêncuộndâythuầncảm đạtcực đạithì: () 222222 CCC22 L C CC RZRZRZ ZLRZC ZZ1 . C +++ =  ===+ ω ω ω (1) Mặckhác: 121212 LL1L2LLL 12 UU UUIZIZZZ ZZ =⇔=⇔= () () 12 2222 1C2C LL RLZRLZ ωω ⇔= +ω−+ω−

DẠYKÈMQUYNHƠNOFFICIAL 309 2 2 1 2 22222222 1 2 1C2C LL LL RL2ZRL2Z CC ⇔= +ω−++ω−+ 2222222222 2 1 2C11C2 LL RL2ZLRL2ZL CC  ⇔+ω−+=+ω−+   ()() ()222222 12C1221 2 LLRZLLLL C ⇔−+=− ()()() ()22 1212C1212 2 LLLLRZLLLL C ⇔+−+=− ()() 22 12C12 2 LLRZLL C ⇔++= () 22 12 C 12 2LL RZC LL ⇔+= + (2) Từ (1)và (2)suyra: 12 12 31 2LL2..6 2 LH 31 LL7 2 ππ === +π + ππ .  Chọn B Cách giải 2: Bài toán xét sự phụ thuộc của UL theo L nên ta có: () () L LL 222 LC 22 CC LL UZU UIZ RZZ11 RZ2Z1 ZZ === +−  +−+   Nhận thấy ngay, UL phụ thuộc kiểu hàm bậc hai theo L 1 Z , vì vậy phải có mối quan hệ hàm bậc hai: ()CT12 1 xxx 2 =+ tức là: 12 12 LLL12 312LL2.. 11116 2 LH 31 Z2ZZLL7 2  =+ππ  ===  +π + ππ .   Chọn B Chú ý: Tương tự cho bài toán khi C biến thiên, có hai giá trị C1, C2 làm cho hiệu điện thế trên tụ trong hai trường hợp bằng nhau. Tìm C để hiệu điện thế trên tụ đạt cực đại, theo phương pháp đánh giá kiểu quan hệ hàm số ta thu ngay được kết quả như sau: () () C CC 222 LC 22 LL CC UZU UIZ RZZ11 RZ2Z1 ZZ === +−  +−+   Nhận thấy ngay, UC phụ thuộc kiểu hàm bậc hai theo C 1 Z , vì vậy phải có mối quan hệ hàm bậc hai: ()CT12 1 xxx 2 =+ tức là: () 12 12 CCC 11111 CCC Z2ZZ2  =+  =+   .

DẠYKÈMQUYNHƠNOFFICIAL 310 Câu 6: Đặt điện áp u = U0cos100πt (V) vào đoạn mạch R, L, C nối tiếp trong đó cuộn cảm thuần và L thay đổi được. Khi 1 3 LLH 2 == π hoặc 2 17 LLH 2 == π thì hiệu điện thế 2 đầu cuộn cảm bằng nhau. Khi 3LL = thì ( )LC max SU2U125V =+= và mạch tiêu thụ công suất là P1. Khi L = L4 thì điện áp hiệu dụng 2 đầu cuộn cảm đạt giá trị cực đại và khi này mạch tiêu thụ công suất là P2. Biết rằng 2 1 P 25 P153 = . Khi L = L5 thì công suất tiêu thụ trên toàn mạch đạt giá trị cực đại và giá trị cực đại đó có giá trị xấp xỉ là: A. 175VB. 168VC. 191VD. 182V Hướng dẫn: Cách giải 1: Ta có: 1 12 2 L1 LL L2 3 ZL100.150 2 UU 17 ZL100.850 2  =ω=π=Ω  π  =  =ω=π=Ω π Để ULmax thì: Lm L1L2LmL1L2 112111111 +=Z++255 ZZZ2ZZ2150850    ===Ω    (1) Mặt khác: () LC LC 22 LC SU2UU(Z+2Z) R+(ZZ) =+= Xét biểu thức 2 LC 22 LC U(Z+2Z)YS R+(ZZ) == . Để Smax thì Ymax nên ta xét Y’. Đạo hàm ta được 222 LCCLC 222 LC 2U(Z+2Z)(R+3Z3ZZ) '0 R+(ZZ) ==   Y 22 22 C CLCL C R+3Z R+3Z3ZZ0Z= 3Z  −=  (2) Thay vào S ta được Smax = 22 C U 9Z+R R = 125V (3) Và P1 = 2 2 2 C UR R R+ 3Z    (4) Với ZL4 để UL max ⇔ ZL4 = ZLm = 255Ω 22 C C R+Z = Z (5) Thay vào công thức của công suất ta được P2 = 2 2 2 C UR R R+ Z    (6)

DẠYKÈMQUYNHƠNOFFICIAL 311 Từ (4) và (6) ta có 2 2 2C 2 1 2 C R 1+ P9Z 25 == R P153 1+ Z  R = 4ZC Thay vào (5)  ZC = 15Ω, R = 60Ω, thay vào (3)  U = 100V. Vậy khi L thay đổi để Pmax thì 22 max U100 P166,67W. R60 ===   Chọn B Cách giải 2: Thay đổi L để UL max Ta có: L LL 222 2 LC C 2 LL UZU UIZ R(ZZ) ZR 1 ZZ === +−  +−  Đặt 22 C 2 LL RZ y1ZZ  =+−  Để ULmax thì ymin Đặt L 1 x Z = thì 222 CC y(RZ)x2Zx1 =+−+ . Vì 22 C aRZ0 =+> nên: C min 22 C bZ yx 2aRZ ⇔=−= + 22 C Lmax C RZ Z Z +  = . Khi đó: 222 2222 C LC C C RZ ZR(ZZ)RZ Z  + =+−=+−  222222 2 C22 C 2 CCC RZ RR RZRR1 ZZZ  + =+−=+=+  Công suất tiêu thụ: 222 2 2 22 2 22 CC UURU PIRR Z RR 1R1R ZZ ====  ++   Khi L1L2 L1L21L12L2 12 UZUZ UUIZIZ ZZ =⇔=⇔= L1L2 2222 L1CL2C ZZ R(ZZ)R(ZZ) ⇔= +−+− 2 2 L1 L2 222222 L1L1CCL2L2CC ZZ RZ2ZZZRZ2ZZZ ⇔= +−++−+ Theo như trên thay 22 CLCRZZZ += trong đó L sao cho ULmax ta có: 22 L1L2 22 LCL1L1CLCL2L2C ZZ ZZZ2ZZZZZ2ZZ = +−+− ( ) ( )2222 L1LCL2L2CL2LCL1L1C ZZZZ2ZZZZZZ2ZZ ⇔+−=+−

DẠYKÈMQUYNHƠNOFFICIAL 312 2222 L1LCL1L2CL2LCL2L1C ZZZ2ZZZZZZ2ZZZ ⇔−=− ( ) ( )22 L1L2LCL1L2CL1L2 ZZZZ2ZZZZZ ⇔−=− Vì L1L2ZZ ≠ nên suy ra L1L2 L L1L2 2ZZ Z ZZ ⇔= + Thay đổi L để ( )LC max SU2U =+ Ta có: () LC LCLC LC U(Z2Z) U SU2UIZ2Z ZZ Z2Z + =+=+== + 22222 LCLLCC 222 LCLLCC UUU R(ZZ)RZ2ZZZA (Z2Z)Z4ZZ4Z === +−+−+ +++ Đặt 222 LLCC 22 LLCC RZ2ZZZ A Z4ZZ4Z +−+ = ++ . Để Smax thì Amin. Đặt LtZ = (t > 0). Thì 222 CC 22 CC t2ZtRZ A t4Zt4Z −++ = ++ Lấy đạo hàm hàm số trên với biến t ta được: () ( ) () 22232 CCCC 222 CC 6Zt6Z2Rt12Z4RZ A't t4Zt4Z = ++ . ( ) ( ) 22232 CCCC A't06Zt6Z2Rt12Z4RZ0 =⇔−−−−= (1) Ta có: 42222222 CCC C 324Z72RZ(18Z2R)018Z2R∆=+=+>  ∆=+ Phương trình (1) có 2 nghiệm phân biệt: 222222 CCC 1 CC 2222 CC 2 C C 2R6Z18Z2RR3Z t 0 12Z3Z 2R6Z18Z2R t2Z0 12Z  −+++ ==>   ==−<   Ta thấy vì t > 0 nên chỉ nhận nghiệm t1 vì C a6Z0 => và 12tt >  hàm số đạt giá trị cực tiểu tại 22 C 1 C R3Z tt 3Z + == . Khi đó: 22 C 222C CCCC min 22 22 CCC C C C R3Z 22Z A(t2ZtZR)'2t2Z3Z (t4Zt4Z)'2t4Z R3Z 24Z 3Z  +  −++−  === +++  + + 

DẠYKÈMQUYNHƠNOFFICIAL 313 222 CC 2 2 C 222 22 CC C 2 C 2R6Z6Z 9Z R 2R6Z12Z R9Z 9Z +− == ++ + . Suyra: () 2 C maxLC max2 2 22 C U9Z SU2UU1. RR R9Z =+==+ + Khi đótacó: 222 42 2222 C22 LC C 22 CCC R3Z RR ZR(ZZ)RZRR1 3Z9Z9Z  + =+−=+−=+=+  Lúcnày 222 2 2 22 2 22 CC URURU PIR Z RR 1R1R 9Z9Z ====  ++   Tacó: 1 2 L1 L2 3 ZL100.150 2 17 ZL100.850 2  =ω=π=Ω  π  =ω=π=Ω π L1L2 L4 1L2 2ZZ Z225. ZLZ  ==Ω + Mặtkhác: 2 2 2C 2 1 2 C R 1+ P9Z 25 == R P153 1+ Z Giảiphươngtrìnhtrênvới ẩnlà C R Z ,suyra CR4Z = . Khi đó: () 2 C maxLC max2 9Z 5 SU2UU1UU100V. R4 =+=+=  = Suyra: 2 2 22 C L4 C R RZR 1617R ZR60. R Z4 4 + + ===  =Ω Thay đổiL để Pmax màP=I2RcóRkhông đổi  Pmax khiImax. Khi đómạchxảyrahiệntượngcộnghưởng  2 max U P166,7W. R == Chọn B Câu 7: Cho mạch điện nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L thay đổi được, tụ điện C và điện trở R. Điện áp đặt vào hai đầu đoạn mạch ( )u1006cos100t V=π . Khi ULmax thì điệnáphiệudụngtrên đoạnmạchchứaRClà100V.Tínhgiátrị ULmax ?

DẠYKÈMQUYNHƠNOFFICIAL 314 Hướng dẫn: KhiLthay đổi để ULmax thì 22 C RC4 Lmax RLmaxRC R URZ U.U UUUU.U3.10 RU + ==  == (1) Mặtkháctalạicó: ()2 22222 RLmaxCRLmaxCLmaxC UUUUUU2UUU =+−=+−+ 22 RCCLmaxLmax U2UUU =−+ 24 LmaxCLmax U2UU2.10 −= (2) Mà 2224 RCRC UUU10 =+= (3) Giảihệ (1),(2)và(3)tacóUR =86,6024V  ULmax =200V. Câu 8: Đặt điệnápxoaychiềucófkhông đổivàohai đầu đoạnmạchABgồm điệntrở thuầnR, tụ điệnCvàcuộncảmthuầnL(Lthay đổi được).KhiL=L0 thìULmax .KhiL=L1 hoặcL= L2 thì điện áp hiệu dụng giữa hai đầu cuộn cảm có giá trị như nhau và bằng UL. Biết rằng L Lmax U k U = .Tổng hệ số công suất củamạch AB khiL =L1 vàL =L2 lànk.Hệ số công suất củamạchABkhiL=L0 cógiátrị bằng? A.n 2 B. n 2 C. n 2 D.n Hướng dẫn: KhiL=L0 thìUL =ULmax: 0 22 C L C 22 C Lmax RZ Z Z URZ U R  + =   + =  (1) Khi L=L1 vàL=L2 thìUL1 =UL2 =UL: L1 22 L1C Z R(ZZ) +− = L2 22 L2C Z R(ZZ) +−  22 L1C 2 L1 R(ZZ) Z +− = 22 L2C 2 L2 R(ZZ) Z +−  22 C 2 L1 RZ Z + C L1 2Z Z = 22 C 2 L2 RZ Z + C L2 2Z Z  (R2 + 2 CZ )( 2 L1 1 Z 2 L2 1 Z )=2ZC( L1 1 Z L2 1 Z )  L1 1 Z + L2 1 Z = C 22 C 2Z RZ + = L0 2 Z  L0 2 Z = L1 1 Z + L2 1 Z (2) Tacó: UL =I1ZL1 = L1 1 UZ Z = L2 2 UZ Z Mặtkhác: L Lmax U U = 1 R Z L1 22 C Z RZ + = L1 22 C Z RZ + cosϕ1 =k  cosϕ1 = 22 C L1 kRZ Z +

DẠYKÈMQUYNHƠNOFFICIAL 315 L Lmax U U = 2 R Z L2 22 C Z RZ + = L2 22 C Z RZ + cosϕ2 =k  cosϕ2 = 22 C L2 kRZ Z + Suyra:cosϕ1 +cosϕ2 = 22 C L1 kRZ Z + + 22 C L2 kRZ Z + =nk  L1 1 Z + L2 1 Z = 22 C n RZ + (3) Mà:cosϕ0 = 0 R Z = () 22 L0C R RZZ +− = 222 2 C C C R RZ RZ Z  + +−  = 4 2 2 C R R R Z + = C 22 C Z RZ + Từ (2)và(3) 22 C n RZ + = L0 2 Z  22 C L0 RZ Z + = n 2 cosϕ0 = C 22 C Z RZ + = 22 CC 22 C ZRZ RZ + + = 22 C L0 RZ Z + = n 2 Chọn C Câu 9: Cho mạch điện như hình vẽ. Trong đó 410 R1003, CF 2π =Ω= .Cuộndâythuầncảmcó độ tự cảmLthay đổi được. Điệnápgiữahai đầu đoạnmạchlàu=200cos100πt(V).Xác định độ tự cảmcủacuộndâytrongcáctrườnghợpsau: a.Hệ số côngsuấtcủamạchcosφ =1. b.Hệ số côngsuấtcủamạchcosφ = 3 2 . c. ĐiệnáphiệudụngtrêncuộncảmLlàcực đại. Hướng dẫn: Tacó C 4 R1003 11 Z200. 10ωC100π 2π  =Ω   ===Ω    a.Hệ số côngsuất LC 24 2 R112 cos11RZZZL ZC10 (100). 2 ϕ=⇔=⇔=⇔=  === ωπ π π H C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 316 b.Khi 3R3 cos2R3Z 2Z2 ϕ=⇔=⇔= 222222 LCLC 4R3Z3R(ZZ)R3(ZZ)  ⇔==+−⇔=−  L LC L 3 LHZ300R ZZ Z10013 LH  ==Ω π  −=±⇔⇔  =Ω  = π c.Theochứngminhtrênta đượckhi 22 22 C L C RZ (1003)20035 Z350LH Z20010 + + ===Ω  = π thì điệnáphiệudụnghai đầuL đạtcực đại.Giátrị cực đại: 2222 LmaxC U100210042 URZ(1003)200V. R 31003 =+=+= Câu 10: Cho mạch điện RLC, L có thể thay đổi được, điện áp hai đầu mạch là u1702cos100t (V)=π .Cácgiátrị 410 R80, CF 2π =Ω= .TìmL để: a.Mạchcócôngsuấtcực đại.TínhPmax b.MạchcócôngsuấtP=80W. c. Điệnáphiệudụnggiữahai đầuL đạtcực đại.Tínhgiátrị cực đại đó. Hướng dẫn: Tacó C 4 R80 11 Z200 10ωC 100π 2π =Ω   ===Ω    a. Công suất củamạch P = I2R. Do R không đổi nên: maxminLCLC 2 PZZZ0ZZ200LH ⇔⇔−=⇔==Ω  = π Khi đó: 222 2 maxmax 2 UU170 PIRRW. RR80 ==== b. Tacó: 22 2L 222 LL U170.80Z350 PIR80R8080 Z80(Z200)Z50 =Ω ==⇔=⇔=⇔  +−=Ω  Từ đó tatìm đượchai giá trị củaL thỏamãn đề bài là: 3,5 LH 1 LH 2  = π  = π

DẠYKÈMQUYNHƠNOFFICIAL 317 c. Điện áp hiệu dụng hai đầu L đạt cực đại khi 22 22 C L C RZ 80200232 Z232LH. Z200100 + + ===Ω  = π Giátrị cực đại 2222 LmaxC U170 URZ802008529V. R80 =+=+= Câu 11: Cho mạch điện xoay chiều gồm RLC mắc nối tiếp,cuộn cảm thuần có độ tự cảm thay đổi được. Đặt vào hai đầu đoạn mạch điện áp xoay chiều u=100cos100πt. Điều chỉnh độ tự cảm để điện áp trên hai đầu cuộn cảm đạt giá trị cực đại là ULmax thì điện áp hiệu dụng trên hai đầu tụ điện làUC =200V. Giátrị ULmax là A. 300V B. 100V C. 150V D. 250V Hướng dẫn: Cách giải 1: Nhận thấy UL =ULmax khi 22 C L C RZ Z Z + =  ULUC =UR 2 +UC 2 (1) U2 =UR 2 +(UL – UC)2 =UR 2 +UL 2 +UC 2 – 2ULUC (2) Từ (1)và (2): U2 =UL 2 – ULUC  (100)2 =UL 2 – 200UL  UL 2 – 200UL – 30000 =0  ULmax =300V.    Chọn A Cách giải 2: L thay đổi để ULmax khi đó: uRC lệch phavới u là 2 π . Dùng giản đồ: hệ thứclượng đường cao trong tam giácvuông: U2 =UL(UL – 200). Suy ra: ULmax =300 V. Chọn A Câu 12: Đặt điện áp xoay chiều có giá trị hiệu dụng vào hai đầu đoạn mạch RLC có L thay đổi. Khi điện áp hiệu dụng ULmax thì UC =200V. Khi đó ULmax có giátrị: A. 300V B. 150V C. 250V D. 400V Hướng dẫn: Cách giải 1: L thay đổi màULmax thì: (1) Khi đó: 22 C2222 LLCCLCRC C RZ ZZZRZUUUU Z + =⇔=+⇔=+ (2) Thay (2)vào (1): 2224L LLCLL L U300V UUUUU200U3.100( U100V ( = =+⇔−−=   =− nhaän) loaïi)   Chọn A Cách giải 2: Tacó: () 2 L L 22 LC UZ U RZZ = +−  UL =ULmax khi 22 C L C RZ Z Z + = Khi đó CLmax CCC CLC UU UU10033 ZZZZ ZZZU2002 ==⇔=== 6 3 U1003V = 2222 LRC UUUU =++

DẠYKÈMQUYNHƠNOFFICIAL 318 ()2 222222 LCCLLCCC 33 RZZZRZ2ZZZZ0 44 ⇔+−=⇔+−+−= 22 LLCCLC 33 ZZZZ0ZZ 42 ⇔−−=⇔= Vậy CLmaxC LmaxLC CLC UUU 3 UZU300V. ZZZ2 =⇔===    Chọn A Câu 13: Đặt điện áp xoay chiều u = U0cos100πt (V) vào hai đầu đoạn mạch mắc nối tiếp gồm R, C và cuôn dây thuần cảm L thay đổi được. Điều chỉnh L để điện áp hiệu dụng ở hai đầu L đạt giá trị cực đại và bằng 100V, khi đó điện áp 2 đầu tụ bằng 36V. Giá trị hiệu dụng 2 đầu đoạn mạch là: A. 64V B. 80V C. 48V D. 136V Hướng dẫn: Cách giải 1: Điều chỉnh L để điện áp hiệu dụng ở hai đầu L đạt giá trị cực đại 22 C 22 LmaxLmaxRC R RZ U UUUUU RU + =⇔=+ Mạch RLC (cuộn dây thuần cảm) có L thay đổi và UL max thì taluôn luôn có: 22 LCRC UUUU =+ và 22 LmaxRC R U UUU U =+ Tadùng công thức: 22 LCRC UUUU =+ suy raUR =48V. Từ công thức: 2222 LmaxRC R UU UUU1004836U80V. U48 =+⇔=+  =    Chọn B Cách giải 2: Khi L biến thiên màULmax tacó giản đồ như hình bên. Theo hệ thứclượng củatam giácvuông tacó:  =80(V).  Chọn B Câu 14: Đoạn mạch xoay chiều AB gồm điện trở R nối tiếp cuộn dây thuần cảm có L thay đổi được, điện áp hai đầu cuộn cảm được đo bằng một vôn kế có điện trở rất lớn. Khi L = L1 thì vôn kế chỉ V1, độ lệch pha giữa điện áp hai đầu đoạn mạch với dòng điện là ϕ1, công suất của mạch là P1. Khi L = L2 thì vôn kế chỉ V2, độ lệch pha giữa điện áp hai đầu đoạn mạch và dòng điện là ϕ2, công suất của mạch là P2. Biết ϕ1 + ϕ2 = 2 π và V1 = 2V2. Tỉ số 2 1 P P là: A. 4 B. 6 C. 5 D. 8 2 RCCL 222 RCL UU.U UUU  =  =−  2 LCLUUUU =− LU RU CU U

DẠYKÈMQUYNHƠNOFFICIAL 319 Hướng dẫn: Tacó: L1 1 L2 212 2 12 Z tan R Z 1 tantancotan Rtan 2  ϕ=   ϕ=  ϕ=ϕ= ϕ π ϕ+ϕ=  . Suy raR2 =ZL1ZL2 Gọi U là điện áp hiệu dụng đặt vào hai đầu đoạn mạch () () 1 22 1 L1L1L2L1 2 22 2 L2L2L2L1 UUU I ZZZZ RZ UUU I ZZZZ RZ  === ++   === ++ () () L1 11L1 L1L1L1 L2 22L2 L2L1L1 UZ UIZ ZZZ UZ UIZ ZZZ  == +   == + Mặt khác: 12L1L2L1L2 U2UZ2ZZ4Z =⇔=⇔= Mà: 2 2 11 22L1L2 22 2211L2L2 PIR PIZ4Z 4. PIZZPIR  =  ==== =  Chọn A Câu 15: Đặt điện áp xoay chiều có giá trị hiệu dụng và có tần số không thay đổi vào hai đầu đoạn mạch gồm điện trở R, cuộn cảm thuần L và tụ điện C ghép nối tiếp. Giá trị của R và C không đổi. Thay đổi giá trị của L nhưng luôn có 2 2L R C < thì khi L = L1 = 1 2π H, điện áp hiệu dụnggiữahai đầucuộncảmthuầncóbiểuthứclàuL1 =U1 cos(ωt+ ϕ1);khiL=L2 = 1 π H, thì điện áp hiệu dụng giữa hai đầu cuộn cảm thuần có biểu thức là uL2 = U1 cos(ωt + ϕ2); khi L = L3 = 2 π H, thì điện áp hiệu dụng giữa hai đầu cuộn cảm thuần có biểu thức là uL3 = U2 cos(ωt + ϕ3). So sánh U1 và U2 ta có hệ thức đúng là: A. U1 < U2 B. U1 > U2 C.U1 = U2 D. U1 = U2 Hướng dẫn: Ta có L LL 22 LC UZU UZ Z R(ZZ) == +− Do L2 = 2L1  ZL2 = 2ZL1 = 2ZL L3 = 4L1  ZL3 = 4ZL1 = 4ZL 2 2 2 2

DẠYKÈMQUYNHƠNOFFICIAL 320 U1 = UL1 = UL2  L 22 LC UZ R(ZZ) +− = L 22 LC 2UZ R(2ZZ) +−  4[R2 +(ZL – ZC)2] = R2 +(2ZL – ZC)2  3R2 + 3ZC 2 – 4ZLZC = 0  3(R2 + ) = 4ZLZC Mặt khác: U2 = UL3 = L 22 LC 4UZ R(4ZZ) +− Để so sánh U1 và U2 ta xét hiệu A = U1 2 – U2 2 = U2ZL 2 2222 LCLC 116 R(ZZ)R(4ZZ)   +−+−  Dấu của biểu thức A tương đương với dấu của biểu thức: B = R2 + (4ZL – ZC)2 – 16[R2 + (2ZL – ZC)2] = 24ZLZC – 15(R2 + ) = 24ZLZC – 20ZLZC = 4ZLZC > 0 Vì do 2 2L R C <  0 < R2 < 2ZLZC Từ đó suy ra B > 0  A > 0  U1 2 – U2 2 > 0  U1 > U2    Chọn B Câu 16: Đặt điện áp xoay chiều u1102cost =ω (V) luôn ổn định vào hai đầu đoạn mạch AB gồm điện trở thuần R, tụ điện có điện dung C không đổi và cuộn cảm thuần có hệ số tự cảm thay đổi được mắc nối tiếp theo thứ tự trên. M là điểm nối giữa điện trở R và tụ điện C. Khi L = L1 thì điện áp hiệu dụng giữa hai đầu MB là U1; khi L = L2 thì điện áp hiệu dụng giữa hai đầu MB là 21 U3U = và pha của dòng điện trong mạch thay đổi một lượng 900 so với khi L = L1. Điện áp hiệu dụng giữa hai đầu điện trở thuần R khi L = L1 là: A. 110V. B. 110 3 V. C. 55 3 V. D. 55V. Hướng dẫn: Ta đi xét bài toán tổng quát như sau: ()()( ) ()() π ϕϕ=   = i1i2 MB2MB1 ; 2 UkU Ta có: + ( ) =+−=+ 2 2222 RLCRMB UUUUUU + ()()( ) ππ ϕϕ=  ϕ+ϕ=  ϕ+ϕ=22 i1i21212 ;coscos1 22 () () ()()⇔+=⇔=+ 22 R1R2 222 22R1R2 UU 1UUU UU Suy ra: ()() ( ) ()()=+−⇔= 222222 R1MB2R1MB2UUUUUU ()()() ()⇔=⇔= 2 2222R1 R1MB1MB1 2 U UkUU k Mặt khác: ()()() () ()=+=+  = + 2 2222R1 R1MB1R1R1 2 2 U kU UUUUU k k1 Vậy: ()() () ()  =  =  == =  + 21 R1 2 MB2MB1 U3U 1103 k3U553V. UkU 31    Chọn C 2 CZ 2 CZ

DẠYKÈMQUYNHƠNOFFICIAL 321 Câu 17: Đặt điện áp xoay chiều ổn định 220V – 50Hz vào 2 đầu mạch AB gồm điện trở thuần R = 50Ω, tụ điện có dung kháng C = 100Ω và cuộn cảm thuần L nối tiếp, L thay đổi được. Thay đổi L để điện áp hiệu dụng URL max. Giá trị URL max có giá trị bằng bao nhiêu? A. 431V B. 401V C. 531V D. 501V Hướng dẫn: Ta có: RLmax 2222 CC 2UR2.220.50 U 531V. ZZ4R1001004.50 == −++−++ ≃    Chọn C Câu 18: Cho đoạn mạch RLC mắc nối tiếp, cuộn dây thuần cảm có độ tự cảm L thay đổi được. Hiệu điện thế xoay chiều 2 đầu đoạn mạch có biểu thức u2002cos100tV 8 π =π+  . Khi 1 1 LH = π hoặc 2 3 LH = π thì thấy cường độ dòng điện trong mạch có giá trị hiệu dụng bằng nhau và bằng 2A . Điều chỉnh L để hiệu điện thế hiệu dụng URL min , giá trị cực tiểu này bằng bao nhiêu? Hướng dẫn: Ta có: 1 2 L1 L2 1 ZL100.100 3 ZL100.300  =ω=π=Ω  π  =ω=π=Ω π Vì tồn tại hai giá trị của L làm cường độ dòng điện qua mạch bằng nhau nên ta có 12 LL C ZZ100300 Z200. 22 + + ===Ω Mặt khác: () 2222 LC U200 I2R100. RZZR100 ===  =Ω +−+ Khi thay đổi L để RLminU thì ta lại có: RLmin 2222 C UR200.100 U405V. RZ100200 === ++ Câu 19: Cho đoạn mạch RLC mắc nối tiếp, cuộn dây thuần cảm có độ tự cảm L thay đổi được. Điều chỉnh giá trị của L để tổng điện áp ( )LRC max UU + thì ( )LRC max UU3U += . a. Hệ số công suất của mạch có giá trị bằng bao nhiêu? b. Biết công suất tiêu thụ của đoạn mạch là 100W. Khi điều chỉnh L để Pmạch max thì Pmạch max có giá trị bằng bao nhiêu? Hướng dẫn: a. Ta có: () LRC max C U2 UU3U R 1cosarctan Z +==    .

DẠYKÈMQUYNHƠNOFFICIAL 322 Đẳng thức xảy ra LCZZ⇔− Với C LC C R7 tanarccos Z9 9 ZZ 7 7 RtanarccosZ 9   =    =    =   Suy ra: () C 2 2 22 LC CCC 7 tanarccosZ R 229 cos . 3RZZ 79 tanarccosZZZ 97    ϕ=== +−  +−   b. Khi điều chỉnh L để Pmạch max thì Pmạch max có giá trị bằng max 22 P100 P112,5W. cos 22 3 === ϕ    Nhận xét: Khi điều chỉnh L để Pmạch max thì Pmạch max được xác định theo công thức: () max 2 2 LRC 2max PP P . cos U2 arccos1 UU cos 2 == ϕ         +         Áp dụng cho bài toán trên ta có: max 2 2 2 P100 P 112,5W. cos arccos1U2 3U cos 2 === ϕ                II. Sự thay đổi C trong mạch RLC mắc nối tiếp Xét mạch điện xoay chiều có hiệu hiệu thế hai đầu ổn định: 0u uUcos(t) =ω+ϕ (V), với R là điện trở L là một cuộn dây thuần cảm không đổi và C có giá trị thay đổi. Nhận xét: Vì trong công thức tổng trở 2222 LCCL ZR(ZZ)R(ZZ) =+−=+− , do đó ta thấy rằng bài toán thay đổi giá trị C cũng giống như bài toán thay đổi giá trị L. Biểu thức tính LmaxCmaxU, U và LCU,U của hai bài toán trên có dạng tương tự, chỉ đổi vai trò của LU và CU cho nhau. A B CR L

DẠYKÈMQUYNHƠNOFFICIAL 323 1. Khảo sát sự biến thiên của công suất theo dung kháng Ta có công suất toàn mạch là: 2 22 LC UR P R(ZZ) = +− , với R, L là các hằng số, nên công suất của mạch là một hàm số theo biến số ZC. Đạo hàm của P theo biến số ZC ta có: ( )2 CL C 222C LC 2RUZZ P'(Z)P'(Z)0 R(ZZ) =  =  +−  khi LCZZ = Bảng biến thiên: CZ -∞ 0 LCZZ = +∞ ( )CP'Z - 0 + ( )CPZ = 2 max U P R 2 22 L U PR RZ = + 0 Đồ thị của công suất theo giá trị ZC: 2. Có hai giá trị C1 ≠ ≠ C2 cho cùng giá trị công suất Với hai giá trị C1 và C2 cho cùng giá trị công suất ta có 12 0 12 0 CC 12 LC 2 12 CC C2 ZZ CC ZZ 211 2L CC  =+ +==⇔  ω=+  Với giá trị C0 là giá trị làm cho công suất mạch cực đại. 3. Giá trị ZC để hiệu điện thế UCmax Khi 22 L C L RZ Z Z + = thì 22 L Cmax URZ U R + = và 2222 CmaxRL 22 CmaxLCmax UUUU UUUU0  =++  −−=  vì uRL vuông pha với hiệu điện thế hai đầu mạch. ZC ZL = ZCO P Pmax

DẠYKÈMQUYNHƠNOFFICIAL 324 4. Có hai giá trị C1 ≠ C2 cho cùng giá trị UC, giá trị ZC để UCmax tính theo C1 và C2 Khi có hai giá trị C = C1 hoặc C = C2 cho cùng giá trị UC thì giá trị của C làm cho UCmax khi 12 12 CCC 1111CC C Z2ZZ2  + =+  =   Trong đoạn mạch RLC mắc nối tiếp với C có giá trị thay đổi được. Nếu ta gọi ϕ là độ lệch pha của điện áp so với dòng điện, khi ta điều chỉnh giá trị của C thì UCmax ứng với góc ϕmax. Khi đó hai giá trị C1 và C2 của C thì UC đều cho giá trị như nhau và ứng với góc ϕ1 và ϕ2 qua hệ thức liên hệ: ϕ ϕϕ ϕ1 + ϕ ϕϕ ϕ2 = 2ϕ ϕϕmax (đúng với cả trường hợp L có giá trị thay đổi) Chứng minh công thức: ϕ ϕϕ ϕ1 + ϕ ϕϕ ϕ2 = 2ϕ ϕϕmax Xét bài toán tổng quát: Mạch RLC với C biến đổi, mạch chịu tác dụng của điện áp xoay chiều có U và ω không đổi. Gọi ϕ1, ϕ2, ϕ0 là góc lệch pha ứng với ZC1, ZC2, ZC0 ứng với UC1, UC2 = UC1 , UCmax. Khi đó: 2ϕ0 = ϕ1 + ϕ2. 1. Phương pháp hình học: Vẽ (d’) // (d)  xác định 2 vị trí có cùng CU (m) U là vecto U khi CmaxU  (m) U ⊥ (d) và (d’)  ( (m) U , (1) U ) = ( (m) U , (2) U ) = α Khi đó: ϕ0 = β + α, ϕ1 = β , ϕ2 = β + 2α  ϕ1 + ϕ2 = 2ϕ0. 2. Phương pháp giản đồ vecto: (d) (d’) α α β UC sin(ϕ+ϕRL) = U cosϕRL (1) ϕRL ϕ0 UCmax sin(ϕ0+ϕRL) = UCmax = U cosϕRL ϕRL ϕ0

DẠYKÈMQUYNHƠNOFFICIAL 325 Từ (1) suy ra: sin(ϕ + ϕRC) = UCcosϕRL U = UC UCmax = sinα (xác định với mỗi giá trị của UC) Suy ra: RL1RLRL RL2RL ϕ+ϕ=αϕϕ=α−ϕ    ϕ+ϕ=π−αϕ=π−α−ϕ   ϕ1 + ϕ2 = 2ϕ0 3. Phương pháp đại số: Cách giải 1: Ta có: 2 ZC0 = 1 ZC1 + 1 ZC2 Với: tanϕ0 = – cotϕRL = –R ZL tan2ϕ0 = 0 2 0 2tan 1tan ϕ −ϕ = L 22 L 2RZ ZR Mặt khác: tan(ϕ1+ ϕ2) = 12 12 tantan 1tantan ϕ+ϕ −ϕϕ = ( ) ()() C1C2L 2 LC1LC2 ZZ2ZR RZZZZ +− = C1C2 22L L 222C1C2 LLC1C2 22 L ZZ 12ZR ZR ZZ RZ2ZZZ ZR   +   −+−  +  = () C1C2 22L L 2222 C1C2 LL 22 L ZZ 12ZR ZR ZZ RZZR ZR   +   −+−  +  = () C1C2 22L L 22C1C2 L22 L ZZ 12ZR ZR ZZ RZ1 ZR   +    +  = L 22 L 2Z ZR = tan2ϕ0  ϕ1 + ϕ2 = 2ϕ0 Cách giải 2: Ta có: UC = U Z .ZC = U Z [ZL – (ZL – ZC)] = U Z.R(tanϕRL – tanϕ) = Ucosϕ(tanϕRL – tanϕ) = U sin(ϕRL ϕ) cosϕRL Áp dụng công thức: ULmax = U cosϕRL (vì ϕRL – ϕ0 = π 2 ) L = L1  ϕ = ϕ1 và UL = UL1 L = L2  ϕ = ϕ2 và UL = UL2 = UL1 Khi đó: UL1 = U cosϕRL sin(ϕRL – ϕ1) = U cosϕRL sin(ϕRL – ϕ2) = UL2  ϕRL – ϕ1 = π + ϕ2 – ϕRL ϕ2 + ϕ1 = 2(ϕRL–π 2) = 2ϕ0 5. Giá trị ZC để hiệu điện thế URC max Khi 22 LL C Z4RZ Z 2 ++ = thì RCmax 22 LLL C 2URU U Z4RZZ 1 Z == +− (Với điệntrở Rvàtụ điệnCmắcgầnnhau). Khi C Z0 = thì RCmin 22 L UR U RZ = + (Với điệntrở Rvàtụ điệnCmắcgầnnhau).

DẠYKÈMQUYNHƠNOFFICIAL 326 BÀI TẬP VẬN DỤNG Câu 1: Mạch điện như hình vẽ. Cuộn dây thuần cảm có độ tự cảm L = 0,318H, R = 100Ω, tụ C là tụ xoay. Điện áp đặt có biểu thức u2002cos100t =π (V) vàohai đầu đoạnmạch. a.TìmC để điệnápgiữahai đầubảntụ đạtgiátrị cực đại,tínhgiátrị cực đại đó. b.TìmC để điệnáphai đầuMB đạtcực đại,tínhgiátrị cực đại đó. Hướng dẫn: a.Cảmkháng: L 1 ZL100.0,318100.100. =ω=π=π=Ω π Cách giải 1: Phương pháp đạo hàm: Tacó: () () C CC 22 22 LC LL 2 CC UZ UU UIZ RZZ11y RZ2Z1 ZZ ==== +− +−+ Đặt () () 22222 LLLL 2 CC C 11 yRZ2Z1RZx2Zx1 ZZ 1 x Z  =+−+=+−+    =  NhậnthấyUCmax khiymin.Khảosáthàmsố: ( ) 222 LL yRZx2Zx1 =+−+ Đạohàm: ( )22 LL y'2RZx2Z =+− () 22 L LL 22 CL 1Z y'02RZx2Z0x ZRZ =  +−=  == + Bảngbiếnthiên: x ∞ 0 L 22 L Z x RZ = + +∞ ( )y'x - 0 + ( )yx miny  ymin khi 2222 LL 22C LL ZRZ100100 xZ200. RZZ100 ++ =  ===Ω + 5 C 115.10 CF. Z100.200  === ωππ Và 22 22 L Cmax URZ 200100100 U 2002V. R100 + + === L M N BA V CR V’

DẠYKÈMQUYNHƠNOFFICIAL 327 Cách giải 2: Phương pháp dùng tam thức bậc hai. Tacó: () () C CC 22 22 LC LL 2 CC UZ UU UIZ RZZ11y RZ2Z1 ZZ ==== +− +−+ Đặt ()222 LL 2 CC 11 yRZ2Z1axbx1 ZZ =+−+=++ với C 22 L L 1 x Z aRZ b2Z  =   =+  =−   NhậnthấyUCmax khiymin.Vìhàmsố ycóhệ số góca>0,nêny đạtcựctiểukhi: b x 2a =− hay 2222 LL 22C CLL ZRZ 1100100 Z200. ZRZZ100 ++ =  ===Ω + 5 C 115.10 CF. Z100.200  === ωππ Và 22 22 L Cmax URZ 200100100 U 2002V. R100 + + === Cách giải 3: Phương pháp dùng giản đồ Fre-nen. Tacó: RLC UUUU =++ Ápdụng địnhlýhàmsố sin,tacó: C C U Usin UU sinsinsin β =  = αβα VìUvà R 22 1 L UR sin U RZ α== + không đổinênUCmax khi: ()max sinsin1 2 β⇔β=π  β= L1L1 1C1C UUZZ cos UUZZ α==  = hay 22222 1L C LL ZRZ100100 Z200. ZZ100 ++  ====Ω 5 C 115.10 CF. Z100.200  === ωππ Và 22 22 L Cmax URZ 200100100 U 2002V. R100 + + === b. Tacó: 22 C MBMB 2222 LLCCLLC 22 C URZ UU UIZ RZ2ZZZZ2ZZy 1 RZ + ==== +−+− + + 1I CU 1U LU RU U β α O P Q

DẠYKÈMQUYNHƠNOFFICIAL 328 Đặt 2 2 LLC LL 2222 C Z2ZZ Z2Zx y11 RZRx =+=+ ++ (vớix=ZC) NhậnthấyUMBmax khiymin.Khảosáthàmsố y: 2 LL 22 Z2Zx y1 Rx =+ + Đạohàm: ( ) () 22 LL 222 2Zx2ZxR y' Rx = + Tacó: 22 LL C 22 L 22 LL C ZZ4R xZ> 0 y'0x2ZxR02( ZZ4R xZ< 0 2(  ++ == =⇔−−=   −+ ==  nhaän) loaïi) () 22 22 LL C ZZ4R 1001004.100 Z 5015162. 22 ++ ++  ===+=Ω 6 C 11 C19,7.10F. Z100.162  === ωπ Lậpbảngbiếnthiên: x ∞ 0 162 +∞ ( )y'x - 0 + ( )yx miny ( ) 2 2 min 22222 22 LLL LL 4R4R y 4R2Z2ZZ4R ZZ4R  == +++ ++ Khi đó: ( ) ( )2222 LL MBmax min UUZZ4R2001001004.100 U 324V. y2R2.100 ++++ ==== Câu 2: Đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch RLC mắc nối tiếp(Llàcuộncảmthuần).Thay đổi điệndungCcủatụ điện đếngiátrị C0 thì điệnáphiệu dụng giữahai bản tụ điện đạt giátrị cực đại vàUC =2U. Khi C =C0, cảm kháng củacuộn cảmcógiátrị là: A. LC0ZZ = B. L ZR = C. LC0 3 ZZ 4 = D. L 2 ZR 3 = Hướng dẫn: Tacó: () () C C 22 22 LC LL 2 CC UZ U U 11RZZ RZ2Z1 ZZ == +− +−+

DẠYKÈMQUYNHƠNOFFICIAL 329 NhậnthấyUC =UCmax khi 22 L C0 L RZ Z Z + = Mặtkhác: () () C0222 Cmax 22C0LC0 LC0 UZ U2U2UZ4R4ZZ RZZ =⇔=⇔=+− +− 222222222 C0LLC0C0LLC0 Z4R4Z8ZZ4Z4R4Z8R8Z4Z ⇔=+−+=+−−+ ( ) 222 222L 22 LC0 2L L RZ 4R4Z3Z034R4Z0 Z + ⇔−−+=⇔−−= 422422 LLLL Z2RZ3R0Z3RZ3R. ⇔−−=⇔=  = Khi đó 22 L C0 C0 L RZ43 ZRRZ. Z4 3 + ==  = Do đó LC0 3 ZZ. 4 =    Chọn C Câu 3: Cho mạch điện RLC có 1 R100Ω,LH π == , C thay đổi. Điện áp hai đầu đoạn mạch u1002cos100t (V)=π .TìmC để UC max Hướng dẫn: Tacó: L R100 1 ZL100.100 =Ω   =ω=π=Ω π NhậnthấyUCmax khi: 22224 L C L RZ10010010 Z200CF. Z1002 ++ ===Ω  = π Khi đó: 2222 CmaxL U100 URZ1001001002V. R100 =+=+= Nhận xét : Trong hai trường hợp L thay đổi và C thay đổi chúng ta thấy vai trò của L và C là bình đẳng nên hoán đổi vị trí của L và C ta sẽ được kết quả. Vậy nên trong trắc nghiệm chúng ta chỉ cần nhớ kết quả với C hoặc L. 22 22 max 22 22 max  + =+=   + =+=  L CLC L C LCL C RZU URZkhiZ RZ RZU URZkhiZ RZ Câu 4: Đặt điện áp xoay chiều vào hai đầu đoạn mạch R, L, C nối tiếp có C thay đổi thì thấy khi 4 1 10 CF π = và 4 2 10 CF 2π = thì điện áp hiệu dụng đặt vào tụ C không đổi. Để điện áp hiệudụng đó đạtcực đạithìgiátrị Clà: A. 43.10 CF 4π = B. 410 CF 3π = C. 43.10 CF 2π = D. 42.10 CF 3π =

DẠYKÈMQUYNHƠNOFFICIAL 330 Hướng dẫn: Tacó C1 C1 22 LC1 C2 C2 22 LC2 UZ U R(ZZ) UZ U R(ZZ)  = +−   = +− Theogiả thuyết: 22 C1C2 C1C2 2222 LC1LC2 ZZ UU R(ZZ)R(ZZ) =⇔= +−+− 222222 C1LC2C2LC1 222222 C1C2LC1C2LC1C2C1C2 Z(R(ZZ)Z(R(ZZ) R(ZZ)Z(ZZ)2ZZZ(ZZ)  +−=+−  −+−=− DoZC1 ≠ ZC2 nêntacó: 22 LC1C2 L C1C2 2ZZZ RZ ZZ += + MặtkháckhiCthay đổiUC cógiátrị cực đạithì 22 LC1C2 C LC1C2 2ZZRZ Z ZZZ + == + Từ đósuyra: 44 4 12 1010 CC3.10 π 2π CF. 224π + + ===   Chọn A Câu 5 (THPT Chuyên ĐH Vinh – 2015): Đặt điện áp u = 200 2 cos100πt (V) vào hai đầu đoạn mạch AB gồm đoạn mạch AM mắcnối tiếp với đoạn mạch MB, trong đó đoạn mạch AMchứacuộndây điện trở r=20Ω, đoạnmạch MBchứa điện trở thuần R=50Ω nốitiếp vớitụ điệncó điện dung Cthay đổi.Khi 1 200 CCF ==µ π thìtrongmạchxảy rahiệntượng cộnghưởng. ĐiềuchỉnhC=C2 thìUMB max,giátrị cực đại đóxấpxỉ bằng: A.323,6V B.262,6V C.225,8V D.283,8V Hướng dẫn: Tacó: 22 C MB 222 CC 22 C 20050Z 200200 U 70(50Z)70100Z1y 1 Z50 + === ++−+ + + với 2 2 70100 50 = + C 2 C Z y Z Để UMB max thìymin vớiZC lànghiệmcủaphươngtrìnhy’=0. ĐạohàmytheoZC hàmsố y ta được y’= () 2 CC 222C C 100Z9800Z250000 0Z119 Z50 =  ≈Ω + (dựa vào sự đổi dấu của y’ khi qua giátrị này để kếtluậnymin). Suyra:UMB max ≈ 262,645V.   Chọn B

DẠYKÈMQUYNHƠNOFFICIAL 331 Câu 6: Mạch điện RCL nối tiếp có C thay đổi được. Điện áp hai đầu đoạn mạch u1502cos100t =π (V).Khi 1 62,5 CCF ==µ π thìmạchtiêuthụ côngsuấtcực đạiPmax =93,75 W. Khi 2 1 CCmF 9 == π thì điện áp hai đầu đoạn mạch RC và cuộn dây vuông pha với nhau, điệnáphiệudụnghai đầucuộndâykhi đólà: A.90V B.120V C.75V D.75V Hướng dẫn: Cách giải 1: Tacó: 1 2 C 6 1 C 3 2 11 Z160 C62,5.10 100. 11 Z90 C10 100.  ===Ω ω π π  ===Ω ω π π KhiC=C2 thìURC vuôngphavớiUdây nêncuộndâycó điêntrở r. KhiC=C1 mạchtiêuthụ côngsuấtcực đại,trongmạchcósự cộnghưởng điện ZL =ZC1 =160Ω. Pmax =I2(R+r)= 2U Rr +  R+r= 2 max U P = =240Ω. KhiC=C2: ()() () 222 2 LC1 ZRrZZ24016090250 U150 I0,6A Z250  =++−=+−=Ω   ===  Suyra 2 22222222 RCdABRCLr 2222 CC 2222 LL UUUUUUU150 UIZ54 UIZ96  +=⇔+++=  ==  == ( )2 22222 RL UU1505496722 +=−−= (1) Mặtkhác:UR + r =UR +Ur =I(R+r)=0,6.240=144(V)  (UR +Ur )2 = 22 RLUU + +2URUr =1442 (2) Từ (1)và(2),ta được:UR =Ur =72(V). Do đó điệnáphiệudụnghai đầucuộndây: 2222 drL UUU72160120V. =+=+=    Chọn B Cách giải 2: KhiZC1 =160Ω thìPmax  CộnghưởngvàP= U2 R+r=93,75  R+r=240Ω vàZL =ZC1 =160Ω (1) KhiZC2 =90Ω thìUAM ⊥ UMB  tanϕAMtanϕMB =-1  Rr=ZLZC2 =14400 (2) Từ (1)và(2)tacóR,rlànghiệmphươngtrình:X2 -SX+P=0  R=r=120Ω Vậykhi đótacóUMB =IZLr = U (R+r)2 +(ZL -ZC2)2. ZL 2 +r2 =120V.   Chọn B 2 93 150 2

DẠYKÈMQUYNHƠNOFFICIAL 332 Câu 7: Cho đoạn mạch xoay chiều AB gồm tụ điện có điện dung C thay đổi được, cuộn dây có điện trở thuần r = 10Ω và độ tự cảm L, điện trở thuần R = 30Ω mắc nối tiếp theo đúng thứ tự trên, rồi mắc vào điện áp xoay chiều u = 100 2sin2πft (V). Người ta thấy rằng khi C = Cm thì điện áp hiệu dụng giữa hai đầu đoạn mạch chứa cuộn dây và tụ điện đạt cực tiểu.Giátrị cựctiểu đólà: A.50V B.25V C.25 2V D.50 2V Hướng dẫn: VớiUAB =100V,r=10Ω vàR=30Ω. KhichỉnhC=Cm mà điệnáp CLrmaxU  cộnghưởng  I= U R+r Vậykhi đóUCLr =Ir(dochỉ cònrvìZL =ZC)= U.r R+r=25V.    Chọn B Câu 8: Trong giờ thực hành, một học sinh mắc đoạn mạch AB gồm điện trở thuần 40Ω, tụ điệncó điệndungCthay đổi đượcvàcuộndâycó độ tự cảmLnốitiếpnhautheo đúngthứ tự trên. Gọi M là điểm nối giữa điện trở thuần và tụ điện. Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều có giá trị hiệu dụng 200V và tần số 50 Hz. Khi điều chỉnh điện dung của tụ điện đến giá trị Cm thì điện áp hiệu dụng giữa hai đầu đoạn mạch MB đạt giá trị cựctiểubằng75V. Điệntrở thuầncủacuộndâylà A.24Ω. B.16Ω. C.30Ω. D.40Ω Hướng dẫn: Tacó: () ()() () 22 LC MBMB 222 LC 22 LC UrZZ U UIZ RrZZR2Rr 1 rZZ +− === ++−+ + +− Để UMB min thìmạchxảyracộnghưởng LCZZ = ,khi đó MBmin 22 2 2 U200 U75r24. 11R2Rr402.40r rr =⇔=  =Ω ++ ++   Chọn A Câu 9: Cho đoạn mạch điện xoay chiều ANB, tần số dòng điện 50Hz, đoạn AN chứa R = 10 3 Ω và C thay đổi, đoạnNBchứaL=0,2 π H.TìmC để ANmaxU : A.106 Fµ B.200 Fµ C.300 Fµ D.250 Fµ Hướng dẫn: Cảmkháng: L 0,2 ZL100.20. =ω=π=Ω π Khi 22 LL C Z4RZ Z 2 ++ = thì RCmax 22AN LL 2UR UU 4RZZ == +− (RvàCmắcliêntiếpnhau). N C A B R L,r

DẠYKÈMQUYNHƠNOFFICIAL 333 Dungkháng: 22 LL C Z4RZ Z 2 ++ = 22204(103)20 30. 2 ++ ==Ω Mà 3 C C 11110 ZCF C.Z100.303 =  === ωωππ =106 F.µ    Chọn A Câu 10: Trong giờ thực hành, một học sinh mắc đoạn mạch AB gồm điện trở thuần 40Ω, tụ điệncó điệndungCthay đổi đượcvàcuộndâycó độ tự cảmLnốitiếpnhautheo đúngthứ tự trên. Gọi M là điểm nối giữa điện trở thuần và tụ điện. Đặt vào hai đầu đoạn mạch AB một điện áp xoay chiều có giá trị hiệu dụng 200V và tần số 50 Hz. Khi điều chỉnh điện dungcủatụ điện đếngiátrị Cm thìUMB min vàbằng75V. Điệntrở thuầncủacuộndâylà A.24 Ω. B.16 Ω. C.30 Ω. D.40 Ω. Hướng dẫn: Tacó: 22 LC MBMBMB 22 LC UIZZUUr(ZZ) Z (rR)(ZZ) +− === ++− 222 LC 22 22 LC LC UU (rR)(ZZ)R2Rr 1 r(ZZ) r(ZZ) == ++−+ + +− +− Để UMB min thìmạchxảyracộnghưởng ( )LCZZ = khi đó: MBmin 2 2 U U R2Rr 1 r = + + 2 2 200 75r24. 4080r1 r ⇔=  =Ω + +   Chọn A Câu 11 (VLTT Số 01 – 2014): Mạch điện AB gồm đoạn AM nối tiếp MB. Đặt vào hai đầu mạch u = 150 2 cos100πt (V). Điện áp ở hai đầu đoạn AM sớm pha hơn cường độ dòng điện một góc 300 . Đoạn MB chỉ có một tụ điện có điện dung C thay đổi được. Điều chỉnh C để tổng điệnáphiệudụng ( )AMMB max UU + .Khi đó điệnáphiệudụng ở hai đầutụ điệnlà: A.150V. B.75 3 V. C.200V. D.75 2 V. Hướng dẫn: Dựavàogiản đồ vectơ: AMMBAMMB 2121 UUUUU sinsinsinsinsin 3 + === π ϕϕϕ+ϕ () +=ϕ+ϕ π  π  =−ϕ+ϕ  π   AMMB21 11 U UUsinsin sin 3 U2 sinsin sin3 3 φ1A π/6 UC U=150 π/3 φ2 M B

DẠYKÈMQUYNHƠNOFFICIAL 334 1 U =2sincos sin33 3 ππ −ϕ π  AMMBmax1 (UU)cos1 3 π   +⇔−ϕ=   1233 ππ ⇔ϕ=  ϕ= Khi đó:U=150V.   Chọn A Câu 12: Mạch điện xoay chiều AB gồm đoạn mạch AM và MB. Điện áp hai đầu đoạn mạch ổn định với điện áp cực đại U0 Điện áp ở hai đầu đoạn mạch AM sớm pha 6 π so với cường độ dòng điện. ĐoạnmạchMBchỉ chứatụ điệnvới điệndungCthay đổi được. Điều chỉnh giá trị của C sao cho tổng ( )AMMB max UU + . Khi đó điện áp hiệu dụng ở hai đầu tụ điệnlà A. U B. 0U C. U2 D. U3 Hướng dẫn: Cách giải 1: Phương pháp truyền thống (biến đổi đại số) ĐoạnmạchAMcóR,L,C1 mắcnốitiếp. Tacó: 1LCZZ 1 tantan. R6 3 π ϕ=== Theobất đẳngthứ Cauchy-Schwarz: ()2 AMMB 22 AMMB UU UU 2 + ≤+ trong đó: ( ) 11 2 2222 AMMBRLCC UUUUUU +=+−+ ()() ( ) () 1 1 1 1 2 2LCC 2 RLCCLCC 22 LCC ZZZ UUUU2UUUU1 RZZZ  =+−−+−=+ +−−  Do đó, ( )AMMB max UU + khi () 1 C 22 LCC max Z RZZZ    +−−  Mà () () ()1 1 1 C 2222 LCCLC CLC C Z 1 RZZZRZZ Z2ZZ Z = +−−+− +−− () () () 1 11 22 LC LCLC 11 2RZZ2ZZ2ZZBÑT Coâsi ≤= +−−− Suyra ( )AMMB max UU + ( ) ( ) ( )1 1 1 2222 LCCLCCLC RZZZ4ZZZ2ZZ +−==−  =−

DẠYKÈMQUYNHƠNOFFICIAL 335 Khi đó: () 1 C C 22 LCC UZ UU. RZZZ == +−−  Chọn A Cách giải 2: Phương pháp giản đồ véctơ Tacó: AMMBAMC UUUUU. =+=+ Theogiả thuyết ( )AMC 2 U,U 3 π = ( ) ( ) AMMBAMCmaxmax UUUU +=+ khivàchỉ khi AMCOUU∆ làtam giác đều C UU = Thậtvậy,gọi α làgóctạobởiIvàu.Khi đó: C C AM AM UU sinU2Usin sin 36 6 UU U2Usin sin2 sin 32  = π  ππ  α+=α+       π  = =−απ  π  −α   CAM UU2Usinsin4Usincos 6236  ππ  ππ   +=α++−α=α−   Vì U = const () CAM max UUcos1 66 ππ  +⇔α−=  α=   AMCOUU∆ là tam giác đều. Chọn A Cách giải 3: Do đoạn mạch AM chỉ có R và ZL nên: ( ) () () 22 LC LC AMMB 2222 LCLLCC URZZ U2ZZ UU RZZ4Z2ZZZ ++ + +== +−−+ (1) Sau đóta đikhảosát(1)vớibiếnZC (hoặcbìnhphươnghaivế rồidùng đồ thị bậchai). Khi đó ta vẫn có kết quả UC = U.   Chọn A Cách giải 4: Do đoạn mạch AM chỉ có R và ZL nên: ( ) () 22LC22222 LCCL AMMB 22222 LCLCLC URZZ RZZ2ZRZ UUU RZZRZZ2ZZ ++ ++++ +== +−++− 22 CLLC LCLC 22222 LCLCLCLC ZRZZZ2ZZZZ U12.U12. RZZ2ZZ4ZZ2ZZ ++ + =+=+ ++−+− LC CL 33 U12.U12.2U. ZZ 4242 ZZ BÑT Coâsi =+≤+= +− 300 600

DẠYKÈMQUYNHƠNOFFICIAL 336 Đẳng thức xảy ra khi và chỉ khi CLC Z2ZUU. =  =  Chọn A Cách giải 5: Dùng tính chất bất đẳng thức Vì U = const nên 22 2222 AMMBAMMBAMMBAMMB 2 UU2UUcos220UUUU220. 3 π ++=⇔+−= Theo AM-GM: 2 AMMB AMMB UU UU 2 + ≤   Theo bất đẳng thứ Cauchy-Schwarz: ()2 AMMB 22 AMMB UU UU 2 + ≤+ Đẳng thức xảy ra khi và chỉ khi AMMBCAM UUUUU. =  == Chọn A Câu 13: Mạch điệnxoaychiềuABgồm đoạnmạchANchứacuộndây, đoạnNBchứatụ điệnCcógiátrị thay đổi được. Đặtmộthiệu điệnthế không đổi vàohai đầu đoạnmạch AB. Điệnáphai đầu đoạnmạchANluônsớmphahơncường độ dòng điệnmộtgóc ϕ. Điều chỉnh C để tổng ( )ANNB max UU + . Khi đó hệ số công suất của đoạn mạch có giá trị A. 2 1 1 1tan cos  +ϕ− ϕ  B. 2 1 1 1tan sin  +ϕ− ϕ  C. 2 1 1 1cot cos  +ϕ− ϕ  D. 2 1 1 1cot sin  +ϕ− ϕ  Hướng dẫn: Điệnáphai đầu đoạnmạchANluônsớmphahơncường độ dòng điện mộtgóc ϕ (cuộn dây có chứa r) nên L L Z tanZrtan r ϕ=  =ϕ . Ta có: ( ) () 22 CL ANNBrLC 22 LC UZrZ UUUU rZZ ++ +=+= +− Đặt: CxZ = , ta xét hàm số: () 22 L 22 L xrZ y rZx ++ = +− Đạo hàm: ( ) ()() 222222 LLLLL 2222 LL rZZrZZrZx y' rZxrZx +++−++ = +−+−

DẠYKÈMQUYNHƠNOFFICIAL 337 Đạo hàm: ( )222222 LLLLL y'0rZZrZZrZx0 =⇔+++−++= 22 LxrZ =+ Bảng biến thiên: x ∞ 0 22 LxrZ =+ +∞ ( )y'x + 0( )yx maxy Từ bảng biến thiên suy ra: ⇔=+= ϕ 22 maxCL r yZrZ cos Hệ số công suất của mạch: ()2 222 LC2 rrr1 k Z rZZ r1 rrtan1tan coscos ==== +−  +ϕ−+ϕ−  ϕϕ   Chọn A Câu 14: Mạch điện xoay chiều AB gồm đoạn AN và đoạn NB mắc nối tiếp. Điện áp ở hai đầu mạch ổn định u = 150cos100πt (V). Điện áp ở hai đầu đoạn AN sớm pha hơn cường độ dòng điện một góc 6 π . Đoạn NB chỉ có một tụ điện có điện dung C thay đổi được. Chỉnh C để tổng ANNB min 11 UU  +   . Khi đó điện áp hiệu dụng ở hai đầu tụ điện là A. 220V B. 110V C. 150V D. 110V Hướng dẫn: Theo hệ quả của bất đẳng thức AM-GM thì 114 abab +≥ + . Đẳng thức xảy ra khi và chỉ khi a = b. Áp dụng vào bài toán trên ta có: ANNBANNB 114 UUUU +≥ + Khi đó () ANNB max ANNB min 11 UU UU  +⇔+  Vẽ giãn đồ véctơ như hình vẽ Theo định lý hàm số sin ta có: ANNBANNB 2112 UUUUU sinsinsinsinsin 3 + +== π ϕϕϕ+ϕ 2 3 2

DẠYKÈMQUYNHƠNOFFICIAL 338 Suy ra: 12 ANNB sinsin UUU sin 3  +=ϕ+ϕ π   11 1 1 2 sinsin2sincos 333UU2Ucos 3sinsin 33  π  ππ  ϕ+−ϕ−ϕ   π  ===−ϕππ    Khi đó: ()ANNB112 max UUcos1. 33 ππ +⇔−ϕ=  ϕ=ϕ=  Vậy điện áp hiệu dụng ở hai đầu tụ điện là 150V.    Chọn C Câu 15: Mạch điện xoay chiều AB gồm đoạn AM và đoạn MB. Điện áp ở hai đầu mạch ổn định u = 220cos100πt (V). Điện áp ở hai đầu đoạn AM sớm pha hơn cường độ dòng điện một góc 300 . Đoạn MB chỉ có một tụ điện có điện dung C thay đổi được. Chỉnh C để tổng ( )AMMB max UU + . Khi đó điện áp hiệu dụng ở hai đầu tụ điện là A. 440V B. 220V C. 220V D. 220V Hướng dẫn: Cách giải 1: Vẽ giãn đồ véctơ như hình vẽ Đặt Y = (UAM + UMB)2 Tổng ( )AMMB max UU + khi Y đạt giá trị cực đại Y = (UAM + UMB)2 = (UAM + UC)2 = 2 AMU + 2 CU + 2UAMUC (1) Mặt khác theo giãn đồ ta có: U2 = 2 AMU + 2 CU – 2UAMUC cos600 = 2 AMU + 2 CU – UAMUC U2 = 2 AMU + 2 CU – UAMUC (2) Z2 = 2 AMZ + 2 CZ – ZAMZC (3) Thay (2) vào (1) ta được: Y = U2 + 3UAMUC (4) Nhận thấy Y = Ymax khi X = UAMUC có giá trị lớn nhất X = Xmax X = UAMUC = I2ZAMZC = 2 AMC 2 UZZ Z = 22 AMAM 222 AMCAMCAM CAM CC UZUZ ZZZZZ ZZ ZZ = +− +− X = Xmax khi mẫu số cực tiểu,  ZC = ZAM  X = U2 (5) và UC = UAM Từ (4) và (5): Y = (UAM + UC)2 = U2 + 3U2 = 4U2  UAM + UC = 2U  2UC = 2U  UC = U = 220V.  Chọn C Cách giải 2: Từ giản đồ véctơ, nhận thấy khi ZC = ZAM suy ra UC = UAM. Khi đó tam giác OUAMU là tam giác đều  UC = U = 220V.    Chọn C Câu 16: Một cuộn dây không thuần cảm nối tiếp với tụ điện C trong mạch xoay chiều có điện áp u = U0cosωt (V) thì dòng điện trong mạch sớm pha hơn điện áp u là φ1 và điện áp hiệu 2 3 2 300 600

DẠYKÈMQUYNHƠNOFFICIAL 339 dụng hai đầu cuộn dây là 30V. Nếu thay C1 = 3C thì dòng điện chậm pha hơn u góc φ2 = 900 – φ1 và điện áp hiệu dụng hai đầu cuộn dây là 90V. Tìm U0. A. 60 5 V B. 30 5 V C. V D. V Hướng dẫn: Ta có: Z2C = 1 3 ZC. I2 = 3I1  i1 sớm pha hơn u; i2 trễ pha hơn u; Hình chiếu của U trên I là RU U2LC = U2L – U2C = U1R  3ZL – ZC = R (1) U1LC = U1C – U1L = U2R  ZC – ZL = 3R (2) Từ (1) và (2)  L C Z2R Z5R =  = Ban đầu U = V  U0 = 60V.  Chọn D Câu 16 (THPT Quốc gia – 2016): Đặt điện áp 0 uUcosωt= (V) (với 0U và ω không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm: điện trở, cuộn cảm thuần và tụ điện dung C thay đổi được. Khi C = C0 thì UC max và công suất của đoạn mạch bằng 50% công suất của đoạn mạch khi có cộng hưởng. Khi C = C1 thì điện áp giữa hai bản tụ điện có giá trị hiệu dụng là U1 và trễ pha 1ϕ so với điện áp hai đầu đoạn mạch. Khi C = C2 thì điện áp giữa hai bản tụ điện có giá trị hiệu dụng là U2 và trễ pha 2ϕ so với điện áp hai đầu đoạn mạch. Biết U2 = U1 và 21 3 π ϕ=ϕ+ . Giá trị của 1ϕ là A. 12 π B. 6 π C. 4 π D. 9 π Hướng dẫn: Cách giải 1: Phương pháp truyền thống Khi C = C0 thì UC = Ucmax  ZC0 = 22 L L RZ Z + Công suất của mạch P = I2R = 2 2 U Z R. Ta có: C0 ch P P = 2 ch 0 Z Z    = 0,5  R2 = 0,5R2 + 0,5( ZL – ZC0)2  R = |ZL – ZC0|= ZC0 ZL = 22 L L RZ Z + – ZL = 2 L R Z  ZL = R và ZC0 = 2R (1) Khi UC1 = UC2  C0 2 Z = C1 1 Z + C2 1 Z (2) 302 60 12II ⊥ () 22 22 303010R2R5R302 R4R5 ×+−== +

DẠYKÈMQUYNHƠNOFFICIAL 340 Từ (1) và (2) ta có: 1 R = C1 1 Z + C2 1 Z Gọi φ’ là góc lệch pha giữa u và i. Ta có: tanφ’ 1 = LC1ZZ R = 1 – C1Z R = 1 – ZC1 C1C2 11 ZZ  +   = –2 1 C C Z Z (3) tanφ’ 2 = LC2ZZ R = 1 – C2Z R = 1 – ZC2 C1C2 11 ZZ  +   = –1 2 C C Z Z (4) Từ (3) và (4) suy ra: tanφ’ 1 tanφ’ 2 = 1  – φ’ 1 – φ’ 2 = 2 π  φ’ 1 + φ’ 2 = –2 π (5) Góc lệch pha giữa giữa u và uC: φ1 = 2 π + φ’ 1  φ’ 1 = φ1 –2 π (6) φ2 = 2 π + φ’ 2 = φ1 + 3 π  φ’ 2 = φ1 + 3 π –2 π (7) Từ (5), (6) và (7) ta được: 2φ1 + 3 π – 2. 2 π = –2 π  φ1 = 12 π .  Chọn A Cách giải 2: Phương pháp đường tròn Ta có: 2 0 0ch000 ch P 1 PPsinsin. P4 2 π =α  α==  α= Mặt khác: 21 1 2102 3 12 5 2 32 π π  α−α= α=     ππ α+α=α=α=   Chọn A Câu 18: Một đoạn mạch gồm cuộn cảm có độ tự cảm L và điện trở thuần r mắc nối tiếp với tụ điện có điện dung C thay đổi được. Đặt vào hai đầu mạch một hiệu điện thế xoay chiều có giá trị hiệu dụng U và tần số f không đổi. Khi điều chỉnh để điện dung của tụ điện có giá trị C = C1 thì điện áp hiệu dụng giữa hai đầu tụ điện và hai đầu cuộn cảm có cùng giá trị và bằng U, cường độ dòng điện trong mạch khi đó có biểu thức 1 i26cos100tA 4 π  =π+  . Khi điều chỉnh để điện dung của tụ điện có giá trị C = C2 thì điện áp hiệu dụng giữa hai bản tụ điện đạtgiátrị cực đại.Cường độ dòng điệntứcthờitrongmạchkhi đócóbiểuthứclà A. 2 5 i22cos100tA 12 π  =π+  B. 2 i22cos100tA 3 π  =π+  C. 2 5 i23cos100tA 12 π  =π+  D. 2 i23cos100tA 3 π  =π+  Hướng dẫn: Khi C = C1 ta có: UD = UC = U  Zd = ZC1 = Z1 UC max A B M1 M2 M0 α1 α0 α2

DẠYKÈMQUYNHƠNOFFICIAL 341 ()2 222 C1 LC1LLC1LL Z rZZrZZZZZ 2  +−=+  −=±  = (1) Khi Zd = ZC1  r2 + 2 LZ = 2 C1Z  r2 = 2 C1 3 Z 4  r = C1 3 Z 2 (2) C1 C1 LC1 1 1 C1 Z ZZZ tan21 . r6 33 Z 2 π ϕ===−  ϕ=− Khi C = C2 ta có: UC = UCmax khi ZC2 = 222 LC1 C1 LC1 rZZ 2Z ZZ 2 + == Khi đó () 2 22 C12 C2LC2C1C1C1 3Z ZrZZ2Z3Z3Z 42  =+−=+−==   C1 C1 LC2 2 2 C1 Z ZZ2Z 2 tan3. r3 3 Z 2 π ϕ===−  ϕ=− Hiệu điện thế hai đầu đoạn mạch: U = I1Z1 = I2Z2  111 2 2 IZI 23 I2A Z 33 ==== Cường độ dòng điện qua mạch: 22 5 iI2cos100t22cos100tA. 46312 ππππ  =π+−+=π+    Chọn A Câu 19: Một cuộn dây không thuần cảm nối tiếp với tụ điện C thay đổi được trong mạch điện xoay chiều có điện áp u = U0 cosωt (V). Ban đầu dung kháng ZC, tổng trở cuộn dây Zd và tổng trở Z toàn mạch bằng nhau và đều bằng 100Ω. Tăng điện dung thêm một lượng ∆C = 30,125.10 π (F) thì tần số dao động riêng của mạch này khi đó là 80π rad/s. Tần số ω của nguồn điện xoay chiều bằng: A. 80π rad/s. B. 100π rad/s. C. 40π rad/s. D. 50π rad/s. Hướng dẫn: Do ZC = Zd = Z  UC = Ud = U = 100I Vẽ giãn đồ véctơ như hình vẽ. Suy ra UL = 1 2 Ud = 50I  2ZL = Ud = 50I  ZL = 50Ω Với I là cường độ dòng điện qua mạch

DẠYKÈMQUYNHƠNOFFICIAL 342 Ta có: L LC C ZL L 1ZZ5000ZC C =ω   == = ω ω’ = 1 L(CC) +∆ = 80π  L(C + ∆C) = 2 1 (80) π  5000C(C + ∆C) = 2 1 (80) π  C2 + (∆C)C – 2 1 (80).5000 π = 0  C2 + 30,125.10 π C – 2 1 (80).5000 π = 0  C2 + 310 8π C –6 2 10 8.4 π = 0  C = 310 8π F Suy ra: ZC = 1 Cω = 100 Ω  ω = ZC C 1 = 80π rad/s.  Chọn A III. Sự thay đổi ω ωω ω trong mạch RLC mắc nối tiếp Xét mạch điện xoay chiều có hiệu hiệu thế hai đầu ổn định: 0u uUcos(t) =ω+ϕ . ω có giá trị thay đổi; R, L và C không đổi. 1. Khảo sát sự biến thiên công suất theo ω ωω ω. Ta có: 2 2 2 2 UR PIR 1 RL C == +ω− ω  Việc khảo sát hàm số P theo biến số ω bằng việc lấy đạo hàm và lập bảng biến thiên rất khó khăn vì hàm số này tương đối phức tạp. Tuy nhiên, ta có thể thu được kết quả đó từ những nhận xét sau:  Khi ω = 0 thì C 1 Z C =→∞ ω làm cho P = 0.  Khi 0 1 LC ω=ω= thì mạch cộng hưởng làm cho công suất trên mạch cực đại.  Khi ω→∞ thì L ZL=ω→∞ làm cho P = 0. Từ những nhận xét đó ta dễ dàng thu được sự biến thiên và đồ thị: ω ∞ 0 0 1 LC ω=ω= +∞ ( )P' ω - 0 + ( )P ω = 2 max U P R 0 0 0 ω P Pmax

DẠYKÈMQUYNHƠNOFFICIAL 343 Nhận xét đồ thị: Từ đồ thị ta thấy rằng sẽ có hai giá trị ω1 ≠ ω2 cho cùng một giá trị công suất, điều này phù hợp với những biến đổi ở phần trên. 2. Giá trị ω ωω làm cho Pmax, Imax, Umax Ta có 2 2 2 2 UR PIR 1 RL C == +ω− ω  , từ công thức này ta thấy rằng công suất của mạch đạt giá trị cực đại khi: 0 11 L0 C LC ω−=  ω=ω= ω . Với = 2 max U P R Khi đó Zmin = R và hiệu điện thế giữa hai đầu mạch và cường độ dòng điện qua mạch đồng pha nhau. 3. Có hai giá trị ω ω1 ≠ ≠≠ ≠ ω ωω2 cho cùng công suất (cộng hưởng) và giá trị ω ω làm cho Pmax tính theo ω ωω ω1 và ω ωω ω2 Nếu có hai giá trị tần số khác nhau cho một giá trị công suất thì: 22 22 22 12 12 URUR 11 RLRL CC =⇔=  +ω−+ω−  ωω  12P P 22 22 12 12 11 RLRL CC  ⇔+ω−=+ω− ωω  22 12 12 12 12 12 12 11 LL(1) 11CC LL CC11L(L)(2) CC  ω−=ω− ωω  ⇔ω−=ω−⇔  ωω  ω−=−ω− ωω Vì ω1 ≠ ω2 nên nghiệm (1) bị loại. Khai triển nghiệm (2) ta thu được : 12 1 LC ωω= Có hai giá trị của ω để mạch có P, I, Z, cosφ, UR giống nhau thì: 2 12ch 1 LC ωω=ω= Với ω = ω1 hoặc ω = ω2 thì I hoặc P hoặc cosφ hoặc UR có cùng một giá trị thì: Imax hoặc Pmax hoặc UR max khi 1212 1 LC ω=ωω  =ωω hay 12fff = . 4. Giá trị ω ωω làm cho hiệu điện thế ULmax

DẠYKÈMQUYNHƠNOFFICIAL 344 Ta có: () L LL 2 22 LC 22422 UZ UU UIZ RZZ11R21y 1 LCLLC ==== +−  +−+  ωω  Nhận thấy LmaxminUy ⇔ Xét hàm số 2 22422 11R21 y1 LCLLC  =+−+ ωω  là một hàm bậc hai theo biến 2 1 ω và 22 1 a0 LC => nên hàm số đạt cực tiểu tại: ( )2 2L 22 2 2LRCC 1b212 2Lω 2a22LCRCC R C =−=  ω== Tần số góc: 2 2 L 222 L 21LR C 2LCRCC2  ω=  =− −ω  () 222 2 22CLCCLC L 1LRRR ZZZZZZ CC222 ⇔=−⇔=−⇔−= ω ( )CLC CLC 2RC ZZZ ZZZ 111 tantan. R2RR22 ⇔=⇔=⇔ϕϕ= Và 22 222 242 min 2 22 R21 4 LLCLC 4RLCRC y 1 4a4L 4 LC   ∆−  =−=−= Khi đó: Lmax 24224222 min 2 UU2UL2UL U y 4RLCRC4RLCRCR4LCRC 4L ==== Hay Lmax 22 2 C 444422 2 L UUU U . 1 LCZ11 1 LCLC Z === ωω 5. Giá trị ω ωω làm cho hiệu điện thế UCmax Ta có : () () C CC 2 2224222 LC UZ UU UIZ RZZLCRC2LC1y ==== +−ω+−ω+ Nhận thấy CmaxminUy ⇔ . Xét hàm số ( ) 224222 yLCRC2LC1 =ω+−ω+ là một hàm bậc hai theo biến 2 ω và 22 aLC0 => nên hàm số đạt cực tiểu tại:

DẠYKÈMQUYNHƠNOFFICIAL 345 2 2222 2 22222 2L bRC2LC2LCRCR Cω 2a2LC2LC2L =−=−== 22 C 2 2L2L RR 1 CC 2LL2  ω== Tần số góc: 2 2 2 CCLC 2 2L R 11LR1 C L2LC2LC  ω=  ω=−  ωω=  2 LC0 ωω=ω Ta có: 2222 222 LLC 1LRLRLRR LLZZZ LC2C2C22 ω=−⇔ω=−⇔ω=−⇔=− () ( )2 LLC LLC 2 ZZZ R1 ZZZ 2R2 ⇔−=−⇔=− LLC RL ZZZ 11 tantan. RR22 ⇔=−⇔ϕϕ=− Và ( )2 2222 242 min 222 RC2LC4LC 4RLCRC y 4a4LC4L ∆− =−=−= Khi đó: Cmax 24224222 min 2 UU2UL2UL U y 4RLCRC4RLCRCR4LCRC 4L ==== Hay Cmax 22 2 C 444422 2 L UUU U 1 LCZ11 1 LCLC Z === ωω Chú ý: - Cho ω = ω1, ω = ω2 thì UC như nhau. Tính ω để UCmax Điều kiện để UCmax khi: () 2 222 C12 2 1LR1 LC22  ω=−=ω+ω   với 2LR 0 C2 −> - Cho ω = ω1, ω = ω2 thì UL như nhau. Tính ω để ULmax Điều kiện để ULmax khi: 2 2 2 22 L12 1LR111 C C22  =−=+ ωωω   với 2LR 0 C2 −> BÀI TẬP VẬN DỤNG Câu 1: Cho mạch AB chứa RLC nối tiếp theo thứ tự (L thuần cảm). Gọi M là điểm nối giữa L và C. Cho điện áp 2 đầu mạch là u = U0cosωt (V). Ban đầu điện áp uAM và uAB vuông pha. Khi tăng tần số của dòng điện lên 2 lần thì uMB: A. Tăng 4 lần B. không đổi C. Tăng D. giảm Hướng dẫn: Ban đầu với tần số ω0 đề cho điện áp đoạn AM vuông pha với điện áp đoạn AB suy ra: M C A B R L

DẠYKÈMQUYNHƠNOFFICIAL 346 L0C0L02222 L0L0C0L0L0C0 ZZZ .1ZZZRZRZZ RR =−⇔−=−  += (1) Lúc sau tăng ω = 2ω0 thì LL0 CC0 Z2Z 1 ZZ 2 =   =  (2) Mà Z = 22 LC R(ZZ) +− = 222 LLCC RZ2ZZZ +−+ (3) Thế (1) vào (2) ta được: Z0 = 2 C0L0C0ZZZ (4) Ta có lúc đầu : UMB0 = I0ZC0 = C0 0 U Z Z = C0 22 L0C0 UZ R(ZZ) +− (5) Ta có lúc sau : UMB = IZC = C U Z Z = C 22 LC UZ R(ZZ) +− (6) Thế (2) vào (6): UMB = C0 2 2 L0C0 UZ 1 2R2ZZ 2 +−  = C0 222 L0L0C0C0 UZ 1 2R4Z2ZZZ 4  +−+   = C0 222 L0L0C0C0 UZ 4R(16Z8ZZZ) +−+ (7) Thế (1) vào (7): UMB = C0 222 L0L0C0C0 UZ 4R(16Z8ZZZ) +−+ Mặt khác: UMB= 2 U 1LC −ω . Khi ω tăng 2 lần thì ω2 tăng 4 lần. Suy ra mẫu số giảm nên UMB tăng.    Chọn C Câu 2: Đặt điện áp xoay chiều u = U0cosωt có U0 không đổi và ω thay đổi được vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Thay đổi ω thì cường độ dòng điện hiệu dụng trong mạch khi ω = ω1 bằng cường độ dòng điện hiệu dụng trong mạch khi ω = ω2. Hệ thức đúng là: A. 12 2 LC ω+ω= . B. 12 1 . LC ωω= . C. 12 2 LC ω+ω= . D. 12 1 LC ωω= Hướng dẫn: Cách giải 1: Ta có: () ()1122 12 2222 LCLC UU II RZZRZZ =⇔= +−+− ( ) ( )1122 22 LCLC ZZZZ ⇔−=− Vậy xảy ra 2 khả năng, biến đổi ta được:

DẠYKÈMQUYNHƠNOFFICIAL 347 () 1122 1122 12 LCLC 12 LCLC 12 12 11 LL ZZZZ CC ZZZZ11 LL CC  ω−=ω−−=− ωω   −=−−  ω−=−ω−  ωω  () () 1212 1212 12 12 21 12 11111LLL CCC 11 LL111 CCL C   ω−ω=−ω−ω=−   ωωωω   ω+ω=+  ω+ω=+ ωω  ωω  () () 21 12 12 12 21 12 1212 1 L1 LC C 11LLC C   ω−ω ω−ω= =−  ωω ωω    ω+ω = ω+ω=  ωω ωω  Chỉ có trường hợp 12 1 LC = ωω (1) là thỏa mãn yêu cầu bài toán. Khi I1 = I2 thì mạch xảy ra hiện tượng cộng hưởng điện, lúc đó 2 11 L CLC ω=⇔ω= ω (2) Từ (1) và (2) ta được: 2 12 1 LC ω=ωω=    Chọn D Cách giải 2: Bài toán này xét về sự phụ thuộc của I theo ω nên ta viết: 12 22 22 12 12 UU II 11 RLRL CC =⇔=  +ω−+ω−  ωω  Ta thấy ngay I phụ thuộc kiểu “hàm phân thức” đối với ω vì vậy phải có quan hệ hàm phân thức: CT12 xxx = , tức là 12ω=ωω hay 2 12 1 LC ω=ωω=    Chọn D Chú ý: 1. Khi bài toán có ωthay đổi, thấy có hai giá trị ω= ω1 và ω= ω2 cũng cho cùng một cường độ dòng điện, hoặc cho cùng độ lớn của độ lệch pha giữa u và i, hoặc cùng UR, ... Tìm ω để có cộng hưởng điện (hay I = Imax, ui ϕ=ϕ , ui 0ϕ=ϕ−ϕ= , ( )max cos1 ϕ= , max PP = , RRmaxUU = , ...) thì ta nên vận dụng phương pháp đánh giá kiểu hàm số để có kết quả nhanh 12ω=ωω . 2. a. Hàm số bậc hai: 2 yf(x)axbxc ==++ Giá trị của x làm f(x) đạt cực trị ứng với tọa độ đỉnh CT b x 2a = (1)

DẠYKÈMQUYNHƠNOFFICIAL 348 Hai giá trị x1, x2 cho cùng một giá trị của hàm f(x), theo hệ thức Vi-et thì 12 b xx a += (2) Từ (1) và (2) ta có mối liên hệ giữa x1, x2 và xCT như sau: ()CT12 1 xxx 2 =+ và gọi đây là kiểu quan hệ hàm bậc hai. b. Hàm số bậc hai: b yf(x)ax x ==+ Giá trị của x làm f(x) đạt cực trị ứng với b ax x = hay là CT b x a = (1) Hai giá trị x1, x2 cho cùng một giá trị của hàm f(x), theo hệ thức Vi-et thì 12 b xx a = (2) Từ (1) và (2) ta có mối liên hệ giữa x1, x2 và xCT như sau: CT12 xxx = và gọi đây là kiểu quan hệ hàm phân thức. Trong các bài toán về điện xoay chiều, mặc dù các đại lượng như I, P, UL, ... không phụ thuộc vào các đại lượng ω, ZL, ... tường minh là hàm bậc hai hay là hàm phân thức chính tắc như trong toán học, nhưng nó chỉ có dạng biểu thức tương tự theo một hàm mũ hoặc kèm theo một hằng số nào đó. Câu 3: Đặt điện áp xoay chiều u = U0cosωt (U0 không đổi và ω thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc nối tiếp, với CR2 < 2L. Khi ω = ω1 hoặc ω = ω2 thì điện áp hiệu dụng giữa hai đầu cuộn cảm có cùng một giá trị. Khi ω = ω0 thì UL max. Hệ thức liên hệ giữa ω1, ω2 và ω0 là : A. 222 012 1 2()ω=ω+ω B. 012 1 2()ω=ω+ω C. 222 012 1111 2  =+ ωωω D. 012 ω=ωω Hướng dẫn: Cách giải 1: Điện áp hiệu dụng giữa hai đầu cuộn cảm có cùng một giá trị: 12 LL 1 22 2 2 2 1 2 1 2 UU UU.L.L 11 RLRL CC =⇔ω=ω  +ω−+ω−  ωω  22 12 22 22 12 12 11 RLRL CC ωω ⇔=  +ω−+ω−  ωω  22 242242 1122 R2R2LL11 CC CC ⇔+=+ ωωωω 2 224242 2121 L1111 2R CCC  ⇔−−=− ωωωω  2 22 22222 1212 L11111L 2RC2R CCC   ⇔−=+  +=−  ωωωω   (1)

DẠYKÈMQUYNHƠNOFFICIAL 349 Ta có: LL 2 22 222 ULUL UIZ 11L1y R2L CC === +−+ ωω  Đặt 2 2 1 xyaxbxd =  =++ ω Tức là khi 22 2 0 11L 2RC 2C  =−ω  (2) Từ (1) và (2) ta được: 222 012 1111 2  =+ ωωω   Chọn C Cách giải 2: Bài toán xét sự phụ thuộc của UL vào ω nên ta có: L LL 222 LC 22 222 UZ UL UIZ R(ZZ) 11L1 R2L CC === +− +−+ ωω  Và ta thấy ngay UL phụ thuộc kiểu hàm bậc 2 đối với 2 1 ω nên ta có ngay mối liên hệ giữa ω1, ω2 và ω0 là 222 012 1111 2  =+ ωωω . Chọn C Chú ý: Khi ω = ω1 hoặc ω = ω2 thì điện áp hiệu dụng giữa hai đầu tụ điện có cùng một giá trị. Khi ω= ω0 thì điện áp hiệu dụng giữa hai đầu tụ điện có giá trị cực đại. Ta có ngay biểu thức: C CC 22 LC2422 2 UZ 1U UIZ C L1R(ZZ) LR2 CC === +−  ω+−ω+   Và ta thấy ngay UC phụ thuộc kiểu hàm bậc 2 đối với 2ω nên ta có ngay mối liên hệ giữa ω1, ω2 và ω0 là ()222 012 1 2 ω=ω+ω . Câu 4 (THPT Quỳnh Lưu - Nghệ An lần 3 - 2012): Mạch điện xoay chiều mắc nối tiếp gồm điện trở thuần R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C. Điện áp ở hai đầu đoạn mạch là u = U 2cosωt (V). Chỉ có tần số góc thay đổi được. Điều chỉnh ω thấy khi giá trị của nó là ω1 hoặc ω2 (ω1 > ω2) thì cường độ dòng điện hiệu dũng đều nhỏ hơn cường độ dòng điện hiệu dụng cực đại n lần (n > 1). Biểu thức tính giá trị R là: A. R = L(ω1 - ω2) n2 - 1 B. R = Lω1 ω2 n2 - 1 C. R = Lω1 ω2 n2 - 1 D. R = L(ω1 - ω2) n2 - 1 Hướng dẫn:

DẠYKÈMQUYNHƠNOFFICIAL 350 Cách giải 1: Ta có khi ω = ω1 và ω = ω2 thì mạch có cùng I với I1 = I2 = I = Imax n (n > 1) với Imax là cường độ cộng hưởng  ω1ω2 = ω2 = 1 LC Khi đó R = U Imax = I1Z1 nI1 = Z1 n = R2 + (ZL1 - ZC1)2 n  (nR)2 = R2 +    Lω1 –1 Cω1  2  (n2 – 1)R2 = (LCω1 2 - 1)2 (Cω1)2 (1) (Thay LC = 1 ω1ω2 và Cω1 = 1 Lω2 vào biểu thức (1)) (1)  (n2 – 1)R2 = L2(ω1 – ω2 )2  R = L(ω1 - ω2) n2 - 1 với (ω1 > ω2)  Chọn A Chú ý: Tương tự nếu ta viết biểu thức theo C thì ta thay LC = 1 ω1ω2 vào (1) Ta được (n2 – 1)R2 = (ω1 - ω2)2 C2ω1 2ω2 2  R = |ω1 - ω2| Cω1ω2 n2 - 1 . Cách giải 2: Theo giả thuyết: 121212 12 11 IIZZLL CC =  =  ω−=−ω− ωω 212 1 11 L CLC  ω=  ωω= ω Mặt khác: max 1 2 2 1 1 I U1U I nnR 1 RL C =  =  +ω− ω  () 2 22222 112 1 1 nRRLRLL C   =+ω−=+ω−ω  ω  () () ( )2 22212 12 2 L n1RLR. n1 ω−ω  −=ω−ω  =  Chọn A Câu 5 (Chuyên Nguyễn Quang Diệu lần 3 – 2014): Đặt điện áp xoay chiều có tần số góc ω thay đổi được vào hai đầu đoạn mạch RLC nối tiếp. Khi thay đổi đổi ω thì cường độ hiệu dụng trong mạch đạt giá trị cực đại là Imax và khi đạt hai giá trị 1ω , 2ω thì cường độ hiệu dụng trong mạch đạt giá trị đều bằng max I 5 . Cho 12 12 ωω 60 ωω C =Ω . Tính R: A. R = 30 Ω B. R = 60Ω C. R = 120 Ω D. R = 100 Ω Hướng dẫn: Ta có:

DẠYKÈMQUYNHƠNOFFICIAL 351 () ()22 LC1212 12 12 12 U I 11111 LLLRZZ CCC II  =  ⇔ω−=−ω+  +−ω+ω=+  ωωωω  = 2 1 21 max1 12 1 1 1 L C 5UU1 L2R IRCI1 5RL C  ω= ω  ⇔=  ω−= ω = +ω−  ω  () 12 1212 12 12 LL2RR30 LCL60. CC  ω−ω=  =Ω   ω−ωω−ω ==ω−ω=Ω ωω Chọn B Chú ý: Khi ω thay đổi 0ω thì cường độ hiệu dụng trong mạch đạt giá trị cực đại là Imax và khi đạt hai giá trị 1ω , 2ω thì cường độ hiệu dụng trong mạch đạt giá trị đều bằng max12 2 LI R. n n1 ω−ω  = Câu 6: Cho đoạn mạch xoay chiều R, L, C nối tiếp. Đặt vào 2 đầu mạch điện áp xoay chiều u = U0cosωt (V), với ω thay đổi được. Thay đổi ω để ULmax. Giá trị ULmax là biểu thức nàosau đây: A. ULmax = 2 C 2 L U Z 1 Z B. ULmax = 22 2UL 4LCRC C. ULmax = 2 L 2 C U . Z 1 Z D. ULmax = 22 2U R4LCRC Hướng dẫn: Ta có: UL = L 22 LC UZ R(ZZ) +− = 22 UL 1 R(L) C ω +ω− ω = 222 22 2 UL L1 RL2 CC +ω−+ ω ω = 22 242 UL 11L1 R2L CC  +−+  ωω  Nhận thấy UL = ULmax khi ω2 = 22 1 LCCR 2  ω = C 1 2 1 LR C2

DẠYKÈMQUYNHƠNOFFICIAL 352 và ULmax = 22 2UL R4LCRC Biến đổi: ULmax = 22 U R 4LCRC 2L = 2 22 2 U R 4L(4LCRC) = 242 2 U RCRC L4L = 242 2 U 11RCRC L4L  −−+  = 22 U 11RC 2L    = 2 22 2 U L 2RC 1C 4L    = 2 2 22 4 U L 2R C 1LC 4L    Biến đổi biểu thức A = 2 2 4 L 2R C 4L    = 2 22 2 4 2RC LC C2 4L       = 222 44 LCRC 2 CL    = 444 1 CLω Do đó ULmax = 22 444 U 1LC LCω = 422 U 1 1 LCω = 2 C 2 L U Z 1 Z .  Chọn A Chú ý: Tính toán hoàn toán tương tự cho bài toán C thay đổi cho Ucmax và thu được UCmax = 2 L 2 C U Z 1 Z Câu 7: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm, biết 2LCR = . Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều có f thay đổi được. Khi tần số góc của dòng điện là ω1 hoặc ω2 thì hệ số công suất trong mạch có giá trị bằng nhau. Giá trị bằng nhau đó là: A. 12 12 12 coscos ωω ϕ=ϕ= ω−ω B. 12 12 22 1122 coscos ωω ϕ=ϕ= ω+ωω+ω C. 12 12 12 coscos ωω ϕ=ϕ= ω+ω D. 12 12 22 1122 coscos ωω ϕ=ϕ= ω−ωω+ω Hướng dẫn: Theo giả thuyết, khi tần số góc của dòng điện là ω1 hoặc ω2 thì hệ số công suất trong mạch có giá trị bằng nhau hay 12coscosϕ=ϕ .

DẠYKÈMQUYNHƠNOFFICIAL 353 Ta có: 2 2 1 1 22 1 22 11 11 RRR coscos Z 11 RLRL CC ϕ==  ϕ=  +ω−+ω−  ωω  Mặc khác 22 L LCRR C =  = nên 2 1 2222 112222 11 LL cosCC LL1L1 L2L CCCCC ϕ== +ω−+ω−+ ωω . Theo phương pháp đánh giá hàm số, ta có: 2 12012 12 11 C LCL ωω=ω  ωω=  = ωω Nên: 2 2 1212 1 2222222 11221122 L cos LLL ωωωω ϕ== ω−ωω+ωω−ωω+ω 12 1 22 1122 cos ωω  ϕ= ω−ωω+ω Chọn D Chú ý: Mở rộng kết quả cho những bài toán tương tự khác. Kết quả bài toán có thể viết lại như sau: ( ) 12max 1 22 22 1122 1212 2121 1cos cos 11 ωωϕ ϕ=== ω−ωω+ω  ωωωω +−+−  ωωωω  Từ đó mở rộng cho bài toán có hai giá trị của ωcho cùng I, UR, P các giá trị đó sẽ có biểu thức tương tự: max 2 12 21 I I 1 =  ωω +− ωω  vì U I Z = giống như R cos Zϕ= Rmax R 2 12 21 U U 1 =  ωω +− ωω  vì R U UIRR Z == giống như R cos Zϕ= . Nhưng max 2 12 21 P P 1 =  ωω +− ωω  vì 2 2 U PIRR Z  ==   giống như 2 2 R cos Z  ϕ=   Câu 8: Mạch điện xoay chiều gồm cuộn dây có (Ro, L) và hai tụ điện C1, C2 . Nếu mắc C1 song song với C2 rồi mắc nối tiếp với cuộn dây thì tần số cộng hưởng là ω1 = 48π rad/s. Nếu mắc C1 nối tiếp với C2 rồi mắc nối tiếp với cuộn dây thì tần số cộng hưởng là ω2 = 100π rad/s. Nếu chỉ mắc riêng C1 nối tiếp với cuộn dây thì tần số cộng hưởng là A. ω = 74π rad/s. B. ω = 60π rad/s. C. ω = 50π rad/s. D. ω = 70π rad/s. Hướng dẫn:

DẠYKÈMQUYNHƠNOFFICIAL 354 Cách giải 1: Do C1 // C2 nên C = C1 + C2 Khi đó: 2 ss 2222 12ss12 111111 LCLCLC(48) ω==  =+= +ωωωπ (1) Do C1 nt C2 nên 12 111 CCC =+ Khi đó: 2 2222 nt nt12 1212 111111 LCLCCLCLC()(100)ω==+=+  ω=ω+ω=π (2) Giải hệ (1) và (2) ta được: 1 60 ω=π rad/s.  Chọn B Cách giải 2: Ta có: Cnt = 2 2 1 ω L  12 12 CC CC + = 2 2 1 ω L  C1C2 = 2 2 1 ω L . 2 1 1 ω L = 222 12 1 ωω L (2) Từ (1) và (2) ta được: C1 + 222 12 1 ωω L . 1 1 C = 2 1 1 ω L (3)  C1 = 2 1 ω L (4) Thay (4) vào (3) 2 1 ω L + 2 222 12 ω L ωω L = 2 1 1 ω L  2 1 ω + 2 22 12 ω ωω = 2 1 1 ω  22 12ωω + 4 ω = 22 2ωω  4 ω 22 2ωω + 22 12ωω = 0 Phương trình có hai nghiệm ω = 60π rad/s và ω = 80π rad/s.  Chọn B Câu 9: Mạch điện xoay chiều nối tiếp gồm cuộn dây thuần cảm L, điện trở R1503=Ω và tụ điện C. Đặt vào hai đầu đoạn mạch hiệu điện thế 0 uUcos2ft =π (V). Khi f = f1 = 25Hz hay f = f2 = 100Hz thì cường độ dòng điện trong mạch có giá trị hiệu dụng như nhau nhưng lệch pha nhau 2π 3 . Cảm kháng của cuộn dây khi f = f1 là? A. 1 H π B. 5 H π C. 3 H π D. 4 H π Hướng dẫn: Đề cho khi f = f1 thì: 1 22 1L1C U I R(ZZ) = +− (1) Khi f = f2 thì: 21 22 2L2C U II R(ZZ) == +− (2) Từ (1) và (2) ta được: 22 1L1C2L2C (ZZ)(ZZ) −=− (3) Do f1 < f2 nên Z1L < Z2L : ϕ1 < 0  ϕ2 > 0  2L2C1C1L1L2L1C2C ZZZZZZZZ −=−  +=+ (3’)  (ω2 +ω1)L = 12 111 C ωω  +   = 12 12 ωω1 C ωω  +    2 12 11 LC ωωω == (4) Đặt: 12ωωω 25.2π.50.2π 100π rad/s=== hay f = 50Hz (cộng hưởng).

DẠYKÈMQUYNHƠNOFFICIAL 355 Đề cho: 21 2 3 π ϕ+−ϕ= . Do tính chất đối xứng 2 12 1 3 3 π ϕ=  ϕ=−ϕ   πϕ=−  (5) Mặt khác: 11C1L 21 2 2L2C f25HzZ4Z f4f f100HzZ4Z ==   =   ==  (6) Từ (5) ta có : 1L1C 1 2L2C 2 ZZ π tanφ tan3 R3 ZZ π tanφ tan3 R3   ==−=−    ===   Do (6) ta thu được: 1L1C 1L1L1L 1L ZZZ4Z3Z3 3ZR RRR3 ===−  = 1L 1L 1 Z 31503 Z1503150LH. 3 ω 25.2ππ  ==Ω  === Khi Z1C = 4Z1L = 600Ω suy ra: 4 1C1 11110 CFF Z600.25.230000.3 ==== ωπππ . Tương tự, lúc sau : Z2L = 600Ω; Z2C = 150 Ω ta cũng tính được 3 LH π = .   Chọn C Chú ý: Bài toán có thể mở rộng: Có hai giá trị của ω để mạch có P, I, Z, cosφ, UR giống nhau thì 2 12m 1 ωωω LC == . Thay đổi f có hai giá trị 12ff ≠ biết 12 ffa += và 12 II? = Ta có : 11 22 121L1C2L2C ZZ(ZZ)(ZZ) =⇔−=−  2 12ch 12 1 LC 2a  ωω==ω  ω+ω=π hay 1212 1 ωωωωω LC =  =  tần số 12fff = . Câu 10: Cho đoạn mạch điện MN gồm một điện trở thuần R = 100Ω, cuộn dây thuần cảm có độ tự cảm 1 LH π = , tụ điện có điện dung 410 CF 2π = , mắc nối tiếp. Mắc hai đầu M, N vào nguồn điện xoay chiều có điện áp tức thời MN u1202cos2πft (V)= , tần số f của nguồn điện có thể điều chỉnh thay đổi được. a. Khi f = f1 = 50 Hz, tính cường độ hiệu dụng của dòng điện và tính công suất tiêu thụ P1 trên đoạn mạch điện MN. Viết biểu thức cường độ dòng điện tức thời chạy trong đoạn mạch đó. b. Điều chỉnh tần số của nguồn điện đến giá trị f2 sao cho công suất tiêu thụ trên đoạn mạch điệnMNlúc đólàP2 =2P1.Hãyxác địnhtầnsố f2 củanguồn điệnkhi đó.Tínhhệ số côngsuất. Hướng dẫn:

DẠYKÈMQUYNHƠNOFFICIAL 356 a. Khi f = f1 = 50Hz: L C 4 1 ZL100π.100 π 100 11 Z200 C10 100π 2π  =ω==Ω  ω=π   ===Ω ω  Tổng trở: ()2 222 LC ZRZZ1001001002 =+−=+=Ω Cường độ hiệu dụng của dòng điện trong mạch là: U1201,2 IA Z 10022 === Công suất tiêu thụ trên đoạn mạch điện là: 2 2 1 1,2 PIR.10072W 2  ===   Độ lêch pha của u và i trong mạch: LC uii ZZ 100 tan1 R10044 −ππ ϕ===−  ϕ=−=ϕ−ϕ  ϕ= Biểu thức của cường độ dòng điện trong mạch là: i1,2cos100tA 4 π =π+  b. Khi thay đổi f để P2 = 2P1 tức P2 = 144W. Ta có: 2 2 22 2 2 2 2 UR PIR144144 1 RL C ==⇔=  +ω− ω  2 22 2 11 L0 CLC  ⇔ω−=  ω= ω  Đây là trường hợp xảy ra cộng hưởng điện, thay số ta tìm được: 4 11 f502Hz 2LC 2.110 2 === π π ππ Hệ số công suất khi đó: R cosφ 1. Z == Câu 11: Cho mạch điện xoay chiều RLC mắc nối tiếp, cuộn dây thuần cảm ( 22LCR > ). Đặt vào hai đầu đoạn mạch điện áp xoay chiều ổn định uU2cos2ft(V). =π Khi tần số của dòng điện xoay chiều trong mạch có giá trị 1 f302Hz = hoặc 2 f402Hz = thì điện áp hiệu dụng giữa hai đầu tụ điện có giá trị không đổi. Để UC max thì tần số dòng điện bằng A. 206Hz. B.50Hz. C. 502Hz. D.48Hz. Hướng dẫn: Ta có: UC = C 22 LC UZ R(ZZ) +− = 2 2 U 1 CRL C ω+ω− ω  Khi UC1 = UC2 thì ω1 2 2 2 1 1 1 RL C    +ω− ω    = ω2 2 2 2 2 2 1 RL C    +ω− ω   

DẠYKÈMQUYNHƠNOFFICIAL 357 ⇔ 22422 111 2 L1 RL2 CC ω+ω−ω− = 22422 222 2 L1 RL2 CC ω+ω−ω− ⇔ ()() 22244 1212 L R2L C  −ω−ω=−ω−ω  ⇔ 22 222 12 22 L1R1R R222 CLCLLC2L  −ω+ω=−=−    (1) Suy ra UC = UCmax khi ω2 = 2 2 1R LC2L (2) Từ (1) và (2) ta thu được: 222222 1212 22fff ω=ω+ω  =+ () () 22 22 12 11 fff30240250Hz. 22  =+=+=  Chọn B Câu 12 (THPT Nam Đàn I lần 3 – 2016): Đặt điệnápxoaychiềucógiátrị hiệudụngU =120 V, tần số f thay đổi được vào hai đầu đoạn mạch gồm cuộn dây thuần cảm L, điện trở thuần R và tụ điện C mắc nối tiếp theo thứ tự đó. Khi tần số là f1 thì điện áp hai đầu đoạn mạch chứa RC và điện áp hai đầu cuộn dây L lệch pha nhau một góc 1350. Khi tần số là f2 thì điện áp hai đầu đoạn mạch chứa RL và điện áp hai đầu tụ điện lệch pha nhau một góc 1350 Khi tần số là f3 thì xảy ra hiện tượng cộng hưởng. Biết rằng 2 2 22 31 ff962 ff25   −=   . Điều chỉnh tần số đến khi điện áp hiệu dụng hai đầu tụ điện đạt giá trị cực đại là UCmax. Giá trị UCmax gần giá trị nào nhất sau đây? A. 123 V. B. 223 V. C. 130 V. D. 180,3 V. Hướng dẫn: Khi 1ff = thì 0 RCL(u; u)135 =  vẽ giãn đồ racó được: 1C1 1 ZR RC =  ω= và 1 1 C R = ω (1). Khi 2ff = thì 0 RLC(u; u)135 =  vẽ giãn đồ ra có được: 2L2 R ZR L =  ω= và 2 R L = ω (2). Khi 3ff = thì cộng hưởng 3 1 (3). LC  ω= Từ (1), (2) và (3) suy ra được: 2 312 ω=ωω (4). Mặt khác: 2222 2222 3131 ff9696 24. ff2525  ωω −=  −= ωω  Thay (4) vào được: 2 22 11 4.96 25 ωω −=  ωω (5)

DẠYKÈMQUYNHƠNOFFICIAL 358 Thay đổi f để CU đạt cực đạt thì Cmax 22 2U.L U R4LCRC = Thay (1) và (2) vào ta được: Cmax 2 22 11 2U U 4. = ωωωω . Thay (5) vào ta được: Cmax 2.120 U122,48 V 96 25 == .  Chọn A Câu 13: Cho mạch điện xoay chiều gồm các phần tử R, L, C mắc nối tiếp, cuộn dây thuần cảm, với tần số của dòng điện thay đổi. Khi tần số của dòng điện là 1 ff66Hz == hoặc 2 ff88Hz == thấy rằng hiệu điện thế hiệu dụng hai đầu cuộn cảm không thay đổi. Khi tần số bằng 3ff = thì LLmaxUU = . Giá trị của 3f là: A. 45,2 Hz. B. 23,1 Hz. C. 74,7 Hz. D. 65,7 Hz. Hướng dẫn: Ta có: UL = L 22 LC UZ R(ZZ) +− = 2 2 UL 1 RL C ω +ω− ω  Khi UL1 = UL2 thì 2 22 21 1 1 RL C   ω+ω− ω    = 2 22 12 2 1 RL C   ω+ω− ω    ⇔ 2 222222 2 2212 22 1 L1 RL2 CC ω ω+ωω−ω− ω = 2 222222 1 1211 22 2 L1 RL2 CC ω ω+ωω−ω− ω ⇔ () 22 222 12 21 222 21 L1 R2 CC  ωω −ω−ω=−  ωω  ⇔ 2222 22 12 11L 2RC2LCRC C  +=−=− ωω  (1) Nhận thấy UL = ULmax khi 2 11 ω C LR C2 =  2 1 ω = C2 2LR C2    = 2 1 ( 2LC – R2C2) (2) Từ (1) và (2) suy ra: 222222 1212 211211 fff =+  =+ ωωω 22 2222 12 ff266.88.2 f74,67Hz. ff6688  === ++   Chọn C Câu 14: Đặt điện áp xoay chiều u = U 2cosωt (V), có tần số góc thay đổi vào hai đầu mạch AB không phân nhánh gồm điện trở thuần R = 100Ω, cuộn cảm thuần L, tụ điện có điện

DẠYKÈMQUYNHƠNOFFICIAL 359 dung C. Gọi N là điểm nối giữa điện trở và cuộn cảm thuần. Thay đổi ω = ω1 thì điện áp ở hai đầu đoạn mạch NB bằng 0. Khi ω = ω2 thì UC max. So sánh ω2 và ω1, ta có: A. ω1 = ω2 B. ω1 < ω2 C. ω1 > ω2 D. ω1 = ω2 2 Hướng dẫn: Khi ω = ω1 thì UNB = 0  ZL = ZC  cộng hưởng  ω1 2 = 1 LC (1) Khi ω = ω2 thì UCmax Ta có:UC = IZC = U ZC Z = C 2 2 2 2 UZ 1 RL C  +ω− ω  = U R2C2ω2 2 + (LCω2 2 - 1)2 Đặt y = R2C2ω2 2 + (LCω2 2 - 1)2  Y = R2C2ω2 2 + L2C2ω2 4 - 2LCω2 2 + 1 Để UCmax khi Zmin  ymin  theo tính chất của parabol thì khi đó ω2 2 = 2LC - R2C2 2L2C2 = 1 LCR2 2L2 < 1 LC = ω1 2  ω2 2 < ω1 2  ω2 < ω1   Chọn C Bài 15: Đoạn mạch AB gồm 2 cuộn dây và một tụ điện mắc nối tiếp. M là điểm nối 2 cuộn dây, N là điểm nối cuộn dây 2 với tụ điện. Cuộn 1 thuần cảm. Khi đặt điện áp uAB = Ucosωt (V) thì cảm kháng cuộn 1 bằng dung kháng tụ điện C, điện áp uAN sớm pha hơn uMB một góc 3 π và có giá trị hiệu dụng UAN = 2UMB. Tỉ số độ tự cảm của 2 cuộn dây 1 2 L L là? A. 1 B. 2 C. 3 D. 4 Hướng dẫn: Để UAN nhanh pha hơn UNB một góc 3 π thì cuộn dây 2 phải có điện trở R. Do UAN = 2UMB nên ZAN = 2ZMB Ta có ZL1 = ZC ( ) ( ) 222 2 L1L2CL2 RZZ4ZZ4R ⇔++=−+ (1) ( ) ( ) 222 L1L2CL2 3RZZ4ZZ ⇔=+−− Giãn đồ véctơ như hình bên. Ta lại có: () 12coscos 3 π =ϕ+ϕ 1212 1 coscossinsin 2 ⇔=ϕϕ−ϕϕ O

DẠYKÈMQUYNHƠNOFFICIAL 360 L1L2CL2 ANMBANMB 1RRZZZZ .. 2ZZZZ +− ⇔=− () ( ) () 222 L1L2 2222 L1L2L1L2 1R2ZZ 2RZZRZZ ⇔=− ++++ ( ) ( )2 222 L1L2L1L2 3RZZ4ZZ ⇔=++− (2) Từ (1) và (2) suy ra: () 222 1 L1L2L1L2L1L212 2 L ZZZZZZLL1. L −=−+  =  =  = Chọn A Câu 16: Cho đoạnmạchxoaychiềuRLCmắcnốitiếp. Đặtvào2 đầumạch1 điệnápxoaychiềucó tần số thay đổi được. Khi tần số của điện áp 2 đầu mạch là f0 = 60Hz thì UL max. Khi tần số của điện áp 2 đầu mạch là f = 50Hz thì điện áp 2 đầu cuộn cảm là uL = UL 2 cos(100πt + ϕ1) (V). Khi f = f’ thì điện áp 2 đầu cuộn cảm là uL = U0L cos(ωt + ϕ2) (V). Biết 0L L U U 2 = . Giá trị của ω’ bằng: A. 160π rad/s B.130π rad/s C.144π rad/s D. 20 30 π rad/s Hướng dẫn: Ta có: UL = IZL = 2 2 UL 1 RL C ω +ω− ω  = 2 2 2 UL 1 RL C +ω− ω  ω Nhận thấy UL = UL max khi 2 2 min 2 min 1 RL C y  +ω−   ω  =  ω   () 2 2 2 0 1C 2LRC 2  =− ω (1) Với ω0 = 120π rad/s. Khi f = f và f = f ’ ta đều có U0L = UL 2 Suy ra: UL = U’L ⇔ 2 2 22 ' RLR'L11 C'C ωω =  +ω−+ω−  ωω  2 2 222211 R'L'RL 'CC   ⇔ω+ω−=ω+ω−  ωω    ()() () 22 222 22 222222 1'111 '2LRC' C'C'  ωω  ⇔ω−ω−=−=ω−ω+  ωωωω  ()22 22 11 C2LRC '  ⇔−=+ ωω  (2)

DẠYKÈMQUYNHƠNOFFICIAL 361 Với ω = 100 rad/s. Từ (1) và (2) ta có: 22 2 0 22222 0 0 211 ' '2 ωω =+  ω= ωωωω−ω ()() 0 2222 0 100.120 '160,36 rad/s. 22100120 ωω ππ  ω===π ω−ω π−π    Chọn A Câu 17 (ĐH - 2013): Đặt một điện áp xoay chiều u = 1202cos2ft π (V) (f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở R và tụ điện có điện dụng C, với CR2 < 2L. Khi f = f1 thì UC max. Khi f = f2 = 1 f2 thì UR max. Khi f = f3 thì UL max. Giá trị của ULmax gần giá trị nào nhất sau đây? A. 173 V B. 57 V C. 145 V D. 85 V. Hướng dẫn: Cách giải 1: Áp dụng công thức: 22 2 0 2 LmaxL U 1 U  ω += ω  hay 2 2 C 2 LmaxL Uf 1 Uf  +=  Với f3f1 = f2 2 nên f3 = 2f1 hay fL = 2fC  UL max= 803V = 138,56V.    Chọn C Cách giải 2: Nếu ta đặt 22 1 f n f ω == ω thì 2 LmaxCmax 4 nU UU n1 == Khi đó: ( ) () 2 LmaxCmax 4 2.120 UU803V138,56V. 21 ====   Chọn C Cách giải 3: Ta có: fC max = f1 = 1 2π 2 2 2LRC 2LC fR max = f2 = 1 2π 1 LC = f1 2 = 1 2π 2 2 2LRC 2LC 2  2 2LRC L = 1  2L – R2C = L  L = R2C Vậy ULmax = 22 2UL R4LCRC = 2 2222 2URC R4RCRC = 2U 3 = 139 V.    Chọn C Câu 18: Cho mạch RLC nối tiếp, cuộn cảm thuần, ω thay đổi được. Đặt điện áp xoay chiều ổn định vào hai đầu mạch. Điều chỉnh 0ω=ω để công suất của mạch đạt cực đại. Điều chỉnh L 48rad/sω=ω=π thì UL max. Ngắt mạch RLC ra khỏi điện áp rồi nối với một máy phát điện xoay chiều một pha có 1 cặp cực nam châm và điện trở trong không đáng kể. Khi tốc độ quay của roto bằng n1 = 20 vòng/s hoặc n2 = 60 vòng/s thì điện áp hiệu dụng hai đầu cuộn cảm bằng nhau. Giá trị của 0ω gần với giá trị nào nhất sau đây? A. 149,37 rad/s B. 156,1 rad/s C. 161,54 rad/s D. 172,3 rad/s Hướng dẫn:

DẠYKÈMQUYNHƠNOFFICIAL 362 Điều chỉnh 0ω=ω thì Pmax 2 02 0 11 LC LC ⇔ω=⇔= ω (1) Điều chỉnh Lω=ω thì UL max ()2 22 L 222 L 22 2LCRC 2 2LCRC ⇔ω=⇔−= −ω Ta có: LL 2 222 2642 ENBSLNBSL U.Z Z 111L11 2RLR2L CCC ωω ===  +ω−+−+ ωωω ω  Đặt 2 1 x = ω xét 3222 2 1L f(x)xR2xLx CC  =+−+   Áp dụng Viét ta có: () () 2 22 123 2 2 122313 LR2 bC xxx2LCRC a13 C c xxxxxxLC a    ++=−=−=−    ++==  Thay (1) và (2) vào (3) ta được : 11 22 L 2222n2040 rad/s 123L3 n20120 rad/s 48 rad/s 0 2222224 1223130 1111 238,43 rad/s 1111111156,12 rad/s = ω=π = ω=π ω=π  ++=ωωωωω=  →  ω= ++=ωωωωωωω   Chọn B Câu 19: Một mạch điện xoay chiều có hiệu điện thế hiệu dụng hai đầu mạch không đổi, tần số góc ω thay đổi được. Mạch gồm các phần tử điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Biết rằng biểu thức L = CR2 Điều chỉnh ω đến giá trị ω = ω1 và ω = ω2 = 9ω1 thì mạch có cùng hệ số công suất. Giá trị của hệ số công suất là: A. 2 13 B. 2 21 C. 4 67 D. 3 73 Hướng dẫn: Cách giải 1: Khi chỉnh ω đến 2 giá trị ω1 và ω2 thì mạch có cùng hệ số công suất  cosϕ2 = cosϕ1  Z1 = Z2  | ZL1 – ZC1 | = | ZL2 – ZC2 | ⇔ ω1ω2 = 1 LC  9ω1 2 = 1 LC và L = CR2 ⇔ LC = R2C2 = 1 9ω1 2 và CR = 1 3ω1 (1) Xét cosϕ1 = R R2 + (ZL1 - ZC1)2 = RCω1 R2C2ω1 2 + (LCω1 2 - 1)2

DẠYKÈMQUYNHƠNOFFICIAL 363 Thay các giá trị từ (1) ta được: 1 2 1 33 cos. 1173 1 99 ϕ== +−     Chọn D Cách giải 2: Tổng quát bài toán: Mạch RLC có ω thay đổi. U = const. Khi điều chỉnh ω = ω1 và ω = ω2 =nω1 thìmạchtiêuthụ cùnghệ số côngsuất,nghĩalàcosϕ2 =cosϕ1 vớiL=CR2 Tương tự từ đề ta có: cosϕ2 = cosϕ1 | ZL1 - ZC1 | = | ZL2 - ZC2 | ⇔ ZL1 + ZL2 = ZC1 + ZC2 (1) ⇔ LC = 1 ω1ω2 (2) Từ (1)  Lω1 = 1 Cω2 ⇔ ZL1 = ZC2  ZL2 = ZC1 (do (1)) Lúc này ta xét tanϕ1 = ZL1 - ZC1 R = ZL1 - ZL2 R ⇔ tanϕ1 = L(ω1 - ω2) R = CL(ω1 - ω2) CR ⇔ tan2ϕ1 = (LC)2.(ω1 - ω2)2 (CR)2 = (LC)2(ω1 - ω2 )2 C.CR2 = (LC)2( ω1 - ω2 )2 LC (vì L = CR2) ⇔ tan2ϕ1 = LC(ω1 - ω2)2 = 1 ω1ω2 (ω1 2 - 2ω1ω2 + ω2 2) =   ω1 ω2 – 2 + ω2 ω1   = 2 12 21  ωω   ωω  ⇔ 1212 1 2121 ff tan ff ωω ϕ=−=− ωω (công thức này chỉ áp dụng khi L = CR2) Từ tỉ lệ giữa ω1 và ω2 ta tính dễ dàng ra tanϕ1 rồi dùng máy tính cầm tay suy cosϕ1. Hoặc có thể áp dụng công thức 1 + tan2ϕ = 1 cos2ϕ . Áp dụng cho bài trên ta có 11 1983 tancos. 91973ϕ=−=−  ϕ=    Chọn D 6. Khi ω thay đổi URL hoặc URC cực đại a. Khi ω thay đổi để URLmax Phương pháp 1: Ta có: + === +−+ + + 22 RLL RL2222 LLCCCLC 22 L UZRZU UU ZRZ2ZZZZ2ZZ 1 RZ Thay === ωω C L 1L1L1 Z CCLCZ . Đặt  =  =  2 LxZ L a 2C

DẠYKÈMQUYNHƠNOFFICIAL 364 == −+ −++ ++ + RL 2 L 22 422 LL UU U Lxa 12LZ14a2CxRx CZRZ Xét hàm −+−+ == +++ 2 2222 xa0.xxa y. xRxxRx0 Để RL maxU thì ymin. Ta có () () ++ === ++ 2 22 22 2 22222 010a1a x2x 1R10R0 x2axaR y' 0 xRxxRx  =−+<   =++>  22 1 22 2 xaaaR0 xaaaR0 Ta có bảng biến thiên x -∞ x1 0 x2 +∞ y’ - 0 + y +∞ +∞ ymin RLU () + = +− 22 L RL max2 2 LC RZ UU RZZ 0 U Vậy, RL maxU khi và chỉ khi   ==++  ω=++   ==   ++  2 2 2 2 L RL C L2 2 LLL1LLL ZxRR 2C2C2CL2C2C2C L1L1 Z CZC LLL R 2C2C2C Khi đó: () + = +− 22 L RLmax 22 LC RZ UU RZZ Phương pháp 2: Ta có: + == +−+ 22 RLL RL 222 LLCC UZRZ UU ZRZ2ZZZ == + +ω + +ω 2 CLC 2222 L 222 UU Z2ZZ12L 1 RZCC 1 RL Xét hàm số −−+ == ++ 22 22222 112L2L1 x yCxCCC RLxLxRx với =ω2 x Để RLmaxU thì  = min yy'0 .

DẠYKÈMQUYNHƠNOFFICIAL 365 Ta có: () () ++ = == ++ 2 22 322 2 2222 22 2 2222 222 2L12L1 00 x2x CCCC 2L2LR y'LRL0R0xxCCC 0 LxRxLxRx Với ∆=+>  ∆=+ 432 2 2 43 2 L2LLL2L 'R0'R CCCCC  ++  =ω=>      −+ =ω=<    22 2 22 2 1 3 22 2 22 2 2 3 LLL2L R CCCC x0 2L C LLL2L R CCCC x0 2L C Ta có bảng biến thiên x -∞ x1 < 0 0 x2 > 0 +∞ y’ - 0 + y +∞ 0 0 ymin RLU () + = +− 22 L RLmax 22 LC RZ UU RZZ 0 U Biến đổi nghiệm ++++ =ω=  ω= 22 2 2 2 22 2 2 2 1 3 2 LLL2LLL2L RR CCCCCCC x 2L 2L C (1) Nhân cả hai vế (1) cho 2L , ta được ++ =ω= 2 2 2 222 L LL2L R ZLCCC 2 hay  =++   2 2 L LLL ZR 2C2C2C Nhân cả hai vế (1) cho 2C rồi nghịch đảo, ta được == ω ++ 2 2 2 C 22 2 2 2 L 12 ZC C LL2L R CCC hay =  ++   C 2 2 L ZC LLL R 2C2C2C

DẠYKÈMQUYNHƠNOFFICIAL 366 Khi đó: () + = +− 22 L RLmax 22 LC RZ UU RZZ b. Khi ω thay đổi để URCmax Phương pháp 1: Ta có: + === +−+ + + 22 RCC RC 222 2 LLCC LLC 22 C UZRZ U UU ZRZ2ZZZ Z2ZZ 1 RZ Thay =ω=ω=L C LL1 ZLC CCZ . Đặt  =  =  2 CxZ L a 2C == −+ −++ ++ + RC 2 C 22 422 CC U1 UU Lxa 12LZ14a2CxRx CZRZ Xét hàm −+−+ == +++ 2 2222 xa0.xxa y. xRxxRx0 Để RC maxU thì ymin. Ta có () () ++ === ++ 2 22 22 2 22222 010a1a x2x 1R10R0 x2axaR y' 0 xRxxRx  −−+  =−+=<    −++ =++>  22 2 22 22 1 22 22 2 22 22 2 22 LLL2L R CCCC xaaaR0 LR LLL2L R CCCC xaaaR0 LR Ta có bảng biến thiên x -∞ x1 0 x2 +∞ y’ - 0 + y +∞ 0 0 ymin RCU () + = +− 22 C RCmax 22 LC RZ UU RZZ 0 U Vậy, RC maxU khi và chỉ khi

DẠYKÈMQUYNHƠNOFFICIAL 367   ==++  ω=   ++    ==  ++   2 2 C RC 2 2 L C2 2 LLL1 ZxR 2C2C2C LLL CR 2C2C2C L1L1 Z CZC LLL R 2C2C2C Khi đó: () + = +− 22 C RCmax 22 LC RZ UU RZZ Phương pháp 2: Ta có: + == +−+ 22 RCC RC 222 LLCC UZRZ UU ZRZ2ZZZ == +ω− + + + ω 2 LLC22 22 C 2 22 UU Z2ZZ2L1L RZC 1 1 R C Xét hàm số == ++ 222 22 22 12L2L LLxx yxCC 11 RxRx CC với =ω2 x . Để RCmaxU thì  = min yy'0 Ta có: ++ +− = ==  ++   2 2 2 2 2 2 2222 2 23 2 2 2 2 2L2L LL00 Cx2xC 1 1 0R02L2L R CLRxx C y'CC 0 11 RxRx CC Với ∆=+>  ∆=+ 432 2 2 43 2 L2LLL2L 'R0'R CCCCC  −−+  =ω=<    −++ =ω=>  22 2 22 2 1 22 22 2 22 2 2 22 LLL2L R CCCC x0 LR LLL2L R CCCC x0 LR Ta có bảng biến thiên x -∞ x1 < 0 0 x2 > 0 +∞ y’ - 0 +

DẠYKÈMQUYNHƠNOFFICIAL 368 y +∞ 0 0 ymin RCU () + = +− 22 C RCmax 22 LC RZ UU RZZ 0 U Biến đổi nghiệm −++ =ω=  ω=  ++    22 2 2 22 2 2 2 1 22 2 22 2 LLL2L RL 2 CCCC xC LR LL2L LR CCC (1) Nhân cả hai vế (1) cho 2L , ta được =ω= ++ 2 2 222 L 2 2 2 L 2 ZLC LL2L R CCC hay =  ++   L 2 2 L ZC LLL R 2C2C2C Nhân cả hai vế (1) cho 2C rồi nghịch đảo, ta được ++ == ω 2 2 2 2 C 22 LL2L 1RZCCC C2 hay  =++   2 2 C LLL ZR 2C2C2C Khi đó: () + = +− 22 C RCmax 22 LC RZ UU RZZ BÀI TẬP VẬN DỤNG Câu 1: Cho đoạn mạch AB gồm cuộn dây thuần cảm 1 LH = π , điện trở 100 R 3 =Ω và tụ điện có điện dung 47.10 CF 6 = π theo thứ tự mắc nối tiếp. Điểm M nằm giữa cuộn cảm và điện trở, điểm N nằm giữa điện trở và tụ điện. Đặt vào hai đầu AB một điện áp xoay chiều không đổi và tần số f thay đổi. Khi UAN max thì giá trị của tần số bằng bao nhiêu? A. 60Hz B. 50Hz C. 40Hz D. 30Hz Hướng dẫn: Khi f thay đổi để UAN max nghĩa là URL max nên:

DẠYKÈMQUYNHƠNOFFICIAL 369 2 2 LC LLL ZZR 2C2C2C  ==++   2 2 444 111 100 .100. 7.107.107.10 2.2.2.3 666   πππ =++=Ω     πππ  Tần số: L RL Z 100 f50Hz. 2L1 2. === π π π    Chọn B Câu 2: Cho đoạn mạch AB gồm cuộn dây thuần cảm L , điện trở R502=Ω và tụ điện có điện dung 310 CF 8 = π theo thứ tự mắc nối tiếp. Với L = nR2C, n > 0,5. Điểm M nằm giữa cuộn cảm và điện trở, điểm N nằm giữa điện trở và tụ điện. Đặt vào hai đầu AB một điện áp xoay chiều không đổi U903V = và tần số f thay đổi. Khi 1 400 ffHz 55 == thì UAM max Khi 20fff == thì UAN max, đồng thời UNB khi đó gần giá trị nào nhất sau đây? A. 130V B. 150V C. 170V D. 200V Hướng dẫn: Khi UAN max thì ()2 2 C 3 502LRL Z 10 C22 8 =−=− π () L 2 X 3 3 140011 fLH. 2CZ55502 10L2. 10 82 8  =⇔=  = π π π− π π Khi 20fff == thì UAN max,suyra  =++   =Ω  =++  =Ω   =   =   2 2 C 2C L L C LLL ZR 2C2C2C Z80 111R kZ100 242L C5 k Z4 Z k

DẠYKÈMQUYNHƠNOFFICIAL 370 Khi đó: () ( ) () C NBC 222 2 LC UZ 903.80 UU 1202V170V. RZZ 50210080 ==== +− +− ≃  Chọn C Câu 3 (Chuyên Lê Khiết lần 1 – 2014): Cho đoạn mạch AB gồm cuộn dây thuần cảm L có điện trở thuần r = 4Ω, điện trở R26=Ω và tụ điện có điện dung C theo thứ tự mắc nối tiếp. Điểm M nằm giữa R và C, điểm N nằm giữa điện trở và tụ điện. Đặt vào hai đầu AB một điệnápxoay chiềukhông đổi U120V = vàtầnsố fthay đổi.Thay đổi tần số dòng điện cho đếnkhi UMB min (chứatụ điệnvàcuộndâydẫn).Giátrị của UMB min là A.16V B.24V C.60V D.32V Hướng dẫn: Trước khi giải bài toán này, ta đi giải bài toán tổng quát tìm điện áp hiệu dụng hai đầu đoạn mạch LrC sau đây: Phương pháp 1: Ta có: () ()() 22 LC LrCLrC 22 LC UrZZ UIZ RrZZ +− == ++− Xét biểu thức () () () 2 2 2 LC fxrx Rrx xZZ0  + = ++  =−≥ . Ta có: ( )LrCmin min Ufx ⇔   . Khảo sát f(x) trong miền giá trị x0 ≥ ta có ( ) minLC fxx0ZZ ⇔=⇔=  , mạch khi đó xảy ra hiện tượng cộng hưởng điện. Khi đó: LrCmin Ur U Rr = + Phương pháp 2: Ta có: () 22 LrCrLC UUUU =+− Theo tính chất cơ bản của bất đẳng thức thì x0 ≥ nên ()2 22 rLCr UUUU +−≥ . Đẳng thức xảy ra khi và chỉ khi LCUU = . Do đó: LrCminLC UUU. ⇔= Cường độ dòng điện qua mạch: U I Rr = + Hiệu điện thế hai đầu mạch LrC khi đó: LrC Ur UIr. Rr == + Vậndụngvàobài toántrên. Dòng điệnquamạch: U120 I4A. Rr264 === ++ Hiệu điệnthế hai đầumạchMB (LrC)khi đó: MBLrC UUIr4.416V. ====    Chọn A Chú ý:

DẠYKÈMQUYNHƠNOFFICIAL 371 Các công thức tính nhanh về góc: Giả sử: ω = ω RL RC n . Ta có: ++ω  = ω 2 2 RL RC LLL R 2C2C2C L C và ω = ω ++  RC 2 RL 2 L C LLL R 2C2C2C và ωω=ω2 RCRLR Khi ω=ωRL hay ω == ω RLL RCC Z n Z thì  ϕϕ=   ϕϕ=−   ϕ=  RL RC 1 tantan 2n 1 tantan 2n 1n1 tan n2 Khi ω=ωRC hay ω == ω RLC RCL Z n Z thì  ϕϕ=   ϕϕ=−   ϕ=−  RC RL 1 tantan 2n 1 tantan 2n 1n1 tan n2 Với ++ω  === ω 2 2 RLC RCL LLL R Z2C2C2C n ZL C 2111R n L242 C  =++ Câu 4: Mạch điệnxoay chiềuAB gồm cuộncảm thuầncó độ tự cảm L, điệntrở thuần R vàtụ điện có điện dung C mắc nối tiếp. Gọi M là điểm nằm giữa cuộn dây và điện trở, N là điểm nằm giữa điện trở và tụ điện. Biết rằng điện áp hiệu dụng hai đầu AB không đổi và mạch có tần số góc ω thay đổi được. Chỉnh ω đến giá trị ω1 rad/s thì UAN max. Từ giá trị ω1 đó giảm tầnsố góc đi 40rad/sthì UMB max vàkhi đóhệ số côngsuất củamạch bằng 3 10 .Biết rằng ω1 nhỏ hơn100rad/s.Giátrị của ω1 gần với giá trị nào nhất sau đây A.48rad/s. B.76rad/s. C.89rad/s. D.54rad/s. Hướng dẫn: Tacó: ωω == ωω− RL1 RC1 n 40

DẠYKÈMQUYNHƠNOFFICIAL 372 Mà: ϕ= 3 cos 10 nên =  ω= ϕ==   =  ω=  1 1 n360 11n1rad/s tan33n2n120 rad/s 2  Chọn D Chú ý: Các công thức tính nhanh về góc: Giả sử: ω = ω RL RC n . Ta có: ++ω  = ω 2 2 RL RC LLL R 2C2C2C L C và ω = ω ++  RC 2 RL 2 L C LLL R 2C2C2C và ωω=ω2 RCRLR Khi ω=ωRL hay ω == ω RLL RCC Z n Z thì  =++⇔=++  2 2 22 2 L L LLLLLL ZRZR 2C2C2C2C2C2C ⇔=++2222 LLCLCLC 2ZZZZZ2ZZR ( ) ⇔−=+ 2 2222 LLCLCLC 2ZZZZZ2ZZR ⇔=+322 LLCC 2Z2ZZZR ⇔=LCLC L ZZZZ RR2Z ⇔ϕϕ== C RL L Z 1 tantan 2Z2n Khi ω=ωRC hay ω == ω RLC RCL Z n Z thì  =++⇔=++  2 2 22 2 C C LLLLLL ZRZR 2C2C2C2C2C2C ⇔=++2222 CLCLCLC 2ZZZZZ2ZZR ( ) ⇔−=+ 2 2222 CLCLCLC 2ZZZZZ2ZZR ⇔=+322 CCLL 2Z2ZZZR ⇔=LCCL C ZZZZ . RR2Z ⇔ϕϕ== L RC C Z 1 tantan 2Z2n Ta có bảng chuẩn hóa ω LZ CZ ωRC 1 n ω=ωRLRC n n 1 Khi ω=ω⇔ϕϕ== L RLRC C Z 1 tantan 2Z2n

DẠYKÈMQUYNHƠNOFFICIAL 373 ⇔=⇔=−  ϕ== n1n1n11n1 .Rnn2tan RR2nn2 nn2 Vậy: ϕ=  ϕϕ= RC 1n11n11 tantantan. n2n2 nn2 Nên ϕϕ=− RC 2 1 tantan 2n Khi ω=ω⇔ϕϕ== C RCRL L Z 1 tantan 2Z2n −−−+− ⇔=⇔=−  ϕ==− n1n1n11n1 .Rnn2tan RR2nn2 nn2 Vậy: ϕ=−  ϕϕ=− RL 1n11n11 tantantan. n2n2 nn2 Nên ϕϕ=− RL 2 1 tantan 2n Tìm biểu thức RLmaxU và RCmaxU theo ω = ω RL RC n = + + RLmax 2 CLC 22 L U U Z2ZZ 1 RZ . Theo chuẩn hóa  =−  =  = L C Rnn2 Zn Z1 Từ đó ta có: () === +− −+ RLmax 2 222 UUn UU 12.n.11 11n1 nn2nn Tương tự, ta cũng có: = RCmax2 n UU n1 Vậy == RLmaxRCmax2 n UUU n1 Tìm biểu thức liên hệ Khi ω=ωRL hay ω === ω RLLL RCCC ZU n ZU Ta có =  += 22 22 RLmax 222 RLmax nU1 UU1 n1Un

DẠYKÈMQUYNHƠNOFFICIAL 374 Suy ra: += 22 C 22 RLmaxL UU 1 UU và ω += ω 22 RC 22 RLmaxRL U 1 U Khi ω=ωRC hay ω === ω RLCC RCLL ZU n ZU Ta có =  += 22 22 RCmax 222 RCmax nU1 UU1 n1Un Suy ra: += 22 L 22 RCmaxC UU 1 UU và ω += ω 22 RL 22 RCmaxRC U 1 U Câu 5: Mạch điệnxoay chiềuAB gồm cuộncảm thuầncó độ tự cảm L, điệntrở thuần R vàtụ điện có điện dung C mắc nối tiếp. Gọi M là điểm nằm giữa cuộn dây và điện trở, N là điểm nằm giữa điện trở và tụ điện. Biết rằng điện áp hiệu dụng hai đầu AB là 1003V và mạch có tần số góc ω thay đổi được. Thay đổi ω=ω0 thì UAN max và khi đó hiệu điện thế hai đầu MB lệch pha với cường độ dòng điện một góc α với α= 1 tan 22 . Giá trị hiệu dụng của hiệu điệnthế hai đầuAN gần giá trị nào nhất? A.105V. B.185V. C.200V. D.300V. Hướng dẫn: Tacó: ϕϕ=− RC 2 1 tantan 2n với ω  = ω    ϕ=  =   α=ϕ==    RL RC RC n 1n1 tann2. n2 112 tantan 222nn1 Mặt khác: ===  = ANRLmaxAN 22 n2 UUU1003.U200V. n121  Chọn C Chú ý: Khi làm những dạng toán liên quan đến góc khi ω thay đổi để RLmaxU , RCmaxU . Nếu không nhớ được các công thức về tan thì có thể sử dụng các đại lượng sau khi đã chuẩn hóa: + Khi ω=ωRL thì  =−  =  = L C Rnn2 Zn Z1 + Khi ω=ωRC thì  =−  =  = L C Rnn2 Z1 Zn Với ω = ω RL RC n  =++ 2111R n 242L C .

DẠYKÈMQUYNHƠNOFFICIAL 375 Câu 6: Mạch điệnxoay chiềuAB gồm cuộncảm thuầncó độ tự cảm L, điệntrở thuần R vàtụ điện có điện dung C mắc nối tiếp với 3L = 2CR2. Gọi M là điểm nằm giữa cuộn dây và điện trở, N là điểm nằm giữa điện trở và tụ điện. Biết rằng điện áp hiệu dụng hai đầu AB không đổi và mạch có tần số góc ω thay đổi được. Thay đổi ω=ω0 thì UAN max. Hệ số công suất củamạch cógiátrị gần giá trị nào nhất sau đây? A.0,75. B.0,82. C.0,89. D.0,95 Hướng dẫn: Tacó: =  = 2 2 R3 3L2CR L 2 C nên =++=++= 2 111R11133 n... L 24224222 C Cách giải 1: Tacó: = ANmaxRLmaxUU . Chuẩnhóa  =−=−=   ==  =   L C 333 Rnn22 222 3 Zn 2 Z1 Suyra: () ϕ=== +−  +−    ≃ 2222 LC 3 R3cos2 0,95. RZZ3310 1 22    Chọn D Cách giải 2: Khi = ANmaxRLmaxUU thì  ϕ==  ϕ===   1n1113 tancoscosarctan0,95. n233 10  Chọn D Câu 7: Mạch điệnxoay chiềuAB gồm cuộncảm thuầncó độ tự cảm L, điệntrở thuần R vàtụ điện có điện dung C mắc nối tiếp. Gọi M là điểm nằm giữa cuộn dây và điện trở, N là điểm nằm giữa điệntrở vàtụ điện.Biết rằng điện áphiệudụnghai đầuAB làkhông đổi vàmạch có tần số góc ω thay đổi được. Thay đổi ω=ω0 thì UAN max và khi đó hiệu điện thế hai đầu MB lệch pha với cường độ dòng điện một góc α với α= 1 tan 22 . Hệ số công suất của mạchcógiátrị gần giá trị nào nhất sau đây? A. 22 3 . B. 3 3 . C. 2 3 . D. 23 3 . Hướng dẫn: Tacó: α=ϕ===  = C RC Z 11 tantann2. R n2n222

DẠYKÈMQUYNHƠNOFFICIAL 376 Chuẩnhóa  =−=−=  ==  = L C Rnn222222 Zn2 Z1 Suyra: () () () ϕ=== +− +− 222 2 LC R2222 cos . RZZ3 2221   Chọn A Câu 8: Mạch điệnxoay chiềuAB gồm cuộncảm thuầncó độ tự cảm L, điệntrở thuần R vàtụ điện có điện dung C mắc nối tiếp. Gọi M là điểm nằm giữa cuộn dây và điện trở, N là điểm nằmgiữa điệntrở vàtụ điện.Biếtrằng điệnáphiệudụnghai đầuABlàkhông đổivàbằngU và mạch có tần số góc ω thay đổi được. Khi ω=ω1 thì mạch tiêu thụ công suất bằng P1 = 100W với hệ số công suất bằng 1. Khi ω=ω2 thì điện áp hiệu dụng UMB max, đồng thời mạch tiêu thụ công suất bằng P2. Sau đó, giữ nguyên giá trị ω2 và tiến hành thay đổi L (hoặc C). Giá trị củaP2 không thể làkết quả nàodưới đây? A.88,9W. B.88,3W. C.89,2W. D.94,3W. Hướng dẫn: Tacó: () ()ϕ=  ϕ= +−+− 2 2 2222 LCLC RR coscos. RZZRZZ Chuẩnhóa  =−  ==  = L C Rnn2 Zn2 Z1 Suyra: () () () ϕ====≤  + +   2 2 2 222 11118 cos n1111 n1911191112n2nn 2nn182n2 Nhậnthấy ()ϕ=2 min 8 cos 9 khi n=2. Chọn A 7. Bài toán tần số thay đổi đến ω1 và ω2 thì RLU hoặc RCU có cùng giá trị Ýtưởngbắt nguồntừ côngthức đãthiết lập  =++⇔−=+   22 2111R111R n.n. 242242LL CC Talưuýrằng ω = ω RL RC n ,kết hợpvới ωω=ω2 RLRCR ta được ωω == ωω 22 RLR 22 RRC n a. Khi thay đổi đến ω1 và ω2 thì RLU có cùng giá trị

DẠYKÈMQUYNHƠNOFFICIAL 377 Tacó: = +ω +ω RL 22 222 U U 12L 1CC RL Từ đóta đặt ω  ==  ω=+ω ω  2 22 2R R 11 tt 22 thayvàohàm số ω = +ω 22 222 12L yCC RL +ω  =  ++ω   22 R 222 R 12L 1 tCC 2 y 1 RtL 2 ,kết hợpvới ω= 2 R 1 LC ,ta được: = + +++ 2 2 2L yC RL LL 24C tR CtC . Để RLmaxU thì  +   +     2 min max RL L yt24C Ct . Hàm nàycódạng = b at t nêntacómối liênhệ sau: Gọi ω =− ω 2 RL 0 2 R 1 t 2 ứng với khi RLmaxU và ω =− ω 2 1 1 2 R 1 t 2 , ω =− ω 2 2 2 2 R 1 t 2 ứng với RLU có cùng giátrị,khi đó:  ωωω  =⇔−=−−=−=+  ωωω  2 2222 2 2 RL12 012 222 RRR 111111R ttt n. 222242L C Khi đó: ===  ω  ωωωω  RL1RL2 22 2 0 1212 UU UU 1 11 LC Chú ý: Chứng minh hoàn toàn tương tự cho kết quả hai giá trị của ωcho cùng UC ===  ω  ωωωω  L1L2 22 2 0 1212 UU UU 1 11 LC b. Khi thay đổi đến ω1 và ω2 thì RCU có cùng giá trị

DẠYKÈMQUYNHƠNOFFICIAL 378 Tacó: = ω− + + ω RC 22 2 22 U U 2L L 1C 1 R C Từ đóta đặt ωω ==  ω= ω + 22 2 RR 2 1 t 21 t 2 thayvàohàm số ω− = + ω 22 2 22 2L L yC 1 R C ω +  = + ω + 2 R2 2 2 R2 2L .L t1C y21 R .C 1 t 2 ,kết hợpvới ω= 2 R 1 LC ,ta được: = + +++ 2 2 2L yC RL LL 24C tR CtC . Để RCmaxU thì  +   +     2 min max RL L yt24C Ct . Hàm nàycódạng = b at t nêntacómối liênhệ sau: Gọi ω =− ω 2 R 0 2 RC 1 t 2 ứng với khi RLmaxU và ω =− ω 2 R 1 2 1 1 t 2 , ω =− ω 2 R 2 2 2 1 t 2 ứng với RCU có cùng giátrị,khi đó:  ωωω  =⇔−=−−=−=+  ωωω  2 2222 2 2 RRR 012 222 RC12 111111R tttn. 222242L C Khi đó: () === −ωω  ωω  ω  RC1RC2 22 12 12 2 0 UU UU 1LC 1 Chú ý: Chứng minh hoàn toàn tương tự cho kết quả hai giá trị của ωcho cùng UC

DẠYKÈMQUYNHƠNOFFICIAL 379 () === −ωω  ωω  ω  C1C2 22 12 12 2 0 UU UU 1LC 1 Câu 1: Mạch điệnxoay chiềuAB gồm cuộncảm thuầncó độ tự cảm L, điệntrở thuần R vàtụ điện có điện dung C mắc nối tiếp thỏa mãn 11L = 50CR2. Gọi M là điểm nằm giữa cuộn dây và điện trở, N là điểm nằm giữa điện trở và tụ điện. Biết rằng điện áp hiệu dụng hai đầu AB không đổi và mạch có tần số thay đổi được. Khi = f3011Hz thì UAN max. Khi = 1 ffHz và == 21 3 fff Hz 4 thì hiệu điện thế hiệu dụng giữa hai đầu MB bằng nhau. Giá trị của 1f gần giá trị nào nhất sau đây? A.108Hz. B.176Hz. C.89Hz. D.154Hz. Hướng dẫn: Tacó: = ANmaxRLmaxUU .Với  =++    =  =  2 2 111R n.11 242L n. C10 11L50CR Mặt khác: =  === 2 RLRL 2R R ff3011 nf3010 Hz. fn11 10 Khi đó:  −=−=−−    22222 RRR 222 RC12 fff 1111 n 2f2f2f2 () ()    ⇔−=−=−−       22 22 2 R 22 RC12 1 f300300 111111 9 102f2f22 f 14  = 1 f100 Hz.   Chọn A Câu 2: Mạch điệnxoay chiềuAB gồm cuộncảm thuầncó độ tự cảm L, điệntrở thuần R vàtụ điện có điện dung C mắc nối tiếp thỏa mãn L = nCR2. Gọi M là điểm nằm giữa cuộn dây và điện trở, N là điểm nằm giữa điện trở và tụ điện. Biết rằng điện áp hiệu dụng hai đầu AB không đổi và mạch có tần số thay đổi được. Khi = 39335 fHz 5 thì UAN max. Khi = f6131Hz và == 2 1316 ff Hz 5 thì hiệu điện thế hiệu dụng giữa hai đầu MB bằng nhau. Giátrị củan gần giá trị nào nhất sau đây? A.0,69. B.0,86. C.0,91. D.0,96. Hướng dẫn: Giả sử:  =  −=−    22 2 RLR 2 RCRC ff11 kk f2f2 với =++ 111 k 242n

đổi điện dung. Mắc vôn kế thứ nhất vào AM, vôn kế thứ hai vào NB. Điều chỉnh giá trị của C thì thấy ở cùng thời điểm số, chỉ củ

DẠYKÈMQUYNHƠNOFFICIAL 380 Mà  =−=−−  2 2222 2 RLRRR R 222 RC12 ffff111 f kf2f2f2 Khi đó: 2 22 RLRL 22 12 ff 111 k 2kf2kf2  −=−−    () 22 22 3933539335 5511 k1,4. 22k61311316 k 5        =−−  =        Suyra: =++  = 11125 1,4n. 242n28  Chọn C CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Đặt vào hai đầu một tụ điện một điện ápxoay chiều có giá trị hiệu dụng U không đổi vàtầnsố fthay đổi.Khi f=50Hzthì cường độ hiệudụngqua tụ là2,4A. Để cường độ hiệu dụngquatụ bằng3,6Athì tầnsố củadòng điệnphải bằng: A.25Hz B.75Hz C.100Hz D.50Hz Câu 2: Cho mạch điện xoay chiều gồm ba đoạn mắc nối tiếp. Đoạn AM gồm điện trở thuần R, đoạn MN gồm cuộn dây thuần cảm, đoạn NB gồm tụ xoay có thể thay

a V1 cực đại thì số chỉ của V1 gấp đôi số chỉ của V2. Hỏi khi số chỉ củaV2 cực đại vàcó giátrị V2 max =200Vthì số chỉ củavônkế thứ nhất là A.100V. B.120V. C.50V. D.80V. Câu 3: Cho mạch điện RLC mắc nối tiếp theo thứ tự R, L, C trong đó cuộn dây thuần cảm có độ tự cảm L thay đổi được, điện trở thuần R100=Ω . Thay đổi L người ta thấy khi 1LL = và khi 1 2 L LL 2 == thì công suất tiêu thụ trên đoạn mạch như nhau nhưng cường độ dòng điệntứcthời vuôngphanhau.Giátrị L1 và điệndungC lầnlượt là: A. 4 1 43.10 LH, CF 2 == ππ B. 4 1 410 LH, CF 3 == ππ C. 4 1 210 LH, CF 3 == ππ D. 4 1 13.10 LH, CF 4 == ππ Câu 4: Cho mạch điện nối tiếp gồm cuộn dây thuần cảm có độ tự cảm L thay đổi được, tụ điện có dung kháng 60 Ω và điện trở thuần 20 Ω. Điện áp đặt vào hai đầu đoạn mạch ( )u205cos100tV =π .Khi cảm khángbằngZL thì LmaxU .Giátrị ZL và LmaxU lầnlượt là A. 200 3 Ω và200V. B. 200 3 Ω và100V. C.200 Ω và200V. D.200 Ω và100V.

DẠYKÈMQUYNHƠNOFFICIAL 381 Câu 5: Đặt điện áp xoay chiều uU2cos100t =π (V) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, tụ điện có điện dung C và cuộn cảm thuần có độ tự cảm L thay đổi được. Điều chỉnh L để LmaxU thì lấy giá trị cực đại đó bằng 100 V, điện áp hiệu dụng ở hai đầutụ điệnbằng36Vvà điệnáphiệudụngtrênR làUR.TínhUvàUR. A.U=80Vvà UR =48V. B.U=136VvàUR =48V. C.U=64VvàUR =48 V. D.U=48Vvà UR =80V. Câu 6: Đặt điện áp u = U 2cosωt (V) vào hai đầu đoạn mạch nối tiếp gồm R = 100 Ω, tụ điện C và cuộn cảm có độ tự cảm L thay đổi được. Khi L = L1 = 1 π H thì cường độ dòng điện qua mạch cực đại. Khi L2 = 2L1 thì điện áp ở đầu cuộn cảm thuần đạt cực đại. Tần số ω bằng: A.200π rad/s B.125π rad/s C.100π rad/s D.120π rad/s Câu 7: Cho mạch điện xoay chiều L, R, C mắc nối tiếp theo thứ tự đó (cuộn cảm thuần có độ tự cảm L thay đổi được). Điều chỉnh L để LmaxU thì R U503 = V. Lúc này, khi điện áp tức thời ở hai đầu đoạn mạch là 1502 V thì điện áp tức thời giữa hai đầu đoạn mạch chứaRC là 502 V.Tínhtrị hiệudụngcủa điện áp ở hai đầu đoạnmạchAB. A. 1003 V. B.615V. C.200V. D.300V. Câu 8: Cho mạch điện xoay chiều mắc nối tiếp gồm các phần tử điện trở thuần R, cuộn dây thuần cảm có độ tự cảm L và tụ điện có điện dung C. Mạch chỉ có tần số góc thay đổi được. Khi ω = ω1 = 100π rad/s thì UL max. Khi ω = ω2 = 2ω1 rad/s thì CmaxU . Biết rằng khi giá trị ω = ω1 thì ZL +3ZC =400Ω.Giátrị Llà: A. 4 7π H B. 3 4π H C. 4 3π H D. 7 4π H Câu 9: Một đoạn mạch RLC, khi f1 = 66 Hz hoặc f2 = 88 Hz thì hiệu điện thế giữa hai đầu cuộncảm không đổi. Để ULmax thì fcógiátrị là A.45,21 B.23,12 C.74,76 D. 65,78 Câu 10: Cho mạch điện xoay chiều RLC có cuộn thuần cảm có độ tự cảm L có thể thay đổi được.Dùngbavôn kế xoaychiều có điệntrở rất lớn để đo điệnáp hiệudụngtrênmỗi phần tử. Điềuchỉnhgiátrị của Lthì thấy = LmaxRmaxU2U .Tínhtỉ số Lmax Cmax U U ? A.3. B.4. C.3. D. 2 3 . Câu 11: Cho đoạn mạch điện xoay chiều ANB, đoạn AN chứa R và C thay đổi, đoạn NB chứaL=1,5 π H.Biết f=50Hz,người tathay đổi C saocho ANmaxANU2U = .Tìm R vàC: A. CZ =200 Ω ; R =100 Ω B. CZ =100 Ω ; R =100 Ω C. CZ =200 Ω ; R =200 Ω D. CZ =100 Ω ; R =200 Ω

DẠYKÈMQUYNHƠNOFFICIAL 382 Câu 12: Đặt điện áp ( ) 00uUcost V (U=ω và ω không đổi) vào hai đầu đoạn mạch mắc nối tiếpgồm điệntrở R,tụ điệncó điệndung C,cuộn cảm thuần có độ tự cảm Lthay đổi được. Khi L=L1 thì LmaxU vàlúcnày RLmaxU0,5U = .Khi L=L2 thì CmaxU .Tínhtỉ số Lmax Cmax U U ? A.0,41. B. 2 . C. 3 . D.2. Câu 13: Mạch điện R1L1C1 có tần số cộng hưởng ω1 và mạch R2L2C2 có tần số cộng hưởng ω2, biết ω1 = ω2. Mắc nối tiếp hai mạch đó với nhau thì tần số cộng hưởng của mạch sẽ là ω.Khi đó ω liênhệ với ω1và ω2 theocôngthứcnào? A. ω =2ω1. B. ω =3ω1. C. ω =0. D. ω = ω1. Câu 14: Cho một đoạn mạch RLC không phân nhánh, cuộn dây thuần cảm, độ tự cảm của cuộn dây có thể thay đổi được. Khi thay đổi giá trị của L thì thấy ở thời điểm UR max thì điện áp này gấp bốn điệnáp hiệu dụng giữa hai đầu cuộn dây. Khi UL max thì điện áp này so với điệnáphiệudụnggiữahai đầu điệntrở khi đógấp: A.4,25lần. B.2,5lần. C.4 lần. D.4 lần. Câu 15: Đặt điện áp ( ) u9010costV( =ωω không đổi) vào hai đầu mạch điện AB nối tiếp theo đúngthứ tự gồm R, C vàcuộn cảm thuầncó độ tự cảm Lthay đổi được.Khi LL1ZZ = hoặc LL2ZZ = thì L1L2 UU270 == V. Biết L2L1 3ZZ150 −= Ω và tổng trở của đoạn mạch RC tronghai trườnghợplà 1002 Ω.Giátrị LmaxU gần giá trị nào nhất sau đây? A.150V. B.180V. C.300V. D.175V. Câu 16: Đoạn mạch RLC mắc nối tiếp gồm điện trở thuần có giá trị 100Ω, cuộn cảm thuần L và tụ điện C. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có giá trị ổn định, có tần số góc thay đổi được. Thay đổi tần số góc, khi ω = ω1 = 200π rad/s thì UL max, khi ω = ω2 = 50π rad/sthì UC max. Độ tự cảm củacuộndây cógiátrị A. 21 H 3 π B. 4 H 9π C. 2 H 3π D. 31 H 2 π Câu 17: Đặt điệnápxoaychiều ( )uU2cos100tV =π vàohai đầu đoạnmạchnốitiếpgồm điện trở thuầnR,tụ điệnCvàcuộncảmthuầncó độ tự cảmLthay đổi được.KhiL=L1 = 1 π (H) thì usớm phahơni là 4 π .Khi L=L2 = 2 π (H)thì LmaxU =200V.TínhU. A.184,776V. B.76,537V. C.200V. D.150V. Câu 18: Cho mạch RLC nối tiếp: Điện trở thuần R, L thay đổi được, tụ điện có điện dung C. Điện áp xoay chiều đặt vào 2 đầu mạch u = U0cos(ωt) (V). Khi thay đổi độ tự cảm đến 1 1 LH = π thì cường độ dòng điện hiệu dụng qua mạch cực đại, lúc đó công suất của mạch bằng200W.Khi thay đổi đến 2 2 LH = π thì UL max =200V. ĐiệndungC cógiátrị: 2

DẠYKÈMQUYNHƠNOFFICIAL 383 A. 200 Fµ π B. 50 Fµ π C. 150 Fµ π D. 100 Fµ π Câu 19: Cho mạch điện nối tiếp gồm điện trở 20 Ω cuộn dây có độ tự cảm 1,4 π H và điện trở thuần 30 Ω và tụ xoay có điện dung thay đổi C. Điện áp giữa hai đầu đoạn mạch: ( )u1002cos100t V.=π Tìm C để CmaxU .Tìm giátrị cực đại đó. A. Cmax U290V = và 5 C2,23.10F = . B. Cmax U297V = và 5 C2,23.10F = . C. Cmax U297V = và 6 C2,23.10F = . D. Cmax U290V = và 6 C2,23.10F = . Câu 20: Đặt điện áp u = U 2 cosωt (V) (U và ω không đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn dây và tụ điện. Biết cuộn dây có hệ số công suất 0,8 và tụ điện có điện dung C thay đổi được. Gọi Ud và UC là điện áp hiệu dụng hai đầu cuộn dây và hai đầu tụ điện. ĐiềuchỉnhC để ( )dC max UU + ,khi đótỉ số củacảmkhángvớidungkhángcủa đoạnmạchlà: A.0,60. B.0,71. C.0,50. D.0,80. Câu 21: Chomạch điệnnốitiếpgồm điệntrở 302 Ω cuộndâycó độ tự cảm ()0,32 H π và điện trở thuần 302 Ω và tụ xoay có điện dung thay đổi C. Điện áp giữa hai đầu đoạn mạch: ( ) u2402cos100tV. =π Khi C =Cm thì = CmaxmUU .Giátrị củaCm vàUm lầnlượt là A.16µFvà158V B.15µFvà158V C.16µFvà120V D.12µFvà120V Câu 22: Cho mạch điện RLC mắc nối tiếp. Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều có f thay đổi được. Khi tần số góc của dòng điện là ω1 hoặc ω2 thì dòng điện hiệudụngtrongmạchcó giátrị bằngnhau max 12 I II n == .Giátrị của điệntrở A. 12 2 L R n1 ω−ω = B. 12 2 L R n1 ω−ω = + C. 12 2 L R n1 ω−ω = + D. 12 2 L R n1 ω−ω = Câu 23: Cho mạch điện xoay chiều R, L, C mắc nối tiếp theo thứ tự đó (cuộn cảm thuần). Điện dung C có thể thay đổi được. Điều chỉnh C để điện áp ở hai đầu C là lớn nhất. Khi đó điện áp hiệu dụng ở hai đầu điện trở R là 150 V. Khi điện áp tức thời hai đầu đoạn mạch là 1003 V thì điện áp tức thời giữa hai đầu đoạn mạch chứa RL là - 300 V. Tính trị hiệu dụngcủa điệnáp ở hai đầu đoạnmạch AB. A. 1003 V. B.615V. C.200V. D.300. Câu 24: Một đoạn mạch xoay chiều mắc nối tiếp gồm điện trở thuần R, tụ điện C và cuộn dây thuần cảm có độ tự cảm L thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ổn định, khi điều chỉnh độ tự cảm của cuộn cảm đến giá trị L0 thì điện áp hiệu dụng hai đầu các phần tử R, L, C có giá trị lần lượt là 30 V, 20 V và 60 V. Khi điều chỉnh độ tự cảm đếngiátrị 2L0 thì điệnáphiệudụnghai đầu điệntrở bằngbaonhiêu? A. 50V B. 50 V 3 C. 150 V 13 D. 100 V 11

DẠYKÈMQUYNHƠNOFFICIAL 384 Câu 25: Đặt điện áp: ( )uU2costV =ω vào đoạn mạch AB nối tiếp gồm cuộn cảm và tụ điện có điện dung C thay đổi được. Khi C = C0 thì CmaxRL1 U,UU = đồng thời u trễ hơn i là α (α > 0). Khi C =C1 thì UC = 470 V đồngthời u sớm hơni là α. Khi C =C2 thì UC = 470 V, RL1 UU140V =− .Giátrị U gần giá trị nào nhất sau đây? A.70V. B.140V. C.210V. D.280V. Câu 26: Đoạn mạch AB nối tiếp gồm hai đoạn mạch AM và MB. Đoạn mạch AM là một cuộn dây có điện trở thuần R403 = Ω có độ tự cảm L = 0,4 π H, đoạn mạch MB là một tụ điện có điện dung C thay đổi được, C có giá trị hữu hạn và khác không. Đặt vào AB một điện áp: ( )AB u1202cos100tV =π . Điều chỉnh C để tổng điện áp hiệu dụng ( )+ AMMBmaxUU .Cực đại củatổngsố này cógiátrị. A.240V. B. 1203 V. C.120V. D. 1202 V. Câu 27: Một mạch điện xoay chiều gồm các linh kiện lý tưởng R, L, C mắc nối tiếp. Tần số riêng của mạch là ω0, điện trở có thể thay đổi. Hỏi cần phải đặt một điện áp xoay chiều có giá trị hiệu dụng không đổi, có tần số góc ω bằng bao nhiêu để điện áp hiệu dụng URL khôngphụ thuộcvàoR? A. ω = ω0 2 B. ω = ω0 C. ω = ω0 2 D. ω =2ω0 Câu 28: Đặt điện áp xoay chiều vào hai đầu đoạn mạch nối tiếp gồm điện trở R, cuộn cảm thuần L và tụ điện có điện dung C thay đổi được. Khi C thay đổi thì điện áp hiệu dụng cực đại trênR,LvàC lầnlượt làx,y,z.Nếu x y =3thì z x bằng A. 22 3 . B. 0,752. C. 0,75. D. 22. Câu 29: Cho mạch điện xoay chiều không phân nhánh gồm 3 phần tử: điện trở R, cuộn cảm thuần có 1 LH π = và tụ điện có điện dung C. Điện áp tức thời giữa hai đầu mạch điện là πu90cos ωt+(V) 6  =   . Khi 1ωω = thì cường độ dòng điện qua mạch là πi2cos240πt(A) 12  =−  , t tính bằng s. Cho tần số góc ω thay đổi đến giá trị mà trong mạchcócộnghưởng điện,biểuthức điệnápgiữa hai bảntụ điệnlúc đólà: A. C πu452cos100πt(V) 3  =−  B. C πu452cos120πt(V) 3  =−  C. C πu60cos100πt(V) 3  =−  D. C πu60cos120πt(V) 3  =−  C A B R L M

DẠYKÈMQUYNHƠNOFFICIAL 385 Câu 30: Đặt điện áp xoay chiều 0 uUcost =ω (V) vào hai đầu đoạn mạch RLC nối tiếp (cuộn dây thuần cảm). Khi chỉ thay đổi L đến giá trị L1 còn C và R giữa nguyên thì LmaxU . Nếu giữ nguyên L, R thay đổi C đến giá trị C1 thì CmaxU = 80 V. Biết L1C1Z2Z = và CLZ5Z = Giátrị LmaxU gần giá trị nào nhất sau đây? A.300V. B.260V. C.380V. D.100V. Câu 31: Cho mạch điện xoay chiều gồm RLC mắc nối tiếp,cuộn cảm thuần có độ tự cảm thay đổi được. Đặt vào hai đầu đoạn mạch điện áp xoay chiều u1002cos100t =π (V). Điều chỉnh độ tự cảm để điện áp trên hai đầu cuộn cảm đạt giá trị cực đại là ULmax thì điện áphiệudụngtrênhai đầu tụ điệnlàUC =100V.Giátrị ULmax là A.300V B.241V C.200V D.250V Câu 32: Đặt điện áp xoay chiều ổn định vào hai đầu đoạn mạch AB nối tiếp gồm cuộn cảm thuần có độ tự cảm L thay đổi, điện trở thuần R = 30 Ω và tụ điện có dung kháng 80 Ω. Thay đổi L để RLmaxU .Cảm khángcủacuộn cảm thuầnlúcnày A.50 Ω. B.180 Ω. C.90 Ω. D.56 Ω. Câu 33: Đặt điện áp ( )u1002cos100tV =π vào hai đầu đoạn mạch nối tiếp RLC có R503 = Ω, 410 CF = π , cuộn cảm thuần có độ tự cảm L thay đổi. Điều chỉnh L = L1 thì LmaxU . Khi L = L2 thì RLmaxU . Khi L = L3 thì CmaxU . Khi điều chỉnh cho L = L1 + L2 – L3 thìcôngsuất tiêuthụ củamạch gần giá trị nào nhất trongsố cácgiátrị sau đây? A.55W. B.90W. C.60W. D.40W. Câu 34: Đặt điện áp ( )uU2cos100tV =π vào hai đầu đoạn mạch mắc nối tiếp theo đúng thứ tự gồm cuộn cảm thuần có cảm kháng 120 Ω, điện trở thuần R và tụ điện có điện dung C thay đổi.Khi C =C0 thì = RCmax U2U .Dungkhángcủatụ điệnlúcnàylà A.160 Ω. B.100 Ω. C.150 Ω. D.200 Ω. Câu 35: Đặt điện áp ( )=π uU2cos100tV vào hai đầu đoạn mạch mắc nối tiếp theo đúng thứ tự gồm cuộn cảm thuần có độ tự cảm L thay đổi được, điện trở thuần R và tụ điện có điện dung C. Khi L = L1 thì = RLmax U2U , đồng thời hệ số công suất toàn mạch là k1. Khi L=L2 thì hệ số côngsuất củamạchlàk2.Chọncácphươngán đúng A. 1 2 2 k 5 k3 13  =    =  B. 1 2 k5 2 k13 3  =    =  C. 1 2 k3 5 2 k 13  =    =  D. 1 2 k13 2 k5 3  =    =  Câu 36: Đặt một điện áp xoay chiều có biểu thức ( )u1002cos100tV =π vào hai đầu đoạn mạch AB gồm hai đoạn AM và MB mắc nối tiếp. Đoạn AM gồm điệntrở R nối tiếpvới cuộncảm thuần có độ tự cảm Lthay đổi. Đoạn MB chỉ cótụ điện có M C A B LR

DẠYKÈMQUYNHƠNOFFICIAL 386 điện dung C. Điều chỉnh L = L1 để MB U50V, I0,5A== và dòng điện trong mạch trễ pha hơnulà600 ĐiềuchỉnhL=L2 thì AM maxU .TínhL2 A. 12 H. + π B. 13 H. + π C. 23 H. 2 + π D. 15 H. 2 + π Câu 37: Đặt hiệu điện thế xoay chiều ( )u1002cos100tV =π vào hai đầu đoạn mạch nối tiếp theo thứ tự gồm cuộn thuần cảm L thay đổi được, điện trở R và tụ điện C. Khi L = L1 thì I = 0,5 A, UC = 100 V đồng thời uC trễ pha hơn u là 600. Khi L = L2 thì RLmaxU . Tìm L2 A. 2 H. π B. 3 H. π C. 4 H. π D. 5 H. π Câu 38: Cho đoạn mạch xoay chiều RLC mắc nối tiếp. Đặt vào 2 đầu mạch 1 điện áp xoay chiều có tần số thay đổi được. Khi tần số của điện áp 2 đầu mạch là 0 f60Hz = thì UL max Khi tần số của điện áp 2 đầu mạch là f = 50Hz thì điện áp 2 đầu cuộn cảm là ( )LL1 uUcos100t=π+ϕ V. Khi f = f ’ thì điện áp 2 đầu cuộn cảm là ( )L0L2 uUcos100t=π+ϕ V.Biết 0L L U U 2 = .Giátrị của ω’bằng: A.160π rad/s B.130π rad/s C.144π rad/s D.20 30 π rad/s Câu 39: Đặt điện áp xoay chiều có giá trị hiệu dụng U và tần số không thay đổi vào hai đầu đoạn mạch AB nối tiếp theo đúng thứ tự gồm: cuộn cảm thuần có độ tự cảm L xác định; điệntrở Rvàtụ điệncó điệndungCthay đổi được. Điềuchỉnh điệndungC để URC min =U1 và URC max =U2.Nếu 2 5 UU 3 = thì U1 là A.0,43U. B.0,64U. C.0,68U. D.0,72U. Câu 40: Cho đoạn mạch AB gồm AM chứa điện trở thuần, MN chứa cuộn cảm thuần L, NB chứa tụ điện C có điện dung thay đổi được. Điện áp AB0 uUcost (V)=ω . Điều chỉnh điện dung C để UC max, khi đó điện áp tức thời cực đại trên R là 12a. Biết khi điện áp hai đầu mạchlà16athì điệnáptứcthời hai đầutụ là7a. Chọnhệ thức đúng. A.4R =3ωL. B.3R =4ωL. C.R =2ωL. D.2R = ωL. Câu 41: Cho mạch điện xoay chiều nối tiếp RLC với C thay đổi. Điều chỉnh C sao cho CmaxU khi đó R U75 = V.Khi = u756V thì = RL u256V .Tìm điệnáphiệudụngtoànmạch A. 756 V. B. 753 V. C.150V. D. 1502 V. Câu 42: Mạch điệnxoaychiềuRLCmắcnốitiếp, đặtvàohai đầumạchmột điệnápxoaychiều u = U0cosωt (V). Điều chỉnh C = C1 thì công suất của mạch đạt giá trị cực đại Pmax = 400W. ĐiềuchỉnhC =C2 thì hệ số côngsuất củamạchlà 2 3 .Côngsuất củamạchkhi đólà

DẠYKÈMQUYNHƠNOFFICIAL 387 A.200W B.200 3 W C.300W D.150 3 W Câu 43: Đặt điện áp xoay chiều ( ) 00uUcost V (U,:=ωω không đổi) vào hai đầu đoạn mạch R, L, C mắc nối tiếp (cuộn dây thuần cảm) với R thay đổi được. Khi R = 20 Ω thì Pmax, đồng thời nếu thay tụ C bằng bất kì tụ nào thì điện áp hiệu dụng trên tụ đều giảm. Dung khángcủatụ lúcnàylà: A.60 Ω. B.40 Ω. C.30 Ω. D.50 Ω. Câu 44: Đoạn mạch AB nối tiếp gồm hai đoạn mạch AM và MB. Đoạn mạch AM là một cuộn dây có điện trở thuần R = 40 Ω và độ tự cảm 0,4 LH = π , đoạn mạch MB là một tụ điện có điện dung C thay đổi được, C có giá trị hữu hạn và khác không. Đặt vào hai đầu đoạn mạch AB một điện áp: ( )AB0 uUcos100t V=π Điều chỉnh C để tổng điện áp hiệu dụng ( ) AMMBmaxUU + .Tìm độ lệchphagiữa điệnáptứcthời trên AM vàtrênAB. A. 6 π . B. 3 16 π . C. 3 8 π . D. 4 π . Câu 45: Đoạn mạch AB nối tiếp gồm hai đoạn mạch AM và MB. Đoạn mạch AM là một cuộn dây có điện trở thuần R = 51,97 Ω và độ tự cảm 0,3 LH = π , đoạn mạch MB làmột tụ điện có điện dung C thay đổi được, C có giá trị hữu hạn và khác không vào hai đầu đoạn mạch AB một điện áp: ( )AB uU2cos100tV =π . Điều chỉnh C để tổng điện áp hiệu dụng ( ) AMMBmaxUU + .Tìm UAM. A.2U. B.U. C.0,5U. D.0,25U. Câu 46: Đặt điện áp ( )uU2costV =ω vào đoạn AB gồm cuộn dây và tụ điện mắc nối tiếp. Biết hệ số công suất của cuộn dây là 0,8 và điện dung của tụ thay đổi được. Điều chỉnhC saocho ( ) cdCmaxUU + .Khi đó,tỉ số L C Z Z bằng: A.0,50. B.0,8. C.0,60. D.0,71. Câu 47: Đặt điện áp u = U 2cos2πft vào 2 đầu mạch điện gồm cuộn dây có điện trở thuần 100 Ω , độ tự cảm 1 L π = H mắc nối tiếp tụ điện có điện dụng 410 C 2π = F. Thay đổi tần số f, khi UCmax thì fcógiátrị bằng: A.25Hz B.25 2 Hz C.50Hz D.25 6 Hz Câu 48: Đặt điện áp xoay chiều ( )=π 0 uUcos100t V vào hai đầu đoạn mạch nối tiếp theo đúng thứ tự gồm, cuộn cảm thuần có độ tự cảm L, điện trở R, tụ điện có điện dung C thay đổi được.Ban đầu điều chỉnh RCmax U, sau đógiảm giátrị này đi 3lầnthì CmaxU .Giátrị của L R Z gần giá trị nhất nàosau đây? A.3,6. B.2,8. C.3,2. D.2,4.

DẠYKÈMQUYNHƠNOFFICIAL 388 Câu 49: Đặt hiệu điện thế xoay chiều ( )=π u1002cos100tV vào hai đầu đoạn mạch nối tiếp theo thứ tự gồm cuộn thuần cảm có độ tự cảm L thay đổi được, điện trở R và tụ điện C. Khi L = L1 thì I = 0,5 A, UC = 100 V đồng thời uC trễ hơn u là π 6 . Khi L = L2 thì RLmaxU . Tìm L2. A. 3 H. π B. 3 H. π C. 2,414 H. π D. 1,414 H. π Câu 50: Đạt điện áp xoay chiều ổn định vào 2 đầu đoạn mạch AB gồm cuộn dây có điện trở thuầnrvàtụ điệnmắc nối tiếp,trong đó2r= 3 ZC.Chỉ thay đổi độ tự cảm L, khi UL max thì cảm khángcủacuộndây là: A.ZL =ZC B.ZL =2ZC C.ZL =0,5ZC D.ZL =1,5ZC Câu 51: Cho mạch điện xoay chiều RLC có cuộn thuần cảm có độ tự cảm L có thể thay đổi được. Điềuchỉnhgiátrị củaLthì thấy = LmaxCmaxU3U .Tínhtỉ số Lmax Cmax U U ? A.3. B. 5 2 . C.3. D. 2 3 . Câu 52: Đặt điện ápxoaychiềucó giátrị hiệudụngU=30 2 Vvàohai đầu đoạnmạchRLC mắcnối tiếp.Biết cuộn dâythuầncảm,có độ cảm Lthay đổi được. Khi UL max thì hiệu điện thế hiệudụnghai đầutụ điệnlà30V.Giátrị của UL max là: A.60V B.120V C.30 2 V D.60 2 V Câu 53: Đoạn mạch AB gồm AM nối tiếp với MB. Đoạn AM gồm điện trở thuần R nối tiếp với cuộn cảm thuần có độ tự cảm L, đoạn MB chỉ có tụ điện có điện dung C với 2 CR2L < . Đặt vào AB một điện áp AB uU2cost =ω (V), U ổn định và ω thay đổi. Khi Cω=ω thì UC max, khi đó điện áp tức thời hai đầu đoạn mạch AM và hai đầu đoạn mạch AB lệch pha sovới dòng điệnlầnlượt là RLϕ và ϕ .Giátrị của RL tantanϕϕ là: A. 1 2 . B.2. C.1. D. 1 . Câu 54: Đặt điện áp ( )uU2cos2ftV =π (f thay đổi) vào hai đầu đoạn mạch AB mắc nối tiếp theo đúng thứ tự gồm điện trở R, cuộn cảm thuần L có độ tự cảm L và tụ điện có điện dungC,với 2 LRC. = Khif=f0 thì CmaxU vàkhi 0 ff502 =+ Hzthì LmaxU .Giátrị củaf0. A. 252Hz . B. 50Hz . C. 502Hz . D. 25Hz . Câu 55: Đặt vào hai đầu RLC mắc nối tiếp một điện áp xoay chiều có U không đổi và f thay đổi được. Khi điều chỉnh tần số đến giá trị f = f1 và f = f2 thì mạch tiêu thụ cùng một công suất. Biết rằng f1 + f2 = 125Hz, độ tự cảm L = 1 π H và tụ điện có điện dung C = 10-4 π F. Giá trị củaf1 vàf2 là: A.72Hzvà53Hz B.25Hzvà100Hz C.50Hzvà75Hz D.60Hzvà65Hz

DẠYKÈMQUYNHƠNOFFICIAL 389 Câu 56: Cho đoạn mạch RLC nối tiếp cuộn dây thuần L và có thể thay đổi được, R, C xác định. Mạch điện mắc vào nguồn có điện áp 0 uUcost =ω (V) không đổi. Khi thay đổi giá trị Lthì Rmax Lmax U 2 U = .Giátrị củaUC max là: A. 2U B. U3 C. U3 2 D. 2U 3 Câu 57: Đặt điện áp ( )uU2cos2ftV =π (f thay đổi) vào hai đầu đoạn mạch AB mắc nối tiếp theo đúng thứ tự gồm điện trở R, cuộn cảm thuần L có độ tự cảm L và tụ điện có điện dung C, với 25 LRC 9 = . Khi f = x Hz thì CmaxU , khi 2 fx1200 =− Hz thì LmaxU và khi f = y Hzthì RmaxU .Chọncácphươngán đúng A. x30 y405 =   =  B. x30 y4010 =   =  C. x40 y405 =   =  D. x40 y4010 =   =  Câu 58: Đặt điện áp ( )uU2cos2ftV =π (f thay đổi) vào hai đầu đoạn mạch AB mắc nối tiếp theo đúng thứ tự gồm điện trở R, cuộn cảm thuần L có độ tự cảm L và tụ điện có điện dung C. Gọi M và N lần lượt là điểm nối L với R và điểm nối R với C. Biết uAN luôn luôn vuôngphavới uMB vàkhi f=50Hzthì CmaxU .Khi mạchxảyracộng hưởngthì fcógiátrị. Câu 59: Cho mạch điện xoay chiều AB gồm R, L, C mắc nối tiếp. Cuộn cảm thuần có độ tự cảm thay đổi được. Đặt vào hai đầu đoạn AB một điện áp xoay chiều ổn định u =100 6 cos100πt (V). Điều chỉnh độ tự cảm để ULmax thì điện áp hiệu dụng hai đầu tụ điệnlà200V.Giátrị của ULmax A.100V B.150V C.300V D.250V Câu 60: Đặt điện áp ( )uU2cos2ft V=π (f thay đổi) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở R, tụ điện có điện dung C, cuộn cảm thuần có độ tự cảm L (với 2 2LRC). > Khi f = f0 thì UC = U và ( )( ) ( )LLCC 6RZZZ7RRZ. ++=+ Khi f = f0 + 75 Hz thì UL = U. Tínhf0. A.50Hz. B.60Hz. C.75Hz. D.100Hz. Câu 61: Đặt điện áp xoay chiều có giá trị hiệu dụng là U vào 2 đầu mạch AB gồm điện trở thuần R = 50Ω, tụ điện có dung kháng C = 100Ω và cuộn cảm thuần L nối tiếp, L thay đổi được. Khi thay đổi L = L0 thì điện áp hiệu dụng URL max. Cảm kháng của cuộn cảm có giá trị bằngbaonhiêu? A.120,7Ω B.120,5Ω C.120,3Ω D.120,1Ω Câu 62: Đặt điện áp ( )uU2cos2ftV =π (f thay đổi) vào hai đầu đoạn mạch AB mắc nối tiếp theo đúng thứ tự gồm điện trở R, cuộn cảm thuần L có độ tự cảm L và tụ điện có điện dung C (với 2 2LRC). > M là điểm nối giữa cuộn cảm và tụ điện. Khi f = f0 thì UC = U và ( )( ) ( )LLCC 6RZZZ7RRZ. ++=+ Khi 0 ff75 =+ Hz thì UL = U. Tìm f để UAM không phụ thuộcR (nếuR thay đổi). A.50Hz. B. 502 Hz. C.75Hz. D. 255 Hz.

DẠYKÈMQUYNHƠNOFFICIAL 390 Câu 63: Đặt điện áp ( )u502costV =ω (ω thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở R và tụ điện có điện dung C, với 2 2LCR. > Khi ω = 100 π rad/s thì CmaxU . Khi ω = 120π rad/s thì UL max. Giá trị của CmaxU gần giá trị nào nhất sau đây? A.85V. B.145V. C.57V. D.173V. Bài 64: Một mạch điện xoay chiều gồm cuộn dây không thuần cảm và hai tụ điện có điên dung lần lượt là C1 và C2. Nếu mắc C1 song song C2 rồi mắc nối tiếp với cuộn dây thì tần số góc cộng hưởng là ω1 = 48π rad/s. Nếu mắc C1 nối tiếp C2 rồi mắc nối tiếp với cuộn dây thì tần số góc cộng hưởng là ω2 = 100π rad/s. Nếu chỉ mắc riêng C1 nối tiếp với cuộn dây thì tầnsố cộnghưởnglà: A.60π rad/s B.74π rad/s C.50π rad/s D.70π rad/s Câu 65: Đoạn mạch xoay chiều R, L, C có cuộn thuần cảm L có giá trị thay đổi được. Dùng ba vôn kế xoay chiều có điện trở rất lớn đo điện áp hiệu dung trên mỗi phần tử Điều chỉnh giá trị của L thì thấy UL max lớn gấp hai lần UR max. Hỏi UL max gấp bao nhiêu lần điện áp hiệudụngtrêntụ? A. 3 4 B.4 C. 3 D. 4 3 Câu 66 (ĐH – 2013): Đặt điện áp ( )u1202cos2ftV =π (f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở R và tụ điện có điện dung C, với 22L>CR . Khi f = f1 thì C maxU . Khi 21 fff2 == thì RmaxU . Khi f = f3 thì LmaxU . Giátrị của LmaxU gần giá trị nào nhất sau đây? A.85V. B.145V. C.57V. D.173V. Câu 67: Đặt điện áp xoay chiều =ω uU2cost (V), (U không đổi còn ω thay đổi được) vào mạch nối tiếp RLC với cuộn dây thuần cảm và <2 CR2L . Điều chỉnh giá trị của ω để CmaxU khi đó = Cmax U90 Vvà = RL U305 V.Giátrị củaU. A.65V. B. 902 V. C. 602 V. D.73V. Câu 68:Mạch điệnxoaychiềugồmcuộndâycóL= 0,4 π Hmắcnốitiếpvớitụ điệnC. Đặtvàohai đầu đoạn mạch điện áp u = U 2 cosωt (V). Khi C = C1 = 42.10 π F thì UCmax = 100 5 V. Khi C = 2,5C1 thì cường độ dòng điện trễ pha 4 π so với điện áp hai đầu đoạn mạch. Giá trị củaUlà A.50V B.100V C.100 2 V D.50 5 V Câu 69: Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi 150V vào 2 đầu mạch AB gồm AM chỉ chứa R, đoạn mạch MB chứa tụ C và cuộn cảm thuần L nối tiếp, L thay đổi được. Biết sau khi thay đổi L thì điện áp hiệu dụng 2 đầu mạch MB tăng 22 lần và dòng

DẠYKÈMQUYNHƠNOFFICIAL 391 điệntrướcvàsaukhi thay đổi Llệchphanhau π 2 . Điệnáphiệu dụng ở 2 đầu mạchAM khi chưathay đổi Llà A.100 3 V B.120V C.100V D.100 2 V Câu 70: Đặt điện áp xoay chiều ()π  =ω+  u2002costV 6 với ω biến thiên vào hai đoạn mạch RLC nối tiếp với cuộn dây thuần cảm. Thay đổi ω cho đến khi tỉ số = L C Z 9 Z41 thì CmaxU .Xác địnhgiátrị CmaxU đó? A.200V. B.205V. C.320V. D.400V. Câu 71: Đặt điệnápxoaychiều ( )=ω uU2costV (ω thay đổi được)vào đoạnmạchAB nối tiếptheothứ tự gồm cuộncảm thuầnL = π 1 H, điệntrở thuần = R1002 Ω vàtụ điện C = π 0,2 mF.Gọi ωRL và ωRC lầnlượt làcácgiátrị của ω để URL max vàURC max.Chọnkết quả đúng. A. ω=π RL 50 rad/s. B. ω=π RC 100 rad/s. C. ω+ω= RLRC 160 π rad/s. D. ω−ω=π RLRC 50 rad/s. Câu 72: Đặt điện áp xoay chiều ( )=ω u1002costV (ω thay đổi được) vào đoạn mạch AB nối tiếp theo thứ tự gồm đoạn AM chứa cuộn cảm thuần L = π 1 H, đoạn MN chứa điện trở thuầnR =50 Ω và đoạn NB chứatụ điệnC = π 0,2 mF. Gọi ωωωωRLCRL ,,, và ωRC lầnlượt làcácgiátrị của ω để RLRLU,U,U và RC maxU Trongsố các kết quả: π ω=πω=ω=π RLC 200 502 rad/s,rad/s,253 rad/s, 3 ω=π+ω=π−+ RLC 5025 rad/s,10025 rad/s. Số kết quả đúng là A.5. B.3. C.4. D.1. Câu 73: Đặt một điện áp xoay chiều u = U0cosωt (V) vào hai đầu một đoạn mạch AB gồm điện trở R, cuộn dây cảm thuần L và tụ điện có điện dung C mắc nối tiếp. Tụ C có điện dungthay đổi được.Thay đổi C,khi ZC =ZC1 thì cường độ dòng điệntrễ pha 4 π sovới điện áphai đầu đoạnmạch,khiZC =ZC2 =6,25ZC1 thìUC max.Tínhhệ số côngsuấtcủamạch. A.0,6 B.0,8 C.0,7 D.0,9 Câu 74: Mạch điện R1L1C1 có tần số cộng hưởng ω1 và mạch R2L2C2 có tần số cộng hưởng ω2, biết ω1 = ω2. Mắc nối tiếp hai mạch đó với nhau thì tần số cộng hưởng của mạch sẽ là ω.Khi đó ω liênhệ với ω1 và ω2 theocôngthức nào?

DẠYKÈMQUYNHƠNOFFICIAL 392 A. ω =2ω1. B. ω =3ω1. C. ω =0. D. ω = ω1 Câu 75: Đặt điện áp xoay chiều ( )=ω uU2costV (U không đổi còn ω thay đổi được) vào đoạn mạch AB nối tiếp theo thứ tự gồm đoạn AM chứa điện trở thuần R, đoạn MN chứa cuộn cảm có độ tự cảm L = π 2 3 H, có điện trở r và đoạn NB chứa tụ điện có điện dung C. Khi ω = ω1 và ω = ω2 thì dòng điện hiệu dụng qua mạch có cùng giá trị I1. Khi ω=ω=π 3 1003 rad/sthì UMB min vàdòng điệnhiệudụngqua mạchbằng = 21 21 II 3 .Khi ω=ω=ω 43 k thì UAN max.Biết ω−ω=ω 222 123 6. Giátrị củak. A.1,17. B.1,5. C.2,15. D.1,25. Câu 76: Cho đoạnmạch xoaychiềunối tiếpgồm cuộndâythuầncảm có độ tự cảm Lthay đổi được,tụ điệncó điện dungC và điệntrở R.Cóhai giátrị khácnhau của LlàL1 vàL2 thì điệnáphiệudụngtrêncuộncảm có cùngmột giátrị.Giátrị củaL để UL max là A. 12 LLL. =+ B. () 12 1 LLL 2 =+ . C. 12 12 2LL L. LL = + D. 12 12 LL L. LL = + Câu 77: Đặt một điện áp xoay chiều u2202cos2ft (V)=π với f thay đổi được vào hai đầu đoạn mạch AB gồm điện trở R, cuộn dây cảm thuần L và tụ điện có điện dung C biến đổi mắc nối tiếp. R= 100Ω; 1 LH = π . Điều chỉnh C = Cx, sau đó điều chỉnh tần số, khi f = fx thìUC max và Cmax 5 U 3 = lần điệnáphiệudụnggiữahai đầu đoạnmạchAB.Giátrị Cx vàfx bằng: A. 5 4.10F; 502Hz π B. 5 4.10F; 50Hz π C. 4 3,6.10F;50Hz π D. 4 3,6.10F;502Hz π Câu 78: Mạch điện xoay chiều RLC không phân nhánh, dung kháng bằng 50 Ω, điện trở thuần R và cuộn cảm thuần có cảm kháng ZL thay đổi. Người ta nhận thấy khi ZL có giá trị ứngvới 100Ω và300Ω thì điệnáphiệudụngtrên cuộncảm có cùngmột giátrị.TínhR. A.25 Ω. B.19 Ω. C. 502 Ω. D.50 Ω Câu 79: Một mạch điện xoay chiều nối tiếp gồm cuộn cảm và tụ điện có điện dung C thay đổi. Dùng vôn kế có điện trở rất lớn mắc vào hai đầu tụ điện. Thay đổi C người ta thấy khi C =40µFvàC =20µFthì vônkế chỉ cùngtrị số. Tìm C để vônkế chỉ giátrị cực đại. A.20µF. B.10µF. C.30µF. D.60µF. Câu 80: Cho mạch điện RLC mắc nối tiếp, cuộn dây thuần cảm có độ tự cảm 6,25 LH = π , tụ điện có điện dung 310 CF 4,8 = π . Đặt vào hai đầu mạch điện áp xoay chiều ( ) u2002costV =ω+ϕ có tần số góc thay đổi được. Thay đổi , thấy rằng tồn tại

DẠYKÈMQUYNHƠNOFFICIAL 393 1 302ω=π rad/s hoặc 1 402ω=π rad/s thì điện áp hiệu dụng trên cuộn dây có giá trị bằngnhau.Giátrị củaUL max là: A. 1205V B. 1502V C. 1203V D. 1002V Câu 81: Đặt một điện áp xoay chiều 0 uUcos100t =π (V) vào đoạn mạch RLC có R1002 = Ω, cuộn cảm thuần có độ tự cảm L < 1,5π H và tụ điện có điện dung C thay đổi được. Khi điện dung tụ điện lần lượt là 1 25 CF =µ π và 2 125 CF 3 =µ π thì điện áp hiệu dụng trên tụ có cùnggiátrị. Để UR max thì giátrị củaC là A. 50 π µF. B. 200 3π µF. C. 20 π µF. D. 100 π µF. Câu 82: Cho đoạn mạch AB gồm 2 hộp đen X, Y nối tiếp (trong mỗi hộp chỉ chứa 1 trong các phần tử: điện trở thuần, cuộn dây hoặc tụ điện). Đặt vào 2 đầu mạch điện áp u = 100 6 cos2πft (V). Ban đầu, f = f1 thì điện áp hiệu dụng hai đầu các hộp đen X, Y lần lượt là UX = 100V, UY = 200V. Sau đó, nếu tăng f thì cường độ dòng điện hiệu dụng I qua mạch giảm. Hệ số côngsuấtcủamạchlúc đầu A. 2 2 . B. 1 3 . C. 1. D. 3 2 Câu 83: Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB nối tiếp gồm điện trở R, cuộn dây cảm thuần L và tụ điện có điện dung C thay đổi được. Khi C = C1 thì dòng điện trễ pha 4 π so với điện áp hai đầu đoạn mạch. Khi 1C C 6,25 = thì UC max. Tính hệ số công suất mạch AB khi đó. A.0,6. B.0,7. C.0,8. D.0,9. Câu 84: Cho mạch điện RLC, với C thay đổi được. Điện áp đặt vào hai đầu đoạn mạch có dạng uU2cost (V).=ω Cảm kháng 2 LH π = . Khi 4 1 10 CCF == π thì cường độ dòng điện i trễ pha π 4 sovới u.Khi 4 2 10 CCF 2,5 == π thìUC max.Giátrị củatầnsố góc ω . A. 200π rad/s B. 50π rad/s C. 10π rad/s D. 100π rad/s Câu 85: Đặt điện áp xoay chiều vào hai đầu đoạn mạch AB nối tiếp gồm điện trở R, cuộn dây cảm thuần 2 L = π H và tụ điện có điện dung C thay đổi được. Khi 1 CC0,1 == π mF thì dòng điện trễ pha 4 π so với điện áp hai đầu đoạn mạch. Khi 1C C 2,5 = thì UC max. Tính tần số góc củadòng điện. A.200π rad/s. B.50π rad/s. C.100π rad/s. D.10π rad/s.

DẠYKÈMQUYNHƠNOFFICIAL 394 Câu 86: Đặt điện áp uU2cos2ft =π (V) (f thay đổi được và U tỉ lệ với f) vào hai đầu đoạn mạch RLC nối tiếp. Khi f = f1 hoặc f = 4f1 thì mạch tiêu thụ cùng công suất. Khi f = 150 Hzthì côngsuất củamạchlàcực đại.Giátrị của f1 gần giá trị nào nhất sau đây? A.74Hz. B.60Hz. C.51Hz. D.109Hz. Câu 87: Cho mạch điện xoay chiều như hình vẽ. Cuộn dây có độ tự cảm 3 L π = H, điện trở thuần r = 100Ω. Đặt vào hai đầu đoạn mạch một điện áp AB u1002cos100πt= (V). Tính giá trị của C để vôn kế có giá trị lớn nhất và tìm giá trị lớn nhất đócủavônkế. A. 443 C.10 π = FvàUCmax =120V B. 43 C.10 4π = FvàUCmax =180V C. 43 C.10 4π = FvàUCmax =220V D. 43 C.10 π = FvàUCmax =220V Câu 88: Đặt điện áp uU2cos2ft =π (V) (f thay đổi được và U tỉ lệ với f) vào hai đầu đoạn mạch RLC nối tiếp. Khi f = f1 hoặc f = 4f1 thì điện áp hiệu dụng trên tụ có cùng giá trị. Khi f=150Hzthì UC max.Giátrị củaf1 gần giá trị nào nhất sau đây? A.77Hz. B.60Hz. C.51Hz. D.109Hz. Câu 89: Đặt điện áp xoay chiều ( )uU2cos2ftV =π (U không đổi còn f thay đổi trong phạm vi từ 0 đến ∞) vào đoạn mạch AB nối tiếp theo thứ tự gồm cuộn cảm thuần có độ tự cảm L, điện trở thuần R = 200Ω và tụ điện có điện dung 200 C = π µF. Khi f thay đổi người tanhậnthấycónhữnggiátrị UL tương ứngvới hai giátrị f1 vàf2 củaf.Giá trị Lcóthể là A. 3 π H. B. 1 π H. C. 2 π H. D. 4 π H. Câu 90: Đoạn mạch xoay chiều AB theo đúng thứ tự gồm: điện trở thuần R, cuộn cảm thuần L và tụ điện C nối tiếp, với 2 CR2L < . Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểu thức uU2cost =ω (V), trong đó U không đổi và ω thay đổi được. Điều chỉnh giá trị của ω để CmaxU .Khi đó CmaxU =1,25U.Hệ số côngsuất đoạnmạchAB khi đólà A. 2 7 . B. 3 2 . C. 5 6 . D. 1 3 Câu 91: Một đoạn mạch AB gồm điện trở thuần R nối tiếp với cuộn dây thuần cảm có độ tự cảm 0,4 LH = π và mắc nối tiếp với tụ điện có điện dung có thể thay đổi. Đặt vào hai đầu mạch AB một điện áp 0 uUcost =ω (V). Khi 3 1 10 CCF 2 == π thì dòng điện trong mạch trễ pha 4 π sovới điệnáphai đầu đoạnmạchAB.Khi 3 2 10 CCF 5 == π thì CmaxU .Giátrị củaRlà: L,r M C V BA

DẠYKÈMQUYNHƠNOFFICIAL 395 A.50Ω B.40Ω C.10Ω D.20Ω Câu 92: Đoạn mạch xoay chiều AB theo đúng thứ tự gồm: điện trở thuần R, cuộn cảm thuần L và tụ điện C nối tiếp, với 2 CR2L < Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểu thức uU2cost =ω (V), trong đó U không đổi và ω thay đổi được. Gọi M là điểm nối giữa L và C. Điều chỉnh giá trị của ω để CmaxU . Khi đó CmaxU = 1,25U. Hệ số công suất đoạnmạchAM khi đólà A. 1 3 . B. 1 3 . C. 5 6 . D. 2 7 . Câu 93: Đặt điện áp xoay chiều uU2cost =ω (V), (U không đổi còn ω thay đổi được) vào mạch nối tiếp RLC với cuộn dây thuần cảm và 2 CR2L < Điều chỉnh giá trị của ω để CmaxU khi đó Cmax U250 = Vvà RL U5021 = V.Giátrị củaU. A.200V. B.150V. C. 1002 V. D. 2410 V. Câu 94: Đoạn mạch xoay chiều gồm RLC nối tiếp, cuộn dây thuần cảm với 2 CR2L < Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có giá trị hiệu dụng U có tần số f thay đổi. Khi f = fL thì LmaxU và lúc này UC = U. Khi f = fC thì CmaxU = 1,5U. Khi f = fL thì hệ số côngsuất củamạchAB gần giá trị nào nhất sau đây? A.0,6. B.0,8. C.0,75. D.0,96. Câu 95: Đoạn mạch xoay chiều AB theo đúng thứ tự gồm: điện trở thuần R, cuộn cảm thuần L và tụ điện C nối tiếp, với 2 CR2L < . Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểu thức uU2cost =ω (V), trong đó U không đổi và ω thay đổi được. Gọi M là điểm nối giữa L và C. Điều chỉnh giá trị của ω để CmaxU . Khi đó Cmax U1,25U = . Hỏi điện áp hai đầuAB sớm phahaytrễ phahơndòng điệnbaonhiêu? A.sớm hơn 3 π . B.sớm hơn 6 π . C.trễ hơn 3 π . D.trễ hơn 6 π Câu 96: Đặt điện áp xoay chiều uU2cost =ω (V), (U không đổi còn f thay đổi được) vào mạch nối tiếp RLC với cuộn dây thuần cảm và 2 CR2L < . Khi f = f1 thì CmaxU và mạch tiêu thụ côngsuất max 3 PP 4 = .Khi 1 ff100 =+ Hzthì LmaxU .Giátrị củaf1. A.125Hz. B. 755 Hz. C.150Hz. D. 752 Hz. Câu 97: Đặt điện áp xoay chiều uU2cost =ω (V), (có giá trị hiệu dụng U không đổi, tần số f thay đổi được) vào 2 đầu đoạn mạch gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Khi f = f0 Hz thì điện áp hiệu dụng hai đầu tụ điện UC = U. Khi 0 ff75 =+ Hz thì điện áp hiệu dụng hai đầu cuộn cảm L UU = và hệ số công suất của toàn mạch lúc này là 1 3 .Hỏi f0 gần giá trị nào nhất sau đây? A.75Hz. B.16Hz. C.25Hz. D.180Hz.

DẠYKÈMQUYNHƠNOFFICIAL 396 Câu 98: Đoạn mạch xoay chiều R, L, C nối tiếp (cuộn dây thuần cảm), tần số dòng điện thay đổi được. Khi f = f1 thì = CmaxmaxUU . Khi f = f2 thì LmaxU , lúc này điện áp hai đầu tụ là max 2 U 3 .Hệ số côngsuất củamạchkhi f=f1 vàf =f2 gần giá trị nào nhất sau đây? A.0,6. B.0,8. C.0,7. D.0,9. Câu 99: Đặt vào hai đầu đoạn mạch điện áp xoay chiều, mạch RLC nối tiếp, điện dung C thay đổi được. Khi C = C1 điện áp hiệu dụng giữa hai đầu tụ điện là 40V và trễ pha hơn điện áp giữa hai đầu đoạn mạch góc ϕ1. Khi C = C2 điện áp hiệu dụng giữa hai đầu tụ điện là40Vvàtrễ phahơn điệnápgiữahai đầu đoạnmạchgóc ϕ2 = ϕ1 + π 3.KhiC=C3 thìUC max, và mạch thực hiện công suất bằng 50% công suất cực đại mà mạch xoay chiều đạt được. Điện áphiệudụnggiữahai đầu đoạnmạchlà: A. 80 6 V. B. 40 6 V. C. 40 3 V. D. 80 3 V. Câu 100: Đặt điện áp uU2cost =ω (V) vào hai đầu đoạn mạch RLC nối tiếp, cuộn dây thuầncảm và 2 CR2L < ,với tầnsố thay đổi.Khi ω = ωC thì CmaxU .Khi ω = ω0 thì C UU = Chọnhệ thức đúng. A. 0 C 2 ω ω= B. 0 C 3 ω ω= C. 0 C . 2 ω ω= D. C0 2.ω=ω Câu 101: Đặt điện áp uU2cost =ω (V) vào hai đầu đoạn mạch RLC nối tiếp, cuộn dây thuầncảm và 2 CR2L < ,với tầnsố thay đổi.Khi ω = ωL thì LmaxU .Khi ω = ω0 thì L UU = . Chọnhệ thức đúng. A. 0 C . 2 ω ω= B. 0 C . 3 ω ω= C. 0 C . 2 ω ω= D. C0 2.ω=ω Câu 102: Đặt điện áp xoay chiều ( )u4526costV =ω với ω biến thiên vào hai đoạn mạch RLC nối tiếp với cuộn dây thuần cảm và 2 CR2L < . Thay đổi ω cho đến khi tỉ số L C Z 2 Z11 = thì UC max.Xác địnhgiátrị UC max đó? A.200V. B.165V. C.172V. D.210V. Câu 103: Đặt điện áp ( )uU2cos2ft V=π (f thay đổi được) vào hai đầu đoạn mạch AB mắc nối tiếp theo đúng thứ tự gồm điện trở R, tụ điện có điện dung C và cuộn cảm thuần có độ tự cảm L, với 2 CR2L < . M là điểm nối giữa cuộn cảm và tụ điện. Khi f = f0 thì UC = U và lúcnàydòng điệntrong mạchsớm phahơnulà α (tanα = 0,75).Khi f =f0 +45Hzthì UL = U.Tìm f để UAM khôngthụ thuộcR (nếuR thay đổi). A.50Hz. B. 305 Hz. C.75Hz. D. 255 Hz. Câu 104: Đặt điện áp ( )uU2cos2ft V=π (ω thay đổi được) vào hai đầu đoạn mạch mắc nốitiếpgồm điệntrở R,tụ điệncó điệndungC,cuộncảmthuầncó độ tự cảmL.Khi ω =2ω1 thì CmaxU và ω =3ω1 thì LmaxU =300Vthì U gần giá trị nào nhất sau đây:

DẠYKÈMQUYNHƠNOFFICIAL 397 A.200V. B.170V. C.190V. D.220V. HƯỚNG DẪN GIẢI Câu 1: ChọnB.Tacó: 12 11C22C 21 12 II UIZIZ2,4f3,6f 2fC2fC ==⇔=⇔= ππ .Suyraf2 =75Hz. Câu 2: ChọnD. Khi UV1 =URmax thì trongmạchcócộnghưởng,khi đó UV2 =UC =UL = RmaxU 2  ZL = R 2 Khi UV2 =UCmax thì ZC = 22 L L RZ Z + =2,5R. Suyra: 12max2max2max 1 VVVV V C UUUU 200 U80V. RZ2,5R2,52,5 ==  === Câu 3: ChọnB.Tacó: ( ) ( )12 22 21212LCLC PPIIZZZZZZ =⇔=⇔=⇔−=− Vì 12 LLZZ ≠ nên () 1 12 1 L LCLCCLC Z 3 ZZZZZZ2Z 22 −=−−=−  = (1) Mặckhác: 11 1 2 1 LCL 1 L C LCL 2 12 12 ZZZ tan R4R Z Z ZZZ 2 tantantan1 RR4R 2  ϕ==      ϕ===−  ϕϕ=−  π  ϕ+ϕ=     1 11 1 22L LL1 4 CL C Z4004 Z16RZ4R400LH 100 31110 ZZ300CF 4Z100.3003  =  ==Ω  === ωππ    ==Ω  === ωππ . Câu 4: Chọn B.Ta có: 22 22 C C LmaxL C URZRZ UZ RR + + =⇔= 22 Lmax 22 10102060 U100V 20 2060200 603  + ==    + ==Ω  LZ Câu 5: Chọn A. LmaxRCUUU ⇔⊥ ,ápdụnghệ thứclượngtrongtam giác vuông 2 bab' = và 2 hb'c' = ta được: α A B M α

DẠYKÈMQUYNHƠNOFFICIAL 398 ( ) ( ) ()() 2 LLC 2 RCLC UUUU1001003680V UUUU361003648V  =−=−=  =−=−=  Câu 6: Chọn C. Khi L = L1 thì I max  cộng hưởng  ZL1 = ZC Khi L = L2 = 2L1 (nghĩa là ZL2 = 2ZL1) thì ULmax  ZL2 = R2 + ZC 2 ZC  ZC = ZL1 = R = 100  ω = 100π Câu 7:Chọn A. Khi L thay đổi để LmaxU thì RC UU ⊥ (URC và U là hai cạnh của tam giác vuông còn LmaxU là cạnh huyền, UR là đường cao thuộc cạnh huyền): ()  +=    +=   +=     =  +=  2 2 RC RC 222 RCR 2 2 RC 222 RC u u 1 U2U2 111 UUU 5021502 1 U2U2 U1003V 111 UU50.3 Câu 8: Chọn A. Khi ω1 = 100π thì UL max  ω1 2 = 2 2LC - R2C2 Khi ω2 = 200π thì UC max  ω2 2 = 2LC - R2C2 2L2C2 Từ đây suy ra ω1ω2 = 1 LC  LC = 1 ω1ω2 (1) Măt khác ZL + 3ZC = 400  LCω1 2 + 3 = 400Cω1 (2) Thay LC =1 ω1ω2 vào (2)  C =8,75.10-5 π F, thế ngược trở lại vào (2)  L = 4 7π H. Câu 9: Chọn C. Để ULmax thì 2 2 ω = 2 1 1 ω + 2 2 1 ω hay 2 2 f = 2 1 1 f + 2 2 1 f Suy ra : f = 12 22 12 ff2 ff + = 74,67 Hz. Câu 10: Chọn D. Khi L thay đổi thì RmaxU và CmaxU ⇔ cộng hưởng B M N A

DẠYKÈMQUYNHƠNOFFICIAL 399 Rmax max CmaxmaxCC UU U IU RUIZZ R =  ⇔=   ==  22 C Lmax URZ U R +  = Theo bài ra: LmaxRmaxU2U = hay 22 C C URZ 2UZR3 R + =  = Khi đó: 22 22 LmaxC CmaxC URZR3R2 . UZR33 + + === Câu 11: Chọn A. Khi 22 LL C Z4RZ Z 2 ++ = thì RCmax 22 LL 2UR U 4RZZ = +− (R và C mắc liên tiếp nhau). Vì ANmaxANU2U = suy ra: 22 LL R 1 4RZZ = +− 222222 LLLL 4RZ2Z4RZZR +−++= 22224224222 LLLLLLL 3R2Z2Z4RZ9R12(RZ)4Z4Z(4RZ)⇔+=+  ++=+ 4222 LL 9R(12Z16Z)R0 ⇔+−= 422 L 9R4ZR0⇔−= 222 L (9R4Z)R0 ⇔−= Do R0 ≠ nên 222 L (9R4Z)R0 −= 22 LL 22 9R4Z0RZ150100. 33 ⇔−=  ===Ω Khi đó: 22 LL C Z4RZ Z 2 ++ = 221504100150 200. 2 ++ ==Ω Câu 12: Chọn B. Khi L = L1 thì LmaxU và lúc này RLmaxU0,5U = : 22 22 C C LmaxLC C Lmax LmaxR RZRZZRUUZ RZ UU2 U2U  + + = =⇔=   =  = Khi L = L2 thì CmaxU ⇔ Mạch cộng hưởng CmaxmaxCC U UIZZU R  === Lmax Cmax U 2. U  = Câu 13: Chọn D.

DẠYKÈMQUYNHƠNOFFICIAL 400 Ta có: 2 12 12 12 2 11 2 1111 2 22 2 2222 11 CCLC (LL)CC 11 L LCC 11 L LCC  ω== + +   ω=  = ω  ω=  = ω Khi đó: 12 12 2222 1122112112 111111CC LL CCCCCC  +=+=+=  ωωωω+  (vì ω1 = ω2) 2 2 1 1 12 12 12 1 (LL)CCCC  ω==ω  ω=ω + + . Câu 14: Chọn A. Khi URmax (mạch có cộng hưởng), ta có: UL = UC và URmax = U = 4UL  R = 4ZC (1) Khi ULmax ta có: 22 RC Lmax C UU U U + = (2) Từ (1) suy ra UR = 4UC (3) Tà (2) và (3) suy ra ULmax = 4,25 UR . Câu 15: Chọn C. Điện áp hiệu dụng trên cuộn cảm: () () 2 L222 LL 222LCLC L LC UZU UIZ1Z2ZZRZ0 RZZU  ==  −−++= +− 2 22 2LCLRC L U 1Z2ZZZ0 U   −−+=  () 2 2 2 LCL 905 1Z2ZZ10020 270   −−+=      Theo định lý Viet: L2L1 L1L2CL2 3ZZ150 L1 L1L2 C bZ150ZZ4,5Z aZ300 c ZZ45000Z100 a −=  =Ω+=−= →=Ω  == =Ω  Thay vào ( )2 22222 RCC ZRZ1002R100R100. =+  =+  =Ω Giá trị 22 22 C Lmax RZ100100 UU9059010284,6V. R100 + + ===≈ Câu 16: Chọn A. Khi ω1 = 100π thì UL max  ω1 2 = 2 2LC - R2C2 (1)

DẠYKÈMQUYNHƠNOFFICIAL 401 Khi ω2 = 200π thì UC max    ω2 2 = 2LC - R2C2 2L2C2 (2) Từ đây suy ra ω1ω2 = 1 LC  LC = 1 ω1ω2 (3)  12 2 2LC = ωω (4) Thế R = 100 Ω và (4) vào (1), ta được: 2 1222 1 1 22 2 12 22. 100.C2 2 100C ω ω==>−ω= ω ωω  4 2 224 11 666106 CCF 1001002.102 ==>=== ωωππ (với ω1 = 200rad/s) Từ (3) Suy ra: 4 12 11221 L .H C3 1066200.50 2 ==== ωωπ π ππ π Câu 17: Chọn A. Khi L = L1 = 1 π (H): L1CL1C L1C ZZZZ tantanZZR. R4R π ϕ=⇔=  =+ Khi L = L2 = 2 π (H): () () () 2222 C C L2L1CC C C 2 2222 C Lmax RZRZ Z2Z2ZRZ21R ZZ R21RRZ UU.200U.U184,776V. RR  ++ ==⇔+=  =−    ++− =⇔=  ≈  Câu 18: Chọn D. Khi thay đổi độ tự cảm cường độ dòng điện hiệu dụng qua mạch cực đại thì xảy ra cộng hưởng: ZC = ZL1  CL1C1 1 ZZZL C =  ==ω ω (*) Lúc đó: 2 max U PP R == (1)  maxmax URP = (2) Khi thay đổi đến 2 2 LH = π thì: 22 C Lmax RZ UU R + = (3) Lấy (1) chia (3), ta được: max 222222 Lmax CCC P U200UU 1 U200RZRZRZ =⇔=⇔= +++ (4) Thế (2) vào (4): max 22 22Cmax C RP 1RZRP RZ =⇔+= + (5)

DẠYKÈMQUYNHƠNOFFICIAL 402 Ta có lúc đầu công hưởng: CL1ZZ = (6) với 1 1 LH = π Và ta có lúc sau ULmax với: 22 C L2 C RZ Z Z + = (7) với 2 2 LH = π Lấy (7) chia (6), ta được: 22 C222 2CCC C RZ 22ZRZZR Z + =  =+  = (8) Thế (8) vào (5): max CmaxC P 200 2ZPZ100. 22 =  ===Ω Từ biểu thức (*) ta có: C 1 Z 100 100π rad/s. L1 ω=== π Suy ra: 4 C 1110100 CFF. Z100π.100 ππ ====µ ω Câu 19: Chọn B. Ta có: 22 22 L Cmax 22 22 L C 2 L 5 C URZ 10020140 U297V R20 RZ 201401000 Z Z1407 11 C2,23.10F Z1000 100. 7   + + ==≈   + + ===Ω    ==≈ ω π  Câu 20: Chọn B. Ta có: cosϕd = d R Z = 0,8  Zd = R 0,8 = 5R 4  ZL = 22 d ZR = 3R . 4 Đặt Y = (Ud + Uc)2 . Tổng (Ud + Uc)max khi Ymax Y = (Ud + Uc)2 = I2( Zd + ZC)2 = 22 dC 22 LC U(ZZ) R(ZZ) + +− = 22 dC 222 LCLC U(ZZ) RZZ2ZZ + ++− Để Y = Ymax thì đạo hàm Y’(ZC) = 0 ⇔ ( 222 LCLC RZZ2ZZ ++− )2(Zd + ZC) – (Zd + ZC)2 2(ZC – ZL) = 0. Do (Zd + ZC) ≠ 0 nên ( 222 LCLC RZZ2ZZ ++− ) – (Z + ZC)(ZC – ZL) = 0 ⇔ (Zd + ZL)ZC = R2 + ZL 2 + ZdZL (1) Thay Zd và ZL vào (1) ta được: 2RZC = 2,5R2  ZC = 5R . 4 Do đó L C Z Z = 5 3 = 0, 6. Câu 21: Chọn B. Cảm kháng: L ZL302=ω=Ω

DẠYKÈMQUYNHƠNOFFICIAL 403 () () () () () () 22 2 2 L Cmax 22 2 2 L C L URrZ100602302 U 158V Rr 602 RrZ602302 Z 1502 Z 302  +++ ==≈  +  +++ ===Ω  Điện dung của tụ: 6 C 1 C15.10F15F. Z ===µ ω Câu 22: Chọn D. Do max 1212min I IIZZnZnR n ==  === () 2 2 222222 11 1 1 1 11 ZRLnRn1RL CC   =+ω−=  −=ω−  ωω  (1) Theo phương pháp đánh giá hàm số, giữa các tần số góc ω1, ω2 và ω0 có mối liên hệ 2 120 ωω=ω mà 2 0 1 LC ω= nên 12 12 11 C LCL ωω=  = ωω (2) Từ (1) và (2) ta được: () ()() 2 2222 2 11212 1 12 1 n1RLLLL 1 L    −=ω−=ω−ω=ω−ω  ω  ωω  () 22 21212 22 LL RR n1n1 ω−ωω−ω  =  = Câu 23: Chọn A. Khi C thay đổi để CmaxU thì RL UU ⊥ (URL và U là hai cạnh của tam giác vuông còn CmaxU là cạnh huyền, UR là đường cao thuộc cạnh huyền): 22 RL RL 222 RLR u u 1 U2U2 111 UUU  +=    +=   +=     =  +=  22 RL 222 RL 30010031 U2U2U1003V 111 UU150 Câu 24: Chọn C. N M A B

DẠYKÈMQUYNHƠNOFFICIAL 404 Khi điều chỉnh L = L0: Điện áp hiệu dụng đặt vào hai đầu mạch: () 22 R1L1C UUUU50V =+−= Do R1 C L1 L1 C1 U30V Z2R U20V 2R Z U60V 3 = =  =   = =  Khi điều chỉnh L2 = 2L0: L2L1 4R Z2Z 3 == . Khi đó tổng trở của mạch: () 2 2 22 RL2C 4R13 UUUUR2RR 33  =+−=+−=   Điện áp hiệu dụng hai đầu điện trở bằng: R2 U150 URV Z 13 == Câu 25: Chọn B. Áp dụng định lý hàm số sin cho tam giác ANB: () RLC RL RL UUU sinsinsin 22 == ππ ϕ−ϕ −ϕ+ϕ   Khi C = C0: () () π == ππ ϕ+α −ϕ−α   π ϕ=−α     = αα 1Cmax RL RL 2 RL 1 UUU sinsinsin 22 21 UU sincos Khi ()1 U470470 CC: 2 sincos2 sin2 2 === π αα  −α   Khi () ()1 2 2 22 U140U470470 CC: 3 sincossinsin 22 ==== αα+ϕππ −α−ϕ+ϕ   Từ (2) và (3) suy ra: 2223α+ϕ=−α  ϕ=−α thay vào (1), (2) và (3): 11 UU140cos0,966U470140 sincos2coscos3coscos3U140,3V α= ====   ααααα−α≈  Câu 26: Chọn A. Cảm kháng: L 0,4 ZL100.40. =ω=π=Ω π M A B

DẠYKÈMQUYNHƠNOFFICIAL 405 Góc lệch pha: R LL U R arctanarctan. UZ3 π α=== Áp dụng: () RLC max U UU240V. sin 2 +== α Câu 27: Chọn A. Ta có: () () 22 L RL222 22 LCLCCLC 2222 LL URZUU U RZZRZZZ2ZZ 1 RZRZ + === +−+− + ++ Để URL không phụ tuộc R thì 2 CLCLC Z2ZZ02ZZ −=  = 011 2L C2LC2 ω  ω=  ω== ω . Câu 28: Chọn B. Nhận thấy RmaxU và LmaxU cộng hưởng Rmax max LmaxmaxLL xUU U IU RyUIZZ R ==  ⇔=   ===  Mà: 22 Lz3y22 CmaxLLL URZR zURZ3ZZ R22 = + ==→+=  = 22 L uRZz z0,752U0,752. Rx +  ==  = Câu 29: Chọn D. Từ biểu thức của i khi ω = ω1 ta có ω1 = 240π rad/s, suy ra 1L 1 Z240.60. 4 =π=Ω π Góc lệch pha giữa u và i lúc đó: ui tan1 6124 πππ  ϕ=ϕ−ϕ=−−=  ϕ=  Ta có: 1 U452 Z452 I1 ===Ω Mặt khác: () 11 2 222 1LC LC ZRZZ2R R45 RZZ =+−=   =Ω =−   . Suy ra: 1 1 C 11C 1111 ZCF CZ240.153600 =  === ωωππ . Khi mạch có cộng hưởng: 2 2 2 2 11 (120)120π rad/s. LC11 . 43600 ω===π  ω= ππ Do mạch cộng hưởng nên: 22 CL2 1 ZZL120.120 ==ω=π=Ω π

DẠYKÈMQUYNHƠNOFFICIAL 406 2 U452 I2A R45 === ; uc chậm pha hơn i2 tức chậm pha hơn u góc 2 π . Pha ban đầu của 2Cu : π 623 ππ −=− . Ta có : 22 C2C UIZ302V == . Vậy C πu60cos120πt(V) 3  =−  . Câu 30: Chọn B. Khi L thay đổi: 22 C Lmax 22 C L1 C URZ U R RZ Z Z  + =  + =  Khi C thay đổi: 22 C Cmax 22 L C1 L URZ U80V R RZ Z Z  + ==  + =  Từ L1C1Z2Z = suy ra: CL 2222 CLZ5Z CL RZRZ 2. ZZ =++ =→ LC ZR0,6Z50,6R. =  = Xét tỉ số: 2222 LmaxC 2222 CmaxL URZR25.0,6.R10. URZR0,6.R + + === ++ Vậy: Lmax U252,98V. ≈ Câu 31: Chọn B. Ta có: 22 RC 22 Lmax RCCLmax C 22 2222LmaxCLmax RLmaxCLmaxC UU U UUUU U UU2UU UUU2UUU  + =  += ⇔  = =+−+ 22 LmaxCLmax U2UUU0 ⇔−−= 22Lmax LmaxLmax Lmax U241V U200U1000( U41V ( = ⇔−−=   =− nhaän) loaïi) Câu 32: Chọn C. Thay đổi L để điện áp hiệu dụng trên đoạn mạch chứa RL đạt cực đại 2222 CC RLmaxL ZZ4R80804.30 UZ90 22 ++ ++ ⇔===Ω . Câu 33: Chọn D. Dung kháng C 1 Z100. C ==Ω ω .

DẠYKÈMQUYNHƠNOFFICIAL 407 Khi L thay đổi: 22 C LmaxL1 C 22 CC RLmaxL2 CmaxL3C RZ UZ175 Z ZZ4R UZ150 2 UZZ100  + ⇔==Ω   ++ ⇔==Ω  ⇔==Ω    Khi 123 LLLL =+− thì ( )L123 ZLLL225 =ω+−=Ω Công suất tiêu thụ của mạch () () 22 2 2222 LC UR100.503 PIR37,45W. RZZ50.3225100 ==== +−+− Câu 34: Chọn A. Điện áp hiệu dụng trên đoạn mạch chứa RC đạt cực đại RCmax2222 LL URUR U2UR80. ZZ4R1201204R 22 =  =  =Ω −++−++ Dung kháng của tụ lúc này: 22 LL C ZZ4R Z160 2 ++ ==Ω Câu 35: Chọn A. Khi L = L1 thì: L1L1 RLmaxL1 2222 CCCC L1C UZUZ U2UZ2R RR ZR4RZR4R Z2RZ1,5R 22  =⇔=  =   ++++ =⇔=  =  () 11 22 L1C R2 kcos. RZZ5  =ϕ== +− Khi L = L2 thì: ( ) 2222 C LmaxL2 C RZR1,5R13 UZR. Z1,5R6 ++ ⇔=== () 2 2 22 LC2 kcosRR3 . RZZ1313 RR1,5R 6  =ϕ=== +− +−  Câu 36: Chọn D.

DẠYKÈMQUYNHƠNOFFICIAL 408 Khi L = L1 thì: () () () MB C L1CL1C 2 22 2 L1CL1 U 50 Z100 I0,5 ZZZ100Z100 tantan R3R R100 U ZRZZRZ100200 I  ===Ω  =Ωπ ϕ=  =   =Ω  =+−=  +−=  Khi L = L2 thì: () 22 CCL RLmaxL ZZ4RZ15 UZ5015LH 22 ++ ⇔==+Ω+  == ωπ . Câu 37: Chọn B. Khi L = L1 vì uC trễ hơn u là 600 mà uC luôn trễ hơn i là 2 π nên u trễ hơn i là 6 π : () L1C CC C 22 L1C ZZ tantan R6 UZ200 100 Z I0,5 R1003 U100 ZRZZ200 I0,5  π  ϕ==−   =Ω  ==   =Ω   =+−===  Khi L = L2 thì RLmaxU nên 2222 CC L2 ZZ4R2002004.100.3 Z300 22 ++ ++ ===Ω L2 2 Z3 LH == ωπ . Câu 38: Chọn A. Ta có: UL = IZL = 22 UωL 1 R(L) C +ω− ω UL = UL max khi y = 22 2 1 R(L) C ω +ω− ω = ymin  2 0 1 ω = 2 2CL 2R 2C    (1) Với ω0 = 120π rad/s. Khi f = f và f = f ’ ta đều có 0L L U U 2 = . Suy ra: UL = U’L  22 ω 1 R(L) C +ω− ω = 22 ' 1 R('L) 'C ω +ω− ω  ω2 2 2 1 R'L 'C  +ω−   ω    = ω’2 2 2 1 RL C  +ω−   ω   

DẠYKÈMQUYNHƠNOFFICIAL 409  (ω2 – ω’2) 2L 2R C    = 22 222 1' C'  ωω  ωω  = 2 1 C (ω2 – ω’2) 22 11 '  +  ωω   C2 2L 2R C    = 22 11 ' + ωω (2) Với ω = 100 rad/s. Từ (1) và (2) ta có: 2 0 2 ω = 2 1 ω' + 2 1 ω  ω’2 = 22 0 22 0 ω 2 ω ω−ω  ω’ = 0 22 02 ωω ω−ω = 2222 100.120 160π rad/s 2.100120 ππ π−π ≃ Câu 39: Chọn C. Điện áp hiệu dụng giữa hai đầu đoạn mạch RC: () 22 C RCRC2 2 LC RZ UIZU RZZ + == +− Nhận thấy: () ∞  ++ =−  === −++−++  =∞  =  22 LL C2RCmax222 LL CRC ZZ4R2UR2U ZUU 2ZZ4Rxx4 ZUU () ∞  =  ==<  = + ++ = 2 C1RC2222 L L RUU Z0UUUU RZ1x1x §ÆtZxR Theo bài ra: 2 12 52U16 Ux 315 xx4 U U0,68U 116 15  =  = −++   =≈  +   Câu 40: Chọn B. Khi 222 00RL0R Cmax00RL22 RL 00RL 111 UUU UUU uu 1 UU  +=   ⊥    += 

DẠYKÈMQUYNHƠNOFFICIAL 410 () 0RL RLC 222 00RL U12a0RL uuu9a22 0 00RL 111 UU12aU15a 16a9aU20a 1 UU = =−=  += = →   =  +=  Mà 222 0RL0R0LUUU =+ ( ) ( ) 222 0L0L 15a12aUU9a. =+  = Từ 0R U12a = và 0L U9a = , suy ra: L R12 Z9 = 4L3R ω= . Câu 41: Chọn C. Khi Cmax00RLUUU ⇔⊥ 222 00RL0R 22 RL 00RL 111 UUU uu 1 UU  +=     +=  ()0R RL 222 00RL U752V0RL u756V; u256V22 0 00RL 111 UU 752 U150V 756256U150V 1 UU = ==  +=  = →   =  +=   Câu 42: Chọn C. Khi C = C1: Pmax = UI1 (1) Khi C = C2: P = UI2 cosϕ (2) Từ (1) và (2) ta có: max P P = 2 1 Icos I ϕ  P = Pmax 2 1 Icos I ϕ (3) Mặt khác: 1 1 2 1 2 2 UU I ZR I cos UU I Icos ZR  ==    =ϕ ==ϕ  (4) Từ (3) và (4) ta được: P = Pmax 2 cos ϕ = 400. 2 3 2     = 300 W. Câu 43: Chọn B. Nhận thấy mạch xảy ra cực đại kép: maxLC 22 2 L CmaxCLL LL PRZZ RZ R UZZZ ZZ  ⇔=−   + ⇔==+> 

DẠYKÈMQUYNHƠNOFFICIAL 411 2 CLLLL 22K 2 L 22 2 CL L LLCL LL R RZZRZZZR20 Z RZ R ZZ RZ R ZZZZ40 ZZ  =+−  =−==Ω    +  ==+ + ==+=Ω   Câu 44: Chọn C. Sử dụng định lý hàm số sin cho tam giác AMB: AMMBAMMBAMMBAMMB UUUUUUUUU sinsinsinsinsin 2sincos2coscos 2222 +++ ===== γαβα+βα+βα−βγα−β (Vì α+β+γ=π nên sincos 22 α+βγ = ) Vậy: () AMMB max 3 UU 28 +⇔α=β==π−γπ (Vì L R tan1 Z4 π γ==  γ= ). Câu 45: Chọn B. Sử dụng định lý hàm số sin cho tam giác AMB: AMMBAMMBAMMBAMMB UUUUUUUUU sinsinsinsinsin 2sincos2coscos 2222 +++ ===== γαβα+βα+βα−βγα−β (Vì α+β+γ=π nên sincos 22 α+βγ = ) Vậy: () AMMB max UU 23 +⇔α=β==π−γπ (Vì L R tan3 Z3 π γ==  γ= )  Tam giác AMB đều AM UU = M C A B LR M B A M C A B LR M B A

DẠYKÈMQUYNHƠNOFFICIAL 412 Câu 46: Chọn C. Ta đã biết: ( ) cdCmaxUU + khi ∆AMB cân tại M, suy ra: 2 CRLLRL22 LC RR ZZRZcos0,8 ZRZ ==+  ϕ=== + LL CC Z0,75RZ 0,75R0,6. Z1,25RZ1,25R =  == = Câu 47: Chọn D. Ta có: UC = CUZ Z = 2 2 U 1 CRL C ω+ω− ω  Khảo sát sự biến thiên của UC theo ω ta có UC = UCmax khi ω = 2πf = 1 L 2LR C2 = 50π 6  f = 25 6 Hz. Câu 48: Chọn C. Khi C thay đổi: 22 LL RCmaxC 22 L CmaxC L ZZ4R UZ 2 RZ UZ' Z  ++ ⇔=  + ⇔=  CC 2222 Z'3Z LLL L L RZZZ4RR 3.3,2. Z2Z = +++ →=  ≈ Câu 49: Chọn C. Khi L = L1 vì uC trễ hơn u là 300 luôn trễ hơn i là 2 π nên u trễ hơn i là 3 π : M A B M C A B LR

DẠYKÈMQUYNHƠNOFFICIAL 413 () L1C CC C 22 L1C ZZ tantan R3 UZ200 100 Z I0,5 R100 U100 ZRZZ200 I0,5  π  ϕ==−   =Ω  ==   =Ω  =+−===  Khi L = L2 thì RLmaxU nên () 2222 CC L2 ZZ4R 2002004.100 Z 10012 22 ++ ++ ===+Ω L2 2 Z12 LH +  == ωπ . Câu 50: Chọn C. Ta có: Ud = dUZ Z = 22 L 22 LC UrZ r(ZZ) + +− = 22 LC 22 L U r(ZZ) rZ +− + Nhận thấy Ud = Ud max khi y = 22 LC 22 L r(ZZ) rZ +− + = 1 + 2 CCL 22 L Z2ZZ rZ + = 1 + 2 CCL 22 CL Z2ZZ 3 ZZ 4 + = 1 + 4ZC CL 22 CL Z2Z 3Z4Z + = ymin Nếu: ZC – 2ZL < 0  ZC < 2ZL  ZL – ZC < ZL – 2ZL = – ZL  2ZL < ZC : mâu thuẫn. Nếu: ZC – 2ZL ≥ 0  ZC ≥ 2ZL  ZL – ZC ≤ ZL – 2ZL = – ZL  ZC ≥ 2ZL Do vậy y = ymin khi ZC – 2ZL = 0  ZL = 0,5ZC Câu 51: Chọn B. Khi L thay đổi thì RmaxU và CmaxU xảy ra cộng hưởng Rmax maxCmaxmaxCC 22 C Lmax UU UU IUIZZ RR URZ U R   =  ⇔=  ==   + =  Theo bài ra: 22 C LmaxRmaxC URZ U3Uhay3UZ22R. R + ==  = Khi đó: 22 22 LmaxC CmaxC URZR8R5 UZ2 22R + + ===

DẠYKÈMQUYNHƠNOFFICIAL 414 Câu 52: Chọn A. Khi L thay đổi ULmax khi 22 C L C 22 C Lmax RZ Z Z URZ U R  + =   +   (1) Ta có: C222 22CLC C LCC U U30230 2ZR(ZZ) ZZZ R(ZZ) =  =  =+− +− (2) Thế (1) vào (2) ta được: 422422 CCCC RZR2Z0RZRZ +−=  =  = Do đó ULmax = UR2U260 R == V. Câu 53: Chọn A. Khi tần số thay đổi, 22 CmaxLLC LRR UZZZ C22 ⇔=−=− ( ) LCLLCL 2RL ZZZZZZ11 .tan.tan RRR22  ==−  ϕϕ=− . Câu 54: Chọn C. Cách giải 1: Khi CmaxU thì 22 CLC LRR LZZ C22 ω=−=− Khi LmaxU thì 22 LC L 1LRR ZZ CC22 =−=− ω 22 CC C LLL f 1LR1RC L.1 CC2f2L ω  ω=−  ==− ωω 2 C0L0 LRC0 ff;0 ff502 0 f 1 f502Hz f5022 = ==+ →=  = + . Cách giải 2: Từ 2 22 CC LL 2 LR C2 f LCLR1RC 1 1 fLC22L CLR C2 ω ===−=−  ω  2 C0L0 LRC0 ff;0 ff502 0 f 1 f502Hz f5022 = ==+ →=  = + .

DẠYKÈMQUYNHƠNOFFICIAL 415 Câu 55: Chọn C. Tổng 2 tần số f1 và f2 làm ta nghĩ đến tích của f1f2. Do khi chỉnh đến 2 giá trị f1 và f2 thì mạch tiêu thụ cùng công suất  để Pmax thì mạch lúc có tính cộng hưởng. Vậy ω2 = 1 LC  ω = 100π  f = 50 và f2 = f1f2 = 502 cùng với f1 + f2 = 125Hz. Suy ra f1 = 50 và f2 = 75 hoặc ngược lại. Câu 56: Chọn B. Ta có: R CC UIR UIZ =  = Nhận thấy URmax và UCmax khi Imax suy ra ZL = ZC. Khi đó: Rmax CmaxC 22 LmaxC UU U UZ R U URZ R  =   =   =+  Nếu Rmax Lmax U 2 U = thì ta có 22 C 4ZR =− (loại) Nếu Lmax Rmax U 2 U = thì ta có CCmax ZR3UU3. =  = Câu 57: Chọn D. Theo hệ thức: 2 2 CL 25 CLRCL 9 fx;2 fx1200 LC f40RCx1 1 x40 2Lx120010f400 = ==− =ω =−→=  =   ω−=  Khi mạch cộng hưởng thì: RLC fffy40.4004010 =  == . Câu 58: Chọn B. Vì uAN luôn luôn vuông pha với uMB nên 2 ANMB L tantan1R Cϕϕ=−  = . Cách giải 1: * Khi CmaxU thì: () 2 22L R C CLCCC LRRL1 LZZL 1 C222C2LC = ω=−=−→ω=  ω= Khi LmaxU thì: () 2 22L R C LCL LL 1LRR1L2 ZZ 2 CC22C2CLC = =−=−→=  ω= ωω Từ (1), (2) suy ra: LCLC 2f2fω=ω  = Khi mạch cộng hưởng thì RLCC ffff2502Hz === Cách giải 2: Từ hệ thức: 2 C 2 CCLRC f50HzL LLL f 1RC50 10,5f100Hz. f2Lf = = ω ==−→=  = ω Khi mạch cộng hưởng thì: RLCC ffff2502Hz === .

DẠYKÈMQUYNHƠNOFFICIAL 416 Câu 59: Chọn C. Ta có: UL = 2 L 22 LC UZ R(ZZ) +− Nhận thấy UL = ULmax khi ZL = 22 C C RZ Z + Khi đó U Z = C C U Z = Lmax L U Z  Z = ZC C U U = ZC 200 1003 = 2 3 ZC  Z2 = R2 + (ZL – ZC)2 = 4 3 ZC 2  R2 + ZL 2 + ZC 2 – 2ZLZC –4 3 ZC 2 = 0  ZL 2 – ZLZC –4 3 ZC 2 = 0  ZL = 2 3 ZC Vậy: C C U Z = Lmax L U Z  ULmax = C C U Z ZL = 2 3 UC = 300V. Câu 60: Chọn A. Khi f = f0 thì UC = U nên () ()22 L 22 2 222 L CLCCL L L L Z2R1 C RZx1 ZRZZZZ 2Z2 RxZ  =−  + + =+−  ==   =  Thay giá trị ZC vào ( )( ) ( )LLCC 6RZZZ7RRZ ++=+ ta được: () 22 LLLLLLL x1x2 6xZZZZ7xZxZZ 22  ++ ++=+  ()() ()2 22 x2(6x1x37xx1x7x180 x9( =  ++=+  +−=   =− nhaän) loaïi) () 222 LL CL L xZZ Z2,5Z2 2Z +  == Khi 0 ff75 =+ Hz thì UL = U nên () ()2 2222 LLCC L Z'RZ'Z'Z'2R3 C =+−  =− Từ (1) và (3) ( )LC ZZ'4. = Thay (4) vào (2): () CC0 00 11 Z2,5Z'2,5f50Hz 2f2f75 =⇔=  = ππ+ . Câu 61: Chọn A. Khi URLmax thì 22 22 CC L ZZ4R 1001004.50 Z 120,7. 22 ++ ++ ===Ω

DẠYKÈMQUYNHƠNOFFICIAL 417 Câu 62: Chọn D. Khi f = f0 thì UC = U nên () ()22 L 222 222L CLCCL L L L Z2R1 C RZ x1 ZRZZZZ 2Z2 RxZ  =−  + + =+−  ==   =  Thay giá trị ZC vào ( )( ) ( )LLCC 6RZZZ7RRZ. ++=+ ta được: () 22 LLLLLLL x1x2 6xZZZZ7xZxZZ 22  ++ ++=+  ()() ()2 22 x2(6x1x37xx1x7x180 x9( =  ++=+  +−=   =− nhaän) loaïi) () 222 LL CL L xZZ Z2,5Z2 2Z +  == Khi 0 ff75 =+ Hz thì UL = U nên () ()2 2222 LLCC L Z'RZ'Z'Z'2R3. C =+−  =− Từ (1) và (3) ( )LC ZZ'4. = Thay (4) vào (2): () CC0 00 11 Z2,5Z'2,5f50Hz. 2f2f75 =⇔=  = ππ+ Thay f0 = 50 Hz vào (2), ta được: ()() 211 2,5.100L2,5.1005 100CLC =π  =π π Ta lại có: () 22 L AMRLRL2 2 LC RZ UUIZUR RZZ + ===∉ +− ()() 2 CL 1 Z2Z22f6 LC ⇔=⇔=π Thay (5) vào (6) ta được: ( ) ( ) 22 22f2,5100f255Hz π=π  = . Câu 63: Chọn A. Khi tần số thay đổi: 22 CmaxLLC LC Cmax22 LC LRR UZZZ C22 L ZZC UUU LRR RRZZ C44  ⇔=−=−     ==   Giá trị điện áp hiệu dụng cực đại: Cmax222 2 C L UUU U 90,45V 120RC 111 1 1004L ==== π  ω  π ω  .

DẠYKÈMQUYNHƠNOFFICIAL 418 Câu 64: Chọn A. Cuộn dây không thuần cảm L có r. Hai tụ có điện dung lần lượt C1 và C2. Mắc song song C1 và C2 ta C = C1 + C2 thì có tần số góc cộng hưởng là ω1 2 = 1 LC = 1 L(C1 + C2) (1) Mắc nối tiếp C1 và C2 ta được 1 C' = 1 C1 + 1 C2 và tần số ω2 2 = 1 LC' (2) Khi chỉ mắc C1 thì lúc này tần số góc cộng hưởng là ωx 2 = 1 LC1 . Từ (1) thêm bớt ta thấy 1 ω1 2 = L(C1 + C2) ⇔ 1 ω1 2 = 1 ωY 2 + 1 ωX 2 (3) Với ωX 2 , ωY 2 lần lượt là tần số góc cộng hưởng khi chỉ có C1 hoặc C2 Từ (2) thêm bớt tương tự ta có: ω2 2 = ωX 2 + ωY 2 (4) Từ (3) và (4) ta có hệ phương trình 2 ẩn  ωX = 60π rad/s. Câu 65: Chọn D. Ta có: URmax = UAB  ULmax = 2UAB Mặt khác ta có ULmax khi UAB URC suy ra 222222 LmaxABRCABRC UUUUUU =+=++ và ( )2 2 RCLCLCC UUUUUUU =−=− Suy ra 2222222 LmaxABRCABLCCCABLC LmaxAB UUUUUUUUUUU U2U  =+=+−+=+  =  LmaxC 4 UU. 3  = Câu 66: Chọn B. Ta có: fCmax = f1 = 2 2 12LRC 22LC π fRmax = f2 = 11 2LC π = f1 = 2 2 12LRC 22LC π  2 2LRC L = 1  2L – R2C = L  L = R2C Khi đó: ULmax = 22 2LU R4LCRC = 2 2222 2RCU2U 3R4RCRC = = 139 V. Câu 67: Chọn C. Khi ω thay đổi, ⇔CmaxU =−=− 22 LLC LRR ZZZ C22 ⇔=−⇔−++=⇔−+= 2 222222 LLCLLCLLLCRL R ZZZZ2ZZZR0Z2ZZZ0 2 = ⇔−+=⇔−+=   => 2222L LLCRLLC LRL U30V U2UUU0U2.90U5.300 U150VU Thay = L U30V vào =+  =+  = 222222 RLRLRR UUU30.5U30U60V () =+−= 22 RLC URUU602V. ⊥ 2 2

DẠYKÈMQUYNHƠNOFFICIAL 419 Câu 68: Chọn B. Nhận thấy UC = UCmax khi ZC1 = 22 L L RZ Z + và UCmax = 22 LURZ R + Cường độ dòng điện trễ pha 4 π so với điện áp hai đầu đoạn mạch tanϕ = LC2ZZ R = tan 4 π = 1  R = ZL – ZC2 = ZL – 0,4ZC1 (vì C2 = 2,5C1 nên ZC2 = 0,4ZC1) Suy ra R = ZL – 0,4 22 L L RZ Z +  RZL = ZL 2 – 0,4R2 – 0,4ZL 2  0,4R2 + ZLR – 0,6ZL 2 = 0  R = 0,5ZL hay ZL = 2R Do đó UCmax = 22 LURZ R + = 22UR4R R + = U 5  U = CmaxU 5 = 100V. Câu 69: Chọn D. Ta có: U’MB = 2 2 UMB  LC 22 LC UZ'Z R(Z'Z) +− = 2 2 LC 22 LC UZZ R(ZZ) +−  2 LC 22 LC (Z'Z) R(Z'Z) +− = 8 2 LC 22 LC (ZZ) R(ZZ) +− (1) Dòng điện trong 2 trường hợp vuông pha nhau nên: ( )( ) 2 LCLC tantan'1ZZZ'ZR ϕϕ=−⇔−−=− ⇔ (Z’L – ZC)2 = 4 2 LC R (ZZ) (2). Thay (2) vào (1), ta được: 2 22 LC R R(ZZ) +− = 8 2 LC 22 LC (ZZ) R(ZZ) +− ⇔ (ZL – ZC)2 = 2R 8 Điện áp hiệu dụng ở 2 đầu mạch AM khi chưa thay đổi L: UAM = IR = 22 LC UR R(ZZ) +− = 2 22UR 9R = 22U 3 = 100 2 V. Câu 70: Chọn B. Khi ω thay đổi: () ()  ⇔=−=−     ==   22 CmaxLLC LC Cmax22 LC LRR UZZZ1 C22 L ZZC UUU2 LRR RRZZ C44 Thay = LC 9 ZZ 41 vào (1) suy ra: = C 24 RZ. 41

DẠYKÈMQUYNHƠNOFFICIAL 420 Thay các kết quả vào (2) ta được: ===    CC LC Cmax 2 2 2 C LC CCC 9 ZZZ.Z 41 UU200.205V. RZRZZ24924 4ZZ.Z4141414 Câu 71: Chọn D. Ta có:  ⇔=ω=++  2 2 RLmaxLRL LLL UZLR 2C2C2C ++   ω= 2 2 RL LLL R 2C2C2C L  ++  = =π π 2 2 333 111 .100.2 2.0,2.102.0,2.102.0,2.10 100 rad/s.1 Tương tự:  ⇔==++ω  2 2 RCmaxC RC 1LLL UZR C2C2C2C  ω= ++  RC 2 2 1 LLL CR 2C2C2C = =π  ++π  32 2 333 1 50 rad/s. 0,2.10111 .100.2 2.0,2.102.0,2.102.0,2.10 Câu 72: Chọn D. Khi RmaxU thì mạch cộng hưởng: ω==π R 1 502 rad/s LC Ta có: + ⇔==− ω 2 LmaxC L 1LR UZ CC2

DẠYKÈMQUYNHƠNOFFICIAL 421 π  ω=== π π π L2 32 3 11200 rad/s. 16LR C 0,2.1050C2 0,2.102 + ⇔=ω=− 2 CmaxLC LR UZL C2 π π  ω===π π 2 23 C 1 50 0,2.10 2LR C2 256rad/s.1L Ta lại có:  ⇔=ω=++  2 2 RLmaxLRL LLL UZLR 2C2C2C ++   ω= 2 2 RL LLL R 2C2C2C L ++  = =π+ π 2 2 333 111 .50 2.0,2.102.0,2.102.0,2.10 5012rad/s.1 Tương tự:  ⇔==++ω  2 2 RCmaxC RC 1LLL UZR C2C2C2C  ω= ++  RC 2 2 1 LLL CR 2C2C2C =  ++π  32 2 333 1 0,2.10111 .50 2.0,2.102.0,2.102.0,2.10 =π−+10012rad/s. Câu 73: Chọn B. Ta có: LC1 1 LC1C1L ZZ tantan1RZZZZR R4 π ϕ===  =−  =−

DẠYKÈMQUYNHƠNOFFICIAL 422 Mặt khác: UC2 = UCmax  ZC2 = 22 L L RZ Z +  6,25ZC1ZL = R2 + 2 LZ  6,25( ZL – R)ZL = R2 + 2 LZ  5,25 2 LZ – 6,25RZL – R2 = 0  21 2 LZ – 25RZL – 4R2 = 0  ZL = 4 R 3 Khi đó: 22 22 L C2 L 16 RZRR25 9 ZR 4 Z12 R 3 + + === Hệ số công suất của mạch: 2 2 2 2 RR cos0,8. Z 425 RRR 312 ϕ=== +−  Câu 74: Chọn D. Ta có: () 2 11 2 21111 12 2 12 22 2 12 2222 11 L LCC11 CC LC11 LL L CC LCC  ω=  = ω ω==   + ω=  = +  ω Với: 12 12 12 2222 1122112112 111111CC LL CCCCCC ω=ω   +=+=+=  ωωωω+  () 2 2 1 1 12 12 12 1 CC LL CC ω==ω  ω=ω + + Câu 75: Chọn A. Khi ω=ω3 thì () ()() +− == ++− 22 LC MBMB 22 Lc rZZ UIZU RrZZ Nhận thấy MBminU ⇔=⇔π=  = πππ 5 LC 215.10 ZZ1003.CF. 31003C3 Lúc này, mạch cộng hưởng nên: ==  = 21max1max 213 IIIII. 3 21 Khi ω = ω1 và ω = ω2 thì dòng điện hiệu dụng qua mạch có cùng giá trị = 1max 3 II 21 nên: == 12 21 ZZR 3 () () () ⇔++ω−=++ω−=+  ωω  2 2 2 2 1 2 1 2 1121 RrLRrLRr CC3

DẠYKÈMQUYNHƠNOFFICIAL 423 () ()  ω−=+ ω ⇔  ω−=−+ ω 1 1 2 2 12 LRr C 3 12 LRr C 3 () () ω−ω=ω = π =Ω  ω=π ωω==ω→  ω=π ⇔   ω−ω=+→+=Ω  222 123 261 123 2 2 LH 3 12 r50 300 1rad/s LC100 rad/s 2 LRrRr200 3 Mặt khác: RrL maxU ⇔ () =ω=+++   2 2 LRL LLL ZLRr 2C2C2C () +++    ω=ω= 2 2 4RL LLL Rr 2C2C2C L ()()() 22 200002000020000200 202,44 rad/s.2 3 ++ ==π π Vậy: 4 3 202,44 k1,17. 1003 ω π === ω π Câu 76: Chọn C. Ta có: () () L LL 22 22 LC CC 2 LL UZU UIZ RZZ11RZ2Z1 ZZ === +− +−+ UL phụ thuộc L 1 Z theo kiểu hàm tam thức bậc 2 nên: L1L212 0 L0 12 11 ZZ2LL1 L Z2LL + =  = + . Câu 77: Chọn A. Ta có: UC = IZC = 2 2 U 1 CRL C ω+ω− ω  . Nhận thấy UC = UCmax khi 21LR LC2 ω=− với điều kiện 2 4 2 2 LR2L2.10 02LRCCF. C2R −>  >  <= π Khi đó 48 2 Cmax 222 2UL54.1036.10 UUCC0 325R4LCRC ==  −+= ππ

DẠYKÈMQUYNHƠNOFFICIAL 424 Phương trình có hai nghiệm: 44 54 CF3,6.102.10 > F( 4.102.10 CF< F (  = ππ  = ππ loaïi) nhaän) Vậy: 254 1LR1010 2f1002f502Hz. LC242 ω=−  π=π−=π  = Câu 78: Chọn C. Ta có: () () L LL 22 22 LC CC 2 LL UZU UIZ RZZ11RZ2Z1 ZZ === +− +−+ , UL phụ thuộc L 1 Z theo kiểu hàm tam thức bậc 2 nên: L1L2C 22 L0C 11 ZZZ1 Z2RZ + == + 22 50111 R502 R502100300   =+  =Ω+  . Câu 79: Chọn C. () () C CC 22 22 LC LL 2 CC UZU UIZ RZZ11RZ2Z1 ZZ === +− +−+ , UC phụ thuộc C 1 Z theo kiểu hàm tam thức bậc 2 nên: C1C2L 22 C0L 11 1ZZZ Z2RZ + == + 12CC C30F 2 +  ==µ . Câu 80: Chọn B. Điện áp hiệu dụng trên cuộn cảm thuần: () () L 222 2 2 222 ULUL U 2L1 RL112L1RL C C CC ω == −+ω+ +−+ ω ωω  Với ω = ω1 hoặc ω = ω2 thì điện áp trên cuộn cảm có cùng giá trị, với ω = ω0 thì điện áp trên cuộn cảm cực đại. Ta có quan hệ: 222 012 1111 2  =+ ωωω = 2 2 2LC R C2     ω0 = 48π rad/s.  ZL = 300Ω; ZC = 100Ω; R = 200Ω  ULmax = 150 2 V. Câu 81: Chọn D.

DẠYKÈMQUYNHƠNOFFICIAL 425 Ta có: C1 6 1 C2 6 2 11 Z400 C25.10 100. 11 Z240 C125.10 100. 3  ===Ω ω π π  ===Ω ω π π Theo giả thuyết: () () C CC 22 22 LC LL 2 CC UZU UIZ RZZ11RZ2Z1 ZZ === +− +−+ UC phụ thuộc C 1 Z theo kiểu hàm tam thức bậc 2 nên: C1C2L 22 C0L 11 1ZZZ Z2RZ + == + L 22L L Z 1 Z100. RZ300  =  =Ω + Vậy: RmaxCL C 1100 UZZ100CF Z ⇔==  ==µ ωπ . Câu 82: Chọn B. Vì UY – UX = 100V và U = 1003 V nên mạch không thể chứa LC. Khi f tăng I giảm nên mạch chứa RL. Giả sử: UY = UR  R U2 cos1 U3 ϕ==> (loại) Vậy: UX = UR=100V  R U1 cos1 U3 ϕ==< Câu 83: Chọn C. Khi LC1 11 LC1 ZZ CCtantanRZZ R4 π =  ϕ==  =− Khi () C2C1 12222 LLC1L CmaxC2C1 L L Z6,25Z C C ZZZRZ6,25 UZ6,25Z ZZ =  =  −+ + ⇔=  =  C1L LL C1 L C2 Z8Z Z3Z ZR 44 25Z Z 16  =   =  =   =  Hệ số công suất mạch AB khi đó:

DẠYKÈMQUYNHƠNOFFICIAL 426 () L 2222 LC2LL L 3Z cosR40,8 RZZ3Z25Z Z 416 ϕ=== +−  +−   . Câu 84: Chọn D. Khi 4 1 10 CCF == π thì dòng điện i trễ pha π 4 so u nên: LC1 ZZR −= (1) Khi 4 2 10 CCF 2,5 == π thì điện áp hai đầu tụ điện đạt giá trị cực đại nên: 22 L C2 L RZ Z Z + = (2) Thay (1) vào (2) ta có: 44282 2 50π rad/s (8 9.10100 2 100π rad/s (  ω−ω+π= π   loaïi) nhaän) Câu 85: Chọn C. Khi LC1 11 LC1 ZZ CCtantanRZZ R4 π =  ϕ==  =− Khi () C2C1 12222 LLC1L CmaxC2C1 L L Z2,5Z C CZZZ 2,5RZUZ2,5Z ZZ =  =  −+ + ⇔=  =  4 L22 1 C1 Z210 2LC22100 rad/s Z  =  ω=  ω=  ω=π ππ . Câu 86: Chọn D. Công suất mạch tiêu thụ (với U = kω): 2 2 2 2 2 2 22422 kR PIRkRL 111LR11 RL21 CLCC2L ω ===  +ω−−−+ ωωω  Nhận thấy P phụ thuộc 2 1 ω theo kiểu hàm tam thức bậc 2 nên: 2222221 01211 11111111 f109,33Hz 21502f16f  =+⇔=+  = ωωω Câu 87: Chọn C. Ta có: L 3 ZL100.1003. =ω=π=Ω π

DẠYKÈMQUYNHƠNOFFICIAL 427 Mặt khác: ( )2 222 L CmaxC L rZ1001003 400 UZ Z 10033 ++ ⇔===Ω 4 C 113 C.10F. 400 Z4 100. 3  === ωπ π ()2 222 L Cmax UrZ1001001003 U 200 R100 ++ ===Khi ñoù: V. Câu 88: Chọn A. Điện áp hiệu dụng trên tụ (với U = kω): C CC 22 22 1kUZk. UIZCC Z11 RLRL CC ω ω ====  +ω−+ω−  ωω  Nhận thấy UC phụ thuộc theo hàm kiểu phân thức đối với ω nên: 22 012111150f.4ff75Hzω=ωω⇔=  = Câu 89: Chọn D. Vì có những giá trị UL tương ứng với hai giá trị f1 và f2 của f nên tồn tại LmaxU và đồ thị có dạng như hình vẽ: LL 2 2 UL UIZ 1 RL C ω == +ω− ω  2 2 22422 c a xx b U 11LR11 21 LCC2L =  −−+  ωω  Nhận thấy UL max khi 2 22 2 2 2 LR b1LRRC4 C2 xC0LH 1 2aC22 C  =−⇔==−>  == ω π . Câu 90: Chọn B. Khi ω thay đổi, CmaxC UU ⇔ là cạnh huyền với U và UL là hai cạnh góc vuông, tức là: () 222 CmaxRLC 222U1,25UUUUU CmaxLLR 3 UUUU0,75UUU 2 ==+− =+→=→= Hệ số công suất đoạn mạch AB khi đó: RU R3 cos ZU2ϕ=== . Câu 91: Chọn D. f UL UL max U L1 = U L2 f 1 f 0 f 2

DẠYKÈMQUYNHƠNOFFICIAL 428 Ta có: 3 1 LC1 LC1 LC1 10 CCF 2 ZZR 4ZZ(1) ZZ tantan1 R4  == π −=π ϕ=   > π ϕ===  Ta lại có: 3 1C2C1 22 L C2maxC2 L 105 CCFZZ 22 R20. RZ UZ(2) Z  ==  = π  =Ω +  =  Lập tỉ số (2) và (1), ta được: L2 LC1 1 C1 1 Z L Z2Z22LC2100π rad/s. Z1 C ω =⇔=⇔=⇔ω=  ω= ω Câu 92: Chọn D. Khi ω thay đổi, CmaxC UU ⇔ là cạnh huyền với U và UL là hai cạnh góc vuông, tức là: () 222 CmaxRLC 222U1,25UUUUU CmaxLLR 3 UUUU0,75UUU 2 ==+− =+→=→= Hệ số công suất đoạn mạch AB khi đó: () () R AM 22222 2 LRL U R0,5U32 cos RZUU7 0,5U30,75U ϕ==== ++ + . Câu 93: Chọn A. Khi ω thay đổi, CmaxU ⇔ : 22 LLC LRR ZZZ C22 =−=− 2 222222 LLCLLCLLLCRL R ZZZZ2ZZZR0Z2ZZZ0 2 ⇔=−⇔−++=⇔−+= 2222L LLCRLLC LRL U150V Z2ZZZ0Z2.250Z21.500 U350VU = ⇔−+=⇔−+=   => Thay L U150V = vào 222222 RLRLR UUU50.21U150 =+  =+ () 22 RRLC U1003VUUUU200V =  =+−= Câu 94: Chọn B. Khi f thay đổi CmaxLmaxUU = và theo bài ra thì CmaxLmax UU1,5. == U Khi f = fL thì Cmax U1,5U = và C UU = nên thay vào: ( ) 222 RLC UUUU =+− () 222 R RR U3RU UU1,5UUUcos0,866 2ZU  =+−  =  ==≈ .

DẠYKÈMQUYNHƠNOFFICIAL 429 Câu 95: Chọn D. Khi ω thay đổi, CmaxCUU ⇔ là cạnh huyền và U và LU là hai cạnh góc vuông, tức là: () 222 CmaxRLC 222U1,25UUUUU CmaxLL R 3 UUUU0,75UUU 2 ==+− =+→=→= Độ lệch pha: LCLC R ZZUU 1 tan RU6 3 π ϕ===−  ϕ=− . Câu 96: Chọn C. Khi 2222 L CmaxLLCC L LRR2ZR UZZZZ C222Z + ⇔=−=−  = Từ max 3 PP 4 = suy ra () 22 2 22 LC UR3UR RZZ4R0 = +−+ L 2 222LC 2 L LC L R3 Z 13L 2 ZZ1,25R 4RC2ZR5RRZZ 2Z 23  =   =  == +  +−=    Khi 22 2 LmaxC LRRR3 UZ'1,25R C222 ⇔=−=−= Từ đó suy ra: C 1 1 C1 Zf1005f150Hz Z'f3 + ==  = Câu 97: Chọn B. Gọi ωL và ωC lần lượt là giá trị của ω để LmaxU và CmaxU . Ta đã biết: ()LC 1 1. LC ωω= Từ đồ thị ta thấy: C UU = thì ( )0C 22ω=ω=ω và L UU = thì ()L 0 '3 2 ω ω=ω= Thay (2), (3) vào (1): () ()00 0'150 0 00 11 '2.''150 4 2LCLC ω=ω−πω ω=→ωω−π= U UL 0 U UC 0

DẠYKÈMQUYNHƠNOFFICIAL 430 Khi 0 'ω=ω thì 1 cos 3 ϕ= và L UU = hay () R R 222 RLCC U1U cosU U 33 2 UUUUU1U 3  ϕ==  =    =+−  =−   ()CC 2 LL0 UZ21 1 5 U3Z'LC  =−== ω Từ (4), (5) suy ra: () 2 0000 0 0 0 2 ''150'1'577,15 rad/s 3 577,15150105,91 rad/sf16,86Hz 2   ωω−π=ω−  ω≈    ω ω=−π≈  =≈ π Câu 98: Chọn D. Ta có: L2C1 12 12 C2L1 1ZZ coscos LCZZ = ωω=  ϕ=ϕ = Khi tần số thay đổi: LmaxCmaxmaxUUU == Khi () L2L2max 2 C2L2 C2C2max UIZU 2 ff:ZZ1 23UIZU 3 ==  =  = ==  Mặt khác: () 2 2 LmaxC2C2L2C2 LRR UZZZZ2 C22 ⇔=−⇔=− Từ (1) và (2) suy ra: L2 Z1,5R = và C2 ZR = Do đó: () () 2 2222 L2C2 RR2 cos 0,894 5RZZR1,5RR ϕ===≈ +−+− Câu 99: Chọn A. Sử dụng công thức giải nhanh ta có P = Pmaxcos2ϕ3  cosϕ3 = 1 2  ϕ3 = π 4 Mặt khác khi chỉnh C đến C1 và C2 thì UC1 = UC2 nên ta có công thức: ϕ3 = ϕ1 + ϕ2 2kết hợp ϕ2 = ϕ1 + π 3      ϕ2 = 5π 12 ϕ1 = π 12 Một công thức giải nhanh khác là UC1 = UCmaxcos(ϕ1 – ϕ3) với tanϕ3 = R ZL  40 = U RR2 + ZL 2.cos(π 4 –π 12)  U = 80 6 V. Câu 100: Chọn A.

DẠYKÈMQUYNHƠNOFFICIAL 431 Nhận thấy CmaxU khi () 2 LC LR ZL1 C2 =ω=− Nếu C UU = thì ZC = Z hay 2 2 0 00 11 RL CC  =+ω− ωω () 2 0LLR 2 2C2 ω  =− Từ (1) và (2) suy ra: 0 C 2 ω ω= Câu 101: Chọn A. Ta thấy LmaxU khi () 2 C L 1LR Z1 CC2 ==− ω Nếu L UU = thì ZL = Z hay 2 2 00 0 1 LRL C  ω=+ω− ω  () 2 0 1LR 2 2CC2  =− ω Từ (1) và (2) suy ra: 0 C . 2 ω ω= Câu 102: Chọn A. Khi tần số thay đổi: () () 22 CmaxLLC LC CmaxLmax 22 LC LRR UZZZ1 C22 L CZZ UUUU2 LRR RRZZ C44  ⇔=−=−     ===   Thay LC 2 ZZ 11 = vào (1) suy ra: C 6 RZ. 11 = Thay các kết quả vào (2): C C LC Cmax 2 2 2 CCC LC C 2Z ZZZ 11 UU4513.165V R6Z2ZZRZZ6 4Z1111114 ===    Câu 103: Chọn B. Khi f = f0 thì UC = U nên () ()22 L 22 2 222 L CLCCL L L L Z2R1 C RZ x1 ZRZZZZ 2Z2 RxZ  =−  + + =+−  ==   = 

DẠYKÈMQUYNHƠNOFFICIAL 432 2 LL LC L x1 ZZZZtan0,752 RxZ +  ϕ=⇔−= () L 2 CLL R2Z x22 21 ZZ2,5Z 2 =   =   + ==  Khi f = f0 + 45 Hz thì UL = U nên () ()2 2222 LLCC L Z'RZ'Z'Z'2R 3 C =+−  =− Từ (1) và (3) ( )LC ZZ'4 = Thay (4) vào (2): ()CC 0 00 11 Z2,5Z'2,5.f30Hz. 2f2f45 =⇔=  = ππ+ Thay f0 = 30 Hz vào (2), ta được: ()() 211 2,5.100L2,5605 60CLC =π  =π π Khi đó: () 22 C AMRC 22 LC RZ UIZUR RZZ + ==∉ +− ()() 2 LC 1 Z2Z0,52f6 LC ⇔=⇔=π Thay (5) vào (6): ( ) ( ) 22 0,52f2,560f305Hz π=π  = . Câu 104: Chọn D. Từ công thức: 22 C LC,Lmax U 1 U  ω += ω   222U 1U223,6V. 3300   +=  ≈ 

DẠYKÈMQUYNHƠNOFFICIAL 432 CHỦ ĐỀ 15: MẠCH ĐIỆN XOAY CHIỀU CÓ CẤU TRÚC THAY ĐỔI A. TÓM TẮT LÝ THUYẾT CƠ BẢN I. Nối tắt L hoặc C mà Z không đổi (I không đổi) Ta có kết các quả sau: ϕ+ϕ ϕ==   =−ϕ+ϕ  ϕ=ϕ=  i2i1 u CL LCi2i1 12 Z2Z 2 Z2Z 2 1. Đối với mạch RLC, khi R và ( )=ω+ϕ 0u uUcost(V) giữ nguyên, nếu biểu thức của dòng điện trước và sau khi nối tắt C lần lượt là () ()  =ω+ϕ  =ω+ϕ  1i1 2i2 iI2cost iI2cost thì: ϕ=−α ϕ=α ϕ+ϕ− ϕ=ϕ=   =  →  −ϕ+ϕ  α=ϕ=   1 2 i2i1LC u 1 CL i2i1L 2 ZZ tan Z2Z2R Z tan 2R Chứng minh: Ta có: ( ) ()  =ω+ϕ  =  +−=+  =  0u 2 222 12LCLCL uUcost(V) Tr−ícvµsaukhimÊtCmµIIRZZRZZ2Z + Trước: () ϕ  ϕ==−=−α  ϕ=−α  =ω+ϕ+α   i1 LCL 1 110u ZZZ tantaniicost RR + Sau: ϕ  ϕ==α  ϕ=α  =ω+ϕ−α   i2 L 2220u Z tantaniicost R Suy ra: ϕ+ϕ ϕ=   ϕ−ϕα=  i1i2 u i1i2 2 2 2. Đối với mạch RLC, khi R và ( )=ω+ϕ 0u uUcost(V) giữ nguyên, nếu biểu thức của dòng điện trước và sau khi nối tắt L lần lượt là () ()  =ω+ϕ  =ω+ϕ  1i1 2i2 iI2cost iI2cost

DẠYKÈMQUYNHƠNOFFICIAL 433 thì: ϕ=α ϕ=−α ϕ+ϕ− ϕ=ϕ=   =  →  ϕ−ϕ− α=ϕ=   1 2 i2i1LC u 1 LC i2i1 C 2 ZZ tan Z2Z2R Z tan 2R Chứng minh: Ta có: ( ) ()  =ω+ϕ  =  +−=+  =  0u 2 222 12LCCLC uUcost(V) Tr−ícvµsaukhimÊtLmµIIRZZRZZ2Z + Trước: ϕ  ϕ===α  ϕ=α  =ω+ϕ−α   i1 LCC 1 110u ZZZ tantaniicost RR + Sau: () ϕ  ϕ==−α  ϕ=−α  =ω+ϕ+α   i2 C 2220u Z tantaniicost R Suy ra: ϕ+ϕ ϕ=   ϕ−ϕα=  i1i2 u i2i1 2 2 BÀI TẬP VẬN DỤNG Câu 1: Cho mạch điện như hình vẽ Đặt một điện áp xoay chiều ( )=π uU2cos100tV vào hai đầu đoạn mạch điện AB như hình vẽ. Cuộn dây thuần cảm và R = ZC. Khi K đóng hoặc mở thì cường độ dòng điện hiệu dụng qua mạch không đổi. a. Tính độ lệch pha giữa u và i khi k mở và k đóng. b. Tính hệ số công suất của đoạn mạch khi k mở và k đóng. Hướng dẫn: a. Tính độ lệch pha giữa u và i khi k mở và k đóng. Khi K đóng, mạch chứa R và C nối tiếp: =+= 22 C ZRZR2 ñoùng Khi K mở, mạch chứa RLC: ()=+−22 LCZRZZ môû Do ( )=  ==  +−=+ 2 222 LCC IIZZR2RZZRZ môûñoùngmôûñoùng  == LC Z2Z2R Độ lệch pha: −π ϕ===  ϕ=   −π ϕ===−  ϕ=−  LC C ZZ 2RR tan1 RR4 Z R tan1 RR4 môû môû ñoùng ñoùng K C BA R L

DẠYKÈMQUYNHƠNOFFICIAL 434 b. Tính hệ số công suất của đoạn mạch khi k mở và k đóng. Cách giải 1: Sử dụng công thức: () ϕ== +− 22 LC RR cos ZRZZ Hệ số công suất của đoạn mạch:  ϕ===    ϕ===  RR2 cos Z2 R2 RR2 cos Z2 R2 môû môû ñoùng ñoùng Cách giải 2: Sử dụng phương pháp chuẩn hóa số liệu Chọn R = 1 đơn vị điện trở Ta có: === ZZR22. môûñoùng Hệ số công suất của đoạn mạch:  ϕ==    ϕ==  R2 cos Z2 R2 cos Z2 môû môû ñoùng ñoùng Câu 2: Đặt điện áp xoay chiều ổn định vào hai đầu đoạn mạch C mắc nối tiếp gồm điện trở thuần R = 100 Ω, cuộn cảm thuần có cảm kháng ZL và tụ điện có dung kháng ZC thì cường độ dòng điện qua đoạn mạch là ()π  =π+ 10 iIcos100tA. 4 Nếu ngắt bỏ cuộn cảm (nối tắt) thì cường độ dòng điện qua đoạn mạch là ()π  =π+ 20 3 iIcos100tA. 4 Dung kháng của tụ bằng A. 100 Ω. B. 200 Ω. C. 150 Ω. D. 50 Ω. Hướng dẫn: Ta có: ( ) ()  =ω+ϕ  =  +−=+  =  0u 2 222 12LCCLC uUcost(V) Tr−ícvµsaukhimÊtLmµIIRZZRZZ2Z + Trước: ϕ  ϕ===α  ϕ=α  =ω+ϕ−α   i1 LCC 1 110u ZZZ tantaniicost RR + Sau: () ϕ  ϕ==−α  ϕ=−α  =ω+ϕ+α   i2 C 2220u Z tantaniicost R ϕ−ϕ π  α==  =α=  ==Ωi2i1C C Z tan1ZR100. 24R    Chọn A

DẠYKÈMQUYNHƠNOFFICIAL 435 Câu 3: Cho mạch điện xoay chiều như hình vẽ. UAB = const; f = 50Hz, điện trở các khóa K và ampe kế không đáng kể Điện dung của tụ có giá trị = π 410 CF Khi khóa K chuyển từ vị trí 1 sang 2 thì số chỉ của ampe kế không thay đổi. Tính độ tự cảm L của cuộn dây? A. π 210 H B. π 110 H C. π 1 H D. π 10 H Hướng dẫn: Ta có: ===Ω ω π π C 4 11 Z100. C10 100. Khi khóa K ở vị trí 1 mạch là hai phần tử R và C. Nên ta có: == + ABAB 22 AB C UU I Z RZ (1) Khi khóa K ở vị trí 2 thì mạch bao gồm hai phần tử là R và L. Nên ta có: == + ABAB 22 AB L UU I' Z' RZ (2) Vì I = I’ nên: =⇔+=+ ++ ABAB2222 2222CL CL UU RZRZ RZRZ ⇔==Ω  === ωππ L LC Z 1001 ZZ100LH. 100    Chọn C II. Nối tắt L hoặc C mà Z không đổi (I thay đổi) Khi R và u = U0cos(ωt + ϕ) giữ nguyên, các phần tử khác thay đổi thì  =ϕ    =ϕ=ϕ  2 22 U Icos R U PcosPcos R coäng höôûng Cường độ hiệu dụng tính bằng công thức: ===ϕ UURU I.cos ZRZR Khi liên quan đến công suất tiêu thụ toàn mạch, từ công thức = 2 PIR , thay ===ϕ UURU I.cos ZRZR , ta nhận được: =ϕ=ϕ 2 22U PcosPcos R coäng höôûng K 1 2 CA B R L A

DẠYKÈMQUYNHƠNOFFICIAL 436 BÀI TẬP VẬN DỤNG Câu 1: Đoạn mạch không phân nhánh RLC đặt dưới điện áp xoay chiều ổn định thì cường độ hiệu dụng, công suất và hệ số công suất của mạch lần lượt là 3 A, 90 W và 0,6. Khi thay LC bằng L’C’ thì hệ số công suất của mạch là 0,8. Tính cường độ hiệu dụng và công suất mạch tiêu thụ Hướng dẫn: Từ công thức: Từ công thức:  ϕ  =ϕ  =  =  = ϕ  2 22 2 222 2 11 PcosP PcosU0,8 P160W. RPcos900,6 Câu 2 (THPT Lý Thái Tổ, Bắc Ninh lần 2 - 2016): Cho mạch điện như hình vẽ. Điện áp xoay chiều ổn định giữa hai đầu A và B là u = 1006 cos( t ω+ϕ ) (V). Khi K mở hoặc đóng, thì đồ thị cường độ dòng điện qua mạch theo thời gian tương ứng là im và iđ được biểu diễn như hình bên. Điện trở các dây nối rất nhỏ. Giá trị của R bằng: A. 100Ω. B.50 2 Ω. C. 100 2 Ω. D. 100 3 Ω Hướng dẫn: I1 = Im ; I 2 = Iđ (K đóng) Cách giải 1: Dùng giản đồ véctơ kép Dựa vào đồ thị ta thấy 1 chu kì 12 ô và hai dòng điện lệch pha nhau 3 ô hay T 4 về pha là 2 π (vuông pha). Ta có: m I3I = ñ  R2R1U3U = . Dựa vào giản đồ véctơ hình chữ nhật ta có: LC1R2R1 UU3U == (1) 222 R1R2 UU(1003) += (2) Từ (1) và (2) suy ra: 222 R1R1R1 U(3U)(1003)U503V +=  = Hay R2R1 U3U3.503150V === Giá trị của R: R1 m R2 U R I U R I  =    =  ñ . Thế số: R1 m U5032 R502 I 3 ===Ω    Chọn B K M N LR C BA mI ABU F R2U C2U LC1U UA B E I ñ R1U Iđ t(s) 3 0 i(A) 3 Im 3 3

DẠYKÈMQUYNHƠNOFFICIAL 437 Cách giải 2: Dùng giản đồ véctơ buộc Ta có: m I3I = ñ  R2R1U3U = . Mặt khác: R1 AB R2 AB U cos U U sin U  α=    α=   R2 R1 U tan3 U3 π α==  α=  R1AB 1 UUcos1003503V 2 =α== . Khi đó: R1 m U5032 R502 I 3 ===Ω .  Chọn B Cách giải 3: Dùng giản đồ véctơ tổng trở Tacó: m I3I = ñ  md Z3.Z = .(vìcùngU) m m U10032 Z1002 I 3 ===Ω  U100321002 Z I3 3 ===Ωñ ñ Dùnghệ thứclượngtrongtamgiácvuôngABC: 2222 m 1112 R502 RZZ100 =+=  =Ω ñ .    Chọn B Câu 3: Một đoạn mạch AB gồm hai đoạn mạch AM và MB mắc nối tiếp. Đoạn mạch AM gồm điện trở thuần R1 mắc nối tiếp với tụ điện có điện dung C, đoạn mạch MB gồm điện trở thuần R2, mắc nối tiếp với cuộn cảm thuần có độ tự cảm L. Đặt điện áp xoay chiều có tần số và giá trị hiệu dụng không đổi vào hai đầu đoạn mạch AB. Khi đó đoạn mạch AB tiêuthụ côngsuấtbằng 160Wvà cóhệ số côngsuấtbằng1.Nếunốitắthai đầutụ điệnthị điện áp hai đầu đoạn mạch AM và MB có cùng giá trị hiệu dụng nhưng lệch pha nha π 3 , côngsuấttiêuthụ trênmạchABtrongtrườnghợpnàybằng A.120W. B.160W. C.90W. D.180W. Hướng dẫn: Mạch 12 RCRL cộnghưởng: 2 12 U P RR = + β ABU α R1U LC1U C2U U A α B IR2U β CZ R LZ H mZ A B I Zñ C C A B R1 LR2 M A B R1 LR2 M Nối tắt C 600 B R1U R2U LU IMA E300

DẠYKÈMQUYNHƠNOFFICIAL 438 Mạch 12 RRL : 2 222 12 U P'cosPcos120cos RR =ϕ=ϕ=ϕ + Dùngphươngphápvéctơ trượt,tamgiáccânAMBtính được 030ϕ= nên: 20 P'160cos30120W. ==  Chọn A Câu 4: Đặt điện áp ( )uU2cos2ftV =π vào hai đầu đoạn mạch mắc nối tiếp AB gồm hai đoạnmạchAM vàMB thìmạchAB tiêuthụ côngsuấtlàP1 ĐoạnAM gồm điệntrở thuần R1 mắc nối tiếp với tụ điện có điện dung C. Đoạn MB gồm R2 mắc nối tiếp với cuộn cảm thuần có độ tự cảm L sao cho 22 4fLC1. π= Nếu nối tắt L thì uAM và uMB có cùng giá trị hiệudụngnhưnglệchphanhau 4 π , đồngthờimạchABtiêuthụ côngsuất240W.TínhP1. A.281,2W. B.160W. C.480W. D.381,3W. Hướng dẫn: Mạch 12 RCRL cộnghưởng: 2 12 U P RR = + Mạch 12 RRL : 2 22 max 12 U P'cosPcos RR =ϕ=ϕ + Từ 22 4fLC1 π= suyramạchcộnghưởng 2 LC1max 12 U ZZ: PP RR === + KhinốitắtL,vẽ giản đồ véctơ như hìnhvẽ.Tam giácAMBcântạiMnêncácgóc đáy bằngnhauvàbằng AB 8 π  trễ hơnilà 22 111 P'Pcos240PcosP281,2W. 888 πππ  ϕ=−  =ϕ  =−  =    Chọn A Câu 5 (Chuyên Nguyễn Quang Diệu lần 3 – 2014): Đặt điện áp xoay chiều có giá trị hiệu dụng 60V vào hai đầu đoạn mạch RLC mắc nối tiếp thì cường độ dòng điện qua đoạn mạchlài1 =I0cos ()π100πtA 4  +   .Nếungắtbỏ tụ điệnCthìcường độ dòng điệnqua đoạn mạchlài2 =I0cos ()π100πtA 12    Điệnáphai đầu đoạnmạchlà: A. ()u602cos100tV 6 π  =π−  B. ()u602cos100tV 12 π  =π−  C. ()u602cos100tV 12 π  =π+  D. ()u602cos100tV 6 π  =π+  Nối tắt L C A B R1 LR2 M C A B R1 R2 M π/8 M A B CU R2U R1U π/8 π/4

DẠYKÈMQUYNHƠNOFFICIAL 439 Hướng dẫn: Tacó: 01020LLCLC IIIZZZ2ZZ ==  =−+  = Với ()12 LCL 1 21uiui L 2 ZZ Z tan RR Z tan R  ϕ==−   ϕ=−ϕ⇔ϕ−ϕ=−ϕ−ϕ  ϕ=  12 ii u 212 ϕ+ϕ π  ϕ== Điệnáphai đầu đoạnmạchlà: ()u602cos100tV 12 π  =π+   Chọn C III. Lần lượt mắc song song ampe-kế và vôn-kế vào một đoạn mạch Mắcampekế songsongvớiCthìCbị nốitắt: L 22 AL Z tan R UIRZ  ϕ=   =+ Mắcvônkế songsongvớiCthì: () VC 222 RLC UU UUUU =   =+−  Mắcampekế songsongvớiLthìLbị nốitắt: C 22 AL Z tan R UIRZ  ϕ=−   =+ Mắcvônkế songsongvớiLthì: () VL 222 RLC UU UUUU =   =+−  Câu 1: Chomạch điệnxoaychiềunhư hìnhvẽ Điệndung C có giá trị thay đổi được và cuộn dây thuần cảm. Điều chỉnh giá trị của C thì thấy: ở cùng thời điểm số, chỉ của V1 cực đại thì số chỉ của V1 gấp đôi số chỉ của V2 Hỏi khi số chỉ của V2 cực đại thì số chỉ của V2 gấp bao nhiêulầnsố chỉ V1? A.2lần. B.1,5lần. C.2,5lần. D. 22 lần Hướng dẫn: KhiV1 cực đạithìmạchcộnghưởng:UR =U=2UC =2UL hayR=2ZL (1) KhiV2 cực đạitacó: R URZ U 2 L 2 Cmax + = theo(1)  22 LL Cmax L U4Z+Z U5 U= 2Z2 = (2) Khi đó: L 2 L 2 C Z RZ Z + = theo(1)ta được: ZC =5ZL =2,5R  Z=R 5 (3) Chỉ số củaV1 lúcnàylà R URU U=IR== Z 5 (4) Từ (3)và (4)tacó: Cmax R U 5 ==2,5 U2    Chọn C L A B R C V2V1

DẠYKÈMQUYNHƠNOFFICIAL 440 Câu 2 (Bến Tre – 2015): Cho mạch điện xoay chiều như hình vẽ Điện dung C có giá trị thay đổi được và cuộn dây thuần cảm. Điều chỉnh giá trị của C và ghi lại số chỉ lớn nhất trên từng vôn kế thì thấy UCmax = 3ULmax. Khi đótỉ số Cmax Rmax U U bằng A. 3 8 B. 8 3 C. 42 3 D. 3 42 Hướng dẫn: Cách giải 1: Vì C biến thiên nên: 22 CmaxL U URZ R =+ (1) LmaxmaxLLL min UU UI.Z.Z.Z ZR === (2) (cộng hưởng điện) và Rmax UU = (3) (cộng hưởng điện) 22 CmaxL L LmaxL R+ZU(1) =3=R=Z8 (2)UZ  (4) 22 CmaxL Rmax R+ZU(1) = (3)UR  (5) Từ (4) và (5)  8 3 U U Rmax Cmax =  Chọn A Cách giải 2: Điều chỉnh C để UCmax ta có ZC = R2 + ZL 2 ZL (1) và UCmax = U R R2 + ZL 2 Chỉnh C để ULmax ta có giá trị cộng hưởng ZL1 = ZC1 và U = UR hay chỉnh C để URmax ta có giá trị cộng hưởng và URmax = U. Theo đề bài thì UCmax = 3ULmax ⇔ U R R2 + ZL 2 = 3U R ZL  R = ZL 8  URmax = ULmax 8 = 8 3 UCmax  UCmax URmax = 3 8 .   Chọn A Câu 3: Cho mạch điện xoay chiều như hình vẽ Điện áp hai đầu có tần số f = 100Hz và giá trị hiệu dụng U không đổi. a. Mắc vào M, N ampe kế có điện trở rất nhỏ thì ampe kế chỉ I = 0,3A. Dòng điện trong mạch lệch pha 600 so với uAB, công suất toả nhiệt trong mạch là P = 18W. Tìm R1, L, U. b. Mắc vôn kế có điện trở rất lớn vào M, N thay cho Ampe kế thì vôn kế chỉ 60V đồng thời điện áp trên vôn kế chậm pha 600 so với uAB. Tìm R2, C? NM A R1 L C B R2 V2V1 L A BR C V3

DẠYKÈMQUYNHƠNOFFICIAL 441 Hướng dẫn: a. Mắc Ampe kế vào M, N ta có mạch điện như hình bên (R1 nt L). Áp dụng công thức tính công suất: P18 PUIcosU120V Icos 3.cos 6 =ϕ  === ϕπ Lại có 2 11 22 P18 PIRR200 I3 =  ===Ω . Từ giả thuyết i lệch pha so với uAB một góc 600 và mạch chỉ có R, L nên i nhanh pha so với u vậy ta có: L L L1 1 ZZ 20033 tan3Z3R2003LH 3R 2.50 π ==  ==Ω  === ωππ . b. Mắc vôn kế có điện trở rất lớn vào M, N ta có mạch như hình vẽ: Vì R1, L không đổi nên góc lệch pha của uAM so với i trong mạch vẫn không đổi so với khi chưa mắc vôn kế vào M, N vậy: uAM nhanh pha so với i một góc AM 3 π ϕ= . Từ giả thiết điện áp hai đầu vôn kế uMB trễ pha một góc π 3 so với uAB. Từ đó ta có giãn đồ véctơ biểu diễn phương trình véctơ: ABAMMBUUU =+ Từ giãn đồ véctơ ta có: 22 AMABMBABMB UUU2UUcos603V 3 π =+−= . Áp dụng định luật ôm cho đoạn mạch AM ta có: AM AM U I0,153A Z == Với đoạn MB có: ZMB = 22 MB 2c U 60400 R+Z=== Ω I 0,15.33 (1) Với toàn mạch ta có: 22 AB 2L U 800 (R+R)+(Z)== Ω I 3CZZ =− (2) Giải hệ phương trình (1) và (2) ta được 2 4 C R200 2003.10 ZCF. 34 =Ω   =  = π A LR1 B O AMU ABU 1RU2RU MBU π 3 π 3 NM A R1 L C B R2 V

Chú ý:

1. Bài tập này cho thấy không phải bài tập nào cũng dùng thuần tuý duy nhất một phương pháp. Ngược lại đại đa số các bài toán ta nên dùng phối hợp nhiều phương pháp giải.

2. Trong bài này khi vẽ giản đồ véctơ ta sẽ bị lúng túng do không biết uAB nhanh pha hay trễ pha so với i vì chưa biết rõ. Sự so sánh giữa ZL và ZC. Trong trường hợp này ta vẽ ngoài

DẠYKÈMQUYNHƠNOFFICIAL 442

giấy nháp theo một phương án lựa chọn bất kỳ (đều cho phép giải bài toán đến kết quả cuối cùng). Sau khi tìm được giá trị của ZL và ZC ta sẽ có cách vẽ đúng. Lúc này mới vẽ giản đồ chính xác. Câu 3: Cho mạch điện xoay chiều như hình vẽ. Hiệu điện thế luôn duy trì hai đầu đoạn mạch là AB u200cos100t =π (V). Cuộn dây thuần cảm, có 1 LH = π ; điện trở thuần có R = 100Ω; tụ điện có điện dung C thay đổi được. Vôn kế có điện trở rất lớn. a. Điều chỉnh C để công suất tiêu thụ của mạch đạt cực đại. Tính công suất cực đại đó. b. Với giá trị nào của C thì số chỉ vôn kế V là lớn nhất, tìm số chỉ đó. Hướng dẫn: Ta có: L 0 1 ZL100.100 R100 U200 U1002V 22  =ω=π=Ω π  =Ω   ===   a. Công suất của mạch tính theo công thức: () () 22 2 222 LCLC URU PIR RZZZZ R R === +−− + Ta thấy rằng U và R có giá trị không thay đổi, vậy P = Pmax thì: ()2 LC LC min ZZ RRZZ100 R  +⇔===Ω   Suy ra: 4 C 1110 CF Z100.100 === ωππ và khi đó ( )2 2 max U1002 ZRP200W R100 =  === b.Số chỉ vôn kế là: 22 VAMAML U UUIZRZ Z ===+ . Dễ thấy do U và 22 L RZ1002+=Ω không đổi, nên UAM lớn nhất ⇔ Z nhỏ nhất ⇔ LC RZZ100===Ω Suy ra: 4 C 1110 CF Z100.100 === ωππ và khi đó ZR = L R BCA V M

DẠYKÈMQUYNHƠNOFFICIAL 443 ( )2 2 max U1002 ZRP200W R100 =  === . Số chỉ vôn kế là: VmaxAM U1002 UZ1002200V R100 === . Câu 4: Cho mạch điện như hình vẽ biết UAB = U không đổi, R, C, ω không đổi. Điều chỉnh L để vôn kế chỉ cực đại. a. Tìm giá trị của L. b. Tìm số chỉ cực đại của vôn kế. Hướng dẫn: a. Vẽ giản đồ vectơ. Dựa vào giản đồ véctơ ta có: RC2 π α=−ϕ = hằng số Theo định lý hàm số sin ta có: () ( )LRC L RC UUU.sin U sinsinsin ϕ+ϕ =  = ϕ+ϕαα Mà ()LmaxRC U Usin1 sin =  ϕ+ϕ= α , tam giác AMB vuông tại A, do đó: URC = ULcos α = UL RCLRCcosUsin 2 π  −ϕ=ϕ  22 CLC CL 2222 CC ZZZ RZZ. RZRZ  +=−= ++ ( ) 222 2222 2C CC LL 2 CCC RZRZRZ ZZL ZZZ + ++  =  =  = ω b. Số chỉ của vôn kế khi đó: 22 Lmax C RC UUU URZ sincosR ===+ αϕ H UL - UC LU RU U φ CURCU α A M B RCφ A R C L B V

DẠYKÈMQUYNHƠNOFFICIAL 444 Câu 5: Cho mạch điện xoay chiều như hình vẽ: các máy đo ảnh hưởngkhông đáng kể đến các dòng điện qua mạch. Vôn kế V1 chỉ U1 = 100V. Vôn kế V2 chỉ U2 = 100V. Và vôn kế V chỉ U = 1003 V. Ampe kế chỉ I= 2A. a. Tính công suất mạch. b. Biết biểu thức điện áp hai đầu đoạn mạch là ( )0 uUcos100tV =π . Viết biểu thức dòng điện trong mạch. c. Viết biểu thức điện áp giữa hai điểm MB. Hướng dẫn: a. Chọn trục i làm trục pha ta có giãn đồ véctơ: 1 AMU100V == ; 2 BMU100V == ;ABU1003V == Dùng định lý hàm số cosin cho tam giác AMB ta có: 222 MBAMAB2AM.ABcos =+−ϕ 222 AMABMB cos 2AM.AB +−  ϕ= 222 100(1003)1003 2.1003.1002 +− == . Suy ra công suất tiêu thụ đoạn mạch: 3 PU.I.cos1003.2.300W 2 =ϕ== . b. Dựa vào giản đồ vec tơ ta có:radi22cos100tA 33 ππ ϕ=  =π−  . c. Áp dụng định lý hàm số sin: 2R1R1 2 UUUsin1001 sin.0,5rad sinsinU10026 ϕ π =  α===  α= ϕα . Mặt khác: 2 u221 0rad 66333 πππππ ϕ=ϕ+α=+=  ϕ=ϕ+ϕ=+= Vậy MB2 uu1002cos100tV 3 π  ==π+  . Câu 6: Chomạch điệnnhư hìnhvẽ,R=60Ω,cuộndây thuầncảmcóL=0,255H,UAB =120V,f=50Hz.Clà điệndungbiếnthiêncủamộttụ điện.Khithay đổi điện dung C có một giá trị của C với số chỉ vôn kế cực đại. a. Tính giá trị của C. b. Tính giá trị cực đại của vôn kế. Coi RV = ∞ A M 1RU 2RU LU B I 2U φ U α φ2 V A R1 R2 A;LMB V2V1 A R L C B V

DẠYKÈMQUYNHƠNOFFICIAL 445 Hướng dẫn: a. Đặt góc tạo bởi URL và i là φ,, U và i là φ. Ta có: ZL = 80Ω. Định lý hàm số sin cho: () C , , U U sin sin 2 = π ϕ−ϕ −ϕ   ( ), C , sin UU cos ϕ−ϕ  = ϕ KhiCbiếnthiên φ thay đổi. UC cực đạikhi (),, LC , L sin1 2 ZZ 1R tan tanRZ π ϕ−ϕ=  ϕ−ϕ=    ϕ=−⇔=− ϕ  22 L C LC RZ1 Z125C24,5F ZZ +  ==Ω  ==µ ω b.Số chỉ vônkế: 22 L Cmax , URZ U.U200V cosR + === ϕ . Câu 7: Mạch điệnnhư hìnhvẽ,cácvôn kế:V1 chỉ 75V,V2 chỉ 125V,uMP =100 2 cos100πt (V),cuộncảmLcó điệntrở R.ChoRA =0,RV1 =RV2 = ∞.Biểuthức điệnápuMN A.uMN = 125 2 cos(100πt+ 2 π )(V). B.uMN = 75 2 cos(100πt+ 2 3 π )(V). C.uMN = 75 2 cos(100πt+ 2 π )(V). D.uMN = 125 2 cos(100πt+ 3 π )(V). Vẽ theo quy tắc đa giác UL -UC LU RU RLU U φ CU ϕ’ CU LU RU RLU U UL -UC φ Vẽ theo quy tắc hình bình hành ϕ’

DẠYKÈMQUYNHƠNOFFICIAL 446 Hướng dẫn: Dựavàogiản đồ véctơ cóngayuMN vuôngphauMP.  Chọn C Câu 8: Đặtmộtnguồn điệnxoaychiều ổn địnhvào đoạnmạchnốitiếpgồm, điệntrở R,cuộn cảmthuầnLvàtụ điệnC.Nốihai đầutụ điệnvớimộtampekế lítưởngthìthấynóchỉ 1A, đồng thời dòng điện tức thời chạy qua nó chậm pha 6 π so với điện áp hai đầu đoạn mạch. Nếuthay ampekế bằng mộtvônkế lítưởngthìnóchỉ 167,3V, đồngthời điệnáptrênvôn kế chậm pha một góc 4 π so với điện áp hai đầu đoạn mạch. Điện áp hiệu dụng hai đầu đoạnmạchlà A.175V. B.150V. C.100V. D.125V. Hướng dẫn: Khi mắc ampe kế song song với C thì C bị nối tắt: 0 LR 30.ϕ= Khi mắc vôn kế song song với C thì mạch không ảnhhưởngvà CV UU167,3V. == Vẽ giản đồ véctơ trượt, áp dụng định lý hàm số sin: 00 167,3U U150V. sin75sin60 =  ≈   Chọn B Câu 9: Đặt điện áp xoay chiều 120 V – 50 Hz vào đoạn mạch nối tiếp AB gồm điện trở thuần R, tụ điện và cuộn cảm. Khi nối hai đầu cuộn cảm một ampe kế có điện trở rất nhỏ thì số chỉ của nó là 3 A. Nếu thay ampe kế bằng vôn kế có điện trở rất lớn thì nó chỉ 60 V, đồng thời điện áp tức thời hai đầu vôn kế lệch pha 3 π so với điệnáphai đầu đoạnmạchAB.Tổngtrở củacuộncảmlà A.40 Ω. B. 403 Ω. C. 203 Ω. D.60 Ω. Hướng dẫn: Khi mắc ampe kế song song với Lr thì Lr bị nối tắt: RC U Z403. I ==Ω Khi mắc vôn kế song song với C thì mạch không ảnh hưởng và RLV UU60V. == Vẽ giản đồ véctơ trượt,ápdụng địnhlýhàmsố cos: V2V1 MA N P L,r C 75 125 100 M N P 167,3 U LU CU RU I 045 045 045 030 060 120 RCU RU CU LU rU I 060

DẠYKÈMQUYNHƠNOFFICIAL 447 220 RC U120602.120.60.cos60603V =+−= rLrL rLRC RCRC ZU 6060 ZZ40. ZU 603603  ==  ==Ω    Chọn A Câu 10: Cho đoạn mạch nối tiếp gồm tụ C và cuộn dây D. Khi tần số của dòng điện bằng 1000Hzngườita đo được điệnáphiệudụngtrêntụ là2V,trêncuộndâylà 3 V,hai đầu đoạnmạch1Vvàcường độ hiệudụngtrongmạchbằng1mA.Cảmkhángcủacuộndâylà: A.750 Ω. B.75 Ω. C.150 Ω. D.1500 Ω. Hướng dẫn: () 22 cd L C C L 22 LC U rZ10003 U I Z2000Z1500. I U rZZ1000 I  +== ==Ω  =Ω  +−==     Chọn D CÂU HỎI VÀ BÀI TẬP LUYỆN TẬP Câu 1: Mộtmạch điệnxoaychiềunốitiếpgồm điệntrở thuầnR,cuộncảmthuầnLvàtụ điệnC. Lầnlượtdùngvônkế có điệntrở rấtlớnampekế có điệntrở không đángkể mắcsongsong với cuộn cảm thì hệ số công suất của toàn mạch tương ứng là 0,6 và 0,8 đồng thời số chỉ củavônkế là200V,số chỉ ampekế là1A.Giátrị Rlà A.128 Ω. B.160 Ω. C.96 Ω. D.100 Ω. Câu 2: Đoạn mạch xoay chiều AB có điện trở R1 mắc nối tiếp với đoạn mạch R2C, điện áp hiệu dụng hai đầu R1 và hai đầu đoạn mạch R2C có cùng giá trị, nhưng lệch pha nhau 3 π Nếu mắc nối tiếp thêm cuộn dây thuần cảm thì cosϕ = 1 và công suất tiêu thụ là 200W. Nếukhôngcócuộndâythìcôngsuấttiêuthụ củamạchlàbaonhiêu? A.160W B.173,2W C.150W D.141,42W Câu 3: Một đoạn mạch xoay chiều nối tiếp AB gồm cuộn cảm và tụ điện C. Khi nối hai cực củatụ điện ampekế có điện trở rất nhỏ thì số chỉ củanó là4 A vàdòng điện qua ampe kế trễ phasovới điệnáphai đầu đoạnABlà 4 π .Nếuthayampekế bằngvônkế có điệntrở rất lớn thì chỉ 100 V và điện áp giữahai đầu vôn kế trễ phaso với điện áp hai đầu đoạn mạch ABmộtgóc 4 π .Dungkhángcủatụ là A.50 Ω. B.75 Ω. C.25 Ω. D.12,5 Ω. Câu 4: Cho balinh kiện: điện trở thuần R =60 Ω,cuộn cảm thuần L vàtụ điện.Lần lượt đặt điện áp xoay chiều có giá trị hiệu dụng U vào hai đầu đoạn mạch nối tiếp RL hoặc RC thì biểu thức cường độ dòng điện trong mạch lần lượt là ()π  =π− 1 i2cos100tA 12 và

DẠYKÈMQUYNHƠNOFFICIAL 448 ()π  =π+ 2 7 i2cos100tA 12 . Nếu đặt điện áp trên vào hai đầu đoạn mạch RLC nối tiếp thìdòng điệntrongmạchcóbiểuthức: A. ()π  =π+  i22cos100tA. 3 B. ()π  =π+  i2cos100tA. 4 C. ()π  =π+  i22cos100tA. 4 D. ()π  =π+  i2cos100tA. 3 Câu 5: Cho đoạnmạchxoaychiềuABgồm điệntrở Rvàmộtcuộndâymắcnốitiếp. Điệnáp đặtvàohai đầu đoạnmạchcótầnsố fvàcógiátrị hiệudụngUkhông đổi. Điệnáphai đầu đoạn mạch lệch pha với dòng điện π 4 Để hệ số công suất toàn mạch bằng 1 thì người ta phải mắc nối tiếp với mạch một tụ điện khi đó công suất tiêu thụ trên mạch là200 W.Hỏi khichưamắcthêmtụ thìcôngsuấttiêuthụ trênmạchbằngbaonhiêu? A.100W. B.150W. C.75W. D.170,7W. Câu 6: Đặt điện áp xoay chiều ( )=ω uU2costV vào hai đầu đoạn mạch mắc nối tiếp gồm điệntrở thuầnR,cuộncảmthuầnLvàtụ điệncó điệndungCthay đổi được.Ban đầu điều chỉnh điện dung đến giá trị C1 thì công suất tiêu thụ trong mạch P1,sau đó điều chỉnh điện dung đến giá trị C2 thì công suất tiêu thụ trong mạch là = 21 P1,5P . Khi đó hệ số công suất củamạch đã A.giảm22,47%. B.tăng22,47%. C.tăng60,6%. D.giảm60,6% Câu 7: ĐoạnmạchxoaychiềuABcó điệntrở Rmắcnốitiếpvớicuộndây, điệnáphiệudụng hai đầu cuộn dây vàhai đầu điện trở R cùng giá trị,nhưng lệch pha nhau 3 π .Nếu mắcnối tiếpthêmtụ điệncó điệndungCthìcosϕ =1vàcôngsuấttiêuthụ là100W.Nếukhôngcó tụ thìcôngsuấttiêuthụ củamạchlàbaonhiêu? A.80W B.86,6W C.75W D.70,7W Câu 8: Một đoạn mạch xoay chiều nối tiếp AB gồm điện trở thuần R, tụ điện có dung kháng ZC vàcuộncảmthuầncó cảmkháng LC Z0,5Z. = Khinốihaicựccủatụ điệnmột ampekế có điệntrở rấtnhỏ thìsố chỉ củanólà1Avàdòng điệnquaampekế trễ phasovới điệnáp hai đầu đoạnABlà 4 π .Nếuthayampekế bằngvônkế có điệntrở rấtlớnthìnóchỉ 100V. Giátrị củaRlà A.50 Ω. B.158 Ω. C.100 Ω. D.30 Ω.

DẠYKÈMQUYNHƠNOFFICIAL 449 HƯỚNG DẪN GIẢI: Câu 1: ChọnA. Khimắcampekế songsongvớiLthìLbị nốitắt: 22C C 22 AAC RR3R 0,7cosZ Z4 RZ UIZIRZ1,25R  =ϕ==  =  +  ==+=  Khimắcvônkế songsongvớiLthìmạchkhông ảnhhưởng LV UU200V. == () C 3R Z 4 22L LC R25R 0,6cosZ RZZ12 = =ϕ=→= +− LRL CCR 1212 RZUU96V 2525 3R3 ZUU72V 44  =  ==     =  ==  Thayvàohệ thức: ( ) 222 RLC UUUU =+− ( ) ( ) ( )22 1,25R9620072R128.⇔=+−  =Ω Câu 2: ChọnC. Cách giải 1: Trêngiản đồ vector: 2 21 1 Z 33 cosZZ Z622 π  =−=  =  (1) VìcùngUvàdo(1)nêntacó: 1 2 I 3 I2 = (2) Côngsuất: ( ) () 2 1112 2 2212 PIRR (3) PIRR (4)  =+  =+  Từ (3)và(4)suyra: 22 11 12 22 PI3333 PP.200150W PI2444  ===  ===   Công thức giải nhanh cho dạng này: 2 22 Rmax U PPcos.cos R =ϕ=ϕ Cách giải 2: Vìcosϕ =1(cộnghưởng điện)  () () 2 2 R 12 12 U P100U100RR RR ==  =+ + (1) Mà: 21 C C2 2 222 RCR2C112 Z tan3Z3R(2) 3R UURZRR2R(3) π ==  =   =⇔+=  = π 6 LZ 1Z I CZ 1R 2R 2 RCZ π 3

DẠYKÈMQUYNHƠNOFFICIAL 450 Công suất khi chưa mắc cuộn dây: ( ) () 2 12 2 2 12C URR P RRZ + = ++ (4) Thay (1), (2) và (3) vào (4): ( ) () () 2 22 22 222 1002RR 600 P150W 42RRR3 + === ++ . Câu 3: Chọn C. Khi mắc ampe kế song song với C thì C bị nối tắt: L L 22 AL Z tantanZR R4 UIZ4RZ4R2 π ϕ==  =   ==+= Mắc vôn kế song song với C thì mạch không ảnh hưởng và CV UU100V. == Vì uC lệch pha với với uAB là 4 π nên AB 4 π ϕ=− LC ABC C IR ZZ tanZ2R R U UU50V 2  ϕ=  =     ===  Mà ( ) 222 RLC UUUU =+− ( ) ()() 2 22 C 4R25050100R12,5Z25. =+−  =  =Ω Câu 4: Chọn C. Ta có: ()  ϕ=  ϕ=α =π+ϕ    =  =  =  ϕ=−  ϕ=−α  L 11 0u 1212LCC 22 Z uUcos100t(V)tanR IIZZZZZ tan R π π    =π+ϕ−α  π  ϕ=     π α=  =π+ϕ+α     10u u 12 20u 7 12 iIcos100t 4 iIcos100t3 Mặt khác: ===  == α 12001 R ZZ120UIZ1202V cos Phương trình điện áp: () u1202cos100tV. 4 π  =π+  Khi mạch RLC cộng hưởng thì ()u i22cos100tA. R4 π  ==π+ 

DẠYKÈMQUYNHƠNOFFICIAL 451 Câu 5: Chọn A. Từ công thức: =ϕ=ϕ 2 22U PcosPcos R coäng höôûng π  == 2 P200cos100W. 4 Câu 6: Chọn B. Áp dụng công thức: =ϕ 2 2U Pcos R ϕϕ =  =≈=+ ϕϕ 2 2222 1111 PcoscosP 1,2247100%22,47% PcoscosP . Câu 7: Chọn C. Cách giải 1: Theo đề dễ thấy cuộn dây không cảm thuẩn có r. Với 22 dL ZrZ =+ . Trên giản đồ do cộng hưởng: LC ZZr3 == Theo đề cho: Rdd UURZ2r =  == Lúc đầu: () () () 1 22 2 12 L UUUU I Z 2r3RrZ 2rr3 ==== ++ + (1) Lúc sau: 2 2 UUUU I ZRr2rr3r ==== ++ (2) Từ (1) và (2) ta có: 1 2 I 3 I2 = (3) Công suất: ( ) () 22 111 22 221 PIRr3rI (4) PIRr3rI (5)  =+=  =+=  Từ (3), (4) và (5) ta có: 22 11 12 22 PP3333PP.10075W PI2444  ===  ===   . Cách giải 2: Trên giản đồ vector: 2 1 Z 3 cos Z62 π == (1) Vì cùng U và do (1) nên ta có: 12 21 IZ 3 IZ2 == (2) đa giác tổng trở lúc đầu 1dZRZ =+ đa giác tổng trở lúc sau 2dC ZRZZRr =++=+ ZL - ZC = 0 π 6 LZ1Z I CZ R r dZ π 3

DẠYKÈMQUYNHƠNOFFICIAL 452 Công suất : ( ) () 22 111 22 221 PIRr3rI (3) PIRr3rI (4)  =+=  =+=  Từ (3), (4) và do (2) ta có: 22 11 12 22 PI3333PP.10075W PI2444  ===  ===   Công thức giải nhanh cho dạng này: 2 22 Rmax U PPcos.cos R =ϕ=ϕ Cách giải 3: Vì cosϕ = 1 (cộng hưởng điện)  () 2 2 R U P100U100Rr Rr ==  =+ + (1) Mà: L L 222 dRL Z tan3Zr3 (2) 3r UUrZRR2r (3) π ==  =   =⇔+=  = Công suất khi chưa mắc tụ C: ( ) () 2 2 2 L URr P RrZ + = ++ (4) Thay (1), (2) và (3) vào (4): ( ) () () 2 22 1002rr 300 P75W 42rrr3 + === ++ . Câu 8: Chọn A. Khi mắc ampe kế song song với C thì C bị nối tắt: L L 22 AAL Z tantanZR R4 UIZIRZR2 π ϕ==  =   ==+= Khi mắc vôn kế song song với C thì mạch không ảnh hưởng và CVLCR UU100VU0,5U50VU ==  === () ( ) ()22 222 2 RLC UUUUR25010050R50. =+−  =+−  =Ω

hướng tỉ lệ thì chúng tôi tin chắc rằng cách chuẩn hóa số liệu sẽ làm quá trình tính toán sẽ trở nên đơn giản đi rất nhiều, giảm thiểu tối đa ẩn số. Hi vọng với phương pháp "Chuẩn hóa số liệu" này, việc tính toán của các em sẽ trở nên đơn giản hơn, cũng sẽ phù hợp với tính chất của trắc nghiệm. Mong rằng các em sẽ có một phương pháp để làm được nhiều dạng hơn, chứ không cần mỗi dạng lại phải nhớ một công thức như hiện nay, các em sẽ dần quên đi mối liên hệ giữa các đại lượng, làm mất đi bản chất đẹp của việc giáo dục. Đối với dạng bài trắc nghiệm thì nhớ càng nhiều công thức càng tốt, nhưng qua dạng khác thì công thức ấy không dùng được nữa, lại lập công thức khác để nhớ, còn nếu các em vào thi quên công thức thì coi như tiêu luôn. Với phương pháp "Chuẩn hóa số liệu" này, chúng tôi hi vọ

DẠYKÈMQUYNHƠNOFFICIAL 453 CHỦ ĐỀ 16 PHƯƠNG PHÁP CHUẨN HÓA SỐ LIỆU Trong chuyên đề này chúng tôi chỉ tập trung giới thiệu cách giải cho một số dạng toán trong điện xoay chiều, xây dựng cách chuẩn hóa cho các đại lượng tỉ lệ cùng đơn vị với nhau. Vì vậy, dấu hiệu nhận biết của các bài toán ấy là đề ra sẽ cho biết các tỉ lệ giữa các đại lượng cùng đơn vị; hoặc là biểu thức liên hệ giữa các đại lượng ấy với nhau; hoặc biểu hiện rõ trong công thức mà các em dùng để tính toán chỉ chứa các đại lượng cùng đơn vị; hoặc khi lập tỉ lệ các biểu thức cho nhau thì các đại lượng khác mất đi chỉ còn biểu thức của các đại lượng cùng đơn vị. Sau khi nhận biết được dạng đề cần làm, xác định được "đại lượng chuẩn hóa" thì chúng ta bắt đầu tính toán, việc xác định được "đại lượng chuẩn hóa" thông thường sẽ là đại lượng nhỏ nhất và cho đại lượng ấy bằng 1, các đại lượng khác sẽ từ đó biểu diễn theo "đại lượng chuẩn hóa" này, đối với trường hợp số phức thì có thể chuẩn hóa góc bằng 0, điều này các em sẽ được rõ hơn trong các ví dụ. Một bài toán vật lý sẽ có nhiều cách giải, nhưng nếu đã chọn cách giải theo

ng sẽ là một công cụ giúp đỡ các em vận dụng vào một số dạng bài tập, nếu có lỡ quên công thức thì vẫn còn phương pháp khác để làm bài thi tốt hơn. Có thể nói vắn tắt về phương pháp này như sau: Khi các đại lượng cùng loại phụ thuộc nhau theo một tỉ lệ nào đó, thì có thể chọn một trong số các đại lượng đó bằng 1. Trong chủ đề này chúng tôi giới thiệu cả cách giải về phương pháp chuẩn hóa số liệu bằng cách lập bảng và không lập bảng để bạn đọc hiểu rõ hơn về phương pháp độc đáo và rất hay này. Các bước vận dụng phương pháp chuẩn hóa số liệu: Bước 1: Xác định công thức liên hệ. Bước 2: Lập bảng chuẩn hóa. Bước 3: Thiết lập các phương trình liên hệ và tìm nghiệm.

DẠYKÈMQUYNHƠNOFFICIAL 454 BÀI TẬP VẬN DỤNG Câu 1 (ĐH - 2007): Đặt vào hai đầu đoạn mạch RLC không phân nhánh một điện áp xoay chiều u = U0cosωt (V). Kí hiệu UR, UL, UC tương ứng là điện áp hiệu dụng ở hai đầu điện trở thuần R, cuộn dây cảm thuần L và tụ điện có điện dung C. Nếu RLC 1 UUU 2 == thì dòng điện qua đoạn mạch A. Sớm pha π 2 so với điện áp ở hai đầu đoạn mạch. B. Trễ pha π 4 so với điện áp ở hai đầu đoạn mạch. C. Sớm pha π 4 so với điện áp ở hai đầu đoạn mạch. D. Trễ pha π 2 so với điện áp ở hai đầu đoạn mạch. Hướng dẫn: Cách giải 1: Phương pháp đại số Để tìm góc lệch pha giữa i và u ta dùng công thức: LCLC R ZZUU tan RUϕ== (1) Theo đề cho: RLC 1 UUU 2 == LR CR U2U UU =   = (2) (Các đại lượng UL, UC tính theo ẩn UR) Thế (2) vào (1) ta có: LC RR RR UU 2UU 21 tan1 UU14 −π ϕ==== ϕ= (ẩn số UR bị triệt tiêu do lập tỉ số)  i trễ pha hơn u một góc π 4 .   Chọn B Cách giải 2: Phương pháp chuẩn hóa số liệu Để tìm độ lệch pha giữa i và u ta dùng công thức: LCLC R ZZUU tan RUϕ== (1) Nhận biết dạng ở đây chính là (1) có các đại lượng cùng đơn vị, hơn nữa “dấu hiệu” trong đề cũng đã cho rất rõ tỉ lệ giữa các đại lượng này RLC 1 UUU 2 == Để đơn giản ta chọn một đại lượng để chuẩn hóa, thông thường chọn giá trị của đại lượng nhỏ nhất bằng 1, các đại lượng khác sẽ được tính theo tỉ lệ với đại lượng này. Ta có thể gán bất kì đại lượng nào trong UR, UL, UC để chuẩn hóa. Ví dụ ta gán trị số UR = 1  L CR U2 UU1 =  ==

DẠYKÈMQUYNHƠNOFFICIAL 455 Thay vào (1) ta được: LC R UU 21 tan1 U14 −π ϕ===→ϕ=  i trễ pha hơn u một góc 4 π .   Chọn B Nhận xét: - Ở cách giải 1 UR là một ẩn số bị triệt tiêu trong quá trình tính toán. - Ở cách giải 2 có ưu thế hơn về mặt tính toán vì chọn trước UR = 1 đơn vị điện áp. Câu 2 (ĐH - 2008): Cho đoạn mạch điện xoay chiều gồm cuộn dây mắc nối tiếp với tụ điện. Độ lệch pha của điện áp giữa hai đầu cuộn dây so với cường độ dòng điện trong mạch là 3 π . Điện áp hiệu dụng giữa hai đầu tụ điện bằng 3 lần điện áp hiệu dụng giữa hai đầu cuộn dây. Độ lệch pha của điện áp giữa hai đầu cuộn dây so với điện áp giữa hai đầu đoạn mạch trên là A. 2 3 π . B. 0. C. 2 π . D. 3 π . Hướng dẫn: Cách giải 1: Dùng phương pháp đại số Ta có: L cd L 22222 C CLrCL Z tantg3r3Z3r U3UUZ3(Zr)Z23r ϕ π ===  =   = =+  =+ LC cd ZZ 3r23r2 tan3 rr33 −ππ  ϕ===−  ϕ=−  ϕ−ϕ=⋅    Chọn A Cách giải 2: Dùng giản đồ véctơ và chuẩn hóa số liệu Ta chuẩn hóa Ud = AB = 1  Uc = BC = 3 Do góc lệch pha giữa Ud và i là 3 π  ABC 6 π = Ta thấy ngay rằng ABC là tam giác cân tại A và suy ra góc lệch giữa u và ud là 2 3 π .   Chọn A Cách giải 3: Dùng phương pháp chuẩn hóa số liệu 1 Theo đề ta cần tìm: ϕd – ϕu. Đề đã cho ϕd ta sẽ tìm ϕu. Ta có ud lệch 3 π so với i nên cuộn dây phải có r (vì nếu chỉ có L thì ud = uL ⊥ i). Vậy ta có d π tan φ tan3 3 ==  LZ 3 r =  L Z3r = (1) Theo đề: Cd U3U =  Cd Z3Z = (2) π/3 A B C H 1 1 I dU LU CU rU U 3 π 6

DẠYKÈMQUYNHƠNOFFICIAL 456 Ta tìm độ lệch pha ϕ giữa u và i, rồi suy ra độ lệch pha giữa ud và u. Có nghĩa là dùng công thức: LCZZ tan r ϕ= . Ta nhận thấy các công thức về độ lệch pha đều là tỉ số nên các trở kháng có sự tỉ lệ tương ứng, vậy ta sẽ chuẩn hóa gán số liệu như sau: Chọn L 22 dL Cd Zr33 r1ZrZ2 Z3Z23  ==   =  =+=  ==   LCZZ 323 tan3 r1 ϕ===− 3 π  ϕ=− Nghĩalàutrễ phahơni mộtgóc 3 π ϕ=− nênud sẽ sớmphahơnumộtgóc 2 3 π   Chọn A Cách giải 4: Dùng phương pháp chuẩn hóa gán số liệu 2 Vìcôngthứctanϕ códạngtỉ số nêntagánr=1. Khi đó: L cdL 2 2222 CLrCC Z tantg3Z3 r3 U3UUZ3(31)Z23 ϕ π ===  =   =+  =+  = LC cd ZZ 3232 tg3r133 ϕ −ππ  ===−  ϕ=−  ϕ−ϕ=⋅    Chọn A Cách giải 5: Dùng phương pháp chuẩn hóa gán số phức (chuẩnhóahàm 0 iIcostcost10 =ω=ω=∠ ) Để đơngiảntachọn 0 iIcostcost10 =ω=ω=∠ (ChọnI0 =1Avà ϕi =0) Tacó: [] d dL ud LC ui.Z10X(rZi)10X(13i)2 33 ui.Z10X1(ZZ)i10X1(323)i 3 ππ ==∠+=∠+=∠  ϕ=   π  ==∠+−=∠+−=−   (vớiXlàphépnhânhaisố phức) Tanhậnthấy ud sẽ sớmphahơnugóc 2 3 π   Chọn A Cách giải 6: Dùng phương pháp chuẩn hóa gán số phức khác (chuẩnhóahàmuvới d0d uUcost10 =ω=∠ ). Từ đócácthànhphầncủauC lúcnàylà: Cdud C uC U3U3 335 u3 5 6 0 325 ππ ==∠  ϕ= π  =∠− πππϕ=−−=−  Tacó: dC 52 uuu1031 63 =+=∠+∠−=∠−ππ Nhậnthấyud sẽ sớmphahơnugóc 2 3 π .   Chọn A

DẠYKÈMQUYNHƠNOFFICIAL 457 Nhận xét: Việc khai thác được tối đa một phương pháp phải bắt nguồn từ sự hiểu rõ bản chất của bài tập, học sinh cần phải luyện tập nhiều phương pháp. Chuẩn hóa gán số liệu là một phương pháp giải rất hay và đã hạn chế tối đa được các bước tính toán rườm ra, giúp chúng ta giải nhanh bài toán trắc nghiệm. Câu 3 (ĐH – 2009): Đặt điện áp u = U0cosωt vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R,tụ điện vàcuộn cảm thuần có độ tự cảm L thay đổi được.Biết dung kháng của tụ điện bằng R3 Điều chỉnh L để điện áp hiệu dụng giữa hai đầu cuộn cảm đạt cực đại, khi đó A. Điệnápgiữahai đầutụ điệnlệchpha 6 π sovới điệnápgiữahai đầu đoạn mạch. B. Điệnápgiữahai đầu cuộncảmlệchpha 6 π sovới điệnápgiữahai đầu đoạnmạch. C.Trongmạchcócộnghưởng điện. D. Điệnápgiữahai đầu điệntrở lệchpha 6 π sovới điệnápgiữahai đầu đoạnmạch. Hướng dẫn: Tacó: C C R1 ZR3 Z3 =  =→  =  Chuaån hoùa KhiLthay đổi để UL max nên: ( )2 222 C L C RZ13 4 Z. Z 33 ++ === Khi đó: LC 4 3 ZZ 33 tan. R126 π ϕ===  ϕ=    Chọn D Câu 4 (ĐH – 2009): Một đoạn mạch điện xoay chiều gồm điện trở thuần, cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cảm kháng gấp đôi dung kháng. Dùng vôn kế xoay chiều (điện trở rất lớn) đo điện áp giữa hai đầu tụ điện và điện áp giữa hai đầu điện trở thì số chỉ của vôn kế như nhau. Độ lệch pha của điện áp giữa hai đầu đoạn mạch so với cường độ dòng điệntrong đoạnmạchlà A. 4 π . B. 6 π . C. 6 π . D. 3 π . Hướng dẫn: Tacó: C LC L Z1 Z2Z Z2 = =→  = Chuaån hoùa Khi CRCR UUZZ1 =  == . Khi đó: LCZZ 21 tan1. R14 −π ϕ===  ϕ=    Chọn A

DẠYKÈMQUYNHƠNOFFICIAL 458 Câu 5 (ĐH - 2010): Nối hai cực củamột máy phát điện xoay chiều một phavào hai đầu đoạn mạch AB gồm điện trở thuần R mắcnối tiếp với cuộn cảm thuần.Bỏ qua điện trở các cuộn dây của máy phát. Khi roto của máy quay đều với tốc độ n vòng/phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là 1A. Khi roto của máy quay đề với tốc độ 3n vòng/phút thì cường độ dòng điện hiệu dụng trong đoạn mạch là 3A. Nếu roto của máy quay đều với tốc độ 2nvòng/phútthìcảmkhángcủa đoạnmạch ABlà: A. R 3 . B. R3 . C. 2R 3 . D. 2R3 . Hướng dẫn: Cường độ dòng điệntrongmạch 22 L U I RZ = + . Cầnchúýcác đạilượng tỉ lệ thuậnvớinhau L nfZU. ∼∼∼ Tốc độ củaroto U ZL n 1 1 3n 3 3 2n 2 2 Khi 1 nn = và 2 n3n = thì 21 2222 31 I3I3R3. R3R1 =⇔=  = ++ Khi 3 n2n = thì L3 L3L3 Z 22R Z2Z. R 33 =  =  =    Chọn C Câu 6: Mạch điện xoay chiều không phân nhánh gồm: điện trở thuần R, cuộn dây thuần cảm L và tụ điện C. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có tần số và điện áp hiệu dụng không đổi. Dùng vôn kế có điện trở rất lớn, lần lượt đo điện áp ở hai đầu đoạn mạch, hai đầu tụ điện vàhai đầu cuộn dây thì số chỉ của vôn kế tương ứng làU, UC vàUL.Biết U =UC =2UL.Hệ số công suấtcủamạch điệnlà A.cosφ = 2 2 . B.cosφ = 1 2 . C.cosφ =1. D.cosφ = 3 2 . Hướng dẫn: Nhậnthấymốiquanhệ U=UC = 2UL nêntachuẩnhóa:UL =1  U=UC = 2. Tacó: 22222222 RLCRLC UU(UU)UU(UU)2(12)3 =+−  =−−=−−=  R U3 =  RU 3 cos U2ϕ== .    Chọn D Nhận xét: Khi chuẩn hóa số liệu, bài toán cho dưới dạng tường minh đã trở thành những con số cụ thể, ngắn gọn phù hợp với hình thức thi trắc nghiệm. Câu 7 (ĐH - 2011): Đặt điện áp u = U2cos 2πft (U không đổi, tần số f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Khi tần số là 1 f thì cảm kháng và dung kháng của đoạn mạch có giá

DẠYKÈMQUYNHƠNOFFICIAL 459 trị lần lượt là 6Ω và 8Ω. Khi tần số là 2 f thì hệ sộ công suất của đoạn mạch bằng 1. Hệ thứcliênhệ giữaf1 vàf2 là: A. 21 2 ff 3 = . B. 21 3 ff 2 = . C. 21 4 ff 3 = . D. 21 3 ff 4 = . Hướng dẫn: Giả sử: L1L2 21 C1C2 Z6Z6n 82 fnf6nn. 8 Z8Zn 3 n =  =  =→  =  = =  =  Chuaån hoùa    Chọn A Câu 8 (ĐH - 2012): Đặt điện áp xoay chiều u =U0cosωt (U0 không đổi, ω thay đổi được)vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Khi ω = ω1 thì cảm kháng và dung kháng của đoạn mạch lần lượt là Z1L và Z1C. Khi ω = ω2 thì trong đoạn mạch xảy ra hiện tượng cộng hưởng.Hệ thức đúng là A. 1L 12 1C Z . Z ω=ω . B. 1C 12 1L Z . Z ω=ω . C. 1C 12 1L Z . Z ω=ω . D. 1L 12 1C Z . Z ω=ω . Hướng dẫn: Giả sử: 1L 2L 1L1L 12 1C 1C 2C1C Z Z ZZ nnZn. n ZnZnZ  = ω=ω→  =  =  = Chuaån hoùa  Chọn D Câu 9: Cho mạch điện AB gồm điện trở thuần R,cuộn thuần cảm L và tụ C nối tiếp với nhau theo thứ tự trên, và có CR2 < 2L. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều có biểuthức uU2cost =ω (V),trong đó U không đổi, ω biếnthiên. Điềuchỉnhgiátrị của ω để UC max. Khi đó Cmax 5U U 4 =⋅ Gọi M là điểm nối giữa L và C. Hệ số công suất của đoạn mạchAMlà: A. 2 7 . B. 1 3 . C. 5 6 . D. 1 3 . Hướng dẫn: Cách giải 1: Dùng phương pháp đại số Đề cho: = Cmax 5U U 4  C 5 ZZ 4 = (1) Mặtkháckhi:UCmax tacó: 222 CL ZZZ =+ (2) Từ (1)và(2)suyra: L 3 ZZ 4 = (3) Thay(1)và(3)vàobiểu thứccủatổngtrở 22 LC ZR(ZZ) =+− Ta được: 3 RZ 2 = Hệ số côngsuấtcủa đoạn mạchAM: AM 22L22 3 Z R2cos2 RZ397 ZZ 416 ϕ===⋅ + +   Chọn A

DẠYKÈMQUYNHƠNOFFICIAL 460 Cách giải 2: Dùng công thức vuông pha Côngthức: 2 2 CC CmaxLL U3 1 U5  ωω +=  = ωω Từ 2 C LR L C2 ω=− và 2 L 1LR CC2 =⋅ ω Ta được: 2 C 2 L AM 22 L 2 RCL5 1 (1)2L4 CR R1 cos (2) 1LRZ 2CR  ω =−  = ω   ϕ== +   Thế (1)vào (2)ta đươc: AM 2 cos 7 ϕ= . Cách giải 3: Dùng phương pháp chuẩn hóa số liệu 1 Tacó:UC max = 4 5 U C 5 ZZ. 4  = ChọnZ=4 Ω  Zc=5 Ω. Tacó: 222 CL ZZZ =+ suyra 2222 lc z=zz=54=3Ω Và 2 LCL R Z(ZZ) 2 =− 2 LCL R =2Z(Z-Z)=2.3(5-3)=12=23Ω 2 ⇒ AM 2222 L R23272 cos 7 RZ(23)37 ϕ====⋅ ++    Chọn A Cách giải 4: Dùng phương pháp chuẩn hóa gán số liệu 2 Hệ số côngsuất của đoạnmạchAMlà: 1 AM R cos Z α= Khônglàm ảnhhưởng đếnkếtquả bàitoánvề tỉ số,tacóthể gán: ZC =5 Ω  Z=4 Ω.Khi đó: 22 L Z543=−=Ω LCL R2Z(ZZ)2.3(53)23 =−=−=Ω Suyra:ZAM = 22 L RZ12921 +=+= Tacó: CmaxC 5U5Z UZ 44 =⇔=⋅ Vì 1 AM R232 cos Z 217 α=== Vậyhệ số côngsuấtcủa đoạnmạchAM: 1 AM R2 cos Z 7 α==⋅  Chọn A Nhận xét: Mỗi cách giải đều có cái hay riêng của nó. Nhưng cách giải 3 và 4 có ưu thế hơn về mặt tính toán, thực hiện dễ dàng hơn, công thức đơn giản hơn rất nhiều.

DẠYKÈMQUYNHƠNOFFICIAL 461 Câu 10 (ĐH - 2013): Đặt điện áp u1202cos2ft =π (V) (f thay đổi được) vào hai đầu đoạn mạch mắc nối tiếp gồm cuộn cảm thuần có độ tự cảm L, điện trở R và tụ điệ có điện dung C, với CR2 < 2L. Khi f= f1 thì UC max.Khi 21 fff2 == thì UR max. Khi f= f3 thì UL max. Giá trị củaUL max gần giá trị nào nhất sau đây? A.85V. B.145V. C.57V. D.173V. Hướng dẫn: Khi: 1 21 2 f1 f2f f2 =  =→  =  Chuaån hoùa .Tacó: 2 2 2 1323 1 f ffff2. f =  == Khi đó: 22 1 Lmax Lmax3 Uf 1U803V145V. Uf   +=⇒=    ≃    Chọn B Câu 11 (ĐH - 2014): Đặt điện áp uU2cos2ft =π (V) (f thay đổi được, U tỉ lệ thuận với f) vào hai đầu đoạn mạch AB gồm đoạn mạch AM mắc nối tiếp với đoạn mạch MB. Đoạn mạch AM gồm điện trở thuần R mắc nối tiếp với tụ điện có điện dung C, đoạn mạch MB chỉ có cuộn cảm thuần có độ tự cảm L. Biết 2L > R2C. Khi f = 60Hz hoặc f = 90Hz thì cường độ dòng điệnhiệu dụngtrongmạch có cùng giátrị.Khi f=30Hzhoặcf=120Hzthì điệnáphiệudụnghai đầutụ điệncócùng giátrị.Khif=f1 thì điệnáp ở hai đầu đoạn mạch MBlệchphamộtgóc1350 sovới điệnáp ở hai đầu đoạnmạchAM.Giátrị củaf1 bằng A.80Hz. B.120Hz. C.60Hz. D.50Hz. Hướng dẫn: Cách giải 1: Tacó: () () C CC 22 LC 22 LC UZ UIZ RZZ UU I Z RZZ  == +−   == +− Để đơngiảnhóacácbướctínhtoán,tanênchọnfnhỏ nhất để chuẩnhóa. f U ZL ZC 60 2 2 x 2 90 3 3 x 3 30 1 1 x 120 4 4 x 4 Trườnghợp3và4thấy UC bằngnhaunêntacó () 222 2 1.x4.x 4 x4. R1xx R4 4 =  = +− +− 

DẠYKÈMQUYNHƠNOFFICIAL 462 Trườnghợp1và2thấy Ibằngnhaunêntacó: () 222 2 2325 R. R2243 R3 3 =  = +− +−  ĐiệnápMBlệch1350 với điệnápAMnên C 1 1 25 2530 3 ZRf305Hz80Hz. 34f ==⇒=⇒= ≃   Chọn A Cách giải 2: Nếu đề bài cho L =kCR2 vàtại hai giátrị củatần số góc ω1 và ω2 thì mạch sẽ có cùng hệ số công suất. Khi ấy hệ số công suất sẽ được tính bằng công thức: 2 21 12 1 cos 1k ϕ  ωω +−  ωω  Thế số tacó: 22 112 cos 2005011311112502002 ϕ==  ππ +−+−  ππ     Chọn C Câu 12: Cho mạch điện xoay chiều RLC mắc nối tiếp, cuộn dây thuần cảm. Các giá trị của điện trở R, độ tự cảm L điện dung C thỏa điều kiện 4L= CR2 . Đặt vào hai đầu đoạn mạch điện áp xoay chiều ổn định,có tần số thay đổi được(với f<125 Hz).Khi tần số f1 =60 Hz thì hệ số công suất của mạch điện là k. Khi tần số f2 = 120Hz thì hệ số công suất của mạch điện là 21 5 kk 4 = . Khi tần số là f3 thì hệ số công suất của mạch điện là 3 k60 61 = . Giá trị của f3 gần giá trị nào nhất sau đây? A.65Hz. B.80Hz. C.100Hz. D.110Hz. Hướng dẫn: Đâylàdạngtầnsố thay đổiliênquan đếnhệ số côngsuất.Giả sử f3 =nf. Theobài,tỉ lệ giữacáctầnsố vàchọn đạilượngZL để chuẩnhóa,tacóbảngchuẩnhóasau: f ZL ZC f1 1 x f2 =2f1 2 x 2 f3 =nf1 n x n Theo đề:4L=CR2  R2 =4ZLZC (1) Thế vàobiểuthứctổngtrở: 22222 LCLCLCLLCCLC ZR(ZZ)4ZZ(ZZ)Z2ZZZZZ =+−=+−=++=+

DẠYKÈMQUYNHƠNOFFICIAL 463 Khi 21 5 kk 4 = thì 21 21L2C2L1C1 5R5RR5RR5R coscos... x 4Z4ZZZ4ZZ41x 2 2 ϕ=ϕ⇔=⇔=⇔= +++ + 151x4 . x 241xR4 2 =  =   += + Khi 3 k60 61 = thì: 3 2 3L3C3 R60R60460n60 cos 4 Z61ZZ616161 nn4 n ϕ==⇔=⇔=⇔= + ++ 2 60n244n2400 −+= (1) Phươngtrình(1)có2nghiệm: 13 23 5 nf100Hz 2 12 nf144Hz 5  =  =    =  =  Giả thiếtchof<125Hznênchọngiátrị f3 =100Hz.    Chọn C Câu 13: Mắc vào đoạn mạch RLC không phân nhánh một nguồn điện xoay chiều có tần số thay đổi được. Ở tần số f1 = 60 Hz, hệ số công suất bằng 1. Ở tần số f2 = 120 Hz, hệ số côngsuấtlà 2 2 . Ở tầnsố f3 =90Hz,hệ số côngsuất củamạchbằng A.0,874. B.0,486. C.0,625. D.0,781. Hướng dẫn: Cách giải 1: Phương pháp đại số Khi ==  ϕ=  =→== 11LCLC ff60Hzcos1ZZZZ1 Chuaån hoùa . Khi = ===   = L 21 C Z'2a ff120Hz2f Z'0,5a với ϕ= 1 cos0,52 Suyra: () () =  =  = +−+− 2 22 2 LC RR1 0,52R1,5a RZ'Z'R2a0,5a2 Khi =  ===   =  L 31 C Z''1,5a ff90Hz1,5f 2a Z'' 3 Suyra: () () ϕ= =≈ +− +−  3 2 22 LC2 R1,5a cos 0,874. RZ''Z''2a 1,5a1,5a 3 Chọn A Chú ý: Bài toán trên sẽ đơn giản hơn nếu ta chọn luôn a = 1 ngay từ đầu (chuẩn hóa số liệu), xem cách giải thứ 2 sau đây.

DẠYKÈMQUYNHƠNOFFICIAL 464 Cách giải 2: Phương pháp chuẩn hóa số liệu Nhậnthấytrongtrườnghợp1,hệ số côngsuất bằng1nênlúcnày:ZL =ZC nênchọnbằng 1.Bảngchuẩnhóasố liệunhư sau. Tầnsố Cảmkháng Dungkháng Hệ số côngsuất = 1 f60 Hz 1 1 ϕ= 1 cos1 = 2 f120 Hz 2 0,5 () ϕ= +− 2 22 R cos R20,5 = 3 f90 Hz 1,5 2 3 ϕ= +−  3 2 2 R cos 2 R1,5 3 Theobàira: ϕ= 2 cos0,52 nên () =  = +− 22 R 0,52R1,5 R20,5  ϕ=≈ +−  3 2 2 1,5 cos0,874. 2 1,51,5 3   Chọn A Nhận xét: Phương pháp chuẩn hóa số liệu giúp chúng ta đơn giản hóa bước tính toán đến mức tối thiểu. Phương pháp này rất thích hợp với hình thức thi trắc nghiệm đòi hỏi độ nhanh và chính xác cao. Câu 14: Đặt điện áp =π uU2cos2ft (V) (trong đó U không đổi, f thay đổi được) vào hai đầu đoạn mạch gồm R và C mắc nối tiếp. Khi tần số là f1 hoặc = 21 f3f thì cường độ hiệu dụng qua mạch tương ứng là I1 và I2 với = 21 I2I . Khi tần số là = 1 3 f f 2 cường độ hiệu dụngtrongmạchbằng A.0,5I1. B.0,6I1. C.0,8I1. D.0,87I1 Hướng dẫn: Bảngchuẩnhóasố liệu. Tầnsố Dungkháng Hệ số côngsuất 1f 1 = + 1 22 U I R1 2f 1 3 = +   2 2 2 U I 1 R 3 3f 2 () = + 3 2 2 U I R2

DẠYKÈMQUYNHƠNOFFICIAL 465 Tacó: =  =  = ++   21 222 2 R2R7 I2IR 1R13 R 3 () ()  + +   === + +   2 2 3 22 12 2 7 1 I3 R1 0,8. I R27 2 3    Chọn B Câu 15: Đặt điện áp uU2cos2ft =π (V)(U không đổivàfthay đổi được)vào hai đầu đoạn mạch RL nối tiếp. Lần lượt cho 1 ff20Hz == , 2 ff40Hz == và 3 ff60Hz == thì công suấtmạchtiêuthụ lầnlượtlà40W,32WvàP.TínhP. A.48W. B.24W. C.36W. D.64W. Hướng dẫn: Côngsuấtmạchtiêuthụ: 2 2 22 L UR PIR RZ == + Bảngchuẩnhóasố liệu f U R ZL P 1f 1 1 x 2 1 22 1.1 P 1x = + 2f 1 1 2x 2 2 22 1.1 P 14x = + 3f 1 1 3x 2 1 22 1.1 P 19x = + Khi đó: 2 2 2 1 2 3 231 1 P 1x321 x P14x40 11 1 P1 1x 11 P19x10,6P0,6P24W 19. 11  + ==  = +   + + ===  == + +     Chọn B Câu 16: Đặt điện áp uU2cos2ft =π (V) (f thay đổi được, U không đổi) vào hai đầu đoạn mạch AB nối tiếp theo thứ tự gồm điện trở thuần R, tụ điện C và cuộn cảm thuần L. Khi f = 50 Hz thì UC = U. Khi f = 125 Hz thì UL = U. Để điện áp uRC lệch pha 1 góc 1350 so với điệnápuL thìtầnsố A.62,5Hz. B.31,25Hz. C.75Hz. D.150Hz.

DẠYKÈMQUYNHƠNOFFICIAL 466 Hướng dẫn: Từ biểuthức () ()2 2222 CCLCLCLL L UUZRZZR2ZZZ2Z1 C =⇔=+−⇔=−=− Mặtkhác: () ()2 2222 LLLCLCCC L UUZ'RZ'Z'R2Z'Z'Z'2Z'2 C =⇔=+−⇔=−=− Khi đó: LC f'2,5f LC ZZ' Z'Z = = → = Chuaån hoùa LC 2 LCL LC ZZ'1 R2ZZZ2 Z'Z2,5 ==  =−= == Bảngchuẩnhóasố liệu f(Hz) ZL ZC tanφ 50 1 2,5 125 2,5 1 f1 1 125 f C1 RC 125 Zf tan RRϕ== Khif=f1 thìuL sớmphahơnuRC là1350 màuL sớmphahơnilà900 nênuRC trễ phahơni là450,tứclà 0 RC 45ϕ=− hay 1 RC 1 125 f tan11f62,5Hz. 2ϕ=−  =−  =   Chọn A Câu 17: Cho mạch điện xoay chiều gồm R, L, C mắc nối tiếp. Tần số của hiệu điện thế thay đổi được. Khi tần số là f1 và 4f1 công suất trong mạch như nhau và bằng 80% công suất cực đạimàmạchcóthể đạt được.Khif=3f1 thìhệ số côngsuấtlà: A.0,8 B.0,53 C.0,6 D.0,96 Hướng dẫn: Côngsuất: ()  == +−   =  2 2 22 LC 2 max UR PIR RZZ U P R Hệ số côngsuất: () ϕ= +− 22 LC R cos RZZ Dựatheotỉ lệ giữacáctầnsố vàchọn đạilượngZL để chuẩnhóa,tacóbảngsau f LZ CZ 1f 1 x = 21 f4f 4 x 4 = 31 f3f 3 x 3

DẠYKÈMQUYNHƠNOFFICIAL 467 Khi () =⇔= +− +−  22 12 222 2 URUR PP R1xx R4 4 () ⇔=  = +− +−  222 2 11 x4. R1xx R4 4 Khi () =⇔=  =Ω +− 22 1max 22 URU P80%P0,8R6. R14R Vậy 3 2 2 618 cos0,96. 4349 63 3 ϕ==  +−    ≃   Chọn D Câu 18: Mắcvào đoạn mạch RLC không phân nhánh gồm một nguồn điện xoay chiều có tần số thay đổi được. Ở tần số f1 = 60Hz, hệ số công suất đạt cực đại cosϕ1 = 1 và lúc lúc đó cảmkháng L1 ZR. = Ở tầnsố f2 =120Hz,hệ số côngsuấtnhậngiátrị 2cos ϕ bằngbaonhiêu? A. 2 13 . B. 2 7 . C.0,5. D. 2 5 . Hướng dẫn: Cách giải 1: Dùng phương pháp đại số Dùngcôngthức: 22 LC RR cos Z R(ZZ) ϕ== +− Lúcf1 =60Hzvàcosϕ1 =1nêntacó:ZL1 =ZC1 =R Lúcf2 =120Hz=2f1 thì L2L1 2 Z2Z2R R Z 2 ==   =  Hệ số côngsuất: 2 22LC22 22 RR cos R(ZZ)R R(2R) 2 ϕ== +− +− 222 RR2 3R13R()13R 2 4 ===⋅ +  Chọn A Cách giải 2: Dùng phương pháp chuẩn hóa số liệu Lúcf1 =60Hzvàcosϕ1 =1nêntacó:ZL1 =ZC1 =R Tagánsố liệu:R=ZL1 =ZC1 =1 Lúcf2 =120Hz=2f1 thì L2 2 Z2 1 Z 2 =   =  2 2222 LC2222 R112 cos R(ZZ)13 12113 22 ϕ====⋅ +−  +−+      Chọn A

DẠYKÈMQUYNHƠNOFFICIAL 468 Câu 19: Cho mạch điện xoay chiều RLC mắc nối tiếp, cuộn dây thuần cảm. Các giá trị của điện trở R, độ tự cảm L và điện dung C thỏa điều kiện 4L = CR2 Đặt vào hai đầu đoạn mạch điện áp xoay chiều ổn định,tần số củadòng điện thay đổi được(f < 130 Hz).Khi tần số f1 =60Hzthì hệ số công suất củamạch điện là k1 .Khi tần số f2 =120Hzthì hệ số công suất của mạch điện là = 21 5 kk 4 . Khi tần số là 3f thì hệ số công suất của mạch điện là = 1 60 k 61 .Giátrị củaf3 gần giá trị nào nhất sau đây? A.55Hz B.70Hz C.95Hz D.110Hz Hướng dẫn: Đâyvẫnlàdạngtầnsố thay đổiliênquan đếnhệ số côngsuất.Giả sử f3 =nf1 Tacóbảng chuẩnhóasau f LZ CZ 1f 1 x = 21 f2f 2 x 2 = 31 fnf 3 x n Theogiả thuyết: =⇔== 22 LC L 4LCRR44ZZ C . Tổngtrở: ()() =+−=+ 22 LCLCLC Z4ZZZZZZ Mặtkhác: = =⇔=   += + 21 5R5Rx4 kk. x 441xR4 2 2 Mà  =  =  =⇔=   + =  =  3 1 3 5 nf100Hz 60460 k3 4 616112 n nf144Hz n 5 Vìgiả thiếtchof >130Hznênchọngiátrị f3 =100Hz. Chọn C Câu 20: Đặt điện áp 0 uUcost =ω (V) vào hai đầu đoạn mạch RLC nối tiếp. Lần lượt thay đổi tần số 123ff, ff150Hz, ff50Hz==+=+ thì hệ số công suất của đoạn mạch lần lượt là 1; 3 5 ; 15 17 . Tần số để mạch xảy ra cộng hưởng gần giá trị nào nhất sau đây, biết rằng giá trị f >50Hz? A.60Hz. B.150Hz. C.120Hz. D.100Hz.

DẠYKÈMQUYNHƠNOFFICIAL 469 Hướng dẫn: Hệ số côngsuất: () ϕ= +− 22 LC R cos RZZ . Tìm tần số khi mạch cộng hưởng ( cos1 ϕ= ) có nghĩa là tìm f, khi đó thì LCZZ = . Ta sẽ chuẩn hóa LC ZZ1 == . Chú ý rằng khi tần số tăng thì ZL tăng đồng thời ZC giảm, vì vậy khitầnsố làf2,f3 thì LCZZ > Giả sử rằng 31 fnfnff50nf50(n1)f. ==  +=  =− Nên: 23 1 ff(n1)f f50 3n2. fff ++− ==− Bảngchuẩnhóa f LZ CZ 1f 1 1 ( ) 21 f3n2f =− 3n–2 1 3n2 31ff = n 1 n Phươngán được đưaralàphảitìm đượcn,sau đó suyra 50 f. n1 = Tacó: 2 2 2 3 2 2 R331 cosR3n2 1543n2 R3n2 3n2 R15151 cosRn 1178n Rn n   ϕ==  =−−   +−−     ϕ==  =−   +−   ()() 231151 3n2nn13n11n100 43n28n  ⇔−−=−  −−+=  n2f50Hz 5 nf75Hz 3 =  =    =  =  Theo đề bàithìf>50 Hz,nêntasẽ chọn f=75Hz.  Chọn A Cách giải 2: Vì khi tần số f2, f3 thì LC LC ZZ ZZtan0 R >  ϕ=> , nên ta có thể chuyển bài toántừ cosϕ sangtanϕ bằngcôngthứcsau 2 1 tan1 cos ϕ=− ϕ .

DẠYKÈMQUYNHƠNOFFICIAL 470 Từ đótatính được: 2 2 3 3 4 tan1 tan3n235 3n2 8tan21 tann 15n  ϕ=  ϕ  == ϕϕ=   n2f50Hz 5 nf75Hz 3 =  =    =  =  Theo đề bàithìf>50 Hz,nêntasẽ chọn f=75Hz.    Chọn A Cách giải 3: Tacó: ()2 L1C1 2 1 ZZ2LC. f =  =π Khi đó: () () 2 2 2 2 2L2C222 2 2 3L3C3 33 3 3 2fL12fLC1 tanZZ2fC2fC tanZZ12fL2fLC1 2fC 2fC π− π− ϕ−ππ === ϕ− π−π− π π () () ()() ()() 3 2 22222 2 332 2 222 2 23 23 f 1 fffff50f150f f5 ff1 fff2 f150f50f f ++− ==== ++− n2f50Hz 5 nf75Hz 3 =  =    =  =  Theo đề bàithìf>50 Hz,nêntasẽ chọn f=75Hz.    Chọn A Nhận xét: Qua ví dụ này ta có thể rút ra được công thức tính nhanh cho bài toán sau: Mạch RLC mắc vào nguồn điện xoay chiều có tần số thay đổi được. Khi tần số là f1 thì trong mạch xảy ra cộng hưởng. Khi tần số là f2, f3 thì độ lệch pha giữa u và i lần lượt là ϕ2 và ϕ3. Ta có tỉ số sau: ( ) () 22 2321 22 3 231 tanfff tan fff ϕ = ϕ Câu 21: Hai đoạn mạch nối tiếp RLC khác nhau: mạch 1 và mạch 2 cộng hưởng với dòng điện xoay chiều có tần số góc lần lượt là ω0 và 2ω0. Biết độ tự cảm của mạch 2 gấp ba lần độ tự cảm củamạch 1.Nếu mắcnối tiếp hai đoạnmạch đó với nhau thànhmột mạch thì nó sẽ cộnghưởngvớidòng điệnxoaychiều cótầnsố góclà A. 0 3ω . B. 0 3 2 ω . C. 0 13ω . D. 0 13 2 ω Hướng dẫn: Chúýbàitoánchocộng hưởngthì 1 LC ω= . Theogiả thuyếtL’=3L, đồngthờitagiả sử C’=xC, ω3 =nω0 Ta đichuẩnhóa 0 1 1 LC ω== . Đốivớimạch2,tacó: 0 111 222x. 3L.xC3x12 ω==  =  =