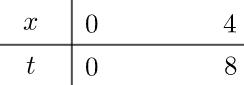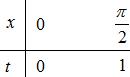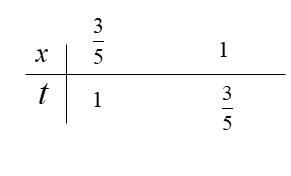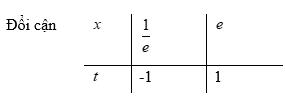CHUYÊN ĐỀ VẬN DỤNGVẬN DỤNG CAO MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection CHUYÊN ĐỀ VẬN DỤNG - VẬN DỤNG CAO LUYỆN THI TỐT NGHIỆP THPT NĂM 2023GIẢI TÍCH 12 - CHUYÊN ĐỀ III NGUYÊN HÀM TÍCH PHÂN ỨNG DỤNG TÍCH PHÂN WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405



CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 1. NGUYÊN HÀM MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO Câu 1: Chohàmsố ( ) 2 1 khi 1 khi<1 x fx x xx = Giảsử F lànguyênhàm f củatrên thỏamãn ( ) 2ln2 F = . Giá trị của ( ) ( )330FF bằng A. ln1921 + . B. ln1921. C. ln31 + . D. ln31. Lời giải Chọn C Ta có ( ) ( ) ( ) 33 3 2 22 1 32ddlnln3ln2 FFfxxxx x −====− . Vì ( )
F = nên
F = Ta
22 2
x −==== . Suy ra
= ( ) ( ) ( ) 1 11 3 2 00 0 1 10dd 33 x FFfxxxx−==== . Suy ra
3
=− Vậy ( ) ( ) 330ln31FF−=+ . Câu 2: Gọi ( ) ( ) 32 xFxaxbxcxde =+++ là một nguyên hàm của hàm số ( ) ( ) 32 2925 xfxxxxe =+−+ . Tính 2222 abcd +++ A. 245 B. 246 C. 248 D. 249 Lời giải Chọn B ( )Fx là một nguyên hàm của hàm số ( )fx nên ta có: ( ) ( ) ' Fxfx = Ta có: ( ) ' Fx ( ) ( ) 23232 xx axbxceaxbxcxde=++++++ CHƯƠNG III NGUYÊN HÀM TÍCH PHÂN ỨNG DỤNG TÍCH PHÂN
2ln2
( ) 3ln3
có ( ) ( ) ( )
1 11 1 21ddlnln2 FFfxxxx
( ) 10 F
( ) 1 0
F
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 3232 xaxabxbcxcde =++++++ Do đó: ( ) ( ) ( ) ( ) 3232 322925xx axabxbcxcdexxxe ++++++=+−+ Đồng nhất hệ số ta có: 2 39 22 5 a ab bc cd = += +=− += 2 3 8 13 a b c d = = =− = 2222 246 abcd +++= Câu 3: Biết ( ) 2 x x c Fxaxbe x =++ là một nguyên hàm của hàm số ( ) 2 2 1 x x fxxe x =++ . Giá trị của biểu thức 2 2 Pabc =− bằng: A. 3. B. 4. C. 1. D. 5. Lời giải Chọn C Vì ( ) 2 x x c Fxaxbe x =++ là nguyên hàm
(
=
Vì ( ) 2 x x c Fxaxbe x =++ là nguyên hàm của ( ) 2 2 1 x x fxxe x =++ nên ta có ( ) ( ) 2 0 201 22021 10 1 c bca Fxfxacbabc ac ab = −== =+==−= == += . Câu 4: Cho hàm số ( )fx xác định trên \1 R thỏa mãn ( ) 1 1 fx x = , ( ) 02021 f = , ( ) 22022 f = Tính ( ) ( )51Sff=−− . A. ln4043 S = . B. 1ln2 S =+ . C. ln2 S = . D. 1 S = . Lời giải Chọn B Trên khoảng ( ) 1;+ ta có ( ) 1 ' 1 fxdxdx x = ( ) 1 ln1xC=−+ ( ) ( ) 1 ln1 fxxC=−+ . Mà 1 (2)20222022 fC== .
của ( ) 2 2 1 x x fxxe x =++ nên ta có
) ( )Fxfx
Mà ( ) ( ) ( ) 222 2232 2211 1.22 xxx xxx ccc Fxaeaxbebcacaxabe xxxxxx
=−++++=+−+++++
Trên khoảng( );1− ta có ( ) 1 ' 1 fxdxdx x = ( ) 2 ln1 xC=−+ ( ) ( ) 2 ln1 fxxC=−+ .
Mà (0)2021 f = 2 2021 C = . Vậy ( ) ln(1)2022khi1 ln(1)2021khi1 xx fx xx −+ = −+ . Suy ra ( ) ( ) ( ) 51ln42022ln220212ln22022ln220211ln2ff−−=+−+=+−−=+
Câu 5: Cho hàm số ( )yfx = có đạo hàm là ( ) 2 122, fxxx =+ và ( ) 13 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 02 F = , khi đó ( )1 F bằng A. 3 B. 1 C. 2 D. 7 Lời giải
Chọn B
Ta có ( ) 2 122, fxxx =+ ( ) ( ) 23 12242 fxxdxxxC =+=++ Vì ( ) 3 134.12.133 fCC=++==− Khi đó ( ) 3 423fxxx=+− Vì ( )Fx là nguyên hàm của ( )fx nên ( ) ( ) 342 4233 FxxxdxxxxC =+−=+−+ Lại có ( ) 022FC== suy ra ( ) 42 32Fxxxx=+−+ Khi đó ( ) 42 1113.121 F =+−+= .
Câu 6: Cho hàm số ( )yfx = có đạo hàm là ( ) 21, x fxexx =++ và ( ) 01 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( )1 Fe = . Tính ( )0 F A. 5 6 B. 1 6 C. 1 6 D. 5 6 Lời giải Chọn A Ta có ( ) 21, x fxexx =++ ( ) ( ) 2 21 xx fxexdxexxC =++=+++ Vì ( ) 0 01010 feCC =++== Khi đó ( ) 2 x fxexx =+++ Vì ( )Fx là nguyên hàm của ( )fx nên ( ) ( ) 232 11 32 xx FxexxdxexxC =++=+++ Lại có ( ) 5 1 6 FeC==− suy ra ( ) 32 5 326 x xx Fxe=++− Khi đó ( ) 0 551 01 666 Fe=−=−=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
Câu 7: Cho hàm số ( ) + = + 2 trên nên ( )Fx là hàm số liên tục tại =1 x Ta có ( ) ( ) 11 limlim xx FxFx +− →→ = ++=++= 23 11 13.112.121 CC Vậy: ( ) ( ) 22328FF−+= Câu 8: Cho hàm số ( )fx xác định trên \0;2 R và thỏa mãn ( ) 2 1 2 fx xx = . Biết rằng ( ) ( ) 240ff−+= và 13 2018 22ff += . Tính ( ) ( ) ( )115Tfff =−++ A. 1 ln51009 2 T =+ . B. 19ln1009 25 T =+ C. 19ln2018 25 T =+ . D. 19 ln 25 T = . Lời giải Chọn B Ta có: ( ) ( ) ( ) 2
231 321 xkhix fx xkhix . Giả sử ( )Fx là một nguyên hàm của ( )fx trên thỏa mãn ( ) = 02 F . Tính giá trị của biểu thức ( ) ( ) −+223FF A. 60 B. 28 C. 1 D. 48 Lời giải Ta có ( ) ( ) ++ == ++ 2 1 3 2 11 1122ddd 222 fxfxdxxxx xxxxxx
31 21 xxCkhix Fxfxdx xxCkhix Theo bài ra ta có ( ) =++== 3 22 0202.022 FCC Vì ( )Fx là một nguyên hàm của ( )fx ====+ 1112 lnln2ln 222 x xxCC x =−+−+=+ ( )
− + =+ +
x Cx x x fxCx x x Cx x Ta có:
12 ln, khi 0 2 12 ln, khi 02 2 12 ln, khi 2 2
1 2 3
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
42
Page 5
tầm
( ) ( ) 1313 111 24ln2ln00 222 ffCCCC −+=+++=+= 222 13111
22223 +=+++== ffCCC ( ) ( ) ( )
TfffCCC =−++=+++++=+ Câu 9: Cho hàm số ( )fx xác đị
35 + Lời giải Chọn A Ta có: ( ) 2 1111 2312 fx xxxx ==− +−−+ Do
) (
2 2 3 1
1
3
xxxx xxCx −−−−+− ==−=−−++− +−−+ −−++ Khi đó ( ) ( ) ( ) ( ) 22 11111 0ln10ln02ln2. 33333fCC=−−++==+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 13 11 330ln13ln32ln31ln320 33 ffCC −−=+−−+−−−++= 1313 2111111 ln2ln2ln50ln2ln5ln. 33333310 CCCC +−+−=−=−−= ( ) ( ) ( ) ( ) 11 111 4ln14ln42ln5ln2 333 fCC −=+−−+=−+ ( ) ( ) ( ) ( ) 2 111121 1ln11ln12ln2ln2ln2 333333fC −=+−−++=++=+
viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu
và biên soạn
ln3ln20181009
123 111319 115ln3ln1lnln1009 222525
nh trên \2,1 thỏa mãn ( ) 2 1 2, fx xx = +− ( ) ( ) 330,ff−−= ( ) 1 0. 3 f = Tính giá trị biểu thức ( ) ( ) ( )414fff −+−− bằng A. 11 ln2. 33 + B. 11 ln20. 33 + C. ln801. + D. 18ln1.
đó, (
) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1
ln1ln2;2 3 11111 dln1ln2;21. 23123
ln1ln2;1
xxCx fxxxxCx
( ) ( ) ( ) ( ) 333 11111 4ln41ln42ln3ln6ln 33332 fCCC =−−++=−+=+ Vì vậy, ( ) ( ) ( )414fff−+−−= 1 11 ln5ln2 33 C −+ + 21 ln2 33 + 3 11 ln 32 C 13 1111112111 ln5ln2lnln5ln2ln 33323333310 CC =+−++−=+++ 11 ln2. 33 =+ Câu 10: Cho hàm số 2 3 khi 1 423kh 2 i ( 1 3 ) xx f x x x xx −+ + = . Giả sử ( )Fx là một nguyên hàm của hàm số ( )fx trên thỏa mãn ( ) 88 3 9 F = . Biết ( ) ( )204 a FF b +=− ( ) ,,1 ab = và , ab là các số nguyên dương. Khi đó, giá trị biểu thức 3 Tab =+ bằng A. 9. B. 11. C. 2021. D. 2024. Lời giải Chọn A Xét ( ) ( ) 04 33
( ) ( ) ( )20433 FFF=+− Mặt khác ( ) ( ) 04 33 2 Ifxdxfxdx =+ ( ) ( ) ( ) 104 313 2 fxdxfxdxfxdx =++
2 Ifxdxfxdx =+ ( ) ( ) ( ) ( )20343 FFFF =−+−
) ( ) ( ) 3 104 22 313 2323230 423 xxdxdxxxdx xx =++++=−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 (
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn −+ . ( ) ( ) ( ) 2043330 FFF +−=− ( ) ( ) ( ) 2 2043033 3 FFF +=−+=− . 9 2;3 a T b = = = . Câu 11: Cho hàm số ( ) 2 3khi1 5 khi1 xx yfx xx + == − . Giả sử F là nguyên hàm của f trên thỏa mãn ( ) F = 320 . Giá trị của ( ) F 1 là A. 11 3 . B. 14 3 . C. 11 6 . D. 17 3 . Lời giải Chọn B
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 3 1 2 2 3 khi 1 3 5+C khi 1 2 x xCx Fx x xx ++ = − . Ta có ( ) 3 11 3 3203.3202 3 FCC =++== . Lại có hàm số ( )yFx = liên tục trên nên liên tục tại x = 1 ( ) (
sử F là một nguyên hàm của f trên thỏa mãn (0)2F = . Tính ( ) ( )4252 FF −+ A. 4051. B. 2020. C. 2021. D. 4036. Lời giải Chọn A Ta có: 2 1 3 2 2021khi1 () 2020khi1 xxCx Fx xxCx ++ = ++ 2 (0)22FC== . Do đó 2 1 3 2021khi1 () 20202khi1 xxCx Fx xxx ++ = ++ Vì 2 1 3 2021khi1 () 20202khi1 xxCx Fx xxx ++ = ++ là nguyên hàm của ()fx nên ()Fx liên tục tại 1 x = , suy ra 11 202220231 CC +== . Vậy 2 3 20211khi1 () 20202khi1 xxx Fx xxx ++ = ++ Do đó, ( ) ( ) ( ) 42524.40465.40474051 FF−+=−+= . Câu 13: Cho hàm số ()fx xác định trên \1;2 thỏa mãn 2 1 () 2 fx xx = , (3)(3)0ff−−= và 1 (0)3 f = . Giá trị của biểu thức (4)(1)(4) fff −+− bằng A. 11 ln2 33 + . B. 1 ln2 3 . C. 1ln18 35 + . D. 1ln80 + . Lời giải
) ( ) limlim xx FxFxF +− →→ == 11 1
31 3.12 3 ++= 2 2 1 5.1+C 2 2 5 C 6 = Vậy ( ) ( ) ( ) .+ = F −=−−− 2 1 514 151 263 Câu 12: Cho hàm số 2 22021khi1 ()32020khi1 xx fx xx + = + . Giả
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
Chọn B
Câu 14: Cho ( )Fx là một nguyên hàm của hàm số ( ) 432 21 2 x fx xxx + = ++ trên khoảng ( ) 0;+ thỏa mãn ( ) 1 1 2 F = . Giá trị của biểu thức ( ) ( ) ( ) ( ) ( )123...20212022SFFFFF =+++++ bằng A. 2022 2023 B. 2022.2024 2023 C. 1 2021 2023 D. 2022 2023 Lời giải Chọn C Ta có ( ) ( ) ( ) 2 432 22 212121 2 21 1 xxx fx xxx xxx xx +++ === ++ ++ +
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Ta có: 2 d111 ()()dd 2321 x fxfxxx xxxx
===− −−−+ ( ) 1 ln2ln1 3 xxC=−−++ Suy ra ( ) ( ) ( ) 1 2 3 1 3ln(2)ln(1)1 1 ()ln(2)ln(1)12 3 1 3ln(2)ln(1)2 xxCkhix fxxxCkhix xxCkhix
−−−−+− =−−++− −−++ ( ) 1 1 (3)ln5ln2 3 fC −=−+ , ( ) 33 12 (3)ln1ln4ln2 33 fCC =−+=+ ( ) 13 12 (3)(3)ln5ln2ln20 33 ffCC −−=−++−= 1313 11 ln100ln10 33 CCCC +−=−=− 22 1111 (0)ln2ln2 3333fCC=+==− ( ) 11 11 (4)ln6ln3ln2 33 fCC −=−+=+ ( ) 3 1 (4)ln2ln5 3 fC =−+ ( ) 22 11 (1)ln1ln2ln2 33 fCC =−+=−+ Suy ra ( ) 123 111 (4)(1)(4)ln2ln2ln2ln5 333 fffCCC −+−=+−+−−− ( ) 11111 ln10ln2ln2ln5ln2 33333 =−+−−−=−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
( ) ( ) (
+ ==
Đặt ( ) (
=+=+ Khi đó (
(
===−+=+
Với ( ) 111 11 222 FCC =−+== Vậy
Fx là một nguyên hàm của hàm số ( ) 1 2x fx + = , thỏa mãn ( ) 2 0 ln2 F = . Tính giá trị biểu thức ( ) ( ) ( ) ( )012...2022TFFFF =++++ . A. 2023 21 ln2 T = B. ( ) 2022 221 ln2 T = C. 2023 22 ln2 T = D. ( ) 2023 221 ln2 T = Lời giải Chọn D Ta có: ( ) ( ) ( ) 1 11 2 d2d2d1 ln2 x xx FxfxxxxC + ++ ===+=+ . Mà ( ) 2 0 ln2 F = ( ) 1 222 0 ln2ln2ln2 x CCFx + +=== . Khi đó: ( ) ( ) ( ) ( )012...2022TFFFF =++++ ( ) ( ) 1232023 22022 2023 2023 22222 ...122...2 ln2ln2ln2ln2ln2 212221 ln212ln2 =++++=++++ == .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) 2 21 1 x Fxfxdxdx xx
+
)121 txxdtxdx
)
) ( ) 2 111 1 FxfxdxdtCC ttxx
+
( ) ( ) 1 1 1 Fx xx =+ +
Suy ra: ( ) ( ) ( ) ( ) ( )123...20212022 111111 1....2022 223320222023 111 1202220212021 202320232023 SFFFFF =+++++ =−−+−+++−+ =−−+=+= Câu 15: Gọi ( )
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 10 Chuyên
thi: Tuyển sinh vào
10 Tốt
THPT
12 Sưu tầm và biên soạn Câu 16: Cho hàm số ( )fx liên tục trên và có đạo hàm ( ) 2 43fxxx =−−− thỏa mãn ( ) ( ) 403ff−+= . Tính giá trị của biểu thức ( ) 5 2 2 Pff =+− A. 21. B. 12. C. 301 24
Lờ
giả
Chọn D Ta có: ( ) ( ) ( ) 2 2 43;;31; ' 43;3;1 xxx fx xxx −−−−−−+ = ++−− Suy ra ( ) ( ) ( ) 3 2 1 3 2 2 3 2 3 23;;3 3 23;3;1 3 23;1; 3 x xxCx x fxxxCx x xxCx −−−+−− =+++−− −−−+−+ Vì ( ) ( ) ( ) 33 limlim3 xx fxfxf−+ →−→− ==− nên 12CC = Vì ( ) ( ) ( ) 11 limlim1 xx fxfxf−+ →−→− ==− nên 23 44 33 CC−+=+ Mà ( ) ( ) 12123 457 4033 362ffCCCCC −+=++==== Vậy ( ) 32 5505301 2. 232424PffCC =+−=−+−+=− Câu 17: Cho hàm số ( )Fx là một nguyên hàm của hàm số ( ) 2 2cos1 sin x fx x = trên khoảng ( ) 0; . Biết rằng giá trị lớn nhất của ( )Fx trên khoảng ( ) 0; là 3 . Chọn mệnh đề đúng trong các mệnh đề sau. A. 334 6 F =− B. 23 32 F = C. 3 3 F =− D. 5 33 6 F =− Lời giải Chọn A Ta có: ( ) 222 2cos1cos1 dd2dd sinsinsin xx fxxxxx xxx ==− ( ) 22 dsin12 2dcot sinsinsin x xxC xxx =−=−++
0984164935
luyện
lớp
Nghiệp
BDKT Toán 10; 11;
. D. 301 24 .
i
i
Do ( )Fx là một nguyên hàm của hàm số ( ) 2 2cos1 sin x fx x = trên khoảng ( ) 0; nên hàm số
( )Fx có công thức dạng ( ) 2 cot sin FxxC x =−++ với mọi ( ) 0; x .
Xét hàm số ( ) 2 cot sin FxxC x =−++ xác định và liên tục trên ( ) 0;
( ) ( ) 2 2cos1 ' sin x Fxfx x ==
Xét ( ) ( ) 2 2cos11 '00cos2 sin23 x Fxxxkk x ====+ .
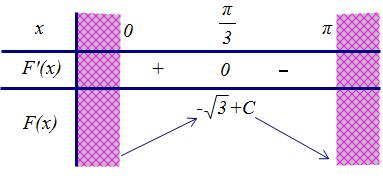
Trên khoảng ( ) 0; , phương trình ( ) '0Fx = có một nghiệm 3 x =
Bảng biến thiên: ( ) ( ) 0; max3 3 FxFC
==−+
Theo đề bài ta có, 3323 CC −+== Do đó, ( ) 2 cot23 sin Fxx x =−++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
11
=−
Câu 18: Giả sử hàm số ( )yfx = liên tục, nhận giá trị dương trên
0;+
ỏ
=
( ) ( ).31fxfxx =+ , với mọi 0 x . Mệnh đề nào sau đây đúng? A. ( ) 354 f B. ( ) 11512 f C. ( ) 10511 f D. ( ) 455 f Lời giải Chọn C Do hàm số ( )yfx = liên tục, nhận giá trị dương trên ( ) 0;+ nên ( ) ( ).31fxfxx =+ ( ) ( ) ( ) ( ) ( ) ( ) 112 ln31* 31313 fxfx dxdxfxxCfxfxxx ===++ ++
Khi đó, 334 6 F
.
( )
và th
a mãn ( )1 fe
,
Ta có: ( )1 fe = nên ( ) ( ) 41 *1** 33 CC =+=− Từ ( )* và ( )** suy ra ( ) ( ) 217 31 333510,31 x fxefe +− == .
Câu 19: Cho hàm số ( )yfx = có đạo hàm liên tục trên thỏa mãn ( )1 fe = và ( ) ( ) , fxfxxx += . Giá trị ( )2 f bằng A. 2 e B. 1 1 e C. 1 1 e + D. 2
Lời giải
Chọn D
Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ... xxxxx fxfxxfxefxexeefxxe +=+== Nên ( ) ( ) .dd xx efxxxex = ( ) . xxx efxxeeC =−+ ( ) xx x
xeeC fx e −+ = . Do ( )1 fe = ( ) 11 1 1 eeC f e −+ = 2Ce= . Suy ra ( ) 2 xx x
xeee fx e −+ = ( ) 222 2 2. 22 eee f e −+ == .
Câu 20: Cho hàm số ()yfx = có đạo hàm là
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 12
2 ()122, fxxx =+ và (1)3 f = . Biết ()Fx là một nguyên hàm của ()fx thỏa mãn (0)2F = , khi đó (1)F bằng A. 3. B. 1. C. 2. D. 7 . Lời giải Chọn B Ta có ( ) 2 ()d122d fxxxx =+ 3 ()42 fxxxC=++ . Mà (1)3 f = 63 C += 3 C =− 3 ()423 fxxx =+− . Ta có ( ) 3 ()d423d fxxxxx =+− 42 ()3 FxxxxC =+−+ . Mà (0)2F = 2 C = 42 ()32 Fxxxx =+−+ . Vậy (1)1F = .
Câu 21: Cho hàm số ( )fx có đạo hàm ( ) 1 fx x = , \0 x và ( ) 12 f = , ( ) 4 fe−= . Giá trị của ( ) ( ) 2 22 ffe bằng A. 8ln2−+ B. 5ln2−+ C. 2ln2−+ D. 1ln2−+ Lời giải Chọn B ( ) ( ) ( ) 1 2
1ln,0 dd ln,0 xCx fxfxxx xCx x
+ === −+
( ) 11 12ln122 fCC=+== ( ) 22 4lne43feCC −=+== Khi đó ( ) ( ) ln2,0 ln3,0 xx fx xx + = −+
( ) ( ) ( ) 2 22ln232225ln2ffe−−=+−+=−+ Câu 22: Cho hàm số ( )yfx = có đạo hàm là ( ) 6sin, fxxxx =+ và ( ) 00 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 03 F = , khi đó ( ) F bằng A. 3 3 . B. 3 3 3 . C. 3 3 2 . D. 3 3. Lời giải Chọn D Ta có 2 1 d6sind3cos fxfxxxxxxxC Mà 00 f nên 1 1 C . Suy ra 2 3cos1fxxx . Lại có 23 2 d3cos1dsin FxfxxxxxxxxC . Hơn nữa, 2 033FC 3 sin3Fxxxx Suy ra 33sin33 F . Câu 23: Cho hàm số ( )yfx = có đạo hàm ( ) 1 6 1 fxx x =+ , ( ) 1; x + và ( ) 212 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa ( ) 26 F = , khi đó giá trị biểu thức ( ) ( )543PFF =− bằng A. 20. B. 24. C. 10. D. 25. Lời giải
Chọn B
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
Trên ( ) 1;+ ta có ( ) ( ) 2 1 6dln13 1 fxxxxxC x =+=−++ .Vì ( ) 212 f = nên 0 C = . ( ) ( ) ( ) ( ) ( ) ( ) 23 1 ln13d1ln11. FxxxxxxxxC =−+=−−−−++ Vì ( ) 26 F = nên 1 1 C =− . ( ) ( ) ( ) 3 1ln1. Fxxxxx =−−+− Vậy ( ) ( ) 54324.PFF=−=
Câu 24: Cho hàm số ( )yfx = có đạo hàm là ( ) 6cos, fxxxx =− và ( ) 03 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 03 F = , khi đó 2 F bằng A. 3 12 2 6 . B. 3 12 2 8 . C. 3 12 2 8 . D. 3 12 2 6 . Lời giải
Chọn C Ta có 2 1 d6cosd3sin fxfxxxxxxxC . Mà 03 f nên 1 3 C Suy ra 2 3sin3fxxx Lại có 23 2 d3sin3dcos3 FxfxxxxxxxxC . Hơn nữa, 2 032FC 3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
14
cos32Fxxxx . Suy ra 33 12 cos3.22 28228 F . Câu 25: Cho hàm số ( )fx có đạo hàm ( ) 1 fx x = , \0 x và ( ) 12 f = , ( ) 4 fe−= . Biết ( )Fx là một nguyên hàm của ( )fx thỏa mãn ( ) 2 2 Fee = , khi đó ( )Fe bằng A. 2 34ee . B. 2 43ee . C. 2 45ee . D. 2 54ee . Lời giải Chọn B Ta có ( ) ( ) ( ) 1 2 1ln,0 dd ln,0 xCkhix fxfxxx xCkhix x + === −+ . Mà ( ) 11 12ln122 fCC=+== ( ) 22 4lne43feCC −=+==
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 15
góc bằng 0. Khi đó ( )1 F bằng A. 7 2 B. 7 2 C. 1 2 D. 1 2 Lời giải Chọn D Vì tiếp tuyến của ( )Fx tại điểm ( )0;2 M có hệ số góc bằng 0 ( ) ( ) ( ) == = 000 02 Ff F Ta có: ( ) ( ) ( ) 32 2 2 d23d3 32 xx fxfxxxxxxC ==−−=−−+ Do ( ) == 000fC Vậy ( ) 32 2 3 32 x f xx x = . Mà ( ) ( ) ( ) 1 0 d10fxxFF =− Suy ra ( ) ( ) ( ) + −+= = = 1 32 0 0 1 21 3d2 322 1d0 F xx x fxxF x Câu 27: Cho hàm số ( )yfx = có đạo hàm là ( ) 6, x fxxex =− và ( ) 02 f =− . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 01 F =− , khi đó ( )1 F bằng A. 1 e . B. 2e . C. 1 e . D. e . Lời giải Chọn D Ta có 2 1 d6d3xx fxfxxxexxeC Mà 02 f nên 1 1 C . Suy ra 2 31 xfxxe .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ( ) ( ) ln20 ln30 xkhix fx xkhix + = −+ . Ta có ( ) ( ) ( ) ( ) 22 2 ln2 ee ee FeFefxdxxdx −==+ ( ) 2 2 2 22 2ln4332 e e e e e e xxdxeexee =+−=−−=− Vậy ( ) 2 43 Feee =− . Câu 26: Cho hàm số ( )yfx = có đạo hàm là ( ) 2 23, fxxxx =−− Biết ( )Fx là nguyên hàm của hàm số ( )fx và tiếp tuyến của ( )Fx tại điểm ( )0;2 M có hệ số
Lại có 23 2 d31dxx FxfxxxexxexC Hơn nữa, 22 01110 FCC . 3 x Fxxex . Suy ra 31 111 Fee .
Câu 28: Cho hàm số ( )fx có đạo hàm ( ) 3 421, fxxxx =−+− và ( ) 00. f = Biết ( )Fx là một nguyên hàm của ( )fx thỏa mãn ( ) 11, F = khi đó ( )2 F bằng A. 131 30 . B. 131 30 . C. 41 30 . D. 41 30 . Lời giải Chọn A
Ta có: ( ) ( ) ( ) 3342 1 421421d fxxxfxxxxxxxC =−+−=−+−=−+−+
Do ( ) 1 000fC== Nên ( ) 42 fxxxx =−+− Suy ra ( ) ( ) 532 d 532 xxx FxfxxC ==−+−+ Mà ( ) 41 11 30 FC== . Hay ( ) ( ) 532 41131 2 5323030 xxx FxF=−+−+=−
Câu 29: Cho hàm số ( )yfx = có đạo hàm là ( ) cos, x fxxex =− và ( ) 03 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 03 F =− , khi đó ( ) F bằng A. 2 e . B. 2 e . C. 2 e . D. 2 e . Lời giải
Chọn A
Ta có 1 dcosdsinxx fxfxxxexxeC .
Mà 03 f nên 11 132 CC Suy ra sin2 x fxxe Lại có 2 dsin2dcos2 xx FxfxxxexxexC Hơn nữa, 22 031131 FCC . cos21 x Fxxex .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
Suy ra 2 Fe
Câu 30: Cho hàm số ( )yfx = có đạo hàm là ( ) 2 623, fxxxx =−+ và ( ) 23 f −= . Biết ( )Fx là nguyên hàm của hàm số ( )fx và ( ) 02 F = . Tính ( ) ( )122FF+− .
A. $26$. B. 314 3 . C. 334 3 . D. 46. Lời giải
Chọn D
Ta có: ( ) ( ) 2 1 32 623d23 fxxxxxxxC =−+=−++
Do ( ) 23 f −= nên 1 29 C = . Khi đó: ( ) 32 2329fxxxx=−++ .
Mặt khác: ( ) ( ) 2 2
432 3 3 2329d29 232 xxx FxxxxxxC =−++=−+++
Do ( ) 02 F = nên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
17
nguyên hàm của ( )fx trên thỏa mãn ( ) 320 F = . Giá trị của ( )1 F là A. 11 3 B. 14 3 C. 11 6 D. 17 3 Lời giải Chọn B ( ) 3 1 2 2 3 khi 1 3 5 khi 1 2 x xCx Fx x xCx ++ = −+ . Ta có ( ) 3 11 3 3203.3202 3 FCC =++== Lại có hàm số ( )yFx = liên tục trên nên liên tục tại 1 x = ( ) ( ) ( ) 11 limlim1 xx FxFxF +− →→ == 32 2 11 3.125.1 32 C ++=−+ 2 5 6 C = Vậy ( ) ( ) ( )2 1514 15.1+ = 263 F −=−−−
2 2 C = , khi đó ( ) 432 3 292 232 xxx Fxx =−+++ Vậy ( ) ( ) 98118 1222.46 33 FF +−=+−=− . Câu 31: Cho hàm số ( ) 2 3khi1 5 khi1 xx fx xx + = − . Giả sử ( )Fx là
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 18
=
.B. 2 412
F
=
. C. 2 3 416 F ++ = D. 2 12 416 F ++ =
Lời giải Chọn B + Ta có ( ) ( ) 2 1 ()2sin12cos22sin2 2 fxxdxxdxxxC =+=−=−+ Vì (0)1 f = nên 1 C = 1 ()2sin21 2 fxxx =−+ + Ta có 2 11 ()2sin21cos2 24 FxxxdxxxxT =−+=+++ Vì (0)1113 44 FTT=+== , nên 2 ()cos213 44 Fxxxx =+++ 2 412 416 F ++ = Câu 33: Cho hàm số ( )yfx = có đạo hàm là ( ) 3 44, fxxxx =+ và ( ) 01 f =− . Khi đó ( ) 1 1 Ifxdx = bằng A. 4 15 B. 26 15 C. 4 15 D. 0 Lời giải Chọn C Ta có: ( ) ( ) ( ) 342 442*fxxxdxxxC =+=++ Thay 0 x = vào ( )* ta có: ( ) 01fC==− . Vậy ( ) 4221fxxx=+− . Khi đó: ( ) ( ) 11 42 11 4 21 15 Ifxdxxxdx ==+−= . Câu 34: Cho hàm số ( )fx xác định trên \1 thỏa mãn ( ) 1 1 fx x = và ( ) ( ) 00,22ff== . Khi đó ( ) ( )13ff −+ bằng: A. 2ln2. B. 2ln2 + . C. 2. D. 22ln2 + . Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 32: Cho hàm số ()yfx = có đạo hàm là 2 ()2sin1, fxxx =+ . Biết ()Fx là nguyên hàm của ()fx thỏa mãn ( ) (0)01Ff== , khi đó 4 F bằng. A. 2 43 416 F ++
416
++
.fxdx =− Tương tự ta cũng có: ( ) ( ) ( ) 3 2
32 fffxdx =+ ( ) 3 2
2 fxdx =+ ( ) ( ) ( ) (
Nên ( ) cos3sin32fxxx =−−− . Ta có ( ) ( ) 1 cos3sin32dsincos32 FxxxxxxxC =−−−=−+−+ Do ( ) ( ) 11 02sin0cos3.02.021 FCC =−+−+== . Vậy ( ) ( ) sincos3212FxxxxF=−+−+=−. Câu 36: Hàm số ( )fx có đạo hàm liên tục trên và:
) ( ) dsin9cos3dcos3sin3 fxfxxxxxxxC ==−=−−+ . Do 1cos3sin3.12 222 fCC
bài
01fxdxff =−− nên suy ra ( ) ( ) ( ) 0 1 ra ta có: ( ) 02 f = 12 C += 1 C = Vậy ( ) 2 e1 x fxx=++
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Chọn D
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
19 ) 03 03 12 12 1322ln1ln122ln2 fffxdxfxdxxx −+=−+=−−+−=+ Vậy ( ) ( ) 1322ln2ff−+=+ . Câu 35: Cho hàm số ( )yfx = có đạo hàm là ( ) sin9cos3, fxxxx =− và 1 2 f = . Biết ( )Fx là một nguyên hàm của ( )fx thỏa mãn ( ) 02 F = , khi đó ( ) F bằng A. 2 B. 22 C. 2 D. 22 + Lời giải Chọn A Ta có ( ) (
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn =−−+==−
Ta có ( ) ( ) ( ) 0 1 ( ) 2 2e1, x fx =+ ( ) ,02xf = . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 3 1 2 F = , khi đó ( )2 F bằng A. 42 ee4 22 −+ B. 42 ee 4 22 ++ C. 42 ee4 22 D. 42 ee4 22 +− Lời giải Chọn A Ta có: ( ) ()d fxfxx = ( ) 2 2e1d x x =+ 2 e x xC=++ Theo
10 fffxdx −=− ( ) 0 1
Mà ( )Fx là nguyên hàm của ( )fx nên ( ) ( ) 222 1 11 e1de 22 xx FxxxxxC =++=+++ ( ) 22 11 3e33e 1 22222 FCC=++==− . Suy ra ( ) 2 2211 e. 222 x e Fxxx =++− Vậy ( ) 42 ee 24 22 F =−+ Câu 37: Cho hàm số ( )fx xác định trên 1 \ thoả mãn ( ) 25 1 x fx x = , ( ) 32 f = và ( ) 04 f = . Giá
trị của biểu thức ( ) ( )325ff bằng A. 14 B. 63ln2 C. 26ln2 D. 14 Lời giải Chọn A
Ta có: ( ) ( ) 253 dd2d23ln1 11 x fxfxxxxxxC xx ===−=−−+ , \1 x
+ Xét trên khoảng ( ) 1;+ ta có: ( ) 3263ln2243ln2 fCC=−+==−+ .
Do đó, ( ) 23ln143ln2fxxx=−−−+ , với mọi ( ) 1; x + .
Suy ra ( ) 5106ln243ln263ln2 f =−−+=− .
+ Xét trên khoảng ( );1− ta có: ( ) 044fC== . Do đó ( ) 23ln14fxxx=−−+ , với mọi ( );1 x− . Suy ra ( ) 366ln2426ln2 f −=−−+=−− . Vậy ( ) ( ) 32514ff−−=− .
Câu 38: Biết ()Fx là một nguyên hàm của hàm số ( ) 2x fxe = và ( ) 00 F = . Giá trị của ( )ln3 F bằng A. 2 B. 6 C. 8 D. 4 Lời giải Chọn D
Ta có: ( ) 22 1 2 xx FxedxeC ==+ ( ) 0 11 00.0 22 FeCC=+==− ( ) 2 11 . 22 x Fxe =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
Khi đó: ( ) 2ln3 11 ln3.4 22 Fe=−= . Câu 39: Cho hàm số ( )fx thỏa mãn ( ) 2 64, fxxx =+ và ( ) 03 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 12 F = , khi đó ( )2 F bằng A. 37 2 B. 37 2 C. 2 37 D. 2 37 Lời giải
Chọn A
( ) ( )d fxfxx = ( ) 23 64d24 xxxxC =+=++ . ( ) 03 f = ( ) 3 3243Cfxxx ==++ ( ) ( ) ( ) 4 32 d243d23' 2 x FxfxxxxxxxC ==++=+++ ( ) ( ) ( ) 4 2 7737 12'232. 2222 x FCFxxxF
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
21
xxxx
==+=++
( ) 222 1636633 FeeeeCeeC =++++=++= . Vậy ( ) 2 63 xxFxee=++ .
( )
F =
ố
=
==−=++−= Câu 40: Cho hàm số ( )yfx = có đạo hàm là ( ) 2 '24, xx fxeex=+ và ( ) 2 112 fee =+ . Biết ( )Fx là một nguyên hàm của ( )fx thỏa mãn ( ) 2 163Fee=++ , khi đó ( )0 F bằng A. 9 B. 10 C. 11 D. 12 Lời giải Chọn B Ta có ( ) ( ) ( ) 22'2412xxxx fxfxdxeedxeeC ==+=++ . ( ) 222 11212120 feeeeCeeC =+++=+= . Suy ra ( ) 2 12 xxfxee =+ Lại có ( ) ( ) ( ) 22126
FxfxdxeedxeeC
.
Khi đó,
010.
Câu 41: Cho hàm s
( )yfx
có đạo hàm ( ) 2 1266fxxx
=++ , x và ( ) 15 f −=− . Biết hàm số ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 18 F =− . Tính ( )1 F A. 10. B. 10. C. 14. D. 8. Lời giải
)fx có đạo hàm ( ) 3 421, fxxxx =−− và ( ) 00. f = Gọi ( )Fx là một nguyên hàm của ( )fx và ( ) 11, F =− khi đó ( )2 F bằng A. 41 . 30 B. 41 . 30 C. 21 . 10 D. 26 . 15 Lời giải Chọn A Ta có: ( ) ( ) 342421 fxxxfxxxxC =−−=−−+ . Do ( ) 000fC== Nên ( ) 42 fxxxx =−− , suy ra ( ) 532 532 xxx FxC =−−+ , mà ( ) 11 11 30 FC=−= . Hay ( ) ( ) 532 1141 2 5323030 xxx FxF=−−−= . Câu 43: Cho hàm số ( )yfx = có đạo hàm là ( ) 2 12182,.fxxxx =++ Gọi ( )Fx là nguyên hàm của ( )fx và thỏa mãn ( ) ( ) 000.fF== Khi đó ( )1 F bằng A. 5. B. 5. C. 2. D. –2. Lời giải Chọn A Ta có ( ) 232 1 (12182)d492. fxxxxxxxC =++=+++ Do ( ) 1 000.fC== Khi đó ( ) 32 492. fxxxx =++ Lại có ( )Fx là nguyên hàm của hàm ( )fx nên ta có ( ) ( ) 32432 2 d(492)d3. FxfxxxxxxxxxC ==++=+++ Mà ( ) 2 00.FxC== Khi đó, ( ) 432 3.Fxxxx =++ Vậy ( ) 432 113.115. F =++= Câu 44: Cho hàm số ( )yfx = có đạo hàm là ( ) 'sin3, x fxxex=+ và 2 2 fe =− . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 03 F = , khi đó ( ) F bằng
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 22
Chọn C Ta
(
(
( ) 11 11 1 32 1 1111
FFfxdxFFfxdx xxxdx −−=−=− =−−+++=− Câu
số (
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
có: ( ) ( ) ( ) 232 1266436 fxfxdxxxdxxxxC
==++=+++
) ( ) 32 1524362 fCfxxxx −=−==+++
) ( ) ( ) ( ) ( ) ( )
8436214
42: Cho hàm
Chọn
Vậy ( ) 1 cos3 3 x fxxe =−−
Ta có ( ) ( ) 1 11 cos3sin3 39 xx FxfxdxxedxxeC ==−−=−++
Với ( ) 0 11 1 03sin032 9 FeCC =−++==
Vậy ( ) 1 sin32 9 x Fxxe
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 2 e −+ . B. 2 e + . C. 2 e . D. 2 e . Lời giải
B Ta có ( ) ( ) ( ) 1 'sin3cos3 3 xx fxfxdxxedxxeC ==+=−−+ Với 222 13 cos0 232 feeCeC =−−−+=−=
=−++ Khi đó ( ) 1 sin322 9 Fee =−++=+ Câu 45: Cho hàm số ()fx xác định trên 1 \ 2 thỏa mãn 2 (); 21 fx x = (0)1 f = và (1)2. f = Tính (1)(3).Pff =−+ A. 3ln3 P =+ . B. 3ln5 P =+ . C. 3ln15 P =+ . D. 3ln15 P =− . Lời giải Chọn C Có 1 2 1 2ln(21)khi2 ()()ddln211 21ln(12)khi2 xCx fxfxxxxC x xCx −+ ===−+= −+ Để 2 1 1 (0)1 (1)22 C f fC = = == Suy ra: 1 ln(21)2 ()khi2 1 ln(12)1khi2 xx fx xx −+ = −+ Do đó (1)(3)3ln3ln53ln15.Pff=−+=++=+ Câu 46: Cho hàm số ( )yfx = có đạo hàm ( ) 2 'cos, 4 fxxx =+ và ( ) 13 0 4 f = . Tính 8 f . A. 2248 16 ++ . B. 16 . C. 28 16 . D. 2248 16 −+ .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 24 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Ta có: ( ) 2 1 cos.1cos2 422 fxxdxxdx =+=++ ( ) 111 .1sin2cos2 222 xdxxxC =−=++ . Vì ( ) 13113 03 444 fCC =+== Khi đó ( ) 11 cos23 22 fxxx =++ , suy ra 112248 cos3 8282416 f ++ =++= Câu 47: Cho hàm số ( )fx xác định trên * có đạo hàm đến cấp hai thỏa mãn ( ) 2 1 fx x =− , ( ) 10 f −= , ( ) 10 f = , ( ) 20 f = , ( ) 3ln3 f −= . Giá trị ( )2 f bằng A. 4ln2 B. 2ln2 C. 12ln2 + D. ln2 Lời giải Chọn D ( )fx xác định trên ( ) * fx xác định trên * Ta có: ( ) 2 1 fx x =− ( ) ( ) ( ) 1 2 2 1 0 1 d 1 0 Cx x fxx x Cx x +
f C f D f −= == = =− = = −= ( ) 22 2ln22ln2fCD −=−+= . Câu 48: Cho hàm số ( )fx có đạo hàm là ( ) sincos, fxxxx =+ và ( ) 0 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa mãn ( ) 23 F = , khi đó ( ) 3 F bằng A. 1 B. 5 + C. 31 D. 35 + Lời giải Chọn B Ta có ( ) ( ) ( ) 1 dsincosdcossin fxfxxxxxxxC ==+=−+ Từ ( ) 11 0cossin01fCC =−+==
=−= + ( ) ( ) ( ) ( ) 11 22 ln0 ln0 xCxDx fx xCxDx ++ = −++ Theo bài ra ta có: ( ) ( ) ( ) ( ) 22 1 1 10 0 10 ln2 20 ln2 3ln3 f CD
=−−++−=+
Câu 49: Cho hàm số ()yfx = có đạo hàm là 2 ()62, fxxx = và (1)2 f = . Biết ()Fx là nguyên hàm của ()fx thỏa mãn (0)0F = , khi đó (2)F bằng A. 2. B. 4. C. 6. D. 8. Lời giải Chọn B
Ta có ( ) 23 ()()6222 fxfxdxxdxxxC ===+
Với 3 (1)22.12.122 fCC =+== Vậy 3 ()222 fxxx = + Ta có ( ) 342 1 ()()222 2 2 FxfxdxxxdxxxxC =++ + == Mà (0)00FC== Vậy 42 1 ) 2 ( 4 Fxxxx −+ = , suy ra (2)4F =
Câu 50: Cho hàm số ()yfx = có đạo hàm là 3 ()122, fxxxx =+ và (1)3 f −= . Biết ()Fx là một nguyên hàm của ()fx thỏa mãn (0)1F =− , khi đó (1)F bằng A. 2 5 . B. 14 15 . C. 1 15 . D. 3 5 . Lời giải Chọn B
Ta có ( ) 3 ()d122d fxxxxx =+ 42 ()3 fxxxC=++ . Mà (1)3 f −= 43 C += 1 C =−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 25
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó ( ) cossin1fxxx=−+ Lại có ( ) ( ) ( ) 2 dcossin1dsincos FxfxxxxxxxxC ==−+=−−++ Từ ( ) 22 23sin2cos22342 FCC =−−++==− Do đó ( ) sincos42Fxxxx =−−++− . Vậy ( ) 3sin3cos33425 F
42 ()31
=+− . Ta có ( ) 42 ()d31d fxxxxx =+− 53 ()3 53 xx FxxC =+−+ Mà (0)1F =− 1 C =− 53 ()31 53 xx Fxx =+−− . Vậy 14 (1) 15 F −=− . Câu 51: Cho hàm số ( )fx thoả mãn 1 2 f = và (
.
ủ
(
fxxx
) ( ) 2 cos6sin1, fxxxx
=−
Biết ( )Fx là nguyên hàm c
a
)fx thoả mãn ( ) 2 0 3 F = , khi đó 2 F
bằng A. 1 3 . B. 2 3 . C. 1. D. 0.
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 26
Lời giải Ch
Ta
(
( ) (
==−=− 2
=−+ Đặ
== Suy
Mà ( ) 33 12sinsin102sinsin 222 fCCfxxx =−+===− Ta có ( ) ( ) ( ) ( ) 32 d2sinsind21cossindcos FxfxxxxxxxxxC ==−=−++ Đặt cosdsind uxuxx ==− Suy ra ( ) ( ) 3 2 21dcos2cos 3 u FxuuxCuxC =−−++=−−++ 3322 2coscoscoscoscos 33 xxxCxxC =−+−+=−+ Mà ( ) ( ) 332222 0cos0cos01coscos1 3333 FCCFxxx =−+===−+ Vậy 3 2 coscos11 2322 F =−+= Câu 52: Cho hàm số ( )yfx = có đạo hàm là ( ) sincos, fxxxxx =+ và ()0 f = . Biết ()Fx là nguyên hàm của ()fx thỏa mãn ()2F = , khi đó (0)F bằng A. . B. 3 . C. . D. 3 . Lời giải Chọn A Ta có ( ) ( ) ( ) d sincosdcoscosdsin fxfxx xxxxxxxxxxC = =+=−+=+ Với ()sin00 fCC +== . Suy ra ( ) sin fxxx = Lại có: ( ) ( )dsindcossin FxfxxxxxxxxC ===−++ Với cossin20 ) 2 (2F CCC −++=++ = == .
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
ọn C
có
)
) ( ) 22 dcos6sin1d6sincoscosd fxfxxxxxxxxx
6sincosdsinxxxxC
t sindcosd txtxx
ra ( ) 233 6dsin2sin2sinsin fxttxCtxCxxC =−+=−+=−+
ọn A
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 27
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra: ( ) 00cos0sin0 F =−++= Câu 53: Cho hàm số ( )yfx = liên tục, nhận giá trị dương trên ( ) 0;+ và thoả mãn ( ) 12 f = ; ( ) ( ) ( ) 2 2 x fx fx = với mọi ( ) 0; x+ . Giá trị của ( )3 f bằng A. 3 34 B. 34 C. 3 D. 3 20 Lời giải
=+=−+++ Vì ( ) ( ) 2 212ln213.2120 fCC =−++== Khi đó ( ) ( ) ( ) 2 ln13,1;fxxxx=−++ Vì ( )Fx là nguyên hàm của ( )fx nên ( ) ( ) 2 ln13 Fxxxdx =−+= ( ) 2 ln13 1 x xxdxxdxC x −−++ ( ) 2 1 ln113 1 xxdxxdxC x =−−+++ ( ) ( ) 3 ln1ln1 xxxxxC =−−−−++ Lại có ( ) 262860 FCC =−++== suy ra ( ) ( ) ( ) 3 ln1ln1 Fxxxxxx =−−−−+
Ch
Ta có ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 . x fxfxfxx fx == với mọi ( ) 0; x+ nên lấy nguyên hàm hai vế ta được ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22233 3 111 .ddd 333 fxfxxxxfxfxxCfxxC ==+=+ Với ( ) ( )3 117 11 333xfCC ==+= Do đó ( ) ( ) ( ) 33 3 3 117 7 333fxxfxx=+=+ . Vậy ( ) 3 334 f = . Câu 54: Cho hàm số ( )yfx = có đạo hàm ( ) ( ) 1 '6,1; 1 fxxx x =++ và ( ) 212 f = . Biết ( )Fx là nguyên hàm của ( )fx thỏa ( ) 6 Fx = , khi đó giá trị biểu thức ( ) ( )543PFF =− bẳng A. 20 B. 24 C. 10 D. 25 Lời giải Chọn B Ta có ( ) ( ) 1 6,1; 1 fxxx x
=++ ( ) ( ) ( ) 2 1 6ln13,1; 1 fxxdxxxCx x
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 28 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ( ) 3 55ln45ln458ln2120 F =−−+=+ ( ) 3 33ln23ln23ln224 F =−−+=−+ Suy ra: ( ) ( ) 54324PFF=−= Câu 55: Cho ( )Fx là một nguyên hàm của hàm số ( )2 e 1 x x y x = + và ( ) 11 F = Hệ số tự do của ( )Fx thuộc khoảng A. 1 ;0 2 B. 1 0; 2 C. 1 ;1 2 D. 1 1; 2 Lời giải Chọn A ( ) ( ) ( ) ( ) 222 1ee eeeddd 1 111 xx xxx x x xxx x xxx +− ==− + +++ ( ) e.e.de.d111e 1111 x xxxxxC xxxx =+==+ ++++ . Do ( ) ee 11110,36 22 FCCC=+==−− . Vậy hệ số tự do của ( )Fx thuộc khoảng 1 ;0 2 . Câu 56: Cho hàm số ( )yfx = biết ( ) ( ) 2 ',0; 2 x fxx x + =+ và ( ) 11 f = . Biết ( )Fx là một nguyên hàm ( )fx thỏa mãn ( ) 1 1 3 F =− , khi đó ( )9 F bằng A. 88ln3 3 + . B. 918ln3 + . C. 927ln3 + . D. 88ln3 3 −+ Lời giải Chọn B Ta có: ( ) ( ) 211 ',0ln 22 x fxxfxxxC xx x + ==+=++ ( ) 110fC== hay ( ) ln fxxx =+ Ta có ( ) ( ) ( ) ( ) 999 111 1 919ln 3 fxdxFFFxdxxdx =−=−++ ( ) 399 11 12 33|ln|918ln3 xxxx =−++−=+
NGUYÊN HÀM CỦA HÀM ẨN HOẶC LIÊN QUAN ĐẾN PHƯƠNG TRÌNH ( ) ( ) ( ) ,, fxfxfx
Dạng 1. Bài toán tích phân liên quan đến đẳng thúrc ' ()()()()() uxfxuxfxhx +=
Phương pháp:
Dễ dàng thấy rằng ()()()()[()()] uxfxuxfxuxfx +=
Do dó ()()()()()[()()]() uxfxuxfxhxuxfxhx +==
Suy ra ()()()d uxfxhxx =
Từ đây ta dễ dàng tính được ()fx
Dang 2. Bài toán tích phân liên quan đến biếu thúrc ()()() fxfxhx +=
Phương pháp:
Nhân hai vế vói x e ta durọc ()()()()() xxxxx efxefxehxefxehx +==
Suy ra ()()dxx efxehxx =
Từ đây ta dễ dàng tính được ()fx Dang 3. Bài toán tích phân liên quan đến biếu thúc ()()() fxfxhx −=
Phương pháp: Nhân hai vế vói x e ta durọc ()()()()() xxxxx efxefxehxefxehx −−−−− −==
Suy ra ()()dxx efxehxx =
Từ đây ta dễ dàng tính được ()fx
Dạng 4. Bài toán tích phân liên quan đến biếu thúrc ()()()() fxpxfxhx +=
fxeehxx
Từ đây ta dễ dàng tính được ()fx Dang 5. Bài toán tích phân liên quan đến biếu thúc ()()()0fxpxfx +=
Phương pháp:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III
TÍCH
TÍCH PHÂN
GIẢI
12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG
Page 29
+==
()()
Phương pháp: Nhân hai vế với () pxdx e ta được ()()()()() ()()()()()() pxdxpxdxpxdxpxdxpxdx fxepxefxhxefxehxe
Suy ra
()()d pxdxpxdx
=
Chia hai vế với ()fx ta đựơc ()()()0()()() fxfx fxfxpxpx
=−=−
Suy ra ()d()dln|()|()d() fx xpxxfxpxx fx
Từ đây ta dễ dàng tính được ()fx
Dạng 6. Bài toán tích phân liên quan đến biểu thức ()()[()]0 n fxpxfx +=
Phương pháp:
Chia hai vế với [()]n fx ta được ()()()0()[()][()] nn fxfx fxfxpxpx +==− Suy ra 1 ()[()]d()d()d[()]1
n n fxfx fxnxpxxpxx −+ =−=− −+
Từ dầy ta dễ dàng tính được ()fx Câu 57: Cho hàm số ( )yfx = đồng biến và có đạo hàm liên tục trên thỏa mãn ( ) ( ) ( ) 2 ., x fxfxex = và ( ) 02 f = . Khi đó ( )2 f thuộc khoảng nào sau đây?
A. ( ) 12;13. B. ( ) 9;10. C. ( ) 11;12. D. ( )1314;. Lời giải Chọn B
Vì hàm số ( )yfx = đồng biến và có đạo hàm liên tục trên đồng thời ( ) 02 f = nên ( ) 0 fx và ( ) 0 fx với mọi ) 0; x+ .
x fx ex fx ( ) ) 2 , 0; x fxeCx=++ với C là hằng số nào đó. Kết hợp với ( ) 02 f = , ta được 21 C =− Từ đó, tính được ( ) ( )2 2219,81fe=+− . Câu 58: Cho hàm số ( )yfx = thỏa mãn ( ) 4 2 19 f =− và ( ) ( ) 32 fxxfxx = . Giá trị của ( )1 f bằng A. 2 3 B. 1 2 C. 1 D. 3 4
=+ Lấy nguyên hàm hai vế, ta được
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 30
+==−
Từ giả thiết ( ) ( ) ( ) 2 ., x fxfxex = suy ra ( ) ( ) ) 2 ., 0;. x fxfxex =+ Do đó, ( ) ( ) ) 2 1 ,0;. 22
11 f =− .
b
) 12ln2 f
)
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn C Ta có ( ) ( ) ( ) ( ) 323 2 fx fxxfxx fx == ( ) ( ) ( ) 4 3 2 1 4 fx x dxxdxC fxfx =−=+ . Mà ( ) 4 2 19 f =− 19163 444 CC =+= . Suy ra ( ) 4 4 3 fx x =− + . Vậy ( )
+== ++++ + . Vậy ( ) ( ) 1 ..dd1dln1 1111 xxxfxfxxxxxxC xxxx ===−=−++ ++++ Do ( ) 12ln2 f =− nên ta có ( ) 1 .11ln2ln21ln21 2 fCCC =−+−=−+=− Khi đó ( ) ( ) 1 ln11 x fxxx x + =−+− . Vậy ta có ( ) ( ) ( ) 333333 22ln311ln3ln3, 222222fab =−−=−=−==− . Suy ra ( ) 22 22 33 229 22 ab +=+−= Câu 60: Cho hàm số ( )yfx = thỏa mãn ( ) 0,0fxx và có đạo hàm ( )fx liên tục trên khoảng ( ) 0;+ thỏa mãn ( ) ( ) ( ) 2 21,0fxxfxx =+ và ( ) 1 1 2 f =− . Giá trị của biểu thức ( ) ( ) ( )12...2020fff +++ bằng A. 2020 2021 B. 2015 2019 C. 2019 2020 D. 2016 2021 Lời giải
Câu 59: Cho hàm số ( )yfx = liên tục trên \1;0 thỏa mãn điều kiện: (
=− và ( ) ( ) ( ) 2 .1. xxfxfxxx ++=+ . Biết ( ) 2.ln3fab =+ ( a ,
). Giá trị (
22 2 ab + là A. 27 4 B. 9 C. 3 4 D. 9 2 Lời giải Chọn B Chia cả hai vế của biểu thức ( ) ( ) ( ) 2 .1. xxfxfxxx ++=+ cho ( )2 1 x + ta có ( ) ( ) ( ) ( ) 2 1 1111 1 xxxx fxfxfx xxxx x
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
Chọn A Ta
(
=+
Mà ( ) 1 1 2 f =− 0
=
=
=−
. ( ) ( ) ( ) ( ) 1 11 2
\1;0 thỏa mãn ( ) 12ln21 f =+ , ( ) ( ) ( ) ( ) ( )121xxfxxfxxx +++=+ , \1;0 x − . Biết ( ) 2ln3fab =+ , với a , b là hai số hữu tỉ. Tính 2 Tab =− A. 3 16 T = . B. 21 16 T = . C. 3 2 T = . D. 0 T = . Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( )121xxfxxfxxx +++=+ ( ) ( ) ( ) 2 1 1 x fxfx xx + += + ( ) ( ) ( ) ( ) 22 2 2 11 1 xx xx fxfx xx x + += ++ + ( ) ' 22 11 xx fx xx =++ ( ) 22 11 xxfxdx xx = ++ ( ) 22 ln1 12 xxfxxxc x =−+++ + ( ) 2 2 1 ln1. 2 xx fxxxc x + =−+++ Ta có ( ) 12ln21 f =+ 1. c = Từ đó ( ) 2 2 1 ln11 2 xx fxxx x + =−+++ , ( ) 33 2ln3. 44 f =+ Nên 3 4 3 4 a b = = Vậy 2 3 16 Tab=−=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
có:
) ( ) ( ) 2 21 fxxfx
=+ ( ) ( ) 2 21 fx x fx
=+ ( ) ( ) ( ) 2 d21d fx xxx fx
( ) 2 1 xxC fx −=++ .
C
( ) 2 1 fx xx
+ 11 1 xx
+
11 2 32 11 3 43 11 2020 20212020 f f f f =− =−
=−
=−
( ) ( ) ( ) 1 12....20201 2021 fff +++=−+ 2020 2021 =− . Câu 61: Cho hàm số ( )yfx = liên tục trên
Câu 62: Cho hs ( )yfx = thỏa mãn 2 yxy = và ( ) 11 f −= thì giá trị ( )2 f là
A. 2 e B. 2e C. 1 e + D. 3 e Lời giải
Ta có 2 yxy = 2 y x y
= 2 dd y xxx y
= 3 ln 3 x yC=+ 3 3 e x C y + = .
Theo giả thiết ( ) 11 f −= nên 1 3 1 e1 3 C C −+ == Vậy ( ) 3 1 33 =e x yfx + = . Do đó ( ) 32e f =
Câu 63: Cho hàm số ( )fx liên tục trên , ( ) 0 fx với mọi x và thỏ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
33
a mãn ( ) 1 1 2 f =− , ( ) ( ) ( ) 2 21xf f x x = + .Biết ( ) ( ) ( ) 12...20191 a fff b +++=− với ( ) ,,,1 abab= .Khẳng định nào sau đây sai? A. 2019 ab−= B. 2019 ab C. 22022 ab+= D. 2020 b Lời giải ( ) ( ) ( ) 2 21xf f x x = + ( ) ( ) 2 21 x fx fx =+ ( ) ( ) ( ) 2 21 dx f xdx fx x =+ ( ) ( ) ( ) ( ) 2 21 dfx xdx fx =+ ( ) 2 1 xxC fx −=++ ( )1 Thay 1 x = vào ( )1 được 1 2 1 2 C +=− 0 C = .Vậy ( ) 11 1 fx xx =− + 111111 (1)(2)...(2019)...213220202019 Tfff =+++=−+−++− 1 1 2020 =−+ . Suy ra: 1 2019 2020 a ab b = −=− = Câu 64: Cho hàm số ( )yfx = liên tục trên ( ) 0;+ thỏa mãn ( ) ( ) 2 23 xfxfxxx += . Biết ( ) 1 1 2 f = . Tính ( )4 f ? A. 24. B. 14. C. 4. D. 16. Lời giải Chọn D
fCCC =+=+= ( ) 2 2 xx fx = . Vậy ( ) 2 44 416 2 f == .
Câu 65: Cho hàm số ( ) 0 fx với mọi x , ( ) 01 f = và ( ) ( ) 1. fxxfx =+ với mọi x . Mệnh đề nào dưới đây đúng? A. ( ) 2 fx B. ( ) 24 fx C. ( ) 6 fx D. ( ) 46 fx Lời giải Ta có: ( ) ( ) 1 1 fx fx x
= + ( ) ( ) 1 dd 1 fx xx fx x
= + ( ) ( ) ln21fxxC=++ Mà ( ) 01 f = nên ( ) ( ) 2122 236 x Cfxefe +− =−==
Câu 66: Cho hàm số ( )yfx = có đạo hàm liên tục trên 2;4 và ( ) 0,2;4fxx . Biế
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 34 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt
THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Trên khoảng ( ) 0;+ ta có: ( ) ( ) ( ) 22 13 2'3' 22 xfxfxxxxfxx x +=+= . ( ) ( ) ( ) ( ) '' 22 33 .. 22 xfxxxfxdxxdx== . ( ) 3 1 . 2 xfxxC=+ ( ) Mà ( ) 1 1 2 f = nên từ ( ) có: ( ) 3 111 1.1.10 222
0984164935
Nghiệp
(
fxx nên hàm số ( )yfx = đồng biến trên 2;4 ( ) ( )2 fxf mà ( ) 7 2 4 f = . Do đó: ( ) 0,2;4fxx . Từ giả thiết ta có: ( ) ( ) ( ) ( ) 33333 441 xfxfxxxfxfx =−+= ( ) ( ) ( ) ( ) 3 3 .41 41 fx xfxfxx fx +== + . Suy ra: ( ) ( ) ( ) ( ) 2 33 d41 1 dd 424141 fx fx x xxxC fxfx + ==+ ++ ( ) 2 2 3 3 41 82 x fxC+=+ ( ) 731 22 422fCC==+=−
t
) ( )
( ) 3 33 7 4,2;4,2 4 xfxfxxxf
=−= . Giá trị của ( )4 f bằng A. 4051 2 . B. 2051 4 . C. 2051 2 . D. 4051 4 . Lời giải Ta có: ( )
0,2;4
uxux xvv == == .ed.eed.ee xxxxx IxxxxxC ==−=−+ . Suy ra ( ) e.ee xxx fxxC =−+ . Theo giả thiết (0)1 f = nên 2 C = ( ) ( ) .ee22 1 ee
x fxf −+ == Câu
xx x
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
Ánh 42
TP
Page 35
Vậy: ( ) ( ) 3 2 4 11 3 4 x fx = (
4 4 f = Câu
Cho ()fx là hàm số liên tục trên thỏ
+= và
( )1 f A. 2 e B. 1 e
Lờ
viên: Huỳnh Văn
Nguyễn Cư Trinh Thuận Hòa
Huế ĐT: 0984164935 68: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) 2 2 11. xfxxfxfx +=− với mọi x dương. Biết ( ) ( ) 111ff == . Giá trị ( ) 2 2 f bằng A. ( ) 2 22ln22 f =+ B. ( ) 2 22ln22 f =+ C. ( ) 2 2ln21 f =+ . D. ( ) 2 2ln21 f =+ . Lời giải Ta có: ( ) ( ) ( ) 2 2 11.";0xfxxfxfxx +=− ( ) ( ) ( ) 2 22 .'11." xfxxfxfx +=− ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 2 ' 2 1 '1." 1 '."1 1 .'1 fxfxfx x fxfxfx x fxfx x +=− +=− =−
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) 4051
67:
a mãn ( ) ( ) , fxfxxx
( ) 01 f = . Tính
C. e D. e 2
i giải ( ) ( ) (1) fxfxx += . Nhân 2 vế của (1) với x e ta được ( ) ( ) e.e..e xxx fxfxx += Hay ( ) ( ) e..ee..ed xxxx fxxfxxx == . Xét .ed x Ixx = . Đặt dd edde xx
69:
Do đó: ( ) ( ) ( ) ( ) ' 1 2 11 .'.d1.d.'. fxfxxxfxfxxc xx =−=++ Vì ( ) ( ) 11 1'11121. ffcc===+=− Nên ( ) ( ) 1 .'.d1.d fxfxxxx x =+− ( ) ( ) ( ) 1 .d1.d fxfxxx x =+− ( ) 2 2 2 ln. 22 fx x xxc=+−+ Vì ( ) 22 11 1111. 22 fcc==−+= Vậy ( ) ( ) 2 2 2 ln122ln22 22 fx x xxf =+−+=+
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 36
Câu
Cho hàm số ()fx thỏa mãn 23 ('())().''()2,
+=−
==
giá trị của 2(2) Tf = A. 43 30 B. 16 15
Lời
ải Có 233
+=−=− 342 1 ().'()(2) 4 fxfxxxdxxxC =−=−+ Từ
== .
.
ậ
Tiế
4224211 2().'()22(())'22 22
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 24253 112 ()(22)2 2103 fxxxdxxxxC =−+=−++ Từ (0)1 f = . Suy ra 1 C = . Vậy 253 12 ()21 103 fxxxx =−++ . Do đó 43 15 T = Câu 70: Cho hàm số ( )fx liên tục và có đạo hàm trên 0; 2 , thỏa mãn ( ) ( ) 3 tan. cos x fxxfx x += Biết rằng 33ln3 36 ffab −=+ trong đó , ab . Giá trị của biểu thức Pab =+ bằng A. 14 9 B. 2 9 C. 7 9 D. 4 9 Lời giải
fxfxfxxxxR
và (0)'(0)1ff
. Tính
C. 43 15 D. 26 15
gi
('())().''()2(().'())'2 fxfxfxxxfxfxxx
(0)'(0)1ff
Suy ra 1 C =
V
y 42 1 ().'()1 4 fxfxxx=−+
p, có
fxfxxxfxxx =−+=−+
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 37
Chọn D ( ) ( ) 3 tan. cos x
x += (
cos x
x += ( ) 2
cos x xfx x = Do đó ( ) 2 sin.dd cos x xfxxx x = ( ) 2
cos x
= Tính 2 d cos x Ix x = . Đặt 2 dd d dtan cos ux ux x vx v x = = = = . Khi đó ( ) 2 dcos dtantandtandtanlncos coscos x x Ixxxxxxxxxxx xx ==−=+=+ Suy ra ( ) .tanlncoslncos sincossin xxxx x fx xxx + ==+ . 22ln2333ln3332ln 36392 3 abff +=−=−−+ 53 ln3 9 =− . Suy ra 5 9 1 a b = =− . Vậy 4 9 Pab=+=− . Câu 71: Cho hàm số ( )yfx = đồngbiếntrên ( ) 0;+ ; ( )yfx = liêntục,nhậngiátrịdươngtrên ( ) 0;+ và thỏa mãn ( ) 4 3 9 f = và ( ) ( ) ( ) 2 '1. fxxfx =+ . Tính ( )8 f A. ( ) 849 f = . B. ( ) 8256 f = . C. ( ) 1 8 16 f = . D. ( ) 49 8 64 f = . Lời giải Chọn A Ta có với ( ) 0; x + thì ( ) 0 yfx= ; 10 x + . Hàm số ( )yfx = đồng biến trên ( ) 0;+ nên ( ) ( ) 0,0;fxx +
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
fxxfx
) ( ) 2 cos.sin.
xfxxfx
sin.
sin.d
xfxx x
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 38 Chuyên
thi:
10
tầm và
Do đó ( ) ( ) ( ) ( ) ( ) ( ) 2 11 fxxfxfxxfx =+=+ (
x
=+ Suy ra ( ) ( ) ( )
fx xxx fx =+ ( )
3
=++ . Vì ( ) 4 3 9 f = nên 28 2 33 C =−=−
= + ( ) 11 1 C fx x x −=−+ + Mà ( ) 11110 fCC ==+= . Vậy ( ) 2 1 x fx x + = ( ) 5 2 2 f = . Câu 73: Cho hàm số ( )yfx = có đạo hàm liên tục trên khoảng ( ) 0;+ , biết ( ) ( ) ( ) 2 210fxxfx ++= , ( ) 0,0fxx và ( ) 1 2 6 f = . Tính giá trị của ( ) ( ) ( )12...2019Pfff =+++ . A. 2021 2020 . B. 2020 2019 . C. 2019 2020 . D. 2018 2019 . Lời giải TH1: ( ) 0 fx = ( ) 0 fx = trái giả thiết.
Hòa
0984164935
luyện
Tuyển sinh vào lớp
Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu
biên soạn
) ( ) ( )1 fx
fx
d1d
( )3 1 1
fxxC
Suy ra ( ) ( ) 2 3 1 12 3 fxx =+− , suy ra ( ) 849 f = . Câu 72: Cho hàm số ( )fx thỏa mãn ( ) 12 f = và ( ) ( ) ( ) ( ) 2 2 2211xfxfxx +=− với mọi x . Giá trị của ( )2 f bằng A. 2 5 B. 2 5 C. 5 2 D. 5 2 Lời giải Chọn D Từ giả thiết ta có: ( ) ( ) ( ) 2 2 2 2 1 .0 1 x fxfx x = + với mọi ( 1;2 x . Do đó ( ) ( ) 110 fxf= với mọi 1;2 x . Xét với mọi 1;2 x ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 2 2222 2 22 2 11 1 11 1dd fxfxxx fxfx x fx x x x xx f x =− +== ++ . ( ) ( ) 2 2 2 1 1 dd 1 fx x xx x x x f = + ( ) ( ) 2 2 d1 d 1 x fx x x x x fx +
..... 122320202020 P =−+−+−= . Câu 74: Cho hàm số ( )yfx = có đạo hàm liên tục trên đoạn 2;1 thỏa mãn ( ) 03 f = và ( ) ( ) ( ) 2 2 .342fxfxxx =++ . Giá trị lớn nhất của hàm số ( )yfx = trên đoạn 2;1 là A. 3 242 B. 3 215 C. 3 42 D. 3 15 Lời giải Ta có: ( ) ( ) ( ) 2 2 .342fxfxxx =++ Lấy nguyên hàm 2 vế của phương trình trên ta được ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22232 .34222 fxfxdxxxdxfxdfxxxxC =++=+++ ( ) ( ) ( ) ( ) ( ) ( ) 3 3 3232 22322 1 3 fx xxxCfxxxxC =+++=+++ Theo đề bài ( ) 03 f = nên từ ta có ( ) ( ) ( ) 3 32 0302.02.02739 fCCC =+++== ( ) ( ) ( ) ( ) 3 3232 3 3229()3229. fxxxxfxxxx =+++=+++ Tiếp theo chúng ta tìm giá trị lớn nhất của hàm số ( )yfx = trên đoạn 2;1. CÁCH 1:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 39
TH2:
(
2
=−+ ( )
=−+ ( ) ( ) ( ) 2
fx xxx fx =−+ ( ) ( ) 2 1
=−++ Ta
6
= 0
=
2 111
xxxx ==− ++ 111112019
Vì ( ) ( ) 32222922250,2;1 xxxxxxx +++=++++− nên ( )fx có đạo hàm trên 2;1 và ( ) ( ) ( ) ( ) 2 2 22 333232 3342 342 0, 332293229 xx xx fx xxxxxx ++ ++ == ++++++ 2;1. x − Hàm số ( )yfx = đồng biến trên ( ) ( ) 3 2;1 2;1max1. 42 fxf −== Vậy ( ) ( ) 3 2;1 max142 fxf== . CÁCH 2: ( ) ( ) 2 3 3 3 3 22 32. 3 223 3229 39 xxx x fx x ++++ =+++= Vì các hàm số 3 22 22 3,2 9 3 33yxyx =+=++ đồng biến trên nên hàm số
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
( ) 0 fx
) ( ) ( )
21. fxxfx
( ) ( ) 2 21 fx x fx
d21d
xxC fx
có: ( ) 1 2
f
C
( )
1 fx
Suy ra, ()fx x là một nguyên hàm của hàm số ( ) g23 xx=+ Ta có ( ) 2 233, xdxxxC +=++ C . Do đó, 2 1 () 3, fx xxC x =++ với 1C nào đó
Vì (1)4 f = theo giả thiết, nên thay 1 x = vào hai vế của ta thu được 1 0 C = , từ đó 32()3 fxxx =+ . Vậy (2)20 f = .
Câu 76: Cho hàm số ( )fx liên tục trên R thỏa mãn các điều kiện: ( ) 022, = f ( ) 0, fx x và ( ) ( ) ( ) ( ) 2 .211, =++ fxfxxfx x . Khi đó giá trị ( )1 f bằng
A. 26 . B. 24 . C. 15 . D. 23. Lời gi
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 40 Chuyên
10 Tốt
12 Sưu tầm và biên soạn 3 3 223 32 39 22 3 yxx =++++ cũng đồng biến trên Do đó, hàm số ( )yfx = đồng biến trên 2;1. Vậy ( ) ( ) 3 2;1 max142 fxf== . Câu 75:
Hòa
0984164935
luyện thi: Tuyển sinh vào lớp
Nghiệp THPT BDKT Toán 10; 11;
Cho hàm số ()fx thỏa mãn (1)4 f = và 32()()23 fxxfxxx =−− với mọi 0 x . Giá trị của (2) f bằng A. 5. B. 10. C. 20. D. 15. Lời giải 32 32 22 1.().()23() ()()2323 fxxfxxxfx fxxfxxxx xxx −=−−==+
Ta
( ) ( ) ( ) (
2 .211 =++ fxfxxfx ( ) ( ) ( ) ( ) 2 21 1 =+ + fxfx x fx Suy ra ( ) ( ) ( ) ( ) 2 . d21d 1 =+ + fxfx xxx fx ( ) ( ) ( ) ( ) 2 2 d1 21d 21 + =+ + fx xx fx ( ) 22 1 +=++fxxxC . Theo giả thiết ( ) 022 = f , suy ra ( )2 1223 +== CC Với 3 = C thì ( ) ( ) ( )2 222 1331 +=++=++− fxxxfxxx
ậ
=
ải
có
)
. V
y ( ) 124
f
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
42
TP Huế
Page 41
Câu 77: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) 2 2 .21fxfxfxxx +=−+ , x và ( ) ( ) 003ff == . Giá trị của ( ) 2 1 f bằng A. 28. B. 22.
.
. Lời giải Ta có ( ) ( ) ( ) ( ) ( ) 2 fxfxfxfxfx =+ . Do đó theo giả thiết ta được ( ) ( ) 2 21fxfxxx =−+ Suy ra ( ) ( ) 2 3 2 32 x fxfxxxC =−++ . Hơn nữa ( ) ( ) 003ff == suy ra 9 C Tương tự vì ( ) ( ) ( ) 2 2 fxfxfx = nên ( ) 2 23 2 29 32 x fxxx =−++ . Suy ra ( ) 23 2342 21 29d18 3233 xx fxxxxxxxC =−++=−+++ , cũng vì ( ) 03 f = suy ra ( ) 3 242 1 189 33 x fxxxx =−+++ . Do đó (
2 128 f = Câu
hàm số ( )fx có đạo hàm trên thỏa mãn ( ) ( ) ( ) ( ) 21ex xfxxfx +++= và ( ) 1 0 2 f = Tính ( )2 f . A. ( ) 2e 3 f = B. ( ) 2e 6 f = C. ( ) 2 2e 3 f = D. ( ) 2 2e 6 f = Lời giải Ta có ( ) ( ) ( ) ( ) 21ex xfxxfx +++= ( ) ( ) ( ) ( ) ( ) 11ex xfxfxxfx ++++= ( ) ( ) ( ) ( ) 11ex xfxxfx +++= ( ) ( ) ( ) ( ) 2e1e1e xxx xfxxfx +++= ( ) ( ) 2e1e xx xfx += ( ) ( ) 2 e1ded xx xfxxx += ( ) ( ) 2 1 e1e 2 xxxfxC +=+ Mà ( ) 1 0 2 f = 0 C = . Vậy ( ) 1e . 21 x fx x = + Khi đó ( ) 2 2e 6 f = Câu 79: Cho hàm số ( )yfx = liên tục trên \0;1 thỏa mãn điều kiện ( ) 12ln2 f =− và ( ) ( ) ( ) 2 1. xxfxfxxx ++=+ . Giá trị ( ) 2ln3fab =+ , với , ab Tính 22ab +
viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa
ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
C. 19 2
D. 10
)
78: Cho
A. 25 4 . B. 9 2 . C. 5 2 . D. 13 4 . Lời giải Từ giả thiết, ta có ( ) ( ) ( ) 2 1. xxfxfxxx ++=+ ( ) ( ) ( ) 2 1 . 11 1 xx fxfx xx x += ++ + ( ) . 11 xx fx xx =++ , với \0;1 x − .
Suy ra ( ) 1 x fx x + d 1 x x x = + hay ( ) 1 x fx x + ln1 xxC=−++
Mặt khác, ta có ( ) 12ln2 f =− nên 1 C =− . Do đó ( ) . 1 x fx x + ln11xx =−+− .
Với 2 x = thì ( ) 2 .21ln3 3 f =− ( ) 33 2ln3 22 f =− . Suy ra 3 2 a = và 3 2 b =− Vậy 22 9 2 ab+= .
Câu 80: Giả sử hàm số ( )yfx = liên tục, nhận giá trị dương trên ( ) 0;+ và thỏa mãn ( ) 11 f = , ( ) ( ).31fxfxx =+ , với mọi 0 x . Mệnh đề nào sau đây đúng? A. ( ) 253 f . B. ( ) 152 f . C. ( ) 455 f . D. ( ) 354 f . Lời giải
= + ( ) ( ) ( ) d 1 d 31 fx x fx x = + ( ) 2 ln31 3 fxxC=++ ( ) 2 31 3 xC fxe ++ = Mà ( ) 11 f = nên 4 3 1 C e + = 4 3
C =− . Suy ra ( ) 4 3 53,794fe= Câu 81:
)
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
42
Cho hàm số ( ) 0 fx thỏamãnđiềukiện (
(
=+
ế
ằ
ổ
(
(
(
(
(
Ta có ( ) ( ).31fxfxx =+ ( ) ( ) 1 31 fx fx x +++++=
= + ( ) ( ) 1 dd 31 fx xx fx x đề
) ( ) 2 23 fxxfx
và ( ) 1 0 2 f =− .Bi
t r
ng t
ng
)
)
)
)
)123...20172018 a fffff b
với ( ) * , ab và a b làphânsốtối giản. Mệnh
nào sau đây đúng? A. 1 a b − . B. 1 a b . C. 1010 ab+= . D. 3029 ba−= . Lời giải Ta có ( ) ( ) ( ) 2 23 fxxfx =+ ( ) ( ) 2 23 fx x fx =+
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 43
( ) ( ) 42 22 31 fx xx fxx +− = ( ) ( ) 42 22 31 +− = dd fx xx xx fxx ( ) ( ) ( ) 42 22 31 +− = d d fx xx x fxx ( ) ( ) ( ) 2 22 1 31 =+− d d fx xx fxx ( ) 3 11xxC fxx =+++ ( ) 3 1 1 fxC xx x =+ ++ . Do ( ) 1 1 3 f =− 0 C = ( ) 42 1 x fx xx = ++ = 22 111 211 xxxx ++−+ ( ) 111 1 231 f =− ; ( ) 111 2 273 f =− ; ( ) 111 3 2137 f =− ;.; ( ) 111 80 264816321 f =− ( ) ( ) ( )1280fff+++= 111 226481 −+ = 3240 6481 . Câu 83: Cho hàm số ( )fx đồng biến có đạo hàm đến cấp hai trên đoạn 0;2 và thỏa mãn ( ) ( ) ( ) ( ) 22 .0fxfxfxfx −+= . Biết ( ) 01 f = , ( ) 62e f = . Khi đó ( )1 f bằng A. 3 2e . B. 3 e . C. 5 2e . D. 2 e . Lời giải Theo đề bài, ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 22 2 . .01 fxfxfx fxfxfxfx fx −+==
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) d23d fx xxx fx
=+ ( ) 2 1 3 xxC fx −=++ Vì ( ) 1 02 2 fC=−= . Vậy ( ) ( )( ) 111 1221 fx xxxx =−=− ++++ Do đó ( ) ( ) ( ) ( ) ( ) 111009 123...20172018 202022020 fffff+++++=−=− Vậy 1009 a =− ; 2020 b = . Do đó 3029 ba−= . Câu 82: Cho hàm số ( ) 0 fx , ( ) ( ) 42 2 2 31 xx fxfx x +− = và ( ) 1 1 3 f =− . Tính ( ) ( ) ( )1280 ... fff +++ A. 3240 6481 B. 6480 6481 C. 6480 6481 D. 3240 6481 Lời giải ( ) ( ) 42 2 2 31 xx fxfx x +− =
== .
Câu 84: Cho hàm số ( )yfx = liên tục trên thỏa mãn ( ) ( ) 2 2.e x fxxfx += , x và ( ) 00 f = Tính ( )1 f A. ( ) 21e f = . B. ( ) 1 1 e f =− . C. ( ) 2 1 1 e f = . D. ( ) 1 1 e f = . Lời giải Chọn D Ta có ( ) ( ) 2 2.e x fxxfx += ( ) ( ) ( ) ( ) 222 e2.e.1e.1 xxx fxxfxfx +== .
Suy ra ( ) ( ) ( ) ( ) 22 2 e.dde. e xx x
xC fxxxfxxCfx + ==+= . Vì ( ) 000fC== Do đó ( ) 2 e x
x fx = . Vậy ( ) 1 1 e f = .
Câu 85: Cho hàm số ( )yfx = thỏa mãn ( ) ( ) 42 '. fxfxxx =+ . Biết ( ) 02 f = . Tính ( ) 2 2 f . A. ( ) 2 313 2 15 f = . B. ( ) 2 332 2 15 f = . C. ( ) 2 324 2 15 f = . D. ( ) 2 323 2 15 f = . Lời giải Chọn B
Ta có ( ) ( ) ( ) 42 '.dd fxfxxxxxC =++ ( ) 2 53 253 fx xx C =++ . Do ( ) 02 f = nên suy ra 2 C = Vậy ( ) 2 328 222 53 f =++ 332 15 =
Câu 86: Cho hàm số ( )fx thỏa mãn ( ) ( ) e, x fxfxx += và ( ) 02 f = . Tất cả các nguyên hàm của ( ) 2 e x fx là A. ()2eexx xC −++ B. ()2 2eexx xC +++ C. ()1ex xC −+ . D. ()1ex xC ++ . Lời giải Chọn D
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 44
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) 2 1ln. 2 fxfx x xCfxCxD fxfx ==+=++ Mà ( ) ( ) 6 012 2e0 f C D f = = = = . Suy ra : ( ) ( ) 2 5 2 22 e1e x x fxf +
Chọn C Xét phương trình ( ) ( ) 22 xfxfxx += ( )1 trên ( ) 0;+ : ( ) ( ) ( ) 1 11 2 fxfx x += ( )2 Đặ
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 45 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) eee1e1e xxxxx fxfxfxfxfxfxxC +=+===+ . Vì ( ) 02 f = nên 2 C = . Do đó ( ) ( ) 2 e2e xxfxx=+ . Vậy: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 ed2ed2de2eed22eed xxxxxxx fxxxxxxxxx =+=+=+−+=+−=
() () 2ee1e xxx xCxC =+−+=++ Câu 87: Cho hàm số ( )yfx = có đạo hàm trên ( ) 0;+ thỏa mãn ( ) ( ) 22 xfxfxx += ( ) 0; x + , ( ) 11 f = . Giá trị của biểu thức ( )4 f là: A. 25 6 . B. 25 3 . C. 17 6 . D. 17 3 . Lời giải
t
x =
ộ
. Ta
Nhân
ả
ế
ủ
=
Lấy
vế
ủ
( ) ( ) ( ) ( ) (
4 4 3 1 1 21411417 .24141 33236xfxxfff =−==+= Vậy ( ) 17 4 6 f = Câu 88: Cho hàm số ( )yfx = có đạo hàm liên tục trên và thỏa mãn điều kiện ( ) ( ) 34 6 2710, xfxfxx +−= và ( ) 10 f = . Giá trị của ( )2 f bằng A. 1. B. 1. C. 7 . D. 7. Lời giải Chọn D
( ) 1 2 gx
, ta tìm m
t nguyên hàm ( )Gx của ( )gx
có ( ) 11 ddlnln 22 gxxxxCxC x ==+=+ . Ta chọn ( ) ln Gxx =
c
2 v
c
a ( )2 cho ( ) e Gx x = , ta được: ( ) ( ) 1 2 xfxfxx x += ( ) ( ) . xfxx
( )3 .
tích phân 2
c
a ( )3 từ 1 đến 4, ta được: ( ) ( ) 44 11 .dd xfxxxx =
)
Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 34 6 22 33
+−=== Do đó ( ) 2 3
111 2710. 3111 fx xfxfx fxfxfxxx
==−+ Suy ra ( ) 3 11 .d361d2 22 fxfxxxxxfxxxx =++=++ ( ) ( ) ( ) ( ) 222217 1011718 22ffff −=−== . Vậy ( ) 2 18 f = Câu 90: Cho hàm số ( )yfx = có đạo hàm liên tục trên ( ) 1;+ và thỏa mãn ( ) ( ) ( ) ( ) 3 2.ln xfxfxxxfx −=− , ( ) 1; x + ; biết ( ) 3 e3e f = . Giá trị ( )2 f thuộc khoảng nào dưới đây? A. 25 12; 2 B. 27 13; 2 C. 23 ;12 2 D. 29 14; 2 Lời giải
111 dd. 1 xxC xx fx ( ) ( ) ( ) ( ) 4 ..1512 fxfxfxfxxx +=+ ( ) ( ) 4 .1512 fxfxxx =+ ( ) ( ) ( ) 452 .1512d36 fxfxxxxxxC =+=++ ( )1 Thay 0 x = vào ( )1 , ta được: ( ) ( ) 0.01ffCC == . Khi đó, ( )1 trở thành: ( ) ( ) 52 .361fxfxxx =++ ( ) ( ) ( ) ( ) 11 11 52263 00 00
11 1 C x fx =−+ Có ( ) 100fC== . Do đó ( ) 3 1 fxx =− Khi đó ( ) 27. f =− Câu 89: Cho hàm số ( )fx thỏamãn: ( ) ( ) ( ) ( ) 2 4 .1512 fxfxfxxx +=+ , x và ( ) ( ) 001ff == . Giá trị của ( ) 2 1 f bằng A. 5 2 B. 8. C. 10. D. 4. Lời giải Chọn B Theo giả thiết, x : ( ) ( ) ( ) ( ) 2 4 .1512 fxfxfxxx +=+
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 46
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Ch
Xét phương trình ( ) ( ) ( ) ( ) 3 2.ln xfxfxxxfx −=− ( )1 trên khoảng ( ) 1;+ : ( ) ( ) ( ) ( ) ( ) ( ) 2 3 12ln 1ln.12ln. lnln xxfxxfxxfxfxxx xxx +−=+= ( )2 Đặt ( ) 12ln ln x gx xx = . Ta tìm một nguyên hàm ( )Gx của ( )gx .
Ta có ( ) ( ) ( ) 12ln12ln1 dddln2dln lnlnln xx gxxxxx xxxx ===− ( ) 2 ln lnln2lnln x xxCC x =−+=+
Ta chọn ( ) 2 ln ln x Gx x =
Nhân cả 2 vế của ( )2 cho ( ) 2 ln e Gx x x = , ta được: ( ) ( ) 23 ln12ln 1 xxfxfx xx += ( ) ( ) 22 lnln 1 xxfxfxxC xx ==+ ( )3 . Theo giả thiết, ( ) 3 e3e f = nên thay 3 e x = vào ( )3 , ta được: ( ) ( ) 3 333 33 22
lne1 .ee3ee0 e3e fCC=+=−= . Từ đây, ta tìm được ( ) ( ) 33 2 2 lnln2 x fxf x == .Vậy ( ) 23 2;12 2 f .
91: Cho hàm số ( )fx có đạo hàm trên thỏa mãn ( ) ( ) ( ) 32 1 2 2 3.e0
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 47
ọn C
Câu
fxx x fx fx −= với x . Biết ( ) 01 f = , tính tích phân ( ) 7 0 .d xfxx A. 11 2 . B. 15 4 . C. 45 8 . D. 9 2 . Lời giải Chọn C Ta có ( ) ( ) ( ) 32 1 2 2 3.e0 fxx x fx fx
−= ( ) ( ) ( ) 3 2 213..e2.e fx x fxfxx + = ( ) ( ) ( ) 3 2 21 3..ed2.ed fx x fxfxxxx + = ( ) ( ) ( ) ( ) 3 2 312 eded1 fx x fxx + =+ ( ) 3 2 1 ee fx x C + =+ . Mặt khác, vì ( ) 01 f = nên 0 C =
Do đó ( ) 3 2 1 ee fx x + = ( ) 32 1 fxx =+ ( ) 3 2 1 fxx =+ . Vậy ( ) 7 0
.d xfxx 7 3 2 0
.1d xxx=+ ( ) 7 3 22 0
1 1d1 2 xx =++ ( ) 7 3 22 0
3 11 8 xx =++ 45 8 = .
Câu 92: Cho hàm số ( )yfx = liên tục và không âm trên thỏa mãn ( ) ( ) ( ) 2 .21fxfxxfx =+ và ( ) 00 f = . Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số ( )yfx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
48
= trên đoạn 1;3 . Biết rằng giá trị của biểu thức 2 PMm =− có dạng ( ) 113,,, abcabc−+ . Tính abc ++ A. 7 abc++= . B. 4 abc++= . C. 6 abc++= . D. 5 abc++= . Lời giả
Câu 93: Cho hàm số ( )yfx = liên tục trên \1;0 thỏa mãn ( ) 12ln21 f =+ , ( ) ( ) ( ) ( ) ( )121xxfxxfxxx +++=+ , \1;0 x − . Biết ( ) 2ln3fab =+ , với , ab là hai số hữu tỉ. Tính 2 Tab =− . A. 21 16 T = B. 3 2 T = C. 0 T = D. 3 16 T =− Lời giải Chọn D Ta có: ( ) ( ) ( ) ( ) ( )121xxfxxfxxx +++=+ , \1;0 x − ( ) ( ) ( ) ( ) 222 2 2 11 1 xxxx fxfx xx x + += ++ + , \1;0 x − ( ) 22 11 xx fx xx =++ , \1;0 x − ( ) 22 d 11 xxxfxC xx =+ ++ , \1;0 x −
i Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 22 .. .2122 11 fxfxfxfx fxfxxfxxdxxdx fxfx =+== ++ ( ) 22 1 fxxC+=+ Mà ( ) ( ) ( ) ( )2 222242 00111112 fCfxxfxxxx ==+=+=+−=+ ( ) 42 2 fxxx=+ Ta có: ( ) ( ) ( ) ( ) ( ) 3 42 1;3 1;3 22 0,1;3max3311;min13 2 xx fxxfxffxf xx + ===== + . Ta có: 261136;1;07 PMmabcabc =−=−===++= .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 49 Chuyên luyện thi:
sinh vào
10 Tốt
THPT BDKT
11; 12 Sưu tầm và biên soạn ( ) 2 1 1d 11 x xxfxC xx −+=+ ++ , \1;0 x − . ( ) 22 ln1 21 xxxxCfxC x −+++=+ + ( ) 22 ln1 21 xxxxCfx x −+++= + , \1;0 x − Ta có:
(
( ) ( ) 23 2 3.. 2 xfxxfx x fx = vì ( ) ( ) 0,0;fxx+ . ( ) ( ) 33 2 22d xxxxxxC fxfx ===+ Mà ( ) ( ) 3 2 1 12 32 x fCfx x === + . Ta có: ( ) ( ) ( ) ( ) 342 2 2 2 6 0,0; 22 xxx fxfxx x x + ==+ + + Vậy, hàm số ( ) 3 2 2 x fx x = + đồng biến trên khoảng ( ) 0;+ Mà ( ) 1;20;+ nên hàm số ( ) 3 2 2 x fx x = + đồng biến trên đoạn 1;2 .
0984164935
Tuyển
lớp
Nghiệp
Toán 10;
( ) 12ln21 f =+ và ( ) 112ln221 fCC =−++= ( ) 22 ln11 21 xxxxfx x −+++= + . ( ) 33 2.ln3 44 f =+ và ( ) 2 2ln3,33933 4416416fababTab=+===−=−= . Câu 94: Cho hàm số ( )yfx = liên tục trên ( ) 0;+ thỏa mãn ( ) ( ) ( ) 223..2 xfxxfxfx −= , với ( ) ( ) 0,0;fxx+ và ( ) 1 1 3 f = . Gọi , Mm lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số ( )yfx = trên đoạn 1;2 . Tính Mm + A. 9 10 B. 21 10 C. 5 3 D. 7 3 Lời giải Chọn C Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 22232 3..23..2. xfxxfxfxxfxxfxxfx −=−=
)
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 50
t cả các nghiệm của phương
( ) 2 FxF = trên khoảng ( ) 0;4 . Tổng S thuộc khoảng A. ( ) 6;9 . B. ( ) 2;4 . C. ( ) 4;6 . D. ( ) 0;2 . Lời giải Chọn Ta có: ( ) ( )( ) ( ) ( ) 222 444 1cossincot1cossin1coscot sinsinsin xxxxxxx Fxdxdxdx xxx ++++ ==+ Gọi ( ) 2 4 1coscot sin xx Adx x + = và ( ) 2 4 1cossin sin xx Bdx x + = Ta có: ( ) ( ) ( ) ( ) 22 3 42 24 1 1coscot12cotcot cot2cot.cot sinsin cotcot 22 xxxx Adxdxxxdx xx xx C ++ ===−+ =−++ ( ) ( ) ( ) 22 2 4 2 1cossin1cossin sin 1cos xxxx Bdxdx x x ++ == Đặt cos tx = , suy ra sin. dtxdx =− . Khi đó:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Suy ra, ( ) ( ) 415 2;1 333MfmfMm ====+= . Câu 95: Cho ( )Fx là một nguyên hàm của hàm số ( ) ( ) 2 3 4x =− x fxex . Hàm số ( ) 2 + Fxx có bao nhiêu điểm cực trị? A. 6 B. 5 C. 3 D. 4 Lời giải Ta có ( ) ( ) = Fxfx ( ) ( ) ( ) ( )( ) ( ) ( ) ( ) 2 2 2 22222.2x14 + +=++=+++− xx Fxxfxxxxxxexx ( ) ( ) ( ) ( )( ) 2 2 22 2x1122 + =+++−++ xx xxexxxx ( ) ( )( )( )( ) ( )2 2 2 1 2x1121202;1;;0;1 2 + =+++−++=−− xx xxxxxxex ( ) 2 0 +=Fxx có 5 nghiệm đơn nên ( ) 2 + Fxx có 5 điểm cực trị Câu 96: Cho ( ) ( )( ) 2 4 1cossincot sin xxx Fxdx x ++ = và S là tổng tấ
trình
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 51 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) 22 2 22222 2 2 11111111 221111.111 111 2cos1cos1 tt BdtdtdtC tt tttt t C xx ++ =−=−=−+=++ −+ −+−+ =++ −+ Do đó: ( ) 24111cotcot 2cos1cos122 xx FxABC xx =+=+−++ −+ Suy ra: ( ) 24111cotcot 22cos1cos122 xx FxFCC xx =+−++= −+ 24 11 cotcot0 cos1cos1 xx xx +−−= −+ 24 224 2coscoscos 0 sinsinsin xxx xxx ++= Với điều kiện sin0 x , ( ) ( ) ( ) 3 223 2 2 cos0 cos0 * cos 2cos021coscos1coscos0 sin cos0 cos0 117 2coscos20cos 4 x x x xxxx x x x x xx x = = −+−+= ++= = = −++= = Theo giả thiết ( ) 0;4 x nên 33 ;;2;2 2222 xxxx ===+=+ ; ;2xx==+ ; ;2xx==+. Khi đó tổng các nghiệm này sẽ lớn hơn 9 . Câu 97: Cho hàm số ( )Fx là một nguyên hàm của hàm số ( ) 2 2cos1 sin x fx x = trên khoảng ( ) 0; . Biết rằng giá trị lớn nhất của ( )Fx trên khoảng ( ) 0; là 3 . Chọn mệnh đề đúng trong các mệnh đề sau. A. 334 6 F =− B. 23 32 F = C. 3 3 F =− D. 5 33 6 F =− Lời giải Ta có:
( ) 222 2cos1cos1 dd2dd sinsinsin xx fxxxxx xxx ==− ( ) 22 dsin12 2dcot sinsinsin x xxC xxx =−=−++
Do ( )Fx là một nguyên hàm của hàm số ( ) 2 2cos1 sin x fx x = trên khoảng ( ) 0; nên hàm số

( )Fx có công thức dạng ( ) 2 cot sin FxxC x =−++ với mọi ( ) 0; x .
Xét hàm số ( ) 2 cot sin FxxC x =−++ xác định và liên tục trên ( ) 0; ( ) ( ) 2 2cos1 ' sin x Fxfx x ==
Xét ( ) ( ) 2 2cos11 '00cos2 sin23 x Fxxxkk x ====+ .
Trên khoảng ( ) 0; , phương trình ( ) '0Fx = có một nghiệm 3 x =
ảng biến thiên:
) ( ) 0; max3 3 FxFC
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 52
B
(
==−+ Theo đề bài ta có, 3323 CC −+== . Do đó, ( ) 2 cot23 sin Fxx x =−++ . Câu 98: Biết Fx là nguyên hàm của hàm số 2 cossin xxx fx x . Hỏi đồ thị của hàm số yFx có bao nhiêu điểm cực trị trên khoảng 0;4 ? A. 2. B. 1. C. 3. D. 0. Lời giải Chọn C Ta có 2 cossin ' xxx Fxfx x trên 0;4
2 cossin '0cossin0 xxx Fxfxxxx x trên 0;4 .
Đặt cossin gxxxx trên 0;4 .
x gxxxx x
Ta có '.sin02 3
Từ đó có bảng biến thiên của gx :
trên 0;4 .
g'(x)
x3 x2 x1 4π 3π 2π π 0 g(x)
+ + 0 0 0
2π π
0 0 0
0 4π -3π
Vì gx liên tục và đồng biến trên ;2 và .20gg nên tồn tại duy nhất 1 ;2 x sao cho 1 0 gx
Tương tự ta có 2 0 gx , 3 0 gx với 2 2;3 x , 3 3;4 x .
Từ bảng biến thiên của gx ta thấy 0 gx khi 1 0; xx và 23 ; xxx ; 0 gx khi 12 ; xxx và 3;4 xx . Dấu của fx là dấu của gx trên 0;4 .
Do đó ta có bảng biến thiên của Fx :
4π 0 x x1 x2 x3 0
f(x) 0 0
CĐ CT F(x)
x + + CT
Vậy hàm số yFx có ba cực trị
Câu 99: Biết ( )Fx là nguyên hàm của hàm số ( ) 2 cos xx fx x = . Hỏi đồ thị của hàm số ( )yFx = có bao nhiêu điểm cực trị? A. 1. B. 2. C. vô số điểm. D. 0. Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 53
Hơn nữa
có
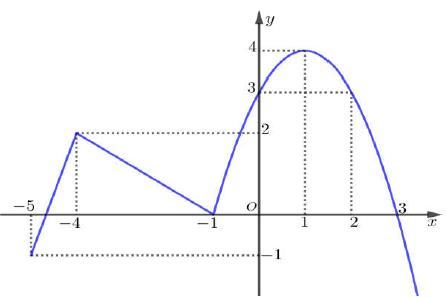

hàm số đồng biến trên toàn trục số.

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 54
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vì ( ) ( ) ( )Fxfx = nên ta xét sự đổi dấu của hàm số ( )fx để tìm cực trị hàm số đã cho. Ta xét hàm số ( ) cos gxxx =− , ta có ( ) 1sin0 gxxx =+ . Vì vậy ( )gx là
ta
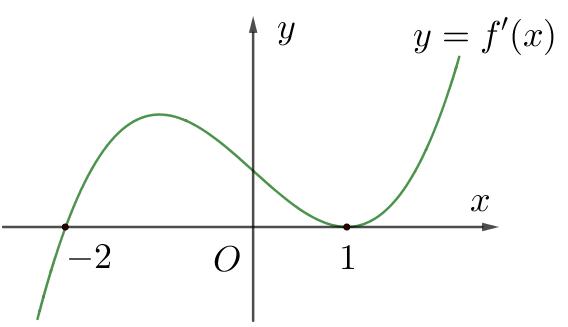
0 22 0 22 g g = −=− , do đó ( ) 0 gx = có duy nhất nghiệm ; 22 − Ta có bảng xét dấu Kết luận hàm số đã cho có một cực trị. Câu 100: Cho hàm số ( )yfx = . Đồ thị của hàm số ( ) ' yfx = trên 5;3 như hình vẽ. Biết ( ) 00 f = , giá trị của ( ) ( )2532 ff −+ bằng A. 33. B. 109 3 C. 35 3 D. 11. Lời giải Chon C
*)Parabol 2 yaxbxc =++ qua các điểm ( ) ( ) ( ) ( ) ( )2;3,1;4,0;3,1;0,3;0 nên xác định được 2 23,1yxxx =−++− suy ra ( ) 3 2 1 3 3 x fxxxC =−+++ . Mà ( ) ( ) 3 2 1 000,3 3 x fCfxxx ===−++ . Có ( ) 5 1 3 f −=− ; ( ) 22 2 3 f =
*)Đồ thị ( ) ' fx trên đoạn 4;1 qua các điểm ( ) ( )4;2,1;0 nên ( ) ( ) ( ) 2 2 22 '1 332 x fxxfxxC =+=++ .
Mà ( ) ( ) 2 2 55212 122 333232 x fCfxx −=−=−+−=−=+− , hay ( ) 14 4 3 f −= .
*) Đồ thị ( ) ' fx trên đoạn 5;4 qua các điểm ( ) ( )4;2,5;1 nên ( ) ( ) 2 3 3 '31414 2 x fxxfxxC =+=++ Mà ( ) ( ) ( ) 2 3 3.4 1414 414.4 323fC −=+−+= suy ra 3 82 3 C = Ta có ( ) ( ) 2 38231 145 236 x fxxf=++−=− . Từ và ta được ( ) ( ) 3135 253222
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
55
ố
(
số ( )yfx = tại điểm có hoành độ 2 x = là A. 1620yx=−− . B. 1620yx=− . C. 1620yx=+ . D. 1620yx=−+ . Lời giải Chọn B ( ) ( ) ( ) ( ) 232 4343 fx fxxxxfxfxxx x +=++=+ Lấy nguyên hàm hai vế ta được: ( ) ( ) 324343d xfxxxxxxC =+=++ . Với 1 x = ta có: ( ) 12 fC =+ . Theo bài ra ( ) 12 f = 220 CC +==
33 ff−+=−+= . Câu 101: Cho hàm s
( )yfx = có đạo hàm liên tục trên ( ) 0;+ thỏa mãn ( ) ( ) 2 43 fx fxxx x +=+ và
) 12 f = . Phương trình tiếp tuyến của đồ thị hàm
Vậy ( ) ( ) 4332 xfxxxfxxx =+=+
Ta có: ( ) 2 32 fxxx =+ ; ( ) 216 f = ; ( ) 212 f =
Phương trình tiếp tuyến của đồ thị hàm số ( )yfx = tại điểm có hoành độ 2 x = là: ( ) 16212yx=−+ 1620yx =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 56



CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 1. NGUYÊN HÀM MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO Câu 102: Biết ( ) ( ) 2020 * 2022 111 d.,1;, 11 b x x xCxab ax x =+ + + Tính giá trị biểu thức a A b = A. 2021. B. 2. C. 3. D. 2020. Lời giải Chọn B Ta có ( ) ( ) ( ) 2020 220202021 20222 11111111 d.dd. 12114022111 x xxxx xxC xxxxxx ===+ ++++ ++ Suy ra 4022 2021 a b = = Vậy 2 a A b == Câu 103: Cho 34 2 34 x fx x =+ + . Khi đó ( ) Ifxdx = bằng A. 2 34 ln 34 x x IeC x + =+ + B. 82 ln1 33 IxxC =−−++ C. 8ln1 33 x IxC =−++ D. 8ln1 3 IxxC =−++ Lời giải Chọn B Đặt: 3481141 1. 343434831 xtt ttx xxxt −−+ =−=== +++− Theo giả thiết: ( ) ( ) ( ) 4110228 .2 3131331 tt ft ttt +− =+==+ Nên: ( ) ( ) 28128.ln1 33133 fxfxdxxxC x =+=−−+ Câu 104: Hàm số 4()(1) =− fxxx có họ các nguyên hàm là CHƯƠNG III NGUYÊN HÀM TÍCH PHÂN ỨNG DỤNG TÍCH PHÂN
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 65 (1)(1)()65=−+ xx FxC . B. 65 (1)(1)()65=++ xx FxC . C. 65 (1)(1)()54=−+ xx FxC . D. 65 (1)(1)()54=++ xx FxC . Lời giải Chọn B Đặt 1 txdtdx =−=− Khi đó ( ) ( ) 445465 11 (1).1.. 65 −=−−=−=−+ xxdxttdtttdtttC Vậy 6565 4 (1).(1)(1)(1)(1) 6565 −=−+=++ xxxx xxdxCC Câu 105: Nếu 1 12() x x e dxfxxC e =−+ + thì ()fx bằng A. e1 x + . B. e x . C. e1 x . D. ( )lne1 x + . Lời giải Chọn D Ta có: 121 112 111 x xxx e dxdxdxdx eee =−=− +++ Đặt: 1 1 1 xx euedxdudxdu u +=== Nên: ( ) ( ) 111 11111 lnlnln1 1111 x x xx ue dxduduCCxeC euuuuue ==−=+=+=−++ +−−+ Vậy: ( ) ( ) ( ) 1 1 2ln12ln1 1 x xx x e dxxxeCexC e =−−++=+−+ + . Câu 106: Xác định các hệ số ,, abc để hàm số ( ) ( ) 2 32 Fxaxbxcx =++− là một nguyên hàm của hàm số ( ) 32 fxxx =− trên khoảng 3 ;. 2 − Lời giải Ta có ( )d32d. fxxxxx =− Đặt 2 2 3 3232dd. 2 u uxuxxxuu =−=−== Nguyên hàm trở thành ( ) 25 243311 ..d3d 2225 uu uuuuuuuC =−=−+
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 3 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( )2 2 2 11 32323232 210 3962 32 21055 217 32. 5510 xxxxC xxxxC xxxC =−−−−−+ =−−+−−+ =−++−+ ( ) 2 2 5 2171 32. 55105 7 10 a Fxxxxb x =− =−++−= = Câu 107: Cho ( )Fx là một nguyên hàm của hàm số ( ) ( )2022 2 .1fxxx=+ thỏa mãn ( ) 1 0 4046 F = , giá trị của ( )1 F bằng A. 20232 . B. 20232 2023 . C. 20232 . D. 20222 2023 . Lời giải Chọn D ( ) ( )2022 2 .1fxxx=+ ( ) ( ) ( ) ( ) ( ) ( ) 2 222202220222023 d11 d.1d =11 22.2023 x fxxxxxxxCFx + =++=++= ( ) ( )2023 2 111 0010 40462.20234046 FCC =++== . ( ) ( ) ( ) 2022 2023 2 12 11 2.20232023 FxxF=+= Câu 108: Khi tính ( )( )3 d 211 x I xx = ++ , người ta đặt ( ) = tgx thì 2d It = . Biết ( ) 3 4 5 = g , giá trị của ( ) ( )01 + gg là A. 236 2 + B. 26 2 + C. 16 2 + D. 36 2 + Lời giải Chọn B Ta có ( )( ) ( ) 3 2 dd 21121 1 1 xx I x xx x x == + ++ + + .
fxfx
fxfx
)
)
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 4
Đặt ( ) (
22 21dd
xxx zzz x xx xx xx + === + ++ ++ ++
21
x
+
+
0
xx
==++=++= ++ (
+
Chọn C Xét ( ) ( ) ( ) 22 .d123d fxfxxxxx =++ ( ) 3 23 3 fx xxxC=+++ Do ( ) 01 f = nên 1 3 C = . Vậy 3 32 ()3331 fxxxx =+++ với 1;2 x − Ta có: ( ) ( ) 2 322 3 963 0,1;2 3(3331) xx fxx xxx ++ =− +++ nên ( )fx đồng biến trên đoạn 1;2 . Vậy ( ) ( ) ( ) 3 3 1;2 1;2 min(1)2,max243 x x fxffxf − − =−=−== . Câu 110: Họ các nguyên hàm của hàm số ( ) ( )( )( ) ( ) 2 12323fxxxxxx =++++ là A. ( ) ( ) ( ) 5 2 2243 3 4 33 53 xx xxxxC + +++++ B. ( ) ( ) 2242 33 xxxxC ++++
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
)
d2d 12121 211 11
Khi đó
2d22 1
IzzCC x
==+=+
Mà
2121 2d222 11
IttCCtCCt xx ++
) ( ) ( ) 00 219 4 15 x tgxgxCgC x
==+=+ + 00 39 0 55 CC =+= . Do đó ( ) ( ) ( ) 21326 011 122 x gxgg x ++ =+=+= + . Câu 109: Cho hàm số ( )fx xác định trên đoạn 1;2 thỏa mãn ( ) 01 f = và ( ) ( ) 22 .123 fxfxxx =++ . Giá trị nhỏ nhất và giá trị lớn nhất của hàm số ( )fx trên đoạn 1;2 là: A. ( ) ( ) 3 3 1;2 1;2 min2,max40 x x fxfx − − == B. ( ) (
3 3 1;2 1;2 min2,max40 x x
− − =−= C. ( ) ( ) 3 3 1;2 1;2 min2,max43 x x fxfx − − =−= . D. ( ) (
3 3 1;2 1;2 min2,max43 x x
− − == . Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 5 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn C. ( ) ( ) ( ) 222543 53312.3 xxxxxxC ++++++ D. ( ) ( ) ( ) 5 2 2243 3 4 33 45 xx xxxxC +−+−+ Lời giải Chọn A ( ) ( )( )( ) ( ) ( )( ) ( ) 2 2 22 d12323d33223d Ifxxxxxxxxxxxxxx ==++++=++++ . Đặt ( ) 2 3d23d txxtxx =+=+ . Suy ra: ( ) ( ) ( ) 2 2 2432 2d2d44d Itttttttttt =+=+=++ 5 43 4 53 t ttC=+++ ( ) ( ) ( ) 5 2 2243 3 4 33 53 xx IxxxxC + =+++++ . Câu 111: Họ các nguyên hàm của hàm số ( ) ( ) ( ) 2020 2022 2021 2022 x fx x = + là A. 2020 12021 20222022 x C x + + . B. 2021 20212021 40432022 x C x + + . C. 2021 12021 4043.20212022 x C x + + D. ( )2021 14043 . 20212022 C x + + Lời giải Chọn C Ta có ( ) ( ) ( ) ( ) 2020 2020 20222 202120211 ddd 2022 20222022 x x Ifxxxx x xx === + ++ Đặt ( ) ( ) 22 2021404311dddd 2022404320222022 x ttxtx x xx === + ++ Suy ra: 2020202111 d 40434043.2021 ItttC ==+ ( ) 2021 d12021 4043.20212022 x fxxC x =+ + . Câu 112: Họ các nguyên hàm của hàm số ( ) 3 3 4 xx fx x = là A. 2 3 2 1 1 C x −+ . B. 4 3 2 31 .1 8 C x −−+ . C. 4 3 2 1 6.1 C x −−+ . D. 4 3 2 31 1 4 C x −−+ . Lời giải Chọn B
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 6 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 3 3 3 2 43 1 1 ddd xx x Ifxxxx xx === . Đặt 322 3 2233 11231 113dddd 2 ttttxttx xxxx =−=−=−−= . Suy ra: 4 234 3 2 33331 .dd.1 2288 IttttttCIC x =−=−=−+=−−+ . Câu 113: Họ các nguyên hàm của hàm số ( ) sin 2sincos x fx xx = + là A. ln2sin xxC ++ . B. 21 .ln2sincos 55 xxxC −++ . C. 21 .ln2cossin 55 xxxC +−+ . D. 12 .ln2sincos 55 xxxC +++ . Lời giải Chọn B ( ) ( ) ( ) 212sincos2cossin sin 55 ddd 2sincos2sincos xxxx x Ifxxxx xxxx +−− === ++ 212cossin212cossin .ddd 552sincos552sincos xxxx xxx xxxx =−=− ++ . Xét 1 2cossind 2sincos xx Ix xx = + . Đặt ( ) 2sincosd2cossind txxtxxx =+=− Suy ra: 11 1 dlnln2sincos IttCIxxC t ==+=++ Vậy: 21 .ln2sincos 55 IxxxC =−++ . Câu 114: ( ) ( ) 2 5473 1cos2d xxx xeexx −+− ++ có dạng ( )2 1 sin2 62 x ab exC + ++ , trong đó , ab là hai số hữu tỉ. Tính ab + . A. 4 B. 3 C. 5 D. 6 Lời giải Chọn A Ta có: ( ) ( ) 2 5473 1cos2d xxx xeexx −+− ++ . ( ) ( ) ( ) 2 5473 1cos2d xxx xexx −++− =++ ( ) ( )2 1 1dcos2d x xexxx + =++
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Để tìm ( ) ( ) 2 54 73 1cos2d xx x xeexx −+ ++ ta đặt ( ) ( )2 1 1 1d x Ixex + =+ và 2 cos2d Ixx = và tìm 12 , II *Tìm ( ) ( )2 1 1 1d x Ixex + =+ . Đặt ( ) ( )(
xxx xeexx −+− ++ ( )2 1 1212 11 sin2 22 x IIeCxC + =+=+++ ( )2 1 11 sin2 22 x exC + =++ Suy ra để ( ) ( ) 2 5473 1cos2d xxx xeexx −+− ++ có dạng ( )2 1 sin2 62 x ab exC + ++ thì 3 a = , 1 b = Vậy 4 ab+= Câu 115: Tính ( ) ( ) 22 2 2 212ln.ln d ln xxxx Gx xxx +++ = + A. 11 ln GC xxx =−+ + . B. 11 ln GC xxx =−++ + . C. 11 ln GC xxx =−+ + . D. 11 ln GC xxx =++ + . Lời giải Chọn A Ta có: ( ) ( ) 22 2 2 212ln.ln d ln xxxx Gx xxx +++ = + ( ) 222 2 2 2lnln d ln xxxxxx x xxx ++++ = + ( ) ( ) ( ) 2 2 2 ln1 d ln xxxx x xxx +++ = + ( )2 2 11 d ln x x x xxx + =+= + ( )2 2 11 dd ln x xx x xxx + + + , đặt ( )2 1 d ln x Jx xxx + = + Xét nguyên hàm: ( )2 1 d ln x Jx xxx + = +
0984164935
) ( ) 2 1;d211d21d txtxxxxx =+=++=+ . ( ) ( ) ( ) 22 11 111 111 1dd 222 xx tt IxexeteCeC ++ =+==+=+ , trong đó 1C là 1 hằng số. *Tìm 2 cos2d Ixx = . 22 1 cos2sin2 2 IxdxxC ==+ . Ta có ( ) ( ) 2 5473 1cos2d
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 8 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn + Đặt: 11 lnd1dd x txxtxx xx + =+=+= 2 111 d ln JtCC ttxx ==+=+ + Do đó: 11 ln GC xxx =−+ + Câu 116: Giả sử ( )Fx là một nguyên hàm của ( ) ( ) 2 ln3 x fx x + = sao cho ( ) (
(
ằ
A.
36 . B.
. C.
36 + . Lời giải Chọn A Cách 1: Ta có hàm số ( )
liên tục trên các khoảng
)
và
+ . Tính ( ) 2 ln3 d x x x + Đặt ( ) 2 ln31dd 3 dd113 33 ux ux x x x v v x xx =+ = + + = =−−=− Suy ra: ( ) ( ) ( ) 2 ln331 dln3d 33 x x Fxxxx xxx + + ==−++ ( ) 31ln3ln 33 x xxC x + =−+++ . •Xét trên khoảng ( )3;0 , ta có: ( ) 1 1 2ln2 3 FC −=+ ; ( ) 1 2 1ln2 3 FC −=+ •Xét trên khoảng ( ) 0;+ , ta có: ( ) 22 48 1ln4ln2 33 FCC =−+=−+ ; ( ) 2 51 2ln5ln2 63 FC =−++ Suy ra: ( ) ( ) 210FF−+= 12 18 ln2ln20 33 CC ++−+= 12 7ln2 3 CC += Do đó: ( ) ( ) 12 251 12ln2ln5ln2 363 FFCC −+=++−++ 2517105 ln2ln5ln2ln2ln2ln5 363336 =−++=− Cách 2: •Xét trên khoảng ( )3;0 , ta có: ( ) ( ) ( ) ( ) 11 2 22 ln3 12dd0,231 x FFfxxxA x + −−−==→ ( )1
) 210FF−+= . Giá trị của
) ( )12FF −+ b
ng
105ln2ln5
0
7ln2 3 . D. 23ln2ln5
fx
(
3;0
( ) 0;
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
1 ln2 2 B. 432 4 C. 322 2 −+ D. ln2 Lời giải Chọn D Ta có ( ) ( ) ( ) 2sin 4sincosdd sin221sincossin221sincos x xx fxxx xxxxxx == ++++++ Đặt sincosd(sincos)d(sincos)dd txxtxxxxxxt =+=−−−=− và 2 sin2x1 t =− khi đó ( ) ( ) ( )2 22 dd11 121211sincos1 1 ttdt fxCC tttttxx t ==−=−=+=+ −+++++++ + Mặt khác 1 0 22 fC == Khi đó ( ) /2/2 00 1 ddln2 sincos1 fxxx xx == ++ . Câu 118: Cho hàm số ( )fx liên tục và thỏa mãn ( ) ( )0,1;3fxx . Biết rằng ( ) ( ) ( ) 23.13.. += xx efxefxfx , ( )1;3 x và ( ) 4 3 2 = fe , khi đó giá trị của 3 2 f thuộc khoảng nào dưới đây? A. 11 ; 32 B. 1 0; 3 C. 12 ; 23 D. 2 ;1 3 Lời giải Chọn B
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn •Xét trên khoảng ( ) 0;+ , ta có: ( ) ( ) ( ) ( ) 22 2 11 ln3 21dd0,738 x FFfxxxB x + −==→ ( )2 •Lấy ( )1 cộng ( )2 theo vế ta được: ( ) ( ) ( ) ( ) ( ) ( ) 1221120,969 FFFFABFFAB −+−−−=+−+=+ Câu 117: Cho hàm số ( )fx có 1 22 f = và ( ) ( ) ( ) 2sin 4;0;sin2+21sincos x fxx xxx = ++ . Khi đó ( ) /2 0 d fxx A.
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 10 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn + Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 23233 .13...12. xxxx efxefxfxefxefx +=+= ( ) ( ) ( ) ( ) 2333 .12.. xxx efxefxefx +=− ( ) ( ) ( ) ( ) 2 33.12. xx efxefx += ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 33 22
=−= + . Suy ra: 31 0,180; 23 f Câu 119: Cho biết 22022222 .ln(+1).(x1).ln(x1)x xxdxabC =++−+ với , ab . Mệnh đề nào sau đây đúng? A. 2 ab = B. ab = C. 1 ab=+ D. 2022 ab = Lời giải Chọn B Ta có: 220222 .ln(x+1)2022.ln(x+1) Mxdxxdx == Đặt 2 2 2 2 ln(x1)dudx . x1 dv2022xdx1011.x x u v = =+ + = = Suy ra 2 22 2 2.1011..x 1011.x.ln(x1)x x1 x Md =+− + 2 222 2 1011.x 1011.x.ln(x1)(x) x1 d =+− + 222 2 1011 1011.x.ln(x1)1011(x) x1 d =+−− + 2222 1011.x.ln(x1)1011x1011.ln(x1) C =+−+++ 222 1011.(x1).ln(x1)1011x C =++−+ . Câu 120: Cho ( ) xFxxe =− là một nguyên hàm của ( ) 2x fxe . Tìm họ nguyên hàm của ( ) 2x fxe A. ( )2 x xeC −+ B. ( ) 21 x xeC−+ C. ( )1 x xeC −+ D. 1 2 x x eC + Lời giải
33 .1.111 .1.122 xx xx efxefx dxdx efxefx ++ == ++ ( ) 3 11 (*) 2 .1 x xC efx =+ + . + Vì ( ) 4 3 2 fe = nên ( ) *113 22 CC =+= + Do đó: ( ) ( ) ( ) 2 3 3 1131 223. .1 x x x xfx xe efx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 11 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn C Theo giả thiết suy ra ( ) ( ) ( ) ( ) 2 .1xxx Fxfxexexe ==−=−+ Tính ( ) 2x Ifxedx = Đặt ( ) ( ) 22 2 xx ueduedx dvfxdxvfx == == ( ) ( ) ( ) ( ) 222121 xxxxx IefxfxedxxexeCxeC =−=−+++=−+ . Câu 121: Phát biểu nào sau đây là đúng? A. esindecosecosd. xxx xxxxx =+ B. esindecosecosd. xxx xxxxx =−+ C. esindecosecosd. xxx xxxxx =−− D. esindecosecosd. xxx xxxxx =− Lời giải Chọn B Đặt sinddcos eded . xx xxvvx uux ==− == Lúc đó, ta có: esindecosecosd. xxx xxxxx =−+ Câu 122: Cho hàm số ( )yfx = thỏa mãn ( ) ( ) ( ) '1e,00 x fxxf=+= và ( ) ( ) dex fxxaxbc =++ với ,, abc là các hằng số. Khi đó: A. 2. ab+= B. 3. ab+= C. 1. ab+= D. 0. ab+= Lời giải Chọn D Theo đề: ( ) ( ) '1ex fxx=+ .
( ) ( ) ( ) ( ) ( ) ( ) 'd1ed1ee 1eee xxx xxx fxxxxfxxdx fxxCxC =+=+− =+−+=+ Mà ( ) ( ) 0 000.e00ex fCCfxx =+=== . ( ) ( ) dedeedee1e xxxxxx fxxxxxxxCxC ==−=−+=−+ Suy ra 1;10abab ==−+= . Câu
Tính 2 lnd xxx . Chọn kết quả đúng? A. ( ) 22 1 2ln2ln1 4 xxxC +++ B. ( ) 22 1 2ln2ln1 4 xxxC −++ C. ( ) 22 1 2ln2ln1 2 xxxC −++ .
22 1 2ln2ln1 2 xxxC +++ . Lờ
giải Chọn B
Nguyên hàm 2 vế ta được
123:
D. ( )
i
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 12
v =
=
=
=
Khi đó ( ) ( ) ( ) ( ) ( ) 332 .1d1.3d fxxxxfxfxxx +=+− ( ) 22 22 26d4 xxxC xx =−−−−=−+ Câu 125: Cho ( )Fx là một nguyên hàm của hàm số ( ) 2 lnsincos sin xx y x = và 1 2 F = . Hệ số tự do của ( )Fx thuộc khoảng A. 5 ;3 2 B. 5 2; 2 C. 3 ;2 2 D. 3 1; 2 Lời giải Chọn A Ta tìm họ các nguyên hàm của hàm số ( ) 2 lnsincos sin xx y x =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt 2 2 1 2ln. ln 2 duxdx ux x dvxdx x
. Khi đó: 1 2 22 lnd.ln.ln 2 I x xxxxxxdx =− Xét 1I có: 2 1 ln 2 dudx ux x dvxdx x v = =
= = . Khi đó: 222 1 1 .ln.ln 2224 xxx IxxdxxC =−=−+ Suy ra: 2222 222 lnd.ln.ln(2ln2ln1) 2244 xxxx xxxxxCxxC =−++=−++ Câu 124: Biết ( ) 2 1 Fx x = là một nguyên hàm của ( )fx x . Khẳng định nào sau đây đúng? A. ( ) ( ) 3 2 2 .1d4 fxxxxC x
+=++ B. ( ) ( ) 3 2 2 .1d4 fxxxxC x +=−+ C. ( ) ( ) 3 2 2 .1d4 fxxxxC x
+=−−+ D. ( ) ( ) 3 2 2 .1d fxxxxC x +=++ Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) 32 22fxfxFxfx xxxx ==−=− . Đặt ( ) 3 1 dd ux vfxx =+ = . Ta có ( ) 2 d3duxx vfx = =
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42
Cư Trinh Thuận
TP Huế
Page 13
tầm và
soạn Đặt 2 lnsincos cossin
1 dd
sin uxx xx ux xx vx vx x ( ) 2 lnsincos
xx x x ( ) ( ) (
1cotlnsincos1cotd
+ =−−−− ( ) ( ) cossin 1cotlnsincosd
xxxx x + =−−− (
Do
FCCC =−+==+ Vậy hệ số tự do của ( )Fx thuộc khoảng 5 ;3 2 Câu 126: Cho 2 () Fxx là nguyên hàm của hàm số 2 (). x fxe . Tìm nguyên hàm I của hàm số 2 '(). x fxe A. 2 2 IxxC B. 2 22
2
.
2 2
. L
Chọn B Ta
+=−++
ọ
Đặt 2 2 3 1 2 = += =− = x x
xu ve edxdv
Nguyễn
Hòa
ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu
biên
dd sincos
cot1
d sin
) cossin
sincos xx xxxxx xx
sin xx
) ( ) ( ) 1cotlnsincoslnsinxxxxxC =−−+−+
1112,57 222
IxxC C.
IxxC
D.
IxC
ời giải
có : 2 () Fxx là nguyên hàm của hàm số 2 (). x fxe ; suy ra : 22'()().2().xx Fxfxexfxe Ta có: 2 '(). x Ifxedx Đặt: 22 2 ()() xx ueduedx dvfxdxvfx Suy ra: 222 ().2().22 xx IfxefxedxxxC Câu 127: Biết ( ) ( ) 22 1 32
xx xedxexnC m với , mn . Khi đó, tổng 22 + mn có giá trị bằng A. 10. B. 65. C. 41. D. 5. Lời giải Ch
n B
dudx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
(
( )
22222
2
3332
+=−++=−+−− =−+−+=−+++=−++
=−++ xxxxx xxxx x xedxxeedxxeedx xeeCexCexC
4765+=+=mn Câu 128: ()Fx là một nguyên hàm của ()cos fxx = trên khoảng ( ) 0;+ và thoả mãn ( ) 2 1 F = . Biết 2 9 a Fc b =+ ( ,, abc là các số nguyên dương và 4 a ), tính abc ++ . A. 7 abc++= . B. 10 abc++= . C. 8 abc++= . D. 13 abc++= . Lời giải Chọn C Ta có ()cosd Fxxx = . Đặt 2 d2d txxtxtt === . cosd2cosd2cosd xxtttttt == Đặt dd dcosdsin. utut vttvt == == cosdsinsindsincos ttttttttttC =−=++ . Vậy ()2sin2cos FxxxxC =++ ( ) 2 12.sin2cos13 FCC =++== Suy ra 2 23sin2cos34 93333 F =++=+ 10 abc ++= . Câu 129: Cho ( )Fx là một nguyên hàm của hàm số ( ) 3 e x fx = và ( ) 02 F = . Hãy tính ( )1 F A. 15 6 e B. 10 4 e . C. 15 4 e . D. 10 e . Lời giải Chọn C Ta có ( ) 3 ded x Ifxxx == . Đặt 3 3 xtxt == 2 d3d xtt= khi đó 3 2 ed3ed xt Ixtt == .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) ( ) ( ) ( )
( )
2222
1111
2224 111117 33 242222 1 27 4
exC Suy ra, 4;7==mn . Vậy 2222
ttttt =−=− . Vậy ( ) 2 3e6ee ttt IttC =−−+ ( ) ( ) 333 3 2 3 3e6ee xxx FxxxC =−−+ Theo giả thiết ta có ( ) 024FC==− ( ) ( ) 333 3 2 3 3e6ee4 xxxFxxx =−−− ( ) 15 14 e F −=−
Ta có ( ) ( ) 2 ., x fxefxx = ( ) ( ) 2 x fx e fx
= ( ) ( ) 2 x fx dxedx fx
= ( ) ( ) ( ) 2 1 x dfxedx fx = ( ) ( )1* x eC fx −=+
Thay 0 x
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42
Cư Trinh Thuận
TP Huế ĐT:
Page 15 Chuyên
10
12 Sưu tầm và biên soạn Đặt 2 2dd eddet t ttu tu v tv = = = = ( ) 2 3e2ed tt Ittt=− 2 3e6ed tt ttt=− . Tính ed ttt Đặt dd edde tt tutu tvv == == edeedee ttttt
số (
=
Nguyễn
Hòa
0984164935
luyện thi: Tuyển sinh vào lớp
Tốt Nghiệp THPT BDKT Toán 10; 11;
Câu 130: Cho hàm
)yfx
liên tục và khác không với mọi x thỏa mãn ( ) 01 f =− và ( ) ( ) 2 ., x fxefxx
= . Giá trị của ( )1 f bằng A. 1 B. e C. e D. 1 e Lời giải Chọn D
= vào ( )* ta được ( ) 0 11 10 01 eCCC f −=+−=+= . Do vậy ( ) ( ) ( ) 111 1 x x efxf fxee −==−=− . Câu 131: Giả sử hàm số ()yfx = liên tục, nhận giá trị dương trên (0;) + và thỏa mãn (1) fe = , ()()31 fxfxx =+ , với mọi 0 x . Mệnh đề nào sau đây đúng? A. 3(5)4 f . B. 11(5)12 f . C. 10(5)11 f . D. 4(5)5 f . Lời giải Chọn C
Do ()yfx = liên tục, nhận giá trị dương trên (0;) + và thỏa mãn (1) fe = , ta có ( ) ( ) ( ) 21 31 33 4121 ln1ln31 3333 x fCCfxxfxe +− =+=−=+−= . ( ) ( ) 7 3 510,312310511. fef = Câu 132: Cho hàm số liên tục trên khoảng và với mọi . Tính tổng biết rằng và . A. B. C. D. Lời giải Chọn D Ta có : Mà Câu 133: Cho hàm số ()fx thỏa mãn (1)2 f = và ( ) ( ) 2 2221()[()]1 ' xfxfxx+=− với mọi (0;) x + Tính giá trị (3) f
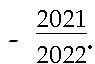
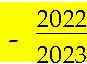
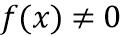
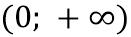
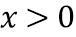

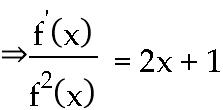
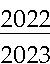
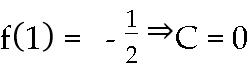
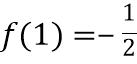

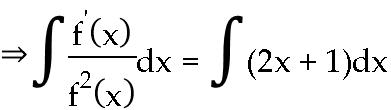
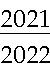
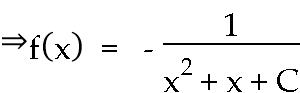
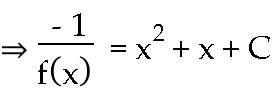

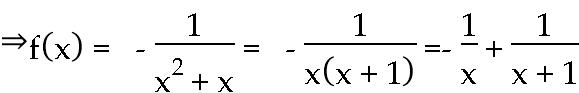
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
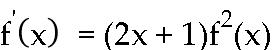
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
=+=++
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 1 2 ()1()1 ()()31 ()()3131 2 ln31ln31. 3 fxfx fxfxxdxdx fxfxxx fxxdxfxxC
=+== ++
A. 8 3 B. 4 C. 10 3 D. 5 Lời giải Chọn C
Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 22 22 2
'1 1'1 1 +=−= + fx x xfxfxx fx x hay ( ) ( ) 2 2
' ' 1 =− + fx x x fx Lấy nguyên hàm hai vế: ( ) 2 1 1 −=−+ + x C fxx . Thay ( ) 2 11 1:0 111 =−=−+= + xCC f suy ra ( ) ( ) 2 110 3 3 + == x fxf x Câu 134: Cho hàm số yfx có đồ thị , C fx có đạo hàm xác định và liên tục trên khoảng 0; thỏa mãn điều kiện 2 ln.,0;.fxxfxx Biết 0,0;fxx và 2. fe Viết phương trình tiếp tuyến với đồ thị C tại điểm có hoành độ 1 x . A. 2 2. 3 yx B. 2 3 y C. 2 1. 3 yx D. 2 3 y Lời giải Chọn D Ta có 2 2 2 1 ln.lnln fx fxxfxxx fxfx 1 lndxlnxxxxC fx Với xe ta có 1 ln eeeC fe mà 2. fe 1 2 C Suy ra 1 1 ln 2
fx xxx Khi đó 2
2 1 3 1ln1.10 f ff Phương trình tiếp tuyến với đồ thị C tại điểm có hoành độ 1 x là: 2 11. 3 yfxxf
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 18 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 135: Cho hàm số ( )fx liên tục trên ( ) 0;+ và thỏa mãn ( ) ( ) ( ) ( ) 2 ln.'2,0;.fxxxfxxfxx=++ Biết ( ) 2 1 fe e = Tính ( )2 f A. ln2 4 B. ln2 2 C. ln2 2 D. ln2 8
Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 2 2 ln.'2ln.'2 1 ln.' 1 ln.'22 ln '2 fxxxfxxfxfxxxfxxfx fxxfx x fxxfxxfxx x fx x x fx =+−= −== = Suy ra ( ) ( ) 2 2 lnln xx xcfx fxxc =+= + Từ có ( ) 2 1 0 fec e == . Suy ra hàm số ( ) 2 ln x fx x = . Khi đó ( ) ln2 2 4 f = . Câu 136: Cho hàm số ( ) 0 fx thỏa mãn điều kiện ( ) ( ) ( ) '2 23. fxxfx =+ và ( ) 1 0 2 f = . Biết tổng ( ) ( ) ( ) ( ) ( )12...201720212022 a fffff b +++++= với * , ab và a b là phân số tối giản. Mệnh đề nào sau đây đúng? A. 1 a b − . B. 1 a b . C. 3035 ab+= . D. 3035 ba−= . Lời giải Chọn D Biến đổi ( ) ( ) ( ) '2 23. fxxfx =+ ( ) ( ) ' 2 23 fx x fx =+ ( ) ( ) ( ) ' 2 23 fx dxxdx fx =+ ( ) ( ) 2 2 11 3 3 xxCfx fxxxC −=++=− ++ . Mà ( ) 1 0 2 f = nên 2 = . Do đó ( ) ( )( ) 2 11 3212 fx xxxx =−=− ++++ Khi đó
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 19 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán
11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( )12...20212022 a ffff b =++++ 1111 ..... 2.33.42022.20232023.2024 =−++++ 11111111 23342022202320232024 =−−+−++−+− 11 22024 =−− 1011 2024 = Với điều kiện , ab thỏa mãn bài toán, suy ra:
a b =− =
ba −= . Câu 137: Cho hàm số ( )fx xác định và có đạo hàm ( ) ' fx liên tục trên đoạn 1;3 và ( ) 0 fx với mọi 1;3 x , đồng thời ( ) ( ) ( ) ( ) ( ) ( ) 2 22 '11 fxfxfxx++=− và ( ) 11. f =− Biết rằng ( ) 3 1 ln3,,.fxdxabab=+ Tính tổng 2Sab =+ A. 1. S =− B. 2. S = C. 0. S = D. 4. S =− Lời giải Chọn A Ta có: 2 2222. 4 '()(1()) '()(1())[(())(1)](1) () fxfx fxfxfxxx fx + +=−==− Lấy nguyên hàm 2 vế ta được 2 2 4 '()(1())(1) () fxfx dxxdx fx + =− 2 2 4 3 432 3 32 23 3 (12()())'() (1) () 111(1) 2(()) ()()()3 111(1) 3()()()3 13()3()(1) 3()3 fxfxfx dxxdx fx x dfxC fxfxfx x C fxfxfx fxfxx C fx ++ =− ++=+ −−−=+ ++− −=+ Mà 1331 (1)1 33fCC −+ =−=−=== 2323 33 3 3 33 3 13()3()(1)113()3()1(1) 3()333()33 (1())11 ()()(1)1(1)(). fxfxxfxfxx fxfx fx xxfx fxfxx ++−++− −=++=− +− =−−+=−= Vậy 33 11 13 ()ln||ln3 1 fxdxdxx x ==−=− . Suy ra 1;0ab=−= hay 1 ab+=−
0984164935
10;
1011 2024
3035.
=−+ .
Suy ra ( ) ( ) 2 3 2 32 x fxfxxxC =−++ . Hơn nữa ( ) ( ) 003ff == suy ra 9 C =
Tương tự vì ( ) ( ) ( ) 2 2 fxfxfx = nên ( ) 2 23 2 29 32 x fxxx =−++ .
Suy ra ( ) 23 2342 1 21 29d18 3233 xx fxxxxxxxC =−++=−+++ , cũng vì ( ) 03 f = suy ra ( ) 3 242 1 189 33 x fxxxx =−+++ . Do đó ( ) 2 128 f = Câu 139: Cho hàm số ( )yfx = dương và liên tục trên ( ) 0;+ , có ( ) 03 f = và thỏa mãn ( ) ( ) ( ) ( ) ( ) ( ) 221'111fxxfxfxxfx++=++− . Khi đó giá trị của ( ) ( )02ff + bằng
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 138: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) 2 2 .21fxfxfxxx +=−+ , x và ( ) ( ) 003ff == . Giá trị của ( ) 2 1 f bằng A. 28. B. 22. C. 19 . 2 D. 10. Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( ) 2 fxfxfxfxfx =+ . Do đó theo giả thiết ta được ( ) ( ) 2 21fxfxxx
B.
ả
Chọn D Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 221'111fxxfxfxxfx++=++− ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 2 2 2 22 2 22 0 00 222 2 11'11 11' 111'1 1 11'1114 32101432124 21223 fxxfxfxxfx fxxfxfx xxfxx fx xfxdxxdxxfx fff ff +++=++ +++ =+++=+ + ++=+++= +−+=+−= +== Vậy ( ) ( ) 0223ff+=
A. 13 +
33 + C. 3 D. 23 Lời gi
i
. Tính 2 Tab =− . A. 21 16 T = . B. 3 2 T = . C. 3 16 T = . D. 0 T = . Lời giải
Chọn C
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 21 Chuyên
thi:
tầm và
soạn Câu 140: Cho hàm số ( )yfx = liên tục trên \1;0 thỏa mãn (
f =+ , ( ) ( ) ( ) ( ) ( )121xxfxxfxxx +++=+ , \1;0 x − . Biết (
fab =+
vớ
,
số hữu tỉ
Hòa
0984164935
luyện
Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu
biên
) 12ln21
) 2ln3
,
i a
b là hai
(
A. 19 2 . B. 21 2 . C. 23 2
D.
Lời giải C
Ta
(
) (
2
4
2
2 xfxxfx
xfxx
= − −=
+ Ta có: ( ) ( ) ( ) ( ) ( )121xxfxxfxxx +++=+ ( ) ( ) ( ) 2 1 1 x fxfx xx + += + ( ) ( ) ( ) ( ) 22 2 2 11 1 xx xx fxfx xx x + += ++ + ( ) ' 22 11 xx fx xx =++ ( ) 22 11 xxfxdx xx = ++ ( ) 22 ln1 12 xxfxxxc x =−+++ + ( ) 2 2 1 ln1. 2 xx fxxxc x + =−+++ + Mặt khác: ( ) 12ln21 f =+ 1. c = Từ đó ( ) 2 2 1 ln11 2 xx fxxx x + =−+++ , ( ) 33 2ln3. 44 f =+ Nên 3 4 3 4 a b = = . Vậy 2 3 . 16 Tab=−=− Câu 141: Cho hàm số ( )fx liên tục và có đạo hàm trên khoảng ( ) 0;+ thỏa mãn
) ( ) 4 2 22xfxxfxx
= , với mọi ( ) 0; x + và ( ) 13 f = . Tính ( )2 f .
.
21 2 .
họn D
có:
) (
) ( ) 3 3 3
4
2
2
x
x xfx x
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 22 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) 233 2 32 22 21 dd 22 2 fx xxxx fxfxxxxC xxxx xfxfx xx x =−=− =−=+ + ( ) 3 1 fxxCx x =++
3 2 1 44144 6 fxdxxdxxxc =+−=+−+ . Vậy 4,13abab ==−+= Câu 143: Cho hàm số ( )fx có đạo hàm cấp hai liên tục trên ( ) 0;+ và thỏa mãn đồng thời các điều kiện ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 '' 1 .3'';'1;11,0,0; 3 fxfxfxfxfffxx−==−=+ . Giá trị ( )2022 f bằng: A. 2020 3 . B. 2018 3 . C. 602. D. 1012. Lời giải Chọn B Từ giả thiết ta có
Do ( ) 3 1 1331.11 1 fCC ==++= , nên ( ) 3 1 fxxx x =++ . Khi đó ( ) 3 121 22. 22 2 f =++= . Câu 142: Cho hàm số ( )yfx = liên tục và xác định trên khoảng 3 ; 4 −+ , thỏa mãn ( ) ( ) ( ) 3 1 fx fxfx = + , ( ) 01 f = và ( ) ( )3 2 1 4 6 fxdxxabxc =+++ . Tính ab + . A. 4 B. 3 C. 2 D. 1 Lời giải Chọn B Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 2 3 1 1..1fxfxfxfx fxfx =+= + Nguyên hàm hai vế ta được: ( ) 2 2 1 4 fx xC + =+ Với ( ) 011fC== Suy ra ( ) ( ) 2 22144441fxxfxx +=+=+− ( ) ( ) ( )
−= == Nguyên hàm hai vế ta được ( ) ( ) ( ) ( ) ( ) 33
fxfxfxfx fxfxfx fxfxfx fxfxfxfx
2 '' 2 '' 4434
.3'' .3'''' '
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
' 1 3 fx C fxfx =−+
' 11 ' 33 3 fx x fxfxD fxfx =−=−=−+ Với ( ) 4 11 3 fD== Suy ra ( ) ( ) 42018 2022 333 x fxf=−+=− Câu 144: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) 2 2 .21fxfxfxxx +=−+ , x và ( ) ( ) 003ff == . Giá trị của ( ) 2 1 f bằng A. 28.. B. 22.. C. 19 . 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
Với ( ) 1 '10 3 fC=−= Suy ra ( ) ( ) ( ) ( ) ( ) ( ) ( ) 33 . D. 10. Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( ) 2 fxfxfxfxfx =+ Do đó theo giả thiết ta được ( ) ( ) 2 21fxfxxx =−+ Suy ra ( ) ( ) 2 3 2 32 x fxfxxxC =−++ . Hơn nữa ( ) ( ) 003ff == suy ra 9 C = . Tương tự vì ( ) ( ) ( ) 2 2 fxfxfx = nên ( ) 2 23 2 29 32 x fxxx =−++ . Suy ra ( ) 23 2342 1 21 29d18 3233 xx fxxxxxxxC =−++=−+++ , cũng vì ( ) 03 f = suy ra ( ) 3 242 1 189 33 x fxxxx =−+++ . Do đó ( ) 2 128 f = .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 24
(
A. 13 + B.
+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 145: Cho hàm số ( )yfx = dương và liên tục trên ( ) 0;+ , có ( ) 03 f = và thỏa mãn
) ( ) ( ) ( ) ( ) ( ) 221'111fxxfxfxxfx++=++− . Khi đó giá trị của ( ) ( )02ff + bằng
33
C. 3 D. 23 Lời giải
( )
( )
(
(
(
(
22 2 2 2 22 2 00 2 2 0 222 2 11'11 11' 1 1 11'1 11'1 114
21223 fxxfxfxxfx fxxfxfx x fx xfxx xfxdxxdx xfx fff ff +++=++ +++ =+ + ++=+ ++=+ ++= +−+=+−= +== Vậy ( ) ( ) 0223ff+= Câu 146: Cho hàm số ( )fx liên tục và có đạo hàm cấp hai dương trên ( ) 0;+ đồng thời thỏa mãn ( ) ( ) 2 ''2''110 fxxfx −+−= với mọi ( ) 0; x+ . Biết ( ) 7 '1 3 f = và ( ) 31 1 30 f = . Tính ( )4 f . A. 376 15 . B. 202 3 . C. 221 15 . D. 179 3 . Lời giải Chọn A Ta viết lại ( ) ( ) ( ) ( ) ( ) ( ) 2 2 2 ''21 ''2''110''1 ''1 fxx fxxfxfxxx fx =+ −+−=−=+ =− Vì hàm số ( )fx có đạo hàm cấp hai dương trên ( ) 0;+ nên ( ) ''21fxx=+ , ( ) 0; x +
Chọn D Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 221'111fxxfxfxxfx++=++−
( ) ( ) ( ) ( ) ( )
( ) ( ) ( )
)
) ( ) ( )
) ( ) ( ) ( )
) ( ) ( ) ( ) ( ) ( ) ( ) ( )
32101432124
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 25
ố (
−=
−=
x
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) 4 ' 3 fxxxxC =++ . Vì ( ) 7 '10 3 fC== . Vậy ( ) ( ) 4 ', 0; 3 fxxxxx=++ . Ta có ( ) 2281 152 fxxxxC =++ . Vì ( ) 31 10 30 fC== Do đó ( ) ( ) 22 81376 4 15215fxxxxf=+= . Câu 147: Cho hàm s
)fx thỏa mãn ( ) 1 ()0,;2 25 fxxf=− và ( ) ( ) 2 3 '4 fxxfx = với mọi x . Giá trị của ( ) ( )10ff bằng A. 1 90 B. 1 90 C. 1 72 D. 1 72 Lời giải Chọn A Vì ()0, fxx nên ( ) ( ) ( ) ( ) ( ) ' 2 333 2 '1 '444 fx fxxfxxx fx fx =−=−=− . Nguyên hàm hai vế ta được ( ) 34 1 4xdxxC fx =−=−+ . Mà ( ) 1 2 25 f =− nên suy ra: 25169 CC −=−+=− ( ) ( ) ( ) ( ) 4 4 11111 910 910990fxxxfxff =−−=−=−+= . Câu 148: Chohàmsố ( )fx cóđạohàm vàliêntụctrên thỏamãn ( ) ( ) 202020212021.2021.. x fxfxxe −= với mọi x
và ( ) 02021 f = . Tính giá trị ( )1 f . A. ( ) 2021 12021. fe = B. ( ) 2021 12022. fe = C. ( ) 2021 12021. fe = D. ( ) 2021 12020. fe = Lời giải Chọn B Ta có ( ) ( ) 20202021 2021.2021. x fxfxxe
( ) ( ) 2020 2021 2021. 2021. x fxfx x e
= ( ) ( ) 202120212020 .2021..2021. xx fxefxex
( ) ( ) 20212020.2021. x fxex
=
Nên ( ) ( ) 20212020.201 d 2. d x f xxxex
= ( ) 2021 2021 . x xC fxe =+ ( ) 2 2021 201
xC fx e + = ( ) ( ) 1 2021 202 x x C e x f =+
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
==
Câu 150: Cho hàm số ( )fx xác định và liên tục trên ( ) 0;+ thỏa mãn ( ) 14 f = và ( ) ( ) 32.23 fxxfxxx =−− . Tính ( )2 f . A. 15. B. 10. C. 20. D. 5. Lời giải Chọn C ▪ Ta có: ( ) ( ) 32.23 fxxfxxx =−− ( ) ( ) 32.23 xfxfxxx −=+ ( ) ( ) 2 . 23 xfxfx x x =+ ( ) 23 fx x x =+ . ▪ Suy ra: ( ) ( ) d23d fx xxx x =+ ( ) 2 3 fx xxC x =++ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ đó ( ) 2 202. 02 10 1 0.0 C fe =+ ( )0 Cf= Theo đề ra ta có: ( ) 02021 f = nên 2021 C = Từ suy ra ( ) ( ) 2021.12021 2021 1120212022. fee =+= . Câu 149: Cho hàm số ( )yfx = có đạo hàm trên ( ) 0;+ thỏa mãn ( ) ( ) 2 23 xfxfxxx += . Biết ( ) 11 f = . Tính ( )4 f ? A. 33 2 . B. 65 2 . C. 33 4 . D. 65 4 . Lời giải Chọn D Trên khoảng ( ) 0;+ ta có: ( ) ( ) ( ) ( ) 22 13 23 22 +=+= xfxfxxxxfxfxx x . ( ) ( ) ( ) ( ) 22 33 ..dd 22
xfxxxfxxxx ( ) 3 1 . 2 =+xfxxC . ( ) Mà ( ) 11 = f nên từ ( ) ta có: ( ) 3 111 1.1.11 222 =+=+= fCCC Suy ra ( ) 2 1 22 =+ xx fx x Vậy ( ) 2 441165 416 244 24 =+=+= f
▪ Do ( ) 14 f = nên ( ) 2 1 13.10 1 f CC =++= . ▪ Khi đó: ( ) ( ) 2 2 23.2220 2 f f =+= .
Câu 151: Biết 32 ()2gxxx=++ là một nguyên hàm của ().e x fx trên , ()Fx là một nguyên hàm của '()e x fx trên và thoả mãn (0)2F =− , giá trị (1)F bằng A. 1. B. 2 e . C. 3. D. 5. Lời giải
Chọn D
Ta có ( ) 22 '()()e32()e()32e xxx gxfxxxfxfxxx =+==+ . Suy ra ( ) 2 '()382ex fxxx=++
Ta có ( ) 232 ()'()ed()382d42
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
27
x FxfxxFxxxxxxxC ==++=+++ Vì (0)22FC=−=− . Vậy (1)14225F =++−= . Câu 152: Cho hàm số yfx có đạo hàm là 312, fxxx và 212 f . Biết Fx là nguyên hàm của fx thỏa mãn 01 F , khi đó 2 F bằng A. 9 B. 4 C. 7 D. 26 Lời giải Chọn A Ta có 2 1 3 d312d12 2 fxfxxxxxxC . Mà 212 f nên 2 11 3 .212.21218 2 CC . 2 3 1218 2 fxxx Lại có 232 2 31 d1218d618 22 FxfxxxxxxxxC . Hơn nữa, 2 011FC 32 1 6181 2 Fxxxx Suy ra 32 1 2.26.218.219 2 F .
hàm số ( )fx liên tục trên đoạn 1;2 và thỏa mãn ( ) ( ) ( ) 221.2.210xfxxfxxx ++−−−= và ( ) 43 1. 24 f = Khi đó ( )2 f bằng A. 119 60 B. 26 15 C. 119 60 D. 119 36 Lời giải Chọn A ( ) ( ) ( ) ( ) ( ) 2222 1.2.2101.21 xfxxfxxxxfxxx ++−−−=+=++ . ( ) ( ) ( ) ( ) 33 2222 1.d1. 33 xx xfxxxxCxfxxxC +=++++=+++ Theo giả thiết ( ) 75 21 34
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
fCC=+= Vậy ( ) ( ) 3 2 2 5 119 34 2 160 x xx fxf x +++ == + . Câu 155: Cho hàm số ( )yfx = có đạohàm ( ) 2 2ee, xx fxx =+ và ( ) 00 f = .Biết ( )Fx lànguyên hàm của hàm số ( )fx thỏa mãn ( ) 02022 F = , khi đó ( )1 F bằng? A. 2 e4035 e 22 ++ B. 2 e4037 e 22 ++ C. 2 4037 ee 2 ++ D. 2 ee2020 ++ Lời giải Chọn B Ta có ( ) ( ) ( ) 22 d2eedee xxxx fxfxxxC ==+=++ Vì ( ) 00 f = nên 2.00 ee02 CC ++==− Suy ra ( ) 2 ee2 xx fx =+− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 153: Cho hàm số ( )yfx = có đạo hàm liên tục trên 1;2 thỏa mãn ( ) 14 f = và ( ) ( ) 3223 fxxfxxx =−− . Tính ( )2 f . A. 5. B. 20. C. 10. D. 15. Lời giải Chọn B Do 1;2 x nên ( ) ( ) ( ) ( ) ( ) 32 2 232323 xfxfxfx fxxfxxxxx xx =−−=+=+ ( ) 2 3 fx xxC x =++ Do ( ) 14 f = nên 0 C = ( ) 32 3 fxxx =+ Vậy ( ) 220 f = Câu 154: Cho
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 29
với mọi 1 x . Biết ( )Fx là một nguyên hàm của ( )fx thoả mãn ( ) 23 F = . Khi đó ( )3 F bằng A. ( ) 1 3ln23 2 F =−+ . B. ( ) 1 3ln23 2 F =+ . C. ( ) 3ln23 F =+ . D. ( ) 3ln23 F =− . Lời giải Chọn A Ta có ( ) ( ) ( ) 2 2 '() '22 fx fxfx fx == Do đó ta có ( ) 1 2 '()1 () =+ fx dxC fx fx và 2 22dxxC =+ . Suy ra 1 2 () xC fx =+ Mặt khác 1 ()1 2 f = nên ta có 2 C =− Vậy 1 () 22 fx x =− . ( )fx
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó ( ) ( ) ( ) 22 1 dee2dee2 2 xxxx FxfxxxxD ==+−=+−+ . Vì ( ) 02022 F = nên 2.00 14041 ee2.02022 22 DD +−+== . Suy ra ( ) 2 14041 ee2 22 xx Fxx=+−+ . Vậy ( ) 2 2.11 14041e4037 1ee2.1e 2222 F =+−+=++ Câu 156: Cho hàm số ( )yfx = có đạo hàm liên tục trên 1;2 thỏa mãn ( ) 14 f = và ( ) ( ) 32'23 fxxfxxx =−− . Biết ( )Fx là một nguyên hàm của ( )fx thoả mãn ( ) 1 1 4 F −= . Khi đó ( )1 F bằng A. 9 4 B. 1 4 C. 4 D. 2 Lời giải Chọn A Xét 1;2 x , ta có ( ) ( ) ( ) ( ) ( ) ( ) ' 32 2 ' 232323d3 xfxfxfxfxxxxxfxxxCx xxx =+=+=+=++ Vì ( ) 14 f = nên 0 C = hay là ( ) 32 3 fxxx =+ . ( ) ( ) 4 323 3 4 x FxxxdxxC =+=++ ( ) 1 1 4 F −= 1 C = ( ) ( ) 4 3 9 11 44 x FxxF =++= Câu 157: Cho hàm số thỏa mãn 1 ()1 2 f = và ( ) ( ) 2 '2 fxfx =
4 f ? A. 24. B. 14. C. 4. D. 16. Lời giải Chọn D
Trên khoảng ( ) 0;+ ta có: ( ) ( ) ( ) ( ) 22 13 2'3' 22 xfxfxxxxfxfxx x +=+= ( ) ( ) ( ) ( ) '' 22 33 .. 22 xfxxxfxdxxdx== . ( ) 3 1 . 2 xfxxC=+ . ( ) Mà ( ) 1 1 2 f = nên từ ( ) có: ( ) 3 111 1.1.10 222 fCCC =+=+= ( ) 2 2 xx fx = Vậy ( ) 2 44 416 2 f == Câu 159: Cho hàm số ( )fx thỏa mãn ( ) ( ) ', x fxfxex+=
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 30
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 11 ln1 222 FxdxxC x =−=−−+ . ( ) 23 F = 3 C = ( ) 1 ln13 2 Fxx =−−+ ( ) 1 3ln23 2 F =−+ Câu 158: Cho hàm số ( )yfx = liên tục trên ( ) 0;+ thỏa mãn ( ) ( ) 2 2'3 xfxfxxx += . Biết ( ) 1 1 2 f = Tính ( )
và ( ) 02 f = .
ọ nguyên hàm của
số ( ) 2x fxe là A. x xexC ++ B. ( )1 x xeC ++ C. x xexC ++ D.
x xeC −+ Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ''1'1' xxxxx fxfxeefxefxefxefxdxdx +=+=== ( ) ( ) 1 1 x x xC efxxCfx e + =+= Theo giả thiết ( ) 02 f = , ta có ( ) 1 1 0 0 022 C fC e + === . Vậy ( ) 2 x x fx e + = Khi đó ( ) ( ) ( ) ( ) 22 2 221 xxxxxx x x fxedxedxxedxxeedxxeC e + ==+=+−=++
H
hàm
( )1
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 31
ế ta có: ( ) 2 .12ln2 222 xx fxdxdxdxxxC xxx ==−=−++ +++ ( ).2ln2 2 x fxxxC x =−++ + Vì (1)6ln3 f =− Nên ( ) 1 112ln3 3 fC =−+ 1 3.(6ln3)12ln3 1 C C −=−+ =− Khi đó: 31010 (3)32ln51(3)ln5 533 ff=−−=− Suy ra 1010 ; 33 ab== Vậy: 101020 333 ab−=+= . Câu 161: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) 2 21 fxxfx =+ với mọi 0 x và ( ) 1 1 2 f =− . Giá trị của biểu thức ( ) ( ) ( ) ( )123...2022Tffff =++++ thuộc khoảng nào sau đây? A. ( )1;0 B. ( )3;2 . C. ( )2;1 . D. ( )0;1 .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 160: Cho hàm số ()yfx = liên tục trên \{2;0}thỏa mãn ( ) 2 .2.()2()2 xxfxfxxx ++=+ và (1)6ln3 f =− . Biết (3).ln5(,) fabab=+ . Giá trị của ab bằng A. 20. B. 10. C. 10 3 . D. 20 3 . Lời giải Chọn D Ta có: ( ) ( ) ( ) 2 .2.22 xxfxfxxx ++=+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 1 2 .2 22 2 22 fx fx xx xfxfx x xx x xx fx xx += + += ++ + =++ Nguyên hàm hai v
'2 '121 11 fx x fxxxfx fx x +=+= + + Nên ( ) ( ) 2 =−
'2 dd 11 fx x xx fx x = + + ( ) ( ) ( ) ( ) 2 2
( ) 2 2121fxxC +=++ . Mà ( ) 000fC==
d1 d1 11 fx x fx x =+ + +
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Ta có: ( ) ( ) ( ) 2 21. fxxfx =+ ( ) ( ) 2 21 fx x fx =+ ( ) ( ) ( ) 2 d21d fx xxx fx =+ ( ) 2 1 xxC fx −=++ ( ) 2 1 xxC fx =−−− Lại có: ( ) 10,5 f =− 2 211 C −=−−− 0 C = . Vậy ( ) (
) ( ) 2 1 1 xxxx fx =−+=−+ hay ( ) ( ) 1 1 fx xx −= + . Ta có: ( ) ( ) ( ) ( )123...2022 ffff 1111 1.22.33.42021.2022 =++++ 1111111112021 ...1. 1223342021202220222022 =−+−+−++−=−= Do đó 2021 2022 T =− Câu 162: Cho hàm số ( )fx có đạo hàm trên , thoả mãn ( ) 1 fx − và ( ) ( ) 2 '121, fxxxfxx +=+ . Biết rằng ( ) 00 f = , khi đó ( )2 f có giá trị bằng A. 0. B. 4. C. 8. D. 6. Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) 2 2 ( ) 2 11fxx +=+ nên ( ) ( ) 2 24 fxxf== . Câu 163: Cho hàm số ( )yfx = thỏa mãn ( ) 1 0, 2 fxx và có đạo hàm ( )fx liên tục trên khoảng 1 ,2 + thỏa mãn ( ) ( ) 2 1 8.0, 2 fxxfxx += và ( ) 1 1 3 f = . Tính tổng: ( ) ( ) ( ) 12...1011.fff +++ A. 12022 22023 . B. 2021 2043 . C. 2022 4045 . D. 12021 22022 . Lời giải Từ giả thiết ta có: ( ) ( ) 2 8.0fxxfx += ( ) ( ) 2 8 fx x fx
=− ( ) ( ) ( ) 2
d 8d fx xx fx =− ( ) 2 1 4xc fx =+ ( ) 2 1 4 fx xc = + Có ( ) 1 1 3 f = nên 2 11 1 4.13 c c ==− + . Vậy ( ) 2 1 41 fx x = 111 22121 xx =− −+ ( ) 11 11 23 f =− ( ) 111 2 235 f =− ( ) 111 3 257 f =− …………………… ( ) 111 2011 220212023 f =− Cộng vế với vế ta được: ( ) ( ) ( ) 11 12...10111 22023 fff ++=− 12022 . 22023 = Câu 164: Cho hàm số ( )fx liên tục trên thỏa mãn ( ) ( ) ( ) ( ) 1 1211xxfxxfx x
+++=− và ( ) 11 f = . Biết ( ) 2ln2fab =+ . Khi đó ab + bằng A. 1 6 . B. 3 2 . C. 1 3 . D. 1 2 . Lời giải
Lấy nguyên hàm hai vế ta được ( ) ( ) 2 d8d fx xxx fx
họn C Từ giả thiết: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 11 12111xxfxxfxxxfx xx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 33
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn C
+++=−+=− Lấy nguyên hàm hai vế ta được: ( ) ( ) 2 1 1dln xxfxxxxC x +=−=−+ . Vì ( ) 11 f = nên ( ) 2.1ln113 fCC=−+= Do đó ( ) 2 ln3 xx fx xx −+ = +
= Vậy phương trình đã cho có hai nghiệm.
Câu 166: Cho hàm số ( )yfx = đồng biến và có đạo hàm liên tục trên thỏa mãn ( ) ( ) ( ) 2 .e, x fxfxx = và ( ) 02 f = . Khi đó ( )2 f thuộc khoảng nào sau đây?
A. ( )12;13 . B. ( )9;10 . C. ( )11;12 . D. ( )1314 ; . Lời giải
Chọn B
Vì hàm số ( )yfx = đồng biến và có đạo hàm liên tục trên đồng thời ( ) 02 f = nên ( ) 0 fx và ( ) 0 fx với mọi ) 0; x+
Từ giả thiết ( ) ( ) ( ) 2 .e, x fxfxx = suy ra ( ) ( ) ) 2 .e, 0;. x fxfxx =+ Do đó, ( ) ( ) ) 2 1 e, 0;. 2 2
x fx x fx
=+ Lấy nguyên hàm hai vế, ta được ( ) ) 2 e, 0; x fxCx=++ với C là hằng số nào đó. Kết hợp với ( ) 02 f = , ta được 21 C =− . Từ đó, tính được ( ) ( )2 2e219,81 f =+− .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 34 Chuyên
thi:
sinh vào
10 Tốt
10; 11; 12 Sưu tầm và biên soạn Vậy: ( ) ln211111 2ln2 66663 fabab + ==+==+= . Câu 165: Cho hàm số ( ) 0 yfx= liên tục trên và ( ) 3 1 fe = . Biết ( ) ( ) ( ) 23,
=− Hỏi phương trình ( ) 4 234 xx fxe −+ = có bao nhiêu nghi
0984164935
luyện
Tuyển
lớp
Nghiệp THPT BDKT Toán
fxxfxx
ệm A. 4 B. 3 C. 2 D. 0 Lời giải Chọn C +) Sử dụng giả thiết ()0fx và liên tục x , ta biến đổi: ( ) ( ) ( ) '() 2323 () fx fxxfxx fx =−=− 2 ln()3fxxxC=−+ 2 3 () xxCfxe −+ = +) Từ giả thiết 323 (1)5 C feeeC −+ === . Suy ra 2 35 () xxfxe −+ = +) Xét phương trình ( ) 4 234 xx fxe −+ = 243523442210 xxxx eexx −+−+ =−−= 1 x
Câu 167: Cho hàm số ()fx thỏa mãn: ( ) ( ) ( ) 2 230fxxfx −+= và ( ) 0 fx với mọi 0 x và ( ) 1 1 6 f =− . Giá trị của biểu thức: ( ) ( ) ( ) ( )123...2022Tffff =++++ thuộc khoảng nào sau đây? A. ( )0;1 B. ( )2;1 C. ( )3;2 D. ( )1;0 Lời giải Chọn D Ta có: ( ) ( ) ( ) 2 230fxxfx −+= mà ( ) 0 fx ,0 x nên ( ) ( ) 2 23 fx x fx
=+ Lấy nguyên hàm 2 vế, ta đượ
35 c: ( ) ( ) 2 (23) fx dxxdx fx =+ , suy ra: ( ) 2 1 3 xxc fx =++ Mà ( ) 1 1 6 f =− suy ra 2 c = . Vậy ( ) 2 111 . 3221 fx xxxx ==− ++++ Ta có: ( ) ( ) ( ) ( ) 11 1 32 11 2 43 11 3 54 11 2022 20242023 f f f f =− =− =− =− Suy ra: ( ) ( ) ( ) ( ) ( ) 111011 123...20221;0 202422024 Tffff =++++=−=− Câu 168: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) ( ) 2 3 .2, fxfxfxxxxR +=− và ( ) ( ) 001ff == . Tính ( ) 2 1 f A. ( ) 2 43 1 15 f = B. ( ) 2 26 1 15 f = C. ( ) 2 47 1 30 f = D. ( ) 2 73 1 30 f = Lời giải Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 2 33 .2.2 +=−=− fxfxfxxxfxfxxx ( ) ( ) ( ) 4 32 1 .2 4 x fxfxxxdxxC =−=−+
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
C
họn B
Ta
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 36
Theo
ả thiết ( ) ( )
ff == nên
C = Suy
) ( ) (
22
42 xx
=−+=−+ ( ) 4 2222 2 x
=−+ ( ) 453 22 2 2 222 2103 xxx fxxdxxC =−+=−++
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
gi
001
1 1
ra: (
) ( ) 44
.12.22
fxfxxfxfxx
fxx
Do ( ) 01 f = nên 2 1 C = . Suy ra ( ) 53 2 2 21 103 xx fxx=−++ Vậy ( ) 2 1273 121 10330 =−++= f . Câu 169: Cho hàm số ( )yfx = có đạo hàm trên và ( ) ( ) ( ) 3 1 x fxfxxe −=+ , với mọi x . Biết ( ) 5 0 4 f = , giá trị ( )1 f bằng A. 3 5 4 ee + . B. 3 3 4 ee + . C. 3 3 4 ee . D. 3 5 4 ee . Lời giải
V
Câu 170: Cho hàm số ( )fx liên tục và có đạo hàm trên 0; 2 , thỏa mãn ( ) ( ) 3 tan. cos x fxxfx x += . Biết rằng 33ln3 36 ffab −=+ trong đó , ab . Giá trị của biểu thức Pab =+ bằng A. 14 9 . B. 2 9 . C. 7 9 . D. 4 9 . Lời giải Chọn D
có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 322 111 xxxxxx fxfxxeefxefxxeefxxe −=+−=+=+ Khi đó: ( ) ( ) ( ) 222 11 1d1 24 xxxx efxxexxeeC =+=+−+ Do ( ) 5 0 4 f = nên 1 C =
ậy nên ( ) ( ) ( ) ( ) ( ) 22333 11113 1111 24244 xxxxxx efxxeefxxeeefee =+−+=+−+=+
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 37 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 3 tan. cos x fxxfx x += ( ) ( ) 2 cos.sin. cos x xfxxfx x += . ( ) 2 sin. cos x xfx x = Do đó ( ) 2 sin.dd cos x xfxxx x = ( ) 2 sin.d cos x xfxx x = Tính 2 d cos x Ix x = Đặt 2 dd d dtan cos ux ux x vx v x = = = = . Khi đó ( ) 2 dcos dtantandtandtanlncos coscos x x Ixxxxxxxxxxx xx ==−=+=+ . Suy ra ( ) .tanlncoslncos sincossin xxxx x fx xxx + ==+ 22ln2333ln3332ln 36392 3 abff +=−=−−+ 53 ln3 9 =− . Suy ra 5 9 1 a b = =− Vậy 4 9 Pab=+=− Câu 171: Cho hàm số ( )fx thỏa mãn ( ) 1 0, 2 fxx và có đạo hàm ( )fx liên tục trên khoảng 1 ; 2 + thỏa mãn ( ) ( ) 2 1 80, 2 fxxfxx += và ( ) 1 1 3 f = . Tính ( ) ( ) ( )12...1011fff +++ A. 12022 . 22023 . B. 2021 2043 . C. 2022 4045 . D. 12021 . 22022 . Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 22 1 808d8d4 fxfx fxxfxxxxxxC fxfxfx +====+ . Mà ( ) ( ) 2 11111 11 34122121fCfx xxx ==−==− −−+ . Ta có:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 38
( ) ( ) (
(
11 11
....
220212023 f
Tfff
=− =− =+++=−=
+= Khi đó 3 2 f thuộc khoảng A. 1 ;1. 2 B. 1 0;. 2 C. 5 2;. 2 D. ( ) 1;2. Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) 3 ee3.,1;3. xxfxfxfxx += ( ) ( ) 2 33e12e xxfxfx += ( ) ( ) ( ) ( ) 2 3333e2e12e2e xxxx fxfxfxfx ++=+ ( ) ( ) ( ) ( ) 3 2 33 2 3 e 1 e12e 2 e1 x xx x fx fxfx fx +== + ( ) ( ) 33 1111 22e1e1 xx xC fxfx =−=−+ ++ Mà ( ) 4 3 2e f = nên ( ) ( ) 3 3 3132 e1 223 e1 x x x Cfx x fx ==+= + ( ) ( ) ( ) ( ) ( ) 2 333111 e 33e3e x xxfxfxfxxxx xxx === Khi đó 3 0,18 2 f Câu 173: Cho hàm số ( )yfx = liên tục trên \1;0 thỏa mãn điều kiện: ( ) 12ln2 f =− và ( ) ( ) ( ) 2 .1. xxfxfxxx ++=+ . Biết ( ) 2.ln3fab =+ ( a , b ). Giá trị ( ) 22 2 ab + là A. 27 4 B. 9 C. 3 4 D. 9 2 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
)
) ( ) ( )
23 111 2 1112022 12...10111. 235 2202322023
111 1011
f
f
=− Câu 172: Cho hàm số ( )fx liên tục và luôn nhận giá trị dương trên khoảng ( )1;3 , thỏa man ( ) 4 3 2e f = và ( ) ( ) ( ) ( ) 3 ee3.,1;3. xxfxfxfxx
xxxfxfxxxxxxC xxxx
===−=−++ ++++
Do ( ) 12ln2 f =− nên ta có ( ) 1 .11ln2ln21ln21 2 fCCC =−+−=−+=−
đó
fxxx
)
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 39
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn B Chia cả hai vế của biểu thức ( ) ( ) ( ) 2 .1. xxfxfxxx ++=+ cho ( )2 1 x + ta có ( ) ( ) ( ) ( ) 2 1 .. 1111 1 xxxx fxfxfx xxxx x +== ++++ + Vậy ( ) ( ) 1 ..dd1dln1 1111
Khi
( ) (
1 ln11 x
x + =−+− . Vậy ta có ( ) ( ) ( ) 333333 22ln311ln3ln3, 222222fab =−−=−=−==− Suy ra ( ) 22 22 33 229 22 ab +=+−= . Câu 174: Cho hàm số ( )yfx = thỏa mãn ( ) 0,0fxx và có đạo hàm ( )fx liên tục trên khoảng ( ) 0;+ thỏa mãn ( ) ( ) ( ) 2 21,0fxxfxx =+ và ( ) 1 1 2 f =− . Giá trị của biểu thức ( ) ( ) ( )12...2020fff +++ bằng A. 2020 2021 . B. 2015 2019 . C. 2019 2020 . D. 2016 2021 . Lời giải Chọn A Ta có: ( ) ( ) ( ) 2 21 fxxfx =+ ( ) ( ) 2 21 fx x fx =+ ( ) ( ) ( ) 2 d21d fx xxx fx =+ ( ) 2 1 xxC fx −=++ . Mà ( ) 1 1 2 f =− 0 C = ( ) 2 1 fx xx = + 11 1 xx =− +
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 40 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) 1 11 2 11 2 32 11 3 43 11 2020 20212020 f f f f =− =− =− =− ( ) ( ) ( ) 1 12....20201 2021 fff +++=−+ 2020 2021 =− . Câu 175: Cho hàm số ( )yfx = liên tục trên \1;0 thỏa mãn ( ) 12ln21 f =+ , ( ) ( ) ( ) ( ) ( )121xxfxxfxxx +++=+ , \1;0 x − . Biết ( ) 2ln3fab =+ , với a , b là hai số hữu tỉ. Tính 2 Tab =− A. 3 16 T = . B. 21 16 T = . C. 3 2 T = . D. 0 T = . Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( )121xxfxxfxxx +++=+ ( ) ( ) ( ) 2 1 1 x fxfx xx + += + ( ) ( ) ( ) ( ) 22 2 2 11 1 xx xx fxfx xx x + += ++ + ( ) 22 11 xx fx xx =++ ( ) 22 11 xxfxdx xx = ++ ( ) 22 ln1 12 xxfxxxc x =−+++ + ( ) 2 2 1 ln1. 2 xx fxxxc x + =−+++ Ta có ( ) 12ln21 f =+ 1. c = Từ đó ( ) 2 2 1 ln11 2 xx fxxx x + =−+++ , ( ) 33 2ln3. 44 f =+ Nên 3 4 3 4 a b = = Vậy 2 3 16 Tab=−=−



CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 2. TÍCH PHÂN MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO Câu 1: Cho hàm đa thức bậc ba ()yfx = có đồ thị hàm số ()yfx = được cho bởi hình vẽ sau. Giá trị biểu thức ( ) ( )32ff bằng A. 20. B. 51. C. 64. D. 45. Lời giải Chọn A Giả sử ( ) 2 fxaxbxc =++ trong đó 0 a có đồ thị ( )C . Hàm số ()yfx = đạt cực trị tại 0 2 b x a =−= suy ra 0 b = . ( ) ( ) 0;1 C suy ra 1 c = . ( ) ( ) 1;4 C suy ra 3 a = . Do đó ( ) 2 31fxx =+ . Vậy ( ) ( ) ( ) 3 2 2 3231d20 ffxx −=+= . Câu 2: Cho hàm số ( )fx liên tục trên khoảng ( ) 0;+ và thỏa mãn ( ) 1 2 fxxfx x += với mọi 0 x CHƯƠNG III NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 2
) 1 422 fxxfx x += Lấy trừ ta được: ( ) ( ) 1 21 3 fxx=− Do đó: ( ) ( ) ( ) 2 22 2 1 11 2 22 113 21 334fxdxxdxxx=−=−= Câu 3: Cho ( ) 2 5 * 0 1 ln,,, 3 xx c Idxbabc xaa ==+ + . Tổng abc ++ bằng A. 17. B. 15. C. 13. D. 16. Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) 2 51515 22 00101 1155 0011 15 01 1212 44 33333 1212 44 33 713 12ln3412ln312ln 222 xx xxxx Idxdxdxxdxxdx xxxxx xdxdxxdxdx xx xx ==−+=−−++−+ +++++ =−−−+−+ ++ =−+−++=+ Suy ra: 2;12;317abcabc ===++=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn . Tính ( ) 2 1 2 .fxdx A. 7 4 B. 7 12 C. 9 4 D. 3 4 Lời giải Chọn D Xét ( ) 1 2 fxxfx x += Thay 1 x x = ta có: ( ) ( ) 111 12.ffx xxx += ( ) 111 2.. xffxx xxx += ( ) 1 21 xffx x += Mặt khác: ( ) ( ) 1 1222 fxxfx x += (
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 3 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 4: Cho hàm số ( )fx liên tục trên và ( ) ( ) 13 01 d6;d4fxxfxx== . Tính tích phân ( ) 1 1 21d Ifxx =− . A. 3 I = B. 8 I = C. 14 I = D. 6 I = Lời giải Chọn B * Ta có: ( ) ( ) ( ) 1 11 2 12 1 11 2 21d12d21d
== ( ) ( ) 11 2 00 11 dd3. 22 Ifvvfxx === * Vậy 12 8 III=+= . Câu 5: Cho hàm số ( )fx liên tục trên và có ( ) 2024 0 d8fxx = , ( ) 6064 0 d10fxx = . Tính ( ) 2022 2022 22020d Ifxx =− A. 18 I = . B. 2 I = . C. 9 I = . D. 5 I = . Lời giải Chọn C ( ) ( ) ( ) 202210102022 12 202220221010 22020d22020d22020d IfxxfxxfxxII =−=−++−=+ ( ) ( ) ( ) 101006064 1 202260640 -dt11 22020dd.105 222Ifxxftfxx =−+==== ( ) ( ) ( ) 202220242024 2 101000 dt11 22020dd.84 222Ifxxftfxx =−==== . Do đó, 549 I =+= .
IfxxfxxfxxII =−=−+−=+ * Tính ( ) 1 2 1 1 12d Ifxx =− . Đặt 12d2d uxux =−=− . Đổi cận: 13 1 0 2 xu xu =−= == . ( ) ( ) ( ) ( ) ( ) 03313 1 30001 1111 ddddd5 2222 Ifuufuufxxfxxfxx ====+= * Tính ( ) 1 2 1 2 21d Ifxx =− . Đặt 21d2d vxvx =−= . Đổi cận: 11 1 0 2 xv xv ==
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 6: Tính tích các giá trị của số thực m để tích phân 1 0 22Ixmdx=−= A. 6. B. 3. C. 2. D. 4. Lời giải Chọn A Th1. 0200;1mxmx − ( ) ( ) 1 1 2 0 0 21 121. Ixmdxxmxm mm =−=−=− −==− Th2. 2200;1mxmx − ( ) ( ) 1 1 2 0 0 21. 123 Imxdxmxxm mm =−=−=− −== Th3. 02 m ( ) ( ) ( ) ( ) ( ) 1 222 2 1 22 2 0 2 0 2 2211 442 m m m m mmm Imxdxxmdxmxxxmxmm =−+−=−+−=+−+=−+ 2 2 13 12220 213 m m mmm m =+ −+=−−= =− Câu 7: Tích các giá trị của m là 1.33−=− .Cho hàm số ( )yfx = liên tục trên và có đồ thị hàm số như hình vẽ bên. Tích phân ( ) 1 0 21d fxx bằng A. 8. B. 4. C. 2. D. 1. Lời giải Chọn B Đặt 21d2d txtx =−=
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
Đổ
. Vậy ( ) 1 0 21d4fxx −= . Câu 8: Cho hàm số ()yfx = liên tục trên và có 3 0 ()d18fxx = , 5 0 ()d3.fxx = Giá trị của ( ) 1 1 41d fxx bằng A. 9 4 . B. 21 4 . C. 21. D. 15 4 . Lời giải Chọn B Ta có ( ) ( ) ( ) 1 11 4 1 11 4 41d14d41d Ifxxfxxfxx =−=−+− +) Tính ( ) 1 4 1 1 14d Ifxx =− : Đặt d 14d 4 t txx =−=− . Đổi cận: 1 15; 0 4 xtxt =−=== . Khi đó ( ) ( ) 05 1 50 11 dd 44 Ifttftt =−= . +) Tính ( ) 1 2 1 4 41d Ifxx =− : Đặt 41dd 4 t txx =−= . Đổi cận: 1 0; 13 4 xtxt ==== . Khi đó ( ) 3 2 0 1 d 4 Iftt =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
i cận: 01;11xtxt ==−== . Khi đó ( ) ( ) ( ) 111 011 11 21ddd 22 fxxfttfxx −== Từ đồ thị hàm số ( )yfx = ta có: + ( ) 0,1;0fxx − + ( ) 0,0;1fxx Do đó ta có: ( ) ( ) ( ) 101 110 11 ddd 22fxxfxxfxx =−+ ( ) ( ) 01 10 11 22fxfx=−+ ( ) ( ) ( ) ( ) ( ) ( ) 11 0110 22ffff =−−−+− ( ) ( ) ( ) 11 21324 22 =−−−+−−=
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
2khi2 () 21khi2 xx yfx xx == + . Tính
A. 79. B. 78. C. 77. D. 76. Lời giải Chọn A Đặt 22211dd txtxttxx =+=+= . Đổi cận 01xt== và 32xt== . Đặt 222 1 1ed2edded 2 xxx uuxux =+== Đổi cận ln25xu== và ln310xu== Như vậy 210210 1515 ()d()d(21)d2d79.Ifttfuuttuu =+=++= Câu 11: Cho hai hàm số ( ) ( ) , fxgx liên tục trên 0;1 thỏa mãn điều kiện ( ) ( ) 1 0 d8fxgxx += và ( ) ( ) 1 0 2d11fxgxx += . Giá trị của biểu thức ( ) ( ) 1 2022 3 20210 2022d53d fxxgxx −+ bằng.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy ( ) ( ) 1 1 4 12 1 1 4 31821 14d41d 444 IfxxfxxII =−+−=+=+= . Câu 9: Cho hàm số ( )fx liên tục trên đoạn 1;4 thỏa mãn ( ) ( ) 21lnfx x fx x x =+ . Tính ( ) 4 3 d fxx . A. 2 32ln2 + B. 2ln2 C. 2 2ln2 D. 2 ln2 Lời giải Chọn C Từ đẳng thức đã cho, lấy tích phân cận từ 1 tới 4 cho hai vế, ta được ( ) ( ) 444 111 21ln ddd fx x fxxxx x x =+ Xét tích phân ( ) ( ) ( ) ( ) 443 111 21 d21d21d fx xfxxfxx x =−−= . Xét tích phân ( ) 4 44 2 2 11 1 lnln dlndln2ln2 2 xx xxx x === . Câu 10: Do đó ( ) ( ) ( ) 434 22 113 (*)dd2ln2d2ln2 fxxfxxfxx =+= .Cho hàm số
tích phân ( ) ( ) 2 3ln3 22 2 0ln2 1 d2e1ed 1 xx xfx Ixfx x + =++ + .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 10. B. 0 C. 20 D. 5 Lời giải Chọn A Ta có hệ sau: ( ) ( ) ( ) ( ) ( ) ( ) 11 00 11 00 d8d5 2d11d3 fxgxxfxx fxgxxgxx +== +== . Xét ( ) ( ) ( ) ( ) 202211 202100 2022d2022d2022d5 fxxfxxfxx −=−−== . Xét ( ) ( ) ( ) ( ) 1 11 3 000 555 53d3d3d.35 333gxxgxxgxx==== Vậy ( ) ( ) 1 2022 3 20210 2022d53d5510 fxxgxx−+=+= . Câu 12: Cho hàm số ( )fx liên tục trên và thỏa ( ) ln2 0 5 1 2 xx feedx+= . Tính ( ) 3 0 12cossin fxxdx + . A. 5 4 . B. 5. C. 5. D. 5 4 . Lời giải Chọn A Đặt 1 xx tedtedx =+= . 02;ln23xtxt ==== Khi đó ta được ( ) ( ) ln23 02 5 1 2 xx feedxftdt+== Đặt 12cos2sin uxduxdx =+=− 03;2 3 xuxu ==== Khi đó ta được ( ) ( ) ( ) 33 3 022 115 12cossin 224fxxdxfuduftdt +=== . Câu 13: Biết 2 2 1 153 241 x Idxabc xx ==++ +− , với a , b , c là các số hữu tỷ, tính Pabc =++ . A. 14 3 . B. 17 3 . C. 14 3 . D. 11 3 . Lời giải Chọn D Ta có: ( ) ( ) 2 222 22 22 2 111 241 241 241441 xxx x Idxdxxxxdx xx xx ===−− −+ +−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 8 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 222 2232 1 111 2 24141 3 Ixdxxxdxxxxdx =−−=−− Đặt 2 2 4 41 414 xt xtdxdtxdxdt x −=== 15 15 23 3 3 14141451 153 34312344 Idttt =−=−=−+ Vậy: 145111 ,, 3443 abcPabc ==−==++= Câu 14: Biết ( ) ln3 0 d1 2lnln e3e4 xx x Iab a ==− ++ với , ab là các số nguyên dương và a là số nguyên tố. Tính giá trị biểu thức 2. Pab =− A. 4. P = B. 1 P =− C. 4 P =− D. 1 P = Lời giải Chọn D * Ta
xxxx xx
== ++++ *
t eded xx ttx == . Đổ
ận 01
xt xt == == . Suy ra ( )( ) 3 3 11
t It
==− ++++ ( ) ( ) ( ) 3 1 111 ln1ln3ln4ln6ln2ln43ln2ln6 222 tt =+−+=−−+=− ( ) 1 2ln2ln3. 2 =− Khi đó 2,322.231.abPab ===−=−= Câu 15: Biết rằng 4 0 4cos2sindln2ln3 sin3cos2 xxaxbc xx =+− + , với ,, abc . Tính Pabc = A. 3 4 P = . B. 3 4 P = . C. 0 P = . D. 2 3 P = . Lời giải Chọn B Ta có ( ) 444 000 4cos2sinsin3coscos3sinsin3cos dd1d sin3cossin3cossin3cos xx xxxxxx xxx xxxxxx + −++−==+ +++
có ln3ln3 2 00 ded e3e4e4e3 x
I
Đặ
i c
ln33
d111 d 13213
tttt
( ) ( ) 4 4 0 0
13 lnsin3cosln22ln3.ln2ln3 4222 xxx =++=+−=+−
Từ đây ta có 13 ,,1 22 abc=== nên 3 4 P = .
Câu 16: Biết ( ) ( ) 22 2 22 0
xxx xabc x
1ee22 delne1 e2
xx x
++++ =+−+ + Tính giá trị của biểu thức 222 2 Tabc =+− A. 12. B. 11. C. 5. D. 10. Lời giải
xexexxxx x x xex
xxxxx x x xxx
Khi đó 3 a = , 1 b = , 222 1210cabc =+−= Câu 17: Tính tích phân 1 0
22 222 000 2 2 0 2 22 de1dd e2e2 de2 2 e 0 2e2 2 3elne2 0 3elne1.
xxx x xxxx xx x x x x x
1ee221e xx x x xx x x x x
++++ + =++− ++ + =++− + =+−+ =+−+
+++++++−+ + ==++− +++ . Khi đó ( ) ( ) ( ) ( ) ( ) ( )
31 5 x dx x + . Lời giải Đặt 2 2 313123 3 udu uxuxududxdx =+=+== . Ta có 2 2 1 31 3 u uxx=+= ( ) 2 2 12222 2 22 22 01111
2 31.1616 33222 116 51616 5 33
uduudu u udu xudu dx uu xuu
−+ + ==== ( )( ) ( )( ) 2222 2 1111
16168 212122 164444 dudududu uuuuu =+=+=+ −−+−+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
Chọn D Ta có ( ) ( )( ) ( ) ( ) 22122e2e11e1e e1 2e2e2
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
Văn
42
Page 10
( )( ) ( ) ( ) ( )( ) 222 111 2244811 242424 11444444 uu uduududu uuuuuu +−− =+=+=+− −+−+−+ 2 4135 24ln24lnln24ln. 1
u u =+=+−=+ +
Câu
1 2 0 ln(1)
Đặ
=−
=+−==−+ + Suy ra: ln2..ln2 48 III =−= Câu
4 2 2
x Ixabc xx + ==++ + , với ,, abc là các số nguyên. Tính giá trị biểu thức 234 Pabc =++ . A. 9 P = . B. 3 P =− . C. 1 P = . D. 3 P = . Lời giải Chọn D Đặt ( ) 2 d21d txxtxx =+=+ Đổi cận: 26 420 xt xt == == . Khi đó 420 20 2 6 26 1 21ddlnln20ln6ln2ln5ln31 1 a xt Ixtb xxt c = + ====−=+−=− + = . Suy ra 2343Pabc=++= Cách khác: Ta có ( ) ( ) 44 4 22 22 2 22 211 ddlnln20ln6ln2ln3ln5 x xxxxx xxxx + =+=+=−=−+ ++ Suy ra 1;1;12343 abcPabc ==−==++= .
viên: Huỳnh
Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
4359
18: Tính tích phân
1 x dx x + + Lời giải Đặt tan tx = ta có 2 (1tan) dxxdx =+ 1 4 2 00 ln(1) ln(1tan) 1 x Idxtdt x
+ ==+ +
t 4 tu
, suy ra 4444 0000 2 ln1tanlnln2ln(1tan) 41tan Iudududuudu u
19: Biết
21 dln2ln3ln5
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 11
) e 2 1 2ln1 dln ln2 xac x bd xx + =− + với a , b , c là các số nguyên dương, biết ; ac bd là các phân số tối giản. Giá trị abcd +++ bằng A. 18. B. 15. C. 16. D. 17. Lời giải Chọn C Đặt lnddx txt x == Đổi cận: 10;e1 ==== xtxt . Khi đó: ( ) ( ) e1 22 10 2ln121 dd ln22 xt Ixt xxt ++ == ++ ( ) 1 1 2 0 0 32391 d2ln2ln 22242 tt tt t =+=++=− ++ + . Vậy 941216 abcd+++=+++= Câu 22: Biết 2 2 1 d3 1 x xab xx =+ +− với a , b là các số hữu tỷ. Tính 35 Pab =− . A. 12 B. 2 C. 2 D. 5 3 Lời giải Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 20: Cho hàm số ( )fx liên tục trên đoạn 0;10 thỏa mãn ( ) 10 0 d20fxx = và ( ) 10 8 d6fxx = . Tính ( ) 4 0 2d Ifxx = A. 7 I = B. 14 I = C. 3 I = D. 12 I = Lời giải Chọn A ( ) 4 0 2d Ifxx = Đặt 2d2d txtx == . Đổi cận: ( ) ( ) ( ) ( ) ( ) ( ) 488108 000010 1111 2ddddd206 2222 Ifxxfttfxxfxxfxx ====+=− Vậy 7 I = . Câu 21: Cho (
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 12
A. 7. B. 2. C.
C
D Đặt 2 112 =+=−= txxtdxtdt . Với 01==xt , với 32==xt . Khi đó tích phân đã cho bằng 222 23 2 111 16 .223 4222 ==−+− +++ ttttdtdtttdt ttt 2 3 2 1 7 36ln212ln26ln3 33 =−+−+=−+ t ttt Suy ra 7,12,61 ==−=++= abcabc . Câu 24: Biết ln6 ln3 d3lnln 23xx x ab ee =− +− với , ab là hai số nguyên dương. Tích Pab = bằng A. 10 P = B. 10 P =− C. 20 P = D. 15 P = Lời giải Chọn A
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có 2 2 1 d 1 x x xx+− ( ) 2 2 1 1d xxxx=−− ( ) 2 22 1 1d xxxx=−− 22 22 11 d1d xxxxx=−− 2 2 3 2 1 1 1d 3 x xxx=−− 2 2 1 71d 3 xxx=−− Tính 2 2 1 1d xxx . Đặt 2 1 xt −= 22 1 xt−= dd xxtt= Khi 1 x = thì 0 t = ; khi 2 x = thì 3 t = . Khi đó 2 2 1 1d xxx 3 3 3 2 0 0 d 3 t tt == 3 = . Vậy 2 2 1 7 d3 13 x x xx =− +− 7 3 a = , 1 b =− Vậy 3512.Pab=−= Câu 23: Cho 3 0 ln2ln3 4213 =++ ++ xadxbc x với ,, abc là các số nguyên. Giá trị ++ abc bằng
9. D. 1. Lời giải
họn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
ị
ủ
i giải Chọn C Ta có 444 2 222322 000 sinsintan1 dd.d cos cos2sin3coscos2tan32tan3 xxx Ixxx x xxxxxx === +++ . Đặt 2 2 11 2tan3tan.d d 2 cos xtxxtt x +== ; 03;5 4 xtxt ==== 55 33 1153 d 222 Itdtt t === 5,3,223427abcabc ===++= Câu 26: Biết ( ) ( ) 2 2 01 sincos1dlndln3 2 e x xfxxfxx x +== và ( ) 2 0 a fxx b = d Biết tích phân ln6 0 dln2ln3 13 x x e xabc e =++ ++ với ,, abc là các số nguyên. Giá trị của biểu thức Tabc =++ là A. 1 T =− B. 1 T = C. 2 T = D. 0 T = Lời giải Chọn D
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét tích phân: ln6ln6 2 ln3ln3 dd 2332 x xxxx xex I eeee == +−−+ . Đặt ddxx tetex == . Đổi cận ln66 ln33 xt xt == == . Suy ra: ( ) 66 6 2 3 33 d11 dln1ln23ln2ln5 3212 t Ittt tttt ==+=−−+−=− −+−− Do đó: 2,5ab== . Vậy 10 Pab== . Câu 25: Biết 4 222 0 sin cos2sin3cos xab dx c xxx
= +
, giá tr
c
a 234abc ++ bằng A. 20. B. 24. C. 27. D. 35. Lờ
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
3 Lời giải Chọn C Đặt 2 11d2d txxtxtt =+=−= . Với 01 12 xt xt == == . Khi đó ( ) ( ) ( ) 2 222 2 111 42 2222 dtdt=dt 3211 tt tttt I tttt == ++++ ( ) 2 22 1 1 6 26dt=66ln136ln36ln2 1 tttt t =−+−++=−+− + 6,6,33abcabc ===−++=− Câu 28: Tính tích phân ( )2017 2 2019 1 2 d x Ix x + = . A. 2018201832 2018 . B. 2017201832 40372017 . C. 2018201832 4036 . D. 2021202132 4040 . Lời giải Chọn C Ta có ( )2017 22220172017 201922 111 2 2121 dd1d x x Ixxx xxxxx + + ===+ Đặt 22 2211 1dddd 2 ttxtx xxx =+=−−= . Đổi cận: 13;22xtxt ==== . Khi đó 3 23 20182018 20172017 32 2 2018 .d1132 2240364036 t Itttdt =−===
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét tích phân ln6 0 d 13 x x e Ix e = ++ . Đặt: 2 332dd xxx tetettex =+=+= . Đổi cận: 02 ln63 xt xt == == . Suy ra: ( ) 33 3 2 22 2d121d2ln124ln22ln3 11 tt Ittt tt ==−=−+=−+ ++ . Do đó: 2,4,2abc==−= . Vậy 0 Tabc=++= Câu 27: Giá trị của tích phân 3 0 3dln3ln2 313 x xabc xx =−+ +++ , với ,, abc . Tổng abc ++ bằng: A. 6 B. 9 C. 3 D.
Câu 29: Cho ( ) ( ) 1 10 0
1 1d 1 xxx aa −= + . Giá trị của a thuộc khoảng nào sau đây? A. ( )11;13 . B. ( )9;11 . C. ( )12;14 . D. ( )10;12 . Lời giải Chọn D Đặt 1dd txtx =−= và 1. xt=+ Đổi cận: 01.xt==− 10.xt== Ta có: ( ) ( ) ( ) 0 100 1112 10 101011 011 1
1 1d1d =+td+ 111211.12 tt xxxttttt −=+== Vậy 11 a =
Câu 30: Cho ( ) ( ) 3 2 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 15
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
22 ab =−−−===− Vậy 231Sab=+= Câu 31: Cho ( ) 1 32 0 1 .1d,,,, ab xxxabc c + += a c là phân số tối giản. Tính Sabc =++ A. 18. B. 17 . C. 16. D. 19. Lời giải Chọn D Đặt 222 22 dd 11 1 ttxx txtx xt = =+=+ =− Đổi cận: 01xt== .
1ln2ln3d,, 2 1 ab xab xx + = . Giá trị của 23 Sab =+ bằng A. 9 B. 11 C. 19 D. 1 Lời giải Chọn D Ta có: ( ) ( ) 33 222 22 1 dd 11 x xx xxxx = . Đặt 2 1d2d txtxx =−= và 2 1 xt=+ Đổi cận: 23xt== . 38xt== . Ta có: ( ) ( ) ( ) ( ) 3388 8 222 3 2233 1111111 ddddlnln1 21212 11 x xxtttt tttt xxxx ===−=−+ ++ ( ) ( ) 15ln23ln3 ln8ln9ln3ln45,3
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 16 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 12xt== Ta có: ( ) ( ) 2 1122 53 3222242 0011 1 .1d.1.d1dd 53 tt Ixxxxxxxttttttt =+=+=−=−=− ( )221 2,2,1519 15 abcSabc + =====++= Câu 32: Cho 3 4 0 4cosd1 1sin x xab x =− + với , ab . Tính Tab = A. 1 T = . B. 2 T = . C. 3 T = . D. 4 T = . Lời giải Chọn D Ta có: 2 4 0 4cos.cosd 1sin xx Ix x = + Đặt sindcosd txtxx == Đổi cận: 00xt== . 2 42 xt == Ta có: ( ) ( ) 22 2 2 2 22 2 00 0 41 d41d42212,24 12 t t IttttabTab t ==−=−=−==== + Câu 33: Biết ln8 2 ln3 11 d1ln 2 e1e xx b xaab a =++− +− với , ab + . Tính Pab =+ ? A. 1 P =− B. 1 P = C. 3 P = D. 5 P = Lời giải Chọn D Ta có: ( ) ln8ln8ln8ln8 22 2 ln3ln3ln3ln3 1 de1ede1ded e1e xxxx xx Ixxxx ==++=++ +− ln8 ln8 ln3 ln3 ede223 xx x ==− ln8 2 ln3 e1d. x x + Đặt 222 e1e1 xxtt =+=+ suy ra 2 22 2d2edddd e1 x x tttt ttxx t === Đổi cận: ln32 ln83 xt xt =→= =→=
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 17 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó 3 2 ln833 2 ln32222 2 11113 e1dd1dln1ln 112122 x tdtt xttt ttt +==+=+=+ −−+ Vậy 2 13 1ln2235 3 22 a IPab b = =++−=+= = Câu 34: Cho hàm
ố ( )yfx = đi
m ( )
m ( )2;2
làm
i xứng.
trị của
3 1 2
ằng A. 8 3 B. 16 3 C. 16 3 D. 8 3 Lời giải Chọn B Cách 1. Đặt 4 txdtdx =−=− . Đồ thị hàm số ( )yfx = có ( )2;2 I là tâm đối xứng nên ( ) ( ) 4 2 2 fxfx +− = Như vậy ( ) ( ) ( ) ( ) ( ) ( ) 44404, fxfxfxfxfxfxx +−=−−==− Ta có ( ) ( ) ( ) 3 1 2 Ixxfxfxdx =−+ ( )( ) ( ) ( ) 3 1 4244ttftftdt =−−−+−
số ( )fx liên tục trên ) 0;+ và ( ) 3 0 18fxdx+= . Tính tích phân ( ) 2 1 Ixfxdx = A. 8 B. 2 C. 16 D. 4. Lời giải Chọn D Đặt 1 12 21 uxdudxududx x =+== + Đổi cận: 01 32 xu xu == == ( ) 3 0 18fxdx+= ( ) ( ) ( ) 222 111 2..8.4.4. ufuduufuduxfxdx === Câu 35: Cho hàm số ( )fx liên tục trên , đồ thị hàm s
qua điể
1;0 A và nhận điể
I
tâm đố
Giá
( ) ( ) ( )
xxfxfxdx
−+
b
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 18
ttdttftftdtttftdt =−++−++−+ ( ) ( ) ( ) ( ) ( ) 333 22 111 682444 ttdttftdtttftdt =−++−+−+ ( ) ( ) 3 3 3 22 1 1 16 3844 33 t ttttft =−++−+= . Cách 2. Chọn hàm ( ) ( )3 22 fxax=−+ . Ta có ( )1;0 A đồ thị ( ) ( ) : Cyfx = Khi đó ( ) ( ) ( ) 33 1202222aafxx −+===−+ và có ( ) ( )2 62fxx =− Do đó ( ) ( ) ( ) ( ) ( ) ( ) 33 32 11 16 222262 3 xxfxfxdxxxxxdx −+=−−+−= Câu 36: Số thực dương m thỏa mãn 4 22 44 21 44 m m xm Idx xm == + có thể biểu diễn về dạng ln5ln13ab . Giá trị của biểu thức 2021 ab + là A. 2020. B. 2021. C. 2022. D. 2023. Lời giải Chọn D Ta có biến đổi sau x y O A I 2 3 2 1
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 3 2 1 684 ttftftdt =−+−+ ( ) ( ) ( ) ( ) ( ) ( ) 333 222 111 468242.268 ttdttttftftdtttftdt =−+−−−−++−+ ( ) ( ) ( ) ( ) ( ) ( ) 333 22 111 2.682268
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 19 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 22 4,5 444 22 22 42 4422 2 2 3 2 2 4,5 3 22 11 21 4 44 2 4 12151125 lnlnlnln. 424135413 m mmm mmmm m m mm xm xx Idxdxdxdt m xmtm m x xm x x tm mtmmm ===== +− + +− − ==−= + Như vậ
Ta
(
( ) (
ln5ln132ln5ln132ln51ln13 1 1 2 . 1 2
−=−−=− = = = Trường hợp ( )2 loại vì VT là số hữu tỉ
ố vô
ỉ. Vậ
==
+= Câu
( ) ( ) ( ) 1 2 0 32d, fxxxfxfxxx =−+ . Tìm giá trị thực dương của a để ( ) 0 4 d 5 a fxxa = A. 9 2 . B. 3 2 . C. 1 2 . D. 2. Lời giải Chọn A Đặt ( ) ( ) 1 0 d mfxfxx = . Khi đó ( ) 2 32, fxxxmx=−+ . Suy ra ( ) 23fxx =− . Vậy ( )( ) 1 2 0 3223d mxxmxx =−+− . Đặt ( ) 2 32d23d txxmtxx =−+=− . Do đó 2 2 2 22 22 2 d42 25 m m m m t mttmmmm =−=−=−+= Vậy ( ) 2 4 3 5 fxxx=−+ . Ta có ( ) 232 00 44413449d3d 55532552 aa fxxaxxxaaaaaa =−+=−+==
y 11251ln2ln5ln13. 44134 Im m ===−
có
) ( )
)
2ln13 1ln5 abab b a b a b
, VP là s
t
y 2,1ab
.Suy ra 20212023ab
37: Cho hàm số ( )fx có đạo hàm liên tục trên thỏa:

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 20 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 38: Cho hàm số ( )fx liên tục trên thoả mãn ( ) ( ) 1 22 0 2313d fxxxfxx =−++ . Tính ( ) 2 0 d fxx Lời giải ( ) ( ) ( ) ( ) ( ) 1122 222 0011 111 13d13d13dd 633 xfxxfxxufuuxfxx +=++== Đặt ( ) 2 1 d xfxxa = ( ) 2 1 23 3 fxxa=−+ ( ) 2 22 1 1 3d621 3 axxaxafxx =−+==− ( ) ( ) 22 2 00 10 d21d 3 fxxxx =−= . Câu 39: Cho hàm số ( )yfx = có đạo hàm liên tục trên đoạn 0;1 thỏa mãn ( ) 10 f = và ( ) 1 2018 0 2 xfxdx = . Giá trị của ( ) 1 2019 0 xfxdx bằng A. 4038. B. 2 2019 . C. 4038. D. 2
. Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) 111 1 2019201920192018 0 000 2019 Ixfxdxxdfxxfxxfxdx ===− ( ) ( ) 1 2018 0 12019 fxfxdx=− 02019.24038=−=− . Câu 40: Cho hàm số ()yfx = có đạo hàm ()fx liên tục trên
=−+ .
.
2019
. Miền hình phẳng trong hình vẽ được giới hạn bởi đồ thị hàm số ()yfx = và trục hoành đồng thời có diện tích Sa = . Biết rằng 1 0 (1)()d xfxxb
+= và (3) fc = . Tính 1 0 ()d Ifxx = . A. Iabc
B. Iabc =−+−
C. Iabc =−++ . D. Iabc =−− .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 21 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Ta có 13 01 ()d()d2(1)(0)(3)2(1)(0). Safxxfxxafffaffac =−=−−=−=+ Áp dụng công thức tích phân từng phần với 1 ux=+ và d()d vfxx = , ta được 11 1 0 00 (1)()d(1)()()d 2(1)(0) | xfxxbxfxfxxb ffIbacIbIabc +=+−= −−=+−==−+ Câu 41: Biết tích phân ( ) 10 2 1 log log2log11 1 x Idxabc x ==++ + , trong đó , , abc là các số hữu tỷ. Tính 1123 Sabc =++ . A. 11. B. 9. C. 9. D. 11. Lời giải Chọn B Đặt ( )2 log1 1ln10 1 1 1 ux dudx x dvdx v x x = = = =− + + ( ) ( ) ( ) ( ) ( ) 101010 2 111 10 log111111 log1 1ln10111ln101 1 10 111110lnln1ln10ln11ln2log2log11 1 11ln1011ln1011 xdx Idxxdx xxxxx x xx ==−+=−+− +++ + =−+−+=−+−+=+− Do đó suy ra ( ) 10 11 10 111.2.13.19 11 1 a bS c = ==++−= =− . Câu 42: Cho hàm số ( )fx thỏa mãn ( ) ( ) .1fxfx = , với mọi x Biết ( ) 2 1 d fxxa = và ( )1 fb = , ( )2 fc = . Tích phân ( ) 2 1 d x x fx bằng A. 2cba B. 2abc C. 2cba −+ D. 2abc −+ Lời giải Chọn A Ta có ( ) ( ) .1fxfx = ( ) ( ) 1 fx fx = suy ra ( ) ( ) 22 11 dd x xxfxx fx = ( ) 2 1 .d xfx =
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 22 Chuyên
thi:
Sưu tầm và
( ) ( ) 2 2 1 1 d xfxfxx=− ( ) ( ) ( ) 2 1 221d fffxx=−− 2
=−− Câu
Cho ( ) ( ) 4 2 0 ln9dln5ln3,,, Ixxxabcabc =+=++ . Giá trị của biểu thức abc ++ bằng A. 7 . B. 8. C. 9. D. 10. Lời giải
ln9dd
ux
vxx v = =+ + + = =
=
=−
Giả sử rằng ( ) 2 2 0 cos.d a xfxx bc =− Khi đó abc ++ bằng. A. 32 B. 5 C. 21 D. 31 Lời giải Chọn D Áp dụng tích phân từng phần, đặt ( ) ( ) d'd ufxufxx == , dcosdvxx = nên chọn sin vx = Ta có: ( ) ( ) ( ) ( ) 222 2 2 0 000 cos.dsin.sin.d.sind 2 xfxxxfxxfxxfxxx =−=− ( ) 222 000 1cos2 1 3d3d.cos2d 222 xx x xxxxx=−=−+ Với tích phân 2 0 cos2d xxx , ta đặt dd,dcos2d uxuxvxx === nên chọn 1 sin2 2 vx =
Hòa
0984164935
luyện
Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12
biên soạn
cba
43:
Chọn B Đặt ( ) 2 2 2 2
9 dd9 2 x ux
x x
Ta có: ( ) 4 4 22 2 2 0 0 992 ln9.d 229 xxx Ixx x ++ =+− + 4 0 259ln25ln9d 22 xx =−− 259ln25ln98 22 =−− 25ln59ln38 =−− ln5ln3 abc =++ . Suy ra: 25 98 8 a babc c
=−++=
Câu 44: Cho hàm số ( )fx có 3 2 f =
và ( ) sin fxxx
= .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 23
Sưu tầm và
soạn Khi đó ta có: 22 00 1 3d.cos2d 22 x xxxx−+ 2 2 2 0 0 111 3.sin2sin2d 16222 xxxx =−+− 222 2 0 111111 30cos23. 16241622416 x =−++=−+−=− 11
a
c = =++= = .
phân ( ) 1 2 0 1d x Ixexaeb =+=+ với , ab Tổng Sab =+ bằng A. 1 B. 1 C. 3 D. 3 Lời giải Chọn A Đặt ( ) ( ) 2 d21d 1 e ded x x uxx ux v vx =+ =+ = = Do
Tính
Đặt 1dd dede xx uxux
=+= ==
Hòa
0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12
biên
431 16
babc
Câu 45: Cho tích
đó ( ) ( ) 1 1 2 0 0 1e21d xx Ixxex =+−+
( ) 1 412 eI=−− . ( )1
( ) 1 1 0 1d x Ixex =+
vxv
. Do đó ( ) 1 1 1 0 0 1ed xx Ixex =+− ( ) 1 0 1exx xe =+− ( ) ( )211 eee =−−−= . ( )2 Từ ( )1 và ( )2 ta được 21Ie=− Khi đó 2 1 a b = =− . Vậy 211 Sab=+=−= Câu 46: Cho hàm số ( )fx có đạo hàm trên và thỏa mãn ( ) 'cossin fxxxx =− . Biết ( ) 2 0 d1fxx =− . Tính ( )0 f . A. ( ) 01 f = . B. ( ) 00 f = . C. ( ) 02 f = . D. ( ) 01 f =− . Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 24 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn D Ta có ( ) ( ) cossincoscoscos xxxxxxxxx −=+= Nên ( ) ( ) cos fxxx = hay ( ) cos fxxxC =+ . Với ( ) ( ) 22 00 dcosd fxxxxCx =+ , ta đặt dd uxux == dcosdvxx= chọn sin vx = Khi đó ( ) 222 2
liên tục trên
ỏ
.
Chọn D Theo
ả
ế
( ) 111 12 000 tt ctecdttedtctdtII =+=+=+
Vì 111 11 100 000 ()()()(1)1ttttt Itedttdeteedteeee ===−=−=−−= ,
===
nên 12 12 2 c cIIcc =+=+= . Vậy ()2, x fxex=+ Do đó ln2022 (ln2022)2202222024 fe=+=+= . Câu
Cho 2 2 1 ln(12)dln5ln3ln2 2 xaxbc x + =++
với
abc . Giá trị
2()
A. 3. B. 0.
.
.
Chọn D
0 000 cosdsinsindCd1 22 xxCxxxxxxC +=−+=−+ . Từ ( ) 2 0 d1fxx =− , ta có 111 22 CC −+=−=− Vậy ( ) cos1fxxx=− nên ( ) 01 f =− Câu 47: Cho hàm số ()fx
th
a mãn 1 0 ()(), x fxetftdtx=+
Tính (ln2022) f A. 2022 B. 2021 C. 2023 D. 2024 Lời giải
gi
thi
t, ta có: () x fxec =+ , với 1 0 () ctftdt = là hằng số. Khi đó:
, với 1 1 0 t Itedt = , 1 2 0 Ictdt =
1 2 1 20 0 ()22 ctc Ictdt
48:
,
, ,
của
abc ++ là:
C. 9
D. 5
Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 25
Đặt
ln(12)2
ux
v x xx =+ =
−+ = =−−=
. 5; 3; 2 abc =−== . Vậy 2()5abc++= . Câu 49: Cho hàm số ( )fx liên tục và có đạo hàm trên 0;1 . Biết ( ) ( ) 1 0 2d5Ixfxx =+= và ( ) ( ) 017ff== . Giá trị của tích phân ( ) 1 0 d fxx bằng A. 7. B. 5. C. 2. D. 1. Lời giải Chọn C Đặt ( ) ( ) 2dd dd uxux vfxxvfx =+= == Khi đó ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 0 1 0 1 0 1 0 1 2d5 0 3120d5 3.72.7d5 d2 Ixfxfxx fffxx fxx fxx =+−= −−= −−= = Câu 50: Cho hàm số ( )fx thỏa mãn ( ) ( ) .1fxfx = , với mọi x . Biết ( ) 2 1 d3 fxxa = và ( ) 11fb=+ , ( ) 21fc=− . Tích phân ( ) 2 1 d x x fx bằng A. 23 cba . B. 23 abc . C. 233 cba . D. 23 abc−++ . Lời giải Chọn C Ta có ( ) ( ) .1fxfx = ( ) ( ) 1 fx fx = suy ra ( ) ( ) 22 11 dd x xxfxx fx = ( ) 2 1 .d xfx =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
2
dd 12 11(21)dd2
ux x x vx
+
Khi đó 2 2 1 ln(12)d x x x + = ( ) 2 2 1 1 (21)2 .ln12d x xx xx −+ ++ 5ln53ln32ln2 2 =−++
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 26
( ) ( ) 2 2 1 1 d xfxfxx=− ( ) ( ) (
2 1 221d
=−−
=−−− Câu
t ( ) 4 0
a Ixxdxc
=+=− vớ
Tabc =++ . A. 64 T = .
Chọn D Áp dụng công thức tích phân từng phần ta có: ( ) 44 222 00 4 2 ln218ln9 0 222121 xxx Ixdxdx xx =+−=− ++ 4 0 1111 8ln9 24421 Ixdx x =−−+ + ( ) 2 4 1 8ln9ln2x1 0 448 xx =−−++ 1 8ln93ln9 8 6363ln93ln33 84 =−+ =−=− Suy ra 63,4,3634370.abcTabc =====++=++= Câu 52: Cho ( ) 2 1 2ln e xxdxaebec +=++ với ,, abc là các số hữu tỉ. Mệnh đề nào sau đây đúng? A. abc −= . B. abc +=− . C. abc += . D. abc −=− . Lời giải Chọn A Ta có: ( ) 1 111 2ln2ln222 eee e xxdxdxxxdxxIeI +=+=+=−+ . Tính I : Đặt 2 1 ln. 2 uxdudx x x dvxdxv == == 22222222 11 1 1 111 .ln. 22222424444 e e ee Ixdxdxxxexexeee x =−=−=−=−+=+
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
)
fffxx
233 cba
51: Biế
ln21ln3
b
i ,, abc là các số nguyên và a b là phân số tối giản. Tính
B. 68 T = . C. 60 T = . D. 70 T = . Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 27
Vậy ( ) 22 1 172ln222 4444 e ee xxdxee +=−++=+− 17
===− .
(
0
= A. 8 . 3 I = B. 8 3 I =− . C. 10 3 I = . D. 24 I = . Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3333 3 0 0000 'ddd33d10 xfxxxfxxfxfxxffxx ==−=−= Suy ra ( ) 3 0 d8fxx = . Đặt 3d3d xttx == . Ta có ( ) ( ) ( ) 133 000 1118 3ddd.8. 3333Ifxxfttfxx ===== Câu 54: Hàm số ( )fx liên tục và thỏa mãn ( ) 02 f = và ( ) ( ) 2 0 24d0 xfxx −= . Tính ( ) 1 0 2d Ifxx = . A. 2 I =− . B. 4 I = . C. 0 I = . D. 2 I = . Lời giải Chọn D Đặt ( ) ( ) 242 uxdudx dvfxdxvfx =−= == . Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 222 2 0 000 24d242d82d xfxxxfxfxxfxx −=−−=− Lại có ( ) ( ) 2 0 24d0 xfxx −= . Suy ra ( ) ( ) 22 00 82d0d4 fxxfxx −== . Đặt 1 22 2 txdtdxdxdt === . Đổi cận: 01 02 x t
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
;2; 44 abc
Câu 53: Cho hàm số ( )fx có đạo hàm trên thỏa mãn ( ) 3 0 'd10xfxx = và ( ) 36 f = . Tính
) 1
3d Ifxx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
(
= . A.
= B.
( ) ( ) ( ) 33 00 233dd624 ffxxfxx =−=−= Câu 56: Biết tích phân ( ) 4 0 1 1cos2d Ixxx ab =+=+ , , ab . Giá trị của ab + bằng A. 24 B. 32 C. 12 D. 4 Lời giải Chọn C . Đặt 11 cos2sin2x 2 dudx ux dvxdx v = =+ = = ( ) ( ) 44 4 00 0 4 0 1 1 1cos2dsin2sin2 22 111 cos2 28448 x Ixxxxxdx x + =+=− =++=+ 4,8ab== vậy 12 ab+= Câu 57: Cho hàm số ( )fx liên tục và có đạo hàm trên 0;1 . Biết ( ) ( ) 1 0 2d5xfxx += và ( ) ( ) 017ff== . Giá trị của ( ) 1 0 d fxx bằng A. 7. B. 5. C. 2. D. 1.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ( ) ( ) ( ) 122 000 111 2ddd.42 222Ifxxfttfxx ===== . Câu 55: Cho hàm số ( )yfx = liên tục trên đoạn 0;3 thỏa mãn ( ) 3 0 d=2xfxx và ( ) 32 f = . Tính
) 3 0 d Ifxx
4 I
3 I =− C. 4 I =− D. 6 I = Lời giải Chọn A Đặt ( ) dd ux vfxx =
= ta có ( ) ddux vfx = = . Do đó: ( ) ( ) ( ) 33 3 0 00 dd xfxxxfxfxx =−
hàm số ( )fx nhận giá trị dương, có đạo hàm liên tục trên 0;2 . Biết ( ) 01 f = và ( ) ( ) 2 24 2 xx fxfxe −= với mọi 0;2 x . Tính tích phân
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 29 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn C Đặt 2 ux=+ , ( ) dd vfxx = , Suy ra ddux = và ( )vfx = ( ) ( ) ( ) ( ) ( ) 11 1 0 00 2d52d5 xfxxxfxfxx +=+−= ( ) ( ) ( ) 1 0 3120d5 fffxx −−= ( ) 1 0 d752fxx =−=
=
A. 14 3 I =− B. 32 5 I =− C. 16 5 I =− D.
3
=− Lờ
Câu 58: Biết ( ) ( ) 1 1 2 2 ln1 de 1 e x xab x + =+ ( ) , ab , chọn khẳng định đúng trong các khẳng định sau: A. 2 234 ab−= B. 2 238 ab−= C. 2 234 ab−=− D. 2 238 ab−=− Lời giải Chọn B Đặt ( ) ( )2 ln1 1 dd 1 ux vx x =− = 1 dd 1 1 1 ux x v x = =− Áp dụng công thức tính tích phân từng phần, ta có ( ) ( ) e1 2 2 ln1 d 1 x x x + ( ) ( ) e1 e1 2 2 2 ln11 d 11 x x x x + + =−+ ( ) e1 e1 2 2 ln1 1lne1 1 11ee x xx + + =−−=−−− 1 2 112.e e =−+=− Suy ra 1;2ab==− ( ) 22 232.13.28 ab −=−−= . Câu 59: Cho
( ) ( ) ( ) 32 2 0 3 xxfx Idx fx
16
I
i giải Chọn C Vì hàm số ( )fx nhận giá trị dương, có đạo hàm liên tục trên 0;2 và ( ) ( ) 2 24 2 xx fxfxe −= nên thay 0 x = , ta có: ( ) ( ) 0.21ff = mà ( ) 01 f = ( ) 21 f = . Đặt:
=− =
32 3 dd
uxx fx vx fx
( ) ( )
=− = ( ) ( ) 2 d36d ln uxxx vfx
uxxx vfx
( ) ( ) 2 d36d ln
=− =
Suy ra: ( ) ( ) ( ) ( ) 2 2 322 0 0
3ln36lnd Ixxfxxxfxx =−−− ( ) ( ) 2 2 0
36lnd xxfxx=−− ( )1
Đặt 2 xt =− dd xt=− .
Khi 02xt=→= và 20xt=→= . Khi đó, ( ) ( ) 0 2 2 36ln2(d) Jttftt =−−−− ( ) ( ) 2 2 0
36ln2d ttftt=−−− .
Vì tích phân không phụ thuộc vào biến nên ( ) ( ) 2 2 0
36ln2d Ixxfxx =−−− ( )2
Từ ( )1 và ( )2 , ta cộng vế theo vế, ta được: ( ) ( ) ( ) 2 2 0
236lnln2d Ixxfxfxx =−−+− . Hay ( )( ) 2 22 0
116 3624d 25 Ixxxxx =−−−=−
Câu 60: Cho ( )fx liên tục trên và thỏa mãn ( ) 216 f = và ( ) 1 0
2d2fxx = .
Tính tích phân ( ) 2 0
d Ixfxx = . A. 30 I = B. 28 I = C. 36 I = D. 16 I = Lời giải Chọn B Xét tích phân ( ) 1 0
2d Jfxx = Đặt 2dd 2 t txx== Đổi cận : 00xt== ; 12xt== Ta có ( ) 2 0
1 d2 2 Jftt== ( ) 2 0
d4ftt = ( ) 2 0
d4fxx = .
Tính tích phân ( ) 2 0
d Ixfxx =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 30
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 31
Đặ
==
==
xt== , 13xt== Ta có ( ) 1 2 2 0 ed 2 x x Ix x = + ( )2 2 3 2 2 2e d t t t t = 3 2 2 2 44 1ed t t tt =−+ 33 22 2 22 44 eded tttt tt =+−+ Tính 3 2 1 2 ed t It = 3 2 2 ee1 t ==− . Xét tích phân 3 2 2 4 .ed t t t Đặt 2 22 44 dd dede tt uut tt vtv ==− == Ta có 33 333 22222 22 22 222 444444 ed.eed.eed ttttt ttt tttttt =+−=−+ Ta suy ra 3 2 2 2 2 44 ed t It tt =−+ 4 e2 3 =−+ . Suy ra 1 e1 3 I =−+ 1 a =− , 3 b = , 1 c = . Vậy 3 abc−+=− Câu 62: Cho hàm số fx liên tục trên và 4 2 10 d20, sincosd4. fx xfxxx x Tính tích phân 2 0 d.Ifxx A. 2. I B. 6. I C. 4. I D. 14. I
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
t ( ) ( ) dd dd uxux vfxxvfx
Khi đó ( ) ( ) 2 2 0 0 d Ixfxfxx =− ( ) 2242.16428 f =−=−= Câu 61: Cho biết ( ) 1 2 2 0 d. 2 x xea xec b x =+ + với a , c là các số nguyên, b là số nguyên dương và a b là phân số tối giản. Tính abc −+ A. 3. B. 0 . C. 2. D. 3. Lời giải Chọn D Đặt 2dd txtx =+= Đổi cận : 02
Lời giải Chọn D Xét 4 1
d20 fx x x Đặt 2 ,txtx suy ra 2dd. ttx
Đổi cận 11 42 xt xt Suy ra 4222 1111
sincosd4.fxxx Đặt sin,ux suy ra dcosd. uxx
20d2dd10.dx10 fx xfttfttfx x Xét 2 0
xu xu Suy ra 11 2 000
4sincosdddx=4. fxxxfttfx Vậy 212 001
ddd14.Ifxxfxxfxx Vậy chọn đáp án D. Câu 63: Cho hàm số ( )yfx = cóđạo hàm ( )f'x liêntụctrên vàthoảmãn ( ) ( ) 1 0 xf'xdx+= và ( ) ( ) 4102028 ff−= . Giá trị của ( ) 1 4 0
312022 4 Ifxdx = là A. 1 . 2 B. 1 . 4 C. 2022 . 3 D. 2. Lời giải Chọn A Tính ( ) 1 4 0
4 Ifxdx = . Đặt 4 tx = suy ra 4 dtdx = , đổi cận 00xt== ; 1 1 4 xt== . Khi đó ( ) ( ) ( ) 1 11 4 000
11 4 44 Ifxdxftdtfxdx === Xét tích phân ( ) ( ) 1 0
31xf'xdx + . Đặt ( ) ( ) 313 uxdudx dvf'xdxvfx =+= == . Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1111 1 0 0000
31313410320283 xf'xdxxfxfxdxfffxdxfxdx +=+−=−−=− Theo giả thiết ( ) ( ) 1 0
312022 xf'xdx+= . Suy ra ( ) 1 0
2 fxdx = . Do đó 1 2 I = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
Đổi cận 00 1 2
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 33 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 64: Cho ( )fx là hàm số liên tục trên thỏa mãn ( ) 11 f = và ( ) 1 0 1 d 3 ftt = Tính ( ) 2 0 sin2sind Ixfxx = . A. 2 3 I = B. 1 3 I = C. 4 3 I = D. 2 3 I =− Lời giải Chọn C ( ) ( ) ( ) ( ) ( ) 1 222 0000 sin2.sind2sin.cos.sind2sin.sindsin2.d Ixfxxxxfxxxfxxtftt ==== Đặt ( ) ( ) dd dd utut vfttvft == == Suy ra ( ) ( ) ( ) 1 0 1124 22d212.2.1 0333Itftfttf =−=−=−= . Câu 65: Cho ( ) 4 4 0 lnsincos cossin1.ln2ln coscos1cos x xx xxa Idxec xexxb + =+=−+ + với ,, abc là các số nguyên dương, a b là phân số tối giản. Tổng 23Sabc =+− bằng A. 7. B. 1. C. 9. D. 3. Lời giải Chọn B . Ta có ( ) ( ) 1 2 44 12 2 00 lnsincoscossin coscos1cos x I I xx xx IdxdxII x exx + =+=+ + Tính ( ) 4 1 2 0 lnsincos cos xx Idx x + = . Đặt ( ) 2 lnsincoscossin sincos sincos costan1 cos xx uxx dudx xx dx xx dv vx x x =+ = + + = =+= Suy ra ( ) ( ) ( ) 4 1 0 sin3 tan1lnsincos1ln2lncosln2 44 cos2400 x Ixxxdxxx x =++−−=−+=− Tính ( ) ( ) ( ) 44 2 00 cossincossin cos1coscos1.cos x xxx exx xx Idxdx exxexex == ++ .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 34
Đặt
2 2 ln1 1 x uxdudx x dvdxvx =+= + == Lúcđó: 111 22 1 2 222 0 000 1 1 2 0 0 11111 ln1ln2ln21
111 ln2ln21 212 xx Ixxdxdxdx xxx xdxA x +− =+−=−=−− +++ =−+=−+ + Tính 1 2 0 1 1 Adx x = + Đặt tan 22 xtt = ( ) 2 1tan. dxtdt=+ Đổi cận : 00 1 4 xt xt == == Do đó : ( ) 2 44 4 2 0 00 1tan 1tan4 t Adtdtt t + ==== + Vậy : 1 ln21 24 I =−+ Câu 67: Cho hàm số () = yfx có đạo hàm là 2021 ()2022, fxxx =+ và (1)1011 f = . Giá trị của 2 0 d 2 x fx bằng A. 1 2023 . B. 1 4046 . C. 2 2023 . D. 1 2023 . Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
( ) coscossin xx texdtexxdx ==− Đổi cận: 4 2 01; 42 xtxte =→==→= Suy ra ( ) 4422 22 4 4 2 11 4 2 112 lnln 2 111 12 ee dtte e Idt ttttt e
==−== +++ + Vậy 4 4 12 4 325 ln2lnln2ln2 242 2 e IIIe e =+=−+=−+ + . Suy ra 5,2,2abc=== 23235221 Sabc =+−=+−= . Câu 66: Tính 1 2 0 ln1 Ixdx =+ Lời giải Đặt
12121
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 35 Chuyên
thi:
10 Tốt
12 Sưu tầm và biên soạn Chọn C Đặt d2d 2 x txt == . Đổi
xt=→=
21xt=→= Ta
21 00 d2()d 2 x Ifxftt == . Đặt ()d()d dd uftuftt vtvt == == . Khi đó: ( ) 111 1 2021 0 000 11 ()d.().()d(1)2022d10111011
ftttfttfttfttt =−=−+=−+=− Suy ra: 2 2023 I =− Câu 68: Cho hàm số ( )yfx = liên tục trên đoạn 11 ; và thỏa mãn ( ) ( ) ( ) 1 1 3 2d 2 fxxtftt +=+ với 11x;− . Khi đó ( ) 1 1 d Ifxx = bằng A. = 3. I B. = 4. I C. = 2. I D. = 1. I Lời giải Chọn C Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 111 111 333 2ddd2 222 fxxtfttfxx.ftttftt +=+=+− ( ) fxAxB,=+ với ( ) ( ) 11 11 33dd2 22 Aftt,Btftt ==− Giả sử ( ) ( ) fxaxb,a,b. =+ Theo giả thiết ta có: ( )( ) ( ) 1 2 1 33 2d112d 22 axbxtatbt,x;axbaxtbxatbtt ++=++−++=+++ 1 232 1 332 22211 223223 axtatbta axbbxtaxbbx,x; ++=+++++=+− ( ) 3 231 231 3223 2 23 .ba abb fxx. aba .ab = == =+ =+= =+
Hòa
0984164935
luyện
Tuyển sinh vào lớp
Nghiệp THPT BDKT Toán 10; 11;
cận: 00
;
có:
20232023
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 36
1 11 2 11 1 333
x Ifxxxxx. ==+=+=+−−=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: ( ) ( )
d31d112 222



CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
MỨC ĐỘ VẬN DỤNG
ỤNG CAO Câu 69: Cho hàm số ( )fx liên tục trên và thỏa mãn ( ) 1 5 d9fxx = . Tích phân ( ) 2 0 139d fxx −+ bằng A. 15 B.
ận
Câu
Cho hàm số ( )fx liên tục trên đoạn 0;10 thỏa mãn ( ) ( ) 1010 02 d7,d1fxxfxx== . Tính ( ) 1 0 2d Pfxx = A. 6 P = B. 6 P =− C. 3 P = D. 12 P = Lời giải Chọn C Ta có: ( ) ( ) ( ) 21010 002 ddd6fxxfxxfxx =−= Xét ( ) 1 0 2d Pfxx = . Đặt 1 2d2ddd 2 txtxxt === . CHƯƠNG III NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
0984164935
BÀI 2. TÍCH PHÂN
VẬN D
27 C. 75 D. 21 Lời giải Chọn D Ta có ( ) ( ) 222 000 139d13d9d fxxfxxx −+=−+ ( ) 2 0 13d18fxx =−+ Xét ( ) 2 0 13d fxx , đặt 13 tx =− d d3dd 3 t txx =−=− Đổi c
khi 01xt== ; 25xt==− . Suy ra ( ) 251 015 11 13d()d()d 33 fxxfttftt −=−= . Khi đó ( ) 211 055 11 139d()d18()d1821 33 fxxfttfxx −+=+=+=
70:

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 2
Đổ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
i cận: Lúc đó: ( ) ( ) ( ) 122 000 11 2ddd3 22 Pfxxfttfxx ==== Câu 71: Cho ( ) 5 1 d26Ifxx== . Khi đó ( ) 2 2 0 11d Jxfxx =++ bằng A. 15. B. 13. C. 54. D. 52. Lời giải Chọn A + Ta có: ( ) 2 2 0 11d Jxfxx =++ ( ) 22 2 00 d1d xxxfxx=++ + Xét 2 0 d Axx = . 2 0 d Axx = 2 2 0 2 2 x == . + Xét ( ) 2 2 0 1d Bxfxx =+ Đặt 2 1 tx=+ d2dtxx= . Đổi cận: ( ) 2 2 0 1d Bxfxx =+ ( ) 5 1 1 d 2 ftt = ( ) 5 1 1 d 2 fxx = Ta có: 1 .2613 2 == Vậy 15 JAB=+= . Câu 72: Cho hàm số ()yfx = liên tục trên thỏa mãn ( ) 9 1 4 fx dx x = và ( ) 2 0 sincos2.fxxdx = Tích phân 3 0 () Ifxdx = bằng A. 8 I = B. 6 I = C. 4 I = D. 10 I = Lời giải Chọn C x 0 2 t 1 5
537d Pfxx =−+ ( ) 22 00
53d+7d fxxx=− ( ) 1 2 0 5
24d 2 Ifxfxx =+− A. 0 I = B. 2018 I = . C. 4036 I = D. 1009 I
d 7 3 t ftx=+ ( ) 5 1 Đặ
1 d14 3 ftt =+ 1 .151419 3 =+= Câu 74: Cho ( ) 4 0 ậ
= Lời giải Ta có ( ) ( ) 22 00 242dd IfxxfxxHK =+−=+ Tính ( ) 2 0 2 Kfxdx = .
n: 02;24xtxt ==== . Nên ( ) 4 0 1 100 d9 2 Kftt== Tính ( ) 2 0 d 42 Hfxx =− ,
208d1fxx = . Tính tích phân ( ) ( ) 2 0 Đặ
t d 22d txtx == ; đổi c
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt 1 txdtdx 2x == . Khi đó 11;93xtxt ==== Suy ra ( ) 933 111 2()4()2. fx dxftdtftdt x === Đặt ;cos 2 sin; 2 tx xdtdx −= = . Khi đó. 00;1 2 xtxt ==== Suy ra 313 001 ()()()224. fxdxfxdxfxdx=+=+=
Câu 73: Cho biết ( ) 5 1
d15fxx = . Tính giá trị của ( ) 2 0
537d Pfxx =−+ . A. 15 P = . B. 37 P = . C. 27 P = . D. 19 P = . Lời giải Đặt 53 tx =− d3dtx=− 1 d=d 3 xt− Đổi cận: 0 x = thì 5 t = ; 2 x = thì 1 t =− . Ta có: ( ) 2 0
t 422 txdtdx =−=− ; đổi cận: 04;20xtxt ==== . Nên ( ) 4 0 1 100 d9 2 Hftt==
Suy ra 2018 IKH=+= . Câu 75: Cho ( )yfx = là hàm số chẵn, liên tục trên 6;6 . Biết rằng ( ) 2 1
d8fxx = ; ( ) 3 1
2d3fxx−= Giá trị của ( ) 6 1
d Ifxx = là A. 5 I = B. 2 I = C. 14 I = D. 11 I = Lời giải
Ta có ( )yfx = là hàm số chẵn, suy ra ( ) ( ) 22 fxfx −= . Khi đó: ( ) ( ) 33 11
2d2d3fxxfxx −== . Xét tích phân: ( ) 3 1 1
2d Ifxx = . Đặt 1 2d2ddd 2 txtxtx === . Đổi cận: 12xt== ; 36xt== . ( ) ( ) ( ) 666 1 222
11 .dd3d6 22 Ifttfttftt ==== ( ) 6 2
d6fxx = . Vậy ( ) ( ) ( ) 626 112
ddd8614Ifxxfxxfxx ==+=+= . Câu 76: Cho hàm số ( )fx liên tục trên và ( ) 2 0
d2018fxx = , tính ( ) 2 0
d.Ixfxx = A. 1008 I = . B. 2019 I = . C. 2017 I = . D. 1009 I = . Lời giải Xét ( ) 2 0
d.Ixfxx = Đặt 2 1 d2ddd. 2 txtxxxxt === Đổi cận: 2 00;.xtxt ==== Khi đó ( ) ( ) 22 00
11 dd1009. 22 Ifttfxx === Câu 77: Cho ( ) 2 1
d2fxx = . Khi đó ( ) 4 1
d fx x x bằng A. 1 B. 4 C. 2 D. 8 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
Đặt xt = 1 dd 2 xt x = 1 d2dxt x = . Khi 1 x = thì 1 t = ; 4 x = thì 2 t = .
Suy ra ( ) ( ) ( ) 422 111
d.2d2d2.2 fx xfttftt x === 4 = Vậy ( ) 4 1
d4 fx x x =
Câu 78: Cho ( ) d fxxx+= 2 2 1 12 . Khi đó ( )d Ifxx = 5 2 bằng A. 2. B. 1. C. 4. D. 1. Lời giải Đặt d ddd. t xtxxtxx +=== 2 12 2 Đổi cận ;.xtxt ==== 1225 Suy ra: ( ) ( ) 2
2 1
5 2 1 dd 2 21 xftt fx = =+ ( ) 5 2
d4 ft t = ( )d Ifxx == 5 2 4 .
dx+3dx=10fxgx (
được
Tính ( ) 3 1 4dxfx
trình: 310 26 uv uv
. ( ) ( ) 3 1 2dx=6 fxgx ( ) ( ) 33 11 2dx-dx=6 fxgx .
t ( ) ( ) 33 11 dx; v =dxufxgx = +
2 u
) ( ) 3 1 3 1 dx=4 dx=2 fx gx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
Câu 79: Cho , fg là hai hàm số liên tục trên 1;3 thỏa mãn điều kiện ( ) ( ) 3 1 Đặ
3dx=10fxgx + đồng thời ( ) ( ) 3 1 Ta
2dx=6 fxgx . Tính ( ) 3 1 hệ phương
4dxfx +2 ( ) 2 1 += −= 4
21dxgx A. 9. B. 6. C. 7. D. 8. Lời giải Ta có: ( ) ( ) 3 1 v
3dx=10fxgx + ( ) ( ) 33 11 = =
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
Đặ
22
−===
Vậy ( ) 3 1 4dx
+2
2 1
.
Cho
số ( )fx liên tục trên thỏa ( ) 1 0 d2fxx = và ( ) 2 0 31d6
+= .
7
Ifxx =
.
(
(
37 73
=−−−=−−
(
( ) ( )
777
=−=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
t 4dtdx;13;31 txxtxt =−=−==== . ( ) ( )( ) ( ) ( ) 3133 1311 4ddtdtdx4 fxxftftfx −=−=== . + Tính ( ) 2 1 21dxgx Đặt 21dz2dx;11;23 zxxzxz =−===== ( ) ( ) ( ) 233 111 11 21ddzdx1.
gxxgzgx
fx
( )
21dx = 6 gx
Câu 80:
hàm
fxx
Tính ( )
0 d
. A. 16 I = B. 18 I = C. 8 I = D. 20 I = Lời giải ( ) 1 0 d2Afxx== , ( ) 2 0 31d6Bfxx=+= đặt 313 txdtdx =+= Đổi cận : 01 27 == == xt xt Ta có: ( ) ( ) ( ) 777 111 1 dt6dt18d=18 3 Bftftfxx === Vậy ( ) ( ) ( ) 717 001 ddd20Ifxxfxxfxx ==+= . Câu 81: Cho ( )fx liên tục trên thỏa mãn ( ) ( ) 10 fxfx =− và ( ) 7 3 d4fxx = . Tính ( ) 7 3 d Ixfxx = A. 80 B. 60 C. 40 D. 20 Lời giải Đặt 10 tx =− . Khi đó ddtx =−
Đổi cận: 37xt== . 73xt== . Khi đó
)
) ( ) ( )
1010d1010d Itftttftt
( ) ( ) 7 3 1010d xfxx=−−
)
( )
333 10d10dd xfxxfxxxfxx
( ) 7 3 10dfxxI=−
Suy ra ( ) 7 3
210d10.440 Ifxx=== . Do đó 20 I =
Câu 82: Cho ( ) 1 0
d9fxx = Tính ( ) 6 0
sin3cos3d Ifxxx
= A. 5 I = . B. 9 I = . C. 3 I = . D. 2 I = . Lời giải Đặt sin3d3cos3.d txtxx == Đổi cận: 00 1 6
xt xt == == ( ) ( ) 1 6 00
====
11 sin3cos3dd.93 33Ifxxxftt
Câu 83: Cho tích phân ( ) 4 0
d32.== Ifxx Tính tích phân ( ) 2 0
2d. = Jfxx A. 32 J = B. 64 J = C. 8 J = D. 16 J = Lời giải Đặt d 2d2dd. 2 === t txtxx Đổi cận: 00;24. ==== xtxt ( ) ( ) ( ) 244 000
111 2ddd16. 222 ===== JfxxfttfttI
Câu 84: Biết ( )fx là hàm liên tục trên và ( ) 9 0
d9fxx = . Khi đó giá trị của ( ) 4 1
33d fxx là A. 0 B. 24 C. 27 D. 3 Lời giải Xét ( ) 4 1
33d Ifxx =− Đặt 33d3d txtx =−= . Đổi cận: 49 10 xt xt == == . Vậy ( ) ( ) 99 00
111 dd.93 333Ifttfxx ==== .
Câu 85: Cho hàm số ()fx thỏa mãn 1 0 (2)2fxdx = .Tích phân 2 0 () fxdx bằng A. 8. B. 1. C. 2. D. 4.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 7
Lời giải Đặt 2 tx = 2 dtdx = 2 dt dx = , 00 12 xt xt == == Ta có 122 000
()1 2(2)() 22 ftdt fxdxftdt=== 2 0 ()4ftdt = Theo tính chất tích phân 22 00 (x)(t)4 fdxfdt== Vậy 2 0 ()4fxdx =
Câu 86: Cho hàm ( )fx thỏa mãn ( ) 2017 0
d1fxx = . Tính tích phân ( ) 1 0
2017d Ifxx =
A. 1 2017 I = . B. 0 I = . C. 2017 I = . D. 1 I = . Lời giải Đặt 2017d2017d txtx == 1 dd 2017 xt= Đổi cận: 00;12017xtxt ==== Vậy ( ) ( ) 20172017 00
111 .dd 201720172017Ifttftt === Câu 87: Cho tích phân ( ) 2 1 d fxxa = . Hãy tính tích phân ( ) 1 2 0 1d Ixfxx =+ theo a A. 4 Ia = . B. 4 a I = . C. 2 a I = . D. 2 Ia = . Lời giải Đặt 2 1d2d txtxx =+= . Đổi cận ( ) ( ) ( ) ( ) 1222 2 0111
d11 1d.dd 2222 Ixfxxftfttfxxta =+==== .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
Câu 88: Cho hàm số ( )fx liên tục trên và thỏa mãn ( ) 4 2 0
tan.cosd2 xfxx
fx x xx = Tính ( ) 2 1 4
= và ( ) 2 2ln d2 ln
e e
2 d fx x x . A. 0 B. 1 C. 4 D. 8 Lời giải * ( ) ( ) 2 44 2 1 2 00
cos 1 tan.cosd.sin2d 2cos fx Ixfxxxx x
== Đặt 2 cos xt = sin2dd xxt=− . Đổi cận x 0 4 t 1 1 2 Khi đó ( ) 1 2 1 1
1 d 2 ft It t =− ( ) 1 1 2
d4 ft t t = . * ( ) ( ) 22 ee22 2 2 ee
lnln12ln d.d ln2ln fxfx x Ixx xxxx == Đặt 2ln xt = 2ln dd x xt x = . Đổi cận x e 2 e t 1 4 Khi đó ( ) 4 2 1
1 d 2 ft It t = ( ) 4 1
d4 ft t t = . * Tính ( ) 2 1 4
2 d fx Ix x = . Đặt 2xt = 1 d 2 xdt= . Đổi cận x 1 4 2 t 1 2 4
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
Khi đó ( ) ( ) ( ) 414 11 1 22
ddd448ftftft Ittt ttt ==+=+= .
hàm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 10
Đổ
x
1 Ta
(
2
dddd
=−===+=+=−= Vậy ( ) ( ) 1 2 00 2sincos332931 d 2 d 2 Ifxxxfxx =+−=+= . Câu 90: Cho ( ) 2 1 d2Ifxx== . Giá trị của ( ) 2 0 sin3cos1 d 3cos1 xfx x x + + bằng A. 2. B. 4 3 . C. 4 3 . D. 2. Lời giải Đặt 2 2 3cos13cos1dsind. 3 uxuxuuxx =+=+−= Đổi cận 1 2 02 xu xu == ==
Câu 89: Cho
số ( ) 223;1 5;1 xxx yfx xx + == − . Tính ( ) ( ) 1 2 00 2sincos3dd 32 Ifxxxfxx =+− . A. 71 6 I = . B. 31 I = . C. 32 I = . D. 32 3 I = . Lời giải Xét tích phân ( ) 2 1 0 sincod s Ifxxx = .Đặt sind dcos txtxx == Đổi cận x 0 2 t 0 1 Ta có ( ) ( ) ( ) 1 111 2 1 000 0 ddd9 55 22 x Ifttfxxxxx ===−=−=
Xét tích phân ( ) 1 2 0 32 d Ifxx =− .Đặt 322 d dd 2 d t txtxx =−=−=
i cận
0 1 t 3
có
) ( ) ( ) ( ) 3 1333 3 2
0111 1
111111022 323318 22223233 x Ifxxfttfxxxxx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 11 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó ( ) ( ) ( ) ( ) 122 2 0211 sin3cos1 2 224 dddd. 3333 3cos1 xfx ufu xufuufxx u x + ==== + Câu 91: Biết ( ) 4 1 5 fxdx = và ( ) 5 4 20 fxdx = . Tính ( ) ( ) 2ln2 22 10 43 xx fxdxfeedx A. 15 4 I = B. 15 I = C. 5 2 I = D. 25 I = Lời giải Chọn A Đặt 434 txdtdx =−= thì ( ) ( ) ( ) ( ) ( ) 2545 1114 11125 43520 4444fxdxftdtftdtftdt −==+=+= Đặt 22 2 xx ueduedx == thì ( ) ( ) ln24 22 01 15 22 xx feedxfudu== . Vậy 25515 424 I =−= . Câu 92: Cho ()fx là hàm số liên tục trên thỏa mãn 2 ()(2)., x fxfxxex +−= . Tính tích phân 2 0 () Ifxdx = . A. 4 1 4 e I = . B. 21 2 e I = . C. 4 2 Ie=− . D. 4 1 Ie=− . Lời giải Đặt 2 xtdxdt =−=− ( )( ) ( )( ) ( ) 022 200 222 Iftdtftdtfxdx =−−=−=− . ( ) ( ) ( ) 222 222 4 22 0 000 111 22 222 xxx e Ifxfxdxxedxedxe =+−==== . Vậy 4 1 4 e I = .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
Page 12
Câu
ố (
ục trên
ỏ
=
x
ế
rằ
1
= Tính
2
= A.
= B.
=
. Ta
( ) ( )
Đặ
(
=== ( ) 2 0 d6, fxxx= ( ) ( ) 12 01 dd6, fxxfxxx += . ( ) 2 1 1d6,fxxx += . ( ) 2 1 d5, fxxx = Câu 94: Cho hàm số ()fx liên tục trên thỏa mãn 8 3 3 2 01 () tan.(cos)6 fx xfxdxdx x == . Tính tích phân 2 2 1 2 ()fx dx x A. 4 B. 6 C. 7 D. 10 Lời giải +) Đặt 32 3 3 txtxtdtdx === Đổi cận 11xt== và 82xt== . Khi đó 822 3 2 3 111 ()(t)(t)336fxffdxtdtdt xtt === 2 1 (t)2 f dt t = +) Đặt 22 1 cos2cossin2costantan 2 txdtxxdxdtxxdxxdxdt t ==−=−=− Đổi cận: 01xt== và 1 34 xt == .
viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
93: Cho hàm s
)fx liên t
th
a mãn ( ) ( ) 23 fxfx
,
. Bi
t
ng ( )
0 d1fxx
tích phân ( )
1 d Ifxx
5 I
6 I
C. 3 I = D. 2 I = Lời giải
có:
( ) ( ) ( ) 1111 0000 1 33.13.d3d2d2d2, 2 fxxfxxfxxfxxx ===== .
t ( ) 2d2d xtxt == , với 00xt== ; 12xt== .
) ( ) ( ) ( ) 122 000 111 32d2dd, 222fxxfttfxxx
Câu 95: Cho hàm số ( )fx liên tục trên thỏa ( ) 2018 0
d2fxx = . Khi đó tích phân ( ) ( ) 2018 e1 2 2 0
ln1d 1 x fxx x + + bằng A. 4. B. 1. C. 2. D. 3. Lời giải Đặt ( ) ( ) 2018 e1 2 2 0
ln1d 1 x Ifxx x =+ + Đặt ( ) 2 ln1tx=+ 2 2 dd 1 x tx x = + Đổi cận: 0 x = 0 t = ; 2018 e1 x =− 2018 t = . Vậy ( ) 2018 0
d Iftt = ( ) 2018 0
d2fxx == .
Câu 96: Cho hàm số ( )fx liên tục trên thỏa mãn ( ) 4 0
= và ( ) 2 1 2 0
d1. 1 xfx x x = + Tính ( ) 1 0
tand3fxx
d.Ifxx = A. 2 I = . B. 6 I = . C. 3 I = . D. 4 I = . Lời giải Ta có ( ) 4 0
== . Đặt ( ) 2 2 1 tanddtand1d cos xttxxtx x ====+ . Vậy ( ) ( ) 11 22 00
tand3Kfxx
11 .d.d3 11 Kfttfxx tx === ++
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó 1 1 3 4 2 1 01 4 1(t)(t) tan.(cos)612 2 ff xfxdxdtdt tt
=−== +) Đặt 22 1 22 2 dxdxdt txdtxdxdtx xxt ==== Đổi cận: 11 24 xt== và 22xt== Khi đó 2212 2 111 1 244 ()1(t)1(t)1(t)2127 2222 fxfffdxdtdtdt xttt + ==+==

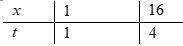
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
Lại có ( ) ( ) ( ) ( )
) 2 1111 222 0000 11 dddd 111 xfx xfxfxxfxxfxx xxx =−=− +++ Vậy
ra (
==
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
(
suy
) 1 0 d4Ifxx
Câu 97: Cho hàm số ( )fx liên tục trên và thỏa mãn ( ) ( ) 16 2 2 1 4 cot.sindd1 fx xfxxx x == . Tính tích phân ( ) 1 1 8 4 d fx x x A. 3 I = . B. 3 2 I = . C. 2 I = . D. 5 2 I = . Lời giải Đặt ( ) 2 2 1 4 cot.sind1Ixfxx == , ( ) 16 2 1 d1 fx Ix x === Đặt 2sin tx = d2sin.cosd txxx= 2 2sin.cotdxxx = 2.cotdtxx = . ( ) 2 2 1 4 cot.sind Ixfxx = ( ) 1 1 2 1 .d 2 ftt t = ( ) 1 1 2 1 d 2 ft t t = ( ) ( ) 1 4 1 8 4 1 d4 24 fx x x = ( ) 1 4 1 8 4 1 d 2 fx x x = . Suy ra ( ) 1 4 1 1 8 4 d22 fx xI x == Đặt tx = 2ddttx= . ( ) 16 2 1 d fx Ix x = ( ) 4 2 1 2d ft tt t = ( ) 4 1 2d ft t t = ( ) ( ) 1 1 4 4 2d4 4 fx x x = ( ) 1 1 4 4 2d fx x x = . Suy ra ( ) 1 2 1 4 4 11 d 22 fx xI x == Khi đó, ta có: ( ) ( ) ( ) 1 11 4 111 884 444 ddd fxfxfx xxx xxx =+ 15 2 22 =+= .
1
2
( )
1
ftdtftdt
24.
( )
3 fxdx =− Lời giải Chọn D Đặttx=− ( ) ( ) ( ) 001 110 fxdxftdtftdt =−−=− ( ) 1 0 3
1 ftdt = = . Lời giải Chọn A Đặt sin,dcosd txtxx == . Đổi cận
( ) ( ) ( ) 212 001 143. fxdxfxdxfxdx=+=−=−
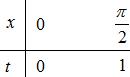
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 15
Đặt ( ) ( )
112 11
22
222
txfxdxfxdxftdt =−=−= ( )
22 11 1
2
==−
Vậy
Câu
Cho ( )fx là
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 số liên tục
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ỏ
Câu 98: Cho hàm số ( )fx liên tục và là hàm số lẻ trên đoạn 2;2 . Biết rằng ( ) ( ) 01 1 1 2 =
1,22fxdxfxdx=−−= .Mệnh đề nào sau đây đúng? A. ( ) ( ) 22 20 = .
2 fxdxfxdx = . B. ( ) 1 1 2 ( ) 2 0
4 fxdx =− . C. ( ) 1 0 sin2.sind Ixfxx
1 fxdx =− D. ( ) 2 0 = A. 4 3 I = . B. 2 3 I = . C. 2 3 I =− D.
99:
hàm
trên th
a ( ) 11 f
và ( ) 1 0 1 d 3 ftt
Tính
1
I
Câu 100: Cho hàm số fx liên tục trên và 9 2 10 d4,sincosd2 fx xfxxx x . Tính tích phân 3 0
d Ifxx A. 6 I = B. 4 I = C. 10 I = D. 2 I = Lời giải Chọn B
Ta có: 993 111
d2d2d fx xfxxftt x Mà 9 1
d4 fx x x nên 33 11
2d4d2 fttftt Vì tích phân không phụ thuộc vào biến số nên 33 11
d2d2fttfxx
Ta có: 1 22 000
sincosdsindsind fxxxfxxftt Mà 2 0
sincosd2fxxx nên 1 0
d2ftt Vì tích phân không phụ thuộc vào biến số nên 11 00
d2d2fttfxx Khi đó 313 001
ddd224Ifxxfxxfxx .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 1 2 00 sin2.sind2.d Ixfxxtftt == Đặt ( ) ( ) 2d2d dd utut vfttvft == == ( ) ( ) ( ) ( ) 1 0 114 2.2d2.12. 033Itftfttf =−=−=
8080.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
Câu 102: Cho hàm số ()yfx = liên tục trên và thỏa mãn 23 3 4()6(2)4 5 xfxfxx+=+ . Giá trị 4 0 ()d fxx bằng A. 52 25 B. 52 C. 48 25 D. 48 Lời giải Chọn A 22 2323 00 2244 22 0000 4444 0000 33 4()6(2)44()6(2)d4d 55 52522()d()3(2)d(2)2()d3()d55 5252522()d3()d5()d()d5525 xfxfxxxfxfxxxx fxxfxxfttfuu fxxfxxfxxfxx +=++=+ +=+= +=== Câu 103: Cho ( )fx liên tục trên và thỏa mãn ( ) ( ) 1 0 216,2d2ffxx== . Tích phân ( ) 2 0 d xfxx bằng A. 30. B. 28. C. 36. D. 16. Lời giải Chọn B Ta có: ( ) ( ) ( ) ( ) 112 000 1 2d22d22d4 2 fxxfxxfxx === .
Câu 101: Cho ( )fx liêntụctrên thỏamãn ( ) ( ) 2020 fxfx =− và ( ) 2017 3 x4.fxd = Khiđó ( ) 2017 3 xxfxd bằng A. 16160. B. 4040. C. 2020. D.
Lời giải Chọn B Đặt 20202020 uxxu =−=− . Ta có x ddu =− . Với 3 x = thì 2017 u = . Với 2017 x = thì 3 u = . Khiđó ( ) 2017 3 xxfxd = ( ) ( ) ( ) ( ) 20172017 33 202020202020ufuduxfxdx −−=− Suy ra ( ) ( ) 20172017 33 2x = 2020x = 8080. xfxdfxd Do đó ( ) 2017 3 x = 4040. xfxd
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 18 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ( ) ( ) dd ddx uxux vfxvfx == == ( ) ( ) ( ) ( ) 22 2 0 00 dd22432428xfxxxfxfxxf =−=−=−= Câu 104: Cho hàm số ( )fx liên tục trên đoạn 0;1 và ( ) 2 0 sind5fxx = . Tính ( ) 0 sind Ixfxx = A. 5 2 I = B. 10 I = C. 5 I = D. 5 I = Lời giải Chọn D Ta có ( ) ( ) ( ) 2 00 2 sindsindsind Ixfxxxfxxxfxx ==+ , Tính ( ) 2 sind xfxx Đặt xt =− ddt x =− ( ) ( ) ( ) ( ) ( ) ( ) sindsindtsindt xfxxtfttft =−−−=− Đổi cận 22 0 xt xt == == ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 2222 0000 22 sindsindtsindtsindtsindsind xfxxtftfttftfxxxfxx =−=−=− Do đó ( ) ( ) ( ) ( ) 22 000 2 sindsindsindsind5 Ixfxxxfxxxfxxfxx ==+== Vậy Chọn D Câu 105: Cho hàm số ()yfx = liên tục trên 1 ;3 3 thỏa mãn 3 1 (). fxxfxx x +=− . Giá trị tích phân 3 2 1 3 ()fx Idx xx = + bằng:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 19 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 8 9 B. 16 9 C. 2 3 D. 3 4 Lời giải Chọn A 3 2 1 1() ().1 1 f fx x fxxfxxx xxxx +=−+=− ++ 333 2 111 333 1 ()16 dd(x1)d19 f fx x xxx xxx +=−= ++ Xét 3 1 3 1 'd 1 f x Ix x = + Đặt 22 11d ddd t txtx xxt === . 1 333 3 222 111 3 333 1 ()d()() 'dd 1 1 1 f fttftfx x IxdtxI xtttxx t ===== +−++ + . Suy ra 168 2 99 II== Câu 106: Cho ( )fx là hàm số có đạo hàm liên tục trên 0;1 và ( ) 1 1 18 f =− , ( ) 1 0 1 .d 36 xfxx = . Giá trị của ( ) 1 0 d fxx bằng A. 1 12 . B. 1 36 . C. 1 12 . D. 1 36 . Lời giải Chọn A Đặt ( ) ( ) dd d uxux dvfxxvfx == == , khi đó ta có ( ) ( ) ( ) ( ) ( ) 111 1 0 000 1 .d.d1d 36 xfxxxfxfxxffxx =−=−= ( ) ( ) 1 0 11 d1 3612 fxxf =−=− . Câu 107: Cho hàm số ( )fx có ( ) 2 1 fe = và ( ) 2 2 21 x x fxe x = với mọi x khác 0. Khi đó ( ) ln3 1 d xfxx bằng A. 2 6 e B. 2 6 2 e C. 2 9 e D. 2 9 2 e Lời giải Chọn D
Khi đó, ta có ( ) ( ) ( ) ln3 ln3ln3ln3 2 2222 111 1
x xxx e xfxxxexexexe =−+===− .
1 d122dd9 22
Câu 108: Cho hàm số ()yfx = có đạo hàm liên tục trên và thỏa mãn 2 0 (2)16,()4 ffxdx== . Tính 1 0 (2) Ixfxdx = . A. 20 I = B. 7 I = C. 12 I = D. 13 I = Lời giải Ta có: ( ) ( ) ( )
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét tích phân ( ) 2 2 21 dd x x fxxex x = Đặt ( ) 2 2 2 21 d4d 1 1 dd x x uxe uxex v vx x x =− = =− = , khi đó ( ) ( ) 222 2 211 dd214d xxx x fxxexxeex xx ==−−+ ( ) 22 1 212xx xeeC x =−−++ Do ( ) 2 10feC== . Vậy ( ) ( ) 22 1 212xxfxxee x =−−+
1 111 0 000 1111 (2)22d(2)2d2 2224 Ixfxdxxfxfxxffxx ==−=− 2 0 1111 (2)().16.472424Iffxdx =−=−= . Câu 109: Cho hàm số fx có đạo hàm liên tục trên 0;1 thỏa mãn ( ) 1 2 0 1 21 xfxdx =− , ( ) 10 f = và ( ) 1 2 0 1 ' 7 fxdx = . Giá trị của ( ) 1 0 fxdx bằng A. 5 12 B. 1 5 C. 4 5 D. 7 10 Lời giải Đặt ( ) ( ) 3 2 ' 3 dufxdx ufx x dvxdx v = = = = ( ) 111 21 0 000 1 21 xfxdxudvuvvdu−===− ( ) ( ) 33 1 1 0 0 ' 33 xxfxfxdx=− ( ) 1 3 0 1 ' 3 xfxdx =− ( ) 1 3 0 1 ' 7 xfxdx = .
( )
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 21 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) 1111 2 2 363 0000 111 '2''2.0 777 xfxdxxdxxfxdxfxdx −=−+=−+= ( ) ( ) ( ) 2 33 '0,0;1',0;1 fxxxfxxx −== . Kết hợp điều kiện ( ) 10 f = ta có ( ) ( ) 4 1 1;0;1 4 fxxx=− Vậy ( ) ( ) ( ) 11144 000 111 11 445fxdxxdxxdx=−=−=− . Câu 110: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 01 ; thỏa mãn ( ) 10 f = , ( ) 1 2 0 1 3 xfxdx = Tính ( ) 1 3 0 '.xfxdx A. 1 B. 1 C. 3 D. 3 Lời giải Chọn A 3 2 ()'() 3 ufxdufxdx x dvxdxv == == 11 3333 00 11 33 00 1 1 ()'()(1)0.(0)'() 0 3333 11 '()'()1 33 xxx Ifxfxdxfffxdx xfxdxxfxdx =−=−− ==− Câu 111: Cho hàm số ( )yfx = có đạo hàm liên tục trên đoạn 0;1 và ( ) ( ) 010ff+= . Biết ( ) ( ) ( ) 11 2 00 1 d,cosd 22fxxfxxx == . Tính ( ) 1 0 d fxx A. B. 3 2 C. 2 D. 1 Lời giải Xét tích phân ( ) ( ) 1 0 cosd 2 Ifxxx == Đặt ( ) ( ) ( ) ( ) cossin ' uxduxdx dvfxdxvfx ==− == , ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 111 1 0 000 cossin10sinsin Ifxxfxxdxfffxxdxfxxdx =+=−−+= Mà ( ) ( ) ( ) ( ) 11 00 1 sinsin 222 Ifxxdxfxxdx ===
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 22 Chuyên
thi:
sinh vào
10 Tốt
THPT
12 Sưu tầm và biên soạn Mặt khác: ( ) ( ) ( ) 1 11 2 00 0 1111 sin1cos2sin2 2222 xdxxdxxx =−=−= ( ) ( ) ( ) ( ) 1 22 0 111 2.sinsin2.0 222 fxfxxxdx −+=−+=
(
nên
( ) ( ) ( ) ( ) sin0sin
−== . Do đó ( ) ( ) ( ) 1 11 0 00 12 dsincos fxxxdxx==−= Câu
Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 thỏa mãn ( ) 10 f = , ( ) 1 2 0 d7fxx = và ( ) 1 2 0 1 d 3 xfxx = . Tích phân ( ) 1 0 d fxx bằng A. 7 5 B. 1 C. 7 4 D. 4 Lời giải Từ giả thiết: ( ) 1 2 0 1 d 3 = xfxx ( ) 1 2 0 3d1= xfxx Tính: ( ) 1 2 0 3d = Ixfxx Đặt: ( ) ( ) 23 dd d3d == == ufxufxx vxxvx . Ta có: ( ) ( ) ( ) 11 1 233 0 00 3d.d ==− Ixfxxxfxxfxx ( ) ( ) ( ) 1 3 0 1.10.0.d =−− ffxfxx ( ) 1 3 0 .d =− xfxx . Mà: ( ) 1 2 0 3d1 = xfxx ( ) 1 3 0 1.d =− xfxx ( ) 1 3 0 .d1 =− xfxx ( ) 1 3 0 7.d7 =− xfxx ( ) ( ) 11 2 3 00 7.dd =− xfxxfxx , ( ) ( ) ( ) 1 2 3 0 7.+d0 = xfxfxx ( ) ( ) 1 3 0 7+d0 = fxxfxx
0984164935
luyện
Tuyển
lớp
Nghiệp
BDKT Toán 10; 11;
Khi đó
) ( ) 1 2 0 sin0fxxdx −=
Vì ( )fx có đạo hàm liên tục trên đoạn 0;1 và ( ) ( ) 2 sin0,0;1fxxx −
ta suy ra
fxxfxx
112:
45 =−− x x 7 5 =
Câu 113: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 thỏa mãn ( ) 14 = f , ( ) 1 2 0
d36 = fxx và ( ) 1 0
1 .d 5 = xfxx . Tích phân ( ) 1 0
d fxx bằng A. 5 6 B. 3 2 C. 4 D. 2 3 Lời giải Từ giả thiết: ( ) 1 0
1 .d 5 = xfxx ( ) 1 0
5.d1= xfxx
( )
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
(
=
=−
=−+
V
.
V
1
7
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
) 3 7+0
xfx ( ) 3 7
fxx ( ) 4 7 4
fxxC
ới ( ) 10 = f 4 7 .10 4 −+= C 7 4 = C
Khi đó: ( ) 4 77 44 =−+fxx .
ậy: ( ) 11 4 00 77 dd 44 =−+
fxxxx
5 0
=
=− fxfxx ( ) 1 2 0 5 10.d 2 =− xfxx , Mà: ( ) 1 0 5.d1== Ixfxx ( ) 1 2 0 5 110.d 2 =− xfxx ( ) 1 2 0 18 .d 5 = xfxx ( ) 1 2 0 10.d36 = xfxx ( ) ( ) 11 2 2 00 10.dd = xfxxfxx , ( ) ( ) 1 2 2 0 10.d0 −= xfxfxx ( ) ( ) 1 2 0 10d0 −= fxxfxx ( ) 2 100 −= xfx ( ) 2 10 =fxx ( ) 3 10 3 =+ x fxC
Tính:
1 0 5.d = Ixfxx Đặt: ( ) ( ) 2 dd 5 d5d 2 = =
= ufxx ufx vxx vx Ta có: ( ) ( ) ( ) 1 11 22 0 00 55 5.d..d 22 ==− Ixfxxxfxxfxx ( ) ( ) 1 2 0 55.1.d 22
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 24
== ufxufxx vxxvx . Ta có: ( ) ( ) ( ) 22 2 233 0 00 3d..d ==− Ixfxxxfxxfxx ( ) 2 3 0 24.d =− xfxx, Mà: ( ) 2 2 0 3d1== Ixfxx ( ) 2 3 0 124.d =− xfxx ( ) 2 3 0 .d23 = xfxx ( ) 2 3 0 4 .d4 23 = xfxx ( ) ( ) 22 2 3 00 4 .dd 23 = xfxxfxx , ( ) ( ) 2 2 3 0 4 .d0 23 −= xfxfxx ( ) ( ) 2 3 0 4 d0 23 −= fxxfxx ( ) 3 4 0 23 −= xfx ( ) 3 4 23 =fxx ( ) 4 1 23 =+fxxC Với ( ) 23 = f 16 3 23 =+ C 53 23 = C
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Với ( ) 14 = f 10.1 4 3 =+ C 2 3 = C Khi đó: ( ) 3 102 33 =+ x fx . Vậy: ( ) 11 3 00 102 dd 33 =+ x fxxx 1 4 0 523 632 =+= x x Câu 114: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;2 thỏa mãn ( ) 23 = f , ( ) 2 2 0 d4 = fxx và ( ) 2 2 0 1 d 3 = xfxx . Tích phân ( ) 2 0 d fxx bằng A. 2 115 B. 297 115 C. 562 115 D. 266 115 Lời giải Từ giả thiết: ( ) 2 2 0 1 d 3 = xfxx ( ) 2 2 0 3d1= xfxx . Tính: ( ) 2 2 0 3d = Ixfxx Đặt: ( ) ( ) 23 dd d3d ==
)
.d
Ixfxx
) 2 dd 1
2
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 25 Chuyên
10 Tốt
12 Sưu tầm và
soạn Khi đó: ( ) 4 153 2323 =+fxx Vậy ( ) 22 4 00 153 dd 2323 =+ fxxxx 2 5 0 153562 11523115 =+= xx Câu 115: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn
= . Đặt: (
(
dd
Hòa ufxx ufx vxx vx = = = = Ta
0984164935 =−
luyện thi: Tuyển sinh vào lớp =−
Nghiệp THPT BDKT Toán 10; 11; ( ) 1 0 1 .d 2 xfxx =− ( ) 1 2 0 11 2d 22 −=− xfxx ( ) 1 2 0 d5 = xfxx , ( ) ( ) 11 2 2 00 dd= xfxxfxx ( ) ( ) ( ) 1 2 2 0 d0 −= xfxfxx ( ) ( ) 1 2 0 .d0 −= fxxfxx ( ) 2 0 xfx −= ( ) 2fxx = ( ) 3 1 3 fxxC =+ Với ( ) 14 = f 11 3 C = . Khi đó: ( ) 3 111 33fxx=+ . Vậy ( ) 11 34 00 1 11111115dd 0 331234 =+=+= fxxxxxx . Câu 116: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;2 thỏa mãn ( ) 26 f = , ( ) 2 2 0 d7fxx = và ( ) 2 0 17 .d 2 xfxx = . Tích phân ( ) 2 0 d fxx bằng A. 8 B. 6 C. 7 D. 5 Lời giải
biên
0;1 thỏa mãn ( ) 14 = f , ( ) 1 2 0
d5 = fxx và ( ) 1 0
1 .d 2 xfxx =− . Tích phân ( ) 1 0
d fxx bằng A. 15 19 B. 17 4 C. 17 18 D. 15 4 Lời giải Tính: ( ) 1 0
có: ( ) ( ) 1 22 0 1 11 .d 0 22 Ixfxxfxx
( ) 1 2 0 1 2d 2 xfxx
, Mà:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
=
xfxfxx −= ( ) ( ) 2 2 0 .d0fxxfxx −= ( ) 2 0 xfx −= ( ) 2 =fxx ( ) 3 1 3 =+fxxC . Với ( ) 26 f = 10 3 C = . Khi đó: ( ) 3 110 33fxx=+ Vậy ( ) 22 34 00 2 110110 dd8 331230 =+=+= fxxxxxx Câu 117: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;3 thỏa mãn ( ) 36 f = , ( ) 3 2 0 d2 = fxx và ( ) 3 2 0 154 .d 3 = xfxx . Tích phân ( ) 3 0 d fxx bằng A. 53 5 B. 117 20 C. 153 5 D. 13 5 Lời giải Tính ( ) 3 2 0 .d Ixfxx =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Tính: ( ) 2 0 .d Ixfxx = Đặt: ( ) ( ) 2 dd 1 dd 2 ufxx ufx vxx vx = = = = Ta có: ( ) ( ) 2 22 0 2 11 .d 0 22 Ixfxxfxx =− ( ) 2 2 0 1 12d 2 xfxx =− ,. Theo giả thiết: ( ) 2 0 17 .d 2 xfxx = ( ) 2 2 0 17112d 22 =− xfxx ( ) 2 2 0 d7
xfxx
( ) ( ) 22 2 2 00 dd xfxxfxx
= ( ) ( ) ( ) 2 2 2 0 d0
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 27 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT
10; 11; 12 Sưu tầm và biên soạn Đặt ( ) ( ) 3 2 dd 1 dd 3 ufxx ufx vx vxx = = = = . Ta có ( ) ( ) 3 33 0 3 11 .d 0 33 Ixfxxfxx =− ( ) 3 3 0 1 54d 3 =− xfxx ,. Theo giả thiết: ( ) 3 2 0 154 .d 3 = xfxx ( ) 3 3 0 154154d 33 =− xfxx ( ) 3 3 0 d8 = xfxx ( ) ( ) 33 2 3 00 d4d= xfxxfxx ( ) ( ) ( ) 3 2 3 0 4d0 −= xfxfxx ( ) ( ) 3 3 0 4d0 −= fxxfxx ( ) 3 40 −= xfx ( ) 3 4 = x fx ( ) 4 16 =+ x fxC Với ( ) 36 f = 15 16 = C Khi đó: ( ) 4 15 1616 =+ x fx . Vậy ( ) 33 45 00 3 115115117dd 0 1616801620 =+=+= fxxxxxx . Câu 118: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 thỏa mãn ( ) 12 f = , ( ) 1 2 0 d8fxx = và ( ) 1 3 0 .d10xfxx = . Tích phân ( ) 1 0 d fxx bằng A. 2 285 B. 194 95 C. 116 57 D. 584 285 Lời giải Tính: ( ) 1 3 0 .d Ixfxx = . Đặt: ( ) ( ) 4 3 dd 1 dd 4 ufxx ufx vx vxx = = = = . Ta có: ( ) ( ) 1 44 0 1 11 .d 0 44 Ixfxxfxx =− ( ) 1 4 0 11 d 24 xfxx =− ,
Toán
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 28 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Theo giả thiết: ( ) 1 3 0 .d10xfxx = ( ) 1 4 0 d38xfxx =− ( ) 1 4 0 8.d38.8 =− xfxx ( ) ( ) 11 2 4 00 8.d38.d =− xfxxfxx ( ) ( ) ( ) 1 2 4 0 838d0 += xfxfxx ( ) ( ) 1 4 0 .838d0 += fxxfxx ( ) 4 8380 +=xfx ( ) 4 4 19 =− fxx ( ) 5 4 95 =−+ fxxC . Với ( ) 12 f = 194 95 = C . Khi đó: ( ) 5 4194 9595 =−+fxx Vậy ( ) 11 56 00 1 41942194116dd 0 95952859557 =−+=−+= fxxxxxx Câu 119: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 thỏa mãn ( ) 10 f = và ( ) ( ) ( ) 11 2 2 00 1 d1ed 4 x e fxxxfxx =+= Tính tích phân ( ) 1 0 d Ifxx = A. 2e I =− . B. e2 I =− . C. e 2 I = . D. e1 2 I = . Lời giải Xét ( ) ( ) 1 0 1ed x Axfxx =+ Đặt ( ) ( ) d1d x ufx vxex = =+ ( ) dd e x ufxx vx = = Suy ra ( ) ( ) 1 1 0 0 eed xx Axfxxfxx =− ( ) 1 0 d x xefxx =− ( ) 1 2 0 1 d 4 x e xefxx = Xét 1 22 0 dx xex 1 22 0 111 224 x exx =−+ 2 1 4 e = Ta có : ( ) ( ) 111 2 22 000 d2dd0 xx fxxxefxxxex ++= ( ) ( ) 1 2 0 d0 x fxxex += Suy ra ( ) 0,0;1 x fxxex += ( ) xfxxe =− ( ) ( ) 1 x fxxeC=−+
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 29
= .
ế
4
0
= , ( ) 4 0 sin2d 4 fxxx =− . Tính tích
(
8 0
= A. 1 I = . B. 1 2 I = . C. 2 I = . D. 1 4 I = . Lời giải Tính (
4 0 sin2d 4
=− . Đặt ( ) (
sin22cos2dd dd xuxxu fxxvfxv == == ,
đó ( ) ( ) (
44 4 0 00 sin2dsin2.2cos2d
=− ( ) ( ) 4 0 sin.sin0.02cos2d 24fffxxx =−− ( ) 4 0 2cos2d fxxx =− Theo đề bài ta có ( ) 4 0 sin2d 4 fxxx =− ( ) 4 0 cos2d 8 fxxx = Mặt khác ta lại có 4 2 0 cos2d 8 xx = Do ( ) ( ) ( ) 44 2 22 00 cos2d2.cos2cos2d fxxxfxfxxxx −=−+ 20 888 =−+= nên ( ) cos2 fxx = Ta có 8 8 0 0 11 cos4dsin4 44 Ixxx === . Câu 121: Cho hàm số ( )yfx = có đạo hàm liên tục trên đoạn 0;1 và ( ) ( ) 010ff+= . Biết ( ) ( ) ( ) 11 2 00 1 d,cosd 22fxxfxxx == . Tính ( ) 1 0 d fxx A. B. 1 C. 2 D. 3 2 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do ( ) 10 f = nên ( ) ( ) 1 xfxxe =− Vậy ( ) ( ) ( ) 11 1 0 00 d1d22 xx Ifxxxexxee ==−=−=− Câu 120: Chohàmsố ( )yfx = cóđạohàmliêntụctrênđoạn 0; 4 và 0 4 f
Bi
t ( )
2
d 8 fxx
phân
)
2d Ifxx
)
fxxx
)
khi
)
fxxxxfxfxxx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 30 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ( ) ( ) ( ) ( ) cosdsind dd uxuxx vfxxvfx ==− == . Khi đó: ( ) ( ) ( ) ( ) ( ) ( ) 11 1 0 00 cosdcossind fxxxxfxfxxx =+ ( ) ( ) ( )
(
2
=−+==
1
BĐT Holder. ( ) ( ) ( ) ( ) 2 22 dd.d bbb aaa fxgxxfxxgxx . Dấu “=” xảy ra ( ) ( ) ,; fxkgxxab= Áp dụng vào bài ta có ( ) ( ) ( ) ( ) 2 111 22 000 11 sindd.sind 44 fxxxfxxxx == , suy ra ( ) ( ) sin fxkx = Mà ( ) ( ) ( ) ( ) ( ) 11 2 00 11 sindsind1sin 22 fxxxkxxkfxx ==== . Vậy ( ) ( ) 11 00 2 dsind fxxxx == . Câu 122: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 thỏa mãn ( ) 11 f = , ( ) 1 2 0 d9fxx = và ( ) 1 3 0 1 d 2 xfxx = . Tích phân ( ) 1 0 d fxx bằng: A. 2 3 B. 5 2 C. 7 4 D. 6 5 Lời giải
( ) ( ) ( ) ( ) ( ) ( ) 111 000 1 10sindsindsind 2 fffxxxfxxxfxxx =−++== Cách 1: Ta có
) ( ) ( ) ( ) ( ) ( ) 1111 2 222 0000 sindd2sindsind fxkxxfxxkfxxxkxx −=−+
1 01 22 k kk
Do đó ( ) ( ) ( ) ( )
2 0 sind0sin fxxxfxx −== . Vậy ( ) ( ) 11 00 2 dsind fxxxx == . Cách 2: Sử dụng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 31
( ) 1 4 0 9d0fxxx += ( ) 1 4 0 .9d0 fxxx += Hay thể tích khối tròn xoay sinh bởi hình phẳng giới hạn bởi đồ thị hàm số ( ) 4 9 yfxx =+ , trục hoành Ox , các đường thẳng 0 x = , 1 x = khi quay quanh Ox bằng 0 ( ) 4 90fxx += ( ) 4 9 fxx =− ( ) ( ).d fxfxx = 4 9 5 xC=−+ . Lại do ( ) 11 f = 14 5 C = ( ) 5 914 55fxx =−+ ( ) 1 0 d fxx = 1 5 0 914 d 55 xx −+ 1 6 0 3145 1052 xx =−+= Câu 123: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 1;2 thỏa mãn ( ) ( ) 2 2 1 1 1d 3 xfxx−=− , ( ) 20 f = và ( ) 2 2 1 d7fxx = . Tính tích phân ( ) 2 1 d Ifxx = A. 7 5 I = B. 7 5 I =− C. 7 20 I =− D. 7 20 I = Lời giải
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có: ( ) 1 2 0 d9fxx = ( )1 Tính ( ) 1 3 0 1 d. 2 xfxx = Đặt ( ) 3 d.d ufx vxx = = ( ) 4 dd 4 ufxx x v = = ( ) 1 3 0 1 d 2 xfxx = ( ) 1 4 0 . 4 x fx = ( ) 1 4 0 1 .d 4 xfxx ( ) 1 4 0 11 .d 44 xfxx =− ( ) 1 4 0 .d1xfxx =− ( ) 1 4 0 18.d18 xfxx =− ( )2 Lại có: 1 1 9 8 0 0 1 d 99 x xx == 1 8 0 81d9 xx = ( )3 Cộng vế với vế các đẳng thức ( )1 , ( )2 và ( )3 ta được: ( ) ( ) 1 2 48 0 18.81d0fxxfxxx ++=
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
=− 7 5 =− Câu 124: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 thỏa mãn: ( ) ( ) 1 2 0 10,d7ffxx == và ( ) 1 2 0 1 .d 3 xfxx = . Tính tích phân ( ) 1 0 d Ifxx = . A. 1 I = B. 7 5 I = C. 4 I = D. 7 4 I = Lời giải Xét tích phân ( ) 1 2 0 .d xfxx . Đặt ( ) ( ) 3 2 dd dd 3 ufxx ufx x vxx v = = = = ( ) ( ) ( ) 11 3 23 00 1 11 .dd 0 333 x xfxxfxxfxx ==− ( ) 1 3 0 1 d 3 xfxx =− ( ) 1 3 0 d1xfxx =− 1 6 0 1 7 xdx = Ta có: ( ) ( ) 111 2 36 000 d14d49d0fxxxfxxxx ++= ( ) ( ) 1 2 3 0 7d0fxxx +=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ( ) ( ) dd ufxufxx == , ( ) ( )3 2 1 d1d 3 x vxxv =−= Ta có ( ) ( ) 2 2 1 1 1d 3 xfxx−=− ( ) ( ) ( ) ( ) 2 33 2 1 1 11 .d 33 xx fxfxx =− ( ) ( ) 2 3 1 11 1d 33 xfxx −=−− ( ) ( ) 2 3 1 1d1xfxx −= ( ) ( ) 2 3 1 2.71d14 xfxx −−=− Tính được ( ) 2 6 1 491d7 xx−= ( ) 2 2 1 d fxx ( ) ( ) 2 3 1 2.71d xfxx ( ) 2 6 1 491d0 xx +−= ( ) ( ) 2 2 3 1 71d0 xfxx −−= ( ) ( )3 71fxx =− ( ) ( )4 71 4 x fxC=+ . Do ( ) 20 f = ( ) ( )4 717 44 x fx =− Vậy ( ) 2 1 d Ifxx = ( )4 2 1 71 7 d 44 x x
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 33 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Mà ( ) ( ) 1 2 3 0 7d0fxxx + . Dấu “=” xảy ra khi ( ) ( ) 33 707 fxxfxx +==− ( ) ( ) 3 d7d fxfxxxx ==− 4 7 4 x C =−+ ( ) 7 10 4 fC== ( ) 4 77 44 x fx =−+ . ( ) 1 0 d Ifxx = 1 45 0 777711 d 4420400 xxx x =−+=−+ 777 2045 =−+= . Câu 125: Cho hàm số ( )yfx = có đạo hàm liên tục trên 0;1 thỏa mãn ( ) ( ) 1 2 0 4 13, 11 ffxdx == và ( ) 1 4 0 7 11 xfxdx = . Giá trị của ( ) 1 0 fxdx là A. 35 11 B. 65 21 C. 23 7 D. 9 4 Lời giải Xét ( ) 1 4 0 7 11 xfxdx = Đặt ( ) ( ) 5 4 5 dufxdx ufx x dvxdx v = = = = ( ) ( ) ( ) 1 11 455 0 00 11 55 xfxdxxfxxfxdx =− ( ) 1 5 0 31 55 xfxdx =− ( ) 1 5 0 372 5 51111 xfxdx =−=− . Xét ( ) ( ) 1 2 0 1 5 0 1 1 1011 0 0 4 11 2 11 11 1111 fxdx xfxdx xdxx = =− == ( ) ( ) 111 2 510 000 440fxdxxfxdxxdx ++= ( ) ( ) 1 2 5 0 20fxxdx += ( ) ( ) 6 5 2 3 x fxxfxC =−=+ . Do ( ) 10 13 3 fC== nên ( ) 11 6 00 1023 337 x fxdxdx =+=
0984164935
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 34 Chuyên
thi:
Tốt
Câu
Cho hàm số ()fx có đạo hàm liên tục trên 0;1 thỏa mãn ( ) 01 f = ; ( ) 1 2 0 1 d
= và ( ) ( ) 1 0 1 21d 30 xfxx−=− . Tích phân ( ) 1 0 d fxx bằng A. 11 30 . B. 11 12
(
=− =−
( ) ( ) ( ) ( ) (
11
22 0 00 21dd xfxxxxfxxxfxx −=−−− ( ) ( ) 1 2 0 d xxfxx =−− ( ) ( ) 1 2 0 1 d 30 xxfxx −= Ta có: ( ) ( ) 11 2 2432 00 d2d xxxxxxx −=−+ 1 543 0 523 xxx =−+ 1 30 = . Do đó, ( ) ( ) ( ) ( ) 111 2 2 22 000 d2dd0 fxxxxfxxxxx −−+−= ( ) ( ) 1 2 2 0 d0fxxxx −−= ( ) 2 fxxx =− ( ) 32 32 xx fxC=−+ . Vì ( ) 01 f = nên 1 C = ( ) 32 1 32 xx fx =−+ . Vậy ( ) 11 32 00 d1d 32 xx fxxx =−+ 1 43 0 126 xx x =−+ 11 12 = . Câu 127: Chohàmsố ( )yfx = cóđạohàmliêntụctrênđoạn 0; 4 và 0 4 f = .Biết ( ) 4 2 0 d 8 fxx = , ( ) 4 0 sin2d 4 fxxx =− . Tính tích phân ( ) 8 0 2d Ifxx = . A. 1 I = . B. 1 2 I = . C. 2 I = . D. 1 4 I = . Lời giải Ta có ( ) ( ) 44 00 sin2dsin2d fxxxxfx = ( ) ( ) 4 4 0 0 sin2dsin2 fxxfxx =−
Hòa
0984164935
luyện
Tuyển sinh vào lớp 10
Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
126:
30 fxx
. C. 11 4 . D. 1 30 . Lời giải Đặt
) ( ) ( ) 2 dd d21d ufxx ufx vxx vxx
= =
Suy ra
) ( )
1
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 35 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 4 0 sin2.0sin2.02cos2d 44 fffxxx =−− ( ) 4 0 2cos2d 4 ffxxx =− ( ) 4 0 2cos2d fxxx =− Do đó
=
=+
= . Bởi vậy: ( )
444 22 000 d2cos2dcos2d
−+=−+ ( ) ( ) 4 22 0 2cos2cos2d0fxfxxxx −+= ( ) ( ) 4 2 0 cos2d0cos2 fxxxfxx −== . Nên: ( ) 8 0 2d Ifxx = 8 0 cos4dxx = 8 0 11 sin4 44 x == . Câu 128: Cho hàm số ( )fx liên tục, có đạo hàm trên , ( ) 216 f = và ( ) 2 0 4 fxdx = . Tích phân 4 0 2 x xfdx bằng A. 112. B. 12. C. 56. D. 144. Lời giải Đặt 22 2 x txtdxdt === . Đổi cận: 00 42 xt xt == == . Do đó ( ) ( ) 422 000 44 2 x xfdxtftdtxfxdx == . Đặt ( ) ( ) 44 uxdudx dvfxdxvfx == == . Suy ra ( ) ( ) ( ) ( ) 222 2 0 000 44()48248.164.4112. xfxdxxfxfxdxffxdx =−=−=−=
( ) 4 0 2cos2d 4 fxxx
Mặt khác: ( ) 44 2 00 1 cos2d1cos4d 2 xxxx
4 0 11 sin4 28 xx
=+ 8
( )
848 fxxfxxxxx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 36 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 129: Cho hàm số ( )fx liên tục trên và ( ) ( ) 2 0 216,d4ffxx== . Tính ( ) 1 0 .2d Ixfxx = A. 7 B. 12 C. 20 D. 13 Lời giải Đặt 2 tx = d2dtx= . Với 00xt== ; Với 12xt== .
==
= Đặt ( ) ( ) dd dd uxux vfxxvfx == == . Ta
( ) ( ) (
2 0 2
0 44 Ixfxfxxff =−=−− ( ) 1 2.1647 4 =−= . Câu 130: Cho hàm số ( )fx liên tụctrên 0;1 thỏamãn ( ) ( ) 23 6 16 31 fxxfx x −=− + .Khiđó ( ) 1 0 d fxx bằng A. 4. B. 1. C. 2. D. 6. Lời giải Chọn A Ta có ( ) ( ) 23 6 16 31 fxxfx x −=− + ( ) ( ) 23 6 16 31 fxxfx x −−=− + ( ) ( ) 111 23 000 6 1d6dd 31 fxxxfxxx x −−=− + ( )*
3131 fxxfxxxfxxx xx −=−== ++ Vậy ( ) 1 0 d4fxx = . Câu 131: Cho hàm số ( )fx xác định và liên tục trên \0 thỏa mãn ( ) ( ) ( ) ( ) 22'211xfxxfxxfx+−=− , với mọi \0 x đồng thời thỏa ( ) 12 f =− . Tính ( ) 2 1 d fxx
Suy ra: ( ) ( ) 22 00 d1d 224 tt Ifttftt
( ) 2 0 1 d 4 xfxx
có
) ( )
11 d22004
. Ta có ( ) ( ) ( ) ( ) ( ) 1101 1 0010 1d1d1dd ux fxxfxxfuufxx =− −=−−−=−= . Và ( ) ( ) ( ) ( ) ( ) 3 1111 2333 0000 6d2d2d2d ux xfxxfxxfuufxx = === Ta có ( ) ( ) ( ) ( ) 11111 00000 11 *d2d6dd6d4
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 37 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. ln2 1 2 B. 1 ln2 2 C. ln23 2 D. ln23 22 Lời giải Chọn D Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2' 22'2111 xfxxfxxfxfxxfxxfx ++=++=+ Do đó ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) '' 22 111 11 111 xfxxfx dxdxxc xfx xfxxfx ++ ==−=+ + ++ ( ) 1 1 xfx xc +=− + Mặt khác ( ) 12 f =− nên ( ) ( ) 2 1111 2101 1 cxfxfx cxxx −+=−=+=−=−− + Vậy ( ) 22 2 1 2 11 1111 dln|ln2 2 fxxdxx xxx =−−=−+=−− . Câu 132: Cho hàm số ( )fx liên tục trên thỏa mãn ( ) ( ) 23532 133 14576, 442 fxxfxxxxxxx +−−−=−−++ . Tích phân ( ) 2 1 d fxx bằng A. 1 7 B. 1 3 C. 7 D. 19 3 Lời giải Mặt khác : ( ) ( ) ( ) 222 23532 111 133 (*)d1d4576 442d fxxxfxxxxxxxx +−−−=−−++ ( ) 22 33 11 41331331dd 34424423fxxfxxxx +−−−−= ( ) ( ) ( ) 222 111 411 ddd 337fxxfxxfxx +== . Câu 133: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 thỏa mãn ( ) 11 f = và ( ) ( ) ( ) ( ) 2 2642 461.4044324,0;1fxxfxxxxx +−=−+− . Tích phân ( ) 1 0 fxdx bằng? A. 23 15 . B. 13 15 . C. 17 15 . D. 7 15 . Lời giải Chọn B ( ) ( ) ( ) ( ) 2 2642 461.4044324fxxfxxxx +−=−+−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 38 Chuyên luyện thi: Tuyển sinh vào
10 Tốt
THPT
12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) 111 2 2642 000 461.4044324.1 fxdxxfxdxxxxdx +−=−+− Xét ( ) ( ) ( ) ( ) 11 22 00 461.244 Ixfxdxxfxdx =−=− . Đặt ( ) ( ) ( ) 2 3 24484 ufx dufxdx dvxdx vxx = =
−−+−=−+− ( ) ( ) ( ) (
1 2
0 42042. fxxxdxfxxxfxxxc −−==− =−+
fxdxxxdx=−+= Câu 134: Cho hàm số có đạo hàm liên tục trên và thỏa
và . Tích phân bằng A. . B. . C. . D. Lời giải Chọn D Cách 1. Áp dụng công thức tích phân từng phần, ta có: Từ Thay vào ta được Xét Đặt , đổi cận: ()fx (0)3 f = 2 ()(2)22, fxfxxxx +−=−+ 2 0 ()d xfxx 4 3 2 3 5 3 10 3 22 2 0 00 ()d()()d xfxxxfxfxx =− ( ) 2 ()(2)22,1 fxfxxxx +−=−+ 0 x = ( )1 (0)(2)2(2)2(0)231 ffff+==−=−=− 2 0 ()d Ifxx = 2 xtdxdt =−=− 02 20 xt xt == ==
0984164935
lớp
Nghiệp
BDKT Toán 10; 11;
=− =− . ( ) ( ) ( ) ( ) ( ) ( ) 11 1 333 0 00 84.84.= 4242.. Ixxfxxxfxdxxxfxdx =−−−−− Do đó: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1111 2 2 33642 0000 1242.425660368. fxdxxxfxdxxxdxxxxdx
)
3342
Mà ( ) 111fc== ( ) 42 1. fxxx=−+ Do đó ( ) ( ) 11 42 00 13 1. 15
mãn
Khi đó
Do đó ta có Vậy Cách 2. Từ Thay vào ta được Xét hàm số từ giả thiết trên ta có Vậy suy ra .
Câu 135: Cho hàm số ( )yfx = có đạo hàm liên tục trên 2;4 và ( ) 0,2;4fxx . Biết ( ) ( ) ( ) 3 33 7 4,2;4,2 4 xfxfxxxf =−= . Giá trị của ( )4 f bằng A. 4051 2 . B. 2051 4 . C. 2051 2 . D. 4051 4 . Lờ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 39
i giải Chọn D Ta có: ( ) 0,2;4fxx nên hàm số ( )yfx = đồng biến trên 2;4 ( ) ( )2 fxf mà ( ) 7 2 4 f = . Do đó: ( ) 0,2;4fxx Từ giả thiết ta có: ( ) ( ) ( ) ( ) 33333 441 xfxfxxxfxfx =−+= ( ) ( ) ( ) ( ) 3 3 .41 41 fx xfxfxx fx +== + Suy ra: ( ) ( ) ( ) ( ) 2 33 d41 1 dd 424141 fx fx x xxxC fxfx + ==+ ++ ( ) 2 2 3 3 41 82 x fxC+=+ ( ) 731 22 422fCC==+=− 022 200 (2)(2)(2) IftdtftdtIfxdx =−−=−=− ( ) ( ) 2222 2 0000 84 ()(2)d22d2()d()d. 33fxfxxxxxfxxfxx +−=−+== 22 2 0 00 410 ()d()()d2.(1). 33 xfxxxfxfxx =−=−−=− ( ) 2 ()(2)221 (0)3 fxfxxx f +−=−+ = 0;1xx== ( )1 1 (2)1;(1)2ff=−= 2 () fxaxbxc =++ 33 11 22 4213 cc abca abcb == ++== ++=−=− 2 1 ()33()3 2 fxxxfxx =−+=− ( ) 22 00 ()d3d10 3 xfxxxxx =−=−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 40
)
vx = = (
vx = =− . ( ) (
)
22 2
11
=−−−=−− . Ta
2 2
+=−+ ( ) ( ) ( ) 22 2 11 d22d fxxfxx + ( ) 2 2 1 83228d xxx=−+ ( ) ( ) ( ) ( ) ( ) 222 2 2 111 d224d24d fxxxfxxxx −−+− ( ) ( ) 22 2 2 11 83228d24d xxxxx=−++− ( ) ( ) 2 2 1 24d0fxxx −−= ( ) 24fxx =− ( ) 2 4 fxxxC=−+ , C . Mà ( ) 103fC== ( ) 2 43fxxx =−+ ( ) ( ) 11 2 00 4 d43d 3 fxxxxx =−+= Câu 137: Cho hàm số ( )fx liên tục trên 0;1 và ( ) ( ) 2 23 1 1 xx fxfx x ++ +−= + , 0;1 x . Tính ( ) 1 0 d fxx A. 32ln2 4 + B. 3ln2 + C. 3ln2 4 + D. 32ln2 2 + Lời giải Chọn C
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy: ( ) ( ) 3 2 4 11 3 4 x fx = ( ) 4051 4 4 f = . Câu 136: Cho hàm số ( )fx có đạo hàm liên tục trên 0;2 và thỏa ( ) 10 f = , ( ) ( ) ( ) 2 2 483228fxfxxx +=−+ với mọi x thuộc 0;2 . Giá trị của ( ) 1 0 d fxx bằng A. 5 3 B. 4 3 C. 2 3 D. 14 3 Lời giải Chọn B Đặt ( ) 2 1 2d Ifxx = . Dùng tích phân từng phần, ta có: (
d2d ufx
) dd 24 ufxx
) (
( ) ( ) ( )
1
2424d24d Ixfxxfxxxfxx
có ( ) ( ) ( )
483228fxfxxx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
+−= . Lại có ( ) 1 2 11 2 00 0 1223d1d2ln12ln2 1122 x x xxxxx xx ++ =++=+++=+ ++ Từ, và suy ra ( ) ( ) 11 00 33 2d2ln2dln2 24fxxfxx=+=+ Câu 138: Cho hàm số ()yfx = liên tục trên thỏa mãn ( ) ( ) ( ) 2 21 3221e4 xx fxfxx −+ +−=−+ . Tính tích phân ( ) 2 0 d Ifxx = ta được kết quả:
−=−−−=
vậy ( ) ( ) ( ) 22 00 32d4d
+−= . Hơn nữa ( ) ( ) 222 22 2
00
xexxx −+−+−+ −=−+== và
= Suy ra ( ) ( ) 22 00 4d8d2 fxxfxx== Câu 139: Cho hàm số ( )fx liên tục trên và thỏa
( ) (
+=+−− vớ
x . Tính
phân ( ) 1 0 d xfxx A. 1 4 B. 5 4 C. 3 4 D. 1 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
41 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Theo giả thiết, ta có: ( ) ( ) 2 23 1 1 xx fxfx x ++ +−= + , 0;1 x và ( )fx liên tục trên 0;1 nên ( ) ( ) 11 2 00 23 1dd 1 xx fxfxxx x ++ +−= + ( ) ( ) ( )2 111 000 12 d1dd 1 x fxxfxxx x ++ +−= + Đặt 1 xt−= thì dd xt =− , với 01xt== , với 10xt== Do đó: ( ) ( ) ( ) ( ) 1011 0100 1dddd fxxfttfttfxx −=−== ( ) ( ) ( ) 111 000 d1d2d fxxfxxfxx
A. e4 I =+ . B. 8 I = . C. 2 I = . D. e2 I =+ . Lời giải Chọn C Theo giả thuyết ta có ( ) ( ) ( ) ( ) 2 22 21 00 32d21e4d* xx fxfxxxx −+ +−=−+ Ta tính ( ) ( ) ( ) ( ) 222 000 2d2d2d fxxfxxfxx
. Vì
fxfxxfxx
2121221 0
21ded21e0 xxxxxx
2 0 4d8 x
mãn
) 273 2231fxxfxxxx
i
tích
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 42
( )* ta được ( ) 1 0 15 d1 44 xfxx =+=
Cho hàm số ( )fx liên tục trên thỏa mãn ( ) 43 2 2244 12,0,1 −−++− −+= xxxx xfxfxx xx . Khi đó ( ) 1 1 d fxx có giá trị là A. 0 . B. 1. C. 1 2 . D. 3 2 . Lời giải Chọn A Từ giả thiết suy ra ( ) 43 23 22244 1 −−++− −+= xxxx fxf xxx Ta có: ( ) 222 43 23 111 22244 1d.dd xxxx fxxfxx xxx −−++− −+= ( ) ( ) 222 23 111 222244 1d1d1d −−−+=−++− xx fxxfxx xxxx ( ) ( ) 11 2 2 00 422 dd 1 2 −+=−+−+ x fttfttx xx ( ) ( ) 01 10 dd0+= fttftt ( ) 1 1 d0= ftt Vậy ( ) 1 1 d0 = fxx Cách trắc nghiệm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn B Áp dụng công thức tích phân từng phần, ta có: ( ) ( ) ( ) ( ) 11 00 1 dd* 0 xfxxxfxfxx =− Từ ( ) ( ) ( ) 273 22311fxxfxxxx +=+−− Thay 1 x = vào ( )1 ta được ( ) ( ) ( ) ( )1213112fff+== Mặt khác từ ( )1 ta có ( ) ( ) ( ) 111 273 000 d2d231d fxxxfxxxxxx +=+−− ( ) ( ) ( ) ( ) ( ) ( ) 1111 22 0000 111 dd2dd3 224fxxfxxfxxfxx +=−=−=− Thay ( ) ( )2,3 vào
Câu 140:
Ta có: ( ) 43 2 2244 12,0,1 xxxx xfxfxx xx −−++− −+= ( ) 43 2 2244 12,0,1 xxxx xfxfxx xxx −−+− −+=+ ( ) ( ) 222222 1212,0,1 xx xfxfxxxx xx −+=−+
Chọn ( ) ( ) 11 11 .d.d0fxxfxxxx === .
Câu 141: Cho hàm số ()yfx = thỏa mãn 2 '''3 ()().()2, fxfxfxxxxR +=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
43
==
ị củ
2
=
Chọn B
fxfxxxxR =− Lấy
vế ta
(
'
4 '2
().()4 fxfxdxxxdx x
=− =−+ Theo đề ra ta có: '(0).(0)4ffC== Suy ra: 22 4 '2 00 ().().4 4 x fxfxdxxdx =−+ 2 2 0 ()104 215 fx = 2(2)268 15 f = Câu 142: Cho fx là hàm số liên tục trên tập xác đinh và thỏa mãn 2 312fxxx . Tính 5 1 d Ifxx A. 37 6 . B. 527 3 . C. 61 6 . D. 464 3 .
và ' (0)(0)2ff
Tính giá tr
a
(2) Tf
A. 160 15 B. 268 15 C. 4 15 D. 268 30 Lời giải
Ta có: 2 '''3 ()().()2, fxfxfxxxxR +=− ( )' '3 ().()2,
nguyên hàm hai
có:
) ( )
'3
().()2
fxfxxC
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 44 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán
11; 12 Sưu tầm và biên soạn Lời giải Chọn C 2 2 11 2 00 312 2331232 61 2331d232d 6 fxxx xfxxxx xfxxxxxx Đặt 2 31d23d txxtxx x 0 1 t 1 5 Suy ra 5 1 61 d 6 ftt . Câu 143: Cho hàm số ( )yfx = liên tục, có đạo hàm trên R thỏa mãn điều kiện ( ) 2 ()()2sincos, fxxfxxxxxR +−= và 22 f = .Tính ( ) 2 0 xfxdx A. 0 B. 2 C. 1 D. Lời giải Chọn A Từ giả thiết ( ) 2 ()()2sincos fxxfxxxx +−= ( ) ( ) ( ) ( ) 2 2 2 ()()cos2sin sin sin fxxfxxxxx xfxxx xfxxxC +=+ = =+ Mặt khác: ( ) 0sin. 22 fCfxxx === Ta có: ( ) ( ) ( ) ( ) 22 2 22 00 00 cos2sin2 xfxdxxfxfxdxxxxxfx =−=+− 2 2 0 2 2 0 cos2sin2sin cos0 xxxxxx xx =+− ==
0984164935
10;
phân hai vế, ta có ( ) ( ) ( ) 11 22 00
Xét tích phân
4.31d1d* xfxfxxxx +−=−
xtxtt
Khi đó, ta có
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 45
10 Tốt
Câu 144: Cho hàm số ( )fx liên tục trên đoạn 0;1 thỏa mãn ( ) ( ) 224.311 xfxfxx +−=− . Tính ( ) 1 0 d Ifxx = . A. 4 . B. 16 . C. 20 . D.
. Lời giải Chọn C Lấy tích
Hòa
0984164935
Chuyên luyện thi: Tuyển sinh vào lớp
Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
6
Vậy ( ) ( ) ( ) 11 00 *5dd 420fxxfxx == Câu 145: Cho hàm số ( )fx liên tục trên khoảng ( ) 0;. + Biết ( ) 33 f = và ( ) ( ) ( ) 3 '2121,0;. xfxfxxx+−+=+ Giá trị của ( ) 5 3 fxdx bằng A. 914 3 . B. 59 3 . C. 45 4 . D. 88. Lời giải Chọn B Ta có:
1 2 0 1d Jxx =− . Đặt sindcosd
== .
1 22 222 000 1d1sin.cosdcosd Jxxttttt =−=−= ( ) 2 2 0 0 11sin2 1cos2d 2224 t ttt =+=+= Xét tích phân ( ) 1 2 0 4.d Kxfxx = . Đặt 2 d2d txtxx == . Khi đó, ta có ( ) ( ) ( ) 111 2 000 4.d2d2d Kxfxxfttfxx === . Xét tích phân ( ) 1 0 31d Lfxx =− . Đặt 1dd txtx =−=− . Khi đó, ta có ( ) ( )( ) ( ) ( ) 1011 0100 31d3d3d3d Lfxxfttfttfxx =−=−== .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 46 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 3 4 22 ' 2'21221 '21212,0;. 2121 22.1 xfxxfx xfxfxxx x fxfx xC xx +−+ +−+==+ ++ ==+ Cho 1 x = từ ( )1 ( ) ( ) ( ) 232 22 33 2.12.1121212. 11 f CCCfxxxxx =+=+=+=+=+ ( ) ( ) 2 22 43 32 11 1 59 2122. 436 xx fxdxxxdx +=+=+= ( ) ( ) 52 31 59 221. 3 fxdxfxdx =+= Câu 146: Cho hàm số ( )fx có đạo hàm và đồng biến trên 1;4 , thỏa mãn ( ) ( ) 2 2 xxfxfx += với mọi 1;4 x . Biết ( ) 3 1 2 f = , tính ( ) 4 1 Ifxdx = A. 1188 45 . B. 1187 45 . C. 1186 45 . D. 9 2 . Lời giải Chọn C Do ( )fx đồng biến trên 1;4 nên ( ) ( ) 31 1 22 fxf=− , ngoài ra ( ) 0,1;4fxx . Khi đó ta có biến đổi sau: ( ) ( ) ( ) ( ) 2 2 21 fx xxfxfxx fx +== + ( ) ( ) ( ) 3322 2121 33 fxxCfxxC +=++=+ Mà ( ) 34 1 23fC== ( ) 2 3 33 24 1 287 33 29918 x fxxx +− ==++ . Vậy ( ) 4 4 42 1 1 11671186 18451845Ifxdxxxxx ==++= . Câu 147: Cho hàm số ()yfx = có đạo hàm liên tục trên thỏa mãn 2 .().'()(), xfxfxfxxx=− và có (2)1 f = . Tích phân 2 2 0 () fxdx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 47 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 3 2 B. 4 3 C. 2 D. 4 Lời giải Chọn C Ta có: ( ) ( ) 22 222 2222 000 2 .().'()()2.().'()2()2 2.().'()()3()2.()'x3()2 2 .()342342 0 xfxfxfxxxfxfxfxx xfxfxfxfxxxfxdfxdxxdx xfxIII =−=− +=−=− =−=−= Câu 148: Cho hàm số ( )fx nhận giá trị không âm và có đạo hàm liên tục trên thỏa mãn ( ) ( ) ( ) 2 21, fxxfxx =+ và ( ) 01 f =− . Giá trị của tích phân ( ) 1 0 d fxx bằng A. 1 6 B. ln2 C. 3 9 D. 23 9 Lời giải ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 21,21, 1 21, fx fxxfxxxx fx xx fx =+=−+ =−+ Vậy ( ) ( ) ( ) 2 2 11 21dxxxxCfx fxxxC =−+=−−+= −−+ . Do ( ) 011fC=−=− . Vậy ( ) 2 1 1 fx xx =− ++ ( ) 111 2 2 000 11 ddd 1 13 24 Ifxxxx xx x ==−=− ++ ++ . Đặt 13 tan,; 2222 xtt += . Suy ra ( ) ( ) 2 33 2 66 3 1tan233 2dtdt. 339 1tan 4 t I t + =−=−=− + Câu 149: Cho số thực 0 a . Giả sử hàm số ()fx liên tục và luôn dương trên đoạn 0;a thỏa mãn ().()1fxfax−= . Tính tích phân ( ) 0 1 d 1 a Ix fx = + ? A. 2 3 a I = B. 2 a I = C. 3 a I = D. Ia =
Lời giải Đặt dd taxtx =−=−
Thay vào ta được ( ) 0
1 d 1
a Ix fx = + ( ) 0
1 dt 1
a fat = +− ( ) 0
a faxfx x fxfax = ++− =+ ( ) ( ) ( ) 22 00
1 d 1
a x fax = +−
, do hàm số ()fx liên tục và luôn dương trên đoạn dd fx xxCx fx
, trên đoạn 0;a Mà ().()1fxfax−= ( ) 1 fx = . Vậy 0 1 d 22 a a Ix== Câu 150: Cho hàm số ( )fx đồng biến, có đạo hàm đến cấp hai trên đoạn 0;2 và thỏa mãn ( ) ( ) ( ) ( ) 22 .0fxfxfxfx 1 d 2 x fxCx fx =+ ( ) 2 0
0;a . Suy ra ( ) ( )faxfx =+ ( ) ( ) ( ) 2 2 2 0 0
. Biết ( ) 01 f = , ( ) 6 2 fe = . Khi đó ( )1 f bằng A. 2 e B. 3 2e C. 3 e D. 5 2e Lời giải Theo bài ra ta có hàm số ( )fx đồng biến trên 0;2 ( ) ( ) 010 fxf = do đó ( ) 00;2fxx Ta có ( ) ( ) ( ) ( ) ( ) ( ) 2 2 fxfxfx fx fx fx = Theo đề bài ( ) ( ) ( ) ( ) 22 .0fxfxfxfx ln22fxC=+ 6 lneln1222 CC −=+= ( ) ( ) 2 fx x fx
=+ Do đó ( ) 11 2 00
fxfxfxfx ln2 2 x fxx =+ ( ) ln15 2 f = ( ) 5 21e f = Câu 151: Cho hàm số ( )yfx = là hàm số lẻ trên và đồng thời thỏa mãn hai điều kiện ( ) ( ) 11fxfx+=+ , x và ( ) 2 1 fx f xx = , 0 x . Gọi ( ) ( ) 1 2 0
( ) 1 fx fx .d 1 fx Ix fx = + . Hãy chọn khẳng định đúng về giá trị của I
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 48
−=
−+=
−+=
( ) ( ) ( ) ( ) 22
Suy ra ( ) ( ) ( ) ( ) ( ) ( ) 0 −= ( )
0d 11 = ( ) ( ) fx xC fx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 49 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. ( )1;0 I − . B. ( )1;2 I . C. ( )0;1 I . D. ( )2;1 I −− . Lời giải Đặt ( )yfx = . Khi đó từ giả thiết ta có : ( ) 11fxy+=+ , ( )2 11 1 1 y f x x + = +
Suy ra 1 1 11 x ff xx =−+ ++
=−+
+
2
x +− = +
1 Và 11 1 x ff xx + =+ 2 1 11 y f xx =+=+ 2 2 xy x + = , 1 11 x ff x x x = + + 2 2 22 1 11 x xy f x x xx xx + + == ++ ( ) 2 2 1 xy x + = + ( )2 Từ ( )1 và ( )
V
ố
ụ
( ) (
cos
.
Chọ
Giả thiết ( ) (
cos
+=
xxfxxfxx += ( ) cos e.cos x fxx = ( ) cos 1 e.sin x fxxC=+ . Do ( ) 02e f = , thế vào ta được 1 2 C = suy ra ( ) ( ) cos2sine x fxx =+ . Dùng máy tính thì ( ) ( ) cos 00 d2sin.ed10,30532891 x Ifxxxx ==+ . Câu 153: Cho hàm số ( )fx liên tục và nhận giá trị dương trên 0;1 . Biết ( ) ( ) .11fxfx−= với 0;1 x . Tính giá trí ( ) 1 0 d 1 x I fx = +
+ , ( )2 11 1 1 y f x x + −=− + + .
1 1 1 f x
+ ( )2 1 1 1 y x + =−+
( )
2 2 1 xxy
( )
2 suy ra : ( ) ( ) 22 22 2 11 xxyxy xx +−+ = ++ 22 2 xxyxy +−=+ yx= hay ( ) fxx = Do đó: ( ) ( ) 1 2 0 .d 1 fx Ix fx = + 1 2 0 .d 1 x x x = + ( ) 2 1 2 0 d1 1 21 x x + = + ( ) 1 2 0 1 ln1 2 x =+ 1 ln20,35 2 =
ậy ( )0;1 I
. Câu 152: Cho hàm s
( )fx có đạo hàm liên t
c trên
0; . Biết ( ) 02e f = và ( )fx thỏa mãn hệ thức
)
sin.cos.e,0; x fxxfxxx += . Tính ( ) 0 d Ifxx = A. 6,55 I
B. 17,30 I
. C. 10,31 I . D. 16,91 I . Lời giải
n C
)
sin.cos.e x fxxfxx
( ) ( ) coscos e.e.sin.cos
. Khi đó ( ) ( ) ( ) ( ) ( ) 0111 1000
dddd 1111111 fxx ttx I ftftfxfx =−=== +−+−+−+ Mặt khác ( ) ( ) ( ) ( ) 1111 0000
dd1dd1 111() fxxfx x xx fxfxft + +=== +++ hay 21 I = . Vậy 1 2 I = . Câu 154: Cho hàm số ( )yfx = có đạo hàm trên khoảng ( ) 0;+ thỏa mãn ( ) ( ) ( ) 3 .ln .
x fxx xfxfx = và ( ) 10 f = . Tính tích phân ( ) 5 1
d Ifxx = . A. 12ln1313. B. 13ln1312. C. 12ln1313 + . D. 13ln1312 + . Lời giải
= ( ) ( ) .e fx x fx x x = fx x xx fxx ++ == với ( ) 0; x+ . ( ) 55 2 11
Lấy nguyên hàm hai vế của suy ra ( ) 2 e 2 fx x x C =+ . Do ( ) 1 d.lnd 2 x Ifxxxx + == . Đặt 2 2 12 lndd 21 xx uux x + == + ; ddvxx = , chọn 2 1 2 x v + = . Theo công thức tích phân từng phần, ta được: 5 5 5 222 1 1 1
11 .lnd13ln13 222 xxx Ixx ++ =−=− 13ln1312=− .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 50
A.
B. 1
C.
D.
L
i Ta
= −++ Xét ( ) 1 0 d 1 x I
= + Đặ
11 txxt =−=− dd xt=− .
ậ
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
3 2
2
1
2
ời giả
có: ( ) ( ) ( ) ( ) .11 fxfxfxfx −+=+ ( ) ( ) ( ) 1 111 fx fxfx
fx
t
Đổi c
n: 01xt== ; 10xt==
Chọn B Từ giả thiết và ( ) ( ) ( ) 3 .ln x fxx xfxfx = ( ) ( ) ( ) 3 ln fx x xxfxfx = ( ) ( ) ( ) 3 e fx x x xfxfx = ( ) ( ) ( ) 2 . .e fx x xfxfx x x 10 f = 1 2 C = , nên ( ) ( ) 2211 eln 22
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 51
ọn
ố (
=
( ) ( ) ( ) 2 132xxfxfxxx ++=++ ( ) ( ) ( ) ( ) 2 12 11 1 2 11 xx fxfx xx x xx fx xx + += ++ + + =++ ( ) ( ) ( ) ( ) ( ) ( ) 22 11 2 1 2 11 3 1ln 12 213 211ln 322 23332ln21ln2ln3. 3222 xxfxdxdx xx x fx x ff ff + =++ =+ + −=+ −=+=+ 22 39 . 22 abab ==+= Câu 156: Cho hàm số ()yfx = liên tục trên thỏa mãn: 2 21 3()(2)2(1)4, xx fxfxxex −+ +−=−+ Tính giá trị của tích phân 2 0 () Ifxdx = . A. 2 Ie=+ B. 24Ie=+ C. 2 I = D. 8 I = Lời giải Chọn C Cách 1: 2 21 3()f(2)2(x1)e4, xx fxxx −+ +−=−+ 2 22 22 21 00 00 3()d(2)d(22)d4d(1) xx fxxfxxxexx −+ +−=−+ . Đặt 2022 0200 2(2)d()()d()d()d(2) txfxxfttfttfxx =−−=−== .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 155: Cho hàm số ( )yfx = liên tục trên \0;1 thỏa mãn điều kiện ( ) 12ln2 f = và ( ) ( ) ( ) 2 1.32xxfxfxxx ++=++ Giá trị ( ) 2ln3fab =+ , với , ab . Tính 22ab + A. 5 2 . B. 13 4 . C. 25 4 . D. 9 2 . Lời giải Ch
D Do hàm s
)yfx
liên tục trên \0;1 nên
Đặt 2 21 221 01 21d(22)d(22)dd0(3) xxu uxxuxxxexeu −+ =−+=−−==
Thay (2) và (3)vào (1) 2 2 0 0 4()d4d fxxx= 2 0 ()d2Ifxx == . Chọn phương án C
Cách 2: Do 2 21 3()f(2)2(x1)e4,(1) xx fxxx −+ +−=−+
2 2 21 21 9()3f(2)6(x1)e12 ()3(2)2(x1)e4 xx xx fxx fxfx −+ −+
+−=−+
( ) 0 d a fxx
fxxx fxfxx aaktkx ktkx
−+ −+ +−=−+ +−=−−+ xx== ++
1e a kx a fx x + bằng
( )d a a fxx C. ( ) 2d a a fxx D. ( ) 0 2d a fxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 52
+−=−−+ 2 21 ()2(x1)e1 xx fx −+ =−+ ( ) 2 22 21 00 ()d2(x1)e1d2 xx fxxx −+ =−+= Câu 157: Cho ( )fx là hàm số chẵn trên đoạn ; aa và 0 k . Giá trị tích phân ( ) d
A.
B.
L
Ta
(
fxfxfx
+++
Xét
(
0
+ . Đặt txxt =−=− dddd
=−−= Đổ
cận: xata =−= 00xt== Khi đó, ( ) ( ) ( ) ( ) 00 dd 1e1e kx kt aa fxftxt =− + + ( ) 0 d
Thay 2 xx =− vào (1) ta có: 2 21 3(2)()2(x1)e4,(2) xx fxfxx −+ −+=−−+ Từ (1) và (2) ta có hệ phương trình: 2 2 a kt
21 21 t = + ( )
3()f(2)2(x1)e4, ()3(2)2(x1)e4, 00
xx xx e.e. dd 1e1e
ời giải
có
) ( ) ( ) 0 0 ddd 1e1e1e aa kxkxkx aa
xxx =+
tích phân
)
d 1ekx a fx x
txtx
i
1e
ft
( )
ftfx
Do đó, ( ) ( ) ( ) 00
e1 dd 1e 23 4 dx fxfxdx x +−= + ( )1 Đặt ( ) ( ) ( ) ( ) ( ) 222 222
kx aaa kxkxkx a
e. ddd 1e1e1e
fxfxfx xxx =+ +++ ( ) ( ) ( ) 00 + nên ta có: ( ) ( ) ( ) 22 2 22
kx aa kx fx xfxx + == + Câu 158: Cho ( ) ( ) , fxfx liên tục trên và thỏa mãn ( ) ( ) 2 1 23 4 fxfx x +−= + . Biết ( ) 2 2 Ifxdx m == . Khi đó giá trị của m là A. 2 m = . B. 20 m = . C. 5 m = . D. 10 m = . Lời giải Hàm số ( ) ( ) , fxfx liên tục trên và thỏa mãn ( ) ( ) 2 1 23 4 fxfx x +−= 2323 Kfxfxdxfxdxfxdx =+−=+− Đặt ( ) ( ) ; xtdxdtfxft −==−−= , 22;22xtxt =−===− Do đó ( ) ( ) ( ) ( ) ( ) 2222 2222
. fxdxftdtftdtfxdx −=−== ( ) ( ) ( ) ( ) ( ) 22222 22222
23235 Kfxdxfxdxfxdxfxdxfxdx =+−=+= ( )2 Đặt 2 2 2 4 dx J x = + ; 2tan x = , ; 22 − , Ta có: ( ) ( ) 2 2 2 2tan21tan cos d dxdd ===+ Với 2 4 x =−=− ; Với 2 4 x == Do đó ( ) 2 44 4 2 4 44
+ ==== + ( )3 Từ ( )1 , ( )2 và ( )3 , ta có ( ) ( ) 22 22
21tan 1 4tan4224 d Jd
5 420KJfxdxfxdx === Mà theo giả thiết, ( ) 2 2 Ifxdx m == nên 20 20 m m == . Chú ý: Có thể tính nhanh 2 2 2 4 dx x + bằng công thức: 22 1 arctan dxx C xaaa =+ +
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 53
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
159: Chohàmsố ( )yfx = làhàmlẻvàliêntụctrên 4;4 biết ( ) 0 2
d2fxx−= và ( ) 2 1
2d4fxx−= . Tính ( ) 4 0
d Ifxx = . A. 10 I =− B. 6 I =− C. 6 I = D. 10 I = Lời giải Xét tích phân ( ) 0 2
d2fxx−= Đặt xt−= ddt x =− . Đổi cận: khi 2 x =− thì 2 t = ; khi 0 x = thì 0 t = do đó ( ) ( ) 00 22
ddtfxxft −=− ( ) 2 0
dt2 ft = ( ) 2 0
d2fxx = .
dt ft = ( ) 2 0
Do hàm số ( )yfx = là hàm số lẻ nên ( ) ( ) 22 fxfx −=− .
Do đó ( ) ( ) 22 11
2d2d fxxfxx −=− ( ) 2 1
2d4fxx =− .
Xét ( ) 2 1
2d fxx .
Đặt 2xt = 1 ddt 2 x = .
Đổi cận: khi 1 x = thì 2 t = ; khi 2 x = thì 4 t = do đó ( ) ( ) 24 12
dt8 ft =− ( ) 4 2
d8fxx =− . Do ( ) 4 0
1 2ddt4 2 fxxft==− ( ) 4 2
d Ifxx = ( ) ( ) 24 02
dd fxxfxx=+ 286=−=− . Câu 160: Cho hàm số ( )fx liên tục trên đoạn ln2;ln2 và thỏa mãn ( ) ( ) 1 1 x fxfx e +−= + . Biết ( ) ln2 ln2
dln2ln3fxxab =+ ( ) ; ab . Tính Pab =+ A. 1 2 P = . B. 2 P =− . C. 1 P =− . D. 2 P = . Lời giải Gọi ( ) ln2 ln2
d Ifxx =
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 54
T
==−−=−−=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
ừ đó: 2 1 arctan 422 dxx C x =+ + ( ) ( ) 2 2 2 2 2 111 arctanarctan1arctan1 42222444 dxx x
+ Câu
Đặt tx =− dd t x =− .
Đổi cận: Với ln2 x =− ln2 t = ; Với ln2 x = ln2 t =− .
Ta được ( ) ln2 ln2
d Iftt =−− ( ) ln2 ln2
d ftt=− ( ) ln2 ln2
d fxx=−
Khi đó ta có: 2I ( ) ( ) ln2ln2 ln2ln2
dd fxxfxx=+− ( ) ( ) ln2 ln2
d fxfxx==+− ln2 ln2
1 d e1 x x = + .
Xét ln2 ln2
1 d e1 x x + . Đặt e x u = ded x ux =
Đổi cận: Với ln2 x =− 1 2 u = ; ln2 x = 2 u =
đượ
d ee1
)
1
x
) ln2
d 1 u
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 55
Ta
c ln2 ln2 1 d e1 x x + (
ln2 ln2 e
x xx
= + (
ln2 1
uu = + ln2 ln2 11 d
u uu =− + ( ) 2 1 2 lnln1 uu =−+ ln2 = Vậy ta có 1 2 a = , 1 0 2 bab=+= . Câu 161: Cho ( )yfx = là hàm số chẵn và liên tục trên . Biết ( ) ( ) 12 01 1 dd1 2 fxxfxx== . Giá trị của ( ) 2 2 d 31 x fx x + bằng A. 1 B. 6 C. 4 D. 3 Lời giải Do ( ) 1 0 d fxx = ( ) 2 1 1 d1 2 fxx = ( ) 1 0 d1fxx = và ( ) 2 1 d2fxx = ( ) ( ) 12 01 dd fxxfxx+ ( ) 2 0 d3fxx == . Mặt khác ( ) 2 2 d 31 x fx x = + ( ) ( ) 02 20 dd 3131 xx fxfx xx + ++ và ( )yfx = là hàm số chẵn, liên tục trên ( ) ( ) fxfxx −= . Xét ( ) 0 2 d 31 x fx Ix = + . Đặttxdxdt =−=−
d 31 x fx Ix == + ( ) 0 2
d = 31 t ft t + ( ) 2 0
( ) 0 2
ft t + ( ) 2 0
d = 1 1 3t
d 31 x fx x = + ( ) ( ) 02 20
d3fxx =
3 d= 31
t t ft t + ( ) 2 0
3 d 31
x x fx x + ( ) 2 2
dd 3131 xx fxfx xx+= ++ ( ) ( ) 22 00
3 dd 3131
Câu 162: Hàm số ( )fx là hàm số chẵn liên tục trên và ( ) 2 0
x xx fxfx xx+= ++ ( ) ( ) 2 0
31 d 31
x x
fx x + = + ( ) 2 0
d10fxx = . Tính ( ) 2 2
d 21 x fx Ix = + A. 10 I = B. 10 3 I = C. 20 I = D. 5 I = Lời giải
Đặt tx =− ddtx=− . Đổi cận: 22xt=−= , 22xt==− . ( ) 2 2
d 21 t ft It = + ( ) 2 2
2 d 21
2d 21 x fx Ix= + ( ) 2 2
t t ftt = + ( ) 2 2
2 d 21
x x fxx = + ( ) 2 2
2 d 21
x x fxx + + ( ) 2 2
d fxx = ( ) ( ) 02 20
dd fxxfxx=+ ( ) 0 2
d10fxx =+
d Jftt=− ( ) 2 0
d Jfxx = , đặt dd txtx =−=− ( ) 2 0
d fxx=− ( ) 2 0 1;1 và ( ) 1 1
d10fxx == 220 I = 10 I = . Câu 163: Cho hàm số ( )yfx = là hàm số chẵn, liên tục trên đoạn 6 fxdx = . Kết quả của ( ) 1 112018x fx dx + bằng A. 2. B. 3. C. 4. D. 5. Lời giải Xét tích phân ( ) 1 112018x fx dx + . Đặt xt =− ; dxdt =− ; 11xt=−= ; 11xt==− ( ) 1 112018x fx dx + = ( ) 1 1 12018 t ft dt + = ( ) ( ) 11 11
2018 12018
2018. 1112018 2018
t t t
x x fx dx + = ( ) 1 1 fxdx = 6
2018 12018
ftftdtdt = + + = ( ) 1 1
x x fx dx + . Vậy ( ) 1 112018x fx dx + + ( ) 1 1
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 56
Mặt khác do ( )fx là hàm số chẵn nên ( ) ( )fxfx −= . Xét ( ) 0 2
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
42
Page 57
Do đó ( ) 1 112018x fx dx + = 1 .63 2 =
2 2020 2 2 .d 1 a x x x eb = + .
tổng Sab =+ A.
= . B.
= .
= . Lời giải Chọn D Xét 2 2020 2 .d 1 x x Ix e = + Đặt dd xtxt =−=−
x xx xxex IIIxxxx ee =+=+==== ++
20212 2021
= .
ra 2021 ab== . Vậy
ố ( )
ục
. Biết ( ) ( ) ln2 ln2 dln2ln3,, fxxabab =+ . Tính Pab =+ A. 2 P =− B. 1 2 P = C. 1 P =− D. 2 P = Lời giải Chọn B Từ giả thiết suy ra ( ) ( ) ln2ln2 ln2ln2 1 dd e1 x fxfxxx +−= + . Ta có ( ) ( ) ( ) ( ) ( ) ( ) ln2ln2ln2ln2 ln2ln2ln2ln2 ddd2d fxfxxfxxfxxfxx +−=−−−= Mặt khác ( ) ( ) ( ) ln2ln2ln2 ln2ln2ln2 1111 ddede e1ee1 e1e xx xxx xx x ==− ++ + ( ) ( ) ( ) ln2ln2 ln2 ln2 ln2 ln2 ln2ln2 113 dede1lne1ln2ln2ln3lnln2 ee12 xxx xx x =−+=−+=+−+= + . Suy ra ( ) ln2 ln2 1 dln2 2 fxx = 11 ,0 22 abab ==+=
Giáo viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Câu 164: Tích phân
Tính
0 S
2021 S
C. 2020 S = . D. 4042 S
. Đổi cận 22;22xtxt =−===− Ta được ( ) ( ) 2020 2222202020202020 2222 .. .d.d.d.d 1 111 1 tx ttx t t ttexe Itttx eee e =−=== +++ + Suy ra ( ) 2 2021 2021 2222020202020212022 2020 222 2 22 .22.d.d.d 11202120212021
Do đó
I
Suy
4042 Sab=+= Câu 165: Cho hàm s
fx liên t
trên đoạn ln2;ln2 và thỏa mãn ( ) ( ) 1 e1 x fxfx+−= +
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 58 Chuyên
Sưu tầm và
soạn Câu
Cho ( )fx là hàm số chẵn và ( ) 1 0 2 fxdx = . Giá trị của tích phân ( ) 1 112019x fx dx + là A. 2 . 2019 B. 2 C. 4 D. 0 Lời giải Chọn B ( ) 1 112019x fx Idx = + Đặt txdtdx =−→−= Cậ
t tt
t ttt ftftft
=−==
++
=+= +++ ====
Cho a là số thực dương, tính tích phân 1 d a Ixx = theo a A. 2 1 2 a I + = B. 2 2 2 a I + = C. 2 21 2 a I −+ = D. 2 31 2 a I = Lời giải Chọn A Vì 0 a nên 0 22 10 11 222 a aa Ixdxxdx + =−+=+= Câu 168: Cho số thực 1 m thỏa mãn 1 211 m mxdx−= . Khẳng định nào sau đây đúng? A. ( )4;6 m . B. ( )2;4 m . C. ( )3;5 m . D. ( )1;3 m . Lời giải Do 1 1221 2 mm m . Do đó với 1,1;210mxmmx− Vậy ( ) ( ) 233 11 2121121 1 mm m mxdxmxdxmxxmmmmm −=−=−=−−+=−+ 1 1 -1 -1 t x
Hòa
0984164935
luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12
biên
166:
n ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) 111 111 111 111 11 10 2019 12019 1201912019 2019 201912019 2 120191201912019 222.22. t
t t
Idtdtdt ft ftft Idtdtdt IftdtftdtI
+
+
Câu 167:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 59
B.
(
(
525 112 25 12
xxx xxx xxx xx xx xxxx =−+ +++ =−−+− ++ =−−++−+ =−−+−+−−+ =−+ Vậy 2,6,336abcPabc ==−===− Câu 170: Tính tích phân 1 1 22xx Idx =− . A. 1 ln2 . B. ln2. C. 2ln2. D. 2 ln2 . Lời giải 1 1 22xx Idx =− ta có 220 xx −= 0 x = . ( ) ( ) 10101 11010 2222222222 xxxxxxxxxx Idxdxdxdxdx =−=−+−=−+− 01 10 22221 ln2ln2ln2 xxxx ++ =+= Câu 171: Cho hàm số ( )fx liên tục trên và có ( ) 1 0 d2fxx = ; ( ) 3 0 d6fxx = . Tính ( ) 1 1 21d Ifxx =− A. 8 I = B. 6 I = C. 3 2 I = D. 4 I = Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ đó theo bài ra ta có 3 0 211 2 m mm m = −+=
=
. Do 1 m vậy 2 m = . Câu 169: Cho tích phân 5 1 2 ln2ln3 1 x dxabc x =++ + với a, b, c là các số nguyên. Tính P = abc. A. 36 P =−
0 P = C. 18 P =− D. 18 P = Lời giải Chọn A Ta có
) ( )
)
25 12 222 ddd 111 33 1d1d 11 3ln13ln1 23ln313ln253ln623ln3 26ln23ln3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 60
Chọn D
( ) ( ) 11 00 11 dd1 22fttfxx === Vậy 12 4 III=+= Câu 172: Cho hàm số ()fx liên tục trên và có 3 0 ()8fxdx = và 5 0 ()4.fxdx = Tính 1 1 (41). fxdx A. 9 . 4 B. 11 . 4 C. 3. D. 6. Lời giải Ta có 1 11 4 1 11 4 (41)(41)(41) fxdxfxdxfxdx −=−+− 1 1 4 1 1 4 (14)(41) fxdxfxdx=−+− IJ=+ +) Xét 1 4 1 (14). Ifxdx =− Đặt 144; txdtdx =−=− Với 1 15;0. 4 xtxt =−=== 1 055 4 1500 111 (14)()()()()1. 444 Ifxdxftdtftdtfxdx =−=−=== +) Xét 1 1 4 (41). Jfxdx =− Đặt 414; txdtdx =−=
( ) ( ) ( ) 1 11 2 12 1 11 2 21d12d21d IfxxfxxfxxII =−=−+−=+ . Xét ( ) ( ) ( ) 11 22 1 11 1 12d12d12 2 Ifxxfxx =−=−−− ( ) ( ) 33 00 11 dd3 22fttfxx === . Xét ( ) ( ) ( ) 11 2 11 22 1 21d21d21 2 Ifxxfxx =−=−−
Với 1 13;0. 4 xtxt ==== 1333 1 000 4
111 (41)()()()()2. 444 Jfxdxftdtftdtfxdx =−==== Vậy 1 1 (41)3.fxdx−=
Câu 173: Cho hàm số ( )fx liên tục trên thỏa ( ) 1 0
2d2fxx = và ( ) 2 0
6d14fxx = . Tính ( ) 2 2
52d fxx + . A. 30 B. 32 C. 34 D. 36 Lời giải
+ Xét ( ) 1 0
2d2fxx = .
Đặt 2d2d uxux == ; 00xu== ; 12xu== . Nên ( ) 1 0
22dfxx = ( ) 2 0
1 d 2 fuu = ( ) 2 0
d4fuu =
+ Xét ( ) 2 0
6d14fxx = .
Đặt 6d6d vxvx == ; 00xv== ; 212xv== Nên ( ) 2 0
146dfxx = ( ) 12 0
1 d 6 fvv = ( ) 12 0
d84fvv = .
+ Xét ( ) 2 2
52d fxx + ( ) ( ) 02 20
52d52d fxxfxx=+++ Tính ( ) 0 1 2
52d Ifxx =+ Đặt 52tx=+ Khi 20 x − , 52tx=−+ d5dtx=− ; 212xt=−= ; 02xt== . ( ) 2 1 12
1 d 5 Iftt = ( ) ( ) 122 00
1 dd 5 fttftt =− ( ) 1 84416 5 =−= Tính ( ) 2 1 0
52d Ifxx =+ . Đặt 52tx=+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
61
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 62 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi 02 x , 52tx=+ d5dtx= ; 212xt== ; 02xt== . ( ) 12 2 2 1 d 5 Iftt = ( ) ( ) 122 00 1 dd 5 fttftt =− ( ) 1 84416 5 =−= Vậy ( ) 2 2 52d32fxx+= Câu 174: Cho số thự
= − .
A.
B.
+
Lờ
Chọn A Ta thấy, ( ) ( ) ( ) (
10101 2 11010 2 fxdxfxdxfxdxxdxaxxdx =+=+− ( ) 1 23 0 2 1 0 1 11 2366 xxa xaa =+−=−+=−
0 23khi 0 x mx fx xxx + = + liên tục trên và ( ) 1 1 d=e3 fxxabc ++ , ( ) ,, abcQ . Tổng 3 abc ++ bằng A. 15. B. 10. C. 19. D. 17. Lời giải Ta có ( ) ( ) 00 limlime1 x xx fxmm++→→ =+=+ , ( ) ( ) 2 00 limlim230 xx fxxx →→ =+= và ( ) 01fm=+ . Vì hàm số đã cho liên tục trên nên liên tục tại 0 x = . Suy ra ( ) ( ) ( ) 00 limlim0 xx fxfxf+−→→ == hay 101mm+==− Khi đó ( ) ( ) ( ) ( ) 10101 222 11010 d=23de1d=3d3e1d xx fxxxxxxxxx ++−+++− ( ) ( ) 0 1 22 0 1 222 =33ee23 33 x xxx +++−=+− . Suy ra 1 a = , 2 b = , 22 3 c =− Vậy tổng 319abc++=− .
c a và hàm số ( ) ( ) 2 20 0 xkhix fx axxkhix
Tính tích phân ( ) 1 1 fxdx bằng:
1. 6 a
2 1. 3 a
C. 1. 6 a + D. 2 1. 3 a
i giải
)
Câu 175: Cho hàm số ( ) 2 ekhi
Câu 176: Tính tích phân 1 12 0 max, xx eedx
A. 1 e . B. ( ) 3 3 2 ee . C. 3 ee . D. 11 2 e e . Lời giải
Ta có: 12 1 12 3 xx eexxx . Suy ra: 12 12
1 0 3 max,1 1 3
ekhix ee ekhix Do đó
x xx x
1 max, 2 xxxxxx Ieedxedxedxee 11 3 33 113 222 eeeeee .
1 11 3 1 1 121212 3 1 0 3 1 00 3
Câu 177: Cho hàm số 2 31 51 xkhix yfx xkhix . Tính 1 2 00
A. 71 6 I . B. 31 I . C. 32 I . D. 32 3 I . Lời giải Chọn B + Xét tích phân: 2 1 0
2sincos332 Ifxxdxfxdx
2sincos Ifxxdx
. Đặt: sincos txdtxdx Đổi cận: với 0 x thì 0 t , với 2 x thì 1 t 111 2 1 2 1 0 0000
+ Xét tích phân: 1 2 0
2sincos2225109 Ifxxdxftdtfxdxxdxxx
332 Ifxdx . Đặt: 1 322 2 txdtdxdxdt Đổi cận: với 0 x thì 3 t , với 1 x thì 1 t
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 63
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 64
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 111 2 033 1 1 23 3 3 33 332 22 319 322. 222 Ifxdxftdtfxdx xdxxx Vậy: 1 2 00 2sincos33292231 Ifxxdxfxdx



CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 2. TÍCH PHÂN MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO Câu 178: Cho hàm số ( )fx có đạo hàm liên tục trên và thỏa mãn các điều kiện ( ) 02 f =− và ( ) ( ) ( ) 2 1 xfxxfxx ++=− , x . Tính tích phân ( ) 3 0 d Ixfxx = A. 4 3 I =− . B. 1 2 I =− . C. 3 2 I =− . D. 5 2 I =− . Lời giải Chọn D Ta có: ( ) ( ) ( ) 2 1 xfxxfxx ++=− ( ) ( ) 2 22 1.. 11 xfxfxxx xx ++=− ++ ( ) ( ) 221.1xfxx +=−+ ( ) 221.1 xfxxC +=−++ ( ) 2 1 1 C fx x =−+ + . Vì ( ) 02 f =− nên 2 211 01 C C −=−+=− + . Do đó ( ) 2 1 1 1 fx x =−− + Khi đó ( ) ( ) 3 33 22 2 00 0 135 13101 222 1 dd x Ixfxxxxxx x ==−−=−−+=−−+−−−=− + . Câu 179: Cho hàm số ( )fx liên tục trên đoạn 1;5 và thỏa mãn ( ) ( ) 22433ln fx x fx x x =− . Tính tích phân ( ) 5 4 d Ifxx = . A. 3 3ln4 B. 3 3ln4 2 C. 3 ln4 D. 3 9ln4 CHƯƠNG III NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Lời giải
Chọn C
Ta có: ( ) 4 2 1
243 3ln d fx x x x x
=− ( ) ( ) 444 2 111
2433lnddd fx x xxfxx x x =−
Xét ( ) 4 1
243 d fx Hx x = Đặt 43tx=− d2dx t x =
Đổi cận: ( ) 5 1
d Hftt= ( ) 5 1
d fxx = . Xét 4 2 1
3ln d x Kx x = ( ) 4 2 1
3lndlnxx = 4 33 1 lnln4 x == Khi đó ta được ( ) ( ) 45 3 11
ddln4fxxfxx=− ( ) 5 3 4
dln4fxx = . Câu 180: Cho hàm số ( )yfx = liêntụctrên vàcóđạohàm thỏa ( )1 fe = và ( ) ( ) ', fxfxxx+= . Giá trị của ( )2 f bằng A. 2 e B. 1 1 e C. 1 1 e + D. 2 Lời giải Chọ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 2
n D ( ) ( ) ( ) ( ) ''xxx fxfxxefxefxxe +=+= ( ) ( )' xx efxxe= ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 22 11 '21.2122xx efxdxxedxefefeeffef =−=−== Câu 181: Cho hàm số ()fx có đạo hàm liên tục trên , thỏa mãn ()()ex fxfx −= và (0)1 f = . Tính (1) f A. (1)e f = . B. (1)2e f = . C. (1)e1 f =+ . D. (1)e1 f =− . Lời giải Chọn B
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 3 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ' 111 22 000 11()()() () ()()e xxxx x x xx f fx dxdxdx ee efxefxefxefx xfx e === −= ( ) ( ) ( ) ( ) 1 0 10 |1112 1 x fxff fe ee =−== Câu 182: Cho hàm số ( )fx liên tục trên 0;1 thỏa ( ) ( ) ( ) 11 22 00 2 2ln2ln1 fxdxfxxdx e +=+ . Tích phân ( ) 1 0 Ifxdx = A. ln 4 e I = . B. ln 2 e I = . C.
với ( ) ( ) ( ) ( ) 1 2 0 ln10ln1 fxxdxfxx −+=+ , 0;1 x . Suy ra ( ) ( ) 11 00 4 ln1lnfxdxxdx e =+= . Câu 183: Cho hàm số ( )fx là hàm số liên tục và là hàm số lẻ trên đoạn 1;1 . Biết ( ) 1 0 .d6fxxx = Tính tích phân ( ) 1 2 1 d 4 fx Ix xx = +− . A. 12 I = B. 9 I = C. 3 I = D. 18 I = Lời giải Chọn C ( ) ( ) ( ) ( ) 2 1111 2 22 2 1111 4 11 dd.4d.d 444 4 fxxx fx Ixxfxxxfxxx xx xx ++ ===++ +− +− ( ) ( ) ( ) ( ) 0101 22 1010 1111 .4d.4d.d.d 4444 fxxxfxxxfxxxfxxx =+++++ . Đặt dd xtxt =−=− , ta có ( ) ( ) ( ) 001 222 110 .4d.4d.4d fxxxftttfxxx +=−−+=−+ ; ( ) ( ) ( ) ( ) 001 110 .d.d.d fxxxftttfxxx =−−−= Suy ra
4 ln I e = . D. 2 ln e . Lời giải Chọn C Bằng phương pháp tích phân từng phần ta tính được ( ) 11 222 00 22 ln12ln2lnxdxdx ee +== Do đó giả thiết tương đương
fx có
hàm
và
ỏa mãn ( ) 2 1 2 x fx x −= . Tính tích phân ( ) 2 2 0
12cos cossin2dsin2dd
t Iftttttt ttt
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
(
( ) (
1111
=−+++++ (
1
==
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 sinsin2sin2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn === Đặt sincosd utdutt == Đổi cận: 00; 1; 2 tutu ==== ( ) 1 1 2 0 0 22 d1 2 2 Iu u u === Câu 185: Cho hàm số ( )fx liên tục trên và thỏa ( ) ( ) 2532 12 fxxfxxxxx ++=+++ . Tính giá trị của ( ) 2 1 fxdx biết ( ) 2 0 8 3 fxdx = A. 7 3 B. 7 6 C. 7 6 D. 7 3 Lời giải Chọn D Lấy tích phân từ 0 đến 1 hai vế của đẳng thức đề bài cho ta được ( ) ( ) ( ) 111 2532 000 12 fxdxxfxdxxxxxdx ++=+++
)
) ( )
22 0000 1111 .4d.4d.d.d 4444 Ifxxxfxxxfxxxfxxx
)
0 1 .d3 2 fxxx
Câu
184: Cho hàm
số ( )
đạo
trên 1;1
th
cossin2d Ifxxx = A. 2 I = . B. 1 I = . C. 1 2 I = . D. 3 2 I = . Lời giải Chọn B Lấy đạo hàm hai vế của phương trình ( ) 2 1 2 x fx x −= ta được ( ) ( ) ( ) ( ) 22 22 21 211 22 xfxfx xxx −−=−= Đặt sin xt = ta có ( ) ( ) ( ) ( ) 22 22 11 1sincos sinsin2sinsin2 ftft tttt −== . Khi đó ( ) ( ) ( ) 222 2 22 000
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 5 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt 2 12 txdtxdx =+= 01;12xtxt ==== . Khi đó ta được ( ) ( ) 12 6432 1 0 01 1 2. 26432 | xxxx fxdxftdt +=+++ ( ) ( ) 12 01 13 22fxdxfxdx += ( )1 Ta có ( ) ( ) ( ) 212 001 88 33fxdxfxdxfxdx =+= ( )2 Lấy ( )2 trừ ( )1 vế theo vế ta được ( ) ( ) 22 11 177 263 fxdxfxdx== Câu 186: Cho hàm số ( )yfx = có đạo hàm liên tục trên 0;4 thỏa mãn (
f = và ( ) ( ) ( ) ( ) 212121 xfxfxxx +−=++ . Tính (
4 f A. 27 B. 20
15 Lời giải Chọn D Từ giải thiết: ( ) ( ) ( ) ( ) 212121 xfxfxxx +−=++ ( ) ( ) 1 21 21 1 21 xfxfx x x +− + = + ( ) 1 21 fx x = + . ( ) 44 00 d1d 21 fx xx x = + ( ) 4 0 4 21 fx x = + ( ) ( )40 4 31 ff −= ( ) 415 f = Câu 187: Cho hàm số ()yfx = có đạohàm liêntụctrên thỏamãn 223 .().'()14(), xfxfxxfxx+= và có (2)2 f = . Tích phân 2022 0 1 2022()dfxx có giá trị là: A. 1. B. 2. C. 1011. D. 2022. Lời giải Chọn C Ta có: 223 .().'()14(), xfxfxxfxx+= 42332 .().'()4.() xfxfxxfxx −=− 4233 42 .().'()4.()1 xfxfxxfx xx =− ' 3 42 ()1fx xx =− 3 4 ()1fx C xx =+ Ta có: 33 44 (2)1210 2222 f CCC =+=+= .
) 01
)
C. 10 D.
Suy ra: 33()() fxxfxx == . Vậy 20222022 00
11 ()dd101120222022fxxxx==
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
Chọn C Ta
(
11 11 33
22
( ) ( ) ( ) 33
22
=+− ( ) ( ) 2 33 2,2 22 xfxAxBxx=+− . Lấy tích phân từ 1 đến 1 của ( )1 và ( )2 ta được ( ) ( ) 1 2 11 111 111 32 2 2 11 1 3333234d.2d 2242 2 333.d2d 2224 AxBx AxB fxxxABx AB AxBx xfxxAxBxxx BxA =+−=− =+− == =+− =+−= Vậy ( ) 1 1 d2IAfxx === Câu 189: Xét hàm số 1 0 ()() x fxexfxdx =+ . Giá trị của (ln(2021)) f bằng A. 2021 B. 2022 C. 2021 e D. 2022 e Lời giải Chọn B Ta có 11 00 ()()()(). xxxx fxexfxdxfxefxexedx =+==+ Đặt dudx dvdxxx ux eve == == ( ) 11 11 00 00 dxdx11. xxxx xexeeeeee =−=−=−−= ()1 xfxe =+ . Vậy ( ) ( )ln2021 (ln2021)1202112022 fe=+=+= .
Câu 188: Cho hàm số ( )fx liên tục trên 1;1 thoả ( ) ( ) ( ) 1 1 3 2d,1;1 2 fxxtfttx+=+− . Tính ( ) 1 1 d Ifxx = ? A. 4 I = . B. 3 I = . C. 2 I = . D. 1 I = . Lời giải
có ( )
) ( ) ( )
d.d2,*
fxxftttftt =+− . Đặt ( ) ( ) 11 11 d,.d AfttBtftt == .
*.2,1
fxxAB
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 190: Cho hàm số ( )fx liên tục trên và thoả mãn ( ) ( ) ( ) 1 0 23' x fxxefxfxdx =+++ . Biết tích phân ( ) 1 2 0 ee Ifxdxabc ==++ Tính 22242 Tabc =+− A. 10 B. 12 C. 15 D. 8 Lời giải Chọn D Đặt ( ) ( ) 1 0 2'd mfxfxx =+ Ta có ( ) e2 x fxxm =++ và ( ) ( ) '1ex fxx=+ . Suy ra ( ) ( ) ( ) ( ) ( ) 111 000 3'3e21e41e63 xxx mfxfxdxxmxdxxmdx =+=++++=+++ . Xét tích phân ( ) 1 0 41ex xdx + Đặt 41d4d dede xx uxux vxv =+= == ( ) ( ) ( ) 11 00 11 41ed41e4ed5e14e5e24e1e2 00 xxxx xxxx +=+−=−−=−−−=+ . Suy ra ( ) ( ) ( ) 11 00 1e 41ed63de263e2633e84 02 x mxxmxmxmmm =+++=+++=+++=++=−− Vậy ( ) ee e24e2 22 xxfxxx=+−−=−− Suy ra ( ) ( ) 22 2 00 22ee de2d1e2ee4. 0022 xx fxxxxxx =−−=−−+=−− Do đó 1 a = ; 1 b =− ; 222 442421610cTabc =−=+−=+−=− Câu 191: Cho hàm số ( )fx liên tục trên thoã mãn ( ) 3 2 x ffx = , x . Biết rằng ( ) 4 0 1 fxdx = . Tính tích phân ( ) 4 2 Ifxdx = A. 5 2 I = . B. 3 2 I = . C. 1 2 I = . D. 1 2 I =− . Lời giải Chọn D
192:
hàm
(
fx
02022
hàm
Tính giá
thoã
fxfxxe
( ) ( ) 20212022'20222022.
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét tích phân ( ) 2 0 d Jfxx = . Đặt 1 dd 22 t xxt == . Với 00;24xtxt ==== . Ta có ( ) ( ) 444 000 1133 d3dd 22222 t Jftfttftt ==== Mặt khác ( ) ( ) ( ) ( ) 4244 0022 31 dddd1 22 fxxfxxfxxfxx=+=−=−
==− Nên ( ) ( ) ( ) 1 1 20222022 0 0 'd xx Jfxeefxx =−+ . ( ) ( ) ( ) ( ) (
1111
00
( ) ( ) 2022 20222022 1012022 12023 f fe ee + + === . Cách 2: Ta có ( ) ( )
x
−=
( ) ( )
.'2022. x fxex= ( )
=+ Với 0 x = ta có 2022.102022 CC =+=
Câu
Cho
số ( )
có đạo
trên
mãn
x
−= với x và ( )
f = .
trị ( )1 f A.
) 202112022e f = . B. ( ) 2022 12022.e f = . C. ( ) 202212023.e f = . D. ( ) 202212021e f = . Lời giải Chọn C Cách 1: Ta có ( ) ( ) 20212022'20222022. x fxfxxe −= ( ) ( ) 2021 2022 '2022 2022. x fxfx x e = ( ) ( ) 11 2021 2022 00 '2022 d2022d1 x fxfx xxx e == . Ta có ( ) ( ) ( ) ( ) 111 20222022 2022 000 '2022 d'.d2022.d xx x fxfx Ixfxexefxx e ==− . Tính ( ) 1 2022 0 2022d x Jfxex = Đặt ( ) ( ) ( ) 20222022 'd 2022edxx ufxdudfxfxx dvxve ===
) ( ) ( ) ( )
20222022202220222022 00
'd'd1.01 xxxx Ifxexfxefxexfxefef =+−==−=
20212022'20222022.
fxfxxe
( ) ( ) 2021 2022 '2022 2022. x fxfx x e =
20222021
20222022 x fxexC
Với 1 x = ta có ( ) 2022 1.120222023fe =+= ( ) 2022 12023. fe= Câu 193: Cho hàm số ()fx có đạo hàm dương trên 1 ; 2 −+ và thỏa mãn 3 2 1 (21)()(()1),. 2 xfxfxx +=+− Biết (0)0 f = . Giá trị của 4 0 ()d fxx thuộc khoảng nào dưới đây? A. ( )0;3 B. ( )3;7 C. ( )7;10 D. ( )10;15 Lời giải Chọn C Vì ()0fx , 1 2 x ()1dd (()1)21 fx xx x fx
= + + . Đặt ()tfx = d()d tfxx = Khi đó 3 2 3 2 3 2 3 2 3 3 2 3 3
Theo giả thiết (0)0 f = , suy ra 3 3(0)139 44fCC+=+= . Do đó ( )3 2 3 1 ()(21)31 64 fxx=++− . Vậy 4 0 ()d9,34fxx .
= + + =++ + +=++ +=++
()1dd (()1)21 d3 (21) (1)4 3 31(21) 4 3 3()1(21). 4
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn +=+=− + + Lấy nguyên hàm hai vế ta được 3 2 3
9 ()11 (21)()(()1),. (()1)212 fx xfxfxx x fx
fx xx x fx t xC t txC fxxC
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 − nên ()10fx + , 1 2 x − . Ta có 3 2 3 2 3
Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
=−++ +=+ +=+ =+
'3.1512. '3.1512. '.3.1512 .1512.
t
3 3 33 3
24 24 24 ' 4
x x xx x
fxxfxxxe fxxfxxxe efxexfxxx efxxx Nguyên hàm hai vế ta được: ( ) 3 52.36=++ x efxxxC . Khi 1= x ta được: ( ) .190 =+=efCC . Suy ra: ( ) ( ) 33
23 52 3632 + + == xx
xx xx fx ee .
xx fxxx e Đặt 32d3d== txtxx . Đổ
được: 1 0 2 d + = t t It e
i cận 00;11 ==== xtxt
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 10 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 194: Cho hàm số ( )fx thỏa mãn ( ) 9 1 = f e và ( ) ( ) ( ) 3 24 '3.1512.,=−++ x fxxfxxxex . Biết ( ) 1 0 d =− b fxxa e , với , ab . Tính 22=+ Sab A. 14 S = . B. 7 = S . C. 25 = S . D. 1 S = . Lời giải Chọn C
Ta
Đặ
2
= = =− t
Câu
ố
Ta có: ( ) ( ) 3 (
23 11 00 .'
32 dd + = x A. 27 4 B. 219 8 C. 357 4 D. 27 8
1 =+
t ut dudt dvdt ve e Khi đó: ( ) ( ) 1 111 000 0 4 223 =−++=−+−=−
tttt Ietedtete e Suy ra 3,4==ab . Vậy 25 = S .
195: Cho hàm s
( )fx có đạo hàm trên và thỏa mãn ( ) 3232, fxxxx+=+ . Tính
) 4 2 0
xfxdx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
2 2 112 Ie e =−=− Câu 197: Cho hàm số ( )yfx = có đạo hàm trên đoạn 1;2 thỏa mãn ( ) ( ) 12,21ff== và ( ) 2 2 1 d2.xfxx = Tích phân ( ) 2 2 1 d xfxx bằng A. 4 B. 2 C. 1 D. 3 Lời giải Chọn D Ta có: ( ) ( ) 2 22 2 2 1 1 11 44 d2; d1xfxxfx xx =−===− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 11 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Ta có ( ) 3232, fxxxx+=+ nên ( ) 43 f = Mặt khác ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 44444 4 222 0 00000 .'.21642.482 xfxdxxdfxxfxfxxdxffxxdxxfxdx ==−=−=− Ta tính ( ) ( ) 44 00 Ixfxdxtftdt == Chọn ( ) 32333 txxdtxdx =+=+ Mà ( ) 3232fxxx+=+ nên ( )( ) ( ) ( )( )( ) 233232 33333332 xxxfxxxxxx +++=+++ Suy ra ( )( ) ( ) ( )( )( ) 11 233232 00 165 33333332 8 xxxfxxdxxxxxdx +++=+++= Hay ( ) 4 0 165 8 tftdt = nên suy ra ( ) ( ) 44 2 00 27 .'482482 4 xfxdxxfxdxI =−=−= . Câu 196: Cho hàm số ( )fx liên tục trên và có ( ) 22 f −= ; ( ) 01 f = . Tính ( ) ( ) 0 2 x fxfx Idx e = . A. 2 12 Ie =− B. 2 12 Ie =− C. 2 12 Ie =+ D. 2 12 Ie =+ Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0 000 22 222 2 ..2 0 xx xxxx fxfxfxefxefxfxf Idxdxdxf eeeee =====− Do ( ) 22 f −= ; ( ) 01 f = nên 2
đúng?
A. ( ) 2 24 f = B. ( ) 2 25 f = C. ( ) 2 26 f = D. ( ) 2 23 f = Lời giải
Chọn B
Ta có ( ) ( ) ., fxfxxx = Lấy nguyên hàm hai vế ta được ( ) ( ) ( ) ( ) ( ) ( ) 222111 .ddd 222 fxfxxxxfxfxxCfxxC ==+=+
Với 0 x = ( ) 22 111 0.0 222 fCC =+= . Suy ra ( ) ( ) 2222111 1 222fxxfxx=+=+ .
Vậy ( ) 2 25 f =
Câu 199: Xét hàm số ( ) 2 1
1 d 1
x t Fxt tt + = ++ . Trong các giá trị dưới đây, giá trị nào là nhỏ nhất?
A. ( )1 F B. ( )2021 F C. ( )0 F D. ( )1 F Lời giải Chọn D
Gọi ( )Gt là một nguyên hàm của hàm số ( ) 2
1 1 t ft tt + = ++ , ta có ( ) ( ) ( ) ( ) 1 1 x FxGtGxG ==− ( ) ( ) ( ) ( ) 2
1 1 1 x FxGxGGx xx
+ =−== ++ ; ( ) 01Fxx==− . Bảng biến thiên của hàm số ( )Fx :
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
12 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vì ( ) ( ) ( ) 2 2 2 1 4 4d0xfxfxx x ++= nên ( ) 2 2 1 2 d0xfxx x += ( ) ( ) 2 22 fxfxC xx =−=+ Mà ( ) ( ) 2 120 fCfx x === . Khi đó ( ) 22 2 22 2 1 11 2 d.d23.xfxxxxx x ===
Câu 198: Cho hàm số ( )yfx = có đạo hàm trên và thỏa mãn ( ) ( ) ., fxfxxx = . Biết ( ) 01 f = , khẳng định nào sau đây
Dựa vào bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số là ( )1 F
200: Cho hàm số ( )fx có đạo hàm và liên tục trên \0;1 , thỏa mãn
) ( ) ( ) 2 1 xxfxfxxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 13 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
+=
=
=
=−
=−++ + Mà ( ) 12ln2 f =− suy ra 1 2ln2.1ln21. 2 CC −=−+=− Ta có ( ) ( ) 233 2.2ln312ln3. 322ff=−−=− Vậy 22 22 339 . 222 Pab =+=+= Câu 201: Cho hàm số ( )yfx = liên tục trên 3 ;1 5 và thoả mãn ( ) 2 3 351 5 fxfx x +=+ . Tính tích phân ( ) 1 3 5 d fx Ix x = 1 ∞ F( 1) F(x) +∞ +∞ + 0 +∞ F'(x) x
Câu
(
++=+ với mọi \0;1 x− và ( ) 12ln2 f =− . Biết ( ) 2ln3fab =+ với , ab , tính 22Pab =+ A. 3 4 P = B. 9 2 P = C. 13 4 P = D. 1 2 P = Chọn B Ta có: ( ) ( ) ( ) 2 1 xxfxfxxx ++=+ ( ) ( ) ( )2 1 . 11 1 xx fxfx xx x
++ + . ( ) ( ) ( ) ( ) 11 11 1 .1. 11 .ln1. 1 xx fx xx xx fxdx xx x fxdx xx x fxxxC x
++
++
++
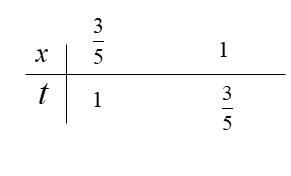
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 14 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 113 ln 2585 I =+ . B. 813 ln 2585 I =− . C. 213 ln 2585 I =+ . D. 113 ln 2585 I =− . Lời giải Chọn D Đặt 3 5 x t = 2 3 ddt 5 x t =− . Đổi cận: Khi đó 3 5 2 1 3 3dt 5 53 5 f t I t t =− 11 33 55 33 55dtdff tx x tx == .
+ = 1 2 3 5 1 d x x x + = 1 3 5 1 d xx x =+ 2 1 3 5 ln 2 x x =+ 83 ln 255 =− 113 ln
=− Vậy 113 ln
=− .
Cho hàm số ( )yfx = là hàm liên tục có tích phân trên 0;2 thỏa điều kiện ( ) ( ) 2 24 0 6d fxxxfxx =+ . Tính ( ) 2 0 d Ifxx = . A. 32 I =− B. 8 I =− C. 6 I =− D. 24 I =− Lời giải Chọn A Ta có ( ) ( ) 2 24 0 6d fxxxfxx =+ . Đặt ( ) 2 0 d xfxxa = . Khi đó ( ) ( ) 242 66 fxxafxxa =+=+ . Do đó ( ) ( ) 22 2 00 d6d axfxxxxax ==+ 2 2 4 0 3 24224 22 ax axaaa =+=+=− Nên ( ) 2 624fxx=− . Vậy ( ) ( ) ( ) 22 2 23 0 00 d624d22432Ifxxxxxx ==−=−=− .
Suy ra 35II+= ( ) 11 33 55 3 5 3d5d f fx x xx xx + ( ) 1 3 5 353 5d fxf x x x
2585 I
2585 I
Câu 202:

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 15 Chuyên
thi:
10 Tốt
12 Sưu tầm và biên soạn Câu 203: Cho hàm đa thức ( )fx thỏa mãn ( ) ( ) 32 2461814, fxxfxxxxx −−=−+−+ . Tích phân ( ) 2 0 d fxx bằng A. 4 B. 10 C. 12 D. 18 Lời giải Chọn B ⬥ Từ giả thiết ( ) ( ) 32 2461814,
Câu
ố (
(
d
=
ằ
A. 2 3 . B. 2 3 . C.
2
D.
2
Lời giải Chọn B Xét ( )
d Axfxx =
Hòa
0984164935
luyện
Tuyển sinh vào lớp
Nghiệp THPT BDKT Toán 10; 11;
fxxfxxxxx −−=−+−+ : Với 0 x = ta có ( ) 214. f = ⬥Ta có ( ) ( ) ( ) 22 32 00 2d461814d fxxfxxxxxx −−=−+−+ ( ) ( ) ( ) 22 00 2dd8*.fxxxfxx −−=− + Với ( ) 2 0 2d Ifxx =− . Đặt 2dddd. txtxtx =−=−−= Đổi cận Khi đó ( ) ( ) ( ) 022 200 dt=dt=d. Iftftfxx =− + Với ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2222 2 0 0000 ddd22d Jxfxxxfxxfxfxxffxx ===−=− + Khi đó trở thành ( ) ( ) ( ) 22 00 d22d8fxxffxx−+=− ( ) ( ) ( ) 22 00 2d82282.1420d10. fxxffxx =−+=−+==
204: Cho hàm s
)fx liên tục trên đoạn 0;1 thỏa mãn ( ) ( ) 1 22 0 12d fxxxfxx =+ . Giá trị của
) 1 0
Ifxx
b
ng
3
.
3
.
1 2 0
2 d2d txxtxtt ===
3 fxxIfxxIxx =−===−=− .
2d. Ixfxx = A. 1 I = B. 12 I = C. 4 I = D. 17 I = Lời giải Chọn A Đặt 2 tx = , suy ra d d 2 t x = , với 0 cosd5fxxx
x = thì 0 t = ; với 2 x = thì 4 t = . Do đó ta có = và ( ) 01. f = Khi đó ( ) 2 0
111 ()d()()d(4)41.444 | xfxxxfxfxxf sin2d fxxx
Câu 207: Cho hàm số ( )fx bằng A. 6 B. 8. C. 7. D. 7. Lời giải Xét ( ) 2 2 0
= , đặt ( ) ( ) 2 cosdsin2d . d'd uxx ux vfx vfxx =− = = =
'cosd10fxxx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
Đặt ,
xtxt ==== ( ) 1 5 0 2d
= Theo
(
222 0
(
11
11
==+=+=− Khi
( ) ( ) ( ) 11 22 00 2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
00;11
Atftt
giả thiết ( )
) ( ) 1
12d12 fxxxfxxfxxA =+=+
) ( )
552 00
2d212d4 412AtfttttAtAA
đó
1d1d
4 0 ()d 22 Ifttt == 44 4 0 00
Câu 205: Cho hàm số ( )fx có đạo hàm là ( ) 23,\2 2 x fxx x = thỏa mãn ( ) 11 f = và ( ) 32 f = Giá trị của biểu thức ( ) ( )024ff + . A. 3. B. 5. C. 57ln2−+ . D. 73ln2 + . Lời giải Chọn D Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 14 03 =−=−=
0241d2d373ln2 ffffxxfxxf +=−++=+ Câu 206: Cho hàm số ()fx liên tục trên và (4)2 f = , 4 0 ()d4fxx = . Tính tích phân ( ) 2 0 có đạo hàm liên tục trên 0;, 2 thỏa mãn ( ) 2 2 0
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
42
Page 17
tầm và
Khi đó ( ) ( ) ( ) 22 22 2 0 00 5'cosdcossin2d fxxxxfxfxxx ==+ ( ) ( ) ( ) ( ) 22 00 50sin2dsin2d506. ffxxxfxxxf =−+⎯⎯→=+= Câu 208: Cho ( )fx là hàm số liên tục trên thỏa mãn ( ) ( ) 2 2, x fxfxxex +−=
( ) 2 0 Ifxdx = A. 4 1 Ie=− B. 4 2 Ie=− C. 21 2 e I = D. 4 1 4 e I = Lời giải Chọn D Ta có: ( ) ( ) 2 2, x fxfxxex +−= ( ) ( ) 2 222 000 2 x fxdxfxdxxedx+−=
Đặt 2
=−=− . Đổi cận: 02 20 xt xt == == ( ) ( ) ( ) (
2022
2
−=−==
( ) 22
22
xx IfxdxxedxIxedx=== ( ) 22 2 4 2 2 0 0 111 444 | xx e Iedxe === . Câu 209: Cho hàm số 1 3 0 ()44() fxxxfxdx =− và (1)0 f . Giá trị (4) f bằng A. 256 B. 248 C. 240 D. 252 Lời giải Chọn B Đặt: 1 0 () afxdx = , a . Khi đó 3 ()44 fxxax =− Ta có: (1)0(1)44a01 ffa =− Xét phương trình 32 2 0 ()444()0 x fxxaxxxa xa = =−=−= = Xét: 2 xa = Với 01 a thì 0 ()0 x fxxa xa = == =− khi đó
viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu
biên soạn
. Tính tích phân
txdtdx
)
0200
fxdxftdtftdtfxdx
222 000 1
2
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 18
1 2 a = , 3 (x)4x2(4)248 fxf=−= thỏa yêu cầu bài toán Câu 210: Cho hàm số ( )yfx = liên tục trên ( ) 0;+ thỏa mãn ( ) ( ) 2 23 xfxfxxx += . Biết ( ) 1 1 2 f = . Tính ( )4 f . A. 16. B. 4. C. 24. D. 14. Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) 2 2 23 23 22 xfxfx xx xfxfxxx xx + +== ( ) ( ) 2 13 22 xfxfxx x += ( ) ( ) 44 22 11 33 ..dd 22 xfxxxfxxxx == ( ) ( ) ( ) ( ) 4 1 6363 .241416 22 xfxfff =−== Câu 211: Cho hàm số ( )fx liên tục trên biết ( ) 3 0 dx8 fx = và ( ) 5 0 dx4 fx = . Tính ( ) 1 1 41dxfx A. 11 4 . B. 3. C. 9 4 . D. 6. Chọn B
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) 1133424201 00 ()444422 a aa a fxdxxaxdxxaxdxxaxxaxa =−−+−=−+−= 222 1 1 122310 1 2 2 a aaaaaaa a = +−+=−+== = Vậy 3 (x)4x2(4)248 fxf=−= Với 0 a thì 2 xa = vậy ()00 fxx== khi đó ( ) ( ) 11 1 342 0 00 1 ()442123 fxdxxaxdxxaxaaaa =−=−=−== Với 0 a = thì ()00 fxx== ( ) ( ) 11 1 342 0 00 1 ()442123 fxdxxaxdxxaxaaaa =−=−=−== Vậy
5 50 = ,
Ifx = . Đặt 41 4 dt txdx =−= . Thế cận 1 1 4 03 x t . Suy ra: fx x xx = . Tính tích phân 2 1 4
41dx e e
dt2 1 4 Ift xt xt == == Khi đó
ậy ( ) ( ) ( ) 1 11 4 1 11 4 41dx14dx41dx123 fxfxfx−=−+−=+= Câu 212: Cho hàm số ()fx 1()1()1()() 1dddd2 222 ftftfxfx Attxx ttxx ==−===
) (2)dfx Ix x = A. 1 I = . B. 2 I = . C. 3 I = . D. 4 I = . Lời giải Chọn D ⚫ Xét 4 2 0 tan.(cos)d1Axfxx
1 == Đặt 2 cos tx = 2 d d2sincosd2costand2.tandtand 2 t txxxxxxtxxxx t =−=−=−=− Đổi cận: 01 1 42
= . 1 111 2 111 1 222
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 (
19 0
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 3
Ta có ( ) ( ) ( ) 1 11 4 1 11 4 =
41dx14dx41dx fxfxfx −=−+− . Xét ( ) 1 4 1 1 14dxIfx = . Đặt 14 4 dt txdx =−=− . Thế cận 1 1 4 50 V
x t . Suy ra: ( ) ( ) 0 1 liên tục trên và thỏa mãn 4 2 0 tan.(cos)d1 xfxx
1 dtdt 1 4 1 4 Iftft = = = . Xét ( ) 1 2 1 4 2 2 (ln)d1 ln
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 20 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ⚫ Xét 2 2 (ln)d1 ln e e fx Bx xx == . Đặt 2ln ux = 2 2ln2ln2dd dddd. lnlnln2 xxuxu uxxx xxxxxxxu ==== Đổi cận : 2 e1 e4 xu xu == == . Khi đó 444 111 1()1()() 1ddd2 22 fufxfx Buxx uxx ==== . ⚫ Xét 2 1 4 (2)dfx Ix x = . Đặt 1 dd 22 2 xv vx v x = = = . Đổi cận: 11 42 24 xv xv == == Khi đó 4414 111 1 222 ()()()() dddd224fvfxfxfx Ivxxx vxxx ===+=+= . Câu 213: Cho hàm số ()yfx = liên tục trên ( ) 0;+ thỏa mãn 2.'()()4. xfxfxxx += Biết (1)2 f = Giá trị của (4) f bằng A. 15 4 . B. 17 4 . C. 15 2 . D. 17 2 . Lời giải Chọn D Với mọi ( ) 0; x+ ta có: ( ) 1 2.'()()4.'().()2.()'2 2 xfxfxxxxfxfxxxfxx x +=+== Lấy nguyên hàm hai vế của ta có: 22(.())'2.() xfxdxxdxxCxfxxC ==+=+ Mà (1)2 f = suy ra: 1 C = . Vậy: 22 .()12.(4)41(4)17 2 xfxxff=+=+= Câu 214: Cho hàm số ( )fx liên tục trên đoạn 0;1 , có đạo hàm ( )fx thỏa mãn ( ) ( ) 1 0 21d10 xfxx += và ( ) ( )031ff = . Tính ( ) 1 0 d Ifxx = . A. 5 I =− . B. 2 I =− . C. 2 I = . D. 5 I = .
Lời giải Chọn A Đặt: 21d2d uxux =+= , ( ) dd vfxx = chọn ( )vfx = . Ta có: ( ) ( ) 1 0
3102d10 fffxx −−= ( ) 1 0
1 212d10 0 xfxfxx +−= ( ) ( ) ( ) 1 0
21d10 xfxx += ( ) ( ) ( ) 1 0
02d10 fxx −= ( ) 1 0
d5fxx =−
Câu 215: Cho hàm số ( )yfx = liên tục trên đoạn 0; 2 thỏa mãn: ( ) ( ) 2cos.14sinsin2.32cos2sin44sin24cos xfxxfxxxx +−−=+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 21 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Khi đó ( ) 5 1 Ifxdx = bằng A.
.
. Lờ
ả
Chọn B Ta
(
ừ
(
222
( ) ( ) ( ) ( ) ( ) ( ) 22 00 5555 1111 11 14sin(14sin)32cos2(32cos2)024 11 000 24 fxdxfxdx ftdtftdtftdtfxdx ++−−−= −=== Vậy ( ) 5 1 Ifxdx = = 0. Câu 216: Cho hàm số ( )fx liên tục trên 3;7 thỏa mãn ( ) ( ) 10 fxfx =− với mọi 3;7 x và ( ) 7 3 4 fxdx = . Tích phân ( ) 7 3 Ixfxdx = bằng A. 80. B. 60. C. 20. D. 40. Lời giải
, 0; 2 x
2. B. 0. C. 8
D. 16
i gi
i
có:
) ( ) 2cos.14sinsin2.32cos2sin44sin24cos(*) xfxxfxxxx +−−=+− Lấy tích phân t
0 đến 2
hai vế của (*) ta được:
) ( ) ( )
000 2cos.14sinsin2.32cos2sin44sin24cos xfxdxxfxdxxxxdx
+−−=+−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 22 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn C Đặt 10 txdtdx =−=− Đổi cận 37 73 xt xt == == Khi đó ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 77377 33733 77 33 101010 1010.4 24020 Ixfxdxxfxdxtftdtftdttftdt fxdxxfxdxI II ==−=−−=− =−=− == Câu 217: Cho hàm số ( )fx là hàm số có đạo hàm liên tục trên 0;1 và ( ) ( ) 1 0 2 11, 3 fxfxdx == . Tính tích phân ( ) 1 2 0 xfxdx bằng A. 1 6 . B. 1 3 . C. 1 6 . D. 1 3 . Lời giải Đặt ( ) ( ) uxdudx dvfxdxvfx == == Khi đó ( ) 1 0 2 3 xfxdx = ( ) ( ) 1 1 0 0 2 3 xfxfxdx −= (
1
2
−=
0
3 fxdx = Ta lại có đặt 2 2 txdtxdx == Đổi cận: 00;11xtxt ==== . ( ) ( ) 11 2 00 1111 2236xfxdxftdt=== Câu 218: Xét hàm số ( )fx liên tục trên đoạn 0;1 và thỏa mãn điều kiện ( ) ( ) 2311 fxfxxx −−=− . Tính tích phân ( ) 1 0 d Ifxx = A. 4 75 I = . B. 1 15 I =− . C. 1 25 I = . D. 4 15 I =− . Lời giải Chọn D Lấy tích phân hai vế từ 0đến 1 của ( ) ( ) 2311 fxfxxx −−=− ta được:
)
0
1 3 fxdx
( ) 1
1
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Tính ( ) 2 2 1 3d xfxx Đặt 2 3d2d txtxx =−=− ; Đổi cận: 12xt=−= ; 21xt==− ( ) ( ) ( ) 212 2 121 111 3ddd 222 xfxxfttfxxI −=−== Vậy I = 141 32 I + 28 3 I = . Câu 220: Cho hàm số ( )fx có đạo hàm liên tục trên . Biết ( ) 51 f = và ( ) 1 0 5d1xfxx = , khi đó ( ) 5 2 0 d xfxx bằng A. 25. B. 123 5 . C. 23. D. 15. Lời giải Chọn A Ta có: ( ) ( ) 1 0 5d1xfxx =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 23 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 11 00 231d1d fxfxxxxx −−=− ( ) ( ) 11 00 4 2d31d 15 fxxfxx −−= Xét ( ) ( ) ( ) ( ) ( ) 1101 1 0010 1d1d1dtd Ifxxfxxftfxx =−=−−−=−= Thay vào ta được ( ) ( ) ( ) 111 000 44 2d3dd 1515fxxfxxfxx−==− . Câu 219: Cho hàm số ( )fx liên tục trên 1;2 và thỏa mãn ( ) ( ) 2 23 fxxxfx =++− . Tính tích phân ( ) 2 1 d Ifxx = A. 14 3 I = . B. 4 3 I = . C. 28 3 I = . D. 2. Lời giải Chọn C ( ) 2 1 d Ifxx = = ( ) ( ) 2 2 1 23d xxfxx ++− = ( ) 22 2 11 2d3d xxxfxx ++− = ( ) ( ) ( ) ( ) ( ) ( ) 2222 13 22222 1111 2 214 2d23d23d3dx 1 33 xxxfxxxxfxxxfx +++−=++−=+−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 24
Đặ
(
trở
Gọi (
5 2
= Đặ
( )
2
. dd
ux vfx
= =
0; 2 thoã mãn ( ) 2 2 0 cos2fxxdx = và ( ) 01 f = . Khi đó ( ) 2 0 sin2 fxxdx bằng A. 3 B. 5 C. 3 D. 2 Lời giải Chọn A Ta có ( ) 2 0 sin2 Ifxxdx = đặt ( ) ( ) 1 sin2sin22 2 ufxdufxdx xdxdvvxdxcosx == ===− , ( ) ( ) ( ) 22 2 0 00 11 sin2cos2.cos2 22 Ifxxdxxfxfxxdx ==−+ ( ) ( )( ) 2 2 0 11 02cos1 222fffxxdx =−−−+− ( ) ( ) 22 2 00 11 1cos 222ffxxdxfxdx =−−−+− ( ) ( ) 2 2 2 0 0 11 1cos 222ffxxdxfx =−−−+− ( ) 1111 12023 222222 fff =−−−+−−=++=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
t: 1 5d5ddd. 5 txtxtx ===
)
thành: ( ) ( ) 55 00 1 dt1d25. 55 t ftxfxx==
)
0 d Ixfxx
t:
( )
d2d
uxx
vfxx
=
=
( ) ( ) ( ) 5 5 2 0 0 .2d25.52.2525.15025. | Ixfxxfxxf =−=−=−=− Câu 221: Cho hàm số ( ) 0; 2 yfx = có đạo hàm liên tục trên
Câu 222: Cho hàm số ()yfx = có đạo hàm không âm trên 0;1, thỏa mãn ()0fx với mọi 0;1 x và ( ) 2 222 2 ().'()11() fxfxxfx +=+ . Nếu (0)3 f = thì giá trị (1) f thuộc khoảng nào sau đây? ().'()1 1()1 fxfx dxdx x fx = + + + Nếu đặt 2 21()().'() 1() fxfx tfxdtdx fx =+= + VT = ( ) ( ) 2 11 2 2
7 3; 2 112 f dtf + =+− + Nếu đặt tan xu = ( ) 21tan dxudu=+ VP = ( ) 4 2 2 0
1 1tan 1tan4 udx u
5 2; 2 C. 5 ;3 2 += + ( ) 2 112 f +− 4 = ( ) 2 132,6 16 f =++ 5 ;3 2 Câu 223: Cho hàm số ( )yfx = có đạo hàm liên tục trên ( ) 0; thỏa mãn ( ) ( ).cot2.sin fxfxxxx =+ Biết 2 24 f = . Tính 6 f A. 2 36 . B. 2 72 . C. 2 54 . D. 2 80 . Lời giải Chọn B ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
=+−+ −== == =−−
3 ;2 2 2 2 2 ' 222 2 2 2 6 666 22 2 6
fxfxxxxxfxfxxxx sxfxfxx xfxfxxxxx x sxfxfxxfxdxxdxdxx xx ff fx x
Page ().'()1 1()1 fxfx fx x = + + 2 2 ().'()1 1()1 fxfx x fx = + + 11 2 2 00
.cot2.sinsin..cos2.sin in..cos sin..cos2.sin2 sin in..cos 2. sinsin 26 sin4361
222 1436672 2 f =−=
25 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ().'()1 1()1 fxfx dxdx x fx = + + 11 2 2 00
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
A.
B.
D.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Lời giải Chọn C Ta có: ( ) 2 222 2 ().'()11() fxfxxfx +=+ ( ) 22 22 2
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
Câu
32
=+++
( ) ( ) ( ) ( )gxfxfxfx =++
A. 2. B. 6. C.
. D.
.
ọn
Ta có: ( ) 32 fxxaxbxc =+++ ( ) ( )
2
=++=+= Do ( ) ( ) ( ) ( )gxfxfxfx =++ ( )1 ( ) ( ) ( ) ( )gxfxfxfx =++ ( )2 Từ ( )1 và ( )2 suy ra ( ) ( ) ( ) ( )gxfxgxfx =+− ( ) ( ) ( ) 666 xfxgxgxx −=−−+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 1 11 10 00 0 66 6 66 66 6661600 2 xx xx xxx xxx gxgxx xfx ee gxegxxe xfxgxx eee xfxgxxgxxgg xx eeeee = == ===−=− dd Câu 225: Cho hàm số ( ) ( ) 32 0 fxaxbxca=++ với ,, abc là các số thực. Biết rằng hàm số ( ) ( ) ( ) ( )gxfxfxfx =++ thỏa mãn ( ) ( ) 21,11gg−=−−= . Giá trị của tích phân ( ) 1 2 6 d e x afx x bằng A. 2 1e e + B. ( )e1e + C. 2 e1 e D. ( )e1e Lời giải Chọn B Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 6 gxfxfxfxgxfxfxa =++=++ ( ) ( ) ( ) ( ) ( ) ( ) 6 6 xx gxgxafx gxgxafx ee −=−= ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1111 2 2222 2 6.. dxdx=dx=.dx xx xxxx x afxgxgxgxegxegxgx eeee e ==
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
224: Cho hàm số ( )
fxxaxbxc
với a , b , c là các số thực. Đặt
, biết ( ) ( ) 02,16gg== , tính tích phân ( ) 1 0 6 d x xfx x e
2
4
Lời giải Ch
A
( )
32,62,6fxxaxbfxxafx
( ) 2 12 11 1 eeee ee =−=+=+ .
ln2 ln5ln6ln23 69 fx dxabc fxfx + =+++ −+ với ,, abc là các số hữu tỉ. Giá trị của biểu thức Tabc =++ thuộc khoảng nào sau đây? 22 ' 22 232
+=++=+ =+ =++ Vì ( ) ( ) 1605 fCfxx ===+ ( ) ( ) 4 2 1
2'3102'310 310 5
fxxfxxxfxxfxxx xfxxx xfxxxC
++ = + Đặt ( ) ( )2
x Idx x
ln25 2
11 ln25 . 2525 1 11 1 2 22
ux dudx xx x dvdx v x xx
=++ = +++ −+ = =+= + ++ ( ) ( ) 4 1
4 111 ln25. 1 22 2525 xx Ixdx xx xx ++ =++− ++ +++ ( ) ( )
443 2 112 2
+−+−− =−=−+=− ++− + =−−+=−++ +
552155252 ln5.ln5.5ln5 626263 25 33 5123511 ln5ln3lnln5ln6ln32. 22 62622333
xxtdxxdxdt xxt x t t t
= =−++= =
a babc c
5 6 12 23 1 3
.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 27 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Chú thích: Hàm ( )fx trong bài toán nêu trên là ( ) 3223fxxx=++ Câu 226: Cho hàm số ( )fx có đạo hàm liên tục trên , thỏa mãn ( ) ( ) 2'310, fxxfxxx +=+ và ( ) 16 f = Biết ( ) ( ) ( ) ( ) ( ) 4 2 1 A. ( )1;2 B. ( )2;3 C. ( )0;1 D. ( )1;0 Lời giải Chọn C ( ) ( ) ( ) ( ) ( ) ( ) ( )
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 28 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 227: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) ( ) ( ) 3 4'2,00 x efxfxfxfxx += và ( ) 01 f = . Tính ( ) ln2 0 fxdx A. 201 640 B. 11 24 C. 209 640 D. 1 12 Lời giải Chọn C Ta có: ( ) ( ) ( ) ( ) 3 4'2 x efxfxfx +=
x
+= ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 3 2 2 2 2 2 ' 41 22 ' 21 2 .' 2 2 ' x x x xx xx xx xx fxfx e fxfx fx efx fx efx efxe fx efxe efxedx efxeC += += += = = =−+ Vì ( ) 01 f = nên ( ) 0002efeCC =−+= Suy ra ( ) ( ) ( )2 3232 22 xxxx fxeefxee =−+=−+ ( ) ( ) ln2ln2 2 32 00 209 2 640 xx fxdxeedx =−+= . Câu 228: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) ( ) ( ) 3 4'2 ,0 0 x efxfxfx x fx += và ( ) 01 f = . Tính ( ) ln2 0 d Ifxx = . A. 11 24 I = . B. 1 12 I =− . C. 209 640 I = . D. 201 640 I = . Lời giải Chọn C Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )' 3222'11 4'22 2 xxxx xx fx efxfxfxefxeefx ee fx +=+==
( ) ( ) ( ) ( ) 3 4'2
efxfxfx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 29 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó ( ) 2x efx là một nguyên hàm của 1 x e , tức ( ) 2 1 x x efxC e =−+ Thay 0 x = vào ta được 2 C = . Tìm được ( ) 2 23 21 xx fx ee =− ( ) 2 ln2ln2ln2 23456 000 21441209 640 xxxxx Ifxdxdxdx eeeee ==−=−+= .
Khi đó giá trị của m là A. 10. m = B. 20. m = C. 5. m = D. 25. m = Lời giải Chọn B Hàm số ( ) ( ) , fxfx liên tục trên và thỏa mãn ( ) ( ) 2 1 23 4 fxfx x +−= + nên ta có: ( ) ( ) ( ) 22 2 22 23 4 dx fxfxdx x +−= + ( )1 Đặt ( ) ( ) ( ) ( ) ( ) 222 222 2323 Kfxfxdxfxdxfxdx =+−=+− Đặt ( ) ( ) ; xtdxdtfxft −==−−= , 22;22xtxt =−===− Do đó ( ) ( ) ( ) ( ) ( ) 2222 2222 . fxdxftdtftdtfxdx −=−== ( ) ( ) ( ) ( ) ( ) 22222 22222 23235 Kfxdxfxdxfxdxfxdxfxdx =+−=+= ( )2 Đặt 2 2 2 4 dx J x = + ; 2tan x = , ; 22 − , Ta có: ( ) ( ) 2 2 2 2tan21tan cos d dxdd ===+ . 2 4 x =−=− ; Với 2 4 x == Do đó ( ) 2 44 4 2 4 44 21tan 1 4tan4224 d Jd + ==== + ( )3
Câu 229: Cho ( ) ( ) , fxfx liên tục trên và thỏa mãn ( ) ( ) 2 1 23. 4 fxfx x +−= + Biết ( ) 2 2 Ifxdx m ==
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 30 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Từ ( )1 , ( )2 và ( )3 , ta có ( ) ( ) 22 22 5 420KJfxdxfxdx === Mà theo giả thiết, ( ) 2 2 Ifxdx m == nên 20 20 m m == . Câu 230: Cho hàm số ( )fx liên tục trên đoạ
Tích
2 0 d 2 x xfx bằng A.
B. 1 5 C.
.
Lời giải Chọn C Ta có: ( ) ( ) 2 231fxfxxx +−=− , 0;1 x ( ) ( ) ( ) ( ) ( ) ( ) 20310 100 21300 ff ff ff += == += Nhận xét: ( ) ( ) ( ) 111 000 1dddx fxxfuufx −== ( ) ( ) (
111 2 000 5d231dd 8 fxxfxfxxxxx =+−=−= ( ) 1 0 0 d 4 fxx = Nên ( ) ( ) ( ) ( ) ( ) ( ) 2111 1 0 0000 d22d=4d44d414. 24010 x xfxtftttfttftfttf ==−=−=− Câu 231: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 thỏa mãn ( ) 10 f = , ( ) 1 2 0 d5fxx = và ( ) 1 0 1 d 2 xfxx = . Tích phân ( ) 1 0 d fxx bằng A. 10 9 B. 11 4 C. 10 9 D. 11 4 Lời giải Chọn A + Theo giả thiết, ta có ( ) 1 0 1 d 2 xfxx = Đặt: ( ) ( ) 2 dd dd 2 ufxx ufx x vxx v = = = = .
0984164935
n
0;1 thỏa mãn ( ) ( ) 2 231fxfxxx +−=− , 0;1 x
phân
5
10
D. 1 10
)
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
( ) 1 2 0 .d1xfxx =− ( ) ( ) 1 2 0 10.d101 xfxx =− ( ) ( ) 1 2 0 25.d10. xfxx =− ( ) 1 2 2 0 5d5 xx −= + Từ đó, ta có ( ) ( ) ( ) ( ) 111 2 2 22 000 d25.d5d5105.fxxxfxxxx ++=−+ ( ) 1 2 2 0 50fxxdx += ( ) ( ) ( ) 223 5 505 3 fxxfxxfxxC +==−=−+ + Mà ( ) 55 100 33fCC ==−+= Khi đó: ( ) 2 55 33fxx=−+ + Vậy: ( ) 11 2 00 55 dd 33 fxxxx =−+ 1 3 0 55 93 xx =−+ 10 9 = . Câu 232: Cho hàm số ()yfx = có đạo hàm và liên tục với 1;2 x . Với , ab là những số thực và ( ) ( ) ( ) ( ) ( ) 2 21 2 1 '2'.. d fxff Ifxxxfxexaebe =++=+ .Tính giá trị 25Sab =+ A. 7 S =− . B. 9 S =− . C. 9 S = . D. 7 S = . Lời giải Chọn A Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2222 22 1111 ddd .'2'.'2.'.d fxfxfxfx Ifxxxfxexfxexxexxfxex =++=++ ( ) ( ) ( ) ( ) ( ) 22 2 ()(2)(1) 1 1 11 '. d' d fxfx fxff Ifxexefxeee ====− ( ) 2 2 1 2d . fx Ixex = ( ) ( ) ( ) ( ) ( ) 22 22 3 11 '. dd . fxfx Ixfxexxefx == .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) 1 1122 00 0 1 d.d 222 xx xfxxfxfxx ==− ( ) 1 2 0 1 0.d 22 x fxx −= ( ) 1 2 0 1 .d 22 x fxx −= ( ) 1 2 0 .d1.xfxx =− + Ta có ( ) 1 2 0 d5fxx =
2 2 d.d 31 x Ifxxx xx == ++ . Đặt ux =− ddux=− . Đổi cận: 33xu=−= và 22xu==− . Khi đó ( ) ( ) ( ) ( ) 2333 62 6262 3222
( )2 , ta được ( ) 62 2 . 31 x fx xx 222 .d.d.dd 33131 1 uux Iuuxfxx uuxx uu =−=== ++++ −+−+ . Vì ( ) ( ) ( ) 2 3
++ v d23Ifxxff ==−− và ( ) ( ) ( ) 3 2
i d32Ifxxff ==−− Do đó: ( ) ( ) ( ) ( )2332ffff−−=−− ( ) ( ) ( ) ( )2332 ffffba −−=−−=− Câu 234: Cho hàm số ( )yfx = liên tục trên đoạn 0;1 và thoả mãn ( ) ( ) 35 1.4.1 xxfxfxx +−−= . Tích phân ( ) 1 0
d Ifxx = có kết quả dạng 2 ab c + , ( ,, abc , a c , b c là phân số tối giản). Giá trị 23 Tabc =−+ bằng A. 89 T = B. 27 T = C. 35 T = D. 81 T = Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 32 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ( ) ( ) ( ) 2 dd fx ux vefx = = ( ) d2d fx uxx ve = = ( ) ( ) 22 2 2()(2)(1) 3 1 11 .24.dd.2 fxfffxfx Ixexexeexex =−=−− . ( ) ( ) 22 (2)(1)(2)(1)(2)(1) 123 11 2.42
V
ố (
=
0984164935
dd2.5fxfx ffffff IIIIeexexeexexee =++=−++−−=−
ậy ( )5 2 5,2527abS==−=+−=− Câu 233: Cho hàm s
)yfx
xác định trên và thỏa mãn ( ) ( ) 62 2 2 1 x fxfx xx +−= ++ với x . Giả sử ( )2 fa = , ( )3 fb −= . Tính ( ) ( )23Tff =−− A. Tba =− B. Tab =+ C. Tab =−− D. Tab =− Lời giải
2 1 x fxfx xx +−= ++ ( )1 , ta được ( ) ( ) ( ) ( ) 62 2 2 1 x fxfx xx −+= −+−+ hay ( ) ( ) 62 2 2 1 x fxfx xx −+= ++ ( )2 . Nhân hai vế của ( )1 với 2 sau đó trừ theo vế cho
=
ớ
Chọn A Với x , thay x bởi x vào biểu thức ( ) ( ) 62 x . Xét tích phân ( ) 22 62 33
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 33
Chọn A
+
=−=−=−+=
+ 1 5 3 0
x
x = + Đặ
=+=+= V
xuxu ==== Khi đó ( ) ( ) 2 2 22 3 2 11 1 2 1. 22422 3 d1d 3339 uu u Buuuu u ==−=−= Do đó, ( ) ( ) ( ) 11 00 422422 3dd 927 ** fxxfxx == Suy ra 4,2,272389abcabc ==−=−+= Câu 235: Cho hàm số ( )fx liên tục trên đoạn 1 0; 2 và thỏa mãn ( ) ( ) ( )2 2 2 1 1 ln121. 2 1 x xxfx x + +++−= Tính ( ) 1 2 0 d.Ifxx = Lời giải Ta có ( ) ( ) ( ) ( ) ( ) 2 2 2 22 1ln1111 ln121 2221 121 f xx xxfxx x xx ++ +++−=−=− + ( ) ( ) ( ) 111 222 2 2 000 1dln1dd* 221 21 x x fxxx x x + −=− + Tính 1 2 1 0 1 d. 2 Ifxx =− Đặt 1 dd. 2 uxux =−=− Đổi cận: 11 0;0. 22 xuxu ====
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Ta có ( ) ( ) 35 1.4.1 xxfxfxx +−−= ( ) ( ) 5 3 4.1 1 x xfxfx x −−= + Từ ta có ( ) 00 f = Lấy tích phân hai vế ta được: ( ) ( ) 111 5 3 000 4.1ddd 1 x xfxxfxxx x −−= +
( ) ( ) ( ) ( ) ( ) ( ) ( ) 1111 1 0 0000 4.1d41.d41.4d4d Axfxxtftttftfttftt
d 1
Bx
t 3232 112d3d uxuxuuxx
ới 01;12
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 34 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 1 0 2 1 1 0 2 dd. Ifuufxx=−= Tính 1 2 2 2 0 d 21 x I x = Đặt sindcosd. xtxtt == Đổi cận: 1 00;. 26 xuxu ==== 66 2 2 00 cosdd 26 21sin txx I x === Tính ( ) ( ) 1 2 3 2 0 ln1 d. 21 x Ix x + = + Đặt ( ) ( ) ( ) 2 ln1d d 1 11dd 2121 x ux u x vx v x x =+ = + = =− + + ( ) ( ) ( ) ( ) 1 11 2 22 3 2 0 00 ln1d1311311131 lnlnln. 2132213232326 21 x x I xx x + =−+=−−=−−=+ ++ + Từ ( ) ( ) 1 2 0 131 *dln. 6326 fxx =−− Câu 236: Cho ( )yfx = là hàm đa thức có các hệ số nguyên. Biết ( ) ( ) ( )2 2 54, fxfxxxx −=++ . Tính ( ) 1 0 fxdx . A. 3 2 . B. 4 3 . C. 5 6 . D. 11 6 . Lời giải Chọn D Theo bài ra ta có ( ) ( ) 2 2 fxaxbxcfxaxb =++=+ Thay vào ( ) ( ) ( )2 2 54, fxfxxxx −=++ ta được ( ) ( )2 22 524 axbxcaxbxx ++−+=++ ( ) ( ) 2222 545454 aaxbabxcbxx −+−+−=++
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 35 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 2 2 2 1 11 11 54141 5415414 541 54 4 13 16 a a b c a aa a babab cb cb b c = = = = = −= = −=−= −= =+ = = Giả thiết suy ra ( ) 2 11abcfxxx ====++ và ( ) ( ) 11 2 00 11 1 6 fxdxxxdx=++= Câu 237: Cho hàm số ( )fx liên tục trên đồng thời ( ) 33 sincos1, 2 fxfxxxx +−=++ . Tích phân ( ) 2 0 b fxdx ac =+ với * ,, abc , b c là phân số tối giản. Khi đó 2abc +− bằng A. 5. B. 7. C. 9. D. 8. Lời giải Chọn B Xét 2 0 2 fxdx . Đặt 2 txdxdt =−=− Đổi cận: 0;0 22 xtxt ==== Khi đó ( ) ( ) ( ) 0 222 000 2 2 fxdxftdtftdtfxdx −=−== Theo giả thiết, ( ) ( ) ( ) 222 3333 000 sincos1sincos1 22 fxfxxxfxdxfxdxxxdx +−=+++−=++ ( ) ( ) ( ) ( ) 2222 3333 0000 1 2sincos1sincos1 2 fxdxxxdxfxdxxxdx =++=++ Ta có ( ) ( ) 2 3 222 322 000 0 sinsin.sin1coscoscoscos2 33 x xdxxxdxxdxx ==−−=−= .
Câu 238: Suy ra 4,2,3abc=== . Khi đó 27 abc+−= .Cho hàm số ( )yfx = nhận giá trị dương và có đạo hàm liên tục trên đoạn 0;3. Biết rằng (
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 36
( ) ( ) 2 3 222 322 000 0
coscos.cos1sinsinsin
==−=−= 2 2 0 0 2 dxx == . Thay,,
ta
( ) 2 0 1222 233243 fxdx =++=+
=
(
ằ
fx =+= + . Ta đi tìm số kR sao cho: ( ) ( ) ( ) ( ) ( ) 2 333 2 000 2.01. 11 fx fx dxkdxkdx fx fx −+= + + ( ) 2 42 1430. 33 kkk −+== Khi đó ( ) ( ) ( ) ( ) ( ) 2 333 000 44 10 19 31 fx fx dxdxdx fx fx −+= + + ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 3 0 222 002 333 111 fxfxfx dx fxfxfx −=−== +++ . Lấy nguyên hàm hai vế của ( )2 ta được: ( ) ( ) 2 13 fx dxdx fx = + ( ) ( ) 2 2 211. 332 fxCfxxxC +=+=+− Theo đề bài ta có ( ) ( ) 2 03421 3 x fCfx ===+− Vậy ( ) 55 2. 9 f =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
sin2
33 x xdxxxdxxdxx
vào
có
) ( ) 2 3 0 4 13 fx dx fx
+
và ( ) ( ) 03,38.ff== Giá trị của
)2 f b
ng bao nhiêu? A. 50 9 B. 3. C. 55 9 D. 2 3 Lời giải Chọn C Ta có: ( ) ( ) ( ) 3 0 3 2.12 10 fx dxfx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
(
(
2 2
2
xx
+ =+ ( ) ( ) (
) 2 3 2 2.
2 fxfx xx x
+ = +
(
( ) 2 3 2 2. 32 dd 3 2 fxfx xx xx fx + = + ( ) ( ) ( ) ( ) 2 2 3 2 d232 d 23 fx xx x fx + + = + ( ) 32 2 2 23 xx C fx + −=+ + Theo giả thiết ( ) 02 f = suy ra ( ) ( ) 2 2 1 22 CC −==− + Với 1 C =− thì ( ) 32 2 2 1 233 xx fx −=+− + ( ) 2 211 1 2133 f −=+− + ( ) 134 f = Vậy 1 0 () fxdx = ( )2171 Câu 240: Cho hàm số yfx có đạo hàm trên đồng thời thoả mãn đẳng thức sau ( ) ( ) ( ) 2532 422148103012,. xfxfxxxxxxfxx ++=++++− Giátrị của ( ) 3 0 d fxx bằng A. 10. B. 1. C. 27. D. 1. Lời giải Chọn C Ta có: ( ) ( ) ( ) ( ) 2532 422148103012,.* xfxfxxxxxxfxx ++=++++− ( ) ( ) ( ) ( ) 0000 2532 1111 4d221d48103012dd xfxxfxxxxxxxxfxx ++=++++−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 37 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 239: Cho hàm số ( )fx có đạo hàm liên tục trên đoạn 0;1 , đồng biến trên đoạn 0;1 thỏa mãn các điều kiện: ( ) 02 f = , x và 4. ( ) ( ) ( ) ( ) 2 2 3 2 22 32 .2 3 xx fxfxfx + =+ , 0;1 x Tính 1 0 ()d fxx A. ( )2171 . B. 34 . C. ( )2117 . D. 22 . Lời giải Chọn A Ta có : 4.
)
) ( )
3
22 32 .2 3
fxfxfx
) (
32 ,0;1 3
fx
Suy ra:
) ( ) ( )
7
2d21d21d 3 fxxfxxxfxfxx+++=−+
( ) ( ) ( ) ( ) ( ) ( ) 000 0 22 1 111
( ) ( ) ( ) ( ) 010 0 1 111
7
77 2dd1d1d1 33 fxxfxxffxxffxx +=−−+−=−+
2ddd 3 fttfuuxfxfxx+=−+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) 0101 1110
Ta có: ( ) ( ) ( ) 2532 422148103012,. xfxfxxxxxxfxx ++=++++−
4d221d48103012dd xfxxfxxxxxxxxfxx ++=++++−
( ) ( ) ( ) ( ) 1111 2532 1111
( ) ( ) ( ) ( ) ( ) ( ) 111 1 22 1 111
92
92 2ddd 3 fvvfhhxfxfxx+=−+
2d21d21d 3 fxxfxxxfxfxx+++=−+ ( ) ( ) ( ) ( ) 131 1 1 111
9292 d11dd112 33 fxxfffxxfxxff =−−−+=−−−
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 313 111
927 d1dd33127 33 fxxffxxfxxf=−+−=−= Thay 0 x = vào ( )* ta có được ( ) 16 f = ( ) 3 0 o hàm cấp hai, liên tục và nhận giá trị dương trên đoạn [0; 1] thỏa mãn 2 11 '()2().'()2.'()(1)''()0,[0;1],'1. 2 . 2 fxfxfxxfxxfxxff −+++=== Biết tích phân ( ) 2 1 0
d27fxx = . Câu 241: Cho hàm số ()fx có đạ a fxdx b = , giá trị của ab + bằng A. 181. B. 25. C. 10. D. 26. Lời giải Chọn B 2 2 2
fxfxfxxfxxfx fxfxxfxxfxfxfxfx xfxxfxfxfxfx
()2()()2.()(1)()0 ()()2()(1)()2()()() (22)()(1)()2()()()
−+++= ++++=+ +++=+ 2 (22)()(1)()2()()() xfxxfxfxfxfx +++=+ 2 (1)()[2()1]() xfxfxfx +=+ 22 1 (1)()()() xfxfxfxC +=++ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 38 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Từ ( ) ( )1,2 ta có được ( ) ( ) ( ) ( ) ( ) 313 100
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 39 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Theo giả thiết: 11 1191 12 2244 ffCC ===+= 22 1 (1)()()()4 xfxfxfx +=++ 2 2 ()1(()0) 1(1) ()() 4 fx fx x fxfx = + ++ . Do đó 2 2 2 ()d111 d 1 (1)(1) 1 () () 2 2 fxx xC xx fx fx ==+ ++ + + Theo giả thiết: ( ) ( ) 1122 2 00 11111113 10 1 22(1)2212 () 2 ffCfxxfxdxxdx x fx =====+=+= + + 13 25 12 a ab b = += = Câu 242: Cho hàm số ( )yfx = xác định và liên tục trên \0 và thỏa mãn ( ) ( ) ( ) ( ) 22 211xfxxfxxfx +−=− vợi mọi \0 x và ( ) 12 f =− . Tính ( ) 2 1 d fxx . A. 1 ln2 2 . B. ln2 1 2 . C. 3ln2 2 . D. 3ln2 22 . Lời giải Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 222221121 xfxxfxxfxxfxxfxfxxfx +−=−++=+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 2 11 1 fxxfx xfxfxxfx xfx + +=+= + ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 11 111 xfx fxxfx xxxxC xfx xfxxfx + + ==−=+ + ++ d ddd Do ( ) ( ) 1 1210 1.11 fCC f =−−=+= + Vậy ( ) ( ) 2 111 1 xfx xfxx x −==−− + . Do đó ( ) 2 22 2 1 11 1111 lnln2 2 fxxxx xx x =−−=−+=−− dd Câu 243: Cho hàm số ( )yfx = có đạo hàm xác định trên ) 0;+ và thỏa mãn ( ) ( ) ( ) 1 xfxxxfx +=+ ; ( ) 1e1 f =+ . Biết rằng ( ) 1 0 d a fxx b = ; trong đó a ; b là những số nguyên dương và phân số a b tối giản. Khi đó giá trị của ( ) 2ab + tương ứng bằng
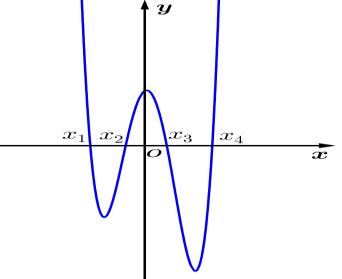
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 40 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 5. B. 8. C. 4. D. 7. Lời giải Chon B ( ) ( ) ( ) ( ) ( ) ( ) 2 1 xfxxxfxxfxxfxfxx +=+−−=− Với 0 x = ta có: ( ) 00 f = Với 0 x , chia hai vế phương trình cho 2 x ta được ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 11.ee.e xxxxfxfxfxfxfxfxfx xxxxx x −=−−=−−=− ( ) ( ) ( ) .ee.ee xxxxfxfx C xx ==+ Thay 1 x = ta được ( )
1111
.
( )
x
Ta
(
11
00
ded1e1
xx
bởi đồ thị
)
=
ụ
ng
ẳ
xx = , 4xx = . Khi đó S được tính bởi công thứ
A. ( ) ( ) ( ) 4 1 ddd x mn xmn Sgxxgxxgxx =++ ( ) ( ) ( ) 23 ;0,0; mxnx . B. ( ) ( ) ( ) 4 1 ddd x mn xmn Sgxxgxxgxx =−+ ( ) ( ) ( ) 23 ;0,0; mxnx . C. ( ) ( ) 4 1 dd x p xp Sgxxgxx =− ( ) ( ) 12 ; pxx
( )
1.eee1ee1 fCCC =+=+−=
Suy ra
( ) .ee1e xxx fx fxxx
=+=+ .
có
) ( ) ( ) ( )
2
1 113
0 222
fxxxxxxx =+=+−=−−= . Vậy 3 a = ; 2 b = và 28 ab+= . Câu 244: Cho hàm số ( ) 432 8 fxaxxxdxe =−−++ ( ) ,, ade có đồ thị cắt trục Ox tại bốn điểm phân biệt có hoành độ lần lượt là 1234 ,,, xxxx như hình vẽ. Xét hàm số ( ) ( ) ( ) ( ) 2 gxfxfxfx =− . Gọi S là diện tích hình phẳng giới hạn
(
ygx
, tr
c Ox và các đườ
th
ng 1
c nào trong các công thức sau?
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 41 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn D. ( ) ( ) 4 1 dd x q xq Sgxxgxx =− ( ) ( ) 34 ; qxx . Lời giải Chọn A Ta có ( ) ( )( )( )( ) ( ) 1234 ,0fxaxxxxxxxxa =−−−− ( ) ( )( )( ) ( )( )( ) ( )( )( ) ( )( )( 123234134124 fxaxxxxxxxxxxxxxxxxxxxxxxxx =−−−+−−−+−−−+−−− ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ' 2222 1234 1234 11111111 0 fxfx fxxxxxxxxxfx xxxxxxxx =+++=−−−− ( ) ( ) 0 fx fx ( ) ( ) ( ) ( ) 2 2 " 0 fxfxfx fx ( ) ( ) 140,; gxxxx ( ) 4 1 d x x Sgxx= . Câu 245: Cho hàm số ()fx liên tục trên và thỏa mãn: 22 ()[2()1]2()[()1]2,1. xfxfxfxfxxx−=−++−− Biết ( ) ( ) 1 2 1 2 2 11 6ln24ln 41 41 x x x fdxab −=− + + ; Giá trị 2 Tab =+ là A. 5 T = B. 6 T = C. 4 T = D. 0 T = Lời giải Chọn C Xét ( ) ( ) 1 2 1 2 2 11 6ln24 41 41 x x x Ifdx =− + + Đặt 44.ln4.2ln2.ln2. 2 xx dt tdtdxtdxdx t ==== Với 11 22 xt=−= và 1 2 2 xt== . Khi đó, ( ) ( ) 2 1 2 2 11 3 11 ft Idt tt t =− + + ( ) ( ) ( ) ( ) 22 1122 22 33 11 ftfxdtdx tx == ++ Ta có: 22 ()[2()1]2()[()1]2,1. xfxfxfxfxxx−=−++−− 3232 2()()2()2()20 xfxxfxfxfxx −++−+= ( )( ) 322 12()()13()30 xfxfxfx +−−++=
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 42 Chuyên luyện thi: Tuyển sinh vào
10 Tốt Nghiệp THPT BDKT
10; 11; 12 Sưu tầm và biên soạn Dễ thấy, ()1,1fxx=− không thoả mãn Do đó, 2 32 (*)13()32()()1 fx x fxfx + +=− Đặt ( ) ( ) 42 2 2 32 32 63 33 1 21 () 21 u u uu u xdxd uu uu fx = + + +=−= Với 1 1 2 xu==− và 20xu== Suy ra ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2
53 200 1 2222 11 2322 2 21633 33..2ln2. 191211 uuuu fx uu Idxududu x uuuu −−+ + ====− + +−−+ Do đó,
== . Vậy 22.124Tab=+=+= Câu
số 32
, với ,, abc là số thực. Biết rằng ''' gxfxfxfx thỏa mãn 31,21gg . Tính tích phân 2 3 12 2 x afx Idx e . A. 2 1.Iee B. 1 2 ee I C. 2 1 2 ee I D. 2 1 2 ee I Lời giải Ta có: 2 '62 fxaxbx ; "122 fxaxb ; "'12 fxa . 2222 1 3333 12 11 66 22 2 xxx x afx IdxaedxefxdxaedxI e , với 2 1 3 x Iefxdx Đặt ' xx ufxdufxdx dvedxve 2 2 13 3 |'xx Iefxefxdx Tương tự, sử dụng tích phân từng phần cho các tích phân tiếp theo ta có: 2 22 133 3 |'|'' xxx Iefxefxefxdx
0984164935
lớp
Toán
3242
1,2ab
246: Cho hàm
20fxaxbxca
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
32
22
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 43 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 222 333 3 |'|''|''' xxxx efxefxefxefxdx 2 222 333 3 |'|''|12 xxxx efxefxefxaedx 2 2 3 3 '''|12 xx efxfxfxaedx 2 2 3 3 |12 xx egxaedx 2 23 3 2312 x egegaedx 2 23 3 12 x eeaedx Vậy 2 22 2323 33 1 11 612 222 xx ee Iaedxeeaedxee Câu 247: Cho hàm số fx nhận giá trị dương, có đạo hàm liên tục trên 0;2 . Biết 01 f và 2 242e xx fxfx với mọi 0;2 x . Tính tích phân 32 2 0 3' d xxfx Ix fx . A. 14 3 I . B. 32 5 I . C. 16 3 I . D. 16 5 I . Lời giải Chọn D Từ giả thiết 2 242e xx fxfx , cho 2 x , ta có 21 f . Ta có
2 0 3' d xxfx Ix fx . Đặt 32 2 3 d36d ' dd ln uxx uxxx fx vx vfx fx Khi đó, ta có
32222 0 00 3ln36lnd32lnd3 IxxfxxxfxxxxfxxJ . 20 2 2 2 02 2lnd222ln2d2 xt Jxxfxxttftt Suy ra
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 44 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 222 222 000 22lnd2ln2d2ln2d Jxxfxxxxfxxxxfxfxx 2 22 22422 00 32 2lned224d 15 xx xxxxxxxx 16 15 J . Vậy 16 3 5 IJ . Câu 248: Cho hàm số ( ) 0 fx có đạo hàm liên tục trên , thỏa mãn ( ) ( ) ( ) 1 2 fx xfx x += + và ( ) 2 ln2 0. 2 f = Giá trị ( )3 f bằng A. ( )2 24ln2ln5 . B. ( )2 1 4ln2ln5 2 . C. ( )2 44ln2ln5 . D. ( )2 1 4ln2ln5 4 . Lời giải Chọn D Xét 0;3. x Ta có ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) 111 1 21212 fx fxfx xfxdxdx xxxxx fxfx +===− +++++ ( ) ( ) ( ) ( ) 1 2ln1ln22ln 2 x fxxxCfxC x + =+−++=+ + . Thay ( ) ( ) 2 1ln21 0:20ln2ln22ln22ln2ln2 222 x xfCCCfx x + ==+=−+==+ + ( ) ( ) ( ) 22 2 11141 ln2ln23ln2ln24ln2ln5 42454 x fxf x + =+=+=− + . Câu 249: Cho hàm số ( )yfx = thỏa mãn ( ) 0,0fxx , và có đạo hàm ( )fx liên tục trên đoạn ( ) 0;+ , thỏa mãn ( ) ( ) ( ) 2 21,0fxxfxx =+ và ( ) 1 1 2 f =− . Giá trị của biểu thức ( ) ( ) ( )12...2022fff +++ bằng A. 2020 2021 B. 2022 2023 C. 2019 2020 D. 2021 2022 Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
42
Page 45
Chọn B Ta
( ) ( ) ( ) ( ) ( ) 2 1 21,021 fx xxxdx fxfx =+=−− ( ) ( ) 2 1 xxC fx =−++ ( ) 1 10 2 fC=−= . Nên ( ) ( ) 2 11 1 fx xxxx =−=− ++ . Suy ra: ( ) 111 2 2.323 f =−=−+ , …, ( ) 111 2022 2022.202320222023 f
ậy ( ) ( ) ( )
12...2020...1 223342022202320232023 fff+++=−−+−+−+=−+=− Cho hàm số có đạo hàm cấp hai, liên tục và nhận giá trị dương trên đoạn 0;1 , thỏa mãn 2 ()2()()2()(1)()0,[0;1], fxfxfxxfxxfxx −+++= 11 1 22ff == .Biết ( ) 1 2 0 d a fxx b = Giá trị của bằng A. 26. B. 25. C. 10. D. 181. Lời giải Chọn B Ta có với mọi x thuộc đoạn 0;1 thì 2 ()2()()2()(1)()0 fxfxfxxfxxfx −+++= Suy ra ( ) 2 22()(1)()()2()() xfxxfxfxfxfx +++=+ ( ) ( ) ( ) ( ) 2 2 1 xfxfxfx +=+ . Suy ra ( ) ( ) ( ) ( ) 2 2 1 xfxfxfxC +=++ . Thay 1 2 x = vào đẳng thức trên ta được: 2 91111 42224 fffCC =++= Suy ra ( ) ( ) ( ) ( ) 2 2 1 1 4 xfxfxfx +=++ ( ) ( ) ( ) 2 2 1 1 2 xfxfx +=+ . Hay ( ) ( ) ( ) 22 1 1 1 2 fx x fx = + + ( )fx ab +
viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
có:
=−=−+ Câu 250: V
111111112022
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 46
Lấ
2 vế ta được: ( ) ( ) ( ) 22 1 dd 1 1 2 fx xx x fx = + + ( ) 11 1 1 2 D x
−=−+ + + . Thay 1 2 x = vào đẳng thức trên ta được: 1111 0 11111111 22222
? A.
B.
C.
D.
Lời giải Chọn B Ta có ( ) 32 432 fxaxbxcxd =+++ và ( ) 2 gxmxn =+ ( ) ( )00 fgep == Có ( ) ( ) ( ) 32 432 fxgxaxbxcmxdn −=++−+− Dựa vào đề bài ta có ( ) ( ) ( )( ) 32 555 4114 222 fxgxaxxxaxxx −=++−=+−− Đồng nhất hệ số ta có: 10 3 ba = , 2 cma −=− , 10 dna −=− Vậy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
y nguyên hàm
fx
DDD f −=−+−=−+= +++ + Suy ra ( ) 11 1 1 2 x fx −=− + + ( ) ( ) 11 1. 22fxxfxx +=+=+ Khi đó ( ) 1 3 2 11 2 00 0 1 113 2 dd 2312 x fxxxx + =+== . Suy ra 13,12ab== Vậy 25 ab+= Câu 251: Cho hàm số ( ) 432 fxaxbxcxdxe =++++ và ( ) 2 gxmxnxp =++ ( ) ,,,,,,,. abcdemnp Các hàm số ( )fx và ( )gx giao nhau tại 3 điểm có hoành độ lần lượt là 5 ,1 2 và 1. Có ( ) ( )00fg = . Tính giá trị tích phân sau ( ) ( ) ( ) ( ) 2 1 fxgx dx fxgx
12ln2.
ln2.
12ln3.
6ln3.
. Câu 252: Cho hàm số ( )fx có đạo hàm và liên tục trên , thỏa mãn ( ) ( ) 2 2 x fxxfxxe += và ( ) 02. f =− Tính giá trị ( ) 1. f A. ( ) 2 1. f e =− B. ( ) 2 1. f e = C. ( ) 1. fe =− D. ( ) 1 1. f e =− Lời giải
Chọn D Ta có ( ) ( ) 2 2.2e x fxxfxx += ( ) ( ) ( ) ( ) 222 e2.e.2e.2 xxx fxxfxxfxx +== Suy ra ( ) ( ) ( ) ( ) 22 2
Câu
2 2 e.d2xde. e xx x
xC fxxxfxxCfx + ==+= . Vì ( ) 022fC=−=− Do đó ( ) 2
2 2 e x
x fx = . Vậy ( ) 1 1. e f =−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 47 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 1 2 1 ln ln22ln11 4422 lnlnln2 33 fxgx dx fxgx fxgx fgfg aa
=− =−−− =−=
80 D. 40 Lời giải Chọn A Dohàm sốliêntục trên nênhàm sốliêntụctại ( ) ( ) ( ) 00 0limlim01 xx xfxfxfm −+→→ ==== Khi đó ta có ( ) ( ) ( ) ( ) 20202 2 11010 dddd1d x fxxfxxfxxexxx =+=++ 2 0 222 2 1 0 191 4 222222 x exe x e =++=−+=− . Do đó 91 ; 22 ab==− .
253: Cho hàm số ( )fx liên tục trên thỏa mãn ( ) 2 ,0 ,0 x xmx fx ex + = . Biết ( ) 2 2 1 d b fxxa e =+ trong đó , ab là các số hữu tỉ. Tính 2 24ab + A. 10 B. 4 C.
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 48 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy 2 2410 ab+= . Câu 254: Cho hàm số ( ) 2 sin2khi0 2coskhi0 xx fx xx + = . Giả sử F là nguyên hàm của f trên thỏa mãn 3 F = . Giá trị của 2 664 FFF −+− bằng A. 133 2 ++ . B. 1313 2212 ++ . C. 13663 12 +− . D. 13 2212 −+ . Lời giải Chọn C Ta có: 2 664 FFF −+− ( ) ( ) 0033222 6664433 FFFFFFFFF =−−+−+−+−+ ( ) ( ) ( ) ( ) 0 643 0 6 64 dd3d2d2 3 fxxfxxfxxfxxF =−−−−+ ( ) 0 643222 0 6 64 sin2d2cosd32cosd22cosd2 3 xxxxxxxxF =−+−−−+ ( ) ( ) ( ) ( ) 0 643 0 6 64 sin2dcos21d3cos21d2cos21d2 3 xxxxxxxxF =−+−+−+−++ ( ) 643 0 6 0 64 111 cos2sin23sin22sin22 2223 xxxxxxxxF =−−+−+−+−++ 331331 1322 234624124212 =−−−+−−+−−++ 1313 2212 =−+ Câu 255: Cho hàm số ( ) 2 30 sin2cos0 xakhix fx xxbkhix + = +− liên tục và có nguyên hàm F liên tục trên thỏa mãn ( ) 210 2 FF −−= với , ab là tham số thự C. Giá trị ( ) 1 6 4 m fxdx = , với m là một số thự C. Khi đó 2m bằng A. 9 2 B. 9 4 C. 9 D. 18 Lời giải Chọn D Hàm số ( )fx liên tục trên nên 1 ab =−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 49 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Mặt khác ( ) 210 2 FF −−= ( ) 2 2 10 fxdx = ( ) ( ) 02 2 0 2 sin2cos310 xxbdxxadx +−++= ( ) 0 2 3 0 2 1 cos2sin-b10 2 xxxxax −+++= 22 2 b a −= Suy ra 1 1 0 22 2 ab a b b a += = = −= Hay ( ) 2 310 sin2cos0 xkhix fx xxkhix + = + . Ta được ( ) ( ) ( ) ( ) 0 101 1 23 0 0 6 66 119 sin2cos31cos2sin2 244fxdxxxdxxdxxxxx =+++=−+++=+= Suy ra 9 m = Vậy 218 m = Câu 256: Cho hàm số ( ) 2 230 230 xkhix fx xxkhix + = −+ Giả sử F là nguyên hàm của f trên thỏa mãn ( ) 30 F = . Giá trị của ( ) ( )2132 FF −+ bằng A. 17. B. 32. C. 22 3 . D. 35. Lời giải Chọn D * Ta có ( ) ( ) ( ) ( ) 2 202 3 0 222 1 110 0 1420 d23d23d332. 333 x fxxxxxxxxxxx =++−+=++−+=+= Mà ( ) ( ) ( ) ( ) 2 2 1 1 d21fxxFxFF==−− nên ( ) ( ) 20 21 3 FF−−= . * Mặt khác ( ) ( ) 2 1 3 2 2 30 d 30 3 xxCkhix Fxfxx x xxCkhix ++ == −++ .
Vì ( ) 30 F = nên 2 9990 C −++= . Suy ra 2 9. C =− Vậy ( ) 2 813 223.29. 33 F =−+−=− Thay ( ) 13 2 3 F =− vào ta được ( ) 111. F −=−
Suy ra ( ) ( ) ( ) 13 21322.113.35. 3 FF −+=−+−=−
51 41 xxCkhix Fx xxCkhix ++ = ++ . Tính ( ) 2 0 tục tại 1 x = ( ) ( ) ( ) 11 limlim1 xx FxFxF +− →→ == 23 1215.114.1CC++=++ 12 1 CC −=− Ta có: ( ) ( ) ( ) ( ) 2 23 12 0
d?fxx A. 14. B. 13. C. 15. D. 16. Lời giải Chọn B Vì hàm số ( )Fx liên d=F2025.204.0 fxxFCC −=++−++ ( ) 2 12 0
d=14+C14113fxxC −=−= Câu 258: Cho hàm số ( ) 2 3210 120 xxkhix fx xkhix −+ = − . Giả sử F là 1nguyên hàm của f trên thỏa mãn ( ) ( ) 20201202122022 FF−+=− . Giá trị ( )1 F nằm trong khoảng nào? A. ( )2;1 B. ( )1;0 C. ( )0;1 D. ( )1;2 Lời giải Chọn A Ta có ( ) ( ) ( ) 12 11 2020()d2021()d202012021240411 IfxxfxxFFF =+=−+− . ( ) ( ) ( ) 404112020120212. FFFI =−+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 50 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Câu 257: Cho hàm số ( )yfx = có nguyên hàm trên là ( ) 2 1 3 2
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 51 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Mà ( ) ( ) 10101 2 11010 ()d()d()d12d321d3 fxxfxxfxxxxxxx =−+=−−+−+=− . và ( ) 22 2 11 ()d321d5 fxxxxx =−+= Suy ra ( ) 2020.32021.54045 I =−+= Vậy ( ) ( ) ( ) ( ) 6067 40411202012021260671. 4041 FFFIF=−+−=−=− Câu 259: Cho hàm số ( ) 2 321 3241 xkhix fx xxkhix − = +− . Giả sử ( )Fx là nguyên hàm của ( )fx trên thỏa mãn ( ) 24 F = . Giá trị của ( ) ( )243FF bằng A. 16 B. 8 C. 18 D. 2 Lời giải Chọn D ( ) 2 321 3241 xkhix fx xxkhix − = +− ( ) 2 1 32 2 31 41 xxCkhix Fx xxxCkhix −+ = +−+ . Vì ( ) 1 242FC== ( ) 2 32 2 321 41 xxkhix Fx xxxCkhix −+ = +−+ Hàm số liên tục trên ( ) ( ) 11 limlim xx fxfx+− →→ = . ( ) ( ) 232 2 11 2 2 lim32lim4 312114 6 xx xxxxxC C C +− →→ −+=+−+ −+=+−+ = ( ) 2 32 321 461 xxkhix Fx xxxkhix −+ = +−+ . Vậy ( ) ( ) 243104.22FF−−=−= . Câu 260: Cho hàm số ( ) 2 21 31 xakhix fx xbkhix + = + thỏa mãn ( ) 2 0 d13fxx = . Tính Tabab =+− ? A. 11 T =− B. 5 T =− C. 1 T = D. 1 T =− Lời giải Chọn A Để tồn tại ( ) ( ) 2 0 d fxxfx liên tục trên đoạn 0;2 ( )fx liên tục tại 1 x =
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 52 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) 11 limlim12311 xx fxfxfabab+− →→ ==+=+=+ Ta có ( ) ( ) ( ) ( ) ( ) ( ) ( ) 21212 12 232 01 00101 32 4 fxdxfxdxfxdxxbdxxadxxbxxax ab =+=+++=+++ =++ Mà ( ) 2 0 13 fxdx = 9 ab += Từ và suy ra 5;4ab== 11 Tabab
. Câu 261: Cho hàm số 2 24 khi1 ()33 khi1 xx fx xx + = + . Tích phân ( ) ( ) 2 0 24.d Ixfxx =− bằng A. 10 B. 10 C. 8 D. 8 Lời giải Chọn A Ta có: ( ) ( ) 2 0 24.d Ixfxx =− Đặt ( ) 24 dd ux vfxx =− = ( ) d2dux vfx = = Nên ( ) ( ) ( )
22 2
00 24.d24.2d
=−=−−
Suy ra (
212 001 4.02()d122()d()d
=−=−+ 12 2 01 122(33)d(24)d10 xxxx =−+++=− Câu 262: Cho hàm số 2 1 khi2 ()1 khi2 xx fx xx + = − . Giá trị của tích phân ( ) e 1 12ln d fx x x + bằng A. 31 6 . B. 47 12 . C. 47 6 . D. 79 12 . Lời giải Chọn B +) Đặt 211 12lndt=ddt=d 2 txxx xx =+ . Đổi cận: 11xt== , e3xt== . Khi đó ( ) ( ) ( ) e33 111 11 dtd 2 12ln d 2 I x ft f fxx x x == + =
=+−=−
( ) ( )
0
Ixfxxxfxfxx
; ta có (0)3 f =
)
Iffxxfxxfxx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
Huỳnh
Ánh 42
Trinh Thuận
TP Huế
Page 53 Chuyên
Tốt
12 Sưu tầm và
soạn ( ) ( ) ( ) ( ) 2323 2 1212 11 dd1d1d 22fxxfxxxxxx =+=++− = 47 12 Câu
Cho hàm số ( ) 2 2 1khi 0 . 21khi 0 xx fx xx + = + Tích phân ( )
Đặ
=
= = =
e
e
e
Câu 264: Cho hàm số ( )3 23 0 () e 0 1 x khix fx k x h m i x x = + + . Biết hàm số ()fx liên tục trên và tích phân 1 1 ()d. b fxxae c =− với * ,,; a abc b tối giản ( 2,718281... e = .). Biểu thức abcm +++ có giá bằng A. 11. B. 35. C. 13. D. 36. Lời giải Chon B Vì hàm số liên tục trên nên hàm số liên tục tại điểm 0. x = ( ) ( ) 233 0000 ()()(0)(1)11 x xxxx LimfxLimfxfLimemLimxxmm +−++ →→→→ ==+=+=+=− Ta có: ( ) 10111 110 3 2 0 3 0 1 ()d()d()23 dd()2 e- d 1 1 x x fxxfxxfxxxx x e + =+=+=− .
viên:
Văn
Nguyễn Cư
Hòa
ĐT: 0984164935
luyện thi: Tuyển sinh vào lớp 10
Nghiệp THPT BDKT Toán 10; 11;
biên
263:
e 1 e lnln d fxx Ix x = bằng A. 14 3 . B. 14 3 . C. 4. D. 2. Lời giải Chọn D
t ( ) ( ) 1 ln dd ln dd ln ux ux x fx vx vfx x
Ta có ( ) ( ) e e 1
1
ln lnlnd fx Ixfxx x =−
( ) ( ) ( ) ( )
1 e 1.11lndln Ifffxx=+−− ( ) 1 1 23d Iftt=+− ( ) ( ) ( ) ( ) 0101 22 1010 5dd521d1d2. Ifttfttxxxx =−−=−+−+=
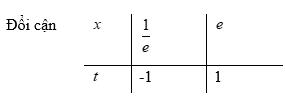
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Ta có: ( ) 000 22 1 111 231231 Ixxdxxxdxdx =++=++ ( ) 10 22 01 33 xdxdx=+++ ( ) 0 3 0 2 2 1 1 213 323. 33 xx =++=− Ta có: ( ) 1 2 2 0 3ln1 Ixxdx =+ Đặt ( ) 23 1 ln1 1 3 uxdudx x dvxdxvx =+= + == ( ) 1 3 1 3 2 0 0 ln1 1 x Ixxdx x =+− + = ( ) 1 2 0 1 ln21 1 xxdx x −−+− + ( ) 1 32 1 0 0 ln2ln1 32 xx xx =−−+++ = 5 2ln2. 6 Ta lại có 12 13531 232ln2232ln. 366 III =+=−+−=++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 54 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy 1 23 12 a b c = = = 35 abcm+++= . Câu 265: Cho hàm số ( ) ( ) 2 2 3ln1khi 0 231khi 0 xxx fx xxx + = ++ . Biết ( ) 1 ln 3ln2 e e fx dxabc x =++ với ,, abc . Giá trị của 6 abc ++ bằng A. 35 B. 14 C. 27 D. 18 Lời giải Chọn A Với ( ) 1 ln e e fx Idx x = đặt 1 ln xtdtdx x == ( ) ( ) ( ) 101 22 12 110 2313ln1 IftdtxxdxxxdxII ==++++=+
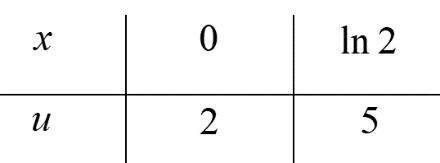
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
xxx
−+
Xét
=
. Đặt 1
x =−= .
cận 2
xu e xeu ==− == . Khi đó ( ) ( ) ( ) ( ) 1101 2220 Ifudufxdxfxdxfxdx ===+ ( ) ( ) 01 2 20 221 x xxdxedx=−+++ ( ) 0 1 32 0 2 132 2 33 x xxxexe =−+++=+ . Do
32,3,136
===++= Câu 267: Cho hàm số 2 1 khi 3 ()75 khi 3 xx fx xx − = − . Tính tích phân ( ) ln2 0 31d xx feex . A. 13 15 B. 94 9 C. 102 33 D. 25 9 Lời giải Xét ( ) ln2 0 31d xx Ifeex =− . Đặt 31 x ue=− d3d x uex = 1 dd 3 x exu = Đổi cận: ( ) ( ) ( ) ( ) ( ) ( ) 553535 2 222323 1111 dddd1d75 d 3333 Ifufxfxfx uxxx xxxx ===+=−+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 55 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy 31 2;2; 6 abc=== . Giá trị 635abc++= . Câu 266: Cho hàm số ( ) 2 1khi 0 22 khi 0 x ex yfx
+ ==
. Tích phân ( ) 2 1/ ln1 e e fx a Idxce xb ==+ biết ,, abcZ và a b tối giản. Tính ?abc ++ A. 35. B. 29. C. 36. D. 27. Lời giải Chọn C
( ) 2 1/ ln1 e e fx Idx x
ln1 uxdudx
Đổi
1 2 1
đó
abcabc
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 56 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 3235 23 194 75 3329 xx Ixx =−+−=− Câu 268: Cho
số ( ) 2 1khi3 75khi3 xx fx xx − = − Tính tích phân ( ) ln2
Chọn B Đặt 1 3e1ded 3 xx uux =−= . Đổi cận 02xu== ;
xu== Ta
( ) ( ) ( )
ln2535 2 0223
3e1edd1d75d
xx fxfuuuuuu −==−+−=− .
số ( ) 2 1,0 23,0 xxkhix fx xkhix ++ = − . Biết ( )
2 2 0
e
−+=
số tối giản. Giá trị của tổng ab + bằng A. 350. B. 305. C. 350. D. 19. Lời giải Chọn D Đặt ( ) ( ) 2 2 12 0 ln 2sin1cos e e fx a IIIfxxdxdxxb =+=−+= . Với ( ) 2 1 0 2sin1cos Ifxxdx =− Đặt 1 2sin12coscos 2 txdtxdxdtxdx =−== Ta có: 01;1 2 xtxt ==−== . Suy ra ( ) ( ) ( ) ( ) 1101 1 1110 111 222 Iftdtfxdxfxdxfxdx ===+ ( ) ( ) 01 2 10 111113 2314 22612 xdxxxdx =−+++=−+=− . Với ( ) 2 2 ln e e fx Idx x =
0984164935
hàm
0 3e1ed xx fx A. 13 15 B. 94 9 C. 102 33 D. 25 9 Lời giải
ln25
có
( )
11194
3339
Câu 269: Cho hàm
( )
ln 2sin1cos
e fx a fxxdxdxxb
với a b là phân
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 57 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đặt ln dx txdt x == Ta có 2 1;2xetxet ==== Suy ra ( ) ( ) 222 2 2 111 ()129 6 Iftdtfxdxxxdx ===++= Suy ra 12 132915 1264 a III b =+=−+== . Vậy 15419 ab+=+= . Câu 270: Cho hàm số ( ) −− = − 32neáu1 5neáu1 xx fx x . Tích phân ( ) 2 2 sinx1cosd fxx bằng A. 9. B. 1. C. 9. D. 1. Lời giải Chọn C ( ) 2 2 sin1cos =− Ifxxdx Đặt sinx1cosd=−= tdtxx Đổi cận. 0;2 22 ====− xtxt . Khi đó. ( ) ( ) ( ) ( ) 001 0 1 222 dddd===+ Ifttfxxfxxfxx ( ) ( ) 10 0 1 2 2 1 21 5d32d53549 =+−=+−=+= xxxxxx . Câu 271: Cho hàm số ( )fx dược xác định với mỗi số thực x , gọi ( )fx là giá trị nhỏ nhất trong các số ( ) 1 21gxx=+ , ( ) 2 2 gxx=+ , ( ) 3 314gxx=−+ . Tính ( ) 4 0 fxdx . A. 31 2 . B. 30. C. 27 2 D. 36. Lời giải Chọn C
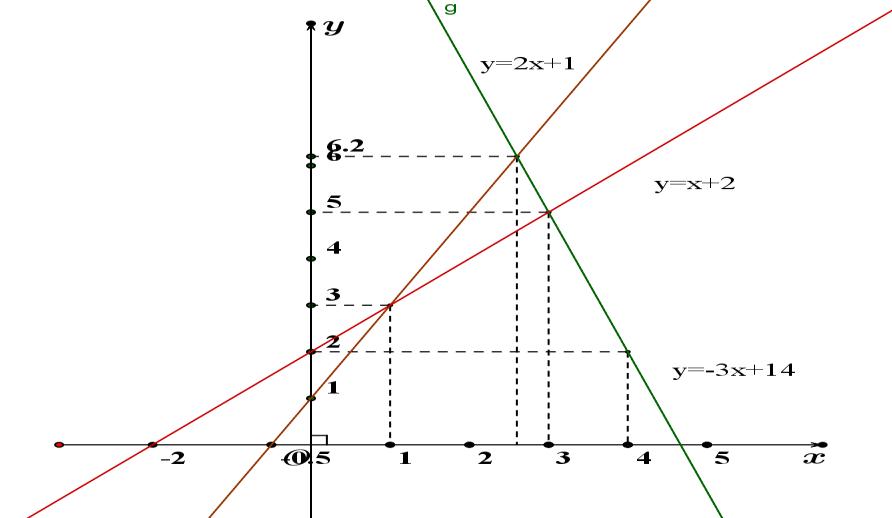
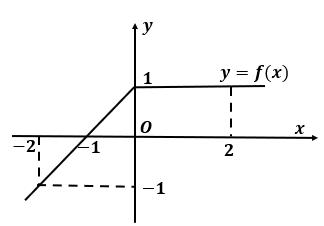
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 58 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Dựa vào đồ thị ta có ( ) ( ) ( ) ( ) ( ) 4134 22 2134 013 0013 212314|2|14|327 222 xx fxdxxdxxdxxdxxxxx =++++−+=+++++= . Câu 272: Cho hàm số ()yfx = . Đồ thị ()yfx = trên [3;0] như hình vẽ sau Hàm số ( )yfx = có đồ thị như hình vẽ bên. Giá trị của ( ) 2 2 fxdx bằng A. 2 B. 1 C. 3 D. 4 Lời giải Chọn A Ta có: ( ) ( ) 02 2 2 2 20 02 112 220 x fxdxxdxdxxx =++=++= . Câu 273: Cho hàm số ( )yfx = có đồ thị hàm số ( )yfx = cắt trục Ox tại ba điểm có hoành độ bằng ,, abc như hình vẽ bên. Khẳng định nào dưới đây đúng?
A. ( ) ( ) ( )fafcfb B. ( ) ( ) ( )fcfafb
C. ( ) ( ) ( ). fcfbfa D. ( ) ( ) ( )fafbfc Lời giải
Chọn A
Trên ( ) , ab hàm số ( )yfx = nghịch biến, trên ( ) , bc hàm số ( )yfx = đồng biến. Suy ra ( ) ( )fafb và ( ) ( )fcfb
Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số, trục hoành và hai đường thẳng , xaxb == . ' S là diện tích hình phẳng giới hạn bởi đồ thị hàm số, trục hoành và hai đường thẳng , xbxc == .
Ta có ' SS suy ra ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) dd ac bb fxxfxxfafbfcfbfafc −− Từ và suy ra ( ) ( ) ( )fafcfb
Câu 274: Cho hàm số ( )yfx = liên tục và không âm trên khoảng ( ) 0;+ . Biết rằng diện tích hình thang cong giới hạn bởi các đường ( );0;1;9yfxyxx ==== bằng 12. Tính ( ) 3 2 1 Ixfxdx = A. 6 I = . B. 24 I = . C. 122 I = . D. 23 I = . Lời giải
12 Sfxdxfxdx === .
Đặt 2 2 txdtxdx ==
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 59 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
. Đổ
ận: 11 39 xt xt == == . Ta có ( ) 9 1 11 .126 22Iftdt=== Câu
Trong mặt phẳng toạ độ Oxy , gọi C là đường
có đỉnh 1;2
đi qua
độ
trụ
Ox
ớ
Chọn A Hàm số ( )yfx = liên tục và không âm trên khoảng ( ) 0;+ suy ra diện tích hình thang cong giới hạn bởi các đường ( );0;1;9yfxyxx ==== bằng ( ) ( ) 99 11 ọ
i c
275:
tròn tâm 1;0 I bán kính 1 R và P là parabol
I ,
gốc toạ
O . Biết đồ thị yfx trùng với nửa đường tròn C dưới
c
v
i m
i 2;0 x và trùng với P với mọi 0;2 x .
Nếu 2 2
d b Ifxx ac với a , b , c là các số nguyên và b c là phân số tối giản, hãy tính abc A. 13. B. 9. C. 10. D. 11. Lời giải Chọn B Gọi 2 : Pymxnxp Theo giả thiết ta có hệ phương trình 2
2 2 14:24 2 00
mnp m n nPyxx m p p Ta có: 2022 2 2200
8 ddd24d 223Ifxxfxxfxxxxx 2839 abc Câu 276: Cho hàm số ( )yfx = . Đồ thị ( )yfx = trên đoạn như hình vẽ bên Cho hàm số ( )fx với đồ thị là Parabol đỉnh I có tung độ bằng 7 12 và hàm số bậc ba ( )gx . Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ 123 ,, xxx thoả mãn 123 1855 xxx =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 60 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Diện tích miền tô đậm gần số nào nhất trong các số sau đây?
A. 5,7 B. 5,9. C. 6,1. D. 6,3 Lời giải
Chọn A
Dễ thấy 17 , 212 I và ( ) ( )( ) 7 12 27 fxxx=+− .
Hàm số ( )gx đạt cực trị tại 1,2xx=−= nên ( ) ( )( ) ( ) 32 '122 32 xx gxaxxaxb gx =+−=−−+
Đồ thị hàm số ( )gx đi qua I nên 17713 2121212, gab =−−=−+ ( )1
Phương trình hoành độ giao điểm: ( ) ( ) ( )( ) 32 7 212 3227 xx fxgxaxbxx =−−+=+−
Theo định lý viet ta có: 123
14 2855 27 185518.5518, 33 3
+ =−=−+=− ( )2 Từ ( )1 , ( )2 ta được ( ) 32 11 1,2 2322 xx abgxx ===−−+ . Từ đó suy ra diện tích miền tô đậm sấp sỉ 5,7.
b a xxxb a
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 61 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH
NGUYÊN HÀM TÍCH PHÂN
ỨNG DỤNG TÍCH PHÂN
12
-



CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT
10; 11; 12 Sưu tầm và biên soạn BÀI 3. ỨNG DỤNG
MỨC ĐỘ VẬN DỤNG – VẬN DỤNG CAO Câu 1: Cho hàm số ( )yfx = là hàm đa thức bậc bốn và có đồ thị như hình vẽ bên. Hình phẳng giới hạn bởi đồ thị hai hàm số ( )yfx = , ( )yfx = có diện tích bằng A. 127 40 . B. 107 5 . C. 87 40 . D. 127 10 . Lời giải Chọn B Ta thấy đồ thị hàm số ( )yfx = tiếp xúc với trục hoành tại hai điểm có hoành độ bằng 2 và 1 nên hàm số có dạng ( ) ( ) ( ) 2221fxaxx=+− Mà đồ thị hàm số ( )yfx = đi qua điểm ( ) ( ) ( ) ( ) 22 11 0;14121 44 Aaafxxx ===+− ( ) ( )( )( ) 1 2121 2 fxxxx =+−+ Xét phương trình hoành độ giao điểm của ( )yfx = và ( )yfx = : CHƯƠNG III NGUYÊN HÀM TÍCH PHÂN ỨNG DỤNG TÍCH PHÂN
0984164935
Toán
TÍCH PHÂN
=−
( ) ( ) ( )( )( ) 22
x x xxxxx x x
=
+−=+−+
2 111 212121 421 4
Hình phẳng giới hạn bởi đồ thị hai hàm số ( )yfx = , ( )yfx = có diện tích là ( ) ( ) ( )( )( ) 4 22 2
11 212121 42 Sxxxxx =+−−+−+= 107 5 . Câu 2: Cho hình thang cong ( ) H giới hạn bởi các đường ,0,0,4yxyxx ==== . Đường thẳng ( )04xkk= chiahình ( ) H thànhhai phầncódiệntíchlà 1S và 2S nhưhình vẽ.Để 12 4 SS = thì giá trị k thuộc khoảng nào sau đây? A. ( )3,1;3,3 B. ( )3,7;3,9 C. ( )3,3;3,5 D. ( )3,5;3,7 Lời giải Chọn C ( ) 3 3 2 2 1 0 0
k k x Sxxk === ( ) 4 3 4 33 2 22 2 22 d.4.. 333 2 k k

2 d. 33 2
(C) C O
y x
B A
x Sxxk ===− Suy ra 333 222 12 222 44.4.3.447 333 SSkkk ==− . Câu 3: Cho hàm số ln yx = có đồ thị ( )C như hình vẽ. Đường tròn tâm A có duy nhất một điểm chung B với ( )C . Biết ( )0;1 C , diện tích của hình thang ABCOgần nhất với số nào sau đây. A. 3,01 B. 2,91 C. 3,09 D. 2,98
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 2
=− =
Lời giải Chọn B
C e O
1 B A
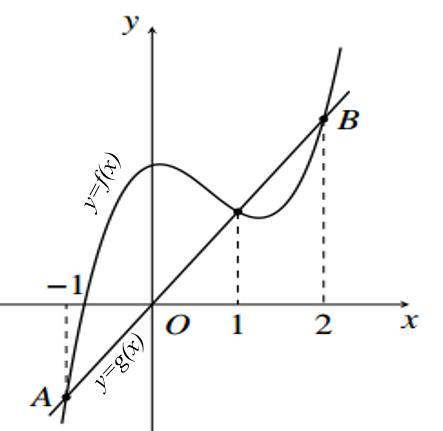
y x
d (C) e+ 1 e
Đường thẳng đi qua ( )0;1 C và song song với trục hoành cắt đồ thị () C tại (;1)Be . Gọi () d là tiếp tuyến của () C tại (;1)Be thì phương trình () d là x y e = () C tiếp xúc với đường tròn tâm A tại (;1)Be thì () d là tiếp tuyến chung của () C và đường tròn tâm A 1 ()(;0)ABdAe e ⊥+ Hình thang ABCO có: 1;;1OAeCBeOC e =+== . Vậy 2,91. ()1 22 OACBOC e ABCO e S + ==+ Câu 4: Cho đồ thị hàm số bậc ba ( ) 32 1 3 yfxaxbxxc ==+++ và đường thẳng ( )ygx = có đồ thị như hình vẽ sau: Biết 5 AB = , diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = , trục hoành và hai đường thẳng 1 x = , 2 x = bằng A. 17 11 . B. 19 12 . C. 5 12 . D. 7 11 . Lời giải Chọn B
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
+−+=−−+ , Đồng nhất hệ số ta đươc 1 a = , 2 b =− , 2 c = . Vậy ( ) 32 1 22 3 yfxxxx ==−++ . Diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = , trục hoành và hai đường thẳng 1 x = , 2 x = bằng 2 32 1
119 22d. 312 Sxxxx =−++= Câu 5: Cho hàm số ( ) 5432 36 fxxaxbxcxdx =+++++ . Biết đồ thị hàm số ( ) ( ) , yfxyfx == và Ox giao nhau tại hai điểm phân biệt có hoành độ lần lượt là 2,3. Diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = và Ox bằng m n là một phân số tối giản với * , mn . Tổng mn + bằng A. 846. B. 845. C. 848. D. 847. Lời giải Chọn D Do 2,3 là nghiệm của phương trình ( ) ( ) 0,0fxfx == nên ( ) ( ) ( ) ( ) 2223 fxxxxm =−−− . Ta có ( ) 0361fm==− . Vậy ( ) ( ) ( ) ( ) 22 231fxxxx =−−+ . Diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = và Ox là ( ) ( ) ( ) 3 22 1
832 231847 15 Sxxxmn =−−+=+= Câu 6: Diện tích hình phẳng giới hạn bởi parabol 2 21yxx=++ và đường thẳng (1)5ymx=++ có giá trị nhỏ nhất bằng A. 16 3 . B. 48 3 . C. 64 3 . D. 32 3 . Lời giải Chọn D Phương trình hoành độ giao điểm là: 2221(1)5(1)40xxmxxmx ++=+++−−= Gọi hai nghiệm của phương trình này là a và b () ab . Theo Vi et, có 1,4abmab+=−=−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
Gọi ( ) ( )
gxmxm= . Ta
(
2
=
=−
(
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
0
có ( ) 1; Am ; ( ) 2;2 Bm Khi đó
) ( )
4 9953 4 3 mtm ABm ml
=+=
Ta có ( ) ( ) 32 0 fxgxaxbxxc =+−+= . Mặt khác
)( ) 322 12axbxxcaxx +−+=−− 323222 axbxxcaxaxaxa
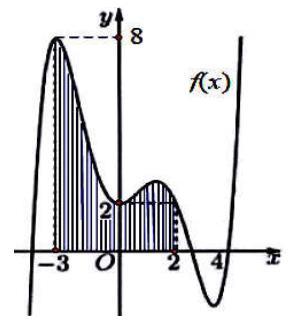
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
Khi
b b a a
(
(
(
c xảy ra khi và chỉ khi 1 m = . Vậy 32 min 3 S = Câu 7: Cho hàm số ( )yfx = liên tục trên có đồ thị như hình vẽ. Giả sử diện tích phần kẻ dọc trên hình vẽ có diện tích bằng a . Tính theo a giá trị của tích phân ( ) ( ) 2 3 21d Ixfxx =+ ? A. 502 Ia =− . B. 50 Ia =− . C. 302 Ia =−− . D. 302 Ia =−+ . Lời giải Chọn A Từ đồ thị suy ra ( ) 2 3 d Sfxxa == và ( ) ( ) 38;22ff−== Ta có ( ) ( ) 2 3 21d Ixfxx =+ ( ) ( ) ( ) 2 3 21dxfx=+ ( ) ( ) ( ) 2 2 3 3 212d xfxfxx=+− ( ) ( ) 52532 ffS=+−− 5.25.82a =+− 502a =− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
đó, diện tích hình phẳng cần tìm là: 3 22 (1) (1)44 32 d
xm Sxmxxxx =+−−=+−
) ( ) ( ) 332211 4 32 m bababa =−+−−−
) ( ) ( ) 22 11 4 32 m babbaaab =−++++−
) ( ) ( ) 2211 4.4 32 m ababababab =+−+−++− ( ) ( ) ( )2 2211 116.144 32 m mm =−+−+−− ( ) ( )2 2 1 8 116. 63 m m =−++ 832 4. 33 SS . Đẳng thứ
Vậy 502 Ia =− . Câu 8: Cho hàm số ( ) 32 fxxbxcxd =+++ với b , c , d là các số thự C. Biết hàm số ( ) ( ) ( ) ( ) 23 gxfxfxfx =++ có hai giá trị cực trị là 6 và 42. Tính diện tích hình phẳng giới hạn bởi các đường ( ) ( ) ( ) ( ) 18 fxfxfx y gx ++ = + và 1 y = A. ln5 B. ln7 C. 2ln6 D. 2ln5 Lời giải Chọn A Hàm số ( )fx là hàm số bậc 3 nên ( )gx là hàm số bậc 3 suy ra ( )gx là hàm số bậc hai. Ta có ( ) ( ) 3 33.3!18 fx == ; ( ) ( ) ( ) 218gxfxfx =++ có hai nghiệm 1x , 2x và ( )1 42 gx = , ( ) 2 6 gx =− . Xét phương trình tìm cận của tích phân để tính diện tích: ( ) ( ) ( ) ( ) ( ) ( ) ( ) 218 10 1818 fxfxfxfxfx gxgx
++++ == ++ Suy ra ( ) ( ) ( ) 1 2 21800 xx fxfxgx xx
= ++== = Diện tích hình phẳng ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 222 111
xxx xxx
1 181818
fxfxfxgxgx Sdxdxdx gxgxgx ++ =−== +++ Đặt ( ) ( ) 18 tgxdtgxdx =+= . Đổi cận ( ) ( ) 111 222
18 18 xxtgx xxtgx ==+ ==+ Do đó 12 12 60 60
12 lnln12ln60lnln5ln5 60 dt St t ===−==−= .
Câu 9: Cho hai hàm số ()yfx = và ()ygx = , biết rằng hàm số 32 () fxaxbxcxd =+++ và 2 () gxqxnxp =++ với , 0 aq có đồ thị như hình vẽ và diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()fx và ()gx bằng 10 và (2)(2).fg = Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()yfx = và ()ygx = bằng a b . Tính Pab =+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 11. P B. 19. P C. 24 P D. 21. P Lời giải Chọn B Ta có: 32 ()12 fxgxaxbqxcnxdpaxxx Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()fx và ()gx bằng 10 nên: ( ) ( ) ( ) ( ) 12 01 dd10Sfxgxxgxfxx =−+−= ( )( ) ( )( ) 12 01 dd101212axxxa Sxx xxx =−= ( )( ) ( )( ) 12 01 1 dd101020 2 4 1 4 2 aa S xxx axaxa xxx =−=−−== Khi đó: ()2012 fxgxxxx () fxgxfxgxdx 432 201252020. xxxdxxxxC Mà 220fg nên: 432 5.220.220.200 CC 43252020 x g x xx x f Câu 10: Suy ra 432 2 0 52020 3 16 d S x x xx = + = . Do đó 19. P Cho hàm số bậc bốn ( )yfx = có đồ thị ( )C như hình vẽ.
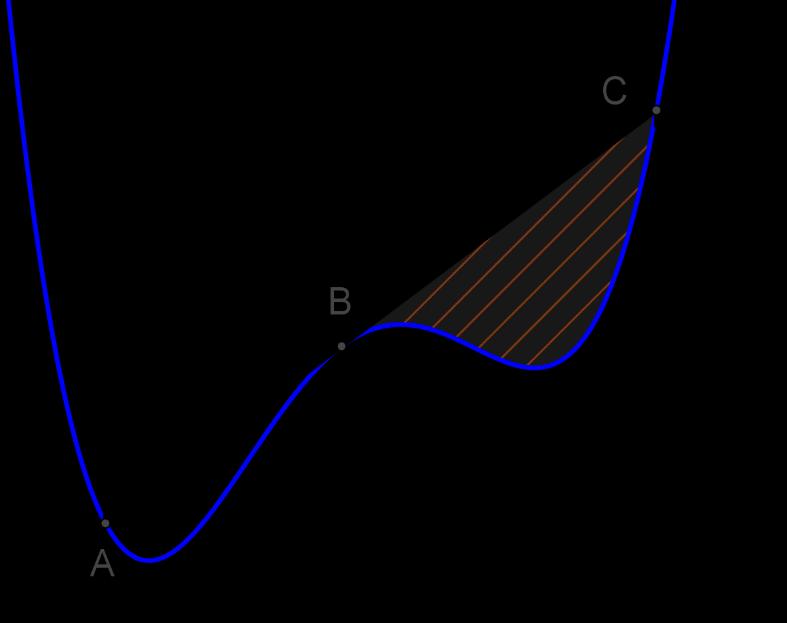
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
Theo
(
( )
) ( )( ) ( ) ( )( ) ( ) 22111 215215 24424 fxgxxxxkxxxx =++−−=+++−− * Gọi 111 2;2,1;,5;5 444 AkBkCk −−++ ( ) ( ) 2222 3 554 4433 443 4 k BCABkk k = −=+−+= =− Đường thẳng nằm ở góc phần tư thứ nhất và thứ ba nên hệ số góc là dương nên ta chọn 3 4 k = Vậy ( ) ( )( ) ( ) 2 311 215 4424 fxxxxx =+++−− Và ( ) 1 2 321 160 fxdx =− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Đường thẳng 1 : 4 dykx=+ có đúng ba điểm chung với ( )C là ,, ABC và 5 . 4 BCAB−= Biết diện tích hình phẳng S là 24 . 5 Giá trị của ( ) 1 2 fxdx bằng A. 2. B. 321 160 . C. 161 80 . D. 159 160 . Lời giải Chọn C Phương trình giao điểm của ( )C và d là: ( ) ( ) ( )( ) ( ) 2 215fxgxaxxx −=+−−
giả thiết, ta có:
)( ) ( ) 5 2 1 24241 215 5524 Saxxxdxa =−+−−==
(
Câu 11: Tính diện tích hình phẳng giới hạn bởi parabol ( ) 2 :4Pyx=+ và hai tiếp tuyến của ( )P tại các điểm , AB có hoành độ lần lượt là 1 và 1.
A. 4 3 B. 1 3 C. 1 2 D. 2 3 Lời giải
Chọn D
Xét hàm số 2 42 yxyx =+=
Ta có ( ) ( )1;5,1;5AB là hai điểm thuộc ( )P
Tiếp tuyến của ( )P tại ( )1;5 A là: ( ) 21523yxyx =−++=−+ .
Tiếp tuyến của ( )P tại ( )1;5 B là: ( ) 21523yxyx =−+=+
Hoành độ giao điểm của hai đồ thị hàm số 23,23yxyx =+=−+ là nghiệm của phương trình:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
xxx +=−+= Khi đó diện tích hình phẳng giới hạn bởi ( )P và hai tiếp tuyế
ủ
ạ
( ) ( ) 01 01 223232 10 10 112 423d423d 333 Sxxxxxxxxxxxx =++−++−−=+++−+= . Câu 12: Diện tích hình phẳng giới hạn bởi ba đồ thị hàm số 1 2,1,24 2 x yyxyx ==−+=−+ bằng A. 2 loge B. 2 loge1 + C. 2 loge1 D. 2 2loge Lời giải Chọn A x y O y = 2x +3 y = x2 +4 y =2x +3 4 3 1
23230
n c
a ( )P t
i , AB là:
Hoành độ giao điểm của hai đồ thị hàm số 1 1,24 2 yxyx =−+=−+ là nghiệm của phương trình: 1 1242 2 xxx −+=−+=
Hoành độ giao điểm của hai đồ thị hàm số 1 2,1 2 x yyx==−+ là nghiệm của phương trình: 11 212100 22 xx xxx =−++−== .
Hoành độ giao điểm của hai đồ thị hàm số 2,24 x yyx==−+ là nghiệm của phương trình: 22422401 xx xxx =−++−==
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 10
diện
ớ
12
01
11211 21d241d4 22ln244 x x Sxxxxxxxxxxx =+−+−++−=+−+−++− 2 loge = Câu 13: Diện tích miền phẳng giới hạn bởi các đường: 2,3 x yyx==−+ và 1 y = là: A. S = 11 ln22 B. 1 1 ln2 S =+ C. 47 50 S = D. 1 3 ln2 S =+ Lời giải Chọn A x y y = 2x +4 y =2x y = 1 2 x +1 2 2 1 1
. Khi đó
tích hình phẳng gi
i hạn bởi ba đồ thị hàm số trên là: 1 2
222
1 0

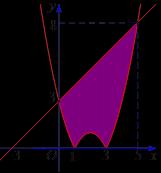
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 11 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét phương trình hoành độ giao điểm của các đường. Ta có: • 231 x xx =−+= • 210 x x == • 312xx −+== Diện tích cần tìm là: ( ) ( ) 12 12 2 01 01 211 21312 ln22ln22 dd x x x Sxxxxx =−+−+−=−++=− Câu 14: Cho hình phẳng ( ) H giới hạn bởi các đường 2 43yxx=−+ , 3 yx=+ . Diện tích của ( ) H bằng A. 37 2 B. 109 6 C. 454 25 D. 91 5 s Lời giải Chọn B Diện tích của ( ) H là

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 12 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 5 2 0 433d Sxxxx =−+−+ ( ) 5 2 0 343d xxxx=+−−+ ( ) ( ) ( ) ( ) 5135 222 0013 3d43d43d43d xxxxxxxxxxx =+−−+−−++−+ 23335135 222 0013 3232323 2333 xxxx xxxxxxx =+−−+−−++−+ 554420 2333 =−++ 109 6 = Câu 15: Cho hàm số ( ) 42 0 yaxbxca =++ và hàm số ( ) 2 0 ymxnxpm =++ có đồ thị là các đường cong như hình vẽ bên. Gọi S là diện tích của hình phẳng được tô đậm. Khẳng định nào sau đây đúng? A. 6264 ; 1515 S B. 2113 ; 53 S C. 21 4; 5 S D. 1367 ; 315 S Lời giải Chọn B Từ đồ thị ta thấy đồ thị hàm hàm số ( ) 42 yfxaxbxc ==++ đi qua các điểm ( )1;3 A , ( )0;2 B và đạt cực trị tại 1 x = ( ) ( ) ( ) 133 022 10420 f abc fc ab f = ++= == += = 1 2 2 a b c =− = = ( ) 4222fxxx =−++ . Từ đồ thị ta lại thấy đồ thị hàm số ( ) 2 ygxmxnxp ==++ đi qua các điểm ( )0;1 C , ( )1;3 A và ( )1;3 D ( ) ( ) ( ) ( ) 2 0111 133441 1330 f pp fmnpmgxx mnpn f =− =−=− =++===− −+== −= Diện tích hình phẳng được tô đậm là
( ) ( ) 1 422 1
2241d Sxxxx =−++−− ( ) 1 42 1
23d xxx=−−+ 1 5 3 1

264 3 5315 x xx =−−+=
Câu 16: Trong mặt phẳng Oxy , cho parabol ( ) ( ) 2 :0Pyaxbxca=++ và đường thẳng ( ):0dymxnm=+ . Tính diện tích hình phẳng ( )D giới hạn bởi ( )P , d và đường thẳng :4 y = như hình vẽ bên. A. 25 6 B. 16 3 C. 19 6 D. 10 3 Lời giải Chọ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
n A Từ đồ thị ta thấy parabol ( ) ( ) 2 :0Pyaxbxca=++ đi qua các điểm
( )0;0 O 01 4240 00 ca abcb bc == ++== == 2 yx= Từ đồ thị ta lại thấy đường thẳng ( ):0dymxnm=+ đi qua các điểm ( )2;0 B và ( )0;2 C 201 22 mnm nn +==−== 2 yx =−+ . Diện tích hình phẳng ( )D là: ( ) ( ) ( ) 12 2 01 42d4d Sxxxx =−−++− ( ) ( ) 12 2 01 2d4d xxxx=++− 12 23 01 25 24 236 xx xx =++−= Câu 17: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số x ye = , ln yx = , 1 yxe=−++ với các trục tọa độ
( )2;4 A và có đỉnh là
2 25 2 ee+− B. 2 2 e C. 2 24 3 ee+− D. 2 3 e Lời giải Chọn A Vì hàm x ye = đồng biến và hàm 1 yxe=−++ nghịch biến, nên phương trình 1 x exe=−++ có nghiệm duy nhất 1 x = Tương tự hàm ln yx = đồng biến và hàm 1 yxe=−++ nghịch biến, nên phương trình ln1 xxe=−++ có nghiệm duy nhất xe = Diện tích hình phẳng cần tính là
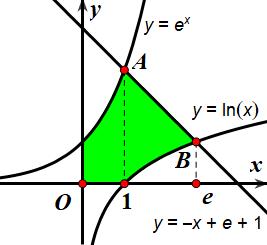
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
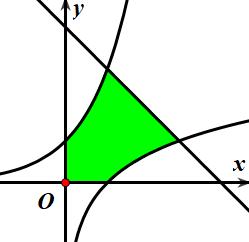
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
( ) ( ) 11 0101 dln1dd1lnd ee xx Sexxxexexxexx =+−−++=+−++− ( ) 2 1 0 1 1 1lnd 2 e e x x eexxx =+−++− ( ) ( ) 2 1 1 1ln 22 e e exxx =−+−−− 2 25 2 ee+− = Câu 18: Cho Parabol ( )P có đồ thị như hình vẽ. Tính thể tích của khối tròn xoay tạo thành khi quay hình ( ) H quanh trục Ox .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
A.
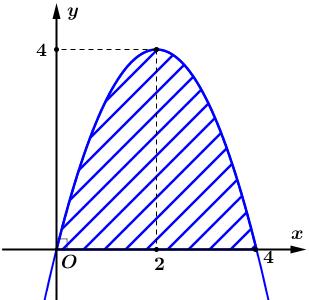
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 15 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 512 15 . B. 512 15 . C. 32 3 . D. 32 3 . Lời giải Chọn B Nhìn vào đồ thị ta thấy, hàm số 2 yaxbxc =++ có đỉnh ( )2;4 I và đi qua 2 điểm ( )0;0 O , ( )4;0 A nên ta có hệ phương
2 2 2 4.2.24241 0.0.0044 0.4.416400 abcabca abccbyxx abcc abc =++++==− =++===−+ ++== =++ Vậy thể tích khối tròn xoay cần tình là: ( ) 4 2 2 0 4d Vxxx =−+ ( ) 4 432 0 816d xxxx =−+ 4 53 4 0 16512 2 5315 xx x =−+= Câu 19: Gọi 1S là diện tích của mặt phẳng giới hạn bởi đường thẳng ymx = với m < 2 và parabol ( )P có phương trình ( ) 2 yxx =− . Gọi 2S là diện tích giới hạn bởi ( )P và Ox . Với trị số nào của m thì 12 1 2 SS = ? A. 3 24 B. 3 22 + C. 2 5 D. 1 4 Lời giải Chọn A * Tính 2S Phương trình hoành độ giao điểm ( ) 0 20 2 x xx x = −= = .
trình:
hoành độ giao điểm của hai đồ thị là : 2 xmx = 0 x xm
Do đó diện tích hình phẳng ( ) H là: 2 0
= =
d m Sxmxx =− ( ) 2 0
d m mxxx=− 23 0 23
m xx m =− 3 6 m =

Theo đề bài: 20 S 3 20 6 m 3 120 m 4.9324... m
Do m là số nguyên dương nên 1;2;3;4 m = Vậy có 4 giá trị m thỏa mãn.
Câu 21: Cho hàm số ( )yfx = . Hàm số ( )yfx = có đồ thị như hình vẽ. Biết phương trình ( ) 0 fx = có bốn nghiệm phân biệt a ,0,b , c với 0 abc .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 16 Chuyên
thi:
10
12 Sưu tầm và biên soạn Do đó 2 2 2 0 4 2d 3 Sxxx=−= . * Tính 1S Phương trình hoành độ giao điểm ( ) 22 0 220 2 x mxxxxmx xm = =−+−= =− . Do đó ( ) ( ) ( ) ( ) 2 3 2 22 3 22 1 00 0 22 2d2d 326 m mm mxm x Sxxmxxxmxx
* ( )
12
.24
m SSm ===−
ẳ
ớ
ạ
ởi
Hòa
0984164935
luyện
Tuyển sinh vào lớp
Tốt Nghiệp THPT BDKT Toán 10; 11;
=−−=−+−=−+=
.
3 3
2 114
2623
. Câu 20: Cho hình ph
ng ( ) H gi
i h
n b
đồ thị hàm số 2 yx = và đường thẳng ymx = với 0 m . Hỏi có bao nhiêu số nguyên dương m để diện tích hình phẳng ( ) H là số nhỏ hơn 20. A. 5 B. 4 C. 6 D. 3 Lời giải Chọn B Ta có phương trình

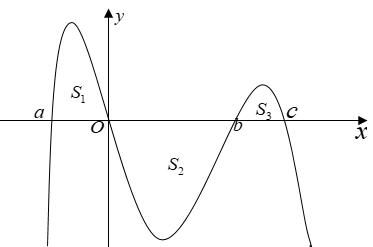



CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
ọi 123 ,, SSS lần lượt là các phần diện tích giới hạn bởi đồ thị hàm số ( )yfx = và trục
( ) ( ) ( ) ( ) ( ) ( ) 0 0 213 0 0 ddd bc bc ab ab SSSfxxfxxfxxfxfxfx +−+−+ ( ) ( ) ( ) ( ) ( ) ( ) 00 ffbffafcfb −−+− ( ) ( )fafc Từ và suy ra ( ) ( ) ( )fafcfb . Câu 22: Cho hàm số ( ) ( ) ( ) 1 2 0 yfxxxufudu ==++ có đồ thị ( )C . Khi đó diện tích hình phẳng giới hạn bởi ( )C , trục tung, tiếp tuyến của ( )C tại điểm có hoành độ 1 x = là A. 1 4 S = B. 1 3 S = C. 2 3 S = D. 1 6 S = Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. ( ) ( ) ( )fafbfc B. ( ) ( ) ( )fafcfb C. ( ) ( ) ( )fcfafb .D. ( ) ( ) ( )fbfafc . Lời giải Chọn B Bảng biến thiên của ( )yfx = : Do đó ta có ( ) ( )fcfb Ta g
hoành như hình bên.
x fxgxaxxxx x
Câu 23: Cho hàm số ( ) 42 yfxaxbxc ==++ có đồ thị ( )C và cắt trục hoành tại điểm có hoành độ bằng 1. Tiếp tuyến d tại điểm có hoành độ 1 x =− của ( )C cắt ( )C tại 2 điểm khác có hoành độ lần lượt là 0 và 2. Gọi 12 , SS là diện tích các phần hình phẳng giới hạn bởi d và ( )C Tỷ số 1 2 =− −=+−== = . Do đó ( ) ( ) 0 2 1 1
S S bằng A. 1 14 B. 1 28 C. 2 25 D. 1 5 Lời giải Chọn B Giả sử phương trình tiếp tuyế 12d 5 a Saxxxx =+−= ; ( ) ( ) 2 2 2 0
khác 28 12d 5 a Saxxxx =+−= . Suy ra 1 2
hoành 1 28 S S =
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 18 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn B Hàm số ( )fx có dạng ( ) 2 fxxaxb =++ , với 1 0 () afudu = và 1 0 (). bufudu = 1 5 32 117 4326 a a ab ab b b =− =++ = =++ Suy ra ( ) 2 17 5;()25. 6 fxxxfxx =−−=− ( ) 41 1;;(1)3. 6 MCf −=− Phương trình tiếp tuyến của ( )C tại : M ( ) 4123 313. 66yxx =−−−=−− Diện tích hình phẳng cầ
n là ( )ygx = . Do tiếp tuyến d tại điểm có hoành độ 1 x =− của ( )C cắt ( )C tại 2 điểm
n tìm là: ( ) 11 22 00 có
17231 5321. 663 Sxxxdxxxdx =−−−−−=−+= độ lần lượt là 0 và 2 nên ta có phương trình hoành độ giao điểm của d và ( )C là: ( ) ( ) ( ) ( ) 2 1 1200 2
fxxxi fx gx fx fx fx
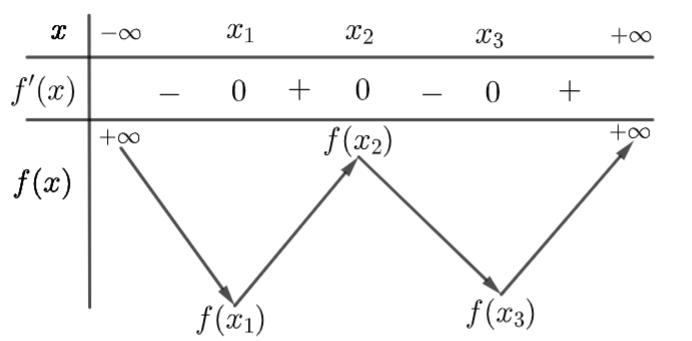
=== == +) Diện tích cần tìm là ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 2 23 12 12 213 dd224226. x x xx xx xx fxfx Sxxfxfxfxfxfx fxfx =−=−=−−= Câu 25: Biết đồ thị
)
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 19
Câu 24: Cho hàm số ( ) 432 fxxbxcxdxe =++++ ( ,,, bcde ) có các giá trị cực trị là 1,4 và 9. Diện tích hình phẳng giới hạn bởi đồ thị hàm số ( ) ( ) ( ) fx gx fx ( )C của hàm số ( ) ( ) 42 , fxxbxcbc=++ có cực trị là ( )1;0 A . Gọi (
= và trục hoành bằng A. 4. B. 6. C. 2. D. 8. Lời giải Chọn B +) Gọi 123 xxx là ba điểm cực trị của hàm số ( )fx . Ta có bảng biến thiên: +) Phương trình hoành độ giao điểm của đồ thị hàm số ( )gx và trục hoành là: ( ) ( ) ( ) ( ) ( ) ( ) 0(1,2,3) 0 0 0(TM) i i P là parabol có đỉnh ( )0;1 I và đi qua điểm ( )2;3 B . Diện tích hình phẳng giới hạn bởi ( )C và ( )P thuộc khoảng nào dưới đây? A. ( )0;1 B. ( )2;3 C. ( )3;4 D. ( )1;2 Lời giải Chọn B Đồ thị ( )C của hàm số ( ) ( ) 42 , fxxbxcbc=++ có cực trị là ( ) ( ) 1;01 AACbc+=− ( ) 3 42 fxxbx =+ vì ( )1;0 A là cực trị nên ( ) 1042021. fbbc =+==−= ( ) ( ) 42 :21Cfxxx=−+ Gọi ( ) ( ) 2 1111 :0Pyaxbxca=++
( )P là parabol có đỉnh ( ) ( ) 1 0;11 IIPc−=− Hoành độ đỉnh ( )P : 1 1 1 00 2 I b xb a =−== . ( )P đi qua điểm ( ) 1111 2;33421 Babca =++= ( ) 2 :1Pyx=− Phương trình hoành độ giao điểm của ( )C và ( )P : 42242 1 211320 2 x xxxxx x
=
= Diện tích hình phẳng: 2 42 2 32d2,537Sxxx =−+ . Câu 26: Cho hàm số ( )yfx = liên tục và nhận giá trị không âm trên 1;2 và thỏa mãn ( ) ( ) 1,1;2.fxfxx=−− Đặt ( ) 2 1 1
d Sxfxx = , 2S là diện tích hình phẳng được giới hạn bởi đồ thị hàm số ( )yfx = , trục Ox và hai đường thẳng 1,2xx=−= . Khẳng định nào dưới đây là đúng? A. 12 2 SS = B. 12 3 SS = C. 12 2SS = D. 12 3SS = Lời giải Chọn C Ta có ( ) 2 1 1
d Sxfxx = Đặt 1dd txtx =−=− Đổi cận 12;21xtxt =−===− Suy ra ( ) ( )( ) 1 1 2
11d Stftt =−−− ( ) ( ) 2 1
dd ftttftt=− ( ) ( ) 22 11
1d tftt =− ( ) ( ) 22 11
dd fxxxfxx=− 21SS=− . Vậy 12 2SS = . Câu 27: Tính diện tích hình phẳng giới hạn bởi hai đường 2 4 yx=− ; 2 yx=− như hình vẽ bên dưới là
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
−+=−−+=
A. 9 2 S = . B. 33 2 . C. 9 2 . D. 33 2 . Lời giải

Chọn C Ta có phương trình hoành độ giao điểm 224220xxxx−=−−−= 1;2xx =−= . Dựa vào hình vẽ ( ) ( ) ( ) ( ) 22 22 11
9 242 2 Sxxdxxxdx =−−−=−++=
Câu 28: Cho hàm số ( ) ( ) 32 360;a,, fxaxbxxcabc =+−+ có hai điểm cực trị là 6 và 2. Gọi ( )ygx = là đường thẳng đi qua hai điểm cực trị của đồ thị hàm số ( )yfx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 160 B. 128. C. 64 D. 672 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
21
ọ
(
(
=+−+=+− Theo bài ta được ( ) ( ) ( ) ( ) ( ) (
2 2
20
fab f ab −=−+−−= = +−= 931 396 aba abb −−==+== ( ) ( ) 322636;31236fxxxxcfxxx =+−+=+− ; Đường thẳng đi qua hai điểm cực trị của hàm số ( ) ( ) 2 12 31236.32x24 33 yfxxxxc ==+−+−++ là ( ) 3224ygxxc ==−++ . Xét phương trình hoành độ giao điểm hai đồ thị 32 6 63632242 2 x xxxcxcx x =− +−+=−++=− = Vậy diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng
Ch
n B
)
) 322363236fxaxbxxcfxaxbx
)
60362.6360
322.2360
( ) ( ) ( ) ( ) 222 323232 662
636322464246424 Sxxxcxcdxxxxdxxxxdx =+−+−−++=+−−++−− 128=
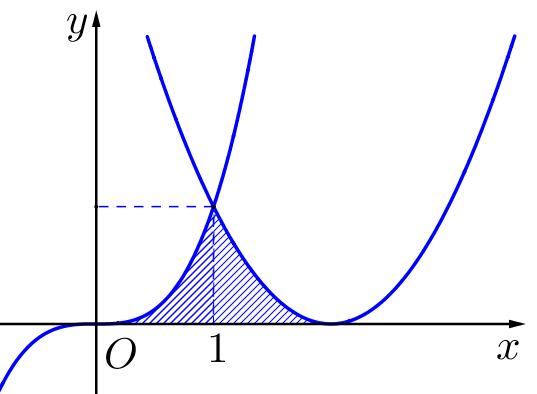
Câu 29: Cho hình ( ) H là hình phẳng giới hạn bởi đồ thị các hàm số 2 44yxx=−+ , đường cong 3 yx = và trục hoành. Tính diện tích S của hình ( ) H . A. 11 2 S = B. 7 12 S = C. 11 2 S =− D. 20 3 S = Lời giải Chọn B + Phương trình hoành độ giao điểm của 3 yx = và 2 44yxx=−+ 32 44xxx=−+ 32 440 1 xxx x −+−= = + Phương trình hoành độ giao điểm của 2 44yxx=−+ và trục hoành 2 4402xxx−+== + Diện tích hình phẳng cần tìm là ( ) 12
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
22
01
2 1 43 2 0 1 24 43
=+−+ 7 12 = Câu
Cho biết
phẳng giới
ạn
ở đó m n
32
d44d Sxxxxx =+−+
xx xx
30:
hình
h
bởi ba đường ln,1 yxyex ==+− và trục hoành có diện tích là
là phân số tối giản và , mn . Tổng mn + bằng A. 13. B. 12. C. 7 . D. 5. Lời giải Chọn D m S n =
Xét phương trình ln1xex =+− Ta thấy xe = là một nghiệm của phương trình Mặt khác hàm số ln yx = đồng biến trên ( ) 0; + ; hàm số 1 yex =+− nghịch biến trên ( ) 0; + . Do đó phương trình có nghiệm duy nhất xe = .
Xét phương trình 101 exxe +−==+
e eee e e e 3;25mnmn ==+= . Câu
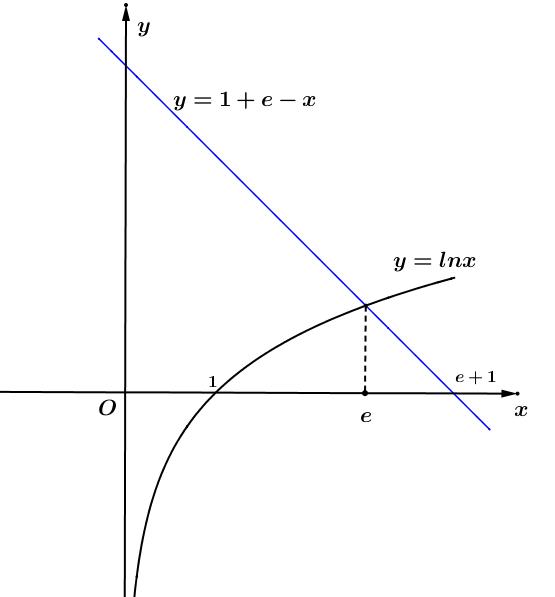
x Sxxexxxxxxexee + +
.
31: Cho hai hàm số ( ) 32 fxaxbxcxd =+++ , ( ) ( ) 2 ,,,,;0gxaxbxeabcdea =++ có đồ thị lần lượt là hai đường cong ( ) ( ) 12 , CC ở hình vẽ bên. Diện tích hình phẳng giới hạn bởi hai đồ thị ( ) ( ) 12 , CC bằng 8 3
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
Suy ra diện tích hình phẳng cần tìm là ( ) 1 1 2 1 11
lnd1d.lnd1113 222 =++−=−++−=++−−=

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 24 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Tính ( ) ( )21fg A. ( ) ( ) 2126fg−−=− B. ( ) ( ) 2124fg−−=− C. ( ) ( ) 2128fg−−=− D. ( ) ( ) 2130fg−−=− Lời giải Chọn C Ta có: ( ) 2 32 fxaxbxc =++ Dựa vào đồ thị, ta có: +) ( ) ( )( )313fxaxx =−− 6;9
=−= Ta
( ) ( )11
==− và ( ) ( ) 3 1 8 3414126618 3 17734 Sfxgxdxabcde abc =−=+++−= ++= 62 912 1773418 baa cab abcc =−= ==− ++== ( ) ( ) ( ) ( ) 322 2121818;212 214 114 fxxxxegxxxe fe ge =−++−=−+ =− −=+ ( ) ( ) 2128fg −−=−
baca
có:
fgdec
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 25 Chuyên luyện thi: Tuyển sinh
10 Tốt
THPT
11; 12 Sưu tầm và biên soạn Câu 32: Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng ( )2022;2022 sao cho bất phương ( ) ( ) 22 loglog1 0 21 xmx x có nghiệm? A. 4042 B. 2022 C. 2020 D. 2023 Lời giải Chọn A Điều kiện: ( ) ( ) 22 loglog10 0 10 210 xmx x x x −− − − ( ) ( ) 22 loglog10 11 0;;1 22 xmx x −− +)
(
−=
33: Cho hàm số ( ) 432 2 fxxaxbxcxd =++++ ( ) ,,, abcd có ba điểm cực trị là 1,1 và 3. Gọi ( )ygx = là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ( )yfx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 256 15 B. 265 15 C. 128 15 D. 182 15 Lời giải Chọn A Ta có ( ) ( )( )( ) ( ) 32 '8113833 fxxxxxxx =+−−=−−+ ( ) 432 28424 fxxxxxd =−−++
0984164935
vào lớp
Nghiệp
BDKT Toán 10;
TH1: Xét 1 0; 2 x
, khi đó 210 x − và
) ( ) ( ) ( ) 22 22 loglog1 210loglog10 xmx xmx x −−= ( ) 2 2 log10 log0 x xm −=
(v«nghiÖm) 2 log2m mxx == do 11 0;0212021;2020;...;2 22 m xmm −−−− +) TH2: Xét 1 ;1 2 x , khi đó 210 x − và 2 log(1)0 x − và ( ) ( ) ( ) ( ) 22 22 loglog10loglog10 21 xmx xmx x −− 22 log0log10;1;2;...;2021 xmmxmm −− Kết luận: Có 4042 giá trị. Câu
Ta có ( ) ( ) ( ) 2 1 '.18166 4 fxfxxxxd =−−+++ Giả sử ( ) , iii Axy là điểm cực trị của đồ thị hàm số ( )yfx = thì ( ) 2 8166iiii yfxxxd ==−+++
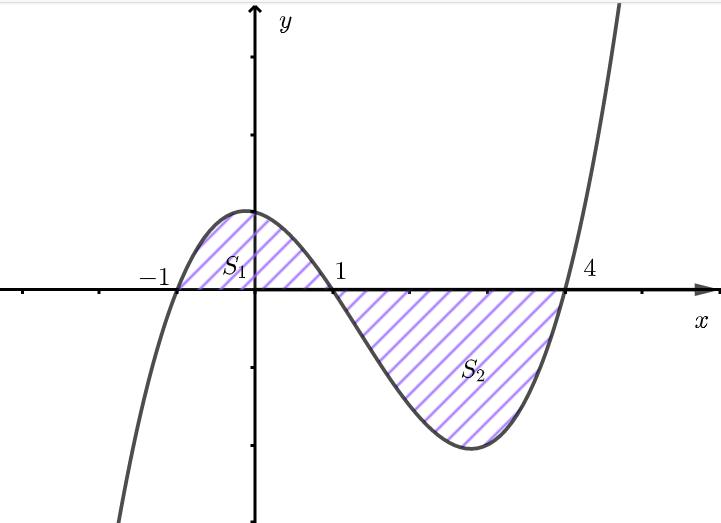
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
=−
n bởi hai đường ( )yfx = và ( )ygx = bằng ( ) ( ) 3 1 256 d 15 Sfxgxx =−= Câu 34: Cho hàm số ()yfx = có đồ thị như hình vẽ Biết diện tích hai phần gạch chéo lần lượt là 125,12SS== . Tính ( ) 10 03(21)4 Ifxdxfxdx =−++ A. 19 2 B. 29 2 C. 17 D. 7 Lời giải Chọn A Ta có 14 1112 ()5,()12 fxdxSfxdxS===−=− Vậy ( ) 1014 0311 (21)4()().5121119 222Ifxdxfxdxfxdxfxdx =−++=+=−=− Câu 35: Cho hàm số bậc ba ( )yfx = có đồ thị là đường cong ở hình bên dưới. Gọi 12 , xx lần lượt là hai điểm cực trị thỏa mãn 21 2 xx=+ và ( ) ( ) 1230.fxfx−= và đồ thị luôn đi qua 00 (;())Mxfx trong đó 01 1 xx=− ()gx là hàm số bậc hai có đồ thị qua 2 điểm cực trị và M. 0 1 1 xx=+ . Tính
Do đó đồ thị hàm số bậc hai qua ba điểm cực trị của đồ thị hàm số ( )yfx = là ( ) 2 8166 ygxxxd ==−+++ Khi đó ( ) ( ) 432 3 2848601 1 x fxgxxxxxx x = −=−++−==
Diện tích hình phẳng giới hạ
tỉ số 1 2
S S ( 1S và 2S lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai hàm (),()fxgx như hình vẽ ). A. 5 32 B. 6 35 C. 7 33 D. 4 29 Lời giải Chọn A Nhận thấy hình phẳng trên có diện tích không đổi khi ta tịnh tiến đồ thị sang trái sao cho 0 0 x = Khi đó ta có 121,3,xx== Xét hàm 32 () fxaxbxcxd =+++ và 2 g()xmxnxp =++ Vì 121,3,
27 xx== là các điểm cực trị nên ta có: (1)0320 (1)(3)02760 fabc fabc =++= =++= Hơn nữa, ta có (1)3(3)2793.(2) ffabcdabcd =+++=+++ Từ và suy ra 6 9 2 ba ca da =− = = Mặt khác dựa vào đồ thị ta thấy: (0)(0)2 (1)3(3)2 (0)(3)3 gfpa ggma ggna == ==− −=− Suy ra 32 ()(692) fxaxxx =−++ , 2 g()(262) xaxx=−++ Khi đó ta có: 1 32 1 0 5 43 12 Saxxxdxa =−+= 3 32 2 1 8 43 3 Saxxxdxa =−+= Do đó, 1 2 5 32 S S =

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Câu 36: Cho hai hàm số ( ) 32 1 2 fxaxbxcx=++− và ( ) 2 1 gxdxex=++ ( ) ,,,, abcde . Biết rằng đồ thị của hàm số ( )yfx = và ( )ygx = cắt nhau tại ba điểm có hoành độ lần lượt là 3; 1; 1
dd Sfxgxxgxfxx =−+− ( ) ( ) ( ) ( ) 11 3232 31 . Trong đó phương trình ( ) ( ) 32 3 0 2 axbdxcex+−+−−= ( )* là phương trình hoành độ giao điểm của hai đồ thị hàm số ( )yfx = và ( )ygx = . Phương trình ( )* có nghiệm 3; 1; 1 nên ( ) ( ) ( ) ( ) ( ) ( )
−+−−−−= −+−−−−= +−+−−=
abdce abdce abdce
abdce abdce abdce
33 dd 22 axbdxcexxaxbdxcexx =+−+−−−+−+−− 3 27930 2 3 0 2 3 0 2
−+−−−= −+−−−= +−+−=
3 2793 2 3 2 3 2
( ) ( ) ( ) ( ) ( ) ( )
= −= −=−
( ) ( )
a bd ce
1 2 3 2 1 2
. Vậy 11 3232 31
13131313 dd 22222222 Sxxxxxxxx =+−−−+−− ( ) 224=−−=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. 9 2 . B. 8. C. 4. D. 5. Lời giải Chọn C Diện tích hình phẳng cần tìm là ( ) ( ) ( ) ( ) 11 31
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 29
c Ox là: ( ) 0 20 2 x xx x = −= = . Do đó 2 2 2 0 4 2d 3 Sxxx=−= * Tính 1S Phương
m của của ( )
v
=
( ) 22 0 220 2 x mxxxxmx xm = =−+−= =− . Do đó ( ) ( ) 22 22 1 00 2d2d mm Sxxmxxxmxx =−−=−+− ( ) 2 2 3 0 2 32 m mx x =−+ ( )3 2 6 m = . * Khi đó 12 1 2 SS = nên ( )3 3 214 .24 623 m m ==− Câu 38: Hình phằng ( ) H được giới hạn bởi đồ thị ( )C của hàm đa thức bậc ba và parabol ( )P có trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 37: Gọi 1S là diện tích của hình phẳng giới hạn bởi đường thẳng ymx = và parabol ( )P : ( ) 2 yxx =− . Gọi 2S là diện tích hình phẳng giới hạn bởi ( )P và trục Ox . Với trị nào của tham số m thì 12 1 2 SS = ? A. 3 24. B. 3 22 + . C. 2 5 . D. 1 4 . Lời giải Chọn A * Tính 2S Phương trình hoành độ giao điểm của ( )P với trụ
trình hoành độ giao điể
P
ới đường thẳng ymx
là:
A. 37 12 . B. 7 12 . C. 11 12 . D. 5 12 . Lời giải
Chọn A
Giả sử ( ) ( ) 32 :0Cyaxbxcxda =+++
Vì ( )C đi qua các điểm ( ) ( )1;2,0;2AB , ( ) ( )1;0,2;2CD ,ta có hệ phương trình: ( ) 32
−+−+=−= ==− =−+ +++== +++=−=
21 23 :32 00 84222
abcda db Cyxx abcdc abcdd
Giả sử ( ) ( ) 2 :0Pymxnxqm=++
Vì ( )P đi qua các điể
.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
30
D
thị của ( )C và( )P ,ta có diện tích hình phẳng cần tìm là: ( ) ( ) 12 322232 11 12 3232 11 3232 37 2222. 12 hp Sxxxxdxxxxxdx xxxdxxxxdx =−+−−++−+−−+= =−−++−++−= Câu 39: Cho hàm số 2x y = có đồ thị ( )C Diện tích miền phẳng giới hạn bởi các đường ( )C , tiếp tuyến của đồ thị hàm số 3 2 8 33 x yx=−+ tại điểm ( )1;2 M và đường thẳng 1 y = là: A. 11 ln22 S =− . B. 1 1 ln2 S =+ . C. 47 50 S = . D. 1 3 ln2 S =+ . Lời giải
m ( ) ( )1;2,1;0AE , ( )2;2 D ,ta có hệ phương trình: ( ) 2 21 01: 4220 mnqm mnqnPyxx mnqq −+=−=− ++===−+ ++=−= .
ựa vào đồ
x x x Sxxxxx =−+−+−=−+−+=−

211 21d31d2 ln22ln22
Phương trình tiếp tuyến của đồ thị hàm số 3 2 8 33 x yx=−+ tại điểm ( )1;2 M là ( )( ) ( ) 1113yyxyx =−+=−+ Xét phương trình hoành độ giao điểm của các đường. Ta có: +) 231 x xx =−+= +) 210 x x == +) 312xx −+== Diện tích cần tìm là: ( ) ( ) 12 12 2 01 01
Câu 40: Cho hàm số ( ) 432 6 ==++++ yfxxaxbxcxd ( ) ,,, abcd . Biết đồ thị hàm số ( )yfx = có ba điểm cực trị có hoành độ lần lượt là 2;1;2 và hàm số ( )ygx = là hàm bậc hai có đồ thị đi ba điểm cực trị đó. Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = thuộc khoảng nào sau đây? A. ( )71;72 B. ( )72;73 C. ( )73;74 D. ( )74;75 Lời giải Ch
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 31
ọn D Ta có ( ) 32 ''2432 ==+++ yfxxaxbxc. Do đồ thị hàm số ( )yfx = có ba điểm cực trị có hoành độ 2;1;2 nên phương trình ( ) '0fx = có ba nghiệm phân biệt 2;1;2 Suy ra ( ) ( )( )( ) ( ) 32 '24212'24249696 fxxxxfxxxx =+−−=−−+ ( ) 432 684896 fxxxxxd =−−++
( ) 2 4322 2 6848962664874,63. =−−++−−+++ xxxxdxxddx
Câu 41: Cho hai hàm số ( ) = yfx và ( ) = ygx liên tục trên . Biết hàm số ( ) 32 =+++ fxaxbxcxd , ( ) 2 =++ gxpxqxr với ,0 ap có đồ thị như hình vẽ. Đồng thời diện tích giới hạn bởi hai đồ thị hàm số ( ) = yfx và ( ) = ygx bằng 2 và ( ) ( ) 111 −=−+fg . Biết rằ

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Ta có ( ) ( ) ( ) 22 11 '2664826648 412 fxxfxxxdgxxxd =−−+++=−+++ . Vậy diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = là ( ) ( ) 2 2 Sfxgxdx =− ( )
phẳng giới hạn bởi hai đồ thị hàm số ( ) = yfx và
ằ
ị
ằ
A. 28. B. 29. C. 30. D. 31. Lời giải Chọn D Dựa vào đồ thị ( ) ( ) ( )( )21 −=++fxgxaxxx và 0 a Theo đề ( )( ) ( )( ) 00 22 21d21d Saxxxxaxxxx =++=++ 1 2.4 2 aa == . Ta có: ( ) ( ) ( )( ) d421d fxgxxxxxx −=++ ( ) ( ) 432 44 fxgxxxxC −=+++ Theo đề: ( ) ( ) ( ) ( ) 111111fgfg −=−+−−−= 11440 CC =−++=
ng diện tích hình
( ) = ygx b
ng m n . Giá tr
+ mn b
ng:
=− +−= = . Diện tích hình phẳng cần tìm là 1 42 1
64 23d 15 Sxxx =+−= .
Câu 43: Cho hàm số 432 ()3(,,,) fxxaxbxcxdabcd =++++ có ba điểm cực trị là 2, 1 và 1. Gọi 32 ()(,,,) gxmxnxpxqmnpq =+++ là hàm số đạt cực trị tại điểm 2 và có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ()yfx = . Diện tích hình phẳng giới hạn bởi hai đường ()yfx = và ()ygx
16 2d 15 m Sxxx n =+== Vậy giá trị 31 mn+= . Câu 42: Cho số ( )yfx = có đạo hàm là ( ) 2 124, fxxx =+ và ( )Fx là một nguyên hàm của ( )fx , ( ) ( ) 010fF== . Tính diện tích hình phẳng S giới hạn bởi đồ thị hàm số ( )yFx = và trục Ox . A. 64 15 S = . B. 116 15 S = . C. 576 5 S = . D. 32 15 S = . Lời giải Chọn A +) Ta có ( ) ( ) ( ) 23 1 d124d44 fxfxxxxxxC ==+=++ . Do ( ) 00 f = nên 1 0 C = , suy ra ( ) 3 44 fxxx =+ ( ) ( ) ( ) 342 2 d44d2 FxfxxxxxxxC ==+=++ Do ( ) 10 F = nên 2 3 C =− , suy ra ( ) 4223Fxxx=+− +) Xét phương trình 42 1 230 1 x xx x 87 321 5 Sfxgxdxxxdx =−=+−=
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn =
b
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
33
( ) ( ) ( ) ( )2 432222 44442 fxgxxxxxxxxx −=++=++=+ Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ( ) = yfx và ( ) = ygx ( ) 0 2 2 2 ằng A. 87 5 B. 81 5 C. 79 5 D. 78 5 Lời giải Chọn A Vì ()gx là hàm số đạt cực trị tại điểm 2 và có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ()yfx = nên phương trình ()()0fxgx có nghiệm 2; 1;1 Suy ra 2 2 ()321fxgxxx ( ) ( ) ( ) ( ) 11 2 2 22
Câu 44: Cho hàm số 432 ()3(,,,) fxxaxbxcxdabcd =++++ có ba điểm cực trị là 2, 1 và 1. Gọi 32 ()(,,,) gxmxnxpxqmnpq =+++ là hàm số đạt cực trị tại hai điểm 2 và 1 và có đồ thị đi qua hai điểm cực trị với hoành độ 2 và 1 của đồ thị hàm số ()yfx = . Diện tích hình phẳng giới hạn bởi hai đường ()yfx = và ()ygx = bằng A. 175 5 B. 243 10 C. 258 10 D. 132 5 Lời giải Chọn B Vì ()gx là hàm số đạt cực trị tại điểm 2;1 và có đồ thị đi qua hai điểm cực trị với hoành độ 2 và 1 của đồ thị hàm số ()yfx = nên phương trình ()()0fxgx có nghiệm 2; 1 Suy ra ( ) ( ) 22()()321 fxgxxx −=+− . Vậy diện tích hình phẳng cần tìm là ( ) ( ) ( ) ( ) 11 22 22
243 321. 10 Sfxgxdxxxdx =−=+−=
Câu 45: Cho hàm số ( ) ( ) 432 ,,, fxxaxbxcxdabcd =++++ có ba điểm cực trị là 1,1,2. Hàm số ( ) ( ) 32 ,,, gxmxnxpxqmnpq =+++ là hàm số đạt cực trị tại 1;1 và và có đồ thị đi qua hai điểm cực trị có hoành độ 1;1của đồ thị hàm số ()yfx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 15 16 B. 36 5 C. 2932 405 D. 16 15 Lời giải Chọn D Vì ()gx là hàm số đạt cực trị tại điểm 1;1 và có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ()yfx = nên phương trình ()()0fxgx có nghiệm 1; 1. Suy ra 22()11fxgxxx ( ) ( ) ( ) 11 2 2 2
16 1 15 Sfxgxdxxdx =−=−= Câu 46: Cho hàm số 32 ()4 fxaxbxcx=+++ và 2 () gxmxnx =+ có đồ thị cắt nhau tại các điểm có hoành độ là 1;1;2. Diện tích của hình phẳng giới hạn bởi đồ thị của hai hàm số trên bằng A. 9 4 B. 9 2 C. 37 12 D. 37 6 Lời giải Chọn D Do hàm số ()fx và ()gx có đồ thị cắt nhau các điểm có hoành độ là 1;1;2, nên ()() fxgx là hàm số bậc ba. Suy ra ta có: ()().(1)(1)(2) fxgxkxxx −=+−− Mặt khác ta có: (0)(0)42 fgk−== 32 ()()2(1)(1)(2)2424 fxgxxxxxxx −=+−−=−−+ Vậy ta có diện tích là:
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 34

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 35
22 32
hình vẽ sau: Biết 5 AB = , diện tích hình phẳng giới hạn bởi đồ thị
số
=
ục
thẳng 1 x = , 2 x = bằng A. 17 11 . B. 19 12
=+−+= Mặt khác ( )( ) 322 12axbxxcaxx +−+=−− 323222 axbxxcaxaxaxa +−+=−−+ , Đồng nhất hệ số ta đươc 1 a = , 2 b =− , 2 c = . Vậy ( ) 32 1 22 3 yfxxxx ==−++ . Diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = , trục hoành và hai đường thẳng 1 x = , 2 x = bằng 2 32 1 119 22d. 312 Sxxxx =−++= Câu 48: Cho đồ thị hàm số ( )yfx = và ( )ygx = như hình vẽ bên dưới
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
11 ()()2424d Sfxgxdxxxxx =−=−−+
12 3232 11 16537 (2424)d(2424)d366 xxxxxxxx =−−+−−−+=+=
Câu 47: Cho đồ thị hàm số bậc ba ( ) 32 1 3 yfxaxbxxc ==+++ và đường thẳng ( )ygx = có đồ thị như
hàm
( )yfx
, tr
hoành và hai đường
. C. 5 12 . D. 7 11 . Lời giải Chọn B Gọi ( ) ( )0 gxmxm= . Ta có ( ) 1; Am ; ( ) 2;2 Bm Khi đó ( ) ( ) 2 4 9953 4 3 mtm ABm ml = =+= =− Ta có ( ) ( ) 32 0 fxgxaxbxxc
Biết đồ thị của hàm số ( )yfx = là một Parabol đỉnh I có tung độ bằng 1 2 và ( )ygx = là một hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là 123 ,, xxx thỏa mãn 123..6xxx =− . Diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số ( )yfx = và ( )ygx = gần nhất với giá trị nào dưới đây? A. 6 B. 8 C. 5 D. 7 Lời giải
1 0 2 1 4201. 2 0 41 42
= ++==−=− = =− Giả sử ( ) 32 gxaxbxcxd =+++ thì đồ thị của nó đi qua 1 1; 2 I và có a abcd c b gxxx abc c d xxx d a
= 11 28 03133 8 1240884 0 ..63 4
a c abcbfxxx c acb a 2 cực trị có hoành độ bằng 0 và 2, tức là phương trình ( ) 2 320gxaxbxc =++= có 2 nghiệm là 0 và 2 Kết hợp với giả thiết ta có hệ phương trình ( ) 32 123
=− +++=− = = =−+− ++= = =−=− =− Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 36
Chọn A Gọi phương trình của Parabol là 2 yaxbxc =++ , từ dữ kiện đề bài ta có hệ phương trình ( ) 2 2
. Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng A. 316 15 . B. 191 9 . C. 253 12 . D. 97 6 . Lời giải Chọn C Xét phương trình hoành độ giao điểm của hàm số ( )yfx = và ( )ygx = : ( ) ( ) ( ) 32 60 hxaxbdxcex=+−+−−= Hàm số ( )yfx = và ( )ygx = cắt nhau tại 3 điểm có hoành độ lần lượt là 3;1;2 nên ( ) ( )( )( ) 3120hxaxxx=++−= . Xét ( ) ( ) 06.3.1.261 haa =−−=−= Vậy hàm số: ( ) ( )( )( )312hxxxx =++− Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng: ( ) ( )( )( ) 22 33
253 d312 12 Shxxxxx ==++−= . Câu 50: Cho hàm số 43 ()22 fxaxxx=−++ và hàm số 32 ()2 gxbxcx=−+ , có đồ thị như hình vẽ bên. Gọi 12 ; SS là diện tích các hình phẳng gạch chéo trong hình vẽ, biết 1 221 640 S = . Khi đó 2S bằng:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 37 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 232 1 2 3 1133 2884 17 1 17 xxxx x x x −=−+− =−− = =−+ Vậy diện tích hình phẳng giới hạn bởi 2 đồ thị hàm số ( )yfx = và ( )ygx = bằng ( ) ( ) ( ) ( ) 117 1 17 1173232 1 17 dd 33 dd 884884 6,22. Sfxgxxgxfxx xxxx xxxx −+ −+ =−+− =+−++−−+− Câu 49: Cho hai hàm số ( ) 32 4 fxaxbxcx=++− và ( ) ( ) 2 2,,,,, gxdxexabcde =++ .Biết rằng đồ thị hàm số ( )yfx = và ( )ygx = cắt nhau tại 3 điểm có hoành độ
ần
l
lượt là 3;1;2

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42
Cư Trinh Thuận
TP Huế ĐT:
Page 38 Chuyên
thi:
10 Tốt
Sưu tầm và biên soạn A. 1361 640 . B. 271 320 . C. 571 640 . D. 791 640 . Lời giải Chọn D Từ đồ thị ta thấy hoành độ giao điểm của đồ thị hàm số ()gx với trục hoành chính là điểm cực trị của hàm số ()
. Do
=
−+=−+ Suy
1
3 k ba c = = = .
=++++ thỏa
=
hàm số ( ) ( ) 2 1 fx gx x = + . Biết đồ thị
ố
=
( ) ( ) 0;0Bg , ( ) ( ) 1;1Cg . Gọi ( )yhx = là hàm số bậc hai có đồ thị qua ba điểm ,
và ( )2,5Db + . Diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = và ( ) ( ) 2 11yxhxx =++− bằng A. 44 15 . B. 56 15 . C. 46 15 . D. 64 15 . Lời giải Chọn A ( ) 32 '432 xxaxbxc f =+++ ( ) 2 ''1262 f xxaxb =++
Nguyễn
Hòa
0984164935
luyện
Tuyển sinh vào lớp
Nghiệp THPT BDKT Toán 10; 11; 12
fx
đó: ().() fxkgx
. Hay: ( ) 3232 4322 axxkbxcx
ra:
3
Hay: 32 ()432 gxaxx=−+ , suy ra: ( ) 4332432 ()()224321432 fxgxaxxxaxxaxaxxx −=−++−+−=−+++ Khi đó: ( ) 1 2 1 0 ()() Sfxgxdx =− ( ) ( ) 1 2 432 0 2211 1432 6404 axaxxxdxa =−+++== Vậy 2 43 2 3 2 1791 22. 4640 Sxxxdx =−++= Câu 51: Cho hàm số ( ) ( ) 432 ,,, fxxaxbxcxdabcd
mãn ( ) 1 min'''' 4 ff x
và
hàm s
( )ygx
có ba điểm cực trị là ( ) ( ) , Amgm ,
AC
Cg
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 39
Vì ( ) 1
x
=
=− . (
2 2 2 1'2.
gx x +− = + đồ
ị
ố
=
== = += ==
( )ygx = có điểm cực trị là (
(
thị
số ( )
32 2 2 '
22
yxxb x x −+ ===−+ +
Mà
+
=++−−= Câu 52: Cho hai hàm số ( ) 432 3 fxaxbxcxx =+++ và ( ) 32 gxmxnxx =+− với ,,,, abcmn . Biết hàm số ( ) ( )yfxgx =− có ba điểm cực trị là 3;1 và 4. Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 935 36 . B. 941 36 . C. 937 36 . D. 939 36 . Lời giải Chọn C Vì ( ) 432 3 fxaxbxcxx =+++ và ( ) 32 gxmxnxx =+− nên hàm số ( ) ( )yfxgx =− có bậc lớn nhất là bậc 4. Mặt khác hàm số ( ) ( )yfxgx =− có ba điểm cực trị là 3;1 và 4.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
min'''' 4 ff
nên 1 a
) ( ) ( ) ( ) ( )
' 1 xfxxfx
th
hàm s
( )ygx
có ba điểm cực trị là ( ) ( ) , Amgm , ( ) ( ) 0;0Bg , ( ) ( ) 1;1
nên ( ) ( ) ( ) ( ) ( ) '00'000 '10'111 gf c bd gff
Suy ra ( ) ( ) 432432111 fxxxbxbxxxb =−+++=−+++ Lại có đồ thị hàm số
)
) , Amgm , ( ) ( ) 1;1Cg nên , AC thuộc đồ
hàm
( )
4323 2
1' fx xxbx
.
( )2;5Db
cũng thuộc đồ thị hàm số trên nên hàm số ( )yhx = có phương trình dạng 2 3 2 2 yxxb =−+ . Phương trình hoành độ giao điểm của đồ thị hàm số ( )yfx = và ( ) ( ) 2 11yxhxx =++− : ( ) ( ) 43222 3 11121 2 xxxbxxxbx −+++=+−++− 432111 20 221 x xxxx x = ++−−= =− . Diện tích hình phẳng cần tìm 1 432 1 1144 2d 2215 Sxxxxx
do là 4, vậy 1 3 k = .
Do đó: ( ) ( ) ( )( )( ) 1 314 3 fxgxxxx −=+−− .
Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = là: ( ) ( ) ( )( )( ) 44
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 40
=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó ( ) ( )yfxgx
có đúng ba nghiệm đơn 3;1 và 4 Suy ra ( ) ( ) ( )( )( )314fxgxkxxx −=+−− Từ dạng hàm số ( )fx và ( )gx suy ra ( ) ( )fxgx có hệ số tự
33 1 d314d 3 Sfxgxxxxxx =−=+−− ( )( )( ) ( )( )( ) 14 31 11937 314d314d 3336 xxxxxxxx =+−−−+−−= Câu 53: Cho hàm số ( )yfx = xác định và liên tục trên đoạn 3;3 . Biết diện tích hình phẳng 12 , SS giới hạn bởi đồ thị hàm số ( )yfx = và đường thẳng 1 yx=−− lần lượt là , Mm . Tính tích phân ( ) 3 3 fxdx bằng? A. 6 mM+− . B. 6 mM . C. 6 Mm−+ . D. 6 mM . Lời giải Chọn D ( ) ( ) ( ) ( ) ( ) 1111 3333 11 MxfxdxMxdxfxdxfxdxM =−−−=−−−=− ( ) ( ) ( ) ( ) ( ) 3333 1111 116 mfxxdxmxdxfxdxfxdxm =++=++=− 313 331 ()()()6 fxdxfxdxfxdxMm =+=−+− .
2019. B. 2020. C. 2021. D. 2018 Lời giải Ta có 2221(1)22 xxxxR +−=+−− ; dấu bằng xảy ra khi 1 x =− Suy ra 2 213[0;1]xxx+−− và vì [4040;3] m−− nên:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
( ) ( ) ( ) 11 22 00 11 2 00 2121 1 21 3 Sxxmdxxxmdx xxdxmdxm =+−−=+−− =+−−=− 16062 20212021. 33 Smm − {2020;.....;3} m −− Vậy
ị
ủ
ọ
;
=
Vậy ( ) 11 22 00 21x21x Sxxmdxxmd =+−−=+−− . 1 3 2 0 1 x 33 x Sxxmm =+−−=− . Thỏa mãn yêu cầu 4040;3 1 20213 3 1 2021 3 m m m m m −− −− − . Vậy có 2018 giá trị m . Câu 56: Cho ( ) ( ) 32 0 fxaxbxcxda =+++ là hàm số nhận giá trị không âm trên đoạn 2;3 có đồ thị ( )fx như hình vẽ. Biết diện tích hình phẳng giới hạn bởi các đồ thị của các hàm số ( ) ( ) 2 gxxfx = ; ( ) ( ) ( ) 2 hxxfxfx =− và các đường thẳng 2;3xx== bằng 72. Tính ( )1 f
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
41 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 54: Gọi S là diện tích hình phẳng giới hạn bởi parabol 2 21yxx=+− và các đường thẳng ;0;1ymxx=== . Có bao nhiêu giá trị nguyên của tham số [4040;3] m−− để 2021 S A.
có 2018 giá tr
nguyên c
a m Câu 55: Goị S là diện tích hình phẳng giới hạn bới parabol 2 21yxx=+− và các đường thẳng ym = ; 0 x = ; 1 x = . Có bao nhiêu giá trị nguyên của tham số 4040;3 m−− để 2021 S A. 2019 B. 2020 C. 2021 D. 2018 Lời giải Ch
n D S là diện tích hình phẳng giới hạn bới parabol 2 21yxx=+− và các đường thẳng ym = ; 0 x =
1 x
;

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 42 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. ( ) 12 f = . B. ( ) 11 f =− . C. ( ) 11 f = . D. ( ) 62 1 5 f = . Lời giải Chọn A Từ hình vẽ ta có được ( ) ( ) ( ) 232 32363 fxxxxxfxxxC =−=−=−+ . Diện tích hình phẳng là: ( ) ( ) ( ) ( ) ( ) 33
d32224 2222 SxfxxxfxffCC ===−=−− Mà ( )2 2 4 9 72247252 2 5 C SCC C = =−−= = Do ( ) ( ) ( ) 32 0,2;33412fxxfxxxf=−+= . Câu 57: Cho hình phẳng D được giới hạn bởi các đường 2 2;yxx =− 1; y = yx = , như hình vẽ. Diện tích của D là A. 782 6 + B. 722 6 C. 722 6 + D. 732 6 Lời giải Chọn A
22 22 dd Sgxhxxxfxxfxfxx =−=+ Do ( ) ( ) ( ) 22 0,2;3xfxxfxfxx + nên ( ) ( ) ( ) 3 22 2 d Sxfxxfxfxx =+ Ta có: ( ) ( ) ( ) ( ) ( ) 3 3 2 2222222 2 2 1199
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 43 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Xét phương trình hoành độ giao điểm: i) 2 12 21 12 x xx x =+ −= =− ii) 22 3 230 0 x xxxxx x = −=−= = . iii) 1 x = . Ta có: ( ) ( ) 112 22 01 2d12d Sxxxxxxx + =−−+−− ( ) ( ) 112 22 01 3d21d xxxxxx + =−++−++ ( ) ( ) 112 22 01 3d21d xxxxxx + =−++−++ 112
131 323 xxxxx + =−++−++ 742
=+ 782 6 + = . Vậy 782 6 S + = . Câu 58: Cho hai hàm đa thức ( ) 32 fxaxbxcxd =+++ và ( ) 2 gxmxnxp =++ . Biết rằng đồ thị hai hàm số ( )yfx = và ( )ygx = cắt nhau tại ba điểm có hoành độ lần lượt là 1;2;4 đồng thời cắt trục tung lần lượt tại , MN sao cho 6 MN = .
3232 01
63
Hình phẳng giới hạn bởi đồ thị hai hàm số đã cho có diện tích bằng A. 125 8 B. 253 24 C. 253 16 D. 253 12 Lời giải Chọn C Phương trình hoành độ giao điểm của đồ thị ( )yfx = và ( )ygx = là: ( ) ( ) 32232 0 axbxcxdmxnxpaxbmxcnxdp +++=+++−+−+−= Do đồ thị hai hàm số ( )yfx = và ( )ygx = cắt nhau tại ba điểm có hoành độ lần lượt là 1;2;4 nên ta được ( )( )( ) ( ) ( ) 32 124 axxxaxbmxcnxdp +−−=+−+−+− . Mà ( ) ( ) 006 Mn fgyyMN −=−== . Suy ra 3 4 a = . Do đó: ( ) ( ) ( )( )( ) 3 124 4 fxgxxxx −=+−− Khi đó: ( ) ( ) ( )( )( ) 44 11
3253 124 416Sfxgxdxxxxdx =−=+−−= Câu 59: Cho hàm số x ye = có đồ thị ( )C . Diện tích hình phẳng giới hạn bởi ( )C , tiếp tuyến của ( )C tại điểm ( ) 1; Me và đường thẳng 1 yx e =− bằng A. 1 21 2 e e B. 24 33 e e C. 3 1 22 e e −+ D. 3 22 e e −+ Lời giải Chọn D Ta có phương trình tiếp tuyến của ( )C tại điểm ( ) 1; Me là ( )( ) 11. yyxeex =−+= .
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 44
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
giải Chọn D Phương trình hoành độ giao điểm: ( )( )( ) 322 1 13110 2 ++−=++++−= axbxcxdxexaxxx . Ta có: ( ) ( ) ( )( )( ) 32 3 311 2 +−+−−=++− axbdxcexaxxx Cho 0 x = ta có: 31 3 22 aa −=−= . Khi đó: diện tích cần tìm là: ( )( )( ) 1 3
1 3114 2 Sxxxdx =++−= . Câu 61: Cho đường cong ( )C 3 827 yxx =− và đường thẳng ym = cắt ( )C tại hai điểm phân biệt nằm trong góc phần tư thứ nhất của hệ tọa độ Oxy và chia thành hai miền phẳng có diện tích 12SS = như hình vẽ dưới. Mệnh đề nào sau đây đúng?


CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 45 Chuyên
thi: Tuyển sinh vào
10 Tốt
THPT BDKT
11; 12 Sưu tầm và biên soạn Xét phương trình 1 .1;1xx eexxexx e ===−=− và 1 .0 exxx e =−= . Từ đồ thị ta có ( ) 01 2 10 1101 d.d. 1022 xxxx e Sexxeexxexex ee =++−=++−
=
ắt
phẳng giới hạn bởi 2 đồ thị
cho
ằ
0984164935
luyện
lớp
Nghiệp
Toán 10;
113 11 2222 ee e eee =−−+−−=− Câu 60: Cho hai hàm số ( ) 32 1 2 fxaxbxcx=++− và ( ) 2 1 gxdxex=++ (,,,,) abcde . Biết rằng đồ thị hàm số ( )yfx = và ( )ygx
c
nhau tại 3 điểm có hoành độ lần lượt là 3; 1; 1. Hình
đã
có diện tích b
ng A. 8 B. 5 C. 9 2 D. 4 Lời

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 46 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 1 0 2 m . B. 1 1 2 m . C. 3 1 2 m . D. 3 2 2 m . Lời giải Chọn C Giả sử đường thẳng ym = cắt đồ thị ( )C tại điểm có hoành độ ( ) ,0 abab Ta có: 3 3 827 827 aam bbm −= −= . Phương trình hoành độ giao điểm: 33 8278270 xxmxxm −=−−= Xét hàm số 3 ()827 fxxxm =−− có ( ) 24 27 ()d4 4 FxfxxxxmxC ==−−+ Lại có: 1 00 ()d()d(0)() aa SfxxfxxFFa ==−=− . 2 ()d()d()() bb aa SfxxfxxFbFa ===− . Theo bài 12 (0)()()()()(0) SSFFaFbFaFbF =−=−= . Vì vậy ( ) 24 27 40 4 Fbbbmb =−−= Do đó 4 2 3 27 40 4 827 b bmb bbm −−= −= 4 9 32 27 b m = = . Chọn đáp án C. Câu 62: Cho đường thẳng yxa =− và đồ thị hàm số yx = . Gọi 12 , SS lần lượt là diện tích hai hình phẳng được gạch chéo trong hình vẽ bên. Khi 12 5 3 SS = thì a thuộc khoảng nào dưới đây? A. 58 ; 23 B. 39 ; 25 C. 95 ; 52 D. 23 ; 32 Lời giải Xét phương trình tương giao giữa đường thẳng yxa =− và hàm số yx = ta có:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 47 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 0 xaxxxa −=−−= ( 0 x ) 2 1111 112424 241111 0(0) 2424 xaxa xa xaxadoa −=+=++ −=+ −=−+=−+ 2 1111111 2444424 xaaaaab =++=++++=+++= Ta có: 21222 000 58 33 bbb xdxSSxdxSSxdxS −==+= ( ) 22 2 2828 . 333322 b a ba bbxadxbbaba =−=−−− ( ) ( ) 2 1 4..2.(0) 2 bbbabbadobba =−=−=− 2 ba= 1111 2 2424 aaaaa +++=−=+ 2 2 11 0 22 2 11 2 44 a a a aaa aa − = −+=+ = Vậy 95 2; 52 a = Câu 63: Tính diện tích S của hình phẳng giới hạn bởi đồ thị hai hàm số 3 33yxx=++ và 2 53yxx=++ Lời giải Ta có 3232 0 3353201 2 x xxxxxxxx x = ++=++−−==− = . ( ) ( ) ( ) ( ) 2202 32323232 1110 02 4343 22 10 3353d2d2d2d 37 . 434312 Sxxxxxxxxxxxxxxxxx xxxx xx =++−++=−−=−−−−− =−−−−−=


CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 48 Chuyên
10
12
tầm và
soạn Câu 64: Diện tích của hình phẳng giới hạn bởi đồ thị của hàm số 2 4 yx=− và đường thẳng 24yx=− bằng A. 36 B. 36 C. 4 3 D. 4 3 Lời giải Chọn C Phương
22
2 x xxxx x = −=−−= = . Diệ
tích
phẳng
ần tính là ( ) 22 22 00 2d2d Sxxxxxx =−=−− 2 3 2 0 4 33 x x =−−= Câu 65: Cho đồ thị ( ) ( ) : Cyfxx == . Gọi ( ) H là hình phẳng giới hạn bởi đồ thị ( )C , đường thẳng 9 x = và trục Ox . Cho điểm M thuộc ( )C và điểm (
9;0
. Gọi 1V
ể
ố
( )
trục Ox
trục Ox .
ết rằ
=
ng thẳng OM A. 4 3 . B. 273 16 . C. 3. D. 33 2 . Lời giải Chọn B Ta có: 9 1 0 81 .d 2 Vxx ==
Hòa
0984164935
luyện thi: Tuyển sinh vào lớp
Tốt Nghiệp THPT BDKT Toán 10; 11;
Sưu
biên
trình hoành độ giao điểm đồ thị hàm số 2 4 yx=− và đường thẳng 24yx=− là
0 42420
n
hình
c
)
A
là th
tích kh
i tròn xoay khi cho
H quay quanh
, 2V là thể tích khối tròn xoay khi cho tam giác AOM quay quanh
Bi
ng 12 2 VV
. Tính diện tích S phần hình phẳng giới hạn bởi đồ thị ( )C và đườ
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 49 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Giả sử ( ) ; Maa , ta có 2 2 11 ..93 33 VMHOAaa === 12 2 VV = 81 6 2 a = 27 4 a = Suy ra 2733 ; 42 M , Phương trình đường thẳng OM là 23 9 yx = Diện tích
=−=−=
, SS lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi 12SS = thì a thuộc khoảng nào sau đây A. 3 0; 16 . B. 37 ; 1632 . C. 19 ; 432 . D. 71 ; 324 . Lời giải Chọn B Phương trình hoành độ giao điểm 2 31 42 xxa =+ 2213 02340 24 xxaxxa −+=−+= Ta có: 932a =− , theo giả thuyết 9 00 32 a Khi đó hoành độ giao điểm là 1 2 3932 4 3932 4 a x a x = +− = Ta có 12 1 22 12 0 1331 2442 xx x SSxaxdxxxadx =+−=−−
cần tính là 27 27 24 4 0 0 23223273 d. 939216 x Sxxxxx
Câu 66: Cho đường thẳng 3 4 yx = và parabol 2 1 2 yxa =+ , Gọi 12
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 50 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 12 1 3223 0 33 6886 xx x xxxx axax +−=−− 322323 112211 121 333 688686 xxxxxx axaxax +−=−−−++ 23 22 2 3 0 86 xx ax −−= 2 22 3 0 86 xx a −−= ( )2 3932 93932a 0 3296 a a +− +− −−= 27993296932932960 aaaa +−−−−−+−= 3932649 aa −=−
aa −=−+ 2 0 40968640 27
a aa a = −= =
Chọn D Ta có ( ) ( )fxgx là hàm bậc 4 nên ( ) ( ) 432 4 fxgxAxBxCxx −=+++ ( ) ( ) 32 4324fxgxAxBxCx −=+++ . Hàm số ( ) ( )yfxgx =− có ba điểm cực trị là 1; 3 và 4 nên ta có hệ phương trình: 1 12 43240 2 10827640 3 25648840 5 6 A ABC ABCB ABC C = −+−+= +++== +++= = ( ) ( ) 32 15 24 33 fxgxxxx −=−++ Diện tích của hình phẳng giới hạn bởi hai đồ thị hàm số ( )yfx = và ( )ygx = bằng
2 8128840961152a81
128
Do a là số thực dương nên 2737 ; 1281632 a = Câu 67: Cho hai hàm số ( ) 432 3 fxaxbxcxx =+++ và ( ) 32 gxmxnxx =+− ; với ,,,, abcmn . Biết hàm số ( ) ( )yfxgx =− có ba điểm cực trị là 1; 3 và 4. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ( )fx và ( )ygx = bằng A. 32 3 . B. 64 9 . C. 125 12 . D. 131 12 . Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
51
4 32 1 15131 24d 3312 Sxxxx =−++=
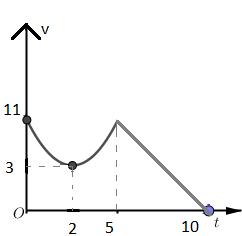



CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 3. ỨNG DỤNG
MỨC ĐỘ VẬN DỤNG VẬN DỤNG CAO Câu 68: Chất điểm chuyển động theo quy luật vận tốc ( )( ) / vtms có dạng đường Parapol khi ( ) 05ts và ( )vt có dạng đường thẳng khi ( ) 510ts .Cho đỉnh Parapol là ( )2,3 I . Hỏi quãng đường đi được chất điểm trong thời gian ( ) 010ts là bao nhiêu mét? A. 181 2 B. 90 C. 92 D. 545 6 Lời giải Chọn D Gọi Parapol ( ) 2 : Pyaxbxc =++ khi ( ) 05ts Do ( ) 2 : Pyaxbxc =++ đi qua ( ) ( )3;2;0;11IA nên 4232 118. 4011 abca cb abc ++== ==− +== Khi đó quãng đường vật di chuyển trong khoảng thời gian từ ( ) 05ts là ( ) ( ) 5 2 0 115 2811 3 Sxxdxm =−+= Ta có ( ) 521 f = Gọi : dyaxb =+ khi ( ) 510ts do d đi qua điểm ( )5;21 B và ( )10;0 C nên: CHƯƠNG III NGUYÊN HÀM TÍCH PHÂN ỨNG DỤNG TÍCH PHÂN
0984164935
TÍCH PHÂN
lái
p phanh, từ thời điểm đó ô tô chuyển động ch
m d
đề
i v
n t
52040 stdtm =−+= .
c ( ) ( ) 520/ vttms =−+ , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét ( m )? A. 20 m. B. 30 m . C. 10 m . D. 40 m. Lời giải Khi ô tô dừng hẳn thì: ( ) ( ) 052004 vttts =−+== . Vậy từ lúc đạp phanh đến khi dừng hẳn, ô tô di chuyển được: ( ) ( ) 4 0
Câu 70: Một ô tô đang chạy với vận tốc là 12 ( ) / ms thì người lái đạp phanh; từ thời điểm đó ô tô chuyển động chậm dần đều với vận tốc ( ) 612vtt=−+ ( ) / ms , trong đó t là khoảng thời gian tính bằng giây kể từ lúc đạp phanh. Hỏi từ lúc đạp phanh đến lúc ô tô dừng hẳn, ô tô còn di chuyển được bao nhiêu mét? A. 8m. B. 12m. C. 15m. D. 10m. Lời giải Lấy mốc thời gian ( )0 t = là lúc đạp phanh. Khi ô tô dừng hẳn thì vận tốc ( ) 0 vt = , tức là ( ) 6120vtt=−+= 2 t = .
Vậy từ lúc đạp phanh đến lúc ô tô dừng hẳn, ô tô còn di chuyển được quãng đường là ( ) 2 0
612d tt−+ ( ) 2 2 0 31212 tt =−+= ( )m
Câu 71: Một chiếc ô tô đang chạy với vận tốc 15m/s thì người lái xe hãm phanh. Sau khi hãm phanh, ô tô chuyểnđộngchậm dần đềuvới vậntốc ( ) ( ) 315 m/s vtt=−+ ,trongđó t Hỏi từlúchãm phanh đến khi dừng hẳn, ô tô di chuyển được bao nhiêu mét? A. 38m. B. 37,2m. C. 37,5m. D. 37m. Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 51121 . 5 10042 ab a ab b += =− += = Khi đó quãng đường vật di chuyển trong khoảng thời gian từ ( ) 510ts là ( ) 10 5 26105 52 52 Sxdxm =−+= Quãng
c
ất
Câu
ột
y
ớ
đường đi đượ
ch
điểm trong thời gian ( ) 010ts là 115105545 . 326 S =+=
69: M
ô tô đang chạ
v
i tốc độ ( ) 20/ms thì người
đạ
ậ
ần
u vớ
ậ
ố
Chọn C
Khi xe dừng hẳn thì ( ) 05vtt== Khi đó quảng đường xe đi được tính từ lúc bắt đầu hãm phanh đến khi dừng hẳn là: ( ) 5 5 2 0 0
3 3151537,5 2 d t Sttt =−+=−+= m
Vậy ta chọn đáp ánC.
Câu 72: động chậm dần đều với vận tốc ( ) 1020vtt=−+ , trong đó t là khoảng thời gian tính bằng giây, kể từlúc bắt đầuđạp phanh. Hỏi từ lúcđạp phanh đến khi dừng hẳn, ôtô còn di chuyển bao nhiêu mét? A. 5 m B. 20 m C. 40 m D. 10 m Lời giải
Chọn B
Lúc bắt đầu đạp phanh, ô tô có vận tốc 20/ms ( ) 0001020200vttt =−+== Ô tô dừng hẳn khi đó vận tốc ( ) 1110201002vttt=−== . Do đó ô tô di chuyển được thêm là: ( ) ( ) ( ) 2 22 0 0
201020520tdtttm−=−=
Câu 73: Một ô tô đang chạy với vận tốc 10/ms thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động chậm dần đều với vận tốc ( ) ( ) 210/ vttms =−+ , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Tính quãng đường ô tô di chuyển được trong 8 giây cuối cùng. A. 55m B. 25m C. 50m D. 16m Lời giải
Ta có 21005 tt −+== Thời gian tính từ lúc bắt đầu đạp phanh đến khi dừng hẳn là 5 giây. Vậy trong 8 giây cuối cùng thì có 3 giây ô tô chuyển động với vận tốc 10/ms và 5 giây chuyển động chậm dần đều với vận tốc ( ) ( ) 210/ vttms =−+ . Khi đó quãng đường ô tô di chuyển là ( ) 5 0
3.10210302555 Stdtm =+−+=+= .
Câu 74: Một chất điểm bắt đầu chuyển động thẳng đều với vận tốc 0v , sau 6 giây chuyển động thì gặp chướng ngại vật nên bắt đầu giảm tốc độ với vận tốc chuyển độ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
ng 5 ()(/),(6) 2 vttamst =−+ cho đến khi dừng hẳn. Biết rằng kể từ lúc chuyển động đến lúc dừng thì chất điểm đi được quãng đường là 80m. Tìm 0v . A. 0 35/ vms = B. 0 25/ vms = C. 0 10/ vms = D. 0 20/ vms = Lời giải Tại thời điểm 6 t = vật đang chuyển động với vận tốc 0v nên có 0 (6) vv = 00 5 .615 2 avav −+==+ , suy ra 0 5 ()15 2 vttv=−++
ng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc 35 a =− ( ) 2m/s . Tính quãng đường của ô tô đi được từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn? A. 87.5 mét B. 96.5 mét C. 102.5 mét D. 105 mét Lời giải
Quãng đường ô tô đi được trong 5 ( )s đầu là 5 5 2 1 0 0 7d787,5 2 t stt=== .
3535 2 t t =− 17.5
= . Vậy quãng đường của ô tô đi được từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là 12sss =+ 87.517.5=+ 105= . Câu 76: Một chất điểm đang
68,25m
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 4 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Gọi k là thời điểm vật dừng hẳn, vậy ta có ( ) 0 0 2 2 ()0.156 55 v vkkvk==+=+ . Tổng quãng đường vật đi được là 00 6 5 806.15 2 k vtvdt =+−++ ( ) ( ) 2 00 6 22 00 2 0 000 00 2 00 0 5 806..15 4 5 806.(6).(6)15(6) 4 42422 5 806..15. 425555 36.4000 10 k vtvtt vkvkk v vvv vv vv v =+−++ =−−+−+− =−+++ +−= = Câu 75: Một ô tô chuyển động nhanh dần đều với vận tốc ( ) 7 vtt = ( )m/s . Đi được 5 ( )s người lái xe phát hiện chướ
chuyển động với vận tốc 0 15m/s v = thì tăng tốc với gia tốc ( ) ( ) 22 4m/sattt =+ . Tính quãng đường chất điểm đó đi được trong khoảng thời gian 3 giây kể từ lúc bắt đầu tăng vận tốc. A. 70,25m. B.
. C.
Phương trình vận tốc của ô tô khi người lái xe phát hiện chướng ngại vật là ( ) ( ) 2 3535 vtt =− Khi xe dừng lại hẳn thì ( ) ( ) 2 0353501vttt =−== Quãng đường ô tô đi được từ khi phanh gấp đến khi dừng lại hẳn là ( ) 1 2 0 .
3535d stt =− 1 2 0 . Lời giải
67,25m
D. 69,75m
theo phương trình ( ) 23 109 stttt =++− trong đó s tính bằng mét, t tính bằng giây. Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất là A. ( )6s t = . B. ( )3s t = . C. ( )2s t = . D. ( )5s t = . Lời giải ( ) ( ) 2 3181vtsttt ==−++
Dễ thấy hàm số ( )vt là hàm bậc hai có đồ thị dạng parabol với hệ số 30 a =− .
Do đó max v đạt tại đỉnh ( )3;28 I của parabol.
Vậy Thời gian để vận tốc của chất điểm đạt giá trị lớn nhất ( )3s t = .
Câu 78: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc ( ) ( ) 1 7m/svtt = . Đi được 5s, người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc ( ) 2 70 m/s a =− . Tính quãng đường S đi được của ô tô từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn. A. ( ) 96,25 m S = . B. ( ) 87,5 m S = . C. ( ) 94 m S = . D. ( ) 95,7 m S = . Lời giải Chọn gốc thời gian là lúc ô tô bắt đầu đi. Sau 5s ô tô đạt vận tốc là ( ) ( )535m/s v = . Sau khi phanh vận tốc ô tô là ( ) ( )35705vtt=−− Ô tô dừng tại thời điểm 5,5s t = . Quãng đường ô tô đi được là ( ) ( ) 5,5 5 05 7d35705d96,25mStttt =+−−= .
Câu 79: Một ô tô bắt đầu chuyển động nhanh dần đều với vận tốc ( ) ( ) 1 2m/svtt = . Đi được 12 giây, người lái xe gặp chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc ( ) 212m/s a =− . Tính quãng đường ( )m s đi được của ôtô từ lúc bắt đầu chuyển động đến khi dừng hẳn? A. ( )168m s = . B. ( )166m s = . C. ( )144m s = . D. ( )152m s = . Lời giải Giai đoạn 1: Xe bắt đầu chuyển động đến khi gặp chướng ngại vật. Quãng đường xe đi được là:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
(
2
=+ (
3 2
==++ (
Mà
==
=++ Vậy 3 3 2 0
3
=++=
ất
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
)
4 attt
) ( )
d2 3 t vtatttC
) C
( ) 015vC
( ) 3 2 215 3 t vtt
215d69,75m
t Stt
Câu 77: Một ch
điểm chuyển động
( ) 12 11 0
d Svtt = 12 0
2dtt = 12 2 0 t = ( )144m= Giai đoạn 2: Xe gặp chướng ngại vật đến khi dừng hẳn. Ôtô chuyển động chậm dần đều với vận tốc ( ) 2 d12 vtattc ==−+ .
Vận tốc của xe khi gặp chướng ngại vật là: ( ) ( ) ( ) 210122.1224m/svv=== . 12.024 c −+= 24 c = ( ) 2 1224vtt =−+
Thời gian khi xe gặp chướng ngại vật đến khi xe dừng hẳn là nghiệm phương trình: 12240 t −+= 2 t = . Khi đó, quãng đường xe đi được là: ( ) 2 22 0
1224d tt=−+ ( ) ( ) 2 2 0 62424m tt =−+= Vậy tổng quãng đường xe đi được là: ( ) 12 168m SSS=+= . Câu 80: Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1m . Một ô tô A đang chạy với vận tốc 16m/s bỗng gặp ô tô B đang dừng đèn đỏ nên ô tô A hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức
d Svtt = ( ) 2 0
( ) 164 A vtt =− , thời gian tính bằng giây. Hỏi rằng để có 2 ô tô A và B đạt khoảng cách an toàn khi dừng lại thì ô tô A phải hãm phanh khi cách ô tô B một khoảng ít nhất là bao nhiêu? A. 33. B. 12. C. 31. D. 32. Lời giải
Ta có: ( ) 016m/s Av =
Khi xe A dừng hẳn: ( ) 0 A vt = 4s t =
Quãng đường từ lúc xe A hãm phanh đến lúc dừng hẳn là ( ) 4 0
164d stt =− 32m =
Do các xe phải cách nhau tối thiểu 1m để đảm bảo an toàn nên khi dừng lại ô tô A phải hãm phanh khi cách ô tô B một khoảng ít nhất là 33m.
Câu 81: Một vật chuyển động với vận tốc 10m/s thì tăng tốc với gia tốc được tính theo thời gian là ( ) 2 3 attt =+ . Tính quãng đường vật đi được trong khoảng thời gian 6 giây kể từ khi vật bắt đầu
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 6
B.
C.
D.
Lời giải Ta
( )
v = và ( ) ( ) 0 d t vtatt = ( ) 2 0 3d t ttt=+ 32 0 3 32 t tt =+ 3213 32 tt=+ . Quãng đường vật đi được là ( ) 6 0 d Svtt = 6 32 0 13 d 32 ttt =+ 6 43 0 11 122 tt =+ 216m =
tăng tốc. A. 136m.
126m.
276m.
216m.
có
010m/s
Câu 82: Một chiếc máy bay chuyển động trên đường băng với vận tốc ( ) 2 10 vttt =+ ( ) / ms với t là
thời gian được tính theo đơn vị giây kể từ khi máy bay bắt đầu chuyển động. Biết khi máy bay đạt vận tốc ( ) 200/ms thì rời đường băng. Quãng đường máy bay đã di chuyển trên đường băng là A. ( ) 2500 3 m . B. ( ) 2000 m . C. ( ) 500 m . D. ( ) 4000 3 m . Lời giải Thời điểm máy bay đạt vận tốc ( ) 200/ms là ( ) 2 10 2001020010 20 t vtttt t = =+== =− Quãng đường máy bay đã di chuyển trên đường băng là
83:
đầ
chuyển động theo một đường thẳng với gia tốc ( ) ( ) 2 62/ attms =− , trong đó t là khoảng thời gian tính bằng giây kể từ lúc ôtô bắt đầu chuyển động. Hỏi quảng đường ôtô đi được từ lúc bắt đầu chuyển động đến khi vận tốc của ôtô đạt giá trị lớn nhất là bao nhiêu mét? A. 18m B. 36m C. 22,5m D. 6,75m Lời giải ( ) ( ) 2 62/ attms =− ( ) ( ) 2 626 vttdtttC =−=−+
Xe dừng và bắt đầu chuyển động nên khi 0 t = thì 00vC== ( ) 2 6 vttt =− . ( ) 2 6 vttt =− là hàm số bậc 2 nên đạt GTLN khi ( ) 3 2 b ts a =−= Quảng đường xe đi trong 3 giây đầu là: ( ) 3 2 0
618 Sttdtm =−= .
Câu 84: Một vật chuyển động trong 6 giờ với vận tốc ( ) / vkmh phụ thuộc vào thời gian ( )th có đồ thị như hình bên dưới. Trong khoảng thời gian 2 giờ từ khi bắt đầu chuyển động, đồ thị là một phần đường Parabol có đỉnh ( )3;9 I và có trục đối xứng song song với trục tung. Khoảng thời gian còn lại, đồ thị vận tốc là một đường thẳng có hệ số góc bằng 1 4 . Tính quảng đường s mà vật di chuyển được trong 6 giờ?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 7
( )
10 3 10 2 0 0
=+=+=
( )
2500 10d5 33 t sttttm
. Câu
Một ôtô đang dừng và bắt
u
A. ( ) 130 3 km . B. ( ) 9 km . C. ( ) 40 km . D. ( ) 134 3 km . Lời giải
Chọn A
+ Vì Parabol đi qua O và có tọa độ đỉnh ( )3;9 I nên thiết lập được phương trình Parabol là ( ) ( ) 2 :6;0;2Pyvtttt==−+
+ Sau 2 giờ đầu thì hàm vận tốc có dạng là hàm bậc nhất 1 4 ytm =+ , dựa trên đồ thị ta thấy đi qua điểm có tọa độ ( )6;9 nên thế vào hàm số và tìm được 15 2 m = . Nên hàm vận tốc từ giờ thứ 2 đến giờ thứ 6 là 115 42;[2;6]ytt=+ + Quảng đường vật đi được bằng tổng đoạn đường 2 giờ đầu và đoạn đường 4 giờ sau. ( ) ( ) 26 2 12 02
115130 6 423 SSSttdttdtkm =+=−+++=
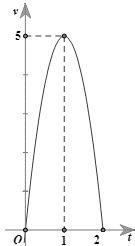
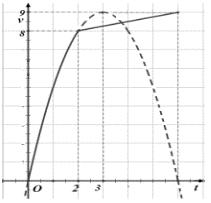
Câu 85: Một người chạy trong 2 giờ, vận tốc v phụ thuộc vào thời gian t có đồ thị là 1 phần của đường Parabol với đỉnh ( )1;5 I và trục đối xứng song song với trục tung Ov như hình vẽ. Tính quảng đường S người đó chạy được trong 1 giờ 30 phút kể từ lúc bắt đầu chạy
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
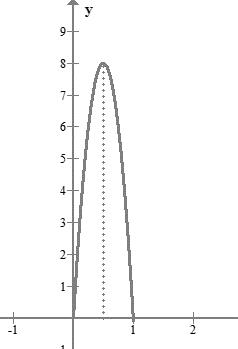
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
Đồ
=−=− −= =−+ +== +=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 2,11km B. 6,67km C. 5,63 km. D. 5,63km Lời giải Ta có 1 giờ 30 phút = 1,5 giờ 1,5 0 ()d Svtt= Đồ thị ()vvt = đi qua gốc tọa độ nên ()vt có dạng 2 () vtatbt =+ .
thị ()vvt = có đỉnh là I nên 2 125 2()510 5510 b baa vttt a abb ab
( ) 1,5 2 0 45 510d5,63 8 Sttt=−+= . Câu 86: Một người chạy trong thời gian 1 giờ, với vận tốc v ( )km/h phụ thuộc vào thời gian ( )h t có đồ thị là một phần của parabol có đỉnh 1 ;8 2 I và trục đối xứng song song với trục tung như hình vẽ. Tính quãng đường S người đó chạy được trong thời gian 45 phút, kể từ khi bắt đầu chạy. A. 5,3 ( )km . B. 4,5 ( )km . C. 4 ( )km . D. 2,3 ( )km . Lời giải Trước hết ta tìm công thức biểu thị vận tốc theo thời gian, giả sử ( ) 2 vtatbtc =++ Khi đó dựa vào hình vẽ ta có hệ phương trình
Câu 87: Một vật chuyển động trong 4 giờ với vận tốc (km/h) v phụ thuộc thời gian (h) t có đồ thị là một phần của đường parabol có đỉnh (1;1)I và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 10
= ++= ++=
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2 0 11 8 22 0 c abc abc
32 32 0 a b c =− = = . Do đó quãng đường người đó đi được sau 45 phút là ( ) 45 60 2 0 32324,5Sttdt=−= ( )km
A.
s = B.
s =
Lời giải Hàm biểu diễn vận tốc có dạng ( ) 2 vtatbtc =++ . Dựa vào đồ thị ta có: ( ) 2 2 1 1222 2 12 c a b bvttt a c abc = = ==−=−+ = ++= Với ( ) 4410tv== . Từ đó ( ) ( ) 4 2 0 40 22 3 sttdtkm =−+= . Câu 88: Một cái cổng hình Parabol như hình vẽ sau. Chiều cao 4 GHm = , chiều rộng 4 ABm = , 0,9 ACBDm == . Chủ nhà làm hai cánh cổng khi đóng lại là hình chữ nhật CDEF tô đậm
6(km).
8(km).
C. 40(km). 3 s = D. 46(km). 3 s =
có

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 11
A.
đồ
Lờ
giải Chọn A Gắn hệ trục tọa độ Oxy sao cho AB trùng Ox , A trùng O
đó
có đỉnh ( )2;4 G và đi qua gốc tọa độ. Giả sử phương trình của parabol có dạng ( ) 2 0 yaxbxca =++ . Vì parabol có đỉnh là ( )2;4 G và đi qua điểm ( )0;0 O nên ta có 2 0 2 2 .2.24 c b ab a c = −= ++= 1 4 0 a b c =− = = . Suy ra phương trình parabol là 2 () 4 yfxxx == + . Diện tích của cả cổng là ( ) ( ) 4 4 3 222 0 0 32 4d2m 33 x Sxxxx =−+=−+= Mặt khác chiều cao ( ) 0,92,79(m) CFDEf=== ; ( )42.0,92,2m CD =−= . Diện tích hai cánh cổng là ( ) 2.6,138m CDEF SCDCF== .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn giá là 1200000 đồng 2 /m , còn các phần để trắng làm xiên hoa có giá là 900000 đồng 2 /m . Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
11445000
ng. B. 4077000 đồng. C. 7368000 đồng. D. 11370000 đồng.
i
khi
parabol
Diện tích phần xiên hoa là ( ) 2 326793 6,14m 31500 xhCDEFSSS=−=−= . Vậy tổng số tiền để làm cổng là 6793 6,138.1200000.90000011441400 1500 += đồng. Câu 89: Một biển quảng cáo với 4 đỉnh ,,, ABCD như hình vẽ. Biết chi phí để sơn phần tô đậm là 2 200.000(đ/m)sơn phần còn lại là 2 100.000đ/m . Cho 8;10;4 ACmBDmMNm === Hỏi số tiền sơn gần với số tiền nào sau đây: A. 12204000. đ B. 14207000. đ C. 11503000. đ D. 10894000. đ Lời giải elip có phương trình là: 22 1 1625 xy+= . Vì
= ==
y MNx y
53 422 53 2
N N N
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
12
= Diện tích phần tô đậm là 53 2 22 1 53 2 4 22559,21() 5 Sydym =− Diện tích elip là 2 .4.520()Sm == Diện tích phần trắng là 2 21 3,622()SSSm =− Tổng chi phí trang chí là: 59,21.2000003,622.10000012204200 T đ =+= . Câu 90: Một họa tiết hình cánh bướm như hình vẽ bên.
Phần tô đậm được đính đá với giá thành 2 500.000đ/m . Phần còn lại được tô màu với giá thành 2 250.000/đm . Cho 4;8. ABdmBCdm == Hỏi để trang trí 1000 họa tiết như vậy cần số tiền gần nhất với số nào sau đây. A. 105660667đ . B. 106666667đ . C. 107665667đ . D. 108665667đ . Lời giải Vì 4;8. ABdmBCdm == (2;4),A − B(2;4),C(2;4),D(2;4) parabol là: 2 yx = hoặc 2 yx =− Diện tích phần tô đậm là 2 22 1 0
32 4() 3 Sxdxdm ==
Diện tích hình chữ nhật là 2 4.832()Sm == Diện tích phần trắng là 2 21 3264 32() 33 SSSdm =−=−= Tổng chi phí trang chí là: 3264 .5000.2500.1000106666667 33 T đ =+
4m
4m 4m
Câu 91: Một khuôn viên dạng nửa hình tròn, trên đó người thiết kế phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm và có trục đối xứng vuông góc với đường kính của nửa hình tròn, hai đầu mút của cánh hoa nằm trên nửa đường tròn và cách nhau một khoảng bằng ( ) 4 m . Phần còn lại của khuôn viên dành để trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ, chi phí để trồng hoa và cỏ Nhật Bản tương ứng là 150.000 đồng/m2 và 100.000 đồng/m2 Hỏi cần bao nhiêu tiền để trồng hoa và trồng cỏ Nhật Bản trong khuôn viên đó? A. 3.738.574. B. 1.948.000 C. 3.926.990 D. 4.115.408 Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
Chọn hệ trục Oxy như hình vẽ, ta có bán kính của đường tròn là 22 4225 R =+=
Phương trình của nửa đường tròn ( )C là: 222 20,020 xyyyx +==−
Parabol ( )P có đỉnh ( )0;0 O và đi qua điểm ( )2;4 nên có phương trình: 2 yx =
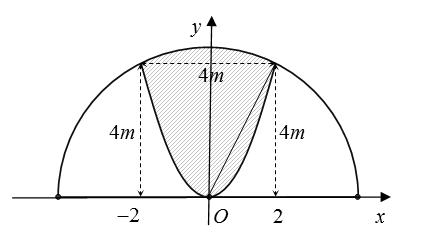
Diện tích phần tô màu là: 2 22 1 2 20d11,94Sxxx =−− ( ) 2 m .
Diện tích phần không tô màu là: ( )2 21 1 ..251011,94 2 SS =−− ( ) 2 m . Số tiền để trồng hoa và trồng cỏ Nhật Bản trong khuôn viên đó là: ( ) 150000.11,94100000.1011,943.738.593 +− Câu 92: Người ta cần trồng một vườn hoa Cẩm Tú Cầu Biết rằng phần gạch chéo là hình phẳng giới hạn bởi parabol 2 21yx=− và nửa trên của đường tròn có tâm làgốc tọa độ và bán kính bằng ( ) 2 m Tính số tiền tối thiểu để trồng xong vườn hoa Cẩm Tú Cầu biết rằng để trồng mỗi 2 m hoa cần ít nhất là 250000 đồng.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
14
A. 32 250000 6 π . B. 310 250000 6 + π . C. 310 250000 3 + π . D. 32 250000 6 + π Lời giải Chọn B Ta có phương trình đường tròn
ốc tọa
ằng
+= . T
xy
=−= =− == =−
tâm g
độ và bán kính b
( ) 2 m 22 2 xy
ọa độ giao điểm của Parabol và đường tròn là nghiệm hệ 2 2 21 21,1 1,1 yx
yx xy
Diện tích vườn hoa là ( ) 2 1
2 1 310 d 6 221 xx S x + =+= số tiền tối thiểu để trồng xong vườn hoa Cẩm Tú Cầu là 310 250000 6 + π


Câu 93: Nhàtrườngdựđịnhlàmmột vườn hoadạngelipđượcchiaralàmbốnphầnbởi hai đườngparabol có chung đỉnh, đối xứng với nhau qua trục của elip như hình vẽ bên. Biết độ dài trục lớn, trục nhỏ của elip lần lượt là 8 m và 4 m, 1, F 2F là hai tiêu điểm của elip. Phần A , B dùng để trồng hoa, phần C , D dùng để trồng cỏ. Kinh phí để trồng mỗi mét vuông hoa và cỏ lần lượt là 250.000 đ và 150.000 đ. Tính tổng tiền để hoàn thành vườn hoa trên A. 5.676.000 đ. B. 4.766.000 đ. C. 4.656.000 đ. D. 5.455.000 đ. Lời giải Gắn hệ trục tọa độ như hình vẽ. Do elip có độ dài trục lớn 284 aa== , độ dài trục nhỏ 242 bb== Diện tích của ( )E là: ( ) 8 E Sab== . Phương trình chính tắc ( )E là: 22 1 164 xy+= . Suy ra 2 1 16 2 yx =− Ta có 22 23 cab=−= ( ) 2 23; 0 F . Do N và 2F có cùng hoành độ ( ) 23; 1 N . Gọi ( ) 2 : Pykx = là parabol nằm ở phía trên trục Ox
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 15
phần C , D là:

SS
E SSS
) ( )
843 3
đó tổ
s
tiền để hoàn thành vườn hoa trên là: 1643843 .250000.1500005676000 33
+ đ. Câu 94: Người ta xây một sân khấu với mặt sân có dạng hợp của hai hình tròn giao nhau. Bán kính của hai của hai hình tròn là 20 mét và 15 mét. Khoảng cách giữa hai tâm của hai hình tròn là 30 mét. Chi phí làm mỗi mét vuông phân giao nhau của hai hình tròn là 300 ngàn đồng và chi phí làm mỗi mét vuông phần còn lại là 100 ngàn đồng. Hỏi số tiền làm mặt sân của sân khấu gần với số nào trong các số dưới đây?
A. 202 triệu đồng. B. 208 triệu đồng. C. 218 triệu đồng. D. 200 triệu đồng. Lời giải.
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 16 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do ( )NP ta có ( )2 1 123 12 kk == . Suy ra ( ) 2 1 : 12 Pyx = . Diện tích phần A là 23 22 23 11 16d 212 A Sxxx =−− 23 22 0 11 216d 212 xxx =−− 2323 22 00 1 16dd 6 xxxx=−− . *
2 1 0
=− .
Đổ
ận: Khi
3 2 1 0 1616sin.4cosd
=− 3
=
=+ 3 8 34 =+ . * Ta có 23 2 2 0 1 d 6 Ixx = 23 3 0 1 18 x = 43 3 = Suy ra: 12 823 3 A SII + =−= 1643 2 3 ABA SSS + +== Tổng diện tích
Xét 23
16d Ixx
Đặt 4sind4cosd xtxtt ==
i c
đó
Ittt
2 0 16cosdtt
( ) 3 0 81cos2dtt
=+
3 0 1 8sin2 2 tt
CD
+= (
AB
−+=
Khi
ng
ố
+−
= +=
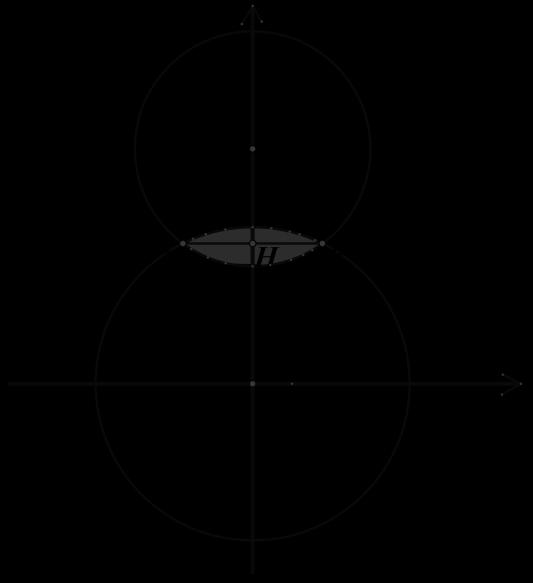
Gọi , OI lần lượt là tâm của các đường tròn bán kính bằng 20 mét và bán kính bằng 15 mét. Gắn hệ trục Oxy như hình vẽ, vì 30 OI = mét nên ( )0;30 I . Phương trình hai đường tròn lần lượt là 222 20 xy+= và ( )2 22 3015 xy+−= . Gọi , AB là các giao điểm của hai đường tròn đó. Tọa độ , AB là nghiệm của hệ ( ) 222 2 22
x xy xy y
5455 20 12 215 3015 12
Tổng diện tích hai đường tròn là ( ) 22 2015625 += . Phần giao của hai hình tròn chính là phần hình phẳng giới hạn bởi hai đồ thị 223015 yx =−− và 2220 yx =− . Do đó diện tích phần giao giữa hai hình tròn là ( ) 5455 12 2222 5455 12
201530d60,2546Sxxx =−+−−
Số tiền để làm phần giao giữa hai hình tròn là 300.000x60,254618.076.386 .
Số tiền để làm phần còn lại là ( ) 100.000x 6252x60,2546184.299.220 −=
Vậy tổng số tiền làm sân khấu là 184.299.22018.076.386202.375.606 + .
Câu 95: Người ta xây một sân khấu với sân có dạng của hai hình tròn giao nhau. Bán kính của hai hình tròn là 20 m và 15 m. Khoảng cách giữa hai tâm của hai hình tròn là 30 m. Chi phí làm mỗi mét vuông phần giao nhau của hai hình tròn là 300 nghìn đồng và chi phí làm mỗi mét vuông phần còn lại là 100 nghìn đồng. Hỏi số tiền làm mặt sân khấu gần với số nào nhất trong các số dưới đây?
A. 218 triệu đồng. B. 202 triệu đồng. C. 200 triệu đồng. D. 218 triệu đồng.
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
+−=
=
Lời giải Gọi 1O , 2O lần lượt là tâm của hai đường tròn bán kính 20 m và 15 m. A , B là hai giao điểm của hai đường tròn.
Ta có 11 20m OAOB== ; 22 15m OAOB== ; 12 30m OO = 222 1122 12 112
43 cos 2.48 OBOOOB BOO OBOO +− == 12 2623 BOO
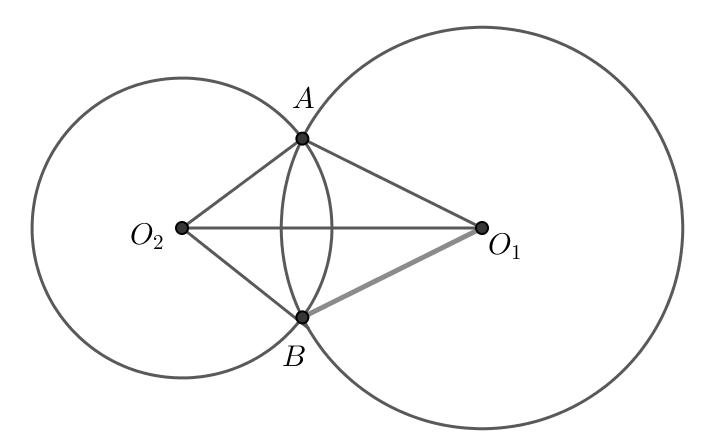
Theo tính chất hai đường tròn cắt nhau ta có 12OO là tia phân giác 1 AOB 121252,77AOBOOB == .
Suy ra diện tích hình quạt tròn 1 OAB là ( ) 1
22 52,77 .20.184,2m 360 OABS = ( ) 1
2 111 1 ..sin159,2m 2 OAB SOAOBAOB = . Gọi 1S là diện tích hình giới hạn bởi dây AB và cung AmB trong đường tròn ( )1O . ( ) 11
2 1 25m OABOABSSS =−=
Chứng minh tương tự ta được diện tích hình giới hạn bởi dây AB và cung AmB trong đường tròn ( ) 2O là ( ) 2 2 35m S .
Suy ra diện tích phần giao nhau là ( ) 2 12 60m SSS=+= . Chi phí làm sân khấu phần giao nhau 60.30000018000000 = . Tổng diện tích của hai hình tròn là ( ) 222 20151963m S =+ Diện tích phần không giao nhau là ( ) 21903m SS −= . Chi phí làm sân khấu phần không giao nhau 1903.100000190300000 = Số tiền làm mặt sân là 18000000190000000208300000 += 208,3 = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
18
Câu 96: Bác Năm làm một cái cửa nhà hình parabol có chiều cao từ mặt đất đến đỉnh là 2,25mét, chiều rộng tiếp giáp với mặt đất là 3 mét. Giá thuê mỗi mét vuông là 1500000 đồng. Vậy số tiền bác Năm phải trả là: A. 33750000 đồng. B. 3750000 đồng. C. 12750000 đồng. D. 6750000 đồng. Lời giải Gọi phương trình parabol ( )
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
19
ứ
ủ
hệ trục tọa độ Oxy sao cho
đỉnh IOy . Ta có hệ phương trình: ( ) ( ) ( ) ( ) ( ) ( ) 9 4, 93 0 42 93 0 42 cIP abcAP abcBP = −+= ++= 9 4 1 0 c a b = =− = Vậy ( ) 2 9 : 4 Pyx=−+ . Dựa vào đồ thị, diện tích cửa parabol là: 3 2 2 3 2 9d 4 Sxx =−+ 3 2 2 0 9 2d 4 xx =−+ 9 3 4 0 9 2 34 x x =+ 2 9 m 2 = . Số tiền phải trả là: 15000006750 9 2 000 = đồng. Câu 97: Một người có miếng đất hình tròn có bán kính bằng 5 m. Người này tính trồng cây trên mảnh đất đó, biết mỗi mét vuông trồng cây thu hoạch được 100 nghìn. Tuy nhiêncần có 1 khoảng trống để dựng 1 cái chòi và để đồ dùng nên người này bớt lại 1 phần đất nhỏ không trồng cây, trong đó 6 ABm = . Hỏi khi thu hoạch cây thì người này thu được bao nhiêu tiền ? 3 ;0 2 B 3 ;0 2 A 9 0; 4 I O 1 1 1 2 y x
2 : Pyaxbxc =++ . Do tính đối x
ng c
a parabol nên ta có thể chọn
( )P có
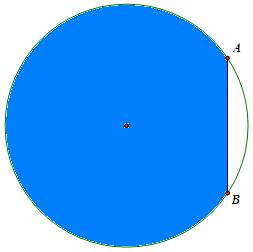

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 20 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 3722 nghìn đồng. D. 7445 nghìn đồng. C. 7446 nghìn đồng. B. 3723 nghìn đồng. Lời giải Diện tích miếng đất là 2 1 π25πSR== . Chọn hệ trục tọa độ Oxy như hình vẽ. Ta có phương trình của đường tròn biên là 22 25 xy+= 5,34RAHOH=== . Phương trình của cung tròn nhỏ AC là 2 25 yx =− , với 45 x . Diện tích phần đất trống là 5 2 2 4 225 Sxdx =− Diện tích phần đất trồng cây là 5 2 12 4 25π225 SSSxdx =−=−− Số tiền thu được là 5 2 4 100100(25π225)7445TSxdx ==−− . Câu 98: Một mảnh vườn hình elip có trục lớn bằng ( )100m và trục nhỏ bằng ( )80m được chia làm hai phần bởi một đoạn thẳng nối hai đỉnh liên tiếp của elip. Phần nhỏ hơn trồng cây con và phần lớn
hơn trồng rau. Biết lợi nhuận thu được là 2000 mỗi 2 m trồng cây con và 4000 mỗi 2 m trồng rau. Hỏi thu nhập của cả mảnh vườn là bao nhiêu? A. 31904000 B. 23991000 C. 10566000 D. 17635000 Lời giải
Gọi phương trình của elip là 22 22 1 xy ab += .
Theo giả thiết, ta có 210050 aa== ; 28040 bb== .
Diện tích phần trồng cây con bằng 1 4 diện tích của elip trừ đi diện tích tam giác DOF . Do đó diện tích phần trồng cây con là ( ) 2 1 m 42 abab S =− Diện tích phần trồng rau bằng 3 4 diện tích elip cộng với diện tích tam giác DOF . Do đó diện tích phần trồng rau là ( ) 2 2 3 m 42 abab S =+ . Thu nhập của cả mảnh vườn là 3 2000400023991000 4242 abababab −++
Câu 99: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng 10 cm bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết 5 AB = cm, 4 OH = cm. Tính diện tích bề mặt hoa văn đó. A. 2 160 cm 3 B. 2 140 cm 3 C. 2 14 cm 3 D. 250cm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 21
ờ
L
i giải
Đưa parabol vào hệ trục Oxy ta tìm được phương trình là: ( ) 2 1616 : 255 Pyxx =−+
Diện tích hình phẳng giới hạn bởi ( ) 2 1616 : 255 Pyxx =−+ , trục hoành và các đường thẳng 0 x = , 5 x = là: 5 2 0
161640 d 2553 Sxxx =−+=

Tổng diện tích phần bị khoét đi: 1 160 4 3 SS== 2 cm
Diện tích của hình vuông là: 2 100 cm hvS = Vậy diện tích bề mặt hoa văn là: 2 21 160140 100 cm 33 hv SSS=−=−= .
Câu 100: Một viên gạch hoa hình vuông cạnh 40cm. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa.
Diện tích mỗi cánh hoa của viên gạch bằng A. 2800cm . B. 2 800 cm 3 . C. 2 400 cm 3 . D. 2250cm . Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
22
2d 2 x xx
( ) 2 3 3 0 22 2 36 x x =− ( ) ( ) 22 4400dmcm 33 == ( ) ( ) 22 4400dmcm 33 == . Câu 101: Trong chương trình nông thôn mới, tại một xã Y có xây một cây cầu bằng bê tông như hình vẽ. Tính thể tích khối bê tông để đổ đủ cây cầu


CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 23
A.
19m B.
21m C.
18m D.
L
Ch
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 y O
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn hệ tọa độ như hình vẽ, các cánh hoa tạo bởi các đường parabol có phương trình 2 2 x y = , 2 2 x y =− , 2 2 y x =− , 2 2 y x = Diện tích một cánh hoa bằng diện tích hình
phẳng giới hạn bởi hai đồ thị hàm số 2 2 x y = , 2 yx = và hai đường thẳng 0;2xx== . Do đó diện tích một cánh hoa bằng 2 2 0
3
3
3
340m
ời giải
ọn hệ trục Oxy như hình vẽ
x
Gọi ( ) 2 111 : Pyaxb =+ là Parabol đi qua hai điểm ( ) 19 ;0,0;2 2 AB
Nên ta có hệ phương trình sau:
=+ =
2 19 0.2 2 2
a b
a b
1 1
8 361 2
=− = ( ) 2 1 8 :2 361 Pyx =−+
Gọi ( ) 2 222 : Pyaxb =+ là Parabol đi qua hai điểm ( ) 5 10;0,0; 2 CD

Nên ta có hệ phương trình sau: ( )2 2 2
=+ =
5 0.10 2 5 2
a b
a b
2 2
1 40 5 2
=− = ( ) 2 2 15 : 402Pyx =−+ . Ta có thể tích của bê tông là: 19 10 223 2 00
158 5.2d2d40m 402361 Vxxxx =−+−−+= . Câu 102: Để kỷ niệm ngày 26 3. Chi đoàn 12A dự định dựng một lều trại có dạng parabol, với kích thước: nền trại là một hình chữ nhật có chiều rộng là 3 mét, chiều sâu là 6 mét, đỉnh của parabol cách mặt đất là 3 mét. Hãy tính thể tích phần không gian phía bên trong trại để lớp 12A cử số lượng người tham dự trại cho phù hợp. A. 3 30 m B. 3 36 m C. 3 40 m D. 3 41 m Lời giải Chọn B Giả sử nền trại là hình chữ nhật ABCD có AB = 3 mét, BC = 6 mét, đỉnh của parabol là I. Chọn hệ trục tọa độ Oxy sao cho: O là trung điểm của cạnh AB, A, B và I, phương trình của parabol có dạng 2 ,0yaxba=+ . Do I, A, B thuộc nên ta có 2 4 3 3 yx=−+ Vậy thể tích phần không gian phía trong trại là 3 2 2 0
4 6.2(3)36 3 Vxdx =−+=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 24
Câu 103: Săm lốp xe ô tô khi bơm căng đặt nằm trên mặt phẳng nằm ngang có hình chiếu bằng như hình vẽ với bán kính đường tròn nhỏ 1 20 Rcm = , bán kính đường tròn lớn 2 30 Rcm = và mặt cắt khi cắt bởi mặt phẳng đi qua trục, vuông góc mặt phẳng nằm ngang là hai đường tròn. Bỏ qua độ dày vỏ săm. Tính
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
25
A. 23 1250 cm B. 23 1400 cm C. 23 2500 cm D. 23 600 cm Lời giải Thể tích săm xe bằng thể tích của khối tròn xoay sinh bởi hình tròn tâm ( )0;25 I bán kính bằng 5 quay quanh trục Ox . Ta có phương trình đường tròn là ( ) 2 2 2 2 2525 2525,5;5 2525 yx xyx yx =+− +−=− =−− . Vậy ( ) ( ) 555 22 222 555 .2525d2525d100.25d Vxxxxxx =+−−−−=− Ta có 5 2 5 25dxx là diện tích nửa hình tròn tâm ( )0;0 O , bán kính bằng 5 5 22 5 12525d..5 22 xx −== . Suy ra 5 2 5 25100.25d100. 2 Vxx =−== 23 1250 cm Chú ý: Có thể bấm máy tích phân, ta được ( ) ( ) 5522 223 55 2525d2525d3927 Vxxxxcm =+−−−− . Kiểm tra các đáp án ta chọn đáp án A.
thể tích không khí được chứa bên trong săm.
Câu 104: Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng 5 OO = cm, 10 OA = cm, 20 OB = cm, đường cong AB là một phần của parabol có đỉnh là điểm A . Thể tích của chiếc mũ bằng A. 2750 3
Ta gọi thể tích của chiếc mũ là V Thể tích của khối trụ có bán kính đáy bằng 10 OA = cm và đường cao 5 OO = cm là 1V . Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong AB và hai trục tọa độ quanh trục Oy là 2V Ta có 12VVV
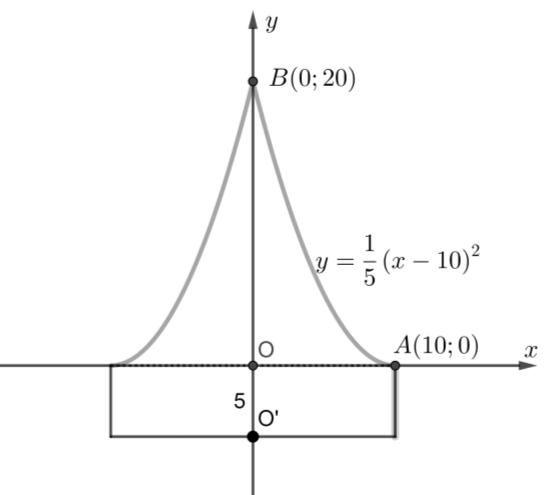
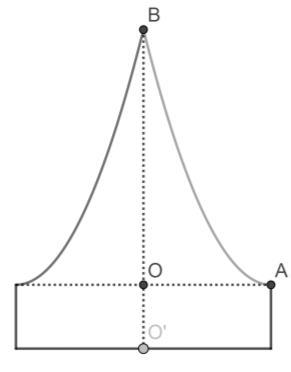
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 26
( ) 3 cm B. 2500 3 ( ) 3 cm C. 2050 3 ( ) 3 cm D. 2250 3 ( ) 3 cm Lời giải Chọn B
=+ 2 1 5.10500 V == ( ) 3 cm Chọn hệ trục tọa độ như hình vẽ. Do parabol có đỉnh A nên nó có phương trình dạng 2():(10) Pyax=− Vì ( )P qua điểm ( )0;20 B nên 1 5 a =
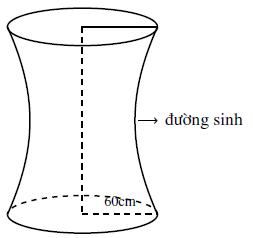

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
27 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do đó, ( ) ( )2 1 :10 5 Pyx=− . Từ đó suy ra 105 xy =− . Suy ra ( ) 20 2 2 0 80001000 105dy3000 33 Vy =−=−= ( ) 3 cm Do đó 12 10002500 500 33 VVV=+=+= ( ) 3 cm Câu 105: Cho chiếc trống như hình vẽ, có đường sinh là nửa elip được cắt bởi trục lớn với độ dài trục lớn bằng 80 cm, độ dài trục bé bằng 60 cm và đáy trống là hình tròn có bán kính bằng 60 cm. Tính thể tích V của chiếc trống. A. 3344963cm V = B. 3344964cm V = C. 3208347cm V = D. 3208346cm V = Lời giải Đặt hệ trục tọa độ Oxy như hình vẽ Gọi ( )E là elip có phương trình 22 1 169 xy+= thì ảnh của ( )E qua phép tịnh tiến theo vectơ ( )0;6 u là elip ( ) E có phương trình ( )2 2 6 1 169 y x += .
Suy ra, phương trình của đường sinh là: 2 3 616 4 yx =−− .
Do đó, thể tích của chiếc trống là: 2 4 2 4
3 616d344,964 4 Vxx =−− ( ) 3dm
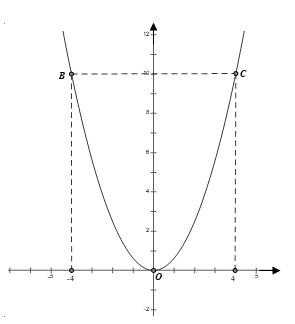

Câu 106: Một cốc
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc là một đường Parabol. Tính thể tích tối đa mà cốc có thể chứa được A. 3 320 Vcm B. 3 1005,31 Vcm C. 3 251,33 Vcm D. 3 502,65 Vcm Lời giải Parabol có phương trình 22 58 85 yxxy == Thể tích tối đa cốc: 10 0 8 .251,33 5 Vydy = .
c thiết diện là một tam giác đều. Thể tích V của vật thể đó là
A. 3 V = B. 33 V = C. 43 3 V = D. V = Lời giải

43 223123 33 x VSdxxx ==−=−= .
Do vật thể có đáy là đường tròn và khi cắt bởi mặt phẳng vuông góc với trục Ox được thiết diện là tam giác đều do đó vật thể đối xứng qua mặt phẳng vuông góc với trục Oy tại điểm O . Cạnh của tam giác đều thiết diện là: 2 21 ax =− . Diện tích tam giác thiết diện là: ( ) 2 2 3 13 4 a Sx ==− . Thể tích khối cần tìm là: ( ) 1 11 3 2 00 0
Câu 108: Sân vận động Sport Hub là sân có mái vòm kỳ vĩ nhất thế giới. Đây là nơi diễn ra lễ khai mạc Đại hội thể thao Đông Nam Á được tổ chức tại Singapore năm 2015. Nền sân là một elip ( )E có trục lớn dài 150m, trục bé dài 90m Nếu cắt sân vận động theo một mặt phẳng vuông góc với trục lớn của ( )E và cắt elip ở , MN thì ta được thiết diện luôn là một phần của hình tròn có tâm I với MN là một dây cung và góc 0 90. MIN = Để lắp máy điều hòa không khí thì các kỹ sư cần tính thể tích phần không gian bên dưới mái che và bên trên mặt sân, coi như mặt sân là một mặt phẳng và thể tích vật liệu là mái không đáng kể. Hỏi thể tích xấp xỉ bao nhiêu?

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 29 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 107: Cho vật thể đáy là hình tròn có bán kính bằng 1. Khi cắt vật thể bằng mặt phẳng vuông góc với trục Ox tại điểm có hoành độ ( )11xx− thì đượ
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 30 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Hình 3 A. 3 57793m . B. 3 115586m . C. 3 32162m . D. 3 101793m . Lời giải Chọn hệ trục như hình vẽ Ta cần tìm diện tích của ( )Sx thiết diện. Gọi ( ) , dOMNx = ( ) 22 22 :1. 7545 xy E += Lúc đó 22 2 2222451901 7575 xx MNy ==−=− 222 2 22 9090 .1.1 75275 22 MNxx RR ==−=−
Câu 109: Một cái thùng đựng dầu có thiết diện ngang là một đường elip có trục lớn bằng 1m, trục bé bằng 0,8m, chiều dài bằng 3m. Đươc đặt sao cho trục bé nằm theo phương thẳng đứng. Biết chiều cao của dầu hiện có trong thùng là 0,6m. Tính thể tích V của dầu có trong thùng.
A. 31,52m V = B. 31,31m V = C. 31,27m V = D. 31,19m V = Lời giải Chọn hệ trục tọa độ như hình vẽ.
Theo đề bài ta có phương trình của Elip là 22 1 14 425
xy+= .
Gọi M , N lần lượt là giao điểm của dầu với elip.

Gọi 1S là diện tích của Elip ta có 1 12 255 Sab ===
Gọi 2S là diện tích của hình phẳng giới hạn bởi Elip và đường thẳng MN
Theo đề bài chiều cao của dầu hiện có trong thùng là 0,6m nên ta có phương trình của đường thẳng MN là 1 5 y = .
Mặt khác từ phương trình 22 1 14 425
xy+= ta có 2 41 54 yx =−
Do đường thẳng 1 5 y = cắt Elip tại hai điểm M , N có hoành độ lần lượt là 3 4 và 3 4 nên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2 222 2 11112025 2.1. 4242275 x SxRRR =−=−=−− Thể tích khoảng không cần tìm là ( ) 75 2 3 2 75 2025 2.1115586. 275 x Vm =−−
có độ sâu là 280cm. Giả sử ( )ht là chiều cao của mực nước bơm được tại thời điểm t giây, biết rằng tốc độ tăng của chiều cao mực nước tại giây thứ t là 3 1 ()3 500 htt =+ và lúc đầu hồ bơi không có nước. Hỏi sau bao
lâu thì bơm được số nước bằng 3 4 độ sâu của hồ bơi? A. 2 giờ 36 giây. B. 2 giờ 34 giây. C. 2 giờ 35 giây. D. 2 giờ 36 giây. Lời giải G
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 32 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 33 44 22 2 33 44 411413 dd 5455410 Sxxxx =−−=−− Tính 3 4 2 3 4 1 d 4 Ixx =− Đặt 11 sindcosd 22 xtxtt == . Đổi cận: Khi 3 4 x = thì 3 t =− ; Khi 3 4 x = thì 3 t = . ( ) 33 2 33 111123 .cosd1cos2d 228832 Itttt ==+=+ Vậy 2 412333 5832101520 S =+−=− Thể tích của dầu trong thùng là 3 .31,52 51520 V =−+= . Câu 110: Người ta thay nước mới cho một bể bơi có dạng hình hộp chữ nhật
ng
ủ
ể
x
Ta có: 3 0 1 3d210 500 x tt+= ( ) 4 3 0 3 3105000 4 x t += 33 (3)333140000 xx ++−= ( )4 3 3 333140000 x +=+ ( )3 3 4 333140000 x +=+ ( )3 3 4 331400003 x =+− 7234,8256 x . Câu 111: Một bác thợ xây bơm nước vào bể chứa nước. Gọi ( )ht là thể tích nước bơm được sau t giây. Cho ( ) 2 62 htatbt =+ và ban đầu bể không có nước. Sau 3 giây thì thể tích nước trong bể là 3 90m , sau 6 giây thì thể tích nước trong bể là 3 504m . Tính thể tích nước trong bể sau khi bơm được 9 giây.
ọi x là thời điểm bơm được số nước bằ
3 4 độ sâu c
a b
(
tính bằng giây ).
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 33
(
3 2 0
(
Từ, 2 3 6 a
= =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 3 1458m . B. 3 600m . C. 3 2200m . D. 3 4200. m Lời giải
)
62d90 atbtt+=
( ) 3 32 0 290 atbt+= 54990 ab+=
) 6 2 0 62d504 atbtt+=
( ) 6 32 0 2504 atbt+= 43236504 ab+=
b
. Sau khi bơm 9 giây thì thể tích nước trong bể là: ( ) 9 2 0 412d Vttt =+ = ( ) 9 323 0 4 61458 3 ttm += . Câu 112: Cho hàm số ( )yfx = có đạo hàm ( )fx liên tục trên đoạn 0;5 và đồ thị hàm số ( )yfx = trên đoạn 0;5 được cho như hình bên. Tìm mệnh đề đúng A. ( ) ( ) ( )053fff = . B. ( ) ( ) ( )305fff = . C. ( ) ( ) ( )305fff D. ( ) ( ) ( )350fff Lời giải Ta có ( ) ( ) ( ) 5 3 530fxxff =− d , do đó ( ) ( )53ff ( ) ( ) ( ) 3 0 300fxxff =− d , do đó ( ) ( )30ff ( ) ( ) ( ) 5 0 500fxxff =− d , do đó ( ) ( )50ff Câu 113: Cho hàm số ( )yfx = có đồ thị ( )yfx = cắt trục Ox tại ba điểm có hoành độ abc như hình vẽ. Mệnh đề nào dưới đây là đúng?


CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 34 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. ( ) ( ) ( )fbfafc B. ( ) ( ) ( )fafbfc C. ( ) ( ) ( )fcfafb . D. ( ) ( ) ( )fcfbfa . Lời giải Chọn A Ta có bảng biến thiên của hàm số ( )yfx = Ta có ( ) ( ) ( ) ( ) 1 bb aa Sfxdxfxdxfbfa ===− ,
2 cc bb
==−=− Vì ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (
12 0 b a SSfbfafbfcfcfa
fxdxfbfa −− Câu 114: Cho hàm số ( )yfx = là hàm đa thức bậc bốn, có đồ thị ( )yfx = như hình vẽ Phương trình ( ) 0 fx = có 4 nghiệm thực phân biệt khi và chỉ khi A. ( ) ( ) 00 ffm . B. ( ) 00 f . C. ( ) ( ) 0 fmfn . D. ( ) ( ) 00 ffn . Lời giải
( ) ( ) ( ) ( )
Sfxdxfxdxfbfc
) ( ) ( )
fcfafb
n tích hình phẳng giới hạn bởi các đồ thị ( );; yfxOyxn ==
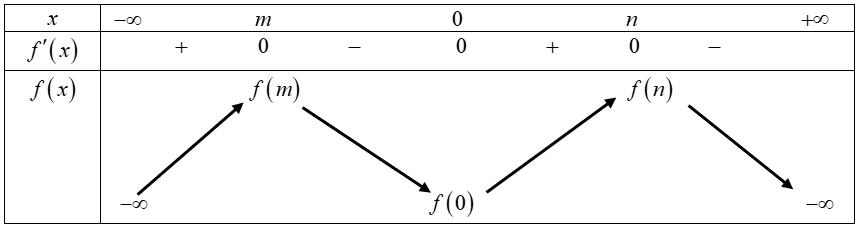

) ( )fnfm
ta thấy
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 35
Chọn A
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
Xét ( ) 0 0 x fxxm xn = == = Bảng biến thiên: Gọi 1S là diện tích hình phẳng giới hạn bởi các đồ thị ( )yfx = ; ;; OxxmOy = Gọi 2S là diệ
Từ hình vẽ ta thấy 21SS ( ) ( ) 0 0 n m fxdxfxdx ( ) ( ) 0 0 n m fxdxfxdx− ( ) ( ) ( ) ( ) 00 fnfffm −−− ( ) ( )fnfm . Từ bảng biến thiên kết hơp với điều kiện (
để phương trình ( ) 0 fx = có 4 nghiệm thực phân biệt ( ) ( ) 00 ffm Câu 115: Cho hàm số ( )yfx = liên tục trên và có đồ thị của hàm số ( )fx như hình bên dưới. Mệnh đề nào sau đây đúng? A. ( ) ( ) ( )021fff− . B. ( ) ( ) ( )012fff − .
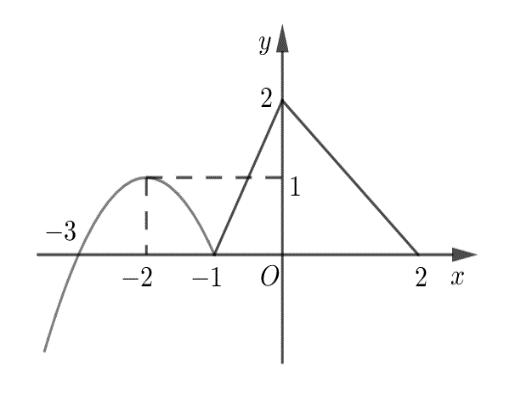
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 36
−−==+ ( ) ( )12ff− ( )2 Từ ( )1 và ( ) ( ) ( ) ( )2012 fff − . Câu 116: Cho hàm số ( )fx Đồ thị của hàm số ( ) = yfx trên 3;2 như hình vẽ Biết ( ) 30,−= f giá trị của ( ) ( )11−+ ff bằng A. 23 6 B. 31 6 C. 35 3 D. 9 2 Lời giải Chọn B Parabol 2 =++ yaxbxc có đỉnh ( )2;1 I và đi qua điểm ( )3;0 nên ta có 2 221 421443. 9303 −=− =− −+==−=−−− −+==− b a a abcbyxx abcc Do ( ) 30−= f nên ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )111001213 −+=−+−−+−−− ffffffff ( ) 101 2 013 ()d()d243d =++−−− fxxfxxxxx ( ) 1 2 12 3 3831 243d1. 236 =++−−−=++= SSxxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn C. ( ) ( ) ( )201fff− D. ( ) ( ) ( )102fff − Lời giải Theo đồ thị, ta có: ( ) ( ) ( ) 0 1 01d0 fffxx −−= ( ) ( )01ff − ( )1 , ( ) ( ) ( ) ( ) ( ) 202 110 21ddd0 fffxxfxxfxx
Với 12 , SS lần lượt là diện tích hình phẳng giới hạn bởi đồ thị hàm số ( ), = yfx trục Ox và hai
đường thẳng 1,0=−=xx và 0,1.==xx Dễ thấy 12 3 1;. 2 ==SS

Câu 117: Cho hàm số ( )yfx = . Đồ thị của hàm số ( )yfx = như hình vẽ. Đặt ( ) ( ) ( )2 21gxfxx=−− .
Mệnh đề nào dưới đây đúng?
A. ( ) ( ) ( )135ggg − . B. ( ) ( ) ( )153ggg − . C. ( ) ( ) ( )513ggg − D. ( ) ( ) ( )351ggg− Lời giải

Ta có ( ) ( ) ( )21gxfxx =−− ; ( ) 0 gx = ( ) 1 fxx =− .
Dựa vào đồ thị ta có các nghiệm sau: 1 3 5
=− = = .
x x x
Ta có bảng biến thiên
Ngoài ra dựa vào đồ thị ta có ( ) ( ) 35 13
11 dd 22gxxgxx − ( ) ( ) 35 13gxgx− ( ) ( ) ( ) ( )3135gggg −−− ( ) ( )51gg −
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
37
Vậy ( ) ( ) ( )351ggg−
c abc abc
= −+= ++=
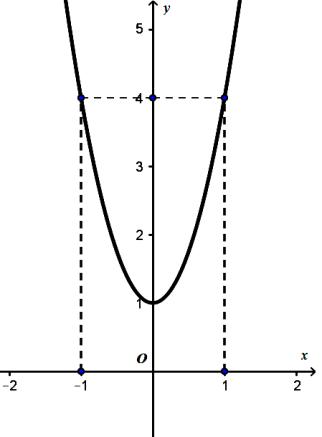
= = 31dx58Sx=+= . Lại có: ( ) ( ) ( ) ( ) 4 4 2 2
3 0 1
a b c = ( ) 2 31yfxx ==+ . Gọi S là diện tích phần hình phẳng giới hạn bởi các đường ( )yfx = , trục Ox , 4, x = 2 x = Ta có ( ) 4 2 2
dx42Sfxfxff ===− . Do đó: ( ) ( ) 4258Hff=−= Câu 119: Cho hàm số ( )yfx = . Đồ thị của hàm số ( )yfx = như hình vẽ bên. Đặt ( ) 2;6 max Mfx = , ( ) 2;6 min mfx = , TMm =+ . Mệnh đề nào dưới đây đúng?
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 38
Câu 118: Cho hàm số ( ) 32 () ,,,,0yfxaxbxcxdabcda ==+++ có đồ thị là ( )C . Biết rằng đồ thị ( )C đi qua gốc tọa độ và đồ thị hàm số '()yfx = cho bởi hình vẽ bên. Tính giá trị (4)(2)Hff =− ? A. 45 H = B. 64 H = C. 51 H = D. 58 H = Lời giải Theo bài ra ( ) 32 () ,,,,0yfxaxbxcxdabcda ==+++ do đó ( )yfx = là hàm bậc hai có dạng ( ) 2 yfxaxbxc ==++ Dựa vào đồ thị ta có: 1 4 4
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
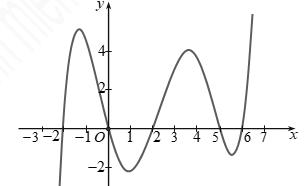
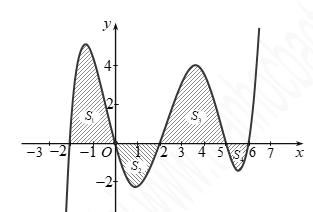
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 39
Quan
vẽ
có ( ) ( ) 02 20 dd fxxfxx − ( )
22
( ) ( ) ( ) ( )0202ffff −−− ( )
22ff− ( ) ( ) 25 02 dd fxxfxx− ( ) (
05 22fxfx ( ) ( ) ( ) ( )0252ffff −− ( ) ( )05ff ( ) ( ) 56 25 dd fxxfxx − ( ) ( ) 55 26fxfx ( ) ( ) ( ) ( )5256ffff −− ( ) ( )26ff Ta có bảng biến thiên
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. ( ) ( )02Tff=+− B. ( ) ( )52Tff=+− C. ( ) ( )56Tff =+ . D. ( ) ( )02Tff =+ . Lời giải Gọi 1S , 2S , 3S , 4S lần lượt là diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = với và trục hoành.
sát hình
, ta
( ) 00
fxfx
( )
)
Dựa vào bảng biến thiên ta có ( ) ( ) 2;6 max5Mfxf == và ( ) ( ) 2;6 min2mfxf==− Khi đó ( ) ( )52Tff=+− . Câu 120: Cho hàm số 432 () fxaxbxcxdxe. Hàm số ()yfx có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
A. 0 ac . B. 0 abcd . C. acbd . D. 0 bdc . Lời giải

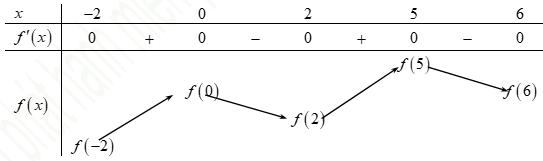
Chọn A
Theo đồ thị ta có (0)00fd và hệ số 0 a
Xét 0 0 1 1 ()() fxdxfxabcd , mà 0 1 ()0fxdx nên ta có 0 abcd
Hay acbd . Do đó ta loại C.
Thay 0 d ta có abc, vì 0 a nên 0 bc . Loại D.
Xét 1 1 0 0 ()() fxdxfxabcd , mà 1 0 ()0fxdx nên ta có 0 abcd
Do đó ta loại B. Từ ta có 0 abcd cộng từng vế với ta có 0 ac
Câu 121: Cho hàm số ( )yfx = có đồ thị gồm một phần đường thẳng và một phần parabol có đỉnh là gốc tọa độ O như hình vẽ. Giá trị của ( ) 3 3 d fxx bằng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
40
A. 26 3 . B. 38 3 . C. 4 3 . D. 28 3 . Lời giải
Chọn D
Ta có, phương trình đường thẳng có dạng yaxb =+ .
Từ hình vẽ, ta thấy đường thẳng đi qua hai điểm ( ) ( )2;0,1;1AB .
Suy ra, ta có hệ phương trình 201 2 12 aba yx abb −+== =+ −+==
Ta có, phương trình parabol có dạng 2,0yaxa= .
Từ hình vẽ, ta thấy parabol đi qua điểm ( ) 2 1;1 Byx −= .
Do đó, hàm số ( ) 2 2,1 ,1 xx yfx xx
+− == − Vậy, ( ) ( ) 313 2 331 d2dd fxxxxxx =++ ( ) 1 3 2 3 1 3
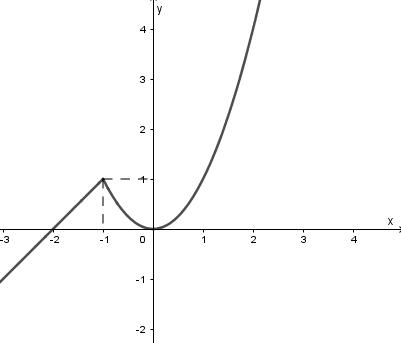
2 11128 9 232233 x x + =+=−++= . Câu 122: Cho hàm số yfx có đạo hàm đến cấp 2 trên . Biết hàm số yfx đạt cực tiểu tại 1 x , có đồ thị như hình vẽ và đường thẳng là tiếp tuyến của đồ thị hàm số tại điểm 2 x . Tính 4 1
2d fxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
41 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
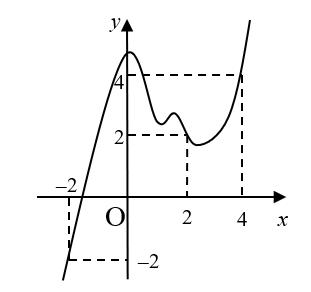
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Ifxxfxx =−++ bằng A. 2. B. 2. C. 6. D. 10. Lời giải Chọn C Xét ( ) ( ) ( ) ( ) ( ) ( ) 4242 0000 '2d'2d'2d2'2d2 Ifxxfxxfxxfxx =−++=−−+++ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 42 00 22224242426. fxfxffffff =−++=−−+−=−−=−−= Câu
Cho hàm số ( )fx liên tục có đồ thị
dưới.
42 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 1. B. 4. C. 3. D. 2. Lời giải Chọn C Dễ thấy đường thẳng đi qua các điểm 0;3 và 1;0 nên :33 yx suy ra hệ số góc của là 323kf Hàm số yfx đạt cực tiểu tại 1 x suy ra 10 f Vậy 4 4 1 1 2d221303fxxfxff Câu 123: Cho hàm số ( )yfx = có đạo hàm liên tục trên và có đồ thị như hình vẽ. Giá trị của biểu thức ( ) ( ) 42 00 '2d'2d
124:
như hình bên
Biết ( ) ( ) ,5;2Fxfxx =− và ( ) 1 3
14 d 3 fxx = . Tính ( ) ( )25FF A. 145 6 . B. 89 6 . C. 145 6 . D. 89 6 . Lời giải Chọn C Dựa vào đồ thị ta nhận thấy, đồ thị hàm số ( )fx liên tục và xác định trên đoạn 5;2 được xây dựng bởi ba hàm số ( ) ( ) ( ) ( )
fxx fxfxx fxx
1 2 3
khi53 khi31 khi12
−− =−− − . Trong đó:. ( ) 1 fx là đường thẳng qua hai điểm ( )5;5 và ( )3;4 có phương trình: ( ) 1 5 2 x fx −+ = ( ) 2 fx có đồ thị là một đường cong nối từ điểm ( )3;4 đến điểm ( )1;2 . ( ) 3 fx là đường thẳng qua hai điểm ( )1;2 và ( )0;3 có phương trình ( ) 3 3 fxx=+
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 43
Vậy: ( ) ( ) ( ) ( ) ( ) ( ) 2312 123 5531 25dddd FFfxxfxxfxxfxx −−==++ . ( ) ( ) 312 2 531 5dd3d 2 x xfxxxx −+ =+++ = 1421145 9 326 =++= .
ố đã cho có diện tích bằng A. 253 48 . B. 235 48 . C. 253 24 . D. 125 24 . Lời giải Chọn C
ành độ giao điể
là
) (




CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 1 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn BÀI 3. ỨNG DỤNG TÍCH PHÂN MỨC ĐỘ VẬN DỤNG – VẬN DỤNG CAO Câu 125: Cho hai hàm số 32 3 () 2 fxaxbxcx=+++ và ( ) 2 3 2 gxmxnx=+− . Biết rằng đồ thị của các hàm số ( )yfx = và ( )ygx = cắt nhau tại ba điểm có hoành độ lần lượt là 2;1;3. Hình phẳng giới hạn bởi hai đồ thị hàm s
V
V
V
i 3 x =
v
(
Do đó ta có hệ ( ) ( ) ( ) ( ) ( ) ( ) 8423 3 27933 abmcn abmcn abmcn −+−−−=− +−+−=− +−+−=− . 1 2 1 5 2 a bm cn = −=− −=− . Suy ra 32 15 ()()3 22 fxgxxxx −=−−+ CHƯƠNG III NGUYÊN HÀM TÍCH PHÂN ỨNG DỤNG TÍCH PHÂN
Ta có phương trình ho
m
32233 22 axbxcxmxnx +++=+− ( ) (
) 32 301 axbmxcnx +−+−+= Ta có phương trình ( )1 có ba nghiệm là 2; x =− 1; x = 3 x =
ới 2 x =− thay vào ta có ( ) ( ) 84230 abmcn −+−−−+=
ới 1 x = thay vào ta có ( ) ( ) 30 abmcn +−+−+=
ớ
thay
ào ta có
) ( ) 279330 abmcn +−+−+=
Chọn C
Ta có ( ) 2 62 fxxmxn =++ , ( ) 122 fxxm =+ , ( ) ( ) 3 12 fx = . Suy ra ( ) ( ) ( ) 32 2621220212 gxxmxnmxnm =++++++++ . ( ) 0 gx = ( ) 2 6262120 xmxnm +++++= . Vì hàm s

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 2 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vậy 3 2 ()() Sfxgxdx =−= 3 32 2 15 3 22 xxxdx −−+ 13 3232 21 1515 33 2222 xxxdxxxxdx=−−++−−+ 638253 8324 =+= . Câu 126: Cho hàm số ( ) 32 22021fxxmxnx=+++ với m , n là các số thực. Biết
số ( )
0984164935
hàm
( ) ( ) ( )gxfxfxfx =++ có hai giá trị cực trị là 2022 12 e và 12 e . Diện tích hình phẳng giới hạn bởi các đường ( ) ( ) 12 fx y gx = + và 1 y = bằng A. 2019 B. 2020 C. 2021 D. 2022 Lời giải
ố (
ự
Ta
ả
Từ đây suy ra ( ) 2022 1 12 gxe=− và ( ) 2 12 gxe=− . Mặt khác ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 12 gxfxfxfx gxfxfxfxfxfx =++ =++=++ . ( ) ( ) ( ) 12 gxgxfx −=− ( ) ( ) ( ) 12 gxgxfx =−+ . Xét phương trình hoành độ giao điểm: ( ) ( ) 1 12 fx gx = + ( ) ( ) ( ) 120 12 −+= − gxfx gx ( ) ( ) 0 12 gx gx = − 1 2 xx xx = = . Khi đó diện tích hình phẳng giới hạn bởi các đường ( ) ( ) 12 fx y gx = + và 1 y = bằng
)gx có hai giá trị c
c trị nên phương trình có 2 nghiệm phân biệt 1x , 2x .
có b
ng biến thiên của hàm số ( )gx như sau:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 3
i ,,, abcd là các số thự C. Biết hàm số ( ) ( ) ( ) ( )gxfxfxfx =++ có 2 giá trị cực trị là 0 và 4. Diện tích hình phẳng giới hạn bởi đường ( ) ( ) 24 fx y gx = + và 1 y = bằng A. ln8 B. ln2 C. 3ln2 D. ln7 6 Lời giải Chọn D ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 4 322 4 432,1262,246,24 2424 241 2424 fxxaxbxcfxxaxbfxxafx gxfxfxfx gxfxfxgxfx gxfxfxfx gx f fxgxgx gxgx =+++=++=+= =++ =++=−+ =++ =−+−= ++ Phương trình hoành độ giao điểm ( ) ( ) 24 fx y gx = + và 1 y = : ( ) ( ) 1 24 fx gx = + ( ) 0 xm gx xn = = = Với ( ) ( ) ( ) ( )gxfxfxfx =++ là hàm bậc ba với hoành độ cực trị là , xmxn == . Giả sử hàm ( )gx có giá trị cực trị tương ứng ( ) ( ) 0,4gmgn== . Khi đó diện tích hình phẳng bởi đường ( ) ( ) 24 fx y gx = + và 1 y = là: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 247 1d1ddln24ln 2424246 nnn n m mmm fxgxgxgx Sxxxgx gxgxgx −+ =−=−==+= +++ . Câu 128: Cho hàm số ( ) 32 fxxaxbxc =+++ với ,, abc là các số thực. Biết hàm số ( ) ( ) ( ) ( )gxfxfxfx =++ có hai giá trị cực trị là 5 và 2. Diện tích hình phẳng giới hạn bởi các đường ( ) ( ) 6 fx y gx = + và 1 y = bằng A. ln3. B. ln7. C. 3ln2. D. ln10. Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) 2 1 1d 12 x x fx Sx gx =− + ( ) ( ) ( ) 2 1 12 d 12 x x gxfx x gx −+ = + ( ) ( ) 2 1 d 12 x x gx x gx = + ( ) 2 1 ln12 x x gx =+ ( ) ( )21 ln12ln12 gxgx =+−+ 120222021=−= Câu 127: Cho hàm số ( ) 432 fxxaxbxcxd =++++ vớ
Chọn C
Xét hàm số ( ) ( ) ( ) ( )gxfxfxfx =++ Ta có ( ) ( ) ( ) ( )gxfxfxfx
Theo giả thiết ta có phương trình ( ) 0 gx = có hai nghiệm , mn và ( ) ( ) 5 2 gm gn
=− = .
(
n m
+ ( ) ( ) ( ) 60 60 fxfx gx ++=
+−=
=
n m
= + (
fxfx x gx ++
n m
=
gx x gx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 4
=++ ( ) ( ) 6 fxfx =++ .
+
xm
(
n m
+ (
Xét phương trình ( ) ( ) 1 6 fx gx = + ( ) ( ) ( ) 60 60 gxfx gx
xn = A. 8 3 B. 8 15 C. 16 3 D. 16 5 Lời giải Chọn C Đặt ()()() hxfxgx =− '()'()'(). hxfxgx =− Xét phương trình hoành độ giao điểm ( ) ( ) ( ) ( ) 0 fxgxfxgx =−=
=
Diện tích hình phẳng cần tính là:
) ( ) 1d 6
fx Sx gx
=−
) ( ) ( ) 6 d 6
gxfx x gx +−
) ( ) ( ) 6 d 6
+ ( ) ( ) d 6
+
) ln6 n m gx =+ ( ) ( ) ln6ln6 gngm =+−+ ln8 = 3ln2 = Câu 129: Cho hai hàm số ()fx và ()gx liên tục trên và hàm số 32 '() fxaxbxcxd =+++ , 2 '() gxqxnxp =++ với ,0aq có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số '()yfx = và '()ygx = bằng 10 và (2)(2)fg = . Tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()yfx = và ()ygx =
Vì hai đồ thị '()yfx = và '()ygx = cắt nhau tại các điểm có hoành độ lần lượt bằng 0;1;2 nên phương trình có các nghiệm là 0; x = 1 x = và 2 x = . Do đó, ta có '()'()'()(1)(2) hxfxgxkxxx =−=−− ( ) 0. k Ta có diện tích hình phẳng giới hạn bởi hai đồ thị hàm số '()yfx = và '():ygx = ( )( ) ( )( ) 212 001 16 ()()d()d52020d. 3 Sfxgxxhxxxxxx =−==−+= Câu 130: Cho hàm số 32 ()2 fxxbxcxd =+++ với b , c , d là các số thực. Biết hàm số ()()()() gxfxfxfx =++ có hai giá trị cực trị là 3 và 6. Diện tích hình phẳng giới hạn bởi các đường thẳng () ()12 fx y gx = + và 1 y = bằng A. 2ln2 B. ln162. C. ln2 D. ln2. Lời giải Chọn D Ta có 322 ()2()62()122()12 fxxbxcxdfxxbxcfxxbfx =+++=++=+= Xét hàm số ()()()() gxfxfxfx =++ Ta có ()()()()()()12 gxfxfxfxfxfx =++=++ . Theo giả thiết ()()()() gxfxfxfx =++ có 2 cực trị là 3 và 6
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn = = Diện tích hình phẳng cần tìm là: 222 432 000
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 5
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 1 '()'()d12d12d. 2 Sfxgxxkxxxxkxxxxk =−=−−−−−= Theo đề: 10 S = . Do đó: 20. k = '()20(1)(2) hxxxx=−− ( ) 4 3232()20(1)(2)d2032d204 x hxxxxxxxxxxxC =−−=−+=−++ Vì (2)(2)fg = (2)(2)(2)0 hfg=−= 0 C = Do đó: 432()52020 hxxxx =−+ Xét phương trình hoành độ giao điểm: ()() fxgx = ()()0fxgx−= ()0hx = 432 520200 xxx−+= 0 2 x x
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 6 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ()0gx = có hai nghiệm phân biệt m , n và ()3 ()6 gm gn =− = Xét phương trình ()1 ()12 fx gx = + ()12()()12()0()()120. xm gxfxgxfxfxfx xn = +=+−=++= = Diện tích hình phẳng cần tính là: ()()12() 1 ()12()12 nn mm fxgxfx Sdxdx gxgx +− =−= ++ ()()()12() ()12 n m fxfxfxfx dx gx +++− = + ()()12() ()12()12 ln()12ln()12ln()12 ln18ln9ln2. nn mm fxfxgxdxdx gxgx n gxgngm m ++ == ++ =+=+−+ =−= Câu 131: Cho hàm số ( )fx thỏa mãn ( ) ( ) ( ) ( ) 22 .ln2,1;xfxxfxxfxx −+=+ , ( ) ( ) 0,1;fxx+ và ( ) 2 1 e e f = . Tính diện tích S hình phẳng giới hạn bởi đồ thị ( ) 2 ,0,, yxfxyxexe ==== A. 3 2 S = . B. 1 2 S = . C. 5 3 S = . D. 2 S = . Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) ( ) 222 2 '1 'ln2ln2 fx xfxxfxxfxxxx fxfx −+=−+= , ( ) 1; x + ( ) ( ) ( ) 2 .ln2,1;xgxxgxxx +=+ với ( ) ( ) 1 gx fx = ( ) ( ) ln2 gx gxxx x += , ( ) 1; x + ( ) ( ) lndd2d gx gxxxxxx x += ( ) ( ) ( ) 2 lndd gxgx gxxxxxC xx −+=+ ( ) 2 ln gxxxC=+ , ( ) 1; x + .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 7 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Do ( ) ( ) 2 2 1 e0 e fgeeC === . Suy ra ( ) 2 ln gxxx = , ( ) 1; x + ( ) ( ) 2 ln0,1; x gxx x =+ ( ) ( ) ln xx yxfx gxx === , ( ) 1; x + Ta có ( ) 22 2 ee 2 ee e ddlnln13 22 e x Sxfxxxx x ==== Câu 132: Cho đường cong 3 ():2 Cyxkx=++ và parabol 2 :2Pyx=−+ tạo thành hai miền phẳng có diện tích 1S , 2S như hình vẽ. Biết rằng 1 8 3 S = , giá trị của 2S bằng A. 1 2 B. 1 4 C. 3 4 D. 5 12 Lời giải Chọn D Phương trình hoành độ giao điểm của () C và d ( ) 322 2 0 220 0. x xkxxxxxk xxk = ++=−+++= ++= Hai đồ thị cắt nhau tại ba điểm phân biệt nên phương trình 2 0 xxk++= có hai nghiệm phân biệt 1x , 2x khác 0 và thỏa mãn 12 0 xx . Do đó ta có 21 2 11 0 1 k xx kxx =−− =−− Trên đoạn 1 [;0] x , 3232220xkxxxxkx ++−+++ . Theo bài ra, diện tích 1 8 3 S = nên


































CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 8
( ) 11 00 432 3232 1 0 dd888 334323 xx xxkx xxxkxxkxxx x ==++= ++++ ( ) ( ) 4324322 11111111 3463234632 xxkxxxxxx −++=++−−=− ( ) 4332 1111111
xxxxxxx +−=+−+−==− Vớ
1222,1xkx=−=−= và 32 20,[0;1]xxxx+−
ta
( ) 1 43 3221 20 0 5 2d. 4312 | xx Sxxxxx =−+−=−+−= Câu 133: Cho hàm số 3213 3 24 yxxx =−++ có đồ thị ( )C và đường thẳng d đi qua gốc tọa độ tạo thành hai miền phẳng có diện tích 1S và 2S như hình vẽ Biết 1 27 4 S = . Khi đó 2 m S n = , giá trị của 2mn bằng A. 143. B. 50. C. 50. D. 142. Lời giải Chọn D Gọi 0 a là hoành độ giao điểm của ( )C và d .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
32320(2)3481602
i
,
có
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 9
=−++−−++ 4322227113133 4842482 aaaaaa =−++−−++ 432711 3 488 aaa =−= . Do đó, 3 : 4 dyx = . Phương trình hoành độ giao điểm của ( )C và d là: 3232 313139 300 424244 xxxxxxx −−++=−−= Phương trình trên có 3 nghiệm: 1 3 x = , 2 0 x =
3
x =− 0 32 2 3 2 139135 d 244128 Sxxxx =−−= Do
135 m = , 128 n = .
−= . Câu 134: Cho hàm số ( ) (
432 3,,,
=++++
ực trị 2,1 và 2. Gọi ( )ygx = là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ( )yfx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = có giá trị thuộc khoảng A. ( )34;35 . B. ( )36;37 . C. ( )37;38 . D. ( )35;36 . Lời giải Chọn C Theo bài ra, ta có: ( ) ( )( )( ) ( ) 32 122121244 fxxxxxxx =+−−=−−+ ( ) 432 342448. fxxxxxd =−−++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó, đường thẳng d có hệ số góc là: 32 2 13 3 13 24 3 24 aaa kaa a −++ ==−++ . Đường thẳng d đi qua gốc tọa độ nên có phương trình là 2 13 :3 24 dyaax =−++
Ta có: 322 1 0 131333d 2424 a Sxxxaaxx =−++−−++ 43222 0 27113133 4842482 a xxxaax
và 3
2
đó:
Vậy: 2142 mn
)
fxxaxbxcxdabcd
có ba điểm c
Biết hàm số ( )fx đạt cực trị tại hai điểm 12 , xx thỏa mãn 21 2 xx=+ và ( ) ( ) 12 0. fxfx+= Gọi 12 , SS là diện tích của hình phẳng như hình bên và 3S là diện tích phần tô đậm. Tính tỉ số 2 3 . S S A. 1 4
3 8
2 16
3 16 Lời giải Chọn D + Tịnh tiến đồ thị hàm số ( )yfx = sang phải một đoạn 12 2 xx + đơn vị ta thu được đồ thị hàm số bậc 3 ( )ygx = nhận gốc toa độ làm tâm đối xứng nên ( )gx là hàm lẻ có dạng ( ) 3 gxaxbx =+ và hàm số ( )gx có hai điểm cực trị là 1 x =− và 1. x =
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
42
Page 10
Khi đó ( ) ( ) ( ) 2112,123,216 fdfdfd −=−=+=+ Giả sử ( ) 2 gxmxnxp =++ Theo
( ) ( ) ( ) ( ) ( ) ( ) 2421124211213 1232332 2421642164 gmnpdmnpd m gmnpdmnpdn pd gmnpdmnpd −=−+=−−+−=− =− =++=+++−==
= = Vậy ( ) 2 432 2 3411164d37,3135837;38.Sxxxxx =−−+− Câu 135: Cho hàm số bậc ba ( )yfx = có đồ th
đường cong
viên: Huỳnh Văn Ánh
Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
bài ra, ta có:
−= =++=+++−= . Do vậy, ( ) ( ) 4322432 34244813323411164 fxgxxxxxdxxpxxxx −=−−+++−−=−−+− . Suy ra ( ) ( ) 2 1 0. 3 1 2 x x fxgx x x =− = −=
ị là
như hình bên dưới.
B.
C.
D.
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
b
(
(
===−−−= Phương trình hoành độ giao
m
ủ
(
axaxxx
= =−= =− ( ) ( ) 2233 3 00 344. Saxxxdxaxxdxa =−+=−= Vậy: 2 3 3 43 416 a S Sa == Câu 136: Cho hàm số bậc ba ( )fx có đồ thị như hình vẽ bên. Biết
12
A. 5 4 B. 3 5 C. 3 8 D. 5 8 Lời giải Chọn B Gọi 0x là
m uốn I của
ố
12
−=−=
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
11 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Có: ( ) ( ) 2 31303. gxaxbgabba =+=+==− Suy ra: ( ) ( ) 3 3.gxaxx =− + Tịnh tiến đồ thị hàm số ( )yhx = sang phải một đoạn 12 2 xx + đơn vị ta thu được đồ thị hàm
ậc nhất ( )ykx = có đồ thị là đường thẳng đi qua gốc tọa độ, điểm
) 21 1 ; 22 g xx A hay
) 1;.Aa Phương trình đường thẳng ( )ykx = là yax = . Ta có: ( ) ( ) ( ) 0 121 1 53 1.1. 44 SgxdxaSgSa
điể
c
a
)gx và ( )kx là: ( ) 3 0 32 2 x
x
hàm số ( )fx đạt cực trị tại hai điểm
; xx thỏa mãn 21 2 xx=+ và ( ) ( ) 12 2 fxfx+= . Gọi 12 ; SS là diện tích của hai hình phẳng được cho trong hình vẽ bên. Tính tỉ số 1 2 S S .
hoành độ điể
đồ thị hàm s
( )yfx = . Do ( )fx đạt cực trị tại hai điểm
; xx thỏa mãn 21 2 xx=+ 1020 1 xxxx
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 12
C
Trong
ra ( )gx là tam thức bậc hai có nghiệm 121;1xx=−= . ( ) ( )( ) ( ) ( ) 2 1110gxaxxaxa =+−=− ( ) 3 3 x gxaxb =−+ Đồ thị hàm số ( )ygx = đi qua điểm ( )0;0 O nên 0 b = ( ) 3 3 x gxax =− . Ta có: 0 342 2 1 05 d 1 312212 Saxxaxxxa =−=−= ( ) 113342 1 00 1 22 1dd 0 33312234 Saxgxaxxaxxaxxxa =−−=−+=−+= Vậy 1 2 3 5 S S = . Câu 137: Cho hàm số ( ) (
432 3,,, fxxaxbxcxdabcd =++++ có ba điểm cực trị là 2, 1 và 1 Gọi ( )ygx = là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ( )yfx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 500 81 B. 36 5 C. 2932 405 D. 2948 405 Lời giải Chọn D ( ) ( ) 43232 31232 fxxaxbxcxdfxxaxbxc =++++=+++ Theo đề ta có: ( ) 2012496.fabc −=−+= ( ) 103212.fabc −=−+= ( ) 103212.fabc =++=−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
ố định đồ thị hàm số ( )fx , tịnh tiến hệ toạ độ Oxy theo véc tơ OI . Khi đó, trong hệ toạ độ mới 12 ; SS không thay đổi so với hệ toạ độ cũ.
hệ toạ độ Oxy mới, đường cong là đồ thị của hàm số bậc ba ( )ygx = . Từ hình vẽ suy
)
Xét hệ phương trình 124968 32126 321224
−+== −+==− ++=−=− .
abca abcb abcc
Khi đó ( ) 32 12241224fxxxx =+−− suy ra ( ) 432 38624 fxxxxxd =+−−+
Lúc này ba điểm cục trị của hàm số ( )yfx = có tọa độ lần lượt là ( ) 2;8 d −+ , ( ) 1;13 d −+ và ( ) 1;19 d −+ . Xét hàm số bậc hai ( ) 2 ,, ymxnxqmnq =++ đi qua ba điểm ( )2;8 , ( )1;13 và ( )1;19 .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 13
mnqm mnqnyxx mnqp −+==− −+==−=−−+ ++=−=
7164. gxxxd =−−++ Ta có ( ) ( ) ( )( )( ) 4322 38843212 fxgxxxxxxxx −=++−−=+−+ . Vậy diện tích giới hạn bởi hai đường ( )yfx = và ( )
=
( ) ( ) ( ) 2 11 3 432432432 2 21 3 3884d3884d3884d Sxxxxxxxxxxxxxxx =−++−−+++−−−++−− 2948 . 405 = Câu 138: Cho hàm số ( )yfx = là hàm bậc bốn có đồ thị như hình bên. Biết diện tích hình phẳng giới hạn bởi đồ thị hai hàm số ( )yfx = và ( ) ' yfx = bằng 214 5 . Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = và trục hoành.
Khi đó ta có hệ phương trình: 2 4287 13167164 194
. Suy ra ( ) 2
ygx
là
A. 81 20 . B. 81 10 . C. 17334 635 . D. 17334 1270 . Lời giải
Chọn A
Từ đồ thị của hàm số ( )yfx = suy ra ( ) ( ) ( ) ( ) 22 21,0fxaxxa =+− . Ta có ( ) ( )( ) ( ) ( ) ( )( )( ) 22 22122122121 fxaxxaxxaxxx =+−++−=+−+
Xét phương trình ( ) ( ) ( )( ) ( )( ) ( ) 21212210fxfxaxxxxx =+−+−−+= ( )( )( ) 2
=− = +−−−= =− =

x x axxxx x x
2 1 21340 1 4
.
Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số ( )yfx = và ( ) ' yfx = là ( )( )( ) ( )( )( ) 44 22 22
428 21342134 5 Saxxxxdxaxxxxdxa =+−−−=+−−−= .
Theo đề bài ta có ( ) 4282141 552 aaTM == ( ) ( ) ( ) 22 1 21 2 fxxx =+− . Vậy diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = và trục hoành là ( ) ( ) 1 22 1 2
181 21 220 Sxxdx =+−= . Câu 139: Cho hàm số 32 () fxxbxcxd =+++ và 2 () gxaxexh =++ ( ) ,,,,, abcdeh . Biết rằng đồ thị hàm số ()và ()yfxygx == cắt nhau tại ba điểm có hoành độ lần lượt là -3; -1; 0 Hình phẳng được giới hạn bởi hai đồ thị đã cho có điện tích bằng A. 37 12
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 14
B. 4 C. 5 13 D. 13 Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 15 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn A Phương trình hoành độ giao điểm của đồ thị hàm số ()và ()yfxygx == : 322 32()()0(1) xbxcxdaxexh xbaxcexdh +++=++ +−+−+−= Theo bài suy ra phương trình có ba nghiệm: 3; 1; 0. Ta có hệ phương trình: 279()3()()04 1()()()03 00 bacedhba bacedhce dhdh −+−−−+−=−= −+−−−+−=−= −=−= . 32 ()()43 fxgxxxx−=++ . Diện tích hình phẳng: 10 31 (()())(()()) Sfxgxdxgxfxdx =−+− 10 44 3232321320 31 31 4343 (43)(43)|| 432432 143812714337 36. 4324243212 xx xxxdxxxxdxxxxx =+++−−−=++−++ =−+−−++−+= Câu 140: Cho hàm số 42 =++ yaxbxc và hàm số 2 =++ ymxnxp có đồ thị là các đường cong như hình vẽ. Diện tích hình phẳng được tô đậm bằng A. 52 . 15 B. 104 . 15 C. 32 . 15 D. 64 . 15 Lời giải Chọn D + Xét hàm số 42 ().==++ yfxaxbxc Ta có 3 ()42.==+ yfxaxbx y x 1 3 4 O 1
Từ đồ thị ta có (0)331 (1)442. (1)04203
===− =++== =+==
fca fabcb fabc Suy ra 42 ()23. =−++fxxx + Xét hàm số 2 ().==++ ygxmxnxp Ta có đồ thị hàm số là parabol có đỉnh ( )0;0 O nên 0 . 0 = = n p Suy ra 2 (). = gxmx

(
111
ddd Sfxgxxxxxxxxx 1 53
=−−+=−−+−+−=
12121264
S S ( 1S và 2S lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai hàm (),()fxgx như hình vẽ ).
5
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 16
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
A.
32 . B. 6 35 . C.
33 . D.
29 . Lời
ả
Hơn nữa, parabol đi qua điểm (1;4) nên 4. = m Do đó 2 ()4. = gxx Diện tích hình phẳng cần tìm là: Chọ
) ( ) ( ) ( ) 111 42242
()()23423 =−=−++−=−−+
1
333. 53535315
xxx Câu 141: Cho hàm số bậc ba ( )yfx = có đồ thị là đường cong ở hình bên dưới. Gọi 12 , xx lần lượt là hai điểm cực trị thỏa mãn 21 2 xx=+ và ( ) ( ) 1230.fxfx−= và đồ thị luôn đi qua 00 (;())Mxfx trong đó 01 1 xx=− ()gx là hàm số bậc hai có đồ thị qua 2 điểm cực trị và M. 0 1 1 xx=+ . Tính tỉ số 1 2
7
4
gi
i
n A
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 17
ừ
( ) 432 346096 fxxxxxd =+−++ Ta có ( ) ( ) 2 11 '.31828 43 fxfxxxxd =+−+−+ Giả sử ( ) , iii Axy là điểm cực trị của đồ thị hàm số ( )yfx = thì ( ) 2 31828iiii yfxxxd ==−+−+ Do đó đồ thị hàm số bậc hai qua ba điểm cực trị của đồ thị hàm số ( )yfx = là ( ) 2 31828 ygxxxd ==−+−+ .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Nhận thấy hình phẳng trên có diện tích không đổi khi ta tịnh tiến đồ thị sang trái sao cho 0 0 x = Khi đó ta có 121,3,xx== Xét hàm 32 () fxaxbxcxd =+++ và 2 g()xmxnxp =++ . Vì 121,3,xx== là các điểm cực trị nên ta có: (1)0320 (1)(3)02760 fabc fabc =++= =++= Hơn nữa, ta có (1)3(3)2793.(2) ffabcdabcd =+++=+++ T
và suy ra 6 9 2 ba ca da =− = = Mặt khác dựa vào đồ thị ta thấy: (0)(0)2 (1)3(3)2 (0)(3)3 gfpa ggma ggna == ==− −=− Suy ra 32 ()(692) fxaxxx =−++ , 2 g()(262) xaxx=−++ Khi đó ta có: 1 32 1 0 5 43 12 Saxxxdxa =−+=
3 32 2 1 8 43 3 Saxxxdxa =−+= Do đó, 1 2 5 32 S S = Câu 142: Cho hàm số ( ) 432 3 fxxaxbxcxd =++++ ( ) ,,, abcd có ba điểm cực trị là 4,1 và 2. Gọi ( )ygx = là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ( )yfx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 3132 5 . B. 4839 10 . C. 8451 10 . D. 28780 81 . Lời giải Chọn D Ta có ( ) ( )( )( ) ( ) 32 '1241212108 fxxxxxxx =+−−=+−+
Khi đó ( ) ( ) 432
=−
=
=
x x fxgxxxxx x x d =− Sfxgxx ( )( )( ) 0 4
=− 1 311d 2 =++− Sxxxx 6 = .
4 1 342914803 1 2 n tích bằng A. 6 B. 9 2 C. 4 D. 11 2 Lời giải Chọn A Ta có: ( ) ( ) ( )( )( )311fxgxaxxx −=++− Suy ra ( )( )( ) ( ) ( ) 32 3 311 2 axxxaxbdxcex ++−=+−+−− . Xét hệ số tự do suy ra: 31 3 22 aa −=−= Do đó: ( ) ( ) ( )( )( ) 1 311 2 fxgxxxx −=++− . Diện tích bằng: ( ) ( ) 0 4
28780 d 81 Sfxgxx =−= . Câu 143: Cho hai hàm số ( ) 32 1 2 fxaxbxcx=++− và ( ) 2 1 gxdxex=++ ( ) ,,,,.abcde Biết rằng đồ thị hàm số ( )yfx = và ( )ygx = cắt nhau tại 3 điểm có hoành độ lần lượt là 3; 1; 1. Hình phẳng giới hạn bởi hai đồ thị đã cho và đường thẳng 4;0=−=xx có diệ
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 18
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
−=+−++=
Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng ( ) ( ) 2 4
42 126164 abc ababc −−= −−=++ ( ) ( ) 4202 281003 abc abc −−−= 255 1 xxx fxfx xx
Mặt khác, diện tích phần tô màu là ( )( ) 2 42 0 28421d 5 abxaxbxcx =−−+−−− −+ += −+ ; ( ) ( ) 102ff−= ; ( ) 1 0
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 3221d Sxxxx =−+−+ ( ) 0 42 1
d0fxx = . Biết diện tích hình phẳng giới
Câu 144: Cho hàm số 42 yaxbxc =++ có đồ thị ( )C , biết rằng ( )C đi qua điểm ( )1;0 A , tiếp tuyến d tại A của ( )C cắt ( )C tại hai điểm có hoành độ lần lượt là 0 và 2 và diện tích hình phẳng giới hạn bởi d , đồ thị ( )C và hai đường thẳng 0 x = ; 2 x = có diện tích bằng 28 5 . Diện tích hình phẳng giới hạn bởi ( )C và hai đường thẳng 1 x =− ; 0 x = có diện tích bằng A. 2 5 . B. 1 4 . C. 2 9 . D. 1 5 . Lời giải Chọn D Ta có 3 42 yaxbx =+ ( )( ):421 dyabx=−−+ Phương trình hoành độ giao điểm của d và ( )C là: ( )( ) ( ) 42 4211 abxaxbxc −−+=++ . Phương trình ( )1 phải cho 2 nghiệm là 0 x = , 2 x = 1 32 5 xxxdx =−−= Câu 145: Cho hàm số ( )yfx = có đạo hàm liên tục trên đoạn 0;1 và thỏa ( ) ( ) ( ) 32 2 2
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 19
++= .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 ( ) 28328 4422 553 ababc=−−−−− ( ) 1123228 24 535 abc ++=− . Giải hệ 3 phương trình ( )2 , ( )3 và ( )4 ta được 1 a = , 3 b =− , 2 c = Khi đó, ( ) 42 :32Cyxx=−+ , ( ):21dyx=+ . Diện tích cần tìm là ( ) 0 42 1
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 20
ố
−+ Mặt khác, ta có ( ) ( ) ( ) ( ) ( ) ( ) 1 1 2 2 0 0 2 2 2 211 dln10d 10 211 11210 0 1 21 dln1 1 x xxxfxx xx x ff xx x xxxC xx =−+== −+ =−−==− −+ =−++ −+ nên suy ra ( ) 2 0 21 1 C x fx xx = = −+ Do đó ( ) 1 2 2 2 0 1 214 dln1lnln4ln3 2 13 0 x Sxxx xx ==−−+==− −+ . Suy ra 4 3 a b = = . Vậy 22 25 Tab=+= . Câu 146: Cho Parabol ( ) 2 :4 Pyxx =−+ có đỉnh I và A là giao điểm khác O của ( )P với trục hoành. M là điểm bất kì trên cung IA, tiếp tuyến của ( )P tại M cắt Ox,Oy lần lượt tại , BC . Gọi 12 , SS lần lượt là diện tích của hai tam giác cong , MABMOC . Tìm M sao cho 12SS + nhỏ nhất. A. ( )4;0 M . B. ( )3;3 M . C. 832 ; 39 M . D. 8160 ; 39 M . Lời giải
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn hạn bởi đồ thị ( ) ( ) : Cyfx = , trục tung và trục hoành có dạng lnln Sab =− với , ab là các s
nguyên dương. Tính 22Tab =+ A. 13 T = B. 25 T = C. 34 T = D. 41 T = Lời giải Chọn B Ta có ( ) ( ) ( ) 32 2 2 255 1 xxx fxfx xx −+ += −+ ( )( ) ( ) 22 2 2 211221 1 xxxxx xx −−+−++ = −+ ( ) ( ) ( ) 2 2 2 2 21221 dddd 11 xxx fxxfxxxx xx xx +=− −+ −+ ( ) ( ) ( ) ( ) 2 2 2 2 2 2 221 d1 21 d dd 1 1 21 xx xx x fxxfxxx xx xx x −+ +=− −+ −+ ( ) ( ) ( ) ( ) 2 2 2 2 22 2 1d1d21 21 d ln1 11 1 21 xx xx x x fxxfxxxC xxxx xx x −+ −+ +=−=−+++ −+−+
Vì M thuộc cung IA nên giả sử ( ) 2 ;4 Mmmm −+ với 24 m .
Tiếp tuyến tại M có phương trình: 2 (24) ymxm =−++ .
Khi đó ( ) 2 2 ;0,0; 24 m BCm m
Gọi 3S là diện tích giới hạn bởi ( )P và Ox, ta có ( ) 4 2 3 0
32 4 3 Sxxdx=−+= .
Diện tích tam giác vuông OBC là ( ) 4 1 . 242 m SOBOC m ==
Ta có: ( ) 4 123 32 423 m SSSS m +=−=− .
Suy ra 12SS + nhỏ nhất khi và chỉ khi ( ) ( ) 4 42 m Sfm m == nhỏ nhất.
Ta có ( ) ( ) ( ) ( ) 3 2 388 ','0 423 mm fmfmm m ===
Lập BBT ta được ( )fm nhỏ nhất khi 8 3 m = .
Vậy 12SS + nhỏ nhất khi 832 ; 39 M Câu 147: Cho hàm số ( ) 42 yfxaxbxc ==++ có đồ thị ( ), C Biết ( ) 10 f −= . Tiếp tuyến d tại điểm có hoành độ 1 x =− của ( )C cắt ( )C tại 2 điểm có hoành độ lần lượt là 0 và 2, Gọi 12 ; SS là diện tích hình phẳng. Tính 2S , biết 1 401 . 2022 S =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 21
Chọn C
A. 12431 2022 . B. 5614 1011 . C. 2005 2022 . D. 2807 1011 .
Lời giải
1;0
trình tiế
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 22
Mà 0,2xx== là nghiệm của suy ra 42 126164 abc ababc −−= −−=++ . Từ và ta có: 2 4233 cabcabca ababbaba =−−=−−= −−=−−=−=− Ta có: ( )( ) ( ) ( ) ( ) 00 4242 1 11 4213221 Saxbxcabxdxaxaxaaxdx =++−−−+=−+−+ ( ) 0 42 1 1 4012005 32. 520222022 a Saxxxdxa =−−=== ( )( ) ( ) ( ) 22 4242 2 00 285614 42132. 51011 a Sabxaxbxcdxaxxxdx =−−+−++=−++== Vậy 2 5614 . 1011 S =
Chọn B Từ đồ thị ( )C nhận thấy 0;0;0abc . Ta có: (1)0 f −= suy ra: 0 abc++= ; gọi ( )
A Phương
p tuyến tại ( )1;0 A là ( ) ( )( ) ( )( ):'11421 dyyxabx =+=−−+ Phương trình hoành độ giao điểm của tiếp tuyến ( ) d và đồ thị ( )C : ( )( ) ( ) 42 421* abxaxbxc −−+=++
Câu 148: Cho hàm số bậc ba ( ) 32 1 2 yfxaxxcxd ==−++ và parabol ( )ygx = có đỉnh nằm trên trục tung. Biết đồ thị ( )yfx = và ( )ygx = cắt nhau tại ba điểm phân biệt ,, ABC có hoành độ lần lượt là 2;1;2 và thỏa mãn 35 2 AB = . Tính diện tích hình phẳng giới hạn bởi hai đồ thị ( )yfx = và ( )ygx = .
A. 238 3 . B. 71 3 . C. 71 6 . D. 13 4 . Lời giải
Chọn C
Parabol ( )ygx = có PT dạng ( ) 2 ,0ykxmk=+ . Ta có ( ) ( ) 2;4,1; AkmBkm −++

Do 22 353511 99. 2242 ABkkk =+=== Suy ra ( ) 2 1 2 ygxxm ==+
Xét phương trình ( ) ( ) ( ) ( ) 32 00fxgxfxgxaxxcxdm =−=−++−= Do PT có 3 nghiệm 2;1;2, suy ra ( ) ( ) ( )( )( )212fxgxaxxx −=+−− . Theo Định lý viet, ta có 123 1 2121 b xxxa aa ++=−−++== . Suy ra di
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
23 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN
ỨNG DỤNG TÍCH PHÂN
-
Page
n tích hình phẳng giới
ởi
( ) (
( )(
22 2 22 71 d14d 6 Sfxgxxxxx =−=−−= . Câu 149: Cho đồ thị hàm số bậc ba ( ) 32 yfxaxbxcxd ==+++ và đường thẳng
vẽ và 12
SS là diện tích
ố
ả
ệ
hạn b
hai đồ thị trên là `
)
)
: dymxn =+ như hình
,
hình phẳng được tô đậm trong hình bên. Biết 1 2 S p Sq = với * , pq là một phân số t
i gi
n. Tính 2022 pq++ .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 24 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 2043. B. 2045. C. 2049. D. 2051. Lời giải Chọn C Ta có ( ) 2 32 yfxaxbxc ==++ . Do đồ thị hàm số ( ) 32 yfxaxbxcxd ==+++ có hai điểm cực trị là ( ) 1; 4 và ( ) 1; 0 nên 3201 3200 43 02 abca abcb abcdc abcdd −+== ++== −+−+==− +++== 2 32yxx =−+ . Vì đường thẳng : dymxn =+ đi qua 2 điểm ( ) ( ) 2 ; 0,0; 2 nên :2dyx=+ Ta có ( ) 11 233 1 00 1 .232d232d 2 Sxxxxxx =+−+=+−+= 1 42 0 311 22 424 xx x =+−+= . ( ) ( ) ( ) ( ) 222 333 2 000 232d232d4d4 Sxxxxxxxxxxx =+−−+=+−+−=−+= . 1 2 11 16 S p Sq == . Vậy 20222049 pq++= . Câu 150: Cho hàm số bậc ba ( )yfx = có đồ thị ( )C như hình vẽ.
Biết rằng đồ thị hàm số đã cho cắt trục Ox tại ba điểm có hoành độ 123 ,, xxx theo thứ tự lập thành cấp số cộng và 31 23 xx−= . Diện tích hình phẳng giới hạn bởi ( )C và trục Ox là S , diện tích 1S của hình phẳng giới hạn bởi các đường ( ) 1 yfx=+ , ( ) 1 yfx=−− , 1xx = và 3xx = bằng A. 43. B. 23 . C. 243 S + . D. 23 S + . Lời giải
Chọn A
Do đồ thị hàm bậc ba cắt trục hoành tại ba điểm có hoành độ 123 ,, xxx theo thứ tự lập thành cấp
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 25
Do
xxxx xxxx fxdxfxdxfxdxfxdxSS
Suy ra: ( ) 2 1 ; 2 x x S fxdx = ( ) 3 2 . 2 x x S fxdx =− Vì đồ thị hai hàm số ( ) 1 yfx=+ và ( ) 1 yfx=−− đối xứng với nhau qua trục hoành nên ta có: ( ) ( ) ( ) ( ) ( ) ( ) 3333 1111 33 2 121 1 31 212122 22 2243. 22 xxxx xxxx xx x xxx Sfxdxfxdxfxdxdx fxdxfxdxdx SS xx =+=+=+ =++ =−+−= Chọn A Câu 151: Cho hai hàm số ( ) 432 fxaxbxcxdxe =++++ với 0 a và ( ) 2 3 gxpxqx=+− có đồ thị như hình vẽ bên dưới. Đồ thị hàm số ( )yfx = đi qua gốc tọa độ và cắt đồ thị hàm số ( )ygx = tại
số cộng nên đồ thị nhận điểm ( ) 2;0 Ax làm tâm đối xứng của đồ thị
đó: ( ) ( ) ( ) ( ) 2233 1212 22
===−=
0 168423 1 3 2 3 3 30 4
e abcpdq

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo
Page 26
bốn
độ lần
t là
và m .
ếp
ếncủađồth
ố
yfxgx =− t
viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 abcpdq abcpdq ambmcpmdqm = −+−−−=− −+−−−=− ++−+−=− ++−+−+= Mặt khác, tiếp tuyến của đồ thị hàm số ( )yhx = tại điểm có hoành độ 2 x =− có hệ số góc bằng 15 2 nên ( ) ( ) ( ) ( ) 1515 232124 5 22habcpdq −=−−+−−+−=− . Từ ( )1 , ( )2 , ( )3 , ( )5 , ta tìm được: 1 2 1 2 7 2 1 2 a b cp dq = =− −=− −= .
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
điểm cóhoành
lượ
2; 1; 1
Ti
tuy
ị hàm s
( ) ( )
ại điểm có hoành độ 2 x =− có hệ số
góc bằng 15 2 . Gọi ( ) H là hình phẳng giới hạn bởi đồ thị hai hàm số ( )yfx = và ( )ygx = . Diện tích của hình ( ) H bằng A. 1553 120 B. 1553 240 C. 1553 60 D. 1553 30 Lời giải Chọn A Đặt ( ) ( ) ( ) ( ) ( ) ( ) 432 3 hxfxgxaxbxcpxdqxe =−=++−+−++ ( ) ( ) ( ) 32 432 hxaxbxcpxdq =++−+− . Phương trình hoành độ giao điểm của 2 đồ thị ( )yfx = và ( )ygx = là: ( ) ( ) ( ) ( ) ( ) 432 030fxgxhxaxbxcpxdqxe ==++−+−++= . Đồ thị hàm số ( )yfx = đi qua gốc tọa độ và cắt đồ thị hàm số ( )ygx = tại bốn điểm có hoành độ lần lượt là 2; 1; 1 và m nên ( ) ( ) ( ) ( ) ( ) 02110 fhhhhm =−=−=== ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 432

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 27
( ) ( ) ( ) 113 211 113581221553 ddd 1201515120 hxxhxxhxx =++=−++−= . Câu 152: Cho hàm số ( )fx liên tục trên và đường thẳng ( ) ( ) :
=+ có đồ thị như hình vẽ. Biết diện tích miền tô đậm bằng 37 12 và ( ) 1 0 19 d 12 fxx = . Tích phân ( ) 0 1 .2d xfxx bằng A. 607 348 . B. 20 3 . C. 5 3 . D. 5 6 . Lời giải Chọn C Ta có: ( ) ( ) ( ) ( ) ( ) 1;332 21. 2;3231 Agxaxb aba gxx abb Bgxaxb =+ +== =+ −+=−= −−=+ Mà ( ) ( ) ( ) ( ) 01 20 3737 21d21d 1212 Sfxxxxfxx =−+++−= ( ) ( ) ( ) ( ) ( ) 01100 20022 372dd21d21dd 123fxxfxxxxxxfxx −++−+== Khi đó ( ) ( ) ( ) ( ) 000 0 2d2ddd 12 d()d() 2 00 122 11 .2d.d.d 44 txtxutut xt vfttvft xt xfxxtftttftftt =→==→= =−→=− =→= =→= ⎯⎯⎯⎯⎯→⎯⎯⎯⎯⎯⎯→− ( ) ( ) ( ) 0 2 1125 22d2.3 4433 ffxx =−−=−−=− .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Thay vào ( )4 : ( )( )( )( ) 432 1171 3031120 2222 mmmmmmmm −−++=−−++= 3 m = . Ngoài ra, ta cũng có: ( ) 432 1171 3 2222 hxxxxx =−−++ . Vậy diện tích hình phẳng cần tính là ( ) ( ) ( ) ( ) 3113 2211 dddd Shxxhxxhxxhxx ==++
dgxaxb
Câu 153: Cho hai đồ thị hàm số ( )yfx = và ( )ygx = như hình vẽ bên dưới. Biết đồ thị của hàm số ( )yfx = là một Parabol đỉnh I có tung độ bằng 1 2 và ( )ygx = là một hàm số bậc ba. Hoành độ giao điểm của hai đồ thị là 123..6xxx =− . Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ( )yfx = và ( )ygx = gần nhất với giá trị nào dưới đây? A. 6. B. 7. C. 5. D. 8. Lời giải Chọn A Parabol cắt Ox tại 0 x = và 2 x = nên 2 ()(2)(2) fxmxxmxx =−=− . Đỉnh I có hoành độ 1 Ix = , suy ra tung độ 11 22 I ymm=−== . Vậy ( ) 2 1 2 yfxxx ==− Hàm số ( )ygx = đạt cực trị tại 0 x = và 2 x = nên ( ) ( ) 2 22 gxaxxaxax

điể
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 28
=−=− Suy ra ( ) 32 3 a gxxaxb =−+ Do đồ thị hàm số ( )ygx = đi qua
m 1
2
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 nên 21 32 ab+= Phương trình hoành độ giao điểm của đồ thị hàm số ( )yfx = và đồ thị hàm số ( )ygx = là 322 1 32 a xaxbxx −+=− 32 1 0 32 a xaxxb −+++= Suy ra 123 3 ..6 b xxx a ==−
1;
I
ện tích hình phẳng giới hạn bởi hai đồ thị hàm số ( )yfx = và ( )ygx = là
32
=−+−=
113299d6,23 88448 Sxxxx
Câu 154: Cho hai hàm số 432 4 ()d3 fxaxbxcxx =+++− (,,,abcd ) và 32 () gxmxnxpx =++ ( ) ,, mnp . Đồ thị hai hàm số ()fx và ()gx được cho ở hình bên dưới. Tính diện tích hình phẳng giới hạn bởi hai đường ()yfx = và ( )2 1 ()2 3 ygxx=+− biết rằng 4 AB = . A. 175 45
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 29 Chuyên
10 Tốt
Sưu tầm và biên soạn 630 ab −= Từ và ta suy ra 3 8 3 4 a b = = Phương trình hoành độ giao điểm của đồ thị hàm số
yfx =
th
ố
ygx =
32 113 0 884 xxx
(
(
1260xxx −+−= 1 17
x x x = =−+ =−−
. B. 14848 1215 . C. 14336 1215 . D.
45
Lờ
giải Chọn B Ta
Hòa
0984164935
luyện thi: Tuyển sinh vào lớp
Nghiệp THPT BDKT Toán 10; 11; 12
( )
và đồ
ị hàm s
( )
là
−+−= 32 860xxx +−+=
)
) 2
17
Di
17
17
−+
512
.
i
thấy đồ thị hàm số ()yfx = và đồ thị hàm số ()ygx = cắt nhau tại đúng ba điểm phân biệt với các hoành độ 1,1,2 nên phương trình ()()0fxgx −= có đúng ba nghiệm phân biệt là 1,1,2. Do đó ta có

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 30 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ()()4(1)(1)(2) fxgxaxxx −=+−− Theo đề 1 4(0)(0)484 2 ABfgaa =−=== . Suy ra ( ) 432 2 ()()()()d2(1)(1)(2)d22 432 xxx fxgxfxgxxxxxxxC −=−=+−−=−−++ Theo đề 4 (0)(0) 3 fg−=− nên 4 3 C =− Suy ra 43224 ()()224323 xxx fxgxx −=−−+− . Đặt ( )2 1 ()()2 3 hxgxx=+− , xét phương trình ()()0fxhx−= . Ta có ( ) ( ) 2 432 2 1 ()()0()()20 3 2 2412 2220. 432333 2 fxhxfxgxx x xxx xxx x −=−−−= =− −−+−−−== = ss Diện tích hình phẳng đã cho là ( ) ( ) ( ) 2 22 432 2 1 241 222 43233 Sx xxx xx fxhdxdx −−+−−− == 4324 2 2 3 2 32 2 3 4416844168 2333323333 xxxxxxxxdxdx = −−+−−−+ + 2 432432 3 2 2 2 3 4416844168 2333323333 dx xxxxxxxx dx = −−+−−−+− + 1433651214848 121512151215 =−+= Câu 155: Cho hai hàm số ( ) ( ) 32232;2 fxaxxbxgxcxxd =−++=−+ có bảng biến thiên như sau: Biết rằng đồ thị của hai hàm số đã cho cắt nhau tại 3 điểm phân biệt có hoành độ 123 ,, xxx thỏa mãn 123 2 xxx++=− . Khi đó diện tích hình phẳng giới hạn bởi các đường ( ) ( ) ;;1;1yfxygxxx ===−= bằng
=−−=−+=−− Do đó: ( ) ( ) ( ) 22

.23626
gxkfxcxxdkaxxbkca
Suy ra: ( ) ( ) 32232;2 3 b fxaxxbxgxaxx =−++=−+ Phương trình hoành độ giao điểm: ( ) ( ) 32232 3223220 33 axxbxaxxaxaxbxbb −++=−++−−+++−= Viet: ( ) 2 123 3 212 3 ab xxxagxxx a + ++==−=−=−−+ đạt giá trị lớn nhất tại 0 1 x =− và giá trị lớn nhất đó bằng ( ) 111101;0 3 b gbcd −=+===−= . Vậy 1 32 1
10 22. 3 Sxxxdx =−−++=
Câu 156: Cho hai hàm số ()fx và ()gx liên tục trên và hàm số 32 '() fxaxbxcxd =+++ , 2 '() gxqxnxp =++ với ,0aq có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số '()yfx = và '()ygx = bằng 10 và (2)(2)fg = . Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()yfx = và ()ygx = bằng
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 10 3 . B. 8 3 . C. 3 4 . D. 1 2 . Lời giải Chọn A Tại các điểm cực trị , của thì ( ) ( ) 0 gg== dó đó ( ) ( )( ) ( ) ( )( ) 2 ;363 gxcxxfxaxxbaxx
1 33
3 k cka
dkbb d = = =−+=−+==
= =
A. 8 3 . B. 8 15 . C. 16 3 . D. 16 5 . Lời giải Chọn B
Đặt ()()() hxfxgx =− ()()(). hxfxgx =− Xét phương trình hoành độ giao điểm: ( ) ( ) ( ) ( ) 0 fxgxfxgx =−= Vì hai đồ thị ()yfx = và ()ygx = cắt nhau tại các điểm có hoành độ lần lượt bằng 0;1;2 nên phương trình có các nghiệm là 0; x = 1 x = và 2 x = . Do đó, ta có: ()()()(1)(2) hxfxgxkxxx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 32
=−=−−−−−= Theo đề: 10 S = . Do
= '()20(1)(2)
=−− (
4
()20(1)(2)d2032d204 x
=−−=−+=−++ Vì
−+= 0 2 x x = = Diện tích hình phẳng cần tìm là: 222 432 000 16 ()()d()d52020d. 3 Sfxgxxhxxxxxx =−==−+= Câu 157: Cho parabol ( ) 2 : Pyx = và hai điểm A , B thuộc ( )P sao cho 2 AB = . Tìm giá trị lớn nhất của diện tích hình phẳng giới hạn bởi parabol ( )P và đường thẳng AB A. 3 2 B. 4 3 C. 3 4 D. 5 6 Lời giải Chọn B x y y=x2 O 1 A B
=−=−− ( ) 0. k Ta có diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()yfx = và ():ygx = ( )( ) ( )( ) 212 001 1 ()()d12d12d. 2 Sfxgxxkxxxxkxxxxk
đó: 20. k
hxxxx
)
3232
hxxxxxxxxxxxC
(2)(2)fg =
(2)(2)(2)0 hfg=−=
0 C = Do đó: 432()52020 hxxxx =−+ Xét phương trình hoành độ giao điểm: ()() fxgx = ()()0fxgx−=
()0hx =
432 520200 xxx
Gọi ( ) 2 ; Aaa và ( ) 2 ; Bbb là hai điểm thuộc ( )P sao cho 2 AB = .
Không mất tính tổng quát giả sử ab .
Theo giả thiết ta có 2 AB = nên ( ) ( )2 2 22 4 baba−+−= ( ) ( ) 22 14 baba −++= .
Phương trình đường thẳng đi qua hai điểm A và B là ( ) ybaxab =+− .
Gọi S là diện tích hình phẳng giới hạn bởi parabol ( )P và đườ
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 33
ng thẳng AB ta có ( ) ( ) ( )3 23 2 d 236 b b a a ba Sabxabxxababxxx =+−−=+−−= . Mặt khác ( ) ( ) 22 14 baba −++= nên ( )2 42bababa −−=− . Vậy ( )3 3 24 663 ba S == Dấu = xảy ra ( ) ( ) ( ) ( ) 22 2 1;1 21 14 01 1;1 ba A baa baba bab B −= −==− −++= +== . Vậy giá trị lớn nhất của diện tích hình phẳng giới hạn bởi parabol ( )P và đường thẳng AB bằng 4 3 . Câu 158: Cho hai hàm số ( ) 32 ==+++ yfxaxbxcxd và ( ) 2 ==++ ygxmxnxk cắt nhau tại ba điểm có hoành độ là 1 1;;2 2 và có đồ thị như hình vẽ Biết phần diện tích kẻ sọc bằng 81 32 . Diện tích phần hình phẳng giới hạn bởi đồ thị ( ) ( ) , yfxygx == và hai đường thẳng 1 ;2 2 xx== bằng A. 79 24 . B. 243 96 . C. 81 32 . D. 45 16 . Lời giải Chọn C
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 34
Ta có
ố
) 54 32 2 27 20123 xx Fxxxx =−−++ là nguyên hàm của hàm số ( )yfx = . Gọi ( )ygx = là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ( )yfx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 3479 1073 . B. 1219 126 . C. 378 5 . D. 3778 1215 . Lời giải Chọn D Ta có ( ) ( ) 43 2 '247 43 xx fxFxxx ==−−++ ( ) 32 '44 fxxxx=−−+ . ( ) 32 77 2;2; 33 2525 '04402;2; 1313 107107 1;1; 1212 xyA fxxxxxyB xyC =−=−−− =−−+=== == . Gọi ( ) 2 ygxaxbxc ==++ là đồ thị đi qua ba điểm cực trị của hàm số ( )yfx = . Ta có: ( ) ( ) ( ) 10710713 1 121212 25258 242 1333 7722 242 333 gabca gabcb gabcc =++==− =++== −=−−+=−= Vậy ( ) 2 13822 1233gxxx=−++
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
( ) ( ) ( ) ( ) ( ) 1 120 2 −=+−− fxgxaxxxa ( ) ( ) ( ) ( ) ( ) ( ) 111 222 1 111 dd 2 d 1181 1212. 264 xx Sfxgxaxxxaxxxa x =−=+−−=+−−= Mà 1 81 32 = S = 2 a Khi đó: ( ) ( ) ( ) ( ) 22 2 11 22 181 212 2 d 2 d 3 Sgxfxxxxxx =−=−+−−= . Câu 159: Biết hàm s
(
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 35 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Phương trình hoành độ giao điểm của ( )fx và ( )gx là: 43 2 2 1 1141 01 431233 3 2 x x xx xx x x = = −−+−= = =− . Diện tích: 2 43 2 2 11413778 4312331215 xx Sxxdx =−−+−= . Câu 160: Cho đồ thị () C của hàm số 43 yxaxd =++ có một điểm cực tiểu 3107 ; 216 A . Gọi () P là đồ thị hàm số ()gx có tọa độ đỉnh 19 ; 48 I và đi qua điểm ( )1;0 B . Diện tích phần đồ thị giới hạn bởi hai đồ thị hàm số () C , () P bằng: A. 72 5 . B. 72 5 C. 62 15 . D. 154 15 . Lời giải Chọn A Do hàm số 43 yxaxd =++ có 42'43 yxax =+ 42 3 '0430 4 a yxaxx =+==− Mà đồ thị hàm số () C có một điểm cực tiểu là 3107 ; 216 A nên 33 2 24 a a −=−= . Thay tọa độ điểm 3107 ; 216 A vào hàm số ta có 5 d =− . Vậy hàm số của đồ thị () C là: 4325yxx=+− Gọi hàm số của 2 ymxnxp =++ ta có: 2 2 1 24 2 11 01 44 1 .(1)(1)0 n m m mnpn p mnp −=− =− ++==− = −+−+= . Vậy hàm số của là: 2 21yxx=−−+ .
ọi hàm số ( )ygx = là hàm số bậc 2 có đồ thị đi qua 3 điểm cực trị của ( )C , S là diện tích của hình phẳng giới hạn bởi 2 đường ( ),()fxgx . S thuộc khoảng nào sau đây: A. ( )1,5;2 . B. ( )2,5;3 . C. ( )0;1 . D. ( )3;4 . Lời giải
Chọn C
Ta có ( )yfx = là hàm số chẵn. Với 0 x ta có bảng biến thiên của hàm số ( ) 2 2 yfxxxc ==−+ là: Lấy đối xứng qua trục tung ta được đồ thị của hàm số ( )yfx = trên là:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 36 Chuyên
thi:
sinh vào
10 Tốt Nghiệp THPT BDKT
10; 11; 12 Sưu tầm và biên soạn Xét phương trình hoành độ giao điểm: 432 1 2260 2 x xxxx x = +++−= =− Vậy diện tích phần đồ thị giới hạn bởi hai đồ thị hàm số 4325yxx=+−
11 432243 22 2521(2125) xxxxdxxxxxdx +−++−=−−+−−+ 1 432 2 (226)72 5 xxxxdx =−−−−+= . Chọn đáp án A. Câu
Cho
số ( ) 2 2|| fxxxc =−+
(
Hòa
0984164935
luyện
Tuyển
lớp
Toán
và 2 21yxx=−−+ là:
161:
hàm
có đồ thị
)C , g
Suy ra đồ thị hàm số ( )yfx = có 3 điểm cực trị là: ( ) ( ) 1;1,(1;1),0; AcBcCc Đồ thị hàm số bậc 2 ( )ygx = đi qua 3 điểm trên suy ra nó có dạng: ( ) 2 gxcax =+ , thay tọa độ điểm B vào ( )ygx = ta được ( ) 2 1 agxxc =−=−+ .
Ta có diện tích hình phẳng giới hạn bởi các đường ( ),()fxgx là: ( ) ( ) ( ) 11 22 00
2 222 3 Sgxfxdxxcxxcdx =−=−+−−+= , vậy ( )0;1 S .
Câu 162: Cho hàm số ( ) 42 yfxaxbxc ==++ cóhai điểmcựctiểu ( ) ( )1;2;1;2 vàđiểm cựcđại ( )0;3 . Hàm số ( ) 2 ygxmxnxp ==++ có đồ thị đi qua các điểm cực trị của đồ thị ( )yfx = . Diện tích hình phẳng giới hạn bởi đồ thị hai hàm số ( )yfx = và ( )ygx = gần bằng giá trị nào nhất trong các giá trị sau A. 1. B. 3. C. 2. D. 5. Lời giải Chọn A Ta có ( ) 423'42 yfxaxbxcyaxbx ==++=+ 2
0 '0 2 x y axb = =
Theo bài ra hàm số ( ) 42 yfxaxbxc ==++ có hai điểm cực tiểu ( ) ( )1;2;1;2 và điểm cực đại ( )0;3 suy ra
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 37
=−
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 38 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) 42 '10 4203 03355103 123210 y abc ycayfxxx abb y = +== =====−+ ++=−=− =− Theo bài ra đồ thị hàm số ( ) 2 ygxmxnxp ==++ đi qua điểm cực trị( ) ( )1;2;1;2 và ( )0;3 suy ra ( ) ( ) ( ) ( ) 2 0333 1232553 12320 y pp ymnmygxx mnn y = == =−++=−=−==−+ −+=−= −=− Phương trình hoành độ giao điểm đồ thị hàm số ( )yfx = và ( )ygx = là 42242 0 5103535501 1 x xxxxxx x = −+=−+−== =− Diện tích hình phẳng cần tìm là ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1101 424242 1110 01 4242 10 555555 4 5555 3 fxgxdxxxdxxxdxxxdx xxdxxxdx −=−=−+− =−+−= Câu 163: Cho hàm số 432 () fxxaxbxcxd =++++ ( ) ,,, abcd có ( ) 01 f = và ba điểm cực trị là 0;1;2. Diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = và đường thẳng đi qua điểm ( )3;10 A có hệ số góc bằng 4 bằng A. 4 B. 106 15 C. 104 15 D. 8 Lời giải Chọn C ( ) 011fd== nên 432 ()1 fxxaxbxcx =++++ . 32 '()432 fxxaxbxc =+++ . Theo bài ra ta có: ( ) ( ) ( ) '0004 '103244 124320 '20 f ca fabcb abcc f = ==− =++=−= ++=−= = suy ra 432 ()441 fxxxx=−++ Đường thẳng đi qua điểm ( )3;10 A có hệ số góc bằng 4 nên có phương trình ( ) 104342yxyx −=−=−
Phương trình hoành độ giao điểm: ( )( )( ) 4322 1 441421310 3 x xxxxxxx x
= −++=−−−+= = Diện tích hình phẳng cần tính là ( ) ( ) 3 432 1
104 44142 15 Sxxxxdx =−++−−= Câu 164: Cho hàm số ( ) ( ) 432 6,,, yfxxaxbxcxdabcd ==++++ . Biết đồ thị hàm số ( )yfx = có ba điểm cực trị có hoành độ lần lượt là 1;1;2 và hàm số ( )ygx = là hàm bậc hai có đồ thị đi ba điểm cực trị đó. Tính diện tích hình phẳng giới hạn bởi các đường ( )yfx = ; ( )ygx = và trục Oy . A. 64 15 S = B. 88 15 S = C. 56 15 S = D. 184 15 S = Lời giải
Chọn A
Ta có ( ) 32 ''2432 yfxxaxbcc ==+++ . Do đồ thị hàm số ( )yfx = có ba điểm cực trị có hoành độ 1;1;2 nên phương trình
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 39
(
Ta
(
(
(
11
46
Vậy diện tích hình phẳng giới hạn bởi các
ng
=
( ) ( ) ( ) ( ) 12 01 Sfxgxdxfxgxdx =−+− 12432432 01 64 61621686162168 15 Sxxxxdxxxxxdx =−++−+−++−= . Câu 165: Cho hàm số ( ) 32 fxxbxcxd =+++ . Biết đồ thi hàm số ( )fx có một điểm cực trị là A có hoành độ bằng 1, đồ thị ( )yfx = cắt trục tung tại điểm B có tung độ là 5. Gọi là đường thẳng đi qua hai điểm A và ( ) ; Ebcd . Tính diện tích hình phẳng giới hạn bởi đường thẳng và đồ thi hàm số ( )fx được tính bởi công thức A. 15 32 1 6d Sxxxdx + =+−+ . B. 1 32 15 62d Sxxxdx =+−+ .
( ) '0fx = có ba nghiệm phân biệt 1;1;2 Suy ra ( ) ( )( )( ) ( ) 32 '24112'24482448 fxxxxfxxxx =+−−=−−+
) 432 6161248 fxxxxxd =−−++
có
)
)
) 22
'1432814328
fxxfxxxdgxxxd
=−−+++=−+++
.
đườ
( )yfx
; ( )ygx = và trục Oy là
diện tích hình phẳng giới hạn bởi đồ thị () C và parabol () P đi qua ba điểm cực trị của đồ thị () C .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 40
−+−= =+−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn C. 1 32 1 6d Sxxxdx =+−+ D. 15 32 15 64d Sxxxx + =+−+ Lời giải Chọn D Ta có: ( ) 2 32 fxxbxc =++ Theo đề ta có: ( ) ( ) 103205 0551 f bcc cb f = ++==− =−=
=− Do đó: ( ) 32 5 fxxxxd =+−+ Khi đó: ( )1;3Ad và ( ) 4; Ed ( ) ( )3;33.1;1 AE == Đường thẳng có một véc tơ pháp tuyến là ( )1;1 n =− Đường thẳng qua ( )1;3Ad và có một véc tơ pháp tuyến là ( )1;1 n =− , nên có phương trình là: ( ) ( ) 130 40 4 xyd xyd yxd −−−+=
Xét phương trình: ( ) 32 32 4 54 640 15 1 15 fxxd xxxdxd xxx x x x =+− +−+=+− +−+= =− = =+ Tính diện tích hình phẳng giới hạn bởi đường thẳng và đồ thi hàm số ( )fx được tính bởi công thức: ( ) 1515 3232 1515 54d64d Sxxxdxdxxxxx ++ =+−+−+−=+−+ . Câu 166: Cho hàm số ( )yfx = là hàm đa thức bậc bốn và có đồ thị () C như hình vẽ. Biết diện tích hình phẳng giới hạn bởi đồ thị hai hàm số ( )yfx = và ( )yfx = bằng 856 5 . Tính
A. 81 20 B. 81 10 C. 81 5 D. 9 20 Lời giải
Chọn A
Theo hình vẽ ta thấy đồ thị () C của hàm số ( )yfx = tiếp xúc với trục hoành tại các điểm
=− = +−=+−−−−++= 2 1 02(4664)02 1

1 1 21(4664)292802 4
x x axxaxxxxxxx x x =− = Theo giả thiết diện tích hình phẳng giới hạn bởi đồ thị của ( )fx và ( )fx là: 856 5 . Nên ta có: 4 432 2 8568564282928d2 555 =−−++== a axxxxxa . Vậy ( ) ( ) ( ) 22221 =+−fxxx ( ) 32 2(4664) =+−− fxxxx Ta có ( ) 32
x fxxxxx x
=− =+−−==− =
. Đồ thị () C có ba điểm cực trị là ( )2;0 A , ( )1;0 B , 181 ; 28 C Giả sử phương trình parabol () P có dạng ( ) 2 (),0 ==++ ygxmxnxpm . Vì () P đi qua ba điểm ( )2;0 A , ( )1;0 B , 181 ; 28 C nên
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
41 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
( )2;0 A , ( )1;0 B nên ( ) ( ) ( ) 22 21,(0)fxaxxa =+− Khi đó ( ) 32 (4664)fxaxxx =+−− Xét phương trình ( ) ( )fxfx = ( ) ( ) 22 32432
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 42 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) 9 2 (2)0 420 9 100 2 81 181 9 428 28 =− −= −+= =++==− = −+= −= a g abc gabcb ab c c g 2 99 ()9 22 ==−−+ ygxxx . Diện tích hình phẳng giới hạn bởi đồ thị () C và parabol () P là ( ) ( ) 1 22 2 2 99812219d 2220 =+−−−−+= Sxxxxx . Câu 167: Cho hàm số 32 1 231 3 yxxx =−+− có đồ thị ( )C . Gọi , MN là hai điểm thuộc ( )C sao cho tiếp tuyến tại , MN song song với nhau. Khi đó diện tích hình
== . Ta có: 32 1122 231()13333 yxxxyxxx =−+−=−−+ , MN thuộc đồ thị ( )C nên ( ) ( ) 12222 11 333333 12222 11 333333 MMMMMM NNNNNN kk yyxxxyx kk yyxxxyx =−−+=−−+ =−−+=−−+ Do đó đường thẳng MN có phương trình: 22 1 333 kk yx =−−+ Mặt khác do 2 OBOA = nên đường thẳng MN có hệ số góc bằng 2 hoặc 2 Suy ra 2 28 33 24 2 33 k k kk −= = =− −=− Ta có: ( ) 2 43yxxx =−+ +) Với 4,MNkxx =− là nghiệm của phương trình
phẳng giới hạn bởi ( )C và đường thẳng MN nằm trong khoảng nào dưới đây? Biết rằng đường thẳng MN cắt trục hoành, trục tung lần lượt tại , AB phân biệt sao cho 2 OBOA = . A. ( )11;12 . B. ( )14;15 . C. ( )12;13 . D. ( )13;14 . Lời giải Chọn D Giả sử ( ) ( ) ;,; MMNN MxyNxy , suy ra ( ) ( ) MN yxyxk


CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 43
=
Từ đó
V
ột miếng đất dạng hình parabol chiều
ều r
2
thẳng
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 22434470xxxx −+=−−+= , phương trình vô nghiệm. +) Với 8,MNkxx = là nghiệm của phương trình 2 11917 4501;,5; 533 x xxMN x =− −−=−−
.
tìm được phương trình đường thẳng MN : 13 2 3 yx=− .
ậy diện tích cần tìm là 5 3 2 1 2d1027 332 x Sxxx =−++= Câu 168: M
dài 18m, chi
ộng 12m. Người ta chia miếng đất bằng
đoạn
song song , ABCD thành ba phần có diện tích bằng nhau Tỉ số AB CD bằng: A. 3 1 2 . B. 3 122 + . C. 1 2 . D. 1 12 + . Lời giải Chọn A Chọn hệ trục tọa độ như hình vẽ: Parabol có dạng 2 = yax , do ( )P đi qua điểm ( ) 1 6;18 2 = a . Diện tích miếng đất là: 6 2 6 18144 2 x Sdx =−= Để diện tích 3 phần bằng nhau thì diện tích mỗi phần là 48 3 S = . Với b, d > 0

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 44
thị hàm số ( )yfx = và ( )ygx = cắt nhau tại 3 điểm có hoành độ lần lượt là 3; 1; 1. Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. 5. B. 9 2 . C. 4. D. 8. Lời giải Chọn C Ta có: ( ) ( ) ( )( )( )311fxgxaxxx −=++− . Suy ra ( )( )( ) ( ) ( ) 32 3 311 2 axxxaxbdxcex ++−=+−+−− Xét hệ số tự do suy ra: 31 3 22 aa −=−= . Do đó: ( ) ( ) ( )( )( ) 1 311 2 fxgxxxx −=++− Diện tích bằng: ( ) ( ) ( ) ( ) 11 31 dd Sfxgxxgxfxx =−+− ( )( )( ) ( )( )( ) 11 31 11 311d311d 22 Sxxxxxxxx =++−−++− 4 = .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Gọi 22 ;;; 22 BbDdbd khi đó = ABb CDd , Ta có: 2223 3 0 0 242472 2226 −=−== b b bxbxxdxb Tương tự ta có 22 3 3 0 1 48144 22 2 −=== d dxAB dxd CD . Câu 169: Cho hai hàm số ( ) 32 1 2 fxaxbxcx=++− và ( ) 2 1 gxdxex=++ ( ) ,,,, abcde . Biết rằng đồ
Câu 170: Cho hàm số ( )fx với đồ thị là Parabol đỉnh I có tung độ bằng 7 12 và hàm số bậc ba ( )gx . Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ 123 ,, xxx thoả mãn 123 1855 xxx =−
ệ
nào nh
5,7. B. 5,9.
t trong các số sau đây?
6,1. D. 6,3.
ời giả
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
45
số ( )gx đạt cực trị tại 1,2xx=−= nên ( ) ( )( ) ( ) 32 '122 32 xx gxaxxaxb gx =+−=−−+ Đồ thị hàm số ( )gx đi qua I nên 17713 2121212, gab =−−=−+ ( )1 Phương trình hoành độ giao điểm: ( ) ( ) ( )( ) 32 7 212 3227 xx fxgxaxbxx =−−+=+− Theo định lý viet ta có: 123 14 2855 27 185518.5518 33 3 b a xxxb a + =−=+= ( )2 Từ ( )1 , ( )2 ta được ( ) 32 11 1,2 2322 xx abgxx ===−−+ .
Di
n tích miền tô đậm gần số
ấ
A.
C.
L
i Chọn A Ta có: 121 22 Ix −+ == Lúc này ta có 17 , 212 I và ( ) ( ) ( )( ):12Pfxaxx=+− . Ta có ( ) 177 , 21227 IPa −= ( ) ( )( ) 7 12 27 fxxx=+− . Hàm
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 46 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Phương trình hoành độ giao điểm là ( )( ) 32 71 122 27322 xx xxx +−=−−+ 1 2 8559 9 8559 9 x x x = + = = Từ đó suy ra diện tích miền tô đậm là ( )( ) 8559 32 9 1 2 71 1225,7 27322 xx Sxxxdx + =+−−++− . Câu 171: Cho hàm số 3243 yxx =− có đồ thị ( )C và đường thẳng d đi qua gốc tọa độ tạo thành hai miền hình phẳng có diện tích 12 , SS như hình vẽ. Khi 2 12 S = thì 1S bằng A. 7 2 B. 3 C. 875 256 D. 865 256 Lời giải Chọn C Phương trình đường thẳng d có dạng ymx = Phương trình hoành độ giao điểm giữa đồ thị ( )C và đường thẳng d là 32 2 0 43 430 x xxmx xxm = −= −−= Gọi b là nghiệm dương của phương trình hoành độ giao điểm trên 2 43bbm−= ( ) 32243243 2 0 0 11 43 22 b b Smxxxdxmxxxmbbb =−+=−+=−+
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT:
Page 47 Chuyên
thi: Tuyển sinh vào
10 Tốt
THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Theo giả thiết 2 12 S = 243 1 12 2 mbbb −+= ( ) 2243 1 4312 2 bbbbb −−+= 43 22402 bbb −−== vì 0 b 10 m = Khi đó phương trình 2 430 xxm−−= trở thành 2 2 43100 5 4 x xx x = −−= =−
=
ắt
ph
ng giới hạn bởi
ng A. 8 B. 5 C. 9 2 D. 4 Lời giải Chọn D Ta có phương trình hoành độ giao điểm là: 322 1 1 2 axbxcxdxex ++−=++ ( ) ( ) 32 3 0 2 axbdxcex +−+−−= Đặt ( ) ( ) ( ) 32 3 2 hxaxbdxcex =+−+−− Dựa vào đồ thị ta có ( ) ( ) ( ) 32 3 2 hxaxbdxcex =+−+−− có ba nghiệm là 3 x =− ; 1 x =− và 1 x = Với 3 x =− ta có ( ) ( ) ( ) 3 2793 1 2 abdce −+−−−=
0984164935
luyện
lớp
Nghiệp
Vậy ( ) 0 32 1 5 4 875 4310d. 256 Sxxxx =−−= Câu 172: Cho hai hàm số ( ) 32 1 2 fxaxbxcx=++− và ( ) 2 1 gxdxex=++ , ( ) ,,,, abcde . Biết rằng đồ thị của hàm số ( )yfx = và ( )ygx
c
nhau tại ba điểm có hoành độ lần lượt là 3; 1; 1 Hình
ẳ
hai đồ thị đã cho có diện tích bằ
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 48
Với
=−
Với
Từ ( ) ( )1,2 và ( )3 ta
( ) ( ) ( ) ( ) ( ) ( ) 3 2793 2 3 2 3 2
−+−−−= −+−−−= +−+−= 1 2 3 2 1 2 a bd ce = −= −=− . Hay ta có ( ) ( ) 1 3 d Sfxgxx =− 11 3232 31 13131313 dd 22222222 xxxxxxxx=+−−++−− 224=+= Câu 173: Hình phẳng được giới hạn bởi đồ thị ( )C của hàm số đa thức bậc ba và parabol ( )P có trục đối xứng vuông góc với trục hoành. Diện
ng
ng A. 5 12 . B. 7 12 . C. 11 12 . D. 37 12 . Lời giải
Gọi ( ) 32 : Cyaxbxcxd =+++
) 2 :
Dựa
hai đường cong này cắt nhau tại ba điểm có hoành độ lần lượt 1;1;2 Do đó: ( ) ( )( ) 2 ()12fxgxaxx −=−− Dựa vào đồ thị, ta có: ( ) ( ) 002fg−= Mà ( ) ( ) 002 fga −= Suy ra ( ) ( ) ( )( ) 2 22112 aafxgxxx ==−=−− Do đó, diện tích hình phẳng cần tìm: ( )( ) ( ) ( ) 212 23232 111 37 122222 12 Sxxdxxxxdxxxxdx =−−=−−++−++−= H H
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
1 x
ta có ( ) ( ) ( ) 3 2 2 abdce −+−−−= .
1 x = ta có ( ) ( ) ( ) 3 3 2 abdce +−+−=
có
abdce abdce abdce
tích hình phẳ
bằ
Chọn D
và (
Pymxnxp =++ ( )0,0am
vào đồ thị nhận thấy
A. 45 4 B. 7 12 C. 32 3 D. 71 6 Lời giải Ch
Câu 174: Cho hàm số 32 ()4 fxaxbxcx=+++ có đồ thị cắt Parabol 2 () gxmxnx =+ tại các điểm có hoành độ là 2; 1; 2. Diện tích của hình phẳng giới hạn bởi hai đồ thị trên bằng = ++=+= += .
49 45771 44d44d 4126 xxxxxxxx =−−+−−−+=+= Câu 175: Cho hàm số ( ) 3 1 fxaxcx=++ và ( ) ( ) 1 gxfx =− có đồ thị như hình vẽ dưới đây. Biết rằng diện tích miền tô đậm bằng 2, với a và c là các số nguyên. Tính giá trị ac ? A. 2. B. 2 C. 1. D. 0. Lời giải Chọn B Đồ thị hàm số ( ) ( ) 1 gxfx =− đi qua điểm ( )2;0 ( ) ( ) 201010 gfac =−=−−+= Do ( ) ( ) 3 limlim1 xx fxaxcx →+→+ =++=− nên suy ra 0 a Phương trình hoành độ giao điểm đồ thị ( )fx và đường thẳng 1 y = : ( ) ( ) 32 2
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 0 110 01 x axcxxaxc axc
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
ọn D Ta có, phương trình hoành độ giao điểm là phương trình
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 nên ()().(2)(1)(2) fxgxkxxx −=+−− Mặt khác: (0)(0)41 fgk−== 32 ()()(2)(1)(2)44 fxgxxxxxxx −=+−−=−−+ . Diện tích là: 22 32 22 ()()44d Sfxgxdxxxxx =−=−−+ ( ) ( ) 12 3232 21
bậc ba có các nghiệm 2; 1; 2
Dựa vào đồ thị hàm số ta thấy đường thẳng 1 y = cắt đồ thị ( )fx tại 3 điểm phân biệt nên phương trình có 2 nghiệm phân biệt khác 0 000cc c aa − Khi đó 2 0 c axcx a +==−
Phương trình hoành độ giao điểm đồ thị ( ) ( ) 1 gxfx =− và đường thẳng 1 y = : ( ) ( ) ( ) ( ) ( ) ( ) 32 2
= −+−+=−−+= −+=
1 1111110 102 x axcxxaxc axc
Dựa vào đồ thị hàm số ta thấy đường thẳng 1 y = cắt đồ thị ( )gx tại 3 điểm
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 50
phân biệt nên phương trình có 2 nghiệm phân biệt khác 1. Khi đó: ( )2 11 10 11 cc xx aa axc cc xx aa −=−=−− −+= −=−−=+− . Diện tích phần tô đậm: ( ) ( ) 1 01 1d11d cc aa Sfxxfxx −+− =−+−− . Xét ( ) 1 1 1 11d c a Ifxx +− =−− . Đặt 1dd txtx =−=− Đổi cận 10xt== , 1 cc xt aa =+−=−− . Suy ra ( ) ( ) ( ) ( ) ( ) 1 00 1 10 11d1d1d1d cc aa cc aa Ifxxfttfttfxx +−−− =−−=−−=−−=−− Như vậy ( ) ( ) 0 0 1d1d c a c a Sfxxfxx =−−− . Do hàm số ( ) 3 1 fxaxcx −=+ là hàm số lẻ nên ( ) ( ) 0 0 1d1d c a c a fxxfxx−−=− suy ra
==
aa fxxaxbxcxxxbb cc
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 51 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) 000 21d21d21d1 ccc aaa Sfxxfxxfxx =−−=−= ( ) 42 42 3 0 0 22 2 d11 4242 14 42 c c a a cc ac aa axcx axcxx cc ca aa +=+=+= −=−= Mà 10 ac −−+= , nên ( ) 22414402121ccccca −=−−+===−=− . Vậy 2 ac =− . Câu
số ( )
432
=++++
hai điểm cực trị 101 ,, . Gọi ( )ygx = là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số ( )yfx = . Diện tích hình ph
176: Cho hàm
( ) =+++=+−=−=− == ( ) 42 2 fxxxd =−+ Ba điểm cực trị hàm số ( )yfx = là ( ) ( ) ( ) 11110 A;d,B;d,C;d. −−+−+ Đồ thị hàm số ( ) ( ) 2 0 ygxmxnxpm ==++ đi qua ba điểm A,B,C nên ta có: ( ) 2 101 110 mnpdnm mnpdmpdngxxd. pdpdpd −+=−+==− ++=−++=−+==−+ === Xét phương trình ( ) ( ) 42242 0 02001 1 x fxgxxxxxxx x = −=−+=−==− = Diện tích hình phẳng giới hạn bởi hai đường ( ) ( )yfx,ygx == là: ( ) 11 4242 11 Sxxdxxxdx =−=−− 1 53 1 4 5315 xx =−−=
fxxaxbxcxda,b,c,d
có
ẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 4 15 B. 2 15 C. 4 13 D. 6 13 Lời giải Chọn A Ta có: ( ) ( )( ) 32 300 432411242 00
Câu 177: Cho hàm số ( ) 32 (),, yfxxaxbxcabc ==+++ có hai điểm cực trị là 1 và 1 Gọi 2 ()(0)ygxmxnxpm ==++ là hàm số bậc hai có cực trị tại 1 x =− và có đồ thị đi qua điểm có hoành độ 1 x = của đồ thị hàm số ( )yfx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = có giá trị nằm trong khoảng nào sau đây?
A. ( )0;1 . B. ( )1;2 . C. ( )2;3 . D. ( )3;4 .
6
52
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Lời
ả
ọn B Hàm
ố 32 yxaxbxc =+++ đạt cự
( ) ( )
y
y = ++== −++==− −=
ố 2
=++
t cực
i t
i
x =−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 (
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
gi
i Ch
s
c trị tại 1 x = nên ta có
102300 102303
aba abb
Hàm s
ymxnxp
đạ
đạ
ạ
1
và cắt đồ thị hàm số
) 32 ,, yxaxbxcabc =+++ tại hai điểm có hoành độ 1 x = nên ta có 202 11 11 mnn abcmnpm abcmnppc −+==− +++=++=− −+−+=−+−= Suy ra ( ) 11 23232 11 4 11;2 3 Smxnxpxaxbxcdxxxxdx =++−−−−=−−++=
A. 10 B. 3 C. 5 D.
Lờ
Chọn D Do hai đồ thị đều đi qua các điểm cực trị của nên phương trình hoành độ chắc chắn đã có các nghiệm x= 1; x=1. Vì vậy ta có 232(x)g(x)(x1)(xk)x fkxxk −=−−=−−+ TH1: Nếu 1 k thì ( ) ( ) 1 323232 111 1 432432 11 42 432432 6243 83 12 kk k Sxkxxkdxxkxxkdxxkxxkdx xkxxxkxx Skxkx kkk Sk =−−+=−−+−−−+ =−−+−−−+ −+− ===
Câu 178: Cho hàm số ( ) 32 yfxxaxbxc ==+++ có đồ thị ( )C đồng thời có 2 điểm cực trị là 1; 1. Biết Parabol( ) 2:(x)mx Pygnxp ==++ đi qua hai điểm cực trị của ( )C . Hỏi có bao nhiêu cặp số nguyên dương ( );pc thỏa mãn 10 cp+ sao cho hình phẳng giới hạn bởi parabol ( ):(x)Pyg = và đồ thị ( )C có diện tích bằng 8?
i giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 53
3232
−=
===
(
1 42 432432 6243 83 12 kk k Sxkxxkdxxkxxkdxxkxxkdx
=−−+=−−+−−−+ =−−+−−−+ =++=
=−+++ có hai điểm cực trị là 1, 5 3 và có đồ thị cắt trục tung tại điểm có tung độ bằng 2. Gọi ( )ygx =
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
(x)g(x)(am)x(bn)xcpx33 3 fxxx cp −=+−+−+−=−−+
Kết hợp 10 cp+ ta được ( ) ( ) ( ) ( );4;15;26;3cp
TH2: Nếu 1 k − thì
) ( ) 111 323232 1 11 432432
xkxxxkxx Skxkx kkk Sk =−−+=−−+−−−+ =−−+−−−+ ===− 3232 (x)g(x)(am)x(bn)xcpx33 3 fxxx cp −=+−+−+−=+−− −=− Kết hợp 10 cp+ ta được ( ) ( ) ( ) ( );4;15;26;3pc === TH3: nếu 1<k<1 thì ( ) ( ) 11 323232 11 1 432432 1 4 2 432432 1 8(vn) 122 k k k k Sxkxxkdxxkxxkdxxkxxkdx xkxxxkxx Skxkx k Sk
Kết luận: có 6 cặp số nguyên thỏa mãn yêu cầu bài toán Lưu ý: 1) do tính đối xứng của đồ thị nên nhận thấy với mỗi số k thỏa mãn điều kiện thì k cũng thỏa mãn điều kiện do đó TH2 có thể suy ra luôn k= 3. 2) có thể đánh giá ( ) 111 3232 111 48Sxkxxkdxxkxxkdxdx =−−++++= nên TH3 không xảy ra Câu 179: Cho hàm số ( ) ( ) 32 ,, fxxbxcxdbcd
là hàm số bậc hai có đồ thị là một Parabol đi qua điểm cực tiểu của đồ thị hàm số ( )yfx = và có đỉnh là ( )1;2 I . Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = có giá trị thuộc khoảng nào sau đây A. ( )8;9 B. ( )9;10 C. ( )7;8 D. ( )3;4
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 54 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Lời giải Chọn A Ta có: ( ) 2 32 fxxbxc =−++ Hàm số ( )fx có hai điểm cực trị là 1 và 5 3 và có đồ thị cắt trục tung tại điểm có tung độ bằng 2 nên ta có: ( ) ( ) 10 32023 1 525101025 005 33333 2 22 02 f bcbc b fbcbcc d dd f −= −−+=−+= = =−++=+== =− =−=− =− Do đó: ( ) 32 52fxxxx=−++− Đồ thị hàm số ( ) 32 52fxxxx=−++− có điểm cực tiểu là ( )1;5 Giả sử, ( ) ( ) 2 0 ygxmxnxpm ==++ Do đồ thị của hàm số ( )ygx =
m cự
u
=
có đỉnh là ( )1;2 I nên ta có hệ phương
7 4 55 7 22 2 20 1 1 2 4 m mnpmnp mnpmnpn nmn p m =− −+=−−+=− ++=++== += −= = Do đó: ( ) 2 771 424ygxxx ==−++ Phương trình hoành độ giao điểm của hai đồ thị của hai hàm số ( )yfx = và ( )ygx = là : 32232 3 77111393 520 4244244 1 x xxxxxxxxx x = −++−=−++−++−== =− Diện tích hình phẳng cần tìm là: 3 33 4 323232 3 11 4 113911391139 ddd 424424424 Sxxxxxxxxxxxx =−++−=−++−+−++−
đi qua điể
c tiể
( )1;5 của đồ thị hàm số ( )yfx
và
trình:

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 55 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 3 3 4 3232 3 1 4 11391139dd8,25 424424 xxxxxxxx =−−++−+−++− Câu 180: Cho hai hàm số ( ) 32 1 fxaxbxcx=++− và ( ) 2 1 2 gxdxex=++ ( ) ,,,, abcde . Biết r
ọ
ng nhất hệ số với phương trình ( ) ( ) 32 3 0 2 axbdxcex+−+−−= suy ra: 31 6 24 aa −=−= ( ) ( ) ( ) 32 1 256 4 fxgxxxx −=+−− Do đó ( )( )( ) 2 3 1253 312d 448 Sxxxx =++−= . --------- HẾT-------Câu 181: Cho hàm số ( ) 32 22022fxxmxnx=+++ với m , n là các số thực. Biết hàm số ( ) ( ) ( ) ( )gxfxfxfx =++ có hai giá trị cực trị là 2022 12 e và 12 e . Diện tích hình phẳng giới hạn bởi các đường ( ) ( ) 12 fx y gx = + và 1 y = bằng A. 2023 B. 2020 C. 2021 D. 2022 Lời giải Chọn C Ta có ( ) 2 62 fxxmxn =++ , ( ) 122 fxxm =+ , ( ) ( ) 3 12 fx =
ằng đồ thị của hàm số ( )yfx = và ( )ygx = cắt nhau tại ba điểm có hoành độ lần lượt 3;1;2 Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. 253 12 B. 125 12 C. 253 48 D. 125 48 Lời giải Ch
n C ( ) ( ) 0 fxgx−= ( )( )( ) 3210axxx +−+= ( )( ) 2 4320axxx ++−= 32 (256)0 axxx +−−= . Đồ
2x Ta
giá trị cực tr
=++=++ (
−+= − ( ) ( ) 0 12 gx gx
= − 1 2
xx xx
x x
1d 12
fx Sx gx =− + ( ) ( ) ( ) 2 1
= = . Khi đó diện tích hình phẳng giới hạn bởi các đường ( ) ( ) 12 fx y gx = + và 1 y = bằng ( ) ( ) 2 1
x x
12 d 12
x x
gxfx x gx −+ = + ( ) ( ) 2 1
gx x gx
d 12
ảng biến gxgx =+−+ 120222021=−= Câu 182: Cho hàm số ( ) 432 2 fxaxbxcxx =+++ và ( ) 32 2 gxmxnxx =+− với ,,,, acbmn . Biết hàm số ( ) ( )yfxgx =− có ba điểm cực trị là 2;1;3. Diện tích hình phẳng giới hạn bởi hai đường ( )yfx = và ( )ygx = bằng A. 131 4 B. 131 6 C. 125 12 D. 125 6 Lời giải Chọn B + Ta có: ( ) ( ) ( ) ( ) ( ) 32 4324.1fxgxaxbmxcnx −=+−+−+
= + ( ) 2 1 ln12 x x gx =+ ( ) ( )21 ln12ln12

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 56
Suy ra ( ) ( ) ( ) 32
gxxmxnmxnm =++++++++ (
= (
2
xmxnm +++++=
(
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
2621220222
) 0 gx
)
6262120
Vì hàm số
)gx có
hai
ị nên phương trình có 2 nghiệm phân biệt 1x ,
có b
thiên của hàm số ( )gx như sau: Từ đây suy ra ( ) 2022 1 12 gxe=− và ( ) 2 12 gxe=− . Mặt khác ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 3 12 gxfxfxfx gxfxfxfxfxfx =++
) ( ) ( ) 12 gxgxfx
−=− ( ) ( ) ( ) 12 gxgxfx =−+ . Xét phương trình hoành độ giao điểm: ( ) ( ) 1 12 fx gx = + ( ) ( ) ( ) 120 12 gxfx gx
+ Mặt khác, vì hàm số ( ) ( )yfxgx =− có ba điểm cực trị là 2;1;3 nên ( ) ( ) ( )( )( ) ( )2132fxgxaxxx −=++−
+ Từ ( ) ( )1,2 suy ra: 2 46 3 aa =−=− . Do đó: ( ) ( ) ( )( )( ) 2 213 3 fxgxxxx −=++−
Vậy diện tích hình phẳng là ( ) ( ) ( )( )( ) 33 22
2131 213 36Sfxgxdxxxxdx =−=++−=
Câu 183: Cho hàm số bậc ba ( ) 32 1 2 yfxaxxcxd ==−++ và parabol (
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
57 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN
ỨNG DỤNG TÍCH PHÂN
-
Page
)ygx = có đồ thị như hình vẽ. Biết đồ thị ( )yfx = và ( )ygx = cắt nhau tại ba điểm phân biệt ,, ABC có hoành độ lần lượt là 2;1;2 và thỏa mãn 35 2 AB = . Tính diện tích hình phẳng giới hạn bởi hai đồ thị ( )yfx = và ( )ygx = A. 71 3 B. 238 3 C. 71 6 D. 13 4 Lời giải Chọn C Ta có: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )2 2 2 2;,1;1221 AB AfxBfxABff −=++−− Theo giả thiết ( ) ( ) 353 21 22ABff=−−= . ( ) 13 822 22 acdacd −−−+−−++= 31 ac +=− . Mặt khác, ( ) ( ) ( )( )( ) ( ) 32 21244 fxgxaxxxaxxx −=+−−=−−+ Nhận xét do đồ thị ( )ygx = là parabol nhận Oy làm trục đối xứng ( ) 2 gxkxm=+ Đồng nhất hệ số của phương trình ( )* ta có: 4 ca =− Từ, suy ra 311 44 aca cac +=−= =−=− . Vậy ( ) ( ) 32 44fxgxxxx −=−−+ . Vậy ( ) ( ) 2 2 71 6 Sfxgxdx =−=
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 58
,
= ,
=
( ) ( ) ( ) 1 fx hx gx = + và trục Ox bằng A. 19 ln 22 . B. 13 ln 22 . C. ln6 2 . D. ln2 2 . Lời giải Chọn A Ta có: ( ) ( ) ( ) ( ) ( ) 2 4 1 2 2 2 1 0 fxxaxb fxxa fx fx =++ =+ = = . Xét: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2.22 gxfxfxfxfxfxfxfx =−+=− . ( ) ( ) 1 2 3 00 xx gxfxxx xx = === = . Xét: ( ) ( ) ( ) 1 fx hx gx = + ; ( ) ( ) 00hxfx== . Do đó: ( ) ( ) ( ) ( ) ( ) ( ) 33 2 112 ddd 111 xx x xxx fxfxfx Sxxx gxgxgx ==+ +++ ( ) ( ) ( ) ( ) 3 2 12 11 .d.d 2121 x x xx gxgx xx gxgx =−+− ++ ( ) ( ) ( ) ( ) 2 3 2 1 11 ln1ln1 22 x x x x gxgx =+++ ( ) ( ) ( ) ( ) ( ) ( ) 2132 11 ln1ln1ln1ln1 22gxgxgxgx =+−+++−+ ( ) ( ) 11 ln2ln3ln6ln2 22 =−+− ( ) ( ) 11 ln3ln2ln6ln2 22 =−+− 19 ln 22 = . Câu này khác đề gốc tý với xem như ( ) 10 gx += vô nghiệm trên 13 ; xx
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Câu 184: Cho hàm số ( ) 32 1 6 yfxxaxbxc ==+++ có đồ thị cắt trục hoành tại 3 điểm phân biệt. Biết hàm số ( ) ( ) ( ) ( ) ( ) 22 2 gxfxfxfxfx =−+ có 3 điểm cực trị 123 xxx và ( )1 2 gx =
( ) 2 1 gx
( ) 3 5 gx
. Diện tích hình phẳng giới hạn bởi đồ thị hàm số
Câu 185: Cho đường cong ( ) 3 :2 =++Cyxmx và parabol ( ) 2 :2 =−+Pyx tạo thành hai miền phẳng có diện tích 1S , 2S như hình vẽ Biết 1 8 3 = S , giá trị của 2S bằng A. 3 4 . B. 1 4 . C. 5 0 32 1 d x
Sxxmxx =++ 1
0 432 8 4323 x
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn = ++= Từ đồ thị ta thấy phương trình () có hai nghiệm trái dấu nên 0 m Và hai nghiệm đó là 1 114 2 m x = , 2 114 2 m x −+− = Ta có ( ) 1
xxmx ++= 432 111 8 4323 xxmx ++= 432 111 34632 xxmx++= 432 114114114 3.4632() 222 mmm m +−+−+− −+= Nhận thấy 2 m =− là nghiệm của phương trình () , nên 2 1 x =
59 0 0() x xxm
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 12 . D. 1 2 . Lời giải Chọn C Xét phương trình hoành độ giao điểm của ( )P và ( )C , có: 32 0 ++=xxmx 2
Câu 186: Vậy ( ) ( ) 2 1 3232 2 00
5 d2d 12
x Sxxmxxxxxx =−−−=−−+= .Cho hàm số ( ) 42 fxaxbxc =++ có đồ thị ( )C , biết ( ) 10 f −= . Tiếp tuyến d tại điểm có hoành độ 1 x =− của ( )C cắt ( )C tại hai điểm có hoành độ lần lượt là 0 và 2. Gọi 12 ; SS là diện tích hình phẳng Tính 2S , biết 1 401 2022 S =
A. 12431 2022 . B. 5614 1011 . C. 2005 2022 . D. 2807 1011 .
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page
60
Chọn B Giả sử tiếp tuyến d có phương trình (
ygxmxn ==+ Tiếp tuyến d tại điểm có hoành độ 1 x =− của ( )C cắt ( )C tại hai điểm có hoành độ lần lượt là 0 và 2, nên ta có: ( ) ( ) ( ) ( ) 2 12,0.fxgxaxxxa −=+− Theo giả thiết: ( ) ( ) ( ) ( ) 0 1 1 0 2 1 401401 20222022 4014012005 12 2022520222022 Sfxgxdx a axxxdxa =−= +−=== Do đó ( ) ( ) ( ) ( ) ( ) ( ) 22 2 2 00 2 2 0 2005 12 2022 20055614 12. 20221011 Sfxgxdxxxxdx xxxdx =−+=−+− =−+−=
Lời giải
)
Câu 187: Cho hàm số bậc ba ( )yfx = có đồ thị như hình vẽ, biết ( )yfx = đạt cực tiểu tại điểm 1 x = và thỏa mãn ( ) ( )1 fx + và ( ) ( )1 fx lần lượt chia hết cho ( )2 1 x và ( )2 1 x + . Gọi 12 , SS lần lượt là diện tích hình phẳng như trong hình dưới. Tính 12 2SS .
A. 3 4 B. 1 2 C. 4 D. 1 4 Lời giải Chọn D
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
61 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN
ỨNG DỤNG TÍCH PHÂN
-
Page
Vậy 1333 12 01 221dd33311 22424 xxxx SSxx −=++=−= . Câu 188: Cho hàm số ( ) 32 2 fxxaxbxc =+++ với ,, abc là các số thực. Biết hàm sồ ()()()() gxfxfxfx =++ có hai giá trị cực trị là 4 và 4. Diện tích hình phẳng giới hạn bởi các đường () ()12 fx y gx = + và 1 y = bằng A. 2ln3. B. ln3. C. ln18. D. ln2. Lời giải Chọn D Ta có ( ) ( ) ( ) ( ) 322 262 12212 fxxaxbxcfxxaxb fxxafx =+++=++ =+= Ta lại có ( ) ( ) ( ) ( ) ( ) ( ) ()()1212 1 ()12()1212 fxgxfxfx fx gxgxfxfxfx −== +++++
Theo bài ra, ta có: ( ) ( )( ) ( ) 2 11,0fxaxbxa =+−− ( ) ( ) ( )( ) ( ) ( )( ) 22 0011111112 fbfxaxxfxaxx ===+−−−=+−− . ( ) ( ) ( )( ) ( )( ) ( ) 32 11151841221 fxaxaxaxa −=++−++−+−− . ( ) ( ) ( ) ( )( ) 3 22113 11210211 222 xx fxxaafxxx −+−===+−−=
) ( ) 2 1
12 81 lnlnlnln2 162 12 gx gx
Câu 189: Cho hai hàm số ()fx và ()gx liên tục trên và hàm số 32 () fxaxbxcxd =+++ , 2 '() gxqxnxp =++ với ,0aq có đồ thị như hình vẽ. Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()yfx = và ()ygx = bằng 5 2 và (2)(2)fg = . Biết diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()yfx = và ()ygx = bằng a b . Tính 22Tab =− .
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 62 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( ) ( ) ( ) ( ) ( ) ( ) ( ) ()12100120 ()1212 fxfx fx fxfx gxfxfxfx −==++= ++++ Ta có ()()()()()()12 gxfxfxfxfxfx =++=++ Suy ra: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ()12 1 121212 fxfxgx fx gxfxfxfxgx −== +++++ Gọi 12 , xx là 2 nghiệm của ()0gx = Khi và chỉ khi 12 , xx là 2 nghiệm của ( ) ( ) 120 fxfx ++= Theo giả thiết ta có ( ) 1 2 ()4 4 gx gx = =− ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 222 2 1 111 12 121212ln12| xxx x x xxx dgx gxgx Sdxdxgx gxgxgx + ====+ +++
(
+ ==== + .
A. 7. B. 55. C. 5. D. 16. Lời giải
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 63
Mặt
( ) (
()'()
Do
5 15 10 0 a bq cn dp = −=− −= −= . Ta có 432()5432 bc fxxxxdxr =++++ , 32()32 qn gxxxpxs =+++ ● ( ) ( ) ( ) ( ) 8 (2)(2)20220 3 fgbqcndprs =+−+−+−+−= . Thế vào ta được 0 rs−= ● ( ) ( ) ( ) ( ) ( ) ( ) 432 5 0 432 bqcn fxgxxxxdpxrs =+++−+−= 432 50 550 42 x xxx x = −+= = Diện tích hình phẳng giới hạn bởi
ố ()yfx = và ()ygx = bằng: ( ) ( ) 22 432 00 54 d55d. 43fxgxxxxxx −=−+= Suy ra 4,3ab== . Vậy 22 7 Tab=−= . Câu 190: Cho hàm số ( ) 42 yfxaxbxc ==++ . Tiếp tuyến d đi qua điểm A có hoành độ 2 x = cắt đồ thị hàm số ( )yfx = tại hai điểm khác A có hoành độ lần lượt là 4 x =− và 0 x = . Gọi 12 , SS lần lượt là diện tích phần gạch sọc Tính tỉ số 2 1 S S
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Chọn A Dựa vào đồ thị ta có: ( )( )( ) ( ) 32 ()'()1232 fxgxaxxxaxxx −=−−=−+ , với 0 a . Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số ()yfx = và ()ygx = bằng: ( ) 22 32 00 5 ()()325 2 fxgxaxxxa −=−+== . Suy ra 32 ()'()51510 fxgxxxx −=−+ .
khác,
) ( ) 32
fxgxaxbqxcnxdp
−=+−+−+−
đó,
hai đồ thị hàm s

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 64
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn A. 3 20 B. 1 28 C. 3 28 D. 1 20 Lời giải Chọn B Gọi phương trình của tiếp tuyến d là ( )ygx = . Phương trình hoành độ giao điểm của đồ thị hàm số ( )yfx = và tiếp tuyến d là: ( ) ( ) ( ) ( ) 4 00 2 x fxgxfxgxx x =− =−== = . ( ) ( ) ( ) ( )2 42fxgxmxxx −=+− với 0 m Theo giả thiết ta có: +) ( ) ( ) ( ) ( ) ( ) ( ) 000 2 1 444 dd42d896 5 m Sfxgxxfxgxxmxxxx =−=−=+−=− . +) ( ) ( ) ( ) ( ) ( ) ( ) 222 2 2 000 dd42d32 5 m Sfxgxxfxgxxmxxxx =−=−−=−+−=− 2 1 1 28 S S = Câu 191: Cho hàm số bậc ba ( ) 32 2 7 yfxaxbxxd ==+−+ và đường thẳng ( )ygx = có đồ thị như hình vẽ bên. Biết 265 7 AB = diện tích hình phẳng giới hạn bởi đồ thị hàm số ( )yfx = và ( )ygx = bằng bao nhiêu?
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận
TP Huế ĐT:
Page 65 Chuyên
10
12 Sưu tầm và biên soạn Lời giải Giả sử : dymxn =+ với 0 m do ( )ygx = là hàm nghịch biến. Do , ABd nên tọa độ hai điểm ( ) ( ) 1;,3;3 AmnBmn ++ Mặt khác ( ) ( ) 22 265265 313. 77 ABmnmn =−++−−= 2 4 265()447 74(/)7 ml m mtm = += =− Suy ra ( ) 4 7 ygxxn ==−+ . Xét phương
( ) ( ) 32 24 77
−=+−+−−+ 32 2 7 axbxxdn =+++− Mà ( ) ( )fxgx ( )( )( ) 32 11333. axxxaxaxaxa =+−−=−−+ Đồng nhất hệ số ta được 2 7 a =− Vậy diện tích hình phẳng giới hạn bởi hai đồ thị là ( )( )( ) 3 1 216 113. 77 Sxxxdx =−+−−= Câu 192: Cho hàm số bậc ba ( )yfx = có đồ thị là đường cong ở hình vẽ bên dưới. Gọi 1x , 2x lần lượt là hai điểm cực trị thoả mãn 21 2 xx=+ và đồ thị luôn đi qua ( ) ( ) 00 ; Mxfx trong đó 01 1 xx=− ; ( )gx là hàm số bậc hai có đồ thị đi qua hai điểm cực tr
ủa đồ th
hàm
=
Hòa
0984164935
luyện thi: Tuyển sinh vào lớp
Tốt Nghiệp THPT BDKT Toán 10; 11;
trình:
fxgxaxbxxdxn
ị c
ị
( )yfx
và điểm M

CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 66
điểm cực đại của hàm số bậc ba như hình vẽ trên. Khi đó 121010;22;11xxxxx ==+==−=− Hàm số ( ) ' yfx = có toạ độ hai điểm cực trị là 1 0 x = và 2 2 x = nên ( ) ( ) ( ) 232'32363 fxaxxaxaxfxaxaxd =−=−=−+ Đồ thị hàm số ( )yfx = đi qua gốc toạ độ nên ( ) 3203 dfxaxax ==−
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn . Tính tỉ số 1 2 S S ( 1S và 2S lần lượt là diện tích hai hình phẳng được tạo bởi đồ thị hai hàm ( )fx , ( )gx như hình vẽ bên) A. 5 32 B. 4 29 C. 7 33 D. 6 35 Lời giải Chọn A Đặt ( ) 32 yfxaxbxcxd ==+++ , suy ra ( ) 2 '32 fxaxbxc =++ Không mất tính tổng quát của bài toán ta có thể tịnh tiến gốc toạ độ trùng với
Chọn A
) 32 4
t tr
5 125 .832 3 abca abcb abcc
c hoành
a S a S == Câu 193: Cho hàm số ( ) 32 4 yfxxaxbxc ==−+++ có đồ thị cắt trục hoành tại ba điểm có hoành độ là ( ) 3,1,1; Fx là một nguyên hàm của ( )fx và ( )ygx = là hàm số bậc hai đi qua ba điểm cực trị của đồ thị hàm số ( )yFx = . Diện tích hình phẳng giới hạn bởi hai đường ( )yFx = và ( )ygx = bằng A. 128 15 . B. 64 15 . C. 16. D. 64. Lời giải −+=−=− −+=−= ++== hay ( ) 32 412412yfxxxx ==−−++ Ta có ( ) ( ) 32432 412412d4212 FxxxxxxxxxC =−−++=−−+++ Mặt khác ta có ( ) ( ) 2 11 483 44 FxxfxxxC =++++− do vậy ( ) 2 483ygxxxC ==++− là hàm số bậc hai đi qua 3 điểm cực trị của đồ thị hàm số ( )yFx = . Xét phương trình hoành độ giao điểm của hai đồ thị hàm số ( )yFx = và ( )ygx = ta có:
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN
Page 67
Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935
Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Vì hàm số (
Ta có ( ) ( ) 124 ffa −==− . Đồ thị parabol ( )P đi qua gốc toạ độ nên có dạng ( ) 2 : Pymxnx =+ ( )P đi qua điểm ( ) 2;4 Aa và ( ) 1;4 Ba nên ta có hệ 4244246122 422842. mnamnamama mnamnanmana +=−+=−=−=− −=−−=−=+= Do đó parabol ( )P có phương trình ( ) 2 :22 Pyaxax =−+ Khi đó ( ) 0 322 1 1 yfxxaxbxc ==−+++ có đồ thị cắ
5 322d 12 a Saxaxaxaxx =−−−+= ; ( ) 2 322 2 0 ụ
8 322d 3 a Saxaxaxaxx =−−−+= Suy ra 1 2 tại ba điểm có hoành độ là 3,1,1 nên ta có hệ phương trình 9310812 44 412
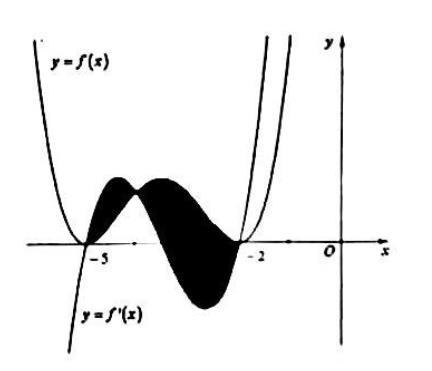
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 68 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ( )( ) ( ) 4322432 2 421248342430 101 1130101 303 xxxxCxxCxxxx xx xxxxx xx −−+++=++−−−−++= −== −−++=+==− +==− Khi đó ( ) ( ) 11 432 33 d4243d SFxgxxxxxxx =−=−−−++ ( ) ( ) 11 432432 31 11 55 432432 31 4243d4243d 22 2323 5353 xxxxxxxxxx xx xxxxxxxx =−−−+++−−−++ =−−+++−−++ 17274717128 155151515 =−+++= Vậy diện tích hình phẳng giới hạn bởi hai đường ( )yFx = và ( )ygx = bằng 128 15 . Câu 194: Cho hàm số ( )fx là hàm đa thức bậc bốn, có đồ thị nhận đường thẳ
=−
xứ
Diện tích hình phẳng giới hạn bởi ( )yfx = và trục hoành bằng A. 81 50 . B. 91 50 . C. 71 50 . D. 61 50 . Lời giải Chọn A Đặt ( ) ( ) ( ) 22 52,0fxkxxk =++ .
ng 7 2 x
làm trục đối
ng. Biết diện tích hình phẳng của phần giới hạn bởi đồ thị hàm số ( ) ( ) , yfxyfx == và hai đường thẳng 5,2xx=−=− có giá trị là 127 50
CHUYÊN ĐỀ III GIẢI TÍCH 12 NGUYÊN HÀM TÍCH PHÂN - ỨNG DỤNG TÍCH PHÂN Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935 Page 69 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn Khi đó ( ) ( )( ) ( ) ( ) ( )( )( ) 22 25225252414 fxkxxkxxkxxx =+++++=+++ Xét hàm ( ) ( ) ( ) ( )( )( ) 2 5234gxfxfxkxxxx =−=+++− Suy ra ( ) 5 2 0 4 1 x x gx x x =− =− = =− = Từ đó ta suy ra ( ) ( ) ( ) ( )( )( ) ( )( )( ) 242 554 42 22 54 52345234 gxdxgxdxgxdx kxxxxdxkxxxxdx =−+ =−+++−++++− 23521271271 10510505 kkkk =+=== Vậy ( ) ( ) ( ) 22 22 55 181 25 550Sfxdxxxdx ==++=