CHUYÊN ĐỀ VẬN DỤNG - VẬN DỤNG CAO LUYỆN THI TỐT NGHIỆP THPT NĂM 2023 - GIẢI TÍCH 12 - SỐ PHỨC

B. 13 C. 2 D. 13

ời giải

, zabiabzabi

có

)

) ( ) 51 5 22 11 abi zi ii zabi

aba abbia bab −==

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

trình ( ) ( ) 2i12i13i zzz +−−=+ và 12 1 zz−= . Tính 1225 Mzz =+ . A. 19 M = B. 39 M = C. 7 M = D. 39 M = Lời giải

zabz =+== Câu 11: Cho hai số phức 1z , 2z thỏa mãn các điều kiện 12 2 zz== và 1224zz+= . Giá trị của 12 2zz bằng? A. 6 B. 26 C. 36 D. 2 Lời giải Chọn B

Ta có: ( )(

Thay ( )1 ,( )2 vào ( )3 ta được 1 acbd+=− ( )4 . Ta có 12 2zz−= ( ) ( ) 2222acbd −+− ( ) ( ) ( ) 2222 44abcdacbd =+++−+ ( )5 . Thay ( )1 ,( )2 ,( )4 vào ( )5 ta có 12 226 zz−=

loaïi 22 1 ab += . Vậy 2 1 z P z = + 1 11 = + 1 2 = . Câu 19: Có bao nhiêu số phức z thỏa 5373 zizi −+=−+ và 3 2 zi zi + là một số thực? A. 0. B. 1. C. 4. D. 2. Lời giải Chọn B Gọi ;, zabiab=+ Ta có: 5373 zizi −+=−+ Suy ra ( ) ( ) ( ) ( ) 2222 53735373 abiiabiiabab +−+=−−+−++=−+−+ ( )41224036* abab +−=+= Lại có: ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) 2 2222

32 2532 33 2 2 22 abiabi aabibb ziabii abii zi abab +−+− +−−−− −+− === −+ + +−+− ( )( ) ( ) ( ) ( ) 2 2222 3225 22 abbab i abab =+ +−+− Vì 3 2 zi zi + là một số thực nên phần ảo ( ) ( )2 2

ab ab

+−   Kết hợp ()() *;** , ta có ( ) ( )2 2 3 250 2 20 5 36 2 ab a ab b ab −=   =−    +−   = +=    

ch

có duy nh

25 0 2 ab ab = +− suy ra ( ) ( ) ( ) 2 2

c

=−+ tho

mãn đề bài.

y 241.xyx+=+=

Câu 26: Có bao nhiêu số phức z thoả mãn 22zi+−= và ( )( ) 313 wzizi =+−++ là số thực? A. 0 B. 2 C. 3 D. 1 Lời giải

Chọn B Gọi zabi =+ Do ( ) ( ) 22 22214ziab +−=++−= , khi đó tập hợp biểu diễn các số phức z là đường tròn ( )C có ( )2;1 I và bán kính 2 R = .

Ta có ( )( ) ( ) ( ) 313.13368 wzizizzizizi =+−++=+++−++ ( )( ) ( )( ) 22 13368 abiabiiabii =+++++−−++ ( ) 22 446228 abababi =++−++−+ . Do ( )( ) 313 wzizi =+−++ là số thực nên 228040 abab −+=−+= , khi đó tập hợp biểu diễn các số phức z là đường thẳng :40 xy −+= Ta có ( ) 1 , 2 dIR = nên  cắt ( )C tại hai điểm phân biệt. Vậy có hai số phức thoả mãn.

Phương trình ( )2 biểu diễn đường tròn ( )'C có tâm ( )3;2 J và bán kính '4R = 25;'2;'6IJRRRR =−=+=

Vì '' RRIJRR −+ nên hai đường tròn ( )C và ( )'C cắt nhau tại hai điểm phân biệt. Vậy hệ phương trình đã cho có 2 nghiệm phân biệt. Câu 28: Cho số phức z thỏa mãn 35zz−=− và ( )( ) 4 zzi +− là số thự C. Tính z . A. 15. B. 15 . C. 20. D. 25 . Lời giải Chọn D Giả sử zabi =+ ( ) , ab . Ta có:

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

A. 0. B. 4. C. 3. D. 2. Lời giải

Chọn C

Gọi số phức zxyi =+ ( ) , xy  có biểu diễn là ; Mxy

Vì ( ) ( ) ( ) 2 2 2 1121xxy y zi   −=−+−  là số thuần ảo ( ) ( )( ) 2 2 10110 xyxyxy −−=+−−−=

Suy ra: Tập hợp điểm biểu diễn của z là hai đường thẳng ( )1 :10 xy +−= , ( ) 2 :10 xy −−= .

Mặt khác: 222zi+−= nên tập hợp điểm biểu diễn của z là đường tròn C có tâm ( ) 2;1,22IR−=

Ta có ( )1 22

211 ,2 11 dIR −+− == +

Vì ( )1 , dIR  nên 1 và C có hai điểm chung.

Lại có ( ) 2 211 ,22 2 dIR === nên 2 và C có một điểm chung. Vậy có 3 số phức thỏa mãn.

Câu 31: Có bao nhiêu số phức z thỏa mãn ( ) ( )2 2 2720zzzz −+−=   ?

4

5

6

3

ời gi

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Vì 2 2 z zz + là số thực nên ( ) 2322 22

0 4040 4 b ababbbaab aba =  −+−=−−+=  +=  Mặt khác: ( )( ) ( ) ( ) ( ) 2222 zziabiabi ++=+++− là số thuần ảo nên ( ) ( ) 220aabb+−−= hay 22 220abab++−= Xét TH1: 00ba== hoặc 2 a =− không thỏa mãn do không tồn tại số phức 2 2 z zz + TH2: 22 2 22

ab ba aba ab aa abab

==  =  +=      == = +=−+     0,0ab== 26 , 55 ab== Vậy ( ) 26 ;,

55 ab

0,0 3 4 26 , 104 22 55       nên

1 55102 2 ab abababab ab 

+=

2

w w là số thuần ảo ( ) 22 22

0 430 =3 a aab ab =  −=   .

Trường hợp 1: 0 a = , thay vào ( )1 ta được: 2 1 21= 2 bb= 

Trường hợp này có 2 số phức thỏa mãn bài toán.

Trường hợp 1: 22 =3 ab , thay vào ( )1 ta được: 2 1 81= 22 bb= , 22 36 =3 84 aba== . Trường hợp này có 4 số phức thỏa mãn bài toán. Vậy có tất cả 6 số phức thỏa mãn yêu cầu bài toán. Câu 38:

= và |3| zim −+= . Số phần tử của S là A. 4. B. 3. C. 2. D. 1. Lời giải Chọn C Dễ thấy 0 m  . Đặt ;, zabiab=+ ta có hệ phương trình 22 222

1 (3)(1) ab abm  +=   −++=  

1 (3)(1) ab abm  +=   −++=   có nghiệm duy nhất

Hai đường tròn này tiếp xúc với nhau

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

C. 40 D. 8

giải Chọn A Gọi ( ) ,, zxyixy=+ . Điều kiện: 6 z  . Ta có ( ) ( ) ( ) ( ) ( ) ( ) 2 2222

6 66 66 66 xyixyi xxyyi zxyi zxyi xyxy

+−− −+− +  === −−+ −+−+ . 6 z z là số thuần ảo ( ) 222 6060xxyxyx −+=+−= ( )1 Gọi ( ) ; Mxy là điểm biểu diễn số phức z

Từ ( )1 ta có M thuộc đường tròn tâm ( ) 113;0,3IR = Từ 2 44zmIM −== , ( ) 2 ;0Im ta có M thuộc đường tròn tâm ( ) 22;0,4ImR =

Vậy  4;4 S =− , nên tích các phần tử thuộc S là 16 Câu 41: Có bao nhiêu số phức z thỏa mãn 122zi−−= và 4410zz++−= ? A. 1 B. 0 C. 2 D. 4 Lời giải Chọn C Áp dụng các tính chất 1212 ; zzzzzz =+=+ ta có 4444zzzz +=+=+=+ Do đó 44104410zzzz ++−=++−= Gọi M là điểm biểu diễn của z . Do 122zi−−= nên M thuộc đường tròn ( )C tâm ( )1;2 I , bán kính 2 R = ( )C có phương trình là ( ) ( ) 22 124xy−+−= . Do 4410zz−++= nên M thuộc đường elip ( )E có hai tiêu điểm là ( ) 1 4;0 F ( ) 2 ;4;0 F và có độ dài trục lớn là 10. ( )E có phương trình là 22 1 259 xy+= . Từ đây có M là giao điểm của ( )C và ( )E . Từ hình vẽ của ( )C và ( )E ta thấy chúng có 2 giao điểm nên có 2 số phức thỏa mãn yêu cầu. Câu 42: . Gọi 12 , zz là hai trong các số phực thỏa mãn 355zi−+= và 12 6 zz−= . Môđun của số phức 12 610 zzi  =+−+ là A. 10  = B. 32  = C. 16  = D. 8  = Lời giải Chọn D Gọi ( ) , zxyixy=+ . Khi đó từ giả thiết 355zi−+= ta có:

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

phức 12 , zz , suy ra M, N nẳm trên đường tròn và từ giả thiết 12 6 zz−= ta có 6 MN = Gọi H là trung điểm của MN suy ra 2222534 IHIMMH=−=−= Ta có ( ) ( ) 1212610353522.48.zziziziIMINIH

n ảo nên ( ) ( ) +++= 110(2)aabb .

Thay ( )1 vào ( )2 ta được. ( ) ++= 2 20voânghieäm bb

Vậy không có số phức z thỏa mãn yêu cầu bài toán. Câu 45: Cho số phức zabi =+ , ( ) , ab thỏa mãn 130zizi++−= . Tính 3 Sab =+ A. 7 3 S = . B. 5 S =− . C. 5 S = . D. 7 3 S =− . Lời giải Chọn B Ta có 130zizi++−= ( ) ( )2 5 13136100 3 zzizzzz =−+−=+−−+== Khi đó 54 131 33 ziii =−−+=−− . Ta được 3145ab+=−−=− .

Câu 46: Có bao nhiêu số phức z thỏa mãn 222zi+−= và ( )2 1 z là số thuần ảo? A. 0 B. 2 C. 4 D. 3 Lời giải Chọn D Đặt zxyi =+ (

Suy ra tập hợp điểm M biểu diễn số phức z là hai đường thẳng 1 :10dxy−−= và 2 :10dxy+−= Ta có ( ) ( ) 1 2 2

2114 ,22 112 dIdR ==== +− và ( ) 2 22

211 ,2 11 dIdR −+− == + nên đường thẳng 1d tiếp xúc với ( )C tại A, và đường thẳng 2d cắt ( )C tại hai điểm phân biệt , BC . Dễ thấy 1d cắt 2d tại điểm ( ) ( ) 1;0 MC  nên ba điểm ,, ABC không trùng nhau. Vậy có 3 số phức thỏa mãn bài toán.

Câu 47: Trên tập hợp các số phức, xét phương trình ( ) 2230zazaa−−++= ( a là tham số thực). Có bao nhiêu giá trị nguyên của a để

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Thay ( )1 ,( )2 ,( )4 vào ( )5 ta có 12 226 zz−= Câu 50: Cho số phức z có phần thực là số nguyên và z thỏa mãn 273 zziz −=−++ . Môđun của số phức 2 1 wzz =−+ bằng A. 445 w = B. 425 w = C. 37 w = D. 457 w = Lời giải Đặt ( ) , zabiab =+ Khi đó: 273 zziz−=−++ 22 2273 ababiiabi ( ) ( ) 22 3730ababi+−++−=

3 5 7 4() 3 3 4 b a a b a . Do a  nên 443421457aziwiw ==+=+= Câu 51: Cho số phức zabi =+ ( ) , ab thoả mãn ( ) 4251 zizii −+−=+ . Tính giá trị của biểu thức Tab =+ A. 2 T = . B. 3 T = . C. 1 T = . D. 1 T =− . Lời giải ( ) ( ) 42514251 ziziiabiiabiii −+−=++−++−=+ ( ) ( ) ( ) 451 252 abi abi  −+=

1 và

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 0 202z020 202 z zizzizzziz ziz =  +=+=+=  += 

+−−−−+− === +− + +− w là một số ảo khi và chỉ khi ( )( ) ( ) 2 2 2

 −−−=  =−    +−  

xyy x xy y yx

21012 107 23 57

222123 w 11 xyixyyxyi zi xyi zi xy = =+     Vậy 1223 77 zi =−+ .Vậy chỉ có 1 số phức z thỏa mãn. Câu 54: Có bao nhiêu số phức z thỏa mãn (2)10zi−+= và .25zz = . A. 2. B. 3. C. 1. D. 4. Lời giải Gọi số phức cần tìm là ( ) , zabiab=+ . Ta có: 2 22 .25 (1) zzzab==+= Lại có: (2)102(1)10 ziabi −+=−+−=

Câu 61: Cho số phức ( ) , zabiab=+ thỏa mãn 255zi++= và .82zz = . Tính giá trị của biểu thức Pab =+ A. 10. B. 8. C. 35. D. 7. Lời giải Theo giả thiết ta có ( ) ( ) ( ) ( )

  = +++=     += +=  

22 22 22

b a ab ab ab

543 2551 2 82822

b bb b

=−   ++=  = 

Thay ( )1 vào ( )2 ta được 2 9 2943015210 169 29

Vì b nên 91ba=−= . Do đó 8 Pab=+=−

Câu 62: Cho M là tập hợp các số phức z thỏa 22ziiz −=+ . Gọi 1z , 2z là hai số phức thuộc tập hợp M sao cho 12 1 zz−= . Tính giá trị của biểu thức 12Pzz =+ . A. 3 P = . B. 3 2 P = . C. 2 P = . D. 2 P = . Lời giải Đặt zxyi =+ với x , y  Ta có: ( ) 22 2222121 ziizxyiyxixy −=++−=−++= Suy ra tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức là đường tròn ( );1O 12 1 zz == . Ta có: ( ) 2222 2 121212233zzzzzzPP ++−=+== . Câu 63: Gọi S là tập hợp các số thực m sao cho với mỗi mS 

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Lời giải

Ta có 2 4 w + ( )2 4 xyi =++ 22 24xyxyi =−++ ( )2 22222 444 wxyxy+=−++ .

Do đó 2 42 ww += ( )2 222222 442 xyxyxy −++=+ ( ) ( ) 2 222222 444 xyxyxy −++=+ ( ) ( ) 4422222222 281644 xyxyxyxyxy +−+−++=+ ( ) ( ) 442222222448120xyxyxyxy ++−+++−+= ( ) ( ) ( ) 2 222222448120xyxyxy +−+++−+= ( ) ( ) 2 222228120xyxy +−+−+= ( ) ( )2 2222 8122 xyxy −+=−+− ( )2 2 2 Pw =−− Câu

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

 −+ =   ++=+−=

ra có hai s

ph

c z thỏa yêu cầu bài toán. Câu 75: Chosốphức ( ),,0=+ zabiaba thỏamãn ( ) .121310 −+−=− zzzzzi .Tính =+ Sab A. 17=− S B. 5 = S C. 7 = S D.

Ta có ( ) 2020505 2019 50510091009(1)(4)11 1(4)()22 1(1)22 i ziii ii +− =+===−−=−+ ++ Phần thực của z bằng 10092 Câu 80: Số phức ( ) ( ) ( ) 2201811...1 ziii =++++++ có phần ảo bằng A. 1009 21 + B. 100912 C. 1009 21 D. ( ) 1009 21−+ Lời giải ( ) ( ) ( ) 22018

11...1 ziii =++++++

) ( ) ( ) 2018 1009 1121

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 1 1 zzz zzz ===   ++=   . Tính giá trị biểu thức 201920192019 123 Szzz =++ A. 1 S =− . B. 20192 S = . C. 1 S = . D. 2019 2 S = . Lời giải Chọn C Đặt ( ) 123 1:1 zzz=== , ( ) 123 2:1 zzz++= .

giải ( )2018 2 1 xx++ 24036 0124036 aaxaxax =++++ . Thay xi = với 2 1 i =− ta được: ( )1009 23403440354036 01234034403540361...aaiaiaiaiaiai−=+++++++ Đối chiếu phần thực ở hai vế ta được: 0246403440361...aaaaaa −=−+−+−+ .

Xét ( ) 22

0 10 a b ab

 =  =   = 

Với 0 a = thì từ ( ) 4 20,1,1 bbbbb ====− ta được 0;; zzizi ===−

Với 0 b = thì từ ( ) 4 20,1,1 aaaaa ====− ta được 0;1;1zzz===− .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Câu 88: Tìm tất cả các giá trị thực của tham số m để số phức 2 2 mi z mi + = có phần thực dương A. 2 m  B. 2 2 m m −     C. 22 m − D. 2 m − Lời giải 2 2 mi z mi + = ( )( ) 2 22 4 mimi m ++ = +

2 22 44 44 mm i mm =+ ++ . Vì z có phần thực dương 2 2 40 2 m m m   −  −  .

Câu 89: Cho hai số phức 34 zi =− và ( ) ( ) '2 zmmim=++ thỏa mãn ' ziz = . Tổng tất cả các giá trị của m bằng A. 1 B. 46 2 C. 0 D. 2 . Lời giải: Chọn D Ta có ( )2 2 '2 zmm =++ và 22 435 iz =+= vậy ta có phương trình ( )2 22 12 4 225242102 2 mmmmmm ++=+−=+=−=−

Câu 90: Biết rằng 2 33(2) zmmmi =−++− , với m , là một số thực. Giá trị của biểu thức 232019 1 Pzzzz =+++++ bằng A. 1. B. 2020. C. 2019. D. 0. Lời giải Chọn B

Ta có 2 33(2) zmmmi =−++− là một số thực khi 202mm−== . Với 21mz== , thay vào biểu thức P , ta được: 23201911111 P =+++++ 2020. = Câu 91: Gọi S là tập tất cả các

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

 +=   +=   có 4 nghiệm phân biệt. Hệ có 4 nghiệm thì đường tròn tâm O bán kính m phải cắt các đường thẳng 1 xy+= tại 4 điểm phân biệt. Các đường thẳng 1 xy+= đôi một cắt nhau tạo thành 1 hình vuông như trên đồ thị. Để đường tròn ( )C : 22 xym += cắt các đường thẳng 1 xy+= tại 4 điểm thì đường tròn sẽ là đường tròn nội tiếp hoặc ngoại tiếp hình vuông với các bán kính tương ứ m m

bán kính  =   =  . Suy ra tổng các giá trị m cần tìm là 3 2 Câu 92: Giá trị của biểu thức 024698100 100100100100100100 ...C CCCCC −+−+−+ bằng A. 1002 . B. 1002 . C. 502 . D. 502 . Lời giải Chọn D Ta có ( )100 0122100100 1001001001001... iCiCiCiC +=++++ ( ) ( ) 02410013599 100100100100100100100100 ... CCCCCCCCi =−+−++−+− Mặt khác ( ) ( ) 50 100211ii +=+  ( )50 2i = Câu 93: Khai triển của biểu thức ( )2018 2 1 xx++ được viết thành 24036 0124036 ... aaxaxax ++++ . Tổng 024640344036 ... Saaaaaa =−+−+−+ bằng: A. 10092 B. 0 C. 10092 D. 1 Lời giải Chọn D

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Ta có ( )2022 224044 01240441... xxaaxaxax ++=++++

Cho xi = ta được ( )2022 2 01234564044 024640441354043

1... ...() iiaaiaaiaaiaa aaaaaaaaai ++=+−−++−−+ =−+−−++−+−+ .

Hay 024640424044 Saaaaaa =−+−+−+ ( ) ( ) ( )1011 20222022 2 111 iii =−++===− .

Câu 94: Tổng 2351Piiii =++++ bằng A. 1. B. i . C. i . D. 1. Lời giải

Chọn D

Tổng P là một cấp số nhân có số hạng đầu 1 ui = và công bội qi = Áp dụng công thức 1 1 . 1

n n q Su q = . Ta có ( ) ( ) 26 26 2 515152 1 1 111 ..1 111111 ii i Puiqiiii qiiiii =======− .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

SỐ PHỨC

; Mxy là điểm biểu diễn số phức zxyi =+ . Bước 2. Biến đổi điều kiện K để tìm mối liên hệ giữa , xy và kết luận. Mối liên hệ giữa x và y Kết luận tập hợp điểm ( ) ; Mxy 0. AxByC++=

Là đường thẳng :0dAxByC++= . ( ) ( ) 22 2xaybR −+−= hoặc 22 220.xyaxbyc +−−+=

Là đường tròn tâm ( ) ; Iab và bán kính 22 Rabc =+− . ( ) ( ) 22 2xaybR −+− hoặc 22 220.xyaxbyc +−−+

Là hình tròn tâm ( ) ; Iab và bán kính 22 Rabc =+− ( ) ( ) 22 22 12 RxaybR −+−

Là những điểm thuộc miền có hình vành khăn tạo bởi hai đường tròn đồng tâm ( ) ; Iab và bán kính lần lượt 1R và 2R . ( ) 2 ,0.yaxbxca =++

một parabol có đỉnh ; 24 b S aa  

c l

n 2, a trục bé 2b và tiêu

Chọn A Ta có: ( )5;5 AB . Đường trung trực của đoạn thẳng AB đi qua trung điểm 13 ; 22 I    có phương trình ( ):20dxy−+= . ( ) ( );22 MdMaazaai +=++ ; ( )2 zaai =−+ . Khi đó ( ) ( )442 waaiaai =++−−+   ( ) ( ) ( )( ) ( )( )424442 aaaaiaaiaa =−−++−+++− w là số thực khi và chỉ khi ( ) ( )( ) 2440aaaa −+++−= 2221608614 aaaabab −−+−==−=−+=− . Câu 3: Cho Gọi () C là tập hợp điểm biểu diễn số phức z thỏa mãn 448zzzz +−+−= . Diện tích hình phẳng được giới hạn bởi () C là A. 24. B. 4. C. 16. D. 8. Lời giải Chọn D Đặt , , zxiyxy=+ . Khi đó, đẳng thức 448zzzz +−+−= 24428 xiy −+= 2288 xy −+= 244xy −+= Ta được đồ thị như hình vẽ bên dưới: Đây là hình thoi có độ dài hai đường chéo là 2 ; 8 nên diện tích bằng: 2 = 8. Câu 4: Cho số phức ( ) 12wiz=++ với 12 izzi+=− . Biết rằng tập hợp các điểm biểu diễn số phức w là đường thẳng  . Khoảng cách từ điểm (1;2)A đến  bằng A. 0 B. 22 C. 2 D. 2 2

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

= 

1 10 z zmzmi =    −++=  ( ) ( )( ) 22

1 1 0 0 = 

1



 −+−=

u diễn số phức ( ) 1 wzi =+ trong mặt phẳng tọa độ ( )Oxy là hình phẳng ( ) H có diện tích bằng A. 9 S  = B. 9 S = C. 18 S  = D. 18 S = Lời giải Chọn C Ta có 123zi

hai

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Gọi ; AB lần lượt là điểm biểu diễn của 12 ; zz . Từ giả thiết 535zi−−= suy ra ; AB thuộc đường tròn tâm ( )5;3 I , bán kính 5 và 12 8 zz−= suy ra 8 AB = . Gọi M là trung điểm của đoạn AB . Khi đó ta tính được 3 IM = .

Mặt khác, M là điểm biểu diễn của số phức 12 2 zz + , I là điểm biểu diễn của số phức 53i + , thay vào ta có biểu thức ( ) 12 12 5331066 2 zz izzi + −−=+−−=

Vậy điểm biểu diễn của 12zz + nằm trên đường tròn tâm ( )10;6 J ; 6 r = .

Khi đó 10 a = ; 6 b = ; 6 r = .

Vậy ( ).96abr+= .

Câu 12: Tập hợp các điểm biểu diễn số phức z thỏa mãn 12 2 23 zi zi +− = −+ là

A. Đường tròn tâm ( )5;8 I bán kính 217

B. Đường tròn tâm ( )5;8 I bán kính 217

C. Đường tròn tâm ( )5;4 I bán kính 25 .

D. Đường tròn tâm ( ) 5 ;4 I bán kính 25 . Lời giải

Chọn C

Gọi zxyi =+  zxyi = ( ) , xy  12 2 23 zi zi +− = −+  12 zi +− = 223 zi −+

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( ) ( ) ( )232 izxyi−=−++ . ( ) ( ) ( ) ( ) 2 432.2 izxyii  −=−+++  . 2821 55 xyxy zi −−++ =+ . Vì 2 z = nên 222821 4 55 xyxy −−++  +=  . 22 641320xyxy +−++= ( ) ( ) 22 3220xy −++= .

Vây tập hợp biểu diễn số phức w là đường tròn tâm ( )3;2 I .

Cách 2 Đặt ;w zabixyi =+=+ . Vì 2 z = nên 22 4 ab+= . Ta có ( ) w322iiz=−+− . ( )( ) 232 xyiiiabi ++−=−+ . ( ) ( ) ( ) ( ) 3222 xyiabbai −++=++− . ( ) ( ) ( ) ( ) 2222 3222 xyabba −++=++− . ( ) ( ) ( ) 22 22 325 xyab −++=+ . ( ) ( ) 22 3220xy −++= .

Vây tập hợp biểu diễn số phức w là đường tròn tâm ( )3;2 I .

Câu 17: Tính tổng của tất cả các giá trị của tham số m để tồn tại duy nhất số phức z thoả mãn đồng thời zm = và 2 43 zmmim −+=

A. 4 B. 6 C. 9 D. 10 Lời giải

Đặt ( ) , zxyixy=+ . Ta có điểm biểu diễn z là ( ) ; Mxy

Với 0 m = , ta có 0 z = , thoả mãn yêu cầu bài toán.

Với 0 m  , ta có:

+ zm= M thuộc đường tròn ( )1C tâm ( ) 0;0, I bán kính Rm =

+ ( ) ( ) 22 244343 zmmimxmymm −+=−++=

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

ng tròn. Bán kính r của đường tròn đó là A. 9 B. 36 C. 6 D. 3 Lời giải Gọi ( ) , wxyixy=+ Theo đề bài ta có: ( ) ( ) ( )( ) ( )181818118 wiziwiizwiizi =++−=+−=++−+ ( )( ) ( ) ( ) ( )( )18181118181 wiiizxyiiz −++=++++−+=++ ( ) ( ) ( ) ( ) ( ) 22222 2 11818.211836 xyxy ++−+=+++−+= Vậy tập hợp các điểm biểu diễn số phức ( )18 wizi =++ là một đường tròn có bán kính 6. r = Câu 19: Cho 12 , zz là hai số phức thỏa mãn điều kiện |z53i|5 −−= đồng thời 12 ||8 zz−= . Tập hợp các điểm biểu diễn số phức 12wzz =+ trong mặt phẳng tọa độ Oxy là đường tròn có phương trình A. 22 (10)(6)36 xy−+−= . B. 22 (10)(6)16 xy−+−= . C. 2253 ()()9 22xy−+−= D. 22 539()()224xy−+−=

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

(10)(6)36

20:

21:

zi

h

điểm

di

ố phức ( ) 235wizi=−−+ là một đường tròn. Xác định tâm I và bán kính của đường tròn trên. A. ( ) 6;4,25IR−−= . B. ( ) 6;4,10IR = . C. ( ) 6;4,25IR = . D. ( ) 6;4,25IR−= . Lời giải

Ta có: ( ) ( )( ) 23521364 wiziwizii =−−+=−+−++ ( )( ) 64213 wiizi −−=−+− ( )( ) 6421325wiizi −−=−+−= Gọi ( ) ; Mxy là điểm biểu diễn số phức ( ) ; wxyixy=+ ( ) ( ) 64256425wixyi −−=−+−= ( ) ( ) ( )2 22 6425xy −+−= Vậy tập hợp điểm biểu diễn số w là đường tròn tâm ( )6;4 I , bán kính 25 R = .

a O qua I suy ra ( )10;6 J và IT là đường trung bình của tam giác OJM , do đó 26JMIT==

Vậy M thuộc đường tròn tâm J bán kính bằng 6 và có phương trình ( ) ( ) 22 10636xy−+−= .

Câu 23: Xét số phức z thỏa mãn 343zi−+= , biết rằng tập hợp các điểm biểu diễn số phức (125)4 wizi =−+ là một đường tròn. Tìm bán kính r của đường tròn đó. A. 13 r = . B. 39 r = . C. 17 r = D. 3 r = . Lời giải Gọi số phức ,wxyi =+ với , xyR  , biểu diễn bởi (;)Mxy (125)4 wizi =−+ (125)4 xyiizi+=−+ (4) 125 xyi z i +− =

(4) 125 xyi z i = + Ta có : 343zi−+= (4)343 125 xyi i i −+= + 63(12)3 125 xyi i +−+ = +

22 22 (63)(12)3 125 xy+++ = + 222 (63)(12)39 xy +++= Vậy 39 r = Câu 24: Cho số phức z thỏa mãn 31 z −= . Biết rằng tập hợp các điểm biểu diễn các số phức ( ) 1312 wizi =−+− là một đường tròn. Tính bán kính r của đường tròn đó. A. 2 r = . B. 1 r = . C. 4 r = . D. 2 r = . Lời giải Gọi =+ wxyi . ( ) 1312

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn wizi =−+− ( ) 1312+=−+− xyiizi ( )12 13 −++ = xyi z i ( ) 13 12 44  =−+++      zxyii ( ) ( ) ( ) ( ) 132213 44 −−+++− =+ xyyx i 3 −= z ( ) ( ) ( ) ( ) 1332213 44 −−+++− + xyyx i 31 z −= ( ) ( ) ( ) ( ) 22 1332213 1 44  −−+++− +=    xyyx ( ) ( )( ) ( ) ( ) ( )( ) ( ) 2222 132313232222133116 −−−+++++++−+−= xxyyyyxx ( ) 22 8463123430 +−++++= xyxy Bán kính ( )2 2 4233123432 =+−−−−= r Câu 25: Cho số phức z thỏa mãn ( )( ) 2225zizi −+−−= . Biết tập hợp các điểm M biểu diễn số phức 223 wzi =−+ là đường tròn tâm ( ) ; Iab và bán kính c . Giá trị của abc ++ bằng A. 18 B. 20 C. 10 D. 17 Lời giải Chọn A Giả sử zabi =+ ( ) ; ab và wxyi =+ ( ) ; xy  . ( )( ) ( ) ( ) 2225212125 ziziabiabi −+−−=−++−−+=  

Suy ra, tập hợp điểm biểu diễn của số phức w là đường tròn tâm ( )2;5 I và bán kính 10 R = . Vậy 17 abc

Câu 26: Xét các s

t cả các điểm biểu diễn c

mãn ( )( )42ziz−+ là số thuần ảo. Biết rằng tập hợp t

a z là một đường tròn. Tìm tọa độ tâm của đường tròn đó. A. ( )1;2 . B. ( )1;2 . C. ( )1;2 . D. ( )1;2 . Lời giải Chọn B Gọi zxyi =+ với , xy  và ( ) ; Mxy là điểm biểu diễn của số phức z Ta có ( )( ) ( ) 22 4224248 zizxyxyyxi −+=++−+−− . ( )( )42ziz−+ là số thuần ảo 22 240xyxy ++−= ( ) ( ) 22 125xy ++−= . Tập hợp các điểm biễn diễn của số phức z là mộ đường tròn có tâm ( )1;2 I ,bán kính 5 R =

27: Cho số phức z thảo mãn ( )( ) 131325zizi +−++= . Biết tập h

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Thay vào ( )* ta được 22 26150xyxy++−−=

Vậy tập hợp các điểm biểu diễn z thuộc đường tròn ( )C có tâm ( )1;3 I và bán kính 5 R = .

Suy ra 1 3 5

=−   =   =  . Vậy 7 abc++= .

a b c

Cách 2: Đặt 0 13 zi =−+ và 5 R = . Ta có 2 00000 zzzzzzzzzz −−=−−=− .

Suy ra 2 22 0000 zzzzRzzRzzR −−=−=−= , với 0 R 

Vậy tập hợp biểu diễn số phức z thuộc đường tròn tâm ( )1;3 I , bán kính 5 R = .

Suy ra 1 3 5

=−   =   =  . Vậy 7 abc++= .

a b c

Câu 28: Xét các số phức z thoả mãn ( ) 1 1 zi zzi −+ ++ là số thực. Tập hợp các điểm biểu diễn của số phức 2 z là parabol có toạ độ đỉnh A. 13 ; 44 I    . B. 11 ; 44 I    . C. 13 ; 22 I    . D. 11 ;

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Số phức 2 z có điểm biểu diễn ; 22 ab M     quỹ tích M là parabol có phương trình 2 1 42 2 yxx=−−

Tập hợp các điểm biểu diễn của số phức 2 z là parabol có toạ độ đỉnh 13 ; 44 I    .

Câu 29: Tính diện tích hình phẳng giới hạn bởi các điểm biểu diễn các số phức thỏa mãn 2410zizi +−+−−= A. 15 . B. 12. C. 20 . D. Đáp án khác. Lời giải

Gọi ( ) ; Mxy là điểm biểu diễn của số phức ( ) ,.zxyixy=+

Ta có: 2410zizi +−+−−= ( ) ( ) 214110.xyixyi ++−+−+−= ( ) ( ) ( ) ( ) 2222 214110xyxy ++−+−+−=

Đặt ( ) ( ) ( )2 2 2;1,4;14206.ABAB−=++=

Khi đó phương trình trở thành: 10. MAMB+=

Khi đó tập hợp những điểm M thỏa mãn phương trình là một elip với.

+ Độ dài trục lớn 10 2105. 2 aa===

+ Tiêu cự 6 263. 2 cABc====

+ Độ dài trục bé 2b với 2222253164.bacb =−=−==

Vậy diện tích hình phẳng giới hạn bởi các điểm biểu diễn các số phức thỏa mãn 2410zizi +−+−−= là diện tích Elip trên: 4.520 Sab===.

Câu 30: Gọi M là điểm biểu diễn của số phức z thỏa mãn 323 zizzi +=+−+ . Tìm tập hợp tất cả những điểm M như vậy. A. Một đường thẳng. B. Một parabol. C.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

ng phức tập hợp những điểm M biểu diễn cho số phức z là? A. ( ) ( ) ( ) 22 :2264Cxy++−= B. ( ) 22 :1 1612 xy E += C. ( ) 22 :1 1216 xy E += . D. ( ) ( ) ( ) 22 :228Cxy++−= . Lời giải

Chọn B Gọi ( ) ; Mxy , 1(2;0) F , 2(2;0) F Ta có 2222 228(2)(2)8 zzxyxy ++−=++++−= 12 8 MFMF += . Do đó điểm ( ) ; Mxy nằm trên elip ( )E có 284, aa== ta có 12 2422FFccc === .

Ta có 222 16412 bac=−=−= . Vậy tập hợp các điểm M là elip ( ) 22 :1 1612 xy E += .

Câu 32: Tìm tập hợp các điểm M biểu diễn hình học số phức z trong mặt phẳng phức, biết số phức z thỏa mãn điều kiện: 4410.zz .

A. Tập hợp các điểm cần tìm là đường elip có phương trình 22 1 925 xy .

B. Tập hợp các điểm cần tìm là những điểm ; Mxy trong mặt phẳng Oxy thỏa mãn phương trình 2222 4412xyxy .

C. Tập hợp các điểm cần tìm là đường tròn có tâm 0;0 O và có bán kính 4 R

D. Tập hợp các điểm cần tìm là đường elip có phương trình 22 1 259 xy . Lời giải

Chọn D

Ta có: Gọi ; Mxy là điểm biểu diễn của số phức .zxyi .

Gọi 4;0 A là điểm biểu diễn của số phức 4. z .

Gọi 4;0 B là điểm biểu diễn của số phức 4. z

Khi đó: 441010.zzMAMB . Hệ thức trên chứng tỏ tập hợp các điểm M là elip nhận , AB là các tiêu điểm.

Gọi phương trình của elip là 22 222 22 1,0, xy ababc ab Từ ta có: 2105. aa 222 28249ABcccbac . Vậy quỹ tích các điểm M là elip: 22 :1. 259 xy E

Câu 33: Cho số phức z thỏa mãn điều kiện: 4410zz++−= . Tập hợp các điểm M biểu diễn cho số phức z là đường có phương trình. A. 22 1 925 xy+= B. 22 1 259 xy+= C. 22 1 925 xy −= D. 22 1 259 xy −= Lời giải

Chọn B

Gọi ( ) ; Mxy biểu diễn số phức ( ) , zxyixyR =+

Từ giả thiết ta có ( ) ( ) 2222 12 441010 xyxyMFMF +++−+=+= với ( ) ( ) 124;0,4;0FF Vậy tập hợp các điểm M biểu diễn cho số phức z là đường Elip có phương trình 22 1 259 xy+= .

Câu 34: Trong mặt phẳng tọa độ Oxy ,gọi( ) H là phần mặt phẳng chứa các điểm biểu diễn các số phức z thỏa mãn 16 z và 16 z có phần thực và phần ảo đều thuộc đoạn  0;1 .Tính diện tích S của ( ) H A. ( ) 326. S =− B. ( ) 164. S =− C. 256. S = D. 64. S  = Lời giải

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Giả sử ( )11111 ; zxyiMxy =+ và ( ) 22222 ; zxyiNxy =+

Theo giả thiết ta có: 3,4,37OMONMN===

Suy ra: tập hợp các điểm biểu diễn 1z là đường tròn ( )1C có tâm 1 ,3OR = tập hợp các điểm biểu diễn 2z là đường tròn ( ) 2C có tâm 2 ,4OR =

Xét tam giác OMN có ( ) 222 0 1 cos120 2..2 OMONMN MONMON OMON +− ==−=

Suy ra M là ảnh của N qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự 3 ,4O V

và phép quay ( ) 0,120O Q hoặc phép quay ( ) 0,120O Q Như vậy ứng với mỗi điểm N ta có 2 điểm M đối xứ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

PHƯƠNG

TRÌNH BẬ

C

HAI

-

BẬC CAO SỐ PHỨ

C VD VDC Xét phương trình bậc hai ( ) 2 0, azbzc++= với 0 a  có: 2 4 bac=− Nếu 0 = thì ( ) có nghiệm kép: 12 2 b zz a ==− . Nếu 0  và gọi  là căn bậc hai  thì ( ) có hai nghiệm phân biệt: 1222 bb zz aa −+−− ==  Lưu ý Hệ thức Viét vẫn đúng trong trường phức : 12 b zz a +=− và 12 c zz a = . Căn bậc hai của số phức zxyi =+ là một số phức w và tìm như sau: + Đặt wzxyiabi ==+=+ với ,,, xyab + ( )2 2 wxyiabi =+=+ ( ) 22 2 ababixyi−+=+ 22 2 abx aby  −=   =  + Giải hệ này với , ab sẽ tìm được a và b wzabi==+ .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

* 0 3 z =− , thay vào phương trình ta được 2 0 2 2 a aa a

=  −  = 

* 0 3 z = , thay vào phương trình ta được 2 260aa−+=

Kết hợp điều kiện 0 a  và điều kiện suy ra 2 a = TH2. 2

    −++  +   

27 2 04830 27 2

a aa a

Khi đó, phương trình có nghiệm phức 0z thì 0z cũng là một nghiệm của phương trình.

Ta có 2 222 0 00 1 .22230 3 a zzaazaaaa a

=−  =−=−−−=  =  Kết hợp điều kiện 0 a  và điều kiện suy ra 3 a = . Vậy có 2 giá trị a dương thỏa mãn là 2 a = ; 3 a = Câu 2: Trên tập hợp các số phức, gọi S là tổng các giá trị thực của m để phương trình ( ) 2 2160mzmzm++−+= có nghiệm 0z thỏa mãn 0 1 z = . Tính S A. 3 B. 4 C. 1 D. 2 Lời giải

Chọn D

Xét phương trình ( ) 2 2160mzmzm++−+= .

TH1: 0 m = Phương trình đã cho có dạng 26033 zzz +==−= không thõa mãn. TH2: 0 m  Ta có ( ) ( ) 2 2 16241mmmmm  =+−−+=−+

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

tham số m để phương trình 2 2980zmzm−+−= có hai nghiệm phức phân biệt 12 , zz thỏa mãn 12zz = . A. 4

Kết hợp với điều kiện 5 3 a − , nhận 22 a =− . Vậy có 2 giá trị của a thỏa mãn.

Câu 5: Trên tập số phức, xét phương trình ( ) 2241420zmzm−+++= ( m là tham số thực). Có bao nhiêu giá trị của tham số m để phương trình đó có nghiệm 0z thoả mãn 0 4 z = ? A. 1 B. 3 C. 4 D. 2 Lời giải Chọn B

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

 =+   =−   . Với 3 o z =− ta có ( )( ) 22 9243806250 mmmm −+−+−=++= + Nếu 03 m  − , khi đó phương trình có hai nghiệm phức 12 ; zz thỏa mãn 12 o zzz == Suy ra 3 o z = 12 .9.9 oo zzzz == 2 8917mm −== . Kết hợp với điều kiện 3 m − suy ra 17 m =− . Vậy tổng các giá trị của m là 34234217617 ++−−=− 13 22 10 13 22

zi zz zi

 =−+   ++=  =−−   Lấy 13 22 zi =−+ , ta có: 2 13 22 zi =−− và 3 1 z = . Suy ra ( )674 20223 1 zz== và ( )673 2021322 13 . 22 zzzzi ===−− Suy ra 131 1231 22 13 22

 =−−−+−+    Suy ra 131133 1231 2222 13 22

Ai i

 =−−−+−+=+    Câu 8: Cho phương trình 2 2680zmzm−+−= . ( m là tham số thực). Có bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm phức phân biệt 12 , zz thỏa mãn 1122 zzzz = ? A. 4 B. 1 C. 3 D. 2 Lời giải Chọn D

Aii i

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Ta có 2 68mm  =−+

TH1: 4 0 2 m m       

Khi đó phương trình đã cho có hai nghiệm thực phân biệt 12 , zz và ( ) ( ) 12 22 11221212 12

0200 zzloai zzzzzzzzmmtm zz = ==+===  =− 

TH2: 024 m  

Khi đó phương trình đã cho có hai nghiệm phức phân biệt 12 , zz 11221211 zzzzzzzz == Mà  3 mm

Vậy có 2 giá trị nguyên của tham số m thỏa mãn bài toán. Câu 9: Trên tập hợp các số phức, xét phương trình 2 28120zmzm−+−= Có bao nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt 12 , zz thỏa mãn 12 ? zz = A. 5 B. 6. C. 3. D. 4. Lời giải

Chọn D

10:

=  =  =−+==   TH2: 026 m   . Phương trình ( )* khi đó có 2 nghiệm 1,2 zmi= luôn thỏa mãn 12zz = . Nên:  3;4;5 m . Vậy các giá trị m th 2 2 2 z z z

a mãn là:  0;3;4;5 m =  =  =−  .

th

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Nếu 0 2 z = thì 2 2100aa−+= không có nghiệm thực a . Nếu 0 2 z =− thì 2 220aa−−= luôn có nghiệm thực a và theo định lý Vi ét tổng hai nghiệm thực này là 2 ( )1 +) Trường hợp phương trình 22320zzaa++−= có nghiệm phức 0z  thì 0z cũng là nghiệm phức của phương trình. Vì 0 2 z = nên 2 000.4zzz== Theo định lý Vi ét ta có 2 2 00 2 .2 1 aa zzaa ==− 2224240aaaa −=−−= ( )*

Phương trình ( )* luôn có hai nghiệm thực phân biệt, theo định lý Vi ét ta có tổng các giá trị của số thực a bằng 2 ( )2 . +) Từ ( )1 và ( )2 suy ra tổng các giá trị của số thực a sao cho phương trình 22320zzaa++−= có nghiệm phức 0z thỏa 0 2 z = là 4

Câu 11: Cho các số thực , bc sao cho phương trình 2 0 zbzc++= có hai nghiệm phức 12 ; zz với phần thực là số nguyên và thỏa mãn 1 321zi+−= và ( )( ) 1222ziz−+ là số thuần ảo. Khi đó, bc + bằng A. 1. B. 12. C. 4. D. 12. Lời giải

Chọn B

Trường hợp 1: Nếu các nghiệm của phương trình là các số thực ; xy thì ( ) ( )2 1 32323421zixix +−=+−=++= mâu thuẫn với giả thiết. Trường hợp 2: Các nghi

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

1222;22 zizi =−+=−− . Vì vậy theo Viet ta có: ( ) ( ) ( ) ( ) 12 12

22224 4812 .22.228 zzbii bc zzcii +=−=−++−−=−   +=+=  ==−+−−=   .

Câu 12: Gọi 1234 ,,, zzzz là 4 nghiệm phức của phương trình ( ) 42440 +−−=zmzm . Tìm tất cả các giá trị m để 1234 6 +++=zzzz . A. 1=− m . B. 2= m . C. 3= m D. 1= m . Lời giải Chọn D

Ta có: ( ) ( )( ) ( ) ( ) 2 4222 2

41 44040 2  =− +−−=+−=  =   z zmzmzzm zm

Ta có: = n n zz . 12 ; zz là nghiệm của phương trình ( )1 . Ta có: 12 42==−=zz . 34 ; zz là nghiệm của phương trình ( )2 . Ta có: 34 == zzm Theo đề ra ta có: 1234 624611 +++=+=== zzzzmmm . Kết luận 1= m . Câu 13: Gọi 12 , zz là hai nghiệm phức của phương trình 2 20 zz−+= . Phần ảo của số phức ( )( ) 2022 12 iziz 

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

2 1212mmm −+=−−+ 0 m = . Vậy có 3 giá trị nguyên của tham số m thỏa mãn đề bài.

Câu 16: Cho các số thực , bc sao cho phương trình 2 0 zbzc++= có hai nghiệm phức 12 , zz thỏa mãn 1 431zi−+= và 2 864zi−−= . Mệnh đề nào sau đây đúng? A. 512. bc+=− B. 54. bc+= C. 54. bc+=− D. 512. bc+= Lời giải

Chọn A

Vì 12 , zz là hai nghiệm phức của phương trình 2 0 zbzc++= nên 12zz = Khi đó ta có

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

dụng định lí Vi ét ta có

4848 ; .36 55

ậy 5483612. bc+=−+=− Câu 17: Trong tập hợp các số phức, cho phương trình ( ) 2 2452016800zaza −−+−= ( a là tham số thực). Có tất cả bao nhiêu giá trị nguyên dương của a để phương trình có hai nghiệm phân biệt 12 , zz sao cho 12zz = A. 7. B. 8. C. 9. D. 10. Lời giải Chọn B Ta có ( ) ( ) 2 2 '45201680109 aaaa =−−−=−+ Th1: 2 1 '01090 9 a aa a   −+   

=  =  =−  ( ) 12 0245045zzaa +=−== Th2: ( ) 2 '010901;9 aaa −+ . Khi đó phương trình có 2 nghiệm phức 12 , zz là 2 số phức liên hợp của nhau, ta luôn có 12zz = . Với  2;3;4;5;6;7;8;45 aa +  . Vậy có 8 giá trị nguyên dương cần tìm. Câu 18: Có bao nhiêu số nguyên m để phương trình 2 210zmz++= có hai nghiệm phức phân biệt 12 , zz thỏa mãn 1233zz+=+ A. 1 B. 2 C. 3 D. 4 Lời giải Chọn B

Với 2 10 m  =− , phương trình 2 210zmz++= có hai nghiệm phức liên hợp 12 , zabizabi =+=− . Khi đó hiển nhiên ( )2 2 12333zabz +=++=+ .

i

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Câu 19: Có bao nhiêu giá trị m nguyên và  2022;2022 m− để phương trình 2 2130zzm−+−= có hai nghiệm phức thỏa mãn 1122 zzzz = . A. 4045. B. 2021. C. 2022. D. 2023 Lời giải Chọn D 44(13)12mm=−−=

TH1. Nếu 00 m 

Khi đó phương trình có hai nghiệm thực 1 13 zm =− và 2 13 zm =+ 1213,13 zmzm=−=+

Ta có ( ) ( ) 22 1122 ..13130 zzzzmmm =−=+= TH2. Nếu 00 m  Khi đó phương trình có hai nghiệm phức 1 13 zim =−− và 2 13 zim =+− 1213,13 zimzim =+−=−−

Mà ( )( ) ( )( ) 1122 ..13131313 zzzzimimimim =−−+−=+−−− 1313mm−=−

Kết hợp hai TH suy ra 0 m  thì phương trình luôn có hai nghiệm phức thỏa mãn 1122 .. zzzz = . Mà  ,2022;2022mZm−  2022;2021;...;1;0 m =−−− .

Vậy có 2023 giá trị m cần tìm. Câu 20: Biết phương trình ( ) 2 0, zazbab++= có một nghiệm là 1 3 zi = và nghiệm còn lại là 2z Mô đun của số phức ( ) 2abz bằng A. 10 B. 9 C. 18 D. 27 Lời giải Chọn D Phương trình ( ) 2 0, zazbab++= có một nghiệm 1 3 zi = thì nghiệm còn lại 2 3 zi =− . Theo Vi et ta có. 12 12

0 .9 zza a zzbb +=− =     ==   Vậy ( ) ( ) 2 9.327abzi −=−−= .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Câu 21: Trên tập hợp các số phức, xét phương trình 2 60zzm−+= ( m là tham số thực). Gọi o m là một giá trị nguyên của m để phương trình có hai nghiệm phân biệt 12 , zz thỏa mãn 1122 zzzz = Trong khoảng ( )0;20 có bao nhiêu giá trị o m A. 11 B. 13 C. 12 D. 10 Lời giải

Chọn D

Xét phương trình 2 60zzm−+= . Ta có '9 m =− . Theo đề bài: 112212 .. zzzzzz == .

Khi '0 phương trình có hai nghiệm thực phân biệt, khi đó: 121212 0 zzzzzz ==−+=

Khi '0 phương trình có hai nghiệm phức phân biệt là hai số phức liên hợp, hay: 909 mm − . Suy ra Trong khoảng ( )0;20 có 10 giá trị o m

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Xét phương trình ( ) 2 21220zmzm−−+−= , ta có: ( ) ( ) 2 2 11.2243mmmm  =−−−−=−+   .

TH1: 0   2 430mm −+ 3 1 m m       .

Phương trình đã cho có hai nghiệm thực phân biệt 1z , 2z

Theo định lí Vi et ta có: ( ) 12 12

21 22 zzm zzm +=−   =− 

Theo đề bài ta có: 1212 zzzz ==− 12 0 zz += ( ) 210 m −= 1 m = TH2: 0   13 m 

Phương trình luôn có hai nghiệm phức 1z , 2z luôn thỏa mãn 12zz = Do đó  2 S = . Vậy tổng các phần tử của tập S là 1.

Câu 24: Có bao nhiêu số nguyên a để phương trình ( ) 2230zazaa −−++= có hai nghiệm phức 12 , zz thỏa mãn 1212 zzzz +=− ? A. 1 B. 2 C. 3 D. 4 Lời giải Chọn D Ta có ( ) ( ) 2 22 343109aaaaa =−−−+=−−+   Trường hợ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

thỏa mãn ( )** . Vậy có 4 số nguyên a thỏa mãn yêu cầu bài toán. Câu 25: Cho số phức w và hai số thực b , c . Biết rằng 2 w + và 34wi là hai nghiệm của phương trình 2 20220 zbzc++= . Tính giá trị biểu thức Pbc =+ bằng A. 4044 P =− . B. 8088 P = . C. 4044 P = . D. 8088 P =− . Lời giải

Ch

ọn B

Nhận xét: Trong tập số phức, phương trình bậc hai 2 0 azbzc++= có hai nghiệm phức 12 , zz thì 2 1 zz = Đặt wxyi =+ ( ) , xy  . Vì , bc  và phương trình 2 20220 zbzc++= có hai nghiệm là 1 2 zw=+ , 2 34 zwi =− nên 2 nghiệm 12 , zz là 2 nghiệm phức có phần ảo khác 0.

Ta có 12 , zz là hai nghiệm của phương trình 2 20 zz−+= nên 12 12

1 .2 zz zz +=   =  . ( )( ) ( ) ( ) ( ) 2022 2022 20222022 2 121212 211 zizizzizziii  −−=−++=−−=−   ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1011 505 21011101110111011101121011 1222212 iiiiiii

đã

có

hai nghiệm của

Theo Viet ta có: ( ) 12 12

1 1 zzm zzm =+   +=  . ( ) 2222 12121212121212 1()21()31 2 zzzzzzzzzzzzzz +=++−=++−= .

Thay ( )1 vào ( )2 ta có: ( ) 22 1 3(1)13404 m mmmmtm m

=−  −+=−−=  =  .

Vậy tổng các giá trị của m là 143−+= . Câu 33: Trên tập số phức, xét phương trình 2 2430zmzm−+−= . Có bao nhiêu giá trị nguyên dương của m để phương trình đó có hai nghiệm phân biệt 1z , 2z thỏa mãn 12 8 zz+= ? A. 0. B. 2. C. 3. D. 1. Lời giải Chọn D Ta có 2 43mm  =−+ . Phương trình có hai nghiệm phân biệt 0   . Nên để phương trình đó có

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Chọn D

trình có hai nghiệm thực, khi đó

Trường hợp 2. '0200 mm === phương trình đã cho là 2 00zz== không thỏa mãn điều kiện 0 2 z = nên 0 m = không là giá trị càn tìm.

Trường hợp 3. '0200 mm  khi đó phương trình có hai nghiệm phức là 212;2 zmmizmmi =−−=+− . Vì hai nghiệm này là hai số phức liên hợp, nên có modun bằng nhau, do đó ta chỉ cần xét một trường hợp. Giả sử 0 2 zmmi =+− khi đó

nguyên của m thuộc khoảng ( )0;20 để phương trình ( )1 có hai nghiệm phân biệt 12 , zz thỏa mãn 1122 zzzz = ? A. 20. B. 11. C. 12. D. 10. Lời giải

C

họn

D Điều kiện để phương trình ( )1 có hai nghiệm phân biệt là: Trường hợp 1: 09 m   Khi đó phương trình ( )* có 2 nghiệm thực phân biệt 12 , zz và 11zz = , 22zz = . Nên 12 22 112212 12

zz zzzzzz zz

=  ==  =− 

Với 12zz = , không thoả mãn yêu cầu phương trình ( )1 có 2 nghiệm phân biệt, nên loại.

Với 1212 0 zzzz=−+= không thỏa mãn, do theo Vi ét, ta có 12 6 zz+= .

909 mm =− ( )0;20 10

Trường hợp 2: 09 m   Khi đó phương trình có hai nghiệm phức phân biệt 1z , 2z và 21zz = , 12zz = . Yêu cầu 11221212 zzzzzzzz == luôn đúng với 9 m  Vậy trong khoảng có số 0m thoả mãn yêu cầu bài toán. Câu 41: Trên tập các số phức, xét phương trình 2 80 zmzm−++= ( m là tham số thực). Có bao nhiêu giá trị nguyên của tham số m để phương trình có hai nghiệm 12 , zz phân biệt thỏa mãn ( ) ( ) 22 1122 8 zzmzmmz +=−− ? A. 12 B. 6 C. 5 D. 11 Lời giải

Khi đó:

    += ++− −=

2 2 12 2 22 1212 2 2 12 2

==    

z c Pzz a acb z

zz z

b z a a

4 4

. Vậy 4c P a =

Cách 2: Trắc nghệm. Cho 1,0,1abc=== , ta có phương trình 2 10 z += có 2 nghệm phức là 12 , zizi ==− . Khi đó 22 1212 4 Pzzzz =+ = + . Thế 1,0,1abc=== lên các đáp án, ta thấy chỉ có đáp án C cho kết quả giống.

Câu 43: Gọi S là tổng các số thực m để phương trình 2 210zzm−+−= có nghiệm phức thỏa mãn 2. z = Tính .S A. 6. S = B. =10. S C. 3. S =− D. 7. S = Lời giải Chọn D

có:

)

2101 zzmzm

( )1

i 0 m  thì ( ) 11zm= . Do 1 212

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Suy ra ( ) ( ) 20192019 1211zz−+− ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 504504 4222 1.111.1.1 iiiiii =−−−++++ ( ) ( ) ( ) ( ) ( ) ( ) ( ) 504504 5045041010 4.2.14.2.14.2.114.2.22 iiiiiiiii =−−−+−+=−+++==−

zbiAb bcibmnimn zbiBb =−−−−   =−=+=+  =+++   Vậy ( ) ( ) 22 442245.ABbb=+−+++= Câu 48: Cho số phức w và hai số thực a , b . Biết rằng wi + và 21 w là hai nghiệm của phương trình x xx xyixyi yy y

2 0 zazb++= . Tổng Sab =+ bằng A. 5 9 B. 5 9 C. 1 3 D. 1 3 Lời giải =  =−   ++=−− +=− =−    1 2

.  =+=+   =−   =−=−   Theo định lý Viet: 12 22

wxyi 2 1 1 3 1 2 3 211 3

) , xy zwii wi zwi

, ab 22 413 1 99

=−=− +=−     = +==    . Vậy 5 9 Sab=+=− .

và phương trình 2 0 zazb++= có hai nghi aa zza zzb bb

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Câu 49: Số phức zabi =+ , , ab  là nghiệm của phương trình ( )( ) 11 1 ziz i z z

−+ = . Tổng 22Tab =+ bằng A. 4. B. 423 . C. 322 + . D. 3. Lời giải Chọn C Điều kiện: 0;1zz . Ta có ( )( ) ( )( ) ( ) 22 11 11 1 ziz izzizzi z z

−+ =−+=− ( ) ( ) 2211 zizzizzzi +=+=−++ ( ) 2 1 zzz =−++ 2 1 z = hoặc 2 210zz−−= 2 12322zz =+=+ . Vậy 22 322 Tab=+=+ .

Câu 50: Cho các số phức z , w khác 0 thỏa mãn 0 zw+ và 136 zwzw += + . Khi đó z w bằng A. 3 B. 1 3 C. 3 D. 1 3 Lời giải Chọn B Ta có 136 zwzw += + 36wz zwzw + = + ( )( ) 36 wzzwzw++= 22 320 zzww −+= 2 3210 zz ww  −+=   12 33 z i w = 1 3 z w = Câu 51: Cho phương trình 2 40 c xx d −+= có hai nghiệm phức. Gọi A , B là hai điểm biểu diễn của hai nghiệm đó trên mặ

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

ức z thỏa mãn ( ) 10 122. izi z +=−+ Mệnh đề nào dưới đây đúng?

A. 3 2. 2 z  B. 2. z  C. 1 . 2 z  D. 13 . 22 z  Lời giải

Chon D

Câu 53:

  ++−==   Đặt 0. za= ( ) ( ) 2 22 42 2 2

101 2212011. 2 a aaaaaz a a Có bao nhiêu giátrị dương của số thực a sao cho phương trình 22320zzaa++−= có nghiệm phức 0z với phần ảo khác 0 thỏa mãn 0 3. z = A. 3 B. 2 C. 1 D. 4 Lời giải Chọn C Ta có ( ) 22 342348 aaaa=−−=−+ . Phương trình 22320zzaa++−= có nghiệm phức khi và chỉ khi ( ) 22 034804830*. aaaa −+−− Khi đó phương trình có hai nghiệm 12 , zz là hai số phức liên hợp của nhau và 12zz = Ta có

 =  ++−=+−===   =−   

2 2222 1212120 .2.2.22 zzaazzaazzaazaa =−=−=−=− Theo giả thiết có ( ) 2 2 2 2

231 32 233 aaa aa a aa

 =−

). Các giá trị của a thỏa mãn điều kiện ( )* . Vậy có 1 giá trị dương a thỏa mãn yêu cầu bài toán.

Câu 54: Cho phương trình 42 440 zmz++= trong tập số phức và m là tham số thự C. Gọi 1234 ,,, zzzz là bốn nghiệm của phương trình đã cho. Tìm tất cả các giá trị của m để ( )( )( )( ) 2222 12344444324zzzz++++= . A. 1 m = hoặc 35 m =− B. 1 m =− hoặc 35 m =− C. 1 m =− hoặc 35 m = D. 1 m = hoặc 35 m = Lời giải Chọn C Đặt ( ) 42 44fzzmz=++ . Vì phương trình ( ) 0 fz = có 4 nghiệm 1234 ,,, zzzz nên ( ) ( )( )( )( ) 42 1234 444 fzzmzzzzzzzzz =++=−−−− Ta có: ( )( ) 2 111422 zzizi +=−+ ( )( )( )( ) ( ) ( ) 2222 1234 22 4444. 44 fifi zzzz ++++=

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Chọn A * Nếu 3 m = : Phương trình trở thành 2 660zzi +== * Nếu 3 m  : Đặt ( ) zxix= , phương

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

+ Với 0 m  (1)2zim=− . Do đó 0 ||4zm =− 0 ||242 zm=−= 440 mm −== 01616 S =+= . Câu 58: Kí hiệu 0z là nghiệm phức có phần thực và phần ảo đều âm của phương trình 2 250zz++= Trên mặt phẳng toạ độ Oxy , điểm M nào dưới đây là điểm biểu diễn số phức 3 0 wi z = ? A. ( )2;1 M . B. ( )2;1 M . C. ( )2;1 M . D. ( )1;2 M . Lời giải

Chọn A

Ta có ( ) ( ) 22 2 12 25012 12 zi zzzi zi =−+  ++=+=  =−−  .

Theo giả thiết ta có 0 12 zi =−− . Suy ra 0 12 zi =−+ . Từ đó ( ) 3 0 .122 wiziii ==−−+=+ . Suy ra w có biểu diễn là ( )2;1 M .

Câu 59: Biết phương trình 22 20 zmzm++−= ( m là tham số) có hai nghiệm phức 12 , zz . Gọi ,, ABC lần lượt là điểm biểu diễn của các số phức 12 , zz và 0 zi = . Có bao nhiêu giá trị của tham số m để diện tích tam giác ABC bằng 1? A. 2. B. 3. C. 4. D. 1. Lời giải Chọn A

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

n tìm của a bằng 6. Câu 61: Trên tập hợp các số phức, xét phương trình 2 2z20zm−−+= ( m là tham số thực). Gọi T là tập hợp các giá trị của m để phương trình trên có hai nghiệm phân biệt được biểu diễn hình học bởi hai điểm , AB trên mặt phẳng tọa độ sao cho diện tích tam giác ABC bằng 22 , với ( )1;1 C . Tổng các phần tử trong T bằng A. 8. B. 4. C. 9. D. 1. Lời giải

Chọn A

Ta có: ( ) ( ) 2 2 2z2011 1 zmzm −−+=−=− TH1. có hai nghiệm phức  101mm− .

Khi đó, phương trình có hai nghiệm phức 1 11 zmi =+− ; 2 11 zmi =−− .

Gọi A, B lần lượt là hai điểm biểu diễn của 1z ; 2z trên mặt phẳng Oxy ta có: ( ) 1;1 Am ; ( ) 1;1 Bm .

Ta có: 21 ABm =− ; ( ) ( ) ( ) ;;12dCABdCx=== .

Khi đó ( ) 1 .;21221. 2 ABC SABdCABmm  ==−==−

TH2. có hai nghiệm thực phân biệt  101mm− .

Khi đó, phương trình có hai nghiệm 1 11 zm =+− ; 2 11 zm =−− .

Gọi A, B lần lượt là hai điểm biểu diễn của 1z ; 2z trên mặt phẳng Oxy ta có: ( )11;0Am ; ( )11;0Bm +− .

Ta có: 21 ABm =− ; ( ) ( ) ;;1dCABdCOx== .

Khi đó ( ) 1 .;1229. 2 ABC SABdCABmm  ==−== Vậy  1;9 T =− nên tổng các phần tử trong T bằng 8

Câu 62: Biết rằng phương trình 2 20zazb++= (,ab là các số thực dương) có hai nghiệm phức liên hợp 12 , zz . Gọi ,, ABC lần lượt là các điểm biểu diễn của số phức 122,, wzz = . Tính giá trị của biểu thức 4 Tba =− biết rằng ba điểm ,, ABC tạo thành một tam giác vuông có diện tích bằng 9. A. 6 B. 8 C. 9 D. 14 Lời giải

Chọn A

Do phương trình 2 20zazb++= (,ab là các số thực dương) có hai nghiệm phức liên hợp 12 , zz nên từ giả thiết ta gọi tọa độ các điểm biểu diễn cho các số phức 122,, wzz = là (2;0);(;);(;) ABxyCxy với 2,0xy (x2;y);(x2;y)ABAC=−=−− . Do A thuộc Ox , , BC đồi xứng qua Ox Nên theo giả thiết suy ra ABC là tam giác vuông cân tại A 22 .0(2)0(1)ABACxy =−−= Mặt khác 1 . 2 ABC SABAC = 22 1 9(2) 2 xy =−+  Từ và suy ra 53 13 xy xy ==   =−=  Với 5,3xy== ta tìm được 1253;53 zizi =+=− . Với 1,3xy=−= ta tìm được 1213;13 zizi =−+=−− suy ra 1;106abT=== Câu 63: Trên tập hợp các số phức, cho biết phương trình 2 20 c zz d −+= có hai nghiệm 12 , zz . Gọi , AB lần lượt là các điểm biểu diễn hình học của 12 , zz trên mặt phẳng Oxy . Biết tam giác OAB đều, tính giá trị của 4.Pcd =+ A. 19 P = B. 16 P = C. 22 P = D. 14 P = Lời giải Từ giả thiết ( ) ( ) 2 2 2011* cc zzz dd −+=−=− Nếu 10 c d − thì có hai nghiệm thực nên không tồn tại tam giác OAB , không thỏa mãn bài toán.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Nếu 101 cc dd − . Khi đó ( ) 1 2

 =+−      =−−  

c zi d c zi d

11 * 11

.

Suy ra 1;1 c A d     và 1;1 c B d     nên tam giác OAB luôn cân tại O

Gọi I là trung điểm đoạn AB , tam giác OAB đều thì .34 13.1 23 ABcc OI dd ==−= Theo giả thiết , cd  và phân số c d tối giản nên 4 c = và 3 d = . Vậy 444.316.Pcd=+=+=

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Câu 64: Trên tập hợp các số phức, xét phương trình 2 210zzm−+−= Có bao nhiêu giá trị của m để phương trình đó có nghiệm phức 0z thỏa mãn 0 2 z = ? A. 1. B. 3. C. 2. D. 4. Lời giải

Chọn B

Phương trình ( ) 2 2101zzm−+−= có m  = , 1 Pm =− .

Trường hợp 1: 00 m  

Khi đó, phương trình có hai nghiệm thực: 0 1 zm =+ hoặc 0 1 zm =− .

+ Với 0 1 zm =+ . Suy ra 121 mm +== .

+ Với 0 1 zm =− . Suy ra 129 mm −==

Trường hợp 2: 00. m  

Vì ( )1 là phương trình bậc 2 với hệ số thực có 0   nên phương trình ( )1 có hai nghiệm phức liên hợp. Do đó 0002.4zzz== 414Pm =−= 3 m =− Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

thỏa mãn 2 22 000012 1 39.9.9359340 4 m zzzzzzmmmm m

=−  ====−+=−−=  = 

Với 1 m =− thay vào ( )1  2 903 zzi +== thỏa mãn

Với 4 m = không thỏa mãn điều kiện ban đầu. Vậy có 3 giá trị

m m m

1 8 1

=   =   =−  Nên tổng các giá trị của tham số m là 8. Câu 66: Trên tập hợp các số phức, xét phương trình: ( ) 22210zmzm−++= ( m là tham số thực). Có bao nhiêu giá trị của m để phương trình trên có nghiệm 0z thỏa mãn 0 6 z = ? A. 4 B. 3 C. 2 D. 1 Lời giải Chọn B Phương trình ( ) ( ) 22210*zmzm−++= TH1: 0 . z  + Ta có: 0 6 z =  0 0

6 6 z z  =  =−  Với 0 6 z = thay vào ( )*  ( ) 2 361210 mm −++=  623 623 m m

 =+   =−  Với 0 6 z =− thay vào ( )*  ( ) 2 361210 mm +++= Không có m . TH2: 0 \. z  + Phương trình ( ) ( ) 22210*zmzm−++= có 2 nghiệm 0z và 0z

Nếu 0 2 z = thì 2 2100aa−+= không có nghiệm thực a . Nếu 0 2 z =− thì 2 13 220 13 a aa a

 =+ −−=  =−  

TH2: 0z  . Khi đó phương trình 22320zzaa++−= có nghiệm phức 0z nên 0z cũng là nghiệm phức của phương trình. Vì 0 2 z = nên 2 000.4zzz== . Theo định lý Vi ét, ta có: 2 2 00 2 .2 1 aa zzaa ==− . 22 15 24240 15 a aaaa a

 =+ −=−−=  =−   .

Từ và, ta có tổng các giá trị của số thực a thỏa yêu cầu bài toán là: 131315154 ++−+++−= Câu 69: Cho S là tập hợp các số nguyên của tham số m để phương trình ( ) 2230zmzmm −−++= có 2 nghiệm

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

mãn yêu cầu bài toán. Cách 2: Ta có ( ) ( ) ( ) 2 22221450211 1 zmzmmzmm −−+−=−+=+ .

Trường hợp 1: 101mm+−

Khi đó ( ) 211 1 211 zmm zmm

 =−++   =−−+   .

Theo bài ra, phương trình đã cho có nghiệm 0z thoả mãn 0 310 z += . Do đó ( ) ( ) 221103 21 221104

=   +++=      = +−+=     .

mtm mm mtm mm

Trường hợp 2: 101mm+− Khi đó ( ) 211 1 211

zmim zmim

 =−++    =−−+ 

Vậy có 3 giá trị của tham số m thoả mãn yêu cầu bài toán.

Câu 71: Trên tập hợp các số phức, xét phương trình ( ) 22210zmzm+−+= ( m là tham số thực). Có bao nhiêu giá trị m dương để phương trình đó có nghiệm 0z thỏa mãn 0 4? z = A. 1 B. 2 C. 3 D. 4 Lời giải

Chọn A

Ta có: ( )2 2 '121 mmm =−−=−+ .

TH1: Nếu '0 210 m −+ 1 2 m  thì phương trình có hai nghiệm thực: Từ giả thiết: 0 0 0

4 4 4 z z z

=  =  =− 

*Với 0 4 z = thay vào phương trình ta có: ( ) 222 421.40880 mmmm +−+=++= 422 422 m m

 =−+   =−−   .

*Với 0 4 z =− thay vào phương trình ta có: ( ) ( ) ( ) 2 22 421.408240 mmmm −+−−+=−+=

TH2: Nếu '0 210 m −+ 1 2 m  thì phương trình đã cho có 2 nghiệm phức:

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Nếu 0 2 z =− thì 2 220aa−−= luôn có nghiệm thực a và theo định lý Vi ét tổng hai nghiệm thực này là 2 ( )1 . +) Trường hợp phương trình 22320zzaa++−= có nghiệm phức 0z  thì 0z cũng là nghiệm phức của phương trình. Vì 0 2 z = nên 2 000.4zzz== . Theo định lý Vi ét ta có 2 2 00 2 .2 1 aa zzaa ==− 2224240aaaa −=−−= ( )* . Phương trình ( )* luôn có hai nghiệm thực phân biệt, theo định lý Vi ét ta có tổng các giá trị của số thực a bằng 2 ( )2 . +) Từ ( )1 và ( )2 suy ra tổng các giá trị của số thực a sao cho phương trình 22320zzaa++−= có nghiệm phức 0z thỏa 0 2 z = là 4 Câu 73: Gọi S là tổng các số thực m để phương trình 2 210zzm−+−= có nghiệm phức thỏa mãn 2. z = Tính .S A. 6. S = B. 7. S = C. 10. S = D. 3. S =− Lời giải

Chọn B

=  ==  =  . +) Vớ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn



75:

ra







663

phức, cho phưong trình 2 60,(1)zzmm−+= . Gọi 0m là một giá trị của m để phương trình có hai nghiệm phân biệt 12 , zz thỏa mãn 1122 zzzz = . Hỏi trong khoảng (0;20) có bao nhiêu giá trị 0 ? m  A. 10. B. 12. C. 11. D. 13. Lời giải Chọn A 2 60,(1)zzmm−+= . '9 m =− . Để phương trình có hai nghiệm phân biệt 12 , zz + Khi '0909 mm − khi đó phương trình có 2 nghiệm thực phân biệt ( ) 1212 39,39, zmzmzz =−−=+− Ta có 1122 , zzzz == 22 11221212 060 zzzzzzzz ==+== không có giá trị của m + Khi '0909 mm − khi đó phương trình có 2 nghiệm phức phân biệt 1239,39zimzim =−−=+− 22 112212 zzzzzz == luôn thỏ

i zz ii zizi

2124 0 11 132(1)0

+ −−= +−−+= Ta có ( ) ( ) ( ) 22 1 2

2 138121 1 zi iiii zi =  =−++==+  =−+  Vậy tọa độ hai điểm biểu diễn 12 , zz là: ( ) ( )0;2,1;1AB Khi đó

( ) 0.12.1 .2 cos .2.22 OAOB AOB OAOB −+ === Vậy 045 AOB = . Câu 78: Biết phương trình ( ) 2 z0, zmnmn++= có một nghiệm là 13i . Tính 3 nm + A. 4 B. 6  C. 3 V = D. 16 Lời gi

2 2 ải Chọn A Vì phương trình ( ) 2 z0, zmnmn++= có một nghiệm là 13i nên ( ) ( ) 2 1313016930 iminimmin −+−+=−−+−+= ( ) ( ) 8320 mnmi −++−+= 802 34 2010 mnm nm mn −++==−  +=  +== Câu 79: Gọi S làtổngcácsố thực m đểphươngtrình 2 210−+−=zzm cónghiệm phứcthỏamãn 2 = z . Tính S . A. 3=− S B. 7 = S C. 10= S D. 6 = S Lời giải Chọn B ( ) 2 2101−+−=zzm .

Ta

Trường hợp 1: Với 0  m ( )* khi đó phương trình ( )1 có hai nghiệm phức là: 1 1 =+ zm và 2 1 =− zm . Mặt khác 1 1 =+ zm và 2 1 =− zm .

Theo bài ra ta có phương trình ( )1 có nghiệm phức thỏa mãn:

Trườ

Ta l

có

1

. Theo bài ra ta có phương trình ( )1 có nghiệm phức thỏa mãn: 2123

zmm thỏa mãn điều kiện ( )** Vậy   3;1;93197. −=−++=mS Câu 80: Trên tập hợp các số phức, xét phương trình 2 60( zzmm −+= là tham số thực). Gọi 0m là một giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt 12 , zz thỏa mãn 1122 zzzz = . Hỏi trong khoảng ( )0;20 có bao nhiêu giá trị 0m  ? A. 13 B. 11 C. 12 D. 10 Lời giải Ch

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Ta có 2 3109 aa =−−+ . + TH1: 0  , phương trình có 2 nghiệm 1,2 3 2 a z − = , khi đó ( )2 2 1212 0 33440 1 a zzzzaaaa a

=  +=−−=−=+=  =−  Thỏa mãn điều kiện 0  + TH2: 0  , phương trình có 2 nghiệm 1,2 3 2 ai z −− = , khi đó ( )2 2 1212 1 33216180 9 a zzzzaiaaa a

=  +=−−=−−=−+−=  =−  . Thỏa mãn điều kiện 0  . Vậy có 4 giá trị của a thỏa mãn yêu cầu bài toán. Câu 82: Trên tập hợp các số phức, xét phương trình 2 60( zzmm −+= là tham số thực). Gọi 0m là một giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt 12 , zz thỏa mãn 1122 .. zzzz = Hỏi trong khoảng ( )0;20 có bao nhiêu giá trị 0m  ? A. 13 B. 11 C. 12 D. 10 Lời giải

Chọn D

Ta có 9 m  =− Nếu 0909 mm  − thì phương trình có hai nghiệm thực phân biệt 12 , zz và 1122 ; zzzz == nên 22 1122121212 ..0 zzzzzzzzzz ==− = += . Điều này không xảy ra. Nếu 0909 mm  − , thì phương trình có hai nghiệm phức là hai số phức liên hợp. Khi đó 1212 ; zzzz == nên ta luôn có 1122 zzzz = , hay 9 m  luôn thỏa mãn. Vì 0m  và ( ) 0 0;20 m  nên có 10 giá trị 0m thỏa mãn. Câu 83: Trên tập hợp các số phức, xét phương trình

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Khi đó, phương trình đã cho có hai nghiệm thực 1z , 2z phân biệt. Do đó, 1212 2 zzzz +=− ( ) ( )2 2 1212 2 zzzz +=− ( ) 2222 12121212 222 zzzzzzzz++=+− ( ) ( ) 22 1212121212 2224 zzzzzzzzzz +−+=+−  ( )2 121212620zzzzzz +−−= ( ) ( ) 2 46122120 mmm −−+−−+= Nếu 4 m − hoặc 312 m  thì ( ) ( ) 22 6 481202240 4 m mmmm m

=−  −−+=+−=  =  Nếu 12 m  thì ( ) ( ) 22 44120120 mmmm −−+=+−= . Trường hợp 2: 2 012043 mmm  +−− Khi đó, phương trình đã cho có hai nghiệm phân biệt 1z , 2z là hai số phức liên hợp: 2 12 mimm −+−−+ và 2 12 mimm −−−−+ . Do đó, 1212 2 zzzz +=− ( ) 222 212212 mmmmm +−−+=−−+ 2 1212mmm −+=−−+ 0 m = . Vậy có 3 giá trị nguyên của tham số m thỏa mãn đề bài. Câu 84: Cho các số thực , bc sao cho phương trình 2 0 zbzc++= có hai nghiệm phức 12 ; zz thỏa mãn 1 332zi−+= và ( )( ) 1222ziz+− là số thuần ảo. Khi đó bc + bằng: A. 1 B. 12 C. 4 D. 12 Lời gi

phương trình không là các số thực, khi đó với

a mãn 12zz = A. 8. B. 7. C. 6. D. 9. Lời giải Chọn A Ta có: ( ) ( ) 2 2 54310215mmmm =+−+=−− Nếu 2 02150 mm −− thì phương trình có hai nghiệm thự C. Khi đó, 121212 0505zzzzzzmm ==−+=+==− Nếu 2 0215035 mmm −−− thì phương trình có hai nghiệm phức liên hợp nên ta luôn có 12zz = Vậy có 8 giá trị nguyên của tham số m thỏa mãn. Câu 86: Trên tập hợp các số phức, xét phương trình 2 4950zmzm−+−= ( m là tham số thực). Có bao nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt 1z , 2z thỏa mãn

TH2: 5 01; 4 m      , khi đó phương trình đã cho có hai nghiệm phức liên hợp nên luôn có 12zz = Vậy có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán.

Câu 87: Trên tập hợp các số phức, phương trình 2 0 azb z ++= , với , ab có nghiệm 0 23 zi =− . Biết rằng phương trình 2 0 bza z ++= cũng có hai nghiệm phức 12 , zz . Tính 12Szz =+ . A. 4. B. 13. C. 25. D. 185 . Lời giải Ch

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Lời giải

Chọn C

+ TH1: Nếu ( ) '09108 mm −−−

Phương trình có nghiệm thực z , khi đó: 55zz==

Phương trình có nghiệm 5 z = hoặc 5 z =− 2530104 25301056 mm mm −+−==− ++−== 

+ TH2: '0808 mm +−

Khi đó phương trình có nghiệm phức ( )3.8zim=−+

Ta có: ( ) 5982524zmm =−+==− . Vậy có 3 giá trị củ

trình có nghiệm phức 0z thỏa mãn 0 1 z = . Tổng các phần tử của S bằng A. 20. B. 12. C. 14. D. 8. Lời giải Chọn B

2 9610 zzm

h

p 1: ( )

( )

th

099101 mm

)0 zabib

phương trình

9610 zzm

) 099101 mm

cũng là một nghiệm của

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

+ TH1: 0  , phương trình có 2 nghiệm 1,2 3 2 a z − = , khi đó ( )2 2 1212 0 33440 1 a zzzzaaaa a

=  +=−−=−=+=  =−  . + TH2: 0  , phương trình có 2 nghiệm 1,2 3 2 ai z −− = , khi đó ( )2 2 1212 1 33216180 9 a zzzzaiaaa a

=  +=−−=−−=−+−=  =−  Vậy có 4 giá trị của a thỏa mãn yêu cầu bài toán.

Câu 92: Trên tập hợp các số phức, xét phương trình ( ) 2 211280zmzm+++−= ( m là tham số thực), có bao nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt 12 , zz thỏa mãn 1211zz+=+ ? A. 7. B. 8. C. 10. D. 11. Lời giải Chọn B Xét phương trình ( ) 2 211280zmzm+++−= Đặt 1 zw=− ( ) ( )( ) 2 12111280wmwm −++−+−= 2 21090wmwm ++−= 2 109mm =−+ Để phương trình có hai nghiệm phân biệt 12 , zz thỏa mãn 1211zz+=+ thì phương trình có hai nghiệm phân biệt 12 , ww thỏa mãn 12 ww = . TH 1: 2 1 1090 9 m mm m   −+    Phương trình có hai nghiệm thực phân biệt 12 , ww . 121212 0200wwwwwwmm ==−+=== ). TH 2: 2 109019mmm −+ . Phương trình có hai nghiệm phức 12 , ww và 12 , ww  . Ta có 12 ww = suy ra 122 www == Từ suy ra tập hợp các giá trị nguyên của m là   2; 3; 4;5; 6; 7; 8 . Từ 2 trườ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

TH1: Nếu ( ) ( ) 2 2 2 01903100 5 m mmmm m −   −−−−−    . Phương trình có 2 nghiệm thực phân biệt, khi đó: 12 12 12

()zzloai zz zz

=  =  =−  ( ) 12 02101zzmm +=−== . TH2: ( ) 2 031002;5 mmm  −−− . Khi đó phương trình có 2 nghiệm phức 12 , zz là 2 số phức liên hợp của nhau, ta luôn có 12zz = . Với  1;2;3;4 mm +  . Câu 94: Có bao nhiêu giá trị thực của tham số m để phương trình 222z90zmm−++= có nghiệm phức 0z thỏa mãn 0 10 z = ? A. 2. B. 3. C. 4. D. 6. Lời giải Chọn D

+) Trường hợp 0z  . Khi đó 0 0 0

10 10 10 z z z

 = =  =−  

Nếu 0 10 z = thì ta có ( )2 2 1021090 mm −++= , khi đó có 2 giá trị thực của m thỏa mãn.

Nếu 0 10 z =− thì ta có ( )2 2 1021090 mm −+++= , khi đó có 2 giá trị thực của m thỏa mãn.

+) Trường hợp 0z  , điều kiện: 2 '0190(*) mm −−

Khi đó có 2 giá trị thực của m thõa mãn. Vậy có 6 giá trị của m thỏa mãn yêu cầu bài toán.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Câu 95: Trong tập số phức, cho phương trình ( ) 2221320, zmzmmm −+++−= Có bao nhiêu giá trị nguyên của m trong đoạn  2022;0 để phương trình có 2 nghiệm phân biệt 12 ; zz thỏa mãn 12zz = ? A. 2022 B. 2023 C. 0 D. 1 Lời giải

Chọn D

Phương trình có 2 nghiệm phân biệt

TH1: '0303 mm −+

Phương trình đã cho có 2 nghiệm thực phân biệt 12 , zz

Theo định lí Vi ét ta có: ( ) 12 2 12

+=+    =+−  

21 32 zzm zzmm

Theo đề bài ta có: 1212 zzzz ==− 12 0 zz += ( ) 210 m += 1 m =−

TH2: '0303 mm −+

Phương trình luôn có 2 nghiệm phức 12 , zz luôn thỏa mãn 12zz = Mặt khác:  2022;0 m− nên không có giá trị nào của tham số m Vậy có 1 giá trị m thỏa mãn.

Câu 96: Trên tập hợp các số phức, xét phương trình 222(1)30zmzm−++−= . Có bao nhiêu giá trị của m để phương trình có nghiệm 0z thoả mãn 0 6 z = ? A. 1. B. 5. C. 3. D. 6. Lời giải Chọn C 222(1)30zmzm−++−= Ta có: ( ) ( ) 2 2 1324mmm  =+−−=+ TH1: 02402 mm  +−phương trình có nghiệm thực 0z . Khi đó: 0 0 0

6 6 6 z z z

=  =  =− 

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Thay 0 6 z = vào phương trình ta có: ( ) ( ) 2 65 12210 65 mTM mm mTM

 =+  −+=  =−  .

có:

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Theo định lý Vi et ta có ( ) ( ) 12 12

1 . .2 zza zzb +=−    =  

Theo

Thay

ải Chọn D Ta có 2 3109 mm =−−+ . Trường hợp 1: 0  Phương trình có 2 nghiệm 1 3 2 m z −+ = và 2 3 2 m z −− = Khi đó ( )2 2 1212 0 33440 1 m zzzzmmmm m

=  +=−−=−=+=  =−  .

Hai giá trị này thỏa mãn điều kiện 0  . Trường hợp 2: 0  Phương trình có 2 nghiệm 1 3 2 mi z −+− = và 2 3 2 mi z −−− = . Khi đó ( )2 2 1212 1 33216180 9 m zzzzmimmm m

=  +=−−=−−=−+−=  =−  . Hai giá trị này thỏa mãn điều kiện 0  Vậy có 4 giá trị của m thỏa mãn yêu cầu bài toán.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Ta có ( )2 2022 202220  =− nên 12 , zz là hai nghiệm phức không thực.

Suy ra 1221 , zzzz == . Mặt khác theo định lí Vi-ét ta có 2022 12.2zz =

Do đó 22 2220222023 12121122122112....2.2.22Pzzzzzzzzzzzzzz =+=+=+=+=== .

Câu 108: Trên tập hợp các số phức, xét phương trình 2 27100zmzm−+−= ( m là tham số thực). Có bao nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm phân biệt 12 , zz thỏa mãn 1 133zi+−= , 2 355zi−+= ? A. 0. B. 1. C. 2. D. 3. Lời giải

Chọn B

Ta có 2 710mm  =−+ Trường hợp 1: 2 0 5 m m        Khi đó 1122 , zxzx == là các nghiệm thực phân biệt nên ta có: ( )2 2 1113133zix+−=++ . Dấu bằng xảy ra khi 1 1 x =− . ( )2 2 2235355zix−+=−+ . Dấu bằng xảy ra khi 2 3 x =

Vậy phương trình 2 27100zmzm−+−= có nghiệm 121,3zz=−= khi đó 1 m = thỏa mãn. Trường hợp 2: 025 m   . Kết hợp m Với 3 m = ta được phương trình 2 32 6110 32 zi zz zi  =+ −+=  =−   . Không thỏa mãn 1 133zi+−= , 2 355zi−+= nên 3 m = Với 4 m = ta được phương trình 2 42 8180 42 zi zz zi  =+ −+=  =−   Không thỏa mãn 1 133zi+−= , 2 355zi−+= nên 4 m = .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( ) ( ) 22 111222 218424218424 zmzmzzmzmz −++−++=−++−++ 12 2424 zz +=+ ( )1 * Xét 5 0 1 m m  

 

. Khi đó PT có 2 nghiệm thực phân biệt Nên ( )1 ( ) ( ) 1212 242442143 zzzzmm +=−++=−+=−=−

* Xét 015 m   . Khi đó PT có 2 nghiệm phức phân biệt 12 , zz liên hợp của nhau

Nên 12 21,21 zz++ cũng là hai số phức liên hợp của nhau. Suy ra 12 2121 zz+=+ luôn thỏa Vậy có 4 giá trị nguyên của tham số m thỏa mãn đề bài.

Câu 110: Có bao nhiêu giá trị thực của tham số m để trên tập số phức phương trình 222(2)10zmzm++++= có hai nghiêm 12 , zz thỏa 12 4 zz+= . A. 1. B. 3. C. 2. D. 4. Lời giải

Chọn C

44442(2)4 442(2)40 mktm zzzz m zz zzzzm mtm 2 22 121111 ..11 zzzzzmzm ===+=+ ( ) ( ) 22 12

 =−  +=+==  =  Vậy có hai giá trị thực của tham số m thỏa yêu cầu bài toán Câu 111: Có bao nhiêu số nguyên để phương trình có 2 nghiệm phức thỏa mãn ? A. 4. B. 2. C. 1. D. 3. Lời giải

=−  +=+= −+=   +=    −−=+=−−+=− =     TH2: 3 016120 4 mm +− , pthương trình có hai nghiệm là hai số phức liên hợp Ta có: 3 42143 3 mtm zzmm mktm

a ( ) 2230zazaa −−++= 12 , zz 1212 zzzz +=−

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Chọn A

Ta có .

+ TH1: , phương trình có 2 nghiệm , khi đó

. Thỏa mãn điều kiện .

+ TH2: , phương trình có 2 nghiệm , khi đó

. Thỏa mãn điều kiện .

Vậy có 4 giá trị của thỏa mãn yêu cầu bài toán.

Câu 112: Cho phương trình 2 40; c xx d −+= ( , cd  ; c d là phân số tối giản), có hai nghiệm phức. Gọi A , B là hai điểm biểu diễn của hai nghiệm đó trên mặt phẳng Oxy . Biết tam giác OAB đều, tính 2 Pcd =+ A. 18 P = . B. 10 P =− . C. 14 P =− . D. 22 P = . Lời giải Chọn D

Ta có: 2 40 c xx d −+= có hai nghiệm phức  40 c d  =− . Khi đó, phương trình có hai nghiệm phức 1 2 xi =+ ; 2 2 xi =− Gọi A, B lần lượt là hai điểm biểu diễn của 1x ; 2x trên mặt phẳng Oxy ta có: ( )

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

zbiAb bcibmnimn zbiBb =−+−   =−=−=+  =+−+−   Vậy ( ) ( ) 22 334410.ABbb=+−++−−= Câu 117: Cho m là số thực, biết phương trình 2 290zmz−+= có hai nghiệm phức 12 , zz . Có bao nhiêu giá trị nguyên của m sao cho 1221 16 zzzz+ ? A. 3. B. 4. C. 5. D. 6.

Lời giải Chọn C 2 290(*)zmz−+= có 2 9 m  =− . Phương trình (*) có hai nghiệm phức 12 , zz thỏa mãn 1221 16 zzzz+ nên 033 m  − . Áp dụng

zzb zzc +=−   =  Xét ( ) ( ) ( ) 222 2 21211234434434 zzizzzzibci −=−+−=−−=− Khi đó phương trình 2 240zbzc−+= có ( ) ( ) ( )( ) 2 2 343;4 434,, 343;4 A B định lý Vi ét ta có, 12122,9zzmzz+== . Ta có 121212 93 zzzzzz===== và 1122 , zzzz == . ( ) 12211212.3.336 zzzzzzzzm +=+=+=  . Theo đề, 1221 8 16616 3 zzzzmm + . Kết hợp với điều kiện ta được 8 3 3 m − . Mà m nguyên nên  2;1;0;1;2 m−− Vậy có 5 giá trị m thỏa mãn yêu cầu bài toán.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

31 Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( ) 22 1 0210210 2 mmmmm  −−+− . Khi đó phương trình đã cho có 2 nghiệm phức phân biệt. Giả sử 12 zabizabi =+=− . Khi đó 222222 12 0 220 0 a zzababab b =  =+=++=  =  . Suy ra 12 00 zzi ==+ mẫu thuẫn với điều kiện đề bài là phương trình có 2 nghiệm phân biệt. Trên tập hợp các số phức, xét phương trình ( ) 2 2130zmzm−+++= ( m là tham số thực). Có bao nhiêu giá trị của tham số m để phương trình có nghiệm phức 0z thỏa mãn 0 26 z += ?

Với 0 4 z = : thay vào ( )1 , được: 11 7 m = Với 0 8 z =− : thay vào ( )1 , được: 83 17 m =− Nếu 2 02021 mmm  +−− thì phương trình ( )1 có nghiệm phức 2 0 2 0

Chọn D Cách 1: Ta có 1 m  =+ . Trường hợp 1: 101mm+− . Khi đó theo bài ra, phương trình đã 72217450 1322113450

12 12 cho có nghiệm thực 0z thoả mãn 0 0 0

zmimm zmimm 7 310 13 z z z

 =+−+−   =+++−  Khi đó ( ) ( ) 2 22 0 26323627290 zmmmmm +=+++−=+−= : Phương trình có hai nghiệm phân biệt. Vậy có 4 giá trị của tham số m để bài toán thỏa mãn. Câu 122: Trên tập hợp các số phức, xét phương trình ( ) 22221450zmzmm −−+−= ( m là tham số thực). Có bao nhiêu giá trị của tham số m để phương trình có nghiệm 0z thoả mãn ( ) 22 001445310zmzmm+−+−−= ? A. 1. B. 2. C. 4. D. 3. Lời giải =  +=  =−  . Từ đó suy ra ( ) ( ) ( )( ) 22 2 2

mmm mmm

 −−+−=   −−−−+−=  2 2

433630 4471430 mm mm  −+=   −+=  ( ) ( ) 3 21 4

mtm mtm

=     =   Trường hợp 2: 101mm+− . Khi đó phương trình đã cho có hai nghiệm phức là 0z và 0z và thoả mãn 0 310 z += ( )( ) ( ) ( ) 2 2 00000 3310039100453.221910 zzzzzmmm ++=+++=−+−−= ( ) ( ) 2

71601 8 47970 71601 8

mtm mm mktm

 + =−   +−=  =−   Vậy có 3 giá trị của tham số m thoả mãn yêu cầu bài toán. Cách 2: Ta có ( ) ( ) ( ) 2 22221450211 1 zmzmmzmm −−+−=−+=+ .

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Trườ

Theo

Trường hợp 2: 101mm+−

Khi đó ( ) 211 1 211

 =−++    =−−+  .

zmim zmim

Theo bài ra, phương trình đã cho có nghiệm 0z thoả mãn 0 310 z +=

Do đó

22110484110047970

Vậy có 3 giá trị của tham số m thoả mãn yêu cầu bài toán. Câu 123: Trên tập hợp các số phức, xét phương trình 222220zmzmm −+−= ( m là tham số thực). Có bao nhiêu giá trị nguyên của ( )10;10 m− để phương trình đó có hai nghiệm phân biệt 12 , zz thỏa mãn 1222zz−=− ? A. 15 B. 18 C. 16 D. 17

Vậy các giá trị nguyên của thỏa mãn là:  9;8;...;1;3;4;...;9 m−−− nên có 16 giá trị nguyên của ( )10;10 m− thoả mãn.

Câu 124: Trong tập số phức, xét phương trình ( ) 2 2140zmz−−+= . Gọi S là tập hợp các giá trị nguyên của m để phương trình có hai nghiệm phân biệt 12 , zz thỏa mãn 12zz = . Tính tổng các phần tử của tập S A. 3. B.

02101

'0 thì phương trình có 2 nghiệm phức khi đó 1z và 2z là 2 số phức liên hợp nên 12zz = '0 2 230mm −− 13 m −  0;1;2 m  Vậy tổng các phần tử của tập S là: 123 += Câu 125: T rên tập hợp các số phức, xét phương trình 2 23100zmzm−++= ( m là tham số thực). Có bao nhiêu giá trị nguyên của m để phương trình đó có hai nghiệm 12 , zz không phải số thực thỏa mãn 12 8 zz+ ? A. 1. B. 2. C. 3. D. 4

TH2: Nế

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Lời giải Ta có: 1 32 2 3

1 51713023 23

z zzzzi zi

=   =−−= 

m OAOBmmthõamãn m ( ) 22 1 1560( 4 zmzmmm −+−−−=

=   −+−==+   =−  . Khi đó ( ) ( ) ( )1;0;2;3;2;3ABC , suy ra ( ) ( )1;3;1;3ABAC==− . ( ) 11 ;1.31.33 22 ABC SABAC   ==−−=  Câu 129: Trên tập số phức, xét phương trình ( ) 2 2101zmzm+++= ( m là tham số thực thỏa 2 10 mm−− ); 12 , zz là hai nghiệm phức của phương trình ( )1 ; , AB lần lượt là điểm biểu diễn của hai nghiệm phức đó trên mặt phẳng Oxy . Có bao nhiêu giá trị nguyên của m để OAB vuông tại O ? A. 2 B. 1. C. 3 D. 4 Lời giải Chọn B Xét phương trình ( ) 2 2101zmzm+++= Phương trình có hai nghiệm phức khi 2 1515 010 22 mmm −+  −− ( )* Ta có các nghiệm 22 121;1zmimmzmimm =−+−++=−−−++ , AB lần lượt là điểm biểu diễn của hai nghiệm phức 12 , zz nên ( ) 2 ;1Ammm−−++ ; ( ) 2 ;1Bmmm −−−++ . OAB vuông tạiO  ( ) 2 1 .0210* 1 2 =−  Vậy chỉ có 1 giá trị nguyên 1 m = thõa mãn yêu cầu. Câu 130: Trên tập hợp số phức, xét phương trình là tham số thực). Có bao nhiêu số nguyên [10;10] m− đề phương trình trên có hai nghiệm phức 12 , zz thỏa mãn 1212 zzzz +− ? A. 11. B. 10. C. 8. D. 9. Lời giải Chọn B Điều kiện 101mm+− 2 45mm =−−

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

, 15

[10;10]

nên số giá trị m thỏa mãn là 0,1,2,3mmmm

. Vậy có 10 giá trị của m. Câu 131: Trên tập hợp số phức, xét phương trình 2220zzm−+= ( m là tham số thực). Có bao nhiêu giá trị của m để phương trình đó có nghiệm 0z thỏa mãn điểm biểu diễn của 0z thuộc đường E lip có phương trình 2 2 1 4 x y += . A. 2 B. 3 C. 4 D. 1 Lời giải Chọn B Xét phương trình 2220zzm−+= có 2 1 m  =− *) Trường hợp 1: 0    1;1 m − .

Phương trình có các nghiệm là 2 0 11 zm =−− hoặc 2 0 11 zm =+−

Với 2 0 11 zm =−− điểm biểu diễn thuộc E lip 2 2 1 4 x y +=

Do đó ( )2 2 114 m −−= 2 13mm −=

Với 2 0 11 zm =+− điểm biểu diễn thuộc E lip 2 2 1 4 x y +=

Do đó ( )2 2 114 m +−= 2 110 mm −==

Trường hợp này giá trị 0 m = thỏa mãn.

*) Trường hợp 2: 0   ( ) ( ) ;11; m −−+ .

Phương trình có các nghiệm là 2 0 11zim=−− hoặc 2 0 11zim=+−

Điểm biểu diễn thuộc E lip 2 2 1 4 x y +=

Do đó ( ) 2 2 2 1 11 4 m +−= 2 3 1 4 m −= 7 4 m =

Trường hợp này giá trị 7 4 m = thỏa mãn. Vậy có 3 giá trị của m thỏa mãn yêu cầu bài toán.

Câu 132: Trên tập hợp các số phức, xét phương trình ( ) 2 2130zmzm−+++= ( m là tham số thực). Có bao nhiêu giá trị của tham số m để phương trình có nghiệm phức 0z thỏa mãn 0 26 z += ? A. 3 B. 1 C. 4 D. 2 Lời giải

Chọn D

trình

2130zmzm

( m là tham

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

ý: 2 2 22222222222()4. zababiabababzzzz =−+=−+=+=== . Lưu ý: 1212 zzzz ++ dấu bằng xảy ra ( ) 12 0 zkzk = 1212 zzzz −+ dấu bằng xảy ra ( ) 12 0 zkzk = 1212 zzzz +− dấu bằng xảy ra ( ) 12 0 zkzk = 1212 zzzz −− dấu bằng xảy ra ( ) 12 0 zkzk = ( ) 2222 121212 2 zzzzzz ++−=+ 2 2 zzzz == z 

( ) ( ) 22 22 rxaybR −+− hoặc rzabiR −−

Hình vành khăn giới hạn bởi hai đường tròn đồn tâm ( ) ; Iab , bán kính lần lượt là , rR ( ) 2 2 0 yaxbxc c xaybyc  =++   =++ 

Parabol ( ) ( ) ( ) 22 22 11 xayc bd ++ += hoặc 1122 2 zabizabia −−+−−=

( )1 Elip ( )2 Elip nếu ( ) ( ) 11222,,,, aABAabBab  Đoạn AB nếu2aAB = ( ) ( ) 22 22 1 xayc bd ++ −=

Hypebol MỘT SỐ DẠNG ĐẶC BIỆT CẦN LƯU Ý: DẠNG 1: Quỹ tích điểm biểu diễn số phức là đường thẳng.

TQ1: Cho số phức z thỏa mãn zabiz −−= , tìm Min z . Khi đó ta có + Quỹ tích điểm ( ) ; Mxy biểu diễn số phức z là đường trung trực đoạn OA với ( ) ; Aab + 22 0 11 22 22

 ==+     =+  

Min zzab ab zi

TQ2: Cho số phức thỏa mãn điều kiện . zabizcdi −−=−− Tìm min z Ta có +Quỹtíchđiểm ( ) ; Mxy biểudiễnsốphức z làđườngtrungtrựcđoạn AB với ( ) ( ) ;,; AabBcd + ( ) ( ) ( ) 2222 22 , 2 Min

abcd zdOAB acbd

+−− == −+− Lưu ý: Đề bài có thể suy biến bài toán thành 1 số dạng, khi đó ta cần thực hiện biến đổi để đưa về dạng cơ bản. Ví dụ 1: + Cho số phức thỏa mãn điều kiện zabizcdi −−=−− Khi đó ta biến đổi . zabizcdizabizcdi −−=−−−+=−− + Cho số phức thỏa mãn điều kiện . izabizcdi −−=−− Khi đó ta biến đổi . abicdi izabiizcdizzzbaizdci ii −−=−−+=+++=++

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

DẠNG 2: Quỹ tích điểm biểu diễn số phức là đường tròn. TQ: Cho số phức z thỏa mãn điều kiện ( ) 0 0 zabiRzzR −−=−= Tìm , MaxMin zz Ta có + Quỹ tích điểm ( ) ; Mxy biểu diễn số phức z là đường tròn tâm ( ) ; Iab bán kính R + 22 0 22 0

 =+=++=+   =−=+−=−  

zOIRabRzR zOIRabRzR

Max Min

Lưu ý: Đề bài có thể cho ở dạng khác, ta cần thực hiện các phép biến đổi để đưa về dạng cơ bản.

Ví dụ 1: Cho số phức z thỏa mãn điều kiện abiR izabiRz ii −−=+= zbaiR++=

Ví dụ 2: Cho số phức z thỏa mãn điều kiện zabiRzabiR −−=−+=

Ví dụ 3: Cho số phức z thỏa mãn điều kiện ( ) 22

abiRR cdizabiRz cdicdi cd +−−=+== ++ + Hay viết gọn 1 01 00

z R zzzRz zz −=−= DẠNG 3: Quỹ tích điểm biểu diễn số phức là Elip.

TQ1: Cho số phức z thỏa mãn điều kiện ( ) 2, zczcaac −++= Khi đó ta có + Quỹ tích điểm ( ) ; Mxy biểu diễn số phức z là Elip: 22 222 1 xy aac += + 22

 =   =−  

za zac

Max Min

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

−+−=− và 12,, zzcci  ).

Tìm Max, Min của 0Pzz =− Đặt 12 222

2 zzc bac  −=   =−  

Nếu 12 0 0 2 zz z + −= Max Min

Pa Pb =   = 

ế

zzkzz

0102

)

a mãn 1 z = . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 11Pzzz=++−+ . Giá trị của Mm bằng A. 133 4 . B. 133 8 . C. 3 3 . D. 33 8 . Lời giải

Chọn A

Đặt 1 tz=+ 12 z += nên  0;2 t 

Vì 1 z = nên .1zz = . Do đó, ta có: 2 11Pzzz=++−+ 2 1. zzzzz=++−+ 11 zzz=++−+ .

Ta lại có ( ) ( ) 2 2 11.1tzzz =+=++ ( )( )11zz =++ 2 zz=++ .

Suy ra 2 2 zzt+=− . Vậy ( ) 2 3 Pttft =+−= , với  0;2 t  . Dễ thấy ( )ft liên tục trên đoạn  0;2 .

3khi32 3khi03 ttt ft ttt

 +   =  −+  , ( ) 1 0 2 ftt  == Ta có: ( ) 03 f = , 113 24 f  = 

 +−  =  −+   Do đó ( ) 21khi32 21khi03 tt ft tt  , ( ) 33 f = , ( ) 23 f = Vậy giá trị lớn nhất của P là 13 4 M = ; giá trị nhỏ nhất của P là 3 m = . Khi đó 133 . 4 Mm = . Câu 3: Gọi 1z , 2z là các số phức thoả mãn điều kiện 1233zz+= và 12 31 zz−= . Giá trị lớn nhất của biểu thức 12Pzz =+ bằng A. 5 B. 4 9 C. 2 D. 1

Lời giải

Ta có: ( )( ) ( ) 222 121212121212 933393 zzzzzzzzzzzz =+=++=+++ ( )1 ( )( ) ( ) 222 121212121212133393zzzzzzzzzzzz =−=−−=+−+ ( )2 Cộng vế ( )1 và ( )2 ta có: ( ) 2222 1212 10101 zzzz =++= . Ta có: ( ) ( )( ) 2 22 222 1212112Pzzzz =+++= 2 P  Dấu “ = ” xảy ra 12 2 2 zz == Vậy max2 P = .

Câu 4: Cho số phức zabi =+ ( ) , ab thỏa mãn 2 2 z zi + + là một số thuần ảo. Khi số phức z có môđun nhỏ nhất, hãy tính ab + A. 0 ab+= B. 221 ab+=− C. 4 ab+= D. 22 ab+= Lời giải

Chọn A

Ta có ,, zabiab=+ . Gọi ( ) ; Mab là điểm biểu diễn cho số phức z . Có ( ) 22 w 22 zabi ziabi +++ == +++ ( ) ( ) ( )2 2

22 2 abiabi ab ++−+  = ++ ( ) ( ) ( )( ) ( )2 2

2222 2 aabbababi ab ++++−+++  = ++ w là số thuần ảo ( ) ( ) ( ) ( )2 2

aabb ab

2201 20

+++=     ++   Có ( ) 22 1220 abab +++= Suy ra M thuộc đường tròn tâm ( )1;1 I , bán kính 2 R = . Vì đường tròn đi qua gốc tọa độ nên khi số phức z có môđun nhỏ nhất thì điểm ( ) ; Mab trùng gốc tọa độ. Vậy 0 ab+= . Câu 5: Cho số phức z thỏa mãn 343zi+−= và 232 wzi =+− Khi đó w có giá trị lớn nhất bằng A. 635. B. 635 + . C. 7. D. 35. Lời giải Chọn B

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

có 232 wzi =+− ( ) 23436 zii=+−−+ ( ) 23436 zii+−+−+ ( )2 2 636635 =+−+=+ . Câu 6: Xét các số phức ,z w thỏa mãn 2 z = và .1iw = . Khi 34 izwi ++− đạt giá trị nhỏ nhất, w z bằng A. 5 B. 29 5 C. 3 D. 221 5

ời giải Chọn A Cách 1: Ta có ( ) ( ) 343455212izwiiizwizw ++−−−+−+−+= Dấu bằng xảy ra khi ( ) ( ) ( ) ( ) 11 22

 =−+   =−  

340 .340 wkikhik izkikhik =−  

 ==   ==   Giải hệ trên suy ra 2 2 5 k =− ; 1 1 5 k =− Hay ( ) ( )

=−   và 1 2

wiw izz

wi izi i zizi

34 55 2 34 5 286 34 555

Khi đó 12 zwi −=−− w5 z −= Cách 2: Trong mặt phẳng Oxy : Gọi M là điểm biểu diễn của số phức iz 2 OM =  M thuộc đường tròn ( )1C tâm O bán kính 1 2 R = Gọi N là điểm biểu diễn của số phức w 1 ON =  N thuộc đường tròn ( ) 2C tâm O bán kính 2 1 R = Gọi ( )3;4 E . Khi đó 34 Aizwi =++− OMONOE=++ . Ta thấy A đạt giá trị nhỏ nhất khi ,M ,N E thẳng hàng và OM và ON ngược hướng với OE Đường thẳng OE có phương trình là 4 3 yx = . Tọa độ giao điểm của đường thẳng OE và đường tròn ( )1C là nghiệm của hệ phương trình:

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn



Ta có: ( ) 22 2 2

z t ab a zz b zt ab

  = += =  





1 1 1 1 w w2w 0 21 21 21 w

Suy ra: 1wtz== . Khi đó: 222 1 1z+w1z+w14z4z4 z zzz T ==== +++ . Đẳng thức xảy ra khi 1 2 z = . Vậy ( ) 1 MaxT=.2 4 Từ ( )1 và ( )2 , suy ra: 1 MaxT=. 4 Câu 8: Xét các số phức , zw thỏa mãn 221zi++= và 123 wiwi −+=− . Khi 33 zwwi −+−+ đạt giá trị nhỏ nhất. Tính 2 zw + A. 213 B. 7 C. 25 D. 61 Lời giải Chọn D Giả sử điểm biểu diễn của , zw lần lượt là , MF .

Do 221zi++= nên M nằm trên đường tròn ( )C tâm ( )2;2 I , bán kính 1 R = .

Gọi ( ) ( )1;2,0;3AB . Do 123 wiwi −+=− nên F nằm trên đường thẳng :10dxy++= là đường trung trực của đoạn thẳng AB .

Gọi ( )3;3 C .Khi đó 33 zwwiMFFC −+−+=+ .Tađi tìm giátrị nhỏ nhất củatổng hai đoạn thẳng này.

Giả sử ( ) C là đường tròn đối xứng với ( )C qua đường thẳng d . Suy ra ( ) C có tâm ( )3;3 I , bán kính 1 RR  == . Khi đó ứng với mỗi ( )MC  luôn tồn tại ( ) MC  sao cho MFMF  = .

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Suy ra 33 zwwiMFFCMFFC  −+−+=+=+ đạt giá trị nhỏ nhất khi ,,, IMFC  thẳng hàng.

Khi đó F là giao điểm của d và IC  với :3ICx  = . Suy ra ( )3;2 F .

Tương ứng ta có M là giao điểm của đường thẳng IF và đường tròn ( )C , M nằm giữa , IF .

Suy ra ( )1;2 M . Do đó 33 zwwi −+−+ đạt giá trị nhỏ nhất khi 12,32 ziwi =−−=− . Suy ra 256 zwi +=− 261zw += . Câu 9: Gọi S là t

ủa 22 1234 Pzizi =−−− bằng A. 16. B. 8. C. 4. D. 32. Lời giải Chọn C

1 111 33432 2

++ = = +  = ++ ( )( ) ( )( ) ( ) 1 2222 22 12111 3344 433443 Pziziziziziziizzzz =−−−−+=− += P = ( ) ( ) 11112222 33334444 4 izzzzizzzz + = Câu 10: Cho 1, z 2z là hai số phức thỏa mãn 12izi−+= và 12 2 zz−= . Giá trị

+ === + + ++− + ++ ++ w có phần thực là 2 2 22 2 43 211 21 zx zxy zx lớn nhất của biểu thức 12 12 Pzzi =+++ có dạng ab + . Khi đó 2 ab + có giá trị là A. 18 B. 15 C. 19 D. 17 Lời giải Chọn B Đặt 12wiziw=−+= . Với 11 1 wizi =−+ ; 22 1 wizi =−+ thì 1 2 w = ; 2 2 w = . Ta có: ( ) 121212222zzizziww −=−=−= Mặt khác, ( )( ) ( )( ) 22 121212121212 wwwwwwwwwwww −++=−−+++ ( )( ) ( )( ) ( ) ( ) 22 12121212112212 2..2 wwwwwwwwwwwwww =−−+++=+=+ . Do đó ( ) 2222 12121212214.wwwwwwww +=+−−+=

z zxiy z w z z x z z z

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

có 121212 12.122 Pzziizziizizi =+++=+++=+−+ 1212 112 wiwiiwwi =+−++−−+=+− . Lại có: 1212 141 PwwiwwiP =+−+++ Suy ra max114 P =+ . Do đó 1 a = , 14 b = . Vậy 2 15 ab+= Câu 11: Giả sử 12 ; zz là hai trong số các số phức z thoả mãn ( )( ) 68. ziz là một số thực. Biết rằng 12 6 zz−= . Giá trị nhỏ nhất của biểu thức 12 3 zz + bằng

A. 521 B. 20421 C. 573−+ D. 20273 Lời giải

Chon D

Gọi , AB là các điểm biểu diễn cho 21 ; zz Đặt ( )( ) ( ) ( ) 68.6.8 zabizizabibai =+−−=−+−−  Do ( )( ) 68. ziz là một số thực nên ( ) ( ) 22 .680680 aabbabab −−+−=+−−= Suy ra , AB thuộc đường tròn tâm ( )3;4 I , bán kính 5 R = Gọi M điểm thoả mãn 30 MAMB+= Gọi H là trung điểm của AB

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

A. 55 . B. 8. C. 3. D. 2. Lời giải Chọn D

Gọi , MN lần lượt là các điểm biểu diễn số phức 34 zi và 2w. Ta có ( ) ( ) 1343411 zziiMI =−−++== , với (3;4)I Suy ra tập hợp điểm M là đường tròn ( )1T tâm (3;4)I và bán kính 1 1 R = .

Ta có 22 w = nên tập hợp điểm N là đường tròn ( ) 2T tâm O và bán kính 2 2 R = Ta có 234 PzwiMN =−−−= . 12 max5128 POIRR =++=++= . Dấu bằng xảy ra khi 1824 65; 55 OIOMM  =   ; 68 25; 55 OIONN  −=   Khi đó ta có 34 55 i z =− , 34 55 i w =+ nên 2 zw−= Câu 14: Cho biểu thức 123456 =−−+−−+−− Pzizizi

Suy ra: 2 PMN = . Khi đó, minmin2 PMNONb =−= , xảy ra khi và chỉ khi ( )0;2 M . Vậy giá trị nhỏ nhất của P bằng 22 Câu 17: Cho hai số phức 12 , zz thỏa mãn 12 12 1;2 231 zizi zizi −+ == +−−+ . Giá trị nhỏ nhất của 12zz là A. 22 . B. 2 . C. 21. D. 1. Lời giải

Chọn A

Giả sử 111 zxyi =+ với 11 ; xy  . Khi đó: ( ) ( ) ( ) 1 111111 1 123123 23 zi zizixyixyi zi =−=+−+−=++− +− ( ) ( ) ( ) 1

222 2 11111 12330xyxyxy +−=++−−+=  Quỹ tích điểm M biểu diễn số phức 1z là đường thẳng :30 xy −+= Giả sử 222 zxyi =+ với 22 ; xy  . Ta có: ( ) ( ) ( ) 2 222222 2 2211211 1 zi zizixyixyi zi + =+=−+++=−++ −+ ( ) ( ) ( ) 222 222 2222222212114230xyxyxyxy ++=−+++−++=  Quỹ tích điểm N biểu diễn số phức 2z là đường tròn ( ) 22 :4230Cxyxy+−++= có tâm ( )2;1 I và bán kính ( )2 2 2132 R =+−−= . Khoảng cách từ I đến  là: ( ) ( ) ( )2 2

213 ;32 11 dIR −−+ == +−  đường thẳng  và đường tròn C không có điểm chung. Ta có: 12 zzMN −= 12zz− nhỏ nhất khi và chỉ khi MN nhỏ nhất.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

13133311 31 xxyyxyxyi xy N M

M'

−+++++++−−+ = +++ Ta có w là số thần ảo khi: ( )( ) ( )( ) 22 13130240 xxyyxyxy −++++=+++= Vậy tập S các số phức z có tập biểu diễn là đường tròn tâm ( )1;2 I bán kính 5 R = . I N'

, AB và M lần lượt là các điểm biểu diễn số phức 12 , zz và 3i

1331 31 3 31 xyixyi xyii w xyii xy (

−+++−+ ++− == +++ +++ ( )( ) ( )( ) ( )( ) ( )( ) ( ) ( ) ( ) 22 22 22 22 1233 PziziMAMBMAMBMIIAMIIB =−−−=−=−=+−+ ( ) ( ) 2222 2.2.2.2. MIMIIAIAMIMIIBIBMIIAIBMIBA =++−++=−= ( ) ( ) 2..cos,426.cos,426 MIBAMIBAMIBA == Dấu bằng xảy ra khi và chỉ khi MI và BA cùng chiều Vậy min 426. P =

) ( ) 22

Câu 19: Cho hai số phức 12 , zz thỏa mãn 111 51313 zizizi −=+++−− và 2 5 zi+= . Giá trị lớn nhất của biểu thức 12 24 Pzzi =+−− bằng A. 535. + B. 213. + C. 9. D. 545. + Lời giải Chọn D Gọi 11111(;)zxyiMxy =+ 22222(;)zxyiNxy =+ 3 (0;1)ziC = 4 1(1;1)ziA=−−−− 5 13(1;3)ziB =+ Dễ thấy điểm C là trung điểm của AB và 25 AB = Theo công thức đường trung tuyến, ta có: 2222 2222 2 242 MAMBABAB MCMAMBMC + =−+=+ Mặt khác theo bài ra ta có: 111 51313 zizizi −=+++−− 22225331. MCMAMBMAMB=+++

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

c 12 , zz trên mặt phẳng tọa độ thỏa mãn tam giác MON có diện tích bằng 32, khi đó giá trị nhỏ nhất của 12zz + bằng A. 82 . B. 122 . C. 12. D. 16. Lời giải Chọn B 1122 4 zzzz = suy ra 22 1212 42 zzzz == Thay 12 2 zz = vào 1122 4 zzzz = ta có 12 2 zz = suy ra 122 3 zzz + = Giả sử 2 1 ; ,(,)zxyiabia z b =+=+ ta được 2 2 xa yb =   =  và ( ) ( ) ( ) ;;;;; MxyNabNab  lần lượt là các điểm biểu diễn số phức 12 , zz và 2z .

Ta có: ( ) ( ) ;; ; OMxyONab =− , tam giác MON có diện tích bằng 32 nên 64 bxay+= hay 16 ab = . Ta có: 22 1223332.122zzzabab ===

A. 25 B. 5 C. 65 5 D. 1 Lời giải

Chọn C

Ta có ( ) 2 1 22 zaaai =+−+ ( ) 2 ;22Maaa −+ . Gọi ( ) 2 ,; zxyixy=+ Ta có 2226 zizi −−=−− ( ) ( ) ( ) ( ) 2222 2161xyxy −+−=−++ 280 xy −−= Suy ra N thuộc đường thẳng :280dxy−−= Khi đó ( ) ( ) ( )2 2 min 2 2

a aaa MNdMd −+ −+−− === +− Vậy 6 min 5 MN =

26 2228 6 , 55 21

23: Gọi ,, MNP lần lượt là điểm biểu diễn của các số phức 123 ,, zzz thỏa mãn điề

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Xét ( ) ( )1;0,3;0AB , ta có: 4 AB =

Ta có: 33134zz++−= PAPBAB+= nên P thuộc đoạn AB .

Gọi , EF lần lượt là điểm đối xứng của P qua 12 , dd .

Ta có: CECPCF == , MPME = , NPNF = .

Chu vi tam giác MNP là: MPNPMNMENFMNEF ++=++ .

Do tam giác CEF cân tại ( )3;0 C và 2 ECFACB =

Ta có: 222 2...cos EFCECFCECFECF =+− ( ) 2 2..1cosCEECF=− 224..sin 2 ECF CE = 224..sinCEACB = .

Suy ra, EF nhỏ nhất CE  nhỏ nhất CP nhỏ nhất CPAB⊥ . Khi đó, ( )0;0 PO  và 33CPCOCE=== . Lại có: 4,10,32ABACBC === 222 5 cos 2..5 ACBCAB ACB ACBC +− == 20 sin 5 ACB = 125 min2..sin 5 EFCEACB == . Vậy giá trị nhỏ nhất của chu vi tam giác MNP bằng 125 5 Câu 24: Cho số

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Vậy tập hợp các điểm M là đường thẳng Δ:10 xy . Do đó, zOM nhỏ nhất khi M là hình chiếu của O trên Δ . Khi đó, 1 ,Δ 2 zOMdO

Câu 25: Xét các số phức ( ) i,, zxyxy=+ thỏa mãn 24i2izz−−=− và z đạt giá trị nhỏ nhất. Tìm P32xy=− A. 2 B. 10 C. 4 D. 2 Lời giải

Chọn D

Ta có 24i2izz−−=− ( ) (2)(4)i2i xyxy −+−=+− 2222 (2)(4)(2) xyxy −+−=+− 40 xy +−=

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Lời giải

Chọn C Ta có 231zi−−=⎯⎯→ tập hợp các điểm M biểu diễn số phức z thuộc đường tròn có tâm ( )2;3 I , bán kính 1. R = Ta có 111 PziziziMA =++=++=+−= với ( ) 1;1; A ( ) ( ) (

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Dựa vào hình vẽ ta thấy ( ) 326 ;. 13 PzwMNd  =−== Dấu "" = xảy ra khi và chỉ khi M  , NM  và MN ⊥ . Câu 28: Cho số phức 12 ; zz thỏa 1 122zi−−= và 22231 zizi ++=−− . Giá trị nhỏ nhất của 12zz bằng A. 33 10 B. 29 10 C. 9 10 D. 13 10 Lời giải

Chọn D

Gọi 1 zxyi =+ với , xy  khi đó ( ) ( ) 22 1 122124zixy −−=−+−= . Suy ra tập hợp biểu diễn số phức 1z là đường tròn ( )C có phương trình ( ) ( ) 22 124xy−+−= . Gọi 2 zabi =+ với , ab Khi đó: ( ) ( ) ( ) ( ) 2222 22231231168110. ziziababab ++=−−+++=−+−++= Suy ra tập hợp biểu diễn số phức 2z là đường thẳng  có phương trình :68110 xy ++= . Gọi M là điểm biểu diễn số phức 1z và N là điểm biểu diễn số phức 2z trong mặt phẳng phứ c.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi 11111,(,)zabiab =+ 

Ta có: ( ) ( )2 111431431ziab −−=−+−= nên tập hợp điểm biểu diễn cho 1z là đường tròn tâm ( ) 1 4;3 I và bán kính bằng 1 1 R = Gọi 22222,(,)zabiab =+ 

Ta có ( )( ) 2242 zzi là số thuần ảo tương đương ( ) ( ) 2222420aabb−++= ( ) ( ) 22 22215ab −++=

Nên tập hợp điểm biểu diễn cho 2z là đường tròn tâm ( ) 2 2;1 I và bán kính 5 .

Ta thấy hai đường tròn rời nhau vì 1212 IIRR + nên 12zz đạt giá trị lớn nhất là: 1212 351 MIIRR=++=+ 12zz đạt giá trị nhỏ nhất là: 1212 51 mIIRR=−−=− Vậy 45 Mm+=

30: Cho

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi ( ) ; Axy là điểm biểu diễn cho số phức u , khi đó ( ) ( ) 22 422424uixy +−=++−= , nghĩa là quỹ tích các điểm A là đường tròn ( )1C có tâm là điểm ( )4;2 I , bán kính 1 2 R = Gọi ( ) ; Bxy là điểm biểu diễn cho số phức v , khi đó 3121 vivi −+=+− ( ) ( ) ( ) ( ) 2222 31312121 xyxy −++=++− ( ) ( ) 22 112xy −++=

Do đó quỹ tích các điểm B là đường tròn ( ) 2C có tâm là điểm ( )1;1 J , bán kính 2 2 R = .

Gọi ( ) ; Mxy là điểm biểu diễn cho số phức w , khi đó 2222 wwiwi =++=+− ( ) ( ) 22 22 2220xyxyxy +=++−−+=

Do đó quỹ tích các điểm M là đường thẳng ( ):20 xy −+=

Ta có ( ) ( ) ( ) ( ) 12,22;,22 dIRdJR == nên đường thẳng ( ) không có điểm chung với hai đường tròn trên.

Ta lại có , IJ nằm khác phía so với đường thẳng ( ) , do đó ( )1C và ( ) 2C cũng nằm khác phía so với đường thẳng ( )

Ta có ww TuvMAMB =−+−=+ , gọi ,, HKE là các giao điểm

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

3422 2 P =−−+

31: Gọi 1z , 2z là hai số phức thỏa mãn đồng thời hai điều kiện 25 1 5 zi−−= ; 2 zmizm −−=+

i m là số thực tùy ý. Gọi A , B lần lượt là điểm biểu diễn hình học của 1z , 2z . Gọi S là tập các giá trị của m để diện tích tam giác IAB là lớn nhất với ( )1;1 I . Tổng bình phương các phần tử S bằng

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi wxyi =+ với x , y  Ta có ( ) ( ) 5103425 iwizi+=−− ( ) 1243 ziwi=−+−+ . Lại có ( ) 122512431225 ziiwii −+=−+−+−+= ( ) 125525 iwi −+−+= 32wi ++= 32xyii −++= ( ) ( ) 22 314xy ++−= Vậy tập hợp các điểm biểu diễn số phức w là đường tròn tâm ( ) 3;1, I bán kính 2 R = max210 POMROI==+=+ min102 PONOIR==−=− . Vậy maxmin210 PP+= .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Theo bất đẳng thức tam giác ta có ( ) ( ) w2126879268794130 ziziizii =+−=−++−−++−=+ . Vậy giá trị lớn nhất của w là 4130 + . Câu 38: Biết số phức z thỏa mãn 32 izzi −=−− và z có giá trị nhỏ nhất. Phần thực của số phức z bằng: A. 2 5 . B. 1 5 . C. 2 5 . D. 1 5 . Lời giải Đặt zxyi =+ ( x , y  ). Khi đó 32 izzi −=−− ( ) ( ) ( ) 222 2 321xyxy +−−=−+− 210xy ++= 21xy =−− ( )1 .

Lại có 22 zxy =+ ( )2 . Thay ( )1 vào ( )2 ta được: 22 zxy =+ ( )2 2 21yy=−−+ 2 541 yy =++ 2 215 5 555 y  =++  

Dấu đẳng thức xảy ra khi 2 0 5 y += 2 5 y =− Thay 2 5 y =− vào ( )1 suy ra 1 5 x =− . Vậy phần thực của số phức z là 1 5 .

Câu 39: Xét các số phức z thỏa mãn 132zi−−= . Số phức z mà 1 z nhỏ nhất là A. 15 zi =+ B. 1 zi =+ C. 13 zi =+ D. 1 zi =− Lời giải Gọi zxyi =+ , , xy  . Khi đó ( ) ; Mxy là điểm biểu diễn của số phức z

Theo bài ra ta có ( ) ( ) 22 132134zixy −−=−+−= Suy ra tập hợp điểm M là đường tròn tâm ( ) 1; 3 I bán kính 2 R =

Khi đó ( )2 2 11 zxyIM  −=−+= với ( ) 1; 0 I

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

1 z nhỏ nhất khi IM  ngắn nhất hay I , M , I  thẳng hàng, M nằm giữa I và I  Phương trình đường thẳng II là 1 x = . Tọa độ giao điểm của đường thẳng II với đường tròn tâm I bán kính 2 R = là ( ) 1 1; 1 M và ( ) 1 1; 5 M . Thử lại ta thấy ( ) 1 1; 1 M thỏa mãn. Vậy 1 zi =+ .

Câu 40: Cho hai số phức 12 , zz thỏa mãn đồng thời hai điều kiện sau 134,12 zzmizmi −=++=++ và sao cho 12zz là lớn nhất. Khi đó giá trị 12zz + bằng A. 2 B. 10 C. 2 D. 130 Lời giải

Gọi , MN lần lượt là điểm biểu diễn của số phức 12 , zz

Gọi ( ) ,, zxiyxy=+ Ta có 134, zMN −= thuộc đường tròn ( )C có tâm ( )1;0 I , bán kính 34 R = Mà 1212 zmizmixyimixyimi ++=+++++=+++

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( ) ( ) ( ) ( ) 2222 12 xymxmy +++=+++ ( ) ( ) 212230 mxmy −+−−=

Suy ra , MN thuộc đường thẳng ( ) ( ) :212230 dmxmy−+−−=

Do đó , MN là giao điểm của đường thẳng d và đường tròn ( )C

Ta có 12 zzMN −= nên 12zz lớn nhất khi và chỉ khi MN lớn nhất MN  đường kính của ( )C . Khi đó 12 22zzOI+==

Câu 41: Cho số phức z thỏa mãn 221zi−−= . Số phức zi có môđun nhỏ nhất là: A. 52. B. 51. C. 51 + . D. 52 + . Lời giải

Cách 1: Đặt wzizwi =−=+ . Gọi ( ) ; Mxy là điểm biểu diễn hình học của số phức .w

Từ giả thiết 221zi−−= ta được: 221wii+−−= 21wi −−= ( ) ( ) 211xyi −+−= ( ) ( ) 22 211xy −+−=

Suy ra tập hợp những điểm ( ) ; Mxy biểu diễn cho số phức w là đường tròn ( )C có tâm ( )2;1 I bán kính 1 R = .

Giả sử OI cắt đường tròn ( )C tại hai điểm , AB với A nằm trong đoạn thẳng OI

Ta có wOM =

Mà OMMIOI + OMMIOAAI++ OMOA Nên w nhỏ nhất bằng 51 OAOIIA=−=− khi .MA 

Cách 2:

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

2 O D

I B E

5 1 -2 2 -2

• ( ) ( ) ( ) 22 2222; PziPxyPdIN =−−=−+−= với ( )2;2 I Từ hình ta có: ( )1;1 E 22 max 4225 MPID===+= và ( ) ( ) 22 min 21212 mPIE===−+−= Vậy, ( )22534;6 AMm=+=+ . Câu 43: Xét số phức z và số phức liên hợp của nó có điểm biểu diễn là M và M . Số phức ( ) 43 zi + và số phức liên hợp của nó có điểm biểu diễn là N và N . Biết rằng M , M , N , N là bốn đỉnh của hình chữ nhật. Tìm giá trị nhỏ nhất của 45zi+− . y 1

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn x

F C

Ta có M và M ; N và N từng cặp đối xứng nhau qua trục Ox . Do đó, để chúng tạo thành một hình chữ nhật thì MNyy = hoặc MNyy  = . Suy ra 34 yxy =+ hoặc 34 yxy =−− . Vậy tập hợp các điểm M là hai đường thẳng: 1 :0dxy+= và 2 :350dxy+= Đặt ( ) ( ) 224554Pzixy =+−=−++ . Ta có PMA = với ( )5;4 A . ( )minmin1 ; PMAMAdAd = hoặc ( ) 2 ; MAdAd = . Mà ( ) 1 1 ; 2 dAd = , ( ) 2 5 ; 34 dAd = , vậy ( ) min1 1 ; 2 PdAd== .

Câu 44: Cho số phức z thỏa mãn 4. zzzz++−= Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của 22.Pzi =−− Đặt AMm =+ Mệnh đề nào sau đây là đúng? A. ( )34;6 A

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

nhất là 3 10 Cách 2: Trên mặt phẳng tọa độ Oxy , tập hợp điểm biểu diễn số phức z là đường thẳng :4230dxy++= . Ta có zOM = z nhỏ nhất OM  nhỏ nhất M  là hình chiếu của O trên d Phương trình đường thẳng OM đi qua O và vuông góc với d là: 20xy−= Tọa độ của M là nghiệm của hệ phương trình:

. Giá trị nhỏ nhất của 12zz là A. 22 . B. 2 . C. 1. D. 21. Lời giải

Giả sử 111 zxyi =+ với 11 ; xy  . Khi đó: ( ) ( ) ( ) 1 111111 1 123123 23 zi zizixyixyi zi =−=+−+−=++− +− ( ) ( ) ( ) 1

222 2 11112 12330xyxyxy +−=++−−+= .  Quỹ tích điểm M biểu diễn số phức 1z là đường thẳng :30 xy −+= Giả sử 222 zxyi =+ với 22 ; xy  . Ta có: ( ) ( ) ( ) 2 222222 2 2211211 1 zi zizixyixyi zi + =+=−+++=−++ −+ ( ) ( ) ( ) 222 222 2222222212114230xyxyxyxy ++=−+++−++= .  Quỹ tích điểm N biểu diễn số phức 2z là đường tròn ( ) 22 :4230Cxyxy+−++= có tâm ( )2;1 I và bán kính ( )2 2 2132 R =+−−= . Khoảng cách từ I đến  là: ( ) ( ) ( )2 2

N M

I N' M'

213 ;32 11 dIR −−+ == +−  đường thẳng  và đường tròn C không có điểm chung. Quỹ tích các điểm biểu diễn số phức 12zz là đoạn thẳng MN 12zz− nhỏ nhất khi và chỉ khi MN nhỏ nhất. Dễ thấy min 32222 MN =−= . Câu 47: Gọi S là tập hợp các số phức z thỏa mãn 134 z −= và 12 zmizmi ++=++ , Gọi 1z , 2z là hai số phức thuộc S sao cho 12zz lớn nhất, khi đó giá trị của 12zz + bằng A. 2 B. 10 C. 2 D. 130 Lời giải

z

t zxyi =+

đó

( ) ,

Khi đó

( )2 2 134xy −+= ; 12 zmizmi

( ) ( ) 212230 mxmy −+−+=

giao điểm c

đường tròn

:134Cxy−+= và đường thẳng ( ) ( ) :212230 dmxmy−+−+= . Gọi A, B là hai điểm biểu diễn 1z và 2z . Suy ra ( )   , CdAB = . Mặt khác 12 2234zzABR−== do đó ( ) 12 max23421;0zzABRId −== Từ đó ta có 1 2 m =− nên :3530dxy−−= 1 2

) ( )

63 43 zi zi =+    =−−  . Vậy 12 2 zz+= Câu 48: Cho hai số phức , zw thỏa mãn 322 z −= , 4222wi−= . Biết rằng zw đạt giá trị nhỏ nhất khi 0zz = , 0ww = . Tính 00 3zw . A. 22 . B. 42 . C. 1. D. 62 . Lời giải Ta có: + 322 z −= , suy ra tập hợp điểm biểu diễn M biểu diễn số phức z là đường tròn có tâm ( )32;0 I , bán kính 2 r = . + 4222wi−= , suy ra tập hợp điểm biểu diễn N biểu diễn số phức w là đường tròn có tâm ( ) 0;42 J , bán kính 22 R = Ta có minminzwMN −= . + 52;2;22IJIMrNJR =====

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

phức z thoả mãn 1 z = . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2 11Pzzz=++−+ . Tính . Mm A. 133 4 . B. 39 4 . C. 33. D. 13 4 . Lời giải Thay 2 1 z = vào P ta có 2 11Pzzz=++−+ 2 2 1 zzzz=++−+ 2 1. zzzzz=++−+ 11zzzz =+++− 11zzz =+++− . Mặt khác ( )( ) 2 1112 zzzzz +=++=++ Đặt tzz =+ do 1 z = nên điều kiện  2;2 t − . Suy ra 21Ptt=++− . Xét hàm số ( ) 21fttt=++− với  2;2 t − ( ) 1 1 22 ft t  =+ + với 1 t  . Suy ra ( ) 0 ft   với 1 t  .

( ) 1 1 22 ft t  =− + với 1 t  . Suy ra ( ) 0 fx  = 7 4 x = . Ta có bảng biến thiên Từ bảng biến thiên suy ra 13 4 M = tại 7 4 t = và 3 m = tại 2 t = Vậy 133 . 4 Mm = . Câu 51: Cho hai số phức z và abi=+ thỏa mãn 556zz++−= ; 54200 ab−−= . Giá trị nhỏ nhất của z  là A. 3 41 . B. 5 41 . C. 4 41 . D. 3 41 . Lời giải Đặt ( ) 1 5;0 F , ( ) 2 5;0 F , vì 53  nên tập hợp các điểm M biểu diễn số phức z thuộc elip có 222 3 4 5 a bac c

=   =−=  =   suy ra ( ) 22 :1 94 xy E += . Tập hợp các điểm N biểu diễn số phức  thuộc đường thẳng :54200 xy −−= . Yêu cầu bài toán trở thành tìm điểm ( )ME  và N  sao cho MN nhỏ nhất. Đường thẳng d song song với  có dạng :540dxyc−+= , ( )20 c − . d tiếp xúc với ( )E khi và chỉ khi ( )2 22 17 5.94.4289 17 c c c

=  =+−=  =− 

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

721 ; 1010 MH     Lúc đó 4921 77 1010 Sab=+=+= . Câu 53: Cho số phức thỏa mãn . Gọi lần lượt là giá trị lớn nhất, nhỏ nhất của biểu thức . Tính A. . B. . C. . D. . Lời giải: Gọi ,, zxyixy=+ , ta có 4 2824 2 x zzzzxy y , tập hợp ( ) ; Kxy biểu diễn số phức z thuộc cạnh các cạnh của trong hình thoi ABCD như hình vẽ.

đạt giá trị lớn nhất khi KM lớn nhất, theo hình vẽ ta có KM lớn nhất khi

KD  hay ( )4;0 K suy ra 49958 M =+=

đạt giá trị nhỏ nhất khi KM nhỏ nhất, theo hình vẽ ta có KM nhỏ nhất khi KF  ( F là hình chiếu của E trên AB .

Suy ra ( )2;1 F do AEAB = nên F là trung điểm của AB

ra 145 m =+= . Vậy 585 Mm+=+

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Giả sử zxyi =+ , , xy  .Gọi , AB lần lượt là điểm biểu diễn cho các số phức 12 , zz . Suy ra 12 4 ABzz=−=

* Ta có ( )( ) 68 zzi −+ ( ) ( ) 6.8 xyiyxi  =−+−−  ( ) ( ) 22 864868 xyxyxyi=+−−+−− . Theo giả thiết ( )( ) 68 zzi −+ là số thực nên ta suy ra 22 680xyxy+−−= . Tức là các điểm , AB thuộc đường tròn ( )C tâm ( )3;4 I , bán kính 5 R = .

* Xét điểm M thuộc đoạn AB thỏa 3034 MAMBOAOBOM +=+= .Gọi H là trung điểm AB . Ta tính được 2222221;22HIRHBIMHIHM =−==+= , suy ra điểm M thuộc đường tròn ( ) C tâm ( )3;4 I , bán kính 22 r = * Ta có 123344 zzOAOBOMOM +=+== , do đó 12 3 zz + nhỏ nhất khi OM nhỏ nhất.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Suy ra ( ) ( ) ( ) ( ) ( ) 22 22 22 12121212122342.3410zzxxyyxxyy −=−+−+−+−=  . Do đó 22 12 1010 zz −− . Câu 57: Cho hai số phức 12 , zz thoả mãn 1124762zizi+−+−−= và 2 121izi−+= . Tìm giá trị nhỏ nhất của biểu thức 12Tzz =+ A. 21. B. 21 + . C. 221 + . D. 221. Lời giải Gọi M là điểm biểu diễn số phức 1z và ( )2;1 A ; ( )4;7 B lần lượt là hai điểm biểu diễn hai số phức 2 i −+ , 47i + . Ta có 62 AB = . Phương trình đường thẳng AB là :30dxy−+= +) 1124762zizi+−+−−= 62 MAMB += MAMBAB+= . Do đó tập hợp các điểm biểu diễn số

phức 1z là đoạn thẳng AB

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Suy ra 12 221. minzz+=− Câu 58: Cho z là số phức thỏa mãn 2 zzi =+ . Giá trị nhỏ nhất của 1213 zizi −++++ là A. 52 . B. 13 . C. 29 . D. 5 . Lời giải Đặt ( ) , zabiab=+ Ta có: ( )2 222 22zziabab =++=++ 4401 bb +==− zai=− . Xét: 1213112 ziziaiai −++++=−++++ ( ) ( ) 2222 1112 aa =−++++ . Áp dụng BĐT Mincôpxki: ( ) ( ) ( ) ( ) 2222 22 11121112 aaaa −++++−++++ 4913=+= Suy ra: 1213 zizi −++++ đạt GTNN là 13 khi ( ) 1 211 3 aaa −=+= . Nhận xét: Bài toán trên có thể được giải quyết bằng cách đưa về bài toán hình học phẳng. Câu 59: Cho các số phức 1 2 zi =−+ , 2 2 zi =+ và số phức z thay đổi thỏa mãn 22 12 16 zzzz−+−= Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Giá trị biểu thức 22Mm bằng A. 15 B. 7 C. 11 D. 8 Lời giải Giả sử ( ) , zxyixy=+ . Ta có: 22 12 16 zzzz−+−= 22 2216xyiixyii ++−++−−= ( )2 2 14 xy +−=

Suy ra tập hợp điểm biểu diễn của số phức z là đường tròn tâm số phức ( )0;1 I bán kính 2 R = .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

zizi

đườ

( ) 2222 24xyxy

tâm ( )3;3 I và bán kính bằng 1. Biể

Gọi ( ) ; Mxy là điểm biểu diễn số phức z . Do 222zi−−= nên tập hợp điểm M là đường

tròn ( ) ( ) ( ) 22 :224Cxy−+−= . Các điểm ( )1;1 A , ( )5;2 B là điểm biểu diễn các số phức 1 i + và 52i + . Khi đó, PMAMB =+ Nhận thấy, điểm A nằm trong đường tròn ( )C còn điểm B nằm ngoài đường tròn ( )C , mà 17 MAMBAB+= . Đẳng thức xảy ra khi M là giao điểm của đoạn AB với ( )C

Ta có, phương trình đường thẳng :430ABxy−+= . Tọa độ giao điểm của đường thẳng AB và đường tròn ( )C là nghiệm của hệ với 15 y 

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

m = 3313 wi=+ . Vậy 1258 w = .

Câu 63: Cho hai số phức 12 , zz thỏa mãn 1 12zi+−= và 21ziz = . Tìm giá trị nhỏ nhất m của biểu thức 12zz ? A. 21 m =− . B. 22 m = . C. 2 m = . D. 222 m =− . Lời giải Đặt 1 ;, zabiab=+ 2 zbai=−+ ( ) ( ) 12 zzabbai−=++− Nên ( ) ( ) 22 121 2. zzabbaz −=++−= Ta lại có 111 2112 ziziz =+−+−=+ 1 22 z − . Suy ra 1212.222zzz−=−

2 MH +

2 MH

65: Cho các số phức w , z thỏa mãn wi35 5 += và ( )( )5w2i4 z =+− . Giá trị lớn nhất của biểu thức 12i52iPzz=−−+−− bằng A. 67 . B. 4213 + . C. 253. D. 413. Lời giải Gọi izxy =+ , với , xy  . Khi đó ( ) ; Mxy là điểm biểu diễn cho số phức z . Theo giả thiết, ( )( )5w2i4 z =+− ( ) ( )( ) 5wi2i45i z +=+−+ ( )( ) 2iwi32i z −+=−+ 32i3 z −+= . Suy ra ( ) ; Mxy thuộc đường tròn ( ) ( ) ( ) 22 :329Cxy−++= . Ta có 12i52iPzz=−−+−− MAMB=+ , với ( )1;2 A và ( )5;2 B .

Gọi H là trung điểm của AB , ta có ( )3;2 H và khi đó:

322zi−−= 2 MI = ( );2MI với ( )3;2 I = 122252 PziziMAMB =+−+−−=+ với ( )1;2 A = , ( )2;5 B =

Ta có 2 IM = ; 4 IA = . Chọn ( )2;2 K thì 1 IK = . Do đó ta có 2 . IAIKIM = IAIM IMIK = IAM và IMK đồng dạng với nhau 2 AMIM MKIK == 2 AMMK=

Từ đó 2 PMAMB =+ ( ) 2 MKMB=+ 2BK 

Dấu bằng xảy ra khi và chỉ khi M , K , B thẳng hàng và M thuộc đoạn thẳng BK

Từ đó tìm được ( )2;23 M =+

Cách 3:

Gọi ( ) ; Mab là điểm biểu diễn số phức zabi =+ Đặt ( )3;2 I = , ( )1;2 A và ( )2;5 B .

Ta xét bài toán: Tìm điểm M thuộc đường tròn ( )C có tâm I , bán kính 2 R = sao cho biểu thức 2 PMAMB =+ đạt giá trị nhỏ nhất.

Trước tiên, ta tìm điểm ( ) ; Kxy sao cho 2 MAMK = ( )MC Ta có ( ) ( ) 22 22 244 MAMKMAMKMIIAMIIK ==+=+ ( ) ( ) 2222222 2.42.2434 MIIAMIIAMIIKMIIKMIIAIKRIKIA ++=++−=+− ( )* .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Phương trình đường tròn ( ) ( ) ( ) 22 :324Cxy−+−= . Tọa độ điểm M là nghiệm của hệ ( ) ( ) 22

22 32423 x x xy y

=  =     −+−= =+     hoặc 2 23 x y

=    =−   . Thử lại thấy ( )2;23 M + thuộc đoạn BK . Vậy 2 a = , 23 b =+ 43 ab +=+ Câu 67: Biết rằng hai số phức 1z , 2z thỏa mãn 1 34i1 z −−= và 2 1 34i 2 z −−= . Số phức z có phần thực là a và phần ảo là b thỏa mãn 3212 ab−= . Giá trị nhỏ nhất của 1222Pzzzz=−+−+ bằng: A. min 9945 11 P = . B. min 523 P =− . C. min 9945 13 P = . D. min 525 P =+ .

Lời giải Gọi 1M , 2 M , M lần lượt là điểm biểu diễn cho số phức 1z , 2 2z , z trên hệ trục tọa độ Oxy . Khi đó quỹ tích của điểm 1M là đường tròn ( )1C tâm ( )3;4 I , bán kính 1 R = ; quỹ tích của điểm 2 M là đường ( ) 2C tròn tâm ( )6;8 I , bán kính 1 R = ; quỹ tích của điểm M là đường thẳng :32120dxy−−= Bài toán trở thành tìm giá trị nhỏ nhất của 12 2 MMMM++ .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

A. 133 4 B. 39 4 C. 33 D. 13 4 Lời giải

Thay 2 1 z = vào P ta có 2 11Pzzz=++−+ 2 2 1 zzzz=++−+ 2 1. zzzzz=++−+ 11zzzz =+++− 11zzz =+++− . Mặt khác ( )( ) 2 1112 zzzzz +=++=++ . Đặt tzz =+ do 1 z = nên điều kiện  2;2 t − .

Suy ra 21Ptt=++− .

Xét hàm số ( ) 21fttt=++− với  2;2 t − ( ) 1 1 22 ft t  =+ + với 1 t  . Suy ra ( ) 0 ft   với 1 t  ( ) 1 1 22 ft t  =− + với 1 t  . Suy ra ( ) 0 fx  = 7 4 x =

Ta có bảng biến thiên Từ bảng biến thiên suy ra 13 4 M = tại 7 4 t = và 3 m = tại 2 t = Vậy 133 . 4 Mm =

72: Cho số phức z thỏa mãn : 2 zzi =+ . Giá trị nhỏ nhất củ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

t

độ

m M vào vế trái phương trình đườ

th

ng kết quả bằng 0 thỏa ta được đáp án A Tự luận: Ta có ( ) 321333 3233331313 wzzzziziwziAM =−−=+−=+−→=+−= với ( )1;3 A ( ) ; Mxy biểu diễn số phức 3z nằm trên đường thẳng :210dxy−+= và ( )1;3 Ad − Khi đó 3 313 wziAM =+−= đạt giá trị nhỏ nhất khi AM ngắn nhất  AMd ⊥ AMd ⊥ nên AM có phương trình: 210 xy++= Khi đó MAMd = nên 31 ;. 55 M    . Câu 74: Cho số phức z thoả mãn 125−+=zi . Giá trị lớn nhất của 1 ++ zi bằng A. 5 B. 52 C. 20 D. 25 Lời giải Cách 1. Ta có 112212225 ziziizii ++=−++−−++−= .

Đặt ( ) ,, zxyixy=+ thì từ điều kiện ta có: ( ) ( ) 22 125xy−++= Gọi ( ) ; Mxy là điểm biểu diễn cho z và ( )1;1 A là điểm biểu diễn cho số phức 1 i , khi đó 1 ziAM ++= với M thuộc đường tròn ( )C tâm ( )1;2 I bán kính 5 R = Dễ thấy ( )AC  , do đó 225AMR= . Suy ra max125 zi++= , đẳng thức xảy ra khi MK  Cách 3. 125−+=zi ( )* Đặt =+ zxyi ( ) ,  xy , khi ấy, ta có ( ) *125 +−+= xyii ( ) ( ) 125−++= xyi  =     =  

25cos  ak ak

t   =++=−=−        =++==    

) ( ) 22 5sin25cos1 =++− aa 1045sin25cos=+−aa 15sin 25cos  −=   +=   xa ya

xa ya . Ta có ( ) ( )111 ++=+++ zixyi ( ) ( ) 2211=+++ xy    

( ) ( ) 22 125−++= xy   Vì ( ) 1sin1 −− a  với mọi ;  a  101011010 −+++ zi 0125++ zi . Vậy giátrị lớnnhất của 1 ++ zi là 25 .Dấu "" = xảyrakhi ( ) sin1 −= a  2 2 −=+ak   coscos2sin5 25 sinsin2cos25 25

12 21 −=    +=−  x y 3 3 =    =−  x y 33=−zi. Câu 75: Cho số phức z thỏa mãn ( ) ( ) 222 izizi−−+= . Giá trị nhỏ nhất của z bằng

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 25 cos 5 5 sin 5

đó

p hợp điểm biểu diễn của z là đường thẳng :230 xy −−= Ta có ( ) mind, zO= . Gọi d là đường thẳng qua O và vuông góc với  :20dxy += . Gọi 2036

Khi đó, ( ) ( ) ( ) ( ) ( ) 2222 111216430 xyxyxy +++=−+−+−=

Ta thấy đường thẳng :6430dxy+−= không đi qua điểm ( )2;1 N nên tập hợp điểm M là đường thẳng d Ngoài ra, zOM = nên z nhỏ nhất khi OM nhỏ nhất, tức là ( ) 22

3313 d, 26 64 OMOd=== + . Vậy 313 min 26 z = Câu 78: Cho số phức z thỏa mãn ( )( ) 2 251231zzzizi −+=−++− . Tính min, w với 22 wzi =−+ A. 1 min 2 w = . B. min1 w = . C. min3 2 w = . D. min2 w = . Lời giải

Theo giả thiết, ( )( ) 2 251231zzzizi −+=−++− ( )( ) ( )( )12121231 zizizizi −+−−=−++− ( ) 12.12130 zizizi −+−−−−+= ( ) ( ) 1201 12132 zi zizi −+=   −−=−+   . ( ) 112012 zizi −+==− . Khi đó, 12221wii=−−+= ( )3 Đặt zxyi =+ ( , xy  ). Khi đó, ( ) ( ) ( ) ( ) ( )21213 xyixyi −+−=−++ ( ) ( ) ( ) ( ) ( ) ( ) 222222 11 121323 22 xyxyyyyzxi −+−=−++−=+=−=− . ( ) ( )2 3993 22 2442 wxix =−+=−+= x  . ( )4 .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi M là điểm biểu diễn số phức z , ( ) 1 3;2 F , ( ) 2 3;1 F , ( )2;0 A và ( )1;3 B . Ta có 32335zizi +−+−+= và 12 35 FF =  1212 MFMFFF += .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Suy ra tập hợp điểm M là đường tròn C tâm ; I 24 , bán kính R 3 Mặt khác: ; zbiAzAb 1122 Tập hợp điểm A là đường thẳng :.dx 1 2 ;zaiBzBa 22 1 Tập hợp điểm B là đường thẳng :.dy 2 1 Giao điểm của d1 và d2 là ; P 21 Gọi H và K lần lượt là hình chiếu của M trên d1 và . d2 Ta có: TzzzzMAMBMHMKMP 22 22222 12 T đạt giá trị nhỏ nhất khi , AHBK và ,, IMP thẳ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Câu 84: Cho số phức zabi =+ ( a , b  ) thỏa mãn 1 z = . Tìm giá trị lớn nhất của biểu thức 222Azz=++− . A. 10. B. 52 . C. 102 . D. 7. Lời giải Ta có: ( ) 2 2 2 22 zab +=++ ; ( ) 2 2 2 22 zab −=−+ . Suy ra: 2222zz++− ( ) 22 28 ab =++ 2 28 z =+ 10= Ta có: ( ) ( )( ) 2 22 222222122250Azzzz =++−+++−=

Vì 0 A  nên từ đó suy ra 5052 A = Vậy giá trị lớn nhất của A là 52 .

Câu 85: Cho số thực a thay đổi và số phức z thỏa mãn ( ) 2 112 zia aai a = + . Trên mặt phẳng tọa độ, gọi M là điểm biểu diễn số phức z . Khoảng cách nhỏ nhất giữa hai điểm M và ( )3;4 I là A. 6 B. 5 C. 4 D. 3 Lời giải

Ta có: ( ) ( )( ) ( ) 2 2 22 2

aaai zai zz aa a

12 12 111 iaaai ziaz aai aa a == ++ + ( ) ( ) 32 2 22 2

+++ + === ++ + Vậy tập hợp các điểm biểu diễn của số phức z là đường tròn tâm O bán kính 1 R = Ta có: 5 OI = . Do đó: min1 514 OMOMOIR==−=−=

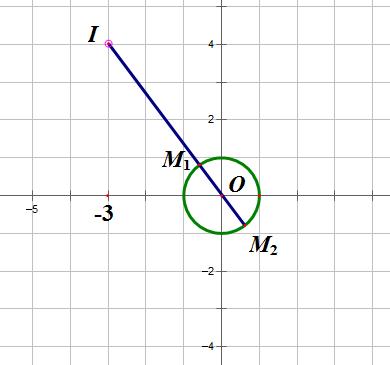
1 1. 11 1

Câu 86: Xét số phức z thỏa mãn 245zi−−= . Gọi a và b lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của z . Giá trị biểu thức 22ab bằng A. 40 B. 45 C. 20 D. 25

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Lời giải Gọi ( ) ; Mxy là điểm biểu diễn số phức zxyi =+ với , xy  . Ta có ( ) ( ) 22 245245zixy −−=−+−=  tập hợp điểm biểu diễn số phức z là một đường tròn có tâm ( )2;4 I và bán kính 5 R =

Kẻ đường thẳng đi qua 2 điểm O và I cắt đường tròn tại 2 điểm M và N như hình vẽ. 22 2425 OI =+= ; 5 IMINR=== Từ hình vẽ ta thấy: min

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( )( ) 68 zzi −+ là số thực. Biết rằng 12 4 zz−= Giá trị nhỏ nhất của 12 3 zz + bằng A. 521 B. 20421 C. 20422 D. 522 Lời giải Giả sử số phức zxyi =+ thỏa mãn ( )( ) 68 zzi −+ là số thực. Ta có: ( )( ) ( ) ( ) ( )( ) ( ) ( ) 686(8)688868 zzixyixyiixyxyxxyyi −+=+−++=−−++−−+−  Để là ( )( ) 68 zzi −+ số thực thì ( ) ( ) ( ) ( ) 22 28680345 xxyyxy −−+−=−+−= Vậy điểm biểu diễn số phức 12 , zz thuộc đường tròn tâm ( )3,4 I , bán kính 5 R = Giả sử 111 zxyi =+ có điểm biểu diễn ( )11 , Axy ; 222 zxyi =+ có điểm biểu diễn ( ) 22 , Bxy . Vì ( ) ( ) 22 121212444 zzxxyyAB −=−+−== Ta xét 1233 zzOAOB +=+ Gọi H là trung điểm ,AB K là trung điểm HB, khi đó ta có:

GTNN của môđun z là min min zOM = 17 OIR =−= ( )1 Đẳng thức xảy ra khi ( )MOIC = và M nằm giữa O và I ( )2

Từ ( )1 và ( )2 ta có M là trung điểm OI nên ( )1;4 M .

Suy ra 1;4ab== . Khi đó: 2 2321210mab=−=−=−

Câu 91: Xét các số phức ( ) , zabiab=+ thỏa mãn 2322zi+−= . Tính 2 Pab =+ khi 1672 zizi +++−− đạt giá trị lớn nhất. A. 3 P = . B. 3 P =− . C. 1 P = . D. 7 P = . Lời giải

Đặt ( ) ( ) ( )1;6,7;28;8ABAB −−= và trung điểm của AB là ( )3;2 K Gọi ( ) ; Mab là điểm biểu diễn số phức z ta có: ( ) ( ) 22 238ab++−= M  thuộc đường tròn ( )C có tâm ( )2;3 I , bán kính 8 R = . Ta thấy ( ) 5;5.0 IKIKABI =−= nằm trên đường thẳng trung trực của AB Xét tam giác 2 222 2 2 AB MABMAMBMK+=+ . ( ) ( )2 222222 244 MAMBMKABMAMBMAMBMKAB +=++++ Ta có 1672 zizi

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Vậy điểm M cần tìm ứng với 2 t =− khi đó ( ) 4 4;52853 5 a MPab b =−  −=+=−+=−  =  Câu 92: Cho số phức z thỏa mãn ( ) 11332 izi ++−= . Giá trị lớn nhất của biểu thức 2623 Pzizi =+++−− bằng A. 56 . B. ( )1516 + . C. 65 . D. 10315 + . Lời giải Cách 1 ( ) 11332 izi ++−= 13 132 1 i iz i ++= + ( ) ( )1231zi −+= . Gọi ( ) ; OMxy = , ( )1;2 OI = là vec tơ biểu diễn cho các số phức zxiy =+ , w12i =+ .

Từ ( )1 có 3 OMOI−= 3 MI = . Suy ra M thuộc đường tròn ( )C tâm ( )1;2 I bán kính 3 R = , ( ) ( ) ( ) 23 :129Cxy−+−= Gọi ( )2;1 OA =−− , ( )2;3 OB = lần lượt là vec tơ biểu diễn cho số phức 2 ai =−− , 23 bi =+ .

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi ( ) ( ) ; MxyC  . ( ) ( )245172,4;5;1;7 AziziMAMBAB =−+++−=+−− . ( ) 5 22,1; 2 AMAMBMAMCC  =+=+−  Ta có: ( ) 33 0; 22 C ICICR  ==   Suy ra, điểm C nằm trong đường tròn ( )C . Vậy, đường thẳng AC cắt đường tròn ( )C tại hai điểm. Do đó, để ( ) 2 AMAMC =+ đạt giá trị nhỏ nhất thì M phải nằm giữa hai điểm A và C .

( ) 513 22, 2 AMAMCACAC =+= . 513 Aab= .

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi ( )111 ; Mxy , ( ) 222 ; Mxy ( ) ( ) 22 121212 8 5 MMxxyy =−+−= . Mà 1z là nghiệm phương trình 63269 iizzi−+=−− ( ) ( ) ( ) ( ) 1111 632629 yxixyi −+−=−+− ( ) ( ) ( ) ( ) 2222 1111 632629 yxxy −+−=−+− 22 111168240xyxy +−−+= ( )111 ; Mxy  đường tròn 22 ():68240 Cxyxy+−−+= . Tương tự ( ) ( ) 222 ; MxyC  . Đường tròn () C có tâm ( )3;4 I , bán kính 1 R = Goị M là trung điểm 12MM 12IMMM⊥ , 2 22 1 43 1 55 IMRMM  =−=−=

46

Vậy: Giá trị lớn nhất của 32 2 T = Câu 96: Cho các số phức z thỏa mãn 2223zz−++= . Tìm giá trị nhỏ nhất của biểu thức 233323 Pzizizi =+++−++− . A. 12 B. 6 C. 8 D. 10 Lời giải Gọi ( ) ; Mxy , ( ) 1 2;0 F

, ( ) 2 2;0 F , lần lượt là điểm biểu diễn cho các số phức zxyi =+ , 2 , 2 Có 2223zz−++= 12 23 MFMF += , có 12 2322 FF = .

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Đặt ( ) 2 23213 fyyyy =+++− , với 11 y − Có ( ) 2

23 1 321 y fy yy +  =− ++ ( ) 0 fy  = ( ) ++=+ 2 321231yyy , Có ( ) −111 y 2 39120 yy +−= ( ) ( ) 1nhaän 4loaïi y y

 =   =−  

Có ( ) 14219 f −=+ , ( ) 112 f = Suy ra ( ) −  = 1;1 12 y Minfy 12 P  Đẳng thức ( )1 xảy ra khi 0,1 231 0 2 33

 ==   ++ =  +  0,1xy == .

xy xy y x

Thử lại: Khi 0,1xy== có 12 P = Vậy

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Cho ( ) ( ) ( ) 12121122 ;,;; aaabbbababab ==+=++ , ta có: ( ) ( ) 22 2222 11221212 ababababaabb +−++++−+ . Dấu “ = ” xãy ra , ab  ngược hướng 1221 11 22

=       

abab ab ab

0 0

Câu 98: Cho số phức zabi =+ ( ) , ab thỏa mãn 4410zz++−= và 6 z lớn nhất. Tính Sab =+ . A. 11 S = . B. 5 S =− . C. 3 S =− . D. 5 S = . Lời giải Trong mp tọa độ Oxy , Ta gọi các điểm biểu diễn của các số phức: zxyi =+ là ( ) ; Mxy ; 40 zi =−+ là ( ) 1 4;0 F ; 40 zi =+ là ( ) 2 4;0 F . Ta có: 4410zz++−= 12 10 MFMF += ( ) ( )

 =++  −=−=  =−+   .

48 16 45 MFxy x MFMFxMFMF MFxy

2 22 1 22 1212 2 22 2

Từ và, suy ra 1 4 5 5 x MF =+ . Mặt khác ( )2 22 1 4 MFxy =++ ( ) 2 22 2 2 4 541 5259 xxy xy  +=+++=  

Vậy, tập hợp các điểm biểu diễn của số phức thỏa mãn 4410zz++−= là Elip có phương trình ( ) 22 :1 259 xy E += Theo đề, ta cần tìm điểm thuộc ( )E sau cho 6 z lớn nhất. Ta gọi các điểm biểu diễn số phức: 60 zi =+ là ( )6;0 A ; zabi =+ là ( ) ( ) ; MabE  ; 50 zi =−+ là ( )5;0 C . Do đó, 6 z lớn nhất khi và chỉ khi MA lớn nhất.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

điểm biểu cho các số phức 2 i −+ và 47i + 62 AB = . Từ đó ta được 62 MAMBAB +== nên tập hợp các điểm M biểu diễn cho số phức 1z là đoạn thẳng AB n

Dễ thấy hình chiếu vuông góc của điểm ( )2;1 I trên đường thẳng ( ) d là điểm ( )0;3 K thuộc đoạn AB suy ra MNKH  với H là giao điểm của IK với ( )C và thuộc đoạn IK .

Do đó ( ) min,221 MNKHdIABR==−=− . Vậy 12 min221 zz+=−

Câu 104: Cho số phức 12,, zzz thỏa mãn 124511ziz−−=−= và 484 zizi +=−+ . Tính 12zz khi 12 Pzzzz =−+− đạt giá trị nhỏ nhất

A. 8 B. 6. C. 41. D. 25 . Lời giải

Gọi A là điểm biểu diễn của số phức 1z . Suy ra A thuộc đường tròn ( )1C tâm ( ) 1 4;5,1IR =

Gọi B là điểm biểu diễn của số phức 2z . Suy ra B thuộc đường tròn ( ) 2C tâm ( ) 2 1;0,1IR =

Gọi ( ) ; Mxy là điểm biểu diễn của số phức zxyi =+

Theo giả thiết 484 zizi +=−+ 4 xy −= . Suy ra M thuộc đường thẳng ( ) 40 dxy−−= Gọi ( ) 2 ' C có tâm ( ) 2 '4;3,1IR−= là đường tròn đối xứng với đường tròn ( ) 2C tâm ( ) 221;0,1IR = qua đườ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

323zi −+=

Suy ra, tập hợp các điểm biểu diễn số phức z là đường tròn ( ) ( ) ( ) 22 :329Cxy−++= .

Gọi ( )MC  .

Ta có: ( ) ( )262;0;2,6;2PziziAMBMAB =−+−−=+ .

Suy ra ( ) 22 2 PAMBM +

Gọi H là trung điểm của cạnh AB .

Ta có: ( ) 2 222222224 2 AB PAMBMMHMHAB  +=+=+  

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Suy ra 222 122331 Pzzzzzz =−+−+− 222 ABBCAC=++ ( ) ( ) ( ) 222 AOOBBOOCAOOC =+++++ ( ) 62...OAOBOBOCOAOC=−++ ( )2 9 OAOBOC=−++ ( )2 93OG =− 2 99 OG =− . Dấu “ = “ xảy ra khi GO  , hay ABC đều. Câu 110: Cho số phức z thỏa mãn 3212. zzzz++− Gọi , Mm lần lượt là giá trị lớn nhất, nhỏ nhất của 43.zi −+ Giá trị của . Mm bằng: A. 28 B. 24 C. 26. D. 20 Lời giải Gọi ;;.zxyixy=+ Xét 3212326.(1) zzzzxy ++−+ Ta có: ( ) ( ) ( ) 22 43432Pzixy =−+=−++ Tập hợp những điểm biểu diễn ;;.zxyixy=+ thỏa mãn là miền trong của hình thoi ABCD với ( )0;3 A ; ( )2;0 B ; ( )0;3 C ; ( )2;0 D tạo bởi 4 đường thẳng 326. xy+= Điểm biểu diễn z thỏa mãn là đường tròn tâm ( )4;3 I bán kính 0 RP= P đạt min, max khi bán kính đường tròn đạt min, max khi xét sự tương giao với miền hình thoi .ABCD

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Ta có đường tròn giao với miền hình thoi điểm gần tâm nhất khi đường tròn tiếp xúc cạnh CD:

3260 xy−−= tương ứng có 22

3.42.36 12 . 13 32 m +− == + Điểm giao xa nhất là đỉnh ( )0;3 A

của hình thoi. Do đó 22 46213. M =+= .24.Mm =

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

tâm

) 1 6;3 I bán kính 1 6. R = Gọi ( ) ; Ncd là điểm biểu diễn số phức 2w

Ta có 1322264wiwi −+=−+= ( ) ( ) ( ) ( ) 22 2642616 cdicd −++=−++= .

Suy ra tập hợp điểm N là đườ

Câu 159: Cho số phức z thỏa mãn đồng thời hai điều kiện 2322zi−+= và biểu thức 7216 Tzizi =+++−− đạt giá trị lớn nhất. Tính giá trị biểu thức ( ) 20212022 Szi =−− . A. 20232 S = . B. 20222 S = . C. 20182 S = . D. 20172 S = . Lời giải

Chọn D

*Gọi M là điểm biểu diễn cho số phức z . Từ giả thiết 2322zi−+= ta suy ra M thuộc đường tròn ( )C tâm ( )2;3 I , bán kính 22 R = *Xét hai điểm ( )7;2 P , ( )1;6 Q , ta thấy 82 IPIQR == nên hai điểm , PQ nằm ngoài đường tròn ( )C và điểm I nằm trên đường trung trực của đoạn PQ . Gọi ( )3;2 J là trung điểm của PQ. Theo giả thiết ta có ( ) 2 222222 2 PQ TMPMQMPMQMJ 

. Ta thấy biểu thức T đạt giá trị lớn nhất khi MPMQ = và MJ lớn nhất, điều này xảy ra khi

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

trị nhỏ nhất của 12 3 zz + bằng A. 20422 . B. 521. C. 20421. D. 522 . Lời giải Chọn A Giả sử zxyi =+ , , xy  .Gọi , AB lần lượt là điểm biểu diễn cho các số phức 12 , zz . Suy ra 12 4 ABzz

Câu 161: Cho số phức z thỏa mãn ( ) ( ) 121242 iziz ++++−= . Gọi max,min mznz == và số phức vmni =+ . Tính 2022 v ? A. 10112 B. 20222 C. 10116 D. 20226 Lời giải Chọn C

Ta có ( ) ( ) 121242114 izizzizi ++++−=+−+−+= M là điểm biểu diễn số phức z , ( ) 1 1,1 F là điểm biểu diễn số phức 1 1 zi =−+ ( ) 2 1,1 F là điểm biểu diễn số phức 1 1 zi =− . Khi đó ta có 12 4 MFMF+= , tập hợp điểm M biểu diễn số phức z là elip nhận 1F , 2F làm 2 tiêu điểm.

Ta có 12 22222FFccc === . Lại có: 2a42 a == Suy ra : 22 422 bac=−=−= . Elip có độ dài trục lớn là 12 4 AA = , độ dài trục bé là 12 22 BB = Mặt khác O là trung điểm 1212 , AABB nên 11 max2,min2 mzOAanzOBb ======== . Do đó 2022 10112266vmniivv =+=+== Câu 162: Gọi S là tập hợp tất cả các số phức z thỏa mãn 12zi−+= Xét các số phức , zz12 thuộc S thỏa mãn 21 22 zz−= . Giá trị lớn nhất của biểu thức 22 122222 Pzizi =−+−−+ bằng A. 6. B. 12. C. 8. D. 9. Lời giải Chọn C

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi I là điểm biểu diễn số phức 1 i. Ta có 12zi−+= ( ) 12zi −−= nên tập hợp các điểm biểu diễn số phức z là đường tròn tâm ( )1;1 I , bán kính là 2. Gọi , AB lần lượt là điểm biểu diễn các số phức , zz12 thuộc S . Do 21 22 zz−= nên 22 AB = . Gọi J là điểm biểu diễn của số phức 22i . 22 122222 Pzizi =−+−−+ ( ) ( ) 22 122222 zizi =−−−−− 22JAJB=−

.

Ch

n A

Ta có: 432zi−−= ( ) ( ) 22 432432xyiixy +−−=−+−=

m ( )4;1 B Gọi E là trung điểm của đoạn AB . Khi đó ta có ( ) 2;2,5EIE = , 25 AB = và 222 2 24 MAMBAB ME + =− Suy ra 22 22222 0 22102 22 ABAB PMAMBMEMEME =+=+=++ Ta có ( ) ( )2 2 2 00 2225214410 MEIEIM=+=+=+ , 2 10 2 AB = Suy ra 144101024410PP +++ . Vậy giá trị lớn nhất của P là max 24410 P =+ . Câu 164: Cho số phức ( ) , zabiab=+ thỏa mãn 13 1 13 zi i −+ = . Tính giá trị của biểu thức 32 Tab =− khi biểu thức 253 Pzizi =−+−+ đạt giá trị nhỏ nhất. A. 2. B. 5. C. 3. D. 2. Lời giải Chọn B Gọi M là điểm biểu diễn số phức ( ) ; zabiMab =+ . Theo giả thiết ( ) ( ) 22 13 11313134 13 zi ziiab i −+ =−+=−−++=

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Khi đó điểm M luôn thuộc đường tròn tâm ( )1;3 I và bán kính 2 R = . Gọi , AB lần lượt là các điểm biểu diễn các số phức 12,53 zizi ==− ta có ( ) ( )0;1,5;3AB .

Do đó 2532 PziziMAMB =−+−+=+

Lấy điểm E thuộc đoạn thẳng IB sao cho 1 IE = Ta có ( )442;3IBIBIEE==− . Mặt khác 2 . IMIEIB = IMIB IEIM = mà MIEBIM = suy ra hai tam giác IME và IBM đồng dạng. 22 MBIB MBME MEIM === ( ) 22245 MAMBMAMEAE +=+= . Do đó 2 PMAMB =+ có giá trị nhỏ nhất là 45 khi M là giao điểm của đoạn thẳng EA và đường tròn tâm I Đường thẳng EAnhậ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

+ Nhận xét: Trường hợp 1 2 x =− suy ra (*) trở thành 50−= . Suy ra tập hợp điểm biểu diễn M của số phức 1z là một hypebol ( ) 43 : 21 x Hy x −+ = + Gọi N là điểm biểu diễn số phức 2z , 3 0; 2 I    . Ta có 22 33 111 22 ii zzNI  +=−−==   .

Suy ra tập hợp điểm biểu diễn N của số phức 2z là đường tròn ( )C tâm 3 0; 2 I    , bán kính 1 R = . Ta có 12 PzzMN =−= .

Suy ra, tập hợp điểm biểu diễn số phức w là đường có tròn tâm ( )1;1 I và bán kính 12 R = Vậy hai điểm , MN biểu diễn hai số phức 12 , ww thuộc đường tròn ( ) ( ) 22 11144xy−++= Ta có: 12 12;2IMINMNzz===−= . Gọi A là điểm biểu diễn số phức 5i . Ta có ( )0;5 A và 37 IA = . ( ) ( ) ( ) 22 22 22 125522. PwiwiIMIAINIAIMINIAIMINIAMN =−−−=−−−=−−−= ( ) ( ) 2..cos.437cos. IAMNIAMNIAMN== . max 437 P = ( ) cos,1 IAMN = Câu 168: Xét các số phức z và w thoả mãn ( ) 122 zwwi −=+ . Gọi S là tập các số phức z sao cho tập hợp các điểm biểu diễn số phức w trên mặt phẳng toạ độ

Oxy là tia Oy . Giá trị lớn nhất của ( ) 123142 Pziizi =−+−+−− với 12 ; zzS  là A. 2. B. 42. C. 2 . D. 22. Lời giải Chọn C Ta có ( ) 2 122 2 z zwwiw zi −=+= + với 2 zi − Gọi ( ) ; Mxy là điểm biểu diễn số phức z Điều kiện 2 zi − tương đương với M không trùng với ( )0;2 A Ta có ( ) ( )  ( ) (

11

Ta có ( ) 123142 Pziizi =−+−+−− ( ) ( ) ( ) 12313 ziizi =−−−+−− ( ) ( ) 12323 zizi =−−−−− Gọi 12;; MME lần lượt là các điểm biểu diễn của số phức 12 ; zz và 3 zi  =−  12 ; MM thuộc nửa đường tròn ( )C ở trên và ( )3;1 E Như vậy 12 2 PEMEM =− Gọi F là giao điểm của đường thẳng EI và nửa đường tròn ( )12;1 F −− Dễ thấy 1 22 EMEFEIR=+=+ ; 2 2 EMEB= .

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Theo giả thiết ( )( ) w zii −+ là số thực nên giả sử ( )( ) w ziik −+= ( ) w w k zii i −= + ( ) 2 w w

ki zi i −= + ( )1 Gọi ( )0;1 I là điểm biểu diễn của số phức i . Từ ( )1 suy ra 2 w

k IAIB i = +  3 điểm ,, IAB thẳng hàng hay AB luôn đi qua điểm cố định ( )0;1 I . Gọi H là trung điểm của AB Ta có 2222 2224215PABAHOAOHOI ===−−= . Dấu bằng xảy ra khi HI  hay OIAB ⊥ Câu 171: Cho số phức ( ) ,, zxyixy=+ thoả mãn 2346zzzzi +−+−+ và 13 zizi −−++ . Gọi , Mm là giá trị lớn nhất và nhỏ nhất của biểu thức 235Pxy=++ . Khi đó Mm + bằng A. 33 5 . B. 17 5 . C. 13 5 , D. 22 5 . Lời giải

Chọn D Gọi ;;.zxyixy=+ Xét 23461363.(1)zzzzixy +−+−+−++

Tập hợp những điểm biểu diễn ;;.zxyixy=+ thỏa mãn là miền trong của hình thoi ABCD với ( )2;2 A ; ( )1;1 B ; ( )4;2 C ; ( )1;3 D tạo bởi 4 đường thẳng 1363.xy−++ Ta có: 13220zizixy −−++++ Tập hợp những điểm biểu diễn z thỏa mãn là nữa mặt phẳng chứa điểm O . Suy ra tập hợp những điểm biểu diễn ;;.zxyixy=+ thỏa mãn và ( )2 là miền trong của ngũ giác EBCDF với 210 ; 77 E    ; ( )1;1 B ; ( )4;2 C ; ( )1;3 D ; 214 ; 55 F   

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( ) ( ) ( ) ( ) 2222 21 xymxmy −++=−++ ( ) ( ) ( ) ( ) 2222 21xymxmy −++=−++ ( ) ( ) 242230 mxmy −+−+=

Do đó S là tập hợp các số phức có điểm biểu diễn là giao của đường tròn ( )C và đường thẳng

d với ( ) ( ) ( ) 22 :1281Cxy++−= và ( ) ( ) :242230 dmxmy−+−+= .

( )C là đường tròn tâm ( )1;2 I , bán kính 9 R = .

Gọi , AB lần lượt là điểm biểu diễn hai số phức 12 , zz . Khi đó 12ABzz =− . Độ dài AB lớn nhất khi AB là đường kính của đường tròn ( )C 12 18 zzAB −== . Ta có I là trung điểm của AB nên có ( ) 222 22222 24 24 OAOBAB OIOAOBOIAB + =−+=+ ( ) 22 22 12 24zzOIAB

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi D thuộc đường tròn ( ) ( )2 2 :14Cxy−+= sao cho BCD đều và EMD  sao cho MBME = . Khi đó ta suy ra ( )3;0 D và nhận định như sau:

Tứ giác DBMC nội tiếp nên 60 DCBDMB== , khi đó ta suy ra BME đều. Lại có tiếp 60 DBECBECBECBMDBECBM +==+= Xét ABE và CBM có: ;; DBBCDBECBM == BDMBCM = , suy ra ( )DBECBMcgc =−− khi đó ta suy ra DECM = Suy ra: 333 Pzizizi =+−+−++ 37 MAMBMCMAMEDEMAMDAD =++=++=+= Dấu bằ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

+ Gọi E là điểm đối xứng với C qua 1d . Đường thẳng 1 qua ( )3;0 C và vuông góc với 1d có phương trình là 3 26260 12 xy xyxy =−+=+−= Khi đó hình chiếu 1H của C lên 1d có tọa độ thỏa mãn 1

5 2410 5 ;1 2 260 2 1

 −−= =      +−=    =  .

xy x H xy y

Vì E đối xứng với C qua 1d nên 1H là trung điểm của CE . Suy ra ( )2;2 E + Gọi D là điểm đối xứng với C qua 2d . Đường thẳng 2 qua ( )3;0 C và vuông góc với 2d có phương trình là 3 26260 12 xy xyxy =−=−−= Khi

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

i gi ===

Câu 175: Cho hai số phức z và w thoả mãn 41 z −= , 223 wiwi −−=++ và 13 wz i −+ là số thự C. Gọi M , m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức Pzw =− . Tổng Mm + bằng A. 42 . nn ABAB nn

B. 410 . C. 815 3 . D. 85 . L  

i

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn 2.42 25 21 I dR  + == +− Suy ra, đường thẳng  không cắt đường tròn ( ) C Ta có: ( ) ( ) . 11 Cos,Sin, 22 AB AB

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

3260 xy−−= . Tập hợp điểm biểu diễn 1z là đường thẳng :3260dxy−−= . 22:322zzi+−= , suy ra tập hợp điểm biểu diễn 2z là đường tròn ( ) ( ) ( ) 22 :324Cxy++−= tâm ( )3;2 I , bán kính 2 r = Số phức 1 zxyi =+ được biểu diễn bởi điểm ( ) ; Axyd  Số phức 2z được biểu diễn bởi điểm (C) B  Gọi điểm. Ta có 112 3 PzizzAMAB =+++−=+ . Gọi 1M

là điểm đối xứng với M qua d , ta có: ( ) 1 3;5 M và

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Từ giả thiết ta có: A thuộc đường tròn tâm ( )0;5 I bán kính 1 22 R = , B thuộc đường tròn tâm ( )1;8 J bán kính 2 2 R = , M thuộc đường thẳng  : 250xy−+=

Bài toán trở thành khi PMAMB =− lớn nhất, tính QOAOM =+ . Nhận thấy I, J ở về hai phía của đường thẳng  . Gọi , BJ là các điểm đối xứng của , BJ qua  . Tính được ( )0;5 J Ta có MBMBM 

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi 111. zxyi =+ có điểm biểu diễn ( )11 ; Axy ; 222. zxyi =+ có điểm biểu diễn ( ) 22 ; Bxy và 3 33 zi =− có điểm biểu diễn ( )3;3 C .

Ta có: ( ) ( ) 22 121212888 zzxxyyAB −=−+−== . Xét 12 33 TzziOAOBOC =++−=++ Gọi H là trung điểm AB 4 AH = và 3 OHABOH⊥= Suy ra: 2.2.2. TOAOBOCOHOCOHOCOHOC =++=++=+ 632 T + . Dấu "" = xảy ra khi OH cùng hướng OC

Câu 182: Gọi S là tập hợp tất cả

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( ) 22 2222

1 22 y i xy xyxyx =+ + ++− . Do w có phần thực bằng 1 2 nên 2222 22

11 11 2 2 xyxy xy =+=+= + . Đặt 111 zxyi =+ ; 222 zxyi =+ 22 11 1 xy += ; 22 22 1 xy+= Từ ( ) ( ) ( ) 222 1 22 1212 1 1 2 212122 2 1121 z xxyyxxy zxxy y y −=−= +++ + + −=  ( ) ( ) 12121212 22121 xxyyxxyy −+=+= ( ) 2222 1212121223xxyyxxyy +++++= ( ) ( ) 22 1212 3 xxyy +++= ( )2 1212333yyyy +−+ . Ta có: ( ) ( ) ( ) 2222 112 2 2 2 2 2 1 1 1142 P xyxy zz y i y i =++++++ + = = + ++ 423 P  + . Dấu "" = xảy ra khi và chỉ khi 12xx =− và 12 3 yy+= . Vậy giá trị lớn nhất của P bằng 423 + . Câu 183: Cho hai số phức , uv thỏa mãn 1 uv−= và 434 uiv −−=− . Gọi , Mm lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 5492 Tuvi =−−+ . Khi đó 2 Mm bằng A. 49. B. 51. C. 50. D. 58. Lời giải Chọn B Ta có: ( )4314543435* iuvuviuvuvi +−++−=+=+−++−=+= Gọi , AB lần lượt là các điểm biểu diễn số phức , uv và điểm ( )4;3 C Theo ( ) *,,, OBBAACOCOBAC++= thẳng hàng theo đúng thứ tự đó.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( )( ) ( ) ( ) ( ) ( ) ( ) 12 1101;1zziacbdiiacbdABOC −−=−+−−−−−=⊥=−   hay AB cùng phương với ( )1;1 u = Ta có ( ) 0,45dAB = nên ( ) ( ) ( ) 12 2.,2,42zzABdAddIdR −==+= Khi đó ( ) ( )5;3,1;1AB nên 12 297130 zzi−=+= Câu 185: Cho hai số phức 12 , zz thỏa mãn 12 122zzi−−−= và 21 6632zzi+−−= . Giá trị lớn nhất của biểu thức 21 35 Pzzi =−−− bằng A. 210 . B. 10 . C. 25 . D. 45 . Lời giải Chọn D Ta có ( ) 21 122zzi−−−= , ( ) 21 15532zzii+−−−−= Đặt ( ) ( ) ( ) 121,,5;552AziBzCOC −−= Khi đó giả thiết tương đương 22,32ABOBAC=+= . Suy ra OCOBBAAC =++ , BA  thuộc đoạn OC và , BAOC cùng hướng.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Ta có ( ) 21 316232 PzziiOBOAOD =−−−−−=−− với ( )3;1 D Gọi 30IBIAI −= thuộc đoạn HK với ( ) ( )1;1,2;2HK 222 POIODDI=−= . Do đó max 245PDH== Câu 186: Cho các số phức 123 ,, zzz thay đổi thỏa mãn ( ) 1 1222 izi −+= , 2 41 iz −= và 3335zz−=− . Giá trị nhỏ nhất của biểu thức 1323 Pzzzz =−+−

bằng

A. 253 B. 743 C. 543 D. 843 Lời giải Chọn B Gọi A, B lần lượt là các điểm biểu diễn số phức 1z , 2z

Ta có: ( ) 1 1222 izi −+= 1 12zi −+= , suy ra A thuộc đường tròn ( )1C tâm ( ) 1 1;1 I bán kính 1 2. R =

Ta lại có: 224141izzi−=+= , suy ra điểm biểu diễn số phức 2z là đường tròn tâm ( )0;4 K bán kính 1 R = . Do đó B thuộc đường tròn ( ) 2C có tâm ( ) 2 0;4 I , bán kính 2 1 R = . Gọi ( ) ; Mxy là điểm biểu diễn số phức 3z

Ta có 3335zz−=− ( ) ( ) 2222 354 xyxyx −+=−+= , suy ra điểm M thuộc đường thẳng :40dx −= . Nhận xét: Hai điểm 12 , II cùng phía với đường thẳng d và đường thẳng d không có điểm chung với hai đường tròn ( ) ( ) 12,.CC

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Gọi ( )3C là đường tròn đối xứng với đường tròn ( )1C qua đường thẳng d , khi đó đường tròn ( )3C có tâm ( ) 3 7;1 I , bán kính 2. R = Khi đó, ứng với mỗi điểm ( )1AC  , tồn tại duy nhất một điểm ( )3 ' AC  sao cho điểm A và A đối xứng với nhau qua đường thẳng d và AMAM  = Ta có: 002312 743. PAMBMAMBMABABIIRR  =+=+=−−=− Dấu “=” xảy ra 000 ;; MMAABB

  . Vậy 743. MinP =−

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

  +−−    −−−

xyxy xyxy xykhixy xykhixy

−+−

( ) 290khi1,1 270khi1,11 2301,1 2501,1 

Gọi Q là điểm biểu diễn của số phức w . 33842626 wiwiQEQF −−+−−=+= , với ( ) ( )3;3,8;4EF . Mà 26 EF = , suy ra tập hợp điểm biểu diễn của số phức w là đoạn thẳng EF . Ta có PzwMQ =−= Dựa vào hình vẽ ta có ( ) 22

32.37 25 min, 5 12 PdEBC +− === + ( ) ( ) 22 max7814234. PFA==−−+−= 25 234 5 mM +=+ . Câu 188: Cho hai số phức , zwphân biệt thỏa mãn 4 zw== và ( )( )ziwi −+ là số thực. Giá trị nhỏ nhất của zw bằng A. 8. B. 23 . C. 215. D. 214 . Lời giải

Chọn C Cách 1: Đầu tiên ta đặt ẩn như sau: azi bwi =−   =−  thì khi đó ta có: 4 aibi+++=

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

( )( ) ( )( ) ( ) ( ) 1 ziwiabiicdiiacbdbdacadbci −+=+−−+=+−−++−−+

Mà do ( )( )ziwi −+ là số thực nên suy ra 1 0 1 ab acadbc cd −−+== . Gọi , AB lần lượt là điểm biểu diễn số phức , zw và điểm ( )0;1 C

Từ đó ta suy ra với hệ thức trên ta có được ,, ACB thẳng hàng. Khi đó ta có hình vẽ như sau:

Ta suy ra 22 max max 241215 zwAB−==−= . Cách 2: Sử dụng cách thuần đại số

Ta có: ( )( ) ( )( ) ( )( ) ( ) ( ) ( )11ziwiziwiziwiRzikwikikwzk −+=−+=−−−=−−=−

Suy ra: ( ) ( ) 22 22 1161 kkwzkwzk −=−−=− . Mà vì 1 k  nên suy ra 0 k  Do đó ( ) ( ) ( ) ( ) 222 2 22 11512 kkwzkwzkzwzwkzwzwkk −=−=+−+−+=−+− Tiếp theo, ta nhận thấy: ( ) ( ) 2 22 1511530150151228 kkkkkk −+=−−−−+− nên suy ra ( ) ( ) ( )28280kzwzwkzwzwk −+−+ . Từ đó ta

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

suy ra: ( )( ) ( ) ( )( ) Rez110 ziwiacbd −+=+−−= . Gọi ( ) ( ) ;,, AabBcd là các điểm biểu diễn số phức , zw với , AB lần lượt thuộc quỹ tích đường tròn tâm O , bán kính bằng 2 và 4. Cùng với điểm ( )0;1 C thì phương trình tương đương với .0ACBC = tức ta có được tam giác ABC vuông tại C . Ta có: ( ) ( ) ;1 ;1 ACab BCcd

 =−   =−   , gọi M là trung điểm AB . Khi đó 2 AB MC = . Từ đó ta có: ( ) ( ) ( ) ( ) 11 22

2221 2221 ABMCCOOMOM ABMCCOOMOM =+=+

Gọi , PQ tương ứng là điểm biểu diễn 124,3zz thì ( )29;229 8,9 QP OPOQ

 =−   ==   .

Gọi ( )1C là đường tròn tâm O bán kính 1 8 R = ( ) 2C là đường tròn tâm O bán kính 2 9 R = ( )3C là ảnh của ( ) 2C qua phép tịnh tiến ( )29;229 v =−

Khi đó ( )3C có tâm ( )29;229 I , bán kính 3 9 R = Có 145 OI = nên 1313 RROIRR −+ , do đó đường tròn ( )3C sẽ cắt đường tròn ( )1C tại 2 điểm phân biệt. Chọn P là điểm tùy ý trong 2 điểm đó.

Khi đó ( ) 3PC  nên theo tính chất phép tịnh tiến, tồn tại điểm ( )1QC  sao cho ( )29;229 QPv==− . Lại có ( )1PC  và ( ) 2QC  nên 8,9OPOQ== Tóm lại tồn tại các điểm , PQ sao cho hệ xảy ra, dẫn tới tồn tại 12 , zz sao cho đẳng thứ

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Câu 192: Cho hai số phức 12 , zz thỏa mãn 1 131zi−−= và 2215 zizi +−=−+ . Giá trị nhỏ nhất của biểu thức 221 1 Pzizz =−−+− bằng A. 101 B. 101 + C. 3 D. 285 1 5 Lời giải

các

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

i ( ) ; zxyixy=+ Do 345zi−−= nên điểm A biểu diễn số phức z thuộc đường tròn tâm ( )3;4 I , bán kính

ại có ( ) 2 222 221 Pxyixyiixyixyi =++−+−=++−+−=

) ( ) 22 22 21423 xyxyxy =++−−−=++

đó điểm A thuộc đường thẳng  : 4230 xyP++−= Để tồn tại x ; y thì ( ) ; dIR   22

4.32.43 5 42 P ++−  +  2310 P −  1333 P  .

max33MP== và min13mP==  22 1258 wMm=+= Câu 194:

hai

mãn 321ziz

, 12 22 zz

và s

ph

c w thoã mãn w241 i

th

c 2123wPziz=−−+− b

ng: A. 10 B. 171 C. 4 D. 26 Lời giải Chọn B Gọi zxyi =+ ta có 321ziz−−=− 30 xy +−= . Gọi điểm biểu diễn 12 , zz lần lượt là , MN thì , MN thuộc đường thẳng :30dxy+−= và 22 MN = Gọi điểm biểudiễnsốphứcw là B .Do w241 i −−= nên B thuộcđườngtròn ( )C tâm ( )2;4 I bán kính 1 R = . Khi đó 2123wPziz=−−+− NAMB=+ . Với ( )2;3 A Dựng hình bình hành ANMC thì ( )0;5 C . Khi đó NAMC = nên NAMB + nhỏ nhất khi MCMB + nhỏ nhất. Ta có đường tròn ( )C và điểm ( )0;5 C nằm về một phía so với đường thẳng d nên gọi ' C là điểm đối xứng với ( )0;5 C qua đường thẳng d thì ( )'2;3C . Khi đó MCMB + nhỏ nhất khi ',, CMB thẳng hàng khi M là giao điểm của đường thẳng ' CI và d

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Giá trị nhỏ nhất của biểu thức 12 2 zzzz −+− bằng A. 23 4 . B. 13 2 . C. 11 2 . D. 5. Lời giải

Chọn A

Gọi điểm ( )11 ; Mxy biểu diễn cho số phức 1 2z ; điểm ( )4;4 I biểu diễn cho số phức 44i + khi đó ta có 11 111 22244 844 ziziMI −−=−−== .Do đó tập hợp điểm M biểu diễn cho số phức 1 2z là đường tròn ( )C tâm ( )4;4 I , bán kính 1 4 R = .

Gọi điểm ( ) 22 ; Nxy biểu diễn cho số phức 2z , điểm ( ) 1 1;0 F biểu diễn cho số phức 1, điểm ( ) 2 1;0 F biểu diễn cho số phức 1, khi đó ta có 2212 112525zzNFNF −++=+= . Do đó tập hợp điểm N biểu diễn cho số phức 2z là elip có hai tiêu điểm 12 ; FF . Gọi điểm ( ) ; Pxy biểu diễn cho số phức z , điểm 5 1; 2 B    biểu diễn cho số phức 5 1 2 zi =−+ , điểm 3 ;3 2 C    biểu diễn cho số phức 3 3 2 i −+ , khi đó 53 22523613 22 ziziziziPBPC +−=+−+−=+−= . Do đó tập hợp điểm P biểu diễn cho số phức z là đường trung trực  của đoạn thẳng BC có phương trình 40 xy−+= . Khi đó ta có 12 2 zzzzPMPN −+−=+ Điểm đối xứng của ( )4;4 I qua đường thẳng  là ( )0;8 I nên đường tròn ( ) C đối xứng với đường tròn ( )C qua đường thẳng  có tâm ( )0;8 I bán kính 1 4 RR  ==

Do đó theo hình vẽ ta có: 123 82 44 PMPNPMPNPMPNMNIORON  ++=+==−−=−−= Vậy giá trị nhỏ nhất của biểu thức 12 2 zzzz −+− bằng 23 4 . Câu 196: Cho hai số phức 12 , zz thỏa mãn 1 321zi++= và 2 21zi+−= . Xét các số phức zabi =+ , ( ) , ab thỏa mãn 20 ab−= . Khi biểu thức 12 2 Tzzzz =−+− đạt giá trị nhỏ nhất thì giá trị biểu thức 22Pab =+ bằng A. 4. B. 9. C. 5. D. 10. Lời giải Chọn C Gọi 12,, MMM lần lượt là các điểm biểu diễn số phức 12,2, zzz Khi đó 1212 2 TzzzzMMMM =−+−=+ . Ta có 1 321zi++=  1M

tâm

41

Ta có 1232 TMMMMMMMMAB =+=+  T đạt giá trị nhỏ nhất khi M là giao điểm của 23II với d . Phương trình đường thẳng 23II là 43100 xy++= Tọa độ điểm M là nghiệm của hệ 20 4310 xy xy

−=   +=−   (1;2) M Do đó 22 5 Pab=+= . Câu 197: Cho các số phức 1z và 2z thỏa mãn các điều kiện 11 1 zizi −=−+ và 2212 zzi −=+ . Giá trị nhỏ nhất của biểu thức 121255Pzzzz =−+−+− thuộc khoảng nào dưới đây A. ( )5;6 B. ( )7;8 C. ( )8;9 D. ( )4;5 Lời giải Chọn A Gọi , MN là điểm biểu diễn các số phức 1 zabi =+

, 2 zcdi =+ ( ) ,,, abcd  .

có ( ) ( ) 11 1111 i z abia zi b i +

36. C. 28. D. 42. Lời giải Chọn B Đặt w1w2 zi =−+= 112212 w1;w1w2;w2 zizi =−+=−+== Ta có: 12125ww5 zz−=−= Vì ( ) 2222 12121212 www+w2www+w11. −+=+= 12121265w1w165ww43

22222 2021 0 abcd acbd  +=+=   +=  Do vậy: ( ) ( ) 2 22 2 12122.202120212zzacbdzz −=−+−=−= Ta có: 12122727202123zzzizzi =−−−−+−−=+ Suy ra 2021,32024abab ==+= . Câu 200: Trong tất cả các số phức z thỏa mãn 24 2 zz z + +=+ , gọi số phức izab =+ ( ) , ab là số phức có môđun nhỏ nhất. Tính 2Sab =+ . A. 5 B. 4 C. 3 D. 2 Lời giải Chọn D Ta có: ( ) ( ) 2222 242424412 2 zz zabiaababa + +=+++=+++=+=+ . ( )2 222 412288zabaaa =+=++=++ . Dấu “=” xảy ra khi ( )2 202aa+==− Do đó z nhỏ nhất khi 2 a =− 2 24ab=−= . Vậy 2 242 Sab=+=−+= . Câu 201: Cho số phức z thỏa mãn 13. z −= Biết

giá trị lớn nhất của biểu thức 2 Pzizi =++−− bằng ab với , ablà các số nguyên dương. Tính .ab + A. 7 . B. 9. C. 12. D. 15. Lời giải

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

222221425xyyxyxy =+++++−−+ Kết hợp với (*) ta được ( ) ( ) 2226222372 Pxyxyxyxy =+++−−=+++−+ Đặt txy =+ thì ( ) 2372 Pfttt ==++− với 37 ; 22 t  − 

Cách 1:. Ta có: ( ) 11 2372 ft tt  =− +− . Xét ( ) 01ftt  == . Mà ( ) 37 125;10;10. 22fff =−==   Vậy ( ) ( ) max125 ftf== xảy ra khi 1. t = Nên 2;5ab== nên 7 ab+= . Cách 2:. Áp dụng BĐT Bunhiacopxki cho 2 cặp số ( )1;1 và ( ) 23;72 tt +− Ta có: ( ) 237211.1025 tt ++−+= . Đẳng thức xảy ra khi 1. t = Câu 202: Cho số phức z thỏa mãn 13. z −= Biết giá trị lớn nhất của biểu thức 2 Pzizi =++−− bằng ab với , ablà các số nguyên dương. Tính .ab + A. 7. B. 9. C. 12. D. 15. Lời giải

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Ta có: ( ) 11 2372 ft tt  =− +− . Xét ( ) 01ftt  == . Mà ( ) 37 125;10;10. 22fff =−==  

Vậy ( ) ( ) max125 ftf== xảy ra khi 1. t = Nên 2;5ab== nên 7 ab+= .

Cách 2: Áp dụng BĐT Bunhiacopxki cho 2 cặp số ( )1;1 và ( ) 23;72 tt +− Ta có: ( ) 237211.1025 tt ++−+= . Đẳng thức xảy ra khi 1. t = Câu 203: Biết số phức z thỏa mãn đồng thời hai điều kiện 345zi−−= và biểu thức 22 2 Mzzi =+−− đạt giá trị lớn nhất. Tính môđun của số phức zi + A. 61 zi+= . B. 52 zi+= . C. 35 zi+= . D. 241 zi+= . Lời giải

ọn A

ọi ( ) ;; zxyixy =+

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Theo đề ta có ( ) ( ) ( ) 22 212111zixy −+=−++= . Khi đó phương trình ( )1 là phương trình đường tròn ( )C có tâm ( )2;1 I và 1 R = . Vậy ( )MC 

Theo đề ta có ( ) ( ) ( ) 222 2 3242232422 Tzzixyxy =−+−+=−++−++ .

Gọi ( ) ( )2;0,2;2AB . Khi đó ( ) ( ) ( ) 222 2 324223434 TxyxyMAMBMAMB =−++−++=+=+ .

Mặc khác ( ) ( ) ( ) 2;0,2;2 ABC − và 22 ABR == vậy AB là đường kính. Suy ra tam giác MAB vuông tại M. Áp dụng bất đẳng th

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

1212122.24zzzzz−+== Vậy giá trị lớn nhất 12zz bằng 4 và dấu bằng xảy ra khi 21 2 zz=−=−

Câu 210: Cho hai số phức , uv thỏa mãn 10 uv== và 3450 uv−= . Tìm giá trị lớn nhất của biểu thức 4386 uvi +−+ . A. 30. B. 40. C. 60. D. 50. Lời giải

Chọn C

Ta có 2 . zzz = . Đặt 34 Tuv =− , 43 Muv =+ . Khi đó ( )( ) 2 3434 Tuvuv =−− ( ) 22 91612uvuvvu=+−+

Tương tự ta có ( )( ) 2 4343 Muvuv =++ ( ) 22 16912uvuvvu=+++ Do đó ( ) 22 22 255000MTuv+=+= Suy ra 22 5000 MT =− 2 5000502500=−= hay 50 M = . Áp dụng zzzz ++ ta có 43864386501060 uviuvi +−+++−+=+= Suy ra max431060 uvi+−= . Câu 211: Xét các số phức , zw thỏa

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

2222 3(1)(3)(1)(5)24 abab   +++=+++  •=+  +=   2 22

=++−++++    . Dấu bằng xảy ra 1,325=−=−ab Câu 214: Cho số phức z thỏa mãn 11 z + . Gọi giá trị lớn nhất và giá trị nhỏ nhất của biểu thức ( ) 12 1 izi P z +++ = + lần lượt là M và m . Khi đó giá trị của ( ) 22Mm + bằng: A. 4. B. 843. + C. 6. D. 2. Lời giải Chọn C +) Ta có: ( ) ( )( ) ( )( ) 12111111 111 zi izizi a abab abbbzi b ab b

 =−    ++=+=−    +−−=−−   = ++=     =−  

 2 1011 2 22 102001 22 (1)1212 2

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn ; ; 00 ababababzz zzzzzzzz aabb aabb ==   •+=+•−=+  + +    Giả sử: ( )( ) ( ) ( )(,)1111 zabiabziababi =+++=+−+++ Mà: 110.i =+ . Do đó: ( )( ) ( )( ) 111111 21 11 zizi P z

.



  Cho số phức z thỏa mãn 57197zi−+= . Giá trị lớn nhất của 47621 zizi −−+−+ thuộc tập hợp nào sau đây? A. ( ) 20;197. B.   30;40. C. 197;2394   D. ( ) 2394;40.

Lời giải

Chọn B

Gọi ( ) ; Mxy là điểm biểu diễn số phức z

Suy ra, ( ) ( ) ( ) 22 :57197MCxy−++= có tâm ( )5;7 I

Gọi ( ) ( )4;7,6;21AB . Ta thấy ( ) , ABC 

Mặt khác, 21972 ABR== AB là đường kính của đường tròn ( )C . ( ) 222 :788MCMAMBAB+== Ta có: ( ) ( ) 2 22 22.7881576MAMBMAMB++== 15762394 MAMB += Ta có: 476212394 ziziMAMB −−+−+=+

Vậy giá trị lớn nhất của 47621 zizi −−+−+ bằng 239439,69.

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chọn B Ta có 13434515146 zizizzz =−+−−=−−− Đặt 2 000435,724 zizzi =−==− . Ta có ( )( ) 22 22 22222 724 ooo Azizzzzzz =+−=+=++ ( )2 442 ..2. oooo zzzzzzzz =+++− Mà ( )( ) 22 1..1 ooooo zzzzzzzzzz ++=+=−− Suy ra ( )2 2 44224212.221201 ooo Azzzzzzzz =++−−−=−+ Hàm số 42 221201ytt=−+ đồng biến trên  4;6 nên 42 2.42.412011681 A −+= . Dấu bằng xảy ra khi và chỉ khi 4 431 z zi =   +−=   Do đó 2 724 zi +− nằm trong khoảng ( )1009;2018

Điều kiện ( ) 22 ||000 zzixyxyix −+−+

Ta có: ( ) ( ) ( ) 22 2 22 222

11 || xyxyi w zixyxyi y z xyx = −−+ == +−+ +−+

−+ −=−−+=+−+ +−+ ( ) ( ) 222222 2424 yxyxyxy +−=++− 22 22

1 8222 8 yxy yxyxyyxy xyxy

 +=    +=  Trường hợp 1: 22 0 0 y xyy x   +=  =  . Trường hợp 2: 2222416xyxy+=+= Gọi 2222 1112221122;16;16zxyizxyixyxy =+=++=+= . Ta có: ( ) ( ) 22 12121224zzxxyy −=−+−= ( )2 12 04 yy − 12 02 yy − . Xét ( ) ( ) ( ) 1 22 12 2222 12212777714Pzizi xyxyyy =+−− =−− −−=−− 12 1428 y P y    . 12 22

4 xy xyy khi 12 2222 11

 =    +=

xx yy xyxy

Dấu "" = xảy ra khi và chỉ 2 16

= +=  Lấy 12 12

15 1 xx yy  ==   =−=   thì 28 P = Vậy giá trị lớn nhất của 28 P = . Câu 227: Cho hai số phức 1z và 2z thỏa mãn 12 34 zzi +=+ và 12 2 zz−= , tìm giá trị lớn nhất của 12Azz =+ . A. 229 B. 29 C. 25 D. 28 Lời giải Chọn B Gọi ( ) 1 ,, zabiab=+ , ( ) 2 ,, zcdicd=+ . Theo giả thiết ta có

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Chọn B Gọi zxyi =+ với , xy  . Ta có: 2222244 zxyyx =+==− , với  2;2 x − . ( ) ( ) 2222231231 Pzzxyxy =++−=+++−+ 84352xx=++− . Xét hàm số ( ) 84352 fxxx =++− trên  2;2 . Có ( )   2113 '302523842;2 11 8452 fxxxx xx =−=−=+=−− +− . Khi đó ( ) 29 f −= , ( ) 27 f = , 13 311 11 f  −=  . Vậy giá trị lớn nhất của P là 311 đạt được khi 13 11 x =− . Câu 230: Cho số phức z thỏa mãn điều kiện 12. z −= Tìm giá

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Suy ra: ( ) ( ) min15 fxf=−= .

Do đó: IM đạt giá trị nhỏ nhất bằng 5 khi 1 x =− Nên MN đạt giá trị nhỏ nhất bằng 51. Vậy 516 mn+=+= .

Câu 232: Xét các số phức z và w thỏa mãn 221zi++= và 23 wiwi +−=− . Khi 33 zwwi −+−+ đạt giá trị nhỏ nhất. Tính 2 zw + A. 25 B. 7 C. 23 D. 61 Lời giải Chọn D

Tacó: 221zi++= nêntậphợpđiểm M biểudiễnsố phức z làđườngtròn ( )C tâm ( )2;2 I , bán kính 1 R = . Gọi ( ) ;; wxyixy=+ 23 wiwi +−=− ( ) ( ) ( ) 222 2 213xyxy ++−=+− ( ) 10. xy +−= Tập hợp điểm N biểu diễn số phức w là đường thẳng ( ) zwMN −= 33 wiNA −+= , với ( )3;3 A . 33 TzwwiMNNA =−+−+=+ . Tham khảo hình vẽ bên dưới

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

Dễ thấy đường tròn ( )C và điểm A thuộc cùng một nửa mặt phẳng bờ 

Dựng đường tròn ( ) C có tâm ( )3;3 I , bán kính 1 R = đối xứng với ( )C qua  .

Gọi M là ảnh của M qua phép đối xứng trục  . Khi đó, với mọi điểm N  , ta có: NMNM = Nên TMNNAMNNA  =+=+ . min ,,, TIMNA   thẳng hàng. Dựa vào hình vẽ trên, suy ra ( ) ( ) 3;21;212 MMzi  −−=−− ; ( ) 3;232 Nwi −=−

Giáo viên: Huỳnh Văn Ánh 42 Nguyễn Cư Trinh Thuận Hòa TP Huế ĐT: 0984164935

Chuyên luyện thi: Tuyển sinh vào lớp 10 Tốt Nghiệp THPT BDKT Toán 10; 11; 12 Sưu tầm và biên soạn

111 1 10821082822 101222  

−==== −+−+  −+ −+  Mặt khác: 2 3 .,0 .34,0

z a w aaaa aa a +−++−−++−++− . Từ ( )3 suy ra 342izwi+−+ . Dấu "" = xảy ra ( ) ( )

32 11122 2 1082 a Twiwiw aa =+=−++−+=+ −+ Dấu “=” xảy ra khi 3 ; 22 ii zw + == Lưu ý: Ở đây sử dụng BĐT zwzw ++ . Dấu “=” xảy ra khi ( )0 zkwk= Câu 236: Xét các số phức , zw thỏa mãn 2 z = và 1 w = . Khi 34 izwi +−+ đạt giá trị nhỏ nhất, zw + bằng A. 3. B. 5 . C. 29 5 . D. 221 5 . Lời giải Ta có 2 izz== . ( ) ( ) ( ) 1 133 2 izwizw izw izwizw  −+  izw whizh izwlil

+ +=  =   +=−+ 

. Dấu "" = ở ( )1 xảy ra khi và chỉ khi ( ) .,0wkizk= ; dấu "" = ở ( )2 xảy ra khi và chỉ khi ( ) .,0whizh= . Ta lại có 3434345 izwiizwiizwiizw h l zi wi

++ 1 2 3 5 86 55 34 55

 =    =−     =−−    =− 

. Vậy 342Minizwi+−+= và 5 zw+= Câu 237: Xét các số phức z ,w thỏa mãn||||1 zw== . Khi |234| zwi đạt giá trị lớn nhất thì || zw bằng A. 55 . B. 8. C. 3 D. 2.