CHUYÊN ĐỀ VẬT LÝ BỒI DƯỠNG HỌC SINH GIỎI Ths Nguyễn Thanh Tú eBook Collection CÁC CHUYÊN ĐỀ MÔN VẬT LÝ ĐẠT GIẢI TẠI HỘI THẢO KHOA HỌC CÁC TRƯỜNG CHUYÊN KHU VỰC DUYÊN HẢI VÀ ĐỒNG BẰNG BẮC BỘ NĂM 2022 WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062424
CÁC CHUYÊN ĐỀ MÔN VẬT LÝ ĐẠT GIẢI TẠI HỘI THẢO KHOA HỌC CÁC TRƯỜNG CHUYÊN KHU VỰC DUYÊN HẢI VÀ ĐỒNG BẰNG BẮC BỘ NĂM 2022
- Giải Nhất: Chuyên đề Hệ cơ liên kết Lý thuyết và phương pháp giải bài tập, tác giả Nguyễn Đức Nhân, trường THPT Chuyên Lê Thánh Tông, Quảng Nam (trang 2 82)
Giải Nhì: Chuyên đề Vận dụng phương trình Lagrange loại II để tìm quy luật của vật trong chuyển động liên kết, tác giả Nguyễn Ngọc Cảnh, trường THPT Chuyên Chu Văn An, Bình Định (trang 83 125)
- Giải Nhì: Chuyên đề Chuyển động liên kết của vật rắn, tác giả Nguyễn Hải Dương, trường THPT Chuyên Lê Hồng Phong, Nam Định (trang 126 230)
- Giải Ba: Chuyên đề Chuyển động liên kết vật rắn, Tác giả Nguyễn Văn Hạnh và Phan Thị Tâm, Trường THPT Chuyên Quốc Học Huế Thừa Thiên Huế (trang 231 284)
Giải Ba: Chuyên đề Xây dựng hệ thống bài toán liên kết trong cơ học vật rắn, Tác giả Phạm Thành Công, Đỗ Thị Hồng Liên, Trường THPT Chuyên Biên Hòa, Hà Nam (trang 285 hết)
DẠYKÈMQUYNHƠNOFFICIAL 1
Chuyên đề
HỆ CƠ LIÊN KẾT LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Tác giả: Nguyễn Đức Nhân THPT Chuyên Lê Thánh Tông, Quảng Nam (Chuyên đề đạt giải Nhất) A. MỞ ĐẦU
1. Lí do chọn đề tài
Từ kinh nghiệm bồi dưỡng học sinh giỏi môn vật lý tôi nhận thấy rằng: cơ học vật rắn nói chung và hệ cơ liên kết nói riêng là một nội dung tương đối khó. Phần lớn học sinh chưa hình dung được chuyển động của các hệ cơ học; chưa nắm rõ ý nghĩa vật lý của các phương trình toán học xuất hiện trong bài toán; nên các em thường gặp các vấn đề sau:
+Lúng túng trong việc xác định các biến số độc lập và lựa chọn hệ toạ độ cho cơ hệ.
+Khó khăn trong việc xác định lực tương tác giữa các vật trong cơ hệ (lực liên kết).
+Khó khăn trong việc xác định liên hệ giữa chuyển động của vật này và vật khác (phương trình liên kết).
+Sai sót trong việc thiết lập và giải tìm nghiệm các phương trình của bài toán. Để khắc phục những khó khăn trên, tôi hướng dẫn học sinh thiết lập quy trình chung khi giải các bài toán cơ liên kết gồm 2 phần : phân tích động học và phân tích động lực học; cụ thể có 5 bước:
B1. Viết các phương trình động học.
B2. Viết các phương trình động lực học.
B3. Viết phương trình năng lượng.
B4. Viết phương trình liên kết.
B5. Giải hệ các phương trình và biện luận nghiệm.
Với mong muốn chia sẻ những kinh nghiệm của mình, tôi viết chuyên đề
“ Hệ cơ liên kết Lý thuyết và phương pháp giải bài tập ” .
DẠYKÈMQUYNHƠNOFFICIAL 2
2. Mục tiêu của đề tài
Mục tiêu của đề tài là tìm kiếm giải pháp khắc phục các khó khăn mà học sinh gặp phải khi học về nội dung hệ cơ liên kết.
3. Nhiệm vụ của đề tài
Hệ thống hoá lý thuyết của hệ cơ liên kết.
Phân loại các dạng bài tập thường gặp trong nội dung hệ cơ liên kết.
Hướng dẫn giải chi tiết các dạng bài tập đã phân loại.
4. Phạm vi của đề tài
- Phần Cơ học Cơ hệ liên kết
5. Cấu trúc đề tài
Ngoài phần mở đầu, kết luận, phụ lục và tài liệu tham khảo, nội dung của đề tài gồm 2 phần:
Phần 1. Tóm tắt lý thuyết Hệ cơ liên kết:
A. Lý thuyết Hệ cơ liên kết.
B. Bài tập ví dụ.
Phần 2. Phân loại và phương pháp giải bài toán Hệ cơ liên kết.
Dạng 1. Liên kế khớp xoay- thanh rắn.
Dạng 2: Liên kết dây treo.
Dạng 3: Liên kết khối cầu trụ lăn.
DẠYKÈMQUYNHƠNOFFICIAL 3
PHẦN I. TÓM TẮT LÍ THUYẾT A. LÍ THUYẾT HỆ CƠ LIÊN KẾT
I. Bậc tự do- Hệ cơ liên kết
1. Bậc tự do Số lượng các toạ độ độc lập dùng để mô tả chuyển động của vật gọi là số bậc tự do của vật đó. Để mô tả chuyển động tự do của vật trong không gian 3 chiều Oxyz sẽ cần 3 toạ độ cho chuyển động tịnh tiến và 3 toạ độ cho chuyển động quay xung quanh các trục đó (Hình1.1); ta nói vật có 6 bậc tự do. Một hệ gồm N vật rắn chuyển động tự do trong không gian 3 chiều sẽ có 6 N bậc tự do.
2. Hệ cơ liên kết. Hệ cơ liên kết là hệ gồm hai hay nhiều vận rắn gắn kết lại với nhau. Trong một hệ cơ liên kết, chyển động vật này ảnh hưởng đến chuyển động của vật kia nên số bậc tự do của mỗi vật sẽ giảm.
II. Phương
DẠYKÈMQUYNHƠNOFFICIAL 4
B. NỘI DUNG
Ví
O x z y x
z
y
r
trình liên kết Phương trình liên kết là phương trình mô tả chuyển động tương đối của các vật trong hệ liên kết.
dụ 1 Trụ rắn trượt Một thanh trượt có thể chuyển động không ma sát dọc theo trục và quay tự do quanh trục Oy như Hình 1.2. Hình 1.1
DẠYKÈMQUYNHƠNOFFICIAL 5
r r = = = . Số bậc tự do của trụ B là 3 : Ví dụ 3 Khối cầu lăn không trượt Khảo sát một quả cầu bán kính a lăn không trượt trên mặt phẳng nằm ngang như Hình 1.4. Hình 1.3 x y z A B Hình 1.2 O x z y y r x z
Các phương trình liên kết của thanh : 0 0 0 0 x z x z r r = = = = . Số bậc tự do của thanh là 2 gồm: y y r Ví dụ 2: Khớp cầu Một thanh trụ B được liên kết với thanh trụ A đứng yên, thông qua khớp cầu như Hình 1.3. Thanh trụ B có thể quay tự do không ma sát trong khớp cầu Số phương trình liên kết của trụ B 3: 0 0 0 x y z r
z y
C x
Cyr Cxr Czr
z y
Hình 1.4
= = =− . Số bậc tự do là 3 : x y z z
z
y
x y
Ví dụ 4: Hệ liên kết phức tạp- Khảo sát một hệ cơ liên kết như Hình 1.5. Từ các ví dụ trên, ta nhận thấy: hệ có số phương trình liên kết là 7 gồm 4 cho khối trụ trượt và 3 cho khớp cầu; số bậc tự do là 2.675 −= gồm y r , , ,, xyz . Tổng quát, số bậc tự do trong một hệ liên kết được xác định 6 MNC =− Trong đó, M là số bậc tự do, N là số lượng vật rắn của hệ, C là tổng số phương trình liên kết. Hình 1.5 x
DẠYKÈMQUYNHƠNOFFICIAL 6
Số phương trình liên kết là 3: ''. ''.
Cz Cxy Cyx O X
ra ra ra Z Y Yr
x
4. Phân loại liên kết
a. Liên kết holonomic
Hệ liên kết có các phương trình liên kết là hàm số theo toạ độ suy rộng và thời gian ( ) 123,,...,,0 n fuuuut = , với iu là toạ độ suy rộng của hệ, được gọi là hệ holonomic. Các hệ cơ được mô tả ở ví dụ 1, ví dụ 2 là hệ holonomic.
b. Liên kết phi holonomic
Hệ liên kết có một trong các phương trình liên kết là hàm số theo toạ độ suy rộng và các vi phân của chúng theo thời gian ( ) 123123 ,,...,,',','...,',0 nn fuuuuuuuut = , được gọi là hệ phi holonomic. Hệ cơ được mô tả ở ví dụ 3 là hệ phi holonomic.
5. Động lực học hệ cơ liên kết Việc phân tích động lực học của hệ cơ liên kết có thể được tiến hành theo các phần sau:
Phần 1: Phân tích động học Bước 1: Viết các phương trình động học + Chọn hệ quy chiếu + Chọn toạ độ suy rộng + Biểu diễn các thành phần vận tốc, gia tốc theo toạ độ suy rộng trong hệ quy chiếu đã chọn.
Phần 2: Phân tích động lực học: Bước 2: Viết các phương trình Newton Euler cho chuyển động của mỗi vật trong hệ.
+ Vẽ sơ đồ tự do, phân tích các thành phần của lực và mômen lực tương ứng.
+ Biểu thành phần phản lực liên kết (chưa biết) theo các lực đã biết và vi phân của toạ độ suy rộng.
Bước 3: Viết phương trình năng lượng cho hệ.
Bước 4: Viết các phương trình liên kết
Bước 5: Giải hệ các phương trình
+ Giải hệ các phương trình từ đó suy ra được thành phần của phản lực liên kết.
DẠYKÈMQUYNHƠNOFFICIAL 7
B. BÀI TẬP VÍ DỤ
Các nội dung lý thuyết đã đề cập ở trên được mô tả cụ thể qua 2 bài tập ví dụ sau.
Ví dụ 1: Một chiếc xe đẩy có khối lượng không đáng kể chuyển động không ma sát trên mặt sàn nằm ngang. Con lắc dạng thanh rắn có khối lượng m, chiều dài L, một đầu được gắn vào trục quay O của thùng xe như Hình 1 6 Cho biết chuyển động của xe trong hệ quy chiếu gắn với đất được xác định bởi hàm ()ut Viết phương trình chuyển động của thanh rắn và biểu thức phản lực do trục O tác dụng lên thanh rắn. Hướng dẫn giải: Số phương trình liên kết: + của xe đầy là 6 gồm () 0 0
x yz xyz
rut rr
= == === + của thanh rắn là 5 gồm 0 0 xyz xy
rrr === ==
Do đó số bậc tự do của hệ: 62111 −= . Toạ độ suy rộng của hệ trong trường họp này là () t .
DẠYKÈMQUYNHƠNOFFICIAL 8
Ch
Ch
Xét
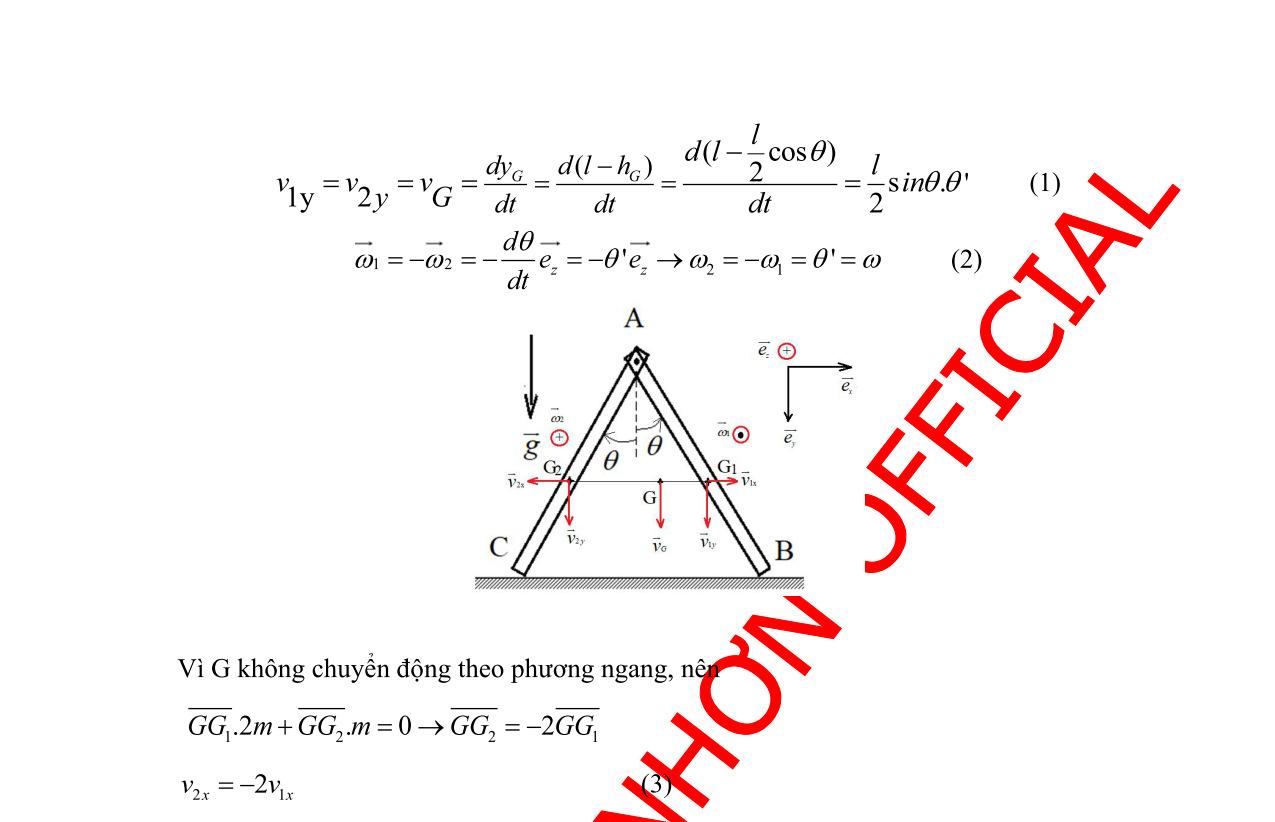
động của xe: ( ) ' O vut = Xét khối tâm C của thanh: ( ) ( ) ( ) 2 '' 2 ''''' 22 Cx Cxr L vutee LL auteee =+ =++− Phân tích động học: Viết các phương trình Newton Euler ( ) ( ) 2''''' 22 '' 2 rryxr C LL FeFemgemuteee L FI +−=++− = Mặt khác: sincos cossin xr yr eee eee =+ =−+ Suy ra: ( )ut , mL g Hình 1.6 x e y e r e e F r F P
Phân tích động học:
ọn hệ quy chiếu gắn với mặt đất.
ọn hệ toạ độ cực gắn với trục quay O
chuyển
M





nh
kh
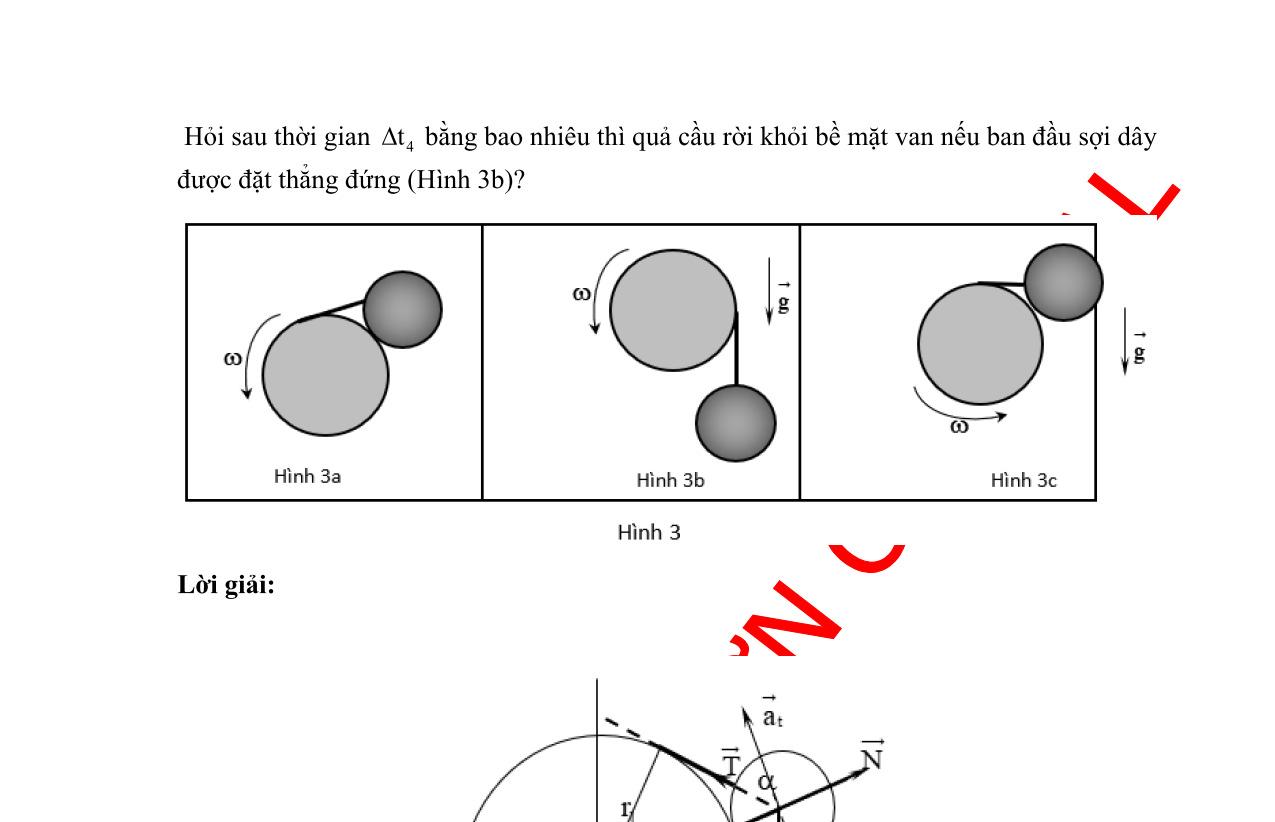
lượng m được đặt lên thành bên trong của một vành trụ mỏng có khối lượng M phân bố đều. Vật nằm trong mặt phẳng thẳng đứng vuông góc với trục của vành trụ và chứa khối tâm của vành trụ. Ban đầu, vành trụ đứng yên trên một mặt phẳng ngang và vật ở vị trí xác định bởi góc lệch 0 so với đường thẳng đứng như Hình 1.7.. Sau đó, thả nhẹ vật cho hệ chuyển động. Giả thiết rằng ma sát giữa vật và vành trụ là không đáng kể, vành trụ chuyển động lăn không trượt trên mặt phẳng ngang. Gia tốc trọng trường là g .
Tìm phản lực của vành tác dụng lên vật lúc vật đến vị trí thấp nhất của quỹ đạo.
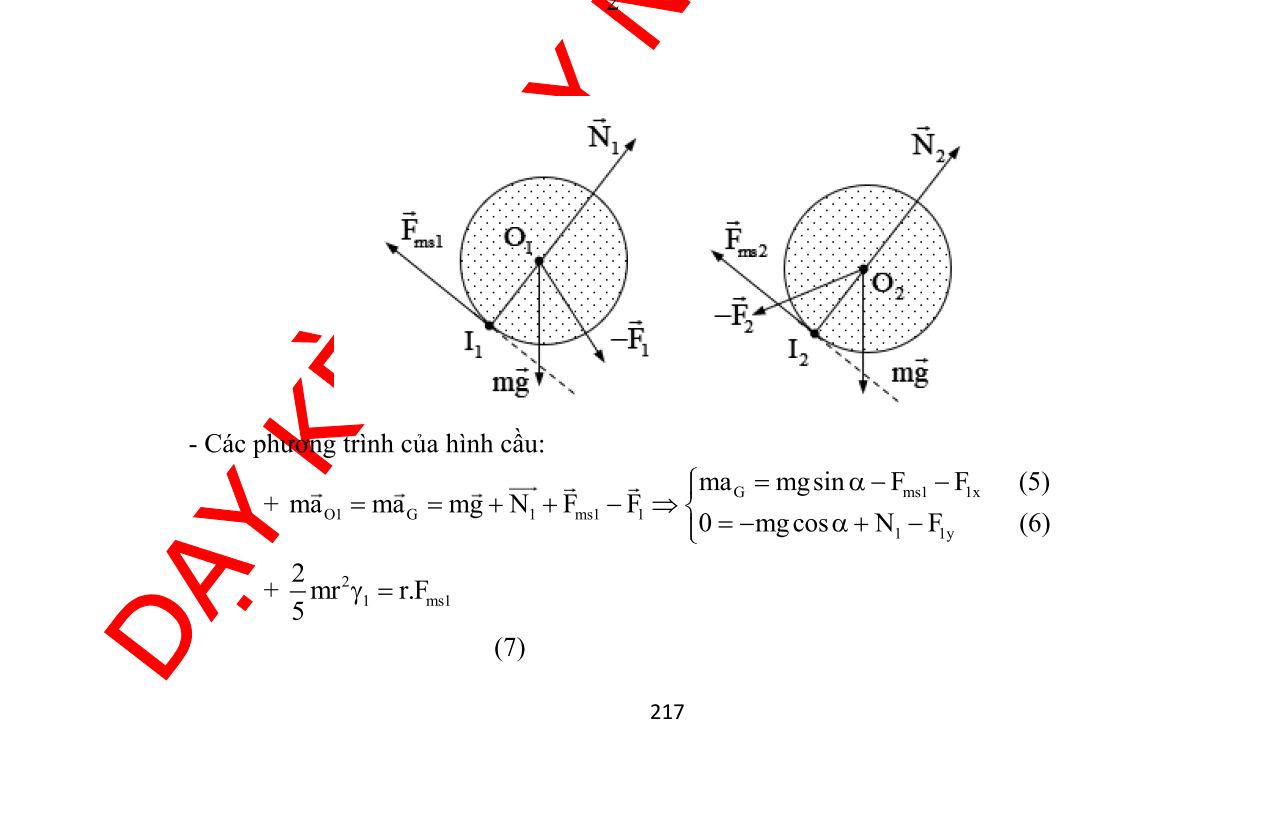
Hướng dẫn giải: Phân tích : Đối với vành: cần xác định toạ độ Gx và góc quay Đối với vật: cần xác đị
DẠYKÈMQUYNHƠNOFFICIAL 9 2 2 ''sin'cos 2 ''cos''sin''cossin'' 24 '' 2 r C C L Fmummg LmL FmummgmumgI L FI =−− =+++=− = Giải
ể
ứ
ẽ
ả
lực
ế
r
Ví
phương trình trên, tìm được bi
u th
c () t s
xác định được các thành phần của ph
n
liên k
t ,
FF
dụ 2:
ột vật
ỏ
ối
nh góc quay Bước 1: Viết phương trình động học - Đối với vật- điểm A ( ) ( ) ( ) 2 '..'. ''..''..'. Ax Axr OAOGGA vueRe aueReRe =+ =+ =++− (1) - Đối với vành điểm G '. 0 ''. Gxx G Gy G Gxx vue xu v yR aue = = = = = Bước 2: Viết phương trình động lực học Vật m:
1.7 g M 0 m e r e G O y x A ()ut
Hình
Xét theo phương Ox: sin rx Fma −= (4)
Xét vành: Gọi KF là lực mà mặt đất tác dụng lên vành theo phương ngang. ( ) ''.''sinKrxKr FFMgMueFMuF +−+==− (5)
Phương trình mômen: ..''.'' KGK FRIFMR== (6)
Bước 3: Viết phương trình liên kết Vì vành lăn không trượt nên: 0.''0'.' K vRuuR =+==− (7) Từ (5)(6)(7), ta suy ra: Ax 2''2' x maMumvMu =−=− (8) Bước 4: Viết phương trình năng lượng Tại vị trí thấp nhất ta có x ee = nên từ (1) ta suy ra '' A vuR =+ (9) Định luật bảo toàn năng lượng cho ta: ( ) 222 0 111 1cos'' 222AG mgRmvMuI −=++ (10)
1cos A G
gR v m M gR m v m M M
0 0 2 2 1cos 2
= + =− + Từ (9), ta suy ra: ( ) 0 .''1cos2 A m RvugR M =−=−+ (11) Thay (11) vào (3) ta được phản lực mà vành tác dụng lên vật ( ) 0 12.1cos r m Fmg M =−++− Dấu “ ” cho biết phản lực này ngược chiều với véc tơ đơn vị r e tại vị trí thấp nhất.
DẠYKÈMQUYNHƠNOFFICIAL 10
( ) ( ) 2 2 cos''sin.' 0 cos''sin.' r AA r FmgmuR Fmgma F FmgmuR +=−− += = =−+−− (3)
Thay (7)(8) vào (10) ta được: ( ) ( )
PHẦN II. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TOÁN HỆ CƠ LIÊN KẾT
Các bài toán Cơ hệ liên kết xuất hiện trong các đề thi học sinh giỏi vật lý thường có 3 dạng sau: liên kết khớp xoay thanh rắn, liên kết dây treo, liên kết khối cầu trụ lăn.
DẠNG 1: LIÊN KẾT KHỚP XOAY- THANH RẮN
1.1. Phương pháp chung:
Kiểu liên kết này xuất hiện giữa hai điểm có khoảng cách không đổi trong quá trình chuyển động của hệ.
Viết biểu thức động học của các điểm trên thanh trong hệ toạ độ Oxy hoặc toạ độ cực.
rrr vvv aaa
BAAB BABA BABA
=+ =+ =+


Viết các phương trình liên kết. - Vẽ các giản đồ véc tơ vận tốc, véc tơ gia tốc (Hình 1.9); hoặc sử dụng khái niệm tâm quay tức thời đề giải bài toán. -Phân tích phản lực liên kết F của thanh thành r F song song và F vuông góc với thanh.Xác định r F , F để tìm F . Trong nhiều trường hợp, việc sử dụng giản đồ véc tơ vận tốc, véc tơ gia tốc sẽ cho lời giải ngắn gọn. 1.2. Bài tập vận dụ

DẠYKÈMQUYNHƠNOFFICIAL 11
ng Bài tập 1: Thanh AB cứng, nhẹ chiều dài L, mỗi đầu có gắn một quả cầu nhỏ khối lượng bằng nhau m, tựa vào tường thẳng đứng như Hình 2.1.1. Truyền cho quả cầu B một vận tốc rất nhỏ để nó trượt trên sàn nằm ngang. Giải thiết rằng trong quá trình chuyển động, B A Av r Aa Av BA vr = Bv Aa 2 r BA ar = ' BA ar = Ba Hình 1.9 A B Hình 2.1.1 O x y B A Ar Br r e e By Ay Ax Bx Hình 1.8
thanh AB luôn nằm trong mặt phẳng thẳng đứng. Bỏ qua mọi ma sát giữa các quả cầu với tường và sàn. Gia tốc trọng trường là g.
a. Xác định góc hợp bởi thanh và tường thẳng đứng vào thời điểm quả cầu A bắt đầu rời khỏi tưởng.
b. Tính vận tốc của quả cầu B khi đó.
Hướng dẫn giải: Lời giải thứ nhất
Phân tích: Số bậc tự do của của vật: 3 bậc: x, y, và góc quay trong mp Oxy, do đó để giải được bài toán cần thiết lập tối thiểu 3 phương trình.
Định hướng: biến đổi các toạ độ x, y, về toạ độ góc quay Điều kiện biên của bài này liên quan đến lực liên kết tại A và tường. Bước 1: Viết các phương trình động học Chọn HQC như hình vẽ.
DẠYKÈMQUYNHƠNOFFICIAL 12
( ) ( ) 2 2 sincos.''sin''cos 222 cossin.''cos''sin 222 GGxGx GGyGy LLL xva LLL yva ===−+ ==−=−+ - Phương trình liên kết: 0;0ABxy== Bước 2: Viết các phương trình động lực học cho khối tâm G Phương trình chuyển động tịnh tiến: ( ) ( ) 2 2 2'sin''cos 2 22'cos''sin 2 A xGGx yGGy B L Nm Fma Fma L Nmgm =−+ = = −=−+ Điều kiện biên của bài toán: đầu A rời khỏi tường thẳng đứng, ta có: ( ) 22 02'sin''cos0'sin''cos 2 A L Nm=−+== (1) Phương trình chuyển động quay cho khối tâm G: / '' B G NG MI = Hay: ( ) ( ) ( ) 2 2 2 2 'cos2sin 22'cos''sinsin'''' 222 1sin Lg LLL mgmm L −+ −+== + (2) Bước 3: Viết các phương trình năng lượng Định luật bảo toàn cơ năng cho ta: ( ) ( ) 2222 112 cos2.''1cos 22GxGyG g mgLmgLmvvI L =+++=− (3) Bước 4: Phương trình liên kết: 0;0ABxy== (đã được sử dụng ở Bước 1) O y x +
-Xét khói tâm G, ta có:
điể
và sàn.
điểm A đi xuố
m
đoạ
) 1sin yL
(1)
nh luật bảo toàn cơ năng cho ta: ( ) ( ) ( ) 222211 1sin 22ABAB mgymvvmglmvv =+−=+ (2) Vì là thanh cứng nên: sincosAB vv = (3) Thay (3) và (2): ( ) ( ) 222 2 11 1sin21sinsin 2sinBB gLvvgL −==− (4)
Khi A chưa rời khỏi tường thì lực gây ra gia tốc và vận tốc theo phương ngang là phản lực của tường tác dụng lên A theo phương ngang. Lực này làm Gxv tăng
DẠYKÈMQUYNHƠNOFFICIAL 13 Bước 5: Giải các hệ gồm các phương trình Từ (1)(2) và (3), ta có: ( ) ( ) ( ) 2 2 2 2 'sin''cos 'cos2sin 2 ''cos 3 1sin 2 '1cos Lg L g L = −+ == + =− Câu b. Ta có: / 'cos'cos.'cos 22 BBxBGxGx LL vvvvL ==+=+= Với 2 cos 3 2 ' 3 g L = = Ta thu được: 8 27 B vgL = Lời giải thứ hai: Gọi
ợ
là góc h
p bởi thanh AB
Tại thời
m bất kỳ,
ng
ột
n (
=−
Đị
dần. Nên khi đầu A rời khỏi tường 0,0 GxNa== nên Gxv đạt giá trị cực đại. Mà 2 BGxvv = nên đạt giá trị cực đại. Xét phương trình ( ) ( ) 22 sinsin21sinsin81sin. 22 B vglgl =−=− Ta nhận thấy: ( ) ( ) 3 1sin.1sinsinsin1sinsin 222722 const −−++= nên Bv đạt giá trị cực đại khi ( ) sin21sinsin 23 −== thay 2 sin 3 = vào (4) ta được 8 27 B vgL = Bài tập 2: Bv
Một thanh AB chiều dài L có đầu A tựa vào tường thẳng đứng và đầu B tiếp xúc với sàn nằm ngang như Hình 2.1.2. Người ta kéo đầu B của thanh dọc theo mặt sàn với vận tốc 0v hướng ra xa tường. Gọi là góc hợp bởi thanh AB và sàn. Xác định gia tốc trung điểm G của thanh khi đầu A vẫn tựa lên tường. Lời giải thứ nhất Phân tích: Số bậc tự do của của vật: 3 bậc: x, y, và góc quay trong mp Oxy, do đó để giải được bài toán cần thiết lập tối thiểu 3 phương trình. Định hướng: biến đổi các toạ độ x, y, về toạ độ góc quay Điều kiện biên của bài này liên quan đến lực liên kết tại A và tường Hướng dẫn giải: Chọn hệ trục toạ độ Oxy gắn với đất và h
DẠYKÈMQUYNHƠNOFFICIAL 14
ng học - Điểm A: 0 ' 0 Ax A OAOBBA vveLe x =+ =+ = (1) Điểm G: 0 2 ' ''' 22 Gx Gr vveLe OGOBBG LL aee =+ =+ =+− (2) Mà 0 Axv = thay vào (1), ta suy ra: 0 0 .'cos0' .cos v vL L −== (3) Từ (3) suy ra: 2 0 3 sin '' cos v L = (4) Từ (4) và (2), ta được: 44 2 222 000 643 sin1 4cos4cos2cos G LLvvv a LLL =+= Vậy: 2 0 32sin G v a L = Lời giải thứ hai Chọn hệ quy chiếu như hình vẽ. Ta có: ABAB vvv =+ (1) Từ hình vẽ, ta suy ra: 0 0 sin sin BA v vv L == (2) A B G O y x r e e 0v '. BA vL = 0 B vv = Av Ga '' 2 G L a = 2 2 G L a ⊥ = A B G 0v Hình 2.1.2
ệ toạ độ cực gắn gới B như hình vẽ. Bước 1: Viết phương trình độ
luôn không đổi, nên Ga luôn hướng thẳng đứng.
ậy
aa LL
GG
A B
2.1.3
Bài tập 3: Một thanh cứng AB có chiều dài L tựa trên hai mặt phẳng P1 và P2 như Hình 2.1.3. Người ta kéo đầu A của thanh lên trên dọc theo mặt phẳng P1 với vận tốc 0v không đổi. Biết thanh AB và vectơ 0v luôn nằm trong mặt phẳng vuông góc với giao tuyến của P1 và P2; trong quá trình chuyển động các điểm A, B luôn tiếp xúc với hai mặt phẳng; góc nhị diện tạo bởi hai mặt phẳng là 0120= . Hãy tính vận tốc, gia tốc của điểm B và tốc độ góc của thanh theo 0v ,L và (góc hợp bởi AB và mặt phẳng P2) Lời giải thứ nhất Chọn hệ trục toạ độ như hình vẽ.
DẠYKÈMQUYNHƠNOFFICIAL 15 Suy ra: 2 0 3 cos '' sin v L = (3) Ta có: GGBGG aaaa ⊥ ==+ (4) Kết quả: 44 2 222 000 643 sin1 4cos4cos2cos G LLvvv a LLL =+= Lời giải thứ ba Tại mọi vị trí của thanh , điểm G luôn cách đỉnh O của góc vuông một khoảng L/2. Do đó G chuyển động trên đường tròn tâm O bán kính L/2. Vận tốc Gv luôn tiếp tuyến với quỹ đạo. Vì thanh cứng, nên hình chiếu của G và B theo hướng của thanh là bằng nhau và bằng 0 0 coscos 2sin GG v vvv == Hình chiếu của gia tốc Ga của điểm G trên bán
OG phải thoả mãn hệ thức 22 0 22sin 2 G vv L L = Nhận
ấy rằng
ếu
ủ
Gv
ủa
( ) 0 coscos
−=−=
kính
th
hình chi
c
a
c
điểm G theo phương ngang
22 GG v vv
V
22 00 23 cos 22sin2sin
vv
−==
0v 2P 1P Hình
Nhận xét: Vật có 3 bậc tự do x y
Bướ
phương
, do đó chúng ta cần 3 phương trình độc lập.
Bước 2: Viết các phương trình động lực học
Bước 3: Viết phương trình
DẠYKÈMQUYNHƠNOFFICIAL 16
= =
=
c 1: Viết các
trình động học Điểm A '' ' cos(sin).' sin cos.' ABAB A A xxLxxL yL yL
=+=+−
(1) Điểm B 0 B B x y
năng lượng. Bước 4: Viết phương trình liên kết Ta có 0 0 A B vv y = = Do đó: 0 00 0 00 1 .cos60 2 3 .sin60 2 Ax Ay vvv vvv == == (2) Bước 5: Giải hệ các phương trình. Từ (1) và (2), ta suy ra: 0 ' 0 ' 0 0 2 0 '' 0 3 3 '. 2cos 1 (sin).' 3 2 .tan 22 3 cos.' 3 2 4.cos B B B v L xLv v xv Lv v x L = +−= =+ = = Lời giải thứ hai Ta có: BBAA vvv =+ (1) Từ hình vẽ, ta suy ra: 0 0 0 0 0 0 0 3 sin60.cos 2.cos cos60.sin 3 .tan 22 B B v vL L vvL v vv = = =+ =+ (2) Suy ra: 2 0 3 3 '. 4.cos BB v av L == (3) Lời giải thứ ba Các thành phần vận tốc của A và B dọc theo thanh bằng nhau nên: A B x y O 0v 2P 1P 060 . BA vL = Bv 0 A vv =
v vv == = (2) Từ (1) và (2), ta suy ra: 0 sin'0BAB vvr =−+= 2 00 23 00 2
== ==
sinsin ' sin 2.sin.cos.'2sin.cos ''
phương
y r e e
==+ Toạ độ của điểm A: ''0 00 3 sincos.cos30 2 AA yLyLvv ==== Tốc độ góc của thanh: 0 ' 00 cos30 3 cos2cos vv LL === Gia tốc của B: 2 ' 0 3 3 4.cos BB v av L == Bài tập 4: Một thanh cứng AC đặt tựa vào vào bậc thềm có độ cao h như Hình 2.1.4. Cho biết đầu A chuyển động từ phải sang trái với vận tốc không đổi 0v . Gọi B là điểm tiếp xúc của thanh và bậc thềm. a. Xác định vận tốc, gia tốc của điểm B. b. Xác định quỹ đạo tâm quay tức thời của thanh. Hướng dẫn giải: Chọn hệ trục toạ độ Oxy gắn với đất và hệ toạ độ cực gắn gới A như hình vẽ vv h h vv hh
0v A
G
C B h Hình 2.1.4 0v A
C B h x O
=+− =− (5)
sin 2sin.cos sinsin sin 2cos.sin.
24 23 0 22 2 0
(3) Từ (1) suy ra: ( ) 2 .''.'. BABABr arere =+− (4) Thay (3) vào (4), ta được: ( )
0
Br Br
v v hh aee hh v aee h
DẠYKÈMQUYNHƠNOFFICIAL 17
( . Các
) 0 0 trình động học 0 .' BxAB OBOAABvvere =+=−+ (1) Vì Bv luôn hướng dọc theo thanh AB, nên: cos 0 BBrA B
cos60 13 tan cos22 A B vvv v
Bài tập 5: Một quả cầu khối lượng m đặt giữa tường thẳng đứng và nêm khối lượng M và góc nêm như Hình 2.1.5. Ban đầu quả cầu ở vị trí đỉnh của nêm tiếp xúc với nêm (mặt nghiêng tiếp tuyến với quả cầu). Nêm đứng yên trên mặt phẳng ngang. Thả để đồng thời quả cầu và nêm cùng chuyển động. Bỏ qua mọi ma sát. Giả sử nêm không bị lật. Tìm gia tốc của quả cầu trong giai đoạn quả cầu còn tiếp xúc với nêm. Hướng dẫn giải: Gọi 1v và 2v lần lượt là vận tốc của quả cầu và nêm.
DẠYKÈMQUYNHƠNOFFICIAL 18 b. Gọi G là tâm quay tức thời của thanh AB. G là giao điểm của đường vuông góc với 0v và Bv . Toạ độ của G : 2 .cot .cot G GG xh x yh yhx h = =+ =+ (6) Biểu thức (6) là phương trình quỹ đạo của tâm quay tức thời G. Một lời giải khác 2 0 0 2 'sin .tan cos ''''' BABABBr BABA BABABr v hOA h vvvvvv avv arere = = =+== =+ =− với sin AB h r = Nên ta rút ra kết quả ( ) 2 0 23 0 2 0 2 0 sin ' 2sin.cos '' cos sin 2cos.sin. BBr Br v h v h vvv v aee h = = == =−
Ta có: 1122 vvv =+ Suy ra: 12 12 tan tan vv aa = = (1) Định luật bảo toàn cơ năng : 22 12 11 0 22mvMvmgy+−= (2) Đạo hàm (2) theo thời gian, lưu ý : 1 ' yv = ; kết hợp với (1) suy ra kết quả: 12v 1v 2
2.1.5
v M m
Hình
Bài tập 6: Trên mặt phẳng ngang nhẵn có hai khối lập phương cạnh H , cùng khối lượng M đặt cạnh nhau (giữa chúng có khe hở nhỏ) như Hình 2.1.6. Đặt nhẹ nhàng một quả cầu có bán kính R , khối lượng mM = lên trên vào khe nhỏ. Bỏ qua mọi ma sát và vận tốc ban đầu của quả cầu. Tìm vận tốc quả cầu ngay trước khi va đập xuống mặt phẳng ngang.
Hướng dẫn giải: Gọi 1v và 22 ,'vv lần lượt là vận tốc của quả cầu, của khối lập phương bên trái và bên phải.
tính ch
DẠYKÈMQUYNHƠNOFFICIAL 19
Đị
ậ
ảo
cơ năng : ( ) 22 12 11 21cos 22mvmvmgR +=− (2) Thay (1) vào (2): ( ) ( ) 2 2 1 2 2 2 2 2 21costan 2tan 21coscos 1cos gR v gR v = + = + (3) Khi quả cầu rời khỏi khối lập phương thì 2v đạt giá trị lớn nhất. Đạo hàm biểu thức 2v theo cosvà cho biểu thức bằng 0, ta được phương trình: 3 cos3cos20 +−= (4). Giải (4), thu được: cos0,596 = Khi đó: ( ) 2 1 cos1cosvgR=− Quả cầu cách mặt đất một đoạn: ( ) 1cos hHR =−− Biện luận: α 2v 1v 12v 12v 1v 2v M M m R H Hình 2.1.6 2 1 2 tan tan g a M m = +
Do
ất đối xứng của hệ, ta suy ra: 1v hướng thẳng đứng từ trên xuống dưới, 22 'vv = Mặt khác: 1122 vvv =+ Suy ra: 12 tan vv = (1)
nh lu
t b
toàn
tập 7: Một thanh đồng chất khối lượng m , chiều dài L có thể quay trong mặt phẳng thẳng đứng quanh một bản lề ở đầu O của thanh. Thanh luôn lựa lên cạnh một khối lập phương cạnh a khối lượng M đặt trên mặt phẳng ngang như Hình 2.1.7. Lúc đầu thanh ở vị trí hợp với phương ngang một góc 0 , thả cho hệ chuyển động không vận tốc đầu. Tìm vận tốc của hộp khi thanh hợp với phương ngang một góc . Bỏ qua mọi ma sát. Hướng dẫn giải: Chọn hệ toạ độ Oxy như hình vẽ. Gọi x là toạ độ khối hộp, v tốc độ của khối hộp, là tốc độ góc của thanh. B là điểm tiếp xúc của thanh và khối hộp. Ta có: 2 2 cotsin
DẠYKÈMQUYNHƠNOFFICIAL 20
ậ
ảo
ậ
ố
( ) 222 2 11 2 1cos22 22 1cos22 RHRH vgRvg RHH ++− == +− Nếu ( )
R =+=−
xa
==−=
Ta
2
B BOB vv v vr a vv = == = O a B y x O a B
Nếu ( ) 1cos0,404 HRR − thì quả cầu chạm đất trước khi rời các hình lập phương, lúc chạm đất thì góc thỏa mãn ( ) 1cos HR =− . Vận tốc ngay trước chạm đất xác định theo định lu
t b
toàn năng lượng và liên hệ v
n t
c.
1cos0,404 HRR − thì sau khi rời khối lập phương, quả cầu chuyển động rơi tự do : 2 01 220,212 H vvghgR
Bài
sin dxadv
dtdta
(1) Hoặc có thể tính cách khác: Vì thanh luôn tiếp xúc với khối hộp nên thành phần vận tốc của điểm B và thành phần vận tốc của khối hộp chiếu theo phương vuông góc với thanh luôn bằng nhau.
có:
.sin .sin
Hình 2.1.7
Định luật bảo toàn cơ năng cho ta: ( ) 22 0 11 sinsin 222 L MvImg+=− (2) Với 2 1 3 ImL = , thay (1) vào (2), ta suy ra: ( ) 0 24 2
gL v ML mD
sinsin sin 3
= +
x vx y = xxl vxl y =+ =+− = (2) - Điểm C: ( ) ' sin' cos sin cos.' CxA CA C Cy
Điểm B: AxBxCx Gx GxA AyByCy Cy Gy
C B A
m Hình 2.1.8
m 2m
vxl xxl yl vl =+− =+ = = (3) - Khối tâm G của hệ: ( ) ' 2 5 sin' 4 4 2 1 cos.' 4 4
m O
vvv v vxl vvv vl v
+
y x
C B A
m 2m
++ = =− ++ = = (4) Bước 2: Viết phương trình động lực học: Phương trình định luật II: |0 0 000 Gxv xGxGx Fav = ==⎯⎯⎯→=
DẠYKÈMQUYNHƠNOFFICIAL 21
= (1) -
Bài tập 8: Hai thanh cứng, nhẹ chiều dài mỗi thanh là 1 lm = nối với nhau bằng bản lề C khối lượng m. Đầu mỗi thanh có gắn các quả cầu A, B có khối lượng 1 2 AB mmm == . Hệ thống được đặt thẳng đứng trên mặt bàn nằm ngang như Hình 2.1.8 Bằng tác động nhỏ, hai quả cầu bắt đầu trượt ra xa nhau sao cho hai thanh vẫn nằm trong mặt phẳng thẳng đứng. Bỏ qua mọi ma sát, gia tốc trọng trường 2 10/ gms = . a. Tìm vận tốc của bản lề tại thời điểm sắp chạm sàn. b. Tìm vận tốc của quả cầu Bm tại thời điểm góc giữa hai thanh là 0260 = Chọn hệ quy chiếu như hình vẽ Bước 1: Các phương trình động học: Điểm A: ' 0 A AA A ( ) ' 2cos 2sin' 0 BA BA B
Suy ra:
=
' ' ' '
xl xl xl yl
A B C C
5 sin.' 4 3 sin.' 4 1 sin.' 4 cos.'
Bước 3: Viết phương trình năng lượng ( ) 2222111 2sin 222ABCxCy mvmvmvvmglmgl ++++= (6)
Bước 4: Viết phương trình liên kết (Đã sử dụng các phương trình liên kết khi viết phương trình động học cho hệ) Bước 5: Giải hệ các phương trình Thay (5) vào (6), ta được: ( ) ( ) ( ) 22 2,75sin.'cos.'21sin llgl +=− (7)
a. Với 00 = , ta suy ra: '2 Cy vlgl == b. Với 060 = , thay vào (7) ta được: ( ) 16 '23 37 g =−− (vì đang giảm) Khi đó ( ) ' 3 sin.'0,6992/ 4
DẠYKÈMQUYNHƠNOFFICIAL 22
=− = = (5)
Lờ
ả
Cv thành hai thành phần , CxCyvv Do tính chất thanh cứng: sinsincos tan Cy BCxCyBCx v vvvvv =+=+ (1) sinsincos tan Cy ACxCyACx v vvvvv =−+=− (2) Do đó: 2 tan 2 BA Cx BA Cy vv v vv v = + = (3), 1 Định luật bảo toàn động lượng theo phương ngang: 20ABCx mvmvmv −++= (4) Định luật bảo toàn cơ năng cho ta:
B xlms =−=
i gi
i khác của bài toán: Gọi là góc tạo bởi thanh và phương thẳng đứng. Phân tích
mglmglmvmvmv vvvvgl
222 2222
111 cos2 222 221cos
ABC ABCxCy
( )
91cos30 91cos 0,6992/ 2114tan2114tan30 B gl gl vms === ++
−=++ +++=− (5) Giải hệ các phương trình (3)(4)(5), ta được ( ) ( ) ( ) ( ) ( ) 0 220
A O K
ta đượ y y y
xrl yrl K K K
= = = (2) Từ (1) và (2), suy ra: 2 0 0 22 22 0 0 2 2 0 3
l r 0 Hình 2.1.9 A O K
l r
=− = = −= = −−+= =−+
sin cos1 sin sin cos ' cos cos'cos0 'sinsin '' sin''cos'sin0 cos sincossin coscos
r l r r l l rl lr rll l rr ll
(3) Từ (1), ta suy ra: 0 22 0 22 2 0 3
xrl xrll r r l
'sin'sin ''cos''sin'cos sincos cos coscos
K K
=−− =−−− =−−−
(4)
D a
y x A B
DẠYKÈMQUYNHƠNOFFICIAL 23
=+ =− (1) -Từ điều kiện liên kết,
Bài tập 9: Một cơ cấu trục khuỷu OA nối với thanh truyền AK, đầu K gắn pittong như Hình 2.1.9 Xác định biểu thức vận tốc và gia tốc của pittong K theo thời gian Cho biết lúc ban đầu trục khuỷu OA nằm ngang và luôn quay với tốc độ góc 0 không đổi. Hướng dẫn giải: Chọn hệ toạ độ Oxy như hình vẽ. - Điểm K: coscos sinsin K K c 0 '0 ''0
Thay t
của các điểm A, B, vận tốc góc của thanh
vào (4) ta thu được kết quả. Bài tập 10: Một cơ cấu gồm 3 thanh rắn CA, AB và BD được gắn kết với nhau trong mặt phẳng thẳng đứng thông qua các khớp xoay như Hình 2.1.10. Thanh CA luôn quay với tốc độc góc không đổi 0 .Tại thời điểm thanh CA hợp với phương ngang góc 045 , xác định vận tố
Bài tập 11: Trong mặt phẳng thẳng đứng cho một hệ cơ gồm trục quay MA gắn với thanh rắn ABC hình thước thợ. Cho biết MA quay quanh M với tốc độ góc '() t , thanh ABC có thể quay tự do quanh trục quay A; trục quay B luôn chuyển động trên mặt phẳng nghiêng góc so với phương ngang Tại thời điểm thanh AM hợp với phương ngang góc như Hình 2.1.11; xác định vận tốc của điểm B, điểm C và gia tốc của B.
DẠYKÈMQUYNHƠNOFFICIAL 24
Hướng dẫn giải: 0 0 2 cos45 2 A AB B BD B BE a v vv v a v a = = = = 0 0 0 0 2 2 A B BD BE va va = = = =
=
c
AB, BD.
0 C A B D 2a Av Bv E A M B l C r l Hình
2.1.11
DẠYKÈMQUYNHƠNOFFICIAL 25 Hướng dẫn giải Chọn hệ quy chiếu như hình vẽ Ta có: BBAA vvv =+ (1) Từ hình vẽ, ta suy ra: 'cos sincos sin 'cos cossin sin tan B BA BBAA BA r v vv r vlv l = = += =− (2) Ta có: CCAA vvv =+ (3) Từ hình vẽ, ta suy ra: ( ) ( ) 22 2 2 '.2..'...cos cos '1sin2cos tan CBABA C vrlrl vr =++ =+−+ (4) Tính gia tốc tại B được xác định bởi biểu thức: ( ) BBAAM1BAABBABAAB BABAAA aaa2v''rr aaaacde ⊥⊥ =++++ =++++++ PP uuruuuruuruuruuuruuuruur rrr r rrrrrr (5) Trong đó: 1 12 2 2.2.'.. .''. . BABA BA cvl drl el == == = (6) Từ hình vẽ ta suy ra: 2 '''.cos'.sin''. cos BA B lrrl a −+−− = (7) Từ (2), ta có : sincos '''sin tan r l =+ (8) Thay (8) vào (7): 2 1sincos''sincos'.sin costan B l arr r − =−−+−− Bài tập 12: Hình vẽ là một kết cấu nằm trên mặt phẳng thẳng đứng tạo thành từ 3 thanh cứng AB, BC, CD. AB và CD có thể chuyển động quanh 2 trục A, D cố định vuông góc với mặt Hình '. A vr = .BABA vl = Bv '. A vr = CABA vl = Cv ''.l '.BABA al = Ba 2 .BABA al ⊥ = ''. A ar = 2 '. A ar ⊥ = 2.'.. BA l 2 .BA l A L 045 B C 045 L D
2.1.12 ; 2 điểm A, D cùng ở trên 1 đường nằm ngang. Hai đầu của thanh BC nối với AB và CD có thể quay quanh chỗ tiếp xúc (tương tự bản lề).
Hướng dẫn giải: Cho AB quay quanh trục A với tốc độ góc tới vị trí như trên hình vẽ, AB ở vị trí thẳng đứng, BC và CD đều tạo với phương nằm ngang góc 045 . Biết rằng độ dài của AB là L , độ dài của
DẠYKÈMQUYNHƠNOFFICIAL 26
BC và CD được xác định
vẽ.
đó hãy tìm giá trị và
ng
ốc Ca của điểm C (biểu diễn qua góc vớ
CD) Hướng dẫn giải: Gia tốc tại C được xác định bởi biểu thức: 22 2 2 r CCBBCBCBB r CBCB CB CB B aaaaaa vv a r L aL =+=++ == = Tá có: 0 / 2 2 / cos45 2 42 CBCB CD r CBC CD L vv v L a CD == == ( ) 0 / 2 2 2 2 // / sin45 2 0 2 2222 BDCB CCDBCD r CBCD CB L vv L vv v L a CB LL == ==== Trong đó: / CBCDv là thành phần theo phương CD của vận tốc tương đối C so với B. Từ hình vẽ ta suy ra: 2 1 222 12 22 2 2 4237 342 2 2 2222 r CCD CCC C L aa aaaL LL aL == =+= =+= Góc giữa phương của Ca với thanh CD là 2 1 tan6 C C a a == Bài tập 13 : 2 B aL = 22 12CCC aaa =+ 1 r CCDaa = CBa r CBa 0 2 cos45 r CCDB aaa =+ BC DC
như trong hình
Khi
hướ
gia t
i thanh
vAB vvv ⊥ =+ Từ hình v B B r B
L L 2
B C
ặt
t
(3) aAB a a
hình v = == Nghĩa là gia tốc của B có hướng dọc theo đường phân giác góc 2. Bài tập 14: Cơ cấu gồm 3 thanh rắn và 4 bản lề như Hình 2.1.14 Cho OAr = ; 2 ABr = ; 1 2 OBr = . Lúc OA thẳng đứng, các
cos2sin2 Bv BCv
L
(5) A
aaa 0v Ba
(4) Ba r Ba BCa r BCa
0v Hình 2.1.13 O
A 0 1O B Hình 2.1.14
DẠYKÈMQUYNHƠNOFFICIAL 27
ẽ: 0 2sin BBC v vv == (1) Trong HQC gắn với A: 2 2 0 24sin r BBB r B B aaa v v a LL =+ == (2) Trong HQC gắn với C: 2 r BCBBBCBC r BC BC aaaaa v a L =+=+ =
M
khác
ừ
ẽ, ta suy ra:
rr BCBB
=−
Từ (1)(2)(3) và (4), ta suy ra: 2 0 2sin2 B v a L =−
Hai thanh cứng, cùng chiều dài L, được nối với nhau ở một đầu bằng một bản lề như Hình 2.1.13. Đầu kia của một thanh được giữ cố định bằng một bản lề, còn đầu kia của thanh thứ hai thì cho chuyển động với vận tốc véctơ v0 không đổi cả về độ lớn lẫn hướng, đồng thời tại thời điểm ban đầu véc tơ vận tốc v0 song song với đường phân giác của góc tạo bởi hai thanh ở thời điểm đó . Hãy tìm độ lớn và hướng của véc tơ gia tốc của bản lề nối hai thanh sau thời điểm ban đầu một khoảng thời gian rất ngắn. Hướng dẫn giải: Ta có: B BBCC Từ (2) và (5), ta suy ra: 2 22 0 sincos sinsin2 r BBB v aaa L + =+= Ta có: ( ) , tantan
DẠYKÈMQUYNHƠNOFFICIAL 28 điểm O , B, 1O cùng nằm trên đường nằm ngang, khi đó thanh OA có vận tốc góc là 0 và gia tốc góc 2 00 3 = . Tìm vận tốc góc và gia tốc góc của thanh AB . Hướng dẫn giải: a. Ta có: 0 0 0 0 0 1 0 2 2 33 3 22 2 A BA A BA BBAA BO BAA r vr r vOA vvr vvv vvr = == ⊥ == =+ = == (1) b. Ta có: TnTnnT BBBBBAAABABA aaaaaaaaa =++=+++ (2) Với 2 0 2 0 2 0 22 0 3 2 3 2 n B n A T A n ABABAB r a ar ar arr = = = == (3) Chiếu (2) lên phương 1OO ta được: 00 .cos30.cos60nTnT B ABABA aaaa =−+ (4) Thay (3) vào (4), ta được: 2 0 2 0 646 2 326 2 AB T BA r a + = + = Bài tập 15: Trục quay OAr = quay đều quanh trục O cố định với vận tốc góc 0 . Đầu B của thanh truyền gắn bản lề với trục của con lăn D có bán kính R , lăn không trượt trên đường nằm ngang như Hình 2.1.15. Biết chiều dài thanh ABL = Tìm vận tốc và gia tốc tại hai điểm I, K trên chu vi con lăn tại thời điểm bán kính BI thẳng đứng và bốn điểm O, A, B, K cùng nằm trên đường thẳng ngang. BAv Bv Av 060 Av O L A 0 1O B T A a n A a n BAa T BAa T Ba n Ba T A a n A a O r A 0 C L B K I Hình 2.1.15
DẠYKÈMQUYNHƠNOFFICIAL 29 Hướng dẫn giải: Điểm A: 0 2 0 0 A n A T A vr ar a = = = Điểm B: 0 0 2 1 0 0 B BAA BA n BA T BA v vvr r L aL a = == = = = Do đó: 2 02 2 2 0 2 0 0 nT BABABA A B n BA T BA aaaa ar r ar r L a L a =++ = =+ = = Điểm I: 22 22 00 2 2 2 0 0 2 0 IK nT IBIBIB BI n IB IB T IBB vv aaaa rr arar LL v a R r aar L == =++ =+=+ == ==+ O A n Aa B K I Av Ba n BAa T IBa T KBa T BAa
DẠYKÈMQUYNHƠNOFFICIAL 30 Điểm K: 2 2 0 2 2 2 0 2 2 0 0 2 0 IK nT KBKBKB B I n IB IB T KBB T BKB vv aaaa r ar L r ar v L a R r aar L aa == =++ =+ =+ == ==+ ⊥ Bài tập 16: Cho cơ cấu như Hình 2.1.16. Trục quay OA quay đều với vận tốc góc 0 4/rads = , 0,5 OAr== m 2 ABr = , 2 BCr = BC = r 2 Hãy tìm: vận tốc góc, gia tốc góc thanh AB và BC. Hướng dẫn giải: Xét thanh AB: 0 2(/) 222(/) 2(/) A BA A AB vOAms vvms v rads AP == == == Xét thanh BC: ( ) 224/ 0,52 B BC v rads BC === Ta có: TnTnnT BBBBBAAABABA aaaaaaaaa =++=+++ Với 2 2 0 2 .82 . .8 0 4 . n BBC T BBC n A T A n ABAB T ABAB aBC aBC aOA a aAB aAB == = == = == = P Av C O A 045 B Bv n Aa n BAa T BAa T Ba n Ba C O A 045 0 B Hình 2.1.16
DẠYKÈMQUYNHƠNOFFICIAL 31 Từ hình vẽ, ta suy ra: ( ) ( ) 2 00 2 122/ cos45.cos45 24/ T B Tnn T BBAB B BC ams aaa a rads BC = =+ == Từ hình vẽ: ( ) ( ) 2 00 2 4/ cos45cos45 4/ T BA TnTn T BBBAA BA AB ams aaaa a rads AB = −=+ == Bài tập 17: Trục quay OA có chiều dài 10 lcm = quay đều với vận tốc góc ( ) 0 6/rads = làm cho con trượt A trượt dọc cần lắc như Hình 2.1.17. Lúc OA nằm và ngang 030 = . Tìm vận tốc trượt của A dọc cần lắc, vận tốc góc 1 của cần lắc. Hướng dẫn giải: 0 1 0 1 0 60/ 1,5/ cos30303/ sin3030/ Ar A rA A vvv vlcms v rads OA vvcms vvcms =+ == == == == Ta có: rC Tn r AC aaaaaaaa +=++=++ Trong đó: 22 0 2 1 2 11 360/ 22903/ 45/ A C n alcms arrcms aOAcms == === == Từ hình vẽ ta suy ra: 2 2 sin135/ sin cos cos903/ n n rA Ar t tn AC C aaacms aaa aaa aaacms =−=− −=−+ =+ =−= A O B 0 1O Av r v v A O B 0 1O r a T a n a Ca Aa A O B 0 1O Hình 2.1.17
DẠYKÈMQUYNHƠNOFFICIAL 32 cần lắc : Vậy gia tốc góc 2 1 1 9034,53/. 20 t a rads OA === Bài tập 18: Cam là một đĩa tròn bán kính R, tâm C quay đều quanh trục cố định qua O với vận tốc 0 làm cho cần đẩy AB chuyển động dọc theo rãnh K như Hình 2.1.18. Độ lệch tâm 2 R OC = . Tìm vận tốc và gia tốc của cần đẩy tại thời điểm ứng với 030 = , 045 = . Hướng dẫn giải: ( ) ( ) ( ) 0 0 00 0 0 3 tan3013 6 .1313 2cos303 Ar A r R vvv vv R v R vOA v =+ ==+ ==+ ==+ Ta có: T rC n ACrr aaaaaaaa +=++=++ A O C r v v Av T r a Ca n r a n a A O C Hình
2.1.18
Bài tập 19: Hai thanh cứng giống nhau mỗi thanh có khối lượng M, chiều dài L nối với nhau bằng một bản lề. Đầu còn lại của thanh thứ nhất được gắn với sàn bằng một bản lề trong khi đầu còn lại của thanh thứ hai có thể trượt không ma sát trên mặt sàn nằm ngang (Hình 2.1.19). Gọi α là góc giữa mỗi thanh và sàn. Bỏ qua ma sát tại các bản lề
Hình 2.1.19
1. Tìm lực mà sàn tác dụng lên thanh thứ hai ngay sau khi thả các thanh ở vị trí có = 450 .
2. Tìm tốc độ góc của hai thanh như là một hàm số của góc khi 0 < <450 .
DẠYKÈMQUYNHƠNOFFICIAL 33 Trong đó: ( ) ( ) ( ) 2 2 2 0 2 0 2 00 13 3 13 2 213 2 3 n r r n Cr R v a R R a R av + == + = + == Từ hình vẽ ta suy ra: ( ) 2 0 2 0 23 tan 0sincossin 9 1 coscos 3 6 3 Tn nT rCr rrC nn ArC A aaaR aaa R aaaa a =−= =+− =+− =+
Xét trong hệ quy chiếu gắn với đất. Gọi G là khối tâm của BC GGBBAAGABBGaaa =+=+ (1) Với 0 2 0 GBGBGB GBGBGB GB aaa L aa v ⊥ ⊥ =+ == = Ga 2 GB L a = BA aL = A L L B C
DẠYKÈMQUYNHƠNOFFICIAL 34 0
BABABA BABABA BA
v
⊥ ⊥ =+
== =
O: 22 11 21524 2212443 L FLPMLMLFPML +=++= (5) +Xét chuyển động quay của thanh AB: Phản lực liên kết 1F do BC tác dụng đã làm quay AB 2 11 2121 221243 L FLPMLFPML −+=−+= (6) Từ (4) (5) và (6), ta suy ra: 7 10 NMg = b. Biểu thức cơ năng của hệ tại vị trí bất kì: 220 0 22 0 11 2sin2sin45 2222 2sin2 A A LL IIMgMg IIMgLMgL ++= ++= (7) Mặt khác: 2 2 0 22 0 1 35cos2 13 . 12 A A IML IIML IMLMOG = +=− =+ (8) Thay (8) vào (7), ta được: A L L B C 2F 1F P N Ga O
0
aaa aaL
Và BACB == (2) + Gọi F1, F2 là hai thành phần lực do thanh AB tác dụng lên thanh BC có phương lần lượt dọc theo BC và vuông góc với BC + Xét phương trình chuyển động của thanh BC: Chuyển động tịnh tiến: 12 GFFPNMa +++= (3). Chiếu (3) lên phương BC, ta được: 1 22 22 FPNML +−= (4) Chuyển động quay quanh tâm quay tức thời
DẠYKÈMQUYNHƠNOFFICIAL 35 ( ) 0 2sin45sin 5 os2 3 g Lc =
DẠNG 2: LIÊN KẾT DÂY TREO
2.1. Phương pháp chung: Kiểu liên kết này xuất hiện khi các vật trong hệ được nối với nhau với sợi dây nhẹ không dãn. Liên kết động học: thành phần vận tốc dọc theo dây của các điểm trên dây là bằng nhau. Lực liên kết trong trường hợp này là lực căng dây T , có phương chiều được xác định. Nên ta có thể phân tích các biểu thức động lực học theo phương sợi dây để tìm T .
Trong trường hợp lực căng dây đóng vai trò là lực xuyên tâm, cần chú ý đến sự bảo toàn mômen động lượng của vật. 2.2. Bài tập vận dụng: Bài tập 1: Một đĩa nặng bán kính R, được treo vào hai dây không dãn quấn quanh nó. Đầu tự do của hai dây. Đầu tự do của hai dây được buộc vào đĩa (Hình 2.2.1) Đĩa đang lăn xuống. Tại thời điểm đang xét, vận tốc góc của đĩa là và góc giữa hai dây là Tìm vận tốc tâm O của đĩa tại thời điểm đó. Cho biết dây luôn luôn căng khi chuyển động. Hướng dẫn giải:
không dãn nên:
DẠYKÈMQUYNHƠNOFFICIAL 36
1 / 1 / 0 0 A Aday B Bday vv vv == == (1) 1 1 AA A B v vBB ⊥ ⊥ Từ đó ta suy ra tâm quay tức thời O1 và hướng của 0v như hình vẽ Vậy: 1 01 OO cos 2 .OO cos 2 R R v = == Bài tập 2: Một khối trụ tròn xoay đồng chất khối lượng M , bán kính R , có thể quay xung quay một trục cố định trùng với trục khối trụ. Một sợi dây dài, nhẹ, không dãn một đầu quấn nhiều vòng vào khối trụ; đầu còn lại được A B 1O 1A 1B Av O Bv 0v Hình 2.2.1
Dây
treo cố định vào điểm treo B. Ròng rọc nhẹ, bán kính r đặt lên sợi dây; ròng rọc có treo mật khối lượng m như Hình 2.2.2 Thả hệ chuyển động với vận tốc ban đầu bằng không. Xác định gia tốc của vật m , cho biết ròng rọc chuyển động lăn không trượt. Hướng d
DẠYKÈMQUYNHƠNOFFICIAL 37
Gọi A, A1 ,A2 lần lượt là các điểm trên sợi dây tiếp xúc với khối trụ và ròng rọc. Dây không dãn nên: 1 2 0 AA AB vv vv = == (1) Vì dây không trượt trên khối trụ và ròng rọc nên: 1 ' 2' A A vR vx = = (2) Do đó: ' ' 2 R x = (3) Chọn mốc thế năng tại vị trí ban đầu. Biểu thức cơ năng của hệ: 2211 ''0 22mxImgx +−= (4) Thay 2 1 2 IMR = và (3) vào (4), ta được: 2 22 1112' '0 222 x mxMRmgx R +−= (5) M m r x M 'x ' r ' r M m R r Hình 2.2.2
ẫn giải:
DẠYKÈMQUYNHƠNOFFICIAL 38 Đạo hàm (5) theo thời gian, ta được: '' 1 2 mg x mM = + Bài tập 3:
gồm 2
ọ
Hướng dẫn: Vì không có hiện tượng trượt trên dây nên: 11 22 A B vr vr = = Mà : '11'22 ; AB vrvr == Gọi C là tâm quay tưc thời trên đĩa. 1122 3 2 AB ACBCACAC vvrr rrrrr == Do đó: 11 3 1122 2 AC r rr rr = + Suy ra: 3 1122 3 2 A AC v rr rr = + = Vận tốc khối tâm C: ( ) 33 1122 2 CAC vrr rr =− = Hình 2.2.3 'A 1 11r 22r 11r 22r 2 1r 2r C A B 'B 1 C 2 1r 2r 3r
Cơ hệ
ròng r
c ròng rọc quay với tốc độ góc lần lượt là 1 , 2 và 1 cái đĩa như Hình 2.2.3. Xác định tốc độ góc và vận tốc khối tâm C của đĩa. Cho biết dây nhẹ, không dãn và không có hiện tượng trượt trên dây.
Bài tập 4: Hai ròng rọc đồng chất A và B có khối lượng lần lượt là 1m và 2m . Quấn sợi dây nhẹ không dãn vào hai ròng rọc. Ròng rọc A quay xung quay trục cố định, ròng rọc B chuyển động tự do trong mặt phẳng thẳng đứng như Hình 2.2.4 Ròng rọc B được thả rơi tự do không vận tốc đầu. Xác định lực căng của dây quấn, gia tốc góc
DẠYKÈMQUYNHƠNOFFICIAL 39
ọ
độ
ủ
ố
ụ B. Hướng dẫn giải: Gọi O là khối tâm của khối trụ B. Ta có: 0112201122 vRRaRR =+=+ (1) Các phương trình động học của hệ: 220 220 1111 222 2 11 22 1 2 1 2 mgTma mgTma TRIT TRI T mR mR −= −= == = = (2) Giải hệ các phương trình trên, ta được: ( ) ( ) 1 2 12 12 2 121 1 122 32 2 32 2 32 T mm g mm m g mmR m g mmR = + = + = + 1 B 2 A Hình 2.2.4
hai ròng r
c, phương trình chuyển
ng c
a kh
i tr
Phương trình chuyển động của khối trụ B: 2 12 1232 S mm gt mm = + + Bài tập 5: Một vật có khối lượng 1m được nối vào sợ dây quấn quanh một ròng rọc O khối lượng 2m , bán kính R. Gắn vào đầu O một thanh cứng OA có khối lượng không đáng kể. Dưới tác dụng của một lực F vuông góc với thanh tại đầu A làm cho ròng rọc quay và kéo vật đi lên (Hình 2.2.5). Xác định gia tốc của vật 1m và sức căng của dây treo. Coi ròng rọc là một đĩa đồng chất. Hướng dẫn giải: Các phương trình động học và động lực học của hệ: ( ) ( ) ( )
Bài tập 6: Tang quay B có hai vành bán kính R, r và momen quán tính đối với trục quay 0I . Vành trong của tang có quấn dây, treo vật nặng D khối lượng m. Khi tang B đang chuyển động với tốc độ góc 0 , người ta ta dụng một lực F vuông góc với cần hãm 1 OA để má hãm E xiết vào vành ngoài của tang B (Hình 2.2.6). Cho biết hệ số ma sát của vành ngoài và má hãm là ,bán kính quán tính của tang đối với trục quay là , các kích thước của cần hãm là 1 OAa = , 1 OEb = . Bỏ qua kích thước của má hãm, ma sát tại các ổ quay, trọng lượng của dây và cần hãm. Xác định gia tốc góc của tang B. Hướng dẫn giải: Gọi L momen động lượng của hệ. Ta có các phương trình động học và động lực học sau:
m Hình 2.2.5 B F m
1O E A Hình 2.2.6
DẠYKÈMQUYNHƠNOFFICIAL 40
−= = −=
1 12 1 2 1 12 2 2 2 2 a aR Tmgma Tm FlTRI FlmgR mmR mgRFl mmR = =
+
+ +
F
M
=+ −= ; vv LImvmv
v LImv NbFa
DB BD
1m
= =− Giải hệ các phương trình trên thu được kết quả: ( ) ( ) 2 0 B aFRmgrb bImr = + Bài tập 7: Hai vật nặng khối lượng 1m và 2m được buộc vào hai dây quấn vào hai tang của một ròng rọc có bán kính r và R . Để nâng vật 1m lên người ta tác dụng vào ròng rọc một mômen quay M (Hình 2.2.7). Tính gia tốc của ròng rọc và gia tốc của hai vật. Cho biết mômen quán tính của ròng rọc đối với trục quay là I . Hướng dẫn giải: Ta có các phương trình động học và động lực học sau: rR ar dL mgrmgRMaR dt MmgrmgR rR mrmrI
r
R M 2m
== = =−++= −+ + = ++
=+
r dL mgrNR dt r 12 1 122 12 1122 22 1122
Hình 2.2.7 m m M Hình 2.2.8
Bài tập 8: Trên một thanh thẳng đặt cố định nằm ngang có hai vòng nhỏ nối với nhau bằng một sợi dây mảnh, nhẹ, không dãn, chiều dài 2 L = mét. Khối lượng mỗi vòng là 1 m = kg. ở điểm giữa của dây có gắn một vật nặng khối lượng 10/9 M = kg (Hình 2.2.8). Lúc đầu giữ vật và hai vòng sao cho dây không căng nhưng nằm thẳng dọc theo thanh ngang. Thả cho hệ vật chuyển động. Bỏ qua ma sát. Lấy giá trị của gia tốc rơi tự do g = 10 m/s2 . a. Tìm tốc độ lớn nhất của vòng.
DẠYKÈMQUYNHƠNOFFICIAL
41
0 0
b. Tìm tốc độ lớn nhất của vật, lực căng của dây ở thời điểm vật có tốc độ lớn nhất. Hướng dẫn giải a. Gọi là góc giữa dây và phương nằm ngang. Gọi v là tốc độ của vật, u là tốc độ của vòng. Vì dây không dãn, hình chiếu vận tốc 2 đầu dây dọc theo dây bằng nhau: cossinuv = (1)
Trong suốt quá trình chuyển động, tốc độ của vòng u luôn tăng vì lực luôn hướng theo chiều chuyển động. Ngay trước khi va chạm với nhau ( = 900) thì chúng có umax còn v = u/tan900 = 0. Định luật bảo cơ năng 2 max 1 . 22 L muMg = (1) max 3,33 u = (m/s). 2. Ta tìm vận tốc v của vật khi dây treo hợp với thanh ngang một góc bấ












DẠYKÈMQUYNHƠNOFFICIAL 42
t kì. Theo định luật bảo toàn năng lượng: 2211 2sin 222 muMvmgL += Suy ra: 2 22 sin100sin 2tan9tan5 MgL v M == ++ (3) Đặt sin x = , ta có: ( ) ( ) ( ) ( ) 2 2 2 1 100 45 '4195 245 xx vyx x xx yx xx == + +− =− + Điệu kiện: ( ) 1 '0 4 yxx== Do đó: max 2,5/ vms = Khi vật M có vmax thì lực tác dụng lên nó bằng 0, vì v’ = gia tốc a = 0, lúc đó mới xảy ra cực trị. 2sin11,1MgTT = (N) Bài tập 9 : Cho một cơ hệ như hình vẽ. Một sợi dây dài, một đầu được giữ cố định ở điểm O, đầu kia vắt qua một ròng rọc nhỏ ở điểm O1 và treo vật khối lượng m. Hai điểm O, O1 ở cùng một độ cao. Một vòng nhỏ được luồn vào dây ở giữa đoạn OO1. Một vật khác có khối lượng cũng là m được treo vào vòng m m M L L 2m 2O O 1m 1O Hình 2.2.9
bằng một đoạn dây ngắn. Các dây không có khối lượng, không dãn. Bỏ qua ma sát. Ban đầu hệ được giữ như Hình 2.2.9, rồi thả không vận tốc đầu. Tìm gia tốc của hai vật khi đi qua vị trí cân bằng tĩnh. Hướng dẫn giải: -Sau khi thả hệ vật với vận tốc ban đầu bằng 0, vật 2 sẽ đi xuống, vật 1 đi lên.
DẠYKÈMQUYNHƠNOFFICIAL 43
Gọ
0l
chiề
ban đầu của sợi dây Tại vị trí cân bằng Biểu thức thế năng của hệ: 0 Wtan2 cos t L mgLmgl =−−− (1) W'0sin1 2 t == (2) Mặt khác 2 2 2 2 2 1 2 tan'' '2' cos sin 2 cos cos ONL vON ON vONL L L = = = =− = =− Biểu thức năng lượng của hệ: ( ) 22 112200 11 tan22 22cos L mvmvmgLmglmglL +−−−=−− Do đó: ( ) ( ) 22 12 12 2 223 33/2 639 8 LL vvgLgL g aa ==−−=− ==− 2 2 12 122 cos ' 2sin. 2sin2cos.' v v L v aav = =− =−− 2P 2O O 1P 1O L L
i
là
u dài
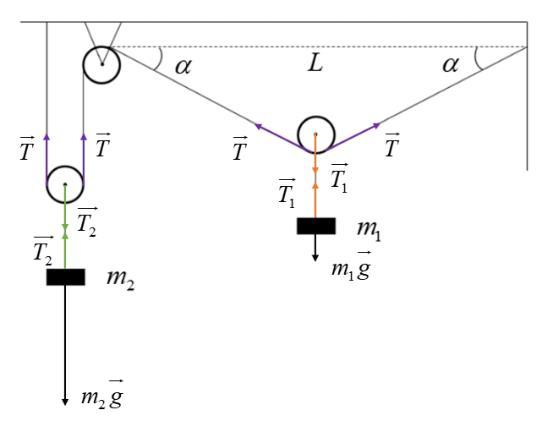
Bài tập 10: Hai vật khối lượng 1m và 2m được bố trí trong một cơ hệ như hình 10L.1 ở nơi có gia tốc trọng trường g. Dây không dãn, các ròng rọc nhẹ và có bán kính rL . Giữ các vật để hệ ở trạng thái cân bằng sao cho góc tạo bởi các sợi dây treo ròng rọc hợp với phương ngang một góc (Hình 2.2.10). Tìm gia tốc tức thời của các vật ngay sau khi thả hệ ra.
Hướng dẫn giải:
Định luật 2 Niu tơn viết cho:
+ Vật m1: 1111 . mgTma += (1)
+ Vật m2: 2222 . mgTma += (2)

+ Ròng rọc gắn với m1: 1 0 TTT++= (3) + Ròng rọc gắn với m2: 2 0 TTT++= (4) Chọn chiều dương của m1 hướng lên, của m2 hướng xuống. Các phương trình véc tơ (1), (2), (3), (4) cho ta các phương trình đại số sau: 1111 Tmgma −= ; 2222 mgTma −= ; 1 20 TsinT−= ; 2 20TT−= (*) 1m dịch chuyển một đoạn rất nhỏ 1x lên trên làm 2m di chuyển một đoạ
DẠYKÈMQUYNHƠNOFFICIAL 44
n 2x xuống dưới (hình vẽ). Khi đó: 211 2 xxcosxsin =−= . Chia hai vế cho thời gian được được mối liên hệ vận tốc của các vật: 21 vvsin = . Lấy vi phân hai vế được mối liên hệ gia tốc: 21 aasin = (**) 2m 2O 1m 1O L Hình 2.2.10
Từ (*) và (**) rút ra: 21 1 2 21 . msinm ag msinm = + và 21 2 2 21 .. msinm agsin msinm = +
Bài tập 11: Một sợi dây nhẹ không giãn được xâu qua một hạt nhỏ có khối lượng m; một đầu sợi dây gắn cố định vào điểm A, đầu còn lại của dây được gắn vào một vành nhẫn nhẹ, có thể trượt không ma sát dọc theo một thanh nằm ngang như Hình 2.2.11. Tại thời điểm ban đầu, hạt được giữ cạnh nhẫn và sợi dây lúc đó là thẳng nhưng chưa căng, sau đó buông hạt. Tìm vận tốc của hạt tại thời điểm dây bị đứt. Biết rằng sợi dây chỉ chịu được sức căng tối đa là 0T . Cho biết chiều dài của sợi dây là L và khoảng cách từ điểm Ađến thanh là h . Bỏ qua mọi ma sát. Hướng dẫn giải: Chọn hệ trục Oxy như hình vẽ Gọi N,B lần lượt là vị trí của vật và của vòng nhẫn. Vì vòng nhẫn không có trọng lượng và trượt không ma sát trên thanh cứng nên BN luôn có phương thẳng đứng. Bước 1: Viết phương trình động học
DẠYKÈMQUYNHƠNOFFICIAL 45
N N
= =
Dựa vào tính chất chiều dài sợi dây
L ta
( ) ( ) ( ) 2 22 2 22 Lhx hyxLyy Lh + −+=−=− (2) Nhận xét: hạt chuyển động trên một nhánh parabol. Từ (1) và (2) ta suy ra ( ) 2 '' ' '.'' .' Nx Nx Ny Ny ax vx xxx xx v a Lh Lh = = −+ = = (3) Bước 2: Viết các phương trình động lực học -Phương trình định luật II: 12 TTmgma ++= (4) Ta có 12 TTT == g h A m L Hình 2.2.11
xPN yBN
(1)
không đổi
suy ra phương trình
Thay (2) vào (7) ta được: 2 22 .' '2'. xxLh xgyxgyLhLy +== (8) Bước 4: Viết các phương trình liên kết Đã sử dụng ở trên Bước 5: Giải các phương trình đã tìm được Thay (2) và (8) vào (6), ta thu được . 2 mgL T Ly = (9) Theo đề bài, sợi dây đứt khi 0TT = , nên 0
DẠYKÈMQUYNHƠNOFFICIAL 46
Từ (3) và (4) ta suy ra ( ) ( ) 2 2 cos cos.'' '. sin1. '.'' sin T Tmx xx m mgTm xxx hL mgTTm Lh −= +−= −+ +−= (5) Với sin hy Ly = và cos x Ly = thay vào (5), ta được 2' 1. hyxxx Tmmg LyhLLyhL −+=− (6) Bước 3: Viết phương trình năng lượng 22 1 02 2 mvmgyvgy −== (7)
=− Chú ý về điều kiện của 0T Vì 0 012 2 Lhhmg y LT + − Nếu 0 12 hmg LT − thì tại thời điểm dây đứt vận tốc của vật bằng 0 21 2 mg vgL T =− Nếu 0 2 mg T thì sợi dây đứt ngay khi vừa thả vật. Nếu 0 1 mgh TL − thì sợi dây không bị đứt trong suốt quá trình chuyển động. Một lời giải khác cho Bài toán: Phân tích lực tại vị trí của vật. Vì sợi dây là lý tưởng và không có ma sát giữa hạt và dây, nên 12 TTT == và lực F hướng theo đường phân giác của véc tơ 1T và 2T
0 1 2 21 2 mg yL T mg vgL T =−
Theo phương tiếp tuyến quỹ đạo, ta có: 2 2coscos v Tmgm R −= (1) với 2 vgy = và R là bán kính cong của Parabol tại điểm N. Ta hãy so sánh chuyển động của hạt ở đây với chuyển động của một vật được ném dưới một góc so với phương ngang (được ném từ C’ ở độ cao H xuống trục X). Khi đó ta sẽ chọn các tham số của chuyển động này sao cho quỹ đạo của vật là Parabol đối xứng với quỹ đạo của hạt qua trục X. Khi đó:
DẠYKÈMQUYNHƠNOFFICIAL 47
=−
cos
==
V
2
xy x y uuu
u
Lh H =+ = =− =− + = (4) Thay (4) vào (3), ta được ( ) 2 cos Ly R = (5) Thay (5) vào (1), ta được kết quả: . 2 mgL T Ly = Chú ý: Nếu ta sử dụng công thức xác định bán kính cong của quỹ đạo 3 2 2 2 2 1 dy dx R dy dx + = , ta cũng tìm được ( ) 2 cos Ly R = , thay vào (1) ta được . 2 mgL T Ly = .
22 2 x OK u t H t g OKLh = =
Suy ra: 22 2 2 x Lh ug H = (2) Gọi vận tốc của vật là u , khi đó gia tốc pháp tuyến của vật tại điểm N’ là 2 '
n u ag R
(3)
ới ( ) ( ) 222 22
2 2 2 2 2 2
Lh
H uLyg ugHy
Bài tập 12: Một động cơ đặt trên bờ có độ cao H so với mặt nước, quấn dây đều vào tời với tốc độ 0v để kéo một chiếc thuyền vào bờ. Tại thời điểm đã cho, dây lập một góc α so với phương ngang, còn vận tốc của thuyền là v. Trên dây người ta có thắt một nút nhỏ và tại thời điểm đang xét, nó cách tời một khoảng lớn gấp 2 lần khoảng cách tới mũi thuyền (Hình 2.2.12). Cho biết sợi dây nhẹ, không dãn. Hãy tìm vận tốc và gia tốc của nút này tại thời điểm đã cho theo H, 0v và α.
DẠYKÈMQUYNHƠNOFFICIAL 48
ọ
Gọ
ị
M là
ị trí
Chú ý: 0 0,0 90 −+= Tại A 0 0 0 2 00 223 ' sin cos '.'.' 'cossin '''1cos sinsin AArA rv vv v vrere LvL vv LL =− =− =+=− = ==− (1) Tại M ( ) ( ) ( ) ' '''2 ' '2' .'. ''.'..'..''.. .'. 02..'.''. MMrM MMrMMMr MMrM MrMM vrere arerererere vrere arerre =+ =++++− =+ =−++ (2) 1. Tính Mv : 22 2 000 22 cot1tan 33 M vvvv =+=+ 2.Tính Ma : 2223 2 00 22 22.cossin ' 3sin3cos M vv r LH == 0v v A M O H L 2 3 L e r e 0v v A M O H L 2 3 L Hình 2.2.12
Hướng dẫn giải: Ch
n hệ toạ độ cực tại O như hình vẽ
i A là v
trí mũi thuyền
v
nút thắt
Bài tập 13: Một sợi dây được quấn vào lõi của một cuộn chỉ. Một đầu dây được vắt qua một đinh cố định. Người ta kéo dây với tốc độ v không đổi (Hình 2.2.13). Hỏi tâm O của lõi chỉ sẽ chuyển động với vận tốc bằng bao nhiêu, tại thời điểm khi dây hợp với phương thẳng đứng một góc . Cho biết cuộn chỉ có bán kính ngoài R, bán kính lớp dây quấn r. Dây không trượt trên cuộn chỉ và cuộn chỉ lăn không trượt trên mặt phẳng ngang. Hướng dẫn giải: Để sợi dây kéo luôn căng có vận tốc v không đổi thì cuộn chỉ phải có chiều quay như hình vẽ. Gọi A là điểm của cuộn chỉ tiếp xúc với sợi dây. 0 A vvOA =+ Vì sợi dây không trượt trên trục chỉ nên hình chiếu của Av lên phương
DẠYKÈMQUYNHƠNOFFICIAL 49
2222 000 cossinsin 2''222 sincoscos M vvv r LLH ==−=− 0 22 22 00 333 sin cossin ''222 3sin3cos3cos M v vv r LLH === Vậy kết quả 0 2 2 22 2322 00 23 sin sinsin 22 2 3coscos3cos M v vv a HHH =+−+
ừ
ẽ
ra:
Điều kiện lăn không trượt: 0v R = Suy ra 0 sin vR v Rr = Biện luận: + 0 0 v nếu sin r R + 0 0 v nếu sin r R 0v r Av OA soiday 2 22 2 0 2 sin 21 tan3 3coscos M v a H =+−+ R v r O A + 0v R v r O Hình 2.2.13
của sợi dây phải bằng v T
hình v
ta suy
0 sin vrv −=
+ 0 0 v = nếu sin r R =
Bài tập 14: Một thanh cứng AB đồng chất, tiết diện đều, khối lượng M, chiều dài AB là L có gắn thêm một vật nhỏ khối lượng 4 M m = ở đầu mút B. Thanh được treo nằm ngang bởi hai sợi dây nhẹ không dãn O1A và O2B (như hình vẽ 2.2.14). Góc hợp bởi dây O1A và phương thẳng đứng là 0 . Cắt đứt sợi dây O2B, tính lực căng dây T của dây O1A và gia tốc góc của thanh ngay sau khi cắt dây. Hướng dẫn giải: Lời giải thứ nhất Chọn hệ toạ độ cực ( ) 11Or gắ
DẠYKÈMQUYNHƠNOFFICIAL
50
n với O1 và ( ) 2Ar gắn với A như hình vẽ Ta có: '''''' GAAGGAAG rrrrrr =+=+ Với ( ) ( ) 2 1 2 2 ''.''.' ''.''.' AAAr AGAGAr rrere rrere =+− =+− Tại thời điểm dây bị cắt: 0,0AGvv== nên: '0,'0== Do đó : ''.''.'' GAAG rrere =+ Viết phương trình động lực học: ( ) '' GFPMmr +=+ Suy ra: ( ) ( ) ( ) 100 cos.''cos r FMmgMmAG ++=+− Vì 1r TF =− hay ( ) ( ) ( ) 00.''coscosTMmAGMmg =+++ Phương trình Mômen: 0 ..cos'' GTGAI −= Với 2 38 ; 515 G LmL AGI== Giải hệ các phương trình trên, ta thu kết quả: A B 1O 2O C m L 0 r e e G e 2r e P T A B 1O 2O C m L 0 Hình 2.2.14
40cos 827cos 45cos '' 827cos
mg T g L GAGA GA GA
( ) ( ) 23 25 MmL AGMmMACmABAGL Mm + +=+== + Các phương trình liên hệ gia tốc: 40cos 827cos 45cos 827cos
= + = + Lời giải thứ hai Tại thời điểm t=0, khi dây O2B vừa bị cắt, vì thanh chưa di chuyển, điểm A có vận tốc bằng 0 và gia tốc Aa hướng theo phương vuông góc với dây O1A. Ta lập phương trình chuyển động của khối tâm G của hệ với gia tốc Ga và chuyển động quay của hệ quanh G với gia tốc . Ta có các phương trình sau: 0 2 0 2 0 2 2 0
aaa a aAG AG =+ == Phương trình mg T g L
= + = +
định luật II Newton: ( ) GPTMma +=+ Chiếu lên phương O1A: ( ) ( ) ( ) 000 .cos.cos..cos GA MmgTMmaMmAG +−=+=+ Phương trình chuyển động quay của hệ quanh khối tâm G 0 ..cos TGG MITAGI == Với 222218 . 1215 G IMLMCGmBGmL =++= Giải hệ các phương trình trên, ta thu kết quả: ( )
DẠYKÈMQUYNHƠNOFFICIAL 51
( )
0 2 0 2 0 2 2 0
Bài tập 15: Một sợi dây quấn nhiều vòng vào vành một bánh xe nặng, đầu kia gắn vào điểm treo. Nếu buông, vành xe sẽ chuyển động xuống dưới. Giải sử có 3 bánh xe như thế mắc “nối tiếp” với nhau, đầu dây của bánh xe sau gắn vào trục của bánh xe trước như hình vẽ 2.2.15. Buông đồng thời tất cả các bánh xe, cả ba sẽ chuyển động. a. Xác định gia tốc của bánh xe trên cùng. b. Bánh xe trên cùng sẽ có gia tốc là bao nhiêu nếu số bánh xe mắc nối tiếp như trên là rất lớn. Hướng dẫn giải: a. Gọi ,,, iiii vhT ,lần lượt là vận tốc chuyển động tịnh tiến của khối tâm, vận tốc góc, quảng đường vành xe thứ i điđược và lực căng của dây “phía trên” tác dụng lên bánh xe thứ i. Ta có phương trình động học:

DẠYKÈMQUYNHƠNOFFICIAL 52
212
vR vvR vvR =
−= −= (1) và 2 11 2 22 2 33 2 2 2 vgh vgh vgh = = = (2) Các phương trình động lực học: Bánh xe 1: 211 222 11122 11 22 mgTTma mvmrmghTh +−= +=+ (3) Bánh xe 2: 322 222 2223221 11 22 mgTTma mvmrmghThTh +−= +=+− (4) Bánh xe :4 32 222 33332 11 22 mgTma mvmrmghTh += +=− (5) Giải hệ các phương trình (1) (2) (3) (4) (5), ta được:
11
323
Hình 2.2.15
221 332
Tma Tmaa Tmaa
và 12 123 23
3 3 2
−+−= −+= (7)
aag aaag aag
1 2 3
8 13 11 13 12 13
ag ag ag
và
Thay (8), (9) vào (7), ta được: 2 51 10 2 +−== Vậy gia tốc của vành thứ nhất trong trường hợp này là: 1 51 2 ag =
1 2 3
8 13 3 13 1 13
Tmg Tmg
= = = b. Giả sử rằng gia tốc của vành đầu tiên: 1 ag = (8),là một hệ số nào đó ta cần xác định. Xét trong hệ quy chiếu chuyển động với gia tốc 1a . Trong HQC sự mô tả chuyển động của tất cả các vành kề từ vành thứ hai là bài toán tương tự như bài toán ban đầu, chỉ với một sự khác biệt là sự chuyển động diễn ra trong trọng trường “hiệu dụng” với gia tốc rơi tự do là : ( ) 1 '1ggag =−=− và tổng số vành bớt đi 1 vành. Vì số vành là rất nhiều nên ta coi gia tốc của vành trên cùng bằng: 1 ''ag = Do đó trong HQC đứng yên, gia tốc của vành thứ hai là ( ) ( ) ' 211 '2aaaggg =+=+=− (9)
DẠYKÈMQUYNHƠNOFFICIAL 53
( ) ( ) 11
= =− =− (6)
−=
=
=
=
Tmg
DẠNG 3: LIÊN KẾT KHỐI CẦU TRỤ LĂN 3.1. Phương pháp chung: Kiểu liên kết này xuất hiện khi khối cầu, khối trụ, vành trụ chuyển động lăn trên một bề mặt. Phương trình liên kết: nếu vật chuyển động lăn không trượt thì véc tơ vận tốc của các vật tại điểm tiêp xúc là bằng nhau về phương chiều và độ lớn. -Phản lực liên kết trong trường hợp này là lực ma sát song song với mặt tiếp xúc và phản lực vuông góc với mặt tiếp xúc. Ta có thể chiếu các biểu thức động lực học theo các phương này để tìm các thành phần của phản lực liên kết.
3.2 Bài tập vận dụng: Bài tập 1: Một đĩa khối lượng m bán kính R dặt trên một xe có khối lượng M. Xe đặt trên một bề mặt không ma sát. Một sợi dây khối lượng không đáng kể quấn quanh đĩa (Hình 2.3.1). Đầu dây được kéo bởi một lực F không đổi như hình vẽ 1)Tìm gia tốc của đĩa và của xe trong trường hợp đĩa lăn không trượt trên xe. 2)Tìm gia tốc của đĩa và xe trong trường hợp đĩa lăn có trượt trên xe, hệ số ma sát trượt là μ. Hướng dẫn giải:
DẠYKÈMQUYNHƠNOFFICIAL 54
Xét chuyển động của đĩa: 1 12 2 1 2 ms ms FFma FI aa R ImR += −= = = (1) Xét chuyển động của xe: 2 ms FMa−= (2) Từ (1) và (2): 1 2 (4) (3) 3 MmF a Mmm F a Mm + = + = + 2) Các lực tác dụng lên đĩa và lên xe như hình vẽ trên. Xét chuyển động của đĩa: 1 ms FFma += (1) Xét chuyển động của xe: 2 ms FMa−= (2) F ms
ms F F
F
Hình 2.3.1
Từ (1) và (2): 1 2
=+ =

















F ag m mg a M
Bài tập 2: Hai trụ đồng chất, cùng chiều cao, có đường kính tiết diện là D và d nằm ngang tiếp xúc với nhau. Hệ số ma sát ở mọi chỗ tiếp xúc là k. Quấn một sợi dây mảnh không dãn quanh trụ lớn và tác dụng vào đầu dây một lực F nằm ngang (Hình 2.3.2). Hỏi hệ số ma sát k phải có giá trị thế nào để có thể di chuyển trụ lớn vượt qua trụ nhỏ. Tính giá trị cần thiết của lực F để thực hiện được di chuyển trên. Biết D=2d, khối lượng trụ lớn là M=10kg; g=10m/s2 . Hướng dẫn giải:
DẠYKÈMQUYNHƠNOFFICIAL 55
-
0 cos
0 cos
2 1 ' 1 2 ' = = F F N F F N => sin 1cos)( 1 + = F N thế vào (2) suy ra 1cos sin + k (3) • Gọi I là tâm quay tức thời Có: F.R(1+cos)=M.g.R.sin => 1cos sin + = Mg F (4) Mặt khác có N2=(M+m)g. Thế (1) và kết hợp (4) ( ) ( ) 1cos sin 1cos sin + + + + m M M k g m M k Mg (5) Vì 1 + m M M nên nếu (3) thỏa mãn thì (5) thoả mãn Vậy k 1cos sin + thay d D d D r R r R + = + = cos F o2 mg o1 F1 F2 N’1 N1 N2 y I F o2 d/2 o1 D/2 Hình 2.3.2
+ vì F2kN2 => FkN2 (1) F1kN1 => FkN1 (2)
Với trụ nhỏ:
sin
sin
Do đó: 0,7 2 1 = D d k

Từ (4) có ) 2( 50 min N D d g M F = = Bài tập 3: Một hình trụ có khối M được bó trí thành cơ hệ như hình vẽ 2.3.3, hệ số ma sát của hình trụ với mặt phẳng ngang là 1, với mặt phẳng ngang là 2 mặt phẳng ngang chuyển động đều về phía trái, cần phải tác động vào mặt phẳng ngang một lực F nhỏ nhất là bao nhiêu để xảy ra điều trên. Hướng dẫn giải:
Giả sử trụ quay: Khi mặt phẳng ngang chuyển động đều thì trụ quay đều và gia tốc của khối trụ bằng không Ta có: + Tổng các Moment lực đối với trục quay qua khối tâm bằng 0: F1 = F2 = F + Theo phương ngang: Nsin - F2 cos -F1 = 0 (1) + Theo phương thẳng đứng: N1 Mg N2cos

DẠYKÈMQUYNHƠNOFFICIAL 56
d D Dd + = 2 cos 1 sin 2
Rút gọn biểu thức ta thu được: FN NMgN 2 12 sin 1cos = + =+ (3) Nhận xét F, N1, N2 phụ thuộc vào 1, 2, và có hai trường hợp có thể xảy ra: • Trường hợp 1. 1 N1 > 2 N2, hình trụ quay, F = 2N2 Khi dó từ (3): 2 2 2 1cos sin N N = + 1.a/ 1cos sin + > 2 => N2 = 0, F = 0 với điều kiện 1N1 > 2N2 với mọi giá trị của 1, 2 1.b/ 1cos sin + < 2 , khi đó hình trụ bị kẹt, điều kiện 1N1 > 2N2 xảy ra với 1 > 2. • Trường hợp 2. 1 N1 < 2 N2, hình trụ không quay được F = 1N1. Hình 2.3.3
F2sin = 0 (2)
1 + Mg Điều kiện 1N1 < 2N2 xảy ra khi 1cos sin 2 + 2N2 > 1 ( N2 + Mg) Đánh giá: Biểu diễn kết quả qua đồ thị, đồ thị biểu diễn mặt phẳng 1, 2 chia làm 3 miền Miền 1: ứng với trường hợp (1.a) Miền 2: ứng với trường hợp (1.b ) và (2.a) hình trụ bị kẹt nên F = - Miền 3: ứng với trường hợp (2.b), F = sin cos 1 1 1 u2
1 + Mg Bài tập 4: Hai bản phẳng song song và thẳng đứng 1 trong số chúng hoàn toàn trơn, cái còn lại rất nhám, được phân bố cách nhau khoảng D (Hình 2.3.4). Giữa chúng có đặt một ống chỉ với đường kính ngoài b ằng D, khối lượng chung bằng M mômen quán tính đối với trục là I. Ổng chỉ bị kẹp chặt bởi 2 bản phẳng sao cho có thể chuyển động xuống dưới khi quay nhưng không trượt so với bản phẳng nhám. Một sợi chỉ nhẹ được buộc với vật nặng khối lượng ma và được quấn vào hình trụ trong của ống chỉ có đường kính d. Tìm gia tốc của vật nặng? Hướng dẫn giải:
sin
u*
(2) u1


DẠYKÈMQUYNHƠNOFFICIAL 57
Từ (3) suy ra: 1 1 2 1cos sin N N = + 1(Mg + N2 ) = N2 1cos sin + . Tìm ra N2 = 1
1 cos 1 sin + * = 1cos
Mg 2.a/ 1cos sin 1 + , khi đó trụ bị kẹt, điều kiện 1N1 > 2N2 khi 1 < 2. 2.b/ 1cos sin 1 + , khi đó F = 1N1 = 1 ( N2 + Mg). Hay: F = sin cos 1 1 1 + (3) (1)
Hình 2.3.4
a m t a M t mga t suy ra a = g 2
a I

+ D
m d D M +
2 4 D M
D D I m d D
+ . Đề bài 5: Đặt trên mặt phẳng nằm ngang nhẵn có một cái nêm hình lăng trụ tam giác đồng chất có góc nghiêng so với mặt nằm ngang, khối lượng M. Trên lăng trụ đặt một khối trụ đồng chất có bán kính R, khối lượng m (Hình 2.3.5). Khối trụ bắt đầu lăn không trượt xuống theo mặt phẳng nghiêng Bỏ qua ma sát lăn. a. Nêm được giữ cố định, tìm gia tốc chuyển động của khối trụ b. Nêm có thể chuyển động tự do. Tìm gia tốc chuyển động của nêm và gia tốc tương đối của khối trụ đối với nêm. a. Phân tích: Vật có 2 bậc tự do: y , do đó cần tìm 2 phương trình độc lập theo y và . Bước 1: Viết các phương trình động học:
Hình 2.3.5
DẠYKÈMQUYNHƠNOFFICIAL 58
gia tốc của vật m là: a0 = a 2 2; ; 2 2 t D d D a h t a H D d D = = . Vận tốc của ổng chỉ và của vật m: v = at, v0 = a0t = a t D d-D . Vận tốc góc của trục chỉ = D t a D v = 22 . Áp
ậ
+
2 2
2
+
2 2 2 2 2 2 2
) D (Dd
Giả sử trong thời gian t khối tâm của ống chỉ đi xuống được một đoạn DH. Lúc này ống chỉ quay quanh khối tâm góc: D H R H = = 2 . Khối m bị cuốn lên một đoạn: D d H d = 2 so với khối tâm của cuộn chỉ. Vậy khối m đi xuống một đoạn: t D d D H D d H H h = = . Gọi a là gia tốc của khối tâm ống chỉ, thì
dụng định lu
t bảo toàn cơ năng: MgH
mg
h = 2 2 2
0
I mv Mv
+ Mga
2
2 ) ( 2 D Dd 2
+ +
=
t
t
- Khối tâm G: ''' 000 GyGy G G GxGx
vSaS yS x va == = = == (1)
Bước 2: Viết các phương trình động lực học:
Phương trình định luật II: sin''sin yGGyyG PFmaFmSP +==− (2)
Phương trình momen: ( ) 2 / 1 ''.''sin.'' 2 y FGG MImSPRmR =−−= (3)
Hay: ( ) 1 ''sin'' 2 SgR −−= (4)
Bước 3: Viết phương trình năng lượng ( ) 22211 0sin' 22 GxGy mgSmvvI =−+++ (5)
y
−−= = vuS yuRS xRS vS =+ =++ =− =− (1) Gọi H là khối tâm của lăng trụ tam giác, ta có:
S u G H
= Câu b. Phân tích: Hệ có 4 bậc tự do: 3 Khối trụ (x,y, góc quay trong mp Oxy), 1 lăng trụ tam giác (x). - Số phương trình cần tìm là 4. Bài tập hệ vật , nên cần xét đến khối tâm của hệ Bước 1: Viết các phương trình động học Chọn hệ quy chiếu Oxy gắn với mặt x O
DẠYKÈMQUYNHƠNOFFICIAL 59
Tiến hành đạo hàm phương trình (5) theo thời gian, ta sẽ thu được phương trình (4). Nên trong bài này, không cần dùng đến bước 3. Bước 4: Phương trình liên kết Vật lăn không trượt nên: ''.''SR = (6) Bước 5: Giải hệ phương trình (4) và (6) ( ) 1 ''sin''2 2''sin ''.''3 SgR Sg SR đất như hình vẽ Gọi G là khối tâm của trụ tròn H là khối tâm của lăng trụ tam giác. Gọi là góc quay của khối trụ quanh khối tâm G. Toạ độ của khối tâm G của trụ: ''.cos .sin.cos .cos.sin 'sin. Gy G G Gx
trí ban đầu của hệ. Ta có biểu thức: ( ) 2222111 0sin'' 222 GxGy mgSmvvIMu =−++++ (4) Bước 4: Phương trình liên kết: Vì lăn không trượt nên: . '.' SR SR = = (5)
Bước 5: Giải hệ các phương trình Thay (5) vào (4) và tiến hành đạo hàm theo t ta thu được: ( ) 2sin '' 32cos2 mMg S Mmm + = +− (gia tốc của khối trụ đối với khối lăng trụ tam giác) Biểu thức gia tốc của khối lăng trụ tam giác đối với đất, ''sin2 32cos2 mg u Mmm
Hình 2.3.6






DẠYKÈMQUYNHƠNOFFICIAL 60 ' 0 Hy Hy vu v = = Gọi J là khối tâm của cả hệ, ta được: ( ) ( ) ''.cos'''''.cos'' .'sin.''sin .. JyJy JxJx muSMumuSMu va MmMm mSmS va MmMm ++++ == ++ == ++ (2) Bước 2: Phương trình động lực học: Phương trình chuyển động tịnh tiến cho khôi tâm J của hệ: yJJy xJJJx Fma Fmgma = −= Với 0 y F = suy ra 0 Jya = Mà ban đầu 0 Jyv = , ta được: ( ) .'.cos ''.cos'' mS muSMuu mM ++= + (3) Bước 3: Viết
ng Chọn mốc thế năng tại vị
phương trình năng lượ
=− +− Bài tập 6: Cho cơ hệ như Hình 2.3.6. Ròng rọc cố định và con lăn cùng khối lượng M, bán kính R. Sợi dây quấn quanh con lăn rồi vắt qua ròng rọc. Một vật khối lượng m được buộc vào đầu tự do của dây. Thả cho con lăn lăn không trượt trên mặt phẳng nghiêng cố định. Biết dây không trượt trên ròng rọc và trên con lăn. Tính gia tốc của vật m. m m M,R M,R
Hướng dẫn giải: Vật m: Định luật II Niutơn mg + T1 = ma (1) Xét ròng rọc B : T1R + T2R = I = R . 2 1 2 a MR -T1 + T2 = 2 Ma (2)
Xét ròng rọc A: IK = 2 2 1 MR + MR2 = 2 2 3 MR MgRsin T2.2R = 'K I = R a MR ' . 2 3 2 (3)
Ta có: a = 2a’ (4) Từ (1)(2)(3)(4) tìm được a = m M m Mg g 54 (sin2) 2 +
Nếu M msin2 thì a>0: vật m đi lên, con lăn lăn xuống và cuốn dây. Nếu M msin2 thì a<0: vật m đi xuống, con lăn lăn lên và nhả dây. Nếu M msin2 = thì a = 0: hệ đứng yên.
Bài tập 7: Hệ như hình vẽ. Con lăn khối lượng m1 và ròng rọc cố định khối lượng m2 đều là những trụ tròn đồng chất cùng bán kính R, dây nhẹ không giãn quấn quanh ròng rọc và buộc vào trục con lăn. Hệ đang cân bằng thì tác dụng vào ròng rọc một ngẫu lực có momen M để kéo con lăn lên (Hình 2.3.7). Biết con lăn luôn lăn không trượt trên mặt phẳng nghiêng. Bỏ qua ma sát tại các trục, hệ số ma sát trượt của con lăn và mặt phẳng nghiêng là k. Cho M=Mo bγ (Mo, b là các hằng số dương, γ là độ lớn gia tốc góc của ròng rọc tại thời điểm t. Biết mặt phẳng nghiêng đủ dài. a/ Tìm biểu thức gia tốc góc của con lăn? b/ Khi con lăn đang có vận tốc thì dây đứt. Xác định qui luật chuyển động của con lăn. Tìm điều kiện của k để con lăn luôn lăn không trượt?
M 1, mR
2, mR
Hình 2.3.7
DẠYKÈMQUYNHƠNOFFICIAL 61
Hướng dẫn giải:
a/ Với con lăn: T- Fms m1gsin = m1a1 (1)
Fms.R = I1 γ1 = m1R2. γ1 (2)










Với ròng rọc: Mo bγ2 T.R = I2 γ2 (3) Với a1=Rγ1=Rγ2 → γ1 = γ2 (4)
Từ 1,2,3,4: ( ) ( ) 01 12 2 21
2sin 23. MmgR bmmR == ++
b/ Sau khi dây đứt, con lăn lăn chậm dần lên và Fms hướng lên.
Fms m1gsin = m1a’ (5) Fms. R = I1γ’ (6)
Từ trên giải được: γ’ = - (7) Thời gian từ lúc dây đứt đến lúc con lăn dừng là: t = = Vẫn chiều (+) hướng lên, hết vận tốc ω thì con lăn lại lăn xuống nhanh dần và lực không thay đổi nên gia tốc không thay đổi. Từ (6) và (7) suy ra Fms = ≤ km1g.cosα ⇒ k ≥ Vậy điều kiện để con lăn lăn không trượt là: k ≥ Bài tập 8: Nêm cố định, bỏ qua ma sát ở các ròng rọc, khối lượng dây và ròng rọc. Biết B là vật hình trụ có bán kính trong r, bán kính ngoài R, có mô men quán tính đối với trục qua tâm là I, khối lượng M (Hình 2.3.8). Biết hình trụ lăn không trượt. Tìm gia tốc của các vật m1, m2 và gia tốc góc của khối trụ Hướng dẫn giải: Chọn hệ quy chiếu đất, Các lực tác dụng vào hình trụ là , ,,,2 ms PNFT , Vật 1 có 11 , PT , Vật 2 có 22 , PT với T1=T2=T
DẠYKÈMQUYNHƠNOFFICIAL 62
a) Giả sử trụ lăn lên trên: Chọn chiều dương như hình vẽ. M m1 + + M m1 A B Hình 2.3.8
bán kính r. Hệ nằm yên cân bằng (Hình 2.3.9). Bỏ qua ma sát giữa hai hình trụ. Cho biết M = 3m, R = 3r.
a. Tính độ lớn lực do nêm tác dụng lên hình trụ nhỏ m.
b. Tìm giá trị nhỏ nhất của hệ số ma sát giữa hình trụ lớn M và mặt nêm.
2. Xét hệ gồm nêm và hình trụ lớn M (Hình b). Nêm có thể dịch chuyển không ma sát trên mặt phẳng ngang. Hình trụ M có thể lăn không trượt trên mặt nêm. Xác định vận tốc khối
DẠYKÈMQUYNHƠNOFFICIAL 63 Gọi aA là gia tốc của ròng rọc A với đất, a1,a2 lần lượt là gia tốc của vật 1 và vật 2 với đất, ta có: 111 222 12 2 A mgTma mgTma aaa −= −= += + Với hình trụ trên mặt phẳng nghiêng, Đối với trục quay qua K với Ik = I + MR2 2 2()sin() TRrMgRIMR−−=+ Gọi B là điểm tiếp xúc với hình trụ của dây. Ta có aA = aB () BA aRra =−= Giải hệ các phương trình trên: 22 112212 22 sin 2()2()2() IMRIMRMgR amamgmmRrRrRr ++ +++=+− Vậy: 2 2 122212 2 1 2 1212 2 sin()()()2()() 2() 2() mMgR IMR gmmmgmmmRrRr a IMR mmmm Rr + −+++− = + ++ 2 1 121112 2 2 2 1212 2 sin()()()2()() 2() 2() mMgR IMR gmmmgmmmRrRr a IMR mmmm Rr + −−+++− =− + ++ 1212 2 1212 2 sin()4 8()() 2() MgR mmmm Rr IMR Rrmmmm Rr −++ = + −++ Bài tập 9: 1. Một khối trụ đặc đồng chất khối lượng M, bán kính R được đặt trên mặt nêm cố định có góc nghiêng α = 300. Một sợi dây nằm ngang, một đầu buộc vào đỉnh nêm, đầu còn lại gắn với M như hình a. Bên cạnh M đặt một khối trụ đồng chất khác có khối lượng m và
tâm C của hình trụ tại thời điểm khi C hạ xuống độ cao h so với vị trí ban đầu. Biết ban đầu cả hai vật đều đứng yên so với mặt đất. Cho biết khối lượng của nêm là M, gia tốc trọng trường là g.
Hình 2.3.9
Hướng dẫn giải:
1. a. Gọi β là góc hợp bởi mặt phẳng chứa hai trục hình trụ và mặt phẳng nghiêng Ta có 0 Rr1 30 R si r2 n==→== + α
β



Vậy hai trục của hai hình trụ ở cùng một độ cao. Gọi 12N và 21N là lực tương tác giữa hai hình trụ, vì bỏ qua ma sát nên hai lực này có phương ngang Phân tích các lực tác dụng lên các hình trụ như hình vẽ
Xét sự cân bằng của hình trụ nhỏ, ta có ba lực 1222N,N,P đều có giá đi qua trục của trụ nên nên không có ma sát giữa hình trụ nhỏ và mặt nghiêng Ta có 1222 NNP0 ++=
DẠYKÈMQUYNHƠNOFFICIAL 64
1P 1N ms1F T 21N12N 2P 2N
Chiếu lên phương song song mặt nghiêng ta được: 21212 1 PsinN.cosNmg. 3 =→= (1)
Chiếu lên phương vuông góc với mặt phẳng nghiêng ta được 2212 NPcosNsinmg..3mg123mg 223 3 =+=+= b. Xét sự cân bằng của hình trụ lớn đối với trục quay là trục hình trụ ms1ms1 T.RF.RFT =→= (2) ms11121 TFPNN0 ++++=
Chiếu lên phương thẳng đứng: 11ms1 PNcosFsin0 −++= (3)
Chiếu lên phương ngang: 211ms1 NNsinFcosT0
DẠYKÈMQUYNHƠNOFFICIAL 65
+−−= (4) Giải hệ phương trình (1), (2), (3), (4) ta được ( ) 1 22 NMmgmg4mg0 33 =+−=− ( ) ms1 Mmg 4 Fmg 3232 + == ++ Ta cần ms1 ms11 1 F FN0,38 N → →μmin = 0,38. 2. α C C h C/Gv Gv Gọi CGv,v là vận tốc của khối tâm hình trụ và nêm. Ta có CC/GG vvv =+ Vì hình trụ lăn không trượt nên ta có C/G vR = với ω là tốc độ góc trong chuyển động quay quanh trục quay qua khối tâm của hình trụ Do đó ta có ( ) ( ) ( ) 22222 CGGGG vvR2vRcos180vR2vRcos =++−=+− (5) Áp dụng bảo toàn cơ năng
( ) 2 2 222 GGG 111MR MvMvR2vRcos.Mgh 2222 ++−+= ( )2 2 GG 3 vRRvcosgh 4 +−= (6)
Bảo toàn động lượng trên phương ngang cho ta ( ) GG MvMvRcos0 −+−+= (7)
Giải hệ phương trình (6), (7) ta được: G R s v 2 co = , 2 2 G 2 ghcos v 3cos = − ,
Thay vào (5) ta được: 2 2 C 2
43cos vgh 3cos − = −
Với 030= ta được C 7gh v 3 =
Bài tập 10: Cho hai quả cầu rắn đồng chất, có cùng khối lượng, bán kính bằng nhau được đặt chồng lên nhau. Quả cầu 1 nằm ở dưới được giữ cố định (Hình 2.3.10). Quả cầu 2 nằm ở trên, ban đầu nằm ở đỉnh quả cầu 1, sau đó bắt đầu lăn xuống. Gọi là góc hợp bởi đường thẳng đứng và đường nối tâm của hai quả cầu, là hệ số ma sát trượt giữa hai mặt cầu. Xác định vị trí tại đó quả cầu 2 bắt đầu trượt trên quả cầu 1. Hướng dẫn giải: Chọn hệ toạ độ c
DẠYKÈMQUYNHƠNOFFICIAL
66
ng
ọ
Xét O2: 2 2 2 2.' 2''.2.' O Or vRe aReRe = =− (1) Gọi F là phản lực liên kết của O2 và O1 Phương trình động lực học: 2OFPma += ( ) ( ) ( ) ( ) 22 sin2.''2.''sin cos2.'2.'cos rr FmgmRFmRmg FmgmRFmRmg +==− −=−=−+ (2) g 1O 2O r e e P F r F g 1O 2O Hình 2.3.10
ực gắn với O1 như hình vẽ. Các phương trình độ
h
c:
Bài tập 11: Một hòn bi bán kinh r, nằm yên tại đỉnh một quả cầu bán kính R (Hình 2.3.11). Khi quả cầu nhận được gia tốc a không đổi nằm ngang thì hòn bi bắt đầu lăn không trượt xuống dưới. Xác định vị trí hòn bi rời quả cầu và tốc độ góc của hòn bi đối với trụ qua tâm của nó. Hướng dẫn giải: Ch
DẠYKÈMQUYNHƠNOFFICIAL 67 Phương trình
2 22'''' 55 FRMRFMR −=−= (3) Phương trình liên kết: '2'0'2'RR −+== (4) Từ (2), (3) và (4): ( ) ( ) 2 2.''sin2'' 5 5sin '' 14 mRmgmR g R −= = (5) Tính ' : Ta có: ( ) ( ) 22 ' 1cos1cos155 ''''' '''277 d gg dt d d RR dt = === = Vật rắn bắt đầu trượt khi: r FF = Do đó: ( ) 1cos 5sin5 2.sin2.cos 147 g g mRmgmRmg RR −=−−+ Ta được phương trình: 2 2sin171sin100 +−−=
.
ực gắn
ới
hình vẽ. Các phương trình động học: Xét O2: ( ) ( ) ( ) 2 .' ''.' C Cr vRre aRreRre =+ =+−+ (1) Gọi F là phản lực liên kết của hai vật Phương trình động lực học: 2qtOFPFma ++= ( ) ( ) 2 sinsin.'' cossin.' r FmgmamRr FmgmamRr ++=+ −+=−+ (2) r e e P F r F O C a qtF O C a Hình 2.3.11
Momen:
Giải phương trình trên ta tìm được
theo
ọn hệ toạ độ c
v
O như
Bài tập 12: Một vật hình cầu bán kính R với mật độ khối lượng của vật phụ thuộc vào khoảng cách r đến tâm của nó theo quy luật 3 3mr 1 7RR =+ , m là một hằng số dương. 1. Tính khối lượng và momen quán tính của vật đối với trục quay qua tâm của nó. 2. Đặt hình cầu trên vào một ống trụ có thành mỏng, bán kính R0, khối lượng M0, mặt trong nhám (Hình 2.3.12). Ống trụ có thể quay quanh trục nằm ngang cố định dọc theo trục của nó. Hình cầu luôn lăn không trượt trong ống trụ. Tìm biểu thức chu kì dao động nhỏ của quả cầu theo R0, R, g trong trường hợp:
DẠYKÈMQUYNHƠNOFFICIAL 68
Đị
T
+ =
2 2 2 17
cos
++
=
+
a. Ống trụ được giữ cố định. b. Ông trụ có thể quay (dao động) tự do, quanh trục của nó. Hướng dẫn giải: 1. Xét phần tử rất nhỏ: dV = r.sinθ.dφ.r.dθ.dr = r2dr.sinθ.dθ.dφ 2 3 3mr dMdV1rdr.sin.d.d 7RR ==+ Khối lượng của vật: R2 2 3 000 3mr M1rdrsinddm 7RR =+= O C Hình 2.3.12
Vì viên bi rời khỏi mặt cầu: ( ) 20cossin.' r FgaRr =−=+ (3) Phương trình liên kết: ' Rr r + = (4)
nh lý biến thiên động năng: ( )( ) ( ) 22 111cossin 22CCC mvImgRrmaRr+=+−++(5)
ừ (3), (4) và (5): 17cos17sin100 gag −−= (5) Thay (5) vào (3) suy ra được : ( ) 2 10 17 Rrg r
Nghiệm của (5):
10189
171 aa gg a g
(2) Phương trình Momen: / '''' FCCC MIFRI
=−= (3) (Dấu “ ” xuất hiện là do M ngược với chiều + đã chọn) Thay (2) vào (3), ta được ( ) 0 44 ''sin'' 105 RRgR −+=− Vì là góc bé, nên
DẠYKÈMQUYNHƠNOFFICIAL 69 Momen quán tính: 22 C Irsin.dM = => R2 432 C 3 000 3mr44 I1rdrsinddmR 7RR105 =+= 2.a Chọn hệ toạ độ cực như hình vẽ. Gọi là góc quay của C quanh tâm O là góc quay của quả cầu quanh tâm C. Bước 1: Viết các phương trình động học: ( ) ( ) ( ) 2 000 '''' CCr vRReaRReRRe =−=−−− (1) Bước 2: Viết các phương
ng lực học: Gọ
F là lực
ết xuất hiện tại vị trí tiếp xúc của quả cầu với
Phương
ật II: (
=−+ =−−−
: ( ) 0 44 ''.'' 105 RRgR −+=− (4) Bước 3: Viết phương trình liên kết: Gọi K là điểm tiếp tiếp xúc của quả cầu với vành trụ Vì quả cầu lăn không trượt và vì vành đứng yên nên: /0 0 Kv = Hay ( ) ( ) ///00 0''0'' KOKCCO vvvRRRRRR =+=−+−==− (5) O C C ( )+ r e e
trình độ
i
liên k
vành.
trình định lu
) ( ) 2 00 ''' Cr FPmaFPmRRemRRe +=+=−−− ( ) ( ) 0 2 0 ''sin 'cos r FmRRP FmRRmg
DẠYKÈMQUYNHƠNOFFICIAL 70
=−
V
V
cầu tại điểm tiếp xúc với vành trụ: ( ) 0 '' K vRRR=−+− Vì khối trụ lăn không trượt nên: ( ) '00 ''' KK vvRRRR =−+−=−
Từ (7)(8)(9), ta có hệ: ( ) ( ) ( ) 0 00 00 44 '''' 105 '''' '''''' mRRmgmR mRRmgMR RRRR −+= −+= −−= ( ) ( ) ( ) ( ) ( ) 00 00 00 0 00 00 0 105105 '''''''' 4444 10544'''''''''' 4410544 '''' 44 '''' 10544 10544 '' 14944 MRMR mRmR MRRR m RRR mMmR mRRmgMR RRgMRR Mm Mmg MmRR =−=− −−−==− + −+= −+=−− + + = +− Vậy ( ) ( ) ( ) ( ) ( ) ( ) 0 0 1054414944 2 1494410544 MmMmRR g T MmRRMmg ++− == +−+ Bài tập 13: O C C ( )+ r e e
Bước 4: Giải hệ các phương trình: Thay (5) vào (4), ta được: ( ) ( ) ( ) 00 0 44 ''.'' 105 '' 149 105 RRgRR g RR
−+=−−
(6) Do vậy: ( ) ( ) 0 0 105149 .2 149105 RR g T RRg == 2.b Gọi là góc quay của ống trụ quanh O. Lực liên kết F gây ra mômen cho khối cầu C: / '''' FCCC MIFRI
=−= (7) Lực liên kết F gây ra mômen cho khối trụ O: /0 '''' FOOO MIFRI
== (8) Phương trình liên kết:
ận tốc điểm K’ của vành trụ tại điểm tiếp xúc với khối cầu: '0 ' K vR =−
ận tốc điểm K trên khối
(9)
Một lồng trụ bằng kim loại đồng chất gồm hai đáy là hai bản kim loại mỏng hình tròn bán kính R và được liên kết với nhau bởi dải kim loại mỏng có bề ngang là R/2 và chiều dài 2R quấn bao quanh rìa của hai bản kim loại như hình vẽ. Lồng trụ có trục quay cố định đi qua tâm và vuông góc với hai đáy. Bên trong lồng trụ có một quả cầu đồng chất bán kính rR/6 = (Hình 2.3.13). Khối lượng lồng trụ và quả cầu cùng bằng m. Quả cầu ban đầu được giữ đứng yên, tiếp xúc với mặt trong khối trụ và điểm tiếp xúc với lồng tại điểm ở độ cao hR/4 = . Tại thời điểm t = 0 thả nhẹ quả cầu và đồng thời tác dụng momen lực M không đổi làm quay lồng trụ, khi đó quả cầu lăn không trượt bên trong lồng trụ và khối tâm của quả cầu đứng yên so với mặt đất. a) Tính momen quán tính của lồng trụ đối với trục quay . b) Tìm M. c) Tìm công của momen lực M đã thực hiện đến thời điểm t. Hướng dẫn giải: Khối lượng riêng của kim loại làm lồng trụ thỏa mãn:
DẠYKÈMQUYNHƠNOFFICIAL 71
F'msn
P
msn
h
γtru γcau 2 2 toanphan2dayxq mmmm R SSS3R 2R.2R 2 ==== + + ( ) 222 truxq2day 222 222 tru 22 R1 III.2R.R2.R.R 22 mR1mmRmR2mR I.2R.R2..R.R 3R223R333 =+=+ =+=+= 2 2 9R R d7 16 sin RR4 === Điều kiện để tâm khối trụ đứng yên: msn PNF0 ++= Chiếu lên phương của lực msn F ta được: msn mg7 Fmgsin 4 == Phương trình chuyển động quay quanh khối tâm của quả cầu: O C Hình 2.3.13
M N
F
3R/4
O
DẠYKÈMQUYNHƠNOFFICIAL 72 2 msncau 2mr F.r. 5 = cau 5gsin 2r = Vì quả cầu lăn không trượt nên gia tốc tiếp tuyến của điểm tiếp xúc của quả cầu phải cân bằng với gia tốc tiếp tuyến của lồng trụ và bằng: tcau 5gsin ar. 2 == t tru a 5gsin57gsin R2R8R === Phương trình chuyển động quay quanh khối tâm của lồng trụ: ' msn trutru F MMI. −= msn 2 Ftrutru MMI..R.mg72mR5gsin27mgR 432R3 =+=+= Tốc độ góc của lồng trụ tại thời điểm t: trutru 5gsin .tt 2R == Gia tốc tiếp tuyến của điểm tiếp xúc của quả cầu = gia tốc tiếp tuyến của trụ tại điểm đó: trucauR.r. = ; cautru R5gsin.t r2r == Công cần thực hiện bằng độ tăng động năng của hệ: 22 22 22 caucautrutru II 12mr5gsin12mR5gsin W..t.t 22252r232R =+=+ 222221035 Wmgsin.tmgt 324 == Bài tập 14: Một vòng có khối lượng M bán kính R,
ề dày không đáng kể, được treo trên một hình trụ đặc đồng nhất bán kính r<R , tâm của trụ tại
như
2.3.14
ả
ử trụ
ố đị
chu
2. Cho rằng trụ vẫ
ể.
3. Giả sử
ụ
O C C
b
O
hình vẽ
. Cho vòng lớn dao động với biên độ góc nhỏ trong mặt phẳng thẳng đứng. Giả sử chuyển động của vòng lớn trên trụ luôn là lăn không trượt. Gia tốc trọng trường là g. 1. Gi
s
c
nh, có bán kính rất nhỏ ( 0 r ). Tính
kì dao động của vòng lớn.
n cố định và có bán kính r đáng k
Tính chu kì dao động của vòng lớn.
tr
có khối lượng m và có bán kính r đáng kể, có thể quay không ma sát quanh trục cố định Hình 2.3.14
trùng với trục của khối trụ. Tính chu kì dao động của hệ
Hướng dẫn giải: Chọn hệ toạ độ cực như hình vẽ. Gọi là góc quay của C quanh tâm O là góc quay của quả vành lớn quanh tâm C. là góc quay của ống trụ quanh O. Ý 1. Phương trình Momen: 2 / ''sin2'' O PO MIMgRMR =−= Vì bé nên sin = Do đó: '' 2 g R =− Vậy 2 2 R T g = Ý 2. Bước 1: Viết các phương trình động học:
DẠYKÈMQUYNHƠNOFFICIAL 73
c học: Gọi F là lực liên kết xuất hiện tại vị trí tiếp xúc của quả cầu với vành. Phương trình định luật II: ( ) ( ) 2''' Cr FPMaFPMRreMRre +=+=−−− ( ) ( ) 2 ''sin 'cos r FMRrMg FMRrMg =−+ =−−− (2) Phương trình Momen: / '''' FCCC MIFRI =−= (3) (Dấu “ ” xuất hiện là do M ngược với chiều + đã chọn)
( ) ( ) ( ) 2'''' CCr vRreaRreRre =−=−−− (1) Bước 2: Viết các phương trình động lự
Thay (2) vào (3), ta được ( ) ''sin''RrgR −+=− Vì là góc bé, nên : ( ) ''.''RrgR −+=− (4) Bước 3: Viết phương trình liên kết: Gọi K là điểm tiếp tiếp xúc của quả cầu với vành trụ Vì quả cầu lăn không trượt và vì vành đứng yên nên: /0 0 Kv = Hay ( ) ( )
(5) Bước 4: Giải hệ các phương trình:
DẠYKÈMQUYNHƠNOFFICIAL 74
−−= =−
Thay (5) vào (4), ta được: ( ) ( ) ( ) ''.'' ''0 2 RrgRr g Rr −+=−− += (6) Do vậy: ( ) ( ) 2 2 2 Rr g T Rrg == Ý 3. Lực liên kết F gây ra mômen cho khối cầu C: / '''' FCCC MIFRI =−= (7) Lực liên kết F gây ra mômen cho khối trụ O: /0 '''' FOOO MIFRI == (8) Phương trình liên kết: Chọn chiều (+) như hình vẽ. Vận tốc điểm K’ của vành trụ tại điểm tiếp xúc với khối cầu: ' ' K vr =− Vận tốc điểm K trên khối cầu tại điểm tiếp xúc với vành trụ: ( ) '' K vRRr=−− Vì khối trụ lăn không trượt nên: ( ) ' ''' KK vvrRRr==−− (9) Từ (7)(8)(9), ta có hệ: O C C e r e F P
/// 0 ''0 '' KOKCCO vvv RRr RRr =+=
DẠYKÈMQUYNHƠNOFFICIAL 75 ( ) ( ) ( ) '''' 1 '''' 2 ''' MRrMgMR MRrMgmr rRRr −+=− −+= =−− ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1 1 '''' '''' 2 2 2 1 '''''''''' 22 1 2 '''' '''' 2 2 2 0 2 mr mr MR MR MRr mr rRr MRMmr MmRr MRrMgmr MRrMg Mm Mm Rrg Mm =− =− =−−−= + −+= −+= + + −+= + Vậy ( ) ( ) 2 2 2 RrMm T gMm −+ = +
Nội dung hệ cơ liên kết là một phần khó, việc giải được các bài tập nâng cao đòi hỏi phải có sự kiên trì, sáng tạo và phải có phương pháp phân tích, lập luận khoa học .
Trong quá trình trực tiếp giảng dạy nội dung này, tôi tuyển chọn các bài tập từ các chuyên đề bồi dưỡng học sinh giỏi, tạp chí vật lý phổ thông, đề thi chọn học sinh giỏi quốc gia, Olimpic vật lý các nước, Olimpic vật lý Quốc tế và phân dạng chúng.
Bài tập đều có hướng dẫn giải theo nhiều cách khác nhau, có phân tích hiện tượng vật lý, lập luận lôgic để học sinh có thể nắm bắt được bản chất các hiện tượng
Hy vọng bài viết này sẽ đáp ứng được phần nào về tài liệu tham khảo, phương pháp giải cùng với hệ thống bài tập được phân dạng
Rất mong được sự góp ý của các bạn đồng nghiệp để đề tài được hoàn thiện hơn, giúp cho công tác giảng dạy, bồi dưỡng học sinh giỏi ngày càng hiệu quả hơn. Xin trân trọng cảm ơn!
Quảng Nam, ngày 10/9/2021
Người viết Nguyễn Đức Nhân
DẠYKÈMQUYNHƠNOFFICIAL 76 C.
KẾT LUẬN
PHỤ LỤC
A. PHƯƠNG TRÌNH ĐỘNG HỌC, ĐỘNG LỰC HỌC TRONG TOẠ ĐỘ CỰC Khi xét các bài toán vật chuyển động trong mặt phẳng, chúng ta sử dụng toạ độ Đềcác Oxy hoặc toạ độ cực ,r . Tuỳ vào bài toán, việc sử dụng một trong hai toạ độ này sẽ giúp giải bài toán một cách dễ dàng hơn so với việc sử dụng hệ toạ độ kia. Từ hình vẽ ta suy ra quan hệ giữa các véc tơ cơ sở của hệ toạ độ cực và hệ toạ độ Đề các như sau: cossin sincos
DẠYKÈMQUYNHƠNOFFICIAL 77
xy
=+ =−+
=−+ =−−
= =−
(
rrr
=++++=−++ '' rr FFeFemr =+= ( ) ( ) 2''' .''2'' r Fmrr Fmrr =− =+ Nhận xét: Số hạng '' mr thể hiện lực tác dụng dọc theo phương bán kính. Số hạng 2' mr thể hiện lực hướng tâm. Số hạng '' mr thể hiện lực dọc theo phương tiếp tuyến. Số hạng 2'' mr liên quan đến lực quán tính Coriolis. B. MỘT SỐ CÁCH KHAI TRIỂN TRONG TOÁN HỌC 1. Định nghĩa và đạo hàm chuỗi mũ Định nghĩa: O x y e r e
rxy
eee eee
Lấy đạo hàm theo thời gian các phương trình trên, ta được: 'sin'cos' 'cos'sin' rxy xy eee eee
Do đó: '' '' r r ee ee
Xét chuyển động của vật có vị trí được xác định bởi ( ) r rrte = Đạo hàm cấp 1 véc tơ vị trị: ''.''.'.' rrr rrererere =+=+ với ' r là vận tốc theo phương bán kính, .'r là vận tốc theo phương tiếp tuyến, thường được viết r
Đạo hàm cấp 2 véc tơ vị trí:
) ( ) 2 ''''''''.'''.'.''''.''2''
rrerererererrerre
DẠYKÈMQUYNHƠNOFFICIAL 78 2n x exx = 1 + x ++...++... 2!n! x phải không có thứ nguyên.; ( ) ( ) 2n x αxαx e= 1 + αx+ +...+ +... 2!n! trong đó phải có thứ nguyên x 1 . Từ đây suy ra rằng: ( ) ( ) ( ) 23 23 x2x αxαx d2α3α e = α+ x+ x...=α1+αx+ ++... =αe dx2!3!2!3! Và tiếp theo : ( ) 2 x2x 2 d e = αe dx Bằng cách lấy loga có dễ dàng suy ra rằng exey = ex+y vì : loge(exey) = logeex + logeey = x + y 2. Khai triển hàm lượng giác, công thức Ơle (Euler) 357246 sinxxxxxxx = x -+-...; cosx = 1 -+-+... 3!5!7!2!4!6! Ta viết chuỗi mũ ix và chú ý rằng 23 i =-1, i= - 1, i= - i,... ( ) ( ) ( ) 234 234 ix 2435 i xixixxixx e= 1 + ix ++++...= 1 + ix --++... 2!3!4!2!3!4! =xxxxix 1 -+-...+ ix -+-...; e= cosx + isinx 2!4!3!5! Đó là công thức Euler. 3. Biểu diễn sinx và cosx theo hàm mũ phức Từ công thức Euler suy ra rằng: e ix = cosx isinx ( ) ( ) ixixixixcosx11 =e+ e; sinx =e22ie 4.Khai triển Ln: 234 n1 n x xxx ln(1x)x.....(1)234n + +−+−++− 5. Khai triển (1x) + : 2n (1x)1x......(1)x(1)...(n1)x 2!n! −−−+ +++++ C. TÍCH VÉC TƠ TRONG TOÁN HỌC 1. Một véc tơ A có thể được xác định bằng một trong hai cách sau đây: Bằng độ dài A và hướng (xác định bởi góc hợp với trục Oz và góc mà mặt phẳng chứa A và Oz hợp với trục Ox) còn gọi là góc phương vị và gọi là góc kinh độ, xem hình P.3.
Bằng 3 toạ độ Ax, Ay, Az tức là ba hình chiếu lần lượt lên các trục Ox, Oy, Oz.
2. Nếu gọi i, j, k lần lượt là vec tơ đơn vị trên các trục Ox, Oy, Oz thì ta có: xyz A = Ai + Aj + Ak
3. Tích vô hướng của hai véc tơ A và B: A.B=ABcosα là góc giữa hai vec tơ A và B Nếu viết biểu thức của tích vô hướng theo hình chiếu thì: xxyyzz A.BABABAB =++ A.BABcos= ; =(A,B)
4. Tích véc tơ (hoặc tích hữu hướng) của hai véc tơ A và B : ABABsin.n = n là véctơ đơn vị trên trục vuông góc với mặt phẳng chứa A và B trục hướng theo chiều chuyển động t
Phương trình vi phân tuyến tính cấp hai có hệ số là hằng số y” + py’ + qy = f(x) (1) y là hàm của x, y’ và y” là đạo hàm cấp một và cấp hai của y theo x; p và q là hai hằng số thực. Phương trình trên là phương trình có vế phải.
Phương trình: y” + py’ + qy = 0 (2) là phương trình không có vế phải hoặc phương trình thuần nhất tương ứng với (2.1). Phương trình đặc trưng của (1) và (2)
DẠYKÈMQUYNHƠNOFFICIAL 79
thì: ( ) ( ) ( ) xyzyzzyzxxzxyyx xyz ijk ABAAAABABiABABjABABk BBB ==−+−+− + Đạo hàm: ddAdB(AB)BA dtdtdt =+ ; ddBdA (AB)AB dtdtdt =+ Toán tử nabna được định nghĩa như sau: iJk xyz =++ Toán tử nabla tác dụng lên một hàm vô hướng f(x, y, z) gọi là gradf fff gradf(x,y,z).fijk xyz ==++
ịnh tiến của một đinh vít thuận khi nó quay theo chiều từ A tới B. Nếu viết biểu thức của tích vô hướng theo hình chiếu
(véc tơ) D. PHƯƠNG TRÌNH VI PHÂN TRONG TOÁN HỌC 1. Định nghĩa
r2 + pr + q = 0 (3)
đó là một phương trình đại số bậc hai, có hai nghiệm thực phân biệt r1 và r2 nếu biệt thức = p2 rq > 0. Khi = p2 4q = 0 thì r1 = r2 là một nghiệm kép. Khi < 0 thì không có nghiệm thực, nếu xét nghiệm ảo thì p Δ r = -±= α ± iβ 22 với p1 α=- ,β= -Δ 22
2. Nghiệm của phương trình thuần nhất (2.2) khi > 0 Định lí: Nếu y1 và y2 là hai nghiệm riêng độc lập tuyến tính của (2) thì: y = C1y1 +C2y2 là nghiệm tổng quát của (2). C1 và C2 là hai hằng số tuỳ ý. Tìm nghiệm riêng: Nếu > 0 thì phương trình đặc trưng (3) có 2 nghiệm thức riêng biệt là r1 và r2.
Có thể thử lại rằng: 12 rxrx 12y= evày= e Là nghiệm riêng độc lập tuyến tính của phương trình thuần nhất (2) Thật vậy: 11 2 11 y'rxrx = re, y" = re Thay vào (2) ta có: ( ) 1111 22 1111 rxrxrxrxre+ pre+ qe= 0; hay er+ pr+ q= 0 Vì r1 là nghiệm của phương trình đặc trưng (3) nên lượng trong dấu ngoặc ( ) ở trên bằng không: Phương trình (2) được nghiệm đúng. Nghiệm tổng quát của (2) sẽ là: 12 12 yrxrx = Ce+ Ce (4) Trong đó C1 và C2 là hai hằng số bất kì, r1 và r2 là thực.
3. Nghiệm của phương trình thuần nhất (2.2) khi < 0 Tìm nghiệm riêng. Khi < 0 phương trình đặc trưng : 2 r+ pr + q = 0 (3) Có hai nghiệm phức: 12 p ΔpΔ r = -+= α + iβ; r = --= α - iβ 2222 Có thể thử lại rằng: ( ) ( ) ( ) ( ) iixx 12 xx y= e= ecosβx + isinβx; y= e= ecosβx - isinβx +− Là hai nghiệm riêng độc lập tuyến tính của phương trình vi phân (2). Nghiệm tổng quát của phương trình vi phân (2) có dạng: y = C1y1
DẠYKÈMQUYNHƠNOFFICIAL 80
+ C2y2 còn có thể viết dưới dạng khác. Thật vậy: ( ) ( ) ( ) 1212 1212 αx y = y+ y= eC(cosβx+isinβx)+Ccosβx- isinβx= αx = eC+ Ccosβx+iC -Csinβx Đặt D1 = C1 + C2 và D2 = i(C1 C2) ta sẽ có: ( ) 12 αx y = eDcosβx + Dsinβx (5) Trong đó D1 và D2 là hai hằng số bất kì, và là hai số thực. 4. Trường hợp riêng : phương trình y” + 2y = 0
Phương trình đặc trưng r2 + 2 = 0 có hai nghiệm ảo r1 = i, r2 = i( = 0, = ). Theo công thức (5) thì nghiệm tổng quát có dạng: y = D1cosx + D2sinx (6) với D1 và D2 là hai hằng số bất kì, là thực. Khi giải phương trình vi phân y” + 2y = 0 có thể chọn ngay hai nghiệm riêng y1 = cosx, y2 = sinx; chọn như thế ta có thể đi đến biểu thức (6) của nghiệm tổng quát. Việc chọn y1 = cosx là nghiệm riêng có thể thử lại một cách dễ dàng. Thật vật y’1 = sinx, y”1 = 2sinx. Thay y”1 và y1 vào phương trình y” + 2y = 0 ta thấy ngay rằng phương trình này được nghiệm đúng. 5. Nghiệm của phương trình thuần nhất (2) khi = 0 Khi đó thì phương trình đặc trưng r2 + pr + q = 0 có một nghiệm kép : 12 rrp 2 ==− Hàm 1 1 rx ye = là một nghiệm riêng của phương trình vi phân thuần nhất (2). Trong trường hợp = p2 4q = 0 ta có thể thử lại rằng nghiệm riếng thứ hai của phương trình vi phân thuần nhất (2) là: 1 2 rx yxe = Thực vậy: 1111 2 21211 rxrxrxrx'" y= e+ rxe; y= rxe+ 2re Thay vào phương trình (2) y” + py’ + qy = 0 ta thấy vế đầu có dạng: ( ) ( ) ( ) ( ) 1111111 22 111111 rxrxrxrxrxrxrxrxe+ 2re+ pe+ rxe+ qxe= xer+ pr+ q+ e2r+p
Vì r1 là nghiệm của phương trình đặc trưng nên: 2 11r+ pr+ q = 0
Vì nghiệm 1 r=p2 nên: 2r1 + p = 0
Từ đó ta thấy rằng vế đầu viết ở trên bằng không, nghĩa là phương trình (2) được nghiệm đúng. 1 rx 2 yc.e = chính là nghiệm riêng độc lập tuyến tính với y1. Nghiệm tổng quát của (2) là: y = C1y1 + C2y2 = (C1 + C2x) 1 rx e (7)
Trong đó C1 và C2 là hai hằng số bất kỳ, r1 là nghiệm kép thực của phương trình đặc trưng.
6. Nghiệm của phương trình vi phân tuyến tính có vế phải: y” + py’ + qy = f(x) (8) Phương trình không vế phải (thuần nhất ) tương ứng là: y” + py’ + qy = 0 (9) Trong lí thuyết phương trình vi phân, người ta đã chứng minh rằng: Nghiệm tổng quát của phương trình vi phân tuyến tính có vế phải (8) thì bằng tổng của nghiệm tổng quát của phương trình không vế phải tương ứng (9) và một nghiệm riêng bất kì của (8). y = y1(x) + y2(x)
DẠYKÈMQUYNHƠNOFFICIAL 81
Nghiệm tổng quát y1(x) của (9) đã tìm được trong các mục trên. Một nghiệm riêng y2(x) của (8) có thể tìm được trong trường hợp vế phải có dạng đặc biệt.
82
DẠYKÈMQUYNHƠNOFFICIAL
TÀI LIỆU THAM KHẢO
[1] David Morin (2015), Cơ học lý thuyết, NXBĐHQGHN.
[2] Phạm Văn Thiều (2020), Bài tập cơ học tập 1 2 , NXBĐHQGHN.
[3] Tô Giang (2012), Bồi dưỡng học sinh giỏi vật lý THPT Cơ học 1,2,3 NXBGD.
[4] Yung Kuo Lim (2008), Bài tập và lời giải Cơ học, NXBGD
[5] Vũ Thanh Khiết, Vũ Đình Túy (2011), Các đề thi học sinh giỏi Vật lý (2001 2010), NXBGD.
[6] Nguyễn Ngọc Tuấn (2016), Tuyển tập các đề thi Olympic Vật lý, NXBĐHQGHN.
DẠYKÈMQUYNHƠNOFFICIAL 83
Chuyên đề VẬN DỤNG PHƯƠNG TRÌNH LAGRANGE LOẠI II ĐỂ TÌM QUY LUẬT CỦA VẬT TRONG CHUYỂN ĐỘNG LIÊN KẾT
Tác giả: Nguyễn Ngọc Cảnh THPT Chuyên Chu Văn An, Bình Định (Chuyên đề đạt giải Nhì)
A. MỞ ĐẦU
I. LÍ DO CHỌN ĐỀ TÀI
Chuyển động liên kết hay còn gọi là chuyển động ràng buộc (Constraint motion) là chuyển động của hệ có từ hai vật trở lên mà giữa chúng có một liên kết nào đó, để khi một vật chuyển động thì liên kết đó kéo theo các vật còn lại chuyển động, hoặc sự có mặt của một vật ràng buộc chuyển động của vật còn lại.
Các bài toán có chuyển động liên kết thường là các bài toán cơ học thuộc loại khó đối với học sinh và nó hay xuất hiện trong các kì thi học sinh giỏi Vật Lý. Mặc dù vậy trong các sách giáo khoa lại không đề cập một cách chi tiết nội dung này, do đó học sinh thường lúng túng không có định hướng khi giải quyết các bài toán có chuyển động liên kết. Để khảo sát chuyển động của một hệ vật hầu như chúng ta khá quen thuộc với việc áp dụng các định luật Newton để giải quyết. Các định luật Newton rất dễ nhớ, tuy nhiên trong thực tế việc triển khai chúng lại rất khó khăn bởi vì:
o Để khảo sát được một hệ có liên kết thì các lực liên kết phải được tính tới, trong thực tế đa số các trường hợp lực liên kết lại phức tạp không dễ dàng tính được.
o Số phương trình cần có cho một cơ hệ n bậc tự do là 3n, cùng với các phương trình mô tả các ràng buộc tương ứng với các liên kết.
o Mọi quan hệ trong các phương trình của Newton đều thể hiện dưới dạng vecto, điều này cũng khiến việc giải các phương trình cũng trở nên phức tạp hơn. Nhận thấy được những hạn chế trên, năm 1788, Lagrange đã phát biểu lại cơ học cổ điển của Newton. Theo Lagrange quỹ đạo chuyển động của hệ vật là nghiệm của các phương trình Lagrange (có hai dạng là loại I và loại II).
Ưu điểm của các phương trình này là chúng chỉ hướng tới những đại lượng vô hướng như động năng, thế năng để mô tả chuyển động của một hệ, điều đó làm cho bài toán trở nên đơn giản hơn nhiều.
Từ những lý do trên tôi chọn chuyên đề “ Vận dụng phương trình Lagrange loại II để tìm quy luật của vật trong chuyển động liên kết”.
CỨ
chuyên
DẠYKÈMQUYNHƠNOFFICIAL 84
II. MỤC ĐÍCH NGHIÊN
U Mục đích của
đề này là xây dựng quy trình chung nhằm vận dụng phương trình Lagrange loại II để tìm ra quy luật chuyển động của một số cơ hệ trong chuyển động liên kết. III. NHIỆM VỤ NGHIÊN CỨU Đề tài này thực hiện các nhiệm vụ nghiên cứu sau:
o Nghiên cứu các khái niệm cơ bản về liên kết, liên kết lí tưởng, tọa độ suy rộng, hàm Lagrange.
o Xây dựng phương trình Lagrange loại II.
o Xây dựng quy trình chung để vận dụng phương trình Lagrange loại II nhằm tìm ra quy luật chuyển động của một số cơ hệ trong chuyển động liên kết.
o Vận dụng quy trình đã xây dựng để tìm quy luật chuyển động của một số cơ hệ liên kết điển hình.
IV. ĐỐI TƯỢNG VÀ PHẠM VI NGHIÊN CỨU
Đối tượng nghiên cứu chuyên đề này là ứng dụng phương trình Lagrange loại II để tìm ra quy luật chuyển động của các cơ hệ.
V. PHƯƠNG PHÁP NGHIÊN CỨU
Nghiên cứu lý thuyết về phương trình Lagrange loại II và vận dụng phương trình Lagrange loại II.
VI. NỘI DUNG CỦA ĐỀ TÀI
Đề tài này gồm 3 phần:
o Phần 1: Cơ sở lý thuyết.
o Phần 2. Vận dụng giải toán. o Phần 3. Bài tập rèn luyện.
VII. PHẠM VI NGHIÊN CỨU
Chuyên đề này chỉ nghiên cứu cho cơ hệ chịu liên kết lí tưởng.
B. NỘI DUNG
PHẦN 1: CƠ SỞ LÝ THUYẾT
I. TỔNG QUÁT 1. Những khái niệm về liên kết. Tọa độ suy rộng 1.1. Số bậc tự do liên kết Ta xét một cơ hệ gồm N chất điểm 123 ,,...., N MMMM chuyển động đối với hệ quy chiếu quán tính. Vị trí của chất điểm i M được xác định bởi bán kính vecto ir hay ba tọa độ Descarter ix , iy và iz . Để xác định vị trí của cơ hệ ta cần N bán kính veto ir , với 1,2,3,..., iN = hay tương ứng 3N tọa độ Descarter. Số thông số độc lập cần thiết để xác định một cách đơn giá vị trí của cơ hệ gọi là số bậc tự do của cơ hệ. Cơ hệ được gọi là tự do nếu những chất điểm tạo thành cơ hệ có thể chiếm những vị trí bất kì trong không gian và có những vận tốc bất kì. Nói cách khác, cơ hệ tự do thì vị trí và vân tốc của những chất điểm tạo nên cơ hệ không bị ràng buộc bởi những điều kiện nào. Số bậc tự do của cơ hệ là 3N . Trong thực tế ta gặp các cơ hệ không tự do, nghĩa là cơ hệ mà vị trí và vận tốc bị hạn chế bởi những điều kiện nào đó.
DẠYKÈMQUYNHƠNOFFICIAL 85
Những điều kiện hạn chế vị trí và vận tốc của các chất điểm của cơ hệ trong không gian gọi là liên kết
Ví dụ 1: Cơ hệ gồm hai chất điểm 1M và 2M nối với nhau bằng một thanh có độ dài l là một cơ hệ không tự do.
Sáu tọa độ Descarter xác định vị trí của hai chất điểm thõa mãn phương trình ( ) ( ) ( ) 222 2 212121 xxyyzzl −+−+−= (1.1)
Chỉ có 5 trong 6 tọa độ Descarter là độc lập. Vậy cơ hệ này có 5 bậc tự do. Ví dụ 2: Cơ hệ gồm hai vật nối với nhau bởi một sợi dây lí tưởng chiều dài l vắt qua ròng rọc trong mặt thẳng đứng là hệ không tự do.
Sáu tọa độ Descarter xác định vị trí của hai vật thõa mãn các phương trình 12 0 zz== , 12 xxConst == , 21 yly =− (1.2) Chỉ có 1 trong 6 tọa độ Descarter là độc lập. Vậy cơ hệ này có 1 bậc tự do. Các phương trình (1.1), (1.2) được gọi là phương trình liên kết. 1.2. Tọa độ suy rộng Để khảo sát được cơ hệ ta cần chỉ ra được liên kết đặt lên cơ hệ. Liên kết này được biểu
DẠYKÈMQUYNHƠNOFFICIAL 86
diễn bởi n phương trình ( ) 123,,,...,,0 N frrrrt = , với 1,2,3,... = Nếu n phương trình này độc lập thì trong số 3N
Descarter
3 sNn =−
tọa độ
có
tọa độ độc lập. Muốn xác định một cách đơn giá vị trí của cơ hệ cần phải xác định s thông số độc lập. Giả sử chúng ta tìm được s thông số 123,,,..., sqqqq liên hệ với các vecto ir , 1,2,3,..., iN = bởi các phương trình ( ) 123,,,...,,0iis rrqqqqt == , 1,2,3,..., iN = 1M 2M • • O x y 1m 2m y O x
Sao cho khi thay vào phương trình trên thì các phương trình trở thành đồng nhất thức ( ) 123,,,...,,0 N frrrrt =
Các thông số 123,,,..., sqqqq được gọi là tọa độ suy rộng của cơ hệ chịu liên kết.
Ví dụ 1: Ta xét chuyển động của một chất điểm trên đường tròn bán kính R xác định.
O x
Đường tròn là liên kết đặt lên chất điểm được biểu diễn bằng phương trình liên kết 222 xyR +=
Số tọa độ độc lập là một. Ta có thể chọn hoặc là x , hoặc là y . Lúc này x hoặc y được gọi là tọa độ suy rộng.
Ví dụ 2: Ta xét chuyển động của một thanh rắn, được cố định một đầu.
Vị trí khối tâm của thanh trong quá trình chuyển động có thể được xác định dựa vào góc . Lúc này được gọi là tọa độ suy rộng.
2. Dịch chuyển khả dĩ và dịch chuyển ảo
2.1. Dịch chuyển khả dĩ
idr
ii rdr + ir
y M M N O
Chất điểm M được xác định bởi vecto vị trí ir . Sau một khoảng thời gian vô cùng bé dt vị trí của chất điểm được xác định bởi ii rdr + . Tập hợp tất cả các vecto dịch chuyển vô cùng bé idr được gọi là những dịch chuyển khả dĩ.
DẠYKÈMQUYNHƠNOFFICIAL 87
2.2. Dịch chuyển ảo Giả sử tại thời điểm t , ta lấy hai hệ thống vecto dịch chuyển khả dĩ idr và idr . Hiệu hai vecto idr và idr là một vecto vô cùng bé, ta kí hiệu là ir . Tập hợp những vecto iii rdrdr =− gọi là những vecto dịch chuyển ảo.
3. Công ảo và liên kết lí tưởng
3.1. Công ảo Giả sử chất điểm i M chuyển động dưới tác dụng của lực iF . Nếu chất điểm này chuyển động tự do thì theo định luật II Newton, ta có i i i
F a m = , với 1,2,3.,..., iN =
NN iiixixiyiyiyiy ii ARrRrRrRr
3.2.
==++
Nghĩa là ( )
DẠYKÈMQUYNHƠNOFFICIAL 88
==
11
NN
==
điểm chuyển động trên một mặt
phản lực liên kết iR vuông góc với dịch chuyển ảo ir , nên 0 ii Rr = . Ví dụ 2: Trong
vật
Khi có liên kết đặt lên hệ thì gia tốc ia có thể không thõa mãn phương trình liên kết. Điều này là do liên kết đã tác dụng lực lên chất điểm i M , ta gọi lực này là phản lực liên kết. Kí hiệu phản lực liên kết tác dụng lên chất điểm i M là iR . Lúc này phương trình chuyển động của chất điểm chịu liên kết i M có dạng iiii maFR =+ , với 1,2,3,..., iN = Công ảo là một đại lượng vật lý được xác định bởi biểu thức ( ) 11 R ir
Liên kết lí tưởng Liên kết được gọi là liên kết lí tưởng nếu tổng công ảo của các phản lực liên kết đặt lên cơ hệ đối với mọi dịch chuyển ảo đều bằng 0.
0
iiixixiyiyiyiy ii ARrRrRrRr
==++=
Ví dụ 1: Một chất
phẳng nhẵn (không ma sát) thì
thực tế, một cơ hệ dù phức tạp đến đâu cũng được cấu tạo từ những cặp
rắn theo các kiểu sau đây: hai vật rắn liên kết với nhau bằng thanh rắn, hoặc chuyển
động quanh một điểm cố định, hoặc tiếp xúc với nhau bằng bề mặt của chúng. Một cơ hệ phức tạp như vậy có thể khảo sát như một cơ hệ chịu những liên kết lí tưởng. Tuy nhiên cũng cần chú ý rằng, trong thực tế không phải mọi liên kết đều là lí tưởng. Ví dụ một vật rắn trượt lên một vật rắn khác, lúc này phản lực R không vuông góc với dịch chuyển ảo. Ta có thể phân tích R thành hai thành phần là N và ms F . Thành phần N vuông góc với dịch chuyển ảo nên 0 Nr = , còn thành phần song song với r ta xem như một lực hoạt động đã biết. Như vậy tác dụng liên kết không lí tưởng bất kì lên cơ hệ tương đương với liên kết lí tưởng và một lực hoạt động bằng lực ma sát.
II. PHƯƠNG TRÌNH LAGRAGE LOẠI II
1. Nguyên lý Dalambert Lagrange
Xét cơ hệ gồm N chất điểm chịu những lực liên kết lí tưởng đặt lên nó, phương trình chuyển động của chất điểm i trong hệ có dạng ir hay iiii maFR −= Nhân hai vế phương trình trên cho ir
) iiiiii maFrRr −= Phương trình chuyển động của tất cả các chất điểm trong cơ hệ
DẠYKÈMQUYNHƠNOFFICIAL 89
(
11
== −=
kết là lí tưởng, theo điều kiện 1 0 N ii i Rr = = , ta được ( ) 1 0 N iiii i maFr = −= (2.1) Biểu thức (2.1) được gọi là nguyên lý Dalambert Lagrange. Trường hợp riêng, khi hệ ở trạng thái cân bằng 0 ia = ta thu được nguyên lý quan trọng của tĩnh học 1 0 N ii i Fr = = (2.2) ir R N ms F
(
)
NN iiiiii ii maFrRr
Vì các liên
Phương trình (2.2) được gọi là nguyên lý dịch chuyển ảo.
2. Phương trình Lagrange loại II
Xét cơ hệ gồm N chất điểm, liên kết đặt lên cơ hệ được biểu diễn bằng n phương trình ( ) 123,,,...,,0 N frrrrt = , 1,2,3,...,n =
Số bậc tự do của cơ hệ là 3 sNn =−
Vị trí của cơ hệ được xác định bởi s tọa độ suy rộng 123,,,..., sqqqq . Các bán kính vecto ir là hàm của 123,,,..., sqqqq và t ( ) 123,,,...,,0iis rrqqqqt == , 1,2,3,..., iN =
Xuất phát từ nguyên lý Dalambert Lagrange (2.1) ta thành lập phương trình chuyển động của cơ hệ trong hệ tọa độ suy rộng.
Trước tiên ta biểu diễn dịch chuyển ảo ir qua biến phân của tọa độ suy rộng.
Giả sử có các tọa độ suy rộng ( ) , kk qqt = trong đó t là biến thời gian và là thông số thực.
Khi 0 = , thì ( ) ( ) ,0 kkk qqtqt == xác định vị trí thực của cơ hệ.
Khi 0 , thì tọa độ suy rộng ( ) , kk qqt = xác định vị trí khả dĩ của cơ hệ phù hợp với liên kết đặt lên nó. Dạng kq thay đổi khi biến số t không thay đổi nhưng thông số thay đổi.
Ta định nghĩa biến phân của tọa độ suy rộng ( ) k qt là đại lượng được xác định bằng biểu thức
DẠYKÈMQUYNHƠNOFFICIAL 90
( ) ( ) ( ) ,, k kkk q qtqtqt =+−= (2.3) Tương tự, ta có biến phân của ir ( ) ( ) ,, i iii r rrtrt =+−= Vì bán kính vecto ir phụ thuộc vào qua hàm ( ) , k qt nên ta có 11 ss iiki ik kkkk rrqr rq qq == === (2.4) Đặt biểu thức ir vào (2.4), ta nhận được ( ) 1 0 s kkk k ZQq = −=
Trong
1,2,3,..., ks = .
1111 NNNN iiiii kiiiiiii iiiikkkk rdrrdrdr Zmammrmr qdtqdtqdtq
(2.5) Ta biết 1 s iii ij j k drrr rq dttq = ==+ (2.6) Từ biểu thức (2.6), ta suy ra ii k drr dtq = , với 1,2,3,..., iN = ; 1,2,3,..., ks = (2.7) Dùng hệ thức (2.6) ta có 22 1 s iiii j j kkjkk rrrdr q qtqqqdtq =
(2.8)
== Đại lượng kQ được gọi là lực suy rộng tương ứng với tọa độ suy rộng. Biến đối kZ về dạng thuận tiện hơn ta được −=
DẠYKÈMQUYNHƠNOFFICIAL 91
đó 1 N i ki i k r QF q = = , 1 N i kii i k r Zma q = = , với
====
===−
=+=
Chú
đến các hệ
11 NN ii kiiii iikk drr Zmrmr dtqq == =− Hay k kk dTT Z dtqq =− , 1,2,3,...,
=
Công nguyên tố của những hoạt lực đối với mọi dịch chuyển ảo bằng 11 Trong đó ( ) 2 1 2 iTmr =
NN i ikk ii k là động năng của hệ Vì các biến phân kq là độc lập tùy ý khác không
r AFQq q == ( ) 1 0 s kkk k ZQq =
ý
thức (2.7) và (2.8) ta có thể viết kZ dưới dạng
ks
(2.9)
(2.10)
nên biểu thức
chỉ thõa mãn khi tất cả các nhân tử kq trong biểu thức đó bằng không. Nghĩa là 0 kk ZQ−= hay kk ZQ = Thay (2.9) vào ta được k kk
dTT Q dtqq −= , với 1,2,3,..., ks = (2.11)
Phương trình (2.11) được gọi là phương trình Lagrange loại II hay phương trình Lagrange trong tọa độ suy rộng Để tìm được phương trình chuyển động của cơ hệ ta chỉ cần giải hệ thống s phương trình Lagrange loại II.
=−
(2.12) Biểu thức lực suy rộng trong trường hợp này có dạng
i rUrU QF qqq r
(2.13) Ta đặt ( ) 123,,,...,, kks rrqqqqt
U F r Trong
DẠYKÈMQUYNHƠNOFFICIAL 92
11 NN ii ki iikkk
==
==−=−
=
k
( ) 123,,,...,, s
= Nên 0 k U q = Ta có ( ) kk TU T qq − = Như vậy
Đại lượng k k dq q dt = được gọi là vận tốc suy rộng; đại lượng 2 2 k k dq q dt = được gọi là gia tốc suy rộng; đại lượng k k 0 kk
T p q = được gọi là xung lượng suy rộng Nếu hoạt lực iF tác dụng lên cơ hệ là lực thế thì ta có i i dLL dtqq −=
thay vào biểu thức của U thì thế năng U chỉ phụ thuộc vào
q và thời gian t
UUqqqqt
phương trình (2.11) bây giờ có dạng
(2.14)
đó
LTU =−
là hàm lagrange của hệ. Phương trình (2.14) là phương trình Lagrange loại II của hệ trong trường hợp hoạt lực tác dụng lên cơ hệ là lực thế.
Từ (2.11) và (2.14), ta tổng quát hóa cho trường hợp hệ chịu tác dụng của các lực thế và không thế thì k kk
dLL Q dtqq −= (2.15) Với kQ là lực suy rộng tương ứng bởi các lực chủ động không thế.
Hoặc 0 kk
dLL dtqq −= (2.16) Với UFdq =− là thế năng của các lực thế và không thế.
Từ (2.11), (2.14), (2.15) và (2.16) ta thấy rằng các phương trình Lagrange loại II không chứa các phản lực liên kết và số phương trình đủ để mô tả chuyển động của cơ hệ là ít nhất đúng bằng số bậc tự do của cơ hệ. Đây là ưu điểm nổi bật của các phương trình Lagrange loại II III. VẬN DỤNG PHƯƠNG TRÌNH LAGRANGE LOẠI II ĐỂ TÌM PHƯƠNG TRÌNH CHUYỂN ĐỘNG CỦA MỘT SỐ CƠ HỆ
1. Quy trình chung
Từ nội dung lý thuyết trên, để vận dụng phương trình Lagrange loại II trong việc tìm quy luật chuyển động của các cơ hệ. Tôi đề xuất một quy trình chung như sau:
o Bước 1: Xác định số bậc tự do của cơ hệ và chọn các tọa độ suy rộng phù hợp.
o Bước 2: Xác định động năng T của hệ qua các tọa độ suy rộng vừa chọn.
o Bước 3: Xác định thế năng của hệ qua các tọa độ suy rộng vừa chọn. Với các lực không thế và các lực thế, thế năng có thể được xác định từ biểu thức tổng quát
UAFdq
Ở bước này, thay vì tính thế năng, ta có thể tính công của các lực hoạt động từ đó suy ra các lực suy rộng tương ứng. Sử dụng phương trình Lagrange dạng (2.11). o Bước 4: Thực hiện các phép toán đạo hàm để thu được phương trình vi phân chuyển động.
DẠYKÈMQUYNHƠNOFFICIAL 93
=−=−
2. Vận dụng cho các cơ hệ điển hình 2.1. Hệ hai vật liên kết với nhau bằng dây lí tưởng
Bài toán 1: Hai vật có khối lượng 1m và 2m được nối với nhau bằng sợi dây mềm, không giãn, chiều dài l vắt qua ròng rọc cố định như hình vẽ. Ròng rọc có momen quán tính là I , bán kính R.
Xác định phương trình chuyển động của các vật 1m và 2m . Hướng dẫn:
Chọn tọa độ suy rộng là x như hình vẽ. Khi đó vị trí của vật 2m được xác định bởi lx
DẠYKÈMQUYNHƠNOFFICIAL 94
. Ta
động quay của ròng rọc 222 1122 111 222 TmvmvI =++ trong đó 1 vx = , ( ) 2 d vlxx dt =−=− , 1 vx RR == → ( ) 22 12 2 11 22 I Tmmxx R =++ Thế năng của hệ ( ) 12 Umgxmglx =−−− Vậy hàm Lagrange của hệ là 1
2
1
2
xây dựng phương trình Lagrange cho cơ hệ. Động năng của hệ là tổng động năng tịnh tiến của hai vật 1m , 2m và động năng trong chuyển
m
m
m
m x
toán
Một
hình trụ bán kính R, trọng lượng
P được quấn xung quanh bởi sợi dây. Dây vắt qua ròng rọc cố định O (ròng rọc lí tưởng) rồi nối với vật nặng A trọng lượng 2P . Vật A trượt trên mặt phẳng ngang với hệ số ma sát . Bỏ qua mọi ma sát.
2P C B 1P
•
Xác định phương trình chuyển động của các vật. Hướng dẫn: Hệ gồm ống trụ tâm C và vật nặng A. Chuyển động của vật A là chuyển động tịnh tiến; ống trụ chuyển động song phẳng. Vậy hệ có hai bậc tự do. Ta chọn tọa độ suy rộng là x và như hình vẽ.
A •
A x
2P 1P B 1P
Xây dựng phương trình Lagrange cho hệ.
DẠYKÈMQUYNHƠNOFFICIAL 95 ( ) ( ) 22 1212 2 11 22 I LTVmmxxmgxmglx R =−=++++− Ta có 12 2 LI
xR =++ → 12
dLI
=++ ( ) 12 L
x =− Vậy
( )
I
++−−=
= ++
mmx
2
mmx dtxR
mmg
phương trình chuyển động của hai vật 1m , 2m là
1212 2 0
mmxmmg R
hay ( ) 12 12 2 mmg x I mm R
Bài
2:
ống
1
DẠYKÈMQUYNHƠNOFFICIAL 96 Động năng của hệ là tổng động năng chuyển động tịnh tiến của vật A và động năng chuyển động song phẳng của vật B 22 2 1 22AA P Tmvx g == 2211 22BO TmvI =+ Ta có BA OB vvx vvR == =+ → O vxR =+ (phương trình phân bố vận tốc) → ( )2 2 1 2 22 B PI TxR gR =++ ( )2 2122 2 222 AB PPI TTTxxR ggR =+=+++ hay 22 2 1211 2 PPPRPR Txx ggg + =++ Thế năng của hệ 211 APxPxPa =−++ → 21 x QPP =−+ và 1 QPR = Thực hiện các phép toán 121 TPPPR x xgg + =+ → 121 dTPPPR x dtxgg + =+ 2 11 2 TPRPR x gg =+ → 2 11 2 dTPRPR x dtxgg =+ Phương trình Lagrange cho chuyển động của hệ 121 21 PPPR xPP gg + +=−+ 11 1 2PPR xPR gg += Từ hai phương trình trên ( ) 12 12 2 2 gPP x PP = + ( ) ( ) 2 12 12 2 gP RPP + = +
2.2. Chuyển động lăn không trượt của vật trên mặt phẳng nghiêng
Bài toán 1: Một đĩa tròn có khối lượng m , bán kính R chuyển động lăn không trượt trên một mặt phẳng nghiêng góc như hình vẽ. Biết momen quán tính của đĩa tròn là I , mặt phẳng nghiêng cố định. Xác định phương trình chuyển động của vật rắn. Hướng dẫn:
Chọn tọa độ suy rộng x như hình vẽ. Ta xây dựng hàm Lagrange cho đĩa. Động năng của đĩa là tổng động năng chuyển động tịnh tiến và chuyển động quay
DẠYKÈMQUYNHƠNOFFICIAL 97
2211 22 TmvI =+ với vx = và v R = → x R = , do đó 2 2 1 2 I Tmx R =+ Thế năng của đĩa sinUmgx =− Vậy, hàm Lagrange của hệ là 2 2 1 sin 2 I LTUmxmgx R =−=++ Ta có x
sin mg x I m R 222111 222MMm TMvmvI =++ Trong đó M vX = , s R =
s
y O x
= + Bài toán 2: Một đĩa tròn có khối lượng m , bán kính R chuyển động lăn không trượt trên một mặt phẳng nghiêng góc như hình vẽ. Biết momen quán tính của đĩa tròn là I , mặt phẳng nghiêng không cố định, khối lượng M . Xác định phương trình chuyển động của đĩa và của mặt phẳng nghiêng. Hướng dẫn: Ta chọn tọa độ suy rộng là X và x như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ Động năng của hệ là động năng chuyển động tịnh tiến của mặt phẳng nghiêng và động năng chuyển động song phẳng của đĩa X
DẠYKÈMQUYNHƠNOFFICIAL 98
2 LI mx xR =+ → 2 dLI mx dtxR =+ sin L mg x = Phương trình chuyển động của đĩa 2
DẠYKÈMQUYNHƠNOFFICIAL 99 cos sin m m xXs ys =+ =− → cos sin m m xXs ys =+ =− → 222 2cos m vXsXs =++ Vậy ( ) 22 2 11 cos 22 I TMmXmsmXs R =++++ Thế năng của hệ sinUmgs =− Hàm Lagrange cho hệ ( ) 22 2 11 cossin 22 I LMmXmsmXsmgs R =+++++ Ta thực hiện các phép toán ( ) cos L MmXms X =++ → ( ) cos dL MmXms dtX =++ 0 L X = 2 cos LI msmX sR =++ → 2 cos dLI msmX dtxR =++ sin L mg s = Phương trình Lagrange cho chuyển động của hệ ( ) cos0MmXms ++= 2 cossin0 I msmXmg R ++−= Từ hai phương trình trên 2 22 sincos cos g X IMm m Rm = + −+ 2 22 sin cos Mmg s IMm m m Rm + = + +− 2.3. Chuyển động của hạt trên một thanh quay Bài toán 1: Một viên bi B, khối lượng m chuyển động dọc theo một thanh nhẹ OA đang quay trong mặt phẳng nằm ngang với tốc độ góc . Bỏ qua mọi ma sát.
Xác định phương trình chuyển động của viên bi. Hướng dẫn:
Chọn các tọa độ suy rộng r và như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ. Động năng của hệ là động năng của vật m ( ) 222 1 2 Tmrr =+ Trong trường hợp này hàm Lagrange chỉ có động năng. Ta thực hiện các phép toán T mr r
DẠYKÈMQUYNHƠNOFFICIAL
100
=
2
=
→ 2 2 dT mrmrr dt =+ 0 T = Phương trình Lagrange cho hệ 2 0 rr −= 20rr += Trường hợp thanh quay với tốc độ góc không đổi Const == và 0 = 2 0 rr −= Phương trình trên cho ta nghiệm dưới dạng O A m O A m r
= → dT mr dtr = 2 T mr r
T mr
Các hằng số 1C và 2C phụ thuộc vào các điều kiện đầu của chuyển động.
Bài toán 2: Một hạt có thể trượt tự do, không ma sát quanh một vòng tròn bánh kính R . Vòng tròn quay với tốc độ góc không đổi quanh một đường kính thẳng đứng. Xác định phương trình chuyển động của hạt. Hướng dẫn:
DẠYKÈMQUYNHƠNOFFICIAL 101
tt
+−
12
rCeCe
=+
suy rộng như hình vẽ. Ta xây phương phương trình Lagrange cho hệ. Động năng của hệ là động năng của vật m ( ) 222221sin 2 TmRR =+ Thế năng của hệ cosUmgR =− Vậy ( ) 22222 1sincos 2 LmRRmgR =++ Ta thực hiện các phép toán 2 L mR = → 2 dL mR dt = m R m R
Chọn tọa độ
Phương trình Lagrange cho chuyển động của hệ 2 sinsincos0RgR +−=


Trường hợp góc nhỏ ( ) 2 0 gR R += Phương trình trên chứng tỏ vật sẽ dao động điều hòa với tần số góc 2 gR R
2.4. Vật chuyển động trên máng tròn Bài toán 1: (HSG Quốc Gia 2005) Cho vật nhỏ A có khối lượng m và vật B có khối lượng M . Mặt trên của B có dạng là một bán cầu, bán kính R như hình vẽ. Lúc đầu B đứng yên trên mặt sàn S , bán kính của mặt cầu đi qua A hợp với phương thẳng đứng một góc 0
( 0 có giá trị nhỏ). Thả cho A chuyển động với vận tốc ban đầu bằng 0. Ma sát giữa A và B không đáng kể. Cho gia tốc trọng trường là g .
a. Giả sử A dao động, B đứng yên (do có ma sát giữa B và sàn S ). Tìm chu kì dao động của vật A
b. Giả sử ma sát giữa B và mặt sàn S có thể bỏ qua. Tính chu kì dao động của hệ. Hướng dẫn: Chọn tọa độ suy rộng như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ. Động năng của hệ là động năng của hạt m
DẠYKÈMQUYNHƠNOFFICIAL 102
22 sincossin L mRmgR =−
=
2 1 2 Tmv = 0
B A C S
B A C S
Trong đó sin cos xR yR = = → cos sin x vR yR = =− → 222vR =
Vậy 22 1 2 TmR = Công toàn phần của các lực chủ động tác dụng lên hệ sin AmgRd =− → sinQmgR =− Ta thực hiện các phép toán 2 T mR = → 2 dT mR dt = 0 T = Phương trình Lagrange cho chuyển động của hạt 2 sinmRmgR =− hay sin0 g R += Trường hợp nhỏ 0 g R += Phương trình trên chứng tỏ hạt dao động điều hòa trong bát hình cầu với tần số góc g R = b. Trường hợp M không cố định. Các tọa độ suy rộng được chọn là x và . Một cách tượng tự ta cũng xây dựng phương trình Lagrange cho hệ Động năng của hệ

DẠYKÈMQUYNHƠNOFFICIAL 103
2211 22MmTMvmv =+ Trong đó B A C S y x O
các thanh cứng, mảnh, nhẹ. Trên hình vẽ, OA và OB là các thanh cứng cùng độ dài R , OAB nằm trong mặt phẳng vuông góc với trục ∆, chứa khối tâm G của vật 1, C là giao điểm của OG và lòng máng. Giữ cho vật 1 luôn cố định rồi đặt trên nó vật 2 là một hình trụ rỗng, mỏng, đồng chất, cùng chiều dài với vật 1, bán
DẠYKÈMQUYNHƠNOFFICIAL 104 M vx = sin cos m m xxR yR =+ = → cos sin x y vxR vR =+ =− → 222vR = Vậy ( ) 22211 cos 22 TMmxmRxmR =+++ Công toàn phần do các lực chủ động tác dụng lên hệ sinAmgR =− → sinQmgR =− Ta thực hiện các phép toán ( ) cos T MmxmR x =++ → ( ) 2 cossin dT MmxmRmR dtx =++− 0 T x = 2 cos T mRxmR =+ → 2 cossin dT mRxmRxmR dt =−+ sin T mRx =− Phương trình Lagrange cho chuyển động của hệ ( ) 2 cossin0MmxmRmR ++−= cossin xRg +=− Trong trường hợp gần đúng ( ) 0 0 MmxmR xRg ++= ++= → 0 Mmg MR + += Phương trình trên chứng tỏ, con lắc dao động nhỏ với tần số góc Mmg MR + = Bài toán 2: (HSG Quốc Gia 2011) Cho vật 1 là một bản mỏng đều, đồng chất, được uốn theo dạng lòng máng
R và được gắn với
O
thành một phần tư hình trụ AB cứng, ngắn, có trục ∆, bán kính
điểm
bằng
kính r () rR , nằm dọc theo đường sinh của vật 1. Kéo vật 2 lệch ra khỏi vị trí cân bằng một góc nhỏ 0 rồi thả nhẹ. Tìm chu kì dao động nhỏ của vật 2. Biết rằng trong quá trình dao động, vật 2 luôn lăn không trượt trên vật 1.


DẠYKÈMQUYNHƠNOFFICIAL 105
Chọn các tọa độ suy rộng và
Động năng của hệ là động năng chuyển động song phẳng của hình trụ 2211 22 TmvI =+ trong đó = và vr = Vậy ( ) ( )( ) 2222211 22 Tmrmrmr =+= Thế năng của hệ ( )cos UmgRr =−− Hàm Lagrange của hệ ( ) 22 cos LTUmrmgRr =−=+− Mặc khác, từ điều kiện lăn không trượt O C B A 0 g O C B A g
Hướng dẫn:
như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ.
chuyển động của hệ ( ) ( ) 2 20 mRrmgRr −+−= → ( ) 0 2 g Rr +=
Phương trình trên chứng tỏ hình trụ dao động điều hòa với tần số góc ( ) 2 g Rr
= 2.5. Dao động của đĩa xoắn
Bài toán 1: (Chọn đội dự tuyển IPho 2004) Hai đĩa tròn A và B đồng tính và giống hệt nhau. Mỗi đĩa có momen quán tính I đối với trục quay đi qua tâm của đĩa và vuông góc với mặt phẳng của đĩa. Đĩa A nằm ngang, tâm của đĩa gắn vào đầu dưới của một sợi dây mảnh thẳng đứng có hằng số xoắn k , đầu trên của dây gắn vào một điểm cố định C Đĩa B cũng nằm ngang và tâm đĩa gắn vào đầu đưới của một sợi dây mảnh khác có hằng số xoắn k , giống như đĩa A, chỉ khác là đầu trên của sợi dây này gắn vào tâm mặt dưới đĩa A, khiến cho hai dây treo nằm trên cùng một đường thẳng đứng. Ở vị trị cân bằng của hai đĩa, hai dây treo không bị xoắn. Kí hiệu 1 và 2 lần lượt là toạ độ góc của mỗi đĩa (vào thời điểm t ) tính từ vị trí cân bằng.
C 1 B
A 2
Viết phương trình vi phân cho chuyển động của từng đĩa Hướng dẫn:
Chọn các tọa độ suy rộng là 1 và 2 như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ.
DẠYKÈMQUYNHƠNOFFICIAL 106
( ) vRrr=−= → ( ) ( ) 2 2 cos LmRrmgRr =−+− Ta thực hiện các phép toán ( )2 2 L mRr =− → ( )2 2 dL mRr dt =− ( ) ( ) sin L mgRrmgRr =−−−− Phương trình Lagrange cho
toán
Berkeley) Cho cơ hệ như hình vẽ. Hai đĩa tròn A và B đồng tính và giống hệt nhau. Mỗi đĩa có momen quán tính I đối với trục quay đi qua tâm của đĩa và vuông góc với mặt phẳng của đĩa. Ba sợi dây thẳng, có momen xoắn được xác định bởi Mk =− . Ở vị trị cân bằng của hai đĩa, hai dây treo không bị xoắn. Kí hiệu 1 và 2 lần lượt là toạ độ góc của mỗi đĩa (vào thời điểm t ) tính từ vị trí cân bằng. C 1 B
A 2
DẠYKÈMQUYNHƠNOFFICIAL 107 Động năng của hệ là tổng động năng chuyển động quay của mỗi đĩa ( ) 2222 1212 111 222 TIII =+=+ Thế năng của hệ được tính bằng tổng thế năng gây ra bởi sự xoắn của hai dây ( ) 2 11 2 221 1 2 1 2 Uk Uk = =− → ( ) ( ) 2 222 1211212 11 22 22 Ukk =+−=+− Vậy, hàm Lagrange của hệ có dạng ( ) ( ) 2222 121212 11 22 22 LTUIk =−=+−+− Ta thực hiện các phép toán 1 1 L I = → 1 1 dL I dt = ( ) 12 1 2 L k =−− 2 2 L I = → 2 2 dL I dt = ( )21 2 L k =−− Phương
(
(
trình Lagrange cho chuyển động của hệ
) 11220 Ik+−=
)221 0 Ik+−= Bài
2: (UC
DẠYKÈMQUYNHƠNOFFICIAL 108 Viết phương trình vi phân cho chuyển động của từng đĩa Hướng dẫn: Chọn
độ suy
là 1 và 2
Động
( ) 2222 1212 111 222 TIII =+=+ Thế năng của hệ được tính bằng tổng thế năng
ra
ba dây → ( )2 22 1221 1 2 Uk =++− Vậy, hàm Lagrange của hệ có dạng ( ) ( )2 2222 121221 11 22 LTUIk =−=+−++− Ta thực hiện các phép toán 1 1 L I = → 1 1 dL I dt = ( ) 12 1 2 L k =−− 2 2 L I = → 2 2 dL I dt = ( )21 2 2 L k =−− Phương trình Lagrange cho chuyển động của hệ ( ) 11220 Ik+−= ( )22120 Ik+−= Biến đổi toán học ( ) ( ) 1212 0 Ik+++= ( ) ( ) 121230Ik−+−= Các phương trình trên cho nghiệm có dạng 1201 cos k AtC I +=++ 1202 3 cos k BtC I −=++
các tọa
rộng
như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ.
năng của hệ là tổng động năng chuyển động quay của mỗi đĩa
gây
bởi sự xoắn của
PHẦN 2: VẬN DỤNG GIẢI TOÁN
Bài tập 1: Cho cơ hệ như hình vẽ. Tìm phương trình chuyển động của vật m . Biết khối lượng của sợi dây và lò xo không đáng kể, momen quán tính của ròng rọc là I , bán kính R, sợi dây không trượt trên ròng rọc, độ cứng của lò xo là k . Bỏ qua mọi ma sát. Hướng dẫn:
Chọn tọa độ suy rộng x như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ. Động năng của hệ là tổng động năng chuyển động tịnh tiến của m và động năng trong chuyển đông
DẠYKÈMQUYNHƠNOFFICIAL 109
rọc 2211 22 TmvI =+ trong đó vx = v R = (dây không trượt) → x R = Vậy 2 2 1 2 I Tmx R =+ Thế năng của hệ là thế năng đàn hồi của lò xo 2 1 2 Ukx = Hàm Lagrange của hệ x
quay của ròng
0 k xx I m R
−= + Vật m dao động điều hòa với tần số góc 2
= + Bài tập 2: Cho cơ hệ như hình vẽ. Vật nặng có khối lượng m , lò xo có độ cứng k . Khung ABCD gồm các thanh có khối lượng không đáng kể, có thể di chuyển được nhờ các khớp ở bốn đỉnh. Tại vị trí cân bằng, khung có dạng hình thoi, góc ở đỉnh là 0 2 . Bóp nhẹ hai đầu AB rồi thả ra.
Xác định phương trình chuyển động của vật m .
k I m R
DẠYKÈMQUYNHƠNOFFICIAL 110
22 2 11 22 I LTUmxkx R =−=++ Ta thực hiện các phép toán 2 LI mx xR =+ → 2 dLI mx dtxR =+ L kx x = Phương trình chuyển động của m 2 0 I mxkx R +−= hay 2
Hướng dẫn: A D C B m
A C C
B m x
2cos0 2sin0 PT Tkl −= −= → 0 0 vị trí vật có li độ x . Ta có ( ) 0 2coscosxAB=− → ( ) .0 2coscos ttruong UmgAB=−− ( ) 0 2sinsinlAB =− (độ biến dạng của lò xo) → 0 0
1 0 tan Pkl −= Tại coscos sinsin l x = → 0 tan 2
x l = + Mặc khác ( ) 0
2cos 2sin0 PTF Tkll −= −+= → 0
k Fx =− + Vì 0 → 2 0 2tan k Fx =− và 0 ttruongU = Thế năng đàn hồi 2 2 0
1 2tan k UFdxx =−= Hàm Lagrange của hệ
1 tan tan 2
DẠYKÈMQUYNHƠNOFFICIAL 111
Chọn tọa độ suy rộng x như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ. Động năng của hệ là động năng chuyển động tịnh tiến cả vật m 2211 22 Tmvmx == Thế năng của hệ là tổng thế năng trọng trường của vật và thế năng đàn hồi của lò xo. Tại vị trí cân bằng của hệ 0 00
các phép

Phương trình Lagrange của hệ 2 0 tan k mxx =− hay 2 0 0 tan k xx m +=
1 tan k m = Bài tập 3: Các vật nặng A và B được nối với nhau bởi một sợi dây không giãn vắt qua ròng rọc D . Khi vật nặng A có trọng lượng 1P hạ xuống thì ròng rọc D có trọng lượng 3P quay quanh ổ trục còn vật nặng B có trọng lượng 2P trượt trên mặt phẳng nghiêng góc so với phương ngang. Biết hệ số ma sát trượt giữa B và mặt phẳng nghiêng là . Ròng rọc D có dạng là một đĩa tròn đồng chất bán kính R. Bỏ qua mọi ma sát. Tìm phương trình chuyển động của vật A.
Hướng dẫn:
DẠYKÈMQUYNHƠNOFFICIAL 112
22 2 0 11 22tan k Lmxx =−
Ta thực hiện
toán L mx x = → dL mx dtx = 2 0 tan Lk x x =−
Phương trình trên cho thấy m dao động điều hòa với tần số góc 0
A D B
DẠYKÈMQUYNHƠNOFFICIAL 113 Chọn tọa độ suy rông x như hình vẽ. Ta xây dựng hàm Lagrange cho hệ. Động năng của hệ là tổng động năng tịnh tiến của các vật A, B và động năng trong chuyển động quay của ròng rọc D 222111 222 AB TmvmvI =++ Trong đó A vx = , ( ) B vlxx =−=− , A vx RR == 2222 123123 1 22422 PPPPPP Txxxx gggggg =++=++ Công toàn phần do các lực chủ động tác dụng lên hệ 122sincos APxPxPx =−− → ( ) 12 sincos x QPP=−+ Ta thực hiện các phép toán 123 2 TPPP x xggg =++ → 123 2 dTPPP x dtxggg =++ Phương trình chuyển động của vật ( ) 123 12 sincos 2 PPP xPP ggg ++=−+ hay ( ) 12 123 sincos 2 PP x PPP ggg −+ = ++ Bài tập 4: Con lăn A lăn không trượt trên mặt phẳng nghiêng góc so với phương ngang, làm vật C có trọng lượng P được nâng lên nhờ một sợi dây vắt qua ròng rọc B. Con lăn A và ròng rọc B đĩa tròn đồng chất có trọng lượng Q và bán kính R. Bỏ qua mọi ma sát. A x A
Hướng dẫn: Chọn tọa độ suy rộng x như hình vẽ. Ta xây dựng hàm Lagrange cho hệ. Động năng của hệ là tổng động năng chuyển động song phẳng của vật A, động năng trong chuyển động quay của ròng rọc B, động năng trong chuyển động tịnh tiến của vật C
DẠYKÈMQUYNHƠNOFFICIAL 114
2211 22 AAA TmvI =+ trong đó A vx = , 22 A A vx RR == → 2 3 4 A Q Tx g = Tương tự như vậy, ta cũng tìm được 2 4 B Q Tx g = và 2 2 C P Tx g = Lực suy rộng của hệ sin x QQP =− Ta thực hiện các phép toán B C A B C A x
Tìm phương trình chuyển động của vật C .
2 2 TQP x xgg =+ → 2 2 dTQP x dtxgg =+ Phương trình chuyển động của vật C 2sin 2 QP xQP gg +=− → ( ) sin 2 QPg x PQ = + Bài tập 5: (Wisconsin) Một vật có khối lượng M được nối với một vòng tròn nhẹ, bán kính a nằm yên trên một bề mặt nằm ngang, không ma sát như hình vẽ. Hạt m chuyển động không ma sát trên đường tròn.
a. Tìm phương trình chuyển động của hạt. b. Trong trường hợp giới hạn, các góc nhỏ. Tường minh phương trình chuyển động của hạt là một hàm theo thời gian. Hướng dẫn: a. Chọn các tọa độ suy rộng x và như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ. Động năng của
động năng trong chuyển động tịnh tiến của M và động năng của
DẠYKÈMQUYNHƠNOFFICIAL 115
hệ là
m 2211 22MmTMvmv =+ Trong đó M vx = sin cos m m xxa ya =+ =− → cos sin m m xxa ya =+ = → ( ) ( ) 22 2 cossin m vxaa=++ Vậy M m M m x
Vậy ( ) 0 Mmg Ma
+ += Phương trình trên chứng tỏ vật m dao động điều hòa với tần số góc ( ) Mmg Ma
+
Bài tập 6: (UC Berkeley) Một thanh mãnh đồng chất chiều dài 2L, khối lượng M được treo vào một sợi dây khối lượng không đáng kể, chiều dài L buộc vào một chiếc đinh như hình vẽ.
DẠYKÈMQUYNHƠNOFFICIAL 116 ( ) 222211 2cos 22 TMxmxaax =+++ Công toàn phần
sin Amgad =− → sinQmga =− và 0 xQ = Ta thực
toán ( ) cos T Mmxma x =++ → ( ) 2 cossin dT Mmxmama dtx =++− 0 T x = 2 cos T mamax =+ → 2 cossin dT mamaxmax dt =+− sin T max =− Phương trình Lagrange
( ) 2 cossin0Mmxmama ++−= cossinaxg +=− b.
( ) 0 0 Mmxma axg ++= ++= → mg x M
F
do các lực chủ động tác dụng lên hệ
hiện các phép
của hệ
Trong trường hợp các góc nhỏ, bỏ qua vô cùng bé bậc 2 trở lên
=
=
lực F nằm ngang, tác dụng vào đầu tự do của thanh. Xác định phương trình chuyển động của thanh, cho rằng trong khoảng thời gian rất ngắn các góc đều rất nhỏ.
DẠYKÈMQUYNHƠNOFFICIAL 117 Một
Chọn
Vị trí khối
xác
bởi sinsin coscos xlL ylL =+ =−− → coscos sinsin x y vlL vlL =+ =+ Động
trong chuyển
( ) 22222222 1111 2cos 2226 TmvIlLLlML =+=++−+ Thế năng trọng trường ( ) coscos tt UMgll=−+ Thế năng gây bởi ngoại lực được xác định bởi → ( ) sin2sin F UFdrFlL=−=−+ Hàm Lagrange của hệ ttFLTUU =−− Thực hiện các phép toán 0 dLL dtqq −= Ta thu được ( ) ( ) 2 cossinsincos0MlMLMLMgF +−+−+−= ( ) ( ) 2 4 cossinsin2cos0 3 MLMlMlMgF +−+−+−= Với điều kiện các góc nhỏ, hệ phương trình trên trở thành x O y
Hướng dẫn:
các tọa độ suy rộng và
như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ.
tâm của thanh được
định
năng của hệ là động năng của thanh
động song phẳng
Bài tập 7: (UC Berkeley) Một con lắc đơn khối lượng m , chiều dài l được gắn trên một vật có khối lượng M như hình vẽ. Vật M có thể trượt không ma sát trên bề mặt nằm ngang. Xác định phương trình chuyển động của hệ. Hướng dẫn: Chọn các tọa độ suy rộng x và như
DẠYKÈMQUYNHƠNOFFICIAL 118
4
3 MlMLMgF
++−= ++−=
0
20
MLMlMgF
hình vẽ. Ta xây dựng hàm
Động năng của hệ là tổng động năng của M và động năng của m . 2211 22MmTMvmv =+ trong đó M vx = sin cos m m xxl yl =+ =− → cos sin xm ym vxl vl =+ = Vậy ( ) 22211 cos 22 TMmxmlxml =+++ Công toàn phần của các lực chủ động tác dụng lên hệ sinAmgl =− → sinQmgl =− Ta thực hiện các phép toán M m M m x
Lagrange cho hệ.
trình trên chứng tỏ rằng con lắc dao động điều hòa với tần số góc Mmg Ml
Bài tập 8: Một hạt có khối lượng m trượt xuống một cái bát hình cầu nhẵn, bán kính R như hình vẽ. Cho rằng hạt vẫn nằm trong mặt phẳng thẳng đứng và cái bát nằm cố định.
a. Xác định phương trình chuyển động của hạt.
b. Gọi M là khối lượng của cái bát, Mm và có thể trượt không ma sát trên bề mặt nằm ngang. Xác định chu kì dao động nhỏ của hạt lúc này. Hướng dẫn:
O x y


Chọn tọa độ suy rộng như hình vẽ. Ta xây dựng hàm Lagrange cho hệ.
DẠYKÈMQUYNHƠNOFFICIAL 119 ( ) cos T Mmxml x =++ → ( ) 2 cossin dT Mmxmlml dtx =++− 0 T x = 2 cos T mlxml =+ → 2 cossin dT mlxmlxml dt =−+ sin T mlx =− Phương trình Lagrange cho
( ) 2 cossin0Mmxmlml ++−= cossinsinsin xxlxg −++=− Trong
( ) 0 0 Mmxml xlg ++= ++= → 0 Mmg
+ +=
=
chuyển động của hệ
trường hợp các dịch chuyển vô cùng bé, ta bỏ qua các vô cùng bé bậc hai trở đi, khi đó
Ml
Phương
+
Động năng của hệ là động năng của hạt m 2 1 2 Tmv = Trong đó sin cos xR yR = = → cos sin x vR yR = =− → 222vR = Vậy 22 1 2 TmR = Công toàn phần của các lực chủ động tác dụng lên hệ sin AmgRd =− → sinQmgR =− Ta thực hiện các phép toán 2 T mR = → 2 dT mR dt = 0 T = Phương trình Lagrange cho chuyển động của hạt
DẠYKÈMQUYNHƠNOFFICIAL
120
2
=−
R
cầu với tần số góc g R = b. Trường hợp M không cố định. Các tọa độ suy rộng được chọn là x và . Một cách tượng tự ta cũng xây dựng phương trình Lagrange cho hệ Động năng của hệ 2211 22MmTMvmv =+ Trong đó M vx = sin cos m m xxR yR =+ = → cos sin x y vxR vR =+ =− → 222vR = Vậy
sinmRmgR
hay sin0 g R += Trường hợp nhỏ 0 g
+= Phương trình trên chứng tỏ hạt dao động điều hòa trong bát hình
DẠYKÈMQUYNHƠNOFFICIAL 121 ( ) 22211 cos 22 TMmxmRxmR =+++ Công toàn phần do các
sinAmgR =− → sinQmgR =− Ta thực hiện các phép toán ( ) cos T MmxmR x =++ → ( ) 2 cossin dT MmxmRmR dtx =++− 0 T x = 2 cos T mRxmR =+ → 2 cossin dT mRxmRxmR dt =−+ sin T mRx =− Phương trình Lagrange cho chuyển động của hệ ( ) 2 cossin0MmxmRmR ++−= cossin xRg +=− Trong
( ) 0 0 MmxmR xRg ++= ++= → 0 Mmg MR +
Xác
.
m
lực chủ động tác dụng lên hệ
trường hợp gần đúng
+= Phương trình trên chứng tỏ, con lắc dao động nhỏ với tần số góc Mmg MR + = Bài tập 9: Một vật có khối lượng m được gắn vào một mặt phẳng nghiêng M bởi một lò xo có độ cứng k như hình vẽ. Cho rằng mặt phẳng nghiêng có thể trượt không ma sát trên bề mặt nằm ngang.
định phương trình chuyển động của m
Hướng dẫn: M
k
DẠYKÈMQUYNHƠNOFFICIAL 122 Chọn các tọa độ suy rộng x và s như hình vẽ. Ta xây dựng phương trình Lagrange cho chuyển động của hệ. Động năng của hệ là tổng động năng của hai vật M và m 2211 22MmTMvmv =+ Trong đó M vx = cos sin m m xxs ys =+ =− → cos sin x y vxs vs =+ =− → 222 2cos m vxsxs =++ Vậy ( ) 2211 cos 22 TMmxmsmxs =+++ Thế năng của hệ Khi vật nằm cân bằng ( ) 0 sin0mgksd −−= → 0 sin mg sd k =+ ( ) ( )2 sin1 2 Umghsksd =−+− Hàm Lagrange của hệ ( ) ( ) ( )2 22 111 cossin 222 LTUMmxmsmxsmghsksd =−=+++−−−− Phương trình Lagrange cho chuyển động của hệ ( ) cos0Mmxms ++= ( ) cossin0 mxmskskdmg ++−+= Bài tập 10: (UC Berkeley) Hai thanh phẳng, có cùng chiều dài l và khối lượng m được nối với nhau bằng một bản lề và một sợi dây nhẹ. Tại thời điểm ban đầu hệ nằm cân bằng như hình vẽ. Tiến hành cắt sợi dây. Bỏ qua mọi ma sát. M m O x y s
Xác định vận tốc của bản lề khi nó chạm sàn.
Hướng dẫn: Chọn tọa độ suy rộng như hình vẽ. Ta xây dựng phương trình Lagrange cho hệ. Vị trí khối tâm của các thanh 1 cos 2 l x = , 1 sin 2 l y = 2 cos 2 l x =− , 2 sin 2 l y = Các thành phần của vận tốc
DẠYKÈMQUYNHƠNOFFICIAL 123
222222 111sinsin 2123 LTUmlmlmglmlmgl =−=+−=− Thực
3 cos0 g l += Vì : 2 1
=
Nên:
=−
y
1 sin 2 l x =− , 1 cos 2 l y = 2 sin 2 l x = , 2 cos 2 l y = Hàm Lagrange cho hệ
hiện các phép toán, ta thu được
2 d d
và 0 = khi 030 =
( ) 3 12sin g l
030 030
O x
Khi bản lề chạm vào mặt sàn 0 = : 3g l =−
PHẦN 3: BÀI TẬP RÈN LUYỆN
Bài tập 1: (Chọn đội tuyển dự IPHO 2011) Một vành trụ mỏng I , đồng chất, khối lượng M , bán kính R . Trong lòng vành trụ có một khối trụ đặc II, đồng chất, khối lượng m , bán kính r , cùng chiều dài với vành trụ. Trong hình vẽ bên, Oxy là mặt phẳng tiết diện vuông góc với trục vành trụ, A và B là giao điểm của mặt phẳng Oxy với hai trục. Tác dụng lực có phương đi qua A vào vành trụ sao cho vành trụ lăn không trượt trên mặt phẳng nằm ngang dọc theo chiều dương trục Ox . Biết khối trụ lăn không trượt trong lòng vành trụ, trục khối trụ luôn song song với trục vành trụ. Ở thời điểm t , góc hợp bởi AB và phương thẳng đứng là ; vận tốc của A là Av , tốc độ góc của AB quanh trục đi qua A là
y x O
I
Xác định quy luật biến đổi của theo thời gian nếu chỉ nhận các giá trị nhỏ. Bài tập 2: (HSG Quốc Gia 2007) Một đĩa tròn đồng chất, khối lượng m , bán kính R , có thể quay quanh một trục cố định nằm ngang đi qua tâm O của đĩa. Lò xo có độ cứng k, một đầu cố định, một đầu gắn với điểm A của vành đĩa. Khi OA nằm ngang thì lò xo có chiều dài tự nhiên. Xoay đĩa một góc nhỏ 0 rồi thả nhẹ. Coi lò xo luôn có phương thẳng đứng và khối lượng lò xo không đáng kể.
Bỏ qua mọi sức cản và ma sát. Tính chu kì dao động của đĩa.
DẠYKÈMQUYNHƠNOFFICIAL 124
.
B R A r k O A
Bài tập 3: Một quả cầu đồng chất khối lượng m , lăn không trượt trên một mặt phẳng nghiêng M , góc nghiêng . Biết rằng mặt phẳng nghiêng có thể trượt không ma sát trên mặt bàn nằm ngang.
a. Xác định phương trình chuyển động của các vật trong hệ.
b. Với trường hợp Mm = và 4 = . Xác định gia tốc của mặt phẳng nghiêng, gia tốc tương đối giữa quả cầu với mặt phẳng nghiêng. Bài tập 4: Cho cơ hệ như hình vẽ. Vật E có khối lượng m , ròng rọc Q có khối lượng không đáng kể. B là một khối trụ có momen quán tính I , bán kính R , khối lượng M Mặt phẳng nghiêng có khối lượng mpn M . Xác định phương trình chuyển động của các vật trong hai trường hợp.
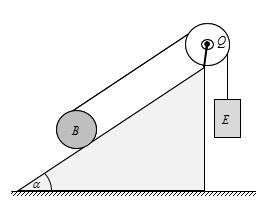
a. Mặt phẳng nghiêng có định. b. Mặt phẳng nghiêng trượt không ma sát trên bề mặt nằm ngang.
C. KẾT LUẬN
Chuyên đề đã trình bày được nội dung cơ sở lí thuyết:
o Phương trình Lagrange loại II.
o So sánh ưu điểm của phương trình Lagrange loại II trong tìm quy luật chuyển động của các cơ hệ chịu liên kết so với sử dụng các phương trình của Newton.
o Xây dựng quy trình chung vận dụng phương trình Lagrange loại II.
o Tìm được quy luật chuyển động của một số cơ hệ điển hình. Tuy nhiên, vì thời gian và trình độ bản thân có hạn, tôi nhận thấy chuyên đề của mình còn nhiều khiếm khuyết. Các dạng bài tập chưa được tổng quát và chưa phong phú.
DẠYKÈMQUYNHƠNOFFICIAL 125
M m
Rất mong được sự góp ý của bạn đọc để đề tài được hoàn thiện hơn, giúp cho công tác giảng dạy, bồi dưỡng học sinh giỏi ngày càng hiệu quả hơn. Xin trân trọng cảm ơn!
D. TÀI LIỆU THAM KHẢO
1. Lê Doãn Hồng Đỗ Sanh. Bài tập cơ học. NXB Giáo Dục 1999.
2. Nguyễn Hữu Mình Tạ Duy Lợi Đỗ Đình Thanh Lê Trọng Tường. Bài tập Vật Lý lý thuyết. NXD Đại Học Quốc Gia Hà Nội 2001.
3. Nguyễn Hữu Mình. Cơ học lý thuyết. NXB Giáo Dục 1986.
4. Lim Yung Kuo. Problems and solution on machenics 1994.
5. G. Gignoux B. Slivestre Brac. Solved Problems in Lagrangian and Hamilton Mechanics.
DẠYKÈMQUYNHƠNOFFICIAL 126
Chuyên đề
CHUYỂN ĐỘNG LIÊN KẾT CỦA VẬT RẮN
Tác giả: Nguyễn Hải Dương
THPT Chuyên Lê Hồng Phong, Nam Định
(Chuyên đề đạt giải Nhì)
MỞ ĐẦU
I. Lí do chọn đề tài Cơ học là khoa học về sự cân bằng và chuyển động của vật thể. Nó làm phong phú thêm kiến thức của chính ta về hàng loạt quy luật cơ bản của thiên nhiên, về các phương pháp nghiên cứu nhiều hiện tượng trong thế giới xung quanh ta. Nó giúp ta bắt các hiện tượng đó phục vụ con người, tạo khả năng phát triển tư duy và xây dựng thế giới quan đúng đắn. Cơ học cũng là phần đầu tiên của chương trình vật lí chuyên. Nó là cơ sở lý thuyết vững chắc của hầu hết các lĩnh vực của nền kỹ thuật.
Theo tính chất của bài toán, người ta phân cơ học thành tĩnh học và động học. Theo tính chất của đối tượng nghiên cứu người ta phân cơ học thành: cơ học chất điểm, cơ học hệ chất điểm, cơ học vật rắn, cơ học các vật thể có khối lượng biến đổi, cơ học vật biến dạng, cơ học chất lưu. Cơ học vật rắn là phần quan trọng bậc nhất trong chương trình Vật lí chuyên; là phần kiến thức gây nhiều khó khăn cho học sinh; cũng là nền tảng cho một số phần kiến thức phía sau; đặc biệt để đánh giá tư duy sáng tạo, quan sát, nhận định trong vật lý. Đặc biệt các bài tập về hệ các vật rắn, các vật rắn liên kết với nhau cần được chú trọng chuyên sâu. Trong chuyên đề này tôi sẽ trình bày tập trung vào các kiến thức và hệ thống bài tập phần “Chuyển động liên kết của vật rắn”.
II. Mục đích của đề tài
Đề tài đề xuất các kiến thức cơ bản đến nâng cao cần truyền đạt cho học sinh về cơ học vật rắn, đồng thời đi sâu hơn vào kiến thức và bài tập chuyển động của các vật rắn có liên kết.
tài mong muốn là giáo trình giảng dạy cho giáo viên chuyên và chuyên đề nghiên c
c
a học sinh. Qua đó học sinh hình thành các kiến thức và kĩ năng giải quyết các vấn
DẠYKÈMQUYNHƠNOFFICIAL 127
Đề
ứu
ủ
đề vật lý.
I - MỞ ĐẦU
1. Định nghĩa Chuyển động phẳng của một vật rắn là chuyển động trong đó mọi điểm của vật chuyển động song song với một mặt phẳng cố định cho trước. Ta quy ước gọi mặt phẳng này là mặt phẳng O, hệ quy chiếu (HQC) gắn với mặt phẳng O là HQC O và người quan sát (NQS) đứng trong HQC O là NQS O.
2. Chuyển động tịnh tiến song song với một mặt phẳng cố định và chuyển động quay quanh một trục cố định là hai dạng chuyển động phẳng cơ bản, độc lập với nhau (đã học trong chương trình trung học phổ thông nâng cao).
3. Vận tốc góc và gia tốc góc Muốn miêu tả đầy đủ chuyển động quay về mặt động học, ta phải coi vận tốc góc và gia tốc góc là những đại lượng đại số hoặc vectơ.
a) Cách biểu diễn đại số (Hình 1.1a)
Chọn một chiều quay làm chiều dương và gọi là góc quay được. • = '(t) > 0 nếu vật quay theo chiều dương. < 0 nếu vật quay ngược chiều dương. • = '(t) cùng dấu với nếu vật quay nhanh dần. trái dấu với nếu vật quay chậm dần. b) Cách biểu diễn vectơ (Hình 1.1b) Chọn trục quay làm phương của vectơ . Chi
DẠYKÈMQUYNHƠNOFFICIAL 128
NỘI DUNG A. CƠ SỞ LÝ THUYẾT1 PHẦN I. KHẢO SÁT CHUYỂN ĐỘNG PHẲNG CỦA VẬT RẮN VỀ MẶT ĐỘNG HỌC
ều của vectơ được xác định bằng quy tắc nắm tay phải (Hình 1.1b) hay quy tắc cái đinh ốc thuận. Vectơ được gọi là vectơ trục. = cũng là vectơ trục. 1 Tô Giang, Cơ học 2, NXB Giáo dục Việt Nam '(t) Hình 1.1a Hình 1.1b
a)
b) Xét một vật mỏng, phẳng (quyển sách mỏng chẳng hạn) đang chuyển động trên mặt bàn (mặt phẳng O). Trong khoảng thời gian rất ngắn t tính từ thời điểm t, vật chuyển động t
vị trí 1 đến vị trí 2 (Hình 1.2). Xét một đoạn thẳng AB bất kì trên vật. Ta có thể dịch chuyển vật từ vị trí 1 sang vị trí 2 theo một trong hai cách sau đây: Cách 1: Thực hiện chuyển động tịnh tiến với vận
DẠYKÈMQUYNHƠNOFFICIAL 129
4. Các công thức (đại số) của chuyển động quay biến đổi đều a) = hằng số b) (
c) =+ 2 0
d)
cùng chiều với nếu vật quay nhanh dần. ngược chiều với nếu vật quay chậm dần. Tuy hai cách biểu diễn là như nhau nhưng ta ưu tiên chọn cách biểu diễn đại số vì sau này ta thường lập và giải hệ phương trình dưới dạng đại số khi làm bài tập.
0 là vận tốc góc ban đầu)
tt/2 ( là góc quay được)
Chuyển động quay đều khi = 0 hoặc = hằng số. II - PHÂN TÍCH MỘT CHUYỂN ĐỘNG PHẲNG TỔNG QUÁT 1. Ví dụ
ố
ể
ậ
ừ
ị
ị
1' (được biểu diễn bằng nét đứt ở
Ta có: Tiếp theo, giữ A' đứng yên và thực hiện chuyển động quay quanh A' để chuyển vật từ vị trí 1' đến vị trí 2. Người ta gọi điểm A' là cực. Theo
ta
0 t=+ 22 0 2 −= Av AA'BB' =
.t.
v t =
ừ
t
c để chuy
n v
t t
v
trí 1 đến v
trí
Hình 1.2a).
Hình 1.2a
có:
A
=
Hình 1.2
Cách 2: Thực hiện chuyển động tịnh tiến với vận tốc để chuyển vật từ vị trí 1 đến vị trí
2' (được biểu diễn bằng nét đứt ở Hình 1.2b). Ta có . Tiếp theo, giữ đứng yên và thực hiện chuyển động quay quanh để chuyển vật từ vị trí 2' đến vị trí 2. Trong trường hợp này, được gọi là cực. Theo Hình 1.2b ta cũng có như ở cách 1. Một chuỗi những chuyển động tịnh tiến và quay kế tiếp nhau như trên miêu tả gần đúng chuyển động thực của vật và càng đúng nếu lấy t càng nhỏ. Trong chuyển động thực thì hai chuyển động thành phần, tịnh tiến và quay, diễn ra đồng thời. Ngoài ra, trong nhiều trường hợp sau này, tác giả sẽ không dùng cách nói đầy đủ là "vật quay quanh một trục vuông góc với mặt phẳng cố định O" mà dùng cách nói gọn là "vật quay quanh một điểm". Khi đó, phải hiểu điểm này là giao điểm của trục quay với mặt phẳng O.
2. Kết luận
a) Chuyển động phẳng tổng quát trong HQC O có thể phân tích thành hai chuyển động thành phần trong HQC đó.
Chuyển động tịnh tiến với vận tốc của một điểm tuỳ ý mà ta chọn làm cực. Chuyển động quay quanh cực đó.
b) Khi phân tích chuyển động phẳng thành chuyển động tịnh tiến và quay thì vận tốc của chuyển động tịnh tiến có thể khác nhau tuỳ thuộc vào việc chọn điểm nào làm cực, nhưng vận tốc góc thì vẫn như nhau.
Tóm lại, chuyển động phẳng tổng quát có thể xem là chuyển động tổng hợp của hai chuyển động thành phần, tịnh tiến và quay hoặc là chuyển động vừa tịnh tiến vừa quay.
III SỰ PHÂN BỐ VẬN TỐC CỦA CÁC ĐIỂM TRONG MỘT VẬT RẮN
DẠYKÈMQUYNHƠNOFFICIAL
130
ậ
ắ
i thời điểm xét, điểm A có vận tốc , điểm B có vận tốc và mọi điểm của vật có một vận tốc góc chung . Ta hãy xét xem , và liên hệ với nhau như thế nào. Nếu chọn điểm A làm cực (Hình 1.3) thì ta có: Lấy đạo hàm theo thời gian ta được: Bv '' 11BBAA = B.t= v ' 1B ' 1B ' 1B t = Av Bv Av Bv OBOAAB. =+ dOBdOAdAB dtdtdt =+
1. Xét một v
t r
n mỏng, phẳng chuyển động trong HQC O. A và B là hai điểm bất kì của vật. Tạ
= +
Hình 1.3
Vì khoảng cách AB không đổi nên là vận tốc của điểm B trong chuyển động quay quanh cực A với vận tốc góc .
Vì thế, = Cuối cùng, ta được: = + (1.1)
Công thức (1.1) cho thấy, vận tốc của một điểm bất kì trên vật bằng tổng vectơ vận tốc của một điểm khác nào đó trên vật mà ta chọn làm cực và vận tốc của điểm ấy trong chuyển động quay quanh cực.
Công thức (1.1) được gọi là công thức phân bố vận tốc.
2. Hệ quả
Công thức (1.1) cũng cho thấy, hình chiếu của vectơ vận tốc của hai điểm lên một trục X đi qua hai điểm ấy luôn bằng nhau (Hình 1.4): (1.2)
Thật vậy, chiếu công thức (1.1) lên trục X thì hình chiếu của vectơ thành phần bằng 0 vì vectơ ⊥ tức là ⊥ trục X.
IV CHUYỂN ĐỘNG QUAY THUẦN TUÝ
1. Tâm quay (hay trục quay) tức thời
Ta tưởng tượng có một mặt phẳng O' gắn với vật và cùng chuyển động với vật (Hình 1.5). Tại mỗi thời điểm ta đều có thể tìm thấy một điểm của mặt phẳng O' này có vận tốc bằng 0 (đối với mặt phẳng O), còn các điểm khác có vận tốc khác 0. Tại thời điểm xét, mặt phẳng O' (bao gồm cả vật) quay quanh điểm này. Ta gọi điểm này là tâm quay tức thời, còn trục đi qua tâm quay tức thời và vuông góc với mặt phẳng O gọi là trục quay tức thời. Tâm quay tức thời có thể nằm trong vật hoặc nằm ngoài vật.
Hình 1.4 Hình 1.5
DẠYKÈMQUYNHƠNOFFICIAL
131
Gọi K là điểm cần tìm ( ). Theo công thức (1), ta có: (a) Bv Av BAv BAv BAv AB Bv Av AB BXAX = vv AB AB AB K 0 = v AK KAKA=+=vv
BK KBKB
=+=
(b)
Các điểm A, B, C... của vật đều quay quanh K với vận tốc góc .
Như vậy, chuyển động phẳng tổng quát còn có thể xem là chuyển động quay thuần tuý quanh tâm quay tức thời.
2. Cách xác định tâm quay tức thời
Hình 1.6
Nếu biết vận tốc của hai điểm của vật, A và B chẳng hạn, thì theo hai công thức (a) và (b), ta suy ra: , và
Từ đó, ta có thể xác định được tâm quay tức thời K bằng cách vẽ.
a) Trường hợp 1: Hai vectơ và khác phương (Hình 1.6a).
KA KB = v v Av Bv Av Bv
b) Trường hợp 2: Hai vectơ và song song với nhau và vuông góc với đoạn thẳng AB (Hình 1.6b và c).
DẠYKÈMQUYNHƠNOFFICIAL 132
V - CHUYỂN ĐỘNG QUAY TƯƠNG ĐỐI vv
A KA ⊥ v B KB ⊥ v A B
1. Như đã biết, trong HQC O, hai chuyển động thành phần, tịnh tiến và quay, xảy ra đồng thời. Muốn nhận ra chuyển động tịnh tiến, NQS O đánh dấu điểm mà người đó chọn làm cực, như điểm A chẳng hạn, rồi theo dõi sự chuyển động của nó. Muốn nhận ra chuyển động quay, NQS O đánh dấu một điểm khác B nào đó rồi theo dõi chuyển động quay của vectơ quanh A. Nhưng việc theo dõi chuyển động này khó hơn vì A luôn chuyển động. Nó chỉ tựa hồ như đứng yên tại mỗi thời điểm mà thôi (Hình 1.7a). Vì thế, NQS phải làm như sau: Chọn một điểm bất kì O1 trong HQC O làm tâm quay, rồi vẽ các vectơ , song song, cùng chiều và cùng độ lớn với các vectơ tại các thời điểm t1, t2... (Hình 1.7b). Chuyển động quay của vectơ quanh O1 miêu tả chuyển động thành phần quay của vật quanh A trong HQC O.
2. Chuyển động quay tương đối Thật là có ích nếu ta tách được chuyển động quay ra khỏi chuyển động tịnh tiến. Muốn thế, ta làm như sau: Chọn HQC O' có gốc toạ độ O' tại cực A còn các trục toạ độ O'x' và O'y' thì có hướng không đổi. Đối với HQC O thì HQC O' là HQC chuyển động tịnh tiến với vận tốc của cực.
Trong HQC O' thì cực đứng yên, tức là chuyển động tịnh tiến bị khử, chỉ còn chuyển động quay của vật quanh cực. Chuyển động quay của vật trong HQC O' là chuyển động quay tương đối (Hình 1.8). 3. Công thức cộng vận tốc Xét chuyển động c
DẠYKÈMQUYNHƠNOFFICIAL 133
ủa một điểm B của vật. là vận tốc tuyệt đối của B trong HQC O. và là vectơ vị trí và vận tốc tương đối của B trong HQC O'. Áp dụng công thức cộng vận tốc, ta có: (1.10) So sánh công thức (1.10) với công thức (1.1) ta suy ra . AB 1 1OB AB 1 1OB Bv O'B ' Bv ' BBAAA vvvv'O'Bv'AB =+=+=+ ' =
1.8
Hình 1.7 Hình
Nói một cách khác, chuyển động quay tương đối của vật trong HQC O' có cùng vận tốc góc và do đó cùng gia tốc góc với chuyển động thành phần quay trong HQC O. VI - CHUYỂN ĐỘNG LĂN KHÔNG TRƯỢT
1. Định nghĩa Một vật rắn (hình cầu hoặc hình trụ) lăn không trượt trên bề mặt S một vật rắn khác, nếu tại mỗi thời điểm vận tốc của điểm K ( ) của vật rắn tiếp xúc với S bằng 0 (xét trong HQC gắn với S). Nếu 0 thì vận tốc này được gọi là vận tốc trượt.
Ví dụ: Bánh xe, thùng phuy, quả bóng lăn không trượt trên mặt đường. Các viên bi lăn không trượt trong các ổ bi. 2. Điều kiện lăn không trượt Ta hãy xét một bánh xe có khối tâm G và bán kính R, lăn không trượt trên mặt đường (Hình 1.9).
a) Trước hết, chuyển động của bánh xe có thể xem làchuyểnđộng tổng hợp của chuyển động tịnh tiến với vận tốc và chuyển động quay quanh G với vận tốc góc (Hình 1.10a, b).
Theo công thức (1.1), ta có: hay viết dưới dạng đại số: (1.11) Lấy đạo hàm theo thời gian (1.11), ta được: (1.12)
Các công thức (1.11) và (1.12) được gọi là điều kiện lăn không trượt. Từ công thức (1.11) và từ Hình 1.10, ta suy ra, trong chuyển động lăn không trượt, đường đi được của khối tâm bằng đường đi được quanh khối tâm của các điểm tiếp xúc của vật với mặt đường.
DẠYKÈMQUYNHƠNOFFICIAL 134
K
K
G
KGKG vvv0 =+= KG vvGK0 =+= KG vvR0 =−= G vR = G
=
v
v
v
aR
Hình 1.10 Hình 1.9
b) Ta có thể tìm ra các công thức trên đây nếu ta coi chuyển động lăn không trượt là chuyển động quay thuần tuý quanh điểm tiếp xúc K. Khi đó các điểm khác, kể cả khối tâm, đều quay quanh K với cùng và như trong chuyển động thành phần quay quanh G.
Thật vậy, ta vẫn có và (Hình 1.10c).
3. Xét về mặt động lực học, khi vật chuyển động lăn không trượt trên mặt của một vật khác S0, thì phản lực của bề mặt của S0 bao gồm một phản lực vuông góc và lực ma sát nghỉ . Còn lực ma sát lăn rất nhỏ bỏ qua. Ví dụ: Ta đẩy một thùng phuy cho chuyển động bằng một lực nằm ngang có giá đi qua khối tâm. Lực chỉ có tác dụng làm cho vật chuyển động tịnh tiến nếu như mặt đường nhẵn. Nhưng vì mặt đường nhám nên nó tác dụng vào thùng phuy một lực ma sát nghỉ giữ cho điểm tiếp xúc K đứng yên và thùng phuy quay quanh nó (Hình 1.11).
Hình 1.11
DẠYKÈMQUYNHƠNOFFICIAL 135
Gv R = Ga R =
msn
F
N
F F
PHẦN II. KHẢO SÁT CHUYỂN ĐỘNG PHẲNG VỀ MẶT ĐỘNG LỰC HỌC I - KHỐI TÂM CỦA
VẬT MOMEN QUÁN TÍNH
1. Khi vật chuyển động dưới tác dụng của lực, người ta phát hiện ra rằng vật có một điểm đặc biệt khác hẳn các điểm còn lại. Ta đã biết điểm này là trọng tâm của vật và kí hiệu là
G. Sở dĩ có tên gọi này là vì khi xét chuyển động của vật trong trường trọng lực là trường lực đều thì ta không thể bỏ qua vai trò của trọng lực và điểm đặt của nó.
Tuy nhiên, trong một số trường hợp khác thì điểm này mất ý nghĩa là trọng tâm của vật. Ví dụ:
Vật chuyển động trong "trạng thái không trọng lượng".
Vật chuyển động trong trường hấp dẫn là trường lực không đều. Trong trường lực này điểm đặc biệt không trùng với trọng tâm của vật.
Vật mỏng, phẳng chuyển động trên mặt phẳng nằm ngang không ma sát dưới tác dụng của những lực nằm ngang. Trong trường hợp này, điểm đặc biệt không mang ý nghĩa là trọng tâm vì trọng lực của từng phần tử của vật đều bị khử bởi phản lực của mặt bàn nên trọng tâm của vật không có vai trò gì đối với chuyển động của vật. Ở phần sau ta sẽ biết vị trí của điểm đặc biệt này chỉ phụ thuộc vào sự phân bố khối lượng trong vật, nên từ nay ta sẽ gọi nó là khối tâm của vật.
2. Tính chất đặc biệt của khối tâm Đặt một vật mỏng, phẳng có khối tâm G đã biết lên một mặt bàn nằm ngang và nhẵn (trong trường hợp này khối tâm trùng với trọng tâm). Buộc sợi chỉ vào một điểm A ở mép vật rồi kéo dây theo các phương khác nhau. Thí nghiệm cho thấy, nếu kéo dây theo phương AG thì vật chuyển động tịnh tiến, còn nếu kéo dây theo các phương khác thì vật vừa quay vừa tịnh tiến. 3. Ta có thể chứng minh rằng trong thí nghiệm trên, tác dụng của lực có giá không đi qua khối tâm (Hình 1.12) tương đương với một lực đặt tại khối tâm và một ngẫu lực. Thật vậy, vật sẽ không chịu thêm một tác dụng nào nữa (xét về mặt chuyển động) nếu ta đặt thêm vào khối tâm một cặp lực cân bằng và , trong đó lực song song, cùng chiều và cùng
DẠYKÈMQUYNHƠNOFFICIAL 136
Momen
M(G) = Fd. F F' F' F' F F F' F F' F
độ lớn với . (Hình 1.13). Như vậy, tác dụng của lực tương đương với một lực đặt tại khối tâm và một ngẫu lực ( , ).
của ngẫu lực này bằng momen của lực đối với khối tâm:
Hình 1.13 Hình 1.12
4. Vị trí của khối tâm Ta coi vật rắn là một hệ chất điểm m1, m2,..., mN có vị trí được xác định bằng các vectơ , ,..., (Hình 1.14). Lí thuyết và thực nghiệm cho thấy, vị trí của khối tâm của vật được xác định bằng công thức sau đây: hay (1.3a) trong đó là vectơ vị trí của khối tâm, còn m = là khối lượng của vật. hay: == GiiGii 11 xmxymy mm (1.3b) Nếu ta chọn gốc toạ độ trùng với khối tâm (Hình 1.15) thì , và công thức (1.3a) trở thành: (1.4)
2 i ir m . Đơn vị I: kg.m2 I phụ thuôc khối lượng và sự phân bố khối lượng. Mômen quán tính của một số vật đồng chất. * Vành tròn hay trụ rỗng bán kính 1r 2r Nr 1122NN G 12N
5. Momen quán tính
R: I = mR2 mrmr...mr r mm...m
đĩa hay trụ đặc bán kính R: I = 1 2 mR2 +++ = +++ Gii 1 rmr m = Gr im G r0 = iiG rr = i iG mr0 = 2 GiiG Imr. =
I = 5 2 mR Hình 1.15
l: I Hình 1.14
DẠYKÈMQUYNHƠNOFFICIAL
137
* Vành
* Hình cầu đặc:
2 * Thanh có tiết diện bé với chiều dài
5.1. Mômen quán tính của vật rắn đối với một trục đặc trưng cho mức quán tính (sức ì) của vật đó đối với chuyển động quay quanh trục đó. Công thức: I = i = 12 1 ml2 5.2. Định lí về trục song song (còn gọi là định lí Stê-nơ Huy-ghen) a) Về lí thuyết, ta có thể tính được momen quán tính của vật rắn đối với một trục qua khối tâm theo công thức đã học
Đối với những vật đồng chất và có dạng hình học đối xứng thì trục đối xứng đi qua khối tâm. Ta đã biết momen quán tính của một số vật này đối với trục của nó (xem SGK nâng cao hay tài liệu tự chọn nâng cao).
Trong khi đó, momen quán tính IK thường không có giá trị xác định vì vị trí của tâm quay tức thời K luôn luôn thay đổi.
Định lí về trục song song cho phép ta tính được IK nếu biết IG. Định lí này được diễn tả bằng công thức sau đây: (1.8) Trong đó d là khoảng cách giữa hai trục quay song song đi qua G và K và vuông góc với mặt phẳng O. b) Ta có thể chứng minh định lí này như sau: Giả sử tại thời điểm xét, K trùng với O. Từ Hình 1.16 ta có: Kết hợp với công thức (1.4) ta được: IK = IG + md2 5.3. Định lí về trục vuông góc a) Xét một vật mỏng, phẳng nằm trong mặt phẳng xy như Hình
DẠYKÈMQUYNHƠNOFFICIAL 138
1.17. Ix, Iy và Iz là momen quán tính của vật đối với các trục x, y và z. Định lí về trục vuông góc được diễn tả bằng công thức sau: Iz = Ix + Iy (1.9) b) Thật vậy, từ Hình 1.13 ta có: . II - CÁC PHƯƠNG TRÌNH ĐỘNG LỰC HỌC CỦA CHUYỂN ĐỘNG PHẲNG 2 KG IImd =+ iGiG rrr =+ ( ) ( ) ( ) 22 2 iGiGGiG rrr2rr =++ 222 iiGGiG rdr2rr =++ 222 KiiiiGGiiG Imrmdmr2rmr ==++ 2 GGiiGmdI2rmr=++ ( ) 2222 ziiiiiii Imxymxmy =+=+ xyII=+ Hình 1.16 Hình 1.17
c I.3 ở trên, tác dụng của hệ lực này tương đương với một lực đặt tại khối tâm và một ngẫu lực có momen .
a) Hợp lực của các lực , ,... đặt tại khối tâm được gọi là tổng của các lực , ... và được kí hiệu là . Sở dĩ gọi như vậy là vì tổng các lực chỉ gây ra gia tốc của chuyển động tịnh tiến giống như toàn bộ khối lượng của vật tập trung tại khối tâm. Vì thế, định luật II Niu tơn cho chuyển động tịnh tiến được viết như sau: (1.5a) hay (1.5b) b) Ngẫu lực có momen bằng tổng các momen đối với khối tâm của các lực , ,... Như đã biết, ngẫu lực không làm cho khối tâm chuyển động mà chỉ làm cho vật quay quanh khối tâm với gia tốc góc . Vì thế phương trình động lực học của chuyển động quay (hay còn gọi là định luật II Niu tơn cho chuyển động quay) được viết như sau: (1.6a)
trong đó IG là momen quán tính của vật
DẠYKÈMQUYNHƠNOFFICIAL 139
1. Xét vật rắn là quả cầu m nhỏ gắn đầu thanh nhẹ, dài r Phân tích: t n F F F
+ = . Xét thành phần Ft: Ft = mat = mr → Ftr = mr2 , vì Ftr = Frcos = Fd = M Vậy: M = F.d = mr2 2. Xét trường hợp vật rắn gồm nhiều chất điểm 2 iii ii MM(mr) == = I.γ Lưu ý: Momen lực là đại lượng đại số, dấu của các momen cho biết mômen lực này làm cho vật rắn quay theo chiều nào. 3. Giả sử vật chịu một hệ lực phẳng , ... song song với mặt phẳng cố định O và đặt vào các chất điểm m1, m2,... Theo mụ
đối với khối tâm hay viết dưới dạng đại số: (1.6b) Biết hệ lực tác dụng vào vật, ta xác định được gia tốc của chuyển động tịnh tiến theo khối tâm G và gia tốc của chuyển động quay quanh khối tâm. 1F 2F F' M F' ' 1F ' 2F 1F 2F F F G F =ma xGx yGy F =ma F =ma M 1F 2F (G) GMI= (G)GMI= Ga
Từ (1.5) và (1.6) ta suy ra: Nếu vật rắn không chịu ngoại lực nào tác dụng hoặc các ngoại lực cân bằng nhau thì khối tâm của vật sẽ đứng yên hoặc chuyển động thẳng đều, còn các điểm khác quay đều quanh khối tâm.
Nếu biết thêm điều kiện ban đầu ( ) ta suy ra được và . Biết và ta suy ra được vận tốc của mọi điểm khác của vật theo công thức (1.1).
c) Ta có thể dùng công thức (1.3a) để suy ra công thức (1.5a).
Thật vậy, lấy đạo hàm theo thời gian của , ta được:
Lấy đạo hàm thời gian của , ta được:
Theo định luật II Niu tơn thì là hợp lực tác dụng vào chất điểm mi, còn . Các nội lực là các lực liên kết giữa các chất điểm tạo nên vật. Chúng xuất hiện từng cặp trực đối nhau nên . Cuối cùng ta có: d) Vì chuyển động phẳng tổng quát còn có thể xem là chuyển động quay thuần tuý quanh tâm quay tức thời K, nên ta có thể áp dụng phương trình động lực học cho chuyển động quay quanh K.
(1.7) trong đó IK là momen quán tính của vật đối với trục quay tức thời K. e) Phương trình động lực học của chuyển động quay tương đối Để tìm gia tốc góc của vật trong chuyển động quay tương đối ta áp dụng phương trình: trong đó IA là momen quán tính của vật đối với cực A, lấy đối với cực A, trong đó có momen của lực quán tính . Nếu chọn HQC O' có gốc đặt tại khối tâm, ta được HQC khối tâm. Trong HQC này ta bỏ qua momen của lực quán tính vì l
DẠYKÈMQUYNHƠNOFFICIAL 140
Tóm lại, muốn xác định gia
ố
ủ
ậ
Cách 1: Chọn khối tâm làm cực: G00 , v Gv Gv Gr Gii 1 m m = vv Gv Gii 1 ama m = i
ngo¹i
néi
ngo¹i
G
a
= (K)K
A AMI= AM q AFma =− GGMI=
ực này đặt tại khối tâm. Đó là ưu điểm của HQC khối tâm.
t
c góc c
a v
t ta có thể chọn một trong các cách sau đây:
ii maF =
lùcnéi lùc ii maFF =+
lùc F0 =
lùc
F
m
MI=
Cách 2: Chọn tâm quay tức thời K làm cực: KKMI=
141
DẠYKÈMQUYNHƠNOFFICIAL
PHẦN III. CÁC ĐỊNH LUẬT BẢO TOÀN I - CƠ NĂNG VÀ ĐỊNH LUẬT BẢO TOÀN CƠ NĂNG
1. Thế năng của một vật rắn
Xét một vật chuyển động phẳng song song với một mặt phẳng O thẳng đứng (Hình 1.18). Chọn mốc thế năng tại z = 0. Thế năng của vật bằng tổng thế năng của các chất điểm tạo nên vật:
Theo công thức (1.3b), ta suy ra: (1.13) Thế năng của một vật rắn bằng thế năng của toàn bộ khối lượng của vật tập trung tại khối tâm. 2. Động năng của một vật rắn chuyển động phẳng tổng quát a) Động năng của một vật rắn bằng tổng động năng của các chất điểm tạo nên vật. Wđ = Đạo hàm công thức (1.4) theo thời gian ta được: (1.14) Kết quả là: Wđ = = (1.15)
Như vậy, động năng của một vật rắn gồm động năng của chuyển động tịnh tiến với vận tốc của khối tâm và động năng của chuyển động quay quanh khối tâm. Mặt khác, nếu ta coi chuyển động của vật là chuyển động quay thuần tuý quanh tâm quay tức thời K thì động năng của vật được tính bằng công thức: Wđ (1.16) b) Định lí biến thiên động năng Độ
DẠYKÈMQUYNHƠNOFFICIAL 142
biến thiên động năng của một vật rắn bằng công của các ngoại lực tác dụng lên vật: Wđ = ngoại lực (1.17) 3. Cơ năng. Định luật bảo toàn cơ năng a) Cơ năng của vật W = Wt + Wđ hay b) Điều kiện để cơ năng của vật được bảo toàn là Không có ma sát và lực cản của môi trường. tiiii Wmgzgmz == tGG Wmgzmgh == ( )2 2 iiiGiG 11 mvmvv 22 =+ 22 GiiiGGiiG 11 vmmvvmv 22 =++ iiG mv0 = 22 GiiG 11 22mvm(r) + 22 GG 11 mvI 22 + 2 K 1 I 2 = A 22 GGG 11 WmghmvI 22 =++ 2 GK 1 WmghI 2 =+ Hình 1.18
Nếu có ma sát thì phải là ma sát nghỉ. Khi ấy, cơ năng của vật được bảo toàn. Nó chỉ biến đổi từ thế năng sang động năng và ngược lại. W = Wt + Wđ = const (1.18a) hay Wđ = Wt (1.18b) II ĐỘNG LƯỢNG. ĐỊNH LUẬT BẢO TOÀN ĐỘNG LƯỢNG
1. Động lượng của một vật rắn bằng tổng động lượng của các chất điểm tạo nên vật.
Số hạng là động lượng của chuyển động quay của vật quanh khối tâm. Theo công thức (1.14) thì nên: (1.19) Động lượng của một vật rắn chuyển động phẳng bằng động lượng của chuyển động tịnh tiến của nó với vận tốc của khối tâm.
2. Định lí biến thiên động lượng
Từ , ta suy ra: hay (1.20)
Độ biến thiên động lượng của một vật rắn bằng tổng xung lượng của các ngoại lực tác dụng lên vật.
3. Định luật bảo toàn động lượng
Từ công thức (1.20), ta suy ra, nếu không có ngoại lực tác dụng vào vật rắn hoặc khi tổng các ngoại lực bằng 0 thì động lượng của vật được bảo toàn: Khi ấy, khối tâm của vật chuyển động thẳng đều, còn các điểm khác thì quay đều quanh
DẠYKÈMQUYNHƠNOFFICIAL 143
khố
III MOMEN ĐỘNG LƯỢNG. ĐỊNH LUẬT BẢO TOÀN MOMEN ĐỘNG LƯỢNG 1. Momen động lượng a) Momen động lượng của một chất điểm m đối với một điểm O được xác định bằng biểu thức: (1.21) trong đó , với M là vị trí của chất điểm. iipmv = ( ) iGiGGiiG pmvvmvmv =+=+ iiGmv iiG mv0 = Gpmv = G pm = v G ngo¹ilùc G m p maF tt === v ngo¹ilùc pF.t = == G pmconst. v O Lrmv = rOM =
i tâm.
Về độ lớn ta có: L = dmv trong đó d là khoảng cách từ điểm O đến giá của vectơ
động lượng (Hình 1.19).
b) Momen động lượng của một vật rắn đối với một trục quay cố định như đã biết là: (1.22a) hay (đại số) (1.22b)
2. Định lí Kơ-níc
Xét một vật chuyển động phẳng trong mặt phẳng O.
Theo định nghĩa, momen động lượng đối với trục Oz và đối với trục G (Hình 1.20) lần lượt là: ;
Theocáccôngthức(1.4)và(1.14)thì và ,nêntacó: (1.23)
Công thức (1.23) được gọi là định lí Kơ níc. Nó cho phép tìm momen động lượng đối với một trục bất kì nếu biết momen động lượng đối với trục đi qua khối tâm. 3. Định lí biến thiên momen động lượng Lấy đạo hàm biểu thức (1.21) theo thời gian, ta được: Vì nên: Mở rộng ra cho vật rắn (hệ chất điể
DẠYKÈMQUYNHƠNOFFICIAL 144
m): Vì , nên: hay (1.24) Độ biến thiên momen động lượng của một vật rắn (hay của hệ chất điểm) bằng tổng các momen xung lượng của các ngoại lực. pmv = LI = LI= O ii i Lrmv = G iGiiGLrmv = ( ) ( ) O GiGiGiG Lrrmvv =++ ( ) ( ) OG GiGGiiGiiGG LrmvrmvmrvL =+++ iiG mr0 = iiG mv0 = OG G LLOGm =+ v dLddrdmv rmvmvr dtdtdtdt ==+ ( ) vmvrF=+ ( ) vmv0, = dL M. dt = ngo¹ilùcnéilùc dL MM dt =+ néilùc M0 = ngo¹ilùc dL M dt = ngo¹ilùc L(M.t)= Hình 1.19 Hình 1.20
4. Định luật bảo toàn momen động lượng Từ (1.24) ta suy ra, nếu thì Nếu không có ngoại lực tác dụng hoặc nếu tổng momen xung lượng của các ngoại lực bằng 0 thì momen động lượng của vật rắn (hay của hệ chất điểm) được bảo toàn. PHẦN IV. MA SÁT LĂN LỰC PHÁT ĐỘNG
1. Ví dụ
Ta hãy xét một quả cầu lăn không trượt trên mặt sàn nằm ngang. Thực tế cho thấy, khi không chịu một lực chủ động nào theo phương ngang thì quả cầu lăn không trượt chậm dần rồi dừng lại. Vận tốc của chuyển động tịnh tiến và vận tốc góc của chuyển động quay quanh khối tâm đều giảm dần đến 0 theo đúng hệ thức vG = R.
Ví dụ trên cho thấy, khi một vật lăn không trượt trên mặt sàn, ma sát lăn xuất hiện cản trở cả hai chuyển động thành phần của vật là chuyển động tịnh tiến với vận tốc của khối tâm và chuyển động quay quanh khối tâm.
2. Giải thích
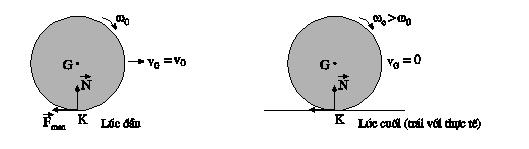
Gv N msnF msnF Gv
a) Ở các phần trước, khi giải các bài toán về chuyển động lăn không trượt, ta đã bỏ qua sự biến dạng của các vật. Còn ở ví dụ trên, nếu ta bỏ qua sự biến dạng này thì sẽ gặp điều nghịch lí. Thật vậy, nếu quả cầu và mặt sàn đều rắn tuyệt đối thì quả cầu chỉ tiếp xúc với mặt sàn ở một điểm. Phản lực và lực ma sát nghỉ đều đặt tại điểm tiếp xúc. Khi ấy, lực dù ngược chiều hay cùng chiều với thì cũng đều dẫn đến kết quả trái với thực tế (Hình 1.24a, b). a)
DẠYKÈMQUYNHƠNOFFICIAL 145
ngo¹ilùc M.t0 = Lconst =
b)
b) Muốn khắc phục điều nghịch lí trên đây thì ta phải từ bỏ khái niệm vật rắn tuyệt đối Thật vậy, ở chỗ tiếp xúc, quả cầu bị dẹt một ít, mặt sàn bị lõm một ít, hình thành một diện tích tiếp xúc. Hơn nữa, trong khi lăn, phần trước của quả cầu ép mạnh vào sàn, còn phần sau do dịch chuyển lên nên ép nhẹ hơn. Do đó điểm đặt của phản lực dịch về phía trước một ít, tạo ra một momen cản chuyển động quay của quả cầu (Hình 1.25). Áp dụng các phương trình động lực học, ta có: (a) (b)
Từ (a) và (b), suy ra: Đối với quả cầu: . Thay vào ta được: (c)
Ta thấy nên giảm cùng với vG theo hệ thức vG = R.
Vậy, ma sát lăn của mặt sàn cản trở chuyển động lăn không trượt bao gồm: Lực ma sát nghỉ giữ cho điểm tiếp xúc không bị trượt và cản trở chuyển động tịnh tiến của vật. Chính lực ma sát nghỉ này bị hiểu sai là lực ma sát lăn. Momen của phản lực đối với khối tâm cản trở chuyển động quay của quả cầu quanh khối tâm (do điểm đặt của phản lực dịch về phía trước một đoạn: KK' = l). Ngườ
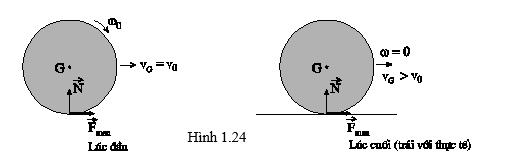
DẠYKÈMQUYNHƠNOFFICIAL 146
i ta gọi là momen ma sát lăn, trong đó KK' = l được gọi là hệ số ma sát lăn. Nó có thứ nguyên của chiều dài. Thí nghiệm cho thấy hệ số l không phụ thuộc vào bán kính của quả cầu hay con lăn và tăng ít khi phản lực tăng. N GmsnMaF =− G msnGG N a FRMII. R −== G msn N 2 I MFR1 MR =+ 2 G 2 IMR 5 = msnNF 7 MM 5 = msnNFMM N N msl MN = l Hình 1.25
Sau đây là một số giá trị của l:
Con lăn bằng gỗ trên gỗ: 0,5 1,5mm.
Bánh xe lửa trên đường ray: 0,5 1mm.
Bánh xe ô tô, xe đạp trên đường nhựa: 10 20mm.
3. Cơ năng và ma sát lăn
a) Lực nào trong hai lực và thực hiện công âm?
msnF N N N N.s N −=− l mslmsl AM.=−
Khi quả cầu lăn không trượt, điểm tiếp xúc K đóng vai trò là tâm quay tức thời. Trong chuyển động quay thuần tuý này, điểm đặt của lực ma sát nghỉ không dịch chuyển trong khi đó thì điểm đặt K' của phản lực dịch chuyển xuống dưới. Do đó, lực ma sát nghỉ không thực hiện công mà chính phản lực mới thực hiện công âm làm giảm cơ năng của quả cầu (Hình 1.26). Amsl = (1.27) trong đó là góc mà vật quay được quanh K (và cũng là góc mà vật quay được quanh G).
b) Trong những trường hơp nào thì bỏ qua ma sát lăn?
Hình 1.26
Khi có mặt của các lực khác tác dụng lên vật, gây ra chuyển động lăn không trượt của vật thì thường thường người ta bỏ qua momen ma sát lăn vì nó quá nhỏ so với momen của các ngoại lực khác. Ví dụ, khi một quả cầu hoặc một xilanh lăn trên một mặt phẳng nghiêng xuống dưới, thì Mmsl = lN nhỏ hơn rất nhiều so với MP của trọng lực. Như thế, trong đa số trường hợp (chứ không phải tất cả), người ta có thể giả thiết rằng quả cầu (hay xilanh) rắn tiếp xúc với mặt sàn rắn tại một điểm và lực ma sát tại đó là lực ma sát nghỉ được tính bằng công thức Fmsn nN.
3. Bánh xe phát động. Phân biệt lực phát động với kéo của đầu tàu.
1. Ta hãy xét sự khởi hành của một đoàn tàu trên một đoạn đường nằm ngang. Để cho đoàn tàu chuyển bánh thì cần phải tác dụng vào đoàn tàu một lực nằm ngang. Các ngoại lực tác dụng lên đoàn tàu chỉ là trọng lực của nó và các phản lực từ phía các đường ray. Chính nhờ các phản lực này mà đoàn tàu chuyển bánh được và các phản lực được sử dụng nhờ vào các bánh xe phát động (Hình 1.27).
DẠYKÈMQUYNHƠNOFFICIAL 147
Hình 1.27 Hình 1.28
Động cơ đốt trong thông qua cơ chế truyền chuyển động để tác dụng vào bánh xe phát động của đầu tàu những lực có xu hướng làm cho bánh xe quay quanh trục của nó. Nhưng do có lực ma sát tại điểm tiếp xúc K với đường ray mà điểm tiếp xúc K được giữ yên, tạo thành tâm quay tức thời để cho tâm O tiến được về phía trước (Hình 1.28). Chuyển động lăn không trượt chỉ xảy ra khi mà phản lực ma sát của đường ray chống lại được sự trượt của bánh xe gây ra bởi chuyển động quay.
Muốn tăng lực ma sát nghỉ này thì ta phải tăng trọng lượng đặt lên các bánh xe phát động. Lực ma sát nghỉ mà đường ray tác dụng lên các bánh xe phát động của đầu tàu hướng về phía trước gọi là lực phát động.
2. Bây giờ ta xét riêng đầu tàu và giả sử rằng tất cả bánh xe đều là bánh xe phát động. Gọi P là trọng lượng của nó, FK là lực kéo của đầu tàu tác dụng vào toa xe thứ nhất. Theo định luật III Niu tơn, đầu tàu chịu một lực cản Fc từ phía toa thứ nhất (Hình 1.28).
Ở giới hạn của cân bằng, lực ma sát nghỉ tác dụng tại điểm tiếp xúc K (tứ
DẠYKÈMQUYNHƠNOFFICIAL 148
c lực phát động) cân bằng với lực cản . Cần nhớ rằng, trong trường hợp này ta bỏ qua momen cản của ma sát lăn vì quá nhỏ so với momen khởi động. Muốn bánh xe không trượt, nói cách khác, muốn có sự khởi
thì phải có: msnF cF cmsn FFP =
hành
Suy ra: FK P ( là hệ số ma sát nghỉ)
Momen phát động cực đại tương ứng: Mpđ = FmsnR = nPR Từ công thức trên, ta suy ra muốn tăng lực kéo cực đại thì phải tăng trọng lượng của đầu tàu và bán kính của các bánh xe phát động. 3. Nếu đầu tàu không kéo các toa mà chạy không tải thì sao? Khi ấy ngoại lực tác dụng vào đầu tàu chỉ là trọng lượng P của nó và phản lực của đường ray. Khi đầu tàu bắt đầu chuyển bánh thì động cơ đốt trong của đầu máy tác dụng vào bánh xe phát động một ngẫu lực có momen phát động lớn đến mức có thể bỏ qua momen ma sát lăn. Khi ấy, mặt đường bị biến dạng làm xuất hiện một phản lực N tại K' và một lực ma sát nghỉ hướng về phía trước. Các định luật động lực học được áp dụng như sau: ; Còn khi đầu tàu chạy đều, thì động cơ đốt trong tác dụng vào bánh xe phát động một ngẫu lực có momen phát động nhỏ, đủ để cân bằng với momen của lực ma sát lăn. Không có lực phát động lẫn lực ma sát lăn. Trong thực tế, sự biến dạng của mặt đường chỉ làm xuất hiện phản lực N tại K' mà thôi. Khi ấy các phương trình động lực học thu về chỉ còn là: Mpđ Mmsl = 0. 4. Xét về phương diện công và năng lượng, thì đầu tàu chạy không tải, động cơ đốt trong thực hiện công để thắng công cản của lực ma sát lăn ở tất cả các bánh xe của đầu tàu. Còn khi kéo các toa thì đầu tàu thực hiện công để thắng công cản của toa thứ nhất. Công của đầu tàu chính là công của lực kéo (A = FKs). Còn công của động cơ bao gồm hai công đó.
msnp® FFma == p®p® a MFRI R ==
DẠYKÈMQUYNHƠNOFFICIAL 149
PHẦN V. CHUYỂN ĐỘNG LIÊN KẾT
Cách giải truyền thống các bài toán cơ học là dùng các công thức động học, động lực học và các định luật bảo toàn. Nhưng có những tình huống trong đó các phương trình không đủ tìm ra nghiệm đơn giá của bài toán. Khi đó cần có những phương trình phụ tính đến các liên kết hoặc các hạn chế đang áp đặt lên chuyển động hệ đang xét. Những hạn chế đó có thể liên quan đến độ cứng của vật, đến tính không dãn của dây, đến chuyển động theo một bề mặt hay sự có mặt các điểm đặc biệt trên quỹ đạo. Biểu diễn các hạn chế đó bằng phương trình cụ thể, mà ta gọi là phương trình liên kết là một nhiệm vụ bắt buộc trong một số bài toán.2
Đối với chất điểm, hệ chất điểm, tuy các liên kết có thể rất đa dạng và phong phú nhưng có thể sử dụng hai phương pháp chính để giải quyết đó là dựa vào liên hệ đường đi hoặc chuyển hệ quy chiếu, ngoài ra cũng có thể sử dụng tính chất của khối tâm hệ vật.
Đối với vật rắn, hệ vật rắn ngoài các phương pháp với chất điểm thì thường phải kết hợp thêm với các kiến thức khác: như chuyển động lăn không trượt, lăn có trượt, định luật bảo toàn và định lí biến thiên mômen động lượng,... nên sẽ tăng thêm tính phức tạp của bài toán.
Bài tập chuyển động liên kết vật rắn có thể chia theo nhiều cách :
- Theo phương trình liên kết (dựa vào liên hệ đường đi, công thức cộng vận tốc do đổi hệ quy chiếu)
Theo dạng liên kết (liên kết bằng dây không dãn, dây dãn, thanh cứng, …) ;
Theo mặt tiếp xúc (vật tròn lăn trên mặt phẳng, vật tròn lăn trên mặt tròn,…);
Theo dạng chuyển động (chuyển động lăn không trượt, lăn có trượt) ;
Theo cách giải quyết với điểm đặc biệt (khối tâm, tâm quay tức thời).
I. DỰA VÀO LIÊN HỆ ĐƯỜNG ĐI
Trong một khoảng thời gian nhỏ, một vật dịch chuyển một đoạn nhỏ nào đó, thì các vật liên kết dịch chuyển các đoạn tương ứng. Từ mối liên hệ hình học giữa chúng, có thể suy ra liên hệ các thông số chuyển động.
Khi có dịch chuyển nhỏ trong khoảng thời gian Ät rất nhỏ thì theo định nghĩa:
DẠYKÈMQUYNHƠNOFFICIAL
150
Vận tốc: 0 lim t rdxdydz vijk tdtdtdt → ==++ 2 Tạp chí Vật lý tuổi trẻ số 161
Trong hệ tọa độ cong (tọa độ địa phương) : ds v dt = , trong đó là vectơ đơn vị tiếp tuyến, s là hoành độ cong tính từ một điểm gốc đã chọn. - Vận tốc góc: d dt = Gia tốc: 222 222 0 lim y x z t
dv dv vdvdxdydz aijkijk tdtdtdt dtdtdt →
==++=++







Hai thành phần gia tốc của chuyển động cong, phẳng: + Gia tốc tiếp tuyến: t dv a dt =
+ Gia tốc pháp tuyến: 2 n v an R = , với n là véc tơ đơn vị pháp tuyến, nó hướng về phía lõm của quỹ đạo. Gia tốc: 22 tnaaa =+ Nếu theo một phương Oz nào đó vận tốc không đổi thì gia tốc theo phương ấy bằng không và gia tốc có phương vuông góc với phương Oz.
Một số liên kết điển hình thường xuất hiện trong bài tập:
Các vật có bề mặt tiếp xúc với nhau: thì dịch chuyển theo phương vuông góc với mặt tiếp xúc bằng nhau.
Các vật nối nhau bởi sợi dây có chiều dài không đổi: Sử dụng phương pháp chiều dài sợi dây không đổi. Từ liên hệ toạ độ của các vật với chiều dài của dây trong quá trình chuyển động rồi đạo hàm hai vế theo thời gian sẽ tìm được liên hệ gia tốc các vật. - Các vật nối nhau bởi sợi dây có chiều dài thay đổi. Đoạn dây thay đổi quấn trên một trục hình trụ: dây có phương tiếp tuyến với mặt trụ và hình chiếu của vận tốc của điểm nằm trên mặt trụ tại tiếp điểm lên phương của dây bằng vận tốc kéo ở đầu dây tự do. - Các vật liên kết bởi thanh cứng nối qua các bản lề hoặc các vật rắn chuyển động. Trong trường hợp này ta sử dụng một số tính chất chuyển động song phẳng của vật rắn như: + Hình chiếu vận tốc của hai điểm trên vật rắn lên đường thẳng nối hai điểm ấy phải có cùng độ lớn.
DẠYKÈMQUYNHƠNOFFICIAL 151
v
v
B
A
B A
I
vAcos = vBcos
+ Tại mỗi thời điểm có thể coi vật rắn đang quay quanh một trục (tâm) quay tức thời. Vị trí trục này có thể xác định được nếu biết phương vận tốc của hai điểm. + Chuyển động lăn không trượt trên mặt phẳng hay trên dây: vận tốc của điểm trên vật tại chỗ tiếp xúc bằng không, có thể coi toàn vật đang quay quanh điểm tiếp xúc, ta có các liên hệ sau của vận tốc và gia tốc của tâm (trục) với vận tốc góc và gia tốc góc của chuyển động quay quanh tâm: v = R., a = R.
II. CHUYỂN HỆ QUY CHIẾU CÔNG THỨC CỘNG VẬN TỐC
Việc thay đổi hệ quy chiếu làm cho chuyển động của các vật trong hệ mới đơn giản và dễ khảo sát hơn. Trong trường hợp này ta thường phải sử dụng quy tắc cộng vận tốc và công thức biến đổi gia tốc. Cần nhắc lại rằng: Chuyển động có tính tương đối.
Theo định nghĩa: tập hợp cứng các điểm cố định đối với một người quan sát kết hợp với một đồng hồ là HQC của người quan sát đó.
Tồn tại vô số hệ tọa độ gắn vào một HQC cho trước, mặc dù chỉ cần một hệ tọa độ không gian gắn vào người quan sát là đủ để đặc trưng cho HQC. Quỹ đạo chỉ được xác định đối với một HQC xác định. Giả sử XOY là một HQC đứng yên, gọi đơn giản là HQC (O) , còn X’O’Y’ là một HQC vừa chuyển động tịnh tiến vừa quay đối với HQC đứng yên, gọi là HQC (O’). M là chất điểm chuyển động, vận tốc của M đối với HQC (O) gọi là vận tốc tuyệt đối, ký hiệu là Ov , còn vận tốc của M đối với HQC (O’) là vận tốc tương đối, ký hiệu là O'v . Ta cần thiết lập liên hệ giữa hai vận tốc nói trên. Trong phầ
DẠYKÈMQUYNHƠNOFFICIAL 152
ển động O’. Các đạ
được
ạ
Các vectơ vị trí của M trong hai HQC là rOMxiyj ==+ và r'O'Mx'.i'y'j' ==+
n này, dấu “ ’ “ không có nghĩa là đạo hàm mà là để chỉ các đại lượng trong HQC chuy
o hàm theo thời gian đều
viết dưới d
ng: d dt .
Theo định nghĩa: O d(OM)drddxdy v(x.iy.j)ij dtdtdtdtdt ===+=+ (lưu ý di 0 dt = và dj0 dt = ) Tương tự đối với người quan sát đứng yên trong HQC (O’) thì cũng phải có: O' d(O'M)dx'dy' vi'j' dtdtdt ==+ (vì đối với người này thì i' và j' là không đổi) Đối với quan sát đứng yên trong HQC (O) thì: d(O'M)dr'd (x'.i'y'.j') dtdtdt ==+ dx'di'dy'dj' i'x'j'y' dtdtdtdt =+++ với lưu ý là: di'i' dt =
DẠYKÈMQUYNHƠNOFFICIAL 153
dtdt +++ = dx'dy'i'j'r') dtdt ++ Ta có ở mọi thời điểm: rOMOO'O'M ==+ nên: O d(OM)d(OO')d(O'M) v dtdtdt ==+ = dx'dy'd(OO')i'j'r') dtdtdt +++ Số hạng O' dx'dy' vi'j' dtdt =+ chính là vận tốc tương đối của M trong (O’), tức là vận tốc mà người quan sát đứng yên trong HQC (O’) nhìn thấy M chuyển động đối với anh ta. Còn tổng của 2 số hạng d(OO')r') dt + được gọi là vận tốc kéo theo. Nó gồm 2 thành phần: + Thành phần d(OO') dt là vận tốc tịnh tiến của HQC (O’) đối với HQC (O). + Thành phần r') là vận tốc quay của HQC (O’) đối với HQC (O). Như vậy:
và dj'j' dt = Thành thử: O' dx'dy' vi'j'x'i'y'j' dtdt =+++ = dx'dy'i'j'(x'i'y'j')
OO' vvv =+ kéo theo tức là ta có công thức tổng quát sau: v tuyệt đối = v tương đối + v kéo theo (1) Các trường hợp đặc biệt:
1) Nếu O’ chỉ chuyển động tịnh tiến (thẳng hoặc cong), thì vận tốc kéo theo chỉ còn thành phần d(OO') dt , như vậy (1) có dạng đơn giản: v tuyệt đối = v tương đối + d(OO') dt hay là 131223 vvv =+ Đây chính là công thức cộng vận tốc trong chương trình vật lý 10, trong đó chỉ mới có thành phần chuyển động tịnh tiến d(OO') dt , chưa có thành phần quay. Có phải lúc nào cũng có 1221vv =− ? 2) Nếu O’ chỉ quay quanh O, tức là OO'const = thì:
= r')
Ta nhận thấy v kéo theo phụ thuộc vào r' nghiã là phụ thuộc vào vị trí của M trong (O’). Công thức tổng quát (1) thường được viết lại là: v
tương đối = v
tuyệt đối + ( v
B. BÀI TẬP CHUYỂN ĐỘNG LIÊN KẾT CỦA CHẤT ĐIỂM
Chuyên đề tập trung vào phần kiến thức chuyển động liên kết của vật rắn, tuy nhiên tôi sẽ dành mục B để trình bày về chuyển động liên kết của chất điểm. Mục đích để học sinh có thể làm quen với các phương trình liên kết, sau đó có thể vận dụng vào với vật rắn, hệ vật rắn phức tạp.
I. DỰA VÀO LIÊN HỆ ĐƯỜNG ĐI
Bài 1: Điểm sáng S cách màn một khoảng L. Một vật chắn sang AB có chiều cao là h chuyển động với vận tốc v0 từ điểm sáng S về phía màn. Hỏi ở thời điểm t thì bóng của đầu B của vật ở trên màn dịch chuyển với vận tốc tức thời là bao nhiêu?
DẠYKÈMQUYNHƠNOFFICIAL 154
v kéo theo
kéo theo ) (2)


DẠYKÈMQUYNHƠNOFFICIAL 155 Lời giải: Tại thời điểm t vật AB cách S là SA = v.t. Trong khoảng thời gian rất nhỏ Ät bóng của B dịch chuyển trên màn: Δs = CC1 = HC HC1 = = LLhLthh v.tv.(tt)v.t.(tt) −= ++ Vậy: 2 t0 o vlimshL tvt → == Bài 2: Một thanh cứng có thể quay trong mặt phẳng thẳng đứng quanh một bản lề ở một đầu của thanh. Thanh tựa lên một hình lập phương có cạnh là a. Cho hình lập phương
chuyển động trên mặt phẳng ngang, ra xa bản lề với vận tốc không đổi là v. Tìm vận tốc góc của thanh khi nó hợp với phương ngang một góc là á.

thanh quay
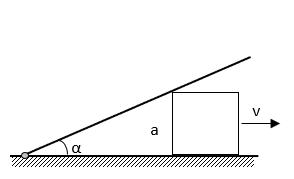
DẠYKÈMQUYNHƠNOFFICIAL 156
giải:
1 AAOA sinsin() = − Do Äá là góc rất nhỏ nên sinΔα ≈Δα. Thay OA = a sin ta được: v.ta sin.sin() = − Vậy 2 t0 limv.sin ta → == Bài 3: Trên mặt đất nằm ngang có một ngọn đèn chiếu sáng một bức tường thẳng đứng. Khoảng cách từ đèn đến bức tường là L. Từ chân tường có một hòn đá nhỏ ném về phía đèn. Quỹ đạo của hòn đá nằm trong mặt phẳng vuông góc với tường và hòn đá rơi sát cạnh đèn. a. Tìm vận tốc ban đầu nhỏ nhất của hòn đá.
Lời
Trong khoảng thời gian rất nhỏ Δt hình lập phương dịch chuyển AA1 = v.Δt còn
góc Δα. ¸ p dụng định lý hàm số sin trong ΔOAA1 ta có
b. Tìm vận tốc dịch chuyển của bóng hòn đá trên tường. Xem là tường đủ rộng. Lời giải a. Từ công thức tầm xa: suy ra vận tốc ban đầu v0 có giá trị nhỏ nhất khi = 450 . Vậy b. Tọa độ của bóng hòn đá trên tường là y1 Vì: . Trong trường hợp α = 450 và thì có: y = x.tanα = Do đó: v1 = v0cosα = . Trong trường hợp tổng quát: x = (v0cosα)t y = (v0sinα)t gt2/2 Do đó:
2 0 vsin(2) L g = 0 vgL = 1 1 yLL yy yLxLx == 0 vgL = 2 22 0
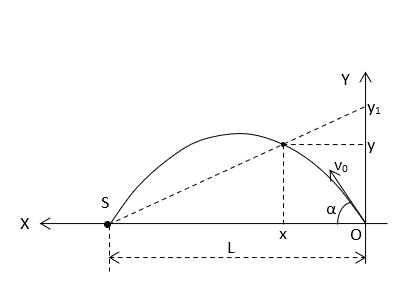
g.x 2.vcos Lx x L 10 yxvcos.t == gL 2 2 10 0
gtLy(vsin.t).2Lvcos.t =− −
DẠYKÈMQUYNHƠNOFFICIAL 157
Vận tốc cần tìm: v1 =
Với trường hợp riêng α = 450 và ta lại thu được kết quả v1 = .
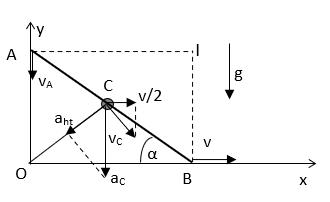

Bài 4: Một thanh cứng nhẹ AB chiều dài 2L trượt dọc theo hai thanh định hướng vuông góc với nhau nằm trong mặt phẳng thẳng đứng: B trượt theo thanh Ox nằm ngang, A theo thanh Oy thẳng đứng. ở trung điểm C của thanh có gắn một vật nhỏ khối lượng m. Đầu B của thanh chuyển động với vận tốc không đổi v từ O. Khi thanh hợp với Ox một góc α, hãy tìm:
a. Tìm phương trình chuyển động của đầu A? b. Tìm vận tốc và gia tốc của m? c. Tìm vận tốc góc của thanh. d. Xác định lực tác dụng của thanh lên vật.
Lời giải
a. Phương trình chuyển động của đầu A là
DẠYKÈMQUYNHƠNOFFICIAL 158
=
00
−+ −
gL
' 1y
2
2 0 L(vsingt)gvcos.t/2L (Lvcos.t)
0 vgL =
2
y = b. Điểm C chuyển động tròn quanh O. Vectơ vận tốc của C vuông góc với OC và hợp với phương ngang một góc 900 α, có hình chiếu lên phương Ox là v/2. vC.cos(900 α) = v/2 → vC = v/(2.sinα) Gia tốc của m hướng theo phương thẳng đứng xuống dưới, có hình chiếu lên phương bán kính là thành phần gia tốc hướng tâm: aht = aC.sinα = Vậy aC = c. ở mỗi thời điểm toàn thanh như một vật rắn đang quay quanh I với vận tốc góc . Như vậy vận tốc của B là vB = v = .RB = .2L.sinα → = v/(2L.siná). d. Gia tốc của vật m là aC hướng theo phương thẳng đứng từ trên xuống và m chịu 2 lực tác dụng: trọng lực P hướng theo phương thẳng đứng và lực N cần tìm (lực tác dụng từ thanh lên vật). Như vậy N cũng hướng phương thẳng đứng. Định luật II Newton cho ta: P N = m.aC. Vậy: N = m
Bài 5: Lõi cuộn chỉ có bán kính trong là r, bán kính ngoài là R. Một sợi chỉ quấn vào lõi trong và vắt qua một cái đinh đóng trên tường. Đầu sợi chỉ được kéo với vận tốc không đổi là v (hình 24). Tìm vận tốc v0 của tâm lõi ở thời điểm khi sợi chỉ hợp với phương thẳng đứng một góc á. Biết rằng lõi cuộn chỉ lăn không trượt trên mặt phẳng ngang. Lời giải

DẠYKÈMQUYNHƠNOFFICIAL 159
2222
x.tgv.t.tg(2L)x(2L)(v.t) ==−=− 2 Cv L 2 3 v 4Lsin 2 3 v g4Lsin
Điểm tiếp xúc B giữa dây và lõi tham gia vào hai chuyển động: tịnh tiến với vận tốc v0 của trục và quay quanh trục với vận tốc góc . Tổng đại số các hình chiếu của các vận tốc trên lên phương của dây phải bằng vận tốc v kéo dây: v = v0sinα .r
Do có sự lăn không trượt nên: v0 .R = 0. Vậy:

Bài 6: Một đĩa nặng bán kính R có 2 dây không dãn quấn vào. Các đầu tự do của dây gắn chặt (hình 22). Khi khối đĩa chuyển động thì dây luôn căng. ở một thời điểm vận tốc góc của đĩa bằng và góc giữa các dây là . Tìm vận tốc của tâm đĩa ở thời điểm này. Lời giải
Gọi v0 là vận tốc của tâm O của đĩa. Tại các điểm tiếp xúc C và D của dây và đĩa vận tốc là: trong đó vD0 và vC0 là các vận tốc của C và D trong chuyển động quay quanh O: vC0 = vD0 = R
Do dây không giãn nên hình chiếu của và lên phương của các dây tương ứng phải bằng không. Chọn hệ quy chiếu gắn với tâm O của đĩa và hai trục song song với hai dây, như vậy góc giữa hai trục này bằng . Chiếu và cho bởi hệ các phương trình (1) lên hai trục ta được:
DẠYKÈMQUYNHƠNOFFICIAL 160
vCx = v0x R = 0 vDy = v0y R = 0 Có nghĩa là hướng
v = 0 R vv
= − C0C0 D0D0 vvv vvv =+ =+ Cv Dv Cv D
0v cos(/2) R
theo phân giác của góc giữa hai dây, và có độ lớn là:
Rsinr
v
Bài 7: Cho hệ như hình vẽ. Các dây nhẹ không giãn và thẳng đứng. Các ròng rọc có khối lượng rất nhỏ. Bỏ qua ma sát. Tìm gia tốc của ròng rọc A khi kéo nó thẳng đứng lên trên bởi lực F đặt vào trục ròng rọc.
Lời giải
Do ròng rọc không có khối lượng nên lực căng dây là T liên hệ với F theo hệ thức F = 2T. Còn liên hệ đường đi của các vật với ròng rọc:
x2 = 2.xA + 2x1. Suy ra mối liên hệ gia tốc: a2 = 2.aA + 2a1.
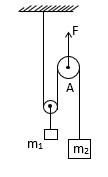
Phương trình định luật II Newton cho từng vật:
m1a1 = 2T P1 = F m1g
m2a2 = P2 T = m2g F/2
3m4m 24mmgF +
12 12
Giải hệ các phương trình cho ta gia tốc ròng rọc A là: aA = Bài 8: Cho hệ như hình vẽ. Các ròng rọc là lý tưởng, bán kính của chúng được chọn sao cho các đoạn dây thẳng đứng (tức là những đoạn dây không chạm ròng rọc). Tìm gia tốc các vật và nút A xoắn trên dây.
DẠYKÈMQUYNHƠNOFFICIAL 161
Lời giải
Do các ròng rọc không khối lượng nên ta có: TA = TB = T; TC = TD; TD = TA = T. Tổng hợp lực tác dụng lên ròng rọc nhỏ nhất: TA + TB TC = T + T T = 0 → T = 0. Vậy các vật đều có gia tốc g vì lực tác dụng lên mỗi vật bằng chính trọng lực. Tổng chiều dài của các đoạn dây thẳng liên quan đến tọa độ x1, x2 và x3 (xem hình vẽ):
L = (x1 0) + (x3 0) + (x3 x1) + (x2 x1) = 2x3 + x2 x1 → 2a3 + a2 a1 = 0
Mà a2 = a3 = g → a1 = 3g. Mặt khác a1 = với aB = g, do đó aA = 5g.

II. CHUYỂN HỆ QUY CHIẾU CÔNG THỨC CỘNG VẬN TỐC
Bài 1: Một tấm gỗ dán mỏng phẳng rơi trong không gian. ở một thời điểm nào đó vận tốc của 2 điểm A và B trên tấm gỗ là và nằm trong mặt phẳng của tấm. Điểm C (tam giác ABC đều: AB = AC = BC = a) có vận tốc 2v. Hỏi những điểm trên tấm gỗ có vận tốc là 3v nằm ở cách đường thẳng AB là bao nhiêu? Lời giải Trong hệ quy chiếu (HQC) chuyển động với vận tốc thì A và B đứng yên còn C
DẠYKÈMQUYNHƠNOFFICIAL 162
. Vậy: .
= =
= =
v
= =
222 3 Cqq vvvvv =+=
quay quanh AB. Như vậy trong HQC gắn với đất: , trong đó là vận tốc C quay quanh AB. Vì và nằm trong mặt phẳng của tấm nên vuông góc với
AB 1(aa)2 + v v v B A
v v v B A
Cq vvv =+ q v
v v B A
q v v
Vận tốc góc của chuyển động quay
Những điểm có vận tốc 3v nằm trên hai đường thẳng song song với AB và cách AB là L, quay quanh AB với vận tốc , trong đó tìm từ phương trình: Như vậy → Bài 2: Trên mặt phẳng ngang nhẵn có hai khối lập phương cạnh H, cùng khối lượng M đặt cạnh nhau (giữa chúng có khe hở nhỏ). Đặt nhẹ nhàng một quả cầu có bán kính R, khối lượng m = M lên trên vào khe nhỏ. Bỏ qua mọi ma sát và vận tốc ban đầu của quả cầu. Tìm vận tốc quả cầu ngay trước khi va đập xuống mặt phẳng ngang. Lời giải
Xét thời điểm quả cầu rơi xuống khối lập phương, ta cần xác định góc á. Liên hệ vận tốc: v1cosá = v

DẠYKÈMQUYNHƠNOFFICIAL 163
2siná → Bảo toàn năng lượng: Để tìm góc á ở thời điểm rời nhau, có thể dùng 2 cách: Cách 1: Tìm v2 rồi xác định cực đại v2. 3 ;2 q v Ra R == ' q vL = ' q v 22'2 (3)() q vvv =+ ' 22 q vvL == L2a = 1 2 v tg v = ( ) 22 12 11 mv2mvmgR1cos22 +=− ( ) 2 1 2 1 v122gR1cos tg +=− ( ) 2 2 1 2 2gR1costg v 2tg − →= +
Lấy đạo hàm theo cosá vµ cho ®ạo hàm bằng 0 ta nhận được phương trình:
Cách 2: Trong HQC chuyển động với vận tốc v2 thì quả cầu chuyển động tròn quanh điểm tiếp xúc, tại thời điểm rời nhau thì HQC trên trở thành HQC quán tính, lúc này thành phần trọng lực đóng vai trò lực hướng tâm: (*)
Thay v1 bằng biểu thức ở trên vào, được phương trình:
Thay vào (*): Còn quả cầu cách mặt đất: * Biện luận: - Nếu thì quả cầu chạm đất trước khi rời các hình lập phương, lúc chạm đất thì
DẠYKÈMQUYNHƠNOFFICIAL 164
góc ö thỏa mãn
Vận tốc ngay
chạm đất xác định theo định luật bảo toàn năng lượng và liên hệ vận tốc. ( ) ( ) 2 2 2 1 2 222 v2gR1cos1coscosv2gRtg2tg1cos −− →=== ++ 3 cos3cos20 +−= 2 mv Rmgcos= 2 11 2 vmv vmgcos sinRsin =→= ( ) 2 22 1 2 2gR1costg vgRcos.sin 2tg − == + 3 cos3cos20cos0,596 +−=→= ( ) 222 1 vgRcos.singRcos1cos ==− ( ) hHR1cos=−− ( ) HR1cos0,404R − ( ) H HR1cos1cos R =−→−= ( ) 22 2 1 2 1cos1cos v2gR1cos2gR1cos1cos ++ =−= + − ( ) 22 1 2 2RH2RH v2g2RHH +− →=
.
trước
- Nếu thì sau khi rơi, quả cầu chuyển động rơi tự do:
Bài 3: Trên mặt phẳng thẳng đứng P có vẽ một vòng tròn C bán kính R tiếp xúc với mặt phẳng ngang. Một chiếc vòng M có bán kính R lăn không trượt trên mặt phẳng ngang tiến về phía vòng tròn C (hình 3). Vận tốc của tâm O1 của vòng M là v. Mặt phẳng của M nằm sát mặt phẳng P. Gọi A là một giao điểm của hai vòng tròn khi khoảng cách giữa tâm của chúng là d < 2R.
Tìm: a. Vận tốc và gia tốc của A. b. Bán kính quỹ đạo và vận tốc của điểm nằm trên vòng M tại A. Lời giải a. Giao điểm A dịch chuyển trên đường tròn C với vận tốc vA tiếp tuyến với C, hình chiếu lên phương ngang là vx = v/2 = vAcosá = vA .


DẠYKÈMQUYNHƠNOFFICIAL 165
)
− 2 f1 R vv2gH2gH10,212H =+=− 22 Rd/4 R A 2 2 v v 21d 4R =
Vậy: . (
HR1cos0,404R
Vì thành phần vận tốc của theo phương ngang không đổi nên gia tốc của A hướng thẳng đứng và thành phần của gia tốc này lên phương bán kính O2A là gia tốc hướng tâm: → a = b) Trong khoảng thời gian rất ngắn quỹ đạo cong của điểm A1 (tại A) trên vòng có thể coi là một cung tròn. Vòng lăn không trượt nên có thể xem như nó đang quay quanh điểm tiếp xúc với vận tốc góc = v/R.
Ta có: IA1 = 2R.cos, với = á/2 → cos = Do đó v1 = .IA1 = v .

Gia tốc của A1 hướng về tâm O1 và có độ lớn là a1 = v2/R.
Gia tốc hướng tâm của A1 lại là: aht1 = a1.cos =
Vậy: R1 = 2R
Bài 4: Hai người đi xe đạp với cùng vận tốc dài v theo các đường tròn bán kính R1 và R2, tâm của các đường tròn là O1 và O2 cách nhau một khoảng là L < R1 + R2, một người đi theo chiều kim đồng hồ, người kia đi ngược chiều kim đồng hồ. Tìm các vận tốc tương đối của mỗi người (trong hệ quy chiếu gắn với người còn lại ) ở thời điểm khi cả hai cùng nằm trên đường thẳng nối tâm tại các điểm (hình 21):
DẠYKÈMQUYNHƠNOFFICIAL 166
a. A1 và A2? b. A1 và B2? Av 2 A ht v aa.cos R == 222 A 3223/2 vvv Rcos4.R.cos4R(1d/4R) == − 2 2 1d 11 2 4R +− 2 2 d 211 4R +− 2 1 1 v R 2 2 d 211 4R +−
Lời giải:

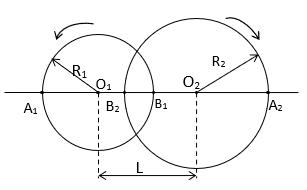
Trong bài, v là vận tốc tuyệt đối. Cần tìm vận tốc tương đối của hai người này. Vận tốc tương đối của người thứ hai là vận tốc đối với hệ quy chiếu gắn với người thứ nhất. Trong hệ quy chiếu này thì người thứ nhất đứng yên. Chọn một hệ quy chiếu có gốc trùng tâm O1, quay với vận tốc góc = v/R1. Vận tốc kéo theo của người thứ hai ở các điểm A2 và B2 là bằng:
Cả hai vận tốc này cùng vuông góc với đường thẳng O1O2 và cùng hướng lên trên. Vận tốc tuyệt đối liên hệ với vận tốc tương đối và vận tốc kéo theo bằng hệ thức vectơ: tuyệt
DẠYKÈMQUYNHƠNOFFICIAL 167 c. B1 và B2? d. B1 và A2?
đối = tương đối + kéo theo → tương đối = tuyệt đối kéo theo 1) Đến đây dễ dàng tìm được vận tốc tương đối của người thứ hai đối với người thứ nhất: k A122 1 2 v vOA(LR) R ==+ k B122 1 2 v vOB(LR) R ==− v v v v v v
-
v
a) và d) Khi người thứ hai ở điểm A2: vận tốc tuyệt đối v2 và có cùng phương chiều (cùng hướng xuống dưới)
vtương đối A2 = v + = v + = hướng xuống dưới.

RRL v R ++
b) và c) Khi người thứ hai ở điểm B2: vận tốc tuyệt đối v2 hướng lên, còn vận tốc hướng xuống dưới:
vtương đối B2 = v = v = hướng lên trên.
k B v 2 2 1 Rv(LR) 12 1
2) Hoàn toàn tương tự có thể tìm được vận tốc tương đối của người thứ nhất đối với người thứ hai:
RRL v R +− 2
v R v
Hệ quy chiếu trong trường hợp này quay quanh O2 với vận tốc góc là ’ = . Các vận tốc kéo theo ( kéo theo) tại các điểm A1 và B1 hướng lên trên, tức là kéo theo hưóng xuống dưới, còn vận tốc tuyệt đối của người thứ nhất tại A1 hướng xuống dưới, tại B1 hướng lên trên (người thứ nhất chuyển động ngược chiều kim đồng hồ). Như vậy:
a) và b) Khi người thứ nhất ở A1: vtương đối A1 = hướng xuống dưới
v 12 2 RRL v R ++ 12 2 RRL v R +−
DẠYKÈMQUYNHƠNOFFICIAL 168
k A
2
c) và d) Khi người thứ nhất ở B1: vtương đối B1 = hướng lên trên. 3) Có thể mở rộng bài toán cho các vị trí khác của hai người. Chẳng hạn tính vận tốc của người thứ nhất đối với người thứ hai khi người thứ nhất ở điểm C như hình vẽ dưới đây. k B v 2
k A v 2 2 1 Rv(LR) + 12 1
Trong trường hợp này vận tốc kéo theo tại C có độ lớn là
vk = ’
và hướng vuông góc với CO2 Ta tính được vận tốc tương đối theo dịnh lý hàm số cosin: vtương đối =
III. BÀI TẬP LUYỆN TẬP
Bài 1: Trục của băng máy cat xet quay trong thời gian t, với vận tốc kéo là v. Bán kính đầu của cuộn băng là R, bán kính cuối (khi hết băng) là r. Tính chiều dày của sợi băng? Đáp số:
Bài 2: Hai thanh cứng chiều dài l1 và l2 nối với nhau qua bản lề A ở một đầu, còn đầu kia chuyển động rời xa nhau với vận tốc v1 và v2 hướng dọc theo một đường thẳng (hình 16). Tìm gia tốc của A ở thời điểm khi góc giữa hai thanh lµ á = 900. Chuyển động của các thanh xảy ra trong một mặt phẳng.
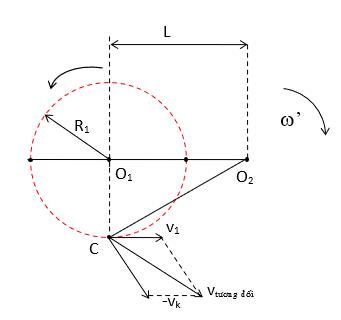
DẠYKÈMQUYNHƠNOFFICIAL 169
2222 11 2 v RLRL R +=+ 22 1 22 RL v1 RR −+ 22dRr v.t =
Đáp số: a =
Bài 3: Cho hệ như hình 17. Biết góc , các khối lượng m1 và m2. Ròng rọc lý tưởng. Bỏ qua mọi ma sát. Tìm gia tốc mỗi vật?
Đáp số: ; a1 = 2a2sin



Bài 4: Ròng rọc gắn trên vật khối lập phương khối lượng m1 có thể trượt tự do trên mặt phẳng ngang. Khi kéo quả cầu ra khỏi phương thẳng đứng góc rồi thả ra thì hệ chuyển động, góc giữa dây với phương thẳng đứng không đổi (hình 18). Tìm gia tốc của khối lập phương và khối lượng của quả cầu?
số:
= g.tgá;
DẠYKÈMQUYNHƠNOFFICIAL 170
Đáp
a
m = 2 66 12 12 22 1212 (vv)ll (ll)ll + + + 1 2 21 amgsin m2.m(1cos) = +− 2 0 2 msin (1sin) −
Bài 5: Cho hệ sau: tấm ván phẳng khối lượng M đặt trên mặt phẳng ngang nhẵn. Hai vật M và 5M đặt trên tấm ván nối với nhau bởi dây vắt qua ròng rọc nhẹ (hình 19). Kéo trục ròng rọc bởi một lực không đổi F hướng theo phương ngang. Hệ số ma sát giữa các vật M và 5M với tấm ván là . Tìm gia tốc a của ròng rọc.
Đáp số: Khi F ≤ 2,8Mg thì a = F/(7M)


Khi 2,8Mg < F < 70Mg thì a =
Khi F ≥ 70Mg thì a =
Bài 6: Một người chạy từ điểm O dọc theo trục Ox với vận tốc không đổi là v1. Con chó của người này lúc đầu (t = 0) ở điểm A, cách O một khoảng là L (OA Ox) bắt đầu chạy với vận tốc không đổi là v2 luôn hướng về phía chủ.
a. Tìm gia tốc của con chó ở t = 0
b. Sau bao lâu con chó đuổi kịp chủ nếu v2 > v1.
c. Giả sử v2 = v1 = v.
+) Tìm khoảng cách giữa con chó và chủ sau thời gian dài.
+) Tìm phương trình quỹ đạo của con chó.
Bài 7: Một hạt cườm khối lượng m được xỏ qua một sợi dây nhẹ, không giãn chiều dài L. Một đầu dây buộc cố định tại điểm A, đầu kia buộc vào một cái vòng rất nhẹ, vòng lại có thể trượt không ma sát trên một thanh ngang (hình 10). ở thời điểm ban đầu, dây được giữ ở cạnh vòng và dây thẳng, không căng. Thả cho hạt cườm chuyển động. Tìm vận tốc của nó ở thời điểm dây bị đứt biết rằng dây chịu sức căng lớn nhất là T0. Khoảng cách từ A đến thanh là h. Bỏ qua mọi ma sát. Bài 8: Ba học sinh: A, B và C đứng trên hai mâm quay với cùng vận tốc góc ù theo chiều kim đồng hồ: A và B trên mâm quay có bán kính là r còn C trên mâm quay bán kính R. Hai mâm quay ở sát cạnh nhau. Tại thời điểm ban đầu vị trí các học sinh như hình 26. Hãy xác định tính chất chuyển động: của C theo quan điểm của B; của A theo quan điểm của C.
DẠYKÈMQUYNHƠNOFFICIAL 171
75 2412 Fg M 3 10 − F g M
⊥
Đáp số
+ B thấy C chuyển động tịnh tiến theo đường tròn tâm O bán kính R + r, trong đó O lại chuyển động trên đường tròn bán kính R có tâm trùng với tâm của mâm quay mà B đứng. + C thấy A chuyển động trên đường tròn tâm O’ bán kính R + r, trong đó O lại chuyển động trên đường tròn bán kính r có tâm trùng với tâm của mâm quay mà C đứng. Bài 9: (Dao động chất điểm – Sử dụng liên hệ đường đi) Bỏ qua khối lượng của ròng rọc, lò xo. Chứng minh vật dao động điều hòa và lập biểu thức tính chu kì dao động trong các trường hợp sau
TH1: Đơn lò xo 2 m T k = TH2: Lò xo song song
k = k1 + k2 + ….. 2 m T k = TH3: Lò xo nối tiếp




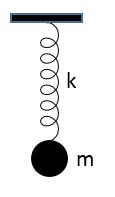

111 ... kkk =++ 2 m T k =
12
DẠYKÈMQUYNHƠNOFFICIAL 172
TH3’:

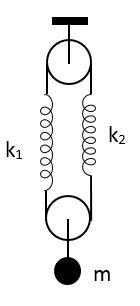

173
DẠYKÈMQUYNHƠNOFFICIAL
Lò xo mắc hỗn hợp k1 nt (k2 // k3) TH4 12 12 (). 2 4 kkm T kk + = TH5 2 9 m T k =
TH6 2 4 m T k =
TH7 21 2 4 m T kk = +
TH8 12 12
4() 2 mkk T kk + =

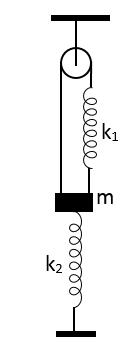

174
DẠYKÈMQUYNHƠNOFFICIAL
TH9 12 12
(4). 2 kkm T kk + =

TH10 2 5 m T k =
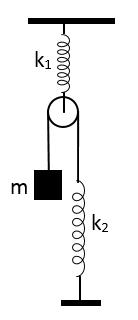
175
DẠYKÈMQUYNHƠNOFFICIAL
C. BÀI TẬP CHUYỂN ĐỘNG VẬT RẮN LIÊN KẾT






PHẦN I. BÀI TẬP VÍ DỤ I. DỰA VÀO LIÊN HỆ ĐƯỜNG ĐI
Bài 1: Một thanh cứng không khối lượng, có chiều dài l quay được tự do trong mặt phẳng hình vẽ nhờ trục quay tại A, đầu trên gắn quả cầu nhỏ khối lượng m. Ban đầu thanh có phương thẳng đứng, quả cầu tiếp xúc với mặt bên hoàn toàn nhẵn của một nêm gỗ có khối lượng M, nêm có thể chuyển động không ma sát trên mặt phẳng nằm ngang. Đẩy nhẹ để hệ bắt đầu chuyển động, tính tỉ số M/m biết rằng m bắt đầu rời khỏi nêm khi góc giữa thanh và mặt phẳng ngang bằng 300 . Lời giải: Xét tại thời điểm vật m bắt đầu rời khỏi bề mặt của nêm, tại thời điểm đó lực tương tác giữa m và M bằng 0. Hình chiếu gia tốc của m trên phương ngang là
DẠYKÈMQUYNHƠNOFFICIAL 176
ta có =→= tt Pcosmaagcos (2). Thế (2) vào (1) →= 2 vglsin (3) Vận tốc của M là == uvsinsinglsin (4) Chọn mặt phẳng ngang làm gốc thế năng, áp dụng định luật bảo toàn cơ năng ta có =++2211 mglmglsinmvMu 22 (5) Thế (3), (4) vào (5) ta được − == 3 M23sin 4 msin Bài 2: Một vật hình trụ rắn khối lượng m và bán kính r trượt xuống mà không lăn trên bề mặt nghiêng, nhẵn của một cái nêm khối lượng M góc nghiêng , nêm có thể tự do chuyển động không ma sát trên mặt phẳng nằm ngang. A
=−= 1tnM aasinacosa - Do m bắt đầu rời khỏi M nên aM = 0 →== 2 tn v asinacoscos l (1) Vào thời điểm đó lực tác dụng lên m có P và phản lực của thanh. Xét theo phương tiếp tuyến
a. Vào thời gian hình trụ trượt xuống tới độ cao h thì cái nêm chuyển động được bao xa?
b. Bây giờ giả sử vật trụ tự do lăn xuống, không trượt trên nêm. Trong trường hợp này, nêm sẽ chuyển động được bao xa?
c. Trong trường hợp nào thì vật hình trụ sẽ xuống tới đáy của nêm nhanh hơn? Điều này phụ thuộc như thế nào vào bán kính hình trụ? Lời giải:
a) Giả sử x0 là khoảng cách giữa khối tâm của hình trụ tại vị trí khảo sát với vị trí ban đầu. Trong một hệ trục tọa độ cố định, giả sử x là tọa độ nằm ngang của khối tâm của nêm. Thành phần vận tốc nằm ngang của vật hình trụ trong hệ quy chiếu này là x’ + x0’.Cos. Vì động lượng của hệ theo phương ngang được bảo toàn, nên từ trạng thái nghỉ ban đầu của hệ, ta có: M.x’ + m.(x’ x0.Cos) = 0 => (M + m). x’ = m.x0’.Cos Đặt x0 = x = 0 tại thời điểm ban đầu t = 0 mà không mất tính tổng quát. Tích phân phương trình trên, ta được: (M + m).x = m.x0.Cos Khi vật hình trụ trượt xuống độ cao h, nó đã dịch chuyển một đoạn x0 = h/Sin và cái nêm đã dịch chuyển một đoạn: x = m.x0.Cos/ (m+M) = m.h.cot / ( M + m) b) Nếu vật hình trụ lăn trên nêm, sự bảo toàn động lượng của hệ theo phương ngang vẫn đúng. Vì vậy, kết quả vẫn giống câu a). c) Sự bảo toàn tổng cơ năng của hệ đúng trong cả hai trường hợp. Vì khối tâm của hình trụ có vận tốc (x’ x0’Cos, x0’Sin) và cái nêm có vận tốc (x’, 0). Đối với trường hợp hình trụ trượt: 1 2 m{(x’ x0’.Cos)2 + x0 ’2.Sin2} + 1 2 M.x’2 = mgx0Sin (1) Đối với trường hợp hình trụ lăn không trượt: 1 2 m{(x’ x0’.Cos)2 + x0 ’2.Sin2} + 1 2 M.x’2 + 1 2 I.’2 = mgx0Sin (2) Với I = mr2/2 , ’ = x0’/r Giải phương trình (1) và phương trình (2), ta thấy hình trụ trượt xuống đáy nêm nhanh hơn. II. ĐỔI HỆ QUY CHIẾU CÔNG THỨC
DẠYKÈMQUYNHƠNOFFICIAL 177
CỘNG VẬN TỐC Bài 3:Hai trụ đồng chất, cùng chiều cao, có đường kính tiết diện là D và d nằm ngang tiếp xúc với nhau. Hệ số ma sát ở mọi
quanh trụ lớn và
trị thế nào
thực hiện đượ
chỗ tiếp xúc là k. Quấn một sợi dây mảnh không dãn
tác dụng vào đầu dây một lực F nằm ngang. Hỏi hệ số ma sát k phải có giá
để có thể di chuyển trụ lớn vượt qua trụ nhỏ. Tính giá trị cần thiết của lực F để
c di chuyển trên. Biết D=2d, khối lượng trụ lớn là M=10kg; g=10m/s2
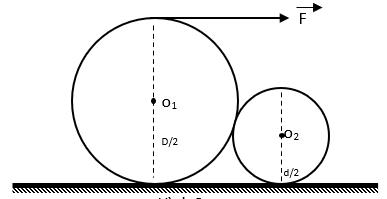

DẠYKÈMQUYNHƠNOFFICIAL 178 Lời giải Xét hệ ở trạng thái cân bằng giới hạn, trụ lớn sắp rời sàn nên phản lực của sàn lên trụ lớn bằng không. F1, F2 lực ma sát ở chỗ tiếp xúc Chọn hệ xoy + Xét trụ nhỏ đứng yên. Chọn 02 là trục quay có 22 1 2 d F d F = Nên F=F2=F1 + vì F2kN2 => FkN2 (1) F1kN1 => FkN1 (2) Với trụ nhỏ: 0 cos sin 0 cos sin 2 1 ' 1 2 ' = = F F N F F N => sin 1cos)( 1 + = F N thế vào (2)
1cos sin + k (3) • Gọi I là tâm quay tức thời Có: F.R(1+cos)=M.g.R.sin =>
1cos sin + = Mg F (4) Mặt khác có N2=(M+m)g. Thế (1) và kết hợp (4) ( ) ( )

1cos sin 1cos sin + + + + m M M k g m M k Mg (5) Vì 1 + m M M nên nếu (3) thỏa mãn thì (5) thoả mãn Vậy k
1cos sin + thay d D d D r R r R + = + = cos d D Dd + = 2 cos 1 sin 2 Vậy 0,7 2 1 = D d k Từ (4) có
2( 50 . min N D d g M F
Bài 4: Một sợi dây vắt qua ròng rọc, ở hai đầu sợi dây có hai người đu vào. Biết khối lượng của mỗi người lớn gấp 4 lần khối lượng ròng rọc. Người A bắt đầu leo theo dây với vận tốc tương đối với dây là u. Tính vận tốc của người B so với mặt đất? coi như khối lượng ròng rọc phấn bố đều trên vành
DẠYKÈMQUYNHƠNOFFICIAL 179
Gọi B là
ậ
thứ
v
)
= =
Lời giải:
v
n tốc của dây đối với đất, (và cùng là vận tốc của người B đối với đất ). Theo công
c cộng vận tốc ta có vận tốc của người A đối với đất là: ( 1)
ABvuv =+
Chiếu ( 1 ) xuống phương chuyển động của A ta được : ( 2 ) Ban đầu cơ hệ đứng yên nên mômen động lượng của hệ đối với trục ròng rọc bằng không: ( 3 )
Khi người A bắt đầu leo lên dây thì mômen động lượng của hệ gồm mômen động lượng của người A, người B và mômen quay của ròng rọc: với Áp dụng định luật bảo toàn mômen độ
DẠYKÈMQUYNHƠNOFFICIAL 180
ng lượng cho hệ : . Giải phương trình tìm được: Vậy vận tốc của người B đối với đất bằng : ABvuv =− 0 L = ' AB LR.m.vR.m.vI. =−− B v R = ,LL = 0 AB R.m.vR.m.vI.−−= 2 0 4 B BB v m R.m.(UV)R.m.v.R. R −−−= 4 9 B u v = 4 9 B u v =
PHẦN II. BÀI TẬP CÓ HƯỚNG DẪN Bài 5: (Lăn không trượt) Hai quả cầu đồng nhất bán kính R, 2R đặt lên một xe lăn sao cho điểm tiếp xúc ở chính giữa một xe lăn. Biết khối lượng của quả cầu nhỏ là m1 = 1kg, quả lớn là m2 = 8kg, xe là M = 6kg. Coi các quả cầu chỉ chuyển động lăn không trượt sao cho góc nối giữa tâm của chúng với phương ngang không đổi α = 600. Chiều dài của xe là
L = 2m.

a. Tìm lực kéo F? b. Sau bao lâu các quả cầu dời khỏi xe? Lời giải Điều kiện lăn không trượt là: v1 = v2 = ω1.R + v = ω2.2R + v ; với v là vận tốc của xe. → ω1 = 2 ω2 → γ1 = 2 γ2.
Phương trình động lực học của hệ 2 quả cầu: Fms = (m1 + m2)a1
Phương trình mômen: F12R = I1. γ1 và 2(Fms F12).R = I2. γ2. với F12 là lực ma sát giữa hai quả cầu.
Phương trình động lực học cho xe: F Fms = M.a. Giải các phương trình trên ta tìm được F = 80N và từ đó tìm được thời gian t = 0,386s. Bài 6: Một hình trụ có khối M được bố trí thành cơ hệ như hình 4, hệ số ma sát của hình tr
DẠYKÈMQUYNHƠNOFFICIAL 181
ụ với mặt phẳng ngang là 1, với mặt phẳng ngang là 2 mặt phẳng ngang chuyển động đều về phía trái, cần phải tác động vào mặt phẳng ngang một lực F nhỏ nhất là bao nhiêu để xảy ra điều trên.
Lời giải: Hình trụ có hai khả năng quay hay không quay. Giả sử trụ quay: Khi mặt phẳng ngang chuyển động đều thì trụ quay đèu và gia tốc của khối trụ bằng không Ta có: + Tổng các Moment lực đối với trục quay qua khối tâm bằng 0: F1 = F2 = F + Theo phương ngang: Nsin F2 cos F1 = 0 (1) + Theo phương thẳng đứng: N1 Mg N2cos F2sin = 0 (2) Rút gọn biểu thức ta thu được:



DẠYKÈMQUYNHƠNOFFICIAL 182
+ = + = (4) (3) 1cos sin 2 1 2 N Mg N N F Nhận xét F, N1, N2 phụ thuộc vào 1, 2, và có hai trường hợp có thể xảy ra: Trường hợp 1. 1 N1 > 2 N2, hình trụ quay, F = 2N2 Khi dó từ (3): 2 2 2 1cos sin N N = + 1.a/ 1cos sin + > 2 => N2 = 0, F = 0 với điều kiện 1N1 > 2N2 với mọi giá trị của 1, 2 1.b/ 1cos sin + < 2 , Khi đó hình trụ bị kẹt, Đkiện 1N1 > 2N2 xảy ra với 1 > 2. * =
Đánh giá: Biểu diễn kết quả qua đồ thị, đồ thị biểu diễn mặt phẳng 1, 2 chia làm 3 miền
Miền 1: ứng với trường hợp (1.a)
Miền 2: ứng với trường hợp (1.b ) và (2.a) hình trụ bị kẹt nên F =
1 + Mg
Miền 3: ứng với trường hợp (2.b), F = sin cos 1 1 1
sau đó đặt lên mặt phẳng nghiêng góc .Con lăn với mặt phẳng nghiêng có hệ số ma sát trượt 1 5tan f = . Vật và mặt phẳng nghiêng là 2 tan f = ,thanh song song với mặt phẳng nghiêng. Bỏ qua khối lương thanh nối và ma sát lăn 1 Mô tả sơ lược định tính chuyển động của hệ thống
DẠYKÈMQUYNHƠNOFFICIAL 183
Trường hợp 2. 1 N1 < 2 N2, hình trụ không quay được F = 1N1. Từ (3) và (4) 1 1 2 1cos sin N N
= + 1(Mg + N2 ) = N2
1cos sin + . Tìm ra N2 = 1 1 cos 1 sin
+ Mg 2.a/
1cos sin 1 +
, khi đó trụ bị kẹt, điều kiện 1N1 > 2N2 khi 1 < 2 2.b/
1cos sin 1 +
, khi đó F = 1N1 = 1 ( N2 + Mg) F =
sin cos 1 1 1 1 + Mg Điều kiện 1N1 < 2N2 xảy ra khi
1cos sin 2 + [ 2N2 > 1 ( N2 + Mg)]
ố
Bài 7: Một vật rắn Khối lượng m được nối cố định vào trục một con lăn hình trụ bán kính R có cùng khối lượng m con lăn quay cùng chiều kim đồng hồ cho đến khi nó có vận t
c 0
ngay
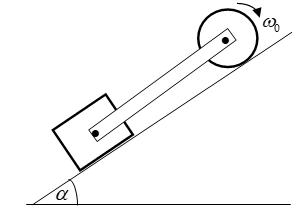

DẠYKÈMQUYNHƠNOFFICIAL 184 2 Tính vận tốc ,gia tốc, quãng đường hệ vật đi được trong từng giai đoạn trên Lời giải: + Do vận tốc dài d vR = > v tịnh tiến của khối tâm nên trụ vừa lăn vừa trượt Khi đó lực ma sát nghỉ trên trụ bằng ma sát trượt và là lực phát động 121 112 22.sin 22.sin()cos msmsmamgFF agffg =−−+ =−+− Suy ra 1 sin ag = Hệ chuyển động nhanh dần đều Vận tốc khối tâm của hình trụ 1 sin. t vatgt == (1) Chuyển động quay của trụ 1 2 ..cos.10sin /0 /2 fmgR g MI mRR ==−=− - Lực ma sát nghỉ làm trụ quay ngược chiều kim đồng hồ với vận tốc góc 0 nên trụ quay với vận tốc nhỏ dần 0 t =+ = 0 10sin. gt R Vận tốc dài của mỗi điểm trên mép trụ . dt vR = (2)

DẠYKÈMQUYNHƠNOFFICIAL 185 Giai đoạn này ngừng khi tdvv = Từ (1) và (2) Ta được 0 1 . 11sin R t g = (3) Khi đó 222 0 111110 1 ./2(.)/11.sin 112tt R vatSvaRg ==→== Giai đoạn 2. Hệ tiếp tục đi lên Hình trụ lăn không trượt ,Lực ma sat lên trụ là lực ma sát lăn 1mslmstff Ta có 2 phương trình sau 221 1 22.sin . mstmsn msn mamgFF IFR =−−− = Từ 2 phương trình trên ta được 2 6.sin 5 ag =− Hệ chuyển động chậm dần cho đến khi dừng lại 222 1010 22 22 5.5. , 66sin21452sin tt vRvR ts agag =−==−= Giai đoạn 3. Hệ đi xuống 321 1 22.sin msmsn msn mamgFF IFR =−−− = 2 3 113 1 ../2 2 msmsn a mRFRFma R →=→= Thay vào ta được 3 2 .sin 5 ag = Bài 8: Một hình trụ bán kính R khối lượng M đặt lên mặt phẳng nghiêng góc với phương ngang và lăn không trượt xuống. Hệ số ma sát giữa hình trụ với mặt phẳng nghiêng là .
a. Tìm điều kiện về góc để hình trụ lăn không trượt trong 2 trường hợp: hình trụ đặc và hình trụ rỗng. b. Tìm gia tốc của tâm hình trụ trong 2 trường hợp trên. c. Đặt vào trong hình trụ rỗng bán kính R, khối lượng M một hình trụ đặc đồng chất có bán kính r = R/2, có khối lượng là m rồi đặt hệ lên mặt phẳng nghiêng góc và thả ra không vận tốc đầu (hình 3). Biết rằng không xảy ra sự trượt giữa các hình trụ và giữa hình trụ với mặt phẳng nghiêng khi hệ lăn xuống. Tìm gia tốc của hệ khi chuyển động ổn định. Lời giải: a.

+ Hình trụ lăn không trượt: tác dụng lên hình trụ gồm trọng lực P, lực ma sát nghỉ F và lực pháp tuyến N của mặt phẳng nghiêng (hình vẽ). + Phương trình động lực học cho chuyển động tịnh tiến: MgFMa sin. −=
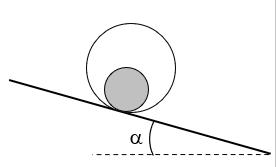
DẠYKÈMQUYNHƠNOFFICIAL 186
+
+
=
+
Phương trình động lực học cho chuyển động quay: a FRII R == , trong đó IMR2 = đối với hình trụ rỗng và IMR2 1 2 = đối với hình trụ đặc.
Suy ra: Mg a MIR2 sin (/)
+ và I FMg MRI 2 sin = +
Điều kiện lăn không trượt ứng với điều kiện về lực ma sát: FNMgcos = .
1) Đối với hình trụ rỗng, IMR2 = thì FMg 1 sin 2 = , điều kiện lăn không trượt tìm được là: 1 tan 2
2)Với hình trụ đặc, IMR2 1 2 = thì FMg 1 sin 3 = , điều kiện lăn không trượt: 1 tan 2
b. Gia tốc lăn không trượt của:
Tâm hình trụ rỗng: ag 1 sin 2 = .
Tâm hình trụ đặc: ag 2 sin 3 = .
c.
Ký hiệu khối lượng của hình trụ rỗng và hình trụ đặc lần lượt là M và m. Khi chuyển động ổn định, cả hai vật có cùng vận tốc tịnh tiến là v và cùng gia tốc tịnh tiến a. Vận tốc góc của hình trụ rỗng là 1 và của hình trụ đặc là 2. Các lực tác dụng lên từng hình trụ như hình vẽ. Từ phương trình R vR12 2 == , suy ra 21 2 = , đồng thời ta cũng có được liên hệ gia tốc góc: 21 2 = . Phương trình động lực học cho chuyển động quay của hình trụ đặc: RRR Fmm 2 2 221 11 2 22224 == Do lăn không trượt nên a R 1 = , suy ra: ma F2 2 = . Phương trình động lực học cho chuyển động quay của hình trụ rỗng: a
DẠYKÈMQUYNHƠNOFFICIAL 187
FFRMRMR
'22 121()−== . Vì FF ' 22 = là lực tương
. Phương
động
ực
ọ
MmgFMma 1 ()sin() +−=+ Thay biểu thức của F1 ở trên vào ta thu được kết quả: aMmg Mm 2()sin 43 + = + Bài 9: Một hình trụ rỗng bán kính R, mặt trong nhám, được giữ thẳng đứng. Một đĩa mỏng đồng chất khối lượng m, bán kính r (r < R), lăn không trượt ở mặt trong của hình trụ sao cho tiếp điểm của nó với hình trụ luôn nằm trên một mặt phẳng nằm ngang. Gọi là hệ số
R
tác giữa hai hình trụ (lực ma sát), nên m FMa 1 2 =+
trình
l
h
c cho chuyển động tịnh tiến của hệ:
ma sát nghỉ giữa đĩa và hình trụ, là góc nghiêng của đĩa so với phương thẳng đứng. Cho gia tốc trọng trường là g, bỏ qua ma sát lăn và lực cản môi trường. Giả sử đĩa lăn đều, không trượt và luôn nghiêng một góc 0= không đổi.
a, Tính vận tốc góc của khối tâm đĩa trong chuyển động quay quanh trục hình trụ.
b, Hỏi 0 phải nằm trong khoảng giá trị minmax , nào thì điều giả sử trên (đĩa lăn không trượt với góc nghiêng không đổi) thỏa mãn?
c, Gọi momen quán tính của đĩa đối với trục quay tiếp tuyến với đĩa và nằm trong mặt phẳng của đĩa là 2 Imr. = Tìm giá trị của . Lời giải a, Các lực tác dụng lên vật: trọng lực mg, phản lực N, lực ma sát Fms. Gọi s0p0 , là vận tốc góc của đĩa quanh trục đĩa và của khối tâm quanh trục hình trụ Điều kiện cân bằng của khối tâm: ( ) ms 2
Tâm quay tức thời của đĩa là A: Đĩa lăn không trượt ( ) s0p00 .r.Rrsin =− (2) Gọi L là momen động lượng của đĩa quanh tâm quay tức thời A. Trọng lực gây ra momen 0 sin = Mmgr hướng vuông góc với mặt phẳng hình vẽ.

DẠYKÈMQUYNHƠNOFFICIAL 188
Fmg
p00
NmRrsin = =−
(1)
ụ thể là chỉ thay đổi hướng với tốc độ thay đổi là 22 // //p00p0s00p00 dL 1 dt2L.L.cos.mrmrcosmgrsin ===+= (3) Từ (2),(3) giải ra được: ( ) 2 0 p0 0 2gtan 3Rrsin = − (4) b, Thay (4) vào (1) tìm ra 0 N2mgtan 3 = . Điều kiện lăn không trượt ms FN
Theo định lý biến thiên momen động lượng dL M dt = . Trong khi chuyển động thì chỉ có thành phần nằm ngang của L biến thiên, c
lượng m,
kính đáy R đang quay đều quanh tr
c c


a nó theo phương ngang với vận tốc góc o . Trụ được đặt nhẹ nhàng lên một sàn xe phẳng, dài nằm ngang. Xe có cùng khối lượng m với trụ và có thể trượt không ma sát trên mặt đất.Ngay sau đó xe chuyển động nhanh dần, nhưng sau một khoảng thời gian xe đạt được vận tốc ổn định và không đổi.
a. Xác định vận tốc ổn định của xe.
b. Xác định năng lượng mất mát từ khi trụ được đặt lên xe đến khi xe đạt vận tốc không đổi.
Lời giải:
HS có thể làm theo một trong hai cách sau đây)
Gọi vận tốc của xe khi ổn định là V. Vận tốc của trụ so với xe khi đó là v, vận tốc quay của trụ khi đó là . Ban đầu trụ trượt trên sàn xe, lực ma sát làm trụ chuyển động tịnh
DẠYKÈMQUYNHƠNOFFICIAL 189 00 33 tanarctan. 222 c,
tính của đĩa với trục nằm trong mặt phẳng đĩa và
O:
i xứng: ( ) 2 2222 xyz 111mr IxdmIydm Ixydm . 2222 =====+= . Chuyển về trục qua A cho ta có 222 // 15 Imrmrmr 44 =+= do đó 5 4 = Bài
ụ
Momenquán
đi qua tâm
Do đố
10: Một tr
đặc có khối
bán
ụ
ủ
DẠYKÈMQUYNHƠNOFFICIAL 190 tiến nhanh dần, chuyển động quay chậm dần đến khi đạt điều kiện lăn không trượt .vR = thì lực ma sát bằng 0 và hệ đạt trạng thái ổn định với các vận tốc không đổ
Cách 1: Sử dụng các định luật bảo toàn: a) Định luật bảo toàn động lượng: ()0mVmVv+−= 2 v V = Định luật bảo toàn mô men động lượng với một trục nằm trên sàn xe vuông góc với mặt phẳng hình vẽ: () o IImvVR =+− Với: 2 2 mR I = và vR = Giải các phương trình ta tìm được: 2 o R v = b) 2 222 () 2222 hptruocsau o hp QWW I ImvVmV Q =− =−++ Với 2 v V = ; .vR = ; 2 2 mR I = mà 2 o R v = . Biến đổi ta được: 22 8 o hp mR Q = Cách 2: Sử dụng phương pháp động lực học: a)Đối với xe: ms V mmaF t == Đối với trụ: 12 qtmsms v mmaFFmaF t ==+=+ o ms IIFR t ==−
i.
Với: 2 2 mR I = và .vR = Biến đổi ta được: 2 o R v = b) () hpmsmsquaymstt QAAA =−=−+
Trong đó: Amsquay là công của lực ma sát trong chuyển động quay của trụ trên xe. Amstt là công của lực ma sát trong chuyển động tịnh tiến tương đối của trụ trên xe. 22 2 12
AFRFR v AF a
o msquaymsms msttms
2 . 2
== = Biến đổi ta được 22 8 o hp mR Q =
Bài 11: Một đĩa đồng chất hình trụ, bán kính R được đặt nằm yên trên mặt phẳng nằm ngang, không ma sát. Một đĩa khác giống hệt nó, đang quay đều quanh trục thẳng đứng (cùng trục với đĩa nằm yên) với tốc độ góc là 0ω và hạ thấp thật chậm để có thể tiếp xúc nhẹ nhàng (không va chạm) råi chồng khít lên đĩa ở dưới. Do có ma sát giữa ở mặt tiếp xúc của hai đĩa nên sau khoảng thời gian t (tính từ thời điểm hai mặt đĩa bắt đầu tiếp xúc), cả hai đĩa quay quanh trục với cùng một tốc độ góc. Hệ số ma sát giữa hai mặt đĩa là μ. Gia tốc trọng trường là g. Tính t ?
DẠYKÈMQUYNHƠNOFFICIAL 191
Lời giải: Xét một phần tử nhỏ của đĩa, được giới hạn bởi 2 hình quạt
là r
r +
ọ
dS và dm lần lượt là diện tích và khối lượng của phần tử . Ta có: 22 21 11 dS = S- S=(r + dr).dα- r.dα 22 = r.dr.dα 2dmmm =dS =.r.dr.dα S πR Gọi ms dF là lực ma sát tác dụng lên phần đĩa có diện tích dS . Ta có: ms dF= μg.dm Gọi CdM là momen cản của lực ma sát do phần tử ms dF gây ra ta có :
bán kính
và
dr. G
i
μmg MdM= dα.r.dr πR td


= = 2 μmg.R3 Phươngtrìnhchuyển độngquay của đĩacódạng: C00 dω M= - I.γ=-I dt .Thayvàota timđược: 2 21dω μmg.R=- mR. 32dt 3R dt=- .dω 4μg → . 0

t0 0 0 ω Lời giải: Câu 4 (4đ): Gọi a1: Gia tốc khối tâm đĩa a2: Gia tốc vật m với đất a3: Gia tốc M với đất Xét chuyển động của đĩa: + Với trục quay đia qua điểm tiếp xúc: T 3 2 R = I Với I = 1/2mR2 + mR2 = 3/2mR2
3ωR 3R t=dt=- dω = 4μg4μg Bài 12: Cho hệ như hình vẽ. Đĩa đồng chất có khối lượng m, bán kính R. Xe đẩy có khối lượng M = 2m chiều dài L = 1m. Xe đẩy có thể chuyển động dễ dàng. Trên đĩa gắn một vành rất nhẹ bán kính 2 R r = , trên vành quấn một sợi dây nhẹ không dãn, đầu kia của dây được nối với vật m qua một ròng rọc nhẹ. Ban đầu đĩa nằm giữa xe đẩy, dây được giữ căng. Sau đó người ta thả nhẹ cho hệ chuyển động. Biết rằng đĩa lăn không trượt trên xe. Cho g = 10m/s2. Xác định thời gian đĩa lăn trên xe và quãng đường vật m rơi xuống tương ứng. T Fms
DẠYKÈMQUYNHƠNOFFICIAL 192
CdM = 2 ms 22 m μmg r.dF= r.μg..r.dr.dα= .r.dr.dα πRπR Từ đó tìm được momen của lực ma sát do toµn bé ®Üa g©y ra lµ : 2πR 2 msms 2 00
2 33 TRmR 22=
T = mR (1)
+ Giả sử Fms tác dụng lên đĩa hướng như hình vẽ: T Fms = ma1 (2) (1)(2) Fms = T ma1 = m(R a1) (3)
Với trường hợp này M nếu chuyển động thì sẽ chuyển động cùng chiều với đĩa a1 R. Kết hợp với (3) Fms = 0
+ Giả sử Fms hướng ngược lại: T + Fms = ma1 (2’) (1)(2)Fms = ma1 T = m(a1 R) (3’)
Với trường hợp này M nếu chuyển động thì sẽ chuyển động ngược chiều với đĩa a1 ≤ R. Kết hợp với (3’) Fms = 0
Vậy Fms=0M không chuyển động. Khi đó a1 = R Xét m: mg T = ma2 = m. 3 R. 2 (4) Thay (1) vào (4) mg mR = 3/2.mR 2g 5R = a1 = R = 2g 5 = 4m/s2 s = L/2 = 0,5m 2s t0,5s a
sàn xe nhờ một cái nêm tiết diện hình tam giác chiều dài OD, góc nghiêng và khối lượng không đáng kể. Các tiếp xúc giữ ống và xe (B và C) không có ma sát, tiếp xúc giữa ống và nêm, giữa nêm và xe có cùng hệ số ma sát k. Cho biết: = 100; m = 50kg; R = 1m; k = 2 và g = 10m/s2. Chọn hệ quy chiếu (Oxyz) là hệ quy chiếu gắn với
DẠYKÈMQUYNHƠNOFFICIAL 193
đồng chất
ối
2 . Ống
==
a2 = 3 R. 2 = 6m/s2 m đi xuống một đoạn: h = 1/2a2t2 = 0,75m Bài 13: Một xe tải dịch chuyển trên con đường thẳng nằm ngang, chở một ống hình trụ
kh
lượng m bán kính R; momen quán tính của ống này đối với trục ống là I = mR
được giữ trên
xe tải, O nằm ở đầu mút của cái nêm, Ox hướng theo mặt nghiêng của nêm, Oy hướng lên vuông góc với Ox trong mặt phẳng thẳng đứng, Oz nằm ngang vuông góc mặt phẳng hình vẽ.
1) Xe khởi động và chuyển động với gia tốc không đổi a . Giả thiết cái nêm và ống được giữ cân bằng. Trong điều kiện đó:
a) Tìm giá trị lớn nhất a1 của gia tốc của xe.
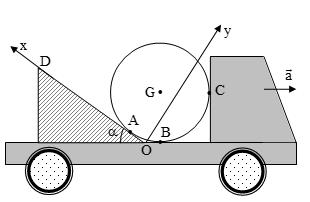
b) Chứng tỏ rằng nêm chỉ đứng yên nếu k lớn hơn một giá trị k1 nào đó mà ta phải xác định.
2) Giả sử k > k1 và cái nêm đứng yên trên sàn xe. Ở thời điểm ban đầu t = 0, xe tải khởi động với gia tốc không đổi a > a1.
a) Giả sử ống lăn không trượt trên nêm, tính gia tốc khối tâm của ống trong hệ (Oxyz).
b) Chứng tỏ rằng ống chỉ có thể lăn không trượt nếu gia tốc của xe không nhỏ hơn một giá trị a2 nào đó mà ta phải xác định.
c) Chứng tỏ rằng thực tế cái nêm chỉ bất động trên sàn xe nếu gia tốc của xe nhỏ hơn một giá trị a3 nào đó mà ta phải xác định.
Lời giải:
1) Giả thiết cái nêm và ống được giữ cân bằng trên xe.
DẠYKÈMQUYNHƠNOFFICIAL 194
Xét trong hệ quy chiếu gắn với xe (hệ phi quán tính). Vì rằng, mg, N, 1N , 2N , và qtF đều có giá qua G nên momen của các lực này đối với G bằng không, do đó momen của ms F cũng bằng không, hay ms F = 0. Định luật II Newton trong hệ quy chiếu (Oxyz): 12 NNNmgma0 +++−= Trong giới hạn 1aa = , các tiếp xúc B, C không có tương tác, 12 NN0 == , chiếu lên Ox và Oy: 1 mgsinmacos0 −+= 1 agtan1,76== m/s2 .
b) Cái nêm có khối lượng không đáng kể, xét trong hệ quy chiếu (Oxyz): Ma sát của ống tác dụng lên nêm bằng không. Ta có: ms00 FNN'0 ++= Chiếu lên Ox và Oy: ms0 FNsin0 −+= 0 NNcos0 −=


195 a)
DẠYKÈMQUYNHƠNOFFICIAL
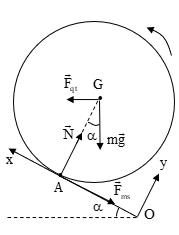
DẠYKÈMQUYNHƠNOFFICIAL 196 Cái nêm cố định nếu ms00 Fk.N 1 kktan0,176== . 2) Giả sử k > k1 và cái nêm đứng yên trên sàn xe. Ở thời điểm ban đầu t = 0, xe tải khởi động với gia tốc không đổi a > a1 a) Định luật II: Gms maFNmgma =++− Gms maFmgsinmacos =−−+ (1) 0Nmgcosmasin =−− (2) Phương trình động lực học của ống đối với G 2 ms I.mRR.F == (3) Khi ống lăn không trượt thì: G aR= (4) Từ (3) và (4) ta có: msGFm.a = , thay vào (1): G 1 a(acosgsin) 2 =− (5) b) Chứng tỏ ống chỉ có thể lăn không trượt nếu 2aa , tìm 2a . Từ (5) ta có: ms 1 Fm(acosgsin) 2 =− (6) Từ (2) ta có: Nm(gcosasin) =+ (7) Chúýrằng: 1 sin aagtang cos == acosgsin0 − ,điềukiện đểống lăn không trượt là: ms 1 |F|m(acosgsin)k|N|km(gcosasin) 2 =−=+

DẠYKÈMQUYNHƠNOFFICIAL 197 a(gcos2ksin)g(2kcossin) −+ 2 sin2kcos
cos2ksin + == − m/s2 (Ta
thể kiểm nghiệm rằng 2
Vì khối lượng nêm là không đáng kể nên ' ms00ms FNN'F0 +−−= Chiếu lên phương ngang, và thẳng đứng: ms0ms FNsinFcos0 −++= (8) 0ms NNcosFsin0 −+=
Thay (6) và (7) vào (8) và (8) ta được: ms0ms 1 FFcosNsinm(acosgsin)cosm(gcosasin)sin 2 =+=−++ 2 2 ms0 sincoscos Fmgasin 22 =++ (10) 0 1 NNcosTsinm(gcosasin)cosm(acosgsin)sin 2 =−=+−− 2 2 0 sinsincos Nmgcosa22 =++ (11) Cái nêm vẫn đứng yên nếu ms00 FkN , tức là khi: 2 2 sincoscos gasink 22 ++ 2 2 sinsincos gcosa22 ++
aag6,2
có
21a6,2 m/sa= ). c)
(9)
22 3 22 k(sin2kcos)sincos aag2,24 (cos2sin)ksincos +− →== +− m/s2 . Bài 14: Hai bánh xe là những đĩa tròn đồng chất có tâm lần lượt là O và O’ nối với nhau bằng dây curoa không dãn, không trượt trên các bánh xe (Hình 4). Bánh xe tâm O đang quay với vận tốc góc 0 thì một má phanh đè vào với áp lực Q, hệ số ma sát k. Biết bánh xe tâm O có khối lượng M và bán kính R, bánh xe O’ có khối lượng M’, dây curoa có khối lượng m.
a) Tìm động năng ban đầu của hệ theo M, M’, m, 0 và R.
b) Tính số vòng bánh xe tâm O quay cho đến khi dừng và gia tốc góc của nó.
Lời giải:
Dây không dãn, công của nội lực bằng 0, ngoại lực tác dụng vào dây là lực ma sát
F = kQ. Khối tâm của các bánh xe và dây không dịch chuyển nên công của trọng lực bằng 0.
Động năng của bánh xe O là K0 = 2
2 0I mà I = 2

2MR nên K0 = 4
2MR 2 0
năng của bánh xe O’ là
DẠYKÈMQUYNHƠNOFFICIAL 198
−+−−
22 22sincossinsincoscos gkcosaksin 2222
Vậy động năng của cả hệ
+
+
(M
+
Động năng
4 1 (M +
Động
K0’ = 4 ' 2 r M ' 2 0 , do 0R = 0’ r K0’ = 4 ' M R2 2 0 Động năng của dây Kd = 2 m R2 2 0 (do V = R0)
K = K0
K0’
Kd = 4 1
+ M’
2m) R2 2 0 (*)
của hệ chuyển thành công của lực ma sát trên n vòng quay
M’ + 2m) R2 2 0 = n.k.Q.2πR
Vậy kQ R m M M n 8 ) 2 ' ( 2 0 + + = Từ (*) ta thấy : Hệ tương đương với 1 bánh xe có bán kính R và khối lượng (M + M’ + 2m) và mô men quán tính tương đương là Itđ, ta có: Itđ = (M+M’+2m) 2
2 R . Gọi là gia tốc góc, ta có phương trình: kQR = Itđ || = td I kQR = 2 ) 2 ' ( 2R m M M

kQR + + = R m M M kQ ) 2 ' ( 2 + +
Bài 15: Một trục quấn dây có thể xem như một hình trụ C khối lượng M = 10 kg, bán kính R = 8cm lăn không trượt trên một mặt phẳng nghiêng làm với phương ngang một góc α = 300 như hình vẽ. Sợi dây quấn trên trục vắt qua ròng rọc B không khối lượng không ma sát, và nối với vật A khối lượng m = 2kg.
a. Tính độ cao mà khối tâm của C đi được khi vật A đi được quảng đường 2m. b. Tính gia tốc khối tâm của C. c. Tính độ lớn lực ma sát nghỉ ở điểm tiếp xúc và tìm điều kiện về hệ số ma sát để C lăn không trượt.
Lời giải:
1. Khi trọng tâm khối trụ lăn không trược theo mặt phẳng nghiêng một đoạn S thì dây xổ ra hoặc cuộn vào được một đoạn đúng bằng S và do đó vật A đi được 2S. Vậy khi vật A đi được 2S = 2m thì khối tâm đi theo mặt phẳng nghiêng S = 1m và theo chiều cao được một đoạn h = S.sinα =0,5m
2. Các lực tác dụng lên hình trụ và vật:
DẠYKÈMQUYNHƠNOFFICIAL 199
DẠYKÈMQUYNHƠNOFFICIAL 200 Các phương trình động lực học: 1mgTma −= s sin m TFMgMa +−= ( ) sm TFRI −= Ta có: 2 1 1 2, , 2 aaaRIMR === Giải hệ ba phương trình trên ta được: 4 83 mM ag mM = + = 0,426 m/s2 Vây khối trụ lăn đi xuống 3. Lực căng dây. ( ) 44() 2a121,3 8383 mMmmM TmgmggN mMmM −+ =−=−== ++ Lực ma sát nghỉ tác dụng lên khối trụ: s 23 2 m Ma FTN =− Điều kiện để khối trụ lăn không trượt: s cos 0,34 cos m ms FNMg F Mg = Bài 16: Ống đồng chất OA dài 3L, khối lượng m quay xung quanh trục thẳng đứng MN. Hai quả cầu nhỏ khối lượng m1 = m2 = m được nối với nhau bằng dây không giãn, không α = 300 B N Fms T mg Mg T
khối lượng, có chiều dài L, có thể trượt không ma sát trong ống. Lúc đầu, khi quả cầu m1 nằm ở vị trí đầu O của ống trùng với trục quay (hình vẽ), truyền cho hệ vận tốc góc ban đầu 0. Bỏ qua khối lượng của trục quay, ma sát ở các ổ trục.
1. Xác định vận tốc góc, gia tốc góc của ống tại thời điểm quả cầu m2 đến đầu A của ống.
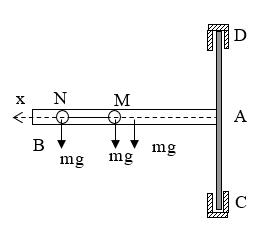
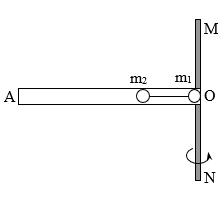
DẠYKÈMQUYNHƠNOFFICIAL 201
+ Tổng các mô men ngoại lực tác dụng lên hệ (hai quả cầu) theo phương MN bằng không nên mô men động lượng theo phương này bảo toàn: LZ = const. + Khi m1 có tọa độ x thì m2 có tọa độ (x + l) , ống có vận tốc góc là L = 2(3) . 3 ml + mx2 + m(l + x)2= 2m(x2 +lx +2l2). Khi: x=0 , L(0) = 4ml20 Khi m2 đến A cách O là 3l thì m1 đến vị trí x = 2l.
2. Tính lực căng T của dây nối hai quả cầu tại thời điểm nói trên. Lời giải:
DẠYKÈMQUYNHƠNOFFICIAL 202 + Gọi vận tốc góc của hệ khi đó là ωA thì :
16ml2A. Từ
=
suy ra vận tốc góc
ủa ống
m2 đến dầu A của ống: A =
/4. + Vận tốc góc của hệ tại thời điểm m 1 ở vị trí x: 2 0 222222 (0)2 2(2)2(2)2 LLl mlxlxmlxlxlxlx === ++++++ ; => gia tốc góc là: 2 0 222 2(2) .' (2) dLxL x dtLxLx + ==− ++ Áp dụng định luật bảo toàn cơ năng: Cơ năng ở O bằng ở A: E0 = EA 2222 2222 0000 .9 2 222.32 mvmlml EIml =+=+= . Vận tốc của các quả cầu tại vị trí bất kỳ là: ( )2 2222 111 ('). nt vvvxx =+=+ , ( )2 2222 222 (')(). nt vvvxxl =+=++ (Chú ý là do dây không giãn nên v1n = v2n = x’) 2 2'222'222 (3)11(9)(4) 2.322 AAA mL Emxlmxl =++++ 2 2'2'2 0 11 222AnA mL mxmx =++ 2 2'2'222 000 11 2 222 AAnA mL EEmxmxml =++= 0 3 2 Ax vl = Gia tốc khi quả cầu m2 tới A là: 2 0 56 64 A =− 2 0 0,2 Xét trong hệ quay chiếu không quán tính gắn với ống OA, chiều dương của Ox hướng ra ngoài. Phương trình chuyển động của quả cầu m2 : " 2mx = T +m(x+L)2 . Phương trình chuyển động của hệ : "''22 12 ()() mxxmxmxl+=++ Vì " Nx = " M x 2 2 mL T = . Khi quả cầu tới A: 2 0 32 AA mL T ==
L(2l) =
L(0)
L(2l)
c
khi
0
Bài 17: Cho một vành trụ mỏng đều, đồng chất, bán kính R và có khối lượng M. Trong lòng vành trụ có gắn cố định ở A một quả cầu nhỏ (bán kính rất nhỏ so với R), khối lượng m. Biết A nằm trong mặt phẳng mà mặt phẳng này vuông góc với trục và đi qua khối tâm C của vành trụ. Người ta đặt vành trụ trên mặt phẳng nằm ngang. Biết gia tốc rơi tự do là g. Giả thiết không có ma sát giữa vành trụ và mặt phẳng. Đẩy vành trụ sao cho AC nghiêng một góc 0 (0 < 900) so với phương thẳng đứng rồi buông ra cho hệ chuyển động với vận tốc ban đầu bằng không.
a. Tính động năng cực đại của hệ.
b. Viết phương trình quỹ đạo của A trong hệ quy chiếu gắn với mặt đất.
c. Xác định tốc độ góc của bán kính AC khi AC lệch góc ( < 0) so với phương thẳng đứng. Lời giải: a) Động năng cực đại của hệ bằng thế năng cực đại: 0 WmgR(1cos) =− b) Kh


DẠYKÈMQUYNHƠNOFFICIAL 203
ối tâm G của hệ nằm trên AC cách C là mR GC Mm = + Do không có ngoại lực tác dụng lên hệ theo phương ngang nên G đứng yên theo phương ngang và chỉ chuyển động theo phương thẳng đứng. Chọn hệ trục Oxy cố định như hình vẽ,
18: Trên mặt phẳng nhám nằm ngang có một vành cứng không trọng lượng. Trên vành có gắn một chất điểm m. Tại thời điểm ban đầu chất điểm nằm ở vị trí cao nhất của vành. Đẩy nhẹ đưa hệ ra khỏi vị trí cân bằng. Xác định sự phụ thuộc của áp lực vuông góc của vành lên mặt phẳng vào góc . Hệ số ma sát nghỉ giữa mặt phẳng và vành bằng hệ số ma sát trượt và bằng k. (Bỏ qua ma sát lăn.)

DẠYKÈMQUYNHƠNOFFICIAL 204 trong đó Oy qua G. AA MR xAGsinsin;yR(1cos) Mm ===− + Đặt 22 22 MRx(yR) AGd1 MmdR ==+= + Quỹ đạo là một đoạn của elip có hai bán trục là d và R. c) Vận tốc của C có phương nằm ngang, của G có phương thẳng đứng. Từ C và G kẻ các đường thẳng vuông góc với véc tơ vận tốc ta xác định được trục quay tức thời là H song song với trục của vành. 22 2 22 G MRmRM2Mm ImMRMR MmMmMm + =++=+++ 2 222 2 HG mRsinM2Mmmsin II(Mm)R MmMm ++ =++=++ Cơ năng bảo toàn nên: 2 0H mgR(coscos)I2 −= Suy ra: 0 222 2m(Mm)g(coscos) (M2Mmmsin)R +− = ++
Bài
giải:

n hệ quy chiếu đất. Giả sử trong quá trình mà ta đang xét, vành lăn không trượt trên mặt sàn.
tương
DẠYKÈMQUYNHƠNOFFICIAL 205
Xét
( ) 2 2 2 0 0 ..cos2.cos 22 ..sin.sin 2 (1cos)Rsin cossin Gxy KG Kxy x y x x y y vvv vvGK vvvGK vKGR vKGR dv aR dt dv aRR dt =+ =+= =++= == =−=− ==+− ==−− (';'') == Xét về mặt Năng lượng. Chọn gốc thế năng tại mặt đất, ta có: 22 2 22 11 (1cos)2 22 1 (1cos)(0) 2 1(1cos) .(1cos) 2(1cos) GG GG mvImgRmgR mvmgRI g mKGmgR R +++= =−= =−= + Xét về mặt động lực học
Lời
Chọ
Xét hệ vành và vật, hệ này
đương với 1 vật rắn.
về mặt động học ta có:

DẠYKÈMQUYNHƠNOFFICIAL 206 PTCĐ quay: sin.(1cos).0 GNRfRI −+== PTCĐ Tịnh tiến của G: x y fma Nmgma = −= 2 2 2 22 2 22 sin (1cos)sin 1cos cossin. sin sin(1cos)sin 1cos (1cos)(1cos)cos.(1cos)sin.(1cos) sin(1cos) .(1cos) (1cos) x y N fmamRmR NmgmamRmR N mRmR NmgmRmR Nmg ===+− + −==−− =+− + +−+=−+−+ ++ −+=− + 222 2 sincos(1cos) 2(1cos)(1cos) 2(1cos)(1cos)2cos Nmgcos mRmR NmgmR Nmgmgmg −+ =+−+ =+−−= =
0
vconst

=> Mâu thuẫn, Nên ngay sau khi vành kết thúc quá trình lăn không trượt trên mặt sàn thì nó sẽ không còn tiếp xúc với sàn nữa, nên khi đó vật m giống như bị ném xiên với quỹ đạo parabol (giữa vật và vành không còn tương tác lực)
Bài 19: Một hình trụ có khối lượng m, bán kính R đang đứng yên. Hình trụ tựa vào một khối hộp và bậc thềm có cùng độ cao như hình 2. Khối hộp được kéo sang trái với vận tốc v không đổi. Lúc đầu, khối hộp ở sát cạnh bậc thềm. Bỏ qua ma sát giữa hình trụ với bậc thềm và khối hộp. Hãy xác định:
a) Dạng quỹ đạo chuyển động của tâm hình trụ so với điểm A ở mép bậc thềm.
b) Điều kiện của vận tốc v để khối hộp vẫn còn tiếp xúc với hình trụ khi khoảng cách giữa hai điểm A và B (ở mép khối hộp) là R 2 .
c) Các lực tác dụng lên thành trụ khi khoảng cách giữa A và B là R 2 .
DẠYKÈMQUYNHƠNOFFICIAL 207 Điều kiện lăn không trượt: 2 222 2222 2 2 sin 1cos sin 1cos 1cos(1cos) 1cos(1cos) (1)cos2cos10 1 cos1 1 N fkN k k k kkk k k = + + −+ −+ +++− + Khi vành bắt đầu lăn có trượt, giả sử nó vẫn còn nén trên mặt sàn và tiếp tục
ển
ng trên mặt phẳng ngang.Phương trình chuyển động quay
ẫn
2 2 sin.(1cos)0 sin1
−+== ==== ++
chuy
độ
v
đúng:
cosons 1cos1 GNRfRI Nk fkNct k
Do
y
Lời giải:
a) Khi hộp vẫn còn tiếp xúc với khối trụ thì khối trụ cũng tiếp xúc với bậc. Suy ra tâm khối trụ luôn cách mép bậc đoạn R, hay nói cách khác tâm khối trụ chuyển động trên cung tròn tâm A, bán kính R.
b) Xét thời điểm khi bán kính AC hợp với phương ngang một góc . Tâm C nằm cách đều khối hộp và bậc, do đó ta dễ thấy: xC = xB/2
Suy ra: vCx = vBx/2 = v/2 (1) Véc tơ vận tốc Cv có phương vuông góc với bán kính quỹ đạo AC. Suy ra Cv hợp với phương thẳng đứng góc . Từ (1) ta có: vC = 2sin v (2) Gia tốc hướng tâm hướng từ C về A có độ lớn: 2 2 24sin C n v v a RR == (3) Tâm C chuyển động đều theo phương ngang nên các phản lực NA và NB bằ

DẠYKÈMQUYNHƠNOFFICIAL 208
ng
Áp dụng phương trình định luật II Newton theo phương CA ta có: NBcos2 + mgsin NA = man (4) Từ (3) và (4) ta có: 2 22 sin 2sin4sin AB mv NNg R ==− Khi AB = R 2 thì = 450. Điều kiện để hộp vẫn tiếp xúc với khối trụ thì: NB 0 Suy ra: 2 vgR
nhau.
Bài 20: Hai quả cầu A và B đặc đồng chất cùng bán kính được đặt chồng lên nhau. Quả cầu A ở dưới có thể quay quanh 1 trục nằm ngang đi qua tâm, quả cầu B ban đầu nằm ở đỉnh của quả cầu A sau đó lăn không trượt từ đỉnh quả cầu A xuống.
a. Chứng minh rằng quả cầu B bắt đầu trượt trên quả cầu A khi hợp bởi đường nối hai tâm của 2 quả cầu và đường thẳng đứng thỏa mãn: sin=(16cos 10). Với là hệ số ma sát trượt giữa hai quả cầu. b. Tính công của lực ma sát nghỉ tác dụng vào cả hệ 2 quả cầu và công của ma sát nghỉ tác dụng riêng vào quả cầu dưới. Lời giải:

DẠYKÈMQUYNHƠNOFFICIAL 209
c) Với 2 vgR thì khi AB = R 2 , lực do khối hộp và bậc tác dụng lên khối trụ là: 2 2 2 AB gv NNm R ==− Ta có phương trình động lực học của chuyển động quay Quả cầu 1: 1 . 1 I M O = 1 2 5 2 . mR R f = (1) Quả cầu 2: 2 . 2 I M O =