BỒI DƯỠNG HSG THPT
MÔN VẬT LÝ
CHƯƠNGI.ĐỘNGHỌCCHẤTĐIỂM
MỤCLỤC
I.1ĐỘNGHỌC.........................................................................................................2
I.2.CHUYỂNĐỘNGNÉM....................................................................................10
I.3.TÍNHTƯƠNGĐỐICHUYỂNĐỘNG............................................................21
I.4ĐỘNGHỌCTOÁNLÝ....................................................................................26
I.1.LỜIGIẢIĐỘNGHỌC.....................................................................................37
I.2.LỜIGIẢICHUYỂNĐỘNGNÉM...................................................................58
I.3.LỜIGIẢITÍNHTƯƠNGĐỐICHUYỂNĐỘNG...........................................94
I.4.LỜIGIẢIĐỘNGHỌCTOÁNLÝ................................................................105
Ths Nguyễn Thanh Tú eBook Collection

CHUYÊN ĐỀ ÔN THI HỌC SINH GIỎI THPT
MÔN VẬT LÝ LỚP 10 - NĂM 2022 - GV
PHẠM VŨ KIM HOÀNG - CÓ LỜI GIẢI CHI
TIẾT (BẢN ĐẸP) (1278 TRANG)
WORD VERSION | 2023 EDITION
ORDER NOW / CHUYỂN GIAO QUA EMAIL
TAILIEUCHUANTHAMKHAO@GMAIL COM
Tài liệu chuẩn tham khảo
Phát triển kênh bởi
Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ
Mobi/Zalo 0905779594
Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon
học thuật : Nguyen Thanh Tu Group
1
vectorstock com/10212086
I.1ĐỘNGHỌC
Bài1.HaivậtchuyểnđộngtừAvàBcùnghướngvềđiểmOvớicùngvậntốc.BiếtAO =20km;BO=30km;Góc .Hãyxácđịnhkhoảngcáchngắnnhấtgiữachúngtrong
060 quáchuyểnđộng?
ĐS: mn53() dcm
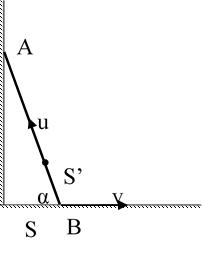
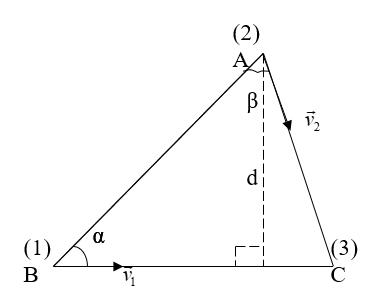
Bài2.Mộtôtôchuyểnđộngthẳngđềuvớivậntốcv1 =54km/h.Mộthànhkháchcáchô tôđoạna=400mvàcáchđườngđoạnd=80m,muốnđónôtô.Hỏi ngườiấyphảichạytheohướngnào,vớivậntốcnhỏnhấtlàbaonhiêu đểđónđượcôtô?
ĐS:HướngtạoABmộtgóc β=900;(v2)min =10,8km
Bài3.Haixechuyểnđộngtrênhaiđườngvuônggócvớinhau,xeAđivềhướngtâyvới tốcđộ50km/h,xeBđivềhướngNamvớitốcđộ30km/h.VàomộtthờiđiểmnàođóxeA vàBcòncáchgiaođiểmcủahaiđườnglầnlượt4,4kmvà4kmvàđangtiếnvềphíagiao điểm.Tìmkhoảngcáchngắnnhấtgiũahaixe.
ĐS:1,166km.
Bài4.HaichuyểnđộngtrênAOvàBOcùnghướngvềOvới .Khikhoảng 10 2;30 3 v v
cáchgiữahaivậtcựctiểulàdmin thìkhoảngcáchtừvậtmộtđếnOlà .Hãy 1303() dcm
tínhkhoảngcáchtừvậthaiđếnO.
ĐS:90(m).
Bài5.MộtconkiếnbámvàođầuBcủamộtthanhcứngmảnhABcóchiều dàiLđangdựngđứngcạnhmộtbứctườngthẳngđứng.Vàothờiđiểmmà đầuBcủathanhbắtđầuchuyểnđộngsangphảivớivậntốckhôngđổiv theosànngangthìconkiếnbắtđầubòdọctheothanhvớivậntốckhông đổiuđốivớithanh.Trongquátrìnhbòtrênthanh,conkiếnđạtđượcđộcaocựcđạilàbao nhiêuđốivớisàn?ChođầuAcủathanhluôntìlênsànthẳngđứng.
ĐS: max2 huL v
Bài6. HaichiếctàubiểnchuyểnđộngvớicùngvậntốchướngtớiđiểmOtrênhaiđường thẳnghợpvớinhaumộtgócα=600.Hãyxácđịnhkhoảngcáchcựctiểuhaitàu.Chobiết banđầuchúngcáchOnhữngkhoảngcáchlàd1 =60kmvàd2 =40km.
ĐS: mn17,32 dkm
Bài7.HaivậtnhỏchuyểnđộngtrênhaitrụctọađộvuônggócOx,OyvàquaOcùngmột lúc.VậtthứnhấtchuyểnđộngtrêntrụcOxtheochiềudươngvớigiatốc1m/s2 vàvậntốc khiquaOlà6m/s.VậtthứhaichuyểnđộngchậmdầnđềutheochiềuâmtrêntrụcOyvới giatốc2m/s2 vàvậntốckhiquaOlà8m/s.Xácđịnhvậntốcnhỏnhấtcủavậtthứnhấtđối vớivậtthứhaitrongkhoảngthờigiantừlúcquaOchođếnkhivậtthứhaidừnglại.
ĐS: v12 đạtgiátrịnhỏnhấtlà8,94m/stạithờiđiểmt=2svàhợpvớiOxgóc26,50
Bài8. TrênđoạnđườngthẳngABdàis=200m,mộtchiếcxekhởihànhtừAchuyểnđộng nhanhdầnđềuvớigiatốca1 =1m/s2 sauđóchuyểnđộngchậmdầnđềuvớigiatốccóđộ lớna2 =2m/s2 vàdừnglạiởB.TínhthờigianngắnnhấtđểxeđitừAđếnB.
ĐS:t=15,63s
Bài9.Từmộtkhícầucáchmặtđấtmộtkhoảng15mđanghạthấpvớitốcđộđềuv1=2m/s, từtrongkhícầungườitaphóngmộtvậtnhỏtheophươngthẳngđứnghướnglênvớivận tốcđầuvo2=18m/sđốivớimặtđất.Tìmkhoảngcáchlớnnhấtgiữakhícầuvàvật.Bỏqua ảnhhưởngkhôngkhílấyg=10m/s2 .
ĐS:20m.
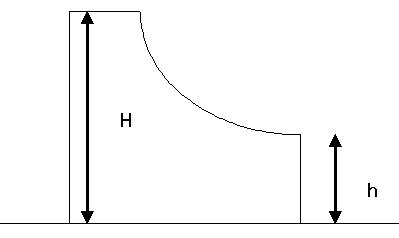
Bài10.Mộtvậtnhỏcóthểtrượtkhôngmasáttừđỉnhmộtcáinêmvàvăngratheophương ngang rồi rơi xuống mặt bàn. Hỏi h bằng baonhiêuthì vật rơi xuống mặt bàn ở xanêm nhất.Biếtrằngkhốilượngnêmrấtlớnsovớikhốilượngcủavật.
ĐS:h= khiđótầmxalmax =H 2 H
2
3
Bài11.HaiôtôđồngthờixuấtpháttừAvàBchuyểnđộngngượcchiềunhau.Ôtôthứ nhất chạy với gia tốc không đổi trên1/3quãng đường AB,1/3quãng đường tiếp theo chuyểnđộngđềuvà1/3quãngđườngcònlạichuyểnđộngchậmdầnđềuvớigiatốccóđộ lớn bằng gia tốc trên1/3quãng đường đầu tiên.Trongkhi đó ôtô thứ hai chuyển động nhanhdầnđềutrong1/3thờigianđitừBtớiA,1/3thờigianchuyểnđộngđều,và1/3thời gianchậmdầnđềuvàdừnglạiởA.Vậntốcchuyểnđộngđềucủahaixelànhưnhauvà bằng70km/h.TìmkhoảngcáchAB,biếtrằngthờigianchạyxethứnhấtdàihơnxethứ hai2phút.
ĐS: 14 ABkm
Bài12.Mộtviênbinhỏchuyểnđộngvớivậntốcv=10m/strongmặt phẳngnằmnganglạigầnmộtchiếchốbằngkimloại.Hốcóhaithành thẳngđứngsongsongvớinhau,cáchnhaumộtkhoảnglàd=5cm.Vận tốcvcủabivuônggócvớithànhhố.ĐộsâucủahốlàH=1m, biva chạmhoàntoànđànhồivàxảyratứcthìvớithànhhố.

1.Tínhsốlầnbivachạmvớithànhhố.
2.Tínhtổngchiềudàiquỹđạocủaviênbitừthờiđiểmbanđầuđếnlúc chạmđáyhố.
ĐS:1.; 2 vH n dg
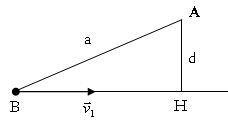
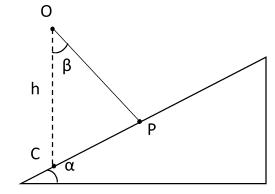
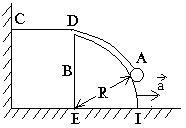
Bài13. Phíatrênmặtphẳngnghiênggócα=300 ,tạiđiểmOcáchmặtphẳngnghiêngmột đoạnOC=h,ngườitađặtmộtmángtrượtthẳngvànhẵn,tựa vàomặtphẳngnghiêngtạiđiểmP(hìnhvẽ).Đểmộtchấtđiểm
từOtrượtkhôngvậntốcđầu,theomángđếnđiểmPcủamặt phẳngnghiêngtrongthờigianngắnnhấtthìgócβgiữaphương thẳngđứngvàmángtrượtphảibằngbaonhiêu? Tìmthờigiantrượtngắnnhấtđótheoh vàgiatốcrơitựdog.Biếtmặtphẳngnghiêngđặtcốđịnh.
ĐS: mn 1,86h t g
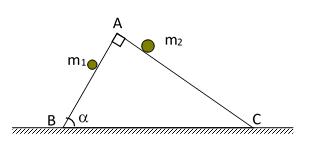
Bài14. MộtnêmcótiếtdiệnlàtamgiácABCvuôngtạiA,vàhaimặtbênlàABvàAC. Chohaivậtm1 vàm2 chuyểnđộngđồngthờikhôngvậntốcđầutừ
Atrênhaimặtnêm.Bỏquamọimasát.Lấyg=10m/s2.(Hìnhvẽ)
a.Giữnêmcốđịnh,thờigianhaivậtm1 vàm2 trượtđếncácchân mặtnêmABvàACtươngứnglàt1 vàt2 vớit2=2t1.Tìm
b.Đểt1 =t2 thìcầnphảichonêmchuyểnđộngtheophươngngangmộtgiatốca0 không đổibằngbaonhiêu?
ĐS:a. =63,40;b.a0 = 7,5m/s2 .

Bài15.Mộtquảcầunhỏchuyểnđộngvớivậntốckhôngđổivtheophương ngangđếnđiểmAtrênmépmộtốnghìnhtrụđặtthẳngđứng,ốngcóchiều caoHđủlớn,bánkínhtiếtdiệnR.KhiđếnAquảcầutạovớiđườngkính miệngốnggóc vàlọtvàoống.
HãyxácđịnhhệthứcliênhệgiữaR;H;vvà đểngaysaukhiquảcầuthựchiệnmộtsố
nguyênlầnvachạmhoàntoànđànhồivớihìnhtrụthìvừavặnthoátratừmiệngốngvới vậntốctheophươngthẳngđứnglúcđóbằng0?Bỏquamọimasátvàlựccản.
ĐS:nRcos =kv,nlàsốvachạm. 2H g
Bài16.Mộtđoàntàukháchđangchạyvớivậntốc thìngườiláitàunhậnthấy 190/ vkmh
ởphíatrước,cáchtàumộtkhoảng cómộtđoàntàuhàngđangchạycùngchiều 140 Lm
với vận tốc . Anh ta dựng phanh cho tàu chạy chậm dần với gia tốc 221,6/ vkmh
21/ ams
Liệucótránhđượcvachạmgiữahaiđoàntàukhông?
ĐS:khôngthểtránhvachạm.
4
5
Bài17. MộtxeôtôchuyểnđộngthẳngtừđịađiểmAđếnđịađiểmBcáchAmộtkhoảng S.Cứsau15phútchuyểnđộngđều,ôtôlạidừngvànghỉ5phút.Trongkhoảng15phút đầuxechạyvớivậntốcv0 =16km/h,vàtrongkhoảngthờigiankếtiếpsauđóxecóvận tốclầnlượt2v0,3v0,4v0,…TìmvậntốctrungbìnhcủaxetrênquãngđườngABtrong haitrườnghợp:
a)S=84km
b)S=91km.
ĐS:a. (km/h);b. (km/h) 43,8bv 44,1tbv
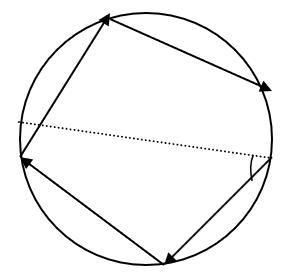
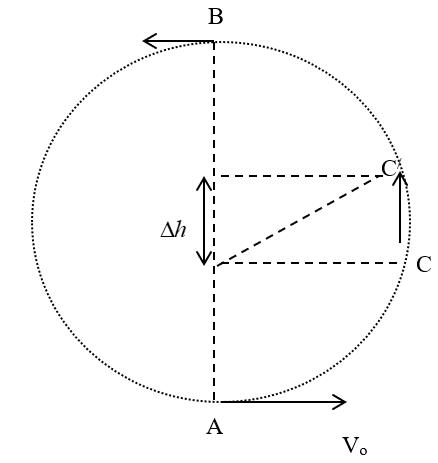
Bài18.Mộtmáybayđangbaynằmngangvớivậntốcvo thìbắtđầungóclêntrênvẽthành
mộtđườngtrònnằmtrongmặtphẳngthẳngđứng.Vậntốccủamáybaykhiđóthayđổitừ
độcaohtínhtừmứcbanđầucủavòngtròntheoquiluật: Ởđiểmcaonhất 222 o vvah
nhiêukhivậtphíatrênđếnchânmặtphẳngnghiêng.Tínhkhoảngcáchtừvịtríhaivậtgặp nhauđếnchânmặtphẳngnghiêng.
ĐS:1. ; ; ;;2.1,2m;3m.

25/ vms 10,6 ts 21 ts
Bài20.TrêntrụcOxmộtchấtđiểmchuyểnđộngbiếnđổiđềutheochiềudươngcóhoành độởcácthờiđiểm tươngứnglà: .Biếtrằng: .Hãytínhgia 123 ;; ttt 123 ;; xxx3221 ttttt tốctheo vàt,chobiếttínhchấtchuyểnđộng. 123 ;; xxx
ĐS: . 321 2 2 xxx a t
củaquĩđạovậntốccủa
nóbằngvo/2. Hãyxácđịnhgiatốccủamáybaykhivậntốccủa nóhướngthẳngđứnglênphíatrên?
ĐS: 109 3c aa
Bài 19. Hai vật nhỏ giống nhau đặt cáchnhaud=1,6mtrên mặt phẳng nghiêng,góc nghiêngsovớiphươngnganglà =300 .VậtởdướicáchchânmặtphẳngnghiênglàL= 90cm(Hình1).Thảđồngthờichohaivậttrượtxuốngkhôngvậntốcđầu.Bỏquamasát.
Lấyg=10m/s2 .
1.Tìmvậntốccủamỗivậtởchânmặtphẳngnghiêngvàthờigiantrượtcủamỗivậttrên mặtphẳngnghiêng.
2. Saukhi đến chân mặt phẳng nghiêngthìhai vật lại trượtsangmặtphẳngngangtheocùngmộtđườngthẳng vớitốcđộkhôngđổibằngtốcđộcủachúngởchânmặt phẳngnghiêng.Hỏikhoảngcáchgiữacácvậtbằngbao
Bài21.HaicầuthủbóngđáAvàBchạytrênmộtđườngthẳngđếngặpnhauvớicùngtốc độ5,0m/s.Đểđiềuhànhtốttrậnđấu,trọngtàichạychổsaocho:luônđứngcáchcầuthủhậu vệA18mvàcáchcầuthủtiềnđạoBlà24m.KhikhoảngcáchgiữaA,Bbằng30mthìvận tốcvàgiatốccủatrọngtàilàbaonhiêu?
ĐS: 25/;3,86/T Vmsams
Bài22.Mộtngườiđứngởsânganhìnngangđầutoathứnhấtcủamộtđoàntàubắtđầu chuyểnđộngnhanhdầnđều.Toathứnhấtvượtquangườiấysauthờigian .Hỏitoathứ 1t nđiquangườiấytrongthờigianbaolâu?
BiếtcáctoacócùngđộdàilàS,bỏquakhoảngnốicáctoa.
ĐS: t 1(1) nnt
Bài23. HaivòngtrònbánkínhR,mộtvòngđứngyên,vòngcònlạichuyểnđộngtịnhtiến sátvòngkiavớivậntốc .TínhvậntốccủađiểmcắtCgiữahaivòngtrònkhikhoảng 0v cáchgiữahaitâm .d 1200
ĐS: 0 224 vR v Rd
6
7
13/ vms
Bài24.Haixeôtôbắtđầuchuyểnđộngthẳng,nhanhdầnđềuhướngđếnmộtngãtư(hình
2).Tạithờiđiểmbanđầu,xe1ởAvới vàcógiatốca1;xe2ởBvới
vàcógiatốca2.Choa1 =3m/s2,x01 =-15m;a2=4m/s2,x02 =-30m.
a)Tìmkhoảngcáchgiữachúngsau5skểtừthờiđiểmbanđầu.
b)Saubaolâuhaichấtđiểmlạigầnnhaunhất?Tínhkhoảngcáchgiữachúnglúcđó.
ĐS:a.6m;b.3,63s.
Bài25.MộtchấtđiểmMchuyểnđộngtrongmặtphẳngthẳngđứngQtheođườngcong
vớivậntốcvt.XácđịnhvậntốcvàgiatốctuyệtđốicủađiểmMdướidạng 652 yxx
hàmcủavt vàOMnếumặtphẳngQquayquanhtrụcquaOvàvuônggócvớiQvớivận tốc khôngđổi.
Bài26.MộtmángđôidạngkhungphẳnghìnhbìnhhànhABCD,mặtkhungđặttrongmặt phẳng thẳng đứng, cócác cạnh AB=DC=avàAD=BC=b.Các cạnh ABvàDCnghiêng mộtgóc sovớiphươngngang,cáccạnhBCvàADnghiêngmộtgóc sovớiphương thẳngđứng.Mángđôiđượcghéptừbốnốngnhỏcùngđường
kínhtrong,mặttrongcủacácốngrấtnhẵn(Hình1).

Haihònbinhỏ1và2cóđườngkínhnhỏhơnđườngkínhtrong củaốngmộtchút,đượcthảcùngmộtlúctừđỉnhA,trượtkhông masátđiđếnCbằnghaiconđường:bi1trượttheomángABC, bi2 trượt theomángADC.Khi đi quacácgócmáng(B,D):
cácbikhôngbịbậtngượclạivàtốcđộcoinhưkhôngbịthayđổi;thờigianvượtquagóc mángkhôngđángkể.
Bỏqualựccảncủakhôngkhí;giatốcrơitựdolàg.
a.TínhthờigiantrượtcủamỗibiđitừAđếnC.
b.TínhtốcđộmỗibikhiđếnCvàhãysosánhhaitốcđộnày.
c.Gọi lầnlượtlàtổngthờigianchuyểnđộngcủabi1vàbi2khiđitừAđếnCvà 12 , CCtt
đặt . 21CCttt
-Hãytìm theo ,a,bvàg. t
-Tìmđiềukiệncủa đểbi2đếnCtrướcbi1.
ĐS:a. ; 1 2(ascos)2sin2 cossin C tginbgaa g g
2 2(ascos)2s2 sins C tginbgbcob g gco
b. =; = 1Cv2(ascos) ginb 2Cv2(ascos) ginb
c.; sinos2sin2s2(ascos)cossin c t gagbcoginb g
8
02OBx
01OAx
9
0045
I.2.CHUYỂNĐỘNGNÉM.
Bài1.Mộtvậtđượcnémtừmặtđấtvớivậntốc 0v
lập với phương nằm ngang một góc.Tìm tầm xa đạtđược,vớigócném nàothìtầmxacựcđại.
ĐS: 045
Bài2.Némmộtvậtvớivậntốcbanđầu lậpvớiphươngnằmngangmộtgóc.Tìm 0v
thờigianđểvậntốccủavậtvuônggócvớiphươngbanđầu.
ĐS: với 0 sin v t g 045
Bài3.VậtAđượcnémthẳngđứnglêntrêntừđộcao sovớimặtđấtvớivậntốc 300m
banđầu .Sauđó vậtBđượcnémthẳngđứnglêntrêntừđộcao sovới 20/ms1s 250m mătđấtvớivậntốcbanđầu Bỏquasứccảnkhôngkhí,lấy Chọn 25/ms g 210/ms gốctoạđộởmặtđất,chiềudươnghướngthẳngđứnglêntrên,gốcthờigianlàlúcném vậtA.
1.ViếtphươngtrìnhchuyểnđộngcủacácvậtA,B?
2.Tínhthờigianchuyểnđộngcủacácvật?
3.Thờiđiểmnàohaivậtcócùngđộcao?Xácđịnhvậntốccácvậttạithờiđiểmđó?
ĐS:
;
Bài 4. Cùng một lúc, từ cùng một điểm O ở độ caohso với mặt đất, hai vật được ném ngangtheohaihướngngượcnhauvớivậntốcđầulầnlượtlàv01 =30m/svàv02 =40m/s.
Bỏquasứccảnkhôngkhí.Lấygiatốcrơitựdog=10m/s2.Chobiếtngaytrướckhiva chạm,vectơvậntốccủahaivậtcóphươngvuônggócvớinhau.Xácđịnhđộcaosovới mặtđấtcủađiểm
ĐS: 0102 260() hvvm
Bài5.Haihạtchuyểnđộngtrongtrọngtrườngđềuvớigiatốctrọngtrườnglà .Banđầu, g haihạtởcùngmộtđiểmvàcácvậntốccóđộlớnlầnlượtlàv01 =3m/s,v02 =3m/s,có phươngđềunằmngangtheohaichiềungượcnhau.Hãyxácđịnhkhoảngcáchgiữahaihạt tạithờiđiểmcácvectơvậntốccủachúngcóphươngvuônggócvớinhauvàthờiđiểmđó.
ĐS: ;L= . 0102vv t g 0102 0102 () vv vv g
Bài6.Mộtvậtnhỏđượcnémlênxiêngóc sovớiđườngnằmngang,vớivậntốcđầucó
độlớnv0 Bỏquasứccảncủakhôngkhí.Hãyxácđịnh:
a.Độđờicủavậttheothờigian .()rt
b.vectơvậntốctrungbình trongthờigian giâyđầutiênvàtrongcảquátrìnhchuyển v động.
ĐS:a. ;b.2 00 1 2
Bài7.Chứngminhrằngởmộtđộcaonàođósovớimặtđấttanémmộtvật,khiđạttầm xacựcđại,vậntốcbanđầuvàvậntốcngaykhichạmđấtvuônggócvớinhau.
Bài8.Mộtvậtđượcnémlêntheophươnghợpvớiphươngngangmộtgócα.Tạithờiđiểm tsaukhiném,véctơvậntốccủavật lệchmộtgócφsovới .Tìmt. v 0v
ĐS: .sin cos v t g
Bài9.Haivậtđượcnémcùngmộtlúcvớivéctơvậntốclầnlượtlà và lầnlượthợp 01v02v vớiphươngngangcácgóc và .Saukhoảngthờigiantthìvéctơvậntốchaivậtsong 12 songvớinhau.Tìmt.
10
5,3 ts , 33/A vms 18/B vms
1.
2.10s;3. 1 2 2 2 300205;25025(1)5(1);1 xttxttt
O. 0v v 2 11
g
rrrvtgt 0 02 () Vvgvg g
ĐS: 010221 011022
sin() (coscos) vv t gvv
Bài10.MộthònđáđượcnémlêntừmặtđấtvớivậntốcbanđầuhướngtớiđiểmA.Hai điểmOvàAcùngnằmtrênmặtphẳngthẳngđứngvàđiểmAcáchmặtđấtmộtkhoảng
bằngAH=h.MộtgiâysaukhinémhònđárơiđúngđiểmH.Bỏquasứccảnkhôngkhí. Lấyg=10m/s2.Tìmh.

ĐS: 5 2 hgm
Bài11.NémmộthònđátừđiểmOtrênmặtđất,saumộtgiâynóđếnđiểmB.Biếtrằng véctơvậntốctạiBvuônggócvớivậntốcbanđầu.XácđịnhkhoảngcáchOB.Bỏquasức cảnkhôngkhí.Lấyg=10m/s2
ĐS:5m.
Bài12.ChúmèoTomởđầumộtnócnhà(điểmBtrênhình)nhảyxuốngvồchuộtJerry.
NhưngJerryởdướiđất(điểmA)pháthiệnvàdùngsúngcaosubắnvàoMèo. Viênsỏi bắnratừsúngcaosucủaJerrycùnglúcTomnhảyxuốngvàđậpvàoTomởchínhgiữa
đoạnAB.TínhđộcaoHcuảnócnhà.BiếtgóchợpbởiABvớiphươngnganglà ,030 vậntốccủasỏibắnratừ súngcủaJerrylà7m/scònTomnhảytheophươngngang.Bỏqua sứccảncủakhôngkhí.Lấyg=10m/s2
Bài13.Haivậtnhỏđượcnémđồngthờitừcùngmộtđiểm:vật(1)đượcnémthẳnglên, vật(2)némxiêngóc =600 (chếchlên)sovớiphươngngang.Vậntốcbanđầucủamỗi vậtcóđộlớnlàv0=25m/s.Bỏquasứccảncủakhôngkhí.Tìmkhoảngcáchgiữahaivật sauthờigian1,7skểtừlúcném?
Đơnvịtính:Khoảngcách(m)
ĐS: d=v0.t 22 cos(sin1)
Bài14.MộthònđáđượcnémtốcđộvtừđộcaoHsovớimặtđấtvớigócnémαsovới mặtphẳngnằmngang.Hònđárơiđếnđấtcánhchỗnémtheophươngngangmộtkhoảng L.
a)Lậpphươngtrìnhquỹđạochuyểnđộngcủavậttheov,H,g,α,L.
b)ChoH=3m,α=450,L=42m,g=10m/s2 Tìmtốcđộvcủahònđákhiném.
ĐS:
Bài15.HaiđiểmA,Bởtrênmặtđất,cáchnhau10(m).TừAbắnvật1vớigócbắn . 030
TừBbắnvật2vớigócbắn (nhưhìnhvẽ).Vậntốc 060 banđầucủahaivậtđềucóđộlớnbằng40(m/s)vàđồng phẳng.Chobiếtvật2đượcbắnsaukhibắnvật1là (s)
vàtrênđườngbayhaivậtsẽvachạmnhauởđiểmM.Lấy
g = 10 2 /.ms

Xácđịnh vàtọađộđiểmM.
ĐS:Với 0,2(s), yM = 7,2(m),xM = 13,8 (m)
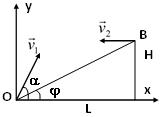
Bài16.Mộtmáybaynémbom,baytheophươngngangởđộcaoH=500msovớimặt đất,chuyểnđộngnhanhdầnđềuvớigiatốca=2m/s2 vàcácquảbomlầnlượtđượcthả
saunhữngkhoảngthờigianbằngnhaut=0,5s.Tìmkhoảngcáchgiữacácđiểmrơicủa
12
ĐS: m gtg Hvtg2,8 (14) 4 2 22 1 13
12 4
= (m/s) 0v
quảbomthứ9vàthứmườimộttrênmặtđấtnếuquảbomthứnhấtđượcthảrakhivậntốc củamáybaylàv0 =100m/s.Chog=10m/s2 vàbỏquasứccảnkhôngkhí.
ĐS: S129m
Bài17 Mộtôtôcủađịchđangleothẳnglênmộtquảđồivớivậntốckhôngđổilà2,5m/s. Đồicósườndốclàmộtmặtphẳngnghiênghợpvớiphươngngangmộtgócbằng300.Trong mặtphẳngthẳngđứngcóchứaôtô,ngườitabắnquảđạnpháotừchândốcvớigócbắn600 sovớiphươngngang.Lúcbắnthìôtôcáchpháo500m.Muốnđạnbắntrúngôtôthìvậntốc củađạnphảilàbaonhiêu?Chog=10m/s2
ĐS:v=88,9747m/s.
Bài18.MộtvậtđượcnémtừđiểmOnàođó,sauthờigian1s
vậtngaytrướckhichạmđấtcóphươngvuônggócvớivậntốclúcném.Tìmkhoảngcách từđiểmnémtớiđiểmchạmđất?
ĐS:4,9(m).
Bài19.Mộtvậtđượcnémlêntừmặtđấtvớivậntốcvo nghiênggóc vớiphươngngang.
Cáchđiểmnémkhoảngnàođócótấmthépthẳngđứng,mặtphẳngquĩđạocủavậtvuông gócvớitấmthép,vachạmgiữavậtvớitấmthéplàtuyệtđốiđànhồi.
1.Cho khoảng cách từ tấm thép tới điểm némlàL. Điểm rơi của vật cách tấm thépbao nhiêu?
2.Nếutấmthépchuyểnđộngvớivậntốcuvềphíavậtvàsauvachạmvậtrơitrởvềđúng
điểmnémthìthờigiantừlúcnémđếnlúcvachạmbằngbaonhiêu?
Bài21 Chứngminhrằngtừmộtđộcaonàođósovớimặtđấttanémmộtvậtthìkhiđạt tớitầmxacựcđại,vậntốcbanđầuvàvậntốcngaytrướckhichạmđấtvuônggócvớinhau.
Gợiý:Sửdụngcôngthức: trongđó làvậntốcbanđầu, làvậntốctạithời 0 vvgt
0v
v điểmt.
Bài22.Từhaiđiểmởcùngđộcaohtrênmặtđấtvàcáchnhaumộtkhoảngl,ngườitađồng thời némhaihòn đá: một hướng lêntrêntheo phương thẳng đứng với vận tốc và một 1v theo phương nằm ngang với vận tốc . Hỏi trongquátrìnhhaihòn đá chuyển động, 2v khoảngcáchngắnnhấtgiữachúngbằngbaonhiêu?Hãyxácđịnhthờiđiểmđó.
Biếtrằngvậntốcbanđầucủahaihònđácùngnằmtrongmộtmặtphẳngthẳngđứng.
ĐS: ; 1
Bài23.Mộtngườiđứngtạichỗnémmộthònđávớivậntốc thìnócóthểrơiđếnmột 0v khoảngcáchkhôngxahơn .Hònđácóthểrơixathêmmộtkhoảngbằngbaonhiêunếu 0x
ngườinémđóđangchạyvớivậntốcvtheohướngném?
Chogiatốctrọngtrườngtạinơinémlàg.Bỏquasứccảncủakhôngkhícũngnhưchiều caocủangườiném.
ĐS: 1.x=Lmax -L = -L; 2.t= 3 0sin2v g 00 0
sincos2 cos vvu vug
Bài20.Mộtthùnghìnhtrụdàilnghiênggóc vớiphươngngang.Mộtquảcầunhỏbay vớivậntốcvo theophươngngangvàothùngvàvachạmđànhồivớithùng.Tìmthờigian quảcầuchuyểnđộngtrongthùng?
ĐS: . 22 02v xvv g
Bài24.NémmộtviênđátừđiểmAtrênmặtphẳngnghiêngvớivậntốc hợpvớimặt 0v phẳngngangmộtgóc =600 ,biết Bỏquasứccảncủakhôngkhí. 030
14
vậtrơixuốngđất.Vậntốc
15 ĐS:
Lthì 22 0cos 2 x v g 02 cot v tg g +Nếu >Lthì 22 0cos 2 x v g 0 1 2 0 2 cot11 cos v gLtgtg g v
+Nếu
22 12 dlv vv 2 22 12 lv t vv
a. TínhkhoảngcáchABtừđiểmnémđếnđiểmviênđárơi.
b. Tìmgóc hợpbởiphươngvéctơvậntốcvàphươngngangngaysauviênđáchạmmặt phăngnghiêngvàbánkínhquỹđạocủaviênđátạiB.
X= 2 02 202 00

ĐS:a. ;b.
2 2 0 0 2 2cossin()2 cos3 v v l g g 2 00 2 30; 33 v R g Bài25. Mộtchiếccôngtenơđặtsaochomặttrênnằmngangđượccầncẩucẩulênthẳng đứng lêncao với gia tốc a=0,5m/s2 Bốn giâysaukhi rời mặt đất người ngồi trên mặt côngtenơnémmộthònđávớivậntốcv0 =5,4m/stheophươnglàmvớimặtphẳngngang côngtenơgóc . 030
a. Tínhthờigiantừlúcnémđáđếnlúcnórơixuốngmặtđất. Biếtcôngtenơcaoh=6(m)
b. Tínhkhoảngcáchtừnơiđáchạmđấtđếnvịtríbanđầucủatấmbêtông(coinhưmột điểm)lấyg=10m/s2 .
ĐS:a. 2s ;b.9,4m t

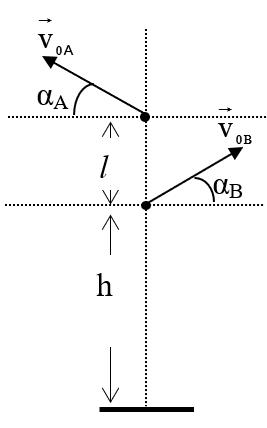
Bài26.Ngườitađặtmộtsúngcốidướimộtcănhầmcóđộsâuh.Hỏiphảiđặtsúngcách váchhầmmộtkhoảnglbaonhiêusovớiphươngngangđểtầmxaScủađạntrênmặtđất làlớnnhất?Tínhtầmxanàybiếtvậntốcđầucủađạnkhirờisúnglà .0v
Bài27.Dướihầmcóđộsâuh,đặtmộtsúngcối.Hỏiphảiđặtsúngcáchváchhầmkhoảng cáchlbằngbaonhiêuvànòngsúngnghiênggóc bằng baonhiêuso với phương ngang để tầm
xatrênmặtđấtslàlớnnhất?Tínhtầmxađó.Vận tốcbanđầucủađạnlàV0.
1gh arccos 2v
Bài28.Mộtbờvựcmặtcắtđứngcódạngmộtphầnparabol(hìnhvẽ).TừđiểmAtrênsườn bờvực,ởđộcaoh=20msovớiđáyvựcvàcáchđiểmBđốidiện trênbờbênkia(cùng độcao,cùngnằmtrong mặtphẳngcắt)mộtkhoảngl=50m,bắnmộtquảđạnpháoxiên lênvớivậntốcv0 =20m/s,theohướnghợpvớiphươngnằmnganggóc =600 .Bỏqua lựccảncủakhôngkhívàlấyg=10m/s2.HãyxácđịnhkhoảngcáchtừđiểmrơiCcủavật đếnvịtríAnémvật.
NhậnxétNếutavẽphác
họaquỹđạochuyểnđộngcủavật
sau
khinémthìthấyđiểmnémvậtvàđiểmvậtrơilàhaigiaođiểm củahaiparabol.Vịtrícácgiaođiểmđượcxácđịnhkhibiết phươngtrìnhcủacácparabol.
ĐS:AC=42,37m
Bài29. HaivậtnhỏAvàBcùngnằmtrênmộtđườngthẳngđứngnhưngcóđộcaochênh lệch nhaul=2m.Ném đồng thời hai vật lêncaotheo phương hợp vớiphươngnằmnganggóc
và .Haivậtchuyểnđộngngượcchiềuvàcóvận 0 A30 0 B45
tốc ban đầu . Bỏ qua sức cản của không 0A v4m/s; 0B v5m/s khívàcoiđộcaobanđầuđủlớn,lấyg=10m/s2.Tínhkhoảngcách giữahaivậtkhivậntốctoànphầncủachúngvuônggócvớinhau.
ĐS: d2,7032m
Bài30.CâubéBđangởbancông.CâubéAđangởdướiđấtvàném
mộtquảbónglên.QuảbóngsaukhivạchmộtđườngcongrơitrúngchâncậubéBvàmất
16
ĐS: 2 0 17
2v1gh1gh.v2ghg2v2v
mộtkhoảngthờigian1s.Biếtrằngcácvéctơvậntốccủaquảbóngkhinémvàlúcrơitrúng châncậubéBvuônggócvớinhau.Lấyg=10m/s2 ,bỏquasứccảncủakhôngkhí.
a)Tínhkhoảngcáchgiữahaicậubé.
b)CâubéBphảinémtrởlạivớitốcđộnhỏnhấtbằngbaonhiêuđểbóngtrúngchâncậu béA,nếubiếtđộcaocủabancônglà3m?
ĐS:a.5m;b.2 5m/s.
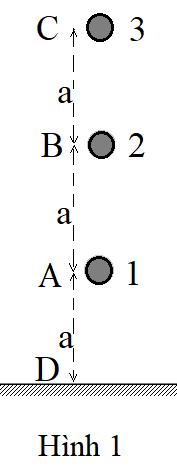

Bài31.Ởmépcủamộtchiếcbànchiềucaoh,cómộtquảcầuđồng
chất bánkínhR=1(cm) . Đẩy chotâmO của quả cầu lệch () Rh
khỏiđườngthẳngđứngđiquaA,quảcầurơixuốngđấtvậntốcban
đầubằng0.Tínhthờigianrơivàtầmxacủaquảcầu(g=10m/s2).
ĐS: ; 101054 33. tgRgRgh g
22 101054 27 R X gRgRgh g
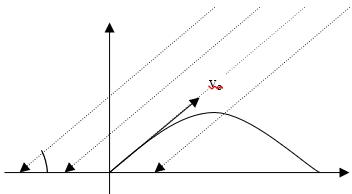
Bài32.Mặttrờinằmởđộcaogóc sovớimặtphẳngngang.Hỏicầnphảinémmộtvật
trongmặtphẳngthẳngđứngđiquamặttrờidướigócném bằngbaonhiêuđểbóngcủa vậtđiđượcquãngđườnglớnnhấttrênmặtđất?
+Khi <450 , Vậytacầnnémvậtthẳngđứng =900
+Khi >450,tacầnnémvậtdướigóc450
Bài33.Cầnnémmộtquảbóngchuyềnbánkínhrtừđộcaoh=2m,cáchrổbóngl=5m theophươngngangtreoởđộcaoH=3mvớigócném nhỏnhấtlàbaonhiêuđểnóbay quarổtừtrênxuốngmàkhôngvachạmvớivòngrổ.ChobánkínhvòngrổlàR=2r.Bỏ quabiếnthiênvậntốcbóngtrongthờigianbayquamiệngrổ.
ĐS: 440
Bài34.TừđiểmAmộtvậtđượcnémxiêngóc,saukhivachạmđànhồitạiđiểmBvới mộtmặtphẳngnghiêng,nónảylênvàlạirơixuốngchínhđiểmA.ThờigianbaytừAđến Blàt1=1,2(s);từBvềAlàt2=1(s).TìmkhoảngcáchAB?
ĐS:6m.
Bài35.Có3viênbinhỏđồngchấtgiốnghệtnhau,đượcthảrơitựdocùngmộtlúc,không vậntốcđầutừbavịtríA(bi1),B(bi2),C(bi3)trêncùngmộtđường thẳngđứng(Hình1).BiếtAD=AB=BC=a,vớiDlàmộtđiểmtrênsàn
màbi1sẽvachạmvớisànởđó.Coicácvachạmtuyệtđốiđànhồixuyên tâm;bỏqualựccảnkhôngkhí;bỏquasựthayđổigiatốcrơitựdogtheo độcao;bỏquathờigianvachạm.Chọnmốcthờigianlúccácbibắtđầu
ĐS:
+Khi =450, tacầnnémvậtthẳngđứng =900 hoặcgóc =450
rơi.Gọi làthờigianrơitựdocủabi1ởđộcaoađếnkhichạmsànlần
1T đầu.
a.Vẽpháchọađồthịtọađộ-thờigiancủacácviênbitrêncùnghìnhvẽtrongthờigian .Hãymôtảđồthịtrênchotừngviênbi.
1023tT
b.Gọi lầnlượtlànhữngthờiđiểmnhỏnhấtbi2vàbi3 nảylênđạtđộcaolớnnhất 23 , TT saunhữngvachạm.Tìm .23 , TT
c.Tìmđộcaolớnnhấtmỗiviênbisaunhiềulầnvachạm.
18
19
I.3.TÍNHTƯƠNGĐỐICHUYỂNĐỘNG.
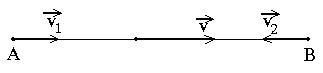
Bài1. Haivậtcáchnhau100mchuyểnđộngtrênmộtđườngthẳngđếngậpnhauvớivận tốclầnlượtlà ,trongkhoảng2vậttrênđoạnthẳngmàchúngchuyển vmsvms 5/;5/12
độngcómộtvậtnhỏluônchuyểnđộngthẳngđềuvớivậntốcv=30m/scùngchuyểnđộng trênđườngthẳngmà2vật(1)và(2)chuyểnđộng.Mỗikhivậttrênđếngặpvật(1)hoặc vật(2)thìvậntốccủanósẽđổihướngngượctrởlạivàcoinhưvẫngiũnguyênđộlớnvận tốccủanó.Hỏikhivật(1)vàvât(2)gặpnhauthìquãngđườngvậtnhỏđiđượccótổng chiềudàilàbaonhiêu?
ĐS:300m.
Bài 2. Hai vật chuyển động với vận tốc không đổi trênhai đường thẳng vuônggóc với nhauchov1 =30m/s,v2 =20m/s.Tạithờiđiểmkhoảngcáchgiữahaivậtnhỏnhấtthìvật mộtgiaođiểm củaquỹđạođoạnS1 =500m,hỏilúcđóvậthaicáchgiaođiểmtrênmột đoạnS2 làbaonhiêu?
ĐS:750m.
Bài3.Mộtôtôđitrongcơnmưavớitốcđộ
54km/h.Gióthổingượcchiềuxechạyvớitốc
độ 3m/s. Một người ngồi trênxe thấy các hạt nước mưa rơi xuống theo phương tạo với đườngthẳngđứngmộtgóc45o
a.Xácđịnhvậntốccủaôtôđốivớigió.
b.Xácđịnhvậntốccủacáchạtnướcmưađốivớimặtđất.
ĐS:a.18m/s;b.18,25(m/s2).
Bài4.HaichấtđiểmchuyểnđộngdọctheotrụcOx.Vậntốccủachấtđiểm(1)và(2)phụ thuộcthờigiantheoquyluật . 121sin2;2sin2 4 vtvt
Trongđóv();t(). / mss
1.Xácđịnhnhữngthờiđiểmmàvậntốchaivậtbằngnhau.
20 ĐS:b. ; ;c. ,, 2 14a22 TT g 3 1 6a 223 TT g 1x ma ha 2x2 ma ha 3x3 ma ha 21
2.Tronghệquychiếugắnvớivật(2)thìvật(1)chuyểnđộngvớivậntốcbaonhiêu.Tìm nhữngthờiđiểmmàđộlớnvậntốcnàylàlớnnhất,nhỏnhất.
ĐS:1. ;2. Độlớnvậntốclớnnhất tại
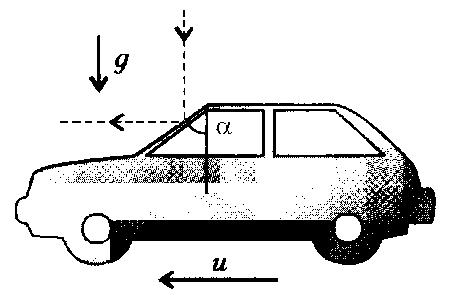
Bài8.Trongkhitrờiđangmưađá,mộtôtôchạytrênđườngnằmngangvớivậntốckhông
đổiu=25km/h.Mộthạtmưađárơixuốngvachạmvớitấmkínhchắngióphíatrướcvà
bật ratheo phương ngangcùng chiều chuyển động của xe.Kính chắn giónghiênggóc sovớiphươngthẳngđứng(H.8).Chorằngtrướckhiva 030
chạmvậntốccáchạtmưacóphươngthẳngđứngvàvachạmlà hoàntoànđànhồi,hãytìmvậntốchạtmưađá:
Bài5.Chovậntốcdòngnướclà vàvậntốccủathuyềnkhinướcđứngyênlà .Hỏi
ngườichèothuyềnphảichèotheohướngnàođểthuyềnbịtrôitheodòngnướclàítnhất?
ĐS:Nếu >uthì .Nếu <uthì dv tduvs/ in tdv vu d s/ in
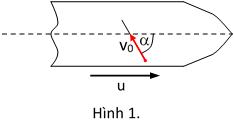
Bài6.Trênboongmộtcontàuthủyđangchuyểnđộngđốivớibờ
sôngvớivậntốcu=15km/hcómộthànhkháchđivớivậntốc
đốivớiboongtàu,theophươnglậpvớitrụcdọccủatàu
góc (xemH.1).Hãytìmvậntốccủahànhkháchđóđốivớibờ.
ĐS: 13km/h. 7 3 u v
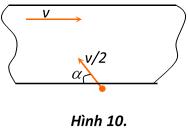
Bài7.Mộtbăngchuyềnchuyểnđộngvớivậntốckhôngđổiv.Băngnằmtrongcùngmặt phẳngvớimặtbàn.Mộthộpnhỏđangchuyểnđộngtrênmặtbànvớivậntốcv/2thìđivào băngchuyềntheohướnglậpmộtgóc (=1/9)vớimépbăng. cos Hệsốmasáttrượtgiữahộpvàbănglà .
1.Độlớnvậntốccủahộpđốivớibăngvàolúcbắtđầuchuyểnđộng
trênbăngchuyềnbằngbaonhiêu?
2.Vớiđộrộngtốithiểucủabăngbằngbaonhiêuđểhộpkhôngđirakhỏibăng?
1.trướckhivachạm;
2.saukhivachạm.
ĐS:1.;2. =75km/h. 1343/ vukmh 23 vu

Bài9.Chocơhệnhưhìnhvẽ.Bchuyểnđộngsangphảivớigiatốc ,cònvậtnhỏAđược a nốivớiđiểmCbằngmộtsợidâykhôngdãnđượcnânglêntheođường dốichínhcủamộtmặttrụcủavậtB.MặtnàycóbánkínhR.Giảsửtại thờiđiểmbanđầuvậtAnằmtrênsànvàđangđứngyên,sợidâyluôn căng.HãytínhvậntốctrungbìnhcủavậtAtrongquátrìnhAđitừsàn lênđếnđiểmcaonhấtcủatrụB(điểmD).
ĐS: v 2 1(48) 2 aR
Bài10.Haivậtm1 vàm2 chuyểnđộngthẳngđềuvớivậntốclầnlượtlà và .Vậtm2 1v2v xuấtpháttừB.
Tìmkhoảngcáchngắnnhấtgiữachúngtrongquátrình
chuyểnđộngvàthờigianđạtđượckhoảngcáchđó? Biết
khoảngcáchbanđầugiữachúnglà vàgócgiữahaiđường l
thẳnglà .
22
*tkkN 122/ vms 2 tkkN Vậntốcnhỏnhất tại 120v *tkkN
u tdv
3
0/vu
0
30
ĐS:1. ;2. 0 7 6 v v . g dv 2 54 75 23
v0 O A
sin 2cos lv vvvv
ĐS: mind 2 2 2 1122
Bài11.Trongphòngcómộtcáiđĩaquayvớivậntốcgóc khôngđổiquanhtrụccốđịnh
Ođiquatâmđĩavàvuônggócvớiđĩa.Mộtconbọdừabòtrênmặtđĩadọctheobánkính
vớivậntốc đốivớiđĩa(H.V).Hãytìmđộlớnvậntốccủaconbọdừađốivớiphòngvào 0v
thờiđiểmnóởđiểmAcáchtrụcOkhoảngR.
ĐS: 222 0 vvR
Bài 12.Bánkính của một hànhtinhr=2000km. Vận tốc các điểm trên xích đạo bằng Một vệ tinh chuyển động trong mặt phẳng ksvm,/061
xíchđạocủahànhtinhtrênquỹđạobánkínhR=3000km,theochiềuquay
củahànhtinhvớivậntốc .Hãytìmvậntốccủavệtinhđốivới ksvm/22 hànhtinh.
ĐS:1,1km/s.
Bài13.MộtđĩanặngbánkínhRcó2dâykhôngdãnquấnvào.
Cácđầutựdocủadâygắnchặt(hình22).Khikhốiđĩachuyển
động thìdâyluôn căng. ở một thời điểm vận tốc góc của đĩa bằng vàgóc giữa cácdâylà .Tìm vận tốc của tâm đĩa ở thờiđiểmnày.
ĐS: cos/2 R v
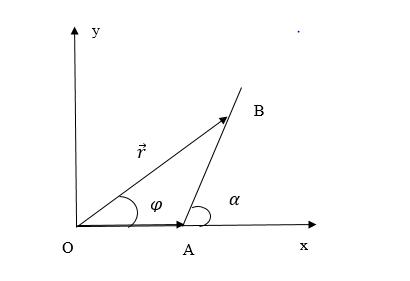
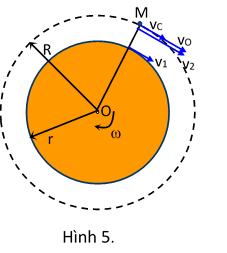
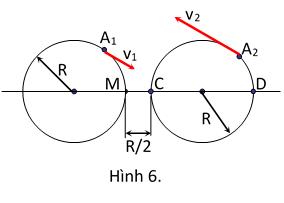
Bài14. TrênhaiđườngtrònbánkínhmỗiđườngbằngR,nằmtrongcùngmộtmặtphẳng, cóhaiôtô và chuyểnđộngvớicácvậntốc và .Kíchthước 1A2A khvvm/201 vv 22
cácôtôrấtnhỏsovớiR.Vàomộtthờiđiểmnàođóthìcácôtô nằmởcácđiểmMvàCcáchnhauR/2(H.6).
1)Hãytìmvậntốccủaôtô đốivớihệquychiếugắnliềnvớiôtô vàothờiđiểmđó. 2A 1A
2)Hãytìmvậntốccủaôtô đốivớihệquychiếugắnliềnvớiôtô khi ởđiểmD. 2A 1A2A
ĐS:1.10km/h;2.110km/h.

I.4ĐỘNGHỌCTOÁNLÝ.
Bài1.ChấtđiểmbắtđầuchuyểnđộngtừAtheođoạnthẳng ABvớivậntốcbấtkì.LấymộtđiểmOngoàiABlàmcực
vàOAlàm trục cực. Tìm phương trình chuyển động của
chấtđiểmdướidạngtọađộcực.
25
ĐS: cos2 0 2 2 sincoscot 1cot rr
Bài2.CóhaitàuAvàBcáchnhaumộtkhoảngađồngthờitàuAvàBchuyểnđộngvới vận tốc không đổi lần lượt làvvàu .TàuB chuyển động trên một đường thẳng vu (đườngthẳngnàyvuônggócvớiđoạnthẳngnốicácvịtríbanđầucủahaitàu,còntàuA luônhướngvềtầuB.HỏisaubaolâutàuAđuổikịptàuB?
ĐS: 22 vu av
Bài3.MộtngườidạochơiCđidọctheomộtconđườngthẳngtrùngvớitrụcOxvớivận tốckhôngđổilàv.Conchócủangườinàyởthờiđiểmbanđầu(t=0)ởđiểmA,cáchO mộtkhoảnglàL(OA Ox)bắtđầuchạyvớivậntốckhôngđổilàuluônhướngvềphía chủ.Saubaolâuconchóđuổikịpchủnếu
Ápdụngkếtquảtíchphân: ;với >1.
ĐS: 02 Lu t
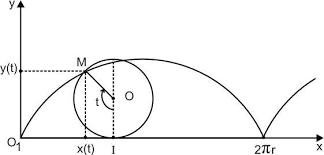
Bài4. Hệtọađộtrụ.Chuyểnđộngxycloit
Xétchuyểnđộnglănkhôngtrượtcủađườngtròntrênđườngthẳng.Giảsửvậntốccủatâm đườngtrònlàv(t)vàbánkínhcủa đườngtrònlàR.
a.Lậpphươngtrìnhchuyểnđộng của một điểm M bất kì thuộc đườngtròn.
b.Khảosátvậntốcvàgiatốccủa Mnhữnglúcnhữngnóởtrên
tròn.
c.GiảsửV=V0=const,khảosáttínhbiếnđổichuyểnđộngtrênmộtcungquỹđạoứngvới
vònglăncủađườngtròn.
ĐS:a. ;b.Vậntốcvx =0vàvy=0;Giatốc:ax=0vàay=
làchuyểnđộngnhanhdần;nếuπ<φ<2πlàchuyểnđộngchậmdần.
Bài5.(ĐềthiHSGQG2005):MộtcanôchuyểnđộngtừbếnAcủabờsôngbênnàysang bờsôngbênkia.Sôngthẳngvàcóchiềurộnglàb.NgườitadựnghệtọađộOxymàgốcO
tạiA,trụcOxvuônggócvớibờsông,cắtbờđốidiệnởB,trụcOyhướngdọcbờsôngtheo chiềunướcchảy.Docấutạocủadòngsông,vậntốcchảyucủanướctạiđiểmcótọađộx phụthuộcvàoxtheoquyluật:
21 [(1)()()] 5552o xxb u hxu bb
Trongđóuo làmộthằngsốdương,còn làhàmHeavisidecủabiến . Hàm () 2 hb x () 2 b x
HeavisidecủabiếnXđượcđịnhnghĩanhưsau:
h(X)=0khiX<0
h(X)=1khi X0
1.Giảsửvậntốccủacanôđốivớinướccóđộlớnvo khôngđổivàluônhướngtheophương vuônggócvớibờsông.
a.Xácđịnhphươngtrìnhquỹđạovàpháchọaquỹđạocủacanô
26
u>v.
2 2 2 0 1x tandx sinx21
u1 v
27
đườngthẳngtựacủađường
một
1 0 sin 1cos 1 M M xR yR Vtdt R 'R c.
tốc: 0V R 0 0 1cos sin x y vV vV 2 0 2 0 sin cos x y V a R V a R
Vậy Vậntốc: ;Gia
Nếu0<φ<π
b.Khicậpbờbênkia,canôcáchBmộtđoạnbaonhiêu?
c.Chứngminhrằnggiatốccủacanôsovớibờsôngphụthuộcbậcnhấtvàovo Tạisao giatốcnàylạiđổihướngđộtngộttạix=b/2
2.Giảsửvậntốccủacanôđốivớinướcluônhướngtheohướngvuônggócvớibờsong nhưngcóđộlớnthayđổisaochocanôcậpbờbênkiaởđiểmcáchBmộtđoạncvềphía hạlưutheomộtquỹđạothẳng.Lậpvậntốccủacanôtheox.
Bài8.Mộtquảbóngbànbắtđầurơitựdotừđộcaohsovớimặtsàn.Saukhivachạm chạmvớimặtsànnólạinảylênnhưngmấtđimộtphầnđộngnăng.Tínhthờigianchuyển độngcủaquảbóngbànnếucoirằngtỉsốcủađộlớnvậntốccủanósauvàtrướcmỗilần vachạmvớimặtsànkhôngđổivàbằnge(e<1).Giatốcrơitựdobằngg.
ĐS: (sốvachạm ) 12 1 eh t eg n
ĐS:1a. ;1b. 2 2 ()1055202 oo ooo oo ooo
uuuxuxubb yxx hx vvbbvvv
21 ()20o o
ubsyb v
Bài9.Mộtđầudâykhônggiãnvắtquaròngrọc cốđịnhtreovậtnhỏB,đầudâykialàđiểmAtrong
tayngườiđitrênmặtphẳngngangtheomộtđường
2. 21 1() 5552 o ubxxb v hx cbb
Bài6.MộtchấtđiểmchuyểnđộngtrongmặtphẳngxOy.Tọađộcủachấtđiểmthayđổi theoquyluật , ,vớiA, làhaihằngsốdương.Hãyxácđịnh: xAsint yA(1cost)
a.Quãngđườngđiđượccủachấtđiểmsauthờigian
b.Gócgiữavectơvậntốcvàvectơgiatốccủađiểmđó.
ĐS:a. ;b. sA(,)2 va
Bài7.Mộthạtchuyểnđộngtheomộtquỹđạophẳngy(x)vớivậntốcvcóđộlớnkhông đổi.Hãyxácđịnhgiatốccủahạtvàbánkínhcongcủaquỹđạotạiđiểmx=0,nếuquỹđạo códạng:
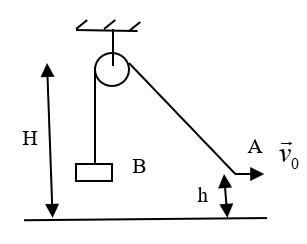
a.Mộtparaboly= x2
thẳngvớivậntốckhôngđổiv0=1m/s.Aluôncách
mặtđấth=1m.Khingườibắtđầuchuyểnđộng,
vậtBởmặtđất,dâyởhaibênròngrọcđềucăng vàcóphươngthẳngđứng.
ĐộcaocủaròngrọclàH=10m.Bánkínhròngrọckhôngđángkể.
a)TìmquanhệhàmsốgiữađộcaocủavậtBvàthờigianngườichuyểnđộng.
b)TìmvậntốccủavậtBkhingườiđiđượckhoảngthờigiant.
c) Để vật chạm tới ròng rọc thì người cần chuyển động trong khoảng thời gian tối thiểu
bằngbaonhiêu?
ĐS:a. ;b. ;c.t=16,73s.
819
Bài 10.HaithanhcứngbằngkimloạicóchiềudàiOA=l1 vàOB=l2 ,liênkếtvớinhau bởikhớpnốiO,đượcđặttrênmặtphẳngnhẵnnằmngang.
b.Mộtelip trongđó , lànhữnghằngsố.
1xy
NgườitakéohaiđầuA,Bcủathanhtheo
cùngphươngABnhưngngượcchiềunhau
vớivậntốckhôngđổilầnlượtlàv1 vàv2.Tìm giatốccủakhớpnốiOlúchaithanhvuônggóc nhau?
28
22
ĐS:a. ;2 R 2a2v 29
B yt
v t
2
281 t
1
A B 2v O
v
() () vvll a llll a
ĐS: Độ lớn gia tốc khớp nối: Hướng của hợp với thanhOB một 266 1212 22 1212
gócα: 2 12 21 tan al al
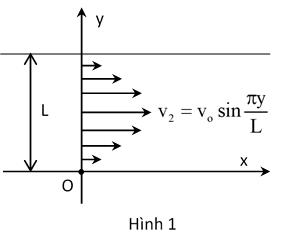
Bài11.MôtchiếccanôxuấtpháttừđiểmAtrênđườngcái,ôtônày cầnđếnđiểmD(trênđồngcỏ)trongthờigianngắnnhất.Biết
thức: (L:chiềurộngconsông),vo vàLlàhằngsố(hình1).Hãytìm: 2o yvvsin L
a)Giátrịvậntốcconthuyềntínhtronghệquychiếugắnvớibờsông.
b)XácđịnhkhoảngcáchtừđiểmOđếnđiểmthuyềncậpbếnởbờbênkiatheophương Ox.
.Vậntốcôtôchạytrênđườngcái(v1)lớnhơnvậntốc
ClAdD C ; ôtôtrênđồngcỏ(v2)nlần.HỏiôtôphảirờiđườngcáitạimộtđiểmBcáchCmộtđoạn xlàbaonhiêu?
ĐS: ,thờigianngắnnhất x 21 l n 1
2 mn 1 v dln t
Bài12.Mộtquảbóngđượcnémxuốngmộtmặtsànnằmngang.Độlớnthànhphầnvận tốc quả bóngtheo phương ngangvà phương thẳng đứng thay đổi sau mỗi va chạm theo quyluật:v0xn+1 = x.v0xn vàv0yn+1 = y.v0yn (Trongđó:v0n,v0n+1 tươngứnglàvậntốcsau lầnvachạmthứnvàthứn+1; x , y làhằngsốvànhỏhơn1).Quãngđườngtheophương ngangvàthờigiantừvachạmđầuđếnkhidừnglạilàLvàt0.Tìmgóchợpbởivậntốc
bóngtheo phương ngangngaysauva chạm đầu tiêntheoL,t0, x và y.Cho biết số va chạmlàrấtlớn.
ĐS:
Bài13.Mộtconthuyềnbơiquasôngtheophươngvuônggócvớidòngchảy,vớivậntốc khôngđổilàv1.Tạimọinơidòngchảyluônluônsong songvớihaibờ,nhưnggiátrịvậntốccủanóphụthuộc vào khoảng cách đến bờ, được biểu diễn theocông
ĐS:a. ;b. 222 1o yvvvsin L o 1
2vL x .v
Bài14.Trênmặtphẳngnằmngangcómột
cộttrụbánkínhRthẳngđứng,ngườitadùng
mộtsợidâychỉmảnhkhôngdãn,khốilượng
không đáng kể để nối một vật nhỏ với một
điểm trênvành trụ, điểm nàysát mặt phẳng
ngang. Ban đầu vật nhỏ nằm yên trên mặt phẳngvàdâyởtưthếcăng,lúcnàychiềudài
dâylàL. Truyền cho vật vận tốc v0 hướng
vuônggóc với dâyvà vật chuyển động trên mặt phẳng ngang cuốn dâyvào trụ. Hỏi sau baolâudâycuốnhếttrụ?Giảthiếttrongkhichuyểnđộngdâyluônnằmngang.Bỏquama sátvàbềdàycủadây.
ĐS:
Bài15.Mộthạtchuyểnđộngtheochiềudươngcủatrụcoxvớivậntốcsaocho (a vax làhằngsốdương).Biếtlúct=0hạtởvịtríx=0.
Hãyxácđịnh:
a.Vậntốcvàgiatốccủahạttheothờigian.
b.Vậntốctrungbìnhtrongkhoảngthờigiantừvịtríx=0đếnvịtríx.

30
1 1 22 0 0 0 1 21 y y x xy vgt tg vL
31
2 02 L t vR
ĐS:a.Vậntốc ;giatốc ;b.

Bài16.Mộtchấtđiểmchuyểnđộngchậmdầntrênmộtđườngthẳngvớimộtgiatốcmà độlớnwphụthuộcvậntốctheođịnhluật trongđóalàmộthằngsốdượng.Tại wav
thờiđiểmbanđầuvậntốccủahạtbằngv0.
Hỏiquảngđườngmàhạtđiđượcchođếnkhidừnglạivàthờigianđiquảngđườngấy?
Bài19.“Runningman”làcâuchuyệnvềmộtcổđộngviêntênlàTiếnchạyđuổitheomột chiếcxebuýtcủađộibóngđámàanhyêuthích.Chpavàblàhaiconđườngthẳngsong songvàngăncáchnhaubởimộtthảmcỏ.TiếnbanđầuởđiểmA,bếnxebuýtởđiểmM, cácđiểmCvàHđượcchọnsaochoACMHlàhìnhchữnhậtcóchiềurộngdvàchiềudài (Hình1). 3 ld
Bài17.MộtchấtđiểmchuyểnđộngchạmdầntrênbánkínhR.saochotạimỗiđiểmgia
tốctiéptuyếnvàgiatốcpháptuyếnluôncóđộlớnbằngnhau.Tạithờiđiểmbanđầut=0, vậntốccủachấtđiểmđólà .0v
Hãyxácđịnh:
a.Vậntốccủachấtđiểmtheothờigianvàtheoquãngđườngđiđược.
b.Giatốctoànphầntheovậntốcvàquãngđườngđiđược.
ĐS:a. ;b. v0
S Rve 2 2 02 s Rve a R
Bài18.Mộtconchóchạyvớitốcđộkhôngđổiv1 đuổitheoconthỏ,conthỏchạydọctheo mộtđườngthẳngvớitốcđộv2.Conchóluônhướngđếnvịtrícủaconthỏ.Tạithờiđiểm banđầucảhaiconvậtcùngởtrênmộtđườngthẳngvuônggócvớihướngchạycủathỏvà cáchnhaumộtkhoảnga.
a)Vậntốccủathỏvàchóphảithỏamãnđiềukiệnnàothìchóđuổikịpthỏ.
b)Trongđiềukiệnchóđuổikịpthỏ,tìmquãngđườngmàmỗiconđiđượcchođếnkhigặp nhau.
1.BiếtđộlớnvậntốcmàTiếnkhichạytrêncácđườnglà cònkhichạytrênthảmcỏlà 1v vớin=2và khôngđổi. 21/ vvn 2v
a)Tiếncầnphảichạytheoquỹđạocódạnggồmcácđoạnthẳngnhưthếnàođểthờigian đếnbếnMlàngắnnhất?
b)KhiquansátthấyxebuýtbắtđầurờibếnMhướngvềCvớivậntốckhôngđổivàcóđộ lớn thì Tiến quyết định chạy theo đường thẳng qua thảm cỏ để gặp xebuýt. Từ 22 Vv
điểmA,Tiếncầnchạytheohướngnàođểgặpđượcxebuýt?
2.Xebuýt chuyển động từ bến M hướng về C với vận tốc không đổi có độ lớn V=36 km/h.TạithờiđiểmxebuýtquađiểmNvới (xemhìnhvẽ)thìTiếnbắt 0 060NAH
đầudichuyểntừđiểmAvớivậntốcbằngkhông.Tiếnchọncáchchạysaochovéc-tơvận tốccủamìnhluônhướngvềxebuýt,cònđộlớnvậntốcluôntăngđểđảmbảomìnhluôn tiếnlạigầnxebuýtvớivậntốckhôngđổi.Tiếncóđuổikịpxebuýtkhông?Vìsao?
ĐS:1a.Chạytrênđườngmộtđoạn sauđóchạytrêncỏ. 2d3 AI 3
1b.TiếnchạytheohướngvuônggócvớiAM
32
2 2 a vt 2 2 a w 2 ax v
.
; 3 2 0 2 3 Sv a 0 2 tv a
ĐS:a.
ĐS:a. ;b.Thỏchạy ;chóchạy 12vv 2 1 122 12 av s vv 12 222 12 avv s vv 33
2.Qũyđạo ;Khiđuổikịpxebus,vậntốccủaTiếnphảiđạt54km/h. 223 rtgLconst 23
Tốcđộnàykhôngthểđạtđược.
Bài20.Mộtvậtnhỏ,khốilượngmnằmtrênmặtphẳngnghiênggóc sovớimặtngang.
Hệsốmasátgiữamvớimặtphẳngnghiênglà Ởthờiđiểmt=0,truyềnchovật tan.k
vậntốcv0 theophươngvừasongsongvớiđáymặtphẳngnghiêngvừasongsongvớimặt nghiêng.Chogiatốctrọngtrườnglàg.ChọntrụcOxnằmtrênmặtphẳngnghiêngvàvuông gócvớivéctơv0 nhưhình.HãyxácđịnhvậntốcVcủavậtkhinótạovớitrụcOxmộtgóc .
ĐS: 0 1cos v v
Bài21.Conđườngngắnnhất
TrênmộtmặtcầubánkínhR,vòngtrònlớn(nghĩalàvòngtrònbánkínhR)làconđường ngắnnhấtgiữahaiđiểm. Gọi làvĩđộvà làkinhđộ. Hãy xácđịnhchiềudàicủaconđườngngắnnhấtgiữaParis(1 = 48052’; 1 =2020’)vàTokyo(2 =35042’; 2 =139030’). Giảthiết,TráiđấtcóhìnhcầubánkínhR=6370km.
ĐS:9709,5km.
Bài22.Tathấyrằngkhiquảpháohoatrongkhôngkhílên đếnđiểmcaonhấtvànổthìdườngnhưtấtcảcácmảnhsáng
đềunằmtrênmộtmặtcầucótâmrơivớivậntốctăngdần. Bằngtínhtoánhãykhẳngđịnhđiềuđó.
ĐS: ; 0 2 11 k k vgg reetj kkk
Bài23.Bốnconrùađứngởbốnđỉnhcủahìnhvuôngcạnha,chúng
bắtđầuchuyểnđộng
vớivậntốckhôngđổi,độlớnvsaochomỗiconrùaluônhướngvềconbêncạnhtheochiều kimđồnghồ.
a.Hỏicácconrùagặpnhauởđâu,saubaolâu?
b. Quỹ đạo chuyển động của mỗi conrùacó dạng như thế nào?Coi mỗi conrùalà một chấtđiểm.
ĐS:a.Bốnconrùagặpnhauởtâmsauthờigian:. t a v
b.Phươngtrìnhquỹđạocủaconrùalàđườngxoắnlogarit:ri= với i=2,3,4là 2 a4e
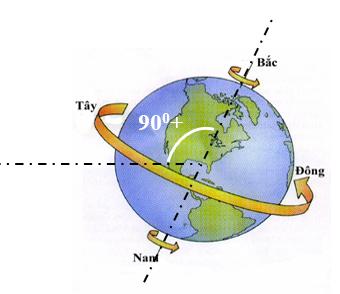

Bài24.Điểmchí
TrụccáccựcBắc–cựcNamhợpvớitrụcMặtTrời–TráiĐấtmộtgóc900 + .
Lúcđôngchí, =23,440
Trong hệ tọa độ Descartes gắn với Trái xyz 0,e,e,e,
Đấtđượcxácđịnhnhưsau:OtrùngvớitâmTráiĐất; : z e trụcnốicáccựcBắc–cựcNam;MặtTrờinằmtrongmặt phẳng(xOz).
a)Hãyxác định tọa độ của các điểm trênTrái Đất lúc MặtTrờimọcvàlúcMặtTrờilặn.
b)TínhthờigiangiữalúcMặtTrờimọcvàMặtTrờilặn
tạimộtđiểmtrênvĩđộ .Đểđơngiản,cóthểbỏquachuyểnđộngquayhằngnămcủaTrái ĐấtchungquanhMặtTrời.
Ápdụng:ởLille(nướcPháp)có =50038’.
34
0 1ktk g vveej k G M 35
d
Bài2
d
GọiClàvịtrígặpnhau 21 ; ACvtBCvt
Ápdụngđịnhlíhàmsốsin
chotamgiácABC
CHƯƠNGI.ĐỘNGHỌCCHẤTĐIỂM
I.1LỜIGIẢIĐỘNGHỌC
Bài1.Xéttạithờiđiểmt:VậtAởA’
VậtBởB’
Khoảngcáchd=A’B’
10 sin2cos.sin 22
Suyra:v2 cógiátrịminkhi()max=1vậy β=900 sin
Dođó (v2)min = 11 sin10,8 d vvkm a

Bài3.Xétchuyểnđộngtươngđốicủavật1sovớivật2tacó
ĐoạnBHvuônggócvớiđườngthẳngchứa
véctơvậntốc chínhlàkhoảngcách 12v ngắnnhấtgiữahaixe. dmin=BH
tan 2 1
3 5 v v 00 5,31 9
dmin=BH=BIsin
=(B0-0I)sin=(B0-0A.tan).sin= 1,166km
36
-----------------
với
d 0120 37 0 0
Tacó: sinsinsin dAOvtBOvt 10 sinsinsinsinsin dBOAO
10sin6053 2cos60sinsin 22
Nhậnxét:dmin(sin)1 2 mn53() dcm
Tacó 21 21 ..sin sinsinsin vtvt vv
11212 2() vvvvv
(3cossin)((3)1)(cossin)2
Bài4.Gọid1,d2 làkhoảngcáchtừvậtmộtvàvậthaiđếnOlúcđầutaxét(t=0).
0 3 sin30sin3sin ddvtdvt
dụngtínhchấtcủaphânthứctacó: 1121211121 3(3)()3 sin3sin3sinsin3sinsin dvtdvtdvtdvtdd


0120
Lúcđó: 0 12 21100 0 sin120390()sin30sin120sin30 dddddm
Vậy,khoảngcáchtừvậthaiđếnOlúcnàylà:d2 ’ =90(m)
Bài5.
KhiBdichuyểnmộtđoạns=v.tthìconkiếnđi
đượcmộtđoạnl=u.t.
Độcaomàconkiếnđạtđược:
với sinsinhlut 222 sinLvt L 2224 . huuLLtvty L
Vóiy= ĐặtX=t2 2224 . Ltvt 22 yvXLX
Nhậnxét: ylàtamthứcbậchaicóa=-v2<0 ymax tạiđỉnhParabol maxmax.hy 2 44 maxmax22 44()4 LL yy avv
tại 4 max2 4 L y v 2 222 bL X av
Vâyđộcaomàconkiếnđạtđượclà: maxmax2 huuL Lyv
Bài6. Chọnhệtrụctọađộkhôngvuônggócnhưhìnhvẽ
GiảsửtàuAchuyểnđộngtrênOyvềO,tàuBchuyểnđộngtrênOxvềO
Phươngtrìnhchuyểnđộngcủachúnglầnlượclà
38
Áp
21
0 0 0 3sin3sin(30)3(sin30coscos30sin) 33cossin 22 21 0 3 sin30311cossinsin 222 dd d 0 21 21(3)sin303 313cossin cossin 22 dd dd d Vậy 212133 3cossin ddddd y Khoảngcáchgiữahaivậtdmin ymax vớiy= 2(3cossin) ÁpdụngbấtđẳngthứcBunhiaCôpski: 39 22222
ymax=2 và 0 3cos cot330 1sing
Ápdụngđịnhlýhàmsintacó: 12 1122 sinsinsinsinsinsin ddddvtdvt d
Vì nêntacó: 1 23 v v
1121
0 3 sin303sinsin ddd
Mặtkhác,tacó: 0 0 sinsin(180)sin()sin(30)
60(1) 40(2) yvt xvt
t=2(s)<4(s). 4a 25 2)(0
Vậyv12 cógiátrịnhỏnhấtkhit=2s.
dOAOBOAOBCOS dxyxy dxyxy
2.60 2cos60 (3)
2221002800(4)dvtvt
Vếphảilàmộttamthứcbậchaicógiátrịnhỏnhấtlà min 30017,32 4 dkm a
Bài7.Chọnmốcthờigianlúc2vậtquaO
-PhươngtrìnhvậntốccủavậtthứnhấttrêntrụcOx:
v1 =v01 +a1t=6+t
-PhườngtrìnhvậntốccủavậtthứhaitrêntrụcOy:
v2 =v02 +a2t=-8+2t
-Khoảngthờigianvậtthứhaidừnglại:v2 =0=>t= 4s
-Vậntốccủavậtthứnhấtđốivớivậtthứhailà:
vvv
112 2
mộttamthứcbậchaicógiátrịnhỏnhấtlà
=>(v12)min = 8,94(m/s)2.21005.20 2
Khiđóv1 =8m/s, .vớiCos =v1/v12 =8/8,94 0,895 (,) 112vv
=> =26,50
-Vậyv12 đạtgiátrịnhỏnhấtlà8,94m/stạithờiđiểmt=2svàhợpvớiOxgóc26,50
Bài8. Gọis1 s2 làquãngđườngxeđitronghaigiaiđoạnứngvớigiatốca1,a
2
; 1 1 1 2s t a 2 2 2 2s t a
tổnggiờigianxeđi
t= . 12 12 12
ÁpdụngbấtđẳngthứcCôsitacó
222 2 ssss aaaa
1212 1212
Đểthờigianxeđilàngắnnhấtthì
1 2(1)sssa aasa
Mặtkhács1 +s2 =200(2) suyra s1=66,67m,s2 =33,33m


Vậyt=15,63s
Bài9.Chọntrụctoạđộthẳngđứngchiềudươngtrênxuống
40
Tạithờiđiểmtkhoảngcáchgiữahaitàulà 222 0 2220 222
Thay(1),(2)vào(3)tađược
1v 2
=>v12 = = 2 2 2 1 vv
12 =
50 2tt
.Do vuônggócvới .
v
22 (6)(82) tt =>v
.2100
là
41
Vếphải
t1,,t2làthờigianxeđitronghaigiaiđoạnứngvớigiatốcs1,s2
tacó
22ss tt aa
1212 1221
Phươngtrìnhchuyểnđôngcủakhícầuvàvật
x1=2t
Phươngtrìnhchuyểnđộngcủavật
x2=-18t+5t2
Phươngtrìnhvậntốccủakhícầu1:v1=2m/s(đ/kt7,5s)

Phươngtrìnhvậntốccủavật2:v2=-18+10t (đ/kt 3s)
Khivậtđangđilênthìkhoảngcáchgiữavậtvàkhícầungàycàngtăng,khivậtlênđên điểmcaonhấtnóđổichiềuchuyểnđôngnhanhdầnđềuđixuống,khoảngcáchgiũavật vàkhícầuvẩntiếptụctăngchođếnkhivậntốccủavậtđạtgiátrịbằngvậntốckhícầu
2m/s.Tacó
v2=-18+10t=2 t=2s
Khoảngcách:dmax=x1-x2=2t-(-18t+5t2)=20m
Bài10.Dokhốilượngcủanêmrấtlớnsovớikhốilượngcủavậtnêntacóthểcoinêm
đứngyên.Ápdụngđịnhluậtbảotoàncơnăngtatínhđượcvậntốccủavậtkhi rờinêm
là:v= 2() gHh
Vậtvăngraxatheophươngnằmngang,khoảngcách
từvậtđếnchânnêmkhivậtchạmsànlàl=v = 2h g
4() hHh
Vậtrơixuốngmặtbànởxanêmnhấtkhil=lmax.Ápdụngbấtđẳngthứccositacól= lmaxkhivàchỉkhi:
h=H -h hay
h= từđótacólmax =H 2 H
Bài11.Vậntốctrungbìnhcủaôtô1trong1/3quãngđườngđầuvàcuối: '0
thờigianchạycủaôtô1: 1 /3/3/35 /2/23 ABABABAB t vvvv
*Tươngtựvậntốctrungbìnhcủaôtô2trong1/3thờigianđầuvàcuốicũnglà ./2v
Và: 222 2 3 233232 vtvttvAB AB t v
*Mà 12 153.1 2 303.702.7030 ABAB ttphuth
14 ABkm
Bài12. Thờigianbirơiđếnđáyhố: 1 2H t g
+Thờigiangiữahailầnvachạm: ,dovậntốctheo 2 d t v
phươngngangkhôngđổinênt2 khôngđổi.
Dođósốlầnvachạm: 1 2
2 tvH n tdg
2.Quátrìnhvachạmdiễnranhanhcoinhưkhôngmấtthời gianvachạm,mặtkhácdovachạmhoàntoànđànhồinên hướngcủavậntốctrướcvàsauvachạmcùnghợpvới phươngnganggócgiốngnhau.Nhưvậyvachạmlàmcho quỹđạoparabolcủaviênbicắtthànhnhữngđoạnnhỏvàđảochiều.Tuynhiênkhiđảo chiềuvàghéplạisẽcóđượcparabolnhưkhôngvachạm.Từđóchiềudàiquỹđạođược xácđịnh:
= 22 0 () t Svgtdt
42
43
2
v v
Bài13. ChọntrụctọađộOxtrùngvớiOP,chiềudươngtừOđếnP.Khichấtđiểmtrượt trênmángkhôngmasátthìgiatốccủanólà:a=gcosβ>0
Chấtđiểmtrượttheománglàchuyểnđộngnhanhdần đềunênthờigianđitừOđếnPlà: (1) 2 cos OP t g
Từhìnhvẽ,xét tacó: OPC
hay (2). cos.os cos(-)cos(-) OChc OP
Thay(2)vào(1)tađược:
2cos4os cosos(-)cos+cos(-2) h hc t gc g
(3)
Đểthờigianvậttrượtlànhỏnhấtthì(3)cómẫusốlớnnhất.Vìgócαcógiátrịxácđịnh
nên(3)nhỏnhấtkhicos(α-2β)=1,hay 2
Thaysốtađượcβ=150. Thayβ=150 vàα=300 vào(3)tađược: = . 0 0 4cos30 (os301) h
Nhưvậyđểthờigianvậttrượtlànhỏnhấtthìβ=150 vàthờigianvậttrượttừOđếnPlà
mn 1,86h
Bài14. a.Giatốccủacácvậttrênmặtphẳngnghiêng:
a1 =gsin,a2 =gcos
AB=(gsin)t2/2vàAC=(gcos)t2/2
t2 =2t1 (1) 4 tan AC AB
Mặtkháctan = (2) tan =2 =63,40 AC AB


b.Đểt1 =t2 thìnêmphảichuyểnđộngvềphíabêntráinhanhnhanhdầnđều
Tronghệquychiếugắnvớinêm:a1n=gsin -a0cos
a2n=gcos +a0sin
Vìt1 =t2 tan = = = =2 AC AB 2 1
n n
a a 0 0
gcos+asin gsinacos
Thaysốtađượca0 = =7,5m/s2 3 4g
Bài15. Theophươngngang,hìnhchiếuđườngđiquảcầuđượcbiểudiễnnhưhình1
+Vìvachạmđànhồinênvậntốctheophươngngangkhôngđổivàdođókhoảngthời
giangiữahailầnvachạmliêntiếpvớithànhốngcũngkhôngđổi: 2cos x R t v
*Theophươngthẳngđứng.
+Tạimépống: voy =0
44
00 sin(90)sin(90) OPOC
g
2
g
g
t c
23 (31)
h
1,86h
45
t g
+Vachạmđànhồinênvậntốctheophươngthẳngđứngngaytrướcvàsauvachạmlà khôngđổi. Thờigianquảcầuđitừmiệngđếnđáybằngthờigianđitừđáylênmiệngvà bằng:
2 y H t g
*Giảsửsaunlầnvachạmvớithành(lầnthứnvachạmởmép)vàklầnvachạmvớiđáy
thìquảcầulêntớimépốngvàlọtrakhỏiống. Tacó: ntx =2kty nRcos =kv
Trongkhiđómuốnkhôngvachạmthỡvậntốctàu1phảikịpgiảmxuống21,6km/h=
6m/s.Dođókhôngthểtránhvachạm.
Bài17.Thờigianmỗilầnxechuyểnđộnglà: 1151/4 tph
Thờigianmỗilầnxenghỉ: 151/12() tph
Trongkhoảngthờigianđầuxeđiđượcquãngđường (km)
Cácquãngđườngxeđiđượctrongcáckhoảngthờigiankếtiếpsauđólà:
GọiSlàtổngquãngđườngmàxeđiđượctrongnlần:
nn v v Ssss n
0 0 12 1 12 442n
Vớiv0=16km/s km (nnguyên)
11 6 21 42 nn S nn
a.KhiS=84km,tacó: 2184Snn
2* H g
Bài16.Gọi và làcácquãngđườngmỗitàuđiđượcchođếnkhitàu1đuổikịptàu 1s2s
2,tacó: (1); (2); (3) 2 11 1 2 svtat 22 svt 21 sLs
Hay: (4) 2382800tt
Gọi v làvậntốccủatàu1khiđuổikịptàu2,thì: (5) 1 125vv tvvv a
Thay(5)vào(4)tađược: (6) 2 2538253800 vv
Phươngtrình(6)có2nghiệm: (bịloại)và 3/ vms 15/ vms
Giảiratađượcn=6(n>0thỏamãn)

NêntổngthờigianxeđitừAđếnBlà: 11 23 65 12 ttth
VậntốctrungbìnhcủaxetrênquãngđườngABlà: (km/h) 43,8b S v t
b.KhiS=91=84+7km
Nhưvậy,sau6lầnđivàdừng,xecònđitiếpquãngđường7kmcònlại,vớivậntốc
v7 =7v0 =112km/h.Thờigianđitrênquãngđườngnàylà:
46
47
0 1014 v svt
; ; ;…; (km) 0 2 2 4 v s 0 3 3 4 v s 0 4 4 4 v s 0 4n nv s
7 7
71 16
Bài19.1.Giatốccủahaivậttrênmặtphẳngnghiêngcócùnggiátrịbằng:
tht v
ThờigiantổngcộngxeđitừAđếnBlà: 117 33 6 16 tttth
VậntốctrungbìnhcủaxetrênquãngđườngABlà: (km/h) 44,1b S v t
Bài18.Theogt:tạiđiểmcaonhấtBvậntốcmáybayvB=vo/2,nênbánkínhquỹđạor
02 12 35/s01ins0 in ms aag
Tốcđộcủahaivậtkhiđếnchânmặtphẳngnghiêng:
vasaLms 22250,93/1111
ms vasaLd222.5.2,55/
thỏamãn: .(1)
222 4 o o v var
+TạiđiểmCnơivậntốccủamáybay
hướngthẳngđứngtừtrênxuống,giatốccủa máybaylàsựtổnghợpcủahaigiatốc:
-giatốchướngtâm:(2) 222 co n vvar a rr
-giatốctiếptuyếnat (3) 22 cn aaa +Đểtínhat,taxétsựdịchchuyểnnhỏcủamáybaytừCđếnC/,khiđó: ,gọi làthờigianmáybayđitừCđếnC/ tacó: 22 22 2()2o c c c vvarhvvah t
,khi thì suyra: 222cc vvah tt
Thờigianchuyểnđộngtrênmặtphẳng nghiêngcủahaivật:
2.Khoảngcáchgiữahaivậtkhicùngchuyểnđộngtrênmặtphẳngngang:
Lúcvật2đếnchânmặtphẳngnghiêngthìvật1cáchvật2mộtđoạn:
1121310,61,2dvtt m
Kểtừkhivật2xuốngđếnmặtngangthìkhoảngcáchgiữahaivậtgiảmdầntheothời giantheobiểuthức:
1211,22 dtdvvtt
Đếnthờiđiểmt=0,6ssau(kểtừkhivật2đếnchânmặtnghiêng)thìvật2bắtkịpvật

1.Vịtríhaivậtgặpnhaucáchchânmặtphẳngnghiêngmộtđoạnbằng:
250,63 lvtm
Bài20.
48
2
22 2 22 109/3 ctc c c vaavaa v aaa r 49
0t / CC
2222
. s a v t0,6 5 3 1 1 1 s a v t1 5 5 2 2 2
Bài21.1.Khikhoảngcáchgiữahaicầuthủlà30m,tamgiácATBvuôngtạiT
Vìkhoảngcáchgiữatrọngtàivàcáccầuthủlàkhôngđổinên:
-vậntốccủatrọngtàiTvàcầuthủAtrênphươngTxbằngnhau;
vậntốccủatrọngtàivàcầuthủBtrênphươngTybằngnhau. 1824
2.XétchuyểnđộngcủatrọngtàitronghệquychiếuquántínhgắnvớicầuthủA:
-cầuthủBchuyểnđộngvớitốcđộ:5+5=10m/s.
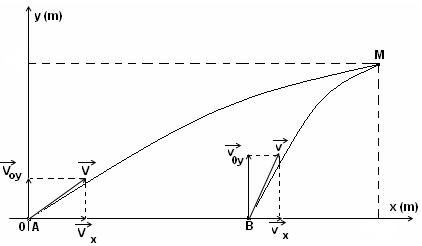
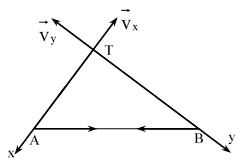
-trọngtàichuyểnđộngtrênđườngtrònbánkínhAT–theophươngBy
. / '2410.8/. 30TAy VVms
Giatốchướngtâmcủatrọngtài–giatốccủatrọngtàitrênphươngTx:
2 232/ 9 TA x V ams AT
Tươngtự:xéttronghệquychiếugắnvớicầuthủB: 2 23/ 2 TBx y
Vậygiatốccủatrọngtàilà: 222 3,86/xy aaams
V ams BT
Bài22.Toathứnhấtvượtquangườiấysauthờigiant1:
ntoađầutiênvượtquangườiấymấtthờigian :n
toađầutiênvượtquangườiấymấtthờigian : 1n 1n t
Toathứnvượtquangườiấytrongthờigian: t
50 2 1 1001 2 2 2002 2 3 3003 1 2 2 2 3 2 at xxvt at xxvt at xxvt 22 21 21021 021 21 4 22 atta xxvtt vtttt 3203232 5 2 a xxvtttt 2 3213221542 .2 22 a a xxxtttttttat 321 2 2 xxx a t Nếu vậtchuyểnđộngnhanhdần. 31 22 xx x
vậtchuyểnđộngchậmdần 31 22 xx x
- Nếu
.3/,.4/ 3030x y VvmsVvms Vậytốcđộcủatrọngtàilà 22 1 5/ xy VVVms 51
2 2 1at s a S t 2 1
; 2 2 n at ns a nS t n 2
t
2 1 2 1 n at ns a nS t n 2(1) 1
.
nn
S
nn
(1) 2 1
a
ttt
Bài23. Chọngốcthờigiant=0lỳc2vòngtrònbắtđầutiếpxúcngoài. Tạimộtthờiđiểm


Sau5s,khoảngcáchgiữachúng:d=30,1m 2 min 366dd
t vaaOMvOM
'cossin8
làvậntốcvàgiatốctươngđốicủaM
t vaaOMvOM r
2 'cossin8
làgiatốccôriolitvà
2 2 2 ... '.cos...sin8
t vaaOMvOM r
làgiatốclytâm
Từhìnhvẽtacó
t vaaOMvOM r
2 'cossin8
Vớirlàbánkínhcong
52
t 1(1) nnt
nàođósau
2 2 0 1 2 c1s1os in 22 0 R d ARRRyC vtd ARxDD Tacó: 0 ' dv Tasuyra: 4 4 2 22Rd y d x 22 0 22 0 24 . 2.24 2' 2 ' 2 1 Rd dv Rd dd v v vd Cy Cx 2 22 0 2 220 . 24 . 2Rd vdv vvvCCy x 0 224 vR v Rd Bài24.PhươngtrìnhchuyểnđộngcủaxeđitừA: 22 1011 1 151,5 2 xxatt PhươngtrìnhchuyểnđộngcủaxeđitừB: 22 2022 1 302 2 xxatt 53 22
44 dxxttttt
gốcthờigianthìtacóphươngtrìnhchuyểnđộngcủađiểm C:
222222422 12 2525 1,515230165112513,236
mn
613,23,63 dts
Ởđây
k
Và 2 2
k
r
Bài25.
2 2 2
r
2 ... '.cos...sin8
t vaaOMvOM
2
k
2
k
2
tk
2
2 2 2 'cossin8 tk t vaaOMvOM r
Kếtquả:
Từ(4):
2 2 2 ... '.cos...sin8 tk t vaaOMvOM r
2 2 2 'cossin8 t tk vaaOMvOM r
2 2 2 ... '.cos...sin8 tk t vaaOMvOM r
2 2 2 'cossin8 tk t vaaOMvOM r
hướngtheo
2 2 2 'cossin8 t tk vaaOMvOM r
Bài26. 1a.Xétchuyểnđộngcủabi1:
Bi1chuyểnđộngtrênABvớigiatốca1,đếnBhếtthời giantB vàđạttốcđộvB: + + (2)
1sinag 2 1 2 2sin B B ta aat g
congvàtrụcOx) Thay(3),(4),(5),(7),(8),(9)và(10)vào(6)tanhậnđược:
1 22sinB vaaga
+ (3)
Bi1chuyểnđộngtrênBCvớigiatốca2,đếnChếttổngthờigiant1C: + (4) 2cosag

Khibi1đếnC: 2 1 12 (() )2CB BCB ttbvtta
Thay(2),(3)và(4)vàotađược: (5) 1 2(ascos)2sin2 cossin C tginbgaa g g
Xétchuyểnđộngcủabi2:
Bi2chuyểnđộngtrênADvớigiatốca2 đếnDhếtthờigiantD vàđạttốcđộvD: + (6) 2 2 2 2cos D D btb at g + (7)
22cosDD vatgb
Bi2chuyểnđộngtrênDCvớigiatốca1,đếnDhếttổngthờigiant2C:
54
Bình
2 2 2 'cossin8 tk t vaaOMvOM r s(9)2in 2 aavOM kct 1)s(0,in OvOMvMt t 1)3)(1272(44 1 126 2 1 1 22 2 3 2 2 3 12 2 2 xx x dx dy dx dy r (làgócgiữatiếptuyếncủađường
55
với
phươngbiểuthứctađược
với
Thay(1),(6),(7)vàotađược (8) 2 2(ascos)2s2 sins C tginbgbcob g gco
Để (bi2đếnCtrướcbi1),khiđó 21CCtt 0sinos45 c
Kếthợpvớiđiềukiệnbàitoán 0045
I.2.LỜIGIẢICHUYỂNĐỘNGNÉM.
Bài1.Theođịnhluậtbảotoàncơnăngthìvậntốc cuốilà 0vv Kếthợpvớihìnhvẽbêntasuyra: .áp 0 ,2.vv
dụngcôngthức:
sins ginbgbcob g gco
2(ascos)2sin2 cossin ginbgaa g g
sinos2sin2s2(ascos)cossin cgagbcoginb g
Bài2.Gọithờigianphảitìmlàt,khiđóvậntốccủavậttạithờiđiểmtlà: 0 vvgt
Tacó: 2 000000.0...0vvvvvgtvvvgt
2 0 00.sin0 sin v vvgtt g
Kếtquảnàychỉcóýnghĩakhi với 0t làthờigianrơicủavật.Vídụnhưvậtđược 0tt némtừmặtđấtthìthờigianrơilà: 0 0 2sin v t g 01 sin45 2
Tứclànếuvậtđượcnémtừmặtđấtthìđểtồntạithờigianthoảmãnđiềukiệnđầubàithì góc phảilớnhơnhoặcbằng450 .
Bài3.1.Viếtphươngtrìnhchuyểnđộngcủacácvật:
56 +
2 2 21 (() )2CD DCD tt avtta
1b.Tốcđộ
Tốcđộ
CCttt
Lưuývớix,y>0thì 2 2() 0xyxyxyxy Dovậy (12) 2sin2s2(ascos)0 gagbcoginb Vậydấucủa phụthuộcvàohiệu hay
cácbi
sau t sinos c phụthuộcvào . 57
bi1đếnClàv1C vàbi2đếnClàv2C: = (9) 121()CBCB vvatt 2(ascos) ginb = (10 212()CDCD vvatt 2(ascos) ginb
haibiđếnCbằngnhau. 1c.Tacó: = - 21
2(ascos)2s2
=…………….
=
việc
đếnCtrướchoặc
khi 2 0 max v L g 0sin2145
2 0 0sin2vvv LL gg
0v v 2
ChọntrụcOxhướnglên,gốctạimặtđất,t=0khinémvậtAtacó;
2 2 2 300205;25025(1)5(1);1 xttxttt
1
2.VậtAchạmđấtkhi 2 10;3002050x tt
Giảipttacó: (loại) 111210;60tsts
VậtBchạmđấtkhi 2 2025025(1)5(1)0x tt
212211;40() tstsloai
ThờigianchuyểnđộngcủaBlà: . 21110 tts
3.Haivậtcùngđộcaokhi: 2 2 1230020525025(1)5(1) xxtttt 5,3 ts
VậntốccủaAkhiđó: 2033/A vgtms
VậntốccủaBkhiđó: 2510(1)18/.B vtms
Bài4.Sauthờigiant,vectơvậntốchaivậtlà
Theođề,vectơvậntốccủahaivậtcóphươngvuônggócvớinhaunên 12.0 vv
Từ(1)và(2),suyra: 0102 260() hvvm g
Bài
Từ(1)và(2)suyra:L= t= 12012) rv 0102 0102 () vv vv g
Vậykhoảngcáchgiữahaihạttạithờiđiểmcácvectơvậntốccủachúngcóphương
vuônggócvớinhaulàL= . 0102 0102 () vv vv g
Bài6.Hạtchuyểnđộngnémvớigiatốctrọngtrường . g
Vậntốchạttạithờiđiểmtlà (1) 0 vvgt
vàđộdờilà (2) ( ởthờiđiểmt=0) 2 00 1 2 rrrvtgt 00 r
58
101 202
vvgt
2
().()0.()()0 vgtvgtvvvvgtgt (1) 0102 22 01020 vv gtvvt g Mặtkhác: (2) 2 h t g 59
vvgt
010201020102
là 101 202 vvgt vvgt Theođề,vectơvậntốccủahaihạtcóphươngvuônggócvớinhaunên 12.0 vv0102 ().()0 vgtvgt (1) 0102 22 01020 vv gtvvt g Mặtkhác: 2 120(120(12)12 1 2 rrvtat Vì và nên 12 a0 012) r0 120(12) rvt Suyra: 120(12) rvt Mà (2) 0(12)0201 vvv0120201vvv
5.Sauthờigiant,vectơvậntốchaivật
Bài10. Cách1:Sửdụngphươngpháptọađộ
ChọnhệtrụcOxynhưhìnhvẽ.Gọi làgócném.
Cácphươngtrìnhchuyểnđộngcủahònđálà
Khit=1sthì:
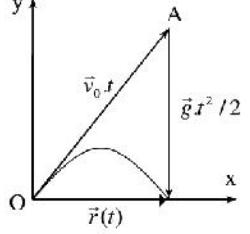
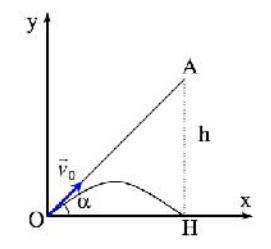
Cách2:Sửdụngphươngphápvéctơ
Véctơvịtrícủahònđá:
60 Tacó: (3) 0 1 2 rr vvgt tt Xétcảquátrìnhnémxiênthì 222 0000 ()()2() vvvgtvgtvvgtgt 2222 002() vvvgtgt Vìv=v0ởt=0vàtoànthờigianchuyểnđộnglàTnên 22 22 0002() vvvgTgT MàT 0suyra (4) 0 2 2() Tvg g Vectơvậntốctrungbình trongthờigian giâyđầutiênlà V 0 02 () Vvgvg g Bài7.Tacó: 0 vvgt Dođó: 00000 vvvvvgtvgt Hay 000cos.g.tvvvgtv Vìtầmbayxacủavậtlà 0cos. Lvt Suyra: 000 ..sin, vvvvvv L gg VậyLđạtgiátrịlớnnhấtkhi và vuônggócvớinhau. v 0v Bài8.Tacó: 0 vvgt Dođó: 00000 vvvvvgtvgt Hay 00 00sincos vvvgt vvvgt 61 sin cos v t g Bài9.Saukhoảngthờigiant,vectơvậntôchaivậtlầnlượtlà: 101 202 vvgt vvgt Theođềbài: 12vv Nên 120102 0 0vvvgtvgt 010201020vvvgtgtv 010221011022
vvvv 010221 011022
vv t gvv
sin()gtcosgtcos0
sin() (coscos)
0 2 0 cos. sint 2 xvt gt yv
0 0 22 0 022 cos 5 2 sin0 0 2 2 L xvLxvOHL g Lhhm g hg yv yv Lh
Từhìnhvẽtasuyra: 2 25() hgtm
Bài11.Cách1:Sửdụngphươngpháptọađộ
ChọnhệtrụcOxynhưhìnhvẽ.Gọi làgócném.
Cácphươngtrìnhchuyểnđộngcủahònđálà
Bài12. Phươngpháptoạđộ
ChọnhệtrụcxOynhưhìnhvẽ. Gọi làgócbắncủaviênsỏi.
Cácphươngtrìnhchuyểnđộngcủasỏilà:
2 s. in cos 2 11 11 yvtgt xvt
CácphươngtrìnhchuyểnđộngcủaTomlà:
GọikhoảngcáchOBlàS.Tacó:
KhiviênsỏiđậpvàoTomởtrungđiểmđoạnABthì:
GọivậntốccủahònbitạiBlà v
Gọi .
DovậntốctạiBvuônggócvớivậntốcbanđầunên:
Bìnhphươnghaivếcủa(1)và(2)rồicộngvớinhau,tađược:
sincos tancotg sin cossin gv v v g Véctơđộdời: 20 00 (t)r(t)r(t).22t gvtvt s vtt Dođó: 0 (t)2 vv st Từhìnhvẽtathấy: Vậy 0t vvgt 2 0 (t)5 22 vvgt stm

62 22 000 11
rrvtgtvtgt
(t)22
0 2 0
2 xvt gt yv
vậtchuyểnđộng
và 0 0 cos sin0 2 xvOHL g yv 0 00 cos sinsin x y vv vvgtvg
cos sin.t
Saukhi
1giây:
(1)
2 2222 00sin 4 g Sxyvvg
,Oxv
(2) 0 0 0 Từ(1)và(2)tathuđược: 5 2 Sgm Cách2:Sửdụngphươngphápvéctơ 63
2 . 2 2 222 yHgt vt tg H xLvt
22 sin 2 c. os 2 2 2 11 112 gyHgt t yvt tg H xvtx s.(2) in c.2(1) os 2 1 12 vtHgt tg H vtx
(3) 2 2 2 22 14 .H tg H vt
Rútttừphươngtrình(2)rồithếvào(3)tađược:
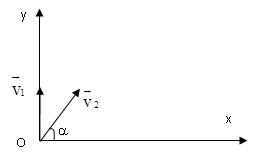
Bài13.ChọnhệtrụctoạđộOxy:gốcOởvịtrínémhaivật,gốcthờigianlúcnémhaivật
Vật
Vật
Khoảngcáchgiữahaivật
d= 22 2121 (xx)(yy)


d= 2 2 000 (vcost)(vsintvt)
d=v0.t 22 cos(sin1)
Bài14.a.x=v0 cos450t
y=H+v0sin450t-1/2gt2
b.Chạmđất 0 c452os 1 45220
Bài15.Chọnhệtrụctọađộ0x,0y,gốctọađộ0trùngvớiđiểmA.
Chọngốcthờigian(t=0)lúcbắtđầuvật1đi.
Theophương0x:
Vậntốcvật1là: = V.cos300 x V
3 40203/ 2 ms
Vậntốcvật2là: 0cos60 x vv
1 4020/ 2 ms
Theophương0y:
Vậntốcbanđầucủavật1là: 01 .sin3040.20/ 2 Oy VV ms
Vậntốcbanđầucủavật2là: 03 .sin6040203/ 2 Oy Vv ms
Theophương0x:
64 m gtg Hvtg2,8 (14) 4 2 22 1 *
222 2 2 2 11AvtgtAB Brvtgt Từhìnhvẽtathấy: (4) 2Hgt (5) 22222 1 c) os()()(2 AB OHvtHK 2 2 2 4tg H H Rútttừ(4)vàthayvào(5)suyra: m gtg Hvtg2,8 (14) 4 2 22 1
Phươngphápvéctơ: VéctơvịtrícủaviênsỏivàTomkhigặpnhau:
0
2 1 x0
1: ;y1=v
t-0,5gt
2: ;y2=v0sin.t-0,5gt2 20 xvcos.t
65 0 0c45 osv x t 220 0 2 0 c452os 1 y45 v x txgHg
0 2 0 v x txgyHg
txH g g
2
4
= (m/s)
x v
445c5 os
00012
Phươngtrìnhchuyểnđộngcủavật1: .203. x XVtt
Phươngtrìnhchuyểnđộngcủavật2: 10 x xvt
2010 t
Giảiphươngtrìnhtađượchainghiệmnhưsau: và (Loại)
Theophương0y:
Phươngtrìnhchuyểnđộngcủavật1: 21 20 2 Htgt
2205tt
Phươngtrìnhchuyểnđộngcủavật2: 21 203 2 htgt
22035tt
Khihaivậtgặpnhauthìtọađộcủachúnggiốngnhau:
Thế(3)vàophươngtrình(2)tađược:
2 2 12121212 2052035 232232232232
Tacóphươngtrìnhbậchaitheo nhưsau:
Với thếvào(3)tađược: (s)
TọađộgiaođiểmMlà:
120,20,4 232 t
2 2 205200,450,47,2Htt m
2032030,413,8Xt m
Bài16. Xácđịnhđược (1) 119SLSS
Tínhđượcthờigianchuyểnđộngcủabom 2H T g
-Viếtđượccôngthứcvậntốccủacácquảbom:
v9 =v0 +8at;v11 =v0 +10at
Tínhđượctầmxacácquảbomkểtừvịtríném (2) 99011110 2H 2H SvT(v8at);SvT(v10at) g g
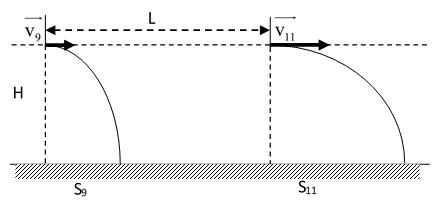
- Gọit’=2tlàkhoảngthờigiankểtừlúcthảquảbomthứ9đếnkhithảquảbomthứ11.
Khiđókhoảngcáchgiữahaivịtríthảquảbomthứ9vàthứ11là:
66
(2) 2
Hhtttt Biếnđổiphươngtrình(1)tađược:
tt
t
(1)
203.2010Xxtt
2 2052035
203.202010
(3) 102012 20320232
67
2 1010370203200
s
s
0,2
2,75
0,2s
- Kếthợp(1),(2),(3)thuđược
2 0 2H S2vt18at2at129m g
Bài17 Chọnhệtrụctọađộ:gốcOtrùngvớinớiđặtpháo,Oytheophươngthẳngđứng
hướnglên,Oxtheophươngnằmngang.Gốcthờigianlàt==làlúcviênđạnđượcbắnra
vớivậntốcv.
Phươngtrìnhchuyểnđộngcủađạntheocáctrụctọađộlà:
x1 =(vcos600).t=0,5vt (1)
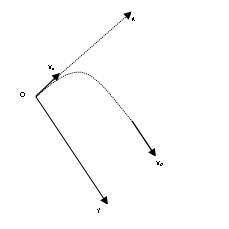
và y1=(vsin600).t–5t2 = .v.t-5t2 (2) 3 2
Phươngtrìnhchuyểnđộngcủaôtôtheocáctrụctọađộlà:
x2 =500cos300 +(2,5.cos300).t=250 +1,25.t (3) 33
y2 =500.sin300 +(2,5sin300).t=250+1,25.t (4)
Khiđạnbắntrúngôtôthì:x1 =x2 vày1 =y2
Suyra:5t2 –2,5.t–500=0(5)
Giảipjươngtrình(5)tađược:t1 =10,25312451
hoặct2=-9,753124512<0loại
Vậyvậntốccủađạnpháolà:từx1 =x2
Suyra:0,5vt1 =250 +1,25.t1 tađượcv=88,9747m/s. 33
Bài18. Chọnhệtrụctoạđộnhư hìnhvẽ,trụcOxtrùngvectơvậntốcbanđầu
+TrongthờigianrơivậntốctheophươngOxgiảmdần,khivậtchạmđấtvậntốctheo
phươngOxbằng0.
+Tạiđiểmchạmđất: x
+Thay(3)vào(1)được:
+KhoảngcáchtừOđếnđiểmchạmđấtlà: OD==4,9(m) 222 1 2dd xygt
Bài19.1.Tấmthépkhônglàmthayđổithànhphầnthẳngđứngcủavậntốc,cònthành phầntheophươngngangđổichiềungượclại. Vìvậyquĩđạonảyratừtấmthép(CE)đối xứngvớiphầnquĩđạokéodàinếucótấmthép(CD). Dođó
điểmrơiEcáchtấmthépđoạn:
3 0sin2 max v
2.Bởivìthờigianchuyểnđộngtrongtrọngtrườngtráiđất(khôngcólựccản)chỉphụ thuộcvàothànhphầnthẳngđứngcủavậntốc,màvachạmlạichỉlàmảnhhưởngđến thànhphầnnằmngangcủavậntốcnênthờigianchuyểnđộngcủavậtkhicótấmthép đangchuyểnđộngđúngbằngthờigianchuyểnđộngcủavậtkhikhôngcótấmthép: (1)
+Xétquátrìnhvachạm:
68 (3) 22 90 1 Lvt'at2vt18at 2
69
0v
đ =vot+gxt2
1 2 yđ = gyt2 (2) 1 2 vđx =vo +gxt=0 vo =-gxt (3)
(1)
xđ = 21 2x gt
xLLL g
0 0
v
g
2sin
t
. Thànhphầnvậntốcvậttheophươngngangngaytrướcvachạmlà: 0cos x vv
. Ngaysauvachạm: TrongHQCgắnvớitấmthép,vậtlaovàovàbắnravớivậntốc: 0cos vu
vv t g gg
*Nếu khiđóquảcầuvachạmvớiđáythùng: 22 0 0 coscos2.sin 2 x
v LvgL g
TrongHQCgắnvớiđất,vậtlaoravớivậntốc:
0cos2 vu
+Gọithờigiantừlúcnémđếnlúcvachạmlàt
TrongHQCgắnvớiđất,quãngđườngtheophươngngangcủavậttrướcvàsauvachạm làbằngnhau:
000 coscos2 vtvutt
sin..cos2 cos vvu t vug
00 0
+vox =vocos; voy =vosin;gx =-gsin; gy = gcos

+DovachạmvớithànhthùnglàđànhồinênthànhphầnvậntốctheophươngOxlà khôngđổi.DođóphươngtrìnhchuyểnđộngtheophươngOxlàkhôngbịthayđổidova chạm. x=vocos.t+ gxt2 và 1 2
0cossin x vvgt
*Nếuvx triệttiêutrướckhix=L: quảcầukhôngvachạmvớiđáythùngmàquaytrởlại. + 22 0 0 coscos2.sin 2 x
1 2 cossincot11 2 cos v gLtgxvtgtLtg
Từphươngtrình: 20 0 1 2 0
Bài21 Gọivậntốcbanđầulà vàvậntốcngaytrướckhichạmđấtlà . 0v
vvgt
0
000000 vvvvgtvvvgt
000cos vvvgtvtg
71
70
(2)
+Thay(1)vào(2)tatìmđược:
Bài20.ChọnOxynhưhìnhvẽ
v LvgL g
+Thờigianchuyểnđộngtrongthùngbằng2lầnthờigianđểvx triệttiêu:
002cos2 cot x
+Trườnghợpquảcầuchỉvachạmvớiđáythùngmộtlầnrồirakhỏithùngthìthờigian chuyểnđộngtrongthùngbằnghailầnthờigiantừkhibayvàothùngđếnkhichạmđáy thùng.
g v
v
Tacó: (tlàthờigianrơicủavật).
Tacó: .
Vìtầmbaycủavậtlà 00 cos. x LvtvtvvgL 000 .sin. vvvvv v L gg VậyLlớnnhấtkhi hayhaivậntốc và vuônggócvớinhau. 0 sin,1 vv 0v v Nhậnxét:Trongvídụnàytađãđưaramộtcôngthứctổngquátlà: 0 vv L g
Vì theo(3),suyra 000vv
Côngthứcnàycóthểápdụngchonhiềubàitoánvàchotacáchgiảimớikháđẹpnhư trongvídụquenthuộcsauđây.
Bài22.chọnH.Q.C.gắnvớihònđáthứnhất.Khiđóchuyểnđộngcủahònđáthứhaisẽ làthẳngđều()vớivậntốc: 01122 aaagg
Điềuđócónghĩalàcácthànhphầnthẳngđứngvànằmngangcủa phảibằngnhau: 1v
00 cossinvvv
hay 2 00 cos1cosvvv
Khoảngcáchnhỏnhấtgiữahaihònđádễdàngtìmđượctừ hình3:
Chúý:Haihònđáđạttớikhoảngcáchngắnnhấtnàysauthờigian:
bìnhphương2vếtađược: 22 2222 00 00 cos2coscos vvvvvv
22 22 00 0 2cos2cos0 vvvvv
(*)
giảiphươngtrìnhtheoẩncos tađược: (1)
Bìnhphươngcủahợpvậntốc 1v thỏamãnhệthức:
saochotớithờiđiểmđóhònđáthứnhấtphải chưarơixuốngđất,tứclàphảithoảmãnđiềukiện:
Đểkếtquảtrêncó
Bài23.Gọi:
+ làvậntốccựcđạicủabàntaytạithờiđiểmném. 0v
+ làvậntốccủangườichạykhiném. v + làvậntốccủahònđá. 1v Đểđạtđượckhoảngcáchxanhấtthìviệcnémphảiđượcthựchiệnsaocho của 10 vvv
hònđáhợpvớiphươngnằmngangmộtgóc .4
(2) 222 1002cosvvvvv
Thay(1)vào(2)tacó: 2222 100 2 vvvvv
Khoảngnémxanhấtkhingườiđóđứngtạichỗlà: . 2 0 0 v x g


Khinémvớivậntốc là: . 1v 2 1v x g
Vậykhichạynémxahơnđượcmộtkhoảng: 0xxx
72
21vvv td
2 2 2 1 1sin vv lv dl
2 2 2 1 2 2 2 2 1 ccos os vv lv vv l v l t td
g
2 2 2 1 2
nghĩacầnphảiđảmbảo
h vv lv2
73
2 00 1 cos2 2 vv vv
22
2.v xvv g
0
Bài24.a.ChọnhệtrụcoxygắnovàođiểmAvàtrụcox songsongvớiphươngngangTrongquátrìnhchuyểnđộng
lựctácdụngduynhấtlàtrọnglực .P
TheođịnhluậtIINewton:
Chiếulên: 0x: x ma00 x a 0y: y Pma ag y
Phươngtrìnhchuyểnđộngcủavậttheohaitrụcoxvàoy:
Khiviênđárơixuốngmặtphẳngnghiêng:
s(4) in c(3) os yl xl
Thế(3)vào(1)tarútratthếvào(2)vàđồngthờithế(4)vào(2)tarútra:
cos0vv x 2 0v
cos 3 2 cos 2 0 g xlv hay ; cos 3 2 cos 2 0 0 g v vt
viênđá: = 3cos 2cos 0 g v t 3 20 g v
vvgt y sin0 323 2 sin00 0 vv vv y = tan 3 1 2 23 0 0 v v v v x y 030

do
0
2 0 cos s)cin(2os g lv
2 0 .cos c)soscin(oscsin2os g lv l g v 3 22 0 75
2
74
Pma
1 s.
c(1)
2 0 0 yvtgt xvt
2(2)
in
os
2
b.TạiBvậntốccủavậttheophươngox là:
Khivậtchạmmặtphẳngnghiêng:
Suyrathờigianchuyểnđộngtrênkhôngcủa
VậntốctheophươngoytạiB:
nênlúcchạmmặtphẳngnghiêng hướngxuống. 23 0V v y v
R v mmFg h 2 cos
LựchướngtâmtạiB:
1342
với 6(/)6,522 vvvms xy
vậy: 214,75 0 ytt
Lúcđárơixuốngđất: y=0 14,750 02 tt 2s t

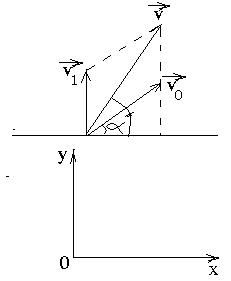
a.Khoảngcáchtừnơiđárơiđếnvịtríbanđầucủacôngtenơ:
22 m
Bài25.Sau4sđộcaocủangườiđứngtrênmậtcôngtenơlà: 1() 0 2 54 6 2
Vậntốccủangườilúcđó: s m vat0,5421
Gọi làvậntốccủaviênđáđốivớingườithìvậntốcviênđáđốivớiđất:
9,4m. 4,7.2Lvt x
Bài26. Phươngtrìnhvậntốccủavậttheophươngox:
Phươngtrìnhvậntốccủavậttheophươngoy:
Phươngtrìnhchuyểnđộng:
Chiếulên:
84,7(/)c5,40.6 os0 ms vv x
0y: 24,7(/)s25,4 in10 ms vvv y
Vậy 045
Chọntrụcoxynhưhìnhvẽgắnvàomặtđất.Phươngtrìnchuyểnđộngcủaviênđátheo phươngoy:
Phươngtrìnhvậntốc:
ĐểtầmxaxlàlớnnhấtthìtạiAvậntốccủavậtphảihợpvớimặtngangmộtgóc450 có nghĩalàtạiA:
76 cos 2 g v R Với:
2 0 22
vvv vvv xy R g v 33 22 0
222
at H
0v 01 vvv
0x:
1
x y v v tg
2
2
77
1sin 0
yvtgt
cos0vv x
vvgt y sin0
; xvt cos0 2 sin 2 0 yvtgt
; cos0vv x vvgt y sin0
Vậyphảiđặtsúngcáchváchhầmmộtkhoảng:

78 (1) 0 scos in v g vvt xy Hơnnữataphảicósauthờigiannày: s2(3) in c(2) os 2 0 0 gh t vt vtl yh xl Từ(2) (3)kếthợpvới(1) (4) cos0v l t c)(oscsin os 2 0 g v l Thayttừ(1)vào(3)tađược: ; 2 1 sin 2 0 2 v gh 2 0 2 2 1 cos v gh Thếvào(4): c)cos(os sin2 2 0 g v l l 2) 1 4 1 ( 2 0 4 0 222 0 v gh v gh g v Từ(1): 2 0 2 0 2 0 00 2 0 2 0 2 1 2 1 2 21 1 2 1 v gh v gh v gh vvv g v gh v gh t y 2 02 1 v gh v y 2)(1) 1 2)( 1 2)( 1 ( 2 20 0 2 0 2 0 2 0 v v gh v gh v gh vv A 79 maxS g v v gh g vA 1 2 12 20 0 2
thì
xacủađạntrênmặtđấtlàlớnnhấtvàtầmxanày 2) 1 4 1 ( 2 0 4 0 222 0 v gh v gh g v l bằng g v v gh.1 2 12 20 0 Bài27. PhươngtrìnhchuyểnđộngcủavậttheotrụcOxvàOy: 0x 2 0y xV.t 1 yVtgt 2 +Điềukiệncủal:Saochoviênđạnvượtrakhỏi miệnghầm x=l ;y=h Tacóphươngtrình Vtgth y 2 02 1 2 0y0y 1 2 0yoy 2 VV2gh t g VV2gh t g *Ứngvớit1:x=l;y=h g lVVVgh oy x ox 20 2
tầm
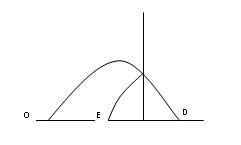
Bài28.ChọnhệtọađộxOyđặttrongmặtphẳng quỹđạocủavật,gắnvớiđất,gốcOtạiđáyvực,Ox nằmngangcùngchiềuchuyểnđộngcủavật,Oy thẳngđứnghướnglên.Gốcthờigianlàlúcném vật.
Hìnhcắtcủabờvựcđượcxemnhưmộtphầnparabol(P1)y=ax2 điquađiểmAcótọa


Suyra20=a(-25)2 a= 4 125
Phươngtrìnhcủa(P1): 24 125 yx
Phươngtrìnhchuyểnđộngcủavật:
Khửtđitađượcphươngtrìnhquỹđạo(P2):
2 12355 2039 2024yxx
ĐiểmrơiCcủavậtcótọađộlànghiệmcủaphươngtrình:
Suyratọađộđiểmrơi:xC =15,63mvàyC =7,82m.
KhoảngcáchgiữađiểmrơiCvàđiểmnémAlà
2242,37ACAB ACxxyym
Bài29. Saukhiđượcném,chuyểnđộngcủahaivậtlàchuyểnđộng
củavậtđượcnémxiên.Trongchuyểnđộngnàyvậtthamgiađồngthời
haichuyểnđộnglàchuyểnđộngthẳngđềutheophươngnằmngang
*Ứngvớit2:x=l+S,y=h *Ứngvớit1:x=l;y=h g SVVgh y x 22 0 2 0 g lVVVgh oy x ox 2 . 0 2 *Ứngvớit2:x=l+S,y=h g SVVgh y x 22 . 0 2 0 Đểtầmxatrênmặtđấtmaxthì nênv0x =v0y=vA 045 A 2 cosv 2 Aox0 v2v2vcos *ĐLBTNLcó: 2 2222 0 A00 11 2mvmghmvv2gh2vcos 2 2 0 1gh cos 2v *Khoảngcách = g lVVVgh oy x ox 2 . 0 2 02 202 00 v1gh1ghv2ghg2v2v Tầmxa: = 22 0y022 0x 0 2V2gh2vcos SV. .vsin2gh gg 2 022 20 0 2v1ghv(1cos)2ghg2v Rútgọncó:S= 2 02
00 2v1gh1ghv2ghg2v2v
202
độ
l
2;
xyh
0 2 2 0 cos1025 2 1 sin510320 2 l xvtt ygtvthtt
với 2 2 1
yx yxx 25,20 xmym
2000 12355 2039 2024
(dobỏqualựccảnkhôngkhí)vàchuyểnđộngvớigiatốcgtheophươngthẳngđứng.
ChọnhệquychiếugồmhệtrụctoạđộOxy(Oycóhướngthẳngđứnglêntrên;Oxnằm nganghướngtheochiềuchuyểnđộngcủavật)chọngốcthờigianlàthờiđiểmkhiném vật
KhảosátchuyểnđộngcủacácvậttheohaiphươngOxvàOy.
vvcos vvsingt AxA AyA
VậtB: 0B0B 0B0B
By Bx
tvvsingt
an vvcos AyA Ax A
A
A A
Trongkhoảngthờigiantừkhinémhaivậttớikhivéctơvậntốctoànphầncủahaivật vuônggócvớinhauthìkhoảngcáchgiữahaivậttheophươngOxvàOylà:
PhươngOy: ) AB yh(vv)t2,0183m BxAx
Bài30.a.ChọntrụctoađộAxynhưhìnhvẽ.
ChuyểnđộngthànhphầntheotrụcAx:
vx =v0cosβ;
x=v0cosβ.t
ChuyểnđộngthànhphầntheotrụcAy:
vy =v0sinβ-gt;
y=v0sinβ.t–gt2/2.
Vì nên 0Bvv 000 .0..0 B xxyy vvvvvv
AB2 =x2 +y2 =(v0cosβ.t)2 +(v0sinβ.t–gt2/2)2 (2)
Thay(1)vào(2)vàt=1s,tađược:
AB2 =-v0sinβ(v0sinβ–g)+(v0sinβ–g/2)2 =5m.
b.QuảbóngdocậubéBnémquaytrởlại.
ChuyểnđộngthànhphầntheotrụcAx:
vx =-v0cosβ;
x=AC-v0cosβ.t

82
VậtA: 00A 00A
vvcos vvsingt Bx By
GọiαA vàαB lầnlượtlàgóchợpbởivéctơvậntốctoànphầncủavậtAvàvậtBso vớiphươngnằmngang.
Tacó: 00A A 00A 0B0B B 0B0B tvvsingt an vvcos
Điềukiệnđểvậntốctoànphầncủahaivậtvuônggócvớinhaulà: 090
tvsingtvsingt antan1
A
Khiđótacó: 00A0B0B AB 00A0B0B 22 00A0B0B00B0A0B
1 vcosvcos gt(vsinvsin)gtvvcos()0
Thaysốtathuđượcnghiệmcủaphươngtrìnhtrênlà: t0,2569 t0,20150() s slo¹i
83
PhươngOx: ABB x(vv)t1,7982m Axx
Suyrakhoảngcáchgiữahaivậttạithờiđiểmđólà: 22 ABAB rxy2,7032m
(v0cosβ)2 =v0sinβ(v0sinβ–gt) (1)
ChuyểnđộngthànhphầntheotrụcAy:
vy =v0sinβ-gt; y=BC+v0sinβ.t–gt2/2.

(2) 2 2 1 cos mmvmgR gR
1 sin 2coscos ACxACx ygv BC v v
Từ(1)và(2)suyra: 3 5sin 3 2 cos
lúcđó: 3
đượcvậntốccủavật
2 2 2 2 2 0 0
tan.tan0* 2 2 gACAgAC C BC v v
22
22
Giảiratađược: 22 0min vgBCACBC
Thaysố: 0min25/. vms
cosp
Theođềbài dovậybanđầutaxem . Rh A0
2
3 5sin 3 2 vgR
(1) c9cos os 2 2 vR R v pm 85
84
Phươngtrìnhquỹđạocủaquảbóng:
2 20 2 0 0
KhiquảbóngrơitrúngchâncậubéA:x=0vày=0
2 22
2 2
C BC vv vv
(*)làphươngtrìnhbậchaivớitanβ.
42 00 00
010 22 AgACgACgACgBC
22 4222 00min 42 00 .2. 1020gACgBCvgBCvgAC vv
VìACvàBCđãxácđịnh,vậytốcđộv0 cógiátrịnhỏnhấtthỏamãn:
Bài31. BanđầuquảcầuxoayquanhtrụcquaytứcthờiA.Lúcbắtđầurơikhỏibànvận tốccủanólàv,phảnlựcNbằng0,lựclàm cho quảcầuquaytrònquanhAlàtrọnglực :
Theođịnhluậtbảotoànnănglượng:
2
Thay vàophươngtrình(1)ta
cos
vgR 3 2
Giaiđoạntiếptheovậtnhưmộtvậtbịnémxiênvớigóc vàvớivậntốcbanđầu: vgR 3 2
2
Chọntrục nhưhìnhvẽ . xy0 A0
1 s. in cos yvtgt xvt
Khichạmđất ,nên:yh ghvtt 2 2 1 sin
Thay vào phươngtrìnhtrêntatìmđược:
Bài32. Xéttrườnghợpgócném : Quãngđườngbóngvậtđiđượcchínhlàtầmxa
+ S2 =2.OA+L=2.OA+ 2 0.sin2v g

+TínhOA: . Phươngtrìnhquĩđạocủavật:
2 22 0 1 2cos g ytgxx v
450,khiđó
0 1max Sv g
*Xéttrườnghợpgócném :Quãngđường bóngvậtđiđượclàS2,gọitầmxalàL
'.2 cos M g tgyxtgx v
222 0 1 ....cos 2. M MOyAx tgtgv tggtg
+Vậy: 2 222 0 2 0 sin21 cos Sv tgtgv ggtg
'2cos21sin22cos2sin21sin2 . Sv vtgtg tg
2'0S 090 0
Khiđó: 2maxmax2cot.Shg
g
t g gghgR R t
S
0() 33 15410 0 33 15410 0 2 1 loai
gghgR R
Vậysau thìvậtsẽrơixuốngđất.
t g gghgR R 33 15410 0
Tầmbayxacủavật: . 3 2 . 3 2 c. os SxvtgR
g gghgR R 33. 15410 0 .
gghgR R g R 15410 0 2 27 2
2
+Nếu
némdướigóc thì 2 0 1max sin2Sv g +Nếu 0 45:
S1max khi
vậtđạtđược.
1 1 sin2Sv g
00 4545
Tathấy:S1 sẽcànglớnnếu càngtăng,suyra
bằng
2
87
. XéttạiđiểmMquĩđạotiếptuyếnvớitiasángmặttrờithì hệsốgóccủatiếptuyếntại Mđúngbằng vàdođó:
22 0
. RútxM từ(2)thayvào(1)được
2222 0 1 cos 2M ytgtgv g
2 2 2 2 0 2 0
ggtg
+TìmS2max tadùngPPđạohàm:
khi (trườnghợp khôngxảyra)
+Khi Vậytacầnnémvậtthẳngđứnghoặcgóc450
45:2sin1SS
Vậytacầnnémvậtthẳngđứng
Vậytacầnnémvậtdướigóc450
Bài33.Gọiv1 làvậntốcbónglúcbắtđầuvàorổvà làgóccủa vớimặtphẳngngang. 1v làgócném.
+Theophươngngangvậntốcbóngkhôngđổinên: 01coscos x vvv
+Theobảotoàncơnăngthì: 22 102 vvgHh
v1 khôngphụthuộcgóc vàdođónếu nhỏnhất
thì cũngnhỏnhất.
+Nhậnthấytrongnhữngquĩđạobóngbayquarổthìquĩ
đạomàbóngxượtqua2méptrướcvàsaucủavòngrổsẽ
cógóc nhỏnhất.
+Từhìnhvẽtacó: 02 sin30 2 rAMMB R
+Chọngốcthờigianlàlúcnémbóng,tlàthờiđiểmbóngxượtquarổ:
x=l=v0cos.t (1)
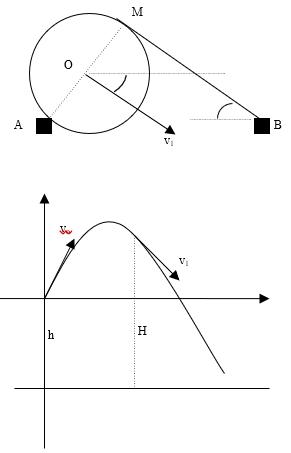
y=H-h=vosin.t- (2) 21 2gt

0 1 sinsinvgtv
01coscosvv
(4)
(3)
+Từ(1);(2);(3);và(4) 2 . Hh tgtgl
Thaysốđược: 044
Bài34. Chọnhệtrụctoạđộnhưhìnhvẽ.
sin;cosx y gggg
+XétquĩđạongượcvớiquĩđạotừAđếnB.
+Dovachạmlàhoàntoànđànhồinênvậntốc
tạiBcủaquĩđạoB2AvàquĩđạongượcA1Blà
đốixứngnhauquaOy.
12
yy xx
12
vv vv
+ 22 1122 22 x x Ax x gg xvttvtt
(1) 122 x x g vtt
+ 22 1122 22 y y Ay y gg yvttvtt
(2) 122 y y g vtt
+Thay(1)và(2)vàocácphươngtrìnhxvàytađược:
22 11212 12 ; 6 22 2 y x A AA gg g xttyttABxyttm
88 21max 2max 2sinS S *
Kếtluận:
02 1max2max
+Khi
02 1max2max
02 1max2max
45:2sin1. SS
+Khi
45:2sin1SS
89
-Thời
Vậybi3đạtđộ
caotốiđaởthờiđiểmgầnnhất:
33 1 6a 2223Tt T g
a. lượtlàh1,h2 vàh3:
1x ma ha
2x2 ma ha
3x3 ma ha
(3)

90
a.Pháchọađồthịtọađộ-thờigianchuyểnđộngcủacácbi Môtả: -Đồthịchuyểnđộngcủabi1a1a2a3a4a5a6a7a8a9a10… -Đồthịchuyểnđộngcủabi2làb1a3 a5c2a6a8c3a10… -Đồthịchuyểnđộngcủabi3làc1c2c3c4 b.Thờigianbi1rơitựdotừđộcaoalà : (1) 1T 2 1 1 2a 2 gT aT g -Thờigianmộtvậtrơitựdotừđộcao2alà 2 12(2a)4a2t T gg
lúc
2 14a22 TT g
Bài35.
Vậybi2đạtđộcaotốiđagầnnhất
(2)
91
gianvậtrơitừdoởđộcao3alà 3 12(3a)6a3t T gg
I.3.LỜIGIẢITÍNHTƯƠNGĐỐICHUYỂNĐỘNG.
Bài1.Vậntốccủavật(1)đốivớimốcvật(2)là:
112 2 vvv (m/s). 10112 2 vvv
v AB t (s)
Thờigiantừbanđầuđếnlúcvật(1)vàvật(2)gặpnhaulà: 10 10 100 12
Quóngđườngvậtnhỏđiđượctổngcộngchođếnlúcvật
(1)vàvật(2)gặpnhaulà:
(m). 3010300svt
Bài2. Gọikhoảngcáchtrênđầucủavật(1)và(2) tớivịtrí giaonhaucủahaiquỹđạolàd1 vàd2.Sauthờigiantchuyển độngkhoảngcáchgiữachúnglà:
2 1122 ()() ddvtdvt
Khiđạtđượckhoảngcáchngắnnhấtgiữahaivậtthì:
Vậy lúchai vật có khoảng cách ngắn nhất thì vật thứ haicáchgiao điểm trên một đoạn 750m
Bài3. Lầnlượtgọicácvật1:ôtô;2:gió;3:mưa;4:mặtđất
-Theođềv14 =15m/s;v24 =3m/s; hợpvớiphươngthẳngđứnggóc450 . 31v
-Biểudiễncácvectơnhưhìnhvẽ
Nếukhôngcógióthìmưarơithẳngđứngnên
32v
a,Theocôngthứccộngvậntốc,vậntốcôtôđốivớigiólà 121442 vvv
Vì nên 1424vv 1442vv
Dođóv12 =v14 +v24 =15+3=18m/s



b.Vậntốcmưađốivớiđất 343224 vvv
Từhìnhvẽtacóv32 =v12 =18m/s(tamgiácvuôngcân)
Và nên =18,25(m/s2) 3224vv 2222 343224183vvv
Bài4.1.Vậntốchaivậtbằngnhau:
1sin22sin2 4 tt
1sin2os2sin2 tctt
* os21 cttkkN
92
= 2 2 2 11221 22 2 2 1 ()2() vvtvdvdtdd mindd 2 2 2 1 1122 vv vdvd t
2 2 2 1 22112 2 2 2 1 1122 111
vv vvdvd vv vdvd Sdv
đó: Sdvt 222 22Sd 2 2 2 1 11221 2 2 2 1 1122 2 () vv vvdvd vv vdvd v 7() 50 20 3500 0 2 11 2 m v vS S
()
Lúc
2S
hướngthẳngđứngxuốngdưới
2.Vậntốctươngđối:
-Vậntốcnhỏnhất 120os21vct *tkkN Bài5.Dễthấyrằng,ởđâytaxéthaiH.Q.C.làhợplý.Yêucầuđảmbảochothuyềnbịtrôi theodòngnướcítnhấtcóliênquantớiH.Q.C.gắnvớibờsông,cụthểlàgóctạobởivận tốc củathuyền(đốivớibờ)lậpvớiđườngvuônggócvớibờlàbénhất.TrongH.Q.C. v gắn liền với dòng nước, người ta đã cho độ lớn vận tốc củatdv thuyềnvàđòihỏitìmhướngcủavậntốcnày,chẳnghạnnhưgóc tạobởivậntốcnàyvàđườngvuônggócvớibờ.Dotrongđiều kiệncủabàitoánkhôngnóigìvềtươngquangiữauvà ,nêntdv taphảixéthaikhảnăng:
a) >u.Trongtrườnghợpnàytacóthềđảmbảochèochothuyềnđitheohướngvuông dv gócvớibờ(tứclàthuyềnkhôngbịtrôitheodòng).Theoquytắccộngvậntốc:
Từhình1biểudiễnphươngtrìnhtrên,tanhậnđược:
b) <u.Phươngtrìnhbiểudiễnquytắccộngvậntốc,bâygiờđượcbiểudiễntrênhình tdv
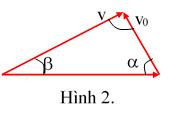


2.Khithay đổi hướng chèo ngọn của vectơ vẽ nên một nửa vòngtròn.Góc cực tiểu tdv
giữavectơ vàđườngvuônggócvớibờtươngđươngvớiđiềukiệnvectơ
v
vớivòngtrònđó.Từđâysuyra:
vu td s/ in
Nhưvậy,khi >uthì ,cònkhi <uthì .Trườnghợp =u tdv tduvs/ in tdv vu td s/ in tdv xindànhchobạnđọcnhưmộtbàitậpnhỏ.


Khixétsựrơitựdocủamộtsốvật,việcchọnH.Q.C.gắnvớimộttrongsố cácvậtđócũngtỏrarấtthuậntiện.TrongH.Q.C.nàychuyểnđộngcủacác vậtsẽlàthẳngđềuđốivớinhau(tấtnhiênởđâybỏquasứccảncủakhôngkhí).Cáchlàm nàythườngđượcgọilà"phươngphápbátướcMunhausen"(bạncóhiểutạisaokhông?).
Tasẽsửdụngphươngphápnàytrongbàitoánsau:
Bài 6. Chúngta lấy bờ sônglàm hệ quy chiếu đứng yênvàtàu thủy làm hệ quy chiếu chuyểnđộng.Khiđó làvậntốctươngđối, làvậntốc 0v
u
kéotheo.Vậntốccủahànhkháchđốivớibờ sẽlàvậntốc v tuyệtđối.Theocôngthứccôngvậntốc:
Sửdụngđịnhlýcosin chúngtatìmđượcđộlớnvậntốcvcủahànhkháchđốivớibờvà góc giữavậntốcnàyvàtrụctàu:
1.Chọnhệquychiếuđứngyêngắnliềnvớibàn,cònhệquychiếuchuyểnđộnggắnliền băngchuyền.Khiđóvậntốccủabăngchínhlàvậntốckéotheo .Lúcbắtđầuchuyển vv C
độngtrênbăngthìvậntốctuyệtđốicủahộpbằngvậntốccủahộp
94
1212
12 1sin22sin2 4 1os2 vvvtt vct
-Độlớnvậntốclớnnhất 122/os21vmsct
2 tkkN
vvu td
tduvs/ in
nàytiếpxúc
+ v0v u
=
13km/h. 3 7 20 2 0 2 u vuvuv cos 0,33; 7 3 2 10 ssin in v v . 019
Bài7.
đốivớibàntrướckhiđivàobăng,vìvậy .
Vậntốctươngđốicủahộpđốivớibăng
lúcbắtđầuchuyểnđộngtrênbănglà .Theoquytắccộngvậntốc(H.11): .
Sửdụngđịnhlýcosinđốivớitamgiáctađược:
2.Đểtrảlờicâuhỏithứhainênchuyểnsanghệquychiếuquántínhgắnliềnvớibăng. Đốivớibăng,hộpcóvậntốcbanđầu theohướnglậpvớimépbăngmộtgóc nàođó Ov vàchuyểnđộngthẳng,chậmdầnđềuvớigiatốc g.Yêucầuđộrộngcủabăngnhỏnhất
màhộpkhôngđirakhỏibăngdẫntớihộpphảidừnglạiởmépbăngđốidiện.Khiđóhộp đi được đoạn đường Đối với chuyển động chậm dần đều của hộp trên băng sin d s
chuyềncóthểviết: Từhaibiểuthứccuốisuyra: .vgs
vàođịnhlýsinđốivớitamgiáctacó:
Thếvàobiểuthứccủadtanhậnđượcđộrộngcựctiểucủabăngchuyềnđể
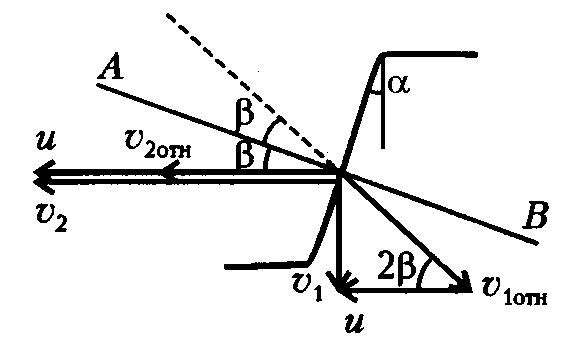
Bài8.Chúngtachọnđườnglàmhệquychiếuđứngyênvà
hệquychiếuchuyểnđộng.Chúngtasẽtìmvậntốc
và củahạtmưađáđốivớiđườngtrước
vàsauvachạm,tứclàcácvậntốctuyệtđối 1v 2v củahạtmưa.Theođềrathì hướngthẳngđứngxuốngdưới,còn hướngnằmngang 1v 2v (H.9).
Ngaysaukhivachạmvậntốctuyệtđối ,vậntốctươngđối và vậntốckéotheocủa 2v Ov2 hạtmưa (cũnglàvậntốccủaôtô)liênhệnhaubởihệthức:
Vì và hướngtheophươngngangnên cũnghướngnằmngang,dođó:
Vậntốctươngđối lậpvớipháptuyếnABcủamặtkínhmộtgóc nàođóchínhlàgóc Ov2 phảnxạ.Từphầnđộnglựchọcchúngtađãbiếttrongvachạmđànhồicủamộtvậtvớibề mặtcủamộtvậtnặng,đứngyênthìgóctớibằnggócphảnxạ,cònđộlớnvậntốctớivà vậntốcphảnxạbằngnhau.Vìvậyvậntốc củahạtmưađáđốivớiôtôngaytrướckhi Ov1 vachạmcũnglậpvớipháptuyếnABcủamặtkínhmộtgóc vàvềđộlớn: =
Trướckhivachạmhệthứcgiữavậntốctuyệtđối ,vậntốctươngđối vàvậntốckéo 1v Ov1 theo là: u
TừH.9dễdàngchứngminhđược vàvậntốctươngđối lậpvớiphươngngang Ov1 mộtgóc2.Sửdụnghình9chúngtacũngtìmđượcvậntốccủahạtmưađátrướcvàsau vachạm: khtumtugvug.().()/ 223431 ==3u=75km/h.
vvuvu OO 221
96
2 v vA
Ov AOC vvv
222 0
OCACA vvvvv 0 7 6 v v
2cos(180)
22 g dv sin2 72 49 Dựa
O A v v s) in( sin 0180
thứccủa
v
21 45
hộpkhôngđirakhỏibang . g dv 2 54 75
ôtôlàm
97
O
;ởđây: .Từđóchúýđếnbiểu
9 45 11 80 2 0 scoss)in in(
và quavtađược: AvO
sin
u =+.2vOv2 u
2vu Ov2 vvu O 22
Ov1Ov2
.
= + . 1v Ov1 u
1 2 1 2
.
uu u
c) os(
c) os(
Giảsửsauthờigian khoảngcáchgiữahaivậtlàngắnnhất.Khoảngcáchđósẽ t là:
'2''cos22BABBBdABB
c)c)2(os(2os


vvvvtlvvtl
= 2 12 22 122 2 1
Taxembiểuthứctrongcănlàmộttamthứcbậchaiẩnsố ,với ,d t 22 2 2 4sin lv
sẽđạtgiátrịnhỏnhấtkhitamthứcđónhậngiátrịnhỏnhất, hay mndd 2 122 2 1
12 2cos c)(os vvvv lvv t

Vàkhoảngcáchbénhấtgiữachúnglúcđósẽlà: a d 4mn
sin 2cos lv vvvv
mind 2 2 2 1122
Bài11 Tấtnhiênlànênchọnphònglàmhệquychiếuđứngyên,cònđĩalàhệquychiếu chuyểnđộng.Khiđó là
vậntốctươngđối.Vậntốckéotheo là 0v Cv vậntốccủađiểmAđốivớiphòng.Vậntốckéotheo hướngvuông Cv
gócvớiphươngbánkínhOAvàcóđộlớnbằng: .Vậntốccủa vR C conbọdừa đốivớiphònglàvậntốctuyệtđối.Theoquytắccộngvận v tốc: = + .Độlớnvậntốccủaconbọdừađốivớiphòngbằng:
Bài 12 Chọn hệ quy chiếu đứng yênlà hệ mà vận tốc và được chotrong đó. Lấy 1v 2v hànhtinhlàmhệchuyểnđộng.Vậntốctuyệtđốicủavệtinhđãchovàbằng .Chúngta2v cầntìmvậntốccủavệtinhđốivớihànhtinhtứclàvậntốctươngđối .Giảsửvàothời Ov điểmnàođóvệtinhđiquađiểmMgắnliềnvớihànhtinhbằngmộtthanhtưởngtượngOM (H.5). Vận tốc của điểm Mtrong hệ quy chiếu đứng yênchínhlà vận tốc kéotheo .Cv Chúngtahãytìmnó.
98
9.KhiAđitừsànlênđếnđiểmcaonhấtcủatrụthìđộdờicủanósẽlà :IA () 2cos22ADIDDAIIDIA A 4 2 2 2 2 22 2 2 2 IRRRRIA A 48 2 2 R IA TacóthờigianđểtrụdịchchuyểntừEđếnFlà: 2 2 1 Eat F
gianđểtrụđitừEđếnFcũngchínhlàthờigianchuyểndờicủavậtnhỏkhiđitừI đếnA: Suyra: a R a R a AD a EF t 2 22.2. VậntốctrungbìnhcủavậtnhỏA: t IA v v 2 1(48) 2 aR Bài
()()2()cos 12 2 2 2 1 dlvtvtlvtvt 99
Bài
Thời
10.
v 0v Cv 222 0 22 0 vvvvR C


















































































