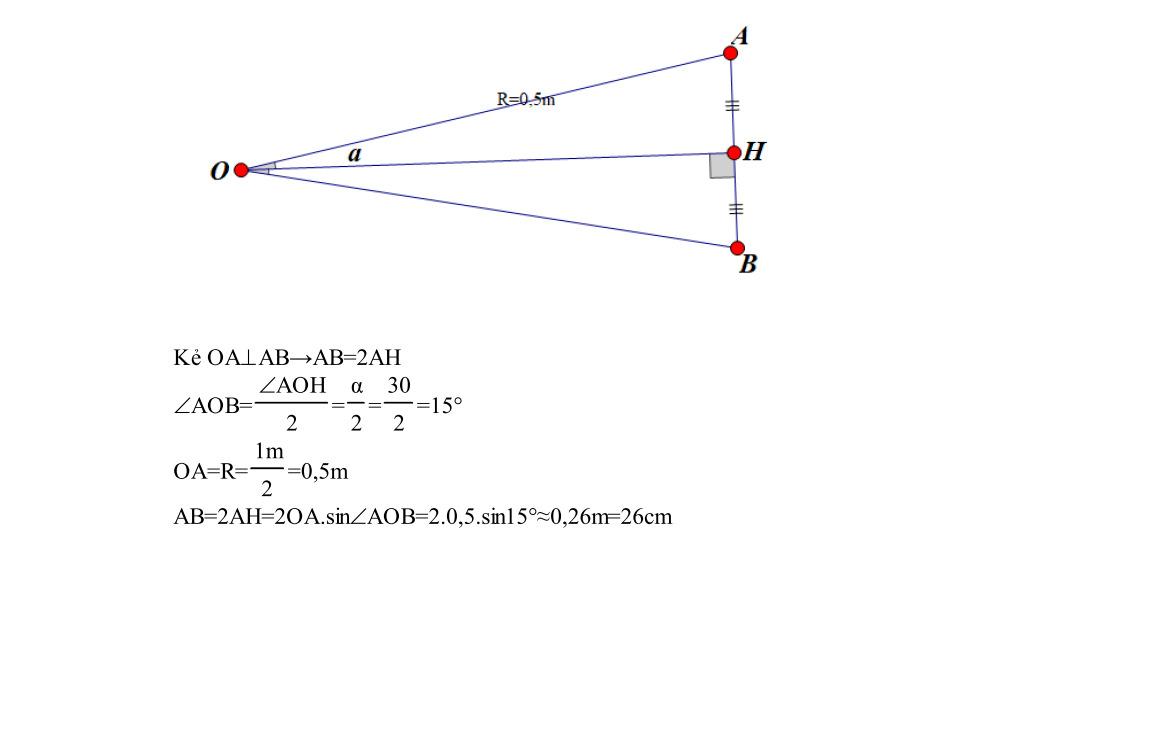
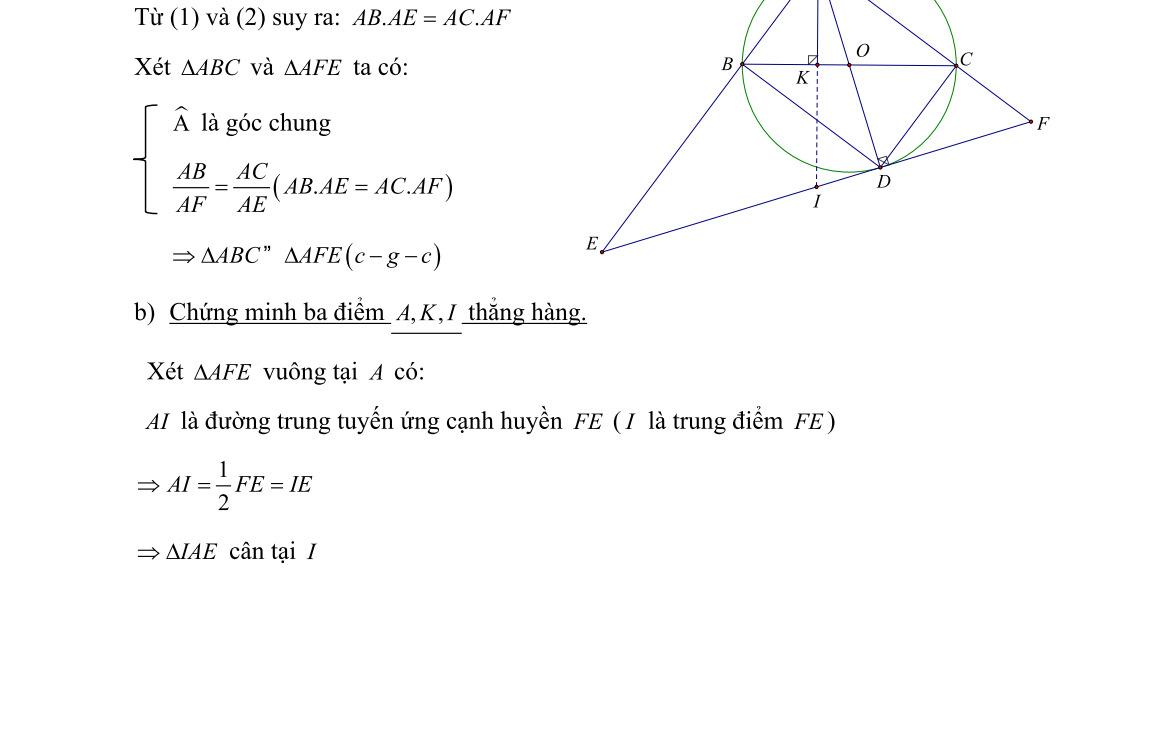
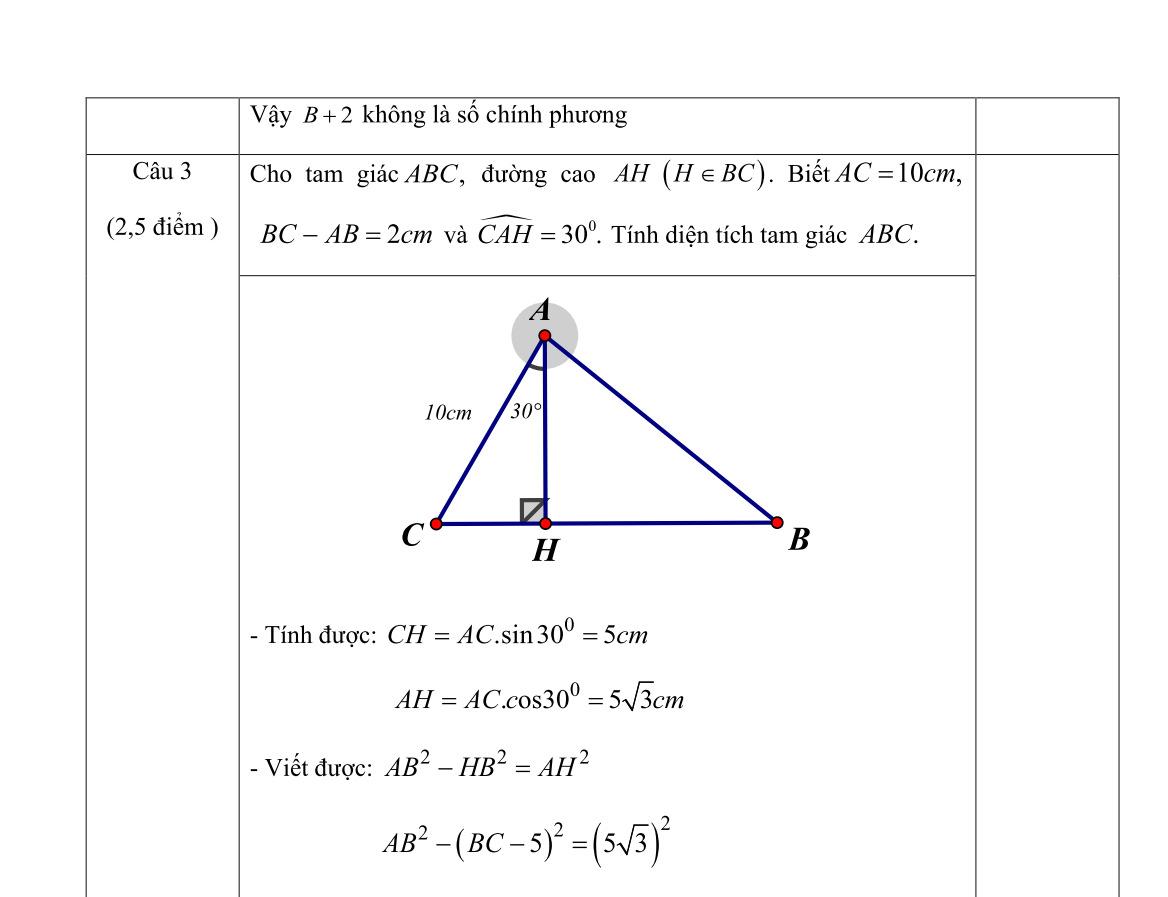
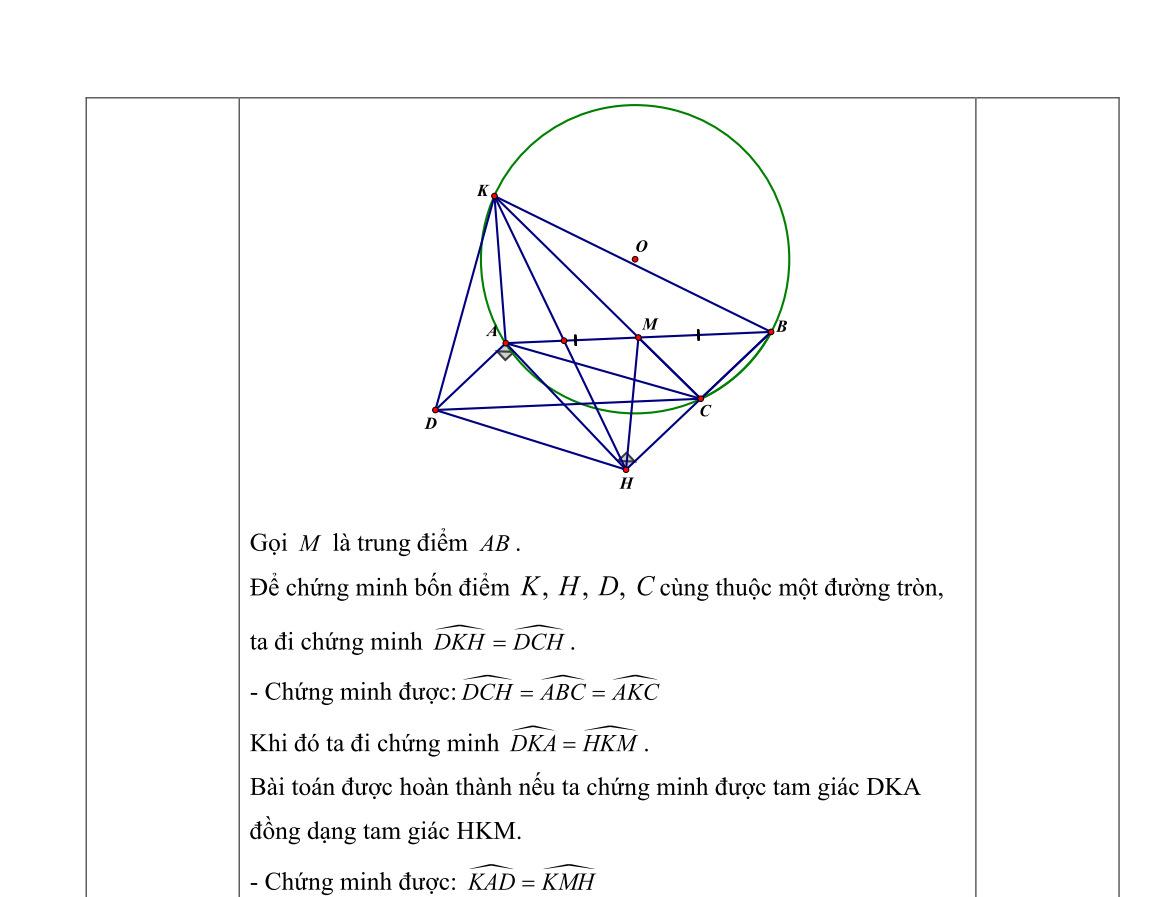
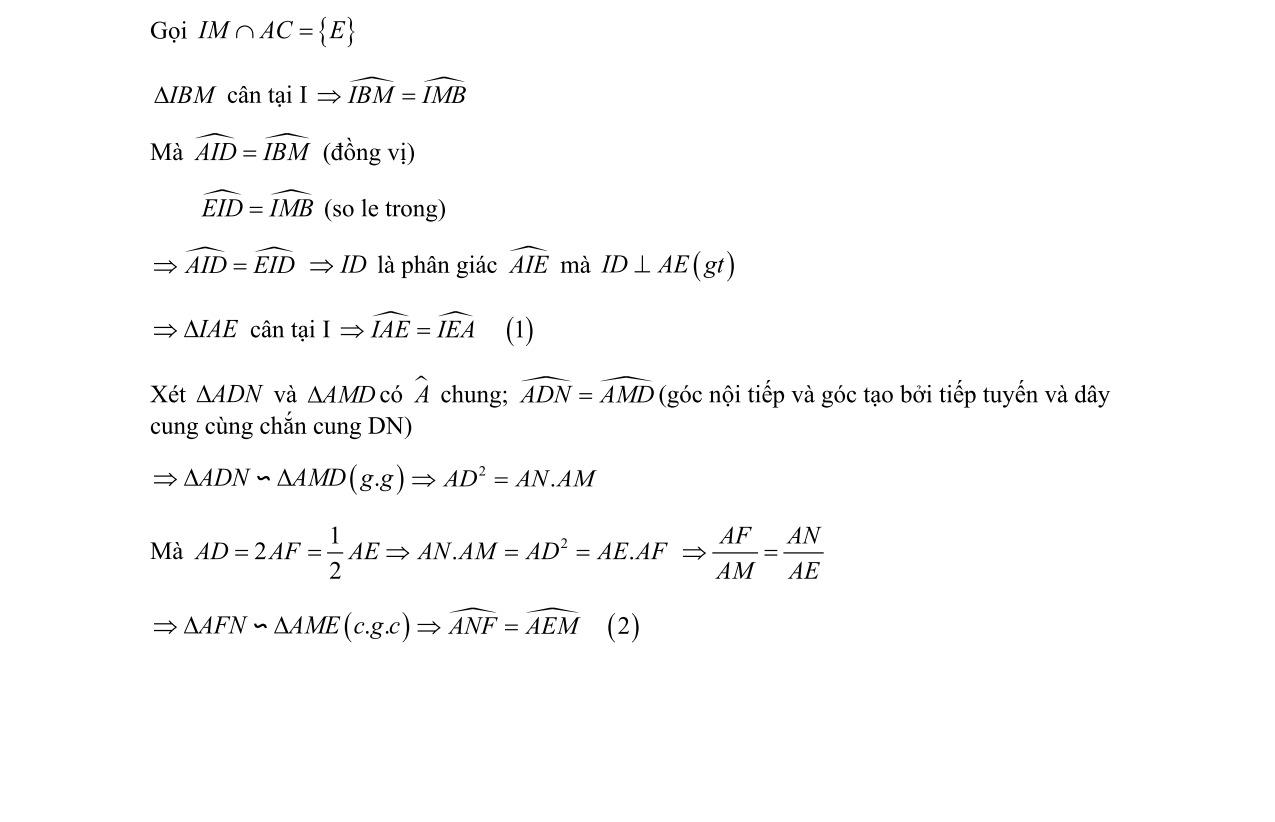ĐỀ CHÍNH THỨC KỲ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2022 – 2023 MÔN TOÁN (CHUYÊN) CÓ LỜI GIẢI by DẠY KÈM QUY NHƠN OLYMPIC

ĐỀ THI TUYỂN SINH LỚP 10 THPT MÔN TOÁN Ths Nguyễn Thanh Tú eBook Collection ĐỀ CHÍNH THỨC KỲ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2022 2023 MÔN TOÁN (CHUYÊN) CÓ LỜI GIẢI CHI TIẾT WORD VERSION | 2023 EDITION ORDER NOW / CHUYỂN GIAO QUA EMAIL TAILIEUCHUANTHAMKHAO@GMAIL.COM Hỗ trợ trực tuyến Fb www.facebook.com/DayKemQuyNhon Mobi/Zalo 0905779594 Tài liệu chuẩn tham khảo Phát triển kênh bởi Ths Nguyễn Thanh Tú Đơn vị tài trợ / phát hành / chia sẻ học thuật : Nguyen Thanh Tu Group vectorstock com/28062405

GIÁO

KỲ THI TUYỂN SINH LỚP 10 TỈNH

Năm học: 2022 - 2023 Môn thi: TOÁN - CHUYÊN

Thời gian làm bài: 150phút (Không kể thời gian phát đề)

1. (2,5 điểm)

Tính giá trị biểu

biết

2. (2,0 điểm)

ChoParabol (

Vẽ đồ thị ( )P và hai điểm

điểm

1;0

( )1;2

trên cùng hệ trục toạ độ.

Viết phương trình đường thẳng ( )d song song với AB và tiếp xúc với ( )P .

Bài 3. (2,0 điểm)

Cho phương trình bậc hai ẩn , xn là tham số: ( ) 2210nxnxn−++=

a)Tìm n để phương trình có hai nghiệm phân biệt 12 , xx . b) Chứng minh rằng 1223xx−≤ với mọi số n nguyên dương.

Bài 4. (2,0 điểm)

Chotamgiác ABC vuông tại C ( )ACBC > ,2 BC = . Biết rằng đường tròn ( )O quaba điểm ,, ABM ( M là trung điểm của BC ) cắt AC tại L với BL là tia phân giác của góc ABC a) Chứng minh.2 CACL = b) Chứng minh ABLCBCLM = c) Tính độ dài cạnh AB

Bài 5. (1,0 điểm)

Một nông dân thu hoạch 100 trái dưa lưới có khối lượng trung bìnhlà1,5kg.Trong 100 trái này có các trái dưa lưới nặng hơn 1,5 kg có khối lượng trung bình là 1,73 kg, các trái dứa lưới nhẹ hơn 1,5 kg có khối lượng trung bình 1,33 kg và các trái dưa lưới nặng đúng 1,5 kg.

a) Tìm biểu thức liên hệ giữa số trái dưa lưới theo khối lượng của chúng.

b) Có ít nhất bao nhiêu trái dưa lưới nặng đúng 1,5 kg?

Website: Liênhệ tàiliệu wordtoánSĐT: Website: SỞ

DỤC VÀ ĐÀO TẠO

AN GIANG

Bài

Cho ( ) ( ) 22 4231013 Axxx =+++−++ a)

thức A khi22 x = . b)Tìm x

9A =− . Bài

) :22 Pyx =− và hai

( )

A ,

B a)

, AB

= = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =

ĐỀ THI CHÍNH THỨC

1. (2,5 điểm)

Tính giá trị

điều

Với

dẫn giải:

giải

(22)10(22)(22)(22)10

(22)642(642)(442)882

Đặt

A trở thành 42 10 Att =−

4222191090190 3 t

Do1 t ≥ nên1 t = hoặc 3t = .

(

t =±

=±

1131303 txxx =⇒++=⇔+=⇔=− (nhận).

313332341 txxxx =⇒++=⇔+=⇔+=⇔= (nhận).

9A =− tìm được các giá trị

2. (2,0 điểm)

( ) :22 Pyx

Vẽ đồ thị ( )P và hai điểm

là3;1

hai điểm ( )1;0A , ( )1;2

trên cùng hệ trục toạ độ.

Viết phương trình đường thẳng ( )d song song với AB và tiếp xúc với ( )P .

giải

đồ thị hàm

có bảng

đường

điểm

Website: Liênhệ tàiliệu wordtoánSĐT: Website: Hướng

Bài

Cho ( ) ( ) 22 4231013 Axxx =+++−++ a)

biểu thức A khi22 x = . b)Tìm x biết 9A =− Lời

Với

kiện 303 xx +≥⇔≥− 2 2242 (13)10(13)(13)10(13) Axxxx  =++−++=++−++  a)

22x = thì23322(12)312 xx +=+=+⇒+=+ Suyra4222

A =+−+=++−  . Do2

A +=+⇒=+−+=+ b)

13(1)txt =++≥ . Biểu thức

( )

)

Atttt

=−⇔−+=⇔−−=⇔ 

Với

Vậy

Bài

ChoParabol

=− và

B a)

, AB

Lời

a) Vẽ

số ( )22 yxP =− , ta

sau: x 21012 22yx =− 82028 (P) A -2 -2 2 -8 -1 B 0 1 x y b) Gọi ( ) ': dyaxb =+ là phương trình

thẳng qua hai

(1;0),(1;2)AB

Khi đó ( )01 ':1 21 aba abbdyx =−+=−  ⇔⇒=−− −=+=− 

Phương trình đường thẳng ( )()//' dd có dạng yxc =−+ ( c là hằng số)

Xét phương trình hoành độ giao điểm của 2 (),():2(*) Pdxxc −=−+ (),() Pd tiếp xúc nhau ⇔ phương trình (*) có nghiệm kép 1 14(2)()0. 8 cc ⇔∆=−−−=⇔=

Vậy 1 ():8 dyx=−+ là phương trình đường thẳng thỏa mãn yêu cầu bài toán.

Bài 3. (2,0 điểm)

Cho phương trình bậc hai ẩn , xn là tham số: ( ) 2210nxnxn−++= a)Tìm n để phương trình có hai nghiệm phân biệt 12 , xx . b) Chứng minh rằng 1223xx−≤ với mọi số n nguyên dương.

Lời giải Phương trình 22(1)0(1)nxnxn−++= là phương trình bậc hai ẩn x nên0 n ≠ .

a) Biệt thức 22 '(1)21 nnn ∆=+−=+ . Phương trình (1) có hai nghiệm phân biệt 12 ; xx

Vậy với

n ≠ thì phương trình (1) có hai nghiệm phân biệt 12 ; xx .

n nguyên dương * n ⇒∈  , tức là 1n ≥ Từ câu 3 a thấy với 1n ≥ , phương trình (1) có hai nghiệm phân biệt 12 ; xx Theo hệ thức Vi ét,tacó:12 2 2xx n +=+ và121 xx = . ( ) 2 1212122 48 44823.xxxxxx

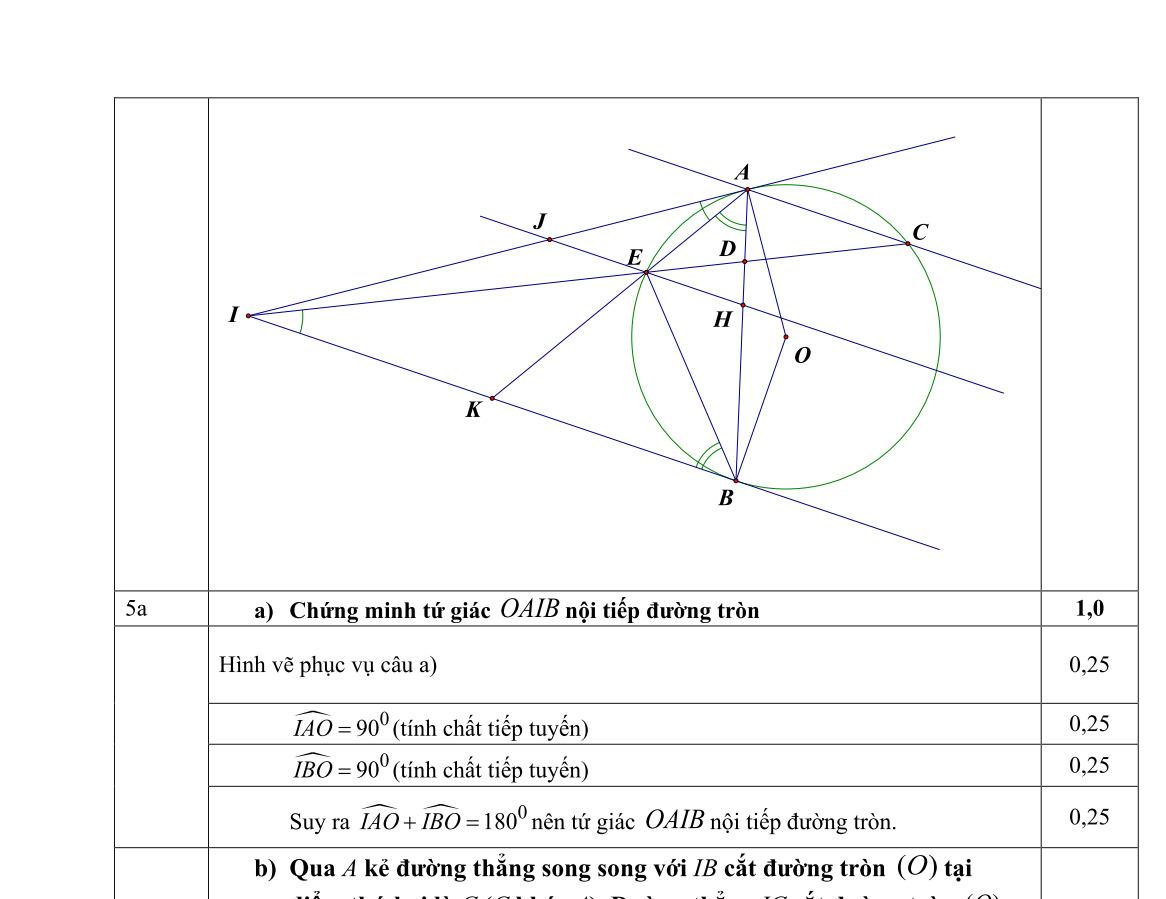
điểm)

ABC ( ABAC < ) nội tiếp trong đường tròn ( )O đường kính AC . Gọi I là một điểm thuộc đoạn OC ( I khác O và C ).Qua I kẻ đường vuông góc với AC cắt BC tại E và AB kéo dài tại D . Gọi K là điểm đối xứng của C qua điểm I .

Chứng minh rằng các tứ giác BDCI và AKED nội tiếp.

Chứng minh .. ICIAIEID = .

giải

Website: Liênhệ tàiliệu wordtoánSĐT: Website:

1 '0210 2

⇔∆>⇔+>⇔>−

1 2

>− và0

b)Do

nn ⇒−=+−=+≤+= Dấu "=" xảy ra khi 1n = . Bài 4. (2,0

Chotamgiác

Lời

kg.

này

lượng trung bình là 1,73 kg, các trái dứa lưới nhẹ hơn 1,5 kg có khối lượng trung bình 1,33 kg và các trái dưa lưới nặng đúng 1,5 kg.

a) Tìm biểu thức liên hệ giữa số trái dưa lưới theo khối lượng của chúng.

b) Có ít nhất bao nhiêu trái dưa lưới nặng đúng 1,5 kg?

Lời giải a) Gọi x, y, z lần lượt là số quả dưa nặng hơn 1,5 kg; bằng 1,5 kg; nhẹ hơn 1,5 kg. (trong đó x, y, z là các số nguyên dương). Khi đó ta có 1,731,51,331,5.100150 xyz++== (1).

Website: Liênhệ tàiliệu wordtoánSĐT: Website: Xét CML∆ và CAB∆ có   (CLMCBA = Tứ giác BMLA nội tiếp)   MCLACB = (gócchung) Nên hai tam giác CML, CAB đồng dạng CMMLCL CAABCB ⇒== (1). a) M là trung điểm 1 2 BCCMBC ⇒= 12 .2 2 CMCBBC ⇒== Từ (1)..2 CLCACMCB ⇒== b) Từ (1) ABLCBCLM⇒= c)BLlàtiaphângiác    ABCMBLABL ⇒= MàB,M,L, A cùng thuộc một đường tròn nên LMLA = . Từ câu 2 ) aLMLAACCLAC AC ⇒==−=− Từ câu ( )2 2 2222 )2 22 BCLMACAC bABACACAC LC ACAC    ⇒====− ABC∆ vuông tại ( )222224266CABACBCACACAB ⇒=+=+=−+=+ (2). Từ (2)(3)(2)03( ABABAB ⇔−+=⇒= vì0) AB > . Bài 5. (1,0 điểm) Một nông dân thu hoạch 100 trái dưa lưới có khối lượng trung bình là 1,5

Trong 100 trái

có các trái dưa lưới nặng hơn 1,5 kg có khối

Website: Liênhệ tàiliệu wordtoánSĐT: Website: b) Theo cách gọi ở câu a),tacó:1001,51,51,5150 xyzxyz ++=⇒++= (2). Từ (1), (2) 17 0,230,170 23 xzxz⇒−=⇔= Vì(17,23)1 = nên đặt ( ) 23*17 zkkxk =∈⇒=  . Từ đó suy ra 10010040. yxzk =−−=− 60 01004002,51;220 ykkky y = ≥⇒−≥⇔≤⇒=⇒  = Vậy có ít nhất 20 trái dưa lưới nặng đúng 1,5 kg.

Câu 1 (3,0

Câu 2 (2,0 điể

minh

trình

luôn

mãn

điể

thực dương ,, xyz thỏamãn ( ) 22223() xyzyxz ++=+ Tìmgiátrị lớnnhấtcủabiểuthức ( )2()22 Pxyzxz =++−+ . Câu 4 (3,0 điểm).

Chotamgiác ABC nhọn() ABAC < nộitiếp đườngtròntâm O và có ba đườngcao

cắtnhaut

i H .Gọi,IJ lần lượt là trung điểmcủa AH và BC .

Website: Liênhệ tàiliệu word toán SĐT (zalo): Website: SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH BÀ RỊA VŨNG TÀU ĐỀ CHÍNH THỨC KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN LÊ QUÝ ĐÔN Năm học: 2022 2023 ĐỀ THI MÔN: TOÁN (Chuyên) Thờigian:150phút(khôngkể thời gian phát đề) Ngàythi:09/06/2022

điểm). a)Rútgọnbiểuthức2 2 222(1) : (1)(1)(1)(1) xxx P xxxx −+− =  −++  với0,1 xx≥≠ . b)Giải phương trình:232(1)250 xxxx−+−−−= . c)Giảihệ phương trinh: 2 2 420 4410 xxyx yxy  ++−= ++−= .

m). a)Chocácsố thực,,,abcd thỏamãn2 ac bd ≥ + .Chứng

phương

cónghiệm ( ) ( ) 220 xaxbxcxd++++= b)Tìmtấtcả cáccặpsố nguyên(;) xy thỏa

phương trình 2 ()(23)220 xyxyxy +++++= . Câu 3 (1,0

m). Vớicácsố

,, ADBECF

ạ

a)Chứngminhrằng IJ vuônggócvới EF và

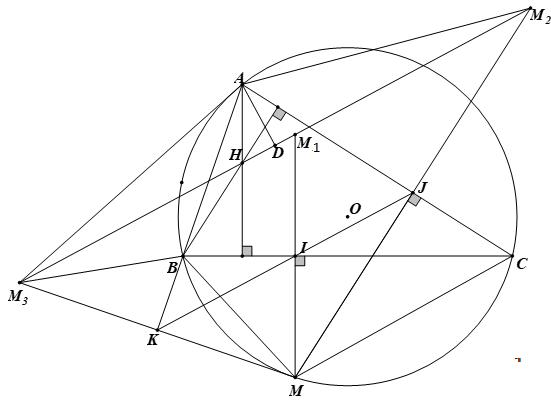
songsongvới OA b)Gọi,KQ lần lượt là giao điểmcủa EF với BC và AD .Chứngminhrằng QEKE QFKF = . c) Đườngthẳngchứatiaphângiáccủa  FHB cắt,ABAC lần lượttại M và N .Tia phângiáccủa  CAB cắt đườngtrònngoạitiếptamgiác AMN tại điểm P khác A . Chứng minh ba điểm,,HPJ thẳnghàng. Câu 5 (1,0 điểm).

Website: Liênhệ tàiliệu word toán SĐT (zalo): Website: Chotamgiác ABC cố địnhcódiệntích S . Đườngthẳng d thay đổi đi qua trọng tâmcủatamgiác ABC cắtcáccạnh,ABAC lần lượttại,MN ,Gọi12 , SS lần lượtlà diệntíchcáctamgiác ABN và ACM .Tìmgiátrị nhỏ nhấtcủa12 SS + HẾT HƯỚNG DẪN GIẢI Câu 1 (3,0 điểm). a)Rútgọnbiểuthức2 2 222(1) : (1)(1)(1)(1) xxx P xxxx −+− =  −++  với0,1 xx≥≠ . b)Giải phương trình:232(1)250 xxxx−+−−−= . c)Giảihệ phương trinh: 2 2 420 4410 xxyx yxy  ++−= ++−= . Lời Giải: a) 22 222 (2)(1)(2)(1)(1)(2)(1) (1)(1)2(1)2(1)(1) xxxxxxx Px xxxxx −+−+−−−− = ⋅==− −+ −−+ b) Điềukiện: 5 2 x ≥ . Phương trình 10(1) (1)(225)0 225(2) x xxx xx −= ⇔−−−−=⇔  −=− . (1)1 x ⇔= (khôngthỏa mãn điềukiện). 22 22 (2)3. (2)25690 xx x xxxx  ≥≥  ⇔ ⇔ ⇔= −=−−+= Vậytậphợpnghiệmcủa phương trình đã cho là {3}S = . c)Cộng hai phương trình đã cho theo vế được 221 (2)2(2)3023 xy xyxy xy += +++−=⇔  +=− . Trườnghợp1:2112 xyxy +=⇔=− thay vào phương trình sau củahệ thu được 2 01 4124101 2 2 yx yyy yx =⇒= +−+−=⇔  =−⇒= Trườnghợp2:2323 xyxy +=−⇔=−− thay vào phương trình sau củahệ thu được

đó cả hai phương trình (1), (2) đềuvô

Website: Liênhệ tàiliệu word toán SĐT (zalo): Website: 22 117517 43241022042 117517 42 yx yyyyy yx  −+−−=⇒= −−+−=⇔+−=⇔  −−−+=⇒=  Vậyhệ phương trình đã cho có 4 nghiệm ( ) 1517117517117 1;0;2;;;;; 22424  −−−+−+−−       . Câu 2 (2,0 điểm). a)Chocácsố thực,,,abcd thỏamãn2 ac bd ≥ + .Chứng minh phương trình sau luôn cónghiệm ( ) ( ) 220 xaxbxcxd++++= b)Tìmtấtcả cáccặpsố nguyên(;) xy thỏa mãn phương trình 2 ()(23)220 xyxyxy +++++= Lời Giải: a) Phương trình đã cho 2 2 0(1) 0(2) xaxb xcxd  ++= ⇔  ++= . Tacó214ab∆=− và224cd∆=− Giả sử phương trình này vô nghiệm, khi

nghiệm.Tứclà 2 2 (1)040;00 (2)04 ba bdbd dc  ∆<  > ⇔⇒>>⇒+> ∆< >  . Lúcnàytheogiả thiếtthì22() acacbd bd ≥⇒≥+ + . Tuy nhiên điềunàyvôlýdo ( )2()122 2 bdacac +>+≥ . Vậyvới điềukiện đề chothìpt ( ) ( ) 220 xaxbxcxd++++= luôncónghiệm b/ Đặt 23 axy bxy =+  =+ Khi đó 2244232 xyxyxy ++=+−−+ ( ) ( ) 423242 xyxyab =+−++=−+ Tacó 2 ()(23)220 xyxyxy +++++= 2420abab ⇔+−+=

Website: Liênhệ tàiliệu word toán SĐT (zalo): Website: ( ) 242abb ⇔+=− 2 24bb ⇒−+  ( ) ( ) ( )2 224bbb ⇒−++  ( ) ( ) ( ) ( )224224bbbb ⇒+−−++  ( )2 84 b ⇒+  ( ) { }244,8b ⇒+∈ Nếu 21 440 2 bba+=⇒=⇒=− 1 2 230 xy xy  +=− ⇒   += 3 2 1 x y  =− ⇒   = (loại) Nếu244 b += 20 1 2 2 ba ba =⇒= ⇒  =−⇒=− *)20 ba=⇒= 0 232 xy xy += ⇒  += 2 2 x y =− ⇒  = (nhận) *)1 2 2 ba=−⇒=− 1 2 232 xy xy  +=− ⇒   +=− 1 2 1 x y  = ⇒   =− (loại) Vậy ( ) 2;2thỏa mãn pt đã cho

Website: Liênhệ tàiliệu word toán SĐT (zalo): Website: Câu 3 (1,0 điểm). Vớicácsố thực dương ,, xyz thỏamãn ( ) 22223() xyzyxz ++=+ Tìmgiátrị lớnnhấtcủabiểuthức ( )2()22 Pxyzxz =++−+ Lời Giải: Tacó: ( ) 22222 3()222() yxzyxzyxz +=++≥++ 22 3()2() yxzyxz ⇒+≥++ 220()3()2 xzyxzy⇒ +++−≤ 2 320xzxz yy  ++ ⇒−+≤   12 xz y + ⇒≤≤ Do đó : 22 2222223113 4()212222 Pxzxzxzxzxzxzxz ≤+−−=+−−≤++−−=−−−−≤   . Đẳngthứcxảyra 1 ;1 2 xzy ⇔=== . Vậygiátrị lớnnhấtcủabiểuthức P là3 2 Câu 4 (3,0 điểm). Chotamgiác ABC nhọn() ABAC < nộitiếp đườngtròntâm O và có ba đườngcao ,, ADBECF cắtnhautại H .Gọi,IJ lần lượt là trung điểmcủa AH và BC . a)Chứngminhrằng IJ vuônggócvới EF và IJ songsongvới OA b)Gọi,KQ lần lượt là giao điểmcủa EF với BC và AD .Chứngminhrằng QEKE QFKF = . c) Đườngthẳngchứatiaphângiáccủa  FHB cắt,ABAC lần lượttại M và N .Tia phângiáccủa  CAB cắt đườngtrònngoạitiếptamgiác AMN tại điểm P khác A Chứng minh ba điểm,,HPJ thẳnghàng. Lời Giải:

Website: Liênhệ tàiliệu word toán SĐT (zalo): Website: a)11 ; 22 IEIFBCJEJFAH ==== IJ⇒ là đườngtrungtrựccủa EF . IJEF⇒⊥ Kẻ đườngkính AT của() O BHCT⇒ làhìnhbìnhhành I⇒ là trung điểmcủa HT . // IJAT⇒ b)Cáctứ giác,,BDHFCDHEBCEF làcáctứ giácnộitiếpnêntacó     EDHHCEHBFHDF === vàdo,HDHKDQDK ⊥⇒ làphângiáctrongvàphângiácngoàicủatamgiác DEF . Đến đây theo tính chất đườngphângiácthì QEKEDE QFKFDF  ==  . Q K T J I H E D F O B C A

Website: Liênhệ tàiliệu word toán SĐT (zalo): Website: c)Tacó       AMHMBHMHBNCHNHCHNA =+=+= AMN⇒∆ cântại A AP⇒ là đườngkínhcủa() AMN //,// PMHCPNHB⇒ . Gọi G là giao điểmcủa,PMHB và L là giao điểmcủa,PNHC Khi đó tứ giác HGPL làhìnhbìnhhành nên HP đi qua trung điểm R của GL Đến đây sử dụng địnhlýTaletvàtínhchất đường phân giác ta được ; GHMFHF GBMBHB == LHNEHE LCNCHC == . Tuynhiênhaitamgiác,HFBHEC đồngdạngnên HFHE HBHC = GHLH GBLC ⇒= // GLBC⇒ Cho HR cắt BC tại I ′ R LG P N M Q K T J I H E D F O B C A

ử dụng địnhlýTaletthì

⇒′=′ II⇒′≡ . Vậy ba điểm,,HPI thẳnghàng. Câu 5 (1,0 điểm).

Chotamgiác ABC cố địnhcódiệntích S . Đườngthẳng d thay đổi đi qua trọng tâmcủatamgiác ABC cắtcáccạnh,ABAC lần lượttại,MN ,Gọi12 , SS lần lượtlà diệntíchcáctamgiác ABN và ACM .Tìmgiátrị nhỏ nhấtcủa12 SS +

Liênhệ tàiliệu word toán SĐT (zalo):

Website:

Website: s

RGARRL IBAIIC == ′′′ IBIC

Lời Giải: Gọi D là trung điểm BC và G làtrọngtâmtamgiác ABC . Tacó: AMNAMGANGAMANSSS ABACSS + ⋅== 11111 22223 AMGANG ABDACD SSAMAGANAGAMAN SSABADACADABAC  =⋅+⋅=⋅⋅+⋅⋅=+  3 ABAC AMAN ⇒+= Mà12 ABNACM ABC SSSSANAM SSACAB ++ = =+ 3.124 SSANAMABAC SACABAMAN +  ⇒=++≥   G D A B C M N

Website: Liênhệ tàiliệu word toán SĐT (zalo): Website: 12 4 3 SSS⇒+≥ Đẳngthứcxảyra//AMANdBC ABAC ⇔=⇔ Vậygiátrị nhỏ nhấtcủabiểuthức12 SS + là4 3 S , đạt đượckhivàchỉ khi//dBC

KỲ THI TUYỂN SINH VÀO LỚP 10 TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 20222023 ĐỀ THI MÔN TOÁN (DÀNH CHO CHUYÊN TOÁN)

Ngày thi: 05 tháng 6 năm 2022

Thời gian làm bài: 150 phút (không kể thời gian giao đề) (Đề thi gồm có 01 trang, 04 câu)

Câu I (3,0 điểm)

1) Rút gọn biểu thức: 322322A =+−−

2) Tìm m để các đường thẳng: 24();35('); yxdyxd =+=+ 23()ymxm=−+−∆ cùng đi qua một điểm.

3) Cho phương trình: 22210 xmxm−+−= ( m là tham số) Tìm m để phương trình có hai nghiệm dương.

Câu II (3,0 điểm)

1) Tìm x, y nguyên thoả mãn: 210xyxy++−=

2) Một cửa hàng điện máy thực hiện chương trình khuyến mãi giảm giá tất cả các mặt hàng 10 % theo giá niêm yết, và nếu hóa đơn khách hàng trên 10 triệu sẽ được giảm thêm 2% số tiền trên hóa đơn, hóa đơn trên 15 triệu sẽ được giảm thêm 4% số tiền trên hóa đơn, hóa đơn trên 40 triệu sẽ được giảm thêm 8% số tiền trên hóa đơn. Ông An muốn mua một ti vi với giá niêm yết là 9 200 000 đồng và một tủ lạnh với giá niêm yết là 7 100 000 đồng. Hỏi với chương trình khuyến mãi của cửa hàng, ông An phải trả bao nhiêu tiền?

3) Giải hệ phương trình: 22 2

26 32 xyxy xyxyx −=  +=+

Câu III (3,0 điểm)

Cho tam giác ABC vuông tại B ( BCAB > ) nội tiếp trong đường tròn tâmO đường kính2ACR = . Kẻ dây cung BD vuông góc với AC, H là giao điểm của AC và BD. Trên HC lấy điểm E sao cho E đối xứng với A qua H. Đường tròn tâm O’ đường kính EC cắt đoạn BC tại I (I khác C).

1) Chứng minh rằng: CI.CA=CE.CB

2) Chứng minh rằng: Ba điểm D, I, E thẳng hàng.

3) Chứng minh rằng: HI là tiếp tuyến của đường tròn đường kính EC.

4) Khi B thay đổi thì H thay đổi, xác định vị trí của H trên AC để diện tích tam giác O’IH lớn nhất.

(1,0 điểm)

cả các cặp số thực ,

dương

mãn điều kiện:

SỞ GD & ĐT HOÀ BÌNH

Câu IV

1) Tìm tất

thỏa

222222 223666362232 xxyyxxyyxy +++++=++ 2)Cho,ab là các số thực thỏa mãn: 22 abab +=+ Chứng minh rằng: 33224 ababab+++≤ Hết Họ và tên thí sinh: Số báo danh: Phòng thi: Giám thị 1: Giám thị 2: ĐỀ CHÍNH THỨC

1 SỞ GD & ĐT HOÀ BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 2022-2023 HƯỚNG DẪN CHẤM MÔN TOÁN (DÀNH CHO CHUYÊN TOÁN) (Hướng dẫn chấm này gồm có 04 trang) Câu I (3,0 điểm) Phần Nội dung Điểm 1 a) Rút gọn biểu thức: 22 (21)(21)A =+−− 0,5 212121212A =+−−=+−+= 0,5 2 Tọa dộ giao điểm của (d) và (d’) là A( 1;2)0,5 Để () ∆ , (d) và (d’) cùng đi qua một điểm khi và chỉ khi A thuộc () ∆ Khi đó ta có 2.(1)32311 3 mmmm −−+−=−⇔=⇔= Vậy m = 1 3 thì 3 đường thẳng đã cho cùng đi qua điểm A(-1;-2) 0,5 3 3) Phương trình 22210 xmxm−+−= có hai nghiệm dương khi và chỉ 2 '210 210 20 mm Pm Sm  ∆=−+≥  =−>  => 0,5 2 (1)0 11 22 0 mm mm m  −≥∀   ⇔>⇒>   >  0,5 Câu II (3,0 điểm) Phần Nội dung Điểm 1 210(2)(y2)30(2)(x1)3 xyxyxyy ++−=⇔+++−=⇔++= 0,5 Vìx,ynguyênnên(y+2)và(x 1) thuộc Ư(3) = { }3;1;1;3 Học sinh tìm được cặp số nguyên (x;y ) = ( 4;3);(2;5);(0;1);(2;1)0,5 2 Tổng giá trị 1 chiếc Tivi và 1 chiếc tủ lạnh ông An mua là 16 300 000 ( đồng) Số tiển ông An phải trả khi được giám giá 10% là. 16300000.90% = 14 670 000 (đồng ) 0,5

2 Vì số tiền trên hóa đơn của ông An là 14700000( đồng) nên ông An được giảm thêm 2% số tiền in trên hóa đơn. Vậy số tiền ông An phải trả là 14670000.98% = 14 376 600(đồng 0,5 3 Giải hệ phương trình: 2 22 26(2)(23)0 3232 xyxyxyxy xyxyxxyxyx −+= −=  ⇔  +=++=+  Với x = 2y ta có 2 2 32 xy xyxyx =  +=+ 22222 2220 1222212201000 xyxyxyx yyyyyyyy = = = =  ⇔ ⇔⇔⇔  +=+−===  0,5 Với 2x = 3y ta có hệ phương trình 2 22 2 2 233 3242 3 33 2 23 30 11707 11 x xyy xyxyxxxxx x y x y x xx x  =−=  ⇔  +=+  −=−+   = =  ⇔⇔=  −=  =  Học sinh giải hệ 2 và kết luận nghiệm (x;y) = ( 0;0); ( 7 11; 14 33) 0,5 Câu III (3,0 điểm) Phần Nội dung Điểm I D O'H O A B E C

ICEchung; ∠ EIC= ∠ ABC=900 ( Góc nội tiếp chắn nửa đường tròn

Suyra(g) CIECBAg ∆∆−

⇒=⇔=

CICACECB

..(dpcm)

Tacó EIBC ⊥ (Do ∠ EIC là góc nội tiếp chắn nửa đường tròn)(1)

VìBD ⊥ AC tại H, và HA = HE; HB = HD nên tứ giác ABED là hình thoi

SuyraDE  AB,màAB ⊥ BCnênDE ⊥ BC(2)

(1) và (2) ta có 3 điểm D,E,I thẳng hàng.

có tứ giác DHIC nội tiếp đường

3 1 XéthaitamgiacCIEvàCBAcó ∠

)0,5



CICE

CBCA

0,5 2

0,5

Từ

0,5 3 Ta

tròn đường kính DC nên ta có ∠ BIH= ∠ BDC=(1800 ∠ HIC) Lại có ∠ BAC= ∠ IEO’ ( đồng vị ); ∠ IEO’= ∠ O’IE ( do tam giác O’IE cân tại O’) Suyra ∠ BIH= ∠ O’IEmà ∠ BIH+ ∠ HIE=900nên ∠ HIE+ ∠ O’IE=900suyraHI ⊥ O’I hay HI là tiếp tuyến của (O’) 0,5 4 Tacó 2 22222 ''2'.''H4 22224OIHOIH AC OIHIORR SOIHIS ∆∆ + =≤===⇒≤ 0,25 Dấu = xảy ra khi 2 '.' 2 '2 R OIHIR OIHI OIHI  = ⇒==  = (DoO’I>0,HI> 0) TacóO’H=R;màO’E=O’I= 2 R suyraAH=HE=R2 R = (21) 2 R Vậy AH = (21) 2 R thì diện tích tam giác O’IH lớn nhất. 0,25

4 Câu IV (1,0 điểm) Phần Nội dung Điểm 1 Tacó:22222 22366(53)3(xy)(53) xxyyxyxy ++=+−−≤+ 22 2236653 xxyyxy⇒++≤+ ( do x, y dương ) Tương tự ta có : 22222 63622(35)3(xy)(35) xxyyxyxy ++=+−−≤+ 22 6362235 xxyyxy⇒++≤+ ( do x, y dương ) Vậy 2222 22366223668() xxyyxxyyxy +++++≤+ (1) 0,25 Tacó22(4)(4)0(,) xyxy −+−≥∀ 2222 8168160328() xxyyxyxy ⇔−++−+≥⇔++≥+ (2) Vậy 222222 223662236632 xxyyxxyyxy +++++=++ 404 40 xy xxy y =  ⇔−=⇒==   −= 0,25 2 Nếu 0ab+= suyra 2200 abab+=⇒== khi đó bất đẳng thức cần chứng minh đúng. Nếu 22 00ababab +≠⇒+=+> Tacó: 22 222 ()()2()() 22 abababababab++ +≥⇒+≥⇔+≥+ Suyra2 ab+≤ 0,25 Tacó:3322222 ()()ab(ab)(ab)ababababaabb +++=+−+++=+ Vì02 ab <+≤ nên2()4 ab+≤ (đpcm) 0,25 * Chú ý: Các lời giải đúng khác đều được xem xét cho điểm tương ứng.

điểm) Cho đườngtròn ( )O vàdâycung CD cố định( CD không là đườngkính). I là một điểmdidộng trên tia đốicủatia DC ( I khôngtrùngvới D ).Qua I kẻ haitiếptuyến , IAIB (,AB làhaitiếp điểm)với đườngtròn ( )O .Gọi H là trung điểmcủa đoạnthẳng CD

Chứng minh năm điểm,,,,AIBHO cùngthuộcmột đườngtròn.

2. Gọi E là giao điểmcủa IO và AB .Chứngminh

DECDOC = .

Chứng minh đườngthẳng AB luôn đi qua một điểmcố địnhkhi I di động. Câu 5. (1,0 điểm) Cho0,0,0 xyz>>> thoả mãn2310 xyz++≥ .Tìmgiátrị nhỏ nhấtcủa

ết

Tỉnh Bắc Kạn Câu 1. (2,0 điểm) Chobiểuthức 15113223 2313 Axxx xxxx −−+ =−− +−−+ 1. Rútgọnbiểuthức. A 2. Tìmcácgiátrị của x để 13 6 A =− Câu 2. (2,0 điểm) 1. Giải phương trình 22929140xxxx+−+−−= . 2. Giảihệ phương trình 2234 . 2 xxyy xyxy  −+=− ++= Câu 3. (2,0 điểm) 1. Trongmặtphẳngtọa độ Oxy ,choparabol ( ) 2 : Pyx = và đườngthẳng ( ) 2 :223dymxmm =−−+ (với m làthamsố).Tìmtấtcả cácgiátrị củathamsố m để ( )d cắt ( )P tại hai điểmphânbiệt,AB cùngnằmbênphảitrụctung. 2. Tìmcácsố nguyêntố ,, xyz thỏamãn ( )5 xyzxyz ++= Câu 4. (3,0

 

391 10 48Pxyz xyz =++++++ . H

10Tuyển sinh vào chuyên Toán

HƯỚNG DẪN GIẢI Câu 1. (2,0 điểm) Chobiểuthức 15113223 2313 Axxx xxxx −−+ =−− +−−+ 1. Rútgọnbiểuthức A 2. Tìmcácgiátrị của x để 13 6 A =− . Lời giải: 1. Rútgọnbiểuthức A Điềukiện:0;1 xx≥≠ ( ) ( ) ( ) ( ) ( ) ( ) 1511323231 13 xxxxx A xx −−−+−+− = −+ ( ) ( ) 572 13 xx xx −+− = −+ ( ) ( ) ( ) ( ) 12525 . 133 xxx xxx = = −++ 2. Tìmcácgiátrị của x để 13 6 A =− . ( ) ( )2513 652133 36 x xx x =−⇔−=+ + 1751 x ⇔= 3x ⇔= 9x ⇔= (TM). Vậy9 x = thì 13 6 A =− Câu 2. (2,0 điểm) 1. Giải phương trình 22929140xxxx+−+−−= 2. Giảihệ phương trình 2234 2 xxyy xyxy  −+=− ++= Lời giải: 1. Giải phương trình 22929140xxxx+−+−−= Điềukiện: 2910xx+−≥ . ( ) 22 19129130 xxxx ⇔+−−+−−= . Đặt ( )291,0txxt =+−≥ . Phương trình trở thành ( ) ( ) 2 1 230. 3 tL tt tTM  =− −−=⇔  =  Với3 t = ta được 221 9139100. 10 x xxxx x = +−=⇔+−=⇔  =− Kếthợpvới điềukiện xác định ta đượctậpnghiệmcủaPT(1)là { }1;10S =−

(với m làthamsố).Tìmtấtcả cácgiátrị củathamsố m để ( )d cắt ( )P tại hai điểmphânbiệt,AB cùngnằmbênphảitrụctung.

Tìmcácsố nguyêntố ,, xyz thỏamãn ( )5 xyzxyz ++= Lời giải:

1. Trongmặtphẳngtọa độ Oxy ,choparabol ( ) 2 : Pyx = và đườngthẳng

( ) 2 :223dymxmm =−−+ (với m làthamsố).Tìmtấtcả cácgiátrị củathamsố m để ( )d cắt ( )P tại hai điểmphânbiệt,AB cùngnằmbênphảitrụctung. Phương trình hoành độ giao điểmcủa ( )d và ( )P là

2232230.xmxmmxmxmm =−−+⇔−++−= (1)

)d cắt ( )P tại hai điểmphânbiệt,AB đềunằmbênphảitrụctungkhivàchỉ khi phương trình(1)cóhainghiệm dương phân

2. Giảihệ phương trình 2234 . 2 xxyy xyxy  −+=− ++= ( ) ( ) ( ) 254 I. 2 xyxy xyxy  +−=− ⇔  ++=  Đặt Sxy Pxy =+  = .Hệ phương trình trở thành 254 2 SP SP  −=−  += (II) (II) 21 560 21 SSS PSP = +−=  ⇔⇔  =−= hoặc 6 . 8 S P =−  = +)Với 1 1 S P =  = ,khôngtồntại,xy thỏamãn. +)Với 6 8 S P =−  = ,tacó ( ) ( ) ( {)};2;4;4;2xy ∈−−−− . Vậyhệ phương trình (I) có tậpnghiệm ( ) ( {)} 2;4;4;2T =−−−− . Câu 3. (2,0 điểm) 1. Trongmặtphẳngtọa độ Oxy ,choparabol ( ) 2 : Pyx = và đườngthẳng ( ) 2 :223dymxmm =−−+

2222

(

biệt. Phương trình (1) có hai nghiệmphânbiệt12 , xx khi 3 '0230. 2 mm ∆>⇔−+>⇔< (*) Khi đó theo địnhlíViéttacó:12 2 12 2 . .23 xxm xxmm +=  =+− Để 12 , xx dương thì 12 2 12 0 020 11. .0230 3 m xxm mm xxmm m > +>>  ⇔ ⇔⇔>> > +−>  <− (**)

ố

AB làhaiti

điể

không là đườngkính) I là

I khôngtrùngvới D ).Qua I kẻ haitiếptuyến

ới đườngtròn ( )O .Gọi H là trung điểmcủa đoạnthẳng CD .

1. Chứng minh năm điểm,,,,AIBHO cùngthuộcmột đườngtròn.

2. Gọi E là giao điểmcủa IO và AB .Chứngminh   DECDOC = .

Chứng minh đườngthẳng AB luôn đi qua một điểmcố địnhkhi I di động. Lời giải:

1. Chứng minh năm điểm,,,,AIBHO cùngthuộcmột đườngtròn.

)90gtIAOIBOo

H là trung điểm CD nên OHCD ⊥ ,suyra

IHOo

ậy năm điểm,,,,AIBHO cùngthuộc đường tròn đườngkính OI .

Từ (*)và(**)suyra 3 1 2 m << thỏamãnyêucầubàitoán. 2. Tìmcácsố nguyêntố ,, xyz thỏamãn ( )5 xyzxyz ++= Vì ( )5 xyzxyz ++= nên5 xyz  . Suyratrong3số ,, xyz cóítnhấtmộtsố chiahếtcho5. Vaitrò,,xyz như nhau, giả sử 5z  ,mà z làsố nguyêntố nên5 z = Khi đó phương trình trở thành ( ) ( ) 51162.31.6xyxyxy ++=⇔−−=== . TH1: 123 134 xx yy −== ⇔  −== .(loạivì,xy làsố nguyêntố) TH2: 112 167 xx yy −== ⇔  −== . Vậy ( ) ( ) ( ) ( ) ( ) ( ) ( {)} ;;2;7;5;2;5;7;5;7;2;5;2;7;7;2;5;7;5;2xyz ∈ làcácgiátrị cầntìm. Câu 4. (3,0 điểm) Cho đườngtròn ( )O vàdâycung CD c

định( CD

một điểmdidộng trên tia đốicủatia DC (

, IAIB (,

ếp

m)v

Tacó   (

== Vì

 90

= .    90 IAOIBOIHOo⇒=== V

độ

2. Gọi E là giao điểmcủa IO và AB .Chứngminh   DECDOC = . Tacó OAOB IAIB =  = . Do đó OI là đườngtrungtrựccủa AB . Suyra OIAB ⊥ Xét OBI∆ có BE là đườngcao,tacó2 . IEIOIB = .(1) IBDICB∆∆ ∽ vì  BIC chungvà   1 2 IBDICB== Sđ  BD . Suyra2. IBID IBICID ICIB =⇔= .(2) Từ (1)và(2)suyra..O IEID IEIOICID ICI =⇔= . IEDICO∆∆ ∽ vì  CIO chungvàO IEID ICI = . Suyra   IEDICO = Như vậy     180 DCOOEDIEDOEDo +=+= Do đó tứ giác CDEO nộitiếp. Vậy   CODCED = . 3. Chứng minh đườngthẳng AB luôn đi qua một điểmcố địnhkhi I di

ng. Gọi J là giao điểmcủa hai đườngthẳng,ABOH . OHIOEJ∆∆ ∽ vì  IOJ chungvà   90 OHIOEJO == . Suyra .. OHOIOIOEOCOD OJ OEOJOHOH =⇔== Vì đườngtròn ( )O ,dâycung CD cố định nên điểm H cố định. Suyra . OCOD OJ OH = không đổi. Do đó J cố định. Vậy đườngthẳng AB luôn đi qua điểm J cố địnhkhi I di động. Câu 5. (1,0 điểm) Cho0,0,0 xyz>>> thoả mãn2310 xyz++≥ .Tìmgiátrị nhỏ nhấtcủa 391 10 48Pxyz xyz =++++++ . Lời giải: Ápdụng BĐT Cô sicho2số dương 1 ,x x ,tacó 1313 2 42 xx xx  +≥⇔+≥   .(1) Đẳngthứcxảyrakhivàchỉ khi1 x =

ết

Ápdụng BĐT Cô sicho2số dương 9 ,4y y ,tacó 9193 3 4242yy yy  +≥⇔+≥   .(2) Đẳngthứcxảyrakhivàchỉ khi 3 2y = . Ápdụng BĐT Cô sicho2số dương 4 ,z z ,tacó 414 41 4 zz zz  +≥⇔+≥   .(3) Đẳngthứcxảyrakhivàchỉ khi2 z = . Theogiả thiếttacó 23z53z5 23z10 424242 xyxy xy ++ ++≥⇔≥⇔++≥ .(4) Đẳngthứcxảyrakhi1 x = , 3 2y = ,2 z = . Cộngtheovế các bđt (1), (2), (3) và (4), ta được 3911333 4822xyzP xyz +++++≥⇔≥ . Đẳngthứcxảyrakhi1 x = , 3 2y = ,2 z = Vậy Min33 2 P = khi1 x = , 3 2y = ,2 z = H

Ỳ THI TUYỂN SINH LỚP 10 CHUYÊN

3: (4 điểm)

cóhainghiệm dương phân

thỏamãn3 abc++= .Chứngminhrằng: 222 222 222 9 . 12 abbccaabc abc ++≥ + Câu 4: (4 điểm) Cho đườngtròntâm O có đườngkính2MNR = .Vẽ đườngkính AB của đườngtròn ( ) ( OA khác M và A khác) N .Tiếptuyếncủa đườngtròn ( )O tại N cắt các đườngthẳng,MAMB lần lượttại các điểm,IK . a)Chứngminhtứ giác ABKI nộitiếp. b) Khi đườngkính AB quayquanhtâm O thoả mãn điềukiện đề bài, xác địnhvị trícủa đườngkính AB để tứ giác ABKI códiệntíchnhỏ nh

abc làcács

Câu

thu

đườngtròn(C khác A và)

SỞ GIÁO

D

ỤC,

KHOA HỌC VÀ CÔNG NGHỆ BẠC LIÊU

Năm học: 2022 2023 Mônthi: TOÁN CHUYÊN Thờigianlàmbài:150phút (Khôngkể thời gian phát đề) Câu 1: (4 điểm) a)Chứngminhbiểuthức ( ) ( )323 (2)15121 Snnnnnn =+++−+−− chiahếtcho120,với n làsố nguyên. b)Tìmnghiệmnguyêncủa phương trình: ( ) ( ) ( ) ( ) 232522. xyxyxyxy +−++−−= Câu 2: (4 điểm) a)Rútgọnbiểuthức 2 135(1)(0,1) 14 aaaa Paa aaaaaa  +− =+>≠  −−+  b)Giảihệ phương trình ( )22 22 400 6400 xxyy xy  +−=  +−=  Câu

a)Tìmtấtcả cácgiátrị củathamsố m để phương trình 2520xxm−+−=

biệt12 , xx thoả mãnhệ thức: 12 113 2xx += . b)Cho,,

ố dương

ất.

5: (4 điểm) Chonửa đườngtròn ( )O đườngkính AB , điểm C

ộ

ửa

B .Gọi I là điểmchínhgiữacung,ACE là giao điểmcủa AI và BC .Gọi K là giao điểmcủa AC và BI . a)Chứngminhrằng EKAB ⊥ . b)Gọi F là điểm đốixứngvới K qua I .Chứngminh AF làtiếptuyếncủa ( )O . c)Nếu  sin6 3 BAC = .Gọi H là giao điểmcủa EK và AB .Chứngminh ( ) 22 KHKHHEHEKE +=⋅ . Hết ĐỀ THI CHÍNH THỨC

nên tích cũng chia hếtcho3.

ạng22 k + với k ∈  . Do đó tích củachúng

1241:8

tcho5nêntíchcủa chúng cũng chia hếtcho5. Vậy S chiahếtcho120.

(

ố nguyênliênti

HƯỚNG DẪN CHẤM Câu 1: a)Tacó ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 432 222 22 5556 1651 156 1123 1123 Snnnnn nnnnn nnnn nnnnn nnnnn =++−− =−++−  =−++ =−+++ =−+++ . Tathấy S làtíchcủa5số nguyênliêntiếpvà1203.8.5 = +)Trong5số nguyênliêntiếpcómộtsố chiahết cho 3

+)Trong5số nguyênliêntiếpsẽ có2số chãnliêntiếpcód

códạng ( )41 kk + mà ( ) ( )

kkkk+⇒+  +)Trong5s

ếpsẽ cómộtsố chiahế

b) ( )

) ( ) ( ) 232522 xyxyxyxy +−++−−= . ( ) ( ) ( ) 23537 xyxyxy ⇔+−+−−+= ( ) ( ) 2537 xyxy ⇔+−−+= Vì ( ) ( ) ( ) ( )71.77.11771 ===−⋅−=−⋅− nên ta có 4 trườnghợpxảyra 1: 10 2513 372 3 x xy xy y   = +−=  ⇔  −+=  =−  (loại) TH2: 10 2573 3116 3 x xy xy y   = +−=  ⇔  −+=  =  (loại) TH3: 2512 378 xyx xyy  +−=−=−  ⇔  −+=−= TH4: 2572 312 xyx xyy  +−=−=−  ⇔  −+=−= Vậy phương trình có hai nghiệmnguyênlà ( ) 2;8và ( )2;2 Câu 2: a) ( ) ( ) ( ) ( ) ( ) 12 35(1) 11114 aaaaa P aaaaa  +− =+⋅  

( ) 2 2 44(1) (1)14 aaa aaa  =+− ⋅  −+  2 2 4(1) (1)4 aa aa =⋅ 1= b) ( ) ( ) ( ) 323222 2222 400601 64006402 xxyyxxyxyy xyxy   +−=+−+= ⇔  +−= +=  ( )322260xxyxyy +−+= 322360xxyxyy ⇔+−−= 322223 22360xxyxyxyxyy ⇔−+−+−= ( ) ( )22 230xyxxyy ⇔−++= 22 2 30 xy xxyy = ⇔  ++= +) Trườnghợp1: 2222113000 24 yy xxyyxxy  ++=⇔++=⇔==   Vônghiệmvì0 xy== khôngthỏa mãn phương trình ( ) 2. +) Trườnghợp2:2xy = thay vào phương trình ( ) 2tacó: 222246404 2 y yyy y = +=⇔=⇔  =− Tacó24;24 yxyx =⇒==−⇒=− Vậyhệ phương trình có 2 nghiệm ( ); xy là ( ) 2;4và ( ) 2;4. Câu 3: a)Theohệ thứcViettacó ( )12 12 5 1. 2 xx xxm +=  =− . Để phương trình đã cho có hai nghiệm dương phân biệtthì 12 12 Δ0 0 0 Sxx Pxx >  =+>  => Thay (1) vào ta được ( )2 (5)42033 504 202 m m mm  −−−>  <  >⇔  −>> Tacó ( )21 2112 1212 1133 23 22 xx xxxx xxxx + +=⇒=⇒+= ( ) 121212429xxxxxx⇒++= Thay (1) vào ta được: ( ) ( ) ( ) 4522929282200.(2) mmmm ⇒+−=−⇒−−−−= t2,0 tmt=−≥ khi đó phương trình ( ) 2trở thành phương trình 2 2() 9820010 9() tn tt tl = −−=⇔  =−  Với2 t = tacó22246 mmm −=⇔−=⇔= thoả mãn điềukiện. Vậy6 m = thoả yêucầubàitoán. b)Bất đẳngthứccầnchứng minh đượcviếtlạithành

( ) ( ) 222 222 222 222 1 29 111 29. abbcca abc abbcca abbcca  +++≥   ⇔+++++≥ Mặtkhácsử dụngbất đẳngthứcCôsibộ basố,tacó 2222 3 22 2222 3 22 2222 3 22 11 33 11 33 11 33 ababababa abab bcbcbcbcb bcbc cacacacac caca ++≥⋅⋅= ++≥⋅⋅= ++≥⋅⋅= . Cộngbabất đẳngthứctrênlạivế theovế, ta được ( ) ( )222 222 111 239. abbccaabc abbcca +++++≥++= Dấu đẳngthứcxảyrakhivàchỉ khi1 abc=== . Câu 4: a)Tacó   MBAMNA = (cùngchắncung MA ) Mà   MNAMIN = (cùngphụ vớigóc  AMN ) Suyra   MBAMIN = .Mà   180MBAABK+=  (haigóckề bù) Nên   180MINABK+=  suyratứ giác ABKI nộitiếpvìcótồng hai góc đốibằng180 b)Tacó  90AMB =  (gócnộitiếpchắnnửa đườngtròn) Xéttamgiácvuông MIK có MN là đườngcao Suyra2MNNKNI =⋅ . Tacó222ABKIMIKMAB SSS =−  ( )22 RIKMAMBRINNKMAMB =⋅−⋅=⋅+−⋅ Ápdụngbất đẳngthứccôsitacó

⇒⊥

tự ACBE ⊥

(gócn

pch

đườngtròn)

có hai đườngcao,ACBI cắtnhautại K K⇒ làtrựctâm AEB

⇒

EKAB⇒⊥ (tínhchất ba đườngcao).

I là điểmchínhgiữ

⇒=⇒= (haigócnộitiếpcùngchắnhaicungbằng nhau).

IACIBC = (haigócnộitiếpcùngch

có AI là đườ

AIBI

ICIACIBA

là đườ

24 INNKINIKR +≥⋅= 222 22 22 MAMBAB MAMBR + ⋅≤== Suyra 222224263 ABKIABKI SRRRRSR ≥⋅−=⇒≥ Dấubằngxảyrakhi;INNKMAMB == y SABKI nhỏ nhấtkhi ABMN ⊥ . Câu 5: a)Tacó  90AIB = 

ộitiế

ắnnửa

BIAE

. Tương

AEB



b)Do

a      ACIAICIBAIBC

Mà  

ắn    )

⇒= . FAK

ngcao ( )

⊥ đồngthời

ngtrungtuyến( F và K đốixứngqua I ) FAK⇒ cântại   AFAIIAK ⇒= Tacó        90 FABFAIIABIAKIABIBAIABAFAB =+=+=+=⇒⊥  tại AAF ⇒ làtiếptuyếncủa ( ) .O c)Tacó  sin KH KAH AK = Mà  sin666 332 KH BACAKHK AK =⇒=⇒= . ABE có BI vừa là đườngcaovừa là đườngphân giác ABE⇒ cântại B nên BI cũng là đườngtrungtrực ( ) .KAKEKBI⇒=∈ 6 1 2 EHEKKHKH  =+=+   Tacó ( )2 KHKHHE + ( ) 622136 2 KHKHKHKH   =++=+      

Và ( ) 662 22136. 22 HEKEHKHKHK

Suyra ( ) 22 KHKHHEHEKE +=⋅

Ghichú:Nếu thí sinh làm bài không theo cách nêu trong đáp án nhung đúng thì vẫn cho đủ số điểmtùng phần nhu hướngdẫn quy định.

 ⋅=+⋅=+   

Hết

THI

Toán (chuyên Toán

igianlàmbài:

Câu 1. (1,5 điểm)

1.Trongmặtphẳng Oxy,cho2 điểm A(2;3); B(7;7).Tìm điểm M thuộctrục Ox để M,A,B thẳnghàng.

2.Cho a lànghiệm phương trình26330 xx+−= .Tínhgiátr ị c ủ abi ể uth ứ c T =12a4 a2+2a Câu 2. (2,0 điểm)

1.Giải phương trìnhsau:2(52)(1310)7 xxxx +−−++−=

++=  ++=  =

xyz xyyzzx xyz

2.Giảihệ phương trìnhsau: 6 11 6

Câu 3. (2,0 điểm)

1.Tìmtấtcả cácnghiệm(x; y; z)của phương trình x(x2+ x +1)= z y 1thỏamãn x, y làcácsố nguyênvà z làsố nguyêntố

2.Tìmtấtcả số thực x thỏamãn2022 x + và32022 x đ ề ulàs ố nguyên. Câu 4. (3,0 điểm)

1. Cho đườngtròn (O) có đườngkính AB.Lấy điểm C thuộc đoạn AO (C khác A, O).Vẽ đườngtròn( I ) đườngkính BC Vẽ tiếptuyến AD vàcáttuyến AEF với đườngtròn( I )(E nằmgiữa A, F )saochotia AO nằmgiữa2tia AD , AE. Đường thẳngvuônggócvới AB vẽ từ C cắt đườngtròn(O)tại 2 điểm,gọimộttrong haigiao điểmlà N saocho N và D thuộchainửamặtphẳng đốinhaubờ AB.

ọi S là giao điểmcủa hai đườngthẳng DI và NB.Gọi R làgiao DN và

AS .Gọi J làtrung điểm SD a)Chứngminhtamgiác AND cân. b)GọiL,Tlần lượtlàtâm đườngtrònngoạitiếpcáctamgiácSBCvà SEF.Chứng minh ba điểm J, L, T thẳnghàng. 2.ChohìnhvuôngABCDcódiệntíchlàS.Tứ giácMNPQcóbốn đỉnh M, N , P , Q thuộc AB, BC, CD , DA và4 đỉnhnàykhôngtrùng4 đỉnhhìnhvuông.Chứngminh rằng: 4 SACMNNPPQQM +++ ≤ Câu 5. (1,5điểm) UBND TỈNH BẮC NINH SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ

VÀO LỚP 10 THPT CHUYÊN NĂM HỌC: 2022-2023 Mônthi:

và Tin) Thờ

150 phút

HẾT

ạnbất kì đề

ả

đấ

đốithủ củamìnhvàkhôngcótrậ

được10bạnthànhmộthàngdọ

1.Cho x,y,z làcácsố thựckhôngâmthỏamãn x3+ y3+ z3=3.Tìmgiátrị nhỏ nhấtcủabiểuthức 333 313131 Pxyz yzx =++ +++ 2.Có10bạnhọc sinh tham gia thi đấubóngbàn.Haib

uph

u vớinhaumộttrận,bạn nào cũng gặp 9

n nàohòa.Chứngminhrằngluônxếp

csao chobạn đứng trướcthắngbạn đứngkề sau.

ÁN VÀO

UBND TỈNH BẮC NINH SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐÁP

LỚP 10 THPT CHUYÊN NĂM HỌC: 2022-2023 Mônthi: Toán (chuyên Toán và Tin) Thờigianlàmbài: 150 phút Câu Đáp án Điểm 1.1 Trongmặtphẳng Oxy,cho2 điểm A(2;3); B(7;7).Tìm điểm M thuộctrục Ox để M,A,B thẳnghàng.1 Gọi ():. dyaxb =+ là đường thẳng đi qua A(2; −3); B(7;7) 232 777():27 aba abbdyx+=−= ⇒⇒⇒=−  +==− 0,5 Do A,M,B thẳnghàngnên M là giao điểmcủa (d) vớitrục Ox nên 7 ;0 2 M    0,5 1.2 Cho a lànghiệm phương trình26330 xx+−= .Tínhgiátr ị c ủ abi ể u th ứ c T =12a4 a2+2a 0,5 Từ giả thiết,suyra 2 231aa =− 422 22 12(1)21 2121 aaaa Taaaa ⇒=−=−+ ⇒=−+−+= Vậy T=1 0,5 2.1 Giải phương trìnhsau:2(52)(1310)7 xxxx +−−++−= (1) 1 ĐKXĐ: 2x ≥ 2 (52)(1310)7 xxxx +−−++−= 52.(1(5)(2)7 52 xx xx xx +−+ ⇔ ++−= ++− 1(5)(2)1 52 xx xx ++− ⇔= ++− Đặt5;2xaxb +=−= với;0 ab ≥ Khi đó phương trình trở thành:11 ab ab + = + 1 (1)(1)0 1 1 abab ab a b ⇔+=+ ⇔−−= = ⇔  = +)Nếu1514() axxktm =⇒+=⇔=− 0,5

+)Nếu1213() bxxtm =⇒−=⇔= Vậy phương trình (1) có nghiệmlàx=3. 0,5 2.2 Giảihệ phương trìnhsau: 6 11 6 xyz xyyzzx xyz ++=  ++=  = 1 Dễ thấy x.y.z=0 nên,,0 xyz ≠ 6 11 6 xyz xyyzzx xyz ++=  ++=  = 6 ()11 6 xyz xyzxy xy z   +=− ⇔++=    =  6 6 (6)11 6 xyz z z xy z   ++=   ⇔−+=    =  0,25 Xét phương trình 6 (6)11 z z −+= 23 6611 zzz⇔−+= (1)(2)(3)0 zzz ⇔−−−= 1 2 3 z z z =  ⇔=   = 0,25 +)Với1 z = thì 5 6 xy xy +=  = (,){(2;3),(3;2)} xy ⇔= +)Với2 z = thì 4 3 xy xy +=  = (,){(1;3),(3;1)} xy ⇔= +)Với3 z = thì 3 2 xy xy +=  = (,){(2;1),(1;2)} xy ⇔= (;;) xyz⇔ làhoánvị của(1;2;3) Vậyhệ phương trình có 6 nghiệm(;;) xyz làhoánvị của(1;2;3) 0,5 3.1 Tìmtấtcả cácnghiệm(x; y; z)của phương trình x(x2+ x +1)= z y 1 thỏamãn x, y làcácsố nguyênvà z làsố nguyêntố 1 Tacó x(x2+ x +1)= z y 1 ⇔ 2 (1)(1) xxzy ++= Vì z làsố nguyêntố nên21;1xx++∈Ζ và2211;11xxx+≥+≥+ 2 1 (;;;) 1 a b xz ababyab xz  += ⇒ ≤+=∈Ν +=  21121 xxx ⇒++⇒+  Mà: { } { }(1)011;20;1 xxx +>⇒+∈⇒∈ +)Nếu010; y xzyzp =⇒=⇒== làsố nguyêntố bấtkỳ 0,5

ấtk

ế

ếu45

y452022 x =±− thỏamãnbài

ỏamãn

Cho đườngtròn (O) có đườngkính AB.Lấy điểm C thuộc đoạn AO (C khác A, O).Vẽ đườngtròn( I ) đườngkính BC.Vẽ tiếptuyến AD vàcát tuyến AEF với đườngtròn( I )(E nằmgiữa A, F )saochotia AO nằm giữa2tia AD , AE. Đườngthẳngvuônggócvới AB vẽ từ C cắt đường tròn(O)tại 2 điểm,gọimột trong hai giao điểmlà N saocho N và D thuộchainửamặtphẳng đốinhaubờ AB.Gọi S là giao điểmcủahai đườngthẳng DI và NB.Gọi R làgiao DN và AS Gọi J làtrung điểm SD .

a)Chứngminhtamgiác AND cân.

b)GọiL,Tlần lượtlàtâm đườngtrònngoạitiếpcáctam giácSBCvàSEF.Chứngminhba điểm J, L, T thẳnghàng.

+)Nếu142;2 y xzyz =⇒=⇒== (thỏamãn) Vậy(;;){(0;0;);(1;2;2)} xyzp = với p làsố nguyêntố b

ỳ 0,5 3.2 Tìmtấtcả số thực x thỏamãn2022 x + và32022 x đ ề ulàs ố nguyên. 1 Đặt2022; xa += 3 2022 b x −= (;) ab ∈Ζ Khi đó 2022;xa=− 3 2022 2022 b a −= 32022(2022)2022 aabb ⇒−−=− 2025()2022 abab⇒−=− Khi đó 2025;;2022 abab −−∈Ζ làsố vôtỷ 20250 45 abab ab ⇒−=−= ⇒==± 0,5 +N

u45 ab== 452022x ⇒=− th

ab==− 452022x ⇒=−− th

0,5 Vậ

4.1

4.1a 0,25 a)Xét ADC∆ và ADB∆ Có   ADCADB =  DAC làgócchung (.)ADCABDgg⇒∆∆  (/)ADAC tc ABAD ⇒= ⇒AD2=AC.AB TamgiácANBvuôngtại N có NC là đườngcaonên AN2=AC.AB (h ệ th ứ c lư ợ ng) T ừ đó AD=AN. Nêntamgiác AND cântại A 0,75 4.1b GọiL,Tlần lượtlàtâm đườngtrònngoạitiếpcáctamgiácSBC vàSEF.Chứngminhba điểm J, L, T thẳnghàng. 1 Tacó:   090ADSANS== Tamgiác AND cântại A nên   SDNSND = Suyratamgiác SDN cântại S nên S thuộctrungtrực ND Hay AS ⊥ ND tại S Chínhvìvậynên AD 2= AR . AS = AE . AF = AC . AB Hay2tứ giác ERSF và CRSB nộitiếpnên L, T cùngnằmtrên trung trực RS (1) 0,5 Tamgiác RSD vuôngtại R có J làtrung điểm SD nên JR = JS Hay J thuộctrungtrực RS (2) Từ (1),(2) ⇒ J,L,Tthẳnghàng. 0,5

4.2 ChohìnhvuôngABCDcódiệntíchlàS.Tứ giácMNPQcóbốn đỉnh M, N , P , Q thuộc AB, BC, CD , DA và4 đỉnhnàykhôngtrùng4 đỉnhhìnhvuông.Chứngminhrằng 4 SACMNNPPQQM +++ ≤ 1 Tacó.. 4 SACMNNPPQQM +++ ≤ 2 4.2.(). ABABMNNPPQQM⇔≤+++ 2.(). ABBCCDDAMNNPPQQM ⇔+++≤+++ Dễ có 222() 2 MQAMAQAMAQ + =+≥ Hay2 MQAMAQ =+ Tương tự 2 MNBMBN =+ 2 PNCPCN =+ 2 PQDQDP =+ Cộngvế vớivế ta được đpcm 5.1 Chox,y,zlàcácsố thựckhôngâmthỏamãn x3+ y3+ z3=3.Tìmgiá trị nhỏ nhấtcủabiểuthức 333 313131 Pxyz yzx =++ +++ 1

. Ápdụngbất đẳngthứcCôsicó: x3+2= x3+1+1 ≥ 3 x y3+2= y3+1+1 ≥ 3 y z3+2= z3+1+1 ≥ 3 z Cộngvế vớivế ta được 333 333(1) 333 Pxyz yzx ≥++ +++ Lạicó 3333 3 (3) 3162 xxyx y + +≥ + 3333 3 (3) 3162 yyzy z + +≥ + 3333 3 (3) 3162 zzxz x + +≥ + Suyra 333 333333 333 115 33316()(2) 16 xyz xyyzzx yzx +++++≥ +++ Mặtkhác 3332 333333()3 3 xyz xyyzzx ++ ++≤= Hay33333313 16()(3) 16xyyzzx −++≥ Từ (1),(2),(3)tacó: 3 4 P ≥ dấu“=”xảyrakhi1 xyz=== Vậy 3 4 MinP = dấu“=”xảyrakhi1 xyz=== . 5.2 Có10bạnhọc sinh tham gia thi đấubóngbàn.Haib ạnbấtkì đềuphải đấuvớinhaumộttrận,bạn nào cũng gặp 9 đốithủ củamìnhvàkhông cótrậnnàohòa.Chứ ngminhrằngluônxếp được10bạnthànhmột hàngdọcsaochobạn đứng trướcthắngbạn đứngkề sau. 0,5 . Xétt ấ tc ả cáccáchs ắ px ế pm ộ ts ố b ạ nthànhm ộ thàngd ọ csao chob ạ n đ ứ ng trư ớ cth ắ ngb ạ n đ ứ ngk ề sau.Cáchs ắ px ế pnàybao

gi ờ cũng t ồ nt ạ ivàs ố cáchs ắ px ế plàh ữ uh ạ n,nênt ồ nt ạ icách s ắ px ế pcónhi ề ub ạ nnh ấ t.

G ọ i123,,,..., kAAAA làcáchs ắ px ế pcónhi ề ub ạ nnh ấ t(1),v ớ i {1;2;3;...;10}k ∈

Gi ả s ử 10k < . Khi đó t ồ nt ạ ib ạ nBkhôngthu ộ cvàohàngtrên 10k <

Theolu ậ t thi đ ấ u,Bph ả i đ ấ uv ớ icácb ạ n123,,,..., kAAAA

+)N ế uBth ắ ng1 A thì123,,,,..., kBAAAA làcáchs ắ px ế pcó1 k + b ạ n vàth ỏ amãnyêuc ầ ubàitoán,mâuthu ẫ nv ớ i (1). Như v ậ yBph ả i thua1 A

+)N ế uBth ắ ng2 A thì123,,,,..., kABAAA làcáchs ắ px ế pcó1 k + b ạ n vàth ỏ amãnyêuc ầ ubàitoán,mâuthu ẫ nv ớ i (1). Như v ậ yBph ả i thua2 A

+)L ậ plu ậ n tương t ự như trên, ta th ấ yBph ả ithua345,,,..., kAAAA . Khi đó ta l ạ icócáchs ắ px ế p123,,,...,, k AAAAB có1 k + b ạ nvàth ỏ a mãnyêuc ầ ubàitoán,mâuthu ẫ nv ớ i(1). Như v ậ y đi ề ugi ả s ử trênlàsai.V ậ y10 k =

THI

Toán (chuyên Toán

igianlàmbài:

Câu 1. (1,5 điểm)

1.Trongmặtphẳng Oxy,cho2 điểm A(2;3); B(7;7).Tìm điểm M thuộctrục Ox để M,A,B thẳnghàng.

2.Cho a lànghiệm phương trình26330 xx+−= .Tínhgiátr ị c ủ abi ể uth ứ c T =12a4 a2+2a Câu 2. (2,0 điểm)

1.Giải phương trìnhsau:2(52)(1310)7 xxxx +−−++−=

++=  ++=  =

xyz xyyzzx xyz

2.Giảihệ phương trìnhsau: 6 11 6

Câu 3. (2,0 điểm)

1.Tìmtấtcả cácnghiệm(x; y; z)của phương trình x(x2+ x +1)= z y 1thỏamãn x, y làcácsố nguyênvà z làsố nguyêntố

2.Tìmtấtcả số thực x thỏamãn2022 x + và32022 x đ ề ulàs ố nguyên. Câu 4. (3,0 điểm)

ọi S là giao điểmcủa hai đườngthẳng DI và NB.Gọi R làgiao DN và

VÀO LỚP 10 THPT CHUYÊN NĂM HỌC: 2022-2023 Mônthi:

và Tin) Thờ

150 phút

HẾT

ạnbất kì đề

ả

đấ

đốithủ củamìnhvàkhôngcótrậ

được10bạnthànhmộthàngdọ

1.Cho x,y,z làcácsố thựckhôngâmthỏamãn x3+ y3+ z3=3.Tìmgiátrị nhỏ nhấtcủabiểuthức 333 313131 Pxyz yzx =++ +++ 2.Có10bạnhọc sinh tham gia thi đấubóngbàn.Haib

uph

u vớinhaumộttrận,bạn nào cũng gặp 9

n nàohòa.Chứngminhrằngluônxếp

csao chobạn đứng trướcthắngbạn đứngkề sau.

UBND TỈNH BẮC NINH SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐÁP ÁN VÀO LỚP 10 THPT CHUYÊN NĂM HỌC: 2022-2023 Mônthi: Toán (chuyên Toán và Tin) Thờigianlàmbài: 150 phút Câu Đáp án Điểm 1.1 Trongmặtphẳng Oxy,cho2 điểm A(2;3); B(7;7).Tìm điểm M thuộctrục Ox để M,A,B thẳnghàng. Giả sử tồn tại ():. dyaxb =+ đi qua A(2; −3); B(7;7) 232 777():27 aba abbdyx+=−= ⇒⇒⇒=−  +==− Khi đó, M là giao điểmcủa (d) vớitrục Ox nên7(;0) 2 M 1.2 Cho a lànghiệm phương trình26330 xx+−= .Tínhgiátr ị c ủ abi ể u th ứ c T =12a4 a2+2a. Từ giả thiết,suyra 2 231aa =− 422 22 12(1)21 2121 aaaa Taaaa ⇒=−=−+ ⇒=−+−+= Vậy T=1 2.1 Giải phương trìnhsau:2(52)(1310)7 xxxx +−−++−= (1) ĐKXĐ: 2x ≥ 2 (52)(1310)7 xxxx +−−++−= 52.(1(5)(2)7 52 xx xx xx +−+ ⇔ ++−= ++− 1(5)(2)1 52 xx xx ++− ⇔= ++− Đặt5;2xaxb +=−= với;0 ab ≥ Khi đó phương trình trở thành:11 ab ab + = + 1 (1)(1)0 1 1 abab ab a b ⇔+=+ ⇔−−= = ⇔  = +)Nếu1514() axxktm =⇒+=⇔=− +)Nếu1213() bxxtm =⇒−=⇔=

Vậy phương trình (1) có nghiệmlàx=3. 2.2 Giảihệ phương trìnhsau: 6 11 6 xyz xyyzzx xyz ++=  ++=  = Dễ thấy x.y.z=0 nên,,0 xyz ≠ 6 11 6 xyz xyyzzx xyz ++=  ++=  = 6 ()11 6 xyz xyzxy xy z   +=− ⇔++=    =  6 6 (6)11 6 xyz z z xy z   ++=   ⇔−+=    =  Xét phương trình 6 (6)11 z z −+= 23 6611 zzz⇔−+= (1)(2)(3)0 zzz ⇔−−−= 1 2 3 z z z =  ⇔=   = Kếthợpvớihệ trêntacó 5 6 xy xy +=  = hoặc 4 3 xy xy +=  = hoặc 3 2 xy xy +=  = (;;) xyz⇔ làhoánvị của(1;2;3) Vậy(;;) xyz làhoánvị của(1;2;3) 3.1 Tìmtấtcả cácnghiệm(x; y; z)của phương trình x(x2+ x +1)= z y 1 thỏamãn x, y làcácsố nguyênvà z làsố nguyêntố. Tabiến đổi được như sau: 2 (1)(1) xxzy ++= Vì z làsố nguyêntố nên21;1xx++∈Ζ và2211;11xxx+≥+≥+ 2 1;1(;;;) ab xzxzababyab ⇒+=+=≤+=∈Ν 21121 xxx ⇒++⇒+  Mà: { } { }(1)011;20;1 xxx +>⇒+∈⇒∈ +)Nếu010; y xzyzp =⇒=⇒== làsố nguyêntố bấtkỳ +)Nếu142;2 y xzyz =⇒=⇒== (thỏamãn) Vậy(;;){(0;0;);(1;2;2)} xyzp = với p làsố nguyêntố bấtkỳ 3.2 Tìmtấtcả số thực x thỏamãn2022 x + và32022 x đ ề ulàs ố nguyên.

.Lấy điểm C thuộc đoạn AO (C

BC.Vẽ tiếptuyến AD vàcát

ới đườngtròn( I )(E nằmgiữa A, F )saochotia AO nằm giữa2tia AD , AE. Đườngthẳngvuônggócvới AB vẽ từ C cắt đường tròn(O)tại 2 điểm,gọimột trong hai giao điểmlà N saocho N và D thuộchainửamặtphẳng đốinhaubờ AB.Gọi S là giao điểmcủahai đườngthẳng DI và NB.Gọi R làgiao DN và AS .Gọi J làtrung điểm SD .

ế

a)Chứngminhtamgiác AND cân.

b)GọiL,Tlần lượtlàtâm đườngtrònngoạitiếpcáctam giácSBCvàSEF.Chứng minh ba điểm J, L, T thẳnghàng.

Đặt2022; xa += 3 2022 b x −= (;) ab ∈Ζ Khi đó 2022;xa=− 3 2022 2022 b a −= 32022(2022)2022 aabb ⇒−−=− 2025()2022 abab⇒−=− Khi đó 2025;;2022 abab −−∈Ζ làsố vôtỷ 20250 45 abab ab ⇒−=−= ⇒==± +Nếu45 ab== 452022x ⇒=− thỏamãn +Nếu45 ab==− 452022x ⇒=−− thỏamãn Vậy452022 x =±− thỏamãnbài 4.1 Cho đườngtròn (O) có đườngkính AB

khác A, O).Vẽ đườngtròn( I ) đườngkính

tuy

n AEF v

Dễ thấy AD làtiếptuyểncủa( I )

AD2= AC . AB = AN 2

Nêntamgiác AND cânt ại A

4.1b GọiL,Tlần lượtlàtâm đườngtrònngoạitiếpcáctamgiácSBC vàSEF.Chứng minh ba điểm J, L, T thẳnghàng.

090ADSANS== Tamgiác AND cântại A nên 

SDNSND = Suyratamgiác SDN cântại S nên S thuộctrungtrực ND Hay AS ⊥ ND tại S Chínhvìvậynên AD 2= AR . AS = AE . AF = AC . AB Hay2tứ giác ERSF và CRSB nộitiếpnên L, T cùngnằmtrên trung tr

làtrung

4.1a

⇒

Tacó:  



ực RS (1) Tamgiác RSD vuôngtại R có J

điểm SD nên JR = JS Hay J thuộctrungtrực RS (2) Từ (1),(2) ⇒ J,L,Tthẳnghàng. 4.2 ChohìnhvuôngABCDcódiệntíchlàS.Tứ giácMNPQcóbốn đỉnh M, N , P , Q thuộc AB, BC, CD , DA và4 đỉnhnàykhôngtrùng4 đỉnhhìnhvuông.Chứngminhrằng 4 SACMNNPPQQM +++ ≤

Tacó 4 SACMNNPPQQM +++ ≤ 2 4.2.(). ABABMNNPPQQM⇔≤+++ 2.(). ABBCCDDAMNNPPQQM ⇔+++≤+++ Dễ có 222() 2 MQAMAQAMAQ + =+≥ Hay2 MQAMAQ =+ Tương tự 2 MNBMBN =+ 2 PNCPCN =+ 2 PQDQDP =+ Cộngvế vớivế ta được đpcm 5.1 Chox,y,zlàcácsố thựckhôngâmthỏamãn x3+ y3+ z3=3.Tìmgiá trị nhỏ nhấtcủabiểuthức 333 . 313131 Pxyz yzx =++ +++

đốith

ất kì đềuph

củamìnhvàkhông

ếp được10bạnthànhmột hàngdọcsaochobạn đứng trướcthắngbạn đứngkề sau. Vìsố cáchxếplàhữuhạn,nênkhitaxếpcácbạnhọcsinh thành1hàng,luôntồntạicáchxếpthỏamãnyêucầu đề bàivà cónhiềunhất m họcsinh.Tasẽ đi chứngminh m =10. Thậtvậy,giả sử m <10.Tứclàtồntại1họcsinh X khôngthể xếpvàohàng.Taxétcác trườnghợpsau:

• NếuXthắng m bạntronghàng.Khinày,taxếp X ở đầuhàng,sẽthỏamãn điềukiện đề bài.

• Xthua m bạntronghàng.Khinày,taxếp X ở cuối hàng,sẽ thỏamãn điềukiện đề bài.

• Xthắng1số bạnvàthua1số bạntronghàng.Lúc đó, luôntồntại2bạnliêntiếpsaochobạn đằng trướcthắng X,bạn đằngsauthua

ỉ cầnxếp X vàogi ữa2bạn đó, sẽ

Ápdụngbất đẳngthứcAM-GMtacó y3+1+1 ≥ 3 y Chứngminh tương tự rồicộngvế vớivế ta được 333 333. 333 Pxyz yzx ≥++ +++ Đặt333(,,)(,,) xyzabc = Khi đó 3abc++= và. 333 abc P bca ≥++ +++ Ápdụngbất đẳngthứcCauchy-SchwarzdạngEngeltacó 2() 3333() abcabc bcaabbccaabc ++ ++≥ ++++++++ Mặtkháctacó222()()()0 abbcca −+−+−≥ 2 ()3() abcabbcca⇒++≥++ 22 2 ()()3 3()()4 33() abcabc P abbccaabcabcabc ++ ++ ≥≥= +++++++ +++ Đẳngthứcxảyrakhi1 abc=== hay1 xyz=== 5.2 Có10bạnhọc sinh tham gia thi đấubóngbàn.Haib ạnb

ả

đấuvớinhaumộttrận,bạn nào cũng gặp 9

ủ

cótrậnnàohòa.Chứ ngminhrằngluônx

X.Khinàytach

thỏamãn đi ềuki ện đề bài.

Như vậy,vớimọi trườnghợp,taluônxếp được X vàohàngsao chothỏamãnyêucầu đề bài.Khinày,số họcsinhtronghàngsẽ

là m +1> m ,tráivớicách đặtban đầu.

Vậygiả sử sai,bàitoán đượcchứngminh.

ngth

:. dyaxb

ng31. yx

ết đường

hàng kinh doanh điệnmáysukhinhậpvề chiếctivi, đã bán chiếc tivi đó; cửahàngthu đượctiềnlãilà10%củagiánhậpvề.Giả sử cửahàngtiếptụcnânggiábánchiếc tivi đó thêm 5% của giá đã bán, nhưng bớt cho khách hàng 245000 đồng, khi đó cửahàngsẽ thu đượctiềnlãilà 12%củagiánhậpvề.Tìmgiátiềnkhinhậpvề củachiếc tivi đó. Bài 3. (3,0 điểm) Cho tam giác đều ABC nộitiếp đườngtròn   ,O điểm D thuộccungnhỏ  AB ( D khác A và B ). Cáctiếptuyếnvới đườngtròn  O tại B và C cắt AD theothứ tự tại E và. G Gọi I là giao điểm của CE và. BG a)Chứngminhrằng:. EBCBCG  b)Tínhsố đo góc BIC Từ đó, hãy chứngminhrằngtứ giác BIDE nộitiếp. c)Gọi K là giao điểmcủa DI và. BC Chứngminhrằng2.. KBKIKD  Bài 4. (3,0 điểm) a)Tìmcácsố thực

Trang 1 BỘ GIÁODỤC VÀ ĐÀO TẠO TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI CỘNG HÒA XÃ HỘI CHỦ NGHĨA VIỆT NAM Độc lập - Tự do - hạnh Phúc ĐỀ THI TUYỂN SINH VÀO TRƯỜNG TRUNG HỌC PHỔ THÔNG CHUYÊN NĂM 2022 Môn thi : Toán Thờigian:90phút(khôngkể thời gian phát đề) Bài 1. (1,5 điểm) Cho1111 : 2121 Axx xxxxx             0;1.xx a)Rútgọn A b)Tìmcácsố nguyên x saocho1 A làsố nguyên dương. Bài 2. (2,5 điểm) a)Trongmặtphẳngtọa độ ,Oxy hãyviết phương trình đườ

ẳng  

 bi

thẳng  d đi qua điểm  2;1A vàsongsongvới đườ

ẳ

 b)Mộtcửa

x saocho2 ax và352 bx đồngthờilàhaisố hữutỉ b)Biếtrằng: phương trình bậchai2110 xaxb cóhainghiệm0 x và1; x phương trình bậchai2220 xaxb cóhainghiệm0 x và2; x … phương trình bậchai2202220220 xaxb cóhainghiệm0 x và2022 x Chứngminrằngsố thực122022 2022 xxx    lànghiệmcủa phương trình bậchai: 21220221220220. 20222022 aaabbb xx           --- Hết ---

đườ

ết đườ

điểm  2;1A vàsongsongvới đườngthẳng31. yx b)Mộtcửa hàng kinh doanh điệnmáysukhinhậpvề chiếc tivi, đã bán chiếc tivi đó; cửahàngthu đượctiềnlãilà10%củagiánhậpvề.Giả sử cửahàngtiếptụcnânggiábánchiếc tivi đó thêm 5% của giá đã bán, nhưng bớtchokhách hàng 245000 đồng, khi đó cửahàngsẽ thu đượctiềnlãilà 12%c

.Tìmgiáti

tivi

Trang 2 HƯỚNG DẪN GIẢI Bài 1. (1,5 điểm) Cho1111 : 2121 Axx xxxxx           với0 x  và 1.x  a)Rútgọn. A b)Tìmcácsố nguyên x saocho1 A làsố nguyên dương. GIẢI a)Với0 x  và 1x  ta có: 1111 : 2121 Axx xxxxx              1211 : 211 Axxxx xxx       321 . 211 Axxx xx            1211 211 xxxx A xx     2 1Ax b)Tacó10 A  và  2 11 1. 1Ax   Vì1 A làsố nguyên dương nên   12 111 x A  Khi0 x  thỏa.Vậy0 x  làgiátrị duynhấtthỏamãnyêucầu. Bài 2. (2,5 điểm) a)Trongmặtphẳngtọa độ ,Oxy hãyviết phương trình

ngthẳng  

dyaxb  bi

ng thẳng  d đi qua

ủagiánhậ

ề

ềnkhinhậpvề củachiếc

đó. GIẢI a)Do  d songsongvới đườngthẳng31 yx nên3 a  và1. b  Mặt khác, do đường thẳng  d đi qua điểm  2;1A nên126, abb tư đó 5b  (thỏamãn1 b  ).Vậy phương trình của đườngthẳng  d cầntìmlà   :35.dyx b)Gọi x (đồng)làgiátiềncủachiếttivilúcnhậpvề.Rõràng0. x  Tacótiềnlãicủachiếctivi đó khi bán là 10% 10 x x  (đồng),suyragiábáncủachiếctivilà11 1010 xx x  (đồng). Nếucửahàngnàynânggiácủachiếctivithêm5%sovới giá đã bán thì số tiềnlãithêmlà 1111 .5% 10200 xx  (đồng).Thế thì, sau khi tăng thêm 5% giá đã bán thì giá mớicủachiếctivi(khi chưa giảmgiá)là1111231 10200200 xxx  (đồng).Khigiảm cho khách hàng 245000 đồngthìgiábánlà

Trang 3 231 245000 200 x (đồng).Vớigiánàythìcửa hàng thu đượclãi12%củagiánhậpvề,tứcbằng 3 12% 25 x x  (đồng). Như vậytacó: 2313 245000. 20025 xx x      Giải phương trình này, ta được7000000. x  Vậygiánhậpvề củachiếc tivilà7000000 x  (đồng). Bài 3. (3,0 điểm) Cho tam giác đều ABC nộitiếp đườngtròn   ,O điểm D thuộccungnhỏ  AB ( D khác A và B ). Cáctiếptuyếnvới đườngtròn  O tại B và C cắt AD theothứ tự tại E và. G Gọi I là giao điểm của CE và BG a)Chứngminhrằng:. EBCBCG  b)Tínhsố đo góc .BIC Từ đó, hãy chứngminhrằngtứ giác BIDE nộitiếp. c)Gọi K là giao điểmcủa DI và BC Chứngminhrằng2KBKIKD  GIẢI a)Dotamgiác ABC đềunên    ,060.ABBCCABACABCACB  Tâm đườngtrònngoại tiếp O cũng là trựctâmcủatamgiác. ABC Do đó .BOAC  Lạicó BE làtiếptuyếntại B của  O nên BEBO  từ đó //.BEAC Tương tự ta cũng có //.CGAB Suyra   AEBGAC  và   BAEAGC  (các góc đồngvị).Từ đó AEBGAC  (gg),dẫn đến BEBA ACCG  Mà ACABBC  nên BECB BCCG  Từ đây, kếthợp với   0 120,EBCGCB ta được EBCBCG  (cgc).(1) b)Từ (1)tacó   BECCBG  Từ đó ,CEBCBI  dẫn đến   0 120.CIBCBE Suyra   00 18060.BIEBIC Dotứ giác ADBC nộitiếp  O nên   0 60,BDEBCA suyra   .BIEBDE  Tứ giác BIDE có   ,BIEBDE  mà hai góc này có đỉnhkề nhaunhìncạnh BE nêntứ giác BIDE làtứ giácnộitiếp. c)Dotứ giác BIDE làtứ giácnộitiếpnên   BDIBEI  (haigócnộitiếpcùngchắncung BI ),mà   BECCBG  nên   .KBIKDB 

trình

ycóhaigiátr

ử dụng địnhlýviet,tacó0

ngthờilàhaisố hữutỉ

và1;

và2;

này đềuthỏamãnyêucầu.

và12.

đó

Trang 4 Xéthaitamgiác KBI và KDB cógóc K chungvà   KBIKDB  nên hai tam giác này đồngdạng (g-g).Suyra KBKD KIKB  từ đó 2 ..KBKIKD  Bài 4. (3,0 điểm) a)Tìmcácsố thực x saocho2 ax và352 bx đồ

. b)Biếtrằng: phương

bậchai2110 xaxb cóhainghiệ

x phương

bậchai2220 xaxb cóhainghiệ

x … phương

bậchai2202220220 xaxb cóhainghiệm0 x và2022. x Chứngminrằngsố thực122022 ... 2022 xxx    lànghiệmcủa phương trình bậchai: 2122022122022......0. 20222022 aaabbb xx           GIẢI a)Tacó:2, xa do đó    3 332 522526321. bxaaaa  Vì,ab làcácsố hữutỉ nên  3212 a làsố hữutỉ.Suyra210, a  tức1. a  Từ đây ta c 12x  hoặc12. x  Thử lại,tathấycácgiátrị

Vậ

ị x thỏamãnyêucầubàitoánlà12 x 

x  b)S

ii xxa  và0 ii xxb  vớimọi1,2,.....,2022. i  Từ

suy ra      12202201220220 ......2022....2022 aaaxxxxx  và   12202201220220 .....2022.bbbxxxxx  Như vậy122022 0 .... 2022 aab x    và122022 0 .... . 2022 bbb x    Do đó, theo định lý viet đảo,cả haisố 0x và  đềulànghiệmcủa phương trình 21220221220220. 20222022 aaabbb x   --- Hết ---

SỞ GIÁO DỤC ĐÀO TẠO KỲ THI TUYỂN SINH VẢO LỚP 10 THPT BÌNH ĐỊNH NÃM HỌC 2022-2023

Môn thỉ chuyên: TOÁN (CHUYÊNTOÁN) Ngày thi: 11/6/2022

phút (không kể thởi gian phát đề)

điểm)

phương

là các số nguyên.

và các nghiệm còn lại của phương trình. Bài 2: (2,5 điểm)

Giải hệ phương trình:

abc là các số nguyên. Đặt 553 (2021)(22022)(32023)232022 ; SabcPabc

Chứng minh rằng S chia hết cho 30 khi và chi khi P chia hết cho 30 . Bài 3: ( 1,0 điểm)

phương

tất cả bao nhiêu đa thức ()Px có bậc không lởn hơn 2 với các hệ số nguyên không âm và thỏa mãn điều kiện (3)100P = . Bài 4: (3,0 điểm)

nhọn (ABAC) < nội tiếp đường tròn (O) , các đường cao AD,BE,CF cắt nhau tại H . Gọi Mlàtrung diểm BC

a) Chứng minh tứ giác DMEF là tứ giác nội tiếp.

b) Đường tròn tâm I đường kính AH cắt đường tròn (O) tại điểm thử hai là P . Kẻ đườngkínhAK của đường tròn (O) . Chứng minh bốn điểm P,H,M,K thẳng hàng.

c) Các tiếp tuyến tại AvàP của đường tròn (I) cằt nhau ở N . Chứng minh ba đường thẳng MN,EF,AH đồng quy.

Bài 5: (1,0 điểm)

2 số , xy thỏa mãn:

giá trị lớn nhất, giá

nhỏ nhất của biều thức:

HẾT

Để chính thức

Thời gian làm bài: 150

Bài 1: (2,5

1. Cho biểu thức: 20222020252017Pxxxxx =⋅−⋅++ Tính giá trị của P khi332525x =+−− 2. Cho

trình 3210 xbxcx+++= trong đó , bc

Biết

trình có nghiệm 025x =+ .Tìm,bc

2 22 ()410 ()2720 xxyyy yxyxy  ++−+= +−−−= 2.Cho,,

=++−++=+++

Có

ChotamgiácABC

Cho

22 2 3 xy xyxy +≤ ++   = Tìm

trị

22 Txyxy =+−

Đáp án Bài 1: (2,5 điểm) 1. Cho biểu th ức 20222020252017Pxxxxx =−++ . Tính giá trị củ a P khi 332525x =+−− 2. Cho phương trình 3210 xbxcx+++= trong đó , bc là các số nguyên. Biết phương trình có nghiệm 025x =+ . Tìm , bc và các nghiệm còn lại của phương trình. Lời giải. 1. Ta có 332525x =+−− ( ) 33333 3 2 (25)(25)32525(2525) 253 (5)520. x xx xxx ⇒=+−−−+⋅−++− ⇒=+ ⇒−−+= Chú ý rằng 2 253520 24 xxx  −+=−+>    nên từ đâ y chỉ có thể 5x = . Thế nên ( ) 202022520172022Pxxxx =−++= . 2. Bằng tính toán trực tiếp, ta tính được 32 0038175;945xx=+=+ . Vì 0x là nghiệm của phương trình 3210 xbxcx+++= nên 32 00010 (38175)(945)(25)10 (3992)(174)50. xbxcx bc bcbc +++= ⇒++++++= ⇒+++++= Ta thấy rằng nếu 1740 bc ++≠ thì 3992 5 174 bc bc ++ = ∈ ++  do , bc là số nguyên, điề u vô lí. Do đó 1740 bc ++= , kéo theo 39920 bc ++= . Giải hệ phương trình 41705 923903 bcb bcc  ++==−  ⇔  ++== . Với (;)(5;3) bc =− thì phương trình trở thành 325310xxx−++= ( ) 241(1)0 25 25 1 xxx x x x ⇔−−−=  =+ ⇔=−   =  Vậy với (;)(5;3) bc =− , ngoài nghiệm 025x =+ thì PT còn nghiệm 125x =− và 21x = . Bài 2: ( 2,5 điểm)

1. Giải hệ phương trinh 2 22 ()410 ()2720 xxyyy yxyxy  ++−+= +−−−= . 2. Cho ,, abc là các số nguyên. Đặt 555 (2021)(22022)(32023)Sabc =++−++ ; 232022Pabc=+++ . Chứng minh rằng S chia hết cho 30 khi và chi khi P chia hết cho 30 . Lời giải. 1. Xét hệ phương trình: ( ) ( ) 2 22 ()4101 ()27202 xxyyy yxyxy  ++−+=  +−−−=  Nhân hai vố phương trình (1) với 2 , ta được ( )22 2228203 xxyyy++−+= Cộng theo vế phương trình (2) và (3) ta được 22 2 ()22150 ()2()150 (3)(5)0 0 3 5 yxyxyyy yxyxy yxyxy y xy xy +++−=  ⇔+++−=  ⇔+−++= =  ⇔=−   =−− Nếu y0 = thay vào phương trình (1) ta được 210x += , không có nghiệm thực. Nếu 3 xy =− , thay vào phương trình (1) ta được 2 (3)3410 yyy −⋅+−+= 22 7100(2)(5)05 y yyyy y = ⇔−+=⇔−−=⇔  = Với 2y = thì 1x = ; với 5y = thì 2x =− . Nếu 5 xy =−− , thay vào phương trình (1) ta được 2 (5)(5)410 yyy −−⋅−+−+= 2260yy ⇔++= , không có nghiệm th ực vì 2 21103260 24yyy  ++=++>   . Vậy hệ phương trình ban đầu có hai nghiệm là (;)(1;2) xy = và (;)(2;5) xy =− . 2. Đặt 2021;22022;32023xaybzc =+=−=+ thì 555 Sxyz =++ và Pxyz =++ . Ta có ( ) ( ) ( )555 SPxxyyzz −=−+−+− . Xét ( )52(1)(1)1.Axxxxxx =−=−++ Ta thấy (1)(1) xxx−+ là tích của ba số nguyên liên tiếp n ên có tích chia hết cho 6 , do vậy A chia hết cho 6. Theo định lý Fermat, ta cũng có 5(mod5)xx = nên A chia hết cho 5. Mà ƯCLN (5,6)1 = nên 5 Axx =− chia hết cho 30 .

Hoàn toàn tương tự ( )5 yy và ( )5 zz cùng chia hết cho 30 . Do vậy () SP chia hết cho 30 . Điều này cho biết S chia hết cho 30 khi và chi khi P chia hết cho 30 . Bài 3: ( 1,0 điểm ) Có tấ t cả bao nhiêu đ a thức ()Px có bậc không l ớn hơn 2 v ới các hệ s ố nguyên không âm và thỏ a mãn điều kiện (3)100P = . Lời giải. - Xét đa thức () PxC = là hằng số thì chỉ có đ a th ức P(x)100 = thỏa mãn. Xét đa thức

iều kiện nên trường h ợp này có tất cả 33

thứ

đề

Xét đa thức

Pxaxbxc

. Theo đề bài ta có 93100 abc++= , mà ,, abc là các số nguyên nên 31ck=+ với k ∈  (với mỗi giá trị củ a k thì ta tìm được duy nhất một gi á trị củ a c ).

Khi đó 333 abk++= hay 3330bka+=−≥ , suy ra 111 a ≤≤ . Với mỗi giá trị a như vậy, có (343) a giá trị nguyên của b nhận từ 0 đến ( 333) a và có duy nhấ t mộ t gi á trị 333 kab =−− thoả mãn sau khi đã chọn a và b . Vậy trường h ợp này có 11 1

1211 (343)34113176 2a

a =

⋅ ∑−=⋅−⋅= cặp (;;) abk thoả mãn, ứng v ới 176 cặp (;;) abc thoả mãn đề bài. Trường h ợp này có 176 đa thức thoả mãn. Từ ba trường h ợp trê n, có tấ t cả 133176210 ++= đa thức ()Px với hệ số nguyên không âm và (3)100P = .

Bài 4: (3,0 điểm)

Cho tam giác ABC nh ọn (AB<AC) nội tiếp đường tròn (O), cá c đường cao AD, BE, CF cắt nhau tại H. Gọ i M là trung điểm BC. a) Chứng minh tứ giá c DMEF là tứ giác nộ i tiếp. b) Ðường tròn tâm I đường kính AH cắ t đường tròn (O) tại điểm thứ hai là P. Kẻ đường kính AK củ a đường tròn (O). Chứng minh bốn điểm P, H, M, K thẳng hàng. c) Các tiếp tuyến tại A và P củ a đường trò n (I) cắt nhau ở N. Chứng minh ba đường thẳng MN, EF, AH đồng quy.

() Pxaxb =+ với 0;0;, abab>≥∈  . Ta có P(3)100 = hay 3100 ab+= , mà * ; ab∈∈ nên 133 a ≤≤ . Với mỗi a như vậy ta tìm được duy nhất 1003 ba =− thỏa mãn đ

đa

c thỏa

bài.

()2

=++ với * ;, abc∈∈

Ta thấy các tứ giác BCEF, ACDF nội tiếp đường tròn đường ki nhh BC, AC. Khi

vậy tứ giác DMEF nội tiếp.

Theo giả thiết KBAB ⊥ và HCAB ⊥ nên // KBHC . Tương tư KCAC ⊥ và HBAC ⊥ nên // KCHB . Tứ giác KBHC có hai cặp cạnh đối di ện song song nhau

ên là hình bình hành. Lại vì M là trung điểm của BC

Lời giải. a)

đó         00 0 180180 180 MEFAEFMECABCMCE FBDBFDBDF =−−=−− =−−= Do

nên H, M, K thẳng hàng. Mặt khác,    90 APHAFHAPK ° === nên P, H, K thẳng hàng. Như vậy H, M, K, P thẳng hàng. c) Gọi R là giao điểm của AD và EF. Vì các tứ giác AFDC, AEDB nội tiếp nên      000 1801802180. EDFFDBEDCBACFIE =−−=−=− Do vậy IEDF là tứ giá c nội tiếp, suy ra .. RERFRIRD = . Mặt khác tứ giác AEHF nội tiếp nên RERFRHRA ⋅=⋅ . Vậy nên ( )1 RARD RIRDRHRA RIRH IAHDIARIRA RIRHHDRHRD ⋅=⋅⇒= ⇒=⇒== Từ chứng minh ở câu b) ta có HMAP ⊥ , lại vì NIAP ⊥ (do NI l à đường trung trực của đoạn AP) nên HM // NI, kết hợp // NADM suy ra   DMHINA = (hai góc nhọn có

Khi

cặp cạnh tương ứng song song). Từ đây DHMAIN∆∆ ∽ (tam giác vuông có hai góc nhọn bằng nhau) ( ).2 IAAN HDDM ⇒= Từ (1) và (2) suy ra RAAN RDDM = . Vậy nên ARNDRM∆∆ ∽ (c.g.c)   ARNDRM⇒= . Vì       0180NRMNRAARMMRDARMARD =+=+== nên M, N, R thẳng hàng, tức là MN cũng đi qua điểm R . Vậy MN, AD, EF đồ ng quy. Bài 5: ( 1,0 điểm ) Cho hai số , xy thoả mãn: 22 2 3 xy xyxy +≤  ++= . Tìm giá trị l ớn nhất, giá trị nhỏ nhất của bi ểu thức: 22 Txyxy =+− . Lời giải. Ta có bất đ ẳng thức 22()()04xy xyxy + −≥⇔≤ . Bởi vậy từ giả thiết, 2 22 () ()330()4. 4 xy xyxyxy + +=+≤+⇒≤+≤ Lại để ý đẳng thức ( ) ( ) 322222 2()xyxyxyxyxy ++−+−=+ hay 2 092()8 Txy ≤−=+≤ , vậy 19. T ≤≤

(;)(1;1) xy = (thoả mãn giả thiết) thì 1T = . Khi (;)(3;3) xy =− (thoả mãn giả thiết) thì 9T = . Kết luận: Giá trị l ớn nhất của T là 9 ; giá trị nhỏ nhất củ a T là 1 .

THI TUYỂN SINH LỚP 10

học:

thi: TOÁN (Chuyên)

gian làm bài: 150phút

Không kể

gian phát đề

1. (2,5 điểm)

(2,0 điểm)

phương trình

Tìm tất cả các giá trị

tham số).

để phương trình có 2 nghiệm phân biệt dương.

Gọi 12 , xx làcác nghiệm của phương trình. Tìm m để biểu thức

2022 6 M xxxx = +− đạt giá trị nhỏ nhất.

Bài 3. (2,0 điểm)

a) Giải phương trình: ( ) 111xxxx +−+−= với x ∈  .

b) Chứng minh rằng: 7 Aaa =− chia hết cho 7 , với mọi a ∈  Bài 4. (3,5 điểm)

tam giác nhọn ABC ( ABAC < ) nội tiếp đường tròn ( )O , M là trung điểm BC ;,BECF là các đường cao ( , EF là chân các đường cao). Các tiếp tuyến với đường tròn tại B và C cắt nhau tại

. Gọi , NP lần lượt là giao điểm

a BS với,EFAS với ( )O ( PA ≠ ). Chứng minh rằng:

1/10 SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ

TỈNH BÌNH DƯƠNG Năm

2022 - 2023 Môn

Thời

(

thời

) Bài

Cho biểu thức 2 : 2 aaaaabab A babaabababab    ++ =+−−     ++++   với a và b là các số thực dương khác nhau. a) Rút gọn biểu thức A b) Tính giá trị của : 2 aaaa B ba abababab    =+−     ++++   khi743 a =− và 743b =+ Bài 2.

Cho

2220 xmxm−+−= ( m là

22 1212

Cho

củ

a) MNBF ⊥ . b) ABCPACBP = c)   CAMBAP = = = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = = ĐỀ

THI CHÍNH THỨC

2/10 Hướng dẫn giải: Bài 1. (2,5 điểm) Cho biểu thức 2 : 2 aaaaabab A babaabababab    ++ =+−−     ++++   với a và b là các số thực dương khác nhau. a) Rút gọn biểu thức A b) Tính giá trị của : 2 aaaa B ba abababab    =+−     ++++   khi743 a =− và 743b =+ Lời giải a) Với , ab là các số thực dương khác nhau, ta có: 2 : 2 aaaaabab A babaabababab    ++ =+−−     ++++   ( ) ( ) ( ) ( ) ( ) ( ) 2 :2 aaaaab abababababab ab  =−+ −+ ++ +− +−+ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2 :2 aabaaabaab abababab ab −−+−+ = + +− ++− ( ) ( ) ( ) ( ) ( ) ( ) 2 :2 aabaaabaab abababab ab −−+−+ = + +− ++− ( ) ( ) ( ) ( ) ( ) ( ) 22 . ababab ababababab ++ = + +− +− ( ) 0 abab abab −+ + =+= Vậy 0A = . b)Theoa),tacó: : 2 aaaaab B ba ababababab    =+−=     ++++   Khi743 a =− và743 b =+ thỏa mãn , ab là các số thực dương khác nhau, ta có: ( ) 2 743232323a =−=−=−=− ; ( ) 2 743232323b =+=+=+=+ ;

(2,0 điểm)

phương trình

Tìm tất

Gọi

nhỏ nhất.

các giá

làcá

nghiệm

phương

Để phương trình

nghiệm

là tham số).

có 2 nghiệm phân biệt dương.

trình. Tìm m để biểu thức

giải

là tham số) (1).

dương

6 M xxxx = +−

giá

3/10 23234223 23232333 B −+−−− ⇒= === ; Vậy 23 3 B = khi743 a =− và743 b =+ . Bài 2.

Cho

2220 xmxm−+−= ( m

cả

trị m để phương trình

của phương

22 1212 2022

đạt

trị

Lời

Cho

trình 2220 xmxm−+−= ( m

(1) có hai

phân biệt

thì: ( ) ( ) 0222 1202017 0 02002 24 2022 0 mmmm bm mmm a mmM c a  ′∆>  −−−>  −+>   −+> >⇔> ⇔>⇔ ⇔>  −> > > >  Vậy 2m > thì (1) có hai nghiệm phân biệt dương. b) Phương trình (1) có 2 17 0 24 m ′ ∆=−+>   với mọi m ⇒ (1) luôn có hai nghiệm phân biệt 12 ; xx với mọi m , theo hệ thức Vi et,tacó:12 12 2 2 xxm xxm +=  =− . ( ) ( ) ( ) 22222 12121212 2022202220222022 64816 8282 M xxxxmm xxxxmm ⇒= = = = +− +−−−−+ ( ) 2 20222022337 4112122 m =≥= −+ Vậy 337 2 MinM = khi1 m = . Bài 3. (2,0 điểm) a) Giải phương trình: ( ) 111xxxx +−+−= với x ∈  b) Chứng minh rằng: 7 Aaa =− chia hết cho 7 , với mọi a ∈  . Lời giải a) ĐKXĐ: 01 x ≤≤ ( ) 111xxxx +−+−= Đặt ( ) 222 011 10121 axabababab bxababab ++= =≥++=   ⇒⇔  += =−≥+−=   ;

phương trình

Với mọi a

tập

}0;1

mãn);

) ( ) ( )7633111Aaaaaaaa =−=−=−+

77aA ⇒  ; Nếu a không chia hết cho 7thì ( ) ( )3 1,2,3,4,5,6mod71,6mod7aa ≡ ⇒≡ 317a ⇒−  hoặc 3177aA +⇒ .

Vậy 7A với mọi a ∈  . Bài 4. (3,5 điểm)

Cho tam giác nhọn ABC ( ABAC < ) nội tiếp đường tròn ( )O , M là trung điểm BC ;,BECF là các đường cao ( , EF là chân các đường cao). Các tiếp tuyến với đường tròn tại B và C cắt nhau tại S . Gọi , NP lần lượt là giao điểm của BS với,EFAS với ( )O ( PA ≠ ). Chứng minh rằng:

Lời giải

4/10 Đặt ( ) ( ) 2 22 1 012220 230 0212113 4 S TM SabSPSPP SS PabSPSPPSS KTM P =   =+≥+=+==  +−= ⇒⇔⇔⇔ =≥ −=−==− =−    =−  Với 1;0SP== tacó 1 0 ab ab += ⇒ = , ab là hai nghiệm của phương trình ( ) 20 010 1 x xxxx x = −=⇔−=⇔  = . Vậy 0;1ab== hoặc 1;0ab== ; Với 0;1ab== 0 0 11 x x x  = ⇒⇔=  −=  (thỏa mãn); Với 1;0

== 1 1 10 x x x  = ⇒⇔=  −=  (thỏa

Vậy

có

nghiệm là {

S = . b)

∈  tacó: (

Nếu

a) MNBF ⊥ . b) ABCPACBP = c)   CAMBAP =

MNBF ⊥

BEC

vuông tại E có EM là trung tuyến

BC EMMBMCMEC⇒===⇒∆ cân tại

giác BFEC

BCFEAABC

(cùng bù với

tứ giác BFEC nội tiếp đường tròn đường kính

MENMECFEAACBABCBAC

lại có

BACCBS

(tổng ba góc trong ABC∆

(góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng

5/10 P

N S

F

E M

O B C

A

. Tacó

∆

  MMECACB ⇒= ; Tứ

có   90BFCBEC==°⇒

 

⇒=

 FEC );   ( )  ( )  180180

⇒=°−+=°−+=

); Ta

 

chắn  BC )   ( )MENCBSBAC⇒== ; Mà   180MBNCBS+=° (hai góc kề bù)   180MENMBN ⇒+=°⇒ tứ giác BMEN nội tiếp   BMNBEN⇒= (hai góc nội tiếp cùng chắn  BN ); Vì   BENBCF = (hai góc nội tiếp cùng chắn  BF )   ( )BMNBCFBEN⇒== , hai góc này lại ở vị trí đồng vị nên // MNCF Dotheo đầu bài ta có CFBFMNBF ⊥⇒⊥ . b) ABCPACBP = . Xét SBP∆ và SAB∆ có:  S chung;   SBPSAB = (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn  BP ); ( ) BPSB SBPSABggABSA⇒∆∆⇒= ∽ (1); Xét SCP∆ và SAC∆ có:  S chung;   SCPSAC = (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn  CP );

6/10 ( ) CPSC SCPSACggACSA⇒∆∆⇒= ∽ (2); Mà theo tính chất hai tiếp tuyến cắt nhau, ta có SBSC = (3); Từ (1), (2) và (3) ta có: .. BPCP ABCPACBP ABAC =⇔= . c)   CAMBAP = . Vận dụng định lý Ptolemy, ta có tứ giác ABPC nội tiếp ( ) OAPBCABCPACBP ⇒=+ ; Theocâub)thì...2..22. ABCPACBPAPBCBPACAPCMBPAC =⇒=⇒= .. APAC APCMBPAC BPCM ⇒=⇒= ; Xét BPA∆ và MCA∆ có:   BPAMCA = (hai góc nội tiếp cùng chắn  AB ); APAC BPCM = (chứng minh trên); ( )   BPAMCAcgcCAMBAP⇒∆∆⇒= ∽ = = = = = = = = = = = = = = = = = = = Hết = = = = = = = = = = = = = = = = = = =

7/10

8/10

9/10

10/10

bánkính

i H làtrự

tâmc

atamgiác

.Gọi,IJ lần lượtlàhìnhchiếucủa M lên các đườngthẳng,. BCCA Đườngthẳng IJ cắt đườngthẳng AB tại K .

ứngminhbốn điểm,,,BKMI cùngthuộcmột đườngtròn.Từ đó suy ra MKAB ⊥ b)Gọi123 ,, MMM lần lượtlàcác điểm đốixứngcủa M qua các đườngthẳng,,. BCCAAB Chứngminhbốn điểm123 ,, MMM và H thẳnghàng. c)Chứngminh khi điểm M di độngtrêncungnhỏ BC taluôncó  234.sin. MMRBAC ≤ Xác địnhvị trícủa điểm M khidấubằngxảyra.

Câu 5. (1,0 điểm)

a)Giải phương

chiahếtcho xy .Chứngminhrằng , xy làcácsố

(1,

xy làcács

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH BÌNH PHƯỚC KỲ THI TUYỂN SINH LỚP 10 NĂM HỌC: 2022 2023 ĐỀ THI MÔN: TOÁN (CHUYÊN ) ĐỀ CHÍNH THỨC (Đề thigồmcó01trang) Thời gian: 150 phút (không kể thời gian phát đề) Ngày thi: 07/06/2022 Câu 1. (2,0 điểm) Chobiểuthức 2312 Pxxxxx xxxxxx +−+ =+− −+ với0,1 xx>≠ a)Rútgọnbiểuthức P b)Tìmgiátrị nhỏ nhấtcủabiểuthức P Câu 2. (1,5 điểm) Cho phương trình ( ) ( ) ( )2 1201xxxm −−+= với m làthamsố.Tìmtấtcả các giátrị củathamsố m để phương trình ( )1 có đúng ba nghiệmphânbiệtthỏamãn 123 1111 3xxx ++= Câu 3. (2,0 điểm) a)Giải phương trình: ( ) ( ) 2 136446xxxx −−+=−+ b)Giảihệ phương trình: 22410121290 5 3222 2 xxyxyy x yxyy  ++−−+=  + −−=−−  Câu 4. (2,5 điểm) Chotamgiác ABC nhọnnộitiếp đườngtròntâm O

R .Gọ

ủ

ABC , M là điểmbấtkìtrêncungnhỏ BC

a)Ch

trình nghiệmnguyên:226270.xyxyyx−++−−= b)Cho,

ố nguyênthỏamãn2220212022xy−+

lẻ vànguyêntố cùngnhau. Câu 6.

0 điểm) a)Cho,ab làcácsố thực dương thỏamãn2 ab+= . Chứngminh: 22 1 11 ab ba +≥ ++ . b)Cho,,abc làcácsố thực dương thỏamãn16 ababc++++= . Tìmgiátrị lớnnhấtcủabiểuthức 212122 112 abc P abc +++ =++ +++ . ………HẾT……… Thísinh không đượcsử dụngtàiliệu. Giámthị coithi không giảithíchgìthêm.

SỞ GIÁODỤC & ĐÀO TẠO BÌNH PHƯỚC ĐỀ CHÍNH THỨC KÌTHITUYỂNSINHLỚP10THPT NĂM HỌC20222023 ĐÁP ÁN THANG ĐIỂM Bài thi: TOÁN (Đáp án thang điểmgồmcó07trang) ĐÁP ÁN VÀ THANG ĐIỂM Câu 1. (2 điểm) Chobiểuthức 2312 Pxxxxx xxxxxx +−+ =+− −+ với0;1 xx>≠ Rútgọnbiểuthức ( ) ( ) ( ) ( ) ( ) ( ) 2312 231111 11 Pxxxxx xxxxxx xxxxxxxx xxxxx +−+ =+− −+ +−+++−+ = +− −+ 0.5 2311 xxxxx xxx +++−+ =+− 0.25 223 xx x ++ = 0.25 Tìmgiátrị nhỏ nhấtcủa P 33 2222.2Pxx xx =++≥+ 262=+ 0.25 0.25 VậyGTNNcủa262 P =+ khivàchỉ khi 33 2 2 xx x =⇔= (thỏa mãn điềukiện) 0.25 0.25 Câu 2. (1.5 điểm) Nộidung Điểm Cho phương trình ( ) ( ) ( )2 1201xxxm −−+= với m làthamsố.Tìmtấtcả cácgiátrị của thamsố m để phương trình ( )1 có đúng ba nghiệmphânbiệtthỏamãn 123 1111 3xxx ++= . Tacó: ( ) ( ) ( ) 2 2 1 120 20* x xxxm xxm = −−+=⇔  −+= Để phương trình ( ) 1cóbanghiệmphânbiệt123 ,, xxx thì phương trình ( ) *phảicó 0.25

hainghiệmphânbiệtkhác1. 0.25 ( ) ( () )2 '101 1 1021 mm m ffxxxmm ∆=−> < ⇔⇔< ≠=−+ ≠  0.25 Dovaitròcácnghiệm như nhau, gọi31 x = và phương trình ( ) *cóhainghiệm phânbiệt12 , xx thỏamãnhệ thứcviet12 12 2xx xxm +=  = Từ yêucầubàitoán: 123 1111 3xxx ++= thì phương trình ( ) *phảicónghiệmkhác0 hay0 m ≠ 0.25 0.125 12 12312 1111222 3 333 xx m xxxxxm + ++=⇔=−⇔=−⇔=− thỏamãn điềukiện 0.375 Câu 3. (2 điểm) Nộidung Điểm a)Giải phương trình: ( ) ( ) 2 136446xxxx −−+=−+ Phương trình đã cho 224644630xxxx ⇔−+−−++= Đặt2460 txx=−+≥ 0.25 Phương trình trở thành:2430 tt−+= 1 3 t t = ⇔  = 0.25 Với2227 3463430 27 x txxxx x  =+ =⇒−+=⇔−−=⇔  =−  0.25 Với ( )22 1461450 txxxxvn =⇒−+=⇔−+= . 0.25 b)Giảihệ phương trình: 22410121290 5 3222 2 xxyxyy x yxyy  ++−−+=  + −−=−−  ĐK: 5 2 3 x y ≥−   ≥  Tacó ( ) ( ) 22 1252121290 xyxyy ⇔++−−+= ( ) '21610xy ∆=+≥ 0.125 21 69 xy xy =− ⇒  =−− 0.125 *Với6913 xy=−−≤− loại.0.125

*Với21 xy=− thay vào phương trình ( )2 ta được: 2 322232 yyyy −−+=−− ( ) ( ) ( )22 2210 322 y yy yy ⇔ −−+= −++ 0.25 ( ) ( ) 2 2 210** 322 y y yy = ⇔  −+= −++ 0.125 +Với23 yx=⇒= (thỏa mãn điềukiện)0.125 + Xét phương trình ( ) **: ( )2 21** 322 y yy =+ −++ Vì 2 3y ≥ nên: 22 322222 3322yy yy −++≥+>⇒ < −++ Mà 4 2112 3y +>+> Vậy phương trình ( ) **vônghiệm. Kếtluận:hệ cónghiệmduynhất ( ) ( );3;2xy = 0.125 Câu 4. (2.5 điểm) Nộidung Điểm Chotamgiác ABC nhọnnộitiếp đườngtròntâm O bánkính R .Gọi H làtrựctâmcủa tamgiác ABC , M là điểmbấtkìtrêncungnhỏ BC .Gọi,IJ lần lượtlàhìnhchiếucủa M lêncác đườngthẳng,. BCCA Đườngthẳng IJ cắt đườngthẳng AB tại K . d)Chứngminhbốn điểm,,,BKMI cùngthuộcmột đườngtròn.Từ đó suy ra .MKAB ⊥ e)Gọi123 ,, MMM lần lượtlàcác điểm đốixứngcủa M qua các đườngthẳng ,, BCCAAB .Chứngminhbốn điểm123 ,, MMM và H cùngthuộcmột đường thẳng. Chứng minh khi điểm M di độngtrêncungnhỏ BC taluôncó  234.sin. MMRBAC ≤ Xác địnhvị trícủa điểm M khidấubằngxảyra. a)

nộitiế

đối)

ứ

ngtròn.0.25

a) Tacó:   ( )090 MICMJCgt == nêntứ giác IJCM

p Do đó:   KIMJCM = (trongbằng ngoài đỉnh

0.125 0.125 T

giác ABMC nộitiếpnên    KBMACMJCM == 0.25 Từ đó suy ra   KIMKBMBIMK =⇒ nộitiếp Vậybốn điểm,,,BKMI cùngthuộcmột đườ

Do   00 9090 BIMBKMMKAB =⇒=⇒⊥ (đpcm) 0.25 Lưu ý: khihọcsinhvẽ điểmMsaochoJn ằmngoàiAC,KnằmtrongABvẫn đạt điểmtối đa. b) Tacó1223 //,//. IJMMJKMM vàtheogiả thiếtcó,,IJK thẳng hàng nên ta có các điểm123 ,, MMM thẳnghàng. 0.125 0.125 tacó    ( )03180 AMBAHBAMBACB +=+− màtacó:   AMBACB = ,nên   03180AMBAHB+= nênnêntứ giác3 AHBM nộitiếp 0.25 từ đó ta có    33 AHMABMABM == 0.125 hoàn toàn tương tự tacó:2 AHCM nộitiếp từ đó ta có    22 AHMACMACM == 0.125 Màtacó:   0180ACMABM+= ,vì ABMC nộitiếp0.125   032180AHMAHM+= Từ đó suy ra 32 ,, MHM thẳnghàng 0.125 C)

Vì23 , MM lần lượt là các điểm đốixứngcủa M qua,ACAB nêntacó 23AMAMAM == haytamgiác23 AMM cântại A . Kẻ đườngcao AD củatamgiác23 AMM suyra AD cũng là phân giác của  23MAM 0.125 Mặtkháctacó       2332222 MAMMAMMAMMABMACBAC =+=+= suyra   3 MADBAC = 0.125 Trongtamgiácvuông3MAD có   333sin.sin MDAMMADAMBAC = = Mà233 2 MMMD =  232.sin MMAMBAC⇒= 0.125 Vậy  234.sin MMRBAC ≤ Vì  sin BAC cố địnhnên23 MM lớnnhấtkhi AM lớnnhấttứclà AM là đường kính. 0.125 Câu 5. (1 điểm) Nộidung Điểm a)Giải phương nghiệmnguyên226270.xyxyyx−++−−= Phương trình đã cho ( ) ( ) 23270xyxyyx ⇔−++−−= ( ) ( ) 2317xyxy ⇔−+−= 0.125 0.125 Từ đó suy ra 2 xy là ướccủa7,tậpcácgiátrị ướccủa7là { } 7;1;1;7.Tacó các trườnghợpsau. * ( )2727 31157 xyxy vn xyy −=−−=− ⇔  +−=−= * 21213 317551 xyxyx xyyy −=−−=−=−  ⇔⇔  +−=−=−=−  (nhận) * ( )2121 31757 xyxy vn xyy −=−= ⇔  +−== * 27275 311551 xyxyx xyyy −=−==  ⇔⇔  +−==−=−  Vậycáccặpnguyên ( ), xy thỏa mãn phương trình là ( ) ( ) 3;1,5;1. 0.125 0.125 b)Cho,xy nguyênvàthỏamãn2220212022xy−+ chiahếtcho xy .Chứngminhrằng , xy làhaisố lẻ vànguyêntố cùngnhau. *Nếu,xy làhaisố chẵnthì2220212022xy−+ khôngchiahếtcho4và xy chia hếtcho4(vôlý). 0.125 Nếu,xy cómộtsố chẵn,mộtsố lẻ thì2220212022xy−+ làsố lẻ và xy làsố chẵn (vôlý). Vậy,xy làcácsố lẻ. 0.125

*Giả sử ( ), xyd = suyra 22 2021 xy và xy chiahếtcho2 d . 0.125 Từ giả thiếtsuyra2022chiahếtcho2 d . Lạido20222.3.337 = nên { }1,2,3,337d ∈ . Nếu1 d > thì2022chiahếtchohoặc 4,9,3372(vôlý).0.125 Câu 6. (1 điểm) Nộidung Điểm a)Chocácsố thực dương , ab thỏamãn2 ab+= .Chứngminhrằng: 22 1 11 ab ba +≥ ++ . * Xét BĐT ( ) 222 abab xyxy + +≥ + với,0 xy > . Biến đổi tương đương ( ) 2222220aybxabxyaybx+≥⇔−≥ (đúng) 0.25 *Khi đó ( ) 222 1 112 abab baab + +≥= ++++ (điềuphảichứngminh). 0.25 c)Cho,,abc làcácsố thực dương thỏamãn16 ababc++++= . Tìmgiátrị lớnnhấtcủabiểuthức 212122 112 abc P abc +++ =++ +++ . Tacó112 6 112 P abc =−−− +++ . Theo BĐT Cauchy ta có ( ) ( ) 1122 116 11 abc ab +≥= ++ ++ Khi đó 22 6 62 P cc ≤−− −+ . Tacó1141 62622 cccc +≥= −+−++ (do06 c << ).Suyra5 P ≤ . Dấubằngxảyrakhi ( ) ( ) 11 3 62 2 116 ab ab cc c abc  +=+ == −=+⇒  = +++=  . Vậygiátrị lớnnhấtcủa P bằng5 đạt đượckhi3,2 abc=== 0.125 0.125 0.125 0.125 Chú ý: Mọi lời giải đúng đều được điểm tối đa của câu hỏi đó.

OKỲ THITUYỂNSINH BÌNHTHUẬNVÀOLỚP10THPTCÔNGLẬP NĂM HỌC20222023

ĐỀ CHÍNHTHỨCMônthi:Toán(lớp10chuyênToán-HS2) (Đề naycó01trang)

Ngàythi:10/06/2022 Thờigian:150phút(khôngkể thời gian phát đề)

ĐỀ:

Bài 1:(2,0 điểm)

Giải phương trình: 62542320

Bài 2:(1,0 điểm)

Haibạn An và Bình đang so về số lượngnhữngviênbimàhaibạnhiệncó.Annóivới Bìnhrằng:“Nếubanchotôimộtsố viênbitừ túicủabạnthìtôisẽ cóviênbigấp6lầnsố viênbicủabạn.Cònnếutôichobạnsố viên bi như thế ,số viênbicủabạnsẽ bằng 1 3 số viên bicủatôi”.Hỏisố viênbiítnhấtmàbạnAncóthể cóbaonhiêu?

Bài 3:(2,0 điểm)

a)Tìmnghiệmnguyêncủa phương trình : 42240 xxyy+−−+=

ố nguyên dương a,b,c thỏamãn222 abc += .Chứngminhrằng:60 abc 

Bài 4:(1,5 điểm)

Chocácsố dương a,b,c thỏamãn3 abc++≤ .Tìmgiátrị nhỏ nhấtcủabiểuthức. 222 12024 P abcabbcca = + ++++

Bài 5:(2,5 điểm)

Cho đườngtròntâmOnộitiếp ABC∆ ,tiếpxúcvớicáccạnhAB,AClần lượttạiDvà E.Gọi I là tâm đườngtrònnộitiếp ADE∆ .

ứngminhA,I,OthẳnghàngvàIlàthuộc đườngtròn ( )O .

ủacácgócBvàCcắt đườngthẳngDElần lượttạiMvàN.Chứng minhtứ giácBCMNnộitiếpvàtamgiácBMCvuông. Bài 6:(1,0 điểm)

Ngườitaviếtcácsố nguyên1,2,3,4,5,6,7,8 lên các đỉnhcủamộtbátgiáclồisaocho tổngcácsố ở mỗi ba đỉnhliêntiếpkhôngnhỏ hơn k ,với k nguyên dương.Tìm giá trị lớn nhấ của k

T

SỞ GIÁODỤC VÀ ĐÀO TẠ

xxx +++=+

b)Cho3s

a)Ch

b)Cácphângiáctrongc

HẾ

túicủabạnthìtôisẽ cóviênbigấp6lầnsố viênbicủabạn.Cònnếutôichobạnsố viên bi như thế ,số viênbicủabạnsẽ bằng 1 3 số viên bicủatôi”.Hỏisố viênbiítnhấtmàbạnAncóthể cóbaonhiêu?

ọi,ab tương ứnglàsố viênbimà2bạnAnvàBìnhhiệncóvà x làsố viênbimàbạnAn nóitới trong đề

đề bàitacóhệ phương trình:

HƯỚNG DẪN GIẢI Bài 1:(2,0 điểm) Giải phương trình: ( )625423201 xxx +++=+ Giải:62542320 xxx +++=+ ĐK: 2505 22 202 xx x x x +≥ ≥−  ⇔⇔≥− +≥  ≥− Đặt25,2 axbx =+=+ 2237abx ⇒+=+ Pt ( ) 164ab ⇔+= 2213ab++ 2269440aabb ⇔−++−+= ( ) ( ) 22 320ab ⇔−+−= 30 20 a b −= ⇔  −= 32532592 2242 22 axxx bxx x    =+=+==  ⇔⇔⇔⇔  = −=+==  (nhận) Vậy phương trình đã cho có nghiệm2 x = Bài 2:(1,0 điểm) Haibạn An và Bình đang so về số lượngnhữngviênbimàhaibạnhiệncó.Annóivới Bìnhrằng:“Nếubanchotôimộtsố viênbitừ

Giải: G

Theo

6()676734 3()34 11 3 axbxabx bxbx axbxabx bx  +=−=−  ⇔⇔−=+ −=+=+ ⇔= Vì,,abx làcácsố nguyên dương nên x bénhấtlàbằng3,suyra11,45 ba== Vậysố viênbiítnhấtmàbạnAncóthể cólà45viên Bài 3:(2,0 điểm) a)Tìmnghiệmnguyêncủa phương trình : 42240 xxyy+−−+= b)Cho3số nguyên dương a,b,c thỏamãn222 abc += .Chứngminhrằng:60 abc  Giải: a)Tacó: ( ) ( ) 422 422 22 2 22 40 1111 2.2.40 2424 11 40 22 140 xxyy xxyy xy xyxy +−−+=  ⇔++−+++=    ⇔+−++=   ⇔−+++= Vì,xyZ ∈ nên ta có các trườnghợpsau: TH1: 22 22 11 142 xyxy xyx −==+ ⇔  ++=−=− (loại) TH2: 22 2 111 1422 xyxyx xyyy =± −=−+=  ⇔⇔  ++=== (nhận) TH3: 2 2 22 22 121 2 xyxy xyx  += −=−  ⇔  ++= =   (loại) TH4: 2 2 22 22 121 2 xyxy xyx  −= −=  ⇔  ++=− =   (loại) Vậy phương trình đã cho có nghiệmnguyên: 1 2 x y =±  = b)Nếu,,abc đềukhôngchiahếtcho3 ⇒ 22 , ab và2 c đều chia cho 3 dư 1 ⇒ 222 abc +≠ do đó có ít nhất1số chiahếtcho3 ⇒ 3abc 

Nếu,,abc đềukhôngchiahếtcho5 ⇒ 22 , ab và2 c đều chia cho 3 dư 1 hoặc4 ⇒ 22ab + chia cho 5 dư 2;0 hoặc3 ⇒ 222 abc +≠ do đó có ít nhất1số chiahếtcho5 ⇒ 5abc  Nếu,,abc làcácsố lẻ ⇒ 22 , ab chiahết cho 4 dư 1 ( )22mod4ab ⇒+= ⇒ 222 abc +≠ Do đó , ab cóítnhất1số chẵn Giả sử alàsố chẵn Nếu b làsố chẵn ⇒ 4abc  Nếu b làsố lẻ mà222 abc += ⇒ c làsố lẻ ⇒ ( ) ( )2 2 222 acbca acbcb =−+ +−  =   ⇒ 2 a chẵn ⇒ 44aabc ⇒  Vậy: ( )3.4.560abc = Bài 4:(1,5 điểm) Chocácsố dương a,b,c thỏamãn3 abc++≤ .Tìmgiátrị nhỏ nhấtcủabiểuthức. 222 12024 P abcabbcca = + ++++ Giải: Vớimọi,,xyz dương ta có: ( )3 31xyzxyz ++≥ và ( )3 1111 32 xyzxyz ++≥ Từ ( ) 1và ( ) 2suyra: ( ) ( )111 93xyz xyz  ++++≥   Đẳngthứcxảyra xyz⇔== Ápdụng ( ) 3tacó: ( )222 222 111 2229abcabbcca abcabbccaabbcca  +++++ ++≥  ++++++ 

ộc đườngtròn ( )O b)CácphângiáctrongcủacácgócBvàCcắt đườngthẳngDElần lượttạiMvàN.Chứng minhtứ giácBCMNnộitiếpvàtamgiácBMCvuông.

Giải:

ứngminhA,I,OthẳnghàngvàIlàthuộc đườngtròn ( )O . Vì O là tâm đườngtrònnộitiếp ABC∆ tiếpxúcvớihaicạnhABvàACtạiDvàE

( ) 2222 129 1 abcabbccaabc ⇒+≥≥ ++++ ++ (do3 abc++≤ ) Mặtkhác: ( ) 2 11 3 33 abc abbcca abbcca ++ ++≤≤⇒≥ ++ Vậy: 222222 1202412202220242027 1 33abcabbccaabcabbccaabbcca  +=++≥+=  ++++++++++  Đẳngthứcxảyra 222 1 3 abcabbcca abcabc abc  ++=++  ⇔==⇔===   ++= Bài 5:(2,5 điểm) Cho đườngtròntâmOnộitiếp ABC∆ ,tiếpxúcvớicáccạnhAB,AClần lượttạiDvà E.Gọi I là tâm đườngtrònnộitiếp ADE∆ . a)ChứngminhA,I,OthẳnghàngvàIlàthu

a)Ch

ODAB OEAC ⊥ ⇒  ⊥ ⇒ AD,AElà2tiếptuyếncủa đườngtròn ( )O ⇒ AO là đườngphângiáccủa  DAE Mà:I là tâm đườngtrònnộitiếp ADE∆ ⇒ A,I,Othẳnghàngvà OIODOE == ⇒ Inằm trên đườngtròn ( )O b)Chứngminhtứ giácBCMNnộitiếpvàtamgiácBMCvuông. Tacó: ADE∆ cântạiA ⇒    0 1800 90 22 BACBAC ADE = =− Mà:      2 ABC ADEABMNMBNMB =+=+ (DoBOlàphângiáccủa  ABC nên   2 ABC ABM = ) ⇒       090 222 BBACABCACB NMBADE + =−=−= Mặtkhác:   2 ACB NCB = (doCOlàtiaphângiáccủa  ACB ) ⇒   NMBNCB = ⇒ Tứ giácBCMNnộitiếp (2 đỉnhkề nhaucùngnhìn1cạnh dướicùnggóc) Bài 6:(1,0 điểm) Ngườitaviếtcácsố nguyên1,2,3,4,5,6,7,8 lên các đỉnhcủamộtbátgiáclồisaocho tổngcácsố ở mỗi ba đỉnhliêntiếpkhôngnhỏ hơn k ,với k nguyên dương.Tìm giá trị lớn nhấtcủa k . Giải: Để tồngcácsố ở 3 đỉnhliêntiếpkhôngnhỏ hơn k ⇒ Để tìmgiátrị lớnnhấtcủagiátrị nhỏ này,talấy2số nhỏ nhất đặtcạnhnhau,2số lớnnhất lần lượtlà7và8 ở 2bêntráiphảicủasố nhỏ nhất ⇒ Gíatrị nhỏ nhất để ba đỉnhkhôngnhỏ hơn k ,ở đây tổngcủa 3 đỉnhnhỏ nhấtlà 71210 ++= ⇒ 10k =

hoànthànhchỉ tiêu đượcgiao?Biếtrằng,mỗigiờ số cây trông đượccủamỗilớplàkhông đổi. Câu 5. (2,0 điểm) Chotamgiác() ABCABBCAC >> .Gọi,MN lần

u ANI và BMK Gọi điểm D là

trung điể

ủa đoạnthẳng IK

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT THÀNH PHỐ CẦN THƠ NĂM HỌC 2022 2023 Khoá ngày 07 tháng 6 năm 2022 MÔN: TOÁN (CHUYÊN) (Đề thicó02trang)Thờigianlàmbài:120phút,khôngkể thời gian phát đề Câu 1. (1,5 điểm) Chobiểuthức 10264 : 1 121 Qxx x xxxxxx  = +  −−+−+  với0 x > và1. x ≠ a)Rútgọnbiểuthức Q b) Đặt ( ) .1.PQxx=−+ Chứngminhrằng1. P > Câu 2. (1,5 điểm) Trongmặtphẳng, Oxy choparabol2 1 ():2 Pyx = và đườngthẳng ( ) ( ) :22.dymxm=+−+ Tìmtấtcả giátrị củathamsố m saocho() d cắt() P tại hai điểmphân biệt ( )11 ; Axy và ( )22 ; Bxy cùngnằmbênphảitrụctung. Câu 3. (2,0 điểm) Giải phương trình và hệ phương trình sau trên tậpsố thực a)21231. xxx+=+− b) 22 2 230 220 xyxyxy xxy  +−−+=  −−+=  Câu 4. (2,0 điểm) a)Tìmtấtcả cáccặpsố nguyên(;) xy thỏamãn 2220652(1)2(30). xyxyyx ++++=− b) Hưởng ứng phong trào “Xanh hóa trườnghọc”,lớp9Avàlớp 9B được nhà trường giaochỉ tiêutrồng 80 cây xanh xung quanh sân vườncủa trường.Nếulớp9Atrồngtrong2 giờ vàlớp9Btrồngtrong1giờ thì được25cây.Nếulớp9Atrồngtrong1giờ vàlớp9B trồngtrong2giờ thì được23cây.Hỏinếucả hailớpcùngtrồngvớinhauthìsaubaolâu

lượt là trung điểmcủa AB và AC Dựngbênngoàitamgiác ABC các tam giác đề

hìnhchiếuvuônggóccủa điểm A lêncạnh, BC điểm E là

a)Chứngminhtứ giác AKBD nộitiếp. ĐỀ CHÍNH THỨC

b)Chứng minh điểm E là tâm đườngtrònngoạitiếptamgiác. IKD c)Tínhsố đo của  .NEM Câu 6. (1,0 điểm) Cho,,xyz làcácsố thực dương. Chứngminhrằng 343 6xzyzx yzzxxy ++ ++≥ +++ ------HẾT-----Ghi chú: Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm. Họ vàtênthísinh:...........................................Số báodanh:................................................... Chữ kýcánbộ coithi1:Chữ kýcánbộ coithi2:

Trong

ĐỀ CHÍNH THỨC

Dành

THI TUYỂN SINH LỚP 10

HỌC PHỔ THÔNG NĂM HỌC 2022 2023

thi: TOÁN (Chuyên)

gian:150phút (không kể thời gian phát đề)

thí sinh thi vào Trường THPT Chuyên Lê Quý Đôn

điểm)

O là gốc tọa độ. Tìm tọa độ hai điểm , AB

O đến AB lớn nhất.

3: (2 điểm

Giải phương trình

Giải hệ phương

(2 điểm)

Tìm tất cả các cặp số nguyên (;)

Cho phương trình

là tham số. Khi phương trình đã cho có hai nghiệm

xx hãy tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 22 121221021Qxxxkxx  . Câu 5: (1,5 điểm)

Cho đường tròn () O bánkính R và điểm A nằm trên đường tròn. Đường tròn (;) AR cắt đường tròn () O tại hai điểm B và C . Gọi M là trung điểm của AB ,tia MO cắt () O tại điểm D .Tia BO cắt AD tại E và() O tại điểm thứ hai là F . Tính độ dài đoạn thẳng DE và diện tích tứ giác ACFE theo R Câu 6: (1,5 điểm) Chotamgiác ABC chọn ABAC  , trực tâm H và nội tiếp đường tròn () O . Gọi M là trung điểm của BC và K là hình chiếu của H trên AM .Tia AM cắt đường tròn ngoại tiếp tam giác BKC tại điểm thứ hai là N . Chứng minh rằng tứ giác ABNC làhìnhbìnhhành.

SỞ GIÁO DỤC VÀ ĐÀO TẠO THÀNH PHỐ ĐÀ NẴNG KỲ

TRUNG

Môn

Thời

(

cho

) Câu 1: (1,5 điểm) Cho biểu thức 31113 : 1112 xxxxx P xxxxxx           với 0x  và1 x  Rút gọn biểu thức P và tìm tất cả các số tự nhiên x để giá trị biểu thức 23 2 xP P là số nguyên tố. Câu 2: (1,5

a) Cho phương trình 2 (5)(3)50 mxnmxm  , với m và n là các tham số. Tìm tất cả các cặp số nguyên(;) mn sao cho phương trình đã cho có nghiệm kép. b)

mặt phải tọa độ Oxy ,choparabol2 2 ():3 Pyx 

với

trên P saochotamgiác OAB vuông tại O và khoảng cách từ

Câu

) a)

210114210 xxx . b)

trình 4322 2222 2143190660 22(1)(2)0 xxyyxy xyxyyyy        . Câu 4:

ab thỏa mãn 32()5abab . b)

222390xxkk , với k

1,2

HƯỚNG DẪN GIẢI Câu 1: (1,5 điểm) Cho biểu thức 31113 : 1112 xxxxx P xxxxxx           với 0x  và1 x  Rút gọn biểu thức P và tìm tất cả các số tự nhiên x để giá trị biểu thức 23 2 xP P là số nguyên tố. Lời giải: Điều kiện xác định : 0x  và1 x  . Tacó:       31113232 :. 1123 11 xxxxxxxxxx P xxxxx xxx              1322 1131 xxxx P xxxxxx    Thay2 1 x P xx   vào biểu thức 23 2 xP P ta được: 23.23 1 232 11 2 22 2 2. 11 x x xPxx xxxx Px xxxx    Do biểu thức 23 2 xP P là số nguyên tố nên 2 2 xx cũng là số nguyên tố Ta đặt: 2 2 xx p   ( p là số nguyên tố)    122 xxp . Để ý: 21xx . Do đó sẽ có hai khả năng:  11 0,1 22 x xp xp        hoặc  12 0,(2,)1,2 2 x xpp xp        . Khả năng 1: 114 222 xx xpp            (nhận). Khả năng 2: 124 25 xx xpp            (nhận). Vậy 2 1 x P xx   vàkhi4 x  và9 x  thì23 2 xP P là số nguyên tố. Câu 2: (1,5 điểm) a) Cho phương trình 2 (5)(3)50 mxnmxm  , với m và n là các tham số. Tìm tất cả các cặp số nguyên(;) mn sao cho phương trình đã cho có nghiệm kép. b) Trong mặt phải tọa độ Oxy ,choparabol2 2 ():3 Pyx  , với O là gốc tọa độ. Tìm tọa độ hai điểm , AB trên P saochotamgiác OAB vuông tại O và khoảng cách từ O đến AB lớn nhất. Lời giải: Điều kiện xác định: 5m  Tacó:22 (3)4(25) nmmm  Để phương trình có nghiệm kép thì: 0 22 (3)4(25)0 nmm  22 (3)4(25) nmm (*) 252 m là số chính phương. Đặt 22 25() maa  

Xét0 a  thì 5và15 5và15 mn mn      Xét1 a  thì224 m  mà 24 không phải là số chính phương nên vô lí Xét24 a  thì221 m  mà 21 không là số chính phương nên vô lí. Xét29 a  thì216 m  nên 4và12 4và12 mn mn      . Xét216 a  thì29 m  nên 3và9 3và9 mn mn      . Xét225 a  thì20 m  nên0và0 mn . Vậy để các cặp số nguyên , mn thỏa đề là: (;)(3;9)(3;9)(4;12)(1;12)(0;0) mn  . Câu 3: (2 điểm) a) Giải phương trình 210114210 xxx . b) Giải hệ phương trình 4322 2222 2143190660 22(1)(2)0 xxyyxy xyxyyyy        . Lời giải: a) 210114210 xxx Điều kiện: 1 2 x  Phương trình (*) tương đương với:  2 2 (4)212 xx  2 2 20 4212221(2)2136 421262160714 (6)21 x xxxxxxx xxxxxx xx          . Vậy phương trình đã cho có tập nghiệm:  36;714S  b) Giải hệ phương trình 4322 2222 2143190660(1) 22(1)(2)0.(2) xxyyxy xyxyyyy        Xét phương trình (2) ta có: 222222(1)(2)0xyxyyyy 222322110xyxyyy  22 (2)(2)20 xyyyy  22 (1)(2)0 xyy  Vì22102 xyy Thay vào (1) ta được: 4322 2143190660 xxyxyxy  432 228124180660 xxxx  432146290330xxxx  43214629033xxxx  432322 81164866324330 xxxxxxxx  2222 (811)6(811)3(811)0 xxxxxxxx  22 (811)(63)0 xxxx  2 2 8110 630 xx xx      . Tự giải phương trình bậc hai ra được các cặp số , xy thỏa đề là :        (;)45;2,45;2,36;2,36;2 xy  Câu 4: (2 điểm) a) Tìm tất cả các cặp số nguyên (;) ab thỏa mãn 32()5abab . b) Cho phương trình 222390xxkk , với k là tham số. Khi phương trình đã cho có hai nghiệm 1,2xx hãy tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 22 121221021Qxxxkxx  . Lời giải:

a) Tìm tất cả các cặp số nguyên (;) ab thỏa mãn 32()5abab . Tacó:32()5abab 335abab  (*)22()()5 abaabbab  . Trường hợp 1: ab   2222 55abaabbab                 2,1(laáy) 1;2(loaïi) 1;2(laáy) 2;2(loaïi) ab ab ab ab . Trường hợp 2: ab  Gọi (,)dab  thìtacó:11221 2 (,)1và adm mmmm bdm        Thay vào (*) ta được: 3333212125dmdmdmm 233(1212)5dmmmmm  2 33 1212 1 (5 d mmmm         Từ đây ta sẽ có được: 33 12125mmmm Nếu 120mm  thì33 12mm  (Vôlí) Do đó 120mm  hay0 a  và0 b  Ta lại có: 32()5abab VT < 0 mà VP > 0 do đó trường hợp này không có cặp số nguyên (;) ab thỏa để Vậy cặp số nguyên (;) ab thỏa để là (;)(2;1)(1;2) ab  b) 22 1(39)03100 kkkk  (5)(2)025 kkk  Theo định lí Viét:1222 2 12 22 39 xxxx xxkk        Thay Q vào ta được: 22 22 (2)(2)10(1) xxxkx  22 2222111(1)1123xxkx  . Vậy min3Q  khi122và1kxx Taxét:221211112102()10xxxkxxxxk  Vì1 x là nghiệm của phương trình 22 11293 xxkk  Thế vào trên 22 93210421 kkkkk  Xét22221xx tương tự như thế 2x cũng là nghiệm của phương trình 222 2221103 xxkk  22421310Qkkkk  (5)(2)(7)(3)(53)(27)62 kkkkkkkk  62Q  Vậy max 62Q  khi29 17 k  Câu 5: (1,5 điểm) Cho đường tròn () O bánkính R và điểm A nằm trên đường tròn. Đường tròn (;) AR cắt đường tròn () O tại hai điểm B và C . Gọi M làtrung điểm của AB ,tia MO cắt () O tại điểm D .Tia BO cắt AD tại E và() O tại điểm thứ hailà F . Tính độ dài đoạn thẳng DE và diện tích tứ giác ACFE theo R . Lời giải:

Tacó: AOACOCAOC  đều mà   22.60120 AOFABFCOF   đều AOFC làhình thoi, AF cắt OC thì I là trung điểm AF . Tacó:  cos.sin60.33 2 AIAOIAORRAFR   132 . 22AOFC SOCAFR Tacó: 11 .. 22AOEABEABO SSSBHAEOMAB  11 .sin75.()sin60.. 22 ABAHHEOBAB   22 13 .sin75.(cos75.sin75.) 24 RABABR  2213 .sin75.(cos75sin75) 24 RR  22 331sin75(cos75sin75) 42AEFCAFOCAOE SSSRR    . Tacó:2EODEDBEDEOEB  ∽ Tacó: OAOBABOAB  đều nên   6030BOABDA    18030 1801806045 2 BEAOBADAB      Kẻ BHAEBHE ⊥ vuôngcân.2 BEBH Tacó:  sinsin18030sin75sin75.sin75. 2 BH BAHBHABR AB      2sin75.2sin751BEREOBERR   2 2sin75(2sin751)EDR  . Câu 6: (1,5 điểm) Chotamgiác ABC chọn ABAC  , trực tâm H và nội tiếp đường tròn () O . Gọi M là trung điểm của BC và K là hình chiếu của H trên AM .Tia AM cắt đường tròn ngoại tiếp tam giác BKC tại điểm thứ hai là N . Chứng minh rằng tứ giác ABNC làhìnhbìnhhành. Lời giải:

chứng minh ABNC

BKCN nội tiếp

vậy, gọi

BBC

,,và ABC lần lượt là

vuôngcó M là trung điểm

ần chứng minh2

AHKB nội tiếp

đường

chứng minh MAMN

lên,,BCACAB

MBMCMB

Cần

làhìnhbìnhhành  cần

 Tacó:

2MKMNMBMCMC Thật

111

chân

cao từ ,, ABC

Tacó:1



BC nên1

 Suyrac

1. MBMKMA  . Tacó:1

     111 AKGABHAKBAHB  11 AHBC nt       111111 180180 AKBAHBBCMMBCAKBMBC     11 MKBMBA 11 MKBMBAMKMA ∽ ,suyra điều phải chứng minh. 

hai điểmmàkho

ấ

4. (1,0 điểm)

ngcáchgi

ả cács

achúngnh

nguyên

hơn hoặcbằng2

ỏamãn:22

ố thực dương ,, abc thỏamãn2324abcabc ++= .Chứngminhrằng: 222

233 16123613412 bca abbcca ++≥ +++ Câu 5. (3,0 điểm)

Cho đườngtròn ( ); OR và hai điểm,PQ nằmngoài ( )O saochogóc POQ vuông, PQ khôngcắt ( )O .Kẻ haitiếptuyến,PAPB với đườngtròn ( )O (,AB làhaitiếp điểm; tia PA nằmgiữahaitia PQ và PO ).Haicáttuyến,PDCQEC thay đổicủa ( )O cùng đi qua C ( D nằmgiữa P và C ; E nằmgiữa Q và C ).Tia PE cắt đườngtròntại điểmthứ hai() FFE ≠ . H là giao điểmcủa AB và OP .Chứngminhrằng:

PEPF không đổi.

AHEAHF =

Đườngtrònngoạitiếptamgiác PDF luôn đi qua một điểmcố định.

ĐỀ THI TUYỂN SINH VÀO LỚP 10 THPT NĂM HỌC 2022 - 2023 TỈNH ĐAK LAK MÔN: Toán chuyên Câu 1. (2,0 điểm) Cho phương trình 22(21)20xmxmm−−+−−= với m làthamsố.Tìmtấtcả cácgiá trị của m để phương trình đã cho có hai nghiệmphânbiệt12 , xx thỏamãn 33 121251015xxxxm +−=+ Câu 2. (2,0 điểm) 1,Giải phương trình: 232532xxxxx ++=+−+ . 2,Giảihệ phương trình: 22 2 24530 109210 xxyyxy xyx  −−+−+=  −++−=  Câu 3. (2,0 điểm) 1,Chohìnhchữ nhật ABCD cóchiềudàibằng47 cm ,chiềurộngbằng43 cm . Chứngminhrằngtrongsố 2022 điểmbấtkìnằmtronghìnhchữ nhật ABCD luôntìm được

ả

ữ

ỏ

cm . 2,Tìmt

ố

dương ,

532024477 xyxy +=−+ Câu

Chobas

1,Tích.

2,  

HẾT

HƯỚNG DẪN GIẢI Câu 1. 1.1 Rútgọnbiểuthức ( )ab ab abba ab aabb A +        + + = :(với abab ≥≥≠ ,,0 0). Tacó: ( )ab ab abba ab ab A +        + + = : ()()3 3 abab abab ab abaabb +        + +++ = ()()()1 ( ) ab aabbab + =++⋅ 1 1= + + = ab ab 1.2 Giải phương trình: ( ) ( )( ) 3 2 12 1 1 1 = ++ + + xxxx (1) Điềukiện:0 >x Tacó: ( ) 1 11 1 1 + = + xxxx ( )( ) 2 1 1 1 12 1 ++ = ++ xxxx Do đó: 3 2 2 11 )1( = + ⇔ xx ( ) ( )32322 ⇒+=+ xxxx ( ) 2460 2 ⇔+= xx ( ) 230 2 ⇔+= xx Đặt tx = ,0 >t ta được phương trình 2230 +=tt Vì0 ++=abc nên1 =t (nhận);3 =t (loại) Với1 =t 11⇒=⇒= xx (thỏa điềukiện). Vậytậpnghiệmcủa phương trình (1) là { }1=S Câu 2. 2.1 Tìm đa thứcbậcba Pxxaxbxc =+++ ()32với abc,,làcáchệ số thực. Biết) ( Px chiahếtcho(x1),) ( Px chiacho(x2)và(x 3) đềucósố dư là 6. Biết:) ).(()(1 PxxAx = ).()6()(2=+PxxBx ).()6()(3=+PxxCx Với) ();();( AxBxCx là các đa thức. Khi1 =x )011( ⇒=⇒++= Pabc Khi2 =x )64222( ⇒=⇒++= Pabc Khi3 =x )693213( ⇒=⇒++= Pabc

+y làsố chẵnnên2 )0(2 22+=⇔=yy thế vào (1) ta được:

(1)05)(122 (2 22

)(2)22)(1 (2 22

)(22 +y làsố chẵnvà1 )(2 22+≤y nên2 )0(2 22+=⇔=yy thế vào (1) ta được: xxxxxxZ +=⇔=⇔=⇔=±⇔=±+∉ 1 5 5 5 5 1 5 1 ))1(1(1)15)(122 (2 222

Vậy:2 ,1 ==xy Câu 3. Cho phương trình (*)(làthamsố thực).

3.1 Giải phương trình khi . Khi , ta được phương trình 6036042 +=xx (1)

Đặt2 tx = ,0 ≥t ta được phương trình 260360 +=tt (2) '8640∆=> nên phương trình (2) có hai nghiệmphânbiệt: 130126 =t (nhận);6 23012 =+t (nhận)

Với6 13012 =t 230126⇒= x 3223)(⇔=± x -Với6 23012 =+t 230126⇒=+ x 3223)( ⇔=±+ x

Vậytậpnghiệmcủa

=±±+

nnghi

3223)

t,,,trong

Tacóhệ:      ++= ++= ++= 9321 422 1 abc abc abc Giảihệ ta được:18 ;;269 ===abc Vậy18 ()926 32 =+ Pxxxx 2.2 Tìmcácsố nguyên xy,thỏamãnbất đẳngthức0 534288 22++++≤xyxyxy Tacó:0 534288 22++++≤xyxyxy 442128810 2222 ⇔+++++++≤ xxyyxxyy )1(2)22)(1 (2 22 ⇔++++≤ xyxy Vì xyN +∈2)2 (; xN ∈)2 (1; yN +∈ )2(22 Nên: xyxyN ++++∈ 222 )(2)22)(1( Do đó: )0(2)22)(1 (2 22 ++++= xyxy hoặc1 )(2)22)(1 (2 22 ++++= xyxy i,0 )(2)22)(1 (2 22 ++++= xyxy (1) Vì2 )(22

)0101

+=⇔=⇔=⇔= xxxxx ii,1

++++= xyxy (2) Vì2

phương trình (1) là { }

3223);((

S 3.2 Tìm để phương trình đã cho có bố

ệmphânbiệ

đó có hai nghiệm,thỏamãn. Đặt,0 ≥t ta có phương trình )9041(24 +=tmtm (3) Để phương trình (*) có bốnnghiệmphânbiệt thì phương trình (3) có hai nghiệm dương phân biệt      > > ∆> ⇔ 0 0 '0 P S [ ]      > > > ⇔ 90 )041(4 )9041( 22 m m mm      > +> ⇔ 4 1 644140 2 m mm (**) Vì2 2 2 13 xx⇒= nên bài toán đưa về tìm m để phương trình (3) có hai nghiệm1 t ,2 t thỏamãn2 13 tt = Tacó:) 41(124 += ttm và ttm 129 ⋅= (hệ thứcViet) )9041( 442 += xmxmm 4=m 4=m m 1x 2x 3x 4x 1x 2x 12 3 xx = 2tx = 12 3 xx =

Biết2 13 tt = )41(34 22 ⇒+=ttm )4141( 442 2 ⇔=⇔=tmtm Do đó: )41(13 = tm Khi đó: )916111041()9341).(41( 32 2 =⇔=⇔+=mmmmmmm (4) Giải phương trình (4) ta được: 32 1157 1 + =m (thỏa(**)) 32 1157 2 =m (khôngthỏa(**)) Vậy32 1157 + =m 3.3 Giảihệ phương trình:      += += 23 23 22 22 yxy xxy )2( )1( Trừ vế theovế của phương trình (1) cho (2) ta được:0 222222+=xyxyxy ()()2()0 ⇔++= xyxyxyyx ()(2)0 ⇔+= xyxyxy i)0 = xyy x ⇔= thế vào (1) ta được:0 23 32+=xx )0233)( (12 ⇔++= xxx *1 10=⇔=xx 1⇒= y *0 233 2 ++=xx , phương trình vô nghiệmvì0 15 ∆=< ii) xyxyxyxy 202 +=⇔+= Đặt SxyPxy =+= ; , điềukiện0 24 ≥SP Ta được: SP 2= Cộngvế theovế của phương trình (1) cho (2) ta được:6 222222+++= xyxyxy ()22()6 2 ⇔+++= xyxyxyxy 2226⇒+= SPSP 4246 22 ⇔+= PPP 8260 2 ⇔= PP      =⇒= =⇒= ⇔ 2 3 4 3 12 PS PS (nhận) *1 ,2 ==SP . Khi đó xy,lànghiệmcủa phương trình 2210 +=XX )01(12 ⇔=⇔= XX Vậy1 ,1 ==xy * 4 3 2, 3 ==SP . Khi đó xy,lànghiệmcủa phương trình 0 4 3 2 23+=XX Giải phương trình ta được 4 321 ; 4 321 12 = + = XX Vậy4 321 ; 4 321 = + = xy hoặc 4 321 ; 4 321 + ==xy Nghiệmcủahệ phương trình: ( )                   + =        = + ∈ 4 321 ; 4 321 ; 4 321 ; 4 321 1;;(,)1 xyyy .

Câu 4. Trong2021số nguyên dương đầutiên,cóbaonhiêusố khôngchiahếtcho7và khôngchiahếtcho11?

Trongcácsố nguyên dương từ 1 đến2021cácsố chiahếtcho7là: 7;14;21;…;2016

Do đó số cácsố chiahếtcho7là:(20167):7+1=288(số)

Trongcácsố nguyên dương từ 1 đến2021cácsố chiahếtcho11là: 11;22;33;…;2013

Do đó số cácsố chiahếtcho11là:(201311):11+1=183(số)

Cácsố chiahếtcho7và11làcácsố chiahếtcho7.11=77(do(7;11)=1)

Trongcácsố nguyên dương từ 1 đến2021cácsố chiahếtcho77là 77;154;…;2002

Do đó số cácsố chiahếtcho77là:(200277):77+1=26(số)

Số cácsố chiahếtcho7hoặcchiahếtcho11là:288+18326=445(số)

Vậytrong2021số nguyên dương đầutiên,số cácsố khôngchiahếtcho7vàkhôngchia hếtcho11là2021445=1576(số)

5.1 Chứng minh tứ giác ABDE nội tiếp. Xác định tâm của đường tròn ngoại tiếp tứ giác ABDE và chứng minh MN // DE Tacó

90AEBADB==° (ADvàBElàhai đườngcao)

Và hai đỉnh D, E là hai đỉnhkề củatứ giácABDE Nêntứ giácABDEnộitiếp. ΔABE vuông tai E nên tâm I của đườngtrònngoạitiếptứ giác ABDE là trung điểmcủacạnhAB.

ABEADE = (gócnộitiếpchắ

 

n  AE )   ABEAMN = (gócnộitiếpchắn  MN ) Do đó   ADEAMN = mà hai góc này đồngvị nênMN//DE. 5.2 Chứng minh: AE. AC. CE = CD. AB. EF ΔCDE và ΔCAB có   DCEACB = (gócchung)và   CDEBAC = (cùngbùvới  BDE ) Nên ΔCDE ∽ ΔCAB(g.g)nên.CDCECACE BC CACBCD =⇒= (1) M N E F D H O I B A C

Tương tự ta có ΔAEF ∽ ΔABC(g.g) nên

=⇒= (2)

=⇒=

Từ (1)và(2)suyra:......

5.3 Gọi K là trung điểm của HC. Chứng minh IHKO là hình bình hành

Kẻ đườngkínhCJtacó:

JA//BH(cùngvuônggócvớiAC)

JB//AH(cùngvuônggócvớiBC)

Do đó Tứ giácAHBJlàhìnhbìnhhành

Mà I là trung điểmcủa AB nên I là trung điểmcủaJH

Talại có O là trung điểmcủa JC nên IO là đườngtrungbìnhcủa ΔJHC nên IO // HC và 2 HC IO = mà K là trung điểmcủaHC

Do đó IO // HK và 2 HC IOHK==

SuyraIHKOlàhìnhbìnhhành.

6. Chobasố thực dương

;y=

,,.Chứngminh:) (2 abc b ca a bc c ab ≥++ + + + + +

. AEEFABEF

ABBCAE

CACEABEF CACEAEABCDEF CDAE

abc

Đặtx= a

b ;z= c suyrax2=a;y2=b;z2=c(x;y;z>0) Khi đó ta cầnchứngminh 222222 2()xyyzzx xyz zxy +++ ++≥++ Tacó: 222222222222 222222333333 xyyzzxxyyzzx zxyzzxxyy xzyzyxxzyzyx zxzyxyxzyzxz +++ ++=+++++  +++ =+++++=++   Tachứngminh33() xzxzxz +≥+ (1) Thậtvậytacó: 222 332233 ()()0()()0 0() xzxzxzxz xzxzxzxzxzxz −+≥⇔−−≥ ⇔+−−≥⇔+≥+ J K M N E F D H O I B A C

Ápdụng(1)tacó: 333333()()()2() xzyzyxxzxzyzyzxyxy xyz xzyzxzxzyzxy ++++++ ++≥++=++ Dấu“=”xảyrakhix=y=z Vậy) (2 abc b ca a bc c ab ≥++ + + + + + khia=b=c

N SINH VÀO LỚP 10 THPT

thi:

(Chuyên)

ảihệ phương

3 (2,0 điểm):

Cho phương trình bậ

2313(2)0

( ) *với m làthamsố.Tìm m để phương trình có 2 nghiệmphânbiệt12 , xx và22121224xxxx+−= .

ấtcả cácnghiệmnguyên ( ); xy của phương trình:

xyxyxy+−−−=

4 (0,5 điểm): Trênbảng đang có haisố 1và2.Thựchiệnghithêmsố lênbảngtheoquy tắcsau:Mỗilầnviếtlênbảngmộtsố cabab =++ vớihaisố a và b đã có trên bảng.Hỏi vớicáchviếtthêmsố như trên sau mộtsố lầnhữuhạncóthể viết đượcsố 2022lênbảng không?

Bài 5 (3,0 điểm): Cho đườngtròn ( )O và điểm M nằm ngoài đườngtròn ( )O .Từ M kẻ 2 tiếptuyến,MAMB đến ( )O (A,B làtiếp điểm).Kẻ cáttuyến MNP (MN<MP).K làtrung điểmcủa NP.

a)Chứngminh các điểm,,,AKOB cùngthuộcmột đườngtrònvà xác địnhtâmcủa đường tròn đó.

b) BA cắt OK tại E và MP cắt AB tại F.Chứngminh KF làphângiáctrongcủa  AKB từ đó suy ra

EAFBEBFA

ngminhkhicáttuy

( 1,0 điể

MNP

đổithìtr

ngtâmtamgiác ANP luônthuộcmột đườngtrònc

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂ

NĂM HỌC 2022 2023 Môn

Toán

Thờigian: 150 phút (khôngkể thời gian phát đề) Bài 1 (1,5 điểm): Chobiểuthức 2 1 11 : 11 xxxPxx xxx   −+ + =− + với0 x > và1 x ≠ . a)Rútgọnbiểuthức P . b)Tínhgiátrị củabiểuthức P với2 32x =− . c) Tìm x để 3P > Bài 2 (2,0 điểm): a)Giải phương trình: (9)(6)(4)(1)56 xxxx −−−−=− b)Gi

trình: 22 22 2259990 222210 xyxyxy xyxy  +−−++=  ++++−=  . Bài

chai: ( ) 22

xmxm−+++=

b)Tìmt

2223130

Bài

= . c)Chứ

ến

thay

ọ

ố định. Bài 6

m): Chobasố thực dương ,, xyz thỏamãn3 xyz++= .Tìmgiátrị nhỏ nhất củabiểuthức: 222 222222 152681526815268 Pxyz xxyyyyzzzzxx =++ ++++++ H ết Thí sinh không đượcsử dụngtàiliệu.Cánbộ coithikhônggiảithíchgìthêm. Họ,tênthísinh:……………………………………Số báodanh:…………………… Chữ kýcủacánbộ coithi1:……………;Chữ kýcủacánbộ coithi2:……………………. Đề thigồm01trang

HƯỚNG DẪN CHẤM MÔN TOÁN Bài 1 (1,5 điểm): Chobiểuthức 2 1 11 : 11 xxxPxx xxx   −+ + =− + với0 x > và1 x ≠ . a)Rútgọnbiểuthức P . b)Tínhgiátrị củabiểuthức P với2 32x =− . c) Tìm x để 3P > . Lời giải a)Rútgọnbiểuthức P . 2 1 11 : 11 xxxPxx xxx   −+ + =− + ( ) ( ) ( ) ( ) 112 1 11 : 11 xxxxxxx xxx  −++−+  −+  + = + ( ) ( ) 2 11: 1 x xxxx x  =++−−+  + ( ) 11 2. 2 xx x xx ++ = = b)Tínhgiátrị củabiểuthức P với322 x =− . Tacó: ( ) 2 32221x =−=− suyra21 x =− Thayvào P tacó: ( )2112.21 22 2121 P −++ == =+ c) Tìm x để 1 3321 x Px x + >⇔>⇔< 1 0 4 x ⇔<< Bài 2 (2,0 điểm): a)Giảiphương trình: (9)(6)(4)(1)56 xxxx −−−−=− . b)Giảihệ phương trình: 22 22 2259990 222210 xyxyxy xyxy  +−−++=  ++++−=  Lời giải a/(9)(6)(4)(1)56 xxxx −−−−=− (1) (1) ( ) ( )221091024560xxxx ⇔−+−++=

Đặt2109 axx=−+ . Suyra ( ) 271556015560 8 a aaaa a =− ++=⇔++=⇔  =− TH1:222 7109710160 8 x axxxx x = =−⇒−+=−⇔−+=⇔  = TH2:22522 8109810170 522 x axxxx x  =+ =−⇒−+=−⇔−+=⇔  =−  Vậy phương trình (1)cótậpnghiệm { }2;8;522;522S =−+ b/Giảihệ phương trình: ( ) ( ) 22 22 22599901 2222102 xyxyxy xyxy  +−−++=  ++++−=  Tacó ( ) (1)(23)230230(3) 230(4) xy xyxy xy −−= ⇔−−−−=⇔ −−=    Đặt22,0. axya=++≥ Suyra22222222axyxya =++⇒+=− ( ) 22122210230 3() a aaaa al = ⇒−+−=⇔+−=⇔  =− Suyra ( )222212105xyxy++=⇔++= TH1: 22 23 2323 1 21020 2 xy xyxy x xyxx x =+=+=+  ⇔⇔ = ++=+−=   =− Suyra 1 1 x y =  =− hoặc 2 5 2 x y =−   =−  TH2: 22 23 2323 1 210450 5 yx yxyx x xyxx x =−=−=−  ⇔⇔ = ++=+−=   =−

Suyra 1 1 x y =  =− hoặc 5 13 x y =−  =− Vậytậpnghiệmcủahệ phương trình là: ( ) ( )5 1;1,2;,5;13 2 S   =−−−−−     Bài 3 (2,0 điểm): a) Cho phương trình bậchai: ( ) 222313(2)0xmxm−+++= ( ) *với m làthamsố Tìm m để phương trình có 2 nghiệmphânbiệt12 , xx và22121224xxxx+−= . b)Tìmtấtcả cácnghiệmnguyên ( ); xy của phương trình: 2223130 xyxyxy+−−−= . Lời giải a/ Cho phương trình bậchai: ( ) 222313(30 2)xmxm−++= + ( ) *với m làthamsố Tìmm để phương trình có 2 nghiệmphânbiệt12 , xx và22121224xxxx+−= *Tacó: ( ) ( ) '22225 311.33296196650. 6 mmmmmmm ∆=+−+=++−−=−>⇔> Tacó:12 2 12 2(31)62 96 xxmm xxm +=+=+  =+ * ( ) 1 222 12121222444xxxxxxxx +−=⇔+−= ( ) ( )22 22 624964 3624436244 mm mmm ⇔+−+= ⇔++−−= 1m ⇔= (TMĐK) Vậy1 m = thì22121224xxxx+−= . b/Tìmtấtcả cácnghiệmnguyên ( ); xy của phương trình : 2223130 xyxyxy+−−−= Tacó:223(2)(23)7 21300 xyxyxyxyxy +−−−==⇔−−−+= Ta xét các trườnghợp TH1: 211 2372 xyx xyy −−== ⇔  −+==− TH2: 2111 23712 xyx xyy −−=−=− ⇔  −+=−=− TH3: 2711 23120 xyx xyy −−==− ⇔  −+==− TH4: 271 2316 xyx xyy −−=−= ⇔  −+=−= Vậytậpnghiệmnguyêncủa phương trình đã cho là: ( ) ( ) ( ) ( {)} 1;2,11;12,11;20,1;6S =−−−− .

Bài 4 (0,5 điểm): Trênbảng đang có haisố 1và2.Thựchiệnghithêmsố lênbảngtheoquy tắcsau:Mỗilầnviếtlênbảngmộtsố cabab =++ vớihaisố a và b đã có trên bảng.Hỏi vớicáchviếtthêmsố như trên sau mộtsố lầnhữuhạncóthể viết đượcsố 2022lênbảng không?

Lời giải

Gọi() cn số viếtlênbảngsaulầnthựchiệnthứ n. Tachứngminh() cn sẽ chia 3 dư 2 vớimọin. Tacócácsố viếtlênbảnglà:5,11,17,23,…

Giả sử trênbảng đang có các số đều chia 3 dư 2vàsố 1. TH1:Tachọn1;32 abk==+ thìsố viếtlênlà3213265 ababkkk ++=++++=+ chia 3 dư 2.

TH1:Tachọn32;32 ambk=+=+ thìsố viếtlênlà (32)(32)32323(3332)2ababmkmkmkkm ++=++++++=++++ chia 3 dư 2. Vậycácsố viếtlênbảng luôn chia 3 dư 2 mà2022chiahếtcho3nênkhôngthể viết được số 2022lênbảng. Bài 5 (3,0 điểm): Cho đườngtròn ( )O và điểm M nằm ngoài đườngtròn ( )O .Từ M kẻ 2 tiếptuyến,MAMB đến ( )O (A,B làtiếp điểm).Kẻ cáttuyến MNP (MN<MP) K làtrung điểmcủa NP. a)Chứngminh các điểm,,,AKOB cùngthuộcmột đườngtrònvà xác địnhtâmcủa đường tròn đó.

b) BA cắt OK tại E và MP cắt AB tại F.Chứngminh KF làphângiáctrongcủa  AKB từ đó suy ra EAFBEBFA = c)Chứngminhkhicáttuyến MNP thay đổithìtrọngtâmtamgiác ANP luônthuộcmột đườngtròncố định. Lờigiải

ếptuyếncủa(O

Suyra A,B,K cùngnhìn MO dướimộtgócvuông Suyra,,,,ABKOM cùngnằmtrênmột đường tròn đườngkính OM Suyra,,,ABKO cùngnằmtrênmột đường tròn đườngkính OM có tâm là trung điểm OM . b/Tacó:

AKMAOM = (Tứ giác AKOM nộitiếp)

= (Tứ giác BOKM nộitiếp)

K N B A O M P a/Tacó:  90MKO =° (K là trung điểm NP)  90MAO =° (AM làtiếptuyếncủa(O))  90MBO =° (BM làti

))

 

  BKMBOM

và   BOMAOM = (Tínhchất2tiếptuyếncắtnhau) Suyra   AKMBKM = suyra KF làphângiáctrongcủa  AKB . Tacó KEKF ⊥ suyra KE làphângiácngoàicủagóc  AKB . Theotínhchất đườngphângiáctrongvàphângiácngoàicủatamgiáctacó: .. EAKA EBKBEAFAEAFBEBFA FAKAEBFB FBKB  =  ⇒=⇒=  =  T G K N B A J O M P c/Gọi J là trung điểm OM,G làtrọngtâmtamgiác ANP và T thuộc AJ saocho2 3 ATAJ = Tacó M,O,A cố địnhnên J,T cố định. Tacó 2 // 3 AGATGT GTKJ AKAJKJ =⇒⇒= Tacó KJ là đườngtrungtuyếntamgiácvuông OKM nên 1 2 KJOM = suyra 1 3 GTOM = Suyra G thuộc đườngtròncố địnhtâm T vàbánkínhbằng 1 3 OM Bài 6 ( 1,0 điểm): Chobasố thực dương ,, xyz thỏamãn3 xyz++= .Tìmgiátrị nhỏ nhất củabiểuthức: 222 222222 152681526815268 Pxyz xxyyyyzzzzxx =++ ++++++ Lời giải Tacó: ( ) ( ) ( ) 22222 15268434343 xxyyxyxyxyxy ++=+−−≤+=+

22 224315268 xx xxyyxy ⇒ ≥ +++ Chứng minh tương tự,tacó: 22 224315268 yy yyzzyz ≥ +++ và 22 224315268 zz zzxxzx ≥ +++ Suyra 222 434343 Pxyz xyyzzx ≥++ +++ Ápdụngbất đẳngthứcCôsitacó: 2243432 2. 434943497 xxyxxyx xyxy ++ +≥= ++ Tương tự 2432 43497 yyzy yz + +≥ + và 2432 43497 zzxz zx + +≥ + Suyra 2() 777 xyzxyzxyzPP ++++++ +≥⇔≥ Mà3 xyz++= suyra 3 7 P ≥ . VậyGTLNcủa P bằng 3 7 khi1 xyz=== .

Câu 1: (2 điểm)

1) Giải phương trình

Giải phương trình:

Giảihệ phương trình

1) Tacó ( )2 54.14810

ờ

TUYỂN SINH VÀO LỚP 10 THPT

HỌC 2022 2023

Môn Toán

gian làm bài 120 phút, đề gồm một trang có năm câu

Lời giải

Phương trình có hai nghiệmphânbiệt1x,2 x , trong đó

59 x2 2 −+ == ,2 59 x7 2 ==−

Vậytậpnghiệmcủa phương trình là { }S2;7 =− .

2) Đặt2 tx = (t0 ≥ )

Phương trình ban đầutrở thành2t8t90 +−= Tacó ( )

Phương trình có hai nghiệ

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH ĐỒNG NAI ĐỀ CHÍNH THỨC ĐỀ THI

NĂM



2 x5x140 +−= 2)

42 x8x90 +−= 3)

2x3y7 x2y7 −=  +=

∆=−−=> nên9 ∆=

2 49250′ ∆=−−=> nên5 ′ ∆=

mphânbiệt1t,2 t trong đó 1 45 t1 1 −+ == (nhận),245t9 1 ==− (loại) Suyra1t1 = nênsuyra2x1 x1 x1 = =⇔  =− Vậytậpnghiệmcủa phương trình { }S1;1 =− . 3) Tacó2x3y72x3y77y7y1y1 x2y72x4y142x4y142x4y14x5 −=−= = == ⇔⇔⇔⇔  +=+=+=+==  Vậytậpnghiệmcủahệ phương trình là ( {)}S5;1 = .  Câu 2: (1 điểm) Rútgọnbiểuthức ( ) ( )28 M35:51 51  =−++   Lời giải Tacó ( ) ( ) ( )288 M35:5135:51 5151   =−++=−++    (vì35 > ) ( ) ( ) ( ) ( ) ( ) ( ) 3551835355845145 :51:51. 515151515151  −−+ =−−++ += +== −+ −+ 4545 5 514 === VậyM5 = .

ẽ đồ

ị hàmsố

ọa độ giao điểmcủaparabol ( ) 12P:yx

và đườngthẳng ( ) d:y2x2 =− bằngphéptính.

(mlàthamsố thực).Tìmtấtcả cácgiátrị củathamsố thựcm sao cho phương trình đã cho có hai nghiệm1x,2xthoả mãn22 1212 xxxx8

phương trình ( )2 xm2x40

ố ( ) 12P:yx

xác định:D

,hàmsố đồngbiếnn

 Câu 3: (2.25 điểm)

( ) 12P:yx 2 = . 2) Tìmt

2 =

3) Cho

++−=

+= Lời giải

Hàms

2 = . Tập

=  1 a0 2 =>

ếux0 > ,hàmsố nghịchbiếnnếux0 < Bảnggiátrị x21012 12 yx 2 = 2 1 2 0 1 2 2 Đồ thị hàmsố 12 yx 2 = là đường cong Parabol đi qua điểmO,nhậnOylàmtrục đốixứng,bề lõm hướng lêntrên. 2) Phương trình hoành độ giao điểmcủa(P)và(d)là:20.5x2x2 =− 2 0.5x2x20⇔−+= (1) Phương trình (1) có nghiệmkép12xx2 == Vớix2 = thìy2 =

cách

địnhvàbiếtrằngsố tấnhàng mỗi ngày đội xe đó chở là như nhau. Vì tình hìnhcấpbáchnênmỗi ngày đội xe đó đã chở nhiều hơn số hàng ban đầulà5tấn hàng, do đó đội xe đã hoàn thành nhiệmvụ đượcgiaosớm hơn 1 ngày. Hỏitheokế hoạch ban đầu độixephảihoànthànhnhiệmvụ trongbaonhiêungày?

2) Tínhdiệntíchxungquanhcủamộthìnhtrụ có bán kính đáy 2 cm và chiềucaogấp3lần bán kính đáy.

ời giải

1) Gọixlàsố ngàytheokế hoạch ban đầu độ

đề bài,tacóbảngsau:

thành.

n/ngày

Đồ thị Parabol(P) và đườngthẳng(d)tiếpxúctại điểm(2;2) 3) Tacó ( ) ( ) ( ) 22 m244m2160 ∆=+−⋅−=++> (đúng vớimọim ∈  Do đó phương trình ( )2 xm2x40 ++−= cóhainghiệmphânbiệt1x,2x. Ápdụng địnhlýViét,tacó12 12 Sxxm2 Pxx4 =+=−−  ==− Tacó ( ) ( )22 12121212 xxxx8xxxx8SP84m28m0 +=⇔+=⇔⋅=⇔−−−=⇔= Vậyvớim0 = thoả mãnyêucầubàitoán.  Câu 4. (1,5 diém) 1) Một đội xe đượcgiaonhiệmvụ vậnchuyển150tấnhàngtiếptế đếnmộtkhuvực có người đang bị

lydodịchCovid19.Theokế hoạchphảihoànthànhtrongmộtthờigiannhất

iphải hoàn

(Đk: * x ∈  và1 x > ) Theo

Số tấnSố ngàySố tấ

Kế hoạch150x 150 x Thựctế 150x1 150 x1 Theo đề bài, ta có phương trình: 150150 5 x1x −= (điềukiện * x ∈  và1 x > ) 2 5x5x150⇔−− ( ) ( )2 14.3012111 ∆=−−−=⇒∆= ( )12 x6,x5l⇒==− Vậytheokế hoạch ban đầu độixelàmtrong6ngày. 2) Chiềucaocủahìnhtrụ là: ( )2.36cm2 = Diệntíchxungquanhcủahìnhtrụ là: ( )2 xqd SCV.h2R.h2.6.224cm ==π=π=π Vậydiệntíchxungquanhcủahìnhtrụ là2 24cm π

Câu 5. (2.5 điểm)

Từ điểmMnằm ngoài đườngtròn ( ) O;R,kẻ haitiếptuyếnMA,MB đến đườngtròn(A,Blàhaitiếp điểm).

1) Chứngminhtứ giácMAOBnộitiếp.

2) Vẽ tiaMxnằmgiữahaitiaMAvàMO.TiaMxcắt đườngtròn ( ) O;Rtại điểmC và điểmD (điểm Cnằmgiữa hai điểmMvàD).ChứngminhhaitamgiácMACvàMDA đồngdạng,rồitừ đó suy ra MCAC2



 

3) GọiH là giao điểmcủaOMvàAB.Kẻ DKvuônggócvớiABtạiK,OPvuônggócvớiCDtạiP, OQvuônggócvớiHDtạiQ.Chứngminhtứ giácHKPQlàhìnhthangcân.

Lời giả



MDAD

i 1) Chứng minh tứ giác MAOB nội tiếp. Tacó  90MAO =° ( MA làtiếptuyếncủa đườngtròn ( ); OR ) Suy ra điểm A thuộc đường tròn đườngkính OM Tacó  90MBO =° ( MB làtiếptuyếncủa đườngtròn ( ); OR ) Suy ra điểm B thuộc đường tròn đườngkính OM . Từ đó suy ra hai điểm A , B cùngthuộc đường tròn đườngkính OM Vậytứ giác MAOB nộitiếp đường tròn đườngkính OM . 2) Chứng minh hai tam giác MAC và MDA đồng dạng, rồi từ đó suy ra MCAC2 MDAD  =   . XétMAC ∆ vàMDA ∆ ,tacó:  BMDlàgócchung   1 MACMDAAC 2  ==  VậyMACMDA ∆∆  (gg) KL F P H Q D B A OM

⇒= 



MC.MDMA MCMA MDMD

MàMAAC MDAD = (cmt) Nên MCAC2 MDAD  =   .

3) Chứng minh tứ giác HKPQ là hình thang cân. Tacó:(Hệ thức lượngMAO ∆ ) MC.MDMH.MO⇒= (kếthợpcâub) MCMH

MOMD ⇒= XétMHC ∆ vàMDO ∆ ,tacó:

MCMH MOMD = (cmt) Vậy ( )MHCMDOcgc ∆∆−−

MHCMDO⇒= OHCD⇒ làtứ giácnộitiếp. Tacó:

DPODQO90 ==° (gt) DPQO⇒ làtứ giácnộitiếp.

PQDPOD90PDO90DCO90DHODHA ⇒==°−=°−=°−= PQ//AH⇒

HayPQHKlàhìnhthang(1)

Có2cáchchứngminhtínhchấtcân. C1:KéodàiHCcắtDKtạiL.

Tacó:

DHA90DHO90MHCAHC =°−=°−=

là đườ

ế

trung điểmDL.

là trung điểmDC(bànkínhvuônggócdâycungCD)

2 2 MAMC MDMA

⇒=



 DMOchung

∽  

 

     

   

AH⇒ làphângiácDHL ∆ MàAH

ngcao(gt) AH⇒ làtrungtuy

n K⇒ là

MàP

NênPK//HC    PFHCHFKHQ⇒== (2) Từ (1),(2)suyraPQHKlàhìnhthangcân. C2:Tacó:HFlàphângiáctrongDHC ∆ vàHMlàphângiácngoài. FCHCMC FDHDMD FCFDFDFCPF MCMDMDMCPC MDPCMFFC FDPFFDPF ⇒== ⇔=== ⇒=⇒= NênPK//HC    PFHCHFKHQ⇒== (2)

Từ (1),(2)suyraPQHKlàhìnhthangcân.

KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN TỈNH ĐỒNG THÁP NĂM HỌC 2022 - 2023 Môn: TOÁN (chuyên) Câu 1. (2,0 điểm) Cho biểu thức 1121 11 Txx xxxx −+ =+ −−+ (với 0,1xx>≠ ). a) Rút gọn biểu thức T . b) Tìm tất cả các giá trị của x để 320 T −= . Lời giải: a) Rút gọn biểu thức T Tacó: ( ) ( ) 11111 1111 x xxxxxxxx + •+=+= 21 1 xx x −+ •= + ( ) 2 1 1 x x + Suyra: ( ) ( ) 2 11 . 11 xx T xxx + = + Vậy 1Tx x = . b) Tìm tất cả các giá trị của x để 320 T −= . 12 3 Tx x == 332xx −= 3x ⇒= 9x ⇒= (nhận) Câu 2. (1,0 điểm) Giải phương trình 2132 xx −=− Lời giải: Điều kiện xác định 1 210 2 xx−≥⇔≥ Phương trình tương đương 22 219124414100 xxxxx −=−+⇔−+= ( ) ( ) 1 5 2 xn xl  = ⇔  =  Vậy tập nghiệm của phương trình là { }1S =

3. (1,0 điểm)

đường

4. (1,0 điểm)

tph

ả cácgiátr

ọa độ Oxy

đườ

. Đường thẳng d vuônggóc với AC tại

Tính độ dài các đoạn

ủ

để đườ

ẳng ( ) ( ) :11dymx=++ ( m làthamsố).

ẳng ( )d cắtparabol

hoành độ lần lượtlà12 , xx (với12 xx < )saocho12 xx > .

giải: Phương trình hoành độ giao điểm của ( )d và ( )

) 2 : Pyx = tại hai điểmphânbiệt

2110 xmx

ệ số 10ac =−< nên phương trình hoành độ giao điểmluôncó2nghiệmphânbiệtvới mọi m haythẳng ( )d cắtparabol ( )P tại hai điểmphânbiệtvớimọi m Theohệ thứcViéttacó12

được

đợt kiểm tra thường xuyên môn Toán,

một trong 3 nhóm:

tiếp tại lớp với hình thức tự luận. NhómB: Kiểm tra trực tuyến với hình thức trắc nghiệm. Nhóm C: Làm bài thu hoạch cá nhân theo chuyên đề đã học. Sau khi kiểm tra, điểm trung bình của các em học sinh được thống kê theo bảng sau: Nhóm ABCAvàBBvàC Điểm trung bình 9,08,08,58,48,2 Biết nhóm A có 10 học sinh lựa chọn. Tính số học sinh và điểm trung bình của lớp đó trong đợt kiểm tra thường xuyên trên (kết quả làm tròn đến hàng phần trăm).

Lời giải:

Câu

Cho hình chữ nhật ABCD có4 AB = dm,2ABAD =

C , đường thẳng d cắt hai

thẳng , ABBD lần lượt tại E và I .

thẳng , BDBE và ID Lời giải: 2216425=+=+=BDABBC . ACE∆ vuông tại C nêntacó: 2 24.1 4 BC BCABBEBE AB =⇒=== . // BECD nêntacó: 11 44 IBBE IBID IDCD ==⇒= 485 33 IDBD ⇒== Câu

Trongmặ

ẳngt

, cho

ngth

Tìmtấtc

ị c

a m

ngth

(

có

Lời

P : ( ) 211 xmx=++ ( )

⇔−+−= . Tacótíchh

1 xxm xx +=+  =− Tacó ( ) ( )2222 121212121200xxxxxxxxxx >⇔>⇔−>⇒+−> Theogiả thiết:12 xx < 120xx ⇔−< do đó 1201 xxm+<⇔<− . Câu 5. (1,0 điểm) Do ảnh hưởng của đại dịch COVID 19, trong một

giáo viên đã chia lớp thành 3 nhóm, mỗi học sinh chỉ

chọn

Nhóm A: Kiểm tra trực

ớ

hệ phương

sinh

6. (1,0 điểm)

Gọi x , y lần lượt là số học sinh của nhóm B, nhóm C ( )* , xy ∈  Ta có hệ phương trình: ( ) 10.9.8 108,4908848,4 8.8,5.88,58,2 8,2 x xxx xyxyxy xy + = ++=+ ⇔  + +=+ = +  Giải

trình: 15 10 x y =  = Số học

của lớp là: 35 Điểm trung bình của lớp là: 8,43. Câu

Giải hệ phương trình 212 3121 xxyxy xyy  ++=+  +−−=  Lời giải: Điều kiện: 1 3 1 x y  ≥−   ≤ Tacó: ( ) ( ) ( )2 1110 xyx ⇔−+−= ( ) ( ) 1 110 1 x xxy xy = ⇔−+−=⇔  += V

i1 x = , phương trình (2) trở thành:2210 yyy −−=⇔= Hệ phương trình có nghiệm ( ) ( );1;0xy = . Với1yx =− , phương trình (2) trở thành3121xxx +−=− ( ) ( ) ( )2 3110 311 xx xxxxxx xx ⇔+−+=−⇔ +−= +++ ( ) 1 10 311 xx xx  ⇔− += +++  01 0 10 xy xx xy =⇒= ⇔−=⇔  =⇒= Hệ phương trình có 2 nghiệm: ( ) ( );1;0xy = ; ( ) 0;1. Câu 7. (3,0 điểm) Chotamgiác ABC nhọn với ABAC < . Ba đường cao ,, ADBECQ cắt nhau tại H (với ,, DBCEACQAB ∈∈∈ ). Gọi M là trung điểm BC , T làgiao của EQ với BC . a) Chứng minh AEDB là tứ giác nội tiếp. b) Chứng minh tứ giác EQDM nội tiếp và .. TDTMTBTC = . c) Chứng minh H là trực tâm của tam giác .ATM Lời giải:

Chứng minh AEDB là tứ giác nội tiếp.

090AEB =

090ADB = Mà,DE là hai đỉnh liền kề trong AEDB . Do đó, tứ giác AEDB nội tiếp.

b) Chứng minh tứ giác EQDM nội tiếp và .. TDTMTBTC = .

tứ giác QHDB , EQBC nội tiếp nên

QDHQBHECQ == . Hơn nữa, HDCE nội tiếp nên

HDEECQ =

đó EQDM nội tiếp. Vìtamgiác TBQ đồng dạng với tam giác TEC nên..TETQTBTC = . Tương tự, TQTETDTM = . Vậy TDTMTBTC = c) Chứng minh H là trực tâm của tam giác .ATM

Gọi K là giao điểm còn lại của TA với đường tròn ngoại tiếp tam giác ABC . Vìtamgiác TKB đồng dạng với tam giác TCA nên..TBTCTKTA = Kết hợp với .. TBTCTETQ = (trongcâu(b)).Suyra..TETQTKTA = Suyratamgiác TKQ đồng dạng với tam giác TEA . Dẫn đến tứ giác AKQE là tứ giác nội tiếp. Mà AQHE cũng là tứ giác nội tiếp. Do đó AKHE nội tiếp. Suy ra  090AKH = Kẻ đường kính AN trong đường tròn ngoại tiếp tam giác ABC . Khi đó

090AKN = .Suyra ,, KHN thẳng hàng. Hơn nữa, BHCN làhìnhbìnhhànhnên,,HNM thẳng hàng. Tóm lại, MK vuônggóc AT . Do đó, H là trực tâm trong tam giác ATM

Vì 



Vì

  

 

. Suyra    2 QDEECHEMQ == Do



điểm)

nghiệm

(2,0 điểm)

Giải phương trình

Giải hệ phương trình

điểm)

lấy điểm

nội

mãn:

đường tròn ( )O , kẻ ba đường cao ,, ADBECF cắt nhau tại

(,MBC

Gọi P là điểm

Họ và tên thí sinh:……………..………………………..……………….; SBD……………… Câu 1: (2,0 điểm) a) Xác định tọa độ giao điểm của parabol ( ) :32Pyx = và đường thẳng ( ) :28dyx=+ b)Cho1111 13355720212023 A =++++ ++++  và202322022.25620 4 B = +−+ . Không sử dụng máy tính cầm tay, hãy chứng tỏ AB > . Câu 2: (2,0

a) Tìm một đa thức bậc ba ( )Px với hệ số nguyên nhận 3 24 3 x + = là một nghiệm và ( ) 16P =− b) Tìm

tất cả các số nguyên , xy thỏa

2222223442410.xyxyxxyxyy−++−+−−= Câu 3:

43143111 xxxxx +−+−−++= b)

222 81440 872020 xyxy yxy xy −−+=  +−+= Câu 4: (3,0

Chotamgiác ABC

tiếp

H ,

M trêncung nhỏ BC

≠ ).

đối xứng với M qua. AB a) Chứng minh:   APBACB = và tứ giác AHBP nội tiếp một đường tròn. b) Chứng minh: H là tâm đường tròn nội tiếp tam giác FDE c)Tìmgiá trị nhỏ nhất của biểu thức . ADBECF T HDHEHF =++ Câu 5: (1,0 điểm) Cho các số thực dương ,, xyz thoả mãn 111 3. xyz ++= Chứng minh rằng 22221. xyzxyz++−≥ HẾT Chữ ký giám thị 1…………………………… Chữ ký giám thị 2…………………..………………… SỞ GIÁO DỤC VÀ ĐÀO TẠO GIA LAI ĐỀ CHÍNH THỨC ( Đề thi có 01 trang) KỲ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN NĂM HỌC 2022 2023 Môn thi: TOÁN (Chuyên) Thời gian làm bài: 150 phút (không kể thời gian giao đề)

Với

được

ta được

HƯỚNG DẪN GIẢI Câu 1: (2,0 điểm) a) Xác định tọa độ giao điểm của parabol ( ) :32Pyx = và đường thẳng ( ) :28dyx=+ b)Cho1111 13355720212023 A =++++ ++++  và202322022.25620 4 B = +−+ . Không sử dụng máy tính cầm tay, hãy chứng tỏ AB > . Lời giải a) Phương trình hoành độ giao điểm của parabol ( )P và đường thẳng ( )d là ( )22 3283280 xxxx=+⇔−−=∗ . Tacó: ( ) ( )2 13.8250′ ∆=−−−=> . Suyra ( ∗) có hai nghiệm phân biệt: ( ) 125 2 3 x −−+ = = và ( ) 1254 33 x = =− .

2x = thì thay vào phương trình của ( )P ta

12y = . Với 4 3 x =− thì thay vào phương trình của ( )P

16 3y = . Vậy tọa độ các giao điểm của parabol ( )P và đường thẳng ( )d là ( ) 2;12và416 ; 33    b)Tacó: ( ) ( ) 122 22, 22 nnnn n nnnnnn +−∗ +− = = ∀∈ ++ +++−  Do đó, 3153752023202120231 22222 A =++++ = . Mặt khác,2022220221.255251 4 B −+ = +−++ ( ) 2 202212 .2551 2  = +−+  ( )20221 .2551 2 =+−+ 20221 2 = . Vì20232022 > nêntacó 2023120221 22 > hay AB >

a) Tìm một đa thức bậc ba ( )Px với hệ số nguyên nhận 3 24 3 x + = là một nghiệm và

16P

b) Tìm nghiệm tất cả các số nguyên , xy thỏa mãn: 2222223442410.xyxyxxyxyy−++−+−−=

giải

a)Tacó ( ) 3 243332324324271812120

xxxxxx + =⇔−=⇔−=⇔−+−= Suy ra đa thức bậc ba ( )Px thỏa đề có dạng ( ) ( )32 27181212Pxkxxx =−+− với k là hằng số.

( ) 16P =− nên362 kk −=−⇔=

Vậy có

Tìm

thỏ

Câu 2: (2,0 điểm)

( )

=− .

Lời

Vì

đa thức cần tìm là ( ) 32 54362424Pxxxx =−+− . b)

nghiệm tất cả các số nguyên , xy

amãn: 2222223442410.xyxyxxyxyy−++−+−−= Tacó2222223442410xyxyxxyxyy−++−+−−= ( ) ( ) ( ) ( ) ( ) ( ) ( ) 222222 22 22 22424410 2423 213 xyxyxxxyyxy xyxxyxy xyxxy ⇔−++++−−−= ⇔−++−++= ⇔−++−= Vì,xy là các số nguyên nên ( ) 2 xyx và ( ) 12xy+− là các số tự nhiên. Do đó, ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 22 22 2 111 213 111211 xyxxy xyxxy xyxyxy −=−=  −++−=⇔ ⇔  +−= +−+−=   ( ) ( ) 22 11 11 xy xy −=  ⇔  +−=−  hoặc ( ) ( ) 22 11 13 xy xy −=−   +−=  . Cả hai trường hợp đều không thỏa mãn. Vậy không tồn tại các số nguyên , xy thỏa mãn đề bài. Câu 3: (2,0 điểm) a) Giải phương trình 43143111 xxxxx +−+−−++= b) Giải hệ phương trình 222 81440 872020 xyxy yxy xy −−+=  +−+= Lời giải a) Điều kiện: 3x ≥ Với điều kiện đó, ta có 43143111 xxxxx +−+−−++=

( ) ( ) 22 34343434 3232 3232 11 11 11 xxxx xx xx x x x −+−+−−−+ −+−− ⇔−++−− ⇔+= ⇔+=− =− Nếu 11x < thì110 x −< , không thỏa mãn phương trình. Nếu 11x ≥ thì320 x −−> ,tacó 2 3232 23 261330 7() 19() 11 11 xx x x xktm xtm x x x −++−− ⇔−= −+= = ⇔  = =− ⇔ Vậy phương trình đã cho có nghiệm duy nhất 19x = . b)Tacó222 81440 872020 xyxy yxy xy −−+=  +−+= . Nếu 0y = thìkhông thỏa mãn hệ. Nếu 0y ≠ thì hệ tương đương với 2 2 2 41 814042140(1) 21 8720022200(2) xx xx yyyy xx x yyyy x  +−−= −−+=    ⇔   +−+= +−−=   . Trừ (2)cho(1) theo vế ta được 2 1 21 11 224260 1 23 x y xx yy x y  +=− +−+−=⇔ +=  TH1: 11 2121 xx yy +=−⇔=−− . Thayvào(1),tacó21145 4(21)14021802 xxxxx −± −−−−−=⇔+−=⇔= . TH1: 11 2323 xx yy +=⇔=−+ . Thayvào(1),tacó2 2 12(23)14023201 2 x xxxx x = −−+−=⇔−−=⇔  =−  . Vậy hệ phương trình đã cho có 4 nghiệm: 1145145 ; 2145    , 1145145 ; 2145  −+   , ( ) 2;1, 11 ; 24    .

điểm)

Chotamgiác ABC nội tiếp đường tròn ( )O , kẻ ba đường cao ,, ADBECF cắt nhau tại H , lấy điểm M trên cung nhỏ BC (,MBC ≠ ). Gọi P là điểm đối xứng với M qua. AB

Chứng minh:

APBACB = và tứ giác AHBP nội tiếp một đường tròn.

b) Chứng minh: H là tâm đường tròn nội tiếp tam giác FDE

Tìm giá trị nhỏ nhất của biểu thức . ADBECF T HDHEHF =++

giải

(1)APBAPMMPBAMPPMBAMB =+=+= . Do  AMB và

a) P đối xứng với M qua AB nên

ACB là các góc nội tiếp cùng chắn cung AB nên

(2)AMBACB =

(1)và(2)suyra

(3)APBACB = . Tứ giác DHEC có

90HDCHEC==° (vì,ADBE là các đường cao của ABC∆ )nên

180(4)ACBAHB+=° Từ (3)và(4)suyra

ECDEHD+=° .Suyra

APBAHB

đó, tứ giác AHBP nội tiếp một đường tròn.

tứ

nội tiếp

Câu 4: (3,0

 

Lời

     



 

Từ

 

  180

 

  180

+=° . Do

b) Dễ thấy, HFAE , AEDB , DBFH là các

giác

nên     HFEHAEHBDHFD === .Suyra HF là đường phân giác của tam giác FDE Tương tự, HD cũng là đường phân giác của tam giác FDE . Vậy H là tâm đường tròn nội tiếp tam giác FDE c) Đặt ,, HBCHCAHAB SxSySz === .Tacó: 1 . 2 1 . 2 ABC HBC ADADBCSxyz HDSx HDBC ++ === . Tương tự, ta cũng có: ; BExyzCFxyz HEyHFz ++++ = = . Suyra3Txyzxyzxyzxyyzzx xyzyxzyxz ++++++  =++=++++++   .

dụng

đẳng

tam giác đều.

tâm

điểm)

minh rằng

Áp

bất

thức AMGM,tacó: 22;22;22 xyxyyzyzzxzx yxyxzyzyxzxz +≥⋅=+≥⋅=+≥⋅= Suyra9 T ≥ Đẳng thức xảy ra khi và chỉ khi 3 3 3 xy yxADHD yzxyzBEHEH zyCFHF zx xz  =  = =⇔==⇔=⇔  = =  là trọng

tam giác ABC Mà H cũng là trực tâm của tam giác ABC nên lúc đó ABC là

Câu 5: (1,0

Cho các số thực dương ,, xyz thoả mãn 111 3. xyz ++= Chứng

22221. xyzxyz++−≥ Lời giải Áp dụng bất đẳng thức AM GM,tacó:2222222;2;2 xyxyyzyzzxzx +≥+≥+≥ . Suyra222xyzxyyzzx ++≥++ Tacó: 111 33xyyzzxxyz xyz ++=⇔++= . Do đó, 2222(1) xyzxyzxyz ++−≥ Dễ dàng chứng minh bất đẳng thức AM GM cho ba số không âm ,, abc : 3 abcabc ++≥ . Áp dụng bất đẳng thức này, ta có 3 111111 33.1(2) xyz xyzxyz =++≥⋅⋅⇔≥ Từ (1)và(2)suyra22221 xyzxyz++−≥ . Đẳng thức xảy ra khi 1xyz===

nhất.

Giải hệ phương trình: ( ) ( ) 2222 2

 −−++=+−++

1.13 6328 xyxyxyxy xyxx

III. (4,0 điểm) Chotamgiác ABC ( )ABAC < cócácgócnhọnnộitiếp đườngtròn

); OR . Các đườngcao,,AKBECF củatamgiác ABC cắtnhautại H vàcắt đườngtròn

; OR tại các điểmlần lượtlà,,MNP ( M khác A , N khác B , P khác C ).

Chứngminh//. EFPN

Chứngminhdiệntíchtứ giác AEOF bằng2 EFR

Tínhgiátrị củabiểuthức. AMBNCP AKBECF ++

Gọi S và Q là chân đườngvuônggóck

Câu I. (2,0 điểm) Chobiểuthức: 2391:(0;1;4). 32623 Axxxxxx xxxxxx  =+− ≥≠≠ +−+−+− 1. Rútgọnbiểuthức A 2. Tìmtấtcả cácgiátrị của x để 2A >− . Câu II. (2,0 điểm) 1. Cho đường thẳng ( )d có phương trình ( ) 221ymxm =−+− (với m là tham số) và điểm ( )1;2A .Tìm tất cả các giá trị của m để khoảng cách từ điểm A đến đường thẳng ( )d đạt giá trị lớn

 +++=−++  Câu

(

( )

ẻ từ điểm K đếncáccạnh,ABAC Đường thẳng QS cắt BC tại G , đườngthẳng GA cắt đườngtròn ( ); OR tại điểm J ( J khác A ).Gọi I là tâm đườngtrònngoạitiếptứ giác BCQS .Chứng minh ba điểm,,IKJ thẳnghàng. Câu IV. (1,0 điểm) Tìm tất cả các cặp số nguyên ( ); xy thỏa mãn: 4322618324200.xxxyxy −+−−++= Câu V. (1,0 điểm) Chobasố thực dương ,, abc thỏamãn222220 abcabbcca +++−−= . Chứngminh: 2222 2223 () abccab ababcab ++ ++≥ ++−+ . --- HẾT--Thí sinh không được sử dụng tài liệu, người coi thi không giải thíchgìthêm. Họ và tên thí sinh:…………………………………...Số báo danh:............................................... Người coi thi số 1: …Người coi thi số 2: UBND TỈNH HÀ NAM SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ CHÍNH THỨC KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN Năm học 2022 2023 Môn: Toán (Đề chuyên) Thời gian làm bài: 150 phút, không kể thời gian giao đề

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NAM ĐỀ CHÍNH THỨC KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN Năm học: 2022 2023 (Hướngdẫnchấmthicó05trang) HƯỚNG DẪN CHẤM MÔN TOÁN (ĐỀ CHUYÊN) Ghi chú: Điểmtoànbàikhônglàmtròn. Cáccáchgiải khác mà đúng cho điểm tương đương. Nội dung Điểm Câu 1 (2,0 điểm) . Chobiểuthức: 2391:(0;4;1). 32623 Axxxxxx xxxxxx  =+− ≥≠≠ +−+−+−  1. (1,5 điểm) Rút gọn biểu thức A . ( ) ( ) 2 (2)(3)(3)91 : (3)(2)31 Axxxx xxxx −−−+−+ = +− +− 0,5 ( ) ( ) 2 (2)(9)91 : (3)(2)31 xxx xxxx −−−−+ = +− +− 0,25 ( ) ( ) 2 (2)1 : (3)(2)31 x xxxx = +− +− 0,25 ( ) ( )2 .3.1 3 x xx x =+− + 0,25 ( ) ( ) 2132xxxx =−−=−+ 0,25 2. ( 0,5 điểm) Tìmtấtcả cácgiátrị của x để 2A >− . 322Axx=−+>− (0;4;1). xxx ∀≥≠≠ 2 37 3400(0;4;1). 24 xxxxxx  ⇔−+>⇔−+>∀≥≠≠   0,25 Vậy 2A >− với0;4;1 xxx ∀≥≠≠ 0,25 Câu 2 (2,0 điểm). 1. ( 1,0 điểm) Cho đường thẳng ( )d có phương trình ( ) 221ymxm =−+− và điểm ( )1;2A Tìm tất cả các giá trị của m để khoảng cách từ điểm A đến đường thẳng ( )d đạt giá trị lớn nhất. Gọi ( )00 ; Mxy là điểmcố địnhnằm trên đườngthẳng d ( ) 00221ymxm ⇔=−+− cónghiệmvới m∀ ( ) ( ) ( ) 000 00 000 2210 202 21032;3 mxxym xx M xyy ⇔+−−−=∀ += =− ⇔ ⇔⇒− −−−==  0,25 Gọi H là hình chiếu của A trên dAHAM ⇒≤ Khoảng cách AH lớn nhất là AM khi HMAMd ≡⇔⊥ 0,25 Phương trình đường thẳng :1AMyx=−+ 0,25 ( ) ( ) 2.113.AMdmm ⊥⇔−−=−⇔= 0,25 2. ( 1,0 điểm) Giải hệ phương trình: ( ) ( ) ( ) ( ) 2222 2 1.131 63282 xyxyxyxy xyxx  −−++=+−++  +++=−++ 

ọnnộitiếp đườngtròn ( ); OR .Các đườ

ại H vàcắt đườngtròn ( ); OR tại các điểmlần lượtlà,,MNP ( M khác A , N khác B , P khác C ).

ủ

2 ĐK: 6 3 x y ≥−  ≥− 0,25 ( ) ( ) ( ) ( ) ( ) 2222 22 22 1.13 2.20 2020, xyxyxyxy xyxy xyxyxy −−++=+−++ ⇔−−++= ⇔−−=++>∀ 0,25 Thay2 yx=− vào phương trình ( )2 2 6128,(1)xxxxx +++=−++≥− ( ) ( ) 2 6312230 33 310 6312 xxxx xx xx xx ⇔+−++−+−−= ⇔++−+= ++++ 0,25 ( ) 11 310 6312 3do1110,1 6312 31. xx xx xxx xx xy  ⇔− +++=  ++++   ⇔= +++>∀≥−  ++++  =⇒= Vậyhệ phương trình có nghiệm ( ) ( );3;1xy = 0,25 Câu III. (4 điểm) Chotamgiác ABC ( )ABAC < cócácgócnh

ngcao,,AKBECF c

atamgiácABCcắtnhaut

1. ( 1,0 điểm) Chứngminh//. EFPN   090BECBFC==⇒ tứ giác BCEF nộitiếp đường tròn đườngkính BC 0,25   CBECFE⇒= (gócnộitiếpcùngchắncung  EC ) 0,25 Mà   CBECPN = (gócnộitiếpcùngchắncung  CN ) 0,25   // CFECPNEFPN⇒=⇒ 0,25

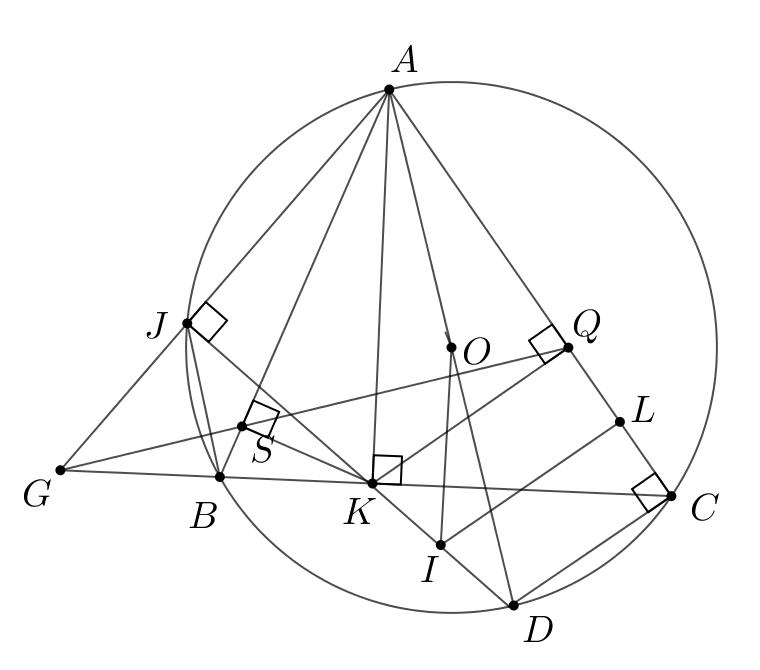
3 2. ( 1,0 điểm) Chứngminhdiệntíchtứ giác AEOF bằng2 EFR   ABNACP = (cùngphụ với  BAC ) ANAP⇒= 0,25 ONOPR == 0,25 , AO⇒ nằm trên đườngtrungtrựccủa PN AOPN⇒⊥ 0,25 Mà// 2AEOF EFR EFPNAOEFS⇒⊥⇒= 0,25 3. ( 1,0 điểm) Tínhgiátrị củabiểuthức AMBNCP AKBECF ++   BAMBCM = (gócnộitiếpcùngchắncung  BM )   BAMBCF = (cùngphụ với  ABC )   BCFBCM⇒= MCH∆ có CK vừa là đườngphângiácvừa là đườngcao ⇒ MCH∆ cântại CK ⇒ là trung điểmcủa MH 0,25 3. AMBNCPAKKMBEENCFFP AKBECFAKBECF KMENFP AKBECF +++ ++=++ =+++ 0,25 BHC ABC KMKHS AKAKS ∆ ∆ == Chứng minh tương tự:;AHCAHB ABCABC SSENFP BESCFS ∆ ∆ ∆∆ == 0,25 3314. BHCAHCAHB ABC AMBNCPSSS AKBECFS ∆∆∆ ∆ ++ ++=+ =+= 0,25 4. ( 1,0 điểm) Gọi S và Q là chân đườngvuônggóckẻ từ điểm K đếncáccạnh,ABAC . Đường thẳng QS cắt BC tại G , đườngthẳng GA cắt đườngtròn ( ); OR tại điểm J ( J khác A ).Gọi I là tâm đườngtrònngoạitiếptứ giác BCQS .Chứng minh ba điểm,,IKJ thẳnghàng.   000 9090180ASKAQK+=+= nênASKQ làtứ giácnộitiếp   ASQAKQ⇒= 0,25

trung

là trung điể

OI là đườngtrungbìnhcủa//AKDOIAKOIBC ∆⇒⇒⊥

= nên OI làtrungtrực BC (3)

KQDC (cùngvuônggóc AC )nên KQCD làhìnhthang.

là đườngtrungbìnhc

⇒⊥

4   AKQBCQ = (cùngphụ với  CKQ ) Do đó   ASQBCQ = Suyra BSQC làtứ giácnộitiếp.   GBSGQC⇒= (.)..(1) GBGS GBSGQCggGBGCGSGQ GQGC ∆∆=>==>= ∽ Vì ASKQ làtứ giácnộitiếpnên:   GQKBAK = Mà   BAKGKS = (cùngphụ với  SBK ) nên   GQKGKS = (.)2.(2) GQKGKSggGQGKGKGSGQ GKGS ∆∆=>==>= ∽ Từ (1)và(2)2.GKGBGC⇒=   .. GJGB GJBGCAGJBGCA GCGA GJGAGBGC ==>∆∆=>= =>= ∽ 2.A GKGJ GKGJG GAGK ⇒=⇒= ⇒   090GKJGAKGJKGKA ∆∆⇒== ∽ ⇒ AJ ⊥ JK 0,25 JK cắt ( )O tại D ( D khác K )thì AD là đườngkínhcủa ( )O Gọi I là

điểm KD , L

m QC Khi đó

Mà OBOC

0,25 Vì//

⇒ IL

ủahìnhthang KQCD ⇒ // ILKQILQC

⇒ IL làtrungtrựccủa QC (4) Từ (3)và(4) ⇒ I là tâm đườngtrònngoạitiếptứ giác BSQC Vậy,,IKJ thẳnghàng. 0,25 Câu IV. (1 điểm) Tìm tất cả các cặp số nguyên ( ); xy thỏa mãn: 4322618324200.xxxyxy −+−−++= 4322 4322 222 618324200 618322444 (2)(26)(2) xxxyxy xxxxyy xxxy −+−−++= <=>−+−+=−+ <=>−−+=− 0,25 Với22 yx=⇒= Với2 y ≠ tacó(y2)2và(x2)2làsố chính phương khác 0 nên 226xx−+ làsố chính phương. Đặt22 26 xxm −+= * () mN ∈ 0,25

5 22(1)5 (x1m)(x1m)5 xm −+= <=>−−−+=− 15 11 (x-1+m>x-1-m) 11 15 3 3 <=> 1 3 xm xm xm xm x m x m −+=   <=>−−=−  −+=  −−=−  =   =  =−  =  0,25 • x=3 ⇒ (y2)2=9 ⇒ y=5hoặcy=1 • x=1 ⇒ (y2)2=81 ⇒ y=11hoặcy=7 Vậycácbộ (x;y)nguyênthỏayêucầubàitoánlà(2;2),(3;5),(3;1),(1;11),(1;7). 0,25 Câu V. (1 điểm) Cho ba số thực dương ,, abc thỏa mãn thỏamãn:222220 abcabbcca +++−−= . Chứngminh: 2222 2223 () abccab ababcab ++ ++≥ ++−+ 2222 2223 () abccab ababcab ++ ++≥ ++−+ 22 2222 () ccab ababcab ⇔++≥ ++−+ Đặt a x c = , b y c = (x,y>0) 222220 abcabbcca +++−−= 222 1220(1) xyxyxyxyxy ⇔+++−−=⇔+−= 0,25 Ápdụngbất đẳngthứcCôsi: 2() 4 xy xy + ≤ Do đó: ( ) ( ) ( ) 2 12()232.202 43 xy xyxyxyxy +  +−≤⇒+−−+≥⇔≤+≤  0,25 22 222 () ccab P ababcab =++ ++−+ 22222 222 1111 (1) 11141 2 22()2() xyxy xyxyxyxyxyxy xy xyxyxyxyxyxyxy =++=++ ++−+++  =+++≥+ +++ +  0,25 2 41 22 22.2 P ≥+= Dấubằngxảyrakhi x=y=1 ⇔ a=b=c 0,25

Ở

DỤC VÀ ĐÀO TẠO HÀ NỘI - ĐỀ THI CHUYÊN TOÁN HÀ NỘI

Ngày thi: 20/06/2022

ời gian: 150 phút.

1. (2 điểm).

1)Giải phương trình

xxx

2)Chocácsố thực,ab và c thoả mãn điềukiện1. abbcca++= Tínhgiátrị củabiểuthức

Bài 2. (2 điểm).

1)Chứngminhnếu n làsố tự nhiênlẻ thì2137 n + chiahếtcho20.

ấtcả cáccặpsố nguyên dương ( ), xy saocho ( ) ( ) ( )22111.yxxxy++=+−

Bài 3. (2 điểm).

1)Tìmhaisố nguyên dương m và n saocho 3 m mn + và 3 n mn + đềulàcácsố nguyêntố.

2)Với,ab và c làcácsố thựckhôngâmthoả mãn điềukiện3 abc++= ,tìmgiátrị lớn nhấtcủabiểuthức233. Pabbccaabc =++−

Bài 4. (3 điểm).

Chotamgiác ABC nhọnvới ABAC < . Đườngtròn ( )I nộitiếptamgiác ABC ,tiếpxúc vớibacạnh,BCCA và AB lần lượttại ba điểm,DE và F

1)Gọi M là giao điểmcủa hai đườngthẳng AI và DF .Chứng minh đườngthẳng CM vuônggócvới đườngthẳng AI

2)Gọi N là giao điểmcủa hai đườngthẳng AI và DE .Gọi K là trung điểmcủa đoạn thẳng BC .Chứngminhtamgiác KMN làtamgiáccân.

3)Cácti

GIÁO

Bài

2422110

−+−+= .

222 2 111 abc P abcabcabc =++− +++++−

2)Tìmt

ếptuyếntại M và N của đườngtròn ( ); KKM cắtnhautại điểm S .Chứngminh đườngthẳng AS songsongvới đườngthẳng ID . Bài 5. (1 điểm). Chotậphợp A gồm70số nguyên dương không vượtquá90.Gọi B làtậphợpgồmcácsố códạng xy + với xA ∈ và yA ∈ (,xy khôngnhấtthiêtphânbiệt). 1)Chứngminh68. B∈ 2)Chứngminh B chứa91số nguyênliêntiếp.

ĐÁP ÁN Bài 1. (2 điểm). 1)Giải phương trình 2422110 xxx−+−+= . 2)Chocácsố thực,ab và c thoả mãn điềukiện1. abbcca++= Tínhgiátrị củabiểuthức 222 2 . 111 abc P abcabcabc =++− +++++− Lời giải 1) Điềukiện 1 2 x ≥ Khi đó phương trình 2242211021212211 xxxxxxx −+−+=⇔−+=−−−+ ( ) ( ) ( ) ( ) 221211*1211 1121** xx xx xx  −=−− ⇔−=−−⇔  −=−− Giải(*):121121 xxxx −=−−⇔=− (điềukiện0 x ≥ ). Khi đó ( ) ( )2221101 xxxxtm ⇔=−⇔−=⇔= Giải(**):1121212 xxxx −=−−⇔−=− (điềukiện2 x ≤ ). Khi đó ( ) ( ) 22 1 2144650 5 xtm xxxxx xkotm = −=−+⇔−+=⇔  =  . Vậy phương trình ban đầucónghiệmlà1. x = 2)Vì1 abbcca++= thayvào P , ta được: 222 2abc P abbccaaabbccababbccacabcabc =++− +++++++++++− ( ) ( ) ( ) ( ) ( ) ( ) ( )2 abcabbcca P abacbcbacacbabcabc ++ =++− ++++++++− ( ) ( ) ( ) ( ) ( ) ( ) ( )2 abcbaccababbcca P abacbcabcabc +++++++ = +++++− ( ) ( ) ( ) ( ) ( )22abbccaabbcca P abbccaabcabc ++++ = +++++− Talạicó ( ) ( ) ( ) 222222 abbccaababbcbccaacabcabc +++=+++++++ 222222 abababcacacabcbcbcabcabc =++++++++−

) ( ) ( ) ababcacabcbcabcabc

) ( ) abcabbccaabc

(Vì1 abbcca++=

vào được0. P

1)Chứngminhnếu n làsố tự nhiênlẻ thì2137 n + chiahếtcho20.

ấtcả cáccặpsố nguyên dương ( ), xy saocho ( ) ( ) ( )22111.yxxxy++=+−

ời gi

1)Vớinlàsố tự nhiênlẻ

ết ( )21 nkk

ừ đó ta được 2143 3737.

Xéttrongmodul4,tacó ( ) ( )4341 311mod4,

)41A

Xéttrongmodul5,tacó:

suyra ( ) 170mod4.A ≡−−≡ Do đó

( )

370mod5,

đó

(

=++++++++− (

=++++− abcabc=++−

). Thay

= Bài 2. (2 điểm).

2)Tìmt

ải

,tavi

=+∈  T

Ank ++ =−=−

kk ++ =−=−

(

( )43 327.817mod5, kk + =≡ suyra

k + −≡ do

( )52A .Mà ( ) 4;51 = nên2137An + =− chiahếtcho20. 2)Vìcácsố cầntìmlàcácsố nguyên dương nên đẳngthắc đã cho tương đương 22111111 . 111 xxy xyyx xyxyxy ++− =⇔+=−⇔−=+ +++ Vì yx−∈  nên 11 . 1 xy +∈ +  Tasẽ chứngminh 112 . 1 mn mnmn == +∈⇔  ==  Trườnghợp1:1 mn== . Khi đó 11 2. mn +=∈  Trườnghợp2: 1 1 m n ≠  = . Khi đó 11 1, mm +∈⇔∈ điềunàyvôlý. Trườnghợp3: 1 1 m n =  ≠ . Khi đó 11 1, nn +∈⇔∈ điềunàyvôlý. Trườnghợp4: 1 1 m n ≠  ≠ . Khi đó 11 . mn mnmn + +∈⇔∈ .

Bởivì.mnmn +≤ nên 2 .. .2 mnm mnmn mnn += ∈⇔+=⇔  =  Vậy 11 11 122 2 x yx xy y +=   = = ⇔  +==   =  Bài 3. (2 điểm). 1)Tìmhaisố nguyên dương m và n saocho 3 m mn + và 3 n mn + đềulàcácsố nguyêntố 2)Với,ab và c làcácsố thựckhôngâmthoả mãn điềukiện3 abc++= ,tìmgiátrị lớn nhấtcủabiểuthức233. Pabbccaabc =++− Lời giải 1) Đặt 33 ; mnab mnmn == ++ và ( ) ,. mnp = Ta được .;.; mkpnlp == trong đó , kl ∈  và ( ) ,1kl = .Từ đó suy ra ( ) 3332 kpkp a pklkl == ++ . Bởivị ( )3 ,1klk+= cho nên ta được 3 .ak  Do a làsố nguyêntố nên1. k = Tương tự như vậytacó1 l = .Suyra 2 2. 2 p abpq ==⇒= Và221.abqq==⇒= takếtluận2. mn== 2)Do,,0 abc ≥ nên 23323 Pabbccaabcabbcac =++−≤++ ( ) ( ) ( ) ( )222 abacbcacabccba =+++=+++ ( ) ( ) 22 27 424 abcabc P ++++ ≤+= Vậy 27 4max P = Dấu“=“xảyrakhivàchỉ khi 3 2 30 abc ac abc abcb =+  == +=⇔  ++== Bài 4. (3 điểm). Chotamgiác ABC nhọnvới ABAC < . Đườngtròn ( )I nộitiếptamgiác ABC ,tiếpxúc vớibacạnh,BCCA và AB lần lượttại ba điểm,DE và. F 1)Gọi M là giao điểmcủa hai đườngthẳng AI và DF .Chứng minh đườngthẳng CM vuônggócvới đườngthẳng AI .

2)Gọi N là giao điểmcủa hai đườngthẳng AI và DE .Gọi K là trung điểmcủa đoạn thẳng BC .Chứngminhtamgiác KMN làtamgiáccân. 3)Cáctiếptuyếntại M và N của đườngtròn ( ); KKM cắtnhautại điểm S .Chứngminh đườngthẳng AS songsongvới đườngthẳng ID . Lời giải 1)Gọi M là giao điểmcủa hai đườngthẳng AI và DF .Chứng minh đườngthẳng CM vuônggócvới đườngthẳng AI . Tacó     180 18018090 22 o oooBB MFABFD=−=−=+ Tacó:  AIC  ( )   1801809090 22 ooooABCB IACICA  =−+=−−=+    Suyra     ; MFAAICBAIIAC == Tacó:    AFMAICAMFACIICB ∆∆⇒==  ,suyratứ giác IDMC nộitiếp. Do đó   90 o IMCIDCCMAMCMAI ==⇒⊥⇒⊥ 2)Gọi N là giao điểmcủa hai đườngthẳng AI và DE .Gọi K là trung điểmcủa đoạn

thẳng BC .Chứngminhtamgiác KMN làtamgiáccân.

Chứngminh,,,,BFIND cùngthuộcmột đườngtròn,suyra//. BNAMBNCM ⊥⇒

Gọi H là giao điểmcủa BN và,ACJ là giao điểmcủa CM và. AB

Tacó:

N là trung điểmcủa BH ( ABH∆ cân)và M là trung điểmcủa CJ ( ACJ∆ cân).

Suyra 11 ;;. 22 KNCHKMBJCHBJ ===

Dovậy KNKMKMN =⇒∆ cân.

3)Cáctiếptuyếntại M và N của đườngtròn ( ); KKM cắtnhautại điểm S .Chứngminh đườngthẳng AS songsongvới đườngthẳng ID .

PMNPCA = Dễ nhậnthấy KN // AC nêntacó

Dựng đườngcao AP thìtacótứ giác APMC nộitiếpsuyra

PCANKPPMNNKP =⇒=

Do đó tứ giác PMKN nộitiếp Vì,SMSN làcáctiếptuyếncủa ( ), KKM nêntacó,,,SMKN cùngthuộc đườngtròn đườngkính SK .Suyra,,,,PSMKN cùngthuộcmột đường tròn đườngkính SK nên

SPKo = , do đó PSBC ⊥ ,mà APBC ⊥ suyra,,APS thẳnghàng.

ASBCIDBCASID ⊥⊥⇒ (đpcm).

ứa70số nguyên dương không vượt quá90( A

vượtquá90)nêncóítnhất1cặpsố thuộc A . Từ đó ta có

2)Ch

ẽ

•

ngminh

ứ

nguyênliêntiế

ố nguyên dương n với4290 n ≤≤ , đềuthuộctập B .

 

    .

 90

Do,//

Bài 5. (1 điểm). Chotậphợp A gồm70số nguyên dương không vượtquá90.Gọi B làtậphợpgồmcácsố códạng xy + với xA ∈ và yA ∈ (,xy khôngnhấtthiêtphânbiệt). 1)Chứngminh68. B∈ 2)Chứngminh B chứa91số nguyênliêntiếp. Lời giải 1)Chứngminh68. B∈ Xét34cặpsố ( ) ( ) ( ) 1;67;2;66;...;34;34dotập A ch

chỉ khôngchứa20số nguyên dương không

68. B∈

ứ

B ch

a91số

p. Tas

ngminhmọis

Với4290 n ≤≤ :Giả sử .nB ∉

-Nếu n làsố lẻ,cáccặpsố ( ) ( ) –1,1;–2;2;nn ...; 11 ;. 22 nn−+    Vì nB ∉ nên

mỗicặpsố đềucóítnhấtmộtsố khôngthuộctập A .Suyracóítnhất 1 21 2 n ≥

số nguyên dương không lớn hơn 90 khôngthuộctập A ,mâuthuẫnvìtập A gồm 70số nguyên dương không vượtquá90.

Nếu n làsố chẵn,xétcáccặpsố ( ( ) –1,1;–2;2; ) nn ...; 11 ; 22 nn−+    vàsố . 2 n

Vì nB ∉ nênmỗicặpsố đềucóítnhấtmộtsố khôngthuộctập A ,ngoàira

2 nA ∉ Suyracóítnhất21 2 n ≥ số nguyên dương không lớn hơn 90 không thuộc

tậ

nguyên dương không vượtquá90. Như

n với4290 n ≤≤ , đềuthuộctập B .

n ≤≤ Giả sử .nB ∉ Nếu n làsố lẻ:xétcáccặpsố ( ) ( ) 90,–90,89;–89;...; nn 11 ;. 22 nn−+    Vì nB ∉ nênmỗicặpsố đềucóítnhấtmộtsố khôngthuộctập A .Suyracóítnhất 1 9121 2 n −≥ số nguyên dương không lớn hơn 90 không thuộctập A ,mâuthuẫn vìtập A gồm70số nguyên dương không vượtquá90. Nếu n làsố chẵn,xétcáccặpsố ( ) ( ) 90;–90;89;–89; nn ...; 22 ; 22 nn+−    và số 2 n Vì nB ∉ nênmỗicặpsố đềucóítnhấtmộtsố khôngthuộctập A ,ngoàira . 2 nA ∉ Suyracóítnhất9121 2 n −≥ số nguyên dương không lớn hơn 90 không thuộctập A ,mâuthuẫnvì A gồm70số nguyên dương không vượtquá90. Như vậy,tấtcả cácsố nguyên dương n với91140 n ≤≤ , đềuthuộctập B -Từ haikếtquả trên, ta suy ra điềuphảichứngminh.

pA,mâuthuẫnvì A gồm70số

vậy,tấtcả cácsố nguyên dương

• Với91140:

Ở

DỤC VÀ ĐÀO TẠO HÀ NỘI - ĐỀ THI CHUYÊN TOÁN HÀ NỘI

Ngày thi: 20/06/2022

ời gian: 150 phút.

1. (2 điểm).

1)Giải phương trình

xxx

2)Chocácsố thực,ab và c thoả mãn điềukiện1. abbcca++= Tínhgiátrị củabiểuthức

Bài 2. (2 điểm).

1)Chứngminhnếu n làsố tự nhiênlẻ thì2137 n + chiahếtcho20.

ấtcả cáccặpsố nguyên dương ( ), xy saocho ( ) ( ) ( )22111.yxxxy++=+−

Bài 3. (2 điểm).

1)Tìmhaisố nguyên dương m và n saocho 3 m mn + và 3 n mn + đềulàcácsố nguyêntố.

2)Với,ab và c làcácsố thựckhôngâmthoả mãn điềukiện3 abc++= ,tìmgiátrị lớn nhấtcủabiểuthức233. Pabbccaabc =++−

Bài 4. (3 điểm).

Chotamgiác ABC nhọnvới ABAC < . Đườngtròn ( )I nộitiếptamgiác ABC ,tiếpxúc vớibacạnh,BCCA và AB lần lượttại ba điểm,DE và F

1)Gọi M là giao điểmcủa hai đườngthẳng AI và DF .Chứng minh đườngthẳng CM vuônggócvới đườngthẳng AI

2)Gọi N là giao điểmcủa hai đườngthẳng AI và DE .Gọi K là trung điểmcủa đoạn thẳng BC .Chứngminhtamgiác KMN làtamgiáccân.

3)Cácti

GIÁO

Bài

2422110

−+−+= .

222 2 111 abc P abcabcabc =++− +++++−

2)Tìmt

) ( ) ( ) ababcacabcbcabcabc

) ( ) abcabbccaabc

(Vì1 abbcca++=

vào được0. P

1)Chứngminhnếu n làsố tự nhiênlẻ thì2137 n + chiahếtcho20.

ấtcả cáccặpsố nguyên dương ( ), xy saocho ( ) ( ) ( )22111.yxxxy++=+−

ời gi

1)Vớinlàsố tự nhiênlẻ

ết ( )21 nkk

ừ đó ta được 2143 3737.

Xéttrongmodul4,tacó ( ) ( )4341 311mod4,

)41A

Xéttrongmodul5,tacó:

suyra ( ) 170mod4.A ≡−−≡ Do đó

( )

370mod5,

đó

(

=++++++++− (

=++++− abcabc=++−

). Thay

= Bài 2. (2 điểm).

2)Tìmt

ải

,tavi

=+∈  T

Ank ++ =−=−

kk ++ =−=−

(

( )43 327.817mod5, kk + =≡ suyra

k + −≡ do

thẳng BC .Chứngminhtamgiác KMN làtamgiáccân.

Chứngminh,,,,BFIND cùngthuộcmột đườngtròn,suyra//. BNAMBNCM ⊥⇒

Gọi H là giao điểmcủa BN và,ACJ là giao điểmcủa CM và. AB

Tacó:

N là trung điểmcủa BH ( ABH∆ cân)và M là trung điểmcủa CJ ( ACJ∆ cân).

Suyra 11 ;;. 22 KNCHKMBJCHBJ ===

Dovậy KNKMKMN =⇒∆ cân.

3)Cáctiếptuyếntại M và N của đườngtròn ( ); KKM cắtnhautại điểm S .Chứngminh đườngthẳng AS songsongvới đườngthẳng ID .

PMNPCA = Dễ nhậnthấy KN // AC nêntacó

Dựng đườngcao AP thìtacótứ giác APMC nộitiếpsuyra

PCANKPPMNNKP =⇒=

SPKo = , do đó PSBC ⊥ ,mà APBC ⊥ suyra,,APS thẳnghàng.

ASBCIDBCASID ⊥⊥⇒ (đpcm).

ứa70số nguyên dương không vượt quá90( A

vượtquá90)nêncóítnhất1cặpsố thuộc A . Từ đó ta có

2)Ch

ẽ

•

ngminh

ứ

nguyênliêntiế

ố nguyên dương n với4290 n ≤≤ , đềuthuộctập B .

 

    .

 90

Do,//

chỉ khôngchứa20số nguyên dương không

68. B∈

ứ

B ch

a91số

p. Tas

ngminhmọis

Với4290 n ≤≤ :Giả sử .nB ∉

-Nếu n làsố lẻ,cáccặpsố ( ) ( ) –1,1;–2;2;nn ...; 11 ;. 22 nn−+    Vì nB ∉ nên

mỗicặpsố đềucóítnhấtmộtsố khôngthuộctập A .Suyracóítnhất 1 21 2 n ≥

số nguyên dương không lớn hơn 90 khôngthuộctập A ,mâuthuẫnvìtập A gồm 70số nguyên dương không vượtquá90.

Nếu n làsố chẵn,xétcáccặpsố ( ( ) –1,1;–2;2; ) nn ...; 11 ; 22 nn−+    vàsố . 2 n

Vì nB ∉ nênmỗicặpsố đềucóítnhấtmộtsố khôngthuộctập A ,ngoàira

2 nA ∉ Suyracóítnhất21 2 n ≥ số nguyên dương không lớn hơn 90 không thuộc

tậ

nguyên dương không vượtquá90. Như

n với4290 n ≤≤ , đềuthuộctập B .

pA,mâuthuẫnvì A gồm70số

vậy,tấtcả cácsố nguyên dương

• Với91140:

KỲ THI TUYỂN SINH VÀO LỚP 10 TRƯỜNG

CHUYÊN HÀ TĨNH NĂM HỌC 2022-2023

CHÍNHTHỨ

1. (2,0 điểm).

a)Choa,b,clàcácsố thựckhác0th

ị củabiểuth

b)Choa,blàcácsố thực dương thỏ

ứngminhrằng:

2. (2,5 điểm).

a)Giải phương trình: ( ) 7

ảihệ phương trình:

Câu 3. (1,5 điểm).

Môn thi: Toán

gian làm bài 150 phút

amãn:1112

và222 abbccaabc

ố nguyên n để A= ( ) ( ) 222 322nnn

làsố chính phương

amãn:20222023 abbccddaa −+−+−+−=+ Tìmsố dư củaphépchia12 a cho16. Câu 4. (2,5 điểm).

ố nguyênth

hai đườngtròn(O)và(O’)cắtnhautại hai điểmphânbiệtAvàB. Trên tia đốicủa tiaABlấy điểmM,kẻ tiếptuyếnME,MFvới đường tròn (O’), trong đó E, F là các tiếp điểm,Fnằm trong đường tròn (O). Hai đườngthằngAEvàAFcắt đườngtròn(O)lần lượt tạiPvàQ(P,QkhácA),tiaEFcắtPQtạiK. a)Chứngminh BKPBFA

SỞ GIÁO DỤC VÀ ĐÀO HÀ

TỈNH

ĐỀ

THPT

Thời

Câu

ỏ

abbcca ++=

++= Tínhgiátr

ức:222222 111 A abbcca =++

amãn:1 abab++= . Ch

( ) ( )2222 1 11211 abab abab + += ++ ++ Câu

231527 xx x ++=+ b)Gi

( ) ( ) 11330 10 xyy yyxx  +−−+=  −++= 

a)Tìms

++++

b)Choa,b,c,dlàcács

ỏ

Cho

∆∆ # b)GọiI,Jlần lượt là giao điểmcủaABvớiOO’vàEF.Chứngminh   IJEIFM = c)Chứngminh22 2 PQOAOK =− Câu 5. (1,0 điểm). Chocácsố thực dương a, b, c thỏamãn:3abcabc ++= . Tìmgiátrị lớnnhấtcủabiểuthức:P = 111 121212 abcbcacab ++ ++++++ Câu 6. (0,5 điểm).Lớp9Acó34họcsinh,cáchọc sinh này đềuthamgiamộtsố câulạc bộ của trường.Mỗihọcsinhcủalớp tham gia đúng mộtcâulạcbộ.Nếuchọnra10học sinhbấtkỳ củalớpthìluôncóítnhất3họcsinhthamgiacùngmộtcâulạcbộ.Chứng minhrằngcómộtcâulạcbộ cóítnhất9họcsinhlớp9Athamgia. Hết./.

Bài giải: Câu 1. (2,0 điểm). a)Choa,b,clàcácsố thựckhác0thỏamãn:1112 abbcca ++= và222 abbccaabc ++= . Tínhgiátrị củabiểuthức:222222 111 A abbcca =++ Giải: Từ 222 2221abbccaabcabbcca abc ++ ++=⇒= (a,b,ckhác0). Tacó: 2 222222222 111111111 A2 abbccaabbccaabcabcabc   =++=++−++    2 2 222 111 222.12 acabbc abbccaabc ++  =++− =−=  b)Choa,blàcácsố thực dương thỏamãn:1 abab++= . Chứngminhrằng: ( ) ( )2222 1 11211 abab abab + += ++ ++ Tacó: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 22 22222222 11 11 1111211211 ababbaabab abababab +++ ++ += ⇔ = ++ ++++ ++ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )22 2222 11 211 11211 ababababab abab ++ + ⇔ = ⇔+=++ ++ ++ ( ) ( ) ( ) 2222222222112421 ababaabbabab ⇔+=++⇔++=+++ ( ) ( ) 222 222 411 aabbababab ⇔++=+⇔+=− (luôn đúng vì từ giả thiếtsuyra 1 abab +=− ) Câu 2. (2,5 điểm). a)Giải phương trình: ( ) 7 231527 xx x ++=+ Ta có: Điềukiện 7 0; 2 xx≠≥ Khi đó: ( ) ( )7 2315272317527 xxxxxx x ++=+⇔++=+ 22 6275276527270 xxxxxxxx ++=+⇔−+++= (*) Đặt27 yx=+ (0 y ≥ ). Khi đó phương trình (*) trở thành: ( ) ( ) 223 650320 2 xy xxyyxyxy xy = −+=⇔−−=⇔  =

+Nếu 2 0 33271 927 x xyxxx xx ≥ =⇔=+⇔⇔=  =+ +Nếu 2 0129 2227 4274 x xyxxx xx ≥ + =⇔=+⇔⇔=  =+ Vậy phương trình đã cho có hai nghiệm: 129 1; 4 xx + == b)Giảihệ phương trình: ( ) ( ) 11330 10 xyy yyxx  +−−+=  −++=  Điềukiện:1 x ≥− , đặt ( )10xtt+=≥ Khi đó hệ đã cho trở thành: ( ) ( ) ( ) ( ) 22 1330330(1) 110(2) tyytyyt yytttyyt −−+=−−+=  ⇔  −+= −+−=   Từ (1)và(2)suyra: ( ) ( )2 0 3011 33 tyyt tyty tyyt −== −+−=⇔⇔−=−=+  +Nếu ty = , thay vào phương trình (1) ta suy ra 2 3301 tt −+=⇔= (vì0 yt=≥ ) suy ra x =0 , được 0 1 x y =  = thỏamãnhệ đã cho. + Tương tự nếu 1 3yt=+ , thay vào phương trình (1) ta được 2 9380 tt+−= 133 6 t −+ ⇒= (vì0 t ≥ )suyra 2 113311332133133 11 3636618ytxt −++ −+ + =+=+=⇒=−=−=−   Vậyhệ đã cho có nghiêm là: (x, y) = ( ) 133133 0;1; 186  ++   Câu 3. (1,5 điểm). a)Tìmsố nguyên n để A= ( ) ( ) 222 322nnn++++ làsố chính phương Tacó:A= ( ) ( ) ( ) ( ) 22222 322211nnnnn ++++=+++  +Xét ( ) 2 202 nnZ +=⇔=−∈ khi đó A = 0 là số chính phương, do đó n= 2thõamãn. +Xét ( ) 2 20n +≠ ,do ( ) 22n + làsố chính phương khác 0, do đó để Alàsố chính phương thì ( ) 2 11n ++ làsố chính phương, đặt ( ) 2211 na ++= (vớialàsố tự nhiên) ( ) ( ) ( )2211111ananan ⇔−+=⇔−−++= Doa,nlàcácsố nguyênnên ( ) ( )1,1anan−−++ là các ướcnguyêncủa1 Suyra:1111 anann −−=++=±⇒=− ,thử lạitathấyn=1thỏamãn;

ệt A và B. Trên tia đốicủa tiaABlấy điểmM,kẻ

đường tròn (O’), trong đó E, F là các tiếp điểm,Fnằm trong đường tròn (O). Hai đườ

ế

ằngAEvàAFcắt đườngtròn(O)lần lượt tạiPvàQ(P,QkhácA),tiaEFcắtPQtạiK.

ứngminh

∆∆

ọiI,Jlần lượt là giao điểmcủaABvớiOO’vàEF.Chứngminh

ứngminh22 2 PQOAOK

Vậy để Alàsố chính phương thì các giá trị nguyênnlà:2;1 nn=−=− b)Choa,b,c,dlàcácsố nguyênthỏamãn:20222023 abbccddaa −+−+−+−=+ Tìmsố dư củaphépchia12 a cho16. Tachứngminhalàsố lẻ: Thậtvậy:vớimọisố nguyênxtacó:22(0) 02(x<0) xx xx ≥ +=     Do đó: ( ) ( ) ( ) ( ) 2 abbccdda ababbcbccdcddada −+−+−+−=   −+−+−+−+−+−+−+−     Từ bàirasuyra:202220232aa +⇒  làsố nguyênlẻ suyra ( ) ( ) 212411akkZakk =+∈⇒=++ ,tathấy ( ) 418 kk +  nên2 a chia 8 dư 1 ( ) ( )26242 181118aaaaa ⇒−⇒−=−++  ,doalẻ nên612 a +  Suyra: ( ) ( )661116aa+−  12116a ⇒−  ,tức 12 a⇒ chia16dự 1. Câu 4. (2,5 điểm). Cho hai đườngtròn(O)và(O’)cắtnhautại hai điểmphânbi

ptuyếnME,MFvới

ngth

a)Ch

BKPBFA

# b)G

  IJEIFM = c)Ch

=− 1 1 K Q P F E B A O' O M

11 A=P(cùngchắncungBQcủa đườngtròn(O))(1); Tacótứ giácAFBEnộitiếp đườngtròn(O’)suyra:

EABEFB = (cùngchắncungBE) Tacótứ giácABQPnộitiếp đườngtròn(O)suyra:

Do đó suy ra:

BQKEAB =

BQKEFB = suyratứ giácBFKQnộitiếp

Từ (1)và(2)suyra (g.g)BKPBFA∆∆ #

b)Từ bàiratacó

MFOMIO

suyratứ giácMFIOnộiti

BKQBFQBKPBFA =⇒= (2)

a)Tacó:  

 

   

  ''90

== 

ếp đường tròn đườngkínhMO’suyra   '180IFMMOI+=  (*) Gọi N là giao điểmcủaMO’vớiEF, theotínhchấttiếptuyếnsuyra:   ''90 MOFEONJOIJ ⊥⇒==  suyra tứ giácO’NJInộitiếpsuyra:   '180MOIIJE+=  (**) Từ (*)và(**)tasuyra:   IJEIFM = c) TachứngminhKlàtrung điểmcủaPQ 1 F E B A O' M N J I F E B A O' O M

Theochứngminhcâuatacó: PKFA BKPBFA BKBF ∆∆⇒= # (1)

Chứng minh tương tự như câu a ta có: (g.g) BAEBQKAEKQ BEBK ∆∆⇒= # (2)

DoMElàtiếptuyếncủa đườngtròn(O’)suyra

Suyra(g.g)

∆∆⇒=

Tương tự :(g.g)

(3);

MBFMFA BFMB ∆∆⇒= # (4),

MBEMEA = (cùngbằng½số đo cung AE)

ếptuyếnkẻ từ M đến đườngtròn(O’)nênME=MF(5)

Từ (1),(2),(3),(4),và(5)suyra: PKQKPKQK

=⇒=

 

EAME MEAMBE BEMB

FAMF

DoE,Flàti

BKBK

nên K là trung điểmcủaPQsuy raOK2222 222 OKPQPQPKOPOKOAOK ⊥⇒==−=− (đpcm). Câu 5. (1,0 điểm). Chocácsố thực dương a, b, c thỏamãn:3abcabc ++= . Tìmgiátrị lớnnhấtcủabiểuthức:P = 111 121212 abcbcacab ++ ++++++ Tacó:111333abcabcabc abcabbcca ++ ++=⇒=⇔++= Đặt: ( )444 111 ;;0,0,0 xyzxyz bccaab ===>>> Từ bàirasuyra:4443 xyz++= Mặtkhác,Ápdụng BĐC Cô si ta có: 33331 abcabcabcabcabcabc =++≥⇒≥⇒≥ Tacó:22444 12144.40 abcabcbcabcabcbcbc ++=+++≥=≥> ( )2 4 11111 .2..1.1 12488 4 xxx abcbc ⇒≤==≤+ ++ (Tasử dụng BĐT 222 xyxy ≤+ ) ( ) ( )24411111 .2..1.13 16816816 xxx =+≤++=+ Tức ( )114 3 1216 x abc ≤+ ++ Tương tự: ( )114 3 1216bcay ≤+ ++ ; ( )114 3 1216 z cab ≤+ ++

tương tương có sử

ụ

abc

ọc sinh này đềuthamgiamộ

ố câulạc

ủa

ớp

gia đúng mộtcâulạcbộ.Nếuchọnra10học sinhbấtkỳ củalớpthìluôncóítnhất3họcsinhthamgiacùngmộtcâulạcbộ.Chứng minhrằngcómộtcâulạcbộ cóítnhất9họcsinhlớp9Athamgia. Dùngphảnchứng: Giả sử cáccâulạcbộ đềukhôngcóquá8họcsinhcủalớp9Athamgia.GọiNlàsố câu lạcbộ có hơn 1 họcsinhcủalớp9A.

NếuN4 > thìtừ 5trongsố cáccâulạcbộ này,tachọnmỗicâulạcbộ 2họcsinhcủalớp 9A, khi đó 10họcsinhnàysẽ khôngthỏamãnbàitoán.

NếuN4 < thìtổngsố họcsinhcủalớp9Athamgiacáccâulạcbộ nàykhôngquá3.824 = , nghĩa là còn có ít nhất3424=10họcsinhcủalớp9A,mỗihọcsinhthamgiamột câulạcbộ màmỗicâulạcbộ nàychỉ có1họcsinhcủalớp9A.Chọn10họcsinhnàythì khôngthỏa mãn điềukiệnbàitoán.

NếuN=4thìsố họcsinhcủalớp9Athamgia4câulạcbộ nàykhôngquá4.8=32, nghĩa là còn có ít nhất2họcsinhcủalớp9A,mỗihọcsinhnàythamgiamộtcâulạcbộ màmỗicâulạcbộ nàychỉ có1họcsinhlớp9A.Chọn2họcsinhtrongsố nhữnghọcsinh cònlạinàyvà4câulạcbộ trênmỗicâulạcbộ chọn2họcsinhcủalớp 9A, khi đó 10 học sinhcủalớp 9A đượcchọnkhôngthỏa mãn điềukiện.Vậy điềugiả sử ở trên sai, nghĩa là tồntạimộtcâulạcbộ cóítnhất9họcsinhcủalớp9Athamgia

Do đó ( ) 1111444123 9 12121216164 abcbcacabxyz++≤+++== ++++++ Dấu“=”xảyrakhix=y=z=11 abc ⇔=== Vậygiátrị lớnnhấtcủaPlà3 4 xảyrakhia=b=c=1. Chú ý: Ngoàicáchgiảitrêncòncáchgiảikhác: Tachứngminh3 4 P ≤ bằng phương pháp biến đổi

ng1

≥ Câu 6. (0,5 điểm).Lớp9Acó34họcsinh,cách

bộ c

trường.Mỗihọcsinhcủal

tham

(2,0 điể

Ỳ THI TUYỂN SINH LỚP

CHUYÊN NGUYỄ

C 2022 2023

thức()2024 Px khôngcónghiệmnguyên.

4 (3,0 điểm).

Cho đường tròn (O) và dây cung AB không đi qua tâm O.Gọi M là điểmchínhgiữacủa cungnhỏ AB; D là 1 điểm thay đổitrêncunglớnAB(DkhácAvàB);DMcắtABtạiC. a.ChứngminhrằngMB.BD=MD.BC; b.ChứngminhrằngMBlàtiếptuyếncủa đườngtrònngoạitiếp tam giác BCD và khi điểmD thay đổi thì tâm đườngtrònngoạitiếptamgiácBCDnằmtrênmột đườngthẳngcố định. 2.ChohìnhthoiABCDcó2 AB = .GọiR1,R2lần lượt là bán kính đườngtrònngoạitiếpcác tamgiácABCvàABD.Ch

SỞ GIÁO DỤC VÀ ĐẠO TẠO HẢI DƯƠNG ĐỀ CHÍNH THỨC K

10 THPT

N TRÃI NĂM HỌ

Môn thi: TOÁN (Chuyên) Thờigianlàmbài:150phút,khôngtínhthời gian phát đề (Đề thicó01trang) Câu 1 (2,0 điểm). a.Sosánhbiểuthức 232 1: 15623 Axxxx xxxxx  +++ =−++  +−+−−  với5 2 b.Tínhgiátrị củabiểuthức 20242023 2 4(1)221 23 xxxx B xx +−++ = + tại13 232232 x =− −+ . Câu 2 (2,0 điểm). a.Giải phương trình: 1 3131 4 x xx x −+=+ b.Giảihệ phương trình: 22 8 111 224 xyxy xxyy ++=   += ++ Câu 3

m). a.Tìmcáccặpsố nguyên(;) xy thỏa mãn phương trình 222562(2)(68) yyyxyyx −+=−+−+ . b. Cho đa thức() Px vớicácsố nguyênthỏamãn(2021).(2022)2023 PP = .Chứngminhrằng đa

Câu

ứngminhrằng122 RR+≥ Câu 5 (1,0 điểm). Cho,,abc làcácsố thực dương thỏamãn2246 abcab ++= .Tìmgiátrị nhỏ nhấtcủabiểuthức 3328 216 abab P bcacc + =++ ++ . ………… HẾT ……….

Lời giải Câu 1 a. ĐKXĐ: 0 4 9 x x x ≥  ≠  ≠ 232 1: 15623 Axxxx xxxxx  +++ =−++  +−+−−  ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1294 : 1232323 132 : 11 23 Axxxxx xxxxxxx Axx xx xx  +− + ⇔= +  +  ⇔= = ++ Tacó: ( ) ( ) ( ) ( ) 525225171 2212121 xx Axx xxx −++ −+ +=+= = + ++ Vì55 00 22 xAA ≥⇒+>⇒>− Vậy 5 2 A >− b.Vì1331 2322322 x =−= −+ nên 31 2 x = lànghiệmcủa đa thức 2 221 xx+− Do đó: 20232 2 2(221)212133 (221)11 xxxxx B xxxx +−+++ = ==− +−+++ . Câu 2. a. ĐKXĐ: 0 1 3 x x >   ≥−  Phương trình đã cho đương đương với: 4(31)1431 xxxxx −+−=+ 2 12(31)431 xxxx ⇔−+=+ Đặt2,31 axbx==+ ta có phương trình 22 32()(3)03 ba ababbaba ba = −=⇔−+=⇔  =− Khi đó 312 316 xx xx  += +=−  +)Với312xx += , điềukiện0 x > ,tacó

22 3123144310 xxxxxx +=⇔+=⇔−−= 1 1 4() x xKTM = ⇔  =−  +)Với316xx +=− , điềukiện 1 0 3 x −≤< ,tacó 2 31636310 xxxx +=−⇔−−= 3153 72 3153() 72 x xKTM  = ⇔  +=  Vậy phương trinh có hai nghiệmlà1 x = , 3153 72 x = b. Tacó 22 8 111 224 xyxy xxyy ++=   += ++ ( ) ( ) 22 (1)(1)9 111 11114 xy xy ++=  ⇔  += +−+− Đặt1,1 uxvy=+=+ Hệ đã cho trở thành 22 9 111 114 uv uv =   +=  , điềukiện: ( )1 1 u v ≠± ∗ ≠± 222222 9 4(2)1 uv uvuvuv = ⇔  +−=−−+ 22 993 18(()) 63 uvuvuv TM uvuvuv = === ⇔⇔⇔∗ +=+=±==−  Từ đó suy ra nghiệmcủahệ phương trình là 24 ; 24 xx yy ==−  ==− Câu 3. a.Tacó:222562(2)(68) yyyxyyx −+=−+−+ 22 2 2 (56)56(2)(2)(4) (2)(3)56(2)(2)(4) (2)(43)56 (1)(2)(3)56 yyyxyyx yyyxyyx yxyxxy xyxy ⇔−++=−+−− ⇔−−+=−+−− ⇔−+−−+= ⇔−−+−= Nhậnthấy(2)(1)3 yxxy −+−=+− ,nêntaphảiphântíchsố 56thànhtíchcủa3số nguyên màtổng2số đầubằng2số cònlại. Như vậy,tacó: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 561.7.8;2;9 567.1.8;8;3 568.1.7;7;3 561.8.7;2;6 568.7.1;7;9 567.8.1;8;6 xy xy xy xy xy xy =⇒= =⇒= =−−⇒=− =−−⇒=− =−−⇒=− =−−⇒=−      

ậy phương trình có

nghiệmtrên.

ả sử đa thức ( )Px có1nghi

mnguyênlàa.

( ) ( ) ( )2024

( ) (

,( ( )Qx là đa thứccóhệ số nguyên)

)2021202420212021

2022202420222022

( ) (

(

2021.20222023

đó 2021

,2022

20212022

làs

) ( )2021,2022

làsố

b.Gi

ệ

Tacó:

PaxaQx −=−

Tacó:

) (

PaQ −=− ( )

) ( )

PaQ −=− Mà

)

PP = làsố lẻ (

PP⇒

lẻ Do

a làcácsố lẻ ( ) ( )

aa⇒−−− làsố chẵn 1⇒−

ố chẵn (điềunàyvôlí) ( ) 2024Px ⇒− khôngcónghiệmnguyên. Câu 4. 1. a.ChứngminhMB.BD=MD.BC Tacó:  1 d 2 MBCsAM =  1 d 2 MDBsMB = Mà:   AMMB = ( vì M là điểmchínhgiữacung  AB )   MBCMDB⇒= Xét MBC và MDB có  BMC gócchung   ()MBCMDBcmt = Do đó, (.)MBCMDBgg ∽ ( )MBBChayMBBDMDBCdpcm MDBD ⇒== b.ChứngminhrằngMBlàtiếptuyếncủa đườngtrònngoạitiếp tam giác BCD và khi điểmD thay đổi thì tâm đườngtrònngoạitiếptamgiácBCDnằmtrênmột đườngthẳngcố định. Gọi (I) là đườngtrònngoạitiếp BCD

   22 BICBDCMBC⇒== (  BIC làgóc ở tâmchắn  BC ,  BDC làgócnộitiếpchắn  BC trong (I))   2 BIC MBC ⇒= Tacó BIC cântạiI   180 2 BIC IBC ⇒=     180 90 22 MBCIBCBICBICo ⇒+=+= MBBI ⇒⊥⇒ MB làtiếptuyếncủa(I),vàI ∈ đườngthẳngvuônggócvớiMB. VìM,Bcố định, nên đườngthẳngvuônggócvớiMBcố định. Do đó, khi điểm D thay đổi thìtâmIcủa đườngtrònngoạitiếptamgiácBCDnằmtrênmột đườngthẳngcố định. 2. Đặt   090 CABxABDx =⇒=− Xét ABC , theo địnhlýsin,tacó:  11 2 2 sin2sin BC RR CABx =⇒= Tương tự,xét ABD ,có: ( ) 022 2 2 2sin902os AB RR xcx =⇒= ( )12 211 090 2sinxcosx RRo x  ⇒+=+<≤   Đặt ( )sinx01 tt =<<

122 ' 2222 211 21 1112 ()() 12(1)1 RR tt ftt ft ttttt  ⇒+=+  =+⇒=−− '2 ()02ftt ⇒=⇔= 12 222 22() 22 RRdpcm  ⇒+≥+=   Câu 5. Tacó: 3328 216 abab P bcacc + =++ ++ ( ) 33 33 28 112 216 118 22 216 abab P bcacc Pabcab bcacc + ⇔=++++− ++ + ⇔=++++−  ++  Tacó:2()0 xy−≥ nên222xyxy +≥ 24()4 xy xyxy xyxy + ⇒+≥⇒≥ + với;0 xy > 114 xyxy ⇒+≥ + Lạicó:22xyxyxy +−≥ nên ( ) ()22() xyxyxyxyxy ++−≥+ 33() xyxyxy⇒+≥+ ( ) 4.2(2) 22 216 2(2)2(2) 2216 Pabcabab bcacc ababab P abcc + ⇒≥++ +− +++ ++ ⇔≥+ ++ Mặckhác:2246 abcab ++= nên2(2)2 abcab −+= 224.24(2) 4 cababccab + ⇒≤⇔=⇒≤ Đặt2tab =+ ,tacó:

2 min 224422 1621621616 2 417 2. 21688 742 6 8216 tttt P ttt t t P t Pkhitt t + ≥+=+=+− ++ + ⇒≥−= + + ==⇔= + 3 26 3 2 2 29 aba abb cab c =+=   ⇔=⇔=   = =  VậyGTNNcủa 73 3,,9 82 Pkhiabc ==== .

diểm)

ABC cân()

nộitiếp đườngtròn ( )O . Các đườngphângiáctrong

BDCE củatamgiác ABC cắtnhautại,IBI cắt ( )O tại FB ≠ . Điểm H đốixứngvới C qua D . Đườngtrònngoạitiếptamgiác HBC cắt BI tại KB ≠ . a)Chứngminhrằng2.DCDIDB = và D là trung điểmcủa đoạnthẳng IK . b)Kẻ KM songsongvới AC với MFC ∈ .Chứngminhrằng M đốixứngvới I qua AC c)Gọi N là giao điể

và,AIJ làtâmcủa đườngtrònngoạitiếptamgiác IBE . Chứ

ng,,,MNJD

mtrênmột đườngtròn.

ĐỀ THI CHUYÊN TOÁN TRẦN PHÚ HẢI PHÒNG 2022 Thời gian làm bài : 150 phút Bài 1:(2 diểm) a) 2 482816 24 Axxxxxxx xxxxxx +−−+− =++ với0,4 xx>≠ . Rútgọn A .Chứngminhrằng8 A > b)Biết phương trình 20axbxc++= với0 a ≠ cóhainghiệm12 , xx thoả mãn120,1 xx ≤≤ . Chứngminhrằng ( ) ( ) ( ) 32 2 4 abac aabc ≤≤ −+ . Bài 2:(2 diểm) a)Giải phương trình 21014221 xxx −+=+ b)Giảihệ phương trình ( ) ( ) 22 22 44331 2345302 xyy xyxyxy  +−=  +−+−+=  . Bài 3:(3

Chotamgiác

ABACBC =>

mcủ

ngminhrằ

cùngnằ

Bài 4:(1 diểm) Cho,,0 xyz > thoả mãn ( )222324 xyyzz ≤++ .Tìmgiátrị nhỏ nhấtcủa 22 22222 4 3201232012() Pyz xxyyxxzzyz =++ +++++ Bài 5:(2 diểm) a)Chứngminhrằngnếu210nab =+ với,,abn + ∈  thoả mãn010 b << thì6 ab 

b)Viếtlênbảng229số tự nhiênliêntiếp1,2,3,,229 … Từ cácsố đã viết xoá đi bốnsố bấtkỳ ,,, xyzt rồiviếtlênbảngsố 2 xyzt +++ (cácsố cònlạitrênbảnggiữ nguyên).Tiếptụcthực hiện thao tác trên đếnkhitrênbảngchỉ cònlại đúng mộtsố,gọisố đó là a .Chứngminhrằng 2022a < . ĐÁP ÁN CHUYÊN TOÁN TRẦN PHÚ HẢI PHÒNG Bài 1: a) 2 482816 24 Axxxxxxx xxxxxx +−−+− =++ với0,4 xx>≠ Rútgọn A .Chứngminhrằng8 A > . Lời giải ( ) ( ) ( ) ( ) ( ) ( ) 4224424 24 xxxxxxx A xxx xx +−++−−+ = ++ 424244 4Axxxxxx xxxx +++−++ =+−=+ 24(2) 840Axx xx +− −=−=≥ Dấubằng24 xx ⇔=⇔= :vôlý. b)Biết phương trình 20axbxc++= với0 a ≠ cóhainghiệm12 , xx thoả mãn120,1 xx ≤≤ . Chứngminhrằng ( ) ( ) ( ) 32 2 4 abac aabc ≤≤ −+ . Lời giải Điềukiện:2Δ40 bac =−≥ TheoViéttacó1212 , bc SxxPxx aa =+=−== với24SP ≥ Chiacả tử vàmẫucho20 a ≠ ta được ( ) ( ) ( ) ( ) ( )12 2123 2 111 bc abacSPPSPAaa aabcbcSPSP aa   +− + = = = =− −+ ++++ −+ Do120,1 xx ≤≤ nên,0 SP ≥ ,suyra2 A ≤

Dấubằng00 Pc ⇔=⇔= Và 335 475S50 414 PSP ASPP SP + ≥⇔≤⇔+−−≤ ++ . Do 2 4 S P ≤ nên ( ) 2 327155 5520 442 S VTSSSSS ≤+−−=−++≤   vì02 S ≤≤ . Dấubằng 2 12 2 41 2 PSba xx ca S  ==− ⇔⇔==⇔  = = . Bài 2: a)Giải phương trình 21014221 xxx −+=+ Lời giải Điềukiện: 1 2 x ≥− ( ) 2816212211PTxxxx⇔−+=++++ 22 (4)(211) xx ⇔−=++ 4211521 4211321 xxxx xxxx   −=++−=+ ⇔⇔  −=++−=+   22 22 21(5)12240 55 21(3)880 11 33 22 xxxx xx xxxx xx  +=−−+=   ≥≥   ⇔ +=−−+=     −≤≤−≤≤    2 2 623 5 623 422422 1 3 2 x x x x x x   =±  ≥   ⇔⇔=+ =±=−   −≤≤   Kếtluận: phương trình có hai nghiệmlà { }623;422 +− b)Giảihệ phương trình ( ) ( ) 22 22 44331 2345302 xyy xyxyxy  +−=  +−+−+=  .

 

3: Chotamgiác ABC cân() ABACBC => nộitiếp đườngtròn ( )O . Các đườngphângiáctrong

BDCE củatamgiác ABC cắtnhautại,IBI cắt ( )O tại FB ≠ . Điểm H đốixứngvới C qua D . Đườngtrònngoạitiếptamgiác HBC cắt BI tại KB ≠ a)Chứngminhrằng2DCDIDB = và D là trung điểmcủa đoạnthẳng IK b)Kẻ

.Chứngminhrằng M đốixứngvới I qua AC c)G

MFC

làtâmcủa đườngtrònngoạitiếptamgiác IBE Chứngminhr

N là

ng,,,

mtrênmột đườngtròn.

Lời giải ( ) ( ) 22 2342530 xyxyy ⇔+−++−+= Xét ( ) 2222 Δ(34)425344(2) yyyyyy =−+−−+=−+=− nên ( ) 342 23 22 342 1 2 yy xy yy xy −+− = =− ⇔  −−+ = =−  Thay23 xy=− vào ( )1 ta được 2221;5 (23)443308162403;3 yx yyyyy yx =−=− −+−−=⇔−−=⇔  == Thay1 xy=− vào ( )1 ta được 222 2;3 (1)44330563201611 ; 55 yx yyyyy yx =−=− −+−−=⇔−−=⇔  ==  Kếtluận:hệ phương trình có bốnnghiệmlà ( ) ( ) ( ) 1116 5;1,3;3,3;2,; 55 

. Bài

KM songsongvới AC với

∈

ọi

giao điểmcủa FC và,AIJ

ằ

MNJD cùngnằ

Lời giải a)Do   DCIDBC = nên ( )DCIDBCgg ∆∼∆− , do đó 2DCDI DCDIDB DBDC =⇒= Xét ( )BHC tacó    DCIDBCDHK == nên//HKIC ,vàdo D là trung điểm CH nên D cũng là trung điểm IK b)Do//KMAC nên   FMKFCA =

Xét ( )O tacó     FCAFBAFBCKBC === Xét ( )BHC tacó   KBCKHC = Do đó   FMKKHC = ,haylàtứ giác KMCH nộitiếp. Suyra KMCH làhìnhthangcân. Theocâua)tacó ( )22 .. ΔΔ DCDIDBDHDIDBDHIDBHcgc =⇒=⇒∼−− . Do đó xét ( )BHC tacó     DHIDBHKCHDHM === . Cuốicùngkếthợpvới   DCIDCM = tasuyra M đốixứngvới I qua AC

c)Gọi AIBCP ∩= là trung điểm BC .Theocâub)tacó     ( )  ( ) 222902180180BNMBDMPNCBDCBCFDBCDCB +=+=−+−−=   Do đó ,,, MNBD cùngnằmtrênmột đườngtròn. Xét ( )BEI vàtheocâub)tacó     22 BJIBEICDIMDI === P Q J N M K H E D F I A O B C

mtrênm

đườngtròn.

,haylà,,MIJ

ời giả

đường tròn (đpcm).

BHC

Màhaitamgiác BJI và MDI đềucântại J và D nênsuyra   BIJMID =

thẳnghàng. Nêntừ   BJMBDM = suyra,,,MBJD cùngnằ

ột

Từ ( ) ( ) 1,2suyra,,,,MNBJD cùngnằmtrênmột

Ghi chú: đường tròn trên còn đi qua cả tâm Q của đườngtròn ( )

. Vì:      2 BQC BQNBHCBMCBMN ==== nên,,,MNBQ cùngnằmtrênmột đườngtròn. Bài 4: Cho,,0 xyz > thoả mãn ( )222324 xyyzz ≤++ .Tìmgiátrị nhỏ nhấtcủa 22 22222 4 3201232012() Pyz xxyyxxzzyz =++ +++++ L

i Dựatrêndấubằng22 xyz⇔== nên ta đánh giá theo hướngsử dụng 2 (2)0 xy−≥ , 2 (2)0 xz−≥ và2()0 yz−≥ Tacó ( ) ( ) 22222222 320124161644(24)(2) xxyyxxyyxxyyxyxy ++=++−−+=+−− 22 3201224 xxyyxy⇒++≤+ Tương tự tacó 22 2 4 2424() Pyz xyxzyz ≥++ +++ Theobất đẳngthứcSvác(Schwarz)tacó ( ) 2 2 ()4 44() Pyz xyzyz + ≥+ +++ . Lạicó ( ) 22222 3242()43() xyyzzyzyzyzxyz ≤++=++≤+⇒≤+ . Do đó 3 222 4443 3.. 8()1616()1616()4 Pyzyzyzyzyz yzyzyz +++ ++ ≥+=++≥ = +++ . Dấubằng 2 22 4 4 2 16() xyz x yz yz yz == = ⇔⇔ +  = == + . Bài 5: a)Chứngminhrằngnếu210nab =+ với,,abn + ∈  thoả mãn010 b << thì6 ab 

ời giải

khichiacho30là2,4,8,16.

Các

ếtlênb

ngsố

ện thao tác trên đếnkhitrênb

(cácsố cònlạitrênbảnggiữ nguyên).Tiếptụcthực

cònlại đúng mộtsố,gọisố

là

.Ch

( )5 22mod30 ≡ nêncácsố dư của2 n

ết3akr =+ với { }0;1;2r ∈ thì ( )2301010mod30 nkrbrb =++≡+ . Do đó { }102;4;8;16 rb+∈ Có các trườnghợp { } { }0,2;4;83,2;4;8 1,631,6 rbakb rbakb  =∈=∈⇔  ===+= .

trườnghợp này đềusuyra6 ab  . b)Viếtlênbảng229số tự nhiênliêntiếp1,2,3,,229.Từ cácsố đã viết xoá đi bốnsố bấtkỳ ,,, xyzt rồivi

ả

2 xyzt +++

ảngchỉ

đó

ứngminhrằng 2022a < Lời giải Xéttổngcủa bình phương các số cònlạitrênbảnglà2222 123229Saaaa =+++…+ . Saumỗilầnthaotácthìtổngnàysẽ không tăng, do 2 2222 2 xyztxyzt +++  ≤+++  theobất đẳngthứcBunhiacopski. Vớitổngcuốicùngvàtổng đầutiêntacó22222229.230.459 123229 6 a ≤+++…+= (ápdụng kếtquả ( ) ( )2222121123 6 nnn n ++  +++…+=   Từ đó suy ra 2022a < .

KỲ THI TUYỂN SINH LỚP 10 THPT, THPT CHUYÊN NĂM HỌC: 2022 - 2023 MÔN THI : TOÁN THPT Thời gian làmbài:90phút, không tính thời gian phát đề

I. Phần trắc nghiệm: (2,0 điểm)

Câu 1. Số nào sau đây la căn bậc hai số học của 4 ? A. 16 B. 16 C. 2 D. 2 Câu 2. Rút gọn biểu thức 82 + A. 22 B. 32 C. 10 D. 16

Câu 3. Giả sử xx12 , là hai nghiệm của phương trình 2 x4x10 −−= . Giá trị của biểu thức xx12 + bằng A. 1. B. 1. C. 4. D. 4. Câu 4. Tìm nghiệm của hệ phương trình A. x y 3 2  =  =−  . B. x y 2 3  =−  =  . C. x y 3 2  =−  =  . D. x y 2 3  =  =−  . Câu 5. Phương trình xx429200 −+= có bao nhiêu nghiệm? A. 4 B. 2 C. 0 D. 1 Câu 6. Tính diện tích S của hình cầu có bán kính Ra 2= A. Sa162=π . B. Sa82=π . C. Sa42=π . D. Sa22=π . Câu 7. Tính chu vi của đường tròn ngoại tiếp tam giác, biết tam giác ABC vuông tại A và BCa 6= A. a6π B.

C. a4

D. a3

8. Cho hình thang có đáy lớn BC , đáy nhỏ AD , ADBCcmACcm 10,52

C. Scm

SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH HẬU GIANG

a3π

π Câu

+== và  ACB 45ο = . Tính diện tích S của hình thang đã cho. A. Scm 5022= . B. Scm252 2 = .

2522= . D. Scm252= . II. Phần tự luận: (8,0 điểm) Câu 1. (2,0 điểm) a) Tính giá trị đúng của biểu thức Axx331=+++ khi x 1= b) Rút gọn biểu thức Bx x 9 , 3 = + với x 0≥ c) Tìm số thực x không âm thỏa mãn x 5= d) Cho biểu thức Daaa a aa 2222 4 22 −+ =++ −+ , với a 04 ≤≠ .Tìm a để D là số nguyên. Câu 2. (2,0 điểm) a) Giải phương trình xx 2 120−−= ĐỀ CHÍNH THỨC (Đề thi gồm 02 trang)

Giải phương trình

Câu 3. (1,5 điểm)

Trong mặt phẳng với hệ tọa độ Oxy , cho hàm số yx 2 =− có đồ thị ( )P và hàm số

có đồ thị là đường thẳng d , với m là tham số.

Vẽ đồ thị ( )P .

b) Tìm m để d cắt ( )P tại hai điểm phân biệt có hoành độ xx12 , thỏa mãn xx12 6

4. (2,0 điểm)

đường tròn ( )O cóbánkính R 3= và điểm M saocho OMR 2= . Từ M , kẻ hai tiếp tuyến MAMB , tới ( )O , với A và B là hai tiếp điểm.

c) Chứng minh tứ giác MAOB nội tiếp Tính diện tích S của tứ giác MAOB

d) Lấy điểm C trên đường tròn ( )O sao cho tam giác ABC nhọn, ABAC < vàcó các đường cao BE, CF. Gọi H là trực tâm tam giác ABC và N, J lần lượt là trung điểm của BC, AH. Chứng minh tứ giác AJNO làhìnhbìnhhànhvà

JEN 90ο = Câu 5. (0,5 điểm) Giải hệ phương trình xyyyyxy

2 32

−+=−−+

21 475190

( ) ( )xxxx 2 5312158 +−−++−=

( ) ymxm561525=−−+

−=

Câu

Cho



xyxyxyxy



 −+−−+=  HẾT

ĐÁP ÁN PHẦN TRẮC NGHIỆM 1C 2B 3D 4D 5A 6A 7A 8D ĐÁP ÁN PHẦN TỰ LUẬN Câu 1. (2,0 điểm) a) Thay x 1= vào biểu thức Axx331=+++ Ta được A 133.1144224. =+++=+=+= b) Tacó: ( ) ( ) ( )xxx x Bx xxx 2 2 9333 3. 333 −+− == = =− +++ c) ( ) xxx 2 52525. =⇔=⇔= d) Xét biểu thức ( ) ( )aa aaa Daa a aaaaa 2 222222222 4 22444 −+−+− =++=++ −+ Daaaaaaa aa 22442434 44 −++++−+ = = , với a 04 ≤≠ . Câu 2. (2,0 điểm) a) Giải phương trình xx 2 120−−= . Tacó: ( ) ( )2 14.1.12490 ∆=−−−=> ⇒ PT có hai nghiệm phân biệt ( ) ( )xx 12 149 149 4; 3 2.1 2.1 −−+ = == =− Vậy { }S 4;3=− . b) Giải phương trình ( ) ( )xxxx 2 5312158 +−−++−= ( )* ĐK: x 3≥ Đặt ( )ax abab bx 52208 3  =+ >≥⇒−= =−  và abxx 2 215=+− PT ( ) ( ) ( ) ( ) ( )abababababab*122 1 110⇔−+=−⇔+=+⇔−−= ( ) ( ) axL bxN 14 14  ⇔=→=− =→=  . Vậy phương trình có nghiệm duy nhất x 4.= Câu 3. (1,5 điểm) a) Bảng giá trị x 2 1 0 1 2 yx 2 =− 4 1 0 1 4

Đồ thị x y -4 -1 2-2 -1 O 1 b) Tìm m Xét phương trình hoành độ giao điểm của ( )P và d : ( ) ( ) ( )xmxmxmxm 2256152556152501 −=−−+⇔+−−+= Tacó: ( ) ( ) mmm 2 2 564.15252564 ∆=−−−+=− Để d cắt ( )P tại hai điểm phân biệt có hoành độ xx12 , ⇔ PT ( )1 có hai nghiệm phân biệt ( )mm 2 648 0* 255 ⇔∆>⇔>⇔> TheoViet,có: xxm xxm 12 12 56 .1525  +=−+  =−+  Xét xx12 6−= ( ) ( ) xxxxxx 22 12 3612124.36⇔−=⇔+−= ( ) ( )mm 2 564152536⇔−+−−+= mm 2 2510002 ⇔−=⇔=± (Thỏa đk ( )* ) Vậy m 2=± . Câu 4. (2,0 điểm) a) Chứng minh tứ giác MAOB nội tiếp. Tính diện tích S của tứ giác MAOB .  Xét tứ giác MAOB ,có:   MAOMBO 90ο == (Do MA, MB lần lượt là tiếp tuyến của đường tròn ( )O ).   MAOMBO 9090180 ⇒+=+=οοο Màhaigóc   MAOMBO , ở vị trí đối nhau, nên tứ giác MAOB nội tiếp 3 3 6 3 B A M O

Áp dụng định lý Pytago vàotamgiác MAO vuông tại

MAMOAO22226333.

Dễ thấy

MAOMBOccc

MAO SSMAAO

2.2...33.393.

Lấy điểm C

Chứng minh tứ giác AJNO làhìnhbìnhhành

Kẻ đường kính AD. Ta c/m được tứ giác BHCD là hìnhbìnhhành.

⇒ là trung điểm HD.

AHD có ON là đường trung bình, nên: ON//AHvà ONAH 1 2 = HayON//AJvà

tứ giác AJNO làhìnhbìnhhành.

 Chứng minh

có EN là trung tuyến của tam giác vuông BEC



=−=−=

( )

∆=∆−− MAOB

2∆ ⇒==== b)

... 

Xéttamgiác

ONAJ = Vậy

 JEN 90ο = Ta

  BENEBN⇒= Tứ giác BCEF nội tiếp   EBNEFC⇒= Tứ giác AFHE nội tiếp   EFCEAH⇒= Mà   EAHJEA = (do JE là trung tuyến tam giác vuôngAEH) Do đó   BENAEJ =       JENJEBBENJEBAEJBEA 90 ⇒=+=+==ο Câu 5. (0,5 điểm) Giải hệ phương trình xyyyyxy xyxyxyxy 2 32 21 475190  −+=−−+  −+−−+=  . Điều kiện: yxy 1 2;0≥+≥ . Xét phương trình: ( ) ( )yxy xyyyyxyyxy yxy 2 21 21 1 21 −−+ −+=−−+⇔−+= −++ ( ) xyy yxy 1 10 21  ⇔−++ = −++  D J N H E F B A M O C D J N H E F B A M O C

( ) yx y yxy 1 1 0* 21  =+ ⇔  += −++ Dễ thấy phương trình ( )* vô nghiệm (do y 1 0 2 ≥> ) Thế yx 1=+ vàopt xyxyxyxy 32475190 −+−−+= xxxx 43233180 ⇔−−−+= ( ) ( ) ( )xxxx 2 32230 ⇔−−++= ( ) ( ) xyN xyN 34 23  ⇔=→= =→=  Vậy hệ pt có nghiệm là ( ) ( ) ( {)}xy;2;3;3;4 ∈ .

KỲ THI TUYỂN SINH VÀO LỚP 10 TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 20222023 ĐỀ THI MÔN TOÁN (DÀNH CHO CHUYÊN NGA PHÁP TRUNG)

Ngày thi: 06 tháng 6 năm 2022 Thời gian làm bài: 150 phút (không kể thời gian giao đề) (Đề thi gồm có 01 trang, 04 câu)

Câu I (3,0 điểm)

1) Giải phương trình: a)23 x

2) Vẽ đồ thị hàm số 24yx

b)352 xx−=+

3) Cho phương trình 2650xxm+−+= (m làtham số) Tìm m để phương trình có hai nghiệm 12 , xx thoả mãn: 22 1222xx+= . Câu II (3,0 điểm)

1) Rút gọn biểu thức: 22 5151 A =− +−

2) Giải hệ phương trình: 122 216 xy xy

 +−=−  ++= 

3)Tìmmột số có hai chữ số. Biết rằng nếu đổi chỗ hai chữ số của nó thì ta được một số mới lớn hơn số đã cho là 36, tổng của số mới tạo thành và số đã cho bằng 88. Câu III (3,0 điểm) Cho nửa đường tròn tâm O đường kính AB, C là điểm chính giữa của cung AB. Lấy điểm E thuộc cung CB (E khác C và B), gọi M là giao điểm của OC và AE

1) Chứng minh rằng: Tứ giác OMEB là tứ giác nội tiếp.

2) Chứng minh rằng: 2 BCAMAE

SỞ GD & ĐT HOÀ BÌNH

−=

=−

 3) Kẻ CI vuông góc với AE (I thuộc AE). Chứng minh rằng OI làtiaphân giác của góc COE 4)Chứngminhrằng: IMEB IEEA  Câu IV (1,0 điểm) Cho các số thực , xy tùy ý thỏa mãn: 2xy+= . Tìm giá trị nhỏ nhất của biểu thức 2222 10422410 Mxxyyxxyy =+++++ Hết Họ và tên thí sinh: ............................................. Số báo danh: ......................... Phòng thi: ....... Giám thị 1: .................................................... Giám thị 2: ............................................................ ĐỀ CHÍNH THỨC

TUYỂN SINH VÀO

1 SỞ GD & ĐT HOÀBÌNH KỲ THI

LỚP 10 TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 2022 2023 HƯỚNG DẪN CHẤM MÔN TOÁN (DÀNH CHO CHUYÊN NGA PHÁP TRUNG) (Hướng dẫn chấm này gồm có 02 trang) Câu I (3,0 điểm) Phần, ý Nội dung Điểm 1 a) Tính đúng nghiệm 11x = 0,5 b) Tính đúng nghiệm 7 2 x = 0,5 2 Xác định được 2 điểm thuộc đồ thị 0,5 Vẽ đúng đồ thị 0,5 3 Phương trình có nghiệm ' 404mm ⇔∆=+≥⇔≥− 0,25 Áp dụng hệ thức Vi ét:12 12 6 5 xx xxm +=−  =− 0,25 ( ) ( ) ( ) ( )2222 12121222222625223 xxxxxxmmTM +=⇔+−=⇔−−−=⇔= KL:...... 0,5 Câu II (3,0 điểm) Phần, ý Nội dung Điểm 1 ( ) ( ) ( ) ( ) 22251251 51515151 A −−+ =−= +− +− 0,5 2522524 1 514 = ==− 0,5 2 ĐK: 1x ≥− 1222144216216 2162165102 xyxyxyxy xyxyyy +−=−+−=−+=−+=−  ⇔⇔⇔  = ++=++==  0,5 2143() 22 xxTM yy  +==⇔⇔==  KL:... 0,5 3 Gọi số ban đầu là (,1199)xxNx∈≤≤ Số mới là (y,1199)yNy∈≤≤ 0,25 Lập được hệ phương trình: ( )3626 8862 yxxTM xyy −== ⇔  +== 0,5 KL:....0,25

2 Câu III (3,0 điểm) Phần, ý Nội dung Điểm M I C A O B E 1Tacó:  090MEB = ( góc nội tiếp chắn nửa đường tròn),  090MOB = 0,5   0180MEBMOB ⇒+= ⇒ Tứ giác OMEB nội tiếp đường tròn 0,5 2 Tacó: CAB∆ vuông tại C, đường cao CO . 2 . BCOBAB⇒= ( hệ thức lượng trong tam giác vuông) 2 . BCOAAB⇒= (1) 0,5 AOM∆ ∽ ( ) ... OAAM AEBggOAABAMAE AEAB ∆⇒=⇒= (2) Từ (1) và (2) 2 . BCAMAE⇒= 0,5 3 Tứ giác ACIO nội tiếp   CAICOI⇒= ( góc nội tiếp cùng chắn cung  IC )0,25  1 2 CAECOE = (góc nội tiếp và góc ở tâm cùng chắn cung  EC )  1 2 COICOEOI =⇒ là tia phân giác của  COE 0,25 4 MOE∆ cóOIlàtiaphângiác IMOMIMOM IEOEIEOA ⇒=⇒= (3)0,25 AOM∆ ∽ ( ). OMEB AEBggOAEA ∆⇒= (4) Từ (3) và (4) IMEB IEEA ⇒= 0,25 Câu IV (1,0 điểm) Phần, ý Nội dung Điểm Tacó: ( ) ( ) ( ) 22222 10423333 xxyyxyxyxyxyxy ++=++−≥+=+≥+ (1) ( ) ( ) ( ) 22222 24103333 xxyyxyxyxyxyxy ++=++−≥+=+≥+ (2) 0,5 Cộng theo từng vế các bất đẳng thức (1) và (2) ta được: ( ) ( ) ( ) 3344.28Mxyxyxy ⇒≥+++=+== Dấu '''' = xảy ra 1xy ⇔== KL: Vậy 81MinMxy=⇔== 0,5 * Chú ý: Các lời giải đúng khác đều được xem xét cho điểm tương ứng.

SỞ GD & ĐT HOÀ BÌNH KỲ THI TUYỂN SINH VÀO LỚP 10 TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 20222023 ĐỀ THI MÔN TOÁN (DÀNH CHO CHUYÊN TIN) Ngày thi: 06 tháng 6 năm 2022 Thời gian làm bài: 150 phút (không kể thời gian giao đề) (Đề thi gồm có 01 trang, 04 câu)

Câu I (3,0 điểm)

1) Rút gọn biểu thức: 11

2) Vẽ đồ thị hàm số

3) Giải phương trình

Câu II (3,0 điểm)

1)Cho đường thẳng ( ) : dyaxb =+ Tìmavà b để đường thẳng ( )d đi qua điểm ( )1;3A và song song với đường thẳng ( ) ’:53dyx=+

2) Để hưởng ứng ngày Tết trồng cây, một tổ có 13 học sinh cả nam và nữ tham gia trồng được 80 cây. Biết tổng số cây mà các bạn nam trồng được bằng tổng số cây mà các bạn nữ trồng được,số cây mà mỗi bạn học sinh nam trồng được nhiều hơn số cây mỗi bạn nữ trồng được là 3 cây. Tính số học sinh nam, học sinh nữ của tổ đó (số cây mỗi bạn nam trồng được là bằng nhau và số cây mỗi bạn nữ trồng được bằng nhau).

3) Cho số thực x dương thoả mãn điều kiện:

Tính giá trị biểu thức: 3 3 1 A x x  Câu III (3,0 điểm)

217x x

Cho đường tròn tâm (O) và một điểm A cố định nằm ngoài đường tròn (O). Vẽ các tiếp tuyến AB, AC tới đường tròn (B, C là các tiếp điểm), vẽ một cát tuyến di động AMN(AM<AN) với (O). Gọi E là trung điểm của MN, CE cắt (O) tại điểm thứ hai là I.

Chứng minh rằng: Năm điểm A, B, O, E, C cùng nằm trên một đườngtròn.

minh

5353 A =+ −+

12 4 yx =

221xx−=−

 

2) Chứng

rằng: BI song song với MN. 3) Chứng minh rằng: EBEI  4) Xác định vị trí của cát tuyến AMN để diện tích tam giác AIN đạt giá trị lớn nhất. Câu IV (1,0 điểm) 1)Cho0,1 ab << , chứng minh rằng: 1aabbab−+−≤ 2) Giải phương trình: 2 35818xxxx −+−=−+ Hết Họ và tên thí sinh: ............................................. Số báo danh: ......................... Phòng thi: ....... Giám thị 1: .................................................... Giám thị 2: .......................................................... ĐỀ CHÍNH THỨC

Phần,

ĐT HOÀ

điểm)

KỲ THI TUYỂN SINH VÀO LỚP 10 TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 20212022 HƯỚNG DẪN CHẤM MÔN TOÁN

dẫn

CHO CHUYÊN TIN)

này gồm có

trang)

Điểm

(loại)

(thỏa mãn).

điểm)

Nội dung Điểm

Đường thẳng ( )d đi qua điểm ( )1;3A nên có phương trình ( )31ab −+= 0,25 Đường thẳng ( )d song song với đường thẳng ( )'d nên ( )5 2 3 a b =  ≠ 0,25

Từ (1)và(2)suyra 5 8 a b =  = (thoả mãn) 0,25 Vậy để đường thẳng ( )d đi qua điểm ( )1;3A và song song với đường thẳng ( ) ':53dyx=+ thì 5

đường thẳng ( ) :58dyx=+

câymà một

phương trình

được

cây

(loại).

1 SỞ GD &

BÌNH

(DÀNH

(Hướng

chấm

Câu I (3,0

Phần, ý Nội dung

1 115353 5353(53)(53) A ++− =+= −+−+ 0,5 25 5 53 A == 0,5 2 Xác định được đúng các điểm thuộc đồ thị 0,5 Vẽ được đúng đồ thị 0,5 3 + Nếu 2x ≥ ta được phương trình: 2211xxx −=−⇔=−

0,5 + Nếu 2x < ta được phương trình: 2211xxx −+=−⇔=

KL…0,5 Câu II (3,0

8 a b =  = hay

0,25 2 Gọi số học sinh nam của tổ là x ( 013 x << , xN ∈ ) ⇒ Số học sinh nữ của tổ là: 13 x 0,25 Số

học sinh nam trồng được là: 40 x (

) Số

học sinh nữ trồng được là: 40 13 x (

) 0,25 Theobàira ta có phương trình: 4040 3 13 xx −= 0,25 Giải

15x = ( TMĐK), 2 104 3 x =

KL… 0,25

tự ta có

Tính chất tiếp tuyến và bán kính)

ra tứ giác ABOC nội tiếp (Tổng hai góc đối bằng 0 180)(1)

E là trung điểm của MN nên

⊥

ra tứ giác AEOB nội tiếp (Tổng hai góc đối bằng 0 180)(2)

(1) và (2) suy ra 5 điểm A, B, O, C, E cùng thuộc một đường tròn đường kính

2 3 Từ giả thiết 2 217x x   suyra:   2 930 11 xxdo xx x      0,5 3 2 3 3 2 21111133 1 xxxxx xxxxx              3 3 1 18 x Ax  0,5 Câu III (3,0 điểm) Phần, ý Nội dung Điểm I K N M E O C B A 1Tacó OBAB ⊥ (

 090ABO ⇒= Tương

 0

ACO = Suy

0,5 Vì

OEMN

 0

AEO ⇒= Suy

Từ

AO. 0,5 2 Trong đường tròn đường kínhAOtacó:   ABCAEC = (cùng chắn cung AC) 0,5 Mà   ABCBIC = ( góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung AC )  AEC⇒ =  // BICBIMN ⇒ 0,5 3Tacó   IBEBEA = (soletrong)0,25 Mà    BEABCABIC == suyra   IBEBEA = nên EBEI  0,25 4////BIMNBIAN ⇒ AINABNSS⇒= ( vì có chung đáy AN và chiều cao hạ từ đỉnh B và đỉnh I bằng nhau). 0,25 Kẻ NK vuông góc với đường thẳng AB 1 2AINABN SSABNK⇒== Ta có AB không đổi SAIN⇒ đạt giá trị lớn khi NK đạt giá trị lớn nhất. Mà max 22 NKNBRNKR ≤≤⇒= khi và chỉ khi N đối xứng với B qua O 0,25

3 Câu IV (1,0 điểm) Phần, ý Nội dung Điểm 1 Vì0,1 ab << nên 1 .1 2 aababab +− −=−≤ Tương tự ta có 1 .1 2 babbaba +− −=−≤ 0,25 Do đó 11 1 22 aabbababba +−+− −+−≤+= (đpcm) 0,25 2 ĐK: 35 x ≤≤ Học sinh chứng minh được: 22 2(ab),, ababR +≤+∀∈ Áp dụng ta được 352(x35x)2,:35 xxxx −+−≤−+−=∀≤≤ 0,25 Tacó22818(x4)22, xxxR −+=−+≥∀∈ Do đó phương trình đã cho tương đương với 2 352 4 8182 xx x xx  −+−= ⇔= −+=  KL… 0,25 * Chú ý: Các lời giải đúng khác đều được xem xét cho điểm tương ứng.

KỲ THI TUYỂN SINH VÀO LỚP 10

TRƯỜNG THPT CHUYÊN HOÀNG VĂN THỤ NĂM HỌC 20222023 ĐỀ THI MÔN TOÁN (DÀNH CHO CHUYÊN TOÁN)

Ngày thi: 05 tháng 6 năm 2022

Thời gian làm bài: 150 phút (không kể thời gian giao đề) (Đề thi gồm có 01 trang, 04 câu)

Câu I (3,0 điểm)

1) Rút gọn biểu thức: 322322A =+−−

2) Tìm m để các đường thẳng: 24();35('); yxdyxd =+=+ 23()ymxm=−+−∆ cùng đi qua một điểm.

3) Cho phương trình: 22210 xmxm−+−= ( m là tham số).Tìm m để phương trình có hai nghiệm dương.

Câu II (3,0 điểm)

1) Tìm x, y nguyên thoả mãn: 210xyxy++−=

3) Giải hệ phương trình: 22 2

26 32 xyxy xyxyx −=  +=+

Câu III (3,0 điểm)

1) Chứng minh rằng: CI.CA=CE.CB

2) Chứng minh rằng: Ba điểm D, I, E thẳng hàng.

3) Chứng minh rằng: HI là tiếp tuyến của đường tròn đường kính EC.

4) Khi B thay đổi thì H thay đổi, xác định vị trí của H trên AC để diện tích tam giác O’IH lớn nhất.

(1,0 điểm)

1) Tìm tất cả các cặp số

là

dương

mãn điều kiện:

SỞ GD & ĐT HOÀ BÌNH

Câu IV

thực

thỏa

222222 223666362232 xxyyxxyyxy +++++=++ 2)Cho,ab

các số thực thỏa mãn: 22 abab +=+ . Chứng minh rằng: 33224 ababab+++≤ Hết Họ và tên thí sinh:............................................. Số báo danh: ......................... Phòng thi: ..... Giám thị 1:........................................................Giám thị 2:..................................................... ĐỀ CHÍNH THỨC

ICEchung; ∠ EIC= ∠ ABC=900 ( Góc nội tiếp chắn nửa đường tròn

Suyra(g) CIECBAg ∆∆−

⇒=⇔=

CICACECB

..(dpcm)

Tacó EIBC ⊥ (Do ∠ EIC là góc nội tiếp chắn nửa đường tròn)(1)

VìBD ⊥ AC tại H, và HA = HE; HB = HD nên tứ giác ABED là hình thoi

SuyraDE  AB,màAB ⊥ BCnênDE ⊥ BC(2)

(1) và (2) ta có 3 điểm D,E,I thẳng hàng.

có tứ giác DHIC nội tiếp đường

3 1 XéthaitamgiacCIEvàCBAcó ∠

)0,5



CICE

CBCA

0,5 2

0,5

Từ

0,5 3 Ta

tròn đường kính DC nên ta có ∠ BIH= ∠ BDC=(1800 ∠ HIC) Lại có ∠ BAC= ∠ IEO’ ( đồng vị ); ∠ IEO’= ∠ O’IE ( do tam giác O’IE cân tại O’) Suyra ∠ BIH= ∠ O’IEmà ∠ BIH+ ∠ HIE=900nên ∠ HIE+ ∠ O’IE=900suyraHI ⊥ O’I hay HI là tiếp tuyến của (O’) 0,5 4 Tacó 2 22222 ''2'.''H4 22224OIHOIH AC OIHIORR SOIHIS ∆∆ + =≤===⇒≤ 0,25 Dấu = xảy ra khi 2 '.' 2 '2 R OIHIR OIHI OIHI  = ⇒==  = (DoO’I>0,HI> 0) TacóO’H=R;màO’E=O’I= 2 R suyraAH=HE=R 2 R = (21) 2 R Vậy AH = (21) 2 R thì diện tích tam giác O’IH lớn nhất. 0,25

; xx làcácsố nguyên.

Tìmcácnghiệmnguyêncủa phương trình 4322216121640xxxyxy −+−+−+= Câu III (2,0 điểm).

ải phương trình 323 1. 11 xx

ảihệ phương trình

Câu IV (3,0 điểm).

33241 21 xyxyxy xyxy ++=+−

Cho ABC∆ nhọn() ABAC < nộitiếp đườngtròn() O . Hai đườngcao BE, CF cắtnhau tại H. Gọi K là giao điểmcủa hai đườngthẳng EF và BC. a)Chứngminhtứ giác BFEC nộitiếp,từ đó suy ra KF.KE=KB.KC. b) Đườngthẳng AK cắt đườngtròn (O) tại điểmthứ hailà M (M khác A).Gọi I làtrung điểmcủa đoạnthẳng BC.Chứng minh ba điểm M,H,I thẳnghàng.

Mộtchitiếtmáygồmhainửahìnhcầubằngnhauvàmộthìnhtr

cchotrênhìnhv

(hìnhvẽ).Hãytính

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÀO LỚP 10 THPT HƯNG YÊN NĂM HỌC 2022 2023 Bài thi: TOÁN ĐỀ CHÍNH THỨC Dành cho thí sinh dự thi vào các lớp chuyên: Toán, Tin học Thờigianlàmbài:150phút,khôngkể thời gian phát đề Câu I (2,0 điểm). Chobiểuthức 221 : 21 Axx xxxxx  + = +  +−−−  a)RútgọnbiểuthứcA. b)Tìmgiátrị của x để A=3 Câu II (2,0 điểm) 1. Trongmặtphẳngtọa độ Oxy,choparabol2 ():Pyx = và đườngthẳng ():(1)5 dymxm=+−+ .Tìmgiátrị củathamsố m để (d)cắt(P)tại hai điểmphânbiệt11(;)Axy , 22 (;)Bxy saocho12

1.Gi

xx −= 2.Gi

{

++=

ụ

thể tíchcủachitiết máy đó theo các kích thướ

ẽ. Câu V (3,0 điểm).Chobasố thực dương x, y, z thỏamãn42324 xyyzxz++= .Tìmgiátrị lớn nhấtcủabiểuthức 222 2 4916 Pxyz xyz =++ +++ . HẾT Thí sinh không đượcsử dụngtàiliệu.Cánbộ coithikhônggiảithíchgìthêm. Họ vàtênthísinh:Phòngthisố: Số báodanh: .................................................Chữ kýcủacánbộ coithi.....................

HƯỚNG DẪN GIẢI Câu I. a)221 : 21 Axx xxxxx  + = +  +−−−  ĐK: 0,1xx≥≠ =(2)21 : (1)(2)()1 xx xxxxx  + +  −+−−  = 21 . (1)1 xx xx  +−    = 2x x + b)233Ax x + =⇔= 23 xx⇔+= 320xx ⇔−+= 11() 24() xxl xxn  ==  ⇔⇔   = =   VậyA=3khix=4 Câu II. 1) Hoành độ giao điểmcủa(P)và(d) 2(1)5 xmxm=+−+ 2(1)50 xmxm ⇔−++−= (*) Tacó2(1)4(5) mm ∆=+−− 2221mm =−+ 2 (1)200 m =−+> Nên (d) luôncắt (P) tại hai điểmphânbiệt A và B Theohệ thứcvi-et12 12 1 .5 xxm xxm +=+  =− (*)25(1) xxmx ⇔−−=− Xét1 x = khôngphảilànghiệmcủa phương trình 5 1 xm x ⇒−= (1) Vì12 ; xxZ ∈ nên1 m + và5 m làcácsố nguyên do đó m cũng là số nguyên Từ (1)tacó mZ ∈ khi5 1 xZ x  −∈  ( ) 1 51 xZ x −∈ ⇒    Suyra3;5 mm=−=

1543 1105 1565 1123 xxm xxm xxm xxm −=−⇔=−⇒=−  −=−⇔=⇒=  −=⇔=⇒=  −=⇔=⇒=− Vậy3;5 mm=−= thỏayêucầubàitoán 2)4322216121640xxxyxy −+−+−+= 43322233448816164 xxxxxxxyy ⇔+−−++++=++ 322 (1)3(1)4(1)8(1)16164 xxxxxxxyy ⇔+++++++=++ 322 (1)(348)(42) xxxxy ⇔+−++=+ 222 (1)(48)(42) xxxy ⇔+−+=+ Vì4201 yzyx ∈⇒+≠⇒≠− Vì,xyz ∈ nên2 (1) x + và2 (42) y + làsố chính phương khác 0 nên 2 (48) xx−+ cũng là số chính phương Đặt248xxm −+= * () mN ∈ 22(2)4 xm⇔−+= 22 (2)4 xm ⇔−−=− (*)(2)(2)4 xmxm ⇔−−−+=− Do22xmxm −−<−+ Nên { { { { { { 241/2 215/2 222 222 217/2 245/2 xmx xmm xmx xmm xmx xmm −−=−= −+= = −−=− =− −+= = −−=−= −+= =   ⇔⇔     2 2(42)4xy=−⇒+= 422400 422441 yyy yyy += == +=−=−=−   ⇔⇔⇔   Vậynghiệmnguyênthỏaycbtlà:(2;0);(2;1) Câu III. 1)3231 11 xx xx −= ĐK: 13 x <≤ 3231 xxx ⇔−−−=− 3213 xxx ⇔−=−+− 32132(1)(3) xxxxx ⇔−=−+−+−− 342(1)(3) xxx ⇔−=−− (*) (*)có điềukiện:3404/3 xx−≥⇔≥ (*)2924164(1)(3) xxxx ⇔−+=−− 22 9241641612 xxxx ⇔−+=−+− (loại) (n) (loại)

2 1340280 2() 14 13() xx xn xl ⇔−+= = ⇔  =  vậynghiệmcủa phương trình: 2x = 2) 33241 21 xyxyxy xyxy  ++=+− ++= 332(1)1 21 xyxyxy xyxy  ++=−− ⇔  +=− 3331(1) 21(2) xyxy xyxy  ++= ⇔  +=− ( ) 322 1()33310 xyxyxyxy ⇔+−−+−= ( ) ( ) ( ) ( ) ( ) 33 2 22 13(1)0 113 110 xyxyxy xyxyxyxy xyxyxyxy ⇔+−−+−= ⇔+−++++−  ⇔+−+−+++= 22 10 10 xy xyxyxy +−= ⇔  +−+++= Với 101 xyxy +−=⇔=− thay vào (2) ta được: ( )2 ⇔ 121(1) yyyy−+=−− ( ) 20yy ⇔−= 01 21 yx yx =⇒= ⇔  =⇒=− Với : 2222102222220xyxyxyxyxyxy +−+++=⇔+−+++= ( ) ( ) ( ) ( ) ( ) ( ) 2222 222 221210 110 xxyyxxyy xyxy ⇔−+++++++= ⇔−++++= 0 101 10 xy xxy y −=  ⇔+=⇔==−   += Vậynghiệmcủahệ phương trình là: (1;0),(2;1),(1;1) Câu IV. 1) a)

090BECCFB==

tứ giác BFEC nộitiếp(2góccùngnhìnmộtcạnhbằngnhau) -xét KEF∆ và KBE∆ có:

K làgócchung

KCFKEB = (2gócnộitiếpcùngchắncungBF) KEF⇒∆ đồngdạngvới KBE∆ KFKC

KFKEKCKB KBKE ⇒=⇔= (đ.p.c.m) (1)

b)Tacó: KIB∆ đồngdạng KBA∆ (g.g)

KIKC KIKAKBKC KBKA ⇒=⇔= (2) Từ (1)và(2)suyra KEKFKIKA = KEKA

KIKF ⇔= Mà  K làgócchung

Suyra KEA∆ đồngdạng KIF∆

KEAKIF⇒= ⇒ tứ giác IAEF nộitiếp(góctrongbằng góc đốingoài) Mặtkhác AEHF nộitiếp đường tròn đườngkínhAH(

090AEHAFH== ) Nên:,,,,IAEFH cùngthuộcmột đường tròn đườngkínhAH

090IHA ⇒= Mà:  090NIA = (gócchắnnữa đườngtròn)

Suyra:,,NIH thẳnghàng

Kẻ đườngkính AN của đườngtròn ( )O ; ( )NO ∈ Xéttứ giác BHCN có: // BHCN (cùngvuônggócvớiAB) // CHBN (cùngvuônggócvớiAC) BHCN⇒ làhìnhbìnhhành Mà M là trung điểmcủaBC MHN⇒∈ Suyra,,MIH thẳnghàng

xéttứ giác BFEC có:  

⇒



 



2) ( ) 32 32 3 4 .20 3 4 .4.20.4. 3 1216 3 VRR cm ππ ππ π =+ =+ =

Câu V: Tacó:423241 6128 xyyzxz xyyzxz++=⇔=== ...1 233424 xyyzxz ⇔++= Đặt0;0;01 234 xyzabcabbcac =>=>=>⇒++= 222 222 434 44991616 2 111 abc P abc abc abc =++ +++ =++ +++ 222 2 abc aabbccababbcaccabbcac =++ +++++++++ ( ) ( ) ( ) ( ) ( ) ( ) 2 abc abacabbcacbc =++ ++++++ ( ) ( ) 2222 ... 22 aabbcc abacabbcbcac =++ ++++++ Tacó: ( ) ( ) ( ) ( ) 2222 2. 22 2. 22 22 2. 22 aaaa abacabac bbbb abbcabbc cccc bcacbcac +≥ ++++ +≥ ++++ +≥ ++++ ( ) ( ) 12222 222 aabbcc pabacabbcbcac  ≤+++++   ++++++  ( ) ( )122 22() 11 22 22 9 4 abacbc P abacbc P P ++  + ⇔≤++ +++  ⇔≤++   ⇔≤ Dấu"" = xảyrakhivàchỉ khi ( ) ( ) 22 2 87 2 87 2 2 aa abacbcbc bbabbab abbc accac cc bcac   = ++ = =  =⇔+=⇔=  ++ +==  = ++  2222111771 1515 abbcacbbbbb ++=⇔++=⇔=⇔=

13 1515 14 1515 714 1515 by cz ax  =⇒=   =⇒=   =⇒= 

1 BÀI GIẢI THAM KHẢO ĐỀ THI CHUYÊN TOÁN LÊ QUÝ ĐÔN KHÁNH HÒA NĂM 2022-2023 (Biên soạn: Nguyễn Bá Vinh; Đặng Mai Quốc Khánh; Lưu Xuân Thắng) Bài 1 (2.00 điểm): a)Rútgọnbiểuthức 3 664211063 32423 A −−+ = + + b)Chocácsố thựca;b;cthỏa222321 aabb−+= , 22342bbcc−+= , 2233ccaa+−= Tínhgiátrị củabiểuthức444 Babc =++ Lời giải: a) ( ) ( ) ( ) ( ) 232 3 2 62211332 116213 12 32321332 13 A +− −+ = +=+=+= −+− + b) ( ) ( ) ( ) 22 22 22 23211 3422 333 aabb bbcc ccaa  −+=   −+=  +−=  Lấy(1)+(2)(3)vế theovế, ta được:2223333330 abcabbcca ++−−−= ( ) ( ) ( ) 222 222 222 0 2222220 0 abcabbcca abcabbcca abbcca abc ⇔++−−−= ⇔++−−−= ⇔−+−+−= ⇔== Khi đó, ( ) 2 11 a ⇔= Từ đó suy ra 4443Babc=++= Bài 2 (2 điểm) a)Trongmặtphẳngtọa độ, cho đườngthẳng:1 dymxm=++ (mlàthamsố).Tìmtấtcả cácgiátrị của m để dcắttrụchoànhtại điểmA,trụctungtại điểmBvàtạothànhtam giácOABcódiệntíchbằng2(Olàgốctọa độ).

2 b)Giảihệ phương trình 3223 22 26520 111 1244430 xxyxyy xyxyy  −+−=  += −+−+ Lời giải: a) Trườnghợp1:0 m = Dễ dàngkiểmtrakhôngthỏayêucầubàitoán Trườnghợp2:0 m ≠ dcắttrụchoànhtại điểmA1;0 Am m +  ⇒−  dcắttrụctungtại điểmB ( )0;1Bm ⇒+ 11 2.2.4.14 2OAB SmOAOBOAOBm m ∆ + =⇔=⇔=⇔−+= ( ) ( ) ( ) 2 2 2 14;01 14 14;0322 mmkhimm mm mmkhimm  +=≥=⇔+=⇔ ⇔  =−± +=−<  Vậy { }1;322m ∈−± lànhữnggiátrị cầntìm. b)Hệ phương trình ( ) ( ) 3223 22 265201 111 2 1244430 xxyxyy xyxyy  −+−=  −= −+−+ . Điềukiện: 2 2 1240 44 0 0 y xy xy              Vì 0y  , phương trình  1 trở thành 3223 333 26520 xxyxyy yyyy  −+−=  32 26520 xxx yyy  ⇔−+−=  

3 Đặt x t y  thì phương trình trở thành3226520 ttt−+−= ( ) ( )2 2 22210 2 2210 2 ttt t tt t ⇔−−+= = ⇔  −+= ⇔= Do đó 22x xy y  Thay vào phương trình  2 , ta được22 4 111 41244430 yyyyy −= −+−+            22 2222 3222432 432 111 4314130 15113312311 15151514518281082 2810520 yyyyy yyyyyyyyyy yyyyyyyyyy yyyy      3 4245410yyyy  2 2 1 450 4 yy y y  2 2 11 450 y y y y              Đặt 1 uy y  với điềukiện 2u  Phương trình trở thành 222450470uuuu  211 211 u u      Với 211u  1 211y y ⇔+=+

4 ( )2 1 2 21110 11 11111411 22 11 11111411 22 yy y y ⇔−++=  =+++ ⇔   =+−+  Nên1 2 11211411 11211411 x x  =+++  =+−+ Với 211u  1 211y y ⇔+=− ( ) 221110 yy ⇔−−+=  2 2114114110  nên phương trình vô nghiệm. Vậynghiệmcủahệ phương trình là 11211411 11 11111411 22 x y               hoặc 11211411 11 11111411 22 x y              Bài 3 (1,50 điểm) a)Chứngminh322310 xx−+≥ vớimọisố thực0 x ≥ b)Chocácsố thựckhôngâm,,xyz thỏa333 1113 1112 xyz ++= +++ .Tìmgiátrị nhỏ nhấtcủabiểuthức222 111 2022 111 Qxyz xxyyzz =+++ −+−+−+ . Lời giải a)Chứngminh322310 xx−+≥ vớimọisố thực0 x ≥ . Tacó ( )32222 2212(1)1Mxxxxxx =−−+=−−− ( ) ( ) ( ) ( ) ( )22 (1)2(1)1121121 xxxxxxxx  =−−−=−−+=−+  Mà 0x  nên210 x +> .

5 Do đó ( ) ( )2 1210,0xxx −+≥∀≥ . Hay322310,0 xxx−+≥∀≥ b)Chocácsố thựckhôngâm,,xyz thỏa333 1113 1112 xyz ++= +++ .Tìmgiátrị nhỏ nhấtcủa biểuthức222 111 2022 111 Qxyz xxyyzz =+++ −+−+−+ . Cách 1. Tacó: 2 23 11 11 xx xxx   ; 2 23 11 11 yy yyy   và 2 23 11 11 zz zzz   222 222 333 111 2022 111 111 2022 111 Qxyz xxyyzz Qxyz xyz     Mặtkhác 32213xx  (câua)nên 22 33 2121 33 x x x x    Suyra      333 333 212121 111 3332022 111 xyz Q xyz          333 333 222222 2022 313131 Qxyz xyz                   3 333 333 333 33 422422422 2022 313131 41112 111 33 111 41112 111 33 111 432 ..32022 323 2022 xyz Q xyz Q xyz Q xyz Q Q                        Vậy min2022Q  khi 1xyz Cách 2.

6 +)Xét 222 222333 111111 111111 Qxyzxyz xxyyzzxyz =++=++ −+−+−++++ 222 333333 111 111111 z Q xyz xyzxy        +)Ápdụng BĐT AM GMtacó: 32 33333 111112131 2 22211111 zz xyzzz    + Tương tự: 2 333 1131 1112 x yzx +≥− +++ và 2 333 1131 1112 y zxy +≥− +++ +)Cộngtheovế cácbất đẳngthứcvới nhau ta được 222 333333 222 333333 333333 333 1113 23 1111112 12111 23 111111 11112111 23 111111 1111 3111 xyz xyzxyz xyz xyzxyz Q xyzxyz Q xyz                          1 0 2        Do đó 2022020222022PQ Dấu“=”xảyrakhi 1xyz Bài 4: (2,50 điểm)Chotamgiácnhọn ABC không cân đỉnhCnộitiếp trong đườngtròn ( )O . Gọi1 d và2 d tương ứnglàtiếptuyếncủa đườngtròn ( )O tại A và B ,cáctiếptuyếnnàycắt nhautại D .Gọi E làhìnhchiếuvuônggóccủa O lên đườngthẳng DC . a)Chứngminhrằng năm điểm,,,,AOEBD cùngthuộcmột đườngtròn. b)Một đườngthẳng d qua C vàsongsongvới AB cắt1 d tại F .Chứngminhrằng tamgiác DAC đồngdạngvớitamgiác DEF . c)Goi K là trung điểmcủa AC .Chứng minh ba điểm,EK và F thẳnghàng. Lời giải

a)Chứngminhrằng năm điểm,,,,AOEBD cùngthuộcmột đườngtròn. Xéttứ giácAOBDcó:

000 9090180OADOBD+=+=

⇒ Tứ giácAOBDnộitiếp đường tròn đườngkínhOD.

⇒ 4 điểmA,O,B,Dcùngthuộc đường tròn đườngkínhOD.

Mặtkhác:  090OED = (vì OECD ⊥ )

Ethuộc đường tròn đườngkínhOD. Vậy 5 điểmA,O,E,B,Dcùngthuộc đường tròn đườngkínhOD.

b) Một đường thẳ

đồ

qua

và

với AB cắt 1d tại F . Chứng minh rằng tam giác

ạ

đường

ới

(gócnộiti

 

⇒

ng d

song song

DAC

ng d

ng v

tam giác DEF . Cách1: Trong

tròn đườngkinhODtacó:   AODAED =

ếpcùngchắn  AD ) Mặtkhác:   AODDAB = (cùngphụ với  OAB ) Dovậy   AEDDAB = ,mà   DABDFC = (đồngvị)nên   AEDDFC = Xét DAE∆ và DCF∆ tacó:  D chung   AEDDFC = (cmt) Do đó DAEDCF∆∆ ∽ (gg) ⇒ DADE DCDF = ⇒ DADC DEDF = Xét DAC∆ và DEF∆ tacó:  D chung DADC DEDF = K E N D F O C AB

∆ cântạiD(tínhchất2tiếptuyếncắtnhau)

DABDBA⇒=

(các gócnộitiếpchắn2cungAD,BDbằngnhau)

ặtkhác,

ộc đường tròn đườngkínhODnên

(đồngvị,//FCAB

đó, AECF làtứ giácnộitiếp

= (2gócnộitiếpcùngchắncungAE)hay

DAC∆ và DEF∆

ACDDFE

8 Do đó DACDEF∆∆ ∽ (cgc) Cách2: DAB

 

VìA,O,E,B,Dcùngthu

    AEDBEDABDBAD ===

  BADDFC =

) Suyra,   AEDDFC = Do

Suyra   ACEAFE

 

= Xét

có:  D chung,   ACDDFE = Do đó DACDEF∆∆ ∽ (gg) c) Goi K là trung điểm của AC . Chứng minh ba điểm , EK và F thẳng hàng. Gọi N là giao điểmcủaCDvà(O). Khi đó KE // AN ( vì KE là đườngtrungbìnhcủa CAN∆ ) Mặtkháctacó   DCADFE = (vì DACDEF∆∆ ∽ ) ⇒ Tứ giácFAECnộitiếp. nên   FECFAC = (gócnộitiếpcùngchắn  FC ) mà   FACANC = (góctạobởitiatiếptuyếnvàdâycungvàgócnộitiếpcùngchắn  AC ) Do đó   FECANC = ⇒ FE // AN ( đồngvị) Qua E ta có KE // AN và FE // AN nên theo tiên đề Ơclit ta suy ra 3 điểmE,K,Fthẳng hàng.

a)Bêntrongmột tam giác đềucạnhbẳng 4 cho năm điểm.Chừngminhrằng trong năm điểm đó có hai điểmmàkhoảngcáchgiữachúngnhỏ hơn 2.

ố tự nhiên,,abc thỏa234 234 abc += .Chứngminhrằng,,abc đềuchiahếtcho6.

ộttậphợp S đượcgọilàcótínhchất T nếu S có đúng bốnphầntử vàvớimọiphầntử

thìítnh

ttronghaiph

hoặ

ba cạnh

ABBCCA

ràng ta có 4 tam giác đều cạnh bằng 2là AMK∆ , BMN∆ , CNK∆ , MNK∆ . Khi cho 5 điểmchovào4tamgiác,theonguyênlýDirchletcóítnhất 2 điểmnằ

9 Bài 5: (2,00 điểm)

b)Chocács

c)M

ủa S

ấ

ộ

ầntừ 1x

c1 x + cũng thuộc S . Chotậphợp{1;2;3;,;2022} X =… .Tínhsố tấtcả cáctậpconcótínhchất T (nêutrên)củatập X . Lời giải a)Bêntrongmột tam giác đềucạnhbẳng 4 cho năm điểm.Chứngminhrằng trong năm điểm đó có hai điểmmàkhoảngcáchgiữachúngnhỏ hơn 2. Gọi ,, MNK lần lượt là trung điểm của

Rõ

mtrongmột tam giác đềunóitrên. Hai điểmnàynằmtrongmột tam giác đềucạnhlà2nênkhoảngcáchgiữachúngnhỏ hơn 2. Vậytồntạiítnhất hai điểmmàkhoảngcáchgiữachúngnhỏ hơn 2. b) Chocácsố tự nhiên ,, abcthỏa 234234 abc += .Chứngminhrằng ,, abc đềuchiahếtcho6. Tacó:234 234 abc += (*) K N M A B C

cũng thuộcS. Chotậ

ả cáctậpconcótínhchất T (nêutrên)củatập

Taxétmộttậphợp S

ồ

abcd .Khôngmấttínhtổngquát,giả sử a<b<c<d thì

d=c+1

10 Từ (*)suyra3b3chẵn ⇒ b3chẵn ⇒ bchẵn ⇒ b  2 ⇒ b3  8 ⇒ 4c43b3  4 ⇒ 2a2  4 ⇒ a2  2 ⇒ a  2 Do đó 2a2  8 ⇒ 4c4  8 ⇒ c  2 Giả sử ckhôngchiahếtcho3. Khí đó 2222 1(mod3)44(mod3)24(mod3)2(mod3) ccaa ≡⇒≡⇒≡⇒≡ (vôlývìsố chính phương khichia3chỉ cósố dư là 0 hoặc1) Vậyc  3 ⇒ 4c43b3  3 ⇒ 2a2  3 ⇒ a2  3 ⇒ a  3 ⇒ 4c42a2  9 ⇒ 3b3  9 ⇒ b3  3 ⇒ b  3 Mà(2,3)=1 Vậy a, b, c đềuchiahếtcho6. c)MộttậphợpS đượcgọilàcótínhchất T nếu S có đúng bốnphầntử vàvớimọixthuộc S thìítnhấtmộttronghaiphầntừ 1 xhoặc 1x +

phợp{1;2;3;,;2022} X =… .Tínhsố tấtc

X .

m { };;;

b=a+1 và

Tachỉ cầnchọn a, c thì b, d cũng xác địnhnêntachỉ cần đếmsố bộ (a,c)saocho { }1,2,...,2019a ∈ ,c>a+1 Với { }1,2,...,2009ak=∈ ⇒ { }2,...,2021ck∈+ ⇒ có 2021(k+2)+1=2020k Chokchạytừ 1 đến2019rồicộnglạithìsố cáchchọn S củaXthỏatínhchất T là: 2019+2018+…+1=2019.20202039190 2 =

Đáp án

Câu 1: Trên đường tròn có bán kính R, độ dàilcủacungcósố đo nº đượctínhtheocông thức nào dưới đây?

A. l=2πR B 360 lRn π = C 180 lRn π = D 2 360 lRn π = Câu 2:Vớimọisố thựca,côngthức nào sau đây đúng?

A. 2 aa = . B. 2 aa =− C. 22 aa = D. 2 aa = Câu 3: Phương trình bậchai250 xx+−= cótổnghainghiệmbằng:

A 1 B 1 C 1 2 D 5 Câu 4: Điểm nào dưới đây thuộc đồ thị 4x2y = ?

A.(1;4) Q . B.(4;1) P . C.(1;4) M . D.(4;1) N . Câu 5:Trongcáchàmsố dưới đây, hàm số nàolàhàmsố bậcnhất?

A 3y = B 32yx = C 2 y x = D 14x6y =+ Câu 6:Cặpsố ( )00 ; xy nào dưới đây là nghiệmcủa phương trình 2xy+= ?

A ( )1;2 B ( )1;1 C ( )2;2 D ( )2;1 Câu 7:Chotamgiác ABC vuôngtại A ,có  030B = và2 BC = (thamkhảohìnhvẽ). Đồ dài cạnhACbằng

SỞ GIÁO DỤC VÀ ĐÀO TẠO KIÊN GIANG KỲ THI TUYỂN SINH VÀO LỚP 10 THPT CHUYÊN NĂM HỌC 2022 2023 ĐỀ CHÍNH THỨC (Đề thicó04trang) MÔN THI: TOÁN Thờigianlàmbài:120phút,khôngkể thời gian chép đề Ngàythi:15/6/2022 Mã đề 101 I.TRẮC NGHIỆM (3.0 điểm; gồm 15 câu hỏi trắc nghiệm một lựa chọn) Thísinhkẻ bản sau đây vào giấy thi và điền đáp án củacâuhỏi tương ứng Câu 123456789101112131415

A 23 3 B 3 C 23 D 15 30° A B C

ucaoh,th

tíchVc

ahìnhtr

trình

Câu 8:Hìnhtrụ có bán kính đáy bằngrvàchiề

ể

ủ

ụ bằng A. 12 3 Vrh =π . B. 2 Vrh =π . C. Vrh =π . D.2Vrh =π . Câu 9:Nếuhaisố cótổngbằng17vàtíchbằng30thìhaisố đó là nghiệmcủa phương

bậc hai nào dưới đây? A 217x300x −−= B 217x+300x −= C 217x+300x += D 217x-300x += Câu 10: Cho đườngtròn(O),haidâyABvàCDcắtnhautại điểm E như hình vẽ bên dưới. Biếtsố đo góc  035AEC = vàsố đo cung nhỏ  DB bằng030.Tínhsố đo cung  AmC . A. sđ  0101AmC = B. sđ  0100AmC = C. sđ  040AmC = D. sđ  065AmC = Câu 11:Ngày04061983,anhemnhàMônggônfiê(Montgolfỉe) ngườiPhápphátminh rakhinhkhícầudùngkhôngkhínóng.Coikhinhkhícầunàylàhìnhcầu đườngkính 11m. Diệntíchmặtkhinhkhícầu đó bằng A. 484 3 π . B. 121 3 π . C.121π . D.484π . Câu 12:ChoParabol(P):2 xya = có đồ thị như hình vẽ bên dướivà(3:3) A thuộc(P) Giátrị củasố thựcalà A 3. B 1 3 C 1 D 1 3 m 35° D B O E A C

Câu 13: Điềukiện để thamsố m củahệ phương trình x31 2x4 my y +=  += cónghiệmduynhấtlà A. 3 2 m ≠ . B.2 m ≠ . C. 2 3 m ≠ . D.6 m ≠ Câu 14:Gọi giao điểmcủa hai đườngthẳng1 yx=+ và24 yx=− là00(;)Mxy .Giátrị của 00xy + bằng A 7. B.11. C.3. D 9. Câu 15:ChotamgiácABCvuôngtạiAcóAB=9cm,AC=12cm(như hình vẽ bên dưới) Độ dài đườngcaoAHbằng A 5cm. B.7,2cm. C.6,4cm D 5,4cm II. TỰ LUẬN (7,0 điểm; gồm có 05 bài) Bài 1 (1,5 điểm) a)Rútgọnbiểuthức ( ) 8122233.M =−−− b)Tínhgiátrị củabiểuthức 11 1: 1 a N aa  =−  (với0;1 aa>≠ )khia=2022. Bài 2 (1,5 điểm).ChoParabol(P):2 2xy = và đườngthẳng(d):10x12 y =− a)Vẽ đố thị (P)trênhệ trụctọa độ Oxy. b)Biết đườngthẳng(d)cắt(P)tại hai điểmphânbiệt.Tìmtọa độ của hai điểm đó. Bài 3 (1,5 điểm). a)Tìmthamsố m để phương trình 2230xxm++−= cóhainghiệm12 , xx thỏamãn 1212 xxxx += . 129 HC B A

b)Tại Đạihộithể thao Đông Nam Á SEAGAMES31diễnra ở ViệtNamtrongtháng5 năm 2022.Bantổ chức đã cho sảnxuấtlinhvậtSaolabằngthúnhồi bông để tặngcho các đoàn thể thao,vận động viên giành huy chương và bán cho các cổ độngviênlàmquà lưu niệm.Một xưởng may đượcBantổ chứcSEAGames31giaosảnxuấtmột lượng linhvậtSaolanhồibôngnhất định. Xưởngmaygồmcóhaitổ sảnsuất,trongtuần đầu hai xưởng đã sảnxuất được1200linhvậtSaolanhồibông.Sangtuầnthứ haitổ thứ nhất sảnxuất vượt20%vàtổ thứ haisảnxuất vượt40%sovớituầnthứ nhất, do đó đếnhết tuầnthứ haisố lượngthúnhồibôngmàhaitổ sảnxuất đượclà1550.Tínhsố lượnglinh vậtSaolanhồibôngmàhaitổ sảnxuất đượctrongtuầndầutiên.

Bài 4 (2,0 điểm). ChotamgiácABCcântạiA,cóbagócnhọnvànộitiếp đườngtròn (O;R). Hai đườngcaoAE,(BF;EBCFAC ∈∈ )cắtnhautạiH,tiaBFcắt đườngtròn(O) tạiM.HaitiaAMvàBCcắtnhautạiS.

a)Chứngminhtứ giácABEFnộitiếptrongmột đườngtròn.

b)Chứngminh

ASBACM =

ọi I là trung điểmcủaAB.ChứngminhIFlàtiếptuyến đườngtrònngoạitiếptam giácFHC.

Bài 5 (0,5 điểm).Cầuthangxoắn ốc(cầuthangcuốntròn)làcầu thang đượcthiếtkế theo hìnhxoắn ốcvớicácbậctừ dướilêntrênxoayquanhmộttrụccố địnhcó phương thẳng đứng.

Vớithiếtkế cầuthangnàygiúptiếtkiệm đượcdiện tích không gian, đặcbiệtcácmẫucầu thangxoắn ốcphùhợpvớinhàphố códiệntíchnhỏ,cótínhthẩmmỹ vàtiếtkiệm đượcchi phíkhixâydựng. Để thiếtkế mộtcầuthangxoắn ốcgồm11bậcthángvớidiệntíchmặt bằngchophépchỉ làmộthìnhvuôngcócạnh 1m ngườithợ đã chia hình tròn đườngkính 1mthành11hìnhquạttrònbằngnhau(mỗimộthìnhquạt tròn tương ứngvớimộtbậccầu tháng), sau đó ngườithợ cố địnhcácbậccủacầuthangquangmộttrụcthẳng đứng,mỗibậc cầuthangcáchnhau15cm(thamkhảohìnhvẽ bên dưới)

Vớidiệntíchmặtbằngvàkhoảngcáchgiữacácbậccầu thang như trên, ngườithợ cầnthiết kế cầuthangxoắn ốcchomột gia đình, biếtrằng ngườicaonhấttrongnhàkhoảng1,70m đứngthẳngtrênbậccầuthangthấpnhất mà đầukhôngbivachạmvớibậccầuthang ở dỉnh đầu đỉnh đầu.Theoyêucầunày,tacầnchiahìnhtrònnàythànhítnhấtbaonhiêuhìnhquạt trònbằng nhau, khi đó hãy tính độ dài đoạnAB?

 

c)G

ĐÁP ÁN I. TRẮC NGHIỆM (3,0 điểm) Câu 123456789101112131415 Đáp án CDACDBDBBBCDDBB Câu 1:.2 360180 nRn lRC π π ==→ Câu 2: 2 aaD =→ dấu“ ” để đảmbảo VP luôn dương Câu 3:121 b xx a +=−=− (Theo ĐL Vi et)Vậy đáp án A Câu 4: Phương án A, B loạivìy<0khôngTM.ThayvàoCvàDtacóCphùhợp Đáp ánC Câu 5: Đáp án D đúng vì hệ số a ≠ 0vàbậc mũ củaxlàbậc1. Câu 6: Đáp án B vì 00112xy+=+= Câu 7:  1 .sin2.sin302.1 2 ACBCBoD ====→ Câu 8:2VrhB π =→ Câu 9: 12 12 x3030 1 1717 1 cc Pxc aB bb Sxxb a  ====→=  →  =+===→=−  Câu 10:       dd00 dEd2.dEd2.3530100 2 sAmCsBDosACsAmCsACsBDB =⇔=+=+=→ Câu 11:2211121 SdC πππ ===→ Câu 12: ( ) ( ) 221 (3;3);:ax3.(3)933 APPyaaaD −∈=→−=−⇔=−→=−→ Câu 13: 3 6 ''21 abm mD ab ≠⇔≠→≠→ Câu 14:00000 12x-45;1516;5611 xxyxxy +=⇔==+=+=+=+= Phương án đúng là D Câu 15: 2 22222222 11111916253636 7,2 12936365 5 AHB AHABAC + =+=+==→===→ II. TỰ LUẬN (7,0 điểm; gồm có 05 bài) Bài 1 (1,5 điểm) c)Rútgọnbiểuthức ( ) 8122233.M =−−−