A Conquista - Matemática - Volume 4

RECURSO EDUCACIONAL DIGITAL

Ensino Fundamental - Anos Iniciais

Área: Matemática

MATEMÁTICA 4

Componente: Matemática

JOSÉ RUY GIOVANNI JÚNIOR

Licenciado em Matemática pela Universidade de São Paulo (USP). Professor e assessor de Matemática em escolas de Ensino Fundamental e Ensino Médio desde 1985.

A conquista – Matemática – Recurso Educacional Digital – 4o ano (Ensino Fundamental – Anos Iniciais)

Copyright © José Ruy Giovanni Júnior, 2021

Direção-geral Ricardo Tavares de Oliveira

Direção de Conteúdo e Negócios Cayube Galas

Direção editorial adjunta Luiz Tonolli

Gerência editorial Natalia Taccetti

Edição Nubia de Cassia de Moraes Andrade e Silva (coord.)

Leticia Mancini Martins, João Alves de Souza Neto

Preparação e revisão de textos Viviam Moreira (sup.)

Adriana Périco, Caline Devèze, Camila Cipoloni, Carina Luca, Fernanda Marcelino, Fernando Cardoso, Graziele Ribeiro, Paulo José Andrade

Gerência de produção e arte Ricardo Borges

Design Daniela Máximo (coord.)

Arte e produção Isabel Cristina Corandin Marques (coord.)

Coordenação de imagens e textos Elaine Bueno Koga

Licenciamento de textos Erica Brambilla

Iconografia Jonathan Santos

Coordenação de audiovisuais Diego Vieira Cury Morgado de Oliveira

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil)

Giovanni Júnior, José Ruy

A conquista [livro eletrônico] : matemática : 4o ano : ensino fundamental : anos iniciais / José Ruy Giovanni Júnior. – 1. ed. – São Paulo : FTD, 2021.

PDF

Área: Matemática.

Componente: Matemática.

ISBN 978-85-96-03237-7 (recurso educacional digital professor – coleção)

1. Matemática (Ensino fundamental) I. Título. 21-90874 CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Cibele Maria Dias - Bibliotecária - CRB-8/9427

EDITORA FTD

Rua Rui Barbosa, 156 – Bela Vista – São Paulo-SP CEP 01326-010 – Tel. 0800 772 2300 Caixa Postal 65149 – CEP da Caixa Postal 01390-970 www.ftd.com.br central.relacionamento@ftd.com.br

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Carta ao professor

Olá, professor! Seja bem-vindo ao Recurso Educacional Digital!

O Recurso Educacional Digital é um material que tem como objetivo auxiliar o seu trabalho e ampliar as possibilidades de planejamento das aulas de Matemática nos Anos Iniciais do Ensino Fundamental O Recurso Educacional Digital em PDF apresenta subsídios para enriquecer o dia a dia em sala de aula, com propostas de abordagens que complementam os materiais já utilizados em sala de aula e que contribuem para a atualização contínua do professor.

Os conteúdos do Recurso Educacional Digital foram formulados com base nos componentes de Literacia e Numeracia da Política Nacional de Alfabetização (PNA), nas competências gerais da Educação Básica, nas competências específicas de Matemática para o Ensino Fundamental, nos objetivos de aprendizagem e nas habilidades correspondentes aos Anos Iniciais do Ensino Fundamental, presentes na Base Nacional Comum Curricular (BNCC)

É importante enfatizar que todas as propostas deste material são sugestões Portanto, o professor tem total liberdade para adequar cada material à sua realidade escolar.

O conteúdo em PDF deste material digital apresenta quatro recursos pedagógicos. São eles:

• Plano de desenvolvimento anual: contém uma proposta de planejamento de conteúdos, de habilidades e de componentes essenciais para a alfabetização, elaborada em formato de um quadro organizado em bimestre, trimestre e semestre A ordem e os conteúdos listados são sugestões elaboradas com o objetivo de fornecer subsídios complementares a outros materiais didáticos. Nesse sentido, este plano pode ser adaptado à realidade da escola ou da turma a critério do professor. O plano, também, contém sugestões de práticas de ensino em sala de aula e texto formativo sobre avaliação.

• Sequências didáticas: contempla duas sequências por bimestre, que consistem em uma proposta de conteúdo para desenvolver competências gerais, competências específicas da área da Matemática e suas Tecnologias, as habilidades dessa mesma área e os componentes essenciais para a alfabetização Cada sequência é composta de um descritivo, uma listagem de objetivos de aprendizagem, um plano de aula - que contém uma listagem das aulas, dos materiais e dos recursos que serão utilizados nas aulas, bem como dos componentes e das habilidades trabalhadas - e a descrição aula a aula do encaminhamento a ser trabalhado, das atitudes e dos procedimentos que os alunos devem realizar sob mediação do professor, de sugestões de atividades.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• Relatórios e indicadores do acompanhamento da aprendizagem: traz subsídios para auxiliar o professor na produção de relatórios e de indicadores do acompanhamento da aprendizagem Os indicadores do acompanhamento da aprendizagem são apresentados em modelos de fichas avaliativas que servem como sugestões para que o professor possa aplicar conforme a realidade da escola e da turma para auxiliá-lo no processo de avaliação coletiva e individual dos alunos. São elas: ficha de avaliação diagnóstica (usada para obter um diagnóstico dos conhecimentos prévios dos alunos), ficha de acompanhamento das aprendizagens (permite observar a evolução de aprendizados ao longo do processo de ensino e aprendizagem), ficha de verificação de resultados (permite observar quais objetivos de aprendizagem foram atingidos ao final do ano letivo) e a ficha de acompanhamento do desenvolvimento de competências socioemocionais (permite observar quais habilidades socioemocionais foram atingidas ao final do ano letivo). Além disso, nesta seção, são apresentadas informações sobre como trabalhar com os dados obtidos, bem como apresentar esses dados para gestores escolares, professores e responsáveis pelos alunos

• Catálogo de audiovisuais: apresenta informações a respeito do conjunto de materiais audiovisuais que acompanha este material. O catálogo tem como objetivo complementar e aprofundar a prática pedagógica e pode ser utilizado de acordo com as características da turma e do planejamento do professor. Para cada audiovisual são apresentadas orientações introdutórias, bem como propostas de atividades que explorem o uso de cada recurso em sala de aula.

A seguir estão listados os principais temas trabalhados neste volume:

• representação e contagem até a ordem de dezenas de milhar;

• adição e subtração;

• multiplicação e divisão;

• medidas de comprimento, de massa e de capacidade;

• medidas de tempo e de temperatura;

• números da forma decimal e fracionária;

• noções de probabilidade e de estatística;

• ângulos;

• simetria

Esperamos que este material possa ser usado para enriquecer o dia a dia em sala de aula, auxiliando na sua prática docente e contribuindo para a formação de seus alunos.

Bom trabalho!

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Instrumentos pedagógicos

Plano de desenvolvimento anual

O Plano de desenvolvimento anual é uma proposta de planejamento elaborada em formato de um quadro organizado em bimestre, trimestre e semestre. Nele, são indicados os conteúdos, as habilidades da Base Nacional Comum Curricular (BNCC) e os componentes essenciais para a alfabetização a serem desenvolvidos em cada período. É importante enfatizar que a organização proposta é uma sugestão e que o professor pode adaptá-la de acordo com a realidade da turma com a qual está trabalhando.

Além do quadro, este plano também contém as seguintes seções:

• Práticas de ensino na sala de aula: são apresentadas sugestões gerais de estratégias e de atitudes que podem ser incorporadas pelo professor para alcançar os objetivos de aprendizagem pretendidos;

• Avaliação: composta de um texto formativo para o professor no qual são apresentadas possibilidades para avaliação diagnóstica, processual e formativa;

• Para saber mais: lista de sugestões complementares de sites , vídeos, livros, artigos, séries, revistas ou filmes que podem ajudar o professor a desenvolver o trabalho em sala de aula.

Freepik.com

O planejamento é uma etapa muito importante das atividades docentes.

º semestre

1º trimestre 1º bimestre

Aprendizagens desenvolvidas no 4º ano

Números e o Sistema de Numeração Decimal

• Compreender a utilização de números naturais para indicar quantidade, ordem e código.

• Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.

• Compor e decompor números naturais até a ordem de dezenas de milhar estabelecendo relação com o Sistema de Numeração Decimal.

• Comparar números naturais até a ordem de dezenas de milhar.

• Estabelecer relação entre números naturais e a reta numérica.

Adição e subtração

• Compreender as ideias da adição (juntar, acrescentar) e da subtração (retirar, separar, comparar e completar).

• Resolver e elaborar situações-problema que envolvam ideias de adição (juntar, acrescentar) e subtração (retirar, separar, comparar e completar).

• Utilizar diferentes estratégias de cálculo de adição e subtração (cálculo mental, algoritmo, estimativas).

• Compreender as relações inversas entre adição e subtração.

Multiplicação

• Compreender ideias da multiplicação (adição de parcelas iguais, disposição retangular, proporcionalidade).

• Resolver e elaborar situações-problema envolvendo a multiplicação e utilizando-se de diferentes estratégias (cálculo mental, algoritmo, estimativa).

• Entender e utilizar o padrão de regularidade nas multiplicações por 10, 100 e 1 000.

• Identificar sequências numéricas compostas de números múltiplos de um número natural.

2º bimestre

• Efetuar a multiplicação de dois números naturais que tenham pelo menos dois algarismos.

Divisão

• Compreender a ideia de repartir em partes iguais da divisão

• Resolver e elaborar situações-problema que envolvam a divisão como repartição em partes iguais e cujo divisor tenha no máximo dois algarismos.

• Utilizar estratégias de cálculo diversas (cálculo mental, algoritmo, estimativa) na resolução de problemas envolvendo a operação de divisão.

• Compreender as relações inversas entre multiplicação e divisão.

• Resolver expressões numéricas envolvendo as quatro operações.

BNCC

EF04MA01

EF04MA02

EF04MA03

EF04MA04

EF04MA05

EF04MA11

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Compreensão de textos.

• Produção de escrita.

BNCC

EF04MA06

EF04MA07

EF04MA08

EF04MA09

EF04MA10

EF04MA12

EF04MA13

EF04MA14

EF04MA15

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento do vocabulário.

• Produção de escrita.

3 º bimestre

Grandeza e medidas

• Ler, interpretar e registrar medidas padronizadas de comprimento, massa e capacidade.

• Realizar comparação de conversão entre unidades de medida de comprimento, de massa e de capacidade.

• Comparar superfícies de figuras por meio de visualização ou sobreposição de desenhos em malhas quadriculadas ou triangulares, incluindo o uso de tecnologias digitais.

• Relacionar e utilizar unidades de medida de tempo (hora, minuto e segundo).

• Explorar o termômetro e reconhecer grau Celsius como medida de temperatura.

• Ler, interpretar e representar dados em tabelas e gráficos de barras ou colunas.

• Coletar, classificar e representar dados de uma pesquisa.

Frações

• Compreender frações em situações que indicam a relação parte-todo.

• Reconhecer frações unitárias mais usuais (1/2, 1/3, 1/5, 1/10 e 1/100).

• Identificar representações de frações na reta numérica.

• Fazer a leitura de um número escrito na forma de fração

Geometria

• Reconhecer ângulos retos e não retos em figuras poligonais por meio de diferentes suportes (dobraduras, esquadros, softwaresde geometria).

• Localizar posições de pessoas ou objetos no espaço com base em diferentes pontos de referência.

• Representar e descrever trajetos representados em diferentes suportes (maquetes, mapas, plantas baixas, esquemas em malha quadriculada).

• Reconhecer características de prismas e pirâmides e associá-los às suas planificações.

• Reconhecer figuras que apresentem simetria, bem como identificar eixos de simetria de uma figura.

Números na forma decimal e probabilidade

• Identificar a escrita de números que representam partes do inteiro.

• Relacionar inteiros, décimos e centésimos entre si.

• Representar na forma decimal uma fração decimal.

• Resolver e elaborar problemas que envolvam números decimais.

• Relacionar números decimais ao sistema monetário

• Ler e interpretar dados em tabelas ou gráficos.

• Analisar eventos aleatórios e identificar resultados que têm maior chance de ocorrência.

BNCC

EF04MA20

EF04MA21

EF04MA22

EF04MA23

EF04MA24

EF04MA27

EF04MA28

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento do vocabulário.

• Compreensão de textos.

• Produção de escrita.

BNCC

EF04MA16

EF04MA17

EF04MA18

EF04MA19

EF04MA25

EF04MA26

EF04MA27

Componentes essenciais para a alfabetização

• Fluência em leitura oral.

• Desenvolvimento do vocabulário.

• Compreensão de textos.

• Produção de escrita.

Práticas de ensino na sala de aula

Nesta seção, serão apresentadas algumas sugestões gerais de estratégias de ensino e de atitudes que contribuem para a aprendizagem dos alunos e promovem o alcance dos objetivos de aprendizagem, das habilidades e das competências desta etapa do Ensino Básico

Oralidade

Nos Anos Iniciais do Ensino Fundamental, é importante que a oralidade seja desenvolvida por meio de atividades que incentivem, por exemplo, a troca de ideias entre os próprios alunos, a explicação ou a justificativa de raciocínios ou resoluções e a socialização de opiniões e reflexões.

Saber se comunicar efetivamente, com objetividade e coerência, é uma habilidade importante não apenas no ambiente escolar mas, também, para a vida cotidiana e para o exercício pleno da cidadania.

A prática da oralidade deve perpassar por diversos atributos: desenvolver a capacidade de ouvir e prestar atenção à fala do colega; respeitar os turnos de fala; identificar e usar corretamente os momentos de interrupção ou de resposta em uma conversa ou discussão; desenvolver a capacidade de recontar histórias ou argumentos, como interagir e reagir a diferentes tipos de situações que envolvam a oralidade (conversar com colegas, fazer apresentação na sala de aula, discutir um assunto sério, fazer uma dramatização e uma exposição para outras turmas ou para os responsáveis).

Sempre que possível, ao realizar discussões, incentivar a manutenção de um ambiente descontraído e agradável, organizando os alunos em uma roda, por exemplo. O uso de roda de conversas é importante para que os alunos possam ser vistos pelos colegas quando exercem sua oralidade. Atividades em que o aluno se levanta e vai até a frente da turma para falar devem ser introduzidas aos poucos até que se tornem parte da rotina da sala de aula.

rawpixel.com/Freepik.com

É importante que a oralidade não seja associada apenas a ir até a frente da turma para falar, mas, também, seja incentivada em atividades lúdicas e em situações de socialização de maneira a favorecer a troca de ideias.

disponibilizado em licença aberta do tipo

Rotina de sala de aula

Além dos conteúdos exigidos pelos documentos norteadores e pelos currículos escolares, os alunos deverão aprender, ainda no Ensino Fundamental, a organizar seus estudos e suas rotinas diárias. Essa prática é, também, chamada de "aprender a aprender", significando o aprendizado de estratégias de organização e de estratégias de estudo que auxiliam diretamente no aprendizado não só do conteúdo de uma área do conhecimento, mas de todas as áreas.

Há diversas atitudes que podem ser tomadas em sala de aula para auxiliar os alunos nessa prática. Por exemplo, apresentar a agenda ou a rotina do dia no início da primeira aula contribui para que os alunos tenham um panorama do que estudarão no dia, entendam como priorizar tarefas e qual é a importância da organização do tempo. Além disso, abre espaço para um diálogo em que os próprios alunos possam fornecer sugestões para o professor, como a troca na ordem de atividades do dia.

Esta proposta, também, ajuda a garantir que a participação dos alunos em sala de aula ocorra de maneira efetiva, pois a rotina da turma deixa de ser algo de responsabilidade apenas do professor e passa a ser uma construção colaborativa de todos os integrantes desse processo: alunos e professores.

A agenda ou rotina da turma pode consistir em uma listagem numerada das atividades programadas para o dia, escrita na lousa ou em outro suporte que permita a visualização por todos. É importante incluir, nessa listagem, os momentos de alimentação e diversão (hora do lanche, visita a um parque, hora da brincadeira ou atividade envolvendo jogos etc.) para que os alunos compreendam a separação entre as situações e as posturas que devem adotar de acordo com cada contexto.

Ao seguir esta proposta, é importante que o tempo reservado para checar a agenda do dia e discuti-la no começo da primeira aula seja breve e objetivo. Ao completar cada aula ou atividade listada, marcar na agenda do dia com um símbolo, que pode ser, por exemplo, o símbolo de checado (✓) para indicar que a atividade foi concluída. Essa atitude fortalece o senso de realização e permite que os alunos ampliem suas noções da passagem do tempo pela observação da sequência de atividades ou aulas realizadas.

A agenda do dia, também, fornece um aprendizado importante sobre rotinas e planejamento: como lidar com mudanças de planos e eventos imprevisíveis. É importante que os alunos entendam que o planejamento da rotina é algo que deve ser usado em favor deles, mas que não deve ser algo imutável. Imprevistos acontecem e eles devem aprender a lidar com isso. Por exemplo, é possível que uma atividade ao ar livre seja programada e chova, impedindo que a atividade seja realizada com segurança naquele dia.

Para lidar com eventualidades, é importante ter um acervo de atividades diversas, individuais ou em grupos, que podem ser utilizadas para ocupar tempos ociosos ou ocupar os alunos que finalizam atividades mais rapidamente, permitindo que os outros alunos tenham tempo para realizar as atividades no tempo deles.

Glossário ou dicionário ilustrado

Para garantir que os alunos se apropriem de nomes e de termos adequados na Matemática é imprescindível usar o vocabulário correto. Nos Anos Iniciais do Ensino Fundamental, ainda, é comum que alguns alunos chamem tudo o que é redondo de círculo ou chamem o cubo de quadrado. Em situações assim, é fundamental corrigir a fala dos alunos com os termos corretos; por exemplo, dizer "cubo" quando algum aluno chamar um cubo de quadrado, até que eles se apropriem do nome e passem a usá-lo de modo correto.

Uma proposta para consolidar esse aprendizado e favorecer o desenvolvimento do vocabulário dos alunos é a criação de um glossário ou dicionário ilustrado da turma. Para isso, pode-se usar uma pasta, um cartaz ou um varal em que o professor escreve a palavra aprendida e um aluno é sorteado para ilustrar o significado da palavra. Sempre que um aluno utilizar o termo incorreto, o glossário pode ser retomado.

KamranAydinov/Freepik.com

Atividades envolvendo criatividade e materiais artísticos enriquecem o repertório dos alunos e favorecem o desenvolvimento de habilidades motoras

Grupos de estudo ou de revisão

Para ter condições de intervir no processo de formação dos alunos de maneira eficaz, é imprescindível acompanhar de modo contínuo as aprendizagens deles, percebendo rapidamente suas dificuldades e seus avanços. No momento em que constatar quais são os alunos que necessitam de maior investimento para alcançar as aprendizagens esperadas, iniciar um trabalho com abordagem diferenciada, para que todos tenham condições de avançar em suas aprendizagens.

Uma estratégia de sala de aula que se mostra bastante eficaz é agrupar os alunos de acordo com as suas necessidades de revisão, em um momento específico da aula, pelo menos uma vez na semana. O intuito disso é retomar o assunto por meio de jogos, de atividades lúdicas ou de situações-problema que tenham como objetivo auxiliar grupos de alunos em suas dificuldades específicas.

Embora essa estratégia exija mais desenvoltura da sua parte, traz resultados nas aprendizagens dos alunos que compensam o investimento de tempo por potencializar o sucesso de todos os envolvidos no processo de ensino-aprendizagem.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Avaliação

O processo de avaliação deve estar presente em todo e qualquer momento em que a aprendizagem escolar estiver envolvida. Antigamente, o processo avaliativo era considerado um procedimento de medida da aprendizagem em que se verificava apenas se o aluno atingiu os requisitos mínimos para progredir com os estudos.

Ao longo do tempo, as avaliações passaram por um processo de ressignificação em que assumiram o papel de verificar o progresso do aluno, ao mesmo tempo que sinalizam a necessidade de novas estratégias para o sucesso do processo de ensino e aprendizagem

Atualmente, é quase consenso a compreensão de que a avaliação escolar não deve apenas verificar se o aluno atingiu os requisitos mínimos para seguir para o próximo ciclo ou se atingiu os objetivos mínimos definidos pelo currículo. Os resultados do processo avaliativo não só representam o panorama da aprendizagem individual dos alunos, como também podem servir como fonte de dados a respeito do trabalho desenvolvido pelos profissionais da escola. Tais dados podem dar direcionamento para a autorregulação do processo de ensino, possibilitando ao professor e demais profissionais da escola refletir sobre suas práticas e procurar estratégias para desenvolvê-las e ampliá-las.

Para que haja um ensino de qualidade, é essencial compreender como os alunos lidam com o conhecimento e quais são as habilidades e necessidades individuais que apresentam, sendo importante que o professor reveja os processos de modo a permitir que os alunos possam superar eventuais dificuldades.

A avaliação não pode se resumir a uma prova isolada no processo de ensino e aprendizagem. É preciso utilizar instrumentos avaliativos diversificados que sejam aplicados ao longo do ano letivo. Além disso, fazer o registro periódico de observações o ajudará a acompanhar o desenvolvimento dos alunos.

Sendo assim, é importante que o processo avaliativo seja, de fato, um processo com diversos e variados momentos passando por: avaliações iniciais que permitam obter um diagnóstico dos conhecimentos prévios; avaliações recorrentes de processo que permitam observar a evolução de aprendizados, bem como identificar pontos de ampliação de conhecimento ou pontos que precisam ser retomados e reforçados; e, por fim, avaliações de resultado que permitam observar o desenvolvimento do aluno fornecendo condições de elaborar estratégias para o ano seguinte.

No processo de avaliação, também, é importante que o aluno conheça os resultados obtidos em seu desenvolvimento individual, ciente do que já é capaz de realizar sozinho e como pode melhorar para avançar, assumindo o papel de protagonista. Nesse sentido, o processo de avaliação inclui, ainda, a autoavaliação do aluno e a participação dos familiares.

A inclusão dos familiares no conhecimento dos resultados do processo avaliativo permite que estejam cientes dos avanços e até mesmo das dificuldades dos alunos, e

poderão cooperar com a escola apoiando adoções de estratégias que favoreçam melhores resultados.

Para auxiliar no processo de avaliação, este material apresenta sugestões de fichas e outros materiais de acompanhamento de aprendizagens na seção Relatórios e indicadores do acompanhamento da aprendizagem

Para saber mais

• ALRØ, Helle; SKOVSMOSE, Ole. Diálogo e aprendizagem em educação matemática Belo Horizonte: Autêntica, 2006. O livro trata da importância do diálogo entre professores e alunos como modo de elevar a qualidade das aprendizagens nas aulas de Matemática.

• BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem teórico-prática Porto Alegre: Penso, 2018. Obra de referência para aprofundar a compreensão do que são as metodologias ativas, do porquê a utilização delas na educação se faz necessária e de como a incorporação delas nas aulas de Matemática é favorável a experiências de experimentação e compartilhamento.

• CARNEIRO, Reginaldo Fernando; SOUZA, Antonio Carlos de; BERTINI, Luciane de Fatima (org.) A Matemática nos anos iniciais do ensino fundamental [livro eletrônico]: práticas de sala de aula e de formação de professores. Brasília, DF: SBEM, 2018. (Coleção SBEM, 11). Disponível em: http://www.sbembrasil.org.br/files/ebook_matematica_iniciais.pdf

Acesso em: 5 dez. 2021.

A publicação, que faz parte da biblioteca do educador matemático da Sociedade Brasileira de Educação Matemática, traz comentários sobre práticas de sala de aula e formação de professores. O diferencial da obra é que, a esses comentários, já constam incorporadas características recomendadas na BNCC.

• CORSO, Luciana Vellinho; DORNELES, Beatriz Vargas. Memória de trabalho, raciocínio lógico e desempenho em aritmética e leitura. Ciências & Cognição, Rio de Janeiro, v 20, n. 2, p. 293-300, 2015.

No artigo, é retratada uma pesquisa cujos resultados indicaram conexões entre raciocínio lógico, leitura e memória de trabalho.

• MALUF, Maria Regina; CARDOSO-MARTINS, Cláudia (org.). Alfabetização no século XXI: como se aprende a ler e a escrever Porto Alegre: Penso, 2013. O texto auxilia a entender como se dá a aprendizagem dos processos de leitura e escrita, sendo uma das obras que embasaram a Política Nacional de Alfabetização (PNA).

• MATEMÁTICA multimídia. Áudios da coleção M3 Podcast Disponível em: https://anchor.fm/matematica-multimidia Acesso em: 5 dez. 2021.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

A coleção de podcastsMatemática Multimídia, produzida pelo Instituto de Matemática, Estatística e Computação Científica (IME) da Unicamp, apresenta diversos recursos educacionais para auxiliar professores.

• MATEMATIZOOM.Podcast Disponível em: https://www.youtube.com/channel/UCY4_E6YSgzjEpyLyJQMFGxQ Acesso em: 5 dez. 2021.

A coleção de podcastsMatematizoom, da Universidade do Estado de Santa Catarina (Udesc), utiliza a cientificidade lúdica para explicar conceitos variados envolvendo situações cotidianas atuais.

• NACARATO, Adair Mendes; CUSTÓDIO, Iris Aparecida (org.). O desenvolvimento do pensamento algébrico na educação básica [livro eletrônico]: compartilhando propostas de sala de aula com o professor que ensina (ensinará) matemática. Brasília, DF: Sociedade Brasileira de Educação Matemática, 2018. (Coleção SBEM, 12) Disponível em: http://www.sbembrasil.org.br/files/ebook_desenv.pdf. Acesso em: 5 dez. 2021. A publicação faz parte da Biblioteca do Educador Matemático da Sociedade Brasileira de Educação Matemática. Trata prioritariamente do desenvolvimento do trabalho com as habilidades relacionadas à unidade temática Álgebra da BNCC nos Anos Iniciais do Ensino Fundamental, visto que esse trabalho constitui um desafio para ser efetivado com adequação à faixa etária.

• NEVES, Iara Conceição B.etal.(org.). Ler e escrever: compromisso de todas as áreas. 9. ed. Porto Alegre: Editora da UFRGS, 2011. O livro esclarece como as atividades, em todas as áreas de conhecimento, podem favorecer de modo integrado a construção da competência leitora e a escrita dos alunos.

• SKOVSMOSE, Ole. Educação crítica: incerteza, matemática, responsabilidade Tradução: Maria Aparecida Viggiani Bicudo. São Paulo: Cortez, 2007. No livro, o autor defende o aspecto de criticidade existente no reconhecimento da potencialidade social que há na Educação Matemática.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Sequências didáticas

Sequência didática 1 • Números naturais até a ordem de dezenas de milhar

Nesta sequência didática, serão apresentadas situações que evidenciam a compreensão do valor posicional dos algarismos em números naturais e do papel do zero no Sistema de Numeração Decimal

Também serão desenvolvidas a leitura, a escrita, a comparação, a ordenação e a decomposição de números naturais de até cinco ordens e será proposto um jogo de bingo para trabalhar com números naturais maiores que 1 000.

Objetivos de aprendizagem

• Reconhecer o valor posicional de cada algarismo em números naturais de até cinco ordens representados na escrita com algarismos ou por extenso

• Comparar e ordenar números naturais de até cinco ordens representados na reta numérica.

• Utilizar o ábaco para compreender o valor posicional dos algarismos em números naturais de até cinco ordens.

• Elaborar um jogo de bingo para trabalhar com números naturais maiores que 1 000.

Plano de aulas

Aula 1: Trabalhar a escrita de números naturais, com mais de três ordens, em algarismo e por extenso. Diagnosticar conhecimentos prévios dos alunos sobre a ordem das unidades de milhar a fim de sanar possíveis dúvidas

Aula 2: Ordenar em ordem crescente números naturais com mais de três ordens Representar esses números naturais no Quadro de ordens e em uma reta numérica. Estabelecer relações entre números naturais e pontos de uma reta numérica. Propor aos alunos a construção de retas numéricas para representar números naturais da ordem das unidades de milhar.

Aula 3: Aprofundar por meio de atividade lúdica a compreensão da ordenação de números naturais de até cinco ordens (até a ordem de dezenas de milhar). Ordenar em ordem crescente os números naturais trabalhados e socializar os critérios adotados para fazer essa ordenação

Aula 4: Representar no ábaco números naturais de até cinco ordens (até a ordem das dezenas de milhar). Explorar no ábaco a decomposição de números naturais de até cinco ordens (até a ordem das dezenas de milhar). Determinar a composição desses números naturais cuja decomposição foi explorada anteriormente

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Aulas 5 e 6: Mobilizar as habilidades matemáticas cujo desenvolvimento foi favorecido ao longo da sequência didática, verificando se os objetivos de aprendizagem trabalhados foram alcançados pelos alunos

Aulas 7 e 8: Confeccionar quadros para utilizar no jogo de bingo, trabalhando sequências de números naturais até a ordem das dezenas de milhar com elementos ausentes a serem identificados e preenchidos

Componentes essenciais para a alfabetização: compreensão de textos e desenvolvimento de vocabulário

Competências gerais da Educação Básica: 1 e 4

Competência específica de Matemática: 3

Habilidades: EF04MA01 e EF04MA02.

Materiais necessários: ábaco, diversas fichas (confeccionadas previamente em folhas de papel sulfite ou outro tipo de papel mais resistente) com os algarismos de 0 a 9 (um algarismo em cada ficha), caixa para colocar essas fichas que serão sorteadas de modo aleatório, folhas de papel sulfite ou cartolina para a elaboração de quadros do jogo de bingo

Aula 1

Iniciar a aula solicitando aos alunos que citem números naturais com mais de três ordens Caso a escola disponha de infraestrutura tecnológica, como computadores ou tablets com acesso à internet, é oportuno propor aos alunos uma pesquisa de dados numéricos referentes a algumas grandezas, como a distância em metro entre duas cidades (dar preferência a cidades próximas da região onde se localiza a escola) ou a diferença em quilograma entre a massa de um elefante adulto e a massa de um elefante filhote

Registrar os dados numéricos na lousa e trabalhar com os alunos a escrita por extenso desses números naturais. Fazer esse registro a fim de realizar um diagnóstico acerca dos conhecimentos prévios dos alunos para sanar possíveis dúvidas sobre características do Sistema de Numeração Decimal até a ordem das unidades de milhar

Retomar que: a cada 10 unidades é formada 1 dezena (10 unidades); a cada 10 dezenas é formada 1 centena (100 unidades); a cada 10 centenas é formada 1 unidade de milhar (1 000 unidades).

Em seguida, propor aos alunos um ditado de números naturais da ordem das unidades de milhar. Pedir que escrevam os números em algarismos e por extenso. Para isso, dar uma pausa entre o ditado de um número e outro. Para esse ditado, por exemplo, sugerem-se os números: 4 000 (quatro mil); 1 000 (mil ou um milhar); 6 000 (seis mil); 9 000 (nove mil); 2 000 (dois mil); 7 000 (sete mil); 3 000 (três mil); 5 000 (cinco mil); 8 000 (oito mil)

Finalizado o ditado, organizar a turma em grupos de quatro integrantes para que compartilhem os registros e estabeleçam comparações entre eles de modo a identificar eventuais inconsistências ou equívocos, bem como fazer a autocorreção da tarefa. Determinar um tempo para essa troca. Incentivá-los a refletir sobre as próprias

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

aprendizagens e a identificar como aplicar esses conhecimentos em diferentes contextos de modo que a competência geral da Educação Básica 1 seja mobilizada

É importante mediar esse momento de modo a validar a correção em todos os grupos. Essa validação pode ser feita por meio da correção registrada na lousa escrevendo as respostas e motivando a participação da turma.

Os aspectos de leitura e escrita de números naturais visam favorecer o desenvolvimento da habilidade EF04MA01 Aproveitar o fim da aula para incentivar os alunos a formularem e a exporem dúvidas que ainda possam ter. Buscar identificar as principais dificuldades enfrentadas por eles e resolvê-las quando surgirem são atitudes que precisam permear toda a aula.

Aula 2

Retomar os números naturais trabalhados na aula anterior e pedir aos alunos que os escrevam em ordem crescente e em algarismos, identificando o valor posicional de cada algarismo. Para isso, solicitar que, no Quadro de ordens, representem na coluna da ordem adequada o algarismo que compõe cada número. Chamar a atenção da turma para que os números sejam representados no Quadro de ordens em ordem crescente. No caso dos números sugeridos no ditado de números na aula anterior, o registro ficaria da seguinte maneira:

Em seguida, traçar na lousa a representação de alguns números naturais em uma reta numérica, conforme o modelo sugerido a seguir.

Propor aos alunos que, um a um, digam um número natural qualquer entre os números já representados na reta numérica. Por exemplo, eles podem dizer: entre 0 e 1 000, qualquer número natural de 1 a 999; ou entre 1 000 e 2 000 qualquer número natural de 1 001 a 1 999; ou entre 2 000 e 3 000 qualquer número natural de 2 001 a 2 999; ou entre 3 000 e 4 000 qualquer número natural de 3 001 a 3 999; e assim por diante até 9 000. A cada número dito por um aluno, fazer a representação na reta numérica na lousa Depois, organizar a turma em duplas e pedir que, no caderno, tracem uma reta numérica como a da lousa para representar números naturais diferentes dos já representados. Um aluno da dupla deve ditar, em ordem crescente, números naturais, e o outro deve escrever por extenso esses números e representá-los na reta numérica na localização mais adequada possível de cada número ditado, conforme a reta numérica na lousa Chamar a atenção dos alunos para o fato de que a proporção na representação é importante. Em um segundo momento da atividade, os alunos trocam de função: o que estava ditando passa a fazer os registros da escrita por extenso e da representação na reta numérica e o outro passa a ditar.

Acompanhar os alunos durante a realização dessa atividade a fim de identificar eventuais dúvidas, fazendo as intervenções e mediações necessárias para que eles compreendam o uso da reta numérica como suporte para a representação e a localização de números naturais.

Concluída a tarefa, pedir às duplas que compartilhem com outras duplas seus resultados. Durante esse processo, identificar novamente eventuais incorreções e dificuldades, avaliando se há necessidade de retomar alguns pontos do conteúdo com a turma.

O objetivo de trabalhar a comparação e a ordenação de números naturais é favorecer o desenvolvimento da habilidade EF04MA01

Para a aula seguinte, é necessário confeccionar conjuntos de fichas com os algarismos de 0 a 9 (um algarismo em cada ficha). Essa confecção poderá ser feita por toda a turma.

Aula 3

O objetivo desta aula é aprofundar o estudo sobre a ordenação dos números naturais de até cinco ordens. Para isso, é sugerida a atividade descrita a seguir

Organizar os alunos em duplas ou grupos de quatro integrantes. Entregar a cada dupla ou grupo um conjunto de fichas com os algarismos de 0 a 9 (um algarismo em cada ficha)

É preciso confeccionar conjuntos de fichas em quantidade suficiente para que fiquem disponíveis além dos que os alunos vão utilizar. Isso porque, em outro momento da aula, esses conjuntos serão usados para compor números com algarismos repetidos nas centenas, nas dezenas e nas unidades (por exemplo, 999, 888 etc.)

Questionar os alunos sobre qual é o maior número natural de quatro algarismos diferentes que pode ser formado com os algarismos do conjunto de fichas que receberam Espera-se que respondam o número 9 876.

Caso isso não ocorra, verificar quais foram as estratégias adotadas e identificar eventuais equívocos. Nesse momento, é importante que os alunos verbalizem como pensaram para indicar as respostas apresentadas, pois, ao formular as justificativas, eles podem reconhecer em quais aspectos cometeram algum engano na formulação do pensamento e assim desenvolver a "própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções", de acordo com a competência específica de Matemática para o Ensino Fundamental 3.

Estimular o compartilhamento de ideias, informações e experiências entre os alunos é importante para mobilizar aspectos da competência geral da Educação Básica 4 durante a condução das aulas.

Em seguida, propor aos alunos questionamentos que os levem a compor outros números com as fichas, como: qual é o menor número natural de quatro algarismos diferentes que pode ser formado com os algarismos do conjunto de fichas que receberam?

Neste momento, disponibilizar para as duplas ou grupos outros conjuntos de fichas e variar os questionamentos, conforme sugerido a seguir:

• Usando os algarismos 3, 7, 8 e 9, sem repeti-los, qual é o maior número natural que pode ser formado e que é um número menor que 4 000? (3 987)

• Usando os algarismos 0 e 5, podendo repeti-los, qual é o número natural que pode ser formado e que é o sucessor de 4 999? (5 000).

A cada questionamento proposto, socializar as respostas entre as duplas ou grupos e pedir que indiquem, de acordo com o valor posicional de cada algarismo e na forma aditiva, a decomposição de cada número natural formado. No caso dessas sugestões de questionamento, espera-se que sejam indicadas as seguintes decomposições:

3 987 = 3 000 + 900 + 80 + 7

5 000 = 5 000 + 0 + 0 + 0

Concluir a aula debatendo com a turma os critérios adotados para a realização das atividades propostas, oportunizando que sejam identificadas dúvidas a serem sanadas

Essas atividades envolvem objetivos de aprendizagem que favorecem o desenvolvimento da habilidade EF04MA02, fazendo com que os alunos:

• marquem a posição dos números naturais na reta numérica de modo adequado;

• reconheçam a ordenação crescente e decrescente dos números naturais na reta numérica;

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

• façam a composição e a decomposição de números de quatro algarismos diferentes ou de quatro algarismos que podem ser repetidos, considerando o valor posicional de cada algarismo

Aula 4

Nesta aula, utilizar um ábaco para explorar com os alunos a representação de números naturais de até cinco ordens (ordem das dezenas de milhar). Por exemplo, escrever na lousa o número 14 587 e colocar no ábaco 7 argolas na haste das unidades, 8 argolas na haste das dezenas, 5 argolas na haste das centenas, 4 argolas na haste das unidades de milhar e 1 argola na haste das dezenas de milhar

Para compreender uma das principais características do Sistema de Numeração Decimal, que é o valor posicional dos algarismos em um número, o ábaco de pinos pode ser um instrumento de grande valia aos alunos, pois permite que eles visualizem nas hastes as ordens numéricas de nosso sistema de numeração.

Providenciar antecipadamente e mostrar aos alunos um modelo de ábaco de pinos Caso a escola não disponha desse material, é possível confeccionar com a turma um modelo feito de material reciclável.

Verificar se todos os alunos conhecem o ábaco e, caso necessário, explicar que, no ábaco, os pinos estão relacionados com a representação, ordem por ordem, como em um Quadro de ordens. Salientar que, no ábaco, as trocas são realizadas à medida que forem colocadas 10 argolas em cada pino. Demonstrar, então, como utilizar o ábaco na decomposição de números até a ordem das dezenas de milhar.

Em seguida, representar no ábaco a decomposição de alguns números naturais da ordem das dezenas de milhar e escolher (ou sortear) alunos (ou pedir que se voluntariem) para que escrevam na lousa, usando algarismos e por extenso, cada número representado

Fazer várias representações no ábaco de modo a permitir a participação de toda a turma. Duas sugestões seriam:

• colocar 5 argolas na haste das unidades, 2 argolas na haste das dezenas, 5 argolas na haste das centenas, 5 argolas na haste das unidades de milhar e 2 argolas na haste das dezenas de milhar, representando o número 25 525;

• colocar 9 argolas na haste das unidades, 9 argolas na haste das dezenas, 9 argolas na haste das centenas, 9 argolas na haste das unidades de milhar e 9 argolas na haste das dezenas de milhar, representando o número 99 999

Observar a participação dos alunos durante a realização da atividade, identificando se eles apresentam dificuldade em entender as representações a fim de escolher, conforme a situação, as estratégias mais adequadas para ajudá-los na superação delas Esse trabalho com o ábaco favorece o desenvolvimento da habilidade EF04MA02

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Aulas 5 e 6

Para o desenvolvimento da atividade sugerida nestas aulas, são necessários os seguintes materiais: o ábaco e as fichas com algarismos de 0 a 9, materiais já utilizados em aulas anteriores, uma caixa de sapatos vazia ou qualquer outro recipiente que possa ser utilizado para o sorteio das fichas.

Colocar as fichas na caixa e explicar aos alunos como a atividade será realizada.

1. Explicar que, em um primeiro momento, serão sorteadas cinco cartelas e, depois, escolher um aluno da turma

2. Com os algarismos que constam nas cartelas sorteadas, o aluno deve formar o maior ou o menor número natural de cinco algarismos diferentes

3. Em seguida, outro aluno representa no ábaco o número formado pelo primeiro aluno e um terceiro aluno o escreve na lousa por extenso

4. Por fim, posicionar o número corretamente na reta numérica já apresentada na lousa (modelo de reta numérica a seguir).

Editoria de arte

Se durante essa atividade os alunos demonstrarem dificuldades, orientá-los e incentivar a participação dos colegas, já que a atividade deve ser realizada com a interação da turma toda

Notar que as etapas dessa atividade mobilizam as habilidades matemáticas cujo desenvolvimento foi favorecido ao longo desta sequência didática: escrita de números usando algarismos e por extenso; decomposição e composição de números naturais até a ordem das dezenas de milhar; ordenação de números naturais; entre outras. Desse modo, pode-se verificar se os objetivos de aprendizagem propostos foram atingidos

No decorrer das duas aulas reservadas para a realização dessa atividade, assegurar que todos os alunos participem dela.

Aulas 7 e 8

Organizar os alunos em duplas e entregar a cada dupla uma folha de papel sulfite. As duplas constroem na folha um quadro com 6 linhas e 4 colunas para ser utilizado como cartela para o jogo de bingo.

Na lousa, fazer um quadro para que os alunos tenham um modelo e escrever algumas sequências com elementos ausentes para serem preenchidos pelas duplas

Registrar cada sequência em uma coluna (na vertical): escrever sequências de números maiores que 10 000. Por exemplo:

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Elaborar e escrever na lousa várias sequências com números naturais entre 10 000 e 11 000, por exemplo, ou outras dezenas de milhar.

Solicitar a cada dupla que escolha três sequências diferentes para copiar no quadro que construíram na folha e preencha as sequências

Depois de as duplas preencherem as sequências e as respostas serem validadas socializando-as entre as duplas, montar as fichas de sorteio, que podem ser confeccionadas em folhas de papel sulfite ou em cartolina.

Nessas fichas, que serão utilizadas para sorteio durante o bingo, devem constar todos os números das sequências que os alunos observaram na lousa, inclusive os números que eles preencheram.

Com todas as fichas em mãos, explicar à turma as regras do jogo:

1. Os números das cartelas correspondem a dezenas de milhar que vão de 10 000 a 11 000.

2. O jogo termina quando uma dupla preencher uma cartela inteira.

3. Quando a dupla completar a cartela, deve dizer "bingo"

Pode-se optar por premiar a dupla vencedora. Nesse caso, é necessário combinar previamente com a turma qual será a premiação. Com as regras devidamente explicadas, iniciar o bingo.

Sortear as fichas e pronunciar em voz alta cada número sorteado para que as duplas possam verificar se o número consta nas cartelas

Caso conste, a dupla pode marcar com lápis ou caneta, da maneira que preferir, sublinhando, fazendo um traço na diagonal ou marcando um X no número sorteado

Quando uma dupla disser "bingo", conferir a cartela.

Se tiver sido estabelecido um prêmio, ele pode ser entregue ao término da conferência.

Sugestões

• BELLOS, Alex. Alex no país dos números. Tradução de Berilo Vargas e Claudio Carina. São Paulo: Companhia das Letras, 2011.

• SMOLE, Katia Stocco; DINIZ, Maria Ignez. Materiais manipulativos para o ensino do Sistema de Numeração Decimal. Porto Alegre: Penso, 2016. (Mathemoteca, v. 1)

• STEWART, Ian. Em busca do infinito: uma história da Matemática dos primeiros números à teoria do caos. Rio de Janeiro: Zahar, 2014.

Sequência didática 2 • Adição e subtração com números naturais até a ordem de dezenas de milhar

Esta sequência didática trabalha a adição e a subtração com números naturais até a ordem de dezenas de milhar usando algoritmos e estratégias pessoais para calcular essas operações, como cálculo mental ou decomposição, por exemplo, bem como explora a resolução e a elaboração de problemas que envolvem adições e subtrações

Objetivos de aprendizagem

• Resolver e elaborar problemas de adição e subtração com números naturais até a ordem de dezenas de milhar

• Aplicar estratégias pessoais e de cálculo mental, fazer estimativas de somas ou diferenças, bem como utilizar a decomposição de números naturais envolvidos na resolução de problemas

• Utilizar algoritmos da adição e da subtração na resolução de problemas

Plano de aulas

Aula 1: Resolver problemas aditivos propostos empregando estratégias diversas de resolução, com e sem o apoio do material dourado.

Aula 2: Ampliar a compreensão do algoritmo da adição como estratégia de resolução de problemas, estabelecendo relações, progressivamente, entre os reagrupamentos realizados no algoritmo e a representação com apoio do material dourado. Elaborar problema de adição de números naturais.

Aula 3: Ampliar a compreensão do algoritmo da subtração como estratégia de resolução de problema, estabelecendo relações, progressivamente, entre as trocas (com ou sem reservas) realizadas no algoritmo e a representação com apoio do material dourado. Elaborar problema de subtração de números naturais. Trabalhar o cálculo de adições e subtrações com base em arredondamentos.

Aulas 4 e 5: Trabalhar a resolução e a elaboração de problemas envolvendo as operações de adição e subtração

Aula 6: Utilizar estratégias pessoais para resolver problemas.

Aulas 7 e 8: Trabalhar o reconhecimento de uma igualdade como equivalência

Componentes essenciais para a alfabetização: compreensão de textos, produção de escrita, fluência em leitura oral e desenvolvimento de vocabulário.

Competências gerais da Educação Básica: 2 e 9

Competência específica de Matemática: 5

Habilidades: EF04MA03 e EF04MA14.

Material necessário: material dourado

Aula 1

Iniciar a aula propondo aos alunos que resolvam alguns problemas envolvendo a adição de números naturais

Para a primeira aula desta sequência didática não são propostos questionamentos a fim de diagnosticar conhecimentos prévios. Isso porque, com os problemas sugeridos a seguir, espera-se que os alunos revelem as estratégias de resolução que já internalizaram para resolver esses tipos de problema.

Além disso, com base nos equívocos que os alunos possam cometer ou nas dúvidas que possam externar durante a realização das propostas sugeridas, é possível identificar o conhecimento que cada aluno, em anos escolares anteriores, já consolidou em relação ao repertório de estratégias de cálculo.

Incentivar os alunos a utilizarem estratégias diversas de resolução, como o cálculo mental, a decomposição dos números naturais envolvidos, entre outras, e solicitar que as descrevam explicando com exemplos a estratégia aplicada em cada resolução.

Pedir o registro por escrito no caderno desse percurso do raciocínio de cada aluno, por meio de esquemas, por exemplo Solicitar que registrem a produção escrita da resposta completa. A seguir, duas sugestões de problemas a serem propostos.

1. Bruna tem 32 bolinhas de gude, e o irmão dela tem 27 bolinhas de gude. Quantas bolinhas de gude os dois têm juntos?

Exemplo de resolução possível:

32 + 27 = 59

Resposta: Os dois irmãos têm juntos 59 bolinhas de gude.

2. João pintou a casa dele usando três cores diferentes Ele utilizou uma lata de tinta amarela de 4 litros, uma lata de tinta azul de 10 litros e uma lata de tinta branca de 6 litros. Ao todo, quantos litros de tinta João utilizou na pintura da casa dele?

Exemplo de resolução possível:

4 + 10 + 6 = 20

Resposta: João utilizou na pintura da casa dele, ao todo, 20 litros de tinta. Após a conclusão das resoluções, socializar com os alunos as estratégias utilizadas por eles nas resoluções dos problemas propostos, pedindo a cada um que as descreva

Verificar quais estratégias eles utilizaram na resolução do problema 1, em que a adição envolve números naturais formados por dois algarismos (números naturais da ordem das dezenas). Por exemplo, alguns alunos podem descrever que a estratégia aplicada foi a

Material disponibilizado em licença aberta do tipo

adição por decomposição e explicar: "primeiro, adicionei 30 a 20 e obtive 50; depois, adicionei 2 a 7 e obtive 9; por fim, adicionei 50 a 9 e cheguei ao resultado, que é 59"

Já na resolução do problema 2, espera-se que os alunos apliquem estratégias de cálculo mental, por exemplo: adicionar 4 a 6 e obter 10 e, em seguida, adicionar as dezenas exatas 10 e 10 e obter 20. Porém, há várias estratégias possíveis, como o apoio do material dourado na resolução dos dois problemas

Demonstrar concretamente, com o material dourado, as adições envolvidas nesses problemas a fim de validar as respostas com a turma. Se necessário, durante a demonstração, questionar os alunos sobre a quantidade que cada peça representa. Em caso de dúvidas, fazer os encaminhamentos adequados para que essa defasagem seja superada, pois no 4º ano é esperado que os alunos já tenham consolidado o conhecimento de que: o cubo grande representa 1 000 unidades; a placa, 100 unidades; a barra, 10 unidades; o cubinho, 1 unidade.

A seguir, são propostas duas situações que podem ser trabalhadas com o material dourado em pequenos grupos ou com a turma toda

3. Uma barra e uma placa do material dourado representam quantas unidades?

Exemplo de resolução possível:

10 + 100 = 110

Resposta: Uma barra e uma placa do material dourado representam 110 unidades.

4. Um cubo grande, uma placa, dois cubos grandes e dez cubinhos do material dourado representam quantas unidades?

Exemplo de resolução possível:

1 000 + 100 + 1 000 + 1 000 + 10 = 3 110

Resposta: Um cubo grande, uma placa, dois cubos grandes e dez cubinhos do material dourado representam 3 110 unidades.

Organizar os alunos em grupos de três ou quatro integrantes Um representante de cada grupo escreve na lousa dois números até a ordem das dezenas de milhar e escolhe outro grupo para representá-los com as peças do material dourado.

O objetivo dessa dinâmica é exercitar a prática reiterada da decomposição de números usando o material dourado, habilidade matemática que favorece o desenvolvimento de estratégias de cálculos mobilizadas na resolução de problemas envolvendo adição e subtração.

Caso a escola disponha de infraestrutura adequada (computadores e acesso à internet), orientar os alunos a utilizarem o material dourado virtual on-line disponível em: https://apps.mathlearningcenter.org/number-pieces/. Acesso em: 5 jan. 2022.

Material disponibilizado em licença aberta do tipo Creative Commons

Atribuição não comercial (CC BY NC – 4.0 International). Perm itida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aula 2

Retomar as trocas da aula anterior sobre as diferentes estratégias utilizadas nas resoluções de problemas, bem como o uso do material dourado Valorizar a importância do acolhimento do ponto de vista do outro com empatia, de modo que a competência geral da Educação Básica 9 seja mobilizada na construção do conhecimento matemático.

Depois, apresentar o problema sugerido a seguir e pedir aos alunos que o resolvam utilizando o algoritmo convencional da adição.

1. As frutas fazem parte dos hábitos alimentares saudáveis de Laura e da família dela. Laura foi à feira e comprou 3 256 gramas de maçãs e 3 984 gramas de laranjas. Quantos gramas de fruta, no total, Laura comprou na feira? 3256 3984 7240 +

Resposta: Laura comprou na feira 7 240 gramas de frutas, no total Sugerir aos alunos um tempo para concluir a resolução do problema proposto e, ao término, explorar com eles a estrutura do algoritmo convencional da adição

Para isso, escrever na lousa o algoritmo e retomar com os alunos os nomes de cada um dos termos da adição. Nesse caso, as parcelas são 3 256 e 3 984 e a soma ou total é 7 240.

Em seguida, ampliar a compreensão do algoritmo da adição, estabelecendo relações, progressivamente, entre as trocas e os reagrupamentos realizados no algoritmo e a representação com apoio do material dourado, como feito na aula anterior

Fazer a gestão dessa demonstração, explicando os reagrupamentos da adição ao juntar e trocar as peças que representam as unidades; depois as que representam as dezenas; em seguida, as das centenas; por último, as das unidades de milhar

Evitar o uso da expressão informal "vai 1", visto que pode induzir os alunos ao erro no entendimento do significado dos reagrupamentos

Durante a explicação, é importante indicar o valor posicional de cada algarismo. Por exemplo, ao adicionar 5 a 8 na ordem das dezenas, ressaltar que está adicionando 50 a 80, obtendo 130, que é adicionado a 10, que foi reagrupado, totalizando, portanto, 140, e registram-se no algoritmo o 4 que corresponde a 40 na ordem das dezenas e o 100 que corresponde a 1 centena, que é indicada pelo número 1 na ordem das centenas. De modo análogo, descrever os outros reagrupamentos realizados nessa adição e verificar se os alunos estão entendendo o uso do algoritmo convencional, incentivando-os a externarem dúvidas para que sejam sanadas.

Para que a dimensão de elaboração de problemas da habilidade EF04MA03 também seja explorada nesta aula, propor aos alunos uma atividade como a sugerida a seguir.

2. Elabore e resolva um problema envolvendo uma adição de números naturais.

Exemplo de problema elaborado: Em uma fazenda, havia uma plantação de 23 486 macieiras e 22 775 laranjeiras. Quantas árvores frutíferas havia nessa plantação?

Exemplo de resolução possível:

23486

22775

Resposta: Nessa plantação, havia 46 261 árvores frutíferas.

A atividade de elaboração de problemas favorece o desenvolvimento da competência geral da Educação Básica 2, pois os alunos recorrem à abordagem própria da Matemática para elaborar problemas com base em conhecimentos adquiridos nessa área, mobilizando habilidades de reflexão e análise.

Aula 3

Iniciar a aula propondo aos alunos que resolvam um problema de subtração de números naturais Com o problema sugerido a seguir, espera-se que os alunos revelem as estratégias de resolução que já internalizaram para resolver esse tipo de problema.

Incentivar os alunos a utilizar estratégias diversas de resolução. Pedir o registro por escrito no caderno do percurso do raciocínio de cada aluno, por meio de esquemas, por exemplo. Solicitar que registrem a produção escrita da resposta completa. A seguir é apresentada a sugestão do problema a ser proposto.

1. Letícia tinha 324 figurinhas na coleção dela. Ela ganhou várias figurinhas e, agora, tem 385 figurinhas na coleção. Quantas figurinhas Letícia ganhou?

Exemplo de resolução possível:

385 - 324 = 61

Resposta: Letícia ganhou 61 figurinhas.

Pedir aos alunos que se organizem em duplas e leiam o enunciado do problema Verificar se eles interpretam adequadamente o enunciado e identificam que a operação a ser realizada é uma subtração.

Caso alguns alunos tenham dúvidas ou dificuldades, enfatizar que é importante ler atentamente o enunciado do problema a fim de identificar os dados e a pergunta, para, só então, determinar a operação que permite resolver a questão

Orientar os alunos a esquematizarem as etapas do processo de resolução do problema em um quadro e montar um na lousa com a turma, por exemplo:

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Quantas figurinhas Letícia tem agora? 385

Quantas figurinhas Letícia tinha? 324

Quantas figurinhas Letícia ganhou? ?

Após organizar as informações, questionar os alunos se é mais fácil determinar a operação a ser realizada com base no esquema feito com as informações do problema. Espera-se que eles concluam que, com essa organização esquemática, fica mais fácil estabelecer relações entre os dados e a questão do problema

Explorar com a turma a estrutura do algoritmo convencional da subtração. Para isso, escrever na lousa o algoritmo e, com os alunos, retomar os nomes dos termos da subtração para que o desenvolvimento do vocabulário matemático deles seja sempre incentivado. Nesse caso, 385 é o minuendo, 324 é o subtraendo e a diferença é o número obtido com o cálculo: 61.

Em seguida, ampliar a compreensão do algoritmo da subtração, estabelecendo relações, progressivamente, entre o cálculo feito no algoritmo e a representação com apoio do material dourado

Propor aos alunos uma atividade como a sugerida a seguir para explorar a estratégia de realizar cálculos fazendo arredondamentos.

2. Em cada subtração, marque um X na opção em que está indicado o resultado mais próximo de cada adição e subtração.

Subtração 1: 5 897 - 1 990

a) 4 000 b) 5 000

Subtração 2: 9 997 - 5 010

a) 3 000 b) 4 000

c) 6 000

c) 5 000

Espera-se que os alunos assinalem a alternativa a na subtração 1 e a alternativa c na subtração 2, fazendo arredondamentos para a unidade de milhar mais próxima

Verificar as respostas com a turma socializando-as. Incentivar os alunos a comunicarem os procedimentos e as diferentes estratégias que utilizaram para realizar essa atividade.

Caso alguns alunos apresentem dúvidas ou dificuldades, orientá-los a estimar o resultado de uma adição ou de uma subtração, arredondando os números envolvidos no cálculo para a ordem mais próxima das dezenas, ou das centenas, ou das unidades de milhar etc. Então o cálculo é feito considerando esses números arredondados de modo a obter um resultado aproximado.

Comentar que essa estratégia é muito utilizada no dia a dia quando fazemos compras e queremos decidir o que é possível comprar, considerando a quantia disponível ou até mesmo para conferir se recebemos o troco correto.

Para que a dimensão de elaboração de problemas da habilidade EF04MA03 também seja explorada nesta aula, propor aos alunos uma atividade como a sugerida a seguir.

3. Elabore e resolva um problema envolvendo uma subtração de números naturais.

Exemplo de problema elaborado: Em uma fábrica, havia no estoque 63 990 bicicletas na segunda-feira da semana passada Nesta semana, na segunda-feira, havia 41 090 bicicletas. Quantas bicicletas essa fábrica vendeu em uma semana?

Exemplo de resolução possível:

63990

41090

22900

Resposta: Em uma semana, essa fábrica vendeu 22 900 bicicletas

Finalizar a aula pedindo aos alunos que, em casa, elaborem um texto de até 20 linhas no qual sistematizem como procedem para elaborar um problema Orientá-los a descrever quais etapas eles seguem para organizar essa elaboração

Essa atividade de produção textual na aula de Matemática visa levar os alunos a refletirem sobre como utilizar processos matemáticos para elaborar e resolver problemas, validando estratégias e resultados, de acordo com a competência específica de Matemática para o Ensino Fundamental 5

Aulas 4 e 5

Iniciar a aula 4 comentando as produções textuais feitas pelos alunos em casa. Pedir a cada um que as leia em voz alta para que todos tomem conhecimento da sistematização feita para retratar a estratégia própria de como elaborar um problema. Essa proposta visa favorecer o desenvolvimento de componentes essenciais para a alfabetização, como compreensão de textos, produção de escrita e fluência em leitura oral.

Em seguida, organizar a turma em grupos de três ou quatro integrantes para trabalhar atividades de elaboração de problemas envolvendo as operações de adição e subtração.

Nas aulas anteriores, os alunos elaboraram problemas envolvendo essas operações separadamente. Nestas aulas, a proposta amplia o grau de complexidade ao explorar a elaboração com as duas operações. Por isso, prever duas aulas para esse trabalho é o mais adequado para gerir e encaminhar esse trabalho.

Caso a escola disponha de infraestrutura como computadores e acesso à internet, pedir aos alunos que pesquisem dados em notícias e busquem informações para subsidiar o contexto do problema que vão elaborar, orientando-os nessa pesquisa sobre a importância de avaliar as fontes utilizadas, principalmente se são fontes confiáveis ou não

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Para orientar os alunos a esse respeito, ler o material "Ferramentas: avaliando a informação", do Programa EducaMídia, que capacita professores para o processo de educação midiática. Esse material está disponível em: https://educamidia.org.br/ recurso/protocolos-para-avaliar-a-informacao Acesso em: 5 jan. 2022.

Na Aula 4, pedir aos grupos que façam essa pesquisa e, depois, elaborem e resolvam dois problemas em que as operações de adição e subtração estejam envolvidas Explicar que, na aula seguinte, os grupos vão trocar os problemas elaborados e um grupo vai validar a resolução do outro. Tudo deve ocorrer com a mediação do professor.

Pedir que escrevam os nomes dos integrantes do grupo em uma folha avulsa e a data em que estão realizando a atividade Registrar os problemas elaborados nessa folha e, em outra folha, a resolução

Apresentar essa proposta de atividade de elaboração de problemas sem fazer uma revisão prévia para que os alunos a realizem de maneira natural. Dessa maneira, os alunos elaboram os problemas sem que enunciados prontos de outros problemas propostos possam direcionar a elaboração.

Caso os alunos recorram a problemas anteriores para se inspirarem na estrutura do enunciado, não há problema, mas é importante deixá-los mobilizar as habilidades matemáticas que possuem em relação à adição e subtração de números naturais, bem como a resolução e elaboração de problemas. A consolidação dessas habilidades é um trabalho contínuo e progressivo.

Transitar entre os grupos e comunicar-se com os alunos durante a elaboração dos problemas, sem interferir no protagonismo deles, mas oferecendo questionamentos que os façam rever posições, se necessário, caso se percebam equívocos.

É muito importante observar se ao elaborar os problemas os alunos fazem perguntas que, para serem respondidas, é preciso fazer o cálculo de uma adição e de uma subtração Podem surgir questões como: O que há mais em uma papelaria: 1 430 livros ou 1 912 agendas?. Embora essa questão esteja relacionada a uma situação, pode ser respondida sem a realização de um cálculo, e apenas pela comparação das quantidades, considerando outras habilidades matemáticas.

Disponibilizar material dourado para que os alunos tenham a opção de utilizá-lo para validar as resoluções como fizeram em aulas anteriores

Na Aula 5, solicitar aos alunos que se organizem nos mesmos grupos, pois vão trocar os problemas com outro grupo a fim de que o outro grupo resolva o problema elaborado. Chamar a atenção para o fato de que as resoluções (os gabaritos) só serão oferecidas ao outro grupo no momento de socializar as respostas entre todos.

Novamente, transitar entre os grupos e comunicar-se com os alunos durante a resolução dos problemas trocados. Dessa vez, observar se os grupos que receberam os problemas interpretam os enunciados de maneira adequada.

São perspectivas diferentes de trabalho: na Aula 4, os alunos assumiram o papel de autores e elaboradores; já na Aula 5, eles assumem o papel de busca da resolução com base em estratégias pessoais.

No momento de socialização das respostas, valorizar o fato, caso ocorra, de algum grupo usar uma estratégia diferente de resolução da que foi pensada pelo grupo elaborador do problema. Comparar as estratégias com os alunos, salientando o fato de que há mais de uma maneira de resolver um problema.

Aula 6

Iniciar a aula motivando os alunos a verbalizarem estratégias que costumam adotar no dia a dia para resolver problemas que envolvam adição e subtração. Debater as situações apresentadas e anotá-las na lousa. Conversar com a turma sobre a vantagem de conhecer diferentes estratégias de resolução e como podem ser utilizadas em diferentes problemas de nossa rotina

Feita essa troca inicial, solicitar aos alunos que resolvam alguns problemas de adição e subtração. Eles podem utilizar a estratégia que preferirem de acordo com tudo que estudaram e compartilharam nas aulas anteriores. Utilizar situações que façam parte do cotidiano da maioria dos alunos é muito importante, por isso os problemas sugeridos a seguir envolvem valores monetários:

1. Natália economizou determinado valor por certo tempo. Hoje, ela foi a uma loja de eletrodomésticos e comprou uma geladeira por 3 200 reais. Do dinheiro economizado de Natália sobrou a quantia de 2 750 reais. Quantos reais Natália tinha economizado?

Exemplo de resolução possível:

3 200 + 2 750 = 5 950

Resposta: Natália tinha economizado 5 950 reais

Verificar se a turma reconhece que, apesar de a ação indicada no enunciado ser a de comprar, o que presume um gasto, a operação envolvida na resolução desse problema é uma adição. Caso alguns alunos realizem uma subtração, isso pode revelar que estão com dificuldades para interpretar o enunciado.

Auxiliá-los na releitura do enunciado pedindo que anotem e organizem os dados em um quadro com perguntas para modelar a situação proposta no problema. Por exemplo:

Quantos reais Natália pagou pela geladeira? 3 200

Quantos reais sobraram após a compra? 2 750

Quantos reais Natália tinha economizado? ?

Desse modo, espera-se que os alunos compreendam, ao completar os dados, que a operação a ser realizada é uma adição, pois envolve a ideia de acrescentar uma quantidade a outra para descobrir o valor desconhecido da quantia inicial em reais que Natália tinha economizado. Nesse caso, a adição: 3 200 + 2 750.

Enfatizar que organizar os dados de um problema ao resolvê-lo é muito importante. Com base nessa estratégia, conversar com a turma sobre outras possibilidades, registrando-as na lousa.

Propor outros problemas envolvendo as operações de adição e subtração, com base nas ideias trabalhadas nas aulas anteriores. A seguir, acompanhar a sugestão de mais um problema a ser proposto nesta aula.

2. Uma cozinheira fez 1 237 empadas de palmito. Em 879 empadas, ela colocou azeitonas misturadas ao recheio, mas, no restante, não vai colocar azeitonas. No total, essa cozinheira precisa fazer 2 568 empadas de palmito. Quantas empadas foram encomendadas sem azeitonas misturadas ao recheio?

Exemplo de resolução possível:

2 568 - 879 = 1 689

Resposta: Foram encomendadas 1 689 empadas sem azeitonas misturadas ao recheio de palmito

Terminar a aula conversando com os alunos sobre esse segundo problema proposto, em que nem todos os dados indicados no enunciado são envolvidos na resolução. Esse é um tipo de problema em que dados a mais são apresentados para verificar a habilidade de interpretação do enunciado que os alunos possuem.

Aulas 7 e 8

A fim de trabalhar o reconhecimento de uma igualdade como equivalência, favorecendo o desenvolvimento da habilidade EF04MA14, sugere-se usar nessas aulas a ideia da balança de dois pratos para que os alunos possam visualizar a representação dessa equivalência.

Iniciar a aula questionando a turma sobre o que aconteceria caso fosse adicionado um quilograma de algo em cada prato de uma balança de dois pratos em situação de equilíbrio. Espera-se que os alunos respondam que, nesse caso, a balança continuará em equilíbrio.

Em seguida, escrever na lousa operações envolvendo adição e subtração que tenham resultados iguais e demonstrar que elas continuam apresentando resultados iguais caso seja adicionada ou subtraída em cada uma delas a mesma quantidade. Por exemplo:

Ampliar esse trabalho, acessando o simulador disponível em: https://phet.colorado.edu/sims/html/equality-explorer-basics/latest/equality-explorerbasics_pt.html. Acesso em: 13 mar. 2023

Nesse simulador, é possível colocar virtualmente diferentes quantidades de objetos, frutas, símbolos ou animais (de acordo com a preferência) sobre os dois pratos de uma balança e, na parte superior da tela, são geradas sentenças matemáticas, demonstrando que a relação de igualdade existente entre dois termos permanece quando se adiciona ou se subtrai um mesmo número a cada um desses termos

O site é em inglês, mas, ao clicar na opção Basics , a proposta é facilmente compreendida por meio do apoio visual das imagens e dos símbolos matemáticos que são familiares aos alunos

Caso a turma esteja em um grau avançado de compreensão desse conteúdo e se queira ampliar o grau de complexidade da proposta, clicar na opção Lab , na qual é possível atribuir valores diferentes de 1 a cada tipo de peça disponível. À medida que as peças vão sendo colocadas na balança, a tela exibe a quantidade de peças usadas em cada prato.

Explorar esse recurso com a turma permite demonstrar diferentes igualdades, pois, ao representar situações em equilíbrio na balança, os alunos podem observar que as igualdades são verdadeiras por ambas indicarem resultados iguais

Verificar se a turma reconhece que a balança continua em equilíbrio quando são adicionadas ou retiradas peças idênticas de ambos os pratos.

Finalizar a aula solicitando aos alunos que produzam no caderno um texto sintetizando as ideias exploradas nesta aula

Sugestões

• DEMO, Pedro. Atividades de aprendizagem: sair da mania do ensino para comprometer-se com a aprendizagem do estudante [recurso eletrônico]. Campo Grande, MS: Secretaria de Estado de Educação do Mato Grosso do Sul – SED/MS, 2018. Disponível em: http://www.sed.ms.gov.br/wp-content/uploads/2018/12/eBookAtividades-de-Aprendizagem-Pedro-Demo.pdf Acesso em: 5 jan. 2022

• NAKASHIMA, Rosária Helena Ruiz; PICONEZ, Stela Conceição Bertholo. Technological PedagogicalContentKnowledge(TPACK): modelo explicativo da ação docente. Revista Eletrônica de Educação, v. 10, n. 3, p. 231-250, 2016. Disponível em: https://www.readcube.com/articles/10.14244%2F198271991605. Acesso em: 20 dez 2021.

• PIRES, Célia Maria Carolino Números naturais e operações. São Paulo: Melhoramentos, 2013. (Coleção Como eu ensino)

Sequência didática 3 • Problemas envolvendo multiplicação com números naturais

Nesta sequência didática, são propostas atividades que abordam a multiplicação com números naturais, bem como os diferentes significados dessa operação matemática, utilizando, para isso, diversas estratégias de cálculo em resolução e elaboração de problemas.

Objetivos de aprendizagem

• Resolver problemas de multiplicação com números naturais, envolvendo diferentes significados, como adição de parcelas iguais, organização retangular e proporcionalidade, utilizando estratégias diversas de cálculo.

• Reconhecer em um jogo a ideia da propriedade comutativa da multiplicação.

• Utilizar o algoritmo da multiplicação em cálculos e na resolução de problemas envolvendo números naturais

• Explorar o cálculo de multiplicações com números naturais por meio da decomposição de acordo com o valor posicional de cada algarismo, aplicando a propriedade distributiva da multiplicação.

• Elaborar problemas de multiplicação com números naturais.

Plano de aulas

Aula 1: Resolver problemas de multiplicação com números naturais, envolvendo diferentes significados, como adição de parcelas iguais, organização retangular e proporcionalidade, empregando estratégias diversas de resolução

Aulas 2 e 3: Explorar de maneira lúdica a operação de multiplicação por meio de dois jogos virtuais on-line , demonstrando compreensão da propriedade comutativa da multiplicação ao reconhecê-la no raciocínio envolvido em um desses jogos

Aula 4: Trabalhar o cálculo de multiplicações de números naturais em que um dos fatores é formado por um algarismo e o outro por três, decompondo em centenas, dezenas e unidades, e aplicando a propriedade distributiva da multiplicação.

Aula 5: Trabalhar o cálculo de multiplicações com base em estimativas e arredondamentos.

Aulas 6 e 7: Ampliar a compreensão do algoritmo da multiplicação como estratégia de resolução de problemas, estabelecendo relações, progressivamente, com a representação do material dourado

Aula 8: Elaborar problema de multiplicação de números naturais com base em multiplicações propostas em um jogo de bingo

Componente essencial para a alfabetização: compreensão de textos.

Competências gerais da Educação Básica: 5 e 9.

Competência específica de Matemática: 2

Habilidades: EF04MA05 e EF04MA06

Materiais necessários: computador com acesso à internet, um baralho de cartas completo e material dourado.

Aula 1

Iniciar a aula conversando com os alunos sobre a multiplicação com base na ideia de uma adição de parcelas iguais. Para tanto, organizá-los em trios e solicitar que resolvam os problemas sugeridos a seguir.

Incentivar a turma a utilizar estratégias diversas de resolução e solicitar que as descrevam explicando com exemplos a estratégia aplicada em cada resolução.

Pedir o registro por escrito no caderno desse percurso do raciocínio de cada aluno. Solicitar que registrem a produção escrita da resposta completa. A seguir, observar duas sugestões de problemas a serem propostos.

1. Na estante do quarto de Tatiana, há 4 prateleiras com 15 livros em cada uma. Quantos livros há na estante do quarto de Tatiana?

Exemplos de resoluções possíveis:

15 + 15 + 15 + 15 = 60 ou 15 × 4 = 60

Resposta: Há 60 livros na estante do quarto de Tatiana.

2. O pai de Tatiana trocou essa estante por duas prateleiras mais compridas presas à parede, em que Tatiana pode colocar 30 livros em cada uma. Quantos livros Tatiana pode colocar nas prateleiras novas?

Exemplo de resoluções possíveis: 30 + 30 = 60 ou 30 × 2 = 60

Resposta: Tatiana pode colocar 60 livros nas prateleiras novas

Após a conclusão das resoluções, solicitar aos alunos que comentem como resolveram os problemas. Pedir que socializem suas estratégias descrevendo-as Questioná-los sobre qual dos problemas tiveram mais facilidade de resolver e o porquê. Alguns alunos podem afirmar que é o problema 2. Verificar se eles utilizaram uma adição de parcelas iguais, por envolver apenas duas parcelas, ou se consideraram que por 30 ser um número múltiplo de 10 o resultado pode ser obtido mentalmente, calculando 3 × 2 = 6 e, em seguida, multiplicando por 10, obtendo 60

Caso os alunos não mencionem, comentar com eles as relações existentes entre os fatores de ambas as multiplicações que podem resolver os problemas propostos: 30 livros correspondem a 2 vezes 15 livros; 2 prateleiras correspondem à metade de 4 prateleiras.

Formule com a turma uma estratégia que favoreça o cálculo mental de uma multiplicação com base nessas relações. Por exemplo: considerar que, ao dobrar um fator e

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

ao dividir o outro pela metade (por 2), é possível obter uma nova multiplicação mais simples de calcular mentalmente

Propor que calculem 25 vezes 6 para aplicar essa estratégia. Nesse caso, os alunos podem realizar esse cálculo mentalmente, dobrando o fator 25 e obtendo 50 e dividindo pela metade o fator 6 obtendo 3. Daí, multiplicar 50 por 3. Como 50 é múltiplo de 10, é possível calcular mentalmente 5 vezes 3 e obter 15 e, em seguida, multiplicar 15 por 10, que é igual a 150.

Não é necessário utilizar a nomenclatura "múltiplo" nesta etapa, pois alguns alunos podem não ter familiaridade com ela. Porém, espera-se que, em ano escolar anterior, ao estudar multiplicação, os alunos tenham explorado as sequências de números formadas ao contar de 2 em 2, 3 em 3, 5 em 5, 10 em 10 etc., o que permite que eles compreendam a estratégia apresentada.

Manter os alunos organizados em trios e propor, também, os problemas sugeridos a seguir, que envolvem a ideia de organização retangular (problema 3) e a de proporcionalidade (problema 4).

3. Aline fez brigadeiros e os colocou em uma bandeja: ela os organizou em 7 linhas com 28 brigadeiros em cada uma (ou pode-se dizer 28 colunas com 7 brigadeiros em cada uma). Quantos brigadeiros Aline fez e colocou nessa bandeja?

Exemplo de resolução possível:

Resposta: Aline fez 196 brigadeiros e os colocou nessa bandeja

4. Patrícia usou 2 laranjas para fazer um copo cheio de suco. De quantas laranjas Patrícia precisa para fazer 3 copos iguais a esse cheios de suco?

Exemplo de resolução possível:

Resposta: Patrícia precisa de 6 laranjas para fazer 3 copos iguais a esse cheios de suco

Durante a resolução dessas atividades, verificar se os alunos precisam de auxílio acompanhando as trocas nos trios e sanando dificuldades de compreensão apresentadas

por eles O objetivo desta aula é favorecer o desenvolvimento da habilidade EF04MA06, com base em uma retomada de algumas ideias da multiplicação.

Aulas 2 e 3

Caso a escola não disponha de infraestrutura adequada como laboratório de informática com computadores para que os alunos possam jogar, providencie, previamente, um computador portátil de modo que organizados em grupos eles possam se revezar para explorar os jogos. Nesse caso, podem ampliar o trabalho jogando em casa também em computadores pessoais (caso possuam) ou em outros dispositivos móveis, comotabletou smartphone

Outra possibilidade é aplicar a metodologia ativa de aprendizagem chamada "sala de aula invertida", solicitando aos alunos, na véspera de cada aula prevista para o trabalho com os jogoson-line, que joguem em casa a fim de explorar na aula o desenvolvimento sugerido a seguir.

Para saber mais a respeito da metodologia ativa de aprendizagem "sala de aula invertida", consulte os materiais indicados em Sugestões, nesta sequência didática

Organizar os alunos em duplas, trios, quartetos ou grupos com mais integrantes, dependendo da quantidade de computadores disponíveis para a realização desta atividade caso ela seja realizada durante as aulas.

Orientá-los explicando que vão explorar habilidades de cálculo mental de multiplicações de modo lúdico em dois jogoson-line

Propor primeiro que acessem o jogo "Cartões flashde multiplicação", disponível em: https://pt.mathigon.org/multiply. Acesso em: 5 jan. 2022.

Nesse jogo, os alunos praticam reiteradamente multiplicações diferentes envolvidas nas tabuadas e com apoio visual das quantidades envolvidas a cada nova multiplicação que surge na tela.

Variar os desafios propondo qual grupo calcula mais rápido todas as multiplicações para eleger um grupovencedor,oque pode tornar omomentomais empolgante e desafiador.

Ressaltar que fazer a contagem um a um da quantidade de elementos representados nos agrupamentos na tela é um procedimento a evitar, pois o objetivo do jogo é desenvolver agilidade no cálculo de multiplicações com base no repertório que os alunos já possuem sobre as tabuadas

Comentar que, nesse jogo, caso não se recordem do produto da multiplicação apresentada na tela, a melhor estratégia é identificar a quantidade de elementos em cada agrupamento formado e a quantidade de agrupamentos, a fim de associar essas quantidades aos fatores da multiplicação.

Observar como os alunos estão se desenvolvendo durante as rodadas do jogo Combinar com eles quantas rodadas serão realizadas na Aula 2, como se fosse um

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

campeonato entre duplas, trios, quartetos ou grupos com mais integrantes, dependendo de como estiverem distribuídos.

Finalizar a aula, socializando as experiências que os alunos tiveram durante o jogo. É importante que sejam exploradas diferentes representações de agrupamentos que apareceram na tela, pois espera-se que um mesmo produto tenha sido obtido em multiplicações distintas como 3 × 4 ou 4 × 3 e 6 × 2 ou 2 × 6.

Com base nessas observações, conversar com a turma sobre a propriedade comutativa da multiplicação, a qual indica que a ordem dos fatores não altera o produto. Verificar se os alunos compreendem essa propriedade pedindo a eles que citem outros exemplos além dos que eventualmente tenham sido identificados durante o jogo. Essa proposta visa favorecer o desenvolvimento da habilidade EF04MA05

Na Aula 3, sugere-se proceder de modo análogo ao descrito para a Aula 2 ao explorar ojogo "Factris", disponível em: https://pt.mathigon.org/factris Acesso em: 5 jan 2022. Esse jogo explora as multiplicações representadas geometricamente, em organização (disposição) retangular

É um jogo elaborado para uma pessoa jogar por vez e desenvolve o raciocínio lógico recorrendo a conhecimentos matemáticos. Além disso, estimula a agilidade de pensamento para reconhecer e investigar agilmente a disposição retangular representada em uma malha mais adequada a ser rotacionada de modo que seja encaixada sem que próximas jogadas sejam bloqueadas.

O trabalho desenvolvido nas Aulas 2 e 3 contempla aspectos da competência específica de Matemática para o Ensino Fundamental 2 As competências gerais da Educação Básica 5 e 9 também são mobilizadas durante o trabalho com esses jogos.

Aula 4

Nesta aula, trabalhar o cálculo de multiplicações de números naturais em que um dos fatores é formado por um algarismo e o outro por três, decompondo em centenas, dezenas e unidades, e aplicando a propriedade distributiva da multiplicação.

Propor aos alunos na lousa a multiplicação de 121 vezes 4, por exemplo.

Com base nesse exemplo, comentar que vão realizar essa multiplicação fazendo a decomposição em centenas, dezenas e unidades.

Iniciar decompondo o número de três algarismos (121) em centenas, dezenas e unidades e, em seguida, multiplicar cada número por 4. O resultado será a adição dos produtos, que é 484.

Na lousa, sugere-se apresentar o desenvolvimento descrito a seguir:

121 × 4 = (100 + 20 + 1) × 4 =

100 × 4 + 20 × 4 + 1 × 4 = 400 + 80 + 4 = 484

Com base nessa proposta, propor aos alunos a atividade sugerida a seguir, que tem como objetivo explorar aspectos da habilidade EF04MA05

1. Calcule as multiplicações a seguir decompondo um dos fatores.

Acompanhar os alunos durante os cálculos de todas as multiplicações dessa atividade Caso eles demonstrem dificuldade ou apresentem dúvidas, disponibilizar material dourado para que representem concretamente as decomposições envolvidas nas multiplicações realizadas, de modo que percebam as relações existentes entre a representação concreta e o registro do cálculo realizado.

Validar com a turma as respostas dessa atividade, representando concretamente com o material dourado.

Aula 5

Nesta aula, com base em estimativas e arredondamentos, trabalhar o cálculo de multiplicações

De início explicar aos alunos que estimar o produto de uma multiplicação é uma estratégia que pode ser empregada no dia a dia para calcular mentalmente uma multiplicação, de modo que seja obtido um resultado aproximado.

Complementar essa colocação, mencionando que, para estimar de maneira adequada, um procedimento é arredondar um dos fatores. Por exemplo: considerar a multiplicação 125 × 11. Em seguida, arredondar para a dezena exata mais próxima o fator 11, a fim de tornar mais fácil calcular a multiplicação por 10. Então: 125 × 10 = 1 250

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Esse produto é uma estimativa adequada e, nesse exemplo, como, ao fazer o arredondamento, foi diminuída 1 unidade de um dos fatores, para chegar ao resultado exato, adiciona-se 125 a 1 250 (pois 1 × 125 = 125), obtendo 1 375.

Os alunos devem chegar a essa conclusão por meio de questionamentos sobre qual dos dois fatores é melhor arredondar. As regularidades envolvidas no produto obtido em uma multiplicação de um número natural por 10, por 100 ou por 1 000 favorecem, neste ano de escolaridade, que essa estratégia seja explorada. Propor, na sequência, a atividade a seguir.

1. Faça uma estimativa do produto de cada multiplicação a seguir, arredondando um dos fatores. Em seguida, explique como é possível proceder o cálculo para chegar ao produto exato.

Sugestões de resposta:

a) 50 × 9

50 × 10 = 500

Exemplo de explicação: Como, no arredondamento, foi acrescentada 1 unidade a um dos fatores, para chegar ao resultado exato, subtrai-se 50 de 500 (pois 1 × 50 = 50), obtendo 450.

b) 15 × 9

15 × 10 = 150

Exemplo de explicação: Como, no arredondamento, foi acrescentada 1 unidade a um dos fatores, para chegar ao resultado exato, subtrai-se 15 de 150 (pois 1 × 15 = 15), obtendo 135.

c) 45 × 9

45 × 10 = 450

Exemplo de explicação: Como, no arredondamento, foi acrescentada 1 unidade a um dos fatores, para chegar ao resultado exato, subtrai-se 45 de 450 (pois 1 × 45 = 45), obtendo 405.

d) 21 × 10

20 × 10 = 200

Exemplo de explicação: Como, no arredondamento, foi diminuída 1 unidade de um dos fatores, para chegar ao resultado exato, adiciona-se 10 a 200 (pois 1 × 10 = 10), obtendo 210.

e) 49 × 9

49 × 10 = 490

Exemplo de explicação: Como, no arredondamento, foi acrescentada 1 unidade a um dos fatores, para chegar ao resultado exato, subtrai-se 49 de 490 (pois 1 × 49 = 49), obtendo 441.

f) 35 × 9

35 × 10 = 350

Exemplo de explicação: Como, no arredondamento, foi acrescentada 1 unidade a um dos fatores, para chegar ao resultado exato, subtrai-se 35 de 350 (pois 1 × 35 = 35), obtendo 315.

Finalizar a aula elaborando com a turma coletivamente na lousa um texto com um resumo das ideias exploradas nesta aula

Aulas 6 e 7

Iniciar a Aula 6 apresentando o problema sugerido a seguir e pedir aos alunos que o resolvam utilizando o algoritmo convencional da multiplicação.

1. Uma escola comprou 573 livros novos para colocar à disposição dos alunos na biblioteca. Sabendo que cada livrou custou 27 reais, quantos reais a escola gastou nessa compra? 573 27 4011 11460 15471 +

×

Resposta: A escola gastou 15 471 reais com essa compra de livros.

Sugerir aos alunos uma previsão de tempo para a resolução do problema proposto e, ao término, explorar com eles a estrutura do algoritmo convencional da multiplicação, estabelecendo relações, progressivamente, entre as multiplicações realizadas no algoritmo e a representação com o apoio do material dourado

Fazer a gestão dessa demonstração indicando o valor posicional de cada algarismo no momento de explicar. Por exemplo, não mencionar “7 vezes 5”, e sim, nesse caso, “7 vezes 500” ou “7 vezes 5 centenas”. Verificar se os alunos estão entendendo o uso do algoritmo convencional, incentivando-os a externar dúvidas para que sejam sanadas.

Na sequência, propor outro problema, conforme sugerido a seguir, envolvendo valores monetários Deixar que os alunos resolvam usando a estratégia que preferirem.

2 A Associação de Pais e Mestres de uma escola decidiu investir em infraestrutura de informática. Para tanto, essa associação realizou um evento no qual foram arrecadadas, no total, 50 cédulas no valor de 50 reais, 80 cédulas no valor de 10 reais e 4 cédulas no valor de 5 reais. Essa associação pretende comprar os seguintes itens cujas condições de pagamento pesquisadas são as descritas:

• um computador portátil (notebook) a ser pago em 5 prestações de 500 reais cada uma;

• um tableta ser pago em 3 prestações de 250 reais cada uma.

De acordo com essas informações, responda às questões.

a) Com o dinheiro que essa associação arrecadou, é possível comprar os dois itens pretendidos?

Exemplo de resolução possível:

Primeiro, pode-se calcular o valor total arrecadado de acordo com as quantidades e os valores das cédulas:

50 × 50 = 2 500 (50 cédulas no valor de 50 reais)

80 × 10 = 800 (80 cédulas no valor de 10 reais)

4 × 5 = 20 (4 cédulas no valor de 5 reais)

Em seguida, os valores parciais obtidos são adicionados:

2 500 + 800 + 20 = 3 320; 3 320 reais.

Na sequência, calcula-se o valor total a ser pago pelos itens:

notebook(5 × 500 = 2 500)

tablet(3 × 250 = 750)

2 500 + 750 = 3 250; 3 250 reais

Comparam-se os valores e nota-se que 3 250 reais é menor que 3 320 reais.

Portanto, com o dinheiro que essa associação arrecadou, é possível comprar os dois itens pretendidos

b) Se essa associação desistisse de comprar o tablet , seria possível comprar 2 notebooks? Justifique sua resposta.

Espera-se que os alunos respondam que não. Exemplo de justificativa: como cada notebookcusta 2 500 reais, 2 notebookscustam 5 000 reais (pois 2 × 2 500 = 5 000), e esse valor é maior que 3 320 reais (valor arrecadado pela associação). Portanto, ainda que essa associação desistisse de comprar o tablet , não seria possível comprar 2 notebooks

Após a resolução desse problema, explorar com os alunos a estrutura do algoritmo convencional da multiplicação, estabelecendo relações, progressivamente, entre as multiplicações realizadas no algoritmo e a representação com o apoio do material dourado Fazer isso com todas as multiplicações envolvidas, inclusive aquelas nas quais um dos fatores é o número 10, a fim de que os alunos observem a representação concreta com o material dourado para atribuir sentido ao que é realizado no algoritmo.

Na Aula 7, organizar a turma em grupos para realizar uma atividade com as cartas de um baralho.

Explicar que, nesta atividade, as cartas do baralho denominadas coringas, valetes, damas e reis são consideradas 0 (zero) quando forem sorteadas

Embaralhar as cartas e, sobre a mesa do professor, colocá-las viradas para baixo organizadas uma ao lado da outra em linhas e colunas

Escolher um aluno, sortear o nome de um ou pedir que algum se voluntarie e pedir que retire 4 cartas cujos números presentes nelas formarão o primeiro fator de uma multiplicação

Orientar que formarão o número na ordem em que forem viradas as cartas. Por exemplo: a primeira carta virada representa um número da ordem das unidades; a segunda, das dezenas; a terceira, das centenas; a quarta, das unidades de milhar.

Registrar na lousa o número formado.

Em seguida, escolher outro aluno, sortear o nome de um ou pedir que algum se voluntarie e pedir que retire 2 cartas cujos números formarão o segundo fator de uma multiplicação. Reforçar a explicação de que formarão o número na ordem em que forem viradas). Registrar na lousa o número formado.

Todos os integrantes dos grupos realizam no caderno a multiplicação a fim de obter o produto e, para isso, fazem os cálculos utilizando o algoritmo convencional

O grupo que finalizar primeiro o cálculo e cuja resposta for validada como correta ganha ponto. Vence o grupo que conseguir juntar mais pontos

Durante a atividade, enquanto os grupos fazem os cálculos, transitar entre eles para verificar se necessitam de algum auxílio e identificar eventuais dúvidas. Disponibilizar material dourado para os grupos que quiserem realizar os cálculos com apoio do material.

Aula 8

Nesta aula, explorar a elaboração de problemas com base na habilidade EF04MA06, propondo aos alunos uma atividade como a sugerida a seguir.

Iniciar a aula de maneira descontraída propondo aos alunos jogar um “Bingo da multiplicação” Para tanto, solicitar a eles que criem cartelas construindo um quadro no caderno composto de 5 colunas por 5 linhas e escrevendo aleatoriamente nos espaços do quadro números naturais entre 1 e 100, conforme a escolha de cada aluno, até preencher com números todo o quadro que representa a cartela do jogo de bingo.

A seguir, constam sugestões com orientações sobre o modo de jogar, algumas regras do jogo, bem como de multiplicações para serem mencionadas nos sorteios.

Sugestõesdealgumasregras:

• Explicar aos alunos que, no bingo da multiplicação, os números das cartelas correspondem ao produto da multiplicação que será dita a cada “sorteio”

• O jogo termina quando algum aluno preencher uma cartela inteira (ou, se preferir, para reduzir a duração do intervalo de tempo do jogo, encerrá-lo quando um aluno preencher alguma linha ou coluna.

• Quando completar a cartela, o aluno precisa dizer “bingo”

Sugestõessobreomododejogar:

• O professor diz em voz alta uma multiplicação (ver exemplos após estas instruções).

• Os alunos calculam o produto da multiplicação e verificam se o número consta na cartela que foi criada. Em caso afirmativo, marcam um X no número na cartela.

• As multiplicações ditas pelo professor são escritas na lousa, na ordem das jogadas, para a conferência da cartela do aluno-ganhador.

• Quando algum aluno falar "bingo", a cartela é conferida coletivamente pela turma.

Seguem sugestões de multiplicações para serem propostas durante esse jogo de bingo:

1. Elabore e resolva um problema envolvendo uma das multiplicações de números naturais que foi anotada na lousa durante os sorteios do bingo

Exemplo de problema elaborado, considerando as sugestões de multiplicações anteriores: Ana comprou 2 estojos e cada um custou 18 reais. Quantos reais Ana gastou nessa compra?

Exemplo de resolução possível:

18 ´ 2 = (10 + 8) ´ 2 =

10 ´ 2 + 8 ´ 2 =

20 + 16 = 36

Resposta: Ana gastou 36 reais nessa compra.

Sugestões

• BERGMANN, Jonathan; SAMS, Aaron. Saladeaulainvertida: uma metodologia ativa de aprendizagem. Tradução de Afonso Celso da Cunha Serra. Rio de Janeiro: LTC, 2018.

Disponível em: https://curitiba.ifpr.edu.br/wp-content/uploads/2020/08/Sala-de-AulaInvertida-Uma-metodologia-Ativa-de-Aprendizagem.pdf Acesso em: 20 dez. 2021.

• SANTANA, Joselane Rodrigues S. de A.; NUNES, Cristiana Gomes; DYSMAN, Michelle. Multiplicação com material dourado. Matemáticacomvida/UFF Disponível em: http:// matematicacomvida.uff.br/2020/01/23/multiplicacao-com-material-dourado/ Acesso em: 5 jan. 2022.

Material disponibilizado em licença aberta do tipo Creative Commons

• SCHNEIDERS, Luís Antônio. O método da sala de aula invertida Lajeado: Univates, 2018. (Metodologias Ativas de Aprendizagem, 99). Disponível em: https://www.univates.br/editora-univates/media/publicacoes/256/pdf_256.pdf Acesso em: 5 jan. 2022

Sequência didática 4 • Problemas envolvendo divisão com números naturais

Nesta sequência didática, é trabalhada a divisão com números naturais cujo dividendo é um número natural de até quatro algarismos e o divisor é um número natural de até dois algarismos. Para isso, são explorados os significados associados à divisão, como repartição equitativa (distribuir igualmente) e medida (quantas vezes cabe), utilizando estratégias de cálculo diversas em cálculos e resolução de problemas.

Objetivos de aprendizagem

• Resolver problemas de divisão com números naturais, envolvendo diferentes significados, como repartição equitativa (distribuir igualmente) e medida (quantas vezes cabe), utilizando estratégias diversas de cálculo

• Utilizar o algoritmo da divisão em cálculos e na resolução de problemas envolvendo números naturais.

• Compreender a relação entre as operações de multiplicação e divisão como operações inversas

• Elaborar problemas de divisão com números naturais

Plano de aulas

Aula 1: Explorar cálculos de divisões exatas e de divisões não exatas com ou sem apoio de material manipulável.

Aulas 2 e 3: Resolver problemas de divisão com números naturais, envolvendo a ideia de repartição equitativa (distribuir igualmente) e medida (quantas vezes cabe), empregando estratégias diversas de resolução

Aula 4: Ampliar a compreensão do algoritmo da divisão, estabelecendo relações, progressivamente, com a representação do material dourado. Utilizar o algoritmo usual da divisão envolvendo dividendo, que é um número natural de até quatro algarismos.

Aula 5: Explorar de maneira lúdica a operação de divisão por meio de jogo virtual on-line . Elaborar problemas envolvendo a divisão com números naturais.

Aula 6: Trabalhar o cálculo de divisões com números naturais envolvendo divisor, que é um número natural formado por dois algarismos.

Aula 7: Utilizar a relação entre dividendo, divisor e quociente na verificação de cálculos de divisão e reconhecer, na resolução de problemas propostos, a relação existente entre a multiplicação e a divisão como operações inversas

Aula 8: Explorar de maneira lúdica a operação de divisão por meio de jogo

Componentes essenciais para a alfabetização: compreensão de textos e produção de escrita. Competências gerais da Educação Básica: 2 e 10.

Competência específica de Matemática: 6

Habilidade: EF04MA07

Materiais necessários: 30 tiras de papel reciclado para cada trio de alunos, material dourado, conjunto de fichas numeradas de 10 a 100 e conjunto de fichas numeradas de 2 a 9 (um número em cada ficha confeccionada, previamente, em cartolina ou papel-cartão), caixa vazia de sapatos identificada com a indicação DIVIDENDOS, caixa vazia de sapatos identificada com a indicação

DIVISORES, lápis de cor, cola e tesoura com pontas arredondadas.

Aula 1

Iniciar a aula organizando a turma em trios. Entregar a cada trio 30 tiras de papel reciclado e escrever na lousa as duas questões sugeridas a seguir. Orientar os alunos a utilizarem as tiras de papel como apoio para manipular e representar concretamente as situações.

1. Se a quantidade de 30 tiras de papel for distribuída igualmente entre 3 alunos, quantas tiras de papel cada aluno vai receber?

Espera-se que os alunos respondam que cada aluno vai receber 10 tiras de papel.

2. Quantos grupos de 5 tiras de papel podem ser formados com as 30 tiras de papel?

Espera-se que os alunos respondam que podem ser formados 6 grupos.

Enquanto os alunos respondem às questões, circular entre eles para identificar de que modo estão procedendo para resolver os problemas: se utilizam o apoio da manipulação das tiras ou se realizam cálculos com base nos conhecimentos que trazem de anos escolares anteriores.

Verificar se entre os alunos que formam os trios há algum que apresenta dúvidas e como eles se ajudam mutuamente na construção do conhecimento. Observar sem intervir nas discussões, mas oferecer questionamentos que os façam repensar se for identificado algum equívoco de compreensão da operação de divisão

Caso os alunos não citem a divisão, explicar a eles que o primeiro problema proposto envolve a ideia de repartição equitativa (distribuir igualmente) e o segundo, a de medida (quantas vezes cabe uma quantidade em outra). Não há sobra de tiras de papel nas divisões envolvidas nas resoluções dos dois problemas. Então, são divisões exatas.

Para aprofundar a aprendizagem, com os alunos ainda organizados em trios, propor uma atividade de cálculo de divisões como a sugerida a seguir.

3. Calcule a divisão apresentada em cada item e indique se é uma divisão exata ou uma divisão não exata.

a) 25 ÷ 6

Quociente: 4; resto: 1; divisão não exata.

b) 28 ÷ 4

Quociente: 7; resto: 0; divisão exata.

c) 23 ÷ 7

Quociente: 3; resto: 2; divisão não exata.

d) 56 ÷ 8

Quociente: 7; resto: 0; divisão exata.

Durante a realização desta atividade, transitar entre os trios de alunos a fim de observar como fazem os cálculos: se fazem desenhos para representar as quantidades, se realizam cálculos com base nos conhecimentos que trazem de anos escolares anteriores ou até mesmo, no caso dos três primeiros itens, se utilizam o apoio de manipulação das tiras

Os alunos podem apresentar dificuldade em calcular a divisão indicada no último item, pois, se optarem por utilizar as tiras, a quantidade que cada trio recebeu não é suficiente, porém é possível que um trio empreste para o outro o conjunto de tiras de modo que as duas quantidades juntas sejam utilizadas adequadamente para fazer as manipulações necessárias.

Se optarem por realizar o cálculo do algoritmo convencional, os alunos podem apresentar dúvidas ao dividirem de maneira exata 5 dezenas por 8 e perceberem que não é possível.

Nesse caso, se nenhum aluno chegar a essa conclusão, orientar que a estratégia mais ágil é pensar qual número que, quando multiplicado por 8, tem produto igual a 56, ressaltando que utilizar os conhecimentos adquiridos com o estudo da tabuada permite obter rapidamente o quociente de uma divisão como a proposta no último item da atividade.

Finalizar a aula elaborando na lousa, com a ajuda da turma, um texto com a síntese das ideias exploradas nesta aula. Pedir aos alunos que copiem o texto no caderno após a construção da produção textual coletiva. Solicitar aos trios que guardem as tiras de papel, pois elas poderão ser utilizadas na próxima aula.

Aulas 2 e 3

Retomar a formação dos trios da aula anterior e propor que resolvam problemas de divisão com números naturais, envolvendo a ideia de repartição equitativa (distribuir igualmente) e medida (quantas vezes cabe), empregando estratégias diversas de resolução, de modo que o desenvolvimento da habilidade EF04MA07 seja explorado

Incentivar os alunos a utilizarem estratégias diversas de resolução e solicitar que as descrevam explicando com exemplos a estratégia aplicada em cada resolução.

Pedir o registro por escrito no caderno desse percurso do raciocínio de cada aluno. Solicitar que registrem a produção escrita da resposta completa. A seguir, há algumas sugestões de problemas a serem propostos aos alunos.

1. Luciana comprou algumas canetas para presentear a mãe dela no Natal. Sabendo que cada caneta custou 6 reais e que Luciana gastou 36 reais, quantas canetas Luciana comprou para a mãe dela?

Exemplo de resoluções possíveis:

36 ÷ 6 = 6

Resposta: Luciana comprou 6 canetas para a mãe dela.

2. Bianca comprou 2 panetones de uma mesma marca e mesmo tipo para a ceia de Natal. Ela gastou, no total, 30 reais nessa compra. Quanto custou cada panetone?

Exemplo de resoluções possíveis:

30 ÷ 2 = 15

Resposta: Cada panetone custou 15 reais.

Durante a elaboração das resoluções, observar como os trios trabalham e quais estratégias utilizam para fazer os cálculos

Avaliar se conseguem identificar qual é a operação que pode ser empregada em cada resolução ou se tentam aplicá-las sem reflexão sobre a pergunta apresentada no problema

Os alunos podem, também, utilizar uma multiplicação para resolver o problema 1, esquematizando os dados, em um quadro, das informações presentes no enunciado. Por exemplo, seguindo a ordem de fluência de leitura dos dados do enunciado, tem-se que:

Quantas canetas Luciana comprou? ?

Quanto custou cada caneta? 6

Quantos reais Luciana gastou? 36

Desse modo, dando continuidade ao trabalho iniciado na aula anterior, os alunos podem pensar em qual número que, quando multiplicado por 6, tem produto igual a 36, e assim identificar o que falta para resolver o problema 1.

Caso algum aluno apresente defasagens em relação ao estudo da tabuada, é importante, nesse momento, antes de avançar para o trabalho sugerido nesta sequência didática, retomar com eles esse conteúdo.

No problema 2, os alunos podem utilizar o apoio do material manipulável (as tiras de papel da aula anterior) para concretamente realizar distribuições de quantidades. Essa prática auxilia os alunos a sistematizarem a compreensão do algoritmo convencional ao realizar uma divisão na qual o dividendo é um número maior que os produtos estudados nas tabuadas. Por exemplo, no problema 2, o número 30 (dividendo) é maior que 20 (produto de 2 × 10 = 20) e, nesse caso, ao dividir 30 por 2, apenas recorrer aos produtos da tabuada não

permite obter diretamente o quociente como nas divisões dos outros problemas propostos até esse momento.

Uma estratégia possível, caso os alunos não a comentem, é orientá-los a decompor o número no dividendo. Por exemplo, no problema 2, decompor 30 em dezenas exatas: decompor 30 em 10 mais 10 mais 10 e dividir cada 10 por 2, obtendo 5 mais 5 mais 5 que é igual a 15 (quociente da divisão de 30 por 2). Ou decompor 30 em 20 mais 10; dividir 20 por 2, obtendo 10; em seguida, dividir 10 por 2, obtendo 5; por fim, adicionar 10 e 5, obtendo 15 (quociente da divisão de 30 por 2)

Os estudos baseados em evidências de pesquisas realizadas com base em práticas pedagógicas revelam muitas estratégias possíveis. Estimular os alunos no exercício da construção de estratégias é o objetivo principal do trabalho organizado em grupos em um esforço produtivo. Essa perspectiva de mentalidade matemática construtiva é preconizada pela pesquisadora britânica Jo Boaler, cuja obra é indicada em Sugestões, nesta sequência didática

Após a conclusão das resoluções, solicitar aos alunos que comentem a maneira como resolveram os problemas. Pedir que socializem as estratégias utilizadas solicitando que as descrevam, motivando a participação de toda a turma

Para aprofundar a aprendizagem, com os alunos ainda organizados em trios, propor uma atividade de cálculo de divisões como a sugerida a seguir para que eles possam aplicar essa estratégia ou outras que foram compartilhadas.

a) 91 ÷ 7

Quociente: 13; resto: 0.

b) 72 ÷ 6

Quociente: 12; resto: 0.

c) 78 ÷ 3

Quociente: 26; resto: 0.

As divisões propostas nessa atividade ajudam os alunos a se apropriarem da estratégia de decomposição do número indicado no dividendo, que foi comentada anteriormente, pois é uma estratégia que permite a eles realizarem mais facilmente divisões de quantidades maiores que o repertório numérico que eles possuem das tabuadas.

Porém, é importante avaliar quais decomposições os alunos realizam para aplicar essa estratégia, pois os termos da decomposição precisam ser números múltiplos do divisor. Os alunos devem construir essa percepção de maneira autônoma sem receber respostas prontas.

3. Calcule a divisão apresentada em cada item.

Aula 4

O objetivo desta aula é ampliar a compreensão do algoritmo da divisão, estabelecendo relações, progressivamente, com a representação do material dourado.

Explorar uma divisão envolvendo dividendo, que é um número natural de três algarismos, e divisor, que é um número natural de um algarismo.

Para isso, escrever na lousa a divisão de 620 por 5 indicando os nomes dos termos da divisão da seguinte maneira: dividendo6205divisor

Fazer a representação usando 6 placas e 2 barras do material dourado e comentar a construção dessa representação, mencionando, por exemplo: "o número 620 indica uma quantidade formada por 6 centenas que podem ser representadas por 6 placas do material dourado e 2 dezenas que podem ser representadas por 2 barras do material dourado".

Em seguida, reforçar que, como a divisão é por 5, devem ser formados 5 grupos com quantidades iguais de peças em cada grupo. Perguntar aos alunos se há possibilidade de os 5 grupos receberem placas. Em caso afirmativo, questionar se vão sobrar placas e, caso sobrem, quantas placas sobrarão

Como há 6 placas e devem ser formados 5 grupos, espera-se que os alunos respondam "sim e vai sobrar 1 placa". Preencher na lousa o registro no algoritmo do que foi representado concretamente com as peças, como sugerido a seguir:

Com a placa restante e as 2 barras, pedir sugestões aos alunos sobre como essas peças podem ser organizadas de modo a dar continuidade aos cálculos.

Debater com os alunos a possibilidade de trocar a placa que representa 1 centena por 10 barras, que representam 10 dezenas.

Fazer a troca e, então, juntar as 10 barras e as 2 barras que sobraram. Ressaltar que agora há 12 barras (12 dezenas) e registrar no algoritmo na lousa essa troca:

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Em seguida, salientar que, como a divisão é por 5, devem ser formados 5 grupos com quantidades iguais, agora, de barras em cada grupo. Perguntar aos alunos se há possibilidade de os 5 grupos receberem barras. Em caso afirmativo, questionar se vão sobrar barras e, caso sobrem, quantas barras sobrarão

Como há 12 barras e devem ser formados 5 grupos, espera-se que os alunos respondam "sim, e vão sobrar 2 barras (2 dezenas)" após serem colocadas 2 barras em cada grupo.

Novamente, preencher na lousa o registro no algoritmo do que foi representado concretamente com as peças:

Dar continuidade à explicação encaminhando de modo análogo ao raciocínio descrito até esse momento, comentando que as 2 barras (2 dezenas) que sobraram podem ser trocadas por 20 cubinhos (20 unidades). Após a troca, fazer o registro no algoritmo:

Em seguida, ressaltar que, como a divisão é por 5, devem ser formados 5 grupos com quantidades iguais, dessa vez, de cubinhos em cada grupo. Perguntar aos alunos se há possibilidade de os 5 grupos receberem cubinhos. Em caso afirmativo, questionar se vão sobrar cubinhos e, caso sobrem, quantos cubinhos sobrarão.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédi to autoral e as criações sejam licenciadas sob os mesmos

Como há 20 cubinhos e devem ser formados 5 grupos, espera-se que os alunos respondam "sim, e não vão sobrar cubinhos" após serem colocados 4 cubinhos em cada grupo.

Complementar e finalizar na lousa o registro no algoritmo do que foi representado concretamente com as peças:

Portanto, 620 ÷ 5 = 124

É importante que todos esses procedimentos sejam feitos com os devidos registros, a fim de que os alunos possam ampliar a compreensão do algoritmo e, assim, possam proceder de modo autônomo quando, individualmente, realizarem os cálculos de divisões usando o algoritmo convencional

Solicitar aos alunos que façam cálculos de divisões com apoio do material dourado e utilizando o algoritmo convencional. Para isso, propor uma atividade como a sugerida a seguir.

1. Calcule a divisão apresentada em cada item.

a) 395 ÷ 3

Quociente: 131; resto: 2.

b) 848 ÷ 4

Quociente: 212; resto: 0.

c) 996 ÷ 3

Quociente: 26; resto: 0.

d) 785 ÷ 7

Quociente: 112; resto: 1

Para que os alunos se tornem matematicamente competentes e adquiram a capacidade de "Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade,

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

resiliência e determinação, tomando decisões", conforme recomendado na competência geral 10 da BNCC, é importante perguntar sempre a eles o porquê das ações que estão fazendo durante a realização das atividades. Incentivá-los a justificar procedimentos faz com que recorram às abordagens próprias da Matemática a fim de compreender mais significativamente o conteúdo estudado e favorecendo o desenvolvimento da competência geral 2

Aula 5

Para que a dimensão de elaboração de problemas da habilidade EF04MA07 também seja explorada nesta sequência didática, nesta aula, sugere-se propor aos alunos uma atividade com a seguinte proposta

Iniciar a aula de maneira descontraída propondo aos alunos o jogo "Avançando com oresto".

Caso a escola disponha de infraestrutura adequada, como laboratório de informática com computadores para que os alunos possam jogar, sugerir a versão virtual desse jogo no app que foi desenvolvido pela equipe da Universidade Virtual do Estado de São Paulo (Univesp), disponível em: https://apps.univesp.br/avancando-com-o-resto/ (acesso em: 5 jan. 2022).

Porém, caso essa infraestrutura não esteja disponível ou se preferir a versão do jogo em papel, há um modelo (com tabuleiros e dados) para imprimir e montar, disponível em: https://www.geogebra.org/m/q8rs9ncy (acesso em: 5 jan. 2022).

Pedir aos alunos que se organizem em duplas, trios ou quartetos, deixando que joguem por determinado tempo. Pedir a eles que anotem no caderno as divisões que calcularem durante o jogo.

Terminada a dinâmica, propor à turma a atividade de elaboração de problemas sugerida a seguir.

1. Elabore e resolva um problema envolvendo uma das divisões de números naturais que foram anotadas no caderno durante o jogo "Avançando com o resto".

Exemplo de problema elaborado considerando uma situação de jogo virtual em que o aluno anotou a divisão de 76 por 4:

Com 76 balas, é possível Denise formar quantos pacotes com 4 balas em cada um? Sobram balas fora dos pacotes?

Exemplo de resolução possível:

Resposta: Com 76 balas, é possível Denise formar 19 pacotes com 4 balas em cada um, e não sobram balas fora dos pacotes

Durante a atividade, verificar se os alunos apresentam dúvidas para que sejam sanadas. Finalizar a aula encaminhando o compartilhamento dos problemas elaborados, bem como as respostas.

Aula 6

Nesta aula, serão trabalhadas as divisões com números naturais cujo divisor é um número natural formado por dois algarismos com base na resolução de problemas

Iniciar a aula solicitando aos alunos que resolvam um problema como o sugerido a seguir, a fim de sondar se realizam a transposição do que foi feito com o material dourado para representar concretamente a divisão de um número da ordem das centenas por um número na ordem das unidades.

Observar o fato de que, nesta aula, é preciso disponibilizar aos alunos peças de cubos grandes para que representem as unidades de milhar envolvidas na divisão e façam as trocas necessárias.

1. Maria comprou um fogão que custou 2 400 reais. Ela vai pagar essa compra em 12 prestações iguais sem acréscimo. Qual é o valor de cada parcela que Maria vai pagar?

Exemplo de resolução possível:

2 400 ÷ 12 = 200

Resposta: O valor de cada parcela que Maria vai pagar é 200 reais

Sugerir aos alunos determinado prazo para concluir a resolução do problema proposto. Em seguida, ampliar a compreensão do algoritmo da divisão, estabelecendo relações, progressivamente, entre a representação com apoio do material dourado e o registro no algoritmo convencional.

Assim como foi feito na aula 4, demonstrar aos alunos a atividade utilizando as peças do material dourado. Fazer a gestão dessa demonstração, explicando as distribuições e trocas Nesse momento, é importante indicar o valor posicional de cada um dos algarismos. Esse trabalho contempla aspectos da competência específica 6 de Matemática e suas Tecnologias.

Após debater com os alunos a resolução desse problema, propor a resolução de outros dois conforme as sugestões a seguir

Acompanhar os alunos durante o registro das resoluções para identificar dúvidas e encaminhar a superação de eventuais dificuldades.

2. Em uma fábrica, há 1 240 latas idênticas de biscoito para serem distribuídas igualmente em 20 caixas iguais. Quantas latas de biscoito serão colocadas em cada caixa?

Exemplo de resolução possível:

1 240 ÷ 20 = 62

Resposta: Em cada caixa, serão colocadas 62 latas de biscoito

3. Carlos anunciou a venda da motocicleta usada dele por 8 550 reais que podem ser pagos em 18 prestações iguais sem acréscimo. Qual é o valor de cada parcela que o comprador dessa motocicleta vai pagar?

Exemplo de resolução possível:

8 550 ÷ 18 = 475

Resposta: O valor de cada parcela que o comprador vai pagar é 475 reais

Finalizar a aula fazendo a correção coletiva e compartilhada desses problemas

Aula 7

O objetivo desta aula é propor atividades em que os alunos utilizem a relação entre dividendo, divisor e quociente na verificação de cálculos de divisão, bem como percebam, na resolução de problemas propostos, a relação existente entre a multiplicação e a divisão como operações inversas

Iniciar a aula retomando algumas estratégias de cálculo e de resolução de problemas de divisão exploradas e compartilhadas nas aulas anteriores

Retomar a ideia já explorada na aula 2 desta sequência didática de que, quando se faz uma divisão, busca-se um dos fatores de uma multiplicação. Escrever na lousa essa ideia com registros pictóricos e cálculos. Por exemplo:

6 44 2 6 4 24 ÷=→×=

44 24 2 66 4 ÷=→×=

♦♦♦♦♦♦♦♦♦♦♦♦

♦♦♦♦♦♦♦♦♦♦♦♦

Em seguida, propor as atividades sugeridas a seguir, a fim de avaliar se os alunos compreendem essa relação apresentada.

1. Luís distribuiu igualmente 12 bombons em 3 caixas: ele colocou 4 bombons em cada caixa. De acordo com essas informações, responda às questões.

a) Qual é a adição de parcelas iguais que representa essa situação?

4 + 4 + 4 = 12

b) Qual é a multiplicação que representa essa situação?

3 × 4 = 12

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

c) Qual é a divisão que representa essa situação?

12 ÷ 4 = 3

2. Em cada item, calcule o quociente da divisão e escreva a multiplicação que indica a relação inversa entre a operação de divisão e a de multiplicação.

a) 48 ÷ 4

Quociente: 12; multiplicação: 12 × 4 = 48

b) 48 ÷ 12

Quociente: 4; multiplicação: 4 × 12 = 48

c) 65 ÷ 5

Quociente: 13; multiplicação: 13 × 5 = 65

d) 65 ÷ 13

Quociente: 5; multiplicação: 5 × 13 = 65

e) 48 ÷ 3

Quociente: 16; multiplicação: 16 × 3 = 48

f) 48 ÷ 16

Quociente: 3; multiplicação: 3 × 16 = 48

Ao término das atividades, coletivamente, validar as respostas incentivando os alunos a socializarem estratégias de resolução.

É importante, no caso da atividade 2, a cada item, representar com peças do material dourado as repartições equitativas das quantidades nos grupos formados Assim, é possível demonstrar, por exemplo, que no item a são 4 grupos com 12 unidades em cada um e, no item b, são 12 grupos com 4 unidades em cada um, de modo que os alunos compreendam a relação entre as operações de divisão e multiplicação, com base na representação concreta das quantidades envolvidas nas operações.

Verificar se os alunos são capazes de aplicar, na resolução de problemas, essa relação entre a operação de divisão e a de multiplicação. Para isso, propor a resolução de um problema como o sugerido a seguir e pedir que comprovem a resposta com uma multiplicação para verificar se está correta

3. Diariamente, Gabriela faz suco natural usando 2 laranjas. Gabriela comprou 22 laranjas. Em quantos dias Gabriela vai consumir todas as laranjas que comprou?

• Resolva e faça uma multiplicação para verificar se a resposta dada está correta. Sugestão de resposta:

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

22 ÷ 2 = 11

Verificação: 11 × 2 = 22

Resposta: Em 11 dias Gabriela vai consumir todas as laranjas que comprou Explorar com os alunos a relação entre essas operações com base na nomeação dos termos dessas operações, mencionando que, por exemplo, nesse problema, o dividendo (22) da divisão é igual ao produto da multiplicação (22) do divisor (2) pelo quociente (11) da divisão:

dividendo = quociente × divisor

Vale ressaltar que, nas propostas anteriores, as divisões envolvidas são exatas. Então, é importante mencionar que, nas divisões não exatas, essa relação também ocorre, porém, ao fazer a verificação, é necessário adicionar o resto da divisão:

dividendo = quociente × divisor + resto

Comentar que essa relação é uma estratégia que pode ser usada na verificação dos cálculos de divisões ou que se pode utilizar uma calculadora

Após a exploração das relações entre a multiplicação e a divisão como operações inversas, finalizar a aula organizando na lousa um texto com uma síntese das ideias exploradas.

Para a aula seguinte, será necessário:

• confeccionar um conjunto de fichas numeradas de 10 a 100 e um conjunto de fichas numeradas de 2 a 9 (um número em cada ficha confeccionada em cartolina ou papel-cartão);

• providenciar uma caixa vazia de sapatos e identificá-la por fora com a escrita do termo DIVIDENDOS;

• providenciar uma caixa vazia de sapatos e identificá-la por fora com a escrita do termo com a indicação DIVISORES

Verificar se essa confecção e as providências necessárias serão feitas por você ou se será um trabalho compartilhado por toda a turma.

Aula 8

Dedicar esta aula à realização de um jogo, organizando os alunos em grupos com até quatro integrantes.

Colocar as fichas numeradas de 10 a 100 dentro da caixa etiquetada externamente com o termo DIVIDENDOS e as fichas numeradas de 2 a 9 dentro da outra caixa etiquetada externamente com o termo DIVISORES.

Explicar aos grupos o modo de jogar, conforme sugerido a seguir

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

• Cada grupo, na sua vez, escolhe um aluno representante para sortear uma ficha de cada caixa

• Em seguida, o grupo do qual o aluno é integrante calcula a divisão e indica verbalmente, em voz alta, para a turma, o quociente e o resto (caso haja) da divisão do maior pelo menor número.

• Anotar na lousa a divisão formada pelos números sorteados e as respostas dadas pelo grupo.

• Orientar que, além de informar o quociente e o resto (caso haja) da divisão, o grupo precisa demonstrar a verificação da resposta apresentada utilizando as estratégias estudadas na aula anterior. Por exemplo: foram sorteados os números 47 e 5; após calcular a divisão, espera-se que os alunos respondam que o quociente dessa divisão é 9 e o resto é 2. Tal verificação seria representada por: 47 = 5 × 9 + 2

Antes de jogar a primeira vez, convidar um aluno para fazer uma simulação de uma situação do jogo para que a turma obtenha uma melhor compreensão da maneira de jogar

Disponibilizar material dourado para que os grupos possam utilizá-lo como apoio para os cálculos das divisões

Neste jogo, os alunos mobilizam as noções desenvolvidas nas aulas anteriores desta sequência didática.

Sugestões

• BOALER, Jo; MUNSON, Jen; WILLIAMS, Cathy. Mentalidades matemáticas na sala de aula: ensino fundamental. Tradução: Sandra Maria Mallmann da Rosa. Porto Alegre: Penso, 2018

• DULLIUS, Maria Madalena; QUARTIERI, Marli Teresinha (org.). Explorando a matemática com aplicativos computacionais: anos iniciais do ensino fundamental. Lajeado: Editora da Univates, 2015. Disponível em: https://www.univates.br/editoraunivates/media/publicacoes/144/pdf_144.pdf. Acesso em: 5 jan. 2022.

Sequência didática 5 • Medindo massas, capacidades e tempo

Nesta sequência didática, são abordadas algumas unidades de medida de massa e capacidade em atividades que abrangem estimativas e medições, bem como a resolução de problemas envolvendo unidades de medida padronizadas mais usuais São também exploradas as unidades de medida de tempo, hora, minuto e segundo, e a relação entre essas unidades de medida.

Objetivos de aprendizagem

• Explorar algumas unidades de medida de massa, capacidade e tempo

• Resolver problemas envolvendo unidades de medida padronizadas mais usuais

• Ler e registrar medidas de tempo em horas e minutos em relógios digitais e em relógios analógicos.

• Ler e registrar duração de intervalos de tempo em situações do dia a dia considerando horários de início e término.

Plano de aulas

Aulas 1 e 2: Reconhecer a importância do uso das unidades de medida de massa (quilograma, grama e miligrama) em situações cotidianas. Estabelecer relações entre essas unidades de medida. Resolver problemas envolvendo medidas de massa utilizando as operações aritméticas fundamentais.

Aulas 3 e 4: Reconhecer a importância do uso das unidades de medida de capacidade (litro e mililitro) em situações cotidianas. Estabelecer relações entre essas unidades de medida. Resolver problemas envolvendo medidas de capacidade utilizando as operações aritméticas fundamentais.

Aulas 5 e 6: Reconhecer a importância do uso das unidades de medida de tempo (hora, minuto e segundo) em situações cotidianas. Estabelecer relações entre essas unidades de medida, explorando relógios analógico e digital virtuais. Resolver problemas envolvendo medidas de tempo em situações cotidianas, utilizando a leitura e o registro de medidas e intervalos de tempo em horas, minutos e segundos para indicar horário de início e horário de término de realização de uma atividade, bem como calcular a duração desse intervalo de tempo

Aulas 7 e 8: Explorar de maneira lúdica algumas unidades de medida por meio de jogos virtuais on-line , demonstrando compreensão das relações de equivalência entre algumas dessas unidades

Componentes essenciais para a alfabetização: compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 1 e 4.

Competência específica de Matemática: 3

Habilidades: EF04MA20 e EF04MA22.

Materiais necessários: computador com acesso à internet e cartelas para bingo

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Aulas 1 e 2

Iniciar a Aula 1 conversando com os alunos, com base no que estudaram em anos escolares anteriores, sobre quais produtos, geralmente, são vendidos em quilogramas ou gramas Escrever na lousa os nomes dos produtos que forem mencionados

Em seguida, solicitar aos alunos que argumentem sobre o motivo de o preço de determinados produtos ser definido de acordo com a massa. Apesar de ser um questionamento de caráter pessoal, espera-se que eles apresentem argumentos, como:

• definir o preço do arroz, feijão, açúcar, sal etc. por unidade não é adequado, pois a contagem dos grãos um a um, em situações do cotidiano, seria uma estratégia muito trabalhosa para obter o valor a ser pago

• no caso de algumas frutas e de alguns legumes, a venda por quilograma ou grama torna-se mais adequada pelo fato de apresentarem pouca uniformidade em relação a características como dimensões (largura e comprimento), o que acarreta falta de uniformidade para que seja estabelecido um preço justo único por unidade ou dúzia.

Essa proposta inicial visa levar os alunos a reconhecer a importância do uso de algumas unidades de medida de massa (quilograma, grama e miligrama) em situações cotidianas

Após essa discussão inicial, explorar com os alunos as relações de equivalência entre as unidades de medida de massa quilograma, grama e miligrama Apresentar na lousa as seguintes equivalências entre essas unidades de medida de massa:

• 1 quilograma (kg) corresponde a 1 000 gramas (g);

• 1 grama (g) corresponde a 1 000 miligramas (mg)

Reforçar com os alunos que a palavra grama, quando relacionada à unidade de medida de massa, é um substantivo masculino, e o correto é dizer "o grama". Quando se diz " a grama " é feita referência à vegetação rasteira presente, por exemplo, em jardins e parques. Em seguida, pedir aos alunos que se organizem em grupos de até quatro integrantes para que resolvam problemas envolvendo medidas de massa, utilizando as operações aritméticas fundamentais e as relações de equivalência

Incentivar os alunos a utilizar estratégias diversas de resolução explicando com exemplos a estratégia aplicada em cada resolução. Pedir que registrem por escrito no caderno esse percurso do raciocínio de cada aluno, por meio de esquemas, por exemplo A seguir, são apresentadas sugestões de problemas a serem propostos.

1. Ana leu no rótulo de um iogurte as seguintes informações sobre sódio e cálcio:

Informação nutricional

Porção de 200 mL (1 copo)

Quantidade por porção

Sódio 110 mg

Cálcio 248 mg

• Quantos copos desse iogurte são necessários para que seja obtido, aproximadamente, 1 grama de cálcio?

Em 1 copo, há 248 mg de cálcio; então, em 4 copos, há 992 mg, pois: 248 × 4 = 992 992 mg correspondem a, aproximadamente, 1 g de cálcio

Portanto, são necessários 4 copos desse iogurte para que seja obtido, aproximadamente, 1 grama de cálcio

2. A Organização Mundial da Saúde (OMS) recomenda que uma pessoa não deve ingerir por dia mais de 5 gramas de sal, que equivalem a 2 gramas de sódio.

• De acordo com essa informação da OMS e a informação nutricional que você leu no enunciado do problema anterior, responda: quantos copos desse iogurte são necessários para que sejam obtidos, aproximadamente, 2 gramas de sódio?

Em 1 copo, há 110 mg de sódio; então, em 19 copos, há 2 090 mg, pois: 110 × 19 = 2 090. 2 090 mg correspondem a, aproximadamente, 2 g de sódio.

Portanto, são necessários 19 copos desse iogurte para que sejam obtidos, aproximadamente, 2 gramas de sódio

A informação apresentada neste enunciado está disponível na notícia "OPAS lança novas metas para reduzir consumo de sal na população e prevenir doenças cardiovasculares", disponível em:

https://www.paho.org/pt/noticias/28-10-2021-opas-lanca-novas-metas-para-reduzir-consumo-sal-napopulacao-e-prevenir-doencas. Acesso em: 3 jan. 2022.

3. Carolina comprou alguns produtos em embalagens com as massas indicadas a seguir. Leia as informações e responda às questões.

• 1 pacote de leite em pó com 400 gramas;

• 1 pacote de arroz com 1 quilograma;

• 1 pacote de milho para pipoca com 500 gramas.

a) Para comprar 1 quilograma de milho para pipoca, Carolina precisaria comprar quantos pacotes como esse que ela comprou?

No pacote de milho para pipoca que Carolina comprou, há 500 g; então, 2 pacotes correspondem a 1 quilograma, pois: 500 × 2 = 1 000 (1 000 g correspondem a 1 kg).

Portanto, para comprar 1 quilograma de milho para pipoca, Carolina precisaria comprar 2 pacotes

b) Faça uma estimativa e responda: se Carolina tivesse comprado 2 pacotes de leite em pó, ela teria comprado mais ou menos de 1 quilograma de leite em pó? Justifique sua resposta.

Espera-se que os alunos respondam menos de 1 quilograma, pois em 2 pacotes de leite em pó há 800 gramas, e 800 gramas é menos que 1 quilograma

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Na Aula 1, as unidades padronizadas de medida de massa mais usuais, o quilograma, o grama e o miligrama, são exploradas a fim de favorecer o desenvolvimento de alguns aspectos da habilidade EF04MA20

Para que os alunos desenvolvam a "própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções", de acordo com a competência específica de Matemática para o Ensino Fundamental 3, neste momento, é importante que verbalizem como pensaram para indicar as respostas apresentadas, refletindo e identificando como aplicar os conhecimentos em diferentes contextos, de modo que a competência geral da Educação Básica 1 seja mobilizada.

Na Aula 2, desenvolver uma atividade de pesquisa que envolve fluência em leitura, bem como habilidades de compreensão de textos e produção de escrita

Considerando o contexto da primeira atividade da Aula 1, desenvolver um trabalho interdisciplinar com Ciências. Comentar que, para manter a saúde dos ossos de nosso corpo, é muito importante que em nossa alimentação sejam inseridos alimentos ricos em cálcio. Pedir aos alunos que, durante a Aula 2, façam uma pesquisa a esse respeito com base na temática da alimentação saudável.

Propor também que explorem essa temática da alimentação saudável por meio do gênero textual história em quadrinhos. Há muitas revistas disponíveis on-line que tratam desse assunto e podem ser acessadas para leitura neste momento. Seguem links com algumas sugestões:

• ALIMENTAÇÃO: como fazer boas escolhas para você e para o planeta. Disponível em: https://turmadamonica.uol.com.br/wwfbrasil/downloads/cartilha_wwf_alimentacao .pdf. Acesso em: 3 jan. 2022.

• A TURMA da Mônica: alimentos saudáveis. Disponível em: https://bvsms.saude.gov.br/bvs/publicacoes/turma_monica_alimentos saudaveis.pdf. Acesso em: 3 jan. 2022.

• TURMA da Mônica: comer sem desperdiçar. Disponível em: https://www.embrapa.br/busca-de-publicacoes/-/publicacao/1115996/turma-damonica-comer-sem-desperdicar Acesso em: 13 mar. 2023

• TURMA da Mônica: receitas para preparar com a turminha em casa Meu pratinho saudável. Disponível em:

https://cangurunews.com.br/wp-content/uploads/2020/05/Receitas-Turma-da-M% C3%B4nica.pdf Acesso em: 3 jan. 2022

Concluir a Aula 2 debatendo com a turma os critérios adotados para a realização da pesquisa proposta, oportunizando que as produções sejam compartilhadas entre os alunos

Aulas 3 e 4

Iniciar a Aula 3 conversando com os alunos, com base no que estudaram em anos escolares anteriores, sobre quais produtos geralmente são vendidos em litros ou mililitros Escrever na lousa os nomes dos produtos que forem mencionados.

Em seguida, solicitar aos alunos que argumentem sobre o motivo de o preço de determinados produtos ser definido de acordo com a capacidade de recipientes, em litro ou mililitro. Apesar de ser um questionamento de caráter pessoal, espera-se que os alunos apresentem argumentos como:

• definir o preço da água de acordo com a capacidade de um recipiente em litro ou mililitro propõe uma uniformização conforme a necessidade, em situações do cotidiano, o que facilita calcular o valor a ser pago. Por exemplo, se uma pessoa precisa de uma garrafa de meio litro de água (500 mililitros), ela adquire a quantidade de líquido que deseja; se, em um consultório médico, o consumo de água é maior, é necessário comprar um garrafão de 20 litros, recipiente com a capacidade adequada para essa necessidade; se em uma casa gasta-se durante um mês a água que é acondicionada em uma caixa-d'água, então o valor a ser pago é calculado com base nesse gasto

• no caso de leite, iogurtes, sucos etc., a venda por litro ou mililitro também se torna mais adequada porque a padronização de recipientes com determinadas medidas de capacidade torna mais fácil estabelecer um preço justo por unidade do recipiente Essa proposta inicial visa levar os alunos a reconhecer a importância do uso de algumas unidades de medida de capacidade (litro e mililitro) em situações cotidianas.

Após essa discussão inicial, explorar com a turma as relações de equivalência entre as unidades de medida de capacidade de litro e mililitro. Apresentar na lousa a seguinte equivalência entre essas unidades de medida:

• 1 litro (L) corresponde a 1 000 mililitros (mL)

Em seguida, pedir aos alunos que se organizem em grupos de até quatro integrantes para que resolvam problemas envolvendo medidas de capacidade, utilizando as operações aritméticas fundamentais e a relação de equivalência.

Incentivar os alunos a utilizar estratégias diversas de resolução explicando com exemplos a estratégia aplicada em cada resolução. Pedir que registrem no caderno esse percurso do raciocínio, por meio de esquemas, por exemplo. A seguir, são apresentadas sugestões de problemas a serem propostos

1. Em cada item, calcule e responda.

a) Um recipiente com capacidade de 500 mL tem o dobro da capacidade de um recipiente com capacidade de 250 mL?

250 × 2 = 500

Portanto, um recipiente com capacidade de 500 mL tem o dobro da capacidade de um recipiente com capacidade de 250 mL.

b) Um recipiente com capacidade de 500 mL tem a metade da capacidade de um recipiente com capacidade de 1 L?

1 L corresponde a 1 000 mL

1 000 ÷ 2 = 500

Portanto, um recipiente com capacidade de 500 mL tem a metade da capacidade de um recipiente com capacidade de 1 L.

c) Viviane fez 1 L de suco de manga. Depois, distribuiu igualmente esse suco em 5 copos idênticos. Quantos mililitros de suco foram colocados em cada copo?

1 L corresponde a 1 000 mL

1 000 ÷ 5 = 200

Portanto, foram colocados em cada copo 200 mililitros de suco.

d) Em uma máquina de uma fábrica de produtos de limpeza, 550 litros de produto são despejados em recipientes com capacidade para 5 litros cada. Sabendo que não ocorre desperdício de produto, quantos recipientes são preenchidos com esses 550 litros de produto?

550 ÷ 5 = 110

Portanto, 110 recipientes são preenchidos com esses 550 litros de produto.

2. Os problemas a seguir foram elaborados com base em informações presentes no infográfico "Como economizar água em cada canto da casa", disponível em: https://turmadamonica.uol.com.br/wwfbrasil/downloads/infografico_agua.pdf (acesso em: 3 jan. 2022). Resolva e responda.

a) Fechar o chuveiro ao se ensaboar pode economizar de 90 L a 162 L de água. Uma pessoa que toma 2 banhos por dia e tem essa atitude pode economizar quantos litros de água por dia?

Exemplo de resolução possível:

90 + 90 = 180

162 + 162 = 324

Portanto, uma pessoa que toma 2 banhos por dia e tem essa atitude pode economizar de 180 litros a 324 litros de água por dia

b) Fechar a torneira ao escovar os dentes pode economizar até 79 L de água, em um apartamento. Considerando que uma pessoa mora em apartamento e escova os dentes 3 vezes por dia e fecha a torneira enquanto escova os dentes. Quantos litros de água, no mínimo, podem ser economizados por dia por essa pessoa?

Exemplo de resolução possível:

79 × 3 = 237

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Portanto, 237 litros de água, no mínimo, podem ser economizados por dia por uma pessoa que mora em apartamento e escova os dentes 3 vezes por dia, fechando a torneira enquanto escova os dentes

c) Ao lavar a louça, fechar a torneira para ensaboar pode economizar até 97 L de uma vez. Uma pessoa que lava louça 4 vezes por dia e fecha a torneira para ensaboar pode economizar quantos litros de água por dia?

Exemplo de resolução possível: 97 × 4 = 388

Portanto, uma pessoa que lava louça 4 vezes por dia e fecha a torneira para ensaboar pode economizar 388 litros de água por dia

d) Lavar o carro com baldes de água, em vez de mangueira, gasta 40 L de água. Com uma mangueira com meia-volta de abertura, são gastos 560 L Uma pessoa que usa baldes pode economizar quantos litros de água cada vez que lava o carro?

Exemplo de resolução possível:

560 – 40 = 520

Portanto, uma pessoa que usa baldes pode economizar 520 litros de água cada vez que lava o carro

Na Aula 3, as unidades padronizadas de medida de capacidade mais usuais, o litro e omililitro, são exploradas a fim de favorecer o desenvolvimento da habilidade EF04MA20

Com base na temática de atitudes sustentáveis para economizar e não desperdiçar água, na Aula 4, considerando o tema contemporâneo transversal Meio ambiente, propor uma atividade de produção textual em que os alunos devem elaborar uma lista dessas atitudes, podendo realizar pesquisas. Explorar também com a turma, por meio do gênero textual história em quadrinhos, a importância das estações de tratamento de água, sugerindo a leitura da revista eletrônica on-linea seguir:

• A TURMA da Mônica: água boa para beber. Disponível em: https://crianca.mppr.mp.br/arquivos/File/publi/turma_da_monica/monica_agua_bo a.pdf Acesso em: 3 jan. 2022.

Essa perspectiva de trabalho, em que as duplas de aulas desta sequência didática estão organizadas, visa estabelecer um trabalho pedagógico alicerçado na proposta de formação integral dos alunos, pois, além do trabalho matemático com o conteúdo estabelecido em uma das aulas desta dupla dedicada a explorar determinadas unidades de medida, na outra aula a proposta envolve temáticas relevantes para a formação cidadã dos alunos.

Aulas 5 e 6

Iniciar a Aula 5 apresentando na lousa as seguintes equivalências entre algumas unidades de medida de tempo:

• 1 hora (h) é formada por 60 minutos (min);

• 1 minuto (min) é formado por 60 segundos (s)

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Em seguida, comentar que:

• 1 dia é formado por 24 horas;

• nos relógios analógicos, essas 24 horas são representadas por números de 1 a 12;

• nos relógios digitais, essas 24 horas são representadas por números de 1 a 24.

Propor aos alunos que explorem a leitura e a representação de horas acessando a versãoon-linede relógios disponíveis em: https://apps.mathlearningcenter.org/mathclock/. Acesso em: 4 jan. 2022

Caso a escola não disponha de infraestrutura adequada, como laboratório de informática com computadores para que os alunos possam jogar, providenciar, previamente, um computador portátil, de modo que possam se revezar para explorar organizados em grupos.

Os alunos podem explorar as funcionalidades desse app para trabalhar com os relógios virtuais. É possível escolher no segundo ícone da esquerda para a direita como se prefere trabalhar com o relógio analógico: com as mãos engrenadas, que ao mover um ponteiro o outro se modifica engrenado, ou com movimentações livres.

O quarto ícone da esquerda para a direita disponibiliza uma versão de display de relógio digital. Já o quinto ícone permite executar o relógio em tempo real, inclusive com o ponteiro dos segundos representado. O sexto ícone é a ferramenta de tempo decorrido, com oqual é possível selecionar e, com uma das mãos, arrastar o ponteiro e visualizar o tempo decorrido do intervalo de tempo representado.

Mais informações a respeito das ferramentas do app estão disponíveis no primeiro ícone da direita para a esquerda, na parte inferior da tela. Mas atenção: é preciso selecionar, ao acessar o link no navegador, a opção de sempre traduzir do inglês para o português, de modo que as informações da página sejam carregadas já traduzidas.

Nesta aula, são sugeridos alguns problemas a serem propostos aos alunos, cuja resolução pode ser validada utilizando também esse app

Durante a resolução dos problemas, verificar como os alunos realizam os cálculos para obter a equivalência de tempo em segundos e em minutos, bem como em minutos e em horas Caso alguns alunos demonstrem dificuldade nesse assunto, explorar com eles, por exemplo:

• uma situação em que se deve indicar quantos minutos correspondem a 3 258 segundos. Demonstrar que uma estratégia possível de resolução é calcular uma divisão de 3 258 por 60, obtendo 54 como quociente e resto 18. Comentar que, neste caso, o 54 obtido no quociente indica os minutos e, como há resto nessa divisão, o 18 corresponde aos segundos. Logo, 3 258 segundos correspondem a 54 minutos e 18 segundos.

Esse mesmo raciocínio pode ser utilizado para esclarecer possíveis dúvidas que os alunos apresentem relacionadas à indicação de quantas horas correspondem a determinada quantidade de minutos, por exemplo:

• supondo que se queira calcular quantas horas correspondem a 1 299 minutos, é possível calcular uma divisão por 60. Ao dividir 1 299 por 60, obtém-se 21 como quociente e 39 como resto. Neste caso, 21 corresponde às horas e 39, indicado no resto, corresponde aos minutos. Então, tem-se que 1 299 minutos correspondem a 21 horas e 39 minutos.

Além desses exemplos, estimular o compartilhamento de ideias, informações e experiências entre os alunos é importante para mobilizar aspectos da competência geral da Educação Básica 4 durante a condução dos problemas sugeridos a seguir, que visam favorecer o desenvolvimento da habilidade EF04MA22.

1. A aula de Paulo no curso de informática começa às 9 horas e 10 minutos com duração de 2 horas e 50 minutos. A que horas termina a aula de informática de Paulo?

Exemplo de resolução possível:

9 horas + 2 horas = 11 horas

10 minutos + 50 minutos = 60 minutos (ou 1 hora)

11 horas + 1 hora = 12 horas

A aula de informática de Paulo termina às 12 horas (meio-dia).

2. Rafael começou, às 17 horas e 15 minutos, a fazer as atividades de Matemática que a professora propôs como tarefa de casa. A duração do intervalo de tempo que Rafael dedicou à realização dessa tarefa foi de 3 horas e 25 minutos. Quando Rafael terminou as atividades, que horas eram?

Exemplo de resolução possível:

17 horas + 3 horas = 20 horas

15 minutos + 25 minutos = 40 minutos

Quando Rafael terminou a tarefa de casa eram 20 horas e 40 minutos

3. Luiz é diretor em uma grande empresa e marcou uma reunião com todos os gerentes cujo horário de início é às 14 horas. Para preparar a sala onde a reunião vai ocorrer, Luiz chegou 40 minutos antes A que horas Luiz chegou à sala de reunião?

Exemplo de resolução possível:

14 horas = 13 horas + 1 hora

1 hora ou 60 minutos

60 minutos – 40 minutos = 20 minutos

Luiz chegou à sala de reunião às 13 horas e 20 minutos.

4. Uma cozinheira colocou às 10 horas e 50 minutos um bolo para assar. Na receita desse bolo está indicado que ele deve ficar assando no forno por meia hora. A que horas esse bolo vai ficar pronto?

Exemplo de resolução possível:

Meia hora ou 30 minutos

10 horas + 50 minutos + 30 minutos = 10 horas + 80 minutos

80 minutos ou 1 hora e 20 minutos (pois: 60 minutos + 20 minutos = 80 minutos)

10 horas + 1 hora + 20 minutos = 11 horas + 20 minutos

Esse bolo vai ficar pronto às 11 horas e 20 minutos.

5. A aula de natação de Laura tem duração de 1 hora e 30 minutos. A quantos minutos esse intervalo de tempo corresponde?

Exemplo de resolução possível:

1 hora corresponde a 60 minutos

60 minutos + 30 minutos = 90 minutos

O intervalo de tempo de 1 hora e 30 minutos corresponde a 90 minutos

Na Aula 6, explorar com a turma os diversos tipos de relógios inventados com o passar do tempo, por exemplo, os relógios de Sol, os relógios de água , os relógios inteligentes conectados aos aparelhos celulares modernos, entre outros. Nesse sentido, desenvolver um trabalho interdisciplinar com História.

Pedir aos alunos que, durante a Aula 6, façam uma pesquisa com base nessa temática. Alguns materiais interessantes são indicados a seguir:

• OBMEP. E haja unidades de medida! Disponível em: http://clubes.obmep.org.br/blog/e-haja-unidades-de-medidas-oficina-2/. Acesso em: 4 jan. 2022.

• SILVA, Mariana Marques da; VIEIRA, Flaviana Tavares. Umrelógioincrível Diamantina: UFVJM, 2018. (Pequenos Curiosos, 29). Disponível em: http://site.ufvjm.edu.br/pequenoscuriosos/files/2013/05/Livro-29-Um-rel%C3% B3gio-incr%C3%ADvel.pdf. Acesso em: 4 jan. 2022.

Ao propor aos alunos que realizem uma pesquisa, é importante orientá-los. A esse respeito, sugere-se a leitura de textos complementes sobre o assunto como: "Avaliandosites e identificando as melhores fontes para pesquisa", na página 7 do material disponível em: https://educamidia.org.br/api/wp-content/uploads/2019/12/MMPapers2_Educacao-paraInformacao_V2-1.pdf. Acesso em: 4 jan. 2021.

Aulas 7 e 8

Nestas aulas, o aspecto lúdico da aprendizagem será explorado por meio de jogos. Durante as partidas dos jogos propostos, acompanhar os alunos, observando se estão interagindo de maneira respeitosa e exercendo a escuta ativa

Permitir que joguem mais de uma partida a cada jogo proposto, a fim de que pratiquem os conteúdos matemáticos envolvidos no jogo.

Para cada aula, sugere-se um jogo.

• Na Aula 7, propor o "Jogo da memória com medidas". Disponível em: https://escola.britannica.com.br/jogos/GM_5_11/index.html. Acesso em: 4 jan. 2021.

• Mais jogos envolvendo outros conteúdos matemáticos podem ser encontrados neste site : Britannica Escola | Capes Ministério da Educação, acessando o link : https://escola.britannica.com.br/se%C3%A7%C3%A3o/jogos/1400/1510. Acesso em: 4 jan. 2021.

• Neste site , há também uma videoteca muito rica e é possível pesquisar por temas em: https://escola.britannica.com.br/. Acesso em: 4 jan. 2021.

• Na Aula 8, sugere-se retomar o uso do app disponível em https://apps.mathlearningcenter.org/math-clock/. Acesso em: 4 jan. 2022.

• Propor aos alunos uma "Batalha de representação de horas em relógios analógicos" Para isso, ditar um horário, e o grupo que primeiro representar corretamente o horário ganha ponto. Vence o grupo que obtiver mais pontos após cinco rodadas.

Ao término de cada partida, conversar com os alunos sobre o jogo e as experiências de aprendizagem obtidas. Embora sejam sugeridos jogos virtuais, pode-se realizar de acordo com a realidade de cada escola uma versão do jogo feita com material concreto

Sugestões

• LUCENA, Rosilângela; RODRIGUES, Anderson; DURÃO, Lúcia; TIBURCIO, Ricardo (org.). As grandezas e medidas em quadrinhos. Recife: Edumatec/UFPE, 2018. Disponível em: https://hal.archives-ouvertes.fr/hal-01857296/document. Acesso em: 23 dez. 2021.

• MOURA, Manoel Oriosvaldo de; LOPES, Anemari Roesler Luersen Vieira; ARAÚJO, Elaine Sampaio; CEDRO, Wellignton Lima. Atividades para o ensino de Matemática nos anos iniciais da Educação Básica: medidas. v. 2. São Paulo: FE-USP, 2019. Disponível em: http://www.labeduc.fe.usp.br/wp-content/uploads/e-book_livro2-Medidas-FINAL-16jan2 019.pdf. Acesso em: 23 dez. 2021.

Sequência didática 6 • Números expressos na forma de fração

Ao longo desta sequência didática, são apresentadas propostas que visam fazer com que os alunos compreendam o significado de frações mais usuais menores que uma unidade Com base em situações do cotidiano dos alunos, o conceito de fração é construído por meio de noções como metade, terça parte, quarta parte, quinta parte, décimos e centésimos.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Perm itida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Objetivos de aprendizagem

• Compreender a ideia de fração.

• Reconhecer a importância da utilização de frações em situações cotidianas.

• Representar uma fração como parte de um inteiro

• Ler, escrever e comparar representações fracionárias.

• Determinar os termos de uma fração: numerador e denominador.

• Identificar frações menores que uma unidade, utilizando a reta numérica como recurso.

Plano de aulas

Aulas 1 e 2: Explorar a ideia de fração com base em situações cotidianas e em modelos visuais contínuos (figuras poligonais divididas em partes iguais). Representar um número expresso na forma de fração. Determinar os termos de uma fração: numerador e denominador Trabalhar a leitura e a escrita de frações menores que uma unidade

Aulas 3 e 4: Representar frações menores que uma unidade, utilizando a reta numérica. Trabalhar a leitura e a escrita de frações menores que uma unidade. Representar frações menores que uma unidade de acordo com representações de figuras poligonais divididas em partes iguais, utilizando aplicativo virtual.

Aulas 5 e 6: Comparar frações menores que uma unidade, utilizando aplicativo virtual

Aulas 7 e 8: Explorar de maneira lúdica a leitura e a escrita de frações por meio de um jogo virtual, demonstrando compreensão da representação dos números expressos na forma de fração ao reconhecê-los no raciocínio envolvido em um desses jogos

Componentes essenciais para a alfabetização: compreensão de textos e produção de escrita Competências gerais da Educação Básica: 5 e 9

Competência específica de Matemática: 5

Habilidade: EF04MA09

Materiais necessários: fichas quadrangulares com medidas de 20 cm por 20 cm, recortadas previamente em folhas de papel sulfite colorido, folhas de papel sulfite colorido, placas emborrachadas e coloridas de EVA, folhas de papel com texturas diferentes, pedaços de barbante com 1 metro de comprimento e computador com acesso à internet

Aulas 1 e 2

Iniciar a Aula 1 debatendo com os alunos em quais situações do dia a dia eles costumam utilizar expressões verbais como "metade de", "um terço de", "um quarto de", " um quinto de", " um décimo de" e " um centésimo de"

Anotar na lousa as respostas dos alunos, que podem fazer referências a situações como: "metade de um chocolate", " um terço de uma torta doce", "um quarto de um sanduíche", "um quinto da bateria do celular está descarregada", "um décimo da distância

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

entre duas cidades já foi percorrido" e "um centésimo das 100 casas deste tabuleiro foi percorrido por esta peça"

Com base nas respostas, verificar o entendimento e a percepção que os alunos têm acerca do significado do uso dessas expressões no dia a dia

Dar continuidade à exploração de situações do cotidiano em que ocorre o uso dessas expressões para levar a turma a compreender a ideia de fração com base em atividades práticas usando recursos manipulativos em um primeiro momento Para isso, solicitar aos alunos que se organizem em duplas

Nas aulas desta sequência didática, o trabalho em pares ou grupos será proposto de modo recorrente, a fim de que a empatia e a cooperação favoreçam o desenvolvimento da competência geral da Educação Básica 9 em prol da construção de conhecimento.

Em seguida:

• distribuir para cada dupla uma ficha quadrangular (com medidas de 20 cm por 20 cm) recortada, previamente, em folha de papel sulfite colorido da cor azul, por exemplo;

• entregar, também, para cada dupla uma folha de papel sulfite colorido do tipo A4 de cor diferente da usada para confeccionar a ficha quadrangular;

• propor as atividades sugeridas a seguir.

1. Dobrem em 4 partes iguais a ficha quadrangular que receberam confeccionada em papel colorido, de modo que sejam feitos vincos que indiquem essa divisão.

Sugestões de respostas: Editoria de arte

2. Dobrem em três partes iguais a folha de papel sulfite que receberam, de modo que sejam feitos vincos que indiquem essa divisão.

Sugestões de respostas:

Editoria de arte

O objetivo é que os alunos percebam algumas maneiras diferentes de dividir igualmente a unidade, o inteiro (neste caso, a folha) em partes iguais, reconhecendo a ideia de um terço como a divisão de um por três.

É importante que os alunos compreendam que a ideia de fração envolve a divisão do inteiro (da unidade) em partes iguais

Vale ressaltar que essas atividades sugeridas podem ser adaptadas para alunos com deficiência visual, confeccionando, em placas emborrachadas e coloridas de EVA ou papéis de texturas diferentes, fichas (ou folhas) inteiras e divididas em partes iguais para que esses alunos possam manipular e compreender por meio do tato o que está sendo trabalhado.

Na Aula 2, ampliar as ideias trabalhadas na aula anterior explicando aos alunos o significado dos termos de uma fração (numerador e denominador) e, para isso, considerar as folhas e dobraduras realizadas nas atividades da Aula 1.

Demonstrar à turma como representar, na forma de fração:

• um quarto, no caso da atividade 1, para indicar cada uma das partes em que a ficha foi dividida;

• um terço, no caso da atividade 2, para indicar cada uma das partes em que a folha foi dividida.

Explicar aos alunos que o número que indica a quantidade de partes:

• em que o inteiro (a ficha ou a folha) foi dividido em partes iguais corresponde ao denominador da fração;

• que são consideradas em relação ao inteiro (a ficha ou a folha) corresponde ao numerador da fração. Nas duas atividades da aula anterior, é considerada cada uma das partes em que foi dividido cada material manipulado para indicar a que fração da ficha (ou a que fração do papel) cada parte corresponde.

Portanto, a escrita do número expresso na forma de fração que representa:

• cada uma das partes iguais em que a ficha foi dividida na atividade 1 é 1 4 ;

• cada uma das partes iguais em que a folha foi dividida na atividade 2 é 1 3

Em seguida, comentar como é feita a leitura dessas frações:

• 1 4 lê-se um quarto;

• 1 3 lê-se um terço.

Depois, entregar a cada dupla um barbante com medida de comprimento de 1 metro para que realizem a atividade sugerida a seguir

3. Cortem em quatro partes iguais o pedaço de barbante que receberam. Mas atenção: não pode ser usado nenhum instrumento de medição, como régua ou fita métrica.

a) Registrem no caderno como fizeram para realizar o que foi pedido no enunciado desta atividade.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

Espera-se que os alunos percebam que, de modo análogo à atividade 1, para obter um quarto do barbante ou a quarta parte, é possível realizar dobras sucessivas. Nesse caso, a primeira dobra seria feita ao meio, obtendo a metade do barbante, e a segunda dobra sucessiva do barbante sobre ele mesmo seria feita para identificar a metade da metade ou a quarta parte do barbante, de modo que seja possível cortá-lo em quatro partes iguais

b) Que fração representa a metade do barbante? Como se lê essa fração?

1 ; 2 um meio.

c) Que fração representa a quarta parte do barbante? Como se lê essa fração?

1 ; 4 um quarto.

Concluir a Aula 2 debatendo com a turma os critérios adotados para a realização das atividades propostas, oportunizando que sejam identificadas dúvidas a serem sanadas.

Aulas 3 e 4

Iniciar a Aula 3 comentando com a turma que as frações são utilizadas para indicar quantidades. Assim como os números naturais são utilizados para indicar quantidades, é importante que os alunos percebam que os números racionais expressos na forma de fração também indicam quantidades relacionadas a um inteiro Sem utilizar essas nomenclaturas, explicar, por exemplo, que, ao ler os ingredientes em uma receita, há indicação de quantidades como:

• 2 ovos e 1 colher de fermento;

• meio litro de leite (neste caso, a quantidade indicada é uma parte, meio litro, de um inteiro, que corresponde a 1 litro de leite)

Com base nessa abordagem inicial, comentar com a turma que é possível representar frações utilizando a reta numérica como recurso, de modo parecido com as marcações que existem em copos medidores graduados, utilizados na cozinha na execução de receitas Depois, propor as atividades sugeridas a seguir

1. É aniversário de Rafaela e Juliana, que são gêmeas. A avó delas, senhora Augusta, fez bolo de cenoura para a festa. Na receita, constavam os ingredientes listados a seguir. Leia-os e responda às questões.

Bolo de cenoura

Ingredientes

1 xícara (chá) de farinha de arroz (integral ou tradicional)

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

1

3 xícara (chá) de açúcar demerara

1 3 xícara (chá) de óleo

1 cenoura grande

2 ovos

3 colheres (sopa) de fécula de batata

2 colheres (chá) de polvilho doce

1 colher (sopa) de fermento químico

a) Que fração é indicada duas vezes nessa receita? Como se lê essa fração?

1 ; 3 um terço

b) Represente em uma reta numérica a fração que é indicada duas vezes nessa receita

Para isso, com o auxílio de uma régua, trace uma reta horizontal para representar o intervalo de 0 a 1 indicando o inteiro. Em seguida, divida o intervalo em três partes iguais. Depois, indique na reta a posição correspondente à fração solicitada.

2. A senhora Augusta também fez rosquinhas de polvilho para a festa das netas Leia os ingredientes utilizados, descritos a seguir, e responda às questões.

Rosquinhas de polvilho

Ingredientes

2 xícaras (chá) de polvilho azedo

1 colher (sopa) de óleo (sugestão: de coco, canola ou de girassol)

1 ovo

1

4 xícara (chá) de água quente

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

1 pitada de sal

a) Que fração de xícara (chá) de água quente consta da receita dessas rosquinhas? Como se lê essa fração?

1 ; 4 um quarto

b) Represente em uma reta numérica a fração de xícara (chá) de água quente que consta da receita Para isso, com o auxílio de uma régua, trace uma reta horizontal para representar o intervalo de 0 a 1 indicando o inteiro. Em seguida, divida o intervalo em quatro partes iguais. Depois, indique na reta a posição correspondente à fração solicitada

3. Para a festa, a avó de Rafaela e Juliana também fez empadas de batata e abobrinha. Leia a lista de ingredientes e responda às questões.

Empadas de batata e abobrinha

Ingredientes

5 unidades de batata inglesa média

1 abobrinha média

2 xícaras (chá) cheias de carne moída cozida e temperada a gosto

1

2 cebola média

1 dente de alho

1 fio de azeite para untar a fôrma e refogar o alho e a cebola

a) Que fração da cebola é utilizada nessa receita? Como se lê essa fração?

1 ; 2 um meio (ou metade)

b) Represente em uma reta numérica a fração de cebola descrita nessa receita Para isso, com o auxílio de uma régua, trace uma reta horizontal para representar o

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

intervalo de 0 a 1 indicando o inteiro. Em seguida, divida o intervalo em três partes iguais. Depois, indique na reta a posição correspondente à fração solicitada

O modo de preparo de cada uma das receitas que foram apresentadas nas atividades sugeridas anteriormente está disponível no material "Vamos brincar de cozinhar? Dicas de receitas para serem realizadas com crianças", disponível em: http://www4.fe.usp.br/wp-content/uploads/cartilhavirtu.pdf. Acesso em: 5 jan. 2022.

Durante a realização das atividades, verificar se os alunos têm dificuldade para medir ocomprimento do intervalo entre 0 e 1 na reta numérica, bem como para dividi-lo em partes iguais. Caso demonstrem dificuldade, é necessário dedicar um intervalo de tempo na aula para que esse aspecto seja trabalhado.

Na Aula 4, amplie o trabalho com frações explorando com a turma as ferramentas "Barras de frações" e "Círculos de fração", disponíveis em: https://pt.mathigon.org/polypad Acesso em: 6 jan. 2022.

Ao utilizar recursos multimídia adequados para apoiar a aprendizagem, está sendo favorecido nos alunos o desenvolvimento da competência geral da Educação Básica 5

Caso a escola não disponha de infraestrutura adequada, como laboratório de informática com computadores para que os alunos possam explorar essas ferramentas, providenciar, previamente, um computador portátil, de modo que organizada em grupos a turma possa explorar os jogos.

Vale ressaltar que as barras de frações e os círculos de fração também podem ser confeccionados previamente em papéis com diferentes cores, texturas e gramaturas para que os alunos os manipulem.

Caso a exploração on-linenão seja possível na escola, os alunos podem ampliar o trabalho iniciado na aula acessando esse linkem casa em computadores pessoais (caso possuam) ou em outros dispositivos móveis, como tabletou smartphone, para realizar as propostas de atividades como tarefa em casa.

Pedir aos alunos que realizem as atividades sugeridas a seguir com o apoio desse recurso virtual.

1. Acessem as "Barras de frações" disponíveis em: https://pt.mathigon.org/polypad Acesso em: 6 jan. 2022. Na barra no canto esquerdo da tela, cliquem no terceiro item, "Frações". Ao clicar nele, duas opções aparecem, e a primeira delas é "Barras de frações" Responda às questões seguintes, utilizando essas barras.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

a) Qual é a cor da barra dividida em duas partes iguais? A que fração do inteiro corresponde cada parte dessa barra? Como se lê essa fração?

Cor laranja; 1 ; 2 um meio.

b) Qual é a cor da barra dividida em três partes iguais? A que fração do inteiro corresponde cada parte dessa barra? Como se lê essa fração?

Cor vermelha; 1 ; 3 um terço.

c) Qual é a cor da barra dividida em quatro partes iguais? A que fração do inteiro corresponde cada parte dessa barra? Como se lê essa fração?

Cor-de-rosa; 1 ; 4 um quarto.

d) Qual é a cor da barra dividida em cinco partes iguais? A que fração do inteiro corresponde cada parte dessa barra? Como se lê essa fração?

Cor roxa; 1 ; 5 um quinto.

e) Qual é a cor da barra dividida em 10 partes iguais? A que fração do inteiro corresponde cada parte dessa barra? Como se lê essa fração?

Cor verde; 1 ; 10 um décimo

2. Acessem os "Círculos de fração" disponíveis em: https://pt.mathigon.org/polypad Acesso em: 6 jan. 2022. Na barra no canto esquerdo da tela, cliquem no terceiro item, "Frações". Ao clicar nele, duas opções aparecem, e a segunda delas é "Círculos de fração". Responda às questões seguintes, utilizando esses círculos.

a) A que fração do círculo inteiro corresponde uma parte de cor laranja? Como se lê essa fração? 1 ; 2 um meio.

b) A que fração do círculo inteiro corresponde uma parte de cor vermelha? Como se lê essa fração? 1 ; 3 um terço.

Material disponibilizado em licença aberta do tipo

Commons

Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

c) A que fração do círculo inteiro corresponde uma parte cor-de-rosa? Como se lê essa fração?

1 ; 4 um quarto.

d) A que fração do círculo inteiro corresponde uma parte de cor roxa? Como se lê essa fração?

1 ; 5 um quinto.

e) A que fração do círculo inteiro corresponde uma parte de cor verde? Como se lê essa fração?

1 ; 10 um décimo.

A utilização das "Barras de frações" e dos "Círculos de fração" nas atividades propostas visa auxiliar os alunos na visualização da representação das frações, de modo mais específico, das frações menores que uma unidade

Explorar com a turma, na atividade 1, a relação que há entre a quantidade de partes em que cada barra foi dividida igualmente e as medidas das partes, levando-os a perceber que, quanto maior a quantidade de partes em que a barra está dividida, menor cada parte é.

Reforçar para os alunos, nas atividades, que a barra e o círculo, em cada caso, correspondem ao inteiro, à unidade, e as partes diferenciadas por cores correspondem às frações menores que um inteiro, menores que uma unidade.

As representações retangulares das barras e as circulares dos círculos nas atividades são utilizadas com o objetivo de os alunos perceberem as mesmas ideias de frações com base em modelos diferentes.

Finalizar solicitando aos alunos que produzam no caderno um texto sintetizando as ideias exploradas nestas aulas

As atividades propostas como sugestão nesta sequência didática exploram aspectos relacionados à habilidade EF04MA09 e, de modo particular, o incentivo à utilização dos recursos on-line apresentados visa fazer com que o aluno possa utilizar "ferramentas matemáticas, inclusive tecnologias digitais disponíveis", a fim de contemplar o aspecto da competência específica de Matemática para o Ensino Fundamental 5.

Aulas 5 e 6

Nas Aulas 5 e 6, dar continuidade ao trabalho iniciado nas aulas anteriores, porém, desta vez, incentivando a utilização de outro recurso on-line

Propor atividades, como as sugeridas a seguir, que envolvem a exploração das frações 1 10 e 1 100 , bem como comparações de frações, para que os alunos, organizados em grupos, respondam a elas usando o app mencionado a seguir

1. Abram o aplicativo disponível em: https://apps.mathlearningcenter.org/fractions/ (acesso em: 6 jan. 2022). Façam o que se pede a seguir e, depois, respondam às questões. No canto inferior da tela, cliquem:

• no segundo ícone da esquerda para a direita para construir cada figura;

• no quinto ícone da esquerda para a direita para colorir cada figura. Explorem as outras ferramentas disponíveis de maneira autônoma!

a) Construam uma figura dividida em 10 partes iguais e pintem, da cor que preferirem, 1 10 dessa figura.

Sugestão de resposta:

Editoria de arte

b) Construam uma figura com a mesma forma e as mesmas medidas da que foi construída no item anterior e a dividam em 100 partes iguais. Depois, pintem da cor que preferirem 1 100 dessa figura.

Sugestão de resposta: Editoria de arte

c) Observem as partes coloridas nas figuras construídas e respondam: um décimo colorido na primeira figura é maior ou menor que um centésimo colorido na segunda figura?

Espera-se que os alunos respondam que um décimo colorido na primeira figura é maior que um centésimo colorido na segunda figura

d) Se tivessem sido coloridos 50 100 da segunda figura, pode-se afirmar que teria sido colorida metade da figura toda? Justifiquem a resposta.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

Espera-se que os alunos respondam que é possível afirmar que teri a sido colorida metade da figura. Os alunos podem justificar a resposta fazendo a construção da figura e colorindo as partes usando o aplicativo:

Editoria de arte

Acompanhar os alunos durante a realização dessa atividade, a fim de identificar eventuais dúvidas, fazendo as intervenções e as mediações necessárias para que compreendam as comparações entre as frações propostas

Na Aula 6, propor aos alunos que, organizados em trios, façam a atividade sugerida a seguir.

2. Usando o mesmo aplicativo da atividade 1, elaborem e escrevam duas afirmações indicando comparações de frações, por exemplo, se uma fração é maior ou menor que outra.

Para elaborar as afirmações, façam no aplicativo a construção de figuras divididas em partes iguais e pintem as partes das figuras construídas que representam as frações da figura. Justifiquem cada afirmação elaborada

Exemplos de afirmações e de justificativas que os alunos podem demonstrar fazendo a construção da figura e colorindo as partes usando o aplicativo:

Afirmação 1: 1 4 é maior que 1 . 8

Editoria de arte

Afirmação 2: 2 10 é menor que 3 10

Editoria de arte

Concluída a tarefa, pedir aos trios que compartilhem com os outros trios as afirmações elaboradas. Durante esse processo, identificar eventuais incorreções e

dificuldades, avaliando se há necessidade de retomar alguns pontos do conteúdo com a turma.

Aulas 7 e 8

Nestas aulas, propor aos alunos que acessem o jogo "Jogo da memória com frações", disponível em: https://escola.britannica.com.br/jogos/GM_4_17/index.html (acesso em: 6 jan. 2022). Nesse jogo, os alunos exploram a leitura e a escrita de números expressos na forma de fração.

Observar como os alunos estão se desenvolvendo durante as rodadas do jogo Combinar com eles quantas rodadas serão realizadas em cada aula, como se fosse um campeonato entre duplas, trios, quartetos ou grupos com mais integrantes, dependendo de como combinarem essa organização. O jogo foi elaborado para um jogador, mas é possível propor que joguem em grupos, de modo que troquem ideias e elejam um aluno para jogar, conforme as ideias do grupo.

Acompanhar a participação da turma, verificando o envolvimento de todos com a atividade lúdica proposta Concluir cada aula debatendo com a turma a contribuição desse tipo de atividade para a aprendizagem matemática deles

Sugestões

• BERTONI, Nilza Eigenheer. Pedagogia: educação e linguagem matemática IV: frações e números fracionários Brasília: Universidade de Brasília, 2009. Disponível em: http://www.sbembrasil.org.br/files/fracoes.pdf Acesso em: 6 jan. 2022.

• MORAIS, Rosilda dos Santos; BERTINI, Luciane de Fatima; VALENTE, Wagner Rodrigues. A matemática do ensino de frações: do século XIX à BNCC. São Paulo: Livraria da Física, 2021. (Histórias da matemática em estudos e no ensino, v. 4).

• SCHASTAI, Marta Burda; SILVA, Sani de Carvalho Rutz da; FARIAS, Elizabeth Regina Streisky de Formação de professores e o ensino de frações nos anos iniciais Curitiba: Appris, 2017.

• SMOLE, Katia Stocco; DINIZ, Maria Ignez (org.) Materiais manipulativos para o ensino de frações e números decimais Porto Alegre: Penso, 2016. (Coleção Mathemoteca, v 3).

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Sequência didática 7 • Ângulos retos e não retos em figuras poligonais, prismas e pirâmides

Ao longo desta sequência didática, é explorado o reconhecimento de ângulos retos e não retos em figuras poligonais, bem como são abordados prismas e pirâmides, analisando e comparando caraterísticas dessas figuras geométricas espaciais a fim de, entre outros aspectos, estabelecer relações de figuras geométricas planas associadas às faces dessas figuras geométricas espaciais.

Objetivos de aprendizagem

• Reconhecer ângulos retos e não retos em figuras poligonais com uso de recursos digitais

• Analisar características de prismas e pirâmides.

• Associar prismas e pirâmides a suas planificações.

Plano de aulas

Aulas 1 e 2: Identificar, em obras de arte, mosaicos e azulejos virtuais inspirados na arte kolam , linhas retas, linhas curvas e figuras poligonais.

Aulas 3 e 4: Trabalhar a ideia de ângulos retos e não retos (ângulo menor que ângulo reto e ângulo maior que ângulo reto). Reconhecer ângulos retos e não retos usando dobradura e esquadro como materiais manipulativos

Aulas 5 e 6: Reconhecer ângulos retos e não retos em figuras poligonais usando esquadro virtual disponível em recurso digital e aplicativo de formas padrão.

Aulas 7 e 8: Reconhecer características de prisma de base hexagonal e pirâmide de base hexagonal por meio de manipulativo virtual

Componentes essenciais para a alfabetização: compreensão de textos, desenvolvimento de vocabulário e produção de escrita.

Competências gerais da Educação Básica: 3, 4 e 5

Competência específica de Matemática: 5

Habilidades: EF04MA17 e EF04MA18

Materiais necessários: folhas de papel quadriculado, esquadros e computador com acesso à internet

Aulas 1 e 2

Nestas aulas, levar os alunos a identificar em padrões artísticos, como mosaicos e arte kolam(arte popular da Índia), e em obras de arte de artistas brasileiros, como Tarsila do Amaral, linhas retas, linhas curvas e figuras poligonais Com isso, esta proposta e outras

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas

propostas desta sequência didática poderão favorecer o trabalho interdisciplinar com a área de Linguagens e suas Tecnologias e com o componente curricular Arte.

Caso a escola disponha de infraestrutura tecnológica, como computadores com acesso à internet, iniciar a Aula 1 encaminhando a turma ao laboratório de informática. Se a escola não dispuser de infraestrutura adequada, providenciar, previamente, um computador portátil, de modo que os alunos, organizados em grupos, possam se revezar para explorar as propostas sugeridas a seguir.

Explicar a eles que vão explorar o reconhecimento de linhas retas, linhas curvas e figuras poligonais (figuras planas fechadas que têm lados formados por linhas retas que não se cruzam) em obras de arte, nesta aula; e em peças e azulejos virtuais inspirados na arte kolam (arte popular da Índia), na Aula 2. Essas propostas visam estabelecer interdisciplinaridade com a disciplina de Arte.

Para o trabalho da Aula 1, sugerir aos alunos que utilizem a galeria virtual com reproduções de obras da pintora brasileira Tarsila do Amaral (1886-1973), disponível em: https://tarsiladoamaral.com.br/obras/ (acesso em: 8 jan. 2022).

De início, pedir que abram a página inicial desse sitee cliquem em Biografia.

Solicitar aos alunos que façam a leitura da biografia dessa artista, estabelecendo um trabalho vinculado a esse gênero textual, que é estudado em Língua Portuguesa.

Complementando esse trabalho com a biografia de Tarsila do Amaral, propor a leitura de imagens e textos presentes na Linha do tempo da vida e obra dessa artista, estabelecendo um trabalho vinculado com História.

Debater com a turma acontecimentos da vida da artista que mais chamaram a atenção deles.

Em seguida, pedir aos alunos que acessem Obras na página inicial desse site, e depois cliquem em Galeria

Explicar à turma que as obras estão organizadas por períodos, em intervalos de tempo determinados em anos, de acordo com o que leram na biografia e observaram na linha do tempo sobre a artista.

Pedir que anotem no caderno os nomes de três obras de arte de Tarsila do Amaral nas quais reconhecerem linhas retas, linhas curvas e figuras poligonais.

Orientá-los a passar o mouse sobre a imagem para conhecerem o nome de cada obra.

Sugestões de respostas: Carnaval em Madureira (imagem P072), A gare (imagem P080), O mamoeiro (imagem P085), entre outras

Encerrar a aula pedindo aos alunos que assistam ao vídeo com a música que é tema do filme de animação Tarsilinha. Esse filme é inspirado na obra de Tarsila do Amaral, e a música foi composta por Zeca Baleiro.

O clipe dessa música é rico em cores e formas e está disponível em: http://tarsiladoamaral.com.br/lancamento-da-musica-tema-do-filme-de-animacao-tarsilinha/ ( acesso em: 8 jan. 2022).

Ao explorar aspectos pessoais, sociais e culturais da vida e obra da artista Tarsila do Amaral, o repertório cultural dos alunos é ampliado, favorecendo o desenvolvimento da competência geral da Educação Básica 3

Na Aula 2, o foco do trabalho é em padrões artísticos e arte kolam(arte popular da Índia). A artekolam, tradicional da Índia, é feita, especialmente, por mulheres que, utilizando pó de arroz ou giz, fazem desenhos de padrões com linhas retas e linhas curvas, formando como se fossem grades ao redor de pontos e criando padrões que seguem determinada regra de repetição.

Sobre artekolam,é pouca a bibliografia já traduzida para oportuguês.Para saber mais a respeito dessa arte, sugere-se a leitura da seguinte obra:

• GERDES, Paulus. Da etnomatemática a arte-design e matrizes cíclicas. Belo

Horizonte: Autêntica, 2010. (Tendências em Educação Matemática, 19)

Encaminhar o trabalho desta aula explorando com a turma recursos multimídia adequados para apoiar a aprendizagem, de modo que o desenvolvimento da competência geral da Educação Básica 5 seja favorecido.

Em um primeiro momento, solicitar aos alunos que acessem o "Tantrix Tiles", disponível em: https://pt.mathigon.org/polypad (acesso em: 8 jan. 2022).

Para isso, orientá-los a clicar na barra no canto esquerdo da tela, no primeiro item, que é "Geometria". Ao clicar nesse item, oito opções aparecem, e a oitava é "Padrões e Arte", na qual o primeiro recurso é "Tantrix Tiles".

Nesse recurso, a identificação visual das linhas retas e das linhas curvas desenhadas nas peças virtuais favorece a percepção de encaixes dessas linhas rotacionando as figuras hexagonais.

Pedir aos alunos que, organizados em grupos, formem na tela um mosaico usando essas peças.

Pode-se propor, como maneira de dinamizar a agilidade de raciocínio dos alunos e tornar a proposta mais desafiadora, que seja cronometrado o tempo de realização dessa tarefa e anotada na lousa a ordem em que os grupos forem concluindo o preenchimento de toda a tela com as peças.

Combinar que, para sinalizar o término, os integrantes do grupo devem erguer as mãos, sem fazer barulho, de modo que não atrapalhem a concentração dos outros grupos Dirigir-se até eles para fazer a conferência dos encaixes sequenciais corretos de linhas retas e linhas curvas de acordo com as cores verde, laranja e roxa que traçam as peças pretas.

Concluída essa atividade, sugere-se passar para a exploração de linhas retas e linhas curvas em azulejos inspirados na artekolam

Pedir aos alunos que acessem os "Azulejos de piscina", também disponíveis em: https://pt.mathigon.org/polypad (acesso em: 8 jan. 2022)

Explicar que, na barra no canto esquerdo da tela, no primeiro item, que é "Geometria", constam as oito opções já verificadas anteriormente, e a oitava é "Padrões e Arte", na qual o terceiro recurso é "Azulejos de piscina".

Reforçar que, desta vez, será usado o terceiro recurso.

Propor a mesma atividade anterior. A variação ocorrida será em relação às peças quadrangulares e às cores diferentes.

Vale ressaltar que o trabalho destas duas aulas favorece o desenvolvimento da habilidade EF04MA18, pois, ao rotacionar, encaixar e reconhecer encaixes de peças que representam figuras poligonais, os alunos iniciam um trabalho intuitivo de reconhecimento de ângulos retos e não retos nessas figuras, fato que será retomado posteriormente nesta sequência didática, para que os alunos compreendam a ideia de ângulos e desenvolvam o vocabulário geométrico tendo contato com essas novas nomenclaturas e seus significados

Aulas 3 e 4

Nestas aulas, os pontos principais do trabalho serão:

• na Aula 3, explorar a ideia de ângulo;

• na Aula 4, usar dobraduras e esquadro para identificar ângulos retos e não retos (ângulo menor que ângulo reto e ângulo maior que ângulo reto) em materiais escolares e no ambiente ao redor.

Na Aula 3, as ideias de ângulo serão exploradas relacionadas:

• à ideia de giro, que envolve um giro em torno de um ponto fixo;

• à ideia de inclinação, que indica uma inclinação em relação a um eixo.

A princípio, na Aula 3, trabalhar com os alunos a ideia de ângulo relacionada ao giro, que envolve um giro em torno de um ponto fixo, e, para isso, sugere-se manipular ponteiros de relógios analógicos.

Essa manipulação pode ser feita nas versões:

• off-line , construindo com os alunos um relógio de ponteiros, usando um modelo para imprimir, colar, recortar e montar em papel mais resistente, como papel-cartão.

• on-line , usando os "Relógios" disponíveis em: https://pt.mathigon.org/polypad (acesso em: 9 jan. 2022) Neste caso, orientar os alunos a acessar esse link ; em seguida, clicar, na barra no canto esquerdo da tela, no sexto item, que é "Jogos e

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Perm itida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas

Aplicativos". Ao clicar nele, três opções aparecem, e a segunda delas é "Relógios" Da esquerda para a direita, pedir aos alunos que selecionem a terceira opção de mostrador de relógios de ponteiros designada por "Movimento livre"

Após decidir se a manipulação será feita off-line ou on-line , sugere-se distribuir aos alunos folhas de papel quadriculado e propor as atividades a seguir.

1. Faça o que se pede em cada item.

a) No relógio de ponteiros, represente o horário de 3 horas.

Espera-se que os alunos posicionem o ponteiro grande apontando para o 12 e o ponteiro pequeno apontando para o 3.

b) Na folha de papel quadriculado:

• marque um ponto sobre o cruzamento de duas linhas para representar o ponto fixo que une os dois ponteiros no relógio;

• depois, trace, a partir desse ponto, uma linha vertical sobre uma linha da malha para representar o ponteiro que marca os minutos;

• em seguida, também, a partir desse ponto, trace outra linha horizontal sobre uma linha da malha para representar o ponteiro que marca as horas;

• por fim, desenhe uma seta para indicar a direção do giro do ponteiro que marca as horas até 3 horas.

Sugestão de desenho/resposta:

Explicar aos alunos que:

• o giro do ponteiro em torno de um ponto fixo do relógio dá a ideia de ângulo;

• esse giro dos ponteiros que marca 3 horas corresponde a um quarto de volta;

• o ângulo de um quarto de volta é chamado de ângulo reto;

• há também ângulos menores e maiores que um ângulo reto.

Pedir aos alunos que representem nos ponteiros do relógio e na folha de papel quadriculado outro horário em que é possível identificar um ângulo reto. Espera-se que os

alunos indiquem o horário de 9 horas, no qual é possível identificar com exatidão um ângulo reto. Por exemplo:

Sugestão de desenho/resposta:

Editoria de arte

Caso alguns alunos apresentem como resposta horários como 12 horas e 15 minutos, 3 horas e 30 minutos, 5 horas e 45 minutos, é importante reforçar que, nesses casos, o ângulo reto não é formado com exatidão pelos dois ponteiros.

Para que os alunos visualizem essa falta de exatidão em situação real de marcação de horário em relógios analógicos, é adequada a utilização do recurso on-line sugerido anteriormente.

Pedir aos alunos que selecionem, da esquerda para a direita, a segunda opção de mostrador de relógios de ponteiros designada por "Engrenado"

Desse modo, ao movimentar um dos ponteiros, o outro se movimenta engrenado, demonstrando com exatidão como é a marcação em um relógio de ponteiros real.

2. Faça o que se pede em cada item.

a) No relógio de ponteiros, represente o horário de 6 horas.

Espera-se que os alunos posicionem o ponteiro grande apontando para o 12 e o ponteiro pequeno apontando para o 6.

b) Na folha de papel quadriculado:

• marque um ponto sobre o cruzamento de duas linhas para representar o ponto fixo que une os dois ponteiros no relógio;

• depois, trace, com base nesse ponto, uma linha vertical sobre uma linha da malha para representar o ponteiro que marca os minutos;

• em seguida, também com base nesse ponto, trace outra linha horizontal sobre uma linha da malha para representar o ponteiro que marca as horas;

• por fim, desenhe uma seta para indicar a direção do giro do ponteiro que marca as horas até 6 horas.

Sugestão de desenho/resposta:

Explicar aos alunos que:

• o giro do ponteiro em torno de um ponto fixo do relógio dá a ideia de ângulo;

• esse giro dos ponteiros que marca 6 horas corresponde à meia-volta;

• o ângulo de meia-volta é um ângulo maior que um ângulo reto;

• há também ângulos menores que um ângulo reto.

Na Aula 4, trabalhar com os alunos a ideia de ângulo relacionada à ideia de inclinação, que indica uma inclinação em relação a um eixo, vinculando a ideia de ângulos menores ou maiores que um ângulo reto.

Para isso, sugere-se utilizar como material manipulativo dobradura e esquadro, de acordo com o encaminhamento das atividades seguintes.

Antes de propor aos alunos estas atividades, faz-se necessário distribuir folhas de papel quadriculado e esquadros.

3. Faça uma dobradura para construir um modelo de ângulo reto, observando as seguintes etapas:

• dobre ao meio no sentido vertical a folha de papel quadriculado que você recebeu;

• dobre novamente o papel ao meio, porém, desta vez, no sentido horizontal, de modo que as bordas retas do papel fiquem sobrepostas exatamente uma sobre a outra;

• desenhe a indicação de ângulo reto e pinte uma pequena região para representar a medida de abertura do ângulo, como no exemplo a seguir:

• Está pronto um modelo de ângulo reto feito de dobradura, que será utilizado para realizar medições na próxima atividade.

4. Utilizando o modelo de ângulo reto feito de dobradura, identifique nos seus materiais escolares ângulos retos e ângulos não retos.

a) Para isso, verifique se, ao sobrepor o modelo de ângulo reto em cada material escolar, os "cantos" coincidem com exatidão

• Se coincidirem, é ângulo reto

• Se não coincidirem, não é ângulo reto.

b) Caso não seja ângulo reto, verifique a inclinação em relação à linha horizontal do modelo de ângulo reto.

• Se a inclinação for maior que a medida da abertura colorida no modelo de ângulo reto, é um ângulo maior que um ângulo reto

• Se a inclinação for menor que a medida da abertura colorida no modelo de ângulo reto, é um ângulo menor que um ângulo reto.

c) Escreva uma lista dos ângulos que foram identificados e em quais materiais escolares. No caso de ângulos não retos, indique se o ângulo é maior ou menor que um ângulo reto.

Sugestões de resposta: ângulos retos foram identificados nos quatro "cantos" da capa retangular de um livro; ângulo maior que um ângulo reto foi identificado na abertura total de uma tesoura com pontas arredondadas

5. Agora, utilizando o esquadro que recebeu, proceda da mesma maneira que fez quando realizou medições com a dobradura do modelo de ângulo reto e identifique no ambiente ao seu redor ângulos retos e ângulos não retos. Escreva no caderno os exemplos que identificou.

Sugestões de resposta: ângulos retos foram identificados nos quatro "cantos" do tampo retangular de uma mesa; ângulo maior que um ângulo reto foi identificado em um relógio de ponteiros marcando o horário de 6 horas; ângulo menor que um ângulo reto foi identificado na medida da abertura entre o batente de uma porta e uma porta quase fechada.

Finalizar a aula solicitando aos alunos que produzam no caderno um texto sintetizando as ideias exploradas nesta aula

O trabalho destas Aulas 3 e 4, bem como das Aulas 5 e 6 seguintes, tem como objetivo desenvolver a habilidade EF04MA18

Aulas 5 e 6

Nestas aulas, o foco será fazer com que os alunos reconheçam ângulos retos e não retos em figuras poligonais usando esquadro virtual disponível em recurso digital.

A cada aula, levar a turma para a sala de informática ou utilizar computador portátil providenciado previamente

Na Aula 5, -pedir aos alunos que acessem os manipulativos virtuais disponíveis em: https://pt.mathigon.org/polypad (acesso em: 9 jan. 2022).

Orientar que, em seguida, cliquem, na barra no canto esquerdo da tela, no primeiro item, que é "Geometria". Ao clicar nesse item, oito opções aparecem A sétima opção é "Utensílios".

Solicitar aos alunos que cliquem nessa opção e selecionem o esquadro virtual, arrastando-o para o centro da tela.

Depois, pedir que cliquem na primeira opção, que é "Polígonos", e arrastem os polígonos representados, um a um, para o centro da tela. Sobreponham o ângulo reto do esquadro virtual de modo que reconheçam ângulos retos e ângulos não retos nas figuras.

Para verificar, orientar os alunos que, ao sobrepor o ângulo reto do esquadro sobre cada figura, os "cantos"” devem coincidir com exatidão

• Se coincidirem, é ângulo reto.

• Se não coincidirem, não é ângulo reto.

Pedir que respondam às atividades sugeridas a seguir, com base nessas investigações e de acordo com as figuras disponíveis nesse recurso digital.

1. Escreva o nome e a cor de uma figura em que é possível identificar apenas ângulos retos.

Sugestão de resposta: quadrado azul.

2. Escreva o nome e a cor de uma figura em que é possível identificar apenas ângulos maiores que um ângulo reto.

Sugestão de resposta: pentágono verde.

3. Escreva o nome e a cor de uma figura em que é possível identificar apenas ângulos menores que um ângulo reto.

Sugestão de resposta: triângulo laranja

Na Aula 6, propor aos alunos que utilizem o aplicativo disponível em: https://apps.mathlearningcenter.org/pattern-shapes/ (acesso em: 9 jan. 2022).

Pedir aos alunos que, na barra cinza, no canto esquerdo da tela, cliquem no último ícone de cima para baixo e escolham uma sombra para preencher totalmente, recobrindo-a

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os

com as figuras poligonais coloridas disponíveis acima, nessa barra. Por exemplo, os alunos podem selecionar:

• o hexágono e preenchê-lo totalmente com triângulos verdes, rotacionando-os e encaixando-os um a um;

• o paralelogramo e preenchê-lo totalmente com paralelogramos azuis, rotacionando-os e encaixando-os um a um;

• o triângulo e preenchê-lo totalmente com trapézios vermelhos, triângulos verdes e paralelogramos azuis, rotacionando-os e encaixando-os um a um; entre outras possibilidades.

Ressaltar para os alunos que:

• não podem sobrepor figuras coloridas para preencher a sombra da figura maior;

• ao dispor as figuras coloridas sobre a figura maior escura, os "cantos" devem coincidir com exatidão.

Para realizar essa atividade, os alunos trabalham a habilidade de reconhecer ângulos retos e não retos nas figuras poligonais disponíveis verificando as possibilidades de encaixe. Além disso, o objetivo é fazer com que os alunos compreendam que a mudança de posição das figuras, ao rotacioná-las para realizar os encaixes, não altera a medida da abertura dos ângulos identificados nelas.

Durante a realização da atividade, incentivar os alunos a se expressarem e partilharem informações, contribuindo com discussões coletivas relacionadas à atividade.

Pedir que façam comentários com base em conclusões extraídas do que estão investigando na atividade, de modo que a competência geral da Educação Básica 4 seja mobilizada.

A perspectiva de ensino híbrido, em que experiências on-line são integradas aos momentos presenciais ou remotos no processo de ensino e aprendizagem, constitui uma abordagem pedagógica que leva a caminhos promissores, por isso a ampliação de competências docentes com base em sugestões que utilizam recursos digitais permeia as aulas ao longo desta sequência didática.

Para saber mais acerca de ensino híbrido e escola conectada, sugere-se a leitura do seguinte material:

• CIEB notas técnicas #18: ensino híbrido e o uso das tecnologias digitais na educação básica. [recurso eletrônico]. São Paulo: CIEB, 2021. Disponível em: https://cieb.net.br/wp-content/uploads/2021/02/Nota-tecnica-18_Ensino-hibrido.pd f. Acesso em: 9 jan. 2022.

Aulas 7 e 8

Nestas aulas, será trabalhado o reconhecimento de características de um prisma de base hexagonal e uma pirâmide de base hexagonal com base na observação da planificação dessas figuras geométricas espaciais utilizando manipulativo virtual

O trabalho de associar esse prisma e essa pirâmide a suas planificações será realizado com o propósito de analisar, nomear e comparar atributos estabelecendo relações entre as representações planas e espaciais. Essa exploração tem como objetivo favorecer o desenvolvimento da habilidade EF04MA17

Ao iniciar a Aula 7, explicar aos alunos que as figuras geométricas espaciais podem ser classificadas em poliedros ou corpos redondos. Complementar que, nos poliedros, todas as superfícies laterais são planas e, nos corpos redondos, há pelo menos uma superfície arredondada.

Com base nessa abordagem inicial, orientá-los a explorar poliedros chamados prismas e pirâmides.

Levar a turma para a sala de informática ou utilizar um computador portátil providenciado previamente, revezando os alunos. virtuais disponíveis em: Pedir que acessem os manipulativos https://pt.mathigon.org/polypad (acesso em: 10 jan. 2022).

Orientar que, em seguida, cliquem, na barra no canto esquerdo da tela, no primeiro item, que é "Geometria". Ao clicar nesse item, oito opções aparecem. A sexta opção é "Sólidos 3D". Solicitar aos alunos que:

• cliquem em "Outros poliedros";

• selecionem e arrastem para o centro da tela o prisma e a pirâmide;

• manipulem esses sólidos geométricos girando-os e observando suas faces;

• respondam às atividades sugeridas a seguir.

1. Descreva algumas características comuns entre o prisma e a pirâmide que podem ser observadas rotacionando-os no manipulativo virtual.

Espera-se que os alunos percebam que tanto no prisma como na pirâmide todas as superfícies laterais são planas, porém, no prisma, há duas bases idênticas, e na pirâmide há apenas uma base. Espera-se também que os alunos reconheçam que, no prisma, todas as superfícies laterais são faces com quatro lados cada, já nas pirâmides, todas as superfícies laterais são faces com três lados cada.

• Caso os alunos demonstrem dificuldade em elaborar a resposta dessa atividade, mostre a planificação do prisma e, em seguida, a da pirâmide. Para tanto, clicar no prisma e, depois, em "Desdobrar", movendo o botão lentamente para que os alunos observem. Repetir esse procedimento com a pirâmide.

• Se não demonstrarem dificuldade em elaborar a resposta dessa atividade, validar essas associações demonstrando-as com a planificação do prisma e, em seguida, da pirâmide. Para tanto, clicar no prisma e, depois, em "Desdobrar", movendo o botão lentamente para que os alunos observem. Repetir esse procedimento com a pirâmide.

Caso na turma haja alunos com deficiência visual, é importante que eles possam compreender o que está sendo discutido passando o dedo no contorno das figuras na tela, por exemplo. Mais sugestões de atividades, nesse caso, podem ser encontradas na seguinte obra:

• BRANDÃO, Jorge. Geometria e deficiência visual... ou matemática para quem não gosta, mas precisa: propostas de atividades para pessoas com deficiência visual e discalculia. Curitiba: CRV, 2018.

Dar continuidade a esse trabalho, questionando os alunos sobre qual é a figura geométrica plana que pode ser identificada nas bases do prisma e na base da pirâmide. Espera-se que os alunos reconheçam que é um hexágono.

Explicar aos alunos que:

• os prismas são nomeados de acordo com a forma de suas bases;

• as pirâmides são nomeadas de acordo com a forma de sua base

Portanto, nesse caso, os manipulativos virtuais utilizados representam um prisma de base hexagonal e uma pirâmide de base hexagonal.

Finalizar a Aula 7 explorando a pirâmide de base triangular, que também é chamada de tetraedro e está disponível no item "Sólidos platônicos". Sugere-se trabalhar o tetraedro de modo análogo ao sugerido anteriormente para o prisma de base hexagonal e a pirâmide de base hexagonal.

Comentar com os alunos que os sólidos são nomeados platônicos em homenagem ao filósofo grego Platão. Pode-se aprofundar um pouco mais a respeito desse filósofo, apresentando informações da linha do tempo disponível em: https://pt.mathigon.org/timeline/plato (acesso em: 10 jan. 2022).

A cronologia com informações sobre outras personalidades importantes para a história da Matemática está disponível em: https://pt.mathigon.org/timeline (acesso em: 10 jan. 2022). É importante selecionar no navegador utilizado a opção de traduzir sempre para oportuguês.

Ao longo desta sequência didática, incentiva-se o uso de recursos digitais a fim de que os alunos possam utilizar "ferramentas matemáticas, inclusive tecnologias digitais disponíveis", contemplando esse aspecto da competência específica de Matemática para o Ensino Fundamental 5

Na Aula 8, explorar com os alunos construções arquitetônicas que se parecem com pirâmides e pedir que pesquisem construções arquitetônicas que se parecem com prismas.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Sobre construções arquitetônicas que se parecem com pirâmides, uma sugestão de indicação para leitura é:

• PIRÂMIDE Britannica Escola Disponível em: https://escola.britannica.com.br/artigo/pir%C3%A2mide/482308. Acesso em: 10 jan. 2022.

Propor atividades de pesquisa nas aulas de Matemática, além de favorecer o desenvolvimento da autonomia e do pensamento crítico dos alunos, leva-os a mobilizar habilidades de leitura e compreensão de textos, bem como de produção escrita na elaboração autoral de produções textuais a serem apresentadas como frutos da pesquisa.

Sugestões

• CAETANO, Danilo Borges. Educação matemática inclusiva: o ensino de geometria plana à luz do desenho universal pedagógico. Curitiba: CRV, 2019.

• OCHI, Fusako Hori etal O uso de quadriculados no ensino da geometria. São Paulo: Caem-IME/USP. (Coleção Ensino Fundamental, 1)

• SANTOS, Cleane Aparecida dos; NACARATO, Adair Mendes. Aprendizagem em geometria na educação básica: a fotografia e a escrita na sala de aula. 2. ed. Belo Horizonte: Autêntica, 2021. (Coleção Tendências em Educação Matemática)

Sequência didática 8 • Números expressos na forma decimal

Nesta sequência didática, são abordadas algumas características do Sistema de Numeração Decimal acerca da representação decimal de um número racional para escrever valores do sistema monetário brasileiro relacionando décimos e centésimos. Operações de adição e subtração de números expressos na forma decimal também são trabalhadas

Objetivos de aprendizagem

• Reconhecer a importância da utilização dos números expressos na forma decimal em situações cotidianas.

• Ler e escrever números expressos na forma decimal.

• Relacionar as frações com denominador 10 (fração decimal) a números escritos na forma decimal (décimos)

• Relacionar as frações com denominador 100 (fração decimal) a números escritos na forma decimal (centésimos).

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

• Representar no Quadro de ordens números expressos na forma decimal maiores que 1, reconhecendo a parte inteira e a parte decimal, e comparar e ordenar esses números para indicar qual é maior e qual é menor.

• Adicionar e subtrair números expressos na forma decimal, realizando as trocas necessárias entre inteiros, décimos e centésimos.

• Resolver problemas que envolvam adição e subtração de números expressos na forma decimal

• Utilizar a representação decimal (inteiros, décimos e centésimos) para escrever valores do sistema monetário brasileiro

Plano de aulas

Aula 1: Explorar números expressos na forma decimal, apresentando a parte inteira e a parte decimal desses números com base na equivalência entre valores de moedas do sistema monetário brasileiro Trabalhar a leitura e a escrita de números expressos na forma decimal.

Aula 2: Explorar números expressos na forma decimal, apresentando a parte inteira e a parte decimal desses números com base em valores de cédulas do sistema monetário brasileiro Trabalhar a leitura e a escrita de números expressos na forma decimal. Explorar de maneira lúdica a correspondência entre representações fracionárias e representações decimais por meio de jogos virtuais on-linesugeridos.

Aula 3: Representar no Quadro de ordens números expressos na forma decimal Comparar números expressos na forma decimal. Ordenar números expressos na forma decimal

Aulas 4 e 5: Calcular a adição de números expressos na forma decimal.

Aulas 6 e 7: Calcular a subtração de números expressos na forma decimal.

Aula 8: Resolver problemas de adição e subtração de números expressos na forma decimal

Componentes essenciais para a alfabetização: Compreensão de textos e produção de escrita.

Competências gerais da Educação Básica: 1 e 7.

Competência específica de Matemática: 3

Habilidade: EF04MA10

Materiais necessários: copos descartáveis biodegradáveis de 200 mL, palitos de sorvete, etiquetas, caneta hidrocor ponta grossa e computador com acesso à internet.

Aula 1

Iniciar a aula conversando com os alunos sobre as cédulas e as moedas do sistema monetário brasileiro Questioná-los se as conhecem e quais estão em circulação no país. Anotar na lousa as respostas que os alunos indicarem. Fazer os registros usando números expressos na forma decimal, a fim de que posteriormente sejam retomados nesta aula.

Neste momento, se possível, apresentar imagens e características de acessibilidade das cédulas e das moedas aos alunos. Uma síntese breve da história das mudanças já ocorridas no sistema monetário brasileiro é uma possibilidade que favorece um trabalho com

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

História No sitedo Banco Central do Brasil, há dois materiais que podem ser utilizados para apoiar essa exploração. São eles:

• DINHEIRO no Brasil. Disponível em:

https://www.bcb.gov.br/content/acessoinformacao/museudocs/pub/Cartilha_Dinh eiro_no_Brasil.pdf Acesso em: 6 jan. 2022.

• SEGUNDA família do Real. Disponível em:

https://www.bcb.gov.br/novasnotas/assets/downloads/materialapoio/2e5/Cartilha.pdf Acesso em: 6 jan. 2022.

Em seguida, na lousa, estabelecer com os alunos algumas relações entre os valores das moedas

A primeira relação que pode ser explorada é a de que 1 centavo de real corresponde a 1 centésimo de real, pois 1 real é formado por 100 centavos. Representar essa relação entre os valores com uma figura dividida em 100 partes iguais e colorir 1 dessas partes.

A representação fracionária da parte colorida dessa figura é 1 100

Portanto, 1 centavo de real corresponde a 1 centésimo de real

Na representação decimal de valores do sistema monetário brasileiro, indica-se este valor: R$ 0,01, que se lê : um centavo.

Destacar que:

• R$ é o símbolo usado para indicar o Real, atual sistema monetário brasileiro;

• antes da vírgula, são escritos os algarismos da parte inteira do número (que, neste caso, não há, pois 1 centésimo é menor que 1 inteiro, conforme a figura demonstra);

• depois da vírgula, são escritos os algarismos da parte decimal do número (que, neste caso, é o centésimo).

Representar no Quadro de ordens o número expresso na forma decimal:

parte inteira parte decimal

Dezenas Unidades , Décimos Centésimos Como se lê: 0 , 0 1 um centésimo

A segunda relação a ser explorada é a de que 1 décimo de 10 centavos é 1 centavo Representar essa relação entre os valores com 1 figura dividida em 10 partes iguais e colorir 1 dessas partes.

Editoria de arte

A representação fracionária da parte colorida dessa figura é 1 10

Portanto, 1 décimo de 10 centavos é 1 centavo

Na representação decimal de valores do sistema monetário brasileiro, indica-se este valor: R$ 0,10, que se lê : dez centavos.

Representar no Quadro de ordens o número expresso na forma decimal:

parte inteira parte decimal

Dezenas Unidades , Décimos Centésimos Como se lê: 0 , 1 0 dez centésimos ou 1 décimo Comentar que a leitura desse número é 10 centésimos ou 1 décimo utilizando partes equivalentes de figuras que podem ser desenhadas na lousa:

Editoria de arte

Propor aos alunos as atividades sugeridas a seguir.

1. Observe as partes coloridas nas figuras em cada item e responda às questões.

a) 1 4 equivale a 25 100 ou 0,25.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos

• Para formar 1 real, são necessárias quantas moedas de 25 centavos?

4 moedas

b) 2 4 equivalem a 1 2 ; 1 2 equivale a 50 100 ou 0,50.

Editoria de arte

• Para formar 1 real, são necessárias quantas moedas de 50 centavos?

2 moedas

• Para formar 50 centavos, são necessárias quantas moedas de 25 centavos?

2 moedas

2. Escreva como se lê os números expressos na forma decimal em cada item.

a) 0,01

Um centésimo.

b) 0,05

Cinco centésimos.

c) 0,10

Dez centésimos ou um décimo.

d) 0,25

Vinte e cinco centésimos.

e) 0,50

Cinquenta centésimos ou cinco décimos.

Nesta aula e nas seguintes, as propostas sugeridas visam favorecer o desenvolvimento da habilidade EF04MA10. Finalizar a aula incentivando os alunos a formular e a expor dúvidas para que possam ser sanadas.

Aula 2

Retomar as ideias exploradas na aula anterior, sobre relações entre valores das moedas do sistema monetário brasileiro, estabelecendo equivalências entre representações fracionárias e representações decimais nas quais 1 real é considerado o inteiro (a unidade), e os valores menores das outras moedas são representados como partes

Para isso, fazer um quadro na lousa, como o sugerido a seguir, e completá-lo coletivamente com a turma

Valor em real de moeda do sistema monetário brasileiro

Como se escreve, na representação decimal e usando o símbolo de real, ovalor dessa moeda?

Esse valor corresponde a que fração de 1 real?

Com base no preenchimento coletivo desse quadro, discutir com os alunos outros exemplos que explorem representações decimais e representações fracionárias correspondentes

Uma possibilidade de explorar de maneira lúdica esse conteúdo é com base em jogos virtuais on-linedisponíveis A seguir, são indicadas duas sugestões de jogos:

• "Conversão de decimais em frações", disponível nolink:

https://escola.britannica.com.br/jogos/GM_3_13/index.html (acesso em: 7 jan.

2022) Orientar os alunos a jogar o nível 1 Os níveis 2 e 3 envolvem milésimos e são adequados para outro momento de escolaridade.

• "Frações e decimais", disponível nolink:

https://escola.britannica.com.br/jogos/GM_5_31/index.html (acesso em: 7 jan.

2022) Orientar os alunos a jogar o nível 1 e utilizar uma calculadora para que realizem

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

as divisões representadas em cada fração e possam relacioná-las às representações decimais correspondentes. Os níveis 2 e 3 envolvem grau de complexidade mais avançado e são adequados para outro momento de escolaridade

Sugere-se também apresentar na lousa um quadro para explorar representações decimais dos valores das cédulas de nosso sistema monetário brasileiro e reforçar com os alunos que, na representação de números expressos na forma decimal, antes da vírgula, os algarismos escritos indicam a parte inteira, e, depois da vírgula, os algarismos escritos indicam a parte decimal

Valor em real de cédula do sistema monetário brasileiro

Como se escreve, na representação decimal e usando o símbolo de real, o valor dessa cédula?

Como se lê esse valor?

Cédula de 2 reais R$ 2,00 dois reais

Cédula de 5 reais R$ 5,00 cinco reais

Cédula de 10 reais R$ 10,00 dez reais

Cédula de 20 reais R$ 20,00 vinte reais

Cédula de 50 reais R$ 50,00 cinquenta reais

Cédula de 100 reais R$ 100,00 cem reais

Cédula de 200 reais R$ 200,00 duzentos reais

Na sequência, propor aos alunos a atividade sugerida a seguir, que explora a leitura e a escrita de números expressos na forma decimal para indicar quantias compostas de cédulas e moedas de nosso sistema monetário brasileiro.

1. Em cada item, escreva como se representa, na forma decimal e usando o símbolo de real, a quantia composta de acordo com a descrição de cédulas e moedas. Depois, escreva como se lê essa quantia.

a) 1 cédula de 10 reais, 7 moedas de 10 centavos e 2 moedas de 1 centavo.

R$ 10,72; dez reais e setenta e dois centavos.

b) 1 cédula de 200 reais, 1 cédula de 20 reais, 1 cédula de 2 reais e 1 moeda de 25 centavos.

R$ 222,25; duzentos e vinte e dois reais e vinte e cinco centavos.

c) 1 cédula de 50 reais, 1 moeda de 50 centavos.

R$ 50,50; cinquenta reais e cinquenta centavos.

d) 2 cédulas de 10 reais, 2 moedas de 10 centavos e 3 moedas de 1 centavo.

R$ 20,23; vinte reais e vinte e três centavos.

Após a conclusão da atividade, validar as respostas com os alunos e, coletivamente, elaborarem na lousa uma síntese, sistematizando o que foi estudado nesta aula e na anterior.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Aula 3

Nesta aula são exploradas a representação, no Quadro de ordens, de números expressos na forma decimal, bem como a comparação e a ordenação desses números, a fim de que os alunos reconheçam que as regras do Sistema de Numeração Decimal podem ser estendidas para a representação decimal de números racionais.

De início, pedir aos alunos que representem no Quadro de ordens os números expressos na forma decimal que escreveram para indicar a quantia em cada item da atividade proposta na aula anterior. Desse modo, espera-se que eles apresentem as seguintes respostas:

parte inteira parte decimal

Em seguida, comparar esses números expressos na forma decimal, de modo que os alunos indiquem qual é o maior e qual é o menor, para que possam ordená-los de modo ascendente (crescente).

Orientar os alunos a primeiro comparar a parte inteira, a fim de reconhecerem mais rapidamente qual é o maior e qual é o menor, pois, neste caso, todos os números decimais apresentados são formados por partes inteiras e partes decimais. Depois, pedir que escrevam em ordem crescente esses números. Espera-se que respondam:10,72 > 20,23 > 50,50 > 222,25

Em seguida, solicitar que escrevam como se lê esses números, pois na aula anterior eles trabalharam a leitura da quantia. Espera-se que respondam: dez inteiros e setenta e dois centésimos; vinte inteiros e vinte e três centésimos; cinquenta inteiros e cinquenta centésimos; duzentos e vinte e dois inteiros e vinte e cinco centésimos.

Questionar os alunos sobre preços de produtos ou serviços que fazem parte do contexto diário deles, como: o preço do pão, o valor da passagem de ônibus, o preço de um pacote de figurinhas etc., e anotar na lousa os valores citados por eles. Em seguida, solicitar que, no caderno, representem em um Quadro de ordens esses números expressos na forma decimal, e, depois, comparem-nos e escrevam em ordem crescente e em ordem decrescente.

Ampliar essa atividade refletindo com os alunos que os valores dos preços mencionados também são uma abordagem importante. Questionar se os alunos acham que os preços mencionados são caros ou baratos, se comprar o mais barato é sempre a melhor opção, entre outras reflexões. Incentivar todos a argumentarem, de modo que a competência geral da Educação Básica 7 seja trabalhada

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Aulas 4 e 5

Nestas aulas, explorar adições com números expressos na forma decimal levando os alunos a compreender trocas necessárias entre inteiros, décimos e centésimos, utilizando o recurso do ábaco

Na Aula 4, solicitar aos alunos que se organizem em grupos de cinco integrantes. Distribuir para cada grupo:

• 5 copos descartáveis biodegradáveis de 200 mL;

• 5 etiquetas;

• 50 palitos de sorvete;

• 1 caneta hidrocor ponta grossa.

Explicar aos grupos que o material disponibilizado será utilizado na confecção de um ábaco, no qual será possível representar números expressos na forma decimal:

• cuja parte inteira seja de até 3 ordens (centenas, dezenas e unidades);

• cuja parte decimal seja de até 2 ordens (décimos e centésimos).

Pedir que escrevam nas etiquetas os nomes dessas ordens e, em seguida, colem uma etiqueta em cada copo. Alertar para o fato de que, na etiqueta da ordem das unidades, precisa ser indicada a vírgula após a palavra, para que seja indicada a separação entre a parte inteira e a parte decimal de cada número.

Com os copos etiquetados, solicitar que os organizem sobre a mesa os copos, um ao lado do outro, na mesma ordem que aparecem em um Quadro de ordens. Pedir que separem os palitos em grupos de 10 em 10 e coloquem 1 grupo de 10 palitos diante de cada copo.

Iniciar a exploração da adição de números expressos na forma decimal, relembrando que, em um ábaco, em cada pino (neste caso, em cada copo) só podem ficar até nove argolas (neste caso, nove palitos de sorvete). Caso contrário, devem ser realizadas trocas.

Solicitar que coloquem dois palitos no copo que representa a ordem dos centésimos na parte decimal. Na sequência, pedir que coloquem mais oito palitos no copo que representa a ordem dos centésimos na parte decimal.

Questionar quantos palitos foram colocados ao todo no copo que representa a ordem dos centésimos na parte decimal e se é necessário trocá-los. Espera-se que os alunos respondam que é necessário trocar os 10 centésimos representados pelos palitos por 1 décimo. Orientar que façam a troca e coloquem apenas 1 palito no copo dos décimos.

Depois, na lousa, representar essa adição em um Quadro de ordens, chamando a atenção para que as vírgulas sejam escritas alinhadas uma embaixo da outra:

Dar continuidade à Aula 4 propondo outras adições seguindo esse mesmo encaminhamento detalhado.

A quantidade de adições a serem calculadas não é o mais importante no objetivo desta proposta, e sim que os alunos compreendam o sentido das trocas que estão sendo feitas, a fim de que reconheçam que as regras das operações fundamentais de números naturais podem ser estendidas para as operações envolvendo números expressos na forma decimal.

Finalizar a Aula 4 solicitando aos alunos que organizem e guardem os copos e os palitos, pois serão utilizados nas próximas aulas. Na Aula 5, com os alunos organizados nos mesmos grupos (ou decidir em parceria com eles se preferem formar novos), trabalhar mais adições com números expressos na forma decimal. Encerrar a Aula 5 solicitando aos alunos que organizem e guardem os copos e os palitos que serão utilizados nas próximas aulas.

Aulas 6 e 7

Nestas aulas, explorar subtrações com números expressos na forma decimal, levando os alunos a compreender trocas necessárias entre inteiros, décimos e centésimos utilizando o recurso do ábaco

Na Aula 6, com os alunos organizados nos mesmos grupos (ou decidir em parceria com eles se preferem formar novos), trabalhar subtrações com números expressos na forma decimal. Encaminhar esse trabalho de modo análogo ao que foi sugerido para a adição de números expressos na forma decimal.

Vale ressaltar, porém, que, primeiro, é necessário solicitar aos alunos que coloquem nos copos a quantidade de palitos da qual será subtraída a outra quantidade, para, somente depois, propor a retirada de palitos envolvida na subtração, e, caso seja necessário, realizar trocas com base na manipulação do ábaco.

Na Aula 6, propor subtrações que não envolvem trocas, por exemplo:

0,09

0,23

2,17

46,75

0,05 = 0,04

0,12 = 0,11

2,10 = 0,07

36,04 = 10, 71

Na Aula 7, ampliar o grau de complexidade propondo outras subtrações em que as trocas são necessárias. Uma possibilidade para variar a proposta de trabalho é propor aos

alunos que resolvam as operações que constam do recurso on-line disponível em: https://escola.britannica.com.br/jogos/GM_3_10/index.html (acesso em: 7 jan. 2022).

Acompanhar os alunos durante a realização dos cálculos, a fim de identificar eventuais dúvidas, fazendo as intervenções e mediações necessárias para que atinjam a compreensão do conteúdo explorado nestas aulas.

Aula 8

Iniciar incentivando os alunos a refletir a respeito das próprias aprendizagens. Para isso, questioná-los sobre como aplicar em diferentes contextos os conhecimentos sobre números expressos na forma decimal, de modo que a competência geral da Educação Básica 1 seja trabalhada Os alunos podem comentar como as muitas situações cotidianas envolvendo ações de compra, venda, troco etc. requerem conhecimentos matemáticos e, em especial, como os números expressos na forma decimal estão envolvidos. Nesse sentido, nesta aula, sugere-se trabalhar a resolução de alguns problemas envolvendo adição e subtração de números expressos na forma decimal. Esse trabalho contempla aspectos da competência específica de Matemática para o Ensino Fundamental 3

A seguir são apresentadas sugestões de problemas a serem propostos. Solicitar aos alunos que registrem no caderno a produção escrita da resolução e da resposta completa de cada problema. Incentivá-los a utilizar estratégias diversas de resolução e pedir que as descrevam, explicando com exemplos a estratégia aplicada em cada resolução.

1. Letícia foi à padaria e comprou pães do tipo francês cujo valor a ser pago é R$ 5,03. Ela também comprou um litro de leite cujo preço foi R$ 2,96. Quanto Letícia gastou nessa compra?

Sugestão de resolução:

5,03 + 2,96 = 7,99

Resposta: Letícia gastou R$ 7,99 nessa compra.

2. Na papelaria, Eliane pagou com R$ 10,00 um caderno que comprou pelo preço de R$ 7,50. Qual valor Eliane recebeu de troco?

Sugestão de resolução possível:

10,00 – 7,50 = 2,50

Resposta: Eliane recebeu R$ 2,50 de troco.

3. Luciana abasteceu o carro e o total a pagar registrado na bomba foi R$ 60,50. Ela entregou ao caixa do posto uma cédula de R$ 100,00 para pagar esse valor. O caixa perguntou se ela teria R$ 10,50 para facilitar o troco, pois ele só tinha cédulas de R$ 50,00 disponíveis. Luciana deu ao caixa os R$ 10,50 solicitados. Quanto Luciana recebeu de troco?

Sugestão de resolução:

Total em dinheiro que Luciana entregou ao caixa do posto: 100,00 + 10,50 = 110,50

Troco recebido: 110,50

60,50 = 50,00

Resposta: Luciana recebeu R$ 50,00 de troco.

Após a conclusão das resoluções dos problemas propostos, pedir aos alunos que socializem as estratégias utilizadas. Neste momento, valorizar se algum aluno usar uma estratégia de resolução diferente da que foi pensada pelos colegas, salientando o fato de que há mais de uma maneira de resolver um problema.

Sugestões

• ALVES, Lynn; COUTINHO, Isa de Jesus (org.). Jogos digitais e aprendizagem: fundamentos para uma prática baseada em evidências. Campinas, SP: Papirus, 2016.

• MUNIZ, Cristiano Alberto; BATISTA, Carmyra Oliveira; SILVA, Erondina Barbosa da. Pedagogia: Matemática e cultura: decimais, medidas e sistema monetário. Brasília: Universidade de Brasília, 2008. Disponível em: http://www.sbembrasil.org.br/files/decimais.pdf Acesso em: 6 jan. 2022.

• ROCHA, Daiana Garibaldi da; OTA, Marcos Andrei; HOFFMANN, Gustavo (org.). Aprendizagem digital: curadoria, metodologias e ferramentas para o novo contexto educacional. Porto Alegre: Penso, 2021.

Relatórios e indicadores do acompanhamento da aprendizagem

Nesta seção, são apresentados subsídios que auxiliam a produção de relatórios e indicadores do acompanhamento da aprendizagem, itens indispensáveis para o processo de ensino-aprendizagem e supervisão sistemática e contínua do desenvolvimento dos alunos São sugestões que podem ser adaptadas à rotina da turma e à realidade escolar do professor.

Produção de relatórios

Os relatórios escolares são importantes ferramentas para fornecer a professores, coordenadores e familiares uma visão global do desenvolvimento e do desempenho dos alunos em sala de aula. Além de aspectos relacionados à aprendizagem de objetos de conhecimento, de habilidades e de competências, os relatórios podem apresentar informações sobre a participação dos alunos nas aulas, a interação deles com os colegas, seu desenvolvimento motor, interesses pessoais, entre outros aspectos.

Esses documentos devem ser produzidos periodicamente, de forma anual, semestral ou bimestral, por exemplo. Dessa maneira, além de monitorar o processo de ensino-aprendizagem, os relatórios podem ser utilizados pela gestão escolar para formular práticas e estratégias, além de promover mudanças nos ambientes e espaços que contribuam para a melhoria dos níveis de aprendizagem.

Para elaborar um relatório, podem-se usar como apoio as fichas apresentadas na seção Indicadores do acompanhamento da aprendizagem. Nessas fichas, são listados conceitos, habilidades, objetos de conhecimento e competências que podem ser diagnosticados e aferidos ao longo do ano letivo. São sugestões às quais o professor pode acrescentar os dados e as informações que julgar convenientes tirachardz/Freepik.com

O trabalho com os dados de indicadores e as análises com base neles trazem reflexões que auxiliam na tomada de decisões para o aprimoramento de estratégias de ensino e aprendizagem.

Os relatórios devem ser redigidos em linguagem adequada e de fácil compreensão, para que sejam compreendidos por familiares, outros professores que acompanham o processo educacional e gestores. Estes podem ser estruturados da seguinte maneira:

• Apresentação dos objetivos da disciplina e como esses objetivos foram trabalhados em sala de aula, ao longo do período;

• Apresentação do acompanhamento de aspectos cognitivos, comportamentais e socioemocionais dos alunos, ao longo do período.

Esses relatórios podem ser acompanhados de apresentações visuais e gráficas que visam facilitar a compreensão das informações. Os dados compilados nas fichas da seção Indicadores do acompanhamento da aprendizagem, por exemplo, possibilitam obter uma boa visão global do desenvolvimento dos alunos, ressaltando os pontos positivos e estabelecendo pontos de atenção em caso de defasagem nas aprendizagens. Pode ser feita, por exemplo, a distribuição percentual dos conceitos atribuídos aos alunos a cada uma das competências gerais, competências específicas e habilidades trabalhadas no período.

Exemplo:

Porcentagem de alunos da turma A de acordo com os conceitos atribuídos a eles em relação às competências gerais trabalhadas no período

Necessita ser consolidado (NC) Em processo de consolidação (PC) Consolidado (C)

É importante ressaltar que os relatórios e os indicadores do acompanhamento da aprendizagem devem ser analisados e utilizados de forma contextualizada, ou seja, em conjunto com as características tanto individuais dos alunos quanto coletivas da turma, tornando-os uma ferramenta eficaz e adequada a cada realidade escolar.

Indicadores do acompanhamento da aprendizagem

Os indicadores de aprendizagem auxiliam no acompanhamento da turma, assim como na investigação das possíveis causas de defasagem nas aprendizagens, favorecendo a revisão de decisões pedagógicas, com o propósito de potencializar o desenvolvimento dos alunos

Os indicadores a seguir foram elaborados com base na BNCC e na PNA e são apresentados na forma de fichas que podem ser aplicadas em diferentes etapas do processo educacional, de modo a diagnosticar e monitorar o desenvolvimento de aprendizagens individuais e coletivas

São apresentadas sugestões de quatro tipos de fichas:

• Ficha de avaliação diagnóstica: permite obter um diagnóstico dos conhecimentos prévios dos alunos.

• Ficha de acompanhamento das aprendizagens: permite observar o desenvolvimento de diferentes aprendizagens ao longo do processo educacional, identificando pontos de sucesso ou que necessitam de novas intervenções para a consolidação das aprendizagens pretendidas

• Ficha de verificação de resultados: permite avaliar o atingimento de objetivos de aprendizagem ao final do ano letivo, podendo também servir de fonte de dados para a elaboração de estratégias para o ano escolar seguinte.

• Ficha de acompanhamento do desenvolvimento de competências socioemocionais: permite acompanhar de forma planejada o desenvolvimento de competências socioemocionais.

wayhomestudio/Freepik.com

gpointstudio/Freepik.com

freepik/Freepik.com

O compartilhamento de informações sobre o andamento e os resultados do desenvolvimento dos alunos é do interesse de gestores escolares, de professores, de pais ou responsáveis e de alunos, e promove momentos de debate e reflexão sobre a prática docente.

Ficha de avaliação diagnóstica

Professor(a):

Turma:

Sugestão de critérios de avaliação

C = consolidado (estudante faz sozinho); PC = em processo de consolidação (estudante precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (estudante não consegue realizar a atividade proposta)

Ficha de avaliação diagnóstica

Números Álgebra Geometria Grandezas e medidas Estatística

Aluno Compor e decompor números naturais (até a ordem da unidade de milhar) identificando características do sistema de numeração decimal.

Utilizar diferentes estratégias de cálculo, incluindo mental ou escrito, para resolver e elaborar problemas de adição e de subtração.

Resolver e elaborar problemas de multiplicação (por 2, 3, 4, 5 e 10) por meio de adição de parcelas iguais.

Identificar regularidades em sequências ordenadas que apresentem adição ou subtração sucessivas de números naturais.

Classificar e comparar figuras planas (triângulo, quadrado, retângulo, trapézio e paralelogramo) em relação a seus lados e vértices.

Reconhecer e descrever características de figuras geométricas espaciais (prismas retos, pirâmides, cilindros e cones), relacionando-as com suas planificações.

Medir capacidade e massa de objetos, utilizando unidades de medida padronizadas (litro, mililitro, quilograma, grama e miligrama).

Ler horas em relógios digitais e em relógios analógicos e reconhecer a relação entre hora e minutos e entre minuto e segundos.

Ler e interpretar dados apresentados em tabelas de dupla entrada, gráficos de barras ou de colunas

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International ). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento das aprendizagens

Professor(a):

Turma:

Aluno:

Sugestão de critérios de avaliação

C = consolidado (estudante faz sozinho);

PC = em processo de consolidação (estudante precisa de apoio de um mediador);

NC = necessita de novas oportunidades de consolidação (estudante não consegue realizar a atividade proposta)

Ficha de acompanhamento das aprendizagens (Matemática)

Habilidades C PC NC Observações

(EF04MA01) Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.

(EF04MA02) Mostrar, por decomposição e composição, que todo número natural pode ser escrito por meio de adições e multiplicações por potências de dez, para compreender o sistema de numeração decimal e desenvolver estratégias de cálculo.

(EF04MA03) Resolver e elaborar problemas com números naturais envolvendo adição e subtração, utilizando estratégias diversas, como cálculo, cálculo mental e algoritmos, além de fazer estimativas do resultado.

(EF04MA04) Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.

(EF04MA05) Utilizar as propriedades das operações para desenvolver estratégias de cálculo.

(EF04MA06) Resolver e elaborar problemas envolvendo diferentes significados da multiplicação (adição de parcelas iguais, organização retangular e proporcionalidade), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

(EF04MA07) Resolver e elaborar problemas de divisão cujo divisor tenha no máximo dois algarismos, envolvendo os significados de repartição equitativa e de medida, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

(EF04MA08) Resolver, com o suporte de imagem e/ou material manipulável, problemas simples de contagem, como a determinação do número de agrupamentos possíveis ao se combinar cada elemento de uma coleção com todos os elementos de outra, utilizando estratégias e formas de registro pessoais.

(EF04MA09) Reconhecer as frações unitárias mais usuais (1/2, 1/3, 1/4, 1/5, 1/10 e 1/100) como unidades de medida menores do que uma unidade, utilizando a reta numérica como recurso.

(EF04MA10) Reconhecer que as regras do sistema de numeração decimal podem ser estendidas para a representação decimal de

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial

(CC BY NC – 4.0 International ). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

um número racional e relacionar décimos e centésimos com a representação do sistema monetário brasileiro.

(EF04MA11) Identificar regularidades em sequências numéricas compostas por múltiplos de um número natural.

(EF04MA12) Reconhecer, por meio de investigações, que há grupos de números naturais para os quais as divisões por um determinado número resultam em restos iguais, identificando regularidades.

(EF04MA13) Reconhecer, por meio de investigações, utilizando a calculadora quando necessário, as relações inversas entre as operações de adição e de subtração e de multiplicação e de divisão, para aplicá-las na resolução de problemas.

(EF04MA14) Reconhecer e mostrar, por meio de exemplos, que a relação de igualdade existente entre dois termos permanece quando se adiciona ou se subtrai um mesmo número a cada um desses termos.

(EF04MA15) Determinar o número desconhecido que torna verdadeira uma igualdade que envolve as operações fundamentais com números naturais.

(EF04MA16) Descrever deslocamentos e localização de pessoas e de objetos no espaço, por meio de malhas quadriculadas e representações como desenhos, mapas, planta baixa e croquis, empregando termos como direita e esquerda, mudanças de direção e sentido, intersecção, transversais, paralelas e perpendiculares.

(EF04MA17) Associar prismas e pirâmides a suas planificações e analisar, nomear e comparar seus atributos, estabelecendo relações entre as representações planas e espaciais.

(EF04MA18) Reconhecer ângulos retos e não retos em figuras poligonais com o uso de dobraduras, esquadros ou softwaresde geometria.

(EF04MA19) Reconhecer simetria de reflexão em figuras e em pares de figuras geométricas planas e utilizá-la na construção de figuras congruentes, com o uso de malhas quadriculadas e de softwaresde geometria.

(EF04MA20) Medir e estimar comprimentos (incluindo perímetros), massas e capacidades, utilizando unidades de medida padronizadas mais usuais, valorizando e respeitando a cultura local.

(EF04MA21) Medir, comparar e estimar área de figuras planas desenhadas em malha quadriculada, pela contagem dos quadradinhos ou de metades de quadradinho, reconhecendo que duas figuras com formatos diferentes podem ter a mesma medida de área.

(EF04MA22) Ler e registrar medidas e intervalos de tempo em horas, minutos e segundos em situações relacionadas ao seu cotidiano, como informar os horários de início e término de realização de uma tarefa e sua duração.

(EF04MA23) Reconhecer temperatura como grandeza e o grau Celsius como unidade de medida a ela associada e utilizá-lo em comparações de temperaturas em diferentes regiões do Brasil ou no exterior ou, ainda, em discussões que envolvam problemas relacionados ao aquecimento global.

(EF04MA24) Registrar as temperaturas máxima e mínima diárias, em locais do seu cotidiano, e elaborar gráficos de colunas com as variações diárias da temperatura, utilizando, inclusive, planilhas eletrônicas.

(EF04MA25) Resolver e elaborar problemas que envolvam situações de compra e venda e formas de pagamento, utilizando termos como troco e desconto, enfatizando o consumo ético, consciente e responsável.

(EF04MA26) Identificar, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem utilizar frações.

(EF04MA27) Analisar dados apresentados em tabelas simples ou de dupla entrada e em gráficos de colunas ou pictóricos, com base em informações das diferentes áreas do conhecimento, e produzir texto com a síntese de sua análise.

(EF04MA28) Realizar pesquisa envolvendo variáveis categóricas e numéricas e organizar dados coletados por meio de tabelas e gráficos de colunas simples ou agrupadas, com e sem uso de tecnologias digitais.

Competências específicas de Matemática para o Ensino Fundamental C PC NC Observações

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas

Material disponibilizado em licença aberta do tipo Creative Commo ns – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Competências gerais da Educação Básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de

C PC NC Observações

vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Componentes essenciais para a alfabetização

Fluência em leitura oral

Desenvolvimento de vocabulário

Compreensão de textos

Produção de escrita

Ficha de verificação de resultados

Professor(a):

Turma:

Sugestão de critérios de avaliação

C = consolidado (estudante faz sozinho); PC = em processo de consolidação (estudante precisa de apoio de um mediador); NC = necessita de novas oportunidades de consolidação (estudante não consegue realizar a atividade proposta)

Ficha de verificação de resultados

Principais objetivos de aprendizagem

Aluno Reconhecer números de até cinco ordens na sua forma numérica e por extenso, bem como identificá-los na reta numérica.

Resolver e elaborar problemas de adição e de subtração com números naturais de até quinta ordem.

Identificar, resolver e elaborar problemas envolvendo multiplicação com números naturais por soma de parcelas iguais, organização retangular e proporcionalidade por estratégias de cálculo diversas.

Analisar e aplicar o algoritmo da divisão.

Resolver problemas envolvendo medidas de massa e capacidade utilizando conversões de unidades de medida quando necessário.

Ler e escrever números expressos na forma de fração e reconhecer equivalências.

Analisar ângulos e vértices de diferentes figuras poligonais.

Identificar e escrever diferentes representações de décimos e centésimos, incluindo valores do sistema monetário brasileiro em representação decimal.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International ). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Ficha de acompanhamento do desenvolvimento de competências socioemocionais

Professor:

Turma:

Período:

Competências socioemocionais Sempre Frequentemente Raramente Nunca

Determinação

Foco

Organização

Persistência

Responsabilidade

Empatia

Respeito

Confiança

Tolerância ao estresse

Autoconfiança

Tolerância à frustração

Iniciativa social

Assertividade

Entusiasmo

Curiosidade para aprender

Imaginação criativa

Interesse artístico

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International ). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Catálogo dos audiovisuais

Esta seção apresenta informações a respeito do conjunto de materiais audiovisuais que compõem a coleção. O material aqui apresentado tem por objetivo complementar e aprofundar a prática pedagógica e pode ser utilizado de acordo com as características da turma e do planejamento do professor. Cada audiovisual apresenta orientações introdutórias, bem como propostas de atividades que explorem o uso de cada recurso em sala de aula. Ressalta-se aqui a necessidade de sempre orientar os alunos quanto aos procedimentos de segurança ao se realizarem alguns dos experimentos propostos.

Audiovisuais da coletânea

O animal terrestre de maior massa

A fim de compreender os significados de algumas unidades de medida de massa e de comprimento, neste audiovisual são apresentadas informações a respeito do animal terrestre de maior massa. Também, as unidades de medida de capacidade são exploradas com base nesse contexto revelando curiosidades a respeito da quantidade de leite que alguns animais recém-nascidos consomem diariamente.

• Medir e estimar comprimentos utilizando unidades de medida padronizadas.

• Medir e estimar massas utilizando unidades de medida padronizadas.

• Medir e estimar capacidades utilizando unidades de medida padronizadas.

• Unidades de medida de comprimento padronizadas: metro e quilômetro

• Unidades de medida de massa padronizadas: quilograma e tonelada

• Unidades de medida de capacidade padronizadas: litro e mililitro.

Programa

Nacional de Imunizações

Neste audiovisual, os alunos são encaminhados a reconhecer a importância da Matemática para a interpretação de dados numéricos, como datas e faixa etária, entre outros veiculados em cartazes de campanhas de vacinação, bem como no calendário e na caderneta de vacinação. Contexto esse associado ao tema contemporâneo transversal Saúde

• Medidas de tempo: duração de eventos e relações entre unidades de medida de tempo

• Coleta e representação de dados de pesquisa realizada

• Ler medidas de tempo em situações relacionadas ao cotidiano, como em cartazes, calendário e caderneta de vacinação.

• Registrar intervalos de tempo com base na duração de eventos, por exemplo, campanhas de vacinação.

• Realizar pesquisa e organizar dados coletados com ou sem uso de tecnologias digitais.

Problemas de contagem

O raciocínio combinatório é o tema principal deste audiovisual, no qual são descritos problemas práticos de contagem com os quais nos deparamos no dia a dia, como determinar a quantidade de senhas numéricas que podem ser formadas com determinada quantidade de algarismos, a fim de escolher uma entre as que são possíveis de se formar.

• Resolver problemas que envolvem a determinação da quantidade possível de agrupamentos que podem ser formados ao combinar elementos de uma coleção com todos os elementos de outra.

• Resolver problemas que envolvam a ideia combinatória da multiplicação.

• Organizar possibilidades em quadros de possibilidades ou em árvores de possibilidades (ou diagrama de árvore).

Todos têm direito à moradia

Neste audiovisual, a Matemática é apresentada em diálogo com o aspecto social do direito que todos têm à moradia por meio da reflexão dos tipos de moradia e do uso de planta baixa no planejamento da construção delas.

• Compreender a representação de uma moradia por meio de uma planta baixa.

• Planta baixa.

• Descrever deslocamentos e movimentação de acordo com pontos de referência representados em planta baixa.

A percepção visual periférica e a central

Um exercício é descrito neste audiovisual para que os alunos testem a própria visão periférica e, desse modo, intuitivamente, reflitam sobre a ideia de ângulo envolvida na visão.

• Desenvolver a noção da ideia de ângulo.

• Reconhecer ângulos retos e ângulos não retos em figuras poligonais.

• Reconhecer ângulos retos comparando-os a um quarto de volta.

• Reconhecer ângulos não retos que sejam maiores que um ângulo reto, comparando-os à meia-volta

Orientações para o uso dos audiovisuais

O animal terrestre de maior massa

Este audiovisual pode ser utilizado como introdução ao trabalho com unidades de medida de comprimento, de massa e de capacidade Nele, são indicadas as massas e as alturas que alguns animais terrestres podem atingir, bem como são exploradas quantidades de leite que alguns animais recém-nascidos consomem diariamente Assim, unidades de medida padronizadas de comprimento, de massa e de capacidade são utilizadas na apresentação dessas informações

Sugere-se que os alunos assistam uma primeira vez a todo o audiovisual completo e seja proposta uma segunda apresentação do trecho em que é citada a massa, em quilograma, do elefante africano e a correspondente massa em tonelada

Explorar com os alunos essa relação de correspondência entre as unidades de medida quilograma e tonelada, explicando que 1 000 quilogramas correspondem a 1 tonelada.

Em seguida, sugere-se explorar relações entre outras unidades de medida apresentadas no audiovisual

Podem ser apresentadas relações como:

• 100 centímetros correspondem a 1 metro;

• 1 000 mililitros correspondem a 1 litro.

Propor aos alunos o questionamento final presente no audiovisual pedindo a eles que comentem o que acharam mais interessante nas informações apresentadas sobre os animais, iniciando uma roda de conversa. Depois, debater com os alunos sobre alguns animais que estão ameaçados de extinção no país Essa abordagem favorece um trabalho interdisciplinar com Ciências Para saber mais sobre alguns animais ameaçados de extinção no Brasil, sugerem-se as seguintes referências para consulta:

• EBC. Animais em extinção. Disponível em: http://memoria.ebc.com.br/animaisemextincao. Acesso em: 12 jan. 2022.

INSTITUTO BRASÍLIA AMBIENTAL (org.). Cerrado dobrado: dobraduras de animais do cerrado ameaçados de extinção. Brasília: Ibram, 2019. (Coleção Eu amo Cerrado).

Disponível em: https://www.ibram.df.gov.br/wp-content/uploads/2019/12/cerradodobrado05dez2019-_web.pdf. Acesso em: 12 jan. 2022.

Sugere-se a proposição das atividades seguintes para completar o trabalho de apoio pedagógico deste audiovisual

Sugestões de atividades

1. De acordo com as informações do audiovisual, responda às questões

a) Qual é o animal terrestre de maior massa?

O elefante africano.

b) Quais são as únicas duas espécies de elefantes existentes atualmente?

O elefante africano e o elefante asiático.

2. Marque um X em cada um dos nomes de unidades de medida de massa.

( ) centímetro ( ) grama ( ) tonelada ( ) mililitro Espera-se que os alunos assinalem o grama e a tonelada

3. Marque um X em cada um dos nomes de unidades de medida de comprimento.

( ) metro ( ) mililitro ( ) quilograma ( ) centímetro Espera-se que os alunos assinalem as opções: metro e centímetro

4. De acordo com informação do audiovisual, um filhote de elefante costuma mamar até os três anos e necessita mamar mais de 11 litros de leite por dia. Quantos litros de leite são necessários para alimentar um filhote de elefante durante uma semana?

Mais de 77 litros de leite.

5. De acordo com informação do audiovisual, um filhote de elefante, ao nascer, pode ter cerca de 100 quilogramas de massa e 90 centímetros de altura. Responda às questões com base nessa informação.

a) Ao nascer, um filhote de elefante tem, aproximadamente, mais de 1 metro ou menos de 1 metro?

Menos de 1 metro.

b) Um filhote de elefante recém-nascido tem massa maior que 1 tonelada ou menor que 1 tonelada?

Menor que 1 tonelada.

6. De acordo com informação do audiovisual, a girafa foi incluída na lista de animais ameaçados de extinção no mundo. Isso porque, nos últimos 30 anos, a quantidade da população de girafas reduziu quase à metade. Em 2015, estimou-se que havia cerca de noventa e sete mil girafas no mundo.

a) Escreva com algarismos o número em destaque no enunciado

97 000

b) O que podemos fazer para evitar que animais sejam ameaçados de extinção? Elabore, no caderno, um texto de até 10 linhas. Se necessário, faça uma pesquisa. Resposta pessoal. Atividade de produção escrita.

Programa Nacional de Imunizações

Por meio deste audiovisual, os alunos tomam contato com um tema que propicia a inserção cidadã deles e de seus responsáveis na assimilação de conhecimentos relacionados ao tema contemporâneo transversal Saúde, pois, no audiovisual, é apresentada a importância do Programa Nacional de Imunizações, da compreensão do calendário básico de vacinação, de dados numéricos registrados em um cartaz no qual são veiculadas algumas informações numéricas acerca de campanhas de vacinação, como a data de início e a data

de término da campanha a fim de identificar a duração desse evento e a faixa etária das pessoas atendidas na campanha

Para esses registros, o uso de algumas unidades de medida de tempo mais usuais é empregado e, por isso, este audiovisual pode ser usado tanto na introdução aos estudos de unidades de medida de tempo como na retomada ou revisão desse conteúdo, considerando que as habilidades para essa compreensão e interpretação mobilizam alguns conhecimentos já explorados em anos escolares anteriores.

Ao término da exibição deste audiovisual, pedir aos alunos que façam a pesquisa proposta na cena final a fim de verificar na caderneta de vacinação se todos foram vacinados contra todas as doenças de acordo com o Calendário Nacional de Vacinação, disponível em: https://www.gov.br/saude/pt-br/assuntos/saude-de-a-a-z/c/calendario-nacional-devacinacao (acesso em: 12 jan. 2022).

Combinar com os alunos como será feita a organização do gráfico cuja construção também é mencionada na cena final do audiovisual: se utilizando tecnologias digitais ou não. No caso de ser feita a opção de utilizar planilhas eletrônicas, é importante reservar uma aula para a realização da atividade.

O objetivo da sequência de atividades sugeridas a seguir é organizar as etapas de realização desta pesquisa em mais de uma aula favorecendo o desenvolvimento da habilidade EF04MA28. Na atividade 1, sugere-se que seja proposta a realização em casa para que os alunos manipulem suas cadernetas de vacinação em conjunto com os responsáveis. Já para a atividade 2, que aborda a pesquisa em si, é adequado, se possível, destinar três aulas para a realização: uma para a coleta de dados, outra para a interpretação deles e, por fim, a última para a organização e construção em um gráfico.

Sugestões de atividades

1. Com o auxílio de um responsável, consulte sua caderneta de vacinação e registre, no caderno, quais das vacinas do calendário nacional de vacinação você já tomou. Resposta pessoal. Atividade de produção escrita.

2. Vamos fazer a pesquisa proposta no fim do audiovisual "Programa Nacional de Imunizações"?

Para organizar, faça o que se pede em cada uma das seguintes etapas.

Etapa 1: Tema

a) Complete: o tema a ser pesquisado é __________________________________.

Vacinação. Espera-se que os alunos se recordem daquilo a que assistiram no audiovisual.

b) Responda: o que se pretende descobrir com esta pesquisa?

Se todos os alunos estão com a vacinação em dia (se todos os alunos foram vacinados contra todas as doenças de acordo com o Calendário Nacional de Vacinação). Espera-se que os alunos se recordem daquilo a que assistiram no audiovisual.

Etapa 2: Público-alvo

c) Responda: quem serão as pessoas participantes entrevistadas na pesquisa?

Todos os alunos da turma.

Etapa 3: Instrumento de pesquisa

d) Combine com o professor e com todos os colegas da turma como serão coletadas as informações dos participantes

A definição depende do consenso entre todos.

Sugestão de resposta: com base na atividade 1, é possível coletar de todos os alunos da turma, por escrito, a listagem das vacinas que cada aluno identificou na própria caderneta de vacinação. Cada aluno registra seu nome e lista as vacinas que já tomou em uma folha avulsa e entrega ao professor, em resposta à seguinte questão, por exemplo: quais vacinas você já tomou? Esse registro pode ser um instrumento de pesquisa usado para formalizar a coleta de dados.

Etapa 4: Organização e tratamento dos dados

e) Responda: os dados serão organizados de que maneira?

Em um gráfico. Espera-se que os alunos se recordem daquilo a que assistiram no audiovisual. É importante decidirem em consenso se o gráfico será construído utilizando tecnologia digital ou não. No caso da utilização de tecnologia digital, uma possibilidade é a construção coletiva com toda a turma. A organização dos dados em uma tabela faz-se necessária anterior à construção do gráfico

Sendo assim, é importante decidirem juntos como será a estrutura dessa tabela, por exemplo:

a) Com quantas colunas? (Uma possibilidade é fazer uma tabela simples composta de duas colunas em que na primeira conste o nome de cada tipo de vacina e, na segunda, seja computada a quantidade de alunos que tomou cada uma )

b) Qual será o título da tabela?

c) Completar a fonte da tabela etc. Incentivar os alunos a se expressarem livremente na tomada dessas decisões fazendo as mediações necessárias.

Com base na tabela, gerar o gráfico com o mesmo título, por exemplo, da tabela sem deixar de indicar a fonte dos dados, que é a mesma

Caso esteja sendo utilizada uma planilha eletrônica, basta selecionar a tabela que o gráfico é gerado automaticamente, no caso de os alunos estarem construindo o gráfico em uma folha de papel quadriculado ou com o auxílio de uma régua, a contagem dos dados precisa ser realizada um a a uma

Etapa 5: Divulgação dos resultados

f) Responda: como apresentar as conclusões da pesquisa?

A definição depende do consenso entre todos.

A interpretação dos dados visa responder ao que se pretende descobrir com a pesquisa. Verificar com os alunos se as colunas indicam quantidades diferentes, pois tal fato indica que alguns tipos de vacina não foram tomados por todos e, nesse caso, propor uma

roda de conversa para debater o resultado que complementa a proposta da pesquisa Nessa roda de conversa, conversar com os alunos sobre a importância das vacinas

Problemas de contagem

Este audiovisual pode ser utilizado como recurso introdutório de apoio pedagógico ao trabalho com problemas de contagem, ou paralelamente ao desenvolvimento desse conteúdo, ou até mesmo como retomada desse conteúdo.

Essa flexibilidade na utilização é possível dado o contexto com base em situações familiares ao cotidiano dos alunos, como a combinação de peças de roupa e a determinação da quantidade de senhas numéricas possíveis de se formar

A ideia combinatória da operação de multiplicação é o tema principal deste audiovisual, por isso, após a exibição, sugere-se retomar com os alunos a identificação das combinações possíveis formadas por 1 calça, 1 camiseta e 1 par de tênis usando as 2 calças, 3 camisetas e 2 pares de tênis disponíveis para compor essas combinações na situação apresentada. Nessa retomada, sugere-se, primeiro, explorar com os alunos quais são as possíveis combinações para, depois, discutir quantas elas são

Em seguida, apoiar o desenvolvimento do raciocínio combinatório dos alunos com base em representações gráficas, como quadros de possibilidades ou em árvores de possibilidades (ou diagrama de árvore). Para isso, sugere-se construir na lousa coletivamente, com os alunos, um quadro de possibilidades ou uma árvore de possibilidades para representar essa situação. Desse modo, espera-se que os alunos relacionem com mais facilidade a resolução desse tipo de problema à operação de multiplicação. Após essa abordagem, a fim de complementar o trabalho de favorecer o desenvolvimento da habilidade EF04MA08, podem-se propor as atividades sugeridas a seguir

Sugestões de atividades

1. Em uma concessionária, estão à venda 3 modelos de carro. Para cada modelo, há 2 opções diferentes de cores disponíveis: preta ou vermelha.

a) De quantas maneiras diferentes é possível, nessa concessionária, um cliente escolher 1 modelo de carro de 1 cor dessas?

De 6 maneiras diferentes (3 × 2 = 6)

b) Se nessa concessionária, para cada um dos 3 modelos, houvesse 4 opções diferentes de cores disponíveis, de quantas maneiras diferentes seria possível um cliente escolher 1 modelo de carro de 1 cor?

De 12 maneiras diferentes (3 × 4 = 12)

2. Marcelo vende tapiocas e oferece 2 tipos diferentes de sabor (doce ou salgada) e 9 tipos diferentes de recheio para cada tipo de sabor. Quantas combinações de 1 tipo de sabor com 1 tipo de recheio Marcelo tem para oferecer?

18 combinações (2 × 9 = 18)

3. No cardápio de um restaurante, há 3 opções de prato principal, 2 opções de salada e 2 opções de sobremesa. De quantas maneiras é possível montar uma refeição nesse restaurante?

De 12 maneiras diferentes (3 × 2 × 2 = 12)

4. Um aluno, para acessar o Ambiente Virtual de Aprendizagem de uma escola, tem de criar uma senha composta de 3 dígitos. Para criar essa senha, a escola orientou que:

• só podem ser usados os algarismos 1, 3 e 5;

• não pode repetir algarismos nem a ordem deles para formar uma mesma senha

De acordo com essas orientações da escola, quantas combinações são possíveis para compor essa senha?

6 combinações (135, 153, 315, 351, 513 e 531)

Todos têm direito à moradia

Neste audiovisual, o cerne é o direito à moradia garantido constitucionalmente para todas as pessoas, favorecendo um trabalho interdisciplinar com Geografia. Com base nesse tema, a Matemática é vinculada a aspectos sociais considerando uma perspectiva de reflexão para além dos conteúdos matemáticos propriamente ditos.

Essa perspectiva de abordagem é inspirada na Educação matemática crítica, e um autor pioneiro dessa discussão é Ole Skovsmose Para saber mais a respeito desse tema, são sugeridas duas referências para leitura:

• SKOVSMOSE, Ole. Educação matemática crítica: a questão da democracia 5. ed. Campinas, SP: Papirus, 2001. (Perspectivas em Educação Matemática, SBEM)

• SKOVSMOSE, Ole. Um convite à educação matemática crítica. Campinas, SP: Papirus, 2014 (Perspectivas em Educação Matemática, SBEM)

Este audiovisual pode ser usado como retomada dos estudos de conteúdos relacionados à unidade temática Geometria, como o de planta baixa Isso porque no audiovisual os alunos são levados à percepção da importância das plantas baixas para o planejamento da construção de moradias.

Após os alunos assistirem ao audiovisual, sugere-se que as atividades apresentadas a seguir sejam propostas para complementar a exploração do trabalho com a habilidade

EF04MA16

Sugestões de atividades

1. Respeitando a cultura local, as moradias podem ser construídas com características diferentes. Elabore, no caderno, um texto de até 15 linhas, descrevendo como é sua moradia, por exemplo: quantos e quais cômodos, posição relativa entre eles (qual fica na frente de qual, qual está à direita de qual etc.), citar alguns móveis maiores, entre outras características principais.

Resposta pessoal. Atividade de produção escrita.

2. Agora, de acordo com o texto elaborado, desenhe, em uma folha avulsa, a planta baixa de sua casa. Para isso, lembre-se de que:

• não é necessário desenhar detalhes, pois uma planta baixa representa de maneira simplificada a vista segundo a perspectiva de cima de um local;

• é importante representar alguns mobiliários ou, até mesmo, alguns objetos para que se tenha ideia da representação da posição entre eles também;

• destacar apenas as linhas de contorno e as linhas internas é importante para indicar a separação dos cômodos.

Se preferir, utilize uma folha de papel quadriculado para fazer essa representação.

Resposta pessoal.

O objetivo desta atividade vinculada ao trabalho com a seguinte é favorecer aspectos da habilidade EF04MA16. Por isso, neste momento, não é necessário cobrar dos alunos rigor em relação à proporcionalidade entre a moradia real e a representação (escala) na representação da planta baixa

3. Novamente, no caderno, elabore um texto de até 15 linhas. Desta vez, descreva no texto, de acordo com a planta baixa que você desenhou na atividade anterior, os deslocamentos que precisam ser realizados para ir do seu quarto até a cozinha de sua casa. Utilize termos como "direita" e "esquerda", "na frente", "atrás", entre outros, para indicar as mudanças de direção e sentido.

Resposta pessoal. Atividade de produção escrita.

A percepção visual periférica e a central

Neste audiovisual, é apresentada como está dividida a percepção visual humana: visão periférica e visão central. A descrição como uma pessoa pode testar a própria visão periférica também é exibida

Este audiovisual pode ser usado na retomada ou na revisão do conteúdo em que os alunos estudam para desenvolver a noção da ideia de ângulo.

Sugere-se que, se possível, este audiovisual seja trabalhado posteriormente e próximo ao momento em que o audiovisual "Todos têm direito à moradia" (que também faz parte da coletânea deste volume da coleção) tenha sido explorado com os alunos.

O desenvolvimento da ideia de ângulo com base na ideia de giros associados a um quarto de volta e meia-volta pode ser explorado na movimentação e deslocamentos em um espaço como em uma moradia representada por uma planta baixa.

Após os alunos assistirem ao audiovisual uma primeira vez, pedir a um aluno que se voluntarie para fazer o teste que é apresentado no vídeo ou fazer um sorteio com os nomes de todos da turma.

Reproduzir uma segunda vez o vídeo fazendo pausas a cada cena para que o teste seja realizado. Aos outros alunos, pedir que observem com atenção

Após esse momento, as seguintes atividades podem ser propostas a fim de trabalhar a habilidade EF04MA18

Sugestões de atividades

1. Durante a realização do teste apresentado no vídeo, é solicitado que seja esticado o braço esquerdo, formando um ângulo reto com o braço direito

Vamos construir quatro ângulos retos usando uma folha de papel sulfite?

Para isso, faça o que se pede em cada item a seguir.

Atividade prática.

a) Pinte os quatro cantos da folha. Um canto de cada cor. Por exemplo: Editoria de arte

b) Em seguida, dobre e desdobre a folha em quatro partes exatamente iguais para fazer vincos da seguinte maneira.

Atenção: ao dobrar, os cantos precisam se sobrepor corretamente e com exatidão.

c) Recorte essas quatro partes. Pronto, estão construídos quatro ângulos retos de papel

2. Agora, utilizando um dos quatro ângulos retos de papel construídos, identifique ângulos retos e ângulos não retos nas figuras poligonais seguintes e faça o que se pede em cada item.

a) Contorne a figura em que é possível identificar ângulos retos Espera-se que os alunos contornem o retângulo

b) Marque um X na figura em que é possível identificar ângulos não retos (ângulos menores que um ângulo reto) Espera-se que os alunos contornem o triângulo

Editoria de arte

3. Elabore, no caderno, a descrição de um caminho a ser feito somente sobre as linhas da malha quadriculada a seguir. Atenção:

• o caminho deve iniciar em qualquer um dos pontos e passar por todos os outros

• Utilize, na descrição, termos como "girar um quarto de volta" (giro que corresponde a um ângulo reto) e "girar meia-volta" (giro que corresponde a um ângulo maior que um ângulo reto).

Trace na malha quadriculada a seguir o caminho que você descreveu.

Sugestão de resposta: começando no ponto vermelho e passando pelos três pontos verdes: Descrição do caminho de acordo com a sugestão de resposta indicada na malha: A partir do ponto vermelho, andar 3 lados de quadrinho da malha.

Girar meia-volta para a direita e andar 7 lados de quadrinho da malha.

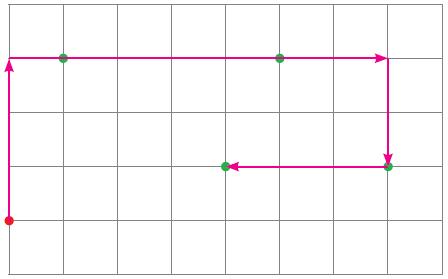
Girar meia-volta para a direita e andar 2 lados de quadrinho da malha.

Girar meia-volta para a direita e andar 3 lados de quadrinho da malha.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédito autoral e as criações sejam licenciadas

BNCC

A Base Nacional Comum Curricular (BNCC) é um documento oficial, homologado em dezembro de 2018, que traz um conjunto de habilidades e competências considerados essenciais para o desenvolvimento dos alunos na Educação Básica (Ensino Infantil, Ensino Fundamental e Ensino Médio).

A BNCC tem por objetivo possibilitar ações escolares que desenvolvam competências e habilidades comuns, garantindo igualdade das aprendizagens a que todos os estudantes brasileiros têm direito.

A seguir, são apresentadas na íntegra as Competências gerais da Educação Básica, as Competências específicas da área de Matemática e suas Tecnologias para o Ensino Fundamental e as habilidades, os objetos de conhecimento e as respectivas unidades temáticas para o 4º Ano do Ensino Fundamental e que podem ser encontrados nas páginas 9, 10, 267, 290, 291, 292 e 293 no documento:

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf

Acesso em: 2 dez. 2021.

Matemática – 4º Ano

Unidades temáticas Objetos de conhecimento Habilidades

Números Sistema de numeração decimal: leitura, escrita, comparação e ordenação de números naturais de até cinco ordens

Composição e decomposição de um número natural de até cinco ordens, por meio de adições e multiplicações por potências de 10

Propriedades das operações para o desenvolvimento de diferentes estratégias de cálculo com números naturais

(EF04MA01) Ler, escrever e ordenar números naturais até a ordem de dezenas de milhar.

(EF04MA02) Mostrar, por decomposição e composição, que todo número natural pode ser escrito por meio de adições e multiplicações por potências de dez, para compreender o sistema de numeração decimal e desenvolver estratégias de cálculo.

(EF04MA03) Resolver e elaborar problemas com números naturais envolvendo adição e subtração, utilizando estratégias diversas, como cálculo, cálculo mental e algoritmos, além de fazer estimativas do resultado.

(EF04MA04) Utilizar as relações entre adição e subtração, bem como entre multiplicação e divisão, para ampliar as estratégias de cálculo.

(EF04MA05) Utilizar as propriedades das operações para desenvolver estratégias de cálculo.

Problemas envolvendo diferentes significados da multiplicação e da

(EF04MA06) Resolver e elaborar problemas envolvendo diferentes significados da multiplicação

divisão: adição de parcelas iguais, configuração retangular, proporcionalidade, repartição equitativa e de medida

(adição de parcelas iguais, organização retangular e proporcionalidade), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

(EF04MA07) Resolver e elaborar problemas de divisão cujo divisor tenha no máximo dois algarismos, envolvendo os significados de repartição equitativa e de medida, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.

Problemas de contagem

(EF04MA08) Resolver, com o suporte de imagem e/ou material manipulável, problemas simples de contagem, como a determinação do número de agrupamentos possíveis ao se combinar cada elemento de uma coleção com todos os elementos de outra, utilizando estratégias e formas de registro pessoais.

Números racionais: frações unitárias mais usuais (1/2, 1/3, 1/4, 1/5, 1/10 e 1/100)

Números racionais: representação decimal para escrever valores do sistema monetário brasileiro

Álgebra Sequência numérica recursiva formada por múltiplos de um número natural

Sequência numérica recursiva formada por números que deixam o mesmo resto ao ser divididos por um mesmo número natural diferente de zero

Relações entre adição e subtração e entre multiplicação e divisão

(EF04MA09) Reconhecer as frações unitárias mais usuais (1/2, 1/3, 1/4, 1/5, 1/10 e 1/100) como unidades de medida menores do que uma unidade, utilizando a reta numérica como recurso.

(EF04MA10) Reconhecer que as regras do sistema de numeração decimal podem ser estendidas para a representação decimal de um número racional e relacionar décimos e centésimos com a representação do sistema monetário brasileiro.

(EF04MA11) Identificar regularidades em sequências numéricas compostas por múltiplos de um número natural.

(EF04MA12) Reconhecer, por meio de investigações, que há grupos de números naturais para os quais as divisões por um determinado número resultam em restos iguais, identificando regularidades.

(EF04MA13) Reconhecer, por meio de investigações, utilizando a calculadora quando necessário, as relações inversas entre as operações de adição e de subtração e de multiplicação e de divisão, para aplicá-las na resolução de problemas.

Propriedades da igualdade (EF04MA14) Reconhecer e mostrar, por meio de exemplos, que a relação de igualdade existente entre dois termos permanece quando se adiciona ou se subtrai um mesmo número a cada um desses termos.

(EF04MA15) Determinar o número desconhecido que torna verdadeira uma igualdade que envolve as operações fundamentais com números naturais.

Geometria Localização e movimentação: pontos de referência, direção e sentido Paralelismo e perpendicularismo

(EF04MA16) Descrever deslocamentos e localização de pessoas e de objetos no espaço, por meio de malhas quadriculadas e representações como desenhos, mapas, planta baixa e croquis, empregando termos como direita e esquerda, mudanças de direção

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial

(CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédi to autoral e as criações sejam licenciadas sob os mesmos

Figuras geométricas espaciais (prismas e pirâmides): reconhecimento, representações, planificações e características

Ângulos retos e não retos: uso de dobraduras, esquadros e softwares

Simetria de reflexão

Grandezas e medidas Medidas de comprimento, massa e capacidade: estimativas, utilização de instrumentos de medida e de unidades de medida convencionais mais usuais

Áreas de figuras construídas em malhas quadriculadas

e sentido, intersecção, transversais, paralelas e perpendiculares.

(EF04MA17) Associar prismas e pirâmides a suas planificações e analisar, nomear e comparar seus atributos, estabelecendo relações entre as representações planas e espaciais.

(EF04MA18) Reconhecer ângulos retos e não retos em figuras poligonais com o uso de dobraduras, esquadros ou softwaresde geometria.

(EF04MA19) Reconhecer simetria de reflexão em figuras e em pares de figuras geométricas planas e utilizá-la na construção de figuras congruentes, com o uso de malhas quadriculadas e de softwaresde geometria.

(EF04MA20) Medir e estimar comprimentos (incluindo perímetros), massas e capacidades, utilizando unidades de medida padronizadas mais usuais, valorizando e respeitando a cultura local.

(EF04MA21) Medir, comparar e estimar área de figuras planas desenhadas em malha quadriculada, pela contagem dos quadradinhos ou de metades de quadradinho, reconhecendo que duas figuras com formatos diferentes podem ter a mesma medida de área.

Medidas de tempo: leitura de horas em relógios digitais e analógicos, duração de eventos e relações entre unidades de medida de tempo

Medidas de temperatura em grau Celsius: construção de gráficos para indicar a variação da temperatura (mínima e máxima) medida em um dado dia ou em uma semana

(EF04MA22) Ler e registrar medidas e intervalos de tempo em horas, minutos e segundos em situações relacionadas ao seu cotidiano, como informar os horários de início e término de realização de uma tarefa e sua duração.

(EF04MA23) Reconhecer temperatura como grandeza e o grau Celsius como unidade de medida a ela associada e utilizá-lo em comparações de temperaturas em diferentes regiões do Brasil ou no exterior ou, ainda, em discussões que envolvam problemas relacionados ao aquecimento global.

(EF04MA24) Registrar as temperaturas máxima e mínima diárias, em locais do seu cotidiano, e elaborar gráficos de colunas com as variações diárias da temperatura, utilizando, inclusive, planilhas eletrônicas.

Problemas utilizando o sistema monetário brasileiro

(EF04MA25) Resolver e elaborar problemas que envolvam situações de compra e venda e formas de pagamento, utilizando termos como troco e desconto, enfatizando o consumo ético, consciente e responsável.

Probabilidade e estatística

Análise de chances de eventos aleatórios

(EF04MA26) Identificar, entre eventos aleatórios cotidianos, aqueles que têm maior chance de ocorrência, reconhecendo características de resultados mais prováveis, sem utilizar frações.

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédi to autoral e as criações sejam licenciadas sob os mesmos parâmetros.

Leitura, interpretação e representação de dados em tabelas de dupla entrada, gráficos de colunas simples e agrupadas, gráficos de barras e colunas e gráficos pictóricos

Diferenciação entre variáveis categóricas e variáveis numéricas Coleta, classificação e representação de dados de pesquisa realizada

(EF04MA27) Analisar dados apresentados em tabelas simples ou de dupla entrada e em gráficos de colunas ou pictóricos, com base em informações das diferentes áreas do conhecimento, e produzir texto com a síntese de sua análise.

(EF04MA28) Realizar pesquisa envolvendo variáveis categóricas e numéricas e organizar dados coletados por meio de tabelas e gráficos de colunas simples ou agrupadas, com e sem uso de tecnologias digitais.

Competências específicas de Matemática para o Ensino Fundamental

1. Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

2. Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

3. Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

4. Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

5. Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

6. Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

7. Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

8. Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

Competências gerais da Educação básica

1. Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social, cultural e digital para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva.

2. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

3. Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

4. Utilizar diferentes linguagens

verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital

, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar

Material disponibilizado em licença aberta do tipo Creative Commons – Atribuição não comercial (CC BY NC – 4.0 International). Permitida a criação de obra derivada com fins não comerciais, desde que seja atribuído crédi to autoral e as criações sejam licenciadas sob os mesmos parâmetros.

informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

5. Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

6. Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao exercício da cidadania e ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

7. Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos, a consciência socioambiental e o consumo responsável em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

8. Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

10. Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

Referências bibliográficas comentadas

• BORBA, Marcelo de Carvalho; SILVA, Ricardo Scucuglia Rodrigues da; GADANIDIS, George. Fases das tecnologias digitais em educação matemática: sala de aula e internet em movimento. Belo Horizonte: Autêntica Editora, 2014. (Tendências em Educação Matemática).

A obra apresenta uma síntese sobre a utilização de tecnologias e internet em favor da Educação Matemática, explorando exemplos de utilização do softwareGeoGebra®, entre outros recursos.

• CARRAHER, Terezinha Nunes (org.). Aprender pensando: contribuições da psicologia cognitiva para a educação. 20. ed. Petrópolis: Vozes, 2012. Nesse livro, é debatida a maneira de pensar das crianças, a fim de proporcionar a elas abordagens significativas das ideias matemáticas.

• COLL, César; TEBEROSKY, Ana. Aprendendo Matemática. São Paulo: Ática, 2006.

Os autores, especialistas em didática e psicologia, tratam de assuntos sobre aprendizagem e ensino de Matemática nos Anos Iniciais.

• D’AMBROSIO, Ubiratan. Educação matemática: da teoria à prática. Campinas: Papirus, 1996.

O autor aborda questões relacionadas à cognição, bem como apresenta ponderações sobre práticas de ensino da Matemática.

• ETCHEVERRIA, Teresa Cristina. O ensino de conceitos aditivos: trajetórias e possibilidades. Curitiba: Appris, 2019. Professoras relatam, nesse livro, um processo de trabalho formativo com a resolução de problemas nos Anos Iniciais do Ensino Fundamental.

• HOFFMANN, Jussara. Avaliação mito & desafio: uma perspectiva construtivista. 44. ed.

Porto Alegre: Mediação, 2014.

A autora relata exemplos da experiência dela com base na avaliação como acompanhamento constante e mediação do processo de ensino e aprendizagem.

• KAMII, Constance. A criança e o número. Tradução de Regina A. de Assis. Campinas: Papirus, 2007.

O livro apresenta uma reflexão sobre as relações estabelecidas pelas crianças na compreensão do conceito de número.

• KISHIMOTO, Tizuko Morchida. Jogos tradicionais infantis: o jogo, a criança e a educação. 18. ed. Petrópolis: Vozes, 2014.

Nesse livro, são descritos estudos acerca dos vínculos existentes entre o jogo, a criança e a educação.

• KRULIK, Stephen; REYS, Robert (org.). A resolução de problemas na Matemática escolar. Tradução de Hygino H. Domingues e Olga Corbo. São Paulo: Atual, 2012. Estão reunidos, nesse livro, artigos de Matemática sobre a resolução de problemas. Esses artigos contribuem para o conhecimento de tendências que valorizam e atribuem valor a esse trabalho.

• PARRA, Cecilia; SAIZ, Irma (org.). Didática da Matemática: reflexões psicopedagógicas. Porto Alegre: Artmed, 1996.

Na obra, há reflexões sobre o ensino do Sistema de Numeração Decimal, o trabalho com cálculo mental e exploração de noções espaciais e Geometria, entre outros assuntos.

• ZUNINO, Delia Lerner de. A Matemática na escola: aqui e agora. 2. ed. Porto Alegre: Artes Médicas, 2007.

Nesse livro, é debatida a importância de os alunos pensarem os cálculos matemáticos que fazem nas aulas, de modo que os relacionem com a aplicação no cotidiano deles.

Documentos oficiais

• BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília: SEB, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pd f. Acesso em: 5 dez. 2021.

Documento normativo no qual está definido o conjunto de aprendizagens essenciais que

os alunos precisam desenvolver durante a Educação Básica, assegurando direitos de aprendizagem e desenvolvimento.

• BRASIL. Ministério da Educação. PNA: Política Nacional de Alfabetização. Brasília: Sealf, 2019. Disponível em: http://alfabetizacao.mec.gov.br/images/pdf/caderdo_final_pna.pdf

Acesso em: 5 dez. 2021.

Política instituída pelo Decreto nº 9.765, de 11 de abril de 2019, com o objetivo de implementar ações a fim de melhorar a qualidade dos processos de alfabetização e combater o analfabetismo no Brasil.

• BRASIL. Ministério da Educação. Relatório Nacional de Alfabetização Baseada em Evidências (Renabe) Brasília: Sealf, 2020. Disponível em: https://www.gov.br/mec/pt-br/media/acesso_informacacao/pdf/RENABE_web.pdf

Acesso em: 5 dez. 2021.

Esse relatório originou-se da primeira Conferência Nacional de Alfabetização Baseada em Evidências (Conabe), que aconteceu em Brasília, em 2019. No Renabe, há uma síntese de pesquisas recentes de especialistas (nacionais e estrangeiros) sobre alfabetização, literacia e numeracia.

Leituras complementares para o professor

• CORSO, Luciana Vellinho; DORNELES, Beatriz Vargas. Qual o papel que a memória de trabalho exerce na aprendizagem da Matemática? Bolema, Rio Claro, v. 26, n. 42b, p. 627-647, abr. 2012.

Artigo sobre a função cognitiva da memória de trabalho no desenvolvimento de habilidades em cálculos aritméticos e leitura.

• MALUF, Maria Regina; CARDOSO-MARTINS, Cláudia (org.). Alfabetização no século XXI: como se aprende a ler e a escrever. Porto Alegre: Penso, 2013.

É uma das obras que embasaram a Política Nacional de Alfabetização (PNA). Auxilia a compreender como se dá a aprendizagem dos processos de leitura e escrita.