A Conquista Matemática - 8º Ano

José Ruy Giovanni Júnior

8

Matemática

MANUAL DO PROFESSOR

ENSINO FUNDAMENTAL ANOS FINAIS COMPONENTE CURRICULAR: MATEMÁTICA

Matemática

COMPONENTE CURRICULAR: MATEMÁTICA

MANUAL DO PROFESSOR

JOSÉ RUY GIOVANNI JÚNIOR

Licenciado em Matemática pela Universidade de São Paulo (USP).

Professor e assessor de Matemática em escolas de Ensino

Fundamental e Ensino Médio desde 1985.

Direção-geral Ricardo Tavares de Oliveira

Direção de Conteúdo e Negócios Cayube Galas

Direção editorial adjunta Luiz Tonolli

Gerência editorial Roberto Henrique Lopes da Silva

Edição João Paulo Bortoluci (coord.)

Alessandra Maria Rodrigues da Silva, Aline Tiemi Matsumura, Bianca Cristina Fratelli, Carlos Eduardo Bayer Simões Esteves, Janaina Bezerra Pereira, Juliana Montagner, Letícia Mancini Martins, Tatiana Ferrari D’Addio

Preparação e Revisão Maria Clara Paes (coord.)

Yara Affonso

Gerência de produção e arte Ricardo Borges

Design Andréa Dellamagna (coord.)

Sergio Cândido

Projeto de capa Sergio Cândido

Imagem de capa Jagerion Caiph/Shutterstock.com

Arte e Produção Isabel Cristina Corandin Marques (coord.)

Debora Joia, Eduardo Benetorio, Gabriel Basaglia, Kleber Bellomo Cavalcante, Rodrigo Bastos Marchini

Diagramação Wym Design

Coordenação de imagens e textos Elaine Bueno Koga

Licenciamento de textos Amandha Baptista

Iconografia Karine Ribeiro de Oliveira

Emerson de Lima, Leticia dos Santos Domingos (trat. imagens)

Ilustrações Alex Argozino, Bentinho, Daniel Bogni, Fabio Eugenio, Hannah Cardoso, Leo Teixeira, Marcos Guilherme, MW Editora e Ilustrações, Pedro Paulo Melara, Roberto Zoellner, Wandson Rocha, Sonia Vaz, Dacosta Mapas

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil)

Giovanni Júnior, José Ruy

A conquista matemática : 8o ano : ensino fundamental : anos finais / José Ruy Giovanni Júnior. – 1. ed. – São Paulo : FTD, 2022.

Componente curricular: Matemática. ISBN 978-85-96-03441-8 (aluno)

ISBN 978-85-96-03442-5 (professor)

1. Matemática (Ensino fundamental) I. Título.

22-114534 CDD-372.7 Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Cibele Maria Dias - Bibliotecária - CRB-8/9427

Reprodução proibida: Art. 184 do Código Penal e Lei 9.610 de 19 de fevereiro de 1998. Todos os direitos reservados à

EDITORA FTD

Rua Rui Barbosa, 156 – Bela Vista – São Paulo – SP CEP 01326-010 – Tel. 0800 772 2300 Caixa Postal 65149 – CEP da Caixa Postal 01390-970 www.ftd.com.br central.relacionamento@ftd.com.br

Em respeito ao meio ambiente, as folhas deste livro foram produzidas com fibras obtidas de árvores de florestas plantadas, com origem certificada.

Impresso no Parque Gráfico da Editora FTD CNPJ 61.186.490/0016-33

Avenida Antonio Bardella, 300 Guarulhos-SP – CEP 07220-020

Tel. (11) 3545-8600 e Fax (11) 2412-5375

Copyright © José Ruy Giovanni Júnior, 2022.

APRESENTAÇÃO

O intuito desta obra é oferecer aos estudantes e professores um material que norteie o trabalho com as ideias matemáticas, levando em consideração as especificidades da faixa etária a que a obra se destina.

Esperamos que este contato com os conceitos matemáticos contribua para que se estabeleça uma relação significativa entre os estudantes e o conhecimento da Matemática, pautada pela curiosidade e pela reflexão.

Ao longo dos volumes desta obra, pretendemos ainda estabelecer um elo entre a Educação Matemática e a formação do sujeito autônomo e consciente de seu papel, tendo em vista que paradigmas em Educação apontam para a formação de um estudante crítico, capaz de analisar, interpretar e participar ativamente na sociedade ao seu redor.

Para descortinar o contexto permeado por múltiplas linguagens e tecnologias em que se inserem, assumindo-se como cidadãos autônomos e conscientes das relações sociais que vivenciam diariamente, nossos estudantes precisam se apropriar dos conhecimentos sócio-historicamente construídos, valendo-se de estratégias e habilidades requeridas pelo mundo contemporâneo. E, no intuito de auxiliar você, professor, a capitanear essa jornada pelo processo de ensino e aprendizagem nos anos finais do Ensino Fundamental, foram elaboradas estas Orientações. Aqui, você encontrará diversas bases e sugestões para o seu trabalho diário junto aos estudantes.

Esperamos que tudo isso possa contribuir para a dinâmica dos atos de aprender e de ensinar, levando a aprendizagens significativas e agradáveis na área da Matemática no Ensino Fundamental.

Aventure-se nessa jornada você também!

O autor

CONHEÇA O MANUAL DO PROFESSOR

Estas Orientações buscam elucidar os caminhos percorridos na elaboração desta obra desde a idealização dela até a efetivação das propostas apresentadas em cada Volume.

Acredita-se ser de grande relevância conhecer os pressupostos teóricos que embasam a obra para, a partir deles, perceber a estrutura e os elementos que a compõem. Além da apresentação desses norteadores, buscou-se promover reflexões acerca do ensino e da aprendizagem de Matemática e as possíveis ações e estratégias que podem ser utilizadas na prática pelo professor. Vale mencionar que muitas explorações aqui apresentadas consistem em sugestões e, portanto, podem ser adaptadas sempre que necessário.

Neste manual, procurou-se utilizar uma linguagem clara e objetiva que permita uma fácil visualização das articulações idealizadas, bem como estratégias de aplicação dos conceitos aqui trabalhados.

Este material está organizado em três partes:

• Na primeira parte, denominada Orientações gerais, são apresentadas reflexões acerca do ensino e da aprendizagem da Matemática e de possíveis instrumentos e ferramentas que podem favorecer a construção do conhecimento matemático nos Anos Finais do Ensino Fundamental e, como mencionado anteriormente, muitas dessas abordagens nortearam a elaboração desta obra.

• Na segunda parte, denominada Orientações específicas do Volume, disposta em formato de U, o professor encontrará o detalhamento das situações e atividades propostas no Livro do estudante, acompanhada de sugestões que possam tornar o processo de ensino e aprendizagem mais rico e proveitoso.

• Na terceira parte, temos a seção de Resoluções comentadas de todas as atividades do Volume e a seção Avaliações oficiais em foco, com uma proposta de avaliação, com questões baseadas em avaliações oficiais de larga escala.

Esperamos que todos esses recursos possam contribuir com o trabalho do professor, dentro e fora da sala de aula, e com o alcance de um objetivo educacional ainda maior: a formação de um estudante crítico, capaz de analisar, interpretar e atuar no mundo de maneira consciente, cooperativa e autônoma.

LUCIOLA ZVARICK/PULSAR IMAGENS

Escola indígena da etnia Waurá da aldeia Piyulaga, em Gaúcha do Norte (MT). Fotografia de 2019. V

Orientações gerais

Considerações sobre o ensino de Matemática

Neste tópico, são apresentados fundamentos teóricos e aplicações de temas relevantes para o ensino de Matemática, como inferência, argumentação, pensamento computacional e resolução de problemas.

A BNCC e o ensino de Matemática

Nesta seção, são apresentadas reflexões e abordagens sobre a Base Nacional Comum Curricular, um dos documentos norteadores desta obra.

A BNCC E O ENSINO DE MATEMÁTICA

Para que possamos iniciar nossas abordagens e reflexões acerca da Base Nacional Comum Curricular (BNCC) e suas indicações, principalmente na área da Matemática, julgamos interessante realizar uma breve apresentação dos movimentos que precedem a homologação desse documento.

Não podemos desprezar as dimensões do país, seja em territorialidade, seja em diversidade, nem ignorar a desigualdade social ainda presente em inúmeras pesquisas e dados estatísticos. Um dos principais desafios, na área da educação, é propiciar oportunidades iguais para todos os estudantes, sem perder a particularidade e a singularidade de cada região ou grupo.

Desde 1988, a Constituição Federal determinava o direito à educação e apresentava os conteúdos mínimos a serem desenvolvidos em todo o território nacional. Nesse mesmo documento, podemos encontrar indicações da necessidade de resguardar os valores culturais e artísticos, nacionais e regionais.

Quase dez anos depois, no ano de 1996, a Lei de Diretrizes e Bases (LDB) estabelece as competências e diretrizes para a Educação Infantil, o Ensino Fundamental e o Ensino Médio, que deveriam nortear os currículos e seus conteúdos mínimos, de modo a assegurar formação básica comum, salientando que os conteúdos deveriam ser complementados com a parte diversificada que garantiria as características locais e regionais.

No Plano Nacional de Educação (PNE) de 2014, essa necessidade é reafirmada, ou seja, em parceria, a União, os estados, o Distrito Federal e os municípios deveriam criar uma Base Nacional Comum Curricular (BNCC) que garantisse a todos os estudantes do território nacional as aprendizagens essenciais, preservando-se as identidades étnicas, culturais e linguísticas. Para isso, cada Secretaria de Educação teria autonomia para pensar e planejar as ações de suas unidades escolares a partir das necessidades locais.

Desse modo, a BNCC, homologada em dezembro de 2017, apresenta um conjunto de aprendizagens essenciais a que têm direito todos os estudantes da Educação Básica. Traz uma perspectiva de igualdade diversidade e equidade para a constituição da ação escolar a partir de uma proposta comum de direitos e objetivos de aprendizagem para os estudantes da Educação Infantil ao Ensino Médio de todo o país. Indica o que deve ser ensinado e desenvolvido, isto é, os conhecimentos e as competências essenciais que devem ser garantidos a todos os estudantes brasileiros em sua vida escolar.

Com o foco no desenvolvimento de competências e no compromisso com a educação integral, o documento apresenta uma abordagem bastante clara no que diz respeito ao desenvolvimento integral dos estudantes (cognitivo e emocional) e a importância da experimentação, articulação e aplicabilidade dos conhecimentos e ao acesso e à utilização consciente da informação e da tecnologia.

As competências O documento apresenta como competência a capacidade de mobilizar conhecimentos, habilidades, atitudes e valores para que se possam resolver os desafios do cotidiano, dentro e fora dos espaços escolares.

Na BNCC, competência é definida como a mobilização de conhecimentos (conceitos e procedimentos), habilidades (práticas, cognitivas e socioemocionais), atitudes e valores para resolver demandas complexas da vida cotidiana, do pleno exercício da cidadania e do mundo do trabalho.

Ao definir essas competências, a BNCC reconhece que a “educação deve afirmar valores e estimular ações que contribuam para a transformação da sociedade, tornando-a mais humana, socialmente justa e, também, voltada para a preservação da natureza” [...].

BRASIL. Ministério da Educação. Base Nacional Comum Curricular educação é a base. Brasília, DF: MEC, 2018. p. 8. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 17 jul. 2022.

São apresentadas dez competências gerais que se inter-relacionam e devem permear os conteúdos apresentados ao longo de todo o percurso escolar da Educação Básica. XXXIX

Uma visão interdisciplinar e os Temas Contemporâneos Transversais

Aqui, são discutidos os Temas Contemporâneos Transversais e algumas sugestões de aplicação de tais temas de modo interdisciplinar nas aulas de Matemática.

O papel do professor

Neste tópico, são apresentadas importantes reflexões sobre o papel fundamental do professor e a prática educativa em Matemática.

Perfis de aprendizagem

Trata-se, aqui, de temas relacionados aos diferentes perfis de aprendizagem apresentados nos diversos contextos escolares brasileiros, e são discutidos modos de lidar com tais diferenças nas aulas de Matemática.

Os conhecimentos matemáticos podem ser encarados como recursos que favorecem a cidadania, dada a ampla gama de aplicações desses conhecimentos nas mais variadas situações da sociedade atual. Para apresentar a Matemática como área a serviço do conhecimento científico e de relevância prática no cotidiano, é necessário que o professor tenha clareza a respeito das relações da Matemática com outras áreas de conhecimento. Para isso, é importante que o professor de Matemática tenha uma formação integral e continuada, apropriando-se das relações e aplicações de conceitos matemáticos em outras áreas do conhecimento e da contribuição da Matemática para construção da cidadania, como destacam Soares e Sheide (2004):

Outra questão crucial é a percepção que o professor tem sobre o conhecimento matemático e as interações que é capaz de estabelecer com esse conhecimento. A sua utilização como ferramenta para a construção da cidadania vai depender da sua capacidade em tratá-lo como um conhecimento articulado aos outros campos do saber e historicamente situado.

SOARES, Marlene Aparecida; SCHEIDE, Tereza de Jesus Ferreira. Professor de Matemática: um educador a serviço da construção da cidadania. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 8., 2004, Recife. Anais […]. Recife: Universidade Federal de Pernambuco, 2004. p. 2. Disponível em: http://www.sbem.com.br/files/viii/pdf/07/CC07289049853.pdf. Acesso em: 13 jul. 2022.

Desse modo, o professor de Matemática, longe de ser um mero transmissor de conhecimentos imutáveis, é um sujeito do conhecimento que compartilha com estudantes conhecimentos esses que devem estar em constante aprimoramento e transformação para serem úteis nas práticas sociais dos estudantes.

Portanto, neste processo de parceria e inter-relação existente entre estudantes e professores, é muito importante que ambos tenham clareza dos objetivos que se quer alcançar, as habilidades a serem desenvolvidas, os processos individuais e coletivos e possíveis caminhos a serem percorridos.

PERFIS DE APRENDIZAGEM

A Base Nacional Comum Curricular trouxe ao centro do debate sobre o processo educativo a necessidade de pensarmos em educação integral. Isso significa considerar cada estudante como indivíduo pleno e complexo, em suas diversas dimensões. Ninguém abandona gostos, características, sonhos, valores e emoções antes de entrar na escola – ao contrário, a sala de aula é composta de diversidade. Na BNCC (2018, p. 14), destaca-se:

[…] Reconhece, assim, que a Educação Básica deve visar à formação e ao desenvolvimento humano global, o que implica compreender a complexidade e a não linearidade desse desenvolvimento, rompendo com visões reducionistas que privilegiam ou a dimensão intelectual (cognitiva) ou a dimensão afetiva. Significa, ainda, assumir uma visão plural, singular e integral da criança, do adolescente, do jovem e do adulto – considerando-os como sujeitos de aprendizagem – e promover uma educação voltada ao seu acolhimento, reconhecimento e desenvolvimento pleno, nas suas singularidades e diversidades. […] BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 14. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 28 jul. 2022.

Essa visão implica reconhecer que ao professor cabe considerar cada estudante em sua singularidade, identificando necessidades, diferentes interesses e modos de aprender. Cada um de nós tem um perfil de aprendizagem. Isso não significa que aprendamos apenas por um canal de aprendizagem, mas, muitas vezes, existem canais mais propícios do que outros e, portanto, reconhecê-los e incentivar o uso deles é muito importante. Existem indivíduos que compreendem melhor a partir de estímulos visuais e, portanto, é interessante recorrer ao uso de gráficos, tabelas, listas e mapas mentais. Há pessoas que compreendem melhor utilizando a leitura (silenciosa) e escrita (listas, textos on-line, artigos, dicionários); LVI

Avaliação

São abordados neste tópico os diversos tipos de avaliação e a importância desse recurso para o processo de ensino e aprendizagem.

Indicações para apoio ao trabalho do professor

Aqui, encontram-se indicações de materiais relevantes para consulta e aprimoramento do professor.

D2_AV1-MAT-F2-2103-V8-MPG-I-LXIV-G24.indd 39

D2_AV4-MAT-F2-2103-V8-MPG-I-LXIV-G24.indd 56

Nesta seção, além dos elementos que compõem o material do estudante, são apresentados os conteúdos de cada Volume. No Livro do estudante, cada Volume desta obra divide-se em nove Unidades e cada Unidade em capítulos.

Aberturas de Unidade

Nesta obra, as aberturas de Unidades têm um papel fundamental: elas propiciam o momento de entrada no grande tema que será tratado. Em cada Volume, a Unidade é introduzida por uma abertura que traz:

• uma imagem (ilustração, fotografia ou infográfico) relacionada com temas que serão estudados ao longo da Unidade e cujo objetivo é instigar os estudantes a uma discussão inicial; • algumas questões para contextualizar os estudantes no assunto da Unidade e mobilizar conhecimentos anteriores.

Capítulos

Nos Volumes desta obra, as Unidades são compostas de uma quantidade variável de capítulos, de acordo com a demanda de cada tema.

Em cada capítulo, os estudantes contarão com diferentes explorações e recursos, como textos, imagens e atividades. Ao longo de cada capítulo, podem ser encontrados seções e boxes que buscam favorecer compreensões, aprofundamentos, reflexões e articulações.

Seções e boxes

Atividades

Nesta seção, os estudantes encontrarão atividades diversificadas que foram organizadas de acordo com os conteúdos apresentados em cada tópico, de modo a facilitar a realização e a conferência. Eventualmente, são apresentadas atividades denominadas Desafio, que apresentam maior nível de dificuldade, permitindo a mobilização de mais habilidades e competências.

POR TODA PARTE

RESPEITO MÚTUO E VALORIZAÇÃO DA DIVERSIDADE Em 1996, a Assembleia Geral da Organização das Nações Unidas (AGNU) declarou o dia 16 de novembro como o Dia Internacional da Tolerância com o objetivo de destacar o compromisso de todos em promover o entendimento entre diferentes povos e culturas. Leia a seguir um trecho do artigo 1 da Declaração de Princípios sobre a Tolerância assinada pelos Estados-Membros da Organização das Nações Unidas para a Educação, a Ciência e a Cultura (Unesco) na 28 reunião da Conferência Geral, realizada em Paris, em 1995.

Artigo 1o – Significado de tolerância

1.1 A tolerância é o respeito, a aceitação e o apreço da riqueza e da diversidade das culturas de nosso mundo, de nossos modos de expressão e de nossas maneiras de exprimir nossa qualidade de seres humanos. É fomentada pelo conhecimento, a abertura de espírito, a comunicação e a liberdade de pensamento, de consciência e de crença. A tolerância é a harmonia na diferença. Não só é um dever de ordem ética; é igualmente uma necessidade política e jurídica. A tolerância é uma virtude que torna a paz possível e contribui para substituir uma cultura de guerra por uma cultura de paz.

Por toda parte

EDUCAÇÃO FINANCEIRA

JUROS CONTRA x JUROS A FAVOR

Os juros são o ponto central do sucesso financeiro. Trata-se de uma questão de escolha: você pode usar os juros contra ou a favor de você! Em síntese, antecipar custa e retardar rende. Se você antecipa com o banco um valor x para pagar por algo que deseja ter, devolverá ao banco x + os juros. Se, ao contrário, retarda o uso de um valor x deixando-o guardado no banco, receberá do banco x + juros quando decidir utilizá-lo. A questão é que esse é

ALERISSATO/SHUTTERSTOCK.COM

um processo por trás do qual existe uma lógica matemática de acumulação, os chamados juros compostos, popularmente definidos como “juros sobre juros”. [...] O problema é que essa é uma moeda de dois lados. [...] Se você faz uma antecipação com o banco, por meio do cartão de crédito, para pagar por um desejo imediato, e não consegue quitar na data, pagará juros sobre juros, e o valor da dívida se multiplicará. Pior ainda, porque a taxa de juros do cartão é, no mínimo, 13 vezes maior do que a taxa de rendimento de uma poupança. Para se ter uma ideia, uma única dívida de R$ 150,00 no cartão de crédito, a uma taxa de 9% ao mês, transforma-se em uma dívida de aproximadamente R$ 4.600.000,00 em dez anos. São os juros contra você! [...]

DOMINGOS, Reinaldo. Ter dinheiro não tem segredo educação financeira para jovens. São Paulo: DSOP, 2013. p. 83-84.

Lígia tem uma conta bancária com cheque especial. Isso significa que ela tem um limite que pode ser utilizado, ou seja, ela pode usar um valor superior ao seu saldo, ficando, assim, com um saldo negativo. Esse saldo negativo é um empréstimo automático, e já aprovado, pelo qual se cobram juros. Para o banco não cobrar mais esses juros, é necessário que o cliente deposite um valor maior ou igual ao da dívida. O gráfico a seguir representa o saldo da conta bancária de Lígia, que inicialmente era devedor em R$ 200,00, e sobre o qual incidirá juro composto de 10% ao mês, caso ela não tome nenhuma providência e quite a dívida.

Responda às questões no caderno.

1. Em quanto tempo a dívida de Lígia dobrará? Entre 7 e 8 meses.

2. O valor da dívida, em reais, é dado pela expressão 200 (1,1) , em que n é a quantidade de meses em que Lígia tem a dívida. Utilizando a expressão e uma calculadora, calcule o valor da dívida de Lígia depois de 5 anos. Aproximadamente R$ 60.896,33.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

Educação financeira

UNESCO, 1997. p. 11. Disponível em: Princ%C3%ADpios%20sobre%20a%20Toler%C3%A2ncia%20da%20UNESCO.pdf.https://www.oas.org/dil/port/1995%20Declara%C3%A7%C3%A3o%20de%20 Acesso em: 4 jul. RAWPIXEL.COM/SHUTTERSTOCK.COM A educação e o acesso à informação são grandes aliados para promover o respeito à liberdade e ao pluralismo de ideias. 280 D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 13/08/22 19:26

1.2 A tolerância não é concessão, condescendência, indulgência. A tolerância é, antes de tudo, uma atitude ativa fundada no reconhecimento dos direitos universais da pessoa humana e das liberdades fundamentais do outro. [...]

É uma seção que apresenta textos, imagens e atividades que proporcionam ao estudante maior contextualização dos assuntos explorados na Unidade. Esta seção busca estabelecer um diálogo entre tópicos de Matemática e de outras áreas do conhecimento, além de oportunizar a ampliação de repertório cultural e perceber a Matemática em variadas situações do cotidiano. Os temas e atividades desta seção possibilitam, ainda, articulações entre os Temas Contemporâneos Transversais e as competências gerais e específicas apresentadas na BNCC.

VIII

Nesta seção, os estudantes encontrarão temas como hábitos conscientes de consumo, controle de gastos, planejamento financeiro e economia. Com base em leituras e reflexões, serão incentivados a repensar ações e atitudes ligadas ao consumo e a lidar com o dinheiro.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd

Tratamento da informação

Nesta seção, que reúne propostas de trabalho com temas associados à probabilidade e Estatística, os estudantes encontrarão textos, gráficos, tabelas e atividades, sempre buscando a contextualização desses temas e a análise e interpretação crítica de dados e informações.

TECNOLOGIAS

286

INFORMAÇÃO TRATAMENTO DA

INTERPRETANDO INFORMAÇÕES

O mercado de trabalho no Brasil e a inclusão de pessoas com deficiência

As pessoas com deficiência enfrentam muitos desafios no dia a dia e, principalmente, no mundo do trabalho. É de fundamental importância para o exercício da cidadania que elas sejam reconhecidas como sujeitos de direito, bem como pela sua força de trabalho, sendo direcionadas a cargos e funções de acordo com suas especificidades e habilidades. Assim, poderão superar desafios e preconceitos. Os direitos ao acesso e à participação no mercado de trabalho precisam ser materialmente garantidos, de modo que muitos espaços que careçam de adaptações sejam ajustados para atender às condições de acessibilidade. O artigo 93 da lei n 8.213 de 1991 especifica a quantidade de vagas que devem ser preenchidas por pessoas reabilitadas ou com deficiência em uma empresa com mais de 100 empregados. Leia a seguir o que diz o referido artigo.

RETOMANDO APRENDEU O QUE

Responda às questões no caderno.

Pessoa com deficiência exercendo atividade laboral em ambiente de trabalho. Fotografia de 2022.

Art. 93. A empresa com 100 (cem) ou mais empregados está obrigada a preencher de 2% (dois por cento) a 5% (cinco por cento) dos seus cargos com beneficiários reabilitados ou pessoas portadoras de deficiência, habilitadas, na seguinte proporção:

I – até 200 empregados....................................2%; II – de 201 a 500..................................................3%; III – de 501 a 1000.............................................4%; IV – de 1001 em diante....................................5%.

BRASIL. Lei n 8.213, de 24 de julho de 1991. Dispõe sobre os Planos de Benefícios da Previdência Social e dá outras providências. Brasília, DF: Casa Civil, 1991. Disponível em: http://www.planalto.gov.br/ccivil_03/leis/l8213cons.htm. Acesso em: 4 jul. 2022.

ARTKIO/SHUTTERSTOCK.COM Com base nessas informações, responda às questões no caderno.

1. Considere uma empresa que tem 1 500 funcioná- rios contratados. De acordo com o artigo de lei citado anteriormente, quantas dessas vagas devem ser ocupadas por beneficiários reabilitados ou pessoas com deficiência habilitadas? No caso de uma empresa com 150 funcionários, qual seria essa quantidade de vagas? 75 vagas; 3 vagas.

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 286

TRANSFORMAÇÕES NO PLANO

Depois do estudo das transformações geométricas no plano, vamos usar ferramentas do software GeoGebra para fazer composições envolvendo simetrias de reflexão, translação e rotação. Considere a seguinte situação. Talita e Fernando estavam usando um software de geometria dinâmica para estudar transformações no plano. Eles foram desafiados a compor um padrão geométrico usando as simetrias de reflexão, translação e rotação. Nesse desafio, eles poderiam usar apenas as seguintes ferramentas:

Mover

Tecnologias

Reta

Reflexão em relação a uma reta Ponto

Polígono Translação por um vetor

Vetor

Intersecção entre dois objetos

Além disso, eles poderiam usar a ferramenta apenas duas vezes. Observe algumas etapas das construções realizadas por Talita e Fernando.

Rotação em torno de um ponto

1 Inicialmente, eles construíram dois triângulos: *BCD e *CEF. Em seguida, os triângulos construídos foram refletidos em relação ao eixo y Depois, refletiram os triângulos CEF e F E C em relação ao eixo x

Fórum

Seção voltada ao desenvolvimento de habilidades relacionadas ao uso de softwares na aprendizagem de Matemática. Com os tutoriais e as atividades desta seção, os estudantes aprenderão a utilizar planilhas eletrônicas, softwares de geometria dinâmica, calculadoras de raízes de equações, entre outros, e a simular situações e a analisar os resultados. Além disso, no fim de cada Volume, há uma seção direcionada às noções de programação, como um dos recursos da obra para favorecer o pensamento computacional a partir do contato com recursos tecnológicos.

Este boxe traz questões que favorecem o debate e possibilitam a troca e o compartilhamento de ideias e conhecimentos, fazendo que os estudantes pratiquem o desenvolvimento de estratégias de argumentação. As propostas podem ou não ser realizadas on-line. Caso a escola possua uma ferramenta desse tipo ou o professor opte por usar uma ferramenta de uso livre na internet, pode-se criar um grupo fechado para realizar essas propostas.

Pense e responda

Neste boxe, serão apresentadas questões que buscam mobilizar conhecimentos e promover reflexões e/ou investigações acerca dos assuntos a serem explorados ou previamente estudados. Aqui, os estudantes terão a oportunidade de exercitar a autonomia e o raciocínio inferencial ao ter de investigar determinado tema antes de observá-lo, generalizá-lo ou sistematizá-lo.

Saiba que

Neste boxe, os estudantes encontrarão um texto objetivo que fornecerá uma dica interessante ou um recado importante para o entendimento de alguma explicação ou para a realização de uma atividade.

Glossário

1. Qual é o número real representado pela letra x que torna verdadeira a igualdade 7x _ [5x + 3 (2x + 1) 10] = _( x + 3)? Alternativa b. a) 11 2 b) 11 3

c) 3 11 d) 3 11

e) 7 3

5. A altura de uma árvore, em metro, é dada por h + 10 100 10 t sendo t a idade da árvore em ano. Se essa árvore tem 6 metros de altura, quantos anos ela tem?

a) 12 anos.

b) 13 anos. c) 14 anos.

d) 15 anos.

e) 16 anos. Alternativa d.

6. De acordo com uma pesquisa, foi constatado que, ao longo de x meses, a quantidade de pessoas que contrairá certo tipo de gripe é dada pela expressão matemática + 13000 10 x 2 Após quantos meses a quantidade de pessoas infectadas por esse tipo de gripe será de 4000?

a) 6 meses.

e) 2 5

2. Observe as equações. =+55 3x x4 3 2 x (x 0, x 4) + 5_5 5 y9 3 y3(y 3, y 3) Resolvendo cada uma dessas equações, oquociente x : y é: Alternativa a. a) 3 5 b) 5 3

c) 3 5 d) 5 3

3. O alugueldeumamotoemumaagência A é 280 reais, acrescido de 3 reais por quilômetro rodado. Em uma agência B o aluguel da mesma moto é 400 reais, acrescido de 1 real por quilômetro rodado. Qual deve ser a quantidade de quilômetros rodados para que o valor do aluguel seja o mesmo em ambas as agências? a) 60 km b) 64 km c) 68 km

d) 70 km e) 72 km Alternativa a.

4. Um número natural n é tal que: + + + + n3 n7 n7 n12

Qual é o valor numérico da expressão + n3? a) 16 b) 25 c) 5

d) 4 e) 3 Alternativa d.

176

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 176

b)

7 meses. c) 8 meses.

d) 9 meses. e) 10 meses. Alternativa c.

7. Em uma loja, a diferença entre o preço de venda e o preço de custo de um produto

é

R$ 5.000,00. Se o preço de custo representa 75% do preço de venda, então, o preço de custo desse produto é

a) R$ 10.000,00.

b) R$ 12.000,00.

c) R$ 15.000,00.

d) R$ 16.000,00.

e) R$ 20.000,00.

8. A quantidade de bolas vermelhas em uma caixa é o triplo da quantidade de bolas pretas. Se tirarmos 2 bolas pretas e 26 bolas vermelhas, a quantidade de bolas de cada cor ficará igual. Quantas bolas vermelhas há na caixa?

a) 8 b) 12 c) 24

Alternativa c. Alternativa d.

d) 36 e) 48

Retomando o que aprendeu

Nesta seção, os estudantes serão convidados a revisitar os conteúdos explorados na Unidade para que possam perceber conquistas e identificar possíveis dúvidas.

Respostas

25/07/22 12:21

Seção final do Livro do estudante, na qual estão todas as respostas diretas às atividades propostas. Trata-se de uma seção voltada para a consulta rápida de respostas.

Apresenta o significado de algumas palavras, auxiliando na leitura e compreensão de textos. Esses significados podem ser ampliados com o incentivo ao uso conjugado com dicionários.

Descubra mais

Boxe com indicações de ampliação do repertório e/ou aprofundamento em determinado tema, como sugestões de livros, vídeos, simuladores, podcasts, artigos etc. para os estudantes.

Um novo olhar

Possibilita aos estudantes retomar os conhecimentos explorados na abertura das Unidades e perceber, por exemplo, as habilidades desenvolvidas e as que precisam ser revistas. Assim, este boxe oportuniza a autoavaliação dos estudantes, ao mesmo tempo que pode ser utilizado pelo professor como ferramenta para o mapeamento de conhecimentos desenvolvidos e a desenvolver na turma.

PICKBIZ/SHUTTERSTOCK.COM

D2-AV1-MAT-F2-2103-V8-U6-178-211-LA-G24.indd

QUADROS DE CONTEÚDOS

Cada um dos quatro volumes da obra é organizado em nove Unidades. O tema principal de cada Unidade está relacionado a uma ou mais Unidades temáticas da BNCC e seguem, em geral, uma ordem de progressão de conteúdos, de acordo com as etapas de aprendizagens previstas para cada um dos Anos Finais do Ensino Fundamental.

Entretanto, o professor tem autonomia para apresentar as Unidades na ordem que julgar mais conveniente para a realidade da turma e de acordo com as ações de planejamento de suas aulas. Por exemplo, se houver mais de uma Unidade consecutiva que trate sobre determinado tema de Números, o professor pode intercalar essas Unidades com uma Unidade, localizada adiante, relacionada a Geometria e, posteriormente, retomar o estudo de Números.

Analogamente, com relação aos conteúdos abordados em cada Unidade, o professor pode seguir a ordem sugerida ou, eventualmente, realizar a sequência de conteúdos que melhor lhe convier. Por exemplo, antes de começar a abordagem teórica proposta em determinada Unidade, o professor pode propor a leitura do texto e o debate sobre o tema de uma seção que traga uma contextualização para aquele conceito matemático a ser trabalhado. Depois da apresentação formal dos conceitos, pode-se propor aos estudantes que retomem a conversa sobre a seção estudada no início da Unidade e que realizem as atividades, analisem as respostas, validem hipóteses etc.

Portanto, o professor tem autonomia em relação aos conteúdos apresentados na coleção, podendo dispor deles, articulá-los e complementá-los de modo a potencializar a construção de conhecimentos e tornar a aprendizagem cada vez mais efetiva.

A fim de auxiliar o professor no planejamento de aulas com apoio didático desta obra, disponibilizamos quadros com a organização trimestral e bimestral de conteúdos da obra por ano, indicando a Unidade, os principais conteúdos abordados nela, além de habilidades, competências e Temas Contemporâneos Transversais da BNCC. 6o ano

Habilidades:

• Sistemas de numeração

• Sistema de Numeração Decimal

• Leitura e interpretação de tabelas e gráficos de colunas

• O conjunto dos números naturais

• Tipos de calculadora

• Operações com números naturais (adição, subtração, multiplicação, divisão e potenciação)

• Tabelas de dupla entrada e gráficos de barras duplas

• Aproximação e estimativa

• Expressões numéricas

• Uso da calculadora para a resolução de expressões numéricas

• Ponto, reta e plano

• Semirreta e segmento

• de reta

• Figuras geométricas

• Sólidos geométricos

• Estimativas e projeções

EF06MA01

EF06MA02

EF02MA32

Competências gerais: 1, 7 e 10

Competências específicas: 1, 2, 4, 5 e 7

Tema Contemporâneo Transversal: Educação Ambiental

Habilidades:

EF06MA03

EF06MA04

EF06MA12

EF06MA14

EF06MA31

EF02MA32

Competências gerais: 4, 7, 9 e 10

Competências específicas: 3, 4 e 6

Temas Contemporâneos Transversais: Direitos da Criança e do Adolescente e Educação para o Consumo

Habilidades:

EF06MA17

EF06MA28

EF06MA31

Competências gerais: 1, 2, 9 e 10

Competências específicas: 1, 2, 3, 6, 7 e 8

Tema Contemporâneo Transversal: Educação em Direitos Humanos

1. Sistemas de numeração

2. Cálculos com números naturais

Bimestre

3. Figuras geométricas

4. Múltiplos e divisores

• Critérios de divisibilidade

• Uso da calculadora para encontrar o resto de uma divisão

• Divisores e múltiplos de um número natural

• Leitura e interpretação de gráficos pictóricos

• Números primos

• Uso de planilha eletrônica na divisibilidade

Habilidades:

EF06MA04

EF06MA05

EF06MA06

EF06MA31

EF06MA32

EF06MA33

EF06MA34

Competências gerais: 1, 3, 4, 5, 6, 7, 8, 9 e 10

Competências específicas: 1, 2, 3, 5, 6, 7 e 8

Temas Contemporâneos Transversais: Diversidade Cultural, Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras e Educação para o Trânsito

5. A forma fracionária dos números racionais

• Fração (comparação, equivalência, simplificação)

• Problemas envolvendo frações

• Adição e subtração de frações

• Forma mista

• Multiplicação com frações

• Fração e porcentagem

• Probabilidade

6. A forma decimal dos números racionais

• Número racional na forma decimal (transformações e comparação)

• Operações com números racionais na forma decimal (adição, subtração, multiplicação, divisão e potenciação)

• Cálculo de porcentagens

• Probabilidade

• Ângulo

• Transferidor

• Uso de software para construir e medir ângulos

• Uso da planilha do LibreOffice Calc para construir gráficos

• Construção de retas paralelas e perpendiculares

Habilidades:

EF06MA07

EF06MA09

EF06MA10

EF06MA13

EF06MA15

EF06MA30

Competências gerais: 4 e 9

Competências específicas: 1, 5 e 6

Habilidades:

EF06MA01

EF06MA08

EF06MA11

EF06MA13

EF06MA30

Competências gerais: 7 e 9

Competências específicas: 3 e 6

Tema Contemporâneo Transversal: Educação Financeira

Habilidades:

EF06MA16

EF06MA18

EF06MA19

EF06MA20

EF06MA21

EF06MA22

EF06MA23

EF06MA25

EF06MA26

7. Ângulos e polígonos

• Polígonos (definição, identificação e nomenclatura)

• Polígonos regulares

• Triângulos (elementos e classificação)

• Quadriláteros (elementos e classificação)

• Plano cartesiano

• Construção de polígonos no plano cartesiano

• Construção e ampliação/redução de polígonos com uso de um software

EF06MA27

EF06MA28

EF06MA31

EF06MA32

EF06MA33

Competências gerais: 1, 2, 5, 7, 8 e 9

Competências específicas: 1, 2, 4, 5, 6, 7 e 8

Temas Contemporâneos Transversais: Educação para o Trânsito, Saúde e Educação Ambiental

2 º Trimestre

º Bimestre

3 º Bimestre

3 º Trimestre

8.

• Unidades de medida de comprimento

• Transformação das unidades de medida de comprimento

• Perímetro de um polígono

• Unidades de medida de superfície

• Transformação das unidades de medida de superfície

• Medidas agrárias

• Área de figuras geométricas planas (retângulo, quadrado e triângulo retângulo)

• Gráfico de segmentos

• Medidas de massa

• Transformação das unidades de medida de massa

• Balança de dois pratos

• Medidas de tempo e de temperatura

• Medidas de volume

Habilidades:

EF06MA24

EF06MA28

EF06MA29

EF06MA31

EF06MA32

Competências gerais: 4, 7, 9 e 10

Competências específicas: 2, 3 e 6

Temas Contemporâneos Transversais: Educação para o Consumo e Educação Ambiental

9.

• Transformação das unidades de volume

• Volume do bloco retangular e do cubo

• Medidas de capacidade

• Transformação das unidades de capacidade

• Pesquisa e fluxograma

7o ano

• Números naturais

• Operações com números naturais

Habilidades:

EF06MA23

EF06MA24

EF06MA33

EF06MA34

Competências gerais: 1, 2, 4, 5, 7, 8 e 9

Competências específicas: 2, 3, 4, 6 e 8

Temas Contemporâneos Transversais: Saúde e Educação Alimentar e Nutricional

1. Números naturais e operações

• Divisores e múltiplos de um número natural

• Números primos

• mmc e mdc

• Gráficos de colunas triplas e de barras triplas

• Os números inteiros

• Os números negativos

• Módulo de um número inteiro

• Comparação de números inteiros

• Operações com números inteiros (adição, subtração, multiplicação, divisão, potenciação e raiz quadrada exata)

• Expressões numéricas

Habilidades:

EF07MA01

EF07MA05

EF07MA07

EF07MA36

Competências gerais: 1, 2, 4, 6, 7 e 9

Competências específicas: 1, 2, 3, 4, 6 e 8

Temas Contemporâneos Transversais: Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras e Vida Familiar e Social

Habilidades

EF07MA03

EF07MA04

EF07MA05

EF07MA06

Competências gerais: 1, 2, 3, 6, 7, 8 e 9

Competências específicas: 1, 2, 3 e 7

Tema Contemporâneo Transversal: Educação em Direitos Humanos

3 º Trimestre 4 º Bimestre

Comprimento e área

Grandezas e medidas

2. O conjunto dos números inteiros

ORGANIZAÇÃO

• Simetria

• Construções feitas com uso das ferramentas de simetria do GeoGebra

• Ampliação

• Transformações no plano cartesiano

Habilidades:

EF07MA06

EF07MA19

EF07MA20

EF07MA21

Competências gerais: 1, 3, 4, 5, 6, 7, 8, 9 e 10

Competências específicas: 1, 2, 3, 4, 6, 7 e 8

Temas Contemporâneos Transversais: Diversidade Cultural e Educação Ambiental

Habilidades:

EF07MA05

• Os números racionais

• Módulo de um número racional

• Comparação de números racionais

• Operações com números racionais nas formas decimal e de fração

• Raiz quadrada exata de números racionais

• Média aritmética

• Média aritmética ponderada

• Análise de tabelas e gráficos com números racionais negativos

EF07MA06

EF07MA07

EF07MA08

EF07MA09

EF07MA10

EF07MA11

EF07MA12

EF07MA35

Competências gerais: 2, 4 e 7

Competências específicas: 2, 3 e 6

Tema Contemporâneo Transversal: Vida Familiar e Social

Habilidades:

EF07MA05

EF07MA06

EF07MA13

• Sequências

• Expressões algébricas

• Igualdade

• Equações (conjunto universo e solução; equivalência)

EF07MA14

EF07MA15

EF07MA16

EF07MA18

e equações

• Equações do 1o grau com uma incógnita

• Equações na resolução de problemas

• Gráficos de linhas (ou de segmentos)

EF07MA36

Competências gerais: 1, 2, 3, 4, 9 e 10

Competências específicas: 1, 2, 3, 4, 5, 6, 7 e 8

Temas Contemporâneos Transversais: Diversidade Cultural, Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras, Educação em Direitos Humanos, Saúde e Vida Familiar e Social

1 º Trimestre

2 º Bimestre

3. Simetria e transformações geométricas

2 º Trimestre

4. O conjunto dos números racionais

5. Linguagem algébrica

• Ângulos

• Retas paralelas cortadas por uma transversal

• Investigação de propriedades de ângulos usando o GeoGebra

• Triângulos (construção, condição de existência e soma das medidas dos ângulos internos)

• Ângulos de polígonos regulares

• Circunferência

• Construções geométricas (circunferência, triângulo e polígono regular)

• Interpretação de gráfico de setores

Habilidades:

EF07MA22

EF07MA23

EF07MA24

EF07MA25

EF07MA26

EF07MA27

EF07MA28

EF07MA33

EF07MA36

EF07MA37

Competências gerais: 1, 5, 7 e 9

Competências específicas: 2, 5, 6 e 8

Temas Contemporâneos Transversais: Processo de Envelhecimento, Respeito e Valorização do Idoso e Saúde

Habilidades:

EF07MA09

EF07MA17

EF07MA29

EF07MA37

• Razão

• Proporção

• Regra de três

• Construção de gráfico de setores

Competências gerais: 2, 3, 4, 6, 7, 8, 9 e 10

Competências específicas: 1, 2, 4, 6, 7 e 8

Temas Contemporâneos Transversais: Educação Financeira, Educação para o Trânsito, Educação Alimentar e Nutricional, Saúde, Educação Ambiental e Educação para o Consumo

• Porcentagem

• Porcentagem com o uso da calculadora

• Probabilidade

• Experimento aleatório

• Média

• Amplitude

• Pesquisa estatística censitária e amostral

• Construção de gráficos usando o LibreOffice

Habilidades:

EF07MA02

EF07MA34

EF07MA35

EF07MA36

Competências gerais: 2, 5 e 7

Competências específicas: 3, 5 e 8

Tema Contemporâneo Transversal: Educação Financeira

Habilidades:

EF07MA29

• Áreas de figuras geométricas planas

• Equivalência entre áreas

• Volume

EF07MA30

EF07MA31

EF07MA32

Competências gerais: 3 e 5

Competências específicas: 2 e 6

Tema Contemporâneo Transversal: Educação Fiscal

2 º Trimestre

3 º Bimestre

6. Figuras geométricas planas

3 º Trimestre

7. Grandezas proporcionais

4 º Bimestre

8. Porcentagem, probabilidade e Estatística

9. Área e volume

ORGANIZAÇÃO UNIDADES PRINCIPAIS CONTEÚDOS BNCC NA UNIDADE

• Operações com números racionais

• Dízima periódica

• Números reais

• Porcentagem e juro simples

• Cálculo de porcentagem usando planilha eletrônica

• Potência com expoente inteiro

• Propriedades da potenciação

• Números quadrados perfeitos

• Raiz quadrada (exata e aproximada) de um número racional não negativo e raízes enésimas

• Potência com expoente fracionário

• Leitura e interpretação de tabelas com intervalos de classes

• Ângulos

• Triângulos

• Altura, mediana e bissetriz de um triângulo

• Congruência de triângulos

• Propriedades dos triângulos

• Construção da bissetriz de um ângulo e da mediatriz de um segmento de reta

• Construção de ângulos notáveis com o GeoGebra

Habilidades:

EF08MA04

EF08MA05

EF08MA23

Competências gerais: 2, 6 e 7

Competência específica: 5

Temas Contemporâneos Transversais: Educação Financeira, Educação Ambiental e Educação para o Consumo

Habilidades:

EF08MA01

EF08MA02

EF08MA24

Competências gerais: 5, 8, 9 e10

Competências específicas: 2, 3, 5, 6, 7 e 8

Temas Contemporâneos Transversais: Ciência e Tecnologia e Vida Familiar e Social

Habilidades:

EF08MA15

EF08MA17

Competências gerais: 3, 5 e 9

Competências específicas: 1, 2 e 5

Temas Contemporâneos Transversais: Diversidade Cultural e Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras

Habilidades:

EF08MA06

EF08MA10

EF08MA11

EF08MA13

• Expressões algébricas

• Valor numérico de uma expressão algébrica

• Monômio (grau, semelhança e operações)

• Polinômios (grau e operações)

EF08MA23

Competências gerais: 1, 3, 6 e 9

Competências específicas: 2, 5 e 6

Temas Contemporâneos Transversais: Educação Financeira, Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras, Educação em Direitos Humanos, Educação para o Consumo e Processo de envelhecimento, respeito e valorização do Idoso

5. Equações

• Equações do 1o grau com uma e com duas incógnitas

• Equação fracionária com uma incógnita

• Equações literais do 1o grau com uma incógnita

• Sistemas de duas equações do 1o grau com duas incógnitas

• Equação do 2o grau

• Uso do Ofi Calc para resolver equações do tipo ax2 + c = 0

Habilidades:

EF08MA07

EF08MA08

EF08MA09

Competências gerais: 1, 2, 5 e 7

Competências específicas: 1, 2, 3, 5, 6 e 8

Temas Contemporâneos Transversais: Educação Ambiental, Educação Financeira e Educação para o Consumo

1 º Trimestre

1 º Bimestre

1. Números reais e porcentagem

2. Potências e raízes

2 º Bimestre

3. Ângulos e triângulos

2 º Trimestre

4. Expressões e cálculo algébrico

ORGANIZAÇÃO

• Polígonos e seus elementos

• Soma das medidas dos ângulos internos e dos ângulos externos de um polígono convexo

• Ângulos de um polígono regular

• Construção do triângulo equilátero e do hexágono regular

• Propriedades dos quadriláteros

• Interpretação de gráficos de setores

• Transformações no plano

• Uso do GeoGebra para fazer composições envolvendo simetrias

• Contagem

• Probabilidade

• População e amostra

• Variáveis

• Média

• Moda

• Mediana

• Amplitude

• Realização de pesquisa estatística

• Construção de gráficos usando o LibreOffice Calc

• Área de figuras planas

• Volume do cubo, do bloco retangular e do cilindro

• Unidades de medida de capacidade

• Equivalência entre decímetro cúbico e litro e entre metro cúbico e litro

• Análise de gráficos

• Grandezas proporcionais e não proporcionais

Habilidades

EF08MA14

EF08MA15

EF08MA16

EF08MA18

EF08MA23

EF08MA24

Competências gerais: 5, 7 e 9

Competências específicas: 2, 4 e 5

Tema Contemporâneo Transversal: Trabalho

9.

• Velocidade média, escala, densidade de um corpo e densidade demográfica

• Grandezas diretamente proporcionais

• Grandezas inversamente proporcionais

• Regra de três simples e composta

Habilidades:

EF08MA03

EF08MA22

EF08MA23

EF08MA25

EF08MA26

EF08MA27

Competências gerais: 1, 2 e 9

Competências específicas: 1, 2, 4 e 8

Temas Contemporâneos Transversais: Saúde e Educação para o Trânsito

Habilidades:

EF08MA19

EF08MA20

EF08MA21

Competências gerais: 1, 2 e 7

Competências específicas: 3, 4 e 6

Temas Contemporâneos Transversais: Ciência e Tecnologia e Educação Ambiental

Habilidades:

EF08MA12

EF08MA13

EF08MA23

Competências gerais: 1, 4 e 9

Competências específicas: 3, 5 e 6

Temas Contemporâneos Transversais: Diversidade Cultural, Trabalho, Ciência e Tecnologia, Educação Ambiental e Educação para o Trânsito

2 º Trimestre

3 º Bimestre

6. Polígonos e transformações no plano

3 º Trimestre

7. Contagem, probabilidade e Estatística

4 º Bimestre

8. Área, volume e capacidade

Estudo de grandezas

ORGANIZAÇÃO UNIDADES PRINCIPAIS CONTEÚDOS BNCC NA UNIDADE

Habilidades:

EF09MA01

EF09MA02

• A Geometria e a descoberta do número irracional

• Os números reais

• Potências

• Notação científica

• Radicais

EF09MA03

EF09MA04

EF09MA07

EF09MA18

Competências gerais: 1 e 7

Competências específicas: 1, 2, 3, 5 e 8

Temas Contemporâneos Transversais: Educação Financeira, Educação para o Consumo e Ciência e Tecnologia

Habilidade:

EF06MA09

Competências gerais: 3, 4, 7, 8 e 9

• Produtos

• Fatoração de polinômios

Competências específicas: 2, 3, 4 e 6

Temas Contemporâneos Transversais: Saúde, Educação para o Consumo e Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras

• Equações do 2o grau com uma incógnita

• Resolução de equações do 2o grau com uma incógnita

• Soma e produto das raízes de uma equação do 2o grau com uma incógnita

• Equações biquadradas

• Importância da representação correta dos gráficos

• Ângulos determinados por retas transversais

• Circunferência e ângulos

• Uso do GeoGebra para verificação da relação entre ângulo inscrito e ângulo central de uma circunferência

• Segmentos proporcionais

• Feixe de retas paralelas

• Figuras semelhantes

• Triângulos semelhantes

Habilidades:

EF09MA03

EF09MA09

EF09MA21

Competências gerais: 1, 2 e 9

Competências específicas: 1, 2, 4 e 5

Tema Contemporâneo Transversal: Educação para o Consumo

Habilidades:

EF09MA10

EF09MA11

Competências gerais: 2, 3, 4 e 5

Competências específicas: 2 e 5

Habilidades:

EF09MA07

EF09MA08

EF09MA10

EF09MA12

Competências gerais: 1, 2 e 7

Competências específicas: 2, 4 e 5

1 º Trimestre

1 º Bimestre

1. Números reais, potências e radicais

2. Produtos notáveis e fatoração

notáveis

2 º Bimestre

3. Equações do 2o grau

2 º Trimestre

4. Relações entre ângulos

5. Proporção e semelhança

6.

• Porcentagem

• Juro simples e juro composto

• Uso do LibreOffice para cálculo de juros e montantes

• Probabilidade

• Análise de gráficos

• Elaboração de pesquisa estatística

• Uso do LibreOffice para construir tabelas e gráficos estatísticos

• O teorema de Pitágoras

• Relações métricas no triângulo retângulo

• Comprimento de arco de circunferência

• Relações métricas na circunferência

• Polígonos regulares inscritos em uma circunferência

• Relações métricas nos polígonos regulares inscritos em uma circunferência

• Área de um polígono regular

• Área do círculo e de um setor circular

• Representações no plano cartesiano

• Figuras espaciais

• Projeções e vistas ortogonais

• Volume de prismas e de cilindros

• Uso do GeoGebra para representação de polígonos regulares

• Leitura e construção de gráficos de setores

Habilidades

EF09MA05

EF09MA20

EF09MA21

EF09MA22

EF09MA23

Competências gerais: 1, 2, 4, 5, 7, 9 e 10

Competências específicas: 2, 4 ,5, 7 e 8

Temas Contemporâneos Transversais: Processo de envelhecimento, respeito e valorização do Idoso, Educação Financeira e Educação Ambiental

Habilidades:

EF09MA13

EF09MA14

Competências gerais: 1, 2 e 7

Competências específicas: 1, 2, 4 e 8

Tema Contemporâneo Transversal: Diversidade Cultural

Habilidades:

EF09MA15

EF09MA16

EF09MA17

EF09MA19

EF09MA22

Competências gerais: 1, 2, 3, 7, 9 e 10

Competências específicas: 2, 5, 6 e 8

Temas Contemporâneos Transversais: Ciência e Tecnologia e Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras

9. Funções

• Função afim

• Função quadrática

• Uso do GeoGebra para construção dos gráficos de funções afins e funções quadráticas

Habilidades:

EF09MA06

EF09MA08

Competências gerais: 1, 2, 3, 4, 5, 7, 9 e 10

Competências específicas: 2, 3, 4 e 8

Temas Contemporâneos Transversais: Trabalho, Educação Financeira, Educação para o Consumo e Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras

2 º Trimestre

3 º Bimestre

Porcentagem, probabilidade e Estatística

3 º Trimestre

7. Relações métricas no triângulo retângulo e na circunferência

4 º Bimestre

8. Figuras planas, figuras espaciais e vistas

ORIENTAÇÕES GERAIS

CONSIDERAÇÕES SOBRE O ENSINO DE MATEMÁTICA

A Matemática não reside apenas no trabalho com os números e as operações; ela vai além. Devemos considerar toda a amplitude que essa área de conhecimento pode oferecer à formação do indivíduo.

Considerando a relevância do ensino de Matemática na esfera escolar, é importante ter em mente que:

O conhecimento matemático é necessário para todos os alunos da Educação Básica, seja por sua grande aplicação na sociedade contemporânea, seja pelas suas potencialidades na formação de cidadãos críticos, cientes de suas responsabilidades sociais.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 265. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 5 jul. 2022.

Desse modo, durante o estudo da Matemática, há uma série de habilidades que podem ser desenvolvidas visando capacitar os estudantes a mobilizar as aprendizagens e a solucionar problemas do cotidiano.

O aprendizado durante esse processo certamente servirá aos estudantes de exercício para o desempenho de seu papel como cidadãos em interação com o mundo que os cerca; afinal, não queremos formar pessoas que apenas saibam, mas que, com seus conhecimentos, possam estabelecer relações com o mundo ao seu redor e fazer intervenções e modificações em seu ambiente de maneira consciente, responsável e eficiente.

Podemos dizer que compreender Matemática é uma tarefa ampla e repleta de variáveis. Quando estamos diante da aprendizagem de um novo conceito, precisamos formular nossas hipóteses, planejar a maneira de resolver determinado problema, confrontar nossas respostas ou hipóteses com as dos outros, antecipar e validar resoluções. Portanto, entre as várias habilidades que são adquiridas ao desenvolver os conhecimentos matemáticos, podemos destacar o raciocínio lógico-dedutivo, que tem papel primordial na formação do sujeito. Todo esse percurso faz acontecer uma aprendizagem mais significativa e abrangente.

A possibilidade de analisar vários modos de resolver determinados problemas e de confrontar e validar hipóteses também propicia uma aprendizagem que extrapola o ensino de Matemática, culminando na formação de um indivíduo mais atuante na sociedade, que se relaciona com grupos e que enfrenta situações-problema buscando soluções, e não se inibindo diante de questões complexas.

Além do raciocínio lógico, merece destaque o trabalho que envolve processos mentais básicos como as noções de correspondência, comparação, classificação, sequenciação, seriação, inclusão e conservação. Esses processos mentais podem ser desenvolvidos com base nas atividades da exploração matemática e contribuem para que os estudantes se tornem capazes de solucionar situações do cotidiano utilizando os conceitos, as diferentes maneiras de proceder e a antecipação de resultados.

Temos assistido, no desenvolvimento de pesquisas em Educação Matemática, a uma forte conexão entre tendências que contextualizam os objetos matemáticos – como modelagem, resolução de problemas, interdisciplinaridade, metodologias ativas e uso de tecnologias digitais – e as justificativas educacionais que sustentam essa conexão, a tal ponto que se torna difícil efetuar, por exemplo, a modelagem matemática aplicada ao ensino de Matemática sem tangenciar outra tendência, e a modelagem matemática torna-se fator de geração de problemas que vão sendo gerenciados por uma ou outra tendência. (MALHEIROS, 2012).

A seguir, apresentaremos algumas ideias acerca dessas tendências e de outros conceitos relentes em relação ao ensino de Matemática.

Letramento matemático

A perspectiva de que todos podem aprender Matemática tem sido um pressuposto dos estudos realizados por educadores matemáticos na busca pelo melhor preparo dos estudantes para viverem e atuarem de modo crítico, solidário e participativo na sociedade contemporânea, visto que é incontestável a presença, cada vez mais significativa, da Matemática no dia a dia. Esse pressuposto também está presente nos documentos oficiais que normatizam a educação brasileira. Entretanto, esse tipo de afirmação gera uma questão importante a ser respondida pelos professores dessa área: O que significa saber Matemática nessa perspectiva?

Ao apresentar a área de Matemática e suas Tecnologias, a BNCC destaca que:

O Ensino Fundamental deve ter compromisso com o desenvolvimento do letramento matemático, definido como as competências e habilidades de raciocinar, representar, comunicar e argumentar matematicamente, de modo a favorecer o estabelecimento de conjecturas, a formulação e a resolução de problemas em uma variedade de contextos, utilizando conceitos, procedimentos, fatos e ferramentas matemáticas. É também o letramento matemático que assegura aos alunos reconhecer que os conhecimentos matemáticos são fundamentais para a compreensão e a atuação no mundo e perceber o caráter de jogo intelectual da matemática, como aspecto que favorece o desenvolvimento do raciocínio lógico e crítico, estimula a investigação e pode ser prazeroso (fruição).

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 266. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 10 jul. 2022.

Essa definição de letramento matemático vem acompanhada da seguinte referência:

Segundo a Matriz do Pisa 2012, o “letramento matemático é a capacidade individual de formular, empregar e interpretar a matemática em uma variedade de contextos. Isso inclui raciocinar matematicamente e utilizar conceitos, procedimentos, fatos e ferramentas matemáticas para descrever, explicar e predizer fenômenos. Isso auxilia os indivíduos a reconhecer o papel que a matemática exerce no mundo e para que cidadãos construtivos, engajados e reflexivos possam fazer julgamentos bem fundamentados e tomar as decisões necessárias.”.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 266 (nota de rodapé). Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 10 jul. 2022.

A referência ao Programa Internacional de Avaliação de Estudantes (Pisa) ocorre por ter sido essa avaliação, que se realiza em âmbito mundial, a cada três anos a partir do ano 2000, que colocou em evidência esse modo de expressar o conhecimento matemático que se espera que jovens de 15 anos apresentem, tendo em vista sua inserção social, cultural e no mundo do trabalho.

Desse modo, ensinar e aprender Matemática não se trata mais de o professor apenas apresentar procedimentos de cálculo, de como resolver equações ou questões de geometria, de como fazer o gráfico de uma função, entre outros, para que os estudantes repitam e repitam ao resolver longas listas de exercícios para apenas decorar o procedimento a ser realizado.

A construção do letramento matemático dos estudantes exige outra postura, tanto do professor como dos estudantes, diante das situações a serem vivenciadas na sala de aula ou fora dela. Para o professor, trata-se de assumir que há necessidade de criar um ambiente de aprendizagem que possibilite aos estudantes sentirem-se à vontade e com tempo para pensar, colocar questões, explorar suas ideias e exprimi-las.

Nesse ambiente, deve ser possível para o professor compreender como os estudantes estão pensando, favorecendo a formulação de questões ou pedidos de explicações para poder acompanhar a utilização das representações matemáticas

e verificar como se expressam sobre elas e, ainda, conferir os recursos que usam para construir sua argumentação. Para os estudantes, trata-se da tomada de consciência de que aprender Matemática significa raciocinar, representar, comunicar-se e argumentar matematicamente e que essas são ações que devem ser realizadas cotidianamente para que se tornem cidadãos críticos, conscientes e capazes de tomadas de decisão bem fundamentadas. Assim, é necessário que ambos, professor e estudante, reconheçam características que podem ser observadas para a avaliação de que o letramento matemático está sendo desenvolvido, apresentadas a seguir.

• Raciocinar: envolve processos de pensamento logicamente encadeados, que exploram e vinculam elementos a partir dos quais é possível realizar inferências, verificar uma dada justificativa, ou fornecer uma justificativa sobre uma afirmação ou sobre soluções alcançadas. É importante considerar ainda que raciocinar matematicamente inclui processos intuitivos, a formulação de novas ideias e a obtenção e validação de conclusões. Segundo D’Ambrosio (2005, p. 30): “As ideias matemáticas, particularmente comparar, classificar, quantificar, medir, explicar, generalizar, inferir e, de algum modo, avaliar, são formas de pensar, presentes em toda a espécie humana.”.

• Representar: utilização de diferentes registros (gráficos, tabelas, diagramas, figuras, equações, fórmulas, materiais concretos) para expressar objetos matemáticos, identificando a possibilidade de transitar de um para o outro de acordo com a necessidade.

• Comunicar: se expressa em ações de leitura, decodificação, interpretações de afirmações, descrição e modelagem matemática de um problema que inicialmente esteja em outra linguagem e quando os estudantes são levados a apresentar a solução ou explicação de determinada situação desafiadora.

• Argumentar matematicamente: processo que se dá pela utilização de conceitos, ideias e entes matemáticos na busca de exercer uma comunicação eficaz e eficiente na aula de Matemática e que deve se aproximar da existente na comunidade matemática. Segundo Grácio (1992), a argumentação envolve simultaneamente a “capacidade de dialogar, de pensar, de optar e de se comprometer” (p. 67). O diálogo promove uma atitude de abertura nas relações com o outro, no momento da comunicação e na disposição para ouvir. O pensar remete a uma atitude crítica e de atenção. A opção traz o comprometimento aliado a uma tomada de decisão para assumir determinada posição em relação a um tema dado.

É possível perceber que os elementos que caracterizam o letramento matemático se entrelaçam e se complementam para uma aprendizagem mais significativa, contribuindo para a construção de uma imagem da Matemática que ultrapassa a do senso e do sentimento comuns de que é uma área de difícil compreensão para muitos, colaborando para o entendimento de que todos podem aprender Matemática.

No trabalho com as propostas desse livro, são várias as oportunidades de o professor acompanhar o desenvolvimento do letramento matemático dos estudantes.

É importante propor discussões sobre as respostas dadas às questões para que os estudantes expressem como pensaram para responder e que relações estabeleceram com as soluções apresentadas anteriormente. Essas relações vão evidenciar como lidaram com a representação usada na resolução dos problemas e como realizaram a leitura, decodificação e interpretação do exposto. Ao apresentarem sua conclusão sobre a questão e defenderem essa tomada de decisão, estão utilizando as capacidades de comunicação e argumentação.

Inferência

A concepção de inferência é amplamente tratada na área de Linguagens por sua importância para os estudos relacionados com a compreensão de textos. No entanto, essa compreensão também é fundamental para os textos matemáticos, apresentados em seus diferentes registros (numérico, algébrico, geométrico, estatístico). Vamos, então, partir de uma concepção geral de inferência para chegar a aspectos mais específicos do raciocínio inferencial em Matemática.

Segundo Santos (2008), há diferentes concepções de inferência por parte de vários autores, mas todas trazem duas características básicas: o acréscimo de informação ao texto e a conexão de partes do texto com o objetivo de preencher lacunas de sentido. A partir dessas características e de suas considerações, essa autora define inferência como “o resultado de uma estratégia cognitiva cujo produto final é a obtenção de uma informação que não está totalmente explícita no texto.” (SANTOS, 2008, p. 65). Portanto, fazer uma inferência significa identificar a presença de informação suplementar não totalmente explicitada no texto.

A inferência está presente no letramento matemático como uma ação inerente ao raciocinar, sendo essencial na tomada de decisão em situações-problema. É ela também que dá suporte ao exercício de criar justificativas lógicas e coerentes na construção de uma argumentação, ou seja, é o uso de informações existentes, de modo explícito ou não, para chegar a novas conclusões.

A realização de inferências em Matemática pode ter um caráter lógico ou pode estar vinculada a processos intuitivos que levam à caracterização de quatro tipos de inferência: indução, dedução, abdução e raciocínio por analogia.

A inferência indutiva está associada a processos de observação a partir do qual são desenvolvidas conjecturas, chegando a um processo de generalização, que indicam uma propriedade, um conceito ou uma ideia de determinado objeto matemático, mas que devem necessariamente ser testadas. É um movimento de análise que se desenvolve do particular para o geral. Esse tipo de inferência é bastante incentivado pelas atividades dos livros desta coleção em propostas para o desenvolvimento do pensamento algébrico, nas quais os estudantes são chamados, por exemplo, a analisar sequências numéricas ou geométricas para escreverem ou obterem um termo qualquer dessa sequência ou uma sentença algébrica que represente todos os seus elementos.

A inferência dedutiva diferencia-se da indutiva por usar a lógica como ferramenta argumentativa, e não a experiência e a observação, desenvolvida do geral para o particular, com uma conclusão necessária e com um papel de validação de conhecimento. As características centrais dessa inferência são a relação necessária entre as premissas e a conclusão e a validade universal da conclusão, desde que a cadeia de deduções esteja isenta de erros. Essa inferência é a mais característica da Matemática; assim, toda vez que o livro tratar da demonstração de alguma propriedade, fórmula ou teorema está sendo desenvolvido esse modo de pensar, e é essencial que o professor chame a atenção dos estudantes sobre essa estruturação formal de encadear asserções de forma lógica e justificar esse encadeamento presente nas demonstrações dedutivas.

A inferência abdutiva é um processo de procura por princípios, explicações ou hipóteses a partir da observação de algo intrigante. Ao contrário da dedução, que parte das hipóteses para verificar que as conclusões são verdadeiras, a abdução parte de uma suposta verdade para encontrar algumas hipóteses das quais ela possa ser deduzida. A criação de hipóteses favoráveis nos leva a investigar a situação e, assim, podemos descobrir fatos novos. O esquema geral da abdução consiste na identificação de uma evidência (um fato ou conjunto de fatos), na apresentação de hipóteses alternativas para explicar tal evidência, seguida de uma avaliação da pertinência e adequação dessas explicações. A hipótese que for considerada a que fornece melhor explicação é tomada como provavelmente verdadeira e assumida como a conclusão da inferência. A procura de explicações a respeito de observações feitas é um processo muito rico na construção do conhecimento e proporciona aos estudantes uma aprendizagem significativa. Esse tipo de inferência é de grande importância para a construção de um pensamento crítico, apoiado em fatos, tendo em vista uma explicação e uma conclusão plausíveis.

O raciocínio por analogia, de acordo com Polya (1954), está estreitamente relacionado com a indução, pois também está ligado à observação e determinação de uma semelhança, mas de nível mais conceitual. Por exemplo, quando pensamos na semelhança entre as propriedades da adição e da multiplicação podemos tomá-las como dois sistemas análogos, ou, ainda, quando fazemos alguma modificação em uma figura geométrica para reconhecer nela uma figura conhecida, estamos buscando situações que possam ser tratadas como análogas.

A identificação dessas diferentes maneiras de agir diante de situações matemáticas põe em relevo que processos intuitivos são válidos em Matemática e são geradores de novas ideias e podem ser utilizados para a obtenção e validação de conclusões.

Argumentação

A formação integral que se pretende para os estudantes, proposta pela BNCC, traz como pressuposto o desenvolvimento de competências e, entre elas, “[...] saber lidar com a informação cada vez mais disponível, atuar com discernimento e responsabilidade nos contextos das culturas digitais, aplicar conhecimentos para resolver problemas, ter autonomia para tomar decisões, ser proativo para identificar os dados de uma situação e buscar soluções [...].” (BNCC, 2018, p. 14) Para que esse desenvolvimento ocorra é necessário que se promova ao longo das aulas a constituição do pensamento crítico dos estudantes.

O pensamento crítico possibilita considerar situações, informações ou atitudes de maneira analítica e racional. Isso envolve entender as origens, as motivações, a coerência, os objetivos e a validade de argumentos para a construção de posicionamentos. Diariamente, precisamos recorrer a esse tipo de pensamento para avaliar se devemos nos convencer da verdade de uma afirmação ou de que o argumento que nos é apresentado é consistente. Também é esse tipo de pensamento que nos permite formular bons argumentos para comunicar e defender nossa posição diante de determinada situação. Em essência, pensar criticamente é saber avaliar e formular uma argumentação. Mas o que é argumentação? Como promover esse desenvolvimento nas aulas?

A teoria da argumentação, em seus primórdios entre os filósofos gregos, estava ligada ao estudo da retórica e da poética, entendidas como a arte de falar bem e escrever belos discursos. Entretanto, com Aristóteles, considerado o pai da teoria da argumentação, amplia-se essa visão. Para ele, ciência, sabedoria, arte, dialética e retórica são formas de racionalidade, dotadas de diferentes graus de exatidão, de rigor ou de precisão, mas todas igualmente caracterizadas pelo argumentar.

Atualmente, defende-se a ideia de que a prática argumentativa está presente em todos os campos da esfera humana e que a argumentação é imprescindível à construção do conhecimento.

Para Japiassú e Marcondes (2001), a argumentação é um

Modo de apresentar e de dispor os argumentos, vale dizer, os raciocínios destinados a provar ou a refutar determinada proposição, um ponto de vista ou uma tese qualquer. Seu objetivo é o de convencer ou persuadir, mostrando que todos os argumentos utilizados tendem para uma única conclusão.

ARGUMENTAÇÃO. In: JAPIASSÚ, Hilton; MARCONDES, Danilo. Dicionário básico de Filosofia. 3. ed. Rio de Janeiro: Zahar, 2001. p. 17. Disponível em: http://raycydio.yolasite.com/resources/dicionario_de_filosofia_japiassu.pdf. Acesso em: 13 jul. 2022.

Para Carnielli e Epstein (2011), um argumento deve ser expresso em uma linguagem clara e direta, por meio de frases chamadas declarativas, de modo que possam ser classificadas em verdadeiras ou falsas e a argumentação é uma

[…] coleção de afirmações, uma das quais se chama “conclusão” e cuja verdade procura-se estabelecer; as outras afirmações chamam-se “premissas”, e estas afirmações pretendem conduzir à conclusão (ou apoiá-la, ou persuadir-nos da sua verdade).

CARNIELLI, Walter Alexandre; EPSTEIN, Richard L. Pensamento crítico: o poder da lógica e da argumentação. 3. ed. São Paulo: Rideel, 2011. p. 8.

O lugar que a argumentação ocupa hoje na escola explicita sua importância para a estruturação e formação do indivíduo, pois ela reflete a liberdade de reflexão e de ação com objetivo democrático, o que leva a pensá-la não apenas do ângulo intelectual mas também do social e do ético.

Ao considerarmos que um dos pilares da construção da Matemática como ciência está em seu processo argumentativo, o qual se consolida nas demonstrações de propriedades e teoremas que, dessa maneira, se tornam verdades a serem utilizadas em diferentes situações, tanto reais como internas à própria área, não se pode deixar de desenvolver nos estudantes a capacidade argumentativa. Ela é tão significativa para essa área que é um dos elementos constitutivos do letramento matemático.

A partir das contribuições da Filosofia e da Educação Matemática, podemos nos aprofundar na valorização do pensamento voltado à explicação e justificação das ações executadas, tendo em vista a construção de significados para conceitos, propriedades e procedimentos matemáticos. A recente valorização de atividades de argumentação nas aulas de Matemática também tem a intenção de encontrar caminhos facilitadores para a aprendizagem de demonstrações. As demonstrações têm um grande poder explicativo na Matemática, e, a princípio, os estudantes podem não reconhecer essa característica e podem também não encontrar sentido nos raciocínios demonstrativos. Para que as demonstrações exerçam seu papel como modo último de justificação matemática, é preciso que os estudantes estejam familiarizados

com padrões de argumentação matemática. As propostas para essa realização apoiam-se na criação e na manutenção de ambientes de aprendizagem que apoiem o fazer Matemática e o falar sobre esse fazer, procurando justificar suas ações.

Na exploração dos livros da coleção, há várias oportunidades para o fazer e o falar sobre Matemática, favorecendo o desenvolvimento da argumentação. Nas aberturas das Unidades, sempre há desafios e novas descobertas a serem feitas; na seção Pense e responda, os estudantes são chamados a usar estratégias próprias e investigativas para as soluções; no boxe Fórum, os estudantes podem expressar entendimentos e exercitar a capacidade argumentativa ao defender ideias nos debates propostos; na seção Retomando o que aprendeu, há a oportunidade de solicitar a eles que expliquem as estratégias de resolução das questões.

No entanto, é preciso lembrar-se de que essas argumentações surgem durante as interações da aula, quando, no decorrer da ação, o professor provoca a turma a justificar estratégias, o uso de determinados procedimentos, que expliquem aos colegas como estão pensando e porque pensaram desse modo. Nessas conversas, é interessante que sejam usados pelo professor termos como argumento, conjectura, plausibilidade da conjectura, inferência, contraexemplo, justificativa e prova matemática para que os estudantes se familiarizem com tais termos e passem a reconhecê-los como parte do conhecimento matemático em construção.

Outro aspecto importante a ser considerado é o da contribuição dos processos argumentativos na elaboração de inferências apoiadas nas relações lógicas que podem ser estabelecidas entre os argumentos, explorando o uso da estrutura condicional “se..., então...”. O pensamento computacional também pode ser acionado, estabelecendo um paralelo no modo de pensar sobre a organização encadeada dos argumentos para se chegar à conclusão e às etapas a serem construídas e seu encadeamento lógico para a solução computacional de uma situação.

O fundamental a se considerar é que “[…] compreender as bases da argumentação correta e do pensamento límpido nos possibilita aproximar da verdade e da justiça, e compreendemos que só quem é realmente incapaz de argumentar bem pode acreditar que maus argumentos produziriam bons resultados.” (CARNIELLI; EPSTEIN, 2011, p. XIV).

Pensamento computacional

Os desafios a serem enfrentados pela humanidade no século XXI têm sido foco de muitas discussões por diferentes órgãos políticos, sociais e educacionais desde o final do século passado e se mantêm até hoje. A capacidade de comunicação e de estabelecer relacionamentos que exige pensar no uso das tecnologias para superar desigualdades e para construir ambientes públicos de direito; as alterações profundas no mundo do trabalho que exigem o domínio de ferramentas digitais e de programas básicos de computação para a maioria dos trabalhadores, as questões éticas e sociais envolvidas no desenvolvimento e uso da inteligência artificial (IA) são apenas alguns exemplos desses desafios. Um dos pontos-chave dessas discussões é a função essencial da educação pela relevância do desenvolvimento da capacidade de agir e pensar de modo criativo e crítico, apoiado pelo conhecimento das diferentes áreas e dos fundamentos da computação aplicados em cada uma dessas áreas. Esses são elementos balizadores para a construção das competências e habilidades dos estudantes tendo em vista a participação deles como cidadãos críticos, conscientes e protagonistas no desenvolvimento da sociedade.

A Unesco, em seu relatório sobre a Educação para a Cidadania Global – preparando alunos para os desafios do século XXI, destaca que:

Em um mundo globalizado, a educação vem enfatizando a importância de equipar indivíduos desde cedo e por toda a vida, com conhecimentos, habilidades, atitudes e comportamentos de que necessitam para serem cidadãos informados, engajados e com empatia. Com essa interconectividade cada vez maior, por exemplo, por meio de TIC e […] redes sociais, as oportunidades para respostas de colaboração, cooperação, aprendizagem compartilhada e coletivas têm aumentado.

ORGANIZAÇÃO DAS NAÇÕES UNIDAS PARA A EDUCAÇÃO, A CIÊNCIA E A CULTURA. Educação para a cidadania global – preparando alunos para os desafios do século XXI. Brasília, DF: Unesco, 2015, p. 11. Disponível em: https://unesdoc.unesco.org/ark:/48223/pf0000234311/PDF/234311por.pdf.multi. Acesso em: 16 jul. 2022.

O pensamento computacional não se refere apenas à computação. Ele parte da mente humana e da capacidade de realizar conexões e resolver problemas de maneira eficiente.

A presença da tecnologia no cotidiano pode ser notada não só para a comunicação, uma vez que

[…] praticamente todos os serviços essenciais da nossa sociedade – dos utensílios do lar às atividades laborais, na saúde, na agricultura, nos automóveis e na crescente automação que vem trazendo enormes desafios sociais e econômicos. Majoritariamente, a informação que a humanidade possui e utiliza contemporaneamente está armazenada digitalmente. O mundo é cada vez mais dependente de tecnologias digitais.

BRASIL. Ministério da Educação. Conselho Nacional de Educação. Normas sobre computação na Educação Básica: complemento à BNCC. Brasília, DF: CNE, 2021. p. 8. Disponível em: http://portal.mec.gov.br/index.php?option=com_docman&view=download&alias=182481 -texto-referencia-normas-sobre-computacao-na-educacao-basica&category_slug=abril-2021 -pdf&Itemid=30192. Acesso em: 16 jul. 2022.

Essas considerações iniciais colocam em relevo a necessidade de a educação escolar incorporar em sua prática discussões e propostas variadas em que se apresentem elementos da Ciência da Computação, tendo em vista o desenvolvimento do Pensamento computacional que

[…] refere-se à habilidade de compreender, analisar, definir, modelar, resolver, comparar e automatizar problemas e suas soluções de forma metódica e sistemática, através do desenvolvimento da capacidade de criar e adaptar algoritmos, aplicando fundamentos da computação para alavancar e aprimorar a aprendizagem e o pensamento criativo e crítico nas diversas áreas do conhecimento.

BRASIL. Ministério da Educação. Conselho Nacional de Educação. Normas sobre Computação na Educação Básica: complemento à BNCC. Brasília, DF: CNE, 2021. p. 10. Disponível em: http://portal.mec.gov.br/index.php?option=com_docman&view=download&alias=182481 -texto-referencia-normas-sobre-computacao-na-educacao-basica&category_slug=abril-2021 -pdf&Itemid=30192. Acesso em: 16 jul. 2022.

No Brasil, a Base Nacional Comum Curricular (BNCC), em seus pressupostos quanto à educação integral dos estudantes, que “se refere à construção intencional de processos educativos que promovam aprendizagens sintonizadas com as necessidades, as possibilidades e os interesses dos estudantes e, também, com os desafios da sociedade contemporânea” (BNCC, p. 14), expressa a preocupação com uma formação escolar que conecte os jovens a essa realidade mundial e os engaje nela. Para isso, é importante evidenciar a importância de os professores do Ensino Fundamental tratarem do desenvolvimento de competências e habilidades dos estudantes que permitirão a eles não se intimidarem diante das novas tecnologias e do uso de recursos computacionais nos ambientes de estudo e, futuramente, de trabalho. No entanto, uma questão se interpõe a esse fato: Como isso pode ser feito se a maioria dos docentes não têm formação específica em computação?

Uma resposta pode ser encontrada quando comparamos as competências e habilidades descritas para Matemática e os elementos básicos do Letramento Matemático com as habilidades fundamentais da era da computação – “pensamento crítico, resolução de problemas, criatividade, ética/responsabilidade, colaboração” (Brasil, 2021, p. 8) e o conceito de pensamento computacional, propostos no documento Normas sobre Computação na Educação Básica (CNE). Dessa comparação, é possível concluirmos que o desenvolvimento do pensamento computacional pode ser feito com o letramento matemático, uma vez que, para ambos, raciocinar, representar, comunicar e argumentar são indispensáveis. Essa possibilidade de abordagem do pensamento computacional e o do letramento matemático aparece de modo explícito na seção Tecnologias, presente em diversos momentos nos livros desta coleção. Essa seção propicia discussões sobre os softwares utilizados e seus recursos, além da apresentação de noções de programação, totalmente pertinentes e de interesse tanto do ponto de vista dos resultados matemáticos a serem obtidos e de seu significado, como do ponto de vista do pensamento computacional identificando a adaptação de algoritmos de uso matemático utilizados em um software ou aplicativo. Há, ainda, outra possibilidade para esse trabalho conjunto – a resolução de problemas.

A resolução de problemas é um dos momentos mais propícios para abordar as relações entre o pensamento matemático e o pensamento computacional, sendo que este tem muito a contribuir para o desenvolvimento daquele. No entanto, cabe ao professor promover discussões com os estudantes, nas quais sejam apresentadas algumas etapas utilizadas em processos computacionais para a resolução de problemas que também são interessantes de serem aplicadas em situações rotineiras de aula.

O Centro de Inovação para a Educação Brasileira (CIEB), em seu documento Currículo de Referência em Tecnologia e Computação (CIEB, 2019), destaca que a resolução de problemas computacionais apresenta as etapas a seguir.

• Decomposição: realiza-se a análise de um problema com o intuito de identificar partes que podem ser separadas, para tornar mais simples a solução de cada uma delas, e de que modo podem ser reconstruídas para a descoberta de uma solução para um problema mais complexo.

• Reconhecimento de padrões: tem um viés um pouco diferente do utilizado na Álgebra, pois está voltado para a identificação de características comuns entre as soluções das partes em que o problema foi decomposto que permita a utilização do mesmo processo ou o reconhecimento de similaridades com outros problemas resolvidos.

• Algoritmo: trata-se de uma sequência de passos, ou seja, conjunto de instruções precisas, ordenadas e necessárias para solucionar um problema, como em Matemática.

• Abstração: refere-se à generalização de padrões e sua classificação, destacando as informações necessárias e organizando-as em estruturas que possam auxiliar na resolução de novos problemas, também se aproximando do movimento de generalização usado em Matemática.

Essa abordagem do pensamento computacional possibilita aos estudantes criarem uma estrutura e um processo de sistematização para analisar uma situação-problema, mobilizando conceitos, procedimentos, fatos e ferramentas matemáticas, que nos permitem afirmar que o pensamento computacional pode ser visto como um suporte analítico para o pensamento matemático com o estabelecimento de maneiras de como um problema pode ser abordado na busca da solução.

Comunicação nas aulas de Matemática

Na escola, todos os dias os estudantes convivem com os colegas, professores e demais componentes da comunidade escolar, e esse processo de interação é de grande importância. Não podemos deixar de mencionar a relevância da comunicação, incluindo as aulas de Matemática.

Os estudantes precisam ser estimulados a se expressar de diferentes modos, por exemplo, falar, ouvir, registrar por escrito, atuar por meio de manifestações artísticas, entre outras, de tal maneira que possam compartilhar vivências, conhecimentos, dúvidas ou hipóteses, conjecturas etc.

Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 9. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 5 jul. 2022.

Falar sobre o que está pensando, os caminhos percorridos, os sentimentos despertados durante as aulas e as estratégias utilizadas em cada situação pode auxiliar não apenas o próprio estudante a reelaborar e organizar seu raciocínio e processo de aprendizagem como também favorecer os demais colegas a validar hipóteses ou a compreender por que pensam de modo diferente ou utilizam estratégias distintas.

Nesse processo de socialização, os estudantes são estimulados a desenvolver diferentes habilidades e competências, incluindo as socioemocionais, ao se relacionar com um ou mais colegas de maneira respeitosa e responsável.

Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 10. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 5 jul. 2022.

Vale destacar, ainda, a importância do desenvolvimento da leitura e da análise de textos matemáticos.

Nas aulas de Matemática, é fundamental que os estudantes sejam incentivados a se familiarizar com o vocabulário, a linguagem e as construções próprias dessa ciência. Além de conhecer termos e símbolos, é importante que consigam articulá-los e analisar criticamente um texto matemático, por exemplo, avaliar a razoabilidade de um resultado, validar ou refutar hipóteses na investigação de situações-problema ou para interpretar uma notícia com dados estatísticos.

Nesse sentido, o desenvolvimento de habilidades, como o raciocínio inferencial e argumentativo e o pensamento computacional, torna-se ferramenta indispensável para uma comunicação eficiente nas aulas de Matemática. À medida que os estudantes desenvolvem a capacidade de elaborar hipóteses, conjecturar, defender ideias e organizar etapas de pensamento, tornam-se aptos a comunicar resultados e entendimentos a respeito dos mais diversos temas, incluindo aqueles de caráter matemático, científico e do cotidiano de modo geral.

Modelagem

Modelagem matemática, em linhas gerais, pode ser entendida como a criação de um modelo, com base em um conjunto de modificações e/ou adaptações de uma estrutura matemática já existente, para solucionar uma dada situação-problema.

Para melhor compreender o significado da modelagem no contexto do ensino e da aprendizagem da Matemática, será preciso recuperar esse conceito no contexto da aplicabilidade da Matemática, aquela exercida por profissionais das mais diversas áreas do conhecimento humano.

Segundo Bean (2001), ao falarmos das raízes da aplicabilidade da Matemática, temos em mente situações-problema complexas e não bem definidas encontradas nas indústrias, no setor da saúde e no meio ambiente, entre outras áreas. Para encaminhamento de uma solução ou de uma melhor compreensão do que ocorre e precisa ser solucionado, será necessário que o profissional responsável crie ou pelo menos modifique modelos matemáticos já existentes, definindo parâmetros, características e relações entre eles.

[…] As características e relações, extraídas de hipóteses e aproximações simplificadoras, são traduzidas em termos matemáticos (o modelo), nos quais a matemática reflete a situação do problema. Durante e depois da criação do modelo, o profissional verifica a coerência da matemática e a validade do modelo no contexto do problema original. […]

BEAN, Dale. O que é modelagem matemática? Educação Matemática em Revista, São Paulo, ano 8, n. 9, p. 51, 2001. Disponível em: http://sbemrevista.kinghost.net/revista/index.php/emr/article/view/1689/1182. Acesso em: 7 jul. 2022.

Ainda de acordo com esse autor, uma transferência do método da modelagem vem sendo implantada na Matemática desenvolvida nas escolas a fim de dar respostas às dimensões socioculturais da educação e ao baixo desenvolvimento dos estudantes em Matemática.

Essa transferência de método se dá com apoio na resolução de problemas aplicados, os quais tratam de questões de relevância que motivem os estudantes a buscar soluções.

Esse autor estudou dissertações e teses de Educação Matemática e afirma que delas surgem duas abordagens: a modelagem como uma metodologia de problematização e a modelagem como aprendizagem baseada em problemas. As duas pretendem enfocar situações de interesse dos estudantes. A primeira problematiza uma situação dada, não bem definida, e é intitulada modelagem; e a segunda, chamada modelação, trabalha uma situação dada já em forma de situação-problema relacionada ao conteúdo a ser ministrado.

Bean (2001) salienta ainda que a modelagem difere da resolução de problemas quando a situação não for bem definida, tal qual proposto por Polya, que será abordado posteriormente nestas Orientações. Para Bean (2001),

A essência da modelagem matemática consiste em um processo no qual as características pertinentes de um objeto ou sistema são extraídas, com a ajuda de hipóteses e aproximações simplificadoras, e representadas em termos matemáticos (o modelo). As hipóteses e as aproximações significam que o modelo criado por esse processo é sempre aberto a críticas e ao aperfeiçoamento.

[…]

BEAN, Dale. O que é modelagem matemática? Educação Matemática em Revista, São Paulo, ano 8, n. 9, p. 53, 2001. Disponível em: http://sbemrevista.kinghost.net/revista/index.php/emr/article/view/1689/1182. Acesso em: 7 jul. 2022.

Sem dúvida, uma vez que o modelo esteja formatado, há de se querer chegar a um resultado, solucionando-o. Daí a aproximação e o afastamento das metodologias – resolução de problemas, modelagem ou modelação – como propostas de ensino da Matemática.

A resolução de problemas, na maioria dos casos, não envolve hipóteses e aproximações simplificadoras na criação de modelos. O problema dado já é bem definido. E, talvez, por causa das diferenças citadas é que a resolução de problemas se torna uma metodologia que costuma ser mais indicada para o Ensino Fundamental de Matemática do que a modelagem matemática e a modelação matemática, que têm sua maior projeção no Ensino Superior.

Resolução de problemas

Muito já se pesquisou desde a apresentação das quatro etapas para se chegar à solução de um problema descritas por Polya, em seu livro intitulado How to Solve It, cuja primeira edição data de 1945. A tendência da Educação Matemática por resolução de problemas avança hoje para além das fronteiras de um método de resolução e passa a ser desenvolvida como uma perspectiva metodológica para o ensino de Matemática.

Onuchic (1999) traz uma retrospectiva do desenvolvimento dessa tendência, evidenciando o trabalho realizado por Schroeder e Lester (1989), que aponta para diferentes modos de abordá-la. De acordo com essa perspectiva, pode-se adotar uma atitude educativa que corresponda a ensinar resolução de problemas. Nessa abordagem, os modelos de

resoluções constituem o foco da atividade. Pode-se, por outro lado, ensinar a resolver problemas; o foco, nesse caso, é concentrar-se no ensino de Matemática e no que dela pode ser aplicado na solução de problemas rotineiros ou não; e, por último, pode-se assumir uma conduta de ensinar Matemática por meio da resolução de problemas, na qual

[...] os problemas são importantes não somente como um propósito de se aprender matemática, mas também, como um primeiro passo para se fazer isso. O ensino-aprendizagem de um tópico matemático começa com uma situação-problema que expressa aspectos-chave desse tópico e são desenvolvidas técnicas matemáticas como respostas razoáveis para problemas razoáveis. [...], deste modo, pode ser visto como um movimento do concreto (um problema do mundo real que serve como exemplo do conceito ou da técnica operatória) para o abstrato (uma representação simbólica de uma classe de problemas e técnicas para operar símbolos).

ONUCHIC, Lourdes de La Rosa. Ensino-aprendizagem de Matemática através da resolução de problemas. In: BICUDO, Maria Aparecida Viggiani (org.). Pesquisa em educação matemática: concepções e perspectivas. São Paulo: Editora da Unesp, 1999. p. 207.

Para Onuchic, essa abordagem é a mais coerente com as indicações apresentadas nos PCN, e estende-se aqui essa coerência à BNCC, pela qual se espera que os estudantes “desenvolvam a capacidade de identificar oportunidades de utilização da matemática para resolver problemas, aplicando conceitos, procedimentos e resultados para obter soluções e interpretá-las segundo os contextos das situações” (BNCC, 2018, p. 265). Onuchic afirma ainda que nessa abordagem “o aluno tanto aprende Matemática resolvendo problemas como aprende Matemática para resolver problemas” (1999, p. 210-211).

Segundo Onuchic e Allevato (2009), durante a aplicação da metodologia surgem sempre oportunidades para avaliar a compreensão dos estudantes dos conceitos que envolvem o problema proposto, possibilitando ao professor perceber o crescimento do conhecimento matemático deles, o que faz a aplicação do método ser um momento de ensino-aprendizagem-avaliação.

Onuchic (1999) alerta para a importância da ação e formação do professor ao aplicar essa metodologia.

[...] vale ressaltar que o sucesso da operacionalização proposta depende, em grande parte, dos professores que irão implementá-la nas salas de aula e de como serão formados esses profissionais nessa perspectiva de trabalho.

ONUCHIC, Lourdes de la Rosa. Ensino-aprendizagem de Matemática através da resolução de problemas. In: BICUDO, Maria Aparecida Viggiani (org.). Pesquisa em educação matemática: concepções e perspectivas. São Paulo: Editora da Unesp, 1999. p. 212.

Embora não haja uma maneira rígida de ensinar por meio da resolução de problemas, passaremos a descrever sucintamente um roteiro metodológico que poderá ser desenvolvido com base em situações-problema propostas em cada volume da obra.

Estudante resolvendo um problema na lousa.

O roteiro apresentado por Onuchic e Allevato (2011) pode ser dividido nas seguintes etapas.

Preparação do problema: nesta primeira etapa, vale ressaltar que o conteúdo matemático necessário para a resolução do problema não foi trabalhado anteriormente com os estudantes. A ideia é que eles mobilizem os conhecimentos que possuem para, a partir disso, construir novos conhecimentos necessários para a resolução.

Leitura do problema: é a etapa em que se promove uma leitura individual do problema, seguida de uma leitura em conjunto, a fim de propiciar esclarecimento de eventuais dúvidas.

Plenária: para esta etapa, são convidados todos os estudantes para discutirem as diferentes resoluções registradas na lousa pelos colegas, defenderem seus pontos de vista e esclarecerem as dúvidas. Nesse processo, o professor se coloca como guia e mediador das discussões, incentivando a participação ativa e efetiva de todos os estudantes.

Resolução do problema: com base no entendimento do problema, sem dúvidas quanto ao enunciado, os estudantes, em grupos, em um trabalho cooperativo e colaborativo, buscam resolver o problema.

Busca do consenso: depois de sanadas as dúvidas e analisadas as resoluções e soluções obtidas para o problema, o professor tenta, com toda a turma, chegar a um consenso sobre o resultado correto.

Observar e incentivar: nesta etapa, o professor se torna um mediador e, portanto, não tem mais o papel de transmissor do conhecimento.

Formalização do conteúdo: nesse momento, denominado formalização, o professor registra na lousa uma apresentação formal – organizada e estruturada em linguagem matemática –, padronizando os conceitos, os princípios e os procedimentos construídos por meio da resolução do problema.

Registro das resoluções na lousa: representantes dos grupos são convidados a registrar e socializar, na lousa, suas resoluções, independentemente de estarem certas ou erradas.

Metodologias ativas

São os estudantes que aprendem. Essa afirmação, tão comentada em debates sobre educação, traz consigo uma concepção do processo de ensino e aprendizagem que, apesar de não ser nova, ainda se apresenta como um desafio às escolas: cada estudante é único e deve ser o motivo, o autor e o protagonista de seu processo de aprendizagem.

Se o principal objetivo da educação é fazer que os estudantes construam conhecimento, que se apropriem de aprendizagens consideradas essenciais e, mais importante, que se tornem competentes em aprender – para que possam fazer isso mesmo quando não estiverem mais no ambiente escolar – a escola é, portanto, para eles e feita deles e por eles. Nesse caso, podemos dizer que são os autores e atores principais.

Os estudantes são os a(u)tores principais do processo porque é deles que devem vir as demandas, o interesse, a curiosidade – uma educação que não considere as especificidades de cada indivíduo/grupo, que não abarque as diferentes formas de ser, os desejos e os projetos desses sujeitos, provavelmente não mobilizará o envolvimento e a dedicação de jovens e crianças que, consequentemente, deixarão de protagonizar essa história.

E, por fim, os estudantes são protagonistas de sua aprendizagem porque pouco se aprende sem interesse e motivação (que é intrínseca), sem inspiração, sem a prática e sem a experimentação. É preciso levantar hipóteses, testá-las, experimentar, errar, explorar, enfim, construir o caminho da própria aprendizagem.

Nessa perspectiva, o modelo de aula que vigora desde tempos remotos – em que o professor “ensina” transmitindo seus conhecimentos e os estudantes os recebem – já não parece mais coerente às necessidades de nossos jovens e crianças, não parece contribuir de forma efetiva com a aprendizagem. É preciso que eles construam o próprio conhecimento – e essa construção relaciona-se ao acesso à informação e sua transformação em algo que faça sentido, em comunhão com seus conhecimentos prévios, emoções e maturidade cognitiva de processamento.

De acordo com o texto “O uso de metodologias ativas colaborativas e a formação de competências”, publicado no site oficial da Base Nacional Comum Curricular, a construção do conhecimento possibilita aos estudantes construir também competências como:

• saber buscar e investigar informações com criticidade (critérios de seleção e priorização) a fim de atingir determinado objetivo, a partir da formulação de perguntas ou de desafios dados pelos educadores;

• compreender a informação, analisando-a em diferentes níveis de complexidade, contextualizando-a e associando-a a outros conhecimentos;

• interagir, negociar e comunicar-se com o grupo, em diferentes contextos e momentos;

• conviver e agir com inteligência emocional, identificando e desenvolvendo atitudes positivas para a aprendizagem colaborativa;

• ter autogestão afetiva, reconhecendo atitudes interpessoais facilitadoras e dificultadoras para a qualidade da aprendizagem, lidando com o erro e as frustrações, e sendo flexível;

• tomar decisão individualmente e em grupo, avaliando os pontos positivos e negativos envolvidos;

• desenvolver a capacidade de liderança;

• resolver problemas, executando um projeto ou uma ação e propondo soluções.

BRASIL. Ministério da Educação. O uso de metodologias ativas colaborativas e a formação de competências. Brasília, DF: MEC, [2019?]. Caderno de Práticas da Base Nacional Comum Curricular. Disponível em: http://basenacionalcomum.mec.gov.br/implementacao/praticas/ caderno-de-praticas/aprofundamentos/202-o-uso-de-metodologias-ativas-colaborativas-e -a-formacao-de-competencias-2?highlight=WyJtZXRvZG9sb2dpYXMiLCJhdGl2YXMiLCJtZXRvZG9s b2dpYXMgYXRpdmFzIl0. Acesso em: 14 jul. 2022.

Mas que metodologias podem ser utilizadas para que os estudantes, de fato, possam construir o conhecimento? Certamente, não há apenas uma maneira e nem sempre todos os estudantes carecem de uma mesma estratégia ou formatação, mas se faz necessário o uso de metodologias que incentivem o protagonismo, que convidem os estudantes à ação, à atuação, ao fazer – e que, fazendo, aprendam, ou seja, as chamadas metodologias ativas.

De acordo com Bacich e Moran (2018):

As metodologias ativas constituem alternativas pedagógicas que colocam o foco do processo de ensino e de aprendizagem no aprendiz, envolvendo-o na aprendizagem por descoberta, investigação ou resolução de problemas. [...]

[...]

As metodologias voltadas para a aprendizagem consistem em uma série de técnicas, procedimentos e processos utilizados pelos professores durante as aulas, a fim de auxiliar a aprendizagem dos alunos. O fato de elas serem ativas está relacionado com a realização de práticas pedagógicas para envolver os alunos, engajá-los em atividades práticas nas quais eles sejam protagonistas da sua aprendizagem. Assim, as metodologias ativas procuram criar situações de aprendizagem nas quais os aprendizes possam fazer coisas, pensar e conceituar o que fazem e construir conhecimentos sobre os conteúdos envolvidos nas atividades que realizam, bem como desenvolver a capacidade crítica, refletir sobre as práticas realizadas, fornecer e receber feedback, aprender a interagir com colegas e professor, além de explorar atitudes e valores pessoais.

É importante ressaltar que as metodologias ativas não se resumem a um conjunto de estratégias com nomes específicos – trata-se principalmente de uma concepção de educação, de um olhar para o processo educativo. Existem inúmeras maneiras de promover a ação dos estudantes, mas é fundamental perceber quais delas são mais adequadas a cada grupo (ou estudante) em cada momento. Em geral, elas não se limitam ao ambiente escolar ou ao momento da aula, ampliando as possibilidades de exploração e envolvimento.

A seguir, são apresentadas algumas estratégias que podem favorecer a aprendizagem ativa e significativa, as quais poderão ser exploradas durante o uso desta coleção.

• Sala de aula invertida: o princípio dessa estratégia é que os estudantes tenham contato com os conceitos e a teoria em um ambiente externo à sala de aula, por exemplo em casa, antes da aula – o que pode ser feito com um vídeo curto, um texto, uma coleta de informações. Desse modo, o tempo didático na escola poderá ser utilizado para a promoção de atividades em grupo, explorações, investigações e debates. De acordo com Bacich e Moran (2018):

[…] os professores podem iniciar com o básico sobre a inversão da sala de aula e, à medida que vão adquirindo experiência, passar a usar a aprendizagem baseada em projetos ou em investigação. Com isso, vão se reinventando, criando cada vez mais estratégias centradas nos estudantes ou na aprendizagem, em vez das aulas expositivas que costumavam ministrar.

BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem téorico-prática. Porto Alegre: Penso, 2018. p. 84.

• Rotação por estações: nessa estratégia, o professor organiza diferentes atividades relacionadas a um mesmo assunto, de modo a explorar habilidades distintas e complementares. Cada grupo trabalhará com uma atividade durante um período e, findado o tempo, passará para a próxima proposta. Durante o tempo de aula, todos os grupos devem ter contato com todas as propostas.

• Aprendizagem baseada na investigação: nessa proposta, a aprendizagem é iniciada com perguntas, problemas ou cenários relacionados à realidade, que deverão ser discutidos para identificação de uma solução. Importante ressaltar que, muitas vezes, não existe apenas uma solução possível, e a experimentação pode ser uma maneira interessante de validar as possibilidades.

BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem téorico-prática. Porto Alegre: Penso, 2018. p. 80-81.

• Aprendizagem em equipe: os estudantes são convidados a trabalhar, durante algum período, em um grupo composto de quatro ou mais membros. As decisões e atividades são realizadas pela equipe, de forma conjunta, o que favorece a interação entre os pares e o desenvolvimento de competências socioemocionais. No fim do período, podem-se trocar as equipes, de modo que cada estudante aprenda a valorizar diferentes perfis e habilidades.

• Jogos: tanto jogar quanto criar jogos são atividades que podem favorecer a aprendizagem ativa. Quando os estudantes jogam, envolvem-se em um contexto que traz significado ao conhecimento e pode mobilizar diferentes habilidades. Desse modo, é importante que o professor crie oportunidades para trabalhar jogos nas aulas e propor análises de estratégias e resultados com base em conhecimentos mobilizados pelos estudantes. Nesta coleção, o professor e os estudantes encontrarão a Matemática contextualizada, voltada para a resolução de problemas muitas vezes em abordagem interdisciplinar, favorecendo a exploração das metodologias ativas. De modo geral, todas as seções da obra, com destaque para as seções Pense e responda e Fórum, podem proporcionar um envolvimento ativo dos estudantes, na investigação por soluções, mobilização de conhecimentos e construção de argumentos baseados nos objetos do conhecimento matemático.

Tecnologias digitais: potencialidades no ensino e na aprendizagem

É inegável a presença das Tecnologias Digitais (TD) na vida privada, no mundo do trabalho e no desenvolvimento do conhecimento gerado na época atual. A intenção nesta obra é promover algumas reflexões acerca das possíveis relações existentes entre as TD e o trabalho desenvolvido na escola, pensando nos principais motivos que podem levar ao fortalecimento dessas relações.

Borba, Scucuglia e Gadanidis (2014), no livro Fases das tecnologias digitais em Educação Matemática, analisam as pesquisas desenvolvidas no Brasil, nos últimos 30 anos, que tratam da presença das tecnologias digitais na Educação Matemática.

[...] Essa tecnologia assumiu nomes distintos que simbolizaram diferentes épocas: Logo, informática, educação matemática on-line, tecnologias da informação, tecnologias da informação e comunicação, internet etc. Os diversificados termos utilizados enfatizaram diferentes aspectos desta tecnologia que, como o título sugere, está em movimento.

BORBA, Marcelo de Carvalho; SILVA, Ricardo Scucuglia Rodrigues da; GADANIDIS, George. Fases das tecnologias digitais em Educação Matemática. Belo Horizonte: Autêntica, 2014. p. 16.

As diferentes maneiras – de como a sala de aula de Matemática tem se transformado com o evento das tecnologias – foram classificadas pelos autores em quatro fases. Passaremos a expor um breve resumo de cada uma das fases por eles descritas. Para uma compreensão mais profunda sobre cada uma das fases e suas fundamentações, recomendamos a leitura do livro.

A primeira fase, nos anos 1980, já discutia o uso de calculadoras simples ou científicas e de computadores. Tecnologia de Informática (TI) era o termo utilizado para se referir a computadores e softwares. No entanto, o uso do software LOGO é que, principalmente, caracterizou essa fase fundamentada no construcionismo, que considerava o potencial da programação do LOGO ao enfatizar relações entre linguagem de programação e pensamento matemático. Havia nessa fase a preocupação com a implantação de laboratórios de informática nas escolas e a formação de professores, pois o papel atribuído às tecnologias era o de catalisador para as mudanças pedagógicas.

A segunda fase teve início em 1990. Nela, existiam muitas perspectivas de como os estudantes, professores e pesquisadores viam o papel dos computadores na vida pessoal e profissional deles. Muitos nem chegaram a usar os computadores, “outros ainda, por perceberem as transformações cognitivas, sociais e culturais que ocorriam com o uso de TI, buscavam explorar possibilidades didático-pedagógicas. Diversos softwares educativos foram então produzidos por empresas, governo e pesquisadores” (BORBA; SCUCUGLIA; GADANIDIS, 2014, p. 22). Nessa fase, os autores destacam o uso de softwares para o ensino de funções (como o Winplot, o Fun e o Graphmathica) e para o de geometria dinâmica (como o Cabri Géomètre e o Geometricks). Esses softwares abrem várias possibilidades didático-pedagógicas apoiadas nas ideias de manipulação, combinação, visualização e construção de objetos matemáticos, tudo minuciosamente descrito pelos autores.

A terceira fase tem início em 1999, com o advento da internet. Em educação, a internet começa a ser utilizada como fonte de informação e como meio de comunicação. Surgem os cursos a distância para formação continuada de professores via e-mails, chats e fóruns. O termo agora utilizado é Tecnologias da Informação e Comunicação (TIC). Em termos de pesquisa, muitas são as questões investigadas, por exemplo: Qual é a natureza do pensamento matemático em cursos on-line? Como a Matemática é transformada em ambientes on-line? Em termos de oportunidades didático-pedagógicas, os pesquisadores colocam em evidência que a interação em ambientes virtuais de aprendizagem oferece nuances cognitivas diversificadas ao investir em multiplicidades de nós e conexões, incentivando a coautoria dos estudantes na atividade proposta.

Atualmente, estamos vivendo a quarta fase, cujo surgimento deu-se em 2014 com a banda larga. Compõem essa fase instrumentos como computador, laptops, tablets, telefones celulares e internet rápida. O termo utilizado para enunciá-la é Tecnologia Digital (TD).

É interessante notar que as fases não se esgotam, muitas das perguntas formuladas em seu início ainda permanecem sendo investigadas e novas questões surgem com o avanço das tecnologias e sua inserção na sociedade.

O que até agora apresentamos nos dá a dimensão da força e da rapidez com que as tecnologias vão sendo implantadas na nossa vida e de como o uso delas nas escolas não pode mais ser retardado. O uso das tecnologias tem um papel preponderante na formação do cidadão ao empreendermos uma visão ampla de educação.

[...] O acesso à informática deve ser visto como um direito e, portanto, nas escolas públicas e particulares o estudante deve poder usufruir de uma educação que no momento atual inclua, no mínimo, uma “alfabetização tecnológica”. Tal alfabetização deve ser vista não como um Curso de Informática, mas, sim, como um aprender a ler essa nova mídia. Assim, o computador deve estar inserido em atividades essenciais, tais como aprender a ler, escrever, compreender textos, entender gráficos, contar, desenvolver noções espaciais etc. E, neste sentido, a informática na escola passa a ser parte da resposta a questões ligadas à cidadania.

BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática Belo Horizonte: Autêntica, 2010. p. 16-17.

Nessa mesma perspectiva sobre o uso das TD em sala de aula, Ponte (2000) afirma que as próprias TIC (na época ainda não iniciada a nova fase) são ferramentas de trabalho pedagógico que podem ser usadas livremente e de maneira criativa por professores e estudantes na realização de diversificadas atividades. Essa ferramenta pode vir a ser articulada ao trabalho por projetos embasados nas diretrizes da interdisciplinaridade, possibilitando um claro protagonismo do estudante na aprendizagem.

No patamar em que os pesquisadores estão colocando as mudanças educacionais que deverão ocorrer em consequência dos problemas contemporâneos, a prática do professor está cada vez mais articulada com o entorno escolar, o que faz dele também um protagonista da construção escolar como um todo.

A importância das tecnologias digitais se intensificou com a pandemia de covid-19, decretada em 2020. Como uma das consequências do isolamento social para conter a doença, aulas presenciais foram suspensas. Com isso, foi necessário reprojetar a rotina escolar no ambiente digital.

Dadas as dificuldades de acesso a recursos digitais ou, ainda, a complexidade inerente ao ensino a distância na Educação Básica, foi necessário grande esforço por parte de professores e estudantes a fim de prosseguir com a vida escolar.

Estudante assistindo a uma aula on-line

Os professores precisaram desenvolver técnicas de aula a distância, bem como modelos de acompanhamento e avaliação digitais. Essa nova realidade ressaltou a necessidade de uma formação integral do professor, incluindo a familiarização com ferramentas de ensino digitais.

Práticas de pesquisa e método científico

A construção do conhecimento é permanente e se dá desde o nascimento de cada indivíduo. É por meio da interação com o meio e com as pessoas, observando as relações sociais, culturais e naturais ao redor, e tirando conclusões sobre elas, que aprendemos. Por esse motivo, de acordo com Pereira (2018, p. 13), “o conhecimento pode ser classificado em popular (senso comum), teológico, mítico, filosófico e científico, com base na forma como é representado”.

O que diferencia o conhecimento científico dos demais tipos é o método, a maneira de conhecer. De acordo com Pereira (2018, p. 18), o conhecimento científico “é necessariamente construído em relação a algo real, por meio da experimentação, é sistemático, aproximadamente exato e verificável”. Destaca-se, contudo, que o conhecimento científico é falível, ou seja, não é absoluto e pode ser contestado e ampliado.

O conhecimento científico é construído por meio da pesquisa científica, que, por sua vez, é um modo de construção do conhecimento. Nela, o pesquisador, a partir de um problema que precisa resolver, algo que quer descobrir, manipula métodos e técnicas para buscar resultados que atendam às suas indagações. De maneira geral, a pesquisa científica tem a seguinte organização:

• identificação do problema;

• enunciação do problema;

• levantamento de hipóteses;

• definição do método ou de estratégias;

• tentativa de solução;

• testagem/comprovação da solução;

• comunicação dos resultados.

Em relação aos métodos científicos, podemos dizer, de acordo com Dias e Fernandes (2000, p. 6), que se trata de “um conjunto de procedimentos adotados com o propósito de atingir o conhecimento”. Ou seja, o método científico consiste nas regras básicas que se devem executar em uma pesquisa para a construção de conhecimento científico. De acordo com Demo (2001, p. 3) “o conhecimento está menos ligado a conteúdos, do que a procedimentos metodológicos de superação dos conteúdos”. O autor amplia a discussão destacando que essa perspectiva leva “à valorização sem precedentes do saber pensar e do aprender a aprender”. Nesse ponto, podemos perceber a imbricada relação entre a pesquisa científica e a educação escolar. De acordo com a BNCC (Brasil, 2018, p. 14):

No novo cenário mundial, reconhecer-se em seu contexto histórico e cultural, comunicar-se, ser criativo, analítico-crítico, participativo, aberto ao novo, colaborativo, resiliente, produtivo e responsável requer muito mais do que o acúmulo de informações. Requer o desenvolvimento de competências para aprender a aprender, saber lidar com a informação cada vez mais disponível, atuar com discernimento e responsabilidade nos contextos das culturas digitais, aplicar conhecimentos para resolver problemas, ter autonomia para tomar decisões, ser proativo para identificar os dados de uma situação e buscar soluções, conviver e aprender com as diferenças e as diversidades.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 14. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 5 jul. 2022.

Desse modo, podemos considerar a pesquisa como uma importante estratégia pedagógica para a construção do conhecimento, em que os estudantes são convidados a identificar e resolver problemas reais, por meio da investigação, construindo – eles mesmos em interação com os demais – sua aprendizagem.

A pesquisa, portanto, pode contribuir para o desenvolvimento do pensamento autônomo e crítico, culminando, inclusive, na capacidade de interpretar informações com clareza, analisá-las e verificar sua veracidade – habilidade tão fundamental em uma época em que há um fluxo incontável de informações disponíveis, muitas delas falsas. De acordo com Demo (2001, p. 10):

[...] Os conteúdos se consomem no tempo, enquanto a habilidade de saber pensar necessita manter-se viva, mais que nunca. Se não sabe pesquisar, não sabe questionar. Não sabendo questionar, não sabe ultrapassar os impasses inevitáveis que toda profissão encontra em sua prática. Assim, o mais importante hoje na pesquisa não é o manejo de instrumentos metodológicos, mas o manejo dos desafios inovadores e por vezes surpreendentes da vida. Saber pensar é ótimo para o mercado, mas é ainda mais essencial para a vida. [...]

DEMO, Pedro. Professor/Conhecimento. Brasília, DF: UnB, 2001. p. 10. Disponível em: http://funab.se.df.gov.br/wp-content/uploads/2018/11/Demo-2001.-Professor-Conhecimento.pdf. Acesso em: 8 jul. 2022.

Nesta coleção, o professor e os estudantes encontrarão noções introdutórias de práticas de pesquisa relacionadas à Matemática, inclusive, em abordagem interdisciplinar e que envolve a história da Matemática e a Etnomatemática, valorizando a construção do conhecimento como um traço cultural e fruto do trabalho de muitos membros, em muitas sociedades. Contextos atuais são apresentados para contribuir com a visão crítica da realidade e com o desenvolvimento de argumentação baseada em conceitos matemáticos.

Cidadania e cultura de paz

Na atualidade, as expressões de violência parecem estar em toda parte. Na voz do âncora do jornal relatando os novos números e desdobramentos de uma guerra, nas mídias sociais em que se escancara a vida pessoal de famosos e anônimos, nas músicas que exploram os abismos provocados pela desigualdade de gênero, no relato de um colega na sala dos professores que não sabe mais como lidar com as dificuldades da vida. E se essa avalanche nos atinge, com flechas vindas de todas as direções, também o faz com os jovens, cujas estruturas, muitas vezes, não são suficientes para lidar com tudo isso.

Em oposição a toda essa violência, faz-se necessária – cada vez mais – a construção e promoção de uma cultura de paz, que, de acordo com D’Ambrósio (2010, p. 48), se estabelece em quatro dimensões: individual, social, ambiental e militar.

A paz individual, relativa ao gerenciamento de emoções e sentimentos de cada indivíduo e que lhe permite ser “dono” de suas ações, em consonância consigo e com as próprias escolhas. Poderíamos dizer que tem estreita relação com as competências e habilidades socioemocionais.

A paz social, que resulta do olhar atento e cuidadoso para o outro, da empatia e do respeito, do reconhecimento e da legitimação da diversidade humana, contribui para a construção de uma convivência harmoniosa e pautada pelos princípios éticos e democráticos.

A paz ambiental, por sua vez, refere-se à impossibilidade de vivermos em conflito com o ambiente, com a natureza; resulta da compreensão de que a manutenção da vida depende de um ambiente sadio e sustentável.

E, por fim, a paz militar, que é violada desde a Antiguidade e ainda hoje, pondo em risco a vida humana. A ausência dela é a materialização da violência, do desrespeito, do descumprimento dos direitos humanos, da falta de empatia e de coerência.

O professor D’Ambrósio (idem) afirma:

[…] Se não contemplarmos a questão da paz na sua multidimensionalidade, estaremos nos iludindo, e este é um ponto fundamental.

Sem paz não haverá sobrevivência. Educar para a paz é educar para a sobrevivência da civilização deste planeta, da humanidade, da espécie – mas a sobrevivência de todos com dignidade. Este é um ponto crucial: a dignidade de o indivíduo ser o que ele é, de poder aderir a um sistema de conhecimentos, de conhecer suas raízes, suas relações históricas, emocionais, sua religião, sua espiritualidade. Um indivíduo é diferente do outro, não há como negar que nós todos somos diferentes. Preservar essa diferença é algo fundamental para que a gente possa falar em uma sobrevivência com dignidade.

D’AMBRÓSIO, Ubiratan. Cultura de paz e pedagogia da sobrevivência. In: ORGANIZAÇÃO DAS NAÇÕES UNIDAS PARA A EDUCAÇÃO, A CIÊNCIA E A CULTURA. Cultura de paz: da reflexão à ação. Brasília, DF: Unesco; São Paulo: Associação Palas Athena, 2010. p. 48. Disponível em: https://unesdoc.unesco.org/ark:/48223/pf0000189919?locale=en. Acesso em: 8 jul. 2022.

A escola, como instância socializadora – em complementaridade com familiares, grupos de convívio e a mídia de massa –, possui papel fundamental para a construção da promoção da cultura de paz. É um espaço privilegiado de desenvolvimento e convivência. É preciso ter, na paz, o percurso e o destino da educação.

Para que isso seja possível, a não violência deve permear todos os processos e ambientes educacionais e envolver os diferentes profissionais que atuam de modo direto ou indireto com os estudantes, além dos familiares e a comunidade do entorno e, claro, os próprios estudantes. A escola deve ser, efetivamente, um espaço de diálogo e civismo, promovendo uma educação compartilhada para a convivência e cidadania.

A Unesco definiu, no texto Cultura de paz no Brasil publicado em seu site, as contribuições da educação para a construção da paz. São elas:

• aprender sobre as nossas responsabilidades e obrigações, bem como os nossos direitos;

• aprender a viver juntos, respeitando as nossas diferenças e similaridades;

• desenvolver o aprendizado com base na cooperação, no diálogo e na compreensão intercultural;

• ajudar as crianças a encontrar soluções não violentas para resolverem seus conflitos, experimentarem conflitos utilizando maneiras construtivas de mediação e estratégias de resolução;

• promover valores e atitudes de não violência - autonomia, responsabilidade, cooperação, criatividade e solidariedade;

• capacitar estudantes a construírem juntos, com seus colegas, os seus próprios ideais de paz.

ORGANIZAÇÃO DAS NAÇÕES UNIDAS PARA A EDUCAÇÃO, A CIÊNCIA E A CULTURA. Cultura de paz no Brasil. Brasília, DF: Unesco, [201-]. Disponível em: https://pt.unesco.org/fieldoffice/brasilia/expertise/culture-peace. Acesso em: 8 jul. 2022.

Todavia, é muito importante não confundir paz com falta de opinião, conflito com confronto. A convivência pressupõe a existência de valores e opiniões diferentes, diversidade de saberes e vivências particulares, interpretadas das mais variadas maneiras, e todos esses elementos podem ser geradores de conflitos, das mais diversas ordens. Contudo, é pela cultura de paz que esses conflitos serão gerenciados com base em princípios democráticos, éticos, solidários e sustentáveis, promovendo o conhecimento – e não o confronto, que conduz à violência.

D’Ambrósio (2010, p. 49) afirma: “trata-se de educar para a paz e a sobrevivência, baseadas na convivência entre diferentes. Esse é o nosso grande desafio.” Para tanto, é preciso promover situações de fala e de escuta, escuta “desarmada”, momentos de debate e de socialização de ideias e sentimentos. Tais proposições poderão favorecer não apenas o autoconhecimento como também a empatia, tão necessários para que os estudantes compreendam que o pluralismo é positivo e necessário. A violência vem da incompreensão, que vem do desconhecimento – assim, conhecer e reconhecer tais pontos é fundamental à cultura de paz.

Como pudemos observar, é imprescindível investir em estratégias pedagógicas que possibilitem e incentivem a identificação e o gerenciamento de sentimentos e emoções, pois as diferentes dimensões da paz se interrelacionam, e tais movimentos favorecem o desenvolvimento de habilidades relativas à autogestão, saúde mental e amabilidade. É preciso auxiliar os estudantes a refletir sobre situações contrárias à paz, como o bullying, e a combater essa e outras formas de preconceitos e discriminação, tal como preconiza a competência geral 9 da BNCC (2018, p. 10):

9. Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 10. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 5 jul. 2022.

Nesta coleção, o professor os estudantes encontrarão propostas que buscam incentivar e promover a fala e a escuta (atenta), o debate, a argumentação e o reconhecimento de diferentes maneiras de pensar e agir. Tais propostas, portanto, objetivam o desenvolvimento de competências necessárias à convivência harmoniosa e à cultura de paz.

A cultura de paz pode ser exercitada nas atividades em grupo, em que os estudantes podem perceber como o diálogo e a mediação de conflitos favorecem a convivência harmoniosa.

A BNCC E O ENSINO DE MATEMÁTICA

Para que possamos iniciar nossas abordagens e reflexões acerca da Base Nacional Comum Curricular (BNCC) e suas indicações, principalmente na área da Matemática, julgamos interessante realizar uma breve apresentação dos movimentos que precedem a homologação desse documento.

Não podemos desprezar as dimensões do país, seja em territorialidade, seja em diversidade, nem ignorar a desigualdade social ainda presente em inúmeras pesquisas e dados estatísticos. Um dos principais desafios, na área da educação, é propiciar oportunidades iguais para todos os estudantes, sem perder a particularidade e a singularidade de cada região ou grupo.

Desde 1988, a Constituição Federal determinava o direito à educação e apresentava os conteúdos mínimos a serem desenvolvidos em todo o território nacional. Nesse mesmo documento, podemos encontrar indicações da necessidade de resguardar os valores culturais e artísticos, nacionais e regionais.

Quase dez anos depois, no ano de 1996, a Lei de Diretrizes e Bases (LDB) estabelece as competências e diretrizes para a Educação Infantil, o Ensino Fundamental e o Ensino Médio, que deveriam nortear os currículos e seus conteúdos mínimos, de modo a assegurar formação básica comum, salientando que os conteúdos deveriam ser complementados com a parte diversificada que garantiria as características locais e regionais.

No Plano Nacional de Educação (PNE) de 2014, essa necessidade é reafirmada, ou seja, em parceria, a União, os estados, o Distrito Federal e os municípios deveriam criar uma Base Nacional Comum Curricular (BNCC) que garantisse a todos os estudantes do território nacional as aprendizagens essenciais, preservando-se as identidades étnicas, culturais e linguísticas. Para isso, cada Secretaria de Educação teria autonomia para pensar e planejar as ações de suas unidades escolares a partir das necessidades locais.

Desse modo, a BNCC, homologada em dezembro de 2017, apresenta um conjunto de aprendizagens essenciais a que têm direito todos os estudantes da Educação Básica. Traz uma perspectiva de igualdade, diversidade e equidade para a constituição da ação escolar a partir de uma proposta comum de direitos e objetivos de aprendizagem para os estudantes da Educação Infantil ao Ensino Médio de todo o país. Indica o que deve ser ensinado e desenvolvido, isto é, os conhecimentos e as competências essenciais que devem ser garantidos a todos os estudantes brasileiros em sua vida escolar.

Com o foco no desenvolvimento de competências e no compromisso com a educação integral, o documento apresenta uma abordagem bastante clara no que diz respeito ao desenvolvimento integral dos estudantes (cognitivo e emocional) e a importância da experimentação, articulação e aplicabilidade dos conhecimentos e ao acesso e à utilização consciente da informação e da tecnologia.

As competências

O documento apresenta como competência a capacidade de mobilizar conhecimentos, habilidades, atitudes e valores para que se possam resolver os desafios do cotidiano, dentro e fora dos espaços escolares.

Na BNCC, competência é definida como a mobilização de conhecimentos (conceitos e procedimentos), habilidades (práticas, cognitivas e socioemocionais), atitudes e valores para resolver demandas complexas da vida cotidiana, do pleno exercício da cidadania e do mundo do trabalho.

Ao definir essas competências, a BNCC reconhece que a “educação deve afirmar valores e estimular ações que contribuam para a transformação da sociedade, tornando-a mais humana, socialmente justa e, também, voltada para a preservação da natureza” [...].

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 8. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 17 jul. 2022.

São apresentadas dez competências gerais que se inter-relacionam e devem permear os conteúdos apresentados ao longo de todo o percurso escolar da Educação Básica.

Vale destacar que tais competências resumem as capacidades e os conhecimentos essenciais ao desenvolvimento de atitudes e valores fundamentais no mundo contemporâneo, como a empatia, a cooperação, a valorização da Ciência e da diversidade, o pensamento crítico e o preparo para o mundo do trabalho. O desenvolvimento desses valores e atitudes objetivam a formação integral dos estudantes como cidadãos críticos e criativos.

As competências gerais, apresentadas a seguir, desdobram-se em competências específicas e habilidades voltadas a cada componente curricular. Entretanto, é importante considerar que tais competências existem por si e podem ser abordadas como tais a qualquer tempo da vida escolar, de modo que estejam presentes frequentemente nas mais variadas atividades e abordagens. Desse modo, pode-se assegurar uma maior apropriação dos conhecimentos, atitudes e valores que essas dez competências preconizam, bem como a aplicação destas nas questões do cotidiano.

As competências gerais da BNCC são:

Valorizar e utilizar os conhecimentos historicamente construídos sobre o mundo físico, social e cultural para entender e explicar a realidade, continuar aprendendo e colaborar para a construção de uma sociedade justa, democrática e inclusiva. Exercitar a curiosidade intelectual e recorrer à abordagem própria das ciências, incluindo a investigação, a reflexão, a análise crítica, a imaginação e a criatividade, para investigar causas, elaborar e testar hipóteses, formular e resolver problemas e criar soluções (inclusive tecnológicas) com base nos conhecimentos das diferentes áreas.

Valorizar e fruir as diversas manifestações artísticas e culturais, das locais às mundiais, e também participar de práticas diversificadas da produção artístico-cultural.

Utilizar diferentes linguagens – verbal (oral ou visual-motora, como Libras, e escrita), corporal, visual, sonora e digital –, bem como conhecimentos das linguagens artística, matemática e científica, para se expressar e partilhar informações, experiências, ideias e sentimentos em diferentes contextos e produzir sentidos que levem ao entendimento mútuo.

Compreender, utilizar e criar tecnologias digitais de informação e comunicação de forma crítica, significativa, reflexiva e ética nas diversas práticas sociais (incluindo as escolares) para se comunicar, acessar e disseminar informações, produzir conhecimentos, resolver problemas e exercer protagonismo e autoria na vida pessoal e coletiva.

Valorizar a diversidade de saberes e vivências culturais e apropriar-se de conhecimentos e experiências que lhe possibilitem entender as relações próprias do mundo do trabalho e fazer escolhas alinhadas ao seu projeto de vida, com liberdade, autonomia, consciência crítica e responsabilidade.

Argumentar com base em fatos, dados e informações confiáveis, para formular, negociar e defender ideias, pontos de vista e decisões comuns que respeitem e promovam os direitos humanos e a consciência socioambiental em âmbito local, regional e global, com posicionamento ético em relação ao cuidado de si mesmo, dos outros e do planeta.

Conhecer-se, apreciar-se e cuidar de sua saúde física e emocional, compreendendo-se na diversidade humana e reconhecendo suas emoções e as dos outros, com autocrítica e capacidade para lidar com elas.

Exercitar a empatia, o diálogo, a resolução de conflitos e a cooperação, fazendo-se respeitar e promovendo o respeito ao outro e aos direitos humanos, com acolhimento e valorização da diversidade de indivíduos e de grupos sociais, seus saberes, identidades, culturas e potencialidades, sem preconceitos de qualquer natureza.

Agir pessoal e coletivamente com autonomia, responsabilidade, flexibilidade, resiliência e determinação, tomando decisões com base em princípios éticos, democráticos, inclusivos, sustentáveis e solidários.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 9-10. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 17 jul. 2022.

Conforme já mencionado, no desenvolvimento de competências é importante uma indicação clara do que os estudantes devem saber (conhecimentos, procedimentos e atitudes) e do que devem saber fazer (mobilização desses conhecimentos, procedimentos e atitudes) diante de cada situação.

Na BNCC, as aprendizagens relativas ao Ensino Fundamental estão distribuídas em cinco áreas do conhecimento (Linguagens, Matemática, Ciências da Natureza, Ciências Humanas e Ensino Religioso), por sua vez, divididas em componentes curriculares. Existem áreas que abrigam mais de um componente curricular, por exemplo, Linguagens, que abrange Língua Portuguesa, Arte, Educação Física e Língua Inglesa.

Os conhecimentos referentes a cada área do conhecimento, como mencionado, estão estruturados em competências gerais, das quais derivam as competências específicas de cada área e/ou componente curricular.

Cada área do conhecimento estabelece competências específicas de área, cujo desenvolvimento deve ser promovido ao longo dos nove anos. Essas competências explicitam como as dez competências gerais se expressam nessas áreas.

[...]

As competências específicas possibilitam a articulação horizontal entre as áreas, perpassando todos os componentes curriculares, e também a articulação vertical, ou seja, a progressão entre o Ensino Fundamental – Anos Iniciais e o Ensino Fundamental – Anos Finais e a continuidade das experiências dos alunos, considerando suas especificidades.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 28. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 17 jul. 2022.

Em Matemática, cumpre destacar que as competências específicas vão ao encontro dos objetivos do letramento matemático e sua importância de tornar significativa a aprendizagem de conhecimentos matemáticos para que estes possam ser utilizados pelos estudantes em questões de estudo e práticas presentes na vida dos estudantes. Observe, a seguir, as competências específicas da área de Matemática na BNCC.

Reconhecer que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diferentes culturas, em diferentes momentos históricos, e é uma ciência viva, que contribui para solucionar problemas científicos e tecnológicos e para alicerçar descobertas e construções, inclusive com impactos no mundo do trabalho.

Desenvolver o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos convincentes, recorrendo aos conhecimentos matemáticos para compreender e atuar no mundo.

Compreender as relações entre conceitos e procedimentos dos diferentes campos da Matemática (Aritmética, Álgebra, Geometria, Estatística e Probabilidade) e de outras áreas do conhecimento, sentindo segurança quanto à própria capacidade de construir e aplicar conhecimentos matemáticos, desenvolvendo a autoestima e a perseverança na busca de soluções.

Fazer observações sistemáticas de aspectos quantitativos e qualitativos presentes nas práticas sociais e culturais, de modo a investigar, organizar, representar e comunicar informações relevantes, para interpretá-las e avaliá-las crítica e eticamente, produzindo argumentos convincentes.

Utilizar processos e ferramentas matemáticas, inclusive tecnologias digitais disponíveis, para modelar e resolver problemas cotidianos, sociais e de outras áreas de conhecimento, validando estratégias e resultados.

Enfrentar situações-problema em múltiplos contextos, incluindo-se situações imaginadas, não diretamente relacionadas com o aspecto prático-utilitário, expressar suas respostas e sintetizar conclusões, utilizando diferentes registros e linguagens (gráficos, tabelas, esquemas, além de texto escrito na língua materna e outras linguagens para descrever algoritmos, como fluxogramas, e dados).

Desenvolver e/ou discutir projetos que abordem, sobretudo, questões de urgência social, com base em princípios éticos, democráticos, sustentáveis e solidários, valorizando a diversidade de opiniões de indivíduos e de grupos sociais, sem preconceitos de qualquer natureza.

Interagir com seus pares de forma cooperativa, trabalhando coletivamente no planejamento e desenvolvimento de pesquisas para responder a questionamentos e na busca de soluções para problemas, de modo a identificar aspectos consensuais ou não na discussão de uma determinada questão, respeitando o modo de pensar dos colegas e aprendendo com eles.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 267. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 17 jul. 2022.

As habilidades

A fim de assegurar que o desenvolvimento das competências específicas de cada área do conhecimento, a BNCC apresenta um conjunto de habilidades. Essas habilidades estão relacionadas a objetos de conhecimento, que, por sua vez, são organizados em unidades temáticas.

Para garantir o desenvolvimento das competências específicas, cada componente curricular apresenta um conjunto de habilidades. Essas habilidades estão relacionadas a diferentes objetos de conhecimento – aqui entendidos como conteúdos, conceitos e processos –, que, por sua vez, são organizados em unidades temáticas. Respeitando as muitas possibilidades de organização do conhecimento escolar, as unidades temáticas definem um arranjo dos objetos de conhecimento ao longo do Ensino Fundamental adequado às especificidades dos diferentes componentes curriculares. Cada unidade temática contempla uma gama maior ou menor de objetos de conhecimento, assim como cada objeto de conhecimento se relaciona a um número variável de habilidades [...].

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 28-29. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 17 jul. 2022.

Cada habilidade pode ser dividida em partes, que abrangem diferentes ações e procedimentos. Compreender cada uma dessas partes e definir os instrumentos adequados de aplicação delas são importantes para garantir a efetiva apropriação das habilidades. Por exemplo, nas habilidades que preveem a resolução e a elaboração de problemas, é necessário dedicar momentos e atividades específicos para cada uma dessas ações a fim de favorecer a aquisição completa dessas habilidades.

Quanto à relação entre as habilidades e as competências, cumpre destacar que uma competência compreende um conjunto de saberes e habilidades. Assim, o fato de os estudantes desenvolverem certa habilidade, ou parte dela, não garante que eles tenham construído a aprendizagem completa de determinada competência. Em Matemática, os estudantes podem, por exemplo, dominar o uso de ferramentas de planilhas eletrônicas, mas isso não significa que eles tenham desenvolvido todos os conhecimentos, atitudes e valores envolvidos na competência geral 5 da BNCC.

No texto da BNCC, a definição de competência aparece como “a mobilização de conceitos (conceitos e procedimentos), habilidades (práticas, cognitivas e socioemocionais), atitudes e valores para resolver demandas complexas da vida cotidiana, do pleno exercício da cidadania e do mundo do trabalho”. É, portanto, a capacidade de mobilizar recursos, conhecimentos ou vivências para resolver questões da vida real, como pensamento crítico e empatia.

Já as habilidades indicam o que aprendemos a fazer e são sempre associadas a verbos de ação, como identificar, classificar, descrever e planejar. No contexto escolar, ler e interpretar um texto, apresentar um trabalho para os colegas e realizar operações matemáticas são exemplos de habilidades que os estudantes desenvolvem ao longo da evolução escolar.

BNCC: você sabe a diferença entre competências e habilidades? Centro de referências em educação integral. [S. l.], 19 fev. 2020, p. 3. Disponível em: https://educacaointegral.org.br/ reportagens/bncc-voce-sabe-diferenca-entre-competencias-e-habilidades/. Acesso em: 17 jul. 2022.

Desse modo, conclui-se que as competências são mais amplas do que as habilidades e que ambas, competências e habilidades, devem ser desenvolvidas de modo articulado por meio dos recursos de aprendizagem presentes em cada componente curricular, os quais devem estar relacionados entre si para garantir a formação integral dos estudantes.

Na abertura de Unidade das Orientações específicas de cada volume, são listadas as competências gerais e específicas, as habilidades e os Temas Contemporâneos Transversais (TCTs) relacionados aos assuntos de cada Unidade. Além disso, ao longo das orientações, são destacados exemplos da coleção que favorecem o desenvolvimento de competências, habilidades e TCTs com o objetivo de facilitar a identificação desses itens pelo professor e auxiliá-lo a tornar ainda mais efetiva a aquisição dos conhecimentos, atitudes e valores previstos pela BNCC.

Quadros de habilidades da BNCC

UNIDADES TEMÁTICAS CONTEÚDOS HABILIDADES

Sistema de numeração decimal: características, leitura, escrita e comparação de números naturais e de números racionais representados na forma decimal

Operações (adição, subtração, multiplicação, divisão e potenciação) com números naturais

Divisão euclidiana

Fluxograma para determinar a paridade de um número natural

Múltiplos e divisores de um número natural

Números primos e compostos

(EF06MA01) Comparar, ordenar, ler e escrever números naturais e números racionais cuja representação decimal é finita, fazendo uso da reta numérica.

(EF06MA02) Reconhecer o sistema de numeração decimal, como o que prevaleceu no mundo ocidental, e destacar semelhanças e diferenças com outros sistemas, de modo a sistematizar suas principais características (base, valor posicional e função do zero), utilizando, inclusive, a composição e decomposição de números naturais e números racionais em sua representação decimal.

(EF06MA03) Resolver e elaborar problemas que envolvam cálculos (mentais ou escritos, exatos ou aproximados) com números naturais, por meio de estratégias variadas, com compreensão dos processos neles envolvidos com e sem uso de calculadora.

(EF06MA04) Construir algoritmo em linguagem natural e representá-lo por fluxograma que indique a resolução de um problema simples (por exemplo, se um número natural qualquer é par).

(EF06MA05) Classificar números naturais em primos e compostos, estabelecer relações entre números, expressas pelos termos “é múltiplo de”, “é divisor de”, “é fator de”, e estabelecer, por meio de investigações, critérios de divisibilidade por 2, 3, 4, 5, 6, 8, 9, 10, 100 e 1000.

(EF06MA06) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor.

Números

Frações: significados (parte/ todo, quociente), equivalência, comparação, adição e subtração; cálculo da fração de um número natural; adição e subtração de frações

(EF06MA07) Compreender, comparar e ordenar frações associadas às ideias de partes de inteiros e resultado de divisão, identificando frações equivalentes.

(EF06MA08) Reconhecer que os números racionais positivos podem ser expressos nas formas fracionária e decimal, estabelecer relações entre essas representações, passando de uma representação para outra, e relacioná-los a pontos na reta numérica.

(EF06MA09) Resolver e elaborar problemas que envolvam o cálculo da fração de uma quantidade e cujo resultado seja um número natural, com e sem uso de calculadora.

(EF06MA10) Resolver e elaborar problemas que envolvam adição ou subtração com números racionais positivos na representação fracionária.

Operações (adição, subtração, multiplicação, divisão e potenciação) com números racionais

Aproximação de números para múltiplos de potências de 10

Cálculo de porcentagens por meio de estratégias diversas, sem fazer uso da “regra de três”

(EF06MA11) Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e a potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem uso de calculadora.

(EF06MA12) Fazer estimativas de quantidades e aproximar números para múltiplos da potência de 10 mais próxima.

(EF06MA13) Resolver e elaborar problemas que envolvam porcentagens, com base na ideia de proporcionalidade, sem fazer uso da “regra de três”, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros.

UNIDADES TEMÁTICAS CONTEÚDOS

Propriedades da igualdade

HABILIDADES

(EF06MA14) Reconhecer que a relação de igualdade matemática não se altera ao adicionar, subtrair, multiplicar ou dividir os seus dois membros por um mesmo número e utilizar essa noção para determinar valores desconhecidos na resolução de problemas.

Álgebra

Problemas que tratam da partição de um todo em duas partes desiguais, envolvendo razões entre as partes e entre uma das partes e o todo

Plano cartesiano: associação dos vértices de um polígono a pares ordenados

Prismas e pirâmides: planificações e relações entre seus elementos (vértices, faces e arestas)

(EF06MA15) Resolver e elaborar problemas que envolvam a partilha de uma quantidade em duas partes desiguais, envolvendo relações aditivas e multiplicativas, bem como a razão entre as partes e entre uma das partes e o todo.

(EF06MA16) Associar pares ordenados de números a pontos do plano cartesiano do 1o quadrante, em situações como a localização dos vértices de um polígono.

(EF06MA17) Quantificar e estabelecer relações entre o número de vértices, faces e arestas de prismas e pirâmides, em função do seu polígono da base, para resolver problemas e desenvolver a percepção espacial.

Geometria

Polígonos: classificações quanto ao número de vértices, às medidas de lados e ângulos e ao paralelismo e perpendicularismo dos lados

(EF06MA18) Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e classificá-los em regulares e não regulares, tanto em suas representações no plano como em faces de poliedros.

(EF06MA19) Identificar características dos triângulos e classificá-los em relação às medidas dos lados e dos ângulos.

(EF06MA20) Identificar características dos quadriláteros, classificá-los em relação a lados e a ângulos e reconhecer a inclusão e a intersecção de classes entre eles.

Construção de figuras semelhantes: ampliação e redução de figuras planas em malhas quadriculadas

(EF06MA21) Construir figuras planas semelhantes em situações de ampliação e de redução, com o uso de malhas quadriculadas, plano cartesiano ou tecnologias digitais.

Construção de retas paralelas e perpendiculares, fazendo uso de réguas, esquadros e softwares

(EF06MA22) Utilizar instrumentos, como réguas e esquadros, ou softwares para representações de retas paralelas e perpendiculares e construção de quadriláteros, entre outros.

(EF06MA23) Construir algoritmo para resolver situações passo a passo (como na construção de dobraduras ou na indicação de deslocamento de um objeto no plano segundo pontos de referência e distâncias fornecidas etc.).

UNIDADES TEMÁTICAS CONTEÚDOS HABILIDADES

Problemas sobre medidas envolvendo grandezas como comprimento, massa, tempo, temperatura, área, capacidade e volume

(EF06MA24) Resolver e elaborar problemas que envolvam as grandezas comprimento, massa, tempo, temperatura, área (triângulos e retângulos), capacidade e volume (sólidos formados por blocos retangulares), sem uso de fórmulas, inseridos, sempre que possível, em contextos oriundos de situações reais e/ou relacionadas às outras áreas do conhecimento.

(EF06MA25) Reconhecer a abertura do ângulo como grandeza associada às figuras geométricas.

Grandezas e medidas

Ângulos: noção, usos e medida

(EF06MA26) Resolver problemas que envolvam a noção de ângulo em diferentes contextos e em situações reais, como ângulo de visão.

(EF06MA27) Determinar medidas da abertura de ângulos, por meio de transferidor e/ou tecnologias digitais.

Plantas baixas e vistas aéreas

Perímetro de um quadrado como grandeza proporcional à medida do lado

Cálculo de probabilidade como a razão entre o número de resultados favoráveis e o total de resultados possíveis em um espaço amostral equiprovável Cálculo de probabilidade por meio de muitas repetições de um experimento (frequências de ocorrências e probabilidade frequentista)

(EF06MA28) Interpretar, descrever e desenhar plantas baixas simples de residências e vistas aéreas.

(EF06MA29) Analisar e descrever mudanças que ocorrem no perímetro e na área de um quadrado ao se ampliarem ou reduzirem, igualmente, as medidas de seus lados, para compreender que o perímetro é proporcional à medida do lado, o que não ocorre com a área.

(EF06MA30) Calcular a probabilidade de um evento aleatório, expressando-a por número racional (forma fracionária, decimal e percentual) e comparar esse número com a probabilidade obtida por meio de experimentos sucessivos.

Probabilidade e estatística

Leitura e interpretação de tabelas e gráficos (de colunas ou barras simples ou múltiplas) referentes a variáveis categóricas e variáveis numéricas

Coleta de dados, organização e registro

Construção de diferentes tipos de gráficos para representá-los e interpretação das informações

Diferentes tipos de representação de informações: gráficos e fluxogramas

(EF06MA31) Identificar as variáveis e suas frequências e os elementos constitutivos (título, eixos, legendas, fontes e datas) em diferentes tipos de gráfico.

(EF06MA32) Interpretar e resolver situações que envolvam dados de pesquisas sobre contextos ambientais, sustentabilidade, trânsito, consumo responsável, entre outros, apresentadas pela mídia em tabelas e em diferentes tipos de gráficos e redigir textos escritos com o objetivo de sintetizar conclusões.

(EF06MA33) Planejar e coletar dados de pesquisa referente a práticas sociais escolhidas pelos alunos e fazer uso de planilhas eletrônicas para registro, representação e interpretação das informações, em tabelas, vários tipos de gráficos e texto.

(EF06MA34) Interpretar e desenvolver fluxogramas simples, identificando as relações entre os objetos representados (por exemplo, posição de cidades considerando as estradas que as unem, hierarquia dos funcionários de uma empresa etc.).

UNIDADES TEMÁTICAS CONTEÚDOS

Múltiplos e divisores de um número natural

HABILIDADES

(EF07MA01) Resolver e elaborar problemas com números naturais, envolvendo as noções de divisor e de múltiplo, podendo incluir máximo divisor comum ou mínimo múltiplo comum, por meio de estratégias diversas, sem a aplicação de algoritmos.

Cálculo de porcentagens e de acréscimos e decréscimos simples

Números inteiros: usos, história, ordenação, associação com pontos da reta numérica e operações

(EF07MA02) Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros.

(EF07MA03) Comparar e ordenar números inteiros em diferentes contextos, incluindo o histórico, associá-los a pontos da reta numérica e utilizá-los em situações que envolvam adição e subtração.

(EF07MA04) Resolver e elaborar problemas que envolvam operações com números inteiros.

(EF07MA05) Resolver um mesmo problema utilizando diferentes algoritmos.

Números

Fração e seus significados: como parte de inteiros, resultado da divisão, razão e operador

(EF07MA06) Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmos procedimentos.

(EF07MA07) Representar por meio de um fluxograma os passos utilizados para resolver um grupo de problemas.

(EF07MA08) Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.

(EF07MA09) Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração 2/3 para expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.

(EF07MA10) Comparar e ordenar números racionais em diferentes contextos e associá-los a pontos da reta numérica.

Números racionais na representação fracionária e na decimal: usos, ordenação e associação com pontos da reta numérica e operaçõe.

(EF07MA11) Compreender e utilizar a multiplicação e a divisão de números racionais, a relação entre elas e suas propriedades operatórias.

(EF07MA12) Resolver e elaborar problemas que envolvam as operações com números racionais.

(EF07MA13) Compreender a ideia de variável, representada por letra ou símbolo, para expressar relação entre duas grandezas, diferenciando-a da ideia de incógnita.

Álgebra Linguagem algébrica: variável e incógnita

(EF07MA14) Classificar sequências em recursivas e não recursivas, reconhecendo que o conceito de recursão está presente não apenas na matemática, mas também nas artes e na literatura.

(EF07MA15) Utilizar a simbologia algébrica para expressar regularidades encontradas em sequências numéricas.

UNIDADES TEMÁTICAS CONTEÚDOS

Equivalência de expressões algébricas: identificação da regularidade de uma sequência numérica

HABILIDADES

(EF07MA16) Reconhecer se duas expressões algébricas obtidas para descrever a regularidade de uma mesma sequência numérica são ou não equivalentes.

Álgebra

Problemas envolvendo grandezas diretamente proporcionais e grandezas inversamente proporcionais

Equações polinomiais do 1o grau

Transformações geométricas de polígonos no plano cartesiano: multiplicação das coordenadas por um número inteiro e obtenção de simétricos em relação aos eixos e à origem

Simetrias de translação, rotação e reflexão

(EF07MA17) Resolver e elaborar problemas que envolvam variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, utilizando sentença algébrica para expressar a relação entre elas.

(EF07MA18) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1o grau, redutíveis à forma ax + b = c, fazendo uso das propriedades da igualdade.

(EF07MA19) Realizar transformações de polígonos representados no plano cartesiano, decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro.

(EF07MA20) Reconhecer e representar, no plano cartesiano, o simétrico de figuras em relação aos eixos e à origem.

(EF07MA21) Reconhecer e construir figuras obtidas por simetrias de translação, rotação e reflexão, usando instrumentos de desenho ou softwares de geometria dinâmica e vincular esse estudo a representações planas de obras de arte, elementos arquitetônicos, entre outros.

Geometria

A circunferência como lugar geométrico

Relações entre os ângulos formados por retas paralelas intersectadas por uma transversal

(EF07MA22) Construir circunferências, utilizando compasso, reconhecê-las como lugar geométrico e utilizá-las para fazer composições artísticas e resolver problemas que envolvam objetos equidistantes.

(EF07MA23) Verificar relações entre os ângulos formados por retas paralelas cortadas por uma transversal, com e sem uso de softwares de geometria dinâmica.

(EF07MA24) Construir triângulos, usando régua e compasso, reconhecer a condição de existência do triângulo quanto à medida dos lados e verificar que a soma das medidas dos ângulos internos de um triângulo é 180°.

Triângulos: construção, condição de existência e soma das medidas dos ângulos internos

(EF07MA25) Reconhecer a rigidez geométrica dos triângulos e suas aplicações, como na construção de estruturas arquitetônicas (telhados, estruturas metálicas e outras) ou nas artes plásticas.

(EF07MA26) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um triângulo qualquer, conhecidas as medidas dos três lados.

Polígonos regulares: quadrado e triângulo equilátero

(EF07MA27) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos.

(EF07MA28) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um polígono regular (como quadrado e triângulo equilátero), conhecida a medida de seu lado.

UNIDADES TEMÁTICAS CONTEÚDOS

Problemas envolvendo medições

Cálculo de volume de blocos retangulares, utilizando unidades de medida convencionais mais usuais

HABILIDADES

(EF07MA29) Resolver e elaborar problemas que envolvam medidas de grandezas inseridos em contextos oriundos de situações cotidianas ou de outras áreas do conhecimento, reconhecendo que toda medida empírica é aproximada.

(EF07MA30) Resolver e elaborar problemas de cálculo de medida do volume de blocos retangulares, envolvendo as unidades usuais (metro cúbico, decímetro cúbico e centímetro cúbico).

Grandezas e medidas

Equivalência de área de figuras planas: cálculo de áreas de figuras que podem ser decompostas por outras, cujas áreas podem ser facilmente determinadas como triângulos e quadriláteros

Medida do comprimento da circunferência

Experimentos aleatórios: espaço amostral e estimativa de probabilidade por meio de frequência de ocorrências

Estatística: média e amplitude de um conjunto de dados

(EF07MA31) Estabelecer expressões de cálculo de área de triângulos e de quadriláteros.

(EF07MA32) Resolver e elaborar problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas.

(EF07MA33) Estabelecer o número p como a razão entre a medida de uma circunferência e seu diâmetro, para compreender e resolver problemas, inclusive os de natureza histórica.

(EF07MA34) Planejar e realizar experimentos aleatórios ou simulações que envolvem cálculo de probabilidades ou estimativas por meio de frequência de ocorrências.

(EF07MA35) Compreender, em contextos significativos, o significado de média estatística como indicador da tendência de uma pesquisa, calcular seu valor e relacioná-lo, intuitivamente, com a amplitude do conjunto de dados.

Probabilidade e estatística

Pesquisa amostral e pesquisa censitária Planejamento de pesquisa, coleta e organização dos dados, construção de tabelas e gráficos e interpretação das informações

Gráficos de setores: interpretação, pertinência e construção para representar conjunto de dados

(EF07MA36) Planejar e realizar pesquisa envolvendo tema da realidade social, identificando a necessidade de ser censitária ou de usar amostra, e interpretar os dados para comunicá-los por meio de relatório escrito, tabelas e gráficos, com o apoio de planilhas eletrônicas.

(EF07MA37) Interpretar e analisar dados apresentados em gráfico de setores divulgados pela mídia e compreender quando é possível ou conveniente sua utilização.

UNIDADES TEMÁTICAS CONTEÚDOS HABILIDADES

Notação científica

Potenciação e radiciação

(EF08MA01) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.

(EF08MA02) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.

Números

O princípio multiplicativo da contagem

Porcentagens

Dízimas periódicas: fração geratriz

Valor numérico de expressões algébricas

Associação de uma equação linear de 1o grau a uma reta no plano cartesiano

Sistema de equações polinomiais de 1o grau: resolução algébrica e representação no plano cartesiano

Equação polinomial de 2o grau do tipo ax2 = b

(EF08MA03) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.

(EF08MA04) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.

(EF08MA05) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.

(EF08MA06) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.

(EF08MA07) Associar uma equação linear de 1o grau com duas incógnitas a uma reta no plano cartesiano.

(EF08MA08) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1o grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.

(EF08MA09) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2o grau do tipo ax2 = b.

Álgebra

Sequências recursivas e não recursivas

(EF08MA10) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.

(EF08MA11) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.

Geometria

Variação de grandezas: diretamente proporcionais, inversamente proporcionais ou não proporcionais

Congruência de triângulos e demonstrações de propriedades de quadriláteros

(EF08MA12) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.

(EF08MA13) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.

(EF08MA14) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.

UNIDADES TEMÁTICAS CONTEÚDOS HABILIDADES

Construções geométricas: ângulos de 90°, 60°, 45° e 30° e polígonos regulares

(EF08MA15) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares.

(EF08MA16) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.

Geometria

Grandezas e medidas

Mediatriz e bissetriz como lugares geométricos: construção e problemas

Transformações geométricas: simetrias de translação, reflexão e rotação

Área de figuras planas Área do círculo e comprimento de sua circunferência

(EF08MA17) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.

(EF08MA18) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.

(EF08MA19) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

Volume de bloco retangular Medidas de capacidade

Princípio multiplicativo da contagem Soma das probabilidades de todos os elementos de um espaço amostral

Gráficos de barras, colunas, linhas ou setores e seus elementos constitutivos e adequação para determinado conjunto de dados

Organização dos dados de uma variável contínua em classes

(EF08MA20) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.

(EF08MA21) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.

(EF08MA22) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.

(EF08MA23) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.

Probabilidade e estatística

Medidas de tendência central e de dispersão

(EF08MA24) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.

(EF08MA25) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.

Pesquisas censitária ou amostral Planejamento e execução de pesquisa amostral

(EF08MA26) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).

(EF08MA27) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.

UNIDADES TEMÁTICAS CONTEÚDOS HABILIDADES

Necessidade dos números reais para medir qualquer segmento de reta

Números irracionais: reconhecimento e localização de alguns na reta numérica

(EF09MA01) Reconhecer que, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade).

(EF09MA02) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica.

Números

Potências com expoentes negativos e fracionários

Números reais: notação científica e problemas

Porcentagens: problemas que envolvem cálculo de percentuais sucessivos

Funções: representações numérica, algébrica e gráfica

Razão entre grandezas de espécies diferentes

(EF09MA03) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.

(EF09MA04) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.

(EF09MA05) Resolver e elaborar problemas que envolvam porcentagens, com a ideia de aplicação de percentuais sucessivos e a determinação das taxas percentuais, preferencialmente com o uso de tecnologias digitais, no contexto da educação financeira.

(EF09MA06) Compreender as funções como relações de dependência unívoca entre duas variáveis e suas representações numérica, algébrica e gráfica e utilizar esse conceito para analisar situações que envolvam relações funcionais entre duas variáveis.

(EF09MA07) Resolver problemas que envolvam a razão entre duas grandezas de espécies diferentes, como velocidade e densidade demográfica.

Álgebra

Grandezas diretamente proporcionais e grandezas inversamente proporcionais

Expressões algébricas: fatoração e produtos notáveis

Resolução de equações polinomiais do 2o grau por meio de fatorações

Demonstrações de relações entre os ângulos formados por retas paralelas intersectadas por uma transversal

(EF09MA08) Resolver e elaborar problemas que envolvam relações de proporcionalidade direta e inversa entre duas ou mais grandezas, inclusive escalas, divisão em partes proporcionais e taxa de variação, em contextos socioculturais, ambientais e de outras áreas.

(EF09MA09) Compreender os processos de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas que possam ser representados por equações polinomiais do 2o grau.

(EF09MA10) Demonstrar relações simples entre os ângulos formados por retas paralelas cortadas por uma transversal.

Geometria

Relações entre arcos e ângulos na circunferência de um círculo

Semelhança de triângulos

(EF09MA11) Resolver problemas por meio do estabelecimento de relações entre arcos, ângulos centrais e ângulos inscritos na circunferência, fazendo uso, inclusive, de softwares de geometria dinâmica.

(EF09MA12) Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes.

UNIDADES TEMÁTICAS CONTEÚDOS

Relações métricas no triângulo retângulo

Teorema de Pitágoras: verificações experimentais e demonstração

Retas paralelas cortadas por transversais: teoremas de proporcionalidade e verificações experimentais

HABILIDADES

(EF09MA13) Demonstrar relações métricas do triângulo retângulo, entre elas o teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos.

(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.

Geometria

Polígonos regulares

(EF09MA15) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um polígono regular cuja medida do lado é conhecida, utilizando régua e compasso, como também softwares

Distância entre pontos no plano cartesiano

Vistas ortogonais de figuras espaciais

Unidades de medida para medir distâncias muito grandes e muito pequenas

(EF09MA16) Determinar o ponto médio de um segmento de reta e a distância entre dois pontos quaisquer, dadas as coordenadas desses pontos no plano cartesiano, sem o uso de fórmulas, e utilizar esse conhecimento para calcular, por exemplo, medidas de perímetros e áreas de figuras planas construídas no plano.

(EF09MA17) Reconhecer vistas ortogonais de figuras espaciais e aplicar esse conhecimento para desenhar objetos em perspectiva.

Grandezas e medidas

Unidades de medida utilizadas na informática

Volume de prismas e cilindros

Análise de probabilidade de eventos aleatórios: eventos dependentes e independentes

Análise de gráficos divulgados pela mídia: elementos que podem induzir a erros de leitura ou de interpretação

(EF09MA18) Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas, tais como distância entre planetas e sistemas solares, tamanho de vírus ou de células, capacidade de armazenamento de computadores, entre outros.

(EF09MA19) Resolver e elaborar problemas que envolvam medidas de volumes de prismas e de cilindros retos, inclusive com uso de expressões de cálculo, em situações cotidianas.

(EF09MA20) Reconhecer, em experimentos aleatórios, eventos independentes e dependentes e calcular a probabilidade de sua ocorrência, nos dois casos.

(EF09MA21) Analisar e identificar, em gráficos divulgados pela mídia, os elementos que podem induzir, às vezes propositadamente, erros de leitura, como escalas inapropriadas, legendas não explicitadas corretamente, omissão de informações importantes (fontes e datas), entre outros.

Probabilidade e estatística

Leitura, interpretação e representação de dados de pesquisa expressos em tabelas de dupla entrada, gráficos de colunas simples e agrupadas, gráficos de barras e de setores e gráficos pictóricos

Planejamento e execução de pesquisa amostral e apresentação de relatório

(EF09MA22) Escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.

(EF09MA23) Planejar e executar pesquisa amostral envolvendo tema da realidade social e comunicar os resultados por meio de relatório contendo avaliação de medidas de tendência central e da amplitude, tabelas e gráficos adequados, construídos com o apoio de planilhas eletrônicas.

UMA VISÃO INTERDISCIPLINAR E OS TEMAS CONTEMPORÂNEOS TRANSVERSAIS

Um dos desafios mais urgentes do ensino de Matemática é fazer que ela interaja com outras áreas do conhecimento e contribua para a formação integral dos estudantes, indo além do conteúdo programático. Estabelecer conexões entre a Matemática e as demais áreas do conhecimento pode ampliar as oportunidades de compreender e utilizar conceitos, tanto da Matemática quanto das demais áreas. Nesse sentido, a interdisciplinaridade (relação entre os componentes curriculares) surge como um dos recursos para tornar a aprendizagem Matemática ainda mais significativa, uma vez que o ensino interdisciplinar prevê a mobilização de aplicações de cada componente de modo integrado para a análise e resolução de uma situação-problema, como destaca-se na BNCC:

[...] a interdisciplinaridade implica um diálogo entre os campos dos saberes, em que cada componente acolhe as contribuições dos outros, ou seja, há uma interação entre eles. [...]

BRASIL. Ministério da Educação. Temas Contemporâneos Transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, DF: MEC, 2019. p. 18. Disponível em: http://basenacionalcomum.mec.gov.br/images/implementacao /contextualizacao_temas_contemporaneos.pdf. Acesso em: 13 jul. 2022.

Faz-se necessário trazer para a Matemática situações contextualizadas que proporcionem ampliação de abordagem, estabelecendo conexões com conteúdos de outras áreas do conhecimento, relevantes para a constituição dos saberes dos estudantes, além de aprofundar as relações da escola com as experiências cotidianas de cada um deles. Aqui, cabe citar a relevância do trabalho transdisciplinar, que prevê o ensino integrado dos conhecimentos de diferentes áreas, como destaca-se na BNCC:

A abordagem transdisciplinar contribui para que o conhecimento construído extrapole o conteúdo escolar, uma vez que favorece a flexibilização das barreiras que possam existir entre as diversas áreas do conhecimento, possibilitando a abertura para a articulação entre elas. Essa abordagem contribui para reduzir a fragmentação do conhecimento ao mesmo tempo em que busca compreender os múltiplos e complexos elementos da realidade que afetam a vida em sociedade.

BRASIL. Ministério da Educação. Temas Contemporâneos Transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, DF: MEC, 2019. p. 18-19. Disponível em: http://basenacionalcomum.mec.gov.br/images/implementacao /contextualizacao_temas_contemporaneos.pdf. Acesso em: 13 jul. 2022.

Para que a prática docente seja organizada, de modo que possibilite a formação de cidadãos críticos, é preciso entender a contextualização como um acontecimento ou uma situação pertencente a um encadeamento de elementos relacionados a recursos disponíveis em cada área de conhecimento.

Para isso, é importante que o professor perceba como manter um diálogo entre as diferentes áreas, trazendo o cotidiano dos estudantes para a aula e aproximando-o do conhecimento científico, desenvolvendo, assim, um ensino capaz de fazer que os estudantes aprendam a relacioná-las a diferentes aplicações do conhecimento matemático. As experiências vivenciadas pelos estudantes e pela escola podem ser utilizadas para dar vida e significado ao conhecimento. Desse modo, é possível abordar questões como problemas ambientais, culturais, políticos etc. que não estejam obrigatoriamente ligados aos estudantes, mas que possam estar relacionados a seus familiares ou a sua comunidade, por exemplo.

Portanto, fazer conexões interdisciplinares entre Matemática, Língua Portuguesa, Arte, Ciências, História, Geografia, Educação Física, Língua Inglesa etc. e transdisciplinar, utilizando-se também os Temas Contemporâneos Transversais, poderá contribuir para que a Matemática e todo o conhecimento envolvido ganhem maior sentido e significado para os estudantes.

É importante ressaltar a importância das explorações que favoreçam a leitura e as reflexões, inclusive nas aulas de Matemática, sobre os conhecimentos construídos em cada momento do processo de aprendizagem.

O uso da escrita como ferramenta que influencia a aprendizagem matemática [...] e outras formas de registrar processos de pensamento estão sendo cada vez mais utilizadas como um veículo importante na compreensão do processo de ensino e aprendizagem. [...] a utilização da escrita, seja nas aulas de matemática, nos processos de formação docente ou na investigação, deve ser vista como um projetos que transforma continuamente a cognição e o aprendizado de quem a produz.

POWELL, Arthur; BAIRRAL, Marcelo. A escrita e o pensamento matemático: interações e potencialidades. Campinas: Papirus, 2006. p. 11-12.

Os Temas Contemporâneos Transversais visam promover a difusão de valores Fundamentais ao interesse social e a formação integral dos estudantes. De acordo com a BNCC, temos que:

[...] os Temas Contemporâneos Transversais têm a condição de explicitar a ligação entre os diferentes componentes curriculares de forma integrada, bem como de fazer sua conexão com situações vivenciadas pelos estudantes em suas realidades, contribuindo para trazer contexto e contemporaneidade aos objetos do conhecimento descritos na BNCC.

BRASIL. Ministério da Educação. Temas Contemporâneos Transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, DF: MEC, 2019. p. 5. Disponível em: http://basenacionalcomum.mec.gov.br/images/implementacao /contextualizacao_temas_contemporaneos.pdf. Acesso em: 13 jul. 2022.

Nesta obra, há seções e atividades que podem favorecer o trabalho com os Temas Contemporâneos Transversais descritos na BNCC e outros que se articulam com eles. Assim, muitos dos conteúdos trabalhados ao longo de cada volume não se encerram em si mesmos, já que podem ser complementados e contemplados com um dos temas contemporâneos como pano de fundo relacionados às competências e habilidades da BNCC.

Para isso, tornam-se de fundamental importância o planejamento e os estudos prévios por parte do professor para se apropriar das relações entre os temas abordados e o conteúdo matemático que será desenvolvido em cada momento e como potencializar essas relações para tornar a aprendizagem ainda mais significativa.

Os Temas Contemporâneos Transversais descritos na BNCC são:

Meio Ambiente

• Educação Ambiental

• Educação para o Consumo

Saúde

• Saúde

• Educação Alimentar e Nutricional

TEMAS CONTEMPORÂNEOS TRANSVERSAIS

Multiculturalismo

• Diversidade Cultural

• Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras

Cidadania e Civismo

• Vida Familiar e Social

• Educação para o Trânsito

• Educação em Direitos Humanos

• Direitos da Criança e do Adolescente

• Processo de envelhecimento, respeito e valorização do Idoso

Ciência e Tecnologia

• Ciência e Tecnologia

Economia

• Trabalho

• Educação Financeira

• Educação Fiscal

BRASIL. Ministério da Educação. Temas Contemporâneos Transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, DF: MEC, 2019. p. 13. Disponível em: http:// basenacionalcomum.mec.gov.br/images/ implementacao/contextualizacao_ temas_contemporaneos.pdf. Acesso em: 13 jul. 2022.

O PAPEL DO PROFESSOR

Certamente, cada professor tem como objetivo principal a aprendizagem de seus estudantes. Para que esse objetivo seja alcançado, é preciso ter clareza sobre o que os estudantes já sabem e como eles aprendem.

Se o professor é um dos grandes responsáveis pela apresentação de um novo conteúdo, de uma nova estratégia, ou ainda difusor de um termo específico desconhecido pela turma, faz-se necessário que ele saiba não só o que vai ensinar, mas também para quem está ensinando.

Nesse sentido, é imprescindível sondar o conhecimento prévio dos estudantes sobre os assuntos que serão formalmente trabalhados na escola, bem como considerar o desenvolvimento das habilidades e a realidade em que vivem e estudam.

Quanto mais o professor ajudar os estudantes a atribuir significados aos conteúdos estudados, mais eles poderão compreender a Matemática e se interessar por ela. Daí a importância de relacionar a Matemática com o cotidiano.

É importante salientar que a Matemática é utilizada, concebida ou tratada de diferentes maneiras nas diversas profissões e ocupações. Por exemplo: o carpinteiro utiliza a Matemática ao medir comprimentos e ângulos para resolver problemas do seu trabalho; o médico a utiliza no diagnóstico, que, na maioria das vezes, é dado por meio da probabilidade estimada com base em sintomas e resultados de exames; o matemático a utiliza como produção de conhecimento científico, entre outros.

Podemos dizer que existem muitas Matemáticas que procuram descrever e produzir uma “leitura de mundo”. A Matemática escolar é uma delas e caracteriza-se pelas maneiras de compreender e resolver as situações-problema, as questões e as atividades por meio da quantificação, da medição, da estimativa, da representação no espaço, do reconhecimento de formas e propriedades, da observação e da manipulação de regularidades e padrões.

O papel do professor é possibilitar o acesso a essas diferentes maneiras de se fazer Matemática e dar suporte para que os estudantes consigam adquirir habilidades e conhecimentos a fim de (res)significar a Matemática experimentada em suas práticas sociais, bem como reconhecer a beleza da Matemática em si.

Além de mediar a aquisição do conhecimento, é importante que o professor trabalhe a cooperação em sala de aula, abrindo espaço para a troca de ideias entre os estudantes, incentivando a valorização e o respeito às diferenças e promovendo a solidariedade e a cooperação no dia a dia escolar.

As pesquisas atuais sobre o ensino da Matemática defendem que é preciso colocar os estudantes no contexto de produção de pensamento e de conhecimento matemático. Desse modo, o foco não é mais os estudantes, o professor ou o conteúdo, mas, sim, a articulação desses três elementos.

Uma vez que as respostas dos estudantes às situações-problema apresentadas desafiam os professores a pensar matematicamente para propor novas questões, cria-se uma parceria nos processos de ensino e aprendizagem. Da mesma maneira, os estudantes são chamados a elaborar novos questionamentos diante do que é proposto/exposto pelo professor. Assim, o conhecimento matemático escolar é redefinido constantemente.

Passos e Romanatto (2010) apontam outros aspectos relevantes para que o professor atinja o objetivo de que seus estudantes aprendam Matemática. Segundo os autores, é necessário que os professores tenham:

[...] o domínio dos conhecimentos atuais sobre a natureza da Matemática, articulado com as ciências da educação, pode resultar em caminhos férteis para que essa área de conhecimento seja apreendida pelos nossos estudantes de forma efetiva e com significado.

PASSOS, Cármen Lúcia Brancaglion; ROMANATTO, Mauro Carlos. A Matemática na formação de professores dos anos iniciais: aspectos teóricos e metodológicos. São Carlos: Editora da UFSCar, 2010. p. 20.

Professor orienta estudantes indígenas da etnia xerente durante aula na Escola Indígena Sakruiwê, na Aldeia Funil, em Tocantínia (TO). Fotografia de 2022.

Os conhecimentos matemáticos podem ser encarados como recursos que favorecem a cidadania, dada a ampla gama de aplicações desses conhecimentos nas mais variadas situações da sociedade atual. Para apresentar a Matemática como área a serviço do conhecimento científico e de relevância prática no cotidiano, é necessário que o professor tenha clareza a respeito das relações da Matemática com outras áreas de conhecimento. Para isso, é importante que o professor de Matemática tenha uma formação integral e continuada, apropriando-se das relações e aplicações de conceitos matemáticos em outras áreas do conhecimento e da contribuição da Matemática para construção da cidadania, como destacam Soares e Sheide (2004):

Outra questão crucial é a percepção que o professor tem sobre o conhecimento matemático e as interações que é capaz de estabelecer com esse conhecimento. A sua utilização como ferramenta para a construção da cidadania vai depender da sua capacidade em tratá-lo como um conhecimento articulado aos outros campos do saber e historicamente situado.

SOARES, Marlene Aparecida; SCHEIDE, Tereza de Jesus Ferreira. Professor de Matemática: um educador a serviço da construção da cidadania. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 8., 2004, Recife. Anais […]. Recife: Universidade Federal de Pernambuco, 2004. p. 2. Disponível em: http://www.sbem.com.br/files/viii/pdf/07/CC07289049853.pdf. Acesso em: 13 jul. 2022.

Desse modo, o professor de Matemática, longe de ser um mero transmissor de conhecimentos imutáveis, é um sujeito do conhecimento que compartilha com estudantes conhecimentos esses que devem estar em constante aprimoramento e transformação para serem úteis nas práticas sociais dos estudantes.

Portanto, neste processo de parceria e inter-relação existente entre estudantes e professores, é muito importante que ambos tenham clareza dos objetivos que se quer alcançar, as habilidades a serem desenvolvidas, os processos individuais e coletivos e possíveis caminhos a serem percorridos.

PERFIS DE APRENDIZAGEM

A Base Nacional Comum Curricular trouxe ao centro do debate sobre o processo educativo a necessidade de pensarmos em educação integral. Isso significa considerar cada estudante como indivíduo pleno e complexo, em suas diversas dimensões. Ninguém abandona gostos, características, sonhos, valores e emoções antes de entrar na escola – ao contrário, a sala de aula é composta de diversidade. Na BNCC (2018, p. 14), destaca-se:

[…] Reconhece, assim, que a Educação Básica deve visar à formação e ao desenvolvimento humano global, o que implica compreender a complexidade e a não linearidade desse desenvolvimento, rompendo com visões reducionistas que privilegiam ou a dimensão intelectual (cognitiva) ou a dimensão afetiva. Significa, ainda, assumir uma visão plural, singular e integral da criança, do adolescente, do jovem e do adulto – considerando-os como sujeitos de aprendizagem – e promover uma educação voltada ao seu acolhimento, reconhecimento e desenvolvimento pleno, nas suas singularidades e diversidades. […]

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. p. 14. Disponível em: http://basenacionalcomum.mec.gov.br/images/BNCC_EI_EF_110518_versaofinal_site.pdf. Acesso em: 28 jul. 2022.

Essa visão implica reconhecer que ao professor cabe considerar cada estudante em sua singularidade, identificando necessidades, diferentes interesses e modos de aprender. Cada um de nós tem um perfil de aprendizagem. Isso não significa que aprendamos apenas por um canal de aprendizagem, mas, muitas vezes, existem canais mais propícios do que outros e, portanto, reconhecê-los e incentivar o uso deles é muito importante. Existem indivíduos que compreendem melhor a partir de estímulos visuais e, portanto, é interessante recorrer ao uso de gráficos, tabelas, listas e mapas mentais. Há pessoas que compreendem melhor utilizando a leitura (silenciosa) e escrita (listas, textos on-line, artigos, dicionários); LVI

outras pessoas são mais auditivas e, nesse caso, participar de conversas, fazer leituras em voz alta, praticar a escuta de podcasts, assistir a palestras e até ouvir músicas podem ser um caminho promissor; temos, também, aqueles mais cinestésicos e, nesse caso, pode ser importante explorar atividades concretas, como simulações, demonstrações, dinâmicas e métodos lúdicos, como a gamificação. É importante salientar que existem ainda pessoas com certa facilidade para se adaptar aos estímulos, os indivíduos chamados multimodais.

Para César Coll (2003, p. 2), é preciso identificar os diversos fatores que se relacionam com a aprendizagem – de natureza cognitiva, emocional, afetiva, social. O autor afirma que:

A qualidade de um sistema educativo está estreitamente relacionada – sobretudo nos níveis correspondentes à educação básica – à sua capacidade de satisfazer as necessidades educativas e de formação de todos os alunos, ou seja, à sua capacidade de diversificar e de ajustar a ação educativa às características individuais e à ampla gama de capacidades, interesses e motivações demonstrados por alunos e alunas diante da aprendizagem escolar. (2003, p. 2)

COLL, Cesar. Atenção à diversidade e qualidade do ensino. Revista Educação Especial, [S. l.], v. 1, n. 1, p. 7-17, 2012. Disponível em: https://periodicos.ufsm.br/educacaoespecial/article/view/5001. Acesso em: 30 abr. 2022.

Há que se considerar as culturas juvenis em sua multiplicidade, a neurodiversidade, os diferentes perfis de aprendizagem. Uma escola que atenda a todos precisa ser inclusiva – não apenas pensando em “minorias”, mas reconhecendo que a diversidade é inerente à humanidade, logo, onde há pessoas, há diversidade. Dessa forma, não há espaço para preconceitos ou discriminações de quaisquer ordens.

Além disso, a escola precisa ser reconhecida pelos estudantes como um espaço de paz para que se sintam seguros e confiantes na construção de seu projeto de vida. Desse modo, é fundamental promover situações que desenvolvam a empatia e a cooperação entre eles e toda a comunidade escolar.

Para que isso aconteça, é preciso buscar novas formas de “fazer educação”, promovendo o protagonismo dos estudantes no processo. As metodologias ativas parecem propícias a essa tarefa, pois favorecem o trabalho coletivo, a reflexão, a convivência e respeitam os diferentes tempos e interesses, bem como a diversidade de formas de aprender.

Sugerimos também a alternância entre agrupamentos e trabalho individual, considerando os objetivos de aula (ou sequência de aulas) e as metodologias empregadas. Em duplas, pequenos grupos, grupos grandes ou até com o grupo-classe. Nos agrupamentos, os estudantes desenvolvem-se a partir da relação com os outros, e, no trabalho individual, o professor pode personalizar o processo, enfocando em habilidades específicas necessárias ao desenvolvimento de cada estudante. Em turmas grandes, o agrupamento pode ser, especialmente, uma estratégia muito útil para contemplar a diversidade e favorecer a aprendizagem de todos.

O professor pode também explorar as tecnologias digitais em suas propostas pedagógicas, com base nas preferências e nos estilos de aprendizagem, valorizando as potencialidades e a integração entre os estudantes. Para além da inclusão das estratégias digitais, convidar os estudantes ao protagonismo, abrindo as portas da escola às culturas juvenis.

Dizemos no plural, culturas juvenis, porque é impossível unificá-las, uma vez que dependem de inúmeros aspectos, como interesses, territorialidades, influências, fatores socioeconômicos. Elas podem ser consideradas como a confluência de modos de vida, práticas sociais, interesses, gostos e saberes específicos que levam às escolhas, linguagens e atuações de cada grupo de jovens, formando identidades. Para desenvolver essas culturas e ampliar a identificação dos estudantes com o processo de aprendizagem, é importante abrir espaço para trocas e aprendizagem coletiva, como promover festivais, saraus poéticos e musicais.

Nesta coleção, são apresentadas propostas diversificadas, que permitem variadas maneiras de exploração e organização do trabalho, favorecendo a organização do trabalho pedagógico e do seu planejamento para atender grupos grandes ou pequenos em suas particularidades.

Grupo de jovens posando para uma fotografia.

AVALIAÇÃO

Em todo trabalho no qual a aprendizagem escolar esteja envolvida, o processo de avaliação estará presente – seja na sala de aula, nas atividades extraclasse, seja nas conquistas pessoais dos estudantes, como o ingresso nas universidades.

A princípio, o processo avaliativo era tido apenas como um procedimento de medida (que definia se os estudantes tinham ou não condições de progredir nos estudos). Atualmente, é quase consenso a compreensão de que a avaliação escolar não deve apenas verificar se os estudantes atingiram os objetivos definidos pelo currículo, com a finalidade rasa de atribuir-lhes uma nota ou um conceito. Desse modo, as avaliações passaram por um processo de ressignificação em que assumiram o papel de um potente instrumento que permite visualizar o progresso de cada estudante e sinalizar possíveis pontos de atenção.

Os resultados avaliativos não só apresentam implicações no processo individual dos estudantes como também produzem dados para a análise do trabalho desenvolvido pelos profissionais da escola, incluindo o professor. Assim, para que haja um ensino de qualidade, devem-se estabelecer relações entre os resultados e as ações da escola, principalmente no que se refere à vinculação do professor com os estudantes. Por isso, é essencial compreender como esses estudantes lidam com o conhecimento, quais são suas habilidades, as dificuldades que apresentam e as necessidades individuais para, junto deles, traçar uma rota de superação dos desafios e avanço nas conquistas.

Nesse contexto, podem ser destacados três tipos principais de avaliação: diagnóstica, formativa de processo ou de resultado. A avaliação diagnóstica, a ser realizada no início do processo de ensino e aprendizagem de determinado conteúdo, é fundamental para esse processo. O professor e os estudantes precisam identificar os conhecimentos já adquiridos para, com base nessa percepção, decidir quais atividades e ações podem ser potencialmente mais interessantes e quais desafios merecem ser ampliados. A clareza dos objetivos a serem alcançados é de fundamental importância, pois, sabendo o ponto a que se quer chegar, é mais fácil perceber se, de fato, chegou-se a esse “lugar”; portanto, é importante compartilhar com os estudantes os objetivos de determinada atividade ou grupo de atividades e o que se pretende avaliar.

No tipo de avaliação formativa de processo, o professor deve lançar mão de diferentes instrumentos avaliativos que sinalizem o desenvolvimento dos estudantes ao longo do processo educativo. Nesse caso, os resultados são parciais e os registros podem nortear a tomada de decisões e o caminho de aprendizagem a ser proposto pelo professor. Desempenho em seminários, participação em debates e capacidade de comunicar e compartilhar estratégias de resolução são indícios do desenvolvimento dos estudantes durante o processo de construção de conhecimentos e podem ser utilizados como meios avaliativos.

A avaliação de resultado ou somativa é aquela realizada ao fim de determinado estudo ou período de estudo para indicar os resultados de desempenho dos estudantes em relação a uma meta de aprendizagem. A prova tradicional é um dos instrumentos mais comuns desse tipo de avaliação, cujo resultado é um índice importante da evolução do nível de aprendizagem dos estudantes, mas não deve ser o único, tampouco analisado isoladamente, sem considerar os resultados dos demais tipos de avaliação realizados.

As questões da seção Avaliações oficiais em foco, baseadas em avaliações oficiais de larga escala (Saeb, Saresp, Pisa, Enem, OBMEP, entre outras), podem ser utilizadas e aplicadas como instrumento avaliativo de um dos tipos de avaliação descritos, de acordo com o planejamento do professor e a realidade de cada turma.

Avaliar o processo

Uma possibilidade é observar a estratégia que os estudantes utilizam para resolver as situações-problema; isso consiste em um recurso valioso para o professor compreender o desenvolvimento deles. Muitas vezes, o modo como produzem algo demonstra o que não compreenderam e possibilita ao professor intervir adequadamente, agindo de maneira eficaz para atender às necessidades reais dos estudantes. Pedir a eles que socializem com os colegas os raciocínios e as estratégias é mais uma maneira de identificar os caminhos e possíveis dificuldades de cada um.

Como já comentamos, é importante incentivar os diferentes registros de representação. Muitas vezes, os estudantes são capazes de compartilhar as estratégias utilizadas oralmente, mas não as representa numericamente. Por isso, é interessante pedir-lhes que registrem o mesmo processo de maneiras distintas para que possam, além de explorar os diferentes registros de representação, conhecer o processo que, para eles, é mais simples ou desafiador.

Autoavaliação

Os estudantes precisam se conscientizar da responsabilidade deles por seu processo de aprendizagem e, para isso, é preciso que percebam a função e a importância dos diferentes instrumentos de avaliação e, mais do que isso, utilizem-nos como molas propulsoras para novas conquistas. Além de identificar e observar o número que indica sua nota, os

estudantes precisam ser motivados a identificar, nos acertos, as conquistas realizadas e, nos erros, possíveis desvios de rota ou rotas inadequadas para aquela situação. Portanto o espaço/tempo para os estudantes se autoavaliarem deve ser fornecido pelo professor.

Nesse processo de autoavaliação, os estudantes podem ser convidados a responder a alguns questionamentos que lhes permitam identificar o uso dos dados corretos, o porquê da escolha de determinada estratégia, o nível de tensão causada em cada resolução e possível interferência no processo de resolução, o que poderia ser melhorado, entre outros.

Nesta obra, os estudantes encontrarão a seção Um novo olhar, que possibilita a retomada dos conhecimentos explorados para que possam perceber, por exemplo, as habilidades desenvolvidas e as que precisam ser recapituladas e, por meio dessas percepções, após a elaboração da autoavaliação, preparar um plano de ações e estudos.

Durante esse processo de mensuração e investigação, é possível utilizar diferentes instrumentos, como: rodas de conversa ou entrevistas; fichas que serão preenchidas pelos próprios estudantes e pelo professor; trabalhos em dupla ou grupos; provas individuais com e sem consulta aos registros pessoais; elaboração e correção de atividades em duplas – um estudante corrige a atividade do outro colega; apresentação dos equívocos cometidos; elaboração de textos e seminários etc. É importante que os estudantes também tomem ciência de como poderão melhorar para avançar, sabendo do que já são capazes de realizar sozinhos, assumindo seu papel atuante.

A avaliação não começa nem termina na sala de aula, ela envolve planejamento e desenvolvimento do processo de ensino, dinamizando oportunidades de ação e reflexão, num acompanhamento permanente do professor, propiciando ao aluno, em seu processo de aprendizagem, reflexões acerca do mundo; formando seres críticos e participativos na construção das verdades formuladas e reformuladas.

CUCCIOLI, Eliana. Superando desafios ao avaliar a aprendizagem matemática. In: LOPES, Celi Espasandin; MUNIZ, Maria Inês Sparrapan. O processo de avaliação nas aulas de matemática. Campinas: Mercado das Letras, 2010. p. 131.

Ao refletir sobre seus avanços, dificuldades e expectativas, os estudantes podem perceber estratégias de aprendizagem que precisam ser modificadas.

Quanto aos familiares, se estiverem cientes das expectativas do professor em relação aos estudantes, poderão cooperar no estabelecimento dessas estratégias.

A avaliação não pode ser considerada um momento isolado no processo de ensino e aprendizagem nem se resumir a uma prova. Como mencionado, é importante que o professor utilize instrumentos avaliativos diversificados e que sejam desenvolvidos ao longo do ano letivo. O registro periódico dessas observações o ajudará a acompanhar o desenvolvimento dos estudantes.

A avaliação assim considerada é contínua e formativa: faz parte do processo de ensino e aprendizagem e tem por objetivo contribuir para a formação dos estudantes.

Diante disso, é interessante destacar um trecho sobre a avaliação em Matemática, descrito nos Parâmetros Curriculares Nacionais (PCN):

Mudanças na definição de objetivos para o ensino fundamental, na maneira de conceber a aprendizagem, na interpretação e na abordagem dos conteúdos matemáticos implicam repensar sobre as finalidades da avaliação, sobre o que e como se avalia, num trabalho que inclui uma variedade de situações de aprendizagem, como a resolução de problemas, o trabalho com jogos, o uso de recursos tecnológicos, entre outros.

Alguns professores têm procurado elaborar instrumentos de avaliação para registrar observações sobre os alunos. Um exemplo são as fichas para o mapeamento do desenvolvimento de atitudes, [...]

Os resultados expressos pelos instrumentos de avaliação, sejam eles provas, trabalhos, postura em sala, constituem indícios de competências e como tal devem ser considerados. [...]

BRASIL. Ministério da Educação e do Desporto. Secretaria de Educação Fundamental. Parâmetros Curriculares Nacionais: Matemática. Brasília, DF: MEC/SEF, 1997. p. 41. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf. Acesso em: 3 ago. 2022.

INDICAÇÕES PARA APOIO AO TRABALHO DO PROFESSOR

DOCUMENTOS OFICIAIS

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/.

BRASIL. Ministério da Educação. Diretrizes Curriculares Nacionais para Educação Básica. Brasília, DF: MEC: SEB: DICEI, 2013. Disponível em: http://portal.mec.gov.br/docman/ julho-2013-pdf/13677-diretrizes-educacao-basica-2013-pdf/file.

BRASIL. Senado Federal. Lei de diretrizes e bases da educação nacional. Brasília, DF: Senado Federal, Coordenação de Edições Técnicas, 2017.

BRASIL. Ministério da Educação. Normas sobre computação na Educação Básica: complemento à BNCC. Brasília, DF: MEC, 2021. Disponível em: http://portal.mec.gov.br/ index.php?option=com_docman&view=download&alias= 182481-texto-referencia-normas-sobre-computacao-na-edu cacao-basica&category_slug=abril-2021-pdf&Itemid=30192.

BRASIL. Ministério da Educação. Pacto Nacional pela Alfabetização na Idade Certa: apresentação. Brasília, DF: SEB, 2014. Disponível em: http://pacto.mec.gov.br/materiais -listagem/item/66-apresentacao.

BRASIL. Ministério da Educação. Parâmetros Curriculares Nacionais: terceiro e quarto ciclos do Ensino Fundamental – Matemática. Brasília, DF: MEC: SEF, 1998. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/matematica.pdf.

BRASIL. Ministério da Educação. Plano Nacional de Educação para o decênio 2014/2024. Brasília, DF: MEC, 2020. Disponível em: https://pne.mec.gov.br/.

BRASIL. Ministério da Educação e do Desporto. Secretaria de Educação Básica. Ensino Fundamental de Nove Anos: orientações para a inclusão da criança de seis anos de idade. 2. ed. Brasília, DF: SEB, 2007. Disponível em: http://portal. mec.gov.br/seb/arquivos/pdf/Ensfund/ensifund9anobase final.pdf.

BRASIL. Ministério da Educação. Temas Contemporâneos Transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, DF: MEC, 2019. Disponível em: http://basenacionalcomum.mec.gov.br/images/implementa cao/contextualizacao_temas_contemporaneos.pdf.

BRASIL. Ministério da Educação e do Desporto. Secretaria de Educação Fundamental. Parâmetros Curriculares

Nacionais: matemática. Brasília, DF: MEC/SEF, 1997. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/livro03.pdf.

Acessos em: 27 jul. 2022.

SITES E PUBLICAÇÕES

A COR DA CULTURA. Disponível em: https://www.cenpec. org.br/tematicas/a-cor-da-cultura-modos-de-brincar.

A EDUCAÇÃO MATEMÁTICA EM REVISTA TEMAS & DEBATES. Disponível em: http://sbemrevista.kinghost.net/revista/index.php/td.

BOLETIM GEPEM (Grupo de Estudos e Pesquisas em Educação Matemática). Disponível em: http://costalima.ufrrj.br/index. php/gepem/index.

CADERNOS DO CAEM. Disponíveis em: https://www.ime. usp.br/caem/publicacoes.php.

CADERNOS – SÉRIE IDEIAS DA FUNDAÇÃO PARA O DESENVOLVIMENTO DA EDUCAÇÃO – FDE. Disponíveis em: https://www.fde.sp.gov.br/PagePublic/Interna. aspx?codigoMenu=253&AspxAutoDetectCookieSupport=1. EDUMATEC. Disponível em: http://www.edumatec.mat.ufrgs.br/.

FACULDADE DE EDUCAÇÃO DA UNIVERSIDADE DE SÃO PAULO (USP)/DEPARTAMENTO DE METODOLOGIA DO ENSINO E EDUCAÇÃO COMPARADA. Disponível em: http://www4. fe.usp.br/feusp/departamentos/edm.

INSTITUTO ALFA E BETO: Ensino da matemática. Disponível em: https://www.alfaebeto.org.br/2019/06/06/ instituto-alfa-e-beto-pensa-sobre-ensino-da-matematica/.

INSTITUTO PAULO FREIRE: Acervo. Disponível em: http:// acervo.paulofreire.org:8080/xmlui/.

LABORATÓRIO DE MATEMÁTICA: Faculdade de Educação da USP. Disponível em: http://www2.fe.usp.br/~labmat/principal.html.

LABORATÓRIO DE PESQUISA MULTIMEIOS. Disponível em: http://www.multimeios.ufc.br/.

MATEMÁTICA EM TODA PARTE – TV ESCOLA – MINISTÉRIO DA EDUCAÇÃO (MEC). Disponível em: https://www.youtube. com/results?search_query=tv+escola+matem%C3%A1ti ca+em+toda+parte.

MINISTÉRIO DA EDUCAÇÃO. Disponível em: https://www. gov.br/mec/pt-br.

NOVA ESCOLA. Disponível em: https://novaescola.org.br/.

PENSAR A EDUCAÇÃO EM REVISTA. Disponível em: https:// pensaraeducacaoemrevista.com.br/.

PORTAL EDUCAÇÃO EM DIREITOS HUMANOS: Educação matemática como formação necessária à cidadania. Disponível em: http://www.dhnet.org.br/dados/livros/edh/br/rs/cidadan/ cap14.htm.

REDE DO SABER. Disponível em: https://deitapecerica.educa cao.sp.gov.br/rede-do-saber/.

REVISTA DO PROFESSOR DE MATEMÁTICA – RPM. Disponível em: https://www.rpm.org.br/.

REVISTA PARANAENSE DE EDUCAÇÃO MATEMÁTICA. Disponível em: https://periodicos.unespar.edu.br/index.php/rpem.

SOCIEDADE BRASILEIRA DE EDUCAÇÃO EM MATEMÁTICA –SBEM. Disponível em: http://www.sbembrasil.org.br/sbembrasil/. Acessos em: 27 jul. 2022.

ENTIDADES DE APOIO À EDUCAÇÃO MATEMÁTICA

Centro de Aperfeiçoamento do Ensino de Matemática – CAEM

Instituto de Matemática e Estatística da Universidade de São Paulo – IME/USP

Rua do Matão, 1010 – Bloco B – sala 167

Cidade Universitária – São Paulo – SP – CEP 05508-090

Fone e fax: (0XX11) 3091-6160

Site: https://www.ime.usp.br/caem/. Acesso em: 27 jul. 2022.

Fundo Nacional de Desenvolvimento da Educação – FNDE

Ministério da Educação – SBS – Quadra 2 – Bloco F

Brasília – DF – CEP 70070-929

Tel.: 0800-616161

Site: https://www.fnde.gov.br/index.php. Acesso em: 27 jul. 2022.

Laboratório de Ensino de Matemática – LEM

Universidade Estadual de Campinas – Unicamp – IMECC

Rua Sérgio Buarque de Holanda, 651 – CEP 13083-859

Fone: (0XX19) 3521-6090

Site: https://www.ime.unicamp.br/lem. Acesso em: 27 jul. 2022.

Laboratório de Ensino de Matemática e Estatística – LEMA

Universidade Federal da Bahia – UFBA – Instituto de Matemática

Avenida Adhemar de Barros, s/n – Salvador – BA – CEP 40170-110

Fone: (0XX71) 3263-6265

Site: http://www.dmat.ufba.br/extensao/lema. Acesso em: 27 jul. 2022.

Núcleo da Informática Aplicada à Educação – NIED

Universidade Estadual de Campinas – Unicamp

Cidade Universitária Zeferino Vaz

Bloco V da Reitoria – piso 2 – Campinas – SP – CEP 13083-970

Tel.: (0XX19) 3788-7136

E -mail: nied@unicamp.br

Site: https://www.nied.unicamp.br/. Acesso em: 27 jul. 2022.

Projeto Fundão – Matemática

Universidade Federal do Rio de Janeiro (UFRJ)

Instituto de Matemática

Centro de Tecnologia – Bloco C – sala 108

Cidade Universitária

Caixa Postal 68530 – CEP 21941-972

Rio de Janeiro – RJ

Fone e fax: (0XX21) 2562-7511

Site: http://www.matematica.projetofundao.ufrj.br/. Acesso em: 27 jul. 2022.

Sociedade Brasileira de Matemática – SBM

Estrada Dona Castorina, 110 – sala 109

Jardim Botânico

CEP 22460-320 – Rio de Janeiro – RJ – CEP 22460-320

Fone: (0XX21) 2529-5073

Site: https://sbm.org.br/. Acesso em: 27 jul. 2022.

RIDO/SHUTTERSTOCK.COM

Estudante resolvendo um problema na lousa.

REFERÊNCIAS BIBLIOGRÁFICAS

ANTUNES, Celso. Jogos para a estimulação das múltiplas inteligências. Petrópolis: Vozes, 2014.

Nesse livro, o autor traz reflexões sobre a importância do jogo no processo de aprendizagem.

BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem téorico-prática. Porto Alegre: Penso, 2018.

Apresenta um conjunto de artigos que abordam estudos e aplicações de metodologias ágeis na educação para o desenvolvimento do protagonismo estudantil de maneira inovadora.

BEAN, Dale. O que é modelagem matemática? Educação

Matemática em Revista, São Paulo, ano 8, n. 9, p. 49-57, 2001. Disponível em: http://sbemrevista.kinghost.net/revista/ index.php/emr/article/view/1689/1182. Aceso em: 27 jul. 2022.

Nesse artigo, o autor diferencia a modelagem matemática de outras aplicações no contexto do ensino de Matemática.

BNCC: você sabe a diferença entre competências e habilidades? Centro de referências em educação integral [S l.], 19 ago. 2020. Disponível em: https://educacaointegral. org.br/reportagens/bncc-voce-sabe-diferenca-entre-compe tencias-e-habilidades/. Acesso em: 17 jul. 2022.

O texto trata sobre as diferenças entre o ensino e a aprendizagem de competências e habilidades no contexto da BNCC.

BOAVIDA, Ana Maria Roque. A argumentação em Matemática: investigando o trabalho de duas professoras em contexto de colaboração. Dissertação (Doutorado em Educação) – Faculdade de Ciências, Universidade de Lisboa, Portugal, 2005. Disponível em: https://repositorio.ul.pt/bits tream/10451/3140/1/ulsd048032_td_Ana_Boavida.pdf. Acesso em: 13 jul. 2022.

A autora descreve e analisa experiências voltadas para o desenvolvimento de estudantes em atividades que envolvem argumentação matemática.

BORBA, Marcelo de Carvalho; PENTEADO, Miriam Godoy. Informática e educação matemática. Belo Horizonte: Autêntica, 2010.

Os autores apresentam o resultado de um trabalho sobre a importância do uso da informática na educação matemática.

BORBA, Marcelo de Carvalho; SILVA, Ricardo Scucuglia Rodrigues da; GADANIDIS, George. Fases das tecnologias digitais em educação matemática: sala de aula e internet em movimento. Belo Horizonte: Autêntica, 2014.

Discute-se, nesse livro, a influência das tecnologias digitais no ensino de Matemática nas últimas décadas.

BOUCINHA, Rafael Marimon. Aprendizagem do pensamento computacional e desenvolvimento do raciocínio Tese (Doutorado) – Centro Interdisciplinar de Novas Tecnologias na Educação, Universidade Federal do Rio Grande do Sul, Porto Alegre, 2017. Disponível em: https://lume.ufrgs.br/ bitstream/handle/10183/172300/001058885.pdf?sequen ce=1&isAllowed=y. Acesso em: 9 jul. 2022.

O autor investiga a relação entre a construção do pensamento computacional e o desenvolvimento do raciocínio dos estudantes.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular: educação é a base. Brasília, DF: MEC, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/. Acesso em: 8 jul. 2022.

Documento oficial composto de orientações que norteiam a (re)elaboração dos currículos de referência das escolas das redes pública e privada de ensino de todo o Brasil. Traz os conhecimentos essenciais, as competências, as habilidades e as aprendizagens pretendidas para crianças e jovens em cada etapa da Educação Básica.

BRASIL. Ministério da Educação. Normas sobre computação na Educação Básica: complemento à BNCC. Brasília, DF: MEC, 2021. Disponível em: http://portal.mec.gov.br/ index.php?option=com_docman&view=download&alias= 182481-texto-referencia-normas-sobre-computacao-na-edu cacao-basica&category_slug=abril-2021-pdf&Itemid=30192. Acesso em: 8 jul. 2022.

Documento que define normas sobre Computação na Educação Básica, em complemento à BNCC.

BRASIL. Ministério da Educação. O uso de metodologias ativas colaborativas e a formação de competências Caderno de Práticas da Base Nacional Comum Curricular. Brasília, DF: MEC, [2019?]. Disponível em: http://basenacionalco mum.mec.gov.br/implementacao/praticas/caderno-de-praticas/ aprofundamentos/202-o-uso-de-metodologias-ativas-cola borativas-a-formacao-de-competencias-2?highlight=WyJt ZXRvZG9sb2dpYXMiLCJhdGl2YXMiLCJtZXRvZG9sb2dpYXM gYXRpdmFzIl0. Acesso em: 14 jul. 2022.

O caderno explora a relevância das metodologias ativas colaborativas para a aprendizagem, abordando conceitos como a Zona de Desenvolvimento Proximal de Vygotsky.

BRASIL. Ministério da Educação. Parâmetros curriculares nacionais: terceiro e quarto ciclos do Ensino Fundamental – Matemática. Brasília, DF: MEC: SEF, 1998. Disponível em: http://portal.mec.gov.br/seb/arquivos/pdf/matematica.pdf. Acesso em: 8 jun. 2022.

Documento que apresenta uma seleção de conhecimentos de cada componente, considerados fundamentais para o exercício da cidadania, além de uma proposta de organização curricular. BRASIL. Ministério da Educação. Temas Contemporâneos Transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, DF: MEC: SEB, 2019. Disponível em: http://basenacionalcomum.mec.gov.br/images/implementa cao/contextualizacao_temas_contemporaneos.pdf. Acesso em: 13 jul. 2022.

Documento explicativo acerca dos Temas Contemporâneos Transversais a serem abordados na Educação Básica.

CARNIELLI, Walter Alexandre; EPSTEIN, Richard L. Pensamento crítico: o poder da lógica e da argumentação. 3. ed. São Paulo: Rideel, 2011.

Os autores apresentam técnicas de como construir bons argumentos e a influência dessa competência no desenvolvimento do pensamento crítico.

CENTRO DE INOVAÇÃO PARA A EDUCAÇÃO BRASILEIRA

(CIEB). Currículo de referência em tecnologia e computação: da Educação infantil ao Ensino Fundamental. São Paulo, 2018. Disponível em: https://curriculo.cieb.net. br/assets/docs/Curriculo_de_Referencia_em_Tecnologia_e_ Computacao.pdf. Acesso em: 20 ago. 2022.

Esse documento propõe uma reflexão sobre os usos das TDICs e apresenta eixos, conceitos e habilidades alinhados à BNCC com o objetivo de favorecer o desenvolvimento de competências de exploração e de uso das tecnologias nas escolas.

COLL, César; MARTÍN, Elena (org.). Aprender conteúdos e desenvolver capacidades. Tradução: Cláudia Schilling. Porto Alegre: Artmed, 2004.

O livro aborda o processo de tomada de decisões que determina o planejamento do currículo, a partir das capacidades e dos conteúdos a serem desenvolvidos.

COLL, César. Atenção à diversidade e qualidade do ensino. Revista Educação Especial, [S. l.], v. 1, n. 1. p. 7-17, 2012. Disponível em: https://periodicos.ufsm.br/educacaoespecial/ article/view/5001. Acesso em: 30 abr. 2022.

O autor compartilha suas reflexões sobre as implicações de uma concepção inclusiva na educação, que considera a diversidade como inerente à condição humana e ao processo de ensino e aprendizagem.

COLL, César. Psicologia e currículo: uma aproximação psicopedagógica à elaboração do currículo escolar. São Paulo: Ática, 2003.

Nesse livro, são apresentadas considerações sobre propostas curriculares que contribuam para o planejamento do ensino, bem como a ação efetiva do processo educativo.

CUCCIOLI, Eliana. Superando desafios ao avaliar a aprendizagem matemática. In: LOPES, Celi Espasandin; MUNIZ, Maria Inês Sparrapan (org.). O processo de avaliação nas aulas de matemática. Campinas: Mercado das Letras, 2010. Esse livro trata sobre a importância de tornar os estudantes partícipes das práticas avaliativas.

D’AMBRÓSIO, Ubiratan. Cultura de paz e pedagogia da sobrevivência. In: Cultura de paz: da reflexão à ação; balanço da Década Internacional da Promoção da Cultura de Paz e Não Violência em Benefício das Crianças do Mundo. Brasília, DF: Unesco; São Paulo: Associação Palas Athena, 2010. Disponível em: https://unesdoc.unesco.org/ark:/48223/ pf0000189919?locale=en. Acesso em: 8 jul. 2022.

Convidado para a palestra magna da série de debates, Ubiratan D’Ambrósio apresenta reflexões acerca da cultura de paz, apresentando-a como necessária à sobrevivência humana.

D’AMBROSIO, Ubiratan. Etnomatemática: elo entre as tradições e a modernidade. Belo Horizonte: Autêntica, 2005.

O autor apresenta reflexões acerca da Etnomatemática, conceito do qual é um dos fundadores, e propicia uma análise da influência cultural da Matemática.

DEMO, Pedro. Professor/Conhecimento. Brasília, DF: UnB, 2001. p. 1-12. Disponível em: http://funab.se.df.gov. br/wp-content/uploads/2018/11/Demo-2001.-ProfessorConhecimento.pdf. Acesso em: 8 jul. 2022.

Nesse artigo, o autor discorre sobre a necessidade da pesquisa científica para a formação humana, destacando ainda as características necessárias ao professor nessa perspectiva.

DIAS, Cláudia; FERNANDES, Denise. Pesquisa e método científicos. Brasília, DF: UFPR, 2000. Disponível em: https:// docs.ufpr.br/~niveam/micro%20da%20sala/aulas/tecnicas_ de_pesquisa/pesquisacientifica.pdf. Acesso em: 8 jul. 2022.

Nessa publicação, as autoras apresentam diferentes definições de ciência, pesquisa e método científicos, buscando traçar um paralelo entre o conhecimento científico e o popular.

FREIRE, Paulo. Pedagogia da autonomia: saberes necessários à prática educativa. 53. ed. São Paulo: Paz e Terra, 2016.

O autor apresenta considerações acerca da formação de professores e de aprimoramento da prática educativa capaz de proporcionar uma aprendizagem eficiente para tornar os estudantes autônomos, críticos e atuantes.

GALVÃO, Eliane Cruz de Santana; ISOTANI, Seiji; TODA, Armando. Pensamento computacional como forma de avançar na aprendizagem de Matemática: um compartilhamento entre o pensamento computacional e a matemática.

In: PÓS-GRADUAÇÃO EM COMPUTAÇÃO APLICADA

À

EDUCAÇÃO, 1., 2020, São Paulo. Anais […]. São Paulo: CAE/ICMC/USP, 2020. Disponível em: https://especializa cao.icmc.usp.br/documentos/tcc/eliane_galvao.pdf. Acesso em: 9 jul. 2022.

Os autores abordam o uso do pensamento computacional como estratégia para resolução de problemas matemáticos.

GRÁCIO, Rui Alexandre Lalanda Martins. Nova retórica e tradição filosófica. Caderno de Filosofias: Argumentação, Retórica, Racionalidades, [S. l.], v. 5, p. 55-69, 1992. Disponível em: https://www.ruigracio.com/pessoal/pdf/NovaRetorica. pdf. Acesso em: 5 jul. 2022.

O artigo traz considerações a respeito da teoria da argumentação do ponto de vista filosófico.

HOFFMANN, Jussara Maria Lerch. Avaliação mediadora: uma prática em construção da pré-escola à universidade. 33. ed. Porto Alegre: Mediação, 2014.

A autora apresenta práticas avaliativas desenvolvidas em vários segmentos de ensino, da Educação Infantil ao Ensino Superior. JAPIASSÚ, Hilton; MARCONDES, Danilo. Dicionário básico de filosofia. 3. ed. rev. e amp. Rio de Janeiro: Zahar, 2001. Disponível em: http://raycydio.yolasite.com/resources/dicionario_de_filoso fia_japiassu.pdf. Acesso em: 13 jul. 2022.

Esse dicionário apresenta o significado de termos e conceitos filosóficos, auxiliando na compreensão desses conceitos.

KOVALSKI, Larissa. O pensamento analógico na matemática e suas implicações na modelagem matemática para o ensino. Dissertação (Mestrado em Educação em Ciências e em Matemática) – Universidade Federal do Paraná, Curitiba, 2016. Disponível em: https://acervodigital.ufpr.br/bitstream/han dle/1884/56193/R%20-%20D%20-%20LARISSA%20KOVALSKI. pdf?sequence=1&isAllowed=y. Acesso em: 27 jul. 2022.

O desenvolvimento do raciocínio matemático por meio da indução, abdução e analogia e as potencialidades desse tipo de pensamento na modelagem matemática.

MACEDO, Lino de. Ensaios construtivistas. São Paulo: Casa do Psicólogo, 1994.

O livro reúne textos baseados na experiência do autor acerca da teoria construtivista aplicada à Psicologia e à Educação.

MALHEIROS, Bruno Taranto. Didática geral. São Paulo: LTC, 2012.

O autor trata dos conceitos básicos da Didática, destacando a diferença entre Educação, Pedagogia e Didática, e mostra métodos práticos e técnicas de aprendizagem.

ONUCHIC, Lourdes de La Rosa. Ensino-aprendizagem de Matemática através da resolução de problemas. In: BICUDO, Maria Aparecida Viggiani (org.). Pesquisa em Educação

Matemática: concepções e perspectivas. São Paulo: Editora da Unesp, 1999. Disponível em: http://www.im.ufrj.br/~ nedir/disciplinas-Pagina/Lourdes_Onuchic_Resol_Problemas .pdf. Acesso em: 27 jul. 2022.

A autora apresenta reflexões acerca do ensino de Matemática por meio de resoluções de problemas.

ONUCHIC, Lourdes de La Rosa; ALLEVATO, Norma Suely Gomes. Pesquisa em resolução de problemas: caminhos, avanços e novas perspectivas. Boletim de Educação

Matemática, Rio Claro, v. 25, n. 41, p. 73-98, dez. 2011. As autoras apresentam os resultados de uma pesquisa sobre a importância e a influência da resolução de problemas na construção de conhecimentos em Matemática.

ORGANIZAÇÃO DAS NAÇÕES UNIDAS PARA A EDUCAÇÃO, A CIÊNCIA E A CULTURA. Cultura de paz no Brasil. Brasília, DF: Unesco, [201-]. Disponível em: https://pt.unesco.org/fieldo ffice/brasilia/expertise/culture-peace. Acesso em: 8 jul. 2022.

A Organização das Nações Unidas para a Educação, a Ciência e a Cultura (Unesco) apresenta orientações para a promoção da cultura de paz na educação.

ORGANIZAÇÃO DAS NACÕES UNIDAS PARA A EDUCAÇÃO, A CIÊNCIA E A CULTURA. Educação para a cidadania global: preparando alunos para os desafios do século XXI. Brasília, DF: Unesco, 2015. Disponível em: https://unesdoc. unesco.org/ark:/48223/pf0000234311/PDF/234311por.pdf. multi. Acesso em: 9 jul. 2022.

O livro trata da importância de uma educação efetiva para a resolução de questões globais e da formação de cidadãos preparados para os desafios do século XXI.

PASSOS, Cármen Lúcia Brancaglion; ROMANATTO, Mauro Carlos. A matemática na formação de professores dos anos iniciais: aspectos teóricos e metodológicos. São Carlos: Editora da UFSCar, 2010.

Esse livro traz uma concepção histórica de alguns assuntos em Matemática com o objetivo de contextualizar situações e facilitar a prática docente.

PEREIRA, Adriana Soares et al Metodologia da pesquisa científica. Santa Maria: UFSM/NTE, 2018. Disponível em: https://www.ufsm.br/app/uploads/sites/358/2019/02/ Metodologia-da-Pesquisa-Cientifica_final.pdf. Acesso em: 8 jul. 2022.

O livro apresenta as principais etapas da pesquisa científica, discorrendo também sobre seus métodos e caracterizando-a como forma de construção do saber.

MATA-PEREIRA, Joana; PONTE, João Pedro da. Promover o raciocínio matemático dos alunos: uma investigação baseada em design Bolema, Rio Claro, v. 32, n. 62, p. 781-801, dez. 2018. Disponível em: https://www.scielo.br/j/bolema /a/JbLWRnZGLJmBYCNYRm4P76J/?format=pdf&lang=pt. Acesso em: 5 jul. 2022.

Nesse artigo, os autores abordam como alguns princípios de design podem favorecer a construção de conhecimentos matemáticos e otimizar a ação do professor.

PERRENOUD, Philippe. Dez novas competências para ensinar. Porto Alegre: Artmed, 2000.

O autor trata da importância do desenvolvimento de um conjunto de competências emergentes que contribuem para a luta contra o fracasso escolar e desenvolvem a cidadania.

POLYA, George. Mathematics and plausible reasoning: Induction and analogy in mathematics. New Jersey: Princeton University Press, 1954a. v. I. Disponível em: https://www.isinj.com/ mt-usamo/Mathematics%20and%20Plausible%20Reasoning%20 I%20-%20Polya%20G.pdf. Acesso em: 27 jul. 2022.

Esse livro trata de aspectos do raciocínio matemático por analogia relacionado ao pensamento inferencial.

PONTE, João Pedro. Tecnologias de informação e comunicação na formação de professores: que desafios? Revista Iberoamericana de Educação, Lisboa, n. 24, p. 63-90, 2000. Disponível em: https://repositorio.ul.pt/handle/10451/3993. Acesso em: 3 ago. 2022.

Nesse artigo, o autor analisa os impactos e as contribuições das tecnologias da informação e comunicação (TIC) na prática docente. POWELL, Arthur; BAIRRAL, Marcelo. A escrita e o pensamento matemático: interações e potencialidades. Campinas: Papirus, 2006. (Perspectivas em educação matemática).

Nesse livro, discute-se como diferentes atividades de escrita podem auxiliar o desenvolvimento da aprendizagem matemática. SANTOS, Márcia Regina Mendes. O estudo das inferências na compreensão do texto escrito. Dissertação (Mestrado em Linguística) – Faculdade de Letras da Universidade de Lisboa, Lisboa, Portugal, 2008. Disponível em: https://repos itorio.ul.pt/bitstream/10451/378/1/19638_ulfl062026_tm.pdf. Acesso em: 7 jul. 2022.

Nesse trabalho, a autora aborda o pensamento inferencial envolvido na leitura e compreensão de textos escritos e como o desenvolvimento desse pensamento pode auxiliar na comunicação de ideia em diversas áreas do conhecimento.

SCHROEDER, Thomas Leonard; LESTER JUNIOR, Frank Klein. Developing understanding in mathematics via problem solving. In: TRAFTON, Paul R.; SCHULTE, Albert P. (ed.). New directions for elementary school mathematics

Reston: NCTM, 1989.

Esse artigo traz reflexões acerca da relevância do método de resolução de problemas na compreensão matemática de estudantes da Educação Básica.

VYGOTSKY, Lev Semionovitch (org.). A formação social da mente: o desenvolvimento dos processos psicológicos superiores. Tradução: José Cipolla Neto, Luís Silveira Menna Barreto, Solange Castro Afeche. São Paulo: Martins Fontes, 2007.

Esse livro reúne alguns dos ensaios mais importantes de Vygotski, organizados e editados por estudiosos da obra desse pensador.

Matemática

JOSÉ RUY GIOVANNI JÚNIOR

Licenciado em Matemática pela Universidade de São Paulo (USP). Professor e assessor de Matemática em escolas de Ensino Fundamental e Ensino Médio desde 1985.

D2_AV1-MAT-F2-2103-V8-INICIAIS-001-011-LA-G24.indd

COMPONENTE CURRICULAR: MATEMÁTICA

Copyright © José Ruy Giovanni Júnior, 2022.

Direção-geral Ricardo Tavares de Oliveira

Direção de Conteúdo e Negócios Cayube Galas

Direção editorial adjunta Luiz Tonolli

Gerência editorial Roberto Henrique Lopes da Silva Edição João Paulo Bortoluci (coord.)

Bianca Cristina Fratelli, Carlos Eduardo Bayer Simões Esteves, Janaina Bezerra Pereira, Juliana Montagner

Preparação e Revisão Maria Clara Paes (coord.)

Yara Affonso

Gerência de produção e arte Ricardo Borges

Design Andréa Dellamagna (coord.)

Sergio Cândido

Projeto de capa Sergio Cândido

Imagem de capa Jagerion Caiph/Shutterstock.com

Arte e Produção Isabel Cristina Corandin Marques (coord.)

Debora Joia, Eduardo Benetorio, Gabriel Basaglia, Kleber Bellomo Cavalcante, Rodrigo Bastos Marchini

Diagramação Wym Design

Coordenação de imagens e textos Elaine Bueno Koga

Licenciamento de textos Amandha Baptista

Iconografia Karine Ribeiro de Oliveira

Emerson de Lima, Leticia dos Santos Domingos (trat. imagens)

Ilustrações Alex Argozino, Bentinho, Daniel Bogni, Fabio Eugenio, Hannah Cardoso, Leo Teixeira, Marcos Guilherme, MW Editora e Ilustrações, Pedro Paulo Melara, Roberto Zoellner, Wandson Rocha, Sonia Vaz, Dacosta Mapas

Dados Internacionais de Catalogação na Publicação (CIP) (Câmara Brasileira do Livro, SP, Brasil)

Giovanni Júnior, José Ruy

A conquista matemática : 8o ano : ensino fundamental : anos finais / José Ruy Giovanni Júnior. – 1. ed. – São Paulo : FTD, 2022.

Componente curricular: Matemática. ISBN 978-85-96-03441-8 (aluno)

ISBN 978-85-96-03442-5 (professor)

1. Matemática (Ensino fundamental) I. Título. 22-114534 CDD-372.7

Índices para catálogo sistemático:

1. Matemática : Ensino fundamental 372.7

Reprodução proibida: Art. 184 do Código Penal e Lei 9.610 de 19 de fevereiro de 1998. Todos os direitos reservados à

Cibele Maria Dias - Bibliotecária - CRB-8/9427 Em respeito ao meio ambiente, as folhas deste livro foram produzidas com fibras obtidas de árvores de florestas plantadas, com origem certificada.

EDITORA FTD

Rua Rui Barbosa, 156 – Bela Vista – São Paulo – SP CEP 01326-010 – Tel. 0800 772 2300

Caixa Postal 65149 – CEP da Caixa Postal 01390-970 www.ftd.com.br central.relacionamento@ftd.com.br

D2_AV1-MAT-F2-2103-V8-INICIAIS-001-011-LA-G24.indd 2

Impresso no Parque Gráfico da Editora FTD

CNPJ 61.186.490/0016-33

Avenida Antonio Bardella, 300

Guarulhos-SP – CEP 07220-020

Tel. (11) 3545-8600 e Fax (11) 2412-5375

APRESENTAÇÃO

Por que estudar Matemática? Quais são as aplicações da Matemática no cotidiano? Essas são dúvidas muito comuns, que você também

pode ter. A Matemática está presente em diversas situações do dia a dia, seja em uma contagem, em uma brincadeira, seja nos mais modernos estudos para auxiliar no desenvolvimento de novas tecnologias. Ela ajuda a decidir se uma compra deve ser paga à vista ou a prazo, a entender as variações da inflação e dos juros, a medir os índices sociais de um país, a compreender e organizar informações, a preservar o meio ambiente, entre outros usos, incluindo as aplicações de figuras geométricas e medidas na arquitetura, na arte e na agricultura.

É importante considerar que a aplicação da Matemática no cotidiano ocorre como resultado do desenvolvimento e do aprofundamento de conceitos nela presentes. Como em todas as áreas do conhecimento, para compreender e aplicar Matemática, são necessários estudo e dedicação.

Nesta coleção, apresentamos a você as bases desse processo de aquisição de conhecimento, com uma linguagem de fácil compreensão, porém com o rigor que a Matemática exige.

Hoje, vivemos em um mundo em constante e rápida transformação, e a Matemática pode nos ajudar a entender essas transformações. Adquirir conhecimento matemático significa estar integrado às mudanças do mundo. Então, vamos entender e fazer Matemática! O autor

CONHEÇA SEU LIVRO

ABERTURA DE UNIDADE

UNIDADE

POLÍGONOS E TRANSFORMAÇÕES NO PLANO 6

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

Todo arquivo digital do tipo bitmap é composto de pixels. Um pixel é a menor unidade de uma imagem representada na tela de um computador. Ao ampliar uma imagem no computador, podemos notar que ela é formada por figuras bem pequenas que lembram quadrados, os pixels. Essas figuras, juntas, formam uma imagem nítida. Somente na ampliação ou na impressão de uma imagem podemos perceber a principal importância da quantidade de pixels que a compõe. Em uma máquina fotográfica digital, por exemplo, conhecemos essa quantidade pelo nome megapixel cujo valor, nesse aparelho, diz quantos pixels vão compor uma fotografia feita nele. Como um pixel não possui medidas definidas, quanto mais megapixels houver em uma fotografia, menores serão as medidas do pixel e mais essa imagem poderá ser ampliada, pois cada pixel sofrerá menos distorção. Observe um exemplo de imagem no qual ampliamos uma parte da fotografia para que possamos perceber os pixels e sua formação poligonal.

178

D2-AV2-MAT-F2-2103-V8-U6-178-211-LA-G24.indd

DENSIDADE DEMOGRÁFICA O cálculo da densidade demográfica de uma região é uma aplicação do conceito de razão entre duas grandezas. Esse resultado é obtido por meio da razão entre a quantidade de habitantes e a área da região por eles ocupada. densidadedemográfica quantidade de habitante área da egião ocupada Acompanhe a situação a seguir. O estado de Tocantins, situado na Região Norte do Brasil, ocupa uma área de aproximadamente 277 424 km2 Em 2021, de acordo com o IBGE, a população estimada desse estado era de 1 607 363 habitantes. Qual era a densidade demográ- fica aproximada desse estado em 2021? Elaborado com base em: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Cidades Estados: Tocantins. IBGE Rio de Janeiro, [2021?]. Disponível em: https://www.ibge.gov.br/cidades-e-estados/ to.html. Acesso em: 6 jul. 2022.

INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA.

De acordo com os dados apresentados, temos: densidade demográfica 1 607363hab 277424 km2 5,8 hab./km

hab./km2

SAIBA QUE

em 2021, a densidade demográfica do estado de Tocantins era de aproximadamente

A cada 10 anos, o IBGE realiza o Censo Demográfico ou Recenseamento Demográfico, que é uma pesquisa para reunir informações sobre a população brasileira. Essas informações são importantes para que ogoverno possa criar políticas públicas mais eficientes para atender às necessidades da sociedade. No Brasil, o primeiro Censo ocorreu em 1872, mas essa ideia de recensear a população e, com base nesses dados, obter informações sobre a sociedade não é recente; romanos e gregos já realizavam censos antes de Cristo. Como não foi possível a realização do Censo no Brasil em 2020, por causa da pandemia de covid-19, o recenseamento ficou previsto para 2022, quando seriam atualizados os dados sobre a população brasileira. Elaborado com base em: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Histórico dos Censos: introdução. Memória IBGE Rio de Janeiro, [2022?]. Disponível em: https://memoria.ibge.gov.br/historia-do-ibge/historico-dos-censos/panorama-introdutorio.html. Acesso em: 6 jul. 2022.

Representação ampliada de um pixel que lembra um quadrado. ED IA RT

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Agora, pense e responda no caderno. Os pixels podem lembrar a forma de quadrados ou retângulos, mas podemos compor imagens no cotidiano com outras figuras poligonais. Em que situações você já se deparou com imagens formadas por outras figuras poligonais?

• De que outras maneiras podemos compor imagens por meio da composição dessas outras figuras poligonais? De acordo com o texto, quanto maior a quantidade de megapixels, maior a qualidade da imagem de uma fotografia. Por quê?

Resposta pessoal. Exemplo de resposta: Podemos justapor figuras poligonais para compor mosaicos. Porque a imagem poderá ser ampliada sem sofrer distorção.

14/08/22 17:19

ATIVIDADES

Responda às questões no caderno.

0,40 kg/dm

1. Um bloco maciço de madeira tem 14 kg de massa e ocupa um volume de 35 dm³. Qual é a densidade desse bloco?

2. Um fio de platina tem um volume de 0,2 cm³. Sabendo que a massa do fio é de 4,3 g, determine a densidade desse metal. 21,5 g/cm

3. A água-marinha é uma das pedras se- mipreciosas mais admiradas em todo omundo. Suponha que uma pedra de água-marinha tenha 8,1 g de massa e 3 cm³ de volume. Qual é a densidade dessa pedra? 2,7 g/cm

4,28 hab./km

4. Uma região do interior do Brasil tem uma população de 64200 habitantes e ocupa uma área de 15000 km². Qual é a densidade demográfica dessa região?

5. A Grécia, país situado no continente europeu, tem cerca de 132000 km² de área. Em 2010, ela tinha uma população aproximada de 11200000 habitantes. Qual era a densidade demográfica aproximada da Grécia nesse ano?

Aproximadamente 84,8 hab./km

ATIVIDADES Imagem da Acrópole de Atenas (Grécia), 2019.

6. Dois bairros de um município, Água Branca e Pedra Azul, têm os seguintes dados referentes à população e à área correspondente. Bairro População Área (em km²) Água Branca 125 000 36 Pedra Azul 85 000 30

8. Caio errou a ordem de grandeza do território argentino, que é de cerca de 2 800 000 km

Qual dos dois bairros tem a maior densidade demográfica? Água Branca.

7. No Rio Grande do Norte, o turismo é a atividade que mais gera empregos no estado. Entre seus inúmeros atrativos, podemos citar a beleza natural, o ar- tesanato (cerâmica, cestaria, rendas e bordados) e a comida típica. Em 2010, esse estado tinha cerca de 3 168 027 habitantes, segundo o Censo do IBGE, e uma área de 52 810 km². Determine a densidade demográfica desse estado. Aproximadamente 59,99 hab./km

No decorrer das Unidades, são apresentadas diferentes atividades. Com elas, você poderá desenvolver estratégias para resolver e elaborar problemas e compartilhá-las com os colegas.

Forte dos Reis Magos. Natal (RN), 2022. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

8. Em 2010, a população argentina

SAIBA QUE

Traz informações complementares importantes, que você pode consultar de maneira prática ao longo dos capítulos.

SOLARYSYS/ALAMY/FOTOARENA

Recife de corais no Mar Vermelho, Egito, 2020. SOLARYSYS/ALAMY/FOTOARENA

D2-AV1-MAT-F2-2103-V8-U6-178-211-LA-G24.indd 179

Com um estilo diferenciado, as páginas de abertura trazem imagens, textos e questões sobre conceitos que serão estudados em cada Unidade.

D2_AV2-MAT-F2-2103-V8-INICIAIS-001-011-LA-G24.indd 4

TRATAMENTO DA INFORMAÇÃO

Nesta seção, você vai observar como a organização e a análise de dados facilitam o entendimento de informações, além de conhecer conceitos de probabilidade e estatística.

286

EDUCAÇÃO FINANCEIRA

JURO ZERO E JURO EMBUTIDO

Atenção, consumidor: ‘juro zero’ é estratégia de marketing Entreumapromoçãoeoutranocomércio,édifícilnãoaderiraumparcelamentoalardeado como juro zero. Impulsionada pelo aumento da renda e pelo avanço no nível de emprego no país, a armadilha dos juros embutidos, escondida no desconto à vista, ganha força no comércio.Aslojascostumamanunciaromesmopreçoàvistaeparaparcelamentosemjuros, masésóchorarumpouquinhoqueoclienteconsegueumdescontosecompraremumavez só. Isso mostra que esse valor menor é o preço real do produto, e o preço cheio embute juros.

[...] O grande risco que o consumidor corre é de fazer das compras a prazo um hábito, pagando juros sem saber e, assim, comprometendo seu orçamento e fazendo dívidas financeiras, em que os juros são mais altos. É melhor juntar e comprar por um preço melhor, já que o juro zero é uma estratégia de marketing do comércio [...].

[...] ROSA, Bruno. Atenção, consumidor: ‘juro zero’ é estratégia de marketing Extra, Rio de Janeiro, 23 jul. 2011.

Disponível em: http://extra.globo.com/noticias/economia/atencaoconsumidor-juro-zero -estrategia-demarketing-2294212.html. Acesso em: 31 maio 2022.

Para entender como são calculados os preços com juro embutido, acompanhe a situação a seguir.

Uma loja oferece duas opções de pagamento na compra de uma mala de viagem como a da imagem. Vamos analisar cada uma das condições.

Se a loja oferece um desconto no pagamento à vista em dinheiro, então, os valores da compra a prazo e da compra à vista são diferentes, ou seja, existe juro embutido no valor da compra a prazo. Vamos calcular o valor e a taxa de juro dessa compra a prazo.

O valor da mala é R$ 500,00 e pode ser pago em duas parcelas iguais de R$ 250,00. Com o desconto de 5%, o cliente paga R$ 500 0,95 R$ 475,00 à vista, em dinheiro.

Para calcular a taxa de juro embutido cobrada pela loja, vamos subtrair de R$ 475,00 os R$ 250,00, que correspondem ao valor da primeira parcela. Essa parcela não tem juro, pois foi paga no ato da compra: R$ 475,00 R$ 250,00 R$ 225,00.

O restante, R$ 225,00, após um mês, com o juro, resulta em uma dívida de R$ 250,00. Portanto, o juro embutido dessa compra é R$ 25,00, e a taxa de juro é aproximadamente 11%.

Responda à questão no caderno.

• Calcule qual seria a taxa de juro embutido no pagamento em duas vezes de R$ 150,00 caso o desconto do pagamento à vista fosse de 8%. Aproximadamente 19%.

TECNOLOGIAS

Nesta seção, você é convidado a utilizar diferentes recursos digitais para resolver e elaborar problemas. São apresentadas, ainda, noções relacionadas à lógica de programação. D2_AV5-MAT-F2-2103-V8-INICIAIS-001-011-LA-G24.indd

INFORMAÇÃO TRATAMENTO

DA

INTERPRETANDO INFORMAÇÕES

O mercado de trabalho no Brasil e a inclusão de pessoas com deficiência

Pessoa com deficiência exercendo atividade laboral em ambiente de trabalho. Fotografia de 2022.

uma empresa com mais de 100 empregados. Leia a seguir o que diz o referido artigo.

As pessoas com deficiência enfrentam muitos desafios no dia a dia e, principalmente, no mundo do trabalho. É de fundamental importância para o exercício da cidadania que elas sejam reconhecidas como sujeitos de direito, bem como pela sua força de trabalho, sendo direcionadas a cargos e funções de acordo com suas especificidades e habilidades. Assim, poderão superar desafios e preconceitos. Os direitos ao acesso e à participação no mercado de trabalho precisam ser materialmente garantidos, de modo que muitos espaços que careçam de adaptações sejam ajustados para atender às condições de acessibilidade. O artigo 93 da lei n 8.213 de 1991 especifica a quantidade de vagas que devem ser preenchidas por pessoas reabilitadas ou com deficiência em

ou pessoas portadoras de deficiência, habilitadas, na seguinte proporção: I – até 200 empregados....................................2%; II – de 201 a 500..................................................3%; III – de 501 a 1000.............................................4%; IV – de 1001 em diante....................................5%. BRASIL. Lei n 8.213, de 24 de julho de 1991 Dispõe sobre os Planos de Benefícios da Previdência Social e dá outras providências. Brasília, DF: Casa Civil, 1991. Disponível em: http://www.planalto.gov.br/ccivil_03/leis/l8213cons.htm. Acesso em: 4 jul. 2022.

Art. 93. A empresa com 100 (cem) ou mais empregados está obrigada a preencher de

2% (dois por cento) a 5% (cinco por cento) dos seus cargos com beneficiários reabilitados

ARTKIO/SHUTTERSTOCK.COM Com base nessas informações, responda às questões no caderno. 1. Considere uma empresa que tem 1500 funcioná- rios contratados. De acordo com o artigo de lei citado anteriormente, quantas dessas vagas devem ser ocupadas por beneficiários reabilitados ou pessoas com deficiência habilitadas? No caso de uma empresa com 150 funcionários, qual seria essa quantidade de vagas? 75 vagas; 3 vagas.

D2_AV1-MAT-F2-2103-V8-U9-262-2 LA-G24 286 13/ 8/

VIKKY MIR/SHUTTERSTOCK.COM

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

para a inserção de pessoas com deficiência no mercado de trabalho? Você considera importante a existência de legislações como essa? 3. Observe o gráfico a seguir e responda às questões.

2. Em seu entendimento, esse artigo de lei tem contribuído, ao longo desses anos,

9% 10,5% 16,1% 17,7%

1,6%

45%

EDITORIA DE ARTE Distribuição dos vínculos formais de trabalho no Brasil, por tipo de deficiência, em 2019 Física Auditiva Visual Reabilitado Mental Múltipla

Elaborado com base em: DEPARTAMENTO INTERSINDICAL DE ESTATÍSTICA E ESTUDOS SOCIOECONÔMICOS (DIEESE). Inclusão da pessoa com deficiência no mercado de trabalho. Nota técnica, São Paulo, n. 246, p. 1-22, 20 nov. 2020. Disponível em: https:// www.dieese.org.br/notatecnica/2020/ notaTec246InclusaoDeficiencia.html.

Acesso em: 4 jul. 2022.

a) Qual era o tipo de deficiência da maioria das pessoas com deficiência com vínculos formais

de trabalho no Brasil em 2019? b) Considerando as pessoas com deficiência visual e as pessoas com deficiência mental, juntas, podemos afirmar que, em 2019, elas correspondiam aproximadamente a um quarto dos

4. Analisando a tabela a seguir, identifique a faixa salarial em que se verificava o rendimento médio da maioria das pessoas com deficiência no Brasil em 2019.

vínculos formais de trabalho ocupados por pessoas com deficiência?

Deficiência física. Sim, pois 16,1% + 9% 25,1%.

De 1 a 2 salários mínimos. Distribuição dos rendimentos médios de pessoas com deficiência no Brasil, em 2019 Faixa salarial (salário mínimo*)

EDUCAÇÃO FINANCEIRA

Conceitos de educação financeira são apresentados para desenvolver reflexões sobre temas relevantes, como consumo consciente, planejamento financeiro, economia etc.

TECNOLOGIAS

RESOLUÇÕES DE EQUAÇÕES UTILIZANDO UM SOFTWARE O Scratch é uma linguagem gratuita de programação em blocos. Voltada para crianças e jovens, essa linguagem foi desenvolvida para facilitar, de modo prático e intuitivo, a criação de programas.

Nesta seção, vamos utilizar algumas ferramentas do Scratch para criar um programa em blocos, que resolve equações de 1 grau, reduzidas na forma ax b (em que a 5 0). Lembre-se de que, conforme estudamos, a solução de equações escritas nessa forma é dada por x b a com a 5 0. No Scratch, vamos nos referir aos coeficientes a e b como variáveis, que são os valores que vamos fornecer ao programa criado para que nos apresente a solução. Acesse a página inicial do Scratch, disponível em https://scratch.mit.edu/projects/editor/? tutorial=getStarted (acesso em: 4 jul. 2022) e realize os passos a seguir.

1 Na aba Código selecione o menu Eventos e arraste o bloco para a janela principal.

2 Para criar as variáveis do programa, que correspondem aos valores que vamos fornecer, selecione o menu Variáveis e clique em Em seguida, digite a no campo Nome da nova variável e clique em OK

3 A variável a está criada. Repita o passo 2 para criar a variável b Feito isso, as variáveis a b deverão constar no menu Variáveis e na tela em que aparece o ator do programa. Para construir a estrutura do algoritmo do programa, vamos utilizar os comandos do menu Sensores e os de mudança de variáveis do menu Variáveis

4 Clique no menu Sensores e arraste o bloco para a tela prin- cipal, encaixando-o no bloco lá existente. Em seguida, digite Insira o valor de a no campo digitável desse bloco.

5 Selecione o menu Variáveis e arraste o bloco para a tela principal, encaixando-o no último bloco colocado nessa tela. Em seguida, clique no menu Sensores e arraste o bloco para o campo digitável de

6 Repita o passo 4 digitando Insira o valor de b no campo digitável; em seguida, repita o passo 5 alterando para no bloco corres- pondente. Você vai obter a estrutura mostrada na Figura 1

Agora, vamos construir o comando que contém a operação de divisão, que possibilita ao ator do programa revelar a solução da equação. 7 Selecione o menu Operadores e arraste a operação para a tela principal. Em seguida, clique no menu Variáveis e arraste as variáveis para esse operador, obtendo

8 Selecione o menu Aparência e arraste o bloco encaixando-o no conjunto construído até então.

9 Para concluir, clique no menu Operadores e arraste o operador para o campo do último bloco encaixado no conjunto. Em seguida, digite A solução da equação é no primeiro campo digitável desse operador e arraste o quociente para o segundo campo, obtendo o algoritmo indicado na Figura 2 Para testar o algoritmo, descubra a solução da equação escrita na forma 2x 5. Clique, inicialmente, em Depois, siga os comandos dados pelo ator e verifique se o resultado obtido é 2,5. Agora, junte-se a um colega, e respondam às questões no caderno.

1. Utilizando o programa criado, obtenha a solução de cada equação a seguir. a) 5x 2 0,4

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd

D2_AV5-MAT-F2-2103-V8-U9-262-291-LA-G24.indd

D2_AV1-MAT-F2-2103-V8-INICIAIS-001-011-LA-G24.indd

MQIMAGENS/SHUTTERSTOCK.COM

D2_AV1-MAT-F2-2103-V8-INICIAIS-001-011-LA-G24.indd

7 8

ENNS/SHUTTERSTOCK.COM D2_AV1-MAT-F2-2103-V8-INICIAIS-001-011-LA-G24.indd

Competências gerais:

• 2, 6 e 7

Competência específica:

• 5

Habilidades:

Números

• EF08MA04 • EF08MA05

Tratamento da informação

• EF08MA23

Temas Contemporâneos

Transversais:

• Educação Financeira

• Educação Ambiental

• Educação para o Consumo

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em quatro capítulos.

O primeiro capítulo aborda o conjunto dos números racionais, discutindo a localização e comparação dos números racionais na reta numérica. Depois, é feita uma retomada das operações com números racionais. No segundo capítulo, inicia-se o estudo com dízimas periódicas simples e compostas. Depois, trabalha-se fração geratriz tanto de dízimas periódicas simples como de dízimas periódicas compostas, contribuindo para o desenvolvimento da habilidade

EF08MA05. No terceiro capítulo, o estudo dos conjuntos numéricos é ampliado, a partir da apresentação dos números irracionais e do conjunto dos números reais. No quarto capítulo, trabalha-se com porcentagem, por meio da resolução de problemas com e sem apoio da calculadora.

NÚMEROS REAIS E PORCENTAGEM 1

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

A educação financeira é um tema importante em qualquer idade, pois, além de planejar gastos, é fundamental saber lidar com a quantidade excessiva de propagandas que oferecem produtos e serviços.

Além das propagandas dos produtos, muitas lojas divulgam as opções de pagamento: parcelado sem juro, parcelado com juro e pagamento à vista. Em alguns casos, há um bom desconto se o produto for pago à vista.

Para ter uma vida financeira saudável, é necessário evitar as compras por impulso e, sempre que possível, comprar apenas o que se pode pagar.

OBJETIVOS

• Retomar os conjuntos numéricos já estudados (naturais, inteiros e racionais) e as operações matemáticas básicas nesses conjuntos.

• Reconhecer uma dízima periódica simples e uma dízima periódica composta.

• Obter a fração geratriz de uma dízima periódica.

• Identificar um número irracional e compreender a formação do conjunto dos números reais.

• Resolver e elaborar problemas envolvendo o conceito de porcentagem.

• Conhecer e aplicar o conceito de juro simples em diferentes situações.

• Utilizar planilhas eletrônicas para resolver problemas relacionados a porcentagens e cálculo de juro.

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

Uma sugestão de encaminhamento para trabalhar com esta abertura de Unidade é incentivar os estudantes a falar sobre a diferença entre desejo e necessidade na hora de comprar de produtos. Outra discussão importante, é falar sobre a importância do planejamento financeiro para conseguir realizar os projetos pessoais. Comentar com eles que um planejamento detalhado deve considerar muitos elementos. Por exemplo, além do preço do item que se deseja, o tempo é um fator importante, é preciso definir se é algo que será conquistado em um período curto, médio ou a longo prazo. Tais abordagens contribuem para o desenvolvimento dos Temas Contemporâneos Transversais Educação Financeira e Educação para o Consumo e da competência geral 6.

Pode-se ainda discutir a diferença entre poupar para comprar à vista com interesse no desconto, geralmente, oferecido pelas lojas no pagamento à vista.

Agora, responda às questões no caderno.

• O que você entende por ter uma vida financeira saudável?

• Qual é a diferença entre comprar algo à vista e comprar a prazo?

• Você sabe o que é juro? Você sabe explicar como ele funciona?

JUSTIFICATIVAS DOS OBJETIVOS

Justificam-se os objetivos desta Unidade dado que são conteúdos que os estudantes aplicam ao analisar acontecimentos no mundo ao redor deles. Por exemplo: na seção Tratamento da informação, debater recursos hídricos permite abordagens do Tema Contemporâneo Transversal (TCT) Educação Ambiental, da competência geral 7 e da habilidade EF08MA23.

A proporção ocupada pela Amazônia é tema da seção Por toda parte, favorecendo o desenvolvimento do TCT Educação Ambiental e da competência geral 2.

Na seção Educação financeira, o tema dos bancos propicia explorar aspectos do TCT Educação Financeira e do TCT Educação para o Consumo. Na seção Tecnologias, o uso das planilhas eletrônicas para calcular juro simples favorece o desenvolvimento da habilidade EF08MA05.

É possível solicitar que calculem o desconto exibido na imagem para um possível produto, como um televisor ou um smartphone Questionar se esse critério é vantajoso para o cliente ou para a loja. Permitir aos estudantes que compartilhem as respostas e, em seguida, solicitar que citem motivos pelos quais alguns estabelecimentos oferecem descontos a partir de determinado preço e que cuidados devem ser tomados diante de ofertas aparentemente “imperdíveis”. Comentar com eles sobre a necessidade de analisar bastante antes de realizar uma compra, desse modo, evita-se a realização de compras por impulso. Esse tipo de encaminhamento contribui para o desenvolvimento da argumentação dos estudantes.

MARCOS GUILHERME

Respostas na seção Resoluções comentadas deste Manual.

ORIENTAÇÕES DIDÁTICAS

Conjunto dos números racionais

Neste capítulo, é feita uma retomada do conjunto dos números racionais para que, na sequência, os estudantes possam explorar os números irracionais e um novo conjunto numérico: o conjunto dos números reais. Para que essa progressão aconteça, é fundamental que eles tenham compreendido os conjuntos numéricos estudados anteriormente (naturais, inteiros e racionais) e as operações fundamentais com esses conjuntos. Além disso, é relevante que os estudantes consigam localizar um número racional na reta numérica e que compreendam como realizar comparações de números racionais, inclusive utilizando a reta numérica.

Discutir com a turma sobre o significado de cada um dos números que aparecem nas situações propostas no Livro do estudante.

Ao abordarem a definição de números racionais, provocá-los sobre a restrição para o denominador. Pode-se, por exemplo, perguntar: Por que esse número deve ser um número inteiro não nulo? Ao questionar os estudantes sobre essa condição, eles são convidados a refletir sobre as implicações dela. Desse modo, contribui-se para o desenvolvimento da inferência e da argumentação

CONJUNTO DOS NÚMEROS RACIONAIS

Os números racionais estão presentes em diversas situações cotidianas. Vamos analisar algumas dessas situações.

Mariana viajou com sua família para o Chile e, no dia 2 de junho de 2022, experimentou uma temperatura de 7 ° C.

Pedro precisava de uma televisão nova. Pesquisou e encontrou uma de 40 polegadas por R$ 1133,99. Ele negociou as condições de pagamento e conseguiu comprá-

Paula está no 8o ano. Em sua turma há 30 estudantes. As meninas correspondem a 2 3 da turma. Dessa quantidade, 20% usam óculos.

AMPLIANDO

Nas situações apresentadas, temos diversos números: 2; 2022; 7; 40; 1 133,99; 5; 8; 30; 2 3 e 20%. Todos esses números pertencem ao conjunto dos números racionais. Os números racionais podem ser positivos ou negativos.

Todo número racional é o resultado de uma divisão de dois números inteiros, sendo o divisor diferente de zero. De modo geral:

São números racionais todos aqueles que podem ser escritos na forma a b , com a e b inteiros e b 5 0.

Os números racionais positivos, negativos e o zero formam o conjunto numérico denominado conjunto dos números racionais. Esse conjunto é representado por q

Vídeo INTRODUÇÃO aos números racionais. 2014. Vídeo (14min54s). Publicado pelo canal Portal da Matemática OBMEP. Disponível em: https://www.youtube.com/watch?v=2Iuw6UZh0_A. Acesso em: 27 jul. 2022. Nesse link, é possível visualizar uma videoaula na qual é resolvido um problema envolvendo números racionais. Depois, é apresentada a definição do conjunto numérico.

-la em 5 vezes sem juros.

A RETA NUMÉRICA

Vamos retomar como localizar números racionais na reta numérica, observando os exemplos a seguir.

1 Representar na reta numérica o número racional 1 4 + Sabemos que o número 1 4 + está localizado entre os números inteiros 0 e +1. Então, vamos dividir o segmento AB, que vai de 0 até +1, em quatro partes iguais e considerar uma dessas partes, a partir do ponto A para a direita.

ORIENTAÇÕES DIDÁTICAS

A reta numérica

2 Representar na reta numérica o número racional 11 3

Vamos escrever o número 11 3 na forma mista: _= 11 3 3 2 3 Esse número está localizado entre os números inteiros 3 e 4. Então, vamos dividir o segmento MN, que vai de 3 até 4, em três partes iguais e considerar duas dessas partes, a partir do ponto M para a esquerda.

Comparação de números racionais

Vamos relembrar como comparar dois números racionais.

• Todo número racional negativo é menor do que todo número racional positivo. 4,6 , 7,8 1 3 , 13 _, 1 5 3 4

• Todo número racional negativo é menor do que zero.

5 , 0 12,4 , 0 _, 6 11 0

• Na comparação de números racionais positivos, basta escrever todos os números na forma decimal, ou escrever todos eles na forma de fração, e fazer a comparação. Vamos comparar, por exemplo, 12,9 e 96 5 . Temos que 96 5 = 19,2. Assim, como a parte inteira de 19,2 é maior do que a parte inteira de 12,9, temos que 19,2 . 12,9.

• Na comparação de números racionais negativos, será maior aquele que possuir o menor módulo. Vamos comparar, por exemplo, 1,4 e 0,2. Sabemos que | 1,4| = 1,4 e | 0,2| = 0,2. Assim, 0,2 possui o menor módulo, o que significa que está localizado mais próximo de zero na reta numérica.

Dessa maneira, 1,4 , 0,2.

20:27 AMPLIANDO

Atividade complementar

Distribuir papel quadriculado para os estudantes e pedir que, com o auxílio de uma régua, tracem um segmento de reta de 11 centímetros. Em seguida, marcar na extremidade esquerda um ponto e indicar o número 0. A 10 cm desse ponto, marcar outro ponto e indicar o nú-

mero 1. Na extremidade direita do segmento, desenhar a ponta de seta para indicar que a reta numérica continua. Depois, subdividir o segmento de reta entre os pontos 0 e 1 em quatro partes iguais e escrever as frações 1 4 , 2 4 e 3 4 nos pontos correspondentes.

A localização de números racionais na reta numérica pode trazer alguns desafios para os estudantes, principalmente relacionados à subdivisão em partes iguais. Explorar o primeiro exemplo e conversar com os estudantes sobre o tipo de fração representada. Retomar o conceito de fração própria, ou seja, aquela que é menor que 1 inteiro. Desse modo, contribui-se para a compreensão de como localizar corretamente um número racional na reta numérica. No segundo exemplo, ao escrever a fração dada na forma mista, permite-se identificar o intervalo no qual ela está localizada. Chamar a atenção dos estudantes para os números racionais negativos.

Comparação de números racionais

Antes de retomar a comparação de números racionais, sugere-se que seja feita uma retomada de como escrever números racionais na forma decimal, na forma fracionária e vice-versa. Alguns estudantes preferem trabalhar com números decimais; outros preferem a forma fracionária, permitir que realizem os cálculos da maneira que preferirem.

Repetir a atividade, subdividindo o segmento de reta em 5 partes iguais.

Questionar os estudantes sobre qual deveria ser a medida de um segmento de reta construído para representar frações com denomina-

dores que não são divisores de 10, como o 3. Espera-se que algum deles responda, por exemplo, que 12 centímetros seria uma boa medida. Ao incentivá-los a se expressarem, contribui-se para o desenvolvimento da capacidade de argumentação.

ILUSTRAÇÕES: EDITORIA DE ARTE

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 15

EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

Operações com números racionais

Inicialmente, é feita uma retomada das operações com números racionais. Na adição e na subtração de números racionais na forma fracionária, pode ser que os estudantes cometam um equívoco bastante comum, que é adicionar (ou subtrair) independentemente os numeradores e os denominadores das frações. Caso façam isso, retomar os procedimentos usados para o cálculo de cada operação para que eles compreendam como devem realizar o cálculo corretamente. Explicar que na adição e na subtração de números racionais na forma decimal é importante que alinhem corretamente os algarismos nas respectivas ordens.

OPERAÇÕES COM NÚMEROS RACIONAIS

Vamos relembrar as operações de adição, subtração, multiplicação e divisão com números racionais, tanto na forma fracionária quanto na forma decimal. Quando queremos realizar operações com dois números racionais, que estão um na forma fracionária e outro na forma decimal, basta transformar todos eles para a forma decimal, ou todos para a forma fracionária, e realizar a operação.

Adição e subtração de números racionais

Na forma fracionária

Temos de estudar dois casos distintos: o primeiro deles refere-se às frações com denominadores iguais. O segundo, às frações com denominadores diferentes.

1o caso: Frações com mesmo denominador.

Para adicionar (ou subtrair) frações com mesmo denominador, mantemos o denominador e adicionamos (ou subtraímos) os numeradores. Observe o exemplo.

2o caso: Frações com denominadores diferentes.

Para adicionar (ou subtrair) frações com denominadores diferentes, devemos obter frações equivalentes às frações dadas, com mesmo denominador. Em seguida, mantemos o denominador comum e adicionamos (ou subtraímos) os numeradores. Acompanhe o exemplo a seguir.

Na forma decimal

Para a adição (ou subtração) de números representados na forma decimal, devemos observar que:

• algarismos que ocupam a mesma ordem devem ficar na mesma coluna, com uma vírgula alinhada à outra;

• adicionamos (ou subtraímos) algarismos de uma mesma ordem entre si;

• colocamos no resultado a vírgula alinhada com as demais. Observe os exemplos a seguir.

AMPLIANDO

Link

PROBLEMAS com soma e subtração de números decimais. Khan Academy. [S l.], c2022. Disponível em: https://pt.khanacademy.org/math/pt-mat-prep-6-ano-1/x908b6fdb043c9ae9:soma-e-subtracao-decimais /x908b6fdb043c9ae9:problemas-de-adicao-e-subtracao-de-numeros-decimais/e/adding_and_subtracting _decimals_word_problems. Acesso em: 27 jul. 2022.

Nesse link, é possível resolver situações-problema envolvendo adição e subtração de números racionais na forma decimal.

Multiplicação de números racionais

Na forma fracionária

Para multiplicar dois números racionais na forma fracionária, multiplicamos os numeradores entre si e os denominadores entre si. Caso seja necessário, simplificamos o resultado até obter a fração irredutível. Observe o exemplo.

Na forma decimal

Para multiplicar um número na forma decimal por outro número na forma decimal, devemos:

• multiplicar os números como se fossem números naturais;

• colocar a vírgula no resultado, de modo que a quantidade de casas decimais seja igual à soma da quantidade de casas decimais dos fatores.

Observe o exemplo a seguir.

4 , 2 1 algarismo na parte decimal

x 2 , 1 1 algarismo na parte decimal

4 2 + 8 4 8 , 8 2 2 algarismos na parte decimal

Divisão de números racionais

Na forma fracionária

Para dividir dois números racionais na forma fracionária, mantemos a primeira fração e a multiplicamos pelo inverso da segunda. Observe o exemplo.

Na forma decimal

Para obter o quociente entre dois números racionais na forma decimal, podemos multiplicar os dois termos por uma mesma potência de 10, a fim de obtermos um número natural como divisor. Observe.

x10

12,66 : 0,3 = 126,6 : 3

ORIENTAÇÕES DIDÁTICAS

Multiplicação de números racionais

Na multiplicação de números racionais na forma fracionária, pode acontecer um engano comum entre os estudantes que é realizar a multiplicação entre numerador e denominador. Caso isso ocorra, retomar o cálculo esclarecendo possíveis dúvidas, fazendo-os perceber a importância de analisar e compreender onde erraram e como devem evitar esse equívoco em outras circunstâncias. Questionar os estudantes sobre o posicionamento da vírgula no produto de dois números racionais na forma decimal.

Divisão de números racionais

Na divisão, verificar se os estudantes compreendem que divisões equivalentes possuem quocientes iguais, ou seja, ao multiplicar (ou dividir) o dividendo e o divisor por um mesmo número, o quociente não é alterado. Se considerar necessário, propor a atividade complementar a seguir para explorar alguns exemplos de cálculos com eles. Pode-se sugerir que, depois de realizarem os cálculos, eles utilizem uma calculadora para verificar os resultados.

Então, dividir 12,66 por 0,3 é o mesmo que dividir 126,6 por 3. Efetuando os cálculos, temos que 12,66 dividido por 0,3 é igual a 42,2.

17

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 17

Atividade complementar

Propor os seguintes cálculos para aprofundar o trabalho com divisões de números racionais na forma decimal.

=

ORIENTAÇÕES DIDÁTICAS

Atividades

Na atividade 1, transitar pela sala de aula e verificar quais estratégias os estudantes escolheram para identificar a posição dos números racionais dados na reta numérica. Nas atividades 2 e 3, discutir estratégias para realizar a comparação dos números racionais. Os estudantes podem escrever as frações na forma de números decimais ou encontrar um denominador comum e escrever frações equivalentes às frações dadas.

Na atividade 4, os estudantes devem efetuar adições e subtrações entre números racionais, tanto na forma decimal quanto na forma fracionária. Observar as estratégias que eles utilizam e, sempre que necessário, ajudá-los nos cálculos.

Depois de realizar as atividades 4, 5 e 6, os estudantes podem verificar a resposta utilizando uma calculadora. Caso considerar necessário, ampliar essa atividade variando a posição da vírgula nos números decimais para que os estudantes percebam a diferença nos resultados.

A atividade 7 requer que os estudantes realizem a subtração de dois números racionais na forma decimal. Verificar como os estudantes realizam os cálculos e incentivá-los a conversar com os colegas para trocarem ideias a respeitos das estratégias que utilizaram.

Responda às questões no caderno.

1. Na reta numérica a seguir, cada um dos quadradinhos representa um número racional. Copie a reta substituindo os quadradinhos por um dos seguintes números.

4. Efetue as operações.

7 8 + 4,5

+ 13 4 19 5

89 7 63 4

7 5 1,4

23,98 23,89

2. Compare os números racionais a seguir, usando os símbolos ., , e = a) 4,9 4,09 b) 15,3 15,3 c) 19 3 23 3

3. (Enem/MEC) Um jogo pedagógico é formado por cartas nas quais está impressa uma fração em uma de suas faces. Cada jogador recebe quatro cartas e vence aquele que primeiro consegue ordenar crescentemente suas cartas pelas respectivas frações impressas. O vencedor foi o aluno que recebeu as cartas com as frações:

que esse aluno apresentou foi:

5. Efetue as multiplicações a seguir.

6. Determine os quocientes das divisões a seguir.

:

:

7. (Prova Brasil) Uma casa tem 3,88 metros de altura. Um engenheiro foi contratado para projetar um segundo andar e foi informado que a prefeitura só permite construir casas de dois andares com altura de até 7,80 metros.

ser a altura máxima, em metros, do segundo andar?

1. Resposta na seção Resoluções comentadas deste Manual.

Em Matemática, muitas vezes, é útil representar números racionais expressos por meio de frações na forma decimal. Para isso, basta dividir o numerador pelo denominador.

Em alguns casos, essa representação decimal é finita. Por exemplo, considerando

ORIENTAÇÕES DIDÁTICAS

Dízimas periódicas

Ao trabalhar esse tópico, sugere-se que os exemplos apresentados no Livro do estudante sejam explorados na lousa, de modo que todos os estudantes possam acompanhar.

Ou seja: 9 20 0,45 _=

Em outros casos, essa representação decimal é infinita e periódica. Vamos con-

Depois, pode-se solicitar a eles que elaborem, no caderno, um exemplo cuja divisão resulte em uma dízima periódica. Nos casos em que a representação decimal é infinita, é importante lembrar aos estudantes que eles podem escrever esse tipo de dízima utilizando a representação abreviada para indicar o período que se repete.

Enfatizar a diferença entre uma dízima periódica simples e uma dízima periódica composta, pois, posteriormente, os estudantes terão de determinar a fração geratriz dessas dízimas.

Ou seja: 7 11 0,636363… =

No segundo exemplo, o resto nunca se anula e fica alternando entre 7 e 4. Assim, os algarismos 6 e 3 continuarão se repetindo indefinidamente no quociente (0,636363…). Como 0,636363… tem uma parte infinita e periódica, dizemos que esse número é uma dízima periódica. A parte que se repete é o período da dízima.

Desse modo, na dízima periódica 0,636363…, o período é o grupo 63, e a representação abreviada desse número é 0, 63. Essa dízima é chamada de dízima periódica simples

Vamos observar a seguinte dízima periódica: 12,1454545…

Nela, o período é 45, e o algarismo 1, que ocupa a casa dos décimos, não se repete; portanto, não pertence ao período. A representação abreviada desse número é 12,145. Nesse caso, a dízima periódica é chamada de composta

ORIENTAÇÕES DIDÁTICAS

Pense e responda

As questões propostas preparam os estudantes para a ideia de como obter a fração geratriz de uma dízima periódica simples. Por meio dessas questões, é possível verificar alguns padrões de repetição ao transformar um número racional expresso na forma de fração em uma representação decimal.

Para encontrar a fração geratriz de uma dízima periódica simples, os estudantes terão, inicialmente, de identificar o período da dízima.

Atividades

Espera-se que os estudantes resolvam a atividade 1, que traz itens em que eles devem realizar divisões por 10, por 100 ou por 1 000. Essa pode ser uma oportunidade para incentivá-los a realizar os cálculos mentalmente.

Na atividade 4, os estudantes devem identificar o período de cada dízima periódica. Avaliar se eles compreenderam como identificar os períodos corretamente; caso eles tenham alguma dúvida, verificar a melhor estratégia para saná-las.

Caso o período da dízima periódica apareça logo após a vírgula, ela é uma dízima periódica simples. Caso haja um ou mais algarismos após a vírgula que não fazem parte do período, temos uma dízima periódica composta

PENSE E RESPONDA

Observe as frações e, com o auxílio de uma calculadora, transforme-as em números racionais na forma decimal.

Agora, no caderno, faça o que se pede.

1. Quais foram os valores obtidos?

0,7777…; 0,131313…; 0,3333…; 2,131313…

2. Quais dos números obtidos são dízimas periódicas? Quais são os períodos delas?

Todos os números são dízimas periódicas; 7; 13; 3; 13.

3. Observe os números na forma de fração e as dízimas periódicas. Você percebe alguma relação entre a quantidade de algarismos do denominador da fração e a quantidade de algarismos do período das respectivas dízimas? Os denominadores das frações têm algo em comum?

Resposta pessoal. Espera-se que os estudantes percebam que a quantidade de algarismos do período de cada uma das dízimas é igual à quantidade de algarismos do denominador da respectiva fração, e que os denominadores das frações são compostos apenas de algarismos 9.

ATIVIDADES

Responda às questões no caderno.

1. Os números racionais a seguir são chamados de frações decimais. Escreva cada um deles na forma decimal.

d) 37 20

e) 35 11

f) 11 9

g) 29 1 000 h) 385 1 000 i) 3 20

j) 13 90 k) 33 4 l) 25 6

3. Classifique cada número decimal da atividade anterior em decimal exato (DE) ou dízima periódica (DP).

4. Identifique o período de cada uma das dízimas periódicas a seguir.

a) 0,02222…

b) 1,77777…

2. Qual é a representação decimal de cada um dos seguintes números racionais?

c) 12,010101…

d) 56,33333…

e) 3,4565656…

f) 1,034034034…

3. a) DE; b) DP; c) DE; d) DE; e) DP; f ) DP; g) DE; h) DE; i) DE; j) DP; k) DE; l) DP

FRAÇÃO GERATRIZ DE DÍZIMAS PERIÓDICAS SIMPLES

Toda dízima periódica é um número racional, pois pode ser escrita na forma de fração. Essa fração é chamada de fração geratriz da dízima periódica, pois, quando transformada em número racional na forma decimal, gera a dízima. Observe, nos casos a seguir, como podemos obter uma fração geratriz de dízimas periódicas simples.

1 Determinar uma fração geratriz da dízima periódica 0,5555…

Para isso, escrevemos a equação x = 0,5555…, que indicaremos por I , em que x é a fração geratriz procurada. Depois, multiplicamos os dois membros dessa equação por 10, obtendo 10x = 5,5555… , que indicaremos por II . Em seguida, subtraímos I de II

10x = 5,5555... II

x = 0,5555... I

9x = 5

Resolvendo a equação, temos:

9x = 5

x = 5 9

Uma fração geratriz da dízima periódica

0,5555… é 5 9

2 Dada a dízima periódica 3,2727…, obter sua fração geratriz.

Para obter uma fração geratriz dessa dízima periódica, escrevemos a equação y  = 3,2727…, que indicaremos por I , em que y é a fração geratriz procurada. Em seguida, multiplicamos os dois membros dessa equação por 100 e obtemos

100y = 327,2727…, que indicaremos por II Depois, subtraímos I de II

100y = 327,2727... II

y = 3,2727... I

99y = 324

Resolvendo a equação, temos:

99y = 324 h== y 324 99 36 11

Logo, uma fração geratriz da dízima periódica 3,2727... é 36 11

Observação:

324 99 , ou qualquer outra fração equivalente a ela, também é uma fração geratriz da dízima periódica 3,2727…

No primeiro caso, multiplicamos a equação por 10, pois o período da dízima contém apenas um algarismo que se repete: o algarismo 5. Ao fazer a subtração das dízimas, as casas decimais, por serem iguais, anulam-se.

O mesmo raciocínio foi aplicado ao exemplo 2, mas dessa vez foi necessário multiplicar a equação por 100, pois o período da dízima é composto de dois algarismos que se repetem: os algarismos 2 e 7.

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 21 30/07/22

Vídeo

CONVERSÃO de dízimas periódicas em frações (parte 1 de 2). Khan Academy. [S l.], c2022. Disponível em: https://pt.khanacademy.org/math/pt-8-ano/numeros-8ano/pt-dzimas-peridicas/v/coverting-repeating-decimals -to-fractions-1. Acesso em: 27 jul. 2022.

Nesse link, é possível assistir a uma videoaula retomando, passo a passo, a construção das equações que levam à fração geratriz de uma dízima periódica simples.

ORIENTAÇÕES DIDÁTICAS

Fração geratriz de dízimas periódicas simples

Explorar os exemplos apresentados no Livro do estudante, que resumem os procedimentos para encontrar a fração geratriz de uma dízima periódica simples. Desse modo, contribui-se para o desenvolvimento da habilidade EF08MA05. No primeiro deles, o período da dízima periódica contém apenas um algarismo que se repete. Assim, foi escrita a equação inicial e, em seguida, ela foi multiplicada por 10. Já no segundo exemplo, o período é constituído por dois algarismos, o que levou à multiplicação por 100 da equação inicial.

ORIENTAÇÕES DIDÁTICAS

Fração geratriz de dízimas periódicas compostas

Propor a leitura coletiva do fluxograma e verificar se os estudantes compreendem cada uma das etapas. A leitura de um fluxograma contribui para o desenvolvimento do pensamento computacional nos estudantes.

Na lousa, escrever algumas dízimas periódicas simples, com períodos compostos de quantidades distintas de algarismos e verificar se os estudantes conseguem seguir as instruções dadas.

Explorar os procedimentos usados para determinar as frações geratrizes de dízimas periódicas compostas. Comentar com os estudantes que os procedimentos são similares aos utilizados no caso de dízimas periódicas simples com uma nova etapa.

Atividades

As atividades propostas nesse bloco contribuem para o desenvolvimento da habilidade EF08MA05. Na atividade 1, os estudantes devem encontrar as frações geratrizes das dízimas periódicas simples indicadas. Sugerir que sigam o fluxograma apresentado no início da página.

Observe a seguir um fluxograma que representa o processo para determinar frações geratrizes de dízimas periódicas simples.

Escolher a dízima periódica simples cuja fração geratriz deseja-se determinar.

Início. Fim.

Determinar o número n de algarismos do período da dízima. Multiplicar a dízima por 10 n

Subtrair a dízima do resultado obtido na etapa anterior.

O valor obtido será o numerador a da fração.

FRAÇÃO GERATRIZ DE DÍZIMAS PERIÓDICAS COMPOSTAS

a b é a fração geratriz da dízima periódica.

Calcular o resultado de: 10 n 1.

O valor obtido será o denominador b da fração.

Assim como é possível determinar uma fração geratriz das dízimas periódicas simples, também podemos determinar frações geratrizes de dízimas periódicas compostas.

Observe o caso a seguir.

Dada a dízima periódica composta 5,6707070…, obter sua fração geratriz. Para isso, primeiro escrevemos a equação x = 5,6707070…, em que x é a fração que queremos encontrar. Em seguida, multiplicamos os dois membros dessa equação por 10 (equação  I ) e por 1 000 (equação II ). Por fim, subtraímos I de II

1 000x = 5670,707070... II

10x =_ 56,707070... I

990x = 5 614

Resolvendo a equação:

=_h=_= 990x 5 614 x 5 614 990 2 807 495

Uma fração geratriz da dízima periódica 5,6707070... é 2 807 495

Nesse exemplo, multiplicamos a equação por 10 para obter uma dízima periódica simples, pois na dízima há um algarismo depois da vírgula que não pertence ao período. Em seguida, multiplicamos a equação por 1 000, a fim de obter outra dízima com mesmo período, pois temos três algarismos até a primeira repetição do período. Por fim, subtraímos as duas equações anulando as casas decimais que se repetem e encontrando a fração procurada.

ATIVIDADES

Responda às questões no caderno.

Exemplos de respostas:

a) 22 9 b) 1 9 c) 161 9 d) 629 99 e) 29 99 f) 700 333

1. Determine uma fração geratriz de cada dízima periódica simples a seguir.

a) 2,4444…

b) 0,11111… c) 17,8888… d) 6,353535… e) 0,292929… f) 2,102102102…

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd

AMPLIANDO

Vídeo

CONVERSÃO de dízimas periódicas em frações (parte 2 de 2). Khan Academy. [S l.], c2022. Disponível em: https://pt.khanacademy.org/math/pt-8-ano/numeros-8ano/pt-dzimas-peridicas/v/coverting-repeating-decimals -to-fractions-2. Acesso em: 27 jul. 2022.

Nesse link, é possível assistir a uma videoaula retomando, passo a passo, a construção das equações que levam à fração geratriz de uma dízima periódica composta.

8. b) Resposta na seção Resoluções comentadas deste Manual.

2. Determine a alternativa que apresenta o valor da expressão: 0,555555... 2 3 +

a) 5 9

b) 7 12

c) 5 99

Alternativa e.

d) 1 e) 11 9

3. Obtenha uma fração geratriz das dízimas periódicas compostas a seguir.

a) 7,15555…

b) 0,53333…

c) 69,0333…

d) 1,17474…

4. Sabendo que 0,11111… = 1 9 , qual é a fração irredutível equivalente a 0,21111…?

a) 10 9

b) 2 19

c) 1 10 d) 19 90

do numerador pelo denominador. Para isso, junte-se a um colega, e façam o que se pede.

a) Construam um quadro, que deve começar como o modelo apresentado a seguir, porém deve ter mais 16 linhas.

ORIENTAÇÕES DIDÁTICAS

Para resolver a atividade 2, os estudantes podem encontrar a fração geratriz de 0,555555... e, em seguida, adicioná-la a 2 3 , pois a resposta está expressa por número na forma de fração. Destacar que a fração da resposta está em sua forma irredutível. Verificar, por exemplo, se eles compreendem que: 0,555555...+=+=+ 2 3 5 9 2 3 5 9 6 9 Uma estratégia para resolver a atividade 4 é decompor o número 0,21111... como 0,1 + + 0,11111...

e) 2 111 10 000

Alternativa d.

5. Considerando os números a = 0,45555…

e b = 0,46, é correto afirmar que:

a) b = a + 0,11111…

b) a = 4 9

c) a não é racional.

d) a , b.

6. Escreva a soma 0,33333… + 0,52222… na forma de fração.

DESAFIOS

Alternativa d. 77 90

7. Junte-se a um colega, e escrevam o passo a passo para obter uma fração geratriz de uma dízima periódica composta qualquer. Depois, representem esse procedimento por meio de um fluxograma.

8. Dado um número racional na forma fracionária, vamos investigar se é possível saber se sua representação decimal será exata ou periódica sem fazer a divisão

7. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

b) Com o auxílio de uma calculadora, dividam o numerador pelo denominador de cada fração e assinalem no quadro se o resultado encontrado é um número decimal exato ou uma dízima periódica, como no caso do exemplo dado, em que a representação decimal de 1 2 é um decimal exato.

c) O que vocês observam em relação aos denominadores de frações correspondentes a números decimais exatos? E de frações correspondentes a dízimas periódicas? Anotem suas hipóteses e debatam com outros colegas e com o professor.

No desafio 7, incentivar os estudantes a compartilhar os fluxogramas que eles elaboraram, a fim de verificarem pontos comuns ou divergentes no momento de sintetizar os procedimentos para encontrar a fração geratriz de uma dízima periódica composta. Se possível, reservar uma aula para realizar a investigação proposta no desafio 8. Atividades como essa contribuem para o desenvolvimento da capacidade de inferência. Uma possibilidade é solicitar a eles que façam a atividade em duplas, desse modo, possibilita-se que eles tenham uma oportunidade de trocar ideias e desenvolver o aspecto da cooperação, uma vez que um pode colaborar com o outro. Ao finalizar a investigação, é importante que os estudantes revejam suas hipóteses iniciais e consigam reconhecer, rapidamente, quando um número racional na forma fracionária terá uma representação exata ou uma representação decimal.

Resposta na seção Resoluções comentadas deste Manual.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

ORIENTAÇÕES DIDÁTICAS

Números irracionais

Ler com os estudantes o texto sobre os números irracionais apresentado no Livro do estudante, destacando o fato de que esses números não podem ser escritos na forma fracionária.

Conjunto dos números reais

Representar os diagramas dos conjuntos numéricos na lousa, explicitando as relações entre eles e destacando a formação do conjunto dos números reais, por meio da união dos conjuntos dos números racionais e dos números irracionais.

NÚMEROS IRRACIONAIS

Observe o seguinte número racional: 0,4545454545…

Esse número é uma dízima periódica, pois possui um número infinito de casas decimais e período igual a 45. Estudamos que as dízimas periódicas podem ser escritas na forma a b , em que a e b são números inteiros, com b 5 0. Nesse caso, 0,4545454545… = 5 11

Agora, analise outro exemplo: 3,8687888990…

Observando a formação desse número, podemos dar continuidade do seguinte modo: 3,868788899091…; 3,86878889909192…; 3,8687888990919293…; e assim por diante. Se continuarmos a preencher as casas decimais desse modo, teremos um número com infinitas casas decimais e sem um período que se repita.

Números como esse não podem ser escritos na forma a b , em que a e b são números inteiros, com b 5 0. Assim, esses números não são números racionais

Ao conjunto de números que apresentam essas características (número infinito de casas decimais e não periódicas), damos o nome de conjunto dos números irracionais. Representamos esse conjunto por i

Número irracional é todo número cuja representação decimal é infinita e não periódica.

São exemplos de números irracionais:

• 2 = 1,414213562373…

• p= 3,1415926535…

• 3 = 1,732050807568…

• 5 = 2,2360679774997…

• 1,707007000700007…

• 0,12345678910111213…

CONJUNTO DOS NÚMEROS REAIS

O conjunto dos números reais, representado por r, é a união do conjunto dos números racionais com o dos números irracionais. O conjunto dos números naturais (n)está contido no conjunto dos números inteiros (z), que está contido no conjunto dos números racionais (q), e todos são subconjuntos de r. Observe, no diagrama, a relação entre esses conjuntos.

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 24

AMPLIANDO

Link

ÁVILA, Geraldo. Cardinalidade: o conjunto dos racionais é enumerável e os dos reais não é. Revista do Professor de Matemática, Rio de Janeiro, 4, [20--]. Disponível em: https://www.rpm.org.br/cdrpm/4/2.htm. Acesso em: 28 jul. 2022.

Neste artigo, há importantes informações sobre aspectos históricos e definições acerca de conjuntos numéricos, como a cardinalidade.

Podemos observar que alguns números pertencem a um conjunto e não a outro, mas todos os números que estudamos até agora pertencem ao conjunto dos números reais. Acompanhe alguns exemplos.

• 5 [r , 5 [q, 5 [z, mas 5 {n e 5 {i

• 7 [r , 7 [q, 7 [z, 7 [n , mas 7 {i

• 2,5 [r , 2,5 [q, mas 2,5 {z, 2,5 {n e 2,5 {i

• 3 [r , 3 [i , mas 3 {q, 3 {z e 3 {n

Em uma reta numérica, podem ser representados todos os números racionais e todos os números irracionais, ou seja, podem ser representados todos os números reais; e cada ponto dessa reta pode ser associado a um único número real.

Essa reta é denominada reta real. Observe a representação de alguns números na reta real.

ATIVIDADES

Responda às questões no caderno.

1. Sabendo que 10 = 3,1622776601683… é um número que tem representação decimal infinita, mas não é dízima periódica, conclui-se que 10 é um número:

a) natural.

b) inteiro.

c) racional.

d) irracional.

e) não real.

Alternativa d.

2. Um exemplo de número irracional é:

a) 4,15151515…

b) 4,501501501…

c) 4,021021021…

d) 4,280281282283…

e) 4,33

ORIENTAÇÕES DIDÁTICAS

Verificar se os estudantes reconhecem os símbolos [ e { ; se considerar necessário, fazer uma retomada desses símbolos e explicar que são usados na relação entre elementos e conjuntos numéricos.

Atividades

As atividades apresentadas nesse bloco têm como principal objetivo levar os estudantes a aplicar os conhecimentos adquiridos a respeito do conjunto dos números reais.

Se considerar oportuno, ampliar a atividade 4 com alguns questionamentos, como:

Alternativa d.

4. Observe os números a seguir.

5

Quais deles pertencem ao conjunto:

a) n?

b) z?

c) z, mas não pertencem a n?

d) q, mas não pertencem a z?

5. A representação decimal de um número pode ser: finita, infinita e periódica ou, ainda, infinita e não periódica. Escreva qual é o caso de cada um dos números a seguir.

• Quais números pertencem ao conjunto dos números reais, mas não pertencem ao conjunto dos números racionais? Resposta: Os números irracionais.

3. (Saresp-SP) A parte decimal da representação de um número segue opadrão de regularidade indicado: 0,12112111211112… Este número é

a) racional não inteiro.

b) inteiro negativo.

c) irracional negativo.

d) irracional positivo.

Alternativa d.

Infinita e periódica. Infinita e não periódica.

a) 27 6 b) 0,23 c) 2

1 4; 0; 1 4 2,3; 1 4 ; 0, 6 Finita.

6. Junte-se a um colega, e criem um exemplo de um número real que seja também racional e esteja escrito na forma fracionária. A representação decimal desse número é uma dízima periódica? Expliquem.

6. Resposta pessoal. Exemplo de resposta: 3 4 ; a representação decimal desse número não é uma dízima periódica.

25 D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd

• Quais números pertencem ao conjunto dos números inteiros não negativos, mas não pertencem ao conjunto dos números inteiros positivos?

Resposta: Apenas o zero.

Na atividade 6, promover um debate e a construção coletiva de uma solução para um problema. Ao fim dessa atividade, pedir aos estudantes que expliquem a escolha do número e verifiquem se acertaram.

ORIENTAÇÕES DIDÁTICAS

Porcentagem

Ao iniciar esse tópico pretende-se favorecer o desenvolvimento da habilidade EF08MA04. Como proposta de encaminhamento, sugere-se que o texto e os exemplos apresentados no Livro do estudante sejam explorados. Outra possibilidade é, antes de iniciar a aula, fazer uma abordagem para compreender os conhecimentos que eles têm a respeito do tema.

Na situação 1, destacar que, como na fração 7 25 o denominador é diferente de 100 (não é uma fração centesimal), determinou-se a forma decimal correspondente, dividindo numerador por denominador, para, depois, indicar a representação percentual.

A expressão por cento, representada pelo símbolo %, faz parte de nosso dia a dia. Podemos encontrá-la facilmente em notícias de jornais e revistas ou da televisão. Nas compras em lojas e supermercados, nas aplicações e nos empréstimos em bancos, enfim, em tudo que se relaciona à economia e às finanças encontramos a expressão por cento. Também usamos comumente essa expressão em gráficos e tabelas.

A expressão por cento significa “por cem”. Assim, por exemplo, 5% (cinco por cento) significa “5 em cada 100”.

Quando dizemos que “Quase 85% da população brasileira vive em áreas urbanas” significa que cerca de 85 em cada grupo de 100 brasileiros vivem em áreas urbanas.

Vitrine de loja exibindo promoção de roupas em shopping. Osasco (SP), 2019.

85% = 85 100 = 0,85

Então, podemos estabelecer a relação a seguir da taxa percentual. representação decimal representação fracionária representação percentual

Quando nos deparamos com uma afirmação como “A Região Norte ocupa uma superfície que corresponde a 45% do território brasileiro” significa que a Região Norte ocupa uma área de 45 km² para cada 100 km² do território brasileiro.

45% = 45 100 = 0,45

Observe como podemos calcular a taxa percentual ou o valor que ela representa nas situações a seguir.

1 Um desconto de 7 mil reais sobre um preço de 25 mil reais representa quantos por cento de desconto?

Inicialmente, temos a razão: = 7 000 25 000 7 25 Podemos fazer o cálculo de dois modos.

1o modo: Usando frações equivalentes:

== 7 25 28 100 28%

2o modo: Escrevendo na forma decimal:

===% 7 25 0,28 28 100 28

Logo, 7 mil reais representam 28% de desconto.

D2_AV4-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 26

Atividade complementar

Ao resolver problemas usando porcentagem, os estudantes vão entrar em contato com diferentes registros, como representação decimal, razão centesimal e representação percentual. Dessa maneira, propor, como atividade complementar, que os estudantes façam no caderno o quadro ao lado e completem os espaços em branco.

Representação percentual 10%

Razão centesimal 12 100

Representação decimal 0,45

DANIEL CYMBALISTA/PULSAR IMAGENS

ORIENTAÇÕES DIDÁTICAS

2 Em uma partida de basquetebol, obtém-se o índice de aproveitamento de lances livres de um jogador calculando a razão percentual entre o número de acertos e o total de lances livres cobrados por esse jogador. Qual é o índice de aproveitamento de um jogador que acertou 12 dos 15 lances livres que cobrou em uma partida?

12

====

15 0,80,80 80 100 80%

O índice de aproveitamento desse jogador foi de 80%.

3 Os estudantes do 8o ano fizeram uma pesquisa com 500 colegas para descobrir a preferência dos estudantes da escola ABC por esportes. O resultado está apresentado no gráfico. Calcular a quantidade de estudantes que prefere cada um dos esportes.

Para calcular a quantidade de estudantes que prefere cada um dos esportes, é necessário verificar a porcentagem correspondente a cada um deles no gráfico e, então, calcular quanto cada porcentagem representa dos 500 estudantes.

• Natação (26%):

26% de 500 ?= 26 100 500130

• Voleibol (14%):

14% de 500 ?= 14 100 50070

• Futebol (25%):

25% de 500 ?= 25 100 500 125

Preferência dos estudantes da escola ABC por esportes

Na situação 2, mostrar que 15 cestas representam o total de arremessos. Portanto, correspondem a 100% dos arremessos, dos quais apenas 12 cestas foram aproveitadas.

Na situação 3, trabalha-se com o cálculo da porcentagem com base na escrita da fração correspondente com denominador 100. Verificar se os estudantes compreendem os cálculos apresentados.

• Handebol (16%):

16% de 500 ?= 16 100 50080

• Basquetebol (19%):

19% de 500 ?= 19 100 500 95

Assim, dos 500 estudantes, 130 preferem natação, 70 preferem voleibol, 125 preferem futebol, 80 preferem handebol e 95 preferem basquetebol.

4 Segundo o Anuário Brasileiro da Educação Básica 2021, produzido pela organização Todos Pela Educação, em 2020 havia no Brasil 3 363 escolas em terras indígenas e, dessas, 1 214 utilizavam materiais pedagógicos específicos para a Educação Indígena. Calcular a porcentagem de escolas em terras indígenas que usavam materiais específicos.

1= 1 214 3 363 0,36136,1%

Logo, aproximadamente 36,1% das escolas em terras indígenas usavam material específico para a Educação Indígena.

Elaborado com base em: TODOS PELA EDUCAÇÃO; EDITORA MODERNA. Anuário Brasileiro da Educação Básica 2021. São Paulo: Todos Pela Educação: Moderna, 2021. Disponível em: https://todospelaeducacao.org.br/wordpress/wp-content/ uploads/2021/07/Anuario_21final.pdf. Acesso em: 17 jun. 2022.

Na situação 4, mostrar que para expressar na forma percentual um número que está na forma decimal basta multiplicá-lo por 100 e acrescentar o símbolo de porcentagem (%). Por exemplo:

• 0,375 = 37,5%

(0,375 100 = 37,5)

• 2,4 = 240%

(2,4 100 = 240)

Estudantes no Centro de Ensino Médio Indígena Xerente Warã (CEMIX), na Aldeia Coqueiro, em Tocantínia (TO), 2022.

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 27

Vídeo

MATEMÁTICA em toda parte: Matemática nas finanças. 2015. Vídeo (27min18s). Publicado pelo canal Matemática do Cotidiano. Disponível em: https://www.youtube.com/watch?v=5wswMJm1fdE&t=3s. Acesso em: 28 jul. 2022.

Nesse link, é possível assistir a uma videoaula relacionando as razões e porcentagens à vida financeira das pessoas.

Fonte: Dados obtidos pelos estudantes do 8o ano.

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades propostas têm como objetivo levar os estudantes a reconhecer o significado do símbolo % (por cento), representar razões em forma percentual e explorar taxas percentuais. Desse modo, pretende-se favorecer o desenvolvimento da habilidade EF08MA04, especialmente em relação à resolução de problemas envolvendo o cálculo de porcentagens.

Desenvolver com os estudantes atividades que utilizam dados que fazem parte do cotidiano deles. Uma sugestão é fazer a análise do consumo de energia elétrica. Usar uma conta de luz para propor que relacionem o consumo de cada mês e verifiquem o aumento ou a diminuição de consumo em relação ao mês anterior, em porcentagem.

Na atividade 4, comentar com os estudantes que a porcentagem aparece com bastante frequência em pesquisas de opinião e análises de pesquisas realizadas. Na atividade, com base na porcentagem de cada opinião, é possível concluir, de modo mais direto, que a maioria das pessoas considerou o show ótimo ou bom.

Na atividade 7, os estudantes precisam elaborar um problema e trocá-lo com seus pares. Atividades como essa possibilitam que os estudantes desenvolvam habilidades de escrita além de precisarem considerar o contexto matemático relacionado ao tema.

ATIVIDADES

3. Respostas pessoais. Exemplos de respostas na seção Resoluções comentadas deste Manual.

Responda às questões no caderno.

1. Um vendedor recebe 8% de comissão nas vendas que realiza. Quanto ele receberá pela venda de um par de tênis de 150 reais?

12 reais.

2. Vilma acertou 76% das 50 questões da prova de Matemática de um vestibular. Quantas questões ela acertou?

38 questões.

3. Analise como Juliana calculou mentalmente 40% de 1 050 reais.

Eu sei que 10% é 100% dividido por 10, então 10% de 1 0 50 é 105. Para determinar quanto é 40%, multipliquei 105 por 4, que resultou em 420.

O que você achou da estratégia de Juliana?

Pense em estratégias para calcular mentalmente e determine o valor de:

a) 25% de 1 080.

b) 5% de 2 700.

c) 50% de 6 340.

d) 2% de 135.

e) 20% de 350.

f) 75% de 1 248.

4. Após uma apresentação de música, 250 espectadores foram entrevistados e opinaram sobre o show. Observe o resultado dessa pesquisa.

Opinião sobre o show

Opinião Quantidade de pessoas

Ótimo 105 Bom 100

Ótimo: 42%.

Bom: 40%.

Regular: 12%.

Ruim: 6%.

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 28

Fonte: Dados fictícios.

7. Resposta pessoal. Exemplo de resposta: “Em uma loja virtual, determinado modelo de tênis é vendido de R$ 150,00 por R$ 120,00. Calcule a porcentagem de desconto em relação ao preço inicial do tênis.”.

Observando a tabela e considerando o total de entrevistados, escreva a taxa percentual correspondente a cada opinião.

5. O primeiro Campeonato Mundial de Voleibol Masculino foi realizado em 1949. Desse ano até 2018, já foram realizados 19 torneios, e o Brasil ganhou três deles. A quantidade de conquistas brasileiras representa quantos por cento da quantidade de torneios realizados?

Aproximadamente 15,8%.

Campeonato Mundial de Voleibol Masculino, em Moscou (Rússia), 1952.

6. No verão de 2022, foi realizada uma análise do resíduo sólido deixado em certa praia. Foram recolhidos 396 kg de plástico, 9 kg de vidro, 18 kg de metal e 27 kg de papel. A partir dessas informações, responda.

a) Quantos quilogramas de resíduo sólido foram recolhidos nessa praia?

b) Os materiais de plástico recolhidos representam quantos por cento desse total?

450 kg 88%

7. Elabore um problema envolvendo o cálculo da porcentagem de desconto oferecido em um produto. Depois, troque seu problema com um colega, e solucionem o problema um do outro.

8. Pesquise em jornais, revistas ou na internet gráficos com dados expressos em porcentagens. Elabore uma atividade baseada em um dos gráficos encontrados

KIBBUTZ GAN SHMUEL ARCHIVE/PICWIKI

Resposta pessoal. A resposta depende dos dados pesquisados.

BENTINHO

AMAZÔNIA OCUPA QUASE 50% DO TERRITÓRIO NACIONAL

[…]

ORIENTAÇÕES DIDÁTICAS

Por toda parte

Área de desmatamento em floresta entre a Amazônia e o Cerrado, em Nova Xavantina (MT), 2021.

Maior reserva de diversidade biológica do mundo, a Amazônia é também o maior bioma brasileiro em extensão e ocupa quase metade do território nacional (49,29%). A bacia amazônica ocupa

2

GLOSSÁRIO

Bioma: conjunto de fauna e flora adaptado a certa região com determinadas condições ambientais, como clima e relevo.

5 da América do Sul e 5% da superfície terrestre. Sua área, de aproxi madamente 6,5 milhões de quilômetros quadrados, abriga a maior rede hidrográfica do planeta, que escoa cerca de 1 5 do volume de água doce do mundo. Sessenta por cento da bacia amazônica se encontra em território bra sileiro, onde o Bioma Amazônia ocupa a totalidade de cinco unidades da federação (Acre, Amapá, Amazonas, Pará e Roraima), grande parte de Rondônia (98,8%), mais da metade de Mato Grosso (54%), além de parte de Maranhão (34%) e Tocantins (9%). [...]

INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. IBGE lança o Mapa de Biomas do Brasil e o Mapa de Vegetação do Brasil, em comemoração ao Dia Mundial da Biodiversidade. Agência IBGE Notícias. Rio de Janeiro, 21 maio 2004. Disponível em: https://agenciadenoticias.ibge.gov.br/agencia-noticias/2013-agencia-de-noticias/ releases/12789-asi-ibge-lanca-o-mapa-de-biomas-do-brasil-e-o-mapa-de-vegetacao-do-brasilem-comemoracao-aodia-mundial-da-biodiversidade.html. Acesso em: 17 jun. 2022. De acordo com o texto e usando uma calculadora, responda no caderno às questões a seguir.

1. A Amazônia ocupa que porcentagem do território brasileiro? Em quais estados esse bioma está presente?

49,29%; Acre, Amapá, Amazonas, Pará, Roraima, Rondônia, Mato Grosso, Maranhão e Tocantins.

2. Sabendo que a área do território brasileiro é de aproximadamente 8 510 000 km², calcule a área aproximada que a Amazônia ocupa no Brasil.

Aproximadamente 4 200 000 km².

3. Faça uma pesquisa e descubra quantos biomas há no Brasil e a porcentagem que cada um deles representa do território nacional.

Resposta na seção Resoluções comentadas deste Manual.

4. O Programa de Monitoramento do Desmatamento da Floresta Amazônica Brasileira por Satélite (Prodes) realiza o monitoramento por satélites do desmatamento por corte raso na Amazônia Legal e produz, desde 1988, as taxas anuais de desmatamento na região, que são usadas pelo governo brasileiro para o estabelecimento de políticas públicas.

Segundo o Prodes, a taxa de desmatamento da Amazônia Legal no Brasil foi de 10 851 km2 em 2020 e de 13 038 km2 em 2021.

Elaborada com base em: BRASIL. Ministério da Ciência, Tecnologia e Inovação. Instituto Nacional de Pesquisas Espaciais. PRODES: Monitoramento do desmatamento da Floresta Amazônica brasileira por Satélite. São José dos Campos: INPE, [2021]. Disponível em: http://www.obt.inpe.br/OBT/assuntos/programas/amazonia/prodes. Acesso em: 18 jun. 2022.

a) Calcule a porcentagem aproximada de aumento no desmatamento de 2020 para 2021.

Aproximadamente 20%.

b) Em seu entendimento, esse aumento é pequeno ou grande? Converse com um colega sobre essa questão.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Ao realizar as atividades propostas nesta seção, os estudantes terão coletado dados sobre os biomas do Brasil, contribuindo para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental.

Essas explorações podem ser ampliadas em outras áreas do conhecimento, como Geografia e Ciências. Se julgar pertinente, providenciar um mapa da América do Sul para que eles possam identificar a localização da Bacia Amazônica.

Propor uma leitura coletiva do texto inicial apresentado no Livro do estudante e, em seguida, propor a eles que respondam às questões. O uso da calculadora como ferramenta de cálculo é indicado nas atividades e contribui para o desenvolvimento da habilidade EF08MA04. Certificar-se de que os estudantes têm acesso a calculadoras simples para a realização dos cálculos.

No item a da questão 4, observar como os estudantes constroem a resolução do problema. Se julgar pertinente, indicar que consultem as situações apresentadas no Livro do estudante.

16/08/22 23:16

D2_AV4-MAT-F2-2103-V8-U1-012-039-LA-G24.indd

AMPLIANDO

Link

INSTITUTO DE PESQUISA AMBIENTAL DA AMAZÔNIA. Amazônia 2018. [S l.]: IPAM, 2018. Escala

1:275. Disponível em: https://ipam.org.br/wp-content/uploads/2018/04/Amazonia_2018_1-1.jpg. Acesso em: 28 jul. 2022.

No site do Instituto de Pesquisa Ambiental da Amazônia (IPAM), é possível encontrar mapas que mostram áreas desmatadas.

Depois de realizarem as atividades, propor aos estudantes que façam uma pesquisa sobre o desmatamento e suas consequências. Selecionar previamente fontes de pesquisa que eles possam usar na sala de aula. Ao terminar, propor um debate com a turma e criar um texto único sobre as atitudes que podem ajudar a conscientizar as pessoas a respeito do tema.

ORIENTAÇÕES DIDÁTICAS

Pense e responda

As atividades desta seção têm como objetivo preparar os estudantes para o trabalho com juro simples e verificar os conhecimentos prévios sobre o assunto. Pedir aos estudantes que reúnam diferentes panfletos com propaganda de mercadorias que contenham ofertas e situações de compra à vista e a prazo.

É importante que os estudantes compreendam as duas maneiras mais comuns de efetuar o pagamento de uma compra: o pagamento à vista, em que o cliente paga o preço total da mercadoria no ato da compra com algum desconto ou não; pagamento a prazo, em prestações, em que o valor da compra é dividido em pagamentos mensais e consecutivos. Nessa modalidade o cliente pode, por exemplo, pagar uma entrada no ato da compra.

Na modalidade de pagamento à vista, o vendedor pode oferecer um desconto para o cliente; na compra a prazo, geralmente, é cobrado um acréscimo (juro) pelo intervalo de tempo decorrido até o vendedor receber o pagamento integral da mercadoria.

Na atividade 1, os estudantes poderão concluir que o juro representa um acréscimo que se paga como compensação pelo pagamento em mais parcelas.

Na atividade 3, discutir com os estudantes diferentes maneiras de se calcular o valor a pagar após o desconto de 10%. Ouvir as estratégias e registrar na lousa. É possível que muitos estudantes saibam que calcular 10% de um valor é equivalente a dividi-lo por 10. Dessa maneira, obtendo o valor do desconto, basta subtraí-lo do valor total. Apresentar, caso nenhum estudante mostre essa estratégia, o cálculo do desconto de 10%, multiplicando o valor

PENSE E RESPONDA

Esta TV é o último lançamento. Vale R $ 1.200,00.

Como eu posso pagar?

Você paga 50% de entrada, e o restante em 3 vezes sem juro.

50% é metade, né? Metade de R $ 1.200,00 é R $ 600,00.

Fica faltando a outra metade, R $ 600,00.

Em 3 vezes sem juro, divido 600 por 3 e obtenho 200. É isso?

Nesse caso, 30% de R $ 1.200,00 são R $ 360,00. Falta pagar R $ 840,00.

Isso mesmo!

Mas no caso de dividir orestante em 10 vezes, há um juro de 5% em cada parcela.

E se eu quiser pagar 30% de entrada e o restante em 10 vezes, posso?

Agora, responda às questões no caderno.

1. Ao acompanhar a história, o que você entendeu por juro?

2. Quanto o comprador pagaria de entrada se desse 40% do valor da TV? Nesse caso, quanto ainda restaria para ele pagar?

R$ 480,00; R$ 720,00

3. Se o comprador pagar à vista, ele ganha 10% de desconto. Nesse caso, quanto custará a TV?

R$ 1.080,00

1. Resposta pessoal. Espera-se que os estudantes percebam que, na história, juro representa um acréscimo que se paga como compensação pelo pagamento em mais parcelas.

total por 0,9. Questionar os estudantes por que essa estratégia funciona e permite que, com apenas um cálculo, o valor a ser pago seja obtido.

AMPLIANDO

Link

PROBLEMAS com descontos, remarcações e comissões. Khan Academy. [S l.], c2022. Disponível em: https:// pt.khanacademy.org/math/pre-algebra/xb4832e56:percent-rational-number-word-problems/xb4832e56:untitled -1026/e/discount_tax_and_tip_word_problems. Acesso em: 28 jul. 2022.

Nesse link, é possível resolver situações-problema envolvendo descontos, acréscimos e comissões.

Então, em vez de R $ 84,00, eu vou pagar R $ 88,20 por mês.

D2-MAT-F2-2103-V8-U1-012-039-LA-G24.indd

Quando uma pessoa pede dinheiro emprestado a um banco, ela paga uma compensação pelo tempo que fica com a quantia emprestada.

Às vezes, quando se compra uma mercadoria à prestação, paga-se um acréscimo pelo tempo correspondente ao número de prestações.

Quando alguém aplica dinheiro em um banco, recebe uma compensação pelo tempo em que está emprestando a quantia ao banco.

Essa compensação ou esse acréscimo a que estamos nos referindo chama-se juro, e corresponde sempre a uma porcentagem do valor do empréstimo ou da compra.

Assim, podemos dizer que:

Juro é toda compensação que se paga, em dinheiro, por uma quantia que se tomou emprestado ou que se recebe por uma quantia que se emprestou.

Quando falamos em juro, consideramos que:

• o dinheiro que se empresta ou que se pede emprestado chama-se capital;

• a taxa em porcentagem que se paga pelo “aluguel” do dinheiro chama-se taxa de juro;

• o total que se paga ao final do empréstimo (capital + juro) chama-se montante Acompanhe, a seguir, algumas situações que envolvem juro.

1 Regina vai a um banco e faz um empréstimo de 12 0 00 reais por 3 meses, com uma taxa de juro simples de 2,7% ao mês. Que quantia ela deverá pagar de juro e qual é o total que Regina terá de pagar ao final do empréstimo?

Vamos indicar por x a quantia que ela deverá pagar de juro e teremos:

x = (2,7% 12 000) 3

x = 0,027 ? 12 000 ? 3 = 972

Ao todo, ela deverá pagar ao banco a quantia de:

12 000 + 972 = 12 972

Regina deverá pagar 972 reais de juro e pagará, no total, 12 972 reais ao final do empréstimo.

2 Uma aplicação feita durante 2 anos, a uma taxa de 12% ao ano, rendeu 1 800 reais de juro simples. Qual foi a quantia aplicada?

Vamos, inicialmente, determinar quanto a aplicação rendeu de juro por ano: 1 800 : 2 = 900.

Representando a quantia aplicada por x, podemos escrever:

12% x = 900

0,12x = 900

== x 900 0,12 7 500

A quantia aplicada foi 7 500 reais.

D2-MAT-F2-2103-V8-U1-012-039-LA-G24.indd

Atividade complementar

Mariana precisa comprar um fogão. Depois de pesquisar bastante, ela encontrou um fogão com duas opções de pagamento: R $ 700,00 à vista ou R $ 800,00 em 4 parcelas de R $ 200,00, pagando a primeira parcela no ato da compra. Sabendo que Mariana possui R $ 800,00 e pretende aplicá-los a juro simples de 4% ao mês, qual tipo de pagamento será mais vantajoso financeiramente? Por quê? Resposta: À vista, pois o valor do rendimento é inferior aos 100 reais de desconto pelo pagamento à vista.

ORIENTAÇÕES DIDÁTICAS

Ressaltar que no regime de juro simples a taxa de juro sempre incide sobre o capital (valor inicial da transação).

Antes de apresentar as situações propostas no Livro do estudante, é interessante fazer uma simulação de juro simples na lousa. Por exemplo, uma aplicação de R $ 10.000,00 a uma taxa mensal de 1% a juro simples. Pedir aos estudantes que calculem o montante (capital + juro) a cada mês de um trimestre. O importante é eles perceberem que o cálculo do juro de cada mês é obtido considerando sempre 1% de R $ 10.000,00.

Propor aos estudantes que façam modificações nas condições de cada situação apresentada para que observem o que ocorre. Por exemplo, eles podem alterar a taxa e o prazo.

Ressaltar que a taxa de juro e o período de tempo considerado precisam ser expressos na mesma unidade de medida de tempo.

ORIENTAÇÕES DIDÁTICAS

Atividades

Nesse bloco de atividades, espera-se que os estudantes utilizem os conhecimentos adquiridos para resolver problemas que envolvem juro simples. Desse modo, pretende-se dar continuidade ao desenvolvimento da habilidade EF08MA04.

Na atividade 1, orientar os estudantes a realizar os cálculos formalmente e, depois, refazê-los com a calculadora, verificando os resultados encontrados. Para calcular o juro simples relativo aos 5 meses, deve-se multiplicar o valor obtido em um mês (R $ 41,40) pela quantidade de meses que renderá juro. Portanto, em 5 meses, renderá: R $ 207,00 (5 ? 41,40). Vale ressaltar que o juro simples não costuma ser praticado no mercado. Mas, em termos didáticos, é bastante útil discuti-lo, pois permite aos estudantes compreender o conceito de juro como acréscimo de um valor.

Na atividade 5, explorar com os estudantes qual seria o valor de juro pago por Pedro após 20 dias de atraso. Pedir aos estudantes que levem para a sala de aula boletos bancários que mostrem a taxa de juro aplicada em caso de atraso. Ressaltar que, nesses casos, o juro aplicado é composto.

Nas atividades 9 e 10, verificar as estratégias que os estudantes utilizam para resolver os problemas propostos, considerando os conteúdos estudados até aqui. Espera-se que os estudantes reconheçam a porcentagem como representação de frações cujo denominador é 100, relacionando a representação de uma porcentagem com a escrita fracionária, bem como empregando a ideia de equivalência com base na compreensão de que 10% = 10 100 = 1 10

Responda às questões no caderno, considerando em todas o regime de juro simples

1. Quanto renderá de juro a quantia de 1 8 00 reais, aplicada durante 5 meses, a uma taxa de 2,3% ao mês?

207 reais.

2. Uma aplicação de 40 0 00 reais rendeu, em três meses, 3 0 00 reais de juro. Qual é a taxa mensal de juro?

7. Uma loja do bairro de Luís colocou o anúncio a seguir na vitrine.

DE SOM

450 reais à vista 468 reais com cheque para 30 dias

Qual é a taxa mensal de juro que essa loja está cobrando para pagamento a prazo?

3. Luís colocou parte de seu 13o salário em uma aplicação que rendia 25,6% de juro ao ano. Sabendo que após dois anos ele recebeu 389,12 reais de juro, qual foi a quantia que ele aplicou?

4. (UFPB) Katienne tem duas opções de pagamento na compra de um fogão: sem juros, em quatro parcelas mensais iguais de R $ 350,00; ou à vista, com 15% de desconto. Nesse contexto, o preço desse fogão, à vista, é:

a) R$ 1.190,00

b) R$ 1.110,00

c) R$ 1.210,00

d) R$ 1.090,00

e) R$ 1.290,00

5. (Saresp-SP) Certo banco cobra juros simples de 0,3% ao dia para contas pagas com atraso de até 30 dias. Pedro pagou uma conta de R $ 50,00 com atraso de 12 dias. O valor pago por Pedro foi de:

a) R$ 51,00

b) R$ 51,40

c) R$ 51,80

d) R$ 52,20

6. (Saresp-SP) Marcos fez um empréstimo de R $ 120.000,00 que deverá ser pago com juros de 1% sobre o valor emprestado a cada mês. Sabendo que pagou R $ 6.000,00 de juros, quantos meses levou para pagar o empréstimo?

8. (Fuvest-SP) Há um ano, Bruno comprou uma casa por R $ 50.000,00. Para isso, tomou emprestados R $  10.000,00 de Edson e R$ 10.000,00 de Carlos, prometendo devolver-lhes o dinheiro, após um ano, acrescido de 5% e 4% de juros, respectivamente.

A casa valorizou 3% durante este período de um ano. Sabendo-se que Bruno vendeu a casa hoje e pagou o combinado a Edson e Carlos, o seu lucro foi de:

a) R$ 400,00

b) R$ 500,00

c) R$ 600,00

d) R$ 700,00

e) R$ 800,00

9. Marina fez um empréstimo bancário de R$ 10.000,00 por 5 meses, com uma taxa de juro de 1% ao mês. Ao mesmo tempo, Leandro fez um empréstimo em outro banco de R$ 5.000,00 por 20 meses.

a) Q ual é a quantia que Marina deverá pagar de juro ao final do empréstimo?

b) Qual é o valor total que Marina terá de pagar ao final do empréstimo?

c) Sabendo que o valor total pago por Leandro ao final do empréstimo foi o mesmo valor que Marina pagou, utilize uma calculadora para determinar a taxa de juro do empréstimo realizado por Leandro.

a) 3 meses

b) 4 meses c) 5 meses d) 6 meses

2,5% 760 reais. Alternativa a. Alternativa c. Alternativa c.

10. A pa rtir da atividade 9, elabore um problema cuja resposta seja “a taxa é de 2% ao mês”. Entregue o problema para um colega resolver e, em seguida, verifique se a resposta dele está correta

Na atividade 10, os estudantes mobilizam conhecimentos estudados até aqui para elaborar um problema dada a indicação de uma resposta. Nesse tipo de proposta de elaboração de problema, os estudantes são desafiados a analisar condições que sejam adequadas para que a resposta obtida seja coerente com a indicação dada.

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd

4% Alternativa c. R$ 500,00

R$ 10.500,00 5,5%

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

EDUCAÇÃO FINANCEIRA

O QUE SÃO OS BANCOS?

Existe um grupo de pessoas que tem dinheiro e quer guardá-lo. Há outro grupo que precisa de dinheiro para investi-lo ou usá-lo em negócios, como construir prédios, abrir comércio e instalar novas fábricas.

Se esses grupos não se conhecem, não é possível realizar negócios entre eles. Mesmo que se conhecessem, poderia não haver confiança entre as pessoas, a ponto de umas pedirem dinheiro emprestado às outras.

Então, os bancos oferecem para aquelas que têm dinheiro uma forma segura de guardá-lo […] e lhes pagam juros ou rendimentos.

E, às pessoas que precisam de dinheiro para investimentos, os bancos fazem-lhes empréstimos e recebem juros pelo serviço.

Dessa maneira, os bancos movimentam o dinheiro. Usam as economias de uns para emprestar a outros.

[…]

Quando as pessoas guardam seu dinheiro no banco, deixam-no depositado por algum tempo. Sabendo disso, os bancos só conservam em seus cofres uma pequena parte de tudo aquilo que recebem, para atender aos clientes que solicitarem alguma quantia. A outra parte, bem maior, é emprestada a outras pessoas. Com a diferença entre os juros que recebem das pessoas que tomam empréstimo e os juros que pagam às pessoas que guardam o dinheiro (em uma conta de poupança, por exemplo), os bancos pagam a seus empregados e obtêm seus lucros.

[…]

BANCO CENTRAL DO BRASIL. Cadernos BC: O que são os bancos? Brasília, DF: BCB, 2002. (Série Educativa, p.14-16). Disponível em: https://www.bcb.gov.br/Pre/educacao/cadernos/bancos.pdf. Acesso em: 18 jun. 2022. Usando o texto e seus conhecimentos sobre porcentagem e juro, responda no caderno.

1. Segundo o texto, qual é o papel dos bancos?

Resposta na seção Resoluções comentadas deste Manual.

2. As aplicações financeiras nos auxiliam a capitalizar nosso dinheiro. Discuta com os colegas as situações a seguir, indicando se uma aplicação financeira ou um empréstimo podem ou não contribuir para:

a) ter um dinheiro extra para aproveitar mais a vida.

b) comprar uma máquina que vai aumentar a produtividade de um negócio.

c) iniciar um negócio cuja previsão de rendimento seja maior do que o juro pago.

d) completar o orçamento doméstico.

e) comprar um objeto cujo valor não está disponível.

DESCUBRA MAIS

Respostas pessoais. Exemplos de respostas na seção Resoluções comentadas deste Manual.

MUSEU DE VALORES – BANCO CENTRAL DO BRASIL. Brasília, DF, [20-?]. Site. Disponível em: https:// www.bcb.gov.br/acessoinformacao/museu/tourvirtual/. Acesso em: 18 jun. 2022.

Faça um tour virtual pelo museu, que reúne diversos materiais interessantes, entre eles, cédulas e moedas brasileiras e estrangeiras, barras de ouro, artefatos ligados à fabricação e à história do dinheiro.

ORIENTAÇÕES DIDÁTICAS

Educação financeira

O texto proposto nesta seção procura explicar o que são os bancos, como funcionam, sua importância e como fazem para guardar e capitalizar dinheiro dos seus clientes. A discussão proposta tem como objetivo contribuir para o desenvolvimento do Tema Contemporâneo Transversal Educação Financeira e da competência geral 2. Pedir aos estudantes que leiam o texto individualmente e façam um resumo no caderno com as informações que considerarem mais importantes.

Depois, pode-se discutir com os estudantes os pontos destacados anteriormente. Explorar as informações destacadas por eles e explicar como os bancos movimentam dinheiro, mostrando que há uma diferença entre o juro pago pelo tomador e o juro recebido por quem investe.

Após a discussão do tema, solicitar aos estudantes que façam as atividades propostas.

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 33

Descubra mais

O boxe Descubra mais propõe um tour virtual pelo Museu de Valores do Banco Central do Brasil. Caso a escola disponha de um laboratório de informática, agendar um horário e levar a turma para explorar o museu. Os estudantes podem fazer isso em duplas. Pedir que registrem no caderno informações interessantes que

30/07/22 20:43

gostariam de compartilhar com os colegas em um momento futuro. Caso não seja possível explorar em pequenos grupos, fazer uma projeção do site na parede da sala de aula, conversando com os estudantes e navegando segundo as solicitações da turma.

Discutir as respostas da atividade 2. Espera-se que os estudantes concluam que as situações dos itens a e d podem ser desvantajosas e que a solução, nesses casos, é adequar gastos e ganhos. Nas situações relativas a negócios, apresentadas nos itens b e c, comentar que muitas vezes essa é a principal escolha para quem está desenvolvendo um negócio, mesmo com o risco de o lucro demorar mais que o previsto ou não acontecer, podendo gerar prejuízos. No item e, discutir a relação entre necessidade e desejo. Nessa situação, uma alternativa é poupar dinheiro durante um tempo para comprar o objeto posteriormente, se for possível aguardar. Essas discussões contribuem para o desenvolvimento do Tema Contemporâneo Transversal Educação para o Consumo e da competência geral 6.

ORIENTAÇÕES DIDÁTICAS

Tecnologias

Nesta seção, é proposta uma exploração de como utilizar o software LibreOffice Calc para realizar cálculos de porcentagem. Desse modo, favorece-se o desenvolvimento da habilidade EF08MA04 e da competência específica 5 da área de Matemática.

Antes de iniciar a atividade garantir que todos os estudantes tenham acesso ao aplicativo. Se possível, instalar nos computadores e notebooks da escola, para que fique disponível para outras situações. Ao iniciar a aula, pode-se propor um momento de ambientação com o software e com algumas ferramentas.

Depois, pode-se explorar a situação apresentada no Livro do estudante. Para dar continuidade, pode-se acompanhar o passo a passo sugerido, de modo que eles consigam acompanhar os cálculos à medida que exploram o uso do software. Nesse momento, é recomendável que a turma esteja organizada em duplas.

Se possível, transitar pela sala de informática para se certificar de que todos estejam acompanhando as etapas.

TECNOLOGIAS

CÁLCULO DE PORCENTAGEM USANDO PLANILHA ELETRÔNICA

Nesta seção, você vai utilizar um software chamado LibreOffice Calc. É possível fazer o download gratuito desse aplicativo no link https://pt-br.libreoffice.org/baixe-ja/libreoffice-novo/ (acesso em: 17 jun. 2022).

A planilha eletrônica LibreOffice Calc é um recurso que auxilia na realização de cálculos e na organização de dados, incluindo a construção de tabelas e gráficos. Entre os tipos de cálculos que podemos fazer nessa planilha estão aqueles que envolvem porcentagem para o cálculo de juro simples.

Abra o LibreOffice Calc e note que as colunas são identificadas pelas letras do alfabeto, as linhas são numeradas e cada célula da planilha é associada a uma coluna e a uma linha. Na imagem a seguir, a célula selecionada corresponde à coluna C e à linha 2, essa célula é indicada por C2.

Acompanhe as etapas a seguir para efetuar cálculos que envolvem juro simples.

• Emerson está pensando em fazer um empréstimo de R$ 6.000,00 no banco e pagar após 6 meses. O gerente de sua conta o informou de que a taxa de juro simples cobrada é de 3,5% ao mês.

Vamos calcular quanto Emerson pagará de juro e o valor final que pagará por esse empréstimo nessas condições.

1 Digite nas células A1, B1, C1, D1 e E1 as respectivas informações: Empréstimo (em reais), Taxa de juro ao mês, Tempo (em mês), Juro e Valor final (em reais). Depois, insira as informações já conhecidas. Na célula A2, abaixo de Empréstimo (em reais), digite 6000; na célula B2, digite 3,5%; e na célula C2, digite 6

D2_AV4-MAT-F2-2103-V8-U1-012-039-LA-G24.indd

2. Resposta pessoal. Espera-se que os estudantes avaliem a possibilidade de Emerson pagar um pouco a mais no total e pagar em mais tempo.

2 Na célula D2, você deverá digitar uma fórmula para calcular o valor do juro, que corresponde ao valor inicial do empréstimo vezes a taxa de juro vezes o tempo. Na planilha eletrônica, digitamos assim:

ORIENTAÇÕES DIDÁTICAS

3 Após digitar a fórmula em D2, pressione Enter, e o valor do juro (1 260) aparecerá automaticamente nessa célula.

4 Na célula E2, você deverá digitar uma fórmula para calcular o valor final a ser pago pelo empréstimo, que se dá pelo valor do empréstimo mais o juro. Na planilha eletrônica, digitamos assim:

5 Após digitar a fórmula em E2, pressione Enter, e o valor a ser pago ao final de 6 meses aparecerá automaticamente.

Portanto, Emerson pagará R$ 1.260,00 de juro e R$ 7.260,00 no total ao final de 6 meses. Agora, utilize a planilha do LibreOffice Calc para resolver as questões a seguir.

1. Emerson tem conta em outro banco e resolveu consultar o gerente dessa outra conta para verificar se conseguiria uma condição melhor. Nesse banco, ele foi informado de que o empréstimo poderia ser pago em 10 meses, a uma taxa de juro de 2,6% ao mês. Faça a simulação desse empréstimo na linha 3 da planilha e verifique quanto Emerson pagaria pelo empréstimo nesse caso.

Emerson pagaria R$ 7.560,00 nesse caso.

2. Comparando o valor a ser pago ao final do empréstimo em cada banco, em seu entendimento, qual dos empréstimos vale a pena Emerson fazer? Justifique.

3. Use a planilha para calcular o montante de um investimento de R$ 1.500,00, a uma taxa de juro simples de 0,5% ao mês por 12 meses. Compare esse montante com o valor a ser pago por um empréstimo no mesmo valor e pelo mesmo tempo com uma taxa de juro simples de 8% ao mês.

No caso do investimento, o montante ao final de 12 meses é de R$ 1.590,00; já no empréstimo, o valor a ser pago é R$ 2.940,00.

No passo 2, os estudantes precisam digitar a fórmula que permite calcular o valor, em reais, do juro. Importante ressaltar para a turma que as fórmulas sempre são iniciadas com o sinal de igual (=). Além disso, destacar que a operação de multiplicação é representada pelo símbolo *. Comentar, ainda, que os estudantes podem digitar as coordenadas das células (A2, B2, C2) ou podem clicar nas células. No passo 3, os estudantes pressionam a tecla Enter e, automaticamente, o valor do juro surge na célula D2. Feito isso, o cálculo do valor final será efetuado com uma nova fórmula, a ser digitada na célula E2, como descrito no passo 4. Novamente, os estudantes devem pressionar a tecla Enter, obtendo o resultado desejado (passo 5). Encaminhar, na sequência, os problemas propostos e verificar se os estudantes preencheram as informações corretamente na planilha. Comumente, os estudantes se esquecem de iniciar a escrita das fórmulas com o sinal de igual. Dessa maneira, o aplicativo não reconhece que deve efetuar um cálculo, o que gera um erro.

FOTOGRAFIAS: REPRODUÇÃO/ LIBREOFFICE CALC

ORIENTAÇÕES DIDÁTICAS

Tratamento da informação

Propor aos estudantes que se reúnam em duplas, incentivando a troca de ideias e de estratégias de resolução. As questões que eles tiverem mais dificuldade podem ser resolvidas na lousa. Esta seção e a discussão do tema proposto podem ser trabalhadas em parceria com o professor de Ciências.

Esta seção aborda o tema água com vários enfoques: distribuição da água no planeta, destino da água retirada das bacias hidrográficas do Brasil, pegada hídrica de um produto e consumo médio de água por brasileiro. Desse modo, busca-se favorecer o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental, da competência geral 7 e da competência específica 5 da área de Matemática. Solicitar aos estudantes que realizem uma pesquisa sobre a importância do consumo diário de água de maneira consciente, os benefícios desse hábito e os malefícios quando não há preocupação com essa recomendação. Todas essas informações poderão ser apresentadas em cartazes a serem expostos na escola para que as informações pesquisadas sejam compartilhadas.

Para a atividade 1, explorar os gráficos que mostram a distribuição da água no planeta. O segundo gráfico dessa atividade apresenta um detalhamento da parte referente à água doce do primeiro gráfico. A análise dos gráficos que são mais adequados para representar determinado tipo de informação também é foco da atividade, contribuindo para o desenvolvimento da habilidade EF08MA23.

INFORMAÇÃO TRATAMENTO DA

RECURSOS HÍDRICOS

A água é uma substância fundamental para a manutenção da vida animal e da vida vegetal. É um recurso natural de extrema importância no desenvolvimento de diversas atividades, como as dos setores agrícola, industrial e econômico.

As atividades a seguir trazem algumas pesquisas e alguns dados sobre a água. Para resolvê-las, é necessário interpretar e construir diferentes tipos de gráfico. Responda às questões no caderno.

1. Os oceanos compõem cerca de 70% da superfície da Terra. Do total de água do planeta, cerca de 97,5% são água salgada, e somente 2,5% são água doce. Observe, no gráfico, como essa água é distribuída e responda ao que se pede em cada item.

Água no planeta

2,5% do total global (água doce)

Geleiras e coberturas permanentes de neve

subterrâneas Rios e lagos

Outros (incluindo umidade do solo, placas de gelo flutuante e pântanos)

Elaborado com base em: BRASIL. Ministério do Meio Ambiente. Agência Nacional de Águas. A Água no Planeta para Crianças. Brasília, DF: ANA, c2014 (slide). Disponível em: http://arquivos.ana.gov.br/institucional/sge /CEDOC/Catalogo/2014/AAguaNoPlanetaParaCriancas2014.pdf. Acesso em: 18 jun. 2022.

a) Explique o significado de cada taxa percentual apresentada no gráfico.

b) Usando uma calculadora, determine a taxa percentual aproximada de água do planeta que corresponde:

• às geleiras e coberturas permanentes de neve;

• aos rios e lagos;

0,0075%

• às águas subterrâneas;

• a outros.

0,75% 0,02%

1.a) Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

O Brasil dispõe de cerca de 12,0% da água doce do Planeta. Mas a distribuição é desigual no território. Há grande disponibilidade na macrorregião Norte, onde vive a menor parcela da população. Em contrapartida, Sudeste e Nordeste, com cerca de 69,0% da população, dispõem de menos de 10,0% do volume disponível para consumo.

Outro fato é que a água doce não se destina apenas para o consumo humano. Dela também dependem atividades como irrigação agrícola e produção industrial, dentre outras. [...] BRASIL. Ministério do Desenvolvimento Regional. Secretaria Nacional de Saneamento. Diagnóstico Temático –Serviços de Água e Esgoto: Visão Geral (ano de referência 2020). Brasília, DF: SNIS, 2021. p. 34. Disponível em: http://www.snis.gov.br/downloads/diagnosticos/ae/2020/DIAGNOSTICO_TEMATICO_VISAO_GERAL_AE_SNIS_2021.pdf. Acesso em: 18 jun. 2022. Observe, no gráfico a seguir, o destino da água retirada das bacias hidrográficas no Brasil, em 2019.

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd

2. Leia o texto a seguir.

De acordo com as informações fornecidas, copie a alternativa incorreta, justificando-a.

a) A proximadamente metade da água retirada destinou-se à irrigação.

b) Os abastecimentos urbano e rural, juntos, correspondem a aproximadamente 26% do destino da água retirada.

c) Foi destinada mais água aos abastecimentos humano e animal do que à irrigação.

d) A s regiões Sudeste e Nordeste têm, juntas, mais da metade da população brasileira e menos de 10% da disponibilidade de água.

Destino da água retirada das bacias hidrográficas no Brasil (2019)

ORIENTAÇÕES DIDÁTICAS

Elaborado com base em: BRASIL. Ministério do Desenvolvimento Regional. Secretaria Nacional de Saneamento. Diagnóstico Temático – Serviços de Água e Esgoto: Visão Geral (ano de referência 2020). Brasília, DF: SNIS, 2021. p. 34. Disponível em: http://www.snis.gov.br/ downloads/diagnosticos/ae/2020/DIAGNOSTICO_TEMATICO_ VISAO_GERAL_AE_SNIS_2021.pdf. Acesso em: 18 jun. 2022.

3. Você sabia que, mesmo quando não consumimos água diretamente, estamos consumindo produtos que precisaram de água para serem produzidos?

A pegada hídrica de um produto é definida como o volume de água consumido, direta e indiretamente, para produzir esse produto ao longo de toda a sua cadeia produtiva. No caso da carne, por exemplo, o cálculo para conhecer a pegada hídrica leva em consideração toda a água usada no processo, desde a quantidade consumida na produção do alimento oferecido ao animal, até a utilizada no abate. Médias globais de pegada hídrica de alguns produtos (em litros de água):

• 1 kg de açúcar refinado: 1 500

• 100 g de chocolate: 2 4 00

• 1 camiseta de algodão: 2 700

• 1 kg de carne bovina: 15 500

Elaborado com base em: PEGADA hídrica dos produtos carne e leite. Embrapa. Brasília, DF, [2018?]. Disponível em: https://www.embrapa.br/busca-de-projetos/-/projeto/208753/pegada-hidrica-dos-produtos-carne-e-leite.

PEGADA hídrica incentiva o uso responsável da água. WWF Brasília, DF, 21 mar. 2011. Disponível em: https://www. wwf.org.br/?27822/Pegada-Hdrica-incentiva-o-uso-responsvel-da-gua#. Acessos em: 18 jun. 2022. Organize as pegadas hídricas dos produtos em uma tabela e construa um gráfico de barras com esses dados.

Resposta na seção Resoluções comentadas deste Manual.

4. Segundo o Sistema Nacional de Informações sobre Saneamento (SNIS), em 2020 o consumo médio de água por habitante no Brasil era de 152,1 litros/dia. De acordo com a Organização das Nações Unidas (ONU), 110 litros/dia é a quantidade de água suficiente para atender às necessidades básicas de uma pessoa.

Elaborado com base em: BRASIL. Ministério do Desenvolvimento Regional. Secretaria Nacional de Saneamento. Diagnóstico Temático – Serviços de Água e Esgoto: Visão Geral (ano de referência 2020). Brasília, DF: SNIS, 2021. p.35-36. Disponível em: http://www.snis.gov.br/downloads/diagnosticos/ae/2020/DIAGNOSTICO_TEMATICO_VISAO_ GERAL_AE_SNIS_2021.pdf.

SÃO PAULO (Estado). Companhia de Saneamento Básico do Estado de São Paulo. Dicas de economia. São Paulo: Sabesp, [20-?]. Disponível em: https://site.sabesp.com.br/site/interna/Default.aspx?secaoId=140#:~:text=De%20acordo%20com%20 a%20Organiza%C3%A7%C3%A3o,mais%20de%20200%20litros%2Fdia. Acessos em: 18 jun. 2022.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Em grupos, pesquisem atitudes que vocês podem ter para economizar água em casa, na escola e em atividades que realizam no dia a dia. Elaborem cartazes e compartilhem com os outros colegas da escola.

2. Alternativa c. A água destinada aos abastecimentos urbano, rural e animal corresponde a 34,3% de toda a água retirada, enquanto a irrigação corresponde a 49,8%.

D2_AV1-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 37

Vídeo

PEGADA Hídrica: Reporter ECO. 2011. Vídeo (5min12s). Publicado pelo canal TV Cultura. Disponível em: https://www.youtube.com/watch?v=J8npPb2ORdA. Acesso em: 28 jul. 2022.

A reportagem pode ser utilizada para ampliar a discussão do conceito de pegada hídrica.

Na atividade 2, auxiliar os estudantes na leitura e interpretação do gráfico de setores. O item a está correto, pois 49,80% da água retirada das bacias hidrográficas brasileiras é destinada à irrigação. Com relação aos abastecimentos urbano e rural, abordados no item b, é correto afirmar que juntos representam aproximadamente 26,0% (abastecimento urbano: 24,30% e abastecimento rural: 1,60%). O item c está incorreto, pois a água destinada aos abastecimentos (urbano e rural) e ao uso animal (24,30% + 1,60% + + 8,40%) corresponde a 34,3% de toda a água retirada, enquanto a irrigação corresponde a 49,80%.

A atividade 3 traz o conceito de pegada hídrica de um produto. Perguntar aos estudantes se eles conheciam esse conceito e se sabiam a quantidade de litros de água utilizada, por exemplo, na produção de 100 g de chocolate. Conversar com eles sobre como devem ser as barras no gráfico que eles devem construir. Espera-se que eles concluam que os comprimentos das barras devem ser proporcionais aos percentuais relativos a cada produto indicado na tabela.

Na atividade 4, os estudantes, reunidos em grupos, devem realizar pesquisas e construir propostas de redução de consumo de água. Para a confecção dos cartazes, providenciar previamente cartolinas, canetas hidrográficas e réguas.

2. a) 34 9 b) 23 90 c) 1206 99 d) 3 973 990

Retomando o que aprendeu

As questões desta seção visam retomar o trabalho com números racionais, porcentagem, juro simples e fração geratriz, o que favorece o desenvolvimento das habilidades EF08MA04 e EF08MA05.

Incentivar os estudantes a socializar as estratégias que utilizaram e trocar ideias com os colegas a respeito de temas sobre os quais ainda tenham dúvida. Acompanhar e orientá-los nesse trabalho. Se necessário, explicar na lousa as dúvidas que ainda persistam.

Orientá-los a consultar o Livro do estudante para tirar dúvidas e buscar informações. Conversar com eles a respeito de acertos e equívocos, indicando as correções com intervenções pontuais. Esse tipo de ação amplia a capacidade de comunicação e argumentação dos estudantes de acordo com a competência geral 7, além de beneficiar a cooperação entre eles.

Após as atividades desta seção, realizar uma discussão com a turma sobre como os conceitos estudados na Unidade podem ser aplicados no dia a dia.

Na atividade 8, verificar se os estudantes compreenderam que é preciso calcular a porcentagem de uma porcentagem, ou seja, é preciso multiplicar as porcentagens dadas no enunciado.

RETOMANDO APRENDEU O QUE

3. a) Sim; 49 7

b) −97; 49 7

c) 3 d) 3 e) 1,25; 49 7 ; 97; 3 5

38

Responda às questões no caderno.

1. A quantidade de casas decimais do produto 3,4 por 1,56 é igual a:

a) 1.

b) 2. c) 3. d) 4. e) 5.

Alternativa c.

2. Determine as frações geratrizes das dízimas periódicas a seguir.

a) 3,77777…

b) 0,255555…

c) −12,181818…

d) 4,0131313…

3. Observe os números a seguir e responda.

6. No colégio do meu bairro há 1 600 estudantes, dos quais 720 são meninos. A quantidade de meninas representa quantos por cento do total de estudantes que há nesse colégio?

a) Alguns desses números pertencem ao conjunto dos números naturais? Quais?

b) Quais números pertencem ao conjunto dos números inteiros?

c) Quais números são irracionais?

d) Quais números são reais, mas não são racionais?

e) Quais números são reais, mas não são irracionais?

4. Uma pesquisa de “boca de urna”, realizada no primeiro turno das eleições para prefeito de um município, indicou que um dos candidatos tinha 1 5 das intenções de voto. Esse número representa quantos por cento das intenções de voto dessa pesquisa?

a) 5%

b) 10% c) 20% d) 25% e) 50%

5. Quinta-feira passada, 5 dos 40 estudantes de uma turma faltaram à aula de Educação Física. Nesse dia, o professor registrou quantos por cento de faltas?

Alternativa c. 12,5%

7. Rafael prepara um copo de suco misturando 120 mililitros de água e 80 mililitros de suco de fruta concentrado. Qual é a porcentagem de água nessa mistura?

8. 30% de 40% de 50% de um número representa quantos por cento do número?

a) 4%

b) 8% c) 5% d) 6% e) 10%

9. Tarcísio tomou emprestados R$ 2.400,00 do banco e vai pagar o empréstimo em 6 vezes, com juro simples de 4% ao mês. A quantia que Tarcísio pagará de juro por mês será:

a) R$ 16,00.

b) R$ 32,00.

c) R$ 96,00.

d) R$ 160,00.

e) R$ 300,00.

10. ( Fuvest-SP) Que número deve ser somado ao numerador e ao denominador da fração 2 3 para que ela tenha um aumento de 20%?

a) 1

b) 2 c) 3 d) 4 e) 5

11. (PUC-RJ) Em um viveiro há várias araras.

• 60% das araras são azuis,

• 4 0% das araras são vermelhas,

• 40% das araras azuis têm bico branco,

• 30% das araras vermelhas têm bico branco.

Que porcentagem das araras do viveiro tem bico branco?

a) 10%

55% 60% Alternativa d. Alternativa c. Alternativa b. Alternativa d.

30/07/22 20:50

Será um decimal exato. Espera-se que os estudantes percebam que o denominador (25) é divisor de 100; logo, podemos escrever uma fração equivalente à fração dada com denominador 100, e, portanto, como um número decimal exato.

12. (Enem/MEC) Após consulta médica, um paciente deve seguir um tratamento composto por três medicamentos: X, Y e Z. O paciente, para adquirir os três medicamentos, faz um orçamento em três farmácias diferentes, conforme o quadro.

X Y Z

Farmácia 1 R$ 45,00 R$ 40,00 R$ 50,00

Farmácia 2 R$ 50,00 R$ 50,00 R$ 40,00

Farmácia 3 R$ 65,00 R$ 45,00 R$ 35,00

Dessas farmácias algumas oferecem descontos:

• na compra dos medicamentos X e Y na Farmácia 2, recebe-se um desconto de 20% em ambos os produtos, independentemente da compra do medicamento Z, e não há desconto para o medicamento Z;

• na compra dos 3 medicamentos na Farmácia 3, recebe-se 20% de desconto no valor total da compra.

O paciente deseja efetuar a compra de modo a minimizar sua despesa com os medicamentos.

De acordo com as informações fornecidas, o paciente deve comprar os medicamentos da seguinte forma:

Alternativa c.

a) X, Y e Z na Farmácia 1.

b) X e Y na Farmácia 1, e Z na Farmácia 3.

c) X e Y na Farmácia 2, e Z na Farmácia 3.

d) X na Farmácia 2, e Y e Z na Farmácia 3.

e) X, Y e Z na Farmácia 3.

13. Elabore uma atividade envolvendo o tema porcentagem de tal modo que, para resolvê-la, seja necessário aplicar os conhecimentos adquiridos nesta Unidade. Utilize tabelas e gráficos para compor a atividade e, se achar necessário, use uma calculadora ou uma planilha eletrônica.

Em seguida, troque sua atividade com a de um colega, resolva a atividade dele e, juntos, corrijam e debatam as duas atividades.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Nesta Unidade, revimos o conjunto dos números racionais e suas operações, conhecemos o conjunto dos números reais e estudamos porcentagem e o sistema de juro simples, com enfoque em aplicações na vida cotidiana e, por consequência, na cidadania. Estudamos também que, ao efetuar qualquer compra, devemos estar atentos para os valores cobrados à vista e em parcelas e cuidar para manter uma vida financeira saudável. Além disso, aprendemos a determinar uma fração geratriz de uma dízima periódica. Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

• Imagine que um colega tenha faltado à aula de revisão das operações com números racionais. Escreva um bilhete para ele explicando como adicionar, subtrair, multiplicar e dividir números racionais. Aproveite para contar-lhe que dificuldades você enfrentou nessa aula e o que fez para saná-las.

Resposta pessoal.

• Ao deparar com uma dízima periódica, você é capaz de identificar seu período? Como você faria isso?

Resposta pessoal. Espera-se que os estudantes respondam que sim, que o período é a parte que se repete na dízima.

• O número racional 6 25 , ao ser escrito na representação decimal, será exato ou será periódico? Você consegue saber sem realizar a transformação para a forma decimal? Explique sua resposta com argumentos matemáticos.

• Em que contextos você consideraria realizar uma compra a prazo, mesmo com juro?

Resposta pessoal. Espera-se que os estudantes descrevam contextos em que o produto/serviço é essencial, mas não há dinheiro suficiente naquele momento; ou em que o valor à vista seria muito alto, como na compra de um imóvel, por exemplo.

D2_AV3-MAT-F2-2103-V8-U1-012-039-LA-G24.indd 39

AMPLIANDO

Link

ORIENTAÇÕES DIDÁTICAS

Um novo olhar

É importante que os estudantes respondam individualmente a cada uma das questões para que possam refletir sobre as aprendizagens e possíveis dúvidas a respeito dos conteúdos estudados. São questões que visam levar os estudantes a refletir sobre as próprias aprendizagens.

A primeira questão pede aos estudantes que escrevam um bilhete a um colega, explicando como resolver as operações com números racionais. Ao pensar em como explicar as operações para um colega, o estudante é convidado a verificar os pontos que ainda trazem dificuldade para expressar o próprio raciocínio. A segunda questão aborda o reconhecimento do período de uma dízima periódica. Espera-se que os estudantes consigam identificar qual é o período de uma dízima, explicitando como procederiam para fazê-lo.

A terceira questão leva os estudantes a refletir sobre como verificar se um número racional escrito na forma fracionária terá representação decimal exata ou periódica, ao ser escrito na representação decimal. Na quarta questão, espera-se que os estudantes descrevam contextos de compra a prazo ou situações como na compra de um imóvel.

14/08/22 23:44

MEDEIROS, Kátia Maria de. A influência da calculadora na resolução de problemas matemáticos abertos.

In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA , 8., 2004, Recife. Anais [...]. Recife: UFPE, 2004. p. 19-28. Disponível em: http://www.sbem.com.br/files/viii/pdf/06/CC77270991472.pdf. Acesso em: 11 ago. 2022.

Nesse artigo, são apresentados vários exemplos de como a calculadora pode ajudar os estudantes na resolução de problemas, em especial nos processos de agilizar as tentativas, de concentração na modelagem e resolução do problema e de melhorar a velocidade de resolução.

BNCC NA UNIDADE

Competências gerais:

• 5, 8, 9 e 10

Competências específicas:

• 2, 3, 5, 6, 7 e 8

Habilidades:

Números

• EF08MA01 • EF08MA02

Probabilidade e estatística

• EF08MA24

Temas Contemporâneos

Transversais:

• Ciência e Tecnologia

• Vida Familiar e Social

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em seis capítulos ; ela apresenta os conteúdos por meio de exemplos e atividades diversificadas, com seções que trazem informações sobre contextos de relevância social, contribuindo para a formação integral dos estudantes e favorecendo o desenvolvimento das competências gerais 5, 8, 9 e 10.

O primeiro capítulo retoma o cálculo das potências com expoentes inteiros. O segundo capítulo retoma as propriedades da potenciação e explora a definição de notação científica. Esse estudo, favorece o desenvolvimento da habilidade EF08MA01. O terceiro capítulo retoma o conceito de números quadrados perfeitos. No quarto capítulo, trabalha-se com a ideia de raiz quadrada exata e raiz quadrada aproximada. No quinto capítulo, expande-se a discussão para outras raízes e faz-se a generalização para raízes enésimas. No sexto capítulo, a relação entre potenciação e radiciação é formalizada a partir do estudo das potências com expoentes fracionários. Esse estudo favorece o desenvolvimento da habilidade EF08MA02.

Lendas são narrativas de origem fantástica ligadas à tradição oral que contam fatos históricos combinados a outros.

Na abertura desta Unidade, apresentamos resumidamente uma lenda que diz como o jogo de xadrez teria sido inventado.

Sissa pediu 1 grão de trigo pela primeira casa do tabuleiro, 2 pela segunda, 4 pela terceira, 8 pela quarta, e assim sucessivamente, até chegar à 64a casa.

OBJETIVOS

Leia a lenda e responda oralmente às questões a seguir.

• Sissa faz um pedido que se mostra impossível de ser atendido. Qual foi esse pedido?

• Que estratégia você utilizaria para calcular a quantidade de grãos que Sissa deveria receber na 30a casa do tabuleiro sem ter de calcular a quantidade de grãos a ser recebida até a 29a casa?

• Outra versão dessa lenda diz que os matemáticos do rei levaram um grande tempo para calcular a quantidade de grãos que deveria ser paga a Sissa. Hoje, existem ferramentas tecnológicas que ajudam a realizar esse cálculo com mais facilidade. Que ferramenta você utilizaria para realizar esse cálculo?

• Converse com um colega sobre as seguintes questões: Você já jogou xadrez? O que você acha desse jogo? Você gosta de jogos de tabuleiro? Qual é seu jogo de tabuleiro preferido?

• Retomar o cálculo de potências com expoentes inteiros e as propriedades da potenciação.

• Compreender as potências de base 10 e aplicá-las na escrita de números em notação científica.

• Retomar o conceito de números quadrados perfeitos e identificá-los por meio da decomposição em fatores primos.

• Calcular raízes quadradas exatas e aproximadas.

• Calcular raízes cúbicas e raízes com índices maiores do que 3.

• Relacionar potenciação e radiciação por meio do cálculo de potências com expoentes fracionários.

• Ler e interpretar tabelas de distribuição de frequência com intervalos de classes.

• Desenvolver atitudes de combate ao bullying e ao ciberbullying.

Respostas na seção Resoluções comentadas deste Manual.

WANDSON ROCHA

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

Sissa, um sábio

Tendo gostado do jogo, o rei prometeu uma recompensa: daria a Sissa qualquer coisa que ele pedisse.

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

Incentivar os estudantes a ler atentamente a lenda apresentada e discutir com eles o papel das lendas na tradição oral e escrita. A narrativa não retrata um fato, mas conta uma história a respeito do jogo de xadrez.

Se houver possibilidade, providenciar tabuleiros de xadrez e alguns grãos de feijão ou de arroz para representar um trecho da história retratada.

Na primeira questão, espera-se que os estudantes respondam que Sissa pediu que lhe fossem dados grãos de trigo pelas casas de um tabuleiro da seguinte maneira: 1 grão pela primeira casa do tabuleiro, 2 grãos pela segunda, 4 pela terceira, 8 pela quarta, e assim sucessivamente, dobrando a quantidade de grãos por casa até chegar à 64 a casa.

JUSTIFICATIVAS DOS OBJETIVOS

Nesta Unidade, apresenta-se o estudo de potencias e raízes, com destaque para a escrita de números em notação científica, favorecendo o desenvolvimento das habilidades EF08MA01 e EF08MA02. Na seção Tratamento da informação, os estudantes leem e interpretam tabelas de distribuição de frequência com intervalos de classes, conforme

Mas feitos os cálculos, verificou‑se que, se juntasse todo o trigo do mundo, ainda não seria possível coletar a quantia que Sissa tinha pedido como recompensa.

Na segunda questão, espera-se que os estudantes percebam que para calcular a quantidade de grãos, eles precisarão calcular uma potência de base 2, cujo expoente varia de 0 a 63. Se considerar pertinente, calcular as dez primeiras casas do tabuleiro. Essa atividade contribui para o desenvolvimento das competências específicas 2 e 3 da área de Matemática.

Na terceira questão, espera-se que os estudantes citem ferramentas como a calculadora ou uma planilha eletrônica, por exemplo.

sugere a habilidade EF08MA24.

No boxe Fórum discute-se bullying e ciberbullying, o que favorece o desenvolvimento do Tema Contemporâneo Transversal Vida Familiar e Social e das competências gerais 8, 9 e 10.

Na seção Por toda parte explora-se a evolução do armazenamento de dados, favorecendo o desenvolvimento do Tema Contemporâneo Transversal Ciência e Tecnologia e da competência específica 3 da área de Matemática.

Na quarta questão há oportunidade de exercitar a capacidade de argumentação e empatia, o que auxilia no desenvolvimento da competência geral 9 e da competência específica 6 da área de Matemática.

O rei ficou espantado perante um pedido que pareceu tão humilde e cedeu imediatamente à sua aparente insignificância.

Segundo a lenda,

indiano, inventou o jogo de xadrez para curar o tédio do rei.

WANDSON ROCHA

ORIENTAÇÕES DIDÁTICAS

Pense e responda

Nessa seção, a atividade proposta utiliza o processo investigativo incentivando os estudantes a fazer levantamento de hipóteses e constatação das hipóteses levantadas. Essa proposta pode contribuir para a compreensão das ideias que envolvem potenciação.

Além disso, eles poderão determinar, por meio da atividade, as sequências numéricas das potências de base 2. Para isso, os estudantes precisarão de folhas de papel sulfite. É conveniente que a atividade dessa seção seja resolvida coletivamente. Eles serão convidados a dobrar e desdobrar as folhas de papel sulfite, mas antes é interessante que levantem hipóteses a respeito da quantidade de dobras e vincos feitos no papel, fazendo inferências para, posteriormente, validá-las ou refutá-las.

POTÊNCIA COM EXPOENTE INTEIRO CAPÍTULO1

PENSE E RESPONDA

Responda às questões no caderno.

4. Resposta pessoal. Espera-se que os estudantes percebam que, a cada dobra ao meio que fazem na folha, a quantidade de partes em que ela fica dividida duplica em relação à quantidade de dobras anterior. Assim, as quantidades de partes podem ser expressas por: 20 (0 dobra), 21 (1 dobra), 22 (2 dobras sucessivas), 23 (3 dobras sucessivas), …

1. Pegue algumas folhas de papel sulfite e siga as orientações a seguir. Dobre uma das folhas ao meio, sucessivamente, por 3 vezes, como mostram as ilustrações.

AMPLIANDO

2a dobra 1a dobra

Então, desdobre a folha. Em quantas partes iguais a folha ficou dividida? 8

3a dobra

2. Dobre outra folha de papel sulfite ao meio, sucessivamente, por 4 vezes. Desdobre-a e responda: em quantas partes a folha ficou dividida? 16

3. Você saberia dizer, antes de fazer as dobras, em quantas partes uma folha de papel sulfite ficaria dividida se fosse dobrada ao meio, sucessivamente, por 5 vezes? E por 6 vezes? Dobre folhas de papel para comprovar suas respostas. 32; 64

4. Você percebe algum padrão na quantidade de dobras sucessivas e na quantidade de partes em que a folha fica dividida? Explique.

Agora, observe uma folha de papel e as dobras feitas nela.

Link

JOGO: Torre de Hanói. Clubes de Matemática da OBMEP. [S l.], [20--]. Disponível em: http://clubes. obmep.org.br/blog/torre-de-hanoi/. Acesso em: 4 ago. 2022.

O jogo on-line Torre de Hanói possibilita aos estudantes explorar a construção da lei geral que determina o número mínimo de movimentos necessários para mover n discos, entre os três pinos disponíveis. Tal lei está associada às potências de 2.

WANDSON ROCHA

• 5 dobras 32 partes

25 = 2 2 2 2 2 = 32

• 6 dobras 64 partes

26 = 2 2 2 2 2 2 = 64

• 7 dobras 128 partes

27 = 2 2 2 2 2 2 2 = 128

• 8 dobras 256 partes

28 = 2 2 2 2 2 2 2 2 = 256

As expressões 20, 21, 22, 23, 24, 25, 26, 27 e 28 são exemplos de potências. E a operação realizada para calcular as quantidades de partes em que cada folha ficou dividida é chamada de potenciação

Em uma potenciação, temos os seguintes termos.

25 = 32 expoente potência (resultado da operação) base

Note que o termo potência é usado tanto para a expressão 25 como para o resultado 32.

Quando a base de uma potência é um número real e o expoente é inteiro, as potências são definidas do mesmo modo que nos casos cuja base é um número racional.

Vamos separar essa definição em duas partes: quando o expoente é um número inteiro não negativo e quando o expoente é um número inteiro negativo.

POTÊNCIA COM EXPOENTE INTEIRO NÃO NEGATIVO

Dado um número real a e um número inteiro n, com n . 1, a potência an representa uma multiplicação de n fatores, em que cada fator é igual ao número a an = a a a a a a n fatores

Quando n = 1, define-se a1 = a.

Quando a 5 0 e n = 0, define-se a0 = 1.

Nesse caso, temos que:

• se o expoente for par, a potência será sempre um número positivo;

• se o expoente for ímpar, a potência terá sempre o mesmo sinal da base

ORIENTAÇÕES DIDÁTICAS

Incentivar os estudantes a elaborar coletivamente um cartaz, que deverá ficar exposto na sala de aula de modo que ele seja constantemente consultado e ampliado ao longo do ano com informações, exemplos e conceitos estudados.

Se considerar necessário, retomar os conceitos de base, expoente e potência. Anotar na lousa um exemplo para cada um dos termos.

Potência com expoente inteiro não negativo

Explicar para os estudantes que qualquer base diferente de zero, elevada ao expoente zero, sempre terá resultado igual a 1.

Caso considerar oportuno, pode-se propor aos estudantes, por exemplo, que construam um fluxograma de como identificar o sinal do resultado de uma potência de acordo com o expoente. A seguir, há uma possibilidade dessa representação.

Início (análise do expoente)

A potência será um número positivo.

Sim

O expoente é par?

Não

A potência terá o mesmo sinal da base.

D2_AV1-MAT-F2-2103-V8-U2-040-051-LA-G24.indd

ORIENTAÇÕES DIDÁTICAS

Explorando potências com a calculadora

Retomar com os estudantes o uso da calculadora no cálculo de potências, utilizando a multiplicação de fatores iguais, mesmo que exista a tecla específica para a potência, caso eles utilizem uma calculadora científica.

É importante ressaltar que os equipamentos tecnológicos são auxiliares na resolução dos cálculos, mas não substituem o raciocínio nem a compreensão da situação ou do problema.

Assim, pela definição:

POTÊNCIA COM EXPOENTE INTEIRO NEGATIVO

Analisemos, agora, o caso em que o expoente é um número inteiro negativo. De modo geral, temos a definição a seguir.

Dado um número real a, com a 5 0, temos:

com n natural.

Note que, para indicar uma potência com expoente inteiro negativo, escreve-se o inverso da base e muda-se o sinal do expoente.

EXPLORANDO POTÊNCIAS COM A CALCULADORA

Para calcular o valor de uma potência, por exemplo, 35, usando uma calculadora simples, podemos fazer deste modo.

AMPLIANDO

Vídeo

POR QUE todo número elevado a zero é igual a 1? 2022. Vídeo (1min25s). Publicado pelo canal Entendendo a Matemática. Disponível em: https://www.youtube.com/watch?v=NHvjdqouH48&t=6s. Acesso em: 4 ago. 2022.

Nesse link é possível acessar uma videoaula para ampliar o estudo proposto neste capítulo.

Responda às questões no caderno.

1. O bserve as multiplicações e escreva cada uma na forma de potência.

a) ( 6) ( 6) ( 6)

b) 0,5 0,5 0,5 0,5 0,5

c) 3 10 3 10

d) ( 1,2) ? ( 1,2) ? ( 1,2) ? ( 1,2)

e) 9 9 9 9

f) 1,1 1,1 1,1 1,1

g) ( 2) ( 2) ( 2) ( 2)

1 ? 1 ? 1 ?? 1

2. Escreva as potências a seguir na forma de multiplicação.

(0,7)3

5. Considerando o como unidade de medida de superfície, use a potenciação para calcular a área da figura a seguir.

ORIENTAÇÕES DIDÁTICAS

Atividades

Orientar os estudantes a realizar as atividades tentando identificar os conhecimentos necessários para a compreensão e a resolução de cada uma delas. Isso auxilia os estudantes a identificar a relação de coerência entre as atividades e a perceber a aplicação dos conceitos estudados. Nesse bloco de atividades, dá-se continuidade ao desenvolvimento da habilidade EF08MA01.

( 0,8)3

3. Cada figura a seguir sugere uma potência. Escreva a potência sugerida.

6. Com cubinhos iguais a este , Lucas compôs o cubo a seguir. Use a potenciação para descobrir quantos cubinhos ele usou

4. Calcule as potências a seguir.

7. Verifique se a expressão (10 + 7) 2 é diferente da expressão 10 2 + 72

8. Considerando que 50% = 0,5, qual é o número decimal que representa o cubo de 50%?

9. Sabe-se que o número decimal A representa o dobro de 1,1, e o número decimal B representa o quadrado de 1,1. Qual é o valor de A B?

10. Escreva a expressão (0,5) 2 na forma: a) decimal. b) percentual (%).

11. Compare os números a e b usando o sinal = , . ou , a) a = 23 ? 22 e b = 26 b) a = 32 52 e b = (3 5)2

12. Sabendo que 10x = 100 e 10 0 = y, calcule ovalor de x + y.

Na atividade 6, antes de resolvê-la, pode-se propor aos estudantes que utilizem peças do Material Dourado para construir um cubo como o apresentado na atividade. A utilização de material manipulável facilita a compreensão do conceito de potência e ajuda os estudantes a perceber que o volume do objeto que está sendo medido pode ser determinado por meio de uma multiplicação.

Para a atividade 12, uma sugestão é que ela seja resolvida coletivamente, favorecendo a troca de ideias entre os estudantes. Eles devem perceber que, nessa atividade, é necessário primeiro interpretar os dados e determinar os valores de x e y, para depois calcular o valor da expressão x + y.

ORIENTAÇÕES DIDÁTICAS

Pense e responda

Com base nas potências de 2 e 3, são propostos diversos cálculos que se relacionam com as propriedades a serem estudadas. No item a, por exemplo, pode-se perguntar aos estudantes o que eles pensam que aconteceu com as potências nessa igualdade. Investigar se eles levantam hipóteses sobre alguma maneira prática de efetuar esse cálculo, favorecendo o desenvolvimento da capacidade de inferência e de argumentação dos estudantes.

Permitir aos estudantes que utilizem as estratégias que julgarem mais interessantes e, após um tempo de exploração (pode ser em duplas), eles devem ser incentivados a verbalizar as hipóteses e conjecturas realizadas durante a atividade proposta. Muitas vezes, eles conseguem chegar às propriedades da potenciação de maneira intuitiva. Nessa seção é possível explorar todas as relações com potências de 2 e 3 e ampliar, por exemplo, para as potências de 5.

Descubra mais

O livro O homem que calculava pode ser explorado em diversas situações. Se possível, utilizá-lo para ampliar o estudo de resolução, leitura e interpretação de problemas. Peças teatrais podem ser encenadas a partir das histórias do livro.

PROPRIEDADES DA POTENCIAÇÃO CAPÍTULO

PENSE E RESPONDA

Observe as potências que Thiago calculou.

AMPLIANDO

Link

Responda no caderno.

1. Usando os resultados obtidos por Thiago, faça as atividades a seguir.

a) Usando o símbolo = ou 5, compare:

• 22 23 e 25

b) Usando o símbolo = ou 5, compare:

• 25 : 23 e 22

c) Determine o resultado de:

• (23)2

• 34 32 e 36

• 35 : 32 e 33

• (23)3 • (32)2

d) Usando o símbolo = ou 5, compare:

• (23)2 e 26

DESCUBRA MAIS

TAHAN, Malba. O homem que calculava. 83. ed. Rio de Janeiro: Record, 2013. Esse livro é um clássico da literatura brasileira que divulga ideias matemáticas. As histórias são repletas de enigmas e personagens curiosos. Um dos capítulos conta a história que inspirou a abertura da Unidade, sobre a lenda do xadrez.

ARAÚJO, Ionara Macêdo de et al. O ensino da matemática através do lúdico por intermédio da metodologia de Malba Tahan. IX Encontro Paraibano de Educação Matemática. Campina Grande, 2016. Disponível em: https://www.malbatahan.com.br/wp-content/uploads/2017/08/Ionara-Mac%C3%AAdo-de

-Ara%C3%BAjoTRABALHO_EV065_MD1_SA4_ID116_29102016225534.pdf. Acesso em: 5 ago. 2022.

O texto sugerido pode proporcionar inspirações para dinamizar algumas rotinas vivenciadas na sala de aula.

CONHECENDO AS PROPRIEDADES DA POTENCIAÇÃO

As propriedades da potenciação podem auxiliar nos cálculos com potências. Para estudá-las, vamos considerar as bases das potências, a e b, números reais diferentes de zero, e os expoentes, m e n, números inteiros.

1a propriedade: Produto de potências de mesma base.

Um produto de potências de mesma base pode ser escrito na forma de uma única potência: conservamos a base e adicionamos os expoentes am an = am + n

Consideremos, por exemplo, o produto de potências de mesma base 23 ? 27

ORIENTAÇÕES DIDÁTICAS

Conhecendo as propriedades da potenciação

Nesse tópico, o objetivo é levar os estudantes a conhecer e aplicar as quatro propriedades da potenciação: produto de potências de mesma base; quociente de potências de mesma base; potência de uma potência; e potência de um produto. Na página 47 do Livro do estudante, são abordadas as duas primeiras propriedades. Construir alguns exemplos na lousa e verificar se os estudantes compreendem como usar as propriedades.

2a propriedade: Quociente de potências de mesma base.

Um quociente de potências de mesma base pode ser escrito na forma de uma única potência: conservamos a base e subtraímos os expoentes

AMPLIANDO

Atividade complementar

Considere que 9 = 32, 27 = 33 e 729 = 3 6 . Usando as propriedades das potências de mesma base, calcule o valor da expressão (9 ? 729) : 27.

Resolução da atividade (9 ? 729) : 27 = (32 ? 3 6) : 33 = (32 + 6 3) = (35) = 243

ORIENTAÇÕES DIDÁTICAS

Nessa página, as propriedades relativas à potência de uma potência e potência de um produto são apresentadas aos estudantes. Ao final, convidá-los a observar todas as propriedades da potenciação e propor que resolvam algumas atividades simples envolvendo a multiplicação e a divisão de potências de mesma base. Se considerar oportuno, as propriedades da potenciação poderão fazer parte do cartaz sugerido inicialmente, incentivando-os a trabalhar em grupos caso tenha optado por adotar a estratégia sugerida.

Potências de base dez e notação científica

Nesse tópico, os estudantes serão levados a identificar as potências de base dez e reconhecer sua utilidade na realização de cálculos e escrita de números muito grandes, como a distância entre planetas medida em quilômetros. O uso de notação científica, tanto para representar números quanto para efetuar cálculos, é bastante importante para o estudo em outros componentes curriculares, como Física e Química. Este tema contribui para o desenvolvimento da habilidade EF08MA01, da competência geral 5 e da competência específica 5 da área de Matemática.

3a propriedade: Potência de uma potência.

Uma potência de uma potência pode ser escrita na forma de uma única potência: conservamos a base e multiplicamos os expoentes

Consideremos, por exemplo, a seguinte potência de potência

52

4a propriedade: Potência de um produto.

Para elevar um produto de dois ou mais números reais a um expoente, elevamos cada fator a esse expoente

Consideremos, por exemplo, a potência de um produto (2 ? 7)3

Essa propriedade também pode ser aplicada para uma potência de um quociente. Observe.

POTÊNCIAS DE BASE DEZ E NOTAÇÃO CIENTÍFICA

Vamos observar como expressar uma potência 10n, para n inteiro. Quando n é um número natural, temos:

D2_AV2-MAT-F2-2103-V8-U2-040-051-LA-G24.indd

Para um expoente natural qualquer:

10n = 1 00000...0 n zeros

Agora, vamos verificar como expressar uma potência 10 n, com n natural.

ORIENTAÇÕES DIDÁTICAS

Realizar a leitura do texto apresentado, destacando as medidas de comprimento apresentadas na tabela ao final da página 48 do Livro do estudante, e deixar claro as diferenças entre as representações de números muito grandes e de números muito pequenos.

Propor alguns exemplos na lousa e solicitar aos estudantes que façam as conversões dos números para a escrita em notação científica.

Temos, nesse caso: 10 0, 00...01 n = n casas decimais

Representar números usando potências de base 10 é muito útil para escrever números muito grandes ou números excessivamente pequenos. Por exemplo:

• 1 200 000 pode ser escrito como uma potência de base 10:

1 200 000 = 12 ? 100 000 = 1,2 ? 10 ? 100 000 = 1,2 ? 1 000 000 = 1,2 ? 106

• 0,000000005 pode ser escrito como uma potência de base 10:

0, 000000005 50, 000000001 510 9 =?=?

Dizemos que os números 1,2 ? 106 e 5 ? 10 9 estão representados em notação científica

Para representar um número em notação científica, escrevemos esse número por meio do produto de dois fatores, no qual um deles é um número maior do que ou igual a 1 e menor do que 10, e o outro fator é uma potência de base 10.

Acompanhe algumas medidas representadas em notação científica.

Algumas medidas aproximadas (em metro)

Distância média de Marte ao Sol 2,28 ? 1011

Distância média de Netuno ao Sol 4,5 1012

Dimensão média do vírus SARS-CoV-2 1,25 10−7

Espessura média de um fio de cabelo fino 6,15 ? 10−5

Elaborada com base em: SILVA, Edna Maria Esteves da. O Sistema Solar. Planetário UFSC. Florianópolis, 3 ago. 2022. Disponível em: https:// planetario.ufsc.br/o-sistema-solar/.

Imagem de microscopia eletrônica do vírus SARS-CoV-2, causador da covid-19 (aumento aproximado de 13 000 vezes quando aplicada com 6 cm de largura; colorida artificialmente).

D2_AV2-MAT-F2-2103-V8-U2-040-051-LA-G24.indd 49

AMPLIANDO

Vídeo

RIO DE JANEIRO (Estado). Secretaria de Ciência, Tecnologia e Inovação. Fundação CECIERJ. Em tempos de pandemia: você tem ideia de quão pequeno é um vírus? Rio de Janeiro: Fundação CECIERJ, 15 out. 2020. Disponível em: https://www.cecierj.edu.br/2020/10/15/em-tempos -de-pandemia-voce-tem-ideia-de-quao-pequeno-e-um-virus/#.

Acessos em: 4 ago. 2022.

14/08/22 16:31

DO MUNDO macroscópico ao microscópico. c2022. Vídeo (3min10s). Publicado por khan Academy. Disponível em: https://pt.khanacademy.org/science/9-ano/fisico-e-quimica-atomica-e-molecular/modelos-atomicos/v/do -mundo-macroscopico-ao-microscopico. Acesso em: 5 ago. 2022.

Nesse link, é possível assistir a uma videoaula sobre os mundos macro e microscópico e sobre as diferenças de escalas.

ORIENTAÇÕES DIDÁTICAS

Por toda parte

O texto apresentado nessa seção aborda algumas mudanças no armazenamento de dados desde os disquetes, usados na década de 1990, até o armazenamento em nuvem, bastante utilizado atualmente. A discussão desse tema contribui para o desenvolvimento do Tema Contemporâneo Transversal Ciência e Tecnologia e da competência específica 3 da área de Matemática.

Para fazer a leitura do texto, os estudantes podem se organizar em duplas ou pequenos grupos. Depois, pedir a alguns estudantes que relatem as principais ideias do texto aos colegas e propor um debate a respeito do assunto. É importante que eles expressem seu entendimento e apresentem argumentos para validá-lo.

Se for possível, providenciar um disquete, um CD-ROM e um pen drive para que os estudantes possam manipular e conhecer melhor esses objetos. A comparação física é bastante interessante e, normalmente, surpreende os estudantes. Ainda em duplas ou grupos, sugerir a eles que resolvam a atividade 1

DO DISQUETE À NUVEM

No fim dos anos 1990 e início dos anos 2000, usávamos corriqueiramente os disquetes para armazenar arquivos de compu tadores e transportá-los a todos os lugares. Eram aqueles disquetes de 3,5 polegadas, revestidos de uma capinha de plástico e com capacidade de 1,44 MB (megabyte). Além da pequena capacidade de armazenamento desses dispositivos removíveis, havia alguns inconve nientes relacionados ao seu uso, como a desmagnetização, a quebra e a grande facilidade de os arquivos neles armazenados serem “cor rompidos”. Em razão dessas limitações, o CD-ROM entrou em cena, armazenando quase 500 vezes mais dados que os disquetes.

Depois do CD-ROM, surgiu o DVD, com capacidades de 4,7 GB (gigabytes) (DVD de uma camada) a 8,5 GB (DVD de dupla camada).

Contudo, os dispositivos que vieram revolucionar o arma zenamento de arquivos foram o pen drive, também chamado de memória USB Flash, e o HD externo, que possui um disco rígido com uma capacidade muito maior de armazenamento. Hoje, existem pen drives com capacidade de até 4 TB ( e HD externos com capacidade de até 16 TB. Além de possuírem mais memória, esses dispositivos têm alta durabilidade, que chega até 10 anos, se conservados adequadamente.

Hoje, por meio da internet, também é possível armazenar dados na nuvem, tecnologia que permite ao usuário armazenar dados em um servidor on-line e acessá-los de qualquer computador, celular ou tablet, sem que haja necessidade de usar qualquer espaço de armazenamento de sua máquina ou de dispositivos.

Você sabe o que é o byte?

O byte é uma unidade de quantidade de informações usada para especificar a capacidade de memórias de computadores, tamanhos de arquivos e discos, entre outros. Um byte equivale a 8 bits

Observe alguns múltiplos do byte

GLOSSÁRIO

Bit : menor unidade de informação que pode ser armazenada ou transmitida.

• 1 quilobyte (KB) é aproximadamente igual a 1 000 bytes ou 103 bytes;

• 1 megabyte (MB) é aproximadamente igual a 1 000 000 bytes ou 106 bytes;

• 1 gigabyte (GB) é aproximadamente igual a 1 000 000 000 bytes ou 109 bytes;

• 1 terabyte (TB) é aproximadamente igual a 1 000 000 000 000 bytes ou 1012 bytes

Responda no caderno.

1. Um CD-ROM com capacidade de 700 MB foi utilizado para gravar dados que ocupam 123 MB. Escreva esses valores em quilobyte, byte e bit, aplicando potências de base 10.

7 ? 10 5 quilobytes; 1,23 ? 10 5 quilobytes; 7 ? 10 8 bytes; 1,23 ? 10 8 bytes; 5,6 ? 10 9 bits; 9,84 ? 10 8 bits

D2_AV2-MAT-F2-2103-V8-U2-040-051-LA-G24.indd

AMPLIANDO

Link

BATISTA, Pollyana. A origem do disquete: entenda sua criação e evolução. Estudo Prático. Belo Jardim, c2022. Disponível em: https://www.estudopratico.com.br/a-origem-do-disquete/. Acesso em: 5 ago. 2022.

No texto, a autora apresenta um breve histórico desde o lançamento comercial do disquete, em 1971, até seu desaparecimento, em meados do século XXI.

THITICHAYA YAJAMPA/SHUTTERSTOCK.COM

ERIC GLENN/ SHUTTERSTOCK.COM

Disquete IMAGENS FORA DE PROPORÇÃO.

ATIVIDADES

9.

Responda às questões no caderno.

1. Aplicando as propriedades da potenciação, escreva cada expressão em uma única potência.

8. Determine o quociente de 1 0242 por 643 .

9. Alguns prefixos indicam determinados números, os quais podem indicar múltiplos e submúltiplos de unidades de medida. Por exemplo: quilograma, milímetro, gigabyte etc. Observe.

• giga: 1 000 000 000 • deca: 10

• mega: 1 000 000 • mili: 0,001

• quilo: 1 000 • micro: 0,000001

ORIENTAÇÕES DIDÁTICAS

Atividades

2. Sabendo que a = 213, b = 27 e c = 25 , determine na forma de potência o valor das expressões.

a) a b b) b : c

c) a : b

d) a2 e) b3 f) a b c

3. Dados x = 102 e y = 10 5 , compare as potências x5 e y2 usando o sinal = ou 5.

4. Transforme cada expressão em um produto de potências.

a) [( 0,6) (1,1)]4

b) (32 ?p)2 c)

5. Calcule o valor da expressão

6.

calcule

7. Aplicando as propriedades da potenciação, calcule o valor das expressões numéricas.

a) : 2  2   2  2 9113

AMPLIANDO

Atividade complementar

• hecto: 100 • nano: 0,000000001 Escreva esses números usando potências de base 10.

10. Escreva os números a seguir em notação científica.

a) 1 350 000

b) 543 000 000

c) 0,0000008

d) 0,00000000000043

11. Considere os números em notação científica e escreva-os com todos os seus algarismos.

a) 6,3 109 b) 9,23 10 4

12. Acompanhe o cálculo a seguir. 3,5 ? 103 + 2,7 ? 105 =

= 0,035

13. Calcule o valor das expressões e dê o resultado em notação científica.

14. Pesquise a população e a área territorial aproximadas do estado em que você mora. Escreva os números correspondentes, inicialmente considerando todos os algarismos e, posteriormente, utilizando notação científica.

Resposta pessoal. A resposta dependerá do estado em que os estudantes moram.

Nesse bloco de atividades, dá-se continuidade ao desenvolvimento da habilidade EF08MA01, de modo que os estudantes terão a oportunidade de aplicar as propriedades da potenciação estudadas. Eles devem identificar as propriedades envolvidas em cada atividade. É essencial que percebam a importância das propriedades das potências como um facilitador dos cálculos.

Propor a seguinte discussão: “O que vocês acham mais simples: resolver as potências e depois efetivar os cálculos ou simplificar a expressão utilizando as propriedades da potenciação antes de efetuar os cálculos?”. É importante salientar que não há certo ou errado nessa discussão, e espera-se que eles concluam que utilizar as propriedades na simplificação antes de efetuar os cálculos facilita a resolução das atividades.

Na atividade 5, propor aos estudantes que a realizem das duas maneiras e comparem as resoluções ao final.

Na atividade 10, se necessário, ajudar os estudantes a perceber que as potências de base 10 facilitam o registro escrito de números com valores muito grandes.

Solicitar aos estudantes que relacionem as potências de 10 com as correspondências entre as unidades de medida.

Retomar a atividade 2 e propor, além dos itens já descritos no enunciado do Livro do estudante, o item indicado a seguir.

Sabendo que a = 213, b = 27 e c = 25, determine na forma de potência o valor das expressões.

ORIENTAÇÕES DIDÁTICAS

Números quadrados perfeitos

O objetivo deste capítulo é preparar os estudantes para fazer a associação entre a Geometria e os números quadrados perfeitos. Pode-se discutir essa relação e começar a identificar quadrados perfeitos com base na variação da medida do lado do quadrado.

Ao iniciar a reflexão a respeito dos quadrados perfeitos, levar os estudantes a pensar no significado do nome utilizado, ou seja, porque eles acreditam que se chama quadrado perfeito e que números poderiam se encaixar nesse conceito. Incentivar os estudantes a trocar ideias com os colegas.

Levar os estudantes a perceber que o processo geométrico para o reconhecimento de um número quadrado perfeito pode ser demorado, principalmente se o número for muito grande. Outro aspecto importante é os estudantes identificarem a relação que existe entre um número quadrado perfeito e a sua raiz quadrada.

NÚMEROS QUADRADOS PERFEITOS

Qual é o número obtido quando elevamos 4 ao quadrado?

O número 16, que equivale a 4 ao quadrado, é chamado de quadrado perfeito.

Observe que é possível mostrar geometricamente que 16 é um número quadrado perfeito.

Consideremos um quadrado com 1 cm de lado. Se usarmos 16 desses quadrados, poderemos formar um novo quadrado.

Os números naturais que são quadrados de outros números naturais são denominados números quadrados perfeitos

Observe, a seguir, alguns números naturais que são quadrados perfeitos.

SANCHES11/SHUTTERSTOCK.COM

COMO RECONHECER SE UM NÚMERO É QUADRADO PERFEITO

Reconhecer se um número é quadrado perfeito pelo processo geométrico pode ser trabalhoso, principalmente se o número for grande. Vamos conhecer outro processo para reconhecer se um número é quadrado perfeito.

Inicialmente, devemos fatorar na forma completa o número e, em seguida, escrever os fatores comuns como potências. Então, se todos os fatores tiverem expoente par, o número será um quadrado perfeito. Caso um dos fatores não apresente expoente par, o número não será um quadrado perfeito. Acompanhe os exemplos.

1 Verificar se 144 é um quadrado perfeito.

2 Verificar se 450 é um quadrado perfeito.

ORIENTAÇÕES DIDÁTICAS

Como reconhecer se um número é quadrado perfeito É importante que os estudantes saibam utilizar o processo de fatoração de um número para verificar se esse número é quadrado perfeito ou não. Nesse momento, verificar se é necessário relembrar o processo de decomposição de um número em fatores primos.

Atividades

24 32

Como todos os fatores obtidos apresentam expoente par, 144 é um número quadrado perfeito.

ATIVIDADES

2 a) É quadrado perfeito.

b)Não é quadrado perfeito.

c)É quadrado perfeito.

d)É quadrado perfeito.

e)Não é quadrado perfeito. f )É quadrado perfeito. g)Não é quadrado perfeito. h)É quadrado perfeito.

Responda às questões no caderno.

1. Desenhe um quadrado de 1 cm de lado e responda.

a) Você pode formar um novo quadrado usando 25 desses quadrados?

Sim.

• Então, 25 é um quadrado perfeito?

b) Se usar 29 desses quadrados, você poderá formar um novo quadrado?

• Então, 29 é um quadrado perfeito?

1 a) • Sim, 25 é um quadrado perfeito. Não. Não, 29 não é um quadrado perfeito.

2. Efetuando a fatoração dos números naturais a seguir, verifique quais deles são números quadrados perfeitos.

a) 225

b) 300

c) 400

d) 729 e) 1 000 f) 1 024

g) 2 000 h) 1 600

3. O número natural A é expresso por:

AMPLIANDO

Vídeo

A = 2 x 116

Indique um número que possa ser colocado no lugar do expoente x para que A não seja um número quadrado perfeito.

Qualquer número ímpar.

4. Quantos números naturais quadrados perfeitos há entre 100 e 300? Dica: para obter os números, calcule 112, 122, ...

5. Qual é o menor número inteiro pelo qual devemos multiplicar 24 ? 32 ? 53 para que esse número se torne quadrado perfeito? a) 2 b) 5 c) 3 d) 10 e) 0

6. O número natural B, cujo algarismo da unidade é 5, é um número quadrado perfeito e está entre 600 e 700. Descubra o valor de B

7 números. Alternativa b. O valor de B é 625.

Nessa seção, prossegue-se o desenvolvimento da habilidade EF08MA01. Na atividade 1, propor aos estudantes que utilizem uma folha de papel quadriculado para representar um quadrado com 25 quadradinhos conforme proposto no item a Para o item b, pedir a eles que tentem formar um quadrado usando 29 quadradinhos. Nesse caso, os estudantes perceberão que não há como montar esse quadrado. Esse trabalho pode ser ampliado com outros números. Na atividade 2, os estudantes devem verificar se um número é quadrado perfeito quando todos os expoentes encontrados em sua fatoração forem pares. Realizar a fatoração dos números apresentados nos itens a e b coletivamente, na lousa. Depois, solicitar aos estudantes que façam individualmente a fatoração dos números dos itens seguintes.

MATEMÁTICA Básica – Aula 8 – Fatoração de números inteiros. 2014. Vídeo (12min37s). Publicado pelo canal Ferretto Matemática. Disponível em: https://www.youtube.com/watch?v=74jrzl0yPlI. Acesso em: 5 ago. 2022.

A videoaula disponível no link pode ser utilizada para revisar ou complementar o conteúdo de fatoração de números inteiros estudado ao longo do capítulo.

Como o fator 2 não apresenta expoente par, 450 não é um número quadrado perfeito.

ORIENTAÇÕES DIDÁTICAS

Raiz quadrada exata

Na primeira situação, comentar com os estudantes que, para determinar a raiz quadrada de 576, pode-se procurar por tentativas um número positivo que, ao multiplicar o algarismo das unidades obtenha-se como resultado o número 6. Por exemplo, ao analisar o resultado de 21 ? 21, é possível perceber que o algarismo das unidades desse produto é igual a 1. Logo, 21 não pode ser a raiz quadrada de 576. Analogamente, o resultado de 22 22 terá como algarismo das unidades 4. Portanto, 22 também não é raiz quadrada de 576. Seguindo o raciocínio, tem-se 24 e 26 como possibilidades, pois 4 ? 4 = 16 e 6 6 = 36.

RAIZ QUADRADA EXATA

A raiz quadrada exata de um número racional não negativo a é o número racional não negativo que, elevado ao quadrado, resulta em a Por exemplo:

• A raiz quadrada de 25 é 5, pois 52 = 5 5 = 25, e 5 . 0. Indica-se: 25 5 =

• A raiz quadrada de 49 é 7, pois 72 = 7 ? 7 = 49, e 7 . 0. Indica-se: 49 = 7.

• A raiz quadrada de 1 4 é 1 2 , pois

1 4 1 2 =

• A raiz quadrada de 0,0625 é 0,25, pois 0,252 = 0,25 0,25 = 0,0625, e 0,25 . 0. Indica-se: 0, 0625 = 0,25.

Note que todo número quadrado perfeito tem uma raiz quadrada exata. Verifique, agora, como determinar a raiz quadrada exata de outros números, analisando os exemplos a seguir.

1 Acompanhe a conversa de Luana e Renato.

Renato, você sabe como podemos fazer para calcular a raiz exata do número 576?

AMPLIANDO

Link

Podemos usar o que já sabemos! Vamos procurar por tentativas um número que elevado ao quadrado dê 576.

O número 576 está entre os números quadrados perfeitos 400 e 900.

A raiz quadrada do número 400 é 20, pois 400 = 20 20 = 202

A raiz quadrada do número 900 é 30, pois 900 = 30 30 = 302 Então, o número que procuramos está entre os números 20 e 30. Por tentativas, calculamos:

212 = 441

222 = 484

232 = 529

242 = 576

QUADRADOS perfeitos – um primeiro estudo. Clubes de Matemática da OBMEP. [S l.], [20--]. Disponível em: http://clubes.obmep.org.br/blog/quadrado-perfeito/quadrado-perfeito-um-primeiro-estudo/. Acesso em: 5 ago. 2022.

Nesse artigo, são apresentadas algumas propriedades e curiosidades sobre os quadrados perfeitos.

Então, pela definição, temos: 576 = 24, pois 242 = 24 24 = 576. Para conferir com a calculadora, basta digitar o número 576 e apertar a tecla 2 Determinar o número na forma decimal que representa a raiz quadrada exata do número 42,25.

Nesse caso, sabemos que o número 42,25 está entre 36 e 49.

36 = 6 6 = 62

49 = 7 7 = 72

Logo, o número que procuramos é um número na forma decimal entre 6 e 7. Daí, temos:

?

=

RAIZ QUADRADA APROXIMADA

Nem todo número racional não negativo tem raiz quadrada exata; quando isso acontece, a raiz desse número é um número irracional, ou seja, é um número com infinitas casas decimais e sem um período que se repita. Por exemplo:

• 3 é um número irracional, pois não existe n racional tal que n2 = 3.

• 1,5 é um número irracional, pois não existe n racional tal que n2 = 1,5.

Em casos como esses, podemos calcular um valor aproximado para essas raízes. Acompanhe as situações a seguir.

1 Observe como as amigas pensaram para calcular a raiz quadrada de 30.

Como vocês calcularam a raiz quadrada do número 30?

Notei que o 30 não é quadrado perfeito. Portanto, a raiz quadrada de 30 não é exata, e vamos ter de fazer aproximações.

Na calculadora, usei a tecla com símbolo de radical e obtive o valor aproximado 5,477225575051661.

ORIENTAÇÕES DIDÁTICAS

Na segunda situação, resolver na lousa o cálculo da raiz quadrada de 42,25, usando o registro na forma fracionária. Dessa maneira, explicar aos estudantes que 42,25 = 4225 100 E que pode-se fazer:

=== 42,25 4225 100 65 10 6,5

Incentivar os estudantes a verificar o resultado utilizando uma calculadora simples.

Raiz quadrada aproximada O exemplo proposto na situação 1 do Livro do estudante pode ser ampliado com o uso de uma calculadora simples, o que pode agilizar o processo dos cálculos e possibilitar aos estudantes que dediquem mais tempo para compreender e explorar o conceito de raiz quadrada aproximada. Reforçar que, se um número não é um quadrado perfeito, sua raiz quadrada não será exata.

ORIENTAÇÕES DIDÁTICAS

Após calcular a raiz quadrada de 30 utilizando uma calculadora, abordar a estratégia das aproximações sucessivas até a casa dos décimos e, em seguida, até a casa dos centésimos, milésimos etc. Construir, passo a passo, cada uma das aproximações apresentadas nesta página do Livro do estudante. Incentivar os estudantes a utilizar uma calculadora comum. Certificar que os estudantes compreenderam o fato de a 30 ser um número entre 5 e 6.

Reforçar a convenção de indicar, como melhor aproximação, o valor que mais se aproxima do número desejado, mas sem ultrapassá-lo.

O valor encontrado na calculadora pode ser escrito com aproximação de uma ou mais casas decimais.

• Aproximação até décimos: 5,5 (a diferença entre o valor encontrado e o aproximado é menor do que 0,1).

• Aproximação até centésimos: 5,48 (a diferença entre o valor encontrado e o aproximado é menor do que 0,01).

• Aproximação até milésimos: 5,477 (a diferença entre o valor encontrado e o aproximado é menor do que 0,001).

É possível, então, determinar a raiz quadrada de 30 com uma aproximação conveniente. Entretanto, nem sempre dispomos de uma calculadora. Nesse caso, como podemos calcular? Podemos determinar o número que expressa a raiz quadrada, com aproximação de uma ou mais casas decimais, fazendo uma estimativa desse valor.

Vamos verificar, então, como estimar a raiz quadrada de 30 com os conhecimentos que temos sobre os números quadrados perfeitos.

• 30 é um número que está entre os quadrados perfeitos 25 e 36.

• Como 25 = 52 e 36 = 62, o número procurado está entre 5 e 6.

• Vamos descobrir que número é esse fazendo tentativas.

Observando os cálculos, verificamos que:

• o número que expressa 30 é maior do que 5,4 e menor do que 5,5;

• 5,4 e 5,5 são os números que representam aproximações para 30 até décimos. Para não termos dois valores, convencionamos que o número procurado corresponde ao menor valor e escrevemos: 30 5, 4 +1 5,4. Assim, a raiz quadrada de 30 é aproximadamente igual a 5,4 se a aproximação for de uma casa decimal (diferença menor do que 0,1).

Caso haja necessidade de uma aproximação de duas casas decimais (diferença menor do que 0,01), fazemos mais tentativas com números entre 5,4 e 5,5.

(5,41)2 = 29,2681 H 29,2681 , 30

(5,42)2 = 29,3764 H 29,3764 , 30

(5,43)2 = 29,4849 H 29,4849 , 30

(5,44)2 = 29,5936 H 29,5936 , 30

(5,45)2 = 29,7025 H 29,7025 , 30

(5,46)2 = 29,8116 H 29,8116 , 30

(5,47)2 = 29,9209 H 29,9209 , 30

(5,48)2 = 30,0304 H 30,0304 . 30

Pela convenção já estabelecida, podemos escrever que 30 5, 47 +1 5,47, ou seja, a raiz quadrada de 30 é aproximadamente igual a 5,47 se a aproximação for de duas casas decimais.

D2_AV1-MAT-F2-2103-V8-U2-052-059-LA-G24.indd 56

AMPLIANDO

Vídeo

APROXIMAÇÃO de raízes quadradas para a segunda casa decimal. c2022. Vídeo (7min15s). Publicado por Khan Academy. Disponível em: https://pt.khanacademy.org/math/pt-9-ano/numeros-9ano/aproximacao-de -numeros-irracionais/v/approximating-square-roots. Acesso em: 5 ago. 2022.

Nesse link, é possível assistir a uma videoaula sobre como aproximar uma raiz quadrada não exata até a segunda casa decimal.

2 Um número positivo x representa a raiz quadrada aproximada, com uma casa decimal, do número 11,3. Descobrir o valor do número x Sabemos que o número 11,3 está entre 9 e 16. Como 9 = 32 e 16 = 42, o número procurado está entre 3 e 4. Vamos, então, fazer os cálculos.

(3,1)2 = 9,61 H 9,61 , 11,3

(3,2)2 = 10,24 H 10,24 , 11,3

(3,3)2 = 10,89 H 10,89 , 11,3

(3,4)2 = 11,56 H 11,56 . 11,3

Então, considerando sempre o menor valor, podemos dizer que a raiz quadrada de 11,3 é aproximadamente igual a 3,3, ou seja, 11,3 1 3,3 (aproximação menor do que 0,1). Portanto, o valor do número x é 3,3.

ATIVIDADES

Responda às questões no caderno.

1. Os números naturais a seguir são quadrados perfeitos. Determine a raiz quadrada exata de cada um deles.

a) 484

b) 625

c) 729

d) 1 156 e) 1 296 f) 1 849

g) 3 025 h) 4 096 i) 10 000

2. Os números na forma decimal a seguir têm a raiz quadrada exata. Determine essa raiz.

4. Obtenha um valor inteiro aproximado que expresse a raiz quadrada de:

a) 172.

b) 200.

ORIENTAÇÕES DIDÁTICAS

Atividades

Essas atividades exploram o cálculo de raízes quadradas aproximadas de números racionais, favorecendo o desenvolvimento da habilidade EF08MA01.

Ao explorar as atividades, pode-se propor que os estudantes elaborem uma lista com os quadrados perfeitos para utilizá-la no processo de obtenção das raízes quadradas aproximadas.

c) 360.

d) 500.

5. Com aproximação até a primeira casa decimal, calcule a raiz quadrada de:

a) 2,56

b) 3,61 c) 5,29 d) 7,84 e) 10,24 f) 37,21

3. A área de um terreno quadrangular é 1 764 m2 . A medida do lado desse terreno representa a raiz quadrada exata desse número. Quanto mede o lado desse terreno? 42 m

6. Calcule a raiz quadrada, com valor aproximado até a primeira casa decimal, de cada um dos números a seguir.

Na atividade 2, organizar os estudantes em duplas para que possam trocar informações a respeito dos procedimentos a serem adotados. Orientar o uso da calculadora como suporte para a realização dos cálculos. No item a, pedir aos estudantes que determinem os dois números inteiros consecutivos que são quadrados perfeitos e têm entre eles o número 2,56. Se necessário, auxiliá-los a concluir que esses números são 1 e 4. Depois de perceber isso, e sabendo que 1 = 1 e 4 = 2, os estudantes devem, por tentativas, determinar um número entre 1 e 2 que, elevado ao quadrado, resulte em 2,56.

(1,1)2 = 1,21

(1,2)2 = 1,44

(1,3)2 = 1,69

(1,4)2 = 1,96

(1,5)2 = 2,25

7. Com valor aproximado até a primeira casa decimal, calcule 5 . 2,2

(1,6)2 = 2,56

Assim, 1,6 é o número decimal que, elevado ao quadrado, resulta em 2,56.

Outra maneira de determinar a raiz quadrada de um número decimal é escrevê-lo como uma fração decimal e fatorar o numerador e o denominador. Se considerar oportuno, explorar essa estratégia na lousa.

ORIENTAÇÕES DIDÁTICAS

Raiz cúbica

Ler a situação inicial com os estudantes, retomando a definição de aresta de um cubo e a relacionando ao conceito de volume dessa figura geométrica espacial. A partir da compreensão desse conceito, introduzir a definição de raiz cúbica de um número racional.

Discutir os exemplos na lousa e destacar que, se o radicando de uma raiz cúbica for negativo, o resultado também será negativo. Isso não ocorre para as raízes quadradas, considerando o conjunto dos números racionais.

Raízes enésimas

A definição de raiz enésima de um número real vale para raízes quadradas e cúbicas; essa definição é a mesma dada para esses casos, com extensão para outros radicandos reais.

OUTRAS RAÍZES CAPÍTULO5

RAIZ CÚBICA

Acompanhe a situação a seguir.

Considere um cubo de volume 8 cm3. Como podemos determinar a medida da aresta desse cubo?

Sabemos que o volume V de um cubo com aresta de medida a é dado por: V = a ? a ? a = a3

Então, para determinar a medida da aresta, em centímetro, de um cubo de volume 8 cm3, devemos obter o número que, elevado ao cubo, resulte em 8. Esse número é 2, pois: 23 = 8. Assim, a aresta do cubo mede 2 cm. Dizemos que 2 é a raiz cúbica de 8. De modo geral, temos:

A raiz cúbica de um número racional a é o número racional que, elevado ao cubo, resulta em a Indica-se a raiz cúbica de a por: a 3 . Acompanhe os exemplos.

• A raiz cúbica de 125 é 5, pois 53 = 5 ? 5 ? 5 = 125. Indica-se: 125 5 3 =

• A raiz cúbica de 729 é 9, pois ( 9)3 = ( 9) ( 9) ( 9) = 729. Indica-se: 729 3 = 9.

• A raiz cúbica de 1 8 é 1 2 , pois

• A raiz cúbica de 0,001 é 0,1, pois 0,13 = 0,1 0,1 0,1 = 0,001. Indica-se: 0, 001 3 = 0,1.

• A raiz cúbica de 0 é 0, pois 03 = 0. Indica-se: 0 3 = 0. Observe que a raiz cúbica pode ser um número racional negativo.

RAÍZES ENÉSIMAS

Além da raiz quadrada e da raiz cúbica, há também outras raízes: raiz quarta, raiz quinta, raiz sexta, raiz sétima etc.

Vamos estender nosso estudo definindo as chamadas raízes enésimas para números reais.

Consideremos um número real a e um número natural n, com n . 1. A raiz enésima do número a é indicada pela expressão:

De modo geral, dado a um número real e n um número natural, com n . 1, temos de considerar dois casos:

• Para n par e a > 0: a n é igual ao número real b, com b > 0, tal que bn = a.

• Para n ímpar: a n é igual ao número real b, tal que bn = a.

Se o número real a for negativo, e o expoente n for par, a expressão a n não está definida no conjunto dos números reais.

Assim, temos:

• A raiz quarta de 16, indicada por 16 4 , é igual a 2, pois 2 . 0 e 24 = 16.

• A raiz quinta de 243, indicada por 243 5 , é igual a 3, pois 35 = 243.

• A raiz sétima de 10 000 000, indicada por 10000 000 7 , é igual a 10, pois ( 10)7 = 10 000 000.

• 2 048 2 11 _= , pois ( 2)11 = 2 048.

• A raiz 16 4 não está definida no conjunto dos números reais, pois 16 é um número real negativo, e 4 é um número par.

ATIVIDADES

Responda às questões no caderno.

1. A figura representa um cubo de volume 1 000 cm3. Calcule a medida, em centímetro, da aresta desse cubo.

3. Calcule o valor da expressão.

10 24 3 _+ 2

ORIENTAÇÕES DIDÁTICAS

Verificar a possibilidade de apresentar alguns exemplos de raízes quartas, quintas etc. para os estudantes, discutindo o sinal da raiz sempre que o radicando for negativo, e o expoente for ímpar.

Atividades

Nesse bloco de atividades, dá-se continuidade ao desenvolvimento da habilidade EF08MA01.

No item b da atividade 4, explicar aos estudantes que a afirmação é falsa, pois, por definição, a raiz quadrada de um número racional é sempre um número não negativo.

Na atividade 5, retomar a relação entre litro e decímetro cúbico e verificar se os estudantes compreendem que precisarão calcular a raiz cúbica de 64.

1000 cm3

2. Calcule o valor das raízes.

4. Observe as afirmações e verifique se são verdadeiras (V) ou falsas (F).

a) 25 é igual 5, pois 5 . 0 e 52 = 25.

b) 25 é igual 5, pois ( 5)2 = 25.

5. Indique a alternativa correta

Um recipiente com a forma de um cubo com 1 dm de aresta tem capacidade de 1 litro. Então, para comportar exatamente 64 litros de água, um recipiente com a forma de cubo deve ter aresta cuja medida é:

10 cm Verdadeira. Falsa. Alternativa a.

a) 4 dm.

b) 8 dm.

c) 16 dm.

d) 64 3 dm.

e) 6 4 dm.

D2_AV1-MAT-F2-2103-V8-U2-052-059-LA-G24.indd 59 06/08/22 09:57

ORIENTAÇÕES DIDÁTICAS

Potência com expoente fracionário

A relação entre as operações de potenciação e radiciação é abordada ao longo deste tema, contribuindo para o desenvolvimento da habilidade EF08MA02.

Construir os exemplos presentes no Livro do estudante na lousa, retomando as etapas da resolução de potências com expoentes fracionários. Verificar se a turma compreende a relação entre essas potências e as raízes enésimas. Propor uma potência com expoente decimal, como 810,25, e discutir com a turma que estratégias eles utilizariam para calcular. Espera-se que proponham escrever 0,25 como 1 4

Atividades

As atividades deste bloco exploram a relação entre as operações de potenciação e radiciação, conforme orienta a habilidade EF08MA02.

Na atividade 1, os estudantes precisam escrever as potências com expoentes fracionários na forma radical. Já na resolução da atividade 2, eles devem realizar a construção inversa, ou seja, deverão escrever os radicais na forma de potências com expoentes fracionários.

POTÊNCIA COM EXPOENTE FRACIONÁRIO CAPÍTULO

6

Estudamos, nesta Unidade, potências como ( 5)2, 6 1 e 20, que são potências com expoentes inteiros cujos resultados já conhecemos. Mas como podemos calcular uma potência com expoente fracionário?

Inicialmente, é importante considerar que as propriedades da potenciação que estudamos para potências de expoentes inteiros também valem quando a base é um número real positivo, e o expoente é fracionário. Em especial, vale a 3a propriedade (potência de uma potência). Acompanhe os exemplos.

Aplicando essa propriedade e a definição de raiz enésima, observe como podemos escrever a potência de expoente fracionário

Utilizando a 3a propriedade de potências, temos:

Então, pela definição de raiz quadrada:

Logo, a potência 3

2 pode ser escrita como uma raiz (ou na forma decimal): 31

Da mesma maneira, podemos escrever outras potências de expoente racional na forma de radical. Então:

Se a é um número real positivo, m é um número inteiro, e n é um número natural, com n . 1, temos: aa m n m n = Acompanhe outros exemplos.

ATIVIDADES

Responda às questões no caderno.

2. Escreva os radicais a seguir na forma de potências com expoente fracionário.

AMPLIANDO

Vídeo

EXPOENTE Fracionário – Relação entre Potenciação e Radiciação | MAB #39. 2016. Vídeo (26min22s). Publicado pelo canal Matemática Rio com Prof. Rafael Procopio. Disponível em: https://www.youtube.com/ watch?v=-UUtj3ZoDuI&t=15s. Acesso em: 5 ago. 2022

A videoaula sugerida aborda as resoluções de potências com expoentes fracionários.

1. Escreva as potências a seguir na forma de radical.

3. Calcule o resultado das expressões a seguir.

a) 64 16

b) 8 0,25

4. Escreva o número 256 5 na forma de uma potência:

a) de base 2.

b) de base 4.

FÓRUM

Bullying

c) de base 16.

d) de base 256.

5. Elabore uma expressão com operações entre potências de expoentes fracionários cujo resultado seja um número natural. Depois, troque com um colega, e um deve resolver a expressão criada pelo outro.

6. Elabore um problema que possa ser solucionado por meio do cálculo do valor da expressão:

Em seguida, entregue o problema para um colega solucionar e resolva o problema elaborado por ele.

ORIENTAÇÕES DIDÁTICAS

Nesse bloco de atividades, dá-se continuidade ao desenvolvimento da habilidade EF08MA01. Pode-se propor outros exemplos para explorar. A seguir há uma possibilidade.

• Geraldo construiu um canteiro retangular cujas medidas do comprimento do lados são 37 m e 9

m. Qual é a medida da área desse canteiro?

Leia e reflita sobre a tirinha a seguir.

Atos indesejáveis e constrangedores, como rir e caçoar dos outros, muitas vezes causam dor e angústia para as vítimas. Atitudes desse tipo podem ser chamadas de bullying.

Você sabe o que é bullying?

De acordo com a Lei no 13.185, de 6 de novembro de 2015, o bullying caracteriza-se quando há violência física ou psicológica em atos intencionais e repetitivos de intimidação, humilhação ou discriminação. Entre os atos característicos de bullying estão ataques físicos, insultos, ameaças, comentários e apelidos pejorativos e expressões preconceituosas.

Elaborado com base em: BRASIL. Lei no 13.185, de 6 de novembro de 2015. Institui o Programa de Combate à Intimidação Sistemática (Bullying). Brasília, DF: Presidência da República, 2015. Disponível em: http://www.planalto.gov.br/ccivil_03/_ato2015-2018/2015/lei/l13185.htm. Acesso em: 28 jul. 2022. O bullying pode acontecer em diversas esferas, como nas escolas e em ambientes virtuais, e todos nós podemos contribuir para combater essa prática.

1. Converse com um colega sobre a tirinha e sobre a ação da menina diante da situação.

2. Vocês já ouviram falar de ciberbullying? Pesquisem o significado desse termo e escrevam, no caderno, um parágrafo para defini-lo.

3. Discuta com um colega, e listem atitudes que vocês podem ter caso sejam vítimas de uma situação de bullying ou a presenciem. Depois, façam um cartaz explicando o que é bullying e como o problema pode ser minimizado na escola.

Respostas pessoais. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Fórum

O tema abordado nesse boxe contribui para o desenvolvimento do Tema Contemporâneo Transversal Vida Familiar e Social, das competências gerais 8, 9 e 10 e das competências específicas 7 e 8 da área de Matemática. Sugere-se que o texto seja explorado coletivamente. Depois, pode-se incentivar uma discussão entre os estudantes promovendo a empatia e o respeito ao próximo. Na atividade 2, uma definição possível é que o ciberbullying é o bullying realizado em diversos meios fazendo uso de tecnologias digitais.

Os cartazes produzidos na atividade 3 podem ser expostos em um local que todos os estudantes da escola tenham acesso. Para ampliar a discussão sobre o tema, pode-se acessar o link https://www.youtube.com/ watch?v=psieH5qBIpk&t=9s (acesso em: 18 ago. 2022), o qual fala sobre oito tipos de bullying que devem ser evitados no ambiente escolar.

BECK, Alexandre. [Bullying]. In: Armandinho cinco Florianópolis: A. C. Beck, 2015. p. 42.

5. Resposta pessoal. Exemplo de resposta:

Exemplo de resposta: Calcule o volume de um cubo cuja aresta tem a mesma medida do lado de um quadrado com 25 cm2 de área.

ORIENTAÇÕES DIDÁTICAS

Tecnologias

Essa seção permite aos estudantes conhecer e explorar um pouco o funcionamento de uma calculadora científica. As atividades propostas nessa seção colaboram para o desenvolvimento do Tema Contemporâneo Transversal Ciência e Tecnologia, da competência geral 5 e da competência específica 3 da área de Matemática.

Caso os estudantes não tenham acesso a uma calculadora científica, comentar que muitos smartphones apresentam as funções desse modelo de calculadora. Além disso, também há sites na internet que apresentam calculadoras científicas on-line. A seguir foram disponibilizados alguns exemplos: • Calculadora Online: https:// www.calculadoraonline.com. br/cientifica. Acesso em: 5 ago. 2022.

• Web 2.0 Calc.com: https:// web2.0calc.com/. Acesso em: 5 ago. 2022.

Se necessário, retomar com os estudantes como inserir na calculadora um número negativo. Por exemplo, para inserir 7 na Web 2.0 Calc.com, pode-se digitar o 7 e clicar na tecla +/ , que troca o sinal do número que está no visor. Vale lembrar que algumas calculadoras possuem uma tecla específica para o sinal negativo.

CALCULADORA CIENTÍFICA

A calculadora foi um dos primeiros instrumentos tecnológicos de fácil acesso e, hoje, pode ser encontrada em diversos modelos. Nesta seção, exploraremos o uso da calculadora científica.

Vale a pena destacar que a calculadora é um instru mento que nos auxilia a entender e a desenvolver nossa capacidade crítica de avaliar um problema; por essa razão, não deve ser utilizada somente para fazer cálculos simples. Existem diversas marcas de calculadora científica; por isso, é possível que o visor e/ou as teclas tenham algumas diferenças nos comandos para determinada função. Para verificar se há diferença, basta executar alguns cálculos cujas respostas você já conhece.

Um modelo de calculadora científica com as teclas das operações de potenciação e radiciação destacadas.

A tecla ^ é utilizada para calcular o valor da potência de um número elevado a um valor qualquer.

Por exemplo: 311. Para fazer esse cálculo, digitamos o 3; em seguida, pressionamos a tecla ^ e digitamos o valor do expoente, 11. Para finalizar, pressionamos = , e aparecerá o valor 177 147.

Há calculadoras em que a tecla ^ é substituída pela tecla xy

A tecla x2 é utilizada para calcular o valor da potência de um número elevado ao quadrado (expoente 2).

Por exemplo: 272. Para realizar esse cálculo, digitamos o valor 27; em seguida, pressionamos a tecla x2 . Para finalizar, pressionamos = , e no visor da calculadora aparecerá 729.

ILLUS_MAN/SHUTTERSTOCK.COM

KATTIKA SEEMORK/SHUTTERSTOCK.COM

3.a) Resposta pessoal. Espera-se que os estudantes percebam que poderiam usar a tecla ^ e elevar o número 258 ao expoente 1 2 .

A tecla log 10x tem como função secundária o cálculo de potências de base 10. Então, será necessário utilizar a tecla Shift , que dá acesso às funções auxiliares.

Para calcular 10 7, por exemplo, realizamos o procedimento a seguir.

Por meio da tecla Shift , habilitamos a função secundária do teclado. Em seguida, pressionamos log 10x . Aparecerá o número 10 no visor. Então, digitamos o expoente, que nesse caso é 7, e, em seguida, pressionamos = , e aparecerá o valor 0,0000001. Algumas calculadoras apresentam diretamente a tecla 10x . Nesse caso, basta digitar ovalor do expoente e acionar a tecla para obter a potência de 10 desejada.

Responda às questões no caderno.

1. Agora, usando uma calculadora científica, calcule o valor das potências a seguir.

a) 2352

b) 1173

c) 395

d) 10 8

2.Resposta pessoal. Espera-se que os estudantes percebam que bastaria calcular 5 5 5 5 5, como apresentado na página 46 desta Unidade.

2. Troque ideias com um colega, e expliquem como vocês fariam o cálculo da potência 5 5 usando uma calculadora simples, sem teclas especiais de potência.

3. Além das teclas apresentadas, a calculadora científica também possui a tecla para calcular a raiz quadrada de um número qualquer. Por exemplo: calcular a raiz quadrada de 5. Para realizar esse cálculo, pressionamos a tecla ; depois, o número do qual se deseja obter a raiz quadrada (nesse caso, 5) e, em seguida, pressionamos = . Aparecerá no visor o valor 2,236067978.

Alguns modelos de calculadora apresentam também as teclas 3 e x para calcular a raiz cúbica de um número e a raiz de índice x, respectivamente.

a) Caso você precisasse calcular a raiz quadrada de 258, mas a tecla de sua calculadora não estivesse funcionando, que procedimento adotaria?

b) Descreva os passos que podem ser executados para calcular uma raiz enésima qualquer a n em uma calculadora científica que não tenha a tecla x

4. Elabore uma atividade que deverá ser resolvida por um colega com o uso da calculadora. Para solucioná-la, deverá ser necessário o uso de algumas das teclas apresentadas e das relações existentes entre elas. Em seguida, corrijam a resolução um do outro, verificando não só a resposta final, mas se o raciocínio aplicado está correto

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

3.b) Resposta pessoal. Espera-se que os estudantes percebam que podem usar a tecla ^ e elevar o número a ao expoente 1 n () 63

ORIENTAÇÕES DIDÁTICAS

Propor aos estudantes outros desafios com a calculadora científica e reservar um tempo de aula para que eles explorem outras funcionalidades, ou seja, um tempo para que eles percebam que as calculadoras científicas realizam muitos outros cálculos além das quatro operações básicas da aritmética. Atividades de exploração desse tipo desenvolvem o pensamento computacional, a capacidade investigativa e desperta curiosidade.

Na atividade 4 os estudantes são desafiados a construir uma atividade que seja resolvida a partir do auxílio de alguma funcionalidade da calculadora científica, preferencialmente relacionada às operações de potenciação e radiciação.

D2_AV1-MAT-F2-2103-V8-U2-060-067-LA-G24.indd 63 06/08/22 10:00

ILUSTRAÇÕES: EDITORIA DE ARTE

ILLUS_MAN/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Tratamento da informação

Nessa seção, os estudantes são apresentados a uma tabela de distribuição de frequência com intervalos de classes. O trabalho com essa seção colabora para o desenvolvimento da habilidade EF08MA24 e da competência específica 6 da área de Matemática.

Na situação apresentada, é importante que reflitam a respeito de possíveis encaminhamentos que a gerência da academia pode fazer com base nos dados coletados, como adequação dos equipamentos às diferentes faixas de altura, por exemplo. Na atividade 1, os estudantes devem ler a tabela de distribuição de frequências com intervalos de classes dada inicialmente, respondendo às questões propostas.

INFORMAÇÃO TRATAMENTO DA

TABELAS COM INTERVALOS DE CLASSES: LEITURA E INTERPRETAÇÃO

Acompanhe a situação a seguir.

A academia Saúde realizou uma pesquisa para conhecer melhor os alunos. Eles responderam a um questionário com várias perguntas, e uma das variáveis pesquisadas foi a altura dos alunos. A gerente da academia organizou os dados na seguinte tabela.

Essa é uma tabela de distribuição de frequências com intervalos de classes. Ela apresenta, na primeira coluna, o que foi pesquisado, neste caso, a altura dos alunos; e na segunda coluna, a quantidade de vezes que esse valor apareceu, ou seja, a quantidade de alunos que apresentam aquela altura. Na primeira coluna, os valores das alturas estão divididos em intervalos numéricos que são chamados de intervalos de classes

Quando utilizamos a representação 1,50 ¿ 1,58, indicamos que o extremo inferior (1,50) estará incluso no intervalo e excluímos o extremo superior (1,58). Assim, para que nenhum número fique de fora, a próxima classe começará com o valor 1,58.

Responda às questões no caderno.

1. Observe as informações na tabela e responda

a) Quantos alunos da academia Saúde foram pesquisados?

1.d) 1,74 ¿ 1,82; significa que a maioria dos alunos pesquisados tem altura maior ou igual a 1,74 m e menor do que 1,82 m. 90 alunos.

b) A altura dos alunos da academia varia entre quais valores?

c) Quantos alunos têm altura entre 1,58 m e 1,66 m, incluindo 1,58 m?

De 1,50 m até 1,98 m. 11 alunos.

d) Qual é o intervalo de classe que apresenta maior frequência? O que isso significa?

e) Quantos alunos têm altura menor do que 1,82 m?

75 alunos.

f) Qual é a porcentagem de alunos que têm altura maior ou igual a 1,90 m?

Agora, consideremos a seguinte situação.

A professora do 8o ano de uma escola listou as notas de seus 35 estudantes na prova final de Matemática. Os resultados estão mostrados a seguir.

AMPLIANDO

Vídeo

TABELA de distribuição de Frequência com intervalo de classes no LibreOffice CALC. 2021. Vídeo (20min3s). Publicado pelo canal Marcelo Zanetti. Disponível em: https://www.youtube.com/watch?v=TJ1Lh6ZaVWc&t=6s. Acesso em: 5 ago. 2022.

Nessa videoaula, é explorado o processo de construção de uma tabela de distribuição de frequências com intervalo de classes usando o software LibreOffice Calc.

Do modo como estão os dados, ela não consegue visualizar rapidamente quantos estudantes ficaram abaixo da média. Decidiu, então, construir uma tabela de distribuição de frequências com os intervalos de classe indicados. Repare que os intervalos de classe sempre têm a mesma quantidade de elementos, ou seja, neste exemplo, cada intervalo corresponde a 2 unidades.

2. Observe as informações dadas e faça o que se pede.

a) Copie a tabela e preencha com a quantidade total de estudantes em cada um dos intervalos de classe

b) Quantos estudantes tiveram nota maior ou igual a 8?

Resposta na seção Resoluções comentadas deste Manual. 9 estudantes.

c) A média para aprovação nessa escola deve ser maior do que ou igual a 6. Quantos estudantes tiveram nota inferior à média na prova de Matemática?

15 estudantes.

d) Qual é a porcentagem de estudantes que têm nota maior do que ou igual a 6?

3. Estas são as idades, em 2022, das atletas da Seleção Brasileira Feminina de Voleibol.

30 32 32 27 20 31

27 21 32 33 30 33

36 29 25 27 24 25

Elaborado com base em: ATLETAS da Seleção Brasileira. Confederação Brasileira de Voleibol [Rio de Janeiro], [20--?]. Disponível em: https://cbv.com.br/ligadasnacoes/selecao -brasileira-feminina.

Acesso em: 25 maio 2022.

Faça o que se pede utilizando as informações fornecidas.

a) Quantas jogadoras compõem a Seleção Brasileira Feminina de Voleibol?

b) Qual é a idade da jogadora mais nova dessa seleção? E da mais velha?

ORIENTAÇÕES DIDÁTICAS

A segunda situação apresentada oferece os resultados de determinada turma de 8 o ano em uma avaliação de Matemática. Os estudantes precisarão preencher a tabela de distribuição de frequências com intervalos de classes.

A atividade 2 é desenvolvida a partir da situação apresentada. Verificar se os estudantes compreendem que os intervalos de classe têm sempre a mesma quantidade de elementos.

Na atividade 3, os estudantes devem construir a tabela de frequências com intervalos de classe, percebendo que o tamanho de cada classe de frequência precisa ser constante. Além disso, a atividade exige que os estudantes interpretem dados coletados, categorizando-os conforme a classe de frequência escolhida, antes de conseguir elaborar a tabela.

c) Construa uma tabela de distribuição de frequências contendo 5 classes de frequências, de modo que a primeira classe seja 20 ¿ 24. Não se esqueça dos dados que toda tabela deve ter, como fonte e título

d) Qual é a faixa de idade em que se concentram mais jogadoras?

e) Quantas jogadoras têm idade maior ou igual a 32 anos?

18 jogadoras. 20 anos; 36 anos. Resposta na seção Resoluções comentadas deste Manual. De 24 a 28 anos. 6 jogadoras.

Notas dos estudantes do 8o ano na prova final de Matemática

Seleção Brasileira Feminina de Voleibol comemorando a medalha de prata nos Jogos Olímpicos de Verão de Tóquio. Japão, 2021.

BOB STRONG/UPI/NEWSCOM/FOTOARENA

ORIENTAÇÕES DIDÁTICAS

Retomando o que aprendeu

O objetivo das atividades dessa seção é propiciar aos estudantes que retomem os conteúdos estudados ao longo da Unidade. Caso seja necessário, fazer retomadas para sanar as dúvidas que podem surgir.

Os estudantes podem fazer esse bloco de questões como uma autoavaliação; por isso, eles devem respondê-las individualmente. É interessante sugerir que realizem essa atividade em sala de aula, assim poderão discutir eventuais dúvidas com os colegas, por exemplo.

Enfatizar a necessidade de resolverem os exercícios individualmente, buscando informações de maneira autônoma, escolhendo suas fontes para chegar aos resultados. Conversar com os estudantes a respeito de seus acertos e erros, indicando a correção com intervenções pontuadas, isto é, dando pistas de quais caminhos eles poderão buscar para encontrar o resultado esperado.

Se ainda persistirem dúvidas, orientá-los a trocar ideias com os colegas e a buscar no Livro do estudante os conceitos que precisarem lembrar.

Dar oportunidade para os estudantes mostrarem como pensaram para resolver as questões, tirando as dúvidas dos colegas.

Responda às questões no caderno.

1. (PUC-RJ) O maior número abaixo é:

a) 331

b) 810

c) 168

d) 816 e) 2434

2. (UFRGS-RS) A expressão (0,125)15 é equivalente a:

a) 545

b) 5 45

c) 245

d) 2 45 e) ( 2) 45

Alternativa a. Alternativa d.

3. ( UFRGS-RS) Por qual potência de 10 deve ser multiplicado o número 10 3 ? 10 3 ? 10 3 ? 10 3 para que esse produto seja igual a 10?

a) 109

b) 1010

c) 1011

d) 1012 e) 1013

7. (Enem/MEC) Medir distâncias sempre foi uma necessidade da humanidade. Ao longo do tempo fez-se necessária a criação de unidades de medidas que pudessem representar tais distâncias, como, por exemplo, o metro. Uma unidade de comprimento pouco conhecida é a Unidade Astronômica (UA), utilizada para descrever, por exemplo, distâncias entre corpos celestes. Por definição, 1 UA equivale à distância entre a Terra e o Sol, que em notação científica é dada por 1,496 x 102 milhões de quilômetros.

Na mesma forma de representação, 1 UA, em metro, equivale a

a) 1,496 x 105 m

b) 1,496 x 106 m

c) 1,496 x 108 m

d) 1,496 x 1010 m

4. (OBM) Dividindo-se o número 4(4 ) 2 por 4 4 obtemos o número:

a) 2

b) 43

c) 4 4

5. O valor da expressão 2 5 16 125 81  3 101 1 000 25333

250 999 é:

a) 7.

b) 10.

c) 13.

Alternativa e. Alternativa e.

e) 1,496 x 1011 m

d) 4 8 e) 412

d) 1 3 e) 2 5

6. (UFRGS-RS) Um adulto humano saudável abriga cerca de 100 bilhões de bactérias, somente em seu trato digestivo. Esse número de bactérias pode ser escrito como

a) 109

b) 1010

c) 1011

d) 1012 e) 1013

Alternativa a. Alternativa c.

8. (Enem/MEC) No depósito de uma biblioteca há caixas contendo folhas de papel de 0,1 mm de espessura, e em cada uma delas estão anotados 10 títulos de livros diferentes. Essas folhas foram empilhadas formando uma torre vertical de 1 m de altura. Qual a representação, em potência de 10, correspondente à quantidade de títulos de livros registrados nesse empilhamento?

a) 102

b) 104

c) 105

d) 106

e) 107

9. Sabe-se que a área de um terreno quadrangular é 1 936 m2. Qual é o perímetro desse terreno?

a) 158 m

b) 168 m

c) 176 m

Alternativa e. Alternativa c. Alternativa c.

d) 186 m

10. Os números x e y representam, respectivamente, as raízes quadradas exatas dos números 51,84 e 40,96. Com o auxílio de uma calculadora, descubra quanto vale x y.

13. Por qual número devemos dividir 105 125 para que o quociente tenha uma raiz quadrada exata?

a) 3

b) 5

ORIENTAÇÕES DIDÁTICAS

d) 15 e) 21

a) 0,08

b) 8 c) 1,8 d) 0,8 e) 2,8

11. Dos números a seguir, qual é quadrado perfeito?

a) 151

b) 453

c) 20,44

a) 3,2.

b) 3,4.

c) 3,3.

d) 24 964

e) 3 804

12. O valor aproximado com uma casa decimal da raiz quadrada de 10 é:

d) 3,1. e) 3,5.

Alternativa d. Alternativa d. Alternativa d.

c) 7

14. Sabendo que x 2 y2 = (x + y) (x y), calcule o valor de 9992 1.

a) 1 000 000

b) 999 999

c) 998 999

d) 998 000 e) 990 000

15. Elabore uma atividade contextualizada que envolva o conceito de notação científica.

Entregue sua atividade para um colega resolver e solucione a atividade criada por ele

Alternativa b. Alternativa d. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Na atividade 15, espera-se que os estudantes elaborem enunciados envolvendo números muito grandes ou muito pequenos. A troca entre os estudantes permite que eles se autorregulem para uma escrita mais clara e coesa e avaliem o nível de dificuldade imposto pela questão.

Um novo olhar

Os questionamentos existentes no encerramento dessa Unidade possibilitam uma retomada dos conteúdos apresentados e reflexões a respeito das aprendizagens individuais.

Nesta Unidade, pudemos conhecer um pouco mais sobre as potências e as raízes, como também aprofundar nossos conhecimentos explorando as propriedades da potenciação e o papel facilitador que ela desempenha nas operações. Trabalhamos com a potência de base 10 e com a notação científica, tópico no qual pudemos perceber algumas aplicações voltadas à escrita de números grandes e de números excessivamente pequenos, como as distâncias no Sistema Solar ou o tamanho de um vírus.

Pudemos relacionar a potência ao jogo de xadrez ao refletirmos sobre a lenda da criação desse jogo, apresentada na abertura. Foi possível perceber o uso do conceito de potência para representar a capacidade de memória e armazenamento de alguns dispositivos.

Estudamos, ainda, os números quadrados perfeitos, a raiz quadrada exata e a raiz quadrada aproximada de números racionais, a raiz cúbica, a raiz enésima de números reais e a relação entre raízes e potências com expoente fracionário.

Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

UM NOVO OLHAR Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

• Foi possível perceber que, além de uma operação, a potência pode ser utilizada para representar números e resultados?

• Quantos bits tem um quilobyte (KB)?

• O que são os números quadrados perfeitos?

8 000 bits ou 8 103 bits Os números naturais que são quadrados de outros números naturais.

• Como a potência de expoente 2 se relaciona com a raiz quadrada?

Determinar a raiz quadrada de um número x é encontrar um número y que, quando elevado ao quadrado, tem como resultado o número x

Se julgar pertinente, retomar a situação do tabuleiro de xadrez, apresentada na abertura da Unidade, e discutir com os estudantes a impossibilidade da realização do pedido de Sissa.

Na primeira questão, espera-se que os estudantes percebam que, além da operação de potenciação, as potências podem ser utilizadas, por exemplo, para representar números em notação científica ou resultados de conversões de unidades de medidas. Na segunda questão, retomar o texto da seção Por toda parte, disponível na página 50 do Livro do estudante.

Na terceira questão, os estudantes precisam recordar o conceito de quadrados perfeitos. Por fim, na quarta questão, devem descrever a relação entre potências de 2 e raiz quadrada.

BNCC NA UNIDADE

Competências gerais:

• 3, 5 e 9

Competências específicas:

• 1, 2 e 5

Habilidades:

Geometria

• EF08MA15

• EF08MA17

Temas Contemporâneos

Transversais:

• Diversidade Cultural

• Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em cinco capítulos; ela apresenta os conteúdos por meio de exemplos contextualizados e atividades diversificadas e traz seções com temas que contribuem para a formação integral dos estudantes favorecendo o desenvolvimento das competências gerais 3, 5 e 9 e competências específicas 1, 2 e 5. No primeiro capítulo, são apresentados os ângulos, suas classificações, ângulos adjacentes, complementares, suplementares, opostos pelo vértice e bissetriz. No segundo capítulo, são apresentados os elementos do triângulo, suas classificações, ângulos, altura, mediana, bissetriz e mediatriz do triângulo e seus pontos notáveis. No capítulo 3, o tema Congruência de triângulos é tratado, apresentando os casos de congruência e sua utilização. No capítulo 4, as propriedades dos triângulos isósceles e equilátero são trabalhadas. Finalmente, no capítulo 5, as construções geométricas da bissetriz de um ângulo e da mediatriz de um segmento de reta são trabalhadas. Esses temas favorecem a apropriação das habilidades EF08MA15 e EF08MA17.

A Unidade também traz seções que abordam contextos de relevância social e cultural, como tecnologia, diversidade cultural e cultura quilombola, os quais colaboram para o desenvolvimento

E TRIÂNGULOS

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

As representações de triângulos são conhecidas e têm sido utilizadas há milênios pelo ser humano em virtude das diversas aplicações dessa figura no cotidiano. Por exemplo, a utilização de objetos com formato de um triângulo retângulo para verificar se o ângulo de uma parede com o chão é 90° Se a medida do ângulo for essa, costuma-se dizer que a parede está “reta”, ou seja, perpendicular ao chão.

Além disso, estruturas triangulares dão mais sustentação a construções, sejam elas metálicas, sejam de pedra, como mostram os exemplos destas fotografias.

Vamos entender o porquê disso?

Construa com palitos de sorvete e percevejos um triângulo e um quadrado deixando os vértices livres para se movimentarem. Observe.

de diversas competências gerais e específicas e Temas Contemporâneos Transversais.

OBJETIVOS

• Identificar ângulos e suas classificações

• Calcular medidas de ângulos

• Examinar as propriedades dos triângulos

• Identificar e empregar elementos de triângulos na resolução de problemas

• Identificar e analisar as propriedades dos triângulos isósceles e equilátero

• Reconhecer características e a importância da cultura quilombola

• Construir ângulos notáveis

• Construir bissetrizes de ângulos e mediatrizes de segmentos

• Resolver problemas usando bissetrizes e mediatrizes

Ponte ferroviária sobre o Canal de Kiel (Alemanha), 2022.

Esta imagem remete à decomposição de uma figura geométrica em triângulos.

PENOFOTO/ SHUTTERSTOCK.COM

Tabuleta babilônica com escrita cuneiforme (c. 18301530 a.C.), Museu do Iraque, Bagdá.

BRIDGEMAN IMAGES/FOTOARENA

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

Agora, segurando em dois vértices do triângulo, puxe-os e empurre-os em sentidos opostos. Faça o mesmo com o quadrado.

• O que você pôde notar? O que aconteceu com o triângulo? E com o quadrado?

O triângulo não pôde ser deformado, diferentemente do quadrado.

Na entrada de algumas construções de antigas civilizações, pode-se verificar um vão triangular provavelmente utilizado para tornar mais leve e estável a estrutura localizada sobre portas.

civil.

Velas triangulares permitem a movimentação de um barco contra o vento, possibilitando maior mobilidade da embarcação.

A abertura desta Unidade aborda algumas situações em que os triângulos são utilizados no cotidiano, mais especificamente na área da construção civil, como no reforço e na estabilidade de estruturas. Uma sugestão de encaminhamento é iniciar a aula solicitando aos estudantes que observem as imagens referentes ao uso do triângulo em outros contextos históricos, de modo que seja possível iniciar uma breve discussão a respeito das imagens observadas.

Em seguida, discutir com a turma quais tipos de estrutura podem ser considerados firmes e algumas características de estruturas que suportam muito mais do que pesam. Essa atividade favorece o desenvolvimento da competência específica 1 e o Tema Contemporâneo Transversal Diversidade Cultural.

Após a discussão, auxiliar os estudantes nas construções propostas na abertura (triângulo e quadrado). Os palitos de sorvete podem ser substituídos por tiras de cartolina com 10 cm de comprimento por 1,5 cm de largura. Nesse caso, é importante que essa troca seja feita por algum material não maleável.

Ao finalizar a abordagem inicial, propor um diálogo com os estudantes e incentivá-los a compartilhar as observações e descobertas a respeito da rigidez do triângulo.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd

JUSTIFICATIVAS DOS OBJETIVOS

Esta Unidade aborda o estudo de ângulos e triângulos, apresentando características e elementos que podem ser usados como ferramenta para resoluções de problemas e que possibilitarão aprofundar o estudo desse tema.

Na seção Tecnologias, pretende-se apresentar a construção de ângulos notáveis utilizando um software de geometria dinâmica. Esse tema colabora para o desenvolvimento da habilidade EF08MA15, da competência geral 5 e da competência específica 5 da área de Matemática.

Na seção Por toda parte, aborda-se a importância das comunidades

tradicionais brasileiras, com destaque para os quilombolas. Desse modo, contribui-se para o desenvolvimento dos Temas Contemporâneos Transversais Diversidade Cultural e Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras e das competências gerais 3 e 9.

KARL ALLEN LUGMAYER/ SHUTTERSTOCK.COM

Os triângulos dão resistência às estruturas. Por isso, eles são muito utilizados, por exemplo, na construção

PENOFOTO/SHUTTERSTOCK.COM

Entrada do túmulo denominado Tesouro de Atreu. Grécia, 2019.

Barco a vela no rio Dnieper. Ucrânia, 2021. OKSANA

ORIENTAÇÕES DIDÁTICAS

Ângulos

Ao iniciar este tópico, solicitar aos estudantes que citem outras situações em que o ângulo aparece no cotidiano, por exemplo, o ângulo formado pela perna ao se sentar em uma cadeira; nesse caso, o joelho representa o “vértice” do ângulo. Essa pode ser uma boa oportunidade para comentar com eles a importância de cuidar da postura. Recomendar que observem como é a postura deles em situações como ao se sentar para estudar, ou mesmo ao fazer uso de aparelhos como celular ou tablet. O cuidado adequado com a postura pode prevenir diversos problemas ortopédicos, entre eles a sobrecarga dos músculos do pescoço que podem atingir a coluna cervical e provocar dores. A seguir há algumas observações importantes que podem ser compartilhadas com eles.

Braços

Os cotovelos devem ser mantidos sempre junto ao corpo, ou seja, nem projetados para frente (braços esticados) e nem em posição de voo (cotovelos erguidos).

Alinhe seus antebraços em um ângulo entre 100 e 110 graus com o teclado. Pense assim: se o seu cotovelo fosse o centro de um relógio, esses graus equivaleriam com o horário 12h20. Já os pulsos devem permanecer sempre retos (relaxados) e alinhados com o resto do braço.

Fonte: VALIN, Alan. Ergonomia: como fazer para se posicionar corretamente em frente ao computador. Tecmundo. [S l.], 16 jan. 2009. Disponível em: https://www.tecmundo.com.br/ educacao/1361-ergonomia -como-fazer-para-se-posicionar -corretamente-em-frente-ao-pc. htm. Acesso em: 6 ago. 2022.

Vamos relembrar o conceito e as classificações de ângulos.

região convexa região não convexa O

Ângulo é toda região do plano, convexa ou não, determinada por duas semirretas de mesma origem.

No ângulo representado nesta figura, destacam-se os elementos a seguir.

• O ponto O, origem das semirretas, é denominado vértice do ângulo.

• As semirretas OA e OB são denominadas lados do ângulo.

Para identificar esse ângulo, utilizamos as notações A OB ou B ˆ OA

Os ângulos podem ser classificados de acordo com sua medida. Vamos relembrar essas classificações.

Em seguida, solicitar a um dos estudantes que siga alguns comandos como se fosse um robô. Essa brincadeira ajuda a desenvolver e retomar as noções de lateralidade. Por exemplo: com o braço esticado para a frente, pedir a ele que gire 90° à direita, depois que gire 180° à esquerda, e assim por diante. Situações como essas podem contribuir para que os estudantes associem a definição de ângulo com a ideia de giro.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 70

Retomar a classificação de ângulos, com relação às medidas, junto aos estudantes. Se considerar pertinente, propor uma atividade rápida de construção de ângulos utilizando régua e transferidor.

ÂNGULOS ADJACENTES

Vamos relembrar: dois ângulos que têm o mesmo vértice e um lado comum são denominados ângulos consecutivos

Na figura, A ˆ OB e B ˆ OC são consecutivos. Eles têm em comum apenas um lado OB () e não têm pontos internos comuns.

Dois ângulos consecutivos que não têm pontos internos comuns são denominados ângulos adjacentes

Portanto, os ângulos A OB e BOC são adjacentes.

BISSETRIZ DE UM ÂNGULO

Vamos considerar o ângulo A ˆ OB da figura, em que med A OB () = 50° A partir do vértice O, traçamos OP, que divide A OB em dois ângulos adjacentes de mesma medida. A semirreta OP é chamada de bissetriz de A ˆ OB. Acompanhe.

ORIENTAÇÕES DIDÁTICAS

Ângulos adjacentes

Relembrar o conceito de ângulos adjacentes com os estudantes e auxiliá-los a identificar quando dois ângulos são consecutivos e quando são adjacentes e a representar dois ângulos consecutivos adjacentes. Por exemplo, na ilustração apresentada no Livro do estudante, os ângulos AÔB e AÔC são consecutivos, mas não são adjacentes.

Pedir aos estudantes que façam a leitura do texto do Livro do estudante de modo atento e individual. Depois, perguntar se compreendem as nomenclaturas “ângulos consecutivos” e “ângulos adjacentes”. Incentivar os estudantes a comentar sobre possíveis dúvidas deles para que juntos possam esclarecê-las.

Bissetriz de um ângulo

Bissetriz de um ângulo é a semirreta de origem no vértice desse ângulo que determina, com os lados do ângulo, dois ângulos adjacentes congruentes.

SAIBA QUE 25°

Dadas duas semirretas de mesma origem, a bissetriz do ângulo formado por elas é o lugar geométrico dos pontos do plano que estão à mesma distância de cada uma dessas semirretas.

P dPA dPB

GLOSSÁRIO

Lugar geométrico: conjunto de pontos que têm uma ou mais propriedades em comum.

71

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 71

AMPLIANDO

Vídeo

PAPMEM – Janeiro de 2020 – Lugares Geométricos – 1. 2020. Vídeo (1h12min27s). Publicado pelo canal Instituto de Matemática Pura e Aplicada. Disponível em: https://www.youtube.com/

watch?v=Nsn1x75KYsg&list=PLo4jXE-LdDTTTEeuzChP9WxQ6xWZswwTo&index=1. Acesso em: 7 ago. 2022. Esse vídeo é parte do Programa de Aperfeiçoamento de Professores de Matemática do Ensino Médio –PAPMEM, do Impa, e apresenta a aula sobre lugares geométricos.

A bissetriz de um ângulo pode ser construída usando-se um software de geometria dinâmica como o GeoGebra. Para isso, construir um ângulo (pode ser uma medida qualquer ou uma medida pré-determinada pelo usuário), e, utilizando a ferramenta bissetriz, selecionar um ponto em um lado do ângulo, o vértice do ângulo e outro ponto no outro lado do ângulo. Esse tipo de exploração favorece o desenvolvimento da habilidade EF08MA15. Se possível, planejar um momento para que os estudantes possam utilizar o laboratório de informática (caso tenham acesso a um laboratório de informática), explorar o software de geometria dinâmica.

Saiba que

O conceito de lugar geométrico é explorado tendo como referência a bissetriz do ângulo formado por duas semirretas de mesma origem. Sugestão de ampliação do tema está disponível na indicação ao lado.

ORIENTAÇÕES DIDÁTICAS

Ângulos complementares, suplementares e ângulos opostos pelo vértice

O objetivo aqui é reconhecer, representar e relacionar ângulos complementares, ângulos suplementares e ângulos opostos pelo vértice. Pretende-se, também, que eles compreendam como determinar, a partir da medida de um ângulo, a medida de seu complemento e de seu suplemento. Solicitar aos estudantes que façam a leitura individual do texto e relatem o que compreenderam. Pedir a eles que anotem a definição de ângulos complementares e suplementares. É interessante que alguns estudantes sejam convidados para ir à lousa explicar como calcular a medida do complemento de um ângulo e a medida do suplemento de um ângulo. Estimular a troca de ideias nesse momento para auxiliar no desenvolvimento da capacidade de argumentação dos estudantes.

Depois, apresentar dois ângulos adjacentes quaisquer na lousa e solicitar aos estudantes que verifiquem se os ângulos dados são complementares e/ou suplementares.

No estudo de ângulos opostos pelo vértice, importante ressaltar a congruência entre eles. Observe a figura a seguir, em que AÔD e BÔC são ângulos opostos pelo vértice.

ÂNGULOS COMPLEMENTARES

Dois ângulos são complementares quando a soma das medidas desses ângulos é igual a 90°

Na figura a seguir, A ˆ OB e B ˆ OC são adjacentes e complementares, e cada ângulo é chamado de complemento do outro.

Assim, se med () A ˆ OB for igual a x, a medida do complemento () B ˆ OC será igual a 90° x.

ÂNGULOS SUPLEMENTARES

Dois ângulos são suplementares quando a soma das medidas desses ângulos é igual a 180°

Na figura a seguir, A ˆ OB e B ˆ OC são adjacentes e suplementares, e cada ângulo é chamado de suplemento do outro.

Desse modo, se med () A OB for igual a x, a medida do suplemento () BOC será 180° x.

ÂNGULOS OPOSTOS PELO VÉRTICE

Consideremos duas retas r e s que se cruzam em um único ponto V formando quatro ângulos: ˆ a, ˆ x, ˆ b e ˆ y , conforme mostra a figura a seguir.

Os ângulos ˆ x e ˆ y são chamados de ângulos opostos pelo vértice (o.p.v.). Também são opostos pelo vértice os ângulos a e ˆ b

Com o auxílio de um transferidor, pode-se verificar que dois ângulos opostos pelo vértice são congruentes, ou seja, têm a mesma medida.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd

• Como AOB e AOD são adjacentes suplementares, temos que m + y = 180° (1).

• Como AOB e BOC são adjacentes suplementares, temos que m + x = 180° (2).

ATIVIDADES

8.a) Bissetriz de um ângulo. Os ângulos formados pela haste azul e cada uma das hastes vermelhas são congruentes.

b) A medida de cada haste verde representa a distância de cada ponto da haste azul até cada uma das hastes vermelhas, de acordo com a definição de bissetriz de um ângulo (é importante considerar que as hastes verdes são perpendiculares a cada haste vermelha). Resposta pessoal.

Responda às questões no caderno.

1. Observe os pares de ângulos suplementares destacados na figura e determine as medidas x e y indicadas.

8. A figura a seguir representa a estrutura de uma rampa de skate cuja sustentação é reforçada pela haste azul e pelas hastes verdes. A haste azul está posicionada à mesma distância de cada uma das hastes vermelhas.

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades deste bloco exploram a aplicação dos conceitos de ângulos adjacentes, bissetriz de um ângulo, ângulos complementares, suplementares e opostos pelo vértice.

x y 100° 50°

2. Determine a medida do complemento de um ângulo de:

a) 66°

b) 74° c) 22° d) 47°

3. Determine a medida do suplemento de um ângulo de:

a) A haste azul representa que elemento relacionado ao ângulo formado pelas hastes vermelhas? O que se pode afirmar sobre o ângulo formado pela haste azul e cada uma das hastes vermelhas?

b) O que indica a medida de cada haste verde? Explique como você pensou para responder.

a) 78°

b) 67° c) 135° d) 139°

4. A medida de um ângulo é igual à medida do complemento dele, acrescida de 70° . Qual é a medida desse ângulo?

5. A medida de um ângulo é igual à terça parte da medida do suplemento dele. Qual é

6. Sabendo que a medida de um ângulo é igual ao quádruplo da medida do complemento dele, determine a medida desse ângulo.

7. Na figura a seguir, calcule as medidas x, y e z indicadas.

9. Determine as medidas x e y indicadas na figura a seguir

No estudo com ângulos, verificar as possíveis dúvidas que os estudantes ainda apresentam em relação à resolução de equações e de instrumentos para obter as medidas de ângulos desconhecidos usando as propriedades estudadas a respeito desse tema. Propor a resolução coletiva, sugerindo a alguns estudantes que façam seus registros na lousa, enquanto o restante da turma descreve o que é exposto, desse modo, favorece-se o desenvolvimento do raciocínio lógico, argumentação e validação de resultados. Esses processos favorecem o letramento matemático e o desenvolvimento das competências específicas 2 e 5 da área de Matemática.

10. D uas retas, AB e CD , são concorrentes em um ponto M, de tal modo que a medida de A ˆ MD representa a terça parte da medida de AMC. Determine as medidas dos quatro ângulos adjacentes indicados na figura, formados com vértice no ponto M

Nas atividades 4 a 6, é importante destacar a importância do registro de uma expressão algébrica por meio de linguagem textual e não simbólica. Verificar se os estudantes conseguem converter o texto em uma expressão com símbolos matemáticos e, se considerar necessário, apresentar outros exemplos.

med(AMC) = 135°; med(BMC) = 45°; med(DMB) = 135° e med(AMD) = 45°.

• Comparando (1) e (2), temos:

Portanto, AOD

e BOC ˆ têm a mesma medida. De modo análogo, é possível concluir que AOB ˆ e COD ˆ são ângulos de medidas iguais.

A atividade 8 apresenta uma aplicação de bissetriz de um ângulo em um contexto que pode ser mais familiar para alguns estudantes, pois trata-se de um problema que cita a estrutura de uma rampa de skate. Se considerar oportuno, aprofundar a ideia de reforços em estruturas, apresentando outros exemplos de estruturas reforçadas, como a estrutura da ponte ferroviária presente na abertura da Unidade.

ORIENTAÇÕES DIDÁTICAS

Triângulos

A definição de triângulo e seus elementos é retomada nesta página. Relembrar com os estudantes como nomear lados, vértices e ângulos de um triângulo. Verificar se eles percebem que o triângulo é um polígono que não possui diagonais.

Ao trabalhar a classificação de triângulos em relação às medidas dos lados e em relação às medidas dos ângulos, verificar se os estudantes ainda têm alguma dúvida a respeito dessas nomenclaturas.

Para aprofundar a exploração a respeito dos triângulos, fazer alguns questionamentos, como: “É possível representar um triângulo com dois ângulos retos?”; “Um triângulo equilátero pode ser obtusângulo?”. Espera-se que os estudantes respondam que em ambos os casos não é possível. Na primeira questão, não é possível que um triângulo tenha dois ângulos retos, pois apenas esses dois ângulos somariam 180°, que é a soma total de todos os ângulos internos de um triângulo. Do mesmo modo, um triângulo equilátero não pode ser obtusângulo, pois um triângulo equilátero possui todos os ângulos de mesma medida. Como a soma dos ângulos internos de um triângulo é 180°, cada ângulo interno de um triângulo equilátero mede 60° (180° : 3). Portanto, o triângulo equilátero é um triângulo acutângulo.

TRIÂNGULOS

ELEMENTOS DE UM TRIÂNGULO

Vamos destacar os seguintes elementos de um triângulo.

• Representação: * ABC

• Vértices: pontos A, B e C

• Lados: AB , AC e BC

• Ângulos internos: ˆ A, ˆ B e ˆ C

• Ângulos externos: ˆ a, ˆ b e ˆ c

CLASSIFICAÇÃO DE TRIÂNGULOS

Classificamos os triângulos em relação às medidas dos lados ou às medidas dos ângulos internos.

Classificação de um triângulo em relação à medida dos lados

Equilátero

Quando os três lados têm medidas iguais.

Isósceles

Quando dois lados têm medidas iguais.

Escaleno

Quando os três lados têm medidas diferentes.

Classificação de um triângulo em relação à medida dos ângulos internos

Acutângulo

Quando os três ângulos internos são agudos (medidas menores do que 90°).

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 74

Retângulo

Quando um dos ângulos internos é reto (medida igual a 90°).

Obtusângulo

Quando um dos ângulos internos é obtuso (a medida é maior do que 90° e menor do que 180°).

ÂNGULOS NO TRIÂNGULO

PENSE E RESPONDA

2. Pela montagem, é possível verificar que, juntos, os três ângulos internos do triângulo formam um ângulo raso. Então: a + b + c = 180° .

Acompanhe como Núbia fez para determinar a soma das medidas dos ângulos internos de um triângulo.

1o passo: Usando uma tesoura com pontas arredondadas, Núbia recortou uma folha de papel para obter uma figura que lembra um triângulo.

2o passo: Em seguida, ela usou lápis de diferentes cores para destacar os três ângulos internos do triângulo e nomeou esses ângulos a, b e c

ORIENTAÇÕES DIDÁTICAS

Ângulos no triângulo

Se considerar necessário, retomar os conceitos de ângulos formados por retas paralelas cortadas por uma transversal: ângulos correspondentes, alternos internos, alternos externos, colaterais internos e colaterais externos. Esses conceitos auxiliaram na compreensão de que a soma das medidas dos ângulos internos de um triângulo é igual a 180°. Pense e responda

3o passo: Depois, Núbia recortou a figura do triângulo, dividindo-o em três partes, com um ângulo em cada parte.

4 o passo: Por fim, ela reposicionou os vértices dos três ângulos, fazendo-os coincidir em um único ponto. ILUSTRAÇÕES:

Agora, faça o que se pede.

1. Utilizando uma folha de papel sulfite, uma tesoura com pontas arredondadas e lápis de cor, faça a mesma atividade que Núbia fez.

Produção pessoal.

2. Depois de finalizar a atividade, responda no caderno: qual é a soma das medidas dos ângulos internos de um triângulo?

Agora, vamos usar os conhecimentos adquiridos sobre ângulos determinados por retas paralelas cortadas por uma transversal para demonstrar algumas relações.

• Consideremos a representação do triângulo ABC seguinte.

a = med () ˆ a

b = med() b

c = med() ˆ c

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 75

Tracemos uma reta r, paralela à reta que contém o lado BC, passando por A. Essa paralela vai formar, com os lados AB e AC, dois ângulos cujas medidas indicaremos por m e n, respectivamente.

11/08/22 21:27

Se possível, reproduzir com os estudantes os passos que a personagem do boxe utilizou para determinar a soma das medidas dos ângulos internos de um triângulo, para que eles relembrem, de maneira intuitiva, a soma das medidas dos ângulos internos de um triângulo. Esse assunto já foi abordado em anos anteriores, a ideia é que seja retomado por meio desta atividade prática para que, depois, eles possam acompanhar a demonstração matemática dessa propriedade. A atividade promove o desenvolvimento da capacidade investigativa, incentivando induções e formulação de conjecturas. Além disso, atividades com uso de dobraduras favorecem o desenvolvimento da competência geral 3.

ORIENTAÇÕES DIDÁTICAS

Nesta página, é apresentada a demonstração da propriedade de que, em qualquer triângulo, a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele. É importante que os estudantes compreendam essa demonstração e a necessidade de realizá-la. Desse modo, aos poucos, eles se familiarizam com a linguagem matemática e abstração necessárias para realizar demonstrações, desenvolvendo assim o raciocínio lógico e a argumentação

Como complemento ao conteúdo das páginas 75 e 76 do Livro do estudante, pode-se entregar uma folha de papel com alguns triângulos desenhados, com espaço suficiente para que eles consigam fazer os prolongamentos dos lados, e pedir a eles que marquem os ângulos internos e tracem seus respectivos ângulos externos.

Depois, na mesma folha com os triângulos desenhados, solicitar a eles que destaquem cada ângulo formado por um ângulo interno e o ângulo externo adjacente a ele, e respondam à pergunta:

“Que tipos de ângulos foram destacados?”.

Espera-se que eles respondam que foram destacados todos os ângulos rasos (180°).

As observações empíricas são importantes para o desenvolvimento de induções e formulações de conjecturas, incentivar os estudantes a participar da aula e trocar ideias entre eles.

Assim: m + a + n = 180°

b + a + c = 18 0°

A soma das medidas dos ângulos internos de um triângulo é igual a 180°

Além dos ângulos internos, um polígono, como o triângulo, tem ângulos externos. Os ângulos externos são aqueles formados por um lado do polígono e pelo prolongamento de um lado consecutivo a esse lado do polígono.

Considerando o triângulo ABC da figura a seguir, temos:

A

• a, b e c são as medidas dos ângulos internos;

• x, y e z são as medidas dos ângulos externos. Analisando a imagem, podemos observar que os ângulos a e ˆ z s ão adjacentes suplementares. O mesmo ocorre com os ângulos b e ˆ y e com os ângulos ˆ c e ˆ x

B

C

Para o triângulo, existe uma relação entre a medida de um ângulo externo e as medidas dos dois ângulos internos não adjacentes a ele. Considerando a figura seguinte, podemos analisar que:

ILUSTRAÇÕES:

B

A C

Assim, temos:

x + c = 180°

• x + c = 180° (adjacentes suplementares);

• a + b + c = 180 ° (soma das medidas dos ângulos internos).

x + c = a + b + c h x = a + b a + b + c = 180° medida do ângulo externo soma das medidas dos ângulos internos não adjacentes a ˆ x

Em qualquer triângulo, a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd

8. med(A) = 64°, med(B) = 68° e med(C) = 48°. Exemplo de resposta na seção Resoluções comentadas deste Manual.

ORIENTAÇÕES DIDÁTICAS

Atividades

Responda às questões no caderno.

1. Em cada caso, identifique o maior lado do triângulo.

SAIBA QUE

Em qualquer triângulo, o maior ângulo opõe-se ao maior lado, e o maior lado opõe-se ao maior ângulo.

2. Considerando as medidas a, b, c e d dos ângulos indicadas no triângulo, qual relação de igualdade podemos formar entre:

R a b d

S

c a) b, c e d? b) a e b? c) a, c e d ?

3. Em um triângulo, as medidas de dois ângulos internos são 72° e 81°. Qual é a medida, em grau, do terceiro ângulo interno desse triângulo?

4. As medidas, em grau, dos ângulos internos de um triângulo são expressas por (3x 48), (2x + 10) e (x 10). Qual é a medida do maior ângulo desse triângulo?

b + c + d = 180° a + b = 180° c + d = a 27° 86°

5. Calcule a medida a indicada no triângulo da figura a seguir. aa

116°

6. Considerando o triângulo ABC da figura, determine o valor de x

7. Em um triângulo ABC, med ˆ A () = 72 ° Sabendo que a medida do ângulo externo no vértice B é 125°, qual é a medida do ângulo interno C ?

8. Considere um triângulo ABC, em que oângulo externo no vértice A mede 116°, med B () = x e med C () = x 20 ° Determine as medidas dos três ângulos internos desse triângulo. Faça um esboço desse triângulo e descreva para um colega a resolução que você fez.

DESAFIO

9. Observe a figura a seguir e calcule o valor da expressão x + y + a + b, aplicando as propriedades de ângulos em um triângulo que forem necessárias.

As atividades deste bloco têm como objetivo levar os estudantes a utilizar as relações da soma das medidas dos ângulos internos e das medidas dos ângulos externos de um triângulo, verificar que cada ângulo interno de um triângulo é suplementar ao ângulo externo adjacente a ele, e que a medida de um ângulo externo é igual à soma das medidas dos dois ângulos internos não adjacentes a ele; e estabelecer as relações de desigualdade entre ângulos e lados de um triângulo. Para o desafio 9, se preferir, propor aos estudantes que se organizem em duplas para discutir como encontrarão as medidas a, b, x e y. Propor, por exemplo, que eles reproduzam a ilustração no caderno, a observem e descrevam os conceitos que podem ser utilizados para determinar as medidas solicitadas. Depois, pedir a eles que destaquem os triângulos que a compõem.

ORIENTAÇÕES DIDÁTICAS

Altura de um triângulo

A partir deste tópico, serão explorados alguns elementos do triângulo, suas definições e suas características. Esses elementos serão muito úteis no desenvolvimento de outros assuntos dentro da Matemática nos anos seguintes de estudo.

É importante que os estudantes compreendam o conceito de cada um dos elementos, para que estejam aptos a construí-los em qualquer triângulo dado.

No caso da altura, reforçar com os estudantes que nem sempre a altura está na região interna do triângulo.

Se possível, levar os estudantes ao laboratório de informática para que eles realizem a construção das alturas de um triângulo utilizando o software de geometria dinâmica GeoGebra. Verificar se eles compreendem que é necessário entender o conceito de altura de um triângulo para realizar a construção.

ALTURA DE UM TRIÂNGULO

Altura de um triângulo é o segmento de reta que une um vértice ao lado oposto (ou ao seu prolongamento), formando um ângulo de 90° com esse lado (ou com seu prolongamento).

Acompanhe os exemplos a seguir.

Utilizamos o símbolo À para relacionar segmentos de retas ou retas concorrentes que são perpendiculares, ou seja, formam um ângulo de 90°.

AH À BC

AH é a altura relativa ao lado BC

AH À BC

AH é a altura relativa ao lado BC

Todo triângulo possui três alturas. O ponto de encontro das retas que contem as alturas é denominado ortocentro. Observe as alturas e o ortocentro nos diferentes triângulos.

AH : altura relativa ao lado BC

‘

BH : altura relativa ao lado AC

CH’ : altura relativa ao lado AB

O: ortocentro do * ABC

Note que, nesse caso, o ortocentro pertence à região interna do triângulo e não coincide com nenhum dos vértices.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd

AMPLIANDO

Link

ABBONDATI, Mario. Alturas do triângulo. GeoGebra [S l.], [20--]. Disponível em: https://www.geogebra. org/m/QvcF2vcb. Acesso em: 6 ago. 2022.

Uma sugestão de encaminhamento, é possibilitar que os estudantes acessem o simulador para visualizarem as alturas e o ortocentro de um triângulo, alterando as posições de seus vértices.

Triângulo acutângulo

AH : altura relativa ao lado BC

‘

BH : altura relativa ao lado AC

CH’ : altura relativa ao lado AB

O: ortocentro do * ABC

ORIENTAÇÕES DIDÁTICAS

Mediana de um triângulo

Note que, nesse caso, o ortocentro não pertence à região interna do triângulo.

Triângulo retângulo

AH : altura relativa ao lado BC

CA : altura relativa ao lado AB

BA : altura relativa ao lado AC

A: ortocentro do * ABC B

Note que, nesse caso, duas das alturas coincidem com os lados AB e AC, e o ortocentro coincide com o vértice A

MEDIANA DE UM TRIÂNGULO

Antes de iniciarmos o estudo da mediana, é preciso compreender o que é o ponto médio de um segmento de reta.

Um ponto M pertencente a AB é denominado ponto médio desse segmento de reta se M divide AB em dois segmentos de retas congruentes. A M B

Nessa figura, M é o ponto médio do segmento AB. Então, AM 2 MB

símbolo de congruência

Agora que sabemos o que é o ponto médio de um segmento de reta, vamos estudar a mediana.

Mediana de um triângulo é o segmento de reta que une um vértice ao ponto médio do respectivo lado oposto.

Inicialmente, apresentar aos estudantes o conceito de ponto médio. Em seguida, explicar a definição e a construção da mediana de um triângulo. Verificar se os estudantes compreendem o conceito ou se ainda têm alguma dúvida.

Se possível, utilizar o recurso do software de geometria dinâmica para auxiliar no processo de aprendizagem do estudante. Para isso, pode-se por exemplo, solicitar a eles que acessem o link: https://www.geogebra.org/m/ fQFRXaaF (acesso em: 6 ago. 2022) e explorem o simulador. Desse modo, eles podem visualizar as medianas e o baricentro do triângulo e alterar a posição dos vértices.

Se considerar oportuno, comentar com os estudantes que o baricentro de um triângulo é também o seu centro de massa. Essa abordagem pode ser feita em conjunto com o professor de Ciências.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd

ORIENTAÇÕES DIDÁTICAS

Bissetriz de um triângulo Assim como foi feito com os elementos anteriores, explicar aos estudantes o conceito e a construção da bissetriz de um triângulo, verificar se eles têm alguma dúvida e fazer as retomadas necessárias antes de dar continuidade ao estudo. Ao explorar este conteúdo, favorece-se o desenvolvimento da habilidade EF08MA15. Verificar se os estudantes percebem alguma semelhança entre a definição de bissetriz de um triângulo e a definição de bissetriz de um ângulo, apresentada na página 71 do Livro do estudante.

Para complementar esse estudo, sugerir que os estudantes acessem o link : https://www.geogebra. org/m/BhZqWYgt (acesso em: 6 ago. 2022), e realizem explorações no GeoGebra envolvendo as bissetrizes e o encentro de um triângulo.

Para auxiliar os estudantes a visualizar a propriedade do triângulo isósceles mencionada, pode-se explorar o simulador disponível no link: https://www. geogebra.org/m/dfpXWbxM

(acesso em: 6 ago. 2022). Nele é possível movimentar os vértices de um triângulo isósceles e verificar que a altura, a mediana e a bissetriz relativas à base desse triângulo coincidem.

Todo triângulo possui três medianas que se encontram em um único ponto denominado baricentro

AM’: mediana relativa ao lado BC

‘

BM : mediana relativa ao lado AC

CM: mediana relativa ao lado AB

G: baricentro do * ABC

O baricentro, diferentemente do ortocentro, é sempre um ponto interno do triângulo.

BISSETRIZ DE UM TRIÂNGULO

Bissetriz de um triângulo é o segmento de reta que une um vértice do triângulo ao respectivo lado oposto, dividindo o ângulo desse vértice em dois ângulos de mesma medida.

BAS 2 C AS

AS é a bissetriz relativa ao ângulo A B ˆ CS 2 S ˆ CA

CS é a bissetriz relativa ao ângulo C

Todo triângulo possui três bissetrizes que se encontram em um único ponto denominado incentro

AS: bissetriz relativa ao ângulo A

‘

BS : bissetriz relativa ao ângulo B

CS’ : bissetriz relativa ao ângulo C

I: incentro do * ABC

Em geral, as alturas, as medianas e as bissetrizes de um triângulo não coincidem, exceto nos triângulos isósceles e equiláteros. Por exemplo, considere o triângulo isósceles ABC a seguir.

Como o triângulo é isósceles, a altura, a mediana e a bissetriz relativas ao lado BC coincidem e correspondem ao segmento AH

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 80

MEDIATRIZ

Já sabemos que o ponto médio de um segmento de reta o divide em dois segmentos congruentes.

ORIENTAÇÕES DIDÁTICAS

Mediatriz

Uma sugestão de encaminhamento é iniciar a aula explicando o conceito de reta mediatriz apresentado no Livro do estudante, para então explicar o conceito e a construção da mediatriz de um triângulo.

SAIBA QUE

Qualquer ponto P da reta mediatriz de AB tem a mesma distância em relação ao ponto A (dPA) e ao ponto B (dPB). Assim, a mediatriz é o lugar geométrico dos pontos do plano que são equidistantes de dois pontos dados, no caso, A e B

Agora, vamos analisar a mediatriz de um lado de um triângulo.

r C B P

A Mediatriz de um lado de um triângulo é a reta perpendicular a esse lado que passa pelo ponto médio desse lado.

A reta r é a mediatriz do lado BC no triângulo ABC.

Todo triângulo possui três mediatrizes que se encontram em um único ponto denominado circuncentro r

s

Na figura, o ponto M, pertencente a AB, é o ponto médio desse segmento, pois AM 2 MB. A reta perpendicular ao segmento AB e que passa pelo ponto M é chamada de reta mediatriz de AB ILUSTRAÇÕES:

r : mediatriz do lado BC

s: mediatriz do lado AC

t : mediatriz do lado AB

O: circuncentro do * ABC

11/08/22 22:05

Verificar se os estudantes compreendem a diferença entre a definição de mediana de um triângulo e de mediatriz de um triângulo. Se considerar oportuno, promover um debate com a turma para que eles possam explicar aos colegas essa diferença. Alguns pontos que podem auxiliar para o desenvolvimento dessa discussão:

• A mediatriz é uma reta; já a mediana é um segmento de reta.

• A mediatriz não passa necessariamente pelo vértice oposto do lado a que ela se refere. Já o vértice e o ponto médio do lado oposto são necessariamente as extremidades da mediana.

• A mediatriz necessariamente passa pelo ponto médio do lado do triângulo e forma um ângulo reto com esse lado. Já a mediana também passa pelo ponto médio do lado do triângulo, mas pode ou não formar um ângulo reto com esse lado.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd

AMPLIANDO

Link

ABBONDATI, Mario. Mediatrizes do triângulo. GeoGebra. [S l.], [20--]. Disponível em: https://www. geogebra.org/m/bePR4ACr. Acesso em: 6 ago. 2022.

Uma sugestão de encaminhamento é possibilitar que os estudantes explorem as mediatrizes e o circuncentro de um triângulo, alterando a posição dos vértices, favorecendo, assim, o desenvolvimento da habilidade EF08MA15.

Ao analisar os triângulos que os estudantes já trabalharam, pode-se, por exemplo, discutir em que condições a reta mediatriz contém a mediana relativa ao mesmo lado. Espera-se que os estudantes compreendam que isso ocorre quando o triângulo é isósceles e, em particular, quando ele é equilátero.

ORIENTAÇÕES DIDÁTICAS

Por toda parte

Com antecedência, solicitar aos estudantes que providenciem os materiais necessários para desenvolver a atividade proposta nesta seção. Por meio da manipulação e da observação de cada etapa, é possível experimentar, explorar, formular conjecturas e perceber os conceitos estudados. Desse modo, busca-se dar continuidade ao desenvolvimento da habilidade EF08MA15. Atividades como essa também favorecem o desenvolvimento da competência geral 3.

Caso considere interessante, solicitar aos estudantes que realizem dobraduras para representar os demais elementos do triângulo estudados anteriormente. As orientações para realizar essa atividade estão na atividade complementar a seguir.

Após o estudo desses elementos, realizar alguns questionamentos como: “Em que condições a mediana, a altura e a bissetriz, relativas ao mesmo lado, coincidem?”. Espera-se que os estudantes cheguem à conclusão de que isso acontece nos triângulos isósceles e equiláteros.

Se considerar oportuno, comentar com os estudantes que o ortocentro, o baricentro, o incentro e o circuncentro são chamados de pontos notáveis do triângulo.

USANDO DOBRADURAS

É possível representar alguns elementos de um triângulo com dobraduras. Nesta atividade, vamos obter as bissetrizes e o incentro de um triângulo.

Você vai precisar de: folha de papel sulfite, tesoura com ponta arredondada, lápis, régua, esquadro e transferidor.

1o passo: Em uma folha de papel sulfite, recorte uma figura que lembre um triângulo qualquer.

2o passo: Para obter a bissetriz de um ângulo do triângulo, dobre-o sobrepondo dois lados. bissetriz bissetriz

3o passo: Obtenha da mesma maneira as três bissetrizes dos ângulos internos do triângulo representado.

Responda às questões no caderno.

4 o passo: Marque o ponto I, no qual as bissetrizes se encontram. Esse ponto é o incentro do triângulo.

Investigação 1: Utilizando um compasso e colocando a ponta-seca no incentro, abra-o até atingir um dos lados e trace a circunferência cujo centro é o incentro, e o raio é a distância do incentro até um ponto pertencente a um dos lados.

• Observe a circunferência traçada e responda: a circunferência intersecta cada lado do triângulo em um só ponto?

Investigação 2: Recorte outra figura que lembre um triângulo e, por dobradura, obtenha a bissetriz de um dos ângulos internos. De um ponto qualquer dessa bissetriz, trace um segmento de reta até um dos lados que forma o ângulo dividido pela bissetriz, de modo que esse segmento de reta seja perpendicular ao lado escolhido.

a) Partindo do ponto escolhido, faça o mesmo procedimento com o outro lado que forma o ângulo. Dobre novamente o triângulo na bissetriz. Os dois segmentos traçados têm o mesmo comprimento?

b) Repita o processo em diferentes pontos da bissetriz. O que é possível concluir? Justifique.

Dica: use esquadro e régua.

Os dois segmentos traçados têm sempre o mesmo comprimento. Isso ocorre porque a bissetriz de um ângulo é determinada pelos pontos do plano equidistantes das semirretas que formam esse ângulo.

AMPLIANDO

Atividade complementar

Acompanhe, em cada sequência a seguir, como representar, por meio de dobraduras, vários elementos de um triângulo. Para fazer estas atividades, será necessário providenciar o material descrito a seguir:

• papel sulfite;

• tesoura com pontas arredondadas;

• lápis;

• esquadro;

• transferidor.

Dobradura 1: Representando alturas/ortocentro

Sim.

Sim.

ATIVIDADES

Responda às questões no caderno.

1. Na figura, AH é uma altura, e BI é outra altura do triângulo ABC. Determine as medidas a, b e c indicadas.

5. 20°. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

segmento está na região de um lago, oque impede essa instalação. Assim, a antena precisará ser deslocada para um novo local ‘C () , que deverá, ainda, atender ao mesmo critério de distância em relação aos municípios A e B. O novo ponto de instalação da antena deve estar localizado:

a) na bissetriz do ângulo formado pelo lado AB e pelo lado ‘AC

ORIENTAÇÕES DIDÁTICAS

Atividades

Neste bloco de atividades, procura-se explorar a resolução de problemas envolvendo os elementos mediana, altura e bissetriz de um triângulo. Desse modo, favorece-se o desenvolvimento das habilidades EF08MA15 e EF08MA17, bem como da competência específica 5 da área de Matemática.

2. O baricentro de um triângulo divide cada mediana em duas partes, de modo que a medida de uma parte é o dobro da medida da outra. Na figura, G é o baricentro, e AM é a mediana relativa a BC

b) na altura de um triângulo definido pelos pontos A, B e C‘

c) na mediatriz do segmento AB

d) em outro ponto qualquer.

4. No *MPQ, MX e PY são bissetrizes. Calcule as medidas a, b e c

Na atividade 4, solicitar aos estudantes que se organizem em duplas e pedir a eles que desenhem no caderno o triângulo apresentado. A troca de ideias entre eles é bastante importante para determinarem a solução do problema, propiciando o desenvolvimento da competência específica 2.

Considerando a figura, qual é a afirmação correta?

Alternativa d.

a) A medida de GM é igual a 2 3 da medida de AM

b) A medida de AG é igual à metade da medida de AM

c) Se GM = 2,89 cm, então AM = 5,78 cm.

d) A medida de AG é igual a 2 3 da medida de AM

3. Uma antena de celular será instalada em um ponto C entre dois municípios, A e B, de modo que fique à mesma distância dos dois municípios. No entanto, representando em um esboço o segmento de reta que liga os dois municípios AB () , p ercebe-se que o ponto médio do

5. Em um * ABC, o ângulo B mede 60 ° , e o ângulo C mede 20 °. Calcule a medida do ângulo formado pela altura relativa ao lado BC e a bissetriz do ângulo ˆ A . Descreva por escrito cada etapa de cálculo que você cumpriu para resolver este problema.

6. Na figura, AD é a bissetriz relativa ao ângulo ˆ A , e AH é a altura relativa ao lado BC . Determine as medidas a, b e c indicadas

• Recorte um triângulo como esse e, por dobradura, represente as três alturas desse triângulo.

• Marque o ponto O onde as três alturas se encontram.

Esse ponto é o ortocentro do triângulo

Investigação: Meça os ângulos que cada altura forma com o lado que contém o seu pé. Quanto mede cada um desses ângulos? Registre no caderno. Resposta: 90°.

Dobradura 2: Representando medianas/baricentro

mediana mediana

ponto médio do lado ponto médio do lado

• Recorte um triângulo e, por dobradura, represente as três medianas.

• Marque o ponto G onde elas se encontram. Esse ponto é o baricentro do triângulo

Investigação: Para cada mediana, meça as distâncias do ponto médio do lado ao baricentro e do baricentro ao vértice. Qual é, nessa ordem, a razão entre essas distâncias? Registre no caderno. Resposta: 1

ORIENTAÇÕES DIDÁTICAS

Figuras congruentes

Nesta página, o conceito de figuras congruentes e polígonos congruentes é apresentado brevemente para que o conceito de triângulos congruentes possa ser apresentado em seguida aos estudantes.

Verificar se os estudantes compreenderam o conteúdo apresentado, pois ele será utilizado como base para a explanação de triângulos congruentes.

Se possível, apresentar aos estudantes o vídeo indicado na seção Ampliando a seguir.

CONGRUÊNCIA DE TRIÂNGULOS

FIGURAS CONGRUENTES

Analise as figuras geométricas a seguir. Vamos sobrepor uma figura à outra.

Percebe-se que as duas figuras, quando sobrepostas, coincidem exatamente. Nesse caso, é possível dizer que as figuras são congruentes

O mesmo pode ocorrer com polígonos, ou seja, dois polígonos com a mesma quantidade de lados são congruentes quando é possível sobrepor um ao outro, de modo que coincidam exatamente.

AMPLIANDO

Vídeo

Os polígonos representados se sobrepõem exatamente, portanto são congruentes. Assim, os lados com a mesma identificação são congruentes, e os ângulos indicados com a mesma cor também são congruentes.

RECONHECENDO figuras congruentes: Parte I. 2020. Vídeo (7min47s). Publicado por Khan Academy Brasil. Disponível em: https://www.youtube.com/watch?v=XSsCVq3AJVc. Acesso em: 8 ago. 2022.

Esse link apresenta uma videoaula sobre figuras congruentes e como determinar quais figuras são congruentes entre si.

ORIENTAÇÕES DIDÁTICAS

TRIÂNGULOS CONGRUENTES

O triângulo, por ser um polígono, também segue essa definição de congruência.

Dois triângulos são congruentes quando têm os lados e os ângulos correspondentes congruentes.

Observe os triângulos ABC e MNP.

Nesse caso, dizemos que:

• Ae Msão â ngulos corre sponde ntes;

• ˆ Be ˆ Nsão â ngulos corre sponde ntes;

• ˆ Ce ˆ Psão â ngulos corre sponde ntes;

• BC eN Psão la dos corre sponde ntes;

• AC eMPsão la dos corre sponde ntes;

• AB eMNsão la dos corre sponde ntes

Como todos os lados correspondentes e todos os ângulos correspondentes são congruentes, os triângulos ABC e MNP também são congruentes.

AMPLIANDO

Link CÁSSIO, Jorge. Congruência de triângulos. GeoGebra. [S l.], [20--]. Disponível em: https://www.geogebra. org/m/fBy4dZmC. Acesso em: 6 ago. 2022.

Se possível, no laboratório de informática, solicitar aos estudantes que resolvam, em duplas, as atividades propostas.

Triângulos congruentes Nesta página, é apresentado o conceito de triângulos congruentes. Verificar se os estudantes compreendem o conceito, pois ele auxilia no desenvolvimento da representação por meio da linguagem simbólica e será bastante utilizado em vários momentos de seu aprendizado nos próximos anos.

ILUSTRAÇÕES: EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

Casos de congruência de triângulos

Para ampliar o estudo sobre os casos de congruência de triângulos, pode-se propor algumas atividades de construção e demonstrações geométricas. Incentivar os estudantes a fazer o levantamento de algumas hipóteses para serem verificadas, desse modo, eles têm a oportunidade de testar conjecturas. A seguir, há uma sugestão de atividade que pode ser desenvolvida com eles, preferencialmente em grupos.

Casos de congruência de triângulos

Para saber se dois triângulos são congruentes, verificamos se os lados e os ângulos correspondentes são congruentes entre si.

No entanto, existem condições que, uma vez satisfeitas, garantem a congruência de dois triângulos sem a necessidade de confirmar a congruência entre os seis elementos (3 lados e 3 ângulos). Essas condições são chamadas de casos de congruência de triângulos. Vamos verificar quais são esses casos.

1o caso: Lado, Lado, Lado (LLL).

São congruentes dois triângulos que têm os três lados correspondentes congruentes.

AMPLIANDO

Atividades complementares

1. Se apenas um par de elementos correspondentes de dois triângulos for conhecido, pode-se afirmar que esses triângulos são congruentes?

2. Saber apenas que dois elementos de um triângulo são congruentes

2o caso: Lado, Ângulo, Lado (LAL).

São congruentes dois triângulos que têm dois lados e o ângulo compreendido entre esses lados correspondentes congruentes.

3o caso: Ângulo, Lado, Ângulo (ALA).

São congruentes dois triângulos que têm dois ângulos e o lado compreendido entre esses ângulos correspondentes congruentes.

a dois elementos correspondentes de outro triângulo é suficiente para determinar que dois triângulos são congruentes?

Resolução das atividades

1. Para responder a essa atividade, pode-se, por exemplo, solicitar aos estudantes que construam dois triângulos com as seguintes características:

• a medida de um lado dos lados deve ser 4,5 cm;

• a medida de um dos ângulos internos deve ser 45°.

Após a construção dos triângulos e a discussão em grupo a respeito das observações, espera-se que eles percebam que há a possibilidade de construir infinitos triângulos não congruentes.

4o caso: Lado, Ângulo Adjacente, Ângulo Oposto (LAAO).

São congruentes dois triângulos que têm um lado, um ângulo adjacente a esse lado e o ângulo oposto a esse lado correspondentes congruentes.

ORIENTAÇÕES DIDÁTICAS

Após a apresentação dos casos de congruência de triângulos, apresentar o caso da congruência no triângulo retângulo. Como aprofundamento, verificar se os estudantes conseguem explicar por que esse caso de congruência só vale para triângulos retângulos.

Caso de congruência no triângulo retângulo

Já estudamos que um triângulo retângulo é aquele que tem um ângulo interno reto (medida igual a 90°).

No triângulo retângulo, os lados recebem nomes específicos.

• O lado oposto ao ângulo reto é chamado de hipotenusa

• Os lados que formam o ângulo reto são chamados de catetos

São congruentes dois triângulos retângulos que têm a hipotenusa e um dos catetos respectivamente congruentes.

2. Para responder a essa atividade, pedir aos estudantes que construam dois triângulos.

• Conhecidos apenas dois lados correspondentes congruentes, de medidas 3,0 cm e 5,0 cm, respectivamente.

• Conhecidos apenas dois ângulos internos correspondentes congruentes, de medidas 45° e 80°, respectivamente.

• Conhecidos apenas um lado e um ângulo interno respectivamente congruentes, de medidas 3 cm e 30°. Espera-se que eles percebam que é possível construir infinitos triângulos não congruentes sabendo apenas que dois elementos de um triângulo são congruentes a dois elementos correspondentes de outro triângulo.

ORIENTAÇÕES DIDÁTICAS

Explorar a situação apresentada no Livro de estudante, discutindo as etapas apresentadas e verificando se os estudantes compreenderam. Esse tipo de demonstração auxilia no desenvolvimento do raciocínio lógico, na formulação de conjecturas, assim como no desenvolvimento da competência específica 2.

Descubra mais

Quanto à sugestão feita no boxe, propor aos estudantes que formem duplas para explorar o livro digital, essa exploração tanto pode ser feita utilizando um smartphone com acesso à internet como no laboratório de informática da escola.

Atividades com geometria experimental podem ser incorporadas para complementar a abordagem. Por exemplo, a superposição de figuras é uma excelente atividade para avaliar congruências.

Utilização dos casos de congruência

Podemos aplicar os casos de congruência para determinar elementos desconhecidos nos triângulos e demonstrar propriedades importantes de Geometria. Acompanhe a situação a seguir.

Na figura, AB ⁄ DE, e C é ponto médio de AD. Determinar os valores de x e y

Como C é ponto médio de AD, AC 2 CD Como A CB e D CE são ângulos opostos pelo vértice (o.p.v.), A CB 2 D CE Vamos, então, comparar os triângulos ABC e DEC.

Observamos que:

• ˆ A 2 ˆ D (60°) (A)

• AC 2 CD C é pontomédiode AD () (L)

• A CB 2 D CE (o.p.v.) (A)

Pelo caso ALA de congruência, temos que * ABC 2*DEC. Logo, os lados correspondentes são congruentes, ou seja, BC 2 EC e AB 2 DE Portanto, x = 5 cm e y = 7 cm.

DESCUBRA MAIS

SOUZA, Nicoly Longaretti de. Propriedades triangulares para o Ensino Básico. GeoGebra. [S l.], c2022. Disponível em: https://www.geogebra.org/m/r7j5qa2x. Acesso em: 21 maio 2022. Esse livro digital apresenta conceitos e definições sobre triângulos e é repleto de atividades interativas e simuladores, úteis na investigação e na análise de padrões e propriedades relacionados aos triângulos.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 88

Responda às questões no caderno.

1. Os triângulos ABC e MNP são congruentes. Pelas indicações, determine o caso de congruência e as medidas x e y

Caso LAL; x = 60° e y = 30°

2. Na figura, ˆ B 2 ˆ E e AB 2 DE . Nessas condições, determine as medidas x e y

x = 4 cm e y = 5 cm.

5.b) Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

5. Os triângulos ABC e DBC da figura apresentam os ângulos congruentes assinalados com marcas iguais.

AD B C

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades deste bloco têm o objetivo de explorar a resolução de problemas que envolvem triângulos congruentes e a utilização dos casos de congruência de triângulos. Desse modo, busca-se favorecer o desenvolvimento do raciocínio lógico e da formulação de conjecturas

3. No * ABC, AB 2 AC e BD 2 DC

Nessas condições, mostre que:

a) x = y.

b) ˆ B 2 ˆ C

Resposta na seção Resoluções comentadas deste Manual.

4. Na figura, AC 2 MN e C 2 ˆ N . Prove que AB 2 MP

Resposta na seção Resoluções comentadas deste Manual.

• Descreva para um colega a resolução que você fez e compare-a com a resolução dele. Vocês resolveram o problema do mesmo modo?

a) Nessas condições, mostre que os triângulos ABC e DBC são congruentes. Justifique por escrito cada etapa da resolução

São congruentes pelo caso LAAO

b) A partir da figura, elabore uma pergunta que envolva congruência de triângulos

Resposta na seção Resoluções comentadas deste Manual.

A M C

D

6. Na figura, A 2 B e AM 2 MB. Prove que M é ponto médio de CD B

Nas atividades 4 a 7, solicitar aos estudantes que se organizem em duplas e compartilhem estratégias que eles utilizarem na resolução. Desse modo, busca-se favorecer o desenvolvimento da competência específica 2 da área de Matemática.

7. A figura mostra um retângulo, no qual M é o ponto médio do lado BC . Prove que o triângulo AMD é isósceles.

M

Resposta na seção Resoluções comentadas deste Manual.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual. 89

D2-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 89

ILUSTRAÇÕES: EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

Propriedades do triângulo isósceles

Uma sugestão para iniciar o estudo deste tópico é pedir aos estudantes que façam uma leitura do texto apresentado no Livro do estudante e observem as ilustrações apresentadas. À medida que avançarem no estudo das propriedades, verificar se os estudantes têm familiaridade com os termos e se compreendem as ilustrações.

Nesse sentido, sugere-se que, no decorrer deste estudo, analise como os estudantes lidam com os conceitos abordados e sempre que considerar oportuno, antes de prosseguir com o conteúdo, retomar os conceitos que eles apresentarem dificuldade.

PROPRIEDADES DOS TRIÂNGULOS

PROPRIEDADES DO TRIÂNGULO ISÓSCELES

Já estudamos que um triângulo isósceles tem dois lados congruentes. Agora, vamos verificar que alguns elementos desses triângulos recebem nomes específicos.

• O lado com medida diferente da medida dos lados congruentes é chamado de base

• Os ângulos adjacentes à base são chamados de ângulos da base

• O ângulo oposto à base é chamado de ângulo do vértice

Os triângulos isósceles apresentam duas propriedades importantes.

1a propriedade: em todo triângulo isósceles, a mediana, a altura relativa à base e a bissetriz do ângulo do vértice coincidem.

Seja o * ABC isósceles, com AB 2 AC , e no qual AM é a mediana relativa à base BC. Vamos demonstrar que AM também é a altura relativa à base BC e a bissetriz do ângulo ˆ A

Comparando os triângulos ABM e ACM, temos:

• AB 2 AC (lados congruentes do triângulo isósceles) (L)

• BM 2 MC M é pontomédiodeBC () (L)

• AM 2 AM (lado comum) (L)

Pelo caso LLL, temos que * ABM 2* ACM.

Como * ABM 2* ACM, então:

a1 = a2 h B ˆ AM 2 C ˆ AM h AM é a bissetriz de ˆ A (ângulo do vértice).

m1 = m2 e m1 + m2 = 180 °h m1 = m2 = 90 °h AM é a altura relativa a BC (base).

2a propriedade: em todo triângulo isósceles, os ângulos da base são congruentes.

O triângulo ABC é um triângulo isósceles com AB 2 AC, e AM é a mediana relativa ao lado BC

Pelo caso LLL, temos que * ABM 2* ACM.

Então, todos os elementos do * ABM são congruentes aos seus correspondentes no * ACM.

Em particular, 2 ˆ B ˆ C (ângulos da base do triângulo isósceles).

PROPRIEDADE DO TRIÂNGULO EQUILÁTERO

Agora, vamos estudar uma propriedade do triângulo equilátero: em todo triângulo equilátero, os três ângulos internos são congruentes e medem 60° cada um. Vamos demonstrar essa propriedade.

Sejam um triângulo ABC equilátero 22ABAC BC () e a mediana AM relativa ao lado BC

ORIENTAÇÕES DIDÁTICAS

Propriedade do triângulo equilátero

O triângulo equilátero é o mais particular de todos os triângulos, pois a altura, a mediana e a bissetriz referentes a todos os seus ângulos internos coincidem, além de todos os ângulos internos serem congruentes.

Comparando os triângulos ABM e ACM, temos:

• AB 2 AC (lados do triângulo equilátero) (L)

• BM 2 MC M éo pontomédiodeBC () (L)

• AM 2 AM (lado comum) (L)

Pelo caso LLL, temos que * ABM 2* ACM. Então, 2

Para ampliar e enriquecer o trabalho com triângulos, propor uma atividade em que os estudantes tenham a oportunidade de rever, discutir e registrar o que aprenderam até esse momento. Organizados em grupos de quatro ou cinco estudantes, solicitar que eles elaborem uma lista, descrevendo tudo o que sabem a respeito dos triângulos. Eles podem, por exemplo, apresentar nessa lista os diversos tipos de triângulo que conhecem e as respectivas propriedades.

Traçamos a mediana BM‘ , relativa ao lado AC. Comparando os triângulos BAM‘ e BCM‘, temos:

• BA 2 BC (lados do triângulo equilátero) (L)

• AM‘2 MC ‘ M éo pontomédiode AC ‘ () (L)

• BM‘2 BM‘ (lado comum) (L)

Pelo caso LLL, temos que *BAM‘2*BCM‘. Então, ˆ A

De 1 e 2 , obtém-se:

Como med A () + med B () + med

() = 180

(soma das medidas dos ângulos internos de um triângulo), temos:

med A () = med B () = med ˆ C () =

Portanto, os três ângulos internos são congruentes, e cada um mede 60°

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd

Assim que terminarem de organizar a lista, pedir a um estudante de cada grupo que relacione na lousa os triângulos que conhecem, bem como suas propriedades já estudadas, comentando e registrando as conclusões do grupo, incentivar a troca de ideias e a argumentação recorrendo aos conhecimentos matemáticos, conforme orienta a competência específica 2 da área de Matemática.

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades deste bloco têm como objetivo que os estudantes apliquem as propriedades estudadas para triângulos isósceles e equiláteros. Desse modo, busca-se favorecer o desenvolvimento da habilidade EF08MA17. No decorrer deste estudo, analisar como os estudantes lidam com os conceitos abordados e sempre que considerar oportuno, antes de prosseguir com o conteúdo, retomar os conceitos que eles têm alguma dúvida e solicitar a alguns estudantes que auxiliem os colegas.

No desafio 8 , pedir aos estudantes que reproduzam a ilustração no caderno e registrem cada etapa necessária para se chegar ao valor da expressão dada. Se preciso, pedir a eles que revejam os conceitos e as propriedades estudadas.

ATIVIDADES

Responda às questões no caderno.

1. Em um triângulo isósceles, um dos ângulos internos mede 106°. Quanto medem os outros dois ângulos desse triângulo?

2. Na figura, o triângulo ABC é isósceles, com AB 2 BC . Calcule as medidas x e y indicadas na figura.

5. 17°. Exemplo de resposta na seção Resoluções comentadas deste Manual.

5. No triângulo isósceles ABC da figura, no qual os lados BA e BC são congruentes, BM é a mediana relativa à base AC . Qual é o valor da medida x indicada? Explique as etapas de resolução deste problema citando as propriedades de triângulos que você utilizou.

3. A figura mostra dois trechos com 600 km de comprimento cada um (linha cheia) percorridos por um avião. Qual é o valor de x, medida do ângulo BCA ?

6. Sabe-se que o pentágono ABCDE da figura é regular (os cinco lados e os cinco ângulos internos são congruentes entre si). Sabendo que a medida do ângulo EAB é 108 °, qual é o valor de x, medida do ângulo AEB indicado na figura?

7. Na figura, temos que AB e CD são paralelos, e o triângulo ACD é isósceles. Determine as medidas a, b e c indicadas na figura.

4. Caio saiu de um ponto A , passou pelo ponto B, caminhou de B até C e retornou ao ponto A , conforme mostra o esquema. Considerando que as distâncias AB e AC são iguais, calcule a medida x do ângulo BAC

8. O quadrilátero ABCD é um quadrado, e o triângulo ABE é equilátero. Nessas condições, calcule o valor da expressão x + y + z.

COMUNIDADES QUILOMBOLAS

Os quilombolas, uma das comunidades tradicionais brasileiras, apresentam características sociais e culturais que colaboram para a construção da identidade do país. Leia o trecho a seguir.

Quilombo é a denominação para comunidades constituídas por [...] [pessoas escravizadas] que resistiram ao regime escravocrata [...]. O que caracterizava o quilombo era a resistência e a conquista da autonomia. [...]

[...] As comunidades remanescentes de quilombo [...] são grupos sociais cuja identidade étnica até hoje os distingue do restante da sociedade. [...] A maneira pela qual os grupos sociais definem a própria identidade é resultado de uma confluência de fatores, escolhidos por eles mesmos: de uma ancestralidade comum, formas de organização política e social a elementos linguísticos e religiosos.

Somente em 1988 – 100 anos após a abolição da escravidão – a Constituição brasileira reconheceu, pela primeira vez, a existência e os direitos dos quilombos contemporâneos. [...] No entanto, a efetivação do direito dos quilombolas às suas terras representa até os dias atuais um enorme desafio.

QUILOMBOLAS no Brasil. Comissão Pró-Índio de São Paulo. São Paulo, c1995-2020. Disponível em: https://cpisp.org.br/direitosquilombolas/observatorio-terras-quilombolas/quilombolas-brasil/. Acesso em: 18 jun. 2022. Algumas comunidades quilombolas enfrentam desafios com relação ao direito ao território que ocupam. O artista paulistano Emol criou um mural na comunidade quilombola de Cumbe, no Ceará, para simbolizar a luta desse grupo pelo direito à terra. Observe a obra do artista.

Considerando os textos e a imagem, responda às questões no caderno.

1. Você conhece alguma comunidade tradicional brasileira? Faça uma pes quisa com o professor e os colegas sobre características e costumes dos quilombolas e de outras comunidades tradicionais. Em seguida, debatam sobre a importância do respeito e da preservação desses grupos.

2. Aplicando seus conhecimentos sobre ângulos e construções geométricas, faça em uma folha avulsa uma releitura do caranguejo representado no mural do Quilombo de Cumbe.

1. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual. Produção pessoal.

ORIENTAÇÕES DIDÁTICAS

Por toda parte

Solicitar aos estudantes que façam a leitura do texto apresentado no Livro de estudante. Depois, promover uma discussão a respeito do tema. A discussão proposta, bem como a resolução das atividades, favorecem o desenvolvimento das competências gerais 3 e 9 e dos Temas Contemporâneos Transversais Diversidade Cultural e Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras. Explicar aos estudantes que a imagem apresentada representa o caranguejo, símbolo do mangue, conforme descrito a seguir.

Atualmente os empreendimentos da [...] (técnica de criação de camarões em viveiros) intensificam a ameaça ao modo de vida [...] no Cumbe. Criam conflitos entre os próprios moradores, poluem as águas e desmatam o mangue, constituindo uma ameaça ambiental, cultural e socioeconômica [...]. Na intervenção que fiz em um dos muros da comunidade está o caranguejo, símbolo do mangue, com o ideograma Akoben pairando sobre sua cabeça (Akoben: chifre da guerra, simboliza a vigilância). Alguns moradores locais nomearam a pintura como “o caranguejo guerreiro pronto pra guerra”.

EMOL. Murais. Emol. [S. l.], [20--]. Disponível em: http:// www.emol.art.br/p/intervencoese-murais.html. Acesso em: 21 maio 2022.

Após a realização das atividades, solicitar aos estudantes que compartilhem com os colegas as respostas e o que sabem a respeito das comunidades quilombolas.

EMOL

EMOL. O caranguejo guerreiro pronto para a guerra. 2016. Mural. Quilombo do Cumbe, Aracati (CE).

ORIENTAÇÕES DIDÁTICAS

Construções geométricas

Para realizar uma aula de construções geométricas, solicitar previamente aos estudantes que tragam régua e compasso para a sala de aula. Antes de iniciar as construções, pedir a eles que se certifiquem de que o grafite do compasso esteja na mesma altura da ponta-seca. Além disso, oideal é trabalhar com a ponta do compasso chanfrada, ou seja, lixada a 45° para fora. Se preferir, distribuir folhas de papel sulfite para que os estudantes realizem as construções.

A construção proposta favorece odesenvolvimento da habilidade EF08MA15, bem como amplia as capacidades de raciocínio, representação e argumentação por meio da linguagem simbólica.

CONSTRUÇÕES GEOMÉTRICAS

Faça, no caderno, as etapas das construções geométricas indicadas a seguir. Para isso, você precisará de lápis, compasso, régua e borracha.

CONSTRUÇÃO DA BISSETRIZ DE UM ÂNGULO

Para construir a bissetriz de um ângulo qualquer, acompanhe os passos a seguir.

1o passo: Desenhe um ângulo qualquer. Com a ponta-seca do compasso no vértice O, trace um arco com uma abertura qualquer e determine os pontos C e D

2o passo: Com a ponta-seca do compasso no ponto C, trace um arco de abertura qualquer entre as duas semirretas que formam oângulo. Mantendo a abertura, coloque a ponta-seca no ponto D, trace um arco que cruze o arco inicial e marque o ponto E

3o passo: Com o auxílio da régua, trace a semirreta com origem no ponto O e que passe pelo ponto E

Agora, vamos realizar uma investigação. Observe a construção final sem os arcos, na qual estão destacados o *OCE e o *ODE. Analisando essa construção, podemos afirmar que:

• OC 2 OD, pois os pontos C e D foram marcados a partir de um mesmo arco de uma circunferência com centro em O;

• CE 2 DE, pois o ponto E foi marcado com o compasso sem modificar sua abertura;

• OE é lado comum aos dois triângulos.

AMPLIANDO

Vídeo

AULA 2: construções geométricas elementares 2. 2015. Vídeo (13min38s). Publicado pelo canal Programa de Iniciação Cientifica da OBMEP. Disponível em: https://portaldaobmep.impa.br/index.php/modulo/ver? modulo=67#. Acesso em: 8 ago. 2022.

Esse vídeo é parte do módulo “Construções geométricas com régua e compasso”, da OBMEP, e apresenta a aula 2 sobre construções elementares, incluindo a construção da bissetriz de um ângulo.

Então, pelo critério LLL, o *OCE e o *ODE são congruentes. Logo, podemos afirmar que

C OE 2 D OE

A semirreta OE tem origem no vértice O vé rtice do â nguloC ˆ OD () e divide o ângulo C ˆ OD em dois ângulos congruentes C ˆ OEeD ˆ OE () . Então, podemos dizer que a semirreta OE é a bissetriz do ângulo C ˆ OD

Assim, por meio dos passos realizados, é possível construir a bissetriz de um ângulo qualquer.

CONSTRUÇÃO DA MEDIATRIZ DE UM SEGMENTO DE RETA

Para construir a mediatriz de um segmento de reta qualquer, acompanhe os passos a seguir.

1o passo: Construa um segmento de reta AB qualquer. Com a ponta-seca do compasso no ponto A e uma abertura maior do que a metade da medida de AB , trace dois arcos.

2o passo: Com a mesma abertura do passo anterior, coloque a ponta-seca do compasso no ponto B, trace arcos que cruzam os anteriores e marque os pontos C e D

ORIENTAÇÕES DIDÁTICAS

Vídeo

AB AB

AMPLIANDO

3o passo: Trace uma reta pelos pontos C e D

C D

A construção da mediatriz de um segmento de reta auxilia no desenvolvimento da habilidade EF08MA15, bem como amplia as capacidades de raciocínio, representação e argumentação por meio da linguagem simbólica. Garantir que os estudantes tragam régua e compasso para a sala de aula. Se preferir, distribuir folhas de papel sulfite para que eles realizem as construções. Fazer a construção da mediatriz com os estudantes e solicitar a eles que verifiquem se a reta construída passa pelo ponto médio do segmento de reta dado, usando uma régua. Em seguida, com o transferidor, solicitar a eles que verifiquem se, de fato, a reta construída é perpendicular ao segmento de reta AB. Essa construção também pode ser feita com o uso de um software de geometria dinâmica.

AB

E s

C D

AULA 1: construções geométricas elementares 1. 2015. Vídeo (12min49s). Publicado pelo canal Programa de Iniciação Cientifica da OBMEP. Disponível em: https://portaldaobmep.impa.br/index.php/modulo/ver ?modulo=67#. Acesso em: 8 ago. 2022.

Esse vídeo é parte do módulo “Construções geométricas com régua e compasso”, da OBMEP, e apresenta a aula 1 sobre construções elementares, incluindo a construção da mediatriz de um segmento.

ORIENTAÇÕES DIDÁTICAS

Atividades

Este bloco de atividades tem como objetivo que os estudantes utilizem o raciocínio e a argumentação por meio da linguagem simbólica a partir da construção de mediatrizes e bissetrizes e resolução de problemas aplicando os conhecimentos de mediatrizes e bissetrizes, o que propicia o desenvolvimento das habilidades EF08MA15 e EF08MA17.

Na atividade 1, verificar se os estudantes percebem que será necessário construir a bissetriz do ângulo entre as pistas 1 e 2.

Na atividade 2, verificar se os estudantes percebem que será necessário construir a mediatriz do segmento compreendido entre os municípios P e Q

No decorrer das atividades é importante analisar se os estudantes compreenderam o conteúdo abordado e verificar as principais dúvidas deles procurando fazer intervenções ou questionamentos que contribuam para saná-las.

2 a) Resposta pessoal. Espera-se que os estudantes percebam que podem indicar qualquer ponto pertencente à mediatriz do segmento PQ

Agora, vamos fazer uma nova investigação. Observe a construção final sem os arcos, na qual estão destacados o *CAD e o *CBD.

Analisando essa construção, podemos afirmar que:

• CA 2 CB 2 AD 2 BD, pois os pontos C e D foram marcados com arcos de duas circunferências de mesmo raio, uma com centro em A e outra com centro em B;

• CD é lado comum aos dois triângulos.

Então, pelo critério LLL, o *CAD e o *CBD são congruentes. Portanto, podemos afirmar que A ˆ CD 2 B ˆ CD . Vamos analisar outros dois triângulos: *CAE e *CBE.

Além de sabermos que CA 2 CB e que A ˆ CD 2 B ˆ CD (da análise anterior), também podemos afirmar que CE é lado comum aos dois triângulos.

Então, pelo critério LAL, o *CAE e o *CBE são congruentes. Desse fato, podemos afirmar:

• AE 2 BE;

• A EC 2 BEC

Como med A EC () + med BEC () = 180°, então med A EC () = 90° e med BEC () = 90° Desse modo, podemos afirmar que a reta CD divide o segmento de reta AB em duas partes de mesma medida e é perpendicular a esse segmento. Portanto, a reta CD é mediatriz do segmento de reta AB

Assim, por meio dos passos realizados, é possível construir a mediatriz de um segmento de reta qualquer.

ATIVIDADES

1. a) Resposta pessoal. Espera-se que os estudantes percebam que podem indicar qualquer ponto pertencente à bissetriz do ângulo determinado pelas pistas.

Responda às questões no caderno.

1. Em um festival de música, o palco será construído na região interna entre duas pistas de dança, de modo que esteja à mesma distância de cada uma dessas pistas.

a) Em que local o palco pode ser construído?

b) Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

60° pista 2 pista1

b) Usando compasso, transferidor e régua, copie a figura e faça uma construção para indicar um local em que o palco possa ser construído. Compare sua resposta com a dos colegas, e verifiquem se o palco pode estar localizado em pontos diferentes daqueles que vocês indicaram.

2. Uma ferrovia deve ser construída à mesma distância de dois municípios P e Q

a) Usando compasso e régua, faça um esboço para indicar o local em que a ferrovia pode ser construída.

b) Esse local é representado por um único ponto? Justifique.

Não, pois esse local pode ser representado por qualquer um dos infinitos pontos da mediatriz do segmento PQ 96 D2_AV2-MAT-F2-2103-V8-U3-068-101-LA-G24.indd

ÂNGULOS NOTÁVEIS NO GEOGEBRA

Os ângulos cujas medidas são 90°, 60°, 45° e 30° são frequentes em estudos de Geometria, por isso são chamados de ângulos notáveis. Vamos mostrar o passo a passo da construção de alguns desses ângulos utilizando o software gratuito GeoGebra, disponível no link https:// www.geogebra.org/classic?lang=pt (acesso em: 20 maio 2022).

Abra o programa e, com o botão direito do mouse, oculte os eixos e a malha da Janela de Visualização. Para isso, clique no símbolo do botão Exibir Eixos e na opção Sem Malha do botão Exibir Malha

°

Construção do ângulo de 90

Para construir os ângulos notáveis, vamos usar construções que já foram estudadas para obter esses ângulos. No caso do ângulo de 90°, faremos a construção da mediatriz de um segmento de reta.

1 Selecione a ferramenta Reta e clique em dois pontos distintos quaisquer, A e B, na Janela de Visualização. Em seguida, selecione a ferramenta Ponto e clique em um ponto qualquer da reta, entre os pontos A e B, para representar o ponto C pertencente à reta inicial. Esse ponto não pode ser o ponto médio do segmento AB

2 Para construir uma circunferência de centro A e raio AC , selecione a ferramenta Círculo dados Centro e Um de seus Pontos e clique nos pontos A e C, respectivamente. (Figura 1)

3 Agora, crie uma circunferência com centro em B e mesmo raio AC da circunferência anterior. Para isso, selecione a ferramenta Compasso, clique na circunferência traçada na etapa anterior e em seguida no ponto B

Por fim, selecione a ferramenta Interseção de Dois Objetos e clique em cada uma das duas circunferências para criar os pontos de intersecção D e E. (Figura 2)

ORIENTAÇÕES DIDÁTICAS

Tecnologias

O estudo proposto nesta seção colabora para o desenvolvimento do pensamento computacional, raciocínio e representação por meio de linguagem simbólica, bem como para o desenvolvimento da habilidade EF08MA15, da competência geral 5 e da competência específica 5 da área de Matemática.

A construção dos ângulos notáveis apresentada no GeoGebra é fundamentada na construção com régua e compasso usuais. Explicar aos estudantes que existem diversas maneiras de construir estes e outros ângulos utilizando o software. Incentivá-los a pesquisar vídeos e sites que exploram recursos do software, favorecendo, assim, o desenvolvimento da autonomia na aprendizagem.

D2_AV1-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 97

AMPLIANDO

11/08/22 22:26

Link

MANUAL. GeoGebra. [S l.], [20--]. Disponível em: https://wiki.geogebra.org/pt/Manual. Acesso em: 13 ago. 2022.

Para aprofundar o conteúdo e explorar outros fatores que o GeoGebra pode oferecer, propor acesso a esse link

Figura 1

Figura 2

FOTOGRAFIAS: REPRODUÇÃO/GEOGEBRA

KARYB/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Após a realização das construções dos ângulos de 90° e 45° questionar os estudantes a respeito da relação entre as construções feitas no software e as construções feitas no papel utilizando instrumentos de desenho. Pode-se, por exemplo, perguntar a eles: “Como construiríamos um ângulo de 90° utilizando régua e compasso?”; “E um ângulo de 45°?”. É importante que eles percebam que as duas construções estão relacionadas à construção das bissetrizes dos ângulos de 180° e 90°, respectivamente. Se considerar conveniente, explorar essas construções utilizando régua e compasso. Ao longo da seção, busca-se favorecer o desenvolvimento do pensamento computacional, da representação por meio de linguagem simbólica, da habilidade EF08MA15, da competência geral 5 e da competência específica 5 da área de Matemática.

4 Selecione a ferramenta Reta e clique nos pontos D e E para criar a reta DE. Note que DE é a mediatriz do segmento de reta AB

Em seguida, com a ferramenta Interseção de Dois Objetos, clique na retas AB e DE para criar o ponto de intersecção F. (Figura 3)

5 Oculte as figuras da Janela de Visualização, exceto as retas AB , DE e os pontos A, B, D e F. Para isso, clique com o botão direito do mouse em cada figura que deseja ocultar e desabilite a opção Exibir Objeto

Em seguida, selecione a ferramenta Ângulo e clique nos pontos B, F e D, nessa ordem. Assim, obtém-se o ângulo BFD cuja medida é 90°. (Figura 4)

Construção do ângulo de 45°

Para construir o ângulo de 45°, utilizaremos a construção do ângulo de 90° e faremos a construção da bissetriz de um ângulo.

1 Repita os passos 1 a 4 da construção do ângulo de 90°. Oculte os objetos da Janela de visualização, mantendo apenas a circunferência de centro A, as retas AB , DE e os pontos A, B, C, D e F

2 Selecione a ferramenta Compasso, clique na circunferência e no ponto F para criar uma circunferência com centro em F

Em seguida, selecione a ferramenta Interseção de Dois Objetos, clique na circunferência de centro F e na reta AB . Repita a operação para obter os pontos de intersecção da circunferência com a reta DF . (Figura 5)

3 Selecione a ferramenta Compasso, clique na circunferência de centro A e no ponto H. Repita a operação, clicando na circunferência e no ponto I, para criar uma circunferência de mesmo raio, mas com centro no ponto I

Em seguida, com a ferramenta Interseção de Dois Objetos, clique nas circunferências traçadas para criar o ponto de intersecção K

Depois, com a ferramenta Semirreta, trace a semirreta com origem no ponto F e que passa pelo ponto K Note que essa semirreta é a bissetriz do ângulo BFD (Figura 6)

D2_AV3-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 98

AMPLIANDO

Link CONSTRUÇÕES geométricas com régua e compasso. Grupo PET Matemática da UFSM. Santa Maria, 2020. Disponível em: https://www.ufsm.br/app/uploads/sites/783/2020/06/Apostila_DesenhoGeom%C3% A9trico_2020.pdf. Acesso em: 8 ago. 2022.

Nesse link, é possível ter acesso a diversas construções geométricas utilizando régua e compasso.

Figura 4

Figura 3

Figura 5.

Figura 6

4 Oculte os objetos da Janela de Visualização, mantendo apenas a reta AB , a semirreta FK e os pontos A, B, F e K. Em seguida, selecione a ferramenta Ângulo e clique nos pontos B, F e K. Desse modo, obtém-se o ângulo B ˆ FK cuja medida é 45°. (Figura 7)

FOTOGRAFIAS: REPRODUÇÃO/GEOGEBRA

Construção do ângulo de 60°

Para construir o ângulo de 60°, vamos considerar o fato de que os ângulos internos de um triângulo equilátero medem 60° e faremos o início da construção do triângulo equilátero.

1 Repita os passos 1 e 2 da construção do ângulo de 90°. Em seguida, selecione a ferramenta Compasso e clique na circunferência, depois no ponto C. Selecione a ferramenta Interseção de Dois Objetos e clique nas duas circunferências para criar os pontos de intersecção D e E (Figura 8)

2 Oculte os objetos da Janela de Visualização, mantendo apenas a reta AB e os pontos A, B e E. Em seguida, selecione a ferramenta Segmento e clique nos pontos A e E, nessa ordem. Por fim, selecione a ferramenta Ângulo e clique nos pontos B, A e E, respectivamente. Assim, obtém-se o ângulo BAE cuja medida é 60°. (Figura 9)

ORIENTAÇÕES DIDÁTICAS

Para resolver as atividades propostas, verificar a possibilidade de trabalhar com os estudantes no laboratório de informática. Caso seja necessário, ajudá-los no processo de construção da bissetriz do ângulo de 60°. Uma sugestão, é orientar os estudantes a realizar os passos da construção utilizando régua e compasso. As instruções apresentadas na seção replicam a construção com régua e compasso feitas no papel, sem utilizar outras ferramentas específicas que o programa fornece.

Responda às questões no caderno.

1. Aplicando as ferramentas do GeoGebra e as estratégias apresentadas nas construções dos ângulos de 90°, 45° e 60°, construa um ângulo de 30°. Descreva a um colega as etapas da resolução que você seguiu e compare-as com as etapas da resolução seguidas por ele.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

2. As construções apresentadas reproduzem os passos das construções geométricas com régua e compasso. No entanto, o GeoGebra possui outras ferramentas de desenho para obter os ângulos desejados. Reúna-se a um colega, investiguem o GeoGebra e apresentem uma ferramenta diferente para obter cada um dos ângulos notáveis

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Figura 7

Figura 8

Figura 9

ORIENTAÇÕES DIDÁTICAS

Retomando o que aprendeu

O objetivo das atividades desta seção é propiciar aos estudantes que retomem os conteúdos estudados ao longo da Unidade, favorecendo o desenvolvimento das habilidades EF08MA15 e EF08MA17. Caso seja necessário, fazer retomadas para sanar as dúvidas que podem surgir.

Os estudantes podem fazer esse bloco de questões como uma autoavaliação, por isso, eles devem respondê-las individualmente. É interessante sugerir que realizem essas atividades em sala de aula, assim poderão discutir eventuais dúvidas com os colegas, por exemplo. Orientá-los a consultar o livro para tirar dúvidas e buscar informações.

Enfatizar a necessidade de resolverem os exercícios individualmente, buscando informações de maneira autônoma, escolhendo suas fontes para chegar aos resultados. Conversar com os estudantes a respeito de seus acertos e erros, indicando a correção com intervenções pontuadas, isto é, dando pistas de quais caminhos eles poderão buscar para encontrar o resultado esperado.

Se ainda persistirem dúvidas, orientar a trocar ideias com os colegas e a buscar conceitos no Livro do estudante ou nos cartazes, caso eles tenham realizado essa construção no decorrer do estudo.

Dar oportunidade para os estudantes explicarem como pensaram para resolver as questões.

Responda às questões no caderno.

1. Em um triângulo isósceles ABC, em que AB 2 AC , o ângulo ˆ A mede o dobro da soma das medidas dos outros dois ângulos. Então, a medida do ângulo ˆ A é:

a) 90°

b) 30°

c) 60°

d) 100° e) 120°

2. Na figura a seguir, o triângulo ABC é isósceles 2 AB BC () . Determine o valor da medida x em grau.

a)

b)

c)

3. (Mack-SP)

Alternativa e. Alternativa c.

4. O triângulo BDC é equilátero. Determine o valor da medida x

Na figura acima, CE é paralelo a BA, a medida do ângulo B ˆ CD é igual a 140° e a medida do ângulo B ˆ AC é 75° Então, os ângulos x, y e z medem, respectivamente,

a) 75°, 75° e 65°

b) 65°, 75° e 65°

c) 75°, 65° e 65°

d) 65°, 65° e 75°

e) 65°, 75° e 75°

D2_AV2-MAT-F2-2103-V8-U3-068-101-LA-G24.indd 100

Alternativa b.

a) 15°

5. O triângulo ABC é equilátero, e M , N e P são, respectivamente, os pontos médios dos lados AB , AC e BC desse triângulo.

b) 18° c) 20° d) 25° e) 27°

a) Quais são as medidas dos ângulos internos do triângulo MNP?

b) Qual é a classificação do triângulo MNP quanto às medidas dos lados?

6. O ângulo BAC de um triângulo isósceles é reto. Sendo CP a bissetriz do ângulo A ˆ CB do triângulo, a medida do ângulo BPC é igual a:

a) 22,5°

b) 45° c) 67,5° d) 112,5° e) 135°

7. Na figura seguinte, as retas t e s são paralelas. Qual é o valor, em grau, da expressão x y?

Alternativa d. 60° cada um. Equilátero. Alternativa d. Alternativa b.

x = 70° y

t s 150°

130°

b) 50° c) 55° d) 60° e) 65°

a) 40°

REPRODUÇÃO/MACKENZIE, 2020.

8. Na figura a seguir, os triângulos ABP e APC são isósceles 22ABAP eAPPC () Sabendo que PQ é a bissetriz relativa ao ângulo APC , determine o valor de x + y.

Alternativa a.

a) 90°

b) 70°

c) 100°

d) 80° e) 60°

9. Uma circunferência que contém todos os vértices de um triângulo é chamada de circunferência circunscrita cujo centro (O) é dado pelo circuncentro do triângulo.

UM NOVO OLHAR

Observe a figura e escolha a afirmativa correta.

Alternativa c.

a) O centro da circunferência circunscrita é oponto de intersecção das medianas.

b) O ponto O é o ponto médio do lado AB

c) O circuncentro é equidistante aos pontos A, B e C

d) A medida do segmento OA é menor do que a medida do segmento OC

180°. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Nesta Unidade, retomamos a definição de triângulo, a soma das medidas dos ângulos internos de um triângulo e as classificações dessa figura geométrica com relação às medidas dos lados e dos ângulos. Estudamos o que são ângulo externo, altura, mediana, bissetriz, mediatriz, além da congruência de triângulos, casos de congruência e as propriedades dos triângulos isósceles e dos triângulos equiláteros.

Com auxílio de régua e compasso, abordamos a construção da bissetriz de um ângulo e da mediatriz de um segmento.

Dada a grande quantidade de conceitos estudados, sugere-se que se faça um fichamento de cada tópico, apontando, de maneira sucinta, as definições. É interessante inserir exemplos para complementar os registros.

Na abertura desta Unidade, foram apresentadas algumas estruturas do passado e do presente, nas quais o triângulo foi utilizado para aumentar a estabilidade e, por consequência, aumentar a carga de sustentação. É importante ressaltar que, quanto mais aprofundado for o conhecimento sobre triângulos, mais possibilidades haverá de se perceber a aplicação deles no cotidiano.

Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

• Qual é o valor da soma das medidas dos ângulos internos de um triângulo? Como você explicaria esse resultado?

• Como os triângulos podem ser classificados?

• Q uais são os casos de congruência de triângulos que foram abordados nesta Unidade?

LLL, LAL, ALA, LAAO e o caso de congruência no triângulo retângulo.

ORIENTAÇÕES DIDÁTICAS

Um novo olhar

Os questionamentos existentes no encerramento desta Unidade permitem um momento específico para que eles possam refletir a respeito das aprendizagens individuais, além de poderem fazer uma breve retomada dos conteúdos abordados ao longo da unidade. É importante que os estudantes respondam individualmente a cada uma das questões para que, desse modo, possam perceber o que aprenderam e as possíveis dúvidas que ainda tenham. Nesta Unidade, pedir aos estudantes que façam um registro dos conceitos abordados em razão das sutilezas inerentes principalmente em relação a alturas, medianas, bissetrizes e mediatrizes do triângulo e, por consequência, seus pontos notáveis.

• Descreva, por meio de um fluxograma, como construir a mediatriz de um segmento de reta

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

De acordo com as medidas dos ângulos internos: triângulo retângulo, triângulo acutângulo ou triângulo obtusângulo. De acordo com as medidas dos lados: triângulo equilátero, triângulo isósceles ou triângulo escaleno.

A primeira questão busca retomar com os estudantes o valor da soma dos ângulos internos de um triângulo; a segunda questão resgata a classificação dos triângulos (observadas as medidas de seus ângulos internos ou as medidas de seus lados). A terceira questão solicita que os estudantes relembrem os casos de congruência de triângulos. A última questão proposta solicita que os estudantes retomem o procedimento de construção da mediatriz de um segmento de reta.

BNCC NA UNIDADE

Competências gerais:

• 1, 3, 6 e 9

Competências específicas:

• 2, 5 e 6

Habilidades:

Álgebra

• EF08MA06

• EF08MA10

• EF08MA11

• EF08MA13

Probabilidade e estatística

• EF08MA23

Temas Contemporâneos

Transversais:

• Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras

• Educação em Direitos Humanos

• Educação Financeira

• Educação para o Consumo

• Processo de Envelhecimento, Respeito e Valorização do Idoso

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em cinco capítulos e apresenta os conteúdos por meio de exemplos contextualizados, atividades e seções com temas e informações sobre contextos de relevância social e humanitária que contribuem para a formação integral dos estudantes, favorecendo o desenvolvimento das competências gerais 1, 3, 6 e 9.

O primeiro capítulo aborda o uso de letras para representar números. Destacar a importância de utilizar a notação algébrica para representar problemas e soluções. No segundo capítulo, são retomadas as expressões algébricas, classificando-as em inteiras, fracionárias ou irracionais.

O terceiro capítulo aborda o cálculo do valor numérico de expressões algébricas, contribuindo para o desenvolvimento da habilidade EF08MA06.

No quarto capítulo, apresenta-se a definição de monômio e alguns conceitos relacionados. No quinto capítulo, inicia-se a discussão sobre polinômios e suas operações.

E CÁLCULO ALGÉBRICO 4

Você consegue imaginar como seria “fazer” Matemática sem o uso da simbologia matemática que conhecemos hoje?

A evolução para o simbolismo atual passou por um processo histórico longo que envolveu diversos nomes em diferentes épocas e locais.

Houve uma época em que toda a Matemática era escrita com palavras, inclusive a representação de números desconhecidos. No Papiro Rhind, já havia problemas envolvendo números desconhecidos, que eram chamados de aha

Foi só no século IV d.C., na obra do matemático grego Diofanto (c. 200-284), que encontramos pela primeira vez o uso de uma letra para representar um número desconhecido; acredita-se que ele usava a letra grega sigma (P).

A diferença principal entre a notação usada por Diofanto e a notação algébrica moderna, bem como a notação exponencial, é a falta de símbolos especiais para operações e relações. Esses elementos foram, em grande parte, contribuição do período que abrange o fim do século XV e o começo do século XVII na Europa.

OBJETIVOS

• Retomar o uso de letras para representar números.

• Identificar expressões algébricas inteiras, fracionárias e irracionais, considerando as restrições impostas por estas últimas.

• Calcular o valor numérico de expressões algébricas.

• Reconhecer monômios e resolver cálculos básicos entre monômios.

Tebas foi uma das principais cidades do antigo Egito e hoje é local de importantes sítios arqueológicos, como o Vale dos Reis, o Templo de Luxor e o Templo de Karnak.

• Reconhecer polinômios e resolver cálculos básicos entre polinômios.

• Resolver sistemas de equações de 1o grau pelo método da adição e pelo método da substituição.

• Refletir sobre a importância do trabalho das mulheres quebradeiras de coco babaçu.

• Compreender a diferença entre juro a favor e juro contra.

Templo de Luxor. Egito, 2022.

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

Fragmento do Papiro Rhind (c. 1550 a.C.), Museu Britânico, Londres (Inglaterra).

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

Esse papiro foi adquirido por volta de 1858, em Tebas, pelo escocês Henry Rhind (1833-1863); por isso, é conhecido como Papiro Rhind ou Papiro Ahmes, em homenagem ao escriba que o copiou, em 1550 a.C., aproximadamente.

Em diversos momentos, os estudantes encontram e utilizam a simbologia matemática sem se preocupar ou se dar conta de que ela nem sempre foi assim. É interessante propor a eles que reflitam a respeito da evolução da simbologia na tentativa de “economizar” e “agilizar” os cálculos. Aqui, a intenção é propiciar a comparação de algumas possibilidades de escrita matemática.

Ao comparar as regras matemáticas escritas na linguagem conhecida com as escritas em outra linguagem, percebe-se que, na realidade, as simbologias utilizadas atualmente passaram por transformações e hoje propiciam uma escrita tida como “mais econômica”. Para que os estudantes percebam isso, apresentar alguns exemplos de expressões matemáticas e sugerir que tentem melhorá-las.

Agora, responda às questões no caderno.

a) Espera-se que os estudantes escrevam algo como: “Sendo n [n , 2n + 1 é ímpar.”.

• Observe esta sentença matemática, escrita apenas com palavras: “Duas vezes um número natural desconhecido adicionado de uma unidade resulta em um número ímpar.”.

a) Represente a afirmação utilizando notação matemática.

b) Substituindo o número desconhecido por 5, que número pode ser determinado pela sentença? O número 11.

• Escreva uma sentença matemática somente com palavras e, depois, reescreva-a usando símbolos matemáticos. Qual das duas maneiras você achou mais simples de escrever?

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

D2_AV3-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

JUSTIFICATIVAS DOS OBJETIVOS

Nesta Unidade, é realizado o estudo das expressões algébricas e discute-se a formação de sequências recursivas e sequências dadas por uma lei de formação, o que contribui para o desenvolvimento das habilidades EF08MA06, EF08MA10 e EF08MA11.

Na seção Por toda parte, discute-se a importância do trabalho das mulheres quebradeiras de

coco babaçu, contribuindo para o desenvolvimento do Tema Contemporâneo Transversal Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras e da competência geral 9. Uma conversa sobre os diferentes tipos de gráfico é proposta na seção Tratamento da informação, cujo assunto abordado contribui para o desenvolvimento do Tema Contemporâneo Transversal Educação em Direitos Humanos e da competência específica 6 da área de Matemática.

Acredita-se que não é necessário contextualizar a teoria dos números, mas é necessário que testem suas operações a fim de verificar a validade delas. Por ser uma atividade dinâmica, é necessário questioná-los o tempo todo, de modo que, se os estudantes perceberam que a simbologia criada vale para a adição, descubram se ela também é válida para a multiplicação. Discutir com eles a dificuldade inerente ao criar um sistema que funcione de maneira universal e explicar-lhes que o atual sistema é um conjunto de pequenas criações de muitos matemáticos ao longo da história da humanidade, contribuindo para o desenvolvimento da competência geral 1.

FRANTIC00/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Pense e responda

As questões dessa seção têm o objetivo de verificar os conhecimentos prévios dos estudantes a respeito das expressões algébricas e o uso de letras. Por meio de argumentos geométricos e de apresentação de fórmulas, eles podem lidar um pouco com esse tema.

Na atividade 2, se julgar pertinente, comentar com os estudantes que uma expressão algébrica é necessariamente composta de números, letras e operações. Já uma expressão numérica não contém letras, como a expressão matemática expressa no item a

USO DE LETRAS PARA REPRESENTAR NÚMEROS CAPÍTULO1

PENSE E RESPONDA

Responda às questões no caderno.

1. Você já estudou que:

• a área de um retângulo equivale ao produto da medida do comprimento pela medida da largura;

• a área de um quadrado equivale ao quadrado da medida de seu lado. Agora, responda: como você representaria a área de cada figura a seguir?

AMPLIANDO

Das expressões que você escreveu para representar as áreas das figuras, quais foram escritas usando:

I) apenas números? A expressão do item a.

II) números e letras? A expressão do item c

III) apenas letras? A expressão do item b

2. Observe as expressões matemáticas a seguir.

a) 3 + 2 + 5 ? 4

b) x + 5y + z

c) 3x 2 + 2y + 4

d) (5 1)2 + 18 : 3 43

Resposta pessoal. Espera-se que os estudantes percebam que as expressões dos itens a e d apresentam apenas números, e as expressões dos itens b e c apresentam letras e números.

Que diferenças você observa entre elas?

O objetivo de representar números desconhecidos por meio de letras é indicar as operações matemáticas de maneira mais simples e sintética. Assim, por exemplo: Indica o quadrado de um número.

Indica o quádruplo de um número.

Indica a metade de um número.

Atividade complementar (Enem/MEC) Num campeonato de futebol de 2012, um time sagrou-se campeão com um total de 77 pontos (P) em 38 jogos, tendo 22 vitórias ( V), 11 empates (E) e 5 derrotas (D). No critério adotado para esse ano, somente as vitórias e empates têm pontuações positivas e inteiras. As derrotas têm valor zero e o valor de cada vitória é maior que o valor de cada empate.

Um torcedor, considerando a fórmula da soma de pontos injusta, propôs aos organizadores do campeonato que, para o ano de 2013, o time derro -

tado em cada partida perca 2 pontos, privilegiando os times que perdem menos ao longo do campeonato. Cada vitória e cada empate continuariam com a mesma pontuação de 2012.

Qual a expressão que fornece a quantidade de pontos (P), em função do número de vitórias ( V), do número de empates (E) e do número de derrotas (D), no sistema de pontuação proposto pelo torcedor para o ano de 2013?

a) P = 3V + E

b) P = 3V 2D

c) P = 3V + E D

Do mesmo modo, se a e b representam dois números reais quaisquer, temos que:

• a + b, ou b + a, representa a soma desses dois números;

• a b representa a diferença entre a e b;

• a ? b, ou b ? a, representa o produto desses dois números;

• a : b, ou a b , com b 5 0, representa o quociente de a por b

Na Geometria, se a representa a medida do lado de um quadrado qualquer, temos que:

• 4 a, ou 4a, indica o perímetro desse quadrado;

• a2 indica a área desse quadrado.

ATIVIDADES

Responda às questões no caderno.

1. Escreva de forma sintética:

a) o quadrado do número real x x 2

b) o cubo do número real y y 3

c) a raiz quadrada do número real a a

d) a quinta potência do número real b b5

e) a soma dos números reais b e c b + c

f) o produto dos números reais a e x ax

g) o dobro do número real y 2y

h) a sexta parte do número real m 1 6 m

i) o quociente entre os números reais z e w, com w 5 0.

j) a metade do número real x 1 2 x

k) a diferença entre os números reais x e y

x y

l) o quíntuplo do número real z 5z

DESCUBRA MAIS

2. Usando duas letras, x e y, por exemplo, escreva uma expressão que represente:

a) o dobro de um número real adicionado ao dobro de outro número real. 2x + 2y

b) o produto da soma pela diferença de dois números reais quaisquer.

c) a soma dos quadrados de dois números reais quaisquer. x 2 + y2

d) a diferença dos quadrados de dois números reais quaisquer. x2 y 2

e) o quadrado da soma de dois números reais quaisquer. (x + y)2

f) a soma da raiz quadrada de um número real com a quinta parte de outro número real.

(x + y)(x y) + x 1 5 y

• AHMES. The Rhind Mathematical Papyrus. 1550 a.C. Papiro, 32 cm x 198,50 cm. Disponível em: https://www.britishmuseum.org/collection/object/Y EA10058. Acesso em: 9 jun. 2022.

• THE BRITISH MUSEUM. Londres, c2022. Site. Disponível em: https://www.britishmuseum.org/. Acesso em: 9 jun. 2022.

Na abertura desta Unidade, você teve acesso a algumas informações a respeito do Papiro Rhind. Esse papiro está localizado na Inglaterra, no Museu Britânico em Londres. Pelo site do museu, é possível conhecer alguns itens de seu acervo, como fotografias, e obter mais informações sobre o Papiro Rhind. Faça uma visita virtual.

ORIENTAÇÕES DIDÁTICAS

Atividades

Após a resolução das questões, propor aos estudantes que confrontem suas respostas com as de um colega. Socializar as diferentes expressões de um mesmo item para validá-las (ou não) coletivamente.

Por exemplo, na atividade 1, no item i é possível escrever de duas maneiras:

z : w ou z w . No item j, os estudantes podem utilizar três registros distintos: 1 2 x ou x 2 ou, ainda, x : 2.

Aproveitar a atividade 2 para discutir com os estudantes algumas situações, por exemplo:

• A igualdade x 2 + y 2 = (x + y) 2 é sempre verdadeira, para x e y reais quaisquer? Não, atribuindo valores reais quaisquer a x e a y, é possível perceber que a igualdade não se mantém.

• A igualdade x 2 + y 2 = (x + + y) 2 é válida para quais números reais x e y? Para que a igualdade seja verdadeira, x ou y precisa ser nulo, isto é, igual a zero.

• Qual é a expressão geral de um número natural (n) par? E de um número natural ímpar? Espera-se que os estudantes identifiquem 2n como par e 2n + 1 como ímpar. Discutir com os estudantes o significado de uma generalização e sua importância para a Matemática e como a linguagem algébrica foi determinante nesse contexto.

Descubra mais

d) P = 3V + E 2D e) P = 3V + E + 2D

Resolução da atividade

Ao resolver o sistema para 2012 ou mesmo analisando as alternativas é possível perceber que a pontuação em caso de vitória é 3 e a pontuação em caso de empate é 1.

Para 2013, mantêm-se as pontuações para vitórias e empates. Como a pontuação em caso de derrota é

2, a expressão correta para a pontuação é: P = 3V + E 2D

Alternativa d.

Se considerar pertinente e houver possiblidade, fazer um tour virtual pelo museu com os estudantes. As explorações das sugestões feitas no boxe favorecem o desenvolvimento da competência específica 2 da área de Matemática.

ORIENTAÇÕES DIDÁTICAS

Expressões algébricas ou literais

É importante que os estudantes se deparem com diversas situações que envolvam expressões algébricas.

Nas situações 1 e 2, os estudantes devem escrever expressões algébricas que representem, respectivamente, o perímetro e a área de regiões poligonais. Uma situação que possibilita desenvolver expressões algébricas e generalizações é o trabalho com sequências numéricas ou geométricas. A seguir, sugerimos uma atividade com uma sequência de figuras recursivas, ou seja, cada nova figura está relacionada com a figura anterior.

EXPRESSÕES ALGÉBRICAS OU LITERAIS

Sabemos que é possível usar as letras do alfabeto (a, b, c, ..., x, y, z) para representar números reais.

Consideremos, então, as seguintes situações.

1 Observe a imagem de uma piscina retangular. Qual é a expressão que representa o perímetro de sua borda?

AMPLIANDO

Atividade complementar

Considere esta sequência de figuras.

Sendo a medida do comprimento da piscina expresso pelo número real x, e a medida da largura da piscina, pelo número real y, o perímetro da borda da piscina é igual a duas vezes a medida do comprimento mais duas vezes a medida da largura. Então, a expressão que representa o perímetro dessa piscina é:

2 x + 2 y ou 2x + 2y

2 Qual é a expressão que representa a área total do terreno da figura?

Podemos imaginar o terreno dividido em duas partes: um retângulo de lados medindo a e b, e um quadrado de lados medindo c. A área total do terreno é igual à soma das áreas dessas partes:

• A área do retângulo é expressa por ab.

• A área do quadrado é expressa por c2 Então, a expressão que representa a área total desse terreno é:

a) Quantos quadrados compõem a 10 a figura?

b) Qual é a expressão geral que determina a quantidade de quadrados da enésima figura (a figura de posição n)? Resolução da atividade

a) Conforme aumenta a posição da figura na sequência, fica muito trabalhoso determinar a quantidade de quadrados dela a partir da figura anterior. Sugere-se, então, determinar a quantidade de quadrados a partir da posição da figura.

S.VIDAL/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

3 Para fazer um carreto, a empresa de Amanda cobra uma taxa fixa de R$ 130,00 e mais R$ 3,50 por quilômetro rodado. Qual é a expressão que representa o valor que essa empresa cobra para fazer um carreto em um percurso de x quilômetros?

S e para cada quilômetro rodado a empresa cobra R $ 3,50, então para x quilômetros o custo será de 3,50x reais. Logo, o valor do carreto é dado pela expressão:

Nas três situações apresentadas, escrevemos expressões matemáticas nas quais aparecem números e letras.

Uma expressão matemática que apresenta números e letras ou somente letras é denominada expressão algébrica ou expressão literal. As letras que aparecem na expressão, que normalmente representam números reais, são chamadas de variáveis

Assim, são exemplos de expressões algébricas ou literais:

• 2x + 2y

• ab + c2

• 130 + 3,50x

MAIS EXPRESSÕES ALGÉBRICAS

A palavra literal vem do latim litteralis, que significa “letra”.

Quando uma expressão algébrica não contém variável ou variáveis no denominador, ela é chamada de expressão algébrica inteira. Exemplos:

Quando uma expressão algébrica contém variável ou variáveis no denominador, ela é chamada de expressão algébrica fracionária. Exemplos:

Quando uma expressão algébrica contém variável ou variáveis no interior de um radical, ela é chamada de expressão algébrica irracional. Exemplos:

Na situação 3, os estudantes precisam construir uma fórmula, relacionando um valor fixo e um valor variável. Problemas envolvendo corridas de táxi seguem a mesma estrutura e podem ser propostos para os estudantes resolverem.

O boxe Saiba que traz a origem latina da palavra literal. Ler com os estudantes e perguntar se eles conhecem outras palavras derivadas do latim.

Mais expressões algébricas

Após apresentar a definição de expressão algébrica para os estudantes, passar exemplos de alguns tipos de expressões algébricas, como as inteiras, as fracionárias e as irracionais. Pedir a eles que, a partir dos exemplos no Livro do estudante, identifiquem as características de cada uma delas.

AMPLIANDO

Vídeo

EXPRESSÕES Algébricas – O que são Expressões Algébricas? –Matemática Básica – Professora Angela. 2020. Vídeo (4min21s). Publicado pelo canal Professora Angela Matemática. Disponível em: https://www.youtube.com/ watch?v=MauV62jWBSI. Acesso em: 6 ago. 2022.

Nessa videoaula, são explorados exemplos relacionados às expressões algébricas.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 107

Verifica-se que a quantidade de parcelas 4 é uma unidade a menos que a posição da figura. Então:

10 a figura H 1 + 9 ? 4 = 1 + 36 = 37

Logo, a 10 a figura é composta de 37 quadrados.

b) A expressão geral que determina quantos quadrados compõem a enésima figura (posição n) é dada por: 1 + (n − 1) ? 4.

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades desse bloco têm como objetivo que os estudantes reconheçam e utilizem expressões algébricas para representar diferentes situações.

É importante trabalhar com atividades que relacionem perímetros e áreas de figuras planas com expressões algébricas, reforçando a integração da Álgebra com a Geometria.

Incentivar os estudantes a desenvolver diferentes estratégias para a resolução dos problemas.

Na atividade 3, por exemplo, os estudantes podem fazer:

• Na figura, cada retângulo pequeno tem área x ? y. Como são 12 retângulos pequenos idênticos, a área do retângulo maior é dada por 12xy;

• O retângulo maior tem lados medindo 4 x e 3 y. Assim, sua área é igual a 4x ? 3y.

Pedir que comparem os resultados obtidos (12xy e 4x ? 3y) e digam a que conclusões podem chegar.

Responda às questões no caderno.

1. Em certa loja, uma caneta custa x reais, e um caderno custa y reais. Caio comprou 5 canetas e 8 cadernos nessa loja. Qual é a expressão algébrica que representa ovalor total pago por ele? 5x + 8y

2. Em uma empresa trabalham h homens e m mulheres.

a) Qu al é a expressão algébrica que representa:

• o total de pessoas que trabalham nessa empresa? h + m

• a diferença entre a quantidade de homens e a quantidade de mulheres que trabalham nessa empresa? h m

• a razão entre a quantidade de homens e a quantidade de mulheres que trabalham nessa empresa?

b) Das expressões algébricas que você escreveu, alguma é fracionária? Qual?

3. Escreva uma expressão algébrica para representar a área do retângulo a seguir, sabendo que ele é formado por 12 retângulos menores com as mesmas dimensões.

5. Escreva a expressão algébrica que representa a área da figura a seguir.

4. Suponha que um terreno tenha o formato desta figura, e suas medidas sejam representadas, em unidade de comprimento, pelas letras x e y Qual é a expressão algébrica que representa o perímetro desse terreno?

6. Caio tinha x reais. Certo dia, foi a uma loja de artigos esportivos e comprou 2 pares de tênis. Cada par custou y reais. Que expressão algébrica pode representar a quantia que sobrou para Caio depois de comprar os pares de tênis?

x 2y

7. Q ual é a expressão algébrica que representa a soma do quadrado de um número x com o triplo do mesmo número x ? x 2 + 3x

EDITORIA

9. Use uma expressão algébrica para responder às questões.

a) Quantos dias há em um período de x semanas mais 20 dias? 7x + 20

108 D2-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 108 09/08/22 11:38

EDUCAÇÃO FINANCEIRA

JUROS CONTRA x JUROS A FAVOR

Os juros são o ponto central do sucesso financeiro. Trata-se de uma questão de escolha: você pode usar os juros contra ou a favor de você! Em síntese, antecipar custa e retardar rende.

Se você antecipa com o banco um valor x para pagar por algo que deseja ter, devolverá ao banco x + os juros. Se, ao contrário, retarda o uso de um valor x, deixando-o guardado no banco, receberá do banco x + juros quando decidir utilizá-lo. A questão é que esse é um processo por trás do qual existe uma lógica matemática de acumulação, os chamados juros compostos, popularmente definidos como “juros sobre juros”.

O problema é que essa é uma moeda de dois lados. [...] Se você faz uma antecipação com o banco, por meio do cartão de crédito, para pagar por um desejo imediato, e não consegue quitar na data, pagará juros sobre juros, e o valor da dívida se multiplicará. Pior ainda, porque a taxa de juros do cartão é, no mínimo, 13 vezes maior do que a taxa de rendimento de uma poupança.

Para se ter uma ideia, uma única dívida de R$ 150,00 no cartão de crédito, a uma taxa de 9% ao mês, transforma-se em uma dívida de aproximadamente R$ 4.600.000,00 em dez anos. São os juros contra você!

DOMINGOS, Reinaldo. Ter dinheiro não tem segredo: educação financeira para jovens. São Paulo: DSOP, 2013. p. 83-84.

Lígia tem uma conta bancária com cheque especial. Isso significa que ela tem um limite que pode ser utilizado, ou seja, ela pode usar um valor superior ao seu saldo, ficando, assim, com um saldo negativo. Esse saldo negativo é um empréstimo automático, e já aprovado, pelo qual se cobram juros. Para o banco não cobrar mais esses juros, é necessário que o cliente deposite um valor maior ou igual ao da dívida.

O gráfico a seguir representa o saldo da conta bancária de Lígia, que inicialmente era devedor em R$ 200,00, e sobre o qual incidirá juro composto de 10% ao mês, caso ela não tome nenhuma providência e quite a dívida.

Responda às questões no caderno.

1. Em quanto tempo a dívida de Lígia dobrará? Entre 7 e 8 meses.

2. O valor da dívida, em reais, é dado pela expressão 200 (1,1) n , em que n é a quantidade de meses em que Lígia tem a dívida. Utilizando a expressão e uma calculadora, calcule o valor da dívida de Lígia depois de 5 anos.

R $ 60.896,33.

AMPLIANDO

Link

VIDA E DINHEIRO. [S l.], c2017. Site. Disponível em: https://www.vidaedinheiro.gov.br/livros-ensino -fundamental/?doing_wp_cron=1659801089.5906779766082763671875. Acesso em: 20 ago. 2022. Nesse link, encontram-se materiais do 1o ao 9 o ano do Ensino Fundamental, nos quais são desenvolvidos diversos conceitos de Educação financeira a partir de jogos colaborativos.

ORIENTAÇÕES DIDÁTICAS

Educação financeira

O objetivo dessa seção é despertar nos estudantes a reflexão sobre como é possível usar o juro a favor ou contra o cidadão. Espera-se que eles percebam que isso pode ocorrer quando o juro é aplicado sobre uma dívida ou em um investimento. As ideias discutidas nessa seção contribuem para o desenvolvimento dos Temas Contemporâneos Transversais Educação Financeira e Educação para o Consumo e da competência específica 5 da área de Matemática.

Pode-se, ainda, conversar a respeito da necessidade e da importância de planejamento financeiro.

Comentar que o cheque especial tem um limite que, depois de atingido, o banco modifica a ação em relação à dívida. Pedir aos estudantes que façam também a interpretação do gráfico de linhas apresentado.

O cálculo solicitado na atividade 2 é apenas ilustrativo da tendência matemática desse tipo de juro. Ressaltar a importância de se manter um controle da vida financeira de modo que esse comportamento dos juros funcione a favor do indivíduo, e não contra. Lembrar os estudantes de que cinco anos são 60 meses. Ressaltar a importância crescente do tempo em uma aplicação a juro composto. No exemplo dado, se a mesma dívida evoluísse a juro simples, o montante após cinco anos seria de R $ 1.400,00. Aproveitar para explorar o uso da calculadora.

ORIENTAÇÕES DIDÁTICAS

Valor numérico de uma expressão algébrica

As generalizações algébricas tratam de modo consistente as situações em que a Aritmética e a Geometria estão envolvidas. Assim, o valor numérico de uma expressão algébrica permite também avaliar situações mais concretas ou particulares. Esse tema contribui para o desenvolvimento da habilidade EF08MA06. Pode-se dar o exemplo a seguir para os estudantes.

Um doce custa x reais. Se forem comprados três doces, a expressão algébrica que representa a quantia que deve ser paga, em real, é 3x. Qual é essa quantia se cada doce custa 5 reais?

Nesse caso, 3x = 3 ? 5 = 15, isto é, 15 reais. Diz-se que 15 é o valor numérico da expressão algébrica 3x quando x = 5.

VALOR NUMÉRICO DE UMA EXPRESSÃO ALGÉBRICA CAPÍTULO3

Vamos analisar duas situações.

1 Ângela, Sandra e Solange vão sempre juntas ao cinema. Se cada entrada para ocinema custa x reais, a expressão algébrica que representa o gasto delas com as entradas é 3x.

• Supondo que no domingo cada entrada custe 23 reais, elas deverão pagar 69 reais pelas três entradas.

3x = 3 ? 23 = 69

Dizemos que 69 é o valor numérico da expressão algébrica 3x para x = 23.

• Supondo que na quarta-feira cada entrada custe 15 reais, elas deverão pagar pelas três entradas 45 reais.

3x = 3 15 = 45

Dizemos que 45 é o valor numérico da expressão algébrica 3x para x = 15.

AMPLIANDO

Atividade complementar

Dobrando a medida a do lado de um quadrado, o que ocorre com a área do novo quadrado obtido? Se esse quadrado tem lado de 5 cm, qual será a área do novo quadrado?

Resolução da atividade

Possibilitar aos estudantes que explorem essa situação. Sugerir que

Vamos supor que:

A área desse terreno é dada pela expressão algébrica:

a a2 + bc

2 O formato e as medidas de um terreno estão representados na figura a seguir. a b c

Área do retângulo de lados medindo b e c Área do quadrado de lado medindo a

• o lado do quadrado meça 20 unidades de comprimento;

• as medidas b e c dos lados do retângulo sejam 16 e 12 unidades de comprimento, respectivamente.

Nessas condições, vamos calcular a área desse terreno.

a2 + bc = 202 + 16 12 = 400 + 192 = 592

A área desse terreno será 592 unidades de área.

O número 592, assim obtido, chama-se valor numérico da expressão algébrica a2 + bc para a = 20, b = 16 e c = 12.

Quando substituímos as variáveis de uma expressão algébrica por números e efetuamos os cálculos indicados, obtemos o valor numérico da expressão algébrica para esses números.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 110

construam um quadro para organizar os dados obtidos. Convidar algumas duplas para ir à lousa anotar a medida de lado escolhida. Ao final, construir coletivamente uma síntese a respeito da situação proposta.

Quadrado original Novo quadrado lado a

Logo, a área do novo quadrado é o quádruplo da área do quadrado original (dobrando a medida do lado, a área se quadruplica).

Se a = 5, então a expressão algébrica 4 ? a 2 tem valor numérico dado por:

4 ? (5) 2 = 4 ? 25 = 100 cm

Ou seja, a área do novo quadrado é 100 cm².

ORIENTAÇÕES DIDÁTICAS

ALGUMAS CONSIDERAÇÕES IMPORTANTES

1 Quando temos expressões algébricas fracionárias, nem sempre é possível obter o valor numérico da expressão para todos os valores que podem ser atribuídos às variáveis. Isso acontece quando esses valores anulam o denominador da expressão; e, como sabemos, não existe divisão por zero. Por exemplo:

• A expressão a x não tem valor numérico quando x = 0.

• A expressão a2 a1 + não tem valor numérico quando a = 1.

Na prática, podemos determinar o valor de uma variável para o qual uma expressão fracionária não apresenta valor numérico, igualando a zero o denominador dessa expressão e resolvendo a equação obtida. Vamos analisar duas situações.

• Para que valor de x a expressão algébrica x3 2x 1 não tem valor numérico?

2x 1 = 0 h 2x = 1 h x 1 2 =

Dizemos que a expressão não tem valor numérico quando x 1 2 =

• Qual deve ser o valor de x, em função de y, para que a expressão algébrica xy xy + não tenha valor numérico?

Igualando o denominador da expressão a zero, temos: x y = 0 h x = y

Dizemos que a expressão algébrica dada não tem valor numérico quando x = y.

2 Já quando temos expressões algébricas irracionais, nem sempre é possível obter o valor numérico da expressão em r . Isso acontece quando os valores atribuídos às variáveis tornam o radicando negativo. Nesse caso, o radical não estará definido no conjunto dos números reais, como vimos na Unidade 2 Por exemplo:

• A expressão 2x não tem valor numérico em r quando x , 0.

• A expressão ab22 + tem valor numérico para quaisquer valores de a e de b, pois ab22 + é sempre maior ou igual a zero.

Investimento

Investimento é a aplicação de algum tipo de recurso, como o dinheiro, com a expectativa de receber no futuro um valor superior ao aplicado. Ao deixar dinheiro em um banco, essa instituição financeira paga juros ao aplicador, que são como um “prêmio” sobre o valor investido.

Os investimentos financeiros são maneiras interessantes de poupar ou assegurar dinheiro para o futuro. É necessário criar no Brasil uma cultura de investimento, pois boa parte das pessoas está mais acostumada a lidar com empréstimos e financiamentos. Em grupos, conversem sobre as seguintes questões. Respondam às questões no caderno.

1. Vocês conhecem algum tipo de investimento? Qual?

2. Por que vocês acreditam que é importante investir?

Respostas pessoais. Exemplos de respostas na seção Resoluções comentadas deste Manual.

Algumas considerações importantes

Para o cálculo do valor numérico de expressões algébricas fracionárias, reforçar com os estudantes as restrições a serem consideradas para o denominador, como mostrado na situação 1 Na situação 2, atentar para o fato de que, em algumas situações, também não será possível determinar o valor numérico de expressões algébricas irracionais, no conjunto dos números reais. Para ampliar a discussão do tema, propor aos estudantes que calculem o valor numérico das expressões (x + y)(x y) e x 2 y 2 , para x = 1,1 e y = 0,8. A ideia é que percebam que o resultado será o mesmo.

Fórum

O tema investimentos abordado no boxe Fórum contribui para o desenvolvimento do Tema Contemporâneo Transversal Educação Financeira e da competência geral 6. Incentivar os estudantes a conversar a respeito do tema e, se possível, pesquisar como funciona algum tipo de investimento. Se houver necessidade, direcionar a pesquisa deles. O site indicado a seguir apresenta algumas informações que podem contribuir para essa pesquisa. • PORTAL DO INVESTIDOR. Rio de Janeiro, [20--?]. Site. Disponível em: https://www.investidor. gov.br/menu/primeiros_passos/ antes_investir/antes_investir. html. Acesso em: 6 ago. 2022.

ORIENTAÇÕES DIDÁTICAS

Atividades

O objetivo dessas questões é levar os estudantes a calcular o valor numérico de uma expressão algébrica quando se atribuem valores às variáveis, bem como utilizar os conhecimentos de cálculo algébrico para resolver problemas.

Ao resolverem as questões envolvendo números racionais na forma fracionária, os estudantes podem encontrar algumas dificuldades. Caso necessário, retomar as operações com números racionais na forma fracionária.

Enquanto eles resolvem as atividades propostas em sala de aula ou quando estiverem realizando a correção, caso eles tenham resolvido as atividades em casa, orientá-los a identificar o uso da expressão algébrica no dia a dia, citando situações do cotidiano em que usamos esse tipo de expressão. Eles podem dizer, por exemplo, que utilizamos expressões algébricas quando:

• fazemos a relação para a compra do material escolar;

• fazemos o planejamento de gastos para determinado passeio;

• tentamos prever o consumo de energia elétrica em um mês.

Na atividade 9, os estudantes são convidados a elaborar um problema envolvendo ideias de proporcionalidade, contribuindo para o desenvolvimento da habilidade EF08MA13.

A atividade 11 favorece o desenvolvimento da habilidade EF08MA06 ao propor aos estudantes que elaborem o enunciado de um problema envolvendo o cálculo do valor numérico de uma expressão algébrica.

Iniciar a atividade explicando aos estudantes que utilizem as letras que preferirem para representar as variáveis, desde que sejam minúsculas.

10. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Responda às questões no caderno.

1. C alcule o valor numérico na forma decimal da expressão algébrica 1 x xx_+ quando x = 4. 1,75

2. Determine o valor numérico da expressão + T M3 , para T = 43,2 e M = 1,5. 9,6

3. Determine o valor numérico de cada uma das seguintes expressões algébricas.

a) a2a a

2 , quando a = 4. 4

7. Um modelo matemático mostra que a quantidade de pessoas que compra determinado produto após t dias de veiculação publicitária é dada por 10 3 +  2  ?  10 t . De acordo com esse modelo, quantas pessoas comprarão um produto após 5 dias de veiculação?

b) m2 2mn + n2, quando m = 1 e n 1 4 =

c) aa x m

2 + , quando a = 8, x = 10 e m = 9.

d) 3(x 2 y 2) 10(x + y) ? (x y), quando x = 2 e y = 2. Zero.

e) (a b)2 c2, quando a 2 3 = , b = 1 e c  = 1.

f) 1x xy 1 2 + , quando x = 0,5 e y = 8.

g) xy xy

33 33 + , quando x = 1 2 e y = 2.

8. Alguns países, como os Estados Unidos, expressam suas temperaturas usando a escala Fahrenheit. Para converter uma temperatura expressa em graus Fahrenheit em graus Celsius, usa-se a expressão f32

1, 8 , em que f é a temperatura em graus Fahrenheit. Qual é a temperatura, em grau Celsius, correspondente a 89,6 graus Fahrenheit?

201 000 pessoas. 32 graus Celsius.

9. P esquise os preços de ingressos de cinema, teatro, ou de alguma outra atividade cultural na cidade ou região em que você mora. Inspirando-se na situação 1 da página 110, elabore uma atividade envolvendo os valores encontrados. A atividade deve envolver o cálculo de valores numéricos de uma expressão algébrica.

n ?+

Calcule o valor numérico dessa expressão, quando p = 10 4 , r = 250 e n = 2.

5. Determine os valores das variáveis para os quais as expressões algébricas a seguir não têm valor numérico.

a) x5 x4 b) ab 13a +

a) x xy + b) xy 2x y + 25 16 4 8 9 0,25 65 63 122 500 x = 4 = a 1 3 =_ x 2 5 b = 1

c) 2x 25x + d) ab 22b

10. Elabore uma atividade com esta ilustração. A atividade deve envolver a escrita de uma expressão algébrica e o cálculo de seu valor numérico. Troque de caderno com um colega; um deve resolver a atividade elaborada pelo outro.

11. Usando um contexto diferente dos utilizados nas atividades 9 e 10, elabore um problema envolvendo o cálculo do valor numérico de uma expressão algébrica. Em seguida, entregue o problema que você elaborou para um colega resolver, enquanto você resolve o problema elaborado por ele.

x EDITORIA DE ARTE 112

Segue um exemplo de problema que pode ser elaborado.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

Sejam x, y e z as quantidades de canetas que Ana, Pedro e Isadora têm.

a) Qual expressão descreve o total de balas que Ana, Pedro e Isadora têm juntos?

b) Se Ana tem 6 canetas, Pedro tem 3 e Isadora tem 4, qual é o total de canetas que os três têm juntos?

Nesse caso, para descobrir a expressão proposta no item a, deve-se utilizar a operação de adição. Desse modo, pode-se escrever x + y + z. Tomando, em particular, x = 6, y = 3 e z = 4 na expressão anterior, chegamos ao valor numérico da expressão 6 + 3 + + 4 = 13. Ou seja, juntos eles têm 13 canetas.

ATIVIDADES

MONÔMIO OU TERMO ALGÉBRICO CAPÍTULO4

PENSE E RESPONDA

Responda às questões no caderno.

1. Observe o retângulo representado a seguir cujas medidas dos lados, expressas em unidade de comprimento, são x e y

1.c) Resposta pessoal. Espera-se que os estudantes percebam que a expressão algébrica do item a é formada por uma multiplicação de variáveis, enquanto a do item b é formada por uma adição com variáveis nas parcelas.

ORIENTAÇÕES DIDÁTICAS

Pense e responda

Nas atividades propostas, explora-se a relação de conceitos geométricos, principalmente perímetros e áreas com o cálculo algébrico. Procurar explorar outras figuras conhecidas pelos estudantes, como quadrados, triângulos, losangos e outros polígonos. A discussão a respeito dessas questões prepara os estudantes para a compreensão dos conceitos que serão trabalhados nos capítulos seguintes desta Unidade.

Agora, responda.

a) Qual é a expressão algébrica que representa a área desse retângulo? xy

b) Qual é a expressão algébrica que representa o perímetro do retângulo?

2x + 2y

c) Entre as duas expressões algébricas que você escreveu nos itens a e b existe uma diferença. Qual é essa diferença?

2. Considere um número real x. Como você representaria:

a) o dobro desse número? 2x

b) o quadrado do número acrescido do próprio número? x 2 + x

Acompanhe as situações.

1 A figura a seguir é a representação de um triângulo equilátero. Seu lado mede d unidades de comprimento. A expressão algébrica que representa o perímetro desse triângulo é 3d.

2 Uma torneira gotejando desperdiça y litros de água em 1 hora. A expressão algébrica que representa a quantidade de água desperdiçada por essa torneira gotejando durante 4 horas é 4y.

ORIENTAÇÕES DIDÁTICAS

Inicia-se com o estudo dos monômios, em seguida, trata-se sobre polinômios, depois, apresenta-se produtos notáveis e fatoração.

Ressaltar que os conceitos e algoritmos matemáticos (e, portanto, a Álgebra) são fundamentais para o desenvolvimento das tecnologias e, principalmente, dos softwares

Se possível, realizar a leitura do item Investigações relativas à Álgebra, do documento Orientações curriculares e proposição de expectativas de aprendizagem para o Ensino Fundamental: ciclo II: Matemática. Nesse documento há informações e orientações a respeito do processo de ensino e aprendizagem relativos à Álgebra .

Um dos pontos a ser destacado desse documento se refere às categorias de erros cometidos pelos estudantes no estudo da Álgebra, conforme o trecho a seguir.

Categorização de erros na álgebra

[...] os estudos de Cortés & Kavafian (1999) apresentam uma classificação de erros e as constatações referentes à persistência deles, que ocorrem no trabalho com a álgebra. O referido estudo levanta por meio de uma pesquisa empírica, os erros cometidos por estudantes franceses (no nível correspondente à 7a e 8a séries no Brasil), quando da resolução de equações. Esses erros são classificados em cinco categorias, construídas a partir da utilização incorreta de determinadas propriedades matemáticas.

Os autores utilizam-se do quadro teórico Invariantes Operacionais, de Gérard Vergnaud (1990), para a elaboração, aplicação e análise da pesquisa.

Foram propostas aos estudantes cinco tipos de tarefas, as quais, segundo os autores, são a origem dos erros na aprendizagem da álgebra:

a c

Denomina-se monômio, ou termo algébrico, todo número ou toda expressão algébrica formada apenas por uma variável ou por uma multiplicação de números e variáveis, em que as variáveis têm como expoentes somente números naturais.

Assim, são exemplos de monômios:

• 3p

• 7 • x 2

• abc

• 4x 3

Em geral, um monômio é formado por duas partes: um número, chamado de coeficiente do monômio, e uma variável ou uma multiplicação de variáveis (considerando seus expoentes), chamada de parte literal Observe.

114

coeficiente parte literal

Observações:

10a3b

coeficiente parte literal

• • • 3x

18 coeficiente (não tem parte literal)

1. Como o número 1 é o elemento neutro da multiplicação, temos que:

• 1x = x • 1a4x 3 = a4x 3

• 1mn2 = mn2

O coeficiente desses monômios é 1.

• 1x = x • 1a4x 3 = a4 x 3 • 1mn2 = mn2

O coeficiente desses monômios é 1.

2. Todo número real é um monômio sem parte literal.

3. Quando o coeficiente de um monômio é 0, o monômio representa sempre o número real zero e é chamado de monômio nulo. Exemplos:

• 0x = 0 • 0a4x 3 = 0

• tarefas envolvendo transformações algébricas com números/coeficientes negativos;

114 12/08/22 19:04

• tarefas envolvendo cálculo numérico com números negativos;

• tarefas envolvendo fatoração e redução de termos semelhantes;

• tarefas envolvendo o tratamento de produto de fatores;

• tarefas envolvendo a passagem dos termos algébricos, de um membro pa-

ra o outro da equação (na resolução de equações do tipo ax + b = cx + d).

Para os autores, a passagem por um erro durante a aprendizagem da resolução de equações algébricas, é quase que necessária para o aluno, principalmente quando ele se depara com uma situação nova, como equações com incógnitas nos dois membros ou quando as equações envolvem produto de fatores.

3 A caixa de presente a seguir lembra um bloco retangular.

ATIVIDADES

10.b) 547,50; 437,50. Esses valores numéricos representam o valor total, em reais, a ser pago por um grupo de 5 adultos, caso realizem o passeio em alta temporada e em baixa temporada, respectivamente.

Responda às questões no caderno.

1. Q ual é o monômio que representa o produto de 7, a e b? 7ab

2. Identifique se as expressões algébricas a seguir são monômios ou não.

a) x 2

b) 10

c) x + 2y

d) 2,1bx 2

e) 3a 2b

f) 5 8 xy 2

g) x y

h) 1 xy

i) x

3. Identifique o coeficiente e a parte literal dos monômios a seguir.

a) 7b3

b) x 2y

c) 0,9c 4

d) a5x 3

e) 6,2a4b2c

f) 4 5

4. Mariana vende carrinhos em miniatura ao preço de x reais cada um. Qual é o monômio que representa o preço de 9 desses carrinhos? 9x

5. Em uma rodovia, o preço cobrado por carro em um dos pedágios é R$ 7,90. Se em determinado dia passaram x carros por esse pedágio, qual é o monômio que expressa a arrecadação, em reais, proveniente desse tipo de veículo nesse dia?

6. Um prédio possui x apartamentos por andar. Se esse prédio tem 20 andares, qual é o monômio que representa a quantidade total de apartamentos? 20x

7. Na V iação Graviola, a viagem de Campina Grande a João Pessoa custa R$ 37,50. Qual é o monômio que representa o valor arrecadado, em reais, com y passageiros que fizeram essa viagem?

8. Para gastar 100 calorias, Caio deve correr x minutos em um terreno plano ou fazer ginástica aeróbica por y minutos.

Se Caio quiser perder 800 calorias, qual é o monômio que representa o tempo, em minuto, que ele deve:

a) correr em um terreno plano? 8x

b) fazer ginástica aeróbica? 8y

9. O volume de um cubo é dado pelo cubo da medida de sua aresta. Qual é o monômio que expressa o volume do cubo da figura?

10. O Cristo Redentor, uma das Sete Novas Maravilhas do Mundo Moderno, fica no município do Rio de Janeiro, e uma das maneiras de chegar a esse monumento é por meio do Trem do Corcovado. Em 2022, o preço desse passeio, ida e volta, para adultos até 60 anos era de R $ 87,50, para baixa temporada, e R$ 109,50, para alta temporada.

a) Escreva o monômio que representa o valor a ser pago, em reais, por um grupo de n adultos para realizar o passeio nesse ano:

• em alta temporada. 109,50n

• em baixa temporada. 87,50n

b) Calcule o valor numérico dos monômios encontrados no item a para n = 5. O que cada um desses valores representa na situação?

ORIENTAÇÕES DIDÁTICAS

Atividades

As questões propostas têm como objetivo trabalhar o conceito de monômio e verificar o que os estudantes compreenderam, além de levantar possíveis dúvidas para serem sanadas.

Eles devem reconhecer um monômio, utilizá-lo para descrever as situações e identificar ocoeficiente numérico e a parte literal.

Na atividade 2, se necessário, lembrá-los de que geralmente um monômio é formado por duas partes – coeficiente e parte literal –, que compõem uma multiplicação (formando um termo) sem que estejam envolvidas adições e subtrações. Ressaltar que existem monômios que não têm parte literal (como no caso do monômio apresentado no item b. Verificar se eles compreendem que, quando o coeficiente é 1 ou 1, ele não aparece expresso no monômio; é o caso, por exemplo, dos monômios apresentados nos itens b e d da atividade 3. Pedir a eles que indiquem oralmente ocoeficiente e a parte literal de cada monômio que identificaram. É importante lembrá-los de que o número real zero também é um monômio, chamado de monômio nulo.

A atividade 11 contribui para odesenvolvimento da habilidade EF08MA10.

SÃO PAULO. Prefeitura Municipal de São Paulo. Secretaria Municipal de Educação. Orientações curriculares e proposição de expectativas de aprendizagem para o Ensino

Fundamental: ciclo II: Matemática. São Paulo:

SME/DOT, 2007. p. 114. Disponível em: https:// acervodigital.sme.prefeitura.sp.gov.br/acervo/ orientacoes-curriculares-e-proposicao-de -expectativas-de-aprendizagem-para-o-ensino -fundamental-ciclo-ii-matematica.

Acesso em: 6 ago. 2022.

AMPLIANDO Vídeo

CORCOVADO train. 2014. Vídeo (8min8s). Publicado pelo canal Oskar Sjostedt. Disponível em: https://www.youtube.com/watch?v=otjIS9TTu7s&t=50s. Acesso em: 6 ago. 2022.

Após a realização da atividade 10, se possível, apresentar o vídeo do trajeto do Trem do Corcovado.

3. e) 6,2; a4 b2c

x 2y

a5x 3

4 5 ; não tem parte literal.

11. C onsidere a sequência numérica (x, 5x, 25x, ...) e escreva os próximos três termos dessa sequência.

Trem do Corcovado e Cristo Redentor. Rio de Janeiro (RJ), 2019.

625x, 3 125x

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

ORIENTAÇÕES DIDÁTICAS

Grau de um monômio

O estudo de monômios serve de referência para o estudo que vem logo a seguir, com os polinômios. A determinação do grau de um monômio, assim como a identificação da parte literal e da parte numérica, contribuem para o entendimento e a construção das noções algébricas.

Monômios semelhantes

O reconhecimento de monômios semelhantes é fundamental para que os estudantes possam efetuar as operações de adição e subtração de monômios.

GRAU DE UM MONÔMIO

O grau de um monômio com coeficiente não nulo é dado pela soma dos expoentes das variáveis. Exemplos:

• O monômio 6x 2y5 é do 7˘ grau. (2 + 5 = 7)

• O monômio 1 3 ab é do 2˘ grau. (ab = a1b1 h 1 + 1 = 2)

• O monômio 5,1y6 é do 6 ˘ grau.

• O monômio 10 é de grau zero.

O grau de um monômio também pode ser dado em relação a uma de suas variáveis. Nesse caso, o grau do monômio corresponde ao expoente da variável considerada. Exemplos:

• O monômio 3x 2y5 é do 2˘ grau em relação à variável x

• O monômio 1 2 ab 3 é do 1˘ grau em relação à variável b

MONÔMIOS SEMELHANTES

Acompanhe.

• 10x 2y e 2 3 xy 2 possuem a mesma parte literal: x 2y.

• 2,5x 3 , 1 2 x 3 e 4x 3 possuem a mesma parte literal: x3

Quando dois ou mais monômios apresentam a mesma parte literal, eles são denominados monômios semelhantes ou termos semelhantes

Assim, são exemplos de monômios ou termos semelhantes:

• 10x 2y e 2 3 xy 2

• 4a2b2 e 7a2b2

• 2,5x 3; 1 2 x 3 e 4x 3

Não são semelhantes, por exemplo, os monômios:

• 6x 2y e 4xy2

• 2x 3; 1 2 x 2 e 5 4 x

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 116 12/08/22 19:05

ADIÇÃO ALGÉBRICA DE MONÔMIOS

Acompanhe as situações a seguir.

1 Qual é o monômio que representa a área do retângulo ABCD da figura?

Para resolver o problema, podemos representar:

• a área do retângulo 1 pelo monômio 5x;

• a área do retângulo 2 pelo monômio 3x.

Então, a área do retângulo ABCD, que é dada pela soma das áreas dos retângulos 1 e 2 , pode ser representada por: 5x + 3x.

Podemos, também, considerar o retângulo ABCD cujos lados medem x e (5 + 3) = 8, e a área será dada por 8x.

Comparando os dois processos, temos:

5x + 3x = 8x ou, ainda, 5x + 3x = (5 + 3)x = 8x.

Assim, 8x é o monômio que representa a área do retângulo ABCD da figura.

2 A figura ilustra a superfície lateral de uma escada com a indicação das medidas dos degraus. Qual é a área dessa superfície?

Para resolver o problema, podemos considerar que:

• a área da figura 1 é dada por x 6y ou 6xy;

• a área da figura 2 é dada por x ? 4y ou 4xy;

• a área da figura 3 é dada por x 2y ou 2xy.

Então, a área da figura toda é dada por:

6xy + 4xy + 2xy = (6 + 4 + 2)xy = 12xy

Assim, a área dessa superfície é dada por 12xy

Uma adição algébrica de monômios é toda expressão algébrica que contém somente adições ou subtrações de monômios, ou ambas as operações.

Podemos dizer que:

Para efetuar a adição algébrica de monômios ou termos semelhantes, adicionamos algebricamente os coeficientes e mantemos a parte literal.

A adição algébrica também pode ser chamada de redução de termos semelhantes Observe os exemplos.

ORIENTAÇÕES DIDÁTICAS

Adição algébrica de monômios

Como sugestão de encaminhamento de aula, explorar, na lousa, os exemplos apresentados no Livro do estudante. Um dos erros que costuma ser comum entre os estudantes é a redução de termos semelhantes, principalmente se os coeficientes dos monômios forem números racionais na forma fracionária. Fazer algumas abordagens na lousa, solicitando aos estudantes que efetuem diversos cálculos envolvendo monômios; assim, poderão discutir eventuais dúvidas.

AMPLIANDO

Vídeo

EXPRESSÕES algébricas parte 4: monômios – Aula 17. 2013. Vídeo (14min11s). Publicado pelo Portal da Matemática OBMEP. Disponível em: https://www.youtube.com/watch?v=LZa7KDgKHmk. Acesso em: 6 ago. 2022.

A videoaula pode ser utilizada para fazer uma retomada do conceito de monômios semelhantes e aplicá-lo na resolução de alguns cálculos.

ILUSTRAÇÕES: EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

Atividades

Algumas das questões apresentadas têm como objetivo que os estudantes determinem o grau de monômios não nulos e o grau de um monômio em relação a uma de suas variáveis.

Na atividade 4, pedir a eles que registrem os seis monômios apresentados, determinando o grau de cada um. Espera-se que os estudantes percebam que a ordem, tanto crescente quanto decrescente, deve ser estabelecida considerando-se os expoentes das partes literais dos monômios apresentados. É importante que eles percebam que o monômio 20 não tem parte literal e, como é não nulo, seu grau é zero.

Outras questões propostas nesse bloco têm como objetivo que os estudantes identifiquem monômios semelhantes e efetuem a adição algébrica de dois ou mais monômios semelhantes.

Na atividade 7, propor a eles que se organizem em duplas para resolver as adições algébricas; desse modo, facilita-se a troca ideias com os colegas.

É importante que eles compreendam o conceito e identifiquem monômios semelhantes, concluindo que esse fato possibilita a redução desses monômios a um único termo.

Quando os estudantes se sentirem confiantes, incentivá-los a realizar o cálculo da soma algébrica dos coeficientes mentalmente, registrando, se houver necessidade, apenas os cálculos intermediários.

Verificar se eles compreenderam as operações de monômios com coeficientes racionais não inteiros (na forma de fração ou na forma decimal), sanando dúvidas quanto às operações com números na forma de fração ou na forma decimal.

Responda às questões no caderno.

1. Entre os monômios a seguir, quais são os que apresentam grau 4?

2 3 mn22 0,5ax 2 1,6ac2 9x 3y

2. Qual é o grau do monômio 15a3x5y?

3. Q ual é o valor que se deve colocar no lugar do expoente x para que o monômio 7,5a2bxc5 seja do 10 ˘ grau? 3

4. Considere os monômios:

f) 1,1ab3 3,5ab3 0,9ab3 + 2,8ab3

g) 1 3 xy 5 6 xy 4 9 xy 2222 22 _+

8. Qual é o monômio que devemos adicionar a 7x 3y3 para obter 2x 3y3? 9x 3 y3

9. Escreva o monômio que adicionado a 2x 2 resulta em:

a) 5x 2 7x 2

b) 4x 2 2x 2

a) Qual é o monômio de maior grau? 2x5

b) Escreva os monômios na ordem decrescente, de acordo com o grau.

5. O s monômios 10an b2 e 20x7 ym são do 8 ˘  grau. Qual é o valor numérico da expressão m + n? 7

6. Considere os

7.

os monômios apresentados, identifique aqueles que são

c) x 2 3x 2 d) 0. 2x 2

10. Fazendo a redução dos termos semelhantes, escreva as expressões algébricas a seguir na forma mais simples.

a) 7x ( 2x + x) + ( 3x + 5x) 10x

b) 5y 2 ( 4y 2 + 7y 2) + ( y 2 + 9y 2 11y 2)

c) 10ab [3ab (ab + 2ab 5ab) 8ab]

d) 2xy + [ 5xy + 2xy (xy + + 4xy 2xy) 8xy] 12xy

11. Considere a expressão algébrica a seguir. 20bc [ 7bc (11bc 40bc 6bc) + 5bc]

a) Escreva o monômio que pode representar essa expressão. 13bc

b) Determine o monômio que se deve adicionar ao monômio obtido no item a para obter 5bc. 18bc

12. Obtenha a forma mais simples de escrita da expressão algébrica a seguir.

3,4a2x2 ( 1,6a2x2 5,8a2x2 3,7a2x2) + + (8,1a2x2 1,9a2x2)

13. Considere esta expressão algébrica. 0,6ay ay + 0,3ay + 0,5ay

a) Escreva essa expressão na forma mais simples.

b) Qual é o valor numérico dessa expressão quando a = 1,4 e y = 0,9? 0,504

14. Elabore um problema envolvendo a adição algébrica de monômios e entregue-o para um colega resolver. Em seguida, verifique se a resolução feita por ele está correta.

Nas atividades 10 e 11, discutir com os estudantes a ordem de eliminação de parênteses e colchetes.

A atividade 14 propõe que os estudantes elaborem um problema, o que favorece o desenvolvimento da habilidade EF08MA06.

14. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

MULTIPLICAÇÃO DE MONÔMIOS

PENSE E RESPONDA

Observe o monômio que representa o volume de cada sólido.

ORIENTAÇÕES DIDÁTICAS

Pense e responda

Essa seção tem como objetivo levar os estudantes a perceber o processo da multiplicação entre monômios. Pedir a eles que expliquem oralmente o que foi feito para determinar o volume do sólido verde, do laranja e do roxo. Verificar se eles descrevem a propriedade de potências de mesma base.

Responda no caderno.

1. Represente o volume dos sólidos a seguir com um monômio.

A atividade proposta também retoma a soma algébrica de monômios.

Inicialmente, vamos recordar a seguinte propriedade: am an = am + n Agora, por meio dos cálculos de área e de volume, vamos verificar como podemos efetuar a multiplicação entre monômios.

O monômio que representa a área desse retângulo é 21x2

O monômio que representa o volume desse bloco retangular é 36x2y

Para multiplicar dois ou mais monômios, multiplicamos os coeficientes entre si e multiplicamos as partes literais entre si.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 119 12/08/22 19:06

AMPLIANDO

Vídeo

MULTIPLICAÇÃO de monômio por monômio – Álgebra básica MAB #72. 2019. Vídeo (13min15s). Publicado pelo canal Matemática Rio com Prof. Rafael Procopio. Disponível em: https://www.youtube.com/watch?

v=-pW8xjVNEqc&t=1s. Acesso em: 6 ago. 2022.

Nessa videoaula, são apresentados alguns exemplos de multiplicação entre monômios que podem contribuir para a ampliação desse estudo.

ILUSTRAÇÕES: EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

O exemplo apresentado nessa página usa a multiplicação de monômios para a construção dos termos de uma sequência algébrica, contribuindo para o desenvolvimento das habilidades EF08MA10 e EF08MA11.

Ler com os estudantes a resolução proposta e verificar se eles compreendem o fluxograma dado ao final da atividade, que mostra as etapas para a construção dos termos da sequência, contribuindo para o desenvolvimento da competência específica 6 da área de Matemática.

Atividades

As questões propostas têm como objetivo que os estudantes efetuem a multiplicação de monômios utilizando as propriedades da multiplicação no conjunto dos números reais e as propriedades da potenciação.

Na atividade 4, que pode ser realizada em duplas, os estudantes precisam pensar em um padrão para formar uma sequência que envolva multiplicação de monômios. Apesar de o tema potenciação de monômios vir mais a frente, se julgar conveniente, o estudo desse tema pode ser antecipado, associando-o à multiplicação de monômios e retomando as propriedades da potenciação com números reais.

Acompanhe mais um exemplo.

Observe os três primeiros termos de uma sequência: 5xy, 10x 3y2, 20x5y3, ... Vamos descobrir opadrão dessa sequência e escrever o 6 ˘ termo.

Primeiro, analisamos o 1˘ e o 2˘ termos da sequência. 5xy 10x 3y2

Observamos que o 2˘ termo é o produto do monômio 5xy (1˘ termo) pelo monômio 2x 2y e que o 3 ˘ termo é o produto do monômio 10x 3y2 (2˘ termo) pelo monômio 2x 2y. Assim, cada termo da sequência, a partir do 2˘ termo, é dado pela multiplicação do termo anterior por 2x2y. Assim, temos:

4o termo: (20x5y3) ? (2x 2y) = 20 ? 2 ? x5 ? x 2 ? y3 ? y = 40x7y4

5o termo: (40x7y4) ? (2x 2y) = 40 ? 2 ? x7 ? x 2 ? y4 ? y = 80x9 y5

6o termo: (80x9 y5) ? (2x 2y) = 80 ? 2 ? x9 ? x 2 ? y5 ? y = 160x11y6

Portanto, o 6o termo da sequência é 160x11y6

Agora, observe como podemos representar a geração de uma sequência desse tipo por meio de um fluxograma.

sim

Início: Escolher oprimeiro termo.

Multiplicar o termo anterior pelo padrão e obter onovo termo.

Fim do processo.

Responda às questões no caderno.

1. Efetue as multiplicações.

a) a4 ? a6 a10

b) (1,5x 2y) ( 0,3xy2) 0,45x 3 y3

c) ( 2,6abc) ( 1,2ab) 3,12a2b2c

d) ( ac) ( a4bc2) a5bc 3

e) ( 0,1y3) ? (+0,2y4) 0,02y7

2. Calcule o resultado das multiplicações.

a) (5a4bc3) ( b2c) (+4a2c) 20a6 b3c5

b) (4,5y2) ? ( 0,3y) ? ( y4) 1,35y7

c) (0,1xy) (100xy2) (0,01x 3) 0,1x5y3

( 12mnp) ?

120

3. Cada ladrilho retangular desta figura tem x unidades de comprimento por 0,5x unidades de largura.

Escreva o monômio que representa a área:

a) de cada ladrilho. 0,5x 2

b) ocupada pelos ladrilhos amarelos. 6x 2

c) ocupada pelos ladrilhos azuis. 6x 2

d) total da figura. 12x 2

2 3 mn 2       ? (5np) 40m3n3p2 ATIVIDADES EDITORIA DE ARTE

120 14/08/22 16:52

SEQUÊNCIAS

Todo grupo de elementos dispostos em determinada ordem é uma sequência. Os elementos, ou termos, de uma sequência podem ser, por exemplo, expressões algébricas, números ou figuras.

Uma sequência pode ou não ter um padrão (ou regra) de formação; neste momento, a nós interessa estudar as sequências que têm um padrão.

Na página anterior, verificamos a sequência 5xy, 10x 3y2, 20x5y3, ...; em que cada termo, a partir do segundo, é gerado multiplicando-se o termo anterior pelo monômio 2x 2y.

Nesse caso, definimos a sequência de forma recursiva, que é o modo de determinar cada termo a partir do termo anterior ou de termos anteriores. Acompanhe outros exemplos.

1 Observe a sequência: 128x2, 64x5, 32x8, ...

Note que, nessa sequência, o 2o termo é igual ao 1o termo multiplicado pelo monômio 0,5x 3 , e o 3o termo é igual ao 2o termo multiplicado pelo monômio 0,5x 3

• 1o termo: 128x 2

• 2o termo: 128x 2 0,5x 3 = 64x5

• 3o termo: 64x5 0,5x 3 = 32x8

Então, podemos gerar o 4o termo a partir do 3o termo, e o 5o termo a partir do 4o termo.

• 4o termo: 32x8 0,5x 3 = 16x11

• 5o termo: 16x11 0,5x 3 = 8x14

2 Consideremos, agora, a sequência: 2, 4, 6, 8, ...

Note que cada termo dessa sequência, a partir do 2o termo, pode ser determinado ao adicionar 2 ao termo anterior; porém, vamos verificar como determinar uma regra de formação para os termos dessa sequência sem recorrer aos termos anteriores.

Vamos chamar os termos da sequência de a1, a2, a3, a4, an, em que n é a posição do termo na sequência. Então:

ORIENTAÇÕES DIDÁTICAS

Por toda parte

O exemplo apresentado na página 120 do Livro do estudante introduz o conceito de sequência definida de forma recursiva. A partir dessa retomada, o exemplo 1 da página 121 propõe a construção de outra sequência recursiva, apoiada na multiplicação de monômios.

O exemplo 2 aborda a construção da sequência de números pares com o objetivo de escrever sua lei de formação. Ambos os exemplos contribuem para o desenvolvimento das habilidades EF08MA10 e EF08MA11 e da competência específica 6 da área de Matemática.

a1 = 2

a2 = 4 a3 = 6 a4 = 8

Observando uma regularidade entre cada termo e sua posição, podemos escrever uma lei de formação ou termo geral da sequência. Acompanhe.

a1 = 1 2 = 2

a2 = 2 2 = 4

a3 = 3 2 = 6

a4 = 4 2 = 8 ; a n = n ? 2 = 2n lei de formação ou termo geral Com essa lei de formação da sequência, é possível determinar qualquer termo da sequência sem precisar determinar os termos anteriores. Se quisermos descobrir o 18o termo dessa sequência, por exemplo, basta calcular o valor numérico da expressão 2n para n = 18. Assim: a18 = 18 ? 2 = 36

Logo, o 18o termo dessa sequência é 36.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

ORIENTAÇÕES DIDÁTICAS

O fluxograma apresenta uma sequência para obter os termos da sequência do exemplo 2 de forma recursiva, contribuindo para o desenvolvimento do pensamento computacional dos estudantes e da competência específica 6 da área de Matemática.

Na atividade 3, sugere-se que os estudantes se organizem em duplas para resolvê-lo no caderno. Circular pela sala de aula, observando as propostas de fluxograma desenhadas pela turma. Finalizar a atividade e pedir a algumas duplas que mostrem como pensaram a organização das etapas. A socialização de estratégias contribui para o desenvolvimento da empatia, do respeito e da capacidade de argumentação

Acompanhe como podemos representar a formação da sequência 2, 4, 6, 8, ... em um fluxograma de dois modos: de forma recursiva e usando a lei de formação.

• De forma recursiva

Início Primeiro termo: a1 2

Início: Atribuir a n o valor 1: n = 1

Calcular o valor numérico de 2n e obter o termo a n da sequência.

sim não

Fim do processo.

Adicionar 2 ao termo anterior e obter o novo termo.

sim

Aumentar n em 1 unidade.

Fim do processo.

3 Agora, observe as quatro primeiras figuras de uma sequência.

Repare que a cada figura pode ser associado um número correspondente à quantidade de quadradinhos menores da figura: 1, 4, 9, 16, ...

Essa sequência é a dos números quadrados perfeitos. Cada termo dessa sequência de números pode ser expresso deste modo:

a1 = 12 = 1

a2 = 22 = 4

a3 = 32 = 9

a4 = 42 = 16 ;

a n = n2

Assim, considerando a sequência de figuras, o termo dessa sequência que ocupa a posição n é composto de n2 quadradinhos, dispostos na forma de um quadrado com n linhas de n colunas de quadradinhos.

Responda às questões no caderno.

1. Descubra os três próximos termos da sequência: 1x, 3x 2, 9x 3, 27x4 , ... 81x5, 243x6 e 729x7

2. Escreva uma sequência de cinco termos, sabendo que sua lei de formação é an = 2n2 + 1.

Resposta pessoal. Exemplo de resposta: 3, 9, 19, 33, 51.

3. Retomando a sequência do exemplo 3, faça o que se pede.

a) Desenhe o 10o termo da sequência.

Respostas na seção Resoluções comentadas deste Manual.

b) Junte-se a um colega, e escrevam um fluxograma para representar a formação dessa sequência.

EDITORIA DE ARTE 122

D2_AV4-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

DIVISÃO DE MONÔMIOS

Vamos recordar a seguinte propriedade: am : an = am n Agora, consideremos alguns exemplos para verificar como podemos realizar a divisão entre dois monômios.

ORIENTAÇÕES DIDÁTICAS

Divisão de monômios

O estudo da divisão entre monômios retoma o estudo realizado anteriormente, envolvendo potências de mesma base e as operações de multiplicação, divisão e potenciação. Se sentir necessidade, fazer um pequeno registro na lousa, resgatando esses conceitos e trazendo exemplos envolvendo expressões literais.

Para dividir um monômio por outro, dividimos os coeficientes entre si e as partes literais entre si.

Observe, agora, o resultado da seguinte divisão.

Nem sempre a divisão de um monômio por outro vai resultar em um monômio, como nesse caso. No entanto, estudaremos apenas a divisão de monômios que tenha como resultado um monômio.

ORIENTAÇÕES DIDÁTICAS

Potenciação de monômios

Escrever na lousa um monômio qualquer elevado ao quadrado e pedir aos estudantes que resolvam, no caderno, como imaginam que seja o correto. Circular pela sala de aula, verificando como eles procedem. Se sentir necessidade, retomar como calcular o quadrado de um número natural qualquer. Desenvolver o produto na lousa e certificar-se de que todos os estudantes compreenderam que, novamente, deverão efetuar multiplicações entre monômios; nesse caso, porém, todos os fatores são iguais.

Atividades

As questões propostas têm como objetivo levar os estudantes a efetuar a divisão entre dois monômios aplicando, para isso, as propriedades da divisão de números reais e as propriedades da potenciação.

Em algumas atividades, trabalha-se a divisão de monômios combinada com a adição e a multiplicação, já vista anteriormente.

Na atividade 1, os estudantes terão a oportunidade de calcular alguns quocientes, o que lhes permitirá verificar se compreenderam o processo e experimentar maneiras diferentes de organizar e realizar os cálculos, podendo, assim, encontrar o caminho que consideram mais rápido e prático para a divisão de monômios. Enfatizar a seguinte estratégia de divisão.

• Dividir os coeficientes entre si.

• Dividir as partes literais entre si, relembrando a seguinte propriedade da potenciação com números: para dividir potências de mesma base diferente de zero, basta manter a base e subtrair os expoentes.

POTENCIAÇÃO DE MONÔMIOS

Considere as situações a seguir.

1 Qual é o quadrado do monômio 10a3?

2 Qual é a 5a potência do monômio 2x 2?

Para tornar esses cálculos mais simples, podemos usar as propriedades das potências:

(am)n = am n (a b)n = an bn

Observe nos exemplos como os cálculos se tornam mais simples:

• ( 10a3)2 = ( 10)2 ? (a3)2 =+100a6

• (2x 2) 5 = (2)5 (x 2) 5 = 32x10

ATIVIDADES

Responda às questões no caderno.

1. Calcule o quociente dos monômios.

a) ( 32abc) : (+8ac) 4b

b) (+40x7y2) : ( 10x4y2) 4x 3

2. Efetue as seguintes divisões.

c) ( 100a3) : ( 25a3) +4

d) (+55a4bc2) : ( 11a2bc) 5a2c

3. Multiplique o monômio 40ax pelo monômio 0,5ax

2. Depois, divida o resultado pelo monômio 10ax. Qual é o monômio que você vai obter? 2ax 2

4. Núbia dividiu o monômio +60x6y3 pelo monômio 12x4y2 . Ao resultado obtido, ela adicionou o monômio +7x 2y e obteve M. Qual é o monômio M ? +2x 2y

5. Se você dividir a expressão 27a4b2 + 7a4b2 pela expressão 10ab + 6ab, que monômio obterá? +5a3b

6. Eduardo efetuou a divisão 10x 3y por 2xy e obteve como resposta 5x 3. A resposta de Eduardo está correta?

Não, pois a resposta correta é 5x 2

7. Se você dividir o cubo da soma ( 7y + 10y + 2y) por ( 10y2 15y2), que monômio encontrará? 5y

8. Efetue a divisão de 1 2 ac25

por

ac49

. Em seguida, adicione o monômio c2 ao resultado. Que monômio você obteve? 2c 2

Caso sinta necessidade, apresentar na lousa a resolução de alguns exemplos.

D2_AV4-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 124

a) a 9 : a

= a 9 _ 5 = a 4

_

b) x 6 : x

= x

= x (relembrar que todo número elevado a 1 é ele mesmo).

c) b 5 : b

= b

_ 5 = b 0 = b (relembrar que todo número (não nulo) dividido por ele mesmo é igual a 1).

Na atividade 2, os estudantes devem calcular quocientes entre monômios que têm coeficientes racionais não inteiros (na forma de fração ou decimal) ou que têm coeficientes inteiros cujo quociente não é inteiro. Se necessário, relembrar com eles esses tipos de quociente entre dois números. Apresentar na lousa a resolução, por exemplo, do item a

POLINÔMIOS

Acompanhe as situações a seguir.

1 Qual é a expressão algébrica que representa a área da figura a seguir?

A área da figura é dada pela soma das áreas das figuras 1 e 2 . Adicionamos, então, as áreas das duas figuras: ab + x 2

A área dessa figura é dada pela soma ab + x 2

2 O esquema a seguir representa uma rodovia, na qual há 4 postos de abastecimento, representados pelos pontos A, B, C e D. A distância de A a B é igual à distância de B a C, e ambas podem ser representadas por x quilômetros. Sabendo que a distância de A a D pode ser representada por y quilômetros, qual é a expressão algébrica que representa a distância de C a D?

ORIENTAÇÕES DIDÁTICAS

Polinômios

Definir polinômio para a turma a partir do conceito de monômio. Alguns estudantes tendem a somar ou subtrair os monômios não semelhantes que compõem um polinômio, juntando suas partes literais. Por exemplo, ao lerem 3x + 4y, alguns estudantes podem escrever 7xy. Esse equívoco é comum e precisa ser discutido com eles.

Observando o esquema, podemos concluir que a distância de C a D é dada pela diferença entre a distância de A a D e a distância de A a C: y 2x A expressão algébrica y 2x representa a distância de C a D

As situações que acabamos de acompanhar nos mostram expressões algébricas que indicam, respectivamente, uma adição e uma subtração de monômios, ou seja, indicam uma adição algébrica de monômios

Qualquer monômio ou adição algébrica de monômios denomina-se polinômio

São exemplos de polinômios as expressões a seguir.

• ab • 9z + 3y • y 2x + 4z 2w

Observação:

• O s monômios que formam um polinômio são denominados termos do polinômio.

Assim:

2xy É um polinômio de um só termo (monômio).

100x + 10y + 2 É um polinômio de três termos: 100x, 10y e 2.

AMPLIANDO

Atividade complementar

A ideia é trabalhar com uma atividade contextualizada, cujo tema faça parte do cotidiano dos estudantes. Para isso, solicitar a eles que tragam uma conta de água para que possam analisar a expressão utilizada para o cálculo do consumo. Esta deve ser uma atividade voluntária, ou seja, é importante que os estudantes se sintam à vontade para levar ou não a conta de água, uma vez que algumas famílias podem não se sentir confortáveis

em enviar a conta. Uma sugestão, se possível, é providenciar cópias de uma conta de água e disponibilizar para os estudantes a fim de que todos possam participar da atividade.

Além da análise de dados, pode-se propor reflexões a respeito de questões importantes, como escassez de água e consumo de água consciente. Ajudá-los a observar que nas contas há um escalonamento de cobrança de água de acordo com o consumo, indicado em metro cúbico (m3).

ILUSTRAÇÕES: EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

Atividades

Nas atividades propostas, os estudantes poderão escrever diversos polinômios, em contextos geométricos e cotidianos, como na atividade 8

A atividade 3 pode ser resolvida com mais de uma estratégia. É importante observar como os estudantes pensam na resolução da questão e compartilhar com a classe as diferenças construídas. Uma estratégia possível é determinar a área da figura completa (x 2) e excluir a área do quadrado de lado y (y2). Assim, a área da figura amarela é x 2 y 2

Mas, eles ainda podem subdividir a figura dada em dois retângulos: um deles, com medidas de lados iguais a (x y) e x e o outro, com medidas de lados iguais a y e (x y).

Assim, a área da figura será x (x y) + y (x y) = = x 2 xy + yx y 2 = x 2 y 2

ATIVIDADES

Responda às questões no caderno.

1. Em uma partida de basquete, uma jogadora fez x cestas de 2 pontos e y cestas de 3 pontos. Escreva o polinômio que representa a quantidade de pontos que essa jogadora marcou nessa partida.

2x + 3y

2. Na bicicleta reclinada da figura a seguir, temos que:

• a medida do raio da roda maior é 3r;

• a medida do raio da roda menor é 2r;

• a distância entre os pontos A e B é d

5. Escreva o polinômio que representa um número formado por:

a) x dezenas e y unidades. 10x + y

b) y dezenas e x unidades. 10y + x

6. Escreva o polinômio que expressa a medida do segmento AB em cada figura.

a)

2a + b

b)

2a b

7. Escreva o polinômio que representa a área da figura a seguir. a2 + 2ab + b2

Escreva o polinômio que expressa a distância entre os centros C1 e C2 das rodas. d + 5r

3. Escreva o polinômio que representa a área da região colorida de amarelo na figura a seguir. x 2 y2

ab a b

8. Uma empresa de aluguel de automóveis cobra uma taxa de R$ 60,00 por dia de aluguel mais R $ 3,00 por quilômetro rodado. Que polinômio vai expressar o valor a ser pago por uma pessoa que aluga um automóvel dessa empresa por y dias e percorre x quilômetros? 60y + 3x

4. Em um estacionamento, há x carros e y motos.

Escreva o polinômio que representa:

a) a quantidade de veículos estacionados

b) a quantidade de rodas dos veículos. x + y 4x + 2y

D2_AV4-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

AMPLIANDO

Atividade complementar

Com base nas atividades 3 e 7 dessa página do Livro do estudante, faça o desenho de um polígono em uma malha quadriculada e represente suas medidas utilizando monômios. Em seguida, troque com um colega e solicite a ele que determine as expressões que representam a área e o perímetro da figura desenhada. Resolução da atividade

Resposta pessoal.

Carros disponíveis para aluguel em pátio de locadora.

POLINÔMIO REDUZIDO

Consideremos o polinômio x 2 + xy + xy + x 2 + xy. Observe que esse polinômio possui termos ou monômios semelhantes. Sabendo que esses termos semelhantes podem ser reduzidos, temos:

x 2 + xy + xy + x 2 + xy =

= x 2 + x 2 + xy + xy + xy = pela propriedade comutativa

= 2x 2 + 3xy soma algébrica de monômios semelhantes

Dizemos que:

2x 2 + 3xy é a forma reduzida do polinômio x 2 + xy + xy + x 2 + xy.

Acompanhe estas outras situações.

1 Escrever na forma reduzida o polinômio 3a 5ab + 8b 2a + 3ab + b.

3a 5ab + 8b 2a + 3ab + b =

= 3a 2a 5ab + 3ab + 8b + b = pela propriedade comutativa

= a 2ab + 9b forma reduzida

2 Escrever na forma reduzida o polinômio 3x2 ( 9x + 4) + ( 7x + x 2 3).

3x 2 ( 9x + 4) + ( 7x + x 2 3) =

= 3x 2 + 9x 4 7x + x 2 3 = Eliminando os parênteses.

= 3x 2 + x 2 + 9x 7x 4 3 = pela propriedade comutativa

= 4x 2 + 2x 7 forma reduzida

Observações:

1. Os polinômios de um só termo são chamados de monômios

2. Um polinômio reduzido de dois termos também recebe o nome de binômio

• 3x + 2y

• 4a b

• xy + 5y2

3. Um polinômio reduzido de três termos também é chamado de trinômio

• x 2 2xy + y2

• x 2 7x + 10

• a + 2b bc

4. Um polinômio reduzido com mais de três termos não tem nome particular.

ORIENTAÇÕES DIDÁTICAS

Polinômio reduzido

Um dos principais erros cometidos pelos estudantes está na redução de termos semelhantes. Isso se agrava se os coeficientes dos monômios forem números racionais na forma fracionária. Se possível, retomar a adição e subtração de números racionais na forma fracionária e, também, na forma decimal. Fazer algumas abordagens na lousa, solicitando aos estudantes que efetuem diversos cálculos envolvendo monômios.

Pedir a eles que registrem, no caderno, o significado das palavras binômio e trinômio, que serão muito usadas nos estudos de Álgebra.

15/08/22 22:32

D2_AV4-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

ORIENTAÇÕES DIDÁTICAS

Grau de um polinômio Ressaltar para os estudantes que um polinômio na forma reduzida não apresenta termos semelhantes. Além disso, não se define grau para o polinômio nulo (aquele que tem todos os coeficientes iguais a zero ou que em sua forma reduzida é igual a zero); se o polinômio for de uma única variável, o grau dele é o maior expoente dessa variável; se o polinômio tiver mais de uma variável, é preciso verificar o grau de todos os monômios e o maior deles é o grau do polinômio.

É importante destacar que o grau de um polinômio só pode ser determinado se esse polinômio estiver na forma reduzida.

Polinômios com uma só variável real Discutir com os estudantes o exemplo a seguir.

O polinômio P = 2x 5 +

+ 3x 4 2x 2 x 2 + x 3 2x 5

aparentemente tem grau 5, mas, depois de reduzir seus termos semelhantes, obtém-se P = 3x 4 + + x 3 3x 2, que é a forma reduzida do polinômio P. Observando P em sua forma reduzida, verifica-se que ele tem grau 4, e não 5, como aparentava. Quase todas as situações modeladas com polinômios recaem em polinômios de uma única variável.

Comentar também com os estudantes que, para escrever polinômios de uma só variável na sua forma completa, eles devem estar na sua forma reduzida e ordenados segundo as potências decrescentes de sua variável. Esse fato é bastante utilizado na divisão de polinômios (assunto que será estudado mais adiante) em que se precisa expressar o polinômio dividendo na sua forma completa.

GRAU DE UM POLINÔMIO

O grau de um polinômio reduzido não nulo é dado por seu termo de maior grau.

• O polinômio a3x 2a4x3 + 9ax2

é do 7o grau.

4o grau 7o grau 3o grau

• O polinômio x3 6x 2y2 2xy

é do 4o grau.

3o grau 4o grau 2o grau

O grau de um polinômio reduzido também pode ser estabelecido em relação a determinada variável. Nesse caso, o grau é dado pelo maior expoente com que a variável considerada aparece nos termos não nulos do polinômio. Assim:

3˘ grau em relação à variável x

O polinômio x 3y + 3x 2y4 é do

4˘ grau em relação à variável y

POLINÔMIOS COM UMA SÓ VARIÁVEL REAL

Considere estes polinômios reduzidos.

• x 2 + 7x 10

• x 3 2x 2 + 4x 1

Polinômios como esses são denominados polinômios na variável x Em Matemática, é comum a escrita de polinômios com os termos em ordem, segundo as potências decrescentes da variável. Observe os exemplos.

• 6x 2 5x 1

• x 3 x 7

• 5x4 7x3 x 2 + 2x 10

Quando um polinômio está assim ordenado, e nele não aparecem uma ou mais potências da variável, dizemos que o polinômio é incompleto. Nesse caso, os coeficientes dos termos que não aparecem no polinômio são zeros. Acompanhe os exemplos:

• x 3 7x 1 é incompleto e pode ser escrito deste modo, em sua forma completa: x3 + 0x 2 7x 1 (forma geral).

• x4 9 é incompleto e pode ser escrito desta maneira, em sua forma completa: x4 + 0x3 + 0x 2 + 0x 9 (forma geral).

D2_AV4-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 128 15/08/22 22:34

AMPLIANDO Link

EXPRESSÕES algébricas e polinômios (videoaulas). Portal da OBMEP. Rio de Janeiro, [2013?]. Disponível em: https://portaldaobmep.impa.br/index.php/modulo/ver?modulo=13. Acesso em: 7 ago. 2022.

Nesse site do Portal da OBMEP, há diversas videoaulas sobre expressões algébricas e polinômios. Elas podem ser utilizadas para complementar ou para ampliar o estudo.

ATIVIDADES

Responda às questões no caderno.

1. Escreva os polinômios a seguir na forma reduzida.

a) 2a 2 x 5a 2 x 2 + 3a 2 x 7ax 2 + + a2x2 2a2x + 5ax 2 3a2x 4a2x 2 2ax 2

b) 6x 5y + 3xy + 2xy 5x + 9y + + 4x xy y 5x + 3y + 4xy

2. Ao resolver uma questão, Fernando chegou ao seguinte polinômio: 0,5a (0,7b 1,2ab) 1,3b + + (0,8a + 2b 0,6ab)

1,3a + 0,6ab É um binômio.

a) Qual é a forma reduzida desse polinômio?

b) O p olinômio é um trinômio ou um binômio?

3. Qual é a forma reduzida de cada um dos polinômios?

a) 8ab (a + 7b 5) + ( 5ab + 2 b) + + (+4a + 2ab 6b) 5ab + 3a 14b + 7

b) 2x2 [2xy + x2 (3xy + y2) + 2y2] xy

DESAFIOS

ORIENTAÇÕES DIDÁTICAS

Atividades

4. Em relação à variável x, qual é o grau do polinômio a seguir? 5 ˘ grau.

2bx 2 7ax5 3cx + abx 3

5. C onsidere o polinômio 10 6x 3 + + x 9x4 + x5 5x2. Escreva-o na forma ordenada e dê o grau do polinômio.

x5 9x4 6x 3 5x 2 + x + 10; 5 ˘ grau.

6. Escreva a forma geral do polinômio c5 1.

c5 + 0c4 + 0c 3 + 0c 2 + 0c 1

7. Qual é o polinômio reduzido que expressa a área da figura?

3ax

Nesse bloco de questões, os estudantes vão aplicar a escrita da forma reduzida e da forma geral (ou completa) de um polinômio e, ainda, determinar o grau de um polinômio.

Na atividade 4, ressaltar que, para obter o grau de um polinômio em relação a determinada variável, deve-se observar o expoente dessa variável em todos os termos do polinômio em que ela aparece. O maior expoente é o grau procurado. No caso do polinômio apresentado, o grau em relação à variável x é 5, maior expoente dessa variável. Perguntar aos estudantes qual é o grau em relação às demais variáveis do polinômio.

8. Todos estes polígonos são regulares e têm lados com a mesma medida x

a) O que representa a expressão algébrica escrita dentro de cada figura dos três primeiros polígonos? O perímetro.

b) Que expressão algébrica deve ser escrita dentro da figura do hexágono?

9. Escreva a expressão algébrica que representa o perímetro de cada um dos hexágonos regulares da figura a seguir.

6x; 6x + 6; 6x + 12

Na atividade 6, inicialmente, perguntar quantas variáveis têm o polinômio dado; espera-se que os estudantes reconheçam apenas uma. Perguntar, ainda, se o polinômio está na forma reduzida, justificando. Espera-se que os estudantes digam que está na forma reduzida porque não há termos semelhantes. Finalizar verificando se os estudantes reconhecem que se trata de um polinômio incompleto.

Assim, os estudantes perceberão o que devem observar para obter a forma geral de um polinômio de uma variável.

Para os desafios 8 e 9, retomar o conceito de polígono regular com os estudantes. Propor a eles que se reúnam em duplas para resolver as questões. Socializar as diferentes estratégias que surjam e fazer a correção coletivamente. Alguns estudantes podem explicar para a classe, oralmente, como pensaram.

Adição algébrica de polinômios

No estudo da adição algébrica de polinômios, os estudantes perceberão que grande parte dos procedimentos aritméticos são válidos no campo algébrico. Discutir cada uma das situações apresentadas no Livro do estudante. A terceira situação mostra uma adição algébrica mais complexa; sugere-se que seja resolvida na lousa. Destacar a inversão dos sinais dos termos do polinômio P3

ADIÇÃO ALGÉBRICA DE POLINÔMIOS

Considere as situações a seguir.

1 Qual é o polinômio que representa o perímetro da figura?

Como o perímetro representa a soma das medidas dos lados, temos:

(2a + 1) + (a + 10) + (a 3) =

= 2a + 1 + a + 10 + a 3 =

= 2a + a + a + 1 + 10 3 =

a EDITORIA DE ARTE

2a +

= 4a + 8 Reduzindo os termos semelhantes. O polinômio que representa o perímetro da figura é 4a + 8

a

Como podemos observar, os preços são expressos de maneiras diferentes. Nessas condições, qual é o polinômio que expressa a diferença entre os preços do videogame nas duas lojas?

A diferença entre os preços das duas lojas pode ser assim escrita:

(2x + 5y) (x + 3y) = subtração de polinômios

= 2x + 5y x 3y = 2x x + 5y 3y = x + 2y

A diferença entre os preços é expressa pelo polinômio x + 2y

3 Considere os polinômios P1, P2 e P3 a seguir.

P1: x 3 + 4x 2 3x + 7 P2: 3x 3 + 6x 5 P3: x 2 + 2x + 3

P3

= =

x3 + 4x 2 3x + 7 + 3x3 + 6x 5 x 2 2x 3 = = x 3 + 3x3 + 4x 2 x 2 3x + 6x 2x + 7 5 3 =

ATIVIDADES

8.a) 6a 15b + 7c

b) 7y2 4ay + 5a2

c) 2a3 + 5a2b ab2 5b3

d) 2x 2 + 2y2 + 4x 2y2

Responda às questões no caderno.

1. Observe as medidas dos lados da figura e escreva o polinômio que expressa o perímetro dela. 13x + 3,1a

e) 0,2a2 0,6b2 0,8c 2

f) 4a2 4ab + 5b2 + 2c 2

g) 0,2x 3 + 0,3x 2 + 0,4x 6

4.a) 9a2x 2 + 7ax + 11a 6x

b) Qual é a soma de A com seu oposto? 0

c) Subtraindo de A o seu oposto, que polinômio obtemos?

18a2x 2 14ax 22a + 12x

5. Considere os polinômios a seguir.

ORIENTAÇÕES DIDÁTICAS

Atividades

2. Q uando adicionamos os polinômios 17x 2 15x + 20 e 13x 2 + 20x 31, obtemos a soma ax 2 + bx + c. Qual é o valor numérico da expressão a + b + c?

3. Em uma partida de basquete, Tiago fez x arremessos de lances livres, dos quais acertou 60% menos 3. Seu companheiro de equipe, Fernando, também arremessou x lances livres e acertou 40% mais 1 desses lances.

Escreva o polinômio que representa:

a) a quantidade de lances livres que Tiago acertou. 0,6x 3

b) a quantidade de lances livres que Fernando acertou. 0,4x + 1

c) a quantidade de lances livres que os dois acertaram juntos. x 2

d) a diferença entre a quantidade de lances livres que Tiago acertou e a quantidade de lances livres que Fernando acertou.

0,2x 4

4. Você sabia que um polinômio tem oposto? Observe as seguintes afirmações.

• x é o oposto de +x.

• 2x y2 é o oposto de 2xy2

• (2a + b) é o oposto de (2a + b).

• (x 2 3x + 1) é o oposto de (x 2 3x + 1).

Seja A o polinômio dado por 9a2 x 2 7ax 11a + 6x, responda:

a) Qual é o oposto do polinômio A?

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

P1: a + b + c

P2: a b + c P3: a + b c

Determine:

a) P1 + P2 + P3 3a + b + c

b) P1 + P2 P3 a b + 3c

c) P1 P2 + P3 a + 3b c

d) P1 P2 P3 a + b + c

6. Um polinômio A adicionado ao polinômio 9x + 3y 10xy x 2 y2 tem como resultado o polinômio a seguir. 3x 2y2 7x + 5y  xy Qual é o polinômio A?

4x 2y2 16x + 2y + 9xy

7. Considere os polinômios P e Q a seguir.

P: x 2 + y2 5xy

Q: 2x 2 + 8xy 3y2

Determine:

a) P + Q 3x 2 + 3xy 2y2

b) P Q x 2 13xy + 4y2

8. Determine os polinômios que representam:

a) (15a 7b + 4c) + ( 8b + 3c 9a)

b) (2y2 3ay + 4a2) (ay 5y2 a2)

c) (3a3 2a2b + 5ab2 6b3) + + (7a2b 5a3 + b3 6ab2)

d) (x2 3xy + y2 x2y2) + (+x2 + 5x2y2 + + y2 + 3xy)

e) (a2 1,6b2 + 0,9c2) (0,8a2 b2 + + 1,7c2)

f) (3a2 5ab c 2 3b2) + ( 6ab + + c2) + (7a2 3ab + 2b2)

g) (0,9x 3 1,8x + 1) + ( 1,3x 2 + + 2,6x 2) (0,7x3 1,6x 2 + + 0,4x + 5)

As questões apresentadas propõem que os estudantes apliquem a adição algébrica de polinômios. Algumas das questões retomam conceitos já estudados, como é o caso do valor numérico de uma expressão algébrica, abordada na atividade 2. Resolver essa atividade na lousa caso julgue necessário. Retomar, na atividade 3, o registro de porcentagens escritas na forma decimal.

Na atividade 4, discutir com os estudantes o conceito de oposto. Comentar que todo polinômio adicionado ao seu oposto resulta no polinômio nulo.

ORIENTAÇÕES DIDÁTICAS

Multiplicação de polinômios

Ao abordar a multiplicação de polinômios, retomar com os estudantes a propriedade distributiva. Verificar se eles compreendem que, na primeira situação apresentada, devem multiplicar o monômio pelos termos do polinômio.

MULTIPLICAÇÃO DE POLINÔMIOS

Multiplicando um monômio por um polinômio

De que maneira podemos representar a área da figura?

Uma das maneiras de representar a área é:

x  (2x + y)

medida do comprimento

medida da largura

A expressão x ? (2x + y) representa algebricamente a multiplicação do monômio x pelo polinômio 2x + y.

Outra maneira de representar a área da figura é adicionar as áreas das figuras que a compõem, ou seja:

x (2x + y) = x 2x + x y = 2x2 + xy

área da figura 1 área da figura 2

Observe que usamos a propriedade distributiva da multiplicação em relação à adição algébrica: x (2x + y) = 2x 2 + xy

Podemos dizer que:

A multiplicação de um monômio por um polinômio é feita multiplicando-se o monômio por cada termo do polinômio.

Acompanhe mais um exemplo.

Qual é o polinômio que representa o produto 5a2m  (3a 2am)?

5a2m (3a 2am) =

= 5a2m 3a 5a2m 2am =

= 15a3m 10a3m2

Nesse caso:

• multiplicamos 5a2m por 3a: 5a2m 3a = 5 3 a2 a m = 15a3m;

• multiplicamos 5a2m por 2am: 5a2m  ( 2am) = 5  ( 2)  a2  a  m  m = 10a3m2;

• adicionando algebricamente ambos os resultados, obtivemos o polinômio 15a3m 10a3m2

D2_AV4-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 132 15/08/22 22:35

AMPLIANDO

Link

DESAFIO de multiplicação de monômios por polinômios. Khan Academy. [S l.], c2022. Disponível em: https:// pt.khanacademy.org/math/algebra-home/alg-polynomials/alg-multiplying-polynomials-by-monomials/e/multiply -monomials-by-polynomials-challenge. Acesso em: 6 ago. 2022.

Uma possibilidade é pedir aos estudantes para explorarem atividades em que se faz a multiplicação de monômios por polinômios acessando a plataforma Khan Academy.

Multiplicando um polinômio por outro polinômio

De que maneira podemos representar a área da figura a seguir?

DIDÁTICAS

Como a figura representada é um retângulo de lados medindo (x + a) e (x + b), uma das maneiras de representar a área é: (x + a) (x + b)

medida da largura medida do comprimento

Note que algebricamente a expressão (x + a) ? (x + b) representa a multiplicação de um polinômio por outro polinômio.

Outra maneira de representar a área da figura é adicionar as áreas das quatro figuras que a compõem, ou seja:

x x + x b + a x + a b = x2 + ax + bx + ab

área 1 área 2 área 3 área 4

Então: (x + a) (x + b) = x x + x b + a x + a b = x2 + ax + bx + ab

polinômio polinômio

Note que usamos a propriedade distributiva da multiplicação em relação à adição algébrica:

• Multiplicamos x por x, o que resultou em x 2

• Multiplicamos x por b, o que resultou em bx.

• Multiplicamos a por x, o que resultou em ax.

• Multiplicamos a por b, o que resultou em ab.

Podemos dizer que:

A multiplicação de um polinômio por outro polinômio é feita multiplicando-se cada termo (ou monômio) de um deles por cada termo (ou monômio) do outro e reduzindo-se os termos semelhantes (se houver).

Ao abordar a multiplicação de dois polinômios, por exemplo, destacar que todos os termos do primeiro devem ser multiplicados por todos os termos do segundo, o que significa aplicar a propriedade distributiva. Para retomar essa propriedade, propor aos estudantes a representação geométrica para, em seguida, realizar multiplicação entre polinômios. Sugerir que pensem na representação geométrica do produto de 12 por 16. Caso eles tenham dúvidas, mostrar que 12 pode ser escrito como 10 + 2 e 16, como 10 + 6.

Depois de discutir com os estudantes as maneiras apresentadas anteriormente, propor a eles que façam a seguinte multiplicação envolvendo dois binômios: (x + 2) ? (x + 6)

Eles podem começar pela representação geométrica.

ORIENTAÇÕES DIDÁTICAS

Atividades

As questões desse bloco exploram a multiplicação de monômio por polinômio.

Na atividade 2, se necessário, esclarecer que deve ser efetuada primeiro a multiplicação entre os monômios e, depois, a multiplicação entre o monômio resultante e o polinômio.

Na atividade 5, antes de os estudantes determinarem a forma reduzida, perguntar a eles qual é o grau do polinômio P. Discutir com eles as possíveis respostas, que serão validadas ao se obter a forma reduzida.

Acompanhe os exemplos.

1 Qual é o polinômio que representa o produto (3a + 2b) (2a 5b)?

(3a + 2b) (2a 5b) = Também podemos fazer assim:

= 3a 2a + 3a ( 5b) + 2b 2a + 2b ( 5b) =

= 6a2 15ab + 4ab 10b2 =

= 6a2 11ab 10b2

O polinômio procurado é 6a2 11ab 10b2

2 Vamos calcular o produto de x + 2 por x2 x 2.

ATIVIDADES

Responda às questões no caderno.

1. Escreva o polinômio que representa a área da região verde da figura.

Outra maneira de se fazer é assim:

4. Em uma loja de produtos esportivos havia a seguinte oferta:

1,2y2

2. A s dimensões de um bloco retangular são 3x, 2y e (2x y). Se o volume de um bloco retangular qualquer é dado pelo produto das medidas de suas três dimensões, escreva o polinômio que representa ovolume desse bloco retangular.

12x 2y 6xy2

3. E screva os polinômios na forma reduzida.

a) 2bx(1 a) + 2x(a b c) 2x(a c)

b) 3a(2a b) [a(6a 3b) b(3a 5b)]

3ab 5b2

AMPLIANDO Vídeo

Sabendo que ontem foram vendidos x pares desses patins, escreva o polinômio que representa a quantia que a loja faturou com as vendas nesse dia.

xy + 4xz a3 + b3

MULTIPLICAÇÃO de polinômio por polinômio e exercícios – Álgebra básica MAB #74. 2019. Vídeo (13min15s).

Publicado pelo canal Matemática Rio com Prof. Rafael Procopio. Disponível em: https://www.youtube.com/ watch?v=tdNYR781hII&t=2s. Acesso em: 7 ago. 2022.

Nessa videoaula, são apresentados alguns exemplos sobre como calcular o produto de polinômios, além da resolução de alguns exercícios.

6. Observe a figura.

a) Escreva o polinômio que representa a área da região verde. 6x 2 xy y2

b) Calcule o valor numérico do polinômio obtido para x = 20 e y = 10. 2 100

7. Escreva o polinômio obtido multiplicando-se o polinômio 1,2x + 0,5y por 1,5x 0,5y. 1,8x 2 + 0,15xy 0,25y2

8. Quando você multiplica 5x2 x 1 por 2x2 + x 5, obtém como produto o polinômio ax4 + bx3 + cx2 + dx + e. Qual é o valor numérico da expressão a + b + c + d + e? 6

9. Escreva o polinômio que representa cada produto.

a) (3a 1,5x)(0,7a 5x) b) (a2 1)(2a2 2a + 1) c) (a + x)(a2 ax + x 2)

10. Usando a multiplicação, escreva o polinômio que representa cada uma das potências a seguir.

a) (x 5y)2 b) (0,6 + 2ax)2 c) (b + y)3

11. Você sabe que o volume de um bloco retangular é dado pelo produto das medidas das três dimensões desse sólido. Determine o polinômio que representa a soma dos volumes das figuras a seguir.

ORIENTAÇÕES DIDÁTICAS

Orientar os estudantes na atividade 8 para que efetuem o produto entre os polinômios dados, façam a redução dos termos semelhantes e, então, identifiquem os coeficientes a, b, c, d e e

O item a da atividade 12 merece atenção especial pelo fato do sinal de menos que separa os dois produtos serem efetuados. Circular pela sala de aula e verificar se os estudantes consideram o sinal ao realizar as multiplicações.

12. Escreva os polinômios na forma mais simples.

a3b

a) (a3 b3 )(a + b) (a2 + b2)(a2 b2) b) (a 2b)[a(b 3) + b(1 a)] DESAFIO

13. Você sabe jogar dominó?

Nesse dominó, também devemos encostar as peças em uma das extremidades abertas. A parte de uma peça em que aparece um polígono deve ficar em contato com a parte de outra peça, na qual apareça uma expressão algébrica que represente a área ou o perímetro desse polígono. Observando o jogo já co meçado, como você o continuaria? Indique em que sequência você colocaria as seguintes peças.

Pela extremidade da esquerda: B, C, D, A. Pela extremidade da direita: A, D, C, B

Para a resolução do desafio 13, pode-se enriquecer esse trabalho de integração com Geometria propondo aos estudantes que, depois de resolvê-lo, construam um dominó com 20 peças (aproveitando as nove já expostas na atividade), que relacionem polinômios com perímetros e áreas de figuras planas e até volumes de sólidos conhecidos.

Organizar a turma em grupos (de 4 ou 5 integrantes) para que cada um deles construa o seu dominó. Discutir com eles se todos os dominós construídos completam o jogo.

Esses jogos podem ficar na escola para serem aproveitados em outros anos.

ab3 3a2 + 7ab 2b2

ORIENTAÇÕES DIDÁTICAS

Divisão de polinômios por um monômio

Resolver na lousa as duas situações propostas no Livro do estudante, certificando-se de que os estudantes compreendem a divisão termo a termo do polinômio pelo monômio dado. Se julgar pertinente, antes de passar para as atividades, propor mais alguns cálculos na lousa e verificar como os estudantes se organizam para a resolução.

Atividades

As questões propostas têm como objetivo levar os estudantes a efetuar a divisão de um polinômio por um monômio não nulo ou de um polinômio por outro polinômio não nulo e aplicar a relação fundamental da divisão: dividendo = quociente x x divisor + resto.

Nos exercícios que envolvem divisão de polinômios por monômios, sugerir aos estudantes que façam a representação das divisões em forma de fração antes de realizar os cálculos, por exemplo:

DIVISÃO DE POLINÔMIOS POR UM MONÔMIO

Efetuamos a divisão de um polinômio por um monômio não nulo fazendo a divisão de cada termo do polinômio pelo monômio.

Observe outra situação.

3 Calcular (12a4b2 28a2b2 + 4ab3) : (4ab). (12a4b2 28a2b2 + 4ab3) : (4ab) =

= (12a4b2) : (4ab) (28a2b2) : (4ab) + (4ab3) : (4ab) =

= 3a3b 7ab + b2

Responda às questões no caderno.

1. Efetue cada uma das seguintes divisões.

:

c) (a2b2c2 + a3bc abc2) : (abc) abc + a2

2. Ao multiplicar um polinômio P por um monômio, você vai encontrar 18a2 x5 + 42a3x4 72a4x 3. Se o monômio é 6a2 x 3, qual é esse polinômio? 3x

D2_AV4-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

+ 7ax 12a2

AS QUEBRADEIRAS DE COCO BABAÇU

As quebradeiras de coco babaçu formam uma das mais importantes comunidades tradicionais brasileiras e lutam para preservar seu território e sua identidade. A seguir, leia o trecho de um texto a respeito dessa comunidade.

Quebradeiras de coco babaçu no povoado de São José de Lagoa. Viana (MA), 2019.

As quebradeiras de coco babaçu têm uma grande importância histórica, econômica, social, política, ambiental e cultural na chamada “região dos babaçuais”, que engloba partes dos estados do Pará, Piauí e Tocantins e, principalmente, do Maranhão. Mais de 300 mil mulheres agroextrativistas exercem a atividade de extrativismo do coco babaçu [...] Os babaçuais nascem espontaneamente na região e hoje ocupam mais de 25 milhões de hectares nos quatro estados, com diferentes densidades. Apesar disso, muitos fazendeiros impedem as quebradeiras de chegarem às palmeiras que estão em suas propriedades. O MIQCB [Movimento Interestadual das Quebradeiras de Coco Babaçu] tem sido o principal movimento articulador na luta pelo acesso aos babaçuais. Por causa da luta organizada, em alguns municípios da região já existem leis que garantem o acesso livre aos babaçuais em terras públicas e privadas para exploração em regime de economia familiar. As chamadas Leis do Babaçu Livre também proíbem as derrubadas indiscriminadas, cortes de cachos e uso de herbicidas. Garantir isso às quebradeiras de coco é não só preservar sua fonte de renda, mas também sua tradição e o equilíbrio do meio ambiente.

Dar visibilidade para a luta das quebradeiras de coco — e a seus desafios e conquistas — é importante para fortalecer a luta pelo direito a terra, território e recursos naturais e, num contexto mais amplo, fortalecer também a luta de outros povos e comunidades tradicionais do país.

MATOS, Francinaldo; SHIRAISHI, Joaquim; RAMOS, Vitória. Acesso à terra, território e recursos naturais: a luta das quebradeiras de coco babaçu. ActionAid Brasil. [Rio de Janeiro], c2015. Disponível em: https://actionaid.org.br/ wp-content/files_mf/1493418575quebradeiras_actionaid_port_rev1.pdf. Acesso em: 10 jun. 2022.

Responda às questões no caderno.

4,28x; 642; Significa que uma quebradeira de coco, que extraiu 150 quilogramas de amêndoa de babaçu, recebeu, no mínimo, 642 reais.

1. Em 2022, a Política de Garantia de Preços Mínimos (PGPM) estabelecia o preço mínimo para o quilograma da amêndoa de babaçu no país em R$ 4,28.

• Escreva uma expressão algébrica para representar o valor mínimo, em reais, recebido por uma quebradeira de coco que produziu mas de amêndoa de babaçu em 2022. Calcule o valor numérico dessa expressão algébrica para x O que significa esse valor numérico?

2. Pesquise quais são os produtos oriundos do babaçu e como eles são produzidos e comercializados. Depois, junte-se a dois colegas, e compartilhem as informações que acharam interessantes.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd 137

AMPLIANDO

Atividade complementar

Em 2020, foram extraídas 47 640 toneladas de coco babaçu no Brasil, e o Maranhão produziu cerca de 93% de todo esse coco. Quantas toneladas de coco babaçu, aproximadamente, foram produzidas por esse estado?

Resolução da atividade

0,93 ? 47 640 1 44 305

Em 2020, foram produzidas, aproximadamente, 44 305 toneladas de coco babaçu no estado do Maranhão.

ORIENTAÇÕES DIDÁTICAS

Por toda parte

Ler o texto da seção Por toda parte, coletivamente, destacando a importância das mulheres quebradeiras de coco babaçu. Esse tema favorece o desenvolvimento do Tema Contemporâneo Transversal Educação para valorização do multiculturalismo nas matrizes históricas e culturais Brasileiras, das competências gerais 6 e 9 e da competência específica 5 da área de Matemática.

Verificar se há palavras desconhecidas no texto. Incentivar os estudantes a procurar o significado em dicionários, físicos ou on-line

Na atividade 1, comentar com os estudantes que a Política de Garantia de Preços Mínimos (PGPM) é uma ferramenta para diminuir variações na renda dos produtores rurais e assegurar uma remuneração mínima por seus produtos.

Organizar os estudantes em duplas ou trios para realizarem a pesquisa proposta na atividade 2 . Incentivar que as apresentações sejam feitas em diferentes plataformas, como na forma de vídeos, cartazes, podcasts etc.

JOÃO

LUIZ BULCÃO/TYBA

RICARDO AZOURY/PULSAR IMAGENS 8-10 cm

ORIENTAÇÕES DIDÁTICAS

Tratamento

da informação

Nessa seção, os estudantes entrarão em contato com uma tabela que apresenta a esperança de vida ao nascer em dez países, em 2020. A saúde é um dos pilares que compõem o Índice de Desenvolvimento Humano (IDH). O texto também aborda noções sobre o Produto Interno Bruto (PIB) de um país. Conversar com os estudantes e verificar se eles compreendem, ainda que parcialmente, o significado de cada um desses conceitos. Essas discussões contribuem para o desenvolvimento do Tema Contemporâneo Transversal Educação em Direitos Humanos

O tema desta seção também possibilita conversas e pesquisas sobre o envelhecimento e os direitos dos idosos, favorecendo o desenvolvimento do Tema Contemporâneo Transversal Processo de envelhecimento, respeito e valorização do Idoso.

Nessa proposta, podem ser abordados diversos assuntos, como a importância de valorizar os idosos e garantir que eles tenham acesso aos direitos como vaga prioritária e atendimento preferencial. Os estudantes podem escolher um local, ou locais, como uma loja, um mercado ou a escola, e verificar se esses direitos estão sendo cumpridos no local.

É importante, também, discutir o papel das entidades governamentais na vida do idoso. O envelhecimento populacional deve ser acompanhado de medidas governamentais que ajudem a lidar com os desafios que essa parte da população enfrentará. Verificar se os estudantes entendem que eles farão parte dessa população um dia; então, lutar pelos direitos dos idosos é lutar pelos próprios direitos. Entre as possíveis medidas a serem discutidas com os estudantes, destacam-se: políticas de

INFORMAÇÃO TRATAMENTO DA

INTERPRETANDO DADOS

2. Menor esperança de vida: 76,08 anos, no Brasil; maior esperança de vida: 84,62 anos, no Japão; variação da esperança de vida: 8,54 anos.

O Índice de Desenvolvimento Humano (IDH) é uma medida resumida do desenvolvimento humano apoiado sob três aspectos: saúde, educação e renda. Ele surgiu com o intuito de oferecer um contraponto ao Produto Interno Bruto (PIB) per capita, que é uma medida econômica e que não reflete a qualidade de vida de uma população. O pilar da saúde utiliza a esperança de vida ao nascer como parâmetro de cálculo.

A tabela a seguir mostra a situação, em 2020, de dez países em relação a esse indicador.

Esperança de vida ao nascer – 2020

País Esperança de vida ao nascer (em ano)

GLOSSÁRIO

Esperança de vida: estimativa, em ano, do tempo médio de vida de uma pessoa.

Elaborada com base em: COUNTRYECONOMY.COM. Esperança de vida ao nascer. Countryeconomy.com [S l.], [2022?]. Disponível em: https:// pt.countryeconomy.com/demografia/ esperanca-vida. Acesso em: 10 jun. 2022.

Responda às questões no caderno.

1. Qual era a média, aproximadamente, da esperança de vida ao nascer entre os países indicados, em 2020?

81,467 anos.

2. Qual é a variação da esperança de vida ao nascer entre os países que ocupam, respectivamente, a primeira e a última colocação na tabela? Identifique quais são esses países.

3. Em 1960, a esperança de vida ao nascer no Brasil era de 54,14 anos. Em quantos anos aumentou a esperança de vida no Brasil de 1960 a 2020? Em 21,94 anos.

Idosos se exercitando ao ar livre. O Japão está entre os países com maior esperança de vida do mundo.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

assistência social e auxílio ao idoso, inclusão do idoso no mercado de trabalho adaptado para complementação da renda, maiores investimentos nos serviços previdenciários e políticas de prevenção de doenças.

Para fomentar essa discussão, os estudantes podem trazer relatos de pessoas idosas da comunidade escolar sobre as dificuldades que enfrentam no dia a dia, ou podem realizar pesquisas estatísticas com essa população a fim

de identificar melhorias no bairro que possam trazer qualidade de vida para eles.

Por exemplo, a criação de um centro de atividades físicas para idosos ou a implantação de aulas comunitárias de alongamento ou pilates em um parque ou praça do bairro apenas para idosos pode ser uma política de melhoria da saúde e qualidade de vida dessas pessoas que também contribui para a comunidade escolar com a criação de empregos.

ORIENTAÇÕES DIDÁTICAS

Taxa de natalidade – 2020

SAIBA QUE

O IDH não contempla todos os índices de desenvolvimento humano de um país. Por exemplo, ele não contempla a taxa de natalidade do país. Essa taxa é o indicativo da quantidade de nascidos vivos a cada 1 000 habitantes no período de um ano. Observe a tabela com esse índice para os mesmos países da tabela Esperança de vida ao nascer – 2020 O símbolo ‰ deve ser lido “por mil”.

Elaborada com base em: COUNTRYECONOMY.COM. Natalidade. Countryeconomy.com [S l.], [2021?]. Disponível em: https://pt.countryeconomy.com/ demografia/natalidade.anio=2020. Acesso em: 10 jun. 2022.

4. Japão e Itália; esses países não são os que têm a menor esperança de vida.

4. Qual dos países da tabela tem a menor taxa de natalidade? Esse país é o que apresenta a menor esperança de vida?

Na primeira questão proposta na página 138, retomar com os estudantes o conceito de média aritmética. Avaliar a possibilidade do uso de uma calculadora simples para efetuar esse cálculo.

5. Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), a população do Brasil em 2020 era de aproximadamente 211 755 0 00. Considerando essa informação e os dados da tabela, calcule a quantidade aproximada de nascidos vivos no Brasil nesse ano.

6. O IBGE é o órgão no Brasil responsável pela coleta, pelo tratamento e pelo armazenamento dos dados relativos à população brasileira. Debata com a turma a importância desse trabalho. A que ele se destina?

Aproximadamente 2 850 222 nascidos vivos. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

7. Os dados sobre a esperança de vida e a taxa de natalidade estão organizados em tabelas. Organize-os em gráficos e, em seguida, faça um texto explicando a escolha pelo tipo de

Conversar com os estudantes, na terceira questão, sobre as hipóteses que eles poderiam levantar para explicar o aumento da esperança de vida ao nascer no Brasil, entre os anos de 1960 e 2020. Ao expor suas ideias, os estudantes desenvolvem a capacidade de inferência, argumentação e o respeito ao posicionamento dos colegas. Dando continuidade ao tema, na página 139 do Livro do estudante, são apresentados dados sobre as taxas de natalidade dos mesmos países já estudados, também em 2020. Destacar para a turma que essa taxa não faz parte do IDH.

As atividades propostas nessa página contribuem para o desenvolvimento da competência específica 6 da área de Matemática.

Na atividade 5, propor o uso da calculadora como ferramenta de apoio para efetuar o cálculo de porcentagem. Discutir com estudantes as diferentes possibilidades de gráficos e permitir que elejam o que julgarem ser o mais adequado na atividade 7, contribuindo para o desenvolvimento da habilidade EF08MA23.

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

AMPLIANDO Link

INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Você foi procurado pelo IBGE? Para que servem as pesquisas do IBGE? Respondendo ao IBGE . Rio de Janeiro, c2022. Disponível em: https://respondendo.ibge. gov.br/voce-foi-procurado-pelo-ibge/para-que-servem-as-pesquisas-do-ibge.html. Acesso em: 1 ago. 2022. Sugerir aos estudantes que consultem esse site do IBGE para obter informações sobre para que servem as pesquisas sobre população.

A taxa de natalidade é um importante indicador para avaliação de questões de saúde pública.

ORIENTAÇÕES DIDÁTICAS

Retomando o que aprendeu

Essas questões visam retomar o trabalho com expressões algébricas e seus valores numéricos. Pode-se propor aos estudantes que tragam de casa algumas questões já resolvidas e desenvolvam outras na sala de aula, com os colegas, fazendo uma autocorreção das questões resolvidas individualmente. As questões em que os estudantes tiverem mais dificuldades podem ser resolvidas na lousa.

Retomar com eles alguns dos tópicos tratados nesta Unidade, dando ênfase para a Educação financeira e o Tratamento da informação. Questioná-los se o tema cálculo algébrico e expressões algébricas se relaciona com esses tópicos. A ideia é fazê-los perceber que os modelos matemáticos utilizados na situação do cotidiano dependem da Álgebra para serem formulados.

Explicar que existem modelos matemáticos que fazem parte do dia a dia de maneira implícita, por exemplo, algoritmos computacionais e fórmulas de juro composto.

Responda às questões no caderno.

1. Determine o valor numérico da expressão 3x 2 5x 1, quando:

a) x = 0. 1

b) x = 1. 7

c) x = 1,2. 2,68

2. Considere a expressão algébrica. ( a b)(a + b) + ab3 a b 2

Sendo a = b = 2, o valor numérico dessa expressão é: Alternativa a.

diretor de marketing dessa empresa verificou que a quantidade vendida desse produto no mês podia ser representada pela expressão algébrica 3 2 x40 + , em que x representa a quantidade de anúncios na televisão durante o mês. Se em determinado mês foram feitas 50 aparições na televisão, então foram vendidas, nesse mês: Alternativa c.

a) 125 unidades.

b) 120 unidades.

d) 110 unidades.

e) 105 unidades.

a) 2.

b) 2. c) 1. d) 1. e) 4.

c) 115 unidades.

Alternativa e.

3. C onsidere a expressão algébrica xy xy . O valor numérico dessa expressão, quando x = 0,4 e y = 0,5 é:

a) 4.

b) 1. c) 1. d) 2. e) 2.

4. (Encceja/MEC) Em uma gincana escolar, as equipes participam de um torneio de perguntas e respostas. São apresentadas 20 perguntas para cada equipe. A cada pergunta respondida corretamente, a equipe recebe 3 pontos; para cada pergunta cuja resposta estiver errada, perde 2 pontos; e para cada pergunta não respondida, perde 1 ponto. Represente por C, E e N as quantidades de respostas corretas, respostas erradas e perguntas não respondidas por uma equipe, respectivamente.

A expressão algébrica que fornece a pontuação final obtida por uma equipe nesse torneio é Alternativa a.

6. U m grupo de estudantes de meteor ologia pesquisou as variações de temperatura em certo município. Após longa coleta de dados, o grupo concluiu que a temperatura podia ser calculada por meio da expressão 1 6 t 2 + 4t + 10, na qual t representa a hora do dia. O grupo calculou a temperatura no município às 12 horas e às 18 horas. Nesse período, a temperatura diminuiu quantos graus Celsius? Alternativa d.

a) 9 °C

b) 8 °C c) 7 °C d) 6 °C e) 5 °C

7. Se o volume da esfera é dado por 4 3 r 3 p

(em que r é a medida do raio da esfera), ovolume correspondente a uma bola maciça com 10 cm de diâmetro, em centímetro cúbico, é: Alternativa e. (Utilize p 1 3,14.)

a) 4 186,66.

b) 500.

d) 418,64. e) 523,33.

a) 3C 2E N

b) 3C 2E + N c) 3C 2E d) 3C 3E

5. O presidente de uma empresa resolveu anunciar um de seus produtos na televisão. A partir de então, constatou-se que houve um aumento nas vendas. O

D2_AV1-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

c) 5 233,33.

8. S abe-se que a x = 10. Então, qual é o valor de A , se A = 4 ax 2a2x?

Alternativa b.

a) 20 0

b) 160

ORIENTAÇÕES DIDÁTICAS

9. A área do triângulo colorido dentro do retângulo a seguir pode ser representada pelo monômio: Alternativa d.

2,5x

5x

12. (Enem/MEC) Um forro retangular de tecido traz em sua etiqueta a informação de que encolherá após a primeira lavagem mantendo, entretanto, seu formato. A figura a seguir mostra as medidas originais do forro e o tamanho do encolhimento (x) no comprimento e (y)na largura. A expressão algébrica que representa a área do forro após ser lavado é (5 x) (3 y).

A atividade 10 retoma a construção de uma sequência, a partir de uma lei de formação dada, contribuindo para o desenvolvimento das habilidades EF08MA10 e EF08MA11.

Um novo olhar

a) 12,5x.

b) 6,25x. c) 12,5x 2 d) 6,25x 2 e) 6,25.

10. C alculando-se os valores da expressão

n (n 1) para n igual a 1, 2, 3, 4, ..., obtém-se qual das sequências a seguir?

Alternativa b.

a) (1, 4, 9, 16, 25, ...)

b) (0, 2, 6, 12, 20, ...)

c) (0, 2, 9, 16, 20, ...)

d) (2, 6, 12, 20, 30, ...)

e) ( 1, 2, 6, 12, 20, ...)

Nestas condições, a área perdida do forro, após a primeira lavagem, será expressa por Alternativa e.

a) 2xy

b) 15 3x

? Alternativa a.

11. Q ual é o 7o termo da sequência xy 4 , xy 2 ,  xy , 2 3

c) 15 5y

a) 16x7y

b) 8x7y c) 16x6y d) 16x5y e) 32x7y

UM NOVO OLHAR

d) 5y 3x

e) 5y + 3x xy

Nesta Unidade, abordamos a introdução ao cálculo algébrico, as expressões algébricas ou literais e o valor numérico das expressões algébricas. Também estudamos os conceitos de monômios, polinômios e suas operações.

Na seção Educação financeira, foi estabelecida uma discussão sobre juros, e na seção Tratamento da informação continuamos o trabalho de análise de dados, determinando qual é o melhor tipo de gráfico a ser utilizado.

Na abertura desta Unidade, buscou-se fazer uma reflexão sobre a simbologia utilizada na escrita matemática, de modo que você pudesse entender que as construções utilizadas nesta Unidade são uma maneira simplificada de se escrever uma expressão matemática. Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

Respostas pessoais. Exemplos de respostas na seção Resoluções comentadas deste Manual.

• Qual é a importância da linguagem algébrica para a Matemática? Com base em seus conhecimentos, como a Álgebra pode auxiliar na resolução de problemas no cotidiano de alguns profissionais? Exemplifique.

• Faça um resumo de todas as operações trabalhadas com monômios e polinômios, garantindo um exemplo para cada operação.

Os questionamentos existentes no encerramento desta Unidade possibilitam, além da retomada dos conteúdos apresentados, reflexões a respeito das aprendizagens individuais e sistematizações. Por isso, é importante que os estudantes respondam individualmente a cada uma das questões para que possam perceber suas próprias conquistas e possíveis dúvidas em cada conteúdo estudado na Unidade.

A proposta de resumo deve-se à quantidade de conceitos que são trabalhados. Para os estudantes, é uma importante retomada de diversos conceitos. Se julgar conveniente, pode-se iniciar esse trabalho em sala de aula, com a mediação do professor, e propondo que o finalizem em casa.

Depois de os estudantes responderem às questões, em uma roda de conversa, pedir a alguns estudantes que exponham o que fizeram para iniciar uma discussão a respeito de cada questão. Em seguida, é possível propor a elaboração coletiva de um diagrama organizando o que foi estudado.

D2-MAT-F2-2103-V8-U4-102-141-LA-G24.indd

AMPLIANDO

Atividade complementar

São dados dois números reais, dos quais o maior é o triplo do menor. Se o menor dos números é expresso por 3,5x, o monômio que representa o produto desses dois números é:

a) 36x 2 b) 36,75x 2 c) 36x d) 36,75x e) 24,5x 2

Resolução da atividade

Menor número: 3,5x

Maior número: 3 3,5x = 10,5x

Produto: 3,5x 10,5x = 36,75x 2 Alternativa b.

REPRODUÇÃO/ENEM, 2012.

BNCC NA UNIDADE

Competências gerais:

• 1, 2, 5 e 7

Competências específicas:

• 1, 2, 3, 5, 6 e 8

Habilidades:

Álgebra

• EF08MA07

• EF08MA08

• EF08MA09

Temas Contemporâneos

Transversais:

• Educação Financeira

• Educação Ambiental

• Educação para o Consumo

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em sete capítulos.

O primeiro capítulo retoma o conceito de equação do 1o grau com uma incógnita, ampliando o estudo para utilizar esse conceito na resolução de problemas. No segundo capítulo, aborda-se a resolução das equações fracionárias. O terceiro capítulo apresenta o estudo das equações literais do 1o grau na incógnita x. O quarto capítulo aborda as equações do 1o grau com duas incógnitas e a representação geométrica delas, contribuindo para o desenvolvimento da habilidade EF08MA07. No quinto capítulo, inicia-se a discussão dos sistemas de equações do 1o grau com duas incógnitas e apresenta-se a solução gráfica de um sistema, o que favorece o desenvolvimento da habilidade EF08MA08. No sexto capítulo, são abordados dois métodos de resolução de sistemas de equações do 1o grau com duas incógnitas, o método da substituição e o método da adição. No sétimo capítulo, aborda-se a resolução de equações do 2o grau com uma incógnita da forma ax 2 + c = 0, o que propicia o desenvolvimento da habilidade EF08MA09.

OBJETIVOS

As novas latas são envasadas e distribuídas para o consumo. Os lingotes são transformados em lâminas de alumínio, usadas para fazer novas latas. D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd

• Retomar a resolução de equações do 1o grau com uma incógnita.

• Reconhecer e resolver equações fracionárias.

• Resolver equações literais do 1o grau na incógnita x

• Identificar a reta como a representação gráfica de uma equação de 1o grau com duas incógnitas.

• Compreender um sistema de equações do

1o grau e identificar sua solução gráfica.

• Reconhecer e resolver sistemas de equações de 1o grau utilizando o método da substituição e o método da adição.

• Compreender e resolver equações incompletas do 2o grau, da forma ax 2 + c = 0.

• Refletir sobre a preservação das tartarugas marinhas e a questão ambiental.

• Compreender a diferença entre juro zero e juro embutido.

Descarte de latas vazias.

JUSTIFICATIVAS DOS OBJETIVOS

Nesta Unidade, apresenta-se o estudo de equações do 1o grau com uma e com duas incógnitas, além de sistemas de equações de duas equações do 1o grau com duas incógnitas. Desse modo, pretende-se favorecer o desenvolvimento das habilidades

EF08MA07 e EF08MA08. Inicia-se, ainda, o estudo das equações incompletas de 2o grau, em especial das equações da forma

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

Inicialmente, conversar com os estudantes sobre a importância da reciclagem de todos os tipos de material. Perguntar se sabiam que o Brasil é um dos países que mais recicla latinhas de alumínio. Tais abordagens contribuem para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental e das competências gerais 2 e 7. Propor uma pesquisa sobre os pontos de coleta de materiais recicláveis disponíveis no município, caso existam.

Destacar a importância das equações para o mundo das Ciências, da pesquisa científica e suas muitas aplicações. Mostrar algumas fórmulas famosas, como a da energia de Einstein (E = mc 2), a equação da reta (y = ax + b), a fórmula de Bháskara, entre outras.

ax 2 + c = 0. Essa abordagem contribui para o desenvolvimento da habilidade EF08MA09. Um exemplo de aplicação dos sistemas de equações é apresentado no boxe Fórum, favorecendo o desenvolvimento da competência geral 5.

A seção Por toda parte apresenta algumas informações sobre o Projeto Tamar e a questão da preservação e proteção das tartarugas marinhas. Esse tema colabora para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental.

O alumínio derretido é moldado em peças chamadas de lingotes

Transporte das latas vazias para os centros de reciclagem

Fardos de latas limpas e prensadas

As latas são trituradas, e o alumínio é fundido à alta temperatura.

ORIENTAÇÕES DIDÁTICAS

Equação do 1o grau com uma incógnita

Neste capítulo, retoma-se o estudo das equações do 1o grau, depois amplia-se o tema, abordando as equações literais, fracionárias e as equações do 1o grau com duas incógnitas. Com isso, é possível o estudo da representação geométrica desse tipo de equação no plano cartesiano e sua utilização como método para resolução de um sistema de equações.

Pense e responda

Espera-se que os estudantes usem o método apresentado anteriormente para resolver os problemas. Depois, pedir a eles que, com os conhecimentos já adquiridos, representem as situações de forma algébrica, esperando que obtenham equações do 1o grau com uma incógnita.

Ao resolverem essas equações, propor uma discussão a respeito de qual processo sentiram mais facilidade para determinar a resposta. É interessante notar que, nesse caso, não há uma única resposta correta, o mais importante é que os estudantes consigam justificar suas escolhas, analisando os pontos positivos e negativos de cada método. Algumas perguntas que podem contribuir para despertar esse raciocínio:

• Qual é a dificuldade que pode apresentar o processo dos antigos egípcios?

• Qual é a possível vantagem de representar problemas como esses por meio de uma equação?

Essas discussões contribuem para o desenvolvimento da competência específica 1 da área de Matemática, além de contribuir para o desenvolvimento da capacidade de argumentação dos estudantes.

EQUAÇÃO DO 1 o GRAU COM UMA INCÓGNITA CAPÍTULO1

Alguns documentos antigos, como os papiros egípcios, traziam inúmeros e curiosos problemas matemáticos; um deles é o Papiro de Rhind, escrito há cerca de 3 000 anos. Acompanhe a tradução de um dos problemas desse papiro.

Uma quantidade, sua metade, seus dois terços, todos juntos são 26. Diga-me: qual é essa quantidade?

Como você faria para resolver esse problema?

Os egípcios não usavam a linguagem algébrica das equações, então, para resolver esse tipo de problema, eles atribuíam à quantidade procurada um valor arbitrário, que fosse divisível, ao mesmo tempo, pelos denominadores das frações que apareciam no problema; nesse caso específico, um valor que fosse divisível por 2 (sua metade) e por 3 (seus dois terços) ao mesmo tempo. Esse valor pode ser 6, 12, 18, 24 ou qualquer múltiplo de 6, pois qualquer um desses números é divisível por 2 e por 3 ao mesmo tempo. Por exemplo, ao atribuir o valor 6 para a quantidade procurada, obtemos:

6 + 1 2 ? (6) + 2 3 ? (6) = 6 + 3 + 4 = 13

Como 13 não é a soma dada no problema, vamos fazer como os egípcios e usar a ideia de proporção. Com os valores 6, 13 e 26, montamos a seguinte proporção:

• Ao valor arbitrário 6 corresponde a soma 13.

• A qual valor vai corresponder a soma 26?

Como 26 representa o dobro de 13, valor encontrado quando atribuímos o valor 6 à quantidade desconhecida, então, pela proporção, a quantidade procurada representará o dobro do valor arbitrário 6. Assim, a quantidade procurada será 2 6, ou seja, 12. Comprovando, temos:

12 1 2 (12) 2 3 (12) 12 6826+?+?=++=

PENSE E RESPONDA

Responda às questões no caderno. Conheça, a seguir, a tradução de outros problemas encontrados no Papiro de Rhind e tente resolvê-los aplicando o processo utilizado pelos egípcios. Depois, explique aos colegas e ao professor como você pensou para resolvê-los.

1. Uma quantidade aumentada do seu um sétimo resulta em 40. Qual é essa quantidade? 35

2. Uma quantidade, sua metade e sua quarta parte, adicionadas, resultam em 56. Qual é essa quantidade? 32

3. Uma quantidade, seus dois terços e seus três quartos são adicionados, e a soma é 145. Qual é essa quantidade? 60

A Álgebra facilita a resolução de problemas que envolvem números desconhecidos, além de favorecer as generalizações.

Ao representar um número desconhecido (ou incógnita) usando uma letra do alfabeto, podemos estabelecer uma relação entre os números conhecidos e os desconhecidos por meio de uma sentença matemática, por exemplo, uma equação.

Aplicando técnicas matemáticas, podemos manipular essa equação até torná-la a mais simples possível, podendo, assim, determinar o número desconhecido.

Considere a seguinte situação.

Desenvolvendo certa velocidade média, uma motorista percorreu, de carro, a distância entre os municípios baianos de Salvador e Mangue Seco em 4 horas. Se a motorista tivesse aumentado em 20 km/h a velocidade média, teria percorrido a mesma distância em uma hora a menos, ou seja, em 3 horas. Como calcular a distância percorrida?

Vamos representar por x a distância percorrida.

Considerando que: = velocidade mé dia distância percorrida te mpo ga sto , podemos montar a equação a seguir para o problema.

Distância entre Salvador e Mangue Seco

x 4 + 20 = x 3

ORIENTAÇÕES DIDÁTICAS

Resolver, parcialmente na lousa, o problema proposto no Livro do estudante. Observar se os estudantes equacionam o problema, com base na situação dada. A transição da linguagem verbal para a linguagem matemática é um ponto a ser observado na sala de aula, pois muitos estudantes costumam apresentar dificuldades nessa mudança de registro.

Verificar se todos compreendem a fórmula para o cálculo da velocidade média. Se necessário, explorar esse conceito com os estudantes.

Se considerar pertinente, levar para a sala de aula um conjunto de problemas, que não serão resolvidos neste momento, apenas para serem apenas equacionados.

Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar 8. ed. Rio de Janeiro: IBGE, 2012.

AMPLIANDO

Link

Centro histórico do Pelourinho, Salvador (BA), 2021.

145 25/07/22 11:29

NEUMANN, Adriana. Matemática em essência. Ciência hoje. Rio de Janeiro, c2022. Disponível em: https://cienciahoje.org.br/acervo/matematica-em-essencia/. Acesso em: 30 jul. 2022.

Nesse artigo, a autora discute o papel da Matemática como decodificadora da natureza.

GURIA QUE VIAJA/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Como resolver uma equação do 1o grau com uma incógnita

Apresentar, na lousa, os passos utilizados na resolução da equação da situação 1:

x 4 20 x 3 +=

1o) Escrever todos os termos como frações de mesmo denominador, usando a equivalência de frações:

3x 12 240 12 4x 12 +=

2o) Efetuar as operações (adições ou subtrações) nos numeradores em cada membro (quando houver):

() 3x 240 12 4x 12 + =

3o) Utilizar o princípio multiplicativo e eliminar os denominadores (multiplicando os dois membros por 12):

() 3x 240 12 12 4x 12 12 + ?=?

3x + 240 = 4x

4 o) Utilizar o princípio aditivo da igualdade:

3x + 240 = 4x

3x 3x + 240 = 4x 3x 240 = x

x = 240

Depois, propor outras equações similares para os estudantes resolverem passo a passo e pedir a alguns deles que mostrem, na lousa, como fizeram. A valorização das diferentes estratégias está relacionada ao pluralismo de ideias. No desenvolvimento da situação 2, destacar a aplicação da propriedade distributiva.

Nesta equação, observamos que:

• o primeiro membro, + x 4 20, é uma expressão algébrica inteira;

GLOSSÁRIO

Expressão algébrica inteira: uma expressão algébrica que não contém variável ou variáveis no denominador.

• o segundo membro, x 3 , também é uma expressão algébrica inteira.

Equações desse tipo são chamadas de equações inteiras do 1o grau na incógnita x Já estudamos que resolver uma equação consiste em encontrar o valor da incógnita que torna a sentença verdadeira, ou seja, encontrar a solução ou a raiz da equação. Estudamos, também, que para resolver equações como a da situação anterior, aplicamos os princípios de equivalência da igualdade até obter uma equação equivalente à equação dada na forma reduzida ax = b, com a, b [r e a 5 0.

Acompanhe outros exemplos desse tipo de equação.

• x + 1 = 7, que pode ser reduzida à forma x = 6.

• 3x + 10 = 5x, que pode ser reduzida à forma 2x = 10.

• 2 ? (3x _ 1) + 5x = 0, que pode ser reduzida à forma 11x = 2.

COMO RESOLVER UMA EQUAÇÃO DO 1 o GRAU COM UMA INCÓGNITA

Vamos retomar a resolução de equações inteiras do 1o grau resolvendo os exemplos a seguir.

1 Considerando a situação apresentada anteriormente, calcular a distância percorrida pela motorista entre os municípios de Salvador e Mangue Seco.

Para isso, calculamos a raiz da equação x 4 20 x 3 += no conjunto r

x 4 20 x 3 +=

+ = 3x 240 12 4x 12

3x + 240 = 4x

Reduzimos todos os termos ao mesmo denominador.

Usamos o princípio multiplicativo para eliminar os denominadores (multiplicando os dois membros por 12).

3x _ 4x = 240 Usamos o princípio aditivo (adicionando 4x e 240 aos dois membros).

x = 240 Usamos o princípio multiplicativo (multiplicando os dois membros por 1).

x = 240

O número real 240 é raiz da equação. Portanto, a motorista percorreu 240 km.

2 Resolver a equação 5 ? (x + 2) _ 3 ? (x + 6) = 40 no conjunto r

5 ? (x + 2) _ 3 ? (x + 6) = 40

5x + 10 _ 3x _ 18 = 40 Eliminamos os parênteses aplicando a propriedade distributiva.

2x _ 8 = 40

2x = 40 + 8 Usamos o princípio aditivo (adicionando 8 aos dois membros).

2x = 48

x = 48 2

x = 24

Usamos oprincípiomultiplicativo multiplicandoosdoismembros por 1 2

O número real 24 é a solução da equação.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 146 25/07/22 11:29

3 Resolver a equação, y3 8 y1 6 y1 12 + + = , em que U =r y3 8 y1 6 y1 12 + + =

3( y3)4(y 1) 24 2( y1) 24 _++ = Reduzimos todos os termos ao mesmo denominador.

3(y _ 3) + 4(y + 1) = 2(y _ 1)

Usamos o princípio multiplicativo para eliminar os denominadores.

3y _ 9 + 4y + 4 = 2y _ 2 Eliminamos os parênteses.

7y _ 5 = 2y _ 2

7y _ 2y = 2 + 5

5y =+3 = y 3 5

ATIVIDADES

Usamos o princípio aditivo.

Usamos o princípio multiplicativo.

A solução da equação é o número real 3 5 Responda às questões no caderno.

1. a) Respostas pessoais. Espera-se que os estudantes concluam que a solução da equação é única e percebam que ao final da resolução devem simplificar a fração obtida, pois não reduziram o denominador usando o mínimo múltiplo comum entre 8, 6 e 12 e, por isso, vão encontrar uma fração equivalente à fração solução da equação.

3. Qual é o valor de x, no conjunto r , na equação (3 + x) _ 1 = (17 _ 4x) _ (3 + x)?

1. Considere a equação resolvida no exemplo 3 e responda.

a) Se ao reduzir todos os termos para o mesmo denominador tivéssemos escolhido o denominador 48 em vez de 24, o que mudaria na resolução dessa equação? Obteria a mesma solução? Explique suas hipóteses aos colegas e ao professor.

b) Resolva a equação reduzindo os termos para o denominador 48 e confirme suas hipóteses. 3 5

2. Considerando U =r , determine a solução das seguintes equações do 1o grau com uma incógnita.

a) 21x _ 17 = 109 6

b) 73x + 100 = 53x 5

c) 1,7 + 2,5x = 4,2 1

d) 23x _ 22 = 19x + 6 7

e) 12x _ 16 = 21 + 10x 2,5

f) 1,9x _ 3,6 = x _ 10,8 8

g) 7(2 + x) = 5(x _ 1,2) + 35 7,5

h) 3(x + 1) _ 2(x _ 1) =_(x + 5) 5

4. Considerando o conjunto r dos números reais, determine a raiz ou solução de cada uma das seguintes equações do 1o grau com uma incógnita.

a) += x 4 20 x 3 240

b) _= 2 5 y 3 4 3 20 y 3

c) 1 x 2 1 3 x2_=_+ 6

d) x10 9 x 6 10 += 40

e) x3 4 x1 3 7 2 + = 29

5. Qual deve ser o número real x para que a expressão x2 4 x1 5 + seja igual a 1?

6. As expressões (x _ 5), (2x _ 9), (3x _ 13) e (4x _ 3) representam números cuja soma é 90. Qual é o maior desses números? 45

ORIENTAÇÕES DIDÁTICAS

Se possível, desenvolver a situação 3 na lousa. Solicitar aos estudantes que, em cada etapa efetuada, descrevam o conceito matemático associado à operação. O uso dos termos corretos auxilia na compreensão dos procedimentos. Assim, “determinar a fração equivalente”, “aplicar o princípio aditivo e/ou multiplicativo”, entre outras, são expressões que devem fazer parte do vocabulário matemático do estudante de 8 o ano.

Atividades

As atividades propostas têm como objetivo fazer com que os estudantes resolvam equações do 1o grau e socializem os diferentes procedimentos desenvolvidos pelos estudantes.

Na atividade 5, observar se os estudantes efetuam corretamente a resolução, pois há uma subtração entre os termos fracionários. É comum que esse tipo de equação possa ser resolvido de maneira incorreta, pois os estudantes podem considerar que o sinal de menos refere-se apenas ao primeiro termo do numerador, e não ao numerador como um todo.

25/07/22 11:32

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 147

AMPLIANDO

Atividade complementar

Considere dois números reais x e y. Multiplicando o número x por 3 4 , ele diminui 5 unidades, e multiplicando o número y por 5 3 , ele aumenta 6 unidades. Nessas condições, quanto vale x y?

Resolução da atividade

xx xx x 3 4 53 42020?=_h=_h=

Na atividade 6, espera-se que os estudantes identifiquem cada expressão entre parênteses como uma parcela da adição cuja soma é 90. Além disso, espera-se que percebam que para identificar qual expressão representa o maior número é preciso, depois de obter o valor de x, determinar o valor de cada uma dessas expressões.

ORIENTAÇÕES DIDÁTICAS

Resolvendo problemas

A resolução de problemas envolvendo o uso de equações é um tema no qual alguns estudantes podem vir a apresentar dificuldades. Propor que organizados em duplas, tentem resolver os problemas propostos nesta página. O trabalho em dupla valoriza a cooperação e desenvolve a empatia nos estudantes.

É possível que alguns tentem resolver os problemas por tentativa e erro. Esse tipo de estratégia está relacionada à inferência e demonstra disposição do estudante para o enfrentamento de problemas.

No problema 1, alguns estudantes podem concluir que 35% do total de partidas corresponde a 21 partidas e, assim, concluir que 5% do total de partidas corresponde a 3. Logo, 100% corresponde a 60 partidas. Observar que, com esse raciocínio, os estudantes não utilizaram a equação como estratégia de resolução. O objetivo aqui é fazê-los construir a equação que traduz a situação-problema. Da mesma forma, é possível determinar uma solução para o problema 2, usando o raciocínio lógico. Confrontar a resolução dos estudantes e apresentar a resolução algébrica.

RESOLVENDO PROBLEMAS

Usando a linguagem das equações, podemos resolver diversos problemas. Acompanhe alguns exemplos a seguir.

1 Uma equipe de futebol disputou algumas partidas em 2022 e obteve o seguinte desempenho: venceu 45% dessas partidas, perdeu 20% e empatou 21 partidas. Quantas partidas essa equipe disputou em 2022?

Vamos representar por x a quantidade de partidas disputadas pela equipe.

Lembre-se: 45% = 0,45 e 20% = 0,20. Assim, podemos escrever esta equação do seguinte modo. quantidade de vitórias quantidade de derrotas quantidade de empates quantidade de partidas disputadas

0,45x + 0,20x + 21 = x

0,45x + 0,20x + 21 = x

0,45x + 0,20x _ x = 21 0,35x = 21

0,35x = 21

x = 21 0, 35 = 60

Logo, essa equipe disputou 60 partidas.

2 Em um estacionamento, há carros e motos, totalizando 14 veículos e 48 rodas. Quantos carros e quantas motos há nesse estacionamento?

Vamos indicar por x a quantidade de carros. A quantidade de motos será indicada por 14 _ x. A equação correspondente ao problema é:

4x + 2 ? (14 _ x) = 48 quantidade de rodas dos carros

quantidade de rodas das motos

quantidade total de rodas

4x + 2(14 _ x) = 48

4x + 28 _ 2x = 48

2x + 28 = 48

2x = 48 _ 28

2x = 20

x = 20 2 = 10 quantidade de carros

14 _ x = 14 _ 10 = 4 quantidade de motos Nesse estacionamento, há 10 carros e 4 motos.

D2_AV2-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 148 14/08/22

AMPLIANDO

Link

SALA de Estudo: Uma maneira diferente de resolver problemas do 1o grau. Clubes de Matemática da OBMEP. [S. l.], [20--]. Disponível em: http://clubes.obmep.org.br/blog/uma-maneira-diferente-de-resolver -problemas-do-1-grau/. Acesso em: 30 jul. 2022.

Nesse artigo, são propostas situações que são resolvidas de maneira intuitiva e, também, usando equações do 1o grau.

OLYA N./SHUTTERSTOCK.COM

PHILIPYB STUDIO/SHUTTERSTOCK.COM

IMAGEM FORA DE PROPORÇÃO. AS CORES NÃO SÃO REAIS.

6. b) Resposta pessoal. Exemplo de resposta: De um mesmo prato dessa balança foram retirados 200 g e 2 maçãs, e no outro prato foi inserida uma maçã. O que precisa ser feito para a balança continuar em equilíbrio? Resposta possível: retirar a maçã que foi inserida e os dois objetos de 200 g cada um, de modo a ficar 2 maçãs em cada prato.

Responda às questões no caderno.

1. Karina participou de um concurso com posto de duas fases. Na 1a fase, ela obteve uma nota, e na 2a fase, obteve 3 pontos a mais do que na 1a. A nota final dos candi datos desse concurso foi calculada assim:

(1 nota) 2(2 nota) 3 aa +? 1a fase: 6; 2a fase: 9.

Sabendo que a nota final de Karina foi 8, que nota ela tirou em cada fase?

Sabendo que nesse mês as três monta doras venderam 7 000 dos 10 000 carros produzidos, qual é o valor de x? x = 80

ORIENTAÇÕES DIDÁTICAS Atividades

As atividades propostas têm como objetivo fazer os estudantes resolverem problemas envolvendo equações do 1o grau em situações variadas.

Estudante em sala de aula.

2. Um prêmio de R$ 165.000,00 deve ser divi dido entre Caio, Pedro e Toni. Pedro deve receber a metade do valor de Caio, e Toni vai receber R$ 20.000,00 a mais do que Caio. Que quantia cada um receberá?

3. Para comprar um computador, Valdir precisa de 200 reais a mais do que tem. Se ele tivesse o dobro da quantia que tem, compraria esse computador e ainda ficaria com 300 reais.

a) Qual é a quantia que Valdir tem?

b) Qual é o preço do computador?

2. Caio: R$ 58.000,00; Pedro: R$ 29.000,00; e Toni: R$ 78.000,00. 500 reais. 700 reais.

4. A produção e as vendas de dezembro das três montadoras de automóveis de uma cidade foram registradas a seguir. Produção e vendas (dezembro de 2022)

Montadora Unidades produzidas

Taxa percentual vendida da produção (%)

Azul 3 000 80

Branca 5 000 60

Vermelha 2 000 x

Fonte: Dados fictícios.

5. Humberto trabalha de segunda a sexta‑feira e recebe mensalmente um auxílio alimentação de R $ 380,00. Ele tem duas opções para almoçar: em um restaurante, onde paga cerca de R$ 15,00 por refeição, ou levando a re feição de casa, ao custo aproximado de R$ 7,00. Sabendo que às sextas feiras Humberto nunca pode levar sua refeição para o trabalho, e considerando que 1 mês tem 4 semanas, responda.

a) O auxílio-alimentação é suficiente para Humberto almoçar todos os dias no restaurante? Sim, pois gastaria R$ 300,00.

b) Em um mês, quantos reais, no mínimo, ele gasta com o almoço no trabalho?

R$ 172,00, no mínimo.

6. Observe a figura seguinte e suponha que todas as maçãs que estão na balança tenham a mesma massa.

Nas situações-problema apresentadas, reforçar o trabalho com leitura e interpretação dos enunciados, para que os estudantes traduzam corretamente as situações para linguagem matemática (neste caso, as equações). Um trabalho interessante pode ser confrontar as equações construídas pelos estudantes e verificar no que se assemelham e no que diferem. Discutir coletivamente os equívocos cometidos é uma estratégia que contribui para a aprendizagem.

Se sentir necessidade, explorar alguns desses problemas oralmente.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 149

a) Determine quantos gramas tem cada maçã

b) Elabore outro problema a partir dessa figura. Depois, entregue para um colega resolver enquanto você soluciona o problema que ele elaborou e, juntos, discutam as respostas obtidas.

DESAFIO

7. Uma tabela tem quatro valores numé ricos. Observa se que, com exceção do primeiro, cada valor corresponde a 2 3 do valor numérico anterior. Sabendo que a soma desses quatro valores é 195, qual é o primeiro valor dessa tabela? E o último?

81 (primeiro valor) e 24 (último valor).

Para finalizar, propor a cada estudante que escreva um texto contando as estratégias utilizadas por ele e pelos colegas e qual estratégia eles julgam ser a melhor para a resolução de cada atividade.

Observar quais estudantes ainda cometem equívocos na resolução das equações, como na troca de sinais ou na divisão, e propor a eles outras estratégias de aprendizagem.

Sugere-se que o desafio 7 seja realizado primeiro individualmente. Em seguida, organizar os estudantes em duplas ou trios para que conversem com os colegas a respeito das estratégias que utilizaram na resolução e quais foram as dificuldades encontradas. Essa abordagem contribui para o desenvolvimento da competência específica 2 da área de Matemática.

PROSTOCK-STUDIO/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Equação fracionária com uma incógnita

Neste momento os conceitos de fração algébrica e equação algébrica fracionária são retomados e aprofundados, bem como o estudo de fatoração, como a redução ao denominador comum. A partir de uma situação cotidiana, os estudantes devem construir a equação que modela o problema e, a partir daí, resolvê-lo. Essa abordagem contribui para o desenvolvimento da competência específica 3 da área de Matemática.

Como resolver uma equação fracionária

Ressaltar a importância de se determinar quais valores a incógnita pode assumir, isto é, o seu conjunto universo. Para as equações fracionárias a restrição são os valores reais que anulam os denominadores. Tais valores não podem pertencer ao conjunto universo da equação original.

EQUAÇÃO FRACIONÁRIA COM UMA INCÓGNITA CAPÍTULO2

Uma fábrica produz, em 1 hora, 2 400 parafusos, que são distribuídos igualmente em x caixas. No fim desse período, constatou-se que os parafusos de 5 caixas estavam com defeitos. Com isso, foi necessário reduzir a quantidade de parafusos em 400 unidades para que as caixas restantes recebessem a mesma quantidade de parafusos que receberiam inicialmente. No início, quantas caixas seriam usadas para distribuir os parafusos produzidos em 1 hora?

Considerando que a quantidade de parafusos em cada caixa é dada por qua ntidadetotal de pa ra fusos qua ntidadedecaixa s , obtemos a seguinte equação, em que x é a quantidade inicial de caixas.

=

2 400 x 2 400 400 x5 quantidade de parafusos em cada caixa depois da redução da quantidade de parafusos e de caixas quantidade de parafusos em cada caixa na situação inicial Nessa equação, observamos que:

• o primeiro membro, 2 400 x , é uma expressão algébrica fracionária, pois apresenta a incógnita no denominador;

• o segundo membro, 2 400 400 x5 , também é uma expressão algébrica fracionária, pois a incógnita aparece no denominador.

Equações desse tipo são chamadas de equações fracionárias na incógnita x Uma equação é fracionária quando tem pelo menos uma incógnita no denominador, sempre fora de radical.

COMO RESOLVER UMA EQUAÇÃO FRACIONÁRIA

Resolvemos as equações fracionárias de maneira similar ao modo que resolvemos outras equações. Devemos, porém, excluir do conjunto solução da equação fracionária os valores da incógnita que anulam o denominador de cada um dos termos da equação. Na situação apresentada, devemos excluir os valores x = 0 e x = 5, que anulam algum denominador da equação.

2 400 x 2 400 400 x5 =

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 150

Máquina que produz parafusos em uma fábrica.

ORIENTAÇÕES DIDÁTICAS

Além disso, somente a solução inteira positiva é solução da situação-problema. Para resolver essa equação, determinamos o mmc (x, x _ 5) = x(x _ 5) e reduzimos as frações ao mesmo denominador.

2 400

x(x5) 2 000 x(x5) 2 400(x 5) x(x5) 2 000 x x(x5) == ⇒

2 400x _ 12 000 = 2 000x

2 400x _ 2 000x = 12 000

400x = 12 000

x 12000 400 == 30

Portanto, no início seriam usadas 30 caixas. Vamos resolver outras equações fracionárias do 1o grau.

1 Determinar o número real x que seja a solução da equação a seguir.

=+ 2x x3 3 x 2 mmc (x, x _ 3) = x(x _ 3) 2x x(x3) 3( x3)2x(x3) x(x3) 2 = _+

Nessa equação, x deve ser diferente de 0 e de 3, pois esses valores anulam algum denominador da equação.

Resolver na lousa as equações fracionárias dadas como exemplo. Na primeira equação, verificar se os estudantes identificam que os valores 0 e 3 são as restrições para os denominadores. Retomar o cálculo do mmc entre x e x 3, considerando que são expressões algébricas distintas e, portanto, devem ser multiplicadas. Pedir que justifiquem cada uma das etapas da resolução, valorizando a capacidade de argumentação dos estudantes.

2x 2 = 3(x _ 3) + 2x(x _ 3)

2x 2 = 3x _ 9 + 2x 2 _ 6x 2x 2 = 2x 2 _ 3x _ 9 h

h 2x 2 _ 2x 2 = 3x _ 9

0 = 3x _ 9 h

h 0 + 3x = 9

3x = 9 x 9 3 =

x = 3

Como 3 não anula nenhum denominador da equação, ele é a raiz ou a solução da equação.

O valor procurado é o número real 3.

Note que t deve ser diferente de 1 e de 1, pois esses valores anulam algum denominador da equação.

Como o número 1 anula os denominadores da equação, ele não é raiz ou solução da equação, portanto, podemos dizer que essa equação não tem raiz ou solução.

D2_AV2-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 151

Já na segunda equação apresentada no Livro do estudante, retomar o caso de fatoração pela diferença de dois quadrados para determinar o mmc entre as expressões algébricas 1 t e 1  t 2. Verificar que o resultado encontrado para t coincide com a restrição para o denominador. Dessa maneira, ressaltar com os estudantes que a equação dada não tem solução real. AMPLIANDO Atividade

universo e resolver a equação fracionária:

Como 7 pertence ao conjunto universo da equação fracionária original (7 não anula o denominador), x = 7.

O conjunto solução dessa equação fracionária é S = {7}.

ORIENTAÇÕES DIDÁTICAS

Atividades

As questões deste bloco têm como objetivo fazer com que os estudantes reconheçam e resolvam equações fracionárias, além de compreender que os valores que anulam os denominadores de uma equação fracionária não podem ser solução da equação.

Procurar resolver algumas questões com e sem a utilização de equações para poder compará-las.

A atividade 8 trata do custo médio de determinado produto. Verificar se conseguem escrever a fórmula do custo médio, ou seja, C C x F8x x médio total == +

Ler o problema com os estudantes e verificar se eles compreendem o que cada uma das variáveis dadas significa.

Responda às questões no caderno.

1. Determine o valor que x não pode assumir nas equações fracionárias a seguir.

7. Em uma colônia de férias A , 128 crianças são distribuídas em x grupos de atividades, e na colônia B, 224 crianças são distribuídas em (x + 6) grupos de atividades. Sabendo que a quantidade de crianças, em todos os grupos, é a mesma para ambas as colônias de férias, qual é a quantidade de grupos de atividades na colônia de férias B? 14 grupos.

2. Qual é o valor real de x que torna verdadeira a igualdade =+ x1 1x

, com

3. Determine o valor real de y para que as expressões 3y y4 e + 3 2 y sejam iguais, sabendo que y 5 0 e y 5 4. 4 5

4. No conjunto r, qual é a solução da equação

8. Chama-se custo médio de produção o custo total dividido pela quantidade produzida. Uma fábrica de camisetas tem um custo total mensal C dado pela fórmula C = F + 8x, em que F representa o custo fixo, e x é a quantidade de camisetas produzidas. Quantas camisetas devem ser produzidas nessa fábrica para se obter um custo médio de R$ 12,00 para um custo fixo de R$ 2.000,00?

5. Determine o conjunto solução das seguintes equações fracionárias.

6. Sabendo que

determine o valor real de

que torna verdadeira essa igualdade.

9. O 8o ano A tem x estudantes. Nessa turma, foram distribuídos 320 livros, de maneira que todos receberam a mesma quantidade. O 8o ano B tem (x _ 2) estudantes. Nessa turma, foram distribuídos 300 livros, e todos os estudantes receberam a mesma quantidade de livros

Quantos estudantes há em cada turma, se cada estudante das duas turmas recebeu a mesma quantidade de livros?

500 camisetas. 32 estudantes no 8o ano A e 30 estudantes no 8o ano B.

POR TODA PARTE

PROJETO TAMAR

A Fundação Projeto Tamar atua no litoral brasileiro desde a década de 80 com a missão de promover a recuperação das tartarugas marinhas, desenvolvendo ações de pesquisa, conservação e inclusão social.

[...]

Está presente [...] em oito estados brasileiros [...]. Desenvolve ações de pesquisa, manejo e proteção das cinco espécies de tartarugas marinhas que ocorrem no Brasil, além de atividades de envolvimento comunitário, inclusão social, sensibilização e educação ambiental, valorização da cultura local e geração de oportunidades de trabalho e renda.

Como resultado desse esforço contínuo vem obtendo conquistas importantes: recuperação das populações comprovada; ampliação do conhecimento científico; apoio das comunidades litorâneas que cessaram o uso direto das tartarugas passando a protegê-las; sensibilização e apoio da sociedade em geral e a geração de recursos próprios (sustentabilidade).

MISSÃO. Fundação Projeto Tamar. [Mata de São João], c2011. Disponível em: http://www.tamar.org.br/interna.php?cod=63. Acesso em: 30 maio 2022.

Litoral baiano e o projeto Tamar

O litoral norte baiano é uma das principais áreas reprodutivas das tartarugas marinhas no país, principalmente para a tartaruga-de-pente (Eretmochelys imbricata), além de importante área de desova das tartarugas-cabeçudas (Caretta caretta) e oliva (Lepidochelys olivacea).

A Fundação Projeto Tamar atua desde Salvador até Mangue Seco, divisa com o Estado de Sergipe e está distribuída em 4 bases de proteção e pesquisa (Arembepe, Praia do Forte, Costa do Sauipe e Conde), um centro de Educação Ambiental em Arembepe e um Centro de Visitantes e de Reabilitação em Praia do Forte.

CAPACITAÇÃO – Bahia. Fundação Projeto Tamar. [Mata de São João], c2011. Disponível em: https://tamar.org.br/interna.php?cod 209. Acesso em: 30 maio 2022. Resolva as equações no caderno, determine os valores de x e y e descubra mais algumas informações sobre o Projeto Tamar.

1. O projeto Tamar tem x bases mantidas em áreas de alimentação, desova, crescimento e descanso das tartarugas marinhas. x = 23; 23 bases.

3x 10 15 57 10 3x 5 _=

2. Instalada em 1991, a base de Sítio do Conde, na Bahia, monitora y quilômetros de praia, entre a foz do rio Inhambupe, ao sul, e a foz do rio Real, ao norte.

=_ 1 4 4 y11 1 2 129 6y 66 y = 81; 81 km

D2_AV2-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 153

AMPLIANDO

Link

PROJETO TAMAR. [S l.], c2011. Site. Disponível em: https://www.tamar.org.br/. Acesso em: 30 jul. 2022. É possível encontrar mais informações sobre o Projeto Tamar no link

ORIENTAÇÕES DIDÁTICAS

Por toda parte

Nesta seção os estudantes aplicarão equações fracionárias que resultarão em valores relacionados a situações reais.

Ler o texto com os estudantes e perguntar a eles se já conheciam o Projeto Tamar e seu papel na preservação das tartarugas marinhas. Escutar as opiniões deles a respeito do projeto e de como devemos proteger os animais. A discussão desse tema contribui para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental, da competência geral 7 e da competência específica 3 da área de Matemática.

Se quiser ampliar a atividade, propor aos estudantes uma pesquisa mais detalhada a respeito das instituições existentes, no estado onde moram, que trabalham com a preservação de animais e do meio ambiente em geral.

Tartaruga­ de ­pente.

IMAGEM CEDIDA PELA FUNDAÇÃO PROJETO TAMAR 1 m

ORIENTAÇÕES DIDÁTICAS

Equações literais do 1o grau na incógnita x

Este é um assunto que pode trazer alguma dificuldade aos estudantes, pois eles não estão acostumados a ter como solução de uma equação uma expressão que contém também letras. Auxilie-os nesse processo de aprendizagem, a fim de que adquiram a maturidade matemática necessária para a compreensão do conceito.

Analisar com os estudantes os exemplos apresentados no Livro do estudante.

Atividades

As atividades propostas têm como objetivo levar os estudantes a reconhecer e resolver equações literais, além de ampliar a compreensão de que a solução de uma equação literal é dada em função das letras consideradas constantes e, por isso, depende dos valores que essas constantes podem assumir.

Reforçar a necessidade de excluir alguns valores que possam ser atribuídos para essas constantes para que não tenhamos um denominador nulo, como nos itens a, b e c da atividade 1 Para complexificar as discussões, propor o seguinte desafio aos estudantes: E se trocássemos a incógnita pela constante e vice-versa? Como ficaria a solução da

EQUAÇÕES LITERAIS DO 1 o  GRAU NA INCÓGNITA X CAPÍTULO3

Observe as seguintes equações, todas do 1o grau na incógnita x

• 3ax = 9 • 2a _ ax = bx • px _ 1 = p2

Nessas equações, aparecem outras letras além da incógnita x. Essas letras figuram na equação como constantes que representam números reais.

Equações desse tipo são denominadas equações literais do 1o grau na incógnita x

COMO RESOLVER UMA EQUAÇÃO LITERAL

DO 1 o GRAU COM UMA INCÓGNITA

Resolveremos as equações literais do 1o grau na incógnita x da mesma maneira que resolvemos outras equações do 1o grau. Acompanhe.

1 Considerando x a incógnita, resolver a equação 8x + 7a = 2x + 25a, em que a [r

8x + 7a = 2x + 25a

8x = 2x + 25a _ 7a

8x = 2x + 18a

8x _ 2x = 18a

6x = 18a

== x 18a 6 3a

A solução da equação é 3a.

2 Considerando x a incógnita, resolver a equação 3(mx + n) _ 2mx = 5n.

3(mx + n) _ 2mx = 5n

3mx + 3n _ 2mx = 5n

mx = 5n _ 3n

mx = 2n h x = 2n m

A solução é o número real 2n m , para m 5 0.

ATIVIDADES

Responda às questões no caderno.

1. Sendo x a incógnita e supondo que os resultados representem números reais, resolva as seguintes equações literais no conjunto r.

a) 5bx + 2a = bx + 3a

b) 3(ax + b) = 2(ax _ b)

c) (x + b)(x _ b) = x ? (x _ b3)

d) (a _ b)x + (a + b)x = 2a

{1}

e) x a = c + x 2a (a 5 0) {2ac}

2. Qual é o conjunto solução da equação 6hx + 14 = 18 + 2hx, em que x é a incógnita e h 5 0?

Assim: x y y x 4 2 2 4 2 1 2 3 2 _=_=_=

EDUCAÇÃO FINANCEIRA

JURO ZERO E JURO EMBUTIDO

Atenção, consumidor: ‘juro zero’ é estratégia de marketing

Entre uma promoção e outra no comércio, é difícil não aderir a um parcelamento alardeado como juro zero. Impulsionada pelo aumento da renda e pelo avanço no nível de emprego no país, a armadilha dos juros embutidos, escondida no desconto à vista, ganha força no comércio. As lojas costumam anunciar o mesmo preço à vista e para parcelamento sem juros, mas é só chorar um pouquinho que o cliente consegue um desconto se comprar em uma vez só. Isso mostra que esse valor menor é o preço real do produto, e o preço cheio embute juros.

O grande risco que o consumidor corre é de fazer das compras a prazo um hábito, pagando juros sem saber e, assim, comprometendo seu orçamento e fazendo dívidas financeiras, em que os juros são mais altos. É melhor juntar e comprar por um preço melhor, já que o juro zero é uma estratégia de marketing do comércio [...].

ROSA, Bruno. Atenção, consumidor: ‘juro zero’ é estratégia de marketing Extra, Rio de Janeiro, 23 jul. 2011. Disponível em: http://extra.globo.com/noticias/economia/atencaoconsumidor-juro-zero -estrategia-demarketing-2294212.html. Acesso em: 31 maio 2022.

Para entender como são calculados os preços com juro embutido, acompanhe a situação a seguir.

Uma loja oferece duas opções de pagamento na compra de uma mala de viagem como a da imagem. Vamos analisar cada uma das condições.

Se a loja oferece um desconto no pagamento à vista em dinheiro, então, os valores da compra a prazo e da compra à vista são diferentes, ou seja, existe juro embutido no valor da compra a prazo. Vamos calcular o valor e a taxa de juro dessa compra a prazo.

O valor da mala é R$ 500,00 e pode ser pago em duas parcelas iguais de R$ 250,00. Com o desconto de 5%, o cliente paga R$ 500 ? 0,95 = R$ 475,00 à vista, em dinheiro.

Para calcular a taxa de juro embutido cobrada pela loja, vamos subtrair de R$ 475,00 os R$ 250,00, que correspondem ao valor da primeira parcela. Essa parcela não tem juro, pois foi paga no ato da compra: R$ 475,00 _ R$ 250,00 = R$ 225,00.

O restante, R$ 225,00, após um mês, com o juro, resulta em uma dívida de R$ 250,00. Portanto, o juro embutido dessa compra é R$ 25,00, e a taxa de juro é aproximadamente 11%.

Responda à questão no caderno.

• Calcule qual seria a taxa de juro embutido no pagamento em duas vezes de R$ 150,00 caso o desconto do pagamento à vista fosse de 8%. Aproximadamente 19%.

ORIENTAÇÕES DIDÁTICAS

Educação financeira

O texto apresentado nessa seção tenta alertar o consumidor a respeito da inexistência do juro zero quando existe um desconto para pagamento à vista. Essa situação contribui para o desenvolvimento dos Temas Contemporâneos Transversais Educação Financeira e Educação para o Consumo, além da competência geral 2 da BNCC. É apresentada uma situação para explicar melhor como são calculados os preços com juro embutido. Nela, o consumidor pode pagar em duas vezes (uma no ato da compra e outra depois de um mês) ou à vista (com 5% de desconto). Explicar aos estudantes que, quando pagamos uma parcela no ato da compra, ela não tem juro embutido e que o valor real da mercadoria é o valor com desconto à vista. Na situação apresentada na atividade complementar no boxe Ampliando a seguir, é apresentada a equação matemática para determinar o valor das parcelas de uma compra que pode ser paga em duas vezes (30 e 60 dias após a compra), com juro embutido.

Promover uma discussão a respeito do tema e questionar os estudantes se já passaram por situações nas quais perceberam que comprar à vista era mais vantajoso.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd

AMPLIANDO

Atividade complementar

Se considerar interessante, apresentar a situação a seguir.

Um comerciante tem um produto cujo preço real é R$ 100,00 e, para vendê-lo em duas parcelas iguais a serem pagas em 30 e 60 dias, vai embutir uma taxa de juro de 5% ao mês. Para isso, ele deve calcular o valor das parcelas com essa taxa.

Resolução da atividade

Vamos representar o valor das parcelas com a incógnita x.

Dívida atualizada após 1 mês: 100 ? 1,05 = 105

Primeira parcela: x

Após o pagamento da primeira parcela, a dívida restante será 105 x.

Para calcular o valor da segunda parcela, aplicamos o juro de 5% sobre a dívida restante, que é (105   x) ? (1,05). Como a segunda parcela deve ser igual à primeira, temos a equação: x = (105 x) ? (1,05)

PEDRO PAULO MELARA

ORIENTAÇÕES DIDÁTICAS

Pense e responda Aqui, os estudantes entrarão em contato com problematizações que envolvem equações do 1o grau com duas incógnitas, iniciando as discussões para o desenvolvimento da habilidade EF08MA07. A ideia é verificar quais estratégias são utilizadas pelos estudantes na busca das soluções e se fazem uso de ferramentas algébricas.

Propor aos estudantes que determinem soluções distintas para uma mesma equação do 1o grau com duas incógnitas. Espera-se que eles percebam que para obter tais soluções devem escolher um valor para uma das incógnitas, substituir esse valor na equação e, assim, determinar o valor da outra incógnita, sempre respeitando as condições dadas sobre os valores que as incógnitas podem assumir. Por exemplo, se as incógnitas representam idades ou quantidades, elas podem assumir somente valores positivos e inteiros, ou seja, devem ser números naturais.

EQUAÇÃO DO 1 o GRAU COM DUAS INCÓGNITAS CAPÍTULO4

PENSE E RESPONDA

Responda às questões no caderno.

1.a) 2x + 16 = 4y

2.a) 4x + 2y = 60

1. Vamos considerar que o retângulo e o quadrado representados a seguir têm perímetros iguais.

8 x

1.b) Sim, pois 2 ? 6 + 16 = 4 ? 7, ou seja, 12 + 16 = 28.

y y

a) Qual é a equação do 1o grau com duas incógnitas que representa esse fato?

b) Se você atribuir para a incógnita x o valor 6 e para a incógnita y o valor 7, esses dois valores satisfazem a equação que você escreveu?

2. Em um estacionamento, há x carros e y motos, totalizando 60 rodas.

a) Qual é a equação nas incógnitas x e y que representa essa situação?

b) Considerando 12 carros e 6 motos, esses valores x = 12 e y = 6 satisfazem a equação que você escreveu no item a?

Sim, pois 4 ? 12 + 2 ? 6 = 60, ou seja, 48 + 12 = 60.

Toda equação que pode ser reduzida a uma equação equivalente na forma ax + by = c, com a, b e c [r e a 5 0 e b 5 0, é denominada equação do 1o grau com duas incógnitas São equações do 1o grau com duas incógnitas:

• x + y = 10 incógnitas x e y

• 3x + 2y = 16 incógnitas x e y

• 7x _ 5y = 9 incógnitas x e y

Dependendo do conjunto universo, uma equação do 1o grau com duas incógnitas, x e y, por exemplo, pode ter infinitas soluções, cada uma delas indicada por um par ordenado de números: o primeiro número representa o valor da incógnita x ; e o segundo representa o valor da incógnita y. Essa ordem precisa ser respeitada. Daí o nome par ordenado Indica-se: (x, y).

Vamos analisar as situações seguintes.

1 O par ordenado (2, 5) é solução da equação 3x + 2y = 16?

3x + 2y = 16

3 ? (2) + 2 ? (5) = 16

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 156

ILUSTRAÇÕES: EDITORIA DE ARTE

6 + 10 = 16 (igualdade verdadeira)

Portanto, o par ordenado (2, 5) é solução da equação 3x + 2y = 16.

2 O par ordenado (5, 2) é solução da equação 3x + 2y = 16?

3x + 2y = 16

3 ? (5) + 2 ? (2) = 16

Como 15 + 4 5 16, o par ordenado (5, 2) não é solução da equação 3x + 2y = 16.

3 Determinar a solução da equação 3x + 2y = 16 quando y = 1.

3x + 2y = 16

3x + 2 ? ( 1) = 16

3x _ 2 = 16

3x = 16 + 2

3x = 18 = x 18 3

x = 6

O par ordenado (6, 1) é solução da equação quando y = 1.

ATIVIDADES

Responda às questões no caderno.

1. Verifique se o par ordenado (5, 2) é uma das soluções das seguintes equações.

a) 5x + 2y = 21 Sim.

b) x _ 9y = 23 Sim.

c) 10x _ y = 48 Não.

d) 6x + 6y = 18 Sim.

e) 3x _ 4y = 23 Não.

f) 0,5x _ 0,3y = 1,9 Não.

2. Considere y = 7x _ 3 e determine o valor da incógnita x nas equações a seguir.

a) 2x + 5y = 59 2

11 16

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades propostas têm como objetivo verificar se os estudantes apresentam uma solução para equações do 1o grau com duas incógnitas e verificam se um par ordenado (x, y) é ou não uma das soluções de uma equação do 1o grau com duas incógnitas.

4. Apresente uma solução para a equação 9x _ 5y = 21 quando:

a) y = 3. (4, 3)

b) x = 6. ( 6, 15)

5. Dada a equação 6x _ y = 42, encontre a solução dessa equação quando:

a) x = 8. (8, 6)

b) y = 30. (12, 30)

6. Analise a afirmação “O par ordenado ( 1, 10) é solução, ao mesmo tempo, das equações 10x _ y = 20 e 5x + 2y = 15” e indique se é verdadeira ou falsa.

No desafio 7, é possível que, com algumas tentativas, até mentalmente, os estudantes cheguem ao par (4, 3). Eles devem perceber que procurar, por tentativas, uma solução de uma equação do 1o grau com duas incógnitas exige que se atribua um valor a uma incógnita e, com isso, se calcule a outra. No caso, a solução deve ser a mesma para as duas equações. Assim, é necessário procurar um valor para uma das incógnitas que forneça, nas duas equações, valores iguais para a outra incógnita.

b) 3x _ y = 21 9 2

c) 5x _ 3y = 2

d) 0,3x _ 0,2y = 1,7 1

3. Determine uma das soluções da equação 0,6x _ 1,5y = 1,5 quando:

a) y = 0,8. ( 0,5; 0,8)

b) y = 1,2. (0,5; 1,2)

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd

DESAFIO

7. Agora, junte-se a um colega, façam tentativas usando apenas números naturais e descubram um par ordenado (x, y) que seja solução, simultaneamente , das equações x + y = 7 e x _ y = 1.

É verdadeira. O par ordenado é (4, 3).

Incentivar os estudantes a procurar mais de um par que seja solução das duas equações simultaneamente. A impossibilidade de encontrar outros pares leva à discussão a respeito da solução de um sistema de equações do 1o grau com duas incógnitas, tema que será estudado na sequência.

ORIENTAÇÕES DIDÁTICAS

Representação geométrica de uma equação do 1o grau com duas incógnitas

A construção da representação geométrica de equações do 1o grau com duas incógnitas pode ser feita utilizando software de geometria dinâmica. É importante ressaltar que a construção feita usando papel quadriculado, régua e lápis é fundamental para que os estudantes compreendam o conceito envolvido. A utilização do software deve ser feita posteriormente, com o objetivo de auxiliar no processo de aprendizagem.

Se sua escola dispuser de computadores, sugere-se que as construções sejam feitas em papel e, em seguida, usando o software. Questionar os estudantes a respeito da inclinação das retas, dos pontos em que a reta intercepta o eixo das ordenadas e o eixo das abscissas. Registrar na lousa as hipóteses dos estudantes, trabalhando tanto a inferência como a argumentação da sua turma.

Atividades

Para a resolução da atividade 2, providenciar com antecedência folhas de papel quadriculado, e solicitar aos estudantes que tragam régua graduada para a sala de aula.

REPRESENTAÇÃO GEOMÉTRICA DE UMA EQUAÇÃO DO 1 o GRAU COM DUAS INCÓGNITAS

A representação geométrica de uma equação do 1o grau com duas incógnitas, em que U =r , é uma reta.

Acompanhe no exemplo como podemos representar uma equação do 1o grau com duas incógnitas no plano cartesiano.

Representar a equação x + y = 3 no plano cartesiano. Inicialmente, construímos um quadro, atribuímos alguns valores para x e calculamos os respectivos valores de y. Com isso, determinamos alguns pares ordenados que são soluções dessa equação.

Depois, localizamos os pontos correspondentes a esses pares ordenados no plano cartesiano. Com o auxílio de uma régua, traçamos a reta que passa por esses pontos.

ATIVIDADES

Responda às questões no caderno.

1. Considere que x assume os valores { 1, 0, 1, 2} e determine os pares ordenados que pertencem à representação geométrica das equações a seguir.

a) 2x + y = 2

b) x _ 3y = 1

Respostas na seção Resoluções comentadas deste Manual.

2. Represente no plano cartesiano as equações a seguir, usando uma folha de papel quadriculado. Respostas na seção Resoluções comentadas deste Manual.

a) x _ y = 2 b) 2x _ y = 5

158

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd

c) x _ 3y = 1

SISTEMAS DE DUAS EQUAÇÕES DO 1 o GRAU COM DUAS INCÓGNITAS

Consideremos o problema dos veículos apresentado na página 148

ORIENTAÇÕES DIDÁTICAS

Sistemas de duas equações do 1o grau com duas incógnitas

Retomar o problema 2 da página 148 do Livro do estudante e as estratégias de resolução adotadas naquele momento. Em seguida, apresentar a resolução proposta nesta página e compará-las.

Podemos resolver essa situação-problema da seguinte maneira: São 14 veículos. Se cada veículo tivesse duas rodas, seriam 28 rodas.

Mas o problema cita que são 48 rodas no total. Então, podemos substituir motos por carros até completar 48 rodas e 14 veículos. 4 ? 2 = 8

10 ? 4 = 40

Promover um debate a respeito dessas estratégias e seus pontos positivos e negativos. Espera-se que os estudantes concluam que o método de tentativa e erro pode ser bastante trabalhoso dependendo da situação e que, por isso, é necessário um novo método para a resolução de sistemas de equações do 1o grau com duas incógnitas, que é o tema que será estudado em seguida, contribuindo para o desenvolvimento da habilidade EF08MA08.

Descubra mais

Quantidade de veículos de 4 rodas: 10

Quantidade de veículos de 2 rodas: 4 14 veículos e 48 rodas

Nesse estacionamento, há 10 carros e 4 motos. Esse modo de resolver o problema pode se tornar trabalhoso e demorado quando as quantidades envolvidas forem muito grandes.

DESCUBRA MAIS

RAMOS, Luzia Faraco. Encontros de primeiro grau. São Paulo: Ática, 2019. (A descoberta da Matemática).

Nesse livro, Rodrigo aprende a resolver problemas que envolvem equações do 1o grau. Entre um problema e outro, ele faz novas amizades.

É possível utilizar o livro para ampliar o trabalho e apresentar novas situações que incentivem os estudantes no trabalho com equações, enriquecendo o estudo desse tema.

Verificar se esse livro está disponível na biblioteca da escola e, em caso afirmativo, organizar um momento de leitura nesse espaço escolar.

25/07/22 11:56

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 159

PANDAPAW/SHUTTERSTOCK.COM

HEMERA; WHITEVECTOR/ SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Atividades

As questões propostas têm como objetivo levar os estudantes a representar uma situação por meio de um sistema de duas equações do 1o grau com duas incógnitas.

Na atividade 1, enfatizar a necessidade de associar cada valor desconhecido a uma incógnita, x ou y, deixando clara essa associação. Por exemplo, no item a:

• Preço de um livro: x

• Preço do outro livro: y

Sistema:

Assim, é importante que os estudantes, na resolução de problemas por meio de sistemas de equações do 1o grau com duas incógnitas, deixem claro qual valor desconhecido está associado a cada uma das incógnitas.

A atividade 4 favorece o desenvolvimento da habilidade EF08MA08 à medida que os estudantes são levados a elaborar um problema que possa ser representado por um sistema de duas equações do 1o grau com duas incógnitas. Para isso, podem usar como base a escrita dos enunciados das situações-problema trabalhadas nesta página.

Alguns estudantes podem encontrar dificuldade em elaborar um problema da maneira proposta. Se isso acontecer, dê alguns exemplos de situações na lousa, de modo que possam assimilar e contextualizar alguma delas.

Para facilitar a compreensão, explique aos estudantes que eles podem usar a letra inicial de cada objeto, alimento ou animal envolvido na situação-problema para representar as incógnitas.

Agora, vamos aplicar os conhecimentos de cálculo algébrico para resolver o problema de outro modo. Inicialmente, indicamos:

• a quantidade de carros que há no estacionamento com x ;

• a quantidade de motos que há no estacionamento com y

Em seguida, a partir dos dados do problema, montamos duas equações.

x + y = 14 e 4x + 2y = 48

2. b) Resposta pessoal. Exemplo de resposta: E a medida da frente é 5 m maior do que a medida do fundo.

quantidade de carros

quantidade de motos Cada moto tem 2 rodas. Cada carro tem 4 rodas.

quantidade total de rodas quantidade de veículos Quando duas equações de 1o grau com duas incógnitas são associadas pelo conectivo e, dizemos que há um sistema de duas equações do 1o grau com duas incógnitas (no caso, x e y).

No exemplo, esse sistema pode ser representado assim: += += xy 14 4x 2y 48

2. a) Resposta pessoal. Exemplo de resposta: Algumas cestas valendo 3 pontos, e outras, 2 pontos, em um total de 56 pontos.

Responda às questões no caderno.

1. Represente por um sistema de duas equações do 1o grau, nas incógnitas x e y, cada uma das situações a seguir.

a) Dois livros custam juntos 60 reais, e o preço de um deles é igual ao dobro do preço do outro.

b) A soma das idades de Lúcio e Fernanda é 9 anos, enquanto a diferença entre essas idades é 3 anos, sendo Lúcio o mais velho.

c) Uma tábua de 3,5 metros de comprimento deve ser cortada em dois pedaços de tal modo que a medida de comprimento do pedaço maior seja igual ao triplo da medida de comprimento do menor menos 0,5 metro.

d) Gabriela tem 10 cédulas, umas de 20 reais e outras de 10 reais, perfazendo um total de 130 reais.

e) A soma de dois números é 100, e o maior deles é igual ao dobro do menor mais 4.

2. Em cada item, complete o enunciado de modo a torná-lo um problema que possa ser representado por um sistema de duas equações do 1o grau nas incógnitas x e y. Depois, represente esse sistema.

a) Em um jogo de basquete, a cestinha do time vencedor fez 24 cestas.

b) O perímetro de um terreno retangular é 22 m.

3. Em um sítio, há bois e patos, totalizando 23 animais e 82 pernas. Use as letras x e y para representar as incógnitas e escreva um sistema de duas equações associado à quantidade de animais (bois e patos) e pernas nesse sítio.

4. A partir das situações apresentadas nesta página, elabore um problema que possa ser representado por um sistema de duas equações do 1o grau com duas incógnitas. Em seguida, entregue-o a um colega para que ele escreva o sistema correspondente. Juntos, façam a correção.

Resposta pessoal. Exemplo de resposta: Em um mercado, 3 quilogramas de tomate e 5 quilogramas de arroz custam 58 reais. Já 1 quilograma de tomate e 1 quilograma de arroz custam 14 reais.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 160

SOLUÇÃO DE UM SISTEMA DE DUAS EQUAÇÕES DO 1 O GRAU COM DUAS INCÓGNITAS

Quando duas equações formam um sistema, embora cada equação tenha infinitas soluções, devemos procurar a solução que satisfaça as duas equações simultaneamente.

A solução de um sistema de duas equações do 1o grau com duas incógnitas, x e y, por exemplo, é um par ordenado (x, y) que é solução tanto da primeira equação quanto da segunda.

Voltemos ao sistema de equações que representa o problema dos veículos da página anterior. += += xy 14

4x 2y 48 

• O par ordenado (10, 4) é solução desse sistema, pois os valores satisfazem as duas equações simultaneamente:

x + y = 14

10 + 4 = 14 (verdadeira)

4x + 2y = 48

4 ? 10 + 2 ? 4 = 48

40 + 8 = 48 (verdadeira)

• O par ordenado (6, 8) não é solução desse sistema, pois satisfaz a equação x + y = 14, mas não satisfaz a equação 4x + 2y = 48:

x + y = 14

6 + 8 = 14 (verdadeira)

4x + 2y = 48

4 ? 6 + 2 ? 8 = 48 (falsa)

24 + 16 5 48

Esse sistema pode ser resolvido geometricamente. Para isso, vamos representar cada uma das equações que o compõe em um mesmo plano cartesiano.

A solução do sistema de equações é o ponto de intersecção das duas retas no plano cartesiano, no caso, o ponto (10, 4).

ORIENTAÇÕES DIDÁTICAS

Solução de um sistema de duas equações do 1o grau com duas incógnitas

Ler o texto apresentado aos estudantes e verificar se eles compreendem que, como cada uma das equações do sistema pode ser representada por uma reta do plano cartesiano, o ponto de intersecção das duas retas é a solução do sistema, pois é solução tanto de uma como da outra equação.

Se possível, propor outros sistemas de equações do 1o grau com duas incógnitas e mostrar a resolução geométrica usando um software de geometria dinâmica.

AMPLIANDO

Vídeo

SISTEMAS de equações com gráficos: soluções exatas e aproximadas. c2022. Vídeo (5min7s). Publicado por Khan Academy. Disponível em: https://pt.khanacademy.org/math/algebra/x2f8bb11595b61c86:systems-ofequations/x2f8bb11595b61c86:introduction-to-systems-of-equations/v/solving-systems-graphically-examples. Acesso em: 30 jul. 2022.

Nesse link, é possível ter acesso a uma videoaula sobre a representação gráfica da solução de um sistema de duas equações com duas incógnitas.

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades propostas têm o objetivo de aplicação dos conhecimentos adquiridos a respeito de um sistema de equações, verificando se um par ordenado é ou não solução de determinado sistema de duas equações do 1o grau com duas incógnitas.

A atividade 3 vai além do que simplesmente uma verificação. Nela, os estudantes devem determinar o par ordenado que é a solução do sistema. Verificar que procedimentos os estudantes usam para resolver essa questão. Ela pode ser feita em duplas ou pequenos grupos, de modo a permitir a troca de ideias e valorizar a cooperação entre os estudantes. Socializar e validar com a turma os diferentes procedimentos que aparecerem.

Responda às questões no caderno.

1. O par ordenado (10, 7) é a solução do sistema _= += 3x2y 16 2x3y 41

? Sim.

2. Verifique se o par ordenado ( 2, 2) é a solução deste sistema de duas equações do 1o grau com duas incógnitas.

3. Faça tentativas e descubra o par ordenado de números naturais que é a solução deste sistema. (4, 2)

4. Pelo regulamento de um torneio de basquete, cada partida que uma equipe vence vale 2 pontos, e cada partida que perde vale 1 ponto. Uma equipe de basquete disputou 8 partidas desse torneio, totalizando 13 pontos. Quantas partidas essa equipe venceu? E quantas ela perdeu? a) Considere que a situação seja expressa por um sistema de duas equações do 1o grau, em que x é a quantidade de vitórias, e y, a quantidade de derrotas, e indique a representação que é solução geométrica desse sistema. Depois, resolva o problema.

AMPLIANDO Link

SOUSA, Aparecido. Sistemas de equações do 1o grau. Geogebra. [S. l.], 2020. Disponível em: https://www. geogebra.org/m/zn4kzuzd. Acesso em: 30 jul. 2022.

O material sugerido apresenta possibilidades para ampliar o estudo. Verificar a possibilidade de propor que determinem pares ordenados que sejam solução de cada uma das equações do 1o grau. Depois, mover o ponto de intersecção para encontrar a solução do sistema de equações.

5. Analise a representação gráfica deste sistema de equações _= += 2x y3 3x 2y 8    , indique as afirmações verdadeiras e corrija as falsas.

Verdadeiras: a e c. Falsa: b. As soluções da equação 2x _ y = 3 são todos os pontos sobre a reta que a representa.

a) Os pontos B e D são soluções da equação 3x + 2y = 8.

b) Os pontos A, C e E são as únicas soluções da equação 2x _ y = 3.

c) A solução do sistema é o ponto A(2, 1).

DESAFIO

6 II. A incógnita x representa a quantia economizada por Bento; e a incógnita y, a quantia economizada por Antônio.

Agora, junte-se a um colega, e resolvam o desafio a seguir.

6. Dois irmãos acabam de contar a quantia que cada um conseguiu economizar.

IMAGEM FORA DE PROPORÇÃO. AS CORES NÃO SÃO REAIS.

Antônio, se você me der um terço do que economizou, eu ficarei com 110 reais.

ORIENTAÇÕES DIDÁTICAS

No desafio 6, incentivar os estudantes a criar estratégias próprias de resolução. Pedir que descrevam como pensaram e socializem as respostas. Discutir com eles a necessidade de uma estratégia eficaz para a resolução de um sistema de equações. Deixar que reflitam um pouco sobre isso.

Para descobrir quantos reais cada irmão conseguiu economizar, responda.

I. Qual dos sistemas a seguir traduz a situação apresentada? Alternativa b.

II. No sistema correto de equações, o que representa a incógnita x? E a incógnita y?

III. Verifique qual dos pares ordenados a seguir é a solução do sistema de equações correto

a) (80, 90)

b) (90, 80)

IV. Qual é a quantia que cada irmão conseguiu economizar?

c) (85, 95)

x = 80 reais (quantia economizada por Bento) e y = 90 reais (quantia economizada por Antônio).

Bento, eu preciso de menos. Basta que você me dê um quarto das suas economias para que eu fique com 110 reais. 163

Alternativa a.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 163 25/07/22 12:03

ORIENTAÇÕES DIDÁTICAS

Método da substituição

Nesta e na próxima página é apresentado o método da substituição para a resolução de sistemas de duas equações do 1o grau com duas incógnitas, contribuindo para o desenvolvimento da habilidade EF08MA08. Ler com os estudantes a explicação e reproduzi-la na lousa, explicando cada passo. Verificar se os estudantes compreendem o que é feito de um passo para outro.

Comentar que esse método é bastante utilizado para a resolução de sistemas desse tipo e que será uma ferramenta muito útil para diversos assuntos que verão em volumes posteriores desta coleção, tanto na Matemática como em outros componentes curriculares.

Pense e responda

Propor aos estudantes que construam um fluxograma com as etapas para a resolução de um sistema de equações pelo método da substituição. Há várias possibilidades de elaboração.

6

RESOLUÇÃO DE SISTEMA DE DUAS EQUAÇÕES DO 1o GRAU COM DUAS INCÓGNITAS

Existem métodos algébricos que permitem calcular o par ordenado (x, y), que é a solução de um sistema de duas equações do 1o grau com duas incógnitas.

Neste capítulo, estudaremos dois desses métodos: o da substituição e o da adição MÉTODO DA

SUBSTITUIÇÃO

Retomemos o problema dos veículos já apresentado.

Em um estacionamento, há carros e motos, totalizando 14 veículos e 48 rodas. Quantos carros e quantas motos há nesse estacionamento?

De acordo com os dados do problema, obtemos o sistema de duas equações do 1o grau com duas incógnitas:

+= += xy 14 4x 2y 48    , em que x representa a quantidade de carros, e y, a quantidade de motos no estacionamento.

Para resolver esse sistema pelo método da substituição, acompanhamos os passos a seguir.

1o passo: Na 1a equação, isolamos a incógnita x

x + y = 14

x = 14 _ y

2o passo: Na 2a equação, substituímos x por 14 y e calculamos o valor de y

4x + 2y = 48

4(14 _ y) + 2y = 48 equação do 1o grau na incógnita y 56 _ 4y + 2y = 48 56 _

2y = 8 h= y 8 2

y = 4 quantidade de motos

PENSE E RESPONDA

Responda no caderno.

Represente os passos da resolução de um sistema de duas equações do 1o grau com duas incógnitas usando um fluxograma. Compare seu fluxograma com o dos colegas.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

164

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 164

3o passo: Substituímos y por 4 na equação x = 14 y e obtemos o valor de x

x = 14 _ y

x = 14 _ 4

x = 10 quantidade de carros

Então, a solução do sistema    += += xy 14 4x 2y 48 é o par ordenado (10, 4)

Há 10 carros e 4 motos no estacionamento.

Acompanhe como aplicar o método da substituição na resolução dos seguintes sistemas.

ORIENTAÇÕES DIDÁTICAS

Retomar a resolução do exemplo 1 na lousa, pois as equações que compõem o sistema exigem algumas transformações iniciais para que fiquem escritas na forma ax + by = c. A partir daí, pode-se aplicar o método da substituição.

    

1 Resolver o sistema _= _+=_

x 2 1 y 3 x3(y 2) 4

1o passo: Inicialmente, devemos preparar as equações, isto é, devemos escrevê-las na forma ax + by = c.

• _= x 2 1 y 3 = 3x 6 6 2y 6 3x _ 6 = 2y 3x _ 2y = 6

x _ 3(y + 2) = 4

_ 3y _ 6 = 4

_ 3y = 2

2o passo: Agora, vamos resolver o sistema equivalente com as equações obtidas no passo anterior.

2y 6 x3y2

• Nesse sistema, vamos iniciar pela 2a equação: x _ 3y = 2

x = 2 + 3y

• Substituímos o valor de x na 1a equação: 3x _ 2y =

• Determinamos o valor de x para y = 0.

x = 2 + 3y

x = 2 + 3 ? (0)

x = 2 + 0

x = 2 A solução do sistema é o par ordenado (2, 0)

D2-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 165

Na primeira equação que compõe o sistema, verificar se os estudantes compreendem a necessidade do cálculo do mínimo múltiplo comum e de como os denominadores foram “eliminados”. Na segunda equação, checar se aplicam a propriedade distributiva corretamente. Alertar o grupo que após esses cálculos iniciais, eles devem aplicar o método da substituição, isolando uma das incógnitas em uma das equações.

22/07/22 17:35

ORIENTAÇÕES DIDÁTICAS

Apresentar o exemplo 2 na lousa e propor aos estudantes que o resolvam antes de observar a resolução apresentada no Livro do estudante. Em seguida, explorar o exemplo na lousa solicitando aos estudantes que comparem com a resolução feita por eles e comentem a respeito dos pontos em que identificaram alguma dificuldade.

Fórum

Ler o texto do boxe com os estudantes e verificar como o controle de tráfego em cruzamentos de ruas com mão única se relaciona aos sistemas de equações. Essa abordagem contribui para o desenvolvimento da competência específica 5 da área de Matemática. A ilustração que acompanha o texto pode auxiliar na compreensão do tema e na construção do sistema solicitado.

2 Determinar o par (x, y), que é a solução do sistema

1o passo: Nesse sistema, devemos ter y 5 0, y 5 1 e x 5 0. Então, vamos reduzir as equações à forma mais simples de cada uma.

2(y _ 1) = 5x 2y _ 2 = 5x h 5x + 2y = 2

2o passo: Em seguida, resolvemos o sistema equivalente    = _+= y3x 5x2y 2

• N esse caso, substituímos a 1a equação, y  = 3x, na 2a e obtemos o valor de x :

5x + 2y = 2

5x + 2 ? (3x) = 2

5x + 6x = 2

x = 2

A solução do sistema é o par ordenado (2, 6)

Uma aplicação de sistemas de equações

Os sistemas de duas equações do 1o grau com duas incógnitas podem ser usados na resolução de diferentes problemas nas mais diversas situações cotidianas. Uma delas é o controle de tráfego em cruzamentos de ruas de mão única.

• Depois, substituímos x = 2 na 1a equação e obtemos o valor de y :

y = 3x

y = 3 ? (2)

y = 6

É possível determinar a média da quantidade de veículos em cada cruzamento de uma via, por exemplo, no horário de maior movimento e, com isso, controlar o tempo de abertura dos semáforos. Acompanhe os cruzamentos A e B representados.

As setas indicam o sentido de cada via. Nessa situação, a quantidade de veículos que chega ao cruzamento é igual à quantidade de veículos que sai dele. Com isso, podemos escrever um sistema de duas equações do 1o grau nas incógnitas x e y e descobrir a quantidade de veículos que passa pelos cruzamentos A e B em determinado horário.

Responda no caderno.

• Junte-se a um colega, escrevam esse sistema e determinem os valores de x e y. Depois, façam uma pesquisa sobre outras aplicações de sistemas de equações.

x = 120 e y = 200. Resposta pessoal. Exemplo de resposta: Os sistemas de equações são usados para dimensionar redes elétricas, no balanceamento de equações químicas, entre outras aplicações.

AMPLIANDO Link

SANTOS. Cleber de Oliveira dos. Álgebra Linear: aplicações de sistemas lineares. [S. l.], [20--?]. Disponível em: https://www.fucap.edu.br/portal/artigos/5.pdf. Acesso em: 31 jul. 2022.

Nesse link, é possível encontrar a descrição de algumas aplicações dos sistemas lineares em situações cotidianas.

ATIVIDADES

3. b) (3, 3) e (1, 5) não são soluções do sistema, pois não pertencem simultaneamente às duas retas.

c) Resposta pessoal. Exemplo de resposta: Uma pessoa comprou 3 lápis e 5 canetas e pagou R$ 26,00. Quanto custa uma caneta nessa papelaria? (R$ 4,00).

Responda às questões no caderno.

1. Determine a solução de cada um dos seguintes sistemas de equações do 1o grau nas incógnitas x e y

a)    += _= xy 22 xy 8 (15, 7)

b)    += _= 2x y26 xy 4 (10, 6)

c)    += _= 3x y5 5x 2y 1 ( 1, 2)

d)    += _= x2y4 3x 2y 20 (4, 4)

e)    += _= x3y3 2x y1,8 (1,2; 0,6)

c) Complete o enunciado do problema a seguir para que ele possa ser resolvido por este sistema.

Ricardo foi à papelaria e comprou um lápis e uma caneta e pagou R$ 6,00.

4. Para alugar uma quadra para uma festa beneficente , 20 pessoas contribuíram com a mesma quantia, mas ficaram faltando 130 reais para atingir o valor necessário. Mais 2 pessoas ingressaram nesse grupo, e, após o acerto final, decidiu-se que todas as pessoas pagariam a mesma quantia, e que as 20 pessoas iniciais deveriam contribuir com mais 3 reais cada uma.

ORIENTAÇÕES DIDÁTICAS

Atividades

Neste bloco, as questões têm como objetivo levar os estudantes a resolver um sistema de equações do 1o grau com duas incógnitas utilizando o método da substituição.

    

f) =_ _=

x 5 10 y 2 xy 8 (20, 12)

g)    _=_+ __+=_ 3x 5y 2( xy )1 6y 3( x3y) 2x (1, 0)

h)  

(6, 3)

2. Uma fração é equivalente a 7 4 . Se adicio narmos 2 ao denominador dessa fração, ela se tornará equivalente a 3 2 Qual é a fração inicial? 21 12

3. Considere o seguinte sistema de duas equações do 1o grau nas incógnitas x e y

3x 5y 26 xy 6 += +=  

a) Resolva-o algebricamente. (2, 4)

b) Em uma folha de papel quadriculado, represente geometricamente esse sistema e a solução dele. Em seguida, a partir da representação que você fez, explique aos colegas e ao professor como você faria para verificar se o ponto (3, 3) é solução desse sistema. E o ponto (1, 5)?

AMPLIANDO

Link

a) Quantos reais as 20 pessoas pagaram antes de as outras 2 pessoas ingressarem?

R$ 32,00

b) Com quantos reais cada uma das 22 pessoas contribuiu no acerto final? R$ 35,00

5. Para embalar 1 650 livros, uma editora usou 27 caixas, umas com capacidade para 50 livros, e outras, para 70 livros. Quantas caixas de cada tipo a editora utilizou?

12 caixas para 50 livros e 15 caixas para 70 livros.

6. Em uma competição esportiva, foram distribuídas apenas medalhas de ouro e de prata. Para efeito de classificação, cada medalha de ouro vale 3 pontos, e cada medalha de prata vale 2 pontos.

a) Se a equipe A conquistou 11 medalhas e obteve 29 pontos no total, quantas medalhas de ouro a equipe A ganhou?

b) A partir do enunciado, elabore um problema envolvendo duas informações indicadas nas fichas.

A atividade 3 favorece o desenvolvimento da habilidade EF08MA08. É provavél que alguns estudantes tenham dificuldade em determinar a solução geométrica proposta no item b, já que podem não recordar o gráfico de equações lineares de duas variáveis. Caso isso aconteça, retome o conteúdo apresentado na página 158 do Livro do estudante.

Caso algum estudante manifestar dificuldade na elaboração proposta no item c, dê alguns exemplos de situações do dia a dia para que eles consigam contextualizar alguma delas. Um exemplo de problema a ser elaborado é o seguinte:  Ricardo foi à papelaria e comprou um lápis e uma caneta. Ele pagou R $ 6,00. Renata foi à mesma papelaria e comprou três lápis e cinco canetas, pagando R $ 26,00. Qual o preço de um lápis e de uma caneta?

obteve 30 pontos obteve 27 pontos conquistou a mesma quantidade de medalhas de prata e de ouro

conquistou 10 medalhas Em seguida, entregue o problema a um colega para que ele possa solucioná-lo. Façam juntos as correções necessárias.

Neste caso, considerando x a quantidade de lápis e y a quantidade de canetas, temos:

3x 5y 26 xy 6 += +=

CÁSSIO, Jorge. Sistemas 2 x 2. Geogebra. [S. l.], 2019. Disponível em: https://www.geogebra.org/m/ gu3ev8hx#chapter/401977. Acesso em: 31 jul. 2022.

Nesse link, há recurso que pode ser explorado com os estudantes para facilitar a compreensão de alguns conteúdos estudados até este momento.

6. a) 7 medalhas de ouro.

6. b) Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 167

ORIENTAÇÕES DIDÁTICAS

Método da adição

Para o método da adição, retomar a aplicação do princípio multiplicativo da igualdade com os estudantes: multiplicando (ou dividindo) os dois membros de uma equação por um mesmo número não nulo, obtemos outra equação equivalente à equação original.

Ressaltar que, para determinar por qual número se deve multiplicar cada equação do sistema ao utilizar o método da adição, deve-se buscar eliminar uma das incógnitas ao se fazer a adição, membro a membro, das duas equações. Facilita eliminar incógnitas que tenham sinais diferentes nas duas equações, em particular, se tiverem coeficientes opostos.

AMPLIANDO

Link

UM GRANDE sistema. Clubes de Matemática da OBMEP [S. l.], 2020. Disponível em: http:// clubes.obmep.org.br/blog/2020/11/ um-grande-sistema/. Acesso em: 30 jul. 2022.

Nesse link, está proposto um sistema de equações do 1o grau, com cinco incógnitas, e é dada uma dica que auxilia na resolução do problema.

MÉTODO DA ADIÇÃO

Vamos estudar como resolver um sistema de duas equações do 1o grau com duas incógnitas usando o método da adição.

Consideremos as situações a seguir.

1 Determinar a solução (x, y) do sistema

1o passo: Como as duas equações apresentam termos opostos (+3y na primeira e 3y na segunda), adicionamos as duas equações membro a membro. Isso permite obter uma única equação, equivalente às equações dadas, sem a incógnita y, pois os termos opostos, quando adicionados, resultam em zero.

2o passo: Substituindo x por 5 em uma das equações do sistema, obtemos o valor de y

5x + 3y = 21

5 ? 5 + 3y = 21

25 + 3y = 21

3y = 21 _ 25

3y = 4 y 4 3 =_

Lembre-se de que o par ordenado que é solução do sistema é solução tanto da primeira equação quanto da segunda.

A solução do sistema é o par ordenado = S5,

2 Resolver o sistema

6

1o passo: Observando as equações do sistema, percebemos que não é viável adicionar membro a membro as duas equações, pois, não havendo termos opostos, nenhuma das incógnitas será anulada. Vamos, então, usar um recurso que é uma aplicação do princípio multiplicativo para deixar o sistema com termos opostos.

Inicialmente, devemos escolher uma das incógnitas, por exemplo, y. Observe que o coeficiente de y na primeira equação é 3, e o coeficiente de y na segunda equação é 2. A ssim, para que os coeficientes de y sejam números opostos, basta multiplicar a primeira equação (5x + 3y = 2) pelo coeficiente de y da segunda equação (2) e multiplicar a segunda equação (4x _ 2y  = 6) pelo coeficiente de y da primeira equação (3). Acompanhe.

2o passo: Agora, temos dois termos opostos: +6y e 6y. Portanto, podemos adicionar membro a membro as equações para obter uma única equação sem a incógnita y

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd

AMPLIANDO

Atividade complementar

Resolva o sistema a seguir pelo método da adição e pelo método da substituição.

Para resolver o sistema aplicando o método da adição, é preciso ter os dois coeficientes opostos no mesmo membro de cada equação. Assim:

Resolução da atividade

• Utilizando o método da adição:

Adicionando membro a membro as duas equações, obtemos: 0 + y = 4 h y = 4

ORIENTAÇÕES DIDÁTICAS

3o passo: Finalmente, vamos substituir x por 1 em qualquer uma das equações do sistema e determinar o valor de y

5x + 3y = 2

5 ? 1 + 3y = 2

5 + 3y = 2

3y = 2 _ 5

3y = 3 y = 1

A solução do sistema é o par ordenado (1, 1)

+=

+=

8 x 6 y 3 2 x 3 y 1       

1o passo: Vamos reduzir as equações à forma mais simples de cada uma.

8 x 6 y 3 8y6x xy 3xy xy 8y6x3xy

+= + = +=

• 8y6x72 +=

Como xy 24, te mos:

8y6x 3(24)

= +=?

• 2y3x24 += += + = +=

= 2 x 3 y 1 2y3x xy 1xy xy 2y3x xy

Como xy 24, te mos:

2o passo: Agora, vamos resolver o sistema equivalente    8y6x72 2y3x24 += +=

Observe que o sistema não apresenta termos opostos, porém, a incógnita x na primeira equação tem coeficiente +6 e na segunda equação tem coeficiente +3. Com isso, usamos o fato de 6 ser o dobro de 3 e concluímos que, para deixar o sistema com termos opostos na incógnita x, basta multiplicarmos a segunda equação por 2. Acompanhe a resolução a seguir.

(2)x_       8y6x72 2y3x24

4y

_

PENSE E RESPONDA

8y6x72 4y6x48

Resposta pessoal. Exemplo de resposta: Multiplicar a segunda equação (2y + 3x = 24) por 4.

Escreva uma maneira de obter termos opostos na variável y nas equações do sistema do exemplo anterior e explique aos colegas e ao professor como você pensou.

Depois que a turma acompanhar os exemplos apresentados no Livro do estudante, fornecer outros na lousa para que eles possam analisar qual dos dois métodos estudados (método da adição ou da substituição) é mais adequado utilizar em cada sistema. Pedir que justifiquem suas escolhas, discutindo a respeito disso com toda a turma. Novamente, ao solicitar que explicitem suas ideias, o professor contribui para o desenvolvimento da argumentação dos estudantes.

Pense e responda

A pergunta proposta no boxe admite diferentes respostas. Ouvir as hipóteses dos estudantes, problematizando na sala de aula a pertinência delas.

169

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 169

Substituindo y por 4 na equação x  3y = 0, temos:

x 3 4 = 0 h x = 12.

Logo, (12, 4) é a solução desse sistema.

• Utilizando o método da substituição:

Observando o sistema original, verifica-se que na primeira equação a incógnita x já está isolada. Assim, basta substituir x por 3y na segunda equação:

2 ? 3y 5y = 4 h 6y 5y = 4 h

h y = 4

Substituindo o valor de y na primeira equação, temos:

x = 3y h x = 3 ? 4 h x = 12

Desse modo, obtemos a solução (12, 4) para o sistema.

ORIENTAÇÕES DIDÁTICAS

Atividades

Neste bloco, as questões têm como objetivo levar os estudantes a resolver um sistema de equações do 1o grau com duas incógnitas utilizando o método que considerarem mais adequado: da adição ou da substituição.

Verificar se os estudantes compreendem que usando o método da substituição ou o método da adição chegarão ao mesmo resultado. Além disso, é interessante fazê-los experimentar a resolução pelos dois métodos, até que identifiquem em qual deles se sentem mais confortáveis para realizar a resolução. Outro ponto a ser considerado é que, além da preferência pessoal para a escolha do método de resolução, em alguns casos, utilizar um ou outro método facilita bastante os cálculos. Auxiliar os estudantes no desenvolvimento dessa habilidade de identificação ao analisar o sistema de equações dado.

Responda às questões no caderno.

1. D etermine a solução de cada um dos seguintes sistemas de duas equações do 1o grau nas incógnitas x e y

5. Em um sorteio, dois números foram premiados. A soma desses dois números é 170, e o maior deles é igual ao triplo do menor mais 2 unidades. Quais foram os números sorteados? 128 e 42.

6. Caio e Pedro são irmãos. Em 2022, a soma das idades dos dois era 22 anos. Como Caio é dois anos mais velho do que Pedro, qual era a idade de Caio em 2022?

7. Em um terreno, há galinhas e ovelhas. São 31 animais e 82 pernas. Quantas galinhas e quantas ovelhas estão nesse terreno?

DESAFIOS

Agora, junte-se a um colega, e resolvam os desafios a seguir.

8. N o quadro, estão indicadas a soma em cada linha e em cada coluna. Descubra os números “escondidos” pelas figuras, sabendo que figuras iguais escondem números iguais.

2. D ois números reais x e y são tais que x4 y3 1 + + = e 2y x2 4 + = Nessas condições, sendo x 5 2 e y 5 3, determine o valor de: a) y _ x 1

b) x : y 3 2

c) (x + y)(x _ y) 5

3. Quando adicionamos 2 aos dois termos de uma fração, ela se torna equivalente a 5 6 ; quando subtraímos 2 dos dois termos da mesma fração, ela se torna equivalente a 1 2 . Qual é a fração considerada? 3 4

4. Cé lia pensou em dois números. A soma entre esses números é 175, e a diferença entre eles é 43. Quais são os números em que Célia pensou? 109 e 66.

9. Carlos e Andrea levaram o cachorro Balu ao veterinário. Lá, encontraram uma balança com defeito, que só indicava corretamente valores superiores a 60 kg. Assim, eles mediram a massa dois a dois e obtiveram os seguintes valores.

• Carlos e Balu, juntos, 87 kg.

• Carlos e Andrea, juntos, 123 kg.

• Andrea e Balu, juntos, 66 kg.

Quantos quilogramas tem cada um?

Carlos tem 72 kg, Andrea tem 51 kg e Balu tem 15 kg.

EQUAÇÃO DO 2 o GRAU CAPÍTULO7

Considere a seguinte situação.

Em um terreno que lembra um quadrado de lado medindo 15 metros, será construída uma piscina retangular cuja medida do comprimento é o dobro da medida da largura. Qual deve ser a medida do comprimento dessa piscina para que restem 153 m² do terreno?

Considerando x a medida da largura da piscina, a situação pode ser representada da seguinte maneira.

A área do terreno é 15 m ? 15 m = 225 m².

A área da piscina é dada por x ? 2x = 2x².

A área restante do terreno é 153 m². Então, podemos escrever 153 = 225 _ 2x² ou, ainda, 2x² _ 72 = 0.

A equação obtida, 2x² _ 72 = 0, tem apenas uma incógnita (x) cujo expoente é 2. Ela é um exemplo de uma equação do 2o grau com uma incógnita da forma ax² + c = 0, em que a 5 0.

SAIBA QUE

Uma equação do 2o grau completa é definida na forma ax² + bx + c = 0, com a 5 0, em que a é o coeficiente que multiplica x², b é o coeficiente que multiplica x, e c é o coeficiente independente. Nesse momento, vamos estudar apenas as soluções de equações do 2o grau incompletas da forma ax² + c = 0.

RESOLVENDO EQUAÇÕES DA FORMA ax² + c = 0

Você já estudou que resolver uma equação significa determinar os possíveis valores que satisfazem a equação em um conjunto universo dado.

Na resolução das equações do 2o grau da forma ax² + c = 0, usaremos a fatoração e a seguinte propriedade dos números reais:

Sendo x e y dois números reais quaisquer e x 2 = y, então, xy =+ ou xy =_

Vamos aplicar essa propriedade para resolver a equação 2x² _ 72 = 0, que obtivemos na situação anterior.

2x² _ 72 = 0 Usamos o princípio aditivo.

2x² = 72

2x 2 72 2 2 = Usamos o princípio multiplicativo.

x² = 36 h x = 36 6 ±=±

ORIENTAÇÕES DIDÁTICAS

Equação do 2o grau

Esse é o primeiro contato dos estudantes com as equações do 2o grau. Aqui serão apresentadas apenas as equações do tipo ax 2 + c = 0, contribuindo para o desenvolvimento da habilidade EF08MA09. Apesar de essa habilidade, na BNCC, referir-se a esse tipo de equação incompleta do 2o grau como ax 2 = b, optou-se por manter a letra c como modo de facilitar a identificação do coeficiente independente pelos estudantes.

Caso os estudantes demonstrem interesse, apresentar, apenas a título de curiosidade, os demais tipos de equação do 2o grau e comentar que essas equações serão estudadas de maneira mais aprofundada no nono ano e no Ensino Médio.

Verificar se os estudantes reconhecem que as estratégias utilizadas para resolver esse tipo de equação do 2o grau são similares às estratégias utilizadas para a resolução de equações do 1o grau.

Saiba que

Utilizamos a notação xa =± para representar xa =+ ou xa =_

A equação tem como soluções x =_6 ou x = 6, que indicamos assim: S = { 6, 6}.

Entretanto, como na situação estudada x representa uma medida, consideramos apenas o valor positivo como resposta do problema.

Assim, a medida da largura da piscina é 6 m, e a medida do comprimento é 12 m.

Apresentar a forma completa da equação de 2o grau, nomear os coeficientes de x 2 (a), de x (b) e o coeficiente independente (c).

Destacar que, nesse momento, o estudo estará centrado em equações incompletas do 2o grau, com b = 0, ou seja, da forma ax 2 + c = 0.

Resolvendo equações da forma ax2 + c = 0

Apresentar aos estudantes a resolução da equação 2x2 72 = = 0, resolvida a partir da fatoração.

Assim, temos:

2x 2 72 = 0

2 ? (x 2 36) = 0

2 ? (x 6) ? (x + 6) = 0

x = 6 ou x = 6

ORIENTAÇÕES DIDÁTICAS

Pense e responda

A partir da análise dos exemplos, espera-se que os estudantes percebam que uma equação incompleta do 2 o grau do tipo ax 2 + c = 0 ou terá duas raízes reais e opostas, ou terá raiz nula, ou não admitirá raízes reais.

Acompanhe outros exemplos de resoluções desse tipo de equação.

1 Resolver a equação 16x 2 _ 1 = 0 no conjunto r

16x 2 _ 1 = 0

16x 2 = 1 Usamos o princípio aditivo.

x 1 16 2 = Usamos o princípio multiplicativo.

=±h=± x 1 16 x 1 4

Logo, os números 1 4 e 1 4 são as soluções da equação. Assim,

2 Determinar os valores reais de x para que se tenha 3x2 _ 60 = 0. Como todos os termos da equação são divisíveis por 3, podemos dividir cada termo da equação por 3 para, depois, determinar os valores de x

3x 2 _ 60 = 0

3x 3 60 3 0 3 x200 2 2

_=h_=

x20x 20 2 =h=±

Como 20 não apresenta raiz quadrada exata, os números 20 e 20 + são as soluções da equação. Assim, {}S20, 20 =_

3 Determinar a solução da equação x 2 + 4 = 0 no conjunto r x 2 + 4 = 0

x² = 4

x4 =±

Como 4 não existe no conjunto r , não temos valores reais para x Logo, a equação não tem raízes reais. Assim, S =@

4 Resolver, no conjunto r , a equação (2y + 1)2 = 8 + 2(2y + 1).

Inicialmente, vamos multiplicar os polinômios e deixar a equação na forma ax² + b = 0 para, depois, resolvê-la:

(2y + 1)² = 8 + 2(2y + 1)

(2y + 1)(2y + 1) = 8 + 2(2y + 1)

4y² + 2y + 2y + 1 = 8 + 4y + 2

4y² + 4y + 1 = 10 + 4y

4y² + 4y _ 4y + 1 _ 10 = 0 Usamos o princípio aditivo.

4y² _ 9 = 0 forma ax² + b = 0

4y² = 9 Usamos o princípio aditivo.

= y 9 4 2 Usamos o princípio multiplicativo.

=± y 9 4 h=± y 3 2

PENSE E RESPONDA

Responda no caderno. Analise as soluções das equações do 2o grau dos exemplos e responda: como podem ser as soluções das equações do 2o grau da forma ax² + c = 0? Explique.

Resposta pessoal. Exemplo de resposta: As soluções podem ser opostas, podem ser iguais a zero ou pode não haver soluções no conjunto dos números reais.

Logo, os números 3 2 e 3 2 são as raízes da equação. Assim, S 3 2 , 3 2 =

172

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 172

ATIVIDADES

4.b) Resposta pessoal. Exemplo de resposta: Pensei em um número natural, elevei esse número ao quadrado e do resultado subtraí 9. Se eu obtive o número 91, em que número pensei? (10).

Responda às questões no caderno.

1. Determine o conjunto solução de cada uma das seguintes equações do 2o grau no conjunto r

a) x 2 _ 1 = 0 { 1, 1}

b) x 2 _ 16 = 0 { 4, 4}

c) x 2 _ 64 = 0 { 8, 8}

d) x 2 + 16 = 0 @

6. A área de um triângulo cuja base mede odobro da altura é 196 cm². Calcule a medida da base desse triângulo. 28 cm

ORIENTAÇÕES DIDÁTICAS

Atividades

e) 9x 2 = 25    

f) x 2 _ 20 = 0

5 3 , 5 3

2. Qual é o conjunto solução de cada uma das seguintes equações do 2o grau, sendo U =r?

a) (x + 5)(x _ 6) = 51 _ x { 9, 9}

b) 2x(x + 1) _ x(x + 5) = 3(12 _ x) { 6, 6}

3. C alcule o conjunto solução de cada equação.

a)

4. Larissa pensou no seguinte desafio.

Pensei em um número natural, elevei esse número ao quadrado e do resultado subtraí 380. Se eu obtive 1 2 20 como resultado, em que número pensei?

a) Resolva o desafio em que Larissa pensou.

b) Elabore um desafio inspirado no desafio de Larissa. Depois, desafie um colega a resolvê-lo, e, juntos, façam as correções necessárias.

5. A área de uma região retangular mede 363 m². Sabendo que a medida do comprimento dessa região é o triplo da medida da largura, determine essas medidas

Medida do comprimento: 33 m; medida da largura: 11 m.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 173

7. B runo tem um terreno cuja área é 400 m², e Lauro tem 4 terrenos que lembram quadrados, todos de mesma área. Sabendo que a área dos 4 terrenos de Lauro é igual à área do terreno de Bruno, responda:

100 m²

a) Qual é a área de cada terreno de Lauro?

b) Qual é a medida do lado de cada terreno de Lauro? 10 m

8. A área de um terreno circular é 314 m². Sabendo que a área do círculo é dada pela expressão p r², em que p= 3,14, então, a medida do raio desse terreno é:

a) 20,0 m.

b) 10,0 m.

c) 12,5 m.

d) 9,0 m.

e) 5,0 m.

DESAFIO Agora, junte-se a um colega, e resolvam o desafio a seguir.

9. (Enem/MEC) A temperatura T de um forno (em graus centígrados) é reduzida por um sistema a partir do instante de seu desligamento (t = 0) e varia de acordo com a expressão T(t) = t 4 2 + 400, com t em minutos. Por motivos de segurança, a trava do forno só é liberada para abertura quando o forno atinge a temperatura de 39 °C. Alternativa d. Qual o tempo mínimo de espera, em minutos, após se desligar o forno, para que a porta possa ser aberta?

a) 19,0

b) 19,8

c) 20,0

d) 38,0

e) 39,0

As atividades têm como objetivo levar os estudantes a determinar o conjunto solução de equações do 2o grau do tipo ax 2 + c = 0. Nas atividades 2 e 3, verificar se os estudantes percebem que precisam realizar algumas manipulações algébricas para que a equação chegue à forma ax 2 + c = 0 e possam resolvê-la com as estratégias estudadas. Por ser um assunto novo para os estudantes, verificar se, durante a execução das atividades, alguém propõe estratégias diferentes da apresentada. Caso isso aconteça, solicitar que explique sua estratégia para que o resto da turma possa validá-la. Desse modo, a construção do conhecimento é feita de maneira coletiva, sempre respeitando a opinião e as ideias dos colegas.

Alternativa b.

4.a) Larissa pensou no número 40.

ORIENTAÇÕES DIDÁTICAS

Tecnologias

As atividades desenvolvidas nesta seção terão como suporte o software Ofi Calc, contribuindo para o desenvolvimento da habilidade EF08MA09 e da competência específica 6. É possível fazer o download gratuito desse aplicativo no link https://www.ofimega.es/ oficalc/ (acesso em: 2 ago. 2022).

Antes de iniciar a atividade, garantir que todos os estudantes tenham acesso ao aplicativo. Se possível, instalar nos computadores e notebooks da sua escola, para que fique disponível para outras situações.

Iniciar a aula apresentando algumas funcionalidades do software, como a conferência da resolução de equações, e mostrar que também pode ser usado como uma calculadora simples.

A seguir, ler as instruções e pedir aos estudantes que as executem uma a uma.

TECNOLOGIAS

UTILIZANDO UM SOFTWARE PARA RESOLVER EQUAÇÕES DO TIPO ax² + c = 0

Nesta seção, vamos utilizar um software chamado Ofi Calc para calcular e estudar as soluções de equações do 2o grau do tipo ax² + c = 0. É possível fazer o download gratuito desse aplicativo no site https://www.ofimega.es/oficalc/ (acesso em: 19 abr. 2022).

Esse recurso pode ser usado para conferir resoluções de equações, fazer outras investigações, explorando as diversas ferramentas disponíveis, bem como utilizar uma calculadora simples.

1 Abra o Ofi Calc, e uma tela como esta aparecerá.

2 Clique na aba Ferram. e selecione a opção Equações – Polinómios, como indicado na imagem.

3 Selecione a aba Equação/Função 2o grau e biquadrada e clique na aba Equações de 2o grau incompleto. Nessa aba, no item *Se falta o termo b: ax2 + c = 0, podemos resolver as equações do tipo ax² + c = 0.

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 174

AMPLIANDO

Link

ÁLGEBRA. Mathway. [S. l.], c2022. Disponível em: https://www.mathway.com/pt/Algebra. Acesso em: 2 ago. 2022.

Outro software que pode ser usado para a resolução de equações é o Mathway. Ele está disponível on-line e na página inicial há um tutorial com algumas orientações de uso.

4 Por exemplo, para resolver a equação 3x² _ 243 = 0, selecionamos 3 em Coef. a:, e 243, em Coef. c: Nessa parte, insira os valores de a e de c

As soluções da equação aparecem aqui.

Agora, com um colega, explore a função do Ofi Calc que auxilia na resolução de equações do 2o grau do tipo ax² + c = 0. Em seguida, resolvam as questões a seguir no caderno.

1. Usando o Ofi Calc, obtenha as soluções das seguintes equações do tipo ax² + c = 0.

a) x 2 _ 9 = 0 3 e 3.

b) 4x 2 + 26 = 0 Não tem raiz real.

c) 4x 2 _ 128 = 0 5,6 e 5,6.

2. Considere as equações de 2o grau a seguir.

I. 2x² _ 3 = 0

II. x² + 1 = 0

III. 3x² _ 5 = 0

IV. x² _ 1 = 0

V. x² + 4 = 0

a) Usando o Ofi Calc, descubra as equações que têm solução em r . Indique as soluções dessas equações. As equações I, IV e V. I: S = { 1,22; 1,22}, IV: S = { 1, 1} e V: S = { 2, 2}.

b) Analise os sinais de a e c nas equações que têm solução no conjunto dos números reais e nas equações que não têm soluções nesse conjunto. O que você observa de regularidades? Use o Ofi Calc para testar suas hipóteses. Depois, conte aos colegas e ao professor suas conclusões.

c) Copie o fluxograma e complete-o para que ele possa ser usado nas resoluções de equações do 2o grau da forma ax² = c.

2. b) Resposta pessoal. Espera-se que os estudantes percebam que a fração c a deve ser um número igual a zero ou maior do que zero. Caso contrário, a equação não tem solução no conjunto dos números reais. Desse modo, se a . 0, então c , 0, ou se a , 0, então c . 0.

ORIENTAÇÕES DIDÁTICAS

Na quarta etapa, os estudantes devem digitar os valores dos coeficientes a e c da equação proposta e verificar a solução. Se considerar pertinente, proponha que efetuem a resolução no caderno e, em seguida, façam a conferência usando o software Ofi Calc.

Na atividade 1, sugerir que identifiquem os coeficientes a e c em cada uma das questões dadas e, em seguida, passem a resolvê-las com o software O fluxograma proposto no item c da atividade 2 contribui para a sistematização da resolução de equações do 2o grau incompletas, da forma ax 2 + c = 0, desenvolvendo habilidades relacionadas ao pensamento computacional

Volte ao início e escreva outra equação.

Escreva a equação do 2o grau que quer resolver. não sim sim

Ela pode ser escrita da forma ax² = c?

A fração a c é maior ou igual a zero?

A equação não tem solução no conjunto dos números reais.

Calcule e escreva a solução do sistema S c a c a =_ 

D2_AV3-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 175 15/08/22

CHARNSITR/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Retomando o que aprendeu

O objetivo das atividades desta seção é propiciar aos estudantes que retomem os conteúdos estudados na Unidade e, caso seja necessário, façam retomadas para sanar as dúvidas que podem surgir.

Se achar conveniente, antes de iniciar as atividades, propor aos estudantes que façam um fluxograma dos conteúdos trabalhados no decorrer desta Unidade, com o objetivo de retomar, organizar e sistematizar as ideias e definições.

Os estudantes podem fazer esse bloco de questões como uma autoavaliação; por isso, eles devem respondê-las individualmente. É interessante sugerir que realizem essa atividade em sala de aula, assim poderão discutir eventuais dúvidas com os colegas, buscando informações de forma autônoma, escolhendo suas fontes para chegar aos resultados. Conversar com os estudantes a respeito de seus acertos e equívocos, indicando a correção com intervenções pontuadas, isto é, dando pistas de quais caminhos eles poderão buscar para encontrar o resultado esperado.

Outra possibilidade é propor aos estudantes que resolvam algumas das questões previamente em casa e que desenvolvam outras em aula, formando duplas ou grupos com os colegas. Essa abordagem contribui para o desenvolvimento da competência específica 8 da área de Matemática. Nessa interação devem aproveitar para fazer a autocorreção daquelas que trouxeram prontas.

Responda às questões no caderno.

1. Qual é o número real representado pela letra x que torna verdadeira a igualdade 7x _ [5x + 3 _ (2x + 1) _ 10] = =_( x + 3)? Alternativa b.

2. Observe as equações.

5. A altura de uma árvore, em metro, é dada por h = + 10 100 10 t , sendo t a idade da árvore em ano. Se essa árvore tem 6 metros de altura, quantos anos ela tem?

a) 12 anos.

b) 13 anos.

c) 14 anos.

d) 15 anos.

e) 16 anos. Alternativa d.

6. De acordo com uma pesquisa, foi constatado que, ao longo de x meses, a quantidade de pessoas que contrairá certo tipo de gripe é dada pela expressão matemática +

13000 10 x 2 Após quantos meses

Resolvendo cada uma dessas equações, oquociente x : y é: Alternativa a.

a quantidade de pessoas infectadas por esse tipo de gripe será de 4 000?

a) 6 meses.

b) 7 meses.

c) 8 meses.

d) 9 meses.

e) 10 meses. Alternativa c.

3. O aluguel de uma moto em uma agência A é 280 reais, acrescido de 3 reais por quilômetro rodado. Em uma agência B, o aluguel da mesma moto é 400 reais, acrescido de 1 real por quilômetro rodado. Qual deve ser a quantidade de quilômetros rodados para que o valor do aluguel seja o mesmo em ambas as agências?

a) 60 km

b) 6 4 km

c) 68 km

d) 70 km e) 72 km Alternativa a.

4. Um número natural n é tal que: + + = + + n3 n7 n7 n12 . Qual é o valor numérico da expressão + n3 ?

a) 16

b) 25

c) 5

AMPLIANDO

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd 176

Atividade complementar

d) 4 e) 3 Alternativa d.

7. Em uma loja, a diferença entre o preço de venda e o preço de custo de um produto é R$ 5.000,00. Se o preço de custo representa 75% do preço de venda, então, o preço de custo desse produto é:

a) R$ 10.000,00.

b) R$ 12.000,00.

c) R$ 15.000,00.

d) R$ 16.000,00.

e) R$ 20.000,00.

(ENEM/MEC) Uma barraca de tiro ao alvo de um parque de diversões dará um prêmio de R$ 20,00 ao participante, cada vez que ele acertar o alvo. Por outro lado, cada vez que ele errar o alvo, deverá pagar R$ 10,00. Não há cobrança inicial para participar do jogo. Um participante deu 80 tiros e, ao final, recebeu R$ 100,00. Qual foi o número de vezes que esse participante acertou o alvo?

a) 30 b) 36 c) 50 d) 60 e) 64

8. A quantidade de bolas vermelhas em uma caixa é o triplo da quantidade de bolas pretas. Se tirarmos 2 bolas pretas e 26 bolas vermelhas, a quantidade de bolas de cada cor ficará igual. Quantas bolas vermelhas há na caixa?

a) 8

Alternativa c. Alternativa d.

Resolução da atividade

Indicando por x a quantidade de acertos e por y a quantidade de erros, podemos escrever duas equações para representar as informações do problema:

9. A s revistas A e B são publicadas por uma mesma editora. A assinatura anual da revista A custa o quádruplo da assinatura anual da revista B, e a assinatura anual das duas revistas juntas custa R$ 260,00. A diferença entre os valores das assinaturas das duas revistas é:

a) R$ 52,00.

b) R$ 156,00.

c) R$ 208,00.

d) R$ 212,00.

e) R$ 218,00.

Alternativa b.

10. J uca pegou um pote cheio de amendoins, com 420 gramas, e comeu a metade deles. Verificou que a massa do pote passou a ser 235 gramas. Quantos gramas tem o pote vazio?

a) 25 g

b) 32 g

c) 40 g

d) 45 g e) 50 g Alternativa e.

11. A bilheteria de um cinema apurou 620 reais vendendo ingressos para 100 pessoas durante uma sessão de

UM NOVO OLHAR

e streia. O preço promocional de cada ingresso é 8 reais, e estudante paga a metade desse preço. Quantos estudantes compraram ingressos nessa sessão?

a) 45

b) 48

c) 50

ORIENTAÇÕES DIDÁTICAS

Um novo olhar

d) 54 e) 55 Alternativa a.

12. Em um grupo de jovens, 25% têm estatura superior a 1,70 m; 45% têm estatura entre 1,65 m e 1,70 m; e 12 desses jovens têm estatura inferior a 1,65 m. Quantos desses jovens têm altura que varia entre 1,65 m e 1,70 m?

a) 40

b) 32

c) 27

d) 25 e) 18 Alternativa e.

13. Uma motocicleta, desenvolvendo certa velocidade, percorre 240 km em t horas. Mantendo essa velocidade média, ela percorrerá 400 km em (t + 2) horas. Qual é essa quantidade t de horas? 3 horas.

Nesta Unidade, realizamos estudos sobre as equações do 1o grau com uma incógnita, equações fracionárias com uma incógnita, equações literais do 1o grau na incógnita  x , equações do 1o grau com duas incógnitas, sistemas de equações do 1o grau com duas incógnitas, tipos de resolução para esse modelo de sistema e equação do 2o grau incompleta do tipo ax 2 + c = 0.

Para que possa perceber suas aprendizagens e possíveis dúvidas, sugerimos a você que faça um roteiro contendo os conceitos abordados nesta Unidade, e não se esqueça de acrescentar alguns exemplos.

Na abertura da Unidade, pudemos estudar um uso de equações do 1o grau. Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

• Na abertura da Unidade, há um valor desconhecido para o qual você fez uma estimativa. Sabendo que, em 2021, foram recicladas 415,5 mil toneladas de latinhas de alumínio, o valor de sua estimativa se aproximou desse valor real?

As questões propostas retomam o assunto abordado no início da Unidade e destacam a importância das equações em outras áreas do conhecimento. É esperado que o estudante perceba como estamos sempre buscando descobrir valores desconhecidos: o valor final da compra de mercado, o preço do frete de uma entrega com base na quilometragem, a quantidade de frutas diferentes que podemos comprar com R $ 10,00, o lucro máximo da empresa, o valor a ser pago com impostos, entre outras situações.

Se possível, utilizar simuladores online de impostos, notas de corte do ENEM, financiamentos, crescimento de plantas e outros, pois eles auxiliam na resolução de problemas e permitem explorar as diferentes incógnitas envolvidas em cálculos de previsão.

• O que devemos excluir do conjunto universo de uma equação fracionária?

• Nesta Unidade, quais foram os métodos estudados que podem ser aplicados para calcular a resolução de um sistema de equações do 1o grau com duas incógnitas?

• Qual é a propriedade dos números reais que aplicamos para resolver equações do 2o grau da forma ax 2 + c = 0?

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual. Os valores da incógnita que anulam o denominador de cada um dos termos da equação. Métodos algébricos da substituição, da adição e método geométrico no plano cartesiano. Sendo x e y dois números reais quaisquer e x2 = y, então xy =+ ou xy =_

D2_AV1-MAT-F2-2103-V8-U5-142-177-LA-G24.indd

Resolvendo o sistema pelo método da adição, temos:

BNCC NA UNIDADE

Competências gerais:

• 5, 7 e 9

Competências específicas:

• 2, 4, e 5

Habilidades:

Geometria

• EF08MA14

• EF08MA15

• EF08MA16

• EF08MA18

• EF08MA23

• EF08MA24

Tema Contemporâneo

Transversal:

• Trabalho

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em sete capítulos e apresenta os conteúdos por meio de exemplos e atividades diversificadas, além de seções que favorecem a reflexão, a argumentação e o uso de diferentes linguagens para expressar informações, contribuindo para o desenvolvimento das competências gerais 5, 7 e 9. Nos capítulos 1 a 4, são retomados os conceitos de polígono e polígono regular, os elementos e a nomenclatura dos polígonos, o cálculo para determinar a quantidade de diagonais, a soma das medidas dos ângulos internos e a soma das medidas dos ângulos externos de um polígono. No capítulo 5, são abordadas algumas construções de polígonos regulares. Esse estudo favorece o desenvolvimento das habilidades EF08MA15 e EF08MA16. No capítulo 6, são exploradas as propriedades dos quadriláteros, desenvolvendo aspectos da habilidade EF08MA14. No capítulo 7, são abordadas as transformações isométricas no plano reforçando aspectos da habilidade EF08MA18.

POLÍGONOS E TRANSFORMAÇÕES NO PLANO 6

Todo arquivo digital do tipo bitmap é composto de pixels. Um pixel é a menor unidade de uma imagem representada na tela de um computador. Ao ampliar uma imagem no computador, podemos notar que ela é formada por figuras bem pequenas que lembram quadrados, os pixels. Essas figuras, juntas, formam uma imagem nítida.

Somente na ampliação ou na impressão de uma imagem podemos perceber a principal importância da quantidade de pixels que a compõe. Em uma máquina fotográfica digital, por exemplo, conhecemos essa quantidade pelo nome megapixel cujo valor, nesse aparelho, diz quantos pixels vão compor uma fotografia feita nele.

Como um pixel não possui medidas definidas, quanto mais megapixels houver em uma fotografia, menores serão as medidas do pixel e mais essa imagem poderá ser ampliada, pois cada pixel sofrerá menos distorção.

Observe um exemplo de imagem no qual ampliamos uma parte da fotografia para que possamos perceber os pixels e sua formação poligonal.

OBJETIVOS

• Compreender a definição de polígono, seus elementos e nomenclatura.

• Determinar a quantidade de diagonais de um polígono convexo.

• Calcular a soma das medidas dos ângulos internos e a soma das medidas dos ângulos externos de um polígono.

• Determinar a medida do ângulo interno de um polígono regular.

• Compreender e construir polígonos regulares.

• Compreender as propriedades dos paralelogramos.

• Interpretar gráfico de setores.

• Reconhecer as transformações isométricas no plano.

• Construir figuras por meio de transformações isométricas no plano.

Representação ampliada de um pixel, que lembra um quadrado.

EDITORIA DE ARTE

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

SOLARYSYS/ALAMY/FOTOARENA

Agora, pense e responda no caderno.

• Os pixels podem lembrar a forma de quadrados ou retângulos, mas podemos compor imagens no cotidiano com outras figuras poligonais. Em que situações você já se deparou com imagens formadas por outras figuras poligonais?

• De que outras maneiras podemos compor imagens por meio da composição dessas outras figuras poligonais?

Resposta pessoal. Exemplo de resposta: Podemos justapor figuras poligonais para compor mosaicos.

• De acordo com o texto, quanto maior a quantidade de megapixels, maior a qualidade da imagem de uma fotografia. Por quê?

Porque a imagem poderá ser ampliada sem sofrer distorção.

JUSTIFICATIVAS DOS OBJETIVOS

Nesta Unidade, apresenta-se o estudo dos polígonos e das transformações isométricas do plano, propiciando, com maior ênfase, o desenvolvimento das habilidades EF08MA14, EF08MA16 e EF08MA18.

Na seção Tratamento da informação, o objetivo é discutir as principais

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

Essa abertura envolve um tema que pode ser de grande interesse para a maioria dos estudantes: a fotografia, hoje em dia amplamente divulgada e presente nas redes sociais. Aqui há o enfoque na ampliação e na redução de imagens, mais especificamente na qualidade de imagem que se obtém e no significado da palavra megapixel (vista com frequência nas características de câmeras digitais, de celulares ou outras).

O pixel é um pequeno quadrado ou retângulo, portanto um polígono, que é utilizado para a formação de imagens; quanto mais megapixel uma câmera tem, mais qualidade a imagem pode ter, pois menores serão os pixels utilizados na formação dessa imagem. Essa diferença é mais visível em fotografias impressas, principalmente quando se deseja uma ampliação.

Se considerar oportuno, comentar com os estudantes sobre o trabalho de Adam Lister, artista americano nascido em 1978 e formado pela Escola de Artes Visuais de Nova York. Adam recriou diversas obras de arte clássicas na forma de pixels, trabalho que originou a série Art History 101 (História da Arte 101, em tradução livre).

características do gráfico de setores, os tipos de variável que estão envolvidos nesse tipo de gráfico, as frequências absoluta e relativa, desenvolvendo aspectos das habilidades EF08MA23 e EF08MA24, bem como exercitar a argumentação, a colaboração e a empatia, favorecendo o desenvolvimento de aspectos relacionados às competências gerais 7 e 9 e da competência específica 4 da área de Matemática.

Na seção Tecnologias, o objetivo é que os estudantes se familiarizem com o software GeoGebra e as ferramentas para a construção de figuras por meio de transformações isométricas no plano.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Recife de corais no Mar Vermelho, Egito, 2020.

SOLARYSYS/ALAMY/FOTOARENA

ORIENTAÇÕES DIDÁTICAS

Polígonos e seus elementos

Esta página retoma o conceito de polígono por meio da visualização e interpretação de uma das obras do artista Paul Klee.

Caso considere interessante, solicitar aos estudantes que pesquisem outras obras desse artista e verifiquem se é possível identificar polígonos nelas também.

A seguir, apresentamos uma possibilidade de trabalho para a retomada do conceito de polígono.

POLÍGONOS E SEUS ELEMENTOS CAPÍTULO1

O pintor e poeta Paul Klee nasceu em 18 de dezembro de 1879, na Suíça. Foi professor da escola de Arte Moderna Bauhaus e da Academia de Belas Artes de Düsseldorf e faleceu em 29 de junho de 1940.

A seguir, reproduzimos a obra Small town among the rocks, de Paul Klee.

Nessa obra, é possível identificar a representação de algumas figuras geométricas planas formadas por linhas fechadas simples, compostas de segmentos de retas, e suas respectivas regiões internas.

KLEE, Paul. Small town among the rocks. 1932. Óleo sobre tela, 44,5 cm x 56,5 cm. Centro Paul Klee, Berna (Suíça).

Observe algumas figuras extraídas dessa obra. Cada uma delas lembra um polígono

Polígono é uma figura geométrica plana formada por uma linha fechada simples, composta apenas de segmentos de retas, e sua região interna.

Quando dois pontos quaisquer pertencentes a um polígono determinam um segmento de reta que fica inteiramente contido em sua região interna, dizemos que opolígono é convexo. Entretanto, se houver um segmento determinado por dois pontos do polígono, de modo que esse segmento não esteja totalmente contido no polígono, dizemos que esse polígono é não convexo

polígono convexo polígono não convexo

D2-AV1-MAT-F2-2103-V8-U6-178-211-LA-G24.indd 180 08/08/22 15:52

AMPLIANDO

Atividade complementar

Organizar os estudantes em grupos para desenvolver uma atividade pela escola levando caderno e lápis. A tarefa será anotar no caderno objetos que identifiquem ter o formato de diversos polígonos. Algumas possibilidades de observação:

• no chão, o tipo de piso;

• no jardim, os formatos que encontram na natureza;

• nas paredes, quadros e painéis;

• no teto, o tipo de luminária;

• nos móveis, os diversos formatos.

Ao retornarem à sala de aula, cada grupo fará um relatório com o desenho dos diversos tipos de polígono que seus integrantes observaram. Se tiverem acesso à internet, eles poderão acessar sites para realizar pesquisas a respeito do uso dos polígonos no cotidiano.

ZENTRUM PAUL KLEE, BERN, BILDARCHIV

ELEMENTOS DE UM POLÍGONO

No polígono representado, podemos destacar os seguintes elementos.

• Os vértices, que são os pontos A, B, C, D e E Nomeamos os polígonos por meio de seus vértices: no caso, temos o polígono ABCDE.

• Os lados, que são os segmentos de retas AB, BC, CD, DE e EA

• Os ângulos internos, que são os ângulos formados por dois lados consecutivos: A BC, BCD, C ˆ DE, D ˆ EA e E AB. Também usamos as letras que indicam os vértices para representar os ângulos internos: A , B , C, D e E Em um polígono, a quantidade de vértices, de lados e de ângulos internos é sempre a mesma. Além desses elementos, destacamos também:

• as diagonais, que são segmentos de retas que unem dois vértices não consecutivos. Na figura a seguir, representamos as diagonais AC, AD, BD, BE e CE

ORIENTAÇÕES DIDÁTICAS

Elementos de um polígono Nesta página, os elementos de um polígono são retomados. Verificar se os estudantes apresentam dúvidas e saná-las. Uma possibilidade é utilizar jogos para explorar o conceito de polígono e identificar seus elementos. Os estudantes podem, por exemplo, montar um jogo de dominó relacionando os polígonos, seus elementos e a nomenclatura (que será retomada na página seguinte).

• os ângulos externos, que são os ângulos formados por um lado do polígono e pelo prolongamento de um lado consecutivo a ele. No polígono da figura a seguir, temos: P ˆ AB, Q ˆ BC, RCD , S ˆ DE e T ˆ EA

Comentar com os estudantes que as manifestações artísticas, como pintura e escultura, são propícias ao desenvolvimento de conceitos geométricos. Propor um trabalho de observação e identificação de polígonos em obras de artistas brasileiros. É interessante realizar esse trabalho integrado com o componente curricular Arte para que os estudantes possam conhecer um pouco mais as obras envolvidas. Pesquisas, visitas a museus e desenhos podem fazer parte da atividade.

ORIENTAÇÕES DIDÁTICAS

Nomenclatura

A nomenclatura dos polígonos é retomada agora no 8 o ano. Comentar com os estudantes os prefixos que nomeiam cada um dos polígonos do quadro e questioná-los se já viram esses prefixos em outros contextos. Eles podem responder terem visto na quantidade de vezes que determinada equipe ganhou alguma competição esportiva. Por exemplo, a seleção brasileira masculina de futebol é pentacampeã mundial, pois ganhou cinco vezes a Copa do Mundo (em 2002, 1994, 1970, 1962 e 1958).

Atividade

A atividade 1 trata do ladrilhamento do plano. A respeito desse assunto, sugerimos o texto escrito pela professora Élvia Mureb Sallum, do Instituto de Matemática e Estatística da Universidade de São Paulo, disponível em: http://clubes.obmep.org.br/blog/ wp-content/uploads/2015/10/ monografia2.pdf (acesso em: 11 ago. 2022).

NOMENCLATURA

Apesar de a origem da palavra polígono estar relacionada à expressão “vários ângulos”, também podemos nomear os polígonos considerando a quantidade de lados que eles têm. Acompanhe no quadro o nome de alguns polígonos.

Polígono Quantidade de lados Nome

3 triângulo (tri = três)

4 quadrilátero (quadri = quatro)

5 pentágono (penta = cinco)

6 hexágono (hexa = seis)

7 heptágono (hepta = sete)

8 octógono (octo = oito)

9 eneágono (enea = nove)

10 decágono (deca = dez)

Existem, ainda, outros polígonos como aqueles que têm:

• 11 lados – undecágono

• 12 lados – dodecágono

• 15 lados – pentadecágono

• 20 lados – icoságono

Os demais polígonos, como o de 13 lados, o de 18 lados, o de 25 lados, entre outros, não recebem nomes particulares.

Responda à questão no caderno.

1. A figura corresponde a um ladrilhamento. Observe que há diferentes tipos de polígonos representados nesse ladrilhamento, porém todos se encaixam perfeitamente, sem sobreposição.

a) Quantos tipos diferentes de polígono você observa nesse ladrilhamento?

b) Como são chamados cada um desses tipos de polígono? Três tipos. Triângulos, quadriláteros e octógonos.

AMPLIANDO

Atividade complementar

Reproduzir esta figura na lousa e pedir aos estudantes que a montem utilizando palitos de mesmo comprimento.

Depois, eles devem resolver as questões propostas.

a) Que polígonos formam essa figura?

b) O que podemos dizer a respeito da medida dos lados desses triângulos?

c) Que nome recebe esse tipo de triângulo?

d) Deslocando apenas três palitos, monte uma figura com seis triângulos equiláteros.

e) Com base na figura original, tente formar seis triângulos equiláteros deslocando exatamente

Você já sabe que todo segmento de reta que une dois vértices não consecutivos de um polígono é chamado de diagonal do polígono

No pentágono representado, os segmentos de retas AC, AD, BD , BE e CE são diagonais desse polígono.

Algumas observações devem ser levadas em conta para traçar as diagonais de um polígono.

• Se quisermos traçar as diagonais a partir do vértice A, por exemplo, não podemos ligá-lo a três vértices do polígono: a ele mesmo (A) e aos vértices consecutivos (B e E ).

• AC , por exemplo, indica a mesma diagonal que CA

Em geral, a quantidade de diagonais não coincide com a quantidade de lados do polígono. A única exceção é o pentágono, que, como acabamos de observar na figura, possui cinco lados e cinco diagonais.

CÁLCULO DA QUANTIDADE DE DIAGONAIS DE UM POLÍGONO

O polígono a seguir representa um octógono (oito lados), no qual estão traçadas todas as diagonais.

Você seria capaz de contar quantas diagonais tem esse octógono?

Traçar uma a uma ou contar as diagonais de um polígono são processos trabalhosos, principalmente se o polígono tiver muitos lados.

Vamos, então, aprender a determinar a quantidade de diagonais de um polígono sem traçá-las.

Note que, em um polígono qualquer de n lados (ou n vértices):

• de qualquer vértice do polígono partem diagonais para todos os vértices (n), exceto para três deles (ele mesmo e os vértices consecutivos a ele). Portanto, de cada vértice partem (n 3) diagonais;

Diagonais de um polígono convexo

Para ampliar o trabalho com diagonais de um polígono, pode-se colocar na lousa o seguinte quadro.

Número de lados do polígono 8 15 10 28 Número de diagonais

Pedir aos estudantes que reproduzam o quadro no caderno e o preencham. Como os polígonos do quadro têm muitos lados, espera-se que os estudantes compreendam que o modo mais prático de realizar a tarefa é utilizando a fórmula apresentada nesta página. No entanto, reforçar que, caso desejassem desenhar o polígono e contar suas diagonais uma a uma, também seria possível, apesar de mais trabalhoso.

Caso tenham dificuldade para manipular a fórmula na realização dos cálculos, ajudá-los a identificar cada uma das incógnitas, a saber: • d indica o número de diagonais; • n indica o número de lados do polígono.

Discutir com os estudantes que esses dois números devem ser naturais não nulos, pois indicam quantidades (de diagonais ou de lados).

quatro palitos. A figura obtida, com seis triângulos equiláteros, forma um novo polígono? Se sim, que polígono é esse?

Resolução das atividades

a) Triângulos.

b) Os lados de cada triângulo têm a mesma medida.

c) Triângulo equilátero.

d) e) Sim, forma um hexágono.

ORIENTAÇÕES DIDÁTICAS

Caso considere necessário, antes de iniciar as atividades, propor o problema a seguir na lousa e realizar a resolução em conjunto com os estudantes.

• Existe um único polígono cujo número de diagonais é igual ao dobro do número de lados. Qual é esse polígono?

Resolução:

• número de lados: n

• número de diagonais: = ?_ d n(n3)

2

• dado do problema: d = 2n Igualando as expressões para d, temos:

= 2n n(n3)

2

4n = n (n 3)

n 3 = 4

n = 4 + 3

n = 7

Logo, o polígono procurado é o heptágono.

Pense e responda

Incentivar os estudantes a explicar aos colegas como pensaram para obter a resposta à questão apresentada. Desse modo, eles exercitam a argumentação e a investigação com base em fatos matemáticos, desenvolvendo a competência geral 7.

Atividades

Para as atividades 7 e 8, verificar se os estudantes percebem que, com a fórmula de determinação do número de diagonais, também é possível determinar o número de lados do polígono, se conhecido o número de diagonais.

• como são n vértices, e de cada um partem (n

3) diagonais, a quantidade total de diagonais seria n ? (n 3). Mas dessa maneira estaríamos contando cada diagonal duas vezes () le mbre-sede que AC eC A, por exemplo, sã oa me smadiagona l . Então, a quantidade de diagonais (d) é dada pela metade de n (n 3).

Assim:

Em um polígono de n lados (ou n vértices), a quantidade de diagonais (d) é dada por:

Consideremos, então, a situação a seguir.

• Quantas diagonais possui o decágono?

10 lados

PENSE E RESPONDA

Responda à questão no caderno. Há um polígono que não possui diagonais. Qual é esse polígono? Explique aos colegas e ao professor como você pensou para responder.

ATIVIDADES

Responda às questões no caderno.

1. Qual é o polígono que possui 2 diagonais?

Triângulo. Espera-se que os estudantes argumentem que o triângulo tem três vértices e que, ao escolher um deles para traçar uma diagonal, os outros dois vértices são consecutivos a ele, e concluam que o triângulo é um polígono que não tem diagonais.

Quantas diagonais tem um polígono regular de 7 lados?

a) 13

2. Quantas diagonais tem um polígono de:

a) 5 lados?

b) 8 lados?

c) 11 lados?

Quadrilátero. 5 diagonais. 20 diagonais. 44 diagonais.

b) 14

d) 16 lados? e) 18 lados?

135 diagonais.

3. A quantidade de diagonais de um octógono é igual a:

a) 13. b) 18. c) 20. d) 23.

4. Um polígono tem 60 cm de perímetro, e todos os lados têm a mesma medida: (5 cm). Calcule a quantidade de lados e a quantidade de diagonais desse polígono

Alternativa c. 12 lados; 54 diagonais.

5. (Saresp-SP) Observe as diagonais dos polígonos regulares de 4, 5 e 6 lados.

2.d) 104 diagonais.

c) 15

d) 16

6. Qual é o polígono cuja quantidade de diagonais é o quádruplo da quantidade de lados?

Alternativa b. Undecágono.

7. (UFSCar-SP) Um polígono regular com exatamente 35 diagonais tem

Alternativa c.

a) 6 lados.

b) 9 lados.

c) 10 lados.

d) 12 lados.

e) 20 lados.

8. (PUC-RJ) Um polígono regular de n lados tem 90 diagonais. O valor de n é:

a) 10.

b) 12.

c) 15.

d) 20.

e) 21.

Alternativa c.

3

ÂNGULOS DE UM POLÍGONO CONVEXO

ÂNGULO INTERNO E ÂNGULO EXTERNO

Consideremos o polígono da figura a seguir. Nele, podemos observar que:

ORIENTAÇÕES DIDÁTICAS Ângulos de um polígono convexo

Para determinar a soma das medidas dos ângulos internos de um polígono convexo, é utilizada a soma das medidas dos ângulos internos do triângulo. Se considerar pertinente, reproduza a atividade a seguir, que mostra uma maneira de determinar a soma das medidas dos ângulos internos de um triângulo.

Um ângulo interno e um ângulo externo de mesmo vértice de um polígono são sempre adjacentes suplementares

SOMA DAS MEDIDAS DOS ÂNGULOS INTERNOS DE UM POLÍGONO CONVEXO

Analisemos, agora, como podemos calcular a soma das medidas dos ângulos internos de um polígono convexo. Vamos partir do conhecimento de que a soma das medidas dos ângulos internos de um triângulo qualquer é igual a 180 ° Quando queremos determinar a soma das medidas dos ângulos internos (Si ) de um polígono convexo, podemos decompor esse polígono em triângulos, uma vez que a soma das medidas dos ângulos internos de um triângulo já é conhecida e é igual a 180°. Fazemos isso traçando as diagonais que partem de um único vértice do polígono. Observe.

• Traçando todas as diagonais a partir de um mesmo vértice, podemos dividir um pentágono em três triângulos.

• Com uma tesoura com pontas arredondadas, recortar um papel em um formato que lembra um triângulo.

• Em seguida, usar lápis de diferentes cores para destacar os três ângulos internos e nomeá-los como a, b e c

• Depois, usando a mesma tesoura, recortar o triângulo, dividindo-o em três partes.

Como a soma das medidas dos ângulos internos de um triângulo é 180°, a soma das medidas dos ângulos internos de um pentágono é 3 180°, ou seja, 540° Esse processo, porém, pode ser longo e demorado, principalmente se o polígono tiver muitos lados.

• Por último, juntar os três vértices em um único ponto.

Pela figura, podemos verificar que, juntos, os três ângulos internos do triângulo formam um ângulo raso ou de meia-volta.

Então: a + b + c = 180°.

ORIENTAÇÕES DIDÁTICAS

Pense e responda

Explorar a relação entre a quantidade de lados do polígono e o número de triângulos em que ele pode ser decomposto. Para essa exploração, pode-se propor aos estudantes que incluam outras linhas nesse quadro, até que percebam que sempre é possível decompor o polígono em n   2 triângulos. Essa abordagem favorece o desenvolvimento do raciocínio por indução, uma vez que os estudantes vão determinar uma regra por meio da observação de regularidades, bem como a investigação, contribuindo para aspectos da competência específica 2 da área de Matemática.

AMPLIANDO

Atividade complementar

a) Resposta pessoal. Espera-se que os estudantes percebam que os polígonos podem ser decompostos em (n 2) triângulos, em que n é a quantidade de lados do polígono. A quantidade de triângulos em que o polígono foi decomposto é multiplicada por 180°. Além disso, os estudantes podem citar que, a cada lado acrescentado ao polígono, a soma das medidas dos ângulos internos aumenta 180 °

PENSE E RESPONDA

Responda às questões no caderno. Observe a quantidade de lados dos polígonos, em quantos triângulos eles foram decompostos e a soma das medidas dos ângulos internos.

Nome Polígono Quantidade de lados Quantidade de

a) Que regularidades você identifica nas informações desse quadro?

b) A partir das regularidades que observou, como você faria para determinar a soma dos ângulos internos de um octógono? Explique aos colegas e ao professor.

A partir do quadro anterior, verificamos que é possível dividir o polígono em uma quantidade de triângulos que coincide com a quantidade de lados do polígono menos dois.

Podemos generalizar esse resultado para um polígono de n lados:

• quantidade de lados: n

• quantidade de triângulos: n 2 (dois a menos do que a quantidade de lados do polígono)

• soma das medidas dos ângulos internos de cada triângulo: 180°

• soma das medidas dos ângulos internos do polígono: (n 2) ? 180°

Sendo Si a soma das medidas dos ângulos internos de um polígono de n lados, temos: S = (n 2) ? 180°

b) Resposta pessoal. Espera-se que os estudantes apliquem as regularidades observadas e concluam que a soma das medidas dos ângulos internos de um octógono é 6 180° = 1 080°

Pedir aos estudantes que, usando o mesmo raciocínio do quadro apresentado no Livro do estudante, determinem a soma dos ângulos internos do octógono (oito lados) e do eneágono (nove lados).

Resolução da atividade

• Octógono

O polígono tem oito lados. Assim, é possível dividir o octógono em (8 2) triângulos, ou seja, em seis triângulos. Logo, a soma das medidas dos ângulos internos do octógono é dada por 6 180° = 1 080°

• Eneágono

O polígono tem nove lados. Assim, é possível dividir o eneágono em (9 2) triângulos, ou seja, em sete triângulos. Logo, a soma das medidas dos ângulos internos do eneágono é dada por 7 ? 180° = 1 260°

Acompanhe como podemos usar a fórmula matemática Si = (n 2) 180 ° para resolver problemas.

1 Um polígono tem 13 lados. Qual é a soma dos ângulos internos?

13 lados n = 13

Si = (n 2) 180°

Si = (13 2) 180° = 11 180° = 1 980°

A soma das medidas dos ângulos internos de um polígono de 13 lados é 1 980°

2 A s oma das medidas dos ângulos internos de um polígono é 1 8 00 °. Quantos lados tem esse polígono?

Nesse caso, temos Si = 1 800°

Como Si = (n 2) 180°, temos:

(n 2) ? 180° = 1 800°

n 180° 360° = 1 800°h n 180° = 1 800°+ 360°h n 180° = 2 160°h=

° ° = n 2 160 180 12

ORIENTAÇÕES DIDÁTICAS

Soma das medidas dos ângulos externos de um polígono convexo

Realizar na lousa os cálculos para a determinação da soma das medidas dos ângulos externos de um triângulo, de um quadrilátero e de um pentágono, como mostrado no Livro do estudante.

O polígono tem 12 lados.

SOMA DAS MEDIDAS DOS ÂNGULOS EXTERNOS DE UM POLÍGONO CONVEXO

Assim como fizemos para os ângulos internos, vamos calcular a soma das medidas dos ângulos externos (Se ) de um polígono convexo.

Sabemos que:

S e = 540

S e = 360° soma das medidas dos ângulos externos de um triângulo

Em seguida, desafiar os estudantes a determinar a soma dos ângulos externos de um polígono de n lados. É esperado que eles procurem estender o raciocínio anterior para um polígono de n lados e escrevam a equação substituindo o número de lados por n. Oriente-os caso apresentem dificuldades nesse processo. Essa abordagem favorece o desenvolvimento da competência específica

2 da área de Matemática, uma vez que os estudantes vão trabalhar o raciocínio dedutivo para concluir que a soma das medidas dos ângulos externos de um polígono é sempre 360°.

ORIENTAÇÕES DIDÁTICAS

Atividades

Nesse bloco de questões, os estudantes aplicarão a soma das medidas dos ângulos internos e a soma das medidas dos ângulos externos de um polígono convexo qualquer.

Caso os estudantes apresentem dificuldades, auxiliá-los, sanando eventuais dúvidas.

Na atividade 1, os estudantes devem lembrar que o polígono pode ser decomposto em n 2 triângulos. Se foram obtidos oito triângulos nessa decomposição, então o polígono tem 10 lados. Esse número pode ser obtido resolvendo a equação n 2 = = 8. Se considerar pertinente, propor outras situações para que determinem a quantidade de lados de um polígono que foi decomposto, por exemplo, em 15 triângulos (17 lados).

Na atividade 4, verificar se os estudantes substituem na equação dada a soma das medidas dos ângulos externos por 360° e a soma das medidas dos ângulos internos por 180(n 2).

Pentágono

um

um polígono de n lados, temos que, em cada vértice, a soma da medida do ângulo interno com a medida do ângulo externo é 180

Se

podemos enunciar a propriedade.

A soma das medidas dos ângulos externos de qualquer polígono é igual a 360°

Responda às questões no caderno.

1. Em um polígono convexo qualquer de n lados, quando traçamos as diagonais que partem de um único vértice, decompomos o polígono em (n 2) triângulos. Sabendo que em determinado polígono obtivemos oito triângulos nessa decomposição, quantos lados tem esse polígono? Como ele é chamado?

10 lados; decágono.

2. Copie o quadro seguinte e preencha-o corretamente.

PentágonoEneágono Icoságono Soma

5. () =° medEAB 54 e () =° medABC 81

3. Como se chama o polígono cuja soma das medidas dos ângulos internos é 1 620° ?

4. Em um polígono, temos que Si + S e = = 1 080 °. Qual é esse polígono?

5. Esta figura é um pentágono não regular. Calcule as medidas dos ângulos E ˆ AB e A ˆ BC

6. Copie o quadro seguinte e complete-o. Soma das

D2-AV1-MAT-F2-2103-V8-U6-178-211-LA-G24.indd

ÂNGULOS DE UM POLÍGONO REGULAR

Sabemos que em um polígono regular:

• todos os lados são congruentes;

• todos os ângulos internos são congruentes.

Como em cada vértice de um polígono a soma das medidas do ângulo interno e seu ângulo externo é 180 °, podemos concluir que os ângulos externos de um polígono regular também são congruentes entre si.

Assim, podemos indicar:

• a medida de cada ângulo interno de um polígono regular por a ;

• a medida de cada ângulo externo de um polígono regular por ae

Para um polígono regular de n lados, temos: a = () == ° a S n n2 180 n i = () == ° a S n n2 180 n i i e a e === ° a S n 360 n e e === ° a S n 360 n e e

Consideremos, então, as seguintes situações.

1 Quais são as medidas do ângulo interno e a do ângulo externo de um hexágono regular?

Hexágono regular: 6 lados.

Cálculo da soma das medidas dos ângulos internos: =_?°h=?°=°S6 2 180 S4 180720 ii ()

Como o hexágono é regular:

DIDÁTICAS

Ângulos de um polígono regular

Nesta página, é apresentado como determinar a medida dos ângulos internos e externos de um polígono regular. Se necessário, retomar com os estudantes o conceito de polígono regular e suas características. A partir dessa retomada é possível incentivar os estudantes a encontrar uma estratégia para determinar a medida do ângulo interno de um polígono regular.

==

° =° a S n 720 6 120 i

° =° a S n 360 6 60 e e , ou, ainda, ae = 180° 120° = 60°

==

O ângulo interno mede 120°, e o ângulo externo mede 60°

2 Qual é o polígono regular cuja medida do ângulo interno é 144°?

Como o polígono é regular: quantidade de lados do polígono =H a S n númerodela dosdopolígonos i i

Se ai = 144°, então:

• =° S n 144 i = 144°

°_ =° 180 n2 n 144 () = 144°

°_ = ° 180 n2 n 144 n n () = °_ = ° 180 n2 n 144 n n ()

Portanto, o polígono é o decágono (10 lados).

D2-AV1-MAT-F2-2103-V8-U6-178-211-LA-G24.indd 189

Começar retomando a fórmula para obter a soma das medidas dos ângulos internos de um polígono e perguntar como determinar a medida de um ângulo interno, dado que todos os ângulos no polígono regular são congruentes. É esperado que concluam que basta dividir a soma das medidas dos ângulos internos pelo número de ângulos internos do polígono regular. Proceda da mesma maneira para que os estudantes obtenham uma estratégia para determinar a medida do ângulo externo de um polígono regular a partir da soma das medidas do ângulo externo. Essa abordagem favorece o raciocínio por indução e o trabalho com a competência específica 2 da área de Matemática. Em seguida, trabalhar na lousa as situações apresentadas, verificando se os estudantes apresentam alguma dúvida a respeito do assunto tratado.

ORIENTAÇÕES DIDÁTICAS

Atividades

Nesse bloco de atividades, os estudantes devem calcular as medidas do ângulo interno e do ângulo externo de um polígono regular. Caso apresentem dificuldade na resolução, orientá-los a consultar no Livro do estudante os conceitos e as relações adequadas para cada item das questões.

Na atividade 8, solicitar aos estudantes que resolvam os itens propostos em duplas. A troca de ideias amplia as interpretações de cada um, o que contribui para um melhor entendimento e enriquecimento da aprendizagem, favorecendo o trabalho com a competência geral 9.

ATIVIDADES

Responda às questões no caderno.

1. Em um polígono convexo qualquer de n lados, podem ser traçadas (n 3) diagonais partindo de cada vértice. Sabendo que em determinado polígono podem ser traçadas sete diagonais de cada vértice, responda.

a) Qual é a soma das medidas dos ângulos internos desse polígono?

b) Qual é a medida de cada ângulo interno, considerando que o polígono é regular?

2. Na figura, ABCDE é a representação de um pentágono regular. Calcule o valor de y   x.

6. Considerando a figura, em que ABC é a representação de um triângulo equilátero, calcule o valor de x

7. Na figura seguinte, AB representa um lado de um hexágono regular, e AC representa um lado de um octógono regular. Qual é a medida de x do ângulo BAC?

3. Na figura, ABCDE é a representação de um pentágono regular. Qual é a medida x do ângulo D FE do triângulo DFE?

4. É dado um polígono regular, no qual a soma das medidas dos ângulos internos é igual ao quádruplo da soma das medidas dos ângulos externos. Qual é esse polígono?

5. Em um polígono, a razão entre a soma das medidas dos ângulos internos e a soma das medidas dos ângulos externos é igual a 7 2 . Quantos lados tem esse polígono?

Decágono regular. 9 lados.

8. O esboço a seguir representa o deslocamento de uma pessoa.

Partindo do ponto A , a pessoa avança 120 m e gira 36° para a esquerda. A seguir, avança outros 120 m e gira 36° para a esquerda. Esse movimento é repetido até que ela retorne ao ponto A, fechando a a linha que representa trajetória.

a) Qual é o polígono regular que essa trajetória limita?

105° Decágono regular.

b) Quantos quilômetros essa pessoa caminha em toda a trajetória?

c) Se em média essa pessoa der 11 passos a cada 8 m, quantos passos ela dará em toda a trajetória?

km 1 650 passos.

CONSTRUÇÕES GEOMÉTRICAS

Neste capítulo, vamos construir com régua e compasso dois polígonos regulares.

TRIÂNGULO EQUILÁTERO

O triângulo equilátero é um polígono regular de três lados; portanto, ele apresenta todos os lados congruentes entre si e todos os ângulos internos também congruentes entre si. Assim, como a soma das medidas dos ângulos internos de um triângulo é 180°, cada ângulo do triângulo equilátero mede 60°

Acompanhe e repita, no caderno, as etapas da construção de um triângulo equilátero.

1o passo: Definimos a medida do lado do triângulo que desejamos construir. Nesse caso, vamos construir um triângulo equilátero cujo lado mede 4 cm.

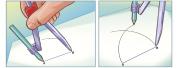
2o passo: Construímos um segmento de reta AB, com 4 cm de comprimento.

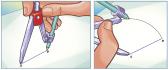
AB

4 cm

3o passo: Colocamos a ponta-seca do compasso no ponto A, abrimos o compasso até o ponto B e traçamos um arco.

ORIENTAÇÕES DIDÁTICAS Construções geométricas

4 o passo: Repetimos o procedimento anterior, mas agora a ponta-seca deve estar no ponto B.

A construção de polígonos regulares, seja com régua e compasso, seja com softwares de geometria dinâmica, é uma habilidade que deve ser desenvolvida, pois auxilia na compreensão das relações e propriedades dos polígonos. Propor aos estudantes que acompanhem as construções no caderno, usando régua e compasso. Depois da construção, incentive-os a justificar por que a figura obtida é um triângulo equilátero. Retomar a definição de circunferência como lugar geométrico de todos os pontos que são equidistantes de um ponto, centro da circunferência. Assim, ao traçar arcos de circunferência com a mesma abertura, garantimos que o ponto de intersecção dos arcos está à mesma distância dos extremos do segmento de reta (base do triângulo). Mostrar que, ao traçar circunferências, e não arcos, obteríamos outro ponto de intersecção delas, abaixo do segmento de reta.

ORIENTAÇÕES DIDÁTICAS

Pense e responda

As questões propostas têm o objetivo de retomar as características do triângulo equilátero: um polígono regular de três lados, ou seja, o triângulo equilátero apresenta os lados congruentes e os ângulos internos também congruentes.

Uma possibilidade para o trabalho com construções geométricas e propriedades dos polígonos é o uso do geoplano. Se possível, providenciar alguns e levá-los à sala de aula. Também é possível construir o seu próprio geoplano. Há também placas prontas com furinhos e hastes de plástico para serem encaixadas. Pode-se, ainda, construir um geoplano com madeira e pregos. Dentro da possibilidade de cada escola, pode-se pedir aos estudantes que construam um em sala de aula ou sugerir que façam em casa, com o auxílio de um adulto.

A seguir, está o material e o procedimento para construir o geoplano. Apresentar essas orientações aos estudantes para que possam efetuar a tarefa.

5o passo: Marcamos o ponto de intersecção dos arcos e o nomeamos como C. Com uma régua, unimos o ponto C aos pontos A e B, determinando o triângulo equilátero.

Depois de traçado o contorno do triângulo, basta colorir a parte interna da figura. Para a construção anterior, utilizamos arcos de circunferências de mesmo raio a fim de garantir que todos os lados do triângulo sejam congruentes. Já estudamos que a circunferência é o lugar geométrico de todos os pontos equidistantes de um ponto, que é o centro da circunferência. Assim, ao construir os arcos, estamos encontrando todos os pontos que distam 4 cm de A e todos os pontos que distam 4 cm de B. Portanto, o ponto de intersecção desses arcos dista 4 cm de A e 4 cm de B

PENSE E RESPONDA

1. O triângulo equilátero tem três lados congruentes entre si.

2. Sim; o fato de que o triângulo equilátero tem três ângulos congruentes entre si.

Responda às questões no caderno.

1. Na construção anterior, que propriedade do triângulo equilátero utilizamos?

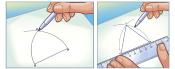
2. Existe outra propriedade dos triângulos equiláteros que pode ser utilizada nessa construção? Qual?

HEXÁGONO REGULAR

O hexágono regular é o polígono de seis lados que apresenta todos os lados congruentes entre si e todos os ângulos igualmente congruentes entre si.

Como a soma dos ângulos internos de um hexágono é 720° [S = (6 2) ? 180° = 720°], cada ângulo interno mede 120° = ° =° a 720 6 120 i

Acompanhe e repita, no caderno, os passos da construção de um hexágono regular.

1o passo: Definimos a medida do lado do hexágono que desejamos construir. Nesse caso, vamos construir um hexágono cujo lado mede 1,2 cm.

2 o passo: Construímos um segmento de reta OA com 1,2 cm de comprimento.

3o passo: Com a ponta-seca do compasso no ponto O e abertura igual à med OA () , traçamos uma circunferência.

Material necessário:

• uma placa de madeira com formato quadrado e pouco mais de 20 cm de lado;

• um lápis de carpinteiro ou lápis preto com grafite mais grossa para traçar uma malha sobre a placa de madeira;

• 64 pregos com cabeça (cada prego medindo cerca de 15 mm de comprimento);

• um martelo;

• elásticos de diversas cores.

Procedimentos:

1. Forme uma malha 8 x 8 sobre a placa de madeira, marcando 64 pontos equidistantes 2,5 cm, tanto horizontal quanto verticalmente.

4o passo: Ainda com a mesma abertura e com a ponta-seca do compasso no ponto A, determinamos o ponto B

ORIENTAÇÕES DIDÁTICAS

5o passo: Com a mesma abertura e a ponta-seca em B, determinamos o ponto C na circunferência. E com a ponta-seca em C e mesma abertura, determinamos o ponto D. Assim seguimos por toda a circunferência, até determinar todos os pontos que correspondem aos vértices do hexágono.

Depois de realizada a construção do hexágono regular, propor aos estudantes que elaborem um fluxograma para a construção de um polígono regular qualquer. Oriente-os a tomar como base os passos descritos nas páginas 192 e 193 do Livro do estudante. Pode-se organizar a turma em duplas para a realização dessa atividade a fim de que possam trocar ideias e validar hipóteses, exercitando a cooperação e favorecendo o trabalho com as competências gerais 7 e 9.

6o passo: Traçamos os lados AB, BC, CD, DE, EF e FA. Para finalizar, colorimos a região interna da figura.

Ao final, pedir às duplas que troquem de fluxograma e construam um polígono regular, por exemplo, de oito lados, seguindo o fluxograma que receberam. Em seguida, pedir que, juntos, façam as correções quando necessárias.

Esse processo garante a construção do hexágono regular desejado, pois:

• o triângulo formado pelos pontos OAB é um triângulo equilátero;

• em um triângulo equilátero, os ângulos internos são congruentes, e cada um mede 60° Assim, construindo dois triângulos equiláteros consecutivos, obtemos o ângulo de 120° , que é a medida do ângulo interno do hexágono regular.

PENSE E RESPONDA

Responda à questão no caderno. Seis triângulos equiláteros.

Em quantos triângulos equiláteros podemos decompor o hexágono? Compare sua resposta com a dos colegas, e, juntos, façam as correções necessárias.

Ao pensar em passos para escrever um fluxograma, os estudantes desenvolvem o pensamento computacional.

Pense e responda

A questão proposta tem como objetivo explorar a argumentação com base nos conhecimentos matemáticos dos estudantes. Espera-se que eles retomem as características de cada polígono e justifiquem que é possível posicionar seis triângulos equiláteros de modo que, dois a dois, formem os lados consecutivos de um hexágono, cujo ângulo interno é 120°.

2. Fixe um prego em cada ponto marcado: você formará oito filas com oito pregos em cada uma.

3. Com o auxílio de um adulto, fixe os pregos na placa utilizando o martelo: cada prego deve entrar 5 mm na madeira, ficando 10 mm de altura para fora dela, o que permitirá o manuseio dos elásticos.

Depois de construir o geoplano, os estudantes devem formar contornos de polígonos com os elásticos e refletir sobre as

propriedades e características de cada polígono formado.

Proponha-lhes:

• observar os vértices, os lados, os ângulos internos e os ângulos externos dos polígonos formados;

• usar elásticos de cores diferentes para indicar as diagonais dos polígonos formados.

Os estudantes devem comparar os perímetros das figuras formadas no geoplano e perceber que há polígonos diferentes com perímetros iguais. Se necessário, recorde a noção de perímetro.

ORIENTAÇÕES DIDÁTICAS

Caso os estudantes já tenham escrito o fluxograma para a construção de um polígono regular usando régua e compasso, pedir que comparem o fluxograma que fizeram com o apresentado na página do Livro do estudante, identificando pontos comuns.

Descubra mais

Propor a exploração do material solicitada na seção, que pode ser realizada em casa. Pedir aos estudantes que observem os parâmetros envolvidos nas representações dos polígonos regulares e verifiquem se estão de acordo com as fórmulas e conceitos estudados nessa unidade. Por meio de softwares de geometria dinâmica, os estudantes podem validar estratégias e resultados, contribuindo para o desenvolvimento da competência geral 5 e da competência específica 5 da área de Matemática.

Na construção do hexágono regular, dividimos a circunferência em seis partes iguais. Agora, vamos representar um círculo e dividi-lo em seis partes iguais. Traçando os segmentos de retas OA e OB, obtemos um setor do círculo, ou setor circular, cujo ângulo central é AOB, como mostra a imagem a seguir.

setor do círculo

ângulo central

No caso da construção do hexágono regular, podemos dividir o círculo em seis setores circulares congruentes cujos ângulos centrais medem °360 6 = 60°

Desse modo, conhecendo a medida do ângulo central e a quantidade de lados de um polígono regular, é possível construí-lo usando régua, compasso e transferidor. Acompanhe os passos dessa construção no fluxograma a seguir.

Início: Escolha a quantidade n de lados do polígono regular.

Determine a medida do ângulo central dividindo 360° por n

Fim: Trace segmentos de retas unindo dois pontos consecutivos até completar o contorno do polígono regular.

DESCUBRA MAIS

Com um compasso, marque na circunferência os demais pontos que a dividem em n setores iguais.

Usando um compasso, construa uma circunferência. Usando um transferidor, marque a medida do ângulo central.

IGM DIGITAL – Instituto Goiano de Matemática. Elementos dos polígonos regulares. GeoGebra. [Goiânia], 6 fev. 2020. Disponível em: https://www.geogebra.org/m/znknpjcf. Acesso em: 2 jun. 2022.

Neste aplicativo, é possível determinar a quantidade de lados de um polígono regular e perceber alguns elementos desse polígono, como o traçado das diagonais, as medidas dos ângulos internos e externos, a soma das medidas dos ângulos internos pela decomposição do polígono regular em triângulos, entre outras representações.

D2-AV2-MAT-F2-2103-V8-U6-178-211-LA-G24.indd 194 14/08/22 17:20

AMPLIANDO

Atividade complementar

Propor aos estudantes que escrevam um fluxograma para determinar, por exemplo, a soma dos ângulos internos de um polígono ou o número de diagonais de um polígono, para que possam exercitar o pensamento computacional. Explicar a eles que vão fixar o fluxograma que construíram no mural da sala e comparar com o fluxograma dos colegas. Com isso, juntos, podem fazer as correções necessárias.

Vamos seguir o fluxograma anterior e construir um octógono regular. Nesse caso, n = 8.

A medida do ângulo central é °360 8 = 45°

Assim, construímos uma circunferência e marcamos o ângulo central de medida 45°

ORIENTAÇÕES DIDÁTICAS

Atividades

Depois, marcamos os pontos dos demais setores circulares. Em seguida, traçamos os segmentos de retas unindo dois pontos consecutivos até completar o contorno do octógono regular.

Caso considere oportuno, orientar os estudantes a resolver as atividades em duplas, assim podem trocar estratégias e validar hipóteses, bem como exercer a cooperação, trabalhando aspectos das competências gerais 7 e 9. Na atividade 3, os estudantes devem se lembrar de que um polígono regular de quatro lados é um quadrado.

Para finalizar, podemos apagar as linhas que usamos na construção, deixando apenas a representação do polígono regular, e colorir a região interna.

ATIVIDADES

Responda às questões no caderno.

3. Espera-se que os estudantes determinem a medida do ângulo central do quadrado fazendo ° 360 4 = 90° , construam uma circunferência, dividam-na em quatro setores circulares congruentes, cujos ângulos centrais medem 90°, e unam os pontos consecutivos por segmentos de retas.

1. A partir da construção de um triângulo equilátero de 5 cm de lado, construa um hexágono regular cujo lado também mede 5 cm.

2. Determine a medida do ângulo central dos seguintes polígonos regulares.

a) Quadrado

b) Pentágono

c) Decágono.

1. G A B 90° 72° 36°

3. Utilizando régua, compasso e transferidor, construa um polígono regular de quatro lados por meio do fluxograma anterior.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

195 D2-AV1-MAT-F2-2103-V8-U6-178-211-LA-G24.indd 195 12/08/22 23:47

ORIENTAÇÕES DIDÁTICAS

Paralelogramos

A congruência de triângulos foi estudada na Unidade 3 deste Volume e dá subsídio para que as propriedades dos quadriláteros, apresentadas aqui, possam ser compreendidas pelos estudantes. Se necessário, retomar os casos de congruência de triângulos.

Uma possibilidade de atividade é solicitar aos estudantes que, utilizando o geoplano construído anteriormente, construam os diferentes tipos de paralelogramo estudados e observem as características de cada um.

Espera-se que os estudantes reconheçam o retângulo como um paralelogramo de ângulos internos congruentes, o losango como um paralelogramo de lados congruentes e o quadrado como um paralelogramo que também é um retângulo e um losango, ou seja, tem os lados e os ângulos internos congruentes.

PROPRIEDADES DOS QUADRILÁTEROS CAPÍTULO6

PARALELOGRAMOS

Considere os quadriláteros representados a seguir.

Todos esses quadriláteros apresentam, em comum, o fato de terem os lados opostos paralelos.

Todo quadrilátero que tem os lados opostos paralelos é denominado paralelogramo

• O paralelogramo EFGH da figura 2, que tem os quatro ângulos internos retos, é denominado retângulo

• O paralelogramo MNOP da figura 3, que tem os quatro lados congruentes, é chamado de losango ou rombo

• O paralelogramo RSTQ da figura 4, que tem os quatro lados congruentes e os quatro ângulos internos retos, é chamado de quadrado

Os paralelogramos apresentam as seguintes propriedades.

1a propriedade:

Em um paralelogramo, os ângulos opostos são congruentes.

• Como a e d são medidas de ângulos colaterais internos, temos: a + d = 180° a = 180° d I

• Como c e d são medidas de ângulos colaterais internos, temos: c + d = 180° c = 180° d II

Comparando I e II , temos: a = c, ou seja, 2 A ˆ C Usando o mesmo raciocínio, podemos mostrar que 2 B D

2a propriedade:

Em qualquer paralelogramo, os lados opostos são congruentes.

Traçando a diagonal AC, obtemos os triângulos ABC e CDA, em que:

• a = c (ângulos alternos internos);

• AC 2 AC (lado comum);

• b = d (ângulos alternos internos).

Então, pelo caso ALA de congruência de triângulos, temos que * ABC 2*CDA. Como consequência, AB 2 CD e BC 2 DA

3a propriedade:

Em qualquer paralelogramo, as diagonais interceptam-se no ponto médio de cada uma delas.

Traçando as diagonais AC e BD, temos:

• a = c (ângulos alternos internos);

• AB 2 CD (lados opostos);

• b = d (ângulos alternos internos).

Então, pelo caso ALA de congruência de triângulos, temos que * AMB 2*CMD.

Como consequência, AM 2 CM e BM 2 DM

Portanto, o ponto M é ponto médio tanto da diagonal  AC como da diagonal BD

Agora, vamos estudar alguns paralelogramos que recebem nomes especiais: retângulo, losango e quadrado

Retângulo

Além das propriedades dos paralelogramos já estudadas, o retângulo apresenta uma propriedade característica: suas diagonais são congruentes.

Decompondo o retângulo nos triângulos ABC e ABD, temos:

• AB 2 AB (lado comum);

• ˆ A 2 ˆ B (ângulos retos);

• BC 2 AD (lados opostos do retângulo).

Pelo caso LAL de congruência de triângulos, temos que * ABC  2* ABD. Como consequência: AC 2 BD

ORIENTAÇÕES DIDÁTICAS

Na lousa, explorar cada uma das demonstrações das propriedades dos quadriláteros, esclarecendo o passo a passo da demonstração. Enfatizar o que precisa ser provado e incentivar a participação dos estudantes por meio de questionamentos. Por exemplo, na 2a propriedade, perguntar quais são os lados opostos no paralelogramo representado no Livro do estudante. Verificar se os estudantes percebem que precisam mostrar que os lados AB e CD são congruentes, bem como os lados BC e AD. Em seguida, iniciar a demonstração traçando a diagonal AC e questionando-os sobre os triângulos formados e se esses triângulos são congruentes. Para ajudá-los, retomar a congruência dos ângulos alternos internos, destacando a congruência dos ângulos a ˆ e c ˆ e dos ângulos b ˆ e d ˆ . Com isso, como o lado AC é comum aos dois triângulos, os estudantes não devem ter dificuldades para concluir que os triângulos ABC e CDA são congruentes e, como consequência desse fato, que os lados opostos de qualquer paralelogramo são congruentes. Proceder dessa maneira para as demais demonstrações e comentar que a demonstração segue um encadeamento lógico e, por isso, ela é válida. Nas demonstrações, os estudantes exercitam o raciocínio por dedução e a argumentação com base em fatos matemáticos.

ORIENTAÇÕES DIDÁTICAS

Losango

Encaminhar a demonstração da propriedade dos losangos que diz que suas diagonais são perpendiculares entre si e estão contidas nas bissetrizes dos ângulos internos. Caso seja necessário, retomar os conceitos de perpendicularidade e bissetriz de um ângulo.

Quadrado

Retomar, com a colaboração dos estudantes, que o quadrado é um paralelogramo, pois é um quadrilátero que tem os lados opostos paralelos, é um retângulo, pois apresenta todos os ângulos retos, e é um losango, pois tem os quatro lados congruentes. Desse modo, as propriedades estudadas para os paralelogramos, os retângulos e os losangos também são válidas para os quadrados.

Losango

Além das propriedades gerais dos paralelogramos, o losango apresenta uma propriedade característica: suas diagonais são perpendiculares entre si e estão contidas nas bissetrizes dos ângulos internos do losango.

Considerando a diagonal DB do losango a seguir, pelo caso LLL de congruência de triângulos, temos que * ABD 2*CBD.

AMPLIANDO

Atividade complementar

Podemos concluir, também, que esses triângulos são isósceles; portanto, os ângulos A DB e A BD e os ângulos CDB e CBD são congruentes. Como os triângulos são congruentes, concluímos que os ângulos A DB, A BD, CDB e CBD são congruentes. Assim, DB é bissetriz de D e B Analogamente, podemos concluir que AC é bissetriz de ˆ A e C Agora, vamos demonstrar que as diagonais do losango são perpendiculares. Considerando os triângulos AMB e AMD, temos que:

• AB 2 AD (lados do losango);

• B ˆ AM 2 D ˆ AM () AC ébisse triz ;

• AM é comum aos triângulos ABM e ADM.

Então, pelo caso LAL de congruência de triângulos, temos que * ABM 2* ADM. Logo, os ângulos A MB e A MD também são congruentes e, como são suplementares, temos que med A ˆ MB () = med A ˆ MD () = 90 °. Portanto, AC e DB são perpendiculares À ACDB ()

Quadrado

O quadrado reúne as propriedades dos paralelogramos, dos retângulos e dos losangos. Como as demonstrações dessas propriedades são análogas às anteriores, elas não serão demonstradas.

DC B A

AC 2 BD

AC À BD

M

AC é bissetriz de A e CA é bissetriz de C

BD é bissetriz de B e DB é bissetriz de D

Para sistematizar esse conteúdo, propor aos estudantes que classifiquem cada afirmação em verdadeira ou falsa e justifiquem as afirmações que julgarem falsas. A construção de argumentos com base em conhecimentos matemáticos é uma habilidade importante a ser desenvolvida nessa etapa da aprendizagem.

Observe as afirmações e verifique se são verdadeiras (V) ou falsas (F).

a) As diagonais de qualquer retângulo são congruentes.

b) As diagonais de qualquer losango são congruentes.

c) As diagonais de um quadrado são congruentes.

d) As diagonais de qualquer retângulo são perpendiculares entre si.

e) As diagonais de qualquer losango são perpendiculares entre si.

f) As diagonais de um quadrado são perpendiculares entre si.

Resolução da atividade

a) V b) F c) V d) F e) V f) V

ATIVIDADES

Responda às questões no caderno.

1. Considere o paralelogramo da figura a seguir. Nele, estão expressas as medidas de dois ângulos opostos. Quais são as medidas dos quatro ângulos desse paralelogramo? 45°, 45°, 135° e 135°

ORIENTAÇÕES DIDÁTICAS

Atividades

2. Determine a medida x no paralelogramo da figura a seguir.

= 47°

3. A figura seguinte é um retângulo.

+ y

De acordo com as indicações, escreva o polinômio que indica:

a) o perímetro do retângulo.

b) a área do retângulo.

4. Esta figura é um quadrado. De acordo com as indicações, escreva o polinômio que indica:

a) o perímetro do quadrado.

b) a área do quadrado.

AMPLIANDO

+ 6y

2 + 7xy + 2y2 20x 4y

y

25x 2 10xy + y2

y

Atividade complementar

Para o trabalho com paralelogramos, como os retângulos, losangos e quadrados, pode-se utilizar o tangram. Pedir aos estudantes que construam quadriláteros usando as peças do tangram. Levantar questões como as a seguir.

a) É possível construir um quadrado com cinco peças do tangram? E com seis peças?

C M D 12 y

x16 20

a) as medidas x e y indicadas.

Nesse bloco, os estudantes deverão identificar os paralelogramos e aplicar as propriedades características destes.

B

5. Observando o losango ABCD, determine: A

b) os perímetros dos triângulos AMB, ABC e ABD

64 e

6. Sabendo que a figura a seguir é um quadrado, calcule as medidas x e y indicadas. x y

7. Se as diagonais de um retângulo formam um ângulo de 114° entre si, quais são as medidas dos ângulos que as diagonais formam com os lados do retângulo?

8. A medida de cada ângulo obtuso de um losango é expressa, em grau, por (2x + 5) °, e a medida de cada ângulo agudo é expressa por (x + 40)°. Nessas condições, determine a medida dos quatro ângulos desse losango.

9. Na figura a seguir, ABCDEF é um hexágono regular, e AFGH é um losango. Determine as medidas x e y indicadas

Resolver com os estudantes a atividade 4, verificando se eles utilizam o produto notável ou a propriedade distributiva para o cálculo da área. Se considerar necessário, aproveitar o momento para recordar os produtos notáveis: quadrado da soma e quadrado da diferença de dois termos.

Para a atividade 9, se necessário, retomar com os estudantes o cálculo da medida do ângulo interno de um polígono regular.

b) É possível construir um paralelogramo com sete peças do tangram?

c) É possível construir um trapézio com cinco peças do tangram?

Resolução da atividade

a) Sim; não.

b) Sim.

c) Sim.

ORIENTAÇÕES DIDÁTICAS

Trapézios

Os trapézios compõem o grupo dos quadriláteros formados por apenas um par de lados paralelos. Estudos mostram que os egípcios já estudavam essa figura.

No Papiro de Rhind, documento egípcio datado de aproximadamente 1650 a.C., encontramos a figura de um trapézio (observe-o na parte esquerda da imagem a seguir). A base maior era designada por um vocábulo cuja tradução seria “boca”; a base menor era a “truncadura”; os lados não paralelos, as “larguras”.

Os romanos denominavam o trapézio mensa, pois achavam que a figura desse quadrilátero lembrava uma mesa.

Somente a partir de meados do século XVII é que o termo trapézio foi adotado definitivamente.

TRAPÉZIOS

Os quadriláteros das figuras seguintes apresentam dois lados paralelos. Quadriláteros com essa característica são chamados de trapézios

Os lados paralelos são as bases do trapézio, e a distância entre as bases é a medida de sua altura

// OP MN é a base maior. OP é a base menor.

Entre os trapézios, destacamos dois casos particulares.

Trapézio retângulo

É o trapézio no qual um dos lados não paralelos é perpendicular às bases.

Na representação, o lado AD é perpendicular às bases AB e CD

Trapézio isósceles

É o trapézio no qual os lados não paralelos são congruentes.

Vamos apresentar duas propriedades dos trapézios isósceles.

1a propriedade:

2a

D2-AV1-MAT-F2-2103-V8-U6-178-211-LA-G24.indd

os

da mesma base são

um trapézio isósceles, as diagonais são congruentes.

Fragmento do Papiro de Rhind, de c. 1650 a.C.

ORIENTAÇÕES DIDÁTICAS

BASE MÉDIA DE UM TRAPÉZIO

O segmento de reta cujas extremidades são os pontos médios dos lados não paralelos de um trapézio é denominado base média do trapézio

D MN

C B A

M: ponto médio do lado AD

N: ponto médio do lado BC

MN: base média do trapézio MN // AB e MN // CD

A medida da base média de um trapézio é igual à metade da soma das medidas das bases do trapézio. = + me dMN me dA Bmed CD 2 () () ()

Responda às questões no caderno.

1. Em um trapézio, três de seus ângulos medem 78 °, 102 ° e 98 °. Determine a medida do quarto ângulo.

82°

2. No trapézio isósceles, os ângulos da mesma base são congruentes. Se em um trapézio isósceles um dos ângulos mede 74°, determine a medida dos outros três ângulos.

6. A figura a seguir é um trapézio isósceles. Sabendo que AM está contido na bissetriz do ângulo A , e BM está contido na bissetriz do ângulo ˆ B, determine a medida x indicada.

O uso do vocabulário adequado é importante na identificação dos quadriláteros. Assim, nas atividades, solicitar aos estudantes que destaquem o trapézio ao qual a questão se refere.

Atividades

As atividades exploram reconhecimento de trapézios, as classificações e as aplicações das propriedades dos trapézios. Incentivar os estudantes a representar a situação descrita por figuras, sempre que possível. Para a resolução das atividades 3 e 4, retomar com a turma que a soma das medidas dos ângulos internos de um quadrilátero é 360°. Se considerar necessário, mostrar que esse resultado é consequência da possibilidade de o quadrilátero ser decomposto em dois triângulos.

3. Determine a medida x indicada na figura.

4. Determine as medidas x e y indicadas na figura.

° , 106° e 106° x = 62° x = 80° e y = 50°

x 106° 106° AB C D M

Nas atividades 7 e 8, os estudantes devem aplicar o teorema da base média para determinar as medidas solicitadas. Caso apresentem dúvidas, retomar o teorema e sua demonstração.

x AB

20,5 cm x

ORIENTAÇÕES DIDÁTICAS

Tratamento da informação

Essa seção contempla gráfico de setores e tabelas e explora a leitura e interpretação de dados nessas representações e o cálculo de porcentagem.

O gráfico de setores é muito utilizado em boletins informativos de órgãos públicos, reportagens, notícias, redes sociais, mídia, entre outros, e tem como característica principal possibilitar a comparação de dados em relação ao todo. Ressaltar o erro comum em gráficos de setores que ocorre quando a soma das frequências relativas não resulta em 100%.

Antes de iniciar, convidar os estudantes a uma reflexão sobre a confidenciabilidade dos dados e apontar os principais elementos que compõem um gráfico, como título, legendas, datas e total das porcentagens.

Destacar a atenção que se deve ter com a fonte dos dados: de onde ela vem, se pode ser considerada confiável, quais interesses poderiam ter as pessoas envolvidas na divulgação de determinados dados, ou seja, se elas não estão utilizando as informações a seu favor. Tudo isso contribui para o letramento estatístico e promove a criticidade dos estudantes.

Além disso, discutir os tipos de variável que estão envolvidos nesses gráficos – no caso, sempre qualitativas ou categóricas –, as variáveis que estão sendo tratadas e como os dados presentes nos gráficos auxiliam para responder às questões e tomar decisões. Explorar frequências absolutas e relativas, desenvolvendo aspectos das habilidades EF08MA23 e EF08MA24.

INTERPRETANDO UM GRÁFICO DE SETORES

Em março de 2021, a Fundação Oswaldo Cruz (Fiocruz) publicou um estudo sobre o impacto da pandemia de covid19 na saúde dos profissionais que atuam na linha de frente no combate ao coronavírus, no município do Rio de Janeiro. O gráfico de setores a seguir expressa, em percentual (%), a quantidade de profissionais de cada categoria dos trabalhadores da saúde que participou do estudo, de acordo com os dados divulgados pela Fiocruz. Responda às questões no caderno.

1. Que categoria profissional teve a maior quantidade de profissionais participando do estudo? Qual foi o percentual dessa participação? Enfermeiros; 27,52%.

2. A menor participação do estudo corresponde a que categoria profissional? Com qual porcentagem?

Psicólogos; 11,24%.

3. Apenas analisando o gráfico, é possível determinar a quantidade de profissionais de cada categoria que participou desse estudo? Por quê?

Não, porque não foi informado o total de participantes do estudo.

Sabendo que a amostra do estudo contou com 258 profissionais, vamos determinar a quantidade de profissionais correspondente a cada categoria.

Categoria profissional dos trabalhadores da saúde que participaram do estudo

Elaborado com base em: NOGUEIRA, Mariana Lima et al Primeiro boletim da pesquisa: monitoramento da saúde, acesso a EPIs de técnicos de enfermagem, agentes de combate às endemias, enfermeiros, médicos e psicólogos, no município do Rio de Janeiro em tempos de covid-19. Rio de Janeiro: EPSJV: FIOCRUZ, fev. 2021. p. 12. Disponível em: https://covid19susrj.fiocruz. br/sites/covid19susrj.fiocruz.br/files/boletim_ pesquisa.pdf. Acesso em: 2 jun. 2022.

x == x 21,71 258 100 56

A partir desses dados, podemos construir uma tabela para indicar, em porcentagem e em valores absolutos, a participação no estudo dos profissionais por categoria da área da saúde. Participação dos trabalhadores da saúde por categoria profissional

ORIENTAÇÕES DIDÁTICAS

Essa seção apresenta um estudo sobre profissionais da área de saúde na pandemia de covid-19 que receberam treinamento nas unidades de saúde sobre manuseio e descarte de EPI. Explicar que EPI são equipamentos de proteção individual, como máscaras e luvas descartáveis, entre outros.

Elaborada com base em: NOGUEIRA, Mariana Lima et al Primeiro boletim da pesquisa: monitoramento da saúde, acesso a EPIs de técnicos de enfermagem, agentes de combate às endemias, enfermeiros, médicos e psicólogos, no município do Rio de Janeiro em tempos de covid-19. Rio de Janeiro: EPSJV: FIOCRUZ, fev. 2021. p. 12. Disponível em: https://covid19susrj.fiocruz.br/sites/covid19susrj.fiocruz.br/files/boletim_pesquisa.pdf. Acesso em: 2 jun. 2022.

Responda às questões no caderno.

4. Ainda com base no estudo anterior, o gráfico de setores mostra a resposta dos 258 profissionais, quando perguntados se as unidades de saúde onde atuam proporcionaram formação/ treinamento sobre o manuseio e o descarte de equipamento de proteção individual (EPI).

a) P ara a pergunta proposta, qual foi a resposta mais citada pelos profissionais? Não proporcionou.

b) Quantos profissionais responderam que a unidade básica proporcionou treinamento, mas foi insuficiente? Dê a resposta em porcentagem e em valores absolutos. 22,6%. 58 profissionais.

Formação/treinamento nas unidades de saúde sobre manuseio e descarte de EPI

Elaborado com base em: NOGUEIRA, Mariana Lima et al Primeiro boletim da pesquisa: Monitoramento da saúde, acesso a EPIs de técnicos de enfermagem, agentes de combate às endemias, enfermeiros, médicos e psicólogos, no município do Rio de Janeiro em tempos de covid-19. Rio de Janeiro: EPSJV: FIOCRUZ, fev. 2021. p. 19. Disponível em: https://covid19susrj.fiocruz.br/sites/covid19susrj.fiocruz. br/files/boletim_pesquisa.pdf. Acesso em: 2 jun. 2022.

c) Você considera importante o treinamento dos profissionais de saúde para o uso correto dos EPIs? Por quê? Conte aos colegas e ao professor Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

AMPLIANDO

Link

A NATUREZA da estatística. In: OBMEP; IMPA (org.). Livro aberto de matemática. [S. l.]: OBMEP/IMPA, [201-]. v. 1. E-book. Disponível em: https://www.umlivroaberto.org/BookCloud/Volume 1/master/view/PE103. html. Acesso em: 11 ago. 2022.

O texto discute conceitos básicos de estatística e como aplicá-los em sala de aula.

Propor o trabalho com outros componentes curriculares, de maneira interdisciplinar, com professores de Ciências, por exemplo. Os professores de outras áreas podem sugerir extensões para complementar as atividades propostas ou propor novas, desenvolvendo o Tema Contemporâneo Transversal Trabalho.

A turma pode ser organizada em pequenos grupos para trabalhar as atividades propostas, de modo que possam trocar ideias e validar hipóteses, exercitando a argumentação, a colaboração e a empatia, favorecendo o desenvolvimento de aspectos relacionados às competências gerais 7 e 9, bem como da competência específica 4 da área de Matemática, uma vez que os estudantes são levados a fazer observações, investigar, organizar e comunicar informações, produzindo argumentos convincentes.

D2-AV1-MAT-F2-2103-V8-U6-178-211-LA-G24.indd

ORIENTAÇÕES DIDÁTICAS

Transformações no plano

Os estudantes, provavelmente, estudaram o conteú do de transformações no plano; então, aproveitar este momento para retomar os conceitos e tirar eventuais dúvidas.

Se considerar necessário que os estudantes realizem as situações apresentadas nestas páginas, pedir a eles que providenciem régua, compasso e papel quadriculado.

NO PLANO CAPÍTULO7

TRANSFORMAÇÕES

Já estudamos que em polígonos e em outras figuras geométricas podem ser aplicadas transformações geométricas no plano. As figuras obtidas por essas transformações são imagens da original e podem ter as medidas dos lados alteradas, assim como sua posição no plano.

REFLEXÃO

Considere a figura representada a seguir. Podemos dizer que II é a reflexão de I em relação à linha vermelha.

AMPLIANDO

Livro

Quando duas imagens são reflexo uma da outra, e esse reflexo se dá em relação a uma linha, dizemos que há simetria de reflexão, ou simetria axial, e a linha é o eixo de reflexão, ou eixo de simetria

TRANSLAÇÃO

O pentágono I foi transladado, na direção e no sentido do vetor u, gerando opentágono II . Para transladar o pentágono, deslocamos os vértices A, B, C, D e E três quadradinhos para a direita e, em seguida, dois quadradinhos para baixo, obtendo os pontos A‘ , B‘ , C‘ , D‘ e E‘, como mostra a figura a seguir.

Transladar: transferir para outro lugar.

A translação é a transformação no plano em que todos os pontos de uma figura são deslocados na mesma direção e no mesmo sentido, preservando as dimensões originais.

BARBOSA, Rui Madsen (org.). Geoplanos e redes de pontos: conexões e educação matemática. Belo Horizonte: Autêntica, 2013 (Série O professor de Matemática em ação, 4).

Esse livro apresenta diferentes maneiras de explorar, brincar, contar, jogar e manusear objetos representados por pontos, quadrados, polígonos, malhas quadrangulares, geoplanos, entre outros. Tudo isso possibilita extrair dessa interação as propriedades conceituais matemáticas.

ROTAÇÃO

Considere a figura a seguir. Nela, I foi rotacionada em torno do ponto O, em 90° no sentido anti-horário, obtendo a figura II Para construir a rotação de uma figura, é preciso definir o ponto em torno do qual essa figura girará, ou seja, um centro de rotação Também é preciso definir um ângulo e um sentido de rotação.

A seguir, acompanhe o passo a passo da rotação do triângulo HIJ em torno do ponto K (centro de rotação) com um ângulo de rotação de 90 ° no sentido horário.

De um dos vértices do triângulo, traçamos uma reta que passa por K, por exemplo, a reta que passa pelos pontos J e K. Construímos uma reta que forma um ângulo de 90° com a reta anterior no sentido horário. Sobre essa reta, marcamos o ponto J‘, de modo que 2‘ JK JK. Repetimos esse procedimento para os demais vértices do triângulo, obtendo os pontos I‘ e H‘

Desse modo, obtemos o triângulo H‘I‘J‘, que é a rotação de 90° no sentido horário do triângulo HIJ em torno do ponto K

ORIENTAÇÕES DIDÁTICAS

Rotação

Aproveitar o contexto e questionar os estudantes sobre onde podemos obter exemplos de transformações do plano no cotidiano. Alguns exemplos que os estudantes podem mencionar: obras de arte, mosaicos, ladrilhos e pisos, logomarcas, entre outros.

Descubra mais

O centro de rotação também pode ser um dos pontos da figura. Na representação, o polígono ABCD foi rotacionado em 180° no sentido horário em relação ao ponto D. Nessa situação, dizemos que D é o ponto fixo dessa rotação.

Sugerimos que a abordagem de polígonos seja feita também por meio da geometria experimental. A interação digital pode ajudar na compreensão de propriedades envolvendo as transformações no plano, pois, ao movimentar as figuras e observar as figuras transformadas sendo modificadas dinamicamente, a relação entre as partes fica evidenciada.

A transformação geométrica rotação consiste em girar determinada figura em torno de um ponto do plano, mantendo o ângulo de deslocamento.

DESCUBRA MAIS

SILVA, Carolina Moura Brasil Carneiro da. Transformações no Plano. GeoGebra. [S l.], 9 set. 2021. Disponível em: https://www.geogebra.org/m/xepu9y9j. Acesso em: 2 jun. 2022.

Esse aplicativo aborda, de maneira tutorial, algumas transformações no plano envolvendo polígonos, como rotações, translações e reflexões. Para cada transformação, há explicações, simulações e atividades interativas.

Propor aos estudantes que acessem o link indicado no Livro do estudante, façam as simulações propostas e anotem o que observaram em cada uma delas. Depois, pedir que apresentem para a turma as anotações que fizeram e, juntos, elaborem um esquema com as principais características de cada transformação.

ILUSTRAÇÕES: EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

Composição de transformações

Verificar se os estudantes compreendem que a composição de transformações são duas ou mais transformações feitas em seguida. É importante que eles percebam que não é uma nova transformação, apenas uma composição das transformações já conhecidas.

Salientar também que, tendo a figura inicial e a final, é possível que mais de uma composição de transformações resulte naquela imagem final.

Se considerar oportuno, reunir os estudantes em duplas, distribuir papel quadriculado e solicitar que tentem reproduzir as figuras presentes no texto. Essa abordagem auxilia na compreensão das etapas necessárias para a obtenção da figura final.

Pense e responda

Organizar os estudantes em pequenos grupos para responder à questão proposta. Se possível, incentivá-los a usar o GeoGebra para fazer simulações. Essa abordagem favorece o desenvolvimento de aspectos das competências gerais 7 e 9, uma vez que os estudantes devem fazer observações, elaborar argumentos convincentes e exercitar a colaboração e a empatia com os colegas.

COMPOSIÇÃO DE TRANSFORMAÇÕES

Algumas figuras podem ser obtidas por meio da composição de transformações geométricas no plano. Acompanhe alguns exemplos.

1 Observe a figura.

O triângulo ABC (figura inicial) passou por duas transformações geométricas para chegar ao triângulo A‘B‘C‘ (figura final). Acompanhe o passo a passo.

1o passo: Reflexão em relação à reta r 2o passo: Rotação de 45° no sentido anti-horário, com centro de rotação no vértice A‘

2 A figura inicial do peixe a seguir passou por uma translação horizontal de três unidades para a direita e, em seguida, uma rotação de 180° em relação ao ponto O

PENSE E RESPONDA

Responda à questão no caderno.

Resposta na seção Resoluções comentadas deste Manual.

Na figura do peixe, é possível chegar à figura final fazendo outros tipos de composição de transformações? Conte aos colegas e ao professor como você chegou a essa conclusão.

1. Resposta na seção Resoluções comentadas deste Manual.

3. Resposta na seção Resoluções comentadas deste Manual.

1. Copie o polígono  ABCDE em uma folha de papel quadriculado e, em seguida, construa a reflexão dele em relação à reta r.

2. Represente o plano cartesiano em uma folha de papel quadriculado e marque os pares ordenados A(3, 2), B(7, 2) e C(5, 5). Em seguida, construa o polígono A‘B‘C‘ refletido em relação ao eixo das ordenadas (eixo y ).

a) Quais são as coordenadas dos pontos A‘ , B‘ e C‘?

b) Deslocar a figura três quadradinhos para a direita e dois quadradinhos para cima.

DESAFIOS

5. Resposta na seção Resoluções comentadas deste Manual.

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades propostas pretendem levar os estudantes a utilizar instrumentos geométricos e trabalhar com as transformações geométricas no plano, percebendo as diferenças na construção de cada uma delas.

O uso de softwares de geometria dinâmica pode auxiliar na construção das isometrias. Mas é importante que essa etapa de construção, usando papel quadriculado, régua, compasso e esquadros, seja trabalhada em sala de aula.

b) Compare as coordenadas dos pontos A, B e C e as respectivas coordenadas dos pontos A‘ , B‘ e C‘. O que você observa com relação às coordenadas desses pontos?

A‘( 3, 2), B‘( 7, 2) e C‘( 5, 5). Resposta na seção Resoluções comentadas deste Manual.

3. Os pentágonos ABCDE e

A‘B‘C‘D‘E‘ são simétricos em relação a uma reta t . Copie os pentágonos em uma folha de papel quadriculado e desenhe a reta t

4. Copie as figuras a seguir em uma folha de papel quadriculado. Em seguida, faça a translação de cada uma delas, de acordo com as instruções.

a) Deslocar a figura quatro quadradinhos para a direita.

Respostas na seção Resoluções comentadas deste Manual.

5. Copie a figura em uma folha de papel quadriculado e, em seguida, complete a rotação dela em torno do ponto O no sentido anti-horário, de um ângulo de 90°. Use régua e jogo de esquadros.

6. Escher (1898-1972), artista holandês de grande renome, utilizou duas transformações no plano para compor a obra a seguir.

O artista holandês Maurits Cornelis Escher trabalhou muito com isometrias em suas obras de mosaicos. Caso considere interessante, apresentar algumas obras do artista, disponíveis em: https://mcescher.com/ ( site em inglês; acesso em: 12 ago. 2022).

ESCHER, Maurits Cornelis. Pássaros/ Peixes (no 22). 1941. Impressão em papel. 34 cm x 45 cm. Que transformações você identifica nessa obra?

7. Em uma folha de papel quadriculado, represente o plano cartesiano e uma figura geométrica qualquer. Depois, aplique uma reflexão em relação ao eixo das ordenadas, seguida de uma translação vertical de três unidades.

Espera-se que os estudantes identifiquem a translação. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

ORIENTAÇÕES DIDÁTICAS

Tecnologias

Reservar com antecedência computadores para os estudantes, caso a escola disponha desses equipamentos. Caso contrário, fazer a demonstração dos comandos na sala de aula. O ideal é que seja em quantidade suficiente para que eles trabalhem em duplas.

É importante salientar que a escolha do software de geometria dinâmica foi feita, entre vários possíveis, por ele ser gratuito e de fácil utilização.

O GeoGebra, além das ferra mentas geométricas, também permite a análise algébrica em diversas situações, como no cálculo de áreas e perímetros.

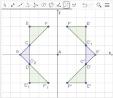
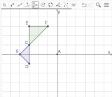
Explorar com os estudantes como funcionam as ferramentas que vão usar durante a realização da proposta e permitir que eles as explorem por algum tempo, de modo que possam se familiarizar com elas. Depois, convidar a turma a reproduzir as construções discutidas nas páginas do Livro do estudante, esclarecendo possíveis dúvidas no processo.

TRANSFORMAÇÕES NO PLANO

Depois do estudo das transformações geométricas no plano, vamos usar ferramentas do software GeoGebra para fazer composições envolvendo simetrias de reflexão, translação e rotação. Considere a seguinte situação.

Talita e Fernando estavam usando um software de geometria dinâmica para estudar transformações no plano. Eles foram desafiados a compor um padrão geométrico usando as simetrias de reflexão, translação e rotação. Nesse desafio, eles poderiam usar apenas as seguintes ferramentas:

Mover Reta

Reflexão em relação a uma reta Ponto

Polígono

Translação por um vetor

Vetor Intersecção entre dois objetos

Rotação em torno de um ponto

Além disso, eles poderiam usar a ferramenta apenas duas vezes. Observe algumas etapas das construções realizadas por Talita e Fernando.

1 Inicialmente, eles construíram dois triângulos: *BCD e *CEF. Em seguida, os triângulos construídos foram refletidos em relação ao eixo y. Depois, refletiram os triângulos CEF e F‘E‘C1‘ em relação ao eixo x

2 Foi realizada uma translação do triângulo BCD, obtendo o triângulo B1‘C3‘D1‘. Em seguida, foi feita uma rotação de 90° desse último triângulo, de centro em A, no sentido horário.

ORIENTAÇÕES DIDÁTICAS

O uso do software para realizar as transformações estudadas anteriormente auxilia o estudante no processo de compreensão dos conceitos.

3 Depois, foi realizada uma translação do triângulo JKI, obtendo o triângulo J‘K‘I‘. Para finalizar, Talita e Fernando refletiram os triângulos JKI e J‘K‘I‘ em relação ao eixo x, obtendo o padrão geométrico que desejavam.

Após a realização das atividades propostas, incentivar os estudantes a testar outras composições de transformações com outras figuras. Desse modo, o raciocínio e o desenvolvimento de novas habilidades são incentivados. Essa abordagem favorece o desenvolvimento de aspectos da competência geral 5 e da competência específica 5 da área de Matemática, uma vez que os estudantes são levados a compreender e utilizar processos e ferramentas matemáticas para validar estratégias e resultados.

Responda à questão 2 no caderno.

1. No GeoGebra, construa o padrão geométrico já apresentado. Você pode seguir o passo a passo que Talita e Fernando usaram, ou realizar as transformações geométricas em outra ordem

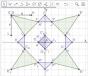
Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

2. Depois de construído o padrão geométrico, usando a ferramenta , clique sobre um vértice de um dos primeiros polígonos construídos e o arraste. Observe a seguir um exemplo.

REPRODUÇÃO/GEOGEBRA

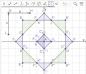
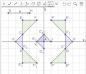
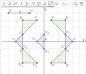
O que você verificou?

FOTOGRAFIAS:

ORIENTAÇÕES DIDÁTICAS

Retomando o que aprendeu

Antes de iniciar a resolução das atividades desse bloco, pedir aos estudantes que façam um resumo dos principais conceitos estudados na Unidade. Se necessário, eles podem consultar o Livro do estudante. Depois, solicitar a eles que citem os principais tópicos estudados na Unidade. Anotar os temas levantados por eles na lousa, de modo que as ideias principais também fiquem expostas. Em seguida, pedir que resolvam as atividades.

Esse bloco de atividades pode ser usado como avaliação de processo. Espera-se consolidar os conhecimentos dos estudantes construídos na Unidade. Sugerir que refaçam algumas atividades anteriores dos assuntos que surgirem dúvidas. Ressaltar tais temas ao corrigir as atividades. Fazer a correção coletivamente, retomando explicações na lousa, quando considerar necessário.

RETOMANDO APRENDEU O QUE

Responda às questões no caderno.

1. Calcule quantas diagonais tem o polígono da representação a seguir.

a) 22

b) 34

c) 44

d) 55

e) 66

2. (Saresp-SP) Seis cidades estão localizadas nos vértices de um hexágono regular, como mostra a figura. Há um projeto para interligá-las, duas a duas, por meio de estradas. Algumas dessas estradas correspondem aos lados do polígono, e as demais correspondem às diagonais. Desse modo, a quantidade de estradas a serem construídas é:

a) 9

b) 15

c) 21

d) 24

e) 27

3. Quantos lados tem o polígono cuja soma das medidas dos ângulos internos

é 2 160° ?

6. Um retângulo e um quadrado têm o mesmo perímetro. No retângulo, um dos lados mede 15 cm, e a medida do outro corresponde a 60% dessa medida. O lado do quadrado mede:

a) 10 cm.

b) 12 cm.

c) 14 cm.

d) 16 cm.

e) 20 cm.

7. No losango ABCD a seguir, temos que:

• med AM () = 40 cm;

• med MC () = x + 3y;

• med BM () = x + y;

• med MD () = 30 cm.

a) Qual é o valor da expressão x y?

b) Em uma folha de papel quadriculado, represente o losango ABCD e:

a) 14

b) 16 c) 17 d) 18 e) 20

4. A representação a seguir é de um hexágono não regular. Determine o valor de x

a) 105°

b) 100°

c) 110°

d) 120°

e) 108°

Alternativa b.

5. Em um polígono regular, a medida de cada ângulo extern o é 24 °. Esse polígono tem:

Alternativa a.

a) 90 diagonais.

b) 105 diagonais.

c) 119 diagonais.

d) 135 diagonais.

e) 170 diagonais.

I. a reflexão dele em relação à reta r

II. a translação desse losango de cinco unidades para a esquerda e três unidades para baixo.

III. a rotação de 180 ° dele em torno do ponto B no sentido anti-horário.

8. Na figura a seguir, o triângulo MBN é isósceles () 2 BM BN . Qual é, em grau, o valor da medida y?

a) 12°

b) 14°

c) 15°

d) 18°

e) 20°

d.

7. b) Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual. Alternativa

9. Na figura a seguir, ABCD é um quadrilátero qualquer, e CD 2 CB. Então, a medida y do ângulo C ˆ BD é:

a) 31°

b) 32°

c) 33°

d) 34°

e) 35°

(OBM)

11. (OBM) Na figura, ABCDE é um pentágono regular, CDFG é um quadrado e DFH é um triângulo equilátero. O valor do ângulo b é:

FH

a) 30°

b) 36°

c) 39°

d) 45°

e) 60°

G D b Alternativa c.

EC

AB

12. (Fuvest-SP) No retângulo a seguir, o valor em graus de a+b é:

40° a

a) A figura ABCD é um quadrado e CE 2 CB Determine a medida do ângulo x

b) Resolva a equação _=

UM NOVO OLHAR

=_ x 4 5

b

ORIENTAÇÕES DIDÁTICAS

Um novo olhar

Os questionamentos existentes no encerramento desta Unidade possibilitam reflexões sobre as aprendizagens individuais, além de uma breve retomada dos conteúdos apresentados. É importante que os estudantes respondam individualmente a cada uma das questões para que, dessa forma, possam perceber o que aprenderam, as dúvidas que ainda tenham e retomar alguns pontos que considerem necessários. Ajudá-los, caso isso ocorra.

a) 50

b) 90

c) 120

Alternativa d.

d) 130

e) 220

Resposta pessoal. Espera-se que os estudantes encontrem durante a pesquisa que a relação entre a quantidade de pixels e a qualidade de uma fotografia não é o que importa. O mais importante para se ter uma fotografia de qualidade são as lentes e os sensores da máquina.

Nesta Unidade, estudamos os polígonos e, em especial, os quadriláteros. Nosso estudo sobre polígonos foi dividido em: elementos de um polígono, nomenclatura utilizada, diagonais de um polígono, relação entre os ângulos internos e externos de um polígono, soma das medidas dos ângulos internos de um triângulo, soma das medidas dos ângulos internos de um polígono convexo e soma das medidas dos ângulos externos de um polígono convexo. Com relação aos quadriláteros, foram abordados: as propriedades de um quadrilátero, os paralelogramos, os trapézios e a base média de um trapézio.

Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

• Na abertura da Unidade, citamos que a quantidade de pixels de uma fotografia é muito importante para sua ampliação. Faça uma pesquisa e verifique qual é a relação entre a quantidade de pixels e a qualidade de uma fotografia.

• Qual é a relação entre o ângulo interno e o ângulo externo adjacente a ele em um polígono regular?

A soma das medidas desses ângulos é igual a 180°

• Que características tem um polígono regular?

• Quais quadriláteros estudados são paralelogramos?

• Que tipos de trapézio foram estudados?

• Que transformações geométricas no plano você estudou?

O retângulo, o losango e o quadrado. Trapézio isósceles e trapézio retângulo. Reflexão, translação e rotação.

Um polígono regular tem todos os lados congruentes entre si e todos os ângulos internos congruentes entre si, o que faz que todos os ângulos externos também sejam congruentes entre si.

A primeira questão faz uma revisita à abertura desta Unidade, retomando a relação entre a quantidade de pixels e a resolução de uma fotografia.

A segunda questão aborda a relação entre o ângulo interno e o ângulo externo adjacente a ele de um polígono qualquer.

A terceira questão busca levar os estudantes a refletir sobre as características que fazem um polígono receber a nomenclatura de polígono regular (todos os lados congruentes entre si e todos os ângulos internos congruentes entre si).

A quarta questão aborda os três tipos de paralelogramo que recebem nomes especiais, levando à observação da relação mais intrínseca existente entre eles, pois todo quadrado também pode ser classificado como losango ou retângulo, sendo a recíproca não verdadeira.

A quinta questão retoma os tipos de trapézio estudados (ressaltamos que os trapézios escalenos não são mencionados, tratamos apenas dos casos especiais de trapézios).

A última questão possibilita aos estudantes se lembrarem das isometrias estudadas na Unidade: reflexão, translação e rotação.

ILUSTRAÇÕES: EDITORIA DE ARTE

Competências gerais:

• 1, 2 e 9

Competências específicas:

• 1, 2, 4 e 8

Habilidades: Números

• EF08MA03

Probabilidade e estatística

• EF08MA22

• EF08MA23

• EF08MA25

• EF08MA26

• EF08MA27

Temas Contemporâneos

Transversais:

• Saúde

• Educação para o Trânsito

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em cinco capítulos e apresenta os conteúdos por meio de exemplos contextualizados e atividades diversificadas, além de trazer seções com temas que colaboram para a formação integral dos estudantes, contribuindo para o desenvolvimento das competências gerais 1, 2 e 9.

O primeiro capítulo retoma o Princípio Fundamental da Contagem, a partir de diferentes situações que favorecem o desenvolvimento da habilidade EF08MA03.

O segundo capítulo discute noções iniciais do cálculo de probabilidade, contribuindo para o desenvolvimento da habilidade EF08MA22. No terceiro capítulo, alguns conceitos de Estatística são explorados, contribuindo para o desenvolvimento da habilidade EF08MA26. No quarto capítulo, abordam-se as medidas de tendência central (média aritmética, moda e mediana), contribuindo para o desenvolvimento da habilidade EF08MA25. No quinto capítulo, exploram-se aspectos relacionados ao planejamento para a realização de uma pesquisa estatística. Esse estudo favorece o desenvolvimento da habilidade EF08MA27.

PROBABILIDADE E ESTATÍSTICA 7

Desde o início da pandemia de covid-19, em dezembro de 2019, variantes do vírus SARS-CoV-2 com alta taxa de transmissão foram detectadas em todas as partes do mundo. Nomeadas com letras do alfabeto grego pela Organização Mundial da Saúde (OMS), as variantes alfa, beta, gama, delta e ômicron foram as mais preocupantes. Felizmente, as vacinas desenvolvidas para combater o vírus também apresentaram eficácia em relação às variantes.

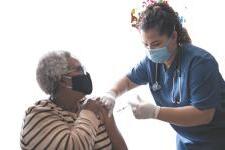
De acordo com dados estatísticos do Instituto Emílio Ribas, em fevereiro de 2022, 82% dos óbitos registrados por covid-19 no estado de São Paulo foram de pessoas não vacinadas ou com esquema de vacinação incompleto. Casos semelhantes ocorreram nos demais estados brasileiros. O estudo também mostrou uma redução de 85% nas mortes por covid-19 desde o início da vacinação no estado, comprovando que a vacinação e os protocolos de saúde são eficazes contra a doença.

As vacinas se mostraram uma alternativa segura e eficaz para controlar a propagação da covid-19. Idosa sendo vacinada. Brasil, 2021.

OBJETIVOS

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 212

• Compreender e utilizar o princípio multiplicativo na resolução de problemas de contagem.

• Calcular a probabilidade de eventos aleatórios.

• Reconhecer pesquisa censitária e amostral, bem como os tipos de amostragem.

• Reconhecer gráficos e tabelas como uma

fonte de informação e avaliar a melhor maneira de representar um conjunto de dados.

• Compreender e calcular média aritmética, moda, mediana e amplitude de um conjunto de dados.

• Planejar, organizar e executar uma pesquisa estatística e apresentar os resultados dela.

• Construir gráficos utilizando planilha eletrônica.

ETAJOE/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

Este gráfico revela que a quantidade de óbitos diminui à medida que a população vai sendo completamente vacinada.

Quantidade de óbitos e proporção da população total vacinada com esquema completo ao longo de 2021

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

JaneiroFevereiro Março Abril Maio Junho Julho AgostoSetembroOutubro

Elaborado com base em: BRASIL. Ministério da Saúde. Boletim Observatório Covid-19 Rio de Janeiro: FIOCRUZ, p. 3, 7 out. 2021. Disponível em: https://portal.fiocruz.br/documento /boletim-extraordinario-do-observatorio-covid-19-6-de-outubro. Acesso em: 13 jun. 2022.

Após leitura do texto e análise do gráfico, pense e responda no caderno.

• Considerando o cenário de distanciamento social, os cuidados com a saúde e as adaptações no modo de vida social, quais foram os maiores impactos da pandemia para você e sua família?

Resposta pessoal.

• Em relação à curva que representa a quantidade de óbitos, o que é possível observar à medida que aumenta a quantidade de vacinados com o ciclo de vacinação completo?

Resposta pessoal. Exemplo de resposta: A quantidade de óbitos vai diminuindo.

JUSTIFICATIVAS DOS OBJETIVOS

Nesta Unidade, apresenta-se o estudo envolvendo contagem e probabilidade. Esse estudo favorece o desenvolvimento das habilidades EF08MA03 e EF08MA22.

As noções de Estatística também estão presentes ao longo da Unidade, discutindo

conceitos como pesquisa censatária e amostral, tipos de amostragem e organização dos dados de uma pesquisa estatística. Desse modo, busca-se favorecer o desenvolvimento das habilidades EF08MA23, EF08MA25, EF08MA26 e EF08MA27.

Na seção Tecnologias, os estudantes são convidados a construir gráficos utilizando planilha eletrônica no software Calc LibreOffice.

Iniciar com a leitura do texto da página 212 do Livro do estudante. Ouvir as experiências dos estudantes na pandemia, incentivando a troca de ideias entre eles, sempre promovendo a empatia e o respeito pela opinião e pelas preferências do outro, contribuindo para o desenvolvimento do Tema Contemporâneo Transversal Saúde, da competência geral 9 e das competências específicas 4 e 8 da área de Matemática. Em seguida, propor a leitura do gráfico de linhas e verificar se os estudantes compreendem as informações presentes nos eixos e a relação entre as duas curvas. Recomenda-se, ainda, reunir outros gráficos e tabelas referentes aos dados sobre vacinação, ocupação de leitos e internações, economia e outros temas relacionados à covid-19. No site do IBGE, é possível encontrar mais informações. Se possível, acessar o link https://covid19.ibge.gov.br/ (acesso em: 8 ago. 2022).

Utilizar os dados para fazer previsões, cálculos de média e interpretação de dados. Destacar a necessidade de verificar as fontes dos dados e a consistência deles, pois podem existir erros de representação como os encontrados no infográfico.

ETAJOE/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Pense e responda

O problema proposto retoma os conhecimentos prévios que os estudantes têm a respeito de possibilidades. Ele pode ser resolvido por meio de um esquema: desenhar as rodovias que partem do município A e chegam ao município B; em seguida, desenhar as rodovias que partem de B e chegam a C

município A

PENSE E RESPONDA

Responda no caderno.

De 12 maneiras distintas.

Imagine que haja quatro possibilidades de meio de transporte para se deslocar de um município A para um município B: aéreo, ferroviário, rodoviário e hidroviário. Por outro lado, o deslocamento do município B para um município C pode ser feito vias aérea, ferroviária ou rodoviária. Utilizando esses meios de transporte, de quantas maneiras distintas é possível se deslocar do município A até o município C , passando por B?

município B

município C

Outro modo de resolver o problema é descrever os elementos dos conjuntos E1 e E2, em que E1 corresponde ao conjunto das estradas que ligam os municípios A e B e E2 ao conjunto das estradas que ligam B a C:

E1 = {x1, x 2, x 3, x4} e

E2 = {y1, y2 , y3}

Há 12 possibilidades (4 3) de sair do município A e chegar ao município C , passando pelo município B

Princípio fundamental da contagem ou princípio multiplicativo

A árvore de possibilidades, também chamada de diagrama de árvore, apresentada na situação de escolha de um suco e um lanche, é um bom recurso para a resolução dos primeiros problemas apresentados aos estudantes. Comentar que esse recurso fica inviável em situações que apresentam número grande de possibilidades.

Apresentar exemplos que mostram uma quantidade maior de possibilidades. Uma sugestão é a formação de números com 4 algarismos distintos, escolhidos entre 2, 3, 7 e 9. Resolver essa

PRINCÍPIO FUNDAMENTAL DA CONTAGEM OU PRINCÍPIO MULTIPLICATIVO

Bárbara e Giovana foram a uma lanchonete para tomar um suco e comer um lanche natural. No cardápio, verificaram que havia três opões de suco (laranja, melancia ou uva) e duas opções de lanche natural (simples ou completo).

De quantas maneiras diferentes cada uma delas pode escolher um suco e um lanche?

Para responder a essa questão, vamos organizar todas as opções em um diagrama, que é chamado de árvore de possibilidades

Observando o diagrama a seguir, percebemos que é possível escolher um suco e um lanche de seis maneiras diferentes.

Opções de suco Opções de lanche natural

situação usando um quadro em que seja possível variar as posições dos algarismos.

Cada opção de suco pode ser combinada com cada opção de lanche natural. Como são três tipos de suco e dois tipos de lanche natural, efetuamos a seguinte multiplicação:

3 2 = 6 quantidade de opções de suco quantidade de possibilidades

quantidade de opções de lanche natural

Portanto, é possível escolher um lanche e um suco de seis maneiras diferentes. Observe outras situações em que podemos aplicar o princípio multiplicativo.

1 Um quiosque de comida italiana oferece em seu cardápio três opções de macarrão: espaguete, pene e talharim. Cada uma dessas opções pode ser servida com uma dentre quatro opções de molho: branco, bolonhesa, pesto e ao sugo. De quantas maneiras distintas é possível compor um prato formado por uma opção de macarrão e uma opção de molho?

Repare que, para cada opção de macarrão, temos quatro possibilidades de escolher o molho. Assim, podemos resolver essa situação utilizando uma multiplicação.

3 4 = 12 quantidade de opções de macarrão

quantidade de opções de molho

quantidade de possibilidades

ORIENTAÇÕES DIDÁTICAS

Ao trabalhar o princípio fundamental da contagem, apresentar situações do dia a dia em que é possível utilizá-lo.

As situações propostas contribuem para o desenvolvimento da habilidade EF08MA03.

Na situação 2, enfatizar que escolher um estudante como representante é diferente de escolhê-lo como suplente. Essa informação é importante ao considerar a resolução, pois influencia a ordem da escolha dos elementos.

Assim, temos 12 maneiras diferentes de compor um prato nesse quiosque.

2 Uma turma de 8 o ano é composta de 25 estudantes. Dois deles serão escolhidos para formar uma comissão, na qual um componente será o representante, e o outro, o suplente. De quantas maneiras distintas essa comissão poderá ser formada?

Observe que qualquer um dos 25 estudantes pode ser o representante, ou seja, temos 25 possibilidades para definir o representante. Escolhido esse estudante, restam 24 opções para ser o suplente. Assim, aplicando o princípio multiplicativo, temos:

25 24 = 600 quantidade de opções para representante

quantidade de opções para suplente

quantidade de possibilidades

Assim, há 600 possibilidades de formarmos uma comissão, na qual um dos membros é o representante da turma, e o outro, o suplente.

ORIENTAÇÕES DIDÁTICAS

Outros problemas de contagem

O primeiro exemplo envolvendo anagrama mostra uma situação em que não há letras repetidas: ROSA. Isso ocorre para que, inicialmente, os estudantes possam compreender como permutar as letras de posição.

Apresentar exemplos de anagramas com letras repetidas. Ao escolher CASA, há duas letras repetidas que, quando permutadas, figuram como se fossem letras diferentes, mas trata-se da mesma letra (A). Desse modo, a contagem da quantidade de anagramas vai precisar levar em consideração esses casos. Uma sugestão é propor aos estudantes que escrevam alguns anagramas de CASA (ou outro qualquer que contenha uma repetição de letras) e tentem determinar a quantidade de anagramas possíveis. Os anagramas geram boas reflexões para escritores e literatos, que buscam, nas palavras escritas, visualizar essas ocorrências. Propor aos estudantes que usem a criatividade para formar diferentes palavras com base em algumas letras e para construir versos ou frases com essas palavras. Por exemplo, com os anagramas ATOR e ROTA pode-se construir frases como “Na rota em que seguia, encontrei um ator.”, “O ator seguiu a rota de seu coração.”.

OUTROS PROBLEMAS DE CONTAGEM

Diversos problemas envolvem a noção de contagem. Observe alguns exemplos.

1 Quantos são os anagramas da palavra ROSA?

A palavra ROSA tem 4 letras, e qualquer uma dessas letras pode assumir a primeira posição na palavra. Escolhida essa letra, sobram outras 3 letras para a segunda posição. Na sequência, há 2 letras disponíveis para a terceira posição e, por fim, 1 letra para a quarta posição. Confira.

Anagrama: permutação das letras de uma palavra formando novas palavras com ou sem sentido.

4 3 2 1 = 24 quantidade de letras para a 1a posição

quantidade de letras para a 2a posição

Assim, há 24 anagramas da palavra ROSA

quantidade de letras para a 3a posição

quantidade de letras para a 4 a posição

2 Em 31 de janeiro de 2020, o Brasil passou a exigir o padrão estabelecido pelo Mercosul para as placas de identificação veicular (PIV) em algumas situações como: registro de veículo zero quilômetro, mudança de município ou estado, dano à antiga placa, entre outras. Também a partir dessa data, foi permitida a troca da antiga placa (cinza) pelo novo modelo, de maneira voluntária, cuidando o proprietário de atualizar a documentação do veículo.

Fonte dos dados: SÃO PAULO (Estado). Departamento Estadual de Trânsito. Informações sobre o novo modelo de placas de identificação veicular – PIV (Padrão Mercosul). São Paulo: DETRAN-SP, [2019?]. Disponível em: https://www.detran.sp.gov.br/wps/portal/portaldetran/cidadao/oquefazerquando/aa929b6b5788-4d32-a91f-0d220a559c47/. Acesso em: 13 jun. 2022. O padrão estabelecido pelo Mercosul para as placas de identificação veicular no Brasil pressupõe o uso de 4 letras e 3 números, conforme imagem a seguir.

De acordo com essas informações e considerando as letras do alfabeto e os algarismos de 0 a 9, quantas placas distintas são possíveis obter?

Repare que nosso alfabeto é constituído de 26 letras (incluindo as letras K, Y e W), e temos disponíveis dez algarismos (de 0 a 9). Assim, aplicando o princípio multiplicativo, temos: 26 26 26 26 10 10 10 = 456 976 000 possibilidades de letras possibilidades de algarismos

Assim, é possível obter 456 976 0 00 placas distintas usando 4 letras e 3 algarismos.

O segundo exemplo aborda os novos modelos de placas de identificação veicular. Aproveitar a situação para discutir questões relacionadas ao Tema Contemporâneo Transversal Educação para o trânsito, explorando a importância da regularização de documentos dos veículos, emplacamento e licenciamento, valorizando a argumentação dos estudantes e desenvolvendo a competência específica 1 da área de Matemática, descrita na BNCC.

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 216

Responda às questões no caderno.

1. Bernardo é o técnico do time masculino de handebol da escola de Mari e vai encomendar os uniformes para o próximo campeonato. Como as cores da escola são azul, amarela, vermelha e branca, a empresa que vai confeccionar os uniformes deu as seguintes opções de escolha: 3 cores de camisetas (vermelha, amarela e branca) e 2 cores de shorts (branco com listra azul e todo azul).

Organize essas opções em uma árvore de possibilidades e responda:

a) De quantas maneiras distintas Bernardo pode compor um uniforme com uma camiseta e um shorts?

6 maneiras.

b) Do total de possibilidades, quantos uniformes podem ser compostos com a camiseta branca?

2

2. As turmas do 8 o ano de certa escola, já pensando na formatura no ano seguinte, farão uma eleição entre os 93 estudantes para a escolha do presidente e do vice-presidente da comissão de formatura. Considere que qualquer um desses estudantes poderá ser o escolhido. De quantas maneiras distintas é possível formar essa comissão?

3. Uma senha bancária é formada por 4 dígitos seguidos de 3 símbolos (#, & e *). De quantas maneiras distintas Ana pode escolher uma senha, se ela não pretende usar o algarismo 0 nem o símbolo #?

4. Quantos números ímpares podemos formar usando uma única vez cada um dos algarismos 3, 4, 7, 8 e 9?

5. (OBMEP) Um estacionamento tem 10 vagas, uma ao lado da outra, inicialmente todas livres. Um carro preto e um carro rosa chegam a esse estacionamento. De quantas maneiras diferentes esses carros podem ocupar duas vagas

AMPLIANDO

Atividade complementar

Desde 2016, na Argentina, as placas de carros (chamadas de chapas patentes) estão sendo formadas no padrão Mercosul: duas letras do alfabeto de 26 letras, seguidas de 3 algarismos, seguidos de duas letras. Quantas placas podemos formar com esse padrão?

de forma que haja pelo menos uma vaga livre entre eles?

ORIENTAÇÕES DIDÁTICAS

Atividades

Caso considere necessário, indicar que algumas atividades sejam feitas em duplas para os estudantes trocarem ideias sobre como raciocinaram a respeito de cada situação.

a) 56 b) 70 c) 71 d) 72 e) 80

6. (Enem/MEC) Uma empresa construirá sua página na internet e espera atrair um público de aproximadamente um milhão de clientes. Para acessar essa página, será necessária uma senha com formato a ser definido pela empresa. Existem cinco opções de formato oferecidas pelo programador, descritas no quadro, em que “L” e “D” representam, respectivamente, letra maiúscula e dígito.

Opção Formato

I LDDDDD

II DDDDDD

III LLDDDD

IV DDDDD

V LLLDD

As letras do alfabeto, entre as 26 possíveis, bem como os dígitos, entre os 10 possíveis, podem se repetir em qualquer das opções.

A empresa quer escolher uma opção de formato cujo número de senhas distintas possíveis seja superior ao número esperado de clientes, mas que esse número não seja superior ao dobro do número esperado de clientes.

A opção que mais se adéqua às condições da empresa é a) I. b) II. c) III. d) IV. e) V.

7. Elabore um problema que envolva o princípio multiplicativo. Em seguida, troque-o com um colega, de modo que um resolva oproblema elaborado pelo outro.

Alternativa d. Alternativa e. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

A atividade 5 impõe uma restrição importante: é preciso existir uma vaga livre entre os carros preto e rosa. Uma maneira de resolver esse problema é considerar que o carro preto está estacionado na primeira vaga. Desse modo, há 8 possibilidades de lugar para estacionar o carro rosa. Isso acontecerá também quando o carro preto estiver na última vaga. Quando o carro estiver em qualquer uma das vagas entre a segunda e a nona, sempre teremos 7 possibilidades de lugar para o carro rosa. Então, há 2 ? 8 + 8 ? 7 = 16 + 56 = = 72 possibilidades de estacionar o carro preto e o carro rosa, respeitando a condição dada.

Na atividade 6, é preciso calcular o número de possibilidades de cada uma das opções de formato de senha para ver qual se adapta às condições dadas.

Na atividade 7, espera-se que o estudante não tenha dificuldade em elaborar o problema proposto. No entanto, se alguma dificuldade se manifestar, peça aos estudantes que consultem as situações e os exemplos propostos nas páginas 215 e 216 do Livro do estudante.

456 976 000

REPRODUÇÃO/ OBMEP, 2018.

ORIENTAÇÕES DIDÁTICAS

Experimento aleatório

Discutir com os estudantes a respeito do que eles sabem sobre experimento aleatório. Esse conceito precisa ser trabalhado cuidadosamente para que os estudantes compreendam que, apesar de não se saber qual será o resultado obtido, é possível descrever todas as possibilidades do experimento.

Espaço amostral

Definir espaço amostral com os estudantes, construindo alguns exemplos e verificando se a turma compreende como descrever todas as possibilidades.

Evento

A ideia de evento é inserida a partir da construção de subconjuntos de um experimento aleatório. Comentar que o estudo de problemas de contagem auxilia na construção de espaços amostrais.

EXPERIMENTO ALEATÓRIO

Quando estudamos probabilidade, um experimento é considerado aleatório se, mesmo ao repeti-lo uma quantidade considerável de vezes da mesma maneira, o resultado obtido for sempre imprevisível.

O lançamento de um dado honesto (todos os resultados têm a mesma possibilidade de ocorrer) e o de uma moeda não viciada (a possibilidade de obter cara é igual à de obter coroa) são exemplos de experimentos aleatórios, pois em cada repetição do experimento o resultado obtido não pode ser previsto.

ESPAÇO AMOSTRAL

Para cada experimento aleatório existe um conjunto de possibilidades de resultados. Ao lançar um dado e observar a face superior, é possível obter um de seis resultados distintos. Os resultados possíveis são: 1, 2, 3, 4, 5 e 6. Já no lançamento de uma moeda, é possível obter um de dois resultados diferentes: cara ou coroa.

Dado um experimento aleatório, o espaço amostral S é o conjunto de todas as possibilidades de resultado daquele experimento.

EVENTO

A partir do lançamento de um dado honesto, vamos, agora, observar os resultados obtidos na face superior.

Desejamos saber, por exemplo, qual é a chance de se obter o número 2 no lançamento desse dado. Ou, ainda, qual é a chance de ser obtido um número primo Essas duas situações descrevem subconjuntos do espaço amostral. Elas correspondem a eventos e são indicadas por E

Na primeira situação, ao lançar o dado e sair o número 2, temos que E = {2} e, assim, a quantidade de elementos de E é representada por n(E) = 1. Na segunda situação, ao lançar o dado e obter um número primo, temos que E = {2, 3, 5}, e, assim, a quantidade de elementos de E é representada por n(E) = 3.

Se não há elementos no conjunto E, correspondente ao evento analisado, dizemos que esse evento é impossível. Por exemplo, ao considerarmos o experimento aleatório “Observar a face superior no lançamento de um dado comum de 6 faces numeradas de 1 a 6”, um evento impossível é “Obter o número 7”.

Quando a quantidade de elementos do evento coincide com a quantidade de elementos do espaço amostral, o evento é chamado de evento certo. Se considerarmos o experimento aleatório “Observar a face superior no lançamento de um dado de 6 faces numeradas de 1 a 6”, a situação “Obter um número menor do que 7” é um evento certo, pois n(S) = 6 e n(E) = 6.

AMPLIANDO

Vídeo

EXPERIMENTO aleatório e o espaço amostral. 2019. Vídeo (4min49s). Publicado pelo canal Khan Academy Brasil. Disponível em: https://www.youtube.com/watch?v=WM-_zN5priE&t=2s. Acesso em: 8 ago. 2022. Nesse link, é possível ter acesso a uma videoaula sobre experimento aleatório e espaço amostral.

ORIENTAÇÕES DIDÁTICAS

Considere a situação a seguir.

Uma urna tem 20 bolas numeradas de 1 a 20. Uma bola é escolhida ao acaso, e observa-se onúmero dela.

Nesse caso, o espaço amostral é dado por:

S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}

Como pudemos analisar, todo evento é um subconjunto do espaço amostral.

O evento “Obter um número maior do que 11” é dado por E = {12, 13, 14, 15, 16, 17, 18, 19, 20}.

O evento “Obter um número múltiplo de 4” corresponde a E = {4, 8, 12, 16, 20}.

PROBABILIDADE

Observamos que, em um experimento aleatório, a probabilidade P de um evento acontecer é dada pela razão entre a quantidade de possibilidades favoráveis ao evento e a quantidade total de possibilidades que podem ocorrer no experimento. Agora, vamos realizar esse cálculo analisando oespaço amostral.

Considerando o experimento aleatório “Retirar uma bola ao acaso de uma urna com bolas numeradas de 1 a 15”, o espaço amostral é S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}.

A probabilidade de ocorrer o evento “Ser retirada a bola de número 8” é de 1 em 15, pois só existe um número 8 no espaço amostral.

Nesse caso, para determinar a probabilidade de um evento ocorrer, podemos determinar a quantidade de elementos do espaço amostral e a quantidade de elementos do evento.

= = = nS 15 nE 1 PE 1 15 () () ()      ⇒

A probabilidade P de um evento E acontecer, a partir de um experimento aleatório, é dada pela razão entre a quantidade de elementos do evento e a quantidade de elementos do espaço amostral.

PE nE nS() () () =

Observe estes exemplos.

1 Uma professora de música vai sortear ao acaso uma dupla de suas alunas para um teste: uma para tocar violão, e outra para cantar. Participarão do sorteio: Gabriela, Helena, Luma, Leila, Bárbara e Lorena. Sabendo que todas cantam e tocam violão, qual é a probabilidade de Helena tocar violão e de Gabriela cantar?

Repare que há 30 maneiras distintas de compor essas duplas, considerando que uma aluna vai tocar violão, e a outra vai cantar. Assim, n(S) = 30. Além disso, E = {(Helena, Gabriela)}.

= = = nS 30 nE 1 PE 1 30 () () ()

Portanto, a probabilidade de Helena tocar violão e de Gabriela cantar é de uma em trinta, ou seja, 1 30

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 219

Ao apresentar a situação da urna com bolas numeradas, verificar se os estudantes compreendem a construção do conjunto de elementos de cada um dos espaços amostrais dados. Propor outras situações, como construir o espaço amostral dos números menores do que 3 ou maiores do que 17. Essa ideia da união de eventos será desenvolvida no Ensino Médio, mas é possível apresentar situações iniciais a respeito desse conteúdo.

Probabilidade

O estudo das probabilidades será desenvolvido em espaços amostrais equiprováveis, ou seja, em que as probabilidades de ocorrência dos eventos são iguais. Considerando os espaços equiprováveis, a soma das probabilidades de ocorrência de todos os eventos de um espaço amostral é sempre igual a 1. Isso será apresentado mais adiante. No exemplo 1, indicar a utilização do princípio multiplicativo para o cálculo da probabilidade pedida. Com isso, mostrar aos estudantes que a análise das possibilidades de ocorrência de um evento é importante antes de pensar no cálculo da probabilidade.

11/08/22 14:40

ORIENTAÇÕES DIDÁTICAS

O exemplo 2 traz a noção intuitiva de eventos complementares e a definição de que a soma das probabilidades de eventos desse tipo é igual a 1. Explorar outros contextos, como os naipes das cartas de um baralho, por exemplo.

2 Considerando os possíveis resultados em um lançamento de um dado honesto, qual é a probabilidade de:

a) se obter o número 4?

Para calcular a probabilidade de esse evento ocorrer, determinamos a quantidade de elementos do espaço amostral e a quantidade de elementos do evento. Temos:

S = {1, 2, 3, 4, 5, 6}

E = {4}

Assim, nessa situação, a probabilidade de se obter o número 4 é

b) não se obter o número 4?

Repare que temos o mesmo espaço amostral do item anterior; porém, a quantidade de elementos do evento é diferente.

S = {1, 2, 3, 4, 5, 6}

E = {1, 2, 3, 5, 6}

Portanto, nessa situação, a probabilidade de não se obter o número 4 é

Observe que a soma das probabilidades calculadas nos itens a e

5 ou 6).

Observe que, no experimento “Lançar um dado honesto de 6 faces numeradas de 1 a 6 e observar a face superior”, a probabilidade de se obter como resultado o número indicado em cada face do dado é sempre igual a 1 6 . Assim, a soma das probabilidades de cada evento que compõe o espaço amostral será igual a 1.

A soma das probabilidades de todos os elementos do espaço amostral é igual a 1. 220

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 220 11/08/22 14:40

AMPLIANDO Link

PROBABILIDADE. Clubes de Matemática da OBMEP. [S l.], [20--]. Disponível em: http://clubes.obmep. org.br/blog/sala-de-estudo-probabilidades/. Acesso em: 9 ago. 2022.

Se possível, compartilhar o texto apresentado com os estudantes. Desse modo, pode-se ampliar o estudo de probabilidade.

ATIVIDADES

1.a) S = {(cara, cara); (cara, coroa), (coroa, cara), (coroa, coroa)}

b) S = {(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6); (2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6); (3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (3, 6); (4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6); (5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6); (6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6)}

c) S = {(M, M, M); (M, M, F); (M, F, M); (M, F, F); (F, F, F); (F, F, M); (F, M, F); (F, M, M)}

2.a) E = {(cara, cara); (coroa, coroa)}

Responda às questões no caderno.

1. Escreva o espaço amostral para cada um dos experimentos a seguir.

a) L ançar uma moeda duas vezes e observar, nessa sequência, o resultado: cara ou coroa.

b) L ançar dois dados de 6 faces de cores distintas e observar o resultado nas faces de cima.

c) A sequência dos sexos possíveis para o nascimento de bebês trigêmeos.

2. Considerando os experimentos e os espaços amostrais da atividade anterior, indique os subconjuntos referentes aos eventos a seguir.

a) N o lançamento das moedas, obter 2 faces iguais como resultado.

b) No lançamento dos dados, obter soma igual a 5.

S = {(1, 4); (2, 3); (3, 2); (4, 1)}

c) Nascerem 2 meninos e 1 menina.

E = {(M, M, F); (M, F, M); (F, M, M)}

3. Um experimento consiste em retirar uma bola numerada de uma urna contendo 25 bolas, numeradas de 1 a 25, e observar o número indicado.

a) Dê o espaço amostral desse experimento.

b) E screva os elementos do evento A , sendo A “Obter um número que é múltiplo de 9”

c) E screva os elementos do evento B, sendo B “Obter um número maior do que 23”

4. Uma urna contém 2 bolas amarelas, 4 bolas azuis e 3 bolas vermelhas. Ao retirarmos uma bola ao acaso, qual é a probabilidade de ela ser azul? E vermelha?

5. Ao sortearmos ao acaso um número de 2 algarismos distintos, qual é a probabilidade de se obter um número par?

6. Considere os números de 1 a 100. Sorteando um número ao acaso, qual é a probabilidade de o número:

a) ser múltiplo de 6?

b) ser múltiplo de 3 e de 5?

7. Em um grupo de 5 adolescentes, há 3 meninas e 2 meninos.

a) Quantas duplas distintas é possível formar com esses adolescentes?

b) Qual é a probabilidade de, sorteando uma dupla ao acaso, essa dupla ser formada apenas por meninas?

8. Utilizando os algarismos 2, 3, 6, 7 e 8, formam-se números de 4 algarismos distintos. Escolhido um desses números ao acaso, qual é a probabilidade de ele ser:

a) par? b) ímpar?

DESAFIO

Junte-se a um colega para resolver o desafio a seguir.

9. (OBMEP) Em uma caixa há cinco bolas idênticas, com as letras O, B, M, E e P. Em uma segunda caixa há três bolas idênticas, com as letras O, B e M. Uma bola é sorteada da primeira caixa e, a seguir, outra bola é sorteada da segunda caixa. Qual é a probabilidade de que essas bolas tenham a mesma letra?

ORIENTAÇÕES DIDÁTICAS

Atividades

A primeira parte das atividades propostas trabalha a construção do espaço amostral e dos subconjuntos relativos a diferentes eventos. Em seguida, é aplicado o cálculo de probabilidades.

Na atividade 6, verificar se os estudantes retomam o conceito de múltiplo de um número natural para concluir que, se um número é múltiplo de 3 e múltiplo de 5, então ele é múltiplo de 15. Com isso, no item b será preciso contar a quantidade de múltiplos de 15 entre 1 e 100.

Na atividade 7, espera-se que os estudantes usem o princípio multiplicativo para resolver o item a e, depois, calculem a probabilidade no item b, a partir do resultado obtido anteriormente.

ORIENTAÇÕES DIDÁTICAS

Conceitos básicos de Estatística

Apresentar a definição de população e amostra e explorar a imagem que ilustra essa definição. A compreensão desses conceitos contribui para o desenvolvimento da competência geral 2. Comentar com os estudantes sobre a importância da amostragem em controle de qualidade na indústria, por exemplo, propondo discussões acerca da inviabilidade de se testar todas as peças produzidas por uma máquina. Discutir os testes de durabilidade de todos os pneus produzidos em um lote. O que aconteceria? Ouvir as hipóteses dos estudantes, fazendo-os refletir sobre o fato de que toda a produção seria deteriorada. Esse tipo de atividade desenvolve as capacidades de inferência e argumentação

Pense e responda

Ao questionar os estudantes a respeito do porquê de todas as pesquisas não serem censitárias, espera-se que eles percebam que esse tipo de pesquisa tem uma grande vantagem, que é a coleta de dados gerais; porém, o custo para isso é muito alto, além de ser necessário um tempo maior para que a pesquisa seja realizada.

CAPÍTULO3 ESTATÍSTICA

CONCEITOS BÁSICOS DE ESTATÍSTICA

A Estatística é uma parte da Matemática em que são estudados métodos para coleta, organização e análise de dados de diferentes áreas do conhecimento, visando à tomada de decisões.

Realizamos uma pesquisa estatística quando pretendemos estudar alguma característica de determinado conjunto de elementos, o qual pode ser de pessoas, resultados, objetos etc. O conjunto de todos os elementos que têm a característica do interesse da pesquisa é chamado de população Quando há muitos elementos na população a ser estudada, podemos realizar a pesquisa por meio de uma amostra que represente essa população.

População é o conjunto de elementos que apresenta alguma característica comum a ser analisada em uma pesquisa.

Amostra é um subconjunto da população, uma parcela representativa da população, ou seja, que apresenta as mesmas características da população.

Para algumas pesquisas, é necessário que toda a população seja investigada. Esse tipo de pesquisa é chamado de censitária No Brasil, a cada dez anos, é realizado o Censo Demográfico pelo Instituto Brasileiro de Geografia e Estatística (IBGE), que tem como objetivo constituir a principal fonte de referência para o conhecimento das condições de vida da população em todos os municípios do país. Por causa da pandemia de covid-19, em 2020 não aconteceu o Censo Demográfico que estava previsto cuja realização foi reprogramada para o segundo semestre de 2022.

PENSE E RESPONDA

Responda no caderno.

AMPLIANDO

Vídeo

Resposta pessoal. Exemplo de respostas: Dificuldade em levantar os dados, custos envolvidos nas pesquisas etc.

Nem todas as pesquisas são censitárias. Em muitos casos, são feitas pesquisas com base em uma amostra da população. Em seu entendimento, por que isso acontece?

RIFO, Laura Letícia Ramos. Probabilidade versus amostra. Coleção Matemática Multimídia. Campinas, [20--]. Disponível em: https://m3.ime.unicamp.br/recursos/1027. Acesso em: 9 ago. 2022.

Para ampliar o estudo, se possível, exibir o vídeo que apresenta um experimento que ajuda a discutir os conceitos de população e amostra.

IMAGENS FORA DE PROPORÇÃO. AS CORES NÃO SÃO REAIS.

O processo de coleta de dados de uma população pode ser muito dispendioso e demorado. Por essa razão, a escolha da amostra é de fundamental importância para a realização de uma pesquisa. A pesquisa censitária é indicada quando a população é pequena ou quando se necessita de um resultado mais preciso.

Por exemplo, em uma campanha eleitoral, as pesquisas de intenções de voto costumam ser atualizadas toda semana. Para que isso seja viável, é feita a pesquisa com uma parte dos eleitores brasileiros, pois se a pesquisa fosse realizada com toda a população, é muito provável que, no dia da eleição, ainda não tivesse sido finalizada a primeira pesquisa.

Ao definir uma amostra, é muito importante garantir que ela seja representativa, ou seja, que considere as mesmas características da população, uma vez que as conclusões são feitas com base nos resultados obtidos por meio da amostra. Existem algumas maneiras de se definir uma amostra, o que conhecemos como amostragem. Entre os métodos de amostragem, vamos estudar três: casual simples, sistemático e estratificado

Amostragem é o processo utilizado para recolher amostras de uma população, de maneira que se possa garantir o acaso nesse processo. Cada elemento da população deve ter a mesma possibilidade de ser selecionado.

Amostra casual simples

A amostra casual simples é caracterizada por um sorteio aleatório. Os elementos de uma população podem ser enumerados e, em seguida, sorteados entre uma quantidade estabelecida previamente.

Por exemplo: O professor de Educação Física vai fazer uma pesquisa sobre o esporte favorito com todos os estudantes do 8o ano de uma escola para decidir os esportes que vai incluir na competição entre turmas. Como a característica da população é ser estudante do 8o ano, independentemente de outras características, como idade e altura, o professor vai definir uma amostra casual simples de 30 dos 300 estudantes matriculados no 8o ano. Para isso, ele vai atribuir um número de 1 a 300 a cada um, escrever esses números em pedaços de papel, colocá-los em uma urna e depois realizar o sorteio.

Amostra sistemática

No caso da amostra sistemática, os elementos da população a ser estudada já se encontram ordenados. São exemplos: produtos de uma linha de produção, prontuários médicos, prédios de uma rua etc. Para a seleção dos elementos que farão parte da amostra, é elaborado um sistema pelo pesquisador.

ORIENTAÇÕES DIDÁTICAS

Comentar a respeito dos exemplos de pesquisas feitas por amostragem e a importância delas para realizar projeções. Tais discussões contribuem para o desenvolvimento da habilidade EF08MA26.

Discorrer a respeito das pesquisas realizadas nas eleições para descobrir a intenção de voto da população. É importante que os estudantes compreendam que esse tipo de pesquisa precisa seguir critérios rígidos preestabelecidos para que o resultado delas não seja enviesado, ou seja, não beneficie candidato X ou Y Comentar, por exemplo, que se a pesquisa tiver uma amostra de 200 pessoas, as quais foram todas entrevistadas em um único bairro, não é possível concluir que aquela é a opinião da maioria das pessoas daquele estado.

Expor aos estudantes que, quanto maior for o tamanho da amostra, melhor serão os dados projetados. Para exemplificar isso, é possível realizar uma pesquisa na própria sala de aula obtendo respostas com diferentes amostragens.

223

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd

AMPLIANDO

Texto

Para complementar o estudo a respeito de pesquisa censitária, apresentar o trecho a seguir.

Para que serve o Censo? – O Censo é a principal fonte de dados sobre a situação de vida da população nos

outras características da população ao longo do tempo.

223

ORIENTAÇÕES DIDÁTICAS

Amostra proporcional estratificada

Ler a definição de amostra proporcional estratificada, resolvendo o exemplo proposto na lousa. Verificar se os estudantes compreendem as relações de proporcionalidade direta construídas para completar a tabela do exemplo.

Pense e responda

Dar um tempo para que os estudantes pensem sobre o melhor tipo de amostragem para o caso de saber o aplicativo de celular preferido dos estudantes. Colher as diferentes respostas e compartilhar entre a turma para que os estudantes avaliem o que consideram mais adequado.

Amostra proporcional estratificada

Na amostra estratificada, a população é dividida em subpopulações chamadas de estratos Esse tipo de amostra é realizado quando outras características da população devem ser levadas em conta. Por exemplo, nas pesquisas de intenção de voto nas campanhas eleitorais, a população estudada são os eleitores, mas é importante considerar na definição da amostra: a região do país onde reside o eleitor, o sexo, a faixa etária, a renda, entre outras características. Assim, o pesquisador deve selecionar uma amostra aleatória de cada estrato.

Observe a situação.

Em um congresso para médicos, 110 pessoas se inscreveram para a palestra sobre cardiologia, 140 para a de obstetrícia e 150 para a de ortopedia. A equipe organizadora do congresso quer fazer uma pesquisa sobre a importância do tema tratado em cada uma dessas palestras com 40 pessoas que participaram delas.

Se for realizada uma amostra simples, existe a probabilidade de os 40 selecionados terem assistido à mesma palestra. Assim, é necessário fazer uma amostra proporcional considerando o público de cada palestra (estrato). Para isso, a equipe organizadora montou este quadro.

Palestra População Amostra

Cardiologia 11011

Obstetrícia 14014

Ortopedia 15015

Total 40040

Para determinar a amostra proporcional de cada estrato, eles utilizaram o total de inscritos no congresso (400), o total de inscritos em cada estrato, o total de pessoas que participarão da amostra (40) e fizeram os seguintes cálculos:

Assim, dos 110 inscritos para a palestra sobre cardiologia serão sorteados 11 para a amostra, dos 140 de obstetrícia serão sorteados 14, e dos 150 de ortopedia serão sorteados 15.

PENSE E RESPONDA

Responda no caderno.

Em seu entendimento, em uma pesquisa sobre o aplicativo de celular preferido dos estudantes do 8 de uma escola, qual é o melhor tipo de amostragem a ser realizada?

Resposta pessoal. Exemplo de resposta: Se considerarmos que todos os estudantes usam aplicativos e que tenham características parecidas, podemos escolher uma amostra casual simples.

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 224

VARIÁVEIS

Quando analisamos certas características da população (e da amostra), como sexo, faixa etária, escolaridade etc., estamos considerando o que chamamos, em Estatística, de variáveis

As variáveis são as características que estão sendo analisadas em uma amostra ou população. Podem assumir valores numéricos ou valores não numéricos, sendo classificadas, respectivamente, em quantitativas e qualitativas

As variáveis quantitativas podem ser expressas usando uma escala numérica. São classificadas em discretas ou contínuas. As variáveis quantitativas discretas podem ser verificadas por meio de contagem e, em geral, são indicadas por números inteiros. Por exemplo: a quantidade de filhos, a quantidade de copos de água ingeridos em um dia, entre outros. Por outro lado, as variáveis quantitativas contínuas representam resultados de medições, como a massa de um indivíduo (em quilograma), o tempo gasto em determinada atividade (em hora) etc.

Já as variáveis qualitativas são as características que não são expressas por valores numéricos. Elas são definidas por categorias ou atributos, ou seja, representam uma classificação dos elementos da população. São designadas como nominais ou ordinais. As variáveis qualitativas nominais não requerem ordenação, como cor dos olhos ou região onde mora. Já as variáveis qualitativas ordinais pressupõem uma ordenação, como grau de escolaridade ou estágio de crescimento de uma planta.

O esquema a seguir sintetiza as variáveis e suas classificações.

ORIENTAÇÕES DIDÁTICAS

Variáveis

O estudo a respeito de variáveis será feito de maneira detalhada, abordando as variáveis qualitativas e as variáveis quantitativas. A partir da compreensão dos tipos de variáveis, os estudantes podem construir melhor a ideia de grandezas discretas e grandezas contínuas.

Pedir aos estudantes que deem outros exemplos de cada tipo de variável estudada. Verificar se eles tiveram contato com algum tipo de situação no dia a dia em que é possível identificar uma variável: quando pedem para avaliar um filme como ótimo, bom, regular ou ruim, por exemplo, há a presença de uma variável qualitativa ordinal.

Descubra mais

DESCUBRA MAIS

ÁUDIOS DA COLEÇÃO M3. (Série Cultura) História da Estatística, [2011?]. Matemática Multimídia. Podcast. Disponível em: https://m3.ime.unicamp.br/recursos/1252. Acesso em: 5 jul. 2022. Neste podcast, são apresentados importantes fatos sobre a História da Estatística que auxiliam a compreender a importância dessa ciência.

A sugestão de podcast aborda a História da Estatística. A duração do áudio é de 8min16s. Se considerar pertinente, proporcionar que todos os estudantes tenham acesso ao áudio, na sala de aula. Depois, propor a eles que troquem ideias sobre os pontos que consideraram mais relevantes. Se sentir necessidade, pode-se ouvir o áudio novamente fazendo pausas propositais e propícias para que ocorra uma discussão proveitosa.

KUBKO/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Organização dos dados

Ao explorar a diferença entre frequência absoluta e frequência relativa, propor a seguinte questão: “Qual é a diferença entre uma pesquisa apresentar os resultados apenas em frequência relativa e outra pesquisa apresentar os dados obtidos usando os dois tipos de frequência?”. Espera-se que os estudantes percebam que, tendo apenas a frequência relativa, é possível realizar conclusões a respeito das porcentagens para cada tipo de resultado; entretanto, ficam faltando informações a respeito da quantidade de elementos da amostra.

ORGANIZAÇÃO DOS DADOS

Para organizar os dados obtidos por meio de uma pesquisa, podemos construir tabelas e gráficos O tipo de tabela e de gráfico que vamos utilizar depende da variável que está sendo analisada. Observe as definições e as tabelas a seguir.

Frequência absoluta é a quantidade de vezes que cada elemento é contado na amostra ou em um intervalo da amostra.

Frequência relativa é a proporção correspondente a cada elemento ou intervalo da amostra, em relação ao todo, expressa em porcentagem.

Considere as tabelas a seguir.

Tabela 1

Esporte preferido dos estudantes do 8o ano A

Esporte Frequência absoluta Frequência relativa (%)

Futebol 9 30

Vôlei 12 40

Basquete 9 30

Total 30 100

Fonte: Dados fictícios.

Tabela 3

Quantidade de filhos dos funcionários da empresa X

Tabela 2

Grau de escolaridade dos funcionários da empresa X

Grau de escolaridade Frequência absoluta Frequência relativa (%)

Ensino Fundamental 6 5

Ensino Médio 3025

Ensino Superior 4840

Pós-graduação 3630

Total 120100

Fonte: Dados fictícios.

Tabela 4

Altura dos clientes de uma academia de ginástica

Repare que na primeira coluna de cada uma das tabelas anteriores estão representados os dados referentes à variável estudada em cada pesquisa.

As tabelas 1 e 2 indicam pesquisas que analisaram variáveis qualitativas. Esporte preferido é uma variável qualitativa nominal, e os dados podem ser organizados como o pesquisador preferir. Grau de escolaridade é uma variável qualitativa ordinal, e os dados indicam uma hierarquia, ou seja, devem ser organizados de acordo com uma ordem.

AMPLIANDO

Atividade complementar

Qual é o tipo de variável estudada em cada uma das pesquisas representadas nas tabelas apresentadas na página 226 do Livro do estudante?

Resolução da atividade

Tabela 1: qualitativa nominal;

Tabela 2: qualitativa ordinal;

Tabela 3: quantitativa discreta;

Tabela 4: quantitativa contínua.

As tabelas 3 e 4 indicam pesquisas que analisaram variáveis quantitativas. Quantidade de filhos é uma variável quantitativa discreta, e os dados são organizados em ordem crescente. Altura é uma variável quantitativa contínua, e os dados são organizados em ordem crescente e em intervalos de classe.

Observe que na tabela 4 os intervalos de classe apresentam o símbolo ¿. Esse símbolo inclui ovalor inicial e não inclui o valor final do intervalo. Por exemplo, no intervalo 1,65 ¿ 1,69, são considerados todos os clientes cuja medida de altura se localiza no intervalo de 1,65 m (inclusive) até 1,69 m. Nesse caso, quem tem 1,69 m de altura será considerado no intervalo seguinte: 1,69  ¿ 1,73. Agora, acompanhe os dados das tabelas anteriores representados em gráficos.

ORIENTAÇÕES DIDÁTICAS

Retomar com os estudantes os três tipos de gráficos apresentados na página 227 do Livro do estudante: os gráficos de colunas, de barras e o histograma, contribuindo para o desenvolvimento da habilidade EF08MA23. Destacar que o histograma é o gráfico que representa a variável quantitativa contínua.

Pense e responda Comentar com os estudantes que as variáveis qualitativas e quantitativas discretas são representadas em gráficos de barras ou de colunas separadas. Já variáveis quantitativas contínuas são representadas em colunas agrupadas.

Fonte: Dados fictícios.

Responda no caderno

Resposta pessoal. Exemplo de resposta: Variáveis qualitativas e quantitativas discretas são representadas em gráficos de barras ou de colunas separadas. Variáveis quantitativas contínuas são representadas em colunas agrupadas.

Considerando os exemplos apresentados, que correspondência podemos fazer entre o tipo de variável e sua representação gráfica?

Os gráficos 1 e 3 são gráficos de colunas, e o gráfico 2 é um gráfico de barras, que já conhecemos. Eles são adequados para representar variáveis qualitativas e variáveis quantitativas discretas. Neles, as barras são separadas e relacionam cada valor com a respectiva frequência absoluta.

O gráfico 4 representa a variável quantitativa contínua e é chamado de histograma. Cada coluna representa um intervalo de valores e, como eles são contínuos, as colunas são agrupadas.

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd

Fonte: Dados fictícios.

Fonte: Dados fictícios.

ORIENTAÇÕES DIDÁTICAS

A construção de um gráfico de setores envolve, além do conhecimento de proporcionalidade, o uso de instrumentos geométricos, como o compasso, a régua e o transferidor.

Se considerar oportuno, propor a construção de um gráfico de setores simples, usando instrumentos geométricos, para que os estudantes possam retomar esse procedimento e calcular os ângulos correspondentes às frequências relativas.

Essa construção também pode ser feita a partir de um software de planilha eletrônica. Se escolher essa opção, acompanhar como os estudantes raciocinam para realizar essa construção. É importante que eles percebam que os softwares nos ajudam a obter resultados mais rápidos, porém é preciso saber o conceito que há por trás da execução dos programas.

Atividades

Após os estudantes realizarem a atividade 1, propor que compartilhem as respostas para que a turma conclua qual seria o melhor tipo de pesquisa escolhido. É importante notar se os argumentos usados pelos estudantes na defesa de suas escolhas são consistentes ou se há algum erro matemático ao se expressarem.

A atividade 3 mostra aos estudantes que uma pesquisa feita com uma amostra específica da população não permite realizar conclusões a respeito de toda a população. Nesse caso, seria melhor que a diretora da escola anotasse as respostas de meninos e meninas.

Já o gráfico de setores, que relaciona cada valor da variável com sua porcentagem, pode ser utilizado para todos os tipos de variáveis. Verifique os gráficos de setores referentes às pesquisas indicadas nas tabelas apresentadas anteriormente.

Gráfico 1

Gráfico 2

Gráfico 3

Gráfico 4

1. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Responda às questões no caderno.

1. Uma fábrica de chocolates decide fazer uma pesquisa para descobrir se seu público prefere os chocolates ao leite ou os amargos. De acordo com seu entendimento, a pesquisa deverá ser censitária ou amostral? Explique.

2. Uma empresa está verificando a pertinência da implantação de uma consultoria nutricional para seus funcionários. Uma das pesquisas realizadas está relacionada à massa (em quilograma) de seus funcionários. Para isso, entrevistaram 50 trabalhadores

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd

2.b) 50 funcionários da empresa.

c) Massa (em quilograma). Variável quantitativa contínua.

dos 250 funcionários registrados na empresa. Com base nessas informações, responda:

a) Qual é a população considerada nessa pesquisa?

250 funcionários da empresa.

b) Qual é a amostra considerada?

c) Qual é a variável analisada nessa pesquisa? Classifique-a.

3. A diretora de uma escola deseja saber qual é o esporte preferido dos estudantes matriculados. Para isso, selecionou uma amostra da população contendo apenas meninos. O que podemos dizer sobre o resultado dessa pesquisa?

3. Resposta pessoal. Espera-se que os estudantes percebam que essa amostra não é representativa e não refletirá a opinião da população correspondente, já que as meninas não foram consideradas na amostra e podem ter opiniões divergentes.

Fonte: Dados fictícios.

Fonte: Dados fictícios.

Fonte: Dados fictícios.

Fonte: Dados fictícios.

GRÁFICOS: EDITORIA DE ARTE

4. Em uma pesquisa, 100 jovens universitários foram entrevistados para saber o consumo diário de água. Copie a tabela a seguir e complete a coluna referente à frequência relativa (em porcentagem). Depois, responda às questões.

6.a)

a) Construa uma tabela que indique a frequência absoluta e a frequência relativa da quantidade de irmãos dos estudantes do 8o ano.

b) Quantos estudantes do 8o ano têm 2 ou mais irmãos?

7. Os gastos dos clientes de uma padaria em um sábado, no período da manhã, estão registrados no histograma a seguir.

Gastos dos clientes da padaria

ORIENTAÇÕES DIDÁTICAS

A atividade 7 apresenta um histograma dos gastos de clientes de uma padaria. No item a, espera-se que os estudantes percebam que não é fácil concluir, a partir da leitura direta do gráfico, quais são as frequências relativas; portanto, é preciso calcular cada uma delas.

Fonte: Dados fictícios.

a) Quantos jovens ingerem, diariamente, no máximo 6 copos (6 ou menos) de água?

b) Qual é o percentual de jovens que segue a recomendação de ingerir no mínimo 8 copos de água por dia?

5. A tabela apresenta os salários dos funcionários de uma empresa. Salários dos funcionários

a) Construa uma tabela de frequências correspondente aos dados representados no gráfico.

b) Q uantos clientes foram à padaria no período em que foi realizada a pesquisa?

8. Este gráfico mostra o resultado de uma pesquisa socioeconômica, na qual foi perguntado a cada um dos 600 entrevistados: Quantos aparelhos de televisão há em sua casa? Aparelhos

Na atividade 8, é apresentado um gráfico que mostra o resultado de uma pesquisa socioeconômica. Conversar com os estudantes sobre os motivos pelos quais se deseja saber a quantidade de televisores nas residências de determinado local. Ouvir as hipóteses dos estudantes e comentar sobre os mapeamentos sociais e econômicos que se pode fazer a partir desses dados, pensando em políticas econômicas ou ações de marketing.

Fonte: Dados fictícios.

a) Quantos funcionários recebem menos do que R$ 1.932,00?

11 funcionários.

b) Q uantos funcionários recebem salário maior ou igual a R$ 2.421,00?

3 funcionários.

6. Em uma pesquisa foi registrada a quantidade de irmãos de cada um dos 30 estudantes do 8o ano. Observe.

3140221100

0223410231

a) Qual é a porcentagem de pessoas que têm 3 ou mais aparelhos de TV?

b) Construa uma tabela com os dados representados no gráfico, indicando as frequências absoluta e relativa.

Resposta na seção Resoluções comentadas deste Manual.

7.a) Resposta na seção Resoluções comentadas deste Manual.

b) 57 clientes.

GRÁFICOS: EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

Média aritmética

Ao explorar o cálculo da média aritmética simples, apresentar outras situações em que ela está presente: determinar a altura média dos jogadores de um time de basquete e calcular o tempo médio do deslocamento de casa até um local ao longo de uma semana são alguns exemplos.

As situações apresentadas contribuem para o desenvolvimento da habilidade EF08MA25. Comentar que muitas pessoas utilizam o termo média sem o rigor matemático. Quando pedem uma pizza, por exemplo, e o atendente diz que ela demorará, em média, 30 minutos para ser entregue, a ideia por trás disso é que, a partir da experiência de entrega de pizzas daquele estabelecimento, o tempo costuma ser em torno de 30 minutos.

CAPÍTULO4 MEDIDAS EM ESTATÍSTICA

As medidas estatísticas podem nos auxiliar a verificar se determinado valor de uma série de dados é representativo. As medidas estatísticas que vamos estudar agora são a média aritmética simples, a média aritmética ponderada, a moda e a mediana

MÉDIA ARITMÉTICA

Média aritmética simples

Considere a situação a seguir.

Marina acompanhou a previsão do tempo no município onde mora. A tabela indica as temperaturas mínimas previstas para a semana de 27 a 31 de agosto de 2022. Temperaturas mínimas previstas para a semana de 27 a 31 de agosto de 2022

Data 27/828/829/830/831/8

Temperatura mínima (em °C) 1011141515

Fonte: Dados fictícios. Podemos calcular a temperatura mínima média desse período considerado adicionando todas as temperaturas e dividindo o resultado por 5, ou seja, pela quantidade de temperaturas registradas na tabela.

Tmín = ++++ 10 111415 15 5 = 65 5 = 13

Dessa maneira, a temperatura mínima média prevista para esse período foi de 13 °C.

A média apresenta, de maneira sintetizada, o conjunto de dados, e o valor calculado representa todos os valores desse conjunto.

A média aritmética simples de uma série de dados é determinada pela soma de todos os valores dividida pela quantidade de valores adicionados.

Média aritmética ponderada

Algumas situações pressupõem o cálculo da média aritmética ponderada. Acompanhe o exemplo a seguir.

Nas aulas de Matemática, Marcos foi avaliado de diferentes maneiras: um trabalho individual com peso 1; duas provas mensais, cada uma com peso 2; e uma prova final, com peso 4. Marcos obteve nota 7,7 no trabalho, 4,8 e 8,4 nas provas mensais e 6,1 na prova final. Qual foi a média de notas obtida por Marcos?

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 230 11/08/22 14:40

AMPLIANDO

Vídeo

A MÉDIA aritmética ponderada. 2018. Vídeo (6min29s). Publicado pelo canal Portal da Matemática OBMEP. Disponível em: https://www.youtube.com/watch?v=2X5FAqqFM_g. Acesso em: 10 ago. 2022.

Nessa videoaula, os estudantes poderão acompanhar a resolução de alguns exemplos de problemas envolvendo a média aritmética ponderada.

Quando uma prova tem peso 2, é como se a nota obtida nessa prova fosse computada duas vezes. Observe como podemos organizar as notas que Marcos obteve.

ORIENTAÇÕES DIDÁTICAS

Desse modo, é como se Marcos tivesse realizado 9 provas, e sua média é dada por:

Outra maneira de calcular a média de notas de Marcos é multiplicar a nota obtida em cada um dos instrumentos avaliativos por seu respectivo peso. Em seguida, dividir pela soma dos pesos.

A média aritmética ponderada de uma série de valores é determinada pela soma de todos os produtos de cada valor pelo respectivo peso, dividindo esse resultado pela soma dos pesos.

A média aritmética ponderada também é utilizada quando os valores estão representados em tabelas. Assim, os pesos são indicados pela frequência absoluta, que apresenta a quantidade de vezes em que o valor aparece. Podemos organizar as notas de Marcos da seguinte maneira.

Ao explorar o exemplo apresentado no cálculo da média aritmética ponderada, notas escolares, discutir com a turma como seria possível descobrir a nota mínima que é necessária obter em uma prova a partir de outras notas já obtidas para ser aprovado. Promover o debate, valorizando cada uma das opiniões dadas, desenvolvendo a empatia e capacidade de argumentação Por exemplo, se a nota mínima de aprovação em Matemática de uma escola é 7, e determinado estudante obteve notas 4 e 6, respectivamente, em provas com pesos 1 e 2, qual deverá ser a nota mínima que ele deve tirar na terceira prova desse sistema de avaliação para ser aprovado, sabendo que a terceira prova tem peso 2? Espera-se que os estudantes elaborem uma equação para resolver essa situação e concluam que a nota mínima, nesse caso, é 9,5.

Saiba que

SAIBA QUE

A soma dos valores das colunas da tabela pode ser indicada pelo símbolo E, que significa “somatório”. Podemos escrever: E (frequência) = 9 e E (nota frequência) = 58,5.

O boxe Saiba que apresenta o símbolo E (somatório) para indicar a soma dos valores de cada uma das colunas do exemplo das notas de Marcos em Matemática, dado no Livro do estudante. Explicar para a turma que esse símbolo representa a letra grega sigma.

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 231

ORIENTAÇÕES DIDÁTICAS

Moda

Conversar com os estudantes o significado de dizer que alguma coisa está na moda. Provavelmente, eles irão associar a um objeto ou costume popular. Fazer o paralelo dessa definição casual para a definição matemática, ou seja, a moda de uma série de dados é o valor que apresenta maior frequência. Ressaltar que uma série de dados pode não ter moda se nenhum valor se repetir.

Saiba que

Ao apresentar essa informação aos estudantes, verificar se eles não trazem uma ideia equivocada a respeito da moda ao considerar que uma série de dados não apresenta moda; registrar que a moda é igual a 0.

Pedir aos estudantes que deem exemplos de situações que podem apresentar mais de uma moda. Por exemplo, uma pesquisa que pergunta a quantidade de moradores por residência. Quanto maior o número de residências investigadas, maiores são as chances de ter modas diferentes.

Mediana

Ler a definição sobre mediana, destacando a necessidade de os dados estarem organizados em ordem crescente ou decrescente. Caso os estudantes não façam isso, podem realizar conclusões erradas a respeito do conjunto de dados analisado.

MODA

A moda também é uma medida utilizada na análise de dados estatísticos. Ela indica o valor que mais se repete entre uma série de valores considerados. Acompanhe os exemplos a seguir.

1 Em um condomínio de casas foi realizada uma pesquisa para verificar a quantidade de habitantes por residência. Observe os resultados.

O número que mais apareceu, ou seja, que teve a maior frequência, indica 3 habitantes por residência. Assim, a moda dessa pesquisa é 3 habitantes.

2 A tabela mostra o resultado de uma pesquisa realizada com estudantes do Ensino Médio de uma escola sobre a quantidade de irmãos de cada estudante. Observe. Para determinar a moda da quantidade de irmãos dessa pesquisa, basta localizar o valor que apresenta a maior frequência. Repare que o número 35 corresponde à maior frequência absoluta, indicando que 35 estudantes têm 2 irmãos. Assim, a moda dessa pesquisa é 2 irmãos.

A moda de uma série de valores é determinada pelo valor que apresenta a maior frequência.

SAIBA QUE

Uma série de valores pode ter mais de uma moda quando diferentes valores apresentam a mesma frequência, ou, ainda, pode não ter moda quando nenhum valor se repete.

MEDIANA

Outra medida utilizada na análise de dados estatísticos é a mediana.

A mediana é a medida estatística que divide uma série de valores em duas partes com a mesma quantidade de termos cada uma, na qual a primeira parte apresenta valores menores ou iguais a ela e, a segunda parte, valores maiores ou iguais a ela.

Considere o exemplo a seguir.

A joalheria Gema Pura vende algumas pedras semipreciosas brutas para colecionadores. Observe na tabela a seguir os preços unitários de venda das pedras semipreciosas dessa joalheria.

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 232

ORIENTAÇÕES DIDÁTICAS

Podemos reorganizar todos os valores em ordem crescente e identificar o preço unitário de venda que separa os demais preços em dois grupos com a mesma quantidade de valores. Verifique uma maneira de fazer essa reorganização.

Tabela de preços

Pedra Preço unitário (R$)

Ágata 80,00

Ametista 10,00

Selenita 30,00

Berilo 190,00

Turmalina 40,00

Topázio 700,00

Quartzo 2,00

2 10 30 40 80 190 700

termo central (Os preços estão em reais.)

Nesse caso, dizemos que a quantidade de preços unitários de venda das pedras da joalheria Gema Pura que são menores ou iguais ao termo central é igual à quantidade de preços unitários de venda que são maiores ou iguais ao termo central. Esse termo central é a mediana desse conjunto de dados.

A mediana dos preços das pedras semipreciosas dessa joalheria é R$ 40,00, ou seja, metade das pedras semipreciosas tem preço menor ou igual a R $ 40,00, e a outra metade das pedras semipreciosas tem preço maior ou igual a R$ 40,00.

Se uma série de dados possui uma quantidade ímpar de valores, a mediana é o termo central da série, organizada em ordem crescente (ou decrescente).

A dona da joalheria Gema Pura também resolveu vender pirita. Observe como ficou a tabela de preços com a inclusão dessa pedra.

A joalheria passou a oferecer 8 pedras, uma quantidade par de itens (e não ímpar, como na tabela anterior). Nesse caso, a mediana é calculada por meio da média aritmética dos termos centrais, de modo que a quantidade de valores que são menores ou iguais à mediana corresponda à quantidade de valores que são maiores ou iguais à mediana.

Com a inclusão da nova pedra, os preços unitários de venda, em reais, em ordem crescente, foram reorganizados do seguinte modo.

2 10 30 40 80 190 700 85

termos centrais

A mediana dos preços de venda passou a ser R$ 60,00,

Tabela de preços

Pedra Preço unitário (R$)

Ágata 80,00

Ametista 10,00

Selenita 30,00

Berilo 190,00

Turmalina 40,00

Pirita 85,00

Topázio 700,00

Quartzo 2,00

= , pois 40 80

Fonte: Joalheria Gema Pura. 233

Após ordenar os valores da série de dados, verificar se a quantidade de dados é par ou ímpar. Se for ímpar, o valor da mediana corresponde ao termo central. Se a quantidade de dados for par, ressaltar que a mediana será dada pela média aritmética dos dois termos centrais.

D2-AV2-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 233

AMPLIANDO

Atividade complementar

Propor aos estudantes uma atividade prática usando tecnologia. Em um conjunto com muitos valores, por exemplo, 200 ocorrências coletadas, como é possível determinar a mediana deles usando uma planilha eletrônica? Construir, com a turma, essa situação em uma planilha eletrônica e mostrar como é possível ordenar os valores do menor para o maior e desse modo descobrir a mediana desejada.

Fonte: Joalheria Gema Pura.

ORIENTAÇÕES DIDÁTICAS

Amplitude

Apresentar o conceito de amplitude e pedir aos estudantes que calculem a amplitude de situações apresentadas anteriormente. No caso da tabela com os preços das pedras de uma joalheria, apresentada na página anterior, a amplitude é R$ 698,00. Questionar os estudantes a respeito do que significa esse valor. Espera-se que eles concluam que isso mostra uma diferença grande entre elementos de um mesmo conjunto de dados: no caso, diferença grande entre os valores cobrados pelas pedras. Se a amplitude, nessa situação, fosse R $ 20,00, a diferença entre os valores das pedras seria bem menor. Comentar que a amplitude nos ajuda a realizar conclusões mais precisas a respeito dos dados de um conjunto, junto à média, à mediana e à moda.

AMPLITUDE

A amplitude de uma série de dados é uma medida que nos auxilia na análise das medidas que acabamos de estudar.

Os dados a seguir apresentam as notas de Lucas e de Mariana em Língua Portuguesa.

Calculando a média, a moda e a mediana das notas de cada um, temos:

Observando esses cálculos, pode-se ter a impressão de que as duas séries de valores são muito parecidas, pois a média, a moda e a mediana das notas de Lucas são iguais às de Mariana. Entretanto, ao analisar esses dados de maneira mais cuidadosa, verificamos que os dois grupos são diferentes. Para analisar melhor essas notas, vamos considerar a diferença entre a maior e a menor nota de cada um.

Lucas

Maior nota: 9,5

Menor nota: 3,5

Diferença: 9,5 3,5 = 6,0

Mariana

Maior nota: 7,5

Menor nota: 5,5

Diferença: 7,5 5,5 = 2,0

A amplitude de uma série de valores é a diferença entre o maior valor e o menor valor observados.

Podemos dizer que, quanto menor for a amplitude dos dados, mais próximos eles estarão da média, da moda e da mediana.

Como a amplitude das notas de Lucas é bem maior do que a amplitude das notas de Mariana, podemos dizer que as notas de Lucas estão “mais espalhadas” do que as notas de Mariana, ou seja, as notas de Mariana ficaram mais próximas das medidas estatísticas calculadas.

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 234

AMPLIANDO

Vídeo

AMPLITUDE e amplitude média. 2013. Vídeo (2min5s). Publicado pelo canal Khan Academy Brasil. Disponível em: https://www.youtube.com/watch?v=ak7c_sEDjFk. Acesso em: 10 ago. 2022.

Nesse link, é possível ter acesso a uma videoaula sobre amplitude e amplitude média de uma série de dados.

ATIVIDADES

Responda às questões no caderno.

1. O quadro mostra as notas de quatro estudantes do 8o ano em Ciências da Natureza.

Bruno 6,57,57,07,56,0

Camila 8,08,07,06,57,5

Marcela 5,05,54,55,56,0

Roberto 4,57,55,05,08,0

a) Determine a média de notas de cada um dos estudantes.

Bruno: 6,9; Camila: 7,4; Marcela: 5,3; e Roberto: 6,0.

b) Para serem aprovados, é necessário obter média maior ou igual a 6,0. Quais desses estudantes foram aprovados?

b) É possível identificar uma moda nesse conjunto de valores? Em caso afirmativo, qual é essa moda?

Possui duas modas: 12 anos e 14 anos.

c) D etermine a mediana dessa série de dados. Lembre-se de organizá-las em ordem crescente ou decrescente.

d) Determine a amplitude desses valores.

13 anos. 10 anos (19 9 = 10).

4. (Enem/MEC) Uma pessoa, ao fazer uma pesquisa com alguns alunos de um curso, coletou as idades dos entrevistados e organizou esses dados em um gráfico.

ORIENTAÇÕES DIDÁTICAS

Atividades

2. Observe, a seguir, a altura dos jogadores de basquete do time do 8o ano do Colégio Y

Artur Bernardo Fernando 1,65 m1,69 m1,79 m

Guilherme Marcelo Otávio Wilson 1,75 m1,63 m1,69 m1,76 m

a) Determine a altura média dos jogadores desse time.

Bruno, Camila e Roberto. A altura média é de aproximadamente 1,71 m.

b) Qual é a mediana das alturas dos jogadores desse time? Explique o significado desse valor.

c) Gustavo também vai fazer parte do time de basquete do 8o ano do Colégio Y. Se sua altura é 1,78 m, quais serão a altura média e a mediana das alturas do time considerando o novo integrante?

A altura média será 1,72 m, e a mediana, 1,72 m.

3. No curso de sapateado de Marina estão matriculados 6 meninas e 4 meninos, de diferentes idades, que compõem a companhia de dança. Observe as idades dos integrantes desse grupo.

1217151412199111410

a) Qual é a média de idade dos participantes desse grupo de dança? 13,3 anos.

As atividades propostas nessa seção contribuem para o desenvolvimento da habilidade EF08MA25. Na atividade 4, os estudantes devem ler o gráfico proposto no enunciado e retirar dele as informações necessárias para determinar a moda. Pelo gráfico, é possível identificar que 21 pessoas entrevistadas tinham 9 anos, 15 pessoas tinham 12 anos, e 12 pessoas tinham 18 anos. Como foram 48 pessoas entrevistadas, e a idade com maior número de ocorrência foi 9, então a moda é 9.

2.b)

9 12 18

Idade (ano)

Qual a moda das idades, em anos, dos entrevistados?

a) 9

b) 12 c) 13 d) 15 e) 21

5. Neste quadro, mostram-se as notas obtidas por dois estudantes do 8o ano de certa escola, acompanhadas dos respectivos pesos de cada avaliação.

Avaliação Peso Notas do estudante 1 Notas do estudante 2

Sabendo que a média para aprovação nessa escola é 6,0, verifique se esses estudantes foram aprovados.

Estudante 1: média = 6,65; Estudante 2: média = 6,57. Ambos os estudantes foram aprovados.

235 D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd

A mediana é 1,69 m. Metade dos jogadores tem altura menor ou igual a 1,69 m, e a outra metade tem altura maior ou igual a 1,69 m.

Alternativa a.

ORIENTAÇÕES DIDÁTICAS

Realizando pesquisas estatísticas

É importante que os estudantes compreendam que toda pesquisa estatística tem um objetivo definido e que conclusões podem ser realizadas a partir dos dados obtidos. Por isso, a pesquisa deve seguir critérios definidos antes de ser executada. Essa abordagem contribui para o desenvolvimento da habilidade EF08MA27 e da competência específica 2 da área de Matemática.

Depois de definir o objetivo, é preciso pensar nas variáveis a serem analisadas, no tamanho da amostra e que perguntas serão elaboradas. Após a pesquisa, definir como os dados serão apresentados: se apenas em tabelas ou, também, em gráficos. Com os dados organizados, calcular as medidas de tendência central, se possível e pertinente, e realizar possíveis conclusões.

Antes de realizar uma pesquisa estatística, é necessário refletir sobre o objetivo da pesquisa e a variável a ser estudada, de modo a identificar a população e a necessidade de se definir uma amostra. Com base nisso, é possível planejar como será feita a coleta dos dados.

Observe a seguinte situação.

Uma escola pretende levar os estudantes do 8o ano e do 9o ano para assistir a uma peça de teatro (objetivo). Para isso, a coordenadora resolveu fazer uma pesquisa para descobrir a qual peça eles gostariam de assistir (variável). Ela entrevistou 60 estudantes (amostra) dos 200 matriculados nas turmas de 8o e 9o anos (população).

Foram pré-selecionadas 3 peças para os estudantes escolherem, que vamos chamar de Peça 1, Peça 2 e Peça 3. Como a população a ser pesquisada tem 120 meninas e 80 meninos, ela trabalhou com uma amostra proporcional estratificada. Acompanhe.

Depois de selecionada a amostra, foi elaborado um questionário para os estudantes responderem.

Nome:

Idade:

Menina ( ) Menino ( )

A que peça de teatro você gostaria de assistir?

Escolha somente uma opção. ( )

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd

AMPLIANDO

Atividade complementar

Para organizar as etapas de realização de uma pesquisa estatística, solicitar aos estudantes que construam um fluxograma.

os dados coletados foram organizados em uma tabela e em um gráfico.

Peça de teatro preferida

Peça teatral Frequência absoluta

Peça 1 28

Peça 2 15

Peça 3 17

Total 60

Fonte: Pesquisa realizada com estudantes do 8o e do 9o ano.

Peça de teatro preferida

ORIENTAÇÕES DIDÁTICAS

Pense e responda

Após analisar os dados da pesquisa, a coordenadora decidiu levar os estudantes ao teatro para assistirem à Peça 1

PENSE E RESPONDA

Não, pois essa pesquisa envolve uma variável qualitativa.

Responda no caderno. É possível calcular a média dos dados dessa pesquisa? Explique sua resposta.

ATIVIDADES

Responda no caderno.

Resposta pessoal. Exemplos de resposta na seção Resoluções comentadas deste Manual.

1. Agora é sua vez! Junte-se a um colega, e realizem duas pesquisas com base nas orientações a seguir.

a) Pesquisa envolvendo uma variável qualitativa nominal.

• Definam um objetivo, a variável a ser analisada, a população e a amostra.

• Realizem a coleta de dados. Em seguida, organizem esses dados em tabela, gráfico de colunas ou de barras ou gráfico de setores.

• Por fim, escrevam um relatório com os resultados. Lembrem-se de colocar a conclusão da pesquisa que vocês fizeram.

b) Pesquisa envolvendo uma variável quantitativa discreta.

• Definam um objetivo, a variável a ser analisada, a população e a amostra.

• Realizem a coleta de dados. Em seguida, organizem esses dados em tabela, gráfico de colunas ou de barras ou gráfico de setores.

• Determinem a média, a moda, a mediana e a amplitude dos dados obtidos e verifiquem como essas medidas estão situadas em relação à amplitude dos dados.

• Por fim, escrevam um relatório com os resultados. Lembrem-se de colocar a conclusão da pesquisa que vocês fizeram.

Verificar se os estudantes concluem que não é possível calcular a média dos dados da pesquisa apresentada, pois eles foram obtidos a partir de uma variável qualitativa: os estudantes da situação precisavam escolher uma peça entre três oferecidas. Nesse ponto, é esperado que os estudantes treinem o olhar crítico a respeito da Estatística e avaliem quando uma ou outra medida de tendência central será utilizada.

Atividades

A atividade proposta leva os estudantes a terem uma postura ativa, pois eles terão que definir as pesquisas que vão realizar a partir do tipo indicado de variável. Acompanhar o processo realizado por eles ao longo dessas pesquisas. A respeito do relatório final, é importante que esteja bem escrito e consiga transmitir ao leitor, que não fez parte da pesquisa, o que pode ser concluído a respeito dela.

Em seguida,

Peça 2 Peça 3

Fonte: Pesquisa realizada com estudantes do 8o e do 9o ano.

ORIENTAÇÕES DIDÁTICAS

Tecnologias

Ao longo da Unidade, os estudantes tiveram contato com diferentes situações, que apresentaram dados possíveis de analisar e calcular, manualmente, as medidas de tendência central relacionada a eles, contribuindo para o desenvolvimento da competência geral 1. Como dito anteriormente, na maioria das situações de pesquisas estatísticas a quantidade de dados pode ser enorme; portanto, é necessário fazer uso de planilhas eletrônicas para auxiliar a organização e a análise dos dados.

Comentar que existem diferentes tipos de planilha eletrônica, mas que nessa seção será desenvolvido o trabalho com a planilha Calc do LibreOffice. Portanto, antes de iniciar esse trabalho, dialogar com os estudantes a respeito do que eles conhecem dessa ferramenta, uma vez que ela já foi utilizada anteriormente na coleção.

CONSTRUINDO GRÁFICOS POR MEIO DE PLANILHA ELETRÔNICA

Nesta seção, você vai utilizar um software chamado LibreOffice Calc para organizar dados em planilhas eletrônicas e construir gráficos. É possível fazer o download gratuito desse aplicativo por meio do link https://pt-br.libreoffice.org/baixe-ja /libreoffice-novo/ (acesso em: 13 jun. 2022).

1 15

2 35

Inicialmente, considere esta tabela. Vamos inserir os dados dessa tabela na planilha eletrônica. Para isso, abra uma nova planilha e digite, na célula A1, o título da tabela: “Quantidade de irmãos dos estudantes do Ensino Médio”. Na célula A2, digite “Quantidade de irmãos”, e, na célula B2, digite “Frequência absoluta”. Em seguida, complete as colunas de acordo com a tabela. Observe a seguir o passo a passo para a construção do gráfico de colunas.

1 Depois de digitar os dados na planilha eletrônica, selecione somente os dados numéricos e clique em Inserir gráfico no menu ou no ícone correspondente ao gráfico.

2 Na janela do Assistente de gráficos, clique em Tipo de gráfico, selecione a opção Coluna e clique em Próximo

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 238

AMPLIANDO

Vídeo

COMO inserir gráfico no LibreOffice. 2016. Vídeo (3min44s). Publicado pelo CANAL_Dicas de Planilha. Disponível em: https://www.youtube.com/watch?v=N2482NKlqUU&t=1s. Acesso em: 10 ago. 2022.

Nessa videoaula, é possível acompanhar algumas dicas de como inserir gráficos em planilhas do LibreOffice.

3 Na mesma tela da etapa 2, clique em Intervalo de dados, selecione Primeira coluna como rótulo e clique em Próximo

4 Na tela da etapa 3, mantenha como está a opção Série de dados e clique em Próximo

5 Na tela da etapa 4, clique em Elementos do gráfico, insira o título do gráfico e o título dos eixos. Se estiver selecionado Exibir legenda, clique para desabilitar.

6 Para concluir, clique em Finalizar. O gráfico estará pronto. Para a construção do gráfico de setores, deve-se inserir na planilha outra coluna com as frequências relativas, em porcentagem, e utilizar o mesmo passo a passo descrito anteriormente. A diferença é que na etapa 1, Tipo de gráfico, seleciona-se a opção Pizza. Para aparecerem os valores das porcentagens, clica-se com o botão esquerdo do mouse em cima do gráfico e seleciona-se a opção Inserir rótulos de dados. Em seguida, repetir o procedimento e clicar em Formatar rótulo de dados e seguir os comandos: selecionar opção Valor como porcentagem ; selecionar

Formato de porcentagem; desabilitar opção Formato de origem; selecionar opção de número com duas casas decimais e clicar em OK; clicar novamente em OK

Responda no caderno.

• Utilize algumas tabelas apresentadas nesta Unidade e explore outras construções de gráficos usando a planilha eletrônica. Repare que você também poderá utilizar a planilha eletrônica para organizar os dados coletados nas pesquisas propostas na atividade da página 237, o que poderá auxiliá-lo na apresentação dos resultados das pesquisas no relatório. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

D2-AV2-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 239

ORIENTAÇÕES DIDÁTICAS

Ao final da seção Tecnologias, verificar se os estudantes ainda têm alguma dúvida a respeito dos procedimentos indicados nesta Unidade.

Para resolverem a atividade proposta, eles precisam fazer uma seleção de quais tabelas da Unidade vão utilizar para construir gráficos no programa indicado. Durante o desenvolvimento da atividade, acompanhar se os estudantes fazem escolhas de modo que construam diferentes gráficos.

Propor aos estudantes que criem o hábito de investigar o funcionamento de qualquer tecnologia que utilizam. Como eles já estudaram a respeito desses gráficos e os procedimentos manuais para construí-los, agora podem utilizar as ferramentas de construção de gráficos para agilizar os procedimentos de análise de pesquisas estatísticas.

15/08/22 22:44

FOTOGRAFIAS: REPRODUÇÃO/LIBREOFFICE

ORIENTAÇÕES DIDÁTICAS

Retomando o que aprendeu

Na atividade 1, a secretária vai usar um tipo de cada peça de roupa; portanto, considerando que ela tem 6 camisas, 4 saias e 3 pares de sapatos, basta calcular a quantidade de maneiras distintas de se arrumar.

Na atividade 2, primeiro é preciso calcular o total de possibilidades do lançamento dos dois dados de seis faces: 6 6 = 36. Depois, analisar os palpites de cada pessoa: para José, a soma deve ser 7; portanto, os casos possíveis são (1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3), ou seja, 6 casos; para Paulo, a soma deve ser 4; portanto, são possíveis os casos (1, 3), (3, 1), (2, 2), ou seja, 3 casos; para Antônio, a soma deve ser 8; portanto, os casos possíveis são (2, 6), (6, 2), (3, 5), (5, 3), (4, 4), com total de 5 casos. Como a probabilidade é calculada pela razão dos casos possíveis pelo total de possibilidades, José tem maior probabilidade de acertar o palpite.

Na atividade 3, os estudantes precisam calcular a média ponderada a partir dos dados do tempo de escolaridade indicado nas duas tabelas. Verificar se eles calculam a média colocando no denominador o número de candidatos.

Responda às questões no caderno.

1. (UEMG) Uma secretária possui 6 camisas, 4 saias e 3 pares de sapatos. O número de maneiras distintas com que a secretária poderá se arrumar usando 1 camisa, 1 saia e 1 par de sapatos corresponde a

a) 13

b) 126

c) 72

d) 54

Alternativa c.

2. (Enem/MEC) José, Paulo e Antônio estão jogando dados não viciados, nos quais, em cada uma das seis faces, há um número de 1 a 6. Cada um deles jogará dois dados simultaneamente. José acredita que, após jogar seus dados, os números das faces voltadas para cima lhe darão uma soma igual a 7. Já Paulo acredita que sua soma será igual a 4 e Antônio acredita que sua soma será igual a 8.

Com essa escolha, quem tem a maior probabilidade de acertar sua respectiva soma é

Alternativa d.

a) Antônio, já que sua soma é a maior de todas as escolhidas.

b) José e Antônio, já que há 6 possibilidades tanto para a escolha de José quanto para a escolha de Antônio, e há apenas 4 possibilidades para a escolha de Paulo.

c) José e Antônio, já que há 3 possibilidades tanto para a escolha de José quanto para a escolha de Antônio, e há apenas 2 possibilidades para a escolha de Paulo.

d) José, já que há 6 possibilidades para formar sua soma, 5 possibilidades para formar a soma de Antônio e apenas 3 possibilidades para formar a soma de Paulo.

e) Paulo, já que sua soma é a menor de todas.

240

3. As tabelas a seguir mostram o tempo de escolaridade de candidatos a uma vaga de vendedor de uma empresa nos anos 2021 e 2022.

Tempo de escolaridade dos candidatos em 2021

Tempo de escolaridade (em ano) Quantidade de candidatos 4 8 8 4 11 5 15 3

Fonte: Dados fictícios.

Tempo de escolaridade dos candidatos em 2022

Tempo de escolaridade (em ano) Quantidade de candidatos 4 10 8 5 11 10 15 12

Fonte: Dados fictícios.

a) Em 2021, qual foi o valor modal do tempo de escolaridade dos candidatos à vaga de vendedor nessa empresa? Qual foi esse valor em 2022?

b) Considere M1 a média, em anos, do tempo de escolaridade entre os candidatos de 2021 e M2 a média, em anos, do tempo de escolaridade entre os candidatos de 2022. Calcule.

• M1 • M2 • M M 1 2

4 anos; 15 anos. 8,2 10 0,82 8 anos; 11 anos.

4. (Enem/MEC) Os candidatos K, L, M, N e P estão disputando uma única vaga de emprego em uma empresa e fizeram provas de português, matemática, direito e informática. A tabela apresenta as notas obtidas pelos cinco candidatos.

ORIENTAÇÕES DIDÁTICAS

Segundo o edital de seleção, o candidato aprovado será aquele para o qual a mediana das notas obtidas por ele nas quatro disciplinas for a maior. O candidato aprovado será

Alternativa d.

a) K. b) L. c) M. d) N. e) P.

5. (Enem/MEC) O quadro apresenta o número de terremotos de magnitude maior ou igual a 7, na escala Richter, ocorridos em nosso planeta nos anos de 2000 a 2011.

Ano 200020012002200320042005200620072008200920102011

Terremotos 151613151611111812172420

Disponível em: https://earthquake.usgs.gov/earthquakes/browse/m7-world.php. Acesso em: 13 ago. 2012 (adaptado).

Um pesquisador acredita que a mediana representa bem o número anual típico de terremotos em um período. Segundo esse pesquisador, o número anual típico de terremotos de magnitude maior ou igual a 7 é Alternativa c.

a) 11. b) 15. c) 15,5. d) 15,7. e) 17,5.

Nesta Unidade, estudamos o princípio fundamental da contagem ou princípio multiplicativo, bem como conceitos relacionados a Probabilidade e Estatística. Em seguida, ampliou-se o trabalho com conceitos básicos de Estatística e como eles estão relacionados à organização dos dados em tabelas e gráficos.

Você percebeu como a Estatística é importante para a tomada de decisões?

Com ela, é possível analisar as características de séries de dados para entender seu comportamento e decidir sobre como utilizar esses dados.

Na seção Tecnologias, você pôde explorar o uso de planilha eletrônica para construir gráficos de colunas e de setores.

A abertura de Unidade teve como tópico principal a evolução da pandemia de covid-19 e a importância da vacinação. Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

• A partir do gráfico apresentado na abertura desta Unidade, faça uma estimativa da amplitude da quantidade de óbitos diários registrados no período de abril a agosto de 2021.

Aproximadamente 2 0 00 óbitos (3 0 00 1 000 = 2 000).

• Em relação aos vacinados com esquema completo de vacinação, também representados no gráfico da abertura desta Unidade, a partir de que mês de 2021 essa variável superou 20%?

A partir de agosto de 2021.

• Em seu entendimento, qual é a importância de organizar um conjunto de dados em gráficos e tabelas? Por que há diferentes tipos de gráficos? Que cuidados precisamos ter ao analisar um gráfico ou uma tabela?

Respostas pessoais. Exemplos de resposta na seção Resoluções comentadas deste Manual.

D2-AV1-MAT-F2-2103-V8-U7-212-241-LA-G24.indd 241

Na atividade 4, verificar se os estudantes não confundem média com mediana. Como a atividade pede a maior mediana nas quatro notas obtidas, é preciso escrever as notas dos candidatos em ordem e calcular a média dos termos centrais. Depois, observar a mediana obtida: K – 33; L – 33,5; M – 35; N – 36; P – 31.

Um novo olhar

As questões propostas retomam o assunto abordado no início da Unidade e revelam a necessidade de analisar, cuidadosamente, os dados apresentados em tabelas e gráficos. Enfatize a importância das fontes e da consistência dos dados. O momento permite elaborar um trabalho interdisciplinar a respeito de temas transversais como cuidados com a saúde, entre outros assuntos. Discussões como essas podem auxiliar na formação crítica dos estudantes para que possam interpretar e questionar, criticamente, as informações que lhes são apresentadas. Retomar a abertura da Unidade e propor aos estudantes que respondam às questões.

Competências gerais:

• 1, 2, e 7

Competências específicas:

• 3, 4 e 6

Habilidades:

Grandezas e medidas

• EF08MA19

• EF08MA20

• EF08MA21

Temas Contemporâneos

Transversais:

• Ciência e Tecnologia

• Educação Ambiental

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em três capítulos e apresenta os conteúdos por meio de exemplos contextualizados e atividades diversificadas, além de trazer seções com temas que contribuem para a formação integral dos estudantes, contribuindo para o desenvolvimento das competências gerais 1, 2 e 7.

O primeiro capítulo retoma o cálculo de áreas de figuras poligonais e introduz o cálculo do perímetro da circunferência e a área de regiões circulares, desenvolvendo, assim, a habilidade EF08MA19.

O segundo capítulo aborda o volume dos sólidos geométricos, em especial, os cubos, os blocos retangulares e o cilindro, o que favorece o desenvolvimento da habilidade EF08MA21. No terceiro capítulo, são abordadas as unidades de medida de capacidade, destacando-se a relação entre litro e decímetro cúbico, a fim de desenvolver a habilidade EF08MA20.

A Unidade é permeada por seções que trazem informações sobre contextos de relevância social e ambiental, como a crise hídrica, o cultivo de hortas em pequenos espaços e as formas

VOLUME E CAPACIDADE

Há muito tempo, faz parte da vida do ser humano a necessidade de determinar medidas de área, volume e capacidade. Alguns povos da Antiguidade como os babilônios, os chineses, os egípcios, os hindus e os gregos calculavam as áreas de algumas figuras geométricas com certa precisão, considerando os meios de que dispunham. Atualmente, a tecnologia é uma grande aliada nos processos de medição de diferentes grandezas.

Nesta imagem, é possível observar o monitoramento do volume de água dos reservatórios que abastecem a Grande São Paulo em março de 2022. Esse monitoramento é feito por empresas especializadas que atuam no abastecimento de água.

Elaborado com base em: HIDROMAPAS. Portal dos Mananciais – Sabesp. São Paulo, [201-]. Dados referentes a 15 mar. 2022. Disponível em: https://mananciais.sabesp.com.br/HidroMapas.

INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018. p. 94. Disponível em: https://biblioteca.ibge.gov.br/visualizacao/livros/liv101627.pdf. Acessos em: 29 jun. 2022.

de energia renováveis e não renováveis, os quais colaboram com o desenvolvimento de diversas competências gerais e específicas e Temas Contemporâneos Transversais.

D2_AV1-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 242

OBJETIVOS

• Resolver problemas envolvendo o cálculo de área de regiões poligonais.

• Calcular o perímetro da circunferência e a área do círculo, aplicando esses conceitos na resolução de problemas.

• Resolver problemas envolvendo o volume de cubos, blocos retangulares e cilindros.

• Conhecer a relação entre decímetro cúbico e litro.

• Analisar gráficos.

Tanque de tratamento de água.

Em 2014, houve uma grave crise hídrica em São Paulo que comprometeu o abastecimento de água da população. No gráfico a seguir, pode-se verificar um comparativo entre o nível de água dos reservatórios no início de setembro de 2013, ano que antecedeu a crise hídrica, e o nível de água no mesmo período de 2021.

Situação dos reservatórios que abastecem a Grande São Paulo –Início de setembro de 2013 e início de setembro de 2021

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

Ao iniciar o trabalho com essa abertura, propor aos estudantes que observem o infográfico e elaborem individualmente um resumo das informações obtidas. Perguntar a eles se sabem o nome do reservatório que atende a região onde moram e qual é o nível atual desse reservatório.

Outras discussões a respeito da economia de água podem ser realizadas durante a aula. Algumas perguntas que podem ser feitas: “Será que há a preocupação com a economia de água em nossa casa?”; “Qual é o tempo médio de banho de cada um de nós?”; “Nós nos lembramos de fechar as torneiras para escovar os dentes?”; “Evitamos lavar carros e calçadas com água própria para o consumo?” etc.

*A construção do Reservatório São Lourenço foi iniciada em 2014. Como esse reservatório entrou em operação em 2018, não há dados de 2013.

Elaborado com base em: SITUAÇÃO dos Mananciais. Portal dos Mananciais – Sabesp. São Paulo, [201-]. Dados referentes a 2 fev. 2013 e 2 set. 2021. Disponível em: https://mananciais.sabesp.com.br/Situacao. Acesso em: 23 jun. 2022.

Responda às questões no caderno.

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

• Você sabe como é realizado o abastecimento de água no município onde mora? Conhece a situação atual de abastecimento desses reservatórios?

Respostas pessoais. Exemplo de resposta na seção Resoluções comentadas deste Manual.

• Compare os dados referentes aos níveis dos reservatórios apresentados no gráfico de colunas duplas. O que você identifica? Em seu entendimento, há motivo para se preocupar com o abastecimento de água dessa mesma região em 2022? Justifique.

Respostas pessoais. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Ao iniciar a leitura do texto que acompanha a imagem, conversar com os estudantes a respeito dos conceitos de capacidade e volume dos reservatórios de água.

D2_AV4-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 243

JUSTIFICATIVAS DOS OBJETIVOS

Nesta Unidade, apresenta-se o estudo de áreas de regiões poligonais e circulares, do volume de cubos, blocos retangulares e cilindros, e das relações entre as unidades de medida de capacidade. Desse modo, favorece-se o desenvolvimento das habilidades EF08MA19, EF08MA20 e EF08MA21.

No boxe Fórum, são apresentadas possibilidades de construção de hortas em pequenos espaços, contribuindo para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental.

Na seção Tratamento da informação, os estudantes são convidados a analisar gráficos, que abordam a questão das energias renováveis e não renováveis.

Na questão 2, espera-se que estudantes observem que, em 2021, os níveis dos reservatórios que abastecem a Grande São Paulo estavam mais baixos do que no mesmo período de 2013, ano que antecedeu a crise hídrica de 2014. Embora um novo reservatório tenha integrado o sistema de abastecimento, é possível estimar que havia motivo de preocupação para o abastecimento em 2022, tomando como base o ocorrido em 2014, mas é necessário observar que isso também depende do período de chuvas na região, que, em geral, costuma ocorrer nos meses de primavera e verão.

DEDMITYAY/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Área de figuras planas

Ler a situação proposta no boxe Pense e responda e garantir um tempo de compartilhamento de impressões e intuições entre os estudantes como alternativa para a prática de argumentação oral e escrita, bem como para o desenvolvimento da competência específica 4 da área de Matemática, da empatia e da cooperação entre eles. Em seguida, reunir os estudantes em grupos e distribuir quadrados de papel para cada grupo, ou confeccionar com eles as peças, para que possam concretizar a atividade. Caso decida construir com os estudantes, separar cartolina, tesoura e régua com antecedência ou solicitar aos estudantes que tragam esse material na data da realização da atividade. É importante que os pedaços quadrados de papel mantenham a proporção das medidas indicadas no problema. Por exemplo, os quadrados de papel podem ter lados de medida 10 cm. O conteúdo abordado no Livro do estudante, bom como a exploração proposta, favorecem o desenvolvimento da habilidade EF08MA19.

PROBLEMAS ENVOLVENDO ÁREA DE POLÍGONOS

Responda à questão no caderno.

Para cobrir parte de um terreno, Marcos vai utilizar placas de grama com formato de quadrado cujos lados têm 1 m de comprimento.

De quantas placas com formato de quadrado ele vai precisar para fazer um gramado retangular de 5 m por 3 m? Compartilhe com a turma o modo como você pensou para resolver esse problema e compare as resoluções. Ele vai precisar de 15 placas.

A prefeitura de um município atendeu às solicitações dos moradores e vai construir uma área para as crianças brincarem na praça principal da cidade. Analisando a imagem aérea da praça, a equipe responsável pelo projeto optou por utilizar uma região em formato de trapézio que não estava gramada.

O arquiteto responsável pela obra pretende destinar um espaço com formato triangular para colocar areia. O espaço total será ampliado, e o parquinho de formato retangular será montado com piso emborrachado conforme indicado no esboço a seguir.

AMPLIANDO

Jogo

CONSTRUTOR de área. PHET Interactive Simulations. Colorado, EUA, c2022. Disponível em: https://phet. colorado.edu/sims/html/area-builder/latest/area-builder_pt_BR.html. Acesso em: 11 ago. 2022.

Esse jogo on-line é composto de seis fases nas quais os estudantes devem construir figuras geométricas poligonais com diferentes desafios propostos, relacionados às áreas dessas figuras.

Acompanhe esta situação. IMAGENS FORA DE PROPORÇÃO. AS CORES NÃO SÃO REAIS.

A equipe responsável pela compra de material para a obra fez algumas perguntas ao arquiteto.

1. Qual é a área do terreno que não está gramada?

2. Qual é a área da região onde será colocada areia?

3. Qual é a área da região destinada ao parquinho com piso emborrachado?

Para responder às perguntas, o arquiteto desenhou uma representação inicial do terreno, que não estava com grama, e uma representação final do terreno, considerando a ampliação, e indicou as medidas de cada lado.

ORIENTAÇÕES DIDÁTICAS

Para determinar a área inicial do terreno, ele utilizou a expressão da área do trapézio:

() A Bb h

2 trapézio = +?

Acompanhe como o arquiteto realizou os cálculos.

A Bb h 2 12 85 2 50 inicial = +? = +? = () ()

Para obter a área da região onde haverá areia, ele utilizou a expressão da área do triângulo:

A bh 2 triângulo =

Para o espaço destinado ao parquinho com piso emborrachado, utilizou a expressão da área do retângulo.

Aretângulo = b ? h

Observe os cálculos do arquiteto.

A bh 2 25 2 5 tanque de areia = ? = ? = e Apiso emborrachado = b h = 10 5 = 50

Assim, ele explicou à equipe de compras que a área inicial do terreno é de 50 m2, a área da região destinada ao tanque de areia é de 5 m2 e a área da região destinada ao parquinho com piso emborrachado é de 50 m2

AMPLIANDO

Link

ÁREA de um trapézio. Khan Academy. [S l.], c2022. Disponível em: https://pt-pt.khanacademy.org/math/ 7ano/xf46753cc3e03cd2f:geometria/xf46753cc3e03cd2f:area-de-quadrilaterios/e/areas_of_trapezoids _rhombi_and_kites. Acesso em: 11 ago. 2022.

Nesse link, é possível ter acesso a problemas envolvendo o cálculo da área de trapézios.

Propor as três perguntas dadas sobre a situação da área destinada ao parque infantil –“Qual é a área do terreno que não está gramada?”, “Qual é a área da região onde será colocada areia?” e “Qual é a região destinada ao parquinho com piso emborrachado?” – e pedir aos estudantes que, em duplas, tentem repondê-las. Circular pela sala de aula e observar os procedimentos adotados por eles para realizar o cálculo de áreas de figuras poligonais. Se considerar pertinente, anotar algumas expressões na lousa, como maneira de apoiar a resolução dos estudantes.

Retomar, também, a expressão para o cálculo da área de losangos, apesar de essa figura não ter sido trabalhada na página 245 do Livro do estudante.

ORIENTAÇÕES DIDÁTICAS

Pense e responda

A investigação proposta no boxe Pense e responda favorece o desenvolvimento da habilidade EF08MA19, incentiva a inferência e a capacidade de argumentação dos estudantes. O levantamento de hipóteses, em duplas, contribui para a troca de ideias e para o desenvolvimento da empatia Espera-se que os estudantes façam estimativas e comparações entre as áreas das respectivas regiões utilizando estratégias pessoais. Circular pela sala de aula, observando como os estudantes interagem e quais são as estratégias construídas por eles. Após a retomada do cálculo da área do círculo, que será feita no próximo tema, retomar a questão e pedir aos estudantes que revejam suas ideias iniciais.

Circunferência e círculo

Antes de introduzir os conceitos de perímetro da circunferência e área do círculo, comentar com os estudantes a equivalência do hectare com o hectômetro quadrado, retomando as unidades de medida de superfície.

Fórum

Organizar a classe para ler as informações do capítulo 2 do livro Horta em pequenos espaços, publicado no site da Embrapa. Nesse capítulo do livro, os estudantes vão aprender os princípios de como cultivar uma horta em pequenos espaços. Esse tema contribui para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental e da competência geral 2.

Em seguida, organizar a turma para discutir e apontar os benefícios de uma horta caseira. Anotar na lousa as sugestões dadas pelos estudantes. As sugestões que eles vão apontar podem ser: levar a uma maneira de se alimentar mais

A equipe responsável pela aprovação e pela execução do projeto perguntou ao arquiteto se uma região de formato circular, de 2 m de diâmetro, não teria a área maior do que a da região triangular, de 2 m de base e 5 m de altura, destinada ao tanque de areia.

PENSE E RESPONDA

Responda à questão no caderno.

Converse com um colega e, utilizando estimativas e comparações entre figuras geométricas planas, respondam ao questionamento proposto ao arquiteto.

• Uma região de formato circular, de 2 m de diâmetro, tem a área maior do que a área de uma região de formato triangular, de 2 m de base e 5 m de altura? Não. Exemplo de resposta na seção Resoluções comentadas deste Manual.

CIRCUNFERÊNCIA E CÍRCULO

De acordo com a Empresa Brasileira de Pesquisa Agropecuária (Embrapa), em 2021, a área de agricultura irrigada no Brasil era de menos de 20% da área total cultivada e produzia mais de 40% dos alimentos, fibras e cultivos bioenergéticos do país. Além disso, a área irrigada por pivôs centrais atingia 1,6 milhão de hectare

GLOSSÁRIO

Hectare: unidade de medida de área, equivalente a 10 000 m2, geralmente utilizada em contextos relacionados à agricultura.

Elaborado com base em: BRITO, Sandra. Área irrigada por pivôs centrais no Brasil atinge 1,6 milhão de hectares. Embrapa. Brasília, DF, 9 mar. 2021. Disponível em: https://www.embrapa.br/busca-de-noticias/-/noticia/59843654/areairrigada-por-pivos-centrais-no-brasil-atinge-16-milhao-de-hectares. Acesso em: 23 jun. 2022.

Observe, na imagem, que a área de plantio tem o formato de círculo, e a linha que contorna essa região dá a ideia de circunferência.

Imagem aérea de região irrigada por sistema de pivô central. Chihuahua (México), 2020.

FÓRUM

Cultivo em locais pequenos

Diferentemente do que se costuma imaginar, não é necessário um espaço grande para cultivar plantas, pois muitas delas podem ser criadas em varandas e até dentro de casas e apartamentos.

Além de plantas decorativas, também é possível ter uma horta dentro de casa! A Embrapa publicou o livro Horta em pequenos espaços, em que ensina os cuidados na hora do cultivo, como preparar a terra, as técnicas para cuidar das plantas e a localização ideal para elas. Esse livro está disponível para download gratuito em: https://www.embrapa.br/busca-de-publicacoes/-/publicacao/927690/horta-em -pequenos-espacos (acesso em: 28 jun. 2022).

• Converse com os colegas sobre os benefícios de cultivar uma horta caseira, além de enfeitar o ambiente Resposta pessoal. Exemplos de resposta: Produzir o próprio alimento; eliminar o uso de agrotóxicos; utilizar o cultivo com fins terapêuticos; economizar nas compras da feira ou do mercado, entre outros.

saudável e de respeito com o meio ambiente, pois o cultivo dessas hortas elimina o uso de agrotóxicos; contato com a natureza, que pode ser terapêutico e tranquilizador; economia, por ser uma maneira mais barata de produzir o próprio alimento; melhoria da relação familiar, entre outras.

D2_AV1-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 246

Depois, os estudantes podem sugerir maneiras e ações específicas para implementar hortas em sua casa ou na de parentes, condomínios ou na própria escola. Para viabilizar essas ações,

é interessante que eles escrevam um manual a respeito da construção de uma horta em pequenos espaços. Essa atividade pode ser feita em pequenos grupos para incentivar a participação de todos e a troca de ideias. É interessante, sempre que possível, promover ações em que os estudantes sejam agentes propagadores do conhecimento adquirido. Se considerar conveniente, convidar o professor de Ciências para um trabalho interdisciplinar.

Comprimento de uma circunferência

Já estudamos que, considerando uma circunferência qualquer cujas medidas do raio e do comprimento da circunferência são r e C, respectivamente, ao dividirmos C por 2r (medida do diâmetro correspondente) obtemos um valor aproximado do número irracional p. Estudamos, também, que isso sempre ocorre, independentemente da circunferência.

C 2r =ph C = 2r ph C = 2p r

Essa fórmula permite calcular o comprimento de qualquer circunferência, conhecida a medida r do raio correspondente.

Se reunirmos à circunferência todos os pontos do interior por ela delimitado, obtemos um círculo. Acompanhe.

ORIENTAÇÕES DIDÁTICAS

Comprimento de uma circunferência

A determinação do comprimento da circunferência é apresentada nessa página. Ler com os estudantes e verificar se eles apresentam alguma dúvida. Auxiliá-los nesse caso.

Área de regiões circulares

A área de um círculo corresponde à medida da superfície ocupada por ele.

Área de regiões circulares

Para determinar a expressão para o cálculo da área do círculo, vamos utilizar a ideia de aproximação por áreas conhecidas. Observe.

Em uma cartolina, desenhamos um círculo e dividimos essa figura em 16 partes iguais, conforme indicado.

Depois, cortamos e separamos cada parte do recorte para reorganizá-las, conforme indica a figura a seguir.

Observe que a superfície do círculo foi reorganizada, e a área correspondente se aproxima da área de uma figura que conhecemos: o retângulo.

AMPLIANDO

Vídeo

Para a verificação da área do círculo, solicitar às duplas que desenhem, em uma folha de papel avulsa, dez circunferências de mesmo raio e tracem polígonos inscritos (aproximados) nessas circunferências com número de lados diferentes. O objetivo é que os estudantes percebam que, quanto maior o número de lados do polígono inscrito, mais o seu perímetro se aproxima do comprimento da circunferência e sua área se aproxima da área do círculo.

Quanto maior a quantidade de partes em que dividimos o círculo, mais o formato da composição obtida se aproxima de um retângulo.

RODA do sonho. 2012. Vídeo (9min). Publicado por Matemática Multimídia. Disponível em: https://m3.ime.unicamp.br/recursos/1173. Acesso em: 11 ago. 2022.

Esse recurso educacional apresenta justificativas para a fórmula de cálculo da área do círculo.

SAIBA QUE

ORIENTAÇÕES DIDÁTICAS

Pense e responda

Retomar as hipóteses levantadas no boxe Pense e responda da página 246 do Livro do estudante e propor aos estudantes que refaçam os cálculos, agora aplicando a fórmula da área do círculo. Validar ou refutar as ideias iniciais.

Atividades

Nessas atividades, os estudantes utilizarão o conhecimento desenvolvido ao longo do capítulo para determinar áreas de círculos e partes de círculos. Desse modo, busca-se favorecer o desenvolvimento de aspectos da habilidade EF08MA19.

Pedir aos estudantes que resolvam as atividades em duplas e, caso considerar necessário, corrigir algumas questões na lousa.

Na atividade 1, verificar se os estudantes efetuam a conversão de unidades de medida de superfície de forma adequada. Destacar que a medida do lado da lajota de cerâmica está dada em centímetro e que a área da sala na qual ela será usada foi dada em metro quadrado.

Assim, podemos calcular a área do círculo multiplicando a medida da base pela medida da altura. Observando novamente a imagem, percebemos que a medida da base é igual à metade da medida do comprimento da circunferência, e a medida da altura é equivalente à medida do raio da circunferência. Com isso, temos:

A = b h =p r r =p r2, ou seja, Acírculo =p r2

Usando a fórmula da área do círculo, vamos resolver a situação a seguir.

Uma folha de papelão tem formato circular de raio 21 cm. Qual é, em centímetro quadrado, a área ocupada por essa folha? (Usar p= 3,14.)

Área =p r² = 3,14 ? (21)² = 3,14 ? 441 = 1 384,74

Assim, a área ocupada por essa folha é de 1 384,74 cm².

PENSE E RESPONDA

Responda no caderno.

Voltando à questão da página 246 sobre a área do tanque de areia para as crianças, qual ocupa maior área: o tanque de formato circular com 2 m de diâmetro, ou o triangular de 2 m de base e 5 m de altura?

O tanque triangular.

ATIVIDADES

Responda às questões no caderno.

1. Uma lajota quadrada de cerâmica tem 15 cm de lado.

a) Qual é a área dessa lajota?

225 cm2

b) Quantas lajotas são necessárias para revestir o piso de uma sala de 45 m2 de área?

2 000 lajotas.

2. Quantas telhas francesas são necessárias para cobrir um telhado formado por duas partes, como a destacada em vermelho e com as medidas indicadas, sabendo que para cada metro quadrado de telhado são usadas 20 telhas?

1 600 telhas.

IMAGENS FORA DE PROPORÇÃO.

3. (OBMEP) Pelo centro do quadrado da Figura 1 traçam-se duas retas perpendiculares, que o dividem em quatro quadriláteros iguais. Esses quadriláteros são rearranjados em outro quadrado maior, como na Figura 2. Qual é a área do quadrado ABCD da Figura 2? Alternativa c.

6. Samuel usou 3,72 m de bordado inglês para fazer o acabamento no contorno de uma toalha de formato circular. Qual é, em metro, a medida do diâmetro dessa toalha? (Use p= 3,1.)

ORIENTAÇÕES DIDÁTICAS

a) 16 cm2

b) 25 cm2

c) 36 cm2

d) 49 cm2

e) 64 cm2

4. Beto deseja pintar as quatro paredes e o teto de uma sala cujas medidas estão indicadas na figura.

Sabendo que com cada lata de tinta é possível pintar 40 m2 de área, quantas latas de tinta Beto terá de comprar?

5. O comprimento do raio de uma circunferência corresponde, em centímetro, a uma das raízes da equação 2x2 32 = 0. Qual é o comprimento dessa circunferência? (Use p= 3,14.)

Quatro latas de tinta. 25,12 cm

AMPLIANDO

Vídeo

Na atividade 5, verificar se os estudantes retomam o cálculo da raiz de uma equação incompleta do 2o grau, da forma ax 2 + c = 0.

7. Um garoto brinca de correr sobre uma linha desenhada no chão, que lembra uma circunferência de 1 m de diâmetro. Que distância o menino percorre ao completar 100 voltas sobre essa linha? (Use p= 3,14.)

8. Um vazamento no tanque de um navio provoca o aparecimento de uma mancha circular de óleo. O raio r da mancha, t minutos depois do início do vazamento, é dado, em metro, pela fórmula = r t 5

a) Qual é, em metro, o raio da mancha após 4 minutos do início do vazamento?

b) Nesse mesmo instante, qual é, em metro quadrado, a área da mancha? (Use p= = 3,14.)

m 314 m 0,4 m 0,5024 m²

9. Considere a figura representada a seguir, composta de um quadrado sobreposto a um círculo.

A atividade 8 apresenta uma fórmula para calcular o raio de uma mancha de óleo em função do tempo de vazamento desse óleo. Ler o enunciado coletivamente e verificar se todos os estudantes compreendem o que cada uma das variáveis significa.

A atividade 9 contribui para o desenvolvimento da habilidade EF08MA19. Incentivar os estudantes a redigir enunciados claros e, ao resolverem os problemas propostos pelos colegas, a exercitar a empatia e a troca de ideias.

Com base nessa figura, elabore um problema que envolva o cálculo de área de figuras planas. Em seguida, troque o problema com um colega de modo que ele resolva o problema que você elaborou, enquanto você resolve o problema elaborado por ele. Por fim, confiram as resoluções e compartilhem as estratégias utilizadas para resolver o problema. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

ÁREA da Coroa Circular – Vivendo a Matemática – Professora Angela. 2017. Vídeo (5min55s). Publicado pelo canal Professora Angela Matemática. Disponível em: https://www.youtube.com/watch?v=jNXOsSgDrxo. Acesso em: 11 ago. 2022.

Se desejar aprofundar o estudo de áreas de regiões circulares com os estudantes, exibir a videoaula na qual é proposto um problema sobre a área de uma coroa circular.

REPRODUÇÃO/ OBMEP, 2017.

ORIENTAÇÕES DIDÁTICAS

Por toda parte

Nessa seção, os estudantes aplicarão os conceitos de áreas estudados. Tais conhecimentos serão empregados na resolução de situações que envolvem dados reais brasileiros com foco nas áreas aproximadas de estados brasileiros representados por polígonos. Esse estudo favorece o desenvolvimento da habilidade EF08MA19.

No item a da questão 1, os estudantes devem calcular a área de um trapézio isósceles. Talvez alguns estudantes não se recordem da fórmula para o cálculo da área de um trapézio. Se considerar oportuno, escrever na lousa essa fórmula. É possível também que eles resolvam o problema usando apenas triângulos e retângulos, resolvendo o problema por composição e decomposição.

Para complementar a atividade, solicitar aos estudantes que, em pequenos grupos, escolham dois estados da federação e, a partir do uso de polígonos simples, calculem a área aproximada desses estados. Nesse momento, eles precisarão retomar o conceito de escala. É uma atividade que entrelaça novos conhecimentos e conhecimentos estudados anteriormente.

ÁREAS PELO BRASIL

Você deve ter percebido que figuras geométricas planas como o quadrado, o trapézio, o triângulo, entre outras, nos possibilitam deduzir fórmulas que facilitam o cálculo de determinada área. No entanto, existem figuras para as quais não há como definir uma fórmula para fazer esse cálculo. Uma possível maneira de obter a área desse tipo de figura é utilizar uma decomposição em figuras para as quais sabemos como realizar o cálculo ou, ainda, trabalhar com áreas aproximadas dessas regiões. Atualmente, há também recursos tecnológicos que são valiosos instrumentos para esse estudo. Considerando, por exemplo, o mapa do Brasil, é possível fazer uma estimativa da área das representações no mapa, relacionando tais regiões a polígonos como triângulos, retângulos, trapézios etc. Observe, a seguir, o mapa do Brasil e uma possível representação fazendo esse tipo de aproximação.

Brasil – Político

Responda no caderno.

1. Utilizando essa estratégia, vamos calcular a área de representação de dois estados brasileiros.

a) A região ocupada pelo estado de São Paulo no mapa é aproximada por dois trapézios isósceles congruentes. Observe a figura com as medidas indicadas em quilômetro e calcule a área aproximada dessa região.

b) Aproximando a região ocupada pelo estado de Sergipe no mapa por um triângulo retângulo isósceles, calcule essa área aproximada.

000 km²

Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas Geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018.

VOLUME DE SÓLIDOS GEOMÉTRICOS

O volume de um sólido geométrico é a medida do espaço ocupado por ele. A unidade padronizada de medida de volume é o metro cúbico

UNIDADES DE MEDIDA DE VOLUME

Além do metro cúbico, existem outras unidades padronizadas de medida para expressar volumes. Confira no quadro essas unidades, dispostas em ordem decrescente, com as respectivas abreviações.

ORIENTAÇÕES DIDÁTICAS

Volume de sólidos geométricos

O estudo do volume do cubo e do bloco retangular foi iniciado em anos anteriores e, neste momento, ele é retomado e ampliado. A ideia é a discussão do volume desses sólidos geométricos em comparação com o cilindro, por exemplo. Além disso, busca-se resolver problemas mais complexos, que exijam um grau de abstração maior e que permitam relacionar este conteúdo a outros temas já estudados.

As unidades mais utilizadas para expressar medidas de volume, além do metro cúbico, são o decímetro cúbico e o centímetro cúbico. Acompanhe alguns exemplos de transformação de unidades.

• Transformar 30 000 cm3 em decímetro cúbico.

km3 hm3 dam3 m3 dm3 cm3 mm3

Como, da direita para a esquerda, cada unidade representa 1 1000 da unidade seguinte, dividimos 30 000 cm3 por 1 000. 30 000 cm3 = (30 000 : 1 000) dm3 = (30 000 0,001) dm3 = 30 dm3

• Quantos centímetros cúbicos há em 1 2 m3?

km3 hm3 dam3 m3 dm3 cm3 mm3

Como, da esquerda para a direita, cada unidade representa 1 000 vezes a unidade seguinte, multiplicamos 1 2 m³ por 1 000 000 (1 000 1 000).

1 2 m³ = 0,5 m3 = (0,5 1 000 000) cm3 = 500 000 cm3

D2_AV1-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 251 12/08/2022 17:56

É importante que os estudantes, nesse momento, consigam diferenciar as medidas lineares (utilizadas para comprimentos) das medidas de superfície (relacionadas ao cálculo de áreas) e também das medidas de volume. Se considerar oportuno, refazer na lousa uma tabela com as medidas.

Caso seja possível, construir um mural permanente com as unidades de medida de comprimento, área e volume mais usuais, seus múltiplos e submúltiplos. Isso facilita, ao longo do tempo, a memorização tanto das unidades de medida quanto de suas relações.

ILUSTRAÇÕES: EDITORIA DE ARTE

ORIENTAÇÕES DIDÁTICAS

Cubo e bloco retangular

Anotar na lousa as expressões para o cálculo do volume do cubo e do bloco retangular, associando o produto das três dimensões (comprimento, largura e altura) à palavra tridimensional. Estudo favorece o desenvolvimento da habilidade EF08MA21.

Cilindro

Para o cálculo do volume do cilindro, retomar com os estudantes o cálculo do comprimento da circunferência e o cálculo da área do círculo. Destacar alguns elementos importantes do cilindro, como suas bases, sua superfície lateral e sua altura.

Se considerar oportuno, conversar com os estudantes a respeito do Princípio de Cavalieri e apresentar a videoaula Princípio de Cavalieri – aula 17, do professor Eduardo Corrêa, com a demonstração desse princípio tão importante na determinação de volume de sólidos geométricos. Disponível em: https://www.youtube.com/ watch?v=wQpi2ZfrITw&t=82s. Acesso em: 11 ago. 2022.

CUBO E BLOCO RETANGULAR

O volume V de um cubo de aresta de medida a é dado por:

V = a3

Conforme estudamos, o cubo é um sólido geométrico cujas arestas têm medidas iguais. Podemos estabelecer uma correspondência entre as arestas destacadas no cubo representado a seguir e as três dimensões dessa figura: comprimento, largura e altura. a a a

O volume de um cubo é igual à medida da aresta correspondente elevada ao cubo.

O volume V de um bloco retangular cujas arestas destacadas na figura anterior têm medidas a, b e c é dado por:

V = a b c

Considere agora um bloco retangular, também chamado de paralelepípedo reto-retângulo. Nesse sólido, as duas bases e as faces laterais são retângulos. a b

c ILUSTRAÇÕES: EDITORIA DE ARTE

Assim como no cubo, o volume de um bloco retangular é igual ao produto das medidas associadas às três dimensões: comprimento, largura e altura. Acompanhe a resolução de um exemplo. Uma siderúrgica produz chapas metálicas maciças, com formato de bloco retangular, cujas medidas são: 3 m de comprimento por 2 m de largura e 0,5 m de altura. Qual é o volume de cada chapa?

V = a ? b ? c h V = 3 ? 2 ? 0,5 h V = 3

O volume de cada chapa é de 3 m3

CILINDRO

Sabemos que o cilindro circular reto é um sólido geométrico, portanto tem volume. Vamos lembrar de algumas características dos cilindros. base altura

base

D2_AV1-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 252

• As bases são dois círculos paralelos congruentes.

• A altura é a distância entre suas bases.

• A superfície lateral é arredondada (não é plana).

ORIENTAÇÕES DIDÁTICAS

Para compreender o cálculo do volume do cilindro, vamos retomar a maneira de calcular o volume de um bloco retangular. Como estudamos, o bloco retangular é um sólido geométrico que tem duas bases retangulares paralelas congruentes e cuja altura é a distância entre essas bases. Nesta figura, por exemplo, as bases do bloco retangular são retângulos de medidas a e b, e a altura do bloco tem medida c

c

ILUSTRAÇÕES:

EDITORIA DE ARTE a b

A área do retângulo correspondente às bases desse bloco retangular é dada por a b (área da base). O volume desse bloco retangular é dado por V = a b c, mas podemos reescrevê-la substituindo a b por Abase (área da base) e c por h (altura). Observe.

Vbloco retangular = a b c Vbloco retangular = Abase h

área da base altura

Utilizando essa estratégia, podemos determinar o volume de outros sólidos geométricos retos que apresentam duas bases paralelas congruentes e cuja altura é a distância entre essas bases.

Assim, o volume de um cilindro reto também é dado pelo produto da área da base pela altura. Como a base do cilindro é um círculo, e lembrando que sua área é A =p r2, temos:

Vcilindro = Abase h Vcilindro =p r2 h

Considere o exemplo a seguir. Calcule o volume de um cilindro reto cuja medida do raio da base é 5 cm, e a medida da altura é 10 cm. Vamos utilizar p= 3,14.

Utilizando a expressão que possibilita calcular o volume do cilindro, temos:

Vcilindro =p r2 ? h = 3,14 ? (5)2 ? 10 = 785

Assim, o volume desse cilindro é de 785 cm3

DESCUBRA MAIS

MATEMÁTICA em toda parte 2 (HD) – Ep. 1: Agricultura. 2021. Vídeo (12min40s). Publicado pelo canal Prof. Leo Akio. Vídeo originalmente produzido pela Segunda Feira Filmes, 2013. Disponível em: https:// www.youtube.com/watch?v=hIoDXbBnkJE&t=3s. Acesso em: 23 de jun. 2022.

O Episódio 1 da série Matemática em toda a parte 2 trata de áreas e volumes de sólidos geométricos no contexto da agricultura. Os conceitos relacionados a blocos retangulares e cilindros são abordados por meio de aplicações na produção de grãos. Explora-se, ainda, a comparação de volumes de sólidos que têm a mesma área lateral.

Estabelecer a relação entre o volume do paralelepípedo e do cilindro, destacando que a base de um cilindro sempre será um círculo. Em seguida, propor a resolução individual, da situação dada no Livro do estudante. Circular pela sala de aula, observando se os estudantes identificam corretamente os valores que serão usados no cálculo.

Descubra mais

Exibir o vídeo indicado como sugestão no boxe Descubra mais Após a exibição, conversar com os estudantes sobre os usos de blocos retangulares e cilindros no armazenamento de grãos. Reflexões sobre agricultura e seus recursos contribuem para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental e da competência específica 3 da área de Matemática.

D2-MAT-F2-2103-V8-U8-242-261-LA-G24.indd

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades desse bloco buscam consolidar o cálculo do volume de cubos, blocos retangulares e cilindros.

Na atividade 1, além do cálculo do volume, os estudantes são convidados a determinar também a área total de cada sólido. Se considerar oportuno, realizar a planificação, na lousa, tanto do cubo quanto do bloco retangular. A visualização dos sólidos “desmontados” contribui para o entendimento do cálculo da área.

A atividade 3 solicita aos estudantes que analisem as dimensões de cada uma das caixas, verificando em qual delas é possível inserir o objeto de 80 cm de aresta. A escolha deve ser feita de modo que sobre o menor espaço livre em seu interior.

Na atividade 6, incentivar os estudantes a trocar os problemas entre si para que um resolva o problema elaborado pelo outro. Por fim, pedir que confiram as resoluções e que compartilhem as estratégias utilizadas para resolver.

ATIVIDADES

Responda às questões no caderno.

1. Calcule o volume de cada sólido geométrico a seguir. a) b)

6. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

5. Determine o volume de cada cilindro a seguir. (Use p= 3,14.)

28,26 cm³

2. O bloco retangular da figura tem 45 cm³ de volume. Determine a medida da altura desse bloco retangular. 3 cm

x 5 cm

3. (Enem/MEC) Um casal realiza sua mudança de domicílio e necessita colocar numa caixa de papelão um objeto cúbico, de 80 cm de aresta, que não pode ser desmontado. Eles têm à disposição cinco caixas, com diferentes dimensões, conforme descrito:

• Caixa 1: 86 cm x 86 cm x 86 cm

• Caixa 2: 75 cm x 82 cm x 90 cm

• Caixa 3: 85 cm x 82 cm x 90 cm

• Caixa 4: 82 cm x 95 cm x 82 cm

• Caixa 5: 80 cm x 95 cm x 85 cm

O casal precisa escolher uma caixa na qual o objeto caiba, de modo que sobre o menor espaço livre em seu interior.

A caixa escolhida pelo casal deve ser a de número

Alternativa c.

b) 2. c) 3. d) 4. e) 5.

a) 1.

4. As medidas das arestas de um cubo medem x cm. Se dobrarmos as medidas das arestas, dobraremos o volume? Justifique sua resposta.

Não, pois o volume ficará multiplicado por 8.

D2-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 254

62,8 cm³

a) b)

6. Considere o molde de acrílico representado, em formato externo cúbico, cortado na parte central da base por um vão em formato de bloco retangular.

13 cm

13 cm 1 13 cm 7 cm 7 cm

Utilizando essa figura, elabore um problema que envolva o cálculo de volume.

7. (Enem/MEC) Uma fábrica brasileira de exportação de peixes vende para o exterior atum em conserva, em dois tipos de latas cilíndricas: uma de altura igual a 4 cm e raio 6 cm, e outra de altura desconhecida e raio de 3 cm, respectivamente, conforme figura. Sabe-se que a medida do volume da lata que possui raio maior, V1, é 1,6 vezes a medida do volume da lata que possui raio menor, V 2.

A medida da altura desconhecida vale

a) 8 cm.

b) 10 cm.

c) 16 cm.

d) 20 cm. e) 40 cm.

Alternativa b.

A capacidade de certo recipiente corresponde à quantidade de líquido que cabe dentro dele. A unidade padronizada de medida de capacidade é o litro

UNIDADES DE MEDIDA DE CAPACIDADE

Além do litro, existem outras unidades padronizadas de medida para expressar capacidades.

Confira no quadro essas unidades, dispostas em ordem decrescente, com as respectivas abreviações.

Múltiplos do litro Unidade fundamental Submúltiplos do litro

Quilolitro Hectolitro Decalitro Litro Decilitro Centilitro Mililitro

ORIENTAÇÕES DIDÁTICAS

Unidades de medida de capacidade

A relação entre as unidades de medida de capacidade e as unidades de medida de volume será feita na próxima etapa. Neste momento, é importante que os estudantes compreendam a relação entre litro e mililitro. Retomar a multiplicação e a divisão de números racionais por potências de 10.

Se considerar oportuno, propor a resolução dos exemplos apresentados, em duplas.

A unidade mais utilizada para expressar capacidades, além do litro, é o mililitro Acompanhe um exemplo de transformação de unidades.

• Expressar 35 litros em mililitros.

35 L = (35 10 10 10) mL = (35 1 000) mL = 35 000 mL

Acompanhe a situação a seguir.

Cristina vai comprar suco de frutas em embalagens de 1 L para servir aos convidados em uma festa. Ela convidou 20 pessoas e estima que cada convidado beba cerca de 3 copos de 200 mL. Quantas embalagens de suco ela terá de comprar?

Repare que cada convidado deverá tomar 600 mL de suco (3 200 = 600).

Como são 20 convidados, o consumo será de 20 600 = 12 000, ou seja, 12 000 mL de suco.

Além disso, 1 L = 1 000 mL; portanto, temos que 12 000 mL = 12 L.

Logo, Cristina precisará comprar 12 embalagens de 1 L de suco.

AMPLIANDO

D2_AV1-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 255

Atividade complementar

(Enem/MEC) Alguns exames médicos requerem uma ingestão de água maior do que a habitual. Por recomendação médica, antes do horário do exame, uma paciente deveria ingerir 1 copo de água de 150 mililitros a cada meia hora, durante as 10 horas que antecederiam um exame. A paciente foi a um supermercado comprar água e verificou que havia garrafas dos seguintes tipos:

• Garrafa I: 0,15 litro

• Garrafa II: 0,30 litro

• Garrafa III: 0,75 litro

• Garrafa IV: 1,50 litro

• Garrafa V: 3,00 litros

A paciente decidiu comprar duas garrafas do mesmo tipo, procurando

atender à recomendação médica e, ainda, de modo a consumir todo o líquido das duas garrafas antes do exame. Qual o tipo de garrafa escolhida pela paciente? a) I b) II c) III d) IV e) V

Resolução da atividade

150 mililitros a cada meia hora = 300 mililitros a cada hora

Em 10 horas, ela deveria ingerir 3 000 mililitros, (3 L). Assim, ela deve

ria comprar 2 garrafas de 1,5 litro.

Alternativa d.

ORIENTAÇÕES DIDÁTICAS

Pense e responda

O objetivo da atividade é mostrar aos estudantes que 1 litro é a capacidade de um recipiente cúbico com 1 dm de aresta. Desse modo, favorece-se o desenvolvimento da habilidade EF08MA20. Solicitar aos estudantes que construam a caixa descrita na atividade. Socializar as ideias e estratégias utilizadas.

Saiba que

Discutir as relações entre as medidas apresentadas no boxe Saiba que, propondo algumas conversões na lousa, para checar o entendimento dos estudantes.

EQUIVALÊNCIA ENTRE O DECÍMETRO CÚBICO E O LITRO

Mariana vai realizar um experimento despejando todo o conteúdo da garrafa de água no recipiente em formato de cubo representado na figura a seguir.

PENSE E RESPONDA

Responda no caderno.

Em seu entendimento, nesse recipiente cúbico cabe todo o conteúdo de água da garrafa? Vai faltar água para encher completamente o recipiente? Ou vai transbordar?

Se possível, construa um modelo de recipiente cúbico como esse, utilizando papelão, revestimento plástico e fita adesiva, e simule essa situação. Anote suas conclusões. Lembre-se de que 1 dm = 10 cm.

Respostas pessoais. Espera-se que os estudantes respondam que todo o conteúdo cabe no recipiente. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Sabemos que o volume de um cubo que tem 1 dm de aresta é 1 dm3. Além disso, podemos verificar que com um litro de água é possível encher, até a borda, um recipiente cúbico com esse formato. Esse fato nos permite escrever a seguinte relação.

1 L = 1 dm3

Acompanhe a seguinte situação.

Brenda estava pesquisando o preço de aquários em uma loja on-line e gostou de um modelo com formato de bloco retangular. Esse modelo tem 50 cm de comprimento, 30 cm de largura e 40 cm de altura. Quantos litros de água cabem nesse aquário?

Para descobrir quantos litros de água cabem nesse aquário, calculamos o volume do bloco retangular associado a ele utilizando as medidas expressas em decímetro.

Como 50 cm = 5 dm, 30 cm = 3 dm e 40 cm = 4 dm, temos:

V = 5 ? 3 ? 4 = 60, ou seja, 60 dm3

Assim, como 1 dm3 = 1 L, concluímos que cabem 60 L de água nesse aquário.

D2_AV1-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 256

AMPLIANDO

Vídeo

Modelo de aquário 50 cm x 40 cm x 30 cm.

SAIBA QUE

Como 1 dm3 = 1 0 00 cm3 e 1 L = 1 0 00 mL, temos que 1 cm3 = 1 mL.

O LITRO e o decímetro cúbico. 2020. Vídeo (5min41s). Publicado pelo canal Francisco de Assis Costa Assis Costa. Disponível em: https://www.youtube.com/watch?v=qnd iLI5Z2g&t=10s. Acesso em: 11 ago. 2022.

Nesse vídeo, é possível ver o experimento com a garrafa PET de 1 litro e o cubo de 1 dm de aresta.

EQUIVALÊNCIA ENTRE O METRO CÚBICO E O LITRO

Um caminhão-pipa está sendo abastecido para distribuir água em uma região. Em cada viagem, esse caminhão distribui 20 metros cúbicos de água.

Quantos litros de água são distribuídos em cada viagem desse caminhão-pipa?

Para responder a essa questão, vamos descobrir quantos litros equivalem a 1 metro cúbico. Para isso, podemos inicialmente explorar a relação entre o metro cúbico (m3) e o decímetro cúbico (dm3).

Sabemos que um cubo de 1 m3 de volume tem arestas de 1 m de comprimento. Além disso, 1 m = 10 dm. Com isso, temos o seguinte:

1 m3 = 1 m ? 1 m ? 1 m = 10 dm ? 10 dm ? 10 dm = 1 0 00 dm3

Como 1 m3 = 1 0 00 dm3 e 1 dm³ = 1 L, concluímos que 1 m3 equivale a 1 0 00 litros.

1 m3 = 1 0 00 L

Assim, como em cada viagem o caminhão-pipa distribui 20 m3 de água, concluímos que são distribuídos 20 0 00 L de água em cada viagem.

ATIVIDADES

Responda no caderno.

1. Ao realizar a leitura do hidrômetro de uma casa, foi verificado que o consumo de água no último mês foi de 18 m3. De acordo com essa informação, responda.

a) Quantos litros de água foram consumidos nessa casa no último mês?

ORIENTAÇÕES DIDÁTICAS

Equivalência entre o metro cúbico e o litro

Propor a situação apresentada no Livro do estudante, solicitando à turma que identifique qual informação desconhecem e que é necessária para a construção da solução. Espera-se que eles identifiquem que ainda não conhecem a relação entre o metro cúbico e o litro. Esse estudo favorece o desenvolvimento da habilidade EF08MA20.

Atividades

Na atividade 1, certificar-se que os estudantes conhecem um hidrômetro e seu funcionamento. Caso sinta necessidade, explicar em sala de aula sua função e seu funcionamento; outra possibilidade de encaminhamento é solicitar que eles realizem uma breve pesquisa a fim de obter essas informações.

18 000 litros. 30 vezes.

b) Sabendo que nessa casa o reservatório de água tem o formato de bloco retangular cujas medidas internas são 1,5 m x 0,8 m x 0,5 m, quantas vezes é possível encher esse reservatório com a quantidade de água consumida no último mês?

AMPLIANDO

Links

• BRASIL. Portaria no 590, de 2 de dezembro de 2013. Brasília, DF: Inmetro, 2013. Disponível em: http://www.inmetro.gov.br/legislacao/rtac/pdf/RTAC00 2050.pdf. Acesso em: 11 ago. 2022.

• POZEBON, Simone; LOPES, Anemari Roesler Luersen Vieira. Grandezas e medidas: surgimento histórico e contextualização curricular. In: CONGRESSO

M odelo de hidrômetro, instrumento utilizado para medir o consumo de água nas residências.

INTERNACIONAL DE ENSINO DE MATEMÁTICA, 6., 2013, Canoas. Anais [...]. Canoas: Universidade Luterana do Brasil, 2013. Disponível em: http:// www.conferencias.ulbra.br/index.php/ciem/vi/paper/ viewFile/971/908. Acesso em: 11 ago. 2022.

Acessar os links para mais informações a respeito das unidades de medida em uso no país e seu surgimento histórico.

Caminhão-pipa sendo abastecido. Salvador (BA), 2017.

JOA SOUZA/SHUTTERSTOCK.COM

JOA SOUZA/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Tratamento da informação

Enfatizar com os estudantes o fato de um gráfico ser mais apropriado do que o outro a depender dos dados neles apresentados, como foi estudado na Unidade 7

A discussão proposta na seção Tratamento da informação refere-se às fontes de energia renováveis e não renováveis, contribuindo para o desenvolvimento dos Temas Contemporâneos Transversais

Ciência e Tecnologia e Educação Ambiental, da competência geral 7 e da competência específica 6 da área de Matemática. Pedir aos estudantes que observem que o gráfico de barras apresenta uma dupla comparação. É possível comparar a participação de cada uma das fontes de energia na oferta interna de energia, observando a relação da parte em relação ao todo e, além disso, esse gráfico permite comparar a OIE no Brasil, no mundo e na Organização para a Cooperação e Desenvolvimento Econômico (OCDE). Destacar que os dados apresentados se referem a anos diferentes e orientar os estudantes a identificar esse tipo de informação no gráfico. Ressaltar que o gráfico de linhas mostra a evolução da participação das fontes renováveis na OIE no Brasil ao longo de 20 anos. Reforçar que esse tipo de gráfico é mais adequado quando se busca mostrar o comportamento de uma ou mais variáveis, a partir dos dados associados a elas, ao longo do tempo. Ele também permite comparar os dados de diferentes variáveis, em um intervalo, simultaneamente.

INFORMAÇÃO TRATAMENTO DA

ANÁLISE DE GRÁFICOS

A produção de energia no Brasil e no mundo ocorre por meio de fontes de energia renováveis, consideradas inesgotáveis, e de fontes de energia não renováveis, consideradas finitas e esgotáveis. São exemplos de fontes de energia renováveis: hídrica, solar, eólica, biomassa, geotérmica e oceânica. Elas são consideradas limpas por emitirem menos gases de efeito estufa se comparadas às fontes não renováveis (petróleo, carvão mineral, gás natural e nuclear).

Acompanhe no gráfico a seguir uma comparação entre a participação dessas fontes de energia na Oferta Interna de Energia (OIE) do Brasil, do mundo e dos países que compõem a Organização para a Cooperação e Desenvolvimento Econômico (OCDE), nos respectivos anos indicados no gráfico.

Comparação internacional da participação das fontes renováveis na Oferta Interna de Energia (OIE)

Fonte: BRASIL. Ministério de Minas e Energia. Atlas da Eficiência Energética – Brasil 2021: Relatório de indicadores. Brasília, DF: MME, [2021?]. p. 15. Disponível em: https:// www.epe.gov.br/sites-pt/publicacoes

-dados-abertos/publicacoes/ PublicacoesArquivos/publicacao-651/ Atlas2021_PT_2022_02_04.pdf. Acesso em: 23 jun. 2022.

Repare, agora, como ocorreu no Brasil, ao longo dos últimos anos, a evolução da participação das fontes renováveis na produção de energia.

Evolução da participação das fontes renováveis na Oferta Interna de Energia (OIE) no Brasil – 2000 a 2020

Fonte: BRASIL. Ministério de Minas e Energia. Atlas da Eficiência Energética –Brasil 2021: Relatório de indicadores. Brasília, DF: MME, [2021?]. p. 15. Disponível em: https://www.epe.gov.br/ sites-pt/publicacoes

-dados-abertos/publicacoes/ PublicacoesArquivos/ publicacao-651/Atlas2021_ PT_2022_02_04.pdf. Acesso em: 23 jun. 2022.

Responda às questões no caderno.

1. Compare os dois gráficos da página anterior e os dados neles apresentados. Embora eles tragam informações referentes à mesma temática, que diferenças podemos verificar entre essas representações?

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

2. No gráfico que mostra a evolução da participação das fontes renováveis na Oferta Interna de Energia no Brasil de 2000 a 2020, em que período podemos identificar a maior queda na participação das fontes renováveis de energia?

De 2009 a 2014.

3. Agora, analise o gráfico a seguir, que apresenta dados referentes à produção de energia elétrica no Brasil, de 2001 a 2019, e a participação das fontes renováveis nessa produção, de acordo com pesquisa da revista Pesquisa FAPESP. Em seguida, responda às questões.

Geração de energia elétrica por tipo de fonte (TWh) e a participação das fontes renováveis (%) – 2001-2019

ORIENTAÇÕES DIDÁTICAS

Fonte: GERAÇÃO de energia elétrica quase dobra de valor desde 2001, mas mantém perfil limpo. Pesquisa FAPESP, São Paulo, ed. 297, nov. 2020. Disponível em: https://revistapesquisa.fapesp.br/geracao-de-energiaeletrica-quase-dobra-de-valor-desde-2001-mas-mantem-perfil-limpo/. Acesso em: 23 jun. 2022.

Maior participação: 2009; menor participação: 2015.

a) Analisando o gráfico de linha, correspondente à participação de fontes renováveis na produção de energia elétrica no Brasil, em qual ano identificamos a maior participação? E a menor?

b) Observe o período de 2011 a 2015, no qual a participação de fontes renováveis na produção de energia elétrica no Brasil continuou a cair, e repare na composição das colunas do gráfico. O que você percebe em relação à produção de energia elétrica no Brasil nesse período e à participação de fontes não renováveis nessa produção?

c) Em seu entendimento, por que foi utilizado o gráfico de linha para indicar o percentual da participação das fontes renováveis na geração de energia elétrica e não outro tipo de gráfico? Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

D2_AV2-MAT-F2-2103-V8-U8-242-261-LA-G24.indd 259

Na questão 3, enfatizar com os estudantes que o eixo da esquerda representa a geração anual de energia elétrica, em Tera Watt-hora e que este eixo orienta a altura das colunas. Por outro lado, o eixo da direita indica a participação de fontes renováveis na geração de energia elétrica, em porcentagem, orientando a evolução da linha no período considerado. Destacar que o gráfico de linha indica uma relação parte-todo ao considerar a participação das fontes renováveis na geração de energia elétrica em comparação com todas as fontes de geração e por isso apresenta dos dados em porcentagem. Nesse sentido, esclarecer que, embora em 2011, 2017 e 2019 as colunas indiquem um destaque para a geração de energia por meio de fontes renováveis, ao considerarmos a relação parte-todo, essa participação ainda não supera o que ocorrera em 2009, com base nos dados representados pela linha. Orientar os estudantes a observar que no período em que a participação de fontes renováveis na produção de energia elétrica no Brasil diminuiu (de acordo com o gráfico de linha), houve aumento no uso de fontes não renováveis; além disso, que uma hipótese para essa redução está relacionada com a crise hídrica no país, visto que as hidrelétricas têm papel predominante na matriz energética brasileira. Comentar que isso também impacta no preço da energia.

17:25

3 b) Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

ORIENTAÇÕES DIDÁTICAS

Retomando o que aprendeu

Nessa seção, exploram-se questões envolvendo os conteúdos desenvolvidos na Unidade. Propor aos estudantes que resolvam as questões desse bloco de atividades em duplas ou trios, discutindo cada questão. Pedir aos estudantes que registrem no caderno o procedimento utilizado em cada caso, resgatando os conceitos trabalhados na Unidade. Mais uma vez, incentivá-los a procurar no Livro do estudante os conceitos em que tiveram dificuldade.

Orientar os estudantes a destacar as informações importantes do enunciado e o que se pede. Se for necessário, eles devem reproduzir os desenhos apresentados ou elaborar outros que traduzam a situação descrita.

Realizar um levantamento das principais dificuldades e retomar os assuntos na lousa. Para a correção, chamar estudantes de diferentes grupos para resolver, na lousa, as questões que geraram mais dificuldades.

Responda às questões no caderno.

1. Sandro vai revestir o piso de uma varanda com lajotas de formato quadrado cuja medida do lado está indicada na figura a seguir.

4. Considerando p= 3,14, calcule a área da figura a seguir, em centímetro quadrado.

Alternativa c.

Sabendo que essa varanda é retangular, de 3,60 m por 6,90 m, quantas lajotas serão necessárias para revestir esse piso?

a) 196 lajotas.

b) 248 lajotas.

c) 256 lajotas.

d) 276 lajotas.

e) 300 lajotas.

2. (OBMEP) O quadrado [a seguir] está dividido em dois triângulos e um quadrilátero. O triângulo amarelo tem o dobro da área do triângulo azul. Qual é a área do quadrilátero rosa?

a) 11

b) 11,04 c) 11,14 d) 11,24 e) 12,14

5. (OBMEP) Na figura temos um retângulo com área igual a 120 cm2, um círculo com área igual a 81 cm2 e um triângulo com área igual a 29 cm2. Qual é a diferença entre a soma das áreas das regiões azuis e a área da região vermelha?

a) 68 cm²

b) 55 cm²

c) 35 cm²

d) 29 cm²

e) 10 cm²

Alternativa a.

a) 36 cm2

b) 48 cm2 c) 52 cm2 d) 56 cm2 e) 60 cm2

3. A medida do raio de uma circunferência, em centímetro, é uma das soluções da equação x 2 25 = 0. Qual é a área do círculo delimitado por essa circunferência? (Considere p= 3,14.)

a) 68,5 cm²

b) 78,5 cm²

c) 88,5 cm²

d) 98,5 cm²

e) 108,5 cm²

Alternativa d. Alternativa c. Alternativa b.

6. (Enem/MEC) A maior piscina do mundo, registrada no livro Guiness, está localizada no Chile, em San Alfonso del Mar, cobrindo um terreno de 8 hectares de área.

Sabe-se que 1 hectare corresponde a 1 hectômetro quadrado.

Qual é o valor, em metros quadrados, da área coberta pelo terreno da piscina?

a) 8

b) 80 c) 800 d) 8 000 e) 80 000

Alternativa e.

7. Observe a imagem a seguir, pense na situação relacionada e elabore um

REPRODUÇÃO/OBMEP, 2019.

REPRODUÇÃO/OBMEP, 2019.

REPRODUÇÃO/OBMEP, 2018.

EDITORIA DE ARTE

7. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

problema que envolva o cálculo de área de figuras planas.

Quantos recipientes serão necessários para acondicionar toda essa quantidade de óleo?

ORIENTAÇÕES DIDÁTICAS

Um novo olhar

Representação de uma região que está sendo loteada.

8. Uma empresa comprou 100 barris contendo 120 litros de óleo em cada barril. Essa quantidade de óleo deverá ser envasilhada em recipientes cuja capacidade de cada um é 750 mililitros.

UM NOVO OLHAR

9. (OBMEP) Cada uma das 5 xícaras da figura está cheia só com café, só com leite ou só com suco. No total, a quantidade de café é o dobro da de suco. Nenhuma das bebidas está em mais de 2 xícaras diferentes. Quais as xícaras que contêm leite?

16 000 recipientes. Alternativa e.

a) apenas a xícara I

b) as xícaras III e IV

c) as xícaras II e V

d) as xícaras III e V

e) as xícaras IV e V

Não. Exemplo de resposta: Para fazer essa afirmação, é necessário conhecer a capacidade de cada reservatório.

Nesta Unidade, aprofundamos o estudo sobre a área de figuras geométricas planas e exploramos o cálculo da área do círculo. Retomamos o estudo do volume de cubos e de blocos retangulares e relembramos as características do cilindro e o cálculo do volume desse sólido geométrico. Além disso, retomamos o estudo da grandeza capacidade e verificamos a equivalência entre as unidades de medida de volume e as unidades correspondentes de medida de capacidade.

Na abertura desta Unidade você foi convidado a refletir acerca da capacidade dos reservatórios de água, que abastecem a região da Grande São Paulo, e dos impactos da crise hídrica para o abastecimento de água nos centros urbanos.

Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

• Considerando apenas as porcentagens registradas no mapa apresentado na abertura desta Unidade, podemos afirmar, por exemplo, que um reservatório com maior porcentagem continha, naquele dia, maior volume de água do que um reservatório cuja porcentagem indicada era menor? Justifique sua resposta.

• Considerando as grandezas e unidades de medida estudadas, quais você costuma utilizar no dia a dia? Como você explicaria a um colega a diferença entre volume e capacidade?

Resposta pessoal. Exemplo de resposta: Espera-se que os estudantes percebam que o volume representa o espaço ocupado por um corpo, enquanto a capacidade de um recipiente está relacionada a quanto esse recipiente é capaz de armazenar.

Os questionamentos existentes no encerramento desta Unidade possibilitam reflexões a respeito das aprendizagens individuais, além de uma breve retomada dos conteúdos apresentados. É importante que os estudantes respondam individualmente a cada uma das questões para que, desse modo, possam perceber o que aprenderam e as possíveis dúvidas que ainda tenham a respeito de determinado assunto abordado.

Um ponto a ser ressaltado no encerramento desta Unidade é a interpretação de textos que envolvem valores numéricos e a utilização de conhecimentos matemáticos para uma correta interpretação dos dados.

AMPLIANDO

Atividade complementar

Um reservatório com capacidade para armazenar 10 m 3 de água estava totalmente cheio quando dele foram retirados 2 200 L de água. Em seguida, foi retirada a metade da quantidade de água que restou. Quantos litros de água ainda restam nesse reservatório?

Resolução da atividade

10 m3 = 10 000

Restam 3 900 L de água no reservatório.

Questionar os estudantes acerca da seguinte situação: “Quem não possui determinados conhecimentos matemáticos consegue realizar uma interpretação de texto ou de gráfico da mesma maneira que uma pessoa que possui?”; “Será que haverá diferença entre essas interpretações? Por quê?”; “Quais são os conhecimentos matemáticos importantes nesse tipo de interpretação?”. O objetivo desses questionamentos é levar os estudantes a notar que a Matemática é uma ferramenta indispensável para o pleno exercício da cidadania, pois sem ela acabamos por fazer uma interpretação fragmentada das informações, o que nos impede de ter uma visão do todo e, portanto, uma análise mais completa da situação. Desse modo, favorece-se o desenvolvimento da competência geral 1.

Competências gerais:

• 1, 4 e 9

Competências específicas:

• 3, 5 e 6

Habilidades:

Álgebra

• EF08MA12

• EF08MA13

Probabilidade e estatística

• EF08MA23

Temas Contemporâneos

Transversais:

• Ciência e Tecnologia

• Diversidade Cultural

• Educação para o Trânsito

• Trabalho

• Educação Ambiental

INTRODUÇÃO À UNIDADE

Esta Unidade está organizada em cinco capítulos e apresenta os conteúdos por meio de exemplos contextualizados e atividades diversificadas, além de trazer seções com temas que contribuem para a formação integral dos estudantes, favorecendo o desenvolvimento das competências gerais 1, 4 e 9.

O primeiro capítulo apresenta os conceitos de razão e proporção e das grandezas diretamente e não proporcionais, iniciando a abordagem da habilidade EF08MA12.

O segundo capítulo aborda algumas razões especiais, como a velocidade média, a escala, a densidade de um corpo e a densidade demográfica. No terceiro capítulo, aprofunda-se o estudo das grandezas diretamente proporcionais e de sua representação gráfica; no quarto capítulo, estudam-se grandezas inversamente proporcionais. O conteúdo desses capítulos favorece o desenvolvimento das habilidades EF08MA12 e EF08MA13. No quinto capítulo, estuda-se regra de três simples e composta.

9 ESTUDO DE GRANDEZAS

Resoluções desta Unidade na seção Resoluções comentadas deste Manual.

O uso de escala na Engenharia e na Arquitetura

Você já teve a oportunidade de analisar a planta baixa de uma edificação ou observar alguma maquete que represente uma construção ou um conjunto de construções como um bairro, por exemplo?

Como nessas representações é impossível usar as reais medidas de comprimento, profissionais que trabalham com Arquitetura, Engenharia Civil, Design, entre outros, utilizam o conceito de escala

Isso possibilita, por exemplo, verificar a relação entre a medida do comprimento de uma parede da sala de aula e a medida do comprimento da representação correspondente em uma planta baixa.

Visitantes observando uma maquete em escala 1 : 25 de edifícios famosos da cidade de Nova York (Estados Unidos), no Parque Temático Tobu World Square. Nikko (Japão), 2016.

A Unidade é permeada por seções que trazem informações sobre contextos de relevância social, como a discussão sobre fake news, a apresentação do Dia Internacional da Tolerância e da lei que indica a quantidade mínima de funcionários reabilitados ou com deficiência que uma empresa deve ter em seu quadro, os quais colaboram com o desenvolvimento de diversas competências gerais e específicas e Temas Contemporâneos Transversais.

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 262

OBJETIVOS

• Compreender os conceitos de razão e proporção.

• Reconhecer grandezas proporcionais e não proporcionais.

• Resolver problemas envolvendo grandezas diretamente proporcionais e identificar essa relação no plano cartesiano.

• Resolver problemas envolvendo grandezas inversamente proporcionais.

CARL COURT/GETTY IMAGES

Converse com os colegas sobre a imagem e responda no caderno às questões a seguir.

• Você já observou uma maquete ou uma planta baixa? Identifique na imagem o que nos permite afirmar que trata-se de uma maquete. Pesquise em quais situações é comum ouso desses recursos.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

• Meça as paredes da sala de aula e faça o esboço de uma delas para representá-la. No desenho, use 1 centímetro para representar 1 metro de comprimento real. Nesse caso, a escala utilizada no esboço é de 1 para 100, a qual é indicada por 1 : 100. Resposta pessoal.

ORIENTAÇÕES DIDÁTICAS

Abertura de Unidade

O tema trabalhado nessas páginas contribui para o desenvolvimento da competência geral 4 e da competência específica 3 da área de Matemática. Conversar com os estudantes a respeito das questões que aparecem na abertura desta Unidade. Ao solicitar a eles que meçam as paredes da sala de aula, verificar como realizam esse procedimento.

Na seção Por toda parte, o Dia Internacional da Tolerância é apresentado aos estudantes, como forma de fazê-los refletir sobre as intolerâncias e injustiças do mundo atual, contribuindo para o desenvolvimento do Tema Contemporâneo Transversal Diversidade Cultural, das competências gerais 1 e 9 e da competência específica 5 da área de Matemática.

Dando sequência ao tema tolerância, na seção Tratamento da informação, os estudantes são convidados a ler e compreender a lei que especifica a quantidade de vagas que devem ser preenchidas por pessoas reabilitadas ou com deficiência em uma empresa com mais de 100 empregados. Essa discussão contribui para o desenvolvimento do Tema Contemporâneo Transversal Trabalho, das competências gerais 4 e 9 e da competência específica 3 da área de Matemática.

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 263

• Resolver problemas de regra de três simples e composta.

• Interpretar informações apresentadas em gráficos de setores e tabelas.

JUSTIFICATIVAS DOS OBJETIVOS

13/08/22 19:07

Nesta Unidade, apresenta-se o estudo das grandezas diretamente proporcionais e inversamente proporcionais, contribuindo para o desenvolvimento das habilidades EF08MA12 e EF08MA13.

No boxe Fórum, discute-se sobre os perigos da propagação das fake news, contribuindo para o desenvolvimento da competência geral 9.

Na seção Tecnologias, os estudantes devem construir um programa em blocos, usando a linguagem Scratch, como forma de desenvolver o pensamento computacional

ORIENTAÇÕES DIDÁTICAS

Razão e proporção

Neste momento, são retomados os conceitos de razão e proporção para que, na sequência, sejam explorados, com mais profundidade, o reconhecimento de relações proporcionais e não proporcionais entre grandezas.

GRANDEZAS CAPÍTULO1

RAZÃO E PROPORÇÃO

Acompanhe a situação a seguir para retomar o estudo dos conceitos de razão e proporção. Bruna contratou uma equipe formada por dois pedreiros e um pintor para realizar uma reforma em sua casa. A equipe deu a ela um prazo de 60 dias para concluir a obra. Desses 60 dias, 15 serão utilizados para fazer a pintura e os últimos ajustes de acabamento. Podemos escrever a razão entre a quantidade de dias utilizados para fazer a pintura e os últimos ajustes de acabamento e o total de dias da reforma. Essa razão é dada por 15 60 ou 15 : 60.

Considerando a e b dois números racionais, com b 5 0, denomina-se razão entre a e b ou razão de a para b o quociente a b ou a : b.

Podemos ler a razão a b ou a : b como razão de a para b ou a está para b ou simplesmente a para b

Analisando a situação anterior, podemos verificar que, de cada 4 dias de reforma, 1 dia é destinado à realização da pintura e de pequenos ajustes de acabamento. Isso também pode ser indicado pela razão 1 4

Repare que essas razões são equivalentes, o que nos permite escrever a seguinte igualdade:

15 60 1 4 =

AMPLIANDO

A

essa

igualdade, damos o nome de proporção

A proporção é uma igualdade entre duas razões. De acordo com a propriedade fundamental das proporções, temos:

a

b c d ad bc =k?=

Verificando a propriedade fundamental das proporções no exemplo anterior, temos: 15 60 1 4 = k 15 ? 4 = 60 ? 1.

Atividade complementar

No Campeonato Anual de Futebol de uma escola, a equipe do 8 o ano A acumulou 36 pontos dos 57 disputados. Qual foi o aproveitamento dessa equipe?

Resolução da atividade

Para calcular o aproveitamento da equipe, os estudantes deverão compor a razão que relaciona o total de pontos acumulados pelo total de pontos disputados: aproveitamento = totald ep ontosacu mu lados totald ep ontosd isputados 36 57 12 19 ==1 0,63 Assim, o aproveitamento dessa equipe foi de, aproximadamente, 63%.

Pintor aplicando a última demão de tinta na parede.

DMITRY KALINOVSKY/SHUTTERSTOCK.COM

GRANDEZAS PROPORCIONAIS

Agora, vamos analisar algumas situações que relacionam grandezas proporcionais.

1 Leandro pesquisou o preço de algumas plantas para decorar a casa dele. A partir das informações levantadas, construiu um quadro com base no preço do vaso de cacto.

ORIENTAÇÕES DIDÁTICAS

Grandezas proporcionais

7,00

14,00

3 21,00

Repare que, quanto maior a quantidade de vasos, maior será o preço total a ser pago. Além disso, esse aumento é proporcional, pois quando dobramos a quantidade de vasos, o preço total a ser pago também dobra; quando triplicamos a quantidade de vasos, o preço total a ser pago também triplica. Com isso, dizemos que a quantidade de vasos e o respectivo preço total a ser pago são grandezas diretamente proporcionais

2 E sta placa de sinalização indica os limites de velocidade na estrada.

Suponha uma situação na qual um automóvel e um ônibus percorram um trecho entre dois municípios com velocidade média correspondente ao limite de velocidade exigido para cada veículo. Se o automóvel levar 4 horas para fazer esse percurso, em quanto tempo a mesma distância será percorrida pelo ônibus?

Construindo um quadro que relacione essas informações, temos:

Repare que o produto entre a velocidade média e o tempo de percurso, em ambos os casos, é igual a 400. Conforme a velocidade média diminui, o tempo de percurso aumenta proporcionalmente. Nesse caso, dizemos que a velocidade média e o tempo de percurso são grandezas inversamente proporcionais

PENSE E RESPONDA

Responda no caderno.

Imagine que um caminhão tenha realizado o mesmo percurso descrito na situação 2 com uma velocidade média de 50 km/h. Em quanto tempo esse caminhão realizou o percurso? Explique como você pensou para resolver.

8 horas. Espera-se que os estudantes verifiquem que precisam descobrir o número que multiplicado por 50 resulte em 400.

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 265

Explorar as situações apresentadas para que os estudantes identifiquem a presença da proporcionalidade e da não proporcionalidade. A situação 1 relaciona a quantidade de vasos de cacto e o preço a pagar, em reais. A situação 2 apresenta a relação entre a velocidade e o tempo de deslocamento de veículos. Se julgar oportuno, pedir aos estudantes que se reúnam em grupos e analisem cada uma dessas situações antes de fazer a leitura do Livro do estudante. Se julgar pertinente, discutir a importância da sinalização de velocidade em estradas e rodovias brasileiras, contribuindo para o desenvolvimento do Tema Contemporâneo Transversal Educação para o Trânsito. Propor aos estudantes que pesquisem porque há diferenças entre limite de velocidade para diferentes tipos de veículos.

Solicitar aos estudantes que, em grupo, pensem e anotem no caderno duas situações proporcionais e duas situações não proporcionais. Depois, propor que socializem com a turma para que possam apresentar suas ideias. Criar um mural de exemplos de situações de proporcionalidade e de situações nas quais as grandezas envolvidas não são proporcionais pode colaborar com o aprendizado da turma.

Pense e responda

13/08/22 19:09

Os estudantes deverão compor uma nova relação de proporcionalidade inversa, pensando, agora, na velocidade de 50 km/h. Observar quais dados anteriores eles usam para compor esse cálculo.

Cada vaso custa R $ 7,00.

Placa de sinalização de limites de velocidade.

RETAN/SHUTTERSTOCK.COM

FATIH YAVUZ/SHUTTERSTOCK.COM

ORIENTAÇÕES DIDÁTICAS

Representação gráfica

A representação gráfica de situações de proporcionalidade direta é uma reta, conforme os exemplos mostrados, mas nem toda reta representa uma relação de proporcionalidade; a representação gráfica de situações envolvendo duas grandezas inversamente proporcionais é uma hipérbole, assunto que será abordado no Ensino Médio. Da mesma maneira, gráficos de funções quadráticas, que representam grandezas não proporcionais (como a relação entre o lado de um quadrado e sua área) também serão revistos mais adiante. Essa abordagem contribui para o desenvolvimento da EF08MA12 e da competência específica 6 da área de Matemática.

AMPLIANDO

Atividade complementar

Se considerar oportuno, construir com os estudantes o gráfico que relaciona a temperatura em graus Celsius e a temperatura em graus Fahrenheit a partir da relação: F = 32 + 1,8 ? C, em que F representa a temperatura em graus Fahrenheit e C representa a temperatura em graus Celsius.

REPRESENTAÇÃO GRÁFICA

As situações que apresentam grandezas proporcionais podem ser representadas por meio de gráficos.

Acompanhe as situações a seguir.

1 Considere um automóvel que, partindo de uma situação de repouso, começa a se deslocar e atinge 6 metros a cada 5 segundos. A seguir, observe os dados sobre esse deslocamento.

(em m)

0 0

5 6 10 12 15 18

Observe que, em todos os pontos, o deslocamento é igual a 1,2 vezes o tempo, pois === 6 5 12 10 18 15 1, 2

Deslocamento de automóvel ao longo do tempo

Considerando o deslocamento como y e o tempo como x, podemos escrever uma expressão matemática para representar essa relação: y = 1,2 ? x. Repare que os pontos estão alinhados, o que nos possibilita traçar uma semirreta começando pela origem do sistema cartesiano.

2 Uma costureira, sabendo que o preço de 1 metro de cetim é R$ 17,90, construiu um quadro a fim de consultá-lo diariamente para saber quanto vai gastar, dependendo da quantidade de cetim que precisará comprar.

Observe o quadro e o gráfico correspondente.

Valor gasto com cetim

17,90

35,80

53,70

Por meio do gráfico, podemos verificar que, se ela precisar de 2,5 m de tecido, deverá gastar cerca de R$ 45,00. Podemos dizer que o valor gasto depende da quantidade de metros. Assim, sendo y o valor gasto, em reais, e x a quantidade de cetim, em metro, obtemos a expressão: y = 17,9 ?

Utilizando essa expressão, verificamos que, ao comprar 2,5 metros de cetim, essa costureira pagará R$ 44,75 (y = 17,9 ? 2,5 = 44,75).

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 266

Destacar aos estudantes que esse gráfico é uma reta que, diferentemente dos outros casos, não passa pela origem do plano cartesiano.

GRANDEZAS NÃO PROPORCIONAIS

Vamos agora analisar algumas situações que relacionam grandezas, porém de maneira não proporcional.

1 Considere o comprimento do lado de um quadrado, cuja medida é expressa em centímetro (cm), e a área correspondente indicada em centímetro quadrado (cm2).

Vamos organizar esses dados em um quadro.

ORIENTAÇÕES DIDÁTICAS

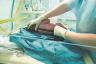
Grandezas não proporcionais

Podemos verificar que, quando dobramos o comprimento do lado do quadrado, a área correspondente quadruplica. Da mesma maneira, triplicando o comprimento do lado, a área correspondente fica multiplicada por 9.

A ssim, podemos concluir que o comprimento do lado de um quadrado e a área correspondente não são grandezas proporcionais. Repare que

2 A escala Fahrenheit de temperatura é muito utilizada nos países de língua inglesa. Para converter uma temperatura expressa em grau Celsius (°C) para grau Fahrenheit (°F), multiplica-se a temperatura em °C por 1,8 e adiciona-se 32.

Observe o quadro a seguir.

Assim, 10 °C correspondem a 50 °F, e 20 °C correspondem a 68 °F. Essas duas escalas termométricas não são proporcionais, pois quando dobramos a temperatura expressa em grau Celsius, o mesmo não acontece com a temperatura correspondente, expressa na escala Fahrenheit.

PENSE E RESPONDA

Responda no caderno.

Um bebê, que nasceu com 3,5 kg e 50 cm, ao completar o primeiro ano de vida estava com 75 cm de altura.

Podemos afirmar que, aos 20 anos, essa pessoa terá 1 500 cm, ou seja, 15 m? Explique seu raciocínio.

Não, pois a idade de uma pessoa e a altura correspondente não são grandezas proporcionais.

O trabalho com grandezas não proporcionais é bastante importante para que os estudantes percebam a não linearidade desses casos. A situação 1 relaciona a medida do lado de um quadrado com a área dele. A situação 2 relaciona a medida de temperatura em graus Celsius com graus Fahrenheit. Nos dois casos não há proporcionalidade entre as grandezas comparadas. As duas situações propostas contribuem para o desenvolvimento da competência específica 3 da área de Matemática. Caso tenha realizado a atividade complementar sugerida anteriormente, poderá resgatá-la. Para ampliar a ideia de não proporcionalidade, propor aos estudantes que tragam para a aula panfletos promocionais que apresentem informações do tipo “Leve 3 e pague 2”. Analisar com a turma a relação entre os preços e a quantidade de itens oferecidos.

Pense e responda

A comparação da altura de uma pessoa relacionada à idade dela é um exemplo explícito de que as duas grandezas não possuem relação de proporcionalidade. Após responder à questão, fazer um levantamento de outras situações em que é explícita a não proporcionalidade. Por exemplo, em uma partida de futebol, o tempo de jogo e a quantidade de gols marcados.

LEVACHINE/SHUTTERSTOCK.COM

Obstetra medindo a altura de um recém-nascido.

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades propostas levam os estudantes a identificar grandezas proporcionais e grandezas não proporcionais e explora a representação gráfica de grandezas diretamente proporcionais.

A atividade 3 apresenta uma situação comum de encontrar no dia a dia: promoção de um produto em quantidades maiores. Espera-se que os estudantes identifiquem que, nesse caso, não se trata de uma situação envolvendo grandezas proporcionais.

Na atividade 4, verificar se os estudantes concluem que o preço a ser pago pela corrida de táxi e o número de quilômetros percorridos não são grandezas proporcionais. Se julgar conveniente, solicitar aos estudantes que escrevam a relação matemática entre essas grandezas: y = 5,50 + 4,00x, em que y indica o valor pago e x, a quantidade de quilômetros percorridos.

ATIVIDADES

2. c) Resposta na seção Resoluções comentadas deste Manual. d) Diminui proporcionalmente. Essas grandezas são inversamente proporcionais.

Responda às questões no caderno.

1. Em uma das situações estudadas, aprendemos que as escalas Celsius e Fahrenheit, utilizadas para expressar medidas de temperatura, não são proporcionais. A relação matemática entre elas é dada pela expressão:

F = 1,8 C + 32, em que F é dado em °F e C é dado em °C.

Com isso, determine:

a) O valor a ser pago por uma corrida de táxi e a quantidade de quilômetros rodados são duas grandezas proporcionais? Explique.

Não, pois o valor é sempre acrescido da bandeirada.

b) Paola pediu um táxi para levá-la ao trabalho. O percurso foi de 12 quilômetros. Quanto ela pagou por essa corrida?

R$ 53,50

5. O gráfico a seguir indica o preço do café em um supermercado.

Preço do café em um supermercado

a) 68 °F em °C b) 25 °C em °F.

20 °C 77 °F

2. Um prêmio de loteria, no valor de R $ 1.530.000,00, será dividido igualmente pelo total de pessoas premiadas.

R$ 306.000,00

a) Quanto cada pessoa receberá, se o prêmio for dividido entre 5 ganhadores?

b) E se forem 6 ganhadores? R$ 255.000,00

c) Construa um quadro relacionando a quantidade de ganhadores (1, 2, 5 e 6) e o valor do prêmio correspondente.

d) Conforme a quantidade de ganhadores aumenta, o que acontece com o valor do prêmio recebido por cada um? O que se pode afirmar sobre essas duas grandezas?

3. Uma livraria está vendendo 2 livros por R$ 49,00 e 5 livros por R$ 90,00. Podemos dizer que a quantidade de livros e o preço a ser pago por eles são grandezas proporcionais? Justifique.

4. A tarifa de táxi é composta de um valor fixo, chamado de bandeirada, adicionado ao valor pago por quilômetro rodado. Sabendo que o valor da bandeirada é de R$ 5,50, e o valor por quilômetro rodado é de R$ 4,00, responda às perguntas.

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd

Preço (R$)

12 345

Fonte: Dados fictícios.

Analisando esse gráfico, responda.

a) Qual é o preço de 2 kg de café? R $ 46,00

b) Quantos reais, aproximadamente, são necessários para comprar 4 kg de café nesse mercado?

Aproximadamente R $ 90,00.

c) Quantos reais alguém vai pagar se comprar 7 kg de café? R$ 161,00

6. Ela bore um problema que envolva grandezas diretamente proporcionais e peça a um colega para resolvê-lo enquanto você resolve o que ele criou.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

3. Não, pois aumentando a quantidade de livros, o preço correspondente a ser pago não aumenta na mesma proporção.

ORIENTAÇÕES DIDÁTICAS

ALGUMAS RAZÕES ESPECIAIS CAPÍTULO2 VELOCIDADE MÉDIA

Hamilton bate recorde e faz volta com a maior velocidade média da história da F1

O hexacampeão de F1, Lewis Hamilton, bateu mais um recorde [...] durante a sessão de classificação para o Grande Prêmio da Itália, e estabeleceu a volta com a maior velocidade média da história da categoria.

O piloto [...] completou os 5 793 metros do circuito de Monza em 1:18,887, com uma velocidade média de 264,362 km/h. [...]

FERRARI, Murillo. Hamilton bate recorde e faz volta com a maior velocidade média da história da F1. CNN BRASIL, São Paulo, 5 set. 2020. Disponível em: https://www.cnnbrasil.com.br/esporte/ hamilton-bate-recorde-e-faz-volta-com-a-maior-velocidade-media-da-historia-da-f1/.

Ai, ai, ai... Que engarrafamento!

Acesso em: 4 jul. 2022.

Demorei duas horas! A velocidade média era de 5 quilômetros por hora.

A velocidade média é a razão entre a distância total percorrida e o tempo gasto para percorrê-la.

velocidade média = distância te mpo

Acompanhe o exemplo a seguir. Um trem percorreu a distância de 453 km em 6 horas. Qual foi a velocidade média do trem nesse percurso?

velocidade média = distância te mpo = 453 km 6h = 75,5 km/h

A velocidade média do trem nesse percurso foi de 75,5 km/h. (Lê-se: 75,5 quilômetros por hora.)

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 269

AMPLIANDO

Link

Velocidade média

Antes de apresentar o cálculo da velocidade média, levantar as opiniões que os estudantes têm a respeito do que seria velocidade média. Concluir que para indicar essa grandeza é necessário relacionar a distância de um percurso e o tempo gasto para realizá-lo. Esse tema contribui para o desenvolvimento da competência específica 3 da área de Matemática. Verificar se os estudantes não confundem a velocidade máxima permitida que aparece nas placas de rua com a velocidade média.

Depois, apresentar a razão: velocidade média = distância te mpo Comentar que, geralmente, a velocidade média é indicada em km/h ou m/s.

13/08/22 19:10

YEUNG, Peter. O exemplo das cidades que passaram a oferecer transporte público gratuito. BBC News Brasil. São Paulo, 15 jul. 2021. Disponível em: https://www.bbc.com/portuguese/vert-cap-57802696. Acesso em: 13 ago. 2022.

No site, é possível ter acesso a informações sobre os impactos do oferecimento de transporte público em uma cidade, contribuindo para a discussão sobre mobilidade e trânsito nas grandes cidades brasileiras.

Lewis Hamilton, piloto de Fórmula 1, 2020.

SBONSI/SHUTTERSTOCK.COM STILLFX/SHUTTERSTOCK.COM

MW EDITORA E ILUSTRAÇÕES

ORIENTAÇÕES DIDÁTICAS

Fórum

Perguntar aos estudantes se eles já desconfiaram de alguma informação que receberam em aplicativos de mensagens ou nas redes sociais. Se sim, pedir que contem para os colegas o que fizeram a respeito. Conversar sobre a importância de sempre fazer a checagem das informações, desenvolvendo a competência geral 9.

Uma fonte interessante para consulta e indicação para os estudantes é o podcast Fake News Não Pod, disponibilizado pelo Jornal da USP. O episódio #01, Como identificar uma fake news, está disponível no link : https://jornal.usp.br/podcast/ fake-news-nao-pod-01-como -identificar-uma-fake-news/ (acesso em: 13 ago. 2022).

Durante a pandemia de covid19, circularam diversas fake news, algumas confundindo a população tanto sobre os sintomas da doença quanto para a adesão à vacinação. Se possível, explorar um pouco o conteúdo dos links indicados a seguir.

• ALÉM da Covid-19, enfrentamos outra epidemia: a de fake news : saiba como se proteger desse “vírus”. Instituto Butantã. São Paulo, 2022. Disponível em: https:// butantan.gov.br/bubutantan/ alem-da-covid-19-enfrentamos -outra-epidemia-a-de-fake -news-saiba-como-se-prote ger-desse-%E2%80%9Cvi rus%E2%80%9D. Acesso em: 13 ago. 2022.

• SAÚDE sem fake news Secretaria Estadual do Distrito Federal. Brasília, DF, 2021. Disponível em: https://www.saude. df.gov.br/web/guest/w/saude -sem-fake-news. Acesso em: 13 ago. 2022.

O perigo das fake news

Com a popularização e acesso facilitado aos meios de comunicação, o conceito de fake news ganhou forma. Empregado às notícias fraudulentas que circulam nas mídias sociais e na Internet, o conceito é aplicado principalmente aos portais de comunicação on-line [...].

[...]

As fake news crescem conforme o número de compartilhamentos, então é necessário repassar somente informações verídicas e sempre se questionar caso veja uma manchete duvidosa. [...]

O compartilhamento de informações fraudulentas tem grandes consequências, apesar de parecer inofensivo. [...]

PARANÁ. Tribunal de Justiça do Estado do Paraná. O perigo das fake news. Curitiba: 2a Vice Presidência do TJPR, [2020?]. Disponível em: https://www.tjpr.jus.br/noticias-2-vice/-/asset_publisher/sTrhoYRKnlQe/content /o-perigo-das-fake-news/14797?inheritRedirect=false. Acesso em: 7 ago.

• Junte-se a alguns colegas, e façam uma pesquisa sobre como identificar se uma notícia é confiável ou não. A seguir, produzam um podcast explicando o que é fake news, a importância de checar uma informação antes de compartilhá-la e fornecendo dicas para identificar se uma notícia é verdadeira.

ESCALA

Uma das aplicações do conceito de razão entre duas grandezas pode ser verificada no uso da escala de redução e da escala de ampliação, conhecidas simplesmente como escala. Por exemplo, ao construir a maquete de um prédio, fazer a planta de um imóvel ou desenhar um novo modelo de carro, determinada escala é utilizada.

A escala de ampliação é um dado importante em análises científicas, como no estudo de microrganismos.

A escala de um desenho é a razão entre a medida do compri mento considerado no desenho e a medida do comprimento real correspondente, expressos na mesma unidade.

escala = me didado comprime nto no de se nho me didado comprime nto real

E xemplo de escala de ampliação na imagem da bactéria Brucella abortus (aumento aproximado de 10 061 vezes quando aplicada com 6 cm de largura; colorida artificialmente).

Em geral, utilizamos as medidas em centímetro para determinar uma escala. Acompanhe a seguinte situação.

Em um mapa, a distância entre dois municípios é de 6 cm. Sabendo que esse mapa foi construído em uma escala de 1 : 50 0 00 0 00, qual é a distância real entre esses municípios?

escala = me didado comprime nto no de se nho me didado comprime nto real h 1 50000000 = 6 x h x = 300 000 000

Logo, se x = 300 0 00 0 00 cm, então x = 3 0 00 km.

A distância real entre esses municípios é de 3 0 00 km.

Escala

D2_AV4-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 270

Ao explorar o conceito de escala, caso os estudantes encontrem dificuldade na escolha da unidade de medida usada e na conversão de unidades de medidas, revisar as unidades de medida de comprimento para construir, em seguida, um quadro que auxilia na conversão de unidades de medidas de comprimento.

km hm dam m dm cm mm

DENNIS KUNKEL

MICROSCOPY/SCIENCEPHOTOLIBRARY/FOTOAR

Respostas pessoais.

ATIVIDADES

Responda às questões no caderno.

1. Um automóvel percorreu uma distância de 280 km em 4 horas. Qual foi a velocidade média desse automóvel nesse percurso? 70 km/h

2. (Enem/MEC) Na construção de um conjunto habitacional de casas populares, todas serão feitas num mesmo modelo, ocupando, cada uma delas, terrenos cujas dimensões são iguais a 20 m de comprimento por 8 m de largura. Visando a comercialização dessas casas, antes do início das obras, a empresa resolveu apresentá-las por meio de maquetes construídas numa escala de 1 : 200. As medidas do comprimento e da largura dos terrenos, respectivamente, em centímetros, na maquete construída, foram de

a) 4 e 10.

b) 5 e 2

c) 10 e 4.

Alternativa c.

d) 20 e 8.

e) 50 e 20.

DENSIDADE DE UM CORPO

3. Antes de iniciar uma viagem, um motorista verificou em um mapa um trecho em linha reta do trajeto a ser percorrido. Sabendo que a escala desse mapa é 1 : 10 000 000, e que esse trecho tem 2 cm de comprimento no mapa, responda:

a) Qual é a distância real a ser percorrida nesse trecho representado em linha reta no mapa?

b) Se nesse trecho do trajeto o motorista viajar a 80 km/h, em quanto tempo ele percorrerá a distância correspondente?

c) Com base no contexto desta atividade, elabore um problema envolvendo escalas e/ou velocidade média. Troque oproblema com um colega para que ele o resolva, enquanto você resolve o problema elaborado por ele. Por fim, confiram as resoluções e expliquem, um ao outro, as estratégias utilizadas.

200 km 2h30min Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Para calcular a densidade de um corpo, também se aplica o conceito de razão entre duas grandezas.

A densidade de um corpo é dada pela razão entre a massa e o volume desse corpo.

= densidade ma ssa  do corpo volume  do corpo

Em geral, a densidade é expressa em quilograma por decímetro cúbico (kg/dm3) ou grama por centímetro cúbico (g/cm3). Acompanhe o exemplo a seguir. Uma escultura de bronze tem 3,5 kg de massa e volume de 400 cm3. Qual é a densidade dessa escultura?

densidade = ma ssa  do corpo volume  do corpo = 3, 5k g 400 cm3 = 3 500 g 400 cm3 = 8,75 g/cm3

Logo, a densidade dessa escultura de bronze é 8,75 g/cm3

ORIENTAÇÕES DIDÁTICAS

Atividades

A atividade 3 favorece o desenvolvimento da habilidade EF08MA13. Para o estudante resolver corretamente o item b, é necessário que ele obtenha a resposta correta do item a. Se alguma dificuldade se manifestar relacionadas a esses dois itens, retome as definições de velocidade média e escala apresentadas nas páginas 269 e 270 do Livro do estudante.

No item c, espera-se que os estudantes consigam elaborar um problema contextualizado, visto que escalas e velocidade média são grandezas encontradas com frequência no dia a dia. Se eles tiverem dúvidas, propor que façam as elaborações em duplas; depois, pode-se explorar, na lousa, os problemas que eles elaboraram, resolvendo-os coletivamente.

Para complementar a atividade, propor aos estudantes que realizem uma pesquisa na internet em fontes confiáveis, em que apareçam notícias apresentando escalas e/ou velocidade média.

Densidade de um corpo

Outra razão importante a ser discutida com os estudantes, refere-se à densidade de um corpo. Anotar a definição de densidade, na lousa, como a razão entre a massa e o volume de determinado corpo. Em seguida, pedir que resolvam a situação proposta no Livro do estudante.

ORIENTAÇÕES DIDÁTICAS

Densidade demográfica

Apresentar densidade demográfica como a razão entre o número de habitantes e a área da região ocupada. Propor aos estudantes que calculem a densidade demográfica do município, do estado e da região brasileira onde está localizada a escola em que estudam, desenvolvendo, assim, a competência específica 5 da área de Matemática.

Para ampliar a ideia de densidade demográfica, propor aos estudantes que calculem a densidade demográfica das salas de aula da escola. Orientá-los a respeito de como fazer uma pesquisa para colher os dados da área de cada sala de aula e da quantidade de estudantes que estudam em cada uma delas. Organizar os estudantes em grupos e dividir as salas de aula entre eles. Depois, elaborar uma tabela para que possam anotar os dados levantados. Após a coleta dos dados, orientar os estudantes a calcular a densidade demográfica de cada sala de aula para que possam analisar os dados.

Saiba que

Incentivar os estudantes a pensar na importância da criação de políticas públicas eficientes. Para que os estudantes ampliem seus conhecimentos a respeito do Censo Demográfico de 2010, pedir que façam uma pesquisa no site do IBGE. Esse trabalho pode ser feito em parceria com o professor de Geografia.

DENSIDADE DEMOGRÁFICA

O cálculo da densidade demográfica de uma região é uma aplicação do conceito de razão entre duas grandezas. Esse resultado é obtido por meio da razão entre a quantidade de habitantes e a área da região por eles ocupada.

densidade demográfica = quantidade de  habitante s área da  região ocupada

Acompanhe a situação a seguir.

O estado de Tocantins, situado na Região Norte do Brasil, ocupa uma área de aproximadamente 277 424 km2 Em 2021, de acordo com o IBGE, a população estimada desse estado era de 1 6 07 363 habitantes. Qual era a densidade demográfica aproximada desse estado em 2021?

Elaborado com base em: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Cidades e Estados: Tocantins. IBGE. Rio de Janeiro, [2021?]. Disponível em: https://www.ibge.gov.br/cidades-e-estados/ to.html. Acesso em: 6 jul. 2022.

Tocantins: localização

Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Atlas geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018. p.161. Disponível em: https://biblioteca.ibge.gov.br/visualizacao /livros/liv101627.pdf. Acesso em: 4 jul. 2022.

De acordo com os dados apresentados, temos: densidade demográfica = 1 607363ha b 277424 km2 1 5,8 hab./km2

Logo, em 2021, a densidade demográfica do estado de Tocantins era de aproximadamente 5,8 hab./km2

SAIBA QUE

A cada 10 anos, o IBGE realiza o Censo Demográfico ou Recenseamento Demográfico, que é uma pesquisa para reunir informações sobre a população brasileira. Essas informações são importantes para que ogoverno possa criar políticas públicas mais eficientes para atender às necessidades da sociedade. No Brasil, o primeiro Censo ocorreu em 1872, mas essa ideia de recensear a população e, com base nesses dados, obter informações sobre a sociedade não é recente; romanos e gregos já realizavam censos antes de Cristo. Como não foi possível a realização do Censo no Brasil em 2020, por causa da pandemia de covid-19, o recenseamento ficou previsto para 2022, quando seriam atualizados os dados sobre a população brasileira. Elaborado com base em: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Histórico dos Censos: introdução. Memória IBGE. Rio de Janeiro, [2022?]. Disponível em: https://memoria.ibge.gov.br/historia-do-ibge/historico-dos-censos/panorama-introdutorio.html. Acesso em: 6 jul. 2022.

D2_AV3-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 272

ATIVIDADES

Responda às questões no caderno.

0,40 kg/dm3

1. Um bloco maciço de madeira tem 14 kg de massa e ocupa um volume de 35 dm³. Qual é a densidade desse bloco?

2. Um fio de platina tem um volume de 0,2 cm³. Sabendo que a massa do fio é de 4,3 g, determine a densidade desse metal. 21,5 g/cm3

3. A água-marinha é uma das pedras semipreciosas mais admiradas em todo omundo. Suponha que uma pedra de água-marinha tenha 8,1 g de massa e 3 cm³ de volume. Qual é a densidade dessa pedra? 2,7 g/cm3

4,28 hab./km2

4. Uma região do interior do Brasil tem uma população de 64 200 habitantes e ocupa uma área de 15 000 km². Qual é a densidade demográfica dessa região?

5. A Grécia, país situado no continente europeu, tem cerca de 132 000 km² de área. Em 2010, ela tinha uma população aproximada de 11 200 000 habitantes. Qual era a densidade demográfica aproximada da Grécia nesse ano?

84,8 hab./km2

8. Caio errou a ordem de grandeza do território argentino, que é de cerca de 2 800 0 00 km2

Qual dos dois bairros tem a maior densidade demográfica? Água Branca.

7. No Rio Grande do Norte, o turismo é a atividade que mais gera empregos no estado. Entre seus inúmeros atrativos, podemos citar a beleza natural, o artesanato (cerâmica, cestaria, rendas e bordados) e a comida típica. Em 2010, esse estado tinha cerca de 3 168 027 habitantes, segundo o Censo do IBGE, e uma área de 52 810 km². Determine a densidade demográfica desse estado. Aproximadamente 59,99 hab./km2

ORIENTAÇÕES DIDÁTICAS

Atividades

As atividades propostas abordam problemas relacionados à densidade de um corpo e à densidade demográfica. Se julgar pertinente, retomar com os estudantes o conceito de área e volume, bem como suas respectivas unidades de medida.

Para resolver as atividades que tratam de densidade de um corpo, basta verificar as unidades que se encontram os dados do problema e calcular a razão entre a massa e o volume ocupado.

Para resolver as atividades que tratam de densidade demográfica, calcula-se a razão entre o número de habitantes e a área ocupada.

8. Em 2010, a população argentina era de aproximadamente 40 100 0 00 habitantes. Sabendo que a densidade demográfica da Argentina nesse ano era de 14,3 hab./km2 , Caio estimou a área do território desse país em 280 000 km2 . A estimativa de Caio está correta? Se não estiver, qual foi oequívoco cometido por ele?

Na atividade 6, comentar com os estudantes que Água Branca é o bairro com maior densidade demográfica, maior número de habitantes e maior área, mas nem sempre isso ocorre. Apresentar dados do Censo 2010 do IBGE de dois locais em que haja essa diferença. Por exemplo:

Rio Branco (Acre) Apuí (Amazonas)

6. Dois bairros de um município, Água Branca e Pedra Azul, têm os seguintes dados referentes à população e à área correspondente.

Bairro População Área (em km²)

Água Branca 125 000 36

Pedra Azul 85 000 30

AMPLIANDO

9. Escolha um dos contextos apresentados nas atividades desta seção e elabore um problema envolvendo razão entre duas grandezas. Troque o problema com um colega para que um resolva oproblema elaborado pelo outro. Em seguida, confiram as respostas e expliquem, um ao outro, as estratégias utilizadas na resolução.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Link DEMOGRAFIA e políticas públicas. O Estado de S. Paulo, São Paulo, ano 141, n. 46332, 24 ago. 2020. Disponível em: https://opiniao.estadao.com.br/noticias/notas-e-informacoes,demografia-e-politicas -publicas,70003410286. Acesso em: 22 ago 2022.

Como sugestão de encaminhamento de aula, explorar a discussão sobre os impactos das mudanças demográficas no estado de São Paulo e algumas adequações que serão necessárias nas políticas públicas.

População: 336 038 pessoas

Área territorial: 8 834,942 km2

Densidade demográfica: 38,03 hab./km2

População: 18 007 pessoas

Área territorial: 54 245,153 km2

Densidade demográfica: 0,33 hab./km2

Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA.

IBGE Cidades. Rio de Janeiro, c2017. Disponível em: https:// cidades.ibge.gov.br/. Acesso em: 22 ago. 2022.

Nesse caso, Rio Branco tem maior densidade demográfica; porém, Apuí tem maior área territorial.

DOTMILLER1986/SHUTTERSTOCK.COM

MQIMAGENS/SHUTTERSTOCK.COM

Imagem da Acrópole de Atenas (Grécia), 2019.

Forte dos Reis Magos. Natal (RN), 2022.

ORIENTAÇÕES DIDÁTICAS

Grandezas diretamente proporcionais

Situações relacionadas à proporcionalidade direta foram abordadas em anos anteriores. Agora, essa noção será retomada, apresentando o gráfico que relaciona duas grandezas diretamente proporcionais.

Explorar a situação 1 que trata da relação entre certa área destinada ao plantio de hortaliças e a quantidade de adubo orgânico necessária. Se julgar pertinente, discutir com os estudantes as vantagens de se usar adubos orgânicos na agricultura, contribuindo para o desenvolvimento do Tema Contemporâneo Transversal Educação Ambiental. Espera-se que os estudantes compreendam que, antes de resolver qualquer equação envolvendo grandezas proporcionais, primeiro, precisa-se analisar se são grandezas diretamente ou inversamente proporcionais. Retomar a relação entre tonelada e quilograma, solicitando aos estudantes que registrem essa informação no caderno.

GRANDEZAS DIRETAMENTE PROPORCIONAIS CAPÍTULO3

Considere as situações a seguir.

Link

AMPLIANDO

GLOSSÁRIO

Tonelada: unidade de medida de massa equivalente a 1 000 quilogramas.

1 N o mês passado, ao preparar uma área de 600 m2 para o plantio de hortaliças, a família de Júlia utilizou 3 toneladas de adubo orgânico. Sabendo que neste mês eles deverão preparar uma área de 1 000 m2 para o plantio e supondo que pretendem utilizar a mesma quantidade de adubo por metro quadrado, quantas toneladas de adubo orgânico serão necessárias?

Essa situação relaciona duas grandezas proporcionais: área (em m2) e quantidade de adubo (em tonelada).

Para responder à pergunta proposta, vamos organizar os dados em um quadro.

Área de plantio (em m2) Quantidade de adubo orgânico (em tonelada)

600 3

1 000 x

Como as grandezas são proporcionais, para obter a quantidade de adubo orgânico necessária para uma área de 1 0 00 m2, utilizamos a propriedade fundamental das proporções.

Cultivo de hortaliças em pequena propriedade. Ibiúna (SP), 2020.

600

1 000 = 3 x h 600 ? x = 1 000 ? 3 h

h x = 3 000 600 = 5

Assim, serão necessárias 5 toneladas de adubo orgânico para preparar 1 000 m2 de área para oplantio.

Observe que, quanto maior a área de plantio, maior será a quantidade de adubo necessária, na mesma proporção. Nesse caso, dizemos que a área de plantio e a quantidade de adubo são grandezas diretamente proporcionais

Duas grandezas são diretamente proporcionais quando variam sempre na mesma razão, ou seja, quando uma aumenta, a outra aumenta na mesma proporção; ou, ainda, quando uma diminui, a outra diminui na mesma proporção.

VANTAGENS e desvantagens do adubo orgânico e inorgânico para a agricultura. Pensamento Verde. [S l.], 2013. Disponível em: https://www.pensamentoverde.com.br/dicas/vantagens-desvantagens-adubo-organico -inorganico-agricultura/. Acesso em: 13 ago. 2022.

Como sugestão de encaminhamento, recomenda-se explorar o texto apresentado no site para ampliar a discussão sobre as vantagens e as desvantagens do uso dos diferentes tipos de adubo na agricultura.

ORIENTAÇÕES DIDÁTICAS

Graficamente, podemos representar a área de plantio em relação à quantidade de adubo orgânico utilizado da seguinte maneira.

Adubo orgânico necessário em relação à área de plantio

2 A g erente de produção de uma fábrica de parafusos verificou no manual de instrução de uma máquina a relação entre a quantidade de parafusos produzida (em unidade) e o tempo de funcionamento correspondente da máquina (em hora).

A nalisando o gráfico, percebemos que essas grandezas são diretamente proporcionais, pois ambas aumentam na mesma razão. Confira.

• Quando a produção de parafusos passa de 600 unidades para 1 200 unidades, varia na razão de = 600 1 200 1 2

• Quando o tempo passa de 4 horas (produção de 600 unidades) para 8 horas (produção de 1 200 unidades), varia na razão de = 4 8 1 2

PENSE E RESPONDA

Responda no caderno.

2 250 parafusos. Exemplo de resposta: Como em 10 horas a máquina produz 1 500 parafusos, em 5 horas são produzidos 750 parafusos. Logo, em 15 horas ela produz a soma desses valores, ou seja, 2 250 parafusos (1 500 + 750 = 2 250).

De acordo com esse gráfico, quantos parafusos essa máquina é capaz de produzir em 15 horas de operação? Explique como você pensou para responder.

Fazer a leitura dos gráficos apresentados, iniciando pela indicação das grandezas representadas em cada um dos eixos. Comentar que os pontos marcados no plano cartesiano, nas duas situações, pertencem a uma reta. Destacar que são retas que passam necessariamente pela origem do sistema cartesiano (0, 0). Esse tema contribui para o desenvolvimento da habilidade EF08MA12 e da competência específica 6 da área de Matemática.

É interessante dizer aos estudantes que problemas envolvendo grandezas diretamente proporcionais podem ser resolvidos a partir de alguns dados apresentados em quadros ou em gráficos, como mostra cada situação apresentada.

Pense e responda

Os estudantes podem desenvolver diferentes estratégias para encontrar a quantidade de parafusos em 15 horas. Uma das estratégias possíveis é encontrar a quantidade de parafusos produzidos em 1h, ou seja, se em 2 horas são produzidos 300 parafusos, em 1 hora, serão 150. Dessa maneira, em 15 horas, basta multiplicar 150 por 15, resultando em 2 250. Há outras possibilidades de resolução. Solicitar aos estudantes que exponham suas ideias, justificando-as, o que contribui para o desenvolvimento da argumentação e da empatia

Fonte: Dados fictícios.

ORIENTAÇÕES DIDÁTICAS

Atividades

Para auxiliar os estudantes na resolução das questões, sugerir que sejam montados os quadros referentes a cada situação, destacando as grandezas envolvidas.

Um modo de resolver a atividade 2 é converter 8 horas em minutos. Depois, verificar a relação que há entre as grandezas: quantidade de pães e tempo de produção. Sugerir a construção do quadro a seguir.

Quantidade de pães Tempo de produção (min) 230 40 x 480

Ao aplicar a propriedade fundamental das proporções, é possível determinar que x = 2 760.

A atividade 8, ao solicitar aos estudantes que elaborem um problema que envolva grandezas diretamente ou inversamente proporcionais, favorece o desenvolvimento da habilidade EF08MA13.

Caso os estudantes tenham dificuldade em elaborar um problema com o tema proposto, fazer algumas perguntas para eles, como: Se um pão custa 2 reais, quanto custam dois pães? E três pães? Depois, pode-se desenhar um quadro na lousa anotando as proporções necessárias.

Responda às questões no caderno.

1. Copie e complete o quadro a seguir considerando que as grandezas envolvidas são diretamente proporcionais.

5. A carga máxima de um caminhão pode ser composta de 600 sacos de cimento ou, ainda, de 7 290 tijolos. Sabendo que esse caminhão já está carregado com 100 sacos de cimento, quantos tijolos ainda poderão ser acomodados nele, de modo a não ultrapassar a carga máxima? 6 075 tijolos.

2. Em uma panificadora são produzidos 230 pães franceses a cada 40 minutos.

6. Amanda tem um cachorro de 4,5 kg. Para tratar uma infecção nas vias urinárias desse pet, o veterinário receitou um antibiótico cuja dosagem é de 6 mL para cada 10 kg de massa do animal. Quantos mililitros de antibiótico Amanda deve dar a seu cachorro?

7. (OBMEP) Para obter tinta de cor laranja, devem-se misturar 3 partes de tinta vermelha com 2 partes de tinta amarela. Para obter tinta de cor verde, devem-se misturar 2 partes de tinta azul com 1 parte de tinta amarela. Para obter tinta de cor marrom, deve-se misturar a mesma quantidade de tintas laranja e verde.

Considerando uma jornada ininterrupta de 8 h, quantos pães são produzidos nessa panificadora? 2 760 pães.

3. Em uma viagem, um automóvel percorre uma estrada com velocidade constante de 110 km/h.

a) Que distância esse automóvel terá percorrido após 3h30min? 385 km

b) Mantendo essa velocidade, uma viagem de 473 km demoraria quanto tempo?

Quantos litros de tinta amarela são necessários para obter 30 litros de tinta marrom?

Alternativa e.

a) 7

b) 8

c) 9

d) 10

e) 11

4. A maquete de um empreendimento imobiliário foi construída na escala de 1 : 120. Sabendo que esse edifício terá 26 andares e que, em média, cada andar tem 3 m de altura, determine a medida da altura desse edifício na maquete.

4,3 h = 4h18min 65 cm

Essa situação simples tem o intuito de nortear os estudantes a elaborar o problema desejado. No momento em que os estudantes trocarem os problemas com os colegas, peça-lhes que façam um quadro com as proporções para facilitar o encaminhamento da resposta.

8. Elabore um problema envolvendo grandezas diretamente proporcionais e troque-o com um colega para que cada um resolva o problema que o outro elaborou. Em seguida, confiram as resoluções e compartilhem entre si as estratégias utilizadas para resolvê-las.

Parte de uma fornada de pães franceses.

2,7 mL

ROCHARIBEIRO/SHUTTERSTOCK.COM

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

GRANDEZAS INVERSAMENTE PROPORCIONAIS CAPÍTULO4

Considere as seguintes situações.

1 Um ônibus faz o percurso do terminal até o centro de um município e depois volta para o terminal. Certo dia, um fiscal registrou a velocidade média desse ônibus e o tempo gasto no percurso de ida até o centro em diferentes turnos. Observe o quadro com os dados coletados pelo fiscal.

Velocidade média (em km/h) Tempo (em minuto)

35 96

Observe que, à medida que a velocidade média aumenta, o tempo gasto para realizar o mesmo percurso diminui. Comparando as razões entre valores correspondentes dessas grandezas, verificamos o seguinte:

35 56 = 5 8 e 96 60 = 8 5 São razões inversas.

35 70 = 1 2 e 96 48 = 2 São razões inversas.

A ssim, dizemos que a velocidade e o tempo são grandezas inversamente proporcionais

Duas grandezas são inversamente proporcionais quando uma varia na razão inversa da outra, ou seja, quando uma aumenta, a outra diminui na mesma proporção; ou quando uma diminui, a outra aumenta na mesma proporção.

ORIENTAÇÕES DIDÁTICAS

Grandezas inversamente proporcionais

Antes de conceituar grandezas inversamente proporcionais, averiguar o entendimento dos estudantes a respeito desse assunto. Verificar se, após terem estudado as grandezas diretamente proporcionais, percebam que, nesse novo caso, se uma grandeza aumenta, então a outra diminui na mesma proporção. Se julgar pertinente, retomar que, quando multiplicamos dois números reais inversos, o produto é igual a 1.

JOA SOUZA/ SHUTTERSTOCK.COM

Passageiros aguardando a saída do ônibus em terminal. Salvador (BA), 2022.

ORIENTAÇÕES DIDÁTICAS

Saiba que Comentar que o gráfico da situação 1 é uma hipérbole, que é um tipo de gráfico a ser estudado no Ensino Médio. Neste momento, é importante que os estudantes identifiquem a característica das grandezas inversamente proporcionais no formato da curva (quando uma grandeza aumenta, a outra diminui proporcionalmente), e não necessariamente que entendam a construção dessa curva. Esse é um procedimento um pouco mais complicado e que será apresentado no Ensino Médio.

Ao explorar a situação 2, verificar se os estudantes têm alguma dúvida quanto ao termo razões inversas. Espera-se que eles percebam que uma fração é o inverso da outra.

Pense e responda Espera-se que os estudantes relacionem o gráfico de duas grandezas diretamente proporcionais há retas que passam pela origem do sistema cartesiano; já o gráfico referente às grandezas inversamente proporcionais é representado pela curva denominada hipérbole.

Graficamente, podemos representar a relação entre a velocidade média e o tempo gasto nos percursos realizados pelo ônibus como indicado a seguir.

Velocidade do ônibus em relação ao tempo de percurso

SAIBA QUE

A curva que representa grandezas inversamente proporcionais é chamada de hipérbole

2 Todo ano, uma empresa faz um desafio a seus funcionários cujo prêmio em dinheiro é R$ 15.000,00. Esse valor é dividido igualmente entre as pessoas que acertarem a pergunta do desafio. Observe o quadro com a relação entre a quantidade de premiados e o valor que cada um recebeu nos últimos três anos.

Quantidade de premiados Valor do prêmio (em R$)

3 5 000

5 3 000

8

1 875

Por meio desse quadro, é possível observar que, quando a quantidade de pessoas premiadas aumenta, o valor do prêmio recebido diminui proporcionalmente. Compare as razões entre valores correspondentes dessas grandezas.

3

5 e 5 000 3 000 = 5 3 São razões inversas.

5 8 e 3 000 1875 = 8 5 São razões inversas.

A ssim, dizemos que a quantidade de premiados e o valor do prêmio recebido são grandezas inversamente proporcionais.

PENSE E RESPONDA

Responda no caderno.

Resposta pessoal. Espera-se que os estudantes percebam que os gráficos que representam grandezas diretamente proporcionais são retas ascendentes (“crescem”) e os que representam grandezas inversamente proporcionais são curvas descendentes (“decrescem”).

Observe as representações gráficas da página 275 e o gráfico desta página. O que podemos verificar quanto às representações gráficas e os correspondentes conceitos de grandezas diretamente proporcionais e grandezas inversamente proporcionais?

Fonte: Dados fictícios.

ORIENTAÇÕES DIDÁTICAS

Responda às questões no caderno.

1. Uma impressora a jato de tinta imprime 100 páginas em 20 minutos. Quatro impressoras iguais a essa devem imprimir essa mesma quantidade de páginas em quanto tempo? 5 minutos.

2. Cinco ope rários levam 20 dias para asfaltar um trecho de uma rodovia. Esse mesmo serviço seria realizado em quantos dias, se houvesse 8 operários trabalhando nessa obra? 12,5 dias.

3. Um ciclista realiza diariamente, em uma hora e meia, um treino cujo percurso tem 48 km.

Com base nessas informações, responda.

a) Qual é a velocidade média desenvolvida por esse ciclista no treino? 32 km/h

b) Para melhorar o tempo de percurso, esse ciclista realizará o mesmo treino, porém com uma velocidade média de 38,4 km/h. Quanto tempo ele gastará? 1h15min

4. Uma equipe de 38 professores foi convocada para corrigir um vestibular bastante concorrido. Estima-se que serão necessários 14 dias para concluir essa tarefa, trabalhando 8 horas por dia. Se forem contratados mais 18 professores, mantendo o mesmo ritmo de trabalho, em quantos dias a equipe conseguirá finalizar esse trabalho de correção? 9,5 dias.

5. Em um livro, a parte correspondente à história narrada tem 150 páginas, e em cada página há 36 linhas de texto. Um editor resolveu reduzir a quantidade de linhas de texto em cada página para 30. Qual será a nova quantidade de páginas do livro? 180 páginas.

7. a

) As grandezas são inversamente proporcionais, porque à medida que a quantidade de trabalhadores aumenta, a quantidade de dias para a conclusão da obra diminui na mesma proporção.

6. (OBM) Anita imaginou que levaria 12 minutos para terminar a sua viagem, enquanto dirigia à velocidade constante de 80 km/h, numa certa rodovia. Para sua surpresa, levou 15 minutos. Com qual velocidade constante essa previsão teria se realizado? Alternativa c.

a) 90 km/h

b) 95 km/h

c) 100 km/h

d) 110 km/h

e) 120 km/h

7. Uma empresa que presta serviços de construção civil fornece um quadro com as seguintes informações:

Quantidade de trabalhadores

Atividades

É importante que os estudantes identifiquem as grandezas envolvidas em cada problema para compreenderem o tipo de relação de proporcionalidade que há entre elas.

Na atividade 1, propor a montagem de um quadro para auxiliar na resolução.

Quantidade de impressoras

Tempo de impressão (em min) 1 20 4 x

Quantidade de dias para conclusão da obra

15

12

10

a) De acordo com esses dados, a quantidade de trabalhadores e a quantidade de dias para conclusão da obra são grandezas diretamente proporcionais ou grandezas inversamente proporcionais? Justifique sua resposta.

b) Utilize esses dados para elaborar um problema envolvendo essas grandezas. Em seguida, troque de caderno com um colega para que um resolva o problema que o outro elaborou. Por fim, verifiquem se as resoluções estão corretas e expliquem, um ao outro, como pensaram para elaborar e resolver os problemas.

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

Observar que, quanto maior a quantidade de impressoras, menor será o tempo de produção. Portanto, trata-se de uma situação de proporcionalidade inversa. A razão entre as quantidades de impressoras é = 1 4 0,25. Como o tempo diminui na mesma proporção, basta calcular esse valor: 20 ? 0,25 = 5. Logo, as quatro impressoras, juntas, imprimem 100 páginas em 5 min.

Na atividade 6, os estudantes devem perceber a relação de proporcionalidade inversa entre a velocidade e o tempo, pois a distância está fixa.

A atividade 7, ao solicitar aos estudantes que elaborem um problema que envolva grandezas diretamente ou inversamente proporcionais, favorece o desenvolvimento da habilidade EF08MA13.

ORIENTAÇÕES DIDÁTICAS

Por toda parte

Iniciar a aula perguntando aos estudantes se eles sabem qual é o Dia Internacional de Respeito à Tolerância. Talvez muitos não saibam que, em 1996, a ONU escolheu o dia 16 de novembro para marcar essa data. Passar, então, à leitura do Artigo 1o , que discute o significado de tolerância.

Conversar sobre o texto, ouvindo as colocações dos estudantes e valorizando, acima de tudo, o respeito ao diferente. Essa abordagem contribui para o desenvolvimento do Tema Contemporâneo Transversal Diversidade Cultural, das competências gerais 1 e 9 e da competência específica 5 da área de Matemática.

Enfatizar que o respeito é algo a ser cultivado desde criança, pois ele deve existir em todos os ambientes que o ser humano possa frequentar.

RESPEITO MÚTUO E VALORIZAÇÃO DA DIVERSIDADE

Em 1996, a Assembleia Geral da Organização das Nações Unidas (AGNU) declarou o dia 16 de novembro como o Dia Internacional da Tolerância com o objetivo de destacar o compromisso de todos em promover o entendimento entre diferentes povos e culturas.

Leia a seguir um trecho do artigo 1o da Declaração de Princípios sobre a Tolerância, assinada pelos Estados-Membros da Organização das Nações Unidas para a Educação, a Ciência e a Cultura (Unesco) na 28a reunião da Conferência Geral, realizada em Paris, em 1995.

Artigo 1o – Significado de tolerância

1.1 A tolerância é o respeito, a aceitação e o apreço da riqueza e da diversidade das culturas de nosso mundo, de nossos modos de expressão e de nossas maneiras de exprimir nossa qualidade de seres humanos. É fomentada pelo conhecimento, a abertura de espírito, a comunicação e a liberdade de pensamento, de consciência e de crença. A tolerância é a harmonia na diferença. Não só é um dever de ordem ética; é igualmente uma necessidade política e jurídica. A tolerância é uma virtude que torna a paz possível e contribui para substituir uma cultura de guerra por uma cultura de paz.

1.2 A tolerância não é concessão, condescendência, indulgência. A tolerância é, antes de tudo, uma atitude ativa fundada no reconhecimento dos direitos universais da pessoa humana e das liberdades fundamentais do outro. [...]

UNESCO. Declaração de Princípios sobre a Tolerância. Tradução: Universidade de São Paulo (USP). Brasília, DF: UNESCO, 1997. p. 11. Disponível em: https://www.oas.org/dil/port/1995%20Declara%C3%A7%C3%A3o%20de%20 Princ%C3%ADpios%20sobre%20a%20Toler%C3%A2ncia%20da%20UNESCO.pdf. Acesso em: 4 jul. 2022.

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 280

A educação e o acesso à informação são grandes aliados para promover o respeito à liberdade e ao pluralismo de ideias.

13/08/22 19:26

Responda às questões a seguir no caderno.

1. No dia a dia, você se considera uma pessoa que age com tolerância? Em seu entendimento, a tolerância contribui para o respeito às diferenças? Justifique sua resposta.

Resposta pessoal.

2. No sistema judiciário brasileiro, os crimes motivados por intolerância e preconceito relacionado à raça, à orientação sexual, ao gênero, à religião e à origem (procedência nacional) são considerados crimes de ódio. Observe os dados representados no gráfico a seguir.

Crimes registrados no Brasil em 2019 associados à intolerância e ao preconceito

sexual Gênero (feminicídio)

Elaborado com base em: BUARQUE, Beatriz; CRETTON, Marcio. Mapa do ódio no Brasil: percepções e recomendações para políticas públicas. Words Heal the World. Reino Unido, 2021. Disponível em: https://www. wordshealtheworld.com/wp-content/uploads/2021/01/HATE-MAP-INPORTUGUESE-2019-final.pdf. Acesso em: 30 jun. 2022.

Com base nesses dados, responda: a cada 1 tolerância, quantos estão relacionados ao preconceito racial?

3. Leia a tirinha a seguir.

BECK, Alexandre. [Respeito]. https://tirasarmandinho.tumblr.com/search/respeito. Acesso em: 30 jun. 2022.

Forme um grupo, e, com base nessa tirinha e no texto sobre tolerân cia, conversem sobre a importância do respeito à diversidade para uma cultura de paz. Registrem em um texto as principais ideias discutidas pelo grupo. Vocês também poderão elaborar um cartaz que possibilite compartilhar com a turma as conclusões do grupo. Resposta pessoal.

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 281

Auxiliar os estudantes na leitura do gráfico de setores proposto na . Ouvir as opiniões dos estudantes diante dos números revelados pelo gráfico, favorecendo assim o desenvolvimento da competência específica 5 da , aproveitar a presença da tirinha de Armandinho para questionar os estudantes a respeito da importância desse tipo de texto para exprimir opiniões diversas. Levantar a relação de quais tirinhas os estudantes

Verificar como os estudantes se organizam para construir o texto e os cartazes solicitados. Esse tipo de trabalho permite que assuntos diversos sejam encontrados e o compartilhamento disso é muito importante para o desenvolvimento das relações humanas entre os estudantes,

ORIENTAÇÕES DIDÁTICAS

Regra de três simples

Por meio da regra de três, os estudantes podem resolver muitos problemas de proporcionalidade, percebendo as relações multiplicativas entre as linhas e as colunas de diferentes quadros construídos a partir das situações apresentadas. Comentar que resoluções de problemas envolvendo regra de três simples também estão presentes em diversas áreas do conhecimento, como Física e Química.

Explorar as duas situações propostas. A situação 1 traz um caso envolvendo grandezas diretamente proporcionais, enquanto a situação 2 mostra a regra de três sendo usada no caso de grandezas inversamente proporcionais.

5

REGRA DE TRÊS

REGRA DE TRÊS SIMPLES

A regra de três simples é uma estratégia utilizada para calcular valores desconhecidos em problemas que relacionam grandezas diretamente proporcionais ou que envolvem grandezas inversamente proporcionais.

Acompanhe as situações a seguir.

1 Camila pagou R$ 8,50 por 2,5 kg de laranjas. Sabendo que Pedro vai comprar 4 kg de laranjas nesse mesmo mercado, quanto ele deverá pagar por essa compra?

Para resolver essa situação, organizamos os dados do problema em um quadro que relaciona as grandezas envolvidas (quantidade de laranjas e preço a pagar).

Sabendo que essas grandezas são diretamente proporcionais, podemos escrever a seguinte proporção.

2,5 4 = 8,5 x h 2,5 ? x = 4 ? 8,5 h x = 34 2, 5 h x = 13,6

Assim, Pedro deverá pagar R$ 13,60 por 4 kg de laranjas.

2 Um automóvel, trafegando em uma rodovia à velocidade constante de 90 km/h, realiza uma viagem em 2,5 horas. Na volta, a viagem é feita a uma velocidade constante de 75 km/h. Qual é o tempo de duração da viagem de volta?

Para resolver essa situação, novamente organizamos os dados do problema em um quadro.

Velocidade (em km/h) Tempo (em h)

Nesse caso, como se trata de grandezas inversamente proporcionais, temos:

Logo, o tempo de duração da viagem de volta é de 3 horas. 282

D2-MAT-F2-2103-V8-U9-262-291-LA-G24.indd

AMPLIANDO

Vídeo

DICA 11 – 3 passos para resolver regra de três simples. 2019. Vídeo (7min04s). Publicado pelo canal Matemática Rio Prof. Rafael Procopio. Disponível em: https://www.youtube.com/watch?v=cUiLE3qg9rM&t=3s. Acesso em: 13 ago. 2022.

Nessa videoaula, os estudantes encontrarão três dicas que poderão auxiliá-los na resolução de problemas de regra de três simples.

Responda às questões no caderno.

1. Para construir um muro de 16 metros de comprimento, Antônio planeja utilizar 2 240 tijolos. Caso o muro tivesse 27 metros de comprimento e a mesma altura, quantos tijolos seriam necessários? 3 780 tijolos.

2. U m pintor mistura tinta branca e tinta vermelha para obter um tom de rosa. Para cada 2,5 L de tinta branca, ele mistura 1,7 L de tinta vermelha. Sabendo que a quantidade de tinta branca e a de tinta vermelha são proporcionais, quantos litros de tinta vermelha ele deve misturar em 3,5 L de tinta branca para obter essa mesma tonalidade? 2,38 L

3. Uma empresa de prestação de serviços de pintura firmou um contrato com um cliente. Em princípio, o serviço seria realizado por 2 pintores, mas seriam necessárias 80 horas de trabalho. Pelo contrato firmado, a obra precisa ser concluída em 16 horas. Nesse caso, pensando no mesmo ritmo de trabalho, quantos pintores serão necessários para cumprir essa meta?

6. Este gráfico indica o preço cobrado por uma operadora de telefonia, em reais, de acordo com o tempo de ligações por minuto utilizado.

ORIENTAÇÕES DIDÁTICAS Atividades

Essas atividades apresentam diferentes situações envolvendo grandezas diretamente proporcionais e grandezas inversamente proporcionais e favorecem o desenvolvimento da competência geral 4 e da competência específica 6 da área de Matemática. Enfatizar o fato de os estudantes terem de avaliar qual é a relação existente entre as grandezas antes de aplicarem a regra de três simples na resolução.

a) Esse gráfico ilustra uma situação de proporcionalidade? Explique.

b) Qual é o preço a ser pago por 45 minutos de ligação? R$ 30,00

c) Com um crédito de R $ 25,00, quantos minutos de ligação é possível fazer?

A atividade 1 relaciona a quantidade de metros de um muro com a quantidade de tijolos necessários para construí-lo. Trata-se de uma relação de proporcionalidade direta, pois, quanto maior for o muro, mais tijolos foram usados para construí-lo. Para resolver, pode-se aplicar a regra de três, assim:

=h= 16 2 240 27 x x3 780

Portanto, seriam necessários 3 780 tijolos.

a) 1 hora. 80 km

b) 2h20min. Aproximadamente 186,7 km.

7. Um filtro de ar retém 0,7 grama de poeira para cada 100 m3 de ar filtrado. Quantos gramas de poeira são retidos quando são filtrados 15 0 00 m3 de ar?

4. U ma motorista dirige a uma velocidade constante. Sabendo que ela viaja 120 km em 1 hora e 30 minutos, calcule a distância que ela viaja em:

5. Co m certa quantidade de arame, pode-se fazer uma tela de 50 m de comprimento por 1,20 m de largura. Aumentando a largura em 1,80 m, qual será o comprimento da nova tela, feita com a mesma quantidade de arame usada na tela anterior?

10 pintores. 20 m

8. Uma escola lançou uma campanha de arrecadação de alimentos não perecíveis para doar a uma comunidade da região. Essa campanha teria a duração de 30 dias, e nos primeiros 15 dias, apenas 20 estudantes aceitaram a tarefa arrecadando 180 kg de alimentos. Nos últimos 15 dias da campanha, 30 novos estudantes se juntaram ao grupo e mantiveram constante o ritmo da coleta. Nessas condições, quantos quilogramas de alimentos foram arrecadados nesses últimos 15 dias? 450 kg

Na situação da atividade 3, quanto maior for o número de funcionários envolvidos na obra, menor será o tempo de execução dela. Portanto, trata-se de um problema envolvendo grandezas inversamente proporcionais. Ao aplicar a regra de três simples nesse problema, obtém-se:

=h= 2 x 16 80 x10

Portanto, serão necessários 10 funcionários para que a obra seja finalizada em 16 h.

Os estudantes podem resolver os itens a e b da atividade 6 a partir da interpretação do gráfico, contribuindo para o desenvolvimento da habilidade EF08MA12 e da competência específica 6 da área de Matemática. Para o item c, podem calcular o valor aproximado a partir da informação obtida anteriormente:

=h= 15 x 10 25 x 37,5

Sim, pois as grandezas variam na mesma razão.

ORIENTAÇÕES DIDÁTICAS

Regra de três composta

Na resolução de problemas envolvendo regra de três composta, é importante que os estudantes percebam a relação entre as grandezas envolvidas no problema para que possam escrever a equação correspondente.

Explorar a situação apresentada e verificar se os estudantes percebem que uma estratégia é fixar uma grandeza e avaliar o comportamento das outras duas, conforme aumenta-se (ou diminui-se) uma delas.

REGRA DE TRÊS COMPOSTA

A regra de três composta também é uma estratégia para o cálculo de valores desconhecidos em problemas que relacionam três ou mais grandezas diretamente proporcionais ou grandezas inversamente proporcionais.

Acompanhe a seguinte situação.

Um trator, ao ser rebocado por cinco pessoas, leva 20 minutos para percorrer uma distância de 120 metros. Em quanto tempo esse mesmo trator percorreria uma distância de 150 metros ao ser rebocado por quatro adultos?

Inicialmente, organizamos as grandezas envolvidas no problema em um quadro. Nesse caso, temos: quantidade de adultos, tempo (em minuto) e distância (em metro).

Quantidade de adultos Tempo (em min) Distância (em m)

5 20 120

4 x 150

• Fixando a quantidade de adultos, analisamos a relação entre as grandezas tempo e distância: aumentando a distância, o tempo para percorrê-la também aumenta proporcionalmente. Logo, concluímos que o tempo e a distância são grandezas diretamente proporcionais.

• Fixando a distância, analisamos a relação entre as grandezas quantidade de adultos e tempo: quanto maior a quantidade de adultos puxando o trator, menor o tempo gasto proporcionalmente. Assim, a quantidade de adultos e otempo são grandezas inversamente proporcionais.

Com isso, o tempo é diretamente proporcional à distância e inversamente proporcional à quantidade de adultos, o que nos permite escrever a seguinte equação.

20 x 120 150 1 5

Portanto, o trator levará 31,25 min (31 minutos e 15 segundos) para percorrer 150 metros ao ser rebocado por quatro adultos.

D2-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 284

ATIVIDADES

Responda às questões no caderno.

1. Na produção de uma fábrica de chocolates trabalham 21 funcionários. Juntos, eles fazem, ao longo da jornada de trabalho de 6 h diárias, 420 barras de chocolate. Próximo de datas comemorativas, a fábrica costuma aumentar a jornada de trabalho para 8 h diárias e faz novas contratações, pois tem como meta a produção de 960 barras de chocolate por dia. Quantos funcionários precisam estar na produção para que essa meta seja atingida? 36 funcionários.

12 máquinas operando 8 horas por dia. Porém, 3 dessas máquinas estão em manutenção e não ficarão prontas nesse período.

Com a redução da quantidade de máquinas, a carga horária diária de operação do maquinário será ampliada para 10 horas. De acordo com essas informações, a gráfica vai conseguir entregar a encomenda no prazo inicial? Se não conseguir, quantos dias a mais serão necessários para concluir esse trabalho?

Não.

ORIENTAÇÕES DIDÁTICAS

Atividades

É possível que surjam dificuldades, por parte dos estudantes, em identificar a relação que há entre as grandezas envolvidas em situações que podem ser resolvidas pela regra de três composta. Caso isso ocorra, relembrar a turma de que a construção de quadros ajuda muito a analisar essas relações.

Na atividade 2, as grandezas envolvidas são: quantidade de crianças, quantidade de castelos de areia e tempo, em hora.

2. Três crianças constroem cinco castelos de areia em 2 horas. Cinco crianças construirão seis castelos de areia em quanto tempo?

Aproximadamente 1h26min.

3. (IFPE) Numa fazenda há 5 cavalos que consomem 300 kg de ração em 6 dias. Suponha que todos eles consomem por dia a mesma quantidade de ração. Com apenas 240 kg de ração, 12 cavalos iguais aos dessa fazenda seriam alimentados durante

a) 1 dia.

b) 2 dias.

c) 3 dias

d) 4 dias.

e) 5 dias.

Alternativa b.

4. Com um automóvel a uma velocidade média de 60 km/h, Beto roda 8 horas por dia e leva 6 dias para fazer certo percurso. Com o mesmo automóvel, mas mantendo uma velocidade média de 80 km/h e rodando 9 horas por dia, em quanto tempo ele faria o mesmo percurso?

5. Uma gráfica recebeu uma encomenda e, para concluir o trabalho em um prazo de 15 dias, pretendia utilizar

6. (Enem/MEC) Uma indústria tem um reservatório de água com capacidade para 900 m³. Quando há necessidade de limpeza do reservatório, toda a água precisa ser escoada. O escoamento da água é feito por seis ralos, e dura 6 horas quando o reservatório está cheio. Esta indústria construirá um novo reservatório, com capacidade de 500 m³, cujo escoamento da água deverá ser realizado em 4 horas, quando o reservatório estiver cheio. Os ralos utilizados no novo reservatório deverão ser idênticos aos do já existente. A quantidade de ralos do novo reservatório deverá ser igual a

Quantidade de crianças

Quantidade de castelos de areia

Tempo (em h) 3 5 2 5 6 x

Alternativa c. Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

a) 2.

b) 4. c) 5. d) 8. e) 9.

7. Com base nos conceitos estudados, elabore um problema envolvendo três grandezas que possa ser resolvido por meio da regra de três composta. Você pode aproveitar algum dos contextos apresentados ou pensar em outros. Em seguida, troque o caderno com um colega, de modo que um resolva oproblema elaborado pelo outro. Por fim, compartilhem as estratégias que utilizaram na elaboração e na resolução dos problemas.

285 D2-MAT-F2-2103-V8-U9-262-291-LA-G24.indd

Observar que a quantidade de crianças e o tempo são grandezas inversamente proporcionais, pois, aumentando o número de crianças, diminui-se o tempo da atividade. Por outro lado, a quantidade de castelos de areia é diretamente proporcional ao tempo, ou seja, mais castelos necessitam de mais tempo para serem construídos. Com isso, é possível montar a equação:

=?h=h= 2 x 5 3 5 6 2 x 25 18 x1,44 h x = 1,44

Ao converter o resultado em horas e minutos, obtém-se, aproximadamente, 1h26min.

Um dia a mais.

ORIENTAÇÕES DIDÁTICAS

Tratamento da informação

Esta seção aborda como tema o mercado de trabalho voltado para pessoas reabilitadas ou com deficiências. Discutir com os estudantes os avanços que a legislação apresentada trouxe para essas pessoas e como isso afeta a vida de milhares de pessoas. Essa discussão contribui para o desenvolvimento do Tema Contemporâneo Transversal Trabalho, das competências gerais 4 e 9 e da competência específica 3 da área de Matemática. Esses temas podem ser propostos para um trabalho de maneira coletiva e colaborativa com os estudantes e entre eles.

Na atividade 1, os estudantes precisam compreender a distribuição das porcentagens com relação à quantidade de funcionários da empresa para realizar o cálculo da quantidade de vagas destinadas às pessoas reabilitadas ou com deficiências. Perceber a necessidade de retomar o cálculo de porcentagens, discutindo algumas estratégias.

INFORMAÇÃO TRATAMENTO DA

INTERPRETANDO INFORMAÇÕES

O mercado de trabalho no Brasil e a inclusão de pessoas com deficiência

As pessoas com deficiência enfrentam muitos desafios no dia a dia e, principalmente, no mundo do trabalho. É de fundamental importância para o exercício da cidadania que elas sejam reconhecidas como sujeitos de direito, bem como pela sua força de trabalho, sendo direcionadas a cargos e funções de acordo com suas especificidades e habilidades. Assim, poderão superar desafios e preconceitos.

Os direitos ao acesso e à participação no mercado de trabalho precisam ser materialmente garantidos, de modo que muitos espaços que careçam de adaptações sejam ajustados para atender às condições de acessibilidade.

Pessoa com deficiência exercendo atividade laboral em ambiente de trabalho. Fotografia de 2022.

O artigo 93 da lei no 8.213 de 1991 especifica a quantidade de vagas que devem ser preenchidas por pessoas reabilitadas ou com deficiência em uma empresa com mais de 100 empregados. Leia a seguir o que diz o referido artigo.

Art. 93. A empresa com 100 (cem) ou mais empregados está obrigada a preencher de 2% (dois por cento) a 5% (cinco por cento) dos seus cargos com beneficiários reabilitados ou pessoas portadoras de deficiência, habilitadas, na seguinte proporção:

I – até 200 empregados....................................2%;

II – de 201 a 500..................................................3%;

III – de 501 a 1 000.............................................4%;

IV – de 1 001 em diante....................................5%.

BRASIL. Lei no 8.213, de 24 de julho de 1991. Dispõe sobre os Planos de Benefícios da Previdência Social e dá outras providências. Brasília, DF: Casa Civil, 1991. Disponível em: http://www.planalto.gov.br/ccivil_03/leis/l8213cons.htm. Acesso em: 4 jul. 2022.

Com base nessas informações, responda às questões no caderno.

1. Considere uma empresa que tem 1 500 funcionários contratados. De acordo com o artigo de lei citado anteriormente, quantas dessas vagas devem ser ocupadas por beneficiários reabilitados ou pessoas com deficiência habilitadas? No caso de uma empresa com 150 funcionários, qual seria essa quantidade de vagas? 75 vagas; 3 vagas.

AMPLIANDO

Link

COMO está a inclusão de pessoas com deficiência no mercado de trabalho? Entrevistadores: Pedro Pontes e Cíntia Cruz. Entrevistada: Rosana Rosa. Brasília, DF: Revista Brasil, 7 ago. 2020. Podcast. Disponível em: https://radios. ebc.com.br/revista-brasil/2020/08/como-esta-inclusao-de-pessoas-com-deficiencia-no-mercado-de-trabalho. Acesso em: 14 ago. 2022.

Nessa entrevista, Rosana Rosa, presidente da Associação Brasileira de Recursos Humanos do Rio de Janeiro (ABRH-RJ), apresenta dados sobre a inclusão de pessoas com deficiência no mercado de trabalho.

ORIENTAÇÕES DIDÁTICAS

2. Em seu entendimento, esse artigo de lei tem contribuído, ao longo desses anos, para a inserção de pessoas com deficiência no mercado de trabalho? Você considera importante a existência de legislações como essa?

Distribuição dos vínculos formais de trabalho no Brasil, por tipo de deficiência, em 2019 45%

Na atividade 2 ouvir os estudantes com relação à legislação apresentada, valorizando a argumentação pautada no respeito ao outro, contribuindo, ainda, para o desenvolvimento da empatia

1,6%

Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual. 9% 10,5% 16,1% 17,7%

Elaborado com base em: DEPARTAMENTO INTERSINDICAL DE ESTATÍSTICA E ESTUDOS SOCIOECONÔMICOS (DIEESE). Inclusão da pessoa com deficiência no mercado de trabalho. Nota técnica, São Paulo, n. 246, p. 1-22, 20 nov. 2020. Disponível em: https:// www.dieese.org.br/notatecnica/2020/ notaTec246InclusaoDeficiencia.html.

Acesso em: 4 jul. 2022.

a) Qual era o tipo de deficiência da maioria das pessoas com deficiência com vínculos formais de trabalho no Brasil em 2019?

Deficiência física.

b) Considerando as pessoas com deficiência visual e as pessoas com deficiência mental, juntas, podemos afirmar que, em 2019, elas correspondiam aproximadamente a um quarto dos vínculos formais de trabalho ocupados por pessoas com deficiência?

Sim, pois 16,1% + 9% = 25,1%.

As atividades 3 e 4 apresentam um gráfico de setores e uma tabela, respectivamente. Destacar para os estudantes o foco na interpretação do significado de informações e no uso e na interpretação desses recursos. Se desejar, trabalhar com os estudantes a transnumeração de tabelas para gráficos, ou vice-versa, podendo ainda utilizar planilhas eletrônicas ou aplicativos como o GeoGebra.

De 1 a 2 salários mínimos.

4. Analisando a tabela a seguir, identifique a faixa salarial em que se verificava o rendimento médio da maioria das pessoas com deficiência no Brasil em 2019.

Distribuição dos rendimentos médios de pessoas com deficiência no Brasil, em 2019

Faixa salarial (salário mínimo*) Frequência relativa (em %)

Até 1 5,94 1 2 54,17 2 3 17,18 3 5 12,48 5 10 7,08 Mais de 10 3,15 Total 100

*Valor do salário mínimo considerado em setembro de 2020. Elaborada com base em: DEPARTAMENTO INTERSINDICAL DE ESTATÍSTICA E ESTUDOS SOCIOECONÔMICOS (DIEESE). Inclusão da pessoa com deficiência no mercado de trabalho. Nota técnica, São Paulo, n. 246, p. 1-22, 20 nov. 2020. Disponível em: https://www.dieese.org.br/notatecnica/2020/ notaTec246InclusaoDeficiencia.html. Acesso em: 4 jul. 2022.

É importante destacar para os estudantes os principais elementos que compõem um gráfico, como título, legendas, eixos horizontal e vertical, datas. Essa seção explora a habilidade EF08MA23.

ARTKIO/SHUTTERSTOCK.COM

Reforçar sempre para os estudantes a atenção que se deve dar à fonte dos dados, verificando de onde ela vem, se pode ser considerada confiável, quais interesses poderiam ter as pessoas envolvidas na divulgação dos dados, ou seja, se essas pessoas estão utilizando as informações a seu favor. Tudo isso promove o letramento estatístico e a análise crítica nos estudantes.

O item b da atividade 3 aborda conceitos sobre aumentos percentuais e porcentagem.

13/08/22 19:31

Na atividade 4, o professor pode rever com os estudantes frequências absolutas, frequências relativas e o significado do conceito de média.

ORIENTAÇÕES DIDÁTICAS

Retomando o que aprendeu

As atividades propostas vão retomar a ideia de proporcionalidade por meio de diferentes situações em que os estudantes precisam analisar a relação que há entre as grandezas apresentadas: se são diretamente proporcionais ou inversamente proporcionais ou se não há relação de proporcionalidade.

A atividade 3 apresenta um problema clássico de analisar diferentes opções de tarifas de locação de quadras de tênis para avaliar qual é a mais adequada para a situação apresentada. Para responder ao item a, os estudantes vão completar o quadro a partir das informações de cobrança de cada tarifa. No item b, eles precisam construir os gráficos de cada uma das tarifas apresentadas para, nos itens c e d, comparar e decidir a tarifa mais vantajosa em cada caso.

Responda às questões no caderno.

1. Em um mapa construído na escala 1 : 15 000, a distância entre duas casas de um vilarejo é representada por um segmento de reta de 1,6 cm. Qual é a distância real entre essas duas casas?

2. Calcule a área de um estado, sabendo que, em 2022, a população era de 10 444 526 pessoas, e a densidade demográfica era de 52,40 hab./km2

3. Uma empresa qu e faz locação de quadras de tênis oferece três opções de tarifa, de acordo com o tempo de uso.

Tarifa 1: R$ 0,40 por minuto de uso. Tarifa 2 : R $ 35,00 para 2 horas de uso, mais R$ 0,40 por minuto de uso adicional.

Tarifa 3: R $ 48,00 para 4 horas de uso, mais R$ 0,40 por minuto de uso adicional.

a) Copie e complete o quadro a seguir.

AMPLIANDO

Atividade complementar

b) No gráfico a seguir, a presentada na cor azul. Copie o gráfico em uma folha de papel quadriculado e, em seguida, represente as e 3 usando as cores vermelha e verde, respectivamente.

D2_AV1-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 288

(Enem/MEC) Na imagem, a personagem Mafalda mede a circunferência do globo que representa o planeta Terra.

Em uma aula de matemática, o professor considera que a medida encontrada por Mafalda, referente à maior circunferência do globo, foi de 80 cm.

Tarifas de aluguel da quadra de tênis

c) Para escolher a tarifa 2, qual seria o melhor tempo de uso? Até 120 minutos.

d) Qual é a tarifa mais barata para 210 minutos de uso da quadra? Tarifa 3.

4. A explosão de um vulcão localizado no mar provoca a formação de um tsunami – onda gigante, de várias dezenas de metros de altura –, que se move a uma velocidade de 138,89 m/s.

a) Transforme essa velocidade em km/h.

b) Em quanto tempo a onda alcançará a casa representada na imagem? 0,16 min ou, aproximadamente, 9,4 s.

Além disso, informa que a medida real da maior circunferência da Terra, a linha do Equador, é de aproximadamente 40 000 km.

QUINO. Toda Mafalda. São Paulo: Martins Fontes, 2008 (adaptado). A circunferência da linha do Equador é quantas vezes maior do que a medida encontrada por Mafalda?

a) 500 b) 5 000 c) 500 000 d) 5 000 000 e) 50 000 000

c) Qual foi a distância percorrida pela onda em 1 s? 138,89 m

d) A ssumindo que a onda leva 18 minutos para chegar à costa, a que distância ela é formada? 150 km

5. Um produtor rural alugou 2 tratores para arar determinada área para o plantio, estimando que essas máquinas vão realizar essa tarefa em 6 horas. Se ele quiser reduzir esse tempo de arado para 4 horas, supondo que as máquinas vão operar em um mesmo ritmo, quantos tratores deverá alugar? 3 tratores.

6. Márcia trabalha em um canil, no qual havia 8 cães que, juntos, consumiam 12 kg de ração em 5 dias. Sabe-se que 3 desses cães foram doados e que a nova embalagem de ração contém 15 kg. Supondo que os cães mantenham esse ritmo de consumo, oconteúdo da nova embalagem de ração é suficiente para quantos dia s?

a) 8 dias.

b) 10 dias.

c) 11,5 dias.

ORIENTAÇÕES DIDÁTICAS

Um novo olhar

d) 12 dias. e) 15 dias. Alternativa b.

Nesta Unidade, retomamos o estudo de grandezas proporcionais. Nesse trabalho, analisamos quando duas grandezas são proporcionais e quando não são. Estudamos, também, o conceito de grandezas diretamente proporcionais e de grandezas inversamente proporcionais, bem como a representação gráfica correspondente a cada uma dessas relações.

Estudamos algumas razões especiais que são utilizadas no dia a dia, como a velocidade média, a densidade de um corpo e a densidade demográfica. Exploramos, também, o conceito de escala e sua aplicação.

Discutimos a importância do respeito mútuo e da valorização da diversidade, refletindo sobre tolerância e situações que podem decorrer da intolerância.

Utilizamos regra de três simples e regra de três composta para resolver situações e elaboramos problemas utilizando a relação entre grandezas. Exploramos, ainda, a questão da inclusão de pessoas com deficiência no mercado de trabalho no Brasil, interpretando informações em diferentes gêneros textuais.

Na abertura desta Unidade, você teve a oportunidade de conhecer um pouco sobre a aplicação do conceito de escala no dia a dia de arquitetos, engenheiros e profissionais que trabalham com representações de edificações.

Vamos, agora, refletir sobre as aprendizagens adquiridas ao longo desta Unidade. Responda no caderno às questões seguintes.

UM NOVO OLHAR Resposta pessoal. Exemplo de resposta na seção Resoluções comentadas deste Manual.

• Como você definiria grandezas diretamente proporcionais? E grandezas inversamente proporcionais?

• O que caracteriza a representação gráfica de duas grandezas diretamente proporcionais? Uma reta.

• Retome o esboço que você fez na abertura da Unidade. Agora, escolha uma escala distinta daquela utilizada e desenhe uma representação da sala de aula em que você estuda. Resposta pessoal.

Os questionamentos dessa seção retomam, brevemente, os assuntos tratados ao longo da Unidade e possibilitam reflexões a respeito das aprendizagens individuais dos estudantes. É importante que eles respondam individualmente a cada uma das questões para que, dessa maneira, possam perceber possíveis dúvidas que ainda existem a respeito de cada um dos assuntos estudados. Espera-se que os estudantes consigam explicar o que são grandezas diretamente proporcionais e grandezas inversamente proporcionais, além de identificar grandezas diretamente proporcionais representadas por meio de gráficos, no caso, retas que passam pela origem.

Resolução da atividade

Convertendo 40 000 km em centímetros, temos:

40 000 km = 4 000 000 000 cm

Dividindo o comprimento total real pelo comprimento medido por Mafalda no globo, temos:

4 000 000 000 cm : 80 cm = 50 000 000

Alternativa e.

ORIENTAÇÕES DIDÁTICAS

Tecnologias

Nessa seção, os estudantes poderão criar um programa em blocos, usando a linguagem Scratch. Essa atividade contribui para o desenvolvimento do pensamento computacional, da inferência, do Tema Contemporâneo Transversal Ciência e Tecnologia e da competência específica 6 da área de Matemática.

Antes de iniciar, explicar os objetivos da proposta, ou seja, construir um programa em blocos que resolve equações do 1o grau da forma ax = b. Nos passos 1 a 5, pedir aos estudantes que identifiquem a aba Código e, em seguida, localizem os seguintes menus: Eventos, Variáveis e Sensores

Circular pela sala de aula verificando se os estudantes localizam os comandos citados no Livro do estudante e se estão com alguma dificuldade.

TECNOLOGIAS

RESOLUÇÕES DE EQUAÇÕES UTILIZANDO UM SOFTWARE

O Scratch é uma linguagem gratuita de programação em blocos. Voltada para crianças e jovens, essa linguagem foi desenvolvida para facilitar, de modo prático e intuitivo, a criação de programas. Nesta seção, vamos utilizar algumas ferramentas do Scratch para criar um programa em blocos, que resolve equações de 1o grau, reduzidas na forma ax = b (em que a 5 0). Lembre-se de que, conforme estudamos, a solução de equações escritas nessa forma é dada por x = b a , com a 5 0. No Scratch, vamos nos referir aos coeficientes a e b como variáveis, que são os valores que vamos fornecer ao programa criado para que nos apresente a solução. Acesse a página inicial do Scratch, disponível em https://scratch.mit.edu/projects/editor/? tutorial=getStarted (acesso em: 4 jul. 2022) e realize os passos a seguir.

1 Na aba Código, selecione o menu Eventos e arraste o bloco para a janela principal.

2 Para criar as variáveis do programa, que correspondem aos valores que vamos fornecer, selecione o menu Variáveis e clique em . Em seguida, digite a no campo Nome da nova variável e clique em OK

3 A variável a está criada. Repita o passo 2 para criar a variável b. Feito isso, as variáveis a e b deverão constar no menu Variáveis e na tela em que aparece o ator do programa. Para construir a estrutura do algoritmo do programa, vamos utilizar os comandos do menu Sensores e os de mudança de variáveis do menu Variáveis

4 Clique no menu Sensores e arraste o bloco para a tela principal, encaixando-o no bloco lá existente. Em seguida, digite Insira o valor de a no campo digitável desse bloco.

5 Selecione o menu Variáveis e arraste o bloco para a tela principal, encaixando-o no último bloco colocado nessa tela. Em seguida, clique no menu Sensores e arraste o bloco para o campo digitável de

D2_AV5-MAT-F2-2103-V8-U9-262-291-LA-G24.indd 290

AMPLIANDO

Link

SCRATCH para educadores. Scratch. [S l.], [20--]. Disponível em: https://scratch.mit.edu/educators/. Acesso em: 14 ago. 2022.

Acessando esse link, é possível obter mais informações e ideias de atividades usando a programação em blocos Scratch.

6 Repita o passo 4 digitando Insira o valor de b no campo digitável; em seguida, repita o passo 5, alterando para no bloco correspondente. Você vai obter a estrutura mostrada na Figura 1

Agora, vamos construir o comando que contém a operação de divisão, que possibilita ao ator do programa revelar a solução da equação.

7 Selecione o menu Operadores e arraste a operação para a tela principal. Em seguida, clique no menu Variáveis e arraste as variáveis para esse operador, obtendo

8 Selecione o menu Aparência e arraste o bloco , encaixando-o no conjunto construído até então.

9 Para concluir, clique no menu Operadores e arraste o operador para o campo do último bloco encaixado no conjunto. Em seguida, digite A solução da equação é no primeiro campo digitável desse operador e arraste o quociente para o segundo campo, obtendo o algoritmo indicado na Figura 2

Para testar o algoritmo, descubra a solução da equação escrita na forma 2x = 5.

Clique, inicialmente, em . Depois, siga os comandos dados pelo ator e verifique se o resultado obtido é 2,5.

Agora, junte-se a um colega, e respondam às questões no caderno.

1. Utilizando o programa criado, obtenha a solução de cada equação a seguir.

a) 5x = 2 0,4

b) 9x 17 = 0 1,888...

2. Construa o algoritmo de um programa que resolva equações de 2o grau, escritas na forma ax 2 + c = 0. Em seguida, teste o programa, determinando a solução da equação 4x 2 100 = 0. Exemplo de resposta na seção Resoluções comentadas deste Manual.

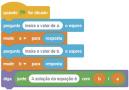
ORIENTAÇÕES DIDÁTICAS

Seguir para os passos 6 a 9, dessa vez pedindo que localizem os menus: Operadores e Aparência

Na atividade 1, os estudantes devem resolver duas equações do 1o grau usando o programa em blocos que acabaram de construir. Se desejar, propor mais algumas equações do mesmo tipo ou pedir aos estudantes que criem outros exemplos e verifiquem se a solução é correta. Na atividade 2, é feito um convite para que os estudantes construam outro programa, a partir do que aprenderam com esse, para a resolução de equações do 2o grau incompletas, da forma ax 2 = c. A ideia aqui é que eles possam experimentar, errar, ajustar e compreender a lógica da resolução.

Figura 1

Figura 2

UNIDADE 1

Números reais e porcentagem

Abertura de Unidade – p. 12

• Resposta pessoal.

• Comprar à vista significa fazer o pagamento do valor integral (ou com desconto) no ato da compra. Comprar a prazo significa pagar o valor em parcelas.

• Resposta pessoal.

1. Conjunto dos números racionais Atividades – p. 18

1.

2. a) 0,5

b) 2,333...

c) 1,8

d) 1,85

e) 3,1818...

f) 1,222...

g) 0,029

h) 0,385

i) 0,15

j) 0,1444...

k) 8,25

l) 4,1666...

3. a) DE; b) DP; c) DE; d) DE; e) DP; f) DP; g) DE;

h) DE; i) DE; j) DP; k) DE; l) DP

4. a) Período: 2

b) Período: 7

c) Período: 01

Atividades – p. 22

1. Exemplos de respostas:

a) 22 9 b) 1 9

2. Alternativa e.

3. Números reais

Atividades – p. 25

1. Alternativa d.

2. Alternativa d.

3. Alternativa d.

4. a) 0; 1

a) . b) , c) , d) , e) =

3. Alternativa a.

29 8

141 20

79 33

6.

12 c) Aproximadamente 68,14.

66,84

32,1 f) 60,3

7. Alternativa a.

2. Dízimas periódicas Pense e responda – p. 20

1. • , = 7 9 0 777 = 0,777...

• , = 13 99 0 131313 = 0,131313...

• , ... = 3 9 0 333 = 0,333...

• , = 211 99 2 131313 = 2,131313...

2. Todos os números são dízimas periódicas; 7; 13; 3; 13.

3. Resposta pessoal. Atividades – p. 20

1. a) 0,7

3,1

0,06

0,11

1,62

0,009

c) 161 9 d) 629 99

3. Exemplos de respostas:

a) 322 45 b) 24 45

d) Período: 3

e) Período: 56

f) Período: 034

e) 29 99 f) _ 700 333

c) 2 071 30 d) 1 163 990

4. Alternativa d. 5. Alternativa d.

6. 77 90

7. Resposta pessoal.

8. a) e b)

b) 4; 0; 1

c) 4 d) 2,3; 1 4 ; 0, 06 ,

5. a) Finita.

b) Infinita e periódica.

c) Infinita e não periódica.

6. Resposta pessoal.

4. Porcentagem

Atividades – p. 28

1. 12 reais.

2. 38 questões.

3. Respostas pessoais.

4. Ótimo: 42%

Bom: 40%

Regular: 12%

Ruim: 6%

5. Aproximadamente 15,8%

6. a) 450 kg

b) 88%

7. Resposta pessoal.

8. Resposta pessoal, que depende dos dados pesquisados.

Por toda parte – p. 29

1. 49,29%; Acre, Amapá, Amazonas, Pará, Roraima, Rondônia, Mato Grosso, Maranhão e Tocantins.

2. A área aproximada é 4 200 000 km2

3. São seis os biomas predominantes no Brasil: Amazônia, ocupando cerca de 49% ; Mata Atlântica, ocupando aproximadamente 13%; Cerrado, cobrindo cerca de 24% do território brasileiro; Caatinga, que ocupa cerca de 10% ; Pampa e Pantanal, ocupando cerca de 2% do território, cada um.

4. a) Aproximadamente 20%.

b) Resposta pessoal.

Pense e responda – p. 30

1. Resposta pessoal.

2. R$ 480,00; R$ 720,00

3 R$ 1.080,00

Atividades – p. 32

1. 207 reais.

2. 2,5%

3. 760 reais.

4. Alternativa a.

5. Alternativa c.

6. Alternativa c.

7. 4%

8. Alternativa c.

9. a) R$ 500,00

b) R$ 10.500,00

10. Resposta pessoal.

c) 5,5%

Educação financeira – p. 33

1. Os bancos oferecem, para quem tem dinheiro e quer guardá-lo, uma forma segura de fazê-lo. Já para as pessoas que precisam de dinheiro para investimentos, os bancos fazem empréstimos, recebendo uma compensação na forma de juro pelo serviço.

2. Respostas pessoais.

Tecnologias – p. 34

1. Emerson pagaria R$ 7.560,00 nesse caso.

2. Resposta pessoal.

3. No caso do investimento, o montante ao final de 12 meses é de R$ 1.590,00; já no empréstimo, o valor a ser pago é R$ 2.940,00.

Tratamento da informação – p. 36

1. a) Resposta pessoal.

b) • às geleiras e coberturas permanentes de neve: 1,72%

• aos rios e lagos: 0,0075%

• às águas subterrâneas: 0,75%

• a outros: 0,02%

2. Alternativa c.

3. Médias globais de pegada hídrica de alguns produtos

1 kg de açúcar refinado

4. Alternativa c.

5. 12,5%

6. 55%

7. 60%

8. Alternativa d.

9. Alternativa c.

10. Alternativa b.

11. Alternativa d.

12. Alternativa c.

13. Resposta pessoal.

Um novo olhar – p. 39

• Resposta pessoal.

• Resposta pessoal.

• Será um decimal exato.

• Resposta pessoal.

UNIDADE 2

Potências e raízes

Abertura de Unidade – p. 40

• Sissa pediu que lhe fossem dados grãos de trigo pelas casas de um tabuleiro da seguinte maneira:

1 grão pela primeira casa do tabuleiro, 2 grãos pela segunda, 4 pela terceira, 8 pela quarta, e assim sucessivamente, dobrando a quantidade de grãos por casa, até chegar à 64a casa.

2. Propriedades da potenciação

Pense e responda – p. 46

1. a) • 22 23 = 25

• 34 32 = 36

b) • 25 : 23 = 22

• 35 : 32 = 33

c)

• 64

• 512

• 81

d) • (23)2 = 26

• (32)2 = 34

• (23)3

5 26

Por toda parte – p. 50

1. 7 105 quilobytes, 1,23 105 quilobytes, 7 108 bytes, 1,23 108 bytes, 5,6 109 bits

e 9,84 ? 108 bits

Atividades – p. 51

1. a) 1 2

10      

b) 206

102

2.

220

26

221 b) 22

225 3. x5 = y2 4.

( 0,6)4 (1,1)4

226

1 500 100 g de chocolate

1 camiseta de algodão

1 kg de carne bovina

2 400

2 700

15 500

Fonte: PEGADA hídrica incentiva o uso responsável da água. WWF. Brasília, DF, 21 mar. 2011. Disponível em: https://www.wwf.org.br/?27822/Pegada-Hdrica-incentiva -o-uso-responsvel-da-gua#. Acesso em: 25 jul. 2022.

Médias globais de Pegada Hídrica de alguns produtos (em litro de água)

• Calcular uma potência de base 2, cujo expoente varia de 0 a 63.

• Resposta pessoal.

• Resposta pessoal.

1. Potência com expoente inteiro Pense e responda – p. 42

16

252

756

9. Giga: 109; mega: 106; quilo: 103; hecto: 102; deca: 101; mili: 10 3;

10 6; nano: 10 9

11.

6 300 000 000

12. a) 8,52 107

13. a) 1,3 108

14. Resposta pessoal.

1 kg de açúcar re nado

100 g de chocolate

1 camiseta de algodão

1 kg de carne bovina

Fonte: PEGADA hídrica incentiva o uso responsável da água. WWF. Brasília, DF, 21 mar. 2011. Disponível em: https://www.wwf.org.br/?27822/Pegada-Hdrica-incentiva -o-uso-responsvel-da-gua#. Acesso em: 25 jul. 2022.

4. Resposta pessoal.

Retomando o que aprendeu – p. 38

1. Alternativa c.

3. a) Sim; 49 7 d) 3 b) −97; 49 7 e) 1,25; 49 7 ; 97; 3 5

c) 3

9,167 106

2 106

3. Números quadrados perfeitos

Atividades – p. 53

1. a) Sim. Sim, 25 é um quadrado perfeito.

b) Não. Não, 29 não é um quadrado perfeito.

2. a) É quadrado perfeito.

b) Não é quadrado perfeito.

c) É quadrado perfeito.

d) É quadrado perfeito.

e) Não é quadrado perfeito.

f) É quadrado perfeito.

g) Não é quadrado perfeito.

h) É quadrado perfeito.

3. Qualquer número ímpar.

4. 7 números.

5. Alternativa b.

6. O valor de B é 625.

4. Raiz quadrada

Atividades – p. 57

1. a) 22

b) 25

c) 27

d) 34 e) 36 f) 43

g) 55 h) 64

i) 100

5.

2. a)

Notas dos estudantes do 8o ano na prova final de Matemática

Nota obtida na prova final de Matemática Quantidade de estudantes

• Os números naturais que são quadrados de outros números naturais.

• Determinar a raiz quadrada de um número x é encontrar um número y que, quando elevado ao quadrado, tem como resultado o número x

UNIDADE 3 Ângulos e triângulos

Abertura de Unidade – p. 68

• O triângulo não pôde ser deformado, diferentemente do quadrado.

1. Ângulos

Atividades – p. 73

1. x = 130° e y = 80°.

2. a) 24°

3. a) 102°

Fonte: Professora do 8o ano.

b) 9 estudantes.

c) 15 estudantes.

d) Aproximadamente 57%

3. a) 18 jogadoras.

b) 20 anos; 36 anos.

c)

6.

5. Resposta pessoal.

6. Resposta pessoal. Fórum – p. 61

1. Resposta pessoal.

2. Resposta pessoal.

3. Resposta pessoal.

Tecnologias – p. 62

1. a) 55 225

b) 1 601 613 c) 90 224 199 d) 0,00000001

2. Resposta pessoal.

3. a) Resposta pessoal. b) Resposta pessoal.

4. Resposta pessoal.

Tratamento da informação – p. 64

1. a) 90 alunos.

b) De 1,50 m até 1,98 m.

c) 11 alunos.

d) 1,74 ¿ 1,82. Significa que a maioria dos alunos pesquisados tem altura maior ou igual a 1,74 m e menor do que 1,82 m.

e) 75 alunos.

f) Aproximadamente 5,56%.

Idade das atletas da Seleção Brasileira Feminina de Voleibol em 2022

Idade (em anos)

Fonte: ATLETAS da Seleção Brasileira. Confederação Brasileira de Voleibol. [Rio de Janeiro], [20--?].

Disponível em: https://cbv.com.br/ligadasnacoes/ selecao-brasileira-feminina. Acesso em: 24 jul. 2022.

d) De 24 a 28 anos.

e) 6 jogadoras.

Retomando o que aprendeu – p. 66

1.

2. Alternativa d.

3. Alternativa e.

b) 16°

c) 68°

d) 43°

4. 80°

5. 45°

6. 72°

b) 113°

c) 45°

d) 41°

7. x = 140°; y = 40° e z = 140°.

8. a) Bissetriz de um ângulo. Os ângulos formados pela haste azul e cada uma das hastes vermelhas são congruentes.

b) A medida de cada haste verde representa a distância de cada ponto da haste azul até cada uma das hastes vermelhas, de acordo com a definição de bissetriz de um ângulo (é importante considerar que as hastes verdes são perpendiculares a cada haste vermelha). Resposta pessoal.

9. x = 130° e y = 20°.

10. med(AMC) = med(DMB) = 135°; med(AMD) = med(BMC) = 45°

2. Triângulos

Pense e responda – p. 75

1. Produção pessoal.

2. Pela montagem, é possível verificar que, juntos, os três ângulos internos do triângulo formam um ângulo raso.

Então: a + b + c = 180°.

Atividades – p. 77

1. a) BC

b) PN

2. a) b + c + d = 180°

b) a + b 180°

c) c + d = a

3. 27°

4. 86°

5. 58°

6. 50°

7. 53°

8. med(A) = 64°, med(B) = 68° e med(C ) = 48°. Resposta pessoal.

9. 180°

Por toda parte – p. 82

1. Sim.

2. a) Sim.

b) Os dois segmentos traçados têm sempre o mesmo comprimento. Isso ocorre porque a bissetriz de um ângulo é determinada pelos pontos do plano equidistantes das semirretas que formam esse ângulo.

Atividades – p. 83

1. a = 30°, b = 30° e c = 60°.

2. Alternativa d.

3. Alternativa c.

4. a = 115°, b = 80° e c = 65°.

5. 20°. Resposta pessoal.

6. a = 90°, b = 50° e c = 95°.

3. Congruência de triângulos

Atividades – p. 89

1. Caso LAL; x = 60° e y = 30°.

2. x = 4 cm e y = 5 cm.

3. a) Demonstração.

b) Demonstração.

4. Demonstração. Resposta pessoal.

5. a) São congruentes pelo caso LAAO

b) Resposta pessoal.

6. Demonstração.

7. Demonstração.

4. Propriedades dos triângulos

Atividades – p. 92

1. 37° cada um.

2. x = 67° e y = 46°.

3. 22,5° ou 22° 30‘

4. 50°

5. x = 17°. Resposta pessoal.

6. x = 36°

7. a = 20°, b = 40° e c = 50°.

8. 165° Por toda parte – p. 93

1. Resposta pessoal.

2. Produção pessoal.

5. Construções geométricas

Atividades – p. 96

1. a) Resposta pessoal.

b) Resposta pessoal.

2. a) Resposta pessoal.

b) Não, pois esse local pode ser representado por qualquer um dos infinitos pontos da mediatriz do segmento PQ

Tecnologias – p. 97

1. Resposta pessoal.

2. Resposta pessoal.

Retomando o que aprendeu – p. 100

1. Alternativa e.

2. Alternativa c.

3. Alternativa b.

4. Alternativa d.

5. a) 60° cada um. b) Equilátero.

6. Alternativa d.

7. Alternativa b. 8. Alternativa a. 9. Alternativa c.

Um novo olhar – p. 101

• 180°. Resposta pessoal.

• De acordo com as medidas dos ângulos internos: triângulo retângulo, triângulo acutângulo ou triângulo obtusângulo. De acordo com as medidas dos lados: triângulo equilátero, triângulo isósceles ou triângulo escaleno.

• LLL, LAL, ALA, LAAO e o caso de congruência no triângulo retângulo.

• Resposta pessoal.

UNIDADE 4

Expressões e cálculo algébrico

Abertura de Unidade – p. 102

• a) Sendo n [n, 2n + 1 é um número ímpar.

b) O número 11.

• Resposta pessoal.

1. Uso de letras para representar números

Pense e responda – p. 104

1. a) 32

b) a b

c) 2x y

I) A expressão do item a

II) A expressão do item c

III) A expressão do item b

2. Resposta pessoal.

Atividades – p. 105

1. a) x2

b) y3

c) a

d) b5

e) b + c

f) ax

3. Valor numérico de uma expressão algébrica

Fórum – p. 111

1. Resposta pessoal.

2. Resposta pessoal.

Atividades – p. 112

1. 1,75

2. 9,6

3. a) 4

b) 25 16

c) 4

4. 122 500

5. a) x = 4

b) a = 1 3

6. a) x = y

b) x = y 2

7. 201 000 pessoas.

8. 32 graus Celsius.

9. Resposta pessoal.

10. Resposta pessoal.

11. Resposta pessoal.

d) 0

e) 8 9

f) 0,25

g) 65 63

c) x = 2 5

d) b = 1

4. Monômio ou termo algébrico

Pense e responda – p. 113

1. a) xy

b) 2x + 2y

2. a) 2x

c) Resposta pessoal.

b) x2 + x

g) 2y h) 1 6 m

i)

Atividades – p. 115

1. 7ab

2. a) Sim.

b) Sim.

c) Não.

d) Sim.

e) Não.

f) Sim.

3. a) Coeficiente: 7; parte literal: b3

b) Coeficiente: 1; parte literal: x2y.

c) Coeficiente: 0,9; parte literal: c4

d) Coeficiente: 1; parte literal: a5x3

g) Não.

h) Não.

i) Não.

D2_AV2-MAT-F2-2103-V8-PFI-292-304-LA-G24.indd

2. a) 2x + 2y d) x2 y2

b) (x + y)(x y) e) (x + y)2

c) x2 + y2 f) x 1 5 y +

2. Expressões algébricas ou literais Atividades – p. 108

1. 5x + 8y

2. a) • h + m • h m • h m

b) Sim; h m

3. 12xy

4. 5x + 3y

5. x2 + ay

6. x 2y

7. x2 + 3x

8. 7x + 10y

9. a) 7x + 20 b) 12y + 10

Educação financeira – p. 109

1. Entre 7 e 8 meses.

2. Aproximadamente R$ 60.896,33.

e) Coeficiente: 6,2; parte literal: a4b2c.

f) Coeficiente: 4

4. 9x

5. 7,90x

6. 20x

7. 37,50y

5 ; parte literal: não tem.

8. a) 8x b) 8y

9. 8a3

10. a) • 109,50n • 87,50n

b) 547,50; 437,50. Esses valores numéricos representam o valor total, em reais, a ser pago por um grupo de 5 adultos, caso realizem o passeio em alta temporada e em baixa temporada, respectivamente.

11. 125x, 625x, 3 125x

Atividades – p. 118

1. 9x3y; 2 3 mn22

2. 9 o grau.

3. 3

4. a) 2x5

b) 2x5; 10x4; 7x3; 8x2; 2,5x; 20

5. 7

6. a) 0,7ax2

b) 20a2x2 c) 5a2x; 0,5a2x d) 10ax; 1 2 ax

7. a) 3x2 e) 2bc

b) 2xy f) 0,5ab3

c) 1,2ab g) 1 18  x y 22

d) 1,3x2y

8. 9x3y3

9. a) 7x2 b) 2x2 c) 3x2 d) 2x2

10. a) 10x

b) y2 c) 13ab d) 12xy

11. a) 13bc b) 18bc

12. 20,7a2x2

13. a) 0,4ay b) 0,504

14. Resposta pessoal.

Pense e responda – p. 119

1. a) 3a3

b) 7a3 c) 14a3 d) 14a3

Atividades – p. 120

1. a) a10

b) 0,45x3y3

c) 3,12a2b2c

d) a5bc3

e) 0,02y7

2. a) 20a6b3c5 c) 0,1x5y3

b) 1,35y7 d) 40m3n3p2

3. a) 0,5x2

b) 6x2

c) 6x2

d) 12x2

4. Resposta pessoal.

Por toda parte – p. 121

1. 81x5, 243x6 e 729x7

2. Resposta pessoal.

3. a)

EDITORIA DE ARTE

6. Não, pois a resposta correta é 5x2

7. 5y

8. 2c2

5. Polinômios

Atividades – p. 126

1. 2x + 3y

2. d + 5r

3. x2 y2

4. a) x + y b) 4x + 2y

5. a) 10x + y b) 10y + x

6. a) 2a + b b) 2a b

7. a2 + 2ab + b2

8. 60y + 3x

Atividades – p. 129

1. a) 3a2x 4a2x2 2ax2 b) 5x + 4xy + 3y

2. a) 1,3a + 0,6ab b) É um binômio.

3. a) 5ab + 3a 14b + 7 b) x2 y2

4. 5o grau.

5. x5 9x4 6x3 5x2 + x + 10; 5o grau.

6. c5 + 0c4 + 0c3 + 0c2 + 0c 1

7. 2x2 + 3ax

8. a) O perímetro. b) 6x

9. 6x; 6x + 6; 6x + 12

Atividades – p. 131

1. 13x + 3,1a

2. 2

3. a) 0,6x 3 b) 0,4x + 1 c) x 2 d) 0,2x 4

4. a) 9a2x2 + 7ax + 11a 6x

b) 0

c) 18a2x2 14ax 22a + 12x

5. a) 3a + b + c

b) a b + 3c

6. 4x2y2 16x + 2y + 9xy

7. a) 3x2 + 3xy 2y2

b) x2 13xy + 4y2

8. a) 6a 15b + 7c

b) 7y2 4ay + 5a2

c) a + 3b c d) a + b + c

c) 2a3 + 5a2 b ab2 5b3

d) 2x2 + 2y2 + 4x2y2

e) 0,2a2 0,6b2 0,8c2

f) 4a2 4ab + 5b2 + 2c2

g) 0,2x3 + 0,3x2 + 0,4x 6

Atividades – p. 134

1. 2xy 1,2y2

2. 12x2y 6xy2

b) Resposta pessoal.

Atividades – p. 124

1. a) 4b

b) 4x3 c) +4 d) 5a2c

2. a) 1 2 ax 3 b) 4an

3. 2ax2

4. +2x2y

5. +5a3b

3. a) 2abx b) 3ab 5b2

4. xy + 4xz

5. a3 + b3

6. a) 6x2 xy y2 b) 2 100

7. 1,8x2 + 0,15xy 0,25y2

10. a) x2 10xy + 25y2

b) 0,36 + 2,4ax + 4a2x2

c) b3 + 3b2y + 3by2 + y3

11. 7x3 + 6x2 + 3x

12. a) a3b ab3

b) 3a2 + 7ab 2b2

13. Pela extremidade da esquerda: B, C, D, A. Pela extremidade da direita: A, D, C, B

Atividades – p. 136

1. a) 0,5a3 + 0,9a4b2

b) 1 3 xy + 5 4

c) abc + a2 c

2. 3x2 + 7ax 12a2

Por toda parte – p. 137

1. 4,28x; 642; Significa que uma quebradeira de coco, que extraiu 150 quilogramas de amêndoa de babaçu, recebeu, no mínimo, 642 reais.

2. Resposta pessoal.

Tratamento da informação – p. 138

1. 81,467 anos.

2. Menor esperança de vida: 76,08 anos, no Brasil; maior esperança de vida: 84,62 anos, no Japão; variação da esperança de vida: 8,54 anos.

3. 21,94 anos.

4. Japão e Itália; esses países não são os que têm a menor esperança de vida.

5. Aproximadamente 2 850 222 nascidos vivos.

6. Resposta pessoal.

7. Resposta pessoal.

Retomando o que aprendeu – p. 140

1. a) 1 b) 7 c) 2,68

2. Alternativa a.

3. Alternativa e.

4. Alternativa a.

5. Alternativa c.

6. Alternativa d.

7. Alternativa e.

Um novo olhar – p. 141

• Resposta pessoal.

• Resposta pessoal.

UNIDADE 5

Equações

8. Alternativa b.

9. Alternativa d.

10. Alternativa b.

11. Alternativa a.

12. Alternativa e.

Abertura da Unidade – p. 142

• Respostas pessoais.

• Resposta pessoal.

• Resposta pessoal.

1. Equação do 1o grau com uma incógnita

Pense e responda – p. 144

1. 35 2. 32 3. 60

Atividades – p. 147

1. a) Respostas pessoais.

b) 3 5

2. a) 6

b) 5 c) 1 d) 7 e) 2,5 f) 8 g) 7,5 h) –5

3. 2

4. a) 240

b) 3 c) 6 d) 40 e) 29

5. 6 6. 45

Atividades – p. 149

1. 1a fase: 6; 2a fase: 9.

2. Caio: R$ 58.000,00; Pedro: R$ 29.000,00; Toni: R$ 78.000,00.

3. a) 500 reais. b) 700 reais.

4. x = 80

5. a) Sim, pois gastaria R$ 300,00.

b) R$ 172,00, no mínimo.

6. a) 100 g b) Resposta pessoal.

7. 81 (primeiro valor) e 24 (último valor).

2. Equação fracionária com uma incógnita

Atividades – p. 152

1. a) 0 b) 0 c) 0 d) −3 e) 1 2 ou 1.

2. a) 4x + 2y = 60

b) Sim, pois 4 · 12 + 2 · 6 = 60, ou seja, 48 + 12 = 60.

Atividades – p. 157

1. a) Sim.

b) Sim. c) Não. d) Sim. e) Não. f) Não.

5. a) (8, 6) b) (12, 30)

6. É verdadeira.

7. O par ordenado é (4, 3). Atividades – p. 158

5. Sistemas de duas equações do 1o grau com duas incógnitas

Atividades – p. 160

1. a) xy 60 x2y    += =

b) xy 9 xy 3    += _=

c) xy 3,5 x3y0,5    += =_

d) += += xy 10 20x 10y 130   

e) xy 100 x2y4    += =+

2. a) Resposta pessoal. b) Resposta pessoal.

3. xy 23 2x 4y 82    += +=

7. 14 grupos.

8. 500 camisetas.

9. 32 estudantes no 8o ano A e 30 estudantes no 8o ano B.

Por toda parte – p. 153

1. x = 23; 23 bases. 2. y = 81; 81 km

3. Equações literais do 1o grau na incógnita x Atividades – p. 154

1.

a 4b , com b

16b

Educação Financeira – p. 155

• Aproximadamente 19%.

4. Equação do 1o grau com duas incógnitas

Pense e responda – p. 156

1. a) 2x + 16 = 4y

b) Sim, pois 2 · 6 + 16 = 4 · 7, ou seja, 12 + 16 = 28.

4. Resposta pessoal.

Atividades – p. 162

1. Sim.

2. Não é solução.

3. (4, 2)

4. a) III. A equipe venceu 5 partidas e perdeu 3.

5. Verdadeiras: a e c. Falsa: b. As soluções da equação 2x y = 3 são todos os pontos sobre a reta que a representa.

6. I) Alternativa b.

II) A incógnita x representa a quantia economizada por Bento; a incógnita y, a quantia economizada por Antônio.

III) Alternativa a.

IV) x = 80 reais (quantia economizada por Bento) e y = 90 reais (quantia economizada por Antônio).

6. Resolução de sistema de duas equações do 1o grau com duas incógnitas

Pense e responda – p. 164 Resposta pessoal.

Fórum – p. 166

x = 120 e y = 200; Resposta pessoal.

Atividades – p. 167

1. a) (15, 7)

b) (10, 6)

c) (−1, −2)

d) (4, 4)

e) (1,2; 0,6)

f) (20, 12)

g) (1, 0)

h) (6, 3)

2. 21 12

3. a) (2, 4)

b) (3, 3) e (1,5) não são soluções do sistema, pois não pertencem simultaneamente às duas retas.

c) Resposta pessoal.

4. a) R$ 32,00

b) R$ 35,00

5. 12 caixas para 50 livros e 15 caixas para 70 livros.

6. a) 7 medalhas de ouro.

b) Resposta pessoal.

Pense e responda – p. 169 Resposta pessoal.

Atividades – p. 170

1. a) (25, 17)

(4, 1) c) (6, 5)

(2, 1)

3. 3 4

4. 109 e 66.

5. 128 e 42.

6. 12 anos.

7. 21 galinhas e 10 ovelhas.

9. Carlos tem 72 kg, Andrea tem 51 kg e Balu tem 15 kg.

7. Equação do 2o grau

Pense e responda – p. 172 Resposta pessoal.

Atividades – p. 173 1.

{}

4. a) Larissa pensou no número 40. b) Resposta pessoal.

5. Medida do comprimento: 33 m; medida da largura: 11 m.

6. 28 cm

7. a) 100 m² b) 10 m

8. Alternativa b.

9. Alternativa d. Tecnologias – p. 174

1. a) 3 e 3.

b) Não em raiz real.

c) 5,6 e 5,6.

2. a) I: S = { 1,22; 1,22}

IV: S = { 1, 1}

V: S = { 2, 2}

b) Resposta pessoal. c)

Escreva a equação do 2o grau que quer resolver

Ela pode ser escrita na forma ax 2 c?

A fração a c é maior ou igual a zero?

sim sim não não

A equação não tem solução no conjunto dos números reais.

Retomando o que aprendeu – p. 176

1. Alternativa b.

2. Alternativa a.

3. Alternativa a.

4. Alternativa d.

5. Alternativa d.

Um novo olhar – p. 177

• Resposta pessoal.

6. Alternativa c.

7. Alternativa c.

8. Alternativa d.

9. Alternativa b.

10. Alternativa e.

Calcule e escreva a solução do sistema:

11. Alternativa a.

12. Alternativa e.

13. 3 horas.

• Os valores da incógnita que anulam o denominador de cada um dos termos da equação.

• Métodos algébricos da substituição, da adição e método geométrico no plano cartesiano.

• Sendo x e y dois números reais quaisquer e x 2 = y, então xy =+ ou xy =_

UNIDADE 6

Polígonos e transformações no plano

Abertura de Unidade – p. 178

• Resposta pessoal.

• Resposta pessoal.

• Porque a imagem poderá ser ampliada sem sofrer distorção.

1. Polígonos e seus elementos

Atividades – p. 182

1. a) Três tipos. b) Triângulos, quadriláteros e octógonos.

2. Diagonais de um polígono convexo Pense e responda – p. 184 Triângulo.

Atividades – p. 184

1. Quadrilátero.

2. a) 5 diagonais.

b) 20 diagonais. c) 44 diagonais. d) 104 diagonais. e) 135 diagonais.

3. Alternativa c.

4. 12 lados; 54 diagonais.

5. Alternativa b.

6. Undecágono.

7. Alternativa c.

8. Alternativa c.

3. Ângulos de um polígono convexo

Pense e responda – p. 186

a) Resposta pessoal.

b) Resposta pessoal.

Atividades – p. 188

1. 10 lados; decágono.

2. Soma das medidas dos ângulos internos

Pentágono 540°

Eneágono 1 260°

Icoságono 3 240°

3. Undecágono.

4. Hexágono.

5. medEAB 54° () = e medABC 81° () =

6. Soma das medidas dos ângulos internos Quantidade de lados do polígono

440°

4. Ângulos de um polígono regular

Atividades – p. 190

1. a) 1 440°

b) 144°

2. 72°

3. 36°

4. Decágono regular.

5. 9 lados.

6. 165°

7. 105°

8. a) Decágono regular.

b) 1,2 km

c) 1 650 passos.

5. Construções geométricas

Pense e responda – p. 192

1. O triângulo equilátero tem três lados congruentes entre si.

2. Sim, o fato de que o triângulo equilátero tem três ângulos congruentes entre si.

Pense e responda – p. 193

Seis triângulos equiláteros.

Atividades – p. 195

1. F

G

A

C B H I

2. a) 90° b) 72° c) 36°

3. O polígono construído deve ser um quadrado.

4. Resposta pessoal.

6. Propriedades dos quadriláteros

Atividades – p. 199

1. 45°, 45°, 135° e 135°.

2. x = 47°

3. a) 10x + 6y

b) 6x2 + 7xy + 2y2

4. a) 20x 4y

b) 25x2 − 10xy + y2

5. a) x = 16 e y = 12.

b) 48, 64 e 72.

6. x = 90° e y = 45°.

7. 33° e 57°.

8. 95°, 95°, 85° e 85°.

9. x = 60° e y = 120°.

Atividades – p. 201

1. 82°

2. 74°, 106° e 106°.

3. x = 62°

4. x = 80° e y = 50°.

5. 100°, 100°, 80° e 80°.

6. x = 106°

7. 20,5 cm

8. x = 32 cm e y = 18 cm.

Tratamento da informação – p. 202

1. Enfermeiros; 27,52%.

2. Psicólogos; 11,24%.

3. Não, porque não foi informado o total de participantes do estudo.

4. a) Não proporcionou.

b) 22,6%. 58 profissionais.

c) Resposta pessoal.

7. Transformações no plano

Pense e responda – p. 206 Sim, um exemplo são duas reflexões se1guidas. r

s Figura inicial

Figura final

REPRODUÇÃO/GEOGEBRA

6. Translação.

7. Resposta pessoal. Tecnologias – p. 208

1. Resposta pessoal.

2. Resposta pessoal. Retomando o que aprendeu – p. 210

1. Alternativa c.

2. Alternativa b.

3. Alternativa a.

4. Alternativa b. 5. Alternativa a. 6. Alternativa b.

• Um polígono regular tem todos os lados congruentes entre si e todos os ângulos internos congruentes entre si, o que faz que todos os ângulos externos também sejam congruentes entre si.

• O retângulo, o losango e o quadrado.

• Trapézio isósceles e trapézio retângulo.

• Reflexão, translação e rotação.

UNIDADE 7

Contagem, probabilidade e estatística

Abertura de Unidade – p. 212

• Resposta pessoal.

• Resposta pessoal.

1. Contagem

Pense e responda – p. 214

De 12 maneiras distintas.

Atividades – p. 217

1. a) 6 maneiras. b) 2 uniformes.

2. 8 556 maneiras.

3. 52 488 maneiras.

4. 72 números.

5. Alternativa d.

6. Alternativa e.

7. Resposta pessoal.

2. Probabilidade

Atividades – p. 221

1. a) S = {(cara, cara); (cara, coroa); (coroa, cara); (coroa, coroa)}

b) S = {(1,1); (1,2); (1,3); (1,4); (1,5); (1,6); (2,1); (2,2); (2,3); (2,4); (2,5); (2,6); (3,1); (3,2); (3,3); (3,4); (3,5); (3,6); (4,1); (4,2); (4,3); (4,4); (4,5); (4,6); (5,1); (5,2); (5,3); (5,4); (5,5); (5,6); (6,1); (6,2); (6,3); (6,4); (6,5); (6,6)}

c) S = {(M, M, M); (M, M, F); (M, F, M); (M, F, F); (F, F, F); (F, F, M); (F, M, F); (F, M, M)}

2. a) E = {(cara, cara); (coroa, coroa)}

b) S = {(1,4); (2,3); (3,2); (4,1)}

c) E = {(M, M, F); (M, F, M); (F, M, M)}

3. a) S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25}

b) A = {9, 18}

c) B = {24, 25}

4. P(A) = 4 9 ; P(V) = 1 3

5. P(E) = 41 81

3. Estatística

Pense e responda – p. 222 Resposta pessoal.

Pense e responda – p. 224 Resposta pessoal.

Pense e responda – p. 227 Resposta pessoal.

Atividades – p. 228

1. Resposta pessoal.

2. a) 250 funcionários da empresa.

b) 50 funcionários da empresa.

c) Massa, em quilograma. Variável quantitativa contínua.

3. Resposta pessoal.

4.

a) 79 jovens.

b) 21%

5. a) 11 funcionários.

b) 3 funcionários.

6. a)

Fonte: Dados fictícios.

Quantidade de irmãos dos estudantes do 8o ano

8. Alternativa d.

9. Alternativa c.

10. a) x = 22°30’ b) x = 4

11. Alternativa c.

12. Alternativa d. Um novo olhar – p. 211

• Resposta pessoal.

• A soma das medidas desses ângulos é igual a 180°.

6. a) P(E) = 4 25

b) P(E) = 3 50

7. a) 10 duplas.

b) P(E) = 3 10

8. a) P(E) = 3 5

b) P(E)

D2_AV3-MAT-F2-2103-V8-PFI-292-304-LA-G24.indd

4. Medidas em Estatística

Atividades – p. 235

1. a) Bruno teve média 6,9; Camila, 7,4; Marcela, 5,3, e Roberto, 6,0.

b) Bruno, Camila e Roberto.

2. a) A altura média é de aproximadamente 1,71 m.

b) A mediana é 1,69 m. Metade dos jogadores tem altura menor ou igual a 1,69 m, e a outra metade tem altura maior ou igual a 1,69 m.

c) A altura média será 1,72 m, e a mediana, 1,72 m.

3. a) 13,3 anos.

b) Possui duas modas: 12 anos e 14 anos.

c) 13 anos.

d) 10 anos.

4. Alternativa a.

5. Ambos os estudantes foram aprovados.

5. Realizando pesquisas estatísticas

Pense e responda – p. 237

Não, pois essa pesquisa envolve uma variável qualitativa.

Atividades – p. 237

1. a) Resposta pessoal.

b) Resposta pessoal.

Tecnologias – p. 238

• Resposta pessoal.

Retomando o que aprendeu – p. 240

1. Alternativa c.

2. Alternativa d.

3. a) 4 anos; 15 anos.

b) • M1 = 8,2

• M2 = 10

Fórum – p. 246

Resposta pessoal.

Pense e responda – p. 248

O tanque de formato triangular ocupa maior área.

Atividades – p. 248

1. a) 225 cm2

b) 2 000 lajotas.

2. 1 600 telhas.

3. Alternativa c.

4. Quatro latas de tinta.

5. 25,12 cm

6. 1,2 m

7. 314 m

8. a) 0,4 m

b) 0,5024 m²

9. Resposta pessoal.

Por toda parte – p. 250

1. a) 240 000 km²

b) 20 000 km²

2. Volume de sólidos geométricos

Atividades – p. 254

1. a) 8 cm³

b) 12 cm³

2. 3 cm

3. Alternativa c.

4. Não, pois o volume ficará multiplicado por 8.

5. a) 62,8 cm³

b) 28,26 cm³

6. Resposta pessoal.

7. Alternativa b.

3. Capacidade

Pense e responda – p. 256

Respostas pessoais.

=

• M M 0, 82 1 2

c) 8 anos; 11 anos.

4. Alternativa d.

5. Alternativa c.

Um novo olhar – p. 241

• Aproximadamente 2 000 óbitos.

• A partir de agosto de 2021.

• Respostas pessoais.

UNIDADE 8

Área, volume e capacidade

Abertura de Unidade – p. 242

• Respostas pessoais.

• Respostas pessoais.

1. Área de figuras planas

Pense e responda – p. 244

Ele vai precisar de 15 placas.

Pense e responda – p. 246

Não.

Atividades – p. 257

1. a) 18 000 litros.

b) 30 vezes.

Tratamento da informação – p. 258

1. Resposta pessoal.

2. De 2009 a 2014.

3. a) Maior participação: 2009; menor participação: 2015.

b) Resposta pessoal.

c) Resposta pessoal.

Retomando o que aprendeu – p. 260

1. Alternativa d.

2. Alternativa c.

3. Alternativa b.

4. Alternativa c.

5. Alternativa a.

6. Alternativa e.

7. Resposta pessoal.

8. 16 000 recipientes.

9. Alternativa e.

Um novo olhar – p. 261

• Não.

• Resposta pessoal.

UNIDADE 9

Estudo de grandezas

Abertura de Unidade – p. 262

• Resposta pessoal.

• Resposta pessoal, que depende das medidas aferidas.

1. Grandezas

Pense e responda – p. 265

8 horas.

Pense e responda – p. 267 Não, pois a idade de uma pessoa e a altura correspondente não são grandezas proporcionais.

Atividades – p. 268

1. a) 20 °C

b) 77 °F

2. a) R$ 306.000,00

b) R$ 255.000,00

c)

2. Algumas razões especiais

Fórum – p. 270 Respostas pessoais. Atividades – p. 271

1. 70 km/h

2. Alternativa c.

3. a) 200 km

b) 2h30min

c) Resposta pessoal. Atividades – p. 273

1. 0,40 kg/dm3

2. 21,5 g/cm3

3. 2,7 g/cm3

4. 4,28 hab./km2

5. Aproximadamente 84,8 hab./km2

6. Água Branca.

7. Aproximadamente 59,99 hab./km2

8. Caio errou a ordem de grandeza do território argentino, que é cerca de 2 800 000 km2

9. Resposta pessoal.

3. Grandezas diretamente proporcionais

Pense e responda – p. 275

2 250 parafusos. Resposta pessoal. Atividades – p. 276

1.

d) Diminui proporcionalmente. Essas grandezas são inversamente proporcionais.

3. Não, pois aumentando a quantidade de livros, o preço correspondente a ser pago não aumenta na mesma proporção.

4. a) Não, pois o valor é sempre acrescido da bandeirada.

b) R$ 53,50

5. a) R$ 46,00

b) Aproximadamente R$ 90,00.

c) R$ 161,00.

6. Resposta pessoal.

2. 2 760 pães.

3. a) 385 km

b) 4,3 h = 4h18min

4. 65 cm

5. 6 075 tijolos.

6. 2,7 mL

7. Alternativa e.

8. Resposta pessoal.

4. Grandezas inversamente proporcionais

Pense e responda – p. 278

Resposta pessoal.

Atividades – p. 279

1. 5 minutos.

2. 12,5 dias.

3. a) 32 km/h

b) 1,25h ou 1h15 min.

4. 9,5 dias.

5. 180 páginas.

6. Alternativa c.

7. a) As grandezas são inversamente proporcionais, porque à medida que a quantidade de trabalhadores aumenta, a quantidade de dias para a conclusão da obra diminui na mesma proporção.

b) Resposta pessoal.

Por toda parte – p. 280

1. Resposta pessoal.

2. 728 crimes.

3. Resposta pessoal.

5. Regra de três

Atividades – p. 283

1. 3 780 tijolos.

2. 2,38 L

3. 10 pintores.

4. a) 80 km

b) Aproximadamente 186,7 km.

5. 20 m

6. a) Sim, pois as grandezas variam na mesma razão.

b) R$ 30,00

c) 37,5 minutos.

7. 105 g

8. 450 kg

Atividades – p. 285

1. 36 funcionários.

2. Aproximadamente 1h26min.

3. Alternativa b.

4. 4 dias.

5. Não. Um dia a mais.

6. Alternativa c.

7. Resposta pessoal.

Tratamento da informação – p. 286

1. 75 vagas; 3 vagas.

2. Resposta pessoal.

3. a) Deficiência física.

b) Sim.

4. De 1 a 2 salários mínimos.

D2_AV3-MAT-F2-2103-V8-PFI-292-304-LA-G24.indd

Retomando o que aprendeu – p. 288

1. 24 000 cm ou 240 m.

2. 199 323,02 km2

3.

Fonte: Dados fictícios.

c) Até 120 minutos.

d) Tarifa 3.

4. a) 500 km/h

b) 0,16 min ou, aproximadamente, 9,4 s.

c) 138,89 m

d) 150 km

5. 3 tratores.

6. Alternativa b.

Um novo olhar – p. 289

• Resposta pessoal.

• Uma reta.

• Resposta pessoal.

Tecnologias – p. 290

1. a) 0,4

b) 1,888...

2. Resposta pessoal.

ALMEIDA, Lourdes Werle de; SILVA, Karina Pessôa da; VERTUAN, Rodolfo Eduardo. Modelagem matemática na Educação Básica. São Paulo: Contexto, 2016.

Esse livro destaca como situações do dia a dia podem contribuir para a motivação do estudo da matemática e para a compreensão e aplicação de vários conceitos trabalhados nessa área.

BACICH, Lilian; MORAN, José (org.). Metodologias ativas para uma educação inovadora: uma abordagem téorico-prática. Porto Alegre: Penso, 2018.

Apresenta um conjunto de artigos que abordam estudos e aplicações de metodologias ágeis na educação para o desenvolvimento do protagonismo estudantil de maneira inovadora.

BOYER, Carl Benjamin; MERZBACH, Uta Caecilia. História da matemática. Tradução: Helena Castro. 3. ed. São Paulo: Blucher, 2012.

Esse livro apresenta episódios da construção histórica do conhecimento matemático destacando a solução de problemas, abertos há muito tempo, e o papel dos computadores na pesquisa em matemática.

BRASIL. Ministério da Educação. Base Nacional Comum Curricular : educação é a base. Brasília, DF: MEC, 2018. Disponível em: http://basenacionalcomum.mec.gov.br/. Acesso em: 8 jun. 2022.

Documento oficial composto de orientações que norteiam a (re)elaboração dos currículos de referência das escolas das redes pública e privada de ensino de todo o Brasil. Traz os conhecimentos essenciais, as competências, as habilidades e as aprendizagens pretendidas para crianças e jovens em cada etapa da Educação Básica. BRASIL. Ministério da Educação. Diretrizes Curriculares Nacionais para Educação Básica. Brasília, DF: MEC: SEB: DICEI, 2013. Disponível em: http://portal.mec.gov.br/docman/ julho-2013-pdf/13677-diretrizes-educacao-basica-2013-pdf/ file. Acesso em: 8 jun. 2022.

As Diretrizes Curriculares Nacionais (DCNs) são normas obrigatórias para a Educação Básica que orientaram a elaboração da BNCC. Elas são discutidas, concebidas e fixadas pelo Conselho Nacional de Educação (CNE).

BRASIL. Ministério da Educação. Normas sobre computação na Educação Básica: complemento à BNCC. Brasília, DF: MEC, 2021. Disponível em: http://portal.mec.gov.br/ index.php?option=com_docman&view=download&alias= 182481-texto-referencia-normas-sobre-computacao-na-edu cacao-basica&category_slug=abril-2021-pdf&Itemid=30192.

Acesso em: 8 jun. 2022.

Documento que define normas sobre Computação na Educação Básica, em complemento à BNCC.

BRASIL. Ministério da Educação. Parâmetros curriculares nacionais: terceiro e quarto ciclos do Ensino Fundamental –Matemática. Brasília, DF: MEC: SEF, 1998. Disponível em: http:// portal.mec.gov.br/seb/arquivos/pdf/matematica.pdf. Acesso em: 8 jun. 2022.

Documento que apresenta uma seleção de conhecimentos de cada componente, considerados fundamentais para o exercício da cidadania, além de uma proposta de organização curricular.

BRASIL. Ministério da Educação. Temas contemporâneos transversais na BNCC: contexto histórico e pressupostos pedagógicos. Brasília, DF: MEC: SEB, 2019. Disponível em: http://basena cionalcomum.mec.gov.br/images/implementacao/contextuali zacao_temas_contemporaneos.pdf. Acesso em: 8 jun. 2022.

Documento explicativo acerca dos Temas Contemporâneos Transversais a serem abordados na Educação Básica.

BUSSAB, Wilton de Oliveira; MORETTIN, Pedro Alberto. Estatística básica. 9. ed. São Paulo: Saraiva, 2017.

Esse material propõe a análise de dados, e apresenta conceitos de probabilidade. Compreende, também, tópicos de inferência estatística.

COSTA, Erick John Fidelis. Pensamento computacional na Educação Básica: uma abordagem para estimular a capacidade de resolução de problemas na matemática. Dissertação (Mestrado em Ciência da Computação) – Centro de Engenharia Elétrica e Informática, Universidade Federal de Campina Grande, Campina Grande, 2017.

Essa dissertação aborda a importância do desenvolvimento de competências relacionadas ao pensamento computacional desde os anos iniciais da educação básica com o objetivo de estimular a capacidade de resolver problemas.

COXFORD, Arthur F.; SHULTE, Albert P. (org.). As ideias da álgebra. Tradução: Hygino Hugueros Domingues. São Paulo: Atual, 1994.

Conceitos de álgebra são explorados nesse livro por meio de ideias fundamentais que auxiliam a aprendizagem do pensamento algébrico.

EVES, Howard. Introdução à história da matemática

Tradução: Hygino Hugueros Domingues. Campinas: Editora da Unicamp, 2004.

Esse livro apresenta uma narrativa da história da matemática baseada em resultados obtidos, obras e dados biográficos de estudiosos, e explicita os panoramas culturais de cada época.

IEZZI, Gelson; DOLCE, Osvaldo; MURAKAMI, Carlos et al Fundamentos de matemática elementar. 8. ed. São Paulo: Atual, 2019. 11 v. (Fundamentos de matemática elementar).

Os livros dessa coleção apresentam conceitos fundamentais de matemática, que servem de introdução a estudos nessa área.

IFRAH, Georges. Os números: a história de uma grande invenção. Tradução: Stella Maria de Freitas Senra. 11. ed. Rio de Janeiro: Globo, 2001.

Esse livro apresenta o desenvolvimento histórico do conceito de números e de outros conceitos matemáticos.

KENSKI, Vani Moreira. Educação e tecnologias: o novo ritmo da informação. 8. ed. Campinas: Papirus, 2012.

Nesse livro, busca-se mostrar como os avanços tecnológicos podem contribuir para as situações de ensino e aprendizagem, discutindo, diversas compreensões do termo tecnologias e sua aplicação.

LINDQUIST, Mary Montgomery; SHULTE, Albert P. (org.). Aprendendo e ensinando Geometria. Tradução: Hygino Hugueros Domingues. São Paulo: Atual, 1994.

O livro apresenta um conjunto de artigos que abordam desafios do ensino de Geometria e recursos para o desenvolvimento do pensamento geométrico.

POLYA, George. A arte de resolver problemas. Tradução: Heitor Lisboa de Araújo. Rio de Janeiro: Interciência, 1978. Nesse livro, a resolução de problemas é apresentada como ferramenta para o desenvolvimento cognitivo.

ROCHA-FILHO, Romeu Cardozo. Grandezas e unidades de medida: o sistema internacional de unidades. São Paulo: Ática, 1988.

Nesse livro são apresentados conceitos fundamentais de grandezas, de unidades de medida, e o surgimento e a importância do Sistema Internacional de Unidades.

ROSALE, André Rodrigues. Argumentação e prova matemática na Educação Básica. Dissertação (Mestrado em Ensino de Matemática) – Instituto de Matemática e Estatística, Universidade de São Paulo, São Paulo, 2017.

Essa dissertação aborda a importância da argumentação matemática para o desenvolvimento da aprendizagem matemática.

ROSEN, Kenneth H. Matemática discreta e suas aplicações 6. ed. [S l.]: McGraw Hill, 2009.

Esse livro apresenta conceitos de matemática aplicada, entre eles a definição de inferência, fundamental para o desenvolvimento do raciocínio matemático.

RESOLUÇÕES COMENTADAS

Unidade 1 • Números reais e porcentagem

Abertura de Unidade – p. 13

• Resposta pessoal. Espera-se que os estudantes citem atitudes, como não fazer dívidas, poupar para emergências e para realizar projetos, bem como fazer o controle e o planejamento dos gastos etc.

• Comprar à vista significa fazer o pagamento do valor integral (ou com desconto) no ato da compra. Comprar a prazo significa pagar o valor em parcelas.

• Resposta pessoal. Juro é toda compensação que se paga, em dinheiro, por uma quantia que se tomou emprestado ou que se recebe por uma quantia que se emprestou.

1. Conjunto dos números racionais

Atividades – p. 18

1.

2. a) . b) , c) , d) , e) = f) .

3. Transformando as frações em números decimais, temos:

= 3 5 0, 6

= 1 4 0, 25

= 2 3 0, 666...

5 9 0,555... =

Colocando os números em ordem crescente, temos:

c) 1 397 : ( 20,5) 1 68,14

d) 501,3 : 7,5 = 66,84

e) 643,284 : 20,04 = 32,1

f) 18 331,2 : 304 = 60,3

7. Seja x a altura do segundo andar:

7,80 = 3,88 + x h x = 7,80 3,88 h x = 3,92

Alternativa a.

2. Dízimas periódicas

Pense e responda – p. 20

1. • = 7 9 0, 777...

• = 13 99 0,131313...

• = 3 9 0, 333...

• = 211 99 2,131313...

2. Todos os números são dízimas periódicas; 7; 13; 3; 13.

3. Resposta pessoal. Espera-se que os estudantes percebam que a quantidade de algarismos do período de cada uma das dízimas é igual à quantidade de algarismos do denominador da respectiva fração e que os denominadores das frações são compostos apenas de algarismos 9.

Atividades – p. 20 1.

1

4 , 5 9 , 3 5 e 2 3

Alternativa a.

Nesta atividade, os estudantes podem ainda determinar um denominador comum aos denominadores das frações e, então, ordená-las.

3. a) DE; b) DP; c) DE; d) DE; e) DP; f) DP; g) DE; h) DE; i) DE; j) DP; k) DE; l) DP

4. a) Período: 2

b) Período: 7 c) Período: 01 d) Período: 3

Atividades – p. 22

1. a) Considere a a fração geratriz do número 2,4444…:

a = 2,4444... I

e) Período: 56 f) Período: 034

Multiplicando ambos os membros dessa equação por 10, temos:

10a = 24,4444... II

Subtraindo I de II : 10a = 24,4444... _ a = 2,4444... 9a = 22 =_ a 22 9

b) Considere b a fração geratriz do número 0,11111…:

b = 0,11111... I

Multiplicando ambos os membros dessa equação por 10, temos:

10b = 1,11111... II

Subtraindo I de II :

10b = 1,11111...

b = 0,11111...

9b = 1

= b 1 9

c) Considere c a fração geratriz do número 17,8888…:

c = 17,8888... I

Multiplicando ambos os membros dessa equação por 10, temos:

10c = 178,8888... II

Subtraindo I de II :

10c = 178,8888...

c = 17,8888...

9c = 161 = c 161 9

d) Considere d a fração geratriz do número 6,353535…:

d = 6,353535... I

Multiplicando ambos os membros dessa equação por 100, temos:

100d = 635,353535... II

Subtraindo I de II :

100d = 635,353535...

d = 6,353535...

99d = 629 =_ d 629 99

e) Considere y a fração geratriz do número 0,292929…:

y = 0,292929... I

Multiplicando ambos os membros dessa equação por 100, temos:

100y = 29,292929... II

Subtraindo I de II :

100y = 29,292929... y = 0,292929...

99y = 29 = y 29 99

f) Considere z a fração geratriz do número 2,102102102…:

z = 2,102102102... I

Multiplicando ambos os membros dessa equação por 1 000, temos:

1 000z = 2102,102102102... II

Subtraindo I de II :

1 000z = 2102,102102102...

z = 2,102102102...

999z = 2 100

z 2 100 999 700 333 ==

2. Primeiro, vamos transformar 0,5555... em fração. Considere x a fração geratriz do número 0,5555…:

x = 0,5555... I

Multiplicando ambos os membros dessa equação por 10, temos:

10x = 5,5555... II

Subtraindo I de II :

10x = 5,5555...

0,5555...

Substituindo a fração obtida na expressão, temos: 0,555555... 2

56 9 11 9

3. a) Considere a a fração geratriz do número 7,15555…:

a = 7,15555...

Multiplicando ambos os membros dessa equação por 10, temos:

10a = 71,5555... I

Multiplicando ambos os membros da equação original por 100, temos:

100a = 715,5555... II

Subtraindo I de II :

100a = 715,5555...

_

71,5555...

b) Considere b a fração geratriz do número 0,53333…:

b = 0,53333...

Multiplicando ambos os membros dessa equação por 10, temos:

10b = 5,3333... I

Multiplicando ambos os membros da equação original por 100, temos:

100b = 53,3333... II

Subtraindo I de II :

100b = 53,3333...

10b = 5,3333...

90b = 48

=_=_ b 48 90 24 45

c) Considere c a fração geratriz do número

69,0333…:

c = 69,03333...

Multiplicando ambos os membros dessa equação por 10, temos:

10c = 690,3333... I

Multiplicando ambos os membros da equação original por 100, temos:

100c = 6 903,3333... II

Subtraindo I de II :

100c = 6 903,3333...

_ 10c = 690,3333...

90c = 6 213

d) Considere d a fração geratriz do número

1,17474…:

d = 1,17474...

Multiplicando ambos os membros dessa equação por 10, temos:

10d = 11,7474... I

Multiplicando ambos os membros da equação original por 1 000, temos:

1 000d = 1 174,7474... II

Subtraindo I de II :

1 000d = 1 174,7474...

_ 10d = 11,7474...

90d = 1 163

d 1163 990 =_

4. Considere x a fração geratriz do número 0,21111…:

x = 0,21111...

Multiplicando ambos os membros dessa equação por 10, temos:

10x = 2,1111...

Escrevendo o número decimal 2,111... como uma adição, para separar a parte inteira da parte decimal, temos:

10x = 2 + 0,1111...

Como 0,111... = 1 9 , temos:

10x = 2 + 1 9

10x =+ 18 9 1 9

x = 19 90

Alternativa d.

5. Analisando cada afirmativa:

a) b = a + 0,11111…

0,45555... + 0,1111... = 0,56666....

Logo, b 5 a + 0,1111... e a afirmativa é falsa.

b) Considerando a a fração geratriz do número 0,45555…:

a = 0,45555...

Multiplicando ambos os membros dessa equação por 10, temos:

10a = 4,5555... I

Multiplicando ambos os membros da equação original por 100, temos:

100a = 45,5555... II

Subtraindo I de II :

100a = 45,5555...

_ 10a = 4,5555...

90a = 41 = a 41 90

Portanto, a = 41 90 e a afirmativa é falsa.

c) Toda dízima periódica é um número racional, pois pode ser escrita na forma de fração; portanto, a é um número racional e a afirmativa é falsa.

d) a , b

0,4555... , 0,46

A afirmativa é verdadeira.

Alternativa d.

6. Primeiro, vamos transformar cada parcela em uma fração.

Considerando x a fração geratriz do número 0,3333…:

x = 0,3333... I

Multiplicando ambos os membros dessa equação por 10, temos:

10x = 3,3333... II

Subtraindo I de II :

10x = 3,3333...

_ x = 0,3333...

9x = 3 == x 3 9 1 3

Agora, considerando y a fração geratriz do número 0,52222...:

y = 0,52222...

Multiplicando ambos os membros dessa equação por 10, temos:

10y = 5,2222... I

Multiplicando ambos os membros da equação original por 100, temos:

100y = 52,2222... II

Subtraindo I de II :

100y = 52,2222...

10y = 5,2222...

90y = 47

= y 47 90

Dessa forma, a soma 0,33333… + 0,52222…, na forma de fração é:

1 3 47 90 30 47 90 77 90 += + =

Para esta atividade, os estudantes poderiam também realizar a adição com os números na forma decimal, obtendo 0,85555... e então determinar uma fração geratriz dessa dízima periódica.

7. Resposta pessoal. Exemplo de resposta:

Início.

O número é uma dízima periódica composta?

Multiplique os membros dessa equação por 10.

8.

Fração Representação decimal Decimal exato Dízima periódica 1 2 x 1 3 x 1 4 x 1 5 x 1 6 x 1 7 x 1 8 x 1 9 x 1 10 x 1 11 x 1 15 x 1 20 x 1 25 x 1 50 x 1 100 x 1 125 x 1 500 x

3. Números reais

1. Como 10 tem representação decimal infinita e não periódica, não pode ser escrito na forma de fração; assim, 10 é um número irracional.

Alternativa d.

Chame essa equação de equação 1.

Não Não

Isole o x

Subtraia a equação 1 da equação 2.

Multiplique os membros dessa equação por 10. Sim Sim

Chame essa equação de equação 2.

O período da dízima periódica passou para o lado esquerdo da vírgula?

2. Entre os números apresentados, o único que tem representação decimal infinita e não periódica é o número 4,280281282283…

Alternativa d.

3. Como a parte decimal da representação de um número é infinita e não periódica, esse número é irracional positivo.

Alternativa d. 4.

a)

0; 1

b) 4; 0; 1

5. a) = 27 6

4,5

Portanto, a representação decimal de

d) 2,3; 1 4 ; 0, 6

b) 0,23

O traço sobre o número 23 indica que 23 é período de uma dízima periódica; portanto, a representação decimal de 0,23 é infinita e periódica.

c) 2

Como 2 não é exata, sua representação decimal é infinita e não periódica.

6. Resposta pessoal. Exemplo de resposta: 3 4 ; a representação decimal desse número não é uma dízima periódica.

4. Porcentagem

Atividades – p. 28

1. ?= 8 100 150 12

Portanto, o vendedor receberá 12 reais pela venda de um tênis de 150 reais.

2. ?= 76 100 50 38

Portanto, Vilma acertou 38 questões da prova de Matemática de um vestibular.

3. Resposta pessoal. Espera-se que os estudantes concluam que a estratégia utilizada por Juliana é útil quando é necessário realizar mentalmente cálculos envolvendo porcentagem.

a) 25% de 1 080.

1 080 : 4 = 270

b) 5% de 2 700. = 5 100 1 20

2 700 : 20 = 135

c)

d)

e)

4. Ótimo: == 105 250  0,4 2  42%

Bom: == 100 250  0,4 0  40%

5. 1= 3 19  0,158 15,8%

Aproximadamente 15,8%.

6. a) 396 + 9 + 18 + 27 = 450

Foram recolhidos 450 kg de resíduo sólido nessa praia.

b) = 396 450  0,8 8

Portanto, os materiais de plástico recolhidos representam 88% dos resíduos sólidos.

7. Resposta pessoal. Exemplo de resposta: “Em uma loja virtual, determinado modelo de tênis é vendido de R$ 150,00 por R$ 120,00. Calcule a porcentagem de desconto em relação ao preço inicial do tênis.”.

150 120 = 30 Então, o desconto é R$ 30,00.

== 30 150 1 5 0,20 Portanto, o desconto no preço do tênis foi de 20%.

8. Resposta pessoal. A resposta depende dos dados pesquisados.

Por toda parte – p. 29

1. 49,29%; Acre, Amapá, Amazonas, Pará, Roraima, Rondônia, Mato Grosso, Maranhão e Tocantins.

2. 8 510 000 49,2 9 100 4 194 579 ?= A área aproximada é de 4 200 000 km2

3. São seis os biomas predominantes no Brasil: Amazônia, ocupando cerca de 49% do território nacional; Mata Atlântica, ocupando aproximadamente 13%; Cerrado, cobrindo cerca de 24% do território brasileiro; Caatinga, que ocupa cerca de 10%; Pampa e Pantanal, ocupando cerca de 2% do território cada um. Elaborado com base em: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Biomas brasileiros. IBGE Educa. Rio de Janeiro c2022. Disponível em: https://educa. ibge.gov.br/jovens/conheca-o-brasil/territorio/18307 -biomas-brasileiros.html. Acesso em: 26 jul. 2022.

4. a) 13 038 10 851 = 2 187 2 187 10 851 0,20 1

Aproximadamente 20%.

b) Resposta pessoal. Espera-se que os estudantes concluam que esse é um aumento grande de um ano para outro.

Pense e responda – p. 30

1. Resposta pessoal. Espera-se que os estudantes percebam que, na história, juro representa um acréscimo que se paga como compensação pelo pagamento em mais parcelas.

2. R$ 1.200,00 0,4 = R$ 480,00; R$ 1.200,00 R$ 480,00 = R$ 720,00 O comprador daria R$ 480,00 de entrada e ainda restariam R$ 720,00.

3. R$ 1.200,00 0,9 = R$ 1.080,00

A TV custará R$ 1.080,00.

Atividades – p. 32

1. 1 800 0,023 5 = 207 Renderá 207 reais.

2. Considerando juro simples, a aplicação rendeu

1 000 reais por mês.

1 000

40 000 0, 025 = Portanto, a taxa mensal de juro é de 2,5%.

3. Seja x a quantia aplicada.

x 2 0,256 = 389,12 h x = 760 Portanto, a quantia aplicada foi de 760 reais.

4. 350 4 (1 0,15) = 1 190

Alternativa a.

5. Juros = 50 12 0,003 = 1,8

Valor pago = 50 + 1,8 = 51,8, ou seja, R$ 51,80.

Alternativa c.

6. Juros pagos ao mês: 120 000 0,01 = 1 200

Seja x o número de meses da dívida.

1 200 x = 6 000 h x = 5

Alternativa c.

7. = 468 450 450 0, 04

A taxa mensal de juro cobrada pela loja é 4% no pagamento a prazo.

8. Valor investido: 30 000 + 10 000 ? 1,05 + + 10 000 1,04 = 30 000 + 10 500 + 10 400 = = 50 900

Valor da casa valorizada: 50 000 1,03 = 51 500

Lucro: 51 500 50 900 = 600

Alternativa c.

9. a) Vamos indicar por x a quantia que Marina deverá pagar de juro e teremos:

x = (1% ? 10 000) ? 5

x = 0,01 10 000 5 = 500

Marina deverá pagar R$ 500,00 de juro ao banco.

b) 10 000 + 500 = 10 500

O valor total que Marina terá de pagar ao final do empréstimo é de R$ 10.500,00.

c) Como, no total, Leandro pagou R$ 10.500,00 e o capital inicial foi de R$ 5.000,00, então o total de juro pago foi de R$ 5.500,00 (10 500 5 000 = = 5 500). Considere y a taxa de juro do empréstimo realizado por Leandro:

5 500 = (y 5 000) 20

y = 5 500 : 100 000

y = 0,055

Portanto, a taxa de juro do empréstimo realizado por Leandro foi de 5,5%.

10. Resposta pessoal. Exemplo de resposta: “Um capital de R$ 10.000,00 foi aplicado durante 50 meses. Sabendo que ao final desse período foi resgatado um montante de R$ 20.000,00, qual é a taxa de juro simples dessa aplicação?”.

Educação financeira – p. 33

1. Os bancos oferecem, para quem tem dinheiro e quer guardá-lo, uma maneira segura de fazê-lo. Já para as pessoas que precisam de dinheiro para investimentos, os bancos fazem empréstimos, recebendo uma compensação na forma de juro pelo serviço.

2. Respostas pessoais. Espera-se que os estudantes percebam que, ao aplicar ou investir uma quantia, o rendimento pode ser utilizado em todas as situações indicadas nos itens. No entanto, realizar um empréstimo exige um bom planejamento e controle financeiro para garantir que conseguirá pagar as parcelas do empréstimo e o retorno desse dinheiro valha a pena. Por exemplo, não é recomendado fazer um empréstimo para ter um dinheiro extra para aproveitar a vida; sugere-se que gastos extras sejam feitos apenas com rendimentos de aplicações ou parte dos ganhos mensais.

Tecnologias – p. 34

1. A tela da planilha eletrônica deve ficar semelhante à reprodução na imagem a seguir. Na linha 3, estão os cálculos para o empréstimo nesse outro banco.

4. Resposta pessoal. Exemplo de resposta: Fechar a torneira ao escovar os dentes, diminuir a quantidade de minutos (duração do intervalo de tempo) de banho, varrer o quintal ao em vez de lavar, reaproveitar a água utilizada na lavagem de roupas para lavar o quintal, entre outras.

Retomando o que aprendeu – p. 38

Portanto, Emerson pagaria R$ 7.560,00 nesse caso.

2. Resposta pessoal. Espera-se que os estudantes avaliem a possibilidade de Emerson pagar um pouco a mais no total e pagar em uma quantidade maior de meses.

3. A tela da planilha eletrônica deve ficar semelhante à reprodução na imagem a seguir. Na linha 2 estão os cálculos para o investimento e na linha 3 estão os cálculos para o empréstimo. No caso do investimento, o montante ao final de 12 meses é de R$ 1.590,00; já no empréstimo, o valor a ser pago é R$ 2.940,00.

Tratamento da informação – p. 36

1. a) Resposta pessoal. Exemplo de resposta:

A cada 100 L de água no planeta, 2,5 L é de água doce e 97,5 L, de água salgada.

A cada 100 L de água doce:

• 68,9 L está em geleiras e coberturas permanentes de neve;

• 0,3 L está em rios e lagos;

• 29,9 L são águas subterrâneas;

• 0,9 L está em outros locais, como pântanos e placas de gelo.

b) A taxa percentual, aproximadamente, de água do planeta correspondente:

• às geleiras e coberturas permanentes de neve: 0,025 0,689 = 0,017225 1 1,72%

• aos rios e lagos: 0,025 ? 0,003 = 0,000075 = 0,0075%

• às águas subterrâneas: 0,025 0,299 = 0,007475 1 0,75%

• a outros: 0,025 0,009 = 0,000225 1 0,02%

2. Alternativa c. A água destinada aos abastecimentos urbano, rural e animal corresponde a 34,3% de toda a água retirada, enquanto a irrigação corresponde a 49,8%.

3. Médias globais de pegada hídrica de alguns produtos (em litros de água)

1. Como a quantidade de casas decimais do produto é igual à soma obtida com a adição das casas decimais dos fatores, temos o primeiro fator com 1 casa decimal e o segundo fator com 2 casas decimais; logo, o produto terá 3 (1 + 2) casas decimais. Alternativa c.

2. a) x = 3,777... I

10x = 37,777... II

Fazendo II I : 9x = 34 h x = 34 9

b) 10x = 2,555... I

100x = 25,555... II

Fazendo II I : 90x = 23 h x = 23 90

c) x = 12,181818... I

100x = 1 218,1818... II

Fazendo II I : 99x = 1 206 h x = 1 206 99

d) 10x = 40,1313.... I

1 000x = 4 013,13.... II

Fazendo II I : 990x = 3 973 h x = 3 973 990

3. a) Sim; 49 7

b) 97; 49 7

c) 3

4. == 1 5  0,2 20%

Alternativa c.

5. == 5 40 1 8 0,125

Portanto, o professor registrou 12,5% de faltas.

6. 1 600 720 = 880 = 880 1600 0,55

Portanto, 55% dos estudantes do colégio são meninas.

7. 120 + 80 = 200 = 120 200 0,6

A porcentagem de água nessa mistura é de 60%.

Fonte: PEGADA hídrica incentiva o uso responsável da água. WWF. Brasília, DF, 21 mar. 2011. Disponível em: https://www.wwf.org.br/?27822/Pegada-Hdrica-incentiva-o-usoresponsvel-da-gua#. Acesso em: 25 jul. 2022.

8. 30 100 40 100 50 100 = 0,06 = 6%

Alternativa d.

9. Juro: 0,04 2 400 = 96

Médias globais de pegada hídrica de alguns produtos (em litros de água)

Médias globais de pegada hídrica de alguns produtos

Alternativa c.

10. Considere x o número que deverá ser adicionado ao numerador e ao denominador.

Fonte: PEGADA hídrica incentiva o uso responsável da água. WWF. Brasília, DF, 21 mar. 2011. Disponível em: https://www.wwf.org.br/?27822/Pegada-Hdrica-incentiva-o-uso-responsvel-dagua#. Acesso em: 25 jul. 2022.

2x

3x 1, 2 2 3

2x

3x 2, 4 3

+ + =? + + = +=+ = =

63x7,2 2, 4x 0, 6x 1, 2 x2

Alternativa b.

11. Porcentagem das araras-azuis com bico branco em relação ao total de araras no viveiro:

0,60 0,40 = 0,24 = 24%

Porcentagem das araras-vermelhas com bico branco em relação ao total de araras no viveiro:

0,40 0,30 = 0,12 = 12%

Porcentagem total de araras no viveiro com bico branco:

24% + 12% = 36%

Alternativa d.

12. Analisando cada uma das alternativas, temos:

a) X, Y e Z na farmácia 1: 45 + 40 + 50 = 135

b) X e Y na farmácia 1 e Z na farmácia 3: 45 + 40 + 35 = 120

c) X e Y na farmácia 2 e Z na farmácia 3: (50 + 50) ? 0,8 + 35 = 115

d) X na farmácia 2 e Y e Z na farmácia 3: 50 + 45 + 35 = 130

e) X, Y e Z na farmácia 3: (65 + 45 +35) 0,8 = 116

Logo, a melhor opção é a apresentada na alternativa c.

13. Resposta pessoal. Exemplo de resposta: Raquel quer comprar uma geladeira nova. Para isso, ela pesquisou os valores e as condições de pagamento em diversas lojas e montou a tabela a seguir.

Preços e condições de pagamento da geladeira

Loja Valor da geladeira Condições de pagamento

Loja A R$ 3.199,00 Parcelamento em 6 vezes sem juro

Loja B R$ 2.899,00 Parcelamento em 10 vezes com juro de 1,2% ao mês

Loja C R$ 2.799,00 Parcelamento em 4 vezes sem juro

Fonte: Dados fictícios.

Sabendo que Raquel pode pagar, no máximo, R$ 600,00 por mês em cada parcela, qual é a loja com a melhor opção para a compra?

Unidade 2 • Potências e raízes

Abertura de Unidade – p. 40

• Sissa pediu que lhe fossem dados grãos de trigo pelas casas de um tabuleiro da seguinte maneira: 1 grão pela primeira casa do tabuleiro, 2 grãos pela segunda, 4 pela terceira, 8 pela quarta, e assim sucessivamente, dobrando a quantidade de grãos por casa até chegar à 64a casa. O pedido se mostra impossível em razão da quantidade de grãos que Sissa teria de receber no total.

• Espera-se que os estudantes percebam que, para calcular a quantidade de grãos a ser recebida por casa do tabuleiro, eles precisarão calcular uma potência de base 2, cujo expoente varia de 0 a 63, da seguinte maneira: 1a casa: 20 grão; 2a casa: 21 grãos; 3a casa: 22 grãos; ...; 30a casa: 229 grãos; ...; 64a casa: 263 grãos.

• Resposta pessoal. Os estudantes podem propor a realização dos cálculos por meio de ferramentas como uma calculadora, uma planilha eletrônica ou outro recurso. Seria interessante pedir a eles que tentassem calcular a quantidade de trigo usando a estratégia para que percebam se ela é viável ou não. Espera-se que percebam que, com uma calculadora, por exemplo, não seria possível, em virtude da quantidade de dígitos que o visor comporta.

• Resposta pessoal. Incentive a troca de ideias entre os estudantes, sempre promovendo a empatia e o respeito pela opinião e pelas preferências do outro.

1. Potência com expoente inteiro Pense e responda – p. 42

1. 8

2. 16

3. 32; 64

(dentro do valor máximo por mês)

Loja B Juro:

Loja C

Valor total: R$ 2.799,00

Valor de cada parcela: R$ 2.799,00 : 4 = R$ 699,75 (acima do valor máximo por mês)

Dessa maneira, a melhor opção para Raquel é comprar a geladeira na loja A

Um novo olhar – p. 39

• Resposta pessoal.

• Resposta pessoal. Espera-se que os estudantes respondam que sim, que o período é a parte que se repete na dízima.

• Será um decimal exato. Espera-se que os estudantes percebam que o denominador (25) é divisor de 100; logo, podemos escrever uma fração equivalente à fração dada com denominador 100 e, portanto, como um número decimal exato.

• Resposta pessoal. Espera-se que os estudantes descrevam contextos em que o produto/serviço é essencial, mas não há dinheiro suficiente naquele momento; ou em que o valor à vista seria muito alto, como na compra de um imóvel, por exemplo.

4. Resposta pessoal. Espera-se que os estudantes percebam que, a cada dobra ao meio que fazem na folha, a quantidade de partes em que ela fica dividida duplica em relação à quantidade de dobras anterior. Assim, as quantidades de partes podem ser expressas por: 20 (0 dobra), 21 (1 dobra), 22 (2 dobras sucessivas), 23 (3 dobras sucessivas), …

5. Como a área de um quadrado é igual a medida dos lados elevado ao quadrado, temos:

132 = 13 13 = 169

Ou seja, a área do quadrado maior é igual a 169 quadrados.

6. Analisando o cubo maior, percebemos que há 8 camadas de cubinhos, cada uma com 8 fileiras com 8 cubinhos em cada fileira. Então, o total de cubinhos utilizado é:

83 = 8 ? 8 ? 8 = 512

Ou seja, Lucas utilizou 512 cubinhos para montar o cubo.

7. Sim, pois (10 + 7)2 = 172 = 289 e 102 + 72 = = 100 + 49 = 149.

8. (50%)3 = (0,5)3 = (0,5) (0,5) (0,5) = 0,125

9. A = 2 1,1 = 2,2

B = (1,1)2 = 1,21

A B = 2,2 1,21 = 0,99

10. a) (0,5)2 = 0,5 ? 0,5 = 0,25

b) 0,25 = 25%

11. a) a = 23 ? 22 = 8 ? 4 = 32

b = 26 = 64

Então, a , b.

b) a = 32 52 = 9 25 = 225

b = (3 5)2 = 152 = 225

Então, a = b.

12. 10x = 100 h 10x = 102 h x = 2 y = 100 = 1

x + y = 2 + 1 = 3

2. Propriedades da potenciação

Pense e responda – p. 46

1. a) • 22 23 = 4 8 = 32

25 = 32

Então 22 23 = 25

• 34 32 = 81 9 = 729

36 = 729

Então 34 32 = 36

b)

• 25 : 23 = 32 : 8 = 4

22 = 4

Então 25 : 23 = 22

• 35 : 32 = 243 : 9 = 27

33 = 27

Então 35 : 32 = 33

c) • 23 2() = 23 23 = 8 8 = 64

• 23 3() = 23 23 23 = 8 8 8 = 512

• 32 2() = 32 ? 32 = 9 ? 9 = 81

d)

• 26 4

3 2 = ()

26 = 64

Então 22 3 2

= ()

Então 33 2 2 4 = ()

• 2 512 3 3 = ()

26 = 64

Então 22 3 3 6 5 ()

Por toda parte – p. 50

1. 700 MB = 700 106 = 700 000 103 =

= 700 000 quilobytes = 7 ? 105 quilobytes

123 MB = 123 106 = 123 000 103 =

= 123 000 quilobytes = 1,23 ? 105 quilobytes

700 MB = 700 106 = 700 000 000 bytes =

= 7 108 bytes

123 MB = 123 106 = 123 000 103 bytes =

= 1,23 108 bytes

Como um byte corresponde a 8 bits, 7 ? 108 bytes será:

8 7 108 = 56 108 bits = 5,6 109 bits

Como um byte corresponde a 8 bits, 1,23 ? 108 bytes

será:

8 1,23 108 = 9,84 108 bits

Atividades – p. 51

14. Resposta pessoal. A resposta dependerá do estado em que os estudantes moram. Orientá-los a fazer a pesquisa em uma fonte confiável, por exemplo, o site do IBGE, com acesso pelo link https://www.ibge.gov. br/cidades-e-estados/ (acesso em: 27 jul. 2022), que apresenta diversas informações fundamentadas e atualizadas sobre cidades e estados brasileiros.

3. Números quadrados perfeitos

Atividades – p. 53

1. a) Sim. Sim, 25 é um quadrado perfeito.

b) Não. Não, 29 não é um quadrado perfeito. 2.

Como o fator obtido apresenta expoente par, 729 é um número quadrado perfeito.

Como todos os fatores obtidos apresentam expoente par, 225 é um número quadrado perfeito. b)

Como os fatores obtidos não apresentam expoente par, 1 000 não é um número quadrado perfeito.

Como o fator 3 não apresenta expoente par, 300 não é um número quadrado perfeito.

Como o fator obtido apresenta expoente par, 1 024 é um número quadrado perfeito.

Como todos os fatores obtidos apresentam expoente par, 400 é um número quadrado perfeito.

Como o fator 5 não apresenta expoente par, 2 000 não é um número quadrado perfeito.

Como os fatores obtidos apresentam expoente par, 1 600 é um número quadrado perfeito.

3. Qualquer número ímpar.

4. 112 = 121

122 = 144

132 = 169

142 = 196

152 = 225

162 = 256

Portanto, são 7 números quadrados perfeitos entre 100 e 300.

5. Para que 24 ? 32 ? 53 se torne um número quadrado perfeito, o expoente de todos os fatores apresentados precisa ser par. Como 5 é o único fator com expoente ímpar, o menor número inteiro pelo qual devemos multiplicar 24 32 53 é o 5. Assim:

24 32 53 5 = 24 32 53 + 1 = 24 32 54 Alternativa b.

6. Como B é um número quadrado perfeito e o algarismo da unidade é 5, o algarismo da unidade dos fatores iguais que multiplicados resultam em B também será

5. Verificando por meio de tentativas, temos:

15 15 = 225

25 ? 25 = 625

35 35 = 1 225

Portanto, o valor de B é 625.

4. Raiz quadrada

Atividades – p. 57

1.

a) 484 = 22

b) 625 = 25

c) 729 = 27

d) 1156 = 34

e) 1 296 = 36

b) 6,9 está entre os quadrados perfeitos 4 (22) e 9 (32), assim o número procurado está entre 2 e 3 e mais próximo de 3. Por meio de tentativas, temos:

2,52 = 6,25

2,62 = 6,76

2,72 = 7,29

Portanto, a raiz quadrada de 6,9 com aproximação de uma casa decimal é 2,6.

c) 13,1 está entre os quadrados perfeitos 9 (32) e 16 (42), assim o número procurado está entre 3 e 4 e mais próximo de 4. Por meio de tentativas, temos:

3,52 = 12,25

3,62 = 12,96

3,72 = 13,69

Portanto, a raiz quadrada de 13,1 com aproximação de uma casa decimal é 3,6.

d) 18,5 está entre os quadrados perfeitos 16 (42) e 25 (52), assim o número procurado está entre 4 e 5 e mais próximo de 4. Por meio de tentativas, temos:

4,22 = 17,64

4,32 = 18,49

4,42 = 19,36

Portanto, a raiz quadrada de 18,5 com aproximação de uma casa decimal é 4,3.

d) 10 está entre os quadrados perfeitos 9 (32) e 16 (42), assim o número procurado está entre 3 e 4 e mais próximo de 3. Por meio de tentativas, temos:

3,12 = 9,61

3,22 = 10,24

Portanto, a raiz quadrada de 10 com aproximação de uma casa decimal é 3,1.

e) 20 está entre os quadrados perfeitos 16 (42) e 25 (52), assim o número procurado está entre 4 e 5 e mais próximo de 4. Por meio de tentativas, temos:

4,32 = 18,49

4,42 = 19,36

4,52 = 20,25

Portanto, a raiz quadrada de 20 com aproximação de uma casa decimal é 4,4.

f) 55 está entre os quadrados perfeitos 49 (72) e 64 (82), assim o número procurado está entre 7 e 8 e mais próximo de 7. Por meio de tentativas, temos:

7,32 = 53,29

7,42 = 54,76

7,52 = 56,25

Portanto, a raiz quadrada de 55 com aproximação de uma casa decimal é 7,4.

2.

a) 2,56 = 1,6

b) 3, 61 = 1,9

c) 5, 29 = 2,3

3. 1764 = 42

f) 1 849 = 43

g) 3 025 = 55

h) 4 096 = 64

i) 10 000 = 100

d) 7, 84 = 2,8

e) 10,2 4 = 3,2

f) 37,2 1 = 6,1

Portanto, o lado desse terreno mede 42 m.

4. a) 172 está entre os quadrados perfeitos 169 (132)

e 196 (142) e está mais próximo de 169, assim o número inteiro aproximado que expressa a raiz quadrada de 172 é 13.

b) 200 está entre os quadrados perfeitos 196 (142) e 225 (152) e está mais próximo de 196, assim o número inteiro aproximado que expressa a raiz quadrada de 200 é 14.

c) 360 está entre os quadrados perfeitos 324 (182) e 361 (192) e está mais próximo de 361, assim o número inteiro aproximado que expressa a raiz quadrada de 360 é 19.

d) 500 está entre os quadrados perfeitos 484 (222) e 529 (232) e está mais próximo de 484, assim o número inteiro aproximado que expressa a raiz quadrada de 500 é 22.

5. a) 2,9 está entre os quadrados perfeitos 1 (12) e 4 (22), assim o número procurado está entre 1 e 2 e mais próximo de 2. Por meio de tentativas, temos:

1,72 = 2,89

1,82 = 3,24

Portanto, a raiz quadrada de 2,9 com aproximação de uma casa decimal é 1,7.

e) 51,2 está entre os quadrados perfeitos 49 (72) e 64 (82), assim o número procurado está entre 7 e 8 e mais próximo de 7. Por meio de tentativas, temos:

7,12 = 50,41

7,22 = 51,84

Portanto, a raiz quadrada de 51,2 com aproximação de uma casa decimal é 7,1.

f) 66,21 está entre os quadrados perfeitos 64 (82) e 81 (92), assim o número procurado está entre 8 e 9 e mais próximo de 8. Por meio de tentativas, temos:

8,12 = 65,61

8,22 = 67,24

Portanto, a raiz quadrada de 66,21 com aproximação de uma casa decimal é 8,1.

6. a) 2 está entre os quadrados perfeitos 1 (12) e 4 (22), assim o número procurado está entre 1 e 2 e mais próximo de 1. Por meio de tentativas, temos:

1,32 =

1,42 =

Portanto, a raiz quadrada de 2 com aproximação de uma casa decimal é 1,4.

b) 3 está entre os quadrados perfeitos 1 (12) e 4 (22), assim o número procurado está entre 1 e 2 e mais próximo de 2. Por meio de tentativas, temos:

1,62 = 2,56

1,72 = 2,89

1,82 = 3,24

Portanto, a raiz quadrada de 3 com aproximação de uma casa decimal é 1,7.

c) 6 está entre os quadrados perfeitos 4 (22) e 9 (32), assim o número procurado está entre 2 e 3 e mais próximo de 2. Por meio de tentativas, temos: 2,32 = 5,29 2,42 = 5,76

2,52 = 6,25

Portanto, a raiz quadrada de 6 com aproximação de uma casa decimal é 2,4.

g) 150 está entre os quadrados perfeitos 144 (122) e 169 (132), assim o número procurado está entre 12 e 13 e mais próximo de 12. Por meio de tentativas, temos:

12,12 = 146,41

12,22 = 148,84

12,32 = 151,29

Portanto, a raiz quadrada de 150 com aproximação de uma casa decimal é 12,2.

h) 450 está entre os quadrados perfeitos 441 (212) e 484 (222), assim o número procurado está entre 21 e 22 e mais próximo de 21. Por meio de tentativas, temos:

21,12 = 445,21

21,22 = 449,44

21,32 = 453,69

Portanto, a raiz quadrada de 450 com aproximação de uma casa decimal é 21,2.

7. 5 está entre os quadrados perfeitos 4 (22) e 9 (32), assim o número procurado está entre 2 e 3 e mais próximo de 2. Por meio de tentativas, temos:

2,12 = 4,41

2,22 = 4,84

2,32 = 5,29

Portanto, a raiz quadrada de 5 com aproximação de uma casa decimal é 2,2.

5. Outras raízes

Atividades – p. 59

1. Para determinar a medida da aresta do cubo de volume 1 000 cm3, precisamos determinar que número elevado ao cubo resulte em 1 000. Esse número é 10, pois 103 = 1 000. Assim, a aresta do cubo mede 10 cm.

2. a) 9 = 3, pois 32 = 9

b) 27 3 = 3, pois 33 = 27

c) 27 3 = 3, pois ( 3)3 = 27

d) 32 5 = 2, pois ( 2)5 = 32

e) 64 3 = 4, pois 43 = 64

f) 64 = 8, pois 82 = 64

3.

h)

i)

4. a) Verdadeira.

b) Falsa, pois, por definição, a raiz quadrada de um número racional é sempre um número não negativo.

5. Um cubo com aresta medindo 1 dm tem volume de 1 dm3 (1 dm 1 dm 1 dm). Assim, 1 dm3 equivale a 1 litro. Pensando de maneira análoga, 64 litros equivalem a 64 dm3

Para determinar a medida da aresta do cubo de volume 64 dm3, precisamos determinar que número elevado ao cubo resulte em 64. Esse número é 4, pois 43 = 64.

Assim, a aresta do cubo mede 4 dm. Alternativa a.

6. Potência com expoente fracionário

6. Resposta pessoal. Exemplo de resposta: Calcule o volume de um cubo cuja aresta tem a mesma medida do lado de um quadrado com 25 cm2 de área.

Portanto, o volume do cubo é igual a 125 cm3

Fórum – p. 61

1. Resposta pessoal. Espera-se que os estudantes percebam que ela não se ofendeu com a atitude do colega que praticava bullying, provavelmente por compreender que as pessoas têm particularidades diferentes umas das outras, e deseja que esse colega entenda isso e ultrapasse a barreira do preconceito na qual parece estar.

2. Resposta pessoal. O ciberbullying é a modalidade virtual do bullying, isto é, quando as intimidações repetidas ocorrem por meio digitais.

3. Resposta pessoal. Exemplos de resposta: Caso a situação de bullying ocorra no ambiente escolar, é importante que o indivíduo que sofreu o bullying ou presenciou contate a coordenação da escola para que tome as atitudes cabíveis. Conversar e apoiar a pessoa que sofreu bullying. Não inventar ou repetir apelidos que difamem o colega ou tenham conotação vexatória. Não fazer ou rir de brincadeiras que humilhem ou causem vergonha ao colega, entre outras.

Tecnologias – p. 62

1.

a) 2352 = 55 225

b) 1173 = 1 601 613

c) 395 = 90 224 199

d) 10 8 =0,00000001

2. Resposta pessoal. Espera-se que os estudantes percebam que bastaria calcular 5 5 5 5 5, como apresentado na página 46 desta Unidade.

3. a) Resposta pessoal. Espera-se que os estudantes percebam que poderiam usar a tecla ^ e elevar o

número 258 ao expoente 1 2

b) Resposta pessoal. Espera-se que os estudantes percebam que podem usar a tecla ^ e elevar o número a ao expoente

4. Resposta pessoal. Exemplo de resposta: Com o auxílio de uma calculadora científica, resolva a expressão a seguir.

Resolução: Utilizando parênteses, é possível realizar o cálculo da expressão todo de uma vez. Contudo, nesse procedimento é preciso atenção aos detalhes. Outra possibilidade é fazer cada etapa da expressão separadamente, ir anotando e depois realizar o cálculo final.

Nesses dois casos, os estudantes utilizarão as teclas de raiz quadrada, de raiz cúbica e de raiz enésima. O cálculo da expressão está indicado a seguir.

21 41 64

Tratamento da informação – p. 64

1. a) 90 alunos.

b) De 1,50 m até 1,98 m.

c) 11 alunos.

d) 1,74 ¿ 1,82; significa que a maioria dos alunos pesquisados tem altura maior do que ou igual a 1,74 m e menor do que 1,82 m.

e) 9 + 11 + 25 + 30 = 75

Portanto, 75 alunos têm altura menor do que 1,82 m.

f) 5 90 0, 055... 0, 056 =1

0,056 100% = 5,6%

Portanto, a porcentagem de alunos com altura maior ou igual a 1,90 m é aproximadamente 5,56%.

2. a) Notas dos estudantes do 8o ano na prova final de Matemática Nota obtida na prova final de Matemática Quantidade de estudantes

Fonte: Professora do 8o ano.

b) 9 estudantes.

c) 2 + 6 + 7 = 15

Portanto, 15 estudantes tiveram nota inferior à média na prova de Matemática.

d) 11 + 9 = 20 20 35  0,5711

0,0571 100% = 57,1%

Portanto, a porcentagem de estudantes com nota maior ou igual a 6 é, aproximadamente, 57%.

3. a) 18 jogadoras.

b) 20 anos; 36 anos.

c) Como o primeiro intervalo de classe foi dado, sabemos que cada intervalo tem uma amplitude

anos. Sabendo que são cinco classes de frequência, a tabela fica como indicada a seguir.

Idade das atletas da Seleção Brasileira Feminina de Voleibol em 2022

Elaborado com base em: ATLETAS da Seleção Brasileira. Confederação Brasileira de Voleibol. [Rio de Janeiro], [20--?]. Disponível em: https://cbv.com.br/ligadasnacoes/ selecao-brasileira-feminina. Acesso em: 24 jul. 2022.

d) De 24 a 28 anos.

e) 5 + 1 = 6

Portanto, 6 jogadoras têm idade maior ou igual a 32 anos.

Retomando o que aprendeu – p. 66

1. Analisando cada alternativa:

a) 331

b) 810 = (23)10 = 230

c) 168 = (24)8 = 232

d) 816 = (34)6 = 324

e) 2434 = (35)4 = 320

Então, 331 é o maior dos números. Alternativa a.

2. ()

3. Aplicando as propriedades da potenciação ao número

7. 1,496 x 102 milhões de quilômetros =

= 1,496 x 102 x 106 quilômetros =

= 1,496 x 108 quilômetros

Agora, transformando essa distância em metro, temos: 1,496 x 108 quilômetros =

= 1,496 x 108 x 103 metros =

= 1,496 x 1011 metros

Alternativa e.

8. Total de títulos de livros registrados =

= 1 000  mm 0,1 mm /folha 10 títulos/folha = 105 títulos

Alternativa c.

9. Seja x a medida do lado do terreno quadrangular.

x = 1 936 = 44

Então, o lado do terreno mede 44 m.

Assim, o perímetro será igual a: 4 44 m = 176 m Alternativa c.

10. x =

4 = 7,2 y =

6 = 6,4 7,2 6,4 = 0,8 Alternativa d.

11. Analisando cada alternativa, temos:

a) O número 151 é primo; logo, não é quadrado perfeito.

b)

Agora, podemos determinar a potência de 10 que deve ser multiplicada pelo número 10

para que o produto seja 10: 10x 10 12 = 101 10x + ( 12) = 101

10x 12 = 101

Precisamos de um número que, ao subtrair 12, resulte em 1, ou seja: x 12 = 1 x = 13

De fato, 1013 12 = 101

Como os expoentes dos fatores obtidos são ímpares, 453 não é um número quadrado perfeito.

c) Sabemos que 16 = 42 e 25 = 52. Como 20,44 está entre os números quadrados perfeitos 16 e 25, então 20,44 não é um número quadrado perfeito.

d)

13. 105 125 5 21 025 5

4 205 5 841 29 29 29

105 125 = 5 5 5 29 29 = 53 292

Como o expoente do fator 5 é ímpar, dividindo o número 105 125 por 5, os expoentes de todos os fatores serão pares, assim o quociente será um número quadrado perfeito.

53 292 : 5 = 53 1 292 = 52 292

Alternativa b.

14. 9992 12 = (999 + 1) (999 1) = = 1 000 998 = 998 000

Alternativa d.

15. Resposta pessoal. Exemplo de resposta: Cada mililitro de sangue de um adulto saudável tem cerca de 5 milhões de glóbulos vermelhos. Com base nesses dados, é correto afirmar que a quantidade de glóbulos vermelhos em uma seringa com 30 mL de sangue é:

a) 1,5 106

b) 150 108

Resolução:

c) 1,5 108

d) 300 108

5 milhões correspondem a 5 106

Se na seringa há 30 mL, temos: 30 5 106 = 150 106 = 1,5 108

Alternativa c.

Um novo olhar – p. 67

• Resposta pessoal. Espera-se que os estudantes percebam que sim, que além da operação de potenciação, as potências podem ser utilizadas, por exemplo, para representar números em notação científica ou resultados de conversões de unidades de medidas.

• 8 000 bits ou 8 103 bits

• Os números naturais que são quadrados de outros números naturais.

• Determinar a raiz quadrada de um número x é encontrar um número y que, quando elevado ao quadrado, tem como resultado o número x

e)

Como os expoentes dos fatores obtidos são pares, 24

é um número quadrado perfeito.

Como os expoentes dos fatores 3 e 317 são ímpares, 3 804 não é um número quadrado perfeito. Alternativa d.

12. O número 10 está entre os quadrados perfeitos 9 (32) e 16 (42), assim o número procurado está entre 3 e 4 e mais próximo de 3. Por meio de tentativas, temos:

3,12 = 9,61

3,22 = 10,24

Portanto, a raiz quadrada de 10 é aproximadamente

3,1.

Alternativa d.

Unidade 3 • Ângulos e triângulos

Abertura de Unidade – p. 68

• O triângulo não pôde ser deformado, diferentemente do quadrado.

1. Ângulos

Atividades – p. 73

1. x + 50° = 180°h x = 130°

y + 100

° = 180°h y = 80°

2. a) 90° 66° = 24°

b) 90° 74° = 16°

3. a) 180° 78° = 102°

b) 180° 67° = 113°

c) 90° 22° = 68°

d) 90° 47° = 43°

c) 180° 135° = 45°

d) 180° 139° = 41°

4. Indicando a medida do ângulo a ser determinada por x, temos:

x = (90° x) + 70°h 2x = 160°h x = 80°

5. Indicando a medida do ângulo a ser determinada por x, temos:

x = 180 x

°_ h 4x = 180°h x = 45°

6. Indicando a medida do ângulo a ser determinada por

x, temos:

x = 4(90° x) h x = 360° 4x h 5x = 360°h

h x = 72°

7. y = 40° (o.p.v.)

x + 40° = 180°h x = 140°

x = z (o.p.v.) h z = 140°

8. a) Bissetriz de um ângulo. Os ângulos formados pela haste azul e cada uma das hastes vermelhas são congruentes.

b) A medida de cada haste verde representa a distância de cada ponto da haste azul até cada uma das hastes vermelhas, de acordo com a definição de bissetriz de um ângulo (é importante considerar que as hastes verdes são perpendiculares a cada haste vermelha). Resposta pessoal.

9. 2x 100° = x + 30° (o.p.v.)

x = 130° Os ângulos de medidas x + 30° e y são suplementares.

Assim, temos:

x + 30°+ y = 180°

Substituindo o valor de x determinado na expressão

anterior, temos:

130°+ 30°+ y = 180°

y = 180° 130° 30°

y = 20°

Portanto, x = 130° e y = 20°

10. A partir da figura e dos dados do enunciado, temos:

()medA ˆ MC = ()medD ˆ MB = x (o.p.v)

()medAMD = ()medB MC = y (o.p.v)

Portanto, a medida do terceiro ângulo interno desse triângulo é 27°

4. (3x 48°) + (2x + 10°) + (x 10°) = 180°h

h 6x = 228°h

h x = 38°

Substituindo o valor de x em cada expressão que representa a medida dos ângulos internos, temos:

(3x 48°) = 3 38° 48° = 66°

(2x + 10°) = 2 38°+ 10° = 86°

(x 10°) = 38° 10° = 28°

Portanto, a medida do maior ângulo é 86°

5. Como em qualquer triângulo a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele, temos:

2a = 116°h

h a = 58°

Portanto, a medida a é igual a 58°

6. Como em qualquer triângulo a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele, temos:

2x + 10° = x + 60°h

h x = 50°

Portanto, x é igual a 50°

7. Com as informações do enunciado e indicando a medida do ângulo interno C por x, podemos montar a figura a seguir.

+ 116° = 180°h () med A = 64°

Portanto, a medida dos ângulos internos do triângulo são 68°, 48° e 64°

A descrição da resolução da questão é pessoal, depende dos processos utilizados pelo estudante. Descrevendo o processo utilizado na resolução apresentada neste Manual, temos:

• fazer um esboço da figura descrita no enunciado;

• utilizar o teorema do ângulo externo para determinar o valor de x;

• efetuar os cálculos das medidas dos ângulos internos;

• verificar a pergunta e dar a resposta.

9. 110°+ y = 135°h y = 25°

135°+ x = 180°h x = 45°

75°+ a = 110°+ 45°h a = 80°

80°+ b + 70° = 180°h b = 30°

Assim: x + y + a + b = 45°+ 25°+ 80°+ 30° =

= 180°

Por toda parte – p. 82

Investigação 1

• Sim.

Investigação 2

()

()medA ˆ MD medAMC 3 =h y x 3 = I

()medAMD + ()medAMC = 180°h y + x =

= 180° II

Substituindo I em II , temos:

x 3 + x = 180°

x3x

3 + = 180°

4x = 540°

x = 135°

Substituindo em I :

y x 3 =h y = 135 3 ° h y = 45°

Portanto:

()medA ˆ MC = ()medD ˆ MB = 135°

()medA ˆ MD = ()medB ˆ MC = 45°

2. Triângulos

Pense e responda – p. 75

1. Produção pessoal.

2. Pela montagem, é possível verificar que, juntos, os três ângulos internos do triângulo formam um ângulo raso.

Então: a + b + c = 180°

Atividades – p. 77

1. a) Em qualquer triângulo, o maior lado é oposto ao maior ângulo; assim, BC é o maior lado, pois é oposto ao maior ângulo, que mede 80°

b) Como o maior lado é oposto ao maior ângulo, PN é o maior lado, pois é oposto ao ângulo de medida 110°

2. a) b + c + d = 180°

b) a + b = 180° c) c + d = a

3. Indicando a medida do terceiro ângulo interno do triângulo por x, temos:

Como em qualquer triângulo a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele, temos:

x + 72° = 125°h

h x = 53°

Portanto, () med C = 53°

8. Com as informações do enunciado, podemos montar a figura a seguir.

a) Sim.

b) Os dois segmentos traçados têm sempre o mesmo comprimento. Isso ocorre porque a bissetriz de um ângulo é determinada pelos pontos do plano equidistantes das semirretas que formam esse ângulo.

Atividades – p. 83

1. Seja O o ortocentro do triângulo ABC. Como AH e BI são alturas do triângulo, então == () () medB ˆ HA medA ˆ IB 90°

No triângulo retângulo BHO:

60°+ 90°+ a = 180°h a = 30°

a = b = 30° (o.p.v.)

No triângulo retângulo AIO:

30°+ 90°+ c = 180°h c = 60°

ILUSTRAÇÕES: EDITORIA DE ARTE

Como em qualquer triângulo a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele, temos:

Portanto, a = 30°, b = 30° e c = 60°

2. De acordo com o enunciado, AM = 2x + x h AM = 3x.

a) Falsa. Como GM mede x, a medida de GM é igual a 1 3 da medida de AM

b) Falsa. Como AG mede 2x, a medida de AG é igual a 2 3 da medida de AM

c) Falsa. Como GM mede x, temos que x = 2,89 cm.

Assim:

AM = 3x h AM = 3 2,89 h AM = 8,67

Portanto, AM = 8,67 cm.

d) Verdadeira. Como AG mede 2x, a medida de AG é igual a 2 3 da medida de AM

Alternativa d.

Esquematizando as informações do enunciado, temos: B C A

Como a mediatriz é o lugar geométrico dos pontos do plano que são equidistantes de dois pontos dados, no caso, A e B, podemos concluir que o novo ponto de instalação da antena será na mediatriz do segmento AB

Alternativa c.

4. Seja I o incentro do triângulo MPQ.

Como MX e PY são bissetrizes do triângulo, então: () () medXMQ medPMX 30 == ° () () medQPY medY PM 35 == °

Aplicando o teorema do ângulo externo no triângulo PIM, temos:

c = 35°+ 30° = 65°

Como ˆ a e ˆ c são suplementares:

c + a = 180°h

h 65°+ a = 180°h

h a = 115°

Agora, aplicando o teorema do ângulo externo no triângulo PIX, temos:

a = b + 35°h

h 115° = b + 35°h

h b = 80°

Portanto, a = 115°, b = 80° e c = 65°

5. Do enunciado, temos:

3. Congruência de triângulos

Atividades – p. 89

1. De acordo com a figura do enunciado:

AB MN 2 (Lado)

A M 2 (Ângulo)

AC MP 2 (Lado)

Então AB CMNP*2* pelo caso LAL de congruência. Com isso, os ângulos correspondentes são congruentes. Então, x = 60° e y = 30°

2. De acordo com as informações do enunciado, os triângulos ABC e DEC são congruentes pelo caso ALA, pois ˆ A ˆ D 2 (ângulos retos). Assim, os lados correspondentes são congruentes e, então, x = 4 cm e y = 5 cm.

3. Como AB 2 AC, BD 2 DC e o lado AD é comum aos triângulos ABD e ACD, então os triângulos são congruentes pelo caso LLL. Assim, os ângulos correspondentes são congruentes e, portanto, x = y e B C 2

4. Como AC 2 MN , C N 2 e A M 2 (ângulos retos), então os triângulos ABC e MPN são congruentes pelo caso ALA. Assim, os lados correspondentes são congruentes e, portanto, AB 2 MP • Resposta pessoal. Um exemplo de resolução está indicado acima.

5. a) De acordo com a figura do enunciado, temos:

• BC é lado comum dos triângulos ABC e DBC;

• ACB DCB 2 (ângulo adjacente ao lado BC );

• ˆ A ˆ D 2 (ângulo oposto ao lado BC ). Então, pelo caso LAAO de congruência, temos AB CDBC*2*

Portanto, x = 67° e y = 46°

3. Na figura, AB 2 BC . Assim, o triângulo ABC é isósceles de base AC

x + x + 135° = 180°h

h x = 22,5° ou 22° 30‘

Assim, a medida de B ˆ CA é igual a 22°30‘

4. Na figura, AB 2 AC . Assim, o triângulo ABC é isósceles de base BC

x + 65°+ 65° = 180°h

h x = 50°

A medida x do ângulo B ˆ AC é igual a 50°

5. Como o triângulo ABC é isósceles de base AC , tem-se que () med C = 73°. Além disso, em um triângulo isósceles, a mediana relativa à base também é altura relativa à base e bissetriz do ângulo do vértice. Então, A ˆ BM C ˆ BM 2 e () ()medA ˆ BM medC ˆ BM x ==

Assim:

73°+ 73°+ 2x = 180°h

h x = 17°

Portanto, x = 17°

Resposta pessoal. Exemplo de resposta:

Para determinar a medida de ˆ C , foi utilizada a 2a propriedade dos triângulos isósceles, que diz que em todo triângulo isósceles os ângulos da base são congruentes.

Para determinar a medida do ângulo CBM , foi utilizada a 1a propriedade dos triângulos isósceles, que diz que em todo triângulo isósceles a mediana, a altura relativa à base e a bissetriz do ângulo do vértice coincidem.

Por fim, calculando a soma das medidas dos ângulos internos do triângulo ABC, foi possível determinar o valor de x

50° x

B 60° 20°

A () () () med Amed Bmed ˆ C 180 ++=°h

E C

h () med A + 60°+ 20° = 180°h

h () med A = 80°

Como AE é bissetriz do ângulo ˆ A , () () medC ˆ AE medE ˆ AB 50 == °

Aplicando o teorema do ângulo externo ao *AEC, temos:

()medAEB = 50°+ 20° = 70°

Como AD é altura relativa a BC , ()medA ˆ DE 90 = 90° e, no *ADE:

x + 90°+ 70° = 180°h x = 20°

Portanto, a medida do ângulo formado pela altura relativa ao lado BC e a bissetriz do ângulo A é 20°

Resposta pessoal. Exemplo de resposta:

Utilizando o teorema do ângulo externo no triângulo

AEC, determinamos ()medAEB . Depois, por meio da soma das medidas dos ângulos internos do triângulo

ADE, determinamos a medida do ângulo formado pela altura relativa ao lado BC e a bissetriz do ângulo ˆ A

6. A altura relativa AH forma com o lado BC um ângulo de 90°; portanto, a = 90°

Considerando o triângulo ABC, temos:

2b + 45°+ 35° = 180°h

h 2b = 100°h

h b = 50°

Considerando o triângulo ACD, temos: 50°+ c + 35° = 180°h c = 95°

Portanto,

b) Resposta pessoal. Exemplo de resposta: Se o ângulo B ˆ CD mede 40°, determine a medida do ângulo B CA Como os triângulos são congruentes, e os ângulos B CD e B CA são correspondentes, eles têm mesma medida; assim, B CA mede 40°

6. Como ˆ A ˆ B 2 , AM 2 MB e A ˆ MC B ˆ MD 2 (o.p.v.), então os triângulos AMC e BMD são congruentes pelo caso ALA. Assim, CM 2 DM . Portanto, M é ponto médio de CD

7. Como M é o ponto médio do lado BC , então CM 2 BM . Além disso, C B 2 (ângulos retos) e CD 2 BA , pois são lados paralelos do retângulo ABCD. Assim, os triângulos DMC e AMB são congruentes pelo caso ALA. Portanto, AM 2 DM

4. Propriedades dos triângulos Atividades – p. 92

1. Como o ângulo dado mede 106°, necessariamente deve ser o ângulo do vértice, pois, se fosse um dos ângulos da base, o outro ângulo da base também mediria 106°, o que seria impossível, visto que a soma das medidas dos ângulos internos de um triângulo é igual a 180°

Então, os dois ângulos a serem determinados são os ângulos da base e têm mesma medida, que indicaremos por x. Assim:

x + x + 106° = 180°h

h 2x = 74°h

h x = 37°

Portanto, cada um dos outros dois ângulos mede 37°

2. Como AB 2 BC , então A C 2 . Assim, x = 67°

°

6. Como ABCDE é um pentágono regular, o triângulo ABE é isósceles de base BE . Assim, () () medAEB medABE x == e podemos escrever:

x + x + 108° = 180°h

h x = 36°

Portanto, o valor de x é 36°

7. • Considerando o triângulo ABC:

20°+ 110°+ c = 180°h

h c = 50°

• Como AB e CD são paralelos, então B ˆ AC ACD 2 (alternos internos). Logo, a = 20°

• Pelo teorema do ângulo externo no triângulo ACD, temos:

b = 2a h

h b = 2 ? 20° = 40°

Portanto, a = 20°, b = 40° e c = 50°

8. Como o triângulo ABE é equilátero, x = 60°. No quadrado:

x + y = 90°h

h y = 30°

Como o triângulo ADE é isósceles de base DE :

z + z + 30° = 180°h

h z = 75°

Logo:

x + y + z = 60°+ 30°+ 75° = 165°

Portanto, o valor da expressão x + y + z é igual a 165°

Por toda parte – p. 93

1. Resposta pessoal. Espera-se que os estudantes citem comunidades quilombolas ou indígenas que conheçam e, caso não conheçam, pesquisem essas comunidades, suas tradições e demais características que julgarem

ILUSTRAÇÕES: EDITORIA DE ARTE

interessantes. No estado do Pará, por exemplo, no município de Oriximiná, encontra-se a Comunidade Remanescente de Quilombo do Jauari, na qual, em 6 janeiro, acontece o Aiuê de São Benedito, festa do padroeiro da comunidade. Nessa festa, comemora-se o santo e as riquezas obtidas durante o ano que passou. Entre as tradições dessa comunidade, pode-se citar a desfeiteira, a valsa, o lundum e a muzarca. Durante a pesquisa, espera-se que os estudantes percebam a importância da preservação das tradições e costumes dessas comunidades, pois fazem parte da manutenção e da história da cultura brasileira.

2. Produção pessoal. Os estudantes podem utilizar os conhecimentos adquiridos sobre os triângulos e fazer a releitura do caranguejo utilizando essa figura geométrica.

5. Construções geométricas

Atividades – p. 96

1. a) Resposta pessoal. Espera-se que os estudantes percebam que podem indicar qualquer ponto pertencente à bissetriz do ângulo determinado pelas pistas.

b) Resposta pessoal. Exemplo de resposta: Espera-se que os estudantes sigam os passos apresentados na página 97 e tracem a bissetriz do ângulo apresentado na atividade. Ou seja, com a ponta-seca do compasso no vértice do ângulo, escolher uma abertura e marcar um ponto em cada semirreta que forma o ângulo. Na sequência, colocar a pontaseca sobre cada um dos pontos marcados nos lados do ângulo e traçar um arco de abertura qualquer na região interna ao ângulo. Com uma régua, traçar uma semirreta a partir do vértice do ângulo e passando pelo ponto formado pela intersecção dos arcos traçados. O palco poderá ser construído em qualquer local da bissetriz, por isso é bem provável que os estudantes indiquem locais diferentes para a construção. pista

2 pista1

2. a) Resposta pessoal. Espera-se que os estudantes percebam que podem indicar qualquer ponto pertencente à mediatriz do segmento PQ

b) Não, pois esse local pode ser representado por qualquer um dos infinitos pontos da mediatriz do segmento PQ

Tecnologias – p. 97

1. Resposta pessoal. Espera-se que os estudantes percebam que para construir o ângulo de 30° podem fazer a construção do ângulo de 60° e, em seguida, realizar a construção da bissetriz de um ângulo, feita na construção do ângulo de 45°. A tela final da construção deve ficar semelhante à apresentada a seguir.

2. Resposta pessoal. Exemplos de resposta:

• Para o ângulo de 90°: ferramenta Reta Perpendicular ou ferramenta Mediatriz;

• Para o ângulo de 45°: ferramenta Reta Perpendicular seguida da ferramenta Bissetriz;

• Para o ângulo de 60°: ferramenta Polígono Regular;

• Para o ângulo de 30°: ferramenta Polígono Regular seguida da ferramenta Bissetriz;

• Para todos os ângulos: ferramenta Ângulo com Amplitude Fixa

Retomando o que aprendeu – p. 100

1 Como a soma das medidas dos ângulos internos de um triângulo é igual a 180° e indicando a medida dos ângulos congruentes por x, temos: () () () med ˆ Amed ˆ Bmed ˆ C 180 ++=°h

h 2 ? 2x + x + x = 180°h

h 6x = 180°h x = 30°

Portanto, () med A = 120°

Alternativa e.

2. ()medMCB + 155° = 180°h ()medMCB = 25°

Como o *ABC é isósceles de base AC , () () medMCB medMAB 25 == °

Como o *ABC é isósceles de base AC , então BM é altura relativa à base e bissetriz do ângulo B . Logo, ()medA ˆ BC = 2x.

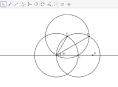
Pelo teorema do ângulo externo no triângulo ABC:

155° = ()medA ˆ BC + ()medM ˆ AB h

h 155° = 2x + 25°h x = 65° Alternativa c.

3. Pelo teorema do ângulo externo no triângulo ABC:

140° = x + 75°h

h x = 65°

Como CE é paralelo a BA , temos:

• os ângulos B AC e A ˆ CE são alternos internos e, portanto, têm a mesma medida. Assim, y = 75°

• os ângulos de medidas x e z são ângulos correspondentes; logo, x = z = 65° Portanto, x = 65°, y = 75° e z = 65°

Alternativa b.

4. Como o triângulo BDC é equilátero, cada um dos ângulos internos mede 60°; assim, temos: () med C = 60°+ 15°h () med C = 75° () med B = 60°+ 20°h () med B = 80°

Considerando o triângulo ABC, temos:

x + 75°+ 80° = 180°h

h x = 25°

Alternativa d.

5. a) 60° cada um. b) Equilátero.

6. Do enunciado, () () med Bmed C4 5 == ° Como CP é bissetriz, ()medP ˆ CA 45 2 22,5 = ° =°

Assim, pelo teorema do ângulo externo no triângulo

ACP: ()medB PC = 90°+ 22,5° = 112,5°

Alternativa d.

7. Como t⁄s:

150° = y + 130°h y = 20°

Assim,

x y = 70° 20° = 50°

Alternativa b.

8. • Como o triângulo ABP é isósceles de base BP , então: () () medABP medAPB z ==

Assim, no triângulo ABP: z + z + 20° = 180°h h z = 80°

• No vértice P, temos ()medAPC + 80° = 180°h h ()medA ˆ PC = 100°

• Como o triângulo APC é isósceles de base AC , então: () ()medPAC medPCA y ==

Assim, no triângulo APC: y + y + 100° = 180°h h y = 40°

• Como PQ é bissetriz de A ˆ PC, então: () x medAPC 2 100 2 50 == ° =°

Assim, x + y = 50°+ 40° = 90°

Alternativa a.

9. Qualquer ponto contido em uma circunferência está a mesma distância do centro da circunferência. Como os vértices A, B e C do triângulo estão sobre a circunferência, eles estão a mesma distância do centro O, que também é o circuncentro do triângulo; portanto, podemos afirmar que os pontos A, B e C equidistam do circuncentro do triângulo. Alternativa c.

Um novo olhar – p. 101

• 180°. Resposta pessoal. Exemplo de resposta: Traçando uma reta r paralela a um dos lados do triângulo e passando pelo terceiro vértice, temos: r A

BC

Analisando a figura, podemos verificar que os ângulos ˆ c e ˆ n são alternos internos e, portanto têm a mesma medida, assim como os ângulos ˆ b e m . Dessa maneira: m + a + n = 180°h b + a + c = 180°

• De acordo com as medidas dos ângulos internos: triângulo retângulo, triângulo acutângulo ou triângulo obtusângulo. De acordo com as medidas dos lados: triângulo equilátero, triângulo isósceles ou triângulo escaleno.

• LLL, LAL, ALA, LAAO e o caso de congruência no triângulo retângulo.

Resposta pessoal. Exemplo de resposta: Início. Fim.

Construir um segmento de reta AB qualquer.

Posicionar a ponta-seca do compasso no ponto

A, escolher uma abertura maior do que a metade da medida de AB e traçar dois arcos, cada um em posição oposta em relação ao segmento de reta AB

Posicionar a ponta-seca do compasso no ponto B, com a mesma abertura da etapa anterior, traçar arcos que cruzam os anteriores e marcar os pontos C e D

Traçar uma reta passando pelos pontos C e D

Unidade 4 • Expressões e cálculo algébrico

Abertura de Unidade – p. 102

• a) Espera-se que os estudantes escrevam algo como:

“Sendo n [n, 2n + 1 é ímpar.”.

b) 2 5 + 1 = 10 + 1 = 11

O número 11.

• Resposta pessoal. Exemplo de resposta:

O dobro do produto entre dois números naturais desconhecidos diferentes é igual a 24.

2 xy = 24

1. Uso de letras para representar números

Pense e responda – p. 104

1. a) 32 b) a b c) 2x y

I) A expressão do item a

II) A expressão do item c

III) A expressão do item b

2. Resposta pessoal. Espera-se que os estudantes percebam que as expressões dos itens a e d apresentam apenas números, e as expressões dos itens b e c apresentam letras e números.

Atividades – p. 105

1. a) x2

b) y3

c) a

d) b5

e) b + c

f) a x = ax

2. a) 2x + 2y

b) (x + y)(x y)

c) x2 + y2

2. a)

3. 4x 3y = 12xy

4. 5x + 3y

5. x2 + ay

6. x 2y

7. x2 + 3x

8. 7x + 10y

9. a) 7x + 20 b) 12y + 10

Educação financeira – p. 109

1. Entre 7 e 8 meses.

2. 5 anos equivalem a 60 meses (5 12 = 60). Então: v = 200 ? 1,1n h h v = 200 1,160 h h v 1 60 896,33 Aproximadamente R$ 60.896,33.

3. Valor numérico de uma expressão algébrica

Fórum – p. 111

1. Resposta pessoal. Exemplos de resposta: poupança, tesouro direto, compra de ações, aplicações em títulos de capitalização de instituições financeiras como bancos, entre outras.

2. Resposta pessoal. Espera-se que os estudantes percebam que investir faz que o dinheiro poupado não perca seu poder aquisitivo e renda uma quantia que pode ser utilizada para realizar projetos futuros, e com o dinheiro em mãos pode-se negociar e fazer as escolhas mais vantajosas.

Portanto, 201 000 pessoas comprarão o produto após cinco dias de veiculação publicitária.

8. f3 2 1, 8 89,63 2 1, 8 32 ==

Portanto, 89,6 graus Fahrenheit correspondem a 32 graus Celsius.

9. Resposta pessoal. A atividade dependerá dos valores pesquisados pelos estudantes. Exemplo de resposta: As estudantes Vânia, Raquel e Isabela foram a um museu cuja entrada inteira custa x reais e estudante paga metade do valor da entrada.

• Escreva a expressão algébrica que representa o gasto delas com as entradas.

x 2 x 2 x 2 3x 2 ++=

• Supondo que cada entrada custe 48 reais, quanto elas deverão pagar pelas três entradas?

3x 2 34 8 2 72 = ? =

Portanto, Vânia, Raquel e Isabela pagarão R$ 72,00 pelas três entradas.

10. Resposta pessoal. Exemplo de resposta: De acordo com a figura, faça o que se pede em cada caso.

• Escreva uma expressão que represente o perímetro do polígono na malha quadriculada.

16x

• Se x = 2 cm, qual é o valor do perímetro desse polígono?

16x = 16 2 = 32

g) 2y h) 1 6 m

i) z w , com w 5 0 j) 1 2 x k) x y l) 5z

d) x2 y2 e) (x + y)2

f) x 1 5 y +

2. Expressões algébricas ou literais

Atividades – p. 108

1. 5x + 8y

Portanto, o perímetro do polígono quando x = 2 cm é igual a 32 cm.

11. Resposta pessoal. Exemplo de resposta: Leonardo foi ao mercado e comprou duas embalagens de pasta dental e três sabonetes.

• Escreva uma expressão que represente o valor gasto por Leonardo na compra desses itens.

Indicando por P o valor de cada pasta dental e por S o valor de cada sabonete, temos:

2 P + 3 S

• Se cada pasta dental custa R$ 5,78 e cada sabonete custa R$ 3,56, com o auxílio de uma calculadora, determine o valor gasto por Leonardo na compra desses itens.

2 ? P + 3 ? S = 2 ? 5,78 + 3 ? 3,56 =

= 11,56 + 10,68 = 22,24

Portanto, com esses valores, Leonardo gastará

R$ 22,24 com a compra.

4. Monômio ou termo algébrico

Pense e responda – p. 113

1. a) x ? y = xy

b) 2x + 2y

c) Resposta pessoal. Espera-se que os estudantes percebam que a expressão algébrica do item a é formada por uma multiplicação de variáveis, enquanto a do item b é formada por uma adição com variáveis nas parcelas.

2. a) 2x b) x2 + x

Atividades – p. 115

1. 7ab

2. a) Sim.

b) Sim.

c) Não.

d) Sim. e) Não. f) Sim.

3. a) Coeficiente: 7; parte literal: b3

b) Coeficiente: 1; parte literal: x2y.

c) Coeficiente: 0,9; parte literal: c4

d) Coeficiente: 1; parte literal: a5x3

e) Coeficiente: 6,2; parte literal: a4b2c.

f) Coeficiente: 4 5 ; parte literal: não tem.

4. 9x

5. 7,90x

6. 20x

7. 37,50y

8. a) 8x b) 8y

9. (2a)3 = 8a3

10.

a)

• 109,50n • 87,50n

b)

• 109,50 5 = 547,50

• 87,50 5 = 437,50

g) Não. h) Não. i) Não.

9. a) 7x2 b) 2x2 c) 3x2 d) 2x2

10. a) 7x ( 2x + x) + ( 3x + 5x) =

= 7x + 2x x 3x + 5x = 10x

b) 5y2 ( 4y2 + 7y2) + ( y2 + 9y2 11y2) =

= 5y2 + 4y2 7y2 y2 + 9y2 11y2 = y2

c) 10ab [3ab (ab + 2ab 5ab) 8ab]

81x5 3x = 243x6

243x6 3x = 729x7

2. Resposta pessoal. Exemplo de resposta:

a1 = 2(1)2 + 1 h a1 = 3

a2 = 2(2)2 + 1 h a2 = 9

a3 = 2(3)2 + 1 h a3 = 19

a4 = 2(4)2 + 1 h a4 = 33

a5 = 2(5)2 + 1 h a5 = 51

3. a)

Esses valores numéricos representam o valor total, em reais, a ser pago por um grupo de 5 adultos, caso realizem o passeio em alta temporada e em baixa temporada, respectivamente.

11. 125x, 625x, 3 125x.

Atividades – p. 118

1. 9x3y; 2 3  m n 22

2. Ao adicionar os expoentes das variáveis da parte literal, temos:

3 + 5 + 1 = 9

Portanto, o monômio 15a3x5y é do 9o grau.

3. Como a soma dos expoentes das variáveis da parte literal precisa ser 10, temos:

2 + x + 5 = 10 h x = 3

4. a) 2x5

b) 2x5; 10x4; 7x3; 8x2; 2,5x; 20.

5. • n + 2 = 8 h n = 6

• 7 + m = 8 h m = 1

m + n = 7

6. a) 0,7ax2

b) 20a2x2 c) 5a2x; 0,5a2x d) 10ax; 1 2 ax

7. a) 7x2 + 2x2 6x2 = 3x2

b) 20xy 17xy 5xy = 2xy

c) 2ab + 1,5ab 2,3ab = 1,2ab

d) 3,1x2y + 4,5x2y 2,7x2y = 1,3x2y

e) 10bc 12bc + 7bc 3bc = 2bc

f) 1,1ab3 3,5ab3 0,9ab3 + 2,8ab3 = 0,5ab3

g) 1 3 xy 5 6 xy 4 9 xy 22 22 22 _+= 1 18  x y 22

8. 9x3y3

+

+ 5,8a2x2 + 3,7a2x2 + 8,1a2x2 1,9a2x2 =

= 20,7a2x2

13. a) 0,6ay ay + 0,3ay + 0,5ay = 0,4ay

b) 0,4ay = 0,4 1,4 ( 0,9) = 0,504

14. Resposta pessoal. Exemplo de resposta:

Determine A + B, se:

A = 2x + 3y

B = 5x + y

(2x + 3y) + ( 5x + y) = 2x + 3y 5x + y

Agrupando os termos semelhantes:

2x 5x + 3y + y = 3x + 4y

Pense e responda – p. 119

1. a) a3 + 2a3 = 3a3

b) a3 + 2a3 + 4a3 = 7a3

c) 2a3 + 2a3 + 2a3 + 4a3 + 4a3 = 14a3

d) 2a3 + 2a3 +

Atividades – p. 120

1.

d) ( ac) ( a4bc2) = a5bc3

e) ( 0,1y3) ? (+0,2y4) = ( 0,1) ? (+0,2) ? (y3) ? (y4) = = 0,02y7

2. a) (5a4bc3) ? ( b2c) ? (+4a2c) = 20a6b3c5

b) (4,5y2) ( 0,3y) ( y4) = 1,35y7

c) (0,1xy) (100xy2) (0,01x3) = 0,1x5y3

d) ( 12mnp)

(5np) = 40m3n3p2

b) Resposta pessoal. Exemplo de resposta:

Início: Em n², atribuir a n o valor 1: n = 1

Primeiro termo: desenhar um quadrado.

Deseja determinar o próximo termo?

Fim do processo.

Aumentar n em 1 unidade.

Considerar a figura do termo n² e dispor a quantidade de quadrados indicada, de modo a formar um quadrado.

Atividades – p. 124

1. a) ( 32abc) : (+8ac) = = ( 32) : (+8) (abc) : (ac) = 4b

b) (+40x7y2) : ( 10x4y2) = = (+40) : ( 10) (x7y2) : (x4y2) = 4x3

c) ( 100a3) : ( 25a3) = ( 100) : ( 25) (a3) : (a3) = =+4

d) (+55a4bc2) : ( 11a2bc) = = (+55) : ( 11) (a4bc2) : (a2bc) = 5a2c 2.

b)

c) 12 0,5x2 = 6x2

d) 6x2 + 6x2 = 12x2

4. Resposta pessoal. Exemplo de resposta: (mn, 3m2n2, 9m3n3, 27m4n4, 81m5n5).

Por toda parte – p. 121

1. Cada termo, a partir do segundo, é obtido multiplicando o termo anterior por 3x; assim, os próximos três termos da sequência são:

27x4 ? 3x = 81x5

6. 10 xy 2xy 5x

7. () () (7y1 0y 2y ) 10 y1 5 y 5y 25y

5. Polinômios

Atividades – p. 126

1. 2x + 3y

2. 3r + 2r + d = d + 5r

3. A área da região colorida da figura é a diferença entre a área do quadrado de lado medindo x e a do quadrado de lado medindo y. Assim, a área é dada por: x2 y2

4. a) x + y b) 4x + 2y

5. a) 10x + y b) 10y + x

6. a) 2a + b b) 2a b

7. a2 + ab + ab + b2 = a2 + 2ab + b2

8. 60y + 3x

Atividades – p. 129

1. a) 2a2x 5a2x2 + 3a2x 7ax2 + a2x2 2a2x + + 5ax2 = 2a2x + 3a2x 2a2x 5a2x2 + + a2x2 7ax2 + 5ax2 = 3a2x 4a2x2 2ax2

b) 6x 5y + 3xy + 2xy 5x + 9y + 4x xy y =

= 6x 5x + 4x + 3xy + 2xy xy +

+ 9y 5y y = 5x + 4xy + 3y

2. a) 0,5a (0,7b 1,2ab) 1,3b + (0,8a + + 2b 0,6ab) = 0,5a + 0,8a 0,7b 1,3b +

+ 2b + 1,2ab 0,6ab = 1,3a + 0,6ab

b) É um binômio.

3. a) 8ab (a + 7b 5) + ( 5ab + 2 b) +

+ (+4a + 2ab 6b) = 8ab a 7b +

+ 5 5ab + 2 b + 4a + 2ab 6b =

= 8ab 5ab + 2ab a +

+ 4a 7b b 6b + 5 + 2 = 5ab +

+ 3a 14b + 7

b) 2x2 [2xy + x2 (3xy + y2) + 2y2] xy =

= 2x2 [2xy + x2 3xy y2 + 2y2] xy =

= 2x2 2xy x2 + 3xy + y2 2y2 xy =

= 2x2 x2 2xy + 3xy xy + y2 2y2 =

= x2 y2

4. 5o grau.

5. 10 6x3 + x 9x4 + x5 5x2 =

= x5 9x4 6x3 5x2 + x + 10 5o grau.

6. c5 1 = c5 + 0c4 + 0c3 + 0c2 + 0c 1

7. x2 + ax + ax + ax + x2 = 2x2 + 3ax

8. a) O perímetro.

b) 6x

9. 6x; 6x + 6; 6x + 12

Atividades – p. 131

1. 3x + 0,5a + 3x + a + 3x + a + 4x + 0,6a =

= 3x + 3x + 3x + 4x + 0,5a + a + a + 0,6a =

= 13x + 3,1a

2. (17x2 15x + 20) + ( 13x2 + 20x 31) =

= 17x2 15x + 20 13x2 + 20x 31 =

c)

b c a b + c = = a + b + c

6. A + 9x + 3y 10xy x2y2 = 3x2y2 7x + + 5y xy h

h A = (3x2y2 7x + 5y xy) (9x + + 3y 10xy x2y2) h

h A = 3x2y2 7x + 5y xy 9x 3y + + 10xy + x2y2 h A = 4x2y2 16x + 2y + 9xy

7. a) P + Q = x2 + y2 5xy + 2x2 + 8xy 3y2 =

= 3x2 + 3xy 2y2

b) P Q =

= x2 + y2 5xy (2x2 + 8xy 3y2) =

= x2 + y2 5xy 2x2 8xy + 3y2 =

= x2 13xy + 4y2

8. a) (15a 7b + 4c) + ( 8b + 3c 9a) =

= 6a 15b + 7c

b) (2y2 3ay + 4a2) (ay 5y2 a2) =

= 2y2 3ay + 4a2 ay + 5y2 + a2 =

= 7y2 4ay + 5a2

c) (3a3 2a2b + 5ab2 6b3) + (7a2b 5a3 + + b3 6ab2) = 2a3 + 5a2 b ab2 5b3

d) (x2 3xy + y2 x2y2) + (+x2 + 5x2y2 + y2 +

+ 3xy) = 2x2 +

Atividades – p. 134

1. 2xy 1,2y2

2. 3x 2y (2x y) = 6xy (2x y) = 12x2y 6xy2

3. a) 2abx b) 3ab 5b2

4. xy + 4xz

5. a(a2 ab + b2) + b(a2 ab + b2) = = a3 a2b + ab2 + ba2 ab2 + b3 = = a3 + b3

6. a) Área da região verde: (3x + y)(2x y) = 6x2 3xy + 2xy y2 = = 6x2 xy y2

b) 6x2 xy y2 = 6(20)2 20 10 (10)2 = = 2 100

7. (1,2x + 0,5y) (1,5x 0,5y) = = 1,8x2 0,6xy + 0,75xy 0,25y2 = = 1,8x2 + 0,15xy 0,25y2

8. (5x2 x 1) ? (2x2 + x 5) = = 10x4 + 5x3 25x2 2x3 x2 + + 5x 2x2 x + 5 = 10x4 + 3x3 28x2 + + 4x + 5

Assim: a = 10; b = 3; c = 28; d = 4; e = 5.

Portanto: a + b + c + d + e = 10 + 3 28 + + 4 + 5 = 6

9. a) (3a 1,5x)(0,7a 5x) = 2,1a2 16,05ax + 7,5x2

b) (a2 1)(2a2 2a + 1) = 2a4 2a3 a2 + + 2a 1

c) (a + x)(a2 ax + x2) = a3 + x3

10. a) (x 5y)2 = (x 5y) ? (x 5y) = = x2 10xy + 25y2

b) (0,6 + 2ax)2 = (0,6 + 2ax) (0,6 + 2ax) =

= 0,36 + 2,4ax + 4a2x2

c) (b + y)3 = (b + y) (b + y) (b + y) =

= b3 + 3b2y + 3by2 + y3

11. Volume do sólido I :

x (3x + 1) 2x = 6x3 + 2x2

Volume do sólido II : (x + 1) x (x + 3) = x (x2 + 4x + 3) =

= x3 + 4x2 + 3x

Assim:

V1 + V2 = 6x3 + 2x2 + x3 + 4x2 + 3x =

= 7x3 + 6x2 + 3x

12. a) (a3 b3)(a + b) (a2 + b2) (a2 b2) =

= (a4 + a3b ab3 b4) (a4 a2b2 + + a2b2 b4) = a4 + a3b ab3 b4 a4 + + a2b2 a2b2 + b4 = a3b ab3

b) (a 2b)[a(b 3) + b(1 a)] =

= (a 2b)(ab 3a + b ab) =

= (a 2b)( 3a + b) =

= 3a2 + 7ab 2b2

13. Pela extremidade da esquerda: B, C, D, A. Pela extremidade da direita: A, D, C, B

Atividades – p. 136

1. a) (2,5a4b 4,5a5b3) : ( 5ab) = 0,5a3 + 0,9a4b2

b)

c) (a2b2c2 + a3bc abc2 ) : (abc) = abc + a2

= 18ax 42ax 72ax

2.

1. 4,28x

4,28x = 4,28 ? 150 = 642

Significa que uma quebradeira de coco, que extraiu 150 quilogramas de amêndoa de babaçu, recebeu, no mínimo, 642 reais.

2. Resposta pessoal. Exemplo de resposta: São diversos os produtos provenientes do babaçu, entre eles podemos citar: o óleo, produzido a partir do fruto, muito utilizado na produção de cosméticos, além de ser comestível; a partir de uma das camadas que envolve o fruto, também é possível produzir uma farinha muito utilizada na indústria farmacêutica; as fibras, utilizadas na confecção de artesanatos, extraídos do talo da palmeira, além da produção de baunilha que se desenvolve naturalmente na palmeira babaçu, como uma espécie de parasita.

Tratamento da informação – p. 138

1 M 84, 62 83,74 84, 00 82,9082,50 81,7580, 90 80,9077, 28 76,08 10

M 814, 67 10

M81, 467

Ou seja, a média da esperança de vida entre os países indicados é 81,467 anos.

2. Menor esperança de vida: 76,08 anos, no Brasil; maior esperança de vida: 84,62 anos, no Japão; variação da esperança de vida: 8,54 anos.

3. 76,08 54,14 = 21,94

Portanto, a esperança de vida do brasileiro aumentou 21,94 anos de 1960 a 2020.

4. Japão e Itália; esses países não são os que têm a menor esperança de vida.

5. 211 755 000 0,01346 = 2 850 222,3

Portanto, aproximadamente 2 850 222 nascidos vivos.

6. Resposta pessoal. Espera-se que estudantes percebam que a coleta e o tratamento desses dados são de grande importância para conhecer o perfil da população brasileira, suas características, principais dificuldades enfrentadas, entre outras informações, muito úteis aos órgãos governamentais para tomada de decisões, elaboração de projetos, políticas públicas etc.

7. Resposta pessoal. Exemplo de resposta:

Gráficos elaborados com base em: INDICADORES econômicos e demográficos. Countryeconomy.com. [S l.], [2021?]. Disponível em: https://pt.countryeconomy.com/demografia/natalidade.anio=2020. Acesso em: 10 jun. 2022.

Em virtude da natureza das informações, foi escolhido o gráfico de colunas verticais para apresentar as informações das duas tabelas, pois a leitura e comparação dos dados fica mais fácil e evidente.

Retomando o que aprendeu – p. 140

1. a) 3(0)2 5(0) 1 = 1

b) 3( 1)2 5( 1) 1 = 7

c) 3(1,2)2 5(1,2) 1 = 2,68

2. ( a b)(a + b) + ab3

( 2)3 () () 2 2

Alternativa a.

3. xy xy 0, 40,5 0, 40,5 2==_

Alternativa e.

4. Sendo C as respostas corretas que valem 3 pontos cada uma, temos: 3C. Sendo E as respostas erradas que valem 2 pontos (perda de 2 pontos) cada uma, temos: 2E.

Sendo N as respostas não respondidas que valem 1 ponto (perda de 1 ponto) cada uma, temos: N.

Dessa maneira, a expressão algébrica que fornece a pontuação final obtida é:

3C 2E N

Alternativa a.

5. 3 2 x4 0 3 2 50 40 115 +=?+=

Alternativa c.

6. • para t = 12h: 1 6 t2 + 4t + 10 = () 1 6 12 2 + 4 12 + 10 = 34

Então, a temperatura medida às 12 h foi de 34 °C.

• para t = 18 h: 1 6 t2 + 4t + 10 = () 1 6 18 2 + 4 18 + 10 = 28

Então, a temperatura medida às 18 h foi de 28 °C.

Portanto, a temperatura diminui: 34 °C 28 °C = 6 °C.

Alternativa d.

7. 4 3 r 4 3 (5) 523,3 3 33 ?p=?p1

Alternativa e.

8. ax = 10

A = 4 ax 2a2x

A = 4 10 2(10)2

A = 160

Alternativa b.

9. 5x 2,5x 2 6, 25 x 2 ? =

Alternativa d.

10. Substituindo n na expressão n ? (n 1) pelos valores indicados (1, 2, 3, 4, ...), temos:

1 (1 1) = 0

2 (2 1) = 2

3 (3 1) = 6

4 (4 1) = 12

5 (5 1) = 20

Alternativa b.

11. Cada termo, a partir do segundo, é o anterior multiplicado por 2x. Desse modo, temos: xy 4 , xy 2 2 , x3y, 2x4y, 4x5y, 8x6y, 16x7y

Alternativa a.

12. A área do forro antes da lavagem:

3 5 = 15

A área do forro após a lavagem: (5 x)(3 y) = 15 5y 3x + xy

A diferença na área do forro:

15 (15 5y 3x + xy) =

= 15 15 + 5y + 3x xy =

= 5y + 3x xy

Alternativa e.

Um novo olhar – p. 141

• Resposta pessoal. Exemplo de resposta: Simplificar a escrita e o cálculo de determinadas situações, o que facilita a generalização e a análise de suas características, entre outras.

• Resposta pessoal. Exemplo de resposta:

Operações com monômios

Adição: 5ax 7ax = 2ax

Multiplicação: (7x) (3x) = 7 3 x x = 21x2

Divisão:

( ) () 20ab 5ab 20ab 5ab 20 5 a a b b 4a b 42 42 42 3 :_===_

Potenciação: (2x2)5 = (2x2) (2x2) (2x2) (2x2) (2x2) =

= 2 2 2 2 2 x2 x2 x2 x2 x2 = 32x10

Operações com polinômios

Adição:

(x3 + 4x2 3x + 7) + (3x3 + 6x 5) (x2 + 2x +

+ 3) = x3 + 4x2 3x + 7 + 3x3 +

+ 6x 5 x2 2x 3 = x3 + 3x3 +

+ 4x2 x2 3x + 6x 2x + 7 5 3 =

= 4x3 + 3x2 + x 1

Multiplicação:

x ? (2x + y) = x ? 2x + x ? y = 2x2 + xy

(x + a) (x + b) = x x + x b + a x + a b =

= x2 + ax + bx + ab

Divisão:

(40x3y2 5x2y3) : ( 10xy) =

40

Unidade 5 • Equações

Abertura de Unidade – p. 142

• Resposta pessoal. Exemplo de resposta: A reciclagem é importante para o meio ambiente, pois reduz o acúmulo de resíduos e a extração de recursos da natureza.

No âmbito social, gera empregos e contribui para a sustentabilidade. Além disso, a reciclagem beneficia a economia com a redução de custos produtivos.

• Resposta pessoal. Espera-se que os estudantes respondam que, a partir de 2020, para calcular a quantidade estimada de latinhas recicladas, em mil toneladas, basta substituir A pelo ano correspondente e efetuar os cálculos. Do mesmo modo, se soubermos a quantidade de latinhas recicladas em um ano, depois de 2020, substituímos esse valor e o ano na expressão e calculamos o respectivo valor de A, resolvendo a equação.

• Segundo as informações e a equação do item anterior, temos que a quantidade de latas recicladas em mil toneladas em 2021, é dada por:

391,5 + 20 (A 2020) =

= 391,5 + 20 (2021 2020) = 391,5 + 20 1 =

= 411,5

Logo, em 2021, estima-se que foram recicladas 411,5 mil toneladas de latas.

1. Equação do 1o grau com uma incógnita

Pense e responda – p. 144

1. Seja x a quantidade, temos:

x + x 7 = 40 h 8x = 7 40 h x = 35

A quantidade é 35.

2. Seja x a quantidade, temos:

x + x 2 + x 4 = 56 h 7x = 4 ? 56 h x = 32

A quantidade é 32.

3. Seja x a quantidade, temos:

x + 2x 3 + 3x 4 = 145 h 29x = 12 145 h

h x = 60

A quantidade é 60.

Atividades – p. 147

1. a) Respostas pessoais. Espera-se que os estudantes concluam que a solução da equação é única e percebam que ao final da resolução devem simplificar a fração obtida, pois não reduziram o denominador usando o mínimo múltiplo comum entre 8, 6 e 12 e, por isso, vão encontrar uma fração equivalente à fração solução da equação.

b) y3 8 y1 6 y1 12 + + =

Reduzimos todos os termos ao denominador 48: () () () 6y 38 y1 48 4y 1 48 _++ =

Eliminando os denominadores:

3) + 8(y + 1) = 4(y _ 1)

e) x3 4 x1 3 7 2 + =h

3x 34 x1 12 67 12 () () h +_ =h

3x 94 x4 12 42 12 h +_+ =h x = 29 h h x = 29

5. Igualamos a expressão a 1 e resolvemos: () ()

Logo, para que a expressão seja igual a 1, x deve ser 6.

6. Do enunciado, temos que a soma das equações é igual a 90. Então: (x 5) + (2x 9) + (3x 13) + (4x 3) = 90 h

h 10x = 120 h x = 12

Substituindo x por 12 nas equações encontramos os números:

• (x 5) = 12 5 = 7

• (2x 9) = 24 9 = 15

• (3x 13) = 36 13 = 23

• (4x 3) = 48 3 = 45

O maior número é o 45.

Atividades – p. 149

1. Chamando a nota da primeira fase de x e igualando a equação à 8, temos:

3.

h 6x = 12 h x = 2

Logo, o valor de x na equação é 2.

4. a) x 4 20 x 3 x 4 x 3 +=h_=

() x2 x3 3 8 x2x6 3 8 3x 18 x6

+?+ =h ++ =h h=h=

Assim, a nota da segunda fase será: x + 3 h

h 6 + 3 = 9

Portanto, a nota na 1a fase foi 6 e a nota na 2a fase foi 9.

2. Sendo C a quantia, em reais, que Caio receberá, P a quantia que Pedro receberá e T a quantia que Toni receberá, temos:

• P = C 2 • T = C + 20 000

Então:

CP T 165 000 C C 2 C2 0 000

++=h+++= =h++=

165 000 C C 2 C

= 145 000 h 5 2 C = 145 000 h C = 290 000 5 h

h C = 58 000

Portanto:

• P = C 2 P 58 000 2 P2 9 000 h=h=

• T = C + 20 000 h T = 58 000 + 20 000 = 78 000

Assim, Caio receberá R$ 58.000,00, Pedro receberá

R$ 29.000,00 e Toni receberá R$ 78.000,00.

3. a) Do enunciado, temos: x + 200 = 2x 300

Logo:

x + 200 = 2x 300 h

h x = 200 + 300 h x = 500

Portanto, Valdir tem 500 reais.

b) Como Valdir precisa de 200 reais, além da quantia que tem para comprar o computador, o valor do computador será igual à quantia que Valdir tem, mais 200 reais. Ou seja:

500 + 200 = 700

Portanto, o preço do computador é 700 reais.

4. 80 100 3 000 60 100 5 000 x 100 2 000 ?+?+=

= 7 000 h 20x = 1 600 h x = 80

O valor de x é 80.

5. a) Como Humberto trabalha 5 dias por semana, ou seja, 20 dias por mês, ele gastaria:

20 R$ 15,00 = R$ 300,00

Portanto, a resposta é sim.

b) Do enunciado, temos que Humberto nunca leva refeição às sextas-feiras. Então, o consumo mínimo mensal é:

16 R$ 7,00 + 4 R$ 15,00 = R$ 172,00

Logo, Humberto gasta, no mínimo, R$ 172,00 por mês com almoço.

6. a) Como a balança está em equilíbrio, temos a igualdade:

2x + 400 = 4x + 200 h 2x = 200 h x = 100 Portanto, cada maçã tem 100 g.

b) Resposta pessoal. Exemplo de resposta: Se uma maçã de um dos pratos for trocada por um peso de 200 g, quantas maçãs devem ser colocadas no outro prato para que a balança fique em equilíbrio?

Resolução:

Representação inicial da balança:

100 + 100 + 200 + 200 = 100 + 100 + 100 +

+ 100 + 200

Representação da balança após a troca (no prato da esquerda):

100 + 200 + 200 + 200 = 100 + 100 + 100 +

+ 100 + 200

Para que a balança fique em equilíbrio acrescenta-

-se uma massa x no outro prato:

700 = 600 + x

x = 100

Assim, no outro prato, deve-se colocar 100 g, ou seja, uma maçã.

Se a troca for feita no prato da direita, o resultado será o mesmo.

7. Seja x o

7. 128 x 224 x6

h 96x = 768 h x = 8

Quantidade de grupos na colônia B:

x + 6 = 8 + 6 = 14

Assim, na colônia de férias B, há 14 grupos.

8. C x F8 x x 12 2 000 8x x = + h= + h

h 12x = 2 000 + 8x h 4x = 2 000 h x = 500

Devem ser produzidas 500 camisetas.

9. 32 estudantes no 8o ano A e 30 estudantes no 8o ano B. Chamando de x a quantidade de estudantes no 8o ano A, temos que:

320 x 300 x2 300 =h x = 320x 640 h

h 20x = 640 h x = 32

Assim, a quantidade de estudantes no 8o ano B é:

x 2 = 32 2 = 30

Logo, há 32 estudantes no 8o ano A e 30 estudantes no 8o ano B.

Por toda parte – p. 153

8 27 x = 8 27 81 = 24

Logo, o primeiro valor é 81, e o último é 24.

2. Equação fracionária com uma incógnita

Atividades – p. 152

1. O x não pode assumir nenhum valor que anule algum denominador da equação. Então, x não pode assumir os seguintes valores: a) 0 b) 0 c) 0 d) x + 3 = 0 h x = 3 e) 2x 1 = 0 h x = 1

1. 3x 10 15 57 10 3x 5 3x 10 3x 5 57 10 15 3x 6x 10 57 150 10 9x 207 x2 3

_=_h+=+h h + = + h=h=

O projeto Tamar tem 23 bases mantidas em áreas de alimentação, desova, crescimento e descanso das tartarugas marinhas.

2. () () ()

=_h h=h

1 4 4 y1 1 1 2 129 6y 66 3y 11 48 12 y1 1 6y 66 258 12 y1 1

h 3y 33 48 = 6y 324 h 3y = 243 h y = 81

A base de Sítio do Conde monitora 81 km de praia, entre a foz do rio Inhambupe, ao sul, e a foz do rio Real, ao norte.

3. Equações literais do 1o grau na incógnita x Atividades – p. 154

1. a) 5bx + 2a = bx + 3a h 4bx = a h x = a 4b       a 4b ,com b0 5

b) ( ) ( ) 3axb 2axb 3ax3b2ax 2b ax 5b x 5b a

+=_h h+=_h h=_h=_

      5b a ,com a0_5

c) (x + b)(x b) = x (x b3) h

h x2 b2 = x2 xb3 h xb3 = b2 h x = 1 b       1 b ,com b 0 5

d) (a b)x + (a + b)x = 2a h

h ax bx + ax + bx = 2a h

h 2ax = 2a h x = 1

{1}

e) x a c x 2a x a x 2a c 2x x 2a c x 2a cx 2ac

=+h_=h h=h=h=

{2ac}

2. 6hx + 14 = 18 + 2hx h 4hx = 4 h x = 1 h

h ,com h0

3. bx 5 bx 3 x 10

+ +=_h

Atividades – p. 158

1. a) 2x + y = 2

6b 6x 10b1 0x 30 3x 30

h ++ =_h

16b4 x3xx 16b

h_=_h=

16b

Educação financeira – p. 155

• Preço à vista: 300,00 (300,00 8%) = 276,00

Logo, R$ 276,00.

Preço a prazo: R$ 300,00.

R$ 276,00, dos quais R$ 150,00 são pagos no ato (sem juros) e sobra R$ 126,00 para pagar.

Como o valor pago na segunda parcela é R$ 150,00, o juro equivale a R$ 24,00.

150

126 1,19, 1 ou seja, o juro é de aproximadamente 19%.

4. Equação do 1o grau com duas incógnitas

Pense e responda – p. 156

1. a) x + x + 8 + 8 = y + y + y + y h 2x + 16 = 4y

b) Sim, pois 2 6 + 16 = 4 7, ou seja, 12 + 16 = 28.

2. a) 4x + 2y = 60

b) Sim, pois 4 12 + 2 6 = 60, ou seja, 48 + 12 = 60.

Atividades – p. 157

1. a) 5 ? 5 + 2 ? ( 2)

b) 5 9 ( 2) = 23

Para x = 1:

2( 1)

3.

?

h x = 0,5 (−0,5; 0,8)

= 1,5 h 0,6x = 0,3 h

b) 0,6x 1,5 ? 1,2 = 1,5 h 0,6x = 0,3 h x = 0,5 (0,5; 1,2)

4. a) 9x 5 3 = 21 h 9x = 36 h x = 4 (4, 3)

b) 9 ( 6) 5y = 21 h 54 5y = 21 h

h y = 15

(−6, −15)

5. a) 6 8 y = 42 h y = 6 (8, 6)

b) 6x 30 = 42 h 6x = 72 h x = 12 (12, 30)

6. • 10 ( 1) 10 = 20 h 20 = 20

• 5 ( 1) + 2 10 = 15 h 15 = 15

Logo, a afirmação é verdadeira.

7. Por tentativa encontramos que o par ordenado é (4, 3).

2. Para representar as equações no plano cartesiano, escolha alguns valores para x, substitua esses valores na equação e determinamos os valores de y. Após obter os pares ordenados, trace uma reta passando por todos

y = 0 ( 1, 0)

Para x = 2: 2 3y = 1 h 3y = 3 h y = 1

1)

ILUSTRAÇÕES: EDITORIA DE ARTE

5. Sistemas de duas equações do 1o grau com duas incógnitas

Atividades – p. 160

1. a) xy 60 x2y    += =

b) xy 9 xy 3    += _=

c) xy 3,5 x3y0,5    += =_

d) xy 10 20 x1 0y 130    += +=

e) xy 100 x2y4    += =+

2. a) Resposta pessoal. Exemplo de resposta: Algumas cestas valendo 3 pontos, e outras, 2 pontos, em um total de 56 pontos.

   xy 24 3x 2y 56 += +=

b) Resposta pessoal. Exemplo de resposta: E a medida da frente é 5 m maior do que a medida do fundo.

   2x 2y 22 xy 5 += =+

Fórum – p. 166

3. xy 23 2x 4y 82

  += +=

4 Resposta pessoal. Exemplo de resposta: Em um mercado, 3 quilogramas de tomate e 5 quilogramas de arroz custam 58 reais. Já 1 quilograma de tomate e 1 quilograma de arroz custam 14 reais.

   3x 5y 58 xy 14 += +=

Atividades – p. 162

1. 3x 2y 16 31 02 71 6 2x 3y 41 21 03 74 1

Sim.

2. y x 2 47 2 2 42 7 x y 2 32 2 2 3

Não é solução.

3. Por tentativa, encontramos que o par ordenado é (4, 2).

4. a) xy 8 2x 1y 13 x8 y 2x 1y 13       += += h =_ +=

• 2(8 y) + y = 13 h 16 2y + y = 13 h y = 3

• x = 8 3 h x = 5

As retas da representação geométrica se cruzam no ponto (5, 3). Portanto, a solução geométrica desse sistema é a III. A equipe venceu 5 partidas e perdeu 3.

5. Verdadeiras: a e c. Falsa: b. As soluções da equação 2x y = 3 são todos os pontos sobre a reta que a representa.

6. I) Para que Bento fique com 110 reais, ele precisa da quantia que já possui mais um terço das economias de Antônio e, para que Antônio fique com 110 reais, ele precisa da quantia que já possui mais um quarto das economias de Bento. Assim, o sistema que traduz essa situação é o da alternativa b.

II) A incógnita x representa a quantia economizada por Bento; e a incógnita y, a quantia economizada por Antônio.

y

III)

Substituindo y na segunda equação: 4(330 3x) + x = 440 h 1 320 12x + x = 440 h 11x = 880 h x = 80

Substituindo x na segunda equação:

y = 330 3 80 h y = 330 240 h y = 90

Logo, o par ordenado (80, 90) é solução do sistema de equações. Alternativa a.

IV) x = 80 reais (quantia economizada por Bento) e y = 90 reais (quantia economizada por Antônio).

6. Resolução de sistema de duas equações do 1o grau com duas incógnitas

Pense e responda – p. 164 Resposta pessoal.

No fluxograma a seguir, consideramos que o sistema tem solução.

(Início)

Observe as equações do sistema e escolha uma delas para isolar uma das incógnitas.

Substitua o valor da incógnita isolada no passo anterior na outra equação.

Faça os cálculos e encontre o valor da incógnita que falta.

• Considerando que, em um cruzamento, a quantidade de veículos que entra nele é igual a quantidade de veículos que sai dele, temos que:

   +=+H +=+H x 125 y4 5cruza mento y5 02 5 225 cruzamento

A B

Da equação que representa o cruzamento B, obtemos:

y = 250 50 h y = 200

Substituindo o valor de y na equação que representa o cruzamento A, temos:

x + 125 = 200 + 45 h x = 245 125 h x = 120

Então, x = 120 e y = 200.

Resposta pessoal. Exemplo de resposta: Os sistemas de equações são usados para dimensionar redes elétricas, no balanceamento de equações químicas, entre outras aplicações.

Atividades – p. 167

1. a)       xy 22 xy 8 xy 22 xy 8 += _= h += =+

• y + 8 + y = 22 h 2y = 14 h y = 7

• x + y = 22 h x + 7 = 22 h x = 15

(15, 7)

b) 2x y2 6 xy 4 2x y2 6 x4 y       += _= h += =+

• 2(4 + y) + y = 26 h 8 + 2y + y = 26 h 3y = 18 h y = 6

• x = 4 + y h x = 4 + 6 h x = 10 (10, 6)

c) 3x y5 5x 2y 1 y5 3x 5x 2y 1       += _= h =_ _=

• 5x 2( 5 3x) = 1 h 5x + 10 + 6x = 1 h 11x = 11 h x = 1

• y = 5 3 ( 1) h y = 5 + 3 h y = 2

( 1, 2)

d)       += _= h =_ _= x2y4 3x 2y 20 x4 2y 3x 2y 20

• 3( 4 2y) 2y = 20 h 12 6y 2y = 20 h 8y = 32 h y = 4

• x = 4 2 ? ( 4) h x = 4 (4, 4)

e) x3y3 2x y1,8    += _= h x3 3y 2x y1,8  

Faça os cálculos e descubra o valor da outra incógnita.

Utilize o valor da incógnita encontrado no passo anterior e substitua em uma das equações.

Refaça os cálculos.

Não Sim

Encontrou o par ordenado (x, y) que satisfaz as equações?

Você encontrou a solução do sistema. (Fim)

• 3x + 2x = 30 h 5x = 30 h x = 6

5y 26

6 3x 5y 26 x6 y

+= += h += =_ • 3(6 – y) + 5y = 26 h 18 3y + 5y = 26 h

• y = 6

Assim: x + y = 6 + 6 = 12

Logo, a equipe B conquistou 12 medalhas. Pense e responda – p. 169

Resposta pessoal. Exemplo de resposta: multiplicar a segunda equação (2y + 3x = 24) por 4.

Atividades – p. 170

EDITORIA DE ARTE

Os pontos (3, 3) e (1,5) não são soluções do sistema, pois não pertencem simultaneamente às duas retas.

c) Resposta pessoal. Exemplo de resposta: Sabendo que outra pessoa comprou 4 lápis e 6 canetas e pagou R$ 30,00, quanto custa uma caneta nessa papelaria?

Resolução:

Considerando x o preço do lápis e y o preço da caneta, temos:

xy 6 4x 6y 30 x6 y 4x 6y 30 += += h =_ +=

• 4(6 y) + 6y = 30 h 24 4y + 6y = 30 h

h 2y = 6 h y = 3

Então, uma caneta custa R$ 3,00.

4. a) 20 x 130 y 22(x 3) y    += +=

Assim:

• 20x + 130 = 22(x + 3) h 20x + 130 =

= 22x + 66 h 2x = 64 h x = 32

Antes de as outras 2 pessoas ingressarem, cada uma das 20 pessoas pagou R$ 32,00.

b) No acerto final, as 22 pessoas contribuíram com R$ 35,00 cada uma.

5. xy 27 50 x7 0y 1 650 x2 7y 5x 7y 165       += += h =_ +=

• 5(27 y) + 7y = 165 h 135 5y + 7y = 165 h

h 2y = 30 h y = 15

• x = 27 15 h x = 12

A editora utilizou 12 caixas para 50 livros e 15 caixas para 70 livros.

6. a)       xy 11 3x 2y 29 x1 1y 3x 2y 29 += += h =_ +=

• 3(11 y) + 2y = 29 h 33 3y + 2y = 29 h h y = 4

• x = 11 4 h x = 7

A equipe A ganhou 7 medalhas de ouro.

b) Resposta pessoal. Exemplo de resposta: Em uma competição esportiva, foram distribuídas apenas medalhas de ouro e de prata. Cada medalha de ouro vale 3 pontos, e cada medalha de prata vale 2 pontos. Se a equipe B conquistou a mesma quantidade de medalhas de prata e de ouro e obteve 30 pontos, quantas medalhas ela ganhou?

Resolução:

 xy 3x 2y 30 = +=

326

1. a) xy 42 xy 8    += _=

Somando as equações, temos: 2x = 50 h x = 25

Substituindo x na 1a equação: 25 + y + 42 h y = 17 (25, 17)

b) 2x 7y 1 2x 3y 11    += _+=_

Somando as equações, temos: 10y = 10 h y = 1

Substituindo y na 1a equação: 2x + 7 ? ( 1) = 1 h 2x = 8 h x = 4 (4, 1)

c)

d)

Somando as equações, temos: 15y = 45 h y = 3

Substituindo na 1a equação:

2.

Somando as equações, temos: x = 3

Substituindo na 1a equação:

( 3) + y = 1 h y = 2

a) y x = 2 ( 3) = 1

b) x : y = 3 2 3 2 =

c) (x + y)(x y) = ( 5) ? ( 1) = 5

x2 y2 5 6 x2 y2 1 2       

+ + = = = _= _= h

6x 5y 2 2x y2 5 ()   

  

_= _+=_

Adicionando as equações, temos: 4x = 12 h x = 3

6 3 5y = 2 h 5y = 20 h y = 4

Logo, a fração considerada é 3 4

4. xy 175 xy 43    += _=

Adicionando as equações, temos: 2x = 218 h x = 109

Substituindo na 1a equação: 109 + y = 175 h y = 66

Carlos pensou nos números 109 e 66.

5. xy 170 x3y2    += =+

• 3y + 2 + y = 170 h 4y = 168 h y = 42

• x = 3 42 + 2 h x = 128

Os números sorteados foram 128 e 42.

6. Seja x a idade de Caio e y a idade de Pedro.

xy 22 xy 2    += =+

• y + 2 + y = 22 h 2y = 20 h y = 10

• x = 10 + 2 = 12

12 anos.

7. Seja x o número de galinhas e y o número de ovelhas. xy 31 2 2x 4y 82 ()    += += h 2x 2y 62 2x 4y 82    =_ +=

Adicionando as equações, temos:

2y = 20 h y = 10

Substituindo na 1a equação:

x + 10 = 31 h x = 21

Estão nesse terreno 21 galinhas e 10 ovelhas.

9.

a) Considere: retângulo = x, trapézio = y, triângulo = z, pentágono = t, losango = k

Da 4a linha, tem-se: 4 + 4 + 4 + x = 20 h x = 8

Da 1a coluna, tem-se: z + 8 + 4 + 4 = 30 h z = 14

Da 3a coluna, tem-se: y + y + 14 + 4 = 22 h y = 2

Da 2a linha, tem-se: 8 + k + 2 + 2 = 18 h k = 6

Da 2a coluna, tem-se: 4 + 6 + t + 4 = 28 h t = 12

Assim: = 8 = 2 = 6 = 12 = 14

CB 87 (I)

CA 123 (II)

AB 66 (III)

Subtraindo (I) de (II): A B = 36 (IV)

Adicionando (III) e (IV): 2A = 102 h A = 51

Substituindo o valor de A em (IV):

51 B = 36 h B = 15

Substituindo o valor de A em (II):

C + 51 = 123 h C = 72

Assim, Carlos tem 72 kg, Andrea tem 51 kg e Balu tem 15 kg.

7. Equação do 2o grau

Pense e responda – p. 172

Resposta pessoal. Exemplo de resposta: As soluções podem ser opostas, podem ser iguais a zero ou pode não haver soluções no conjunto dos números reais.

Nas equações do tipo ax2 + c = 0, as soluções serão sempre a raiz quadrada de um número real: se esse número for positivo, teremos como solução dois números opostos; se o número for igual a zero, teremos solução igual a zero; se o número for negativo, não teremos solução no conjunto dos números reais.

Atividades – p. 173

1. a) x2 1 = 0 h x2 = 1 h x = 1 h x =±1

{ 1, 1}

b) x² 16 = 0 h x² = 16 h x = 16 h x =±4

{ 4, 4}

c) x2 64 = 0 h x2 = 64 h x = 64 h x =±8

{ 8, 8}

d) x2 + 16 = 0 h x2 = 16 (não tem solução no conjunto dos números reais) @ e) 9x2 = 25 h x2 = 25 9 h x = 25 9 h x =± 5

f) x2 20 = 0 h x2 = 20 h x = 20 h x =± 25

5. Seja x a medida da largura e y a medida do comprimento, temos: x y = 363 h x(3x) = 363 h 3x2 = 363 h x2 = 121 h x = 121 h x =±11

Como x . 0, x = 11

Medida do comprimento: 3x = 3 11 = 33

Assim, a medida do comprimento é 33 m e a medida da largura é 11 m.

6. A área de um triângulo é dada por: A = bh 2

Do enunciado, temos que a base mede o dobro da altura: b = 2h

Assim: 196 = 2h h 2 h 196 = h2 h h = 196 h h =±14

Como h . 0, h = 14

Logo, a medida da base é: b = 2 14 = 28

Portanto, 28 cm.

7. a) Como a área dos quatro terrenos quadrados de Lauro medem, juntos, 400 m2, temos:

4x = 400 h x = 100

Portanto, cada terreno de Lauro mede 100 m².

b) Sabendo que cada terreno de Lauro é quadrado, temos:

x2 = 100 h x = 100 h x =±10

Como x > 0, x = 10.

Portanto, o lado do terreno mede 10 m.

8. Do enunciado temos: pr2 = 314 h 3,14r2 = 314

Então: r2 = 314 3,14 h r2 = 100 h r = 100 h r =±10

Como r . 0, r = 10.

Alternativa b.

9. Do enunciado, temos: T(t) = t 4 2 + 400 h 39 = t 4 2 + 400

Então: t2 = 4(400 – 39) h t2 = 1 444 h t = 1444 h t =±38

Como t . 0, t = 38.

Alternativa d.

Tecnologias – p. 174

1. Utilizando o Ofi Calc, obtemos as seguintes soluções:

a) 3 e 3. b) Não em raiz real. c) 5,6 e 5,6.

2. a) Utilizando o Ofi Calc, verifica-se que as equações que têm solução em r são: I, IV e V. I: S = { 1,22; 1,22} IV: S = { 1, 1} V: S = { 2, 2}

b) Resposta pessoal. Espera-se que os estudantes percebam que a fração c a deve ser um número igual a zero ou maior do que zero. Caso contrário, a equação não tem solução no conjunto dos números reais. Desse modo, não haverá solução no conjunto dos números reais se a . 0 e c , 0 ou se a , 0 e c . 0.

c)

(Início) Escreva a equação do 2o grau que quer resolver.

4. a) x2 380 = 1 220 h x2 = 1 600 h x = 1600 h x =±40

Como x é um número natural, x = 40.

Larissa pensou no número 40.

b) Resposta pessoal. Exemplo de resposta: Pensei em um número natural, elevei esse número ao quadrado e do resultado eu subtraí 9. Se eu obtive o número 91, em que número eu pensei?

Resolução:

x2 9 = 91 h x2 = 100 h x = 100 h x =±10

Como x é um número natural, x = 10.

Pensou no número 10.

A equação não tem solução no conjunto dos números reais.

Calcule e escreva a solução do sistema

Volte ao início e escreva outra equação.

ILUSTRAÇÕES: EDITORIA DE ARTE

Retomando o que aprendeu – p. 176

1. 7x [5x + 3 (2x + 1) 10] = ( x + 3) h

h 7x [5x + 3 2x 1 10] = x 3 h

h 7x 5x 3 + 2x + 1 + 10 = x 3 h 4x + 8 =

= x 3 h 3x = 11 h x = 11 3

Alternativa b.

Assim: A B = 208 52 = 156 R$ 156,00. Alternativa b.

Atividades – p. 184

1. Sendo d = 2, temos:

3x x4 3 2 x 3x xx 4

2 () () () ()

=+h= = _+ h

3x x4 2x 4 xx 4

2 22

3x 3x 12x2x8 10 x8 x 4 5

h=_+_h

+= +=

10. PA 420 I P A 2 235 II () ()

Fazendo (I) (II), tem-se: A 2 185 A 370 =h=

Substituindo A em (I): P + 370 = 420 h P = 50 50 g. Alternativa e.

d = n(n3) 2 h 2 = n(n3) 2 h 4 = n2 3n h

h n2 3n 4 = 0

D= ( 3)2 4 (1) ( 4) = 25

n = (3)2 5 21 35 2 ± = ±

n = 8 2 = 4 ou

n = 2 2 = 1

Como n . 0, tem-se que n = 4. O polígono tem 4 lados, portanto, é um quadrilátero.

2. a) Sendo n = 5, temos:

5 y9 3 y3 5y 33 y9

2 2 2

= + h+=__h

5y 33 y9 5y 3

h+=__h+= =_+_h

h=_h=_ () () () () () () () ()

3y 3y 3 53 y3 53y9

= 620 h h 4E = 180 h E = 45 Alternativa a.

h=h=_+h

h=h= Assim: x y

3y 4y 4 3

d = n(n3) 2 h d = 5(53) 2 h d = 10 2 h

h d = 5

Portanto, o polígono de 5 lados tem 5 diagonais.

b) Sendo n = 8, temos:

d = n(n3) 2 h d = 8(83) 2 h

3 5 ==_

Alternativa a.

3. A: 280 + 3x

4 5 4 3

B: 400 + x 280 + 3x = 400 + x h 2x = 120 h x = 60 60 km. Alternativa a.

4. n3 n7 n7 n1 2 + + = + + h n2 + 15n + 36 = n2 + 14n + + 49 h n = 13

12. Seja x o número de jovens. Assim: (100% 25% 45%)x = 12 h 0,3 x = 12 h h x = 40 Então: 0,45 ? 40 = 18 Alternativa e.

13. 240 t 400 t2 400 t = + h= 240t + 480 h t = 3 3 horas.

Um novo olhar – p. 177

• Resposta pessoal. Espera-se que os estudantes tenham chegado a um valor próximo a 415,5 mil toneladas.

• Os valores da incógnita que anulam o denominador de cada um dos termos da equação.

• Métodos algébricos da substituição da adição e método geométrico no plano cartesiano.

• Sendo x e y dois números reais quaisquer e x2 = y, então xy =+ ou xy =_

h d = 40 2 h d = 20

Portanto, o polígono de 8 lados tem 20 diagonais.

c) Sendo n = 11, temos:

d = n(n3) 2 h d = 11(113) 2 h

h d = 88 2 h d = 44

Portanto, o polígono de 11 lados tem 44 diagonais.

d) Sendo n = 16, temos:

d = n(n3) 2 h d = 16(163) 2 h

h d = 208 2 h d = 104

Portanto, o polígono de 16 lados tem 104 diagonais.

e) Sendo n = 18, temos:

d = n(n3) 2 h d = 18(183) 2 h

Substituindo (II) em (I): PV 0,75 PV = 5 000 h 0,25 PV = 5 000 h h PV = 20 000

Substituindo PV em (II):

P0,7 52 0 000 C =?h PC = 15 000

R$ 15.000,00. Alternativa c.

8. Substituindo (I) em (II):

3P 26 = P 2 h 2P = 24 h P = 12

Substituindo P em (I): V = 3 ? 12 = 36 Alternativa d.

Unidade

6 • Polígonos e transformações no plano

Abertura de Unidade – p. 178

• Resposta pessoal. Exemplo de resposta: Figuras formadas por polígonos podem ser encontradas em mosaicos e em vitrais.

• Resposta pessoal. Exemplo de resposta: Podemos justapor figuras poligonais para compor mosaicos.

• Porque a imagem poderá ser ampliada sem sofrer distorção.

1. Polígonos e seus elementos

Atividade – p. 182

1. a) Três tipos. b) Triângulos, quadriláteros e octógonos.

2. Diagonais de um polígono convexo

Pense e responda – p. 184

Triângulo. Espera-se que os estudantes argumentem que o triângulo tem três vértices e que, ao escolher um deles para traçar a diagonal, os outros dois são consecutivos a ele, e concluam que o triângulo é um polígono que não tem diagonal.

h d = 270 2 h d = 135

Portanto, o polígono de 18 lados tem 135 diagonais.

3. Sendo n = 8, temos:

d = n(n3) 2 h d = 8(83) 2 h d = 40 2 h

h d = 20

Portanto, um octógono tem 20 diagonais. Alternativa c.

4. A quantidade de lados é dada por: 60 5 = 12

Logo, o polígono tem 12 lados.

Sendo n = 12, temos:

d = n(n3) 2 h d = 12(1 23) 2 h

h d = 108 2 h d = 54

Assim, o polígono tem 12 lados e 54 diagonais.

5. Sendo n = 7, temos:

d = n(n3) 2 h d = 7(73) 2 h d = 28 2 h

h d = 14

Logo, um polígono de 7 lados tem 14 diagonais. Alternativa b.

6. Do enunciado, temos que d = 4n. Então:

d = n(n3) 2 h 4n = n(n3) 2 h

h 8n = n2 3n h n2 = 11n h n = 11

O polígono tem 11 lados, portanto, é um undecágono.

7. Sendo d = 35, temos:

d = n(n3) 2 h 35 = n(n3) 2 h

h 70 = n2 3n h

h n2 3n 70 = 0

D= ( 3)2 4 (1) ( 70) = 289

n = (3) 289 21 31 7 2 ± ? = ±

n = 20 2 = 10

ou

n = 14 2 = 7

Como n . 0, tem-se que n = 10.

Alternativa c.

8. Sendo d = 90, temos:

d = n(n3) 2 h

h 90 = n(n3) 2 h

h 180 = n2 3n h

h n2 3n 180 = 0

D= ( 3)2 4 (1) ( 180) = 729

n = (3) 729 21 32 7 2 ± = ±

n = 30 2 = 15

ou

n = 24 2 = 12

Como n . 0, tem-se que n = 15.

Alternativa c.

3. Ângulos de um polígono convexo

Pense e responda – p. 186

a) Resposta pessoal. Espera-se que os estudantes percebam que os polígonos são decompostos em (n 2) triângulos, em que n é a quantidade de lados do polígono. A quantidade de triângulos em que o polígono foi decomposto é multiplicado por 180°.

Além disso, os estudantes podem citar que, a cada lado acrescentado ao polígono, a soma das medidas dos ângulos internos aumenta 180°.

b) Resposta pessoal. Espera-se que os estudantes apliquem as regularidades observadas e concluam que a soma das medidas dos ângulos internos de um octógono é

6 180° = 1 080°.

Atividades – p. 188

1. n 2 = 8 h h n = 10 10 lados; decágono.

2.

Soma das medidas dos ângulos internos

Pentágono n = 5 Eneágono n = 9 Icoságono n = 20

S = (n 2) 180°

S = (5 2) 180°

S = 3 180° = 540°

3 Sendo S = 1 620°, temos:

S = (n 2) 180°

S = (9 2) 180°

S = 7 180° = 1 260°

6. Soma das medidas dos ângulos internos 1 440° 1 800°

S = (n 2) 180° h

S = (n 2)

Número de lados do polígono

h 1 440° = (n 2) 180° h

h n 2 = 8 h

h n = 10

4. Ângulos de um polígono regular

Atividades – p. 190

1. a) Sabendo a quantidade de diagonais que parte de cada vértice, determinamos a quantidade de lados do polígono:

n 3 = 7 h n = 10

Depois, calculamos a soma das medidas dos ângulos internos:

S = (n 2) h 180° h S = (10 2) 180° h S = 1 440°

A soma das medidas dos ângulos internos do polígono é 1 440°.

b) Considerando que o polígono é regular e tem 10 ângulos internos, temos:

a = 1440 10 ° = 144°

Cada ângulo interno do polígono mede 144°.

2. Sendo n = 5, calculamos a soma das medidas dos ângulos internos do polígono:

S = (n 2) 180° h S = (5 2) 180° h S = 540°

Se o pentágono é regular, cada ângulo interno mede:

ai = 540 5 ° = 108°

Então: y = 108°

Como a soma dos ângulos internos de um triângulo é igual a 180°, temos no triângulo ABE:

x + x + 108° = 180° h 2x = 72 h x = 36°

Portanto:

y x = 108° 36°

y x = 72°

3. Sendo n = 5, calculamos a soma das medidas dos ângulos internos do polígono:

S = (n 2) 180° h S = (5 2) 180° h S = 540°

Se o pentágono é regular, cada ângulo interno mede:

ai = 540 5 ° = 108°

Assim, cada ângulo externo do pentágono mede:

a e = 180° 108° = 72°

S = (n 2) 180°

S = (20 2) 180°

S = 18 180° = 3 240°

S = (n 2) 180° h 1 620° = (n 2) 180° h n 2 = 9 h n = 11

O polígono tem 11 lados, portanto é um undecágono.

4. Em qualquer polígono, a soma dos ângulos externos vale 360°. Assim:

• S + S e = 1 080° h S + 360° = 1 080° h Si = 720°

• S = (n 2)

? 180° h 720° = (n 2)

? 180° h n 2 = 4 h n = 6

O polígono tem 6 lados, portanto é um hexágono.

5. Sendo n = 5, calculamos a soma dos ângulos internos do polígono:

S = (n 2)

? 180° h S = (5 2) ? 180° h S = 3 ? 180° = 540°

Assim: 2x + 3x + 120° + 135° + 150° = 540° h 5x = 135° h x = 27°

Logo: med (EÂB) = 2x = 2 27° = 54°

med (AB ˆ C) = 3x = 3

? 27° = 81°

Como a soma dos ângulos internos de um triângulo é igual a 180°, temos no triângulo DFE: x + 72° + 72° = 180° h x = 36°

A medida de x é 36°.

4. Do enunciado temos: Si = 4 S e Sabendo que a soma dos ângulos externos é igual a 360°:

S = 4 ? 360° h S = 1 440°

Conhecendo a soma dos ângulos internos do polígono, determinamos a quantidade de lados:

S = (n 2) 180° h 1 440° = (n 2) 180° h

h n 2 = 8 h n = 10

O polígono tem 10 lados, portanto é um decágono regular.

Da figura, temos: x = 360° 6 h x = 60°

Sabendo que a soma das medidas dos ângulos internos de um triângulo é igual a 180°:

Assim, cada ângulo do outro par de ângulos opostos mede 135°.

Portanto, os ângulos do paralelogramo medem 45°, 45°, 135° e 135°. 2.

2y + 60° = 180° h y = 120° 2 h y = 60° Atividades – p. 195

=

5. Do enunciado temos: S S 7 2 i e

Sabendo que a soma dos ângulos externos é igual a 360°:

S 360 7 2 ° =h 2S = 2 520° h S = 1 260°

Determinando a quantidade de lados do polígono:

• Si = (n 2) 180° h 1 260° = (n 2) 180° h

h n 2 = 7 h n = 9

O polígono tem 9 lados.

6. O polígono ABDEFGHI corresponde a um octógono regular. Assim, a medida de cada ângulo interno vale:

a n2 180° n a 82 180° 8 ii () () =h=h

h a = 135°

Assim: x + 135° + 60° = 360° h x = 165°

7. • A medida de cada ângulo interno do hexágono regular vale:

a = n2 180° n a 62 180° 6 () () _? h= _? h

h a = 120°

• A medida de cada ângulo interno do octógono regular vale:

a = n2 180° n a 82 180° 8 () () _? h= _? h

h a = 135°

Assim: x + 135° + 120° = 360° h x = 105°

8. a) a e = 360° n h 36° = 360° n h n = 10

Logo, a trajetória limita um polígono de 10 lados, ou seja, um decágono regular.

b) A distância que essa pessoa caminha na trajetória: 10 120 m = 1 200 m

Logo, a pessoa caminha 1,2 km.

c) 11 passos 8 m

x 1 200 m

x 1 200 11 8 1 650 = ? =

A pessoa dará 1 650 passos.

5. Construções geométricas

Pense e responda – p. 192

1. O triângulo equilátero tem três lados congruentes entre si.

2. Sim, o fato de que o triângulo equilátero tem três ângulos congruentes entre si.

Pense e responda – p. 193

• O hexágono pode ser decomposto em seis triângulos equiláteros.

Demonstração:

1. F G

A

C B H I

2. O ângulo central é dado por: 360° n

a) Como o quadrado possui 4 lados, temos: Medida do ângulo central = 360° 4 = 90°

b) Como o pentágono possui 5 lados, temos: Medida do ângulo central = 360° 5 = 72°

c) Como o decágono possui 10 lados, temos: Medida do ângulo central = 360° 10 = 36°

3. Espera-se que os estudantes determinem a medida do ângulo central do quadrado fazendo 360° 4 = 90°, construam uma circunferência, dividam-na em quatro setores circulares congruentes, cujos ângulos centrais medem 90°, e unam os pontos consecutivos por segmentos de retas.

4.

(Início) n = 9

Calcule a medida do ângulo central: 360° : 9 = 40°

Construa uma circunferência.

Usando um transferidor, marque a medida do ângulo central.

Usando um compasso, marque na circunferência os 9 pontos que a dividem em 9 setores iguais.

Trace segmentos de reta unindo os pontos consecutivos.

(Fim)

6. Propriedades dos quadriláteros

Atividades – p. 199

1. Como em um paralelogramo os ângulos opostos são congruentes, temos:

6x 21° = 4x + 1° h 2x = 22° h x = 11°

Assim, cada ângulo destacado na figura mede:

6x 21° = 6 ? 11° 21° = 45°

Como em um paralelogramo dois ângulos consecutivos são colaterais internos:

180° 45° = 135°

Podemos verificar na figura que: 82° = x + 35°

Logo,

x = 82° 35° h x = 47°

Assim, a medida x é 47°.

3. a) O perímetro é igual à soma de todos os lados.

Então:

P = 2 (3x + 2y) + 2 (2x + y) h

h P = 6x + 4y + 4x + 2y h

h P = 10x + 6y

b) A área é igual ao produto da base pela altura.

Então:

A = (3x + 2y) (2x + y) h

h A = 6x2 + 3xy + 4xy + 2y2 h

h A = 6x2 + 7xy + 2y2

4. a) O perímetro é igual à soma de todos os lados.

Então:

P = 2 (5x y) + 2 (5x y) h

h P = 10x 2y + 10x 2y h

h P = 20x 4y

b) A área é igual ao quadrado do lado. Então:

A = (5x y)2 h

h A = (5x y) (5x y) h

h A = 25x2 5xy 5xy + y2 h

h A = 25x2 10xy + y2

5. a) O ponto M é ponto médio das diagonais AC e BD

Então:

x = 16 e y = 12.

b) • Perímetro do triângulo AMB:

P = y + 16 + 20

P = 12 + 16 + 20 = 48

• Perímetro do triângulo ABC:

P = y + 12 + 20 + 20

P = 12 + 12 + 20 + 20 = 64

• Perímetro do triângulo ABD:

P = x + 16 + 20 + 20

P = 16 + 16 + 20 + 20 = 72

6. No quadrado, as diagonais são bissetrizes dos ângulos internos. Assim: y = 45°

Sabendo que a soma das medidas dos ângulos internos de um triângulo é igual a 180°, temos:

x + y + y = 180° h x + 45° + 45° = 180° h

h x = 90°

Assim: x = 90° e y = 45°.

114° 90° x

Da figura temos que: x + x + 114° = 180° h x = 33°

Assim: 90° x = 90° 33° = 57°

Logo, os ângulos medem 33° e 57°.

8. Como em um paralelogramo dois ângulos consecutivos são colaterais internos, a soma de suas medidas é igual

a 180°:

2x + 5° + x + 40° = 180° h 3x = 135° h x = 45°

Assim, as medidas dos ângulos são:

• 2x + 5° = 2 45° + 5° = 95°

• x + 40° = 45° + 40° = 85°

Portanto, 95°, 95°, 85° e 85°.

9. A medida de cada ângulo interno do hexágono regular vale:

ai = n2 180° n a 62 180° 6 i () () _? h= _? h

h ai = 120°

Assim, da figura, temos que: 120° + x = 180° h

h x = 60°

Como em um paralelogramo dois ângulos consecutivos são colaterais internos, a soma de suas medidas é igual a 180°:

x + y = 180° h 60° + y = 180° h y = 120°

Logo, x = 60° e y = 120°.

Atividades – p. 201

1. Sabendo que a soma das medidas dos ângulos internos de um quadrilátero é igual a 360°, temos:

78° + 102° + 98° + x = 360° h x = 82°

Logo, o quarto ângulo mede 82°.

2. Em um trapézio isósceles, seja x a medida dos ângulos agudos congruentes e y a medida dos ângulos obtusos congruentes.

Assim: x = 74°

Sabendo que x + y = 180°:

74 + y = 180° h y = 180° 74° h y = 106°

Logo, os três ângulos medem 74°, 106° e 106°.

3. A soma das medidas dos ângulos internos de um quadrilátero é igual a 360°, então temos:

x + 118° + 90° + 90° = 360° h x = 62°

Assim, x mede 62°.

4. Da figura temos: x + 30° + 70° = 180° h x = 80°

Da mesma forma: x + y + 50° = 180°

Assim, substituindo o valor de x:

80° + y + 50° = 180° h y = 50°

Portanto, x = 80° e y = 50°.

5. Em um trapézio isósceles, os ângulos agudos (de medida x) são congruentes, e os ângulos obtusos (de medida y) são congruentes.

Assim: x 4 5 y =

Mas, x + y = 180° h

8. Montando um sistema de equações e resolvendo-o pelo método da adição, temos:

= _= h += _= xy 2 25 (2)

xy 14 xy 50 xy 14

Somando as equações:

2x = 64 h x = 32

Substituindo x na primeira equação:

32 + y = 50 h y = 50 32 h y = 18

Assim, as bases medem: 32 cm e 18 cm.

Tratamento da informação – p. 202

1. Enfermeiro. 27,52%.

2. Psicólogos. 11,24%.

3. Não, porque não foi informado o total de participantes do estudo.

4. a) Não proporcionou.

b) Do gráfico, temos que a quantidade de profissionais que responderam que a unidade básica proporcionou treinamento, mas foi insuficiente, representa 22,6%.

Para saber a quantidade de profissionais que deram essa resposta:

Porcentagem Quantidade de profissionais 100% 258 22,6% x x 22,4 8 258 100 58 ==

Logo, 22,6%; 58 profissionais.

c) Resposta pessoal. Espera-se que os estudantes respondam que sim, pois os EPIs protegem os profissionais da saúde dos riscos ao realizar os procedimentos nos pacientes. Além disso, protege os pacientes.

7. Transformações no plano

Pense e responda – p. 206 Sim, um exemplo são duas reflexões seguidas. r s Figura inicial

A’( 3, 2), B’( 7, 2) e C’( 5, 5).

b) Para os respectivos pontos, na figura original e na figura refletida, os valores das ordenadas permanecem iguais e os das abscissas correspondem aos opostos das abscissas da figura original.

°°

h+=h=h h=h=

° °

4 5 yy 180 9y 5 180 y 5 180 9 y 100

Portanto:

x = 4 5 y h x = 4 5 100° h x = 80°

Os ângulos do trapézio medem 100°, 100°, 80° e 80°.

6. Seja t a medida dos ângulos agudos.

Assim:

t + t + 106° + 106° = 360° h 2t = 148 h t = 74°

Portanto:

x + t 2 + t 2 = 180° h x + t = 180° h

h x + 74° = 180° h x = 106°

A medida x é 106°.

7. Utilizando a fórmula: () () () medEF medABmed CD 2 = +

Temos: 16,7 = x1 2, 9 2 + h x = 20,5

Logo, a medida x é 20,5 cm.

6. Espera-se que os estudantes identifiquem

Resposta pessoal. Exemplo de resposta:

6. Do enunciado:

15 cm

0,6 15 cm = 9 cm

Assim, o perímetro do retângulo vale: 15 + 15 + 9 + 9 = 48

Cada lado do quadrado mede: 48 4 = 12

Portanto, 12 cm.

Alternativa b.

7. a) xy xy 34 0 30    += +=

II I

Fazendo (I) (II): 2y = 10 h y = 5

Tecnologias – p. 208

REPRODUÇÃO/GEOGEBRA

Substituindo y em (II): x + 5 = 30 h x = 25

Portanto: x − y = 25 5 = 20 cm

b) I.

2. Resposta pessoal. Exemplo de resposta: As alterações realizadas nos primeiros polígonos construídos acontecem nos demais polígonos obtidos como transformação no plano dos primeiros.

Retomando o que aprendeu – p. 210

1. Sendo 11 a quantidade de lados do polígono, temos:

d = () () nn 3 2 d 11 11 3 2 d4 4 h=h=

Logo, o polígono tem 44 diagonais.

Alternativa c.

2. Para o hexágono, temos n = 6. Então:

d = () () nn 3 2 d 66 3 2 d9h=h=

Assim, o número de estradas será: 9 + 6 = 15

Alternativa b.

3. A soma dos ângulos internos é dada por: S = (n 2) 180°

Assim: 2 160° = (n 2) 180° h n 2 = 12 h n = 14

Portanto, o polígono tem 14 lados.

Alternativa a.

4. A soma dos ângulos internos é dada por: S = (n 2) ? 180°

Sabendo que n = 6, temos:

S = (6 2) ? 180° h S = 720°

Assim: 4x + 160° + 160° = 720° h 4x = 400° h x = 100°

Alternativa b.

5. Sabendo que a medida do ângulo externo é 360° (soma das medidas dos ângulos externos) dividido pela quantidade de lados do polígono, temos:

a e = 360 n 24 360 n n1 5 ° ° ° h=h=

Assim, a quantidade de diagonais é:

d = () () nn 3 2 d 15 15 3 2 d9 0 h=h=

Logo, o polígono tem 90 diagonais.

Alternativa a.

ILUSTRAÇÕES: EDITORIA DE ARTE

8. No quadrilátero ABCD, tem-se:

Verifica−se que: m(ABC) = m(MBN) = 2x = 2 72° = 144°

Assim, no triângulo BMN: y + y + 144° = 180° h 2y = 36 h y = 18°

Alternativa d.

9. No triângulo ABD: 72° + (21° + y) + (21° + y)

Alternativa c.

1.

E 45°

1. Contagem

Pense e responda – p. 214

45° x y y

AB

Assim:       += =_ h += =+ xy 90°

xy 45° xy 90° (I) yx 45° (II)

Substituindo (II) em (I):

x + x + 45° = 90° h 2x = 45° h x = 22,5°

ou 22° 30’

x = 22°30’

b) 3x x4 2 x 3 3x 2x 4 xx 4

Quantidade de maneiras possível de sair do município A e chegar ao município C, passando pelo município B:

4 3 = 12

Portanto, são 12 maneiras distintas de sair de A até chegar em C

Atividades – p. 217

1. a) 3 2 = 6

Portanto, são 6 maneiras diferentes de Bernardo compor o uniforme. b) 2 uniformes.

2. 93 92 = 8 556

superior à quantidade esperada de clientes, mas que essa quantidade não seja superior ao dobro da quantidade esperada de clientes, então a opção que mais se adapta às condições da empresa é a opção V. Alternativa e.

7. Resposta pessoal. Exemplo de resposta: Quantos números de 3 algarismos distintos pares podemos formar com os algarismos 1, 3, 6 e 8, sem repeti-los?

3x x4

() () () ()

2 22

_=h= =h_+=_h

xx 4 3x 2x 83x1 2x

h=_h=_

10 x8 x 4 5

11. • Para o pentágono, n = 5:

ai = n2 180° n a 52 180° 5 i () () h=h

h ai = 108°

• Para o quadrado, n = 4:

ai = n2 180° n a 42 180° 4 i () () _? h= _? h

h ai = 90°

• Para o triângulo, n = 3:

ai = n2 180° n a 32 180° 3 i () () h=h

h ai = 60°

Assim: m(HDE) + 108° + 90° + 60° = 360° h

h m(HDE) = 102°

Como o triângulo HDE é isósceles: b + b + 102° =

= 180° h 2b= 78 hb= 39°

Alternativa c.

12. Do enunciado temos: 40°

Portanto, são 8 556 maneiras distintas de formar a comissão.

3. 9 9 9 9 2 2 2 = 52 488

Portanto, são 52 488 maneiras de Ana escolher a senha bancária.

4. Na ordem das unidades, há 3 possibilidades: 1, 7 e 9. Na ordem das dezenas de milhares, pode ser qualquer algarismo, menos o algarismo colocado na ordem das unidades, ou seja, 4 possibilidades. Na ordem das unidades de milhar, pode ser qualquer algarismo, menos o algarismo colocado na ordem das unidades e das dezenas de milhar, ou seja, 3 possibilidades. Na ordem das centenas, pode ser qualquer algarismo, menos o algarismo colocado na ordem das unidades, das dezenas e unidades de milhar, ou seja, 2 possibilidades. Na ordem das dezenas, pode ser qualquer algarismo, menos o algarismo colocado na ordem das unidades, das dezenas e unidades de milhar e das centenas, ou seja, 1 possibilidade. Assim: 3 4 3 2 1 = 72 Portanto, é possível formar 72 números ímpares com os algarismos fornecidos.

Para a ordem das unidades, há 2 possibilidades (6 e 8). Na ordem das dezenas, pode ser qualquer algarismo, menos o algarismo colocado na ordem das unidades, ou seja, 3 possibilidades. Na ordem das centenas, pode ser qualquer algarismo, menos os algarismos colocados na ordem das unidades e na ordem das dezenas, ou seja, 2 possibilidades. Assim:

2 3 2 = 12

Portanto, utilizando os algarismos 1, 3, 6 e 8, podemos escrever 12 números distintos pares com três algarismos.

2. Probabilidade

Atividades – p. 221

1. a) S = {(cara, cara); (cara, coroa), (coroa, cara), (coroa, coroa)}

b) S = {(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6); (2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (2, 6); (3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (3, 6); (4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (4, 6); (5, 1); (5, 2); (5, 3); (5, 4); (5, 5); (5, 6); (6, 1); (6, 2); (6, 3); (6, 4); (6, 5); (6, 6)}

c) S = {(M, M, M); (M, M, F); (M, F, M); (M, F, F); (F, F, F); (F, F, M); (F, M, F); (F, M, M)}

2. a) E = {(cara, cara); (coroa, coroa)}

5. Primeira possibilidade: o carro preto ocupa uma das vagas a seguir:

b) S = {(1,4); (2,3); (3,2); (4,1)}

c) S = {(M, M, F); (M, F, M); (F, M, M)}

b a 180° a

B

180° b

A D C

Assim, no quadrilátero ABCD:

ILUSTRAÇÕES: EDITORIA DE ARTE

40° + 90° + (180° a) + (180° b) = 360° h

h 490 ab= 360° ha+b= 130°

Alternativa d.

Um novo olhar – p. 211

• Resposta pessoal.

• A soma das medidas desses ângulos é igual a 180°

• Um polígono regular tem todos os lados congruentes entre si e todos os ângulos internos congruentes entre si, o que faz que todos os ângulos externos também sejam congruentes entre si.

• O retângulo, o losango e o quadrado.

• Trapézio isósceles e trapézio retângulo.

• Reflexão, translação e rotação.

Unidade 7 • Contagem, probabilidade e Estatística

Abertura de Unidade – p. 213

• Resposta pessoal.

• Resposta pessoal. Espera-se que estudantes percebam que a quantidade de óbitos vai diminuindo.

As vagas “laranja” correspondem às vagas que não podem ser ocupadas pelo carro rosa. Assim, há 8 7 = 56 possibilidades.

Segunda possibilidade: o carro preto ocupa uma das vagas a seguir:

As vagas “vermelho” correspondem às vagas que não podem ser ocupadas pelo carro rosa. Assim, há 2 ? 8 = = 16 possibilidades

Portanto: 56 + 16 = 72

3. a) S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25}

b) A = {9, 18}

c) B = {24, 25}

4. São 9 bolas na urna ao todo (2 + 4 + 3). Como são 4 bolas azuis, na urna, a probabilidade de retirar uma bola azul é:

P(A) = 4 9

Como são 3 bolas vermelhas, na urna, a probabilidade de retirar uma bola vermelha é:

P(V) = 3 9 = 1 3

5. Quantidade de elementos do espaço amostral: 9 9 = 81

9 possibilidades (0 a 9, menos o anterior)

9 possibilidades (1 a 9)

Quantidade de elementos do evento: 41

Assim: P(E) = 41 81

6.

a) P(E) = 16 100 4 25 =

elementos do evento: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96

b) P(E) = 6 100 3 50 =

elementos do evento: 15, 30, 45, 60, 75, 90

7. a) 10 duplas:

(G1 G2; G1 G3; G2 G3; G1 R1; G1 R2; G2 R1; G2 R2; G3 R1; G3 R2; R1 R2)

b) P(E) = 3 10

8 a) Número de elementos do espaço amostral: 5 4 3 2 = 120

Número de elementos do evento: 4 ? 3 ? 2 ? 3 = 72

P(E) = 72 120 3 5 =

b) Número de elementos do espaço amostral: 5 4 3 2 = 120

Número de elementos do evento: 4 ? 3 ? 2 ? 2 = 48

P(E) = 48 120 2 5 =

9. Como há 5 possibilidades de retirada de bolas na primeira caixa e 3, na segunda, a quantidade total de retiradas de bolas das caixas é: 5 3 = 15

Uma vez que as bolas da segunda caixa são O, B e M, é necessário retirar uma bola com uma dessas letras da primeira caixa, assim, temos 3 possibilidades de retirada na primeira caixa. E como a letra retirada na segunda caixa deve ser igual à retirada na primeira, há apenas uma possibilidade de retirada na segunda caixa. Sendo assim, a probabilidade pedida é:

P(E) 3 15 1 5 ==

Alternativa b.

3. Estatística

Pense e responda – p. 222

Resposta pessoal. Exemplo de respostas: Dificuldade em levantar os dados, custos envolvidos nas pesquisas etc.

Pense e responda – p. 224

Resposta pessoal. Exemplo de resposta: Se considerarmos que todos os estudantes usam aplicativos e que tenham características parecidas, podemos escolher uma amostra casual simples.

Pense e responda – p. 227

Resposta pessoal. Exemplo de resposta: Variáveis qualitativas e quantitativas discretas são representadas em gráficos de barras ou colunas separadas. Variável quantitativa contínua é representada em colunas agrupadas.

Atividades – p. 228

1. Resposta pessoal. Espera-se que os estudantes percebam que a pesquisa mais adequada é a amostral, uma vez que não é possível consultar todos os clientes da fábrica de chocolates e os custos de uma pesquisa censitária são altos, além de demorados.

2. a) 250 funcionários da empresa.

b) 50 funcionários da empresa.

c) Massa, em quilograma. Variável quantitativa contínua.

3. Resposta pessoal. Espera-se que os estudantes percebam que essa amostra não é representativa e não refletirá a opinião da população correspondente, já que as meninas não foram consideradas na amostra e podem ter opiniões divergentes.

4. Consumo de água

Quantidade de copos de água (por dia) Frequência absoluta Frequência relativa

a) 56 + 23 = 79 jovens.

b) 14% + 7% = 21%.

5. a) 9 + 2 = 11 funcionários.

b) 1 + 2 = 3 funcionários.

6. a) Quantidadede irmãos dos estudantes do 8o ano Quantidade

escola.

b) 8 + 4 + 3 = 15; 15 estudantes.

7. a) Gastos dos clientes da padaria

8. a) 14% + 2% = 16%

b) Aparelhos de TV nas residências

4. Medidas em Estatística

Atividades – p. 235

1. a) Bruno: 6,57,577,5 6 5 34,5 5 6, 9  ++++ ==

Camila: 8 876,5 7,5 5 37 5 7, 4 ++++ ==

Marcela: 55,5 4,55,5 6 5 26,5 5 5, 3 ++++ ==

Roberto: 4,57,555 8 5 30 5 6, 0 ++++ ==

b) Bruno, Camila e Roberto foram aprovados.

= ++++++

2.

Portanto, a altura média é de aproximadamente 1,71 m.

b) Ordenando os valores: 1,63; 1,65; 1,69; 1,69; 1,75; 1,76; 1,79

A mediana corresponde ao valor do elemento da quarta posição. Assim, a mediana é 1,69 m. Metade dos jogadores têm altura menor ou igual a 1,69 m e a outra metade tem altura maior ou igual a 1,69 m.

c) M 1, 65 1, 69 1, 79 1, 75

2. Soma dos valores de dois dados:

Das informações anteriores, verifica-se que há 6 possibilidades para formar a soma “7”, 5 possibilidades para formar a soma “8” e apenas 3 possibilidades para formar a soma “4”. Alternativa d.

3. a) 4 anos; 15 anos.

63

76 1, 78 8 13,7 4 8 1, 7175 = +++++++ =1

Assim, a altura média considerando o novo integrante é aproximadamente 1,72 m. Ordenando os valores: 1,63; 1,65; 1,69; 1,69; 1,75; 1,76; 1,78; 1,79

A mediana corresponde à média dos valores dos elementos da quarta e da quinta posição. Assim, a mediana será 1, 69 1, 75 2 1, 72 + =

A altura média será 1,72 m e a mediana 1,72 m.

3. a) M 12 17 15 14 12 19 91 11 41 0 10 133 10 = +++++++++ == 13,3 anos

b) Possui duas modas: 12 anos e 14 anos.

c) Organizando os dados em ordem crescente: 9 10 11 12 12 14 14 15 17 19

A mediana corresponde à média dos valores dos elementos da quinta e da sexta posição. Assim, a mediana será 12 14 2 + = 13, ou seja, 13 anos.

d) 19 9 = 10

4. Como a moda é a variável com maior frequência, a idade de 9 anos é a moda dos dados apresentados no gráfico. Alternativa a.

5. Média do estudante 1:

M 35,5 29,2 10,0 45 ,4 10 66,5 10 6, 65 = ?+?++? ==

Média do estudante 2:

M 36,3 28,7 9, 84 4, 9 10 65,7 10 6,57 = ?+?++? ==

Portanto, ambos os estudantes foram aprovados.

5. Realizando pesquisas estatísticas

Pense e responda – p. 237

Não, pois essa pesquisa trabalhou com uma variável qualitativa.

Atividades – p. 237

1. a) Resposta pessoal. A execução desta pesquisa depende das escolhas dos estudantes.

b) Resposta pessoal. A execução desta pesquisa depende das escolhas dos estudantes.

Tecnologias – p. 239

1. Resposta pessoal. A organização dos resultados vai depender da pesquisa escolhida pelos estudantes na página 237.

Retomando o que aprendeu – p. 240

1. Quantidade de maneiras distintas com que a secretária poderá se arrumar:

6 4 3 = 72

Alternativa c.

b) • M1 = 48 84 11 51 53 20 164 20 8, 2  ?+?+?+ ==

• M2 = 41 08 51 11 01 51 2 20 370 37 10 ?+?+?+? ==

==

• M M 8, 2 10 0, 82 1 2

c) Para 2021, organizamos os dados da seguinte maneira.

Como são 20 vendedores, utilizamos os 10o e o 11o termos (em vermelho).

Mediana = 88 2 + = 8 anos

Para 2022, organizamos os dados da seguinte maneira.

15 15

Como são 37 vendedores, utilizamos os 19o termo (em vermelho).

Mediana = 11 anos.

4. A mediana será a média dos valores intermediários de cada candidato.

Mediana do candidato K: 33 33 2 33 + =

Mediana do candidato L: 33 34 2 33,5 + =

Mediana do candidato M: 35 35 2 35 + =

Mediana do candidato N: 35 37 2 36 + =

Mediana do candidato P: 26 36 2 31 + =

Alternativa d.

5. Organizando os dados, temos: 11 11 12 13 15 15 16 16 17 18 20 24

A mediana corresponde à média dos valores dos elementos da 6a e 7a posições. Assim, a mediana será 15 16 2 + = 15,5.

Alternativa c.

Um novo olhar – p. 241

• Aproximadamente 2 000 óbitos (3 000 1 000 = 2 000).

• A partir de agosto de 2021.

• Resposta pessoal. Espera-se que os estudantes percebam que as tabelas e os gráficos nos auxiliam a transmitir informações de maneira mais simples e rápida. Os diferentes tipos de gráfico servem para transmitir diversos tipos de informação, por exemplo, quando se deseja analisar os dados ao longo de um período, o gráfico de linhas é o mais indicado; quando se deseja comparar parte dos dados com o total, o mais indicado é o gráfico de setores etc. Ao analisar um gráfico e uma tabela, é importante verificar a fonte dos dados, se a escala está correta, se há legenda etc.

Unidade 8 • Área, volume e capacidade

Abertura de Unidade – p. 242

• Resposta pessoal. Espera-se que os estudantes saibam o nome do reservatório que abastece o município em que vivem. Informações sobre o abastecimento, nível do reservatório e a qualidade de água, caso não saibam, podem ser obtidas conversando com amigos e familiares ou fazendo uma pesquisa na internet.

• Resposta pessoal. Espera-se que estudantes observem que, em 2021, os níveis dos reservatórios que abastecem a Grande São Paulo estavam mais baixos do que no mesmo período de 2013, ano que antecedeu a crise hídrica de 2014. Embora um novo reservatório tenha integrado o sistema de abastecimento, é possível estimar que havia motivo de preocupação para o abastecimento em 2022, tomando como base o ocorrido em 2014, mas é necessário observar que isso também depende do período de chuvas na região que, em geral, costuma ocorrer nos meses de primavera e verão.

1. Área de figuras planas

Pense e responda – p. 244

Do enunciado, temos que a área que Marcos vai cobrir é retangular e mede 3 m por 5 m, então, essa região mede:

3 m 5 m = 15 m2

Se cada placa de grama mede 1 m2, temos:

15 m 1m 15 2 2 =

Logo, Marcos vai precisar de 15 placas.

Pense e responda – p. 246

Não. Espera-se que os estudantes façam estimativas e comparações entre as áreas dos respectivos formatos utilizando estratégias pessoais.

Por exemplo, eles podem comparar a área da região circular com a área de um quadrado de 2 m de lado, verificando que a área da região circular é menor do que a área desse quadrado e, em seguida, observar que a área desse quadrado é menor do que a área da região triangular considerada.

Fórum – p. 246

Resposta pessoal. Exemplo de resposta: Produzir o próprio alimento; eliminar o uso de agrotóxicos; utilizar o cultivo com fins terapêuticos; economizar nas compras da feira ou do mercado, entre outros.

Pense e responda – p. 248

Área do tanque em formato triangular: bh 2 25 2 5 ==

Área do tanque em formato circular (considerando p= 3,14): pr2 = 3,14 ? 12 = 3,14

Assim, a área do tanque triangular (5 m2) é maior do que a área do tanque circular (3,14 m2).

Então, o tanque triangular ocupa maior área.

Atividades – p. 248

1. a) A área da lajota quadrada é: l2 h 152 = 225

Portanto, 225 cm2

b) Área do piso em centímetro quadrado: 450 000 cm2

450 000

225 2 000 =

São necessárias 2 000 lajotas.

2. O telhado tem duas áreas retangulares de 4 m por 10 m. Então, a área total é:

A = 2 ? 10 ? 4 = 80

Portanto, o telhado tem 80 m2 de área.

Se a cada metro quadrado de telhado são usadas 20 telhas: 20 80 = 1 600

Logo, são necessárias 1 600 telhas.

3. Marcando o ponto E na Figura 2, temos:

AE BE = AB h 10 4 = 6

Então, se o lado quadrado mede 6 cm, sua área é 62 = 36.

Logo, a área do quadrado ABCD é 36 cm2

Alternativa c.

4. Áreas a serem pintadas:

• Parede do fundo: 4 m 8 m = 32 m2

• Parede da frente com porta: 4 m 8 m 2 m 1,5 m = 32 m2

• Parede lateral com janela: 4 m 5 m 1 m 3 m = 20 m2

3 m2 = 29 m2

3 m2 = 17 m2

• Parede lateral sem janela: 4 m 5 m = 20 m2

• Teto: 5 m 8 m = 40 m2

Assim, a área total a ser pintada mede:

32 m2 + 29 m2 + 17 m2 + 20 m2 + 40 m2 = 138 m2

Dividindo a área total pelo rendimento de cada lata de tinta, temos:

138  m 40  m 3, 45 2 2 =

Logo, terá de comprar quatro latas de tinta.

5. As raízes da equação são: 2x2 32 = 0 x2 = 32 2 x =± 16 x =±4 Como x . 0, x = 4.

Então, o raio da circunferência é 4 cm e seu comprimento é:

2 ?p? r = 2 3,14 4 = 25,12 25,12 cm

6. O comprimento de uma circunferência é dado por:

2 ?p? r

Do enunciado, temos que o comprimento da toalha circular é 3,72 m. Então:

2 ?p? r = 3,72 2 ? 3,1 ? r = 3,72

6,2 r = 3,72

r = 0,6

Como o diâmetro é duas vezes o comprimento do raio: 2 ? 0,6 = 1,2

O diâmetro da toalha mede 1,2 m.

7. C = 2 ?p? 0,5 = 2 ? 3,14 ? 0,5 = 3,14

Em 100 voltas: 100 3,14 = 314

Portanto, ele percorre 314 m.

8. a) Substituindo o tempo na fórmula, temos:

r = t 5 h r = 4 5 r 2 5 0, 4  h==

Após 4 minutos de vazamento, o raio da mancha é 0,4 m.

b) A =pr2 = 3,14 (0,4)2 h A = 0,5024

No mesmo instante, a área da mancha é 0,5024 m2

9. Resposta pessoal. Exemplo de resposta: Sabendo que o contorno do círculo mede 31,4 cm, calcule a diferença entre a área do quadrado e a do círculo.

Resolução:

Para encontrar a área do círculo precisamos saber a medida do raio. Se o contorno do círculo é 31,4 m, temos:

2 ?p? r = 31,4

2 ? 3,14 ? r = 31,4

6,28 ? r = 31,4

r = 5

Calculando a área do círculo:

pr2 = 3,14 52 = 78,5

Logo, a área do círculo é 78,5 cm2

Para determinar o lado do quadrado e calcular sua área, temos, de acordo com a figura, que a diagonal do quadrado é igual ao diâmetro do círculo. Então, a diagonal do quadrado é: 2

Sabendo que a diagonal do quadrado é 2 , temos:

10 = 2 hl= 10 2 2 hl= 52

Calculando a área do quadrado:

() 52 2 = 50

Assim, a área do quadrado é 50 cm2

Portanto, a diferença entre as áreas é

78,5 cm2 50 cm2 = 28,5 cm2

Por toda parte – p. 250

1. a) Em cada trapézio temos que: a altura mede 480 : 2 = 240; a base menor mede 400; a base maior mede 800 200 = 600.

A área do trapézio é dada por: ( ) Bb h 2 +?

Então, a área dos dois trapézios é:

A = 2 ? ( ) 600 400 240 2 +? = 240 000

240 000 km2

b) A área do triângulo é dada por: bh 2

A = 200 200 2 = 20 000

20 000 km²

2. Volume de sólidos geométricos

Atividades – p. 254

1. a) 2 cm 2 cm 2 cm = 8 cm³

b) 3 cm 2 cm 2 cm = 12 cm³

2. 5 3 x = 45

15x = 45 x = 3

Logo, a altura do bloco retangular é 3 cm.

3. O objeto não cabe na caixa de número 2, pois umas das dimensões da caixa é menor que 80 cm.

Sabendo que o objeto cabe nas demais caixas, sobrará menos espaço no interior daquela que tiver menos volume. Então:

Caixa 1: 86 cm 86 cm 86 cm = 636 056 cm3

Caixa 3: 85 cm 82 cm 90 cm = 627 300 cm3

Caixa 4: 82 cm 95 cm 82 cm = 638 780 cm3

Caixa 5: 80 cm 95 cm 85 cm = 646 000 cm3

Assim, a caixa escolhida pelo casal deve ser a de número 3. Alternativa c.

4. Para fazer a verificação, basta calcular os volumes.

• Volume do cubo de aresta x: x ? x ? x = x3

• Volume do cubo de aresta 2x: 2x ? 2x ? 2x = 8x3

Portanto, a resposta é não, pois o volume ficará multiplicado por 8.

5. O volume do cilindro é dado por: Abase ? h

a) V =p r2 h h V = 3,14 22 5 h V = 62,8

O volume do cilindro é 62,8 cm³.

b) V =p r2 h h V = 3,14 (1,5)2 4 h

h V = 28,26

O volume do cilindro é 28,26 cm³.

6. Resposta pessoal. Exemplo de resposta: Fernanda vai fabricar uma peça que lembra um cubo com um vão que lembra o formato de um bloco retangular, como mostra a figura. Qual é o volume dessa peça?

Resolução:

O volume da peça é dado pelo volume do cubo menos o volume do vão. Então:

13 13 13 7 7 13 = 2 197 637 = 1 560

Assim, o volume da peça é 1 550 cm3

7. O volume do cilindro é dado por: V =p? r2 ? h

Do enunciado, temos V1 = 1,6 V2. Então:

p 62 4 = 1,6 p 32 h2

p 144 =p 14,4 h2

h2 = 10

Alternativa b.

3. Capacidade

Pense e responda – p. 256

Resposta pessoal. Exemplo de resposta: Espera-se que os estudantes respondam que todo o conteúdo cabe no recipiente, sem faltar nem transbordar água, pois 1 L = 1 dm3

Atividades – p. 257

1. a) Sabendo que: 1 m3 = 1 000 L 18 m3 = 18 000 L

Nessa casa foram consumidos 18 000 litros de água no último mês.

b) Capacidade do reservatório:

1,5 m 0,8 m 0,5 m = 0,6 m3

Dividindo a quantidade de água consumida no último mês pela capacidade do reservatório, temos:

18 m 0, 6m 3 3 = 30 É possível encher o reservatório 30 vezes.

Tratamento da informação – p. 258

1. Resposta pessoal. Exemplo de resposta: Ambos os gráficos apresentam informações sobre a oferta interna de energia (OIE) em dado período. No entanto, o primeiro é um gráfico de barras, que traz uma comparação entre a OIE no Brasil em 2020, no mundo em 2018 e na OCDE em 2018, considerando em cada barra a participação de fontes renováveis e de fontes não renováveis de energia, em porcentagem, explicitando uma relação parte-todo. O segundo é um gráfico de linha que apresenta, de 2000 a 2020, a evolução na participação das fontes renováveis de energia na OIE apenas no Brasil.

2. A maior queda na participação das fontes renováveis de energia foi no período de 2009 a 2014.

3. a) Maior participação: 2009 (89%); menor participação: 2015 (74%).

b) Resposta pessoal. Exemplo de resposta: Embora a participação de fontes renováveis na produção de energia elétrica no Brasil continuou a cair, a geração de energia elétrica no país aumentou, acompanhada de um aumento da participação das fontes não renováveis de energia nessa produção, o que pode ter compensado a carência de fontes renováveis.

c) Resposta pessoal. Espera-se que os estudantes percebam que, como está representada a evolução da participação das fontes renováveis de energia na geração de energia elétrica ao longo de um período, o gráfico de linha é o mais adequado.

Retomando o que aprendeu – p. 260

1. A área de cada lajota é: 30 cm ? 30 cm = 900 cm2

A área da varanda, em centímetro quadrado, é: 360 cm 690 cm = 248 400 cm2

Para obter a quantidade de lajotas, dividimos a área da varanda pela área de cada lajota. Então: 248 400 900 = 276

Logo, serão necessárias 276 lajotas para revestir a varanda. Alternativa d.

2. Para encontrar a área do quadrilátero, devemos subtrair as áreas dos dois triângulos da área do quadrado. Então, vamos determinar essas áreas.

Área do triângulo amarelo: bh 2 82 2 8 ==

Portanto, 8 cm2

Do enunciado, temos que o triângulo amarelo tem o dobro da área do triângulo azul. Seja x a área do triângulo azul, temos: 8 = 2x h x = 4

Portanto, a área do triângulo azul é 4 cm2

Área do quadrado: 82 = 64

Portanto, 64 cm2

Assim, a área do quadrilátero é: 64 4 8 = 52

52 cm2

Alternativa c.

3. Resolvendo a equação, temos:

x2 25 = 0

x2 = 25

x =±5

Como x . 0, x = 5.

Assim, o raio da circunferência é 5 cm.

Área do círculo delimitada pela circunferência:

A =pr2 h A = 3,14 ? 52 h A = 78,5

78,5 cm2

Alternativa b.

4. A figura está dividida em três partes; dois quadrados de lado 2 cm e 1 4 de círculo de raio 2 cm.

Calculando a área dos dois quadrados juntos, temos: 2 2 2 = 8

Portanto, 8 cm2

Calculando a área do setor circular, temos: r 4 3,14 2 4 22 p? == 3,14

Portanto, 3,14 cm2

Assim, a área da figura é: 8 cm2 + 3,14 cm2 = 11,14 cm2

Alternativa c.

5. Nomeando as partes da figura, temos:

Do enunciado, temos:

• Área do retângulo H A + B = 120 cm2

• Área do círculo H B + C + D = 81 cm2

• Área do triângulo H D + E = 29 cm2

A área azul corresponde à área total da figura menos a área do círculo.

Área azul: A + B + C + D + E (B + C + D)

Área vermelha: C

Diferença entre as áreas azul e vermelha:

AB 120 CD E 29 BC D 81 C () ++++_++_= 68

68 cm2

Alternativa a.

6. Sabendo que 1 hm2 = 10 000 m2, temos: 1 hectare = 1 hm2 = 10 000 m2

Então, se a piscina cobre um terreno de 8 hectares, essa área corresponde a 80 000 m2 Alternativa e.

7. Resposta pessoal. Exemplo de resposta: Marcos comprou um terreno retangular com 12 metros de largura e 28 metros de comprimento. Ele vai construir uma casa que ocupará 160 m2 desse terreno. Qual é a área do terreno que não será ocupada pela construção?

Roteiro de resolução:

Como o terreno é retangular, multiplique a medida da largura do terreno pelo comprimento para obter a área total: 12 m 28 m = 336 m2

Depois, subtraia a área que a casa ocupará da área total do terreno:

336 m2 160 m2 = 176 m2

Dê a resposta: A área que não será ocupada pela construção é de 176 m2

8. Quantidade total de óleo: 100 ? 120 L = 12 000 L = 12 000 000 mL

Dividindo a quantidade total de óleo pela quantidade que será acondicionada em cada recipiente, temos:

12 000 000  mL

750 mL = 16 000

Logo, serão necessários 16 000 recipientes.

9. Nenhuma das xícaras tem o dobro do volume de outra xícara. Somando os valores das xícaras dois a dois, tem-se:

950 + 750 = 1 700

950

Verifica-se que VI + VIII é o dobro de VII

Assim:

• xícaras I e III contêm café;

• xícara II contém suco;

• xícaras IV e V contém leite. Alternativa e.

Um novo olhar – p. 261

• Não. Exemplo de resposta: Para fazer essa afirmação, é necessário conhecer a capacidade de cada reservatório.

• Resposta pessoal. Exemplo de resposta: Espera-se que os estudantes percebam que o volume representa o espaço ocupado por um corpo, enquanto a capacidade de um recipiente está relacionada a quanto esse recipiente é capaz de armazenar.

Unidade 9 • Estudo de grandezas

Abertura de Unidade – p. 262

• Resposta pessoal. Exemplo de resposta: A presença de pessoas observando a maquete e a proporção entre a representação dos prédios e as pessoas. Algumas situações que os estudantes podem relatar: maquetes feitas para representar prédios que serão construídos, localizadas em stands de vendas, panfletos de propaganda com a planta baixa de apartamentos à venda, planta baixa de feiras e exposições com a distribuição dos stands de cada expositor.

• Resposta pessoal, que depende das medidas aferidas pelos estudantes

1. Grandezas

Pense e responda – p. 265

8 horas. Espera-se que os estudantes verifiquem que precisam descobrir o número que multiplicado por 50 resulte em 400.

Pense e responda – p. 267

Não, pois a idade de uma pessoa e a altura correspondente não são grandezas proporcionais.

Atividades – p. 268

1. a) F = 1,8 C + 32 h 68 = 1,8 C + 32 h C = 20

Portanto, 68 °F equivalem a 20 °C.

b) F = 1,8 C + 32 h F = 1,8 25 + 32 h F = 77

Portanto, 25 °C equivalem a 77 °F.

2. a) 1 530 000 5 306 000 =

Cada pessoa receberá R$ 306.000,00.

b) 1 530 000 6 255 000 =

Cada pessoa receberá R$ 255.000,00.

c) Fazendo as contas para dois ganhadores:

1 530 000

2 765 000 =

Então, o quadro ficará assim:

2 765.000

5 306.000

6 255.000

d) Diminui proporcionalmente. Essas grandezas são inversamente proporcionais.

2018.

3. Não, pois aumentando a quantidade de livros, o preço correspondente a ser pago não aumenta na mesma proporção.

4. a) Não, pois o valor é sempre acrescido da bandeirada.

b) V = 5,50 + 4 12 = 53,50

Portanto, Paola pagou R$ 53,50 pela corrida.

5. a) R$ 46,00 (obtido diretamente do gráfico).

b) Analisando o gráfico, conclui-se que são necessários aproximadamente R$ 90,00.

c) Indicando por x o valor a pagar por 7 kg de café, temos:

2 46 7 x x 161 =h=

Portanto, se alguém comprar 7 kg desse café pagará R$ 161,00.

6. Resposta pessoal. Exemplo de resposta:

Jonathan é vendedor de carro em uma loja e recebe de comissão 1,5% do valor de suas vendas. Se no mês de maio ele teve uma comissão de R$ 3.150,00, qual foi o valor das vendas dele nesse mês?

3 150 x 0, 015 x 210 000 =h=

Portanto, Jonathan vendeu R$ 210.000,00 no mês de maio.

2. Algumas razões especiais

Fórum – p. 270

Resposta pessoal. Os estudantes podem citar a importância de sempre identificar a fonte da informação e a autoria, além de pesquisar em outras fontes a mesma informação.

Atividades – p. 271

1. = 280 km

4 h 70 km/h

A velocidade média desse automóvel no percurso foi de 70 km/h.

2. • comprimento: 20 m = 2 000 cm

• largura: 8 m = 800 cm

Dimensões da maquete:

• comprimento: 2 000 cm = 1 200 10  cm

• largura: 800 cm ? 1 200 = 4 cm

Alternativa c.

3. a) 1 10 000 000 2 x x2 0 000 000 =h=

20 000 000 cm = 200 km

Portanto, a distância real a ser percorrida no trecho representado em linha reta no mapa é 200 km.

b) = 200 80 2,5

Ou seja, para percorrer esse trajeto a 80 km/h, ele levará 2h30min.

c) Resposta pessoal. Exemplo de resposta:

Qual deve ser a velocidade média do automóvel para que o motorista faça esse trajeto em duas horas?

200 x 2x 100 =h=

A velocidade média deve ser de 100 km/h.

Atividades – p. 273

1. = 14  kg

35 dm 0, 40 3 kg/dm3

Portanto, a densidade desse bloco de madeira é 0,40 kg/dm3

2. 4, 3 g

0, 2 cm3 = 21,5 g/cm3

Portanto, a densidade desse fio de platina é 21,5 g/cm3

3. 8,1 g 3 cm3 = 2,7 g/cm3

Portanto, a densidade dessa pedra é 2,7 g/cm3

4. 64 200  hab

15 000  km 4,28 2 = hab./km2

Portanto, a densidade demográfica dessa região é 4,28 hab./km2

5. 11 200 000  hab

132 000  km2 1 84,8 hab./km2

Portanto, a densidade demográfica da Grécia naquela época era aproximadamente

84,8 hab./km2

6. • Água Branca: 125 000  hab 36  km 3 472,2 2 1 hab./km2

• Pedra Azul: 85 000  hab 30  km 2 833,3 2 1 hab./km2

Portanto, o bairro Água Branca tem maior densidade demográfica.

7. 3 168 027  hab 52 810  km 59,9 9 hab. /km 2 2 1

Portanto, a densidade demográfica desse estado é de aproximadamente 59,99 hab./km2

8. 40 100 000  hab x km2 = 14,3 hab./km2 h x 1 2 804 196 km2

Logo, Caio errou a ordem de grandeza do território argentino, que é de cerca de 2 800 000 km2

9. Resposta pessoal. Exemplo de resposta: Pesquise a área do município em que você vive e a quantidade de habitantes dele. Com esses dados, calcule a densidade demográfica do município.

A resposta dependerá dos dados pesquisados.

3. Grandezas diretamente proporcionais

Pense e responda – p. 275

2 250 parafusos. Exemplo de resposta: Como em 10 horas a máquina produz 1 500 parafusos, em 5 horas são produzidos 750 parafusos. Logo, em 15 horas, ela produz a soma desses valores, ou seja, 2 250 parafusos (1 500 + 750 = 2 250).

Atividades – p. 276

1.

2. ?? = 230 86 0 40 2760

Portanto, em uma jornada ininterrupta de 8 horas, são produzidos 2 760 pães.

3. a) 110 km/h 3,5 h = 385 km

b) 473 km 110  km/ h = 4,3 h

Ou seja, demoraria 4,3 h ou 4h18min.

4. A altura desse prédio é:

26 3 = 78

Ou seja, o prédio real tem 78 m ou 7 800 cm. Assim, a altura da maquete será:

1 120 x 7 800 x6 5  =h=

Ou seja, 65 cm.

5. • Parcela ocupada pelos sacos de cimento: = 100 600

• Tijolos que ainda podem ser colocados:

Ou seja, 6 075 tijolos.

6. = 4,5   6 10 2, 7

Portanto, Amanda deve dar 2,7 mL de antibiótico para seu cachorro.

7. Escrevendo o que foi fornecido pelo enunciado em forma de esquema, temos: Marrom

30 L

1 parte de cor laranja 15 L

3 partes de tinta vermelha

2 partes de tinta amarela

1 parte de cor verde 15 L

2 partes de tinta azul

1 parte de tinta amarela

9 L

6 L

10 L

5 L Como são necessários 6 litros de tinta amarela para fazer a cor laranja e 5 litros de cor amarela para fazer a cor verde, serão necessários ao todo 11 litros de tinta amarela para fazer a cor marrom.

Alternativa e.

8. Resposta pessoal. Exemplo de resposta:

Em 9 minutos, baixou-se 36% de um arquivo. Mantendo esse ritmo, quanto tempo mais será necessário para terminar de baixá-lo?

= 9   6 4 36 16

Portanto, serão necessários mais 16 minutos.

4. Grandezas inversamente proporcionais

Pense e responda – p. 278

Resposta pessoal. Espera-se que os estudantes percebam que os gráficos que representam grandezas diretamente proporcionais são retas ascendentes (“crescem”) e os que representam grandezas inversamente proporcionais são curvas descendentes (“decrescem”).

Atividades – p. 279

1. x = 20  min 1 imp. 4 imp. 5 min ? =

Quatro impressoras iguais a essa devem imprimir essa mesma quantidade de páginas em 5 minutos.

2. x == 20 5 8 12,5

Portanto, 8 homens levariam 12,5 dias para asfaltar o trecho da rodovia.

3. a) 48  km 1,5 h = 32 km/h

A velocidade média desenvolvida pelo ciclista é de 32 km/h.

b) 48  km 38,4  km/ h = 1,25h ou 1h15 min

O ciclista gastará 1h15min.

4. 38 14 56 = 9,5

A equipe conseguirá realizar o trabalho de correção em 9,5 dias.

5. = 36 150 30 180

O livro terá 180 páginas.

6. x =h= 15 80 12 x 100

Alternativa c.

7. a) As grandezas são inversamente proporcionais, porque, à medida que a quantidade de trabalhadores aumenta, a quantidade de dias para a conclusão da obra diminui na mesma proporção.

b) Resposta pessoal. Exemplo de resposta: Para que a obra seja concluída em cinco dias, quantos trabalhadores a empresa deverá colocar nessa obra?

=h= x 3   2 0 5 x1 2

Portanto, são necessários 12 trabalhadores na obra.

Por toda parte – p. 280

1. Resposta pessoal. Espera-se que os estudantes reflitam sobre suas atitudes e percebam a importância de ser tolerante com as pessoas.

2. ?h= 72,8 100 1000 x 728

Portanto, 728 crimes.

3. Resposta pessoal. Espera-se que os estudantes elaborem cartazes que valorizem a diversidade entre as pessoas.

5. Regra de três

Atividades – p. 283

1. x = 27 2 240 16 3 780 =

Ou seja, seriam necessários 3 780 tijolos.

2. x == 3,51,7 2,5 2, 38

Portanto, ele deve misturar 2,38 L de tinta vermelha.

3. x == 2   8 0 16 10

Para cumprir a meta, serão necessários 10 pintores.

4. a) x = = 120  km   1 h 1,5 h 80  km

b) 2h20min = 2,333... h

x = 80 km/h 2,333… h = 186,666… km

Aproximadamente 186,7 km.

5. Quantidade de arame: 50 m 1,20 m = 60 m²

Nova tela: x ? (1,20 m + 1,80 m) = 60 m²

x = 20 m

Portanto, o comprimento da nova tela será de 20 m.

6. a) Sim, pois as grandezas variam na mesma razão.

b) R$ 30,00 (pela análise do gráfico).

c) x == 25 45 30 37,5 37,5 minutos.

7. x == 15 000  m 0, 7 g 100  m 105 g 3 3

8. x = ? = 180  kg  50  estudantes 20  estudantes 450  kg

Atividades – p. 285

1. =? 21 x 8 6 420 960 h x = 36 São necessários 36 funcionários.

2. =? 2 x 5 3 5 6 h x = 1,44 h

Aproximadamente 1h26min.

3. 6 x 300 240 12 5 6 x 3x 2 =?h=h=

Alternativa b.

4. =?h= x 6 60 80 8 9 x4

Beto faria o percurso em 4 dias.

5. =?h= 15 x 9 12 10 8 x1 6

Portanto, a gráfica não conseguirá cumprir o prazo inicial. Será necessário um dia a mais.

6. =?h= 6 x 4 6 900 500 x5 Alternativa c.

7. Resposta pessoal. Exemplo de resposta: Com um pacote de ração de 10 kg, Renan alimenta seus cinco gatos por 30 dias. Uma amiga deixou seus dois gatos com Renan enquanto viaja a trabalho. Com isso, Renan comprou um pacote de ração de 12 kg. Considerando que todos os gatos comem a mesma quantidade de ração, quanto tempo o pacote de ração comprado por Renan irá durar?

=?h1 30 x 10 12 7 5 x2 5, 7

Portanto, o pacote de ração durará aproximadamente 25 dias.

Tratamento da informação – p. 286

1. 1 500 0,05 = 75 150 0,02 = 3 75 vagas; 3 vagas.

2. Resposta pessoal. Espera-se que os estudantes entendam a importância desse artigo para a inserção de pessoas reabilitadas ou com deficiência habilitadas no mercado de trabalho, pois garante que as empresas disponibilizem vagas para esses profissionais.

3. a) Deficiência física.

b) Sim, pois 16,1% + 9% = 25,1%.

4. De 1 a 2 salários mínimos.

Retomando o que aprendeu – p. 288

1. =h= 1 15 000 1, 6 x x2 4 000

Portanto, a distância real entre essas duas casas é de 24 000 cm ou 240 m.

2. 52,40 =h 10 444 526 A A = 10 444 526 52,4 0 h A 1 199 323,02

Portanto, a área do estado é 199 323,02 km2

b)

Fonte: Dados fictícios.

c) Até 120 minutos.

d) Tarifa 3.

4. a) 138,89 ? 3,6 1 500

Portanto, 500 km/h.

b) x = 1 300 m 138,8 9 m/s 9, 4 1

A onda atingirá a casa em 9,4 segundos ou 0,16 minuto.

c) 138,89 m

d) 138,89 18 60 = 150 001,2

Ou seja, a onda se formou a 150 001,2 m ou aproximadamente 150 km.

5. =h= 2 x 4 6 x3

Portanto, são necessários 3 tratores.

6. =?h= 5 x 12 15 5 8 x1 0

Alternativa b.

Um novo olhar – p. 289

• Resposta pessoal. Exemplo de resposta: Grandezas diretamente proporcionais são aquelas que variam sempre na mesma proporção (quando uma aumenta, a outra aumenta na mesma proporção; ou, ainda, quando uma diminui, a outra também diminui na mesma proporção). Grandezas inversamente proporcionais são aquelas em que uma varia na razão inversa da outra (quando uma aumenta, a outra diminui na mesma proporção; ou, ainda, quando uma diminui, a outra aumenta na mesma proporção).

• Uma reta.

• Resposta pessoal que depende das medidas aferidas pelo estudante.

Tecnologias – p. 290

1 a) Utilizando o programa, obtém-se x = 0,4. De fato:

=h= x 2 5 x0,4

b) Utilizando o programa, obtém-se x = 1,888... . De fato:

=h= x 17 9 x1, 888...

2. Para construir o programa que resolve equações do 2o grau do tipo ax2 + b = 0, vamos primeiro determinar a solução geral para esse tipo de equação. Assim: ax2 + b = 0 h ax2 = b h=_h x b a 2 x b a =_

Então, precisamos criar um programa que, entrando com os valores de a e b, retorne o cálculo b a . Perceba que o início do programa é igual ao programa criado na seção para resolver equações do 1o grau. O que irá mudar é a parte final, com a indicação do cálculo a ser feito. Um exemplo de resposta do passo a passo está indicado a seguir.

1. Repita os passos 1 a 6 indicados nas páginas 290 e 291 da seção Tecnologias

2. Agora, vamos construir o comando que contém a operação de divisão. Selecione o menu Operadores e arraste a operação para a tela principal. Em seguida, ainda no menu Operadores, arraste a operação para a tela principal, encaixando-a no primeiro campo digitável da operação de divisão.

3. No primeiro campo digitável da operação de multiplicação, digite 1 e, no segundo campo, arraste a variável b do menu Variáveis

4. No segundo campo digitável da operação de divisão, arraste a variável a do menu Variáveis. Com isso, construímos o cálculo b a e a estrutura deve ficar como indicada na Figura 1

5. Agora, vamos construir o cálculo da raiz quadrada. Para isso, no menu Operações, arraste o bloco para a janela principal. Dentre as opções da lista do bloco, escolha raiz quadrada e arraste o bloco construído no passo anterior para o campo digitável deste bloco.

6. No menu Aparência, selecione o bloco , encaixando-o no conjunto construído até então.

7. Para concluir, clique no menu Operadores e arraste o operador para o campo digitável do último bloco encaixado no conjunto. Em seguida, digite A solução da equação é no primeiro campo digitável desse operador e arraste o cálculo do passo 5 para o segundo campo. O algoritmo final está indicado na Figura 2

Ao testar o programa para determinar a raiz da equação 4x2 100 = 0, o programa deve devolver a solução 5

Figura 1

Figura 2

AVALIAÇÕES OFICIAIS EM FOCO

QUESTÕES PROPOSTAS

1. (Enem/MEC) Pesquisadores da Universidade de Tecnologia de Viena, na Áustria, produziram miniaturas de objetos em impressoras 3D de alta precisão. Ao serem ativadas, tais impressoras lançam feixes de laser sobre um tipo de resina, esculpindo o objeto desejado. O produto final da impressão é uma escultura microscópica de três dimensões, como visto na imagem ampliada.

os freios são acionados, pode ser obtida com a fórmula:

em que

M é a medida da marca de derrapagem, em metro;

e corresponde à eficiência de frenagem; e C é o coeficiente de atrito.

Em um dos experimentos, ao acionar um freio, um carro teve a marca de derrapagem medindo 30 m, o coeficiente de frenagem de 0,35 e o coeficiente de atrito de 0,6. De acordo com a fórmula, qual era velocidade aproximada desse carro, em quilômetro por hora, quando os freios foram acionados?

a) 7

b) 6,3

c) 3,1

d) 2,5

A escultura apresentada é uma miniatura de um carro de Fórmula 1, com 100 micrômetros de comprimento. Um micrômetro é a milionésima parte de um metro. Usando notação científica, qual é a representação do comprimento dessa miniatura, em metro?

a) 1,0 x 10 1

b) 1,0 x 10 3

c) 1,0 x 10 4

d) 1,0 x 10 6

e) 1,0 x 10 7

2. Um pesquisador fez alguns experimentos para descobrir a relação entre as marcas criadas na pista quando um carro freia de maneira abrupta e a velocidade do carro no momento da freada. Ele obteve um resultado em que a velocidade do carro, em quilômetro por hora, no momento em que

3. (Saresp-SP) Para ingressar na sala segura de um laboratório, Mauro deve apertar 5 botões coloridos na sequência correta. Mauro esqueceu-se da senha, mas lembrou que o primeiro botão a ser apertado era o de cor azul e o último a ser apertado era o de cor verde.

Qual é o número máximo de tentativas que Mauro deve fazer para acessar a sala, sabendo que cada cor é apertada uma única vez?

a) 120

b) 30

c) 12

d) 6

REPRODUÇÃO/ENEM, 2020. REPRODUÇÃO/SARESP

4. (Saresp-SP) Uma máquina fotográfica custava

R$ 400,00. No Dia dos Pais foi vendida com um desconto de 5% e, logo depois, em cima do novo preço sofreu um aumento de 10%. O seu preço atual, em reais, é:

a) 405,00

b) 412,00

c) 418,00

d) 420,00

(Pisa) PINGUINS – Texto base para as questões 5 e 6

O fotógrafo de animais Jean Baptiste fez uma viagem de um ano e tirou inúmeras fotos de pinguins e de seus filhotes. Ele se interessou particularmente pelo crescimento do tamanho de diferentes colônias de pinguins.

6. Jean supõe que a colônia continuará a crescer da seguinte maneira.

• No início de cada ano, a colônia tem um número igual de machos e fêmeas que formam casais.

• Cada casal de pinguins procria um filhote a cada primavera.

• Ao final do ano, 20% de todos os pinguins (adultos e filhotes) estarão mortos.

• Os pinguins com um ano de idade também terão filhotes.

De acordo com as hipóteses acima, qual das seguintes fórmulas expressa o número total de pinguins P ao final de 7 anos?

a) P = 10 000 x (1,5 x 0,2)7

b) P = 10 000 x (1,5 x 0,8)7

c) P = 10 000 x (1,2 x 0,2)7

d) P = 10 000 x (1,2 x 0,8)7

Para resolver a atividade 6, considere um total de 10 000 pinguins (5 000 casais).

5. Normalmente, um casal de pinguins produz dois ovos por ano. Em geral, o filhote que nasce do maior dos dois ovos é o único a sobreviver.

Com os pinguins saltadores, o primeiro ovo pesa em torno de 78 g e o segundo em torno de 110 g.

Em que proporção aproximadamente o segundo ovo é mais pesado que o primeiro?

7. Arthur encontrou a dízima periódica 0,444... efetuando a divisão de dois números inteiros positivos a e b. Em seguida, ele realizou a divisão de b por a. O resultado encontrado foi:

a) 0,55

b) 0,5252...

c) 2,25

d) 2,2525...

8. (Saresp-SP) Numa gincana de Matemática, Hélio calculou mentalmente dois números de modo que sua soma fosse igual a 12 e sua diferença 2. Lúcia utilizou outra estratégia, determinando esses dois números algebricamente. Dessa forma, um possível sistema de equações para indicar o raciocínio de Lúcia é:

a) xy 12 2x 3y 1 += +=   

c) xy 5 xy 7 _= +=  

a) 29% b) 32% c) 41% d) 71%

b) 2x y9 4x 3y 10 _= +=   

d) xy 12 xy 2 += _=

9. (OBMEP) Nas balanças há sacos de areia de mesmo peso e tijolos idênticos.

Quanto deve marcar a última balança? a) 22 kg b) 23 kg c) 24 kg

10. O gráfico a seguir relaciona as variáveis x e y.

25 kg e) 26 kg

Assinale a equação que expressa essa relação.

2x y = 5

11. (OBMEP) Observe a sequência de figuras abaixo, todas elas com a forma da letra Y. Seguindo este padrão, quantas bolinhas terá a 15 a figura?

12. (Saresp-SP) Kátia encontrou um termômetro com marcação numa escala desconhecida. Havia apenas dois números com marcação legível. Para encontrar a temperatura marcada naquele momento, Kátia achou uma boa ideia fazer medições com sua régua, em cm, conforme a figura a seguir.

REPRODUÇÃO/SARESP

Qual o valor que Kátia encontrou para a temperatura x?

a) 31 b) 41 c) 51 d) 61

13. (Enem/MEC) Uma fatura mensal de água é composta por uma taxa fixa, independentemente do gasto, mais uma parte relativa ao consumo de água, em metro cúbico. O gráfico relaciona o valor da fatura com o volume de água gasto em uma residência no mês de novembro, representando uma semirreta.

Observa-se que, nesse mês, houve um consumo de 7 m3 de água. Sabe-se que, em dezembro, o consumo de água nessa residência, em metro cúbico, dobrou em relação ao mês anterior. O valor da fatura referente ao consumo no mês de dezembro nessa residência foi

a) superior a R $ 65,00 e inferior a R $ 70,00.

b) superior a R $ 80,00 e inferior a R $ 85,00.

c) superior a R $ 90,00 e inferior a R $ 95,00.

d) superior a R $ 95,00.

e) inferior a R $ 55,00.

14. Observe o fluxograma com a sequência de comandos na imagem.

Calcule 3x (Início) Insira um número inteiro x

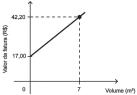
O resultado é menor do que 30?

Calcule 3x 2

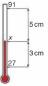
Calcule 3x

Considerando o número 12, após efetuar os passos descritos no fluxograma, o número obtido é:

a) 1 296

b) 144

c) 36 d) 6

REPRODUÇÃO/ENEM, 2020.

15. José possui um terreno triangular ABC, conforme representado na figura a seguir, e deseja separar uma área para o plantio de milho, que está representada pelo quadrilátero CEDF, em que os pontos D, E e F são pontos médios dos lados AB, AC e BC, respectivamente.

Sabendo que a área total do terreno de José mede 450 m2, a área reservada para o plantio de milho, em metro quadrado, é:

a) 360 b) 225 c) 150 d) 100

16. (Enem/MEC) O fenômeno das manifestações populares de massa traz à discussão como estimar o número de pessoas presentes nesse tipo de evento. Uma metodologia usada é: no momento do ápice do evento, é feita uma foto aérea da via pública principal na área ocupada, bem como das vias afluentes que apresentem aglomerações de pessoas que acessam a via principal. A foto é sobreposta por um mapa virtual das vias, ambos na mesma escala, fazendo-se um esboço geométrico da situação. Em seguida, subdivide-se o espaço total em trechos, quantificando a densidade, da seguinte forma:

• 4 pessoas por metro quadrado, se elas estiverem andando em uma mesma direção;

• 5 pessoas por metro quadrado, se elas estiverem se movimentando sem deixar o local;

• 6 pessoas por metro quadrado, se elas estiverem paradas.

É feito, então, o cálculo do total de pessoas, considerando os diversos trechos, e desconta-se daí 1 000 pessoas para cada carro de som fotografado. Com essa metodologia, procederam-se aos cálculos para estimar o número de participantes na manifestação cujo esboço geométrico é dado na figura. Há três trechos na via principal: MN, NO e OP, e um trecho numa via afluente da principal: QR

Segundo a metodologia descrita, o número estimado de pessoas presentes a essa manifestação foi igual a a) 110 000. b) 104 000.

REPRODUÇÃO/ENEM, 2020.

17. (OBMEP) A soma dos números das faces opostas de um dado é sempre 7. O dado da figura é girado sucessivamente sobre o caminho indicado até parar na última posição, destacada em cinza. Nessa posição, qual é o número que está na face superior do dado?

Após o primeiro giro:

a) 1 b) 2 c) 3 d) 4 e) 5

18. (OBMEP) Os quatro dados da figura são idênticos, e há três pares de faces em contato. Qual é o valor da soma dessas faces? a) 73 b) 74 c) 75 d) 76 e) 77

19. (Enem/MEC) Uma casa lotérica oferece cinco opções de jogos. Em cada opção, o apostador escolhe um grupo de K números distintos em um cartão que contém um total de N números disponíveis, gerando, dessa forma, um total de C combinações possíveis para se fazer a marcação do cartão. Ganha o prêmio o cartão que apresentar os K números sorteados. Os valores desses jogos variam de R$ 1,00 a R$ 2,00 conforme descrito no quadro.

Um apostador dispõe de R$ 2,00 para gastar em uma das cinco opções de jogos disponíveis. Segundo o valor disponível para ser gasto, o jogo que oferece ao apostador maior probabilidade de ganhar prêmio é o

a) I. b) II. c) III. d) IV. e) V.

20. (Saresp-SP) Um proprietário de uma casa pretende fazer uma cisterna em forma de paralelepípedo de 5 m de comprimento por 2 m de largura e 1,5 m de profundidade. Qual o volume de água que essa cisterna pode armazenar?

a) 7,5 m3 b) 8,5 m3 c) 10 m3 d) 15 m3

21. (Enem/MEC) Uma empresa deseja construir um edifício residencial de 12 pavimentos, num lote retangular de lados medindo 22 e 26 m. Em 3 dos lados do lote serão construídos muros. A frente do prédio será sobre o lado do lote de menor comprimento. Sabe-se que em cada pavimento 32 m2 serão destinados à área comum (hall de entrada, elevadores e escada), e o restante da área será destinado às unidades habitacionais. A legislação vigente exige que prédios sejam construídos mantendo distâncias mínimas dos limites dos lotes onde se encontram. Em obediência à legislação, o prédio ficará 5 m afastado da rua onde terá sua entrada, 3 m de distância do muro no fundo do lote e 4 m de distância dos muros nas laterais do lote, como mostra a figura.

A área total, em metro quadrado, destinada às unidades habitacionais desse edifício será de a) 2 640. b) 3 024. c) 3 840. d) 6 480. e) 6 864.

22. (Enem/MEC) A Cifra de César é um exemplo de um método de codificação de mensagens usado por Júlio César para se comunicar com seus generais. No método, cada letra era trocada por uma letra que aparecia no alfabeto um número fixo de casas adiante (ou atrás) de forma cíclica. A seguir temos um exemplo em que cada letra é substituída pela que vem três posições à frente.

Para quebrar um código como esse, a análise de frequências das letras de um texto é uma ferramenta importante.

Uma análise do texto do romance O guarani, de José de Alencar, que é composto por 491 631 letras, gerou o seguinte gráfico de frequências:

Após codificar esse texto com a regra do exemplo fornecido, faz-se nova análise de frequência no texto codificado.

As quatro letras mais frequentes, em ordem decrescente de frequência, do texto codificado são

a) A, E, O e S.

b) D, E, F e G.

c) D, H, R e V.

d) R, L, B e X.

e) X, B, L e P.

23. Considere a sequência a seguir, na qual os números inteiros são organizados.

Continuando o mesmo padrão, a soma dos números que compõem a próxima linha superior é:

ORIENTAÇÕES DIDÁTICAS

A questão 1 envolve cálculo com potências e a representação desse valor em notação científica, favorecendo a habilidade EF08MA01. Pode-se aproveitar a oportunidade para valorizar a importância da notação científica como ferramenta para diversas ciências, pois permite representar e operar com números muito grandes ou muito pequenos.

A questão 2 foi elaborada a partir do modelo Saeb (MA9N21 da matriz de referência) e permite explorar o cálculo aproximado da raiz quadrada de 6,3, pelo cálculo de valores que elevados ao quadrado estejam próximos do valor, favorecendo a habilidade EF08MA02. Já a questão 3 favorece a habilidade EF08MA03 ao explorar a quantidade de possibilidades de determinado evento utilizando o princípio multiplicativo. Pode-se explorar a questão 3, apresentando outras condições iniciais, de modo que se possa observar como o cálculo se altera.

Problemas que envolvem o cálculo de descontos e aumentos sucessivos, como na questão 4, favorecem a habilidade EF08MA04. A questão permite discutir que um desconto de 5% seguido de um aumento de 10% não corresponde a um aumento de 5%. Na questão 5, também se aplica o cálculo de porcentagem em uma situação contextualizada, favorecendo igualmente a habilidade EF08MA04.

A questão 6 permite abordar o valor numérico de uma expressão algébrica, permitindo ao estudante formular um modelo matemático de crescimento exponencial, favorecendo a habilidade EF08MA06.

Na questão 7, elaborada no modelo Saeb (MA9N110 da matriz de referência), o estudante deve obter a fração geratriz para a dízima periódica apresentada, favorecendo o desenvolvimento da habilidade EF08MA05.

A questão 8 favorece a habilidade EF08MA08, associando um problema à representação algébrica de um sistema. É interessante aproveitar a oportunidade para explorar a representação também no plano cartesiano a fim de que o estudante faça relações entre diferentes registros de um mesmo problema.

Na questão 9, o estudante pode relacionar a soma dos pesos utilizando as relações obtidas nas duas primeiras balanças, favorecendo as habilidades EF08MA06 e EF08MA12, expressando algebricamente a soma dos pesos e associando ao seu valor numérico.

A questão 10 favorece a habilidade EF08MA07 ao associar uma reta no plano cartesiano a uma equação do 1o grau.

A questão 11 permite aos estudantes identificar

a regularidade da quantidade total de bolinhas de uma sequência figural para um padrão que possibilite encontrar o total de bolinhas de outras figuras, favorecendo a habilidade EF08MA10.

Na questão 12, além da solução apresentada utilizando equações, pode-se trabalhar o fato de que a divisão de 64 (91 27) em oito partes iguais é 8 e então adicionar 24 (3 multiplicado por 8) ao 27. Essa questão explora grandezas proporcionais, o que favorece a habilidade EF08MA13.

A questão 13 favorece as habilidades EF08MA12 e EF08MA13 ao solicitar a expressão algébrica que fornece o valor de uma conta de luz a partir da sua representação gráfica e o valor do consumo (relação de proporcionalidade entre as grandezas envolvidas).

Na questão 14, apresenta-se um fluxograma que realiza cálculos de maneira recursiva, favorecendo a habilidade EF08MA11.

As questões 15 e 16 possibilitam articular o cálculo de áreas utilizando diferentes estratégias. Uma delas é a relação entre semelhança e áreas. Outra é o cálculo por meio do produto das medidas da base e da altura, o que desenvolve a habilidade EF08MA19.

As questões 17 e 18 envolvem o trabalho com a visualização de composição de rotações em evidência, o que favorece a habilidade EF08MA18. Nas duas questões, pode-se aproveitar a oportunidade para explorar outras transformações.

A questão 19 envolve o cálculo de probabilidade, comparando diferentes jogos lotéricos cujos preços podem variar, o que contribui para o desenvolvimento da habilidade EF08MA19.

Ao efetuar o cálculo de volume da questão 20, a habilidade EF08MA21 está sendo favorecida, mas pode-se aproveitar a oportunidade para reforçar a relação entre metro cúbico e litro, relatados na habilidade EF08MA20.

A questão 21 exige interpretar e organizar as informações contidas no texto em combinação com as informações da figura para obter o cálculo de áreas utilizando composições em um terreno retangular, o que favorece a habilidade EF08MA19.

Na questão 22, a partir da análise de frequências e da codificação, identificam-se as quatro letras mais frequentes no texto codificado, favorecendo a habilidade EF08MA24.

A questão 23 trabalha com a formação de sequência, o que favorece a habilidade EF08MA11, e com estratégias de adição de números consecutivos.

RESOLUÇÕES

Questão 1

Um micrômetro é a milionésima parte de um metro, ou seja, corresponde a 10 6 metros. Logo, 100 micrômetros correspondem, em metro, a 102 10 6 = 10 4, ou seja, 1,0 10 4

Alternativa c.

Questão 2

V3 00,3 50,6 6, 3 =??= cujo valor aproximado é 2,5.

Alternativa d.

Questão 3

Considerando que o primeiro botão é azul e o último é verde, ficam três opções de botões entre eles: roxo, vermelho e amarelo. A quantidade de possibilidades será:

= 13 21 16 azul verde possibilidades.

Alternativa d.

Questão 4

95% de 400 correspondem a 380, e 110% de 380 correspondem a 418.

Alternativa c.

Questão 5

Ao dividir 110 por 78, encontra-se aproximadamente 1,41, o que significa que a proporção é de aproximadamente 41%.

Alternativa c.

Questão 6

Na expressão que representa o cálculo da quantidade de pinguins ao final de 7 anos, devem ser observados:

• a quantidade inicial de pinguins: 10 000;

• a população inicial acrescida da taxa de crescimento de 50%: multiplicação por 1,5;

• a perda de 20% de pinguins ao final do ano: multiplicação por 0,8;

• o período de 7 anos: entra como expoente da multiplicação entre 1,5 e 0,8;

• o cálculo se dará por P = 10 000 (1,5 0,8)7

Alternativa b.

Questão 7

A fração geratriz da dízima periódica 0,4444... é 4 9 . Assim, a = 4 e b = 9.

Calculando 9 : 4, encontra-se 2,25.

Alternativa c.

Questão 8

Considerando x e y os números desconhecidos, se a soma deles é 12, tem-se x + y = 12. Ao mesmo tempo, se a diferença entre os números é 2, tem-se x y = 2.

Alternativa d.

Questão 9

Na primeira balança, temos que 3A + 2T = 64 e, na segunda balança, 2A + T = 41.

Subtraindo as duas equações, encontramos que A + T = 23, que corresponde ao peso da última balança.

Alternativa b.

Questão 10

Colocando as equações na forma reduzida, tem-se: y = 2x 5; y = 2x +5; y = 2x + 5; y = 2x 5. Como a reta é crescente e passa pelo ponto (0, 5), então a equação que satisfaz essa condição é a y = 2x 5.

Alternativa a.

Questão 11

A figura 1 é formada por 5 bolinhas (3 + 1 + 1 = 2 + 1 + 1 + 1 = 2 + 3 1).

A figura 2 é formada por 8 bolinhas (4 + 2 + 2 = 2 + 3 2).

A figura 3 é formada por 11 bolinhas (5 + 3 + 3 = 2 + 3 3).

Assim, a figura 15 será formada por 2 + 3 ? 15 = 47 bolinhas.

Alternativa b.

Questão 12

Com base na figura, tem-se: 91 x 5 x2 7 3 =h 3(91 x) = 5(x 27) h

h 273 3x = 5x 135 h 8x = 408 h x = 51

Alternativa c.

Questão 13

O valor da conta de água no mês de novembro foi formado por um valor fixo de R$ 17,00, mais o valor associado ao consumo de 7 m3 de água cujo valor foi de 42,20 17,00 = R$ 25,20. Como o consumo em dezembro foi o dobro do mês anterior, o valor associado ao consumo de 14 m3 de água foi de R$ 50,40. Com isso, o valor da conta do mês de dezembro foi de 50,40 + 17,00 = R$ 67,40, ou seja, superior a R$ 65,00 e inferior a R$ 70,00.

Alternativa a.

Questão 14

Como o número de entrada é 12, tem-se no segundo comando: 3 12 = 36; no terceiro comando: 36 . 30; no quarto comando: 31 23 66?==

Alternativa d.

Questão 15

Como os triângulos BDF e ADE são semelhantes ao triângulo ABC, sendo a razão de semelhança igual a 1 2 , então suas áreas medem, cada uma, 1 4 da área do triângulo ABC, ou seja, juntas medem 1 2 da área do terreno. Consequentemente, a área do paralelogramo DECF mede 1 2 da área do triângulo ABC. Sendo assim, a área destinada ao plantio de milho é 1 2 450 m 225 m 22 ?=

Alternativa b.

Questão 16

De acordo com as condições dadas, tem-se:

Questão 17

A partir das duas primeiras posições e aplicando os giros sucessivos, tem-se:

Após o 3o giro: Após o 4o giro:

Após o 5o giro:

Observa-se que o número da face superior do dado quando ele se encontra na casa cinza é o número 2. Alternativa b.

Questão 18

Após o 6o giro:

Os números escritos nas quatro faces que compartilham um lado com a face de número 10 são: 11, 12, 13 e 14. Observando as rotações do número 10, temos que:

• 11 é oposto a 14;

• 12 é oposto a 13;

• 13 é o número que está mais próximo do algarismo 1 do número 10;

• 12 é o número que está mais próximo do algarismo 0 do número 10.

Assim, a soma dos números das faces em contato é 14 + 13 + 12 + 14 + 11 + 12 = 76.

Alternativa d.

Questão 19

Considerando que, com R$ 2,00, o apostador pode fazer dois jogos II ou dois jogos IV, as probabilidades são:

Observa-se que PV representa o maior valor, portanto o jogo V é o que oferece maior probabilidade de ganhar.

Questão 20

Multiplicando as três dimensões da cisterna para obter seu volume, tem-se:

V = 5 2 1,5 = 15 m3

Alternativa d.

Questão 21

Considerando os dados do enunciado e as medidas representadas na figura, tem-se:

Área das unidades habitacionais: 12 (26 8) (22 8) 12 32 = 2 640 m2

Alternativa a.

Questão 22

As letras mais frequentes no texto do romance, em ordem decrescente de frequência, são A, E, O e S. De acordo com a tabela, no texto codificado, tais letras correspondem, respectivamente, a D, H, R e V.

Alternativa c.

Questão 23

A linha superior é formada pelos números naturais 57 a 65, cuja soma é 549.

Alternativa a.

ISBN 978-85-96-03442-5

9 788596 034425