ClassicalandQuantum ParametricPhenomena
ALEXANDEREICHLERANDODEDZILBERBERG
ETHZurichandUniversityofKonstanz
GreatClarendonStreet,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries ©AlexanderEichlerandOdedZilberberg2023
Themoralrightsoftheauthorshavebeenasserted
Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica BritishLibraryCataloguinginPublicationData Dataavailable
LibraryofCongressControlNumber:2023935805
ISBN9780192862709
DOI:10.1093/oso/9780192862709.001.0001
Printedandboundby CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
Toourwivesanddaughters
Acknowledgments
Weareindebtedtomanycolleaguesforaccompanyingusalongourscientificjourneyandforimprovingourownunderstandingthroughcountlessdiscussions.First, wewouldliketothankallofourcollaboratorsandco-authorsthroughouttheyears. Amongthesemanynames,weespeciallymentionR.Chitra,ToniL.Heugel,and JanKo˘sataforhelpingtoshapethewaywethinkaboutthetopic.Itwasaprivilegeandapleasuretoworkwithyou.Second,welearnedmuchfromtheintelligent questionsofthestudentsattendingourcourseovertheyears,andfromtheinputof ourguestlecturers.SpecialcreditgoestoGiacomoScalari,MartinFrimmer,J´erˆome Faist,andChristopherEichler,whoseguestlecturesonnonlinearoptics,mechanics, andelectronicswereaninspirationforseveralstudentprojects.Third,wearegrateful tomanycolleaguesinthecommunityofnonlineardynamics,whoseguidanceandcommentsprovedinvaluable.SpecificthanksgoMarkDykman,StevenShaw,EvaWeig, GuillermoVillanueva,RonLifshitz,HiroshiYamaguchi,andIacopoCarusotto.For criticalcommentsonthistext,wefurtherthankAlexanderGrimm,RobertChapman, andJavierdelPino.Finally,wewillbeobligedtoeveryreaderhelpingustoimprove thisbookbyprovidingconstructivecriticismandfeedback.
Preface
Thisbookprovidesanoverviewofthephenomenaarisingwhenparametricpumpingisappliedtooscillators.Thesephenomenaincludeparametricamplification,noise squeezing,spontaneoussymmetrybreaking,activatedswitching,catstates,andsyntheticIsingspinlattices.Tounderstandtheseeffects,weintroducetopicssuchasnonlinearandstochasticdynamics,modecoupling,andquantummechanics.Throughout thebook,wekeeptheseintroductionsassuccinctaspossibleandfocusourattention onunderstandingparametricoscillators.Asaresult,wefamiliarizeourselveswith manyaspectsofparametricsystemsandunderstandthecommontheoreticaloriginof nanomechanicalsensors,opticalamplifiers,andsuperconductingqubits.
Parametricphenomenahaveenabledimportantscientificbreakthroughsoverrecent decadesandarestillthefocusofintenseresearchefforts.Ourintentionistoprovide aresourceforexperimentalandtheoreticalphysicistsenteringthefieldorwishingto gainadeeperunderstandingoftheunderlyingconnections.Assuch,wecombineformal andintuitiveexplanations,accompaniedbyexercisesbasedonnumericalpythoncodes. Thiscombinationallowsthereadertoexperienceparametricphenomenafromvarious directionsandtoapplytheirunderstandingdirectlytotheirownresearchprojects. Forlecturers,thebooksuppliesallthematerialnecessaryforanadvancedclasson thetopic.
1.1Newton’sEquationofMotion5 1.2ResponseoftheDrivenResonator7 1.3MatrixFormulation8 1.4ParametricModulation11 1.5FloquetTheory13 Chaptersummary18 Exercises19
4DissipationandForceFluctuations
4.1TheRoleofForceNoise46
4.2TheFluctuation–DissipationTheorem52
4.3TheProbabilityDistributionApproach57 Chaptersummary61 Exercises62
5.1MultistabilityandQuasi-StableSolutions63
5.2ParametricAmplificationbelowThreshold64
5.3ParametricPumpingAboveThreshold68
5.4HierarchyofRelevantTimescales74 Chaptersummary76 Exercises77
ListofImportantSymbols
(inapproximateorderofappearance)
H Hamiltonian
Epot potentialenergy
Ekin kineticenergy
Etot = Epot + Ekin;totalenergy
x displacement
p momentum
t time
m mass
ω0 angularresonancefrequency
ν0 = ω0/(2π);temporalresonancefrequency
k = mω2 0 ;springconstant
T0 =2π/ω0 =1/ν0;unforcedoscillatorperiod
Q qualityfactor
Γ= ω0/Q;dampingrate
τ0 =2/Γ;amplitudedecaytimeconstant
ωΓ = ω2 0 Γ2/4 1/2 ≈ ω0;dissipation-shiftedangularresonancefrequency
µ characteristicexponent
F0 amplitudeofexternalforce
F inChapters1to7:allforcetermsactingonthebareresonator inChapters9and10:= F0 2 /2mω0;rotating-framequantumforceterm
ω angularfrequencyofexternalforce
θ phaseoffsetofexternalforce
χ susceptibilityfunctionofdrivenresonator
X oscillationamplitude
x vectorofasystem’sdegreesoffreedom
G inChapters1to7:matrixcontainingthecoefficientsofthedifferentialequation inChapter10:parametricdriveintherotating-framequantumHamiltonian
W inChapters1to7:Wronskianmatrix
inChapters8to10:Wignerquasiprobabilitydensity
Φstatetransfermatrix
Tp periodofparametricpump
ωp =2π/Tp;angularfrequencyofparametricpump
λ parametricmodulationdepth
λth =2/Q;parametricpumpingthresholdat ωp =2ω0
β3 coefficientofcubic(Duffing)nonlinearity
β2 coefficientofquadraticnonlinearity
β = β3 10 9 β2 2 ω2 ;coefficientofeffectiveDuffingnonlinearity
u in-phaseoscillationquadrature
v out-of-phaseoscillationquadrature
ψ phaseoffsetofparametricpump
η coefficientofnonlineardamping
kB ≈ 1 38 × 10 23 JT 1;Boltzmannconstant
T temperature
Eeq equilibriumenergy
ξ forcenoiseterm
ςD standarddeviationofforcenoise
σx standarddeviationof x (foranyvariable x)
SF powerspectraldensityofforcenoise
Ξu in-phasequadratureofforcenoise
Ξv out-of-phasequadratureofforcenoise
ρ probabilitydensity inChapters8to10:densityoperator
J coefficientofcouplingbetweenresonators
∆k detuningspringforce
U inChapter6:normal-modetransformationmatrix inChapter10:Kerrnonlinearity
ω∆ = J ω0m ;angularexchangerateandspectralsplitting
t∆ = 2π ω∆ ;energyexchangetime
g parametriccouplingmodulationdepth
ωR angularRabifrequency
≈ 1 05 × 10 34 Js 1;reducedPlanckconstant
στ statelifetime
σE energyuncertainty
Ψwavefunction
n inChapters8to10:Fockstatenumber
a =ˆ a;annihilationoperator
a† =ˆ a†;creationoperator
xdl = 1 2 (a† + a);dimensionless x operator
pdl = i 2 (a† a);dimensionless x operator
α amplitudeofcoherentstate
Pj probabilityofmeasuringthesysteminthestate j
κ =Γ;system-environmentcouplingrate
nth meanthermalexcitation
Urot rotating-frametransformationmatrix
∆ ω ω0;angularfrequencydetuning
a annihilationoperatorintherotatingframe
a† creationoperatorintherotatingframe
αR realpartofcoherentstateamplitude
αI imaginarypartofcoherentstateamplitude
∆U =∆+ U ;detuningshiftedbytheKerrnonlinearity
Introduction
“It’sstillmagicevenifyouknowhowit’sdone.”
(TerryPratchett, AHatFullofSky)
AboutThisWork
Thisbookemergedfromamaster-levelcourseon“ParametricPhenomena”thatthe authorsheldtogetheratETHZurichbetween2018and2021,andindividuallyattheir respectiveuniversitiessincethen.Thecoursewasorganizedasareverse-classroom event:studentswouldpreparebyreadingmaterialathome,andthenusethetimein classtosolveexercisesanddiscusswiththeteachingteam.Withthisapproach,we hopedtopresentthetopicinmuchthesamewayasweexperienceitduringourown research,andtoencouragethestudentstoformulate(andsolve)theirownquestions. Inlinewiththisphilosophy,thegradeddeliverablethateverystudenthandedinfor passingthecoursewasaposterthatapproximatedoneparticularsystemasaparametricoscillator,includingphysicalunitsandestimatednumericalvalues.Wesawmany creativeresults,rangingfromanairplanewobblinginthewindandashiprollingin theseatoananoparticletrappedinanopticalpotential,aJosephsonsuperconducting resonator,anopticalringresonator,ayo-yo,andeventhepredator–preydynamics betweenapackofwolvesandaflockofsheep.Thisbookismeanttoprovideallthat isnecessarytoholdsuchacourse,includingthereadingmaterial,exercises,codesto solvetheexercises,andatutorialofhowtomaprealisticphysicalsystemsontothe desiredequations.
Inthisbook,weperformadiagonalcutthroughmanydifferenttopics.Wefollowa pathfromthedeterministicmechanicsofaharmonicoscillatorallthewaytothenondeterministicphysicsofcouplednonlinearquantumoscillators.Alongthistrajectory, weencountermanyideasandconceptsthatcanfillentirebooksoftheirownaccord. Ourdiscussionsoftheseconceptsareguidedbythewishtobuildanunderstanding withoutdealingwithallpossibledetails.Thisbookisclearly not anexhaustiveresource ontopicssuchasnonlinearmechanics,stochasticphysics,orthequantumoscillator. Thesetopicshavebeentreatedinmuchmoredetailinotherarticlesandbookswhich wecitewhereappropriate.Rather,wewanttofocusonthecombinationofallthese fundamentaltheoriestogainabalancedandcomprehensiveviewoftheparametric oscillator.
InChapter1,westartwiththedeterministicbehavioroftheclassicalharmonic oscillatorsubjecttodampinganddriving,andlatertoparametricpumping.Buildingonthisfoundation,weaddnonlinearitiesinChapter2,andcombinethemwith aparametricpumpinChapter3.InChapter4,weintroducefluctuatingforcesfor theexampleoftheharmonicoscillator,whichwegeneralizetothenonlinearparametricoscillatorinChapter5.CouplingbetweenoscillatorsisdiscussedinChapter6
andappliedtostochastic,nonlinearparametricoscillatorsinChapter7.ThequantumharmonicoscillatorfollowsinChapter8,whichleadstothedrivenanddamped quantumharmonicoscillatorinChapter9,andthequantumparametricoscillatorsin Chapter10.Finally,inChapter11weexplainwithseveralexampleshowmechanical, electrical,andopticalsystemscanallserveasparametricoscillators.
0.1HistoricalReview
InthisIntroduction,wereviewhistoricalexamplesofparametricphenomenaand understandwhythistopicisstillthefocusofsomanyresearchfieldstoday.Before wecanembarkonourtourthroughthecenturies,wemustclarifywhatwemeanby theterm parametric.Inourusageoftheword,itreferstoaperiodicmodulationof aresonator’spotential—physically,themodulationcouldoriginatefromachangein thetensionofamechanicalstring,achildalternativelystandingandsquattingona swing,theeffectofwaveshittingashiptochangeitsbuoyancycenter,avariationin theeffectivecapacitanceofanelectricalresonator,oranincreaseofthepolarization ofanopticalmediuminresponsetoelectromagneticwaves.Alloftheseseemingly disparateexamplesobeyverysimilarequations,andmanyofthemcanbeusedfor similartechnologicalapplications(althoughsofarnoapplicationshavebeendeveloped forchildrenonswings...).Thephenomenathatariseasaconsequenceofparametric modulationareasvariedasthephysicalsystemsinwhichtheyappear.Atfirstglance, themenagerieofparametricphenomenamayappearendless,butwewillseethatthey allfollowafewintuitiverulesandcanbeclassifiedaccordingly.
Theearliestexamplesofparametricoscillationarefound,notsurprisingly,inthe mechanicaldomain.Toourknowledge,thefirstexperimentaldescriptionofparametric resonanceisascribedtotheworksofMichaelFaradayin1831[1]andFranzMelde in1860[2].However,applicationsoftheeffectaremucholder:thebigcenser“O Botafumeiro”usedforcertainritualsintheCathedralofSantiagodeCompostela inSpainissetintopendulummotionbyperiodicallymodulating(i.e.parametrically pumping)thelengthofitsrope[3].Asthecenserweightsabout60kgandmoves 20mupanddownduringitslargestoscillations,ateamofoperatorsisneededforthis pumping,andtheiractionshavetobecoordinatedintimetoachievethedesiredeffect. ReportsofparametricpumpingofOBotafumeiroreachbacktothe13thcentury.A mathematicaltreatmentofparametricoscillationwasnotattempteduntil1883,when LordRayleighpublishedhispaper“Onmaintainedvibrations”[4].Heanalyzedthe differenttypesofdrivingthatasystemcanexperienceandshowedthatparametric modulationscanexplainFaraday’sexperimentalobservations[1].
Technologicalapplicationsofparametricpumpinginelectronicsbegantoappear inthe20thcenturywiththedevelopmentoftheMagAmp[5]andtheKlystron[6] amplifiers,bothofwhichwerebasedontime-dependentmodulationofacontrolparameter.TheMagAmpfoundapplicationinearlyradiotelephonesaround1915,and theKlystronallowshigh-powermicrowavegenerationandisstillinusetodayforniche applicationssuchasspacecraftcommunicationandsynchrotrons.Inthesecondhalfof thecentury,inventionslikethe ParametricAmplifier byArthurAshkinandcolleagues in1959[7]andthe Broadbandcavityparametricamplifierwithtuning byClossonin 1962[8]openedupnewperspectivesforelectricalsignalamplification.Itwasun-
derstoodthatamodulationofthereactance(i.e.,thecapacitanceorinductance)of aresonantelectricalcircuitcanleadtostrongsignalamplificationwithoutadding Nyquistnoisewhichisunavoidableinresistor-basedoperationalamplifiers[9,10].
Withtheadventofsuperconductingcircuitsandthepossibilityofastrongnonlinear inductanceimposedbyJosephsonjunctions,theparametricamplifierwasbroughtto itslogicalculmination,offeringsignalamplificationwithnomorenoisethanwhatis absolutelyrequiredbythelawsofquantummechanics[11–13].However,itwasonlyaftertheturnofthemillenniumthatthese Josephsonparametricamplifiers movedfully intothefocusoftheexperimentalquantumphysicscommunity[14–20],enablingexperimentsthatpreviouslywereunfeasible[21].Aroundthesametime,parametricamplification[22–27]andcoupling[28–32]werealsoexploredinthegrowingnanomechanics community.Aparticularlyimportantapplicationarosein cavityoptomechanics,where theparametriccouplingbetweenamechanicalandanopticaldegreeoffreedomcanbe usedforprecisecontroloftheresonatorandforcoolingitdowntoitsquantumground state[33].Parametricsqueezingcanbeusedtoreducefluctuations[22,34–36]andhas beenemployedasameanstogeneratenonclassicaloptical[37,38]ormechanical[39–41]states.Importantly,parametricsqueezinghasbeenproposedasawaytoboostthe sensitivityofopticalinterferometersforgravitationalwavedetection[42–44].
Mostoftheaboveapplicationsareachievedforrelativelyweakparametricmodulation.Bycontrast,whenthepumpingexceedsacertainthreshold,entirelynew phenomenaappear.Understrongparametricpumpingatafrequencyclosetotwice itsresonancefrequency,aresonatorexperiencesanegativeeffectivedamping,such thatitwillringuptolargeamplitudesandbestabilizedonlybynonlinearpotential terms[45].Suchparametricinstabilityappearsinmanycontexts;forinstance,itisheld responsibleforthedreaded parametricrolling ofshipsthathascausedcatastrophic accidents[46].Itisalsoconsideredasapossiblemechanismforparticlecreationin modelsoftheearlyuniverse[47,48].
Beyondtheinstabilitythreshold,theparametricallydrivenresonatorcanselectone oftwooscillationphasesthatareseparatedbyaphaseof π.Thiscausesaspontaneous breakingofthetime-translationsymmetryofthesystem—oscillationswitheither phaseareequivalentsolutionsinresponsetothedrive,butonlyoneofthemcanbe realizedatthesametime(inaclassicalsystem)[45,49].Around1960,EiichiGoto[50] andJohnvonNeumann[51]independentlyrealizedthatthesephasestatesofferaway toencodedigitalinformation.The parametron wasindeedusedasamemoryunitfor electricalcomputersinJapanuntiltheinventionofthetransistorprovidedamore efficientsolution.
0.2PresentandFuture
Overthelastfewyears,thedevelopmentofnovelresonatorsintheelectrical,mechanicalandopticaldomainhasledtoarevivalofinterestintheparametricoscillator1 and theideaof parametronphaselogic,inboththeclassicalandquantumdomains[52–65].Ofparticularinterestistheideaofcouplingmanyparametronsintoaconfigurable
1 Othertermsfortheparametricoscillatorare Kerrparametricoscillator or two-photondrivenKerr resonator
Hopfield-typenetwork[66,67].Here,thephasestatesofasingleparametronrepresent thetwopolarizationstatesofaspin,andtheentirenetworkcanbeusedtosimulatethe behaviorofthecorrespondingmany-bodyIsingmodel[68].Manyoptimizationproblems,suchastheMAX-CUTproblem[69,70]orthenumberpartitioningproblem[71], areisomorphictofindingthegroundstateofanIsingnetwork,andatthesametime arenearlyintractablewithclassical(sequential)computers[72].Recentyearshave thereforeseenasurgeofideasrelatedtoparametronlogiccontrol[55,57,73–77]and parametricnetworkoperation[62,69–71,78–86].
Whetherthecomplexityofamultimodenonlinearoscillatornetworkcanbetamed toenableparallelcomputingandquantumsimulationsisanopenquestionandwill bethesubjectofintensiveresearchoverthecomingyears.Whatissafetopredict isthateverynewphysicalimplementationoftheharmonicoscillatorsoonerorlater rediscoversparametricphenomenaandappliesittoanewpurpose.Aconceptthat issoversatileandusefulwillremainimportantinscienceandtechnology,nomatter whatthefuturebrings.
TheHarmonicResonator
Harmonicoscillatorsareubiquitousinnatureandhavebeentreatedinmanytextbooksindepth[87,88].Webrieflyrepeatinthisfirstchapterthosefeaturesthatare importantfortherestofthebook.Tofacilitateanintuitiveapproach,weadoptthe languageofamechanicaloscillator,butthediscussionmayeasilybetranslatedto anyoscillatingsystem,cf.Chapter11.Exampleswillbecalculatedwithoutunits,to preservethespiritofageneraltreatment.
1.1Newton’sEquationofMotion
Consideramassonaspring,seeFig.1.1.Thesystemhaskineticandpotentialenergy, wherethelatterisstoredinthespringproportionaltothesquareofthedisplacement x,suchthat
Here, H istheHamiltonianofthesystem, p themomentumandcanonicalconjugate ofthedisplacement x, k thespringconstant,and m themass.TheHamiltonianisa functionthatdescribesthetotalkineticandpotentialenergyofaclosedsystem.From Hamiltonianmechanics,wecancalculatetheforcethatactsonthemassatanygiven time t as
wheredotsdenotedifferentiationwithrespecttotime t.Thequadraticpotential, thus,correspondstoalinearspringforce.Combiningeqn(1.1)withthesecondoneof Hamilton’sequationsofmotion(EOM),
weobtainasecond-orderdifferentialequationthatisknownasNewton’sEOM,
Equation(1.4)issolvedusingtheansatz x(t)= xinieiω0t,where xini isdetermined bytheinitialboundaryconditions, ω0 =(k/m)1/2 =2πν0 =2π/T0 istheangular resonancefrequency, T0 istheunforcedperiodicityoftheoscillator,andwereferto
Fig.1.1 (a)Asanexampleofaharmonicoscillator,weuseamassonaspring.Displacing themassfromitsrestpositionby x resultsinarestoringspringforce Fspring = kx.A displacedmassisshowningray.(b)Thepotentialenergyofaharmonicoscillatorisquadratic indisplacement, Epot = 1 2 kx2,cf.eqn(1.2).
ν0 as naturalfrequency.Notethateqn(1.4)describesanoscillatorthatisisolated fromitsenvironment,thatis,Hamiltonianevolutionisenergy-conservinganddoes notfeaturedampingterms.
Findingthemicroscopicoriginofdampingtermsisanimportanttopiconits own[89].Fornow,weassumeaphenomenologicalsourceofdissipationthatenters Newton’sEOMandcanstabilizetheoscillator’smotion,
whereΓisthecoefficientcorrespondingtothedissipative(linear)dampingenacted bytheenvironment.Notethatfromamathematicalpointofview,wecanaccountfor theaddeddampingtermthroughthetransformation[88]
wherewedefineadecaytime τ0 =2/Γ.Theequationofmotionfor y(t)thentakes theformofaclosedharmonicoscillator,
inanexponentiallyexpandingorshrinkingcoordinatesystemandwithaslightly shiftedresonancefrequency
Fromthetransformationineqn(1.6),weobservethatfor2ω0 > Γ > 0theoscillator coordinate x(t)decaysexponentiallyintimeinadditiontoanharmonicoscillation. However,wecanalreadyguessthatsomethingdifferentmusthappenonce2ω0 ≤ Γ. Adirecttreatmentofthehomogeneousdissipativecaseineqn(1.5)ispossible startingfromthesameansatzthatanyparticularsolutionhastheform
Fig.1.2 Thereal(solid)andimaginary(dashed)partsofthecharacteristicexponents, cf.eqn(1.11),asafunctionof(a)dampingcoefficientΓforabareangularresonancefrequency ω0 =2π,andof(b) ω0 forΓ=2π withacomplex characteristicexponent µ ∈.Insertingeqn(1.9)intoeqn(1.5)leads to
which,for x =0,resultsinaquadratic characteristicequation withthetworoots
Thisisidenticaltowhatweobtainedwiththecoordinatetransformationmethodin eqn(1.6),seeeqn(1.8)andthediscussionthereafter.
Wecanidentifyseveraldistinctregimesofmotion:fordampedoscillators(Γ > 0)wedistinguishbetweenoverdamped(ω2 Γ < 0),criticallydamped(ω2 Γ =0),and underdampedmotion(ω2 Γ > 0),whereoscillationappearsonlyforthelatter.1 ForΓ < 0,theoscillatorisunstableandthemotionbecomesunbounded.Thisisvisualizedby plottingtherealandimaginarypartofthecharacteristicexponents µa,b,seeFig.1.2. Notethat,inmanycases,thesmallcorrectiontothebarefrequencyduetothedamping termisneglected,suchthat ω2 Γ ≈ ω2 0
1.2ResponseoftheDrivenResonator
Inlargepartsofourtreatment,wewilluseNewton’sEOMtoanalyzethebehaviorof drivenoscillatingsystems.Forourmassonaspring,wecanwrite
where F = F0 cos(ωt)isanexternaldrivingforcethatturnseqn(1.12)intoaninhomogeneousdifferentialequation.
1 Thecriticallydampedpointisanexampleofan exceptionalpoint wheretherootsaredegenerate andeqn(1.9)isinsufficient[90].
Fig.1.3 Long-timelimitresponseof(a)theamplitude X(ω)and(b)thephase φ(ω)ofa drivenresonator,cf.eqns(1.14)and(1.15),respectively. F0/m =80, ω0 =100andΓ=1 (Q =100).
Foradriven,dampedresonator,weproceedbyFouriertransformingeqn(1.12).
TheFouriercomponentof F at ω issimply F0.Solvingforthefrequency-dependent, complexamplitude x(ω)= X(ω)eiφ(ω) yields
whereweuse χ todenotethesusceptibilityoftheresonator.Notethat x(ω)isa complexnumber,while X(ω)and φ(ω)areassumedtobereal.Inmanycases,we areinterestedinthelong-timelimitresponseoftheresonatortoaforceatasingle frequency,andfind
aswellas
TheamplitudeandphaseresponsefunctionsaredrawninFig.1.3.Experimentally, suchcurvesareoftenusedtoextracttheresonancefrequencyandqualityfactorof aresonator:thefull-width-at-half-maximum(FWHM)ofthe squaredamplitude X 2(ω)isgivenby∆ω =Γ= ω0/Q,with Q thequalityfactor(or,iftemporalfrequency isplotted,∆ν = ν0/Q).Iftheunsquaredresponseismeasured,suchasinFig.1.3(a), onemustextract∆ω or∆ν at 1/2ofthemaximum.
1.3MatrixFormulation
Inthissection,wewillintroducethetechniqueofthestatetransitionmatrixmethod[88]. Generally,any N -orderODEcanbecastintoasetof N coupledfirst-orderODEs. Wewillherecoverthecaseofasecond-orderdifferentialequation.Westartbycasting
eqn(1.12)intotwocoupledfirst-orderdifferentialequations(cf.Hamilton’sEOMs above),whicharewritteninmatrixformas
isastatevectordescribingtheresonatorcoordinates, G(t)isamatrixthatcontains thecoefficients,and f(t)istheforcingvector.Intheconcreteexampleofeqn(1.12), wewrite
1.3.1SolvingtheEquationinMatrixForm
Wecanuseeqn(1.16)foranalternativederivationofthesolutionofthesecond-order differentialequationshownineqn(1.11)[88,91,92].Namely,for f(t)=0andassuming x(t)tobeaparticularsolutionofthegeneralform xinieµt,weknowthat ˙ x(t)= µx(t), thereforeweobtainincombinationwitheqn(1.16)
For xini =0,thisequationisonlyfulfilledif
where |...| standsforthedeterminantofamatrixandtr(...)foritstrace.Equation(1.20)isanotherwaytowritethe characteristicequation whichwehave alreadyseenineqn(1.10)forthecaseofadissipativeharmonicoscillator.Fromthe resultofthecharacteristicequation,wecandeterminewhetherthesystemdecaysin time(µ< 0)orgrowswithoutbound(µ> 0).Notealsothateqn(1.20)isequivalent tosolvingfortheeigenvaluesof G
1.3.2StabilityAnalysis
Equation(1.16)offersasimplewaytofindthestationarypointsofthesystemby imposing ˙ x(t)=0.Inthecaseabovewith f(t)=0,weobtain x =0astheonly stationarypointinthesystem.Thedynamicsaroundthispointarethendescribedby eqn(1.20).
Thisprocedurecanbesimilarlyperformedforotherstationarypoints.Specifically, havingfoundanequilibriumpoint,weaskourselvesifthepointisstableagainst smallperturbationsin x;doesthesystemreturntotheequilibriumpointafterithas beenslightlydisplaced?Thereisasimplemethodtoanswerthisquestion:assuming
(xeq, ˙ xeq)tobeanequilibriumpointwhere ˙ x(t)=0,weTaylorexpandtolinearorder aroundthispoint.Ournewdegreesoffreedomarenow
Similartoeqn(1.19)andeqn(1.20),wecanformulateacharacteristicequationfor δx tofindoutifthesystemgrowsawayfromtheequilibriumpoint(xeq, ˙ xeq)over time(unstablebehavior)orwilldecaytowardit(stable).Apointisonlystableifall realcharacteristicexponentsarenegative.Theunderdampedoscillatorinaquadratic potentialisonlystableat x =0.
1.3.3FromaDifferentialtoanIntegralEquation
Thematrixformulationisusefulnotonlyforanalysisofthesystem’sequilibrium pointsandtheirstabilitytosmallperturbations,butalsoforcalculatingthetime evolutiongivenanyspecificinitialconditionsandexternalforce[88].Inordertoshow this,wefirstdefinetheWronskianmatrix
TheentriesoftheWronskianmatrixinthefirstrow, xa(t)and xb(t),areorthogonal basissolutionstothehomogeneousEOM.Inourcaseofeqn(1.5),wecanchoosefor example xa(t)=cos(ω0t)e Γt/2 and xb(t)=sin(ω0t)e Γt/2.Thedeterminantofthe Wronskianmatrix,whichmustbenonzeroinordertomakethematrixinvertible,is simplycalledthe Wronskian.Forthehomogeneouscase,ageneralsolutionisofthe form x(t)= W (t)d where d isavectorofconstantcoefficientstobedefinedthrough theboundaryconditions.Movingtoaninhomogeneouscasebyapplyinganexternal drive f =0,weuseaso-called variationalansatz thatallowstheprefactorstoalso dependontime.Thisleadsto
Differentiatingthissolution,weobtain
wherethefirsttermontheright-handsidesatisfies
because W (t)is,bydefinition,composedoutofparticularsolutionsofeqn(1.16)for f(t)=0.Therefore,ifweentereqn(1.23)intoeqn(1.16),weobtain
Multiplyingthisequationwith W 1(t)fromtheleftandintegrating ˙ d(t)overtime, wefindthat
with d(0)= W 1(0)x(0)and t denotingtheintegrationvariable.Thetimeevolution of x(t)thenfollowsfromeqn(1.23)as
wherewehaveintroducedthestatetransitionmatrix
Fortheconcretecaseofbasissolutionschosenas xa
sin(ω0t)e Γt/2,weobtain
Thisformalismproducesthesamelong-timelimitsolutionsaseqn(1.13),but furthermoreallowsustostudytime-dependentphenomena.Weunderstandfrom eqn(1.26)thattheroleoftheforceterm f(t)istochangetheentriesoftheweighting vector d overtime;forinstance,aforcemayincreasetheamplitudeofoscillation, whichwillappearasalargerentryin d(t).Theforcecanalsochangethephaseofan oscillation,suchthatitevolvesfrom xa(t)=cos(ω0t)e
Inaddition,theforcingcanlockthemotionoftheoscillatortoanexternaldriving frequency.Intheabsenceofanexternalforce,theevolutionisentirelydeterminedby theinitialcondition,whichcorrespondsto d(0).
Equation(1.28)impliesthatwhenthefundamentalsolutionsbasisandtheinitial conditionsareknown,thecompletetimeevolutionofalineardifferentialequation canbeanalyticallydetermined.Importantly,thisisevenpossibleincaseswherethe entriesof G(t)varyintime,aslongasfundamentalsolutionsareknownatanygiven moment.Theintegrationineqn(1.28)isthenperformedpiecewise.
Theresultofaringdowncalculatedwitheqn(1.28)isshowninFig.1.4(a).Ringdownmeasurementsareusefulinexperimentsbecausetheyallowforaprecisecharacterizationofthedamping.InFig.1.4(b),anexamplewithexternalforcingisprovided. Theevolutiondependscruciallyonthephaseoftheforcerelativetothestartingconditions.However,thelong-timelimitresponseisindependenton x(0)andcorresponds totheresultfoundineqn(1.14).
1.4ParametricModulation
Ourmainfocuswillbeonthestudyofparametricresonators,thatis,systemswhere thehomogeneoustermsofthemodel,suchasthepotentialenergycoefficient(the springconstant),areallowedtovaryperiodicallyintime,seeFig.1.5.Inthissection,
Fig.1.4 (a)Ringdowntimetraceofanundriven,dampedharmonicresonatorcalculated withthestatetransitionmatrixmethod,cf.eqn(1.28),for ω0 =100andΓ=1(Q =100). Theamplitudedecaysexponentiallyas e t/τ0 withadecaytime τ0 =2/Γ=2Q/ω0.(b)The samesystemevolvingundertheinfluenceofanexternalforcewith F0/m =25.Duetothe specificphaseoftheforce,thesystemringsdownfasterthanintheunforcedcase,andthen ringsuptoastableamplitudewithaninvertedphaserelativetothestartingcondition.
wegainafirstimpressionofthebehaviorofsuchsystems.Westartwiththeundamped Hillequation,
whereΨH (t)isafunctionthatisperiodicoveratime Tp,andwhere λ isaconstantthat characterizesthemodulationdepth.ThemostwidelyusedformoftheHillequation isthe Mathieuequation,
with ωp ≡ 2π/Tp andaconstantphase ψ.Thesametransformationasineqn(1.6)can beappliedtotheHillequationtoanalyzedampedsystems.Inlaterchapters,however, wewilltreatdampingexplicitlytofacilitateobservationofthesystemsina labframe. Theeffectofresonantparametricpumpingat ωp ≈ 2ω0 isfundamentallydifferent fromthatofexternalforcingbecausethepumptermislinearin x.Ontheonehand, startingfromtheinitialcondition x =˙x =0thesystemwillundergonoevolutionat all.Ontheotherhand,ifthesystemhasnonzeroinitialconditionsandisoscillating
Fig.1.5 (a)Astringisheldattwoclampingpoints(rounddots).Thefourpicturesshow snapshotsintime.Solidarrowsindicatepositiveandnegativetensionthatisappliedtothe stringattheclampingpoints,whilehollowarrowscorrespondtotheinstantaneouslateral stringvelocity.Themodulatedtensionisaformofparametricpumpingandcanamplifyor dampthemotiondependingontherelativephase.(b)Parametricpumpingcorrespondsto amodulationoftheharmonicpotentialshapeasafunctionoftime,asindicatedbythetwo differentsnapshotsinblackandgray.
as x(t) ∝ cos(ω0t),themultiplicationof x(t)with λ cos(ωpt)willgenerateaneffective drivingterm ∝ cos((ωp ω0)t).Sinceitisproportionaltotheinstantaneousoscillation amplitude,thisparametricpumpingwillactasanadditionalpositiveornegative dampingtermΓp fordifferentrelativephases ψ betweenthevibrationandthepump. Iftheresonatorhasnointernaldamping,thatisΓ=0,theeffectivedampingΓeff =Γ+ Γp willbecomenegativefortwooppositephasesofmotion(twovaluesofthephasethat areseparatedby π).Theresonatorwillthereforeexperienceexponentialamplification inthesephasesandwillbecomeunstable.Inthefollowing,wewilldemonstratethis behaviorusingFloquetanalysis.
1.5FloquetTheory
Whenthecoefficientsofthehomogeneoussystemaresubjecttoperiodicmodulations withaperiod Tp,thesystemmaybecomeunstableeveninthepresenceofpositive damping(Γ > 0)[88].Inordertoinvestigatetheconditionsforstabilityofamodulated system,wefirstnotethatthestatetransitionmatrixΦfulfillsthehomogeneouspart ofeqn(1.16),thatis,
Fromthis,andtakingintoaccountthat G(t)= G(t + Tp),itfollowsthattheoperation thatΦ(t, 0)performsonaninitialstate x(0)canbesplitintorepeatedidenticalparts thatdescribetheoperationoveronemodulationperiod Tp,
Tp, 0)= C. (1.34)
Intheabsenceofforcing,thestateevolutionover n periodscanthensimplybedescribedby
ThisisoneformtoexpressFloquet’stheorem.Itentailsthatitisenoughtounderstand theeffectofthe discretetransitionmatrix C inordertopredictthebehaviorof x(t).Inparticular,Floquettheoryisoftenappliedtoanalyzewhetherasystemis stableornot.Theanalysismakesuseofthecomplexeigenvalues c = e ˆ µTp of C, whicharecalled characteristicmultipliers.Here,ˆ µ arereferredtoascharacteristic exponents,butwehavemarkedthemwithahatsymboltoemphasizethattheyare notidenticaltothecharacteristicexponents µ thatwehavepreviouslyencountered, forexampleineqn(1.11).Indeed, C onlycontainsinformationaboutthediscrete changesthatoccuroverfullperiods Tp,andnotabouttheperiodicevolutionof x(t) withinthesetimesteps.
Forthefamiliarexampleoftheunderdampedharmonicresonator,weusethe naturalperiodicityof Tp =2π/ωΓ.Wethenfindthatthetwoeigenvalues ca,b arereal andequalandamounttotheexponentialdecayfactor e ΓTp/2,suchthatˆ µ = Γ/2. Bycontrast,ifatleastoneofthecharacteristicmultipliershasarealcomponentlarger than1,thesystemwillgrowinfinitely.Inreality,suchgrowthisalwaysboundedby theemergenceofnonlinearities.
Inthelightofeqn(1.33),wewritedownacharacteristicequationsimilarto eqn(1.20)tofindtheeigenvaluesofΦ(Tp, 0)= C.Here,weobtain
Wecanfurtherusetherelationships[88]
Asaconcreteexample,wewillanalyzethestabilityoftheso-calledMeissnerequationwithaddeddamping,
where ψM (t)= 1for0 <t<Tp/2and ψM (t)=1for Tp/2 <t<Tp withineach period Tp.TheMeissnerequationhassimilarpropertiesastheMathieuequationand canbesolvedanalyticallybydefiningstatetransitionmatricesoverpartialperiods. Namely,ifthecoefficientsofanEOMvaryovertime,thediscretetransitionmatrix C canbeobtainedfromthemultiplicationofstatetransitionmatricescoveringsubperiodtimeintervals,
=Φ(Tp, 0)= N
where t0 =0and tN = Tp.NotethatfortheMathieuequation,thisprocedurewould requireinfinitelymanyproductsbecausethepotentialtermchangescontinuously.
Westartwitheqn(1.6)totransformoursystemfromeqn(1.38)into
whereweassume Q 1andtherefore ω0 ≈ ωΓ.TheMeissnerequationallowsusto dividethefullperiod Tp intotwohalfperiodswithconstantcoefficients,
with
Foreachhalfperiod,wecandefinefundamentalsolutionscos
andcorrespondingWronskianmatrices
whichleadustohalf-periodstatetransitionmatrices
Thefinalstatetransitionmatrixisobtainedfrom
wherewerememberthatthecoefficientsinthehalf-periodstatetransitionmatrices assumedifferentvalues,seeeqn(1.42).
Inordertocalculatetheeigenvalues ca,b,weusethecharacteristicequation(1.36). Forasecond-ordersystemwithoutloss,tr(G(t))=0,sowecaninsert |Φ(Tp, 0)| =1 andarriveat
Finally,wetransformbackinto x-coordinatesandfindthecharacteristicexponentsas
Thecharacteristicexponentoftheundampedsystemcanalsobecalculateddirectly[88],yieldingtheexpression
Equation(1.47)or(1.48)canbeusedtomapthestabilityofthedampedMeissner oscillatorasafunctionofthemodulationdepth λ andthedetuningofthemodulation
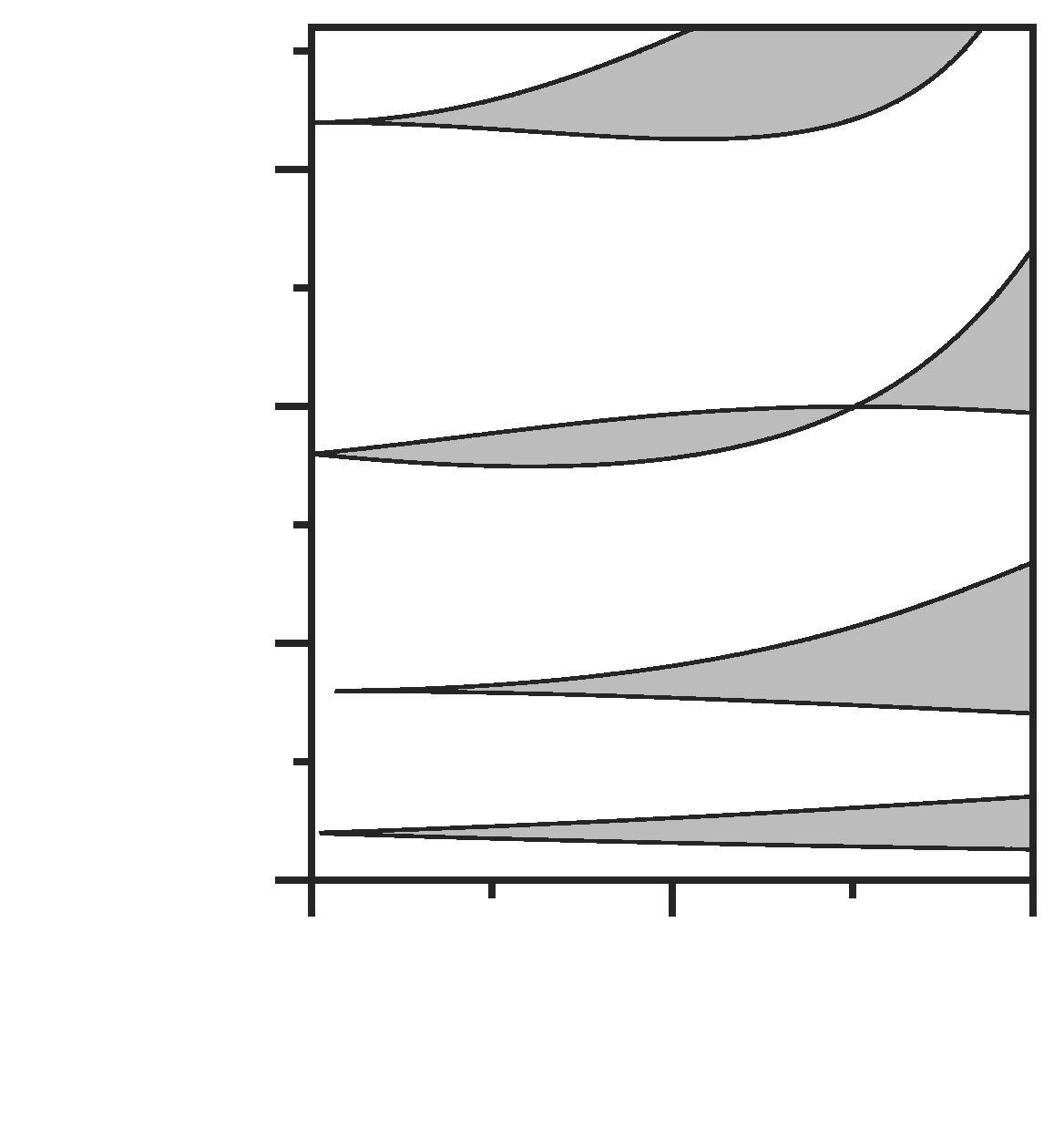
Fig.1.6 (a)StabilitydiagramoftheMeissneroscillator,cf.eqn(1.38),asafunctionof ω 2 0 T 2 p /π 2 and λ.Whiteareascorrespondtoastablesystemwithˆ μa,b < 0,whilegrayareas correspondtoanunstablesystemwithˆ μa,b > 0,cf.eqn(1.48).(b)Thesamesystemwith addeddampingΓ=0 1.Thetonguesareroundedoffbythedampingandnolongerreach λ =0.
Fig.1.7 (a)StabilitydiagramoftheMathieuequation,cf.eqn(1.32),asafunctionof ω 2 0 T 2 p /π 2 =4ω 2 0 /ω 2 p and λ.Whiteareascorrespondtoastablesystemwithˆ μa,b < 0,while grayareascorrespondtoanunstablesystemwithˆ μa,b > 0.(b)Thesamesystemwithadded dampingΓ=0 1.Thetonguesareroundedoffbythedampingandnolongerreach λ =0.
frequency ωp =2π/Tp from ω0 .ThestabilitydiagramsinFig.1.6exhibitdistinct instabilitylobeswherethesystemdivergesundertheinfluenceoftheMeissnermodulation.Thegrayregionsareknownas Arnold’stongues.Foranundampedsystem, theArnold’stonguesstretchallthewayto λ =0,contactingthefrequencyaxisat ω 2 0 /ω 2 p = n2 /4,whereeachnaturalnumber n indexesonetongue.Thisconditionfor thepumpfrequencies ωp whereinstabilitiesoccurisgenerallytrueforanyHillequationaslongastheysharethesameFloquetperiod Tp .InFig.1.7,wecanseethesame setoftonguessolvednumericallyfortheMathieuequationwith ωp =2π/Tp .Inthe
followingchapters,wewillconcentrateonthelowestArnoldtongueoftheMathieu equationwhere ωp ≈ 2ω0