CHAPTER0Preliminaries
0.1 Concepts Review
1. rationalnumbers
2. dense
3. Ifnot Q thennot P.
4. theorems
Problem Set 0.1
1. 42(811)642(3)6 46616 −−+=−−+ =++=
2. ( ) [ ] [] 324712324(5) 32203(22)66 ⎡⎤−−=−− ⎣⎦ = +==
3. –4[5(–312–4)2(13–7)] –4[5(5)2(6)]–4[2512] –4(37)–148 ++ =+=+ ==
4. [ ] [] () () 51(71216)42 51(3)425342 512527 −+−++ =−++=−++ =+=+=
5. 5165758 713919191 ==
6. 331331 472163216 426743 42424242 +−=+−
7. 11111113–41 –3243632126 1111 –32126 114 –32424 131 32424
8. 121111 352352153 3 521515 1212121 352153515 161151 315153159
9. 222 114 33 2 142142146 21212114 5 143296 21734949 ⎛⎞⎛⎞ ⎛⎞ ⎜⎟⎜⎟== ⎜⎟ ⎜⎟⎜⎟ ⎝⎠
=== ⎜⎟⎜⎟
10. 223533 5 77773311 1171662 7777 ⎛⎞⎛⎞⎛⎞ ⎜⎟⎜⎟⎜⎟ ⎝⎠⎝⎠⎝⎠ = ==−=− ⎛⎞⎛⎞⎛⎞ ⎜⎟⎜⎟⎜⎟ ⎝⎠⎝⎠⎝⎠ 11. 11121147 7217777 11121141515 721777 === ++ 12. 1374675 24888885 13746733 2488888 −+−+ = == +−+− 13. 13 22 112321 1–1–1––13333 = === + 14. 333 222 15257 2222 614620 2 7777 +=+=+ +− =+=+=
15. ( ) ( ) ( ) ( ) 22 535–35–3 5–32 += ==
16. () () () () () 222 5352533 521538215 −=−+ =−+=−
17. 2 2 (34)(1)3344 34 xxxxx xx −+=+−− =−−
18. 2 2 2 (23)(23)(23) 4669 4129 xxx xxx xx −=−− =−−+ =−+
19. 2 2 (3–9)(21)63–18–9 6–15–9 xxxxx xx +=+ =
20. 2 2 (411)(37)12283377 126177 xxxxx xx −−=−−+ =−+
21. 2222 432322 432 (31)(31)(31) 933331 96721 tttttt tttttttt tttt −+=−+−+ =−+−+−+−+ =−+−+
22. 3 2 322 32 (23)(23)(23)(23) (4129)(23) 81224361827 8365427 tttt ttt ttttt ttt +=+++ =+++ =+++++ =+++
23. 2–4(–2)(2)2 –2–2 xxx x xx + ==+ ,2 x ≠
24. 26(3)(2)2 3(3) xxxx x xx −−−+ ==+ , 3 x ≠
25. 2–4–21(3)(–7) –7 33 tttt t tt + == ++ ,3 t ≠−
26. 2 322 222(1) 2(21) 2(1) (1)(1) 2 1 xxxx xxxxxx xx xxx x = −+−+ = =−
27. 2 1242 22xxxx ++ + + 124(2)2 (2)(2)(2) 12482620 (2)(2) 2(310) (2) xx xxxxxx xxx xxxx x xx + =++ + ++ ++++ == ++ + = +
28. 2 2 6291 y yy + 2
2(31)(31)(31) 2(31)2 2(31)(31)2(31)(31) y yyy yy yyyy =+ −+− + =+ + −+− 622
2(31)(31) yy yy ++ = + 82 2(31)(31) y yy + = +− 2(41)41 2(31)(31)(31)(31) yy yyyy ++ == + −+−
29. a. 000 ⋅ = b. 0 0 isundefined.
c. 0 0 17 = d. 3 0 isundefined.
e. 5 00 = f. 0 171 =
30. If 0 0 a = ,then00 a = ⋅ ,butthisismeaningless because a couldbeanyrealnumber.No singlevaluesatisfies0 0 a =
31. .083 121.000 96 40 36 4
32. .285714
.294117...
37. x =0.123123123... 1000123.123123... 0.123123... 999123 12341 999333 x x x x = = = ==
38. 0.217171717 x = 1000217.171717... 102.171717... 990215 21543 990198 x x x x = = = ==
39. x =2.56565656... 100256.565656... 2.565656... 99254 254 99 x x x x = = = =
40. 3.929292 x = 100392.929292... 3.929292... 99389 389 99 x x x x = = = =
41. x =0.199999... 10019.99999...
101.99999... 9018 181 905 x x x x = = = ==
42. 0.399999 x = … 10039.99999... 103.99999... 9036 362 905 x x x x = = = ==
43. Thoserationalnumbersthatcanbeexpressed byaterminatingdecimalfollowedbyzeros.
44. 1 , p p qq ⎛⎞ = ⎜⎟ ⎝⎠ soweonlyneedtolookat 1 . q If 25, nm q =⋅ then 111 25(0.5)(0.2). nm nm q ⎛⎞⎛⎞ =⋅=
Theproduct ofanynumberofterminatingdecimalsisalsoa terminatingdecimal,so(0.5)and(0.2), nm andhencetheirproduct, 1 , q isaterminating decimal.Thus p q hasaterminatingdecimal expansion.
45. Answerswillvary.Possibleanswer:0.000001, 12 1 0.0000010819... π ≈
46. Smallestpositiveinteger:1;Thereisno smallestpositiverationalorirrationalnumber.
47. Answerswillvary.Possibleanswer: 3.14159101001...
48. Thereisnorealnumberbetween0.9999… (repeating9's)and1.0.9999…and1represent the same realnumber.
49. Irrational
50. Answerswillvary.Possibleanswers: and, π π 2and2
51. 3 (31)20.39230485 +≈
52. ( ) 4 230.0102051443 −≈
53. 431.123–1.090.00028307388 ≈
54. () 1/2 3.14150.5641979034 ≈
55. 2 8.91–30.000691744752 π+π≈
56. 42(62)3.661591807 ππ−≈
57. Let a and b berealnumberswith ab < .Let n beanaturalnumberthatsatisfies nba < 1/.Let} {: Skknb > = .Since anonemptysetofintegersthatisbounded belowcontainsaleastelement,thereisa kS ∈ 0suchthat knb > 0/but knb ≤ )/(10.Then a n b nn k n k > > = 11100
Thus, ab n k ≤ < 01.If b n k < 01,thenchoose n k r 01 = .Otherwise,choose n k r 02 =
Notethat 1 abr n < −< .
Given ab < ,choose r sothat1arb << .Then choose23 , rr sothat213arrrb < <<< ,andso on.
58. Answerswillvary.Possibleanswer:3 120in ≈
59. ft 4000mi528021,120,000ft mi r =×= equator22(21,120,000) 132,700,874ft rπ π = = ≈
60. Answerswillvary.Possibleanswer: beatsminhrday 70602436520yr minhrdayyear
735,840,000beats ×××× =
61. 2 2 3 16 212(27012) 93,807,453.98in. Vrh ⎛⎞ = π=π⋅⋅ ⎜⎟ ⎝⎠ ≈ volumeofoneboardfoot(ininches): 112121443 in. ××= numberofboardfeet: 93,807,453.98651,441boardft 144 ≈
62. 223 (8.004)(270)(8)(270)54.3ft. V ππ =−≈
63. a. IfIstayhomefromworktodaythenit rains.IfIdonotstayhomefromwork, thenitdoesnotrain.
b. Ifthecandidatewillbehiredthenshe meetsallthequalifications.Ifthe candidatewillnotbehiredthenshedoes notmeetallthequalifications.
64. a. IfIpassthecourse,thenIgotanAonthe finalexam.IfIdidnotpassthecourse, thnIdidnotgetanAonthefinalexam.
b. IfItakeoffnextweek,thenIfinishedmy researchpaper.IfIdonottakeoffnext week,thenIdidnotfinishmyresearch paper.
65. a. Ifatriangleisarighttriangle,then 222 abc += Ifatriangleisnotaright triangle,then222 abc +≠
b. Ifthemeasureofangle ABC isgreaterthan 0oandlessthan90o,itisacute.Ifthe measureofangle ABC islessthan0o or greaterthan90o,thenitisnotacute.
66. a. Ifangle ABC isanacuteangle,thenits measureis45o.Ifangle ABC isnotan acuteangle,thenitsmeasureisnot45o .
b. If22 ab < then ab < If22 ab ≥ then .ab ≥
67. a. Thestatement,converse,and contrapositivearealltrue.
b. Thestatement,converse,and contrapositivearealltrue.
68. a. Thestatementandcontrapositivearetrue. Theconverseisfalse.
b. Thestatement,converse,and contrapositiveareallfalse.
69. a. Someisoscelestrianglesarenot equilateral.Thenegationistrue.
b. Allrealnumbersareintegers.Theoriginal statementistrue.
c. Somenaturalnumberislargerthanits square.Theoriginalstatementistrue.
70. a. Somenaturalnumberisnotrational.The originalstatementistrue.
b. Everycirclehasarealessthanorequalto 9π.Theoriginalstatementistrue.
c. Somerealnumberislessthanorequalto itssquare.Thenegationistrue.
71. a. True;If x ispositive,then2 x ispositive.
b. False;Take2 x =− .Then20 x > but 0 x < .
c. False;Take 1 2 x = .Then xx < = 4 21
d. True;Let x beanynumber.Take 21 yx = + .Then2 yx > .
e. True;Let y beanypositivenumber.Take 2 y x = .Then0 xy<< .
72. a. True; ( )()1:01xxxx + −<++−<
b. False;Thereareinfinitelymanyprime numbers.
c. True;Let x beanynumber.Take 1 1 y x = + .Then 1 y x > .
d. True;1/ n canbemadearbitrarilyclose to0.
e. True;1/2 n canbemadearbitrarilyclose to0.
73. a. If n isodd,thenthereisaninteger k such that21. nk = + Then 222 2 (21)441 2(22)1 nkkk kk = +=++ =++
b. Provethecontrapositive.Suppose n is even.Thenthereisaninteger k suchthat 2.nk = Then2222 (2)42(2)nkkk === . Thus2 n iseven.
74. Parts(a)and(b)provethat n isoddifand onlyif2 n isodd.
75. a. 24333333 =
b. 12443122312or231 = ⋅=⋅⋅⋅
=⋅=⋅⋅
c. 22 510022550221275 223425223585 2235517or23517
=⋅⋅⋅=⋅⋅⋅⋅
=⋅⋅⋅⋅⋅⋅⋅⋅
76. Forexample,let23; Abcd =⋅⋅ then 2246 Abcd =⋅⋅ ,sothesquareofthenumber istheproductofprimeswhichoccuraneven numberoftimes.
77. 2 22 2;22;2;pp qp qq === Sincetheprime factorsof p2mustoccuranevennumberof times,2q2wouldnotbevalidand2 p q = mustbeirrational.
78. 2 22 3;23;3;pp qp qq === Sincetheprime factorsof2 p mustoccuranevennumberof times,2 3q wouldnotbevalidand3 p q = mustbeirrational.
79. Let a, b, p,and q benaturalnumbers,so a b and p q arerational. apaqbp bqbq + += This sumisthequotientofnaturalnumbers,soitis alsorational.
80. Assume a isirrational,0 p q ≠ isrational,and pr a qs ⋅= isrational.Then qr a ps = is rational,whichisacontradiction.
81. a. –9–3; = rational
b. 3 0.375; 8 = rational
c. (32)(52)15430; == rational
d. 2 (13)1233423; +=++=+ irrational
c. x =2.4444...; 1024.4444... 2.4444... 922 22 9 x x x x = = = = d. 1
83. a. Answerswillvary.Possibleanswer:An example is2{:5,arationalnumber}.Sxxx =< Heretheleastupperboundis5,whichis realbutirrational.
b. True
0.2 Concepts Review
1. [1,5);(,2] −∞−
2. b >0; b <0
3. (b)and(c) 4. 15 x ≤≤
Problem Set 0.2 1.
2. a. (2,7) b. [3,4) c. (,2] −∞− d. [1,3]
3. 725 2;(2,) xx x −<− −<−∞
4. () 3546 1;1, xx x −<− <∞
5. 7–293 –52 55 –;–, 22 xx x x ≤+ ≤ ≥∞⎡⎞ ⎟ ⎢ ⎣⎠
6. 5364 1;(,1) xx x −>− >−∞
7. 4325 633 21;(2,1) x x x −<+< −<< −<<−−
8. 34911 6420 33 5;,5 22 x x x −<−< << ⎛⎞ << ⎜⎟ ⎝⎠
9. –31–64 –4–63 2112 –;–, 3223 x x x < ≤ <≤ ⎡ ⎞ >≥ ⎟ ⎢ ⎣ ⎠
10. 4537 132 1221 ;, 3333 x x x < −< −<−< ⎛⎞ >>−−⎜⎟ ⎝⎠
11. x2+2x –12<0; 2 –2(2)–4(1)(–12)–252 2(1)2 –113 x ± ± == =± ( ) ( ) ––113––1–130; xx ⎡⎤⎡⎤ + < ⎣⎦⎣⎦ ( ) –1–13,–113 +
12. 2560 (1)(6)0; xx xx −−> + −> (,1)(6,) ∞−∪∞
13. 2x2+5x –3>0;(2x –1)(x +3)>0; 1 (,3), 2 ⎛⎞ ∞−∪∞⎜⎟ ⎝⎠ 14. 2 4560 3 (43)(2)0;,2 4 xx xx −−< ⎛⎞ +−<−⎜⎟ ⎝⎠
15. 4 0; –3 x x + ≤ [–4,3)
16. 322 0;,(1,)13 x x ⎛⎤ ≥−∞∪∞ ⎜ ⎥ ⎝⎦
17. 2 5 2 50 25 0; x x x x < −< < 2 (–,0), 5 ⎛⎞ ∞∪∞⎜⎟ ⎝⎠
18. 7 7 4 7 70 4 728 0; 4 x x x x ≤ −≤ ≤ () 1 ,0, 4 ⎡⎞ −∞∪∞ ⎟ ⎢ ⎣⎠
19. 1 4 32 1 40 32 14(32)0 32 91223 0;,, 3234 x x x x x x ≤ −≤ ≤ ⎛⎞⎡⎞ ≤−∞∪∞ ⎜⎟⎟ ⎢ ⎝⎠⎣⎠
20. 3 2 5 3 20 5 32(5)0 5 277 0;5, 52 x x x x x x > + −> + −+ > + ⎛⎞ >−−⎜⎟ + ⎝⎠
21. (2)(1)(3)0;(2,1)(3,8) xxx + −−>−∪
22. 31 (23)(31)(2)0;,,2 23 xxx ⎛⎞⎛⎞ +−−<−∞−∪⎜⎟⎜⎟ ⎝⎠⎝⎠
23. 2 (2-3)(-1)(-3)0; xxx ≥ [ ) 3 –,3, 2 ⎛⎤ ∞∪∞ ⎜ ⎥ ⎝⎦
24. () () 2 (23)(1)(3)0; 3 ,11,3, 2 xxx−−> ⎛⎞ −∞∪∪∞ ⎜⎟ ⎝⎠
25. 32 2 –560 (5–6)0 (1)(–6)0; xxx xxx xxx < < + < (,1)(0,6) ∞−∪
26. 32 2 2 10 (1)(1)0 (1)(1)0; xxx xx xx −+> −> + −> (1,1)(1,) ∪∞
27. a. False. b. True. c. False.
28. a. True. b. True.
c. False.
29. a. ⇒ Let ab < ,so 2 abb < .Also,2aab < Thus,22 aabb << and22 ab < . ⇐ Let 22ab < ,so ab ≠ Then () () 222 22 02 22 abaabb babbbba <−=−+ <−+=−
Since0 b > ,wecandivideby2b toget 0 ba−>
b. Wecandivideormultiplyaninequalityby anypositivenumber. 11 1 aba bba <⇔<⇔<
30. (b)and(c)aretrue.
(a)isfalse:Take1,1 ab=−= . (d)isfalse:if ab ≤ ,then ab−≥−
31. a. 3x +7>1and2x +1<3 3x >–6and2x <2 x >–2and x <1;(–2,1)
b. 3x +7>1and2x +1>–4 3x >–6and2x >–5 x >–2and5–; 2 x > () 2, −∞
c. 3x +7>1and2x +1<–4 x >–2and5–; 2 x <∅
32. a. 271or213 28or22 4or1 xx xx xx −>+< >< >< (,1)(4,) −∞∪∞
b. 271or213 28or22 4or1 (,4] xx xx xx −≤+< ≤< ≤< −∞
c. 271or213 28or22 4or1 (,) xx xx xx −≤+> ≤> ≤> −∞∞
33. a. 22 –322 ––32 (1)(2–7)1 35–71 2–5–60 (3)(1)(–2)0 xxxx xxxx xxx xxx ++≥ +≥ +≥ ++≥ [3,1][2,) −∪∞
b. 42 42 22 2 28 280 (4)(2)0 (2)(2)(2)0 xx xx xx xxx ≥ ≥ +≥ + +−≥ (,2][2,) ∞−∪∞
c. 222 22 22 (1)7(1)100 [(1)5][(1)2]0 (4)(1)0 (2)(1)(1)(2)0 xx xx xx xxxx + ++< + −+−< < + +−−< (2,1)(1,2) −∪
34. a. 01.2 1 99.1 < < x xx 01.9912.1 < < 1991 < x and x1201 < 199 1 < x and 201 1 > x 99.1 1 01.2 1 < < x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 199 1 201, 1
b. 01.3 2 1 99.2 < + < x )(201.)13(2 99.2 + < < + xx 981.995.2 < + x and02 .016.13 + < x
299 98.4 < x and 301 02.5 > x
299 498 301 502 < < x ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ 299 498 301, 502
35. 25; 25or25 3or7 x xx xx −≥ ≤−−≥ ≤−≥ (,3][7,) ∞−∪∞
36. 21; x +< –121 –3–1 x x <+< << (–3,–1)
37. 4510; 104510 1545 155155 ;, 4444 x x x x +≤ −≤+≤
−≤≤ −≤≤−⎡⎤ ⎢⎥ ⎣⎦
38. 2–12; x >
2x –1<–2or2x –1>2 2x <–1or2x >3; 1313 –or,–,–, 2222 xx ⎛⎞⎛⎞ <>∞∪∞
39. 2 57 7 22 57or57 77 22 2or12 77 7or42; x xx xx xx −≥ −≤−−≥ ≤−≥ ≤−≥ (,7][42,) −∞−∪∞
40. 11 4 x +< 111 4 20; 4 x x −<+< −<< –8< x <0;(–8,0)
41. 561; 561or561 55or57 77 1or;(,1), 55 x xx xx xx −> −<−−> <> ⎛⎞ <>−∞∪∞⎜⎟ ⎝⎠
42. 2–73; x >
2x –7<–3or2x –7>3 2x <4or2x >10 x <2or x >5;(,2)(5,) −∞∪∞
43. 1 36; 11 36or36 11 30or90 x xx xx −> <−−> + <−> 1319 0or0; 11 ,00, 39 xx xx +− < > ⎛⎞⎛⎞ −∪ ⎜⎟⎜⎟ ⎝⎠⎝⎠
44. 5 21; x + > 55 2–1or21 55 30or10 355 0or0; xx xx xx xx + <+> +<+> ++ < > (–,5–5)–,0(0,) 3 ⎛⎞ ∞ ∪∪∞ ⎜⎟ ⎝⎠
45. 2340;xx −≥ 2 3(–3)–4(1)(–4)35 –1,4 2(1)2 x ± ± === (1)(4)0;(,1][4,) xx + −=−∞−∪∞
46. 2 24(4)4(1)(4) 440;2 2(1) (2)(2)0;2 xxx xxx ±−− +≤== −−≤=
47. 3x2+17x –6>0; 2 –17(17)–4(3)(–6)–17191 –6, 2(3)63 x ± ± === (3x –1)(x +6)>0; 1 (–,–6), 3 ⎛⎞ ∞ ∪∞⎜⎟ ⎝⎠
48. 2 1411150; xx + −≤ 2 11(11)4(14)(15)1131 2(14)28 35 , 27 x x −±−− −± == =− 3535 0;, 2727 xx ⎛⎞⎛⎞⎡⎤ ⎜⎟⎜⎟+−≤− ⎢ ⎥ ⎝⎠⎝⎠⎣⎦
49. 30.5535(0.5)5152.5 xxx −<⇒−<⇒−<
50. 20.3424(0.3)4181.2 xxx +<⇒+<⇒+<
Section 0.2
51. 262612 6 xxx ε ε ε −<⇒−<⇒−<
52. 42428 2 xxx ε ε ε +<⇒+<⇒+<
53. 3153(5) 35 5; 33 xx x x ε ε ε εε δ −<⇒−< ⇒−< ⇒−<=
54. 484(2) 42 2; 44 xx x x ε ε ε ε ε δ −<⇒−< ⇒−< ⇒−<=
55. 6366(6) 66 6; 66 xx x x ε ε ε εε δ +<⇒+< ⇒+< ⇒+<=
56. 5255(5) 55 5; 55 xx x x ε ε ε εε δ +<⇒+< ⇒+< ⇒+<=
57. Cd π = –100.02 –100.02 10 –0.02 100.02 –0.0064 C d d d ≤ π≤
⎛⎞ π≤ ⎜⎟ π ⎝⎠ ≤≈ ππ
Wemustmeasurethediametertoanaccuracy of0.0064in.
58. () 5 501.5,32501.5; 9 CF−≤−−≤ () 5 32901.5 9 1222.7 F F −−≤ −≤
Weareallowedanerrorof2.7F.
59. 22 22 2 ––12–3 –12–6 (–1)(2–6) 2142436 322350 (3–7)(–5)0; xx xx xx xxxx xx xx < < < + <+ +> > 7 –,(5,) 3 ⎛⎞ ∞ ∪∞ ⎜⎟ ⎝⎠
60. () 22 211 (21)1 xx xx −≥+ −≥+ 22 2 44121 360 3(2)0 xxxx xx xx +≥++ −≥ −≥ (,0][2,) ∞∪∞
61. 22 22 2 22310 4610 (46)(10) 16483620100 1568640 (54)(316)0; xx xx xx xxxx xx xx −<+ −<+ −<+ +<++ −< +−< 416 –, 53 ⎛⎞ ⎜⎟ ⎝⎠
62. ()() 22 22 2 3126 31212 (31)(212) 961448144 5541430 511130 xx xx xx xxxx xx xx −<+ −<+ −<+ −+<++ −−< +−< 11 ,13 5 ⎛⎞ ⎜⎟ ⎝⎠
63. ( ) 22 2 222 andOrderproperty:whenispositive. Transitivity xyxxxyxyyyxyxzyzz xy xyxx <⇒≤<<⇔<
⇒< ⇒<=
Conversely, ( ) () () 222222
<⇒<=
222 –0Subtractfromeachside. –0Factorthedifferenceoftwosquares. –0Thisistheonlyfactorthatcanbenegative. Addt xyxyxx xyy xyxy xy xyy
⇒< ⇒+<
⇒<
⇒< oeachside.
64. () () 22 0, abaaandbb <<⇒== so
( ) ( ) 22 , ab < and,byProblem63, abab <⇒<
65. a. –(–)–abababab =+≤+=+
b. –ababab ≥≥ UseProperty4 ofabsolutevalues.
c. () abcabcabc abc ++=++≤++ ≤++
66. 22 2 2 2 1111 2233 11 32 11 32 11 32 xxxx xx xx xx ⎛⎞ −=+−⎜⎟ ++++⎜⎟ ⎝⎠ ≤+− + + =+ + + =+ + + bytheTriangularInequality,andsince 230, x +> 2 11 200,0. 32 x xx +>⇒>> + + 233 x +≥ and22, x +≥ so 2 11 33 x ≤ + and 11 22, x ≤ + thus, 2 1111 3232xx +≤+ + +
67. 22 –2(–2) 99 xx xx + = ++ 222 –2–2 999 xx xxx ≤+ + ++ 2222 –222 9999 xxx xxxx + ≤+= + +++
Since2 2 11 99, 99 x x + ≥≤ + 2 22 99 xx x + + ≤ + 2 –22 99 xx x + ≤ +
68. 22 22727 44715 xxxxx ≤ ⇒++≤++ ≤ ++= and211 x + ≥ so 2 1 1. 1 x ≤ +
Thus, 2 2 22 271 27 11 15115 xx xx xx ++ =++ + + ≤⋅=
69. 4321111 24816 xxxx ++++ 432 432 1111 24816 1111 1since1. 24816 1111 So1.93752. 24816 xxxx x xxxx ≤++++ ≤++++≤ + +++≤<
70. a. 2 20 (1)0 0or1 xx xx xx xx < −< −< <> b. 2 20 (1)0 01 xx xx xx x < −< −< <<
71. 0 a ≠⇒ 2 2 2 11 0––2 aa aa ⎛⎞ ≤=+ ⎜⎟ ⎝⎠ so, 22 22 11 2or2 aa aa ≤++≥ .
72. and 22 2 ab aaababbb aabb ab ab < +<++<+ <+< + <<
73. 22 22 0 and ab aababb aabb aabb << << << <<
74. () ( ) () 22 2222 2 11 2 24 1111 02 4244 1 0()whichisalwaystrue. 4 abababaabb aabbaabb ab ≤+⇔≤++ ⇔≤−+=−+ ⇔≤−
75. Forarectangletheareais ab,whilefora squaretheareais 2 2 2 ab a + ⎛⎞ = ⎜⎟ ⎝⎠ From Problem74, 12 () 22 ab ababab + ⎛⎞ ≤+⇔≤ ⎜⎟ ⎝⎠ sothesquarehasthelargestarea.
76. 2399 10; (,1] xxxx +++++≤ −∞−
77. 1111 102030 R ≤++ 1632 60 111 60 60 11 R R R + + ≤ ≤ ≥ 1111 203040 1643 120 120 13 R R R ≥++ ++ ≥ ≤ Thus,60120 1113 R ≤≤
78. 22 2 2 2 4;4(10)400 44000.01 41000.01 0.01 100 4 ArA r r r π ππ ππ π π === −< −< −< 2 0.010.01 100 44 0.010.01 100100 44 0.00004in r r ππ π π δ −<−< −<<+ ≈
0.3 Concepts Review
1. 22 (2)(3) xy++−
2. (x +4)2+(y –2)2=25 3. 2537,(1.5,5)22 −++ ⎛⎞ = ⎜⎟ ⎝⎠ 4. db ca
Problem Set 0.3
22 (3–1)(1–1)42 d =+==
22 (32)(52)748.60 d =−−++=≈ 3.
22 (4–5)(58)17013.04 d =++=≈
4.
22 (16)(53)49453 7.28 d =−−+−=+= ≈
5. 22 1(52)(3–4)49150d =++=+= 22 2(510)(38)252550
223(210)(48) 14416160 12sothetriangleisisosceles. d d dd =−+−=+= =−−+− =+= =
6. 22 (24)(40)41620 a =−+−−=+= 22 (48)(02)16420 b =−++=+=
22 (28)(42)36440 c =−+−+=+= 222 , abc += sothetriangleisarighttriangle.
7. (–1,–1),(–1,3);(7,–1),(7,3);(1,1),(5,1)
8. () 2222 22 (3)(01)(6)(04); 6101252 642 77,0 xx xxxx x x −+−=−+− −+=−+ = =⇒
9. –24–231 ,1,; 222 ++ ⎛⎞⎛⎞ = ⎜⎟⎜⎟ ⎝⎠⎝⎠ 2 2125 (12)–393.91 24 d ⎛⎞ =++=+≈ ⎜⎟ ⎝⎠
10. midpoint123639 of,, 2222 AB ++ ⎛⎞⎛⎞ ==⎜⎟⎜⎟ ⎝⎠⎝⎠ midpoint4374711 of,,2222 CD ++ ⎛⎞⎛⎞ ==⎜⎟⎜⎟ ⎝⎠⎝⎠ 2237911 2222 4152.24 d ⎛⎞⎛⎞ =−+−⎜⎟⎜⎟ ⎝⎠⎝⎠ =+=≈
11 (x –1)2+(y –1)2=1
12. 222 22 (2)(3)4 (2)(3)16 xy xy + +−= + +−=
13. 222 222 2 22 (2)(1) (52)(31) 91625 (2)(1)25 xyr r r xy −++= −++= =+= −++=
Section 0.3 Instructor’sResourceManual
14. 222(4)(3) xyr −+−= 222 2 22 (64)(23) 415 (4)(3)5 r r xy −+−= =+= −+−=
15. 1337 center,(2,5) 22 ++ ⎛⎞ == ⎜⎟ ⎝⎠ 11 22 radius(1–3)(3–7)416 22 1 205 2 =+=+ == 22 (–2)(–5)5 xy+=
16. Sincethecircleistangenttothe x-axis,4. r = 22 (3)(4)16 xy−+−=
17. 22210–6–100xxyy+++= 22 22 22 2–60 (21)(–69)19 (1)(–3)10 xxyy xxyy xy ++= ++++=+ ++= center(–1,3);radius10 ==
18. 22 22 22 616 (69)169 (3)25 xyy xyy xy +−= +−+=+ +−= center(0,3);radius5 ==
19. 22 –12350xyx++= 22 22 22 –12–35 (–1236)–3536 (–6)1 xxy xxy xy += ++=+ += center(6,0);radius1 ==
20. 22 22 22 10100 (1025)(1025)2525 (5)(5)50 xyxy xxyy xy +−+= −++++=+ −++= ( ) center5,5;radius5052 =−==
21. 22 41615460 xxyy + +++= 22399 4(44)415162164xxyy ⎛⎞ + ++++=−++ ⎜⎟ ⎝⎠ 2 2313 4(2)444 xy ⎛⎞ +++= ⎜⎟ ⎝⎠ 2 2313 (2)416 xy ⎛⎞ +++= ⎜⎟ ⎝⎠ center= 3 2,; 4 ⎛⎞ ⎜⎟ ⎝⎠ radius=13 4
22. 22 22 105 416430 16 4(44)439 464 1059 16 1616 xxyy xxyy ++++= ⎛⎞ +++++⎜⎟ ⎝⎠ =−++ 2 2 2 2 3 4(2)410 8 35 (2)82 xy xy ⎛⎞ + ++= ⎜⎟ ⎝⎠ ⎛⎞ +++= ⎜⎟ ⎝⎠ 3510 center2,;radius 822 ⎛⎞ =−−== ⎜⎟ ⎝⎠
23. 2–1 1 2–1 = 24. 75 2 43 =
25. –6–39 –5–27 = 26. 64 1 02 −+ =
27. 5–05 –0–33 = 28. 60 1 06 = +
29. 21(2) 22 40 yx yx xy =−− −=−+ +−=
30. 41(3) 43 70 yx yx xy =−− −=−+ +−=
31. 23 2–30 yx xy = + +=
32. 05 050 yx xy = + +−=
33. 8–35 ; 4–22 m == 5 –3(–2) 2 2–65–10 5–2–40 yx yx xy = = =
34. 211 ; 844 m == 1 1(4) 4 444 400 yx yx xy −=− −=− −+=
35. 3y =–2x +1; 21 –; 33yx=+ 2 slope–; 3 = 1 -intercept3 y =
36. 456 53 42 yx yx −=− =−+ 53 slope;-intercept42 y =−=
37. 6–210–2 –210–8 –54; yx yx yx = = =+ slope=–5; y-intercept=4
38. 4520 5420 4 4 5 xy yx yx +=− =−− =−− 4 slope;-intercept=4 5 y =−−
39. a. m =2; 32(–3) 2–9 yx yx += = b. 1 –; 2 m = 1 3–(–3) 2 13 22 yx yx += =
c. 236 3–26 2 –2; 3 xy yx yx + = =+ = + 2 –; 3 m = 2 3–(–3) 3 2 ––1 3 yx yx += = d. 3 ; 2 m = 3 3(–3) 2 315 –22 yx yx += = e. –1–23 –; 314 m == + 3 3–(–3) 4 33 44 yx yx += = f. x =3 g. y =–3
40. a. 35 3(3)(1)5 4 xcy c c + = += = b. 0 c = c. 21 21 xy yx + =− = 2; m = 35 35 35 xcy cyx yx cc + = = −+ = −+ 3 2 3 2 c c =− =
d. c mustbethesameasthecoefficientof x, so3. c =
e. 23(3);yx−=+ 1 perpendicularslope; 3 =− 13 3 9 c c −=− =
41. 3 ; 2 m = 3 1(2) 2 3 2 2 yx yx +=+ =+
42. a. 2; m = 310 310 10 33 kxy ykx k yx −= −=−+ =− 2;6 3 k k == b. 1 ; 2 m =− 1 32 3 2 k k =− =−
c. 236 326 2 2; 3 xy yx yx += =−+ =−+ 339 ;; 2322 k mk===
43. y =3(3)–1=8;(3,9)isabovetheline.
44. 0 (,0),(0,);0 ;;1 bb abm aa bbxxyyxbybaaab ==− =−++=+=
45. 234 –35 xy xy + = + = 234 9–3–15 11–11 –1 xy xy x x + = = = = –3(–1)5 2 y y + = =
Pointofintersection:(–1,2) 3–24 24 –33 yx yx = + = + 3 2 m = 3 2(1) 2 37 22 yx yx =+ = +
46. 458 210 xy xy = + =− 458 4220 728 4 xy xy y y = −−= −= = 45(4)8 412 3 x x x −= = =
Pointofintersection: ( ) 3,4; 458 548 48 55 xy yx yx = =−+ = 5 4 m = 5 4(3) 4 531 44 yx yx + =−+ =−−
47. 3–45 239 xy xy = += 9–1215 81236 1751 3 xy xy x x = += = = 3(3)–45 –4–4 1 y y y = = =
Pointofintersection:(3,1);3x –4y =5; –4–35 35 –44 yx yx =+ = 4 –3 m = 4 –1–(–3) 3 4 –5 3 yx yx = =+
48. 5–25 236 xy xy = += 15–615 4612 1927 27 19 xy xy x x = += = = 27 236 19 60 3 19 20 19 y y y ⎛⎞ += ⎜⎟ ⎝⎠ = =
Pointofintersection:2720,; 1919 ⎛⎞ ⎜⎟ ⎝⎠ 525 –2–55 55 –22 xy yx yx −= =+ = 2 –5 m = 20227 19519 25420 –59519 2154 595 yx yx yx ⎛⎞ =−⎜⎟ ⎝⎠ =++ =−+
49. 26–13 center:,(4,1) 22 ++ ⎛⎞ = ⎜⎟ ⎝⎠ 2633 midpoint,(4,3) 22 ++ ⎛⎞ == ⎜⎟ ⎝⎠
inscribed22 circle:radius(4–4)(1–3) 42 =+ ==
22 (–4)(–1)4 xy + = circumscribedcircle: 22 radius(4–2)(1–3)8 =+=
22 (–4)(–1)8 xy + =
50. Theradiusofeachcircleis164. = Thecenters are ( ) ( ) 1,2and9,10.Thelengthofthebeltis thesumofhalfthecircumferenceofthefirst circle,halfthecircumferenceofthesecondcircle, andtwicethedistancebetweentheircenters.
1122 2(4)2(4)2(19)(210)22 82100144 56.37 L ππ π =⋅+⋅+++−− =++ ≈
51. Putthevertexoftherightangleattheorigin withtheotherverticesat(a,0)and(0, b).The midpointofthehypotenuseis,. 22 ab ⎛⎞ ⎜⎟ ⎝⎠ The distancesfromtheverticesare 2222 22 –0–2244 1 2, abab a ab ⎛⎞⎛⎞ ⎜⎟⎜⎟+=+ ⎝⎠⎝⎠ =+ 2222 22 0––2244 1 ,and 2 abab b ab ⎛⎞⎛⎞ ⎜⎟⎜⎟+=+ ⎝⎠⎝⎠ =+ 2222 22 0–0–2244 1 2, abab ab
⎛⎞⎛⎞ ⎜⎟⎜⎟+=+ ⎝⎠⎝⎠ =+ whichareallthesame.
52. FromProblem51,themidpointofthe hypotenuse, ( ) 4,3,,isequidistantfromthe vertices.Thisisthecenterofthecircle.The radiusis1695. + = Theequationofthe circleis 22 (4)(3)25. xy−+−=
53. 22 –4–2–110xyxy+= 22 22 22 22 22 (–44)(–21)1141 (–2)(–1)16 20–12720 (20100)(–1236) –7210036 (10)(–6)64 xxyy xy xyxy xxyy xy +++=++ += +++= ++++ =++ ++=
centeroffirstcircle:(2,1) centerofsecondcircle:(–10,6) 22 (210)(1–6)14425 16913 d =++=+ ==
However,theradiionlysumto4+8=12,so thecirclesmustnotintersectifthedistance betweentheircentersis13.
54. 22 22 22 22 0 44 44 xaxybyc ab xaxyby ab c ++++=
=−++ 2222 22 22 4 224 4 04 4 ababc xy abc abc +− ⎛⎞⎛⎞ ⎜⎟⎜⎟+++= ⎝⎠⎝⎠ +− >⇒+>
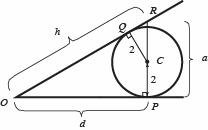
55. Labelthepoints C,P,Q, and R asshowninthe figurebelow.Let dOP = , hOR = ,and aPR = .Triangles OPRΔ and CQRΔ are similarbecauseeachcontainsarightangleand theyshareangle QRC∠ .Foranangleof 30, 3 2 d h = and 1 2 2 aha h =⇒= .Usinga propertyofsimilartriangles,/3/2 QCRC = , 234 2 223 a a =→=+ BythePythagoreanTheorem,wehave 2232347.464dhaa=−==+≈
56. Theequationsofthetwocirclesare 222 222 ()() ()() xRyRR xryrr −+−= −+−=
Let ( ) , aa denotethepointwherethetwo circlestouch.Thispointmustsatisfy 222 2 2 ()() ()2 2 1 2 aRaRR R aR aR −+−= −=
⎛⎞ =±⎜⎟ ⎜⎟ ⎝⎠
Since aR < , 2 1. 2 aR ⎛⎞ =−⎜⎟ ⎜⎟ ⎝⎠
Atthesametime,thepointwherethetwo circlestouchmustsatisfy 222()() 2 1 2 ararr ar +−= ⎛⎞ =±⎜⎟ ⎜⎟ ⎝⎠
Since, ar > 2 1. 2 ar ⎛⎞ =+⎜⎟ ⎜⎟ ⎝⎠
Equatingthetwoexpressionsfor a yields 2 22 11 22 22 112 2 1222 11 222 Rr rRR ⎛⎞⎛⎞ −=+ ⎜⎟⎜⎟ ⎜⎟⎜⎟ ⎝⎠⎝⎠ ⎛⎞ ⎜⎟ ⎜⎟ ⎝⎠ == ⎛⎞⎛⎞ + +− ⎜⎟⎜⎟ ⎜⎟⎜⎟ ⎝⎠⎝⎠ 1 12 2 1 1 2 rR −+ = (322)0.1716 rRR =−≈
57. Refertofigure15inthetext.Givenine1 l with slope m,draw ABC withverticaland horizontalsides m,1.
Line2 l isobtainedfrom1 l byrotatingit aroundthepoint A by90° counter-clockwise. Triangle ABC isrotatedintotriangle AED Wereadoff 2 11 slopeof l mm ==− .
58. 2222 2(1)(1)(3)(4) xyxy −+−=−+− 22 22 4(2121) 69816 xxyy xxyy −++−+ =−++−+ 22 2222 22 2 2 32391644; 217 32317;; 33 21171 3939 152 39 xxy xxyxxy xxy xy −+=+−− −+=−+= ⎛⎞ ⎜⎟−++=+ ⎝⎠ ⎛⎞ ⎜⎟−+= ⎝⎠ 152 center:,0;radius: 33 ⎛⎞ ⎛⎞ ⎜⎟ ⎜⎟ ⎜⎟ ⎝⎠ ⎝⎠
59. Let a, b,and c bethelengthsofthesidesofthe righttriangle,with c thelengthofthe hypotenuse.ThenthePythagoreanTheorem saysthat222 abc += Thus, 222 888 abc πππ += or 222111 222222 abc ⎛⎞⎛⎞⎛⎞ π+π=π ⎜⎟⎜⎟⎜⎟ ⎝⎠⎝⎠⎝⎠
12 22 x ⎛⎞ π ⎜⎟ ⎝⎠ istheareaofasemicirclewith diameter x,sothecirclesonthelegsofthe trianglehavetotalareaequaltotheareaofthe semicircleonthehypotenuse. From222, abc += 222333 444 abc += 32 4 x istheareaofanequilateraltriangle withsidesoflength x,sotheequilateral trianglesonthelegsoftherighttrianglehave totalareaequaltotheareaoftheequilateral triangleonthehypotenuseoftherighttriangle.
60. Seethefigurebelow.Theangleat T isaright angle,sothePythagoreanTheoremgives 222 2222 2 ()() ()2() (2)() PMrPTr PMrPMrPTr PMPMrPT +=+ ⇔ ++=+ ⇔+= 22 sothisgives()()() PMrPNPMPNPT +==
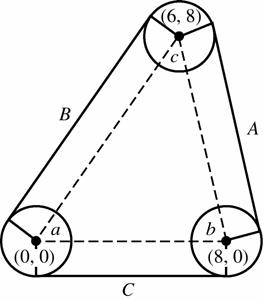
61. Thelengths A, B,and C arethesameasthe correspondingdistancesbetweenthecentersof thecircles: 22 22 (–2)(8)688.2
22 (6)(8)10010 (8)(0)648 A
Eachcirclehasradius2,sothepartofthebelt aroundthewheelsis 2(2a)+2(2b)+2(2c) π πππππ 2[3-()]2(2)4 abc π ππ = ++==
Since a + b + c = π ,thesumoftheanglesofa triangle.
Thelengthofthebeltis8.21084 38.8units. ≈+++π ≈
62 AsinProblems50and61,thecurvedportions ofthebelthavetotallength2. rπ Thelengths ofthestraightportionswillbethesameasthe lengthsofthesides.Thebeltwillhavelength 12 2. n rdddπ + +++
63. A =3, B =4, C =–6 22 3(–3)4(2)(–6)7 (3)(4)5 d ++ == +
64. 2,2,4ABC==−= 22 2(4)2(1)4)1472 (2)(2)82 d −−+ === +
65. A =12, B =–5, C =1 22 12(–2)–5(–1)118 (12)(–5)13 d + == +
66. 22 2,1,5 2(3)1(1)5225 (2)(1)55 ABC d ==−=− === +−
67. 24(0)5 5 2 x x += = ( ) 5 2 22 24(0)–725 (2)(4)205 d + === +
68. 7(0)51 1 5 y y −=− = 22 1 7(0)5657774 (7)(5)7474 d ⎛⎞ ⎜⎟ ⎝⎠ === +−
69. 235 ; 123 m ==− + 3 ; 5 m = passesthrough 213211 ,, 2222 −+− ⎛⎞⎛⎞ =− ⎜⎟⎜⎟ ⎝⎠⎝⎠ 131 252 34 55 yx yx ⎛⎞ −=+⎜⎟ ⎝⎠ =+
70. 0–41 –2;; 2–02 mm=== passesthrough 0240,(1,2)22 ++ ⎛⎞ = ⎜⎟ ⎝⎠ 1 –2(–1) 2 13 22 yx yx = = + 6–01 3;–; 4–23 mm=== passesthrough 2406,(3,3)22 ++ ⎛⎞ = ⎜⎟ ⎝⎠ 1 –3–(–3) 3 1 –4 3 131 –4 223 55 62 3 13(3)322 yx yx xx x x y = =+ +=+ = = = += center=(3,3)
71. Lettheoriginbeatthevertexasshowninthe figurebelow.Thecenterofthecircleisthen ( ) 4,rr ,soithasequation
222 ((4))(). xryrr −−+−= Alongthesideof length5,the y-coordinateisalways3 4 times the x-coordinate.Thus,weneedtofindthe valueof r forwhichthereisexactlyone xsolutionto 2 22 3 (4). 4 xrxrr ⎛⎞ −++−= ⎜⎟ ⎝⎠ Solvingfor x inthisequationgives ()162162476. 25 xrrr =−±−+−⎛⎞ ⎜⎟ ⎝⎠ Thereis exactlyonesolutionwhen2760, rr −+−= thatis,when1 r = or6 r = .Theroot6 r = is extraneous.Thus,thelargestcirclethatcanbe inscribedinthistrianglehasradius1. r =
72. Thelinetangenttothecircleat ( ) , ab willbe perpendiculartothelinethrough ( ) , ab andthe centerofthecircle,whichis ( ) 0,0.Theline through ( ) , ab and ( ) 0,0hasslope 2 02 ; 0 bbar maxbyryxaabb ==+=⇒=−+ so 2 axbyr += hasslope a b andis perpendiculartothelinethrough ( ) , ab and ( ) 0,0,soitistangenttothecircleat ( ) ,.ab
73. 12a +0b =36 a =3 22 336 b += 33 b =± 3–3336 –312 xy xy = = 33336 312 xy xy += +=
74. Usetheformulagivenforproblems63-66,for ()() ,0,0xy = 222 ,1,;(0,0) (0)1(0) (1)1 AmBCBb mBbBb d mm ==−=− −+−− == +−+
75. Themidpointofthesidefrom(0,0)to(a,0)is 000 ,,0 222 aa++ ⎛⎞⎛⎞ = ⎜⎟⎜⎟ ⎝⎠⎝⎠
Themidpointofthesidefrom(0,0)to(b, c)is 00 ,, 2222 bcbc++ ⎛⎞⎛⎞ = ⎜⎟⎜⎟ ⎝⎠⎝⎠ 1 2 212 22 –0 –0 ; ––c ba cc m baba c mmm ba == ===
76. Seethefigurebelow.Themidpointsofthe sidesare
1212 ,,22 Pxxyy ++ ⎛⎞ ⎜⎟ ⎝⎠ 2323 ,,22 Qxxyy ++ ⎛⎞ ⎜⎟ ⎝⎠ 3434 ,,22 Rxxyy ++ ⎛⎞ ⎜⎟ ⎝⎠ and 1414 ,.22 Sxxyy ++ ⎛⎞ ⎜⎟ ⎝⎠
Theslopeof PS is [] [] 1412 42 42 1412 1() 2 1. 2() yyyyyy xx xxxx +−+ = +−+
Theslopeof
QR is [] [] 3423 42 42 3423 1() 2 1() 2 yyyyyy xx xxxx +−+ = +−+ Thus
PS and QR areparallel.Theslopesof SR and PQ areboth31 31 , yy xx so PQRS isa parallelogram.
77. 22(–6)25;xy+= passesthrough(3,2) tangentline:3x –4y =1 Thedirthitsthewallat y =8.
0.4 Concepts Review
1. y-axis 3. 8;–2,1,4
2. ( ) 4,2 4. line;parabola
Problem Set 0.4
1. y =–x2+1; y-intercept=1; y =(1+ x)(1– x); x-intercepts=–1,1 Symmetricwithrespecttothe y-axis
Section 0.4
2. 21; xy=−+ -intercepts1,1; y =− -intercept1 x =
Symmetricwithrespecttothe x-axis.
3. x =–4y2–1; x-intercept=–1
Symmetricwithrespecttothe x-axis
4. 2 41;yx=− -intercept1 y =− 11 (21)(21);-intercepts,22 yxxx =+−=−
Symmetricwithrespecttothe y-axis.
5. x2+ y =0; y =–x2 x-intercept=0, y-intercept=0
Symmetricwithrespecttothe y-axis
6. 22;-intercept0yxxy = −= (2);-intercepts0,2yxxx = −=
7. 7x2+3y =0;3y =–7x2; 72 –3 yx = x-intercept=0, y-intercept=0
Symmetricwithrespecttothe y-axis
8. 2 322;yxx = −+ -intercept2 y =
9. x2+ y2=4
x-intercepts=-2,2; y-intercepts=-2,2
Symmetricwithrespecttothe x-axis, y-axis, andorigin
10. 22 3412; xy+= y-intercepts3,3 =− -intercepts2,2 x =−
Symmetricwithrespecttothe x-axis, y-axis, andorigin
11. y =–x2–2x +2: y-intercept=2 248223 -intercepts–13 –2–2 x ±+± ===±
12. 22 4312; xy+= -intercepts2,2 y =−
x-intercepts3,3 =−
Symmetricwithrespecttothe x-axis, y-axis, andorigin
13. x2 – y2=4
x-intercept=-2,2
Symmetricwithrespecttothe x-axis, y-axis, andorigin
14. 22(1)9;-intercepts2,4xyy+−==−
x-intercepts=22,22
Symmetricwithrespecttothe y-axis
15. 4(x –1)2+ y2=36;
y-intercepts3242 =±=±
x-intercepts=–2,4
Symmetricwithrespecttothe x-axis
16. 22432xxy−+=−
x-intercepts=22 ±
Symmetricwithrespecttothe x-axis
17. x2+9(y +2)2=36; y-intercepts=–4,0
x-intercept=0
Symmetricwithrespecttothe y-axis
18. 441;-intercepts1,1 xyy + ==−
x-intercepts1,1 = Symmetricwithrespecttothe x-axis, y-axis, andorigin
19. x4+ y4=16; y-intercepts2,2 =−
x-intercepts2,2 = Symmetricwithrespecttothe y-axis, x-axis andorigin
20. y = x3 – x; y-intercepts=0; y = x(x2–1)= x(x +1)(x –1);
x-intercepts=–1,0,1
Symmetricwithrespecttotheorigin
21. 2 1 ; 1 y x = + y-intercept=1
Symmetricwithrespecttothe y-axis
22. 2;-intercept0 1 x yy x == +
x-intercept=0
Symmetricwithrespecttotheorigin
23. 22 –22 –22 24312–2
24. () 22 459(2)36;-intercept5 xyx++==
25. y =(x –1)(x –2)(x –3); y-intercept=–6 x-intercepts=1,2,3
26. y = x2(x –1)(x –2); y-intercept=0 x-intercepts=0,1,2
2(21)3(44)–2212
2(–1)3(2)12 xxyy xxyy xy ++= ++++=++ ++=
y-intercepts= 30 –2 3 ±
x-intercept=1
27. 22(1);yxx=− y-intercept=0 x-intercepts=0,1