TimeRegained Symmetry andEvolutionin
ClassicalMechanics
Volume1
SeanGryb
UniversityofGroningen
KarimP.Y.Thébault
UniversityofBristol
GreatClarendon Street,Oxford,OX26DP, UnitedKingdom
OxfordUniversityPressisadepartmentoftheUniversityofOxford. ItfurtherstheUniversity’sobjectiveofexcellenceinresearch,scholarship, andeducationbypublishingworldwide.Oxfordisaregisteredtrademarkof OxfordUniversityPressintheUKandincertainothercountries ©SeanGrybandKarimP.Y.Thébault2024
Themoralrightsoftheauthorshavebeenasserted Allrightsreserved.Nopartofthispublicationmaybereproduced,storedin aretrievalsystem,ortransmitted,inanyformorbyanymeans,withoutthe priorpermissioninwritingofOxfordUniversityPress,orasexpresslypermitted bylaw,bylicenceorundertermsagreedwiththeappropriatereprographics rightsorganization.Enquiriesconcerningreproductionoutsidethescopeofthe aboveshouldbesenttotheRightsDepartment,OxfordUniversityPress,atthe addressabove
Youmustnotcirculatethisworkinanyotherform andyoumustimposethissameconditiononanyacquirer
PublishedintheUnitedStatesofAmericabyOxfordUniversityPress 198MadisonAvenue,NewYork,NY10016,UnitedStatesofAmerica BritishLibraryCataloguinginPublicationData
Dataavailable
LibraryofCongressControlNumber:2023946171
ISBN9780198822066
DOI:10.1093/oso/9780198822066.001.0001
Printedandboundby
CPIGroup(UK)Ltd,Croydon,CR04YY
LinkstothirdpartywebsitesareprovidedbyOxfordingoodfaithand forinformationonly.Oxforddisclaimsanyresponsibilityforthematerials containedinanythirdpartywebsitereferencedinthiswork.
Preface
Thisbookisthefirstvolumeofatwo-partproject, TimeRegained,articulatinga newapproachtotheanalysisoftimeinmodernphysicaltheory.OurparticularconcerniswiththeProblemofTimeasitoccursintheorieswhichfeaturedynamical lawsthatareinvariantundertimereparameterizationsymmetries.Theclassofsuch theoriesincludesbothsimplemechanicaltheoriesandthegeneraltheoryofrelativity andprospectivetheoriesofquantumgravity.Ourgoalistoprovideasolutiontothe problemoftimesuchthatdeterminatetime-orderingstructurecanbereconciledwith reparameterizationsymmetry.Thepresentvolumeisfocusedonanalyticalformulationsofclassicalmechanicaltheory.Thisrestrictedcontextwillallowustodevelop anewframeworkfortheanalysisofsymmetryandstructureinphysicaltheoryand provideafullygeneralandexplicitresolutionoftheclassicalmechanicalproblemof time.Inthesecondvolume,theframeworkwillbeextendedtothecontextofclassical andquantumgravitationaltheoriestowardsbothformalresolutionofthegravitational problemoftimeingeneraltermsandanexplicitsolutionrealizedinthecontextof simplecosmologicalmodels.Thiscosmologicalsolutionwillbefoundtohaveattractive novelconsequencesincludingunitarityandsingularityresolution.
Inthemostgeneralsenseourprojectisoneconcernedwiththe naturalphilosophy oftime.Assuch,weintendourworkasacontributiontobothphysicsandphilosophy. Oursisnot,however,aprojectregardingthe interpretation ofphysicaltheoryorthe metaphysics oftime.Rather,ourprincipalgoalistomotivateandarticulateanovel proposalforthe development ofphysicaltheory.Themainfocusofthepresentvolume istheproblemoftimeasitoccursinclassicalmechanicaltheoriesandourproposal isdesignedspecificallyasaresponsetotheprobleminthatcontext.Firstandforemost,therefore,thisbookisintendedasacontributiontomathematicalphysics.In ordertoformulateandimplementoursolutiontotheclassicalmechanicalproblemof timenewworkonthegeometricfoundationsofmechanicaltheorieswillberequired. Inparticular,wewillprovideaformalismforthecomprehensiveandrigorousanalysisofreparameterizationsymmetriesthatsupersedesthatprovidedbythestandard approachduetoDirac.
Ourformalanalysiswillbebuiltuponthesustainedanalysisofatangledknot ofhistoricalandphilosophicalproblemsrelatingtotimeandsymmetry.Mostsignificantly,wewillconsiderphilosophicalargumentsregardingtime,asfoundinthework ofNewton,Leibniz,andMach,andphilosophicalargumentsregardingsymmetry,as foundintheworkofvariouscontemporaryauthorsinphilosophyandfoundationsof physics.Inthisrespect,thisbookisalsoaresearchmonographinthephilosophyof physicswhichengageswithcoreissuesinthehistoryofnaturalphilosophy.Wedo nottakethemathematicalphysics,philosophical,andhistoricalaspectstobedisconnected.Rather,wewilladoptthemethodologicaloutlookofwhatmightbecalled
vi Preface
a‘three-field’approachtothefoundationsofphysics:aninterdisciplinaryapproach simultaneouslyapplyingmethodsandinsightsfrommathematicalphysics,thehistory ofnaturalphilosophy,andthephilosophyofphysics.
Ourultimategoalisnot,however,merelytoprovideaunifiedphysical,philosophical,andhistoricalanalysisoftheproblemoftimetakeninisolation.Rather,wefind theproblemoftimetobebothadomainofenquiryinitsownrightanda‘resource’, providingtoolsthatcanbeproductivelyappliedtootherdomains,cf.Rickles(2020).
Ontheonehand,wewillviewtheproblemoftimeasaphysical,philosophical,and historicalsubjectinitsownright,withattendantproblems,questionsandformalchallenges.Butontheother,wewillviewtheproblemasanarenafordevelopingnew concepts,tools,andtechniques,whichfindapplicationsinotherdomains.Whenseen fromthisperspective,theproblemoftimegainsconsiderablevalueasatopicofstudy sinceitbringsintoreliefkeyissuesinthestudyoftimeinclassicalmechanicaltheories.
Acknowledgements
SupportandFunding. Thegenesisofthisprojectcanbetracedtoaaprecisespatiotemporalcoincidenceinthetermsofthefirstdiscussionofitstopicinthefirst meetingofitsauthorsataconferenceinBrisbanein2011,anditsdevelopmenthas beenspreadacrossspaceandtimeencompassingAustralia,Canada,theChannelIslands,theNetherlands,Germany,theUnitedKingdom,andRomania.Thedebtswe havejointlyaccruedincompletingthisbookaredifficulttoexhaustivelyexpress.Of particularnoteareearlydiscussionsregardingtheproblemoftimewhichoneorboth authorsprofiteddeeplyfromwithJulianBarbour,OliverPooley,andHansWestman.PartsofthebookhavegreatlyprofitedfromfurtherinteractionswithEdward Anderson,RicArthur,AlexBlum,MartinBojowald,HarveyBrown,JeremyButterfield,AdamCaulton,DavidCobb,ErikCuriel,Ana-MariaCret , u,KarenCrowther, RadinDardashti,RichardDawid,PeteEvans,SamFletcher,SimoneFriedrich,SteffenGielen,HenriqueGomes,JonathanHalliwell,StephanHartmann,PhilippH¨ohn, NickHuggett,LucyJames,TimKoslowski,JamesLadyman,HuwPrice,JamesRead, DeanRickles,BryanRoberts,DonaldSalisbury,SimonSaunders,StevenSavitt,Lee Smolin,TonyShort,DaveSloan,KurtSundermeyer,TzuChienTho,JimWeatherall, andChrisW¨uthrich.WeareparticularlyappreciativetoRicArthurandErikCuriel fordetailedcommentsondraftchaptersofthemanuscript.Materialdevelopedtowards thisbookhasalsoreceivedfeedbackfromawidevarietyofaudiencesinpresentations andfromvariousanonymousreviewersofresearcharticles.KTisgratefultoUniversity ofBristolstudentsonthecourses Space,TimeandMatter and AdvancedPhilosophy ofPhysics forfeedbackonmaterialthathasusedinthepresentbook.
InitialworkonthisprojectwassupportedbythePerimeterInstituteforTheoretical Physics,theCentreforTime(UniversityofSydney),RadboudUniversity,UtrechtUniversity,andtheMunichCenterforMathematicalPhilosophy(Ludwig-MaximiliansUniversit¨atM¨unchen).WearegratefultoHuwPriceandStephanHartmannforfacilitatingthisearlyinstitutionalsupportaswellastotheAlexandervonHumboldt FoundationandtheNetherlandsOrganisationforScientificResearch(NWO)(Project No.620.01.784)forfinancialsupport.KTisparticularlygratefultocolleagues,students,andacademicvisitorsattheBristolDepartmentofPhilosophy.Thisworkcould nothavebeencompletedwithouttherichscholarlyandcollegialatmospherethatBristolhasprovidedoverthelasteightyears.Significantworktowardsthisprojectwas completedbyKTduringaUniversityResearchFellowshipin2018/19,supportedby theUniversityofBristol.ThanksisalsoduetoOxfordUniversityPress,andinparticularSonkeAdlungandGiuliaLipparini,forpatienceandsupportnotwithstanding thesomewhatglacialprogressofthisproject.
AfinalandmostsignificantnoteofthanksisduetoAnaandNienkefortheir constantsupportandencouragement.
PreviouslyPublishedMaterial Thevastmajorityofthematerialpresentedhereis new.Thatsaid,variouselementsbuildindifferentwaysonexistingpublishedworksof theauthors.Whenwearedrawingexplicitlyonpublishedmaterial,thisisindicatedbelow.Therearetwosubstantialtranchesofmaterialthatarereproducedfromprevious work.First,weareparticularlygratefultoElsevierforpermissiontorepublishpartsof
viii Acknowledgements
thearticle‘OnMachonTime’whichwaspublishedin StudiesinHistoryandPhilosophyofSciencePartA,89,84–102whichisincludedinChapter4.Second,Chapter12 featuresmaterialfromthepresubmission,preprintversionofthearticle‘Schr¨odinger EvolutionfortheUniverse:Reparameterization’,philsci-archive.pitt.edu/11299/.Finally,atamoreminorlevel,wearegratefultoOxfordUniversityPressforpermission torepublishseveralparagraphsfromthearticle‘TimeRemains’, BritishJournalfor thePhilosophyofScience,67(3),663–705,whicharereproducedinChapter14.
1Introduction 1
1.1TheObjectsofOurEnquiry1
1.2SymmetryandEvolution4
1.3TransformingStructures10 1.4TimeRegained17
1.5DirectedTimeOrderingandTime’sArrow22
PARTINATURALPHILOSOPHYOFTIME
2OnNewtonOnTime 27
2.1OnNewton’sMethodologyintheScholium27
2.2TheTripartiteNatureofNewtonianTime30
5StructureandPossibility
x Contents
6.4IsolatedSubstructuresandNarrowSymmetries100
6.5NomicStructureofNewtonianMechanics103 6.6ChapterSummary109
7IrregularNomicStructure 110
7.1IrregularLagrangians110
7.2ConstrainedHamiltonianMechanics112
7.3Dirac’sTheorem116
7.4Noether’sSecondTheorem119
7.5ChapterSummary121
8DiagnosingDynamicalRedundancy 122
8.1VariationalSymmetriesofHistories122
8.2Noether’sSecondTheoremRevised125
8.3InitialValueConstraints131
8.4DynamicalRedundancy136
8.5NomicStructureofBarbour–BertottiTheory140 8.6ChapterSummary150
9TheNewFramework 151
9.1TheAIRClassification151 9.2TheNomic-AIRAnalysis156
9.3GlobalandLocalStructures160
9.4ChapterSummary161
PARTIIITHEPROBLEMOFTIMEINCLASSICALMECHANICS
10SpatiotemporalStructureandTheoryRe-Articulation 165 10.1StructuresandHeuristics165 10.2SpatiotemporalStructureinNewtonianMechanics170 10.3SpatiotemporalStructureinBarbour–BertottiTheory175 10.4ChapterSummary177
11LocalTemporalSymmetry 178
11.1TimeReparameterizationInvariance178 11.2DynamicalRedundancyandEvolution181 11.3TemporalLeibnizShifts185 11.4ChapterSummary186
12ReparameterizationInvariantDynamics 187
12.1JacobiActionsasGeodesicPrinciplesonConfigurationSpace187 12.2TotalEnergyasaConstantofMotion189 12.3GeneralizedHamilton–JacobiFormalism192 12.4IntegralsofMotionandCompleteObservables195 12.5ChapterSummary200
13TemporalStructureRegained 201
13.1DifferentiatingDynamicalRedundancyandEvolution201 13.2ADynamicalViewofHamiltonianConstraints204
Introduction
1.1TheObjectsofOurEnquiry
Atoncepossessingaunityofnatureandaninfinitevariegationofform.Singularly constitutiveofhumanexperienceandthesubjectofinexhaustiblydiverseartistic, philosophical,andscientificdiscourses.Suffusedthrougheverythingandyetnothing in-and-ofitself.Timeisproblematic.Weknowpreciselywhatitis,untilwebeginto discussit.Itisthiscombinationofunityandmultiplicity,familiaritiesandintangibility, thatshouldperhapsbedesignatedthemasterproblemoftime,ofwhichallothersare mereshadows.Yet,therecanbenosubstantiveprogressinanyphilosophicalenquiry intothenatureoftimewithoutfirstsettingafirmdelimitationofitsremit.Whatwill wemeanbytheproblemoftime?Whatapproachwillwetaketowardsitsinvestigation? Whatwouldconstituteasolution?
Letusstartbyprovidingabriefcommentonourmethodologicaloutlook,echoingtheremarksofthePreface.Theprimaryrestrictionwewillmakeinwhatfollows istheassumptionofacontemporaryscientificperspectiveinwhichouroutlookon boththeproblemanditssolutionwillbeanchoredinmethodsofmoderntheoretical physics.Ourmethodologywillbeaninherentlyinterdisciplinaryone,drawing,inaddition,upontoolsfromanalyticphilosophy,thephilosophyofphysics,andthehistory ofnaturalphilosophy.Theoverridingapproachwewilladopt,however,willbethat ofmathematicalphysics.Ourgoalwillbetopreciselyformulateandsolveaspecific probleminthearticulationofclassicalmechanicaltheory,understoodfromamodern geometricperspective.Indoingthiswewillberequiredtoconstructnewformalapproachestothegeometricanalysisofsymmetryandevolutioninmechanicaltheory. Thereisnoscopeforapurelyinterpretativesolutiontotheproblemoftimeinclassical mechanics.Anapproachfoundeduponthemethodologicaloutlookofmathematical physicsisthusunavoidable.
Wecanfurtherconstrainthescopeofourinvestigationsbydelimitingtwodimensionsofanalysis.Thefirstdimensionistheaspectsoftimeor,asweshallmore preciselyframethem,the temporalstructures thatwewillconsider.Ourenquiryisa foundationaloneinthesensethatthetargetofourformalexcavationsshallbethe bare substratum oftimeasrepresentedinmechanicaltheory.Wewillfocusoursustained attentionupontheprovisionofamaximallyprecisephysico-mathematicalcharacterizationofthebasicstructuralcharacteristicsoftime.Thelimitationinthescopeofour enquirytobasictemporalstructureallowsustocentreouranalysisuponthetemporal structureofmechanicaltheoriesinwhichthefunctionoftimeandtemporalityisat itsmostminimalintermsofproviding undirectedtimeorderings and durations.The firstwewillcall chronordinalstructure,thesecond chronometricstructure.Athird
keytemporalstructurerelatestotherepresentationof empiricalfeatures oftimeor temporality.Thiswewillcall chronobservable structure.Amajorpreoccupationin whatfollowsshallbetheexplicationandanalysisofchronordinal,chronometricand chronobservabletemporalstructuresasfoundwithinclassicalmechanicaltheories.
Theseconddimensionofanalysisthatwillactasaframeforourinvestigationsis theidentificationoftheproblemitself.Thatis,ourendeavourswillbefocusedupon aspecificchainofinterrelatedissuesintheanalysisofparticularaspectsoftimein classicalmechanicaltheorywhichcantogetherbeidentifiedas the problemoftime. Inordertobetterunderstandtheproblemasitoccursinmodernphysicaltheoryit willserveusparticularlywelltoconsidertwo precursorproblems,eachofwhichcan beidentifiedinhistoricaldebatesregardingthenatureoftime.Inordertopresent theseproblemswemustfirstmaketwocrucialfurtherterminologicalspecifications, eachofwhichwillbeexplicatedinmoredetailshortly.First,temporalstructurethat isunchangedundervariationbetweensymmetryrelateddynamicalmodelsinatheory is invariant structure.Second,temporalstructurethatischangedundervariation betweendynamicallyrelatedmodelsinatheoryis dynamicallyrelative structure. The chronordinalproblem isthentofix determinatechronordinalstructure asboth invariantanddynamicallyrelative.The chronometricproblem istofix determinate chronometricstructure thatis invariantanddynamicallyrelative. Eachoftheseproblemscomesfromadesiretorepresenttemporalstructureas invariantanddynamicallyrelative,inthesensewewilldefinebelow,combinedwitha requirementfortwokeytypesofsuchstructure,chronometricstructureandchronordinalstructure,tobedeterminate.Therequirementfordeterminatechronordinalstructurewillbeunderstoodasa pragmaticnecessity,whiletherequirementfordeterminate chronometricstructurewillbeunderstoodasan empiricalnecessity.Thusineachcase, thesearemorethaninterpretativeproblems;rathertheyarephysico-mathematical problems,relatingtothetemporalstructureswhicharerequiredtobemathematically well-definedinordertoprovideanadequatemechanicalrepresentationofdynamical motions.
Anovelachievementinwhatfollowswillbetheidentificationoftheprecursorproblemsattwocrucialjunctureswithinhistoricaldiscussionsofthenaturalphilosophy oftime.Theprecursorproblemswewillidentifyarefoundwithintheearlymodern debatesregardingthe‘absolute’and‘relative’statusoftimeinmechanicaltheory,in particular,withintheclassicabsolutevsrelativetimedialectic,asexpressedinthe correspondencebetweenLeibnizandClarkeintheearly1700s.Stillinthehistorical naturalphilosophicalcontext,wewillalsofindtheseproblemsperspicuouslyexpressed intheworkofErnstMachtowardstheendofthe1800s.OurdiscussionoftheMachian viewoftimewilltakeplacenotonlyintheparticularcontextofadialecticwiththe originalNewtoniantreatmentbutalsoincomparisonwithworkbyMach’scontemporariesonthereframingofNewtonianabsolutetimeintermsofinertialclocks.Ineach case,wewillargue,theinformalproblemisattheheartofkeydebates,disputes,and ambiguities.Newton,Leibniz,andMachallgrappledwiththeprecursorproblemsof time,andvaluablelessonscanbelearnedfromtheirstruggles.Itwillproveofinvaluableprofittoourconstructiveprojecttodeepenourunderstandthefoundationsof theprogenitorproblemsoftimeasfoundinthewritingsofthesethreethinkers.
DiscussionoftheprecursorproblemsinthecontextofthehistoryofnaturalphilosophyoftimeandtheviewsofNewton,Leibniz,andMachwillbethefocusofPartI ofthismonograph.Thiswillleadintoamoreformalandgeneralanalysisofsymmetry andstructureinphysicaltheorythatwillbedevelopedinPartII,themainideasof whichwillbesummarizedshortly.Theformalizedmodernproblemoftimeisfocusof PartIII.Itwillbeworthwhiletogiveabriefoverviewofhowweproposetoformulate andsolvethisproblemnow.
Thisproblemoftimeoccurswithinallmechanicaltheoriesinwhichthelawsare invariantunderlocaltimerelabelling.Such reparameterizationinvarianttheories are thecontextinwhichthemodernclassicalmechanicalproblemoftimecanbeformally statedandinwhichoursolutionshallbearticulated.Theproblemcanbestatedas follows: theproblemoftimeinclassicalmechanicsisthatthesymmetryproperties ofreparameterization-invarianttheorieswithregardtochronometricandchronobservablestructureenforceindeterminacywithregardtosuchstructureunderthestandard approachtogaugesymmetry.
Oursolutionwillbefirsttodemonstratethatthestandardapproachtogauge symmetryisinadequatetothetreatmentofreparameterizationinvarianttheoriesand secondtoformulateageneralandfullyadequatealternativebaseduponamoreperspicuousanalysisoftemporalsymmetryandstructure.Ourapproachissuchthat reparameterizationinvarianceisdemonstratedtobefullycompatiblewithdeterminatechronordinalstructure.Assuch,thenovelapproachtosymmetryandevolution inclassicalmechanicsthatwewillestablishinthismonographwillprovidearesolution oftheproblemoftimeinclassicalmechanics.Wewillprovideaformalanalysisofthe symmetryandstructureofreparameterizationinvarianttheoriesthatallowsfordeterminateandwell-behavedchronometric,chronobservable,andchronordinaltemporal structures.
Thisworkwillprovideaformalbasistorejectalternativeviewsontheproblemof timeinclassicalmechanics.Mostsignificantly,wewilldemonstratetheformalinadequacyofapproachesbaseduponsupposedequivalencebetweendynamicsandgauge symmetry,whichisoftentakentoleadtowardstheoutrightdenialoftemporalevolution.Thisviewisoftenonlyimplicitlyexpressedintheclassicalmechanicalcontext butisastraightforwardimplicationofthestandardinterpretationofHamiltonian constraintswhenappliedtoreparameterizationinvarianttheories.Theessenceofthis viewhasbeenmostvividlyexpressedintermsofthesloganthat‘motionistheunfoldingofagaugetransformation’(HenneauxandTeitelboim,1992,p.103).That suchparadoxicalstatementscanbefoundwithintextbooktreatmentsofcontemporaryphysicaltheoryiswithoutdoubtremarkable.Onemightplausiblyclassifysuch anunderstandingasthepseudo-problemoftime.Onemajorgoalofourprojectwill betodemonstratethatthepseudo-problemispreciselythat.Supposedequivalence betweenmotionandgaugesymmetryrestsuponaformalconflation.Inparticular, wewillimplementanewformalanalysisthatallowsonetoexplicitlydifferentiatethe generatorsofevolutionand‘gauge’symmetryinreparameterizationinvarianttheories. Fundamentaltimelessnessthusrestsuponamistake.Motionisnottheunfoldingofa gaugetransformation.Withthecorrectmathematicaltoolsonecanclearlydistinguish
thefundamentallydistinctrolesofsymmetryandevolutioninreparameterizationinvarianttheoriesofclassicalmechanics.
Onamoreconstructivenote,weshouldmentionasecondalternativeapproachto theproblemoftimethatworkstowardsadeflationratherthanasolution.Theessence ofthisviewisideathatafunctionallyadequatemechanicscanberecoveredbasedupon arelativizedandunderdeterminedchronordinalstructure.Underthisview,chronordinalstructurecanbebuiltinternallytoamechanicalsystembyreferencetoparticular degreesoffreedomthatplaytheroleofinternalclocks.Thisviewhasbeenadvocated consistentlyinthecontextofreparameterizationinvariantclassicalmechanicaltheoriesbyRovelli.1 Formally,thisapproachwillbeshowntobeacomplementary,yetin acertainspecificsensemorelimited,thanourownanalysis.
1.2SymmetryandEvolution
Ouranalysisofsymmetryandevolutioninclassicalmechanicsisdesignedtobeof independentvalueoutsidetheanalysisofreparameterizationinvarianttheoriesand theproblemoftime.Weconstructanewframeworkfortheanalysisofsymmetry andstructureinmechanicaltheorywhichallowsfortheanalysisofthefullsetof transformationpropertiesofanystructurethatcanbedefinedonthemodelspace ofatheory.Thisframeworkallowsforafine-grainedandunambiguousidentification of‘gaugesymmetries’intermsoftheexistence,ornot,ofinitialvalueconstrains. Moreover,ourframeworkwillalsoallowfortheidentificationofcoreheuristicsfor theoryextensionandre-articulation.Thecoreaspectsofourframeworkcanbeoutlined informallyasfollows.FullformaldefinitionsandproofswillbeprovidedinPartII.
1.2.1ThreeLevelsofTheoreticalStructure
Aphysicaltheorycanbeanalysedintermsofthreelevelsofstructure,eachwith differentformsandfunctions.Atthemostbasiclevel, constitutivestructure isthe mostbasicstructureofatheory.Thisisthestructurethatonemustassumeinorder tobuildthespaceofkinematicallypossiblemodels.Thatis,thespacewhichrepresents thebasic‘pre-nomic’setofpossibilitiesadmittedbythetheory.Eachofthesemodels canbethoughtofassomethinglikeabareuniverse,strippedoflawsanddynamics.The constitutivestructuresarethoserequiredtoformulatethespace, K,of kinematically possiblemodels (KPM)ofthetheory.Forthemostpartwewillassumethatthe constitutivestructuresconsistof:i)amanifoldstructureusedtocharacterizephysical events,andrepresentedbyadifferentialmanifold;ii)geometricstructures,usedto characterizerelationsofordering,distanceandorientationbetweentheevents;and iii)matterstructures,usedtocharacterizethenon-geometricmaterialcontent.
Modelswithdifferenttokensofthesametypeofconstitutivematterandgeometric structurearetypicallyconstitutivelydistinctKPMsofthesametheorydespitethefact thattheysharethesameconstitutivestructure.Thus,forexample,two-andthreebodyparticlemodelscanbeunderstoodashavingthedistincttokensofacommon Newtonianconstitutivestructure.
1 SeeinparticularRovelli(2002,2004,2007).
Thetoken-typedistinctionwillallowustodistinguishbetweenthefollowingtwo cases.FirstwehavestructurecommonbetweenallKPMswhichsharethesame type ofstructure.Suchstructureisconstitutivelyfixed.Constantsofnaturecantypically beunderstoodasanexampleofconstitutivelyfixedstructuresofatheory.Second wehavestructurethatiscommonbetweenallKPMswhichsharethesame token of structurebutwhichvariesbetweenatleasttwodistincttokensofthesametypeof constitutivestructure.Constantsofmotioncantypicallybeunderstoodasanexample ofconstitutivelyfixedstructuresofatheory.Thisdistinctionallowsfordifferentiation betweenthemodalstatusoftwodifferenttypesofstructure.Thatis,structurethat isthesameinallKPMsofthesamemodeltype,andstructurethatcanvarybetween kinematicallypossiblemodelsthatinstantiatedifferenttokensofthattype.
WithregardtoKPMs,ourframeworktakesaformsimilartothatofwhatweshall callthe StandardFormalism usedtocharacterizethemodelspaceofaphysicaltheory. ThestandardformalismisarticulatedintermsofaspecificationofthespaceofKPMs togetherwithasetofsolution-independent‘fixed’(or‘non-dynamical’)fieldscommon toallKPMs,andasetof‘non-fixed’(or‘dynamical’)fieldsnotcommonbetweenall KPMs.Constitutivelyfixedinoursensethuscoincideswithfixedwithinthestandard formalism.WewilldiscussthisrelationshipatlengthinChapter5andreturnbriefly totheconceptoffixedstructureshortly.
Nomicstructureorlaw-likestructureisthestructurethatrepresentsthelawsof aparticulartheory.Inourframeworknomicstructurewillhavetwoimportantand distinctfunctions.Thefirstfunctionofnomicstructureistopickoutapartitionin thespaceofKPMs:thatis,totelluswhichmodelsaredynamicallypossibleand whicharenotdynamicallypossible.Wecanformalizethispartitioningfunctionin termsofanomicstructurethatpartitionsthespaceofKPMsintothepropersubspaceofdynamicallypossiblemodels,orDPMs, D ⊂ K.Thesecondfunctionofnomic structureistoprovideuswithanequivalencerelationbetweenDPMs.Theequivalence relationfunctionprovidesamethodologyfordeterminingwhichDPMsaredynamically distinctandwhicharedynamicallyidentical.Therelevantnotionofdistinctnessand identityishereanomiconeratherthananonticone;thatis,adistinctionbasedupon adifferencethatthelawspickoutbetweentwomodelsandnotadistinctionthatis necessarilyequivalenttoastrongmetaphysicalnotionofdistinctnessandidentity.
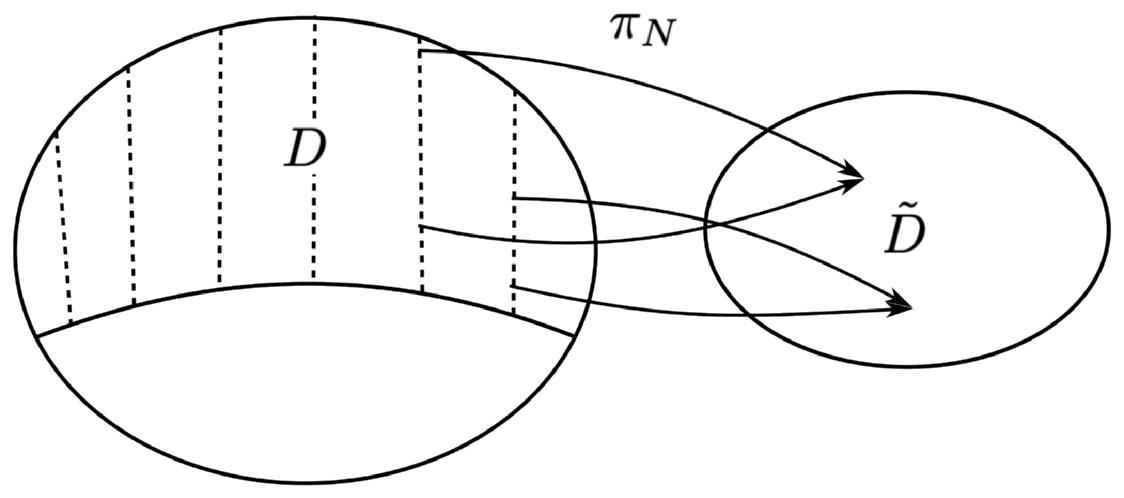
Wecanexplicitlyformalizetheequivalencerelationfunctionofnomicstructurein termsofa ProjectionMap, πN .Thisissomenomicstructurethatservesto‘projectout’ distinctionsbetweenmodelsaccordingtosomedynamicalequivalenceprinciple.We candesignatethespaceofequivalenceclasses D of D thespaceofDistinctDynamically PossibleModels(DDPMs);thisallowsustoconsidertheprojectionfromthespace ofDPMstothespaceofDDPMs: πN : D → ˜ D.Theroleofthenomicstructure canbegivenaschematicrepresentationasperFig.1.1wherewehaveintroducedthe terminologyofa‘fibre’fortheequivalenceclassofDPMs.
1.2.2SymmetryandEquivalence
Theterminologywehaveintroducedthusfaralreadyaffordsusresourcestodemarcate anumberofconceptsofsymmetryandequivalence.Inparticular,wearenowina
namicallypossiblemodels.Thedottedlinesare‘fibres’thatrepresentdynamically equivalentmodelswhichtheprojectionmap, πN ,mapsintosinglepointsinthespace ofdistinctdynamicallypossiblemodels, ˜ D positiontodisambiguatetheideaofasymmetryasatransformationwhich‘maps solutionsintosolutions’viaathreefolddistinction.
Firstwecandistinguish non-symmetrymaps.ThesearemapsbetweenDPMsof atheorythatareconstitutivelydistinctatthetokenlevel;thatis,mapsbetween differenttokensofthesameconstitutivestructure.Thesemapstakesolutionsinto solutionsbutarenotsymmetriesinanyrelevantsensesincetheydonotpreserve constitutivestructureatthetokenlevel.Simpleexamplesincludemappingbetween two-bodyandthree-bodysolutionsinNewtonianmechanicsandmappingbetween SchwarzschildanddeSittersolutionsingeneralrelativity.
Second,wecandistinguish broadsymmetrymaps.Thesearemapswhichtransform betweenDPMsthatareconstitutivelyequivalentatthetokenlevel.Broadsymmetry mapstransformbetweenDPMswiththesametokenoftheconstitutivestructure;for example,mapsthattransformbetweenthedifferentinitialconditionsofathree-body Newtoniangravitationalsystem.
Third,wecandistinguish narrowsymmetrymaps.Anarrowsymmetryisasub-set ofthebroadsymmetrieswhichcorrespondtomapsbetweenDPMswhichareconstitutivelyequivalentanddynamicallyequivalent.Theintuitiveandvaguelyexpressedidea of‘symmetrytransformation’canbeprecisifiedasourconceptofnarrowsymmetry.
FollowingBelot(2013),itisworthmentioningatthisstageofouranalysisthat thestandardapproachestothedynamicalformalisationofsymmetriesintermsof variationalsymmetries,divergencesymmetries,orHamiltoniansymmetrieswillnot ontheirownfurnishareliablenotionofnarrowsymmetry.Thisisbecause,aswill bediscussedinmoredetaillater,therearealwayscaseswheresuchformalisationsof dynamicalsymmetriesleadusto:i)designateasequivalentDPMswhichwewantto thinkofasdynamicallydistinct;andii)designatedistinctDPMswhichwewantto thinkofasdynamicallyequivalent.Ourmethodologywillbetoapproachtheresolutionofsuchproblematicambiguitiesinstages.Thefirststageistheformulationofa deliberatelytooweakpreliminarystancetowardstheclassificationofnarrowsymmetriesbuiltuponanappropriaterefinementofoneofthestandardformalsymmetry
Fig. 1.1: Schematic representation of the nomic structure. D is the partition of dy-
definitions.Thesecondstagewillthenbetomodifythenomicstructuresuchthatthe furtherphysicallywell-motivatednarrowsymmetriescanbestipulated.
Wecanspecifyourweaknotionofnarrowsymmetryviaasufficientbutnotnecessaryconditionasfollows: preliminarystanceonnarrowsymmetries:allbroadsymmetrieswhicharevariationalsymmetries(i.e.transformationsthatleavethevariational probleminvariant)ofthefullsystemunderstudyarenarrowsymmetries. Hereweare usingtheword‘stance’followingapartialinspirationfromvanFraasen’sepistemic voluntarisminthecontextofphysicalreasoningregardingsymmetries,laws,andtheoreticalmodels.Inparticular,wetaketheretobesignificantroomfor‘operationofthe will’whenitcomestoourchoiceofnarrowsymmetryprinciples(vanFraassen,1989; vanFraassen,2008;Okruhlik,2014).Further,thestanceisbydesignapreliminary one,opentorevisionandmodificationbutconstitutingasolidworkinghypothesis thatcanbeusedasafirststepintheanalysisofthenarrowsymmetriesofaphysical theory.
Thepreliminarystanceallowsustoclassifyasnarrowsymmetriesthemostbasic andnaturalexamplesofmapsbetweendynamicallyequivalentmodels.Forexample, time-independentrigidEuclideantransformationsofasetofgravitatingNewtonian pointparticlesarevariationalsymmetriesandthuswewillrecovertheexpectation thatre-embeddingthesamesetofNewtoniangravitationalmotionsinauniformly spatiallyshiftedspacewillleadtoadynamicallyequivalentmodelofthetheory.
Theobviouscomplicationforeventhissimplecasearetime-dependenttransformationssuchasGalileanboosts.Thesearenotvariationalsymmetriesofasetof gravitatingNewtonianpointparticlesandthus,underthepreliminarystance,models relatedbysuchtransformationsaretakentobedynamicallydistinct.However,the physicalproblemathandmayindicatethattherelevanttransformations should be narrowsymmetries.Thisiswherethesecondstagecomesin.Onourapproach,such transformationsmaybepromotedtonarrowsymmetriesbyamodificationofthevariationalprinciple.Thenarrowsymmetriesofatheorycanbeadaptedtotheparticular contextinwhichthetheoryisbeingapplied,butatthecostofexplicitlychangingthe variationalprincipleusedtodefinethesolutionsofthetheory.Explicitconsideration ofthiscasewillbeprovidedin §6.5and §8.5.
1.2.3IrregularNomicStructure
Thephysicalsignificanceoftheambiguitiesinthedynamicaldefinitionofnarrowsymmetryshouldnotbeoverstated.Theprimaryroleofdynamicalequivalenceprinciples, andthusthedefinitionofnarrowsymmetries,withinmechanicaltheoryisinthespecificationofthedynamicalevolutionofagivensystemintermsofwell-posedequations ofmotion.Fromtheperspectiveofthevariationalproblem,themostfundamentalsubdivisionisbetweenthosetheoriesinwhichthenomicstructure enforces aprojection asarequirementforwell-posednessandthosetheoriesinwhichthenomicstructure whichallowsforindependentwell-posedequationsofmotionforallmodelswhichare DPMs.
InthecontextofLagrangianactionprinciplesthisisadistinctionwhichis(almost)entirelybetweenwhatareusuallycalled‘regular’Lagrangiansand‘irregular’ Lagrangians.Withthisinmindwecanintroducethedistinctionbetweenregularand
irregularnomicstructure. RegularNomicStructure isnomicstructurethatenforcesa partitionbutnotaprojection.ForatheorywithregularnomicstructureitisinprinciplepossibletotreatallDPMsasprimefaciedynamicallydistinct.However,thereare typicallygoodphysicalreasonstoapplyaprojectionbasedonpreliminarystance.It is,however,inprinciplepossibletotreatallDPMsasprimefaciedynamicallydistinct, notwithstandingthepreliminarystance.
Bycontrast, IrregularNomicStructure isnomicstructurethatenforcesapartition andaprojection.Foratheorywithirregularnomicstructureitismandatoryto classifyatleastsomeDPMsasdynamicallyequivalentinordertoconstructawellposedinitialvalueproblem.ItisinprinciplethenpossibletotreatallDPMswhichare independentlywell-posedasdynamicallydistinct.However,againtherearetypically goodphysicalreasonstoapplyaprojectionbasedonthepreliminarystance.
Thecrucialphysicalideaisthatintheorieswithregularnomicstructure,alldegreesoffreedomhaveindependentlywell-posedequationsofmotionassociatedwith them.Foratheorywithregularnomicstructure,thereisanimportantsenseinwhich thereis formally noredundancyorunderdeterminedequations.Theclassoftheories withirregularnomicstructureisimportantlydifferent.Inparticular,withafewimportantexceptions,thesetheoriesaresuchthatthereexistdegreesoffreedomwhich donothaveindependentlywell-posedequationsofmotionassociatedwiththem.In suchcircumstances,wetypicallyencounteraperniciousformof dynamicalredundancy whereinthereexisttransformationsofthedynamicalvariablesthatleadtoanunderdeterminationintheequationsofmotion.Suchredundancy must beinterpreted asnarrowsymmetrysinceotherwisetheinitialvalueproblemwillnotbewell-posed. Thestandardterminologyforsuchtransformationsis‘gaugetransformations’andthe underdetermineddynamicalvariablesarestandardlyunderstoodas‘gauge’degreesof freedom.
Theinterconnectedproblemsofunderdetermination,gaugesymmetries,andredundancyhavebeenthesubjectofalargeamountofdiscussioninbothphysicsand thephilosophyofphysics,bothingeneraltermsandinthespecificcanonicalcontext thatisthefocusofthisbook.2 Noneoftheextantaccountsarefullysatisfactory,however.Furthermore,asalreadynoted,wetaketheproblemoffindingsuchanaccount tobethekeychallengetothecorrectdiagnosisandresolutionoftheproblemoftime inclassicalmechanics.
Thestandardtreatmentoftherelationshipbetweensymmetryandredundancy derivesfromtheDiracanalysisofconstrainedHamiltoniansystems.3 Inparticular, thekeydiagnostictoolcomesfromaprescriptionduetoDiracfortheidentification of‘gaugetransformations’andtheassociatedredundancyinsystemswithirregular nomicstructure.Thisapproachisbuiltupontheidentificationof canonicalconstraints asgeneratorsofgaugetransformations.Inbrief,theideaisthatcertainconstraint functionsthatoccurinthederivationofthecanonicalmomentaaretakentogether
2 Extensivereferencetothephysicsliteraturewillbeprovidedinwhatfollows.Keycontributions fromphilosophersare(BelotandEarman,2001;Belot,2003;Earman,2003;Rickles,2004;Rickles, 2007;Pitts,2013;PooleyandWallace,2022).Ourownanalysisprovidedbelowisbaseduponan extensionofthatprovidedin(GrybandTh´ebault,2014;GrybandTh´ebault,2016a).
3 ThetextbooktreatmentsareprovidedinDirac(1964),SudarshanandMukunda(1974),Sundermeyer(1982),GitmanandTyutin(1990),andHenneauxandTeitelboim(1992).
withrelevantconsistencyconditionstoformanalgebrathatexpressesthefailureof thecanonicalsystemtobeindependentlywell-posed.Thesolutionisthentotreat asdynamicallydistinctonlythosesolutionsthatareindependentoftheconstraint algebraintermsofthedirectionsoftheassociatedflowsonphasespace.Conversely, accordingtotheDiracprescription,phasespacepointsthatliealongtheorbitofa constraintshouldbetakentorepresentphysicallyidenticalstatesofaffairs.Thusthe transformationbetweensuchpoints,asgeneratedbytheconstraint,ismeregauge. TherearehowevervariousgeneralconsiderationsthatcallintoquestiontheDirac prescription.Thefirstisthattheprescription,bothinoursketchandinthedetailed presentationbothbyDiracandbysomelaterauthors,elidesthesignificantdifference betweentransformationsofinstantaneousstatesandtransformationsofdynamical histories.Clearly,onewouldliketobeabletomovebackandforthbetweenthe symmetriesdefinedatthelevelofhistoriesandthedynamicalredundancywhich existsattheleveloftheinitialvalueproblem.However,considerablecareisneeded insettingupsuchcorrespondences,andonitsowntheDiracapproachprovestoo coarse-toothedfortherelevantpurpose.Onegoalofourapproachistoprovidea geometricframeworkthatallowsforthedisambiguationoftheconnectionsbetween constraints,redundancy,and‘gauge’symmetriesatboththelevelofhistoriesandthe levelofinstantaneousstates.
ThesecondmorefundamentalissuewiththeDiracprescriptionisitsimplicationfor theorieswhichareinvariantundertimereparameterizations.Ageneralfeatureofsuch theoriesisthattheHamiltonianfunctionisitselfnecessarilyaconstraint.Thisthen meansthattheDiracprescriptionimpliesthattheHamiltonianfunctionisagenerator ofgaugetransformations.However,weofcourseapplytheHamiltonianfunctionalsoin theroleofthegeneratorofdynamicalmotions.Wethenarriveatourparadox:motion istheunfoldingofagaugetransformation!Herethelinesofinterpretationbecome rathercriss-crossed.Dirachimselfinfactneverendorsedsuchaparadoxicalconclusion. Moreover,theargumentthathehimselfprovidedfortheprescriptionclearlydoesnot supporttheconclusioneither.WhatisoftencalledDirac’stheoremwillbeexplicitly reconstructedin §7.3.FollowingonfromthediscussionofBarbourandFoster(2008), itshallbemadeexplicitinourrenditionofthetheoremthattheresultthatisproved byDiracislimitedinscopebytheassumptionthatconstrainedHamiltoniantheory inquestioncontainsanexternaltimevariable.Dirac’stheoremthussimplydoesnot applytoreparameterizationinvarianttheories.
AtthispointitmightbehopedthattheambiguitiesinthissituationcanberesolvedbyappealtoNoether’ssecondtheorem.Thisisbecausethesecondtheorem establishesaconnectionbetweeninvarianceofanactionunderinfinitesimaltransformationsofaninfinitecontinuousgroupparameterizedbyarbitraryfunctionsandthe existenceofgeneralized‘gauge’identitieswhichholdirrespectiveofthesatisfaction oftheEuler–Lagrangeequations.Sincereparameterizationinvarianceispreciselyan invarianceoftheactionunderaninfinitesimaltransformationofaninfinitecontinuous groupparameterizedbyarbitraryfunctions,oneisthusguaranteedtheexistenceofa gaugeidentityinthiscasealso.Onemightexpect,then,thattherelevantgaugeidentitiesallowonetoidentifydynamicalredundancywithintheinitialvalueproblemand thusremovetheambiguityintheDiracprescriptionforthecaseofreparameterization
invarianttheories.
Thesituationisnot,however,sostraightforward.Infact,newworkwillberequiredtoestablishingeneraltermstheconnectionbetweenirregularnomicstructure, Noether’ssecondtheorem,andtheexistenceof initialvalueconstraints.Itisthelatter whichareindicativeofthespecificspeciesofunderdeterminationproblemassociated withdynamicalredundancyandwhicharerequiredfortheisolationofgaugedegrees offreedom.Themajorformalachievementofthismonographistheestablishmentof afirst-ordergeometricformalismthatprovidesgeneralcriteriaforisolatingdynamical redundancy.ThesecriteriageneralizeandsupersedethoseprovidedbyeitherNoether’s secondtheoremortheDiracapproach.Theyarealsoimportantinidentifyingthecrucialambiguityregardingthepreliminarystanceinthecontextofthedistinctionbetweenvariationalsymmetries-over-historiesandvariationalsymmetries-at-an-instant. Asweshallsee,reparameterizationsshouldbeunderstoodasvariationalsymmetriesover-historiesandthusinthatsensearenarrowsymmetries.However,reparameterizationsarenotvariationalsymmetries-at-an-instantandthereforearenotnarrow symmetriesinthatsense.
Ourprojectistoprovidenewandmorefundamentaldiagnostictoolsforinterpretinggaugetheories.Thischallengeshallbetakenupintwostages.ThefirstinChapter 8willbetosetoutourfirst-orderformalismforthecaseoftheorieswithafixed timeparameterization.Theproblemofextendingouranalysistoreparameterization invarianttheorieswillbethesubjectofanextendedanalysisinPartIII.Crucialto interpretingtheimplicationsofthisnewformalismwillbethenewframeworkforthe analysisofsymmetryandstructurethatwewillsummarizebelow.
1.3TransformingStructures
1.3.1AbsoluteandRelativeStructures
Distinctconceptsof‘absolute’and‘relative’areoftenconflatedindiscussionsofthe statusofspaceandtimeinphysicaltheory.Itwillproveessentialtoourdiscussionto differentiate three basiccontrastsinthecontextofourdiscussionsofspatiotemporal structuresinphysicaltheory.HerewearetakinginspirationfromFriedman(1983, II.3).Theseare:i)absolutevsrelationalspatiotemporalstructure,whichisanontologicaldistinctionrelatingtodependencyrelations;ii)absolutevsrelativespatiotemporalstructure,whichisaformaldistinctionrelatingtonon-dynamicaltransformation properties;andiii)absolutevsdynamicalspatiotemporalstructure,whichisaphysical distinctionrelatingtodynamicaltransformationproperties.Forclarity,wewillmakea terminologicalrefinementarenamethetrioofdistinctionsas substantival vs. relational (ontologicaldistinction), invariant vs. surplus (formaldistinction),and dynamically absolute vs dynamicallyrelative (physicaldistinction).Withthisterminologyinhand letusthenconsidereachcontrastinalittlemoredetail.4
4 Thereisavastliteraturethatdiscussesindifferentwaysandusingdifferentterminologieseach ofthesedistinctions.OuraccountismostcloselyrelatedtothatofFriedman(1983,II.3).Further generaldiscussionscanbefoundinSklar1974;Earman1989;Rickles2007;Maudlin2012;Pooley2013; Dasgupta2015.Theliteraturespecificallydealingwithabsoluteandrelativespacetimestructurein thecontextofanalyticalmechanicswillbeintroducedinthecontextofourspecificdetaileddiscussions inPartsIIandIII.
Thefirstcontrastbetweenabsoluteandrelationalrestuponadistinctionwith regardtothe‘onticdependency’betweenmaterialandspatiotemporalentities.FollowingPooley(2013,p.522),asubstantivalistaboutspatiotemporalstructurewill maintainthatacompletecatalogueofthefundamentalobjectsintheuniverselists, inadditiontotheelementaryconstituentsofmaterialentities,thebasicpartsofthe relevantspatiotemporalstructure.Relationalistsmaintainthatspatiotemporalstructuredoesnotenjoyabasic,non-derivativeexistence.Accordingtotherelationalist, claimsapparentlyaboutspatiotemporalstructureareultimatelytobeunderstoodas claimsaboutmaterialentitiesandthepossiblepatternsofspatiotemporalrelations thattheycaninstantiate.
Thecontrastbetweenrelationalismandsubstantivalismcanbeconnectedtodifferentaccountsofhowonecountsdistinctontologicalpossibilities.Thisisonthebasis oftherelationalistadmittingfeweronticpossibilitiesthanthesubstantivalistprecisely becausetherelationalist,butnotthesubstantivalist,deniesthattwostatesofaffairs thatareidenticalintheirrelationalspatiotemporalstructurecanbeontologicallydistinct.Adirectequationoftheviewswithstrategiesforpossibilitycountingrestupon anoversimplificationhowever,sincesomeprominentsubstantivalviewsthatcount possibilitiesinthesamewayasrelationalists.5 Asweshallexplaininmoredetail shortly,wewillseekto‘bracket’theontologicaldistinctionbetweenrelationalismand substantivalisminourdiscussionswheneverpossible.Thattheconnectionbetween possibilitycountingandontologyprovestobesounderdeterminedisarguablyavindicationofsuchastrategy.Inanycase,thesignificanceforourcurrentdiscussionis thatanyontologicaldistinctionbetweenrelationalismandsubstantivalism doesnot haveacorrelateinthetransformationbehaviourofspatiotemporalstructuresunder mapsbetweenDPMsascharacterizedintheframeworkintroducedin §1.2.
Thesecondcontrastcanbecharacterizedpreciselyinourframeworkviathebehaviourofaspatiotemporalstructureundernarrowsymmetriestransformations.As notedabove,forclarity,wewillrefertothe‘absolute’spatiotemporalstructuresthat donotchangeundernarrowsymmetrytransformationsas invariant structuresand the‘relative’spatiotemporalstructuresthatdochangeinawell-behavedmanneras surplus structures.Thisclassificationwill,ofcourse,onlybedefinedinthecontext ofadefinitionofnarrowsymmetriesforaparticulartheory.Itwillthusinheritall thecomplexitiesandqualificationsinthedefinitionofnarrowsymmetriesasperour earlierdiscussions.
Theimportantpointisthatforanygivenspecificationofnomicstructureinterms ofapartitionandprojection,onehasathandanentirelyunambiguousdefinitionof themapsthattransformbetweenDPMswhichareidenticalaccordingtotherelevant nomicstandardofequivalence.Thesetransformationswithinanequivalenceclassare graphicallyrepresentedasmovingalongthe‘fibres’givenbytheverticaldottedlines inFig.1.1.Invariantspatiotemporalstructureisthenstructurewithtransformations thatareentirelytrivialasonemovesalongthefibre.Surplusspatiotemporalstructure
5 Applicationofthisgeneralstrategyforsubstantivalismwithreducedpossibilitycountingcanbe foundforinstanceinMaudlin1988;Butterfield1989;Brighouse1994.SeealsoRickles(2007)and Pooley(2013).
bycontrastisstructurethathasnon-trivial,butwell-definedtransformationproperties asonemovesalongthefibre.
Finally,wecanconsiderthethirdcontrastthatrelatestothetransformationbehaviourofaspatiotemporalstructureunder‘dynamicaltransformations’,definedas thebroadsymmetrieswhicharenotnarrowsymmetries.Wewillrefertospatiotemporalstructuresthatdonotchangeunderdynamicaltransformationsas dynamically absolute andtemporalstructuresthatdochangeinawell-behavedmanneras dynamicallyrelative 6 Itisimportantnoteherethatbyourdefinitionthedynamical transformationsaremapswhichtransformsbetweenDPMsthatareconstitutively equivalentatthetokenlevelandyetdynamicallydistinct.Thisisthecomplementof thenarrowsymmetrieswithinthesetofbroadsymmetries.
Inparalleltothesecond‘formal’distinction,inthecaseofthisthird‘physical’ distinction,itisimportantthatforanygivenspecificationofnomicstructureinterms ofapartitionandprojection,onehasathandanentirelyunambiguousdefinitionof themapsthattransformbetweenDPMswhicharedistinctaccordingtotherelevant nomicstandardofdistinctness.Thesetransformationsbetweenequivalenceclassesare graphicallyrepresentedasmovingbetweenthe‘fibres’givenbytheverticaldotted linesinFig.1.1.Dynamicallyabsolutespatiotemporalstructureisthenstructurethat issuchthatitstransformationsareentirelytrivialbetweenthefibres.Dynamically relativespatiotemporalstructurebycontrastisstructurethathasnon-trivial,butwelldefined,transformationpropertiesasonemovesbetweenthefibres.Movingbetween thefibresinspaceofDPMs D isofcourseequivalenttomovingbetweenpointsin thespaceofDistinctDPMs D,givenbytheprojection πN : D → D.Thusbyour definitionsdynamicallyabsolutestructuredoesnotchangebetweenanypointin ˜ D but dynamicallyrelativestructuredisplayedwell-definedandnon-trivialtransformation propertiesundertransformationsin D.
Asabriefaside,itisworthnotingthatdynamicaltransformationsdonotconstitute thefullsetoftransformationsbetweendistinctDPMs.Thisisbecausewearealso excludingfromourdefinitionofdynamicaltransformationsmapsbetweenDPMsof atheorywhichareconstitutivelydistinct;thatis,mapsbetweendifferenttokensof thesameconstitutivestructure.Thesemapstakesolutionsintosolutionsbutare notsymmetriessincetheydonotpreserveconstitutivestructureatthetokenlevel. Returningtoourfavouriteexamples,considermappingbetweentwo-bodyandthreebodysolutionsinNewtonianmechanicsormappingbetweenSchwarzschildandde Sitteringeneralrelativity.Whilsttheinvarianceornotofspatiotemporalstructure inthecontextofsuchconstitutivelydistinctmodelsisofgreatphilosophicaland physicalsignificance,especiallyinthecontextoftheproblemofprovidingasubstantive definitionofbackgroundindependence,theformalstructureoftransformationsinthis widercontextisnotamenabletotheanalysiswewillprovideandwillthusbetreated asadistinctcasefromdynamicaltransformationswhenrequired.
Torecap,wehaveintroducedthreebinarycontrasts:anontologicalcontrastbetweensubstantivalandrelational;aformaldistinctionbetweeninvariantandsurplus;
6 Dynamicallyabsolutestructuresinoursenseareanalogues,insomeways,toso-calledAbsolute Objects.SeePooley(2017, §7)andCuriel(2019).
AbsoluteRelative
Ontological Substantival Relational Formal Invariant Surplus Physical DynamicallyAbsolute DynamicallyRelative
Table1.1 Tableillustratingthreebinarycontrastsregardingsensesinwhichaspatiotemporalstructuremaybeabsoluteorrelative.Undertheassumptionofindependencethreebinary choicesyieldseightpossibilities.
andaphysicaldistinctionbetweendynamicallyabsoluteanddynamicallyrelative.For easeofreferenceandunderstandingwehavesetoutthesedistinctionsinTable1.1.
1.3.2BracketingOntology
Inprincipleitispossibleforagivenspatiotemporalstructuretobeunderstoodas realizedanyoftheeightpossibilitiesgivenbyarbitrarycombinationsofthethree binarydistinctions.Forexample,inprinciple,onemightholdthatagivenstructure issubstantival,surplus,anddynamicallyrelativeorrelational,invariant,anddynamicallyabsolute.Withinthecontextofourpositiveprojectwewillmakethesignificantmethodologicalchoicetotreatthethreedistinctions,substantivalvsrelational, invariantvssurplus,anddynamicallyabsolutevsdynamicallyrelativeasmutually independentandtofocusouranalysisonthesecondandthirdtotheexclusionofthe firstwhichwillbe‘bracketed’inwhatfollows.
Thisisnottosaythatwedonotrecognizethatadeepconceptualallianceexistsbetween,forexample,relationalismanddynamicalrelativity.Suchconnections willbeconsideredatlengthinourdiscussionoftheviewsofNewtonandLeibniz inPartI.Moreover,ingeneralterms,itisplausiblythecasethatatleastsomekey argumentsareatleastinpartoverlapping.Forexample,epistemologicalarguments infavourofrelationalandinvariantstructure.However,inourviewtherelationalist/substantivalistontologicaldisputecaninfactbelargelydetachedfromwhatwe taketothe physicallysignificant issuesregardingthe formalrepresentation ofspatiotemporalstructureinphysicaltheory.Theseissues,inourview,arealwaysissues regardingtheinvariant/surplusanddynamicallyabsolute/relativedistinctions.Inline withourprogrammaticaimofresolvingtheproblemoftimeinclassicalmechanics, ratherthaninterveningindebatesregardingthemetaphysicsoftime,wewillseek to‘bracket’theontologicaldisputeandfocusourenergiesonthesecondandthird physico-mathematicaldisputes.
Onespecificmeansthatwewillusetoachievethisbracketingistoleaveopenthe representationalrelationshipbetweendistinctDPMsandtheontologytheystandin forintheworld;thatis,wewillrefrainfromassumingan interpretation thatfixes eitheramodel-worldrepresentationrelationorstandardofrepresentationalequivalencebetweenmodels.Itisonlygivenachoiceofaparticularinterpretativeattitude towardsrepresentationthatournotionofdynamicallydistinctmodelscanbetakento fixarelevantnotionof ontological distinctmodels.Inparticular,sofarasthedebate betweenrelationalistsandsubstantivalistsreducestothecorrectonticpossibility,this debateistransformedintoachoiceofattitudetowardsrepresentationthatwerefrain