Measuring Industrial Concentration

depicted in Figure 15.9 consists of a single firm.The total level of pollution emitted by the firm is measured along the horizontal axis,while the unit cost of pollution is measured along the vertical axis.As before,the MSC curve represents the marginal social cost of production,which includes both the marginal private and marginal externality cost.We know that marginal social cost is an increasing function of the firm’s output level.The marginal social cost curve assumes that the firm is operating with a given level of production technology.Pollution is a by-product of production,and the amount of pollution created is a function of the underlying production technology.We will assume that the level of the pollution created varies directly with the level of the firm’s output (i.e.,the greater the level of output,the greater the level of pollution created).

On the surface,it may appear that reducing the level of pollution unambiguously benefits society.Unfortunately,nothing could be further from the truth.Pollution is a by-product of production,which generates social benefits.Thus,while reducing pollution lowers marginal social costs,it also results in a reduction of social benefits.This reduction in social benefits may be viewed as the opportunity cost of pollution abatement.This relationship is illustrated in Figure 15.9,where MCA represents the firm’s marginal cost of pollution abatement.

The position of the MCA curve depends on the firm’s production technology.If the firm switches to a production technology that results in a lower level of pollution,then the MCA curve will shift upward.The marginal private cost of production will also shift upward because of the use of the new,more costly technology,although the marginal social cost curve may be unaffected because of the reduction in negative,third-party effects. It should be clear from Figure 15.9 that with a given production technology, reductions in pollution can be accomplished only through a reduction in output.Contrary to popular belief,therefore,the optimal level of pollution is not zero,since this would imply a zero level of production.This,of course, begs the question:Is there a socially optimal level of pollution?

The optimal level of pollution in Figure 15.9 is r*.To see this,suppose that the firm produced an output level that generated pollution of r¢.At this level,marginal social cost associated with this level of pollution is MSC¢ . Reducing production will,of course,reduce the level of production,but at the cost of lower output.As long as the marginal cost of pollution abatement (i.e.,the marginal loss of social benefits from production) is less than the marginal cost of pollution,society will be made better off by reducing pollution.On the other hand,if the firm is producing at r≤,then society will be better off by accepting higher levels of production (and pollution),since the marginal cost of pollution abatement is greater than the marginal social cost of pollution.Clearly,society’s welfare will be maximized where the marginal social cost of pollution is equal to the marginal cost of pollution abatement,which in Figure 15.9 occurs at pollution level r*.Of course,

there is no a priori reason for the firm depicted to produce at this,or any other,level.Unless there is an incentive to do otherwise,the firm depicted in Figure 15.9 will produce at the output level at which marginal revenue equals marginal private cost.

Suppose that the firm depicted in Figure 15.9 maximizes profit by producing at an output level that results in r¢ pollution.Suppose further that the government has determined that the socially optimal level of pollution is r*.What can government do to reduce pollution by the amount (r¢-r)? The most obvious solution is for the environmental protection agency of the government to mandate that pollution levels not exceed r*.The firm’s management could be discouraged from violating these emission standards by the threat of fines,imprisonment,or some other legal recourse.

Alternatively,government could achieve the same socially optimal level of pollution by imposing an emission penalty fee,a fine levied on the firm per unit of pollution produced.In Figure 15.9,the optimal emission fee is f*.Whenever the marginal revenue to the firm arising from an increase in production is greater than the emission fee,it will be in the firm’s best interest to increase production and pollution until MCA = f*,which would result in the same socially optimal level of pollution r*.

The problem with both emission standards and fees is that these approaches assume that the regulator has complete information about production methods,which is rarely,if ever,the case.To highlight this point,we will relax our earlier assumption that the industry described in Figure 15.8 consists of a single firm.Suppose,instead,that the industry consists of two firms,and each uses a different production technology,which generates different amounts of pollution.This situation is illustrated in Figure 15.10, where firm1 employs a more environmentally friendly technology than firm 2.For this reason,the MCA2 curve lies above MCA1.

Suppose now that the government’s environmental protection agency wants to reduce the average level of pollution from each firm to r*.The

$

MCA 2 MCA 1

Emission standard

MCA 2

MCA 1

0 Pollution *

FIGURE 15.10 Emission

standards and incomplete information.

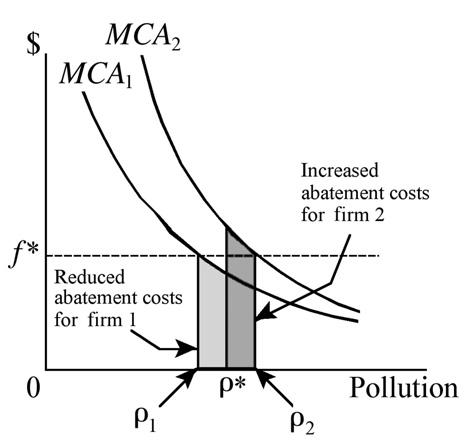
FIGURE 15.11 Emission fees and incomplete information.

government could accomplish this outcome by mandating that each firm’s pollution not exceed r*.In the situation depicted in Figure 15.10,both firms reduce the level of pollution to r*,but the marginal cost of abatement for firm 1 is less than the marginal cost of abatement for firm 2.This outcome is not efficient,however,since neither firm minimizes the cost of abatement. A more efficient solution could be accomplished by charging an emission fee.An alternative approach is for the government to impose an emission fee of f* on both firms.In this way,each firm incurs the same marginal abatement cost,but the levels of pollution produced are different.This outcome is illustrated in Figure 15.11.

Unlike the situation depicted in Figure 15.10,where a mandated emission standard resulted in different marginal abatement costs for the two firms,in this case the marginal abatement costs are the same for both firms, but the amount of pollution is different.As a result of the imposition of the emission fee f*,firm 1 will reduce the amount of pollution produced to r1 while firm 2 will increase the amount of pollution produced to r2.The average pollution produced by the two firms is the efficient level r*.One advantage of charging an emission fee is that it serves as an incentive for the high-cost firms to adopt production technologies that generate lower levels of pollution.

Unfortunately,incomplete information about the firms’ abatement costs could result in large welfare costs to society from incorrectly pricing the emission fee.This situation is illustrated in Figure 15.12,where,because of incomplete information,the government sets the emission fee at f ¢< f*,and the result of this incorrect pricing is a welfare cost to society equal to the area of the shaded region ABC.When incomplete information about abatement costs threatens to result in large welfare costs to society,setting emissions standards may be superior to charging an emission fee as a solution to the pollution problem.