2.2 Black vertices are suspicions about choosing them

1. Neutrosophic Graphs

Fuzzy(neutrosophic)-metric number is n − 2. By G is fixed-vertex, for any given vertices m and m , σ(m) = σ(m ). So fuzzy(neutrosophic)-metric dimension is (n − 2)σ(m) where m is a given vertex. cor55.15 Corollary 1.8.15. Let G be a fixed-vertex strong fuzzy(neutrosophic) wheel. Let n ≥ 3. Then every (n − 2)-set excludes center and a given vertex, is fuzzy(neutrosophic)-resolving set. Every (n − 2)-set excludes center and a given vertex, is fuzzy(neutrosophic)-metric set. Fuzzy(neutrosophic)-metric number is n − 2. Fuzzy(neutrosophic)-metric dimension is (n − 2)σ(m) where m is a given vertex.

Proof. Consider x and y are excluded by a (n − 2)-set. Let m be a given vertex which is distinct from them. By G is wheel, m has a common part with either x or y and not with both of them. It implies d(x, m) = d(y, m). Since if m has a common part with x, then d(x, m) = 1 = 2 = d(y, m). And if m has a common part with y, then d(x, m) = 2 = 1 = d(y, m). Thus m fuzzy(neutrosophic)-resolves x and y. If w is another vertex which is distinct from them, then pigeonhole principle induces at least two vertices have same conditions concerning either being in same part or in different parts. It implies (n − 3)-set isn’t fuzzy(neutrosophic)-resolving set. Therefore, every (n − 2)-set excludes two vertices from different parts, is fuzzy(neutrosophic)-metric set. Fuzzy(neutrosophic)-metric number is n − 2. By G is fixed-vertex, for any given vertices m and m , σ(m) = σ(m ). So fuzzy(neutrosophic)-metric dimension is (n − 2)σ(m) where m is a given vertex.

Fuzzy(neutrosophic) t-partite(bipartite/star/wheel) is also studied but by adding one restriction on these models. Fuzzy(neutrosophic) t-partite gets us one result involving family of them when they’re either fixed-edge or strong fixed-vertex.

Corollary 1.8.16. Let G be a family of fixed-vertex strong fuzzy(neutrosophic) t-partite with fuzzy(neutrosophic) common vertex set. Let n ≥ 3. Then simultaneously fuzzy(neutrosophic)-metric number is n − 2, simultaneously fuzzy(neutrosophic)-metric dimension is (n − 2)σ(m). Every (n − 2)-set excludes two vertices from different parts, is simultaneously fuzzy(neutrosophic)-resolving set for G. There’s an (n − 2)-set which is simultaneously fuzzy(neutrosophic)metric set for G.

Proof. By Corollary (3.31.8), every result hold for any given fixed-vertex strong fuzzy(neutrosophic) t-partite. Thus every result hold for any given fixed-vertex strong fuzzy(neutrosophic) t-partite, simultaneously. Therefore, simultaneously fuzzy(neutrosophic)-metric number is n − 2, simultaneously fuzzy(neutrosophic)metric dimension is (n − 2)σ(m). Every (n − 2)-set excludes two vertices from different parts, is simultaneously fuzzy(neutrosophic)-resolving set for G. There’s an (n − 2)-set which is simultaneously fuzzy(neutrosophic)-metric set for G. Corollary 1.8.17. Let G be a family of fixed-vertex strong fuzzy(neutrosophic) bipartite with fuzzy(neutrosophic) common vertex set. Let n ≥ 3. Then simultaneously fuzzy(neutrosophic)-metric number is n − 2, simultaneously fuzzy(neutrosophic)-metric dimension is (n − 2)σ(m) Every (n − 2)-set excludes two vertices from different parts, is simultaneously fuzzy(neutrosophic)-resolving

36

In this chapter, I introduce some applications concerning new ideas and in this ways, the results make sense more about their impacts on different models. 1.9. Applications

set for G. There’s an (n − 2)-set which is simultaneously fuzzy(neutrosophic)metric set for G.

Proof. By Corollary (3.31.9), every result hold for any given fixed-vertex strong fuzzy(neutrosophic) bipartite. Thus every result hold for any given fixed-vertex strong fuzzy(neutrosophic) bipartite, simultaneously. Therefore, simultaneously fuzzy(neutrosophic)-metric number is n − 2, simultaneously fuzzy(neutrosophic)metric dimension is (n − 2)σ(m). Every (n − 2)-set excludes two vertices from different parts, is simultaneously fuzzy(neutrosophic)-resolving set for G. There’s an (n − 2)-set which is simultaneously fuzzy(neutrosophic)-metric set for G.

Corollary 1.8.18. Let G be a family of fixed-vertex strong fuzzy(neutrosophic) star with fuzzy(neutrosophic) common vertex set. Let n ≥ 3. Then simultaneously fuzzy(neutrosophic)-metric number is n − 2, simultaneously fuzzy(neutrosophic)-metric dimension is (n − 2)σ(m) Every (n − 2)-set excludes center and a given vertex, is simultaneously fuzzy(neutrosophic)-resolving set for G. There’s an (n − 2)-set which is simultaneously fuzzy(neutrosophic)-metric set for G.

Proof. By Corollary (3.31.10), every result hold for any given fixed-vertex strong fuzzy(neutrosophic) star. Thus every result hold for any given fixed-vertex strong fuzzy(neutrosophic) star, simultaneously. Therefore, simultaneously fuzzy(neutrosophic)-metric number is n − 2, simultaneously fuzzy(neutrosophic)metric dimension is (n − 2)σ(m). Every (n − 2)-set excludes two vertices from different parts, is simultaneously fuzzy(neutrosophic)-resolving set for G. There’s an (n − 2)-set which is simultaneously fuzzy(neutrosophic)-metric set for G.

Corollary 1.8.19. Let G be a family of fixed-vertex strong fuzzy(neutrosophic) wheel with fuzzy(neutrosophic) common vertex set. Let n ≥ 3. Then simultaneously fuzzy(neutrosophic)-metric number is n − 2, simultaneously fuzzy(neutrosophic)-metric dimension is (n − 2)σ(m) Every (n − 2)-set excludes center and a given vertex, is simultaneously fuzzy(neutrosophic)-resolving set for G. There’s an (n − 2)-set which is simultaneously fuzzy(neutrosophic)-metric set for G.

Proof. By Corollary (3.31.11), every result hold for any given fixed-vertex strong fuzzy(neutrosophic) wheel. Thus every result hold for any given fixed-vertex strong fuzzy(neutrosophic) wheel, simultaneously. Therefore, simultaneously fuzzy(neutrosophic)-metric number is n − 2, simultaneously fuzzy(neutrosophic)metric dimension is (n − 2)σ(m). Every (n − 2)-set excludes two vertices from different parts, is simultaneously fuzzy(neutrosophic)-resolving set for G. There’s an (n − 2)-set which is simultaneously fuzzy(neutrosophic)-metric set for G.

1.9 Applications

Two applications are posed as follow.

37

1. Neutrosophic Graphs

Located Places

A program is devised for a robot to locate every couple of given places, separately. The number which this program assigns to any place from a given couple of places are unique. Thus every place has an unique number when a couple of places are given. Three numbers are assigned to a place. First number is about a model concerning attributes which titled to be obstacle for locating the place, second number is about a model concerning attributes which titled to be indeterminate for locating the place and sometimes, they’re obstacle but sometimes, they’re determinate to locate that place. Third number is about a model concerning attributes which titled to be determinate for locating the place. For example, (0.2, 0.5, 0.8) is assigned to a place v as information about its location. This is a brief outline of this application. To get it more precisely, I use some steps to clarify about them.

Step 1. (Definition) Located place is a term to categorize places into two classes. Applications for this function are too many but they’ve noticed to some parameters like decreasing costs, precise analysis, decreasing the ranges of analysis, restrictions on cases, low amount of selective data as possible, et cetera. Selective points as possible to distinguish about every couple of points out of them, are optimal case as possibilities allow. Step 2. (Issue) A train has some stops which every stop has some attributes.

A couple of stops are given but they’re impossible to locate by their attributes.

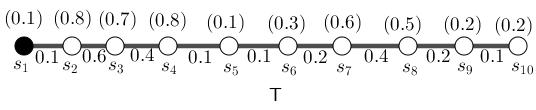
Step 3. (Model) I use attributes of stops to get a model with three numbers chosen from real numbers amid zero and one. Every number illustrates every aspect of their attributes. The first number is obstacle means bad attributes, the second number is indeterminate and third number is determinate means good attributes. But to use sensible clarification, I use a fuzzy model as Figure (1.10). To get it more precisely, consider Table (1.7) as a fuzzy model which assigns to every stations and connections a value, separately. In fact, set of stations and set of connections are used to make fuzzy sets from them.

Figure 1.10: Black vertex {s1} is only fuzzy(neutrosophic)-metric set amid all sets of vertices for fuzzy(neutrosophic) graph T .

Step 4. (Solution) As figure (1.10) shows, I study this fuzzy model. By Proposition (3.31.1), the stop s1 locates every given couple of stations. To get beyond this result, If I’ve a family of fuzzy(neutrosophic) paths excerpt from family of trains with fuzzy(neutrosophic) common and s1 in common, then by Corollary (3.31.4), the stop s1 locates every given

38

F3