3 minute read
Smarandache [4, 8] introduced it in 2022. Let ����be a universe of discourse, H a non-empty subset of ����, and P(����) the powerset of ����. Let a be an attribute, and ����be a set of this attribute-values. Then ����: ����→ ����(����) is called an IndetermSoft Set if: i) the set A has some indeterminacy; ii) or the set P(H) has some indeterminacy; iii) or there exist at least an attribute-value v∈A, such that F(v) = indeterminate (unclear, incomplete, conflicting, or not unique); iv) or any two or all three of the above situations. The IndetermSoft Set has some degree of indeterminacy, and as such it is a particular case of the NeutroFunction [5, 6], defined in 2014 – 2015, which is a function that is only partially well-defined (inner-defined), partially indeterminate, and partially outer-defined. The NeutroFunction is a generalization of the classical function, that is totally well-defined. IndetermSoft Set, as extension of the classical (determinate) Soft Set, deals with indeterminate data, because there are sources [4, 8] unable to provide exact or complete information on the sets A, H or P(H), and on the function F. We did not add any indeterminacy, we found the indeterminacy in our real world. Because many sources give approximate/uncertain/incomplete/conflicting information, not exact information as in the Soft Set, as such we still need to deal with such situations. For more information on IndetermSoft Set consult [4
from Practical Applications of IndetermSoft Set and IndetermHyperSoft Set and Introduction to TreeSoft Se
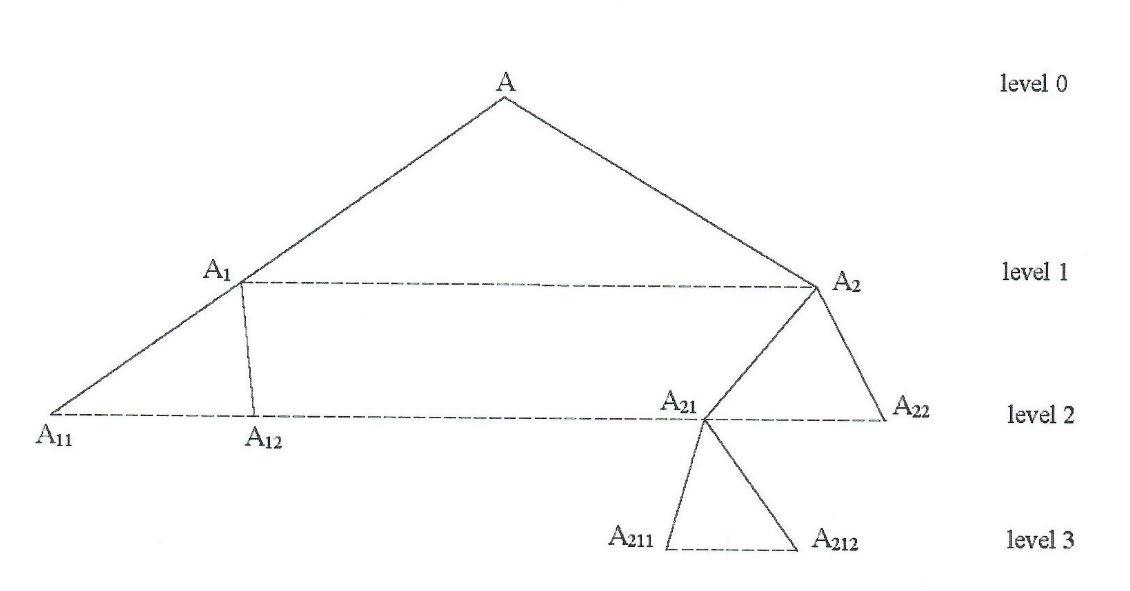
����(����2)=����(����21)∪����(����22)=�����(����211)∪����(����212)�∪����(����22)=����(����211)∪����(����212)∪����(����22) where ����211, ����212, ����22 are all leaves of the SubTree whose root is ����2 {i.e. SubTree(����2)}.
The proof of Theorem 2 is obvious, no matter what graph-tree one has, and it is similar to the below Example:
Advertisement
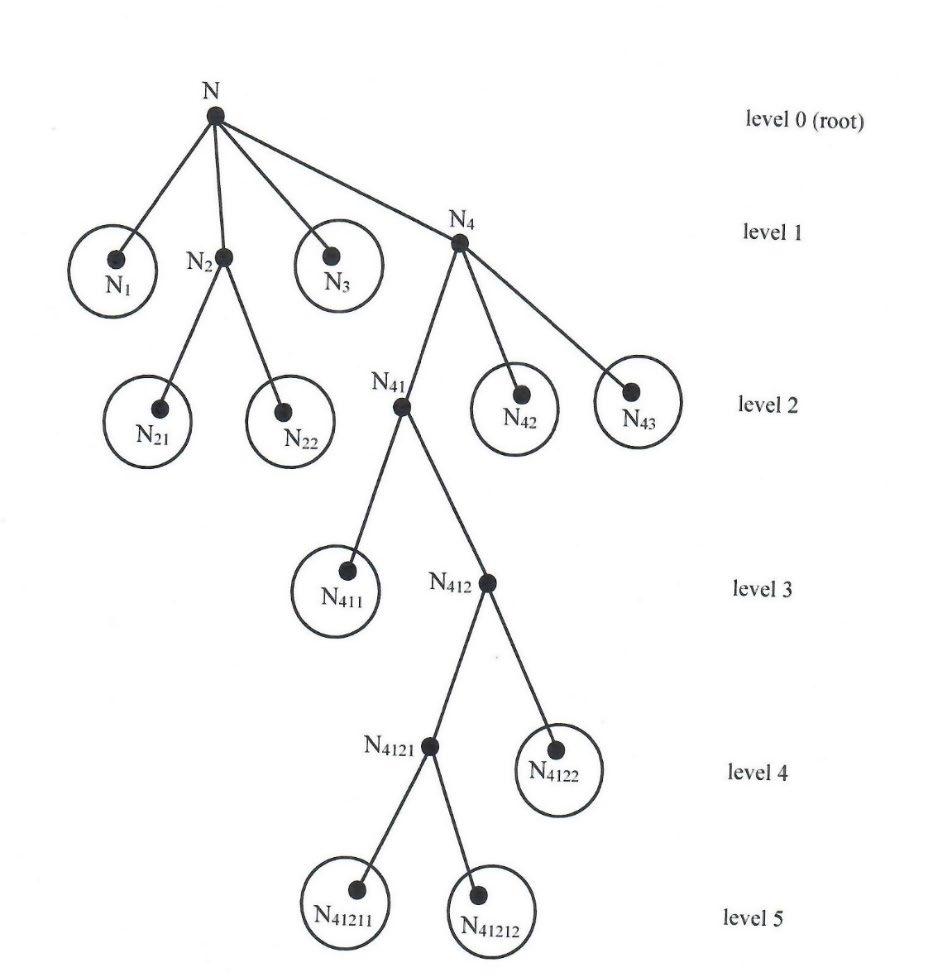
Graph 3: Tree(N)
The circled nodes are the leaves. ����(����) = ����(����1)∪����(����2)∪����(����3)∪����(����4) = ����(����1)∪[����(����21)∪����(����22)∪����(����3)∪����(����41)∪����(����42)∪����(����43)] = ����(����1)∪ ����(����21)∪����(����22)∪����(����3)∪[����(����411)∪����(����412)]∪����(����42)∪����(����43) = ����(����1)∪ ����(����21)∪����(����22)∪����(����3)∪ ����(����411)∪[����(����4121)∪����(����4122)]∪ ����(����42)∪����(����43) = ����(����1)∪ ����(����21)∪����(����22)∪����(����3)∪ ����(����411)∪����(����41211)∪����(����41212)∪����(����42)∪����(����43) which is the union of the soft-values F(.) of all leaves of the SubTree(N). Actually Theorems 1 and 2 are equivalent.
17.3. Theorem 3
�������������1
,��������2,…,�������������=�������������1�∩�������������2�∩…∩������������������,
where ��������1,��������2,…,������������ are nodes of various levels into the TreeSoft Set of ����.
The proof results from the fact that 1 ( ) iFN represents the subset H1 of elements in H that have the attribute-value N 1i , and 2 ( ) iFN represents the subset H2 of elements in H that have the
attribute-value
attribute-value
N2i , and so on ( ) piFN represents the subset Hp of elements in H that have the Nip , therefore to get the elements that have all these attribute-values one needs to intersect these subsets 1 2 ... H H H ∩ ∩ ∩ p .
18. Future Research
To define the operations (complement, intersection, union) for IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set respectively and to use them in real applications.
19.Conclusion
We introduced the TreeSoft Set as an extension of the MultiSoft Set. We presented simple practical applications of IndetermSoft Set, IndetermHyperSoft Set, and TreeSoft Set respectively for better understanding.
Funding: This research received no external funding. Conflicts of Interest: The authors declare no conflict of interest.
References
1. Molodtsov, D. (1999) Soft Set Theory First Results. Computer Math. Applic. 37, 19-31 2. F. Smarandache, Extension of Soft Set to Hypersoft Set, and then to Plithogenic Hypersoft Set, Neutrosophic Sets and Systems, vol. 22, 2018, pp. 168-170 DOI: 10.5281/zenodo.2159754; http://fs.unm.edu/NSS/ExtensionOfSoftSetToHypersoftSet.pdf 3. Florentin Smarandache, Extension of Soft Set to Hypersoft Set, and then to Plithogenic Hypersoft Set (revisited), Octogon Mathematical Magazine, vol. 27, no. 1, April 2019, pp. 413-418 4. Florentin Smarandache, Introduction to the IndetermSoft Set and IndetermHyperSoft Set, Neutrosophic Sets and Systems, Vol. 50, pp. 629-650, 2022 DOI: 10.5281/zenodo.6774960; http://fs.unm.edu/NSS/IndetermSoftIndetermHyperSoft38.pdf 5. F. Smarandache, (2015). Neutrosophic Function, 14-15, in Neutrosophic Precalculus and Neutrosophic Calculus, EuropaNova, Brussels, 2015; http://fs.unm.edu/NeutrosophicPrecalculusCalculus.pdf 6. F. Smarandache, Neutrosophic Function, in Introduction to Neutrosophic Statistics, Sitech & Education Publishing, 74-75, 2014; http://fs.unm.edu/NeutrosophicStatistics.pdf 7. Shawkat Alkhazaleh, Abdul Razak Salleh, Nasruddin Hassan, Abd Ghafur Ahmad, Multisoft Sets, Proc. 2nd International Conference on Mathematical Sciences, pp. 910-917, Kuala Lumpur, Malaysia, 2010 8. F. Smarandache, Soft Set Product extended to HyperSoft Set and IndetermSoft Set Product extended to IndetermHyperSoft Set, Journal of Fuzzy Extension and Applications, 2022, DOI: 10.22105/jfea.2022.363269.1232, http://www.journal-fea.com/article_157982.html
Received: September 16, 2022. Accepted: October 3, 2022