Refresca lo que has aprendido en MATEMÁTICAS
de MATE MÁTICAS 3 . o ESO Rumbo a
2.o muestra
¿Qué encontrarás en este cuaderno?
Refresca tus conocimientos de cálculo, álgebra, geometría, medida, estadística y probabilidad de una manera práctica y amena para empezar el próximo curso con buen pie.
Los contenidos se agrupan en seis semanas de cinco días . Para facilitarte la gestión del tiempo , cada semana se especifican las páginas que puedes hacer diariamente.
MENSAJE SECRETO
Cada semana empieza con un enigma . ¿Lo sabrás resolver?
Y, para saber cómo vas de matemáticas, resuelve las actividades de las siguientes páginas.
El producto de dos números enteros es –285. Si uno es el opuesto de 15, ¿cuál tiene que ser el otro número?
7. ¿Por qué número hay que dividir –350 para obtener –7?
Resuelve mentalmente estas operaciones y anota el tiempo que has tardado en hacerlo (pon el cronómetro en marcha antes de empezar): a) En una base científica de la Antártida, hace una hora el termómetro marcaba –5 °C y ahora marca –13 °C. ¿La temperatura, ha aumentado o ha disminuido? ¿Cuánto ha variado?
b) A las 5 h, un termómetro marcaba –3 °C. La temperatura ha aumentado 10 °C a lo largo de la mañana. ¿Qué temperatura marca el termómetro al mediodía?
c) Una persona vive en la planta 4 de un edificio, y su plaza de parking está en el sótano 5. ¿Cuántas plantas hay entre su vivienda y su plaza de parking?
e) Euclides nació el año 325 a. C. y Pitágoras, 247 años antes. ¿En qué año nació Pitágoras? SIN CALCULADORA 6 PRIMERA SEMANA 1 2 4 5 3 DÍA DÍA DÍA DÍA DÍA
d) Ayer Helena tenía 35 € en su cuenta y hoy está en números rojos, ya que tiene una deuda de 25 € ¿Desde ayer, ha ingresado dinero o ha gastado? ¿Qué cantidad?
Y, además, practica un poco más con las secciones El Reto y Sin calculadora .
5. Describe estas expresiones algebraicas. Hace falta que indiques, en cada caso, el grado y si se trata de un monomio, un binomio o un polinomio. a) 3mn b) y + 2xy –c) 7 + z + 2 d) tzx ty – 2 6. Observa las siguientes expresiones algebraicas y realiza las operaciones indicadas: A = 2 – 5x2 – 2x + 2 B – 3 + x + 2 – 4 a) A B = 2x – 5 – 2x + 2 + – 3x + x + 2 – 4 = x – 4x – 2 Sumamos y restamos los monomios con partes literales iguales. b) A B c) A (–3 = d) B (–2 = POLINOMIO 4x4 + 5x3 + 1 grado: 4 BINOMIO 2xy + z grado: 3 MONOMIO 2x2y2z grado: 2 + 2 + 2 = 6 parte literal coeficiente ¡PISTA! En una sala hay cuatro puertas y por cada puerta entra un niño. ¿De cuántas maneras diferentes pueden salir los niños si todos tienen que salir por una puerta diferente de aquella por donde han entrado y no pue- den salir dos niños por la misma puerta? ¡EL RETO! 39 TERCERA SEMANA 3DÍA 5DÍA 2 DÍA 1DÍA 4DÍA
DHRQRZ N YRF FRG ÇRE NANE N YN ÇVFOVAN ¿LO RESUELVES? ¿Qué mensaje ha enviado Jana a Sergio? ¿Te atreves a enviar un mensaje secreto a un amigo o amiga? No te olvides de darle la clave QUEDAMOS... 4 PRIMERA SEMANA 1 2 4 5 3DÍA DÍA DÍA DÍA DÍA 1. Rellena los huecos con el número entero que corresponda: a) |+7| = = 7 b) = = 5 c) |–4| = = d) = |+2| = 2. Calcula el resultado de las siguientes operaciones. Ten en cuenta los valores absolutos y fíjate en los ejemplos: |+10| = 10 |+4| = 4 |–10|= 10 |–4| = 4 a) –2 + |–5| – 1 = c) –2 |–5| = b) |18 (–3)|= d) |10 – 19 + 3| = 3. Ordena estos números de menor a mayor: 8 3 +7 –4 –11 0 1 –3 17 < < < < < < < < 4. Descompón los siguientes números como suma de dos enteros con diferente signo: a) –7 = b) 8 = c) –2 = d) 11 = 5. La resta de dos números es –4. Si uno de los números es –1, ¿cuál es el otro? –3 –2 –1 0 1 2 3 valor absoluto: |–3| = |+3| = 3 NÚMEROS ENTEROS ¡PISTA! LOS NÚMEROS ENTEROS 5 PRIMERA SEMANA 3DÍA 5DÍA 2DÍA 1 DÍA 4DÍA
6.
REGLA
+ –+ + –– – +
DE LOS SIGNOS ¡PISTA! 3
El opuesto de 4 es –4. ¡PISTA!
Y, si algún contenido te cuesta un poco, no te preocupes: ¡te damos pistas !
¡Experimenta cada semana el desafío de nuevas situaciones de aprendizaje!
3.
4.
5.
Y, cuando te apetezca, haz los pasatiempos que encontrarás en el Cajón de sastre .
El solucionario está al final del cuaderno. Utilízalo correctamente y procura no mirarlo hasta que no hayas hecho las actividades.
ganados:
1 / Expresión numérica: 3 3 + 2 0 + + 1 (–1,5) / Puntos totales: 7,5 Equipo D. Partidos ganados: 2 Partidos empatados: 2 / Partidos perdidos: 2 / Expresión numérica 2 3 + 2 0 + + 2 (–1,5) / Puntos totales: 3 b) Ha ganado la competición el equipo C. c) Entre los cuatro equipos suman 7,5 puntos. d) La diferencia de puntos entre los dos equipos es de 10,5 puntos. 2. a) El mes de más precipitaciones ha sido el mes de septiembre. b) La temperatura más baja registrada es de –11 °C, en los meses de febrero y marzo. c) La diferencia de temperaturas es de 13 °C. d) La diferencia de temperaturas es de 11 °C. e) La oscilación térmica en Bjørnøya es de 14 °C. 3. Nos faltarán 474,95 m para llegar a la cima. 4DÍA Páginas 12 y 13 1. Respuestas correctas a) y b). Ha ahorrado 643,10 € bastante para hacer el curso.
2. b) –5,60102 < 5,6005 < 5,602 < 5,6005 c) –1,05 < –0,025 < 0,02 < 0,07 < 0,12 < 0,8 d) 0,507 < 0,57 < 0,705 < 0,75 e) 0,05 < 0,102 < 0,105 < 0,251 < 0,501 3. a) La medida de la pantalla de un televisor es la longitud díagonal de la pantalla. 27 pulgadas = 68,58 cm; 24 pulgadas = 60,96 cm; 45,725 cm = 18 pulgadas b) Es una medida de superficie. 100 km = 10
1. Clasifica estos poliedros en regulares e irregulares: a) ¿Cómo definirías los poliedros regulares? ¿Y los irregulares? b) Entre los poliedros irregulares, hay uno que es cóncavo. ¿Cuál es? c) ¿Cómo justificarías que se trata de un poliedro cóncavo? Un poliedro es un cuerpo geométrico limitado por polígonos. ¡PISTA! segment interior poliedre convex poliedre còncau segment exterior cara arista vértice LA MEDIDA DEL VOLUMEN Poliedro convexo Poliedro cóncavo segmento interior segmento exterior 65 QUINTA SEMANA 3DÍA 5DÍA 2 DÍA 1DÍA 4DÍA 1 POMPAS DE JABÓN ¿Qué podemos hacer con pompas de jabón? Primero hay que preparar la mezcla: Además, necesitas una pajita de refresco, estructuras hechas de alambre (planas y poliédricas), hilo... ¡y muchas ganas de pasártelo bien! ¿Podrás agujerear una burbuja? ¿Podrás formar una burbuja dentro de una burbuja? ¿Y una burbuja cúbica, la podrás hacer? 1 Si fueran botes de helado, ¿en cuál de los dos cilindros cabría más? 50 % de agua 40 % de jabón 10 % de glicerina ¿EN CUÁL CABRÍA MÁS HELADO? Dobla la hoja por el lado corto. hoja DINA4 (21 cm × 29,70 cm) Dobla la hoja por el lado largo. 78 CAJÓN DE SASTRE PONTE LAS GAFAS MATEMÁTICAS 1 Sal a pasear y... ¡haz fotos de objetos matemáticos! ¿Piensas que encontrarás un banco en forma de cubo? ¿Y una papelera en forma de cilindro? ¿Y uno de los conos que utilizan para tráfico? ¿Y uno de los hexágonos de las baldosas del suelo? ¿Y a simetría en una ventana? 79 CAJÓN DE SASTRE LA ORQUESTA SINFÓNICA Para la fiesta mayor, queremos montar una pequeña orquesta sinfónica formada por las personas que tocan algún instrumento. Para saber cuántos instrumentos hacen falta, algunos jóvenes han preparado un dosier en el cual han descrito cómo es una orquesta sinfónica típica. 1. Determina qué porcentaje de instrumentos hacen falta de cada tipo. Rellena la siguiente tabla: Familia musical Cantidad mínima Cantidad máxima Proporción mínima Proporción máxima Viento-madera 8 8 Viento-metal 7 16 Percusión 5 10 Cuerda 62 74 TOTAL 82 108 2. ¿De qué familia se necesitan más instrumentos? 3. ¿Cuál es la razón entre el número de instrumentos de cuerda y el número del resto de instrumentos? ¿Cuál es la razón entre el número de instrumentos de percusión y el número de instrumentos de SITUACIÓN DE APRENDIZAJE 1 2 4 5 3 DÍA DÍA DÍA DÍA DÍA
Pau y Teresa hacen un trabajo sobre el impacto que ha tenido la crisis en los principales sectores económicos de su ciudad. Han recopilado muchos datos y quieren sacar conclusiones sobre el funcionamiento general de la economía. 1. La siguiente tabla muestra la estructura económica de la ciudad en el año 2020. En la segunda columna se detalla el VAS (valor añadido sucio, en millones de euros). En la cuarta columna se muestran los millares de personas ocupadas en cada sector económico. Queremos saber qué porcentaje respecto del total ocupa cada sector de actividad. Haz los cálculos necesarios y rellena la tabla para determinar qué porcentaje respecto del total representan el VAS y el número de personas ocupadas en cada sector. Sectores de actividad VAS (millones de euros) % respecto del total Ocupados (miles de personas) % respecto del total Agricultura 2 477 53,1 Industria y energía 40 776 604,3 Construcción 10 855 215,7 Servicios 153 704 2 641,7 TOTAL 100 100 2. ¿Cuál es el sector que crea más empleo?
DATOS ECONÓMICOS
¿Qué porcentaje ocupa este sector respecto del total de empleo?
El Departamento de Economía y Hacienda prevé un incremento del 2,8 % en el empleo para el próximo año. ¿Cuántos millones de personas estarán ocupadas, aproximadamente?
¿Qué cantidad total de ocupados habrá en cada sector si se cumplen las previsiones y se mantienen los porcentajes de empleo en cada sector? 31 SITUACIÓN DE APRENDIZAJE 3DÍA 5DÍA 2DÍA 1 DÍA 4DÍA
PRIMERA SEMANA 1DÍA Páginas 4 a 6 MENSAJE SECRETO ¿LO RESUELVES? Quedamos a las siete para ir a la piscina. LOS NÚMEROS ENTEROS 1. a) |+7| = |–7| = 7 b) |+5| = |–5| = 5 c) |–4| = |+4| = 4 d) |–2| = |+2| = 2 2. a) –2 + |–5| – 1 = 2 c) –2 |–5| = –10 b) |18 (–3)| = 6 d) |10 – 19 + 3| = 6 3. –11 < –4 < –3 < 0 < 1 < 3 < +7 < 8 < 17 4. Respuesta abierta, por ejemplo: a) –10 + 3 b) –2 + 10 c) –4 + 2 d) –1 + 12 5. Puede ser –5, porque (–5) – (–1) = –4; también puede ser +3, porque (–1) – (+3) = –4. 6. +19 7. Hay que dividirlo por +50. SIN CALCULADORA a) La temperatura ha disminuido. La variación ha sido de 8 °C. b) Al mediodía, el termómetro marca +7 °C. c) Hay 9 plantas. d) Ha gastado 60 € e) Pitágoras nació el año 572 a. C. 2DÍA Páginas 7 a 9 1. a) –13 b) –6 c) +6 d) +1 2. b) (+4) + (–7) – (+2) + (+6) = +1 c) (+2) – (+8) + (–5) – (–13) – (+1) = +1 d) –5 + (+1) (–4) = –9 e) (+10) (–2) – (–3) = –2 f) [–13 + 6 + (–3)] (–2) = +5 g) –6 – (–8) (–7 + 4 – 2) = –46 3. a) –14 – (+24) (+1 – 9) – (–2 – 3) = –6 b) –5 (–2 + 4) (–2 – 4) 2 = +30 c) +4 + [+2 – (+8) (–5) – (–7 + 6)] =+47 d) +2 – (2 · 2) – [+3 – (+2) (–2 – 5)] = –31 e) 5 [11 – 4 (11 – 7)] = –25 f) (–4) [12 + 3 · (5 – 8)] = –12 g) 4 – (–2) [8 – 3 (5 – 7)] = 32 4. a) 0 b) 15 c) –78.125 d) 512 e) 2 f) 4 ¡EL RETO! 41; 22, 19; –4, 26, –7; –29, (–5) (–3) (–2) LOS NÚMEROS DECIMALES 5. a) 3,75 b) 345 678 c) 1,305 d) 0,01225 e) 94,872 f) 1 952,625 e) 15,36 f) 2 700 g) 0,169 6. 3DÍA Páginas 10 y 11 1. a) Equipo A. Partidos ganados: / Partidos empatados: 3 Partidos perdidos: 2 / Expresión numérica: 1 3 + 3 0 + + 2 (–1,5) / Puntos totales: 0 Equipo B. Partidos ganados: 1 / Partidos empatados: 1 Partidos perdidos: 2 / Expresión numérica: 1 3 + 1 0 + + 4 (–1,5)
3
/ Puntos totales:
Equipo C. Partidos
3 Partidos empatados: 2 / Partidos perdidos:
000 ha c) 3,781855 km; 0,96558 km d) Son 11 toneladas. 5DÍA Páginas 14 y 15 SITUACIÓN DE APRENDIZAJE AMIGOS POR TODO EL MUNDO 1. En Bogotá serán las 15 h del 15 de agosto, y en Pekín, las 4 h del 16 de agosto. 2. Bogotá. Hora de salida: 11 h / Duración prevista: 12 h 15’ Llegada (hora de Londres): 23 h 15’ / Llegada (hora de Barcelona): 0 h 15’ Llegada (hora de la ciudad de destino): 18 h 15’ Pekín. Hora de salida: 13 h / Duración prevista: 14 h 30’ / Llegada (hora de Londres): 3 h 30’ / Llegada (hora de Barcelona): 4 h 30’ Llegada (hora de la ciudad de destino) 11 h 30’ 3 12 2,5 Multiplícalo por 100. 300 200 250 Divide el resultado anterior por 000. 0,3 1,2 0,25 Suma 3,4 al resultado anterior. 3,7 4,6 3,65 Multiplica el resultado anterior por 2,3. 8,51 10,58 8,395 99
MENSAJE SECRETO
DHRQRZ N
YRF FRG ÇRE
NANE N YN
ÇVFOVAN
¿LO RESUELVES?
¿Qué mensaje ha enviado Jana a Sergio?
¿Te atreves a enviar un mensaje secreto a un amigo o amiga? No te olvides de darle la clave QUEDAMOS...
4 PRIMERA SEMANA 1 2 4 5 3DÍA DÍA DÍA DÍA DÍA
LOS NÚMEROS ENTEROS
NÚMEROS ENTEROS
1. Rellena los huecos con el número entero que corresponda:
a) |+7| = | | = 7
b) | | = | | = 5 c) |–4| = | | = d) | | = |+2| =
2. Calcula el resultado de las siguientes operaciones. Ten en cuenta los valores absolutos y fíjate en los ejemplos: |+10| = 10 |+4| = 4 |–10|= 10 |–4| = 4
a) –2 + |–5| – 1 = c) –2 · |–5| = b) |18 : (–3)|= d) |10 – 19 + 3| =
3. Ordena estos números de menor a mayor: 8 3 +7 –4 –11 0 1 –3 17 < < < < < < < <
4. Descompón los siguientes números como suma de dos enteros con diferente signo:
a) –7 =
b) 8 = c) –2 = d) 11 =
5. La resta de dos números es –4. Si uno de los números es –1, ¿cuál es el otro? –3 –2 –1 0 1 2 3 valor absoluto: |–3| = |+3| = 3
¡PISTA!
5 PRIMERA SEMANA 3DÍA 5DÍA 2 DÍA 1 DÍA 4DÍA
6. El producto de dos números enteros es –285. Si uno es el opuesto de 15, ¿cuál tiene que ser el otro número?
7. ¿Por qué número hay que dividir –350 para obtener –7?
SIN CALCULADORA
Resuelve mentalmente estas operaciones y anota el tiempo que has tardado en hacerlo (pon el cronómetro en marcha antes de empezar):
a) En una base científica de la Antártida, hace una hora el termómetro marcaba –5 °C y ahora marca –13 °C. ¿La temperatura, ha aumentado o ha disminuido? ¿Cuánto ha variado?
b) A las 5 h, un termómetro marcaba –3 °C. La temperatura ha aumentado 10 °C a lo largo de la mañana. ¿Qué temperatura marca el termómetro al mediodía?
c) Una persona vive en la planta 4 de un edificio, y su plaza de parking está en el sótano 5. ¿Cuántas plantas hay entre su vivienda y su plaza de parking?
d) Ayer Helena tenía 35 € en su cuenta y hoy está en números rojos, ya que tiene una deuda de 25 €. ¿Desde ayer, ha ingresado dinero o ha gastado? ¿Qué cantidad?
e) Euclides nació el año 325 a. C. y Pitágoras, 247 años antes. ¿En qué año nació Pitágoras?
REGLA DE LOS SIGNOS ¡PISTA! 3 + –+ + –– – + El
¡PISTA!
opuesto de 4 es –4.
6 PRIMERA SEMANA 1
3DÍA DÍA DÍA DÍA DÍA
2 4 5
1. Adivina, en cada caso, de qué número se trata:
2. Resuelve las siguientes operaciones combinadas:
a) Soy negativo, impar, menor que –12 y mayor que –15.
b) Soy mayor que –7 y el triple de mi valor es –18.
c) Soy el opuesto del número anterior.
d) Soy positivo, mi valor absoluto es menor que 9 y mi opuesto es un número negativo mayor que –2.
a) –5 – [+5 – (–5) · (–3) + (–8)] + (–9) : (–3) = –5 – [+5 – 15 – 8] + (–9) : (–3) = –5 – (–18) + 3 = +16
b) (+4) + (–7) – (+2) + (+6) =
c) (+2) – (+8) + (–5) – (–13) – (+1) =
d) –5 + (+1) · (–4) =
e) (+10) : (–2) – (–3) =
f) [–13 + 6 + (–3)] : (–2) =
g) –6 – (–8) · (–7 + 4 – 2) =
DE LAS OPERACIONES ¡PISTA! ( ) x : + –1.O 2.O 3.O
JERARQUÍA
7 PRIMERA SEMANA 3DÍA 5DÍA 2 DÍA 1 DÍA 4DÍA
(–7)2 = 49
2 4 5
(–7)3 = –343
3. Resuelve estas operaciones combinadas:
a) –14 – (+24) : (+1 – 9) – (–2 – 3) =
b) –5 · (–2 + 4) · (–2 – 4) : 2 =
c) +4 + [+2 – (+8) · (–5) – (–7 + 6)] =
d) +2 – (2 · 2)² – [+3 – (+2) · (–2 – 5)] =
e) 5 · [11 – 4 · (11 – 7)]=
f) (–4) · [12 + 3 · (5 – 8)] =
g) 4 – (–2) · [8 – 3 · (5 – 7)] =
4. Resuelve estas operaciones con potencias:
a) 42 + (–42) =
b) (–4)2 – (–40) = c) –5 · (52)3 =
¡EL RETO!
Rellena las casillas vacías. Ten en cuenta que el valor de cada casilla es la suma de los dos valores de las casillas inferiores.
d) 24
27 22 = e)
29 4 )5 = f) [ 23
¡PISTA!
·
(
(–2)2 ]2 =
base negativa exponente impar resultado negativo
base negativa exponente par resultado positivo
–4 –29 (–5)2 (–3)0 (–2)3 8 PRIMERA SEMANA 1
DÍA DÍA DÍA DÍA DÍA
3
LOS NÚMEROS DECIMALES
MULTIPLICACIÓN Y DIVISIÓN CON DECIMALES
1,5 · 2,5 15 · 25 = 375 1,5 · 2,5 = 3,75 4,5678 : 3,5 = 45,678 : 35 = 1,305
MULTIPLICACIÓN Y DIVISIÓN POR LA UNIDAD SEGUIDA DE CEROS
5. Haz las siguientes operaciones:
a) 1,5 · 2,5 = 3,75 d) 12,25 : 1 000 g) 288,1 : 18,73
b) 134,5678 · 10 000 e) 13,4 · 7,08 h) 54 : 0,02 c) 4,5675 : 3,5
6. Realiza las operaciones indicadas y completa esta tabla:
Multiplícalo por 100.
Divide el resultado anterior por 1 000.
Suma 3,4 al resultado anterior.
Multiplica el resultado anterior por 2,3.
¡PISTA!
134,5678
100
13 456,78 12 473
100 = 124,73
·
=
:
¡PISTA!
f) 153,75
12,7 i) 0,325 · 0,52
·
3 12 2,5
9 PRIMERA SEMANA 3DÍA 5DÍA 2 DÍA 1 DÍA 4DÍA
1. Los chicos y las chicas del pueblo donde veraneo hemos organizado una liguilla de voleibol entre cuatro equipos. Si un equipo gana un partido, consigue 3 puntos; si empata, consigue 0 puntos, y si pierde, –1,5 puntos. Cada equipo ha jugado 6 partidos.
Los resultados se muestran en la tabla adjunta.
a) Completa la tabla con las expresiones numéricas correspondientes.
b) ¿Qué equipo ha ganado la competición?
c) ¿Cuántos puntos suman entre los cuatro equipos?
d) ¿Cuál es la diferencia de puntos entre el equipo ganador y el último equipo en la clasificación?
Partidos ganados Partidos empatados Partidos perdidos Expresión numérica Puntos totales Equipo A 1 3 2 Equipo B 1 1 4 Equipo C 3 2 1 Equipo D 2 2 2
10 PRIMERA SEMANA 1
DÍA DÍA DÍA DÍA DÍA
2 4 5 3
2. Observa el gráfico, que corresponde a las temperaturas y las lluvias registradas durante un año en la Isla del Hueso.
Después, responde a las preguntas.
CLIMA POLAR
Temperaturas (ºC)
Isla del Hueso (20 m)
Precipitaciones (mm)
a) ¿Cuál ha sido el mes con las precipitaciones máximas?
b) ¿Cuál es la temperatura más baja registrada?
c) ¿Qué diferencia de temperatura ha habido entre enero y julio?
d) ¿Y entre julio y diciembre?
e) Se entiende por oscilación térmica la diferencia entre la temperatura anual más alta y la más baja. Calcula el valor registrado en la isla del Hueso.
3. Hemos preparado una ruta de senderismo por la montaña. La ruta empieza a 850 m sobre el nivel del mar, se enfila 850,75 m, después baja 220,5 m y, finalmente, vuelve a subir 550,8 m más. Llegados a este punto, todavía estamos lejos de la cima, que se encuentra a 2 506 m sobre el nivel del mar. Calcula los metros de subida que nos faltan para llegar a la cima.
E F M A M J J A S O N D 25 20 15 10 5 0 –5 –10 –15 500 450 400 350 300 250 200 150 100 50 0
11 PRIMERA SEMANA 3DÍA 5DÍA 2 DÍA 1 DÍA 4DÍA
2
1. Este verano, Sergio quiere ahorrar para poder hacer un curso de submarinismo en septiembre.
Ha empezado a trabajar la segunda quincena de junio. Ha cobrado 38,45 € cada semana y ha podido ahorrar todo el dinero que ha ganado.
Durante el mes de julio cobrará 74,50 € semanales.
4 5 3
En agosto trabajará solo tres semanas y cobrará semanalmente un 20 % más que en julio.
Quiere calcular cuánto dinero habrá ahorrado a finales de agosto. ¿Cuál o cuáles de las expresiones siguientes serían las adecuadas para hacer estos cálculos?
a) 2
¿Cuánto ha ahorrado? Si el curso tiene un coste de 500 €, ¿habrá ahorrado bastante para hacerlo?
2. Ordena de menor a mayor los siguientes números decimales:
a) 6,1; 4,22; 4,02; 6,11; 3,99; 3,9 3,9 < 3,99 < 4,02 < 4,22 < 6,1 < 6,11
b) 5,602; 5,611; 5,6005; –5,60102
c) 0,02; –1,05; 0,8; 0,12; –0,025; 0,07
d) 0,75; 0,57; 0,507; 0,705
e) 0,102; 0,05; 0,105; 0,501; 0,251
· 38,45
74,5
3 · 74,5
1,2
· 38,45
· 74,5
3 · [74,5
(74,5 · 20 100 )] =
+ 4 ·
+
·
= b) 2
+ 4
+
+
c) 2 · 38,45 + 4 · 74,5 + 3 · 74,5 + (74,5 · 20 100 ) =
12 PRIMERA SEMANA 1
DÍA DÍA DÍA DÍA DÍA
3. ¡Descubre equivalencias entre medidas!
Responde a estas preguntas y ten en cuenta los decimales:
a) En un televisor, ¿qué medimos en pulgadas?
¿Cuánto mide en centímetros un televisor de 27 pulgadas? ¿Y una de 24 pulgadas? ¿Cuántas pulgadas son 45,725 cm?
b) ¿Qué medirías en hectáreas?
¿Cuántas hectáreas son 100 km2?
Una pulgada equivale a 2,54 cm.
Una hectárea (ha) son 10 000 m2.
Una milla terrestre son 1,6093 km.
c) ¿Cuántos kilómetros son 2,35 millas? ¿Y 0,6 millas?
d) Los elefantes son los animales terrestres mayores que existen. Al nacer, una cría de elefante pesa aproximadamente 120 kg, pero el elefante más grande que se ha visto nunca pesaba 11 000 kg. ¿Cuántas toneladas son?
¡PISTA! 13 PRIMERA SEMANA 3DÍA 5DÍA 2 DÍA 1 DÍA 4DÍA
1 2 4 5 3DÍA
AMIGOS POR TODO EL MUNDO
Judit y Paula han hecho un viaje a Londres este verano para mejorar su inglés. Allí han conocido a Carlos, de Bogotá, y a Huang, de Pekín. Ahora que cada uno volverá a su país, quieren seguir estando en contacto a través del chat, pero tienen que ir con cuidado con las diferencias horarias entre sus países.
1. ¿Las dos chicas vuelven a Madrid el 15 de agosto a las 21 h. ¿Qué hora y qué día será en la ciudad de cada uno de sus amigos?
Ten en cuenta que la franja horaria de Madrid en verano es UTC+2.
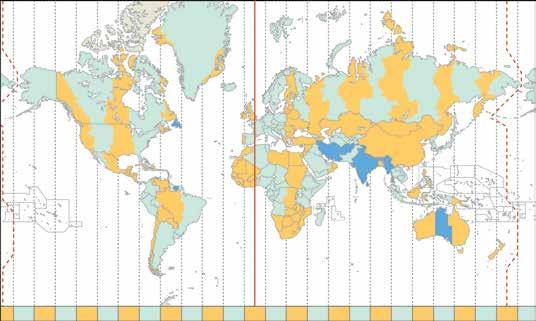
2. Observa esta tabla que ha hecho Paula con los horarios de los vuelos de sus amigos y complétala:
Hora de salida de Londres
Carlos 11 h 12 h 15’
Huang 13 h 14 h 30’
(hora de Londres)
(hora de Madrid)
Llegada (hora de la ciudad de destino)
3. ¿En qué franja horaria, según la hora de Madrid, se podrán comunicar Judit y Paula con sus amigos?
Estos son los horarios de conexión de cada uno:
Duración prevista Llegada
Llegada
-11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 +7 +8 +9 +10 +11 +12- -11 +3,5 +4,5 +5,5 +4,45 +6,5 +8,5 +12 canvi de data internacional canvi de data internacional
14 SITUACIÓN DE APRENDIZAJE
DÍA DÍA DÍA DÍA
Carlos Huang
AJUSTAMOS LAS CUENTAS
Al acabar el ciclo formativo de producción agropecuaria, tres amigos montaron una empresa de cultivo de setas. Se especializaron en el cultivo de xiitake, seta y seta amarilla.
1. Fundaron la empresa en marzo y cada uno aportó 3 500 €. Los primeros gastos fueron de 650 € en concepto de fianza por el alquiler del local, 235 € por la adquisición de mobiliario para el almacén y 2 045,50 € por la compra de cámaras frigoríficas. ¿De cuánto dinero disponían después de hacer todos estos pagos?
2. En abril empezaron a llevar las cuentas en una hoja de cálculo. Pagaron 325,50 € por el alquiler mensual del local y 1 750,75 € por la materia prima, y vendió 10 bandejas de xiitakes a 30,25 € cada una, 12 bandejas de setas a 20,75 € cada una y 18 bandejas de setas amarillas para 25,50 € cada una. Completa la tabla con los ingresos y el saldo correspondiente:
Dinero inicial
Alquiler local
Compra materia prima
Venta xiitakes
Venta setas
Venta setas amarillas
3. Durante el mes de mayo, vieron que los gastos habían aumentado en 200 € con respecto a los gastos del mes de abril y que los ingresos por las ventas se habían multiplicado por 3,2. Calcula el saldo final en el mes de mayo y valora si la actividad les fue rentable.
Concepto Ingresos (€) Gastos (€) Saldo (€)
Coste 15 SITUACIÓN DE APRENDIZAJE 3DÍA 5DÍA 2 DÍA 1 DÍA 4DÍA
Beneficio
EL TRIÁNGULO DE TARTAGLIA
Completa todas las filas. Cada casilla se rellena con la suma de los dos números que tiene justo encima.
¿Qué pasa si sumas todos los números de una fila?
¡Pinta las casillas con números impares y obtendrás un trocito del fractal de Sierpinski!
EL FRACTAL DE KOCH
Y, hablando de fractales, busca un poco de fresco en medio del verano. Dibuja un copo de nieve.
1. Dibuja un triángulo equilátero.
2. Divide cada lado del triángulo en tres partes iguales y dibuja otro triángulo equilátero más pequeño en cada uno de los lados.
3. Repite este procedimiento hasta que... ¡Este proceso es infinito!
4. ¡Los fractales no tienen fin!
1
1
2 3 1 1 2 1 1 1 1
16 CAJÓN DE SASTRE
CAMINOS
Haz caminos para que cada emoticono encuentre su pareja.
¡Cuenta! Los caminos no se pueden cruzar.
EL JUEGO DE LOS RASCACIELOS
¡Diseña una ciudad!
Material
• Tablero cuadriculado 4 × 4
• 16 edificios de diferentes alturas construidos con cubos encajables, dados, latas...
Objetivo
Colocar los 16 edificios, teniendo en cuenta que en cada fila y en cada columna solo puede haber un rascacielos de cada altura. Los números de los alrededores del tablero indican los edificios que se ven desde cada punto de vista.
1
¡Diseña una ciudad!
¿Cómo queda esta ciudad?
1
2 3 1 2 3 1 2 2 2 1 2 2 2 4 1 3 17 CAJÓN DE SASTRE
SOLUCIONARIO
© GRUPO ANAYA, S.A., 2024 - C/ Valentín Beato, 21 - 28037 Madrid.
Reservados todos los derechos. El contenido de esta obra está protegido por la Ley, que establece penas de prisión y/o multas, además de las correspondientes indemnizaciones por daños y perjuicios, para quienes reprodujeren, plagiaren, distribuyeren o comunicaren públicamente, en todo o en parte, una obra literaria, artística o científica, o su transformación, interpretación o ejecución artística fijada en cualquier tipo de soporte o comunicada a través de cualquier medio, sin la preceptiva autorización.