DEDUCCIÓN DE LAS DERIVADAS DE LAS
FUNCIONES
CÁLCULO DIFERENCIAL E INTEGRAL
PROFR. I.Q. IGNACIO ROSALES ORTIZ
1. Dx(c) = 0

1. Comenzamos aplicando el límite:
2. Como f(x) = c
3. La f(x + Dx) = c , ya que como la función no tiene término de x, no hay donde aplicar el incremento:
4. Se eliminan los términos del numerador y nos resulta cero:
5. Y como el cero es un número, el límite de una constante, es la misma constante; por tanto:




2. Dx(x) = 1

1. Comenzamos aplicando el límite:
2. Como f(x) = x
3. La f(x + Dx) = x + Dx , ya que como la función es x, hay donde aplicar el incremento:
4. Se eliminan los términos semejantes del numerador (en este caso se elimina x):
5. Quedándonos Dx/Dx = 1, y el límite de una constante, es la misma constante; por tanto:




3. Dx(x^n) = n x^n-1

1. Comenzamos aplicando el límite:
2. Como f(x) = x^n
3. La f(x + Dx) = (x + Dx)^n , ahora lo que tenemos es un binomio elevado a la npotencia, para esto ocupamos el desarrollo del binomio de Newton:


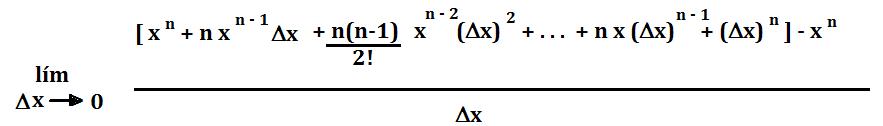

3. Dx(x^n) = n x^n-1 (continuación)
4. Se eliminan los términos semejantes del numerador (en este caso se elimina x^n):
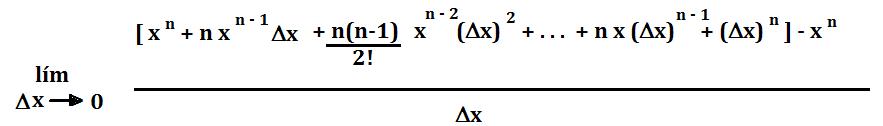
5. Ahora, nos quedan todos los términos que tienen Dx, factorizamos y eliminamos el Dx:

3. Dx(x^n) = n x^n-1
(continuación)

6. Aplicamos el límite y como todos los términos tienen Dx, se eliminan, con excepción del primer término, por tanto, nos queda:
7. La derivada de la función x^n:

4. Dx[c f(x)] = c f´(X)

1. Comenzamos aplicando el límite:
2. Como f(x) = c f(x)
3. La f(x + Dx) = c[f(x + Dx)] , sustituimos :
4. Como en ambos términos se tiene c, factorizamos c :
5. Aplicamos el teorema de los límites, el límite de una constante que multiplica a una función, la constante multiplica al límite de la función :




6. Como obtenemos la definición de la derivada que multiplica a la constante, nos queda: cf´(x)
5. Dx[f(x) ± g(x)] = Dx[f(X)] ± Dx[g(x)]






(continuación)


(continuación)


7. Dx[ f(x) ] = g(x) g(x) Dx[f(X)] - f(X) Dx[g(x)] [g(x)]^2



7. Dx[ f(x) ] = g(x) g(x) Dx[f(X)] - f(X) Dx[g(x)] [g(x)]^2
(continuación)


