VAN
Leerdoelwitte
Aan die einde van hierdie eenheid moet jy: • basiese wiskundige vaardighede kan toepas • afronding, wetenskaplike notasie, persentasies, verhoudings, koers en eweredigheid verstaan en berekeninge kan doen
Deel 1: Afronding
Wanneer ons getalle afrond, moet ons bewus wees van die konteks van die probleem. Konteks is die verband waarin iets voorkom. Dit sal bepaal of ons na onder of na bo afrond en ook tot hoeveel desimale plekke ons moet afrond.
Belangrik
Wanneer ons getalle afrond, kan ons nie net sê dat die oorspronklike getal gelyk is aan die afgeronde getal nie, daarom gebruik ons nie = nie, maar ≈ . ≈ beteken amper gelyk aan OF min of meer gelyk (afgerond OF geskat)
VOORBEELDE
Rond die volgende getalle af tot die aantal desimale plekke tussen hakies aangedui:
1.1 8,25632 (2 desimale plekke)
BASIESE VAARDIGHEDE Sample
Antwoord: ≈ 8,26
Let wel: Kyk na die derde desimaal. ’n Getal kleiner as 4 maak geen verskil aan die tweede desimaal nie. As die derde desimaal 5 of groter is, word die tweede desimale syfer een groter, daarom het die 5 in ’n 6 verander.
1.2 16,89432 (3 desimale plekke)
Antwoord: ≈ 16,894
1.3 428,899 (2 desimale plekke)
Antwoord: ≈ 428,90
Aktiwiteit 1
Rond die getalle af tot TWEE desimale plekke:
1. 4,3568
2. 18,3578
3. 1,9999
4. 45,4386
5. 834,8765
6. 29,99124
7. 492,6324
8. 9,3334
9. 16,448
10. 74,97553
Deel 2: Afronding tot die naaste 10, 100 en 1 000
Gebruik plekwaardes om jou te help om getalle af te rond. As jy byvoorbeeld getalle tot die naaste 10 moet afrond, moet jy na die Ene-kolom kyk.
Duisende Honderde Tiene Ene
Afronding tot die naaste 10
Getalle kleiner as 5 in die Ene-kolom word na die vorige tien afgerond
Getalle groter as 5 in die Ene-kolom word na die volgende tien afgerond.
Afronding tot die naaste 100
Getalle kleiner as 5 in die Tiene-kolom word na die vorige 100 afgerond.
Getalle groter as 5 in die Tiene-kolom word na die volgende 100 afgerond.
Afronding tot die naaste 1 000
Getalle kleiner as 5 in die Honderde-kolom word na die vorige 1 000 afgerond.
Getalle groter as 5 in die Honderde-kolom word na die volgende 1 000 afgerond.
VOORBEELDE
2.1 Rond die getalle af tot die naaste 10:
2.1.1 75 ≈ 80
2.1.2 17 ≈ 20
2.1.3 163 ≈ 160
2.1.4 689 ≈ 690
2.1.5 3 ≈ 0
2.2 Rond die getalle af tot die naaste 100:
2.2.1 75 ≈ 100
2.2.2 2 082 ≈ 2 100
2.2.3 43 ≈ 0
2.3 Rond die getalle af tot die naaste 1 000:
2.3.1 899 ≈ 1 000
2.3.2 3 956 ≈ 4 000
2.3.3 282 ≈ 0
Aktiwiteit 2
Rond die getalle af tot die naaste 10, 100 of 1 000:
1. 48 (naaste 10)
2. 245 (naaste 100)
3. 2 367 (naaste 1 000)
4. 4 356 (naaste 10, 100 en 1 000)
5. 3 835 (naaste 10, 100 en 1 000)
Deel 3: Wetenskaplike notasie
Belangrik
Een miljoen: 1 000 000 (6 nulle)
Een miljard (biljoen): 1 000 000 000 (9 nulle)
Een biljard (triljoen): 1 000 000 000 000 (12 nulle)
Sample
Ons gebruik wetenskaplike notasie om baie groot of baie klein getalle op so ’n manier te skryf dat dit maklik is om te lees Die getal word geskryf deur ’n getal tussen 1 en 10 te gebruik wat dan met ’n mag van 10 vermenigvuldig word.
Om groot getalle in wetenskaplike notasie te skryf, moet jy ’n desimale komma ná die eerste syfer plaas sodat die getal tussen 1 en 10 is. Tel die aantal plekke vanaf die desimale komma tot aan die einde van die getal om vir jou te wys watter mag van 10 jy moet gebruik. Verwyder enige nulle en skryf die getal vermenigvuldig met 10 tot die mag ���� (���� is die aantal plekke van die desimale komma af tot aan die einde van die getal).
Vir baie klein getalle moet jy die aantal plekke vanaf die desimale komma tel tot jy ’n getal tussen 1 en 10 het. Verwyder enige nulle voor die desimale komma en skryf die getal vermenigvuldig met 10 tot die mag negatiewe ����
VOORBEELDE
• Skryf 81 500 in wetenskaplike notasie.
• Skryf 0,0043 in wetenskaplike notasie.
4 3 2 1 1 2 3
notasie
34 000 000 3,4 × 107
734 000 000 000 7,34 × 1011
0,000 0014 1,4 × 10-6
0,000 000 000 03 3,0 × 10-11 674 965,38 6,7496538 × 105
Aktiwiteit 3
8 1 5 0 0 = 8,15 × 104 0, 0 0 4 3 = 4,3 × 10-3 Sample
1. Skryf die getalle in wetenskaplike notasie: 1.1 2 700 000 1.2 4 500 1.3 0,000 000 56 1.4 0,000 18
2. Skryf die volgende as ’n gewone getal: 2.1 6,4 ×
×
Deel 4: Persentasies
’n Persentasie is ’n manier om die aantal dele van ’n geheel (die teller) as ’n getal uit 100 uit te druk. Dit word altyd met die %-simbool agteraan geskryf. ’n Persentasie kan ook in die vorm van ’n breuk geskryf word. Die noemer sal altyd 100 wees. “Persent” is afgelei van die Latynse woord per centum, wat “per honderd” of “vir elke honderd” beteken.
Persentasies kan as ’n gewone breuk of as ’n desimale getal uitgedruk word, bv. 83% = 83 100 OF = 0,83
4.1 Berekening van persentasie
Om ’n persentasie van ’n hoeveelheid te bereken, moet jy die persent as ’n breuk skryf en dit met die hoeveelheid vermenigvuldig.
persent 100 × hoeveelheid
VOORBEELDE
4.1.1 Bereken 25% van R5 000,00.
Onthou: Die woord “van” beteken vermenigvuldiging.
Volgorde op sakrekenaar: (25 ÷ 100) × 5 000 =
4.1.2 Thandi behaal 28 40 in ’n Wiskundige Geletterdheid-toets. Wat is haar persentasie vir die toets?
28 40 × 100 = 70%
Volgorde op sakrekenaar: (28 ÷ 40) × 100 = Sample
4.2 Bepaal nuwe waardes met gegewe persentasies
Soms moet ons die nuwe prys van ’n item of produk bereken nadat dit met ’n sekere persentasie verhoog word, bv. BTW (Belasting op toegevoegde waarde) wat op die oorspronklike prys gehef word
VOORBEELDE
4.2.1 ’n Pakkie koekies kos R15,30 sonder BTW. Hoeveel sal jy betaal nadat BTW bygevoeg word? (Suid-Afrika se BTW-koers is tans 15%)
15
100 × R16,00 = R2,40 OF R16,00 × 115% = R18,40
R16,00 + R2,40 = R18,40
Jy sal R18,40 betaal nadat BTW bygevoeg is.
4.2.2 ’n Handelaar verhoog sy pryse met 8%.
As die oorspronklike prys R45,99 is, wat sal die prys ná die verhoging wees?
8
100 × R45,99 = R3,68 OF R45,99 × 108% = R49,67
R45,99 + R3,68 = R49,67
Die nuwe prys is R49,67.
4.2.3 ’n Skoenwinkel het ’n uitverkoping met 25%-afslag op alle skoene. Wat sal jy vir ’n paar skoene betaal wat oorspronklik R645,00 gekos het?
Sample
25 100 × R645,00 = R163,50 OF 100% – 25% = 75%
R645,00 – R163,50 = R490,50 75% × R645,00 = R490,50
Jy sal nou R490,50 vir die paar skoene betaal.
4.2.4 Die petrolprys daal met 2,5%.
Hoeveel sal motoriste nou vir ’n liter petrol betaal as die prys R14,40/ℓ was?
2,5
100 × R14,40 = R0,36 OF 100% – 2,5% = 97,5%
R14,40 – R0,36 = R14,04
Motoriste sal nou R14,04/ℓ betaal.
97,5% × R14,40 = R14,04
4.3 Bepaal die oorspronklike waarde met nuwe gegewe waardes en persentasies
Soms moet ons die oorspronklike prys van ’n item of produk bereken voordat dit met ’n sekere persentasie verlaag is, bv. afslag op produkte tydens ’n uitverkoping.
Belangrik
Jy moet die oorspronklike waarde bepaal – die vorige bedrag, voordat dit verhoog of verlaag het.
VOORBEELDE
4.3.1
Skottelgoedseep kos R23,10 BTW ingesluit. BTW is 15%.
Wat was die skottelgoedseep se prys voordat BTW bygevoeg is?
P = prys sonder BTW
P × 115% = R23,10
(115% = 100% + 15%)
P = 23,10 115% OF R23,10 ÷ 1,15
P = R20,09
Die skottelgoedseep se oorspronklike prys was R20,09.
4.3.2 ’n Slaghuis verhoog hul pryse met 9%, wat beteken dat biltong nou R195,10/kg kos. Wat was die oorspronklike prys voor die verhoging?
Sample
P: oorspronklike prys
P × 109% = R195,10
P = 195,10 ÷ 109% = R178,99
Die biltong se oorspronklike prys was R178,99.
4.3.3 ’n Rekenaarwinkel hou ’n uitverkoping met alle items teen 25%-afslag. As ’n drukker se verkoopprys nou R1 538,40 is, wat was die oorspronklike prys voor die afslag?
P: oorspronklike prys (100% – 25% = 75%)
P × 75% = R1 538,40
P = R1 538,40 ÷ 75% = R2 051,20
Die drukker het oorspronklik R2 051,20 gekos.
4.4 Persentasiestyging en persentasiedaling
Ons kan die volgende formule gebruik om persentasiestyging of persentasiedaling te bepaal.
Persentasiestyging/persentasiedaling = huidige waarde vorige waarde vorige waarde × 100
VOORBEELDE
4.4.1 In 2019 het ’n skool 1 538 leerders gehad en in 2020 was daar 1 645 leerders. Met watter persentasie het die leerdertal verhoog?
Persentasiestyging =
Persentasiestyging
4.4.2 In 2018 het ’n glasfabriek 796 foutiewe glase vervaardig en in 2019 slegs 675. Met watter persentasie het die foutiewe glase afgeneem?
Persentasiedaling =
Persentasiedaling
Die negatiewe waarde dui ’n afname aan. In hierdie voorbeeld het die persentasie foutiewe glase met 15,20% afgeneem Sample
Aktiwiteit 4
1. Bereken:
1.1 45% van R2 500
1.2 33⅓% van R8 500
2. Thabo behaal 38 75 in ’n Lewenswetenskappetoets. Wat is sy persentasie? Rond jou antwoord af tot die naaste persentasie.
3. ’n Winkelassistent het vergeet om BTW by te voeg toe sy die verkoopprys van verskeie items bereken het
Die volgende items se prys moet herbereken word:
• ’n Paar tekkies teen R189,99
• ’n Denimbroek teen R539,99
• ’n T-hemp teen R125,90
• ’n Serp teen R85,99
Bereken die nuwe prys van elke item. BTW is 15%
4. Pieter koop ’n tweedehandse bakkie teen R185 000, BTW van 15% ingesluit. Wat sou die bakkie gekos het voordat BTW bygevoeg is?
5. Die petrolprys styg met 2,3% en motoriste betaal nou R16,30/ℓ Hoeveel het motoriste voor die styging vir ’n liter petrol betaal?
6. ’n Blu-ray-speler wat eers R1 235,00 gekos het, kos nou R855,00. Bereken die persentasie afslag tot die naaste heelgetal.
7. Watter persentasie is 36 minute van ’n uur?
Sample
8. Ná ’n inflasieverhoging van 8,5% kos ’n sakkie kruideniersware nou R685,00. Wat het dieselfde sakkie kruideniersware voor die verhoging gekos?
9. ’n Maatskappy het 840 werknemers waarvan 195 vroulik is. Watter persentasie van die werknemers is manlik? Rond jou antwoord af tot die naaste heelgetal.
10. Mandla verdien R18 845,00 per maand. Hy het voorheen R16 750,00 verdien. Die gemiddelde salarisverhoging by sy firma was 10%. Wys deur middel van berekeninge of Mandla se nuwe salaris met die firma se gemiddeld ooreenstem
Deel 5: Verhoudings
’n Verhouding is ’n vergelyking tussen waardes wat in dieselfde eenheid gemeet word. Jy moet seker maak dat jy met dieselfde eenhede werk omdat waardes met verskillende eenhede nie as ’n verhouding uitgedruk kan word nie
• Skryfwyse: 2 tot 5 OF 2 : 5 OF 2 5 (Ons lees dit as twee tot vyf.)
• Verhoudings moet altyd in hul eenvoudigste vorm geskryf word, bv. 10 : 25 → 2 : 5 (deel elke getal deur 5)
• Verhoog R12,50 in die verhouding 3 : 5
5 3 × R12,50 = R20,83 (teller hoogste waarde)
• Verlaag R12,50 in die verhouding 3 : 5
3
5 × R12,50 = R7,50 (teller laagste waarde)
Verhoudings bestaan meestal uit twee terme, maar kan ook meer as twee terme hê. Die volgorde van die terme in ’n verhouding is belangrik. ’n Verhouding van 1 : 6 is NIE dieselfde as ’n verhouding van 6 : 1 NIE.
VERDELING VAN VERHOUDINGS
a) R8 000 word tussen Anne, William en Susan in die verhouding 2 : 3 : 5 verdeel. Hoeveel sal elkeen ontvang? Bepaal die geheel deur 2 + 3 + 5 = 10 op te tel.
Anne: 2 10 × R8 000 = R1 600
William: 3 10 × R8 000 = R2 400
Sample
Susan: 5 10 × R8 000 = R4 000
b) ’n Stuk lint van 30 m word in die verhouding 1 : 2 : 3 verdeel. Hoe lank is elke stuk?
Deel 1: 1 6 × 30 m = 5 m
Deel 2: 2 6 × 30 m = 10 m
Deel 3: 3 6 × 30 m = 15 m
Aktiwiteit 5
1. Skryf die volgende verhoudings in hul eenvoudigste vorm:
1.1 54 : 81
1.2 5 dae : 5 weke
1.3 2,5 ℓ : 500 mℓ
2. Die volgende verhouding word op ’n bottel aanmaakkoeldrankkonsentraat gegee: “meng 1 : 4 met water”.
2.1 Wat beteken dit?
2.2 Hoeveel water en hoeveel konsentraat moet jy meng om 1 ℓ-koeldrank vir jouself en ’n paar vriende aan te maak?
3. Verdeel R4 500 tussen Kate, Megan en Sophia in die verhouding 5 : 8 : 12.
4. Vermeerder R168,50 in die verhouding 2 : 3
5. Verminder 520 kg in die verhouding 9 : 7.
Deel 6: Koers
Koers is die verhouding tussen twee waardes van verskillende eenhede. Anders as verhouding waar ons met dieselfde eenheid werk, werk koers met verskillende eenhede. Dink aan die wisselkoers waar die waarde van verskillende geldeenhede met mekaar vergelyk word, bv. die waarde van die rand teenoor die dollar. Nog voorbeelde sluit in km/h, R/kg, m/s en kg/m2.
VOORBEELDE
6.1 Die wisselkoers is R18,45 vir een euro (€) As jy €1 500 het, hoeveel rand het jy?
€1 500 × R18,45 = R27 675,00
Sample
6.2 As jy R100 000 het, hoeveel euro het jy?
R100 000 ÷ R18,45 = €5 420,05
6.3 ’n Watertenk met 100 ℓ-kapasiteit lek teen 1,4 ℓ/min. Hoe lank sal dit neem voordat daar 64 ℓ water in die tenk oor is?
Gee jou antwoord in minute en sekondes.
100 – 64 = 36 ℓ
36 ℓ ÷ 1,4 = 25,71 minute
25 minute en (0,71 × 60)
25 minute 42 sekondes.
Aktiwiteit 6
1. £1 (Britse pond) → R19,65
1.1 Hoeveel rand is gelyk aan £20 000?
1.2 As jy R55 000,00 het, hoeveel Britse pond (£) het jy?
2. 5 kg aartappels kos R45,89. Hoeveel sal 1 kg aartappels kos?
Deel 7: Eweredigheid
Eweredigheid beteken dat twee verhoudings se waardes gelyk aan mekaar is, bv. 1 : 2 = 2 : 4.
Direkte eweredigheid
As een hoeveelheid toeneem, neem ’n ander hoeveelheid teen dieselfde koers toe.
Die verhouding tussen die twee hoeveelhede bly konstant. Die grafiese voorstelling van direkte eweredigheid is ’n reguit lyn wat met dieselfde helling (gradiënt) toeneem.
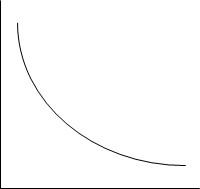
Indirekte (inverse) / omgekeerde eweredigheid
As een hoeveelheid toeneem, neem ’n ander hoeveelheid af.
Die grafiese voorstelling van indirekte of omgekeerde eweredigheid is ’n kurwe wat die toename van een hoeveelheid en die afname van ’n ander hoeveelheid voorstel.
Aktiwiteit 7
1. Piesangs kos R15,99/kg. Voltooi die tabel deur die ontbrekende waardes in te vul:
2. Teken ’n lyngrafiek op ’n benoemde assestelsel om die tabel grafies voor te stel.
3. Watter soort eweredigheid word hier voorgestel? Motiveer jou antwoord.
4. ’n Groep leerders wil ’n bus huur om hulle na Gold Reef City te neem. Die bus se huurkoste beloop R3 000. Die bedrag wat elke leerder moet bydra, hang af van hoeveel mense op die bus gaan wees.
4.1 Voltooi die tabel om die bedrag per persoon aan te dui.
4.2 Teken ’n lyngrafiek om die tabel grafies voor te stel.
4.3 Watter soort eweredigheid word hier voorgestel? Motiveer jou antwoord.
• Omvattende verduidelikings van wiskundige konsepte in eenvoudige taal.
• Praktiese, alledaagse voorbeelde.
• Aktiwiteite wat leerders se toepassing van kennis en hul redeneervermoë uitdaag.
• Die fasiliteerdersgids bevat stapvirstapbewerkings en antwoorde.
• Sluit ’n formuleblad en alfabetiese lys van wiskundige terme in vir maklike verwysing.
• Gebruik in die klaskamer of tuis.
home classroom college workplace