BUHAR SIVI DENGESİ

Buhar sıvı dengesi, adından da anlaşılacağı üzere buhar ve sıvı olmak üzere iki fazın dengede olduğu durumlar için kullanılan ifadedir. Bu kavram, özellikle kimya sektöründe mühendislik

DENGE KAVRAMI

Denge durumu, bir kimyasal etkileşimin söz konusu olduğu bir sistemde, reaktanların ve ürünlerin konsantrasyonlarının artık zamanla değişmediği durum olarak tanımlanır. Bu, reaksiyondaki moleküller arasında artık hiçbir hareket olmadığı anlamına gelmez.[1] Bu durumu makroskopik GIBBS FAZ KURALI Gibbs Faz Kuralı, termodinamik dengedeki çok fazlı bir sistemin serbestlik derecesini tanımlar. Bu ifade, sistem dahilindeki her fazın intensif bağımsız termodinamik özelliklerinin sayısına ve sistemdeki Şeklinde ifade edilir. Bu ifadede Π faz sayısını, N sistemdeki kimyasal tür sayısını, F ise serbestlik derecesini temsil eder. Serbestlik derecesi için bulunan sayı, o problemin tanımlanması için gerekli olan bağımsız değişken sayısını yansıtır. Daha iyi açıklamak gerekirse, serbestlik derecesinin 2 olarak Buhar sıvı dengesini ikili karışım olarak göz önüne alırsak, Gibbs serbestlik derecesi bize tanımlamamız gereken 3 bilinmeyen daha olduğunu söyler. Bu bilinmenler basınç, sıcaklık ve mol fraksiyonudur. uygulamalarında, üretim proseslerinde sıklıkla karşılaşılan ve mühim bir yere sahip olan bir kavramdır.

düzeye uygularsak, yine mikroskopik düzeyde moleküllerarası gerçekleşen etkileşimlerin artık büyük sisteme olan etkisinin ihmal edilebilir düzeyde küçük olduğu görülür. Ulaşılan bu denge durumunda ise basıncın, faz bileşimlerinin ve sıcaklığın sabit

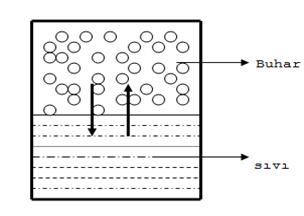
kaldığı görülür. faz sayısına bağlıdır. Kimyasal bir reaksiyonun

Π + F = N + 2

gerçekleşmediği bir sistem için Gibbs Faz Kuralı [2] bulunması, mevcut prosesin çözümlenebilmesi için 2 bağımsız değişken daha tanımlamamız gerektiğini anlatır. Haliyle bir termodinamik problemin çözülebilir olması, o proses için serbestlik derecesinin

BUHAR SIVI DENGESİNİN TÜM OLASILIKLARI

sıfır olması demektir. Sonuç olarak ikili bir buhar sıvı denge karışımının tüm olasılıkları 3-boyutlu grafiklerle ifade edilebilir.

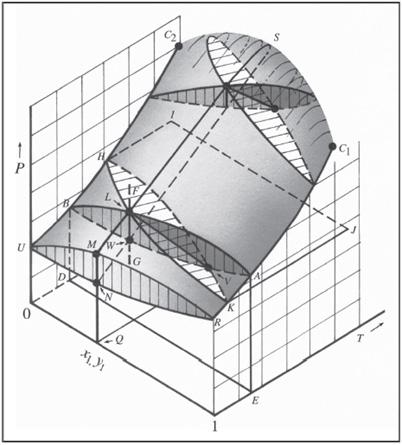
Şekil “Introduction to Chemical Engineering Thermodynamics” kitabından alınmıştır.

Bir maddenin yüksek basınç altında daha yoğun bir fazda olacağı bilindiğine göre; grafikteki basıncın düşük olduğu bölgede bulunan alt yüzeyin doygun buhar yüzeyi, grafikteki basıncın yüksek olduğu üst kısımdaki yüzeyin ise doygun sıvı yüzeyi olduğunu söylemek mümkündür. Bu 3-boyutlu grafiklerden ikili karışımı oluşturan saf bileşenlerin kritik noktalarını, saf bileşenlerin farklı sıcaklıklardaki doygun basınç değerlerini, karışımı habbe ve şebnem noktalarını bulmak mümkündür. PTxy grafikleri daha kolay bir şekilde okunması açısından Pxy veya Txy grafikleri şeklinde de incelenebilir.

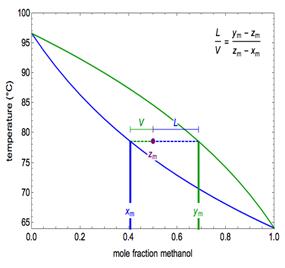
Bu grafiklerden habbe be şebnem noktalarını okumak mümkündür. Habbe noktası, yoğunlaşmanın

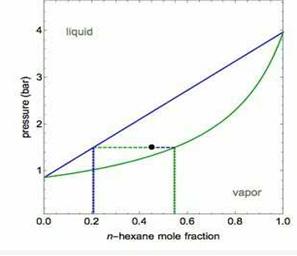
başladığı noktadır. Şebnem noktası ise buharlaşmanın başladığı noktadır.[3]

İDEAL DENGE DURUMU İÇİN MODELLER

RAOULT KANUNU

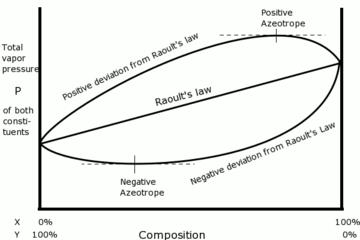
1880’li yıllarda Fransız kimyager François-Marie Raoult, bir maddenin bir çözelti içerisinde çözündüğü zaman çözeltinin buhar basıncının genellikle azalacağını ve bu gözlemin mevcut çözülmüş madde miktarı ile saf çözücünün orijinal buhar basıncına bağlı olduğunu keşfetmiştir.[4] Raoult Kanunu

yalnızca ideal çözeltilerde geçerlidir ve buhar mol fraksiyonu ile basıncın çarpımının , sıvı mol fraksiyonu ile mevcut sıcaklıktaki orijinal buhar

HENRY KANUNU

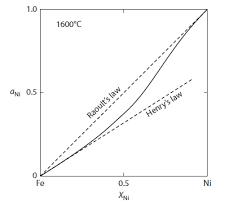
19. Yüzyılın başlarında gazların çözünürlüğü üzerine çalışmalarda bulunan İngiliz kimyager William Henry 1803 yılında su tarafından absorplanan su miktarı ile alakalı yayınında çözünmüş gaz miktarının gaz fazındaki kısmi basıncı ile orantılı olduğunu ifade İdeal olmayan denge durumu için Raoult ve Henry kanunları kullanılmaz. Bunların yerine modifiye Bu modeller temel olarak azeotrop oluşturan ve ideal durumda olmayan ikili çözeltiler için geliştirilmiş, • van Laar Modeli Van Laar denklemi;Van der Waals denkleminden türetilen, sıvı karışımların faz dengesini tanımlamak için 1910-1913 yıllarında Johannes van Laar eder. [5] Bu kanun ise buhar mol fraksiyonu ile basıncın çarpımının, sıvı mol fraksiyonu ile her madde için deneysel olarak tespit edilen Henry sabiti

İDEAL OLMAYAN DENGE DURUMU İÇİN MODELLER

ile çarpımına eşit olduğunu ifade eder. formülleri geliştirilmiştir. basitleştirilmiş yaklaşımlardır.[6]

tarafından geliştirilen bir termodinamik aktivite modelidir.[7]

• Margules Modeli

Gibbs Duhem ilişkisi ile uyumlu olan Margules denklemi, termodinamiğin önemli bir temel denklemidir ve Raoult ve Henry yasalarının bir formülasyonunu verir. Margules denklemi,

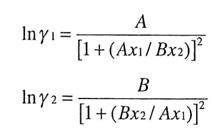
bir çözeltinin aşırı kısmi Gibbs enerjisini temsil edebilecek başka herhangi bir denklemi temsil edebiliyorsa iyonik çözeltilere de uygulanabilir. [8]

• Wilson Modeli

Flory-Huggins denklemine benzer bir ilişkiye dayanarak, Wilson merkezi bir molekülün çevresindeki yerel konsantrasyonların, çevredeki

moleküller ile rekabet eden moleküler etkileşimler nedeniyle yığın konsantrasyonlarından farklı olduğunu varsayarak bu modeli geliştirmiştir.[9

Kaynaklar

[1] https://web.iit.edu/sites/web/files/departments/academic-affairs/academic-resource-center/pdfs/ Equlibrium.pdf [2]https://www.sciencedirect.com/topics/engineering/gibbs-phase-rule [3] https://www.cheric.org/files/education/cyberlecture/e200114/e200114-501.pdf [4] https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps / Supplemental_Modules_(Physical_and_Theoretical_Chemistry) [5] https://www.atmos-chem-phys.net/15/4399/2015/acp-15-4399-2015.pdf [6]https://www.jscimedcentral.com/ChemicalEngineering/chemicalengineering-3-1039.pdf [7]https://en.wikipedia.org/wiki/Van_Laar_equation#: [8] https://link.springer.com/article/10.1007/BF02648369 [9] https://chejunkie.com/knowledge-base/the-wilson-equation-for-excess-gibbs-energy/