







1 ЗА СВЕ РАЗРЕДЕ: • ДИГИТАЛНИ УЏБЕНИЦИ • НАСТАВНЕ ПРИПРЕМЕ • КОНТРОЛНЕ ВЕЖБЕ • ДОДАТНИ НАСТАВНИ МАТЕРИЈАЛИ 2023/2024 Kаталог уџбеника за математику Највећи и највише награђивани домаћи издавач за децу 30 година у образовном издаваштву 8 награда на међународном такмичењу за најбољи европски уџбеник Члан Европског удружења издавача уџбеника од 2006. године
••Препоручени садржаји, који воде остварењу предвиђених исхода, обрађени су кроз шест тематских целина (Природни бројеви и дељивост, Основни појмови геометрије, Угао, Разломци (I део), Осна симетрија и Разломци (II део)).
••Свака наставна тема почиње уводном страном, где се налазе примери из свакодневног живота, понешто из историје математике и кратка најава садржаја који ће се обрађивати, као и кратак тест за проверу претходно усвојених знања, неопходних за успешно савладавање садржаја који следе. ••У оквиру сваке наставне јединице издвојени су и посебним иконичким знацима означени следећи делови: кључни појмови, обрада новог градива, додатна објашњења дефиниција и правила, решени задаци који помажу у разумевању градива и одељак Провери шта знаш, с неколико задатака који се односе на обрађено градиво.

••На почетку сваке лекције дат је занимљив задатак као подсетник на оно што ученик већ зна, а у вези је с градивом које се обрађује.
••Градиво је у уџбенику изложено тако да ученика активно води кроз лекцију: полазећи од једноставних примера, преко правила, решених примера до задатака за вежбу. ••На крају сваке наставне теме налази се рубрика Запамти. То су прегледне систематизације
2
градива обрађеног у оквиру наставне теме. ••На крају уџбеника дати су резултати и упутства за решавање свих задатака. ••Уџбеник је доступан и у дигиталном формату, с мултимедијалним материјалом, интерактивним задацима и проверама знања. Ауторке: Мирјана Стојсављевић-Радовановић Љиљана Вуковић, Јагода Ранчић Уџбеник за 5. разред Математика

















3 1. На сликама су приказане неке од највиших грађевина на свету. Дате су њихове висине и године изградње. а) Код највише грађевине упиши број 1, затим 2 код следеће по висини и тако редом, од највише до најниже, то јест до броја 10. б) Напиши редом године подизања ових грађевина, од најстарије грађевине до најмлађе. в) Које ће године најстарија од ових грађевина прославити један век постојања? ПРИРОДНИ БРОЈЕВИ И ДЕЉИВОСТ Сигурно се нико од вас не сећа тога када је научио да броји. Покушај да замислиш како би свет изгледао када не би постојали бројеви. Могле би да се користе речи мало, много, не баш много и сличне. Бројеви су један од најгенијалнијих изума свих времена. Можда мислиш да су компјутери, свемирски бродови, мобилни телефони и други изуми бољи и моћнији. Али њих не би било без коришћења бројева. На сликама су неке од највиших грађевина на свету. 818 m Бурџ Калифа Дубаи, Уједињени Арапски Емирати, 2010 539 m ТВ торањ Останкино Москва, Русија, 1967 509 m Тајпеј 101 Тајпеј, Тајван, 2004 634 m Toкио Скајтри Токио, Јапан 2012 556 m Лотe светски торањ Сеул, Јужна Кореја 2017 553 m Торањ CN Торонто, Канада, 1975 443 m Емпајер стејт билдинг Њујорк, САД, 1931 520 m Вилис тауер Чикаго, САД, 1974 452 m Куле Петронас Куала Лумпур, Малезија, 1996 632 m Шангајски торањ Шангај, Кина, 2014 2. Једна од највиших зграда на Балкану јесте Пословни центар Ушће Висока је 134 m и има 25 спратова. Просечна висина једног спрата ове зграде је: мања од 5 m 5 m већа од 5 m. Који је одговор тачан? Западна капија Београда нижа је 19 m од Пословног центра Ушће Израчунај њену висину. Београђанка је грађена почетком седамдесетих година ХХ века и дуго је била највиша зграда у овом региону. Њена висина износи једну десетину километра. Израчунај њену висину у метрима. Источна капија Београда има 28 спратова. Просечна висина једног њеног спрата износи око 3 m. Колика је приближна висина те зграде? Поређај ове грађевине по висини, од најниже до највише, и напиши њихове називе. Висина Авалског торња је 205 метара. Колика је разлика у висини између Авалског торња и Пословног центра Ушће? а) Више од 70 m. б) Tачно 70 m. б) Mање од 70 m. У наредном поглављу обновићемо оно што сте већ учили о природним бројевима, а научићете нешто више о скуповима и скуповним операцијама. Научићете још неке особине бројева, па ћете знати како да: примените правила дељивости одредите највећи заједнички делилац и најмањи заједнички садржалац разликујете просте и сложене бројеве. 30 ПРОСТИ И СЛОЖЕНИ БРОЈЕВИ Пре више од тридесет година научници су се запитали какав би то био универзални језик у читавом свемиру који би могла да разумеју ванземаљска интелигентна бића. Закључили су да би то морали бити бројеви. Један од чувених низова бројева: 1, 1, 2, 3, 5, 8, 13, 21… назива се Фибоначијев низ. Правило по којем се бројеви у њему ређају прилично је једноставно: сваки следећи добија се сабирањем претходна два. На пример: 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8, 5 + 8 = 13, 8 + 13 = 21… Сада можете сами да одредите следеће чланове Фибоначијевог низа. Ако пажљиво избројимо љуспе на једној од шишаркиних спирала, добићемо неке од бројева из Фибоначијевог низа, на пример 8, 13 или 21. И сунцокрет је „познавалац“ математике. Бројеви његових семених плодова одговарају члановима Фибоначијевог низа: 55, 89, 144 итд. До сада није пронађена ниједна појава у природи коју бисмо могли да опишемо низом бројева 2, 3, 5, 7, 11, 13, 17… који су дељиви само јединицом и сами собом. Зато су научници изабрали баш те бројеве као поруку Земљана. Сигналима су помоћу моћних радио-телескопа послати далеко у свемир. Сада ослушкујемо и још чекамо одговор на нашу поруку. Број 3 је прост број, а 12 је сложен број. Бројеве 2, 3, 5, 7, 11, 13, 17… називамо простим бројевима. Прост број је природни број који има само два делиоца: 1 и сам тај број. Сложен број је природни број који има више од два делиоца. Број 1 не убрајамо ни у просте ни у сложене бројеве. Који је од датих бројева прост, а који сложен? 9 21 97 19 121 61 224 • прости бројеви • сложени бројеви • Ератостеново сито 31 4 Поступак за одређивање свих простих бројева који се налазе између два природна броја назива се Ератостеновим ситом. Тај поступак је добио име по грчком математичару, астроному и географу Ератостену. Одређујемо све просте бројеве мање од 20. 1. корак Пишемо све бројеве од 1 до 20. Прецртавамо број 1 јер није ни прост ни сложен број. 2. корак Заокружујемо први прост број, а то је 2, и прецртавамо све сложене бројеве дељиве са два (парне бројеве). 3. корак Заокружујемо прост број 3 и прецртавамо све сложене бројеве дељиве са три. Међу тим бројевима постоје и бројеви који су већ прецртани јер су дељиви и са 2 и са 3. То су бројеви 6, 12 и 18. 4. корак Заокружујемо прост број 5 и проверавамо да ли су у датом низу бројева већ прецртани сви бројеви дељиви са 5. Заокружујемо све преостале бројеве који нису прецртани. Заокружени бројеви у датом низу бројева мањих од 20 jeсу прости бројеви: 2, 3, 5, 7, 11, 13, 17 и 19. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 Сви бројеви дељиви са 4 су већ прецртани јер су сложени и дељиви са 2. У овом ситу прецртавај бројеве који су дељиви, редом, бројевима 2, 3, 5 и 7. Напиши све бројеве од 21 до 50. Заокружи све просте бројеве и прецртај све сложене бројеве користећи Ератостеново сито. У датој таблици бројева од 1 до 100 заокружени су сви прости бројеви. Прецртан је број 1 и прецртани су сви сложени бројеви. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 ПРОВЕРИ ШТА ЗНАШ 1. Који су од датих бројева прости, а који сложени? 8 25 83 31 169 79 288 2. Користећи Ератостеново сито, одреди све просте бројеве од 100 до 150. Поступак прецртавања сложених бројева у Ератостеновом ситу завршавамо у кораку у ком заокружујемо прост број који, помножен самим собом, даје број већи од највећег броја у ситу. Сви преостали непрецртани бројеви су прости бројеви. Наставна јединица – обрада Помоћ у решавању и разумевању конкретних ситуација Уводна страна у наставну тему Најава садржаја који ће се обрађивати Кратак тест за проверу претходно усвојених знања Кључни појмови Подаци из разних области Решени задаци Водич кроз уџбеник






















4 86 1 2 3 УГЛОВИ НА ТРАНСВЕРЗАЛИ • трансверзала за паралелне праве • једнаки углови на трансверзали • углови на трансверзали чији је збир 180° Израчунај означене углове на слици. На цртежу су паралелне праве a и b и a2 = 60°. Измери b2 Израчунај означене углове на слици. Који су углови једнаки углу a1? Који су углови једнаки углу a2? Који углови дају збир 180° када се саберу са углом a1? Који углови дају збир 180° када се саберу са углом a2? Сети се особине упоредних углова и особине унакрсних углова. a1 b1 a2 a3 a4 b2 b3 b4 a b c a1 a2 a3 b1 b2 b3 a b c 60° 70° Реч трансверзала у саобраћајној терминологији означава пут који пресеца друге путне правце. Планинари трансверзалом називају означене планинарске стазе које повезују контролне тачке. Знак који користе за обележавање стаза приказан је на слици. Код нас је позната Фрушкогорска трансверзала. Трансверзала је у математици права која сече две праве или више њих. Права c на цртежу јесте трансверзала за праве a и b Углови чије су области осенчене на слици називају се угловима на трансверзали. Ако је a || b, углови осенчени истом бојом међусобно су једнаки, а збир два угла осенчена различитим бојама износи 180°. Важи и обрнуто: ако су углови осенчени истом бојом једнаки, праве су паралелне. a b c Израчунај углове означене луковима на цртежу ако праве: a) a и b јесу паралелне б) m и n нису паралелне. a b c 72° m n c 72° 125° Подсети се: Ако је збир углова 180°, они су суплементни углови. 87 4 5 На којим су цртежима праве p и q паралелне? Ако је t || s, израчунај углове a и b p q a 63° 66° p q a 85° 95° p q a 76° 106° p q a 45° 45° б) а) б) а) в) г) t s α β 125° 110° a b t s c d 42° 92° ПРОВЕРИ ШТА ЗНАШ 1. Нацртај паралелне праве а и b и праву c која их сече. Ако је угао између правих а и c једнак 35°, колики је оштар угао између правих b и c? 2. Нацртај паралелне праве а и b и паралелне праве c и d које их секу. Ако је угао између а и c једнак 50°, колики je угао између правих b и d? 1 УГЛОВИ С ПАРАЛЕЛНИМ КРАЦИМА • jеднакост углова с паралелним крацима углови с паралелним крацима чији је збир 180° • углови паралелограма Нацртај оштар угао xOy и полуправу Ma || Ox као што је приказано на слици. а) Нацртај полуправу Mb || Oy тако да угао aMb буде оштар. Измери углове xOy и aMb б) Нацртај полуправу Mb || Oy тако да угао aMb буде туп. Измери углове xOy и aMb На сликама је дат и пример када је један од углова неконвексан. Иначе, када говоримо о угловима с паралелним крацима, разматрамо само конвексне углове. Углове чији краци припадају паралелним правама називамо угловима с паралелним крацима. На пример, углови a и b на сликама јесу углови с паралелним крацима. a b a b a b a b И ТО ЈЕ МАТЕМАТИКА За одређивање положаја тачке на овом цртежу користе се два броја. На пример, тачка А налази се у пресеку кружнице полупречника 3 и крака угла од 45°, па је њен положај одређен паром 3, 45°. Којим је паром одређен положај тачке B, а којим тачке C? Уцртај тачку D чији је положај одређен паром 2, 225°. Положај било које тачке одређен је растојањем од ње до центра и одговарајућим централним углом. Растојање од центра одређује кружница којој припада та тачка, а централни угао јесте угао чији је један крак увек дата полуправа Ox а други полуправа којој припада дата тачка. Мрежа дата на претходном цртежу назива се поларним координатним системом. Мрежу чине концентричне кружнице чији је центар тачка О и полуправе с почетком у тачки О У решавању неких реалних проблема користи се систем врло сличан поларном координатном систему. На пример: код радара – за одређивање положаја и праћење кретања авиона и бродова. 180° 210° 240° 270° 300° 330° 150° 120° 90° 60° 30° 0° 1 2 3 90° 45° 0° 135° 180° 1 2 3 225° 270° 315° 90° 45° 0° 135° 180° 225° C O B x A 270° 315° 1 2 3 Ox је бројевна полуправа. Вероватно се некада забављаш с другарима играјући ИКС-ОКС (уписујеш X или O у табелу). Ова математичка игра слична је игри ИКС-ОКС 1 2 92 ЗАПАМТИ оштар прав туп опружен неконвексан пун мањи од 90° једнак 90° између 90° и 180° једнак 180° између 180° и 360° једнак 360° Комплементни углови Суплементни углови Суседни углови Упоредни углови Унакрсни углови a + b = 90° a b a + b = 180° a b a b a и b су суседни и суплементни a b a = g b = d a g b d Основна јединица мере за угао је степен. Ознака 1° чита се: један степен 40° 130° t – трансверзала Једнаки су углови који су обојени истом бојом, а суплементни они који су различитих боја. a || b AB DC α β δ γ g = a b = d a + b = 180° Углови с паралелним крацима су једнаки ако су оба угла оштра или ако су оба тупа или ако су оба права. Углови с паралелним крацима су суплементни ако је један угао оштар, а други туп, или ако су оба угла права. ВРСТЕ УГЛОВА УГЛОВИ НА ТРАНСВЕРЗАЛИ УГЛОВИ ПАРАЛЕЛОГРАМА УГЛОВИ С ПАРАЛЕЛНИМ КРАЦИМА Математичке дефиниције Додатни задаци Задаци Провери шта знаш Систематизација градива Водич кроз уџбеник
прати уџбеник и у њој се налазе задаци за даље вежбање. Заступљени су разноврсни задаци, свих типова и нивоа тежине, а поред њих у збирци се могу наћи и додатна објашњења дефиниција и правила, као и решени задаци који помажу у разумевању градива. У рубрици Пробај и ово налазе се задаци намењени оним ученицима који могу и желе да науче нешто више. ••На крају сваке тематске целине у збирци налазе се систематизације дате кроз задатке за проверу знања. Задаци су градирани у три нивоа: основни, средњи и напредни. Одређивање нивоа највећег броја задатака урађено је према документу Општи стандарди постигнућа – образовни стандарди за крај обавезног образовања за предмет математика, а аутори су се ослонили и на исходе дефинисане у програму наставе и учења за осми разред основне школе. ••На крају збирке дати су резултати и упутства за решавање свих задатака. Помоћ у решавању задатка



5 10 Дати су скупови A = {2, 4, 5, 7, 8}, B = {3, 4, 6, 7, 9, 10} и C = {1, 4, 5, 8, 9, 11}. Одреди елементе скупова A ∩ B A ∩ B ∩ C A ∪ B A ∪ B ∪ C (A ∩ B) ∪ C A ∪ (B ∩ C) Скупови S и T представљени су Веновим дијаграмом. Који је скуп њихова унија? а) {3, 2} б) {5, 6} в) {1} г) {5, 6, 1, 3, 2} д) {5, 6, 1, 3, 5, 6} S T 3 2 5 6 1 Доврши Венов дијаграм и упиши елементе скупова. Одреди елементе њихове уније. а) T = {4, m, 9}, S = {m, е, 3} б) T = {4, m, 9}, R = {е, 3} в) T = {4, m 9}, P = {m, 9} T T T S 5 6 7 8 9 1 2 3 4 Елементи скупа A јесу сви природни бројеви мањи од 8 а елементи скупа B сви природни бројеви већи од 4 и мањи од 10. Напиши елементе скупова A B и A ∪ B. Запиши елементе скупова E и F ако је: E ∪ F = {1, 2, 3, 4} 1 ∈E 1 ∈F 2 ∈E ∩ F 3 ∈E 3 ∉F 4 ∉E Задатке овог типа лакше ћеш решавати ако користиш Венове дијаграме. РАЗЛИКА СКУПОВА Изврши назначене скуповне операције: а) {1, 11, 101, 110, 1 011} \ {10, 101, 1 101} б) {10, 101, 1 101} \ {1, 11, 101, 110, 1 011}. а) Одреди и напиши елементе скупова L P R ако је: L – скуп свих једноцифрених парних бројева P – скуп свих једноцифрених бројева већих од 2 R – скуп свих природних бројева већих од 4 и мањих од 11. б) Напиши елементе скупова: L \ R L \ P R \ P R \ L P \ L P \ R Доврши Венов дијаграм и упиши елементе скупова. Одреди елементе њихове разлике. а) T = {а, m, 2}, S = {m, е, 2, 3} б) M = {4, m}, R = {е, 3} в) L = {4, m 9}, P = {m, 9} T S R P Скупови су дати описно: S = {x x ∈N0 и x ≤ 4} P = {x | x ∈N и x < 4}. Запиши скупове набрајањем елемената. а) S б) P в) S ∪ P г) S ∩ P д) S \ P ђ) P \ S 11 6 7 Венови дијаграми могу ти помоћи у учењу других предмета. Када треба да уочиш и запамтиш неке сличности и разлике, можеш да користиш Венов дијаграм. На пример, на следећи начин можеш приказати које су особине Милоша Војиновића и цара Душана поменуте у песми Женидба Душанова сличне, а које различите. храбар духовит мудар пожртвован неопрезан лаковеран осеЋајан поносан Милош Војиновић Цар Душан За било који скуп B одреди: а) B \ B б) B \ Ø в) Ø \ B Одреди и напиши елементе скупова ако је: A – скуп двоцифрених бројева чији је збир цифара 4 B – скуп двоцифрених бројева чији је производ цифара 2. а) A б) B в) A ∪ B г) A ∩ B д) A \ B ђ) B \ A Збир цифара броја 35 је 3 + 5 8, а производ цифара је 3 5 15. СКУПОВИ И СКУПОВНЕ ОПЕРАЦИЈЕ Прикажи Веновим дијаграмом дате скупове и одреди њихов пресек, унију и разлику: а) A = {31, 32, 33, 34, 35}, B = {32, 33, 34, 35, 36, 37} б) A = {m n p}, B = {g f h} в) A = {2, 3, а b, 5}, B = {а, 2, b}. Скуп A чине сви бројеви мањи од 20 које можеш да поделиш са 2 без остатка, а скуп B сви бројеви мањи од 20 које можеш да поделиш са 3 без остатка. а) Запиши елементе тих скупова. б) Одреди елементе скупа A ∩ B, A ∪ B в) Прикажи скупове A и B Веновим дијаграмом. За било који скуп A одреди: а) A ∪ A б) A ∪ Ø в) A ∩ A г) A ∩ Ø. Скупове F = {101, 102, 103, 104, 1055} и G = {103, 104, 105, 106, 107, 108} прикажи Веновим дијаграмом и провери тачност једнакости (F \ G) ∪ (G \ F) = (F ∪ G) \ (F ∩ G). Одреди елементе скупова A B и A ∩ B ако је дато: A ∪ B {Ш, К, О, Л, A} A \ B {Ш} B \ A {A, К}. Ако ти је лакше – цртај. Јована је за свој рођендан направила чоколадну и воћну торту. Позвала је 20 својих пријатеља. Свако од њих пробао је најмање једну торту. Чоколадну торту пробало је њих 15, а обе торте њих шесторо. Колико је њених пријатеља пробало воћну торту? Настави да решаваш задатак у свесци као што је започето. Č – чоколадна торта V – воћна торта Овај задатак можеш решити и применом Веновог дијаграма, тако што ћеш, уместо навођења елемената скупова, као што смо до сада радили, написати њихов број. Č V Задаци
Стојсављевић-Радовановић,
Збирка
Математика
••Збирка
Ауторке: Мирјана
Љиљана Вуковић, Јагода Ранчић
задатака за 5. разред
дигиталних уџбеника Креативног центра може приступити сваки наставник без регистрације, преко адресе www.ekcskola.rs ••Корисници наших штампаних књига могу користити комплетне верзије уџбеника уколико се региструју
7 ВРХУНСКИ ЕВРОПСКИ ОБРАЗОВНИ СОФТВЕР КОЈИ ЋЕ ВАМ БИТИ СВАКОДНЕВНА ПОМОЋ У НАСТАВИ ••Дигитални уџбеници припремљени су у сарадњи с највећим финским произвођачем образовног софтвера, чији су партнери и неки од највећих издавача у Финској и Европи. ••Предност им је лако и интуитивно коришћење и кретање кроз програм, као и модеран и иновативан изглед платформе. ••Могу се користити на телефону, таблету и компјутеру и нема потребе за додатном инсталацијом програма. ••Могу се користити и на електронској табли и погодни су за рад у учионици с већом групом ђака. ••Истовремено могу бити и материјал из којег ученик учи у школи или код куће и помоћно средство намењено наставнику за ефикасније извођење наставе.
на истој адреси. ТОКОМ ПРОТЕКЛЕ ДВЕ ГОДИНЕ ОВАЈ МАТЕРИЈАЛ ЈЕ УСПЕШНО КОРИСТИЛО ВИШЕ ХИЉАДА НАСТАВНИКА. НОВО! Наставник може да прати рад својих ученика тако што ће прегледати резултат који је ученик остварио радећи задатке из одређене лекције или области. e-KC Дигитални материјали
••Демо-верзијама


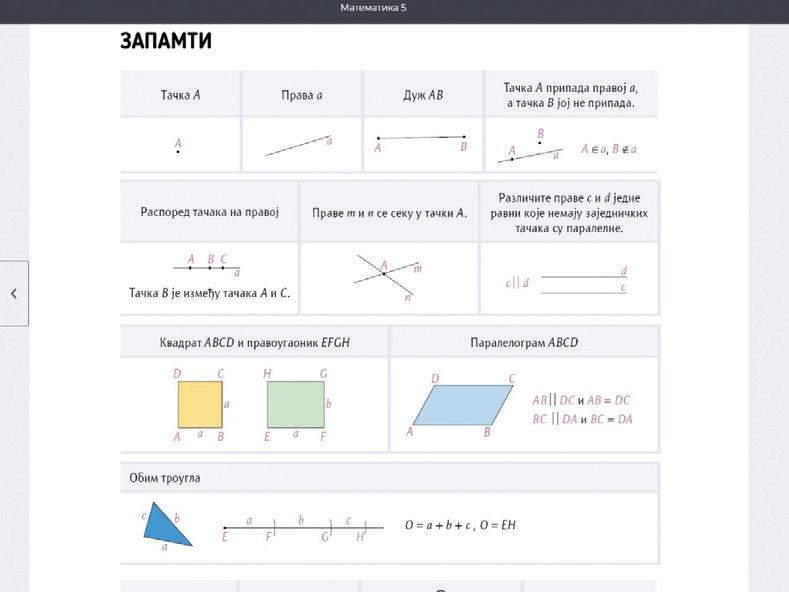
8 ••Уџбеник се састоји од шест поглавља у којима се обрађује градиво предвиђено новим програмом наставе и учења. Провери шта знаш – задаци на крају сваке обрађене целине које ученик може да ради самостално у свесци или на табли и могућност брзе провере тачности резултата Oмогућено је увеличавање делова текста уџбеника, што је изузетно погодно за демонстрацију у учионици, а такође чини материјал прегледним за ученика. Запамти – сумирани појмови који су обрађени у поглављу Дигитални уџбеник за ПЕТИ разред основне школе
Дигитални уџбеник за ПЕТИ разред основне школе
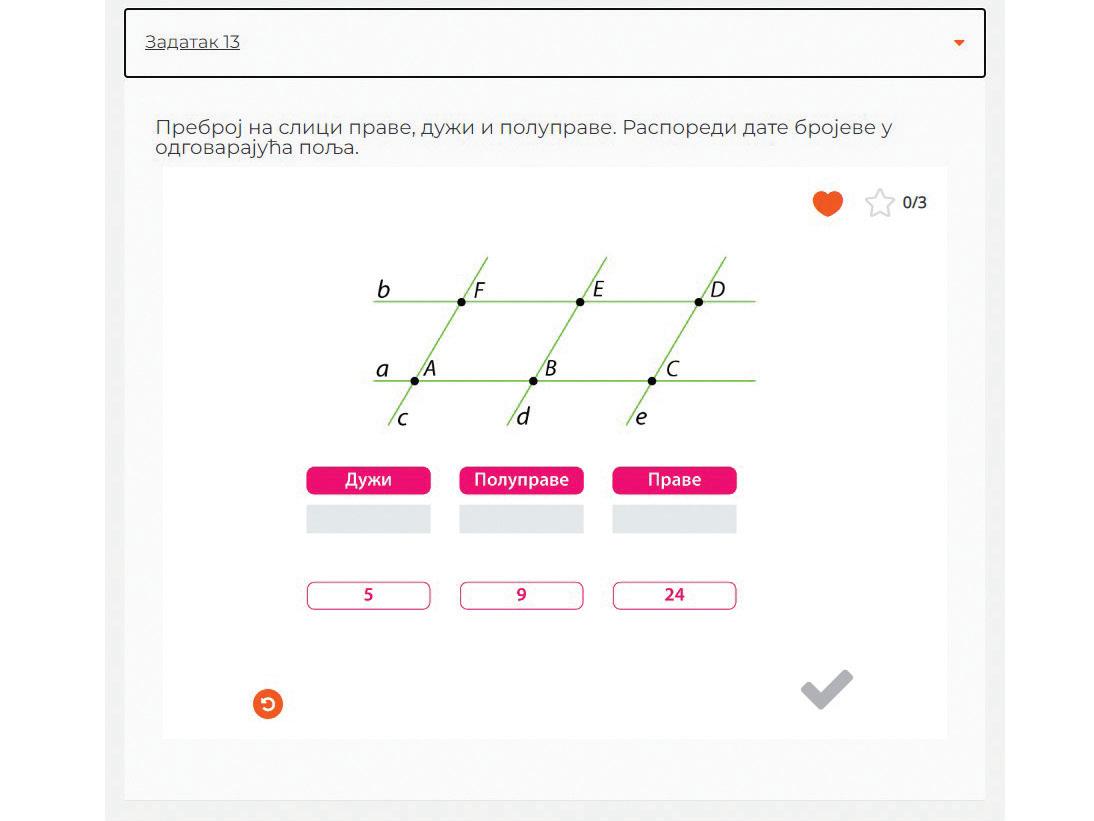
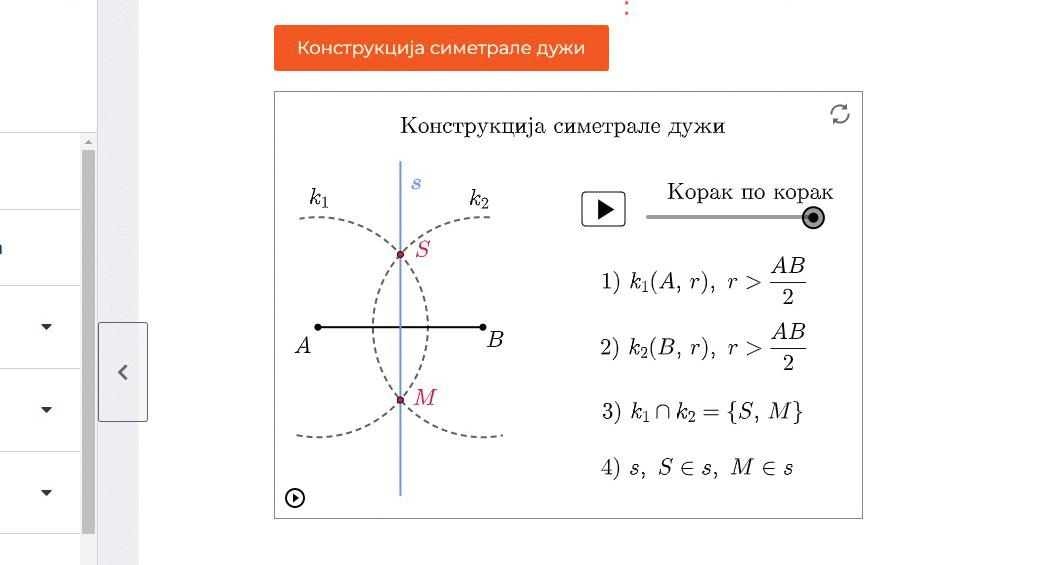



••Различити визуелни прикази који на сликовит начин демонстрирају математичке садржаје који се обрађују 2. 3.
4.

••Тестови – У свакој од девет група налази се 10-15 задатака за рад на компјутеру. Њима се проверава усвојено знање из одређене области, а решења је могуће одмах проверити.
рад.
9
На крају сваке провере знања ученик и наставник имају увид у проценат успешности у решавању, а ученик има могућност да се врати на задатке које није тачно урадио и покуша поново. ••Кретање кроз материјал је једноставно. Систем памти где је ученик последњи пут био како би лакше могао да настави
У задацима се од ученика захтевају различите активности: превлачење, уписивање, повезивање, проналажење парова. Дат је велики број типова задатака, што је разноврсније од уобичајених дигиталних материјала. Задаци се разликују према типу и нивоу знања које се њима проверава. 1.


10 Припреме
час (у електронској
штампаној форми) садрже: Са сликама у збирци наставник уводи положај две кружнице у равни: немају заједничких тачака (два положаја ), имају једну заједничку тачку (два положаја ) и имају две заједничке тачке. Положај две кружнице повезује са одстојањем центара и дужинама полупречнчика. Ученици цртају слике из задатка 16. Наставник обилази. Помаже. Дискутују се задати елементи и дају одговори о очекиваном положају кружница. Завршни део часа (5 минута) За домаћи: 4, 8, 12, 14, 15, задатак са стране 43 и 44 из збирке Анализа часа (запажања наставника) Школа Наставник Разред и одељење V Датум Редни број часа: 21 Наставна тема: OСНОВНИ ПОЈМОВИ ГЕОМЕТРИЈЕ Наставна јединица: Кружница, круг, кружни лук, тетива Циљ часа: обнављање појма кружнице и круга и њихових елемената – центар, полупречник кружни лук и тетива и њихових ознака уочавање односа две кружнице, односно два круга; разматрање на конкретним примерима и задацима стицање навике прецизног и уредног цртања и коришћења математичке симболике Исходи часа: Ученик/ученица је у стању да: -опише основне појмове у вези са кругом (центар, полупречник, тангента, тетива) и одреди положај тачке и праве у односу на круг Стандарди који се реализују у оквиру методске јединице Ученик/ученица уме да: МА.1.3.3. – влада појмовима: круг, кружна линија (издваја њихове основне елементе, уочава њихове моделе у реалним ситуацијама и уме да их нацрта користећи прибор; уме да израчуна обим и површину круга датог полупречника) Тип часа: вежбање Облик рада: индивидуални, фронтални Метода рада: рад на тексту, илустративна Наставна средства: збирка стр. 42, 43 и 44; прибор за геометрију, пројектор Корелација: Ток и садржај часа Уводни део часа (5 минута) Наставник проверава усмено како су ученици урадили задатке за домаћи. Док прегледа њихове свеске поставља питања: Које тачке припадају кружници, а које кругу? Да ли центар припада кружници и да ли припада кругу? Шта је пречник Како обележавамо тетиву, како лук Главни део часа (35 минута) Ученици раде задатак 1. Један ученик даје одговоре. Ученици самостално раде задатак 2 – обележавање кружнице. Задатак 3. Однос тачке и кружнице, круга. Усмена провера Са задатком 5, ученици повезују положај тачке са одстојањем од центра. Задатак 6. ученици мере и записују дужине полупречника, пречника у збирци Цртајући на табли, ученици у свесци, кружница из задатка 7. уводимо појам концентричних кружница Користимо слику задатка 10. ученици одговарају која је тетива најкраћа која најдужа, упоређују тетиве. Задатак 11. ученици цртају у свесци Један ученик излази и црта на табли кружницу и тетиве одређене дужине. Задатак 13. ученици цртају у свесци Наставник обилази и помаже. Дискутује се слика и проверава одговор. •• исходе из којих произлазе компетенције •• образовне стандарде •• структуру часа •• тип часа •• облик рада •• наставне методе •• наставна средства •• корелације •• активности ученика/наставника Пример припреме – 5. разред Наставне припреме за 5, 6, 7. и 8. разред пратећи су део уџбеника Методичка подршка
за
или
Ауторке: Mирјана Стојсављевић-Радовановић, Љиљана Вуковић, Јагода Ранчић
Ауторке: Mирјана Стојсављевић-Радовановић, Љиљана Вуковић, Јагода Ранчић
•• Садржи 670 задатака кључних за разумевање школског градива
Ауторке: Mирјана Стојсављевић-Радовановић, Љиљана Вуковић, Јагода Ранчић
•• Садржи 687 задатака кључних за разумевање школског градива •• Помаже ученицима да поправе оцену из математике •• Садржи 716 задатака кључних за разумевање
Ауторке: Mирјана Стојсављевић-Радовановић, Љиљана Вуковић
•• Садржи 884 задатка кључна за разумевање школског градива
•• Корисна за вежбање и утврђивање градива





11
школског градива •• Припрема ученике за контролне вежбе
ВЕЖБАМ МАТЕМАТИКУ •• Одлична припрема за контролне вежбе и писмене задатке •• Свака област се завршава задацима који систематизују знања на основном, средњем и напредном нивоу (Провера знања) •• Збирка је намењена ученицима који воле математику и који могу да савладају сложеније садржаје од оних што се обрађују на редовним часовима. •• Написана је по плану и програму за додатну наставу. •• На крају збирке дата су решења задатака. За лакше задатке понуђени су само коначни резултати, а за сложеније упутства или комплетна решења. •• У збирци се налазе задаци који подстичу развој логичког и формалног мишљења. Решавање задатака из ове збирке представља одличну припрему за такмичење. Ауторке: Наталија Јекић, Душанка Ковачевић ДОДАТНА НАСТАВА – МАТЕМАТИКА 5 Додатни материјали
•• Садрже 17 кратких контролних вежби подељених у две групе (15 минута по вежби)
•• Садрже 7 контролних вежби (А и Б група) које обухватају све садржаје предвиђене планом и програмом у петом разреду (45 минута по вежби) Ауторке: Злата Ступаревић, Свјетлана Петровић

•• Садрже 18 кратких контролних вежби подељених у две групе (15 минута по вежби)
Садрже 9 контролних вежби (А и Б група) које обухватају све садржаје предвиђене планом и програмом у шестом разреду (45 минута по вежби)

•• Садрже 12 кратких контролних вежби подељених у две групе (15 минута по вежби)
•• Садрже 6 контролних вежби (А и Б група) које обухватају све садржаје предвиђене програмом наставе и учења у седмом разреду (45 минута по вежби)

•• Садрже 17 кратких контролних вежби подељених у две групе (15 минута по вежби)
•• Обухваћени су сви садржаји предвиђени програмом наставе и учења у осмом разреду
Ауторке

••
: Злата Ступаревић, Свјетлана Петровић Ауторке: Злата Ступаревић, Свјетлана Петровић Креативна школаКреативна школа Свјетлана Петровић Злата Ступаревић КОНТРОЛНЕ ВЕЖБЕ ИЗ МАТЕМАТИКЕ за шести разред основне школе 6 Ауторка: Злата Ступаревић www.kreativnicentar.rs CIP – Каталогизација у публикацији Народна библиотека Србије, Београд ISBN 978-86-529-1131-8 COBISS.SR-ID 84417801 Креат ивна ш кола највише награђивани издавач за децу у образовном издаваштву на међународном такмичењу најбољи европски уџбеник Европског удружења издавача од 2006. године За све информације јавите се тиму за вашу територију Креативни центар • Градиштанска 8, 11120 Београд 35 • Тел.: (011) 30 88 446 Продаја: за град Београд – тел. 011 / 24 40 659, 38 20 464 • e-mail: jelena.banjanin@kreativnicentar.rs за Војводину – тел. 011 / 24 00 333 • e-mail: jelena.markovic@kreativnicentar.rs за централну Србију и КиМ – тел. 011 / 38 20 483 • e-mail: jelena.markovic@kreativnicentar.rs Контролне вежбе

























































