ГДЗ Геометрія 10 клас Істер 2023
Розділ 1. Вступ до стереометрії
1.27.

1.28.
1.29. Необхідно з’єднати нитками протилежні ніжки стола (перевернути стіл та з'єднати нитками ніжки по діагоналі).
За теоремою про існування і єдність площини, яка проходить через дві прямі, що перетинаються, якщо дві нитки перетнулися, то ніжки стола лежать в одній площині. 1.30.
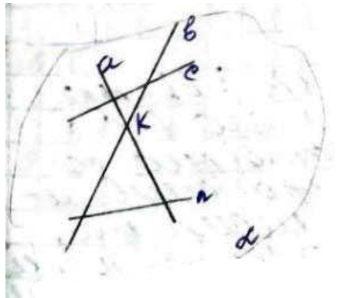
За теоремою про існування і єдність площини, яка проходить через дві прямі, що перетинаються: прямі а і в належать одній площині (наприклад, площині альфа). Проведемо будь-які дві прямі (наприклад, с і n), які не проходять через точку К і
перетинають обидві прямі а і в.
За теоремою про існування і єдність площини, що проходить через пряму і точку, що їй не належить. Через пряму с і точку К можна

провести площину і тільки одну; а оскільки а ∩ с, в ∩ с, а ⊂ α, в ⊂
α, то за теоремою про існування і єдність площини, яка проходить через дві прямі, що перетинаються, с ⊂ α.
Міркуючи аналогічно, можна дійти висновку, що n ⊂ α.
Отже, всі прямі, які не проходять через точку К і перетинають обидві прямі а і в, лежать в одній площині.
1.31.
shkola.in.ua

1.32. Задане взаємне розміщення прямих а, в і с можливе, коли прямі а, в і с перетинаються в одній точці. 1.33.
Оскільки прямі КМ і KL перетинаються з прямою LM в точках М
і L відповідно, то за теоремою про існування і єдність площини, яка проходить через дві прямі, що перетинаються, прямі KM, KL, LM належать одній площині.
За умовою пряма а не лежить з прямими KL і KM в одній площині, а оскільки прямі KL, KM і LM лежать в одній площині, то прямі а в LM не лежать в одній площині, а отже, за теоремою про
існування і єдність площини, яка проходить через дві прямі, що перетинаються, прямі а і LM не перетинаються.
1.34. Проведемо пряму m, яка перетинає прямі а, в і с. Оскільки прямі а, в і с належать одній площині і кожна з них перетинається з прямою m, то за теоремою про існування і єдність площини, яка проходить через дві прямі, що перетинаються, прямі а, в, с і m належать одній площині. Поставимо довільну точку М, яка не належить ні одній з прямих а, в, с, m. За теоремою про існування і єдність площини, що проходить через пряму і точку, що їй не належить через пряму m і точку М можна провести площину, яка перетинається з площиною, в якій лежать прямі а, в, с по прямій m. Звідси випливає, що площина, яка не проходить через точку К і перетинає прямі а, в, с існує.
Оскільки а ⊂ α, а ∩ β = А, то точка А є β, А є α.
Оскільки b ⊂ β, b ∩ α = В, то В є α, В є β.





Оскільки А є β, А є α, В є α, В є β, то за аксіомою СІІІ (якщо дві площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку) АВ ⊂ α і АВ ⊂ β, отже α ∩ β = АВ.
1.36.
Так. Оскільки пряма а ⊂ α і пряма а перетинає площину β, то точка К, в якій а перетинає β належить обом площинам α і β. За аксіомою СІІІ (якщо дві площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку) К є с. Отже, а ∩ с = К.
shkola.in.ua
1.37. За теоремою про існування і єдність площини, що проходить
через пряму і точку, що їй не належить, існує площина (АВМ), яка перетинається з площиною трикутника АВС по прямій АВ.
1.35.
Отже, прямі МА і ВС лежать в різних площинах, тому не перетинаються.
1.38.
Так. За теоремою про існування і єдність площини, яка проходить
через дві прямі, що перетинаються, пряма с належить тій же площині, що і сторони трикутника АВ і АС. Отже, с ⊂ (АВС).
1.39. 1.40.
Так. Нехай А є α, В є α, ВD ∩ АС = 0, О є α. Оскільки BD ∩ АС = 0 і О є α, В є α, то за теоремою про існування і єдність площини, яка проходить через дві прямі, що перетинається, можна стверджувати, що АС ⊂ α, BD ⊂ α, а отже дві інші вершини паралелограма С і D належать площині α. 1.41.
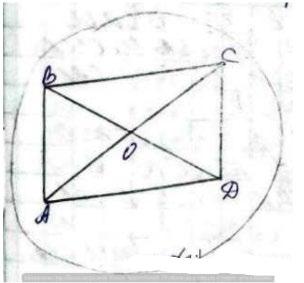
Не правильно. ВС ∩ CD = C, AB ∩ BC = B, CD ∩ AD = D, AB ∩ AD = A, отже за теоремою про існування і єдність площини, яка проходить через дві прямі, що перетинаються, існує площина (АВС), яка перетинається з площиною α в точці А. Отже, точка А спільна для площини α і (АВС). СВ ⊂ (АВС), СD ⊂ (АВС), СВ ∩ α = М, СD ∩ α = N, отже, точки М і N є спільними для площини α і (АВС). За аксіомою С3, точки А, М, N лежать на одній прямій. Отже малюнок виконано невірно.



1.42.
1.43.
ВС ⊂ (АВС), АС ⊂ (АВС), отже AL ⊂ (АВС), ВК ⊂ (АВС). Оскільки АС ∩ β = L, ВС ∩ β = К, то точки L і К є спільними для обох площин β і (АВС). (АВС) ∩ β = D, отже точка D також є спільною точкою для обох площин β і (АВС). За аксіомою С3 (АВС) ∩ β, по прямій, якій належать всі спільні точки D, К, L, отже точки K, L, D лежать на одній прямій.
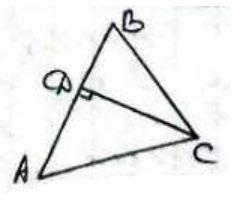
1) Проведемо висоту СD до сторони АВ, отримаємо для
shkola.in.ua
прямокутних трикутника ΔВСD і ΔАСD, в яких АС і ВСгіпотенузи, АD і ВD - катети.
Оскільки гіпотенуза завжди більше катета, то сума двох гіпотенуз
завжди буде більше суми двох катетів.
АD + ВD > ВС + СА; АВ < ВС + СА
Аналогічне доведення для двох інших сторін трикутника. У випадку, коли АВ = ВС + СА - це не трикутник, а відрізок.
2) MN = 5 см; NP = 40 мм = 4 см; MP = 8 см Оскільки виконується нерівність трикутника:
5 < 8 + 4; 8 < 4 + 5; 4 < 5 + 8, то
MNP - трикутник, отже за теоремою про існування і єдність площини, яка проходить
через дві прямі, що перетинаються, через точки M, N, P можна провести лише одну площину.
1.44. Перевіримо нерівність трикутника:
5 ≤ 11 + 6; 6 ≤ 11 + 5; 11 = 5 + 6
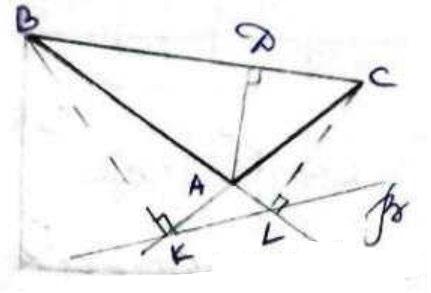
Звідси випливає, що LM - це відрізок, на якому лежить точка К, а через відрізок можна провести безліч площин.
1.45. Випадок 1. Якщо брати прямі попарно (три пари), то за теоремою про існування і єдиність площини, яка проходить через дві прямі, що перетинаються, можна провести три різні площини.
Випадок 2. Якщо брати всі три прямі одночасно і вони перетинається, то через них можна провести лише одну площину (за теоремою про існування і єдиність площини, яка проходить через дві прямі, що перетинаються).
1.46. Так, оскільки бісектриси трикутника перетинаються зі сторонами трикутника та виходять з його вершин, отже за теоремою про існування та єдиність площини, яка проходить через дві прямі, що перетинаються, бісектриси лежать в одній площині з трикутником, а отже з його вершинами.
1.47. Так. Середини сторін трикутника (точки) належать сторонам трикутника, отже сторони трикутника належать площині α. Сторони трикутника перетинаються у вершинах, отже, вершини належать площині α.
1.48.
Ні. Нехай АD, ВК і СL - висоти ΔАВС.
За умовою точки К і L належать площині β.
СL і ВК належать площині (АВС).
Отже, (АВС) ∩ β = KL.
Таким чином в цьому випадку вершини ΔАВС не належать
площині β.
1.49.
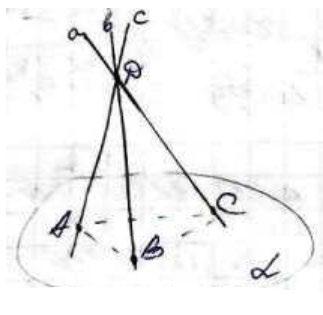
Припустимо, що а ∩ α = А, b ∩ α = В, с ∩ α = С. Точки А, В і С не лежать на одній прямій.
shkola.in.ua
Розглянемо прямі а і b: а ∩ b = D, отже за теоремою про існування і єдиність площини, яка проходить через дві прямі, що перетинаються, прямі а і b утворюють площину (АВD), (АВD) ∩ α = АВ. Аналогічно міркуючи, можна дійти висновку, що існує площина (АСD). ((АСD) ∩ α = АС), та площина (ВСD) ((ВСD) ∩ α = ВС). Отже, прямі а, b і с не лежать в одній площині. Якщо і прямі а, b і с лежали в одній площині, то за аксіомою С3 вони б перетиналися з площиною α по прямій, що проходить через точки А, В і С, а ці точки не лежать на одній прямій за умовою задачі. 1.50.
а ⊂ α, К є α, отже за теоремою про існування і єдність площини, що проходить через пряму і точку, що їй не належить, площина α єдина; b ∩ α = К, отже пряма b лежить в іншій площині, ніж α. З цього випливає, що а не перетинає b.
1.51. Ні, оскільки ця пряма лежатиме в іншій площині, ніж прямі m та n відповідно (за теоремою про існування та єдність площини, яка проходить через дві прямі, що перетинаються, ця пряма утворить з прямою а нову площину).
1.52. Так. За теоремою про існування і єдність площини, яка проходить через дві прямі, що перетинаються, пряма с утворить з а і b дві площини, і пряма d утворить з а і b дві різні площини; тому прямі с і d будуть знаходитися у різних площинах, а отже, не перетнуться. 1.53.
Нехай а ∩ β, тоді за аксіомою С3, точка перетину а і β, належить прямій m. Отже, а ∩ m = К. У випадку, коли а не перетинає β, у прямої а та площини β не буде спільної точки, а отже а не перетинається з m.
Нехай а ∩ b = А, А ∩ с = В, с ∩ d = С. Тоді точки
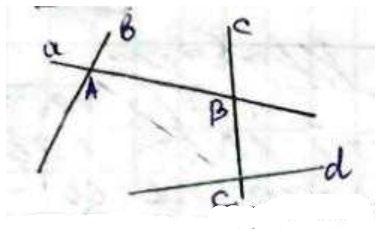




1.54. 1.55. 1.56.
А, В і С не лежать на одній прямій. За аксіомою С4 через точки А, В і С можна провести площину і тільки одну (АВС). Звідси випливає, що прямі а, b, c і d належать площині (АВС).
shkola.in.ua
Аналогічно міркуючи, можна довести для кількості n прямих.
1.57. АВ ∩ А1В1 = Р; ВС ∩ В1С1 = Q; АС ∩ А1С1 = R. Отже, площини (АВС) і (А1В1С1) мають три спільні точки P, Q, R, тобто перетинаються у цих точках.

За аксіомою С3 точки P, Q, R лежать на одній прямій.

shkola.in.ua
1.58. 1.59.























