1.2.2 Creating multiple outcomes defined by a system specific sequence

1.1.2 Creating multiple outcomes defined by a system specific sequence.

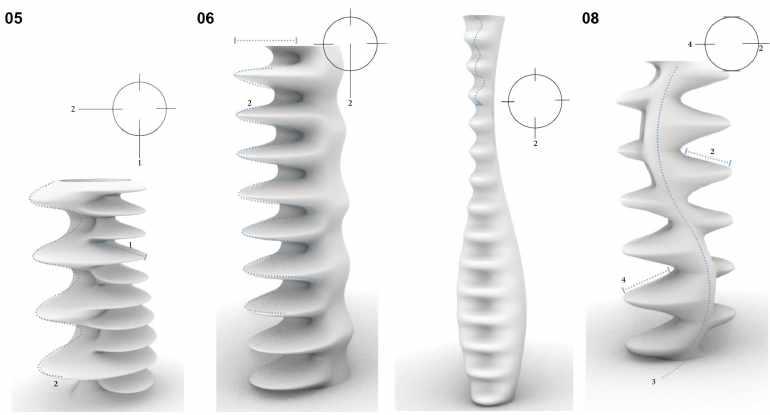
Plethora of Iterations(g) are generated through manipulation of parameters. Students give conclusion by observing change in the behavior of morphology. Also, identifying dominant and appropriate parameters based on design intent. In figure 1-4 the student achieves shell geometry while underlining that the use of sine curve intensity and intervals helps achieves maximum parametric control over desired geometry.

ITERATION 01 :

Changing the direction of the curve. For all sin curves Frequency of the Sin curve : 1 Amplitude : +1

ITERATION 02 :

Varying depths of the third curve. For 3rd sin curve Frequency of the Sin curve : 2 Amplitude : +1

ITERATION 03 :

Varying the heights of the curves and number of sin curves.

ITERATION 04 :

Increasing the number of sin curves and depth of the sin curve. For 3 rd sin curves Frequency of the Sin curve : 6 Amplitude : +3

ITERATION 05 :

Decreasing the height of the curves and increasing the depth of the curve. For 1st sin curves Frequency of the Sin curve : 10 Amplitude : +1

ITERATION 06 :

Decreasing the depth and increasing the depth of sin curves. For 2nd sin curves Frequency of the Sin curve : 9 Amplitude : +1.5

ITERATION 07 :

Decreasing the depth curve with one sin curve count and increasing the depth of curve. For 2nd sin curves Frequency of the Sin curve : 13 Amplitude : +0.5

ITERATION 08 :

Decreasing the depth sin curve and increasing the depth of curve. For 2nd and 4th sin curves Frequency of the Sin curve : 6 Amplitude : +2

Iterations(g) is the repetition of a process in order to generate a sequence of outcomes based on the design approach set by specific rules governing a geometry by parameter and constrain.

Figure 1-4 Iterations- Exploration of surface through sine BOOTCAMP: Exploring geometrical configuration through a set of r curves.(Tejaswini Walunj - M.Arch 2nd year) ules. BOOTCAMP: Exploring geometrical configuration through a set of r Exploration 1: ules. Exploration of surfaces through sine curves