Microeconomics Exam Questions and Answers

Problem

A principal hires an agent at date 0. At date 1, the agent will face one of two tasks, task A or taskB. Neither the principal nor the agent knows at date 0 which task the agent will face at date 1. It will be task A with probability p and task B with probability 1p.  The agent will learn the task at date l; the principal will never learn which task the agent faced. The agent’s effort into either task is private information. The agent’s cost of effort when performing task A is cA(e) = e2 and her cost of effort when performing task B is cB(e) = ae + be2 , where a is a parameter that can be positive or negative and b is positive. The principal’s benefit from task A is B(e) = e. The principal does not benefit from task B. The principal and the agent are both risk neutral. The principal and the agent observe a signal of effort x = e + ε, where ε is a noise term with zero mean (given risk neutrality, the specific distribution is unimportant.) The signal x is observed regardless of which task the agent is performing. The principal pays the agent with a linear contract s(x) = αx + . The agent’s reservation utility is normalized to zero. The fixed payment  can be negative. a.Set up the program that selects the Pareto optimal parameters  and  given the agent’s incentive compatibility and participation constraints. (Note that effort levels are different depending on which task the agent ends up performing). b.What is the optimal value of ? c.Suppose the principal can rule out task B. If task B is ruled out, x is identically zero when task B would have come up (task A still comes up with probability p).

https://www.liveexamhelper.com/

Will it ever be optimal not to rule out task B?

Consider a monopsonistic firm facing a continuum of workers. These workers can be of two types L and H with 0 < L < H < 1. The fraction of workers of each type is pL and pH. Workers of type i that are paid wage w and asked to work h hours receive utility U = u(w  ih), where u is a strictly concave increasing utility function with u(0) = 0. The hours of work h must fall in the (normalized) interval [0, 1]. Both type of workers have u(0) as their opportunity cost of working. The value to the firm from hiring a worker of type i at wage w and hours h is  = h/i w. The workers know their cost parameter i, the firm does not.

a. What is the profit maximizing first-best contract in this situation (ie. when the firm can identify the two types and offer separate contracts to each). Can this contract be implemented?

b. Set up the program that identifies the profit maximizing second-best solution.

c. Use a diagram to identify binding constraints. Characterize the solution to the second- best program as precisely as you can (utilizing the diagram if you wish). One can give an exact answer.

d. When will the low type not be hired at all?

https://www.liveexamhelper.com/

QUESTION 3.

An agent produces output for a principal according to the production function y = e + , where e≥ 0 is the agent's choice of input and is a stochastic productivity  parameter that takes on the value H with probability p (0 < p < 1) and the value L < H with probability (1-p); i > 0 for i = L,H.

The principal can only observe the output y, not the input e nor the productivity parameter . The agent can observe  before choosing his input x.

The agent's utility function is u(m,x) = m c(x), where m is money and c is a strictly convex and increasing cost function with c(0) = 0. The principal is risk neutral and values profit (that is the difference between output y and the payment to the agent w). The principal offers the agent a contract w(y), which the agent can reject or accept after observing the value of . The agent's reservation utility is the same in either state  and is normalized to 0.

a.Set up the program that maximizes the principals expected profit subject to the agent's incentive compatibility and individual rationality constraints (participation constraints).

b.Show that only one of the individual rationality constraints and one of the incentive compatibility constraints will bind. (You can provide an algebraic or a geometrically based argument.)

c.Assume now that  ϵ [0,1] is a continuous parameter. Write down a formula for w()  that implements the first best choice function e *() for  the agent.

Hint: For each type the  agent can be viewed as choosing y rather than e. It is easier to consider y the agent’s choice variable.

https://www.liveexamhelper.com/

Consider the following regulation problem. A firm produces a public good with the cost function c(x,)  = x 2/2 where x is the output and is  a cost parameter that only the firm knows. The social benefit is b(x) = x. The government has to decide on an optimal incentive scheme for the firm. If p(x) is the payment for x, the firm’s profit is p(x) – c(x,).  The firm always has the option not to produce, which yields profit 0.

a.Suppose the government wants to maximize the sum of social benefits and the firm’s profits. Show that in this case there is a simple subsidy scheme that maximizes the government’s objective and thus achieves the first-best outcome.

b.Suppose instead that the government is only interested in maximizing the social benefit b(x) net of the payment p(x) to the firm. Assume the cost parameter  can take two values,  = 1 and  = 2 with Prob ( =1) = p and Prob (=2)  = 1 – p. Set up a program that solves the government’s second-best problem. Draw a diagram that shows the nature of the second-best solution, including the constraints that are binding, the level of firm profit and the second- best distortions in the choice of x.

c.Assume now that  is continuously distributed on the interval [1,2]. Suppose the government wants to implement the solution x()  = 2 – . What payment scheme should it use given the objective in part b?

(a) Here is the program:

The first constraint is the agent’s IC constraint for task A, the second his IC constraint for task B, and the third his participation constraint.

The optimal α is thus

When α < a, eB = 0, and the principal’s payoff is

The optimal value of α is one. When < a < 1, the principal’s payoff is increasing in α when α ≥ a pb+1−p and decreasing in α when α ≥ a. Therefore, the optimal α is a. To sum up,

(c) Assume that B is ruled out. Consider the following contract: α = 1 and β is the minimum salary that satisfies the agent’s participation constraint. Then eA = 1/2 and eB = max{a/(2b), 0}, which are first-best effort levels. In other words, there is no efficiency loss in this contract. Also, the agent’s participation constraint holds with equality, so this is the optimal contract for the principal and beats any contracts that satisfy the agent’s participation constraint. Therefore, it is always optimal to rule out task B. Question 2

(a) For each type, wi = θihi, and thus the profit is hi/θi − θihi. SInce θi < 1, the optimal choice of hi is one, and wi = θi. This is not implementable when types are not observed, because type L prefers to receive wH = θH instead of wL = θL.

(b) There is no uncertainty from the agent’s perspective, so the agent has effective payoff w − θih. Here is the program:

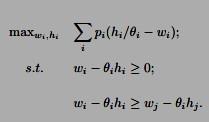
(c) Notice that the agent’s payoff w − θih has strictly decreasing differences in θi and h and strictly decreasing in θi, so the IR constraint for type H and the IC constraint for type L not to immitate type H are the binding constraints. Also, hL > hH. Therefore, The employer chooses hH and hL to maximize

Clearly, h L = 1. Also, when ∗ https://www.liveexamhelper.com/

h = 1, and when the LHS is negative, h H H = 0. When the LHS is zero, the ∗∗ employer is indifferent among all hH. (d) See (c) : the low type (here type H) will not be hired when the LHS of (1) is negative

Question 3

(a) First note the principal can choose y H and y L and set t to be arbitrarily low for any other realized output. Thus the principal’s problem reduces to

(b) We can first eliminate IRH: tH − c(yH − σH) ≥ tL − c(yL − σH) ≥ tL − c(yL − σL) ≥ 0 where the first inequality is ICH, the second follows from the fact that σH > σL and c(·) is increasing, and the third inequality is IRL. Next, it must be the case the IRL binds, otherwise the principal could lower tH and tL by equal amounts to earn profit without affecting the other constraints.

Third, ICH must bind. Otherwise it would be possible to lower tH, which would improve the principal’s profit while slackening ICL and not affecting IRL (which in turn, implies ICH is still satisfied).

Fourth, we can eliminate ICL by first establishing monotonicity. Adding the two IC constraints gives https://www.liveexamhelper.com/

where the conclusion follows from the fact that c(·) has a negative cross-partial w.r.t. y and σ. Using the fact that ICH binds, again due to the negative cross-partial.

(c) Same method as 4.c, alternatively note that for a type σ agent, the first best choice of output, y (σ), is given by y (σ) = arg max y − c(y - σ). y ∗∗ so w(y) = y implements the first best choice of output (note that y*(σ)=e*+σ where c'(e*)=1 so that w(σ) =w(y(σ)) =y(σ) =e*+σ )

Question 4

(a) Consider the scheme p(x) = x + A where A is chosen so that all firms want to produce. Then each firm maximizes x − c(x, θ) = b(x) − c(x, θ) and thus chooses the first-best output

Since the government’s objective function is the social surplus b(x)−c(θ, x), she will implement the first-best.

(b) The program is as follows:

First consider the problem of choosing (t1, t2) given (x1, x2) (where x1 ≥ x2). Notice that the firm’s profit is decreasing in θ, so only the participation constraint of the highest cost type is binding, so t2 = c(2, x − 2). The IC constraint implies that t1 − t2 [c(x1, 1) − c(x2, 1), c(x1, 2) ∈ − c(x2, 2)]. As the government wants to minimize t1, t1 = c(x1, 1) − c(x2, 1) + t2. In other words, the low-cost type is indifferent between choosing x1 and choosing x2. The government’s payoff under (x1, x2) is It is straight forward to show that the optimal choice is x1 = 1 = xF B(1), and x2 = 2−p < xF B(2). Therefore, output by the high-cost type is downward distorted. (c) As before, the binding IR constraint is the constraint for the highest-cost type. Therefore, Therefore, the payment scheme is

https://www.liveexamhelper.com/