Clustering of architectural floor plans: a comparison of shape representations

AutomationinConstruction

Clusteringofarchitecturalfloorplans:Acomparisonof shaperepresentations

EugénioRodrigues a , * ,DavidSousa-Rodrigues b ,MafaldaTeixeiradeSampayo

,AdélioRodriguesGaspar d , ÁlvaroGomes e ,CarlosHenggelerAntunes e

a ADAI,LAETA,UniversityofCoimbra,RuaLuísReisSantos,PóloII,3030-788Coimbra,Portugal

b CentreofComplexityandDesign,FacultyofMathematics,ComputingandTechnology,TheOpenUniversity,MiltonKeynesMK76AA,UnitedKingdom

c CIES,DepartmentofArchitecture,LisbonUniversityInstitute,Av.ForçasArmadas,Lisboa1649-026,Portugal

d ADAI,LAETA,DepartmentofMechanicalEngineering,UniversityofCoimbra,RuaLuísReisSantos,PóloII,Coimbra3030-788,Portugal

e INESCCoimbra,DepartmentofElectricalandComputerEngineering,UniversityofCoimbra,RuaSílvioLima,PóloII,Coimbra3030-290,Portugal

ABSTRACT

Articlehistory:

Generativedesignmethodsareabletoproducealargenumberofpotentialsolutionsofarchitecturalfloor plans,whichmaybeoverwhelmingforthedecision-makertocopewith.Therefore,itisimportantto developtoolswhichorganisethegenerateddatainameaningfulmanner.Inthisstudy,acomparativeanalysisoffourarchitecturalshaperepresentationsforthetaskofunsupervisedclusteringispresented.Threeof thefourshaperepresentationsarethePointDistance,TurningFunction,andGrid-Basedmodelapproaches, whicharebasedonknowndescriptors.Thefourthproposedrepresentation,TangentDistance,calculatesthe distancesofthecontour’stangentstotheshape’sgeometriccentre.Ahierarchicalagglomerativeclustering algorithmisusedtoclusterasyntheticdatasetof72floorplans.Whencomparedtoareferenceclustering, despitegoodperceptualresultswiththeuseofthePointDistanceandTurningFunctionrepresentations, theTangentDistancedescriptor(Randindexof0.873)providesthebestresults.TheGrid-Baseddescriptor presentstheworstresults.

©2017ElsevierB.V.Allrightsreserved.

1.Introduction

Generativedesignmethodsarecommonlyusedinarchitectural design.Thesemethodshaveseveralapplicationsinthedesignof structuralelements,facadelayout,spaceplanning,optimisationof buildingform,replicationofarchitecturalstyles,andurbandesign. Themaingoalistoassistbuildingdesignpractitionersinexploring alargersetofsolutions,whichatraditionaltrial-and-errorprocess couldneverachieve.However,oneofthedrawbacksisthatthey mayproduceanexcessivenumberofsolutionsforahumantocope with;moreover,itisjustnotfeasibletoratesolutionsaccordingto aperformancecriterionandthenselectthetop-rankedones,especiallyforunclearandsubjectiveproblems.Analternativeapproach istoorganisethegenerateddataintogroupsdeterminedbycommonfeatures.Thisallowsthedecision-makertocomparegroup typesbeforeanalysingspecificsolutions.Therefore,tofacilitate thedecision-maker’staskofcomparisonandselection,thispaper

presentsanunsupervisedclusteringtechniqueusingfourdifferent shaperepresentations.Themethodandtheperformanceofthese shapedescriptorsisanalysedinacomputergeneratedarchitectural floorplanshowcase.

Thisisatypicaltaskformachinelearningtechniques.Inthefield ofmachinelearningtherearetwomainsubfieldsdealingwithorganisationofdata:classificationandclustering.Whiletheformerisused tolabeldataaccordingtopre-definedclasses,thelatterdealswith unlabelleddataandthetaskisusuallytocreatepartitionsinthedata whilemakingcoherentgroupsaccordingtosomedefinedmetric. Thisisaprocessofidentifyingstructuresinunlabelleddatasets regardlessofthedatatype.HanandKamber [1] classifiedclustering techniquesintofivecategories:partitioningmethods,hierarchical methods,density-basedmethods,grid-basedmethods,andmodelbasedmethods.

* Correspondingauthor.

E-mailaddress: eugenio.rodrigues@gmail.com (E.Rodrigues).

Clusteringtechniqueshavebeenappliedindiverseareas.Some ofthemostrelevantapplicationsincludetheclassificationof textualdocuments [2],documentnavigationforsearchengine optimisation [3–5],resourceprojectscheduling [6],pointcloud simplification [7,8],timeseriesanalysisandclustering [9],image clustering [10],faceexpression [11],databaseretrievalofmechanical objects [12,13],andsketchrecognition [14] http://dx.doi.org/10.1016/j.autcon.2017.03.017 0926-5805/©2017ElsevierB.V.Allrightsreserved.

Theclusteringofobjects,accordingtotheirshape,hasalsobeen previouslyappliedindiversefields.Thecorrectrepresentationof theshapehasasignificantimpactonthematchingcorrectnessof thealgorithms [15].Forinstance,Changetal. [16] proposedashape recognitionschemewheretherepresentationcorrespondstothe distanceoffeaturepointsintheshape’sboundarytothecentroid. Thisshaperepresentationpresentsthepropertyofbeinginvariant totranslationastheboundaryisfixedinrelationtothecentroid independentlyofitsglobalposition.Asthedistancesofthefeature pointsareorderedanddividedbyaminimumdistance,thisalso resultsininvariancetoscaling,rotation,andreflection.Insteadof onlyconsideringtheshapefeaturepoints,YankovandKeogh [17] usedtheentirecontourfortheshaperepresentationandanonlinear reductiontechniquetoclusterpathologicalcells.

Arkinetal. [18] representedapolygonalshapebyitsturning function.Theshapedescriptorconsistsinmeasuringtheangleof thecounter-clockwisetangenttothe x-axisineachofthefeature pointsinthepolygon.Therefore,thevaluesvarybetween p and p . Asthepolygonisscaledtohavealengthof1,inadditiontobeing translationinvariant,therepresentationisalsoinvarianttoscaling. However,resultsdependonthestartingpointandthepolygon’s rotationandreflection.

SajjanharandLu [19] suggestedagrid-basedrepresentation whereashapeisplaced,rotated,andscaledtofitasquaregrid.For eachcellinthegridabinaryvalueisdetermined:0foremptyand 1forfilled.Althoughthisrepresentationguaranteestranslationand scaleinvariance,ifthegridisadaptive,thescalingisonlyinvariant tooneoftheaxes—therotationinvarianceisdependentontherotationofthegridtomatchthesameshapeorientation.Also,asmaybe expected,theresultsvaryaccordingtothegridsize,asthischanges thecapabilitytocapturetheshape’sdetails.

Siddiqietal. [20] usedashockgraphtocapturetheeffectson theboundingcontoursofthesingularitiesintheshapestructure.The graphisdeterminedaccordingtoasetofrulesinashockgraphgrammarwhichreducesittoarootedshocktree.Arecursivealgorithm isthenusedtomatchtwoshocktrees,startingfromtherootand proceedingthroughthesubtreesinadepth-firstapproach.

Belongieetal. [21] presentedanapproachtomeasuresimilarity ofshapesbyconsideringthedistributionoftheremainingpointsin eachreferencepoint.Ascorrespondingpointsintwosimilarfigures havesimilarcontexts,atransformationisusedtoaligntwoshapes. Thedissimilaritybetweenthemiscalculatedbysummationoverthe errorsbetweenthecorrespondingpointsinthetransformation.

Aimingtoretrieveshapesfromadatabase,whicharesimilarto aqueryshape,Tanetal. [22] proposedanewrepresentationbased onacentroid-radiiapproach.Accordingtotheauthors,thisapproach allowsthemodellingofconvex,concave,andhollowshapes.Therepresentationconsistsofasetofvectors,eachonemeasuredatregular intervalsfromthecentroidofaconcentricring.

InKlassenetal. [23],theshapesareconsideredtobeplanarclosed curvesrepresentedeitherasdirectionfunctionsorascurvature functions.Inthismanner,shapesmaybemodelledasstretchable, compressible,andbendablestringsalongtheirextensionsthatare constructedfromspacesofparametriccurves [24,25].Geodesicsare usedtodeterminethedissimilitudebetweenshapes.

LingandJacobs [26] classifiedshapesbyusinganinner-distance tobuildtheshaperepresentationofthestructureorarticulation parts.Theinner-distanceisthelengthoftheshortestpathbetween tworeferencepointsontheshapeboundaryandallowsthecreation ofarticulationinvariantrepresentations.

Shenetal. [27] proposedamethodtogroupplanarfiguresby theirskeletongraph.Theclusteringiscarriedoutbydeterminingthe commoninternalshapestructurethatbelongstothesamecluster. Thedataisgroupedbyusinganagglomerativeclusteringalgorithm.

Inarchitecture,ChaandGero [28] investigatedshapepatternsto determineifanysimilarities,relationships,andphysicalproperties

couldberecognised.delasHerasetal. [29] usedrunlengthhistogramsasaperceptualrepresentationoffloorplansmadeby architects.Thisapproachallowstheretrievalofdesignswithsimilarpropertiesfromadatabase.Duttaetal. [30] usedagraph-based methodtoidentifysymbolsinfloorplanssuchasfurnitureand openings.

However,despiteallofthementionedapproaches/methods,the useofclusteringtechniqueshasyettobeusedtogroupdesignsin thecaseofautomaticgenerationoffloorplans.Inapreviousstudy, Sousa-Rodriguesetal. [31,32] conductedanonlinesurveydirected atdesignandconstructionexperts—mostlyarchitects,engineersand architectureundergraduates—inwhichthemajorityofrespondents consideredtheoverallshapeoffloorplansasthemostimportant similitudefeature.Thishighlightstheimportanceofhavingperceptuallyaccuratealgorithmsfortheautomationofthistask.

Inthispaper,fourshaperepresentationsarestudiedasfloor plandesigndescriptorsunderthesamesettings.Alldescriptorsare vectors ofsimilarlength,andallareusedtopartitionthesame datasetwiththesameclusteringalgorithm.Threeofthefourshape representationsareknowndescriptors:thesearethedistancetocentroid [16],theTurningFunction [18],andtheGrid-Basedmodel [19] Thefourthandlastshapedescriptorisanovelrepresentationspecificallycreatedtocaptureorthogonalfloorplanshapes.Itconsists incalculatingthedistanceofthetangentlinestothegeometric centreoftheshape.Theclusteringprocedureisanagglomerative hierarchicalalgorithmwithWardlinkage [33] andEuclideandistanceasadissimilaritymeasure.Theadvantagesanddisadvantages ofeachshaperepresentationareanalysedinashowcasewith72 floorplandesigns.Thesedesignsweregeneratedusingaspecific algorithm,namedEvolutionaryProgramfortheSpaceAllocation Problem(EPSAP) [34–36].TheEPSAPalgorithmgeneratesalternative floorplansaccordingtotheuser’sspecifications.

Afterthisintroductorysection, Section2 describesthemethods appliedtotheclusteringofthefloorplansdesigns.In Section3 the resultsforashowcaseofasingle-familyhousearepresentedand comparedtoareferenceclusteringpartition.Thediscussionofthe relevantresultsfollowsin Section4,aswellastheanalysisofthe applicabilityofthedescriptors.Finally,conclusionsaredrawnand futureworkisoutlinedin Section5

2.Methodology

Todeterminethemostsuitableshaperepresentationtobeused intheclusteroforthogonalfloorplans,threeshapedescriptors inspiredbypreviousworksandonenewdescriptorwereimplemented.Thesedescriptorshavethesamevectorlengthandshape matchingalgorithmusingtheEuclideandistancetocalculatethedissimilitudebetweentheshapes.Therefore,thecomputationalburden isequalforthefourapproaches.Aspecificalgorithmgenerateda datasetoffloorplandesigns.Thissyntheticdatasetdoesnotrequire apre-processingmechanismfordenoisingtheshapes,northeapplicationofadimensionalityreductiontechnique.Therefore,thefocus isontheperceptualqualityoftheresultsofeachshapedescriptor.

2.1.Shaperepresentation

Therepresentationofcontinuousfeaturesplaysanimportantrole inmachinelearningtechniques,eitherbecausethemachinelearning techniqueitselfrequiresanominalfeaturespace—nominalfeatures describequalitativeaspectsthatdonotshareanaturalordering relationship—orbecausediscretisationallowsforbetterresultsin themachinelearningtechnique.Theresearchondatasetdiscretisationformachinelearningisvastandbeyondthescopeofthis paper,butitisimportanttomentionthatsuchalgorithmsusually aimtomaximisetheinterdependencybetweendiscreteattribute valuesandclasslabels,asthisminimisestheinformationlossdueto

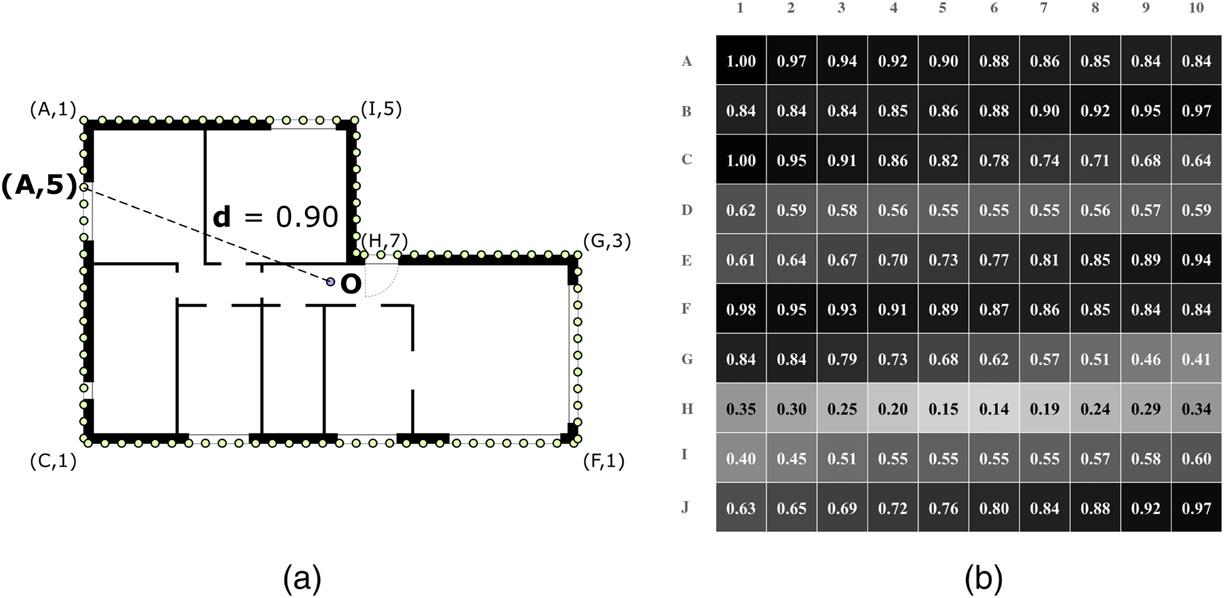
Fig.1. PointDistance(PD)descriptor.(a)Exampleofthenormaliseddistanceforthepoint(A,5)withvalueof0.90,whichcorrespondstoitsrealdistancedividedbythelongest distanceofallsilhouettepoints.Thewallcornersaremarkedwiththematrixindextodepictthecounter-clockwiseorderofthefeaturepoints.(b)Vectorintheformofagradient matrix(whiteis0andblackis1)ofthenormaliseddistances.

thediscretisationprocess.Theprocesshastobalancethetrade-offs betweenthesetwogoalsandmanystudieshaveshownthatseveral machine-learningtechniquesbenefitfromit [37–40].

Inthisstudy,thefourdescriptorsaredesignedtohavesimilarfeatures.Theseareinvarianttotranslationandscalingbutsensitiveto rotationandreflection.Adescriptorvariantthatconsidersindependentscalingofx-andy-coordinateswasalsoanalysed.Thereasonfor thesefeaturesisthat,despitefloorplansbeinggeneratedonablank canvas,humanexpertscontinuetohaveanotionofnorth-southand east-westframework,thusarotatedorareflectedfloorplanisconsideredasanalternativedesign.Buildingshaveastrongrelationwith theirenvironmentandtheirformdependsonthesurroundingbuildings,landscape,solarorientation,andsoon.However,becausethere arenovisualreferencesaroundeachfloorplan,translationdoesnot affectthehumanperceptionofthatshape.Asaresult,rotationand reflectionwereconsideredasfeaturesthatinfluencetheclustering result.Nevertheless,invariancetorotationandreflectioncouldbe easilyachievedbyorderingthedescriptorvectororconsideringthe distributionofthesevalues.

2.1.1.PointDistance(PD)descriptor

BasedonChangetal.’s [16] shaperepresentation,thePointDistance(PD)descriptorhaspointsmarkedontheshapesilhouette atequalsegmentlengths.Thestartingpointisthenearestshape perimeterpointinrelationtothetop-leftcorneroftheshapeboundingboxandthepointsaredistributedinacounter-clockwisedirection.OurimplementationdiffersfromChangetal.’srepresentation asthereferencepointisnottheshape’scentroid,whichisdefinedas theaverageofthe x-and y-coordinatesofallperimeterpoints,but insteadconsidersthegeometriccentreoftheboundingboxasthe referencepoint.Theshapedescriptoristhenavectorofnormalised values—correspondingtothedistancefromthereferencepointtothe orderedperimeterpointsdividedbythelongestpointdistance.

Fig.1aillustratesanexampleofthemarkedperimeterpoint(A,5) anditsnormaliseddistancetothecentre(0.90).Theexamplerepresentsthedescriptorvariantwherethe x-coordinateand y-coordinate scalesarepreserved. Fig.1bdepictstherepresentationvectorofnormalisedvaluesrangingfrom0(white)to1(black)inagradient

matrixform,1 wherethefirstvectorpointis(A,1)andconcludesin point(J,10).Inthefloorplanimage,thewallcornersaremarked withthecorrespondingmatrixpointtodepictthecounter-clockwise orderofthemarkedpoints.

2.1.2.TurningFunction(TF)descriptor

ThesecondshapedescriptorisbasedonArkinetal.’s [18] turning function.Thisconsistsindeterminingthecounter-clockwiseangleto the x-axisofatangentineachfeaturepointalongtheshapecontour. Thefeaturepointsaremarkedatequaldistances.

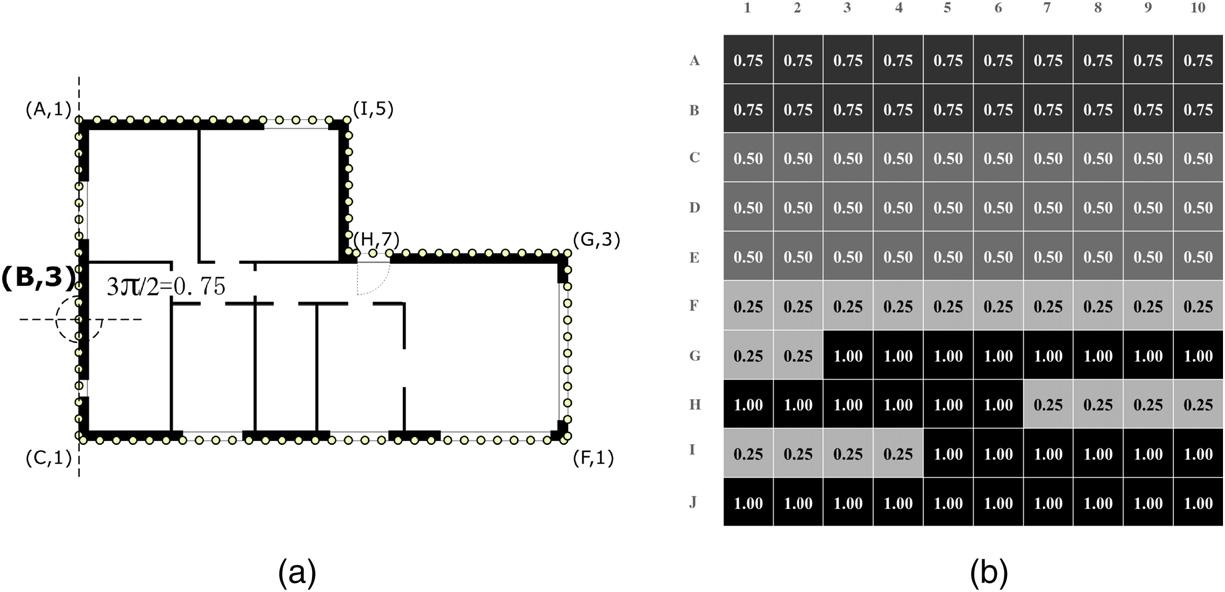
Fig.2adepictsanexamplewheretheturningfunctionangleis measuredatpoint(B,3),withthevalueof3p /2,inthedescriptorvariantofpreservedaspectratio.Thefeaturepointsstartwith theinitialpoint(A,1),whichisthenearestperimeterpointtothe top-leftcorneroftheshapeboundingbox,andcontourstheshape silhouetteinacounter-clockwisemanner.Therefore,thevaluesvary between0and2p thatarethennormalisedtohavevaluesranging from0to1. Fig.2billustratesthevectoroftheTurningFunction(TF) descriptorasagradientmatrix.Asthefloorplansareorthogonal,the shapeedgesonlytakeonfourpossiblevalues {p /2, p ,3p /2,2p } = {0 25,0 50,0 75,1 00}

2.1.3.Grid-Based(GB)descriptor

TheGrid-BaseddescriptorisinspiredonSajjanharandLu’s [19] workandconsistsinplacingtheshapeunderasquaregridparallel totheexteriorwallsofthefloorplans.Foreachcellinthegrid,the centremay(1)ormaynot(0)beoccupiedbytheshapearea.The representationisavectorofbinaryvalueswiththelengthequalto thenumberofcells.Thevaluescorrespondtoreadingthegridfrom left-to-rightandtop-to-bottom.

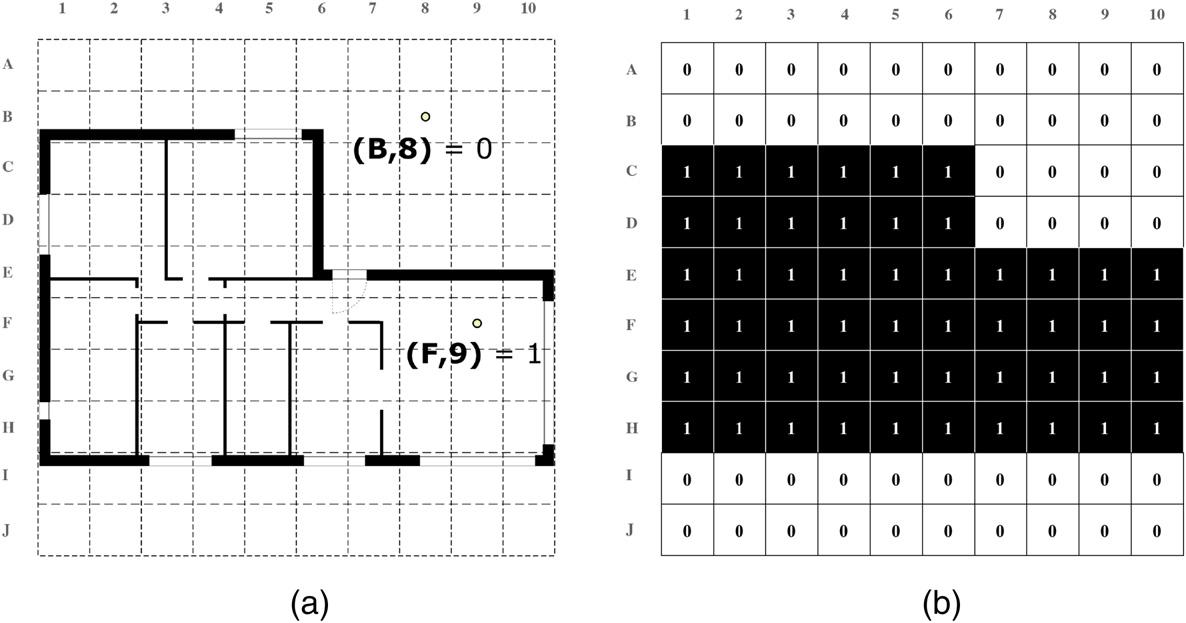
Fig.3aillustratesanexampleofafloorplanoverlaidbyagrid.In theexample,point(B,8)hasavalueof0while(F,9)hasavalueof1 dependingonwhetherthefloorplanareaisunderthatcellcentreor

1 Thegradientmatrixofthefourrepresentationsisusedonlyforvisualcomparison ofdifferentfloorplans.Theagglomerativehierarchicalalgorithmuseseachdatapoint asa1-dimensionalvector.

Fig.2. TurningFunction(TF)descriptor.(a)Exampleofthemeasuringangleinpoint(B,3)thathasthevalueof0.75,whichcorrespondsto3p /2.Thewallcornersaremarked withthematrixindextodepictthecounter-clockwiseorderofthefeaturepoints.(b)Vectorintheformofagradientmatrix,where0iswhiteand1isblack,foranglesranging from0to2p

not. Fig.3brepresentsthecorrespondingbinaryvectorasamatrix. Eachmatrixentryhasthecorrespondingvalueintheoverlaidgridin thefloorplan.

2.1.4.TangentDistance(TD)descriptor

TheTangentDistance(TD)descriptorconsistsindetermining thedistanceofastraight-linetangenttotheshapecontourtothe boundingboxcentre.Asfloorplansareorthogonalshapes,ultimately thetangentlinecoincideswiththeexteriorwall.Theshapehasits perimetermarkedwithpointsatregularlengthintervalsstarting onthenearestpointontheshapeperimetertothetop-leftboundingrectangle.Ineverypoint,astraightlineisdrawntangenttothe

shapeandthedistanceismeasuredtothecentrepoint.Thevector hasitsvaluesnormalised—measureddistancedividedbythelongest distance.

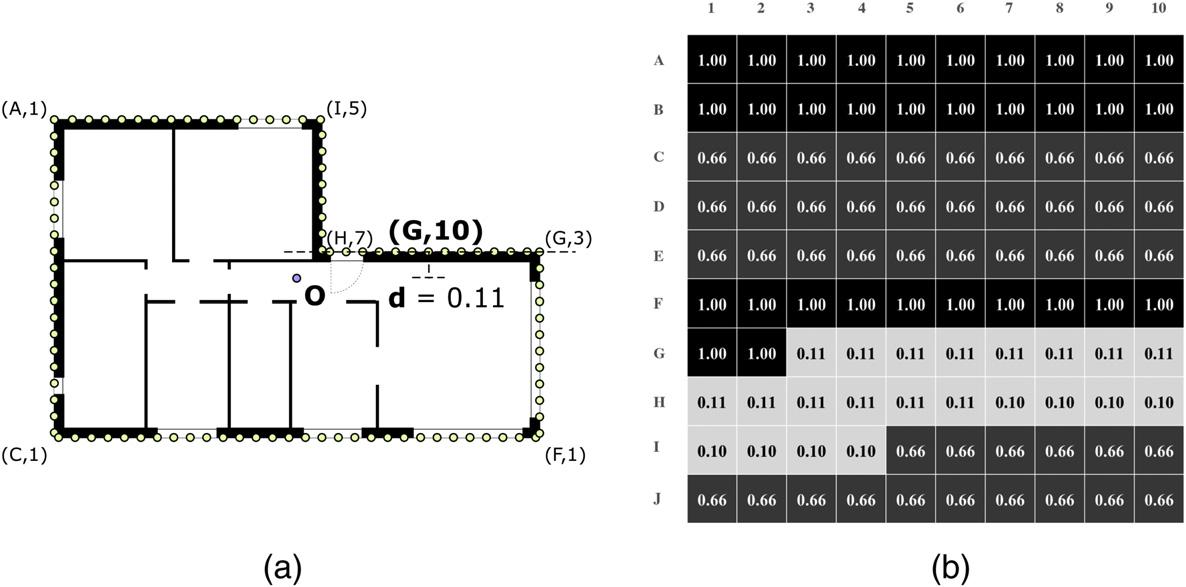
Fig.4adepictsanexampleofthedescriptorvariantforpreserved aspectratio.Thefeaturepoint(G,10)hasanormaliseddistancevalue of0.11ofitstangenttothecentre. Fig.4billustratestheresulting vectorintheformofagradientmatrix.

2.2.Clusteringalgorithm

Thedatasetwasclusteredusinganagglomerativehierarchical algorithmwithWardlinkage [33] andtheEuclideandistanceas

Fig.3. Grid-Based(GB)descriptor.(a)Exampleoftwopointmeasurements.Point(B,8)isoutsidethefloorplanareathushavingthevalueof0.Meanwhile,point(F,9)fallswithin thefloorplanareaandhasavalueof1.(b)Vectorintheformofamatrix(whiteis0andblackis1)depictingthecorrespondingcellvalueintheoverlaidgridinthefloorplan. Onlythecellcentreisusedtomeasurethepresenceofthefloorplan.

thedissimilaritymeasurebetweendifferentfloorplandesigns(featurevectors).Hierarchicalclusteringisbasedontheassumptionthat thereismaximalquantifiableinformationwhenasetofelements isungrouped,andthatthisinformationiscapturedbyanobjective function.Inthecaseofagglomerativehierarchicalclustering,the algorithmstartsbyconsideringasmanyclustersastheavailabledata pointsandplacingeachdatapointinacluster.Itproceedsbymergingtwoexistingclustersthatoptimiseanobjectivefunction.Inthis casethefunctionisavariancecriterionminimisingthetotalwithinclustervariance.Ateachstepoftheagglomerativeprocess,thetwo clusterstobemergedaredependentontheleastincreaseinthetotal within-clustervariance.Theprocessthenproceedsiterativelyuntil allclustersaregroupedintoasingleglobalcluster.

Althoughthelinkagecriterionusedinhierarchicalclusteringcan beofdifferenttypes,Ward’scompletelinkageaimstofindcompact clustersandwasthereforepreferredinthiswork.Asimilarlinkage isthecompletelinkageclustering [41],wherethedistancebetween twodifferentclustersiscalculatedbyconsideringallpair-wiseinteractionsbetweentheelementsinthetwoclusters.Itthenusesthe distanceofthepairofpointsthatisfarthestawayfromeachotheras thedistancebetweenthetwoclusters.Italsoaimstocreatecompact clustersandtocomputefaster.ForlargepopulationsitisanalternativetotheWard’scriterionasitisfaster.Inthiswork,allresults employedtheWard’scriterion.

Thereareseveralmeasuresavailabletodeterminethedissimilitudeoftwodescriptorvectors [42].Inthisworkthedissimilitude betweentwofeaturevectorswascalculatedbytheEuclideandistancefor N-dimensions,with N beingthelengthofthefeaturevector describingthefloorplandesign.

2.3.Syntheticdataset

Thedatasetoffloorplandesignswascreatedusingagenerativedesignalgorithm,namedtheEvolutionaryProgramforthe SpaceAllocationProblem(EPSAP) [34–36].Thisalgorithmcombines anEvolutionStrategy(ES)techniqueandaStochasticHillClimbing(SHC)methodinatwo-stageapproach.TheEPSAPiscapable ofgeneratingmulti-storeyfloorplanswhereparametric,non-rigid,

andnon-fixedverticalcirculationelementsevolveduringthesearch processininteractionwiththeremainingspaces.

Fromasetofrequirementsdefinedbytheuserandgivenas input(see Subsection3.1 foranexampleoftherequiredinput information),thegenerativedesignprocessinitialisesbycreating, atthefirstESgeneration,randomlydistributedanddimensioned rectangles(eachcorrespondingtoaroom)inthe2-dimensional plan—eachstoreyhasitsown2-dimensionalplan.Eachdesignsolutionisevaluatedwithaweightedsumofseveralobjectives.These objectivesareconnectivity(interiordoors),adjacency(proximity betweenrooms),roomdimensionsandarea(accordingtominimum sizeofthesmallestrectanglesideandminimumfloorarea,respectively),compactnessofthefloorplan,roomoverflowinrelationtoa buildingboundary(whenspecifiedbytheuser),openingdimensions (tosatisfyminimumwidthandwindow-to-floorratio),andopening orientation(whenspecifiedbytheuser).

AteveryESgeneration,theSHCmethodiscalledtorandomly transformthedifferentarchitecturalelementsinthefloorplan (rooms,stairs,elevators,clusterofspaces,openings,walls,andthe floorplansasawhole).TheSHCmethodappliesgeometricactions suchastranslation,reflection,rotation,stretching,alignmentofelements,permutationofelementtype,andchangestotheelement’s orientation.Thetransformationactionrandomlyselectstheelement, direction,andmagnitudeofchangefromtheadmissiblegeometric values.Then,thecandidatesolutionsareevaluated.Iftheactionproducesanequalorbettersolution,thechangeispreserved,otherwise itisdiscarded.TheSHCstagecontinuesiterativelyuntilreaching theSHCterminationcriterion—thedifferencebetweenthemoving averageandthelastiterationofthebestindividuals’averageperformanceisgreaterthanadefinedthreshold.Then,solutionshaving betterperformancethantheaverageofthepopulationarepreserved forthenextESgeneration,whiletheremainingonesarediscarded andsubstitutedwithnewrandomlygeneratedones,thusinitiating anewEScycle.WhentheESterminationcriterionisreached,the algorithmstopsanddisplaystheresultstotheuser.

AstheEPSAPproducesalargenumberofalternativefloorplans, somekindofaggregationmechanismisrequiredtohelpuserscompareandanalysethegeneratedsolutions.Thisisthemotivationfor thedevelopmentofthisstudyasdescribedin Subsection2.1.

Fig.4. TangentDistance(TD)descriptor.(a)Exampleofthetangentdistanceforthefeaturepoint(G,10),whichhasthenormaliseddistancevalueof0.11.Thehorizontalwalls cornersaremarkedfollowingthecounter-clockwiseorder.(b)Vectorintheformofagradientmatrix,where0iswhiteand1isblack.

3.1.Showcasespecifications

Asingle-familythree-bedroomhousewasusedasanillustrative example.Inadditiontothethreebedrooms(R6–8 ),ahall(R1 ),a kitchen(R2 ),alivingroom(R3 ),acorridor(R5 ),andtwobathrooms (R4 and R9 )werespecified.Topologically,allspaceshaveconnection tothehallorthecorridor.Thekitchenalsohasaninteriordoorconnectingtothelivingroom.Oneofthebathroomsservesthepublic areaofthehouseandtheotherisconnectedtothecorridorofthe privatepartofthehouse,whichisconnectedtoallbedrooms.The interiorconnectivity(Mcon )isdefinedinMatrix(1),where1representsaninteriordoorconnectingtworoomsand0indicatesthe absenceofdoorsconnectingthem.

0.11mfortheinteriorwall(tiw ).Thefloorplandesign(FPD)must haveaconstructionareainferiorto200m2 (ac ).

Usingtheserequirementsasinput,theEPSAPalgorithmranasingletimetogenerate72alternativefloorplansfromapopulationof 576individuals(eachindividualisacandidatesolution).Thegenerativedesignprocesstook136sina2.8GHzQuad-corecomputerwith 8GBofRAM.Multi-threadingwasused.Thefloorplansimproved overatotalof1790iterationsbyminimisingpenaltiesfornotsatisfyingtheuserspecifications.Thebestindividualhadafitnessof 98,265.1inthefirstiterationand2.2inthelastiteration,which resultedfromnotattainingtheaimedfloorplanarea.

3.2.Clusteringresults

AsthepurposeofthisworkwastoprovidetheEPSAPalgorithm withclusteringcapabilitiestohelptheuserdealwithalargenumber ofgeneratedsolutions,andbecausethetypeofshapesandresultingnumbersarenotknownapriori,anunsupervisedclustering approachwasused.Thatis,thenumberofclustersdoesnotdepend ontherealnumberofdifferentshapesinthegeneratedsetbuton thenumberofalternativesolutionsthattheuserwantsormight analyse.Asthecomplexityofthefloorplansincreases,thenumberofalternativeshapesalsogrows,easilyreachingnumbersthat becomeintractableforthedecision-maker.Theclusteringmechanismisindependentfromthenumberofclustersandthenumber offloorplandesigns,thusmaybescaledupordownonlyaffecting computationtime.Asthevectorineveryclusteringprocesshadthe samelength(100values),thetypeofshaperepresentationdidnot affecttheperformanceofthealgorithm.However,theresultshad significantdifferencesdependingontheshapedescriptor.

Allinteriordoorsmusthave0.90mwideexceptthelivingroom doors,whichare1.40m.Withtheexceptionofthehorizontalcirculationspacesandoneofthebathrooms,allremainingspaceshaveat leastonewindow(thelivingroomhastwo).Thehallhasoneexterior doorfacingnorth(orientationup).Noothertopologicalrequirement wasadded,suchasopeningorientationorspacelocationonthefloor plan.

Thedetailedshowcaserequirementsarepresentedin Table1, wheretheinformationrelatingtoeachroomislisted.Theseinclude spacename(Msn ),spacefunctiontype(Mst ,where0represents circulationspaces,1rooms,and2kitchensandbathrooms),minimumfloorsidedimension(Mfd ),minimumfloorarea(Mfa ),exterior openingwidth(Meow )andheight(Meoh ),spacewindow-to-floorratio (Mwfr ),clearareaintheoutsideofopening(Meoa ),exterioropeningorientation(Meoo ),andinteriordoorsminimumwidth(Midw ). Thethicknessesofwallsare0.32mfortheexteriorwall(tew )and

Duringthepreparatorywork,asurveywasconductedtodeterminewhichclusteringfeatureshumanexpertsusetogroupfloor plans [31,32].Thesurveyanalysisdeterminedthemainfeatures, suchasshapeandindoorroomarrangement.However,human expertsaregenerallyinconsistentduringtheclusteringprocess—for instance,thesameindividualmaysometimesgatherfloorplansby shapeandinothertimesbyindoorspacearrangement.Thisresulted inhavinggroupswhereafloorplanAhassimilarshapeasafloor planBandthelatterhasthesameinternalarrangementasafloor planC.However,ChasnosimilaritywhatsoeverwithA,despitethe threebeinginthesamecluster.Therefore,theresultsofthesurvey werenotusedasagroundtruthduetothischangingbehaviour.As analternative,areferenceclusteringwasdeterminedbytypifying shapesfromdesignsfoundinthedataset. Fig.5 depictssuchpartition(labelledfrom A’ to I’)withthetypifiedshapeontheleftofeach groupletter.

ThereistheO-shape,fourrotatedL-shapes,tworotatedT-shapes, andtworeflectedZ-shapes.Group A’ (O-shape)has7designs; B’

1.20m 2.00m {1.80m,3.00m}North0.90m

1.00m 0.1{3.00m,3.00m} 0.90m

{5.00m,4.00m}{2.40m,2.40m} {3.00m,3.00m} 1.40m

0.90m

0.90m

1.00m 0.1{3.00m,3.00m} 0.90m

1.00m 0.1{3.00m,3.00m} 0.90m

1.00m 0.1{3.00m,3.00m} 0.90m

0.60m 0.60m {3.00m,3.00m} 0.90m

Fig.5. Referenceclusteringandshapetypebygroup.

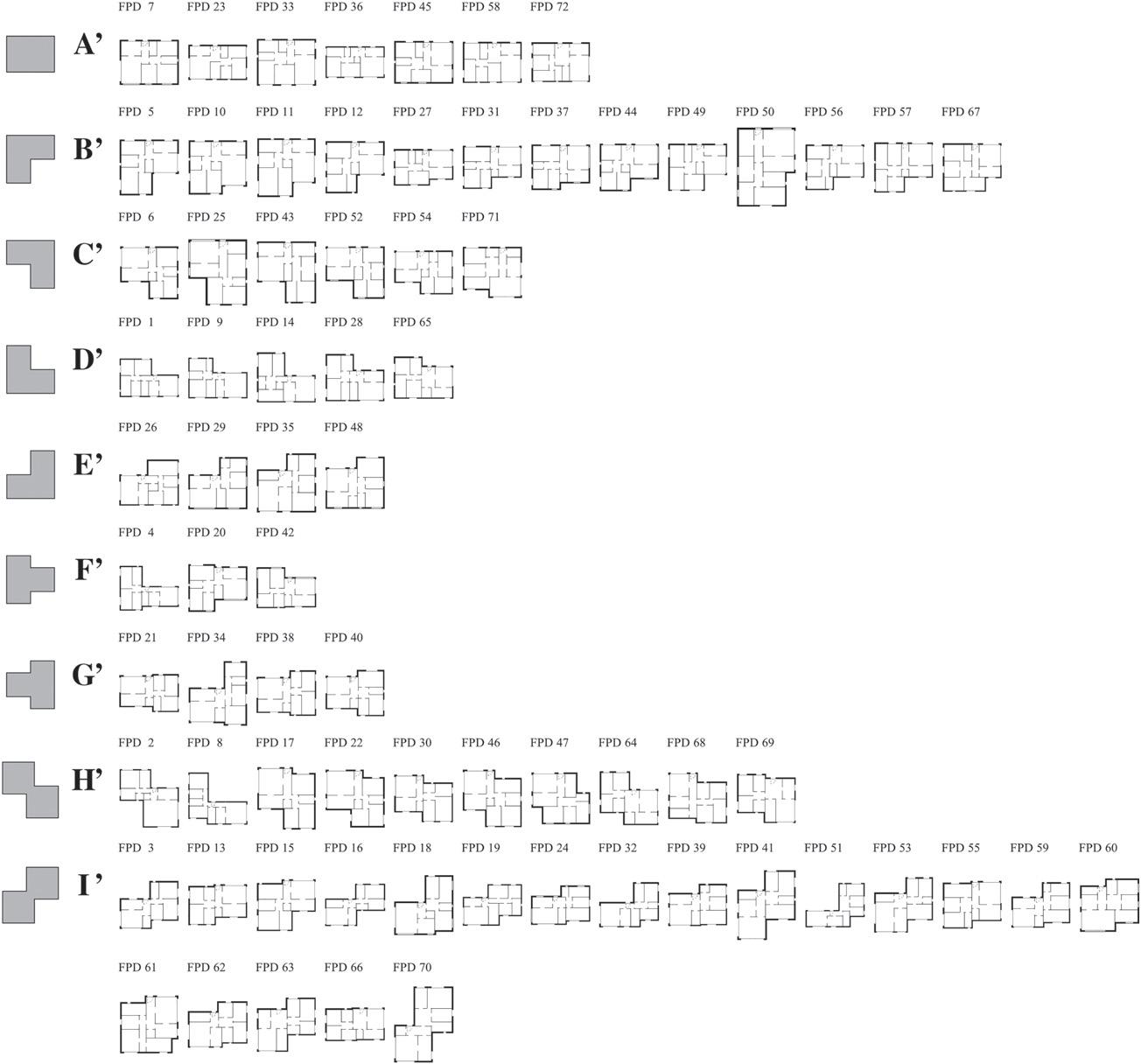
(top-leftL-shape)has13; C’ (top-rightL-shape)has6; D’ (L-shape) has5; E’ (reflectedL-shape)has4; F’ (rotatedleftT-shape)has3; G’ (rotatedrightT-shape)has4; H’ (Z-shape)has10;and,finally, I’ (reflectedZ-shape)has20designs.

Severalmeasureshavebeenproposedtodeterminethequalityof theresultinggroupsandcomparingthoseclusterswithareference groupofthedata.Themeasuresofcomparisonhavetobeableto handleminordataperturbationsaswellasmissingdata,butremain sensitiveenoughwhentwoclusteringmethodsproducedifferent resultsfromthesamedata [43].InRand [43] anindexisproposed thatisbasedonameasureofsimilaritybetweentwodifferentclusteringsofthesamedatasetandconsidershoweachpairofdata pointsisassignedineachclustering.Ifthepairofpoints i, j isplaced together—assignedtothesamecluster—inbothclusterings,orifthey areplacedindifferentclustersinbothclusterings,thisisconsidered asimilaritytraitbetweenthetwoclusterings.Thedissimilarityis observedwhenthepairofpointsisplacedtogetherinoneclustering andseparatedintheother [43].Therefore,foranytwoclusterings

,thesimilaritybetweenthemiscalculatedbyEq.(2),where

=1ifthepairofpoints i, j appearsinboth clusteringsinthesamerelationand

=0ifthepairofpointsdoes nothavethesamekindofrelationsinbothclusterings.

Additionally,eachdescriptor(anditsalternativevariantof non-fixedaspectratio)wasevaluatedaccordingtotheperceptual coherenceofeachgroupandbetweengroups.Agroupisconsidered coherentifitpresentsadominantshape(theshapethatappearsthe highestnumberoftimesinagroup)withalowernumberofoutlier designs.Confusionmatricesareusedtocomparedescriptorvariants. Thesearepresentedinatableformatwheretwoclusteringsfrom thesamedatasetcanbecomparedbyshowingthenumberofelementsthatbelongtotheclustersofbothclusterings,ineachtable

entry.Theseareusuallyusedtocompareaclusteringpredictedby amachinelearningalgorithmandaclusteringthatisareference clustering.Thecolumnsandrowsrepresenteachgroupforthetwo descriptors.

3.2.1.PointDistance(PD)descriptorresults

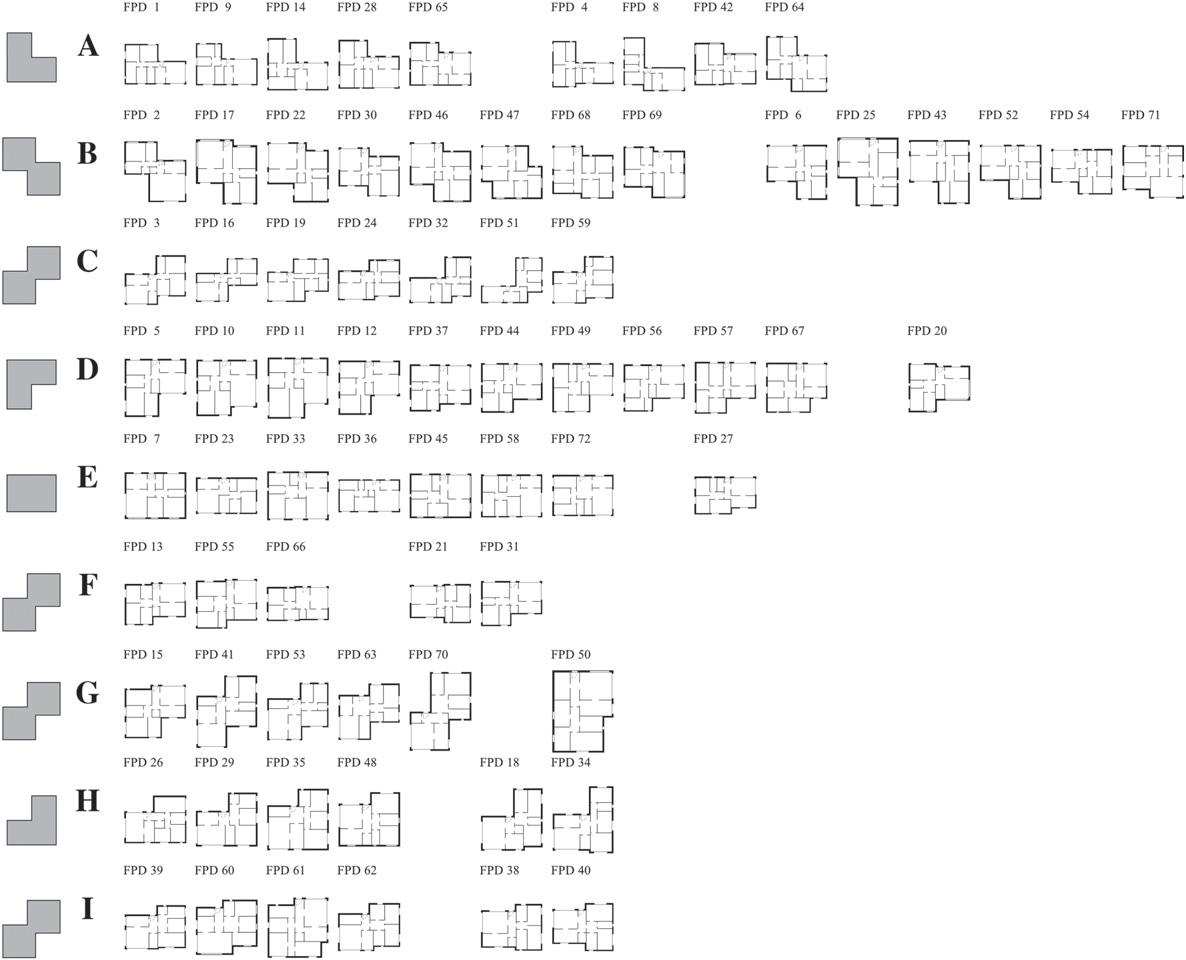
ForPDdescriptor, Fig.6 depictstheclusteringresults(forfixed aspectratio)andthegroup’sdominantshapeatleftofthegroupletter.Thegroupoutlierswereplacedattheendofeachgrouprowfor readability.

Thisdescriptorpresentssixuniquedominantshapesfromatotal ofninepossibleones,noneofthegroupswasfreefromoutliers,clusteringaccuracyof70.83%,andRandindexof0.861.Thenumberof designspergroupvariesbetween4and14.Thegroupwiththehighestnumberofdominantshapedesigns(Nd )wasgroup D with9and thegroupswiththelowestnumberofoutlierswere D, G, H,and I withone.Outliersexistinallgroups.

Fromaperceptualanalysis,whencomparedtothereferenceclusteringpartition,thePDdescriptorisunabletohaveafullycoherent group.Forinstance,group A hastheL-shapeasthedominantshape thetypeandFPD4,8,42,and64asoutliers.Group B followstheZshapetypeandhasasoutliersFPD6,25,43,52,54,and71,which wouldfitbetterinthetop-rightL-shape(dominantshapeabsent

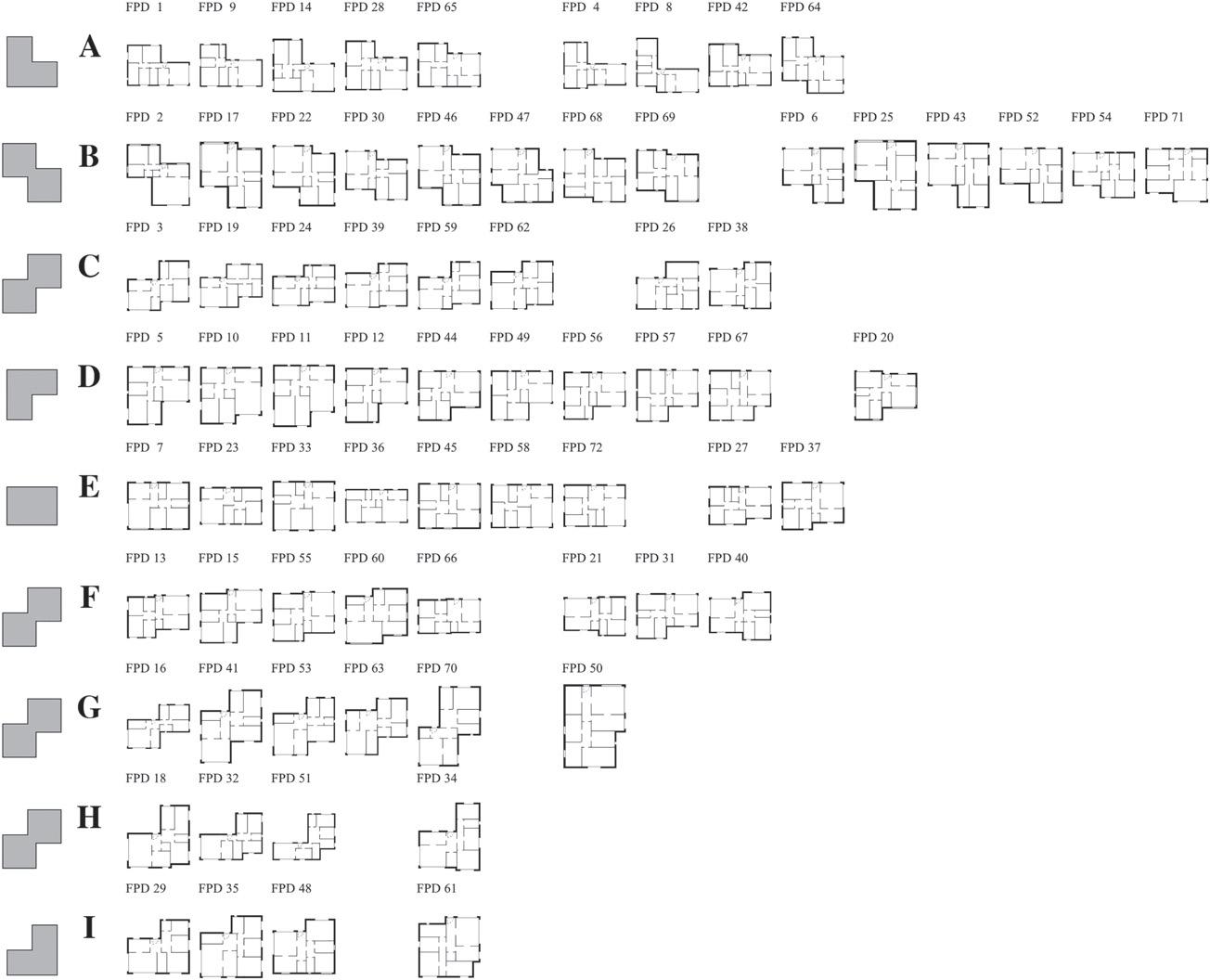
fromthispartition).Group C onlyhas2outliers(FPD26and38) andhasareflectedZ-shape.Thetop-leftL-shapegroup D hasonly 1outlier(FPD20).Group E aggregatestheO-shapetypeandhave2 outliers(FPD27and37)thatwouldfitingroup D.Groups F and H havethesamereflectedZ-shapetypeasgroup C andonlyhaveone incorrectlyassigneddesign(FPD50and34,respectively).Finally,the lastgroup I hasareflectedL-shapewithoneoutlier(FPD61).

Table2apresentstheconfusionmatrixofthisfixedaspectratio descriptorvariantagainstthereferenceclusteringpartition.Itis noticeablethatdesignsinpartitions B’ and I’ aredispersedoverfour ormoregroupsofthedescriptorresults,thusshowingthedifficulty ofthePDdescriptorincorrectlydeterminingthetop-leftL-shapeand thereflectedZ-shapetypes.Itisalsoobservablethatthetop-right L-shape(partition C’),rotatedleftT-shape(F’),androtatedrightTshape(G’)areoutliersinseveraldescriptorgroups(B; A and D;and C, F,and H,respectively).

Comparingthefixedaspectratiovariantofthisdescriptorwith thenon-fixedone(see Fig.A.10 in AppendixA),theperformance decreaseswithanclusteringaccuracy(Ac)to66.67%andRandindex (Ri )to0.852.Despitehavingonegroupwithnooutlier(group C)and findingthesamenumberofuniqueshapegroups(see Table2b),the descriptorwiththisfeaturelosesaccuracyingroups B, E, G, H,and I; however,itimprovesingroups C and D (see Table2c).

Fig.6. ClusteringresultsusingPointDistance(PD)descriptor.

PointDistance(PD)confusionmatrices.

3.2.2.TurningFunction(TF)descriptorresults

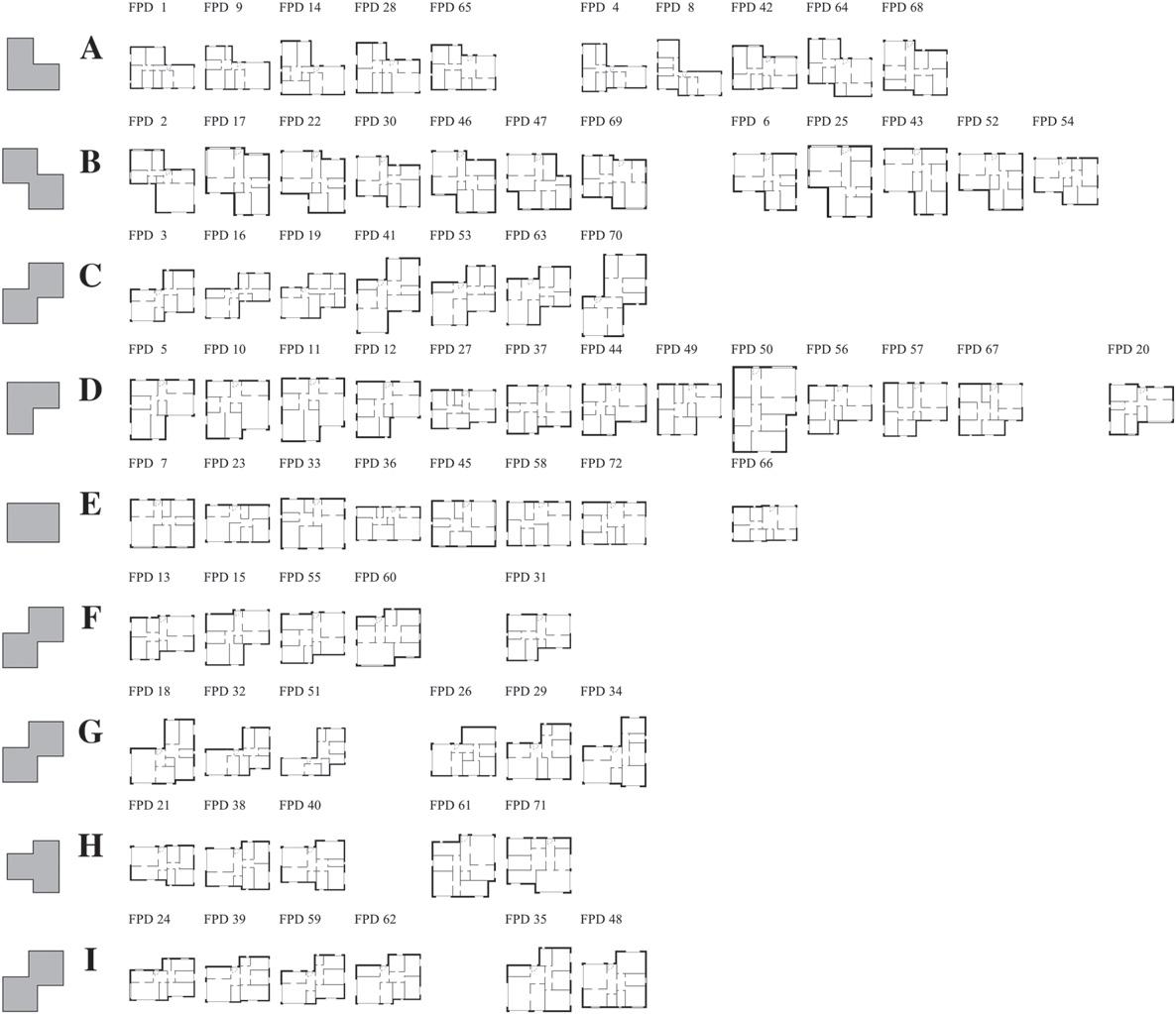
Fig.7 presentstheresultsfortheTFdescriptorandthedominant shapeineachgroup.TheTFdescriptorhas6uniqueshapegroups (Nu ),2groupswithoutanyoutlier(No ),clusteringaccuracyof66.67%, andRandindexof0.842(Ri ).Thenumberofdesignspergroupvaries between4and15.Thegroupswiththehighestnumberofdominant shapedesigns(Nd )were C and D with8.Thegroupswithnooutliers were D and H (Ne ).

Theperceptualanalysisofthegroupcoherenceshowsthatgroup A hastwooutliers(FPD4and8)andthedominantshapetypeisthe L-shape.Group B followstheZ-shapeandhasFPD28,42,and65 incorrectlyassigned. C hasareflectedZ-shapetypeandthelargest numberofoutliers(FPD21,26,29,35,38,40,and48)thatmix reflectedL-shapeandrotatedrightT-shapetypes.Group D hasno outliersanditsshapetypeisthetop-leftL-shape.Group E dominant shapeisthetop-rightL-shapewith4outliers(FPD17,22,46,and69)

Fig.7. ClusteringresultsusingTurningFunction(TF)descriptor.

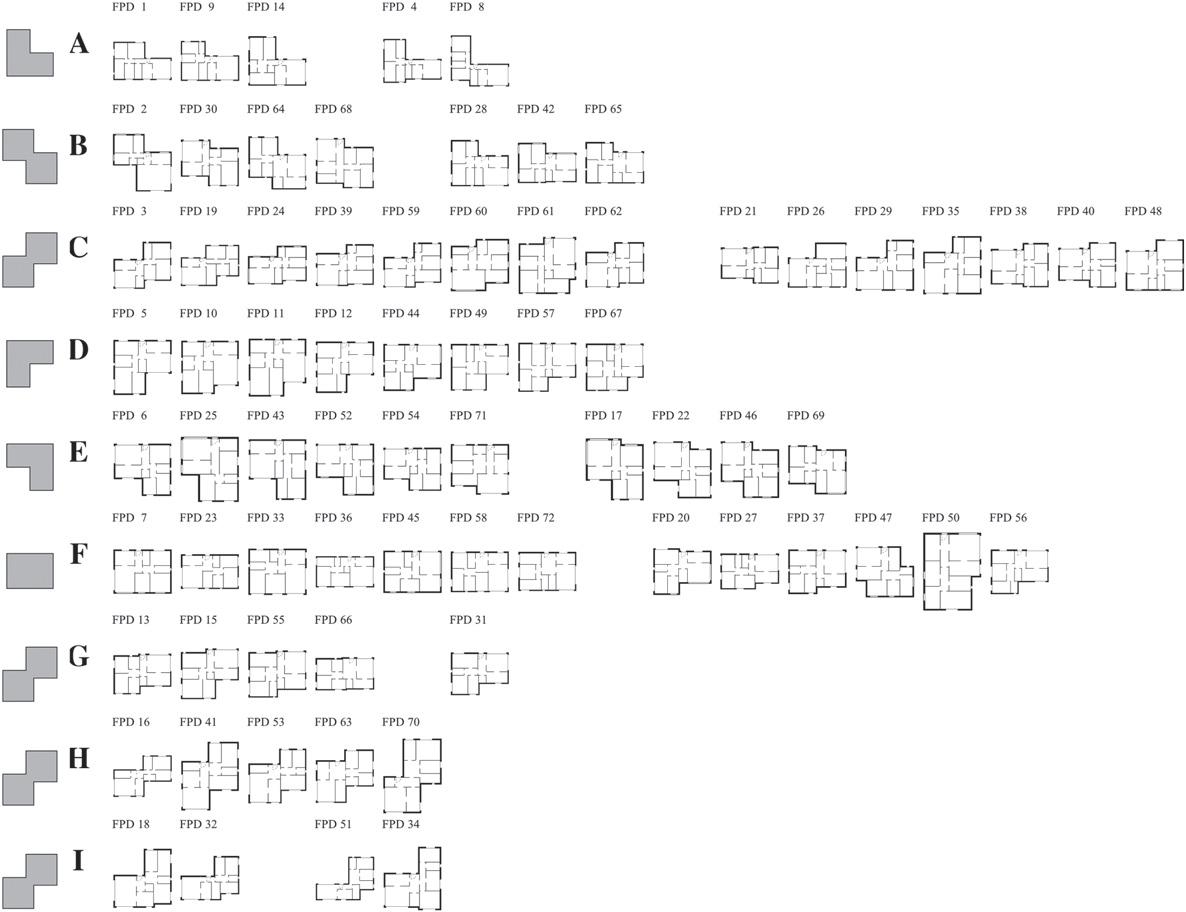
whoseshapefitsingroup B withZ-shapetype.TheO-shapegroup is F andhas6outliers(FPD20,27,37,47,50,and56).Groups G, H, and I havethesamedominantshapeas C (reflectedZ-shape). G only has1outlier(FPD31,atop-leftL-shape)and I has2outliers(FPD51 and34).

Table3acomparesthefixedaspectratiodescriptorvariantwith thereferenceclusteringpartition.Thedesignsinpartitions B’, F’, H’,and I’ arespreadoverthreeormoregroups,thusindicating theTFdescriptor’sdifficultyincorrectlycapturingtheshapetopleftL-shape,rotatedleftT-shape,Z-shape,andreflectZ-shapetypes, respectively.Onemayalsonotethatshapesfrompartitions E’, F’,and G’ wereunabletodominateanygroup.

Whenconsideringthenon-fixedaspectratiodescriptorvariant (resultsaredepictedin Fig.A.13 in AppendixA),theperformanceof Ac increasesto69.44%andthe Ri to0.858.Oneofthetwogroupsthat hadnooutliersisalsolost. Table3bshowstheincreaseofclustering accuracyforshapesinpartitions B’, D’,and F’ anddecreasesin C’ and E’

.Whencomparingbothdescriptorvariantsin Table3c,group I has thelargestshiftofdesigns,capturing8thatwerepreviouslyingroup C.Thegroupsthatacquiredesignsfromothergroupsare A, C, D, F, and H

3.2.3.Grid-Based(GB)descriptorresults

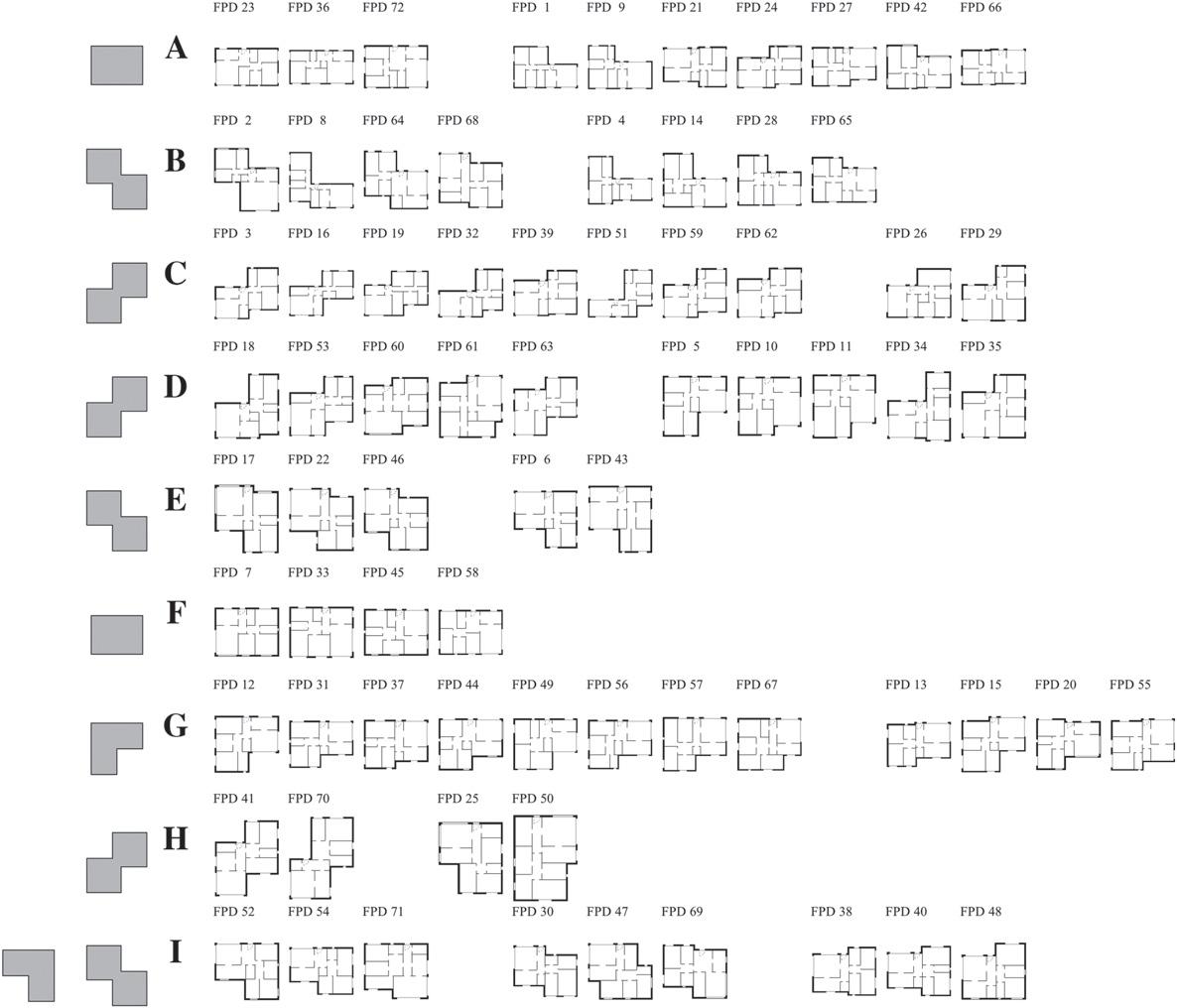
Fig.8 illustratestheGBdescriptorclustering.GBonlyidentifies 5uniqueshapegroups(Nu )andonegroupwasfreefromoutliers (No ).TheclusteringaccuracyandRandindexwerethelowestofall descriptorswithonly55.56%(Ac)and0.824(Ri ),respectively.The numberofdesignspergroupvariesbetween4and12.Thegroups withthehighestnumberofdominantshapedesigns(Nd )were C and G with8.Group F hadnooutliers(Ne ).Group I hastwodominant shapes.

GBdescriptorhasthelowestgroupcoherenceofallthedescriptors’results.Forexample,groups A and I havemoreoutliersthan dominantshapes—A (O-shapetype)hasFPD1,9,21,24,27,42,and 66asoutliers,and B hasFPD38,40,and48,andoneofthetwosets FPD52,54,and71(top-rightL-shape)orFPD30,47,69(Z-shape). TheZ-shapegroups B and E have4(FPD4,14,28,and65)and2outliers(FPD6and43).Groups C, D,and H haveasdominantshapethe reflectedZ-shapetypeandhasdissimilardesignsFPD26and29,FPD 5,10,11,34,and35,andFPD25and50,respectively.Group G,with top-leftL-shapetype,hasFPD13,15,20,and55presentsdiffering designs.

Theconfusionmatrix,depictedin Table4aforfixedaspectratio, showsdesignsdispersedoverallgroups,formingheterogeneouspartitions.Forinstance,referenceclusteringpartitions B’ and I’ have

designsdistributedoverfourormoredescriptorgroups—A, D, G,and H,and A, C, D, G,and H,respectively.Therefore,thefixedaspectratio variantofthisdescriptorcannotaccuratelycapturethedifferences betweenallshapes.

However,ifallowedtochangethedesignaspectratio,theGB descriptorsignificantlyimprovesitsaccuracy,reaching75.00%for Ac (thehighestofalldescriptors)and0.874for Ri .Thegroupdesigns aredepictedin Fig.A.12 in AppendixA.Italsoachieves7unique shapegroups(Nu )andtwogroupswithoutanyoutlier(No ). Table4b showstheperformanceimprovementinallgroupsasdominant shapedesignsincreaseinallpartitions.Thecomparisonofthetwo descriptorvariantsin Table4cillustrateshowdesignsthatinitially wereingroup A arenowassignedtogroups A to F.Otherexamples arethenewgroups B, C, D,and E,whichcapturedesignsthatwere assignedtoseveralgroups.

3.2.4.TangentDistance(TD)descriptorresults

TheresultsfromtheTDdescriptoraredisplayedin Fig.9.Outofall thedescriptorsandvariantsinthisstudy,theTDdescriptorpresents thebestresults.Itwasabletodetermine6uniqueshapegroups(Nu ; similartoPDandTFdescriptors)andonly1grouphadnooutliers. TheclusteringaccuracyandRandindexwerethehighestofthefixed aspectratiosdescriptorsvariantwith73.61%and0.873(Ri ),respectively.Thenumberofdesignsperclustervariesbetween5and14. Thegroupwiththehighestnumberofdominantshapeswas D with 10andthelowestnumberofoutlierswasgroup C withnone.

Thisdescriptorhasthehighestgroupcoherenceofall.However, therearestilloutliers.Forinstance,group A hastheL-shapeasthe dominantshapetypebutalsocaptures4outliers(FPD4,8,42,and 64),threeofthoseduetosmallrecessesinthebottomwall.Itis observablethatFPD64clearlybelongstotheZ-shapetypegroup. Group B has6outliers(FPD6,25,43,52,54,and71)—allfitting thetop-rightL-shapeinsteadofthedominantZ-shapetype.TopleftL-shapeingroup D hasasingleoutlier(FPD20),whichfitsthe rotatedleftT-shapeduetoasmallrecessinthetopwall.Forsimilarreasons,group E withO-shapetypehasFPD27(top-leftL-shape) asanoutlier.Groups F and G havethesamereflectedZ-shapetype. TheoutliersofthesegroupsareFPD21and31andoutlierFPD50, respectively.Despitehavingthesameshapetype,TDdescriptorpartitioneddesignsintotwogroupsbecausetheconcaveturnsinthe wallshavedifferentsizesegments.Group H has2outliers(FPD18 and34)inthedominantshapetypereflectedL-shape.Onceagain, thedescriptordidnotconsiderthesedesignswithadifferentshape despitethesmallrecessinthebottomwall.Finally,thelastgroup I,

Fig.8. ClusteringresultsusingGrid-Based(GB)descriptor.

withreflectedZ-shape,has2outliers(FPD38and40withrotated rightT-shapetype).

Table5apresentstheconfusionmatrixforthisdescriptoragainst thereferenceclustering.Partition A’ designsarefullyincludedin group E.However,partition B’ hasthreeofitsdesignsspreadover threegroups E to G,buttheremaining10designsareassignedto group D.Partitions C’, D’,and E’ arealsoassignedtoacorresponding group—B, A,and H,respectively.Designsinpartitions G’ and H’ are

Table4

Grid-Based(GB)confusionmatrices.

distributedoverthree(F, H,and I)andtwogroups(A and B).Finally, thelargestreferenceclusteringpartition I’ haditsdesignsassigned tofivegroups(C,and F to I).

Whenconsideringthenon-fixedaspectratiodescriptorvariant (Fig.A.13 in AppendixA),thedescriptorunderperformsslightlyin theclusteringaccuracy,whichdecreasesto72.22%,butimprovesin theRandindexto0.876.Referenceclusteringpartitions B’ and G’ are betterpartitionedinthisdescriptorvariant,butaccuracyislostfor

Fig.9. ClusteringresultsusingTangentDistance(TD)descriptor.

partitions C’, E’, G’, H’,and I’ (Table5b).Comparingbothdescriptor variants(Table5c)groups B, C,and E to I haveafewdesignsthat havebeenshiftedtoothergroups.

4.Discussion

Table6 summarisesperdescriptorthenumberofuniqueshapes (Nu ;numberofgroupswithuniqueshapetype),numberofgroups withoutoutliers(No ),thepercentageofclusteringaccuracy(Ac;

Table5

TangentDistance(TD)confusionmatrices.

numberofdominantshapedesignspertotaloffloorplandesigns), andRandindex(Ri ).Italsoliststhenumberofdominantshapes(Nd ) andthenumberofoutliers(Ne )pergroup.Thedescriptorwithbetter Ri isTangentDistance(TD)with0.873and0.876forfixedandnonfixedaspectratiovariants,respectively.However,Grid-Based(GB) presentsthehighestnumberofuniqueshapegroups(Nu )andthe highest Ac of75%forthenon-fixedaspectratiodescriptorvariant.

Thepresenceofoutliers(Ne )inthePointDistance(PD)descriptormayindicatewhysomegroupshavedesignsdispersedbyother

Descriptorsperformance. Group ABCDEFGHI

Descriptor

(a)Fixedaspectratio

Nu No Nd Ne Nd Ne Nd Ne Nd Ne Nd Ne Nd Ne Nd Ne Nd Ne Nd Ne AcRi

PointDistance(PD) 6 054866291725351313170.83%0.861

TurningFunction(TF) 62 32438780647641503166.67%0.842

Grid-Based(GB)5137448255324084223655.56%0.824

TangentDistance(TD) 6 15486701017132514242 73.61% 0.873

(b)Non-fixedaspectratio

PointDistance(PD)61545470101764253332166.67%0.852

TurningFunction(TF)6153405491547431814469.44%0.858

Grid-Based(GB) 72 4252121876471503041 75.00%0.874

TangentDistance(TD)61557570121714133324272.22% 0.876

Nu -numberofgroupswithuniqueshape; No -numberofgroupswithoutoutliers; Nd -numberofdominantshapedesigns; Ne -numberofoutliers; Ac -accuracy; Ri -Randindex. clusters.Thiscanresultfromthefactthat,whenthereisaslight discontinuityoftheexteriorwall,themeasureddistancefromthe pointsintheperimeterdilutessuchdifference.Thisisabenefitin shapesrequiringdenoising;however,indatasetswithnonoisethe resultsarenotsogood.

InthecaseoftheTurningFunction(TF)descriptor,otherproblem occurs.Namely,duetotheabsenceofinformationinthedescriptorvectorresultingfromwallrecessessmallerthanthedistance betweenfeaturepoints—whenthewallturnsasmalldistanceand turnsbacktothesamedirection.Inthissituation,andbecausethis descriptoronlycapturestheangleofthewall,theinformationbefore andafterthewallchangeisthesame.Theonlywaytoinclude thatinformationistohaveafeaturepointoftheshapesilhouette init.Additionally,evenifthewallrecessissomehowcaptured,it onlyrepresentsafewvaluesinthevectorasthemainpartsof thewallcontinuetohavethesameangle.Thiswouldbeavoided onlyifthedescriptoralsomeasuredthewalldistancetoareference point.

IntheresultsfortheGBdescriptortheproblemisdifferent.In thiscase,thedescriptorvectorisverysensitivetothemeasuring pointsinthegrid.Therefore,iftherearesmallvariantsintheshape proportionsthenarowofpointscanturnfrom0to1andvice-versa. Forinstance,awiderrectangle,whenscaledtofitthemeasuringgrid, willresultinasmallerheightthushavinglessareafilledinthegrid. Despitetheshapebeingbasicallythesame,thiswillresultindifferentvectors(comparetheFPD23ingroup A andgroup F in Fig.8 asan exampleofthisissue).However,whendealingwithadjustedaspect ratio,theperformanceimprovesfortheGBdescriptor.

TheTDdescriptorpresentsthebestresultsforbothvariantsofthe aspectratio.Thisisduetothefactthatitincorporatestheadvantages ofthePDandTFdescriptors,namelytheabilitytocapturethedistanceofthesegmentandtheanglechangeofthewalls,respectively. However,whenextendingtheusetoshapessuchastheequilateral triangle,square,pentagon,orotherregularpolygons(evenacircumference),theTDdescriptorwillclassifyalloftheminthesamegroup, asthepolygontangentsallhavethesamedistancetothecentre. Anotherissuewasfoundwiththisdescriptor.Insomecases,when designshavethesameshapetype,itmayconsiderdistinctduetothe sensitivityoverthesizeofthesegmentsineveryturnoftheexterior wall(seegroups F and G in Fig.9 asanexample).

Inthecaseofthedistance-baseddescriptors(PDandTD),itis possibletocontroltheirsensitivitytowallrecessesintheshape perimeterbyexponentiatingthenormaliseddistances.Iftheexponentislowerthan1,therepresentationreducesthesensitivityto smallvariations;otherwise,whengreaterthan1,thisisincreased.

Itisinterestingtoobservethatthedescriptorsthathavethe bestresultsareallperimeter-basedrepresentations.Area-basedrepresentations,suchastheGBdescriptor,aretoosensitivetosmall changesintheproportionsoftheshape.Thisapproachmayhave

betterresultsinshapesthatrequiredenoising.However,insyntheticdatasetssuchastheoneillustratedintheshowcase,areabasedrepresentationisalessreliableapproach.Limitationsofthese descriptorsmaybesummarisedasfollows:

• PD,TF,andGBdescriptorsareinsensitivetosmallrecessesin theperimeter;

• TFdescriptormaynotcaptureperimeterturnsiftheshape’s silhouettestepisbiggerthattheturnsegmentdimension;

• GBdescriptorgreatlydependsonthegridresolutionthus makingitverysensitivetosmallvariationsintheshapeproportions;

• TDdescriptormaysufferfromexcessivesensitivitytothesegmentssizeinwallturns,thusleadingtoclusterdesignsin differentgroupsdespitehavingthesameshapetype;

• TDdescriptorclustersregularpolygons(triangle,square,circle, etc.)asthesameshape;and,

• TDdescriptorisverysensitivetoshapeswithnoiseinthe perimeter.

Thematchingandclusteringoffloorplandesignshassomepossibleapplications.Oneofthoseistouseitasaclusteringmechanism forresultsobtainedfromgenerativedesignmethods—forexample, theEPSAPalgorithmalreadyincludesthesemechanismstoorganisedatatobepresentedtothedecision-maker.Anotherexampleis touseitwithintheevolvingprocessofpopulation-basedmethods. Thismayhavetwopurposes.First,toselectthebestindividualsof eachgrouptobekeptinthenextgeneration,thuspreservingthe populationdiversityandavoidingthedominanceofoneshapetype. Secondly,toconductthegenerativeprocessonsolutionsthatareof interesttotheuseraccordingtotheirdefinedshapetypecriterion. Nowadaysfloorplangenerativemethodsdealwithbuildingboundariesasdefinedpolygons.However,iftheuserisabletochoose theaimedshapeorshapes,themethodmayfocusonlyonthat rangeofcandidatedesigns,thusreducingthecomputationburden byavoidingtheproductionandevaluationofirrelevantsolutions. Finally,apossibleapplicationistouseitasaretrievalprocessof designsinarchitecturaldesigndatabases.

5.Conclusion

Fourshapedescriptorswereusedtocapturetheformofasyntheticdatasetoffloorplandesignsandacomparisonoftheirperformancewascarriedout.Everydescriptorhadthesamevectorlength andthesameclusteringalgorithmwasusedtoaggregatethefloor plans.

Theperceptualanalysiscarriedoutonthefourdescriptors showsthatTangentDistance(TD)capturesbetterfloorplanshapes andpresentsfeweroutliers.Thiswasduetothefactthatthis

descriptornotonlymeasuresthedistancetothegeometriccentrebutalsocapturesthediscontinuitiesinthewalls.Theoutliers resultedfromexcessivesensitivitytosmallwallrecessesinthe perimeterthusshiftingthedesigntoothergroupwithasimilar overallconfiguration.

Inthecaseoftheotherdescriptors,theoppositehappens.The Grid-Based(GB)descriptorpresentstheleastreliableapproachand isverysensitivetodifferentproportionsinthesameshapethus designsaredistributedoverseveralgroupswithdifferentdominant shapes.

Forthefixedaspectratiovariant,theperformanceofthetwo bestdescriptorswasaRandindexof0.861and0.873forthePoint Distance(PD)andTD,respectively.Inthenon-fixedaspectratio descriptorvariant,thedescriptorswiththebestperformancewere theGBandTD,withaRandindexof0.874and0.876,respectively.

Despitethesegoodresults,someissuesstillneedtobetackled. Futureworkincludesextendingtheseapproachestonon-orthogonal

AppendixA.Descriptors’resultsfornon-fixedaspectratio

Figs.A.10,A.11,A.12,and

andmulti-storeydesigns,tostudyotherdescriptorsthatcapturethe innerspacerelationsinthefloorplan,andtotesttheperformanceof descriptorsinothertypesofclusteringalgorithms.

Acknowledgments

Thisworkhasbeendevelopedunderthe EnergyforSustainability Initiative oftheUniversityofCoimbra(UC).Ithasbeenpartially supportedbythePortugueseFoundationforScienceandTechnology(FCT),undertheprojectsPEstINESCCUID/MULTI/00308/2013, SuscityMITP-TB/CS/0026/2013,andbyFCTandEuropeanRegional DevelopmentFund(FEDER)throughCOMPETE2020–Programa OperacionalCompetitividadeeInternacionalização(POCI),underthe projectRen4EEnIEQ(PTDC/SEM-ENE/3238/2014andPOCI-01-0145FEDER-016760respectively).EugénioRodriguesacknowledgesthe supportoftheFCTunderPostDocgrantSFRH/BPD/99668/2014.

displaytheresultingclusteringofeachofthefourshaperepresentationswithnon-fixedaspectratio.

Fig.A.10.

Fig.A.11. ClusteringresultsusingTurningFunction(TF)descriptorwithnon-fixedaspectratio.

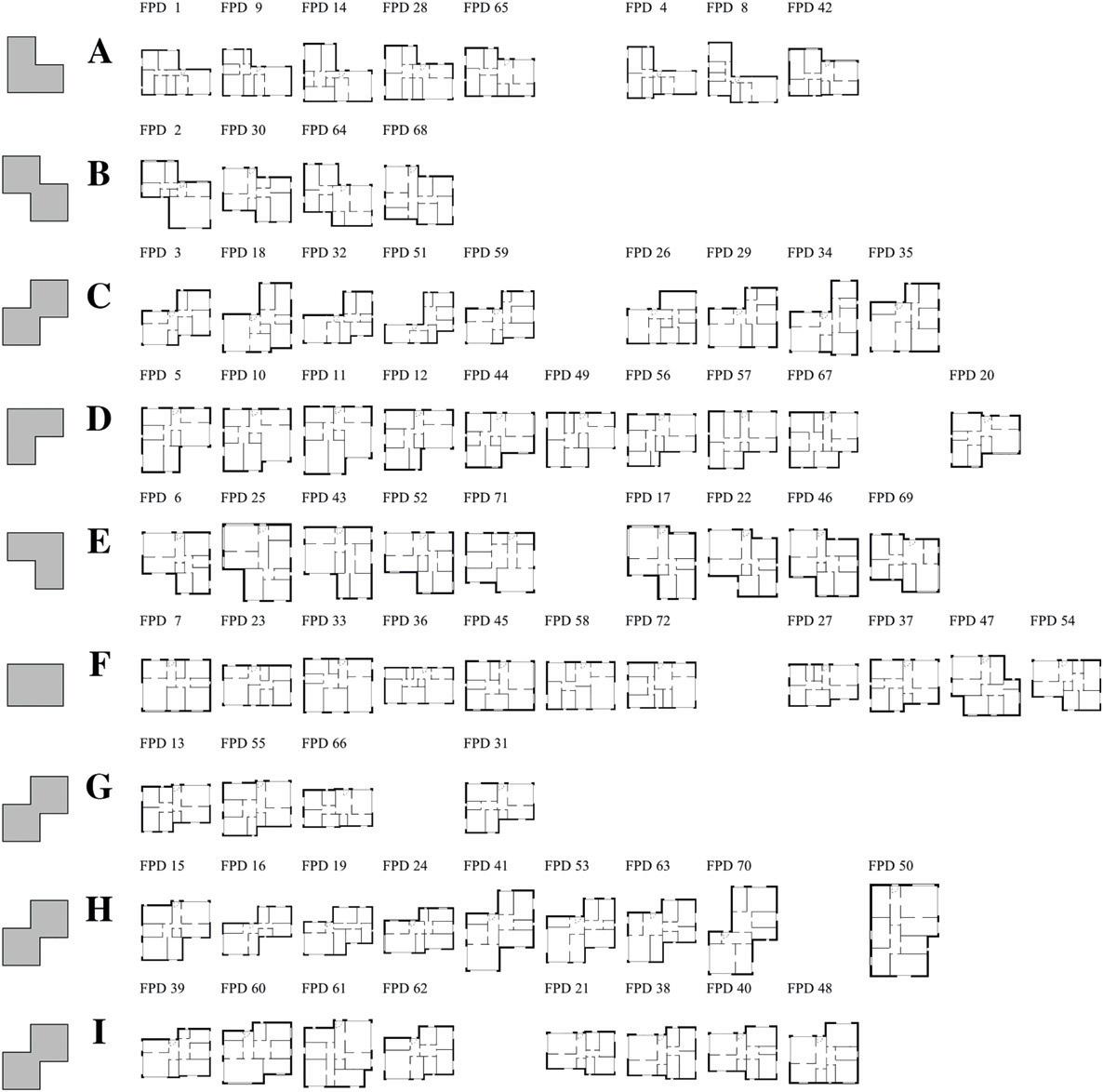
Fig.A.12. ClusteringresultsusingGrid-Based(GB)descriptorwithnon-fixedaspectratio.

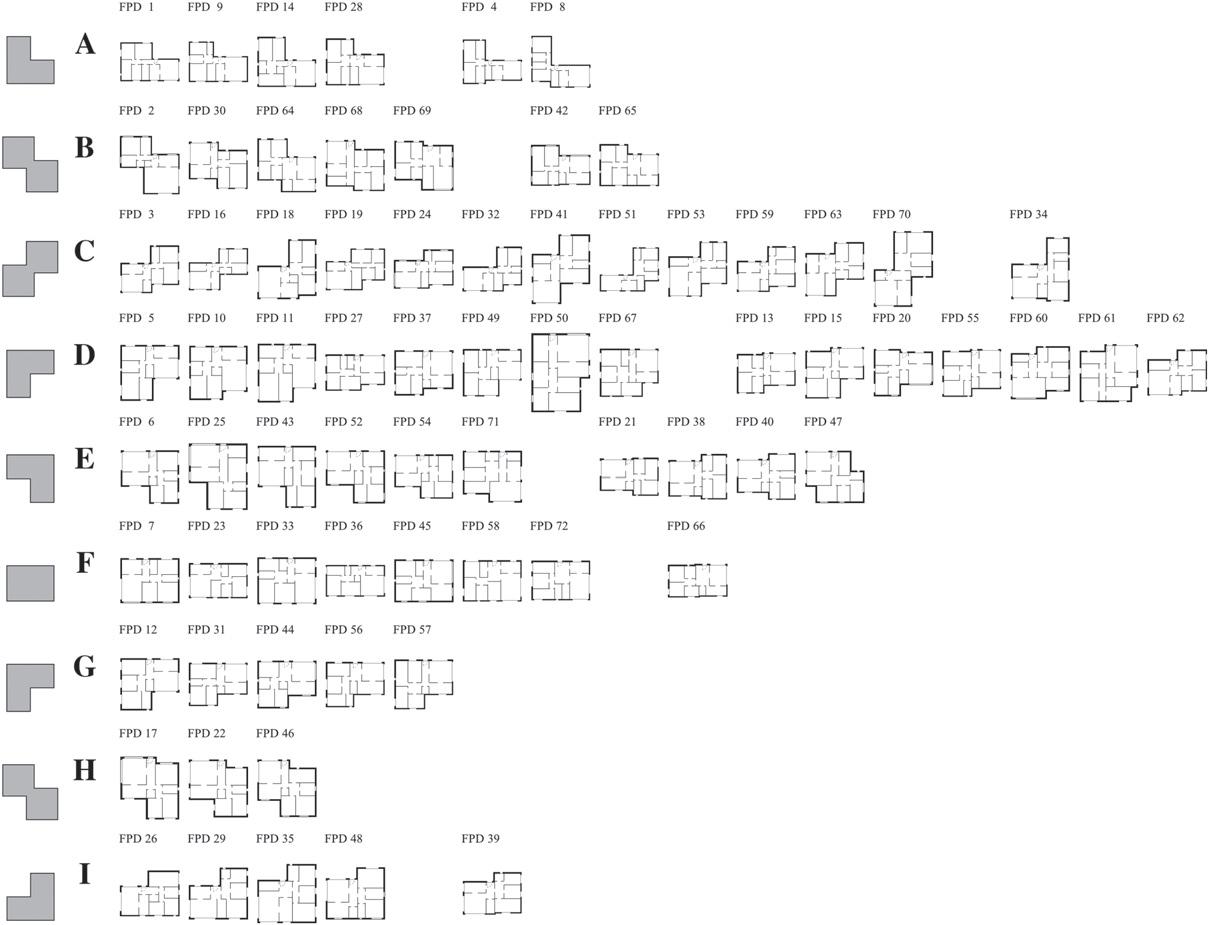
Fig.A.13. ClusteringresultsusingTangentDistance(TD)descriptorwithnon-fixedaspectratio.

References

[1] J.Han,M.Kamber,DataMining:ConceptsandTechniques,2ndedned., MorganKaufmannPublishersInc.,SanFrancisco,CA,2001.978-1-55860-901-3.

[2]M.AlQady,A.Kandil,Automaticclusteringofconstructionprojectdocuments basedontextualsimilarity,Autom.Constr.42(2014)36–49.ISSN09265805. http://dx.doi.org/10.1016/j.autcon.2014.02.006

[3]S.Dumais,H.Chen,HierarchicalclassificationofWebcontent,Proceedings ofthe23rdAnnualInternationalACMSIGIRConferenceonResearch andDevelopmentinInformationRetrieval,SIGIR’00,ACM,NewYork,NY, USA,2000,pp.256–263. http://dx.doi.org/10.1145/345508.345593.1-58113226-3.

[4]F.Beil,M.Ester,X.Xu,Frequentterm-basedtextclustering,Proceedingsof theEighthACMSIGKDDInternationalConferenceonKnowledgeDiscoveryand DataMining,KDD’02,ACM,NewYork,NY,USA,2002,pp.436–442. http://dx. doi.org/10.1145/775047.775110

[5]D.Sousa-Rodrigues,Q-analysisbasedclusteringofonlinenews,Discontinuity NonlinearityComplexity3(3)(2014)227–236.ISSN21646414. http://dx.doi. org/10.5890/DNC.2014.09.002

[6]M.-Y.Cheng,D.-H.Tran,Y.-W.Wu,Usingafuzzyclusteringchaotic-based differentialevolutionwithserialmethodtosolveresource-constrainedproject schedulingproblems,Autom.Constr.37(2014)88–97.ISSN09265805. http:// dx.doi.org/10.1016/j.autcon.2013.10.002

[7]H.Song,H.-Y.Feng,Aglobalclusteringapproachtopointcloudsimplification withaspecifieddatareductionratio,Comput.AidedDes.40(3)(2008)281–292.ISSN00104485. http://dx.doi.org/10.1016/j.cad.2007.10.013.

[8]B.-Q.Shi,J.Liang,Q.Liu,Adaptivesimplificationofpointcloudusingk-means clustering,Comput.AidedDes.43(8)(2011)910–922.ISSN00104485. http:// dx.doi.org/10.1016/j.cad.2011.04.001

[9]T.W.Liao,Clusteringoftimeseriesdata–asurvey,PatternRecogn.38(11) (2005)1857–1874.ISSN0031-3203. http://dx.doi.org/10.1016/j.patcog.2005. 01.025

[10]V.V.Vikjord,R.Jenssen,Informationtheoreticclusteringusingak-nearest neighborsapproach,PatternRecogn.47(9)(2014)3070–3081.ISSN00313203. http://dx.doi.org/10.1016/j.patcog.2014.03.018

[11]S.T.Roweis,L.K.Saul,Nonlineardimensionalityreductionbylocallylinear embedding,Science290(5500)(2000)2323–2326.ISSN00368075. http://dx. doi.org/10.1126/science.290.5500.2323

[12]J.Pu,K.Ramani,Onvisualsimilaritybased2Ddrawingretrieval,Comput. AidedDes.38(3)(2006)249–259.ISSN00104485. http://dx.doi.org/10.1016/j. cad.2005.10.009

[13]S.Jayanti,Y.Kalyanaraman,K.Ramani,Shape-basedclusteringfor3DCAD objects:acomparativestudyofeffectiveness,Computer-AidedDes.41(12) (2009)999–1007.ISSN00104485. http://dx.doi.org/10.1016/j.cad.2009.07.003.

[14]V.Deufemia,M.Risi,G.Tortora,SketchedsymbolrecognitionusingLatentDynamicConditionalRandomFieldsanddistance-basedclustering,Pattern Recogn.47(3)(2014)1159–1171.ISSN00313203. http://dx.doi.org/10.1016/j. patcog.2013.09.016

[15]D.Zhang,G.Lu,Reviewofshaperepresentationanddescriptiontechniques, PatternRecogn.37(1)(2004)1–19.ISSN00313203. http://dx.doi.org/10.1016/ j.patcog.2003.07.008

[16]C.Chang,S.Hwang,D.Buehrer,Ashaperecognitionschemebased onrelativedistancesoffeaturepointsfromthecentroid,PatternRecogn. 24(11)(1991)1053–1063.ISSN00313203. http://dx.doi.org/10.1016/00313203(91)90121-K

[17]D.Yankov,E.Keogh,Manifoldclusteringofshapes,Proceedings-IEEEInternationalConferenceonDataMining,ICDM(2006)1167–1171.ISSN15504786. http://dx.doi.org/10.1109/ICDM.2006.101

[18]E.Arkin,L.Chew,D.Huttenlocher,K.Kedem,J.Mitchell,Anefficiently computablemetricforcomparingpolygonalshapes,IEEETrans.PatternAnal. Mach.Intell.13(3)(1991)209–216.ISSN01628828. http://dx.doi.org/10.1109/ 34.75509

[19] A.Sajjanhar,G.Lu,Agridbasedshapeindexingandretrievalmethod,Comput. J.Multimed.StorageArchivingSyst.29(1997)131–140.

[20]K.Siddiqi,A.Shokoufandeh,S.J.Dickinson,S.W.Zucker,Shockgraphsand shapematching,Int.J.Comput.Vis.35(1)(1999)13–32.ISSN09205691. http:// dx.doi.org/10.1023/A:1008102926703

[21]S.Belongie,J.Malik,J.Puzicha,Shapematchingandobjectrecognitionusing shapecontexts,IEEETrans.PatternAnal.Mach.Intell.24(24)(2002)509–522. ISSN01628828. http://dx.doi.org/10.1109/34.993558.

E.Rodriguesetal./AutomationinConstruction80(2017)48–65

[22]K.L.Tan,B.C.Ooi,L.F.Thiang,Retrievingsimilarshapeseffectivelyandefficiently,MultimediaToolsAppl.19(2003)111–134.ISSN13807501. http://dx. doi.org/10.1023/A:1022142527536

[23]E.Klassen,A.Srivastava,W.Mio,S.H.Joshi,Analysisofplanarshapes usinggeodesicpathsonshapespaces,IEEETrans.PatternAnal.Mach.Intell. 26(3)(2004)372–383.ISSN01628828. http://dx.doi.org/10.1109/TPAMI.2004. 1262333

[24]A.Srivastava,S.H.Joshi,W.Mio,X.Liu,Statisticalshapeanalysis:clustering, learning,andtesting,IEEETrans.PatternAnal.Mach.Intell.27(4)(2005)590–602.ISSN01628828. http://dx.doi.org/10.1109/TPAMI.2005.86

[25]W.Mio,A.Srivastava,S.Joshi,Onshapeofplaneelasticcurves,Int.J.Comput. Vis.73(3)(2007)307–324.ISSN0920-5691. http://dx.doi.org/10.1007/s11263006-9968-0

[26]H.L.H.Ling,D.Jacobs,Shapeclassificationusingtheinner-distance,IEEETrans. PatternAnal.Mach.Intell.29(2)(2007)1–35.ISSN0162-8828. http://dx.doi. org/10.1109/TPAMI.2007.41.

[27]W.Shen,Y.Wang,X.Bai,H.Wang,L.JanLatecki,Shapeclustering:common structurediscovery,PatternRecogn.46(2)(2013)539–550.ISSN00313203. http://dx.doi.org/10.1016/j.patcog.2012.07.023

[28]M.Y.Cha,J.S.Gero,Shapepatternrecognitionusingacomputablepattern representation,ArtificialIntelligenceinDesign’98,SpringerNetherlands, Dordrecht,1998,pp.169–187. http://dx.doi.org/10.1007/978-94-011-51214_9.978-94-011-5121-4.

[29]Runlengthhistogramimagesignatureforperceptualretrievalofarchitectural floorplans,in:B.Lamiroy,J.-M.Ogier(Eds.),GraphicsRecognition.Current TrendsandChallenges:10thInternationalWorkshop,GREC2013,Bethlehem, PA,USA,August20–21,2013,RevisedSelectedPapers,SpringerBerlin Heidelberg,Berlin,Heidelberg,2014,pp.135–146. http://dx.doi.org/10.1007/ 978-3-662-44854-0_11.978-3-662-44854-0.

[30]A.Dutta,J.Lladós,H.Bunke,U.Pal,Aproductgraphbasedmethodfordualsubgraphmatchingappliedtosymbolspotting,in:B.Lamiroy,J.-M.Ogier(Eds.), GraphicsRecognition:CurrentTrendsandChallenges,vol.8746ofLecture NotesinComputerScience,SpringerBerlinHeidelberg,Berlin,Heidelberg, 2014,pp.11–24. http://dx.doi.org/10.1007/978-3-662-44854-0.978-3-66244853-3.

[31] D.Sousa-Rodrigues,M.TdeSampayo,E.Rodrigues,A.R.Gaspar,Á.Gomes,C.H. Antunes,Onlinesurveyforcollectiveclusteringofcomputergeneratedarchitecturalfloorplans,15thInternationalConferenceonTechnologyPolicyand Innovation,17–19June,MiltonKeynes,UK,2015.

[32]D.Sousa-Rodrigues,M.TeixeiradeSampayo,E.Rodrigues,A.R.Gaspar,Á. Gomes,Crowdsourcedclusteringofcomputergeneratedfloorplans,in:Yuhua

Luo(Ed.),The12thInternationalConferenceonCooperativeDesign,Visualization&Engineering,Sept20–23,Springer,Mallorca,Spain,2015,pp.142–151. http://dx.doi.org/10.1007/978-3-319-24132-6_17.978-3-319-24132-6.

[33]J.H.Ward,Jr,Hierarchicalgroupingtooptimizeanobjectivefunction,J. Am.Stat.Assoc.58(301)(1963)236–244. http://dx.doi.org/10.1080/01621459. 1963.10500845

[34]E.Rodrigues,A.Gaspar,Á.Gomes,Anevolutionarystrategyenhancedwith alocalsearchtechniqueforthespaceallocationprobleminarchitecture,part 1:methodology,Comput.AidedDes.45(5)(2013)887–897.ISSN00104485. http://dx.doi.org/10.1016/j.cad.2013.01.001

[35]E.Rodrigues,A.Gaspar,Á.Gomes,Anevolutionarystrategyenhancedwitha localsearchtechniqueforthespaceallocationprobleminarchitecture,part2: validationandperformancetests,Comput.AidedDes.45(5)(2013)898–910. ISSN00104485. http://dx.doi.org/10.1016/j.cad.2013.01.003

[36]E.Rodrigues,A.Gaspar,Á.Gomes,Anapproachtothemulti-levelspaceallocationprobleminarchitectureusingahybridevolutionarytechnique,Autom. Constr.35(2013)482–498.ISSN09265805. http://dx.doi.org/10.1016/j.autcon. 2013.06.005.

[37] J.Dougherty,R.Kohavi,M.Sahami,etal.Supervisedandunsupervised discretizationofcontinuousfeatures,Proceedingsofthe12thInternational ConferenceonMachineLearning,July9–12,TahoeCity,California,USA,1995, pp.194–202.978-1-55860-377-6.

[38] S.Kotsiantis,D.Kanellopoulos,Discretizationtechniques:arecentsurvey, GESTSInt.Trans.Comput.Sci.Eng.32(1)(2006)47–58.

[39] J.L.Lustgarten,V.Gopalakrishnan,H.Grover,S.Visweswaran,Improvingclassificationperformancewithdiscretizationonbiomedicaldatasets,AMIAAnnual SymposiumProceedings,vol.2008,AmericanMedicalInformaticsAssociation. 2008,pp.445–449.ISSN1942597X.

[40]M.Rucco,D.Sousa-Rodrigues,E.Merelli,J.Johnson,L.Falsetti,C.Nitti, A.Salvi,Neuralhypernetworkapproachforpulmonaryembolismdiagnosis, BMC.Res.Notes8(1)(2015)617.ISSN1756-0500. http://dx.doi.org/10.1186/ s13104-015-1554-5

[41]D.Defays,Anefficientalgorithmforacompletelinkmethod,Comput.J.20(4) (1977) 364–366.ISSN14602067. http://dx.doi.org/10.1093/comjnl/20.4.364

[42]E.Deza,M.M.Deza,EncyclopediaofDistances,SpringerBerlinHeidelberg, Berlin,Heidelberg,2009,733. http://dx.doi.org/10.1007/978-3-642-002342.978-3-642-00233-5.

[43]W.M.Rand,Objectivecriteriafortheevaluationofclusteringmethods,J. Am.Stat.Assoc.66(336)(1971)846–850. http://dx.doi.org/10.1080/01621459. 1971.10482356