What Louis Kahn Hid in Plain Site:
Discovering Embedded Classical Geometry at the Salk Institute
Ramon Palos Hernandez
USC School of Architecture
ARCH 470b Architectural Studies Capstone
May 10, 2021
Thesis Advisors:
Lauren Matchison, AIA, Associate Professor of Practice
Geoffrey von Oeyen, AIA, Assistant Professor of Practice
Introduction
Architect Louis Kahn’s seminal 1944 essay on “Monumentality”1 stated that antiquity holds “lessons”2 for modern architecture. In Kahn’s site design for the Salk Institute, the lessons he applied from Greco-Roman influences are hidden in plain site.
Beyond the edges of the Salk Institute’s floor plate, this study finds a phantom geometric framework governing the relationship of the Salk’s footprint to the macro site topography. Site analysis diagrams reveal that Kahn’s embedded geometry in the Salk building footprint aligns proportionally with the site’s macro geometric order. Analysis diagrams suggest that this classical Euclidian3 ratio governs the Salk's horizontal and vertical relationship of the plaza to the shoreline and the natural topography in between. The study diagrams deliver a second discovery: this same geometric template also governs the location, proportions, and relationships of the Salk’s controversial 1992 building expansion.

ton and Co., 2001 Pg. 21 (a reprint of Kahn’s essay first
auty of Mathematics,”Race Point Publishing, 2018, Pg. 8
lopments that apply a graphical analysis to Kahn’s design philosophy. A review of research atical/geometric ordering templates known since
Part 1 - Background and Context






















This study of Louis Kahn’s Salk Institute captures a broader site context for clues to aid our understanding of forces evident and hidden

A second critical question is about Kahn’s sense of spatial order as “an underlying principle and a quality of things,”6 which is perhaps the essential element in the perceived timeless monumentality of the Salk. Entering the plaza elicits sensations similar to entering a sacred space. Diagram studies here explore relationship characteristics with the site, the ocean, and the plaza for clues to hidden geometries to better understand Kahn’s intent and glean insight on his notions of architectural order. Regarding his idea of order, Kahn “only spoke of it in metaphor,”7 enigmatically clarifying that “Order is.”8
Why did Kahn anchor the building where it sits? Why not place the building closer to the ocean or farther away from it, or shift the plaza right or left? A progression of concept site sketches by Kahn’s hand9 bears out that he tried all these moves before settling on the final iconic site layout. A diagram study maps out the evolution of site layouts (Fig. 5). This and other diagram studies here prove instrumental in deciphering what Kahn meant when asking “How close is too close? How far is too far?”10 (Fig. 15-D & 19).
Fig. 5 – Diagram series study demonstrating how Kahn’s earliest site layout concepts evolved, driven by client directives for programmatic revisions while constrained by natural site forces and legal boundary lines. The notable observation is that the axial line of sight was not settled until the last revision.
6 Lobell, John, “Between Silence and Light; Spirit in the Architecture of Louis I. Kahn”, Shambhala, 1979, Pg. 63.
7 Lobell, John, Pg. 63.
8 Ibid.
9 Kieffer, Jeffry, “The Evolution of a Building Complex: Louis I. Kahn’s Salk Institute for Biological Studies”, Artifice Press, Ltd., 2019.
10 Steele, James, “Salk Institute, Louis I. Kahn”, Phaidon Press, 1993, Pg. 7.
11 Williamson, James, “Kahn at Penn: Transformative Teacher of Architecture,” Routledge, (2015), Pg. 2
12 Twombly, Robert, “Louis Kahn Essential Texts”.
13 Ibid
14 Ibid
15 Curtis, William J.R., “Authenticity, Abstraction and the Ancient Sense: Le Corbusier’s and Louis Kahn’s Ideas of Parliament,” Perspecta, 1983, Vo. 20, Pg. 191
16 Steele, James, Pg. 16.
Louis Kahn was an influential architect, teacher, and theorist who broke away from modernist tendencies (“Kahn ‘set his strongest students free’ from the straightjacket of an exhausted International Style model”).11 Kahn's teachings championed the notion of distilling essential concepts and “lessons”12 of “monumentality”13 from Greek and Roman antiquity and injecting them into the sensibilities of a modern context. Another of Kahn’s seminal lessons is capsulized as a rhetorical question: Kahn asks a brick what it wants to be.14 We enter Kahn’s dialogue by deciphering what the site told Kahn what it wanted to be. Exploring site context at a macro scale via graphic diagrams reveals significant fresh insight into palpable site forces and hidden ordering geometries governing the Salk’s relationships. We begin to see the lessons Kahn synthesized, given abundant graphic clues. According to William Curtis, “Classical inspirations were embedded in Kahn’s mind.”15 Ironically, studying a Kahn floor plan is “like discovering a hidden ruin.”16
Part 2 - Research Precedent
A broad body of academic critique and research focuses on the influence that Roman ruins held for Kahn, starting with Kahn himself. In the essay "Monumentality,"17 Kahn states that "monumental structures of the past cannot live again, but we must not discard the lessons these buildings teach for they have the common characteristics of greatness."18
In his 1993 book,24 USC professor James Steele dissects Kahn's technical achievements of the ground-breaking "flexible"25 design of the Salk's laboratory spaces. Prof. Steele emphasizes that while Kahn's monumental spatial elements were masterfully executed, Kahn's hidden structural and building systems are perhaps more important since they are technically advanced.26 Steele then pivots to the significance of the natural site features when citing a meeting at the Salk between Kahn and Mexican architect Luis Barragan in 1966 when the plaza was still “muddy.”27 Barragan noted that the east-west axis as a "line to the sea"28 is a prominent force that would be lost if the courtyard were filled with trees. Kahn “implemented Barragan’s idea”29 for a stark plaza aesthetic.
A 2006 critique by Berkeley Professor Marc Treib provides insightful analysis on the evolving treatment of the plaza landscape design. Prof. Treib is one of a handful of researchers who intuited the influential role site forces played in Kahn’s design choices. He observes that the Y-shaped property line is odd. Study diagrams illustrate that this odd-shaped legal boundary (Fig. 10-A) makes sense only when superimposed on a topographic map (Fig. 10-B) and over an aerial map (Fig 10-C). The Salk plaza’s thin
17 Kahn, Louis, “Monumentality”, 1944.
18 Ibid
19 Scully, Vincent, “Louis I. Kahn and the Ruins of Rome”, Engineering and Science, Winter 1993, Pg. 3
20 Scully, Vincent
21 Ibid
22 Gast, Klaus-Peter, “Louis I. Kahn: The Idea of Order”, 2001, Birkhauser, 2001, Fig. 36-39, Pg. 69
23 Gast, Klaus-Peter, Fig. 20-22, Pg. 49
24 Steele, James, “Salk Institute, Louis I. Kahn”, Phaidon Press, 1993.
25 Steele, James, Pg. 13.
26 Steele, James, Pp. 10-11.
27 Steele, James, Pg. 5
28 Ibid.
29 Steele, James, Pg. 5
One influential scholar was Yale Professor Vincent Scully. In his 1992 essay "Louis I. Kahn and the Ruins of Rome,”19 Scully devotes considerable time describing where and how Kahn's singular sensibilities and predilection for a modern monumental aesthetic developed. He argues that the forms Kahn captured in travel sketches of Roman ruins, medieval towns, and Egyptian pyramids20 had a considerable influence on maturing an aesthetic vocabulary that uniquely informed notions of spatial monumentality.21 Expanding on Scully’s thoughts, study diagrams here suggest that Kahn learned an even more fundamental vocabulary from antiquity, but one that Kahn purposely hid. Scholarly studies reveal that a phantom geometry permeates Kahn’s iconic and seminal masterpieces. For example, the Salk Institute Laboratories22 and the Margaret Esherick House,23 with significant comparative scale differences and uses, share the same phantom Greco-Roman geometric ordering code.
1.4SquareRectangle (√2) 1.6 Rectangle (√3) (Fig. 4-A).
linear water channel was inspired by garden elements in the Alhambra and the Mezquita at Cordoba.30 Prof. Treib also observes that Kahn’s use of formed concrete at the Salk is akin to an “ancient weathered cast,”31 an allusion to Kahn’s affinity for Roman ruins.32
In 2019, architect Jeffrey Kieffer33 published a comprehensive study of the partnership between Salk and Kahn. The book treads the early history of Dr. Jonas Salk's quest to build his laboratory. It delves into detailed explorations of Kahn's office and staff activities before, during, and after the design and construction phases. Kieffer goes further than most researchers in recognizing the palpable role that the site’s natural forces played in Kahn's site design strategy. Kieffer observes that "The topography suggested lines of force which defined the spatial character of the site”34 Kieffer's exhaustive historical research of Salk’s formative phases lays out the spectrum of devilishly contradictory forces Kahn overcame.35
Most published academic research work on Kahn is narrative-based. One divergent research approach applied a graphic analysis method. In 1985, Professors Roger Clark and Michael Pause published “Precedents in Architecture,”36 a seminal guide in comparative architectural graphic analysis. Clark and Pause include a simple list of graphic vocabulary tool sets to aid in this analysis approach. One set under the “Geometry” tool kit, includes the square, the 1.4 rectangle and the 1.6 rectangle37 (Fig. 6). No historical context accompanies this specific tool set, or explains the significance of why the two 1.4 or 1.6 rectangles are even included as critical analysis tools in the first place.
30 Treib, Marc, “To End a Continent: The Courtyard of the Salk Institute”, Journal of the Society of Architectural Historians, 65, No. 3, Sept. 2006, Pp 402-427.
31 Treib, Marc, Pg. 426
32 Steele, James, Pg. 13.
33 Kieffer, Jeffry, “The Evolution of a Building Complex: Louis I. Kahn’s Salk Institute for Biological Studies”, Artifice Press, Ltd., 2019.
34 Kieffer, Jeffry, Pg. 25.
35 Thomas, Leslie, “Things in their best order: Technical aspects of the Salk and their role in its design,” The Journal of Architecture, 8:1, (2003), Pg. 111.
36 Clark, Roger H. and Michael Pause, “Precedents in Architecture,” Van Nostrand Reinhold, (1995).
37 Clark, Roger H., Pg. xi.
Mark A. Reynolds is an art professor and a self-described “Geometer”38 who was first published in 1995. In a 201539 research report, Reynolds explores the Salk’s plan and elevations with a series of diagrams looking for underlying ordering geometries (Fig. 7). Reynolds has opened new research precedents by deploying geometric analysis methods as a critical research tool in studying how Kahn deployed spatial and geometric ordering strategies. Reynolds' research inquiry is compelling and suggests that cultures have deployed the same spatial geometric ordering technique through the ages across continents. Testing his
38 In the tradition of classical and Gothic era geometers who laid out walls and spatial proportions for temples, cathedrals, and civic buildings.
39 Reynolds, Mark, “The Salk: A Geometrical Analysis Supported by Historical Evidence”, Architecture and Mathematics from Antiquity to the Future”, Vol 2., Pg. 435.
method and theory, Reynolds extends his unique visual study approach to explore geometric proportioning device applications in "the pre-Columbian Mesoamerican city of Teotihuacan, Mexico.”40
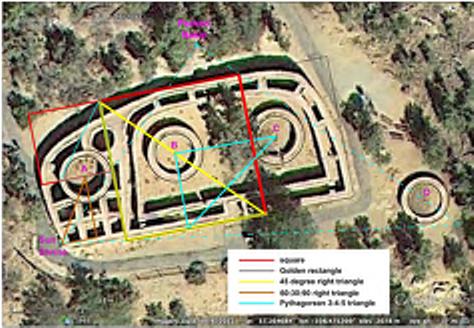
Fig. 7 –Geometrical analysis showing the Pythagorean proportioning template superimposed on a portion of the Salk Institute’s south façade (Image Credit: Reynolds, Fig. 76.5, Pg. 444).

An offshoot from Reynolds’ scholarly research into classical mathematical proportioning concepts is taken by University of Arizona’s professor Sherry Towers studying Pueblo ceremonial sites in the southwestern United States. Published in 2016,41 Towers documents evidence of geometric42 proportioning methods in the Chaco Pueblo site. Towers posits that native American peoples used simple methods for squaring and proportioning spaces with a method that matches the 1.618 (or 0.1618) ratio. The way of embedding the 1:618 classical proportioning ratio at the Pueblo site (Fig. 8) is consistent with geometric site ordering principles embedded in Greek and Roman monuments, Maya temples, Gothic and Renaissance cathedrals, and 20th-century modern masterworks by Mies, Le Corbusier, and Louis Kahn. Site geometry was truly universal, as Reynolds and Towers begin to demonstrate. While Tower’s research into Chaco Pueblo geometries is intriguing and compelling, it is not entirely conclusive.
In a 2010 report, Christopher Powell43 discovered that Maya descendants currently living in the Yucatan peninsula rely on community geometers for laying out plans when constructing traditional thatched-roofed homes. The tradition and geometric knowledge has been handed down through many generations carried by Shaman.44 Powell’s analysis diagrams demonstrate the Maya’s use of basic geometry in transforming a square layout into a rectangle. The resulting spatial proportion is either in the ratio of √2 or √3 (Fig. 9-A-B). The geometric proportioning device, Powell found, also governs the interior
40 Website, Mark Reynolds, www.piorogi2000.com/2015/mark-reynolds-has-three-articles-on-geometric-analysispublished/).
41 Towers, Sherry, “Advanced geometrical constructs in a Pueblo ceremonial site, c 1200 CE”, Journal of Archeological Science: Reports, 2017.
42 Towers, Sherry, Pg. 9.
Powell, Christopher, “The Shapes of Sacred Space: A proposed System of Geometry Used to Lay Out and Design Maya Art and Architecture and Some Implications Concerning Maya Cosmology”, Ph.D. Dissertation, University of Texas at Austin, August 2010.
Powell, Christopher, Pg. vi.
In 2000, Professor Antonio Fernandez-Puertas, published a report unveiling a tantalizing finding in Spain’s Mezquita de Cordoba. Southern Spain’s Arab rulers also applied lessons from antiquity. Greek mathematics and geometry formed the basis of the Mezquita’s expansion (Fig. 10). Starting with a square plan in the “8th-century,”47 by the 10 century the Mezquita’s square plan grew into a rectangle. Like the Maya, the Pythagorean ratio based on the square root of two (√2), he found, governed the rectangle’s proportion Puertas repeated the research technique at another the same Greco-Roman proportioning template intimat Alhambra’s plans and elevations.

The research tendency concentrating on the graphical analysis method takes a striking path with Klaus-Peter Gast. In his 2001 book, “Louis I. Kahn’s most iconic projects. sing Kahn’s hidden use of d as purposeful clear about Salk’s Platonic square
University in Spain. d Proporcional de su Plant General (Siglos VIII-X), Archivo 17.


Klaus-Peter Gast, Geometrical analysis showing Kahn’s application of proportioning ratios as a foundational ordering principle.
er”, 2001, Birkhauser, Fig. 36-39, Pg. 69.






yan ruin complex in Chiapas, Mexico. Temple VIII is The classical and modern Maya’s spatial layout y Pythagoras, Plato…and Vitruvius.”45 The Classical n mathematics, but deployed this geometric
: Gast, Fig. 42 Pg. 71.
: Gast, Fig. 15, Pg. 38.
: Gast, Fig. 21, Pg. 49.)

with √2 at Salk, √3 at the Richards Medical Research tower complex49 (Fig 11-B), and √2 the Margaret Esherick House50 (Fig. 11-C).
The “Foreward” in Gast’s book is written by Anne Griswold Tyng, Kahn’s romantic and professional partner.51 Tying notes, “I am convinced that the Divine Proportion is a safety net to catch chaos in the universe.”52 Anne Tyng’s hidden influence on Kahn’s designs is well documented. Less well known is her 1975 Ph.D. dissertation on the Divine Proportion.53 Tyng informs that the mathematical ratio 1.618 (√3) and its geometric template representation illustrated by Pythagoras was coined during the Renaissance as the “golden mean,” the “golden section,” and by Leonardo da Vinci as the “Divine Proportion.”54
In this vein, Marcus Frings publishes “a treatise on the history and evolution of the Golden Section,” Frings addresses a gap within the academic literature, citing the lack of a “thorough study of the Golden Section in architectural theory.”55 Notably, Frings highlights Le Corbusier as a luminary architect “attracted” to the “scientific analysis of proportions.”56 Gast’s book was already one year old when Frings’ report was published in 2002. Frings may not have been aware that Gast showcased Kahn’s prodigious penchant for silently embedding classical ordering ratios in his floor plans.
Kahn was younger than Le Corbusier by 14 years.57 Given that they were contemporaries, Kahn “respected” Le Corbu, and looked up to him for validation, occasionally asking rhetorically, “How am I doing Corbu?”58 In a 2014, Jean-Louis Cohen publishes a critique on Le Corbusier’s notions of proportioning principles. Cohen traces Le Corbu’s correspondence and sketches (Fig. 12) as he prepared to publish a treatise on the “Modulor”, a system of proportions “codified in 1945.”59 Cohen assesses that “Le Corbusier’s Modulor is probably the most comprehensive proportional system imagined during the 20thcentury.”60 Cohen accounts that Le Corbusier presented his proportioning theory at the 1951 Milan Trienalle where he “introduced, with affirmed modesty, the system of proportional
Fig. 12: Sketch by Le Corbu showing early concept of a “Modular” theory of proportions (Image Credit: J-L Cohen, Fig. 7, Pg. 5).

49 Gast, Fig. 15, Pg. 38.
50 Gast, Fig. 21, Pg. 49.
51 “Anne Tyng, Architect”, Docomomo, Website (https://docomomo-us.org/designer/anne-tyng)
52 Gast, Klaus-Peter, Pg. 7
Tyng, Anne Griswold, “Simultaneous Randomness and Order, The Fibonacci-Divine Proportion as a Universal Forming Principle”, Graduate School of Arts and Sciences, University of Pennsylvania, 1975.
Tyng, Anne Griswold, Pg. 1
Frings, Marcus, “The Golden Section in Architectural Theory”, Nexus Journal, Vol. 4, No. 1, 2002, Pg. 9
Frings, Marcus, Pg. 20
Kahn: (B) Feb. 20, 1901, (D) March 17, 1974; Le Corbusier, (B) Oct. 6, 1887, (D) Aug. 27, 1965.
Williamson, James, Pg. 149.
Cohen, Jean-Louis, “Le Corbusier’s Modular and the Debate on Proportion in France,” Ubiquity Press, Architectural Histories, 2, No. 23, (2014), Pg. 1.
Fig. 13: Diagram study extracting the 1.4 (√2) and 1.6 (√3) ratio proportioning templates from Le Corbusier’s “Modulor” man (Image Credit: J-L Cohen, Fig. 7, Pg. 5).
measurements he had invented.”61 One hand-sketch shows that Le Corbu combined two geometric proportioning templates based on the √2 (1.4 ratio) and √3 (1.6 ratio) into a single diagram,62 and takes a cue from da Vinci by adding a human-scaled figure as a proportional reference device. Le Corbu’s “invented” concept, the “Modulor,” was simply a re-branding of ideas that fused classical Greek math with Renaissance humanistic refinements by da Vinci who anthropomorphized the ratio’s abstract geometric construct from ancient Greece.


The difference between Kahn and Le Corbu was that while Le Corbusier cast the classic proportioning ratios as iconography on the side of his buildings, published essays and books about it, and lectured in international venues, Kahn, in contrast, quietly buried classical Greek proportional ordering devices in his plans, alluding to but never

The study method is modeled on established research precedents that use graphical analysis. Scully, Keiffer, Steele, and Treib rely on written narratives that conjure images of observed site forces. Clark, Reynolds and Gast contribute rigorous geometric studies demonstrating the power of graphical analysis as a research tool in discovering new insights into Kahn’s design approach. However, there is no evidence of research that captures a wide-lens analysis of site forces beyond the Salk’s drip-edge footprint. And yet, diagrams here demonstrate what researchers have intuited. These outside forces play a crucial role in understanding the evolution of Kahn’s development of the Salk’s site parti. The narratives from Kieffer, Steele, Treib, and others provide a framework for setting up a graphical analysis

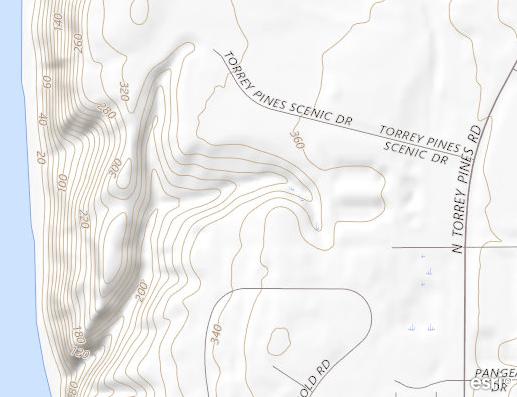

A point of departure for the graphical diagramming exercise starts with analyzing the city-donated land that Louis Kahn was handed63 (Fig. 14-C). The Salk’s legal site boundary comprises a collection of irregular land parcels that splay open facing the sea. There was a reason the city, and the public, gladly gifted in 1960 to Dr. Salk such prime ocean-front property.64 The Salk facility would be a magnet for other research ventures, thus transforming the area into a Biotech hub (a 2018 report ranked San Diego #5 in a top-ten list of national Biopharma clusters).65
A review of the legal parcel map66 (Fig. 14-A) shows an irregular site boundary that yields no obvious point of departure, offering no clues to any self-evident solutions for developing a building parti. A cursory review of topographic67 maps (Fig. 14-B) and aerial images68 (Fig. 14C) asserts the site’s inscrutability while emphasizing the powerful geographic features that tug and push at the site.
63 Steele, James, Pg. 1
64 Kieffer, Jeffry, Pg. 25.
65 Phillippidis, Alex, “Top 10 U.S. BioPharma Clusters”, Genetic Engineering & Biotechnology News, Sept. 23, 2018.
66 County of San Diego Assessor’s parcel map.
67 U.S. Geological Survey Map, Torrey Pines Map Sector.
68 Google Maps, Aerial Image.
Catalyzing the first move, the graphical diagramming exercise starts (Fig. 15-A) by transforming the irregularly shaped site boundary line into an imaginary rectilinear shape that aligns visually with the site’s natural geometric orientation to the ocean. The irregular County Assessor’s polygonal parcel line is distilled as an abstract rectangular shape that is narrow and long (Fig. 15-C). Given the ocean’s proximity and pull, first to emerge is a forceful line of sight that implies a singular central axis running along the east-west cardinal points with the dominant west end touching the ocean’s horizon (Fig. 15-E). On the eastern end, the axis line self-adjusts, comfortably settling into the mid-point of the sidewalk property line. The northsouth dimension of the east property line determines the rectangle’s narrow width. The long dimension is visually set between the west ridgeline
line.

We begin to see the site-driven forces that likely shaped Kahn’s siting of the Salk’s footprint in sequential order. Most of the terrain sandwiched between the Salk’s western edge and the shoreline is public land deeply carved by a stream pattern connected to a more extensive regional watershed system. From ridge line to street line fits the √3 ratio (Fig. 15-D). Flat terrain starts at elevation 340 feet above sea level and 2,000 feet inboard from the shoreline (Fig. 16). The ratio of these two numbers, at
 Fig. 16: Diagram study series showing relationship of 2,000 ft. Horizontal
Fig. 17-C: Horizontal Line of sight vs. Ridge and shoreline. Fig. 15–E: The ridge line acts as critical visual and geometric demarcation point.
Fig. 16: Diagram study series showing relationship of 2,000 ft. Horizontal
Fig. 17-C: Horizontal Line of sight vs. Ridge and shoreline. Fig. 15–E: The ridge line acts as critical visual and geometric demarcation point.
18-C:
natural terrain aligns with Kahn’s geometry start point, setting a hidden order. Where Kahn’s platonic square parti for the Salk eventually settles is revealed as logical, elegant,71 and naturally aligning with a broader geometric and natural order
Salk Plaza and the Ocean
One powerful effect of the processional path when entering the Salk plaza at the east end is experiencing the arresting visual connection to the ocean (Fig. 18-A-D). The ridge blocks the shoreline. Without a visual reference to the shoreline, the barrier sets up a visual trick, seemingly raising the sea level to the ridgeline (Fig. 18-B) and spilling to reach the plaza’s edge (Fig. 18-C). This condition has the visceral sensation that the ocean’s blue waters start immediately where the plaza’s travertine pavers drop off at the western horizon.
18-B:
71 Thomas, Leslie, Pg. 111
72 Evans, Robin, “Mies Van Der Rohe’s Paradoxical Symmetries”, AA Files, Spring 1990, No. 19, Pp. 56-68.
73 Evans, Robin, Pg. 67.
The Salk’s 1992 Addition
The site diagrams reveal this ridgeline condition as pivotal in establishing the visually correct site boundary, though an artificial geometric construct. The mesmerizing ocean horizon effect is a natural illusion concentrated by the plaza’s powerfully singular axial processional path (Fig. 15-E). This effect is not arbitrary or accidental. The phenomenon is experiential. One relevant research precedent focused on diagramming experiential space phenomena was published by Robin Evans in a 1990 critique, “Mies Van Der Rohe’s Paradoxical Symmetries.”72 I draw a parallel between the Salk Institute’s strong axis that forces the vista toward the ocean with Evans’ description of an equivalent effect in his study of Mies’ Barcelona Pavilion: “By virtue of its optical properties, and of its disembodied physicality, the pavilion always draws us away from consciousness of the way we see it.”73
The diagram studies shed insight into a troubled historical episode. The Salk's 1992 expansion project received an avalanche of negative professional peer critique
Dr. Jonas Salk made a critical decision early on that proved pivotal. He partnered with the architecture firm of Anshen and Allan. The firm held a valuable asset: Jack MacAllister,81 the firm’s principal, was a former Kahn employee.82 He had insider knowledge having “led the design of the Salk Institute in La Jolla at the age of 25.”83 MacAllister’s engagement signaled that the Salk’s addition would integrate with Kahn’s design spirit and intent. Macallister held the key that unlocked Kahn’s phantom underlying spatial ordering framework. MacAllister was reponsible for executing Kahn’s “disciplined and rigorous”84 technical details and is deserving of credit as Kahn’s site architect on the original Salk.85
Like the Mezquita de Cordoba, the Salk grew from a square to a rectangle using universal ordering templates (Fig. 19). Defining and anchoring the building addition’s footprint was a simple 3-
74 Crosbie, Michael, “Add and Subtract”, Progressive Architecture, Oct. 1993
75 Lesser, Wendy, “You Say to Brick, The Life of Louis Kahn”, Farrar, Straus & Giroux, 2017, Pg. 30.
76 Giovanni, Joseph, “The Salk Addition”, Architecture Magazine, Vol. 85, Issue #3, March 1996, Pg. 72.
77 Crosbie, Michael, “Add and Subtract”, Progressive Architecture, Vol. 74, Issue 10, Oct. 1993.
78 Ibid.
79 Ibid.
80 Ibid.
81 AIA California, Video of Jack MacAllister interview, Montery Design Conference Website: (http://aiacalifornia.org/monterey-design-conference-speakers/), (2016).
82 Lesser, Wendy, “You Say to Brick, The Life of Louis Kahn”, Farrar, Straus & Giroux, 2017, Pg. 27
83 Lesser, Wendy, Pg.
84 Thomas, Leslie, “Things in their best order: Technical aspects of the Salk and their role in its design,” The Journal of Architecture, 8:1, (2003), Pg. 102.
85 Thomas, Leslie, Pg. 103
Fig. 19 – Diagram series of macro site plan demonstrating how the 1992 Salk addition project by MacAllister’s geometry is tied to Kahn’s original 1965 plan geometry.
led by the American Institute of Architects (AIA).74 Louis Kahn had passed away in 1974.75 By 1990, Dr. Salk’s laboratories needed to expand by an additional 110,000 square feet.76 To grow an iconic 20th-century architectural masterpiece by a revered master was a daunting challenge.77 Any move would be met with intense international scrutiny and critique. A cloud of controversy quickly surrounded Dr. Salk’s expansion project when plans were publicly “unveiled”78 in 1991. Concerned with the proposed expansion design, Dr. Salk was summoned by the AIA to meet with “Richard Meier, Venturi, and Frampton.”79 All three expressed their alarm about design plans showing the proximity of the new addition to the original building. Dr. Salk only conceeded some minor changes.80
Conclusion

The graphical analysis diagrams in this study reveal new insights on the intent of Louis Kahn’s design for the Salk Institute and how powerful site forces likely guided and helped define the most iconic spatial elements. The diagrams are instrumental in discovering essential aspects of the nature and character of Kahn’s architecture. For example, the site study diagrams reveal a clean geometric correlation between natural forces and the Salk’s original building site.
Decoding Kahn’s plan layout at the Salk reveals a “Divine Proportion”86 intentionally embedded, acting as essential
he square part of the Golden Section template over rter radius from end point of the square’s top side the expansion and set the internal proportions for
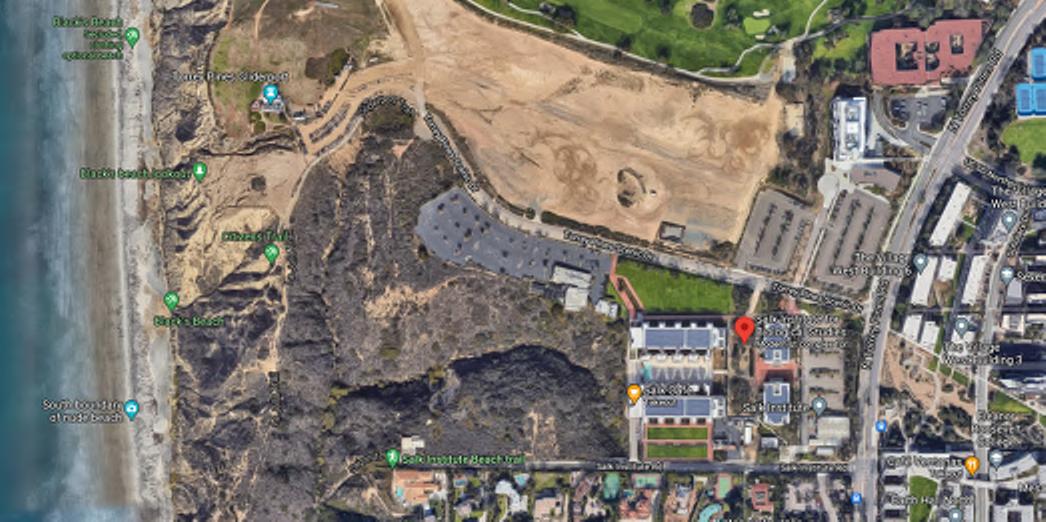
and new Salk buildings are linked in the most intimate way possible, controlled by hidden ordering devices that adhere to Kahn’s original embedded underlying

Fig. 23 – Diagram studies showing the evolution the Salk Institute’s growth, from Kahn’s original 1965 square layout to the 1992 addition that transforms the conceptual square parti into a rectangle that is proportioned by the Greek Ratio of 1.618 (√3).
ssive Architecture, Oct (1993).
l History”, Pg. 246, Thames & Hudson, 4th Edition, 2016.
This diagram study visualizes the critical role that hidden geometric ordering devices played in achieving two objectives: Applying the geometric proportioning device does not alter Kahn’s original plan, and provides a fundamental ordering framework for guiding where to place the limits of the expansion footprint.
Fig. 22 – Diagram showing 1992 addition to the original 1965 Salk building complex. Aerial view is superimposed with the classical proportioning Ratio of 1.618 (√3). Shows proportioning relationship between Salk’s 1965 vs. 1992 building addition. The same ratio governs proportions at 3 scales (Image credit: Google Earth).
Acknowledgements
The idea for this research topic was inspired by lectures on Louis Kahn’s Salk Institute delivered by Professor James Steele in Arch 214 World History of Architecture and Arch 606 Advanced Architectural Theory. James Steele teaches architectural history and theory at the University of Southern California’s School of Architecture. I thank architect and author Jeffry Kieffer for providing critique of an earlier version of this report, which was a term paper submitted to Prof. James Steele in 2018.
Image Credits
All graphic analysis diagrams are by the author unless credited otherwise.
Bibliography
1. Clark, Roger and Michael Pause, “Precedents in Architecture,” Van Nostrand Reinhold, (1995).
2. Cohen, Jean-Louis, "Le Corbusier’s Modulor and the Debate on Proportion in France," Architectural Histories 2, no. 1 (2014).
3. Crosbie, Michael J, "Add and Subtract," Progressive Architecture, No. 10, (1993).
4. Curtis, William J.R., “Authenticity, Abstraction and the Ancient Sense: Le Corbusier’s and Louis Kahn’s Ideas of Parliament,” Perspecta, Vol. 20, (1983).
5. Evans, Robin, “Mies Van Der Rohe’s Paradoxical Symmetries,” AA Files, Spring (1990).
6. Fernandez-Puertas, Antonio, “La Fachada del Palacio de Comeras, Situacion, Funcion y genesis,” (1980).
7. Frampton, Kenneth, “Modern Architecture, A Critical History”, Thames & Hudson, 4th Edition, (2016).
8. Frings, Marcus, "The Golden Section in Architectural Theory," Nexus Network Journal 4, no. 1 (2002).
9. Gast, Klaus-Peter, “Louis I. Kahn: The Idea of Order,” Birkhauser, (2001).
10. Giovannini, Joseph, "The Salk Addition." (1996).
11. Kieffer, Jeffry, “The Evolution of a Building Complex, Louis I. Kahn’s Salk Institute for Biological Studies,” Artifice, (2019).
12. Lesser, Wendy, “You Say to Brick, The Life of Louis Kahn,” Farrar, Straus & Giroux, (2017).
13. Lobell, John, “Between Silence and Light; Spirit in the Architecture of Louis I. Kahn”, Shambhala, (1979).
14. Meisner, Gary B., “The Golden Ratio: The Divine Beauty of Mathematics,” Race Point Publishing, (2018).
15. Pacioli, Luca, “Divina Proportione,” illustrated by Leonardo da Vinci, (1509).
16. Phillippidis, Alex, “Top 10 U.S. BioPharma Clusters,” Genetic Engineering & Biotechnology News, Sept. 23, (2018).
17. Powell, Christopher, “The Shapes of Sacred Space: A proposed System of Geometry Used to Lay Out and Design Maya Art and Architecture and Some Implications Concerning Maya Cosmology”, Ph.D. Dissertation, University of Texas at Austin, August (2010).
18. Reynolds, Mark A, “A New Geometric Analysis of the Teotihuacan Complex,” Springer International Publishing, (2014).
19. Scully, Vincent, “Louis I. Kahn and the Ruins of Rome," MoMA no. 12 (1992).
20. Steele, James, “Salk Institute, Louis I. Kahn,” Phaidon Press, (1993).
21. Thomas, Leslie, “Things in their best order: Technical aspects of the Salk and their role in its design,” The Journal of Architecture, 8:1, (2003).
22. Towers, Sherry, "Advanced Geometrical Constructs in a Pueblo Ceremonial Site,” Journal of Archaeological Science: Reports 12, (2017).
23. Treib, Marc, "To End a Continent: The Courtyard of the Salk Institute," Journal of the Society of Architectural Historians 65, no. 3 (2006).
24. Twombly, Robert, “Louis Kahn Essential Texts,” Norton and Co., (2001) Pg. 21 (a reprint of Kahn’s essay first appearing published in 1944).
25. Tyng, Anne Griswold, “Simultaneous Randomness and Order, The Fibonacci-Divine Proportion as a Universal Forming Principle”, Graduate School of Arts and Sciences, Ph.D. Dissertation, University of Pennsylvania, (1975).
26. Willamson, James, “Kahn at Penn: Transformative Teacher of Architecture,” Routledge, (2015).
27. Yalta, Kenan, Selcuk Ozturk, and Ertan Yetkın, "Golden Ratio and the Heart: A Review of Divine Aesthetics," International Journal of Cardiology, 214, (2015).
Websites:
28. AIA California, Video of Jack MacAllister interview, Monterey Design Conference Website: (http://aiacalifornia.org/monterey-design-conference-speakers/), (2016).
29. County of San Diego Assessor’s parcel map.
30. Cuno, Jim, “The Salk Institute Part 1 – Founding and Forming”, Getty Blog, Arts and Ideas, The Getty, Oct. 31, (2018).
31. Docomomo, “Anne Tyng, Architect,” website: (https://docomomo-us.org/designer/anne-tyng), (2021).
32. Google Maps, Aerial Images.
33. Reynolds, Mark A., Website (www.piorogi2000.com/2015/mark-reynolds-has-three-articles-ongeometric-analysis-published/).
34. U.S. Geological Survey Map, Torrey Pines Map Sector.
Reference Bibliography
35. Crosbie, Michael J., "Dissecting the Salk," Progressive Architecture 74, no. 10, Oct (1993).
36. Aljubori, Luai, Chaham Alalouch. "Finding Harmony in Chaos: The Role of the Golden Rectangle in Deconstructive Architecture," International Journal of Architectural Research 12, no. 3 (2018).
37. Barizza, Elisabetta, Marco Falsetti. Rome and the Legacy of Louis I. Kahn. Milton Park, Abingdon, Oxon: Routledge, an imprint of the Taylor & Francis Group, (2019).
38. Benekikt, Michael, "Between Beakers and Beautitudes." (1993).
39. Burton, Joseph A, "The Aesthetic Education of Louis I. Kahn, 1912-1924," Perspecta 28, (1997).
40. Caldarelli, Mario, “La Ristrutturazione Del Moderno (the Salk Institute East Building),” Milano, L'Arca edizioni, (1997).
41. Ching, Francis, “Architecture Form, Space, and Order”, Third Edition, Wiley, (2007).
42. Clement Falbo, “The Golden Ratio – A contrary Viewpoint”, the College of Mathematics Journal, online, Nov. 28, (2017).
43. Cohen, Preston Scott, “Contested Symmetries and Other Predicaments in Architecture,” New York, Princeton Architectural Press, (2001).
44. Conn, Adam, Ullas V. Pedmale, Joanne Chory, and Saket Navlakha, “High-Resolution Laser Scanning Reveals Plant Architectures that Reflect Universal Network Design Principles,” Vol. 5, Cell Press, (2017).
45. Dabbour, Loai M, "Geometric Proportions: The Underlying Structure of Design Process for Islamic Geometric Patterns," Frontiers of Architectural Research 1, no. 4 (2012).
46. Debnath, Lokenath, "A Short History of the Fibonacci and Golden Numbers with their Applications," International Journal of Mathematical Education in Science and Technology, April 15, (2011).
47. Degnath, Lokenath, “A short history of the Fibonacci and Golden Numbers with their applications,” Int’l Journal of Mathematics Education in Science and Technology, Vol. 42, Issue 3, (2011).
48. Delaine, Janet, “The Baths of Caracalla, A study in the design, construction, and economics of largescale buildings projects in imperial Rome”, Journal of Roman Archeology Supplemental Series Number 25, (1997).
49. Doyle, James A, "Early Maya Geometric Planning Conventions at El Palmar, Guatemala," Journal of Archaeological Science 40, no. 2 (2013).
50. Edmund, Thomas, “Monumentality and the Roman Empire,” Oxford Press, (2007).
51. Elam, Kimberly, “Geometry of Design: Studies in Proporation and Composition,” Princeton Architectural Press, (2011).
52. Fleming, Stevens, "Theorizing Daylight: Kahn's Unitarian Church and Plato's Super-Form, the Good," Arq 10, no. 1 (2006).
53. Fleming, Stevens & Mark Reynolds, "Timely Timelessness: Traditional Proportions and Modern Practice in Kahn’s Kimbell Museum," Nexus Network Journal 8, no. 1 (2006).
54. Frampton, Kenneth, “Louis I Kahn and the new Monumentality”, Design Book Review, Berkeley, (1993).
55. Friedman, Daniel S., “Salk Institute: Louis I. Kahn,” (2017).
56. Ghorbani, H., “The Golden Ratio: The Mathematics of Beauty”, MIR
57. Gideon, Sigfried, “Architecture, You, and Me; The Diary of a Development,” Harvard University Press, (2013).
58. Goldberger, Paul, "Architecture as Object," Why Architecture Matters, 65-108: Yale University Press, (2009).
59. Henein, Michael Y., Ying Zhao, Rachel Nicoll, Lin Sun, Ashraf W. Khir, Karl Franklin, and Per Lindqvist, "The Human Heart: Application of the Golden Ratio and Angle," International Journal of Cardiology 150, no. 3 (2011).
60. Hildner, Jeffrey, "Remembering the Mathematics of the Ideal Villa," Journal of Architectural Education (1984) 52, no. 3 (1999).
61. Howe, Eunice D. & Evans, Robin, “The Projective Cast: Architecture and its Three Geometries" (Book Review)." Renaissance Quarterly 50, no. 3 (1997).
62. Kalman, Dan and Mena Robert, "The Fibonacci Numbers—Exposed," Mathematics Magazine 76, no. 3 (June 1, 2003).
63. Krautheimer, Richard, “The Constantinian Basilica”, Dumbarton Oaks Papers, Vol 21, (1967).
64. Ksiazek, Sarah Williams, "Critiques of Liberal Individualism: Louis Kahn's Civic Projects,” Assemblage No. 31 (1996).
65. Lekson, Stephen and Stephen, H., “The Architecture of Chaco Canyon, New Mexico,” University of Utah Press, (2007).
66. Leslie, Stuart W., "A Different Kind of Beauty, Scientific and Architectural Style in I. M. Pei's Mesa Laboratory and Louis Kahn's Salk Institute,” Historical Studies in the Natural Sciences 38, No. 2 (2008).
67. Leslie, Thomas, “Things in their Best Order: Technical Aspects of the Salk Institute and their Role in its Design,” The Journal of Architecture, Vol. 8. (2003).
68. Lüttge, Ulrich and Gustavo M. Souza, "The Golden Section and Beauty in Nature: The Perfection of Symmetry and the Charm of Asymmetry," Progress in Biophysics and Molecular Biology 146, (2019).
69. Margalith, Dana, "Memory Enabling Dwelling: Remembrance and Amnesia in Louis I. Kahn's Design for the Salk Institute for Biological Studies in La Jolla, California," Journal of Architecture 25, no. 5 (2020).
70. Margalith, Dana, "Memory Enabling Dwelling: Remembrance and Amnesia in Louis I. Kahn's Design for the Salk Institute for Biological Studies in La Jolla, California," Journal of Architecture, 25, No. 5, (2020).
71. Markowsky, George, "Misconceptions about the Golden Ratio," The College Mathematics Journal 23, no. 1 (January 1, 1992).
72. Mattern, Shannon, "Geometries of Reading, Light of Learning: Louis I. Kahn's Library at Phillips Exeter," Nexus Network Journal 12, no. 3 (2010).
73. Miles, Margaret M., “A Companion to Greek Architecture”, John Wiley & Sons, (2016).
74. Moe, Kiel, "Extraordinary Performances at the Salk Institute for Biological Studies,” Journal of Architectural Education (1984-) 61, no. 4 (2008).
75. Mumford, Lewis, “The City in History: Its Origins, its Transformations, and its Prospects,” Harcourt, Brace & World, (1961).
76. Nabavi, Faezeh and Yahaya Ahmad, "Is there any Geometrical Golden Ratio in Traditional Iranian Courtyard Houses?" International Journal of Architectural Research 10, no. 1 (2016).
77. Newman, Morris, “Addition Planned for Kahn's Salk Institute,” Vol. 72. New York: Reinhold, 1991.
78. Niesewand, Nonie. "ARCHITECTURE: Cereal Thrillers, Sacred Geometry and the Magic of Number Seven; Why is Wednesday 7 July so Important?” Independent, (1999).
79. Ostwald, Michael J. Under Siege, “The Golden Mean in Architecture,” Vol. 2.
80. Ozturk, Selcuk, Kenan Yalta, and Ertan Yetkın, "Golden Ratio: A Subtle Regulator in our Body and Cardiovascular System?" International Journal of Cardiology, 223, (2016).
81. Reilly, Michael, “God's Place in a Rational World?” Vol. 196. London: New Science Publications, (2007).
82. Rossi, Corinna, “Architecture and Mathematics in Ancient Egypt,” Cambridge University Press, (2003).
83. Samalavicius, Almantas, “Architecture, City and Mathematics: The Lost Connection” Mathematics Interdisciplinary Research, Journal Vol. 4, Issue 1, Spring (2019).
84. Scriba, Christoph J., Peter Schreiber, and Jana Schreiber, “5000 Years of Geometry: Mathematics in History and Culture,” Springer Basel AG, (2015).
85. Senseney, John R., “The Art of Building in the Classical World: Vision, Craftsmanship, and Linear Perspective in Greek and Roman Architecture” Cambridge University Press, (2011).
86. Senseney, John R., "Idea and Visuality in Hellenistic Architecture: A Geometric Analysis of Temple A of the Asklepieion at Kos," Hesperia 76, no. 3, (2007).
87. Senseney, John R., “Plans, Measurement Systems, and Surveying,” Oxford, Blackwell Publishing Ltd, (2013).
88. Simon, Bennett, "Mondrian’s Search for Geometric Purity: Creativity and Fixation," American Imago 70, no. 3, (2013).
89. SIRY, JOSEPH M., "Roche and Dinkeloo’s Center for the Arts at Wesleyan University; Classical, Vernacular, and Modernist Architecture in the 1960s," Journal of the Society of Architectural Historians 75, no. 3 (2016).
90. Stein, Karen, "The Salk Institute." Architectural Digest, (2013)
91. Velmurugan, C. and R. Kalaivanan, "Existence of the Golden Ratio in Tanjavur Brihadeeshwarar Temple,” Open Journal of Mathematical Sciences 4, no. 1 (2020), Pp. 211-219.
92. Waerden, Bartel L. van der, “Geometry and Algebra in Ancient Civilizations,” Springer, (1983).
93. West, Bruce J. and Jonas Salk, “Complexity, Organization and Uncertainty,” Vol. 30. Amsterdam, Elsevier Science, (1987).
94. Yetkin, Gulay, Nasir Sivri, Kenan Yalta, and Ertan Yetkin, "Golden Ratio is Beating in our Heart,” International Journal of Cardiology, 168, no. 5 (2013).
