Do Derivatives Belong in a Retail Investor’s Portfolio? Russell Kwok, Remove

Do derivatives belong in a retail investor’s portfolio ?

Russell Kwok, Remove

Disclaimer: The author of this essay is not a qualified financial advisor and thus, all content is for informational purposes only and not to be treated as investment advice. Any loss is in no manner the responsibility of the author. It is very important to do your own analysis before making an investment. Derivatives are leveraged and complex securities and may incur substantial losses. To invest in such instruments, please follow all regulations and follow professional advice.

The recent volatility the financial markets, with fastest bear market on record in 19 days (LPL Research, 2020), have brought to mind the 2008 recession, which had led to financial catastrophe for millions of people around the world, in addition to the collapse of many renowned institutions such as Lehman Brothers. The current consensus of economists is that it was catalysed by investors gaining subprime credit exposure through derivatives. (Coghlan, et al., 2018) Thus, they are often derided as risky and complex. That view, however, is overgeneralising and may potentially exclude many opportunities that permit an intelligent investor to increase their returns, while derisking. (Asness, 2010) Truly, what harms investors is a lack of understanding. (Marolia, 2015) In view of these misconceptions, this essay will explore the types and structures of derivatives, the risk-reward ratio compared to other asset classes and examples where such securities are not only profitable, but beneficial for individual investors. Derivatives are defined as “financial securities with a value that is reliant upon or derived from, an underlying asset or group of assets”. (Chen, 2020) This is done through a contract in which a writer promises to deliver some value, or the underlying goods to the purchaser of this agreement. The earliest example of derivatives in use comes from Aristotle’s Politics. He recounts the activities of a fellow philosopher, Thales of Miletus: “he raised a small sum of money and paid round deposits for the whole of the olive-presses… and when the season arrived, there was a sudden demand for a number of presses at the same time… by letting them out on what terms he liked, he realized a large sum of money” (Aristotle, 1981) Thus, many who claim they are recent exploitative inventions of Wall Street are mistaken. In the latter example, derivatives were utilised for speculation, which is often mistakenly portrayed as their primary use in the financial markets.

This belief is fallacious because there are actually multiple uses for such instruments; in fact, their invention was due to a need to facilitate hedging, which is still the most common use. (CFTC, n.d.) It means trying protects oneself against volatile asset prices by using derivatives to offset losses and gains on other securities they own; this is known academically as reducing variance. (Gilson & Black, 1993) Such ‘insurance’ is crucial for farmers and all sorts of businesses around the world who need to lock in prices to ensure costs stability and guaranteed payments. Another use is to adjust your asset allocation without transacting any underlying assets, so as to minimise frictional costs. For intelligent investors, in addition to hedging, one can write (i.e. sell) contracts to generate cash, often without buying or selling equities, and decrease cost basis

which will increase returns. There are many other uses, such as arbitrage (taking advantage of minor market errors), but they are accessible mostly for institutional investors and hence, do not provide any practical value to the retail investor.

Derivatives, as described, are an umbrella term for many different types of securities, such as swaps, futures, options and other more esoteric iterations such as weather derivatives that permit hedging of adverse meteorological conditions that could affect crops. For individual investors though, futures and particularly options, are the main structure for gaining exposure to this asset class. This is because they require relatively little collateral (cash used to backstop investors in case one cannot satisfy the contract) and are simple to understand. Let us first elaborate on their structures, in order to illustrate that their reputation of complexity and opacity is a fallacy, obstructing a path that could lead to not only better, but safer returns.

In essence, futures are “standardized agreements to buy and sell fixed amount of a certain commodity at a specified location at a future time for a predetermined price”. (Rogers, 2007) Given the exceedingly particular verbiage, it would wise to break it down into four sections: the agreement; the location; the time; and the price. The first section is self-explanatory, as derivatives are contracts between two or more counterparties. The second part describes the delivery or settling in cash of the goods one has ordered through the agreement; this can be problematic for retail investors as one needs a warehouse but 95% of commodities with such a mechanism do not take delivery. (Hecht, 2020) This is because, one can ‘roll-over’ one’s contract- in other words, extend the delivery date through a new contract. This is not difficult if one has a competent broker. The time is simply the month in which the contract expires, and delivery occurs, while the price is the agreed value at which to buy or sell the particular goods. One makes a profit in futures by utilising the spread between ‘spot prices’, or current prices, and ‘future prices’, which are prices in the chosen month. If one believes future prices will be higher than the contract price for let’s say, December, one can buy that future and sell it when it converges to your target price.

But why even invest in commodities? Studies have shown that commodity futures returns are negatively correlated with equity and bond returns and are positively correlated with inflation, unexpected inflation, and changes in expected inflation.’ (Rouwenhorst & Gorton, 2004) This means that one could potentially profit during periods of market volatility and tumult, providing better risk-adjusted returns. Even for non-physical futures, such as E-mini S&P 500s, there is no management fees, better liquidity and cheaper margin, reducing overhead expenses, resulting in higher profits.

Options and futures are very similar instruments, but with a slight difference- the former are contracts giving one the right (i.e. an option), rather than the obligation, to purchase or to sell the underlying asset. Thus, this can apply for individual stocks, which makes them, perhaps, more relevant for the individual intelligent investor. As they are rights to buy assets at a certain price, many variations exist, but once again, a proper retail investor should only put money in their circles of competence.

The two main types of ‘plain vanilla’ options, Wall Street jargon for the basic or standard version, which are European and American. The former is less common and is used for indices or currencies rather than individual equities, as they can only be exercised on the expiration date. The latter is an option that can be exercised at any time one desires within the contract period (Hanson, 2008). When one desires to buy or write (i.e. sell) an option, there are some vital specifications to consider. Firstly, one has to determine if it is a right to buy- a call option as if ‘calling in the asset’- or to sell – a put option, as if ‘putting it on the market’-. Then the quantity of a particular asset is agreed on, along with the expiration date, and the strike price. (OCC, 1994) The latter is like the price of the future; that is to say the value at which the transaction is to occur. As it is a right, rolling over is not necessary, as one can leave the option unexercised (albeit losing the premium, which is price of the option). If one does indeed exercise it, either cash or the asset is delivered or for the latter, sold.

Alternatively, options can be compared to a loan. Using this analogy, one can borrow the entire purchase price with only a moderate interest rate (premiums in this case) upfront with minimal collateral; if the investment did not succeed, principal would not have to be returned. (Greenblatt, 1999) Such generous terms cannot be found in any bank in the world, even if one had the highest credit score.

Given the strike price and premium, one can deduce three different situations in which an option holder can be in: in-the-money (ITM); at-the-money (ATM) and out-of-the-money (OTM). ITM options mean that the underlying asset price is under (for a put) or above (for a call) the strike price, so exercising the right would result in profit. ATM option have a current price at strike price, so no loss or profit is incurred if exercised forthwith. OTM is the exact opposite of ITM and results in an immediate loss if exercised; one would purchase them because they are cheaper, and so allow the investor to make greater gains when the stock price exceeds the strike for the option to become ITM. Generally, due to their chance of potential profit being discounted in the price of the option if exercised, so ITM and ATM options are extremely expensive. Thus, in reality, it would be more difficult profit using them.

In every intelligent investment, we have to ensure it is “one which, upon thorough analysis, promises safety of principal and a satisfactory return. Operations not meeting these requirements are speculative.” (Graham & Dodd, 1940) Hence, one needs to examine the risks involved in derivatives before gaining exposure to them. Market risk is probably on the top of one’s mind, as it is most direct and most common, as it is defined as ‘the risk of loss from adverse price movements in the market’. (Krawiec, 1997) This is most dangerous if one enters unhedged transactions, also known as ‘naked’ trades, as one might be forced in a margin call to liquidate other holdings in order to satisfy the contract, realising all losses and eliminating your capital.

This brings to mind the critical concept of margin in this asset class, as it is partly the reason for its popularity. Margin is merely collateral held by one’s broker to ensure one is able to satisfy the contract. (Fortune, 2003) In this way, one can build up a substantial quantity of derivatives with little money; in other words, one can gain leverage. Therefore, intelligent retail investors can boost returns without incurring too large a risk, if one is judicious about the gearing involved. The most severe risks though are often neglected; they are counterparty risk and credit risk, in which the other side of the contract fails to deliver on their promises. Margin aims to mitigate (Cherubini, 2005), as it ensures the other side is faithful to the contract. In actuality, one could view the Great Recession partially as a counterparty risk crisis. (Thakor, 2015) However, this is not a grave concern if individual investors dissociate themselves from large contracts on illiquid markets, which are often fraudulent and exploitative.

Through the examination above, it is demonstrated that many risks associated with derivatives are in fact affecting mainly investors who are institutional, highly leveraged, or engage in less established mechanisms such as illiquid contracts.

Regardless of the veracity of the academic discourse on the merits of derivatives above, what critics of such instruments say are very true if one deals speculatively in them. Consequently, would be prudent to examine some scenarios in which derivatives truly aid the intelligent investor in making safer and better investments. Buying futures is a simple strategy, as it is the only way to gain exposure to commodities, so we will focus on three main strategies to do with options. For simplicity’s sake, they will all be for long positions.

1.) Writing or selling options.

This means one will be on the other side of the trade and will receive a premium for it (i.e. the cost to buy an option). The Chicago Board Options Exchange (CBOE) has

noted that only about 5% of options are actually exercised (Shwager, 1990), implying that most options expire without being exercised, enabling their writers to collect the full premium. Moreover, time decay, a “measure of the rate of decline in the value of an options contract due to the passage of time” (Chen, 2020), is always working against the buyer, so as a seller, you benefit. To reduce the probability that the options writer faces adverse losses during volatile times via forced selling or buying of the stocks on the open market, the writer should always hold underlying stock concerning the options contract. However, this risk can be exploited safely and lucratively if an investor desires to sell or buy some shares of a business; this is because one can effectively be paid to do so.

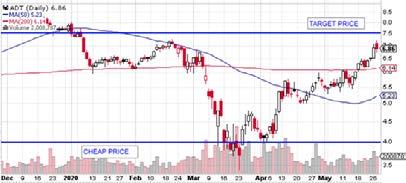
Let us assume one has analysed ADT Inc. (ADT) and recognised that it provides an attractive price at $4, given that it is worth the target price of $7.5. You could sell OTM put options- effectively, allowing someone to sell to you- with exercise price $4, which will allow you to be paid to purchase it. If one’s convictions are correct, the price will revert towards the $7.5 in the fullness of time. When you desire to close one’s position, you can sell an OTM call option- allow someone to buy from you-. It is particularly advantageous as one can pick the strike price as close as possible above the market price to maximise premiums. (Elias, 2001) By doing, it is possible to reduce cost basis towards zero, greatly expanding one’s margin of safety.

Normally, a company’s market value will only gradually reach intrinsic value, with frequent fluctuations. In these scenarios, one can even write call options around 10%- 20% above current price to generate premiums. That said, one should always buy back the calls when it is 25% of the premium obtained (Elias, 2001), or else, the price could exceed the strike price and generate a loss.

2.) Long straddle.

There are many complex ways to construct options in a manner that permits maximum profit for a certain viewpoint; these structures are short-term and constitute as speculation, something an intelligent retail investor should avoid. Nevertheless, there is one, known as a long straddle, which is statistically a profitable and safe method to exploit significant price movements in any direction.(Surur & Isynuwardhana, 2018) This methodology is most appropriate for major news or earnings releases in comparatively volatile businesses, like drug companies.

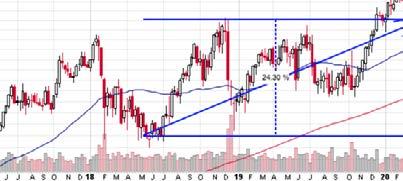
This strategy consists of purchasing a put and a call on the same underlying security with the same expiration date. (CME Institute, n.d.) The only downside, though, is that the total premiums paid is quite large, so only large moves are profitable. One can add the total premium to either side of the current price to discover the range at which the price needs to exceed; when it is so, one can exercise the options and realise the profits. The chart above shows Biogen Inc. (BIIB), a large biomedical corporation releasing news that a landmark drug for Alzheimer’s disease was delayed, resulting in a 12% decline. (Griffin & Lipschultz, 2020) One might notice the start of a recovery at the end; hence, such trades are short-term and need to be closed in 2-3 days once profit is made.

3.) Long-Term Equity Anticipation Securities (LEAPS) or Warrants

These instruments may sound rather byzantine, but they are basically long-term options. LEAPS last for almost 2½ years while warrants are issued by the underlying company and can last for any long period of time, even for perpetuity. (Kumar, 2019) These are traded securities and can be found for most large companies, so they are not illiquid.

One can actually replicate one’s portfolio with these securities, but with extra safety, as it involves less initial capital and limited losses. Even for staid blue chips like Johnson & Johnson (pictured below), such derivatives can boost otherwise unspectacular returns with safe amounts of leverage.

Some might wonder why using LEAPS are more advantageous than utilising margin loans, even when LEAPS have a maximum 100% loss and are time-constrained securities. The key difference is that they are provide non-recourse leverage. (Mishuris, 2017) This means that they do not affect the rest of the portfolio in a worst-case scenario. For example, if one utilises margin loans, a margin call could occur, forcing one to change asset allocation and perhaps increase risk. Using long-term options, the only capital at risk of permanent loss is the premium; this can be equivalent to an equity position many times of the price of the option. The time-constraint aspect of long-term options can be somewhat problematic for the intelligent investor, but like futures, one can roll-over the option, potentially making it last for more than 5 years. (Seagler, n.d.) This is not a difficult procedure if one has a competent broker. However, in behavioural investing, a stock owner is vulnerable to many biases that inhibit returns. One is known as the endowment effect. It leads one to value their holdings more than if they did not own it. (Kahneman, et al., 1991) The second most damaging bias would be anchoring. It is when one’s initial exposure is promoted during analysis, which impedes the inclusion of new evidence. (Boo & Furnham, 2011) Another is loss aversion, in which the investor does not sell suboptimal investments, as doing so would realise a loss and cause discomfort. By holding it, one is in an illusion in which one believes it is a temporary setback. (Kahneman & Tversky, 1979) With an option that has a fixed expiration date, which

is effectively a forced liquidation date, these biases are less likely to impact the investor, since they will force the investor to make a decision of whether it is worth re-establishing the position from a perspective of not owning it and thus be able to take a completely fresh view of the investment.

A successful use of LEAPS would be Wells Fargo (WFC) in 1992, when it was in the midst of a real-estate downturn. (Greenblatt, 1999) One could purchase 2-year LEAPS costing $14, strike price at $80 with current market price of $77. Assuming one has done sufficient research of the business, and estimated intrinsic value at, for example, $160, which is not unreasonable if market conditions normalise and earnings continue to grow. On an investment of $14, if the price does reach the target price, it would imply a profit of $66. This is a risk/reward ratio of 1:5 compared to a 1:2 ratio if one purchased equity only, which is most exceptional.

The approaches detailed above are only three out of tens of options strategies that exist (Cohen, 2005), but the ones illustrated provide lower risk exposure and deserves consideration in the portfolio of the informed investor. Some may wonder why these methods are still profitable if they are already known, given the widespread agreement regarding the assumptions outlined in the Efficient Market Hypothesis; this is because of the dissemination of inaccurate information and negative attitudes towards financial derivatives within society, making this asset class inefficient. (Ackert & Tian, 2001) Furthermore, individual investors have the advantage of being small and agile, with the ability to evade many risks that ensnare larger investors. Opportunities are plentiful, but as always, only proceeding with diligence and caution can profits emerge, allowing for long-term wealth generation.

Bibliography

Ackert, L. F. & Tian, Y. S., 2001. Efficiency in Index Options Markets and Trading in Stock Baskets. Journal of Banking and Finance, 25(9), pp. 1607-1634. Aristotle, 1981. The Politics. 2nd Edition ed. s.l.:Penguin Classics. Asness, C., 2010. Institutional Investor. [Online] Available at: https://www.institutionalinvestor.com/article/b150qd3fhy4cwb/using-derivatives-and-leverage-to-improve-portfolio-performance?Keywords=Asness&OrderType=1&PeriodType=4&StartDay=0&StartMonth=1&StartYear=2010&EndDay=0&EndMonth=12&EndYear=2010&ScopeIndex=0 [Accessed 15 June 2020]. Boo, H. C. & Furnham, A., 2011. A Literature Review of The Anchoring Effect. Journal of Behavioral and Experimental Economics, 40(1), pp. 35-42. CFTC, n.d. Commodity Futures Trading Commission. [Online] 47

Available at: https://www.cftc.gov/LearnAndProtect/EducationCenter/FuturesMarketBasics/index.htm [Accessed 27 May 2020]. Chen, J., 2020. Investopedia. [Online] Available at: https://www.investopedia.com/terms/d/derivative.asp [Accessed 19 May 2020]. Chen, J., 2020. Investopedia. [Online] Available at: https://www.investopedia.com/terms/t/timedecay.asp [Accessed 28 May 2020]. Cherubini, U., 2005. Counterparty Risk in Derivatives and Collateral Policies: The Replicating Portfolio Approach, Bologna: University of Bologna. CME Institute, n.d. CME Group. [Online] Available at: https://www.cmegroup.com/education/courses/option-strategies/straddles.html [Accessed 28 May 2020]. Coghlan, E., McCorkell, L. & Hinkley, S., 2018. Institute for Research on Labor and Employment. [Online] Available at: https://irle.berkeley.edu/what-really-caused-the-great-recession/ [Accessed 18 May 2020]. Cohen, G., 2005. The Bible of Options Strategies: The Definitive Guide for Practical Trading Strategies. 1st Edition ed. s.l.:FT Press. Elias, S., 2001. Generate Thousands in Cash On Your Stocks Before Buying Or Selling Them. 3rd Revised Edition ed. Leawood, KS: Leathers Publishing. Fortune, P., 2003. Margin Requirements Across Equity-Related Instruments: How Level Is the Playing Field?. New England Economic Review, 27 November. Gilson, R. J. & Black, B. S., 1993. The Essentials of Finance and Investment. 1 ed. s.l.:Foundation Press. Graham, B. & Dodd, D. L., 1940. Security Analysis. 2nd Edition ed. New York: McGraw Hill Education. Greenblatt, J., 1999. You Can Be a Stock Market Genius: Uncover the Secret Hiding Places of Stock Market Profits. 1st Edition ed. New York: Touchstone. Griffin, R. & Lipschultz, B., 2020. Bloomberg.com. [Online] Available at: https://www.bloomberg.com/news/articles/2020-04-22/biogen-alzheimer-s-drughits-delays-caused-by-data-covid-19 [Accessed 28 May 2020]. Hanson, W., 2008. InvestorPlace. [Online] Available at: https://investorplace.com/2008/11/option-styles-american-vs-european/ [Accessed 27 May 2020]. Hecht, A., 2020. The Balance. [Online] Available at: https://www.thebalance.com/taking-delivery-of-commodities-via-the-futuresmarket-4118366

[Accessed 27 May 2020]. Kahneman, D., Knetsch, J. L. & Thaler, R. H., 1991. Anomalies: The Endowment Effect, Loss Aversion, and Status Quo Bias. The Journal of Economic Perspectives, 5(1), pp. 193-206. Kahneman, D. & Tversky, A., 1979. Prospect Theory: An Analysis of Decision under Risk. Econometrica, 47(2), pp. 263-291. King, L. W., 2008. Yale Law School: Avalon Project. [Online] Available at: https://avalon.law.yale.edu/ancient/hamframe.asp [Accessed 20 May 2020]. Krawiec, K. K., 1997. More Than Just “New Financial Bingo”: A Risk-Based Approach to Understanding Derivatives. The Journal of Corporate Law, 23(1), pp. 2-63. Kumar, S., 2019. Value Stock Guide. [Online] Available at: https://valuestockguide.com/all/stock-warrants/ [Accessed 28 May 2020]. LPL Research, 2020. LPL Research. [Online] Available at: https://lplresearch.com/2020/03/12/the-fastest-bear-market-ever/ [Accessed 18 May 2020]. Marolia, V., 2015. Derivatives Don’t Kill People... People Kill People, Orlando, FL: Regal Point Capital Management, LLC. Mishuris, G., 2017. Supplement to Q1 2017 Quarterly Letter, s.l.: Silver Ring Value Partners. OCC, 1994. Characteristics and Risks of Standardized Options. 1st Edition ed. Chicago: Options Clearing Corporation. Rogers, J., 2007. Hot Commodities: How Anyone Can Invest Profitably in the World’s Best Market. Reprint Edition ed. New York: Random House Trade Paperbacks. Rouwenhorst, K. G. & Gorton, G., 2004. Facts and Fantasies about Commodity Futures, Cambridge, MA: National Bureau of Economic Research. Seagler, S., n.d. Snider Advisors. [Online] Available at: https://www.snideradvisors.com/blog/when-should-you-roll-over-a-covered-call/ [Accessed 8 Jun 2020]. Shwager, J. D., 1990. Market Wizards. Reissue Edition ed. s.l.:HarperBus. Surur, G. N. I. & Isynuwardhana, D., 2018. Return Analysis on Contract Option Using Long Straddle Strategy and Short Straddle Strategy with Black Scholes. International Journal of Academic Research in Accounting, Finance and Management Sciences, 8(4), pp. 16-20. Thakor, A. V., 2015. The Financial Crisis of 2007–2009: Why Did It Happen and What Did We Learn?. The Review of Corporate Finance Studies, 4(2), p. 155–205.

An introduction to the problem of evil.

Toby Rooth, Shell

The Problem of Evil: Christianity has been scrutinised since it first emerged from Judea. Over the centuries there has been much debate over the key ideas and basis for the religion. Ecclesiastical critics such as philosopher J.L. Mackie and Epicurus make feasible arguments against the church and the concept of God’s omnipotence, omnibenevolence and the existence of evil. Epicurus argued 1 that God’s omnibenevolence, His omnipotence, and the existence of evil could not all be compatible. The problem of evil has been presented consistently by philosophers and theologians throughout time. However, arguably the most succinct explanation is written by the eighteenth-century philosopher, David Hume: “Is He willing to prevent evil, but not able? then He is impotent. Is He able, but not willing? then He is malevolent. Is He both able and willing? whence then is evil?” 2 Hume considered evil to be decisive evidence against the existence of God as do many atheists. Consequently, the problem of evil remains the backbone of many atheist arguments. This put Christian theologians in a position where they either had to admit that God is not both omnipotent and omnibenevolent (being ignorant of the scriptures) or explain the existence of evil. However, the Bible confirms both God’s omnipotence (As well as being referenced in the bible “For His invisible attributes, namely, his eternal power and divine nature, have been clearly perceived” 3 , the Fathers of the early Church considered the fact that God created everything as decisive proof of His omnipotence) and omnibenevolence (referenced in the Bible, “But you, Lord, are a compassionate and gracious God, slow to anger, abounding in love and faithfulness” 4 ) to be true, and as the Bible is divine (“All Scripture is breathed out by God” 5 ,) or at least θεόπνευστος (inspired) by God , evil became the subject of many theodicies. 6 The question is clear, ‘Si deus est, unde malum?’ (‘If God exists, why is there evil?’)” 7 . Moral Evil and Natural Evil: When approaching evil in this way, it is common practice to divide it into two parts: moral evil and natural evil. Moral evil is generally considered to be the acts of mankind which inflict pain and suffering upon ourselves or others. Many Christians believe that this evil was the result of ‘the Fall’ when man fell from grace, as well as some believing it to be bestowed upon oneself from birth or as a result of free will and human agency. “The intent of man’s heart is evil from his youth” 8 . Natural evil is that which happens without human

1 There are no existing texts by Epicurus containing this argument, however, the author Lactantius attributes the Epicurean paradox (a version of the problem of evil) to Epicurus in his work De Ira Dei, 13, 20-21. 2 David Hume, Dialogues Concerning Natural Religion (originally published in 1779), Norman Kemp Smith, ed. (New York: Bobbs-Merrill Co., Inc., 1947), 198. 3 Romans 1.20 4 Psalm 86.15 5 2 Timothy 3.16 6 An attempt to explain the problem of evil 7 Barry L. Whitney, What are they saying about God and evil? Published by Paulist Press (1989), p. 3. 8 Genesis 8.21

involvement, such as earthquakes and tsunamis. The consensus is that natural evil occurs as a punishment from God, as a result of the moral evil that humans create. However, this varies depending on the theodicy in question. The Faith Solution: Throughout time, many a biblical scholar, theologian, and philosopher have pondered the problem of evil. Most of these intellectuals take a rational approach to explaining the problem of evil. However, some theologians prefer to take a much more teleological stance towards the problem, arguing that we should trust in God, as (in the words of Rahner) we must accept the “incomprehensibility of suffering” 9 , understanding that experiencing evil is part of God’s plan, and we should have faith in his providence. In the Bible, Job is tested by God 10 and comes to accept that his suffering is beyond his understanding 11 . “For as the heavens are higher than the earth, so are my [God’s] ways higher than your ways, and my thoughts than your thoughts.” 12 Job maintains faith in God, even when all seems lost, and God rewards him for his faith. This way of explaining evil is perhaps so appealing due to its simplicity, meaning that it’s easily understood and applicable almost every type of evil. Unlike other theodicies, the faith solution grants an instant justification and consolation for one’s suffering, whereas in the case of other theodicies such as Augustine’s, coming to the answer that one’s suffering is just a ‘privation of good’, is not quite as comforting as knowing that their suffering happens for a good purpose. This teaches the Christian to maintain faith in God, just as Job did, to obtain this greater good. Whilst the faith solution has many benefits, it possesses many downfalls and loopholes too. The nature of the solution dictates that it is broadly applicable to all kinds of evil. Paul Schilling makes the point that with this justification of evil, one can claim any action to be justified by God for reasons only He can know by claiming faith in His providence. 13 This same concept applies to natural evil and has a similar effect. Amid a natural disaster, say an earthquake, an operation is coordinated to provide aid to those in need. The faith solution here would remove one’s responsibility and duty to help those people, as their suffering is justified in the eyes of God. However, we are still obliged to help those people, as demonstrates through the teachings of Christ. The answer that the faith solution presents can be frustrating, as it arguably avoids tackling the problem of evil directly. That being said, the faith solution presents a feasible argument as to why we shouldn’t question this problem, however this can feel rather evasive at times and doesn’t give a satisfactory answer to how God can be both omnibenevolent, omnipotent, and allow evil to exist.

9 Karl Rahner, “Why does God allow us to suffer?” p. 10 Job 1.8–12 11 Job 42.1–6 12 Isaiah 55.9 13 Paul Schilling, God and Human Anguish, p. 66-67. 208.

In short, the faith solution can be consoling as it grants instant comfort for one’s suffering, but it also has the potential to make human accountability/responsibility for evil idle, as all evils are justified by God. Moreover, the faith solution can be regarded insubstantial when finding an answer to evil, and keeping faith can be hard, especially when expected to do so blindly. The Augustinian Theodicy: The Augustinian theodicy is one of the most important concepts when it comes to explaining the problem of evil. Augustine’s work is regarded as arguably the most influential after Saint Paul, “shaping biblical exegesis” 15 and creating a lasting theological methodology. The Augustinian theodicy (developed in his books City of God and Confessions) has been adapted and elaborated on by many theologians and philosophers alike (labelled as Augustinian by John Hick). Perhaps the most famous interpretations of Augustine’s theodicy are to be found in the writings of Thomas Aquinas and John Calvin, who further developed the idea. Augustine writings here were heavily influenced by the first chapters of Genesis. The Augustinian theodicy can be outlined in four parts. The first is that Augustine defines evil as ‘privatio boni’, a privation (or corruption) of good. God intended for us to choose good (“For I know the thoughts that I think toward you, saith the Lord, thoughts of peace, and not of evil”) 16 , but as He gave us free will, one has the option to choose evil (“And God said, Let us make man in our image, after our likeness: and let them have dominion over the fish of the sea, and over the fowl of the air, and over the cattle, and over all the earth”) 17 and in doing so corrupts our use of it. Augustine wrote that “evil has no positive nature; but the loss of good has received the name ‘evil’” 18 . Paul Tillich and Martin Heidegger have expressed that evil should be regarded as ‘nonbeing’. 19 God created the world ‘ex nihilo’ (out of nothing), and as God is ideally perfect, one must conclude that He made a perfect world (“God saw everything that he had made, and, behold, it was very good” 20 ). In Genesis, Moses appears to claim that God originally created the world without moral or natural evil. Instead, moral evil enters the world as the result of the original sin, a by-product of his creations. 21 Augustine believed evil to be a distinct lack of good, and evil enters the world in the sense that mankind turns away from good, losing their innocence, and becoming preoccupied with catering for their own desires and needs. It is when this state of total goodness is corrupted that ‘evil’ (or a lack of good) enters the world. It is now when the atheist asks, ‘what does Augustine have to say in response to natural evil?’ Well, Augustine believed that natural evil is the corruption of good in the wills of those who have the ability

14 James O’Donnel, St Augustine, Encyclopaedia Britannica (Feb 19, 2020). 15 Jeremiah 29.11 16 Genesis 1.26 17 Augustine of Hippo, The City of God, Book XI, Chapter 9. 18 See John Hick, Evil and the God of Love, 182ff . 19 Genesis 1.31 20 Stephen Menn, Descartes and Augustine. Cambridge University Press (2002), p. 168.

to affect natural phenomenon, e.g. Satan and his cohorts (fallen angels), who try with all their might to dissuade the Christian from keeping faith in God. At no point is Augustine prepared to suggest that God is responsible for evil in any way. This leads to the third part. Augustine’s theodicy dictates that mankind is solely responsible for the existence of moral evil, and that God is not responsible for evil – it wasn’t created by Him and was “certainly not desired by God” 21 The doctrine of the original sin informs us that all humans are guilty of disobedience through the original sin, expressed by the Apostle Paul “Wherefore, as by one man sin entered into the world, and death by sin; and so death passed upon all men, for that all have sinned” 22 .Augustine’s theodicy explains that God’s omnibenevolence maintains perfection, without responsibility for suffering. As with any theodicy, Augustine’s has its criticism in abundance. John Hick argued that if God made a perfect world, it would have been impossible for it to go wrong (for humans to become immoral). Hick also disputed Augustine’s point that God remains without responsibility for evil. Hick writes that if God knew the choices that humans would make (regarding Augustine’s views on predestination) he must be somehow responsible for them. Furthermore, there has been much criticism of Augustine’s theodicy from a scientific point of view. Hick described the theodicy as “implausible” considering Charles Darwin’s theory of evolution, as it would render the fall from grace inaccurate. 23 Augustine proposes that all men were seminally present in Adam, however if Adam didn’t exist as such, mankind could not be seminally present in him, flawing Augustine’s theodicy. Arvind Sharma has pointed out that natural evil cannot be so in the way that Augustine proposed, as scientific consensus suggests that natural disasters have occurred before the existence of humans, therefore making it impossible for natural evil to occur as a result of sin. 24 Lastly, Augustine believed that God was also omniscient, meaning he reliably knows what people will do. If this is so, as argued by David Ray Griffin, people would not truly be free. With this concept, he proposed that the original sin must itself be indirectly caused by God, rendering any punishment unjust. 25 These are just three of the most basic contradicting arguments among many others.

The Irenaean Theodicy: The work of Saint Irenaeus of Lyons has influenced the theological sphere greatly, as well as being a heated topic of debate. Irenaeus proposed a theodicy which became a major part of considering the problem of evil. His theodicy (like Augustine’s) has been developed and elaborated on over the centuries by countless philosophers, theologians and Christian thinkers, perhaps most notably

21 Barry L. Whitney, What are they saying about God and evil? Paulist Press (1989), p. 29. 22 Romans 5.12 23 Stephen Davis, Encountering evil: live options in theodicy. Westminster John Knox Press. Davis, 2001, p. 54. 24 Sharma, A primal perspective on the philosophy of religion. Springer, 2006, pp. 85-8. 25 David Ray Griffin, God, Power and Evil: A Process Theodicy, (1976).

by Origen, Schleiermacher and Hick (again Hick took the liberty of labelling adaptations of the theodicy as ‘Irenaean’). The Irenaean theodicy can be outlined in three parts. The first part of his theodicy sets the important distinction between humans being in the image of God and humans being in the likeness of God. In the Bible it says “God created man in his own image, in the image of God he created him” 26 , and how this is interpreted is fundamental to the Irenaean theodicy. Irenaeus makes the distinction that we were created in God’s image (in so far as we possess a free will and intellect), but not his likeness. He believed that we are first created in his image, then we develop and into the likeness of God (inheriting his infallibly good characteristics), eventually reaching a point where we live like him.

It’s a two-stage creation process and Irenaeus is proposing that the creation is incomplete as of now. One can think of mankind as a new-born baby. The baby is created in the image of its mother and then grows into her likeness. Mankind is the same. John Hick wrote that to be created in the image God means to have the potential to have knowledge and be in a relationship with God (which we currently have, like a baby being able to develop into the likeness of its mother) however, this is fulfilled when the creation is complete and we come to be in the likeness of God. The second part of the Irenaean theodicy dictates that one experiences suffering for the moral development of mankind. Friedrich Schleiermacher argued that as “God would create flawlessly” it would be illogical for a perfect world to go wrong. Irenaeus saw the world in a very teleological sense, where humans would learn more about good by experiencing evil. This became known as ‘soul-making’. Irenaeus argued that a world without evil and suffering would be less suited to the development of humans, especially without meaningless suffering. He proposed that this was the purpose of natural evil, seemingly meaningless suffering has the divine purpose to develop feelings such as compassion and sympathy. Hick elaborated on this by arguing that suffering is necessary for the development of humans and in response to meaningless suffering, claimed that if all suffering and evil had purpose mankind would be unable to develop feelings of compassion and sympathy. Irenaeus writes “A world without problems, difficulties, perils, and hardships would be morally static. For moral and spiritual growth comes through response to challenges; and in a paradise there would be no challenges.” 27 In the Bible it reads “And God saw everything that he had made, and, behold, it was very good.” 28 Irenaeus (contrary to Augustine) interpreted this as the world being fit for purpose (for the development of humans), rather than without evil. He referenced the Book of Jonah to illustrate how suffering would result in atonement and bring oneself closer to God. Unlike Augustine, Irenaeus believed that God is in part responsible for suffering, as he permits it for soul-making. He believes that for humans to truly learn, we must be

26 Genesis 1.27 27 Irenaeus, Church Fathers: Against Heresies, 28 Genesis 1.31

given free will with the choice to actually do evil. We must learn from real consequences if you will. Lastly, Irenaeus lays out his beliefs of when mankind will become in likeness with God. Influential works have much criticism, and the Irenaean theodicy is no exception. Dewi Phillips presents the argument that, concerning the Holocaust, any theodicy which explains evil to be instrumental or teleological should be treated as inadequate, as the scale on which people suffered is too great to be justified by any means, regardless of what benefits it might bring. 29 However, one can argue that while God permits evil per se, event such as the Holocaust are caused by humans, and not God. C. Robert Mesle also argued that although suffering is sometimes indirectly beneficial, often it does more harm than good. 30 Another Process theologian David Ray Griffin challenged the idea of ‘soul-making’ by proposing that God inflicts pain for his own ends, which he viewed as corrupt.

Summary The problem of evil is a nuanced and complex topic with many details and difficulties. Whilst there is no definitive answer, there are premises with which a conclusion can be drawn. The faith solution provides a consoling answer to the problem of evil as it grants one with the peace of mind that there is a reason for one’s suffering that only God can know. In addition to being easily understood, the faith solution also proposes that we should not question God, (“But let him ask in faith, nothing wavering. For he that wavereth is like a wave of the sea driven with the wind and tossed”) 31 and accept that it is foolish to try to understand His ways. However, although this way of thinking is credible, it’s inherently unsatisfactory when trying to find an answer to evil, regardless of how valid its points may be. Paul Schilling points out that the faith solution grants one the power to do evil without bearing responsibility, as God willed them the do so for a reason they cannot question. The faith solution is thus ill-founded, consequently providing no satisfactory solution to the problem of evil. The Augustinian theodicy presents an argument that has stood for many centuries; a testament to the strong case it exhibits. Augustine writes about his theodicy in great depth, justifying, deliberating, and explaining each principle that led him to his conclusion. However, perhaps being ignorant to the extent which he wrote, I dislike his theodicy (favouring Irenaeus’). The premise for my disliking of his theodicy lies in Augustine avoiding admitting that God has any responsibility for evil, or that evil exists as such. If God did create the world ‘ex nihilo’ then he must have some level of responsibility for his creations, even if their suffering is justified. To further this, if God

29 Hugh Campbell and Michael Wilkinson, Philosophy of Religion: An introduction. Continuum International Publishing Group (2010). 30 C. Robert Mesle, Process theology: a basic introduction, Chalice Press (1993). 31 James 1.6

does have responsibility for his creations, and is truly omniscient, he must, in turn, be indirectly responsible for the original sin, rendering any punishment unjust. The Irenaean theodicy presents a better argument regarding God’s responsibility for evil.

The Irenaean theodicy presents a much more logical answer to the problem of evil. Instead of redefining evil to support God, Irenaeus admits that God is responsible for some suffering, but it’s justified due to it being a ‘soul-making’ necessity. Moreover, the Irenaean theodicy dictates that we are yet to develop into the likeness of God, which is a much more reasonable and satisfying conclusion that is perfectly feasible. The idea that we need to develop and endure difficulties to reach a true state of perfection (or become in the likeness of God) is more true to day to day life as we know it and is a more rational and logical solution. This is why the Irenaean theodicy is the most convincing argument.

Toby Rooth, Shell

My Arcade Cabinet

Rohan Haripaul, Remove

understanding the depths of quantum computing...

Hyunjo Kim and Yikai Zhou, Shell

Definitions:

Information - An interpretation of the particular system’s state - fixed set of distinguishable values

Computation - A physical process where there is a fixed set of states and finite in time

Introduction

Quantum computing can be seen as the ‘gold rush’ of the 21st Century. In 2017 and 2018 alone, there has been an investment of $450 million just from private investments and the US government has authorised $1.2 billion to be invested into quantum information science over the next five years. So, what is causing this boom? In order to find out what this quantum computing frenzy is all about, we need to understand the differences from classical computing. This study will embody the basic studies and ideas of Quantum Physics and Computing, Qubits and Quantum Gates, Deutsch's problem and basic algorithms, Shor’s algorithm.

Classical Computing Classical computing stores and processes information through a binary unit, or bits. (e.g. 11001 can refer to a classical state of 25) We can refer to Figure 1, to understand how classical computing stores information. Specifically, Shannon’s entropy focuses on how many bits are required to store a certain variable. Basically what Shannon’s Entropy actually means is that the summation for each symbol of the probability of that symbol times the logarithm b of one over the probability of that symbol. 1/P can be expressed as P-1 and by using logarithmic identities, we put a negative sign in front of the Σ. To understand this, I will give an example: There is Machine 1 where A, B, C, or D is given as an output. The chance that the next letter will be A is 25%, B is 25%, C is 25%, D is 25%. Machine 2 → A is 50%, B is 12.5%, C is 12.5%, D is 25%. What is the minimum number of questions you need to ask you would expect to ask to find out what the next number is? Here is the answer:

1. Is it A or B? → Through this we can eliminate half of the possibilities → If yes, we will end up with two symbols, A and B (both equally likely).

2. Is it A? → Then, we will know what symbol it is. * Of course, the same will apply if we got C or D

Two Questions are needed for Machine 1 as: 0.25 * 2 + 0.25 * 2 + 0.25 * 2 + 0.25 * 2 = 2

For Machine 2:

1. Is it A? → If it is A, it is complete, but if it is not, we still have B, C, D.

2. Is it D? → If it is D, it is complete, but if it is not, we still have B, C.

3. Is it C? → Then, you will definitely know which symbol it is.

Be careful! The minimum is not three questions… In fact it is 1.75 (on average) questions as: 0.5 * 1 + 0.125 * 3 + 0.125 * 3 + 0.25 * 2 = 1.75

What can we understand from this analogy? Machine 2 is producing less information as there is less uncertainty (smaller amount of questions that needs to be asked). Shannon calls the unit of this entropy as bits and we see in computers that they are in binary. Computers store information using bits because 0s and 1s are like making choices as we can see in the Machine Analogy…

To make things simpler, I will just quickly simplify Shannon’s entropy where all states are equiprobable as that is how classical computing works.

From this simplification, we can now understand how information is stored. For example, if a state has 64 states, there will be 6 bits.

Now, we will look at the computation of classical computing. In order for classical computing to work and compute a function, we need to see if there is an algorithm in place. It should be able to process a number of states, the final state, and understand the parameters which control the behaviour of abstract to controlled models. Although we will not go in detail about the computation of classical computing, we will show you how decisions are made in computers through logic gates. Figure 2; shows an easy representation of logic gates using logic.ly.

Logic gates are the fundamental constituents of digital integrated circuits. They are devices which implement the Boolean functions to accrue one output from two inputs. Boolean algebra is the mathematics we use to peruse digital gates. We implement Boolean laws to diminish and simplify a complex Boolean expression to reduce the number of logic gates required. The various logic gates consist of AND, OR, NOT, NAND, NOR, AOI*, OAI*, E/XOR and E/XNOR gates. Logic gates may be adhered or cascaded together to conceive a logic gate function with any desired number of inputs, or to form combinational and sequential type circuits, or to produce various logic gate compounds from accustomed gates.

The usage of the term 'gate' is eminently suitable as logic gates can be simply appreciated by examining the basic function of a gate: to control a flow. In a computer, a gate controls the flow of electric current through a circuit. The gate consists of transistors. The transistors used in the construction of logic gates are classified into two basic categories, PMOS and NMOS transistors that are found in the ubiquitous CMOS (complementary metal-oxide semiconductor) technology. Logic gates are analogous to taps, permitting and restricting current flow. The current that flows through a gate establishes a voltage at a point in the circuit. This voltage represents a single 'bit' of information. The voltage may either be high (representing the value '1') or low (representing the value '0').

Logic gates within a microchip are conceived of an arrangement of transistors. Regarding modern microchips, the transistors are of the kind called Metal-Oxide-Semiconductor FieldEffect Transistor (MOSFET), and the material used to conceive the semiconductor is silicon. A MOSFET has three components; the three regions are arranged horizontally adjacent to one another. By conjoining MOSFETs, we obtain a microchip. The microchips are further aligned to make up a storage unit in the CPU.

Quantum Computing

We know that as classical computers go to atomic, molecular level, pair injunction does not work and the ideas and the laws that govern classical computing do not work any more as there are now quantum effects. Also, classical computing cannot emulate/simulate quantum phenomena. If classical computing encounters intractable problems, the complexity of the solution will exponentially increase. One of these hard, intractable problems is simulating a quantum realm. Richard Feynman discussed that these quantum-based computers will be able to simulate the quantum realm, and effectively simulate 66

themselves. To give an insight, quantum computers can solve problems 100 million times faster than classical computers.

Now, I will talk about what kind of quantum effects we are talking about: superposition, and entanglement. Superposition is the counterintuitive ability of a quantum object to exist in a multitude of states. Let me give you an example - the double-slit experiment. There are two very narrow slits and photon emitters. Let’s say we put the photon detectors behind the gaps on the metal sheet. The upper detector will be state (1) and the other will be state (0). What will actually happen is that both detectors will detect the photon. This is because of the Heisenberg Uncertainty Principle; Heisenberg told us that we cannot both know the coordinate and the momentum of the particle. As we know the wavelength of the photon, we are unsure about its coordinate. Thus, what is happening now is that we have a probabilistic measurement where one half goes through the upper slit, whilst another half goes to the bottom slit.

Similar to what I just talked about, a similar phenomenon happens in quantum computing. In a bit, the spin of an electron (spin up/spin down) determines if it is a 0 or a 1. In quantum computing, a qubit takes both the value of 0 and 1, these quantum objects will be in two states until it is measured. However, before it is measured, the electron (inside the computer) will exist in something called a ‘quantum superposition’. The fact that the probability varies can be manipulated by quantum operations, but before we go into how quantum operations work, I will talk about entanglement.

Quantum entanglement is when two quantum objects interact. First, I will talk about spin. All fundamental particles have this thing called spin. Although the particles are not actually spinning, they have an angular momentum and an orientation in space. Entangled particles are dependent on each other meaning that the measurement on one partner will affect the other partner immediately. The way it works in quantum computers is that the quantum computer leverages entanglement between qubits and the probabilities according to superposition to execute a series of operations using quantum algorithms that will be demonstrated in the latter sections of our study.

Information

Quantum computers are the pinnacle of human technology at present. By availing the unique phenomena of quantum mechanics, we are capable of making prominent ameliorations in computing speeds. These phenomena incorporate complex probability amplitudes, quantum interference, quantum parallelism, quantum entanglement, decoherence and the unitarity of quantum evolution. We employ these phenomena to permit the secure transmission of classical information (quantum cryptography), the use of controlled quantum evolution for efficient computation (quantum computation, the possibility of preserving quantum coherence in the presence of irreversible noise processes (quantum error correction) and the use of quantum entanglement to permit reliable transmission of quantum states (teleportation). The common theme of all these insights is the use of quantum entanglement as a computational resource. In quantum computation, a quantum algorithm is an algorithm which runs on a realistic model of quantum 67

computation. There’re several quantum algorithms which are in application in quantum computing. Shor’s algorithm, Deutsch algorithm, Simon’s algorithm, Grover’s algorithm, Fourier fishing and many others.

Quantum computers can solve strenuous computational problems such as integer factorisation of astronomical numbers. These computational tasks can execute exponentially faster on a quantum computer than on a classical computer. The aspiration of conceiving a quantum computer was first proposed in 1981 by Nobel laureate Richard Feynman. Feynman envisioned a machine which computes efficiently by simulating quantum mechanical systems. The computational power from quantum computers would have eminent effects on a vast variety of topics, applications to a multitude of problems outside quantum mechanics. Computation has diversified away from its narrow beginnings of facilitating simulations of Newtonian mechanics. The studies of quantum algorithms have diverged greatly from simply simulating quantum physical systems to impact a vast majority of fields, including cryptography, information theory, language theory, and mathematics. There are various models of quantum computing, they incorporate the quantum circuit model, adiabatic quantum computer, quantum Turing machine, one-way quantum computer, and various quantum cellular automata. The mainstream models implement the quantum circuit. Quantum circuits are paved based on quantum bits, also known as qubits. They are analogous to the bit in classical computation. A bit, in its presence, can be of value of 1, or 0. Quantum bits acquire both the characteristics of a mainstream bit, and they can be in a superposition of the 1 and 0 states. However, when qubits are measured the result of the measurement is always either a 0 or a 1; the probabilities of these two outcomes depend on the quantum state that the qubits were in immediately prior to the measurement. Computation is performed by manipulating qubits with quantum logic gates.

About Qubits and Quantum gates

Qubits

A qubit is the minimal amount of information of quantum information. For example, we could look at the polarisation of a single photon in which the two states will be determined by if it is in a horizontal or vertical polarisation, but because of superposition.

Let’s look at some of the mathematical models:

A qubit can be represented as a linear superposition of basis vectors. The vectors are expressed as seen in Figure 3 in the bra--ket notation, formulated by 20th Century Physicist Dirac. These two computational basis states are said to exist within the Hilbert Space (Hilbert Spaces are tools when modelling quantum mechanics mathematically). Figure 4 shows how qubit basis states can be combined to create product basis states. The rule is that if there are n qubits, they have a superposition state vector in 2n dimensional Hilbert space.

What is a pure qubit state? It is where there is a coherent superposition of the basis states. We can derive from this the fact that a single qubit can be represented linearly with “ket 0” and “ket 1”. Look at Figure 5 for the mathematical expression.

I will deconstruct Figure 5 which reads: “ket phi” = alpha “ket 0” plus beta “ket 1”. Both ɑ and are the probability amplitudes which can be complex numbers (a + bi). A probability amplitude describes the relationship between the wave function and the measurement of the system. The probability to find the particle at x at some time t is equal to the modulus squared of the probability amplitude. By referencing to the Born Rule, the probability of outcome “ket 0” with value 0 is modulus ɑ2 and the probability of outcome “ket 1” with value 1 is modulus 2 , because these two equate to probabilities, the equation must equal to 1, so we can come up with this equation: |ɑ|2 + | |2 = 1

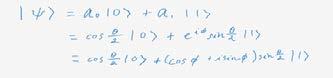
From this we can understand how qubits work. From the equation above, you can see that there is no certain value for 1 and 0. The qubit only contains the probability of one another. Therefore, there is no way to know due to the superposition state if the qubit state is “1” or “0”. The diagram right next here shows the equation of a superposition. It can be written as a superposition of the basis vectors “ket 0” and “ket 1”, where the coefficient are complex numbers. The theta is the coaltitude in respect to the z axis and the phi is the longitude in respect to the x axis. The cosine half angle and the sine half angle can represent the amplitudes, where e^iphi can be expressed in the polar form of a+bi. Until it is measured, the probability of the superposition remains to be equal.

Quantum Gates

A quantum gate is basically a quantum circuit that runs on a small number of qubits. Unlike many classical computers, quantum gates can be reversed. Logic reversibility is where you are able to reconstruct the input from the output of a computation. Quantum logic gates are represented by unitary matrices which is a form of a complex square matrix in which its conjugate transpose is also its inverse. To easily express this, the matrix is flipped over on its diagonal row and the conjugate of the inverse is calculated (Look at deepai.org for more info). In this section about Quantum Gates, we will look at the Hadamard (H) Gate, Pauli-X Gate, Pauli-Y Gate, Pauli-Z Gate, the Phase Shift gate, and the Square root of the SWAP Gate.

The Hadamard Gate as shown in Figure 6 shows the calculations. As we are dealing with quantum gates, there is no definite value of 0 and 1. Therefore, we will assign them as equal probabilities, which then makes the probability amplitude 1/root 2. The H Gate is a combination of “ket 0” and “ket 1”, if we would look at a Bloch Sphere (geometrical representation of a pure state space of a qubit), it would be shown as the combination of two rotations. The effect of a Hadamard Gates is that they expand the range of states it’s possible for the quantum computer to be in. Because of this very expansion, what occurs is that it actually creates the possibilities of short cuts, which may help some computations to become quicker. (Understand that by the term ‘quicker’ we are not referring to the internet or simply typing in a google search engine, but for example you could find the next prime number more quickly) Let me use an analogy… If we are playing chess and we create a new rule that is only in our favour, so the rook can now travel diagonally, we could possibly checkmate our opponent more quickly.

The Pauli-X gate is the quantum equivalent of a NOT gate. A NOT gate in classical computing is where it inverts the value of the input. In Boolean Algebra, the NOT Function follows the Complementation Law of inversion as seen in Figure 7. In the bloch sphere representation, it is a rotation in the x axis by π radians (180 degrees), it can be represented like in Figure 8.

The Pauli-Y Gate rotates around the y axis. It switches the amplitudes and multiplies them by ±i (imaginary number).

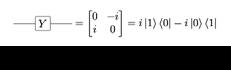
The Pauli-Z, it rotates a single qubit by π around the z axis. These Pauli Gates are the fundamental operations and the easiest of all quantum gates. When we actually use these gates for a programme Pauli Gates prove to be so important. Look at Figure 10 for the representation of the Pauli-Z gate mathematically.

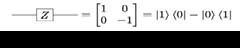
The last quantum gate we will talk about is the Phase Shift Gates. This is a group of single-qubit gates that leave “ket 0” unchanged but changes “ket 1” to e^iphi “ket 1”. This modifies the phase of the quantum state, but does not alter the probabilities of “ket 0” and “ket 1”. To elaborate, waves are characterised by amplitude and phase and in the Bloch sphere, this phase shift gate is equivalent to tracing a horizontal circle by phi radians. These phase shifts helps to unlock different values. The amplitudes and phases will influence the resulting quantum state, and correspond to the same physical state, but they are not interchangeable. From this idea, we can conclude that global phase factors are unphysical, thus undetectable. We can say “ket phi” is equal to “ket e^jphi” which leads us to the equation as seen in Figure 11 where 0<=p<=1 is the probability of the bit being in state 0, whereas 0<=phi<=2π. As aforementioned, the phase shift gate facilitates the process of reaching all values of p and phi.

Lastly, we will look at the implementation of the square root of the SWAP Gate. The SWAP Gate swaps two qubits, with the basis states of “ket 00”, “ket 11”, “ket 10”, “ket 01”. It is represented by a matrix that looks like Figure 13. However, the Square Root of the SWAP Gate performs half-way of the qubit swap. Any many-qubit gate can be constructed using a single qubit gate and this very gate. With more than one application required, it is transformed to a Bell state, where the specific quantum states of two qubits can represent the simplest examples of quantum entanglement. Thus, we can understand the matrix representation from Figure 14. We will look at quantum operations now using quantum algorithms.

Quantum Algorithms

Shor’s algorithm Shor's algorithm is a polynomial-time algorithm utilised in quantum computing or integer factorization, contrived by the renowned mathematician Peter Shor. The mathematical expression for this algorithm is to factor a number N in O [(log N)3] time and O (log N) space (detailed mathematical explanation of the algorithm is provided in the extra information document). No other classical algorithm innovated can factor O [(log N) k] for any value of k in a conceivable amount of time. Au contraire to classical algorithms, Shor’s algorithm can evaluate the factors in polynomial time. It is eminently more efficient as normal computers, which use classical algorithms, which enumerates prime factors of astronomical integers by guessing, inputting a number and to scrutinise if the number is a prime factor of the original integer or not. On the other hand, Quantum computers, with the application of Shor’s algorithm, still inputs a prediction of a factor however can fabricate a better guess for the following predictions.

Deutsch algorithm The Deutsch–Jozsa algorithm is a deterministic quantum algorithm advocated by the renowned physicist, David Deutsch. When a deterministic algorithm derives an input, the output would always be identical. Simon’s algorithm is the first quantum algorithm to show an exponential increase in speed in comparison to the best classical algorithm in solving a specific problem. This quantum algorithm is based on quantum Fourier transform. In the Deutsch–Jozsa algorithm we use an oracle to determine if a binary function f(x) : {0,1}^n {0,1}f(x): {0,1} n→{0,1} is constant or balanced. The motivation is to show a black box problem that can be solved efficiently by a quantum computer with no error, whereas a deterministic classical computer would need many queries to the black box to solve the problem. More formally, it yields an oracle relative to which EQP, the class of problems that can be solved exactly in polynomial time on a quantum computer, and P are different

Simon’s algorithm Simon’s algorithm is the first quantum algorithm to show an exponential increase in speed in comparison to the best classical algorithm in solving a specific problem. This quantum algorithm is based on quantum Fourier transform. Simon’s algorithm is eminently similar to Shor’s algorithm. We are given an unknown black box function which is determined to be either one-to-one or two-to-one, which have the following properties:

Mathematical Explanation

Shor’s algorithm

Furthermore, we need to set up quantum parallelism, which we achieve so by conceiving an entangled state; we need apply a 2-dimensional Hadamard gate (as we have seen in the Quantum Gates section) to output being:

Now we look at the quantum oracle, which is a "black box" operation that is used as input to another algorithm. Often, such operations are defined using a classical function. I will walk you through the input of the quantum oracle.

Initially, we apply linearity to the superposition going into the oracle’s register. Then we set “r” as the period of the function and D as the domain. I assumed that “r” is a divisor of D, as if it isn’t it requires a much more complicated explanation which is not suitable for this part. Utilising the function is periodic injective along with one unknown variable. We can gather from injective periodicity that the domain can be split into many disjoint cosets of size a, each as a sub-domain to the function. With the aid of a bit of group theory we can simplify down the r ≡ [0, a-1] = [0,1,2,...,a-1]. Then we deconstruct our simplified answer. Moreover, we proceed to finalise the output of the oracle.

Finally, we move onto the QFT. We apply the QFT at the output of the oracle then proceed to work out the QFT of the entire superposition.

Order Finding Problem

The input: A positive function where xʳ ≡ (mod N) N≥2. The output: The order “r” for the input function. The order finding problem is used to find the period of a function. We can use Phase Estimation (explained in the section below) to solve the problem, which can be understood as: accumulating an eigenvalue e²^π^i^rho for a unitary operator U and an eigenvector |u ..

We apply the unitary operator into the circuit above and we acclaim the fact that U is unitary and the eigenvector of |u .

** The phase estimation was used for the algorithm to compute the period of the function by securing the eigenvector with its eigenvalues of the Unitary operator.

Phase Estimation We presume a unitary operator of “U” has an eigenvector of alongside an eigenvalue of e^2^π^rho where the known value is the “rho”. Our aspiration is to obtain an estimation for . The input is the eigenvector and controlled U²ʲ operator where “j” is a non-negative integer.

Quantum circuit:

We assume that there is an oracle which is applicable for U²ʲ where the control state is and j is a semiclassical quantum Fourier transform (t-bit). We then proceed to the algorithm

We conceive superposition from the initial state the apply a black-box algorithm to the state. Then we proceed to measure the output. Phase estimation is used to solve the order-finding problem.

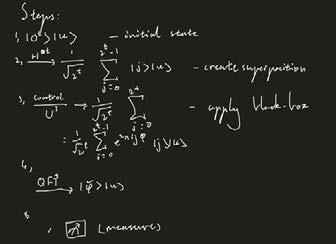
Deutsch-Jozsa Algorithm

Let f: [0,1]ⁿ---> [0,1] be a function where f is a constant if f(x) does not alter for all options of x€[0,1]ⁿ. F is considered balanced when f(x)=0 for half of the outputs and the other half resulting in f(x)=1. This algorithm is used to determine if f is balanced or constant.

The o with a cross denotes tensor product. For more information about tensor products, visit: https://en.wikipedia.org/wiki/Tensor_product

Simon’s Algorithm

Simon’s algorithm is the first quantum algorithm to show an exponential increase in speed in comparison to the best classical algorithm in solving a specific problem. This quantum algorithm is based on quantum Fourier transform. Simon’s algorithm is eminently similar to Shor’s algorithm. We have an input of [0,1]ⁿ---> [0,1]ⁿ and already know that s € [0,1]ⁿ such that [f(x)=f(g)]--->[x o g €[0ⁿ,s]]. Our intention is to find s.

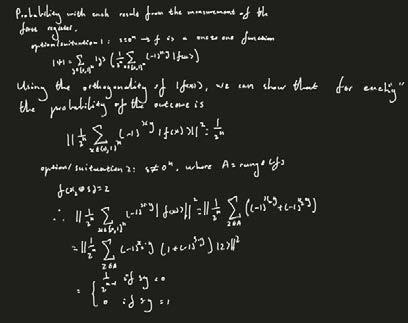
Our initial register is deterministic, and we proceed to utilise the orthogonality of |f(x)>for each value of “y”. Since our output has two situations, we have two various expressions as shown above. We are required to apply two Hadamard transformations and also use a black box algorithm to find the output.

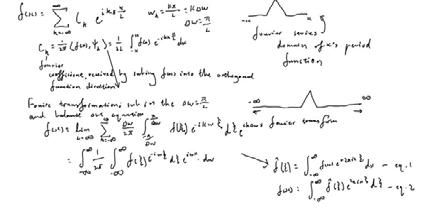
The Fourier transform can be defined as an improper Riemann integral, making it an integral transform. After we obtain the Fourier coefficient, we can substitute it in from the Fourier series into Fourier transform. It can both be expressed as a domain of a period’s function.

Conclusion

Joey and I worked really hard to find the essence of quantum computing whilst working on this project. When we said that we will, ‘Understand the depths of quantum computing…’, we really tried to see the proofs, the mathematical explanations although it was an arduous task for us. But, from our mathematical explanations and the concepts of quantum computation, we can derive that the benefits of quantum computation surely surpass the benefits of classical computation. We challenge more and more people to look at the next technological breakthrough - quantum computation. The prototype built by IBM can be accessed anywhere in the world via the Cloud and everyone can try to engineer quantum softwares. Our goal for this project was not simply to see why quantum computation actually works but to show how efficient quantum computing would be. The future of quantum computation is bright, but it is essential for it to become accessible and we hope that our project helped people to understand the domain of quantum computation.

Bibliography: 1. 2. 3. https://en.wikipedia.org/wiki/Information_theory https://towardsdatascience.com/the-intuition-behind-shannons-entropy-e74820fe980 0 https://www.quantiki.org/wiki/shors-factoring-algorithm

4. 5. 6.

7. 8. 9. https://algassert.com/post/1718 https://en.wikipedia.org/wiki/Shor%27s_algorithm https://en.wikipedia.org/wiki/Quantum_computing#:~:text=Quantum%20computing% 20is%20 the%20use,are%20known%20as%20quantum%20computers. https://uwaterloo.ca/institute-for-quantum-computing/quantum-computing-101 https://www.nature.com/articles/npjqi201523 https://qiskit.org/textbook/ch-algorithms/simon.html

10. https://en.wikipedia.org/wiki/Deutsch%E2%80%93Jozsa_algorithm

11. https://en.wikipedia.org/wiki/Quantum_algorithm#:~:text=In%20quantum%20computi ng%2C%20 a%20quantum,quantum%20circuit%20model%20of%20computation.

12. 13. 14.

https://www.quantum-inspire.com/kbase/deutsch-jozsa-algorithm/ https://qiskit.org/documentation/tutorials/circuits/3_summary_of_quantum_operations .html https://en.wikipedia.org/wiki/Quantum_logic_gate 15. https://dash.harvard.edu/bitstream/handle/1/11084801/Yung_IntroductionQuantum. pdf?sequence%3D1 16. 17. 18. https://www.springer.com/gp/book/9783540785316 https://www.quantiki.org/wiki/quantum-gates https://www.nature.com/articles/s41598-019-49657-1

**All mathematical work in this project has been done by either Joey or Hyunjo

Metal Work Projects

George Beattie, Remove