Secciones eficaces de las reacciones nucleares

TEORÍA DE LOS REACTORES

ESTADO ESTACIONARIO

CONDICIÓN DE CRITICIDAD FACTORES DE MULTIPLICACIÓN

Al realizar el balance neutrónico de un sistema de reacción en cadena, con el fin de determinar su tamaño crítico, es necesario tener en cuenta la absorción de neutrones térmicos y la producción de neutrones de fisión, así como también la pérdida de neutrones por escape. Para que un reactor de tamaño finito pueda mantenerse una reacción en cadena auto sustentada, deben producirse por fisión tantos neutrones, por lo menos, como neutrones se pierden por absorción y por escape.

Una de las propiedades fundamentales de todo sistema multiplicador, en el que se están produciendo neutrones por fisión, es el factor de multiplicación infinito. Se define como la relación entre el número de neutrones que se producen por fisión en cada generación y el número de neutrones absorbidos en la generación anterior, correspondiente a un sistema de tamaño infinito. En un sistema infinitamente grande no hay pérdidas por escape, de modo que la desaparición de neutrones del sistema se produce solamente por absorción, en el combustible, moderador, etc. La condición de criticidad, es decir aquella que hace justamente posible la fisión em cadena auto sustentada, se reduce a un factor de multiplicación infinito kꝎ, sea igual a la unidad; en este caso, el número de neutrones producidos en cada generación sería igual al número de neutrones perdidos en la generación anterior. De este modo podría mantenerse un estado estacionario con densidad neutrónica constante, prosiguiendo la reacción en cadena con una velocidad constante.

Cuando se trata de un sistema de tamaño finito, parte de los neutrones se pierden por escape; la condición de criticidad viene representada, por el factor de multiplicación efectivo, kef, que se define como la relación entre el número de neutrones producidos por fisión en cada generación y el número total de neutrones perdidos por absorción y por escape, en la generación anterior. La condición de criticidad, en un sistema de tamaño finito se reduce a kef = 1, siendo posible en tales circunstancias el mantenimiento de la fisión en cadena, en un régimen de estado estacionario. Si las condiciones son kef < 1, la cadena sería convergente e iría extinguiendo se de modo gradual. Ocurriría que, en cada generación, se perderían de una forma u otra, más neutrones, que los producidos por fisión, y la densidad neutrónica y la velocidad de fisión, disminuiría de modo constante, en este caso sería un sistema subcrítico. Cuando kef > 1, la cadena es divergente y el sistema se denomina supercrítico. Se producirían en cada generación más neutrones de los que se pierden, con el resultado de que tanto la población neutrónica como la velocidad de fisión aumentarían de forma continua.

De las definiciones anteriores, referentes a los factores de multiplicación infinito y efectivo, se deduce que

Kef / kꝎ = Neutrones absorbidos / Neutrones absorbidos + Neutrones que se escapan = P

La relación que define a P constituye, una medida de la probabilidad de que los neutrones no escapen del sistema, sino que permanezcan en el mismo hasta que sean absorbidos.

Kef = KꝎ P

Siendo P la probabilidad de permanencia del sistema. El problema de establecer criticidad le corresponde a kef = 1, se divide en dos partes. La primera consiste en calcular el factor de multiplicación infinito, que es función de los materiales, combustible, moderador, refrigerante, estructuras, etc. que integran el reactor. En el caso de que el combustible y el moderador constituyan un sistema heterogéneo o reticular, también juega un papel importante la forma en que están distribuidos los materiales. La segunda parte consiste en la determinación de la probabilidad de permanencia, que depende parcialmente de la naturaleza de los materiales, pero sobre todo de la geometría del sistema, es decir de su forma y tamaño. Para un reactor de composición determinada, la probabilidad de permanencia aumenta con el tamaño del mismo, teniendo a la unidad para sistemas de tamaño infinito, en cuyo caso K y Kef son idénticos

REACTORES CON REFLECTOR

EFECTOS DEL REFLECTOR

El núcleo de los reactores, la región que contiene el combustible, está rodeado por un reflector, constituido por un material que posea buenas propiedades dispersantes para neutrones. En los reactores térmicos, se utilizan con este objeto, agua pesada, berilio (o su óxido) y grafito. Como la misión del reflector es la de devolver al núcleo del reactor gran parte de los neutrones que, se habrían perdido por escape, el sistema combustible-moderador, puede alcanzar la criticidad, con dimensiones sensiblemente menores que las correspondientes al reactor desnudo. El empleo de reflector conduce, a una disminución de la masa crítica del material fusible.

Aparte de disminuir el volumen y la masa del reactor crítico, la presencia del reflector puede traducirse en un aumento de la potencia media del reactor, para valores determinados de la masa crítica y del pico de flujo neutrónico. El nivel de potencia es proporcional al valor medio de la densidad, o flujo, de neutrones térmicos en el núcleo del reactor. Suponiendo que el flujo, en el centro de un reactor con reflector, tiene el mismo valor que el de un reactor desnudo. Por efecto del retorno de neutrones provocado por el reflector, el valor del flujo en las proximidades de las superficies límites es muy superior al que tendría sino hubiera reflector. Como consecuencia, el flujo medio de neutrones térmicos, referido a todo el volumen del núcleo del reactor y por lo tanto, el nivel de potencia medio, resulta incrementado. Cuando se emplea un reflector, se aprovechan más completamente las propiedades multiplicadoras de las zonas más externas del núcleo del reactor.

El tratamiento del balance neutrónico, por aplicación de la ecuación en régimen estacionario, es más difícil para un reactor con reflector que para un reactor desnudo. La mayoría de los neutrones rápidos que escapan del núcleo de un reactor térmico, serán moderados en el reflector, retornando al núcleo con su energía muy reducida. Como las propiedades absorbentes y difusoras del reflector son, muy distintas de las del núcleo del reactor, resulta muy complicado el cálculo de las pérdidas neutrónicas, por absorción y por escape, que se producen a lo largo del proceso de moderación a energías térmicas.

METODO PARA UN GRUPO DE NEUTRONES

A causa de la complejidad del problema, la ecuación de difusión-edad correspondiente a un reactor con reflector sólo puede resolverse, en general, por medios numéricos. La alternativa es el empleo de aproximaciones por grupos de neutrones, consistiendo la más sencilla en suponer que todos los neutrones pertenecen a un solo grupo. Aunque, los resultados de este método, dista mucho de ser exacto, cuantitativamente las conclusiones generales que se deducen concuerdan con las obtenidas por los métodos más exactos.

Las propiedades del reflector se designan mediante el subíndice r; los símbolos que no llevan subíndice especial, se refieren a propiedades del núcleo del reactor. La ecuación de difusión en estado estacionario, dentro de la teoría de grupo, correspondiente al núcleo del reactor es, por tanto,

Mientras que la correspondiente al reflector, que al no tener material combustible carece de propiedades multiplicadoras, se expresa

En la que k2 r = r  r/Dr. Resolviendo las ecuaciones anteriores y aplicando las condiciones apropiadas en los límites, se puede calcular el efecto del reflector sobre el tamaño crítico de un reactor.

AHORROS POR EL REFLECTOR

Para expresar la reducción que experimentan las dimensiones críticas del núcleo de un reactor por efecto del reflector, se ha introducido el concepto de ahorro por reflector,  , que en el caso de un reactor esférico, se define como

 = R0 - Rc

siendo R0 el radio crítico del reactor desnudo. Siendo R0 =   c, el ahorro por reflector infinitamente grueso es  (reflector infinitamente grueso)  (D/Dr) Lr

Se llega exactamente al mismo resultado, aplicando el método de un grupo a un reactor cúbico o paralelepípedo con reflector infinito. En este caso, la dimensión a que se refieren los ahorros por reflector es la semi longitud de la arista.

En el caso de un reflector, que tenga un espesor finito viene dado por

 = (D/Dr) Lr tanh T/ Lr

Siendo T el grosor del reflector. Para valores grandes de T/ Lr es decir, cuando se trata de un reflector “grueso”, tanh T/ Lr tiende a la unidad, con lo que el ahorro del reflector tiene el mismo valor que un reflector infinitamente grueso. En cambio para valores pequeños de tanh T/ Lr puede reemplazarse por T/ Lr

 (reflector delgado)  (D/Dr) T

Si el reflector de un reactor térmico es idéntico al moderador, los valores de D y Dr no difieren mucho

Cuando se trata de un reflector delgado, de naturaleza idéntica a la del moderador, el ahorro por reflector es aproximadamente igual al propio grosor del reflector Esto implica que se puede retirar combustible de las capas externas de un reactor desnudo, sin que la criticidad se vea afectada de modo apreciable, siempre que el espesor de la capa sea pequeño, comparado con la longitud de difusión de los neutrones térmicos en el moderador.

El concepto de ahorro por reflector es bastante útil, ya que proporciona un método para estimar, de forma aproximada, el tamaño crítico de un reactor.

MÉTODOS DE VARIOS GRUPOS

El método basado en la teoría de un grupo constituye solamente una primera aproximación, pero tiene la ventaja de ser muy sencillo y de llevar a conclusiones cualitativamente correctas. Los valores calculados del ahorro por reflector, sobre la base de un solo grupo de neutrones, son excesivamente bajos, por dos razones. En primer lugar, al admitirse en la teoría de un grupo que todos los neutrones son térmicos, no se tiene en cuenta el hecho de que los neutrones rápidos que escapan del núcleo del reactor, realizan mayor número de colisiones en el reflector que los neutrones térmicos, teniendo la mayor probabilidad de ser contra dispersados. En segundo lugar, los neutrones que llegan a la zona del reflector con energías superiores al nivel de resonancia, son moderados en dicha zona, retornando luego al núcleo del reactor como neutrones térmicos; estos neutrones han eludido totalmente la captura de resonancia, a la que habrían estado sometidos si se hubieran termalizados en el núcleo del reactor. Ambos factores tienden a incrementar la efectividad del reflector, en comparación con lo que cabría esperar si todos los neutrones tuvieran energías térmicas.

En el tratamiento teórico de los reactores con reflector, la segunda aproximación consiste en operar con dos grupos de neutrones. Se postula que todos los neutrones pueden clasificarse en dos grupos energéticos, uno de neutrones rápidos (de fisión) y otro de neutrones lentos (térmicos). Tenemos cuatro ecuaciones diferenciales, dos de ellas análogas a

y otras dos análogas a

que corresponden a las distribuciones de flujo, rápido y lento en el reflector

En la figura aparece ilustrado el carácter general de la variación del flujo neutrónico con la distancia tomando como origen el centro del reactor. El flujo de neutrones térmicos presenta un máximo en la región del reflector, a corta distancia de la superficie límite reactor/reflector. Este máximo puede añadirse el hecho de que, en el reflector, se producen neutrones térmicos por moderación de los rápidos, pero son absorbidos en menor grado que en el núcleo del reactor. A distancias mayores de la superficie de separación, tanto el flujo térmico como el de los neutrones rápidos decrece constantemente, reduciéndose ambos a cero en la superficie límite extrapolada del reflector. En un buen reflector, el flujo de neutrones térmicos puede alcanzar valores tan altos como el núcleo del reactor; ésta es la razón de que algunos reactores térmicos se controlen por introducción de un absorbente en el reflector, en lugar de hacerlo en el núcleo.

La deducción de la condición de criticidad, para un sistema cualquiera, se basa en ecuaciones que representen la distribución de flujo neutrónico en estado estacionario, en función de las coordenadas espaciales y energéticas.

En el cálculo riguroso del tamaño crítico, y de la distribución espacial del flujo neutrónico, exige el empleo de una aproximación por varios grupos, que pueden llegar a ser hasta 30 y más grupos energéticos. En cada uno de ellos, el régimen de estado estacionario se representa mediante alguna aproximación de la ecuación de transporte monoenergética. La solución del sistema de ecuaciones diferenciales resultantes, constituye un problema, que solamente puede lograse con calculadoras de gran velocidad

SISTEMAS REACTORES HOMOGÉNEOS

El tratamiento teórico de los reactores homogéneos, en los que el combustible se encuentra dispersado uniformemente por todo el moderador, y en los cuales la distribución del combustible se ajusta a un esquema geométrico definido o red, dentro de la masa del moderador. El cálculo de ciertos sistemas reticulares, por ejemplo, los de uranio y óxido de uranio ligeramente enriquecido moderados por agua, se lleva a cabo como si tales sistemas fueran homogéneos. Si bien los resultados no son exactos, constituyen una aproximación adecuada.

Las propiedades de un sistema multiplicador homogéneo, hay que considerar primeramente el cálculo de la probabilidad de escape a la resonancia y de la utilización térmica. La probabilidad de escape a la resonancia en un sistema homogéneo, puede representarse mediante la ecuación.

La integral que figura en esta ecuación recibe el nombre de integral de resonancia efectiva y puede representarse por

La probabilidad es

La integración se extiende a todo el intervalo energético de resonancia

Se han determinado los valores de la integral de resonancia efectiva, correspondientes a varias mezclas de uranio natural y diferentes moderadores. A la temperatura de 300º K, los resultados se distribuyen sobre la recta de la figura, que es una representación de la integral de resonancia en función de la sección eficaz de dispersión total, por átomo de combustible.

La utilización térmica de un sistema homogéneo, en ausencia de impurezas es representado por la ecuación.

Con los datos utilizados y con los valores obtenidos mediante las ecuaciones, se han calculado los valores del factor de multiplicación infinita que figuran en la tabla.

Idéntica situación plantean los sistemas homogéneos de uranio natural moderados por agua ordinaria o berilio, pero si el moderador es agua pesada, el sistema puede alcanzar la criticidad para ciertos valores de la relación combustible/moderador. La relación óptima conduce a un valor máximo de 1,03 para el factor de multiplicación infinito, lo que quiere decir que el sistema crítico sería probablemente demasiado grande para tener una aplicación práctica. Se puede construir reactores de tamaño razonable con agua pesada como moderador, utilizando el combustible en forma de bloques o barras.

Otro método para alcanzar la criticidad, con uranio natural como combustible, consiste en aumentar la probabilidad de escape a la resonancia, para un valor determinado de la relación combustible/moderador, utilizando sistemas

reticulares heterogéneos, constituidos por bloques o barras de uranio natural distribuidos en una matriz de moderados.

Si se utilizan materiales muy enriquecidos, los reactores térmicos pueden alcanzar la criticidad con una concentración de combustible muy baja. En este caso, la relación de moderador a combustible es grande lo que trae consigo que la fracción de neutrones capturados en el combustible durante la moderación sea pequeña, ya que la probabilidad de dispersión es muy superior a la de absorción. Aumentando la relación de uranio 235 a moderador, aumenta la utilización térmica y el factor de multiplicación infinito.

CALCULO DEL TAMAÑO CRÍTICO

Una vez determinado el factor de multiplicación infinito, el cálculo del tamaño crítico de un reactor homogéneo consiste en la evaluación de la laplaciana crítica utilizando la ecuación basada en el modelo de difusión-edad. La concentración de combustible en un reactor térmico es relativamente baja, tratándose de sistemas homogéneos, el coeficiente de difusión y la edad de los neutrones térmicos tendrán los mismos valores que el moderador puro. La longitud de difusión en el núcleo del reactor es completamente distinta de la que corresponde al moderador solo.

Una vez determinada la laplaciana crítica, es posible deducir las dimensiones críticas del reactor desnudo, correspondientes a la configuración geométrica de que se trate, esfera, cilindro o cubo

A pesar de que algunos de los razonamientos se refieren a un combustible constituido por Uranio 235 puro, las conclusiones a que se llega son aplicables a todos los tipos de reactores térmicos. Sea cual fuere la naturaleza del combustible o la forma del reactor, siempre existirá, un valor de la relación de moderador a combustible que haga mínima la masa crítica.

SISTEMAS DE REACTORES HETEROGÉNEOS

Cabe la posibilidad de incrementar el factor de multiplicación infinito, por el aumento de la probabilidad de escape a la resonancia, disponiendo el combustible de forma reticular – por bloques, barras, o placas – en una matriz del moderador. La consecuencia es que se puede alcanzar la criticidad, mientras que ello resulta imposible en un sistema homogéneo, aunque se utilicen exactamente los mismos materiales. También el empleo de elementos combustibles en forma de barras o placas, favorece la transmisión del calor generado por fisión, a un refrigerante que se hace circular a través del núcleo del reactor.

Una red de barras de uranio, en un moderador, los neutrones rápidos, que se forman por fisión en el centro de las barras, alcanzan al moderador, donde van perdiendo energía gradualmente, cercanas a los valores de resonancia, y son absorbidos por núcleos de Uranio 238, principalmente en las capas exteriores de las barras Pocos neutrones, se absorben en el interior de las mismas. De todos los neutrones epitérmicos que penetran en las barras de uranio, solamente son capturados los que poseen energías idénticas a los picos de resonancia o muy próximas. Todos los demás tienen una gran posibilidad de atravesar la barra, porque las pérdidas energéticas que experimentan, por las colisiones con los núcleos pesados de uranio son muy pequeñas. Al llegar nuevamente al moderador, los neutrones se moderan todavía más, pudiendo pasar por varias resonancias, antes de ser capturados definitivamente como neutrones térmicos. La probabilidad de escape a la resonancia será mayor, en este sistema que en un sistema homogéneo, de la misma composición. Cuanto mayor sea el radio de la barra, mayor es la proporción de combustible protegida de los neutrones de resonancia, puesto que estos últimos son absorbidos en las capas exteriores. En igualdad de todas las circunstancias restantes, para un valor determinado de la relación combustible/moderador, la probabilidad de escape a la resonancia aumenta con el radio de la barra.

El factor de fisión rápida aumenta también en un sistema heterogéneo, comparado con el de una mezcla homogénea de la misma composición. Los neutrones de fisión, producidos en el interior de la barra de uranio, apenas experimentan moderación. La absorción de estos neutrones rápidos por núcleos de Uranio 238 -y las fisiones resultantes- será mayor en un sistema homogéneo, donde los neutrones son frenados rápidamente en el moderador a energías que hacen imposible la fisión del Uranio 238. Parte de los neutrones rápidos liberados en la fisión del Uranio 238, podrán ocasionalmente, provocar más fisiones de este tipo antes de escapar hacia el moderador, efecto que se sumará al factor de fisión rápida.

El único factor que aparece rebajado en un sistema reticular, en comparación con una mezcla homogénea de la misma composición, es la utilización térmica. Esta disminución está más que compensada por la que experimenta la integral de la resonancia efectiva y el consiguiente incremento de la probabilidad de escape a la resonancia, como consecuencia de la autoprotección de la barra de uranio frente a los neutrones de resonancia.

FACTOR DE FISIÓN RÁPIDA

El cálculo del factor de multiplicación rápida, basado en la teoría de las probabilidades, y exige conocer las secciones eficaces de fisión, de captura y de dispersión inelástica y elástica para neutrones rápidos. Los valores son tanto mayores, cuanto mayor es la probabilidad de que un neutrón de fisión primario realice una colisión de cualquier clase, en el interior de la barra o bloque, en el que ha sido creado. Esta probabilidad aumenta, con la sección eficaz total del material combustible y con el radio de la barra, ocurriendo lo mismo con el factor de fisión rápida. La ventaja que supone el empleo de barras gruesas es relativamente pequeña, debido al incremento que experimenta el factor de fisión rápida. La dependencia con el radio de las barras en el caso de combustible uranio natural, aparece ilustrada en la figura.

DETERMINACIÓN DE LA RED ÓPTIMA

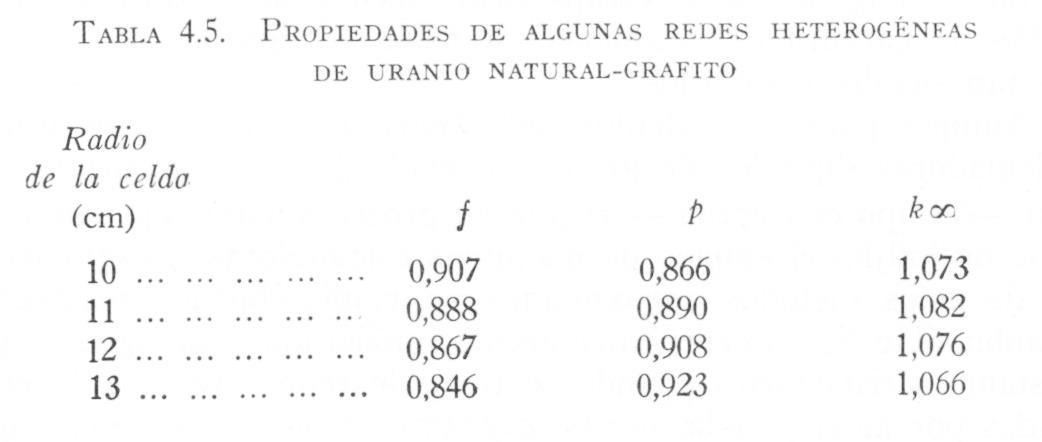
El problema que plantea la construcción de un reactor heterogéneo, es la distribución de combustibles y moderador para un valor máximo del producto p x f El procedimiento consiste en considerar cierto número de redes combustible-moderador, variando el radio de las barras y de la celda unidad (espacio de la red), y calcular para cada una de ellas los valore4s de p, f, e.

Los datos en la tabla, que se obtienen, se refieren a una red de uranio natural-grafito, con barras de combustible cilíndricas de 1,25 cm de radio situadas en celdas de radio variable.