FEBRUARY 2023
INTRODUCTION
Dr Lester Flockton is widely known and respected throughout New Zealand for his curricular knowledge, his extensive experience in the schooling sector, his deep understanding of the work of principals and teachers, and the integrity of his professional observations, insights and commentaries.
Scholastic New Zealand has called on Lester to conduct a further investigation into the suitability of PR1ME Mathematics for supporting teachers and ensuring improvement of student outcomes.
The focus of this report is an examination of evidence that speaks to the appeal and impact of PR1ME Mathematics.
Scholastic New Zealand
The quest for authentic evidence
New Zealand schools are expected to work to the achievement objectives in the national curriculum but there is no mandatory mathematics programme that schools must follow to achieve these outcomes. Schools are free to choose.
However, there are two major obstacles to choice. The Ministry of Education now controls the curricular purse strings, whereas Tomorrow’s Schools always intended that funding be devolved to ‘self-managing’ schools to allow the opportunity to choose programmes and resources considered most effective for their teachers and students.
The recentralisation and capture of funding is one of the most significant changes that has occurred since the initial reforms of education. The effect has been an undermining of choice. Schools must now dip into their own financial resources if they are to commit to and explore opportunities that have the promise of benefiting teaching and learning in preference to what the Ministry provides. Yet numerous schools with genuine commitment to improvement are doing just that, including the large number now using PR1ME Mathematics.
The second major obstacle that schools face is searching out programmes that can benefit their students’ learning. This requires access to balanced, dependable evidence that can be readily interpreted and critiqued. Research that focuses almost singularly on delivery of programmes (pedagogy) without also attending to programme content and structure, for example, has significant limitations for improving curricular outcomes. Balance is absent.
Much mathematics research is conceived, constructed and conducted through an academic lens by a relatively small group of tertiary specialists. Yet despite governmental patronage, their work seldom results in deep and sustained improvements across the system. Too often this is because of a failure to recognise the simple truth that there is no one single approach that will work everywhere and for everyone. It is now widely acknowledged, for example, that the Ministry of Education’s Numeracy Project is a case in point. The heavy concentration of funding and support around this flawed project has denied investment in other, potentially better approaches and has resulted in steady declines in student achievement.
Arguably, some of the most valid research in mathematics is what teachers themselves do in their everyday work. Through repeated observations and thorough evaluations of particular methods and approaches, they are in a position to make informed judgments about the suitability and effectiveness of what they are doing and what they are teaching. This ‘grounded’ research allows them to make informed professional decisions about the kind of changes and improvements that are needed to support student learning.
This report draws on teacher voice, experience, and the judgements they have made about PR1ME Mathematics with the purpose of establishing authentic, grounded evidence of its effectiveness for teaching and student learning. No mathematics research – that is, NO research – accounts for all of the variables and complexities that need to be accounted for when making judgements and considering conclusions. Regardless, this report claims a high level of authenticity – and thus validity.
About PR1ME Mathematics
PR1ME Mathematics is based on three of the top performing maths countries in the world: Singapore, South Korea and Hong Kong. PR1ME was developed alongside the Ministry of Education in Singapore. The programme and its content speak to the universal world of mathematics and mathematics education. It is the one curriculum area whose subject matter is the substantially the same, no matter where on Earth you are.
Key features of PR1ME Mathematics
• Covers junior through to senior year levels of primary education – Years 1 to 8
• Follows a text-based programme that allows ample scope for localised and teacher augmentation
• Ensures a consistent approach to teaching, programme content and sequencing of learning through each year level of the school
• Provides built-in teacher professional development and support for all mathematics concepts and problem solving strategies
• Develops mathematical understandings progressively through concrete, pictorial and abstract approaches
• Builds student confidence through consistent problem-solving strategies
• Mathematical problems are posed in multiple ways
• Knowledge and skills at each step of learning are regularly applied to contextual, real-world problems
• Through a scaffolded approach, mastery of increasingly complex concepts (strategies) and skills is built up from previous steps of learning
• Maintenance and mastery are supported by revisiting and practising concepts and skills previously learned
• Active discussion and engagement among students is key to their learning rather than rote, lock-step approaches
• Supplementary resources and activities that fit with the programme are already available in schools
• Regular assessments provide formative feedback and contribute to summative purposes
Investigating the appeal and impact of PR1ME Mathematics for teaching and learning
The number of schools in New Zealand that have chosen to use PR1ME has steadily grown since its introduction nine years ago. There is now a good number that have been using it consistently over three or more years so this allows a reliable study of its appeal and its impact on teaching and learning. A sample of 47 of those schools, which are delivering the programme to around 12,000 Year 1–8 students, have participated in the survey reported here to help give a picture of whether the programme is performing to expectations.
Number of years schools have been using PR1ME Mathematics
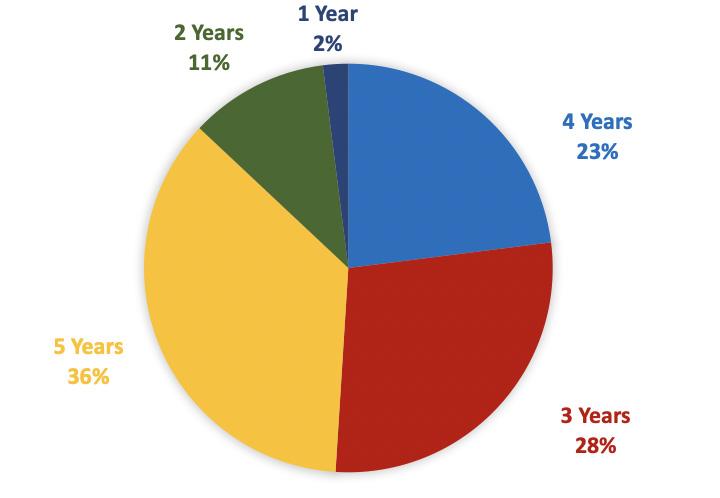
For the purposes of a study that seeks reliable results, it is preferable to obtain information from schools that have been using PR1ME over successive years. It is generally too early to draw definitive conclusions when a new programme such as PR1ME has only been in use for one or two years, even though initial impressions are often helpful. The following data shows the length of time that schools in this study have been using PR1ME Mathematics.
The large majority (87 percent) of schools have been using PR1ME for 3 to 5 years, with the largest percentage having used it for 5 years.
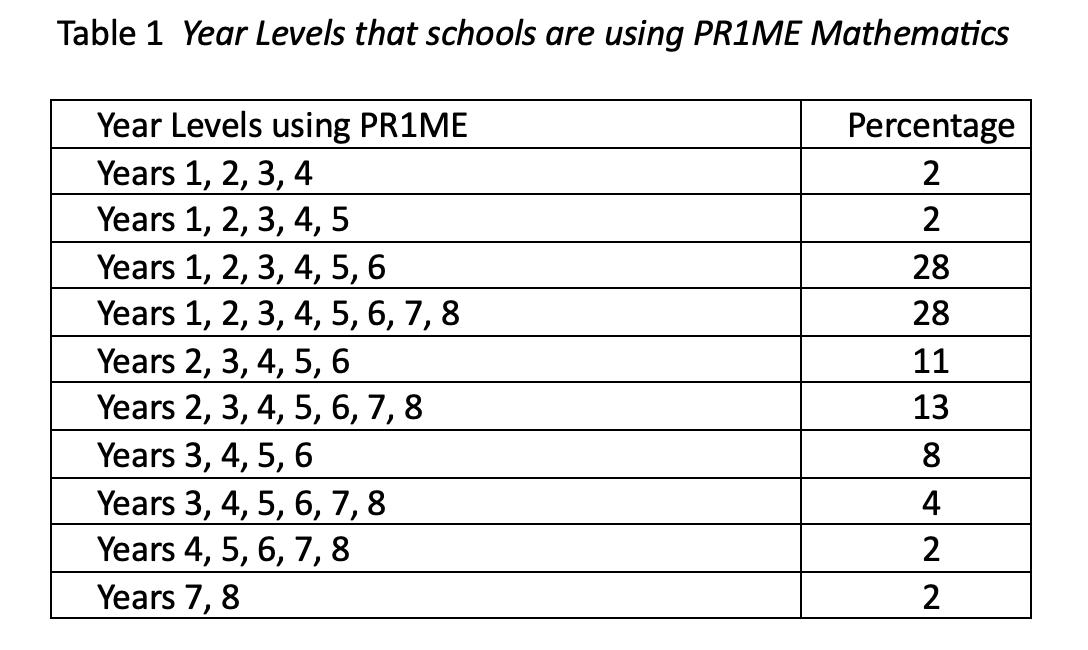
Year levels at which schools are using PR1ME Mathematics
PR1ME Mathematics is a programme that covers Year 1 through to Year 8. In this study it was considered useful to know the extent to which is being used at each year level. Some schools introduce PR1ME successively through the year levels so that students become progressively immersed in the programme. Others introduce the programme simultaneously at the various year levels. In this study, the highest percentage of schools – contributing, full primary and intermediate – are using PR1ME at every year level. The very full coverage across year levels seen in the table below gives a strong basis for the findings of this study.
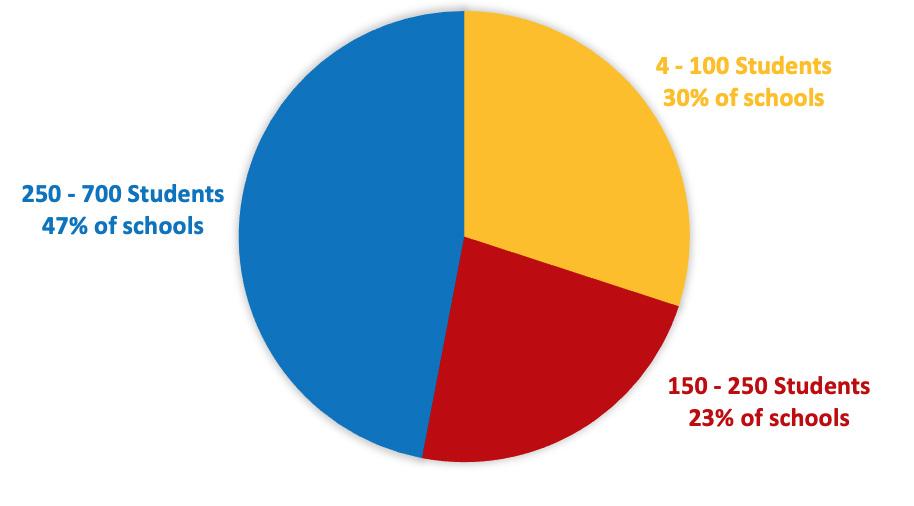
Number of students learning mathematics through PR1ME
The schools included in this study ranged from small, full primary rural schools to large urban schools, including intermediates. Maori and Pasifika students were well represented in the sample. School rolls ranged from 4 students to 700 students with a sample average school roll of 264. The graph below shows a majority of schools were quite large, yet a substantial number were smaller to mid-size schools.
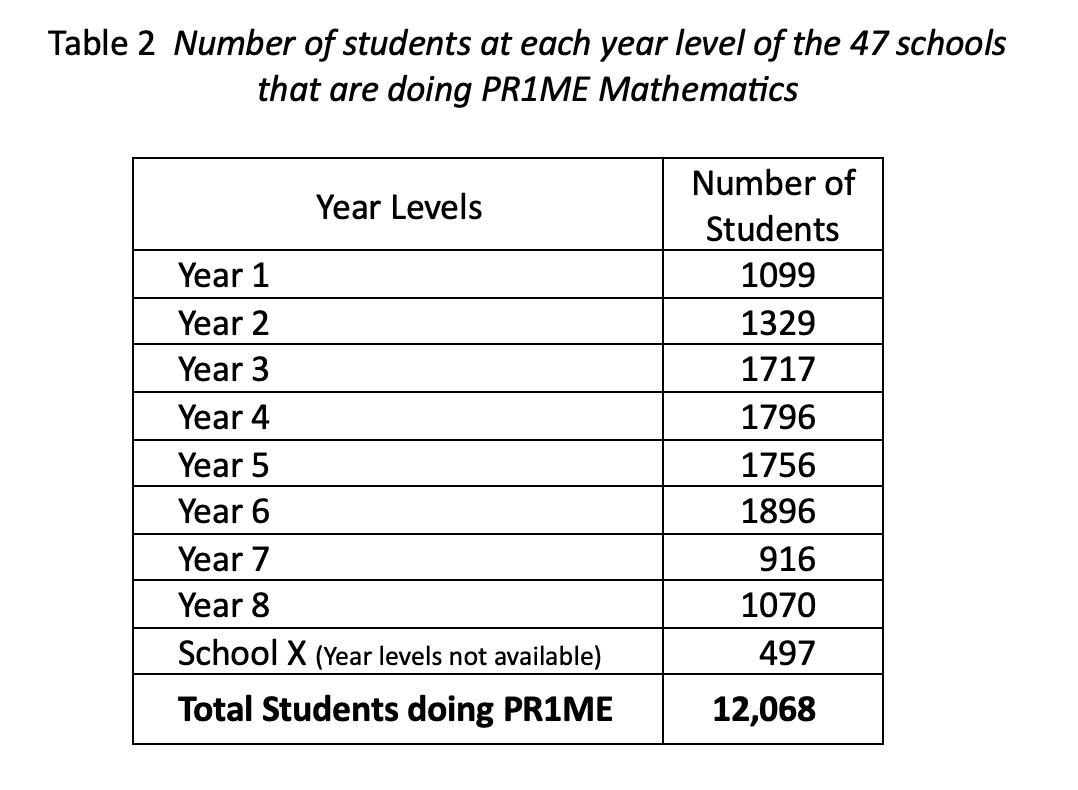
School roll data was accessed from the Ministry of Education’s Education Counts. The numbers of students at each year level, as shown below, provide a strong basis for strength of reliability in the findings of this study.
Representation of
different
levels of Socio-Economic Status (decile rankings) in the sample of participating schools
Studies like this are usually interested in comparing the performance of schools situated in different levels of community socio-economic status because of the strong impact SES has on achievement. Unfortunately, this information is no longer available for individual schools in Education Counts, a government site which provides access to a comprehensive range of education statistics. Former Minister of Education Hekia Parata directed its removal.
The mathematics programme schools used BEFORE they changed to PR1ME
Schools were asked what mathematics programme they were using before deciding to change to PR1ME. One school – a new school – started out on PR1ME five years ago and continues to do so. The majority of schools were following the Ministry of Education’s Numeracy Project approach to teaching mathematics. Others used the New Zealand Curriculum as a guide for their programmes, or a ‘mish-mash’ of approaches with teachers given a choice of what they did. One principal commented that the school had been using a variety of bits and pieces with no clear programme direction. The previous prinicipal had used the Numeracy Project but the new principal wanted something easier to follow.
Reasons
why schools opted for PR1ME over their previous programmes/approaches
Schools were asked why they decided to move away from the mathematics programmes or approaches they had been using. There were three common themes across the responses, with most expressing dissatisfaction with their results from following programmes and approaches directly or indirectly provided by the Ministry of Education.
1. The need for much improved consistency of teaching across all classrooms
• Teaching of maths in the school was very inconsistent and highly dependent on individual teachers’ ability and their enjoyment of teaching maths.
• No consistency across the school. Some were teaching entirely through problem-solving with not enough attention to math skills and knowledge
• Children were not all getting the same level of teaching of concepts, which showed up in achievement results.
2. The need for a well-structured and supportive mathematics programme across all year levels
• We wanted a structured programme that all teachers could access and follow regardless of their experience.
• Needed a well-structured, effective programme that would support both teachers and students.
• Our maths results were not good. Many younger/newly trained teachers struggled to make sense of the resources and support provided by MOE. Many teachers were often frustrated by not knowing what they should be doing and the absence of any clear structure.
3. The need to improve student achievement and engagement in mathematics
• We have a lot of students with learning issues – the Numeracy Project approach did not help them at all.
• Found that a dominant focus on strategy in the Numeracy Project was negatively impacting on the breadth of the learned curriculum and student progress.
• Math results showed students lacked a lot of basic knowledge as the overemphasis on strategy dominated.
• With the Numeracy Project our data on student knowledge and engagement was regressing.
• Our students found DMIC not engaging and motivating whereas with PR1ME they are enjoying math and say math is fun.
• After 7 years on DMIC, our data was actually worsening.
• DMIC was really only useful for problem-solving but didn’t offer enough coverage of the maths curriculum.
Other reasons for changing to PR1ME included the excessive amount of time teachers spent on sourcing and organising maths material for student learning, and concerns about programme coverage and balance.
Programmes schools used in addition to PR1ME Mathematics
The study was interested to learn of any other programmes that schools might be using in addition to PR1ME, since these could potentially have some impact on student achievement.
Most schools were using supplementary resources that they had previously used and were readily available. These were typically used to provide further practice and reinforcement of concepts and skills covered by PR1ME (basic facts, for example) or in some cases to augment the PR1ME programme. Examples of supplementary activities variously used included Mathletics, MoneyTime, Maths Buddy, Numicon, Mathseeds, and resources from NZ Maths and TKI. Most of these activities were used according to individual teachers’ choice rather than being school-wide.
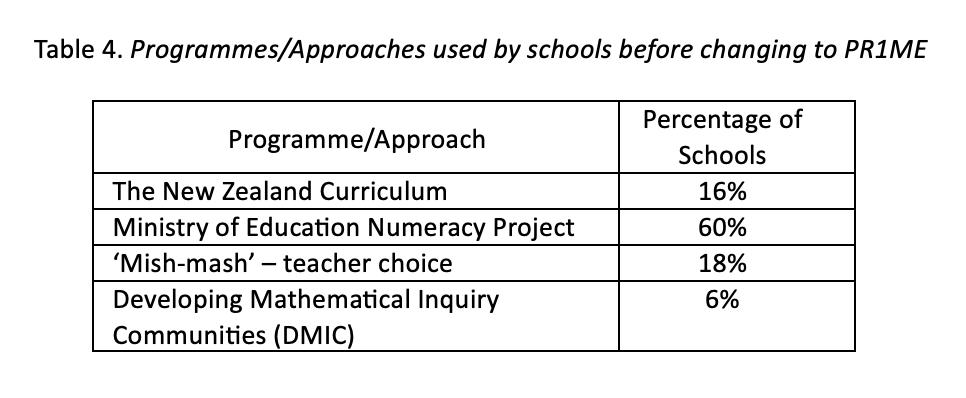
Schools were also asked to give a best estimate of the amount of time that was exclusively focused on the PR1ME programme so that the extent to which supplementary activities were used could be gauged. The following graph shows that for most schools PR1ME was the core programme. A lesser number used supplementary activities for a significant part of their programme.
Teachers’ classroom organisation of student learning
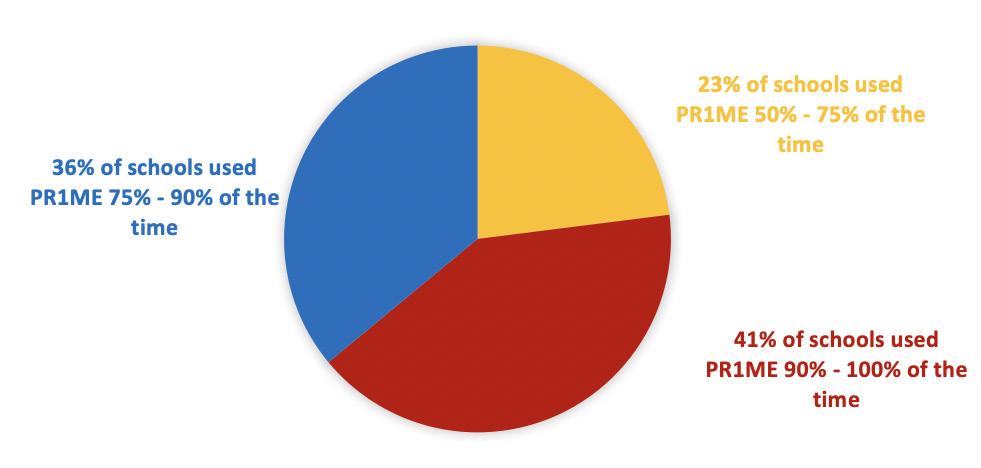
There is debate around teachers’ organisation of student learning and its impact. The tendancy to over-generalise from research can ignore how the same practice (e.g., fixed ability grouping) can work with different effects in different settings: sometimes negative and counterproductive; sometimes positive and productive. Enduring variables in all of this include such things as classroom culture, the teacher’s understanding and responsiveness to an individual student’s learning needs, and pedagogical ‘style’. In this study we asked whether teachers used fixed ability grouping, variable grouping, or no grouping at all (whole class teaching). There are advocates for each of these approaches, yet it can be misleading to say that one is better than the other in all settings. Within the limitations of this survey, there was no evidence to support one form over another form of organisation. Only 2% (i.e. one school) used whole class teaching.
Tools used to summatively measure student learning
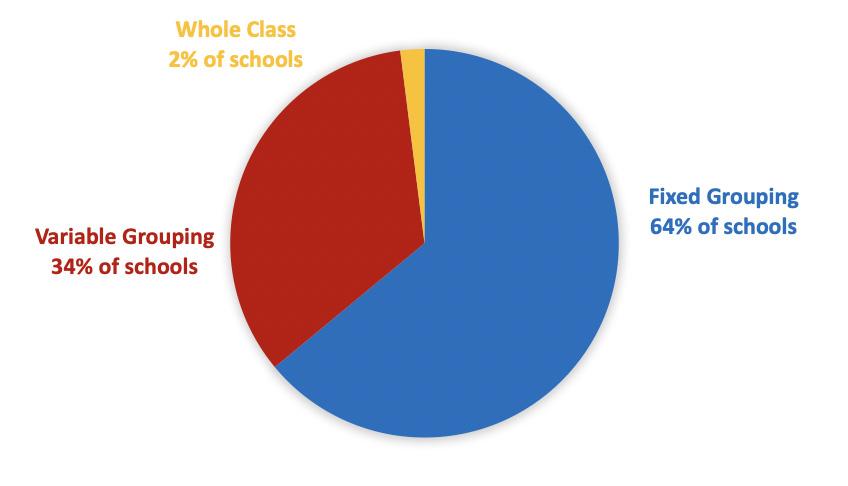
A key purpose of this study is to establish authentic, grounded evidence of PR1ME’S effectiveness for teaching and student learning. Grounded evidence gives credence to teachers’ ongoing classroom assessments and judgements based on repeated observations of students’ work. However, in reaching overall judgements it is expected that results from one or another standardised test will be brought into the mix of information to support judgement making. Accordingly, schools were asked what tools they used to help make summative judgements, and how often such tools were used.
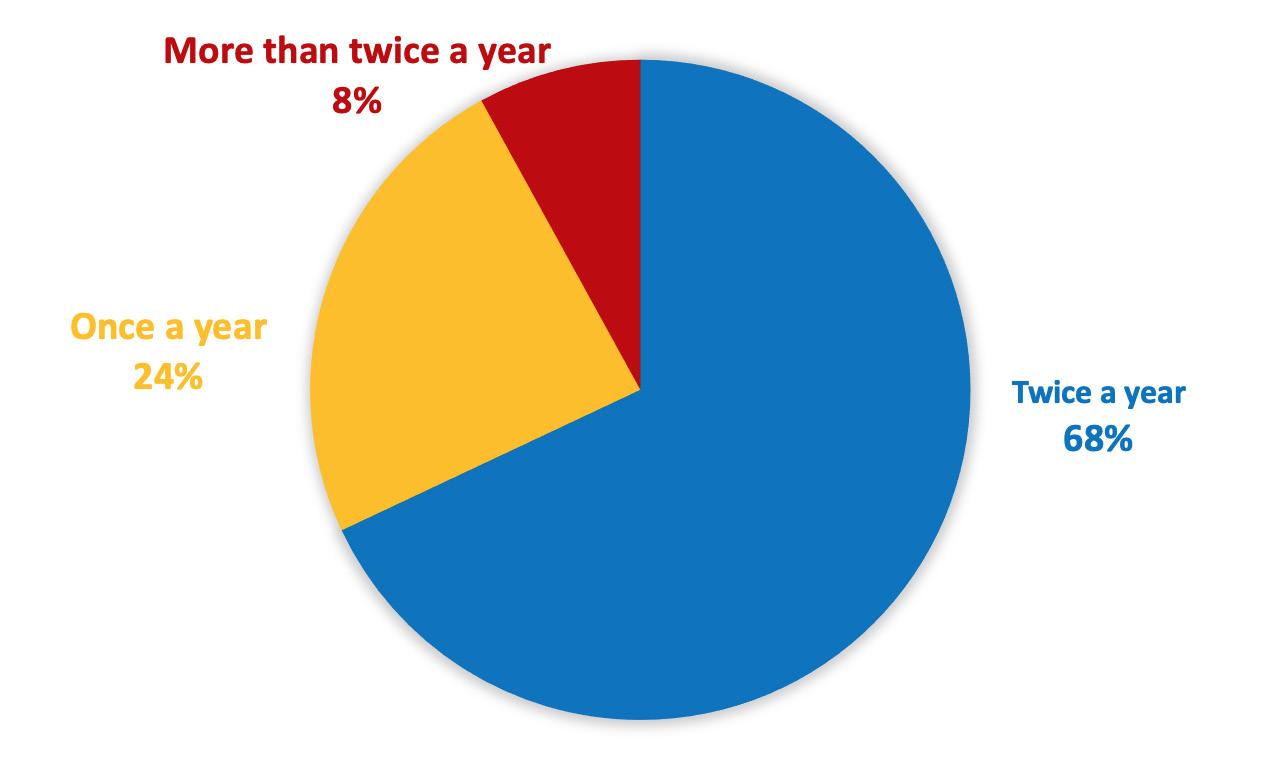
Figure 5 (below) shows almost half of schools are using PAT Mathematics. The other half are also using PAT along with other measures such as basic facts testing, JAM, IKAN, PACT and Gloss. A few schools are using e-asTTle, mostly in combination with other measures. Many schools use the PR1ME summative tests along with PAT or e-asTTle. A small number use only the PR1ME summative tests. What is clear is that the majority of schools are using some form of external testing to assist in their judgements of student learning. Furthermore, as Figure 6 shows, the majority of schools are using summative measures twice a year.
Fig. 6 Frequency of summative measures
The impact of PR1ME Mathematics on student learning and achievement
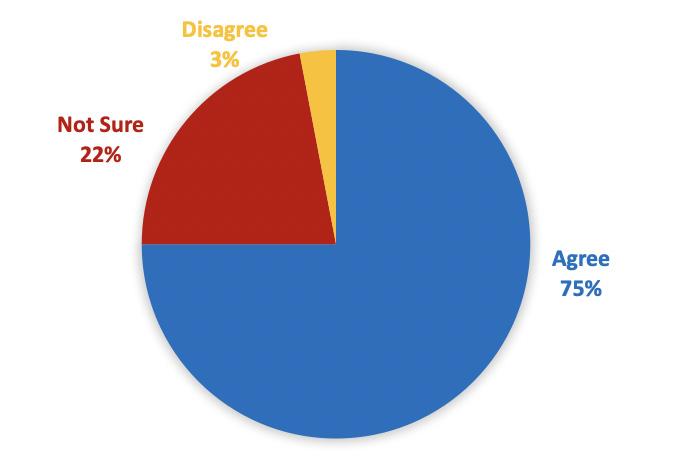
Using evidence-based overall judgements of student learning and achievement in mathematics, schools were asked whether (a) most students are achieving better than pre-PR1ME, (b) about half of students are achieving better than pre-PR1ME, or (c) about a quarter of students are achieving better than pre-PR1ME.
Seventy-five percent said most students were achieving better with PR1ME, whereas 22% were unsure. The schools who were unsure tended to have limited achievement data from pre-PR1ME that allowed them to make a confident judgement. The very small percentage of schools that disagreed nonetheless said that at least half of their students were achieving better with PR1ME.
The graph below speaks for itself; it provides clear evidence of positive results and affirmation of the impact and benefits of PR1ME for students’ learning and achievement. Importantly, it gives justification to schools for discontinuing their previous programmes and approaches in their quest for better teaching and learning outcomes. Schools agreeing that students are achieving better tend to be those that have been using PR1ME longer than those who are not sure.
As a further check on schools’ judgements, they were also asked inverse questions on student achievement. They were asked whether they agreed, disagreed or were unsure whether (a) most students were achieving no better on PR1ME, or (b) about half were achieving no better, or whether (c) about a quarter of students were achieving no better. Figure 8 shows that 85% disagreed that most students were achieving no better, while 15% were unsure.
Fig. 8 Percentage of schools that agree, disagree, or who are not sure that most of their students have not improved their achievement with PR1ME

Student Engagement
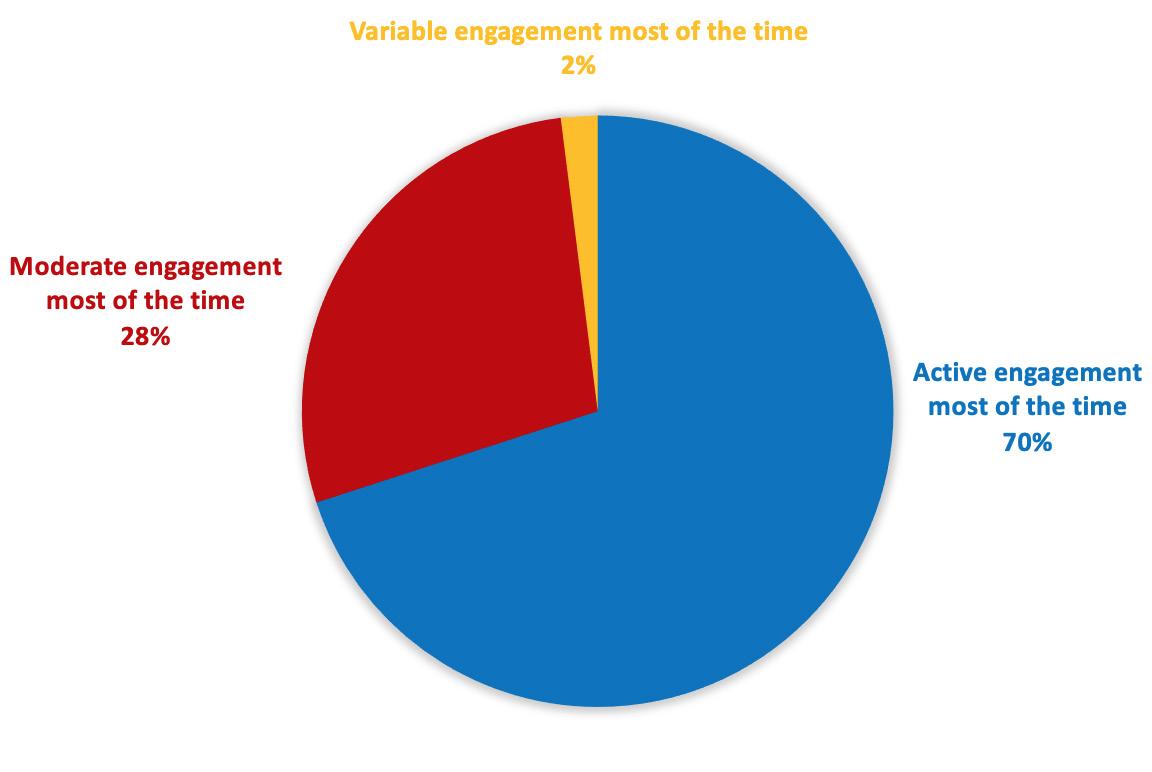
It is well established that student engagement is a key influence on progress and learning outcomes. The more engaged students are, the more likely they are to progress and achieve. The survey therefore enquired into the extent to which most students effectively engage in learning through PR1ME Mathematics. Results showed that the large majority were actively engaged most of the time, whereas about a quarter were moderately engaged most of the time and a very small percentage showed variable engagement. Given the number of variables that impact on engagement beyond PR1ME itself, this is a very positive result.
Schools’ expectations of PR1ME Mathematics
Schools were asked what their expectations were of PR1ME Mathematics when they decided to adopt the programme. There were a number of common themes in response to this question:
• Greater consistency of teaching and curricula coverage across the school.
• Clear planning guidelines and better economies in planning and preparation time.
• Solid teaching and coverage of concepts and knowledge.
• A programme built on solid progressions with regular checkpoints on progress.
• A structure that helps to clarify needs and gaps in learning.
• Improved teacher capability and student learning outcomes.
• Ongoing teacher guidance and support.
• Student confidence and engagement.
• A programme that would extend our capable students and help those not so confident.
• A programme that was easy for both teachers and students to follow.
• A return to explicit teaching.
• Regular feedback for both teachers and students on progress.
• Enjoyment of teaching and learning – bringing the fun back into teaching.
Once PR1ME had been implemented as the core approach to teaching and learning, to what extent were schools satisfied that initial expectations were being met? Over 90% of schools were clearly satisfied. Representative examples of feedback include the following:
• Teachers are finding the programme great to work with.
• We love PR1ME, especially in our small multi-level environment.
• Exceptionally satisfied. Would not use anything else. The programme has proven itself.
• Very pleased with our upward-trending achievement results.
• Highly satisfied. We have much improved student achievement and most significantly our students love maths. Parents are also very supportive of PR1ME.
• Maths knowledge, understanding and confidence have all increased.
• Teachers are much more comfortable teaching maths.
• We are satisfied that more maths is being taught and that the kids are being challenged.
• Our teachers like the ease of PR1ME.
• The ease of planning of maths programmes is clearly beneficial for teachers’ wellbeing and workload.
• We are extremely happy with the programme, the results, and the children’s engagement.
• Very satisfied, especially with much improved student engagement and their sense of achievement.
• PR1ME provides fantastic resources to support teaching.
• It does everything we wanted.
• The kids love it. The teachers love it.
• Our expectations are absolutely being met.
What teachers say they like about PR1ME
Teacher voice is an important part of any study that is concerned with the work they are expected to do. Teachers don’t necessarily speak with one voice, however; their experiences, work environments and the resources available to support their teaching can differ significantly. These factors, along with personal viewpoints, biases and preferences, can influence their position and opinions on a variety of matters. Regardless of potential underlying differences, teacher feedback on PR1ME Mathematics is worthy of attention. As it turns out, there was strong unanimity around a number of common themes in what they like about PR1ME:
• Planning is simplified and ensures expected coverage.
• Planning is more focussed and independent work more controlled.
• Planning is quick and easy to follow. New teachers pick up the programme with relative ease and we don’t have to spend hours finding and putting together resources.
• Teacher guides are easy to follow and highly supportive.
• Everything you need is at hand – none of the hunting stuff out, etc.
• We like all of the PR1ME resources. They meet all of our planning, teaching, assessment, etc. needs.
• We find it very easy to use the course books to unpack new learning with our students. It is easy for me as math leader to do regular PLD with staff as well as introducing new staff to the programme who haven’t done PR1ME before.
• Teachers and students love the course books – no more endless photocopying.
• The clarity. Each concept is explained so well.
• Consistency – teachers feel more confident that concepts and knowledge are being consistently and progressively taught at all levels.
• The math language is consistent at every stage of teaching and learning.
• The approach to problem-solving is consistent throughout the school.
• Builds capacity and capability – lessons are well structured.
• The structure, the ease of use, the curricula coverage.
• The structure is easy to follow and easy to report on.
• The summative assessments and tracking sheets.
• PR1ME is easy to follow, there is a great sequencing of topics, and problem-solving is not abstract.
• It is easy to pick up and follow which is great also for relief teachers.
• The coherence, the spiral approach, curriculum breadth, student engagement, assistance with teacher planning and the structure that supports less confident teachers.
• The spiral approach – learning builds on previous learning all the way.
• Teachers like that it spirals and regularly revisits and re-practises concepts previously covered.
• The students love PR1ME, which is easy to see in their engagement with learning at math time.
The validity of claims about PR1ME by detractors who have not taught or used it
Some who are intent on advocating their preferred approach to teaching mathematics over other programmes (mostly the Numeracy Project) claim that PR1ME provides no real opportunities for discussion and problemsolving, that it keeps students pinned down to mindless drills, and that it is a lock-step approach that stifles teacher creativity in teaching mathematics. These attitudes are further entrenched by an aversion to the use of common texts and failure to make a distinction between text-based and traditional textbook approaches.
Based on their experience in actually using PR1ME in the classroom, schools were asked if such claims have validity. Most were quick to refute such opinions, while some argued that it is not PR1ME itself that has shortcomings, but those individual teachers whose practice can have weaknesses –weaknesses that would apply regardless of which mathematics programme they followed. Responses in this part of the survey were particularly lucid.
Do teachers agree with the detractors?
• Yes and no. We have found it depends on the teacher. Some are more effective than others in promoting a lot of discussion.
• PR1ME allows plenty of opportunities for discussion and problem-solving. Our students enjoy this part of their maths learning.
• Drills are by no means mindless. PR1ME tasks give children time to practise and consolidate what they have been learning.
• Yes and no. It depends on the indiviual teacher, but PR1ME encourages interaction among students and provides plenty of opportunities for discussion. This is a pedagogical matter – how teachers teach and work with students.
• We disagree. We know that students need many opportunities to practise what they have learned. We believe that regula,r meaningful practice is crucial to student progress. It aids with understanding and fluency in maths.
• This is a false claim. We have dedicated times for problem-solving, whole class and in flexible groups, to delve deeply iinto a culture of problem-solving and allowing opportunities for rich engagement and learning.
• Not at all! PR1ME is based on problem-solving. It’s embedded in each concept, in each chapter, and in each review.
• The word problems in PR1ME and others that teachers come up with are great for discussion. The bar model helps students discuss the maths the are learning. The students actually like the balance of learning and time to practise skills.
• Like all programmes, whether PR1ME or somethig else, it depends on the teacher.
• No. We have lots of discussion going on in teaching groups.
• No. For the majority, repetition, revisiting and practice are truly necessary to embed learning. Few students learn with permanence by only visiting a concept or skill once in a while.
• Our teachers do class lessons and basic facts at the beginning of each maths lesson before working on PR1ME.
• Our students are able to decide whether they want to work on their own or with peers. Not all students want to work with peers and not all students want to wait for their peers to catch up to where they are at. Students work at their own rate and PR1ME allows students to progress at their own rate without feeling pressured to achieve or feel like they can’t keep up with others.
• No. The problem-solving discussions during guided teaching sessions are arguably better than they were before we used PR1ME.
• I wish I had had the opportunity to do the bar model for problem-solving when I was a student as I know that this is an area that I struggled with as a youngster.
• I absolutely disagree with such claims. We successfully use PR1ME as our main resource to teach mathematics. It gives clear processes for teaching students the language of maths and a variety of effective strategies to solve equations and word problems.
• I cannot believe such claims. PR1ME allows for open discussion and explanation of what the child is doing.
• No. There are limited ‘drills’ (not really an appropriate word). The practice work is not mindless, it is not overdone, and it is necessary for learning and progressing.
• It depends on the kaiako. Initially this was the case in our school but we worked on growing teachers’ capabilities around maths. They learned that they could ‘stray’ from the so-called script and support children to progress their PR1ME-based learning.
Summing Up
The evidence is clear. PR1ME Mathematics is proven to be an effective and successful teaching programme in the majority of schools surveyed. Most are clear that student learning, progress and engagement have all advanced beyond what they were achieving in their previous programmes. There is no one math programme or approach that works equally well in everyone’s hands but the results here show that PR1ME has considerable appeal across a wide range of New Zealand schools because of what it achieves for teachers and children.
In particular, the survey highlighted:
• The clear and easy-to-follow programme structure that works right across each year level in the school
• The built-in guidance and support for teachers and its basis for teacher professional development
• The consistent and spiral approach to teaching concepts, knowledge and skills from earliest through to more advanced stages of learning
• The confidence given to students through the approach to problemsolving
• The value of students having regular opportunities to build upon, practise and consolidate what they have learned at every stage
• The scope for enriching learning with supplementary activities that are readily available in most schools
• The considerably lessened teacher workload for planning and preparing lessons
• The provision of regular checkpoints for assessing student progress and achievement
• The absence of concerns that a text-based programme limits opportunities for teacher initiatives and culturally enriching contexts for learning
• The enjoyment and satisfaction teachers and students experience in teaching and learning mathematics.
The benefits of text-based mathematics programmes
In years gone by, textbooks were the cornerstone of teaching and learning. In their time they served a purpose. But times have changed. Teachers want scope within their programmes to determine when some concepts or skills need more or less time, attention and practice for students to secure their learning. Teachers want to be in the position where they can exercise professional judgements relative to their particular groups of students. The traditional textbook approach didn’t allow for this, hence teachers became averse to their use. This led to a huge pendulum swing, but as we have seen time and again, pendulum swings seldom work as might be hoped. As with most things ‘education’, balance is critical.
The work of Tim Oates (Cambridge University, a foremost expert on school curriculum) threw into sharp relief the role of high quality texts in realising the aims of national curricula and supporting effective teaching. His research showed that the use of high quality texts is key to ensuring that schools teach the National Curriculum to a standard that matches education systems of top performing countries. Oates argues that there should be coherence between the National Curriculum, the content of texts and the approach to teaching in schools.
The evidence provided in this report goes a long way to upholding and supporting such well-reasoned justifications. PR1ME is nothing like your oldfashioned textbook and shouldn’t be thought of as such.

ABOUT THE AUTHOR
Dr Lester Flockton is a graduate of Dunedin Teachers’ College and the University of Otago. He has extensive experience in New Zealand’s school system as teacher, principal, inspector of schools, Ministry of Education official, researcher, university teacher, educational thinker and leader. Throughout his career in education he has worked on many national curriculum and assessment committees and projects, including major roles in the development and writing of The New Zealand Curriculum (2007). He has led numerous professional development and learning programmes, made dozens of conference presentations here and overseas, and held office in various professional organisations.
Lester Flockton was one of the founding directors of the Educational Assessment Research Unit at the University of Otago, and one of the prime developers and co-directors of New Zealand’s highly regarded National Education Monitoring Project. Lester’s field of expertise combines teaching and learning, curriculum and assessment, and the leadership, governance and management of schools. He has received a number of honours in recognition of his service to education in New Zealand.
