MEDIDAS DE TENDENCIA CENTRAL PARA DATOS NO AGRUPADOS

0; 0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 7; 7; 7; 8; 8; 8; 9; 10; 10.

Con los datos obtenidos, elaborar una tabla de frecuencias con 5 intervalos o

clases.

Solución: ▪ Hallamos el rango: R = X max –X min = 10 –0 = 10. ▪ El número de intervalos (k), me lo da el enunciado del problema: k = 5. ▪ Calculamos la amplitud de clase: A = R/k = 10/5 = 2. ▪ Ahora hallamos los límites inferiores y superiores de cada clase, y elaboramos la tabla de frecuencias.

intervalo Marca de clase Frecuencia absoluta Frecuencia acumulada Frecuencia relativa Frec. relativa acumulada

[0 –2) 1 8 8 0,229 0,229

[2 –4) 3 7 15 0,200 0,429

[4 –6) 5 8 23 0,229 0,658

[6 –8) 6 6 29 0,171 0,829

[8 –10] 9 6 35 0,171 0

total 35 1

Medidas de Tendencia Central para datos no agrupados

para que una calificación tenga significado hay que contar con elementos de referencia generalmente relacionados con ciertos criterios estadísticos.

Supóngase que un determinado alumno obtiene 35 puntos en una prueba de matemática.

Este puntaje, por sí mismo tiene muy poco significado a menos que podamos conocer el total de puntos que obtiene una persona promedio al participar en esa prueba, saber cuál es la calificación menor y mayor que se obtiene, y cuán variadas son esas calificaciones.

Medidas de tendencia central: Son indicadores estadísticos que muestran hacía que valor (o valores) se agrupan los datos.

Existen tres medidas comunes para identificar el centro de un conjunto de datos: la media, mediana y moda. En cada caso, se ubican alrededor del punto en donde se aglomeran los datos.

Media aritmética: Medida de tendencia central usualmente llamada promedio, se define como la división de la suma de todos los valores entre el numero de datos.

MEDIANA: Del conjunto de datos obtenidos es el valor que al organizar los datos en orden ascendente o descenderte a la mitad o centro de los mismos. La posición que ocupa la mediana puede ser determinada mediante la siguiente fórmula:

Mediana =X [(n/2) +1/2]

Ejemplo: Dados los siguientes 8 datos ordenados en orden ascendente: 5,8,8,11,11,11,14,16., encuentra la mediana.

Utilizando la fórmula para ubicar la posición del dato que representa la mediana indica que:

Mediana = (8/2) +1/2 = 4.5

Por lo que la mediana está ubicada entre el dato 4 y 5; el valor del dato 4 es “ 11” y del dato 5 es “ 11”, por lo que al sacar el promedio, da que la mediana de la muestra estudiada es 11.

MODA: Es el dato que ocurre con mayor frecuencia en un conjunto de elementos estudiados. Del ejemplo anterior donde los datos recopilados son: 5,8,8,11,11,11,14,16; el dato que ocurre con mayor frecuencia es el valor 1, siendo este valor la moda.

MEDIA PONDERADA: es una media aritmética, en la cual se considera a cada uno de los valores de acuerdo con su importancia en el grupo.

Mediana Ponderada

En donde:

X = Observación individual

Q= el peso o ponderación asignada a cada observación

Medidas de Tendencia Central para datos agrupados

Cuando se trabaja con datos que han sido agrupados en una distribución de frecuencias, no se sabe con certeza los valores individuales de cada dato. Por lo que se utilizan métodos alternos para aproximar los valores de las medidas descriptivas.

MEDIA PARA DATOS AGRUPADOS: Al calcular la media para datos agrupados, se supone que las observaciones en cada clase son iguales al punto medio de la

clase

MEDIANA: Primero se encuentra la clase mediana, la cual es la clase cuya frecuencia acumulada es mayor o igual a n/2 y puede determinarse mediante la siguiente fórmula:

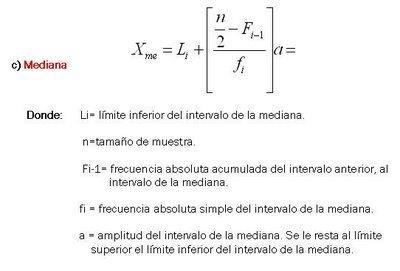
LA MODA es la observación que ocurre con mayor frecuencia, por lo que es necesario identificar la clase modal, esta se localiza encontrando la clase que tenga más frecuencia.